Что такое эквивалентный резистор. Как рассчитать эквивалентное сопротивление для последовательного и параллельного соединения резисторов. Как применять эквивалентные резисторы при анализе и расчете электрических цепей. Какие формулы используются для расчета эквивалентного сопротивления. Где на практике применяется концепция эквивалентного резистора.
Что такое эквивалентный резистор
Эквивалентный резистор — это теоретический резистор, который можно использовать для замены группы резисторов в электрической цепи, не изменяя при этом электрические характеристики цепи. Концепция эквивалентного резистора позволяет упростить анализ сложных электрических схем, сводя их к более простым эквивалентным схемам.
Основные свойства эквивалентного резистора:
- Имеет такое же суммарное сопротивление, как и заменяемая им группа резисторов
- При подключении к той же разности потенциалов пропускает такой же ток, как и исходная группа резисторов
- Рассеивает такую же мощность, как и заменяемые им резисторы
Расчет эквивалентного сопротивления при последовательном соединении
При последовательном соединении резисторов их эквивалентное сопротивление равно сумме сопротивлений отдельных резисторов:

Rэкв = R1 + R2 + R3 + … + Rn
Где Rэкв — эквивалентное сопротивление, R1, R2, R3, …, Rn — сопротивления отдельных резисторов.
Почему это работает? При последовательном соединении через все резисторы протекает один и тот же ток. Согласно закону Ома, падение напряжения на каждом резисторе пропорционально его сопротивлению. Суммарное падение напряжения на всей цепочке резисторов равно сумме падений напряжения на отдельных резисторах. Отсюда и следует правило сложения сопротивлений.
Расчет эквивалентного сопротивления при параллельном соединении
При параллельном соединении резисторов для расчета эквивалентного сопротивления используется следующая формула:
1/Rэкв = 1/R1 + 1/R2 + 1/R3 + … + 1/Rn
Где Rэкв — эквивалентное сопротивление, R1, R2, R3, …, Rn — сопротивления отдельных резисторов.
Эту формулу можно преобразовать к виду:
Rэкв = 1 / (1/R1 + 1/R2 + 1/R3 + … + 1/Rn)
Почему используется такая формула? При параллельном соединении на всех резисторах действует одинаковое напряжение. Ток через каждый резистор обратно пропорционален его сопротивлению. Суммарный ток через всю параллельную цепь равен сумме токов через отдельные резисторы. Отсюда и следует правило сложения обратных величин сопротивлений.
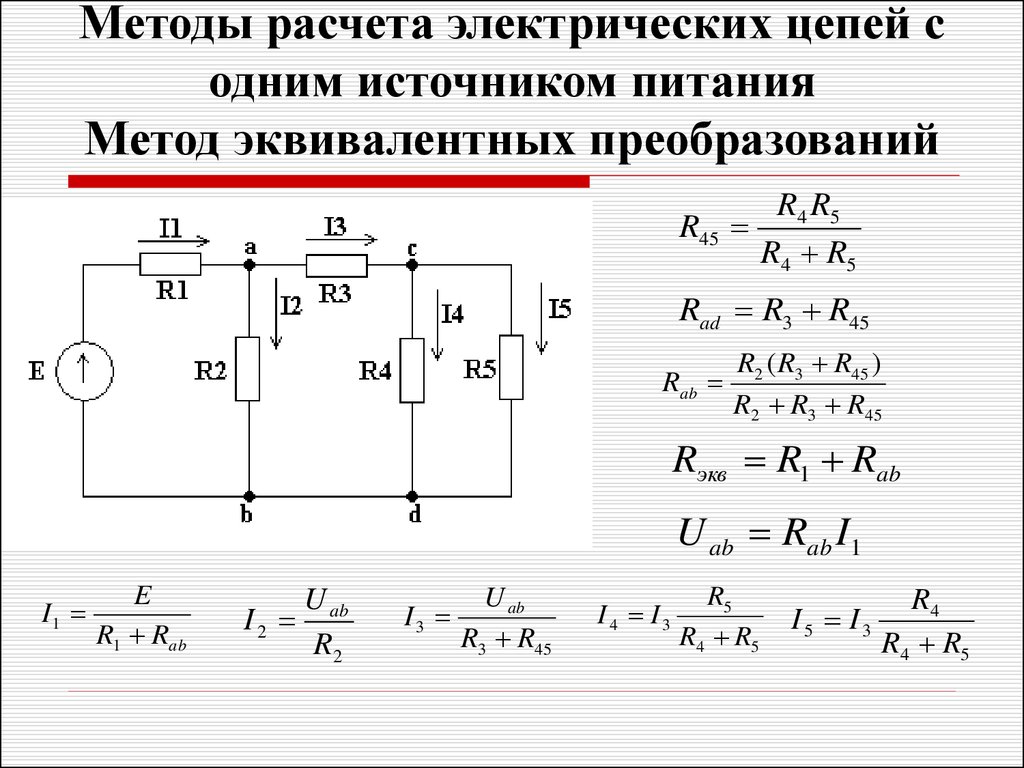
Применение концепции эквивалентного резистора
Концепция эквивалентного резистора широко применяется при анализе и расчете электрических цепей:
- Упрощение сложных схем путем замены групп резисторов на эквивалентные
- Расчет токов и напряжений в разветвленных цепях
- Анализ делителей напряжения и тока
- Расчет мощности, выделяемой на участках цепи
- Согласование сопротивлений в электронных схемах
Рассмотрим несколько примеров применения эквивалентных резисторов на практике.
Пример расчета эквивалентного сопротивления смешанного соединения
Допустим, у нас есть схема из 5 резисторов:
- R1 = 10 Ом и R2 = 20 Ом соединены последовательно
- R3 = 30 Ом, R4 = 40 Ом и R5 = 50 Ом соединены параллельно
- Эти две группы соединены последовательно
Как рассчитать эквивалентное сопротивление всей схемы?
- Найдем эквивалентное сопротивление последовательной группы R1 и R2: R12 = R1 + R2 = 10 + 20 = 30 Ом
- Рассчитаем эквивалентное сопротивление параллельной группы R3, R4 и R5: 1/R345 = 1/30 + 1/40 + 1/50 = 0,0333 + 0,025 + 0,02 = 0,0783 R345 = 1 / 0,0783 ≈ 12,77 Ом
- Теперь у нас две группы соединены последовательно, поэтому: Rэкв = R12 + R345 = 30 + 12,77 = 42,77 Ом
Таким образом, эквивалентное сопротивление всей схемы составляет примерно 42,77 Ом.
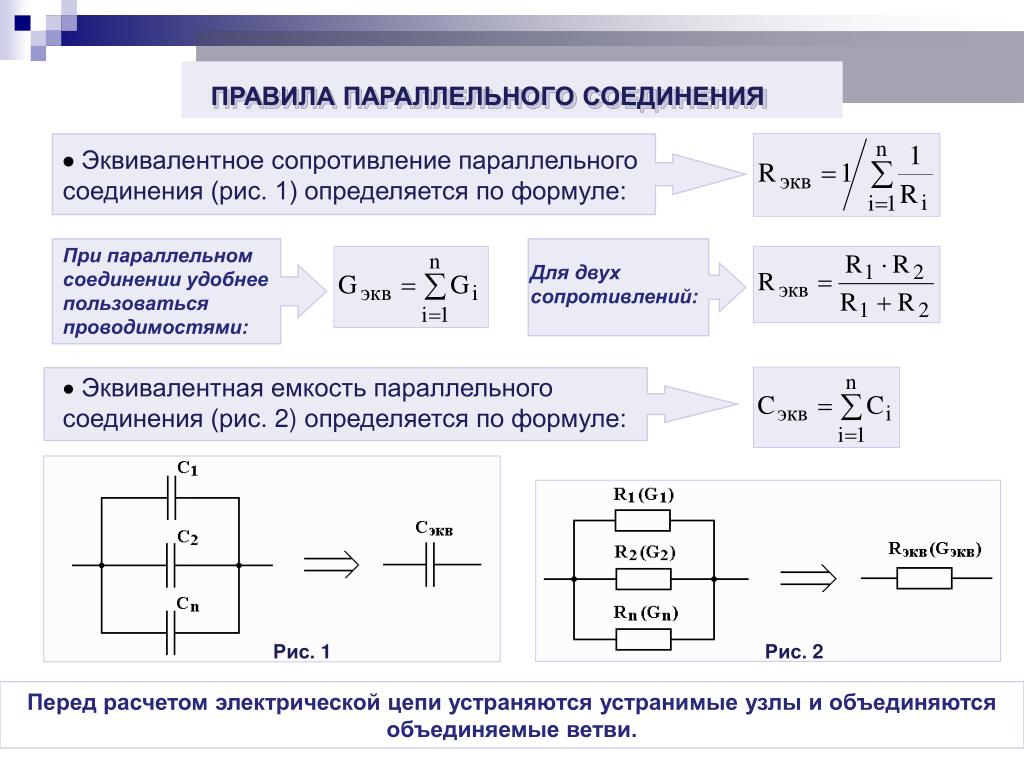
Использование эквивалентных резисторов в делителях напряжения
Делитель напряжения — это схема, которая позволяет получить напряжение, меньшее входного, путем его деления на резисторах. Рассмотрим простой пример делителя напряжения на двух резисторах:
- Входное напряжение Uвх = 12 В
- R1 = 1 кОм
- R2 = 3 кОм
Как рассчитать выходное напряжение на R2?
- Найдем эквивалентное сопротивление цепи: Rэкв = R1 + R2 = 1 кОм + 3 кОм = 4 кОм
- Рассчитаем ток в цепи по закону Ома: I = Uвх / Rэкв = 12 В / 4 кОм = 3 мА
- Найдем выходное напряжение на R2: Uвых = I * R2 = 3 мА * 3 кОм = 9 В
Таким образом, выходное напряжение делителя составляет 9 В.
Эквивалентные резисторы в расчете мощности
Концепция эквивалентного резистора полезна при расчете мощности, выделяемой в электрических цепях. Рассмотрим пример:
- Три резистора R1 = 100 Ом, R2 = 200 Ом и R3 = 300 Ом соединены параллельно
- К ним приложено напряжение U = 12 В
Какая мощность выделяется на этих резисторах?
- Рассчитаем эквивалентное сопротивление: 1/Rэкв = 1/100 + 1/200 + 1/300 = 0,01 + 0,005 + 0,00333 = 0,01833 Rэкв = 1 / 0,01833 ≈ 54,55 Ом
- Найдем ток через эквивалентный резистор: I = U / Rэкв = 12 В / 54,55 Ом ≈ 0,22 А
- Рассчитаем мощность: P = U * I = 12 В * 0,22 А = 2,64 Вт
Таким образом, на всех трех резисторах выделяется мощность 2,64 Вт.
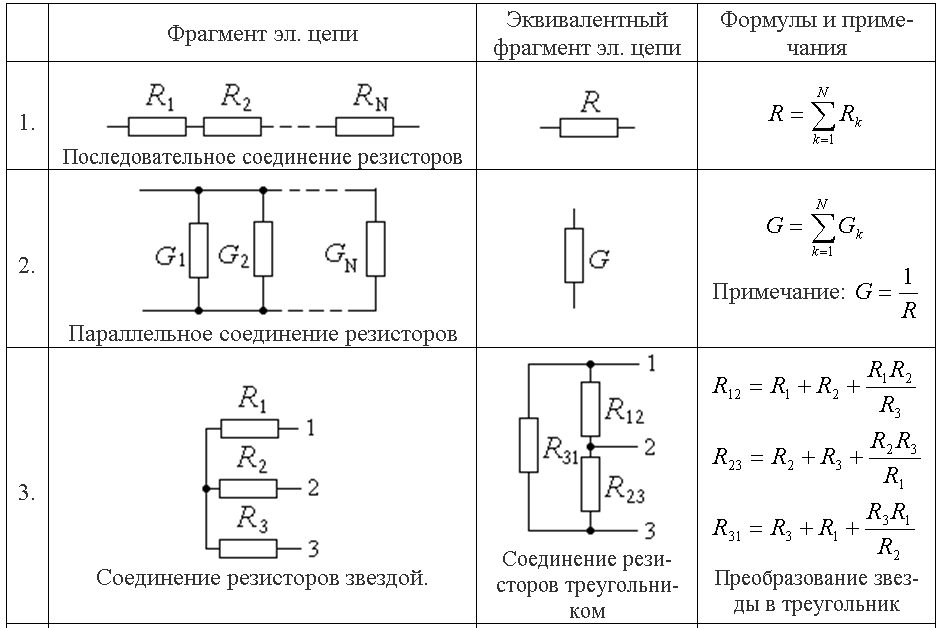
Эквивалентные резисторы в электронных схемах
В электронных схемах концепция эквивалентного резистора часто используется для анализа и проектирования различных узлов:
- Входные и выходные каскады усилителей
- Цепи обратной связи
- Фильтры
- Генераторы сигналов
- Источники питания
Например, при расчете коэффициента усиления транзисторного усилителя часто используют эквивалентную схему, где транзистор заменяется его внутренним сопротивлением. Это позволяет применить методы расчета резистивных цепей для анализа работы усилителя.
Ограничения концепции эквивалентного резистора
Несмотря на широкое применение, концепция эквивалентного резистора имеет ряд ограничений:
- Применима только для линейных цепей
- Не учитывает реактивные составляющие (индуктивность, емкость)
- Не отражает частотные свойства цепей
- Может давать погрешность при работе с резисторами, имеющими существенный разброс параметров
Поэтому при анализе сложных электронных схем, особенно на высоких частотах, часто требуется использовать более сложные модели и методы расчета.
Заключение
Концепция эквивалентного резистора — мощный инструмент для анализа и расчета электрических цепей. Она позволяет упростить сложные схемы, свести их к более простым эквивалентным цепям, что значительно облегчает расчеты токов, напряжений и мощностей. Понимание принципов расчета эквивалентных сопротивлений при последовательном и параллельном соединении резисторов — важный навык для всех, кто работает с электрическими и электронными схемами.
2.3. Эквивалентная схема резистора
Резистор нельзя рассматривать как, элемент, обладающий только активным сопротивлением, определяемым его резистивным элементом.
Помимо сопротивления резистивного элемента он имеет емкость, индуктивность и дополнительные паразитные сопротивления. Эквивалентная схема постоянного резистора представлена на рисунке 2.7.
На схеме RR –
сопротивление резистивного элемента, Rиз – сопротивление изоляции, определяемое свойством защитного покрытия и основания, Rк – сопротивление контактов, LR – эквивалентная индуктивность резистивного слоя и выводов резистора, СR – эквивалентная емкость резистора, CB1 и CB2 – емкости выводов.Активное сопротивление резистора определяется соотношением
Сопротивление
Rк имеет
существенное значение только для
низкоомных резисторов. Сопротивление
Rиз
практически влияет на общее
сопротивление только высокоомных
резисторов. Реактивные элементы
определяют частотные свойства резистора.
Из-за их наличия сопротивление резистора
на высоких частотах становится
комплексным.
Сопротивление
Rиз
практически влияет на общее
сопротивление только высокоомных
резисторов. Реактивные элементы
определяют частотные свойства резистора.
Из-за их наличия сопротивление резистора
на высоких частотах становится
комплексным.
Индуктивность и ёмкость являются распределёнными параметрами. Индуктивность резистора определяется его конструкцией, размерами и размерами выводов. Ёмкость резистора появляется между его различными участками, а также определяется конструкцией выводов и их размерами. Наличие ёмкости и индуктивности вызывает появление реактивной составляющей полного сопротивления, которая приводит к изменению активной составляющей сопротивления.
Параметры резисторов характеризуют эксплуатационные возможности применения конкретного типа резистора в конкретной электрической схеме.
1.Номинальное
сопротивление Rном и
его допустимое отклонение от
номинала ±R
являются основными параметрами
резисторов. Номиналы сопротивлений
стандартизованы в соответствии с ГОСТ
10318, а допустимые отклонения — в соответствии
с ГОСТ 9664. Для резисторов общего назначения
ГОСТ предусматривает шесть рядов
номинальных сопротивлений: Е6, Е12, Е24,
Е48, Е96 и Е192. Цифра указывает количество
номинальных значений в данном ряду,
которые согласованы с допустимыми
отклонениями (смотри таблицу 2.1).
Номинальные значения сопротивлений
определяются числовыми коэффициентами,
входящими в таблицу 2.1, которые умножаются
на
10n, где п – целое
положительное число. Так, например,
числовому коэффициенту 1,5 соответствуют
резисторы с номинальным сопротивлением,
равным 15, 150, 1500 Ом и т.д.
Номиналы сопротивлений
стандартизованы в соответствии с ГОСТ
10318, а допустимые отклонения — в соответствии
с ГОСТ 9664. Для резисторов общего назначения
ГОСТ предусматривает шесть рядов
номинальных сопротивлений: Е6, Е12, Е24,
Е48, Е96 и Е192. Цифра указывает количество
номинальных значений в данном ряду,
которые согласованы с допустимыми
отклонениями (смотри таблицу 2.1).
Номинальные значения сопротивлений
определяются числовыми коэффициентами,
входящими в таблицу 2.1, которые умножаются
на
10n, где п – целое
положительное число. Так, например,
числовому коэффициенту 1,5 соответствуют
резисторы с номинальным сопротивлением,
равным 15, 150, 1500 Ом и т.д.
Таблица 2.1
Е24 |
Е12 |
Е6 |
1,0 |
1,0 |
|
1,1 |
— |
— |
1,2 |
1,2 |
— |
1,3 |
— |
— |
1,5 |
1,5 |
1,5 |
1,6 |
— |
— |
1,8 |
1,8 |
— |
2,0 |
— |
— |
2,2 |
2,2 |
2,2 |
2,4 |
— |
— |
2,7 |
2,7 |
— |
3,0 |
— |
— |
3,3 |
3,3 |
3,3 |
3,6 |
— |
— |
3,9 |
3,9 |
— |
4,3 |
— |
— |
4,7 |
4,7 |
4,7 |
5,1 |
— |
— |
5,6 |
5,6 |
— |
6,2 |
— |
— |
6,8 |
6,8 |
6,8 |
7,5 |
— |
— |
8,2 |
8,2 |
— |
9,1 |
— |
— |
Допустимые
отклонения от номинала для ряда Е6
составляют ±20%, для ряда Е12 – ± 10%, для
ряда Е24 – ± 5%.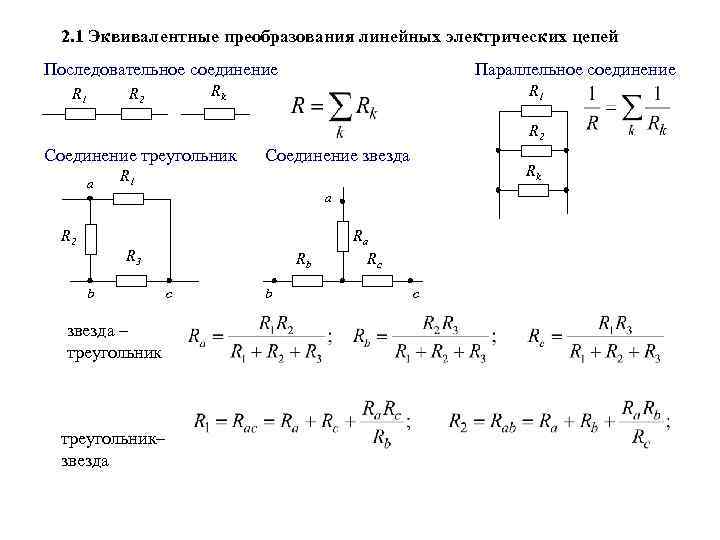 Это значит, что резистор
с сопротивлением 1,5кОм из ряда Е12 может
обладать сопротивлением в пределах от
1,35 до 1,65кОм, а тот же резистор из ряда
Е6 – в пределах от 1,2 до 1,8 кОм. Числовые
коэффициенты, определяющие номинальные
значения сопротивлений, подобраны так,
что образуется непрерывная шкала
сопротивлений, т.е. максимально возможное
сопротивление какого-либо номинала
совпадает (или несколько больше) с
минимальной величиной сопротивления
соседнего номинала. Прецизионные
резисторы имеют отклонения от номинала
±2%; ±1%; ±0,5%; ±0,2%; ±0,1%; ±0,05%; ±0,02% и ±0,01%.
Это значит, что резистор
с сопротивлением 1,5кОм из ряда Е12 может
обладать сопротивлением в пределах от
1,35 до 1,65кОм, а тот же резистор из ряда
Е6 – в пределах от 1,2 до 1,8 кОм. Числовые
коэффициенты, определяющие номинальные
значения сопротивлений, подобраны так,
что образуется непрерывная шкала
сопротивлений, т.е. максимально возможное
сопротивление какого-либо номинала
совпадает (или несколько больше) с
минимальной величиной сопротивления
соседнего номинала. Прецизионные
резисторы имеют отклонения от номинала
±2%; ±1%; ±0,5%; ±0,2%; ±0,1%; ±0,05%; ±0,02% и ±0,01%.
2.Номинальная мощность рассеивания Рном определяет допустимую электрическую нагрузку, которую способен выдержать резистор в течение длительного времени при заданной стабильности сопротивления.
Как уже отмечалось, протекание тока через резистор связано с выделением в нем тепла, которое должно рассеиваться в окружающую среду. Мощность, выделяемая в резисторе в виде тепла, определяется величиной приложенного к нему напряжения U и протекающего тока I и равна
Рвыд= UI |
(2. |
Мощность, рассеиваемая резистором в окружающую среду, пропорциональна разности температур резистора TRи окружающей среды ТO
и зависит от условий охлаждения резистора, определяемых величиной теплового сопротивления RTкоторое тем меньше, чем больше поверхность резистора и теплопроводность материала резистора.
Из условия баланса мощностей можно определить температуру резистора, что наглядно показано на рисунке 2.8а.
откуда TR=UIR.
Следовательно,
при увеличении мощности, выделяемой в
резисторе, возрастает его температура
TR , что может привести
к выходу резистора из строя. Для того
чтобы этого не произошло, необходимо
уменьшить RT, что
достигается увеличением размеров
резистора. Для каждого типа резистора
существует определенная максимальная
температура Тмах,
превышать которую нельзя.
Для каждого типа резистора
существует определенная максимальная
температура Тмах,
превышать которую нельзя.
Температура TR, как следует из вышеизложенного, зависит также от температуры окружающей среды. Если она очень высока, то температура TR может превысить максимальную, чтобы этого не произошло, необходимо уменьшать мощность, выделяемую в резисторе (рисунок 2.8, б). Для всех типов резисторов в технических условиях оговариваются указанные зависимости мощности от температуры окружающей среды (рисунок 2.8, в). Номинальные мощности стандартизованы (ГОСТ 9663) и соответствуют ряду: 0,01; 0,025; 0,05; 0,121; 0,25; 0,5; 1; 1,2; 5; 8; 10; 16; 25; 50; 75; 100; 160; 250; 500.
3. Предельное рабочее напряжение Uпред определяет величину допустимого напряжения, которое может быть приложено к резистору. Для резисторов с небольшой величиной сопротивления (сотни Ом ) эта величина определяется конструкцией резистора и рассчитывается по формуле:
Для
остальных резисторов предельное рабочее
напряжение определяется конструкцией
резистора и ограничивается возможностью
электрического пробоя, который, как
правило, происходит по поверхности
между выводами резистора или между
витками спиральной нарезки.
4.Температурный коэффициент сопротивления (ТКС) характеризует относительное изменение сопротивления при изменении температуры
Он может быть как положительным, так и отрицательным. Если резистивная пленка толстая, то она ведет себя как объемное тело, сопротивление которого с ростом температуры возрастает. Если же резистивная пленка тонкая, то она состоит из отдельных «островков», сопротивление такой пленки с ростом температуры уменьшается, так как улучшается контакт между отдельными «островками». У различных резисторов эта величина лежит в пределах (7…12)10-4.
5.Коэффициент старения βR характеризует изменение сопротивления, которое вызывается структурными изменениями резистивного элемента за счет процессов окисления, кристаллизации и т.д.
В
ТУ обычно указывается относительное
изменение сопротивления в процентах
за определенное время (1000 или 10000 ч).
6.ЭДС шумов резистора. Электроны в резистивном элементе находятся в состоянии хаотического теплового движения, в результате которого между любыми точками резистивного элемента возникает случайно изменяющееся электрическое напряжение и между выводами резистора появляется ЭДС тепловых шумов. Тепловой шум характеризуется непрерывным, широким, практически равномерным спектром. Величина ЭДС тепловых шумов определяется соотношением:
Uт = |
(2.8) |
где k = 1,38 ·10 -23 Д ж/К – постоянная Больцмана; Т – абсолютная температура в градусах шкалы Кельвина; R – сопротивление. Ом; f – полоса частот, в которой измеряются шумы.
Если
резистор включен на входе высокочувствительного
усилителя, то на его выходе будет слышен
характерный шум. Уменьшить уровень этих
шумов можно лишь, уменьшая величину
сопротивления R или температуру T.
Уменьшить уровень этих
шумов можно лишь, уменьшая величину
сопротивления R или температуру T.
Помимо тепловых шумов существует токовый шум, возникающий при протекании через резистор тока. Этот шум обусловлен дискретной структурой резистивного элемента. При протекании тока возникают местные перегревы, в результате которых изменяются контакты между отдельными частицами токопроводящего слоя и, следовательно, флюктуирует (изменяется) величина сопротивления, что ведет к появлению между выводами резистора токовой составляющей шума. Токовый шум, также как и тепловой, имеет непрерывный спектр, но интенсивность его увеличивается в области низких частот.
Поскольку величина тока, протекающего через резистор, зависит от величины приложенного напряжения U, то в первом приближении можно считать, что
UI = KIU, |
(2. |
где KI – коэффициент, зависящий от конструкции резистора, свойств резистивного слоя и полосы частот.
Величину KI указывают в технических условиях (ТУ) и лежит она в пределах от 0,2 до 20 мкВ/В. Чем однороднее структура, тем меньше токовый шум. У металлопленочных и углеродистых резисторов величина Кi 1,5 мкВ/В. У композиционных поверхностных Кi 40 мкВ/В, у композиционных объемных Кi 45 мкВ/В. У проволочных резисторов токовый шум отсутствует. Токовый шум измеряется в полосе частот от 60 до 6000 Гц. Его величина значительно превышает величину теплового шума.
В электрической цепи, содержащей несколько резисторов, напряжение суммарного шума определяется уравнением:
U∑ = |
(2. |
Выбор и расчет пусковых резисторов для силовых цепей
Величину сопротивления пусковых резисторов выбирают таким образом, чтобы избежать бросков тока в процессе пуска, которые могут повредить электродвигатель или другое оборудование электрической сети.
После того, как величина пускового сопротивления была рассчитана, производится выбор резисторов и проверка их на нагрев. Температура резисторов не должна превышать допустимую для данной конструкции.
В процессе пуска электрической машины ток, протекающий через пусковой резистор, изменяется во времени. Если длительность протекания тока через пусковое сопротивление мала, по сравнению с его постоянной времени Т, то расчеты можно упростить и вести их с использованием эквивалентного тока Iэ.т, тепловой эффект от которого будет равен прохождению через резистор реального тока:
tp – время прохождения тока через резистор. В данном случае теплоотдачей можно пренебречь. Температура от эквивалентного тока по теплу и реального тока будет одинакова.
Для определения эквивалентного тока можно использовать реальную кривую тока и построить зависимость i2(t) и провести интегрирование графическим путем.
Наряду с эквивалентным током по теплу Iэ.т существует эквивалентный ток по нагреву Iэ.н. – это ток, который при прохождении через сопротивление нагревает его до такой же температуры, что и реальный ток. В случае допущения tp<<T эквивалентный ток по нагреву равен эквивалентному току по теплу I’э.н. = Iэ.т.
Рассчитав значения Iэ.т и Iэ.н. можно выбрать необходимый резистор из каталога, если в нем приведен ток кратковременного режима работы для заданного времени работы tр.
Как правило, в каталогах приводится длительно допустимый ток нагрузки резистора. В таком случае нужно перейти к эквивалентному длительному току, который нагревает резистор до той же температуры, что и пусковой. Ниже показан пример проверки резистора для пуска шунтового электродвигателя.
Пуск электродвигателя производится раз в смену. Номинальный ток электрической машины равен 120 А, относительный пиковый момент равен Мп = 2, момент переключения Мпер = 0,8; пиковый ток 2Iн, ток переключения 0,8Iн. Первая ступень работает в течении t1 = 1,35 с, вторая ступень t2 = 1,35+0,54 = 1,9 с. Для работы выбран резистор на длительный ток 33 А с постоянной времени Т = 250 с. Поскольку постоянная времени Т значительно больше t1 и t2, то эквивалентный ток по нагреву равен эквивалентному току по теплу. Исходя из этого для первой ступени:
Так как пусковой резистор должен допускать троекратный перегруз, то для первой ступени tpi = 3t1=3·1,35=4,05 c. Воспользовавшись приведенной ниже кривой для tр1/Т = 4,05/250 = 0,015, находим эквивалентный ток резистора: Iэ.дл. = 0,13Ipi = 22,6 A. Для второй ступени резистора: tр2 = 3t2 = 3·1,9 = 5,7 c.
Поскольку ток переключения и пиковый ток такие же, как и для первой ступени, то Iр1 = Iр2. Для данной ступени (tр2/Т) = 0,023. С помощью кривой, приведенной выше, найдем Iэ.дл. = 26 А. Так как длительный ток резистора равен 33 А, то данный резистор проходит проверку по нагреву.
Для перемежающегося режима расчет ведется аналогичным образом. Если постоянная времени Т велика по сравнению со временем цикла tр1 + tр2, то уравнение можно упростить:
При проведении расчетов по формуле (2) нет необходимости в постоянной нагрева Т, данный подход более прост по сравнению с формулой (1) и дает результат с запасом. Формулу (2) можно использовать при проведении предварительных расчетов.
Для повторно-кратковременного режима работы Ip1 = Ip = const, Ip2 = 0. В таком случае для любого tp/T будем иметь:
Если же tp<<T, то формула (3) может быть значительно упрощена:
Эквивалентный по теплу ток Iр.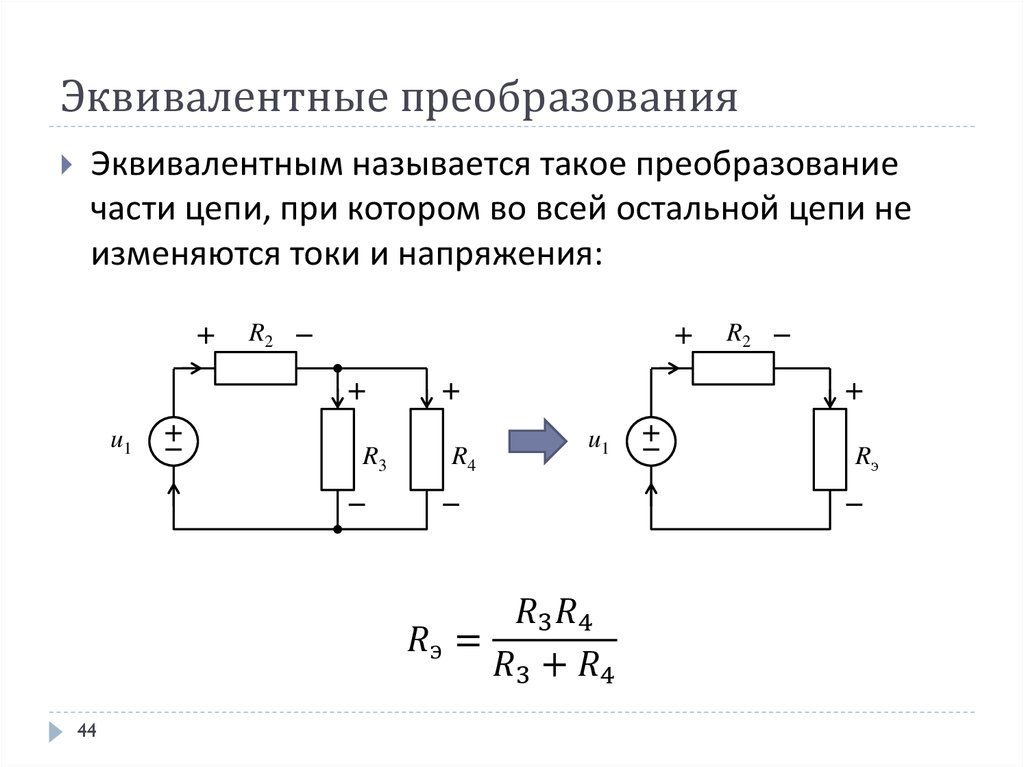 ц за время цикла tp + tп можно найти из равенства:
ц за время цикла tp + tп можно найти из равенства:
Из формул (4) и (4а) следует, что Iэ.н. = Iр.ц.
Отсюда следует вывод, что при принятых допущениях эквивалентный по теплу ток равен эквивалентному току по нагреву за время одного цикла.
Тепловой расчет резисторов является кропотливым и довольно громоздким, поэтому для типовых схем включения рекомендовано выбирать резисторы из специальных таблиц, в которых величины сопротивлений и их ток выражены в зависимости от параметров электродвигателя.
При компоновке резисторов в реостаты и ящики все они должны максимально использоваться по нагреву, так как это позволит уменьшить вес и габарит электрического аппарата. Для максимально эффективного использования резисторов при включении их последовательно все они должны иметь один и тот же длительный ток.
При создании пусковых схем для электрических машин большой мощности приходится использовать параллельное соединение элементов силовой цепи.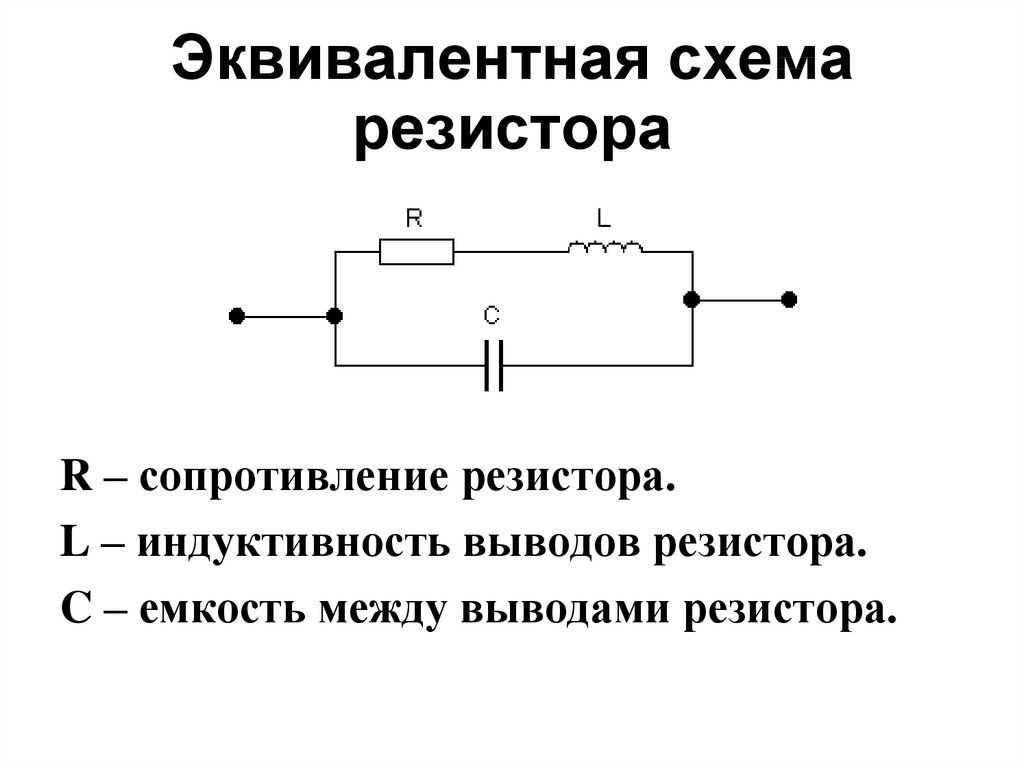
При параллельном соединении резисторов падения напряжений на них равны и для их полного использования нужно, чтобы произведение длительно допустимого тока на сопротивление для всех резисторов было равно.
Например, если один из реостатов имеет ra меньшее, чем у других, а падение напряжение на нем равно iara, то при параллельном соединении это значит, что по нему будет протекать больший ток (поскольку напряжение равно при параллельном соединении для всех элементов). В итоге получим один перегруженный по мощности реостат, а остальные недогружены.
Определение параллельного эквивалентного сопротивления в физике.
(существительное)
сопротивление сети такое, что на каждый резистор действует одна и та же разность потенциалов (напряжение), так что токи через них складываются. В этом случае обратное эквивалентное сопротивление равно сумме обратного сопротивления всех резисторов в сети.
-
Сопротивление и удельное сопротивление
- Разность потенциалов (напряжение) в сети представляет собой сумму этих напряжений, таким образом, всего сопротивление (серия эквивалентна сопротивление ) можно найти как сумму этих сопротивлений :
- Таким образом, можно вычислить эквивалентное сопротивление (Req) сети:
- параллель эквивалент сопротивление можно представить в уравнениях двумя вертикальными линиями «||» (как в геометрии) в упрощенном виде.
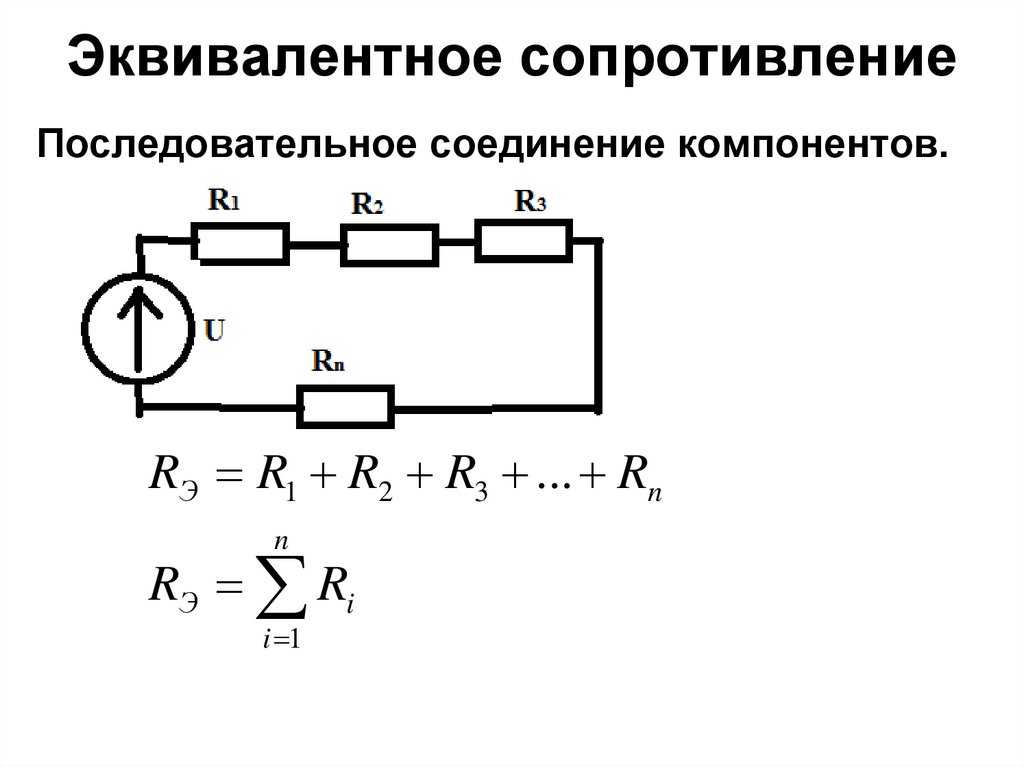
- Для случая двух резисторов, соединенных параллельно , это можно рассчитать с помощью:
- Как частный случай, сопротивление N резисторов, соединенных параллельно , каждый из которых имеет одно и то же сопротивление Ом, определяется как R/N.
-
Комбинированные цепи
- В этом случае провод с сопротивлением включен последовательно с другими сопротивлениями , которые в параллельны .
- На рисунке общее сопротивление можно рассчитать, соединив три резистора друг с другом последовательно или параллельно .
- Для более сложных комбинационных схем различные части могут быть идентифицированы как последовательные или параллельные , сокращены до их эквивалентов , а затем уменьшены до тех пор, пока не останется одно сопротивление , как показано на . Комбинированная цепь
- может быть преобразована в последовательную цепь, основываясь на понимании эквивалентных сопротивлений из параллельных ветвей в комбинированную цепь.
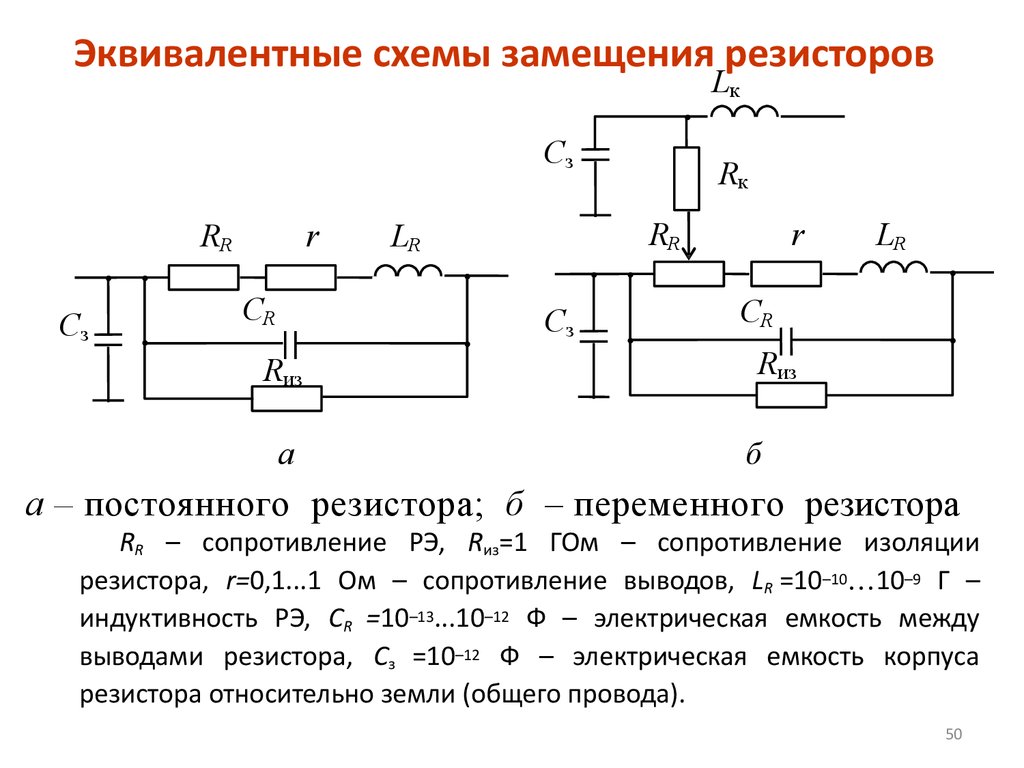
- Каждый идентифицируется и сокращается до эквивалента сопротивления , и они далее уменьшаются до тех пор, пока не будет достигнуто одно сопротивление , эквивалентное .
-
Резисторы параллельно
- Суммарное сопротивление в параллельной цепи равно сумме величин, обратных каждому отдельному сопротивлению .
- Резисторы находятся в параллельно , когда каждый резистор подключен непосредственно к источнику напряжения соединительными проводами, имеющими пренебрежимо малое сопротивление .
- Это означает, что общее сопротивление в параллельной цепи равно сумме величин, обратных каждому отдельному сопротивлению .
- Три резистора, соединенные параллельно с аккумулятором и эквивалентным одинарным или параллельным сопротивлением .
- Рассчитать общее сопротивление в цепи с резисторами, соединенными параллельно
-
Резисторы серии
- Суммарное сопротивление в цепи с последовательно соединенными резисторами равно сумме отдельных сопротивлений .
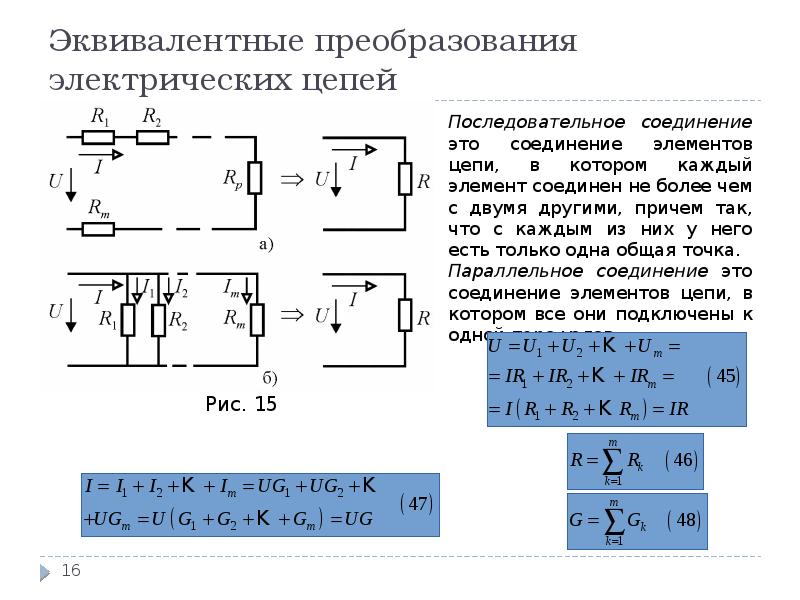
- Простейшими комбинациями резисторов являются последовательное и параллельное соединения.
- Это означает, что общее сопротивление в серии равно сумме отдельных сопротивлений .
- Поскольку весь ток должен проходить через каждый резистор, он испытывает сопротивления каждого, а сопротивления последовательно просто складываются.
- Три резистора, соединенные последовательно с батареей (слева) и , эквивалентные одиночному или последовательному сопротивлению (справа).
- Суммарное сопротивление в цепи с последовательно соединенными резисторами равно сумме отдельных сопротивлений .
-
Зарядка аккумулятора: последовательное и параллельное ЭДС
- При последовательном соединении источников напряжения их ЭДС и внутренние сопротивления складываются; в параллельно они остаются прежними.
- Когда два источника напряжения с одинаковыми ЭДС соединены параллельно , а также подключены к нагрузке с сопротивлением , общая ЭДС будет такой же, как и отдельные ЭДС.
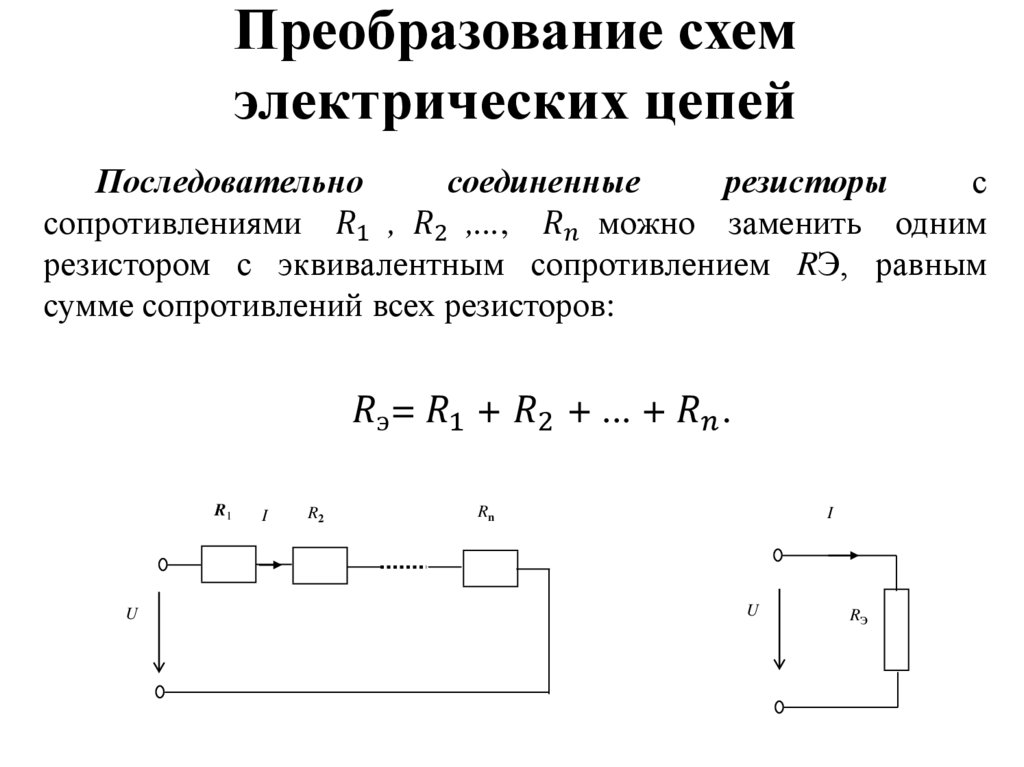
- Но общее внутреннее сопротивление уменьшается, так как внутренние сопротивления находятся в параллельно .
- Два источника напряжения с одинаковыми ЭДС (обозначены буквой E), соединенные параллельно , производят одинаковую ЭДС, но имеют меньшую общую внутреннюю сопротивление , чем отдельные источники.
- Сравните сопротивления и электродвижущие силы для источников напряжения, соединенных в одной и противоположной полярности, а также последовательно и параллельно
-
Резюме
- Три типа эквивалентности (структурная, автоморфная и регулярная) имеют постепенно менее строгие определения того, что означает для двух акторов быть « эквивалентным ».
- Структурная эквивалентность является наиболее «конкретной» формой эквивалентности .
- Чистая структурная эквивалентность может быть довольно редкой в социальных отношениях, но приближения к ней могут быть не такими уж редкими.

- Автоморфный эквивалент немного более расслаблен.
- С помощью автоморфной -эквивалентности мы ищем классы акторов, которые находятся на таком же расстоянии от других наборов акторов, то есть мы пытаемся найти параллельно или заменяемых подструктур (а не заменяемых лиц).
-
Автоморфная эквивалентность
- Несмотря на то, что актер B и актер D структурно не являются эквивалентными (у них действительно один и тот же начальник, но разные работники), они кажутся « эквивалентными » в другом смысле.
- Это разные люди, но два менеджера кажутся почему-то эквивалентными .
- На самом деле актеры B и D образуют «автоморфный» эквивалент класса .
- Идея автоморфной эквивалентности состоит в том, что наборы акторов могут быть эквивалентными , будучи встроенными в локальные структуры, которые имеют одинаковые модели связей — « параллельные » структуры.
- Обратите внимание, что менее строгое определение « эквивалентность » уменьшило количество классов.
-
Как называются скелетные мышцы
- Анатомическое расположение пучков скелетных мышц можно описать как параллель , сходящаяся, перистая или сфинктерная.
- Параллельные мышцы характеризуются пучками, которые проходят параллельно друг другу, и сокращение этих групп мышц действует как продолжение сокращения отдельного мышечного волокна.
- Параллельные мышцы можно разделить на веретенообразные и неверетенообразные в зависимости от их формы.
- Двуглавая мышца плеча является примером веретенообразной параллельной мышцы и отвечает за сгибание предплечья.
- Скелетные круговые мышцы отличаются от гладких мышц эквивалентов своей структурой и тем, что они находятся под произвольным контролем
-
Повторение и параллелизм
- Повторение и параллелизм могут добавить вашей речи ясности и выразительности.
- Точно так же параллелизм представляет собой структурированное использование повторения с использованием идентичных или эквивалентных конструкций в соответствующих предложениях для выражения одного и того же чувства.
- Параллелизм — это особенно эффективная техника для обеспечения структуры, порядка и баланса в вашей речи, в дополнение к прояснению ваших аргументов.
- Параллелизм работает так же, но без механического повторения слов или идей и вместо этого строит их из похожих примеров.
- См. ниже, как параллелизм использовался в этих двух динамиках:
- Повторение и параллелизм могут добавить вашей речи ясности и выразительности.
-
Вольтметры и амперметры
- Чтобы вольтметр мог измерять напряжение устройства, он должен быть подключен к параллельно этому устройству.
- Это необходимо, потому что объекты в параллельно испытывают одинаковую разность потенциалов.
- Общее сопротивление должно быть:
- Тот же гальванометр может работать и как амперметр, если его поместить в параллельно с малым сопротивлением Ом, часто называемым шунтирующим сопротивлением .

- Поскольку R и r параллельны , напряжение на них одинаково.
Видео-вопрос: Определение эквивалентного сопротивления комбинированной цепи
Стенограмма видео
В показанной цепи 𝑅 два равно два 𝑅 один и 𝑅 три равно трем 𝑅 два. Суммарный ток через ток 0,36 ампера. Какое сопротивление 𝑅 один?
В показанной схеме у нас есть три
резисторы параллельно и мы хотим найти значение сопротивления, 𝑅 единица. Чтобы найти сопротивление 𝑅 единицу, мы
можно преобразовать три резистора параллельно в один эквивалентный резистор 𝑅
общий. Это позволит нам найти
полное сопротивление цепи в пересчете на 𝑅 единицы. Поскольку нам даны оба
разность потенциалов, обеспечиваемая ячейкой, и полный ток в цепи,
мы также можем использовать закон Ома для расчета общего сопротивления в цепи. Затем мы можем использовать это значение для
вывести 𝑅 один.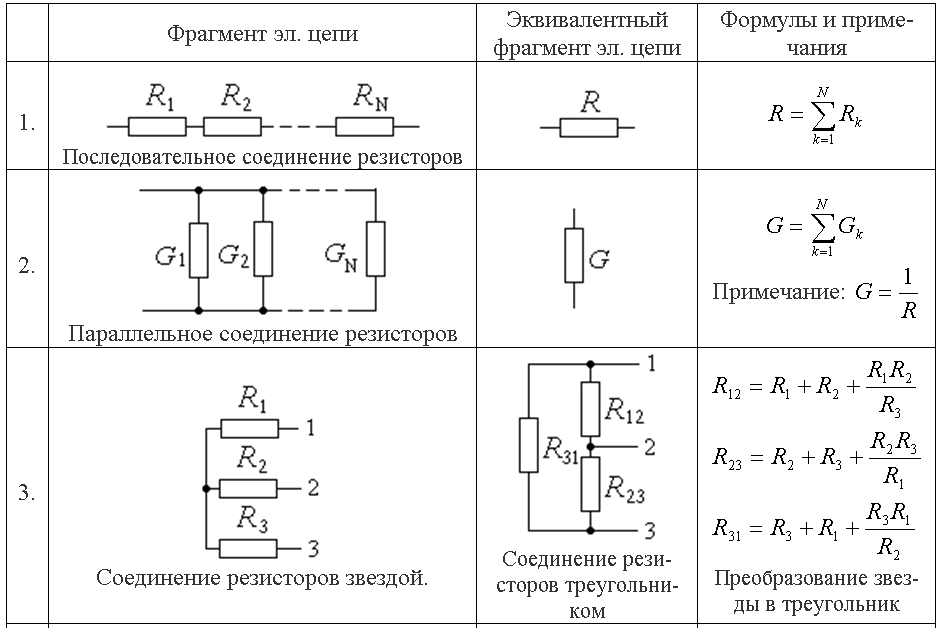
Начнем с поиска эквивалентное сопротивление цепи, 𝑅общ. Напомним, что для любого числа резисторы соединены параллельно, общее сопротивление определяется как 𝑅 total равно единице больше 𝑅 один плюс один больше 𝑅 два и так далее плюс один больше 𝑅 𝑁 в минус один власть. Итак, для этой схемы мы можем заменить три резистора, соединенных параллельно, на один эквивалентный резистор, который будет иметь общее сопротивление 𝑅, равное единице на 𝑅 единицы плюс один на 𝑅 два плюс один на 𝑅 три в отрицательной степени.
Нам дано, что 𝑅 два равно двум
𝑅 один, и нам также дано, что 𝑅 три равно трем 𝑅 двум. Потому что мы пытаемся найти
значение 𝑅 единицы, полезно найти 𝑅 три через 𝑅 единицу. Для этого мы можем заменить
значение 𝑅 два в выражение для 𝑅 три, чтобы получить 𝑅 три равно три раза
два 𝑅 один, что равно шести 𝑅 один.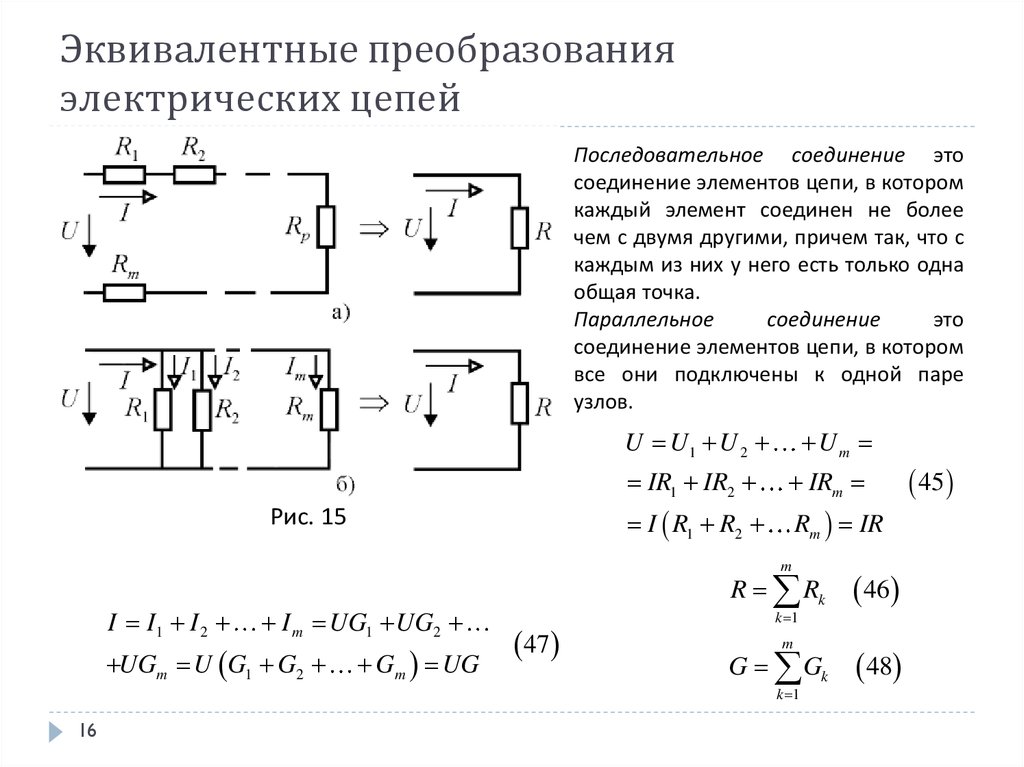 Подставляя значения для
𝑅 два и 𝑅 три, мы можем найти выражение для 𝑅 суммы через 𝑅 один. Мы находим, что 𝑅 всего, что составляет один
больше 𝑅 один плюс один больше 𝑅 два плюс один больше 𝑅 три в отрицательной степени единицы,
равно одному больше 𝑅 одному плюс одному больше двух 𝑅 одному плюс одному больше шести 𝑅 одному больше
отрицательная одна мощность.
Подставляя значения для
𝑅 два и 𝑅 три, мы можем найти выражение для 𝑅 суммы через 𝑅 один. Мы находим, что 𝑅 всего, что составляет один
больше 𝑅 один плюс один больше 𝑅 два плюс один больше 𝑅 три в отрицательной степени единицы,
равно одному больше 𝑅 одному плюс одному больше двух 𝑅 одному плюс одному больше шести 𝑅 одному больше
отрицательная одна мощность.
Манипулируя алгеброй a
немного, мы можем упростить это выражение. Во-первых, мы хотим убедиться, что
все три члена имеют один и тот же знаменатель, шесть 𝑅 один. Для этого умножаем вершину и
внизу первого члена на шесть, чтобы получить шесть больше шести 𝑅 один. Затем мы можем умножить вершину и
внизу второго члена на три, чтобы получить три больше шести 𝑅 один. Это оставляет нам шесть 𝑅 один в
знаменатель всех трех членов. Затем мы можем объединить эти термины
в одну дробь, суммируя числители.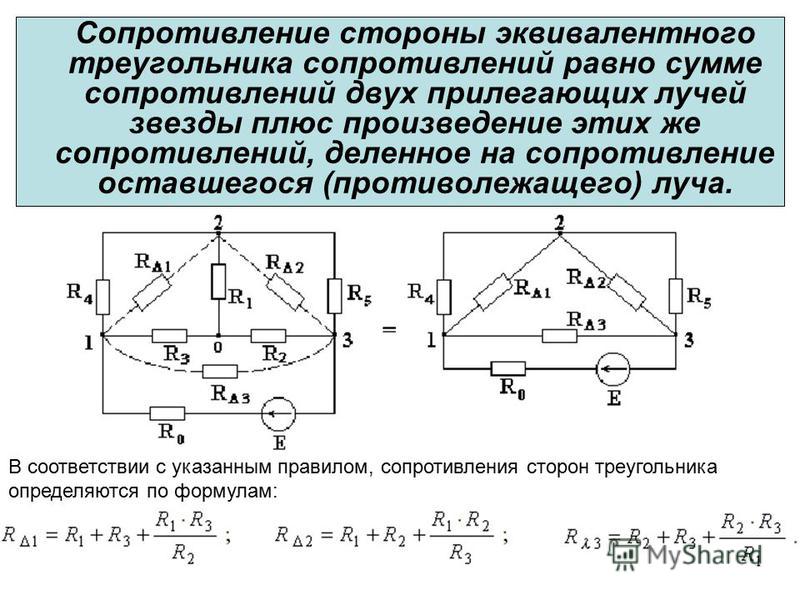 Шесть плюс три плюс один разделить на
шесть 𝑅 один равно 10 разделить на шесть 𝑅 один. Чтобы получить эту дробь в свою
В простейшей форме мы можем сократить в два раза сверху и снизу. Это дает нам пять разделить на три
𝑅 один. Наконец, взяв обратное, мы
найти 𝑅 сумма равна трем 𝑅 один разделить на пять.
Шесть плюс три плюс один разделить на
шесть 𝑅 один равно 10 разделить на шесть 𝑅 один. Чтобы получить эту дробь в свою
В простейшей форме мы можем сократить в два раза сверху и снизу. Это дает нам пять разделить на три
𝑅 один. Наконец, взяв обратное, мы
найти 𝑅 сумма равна трем 𝑅 один разделить на пять.
Итак, мы нашли выражение для полное сопротивление в цепи в пересчете на 𝑅 единицы. Теперь мы можем использовать закон Ома, чтобы найти значение полного сопротивления, которое затем позволит нам определить значение 𝑅 один.
Напомним, что закон Ома может быть
записывается как 𝑉 равно 𝐼𝑅, где 𝑉 — разность потенциалов, 𝐼 — ток,
𝑅 — сопротивление. Здесь мы хотим использовать закон Ома, чтобы
рассчитать значение сопротивления 𝑅 общ. Так что нам нужно переставить это
уравнение, чтобы сделать 𝑅 предметом.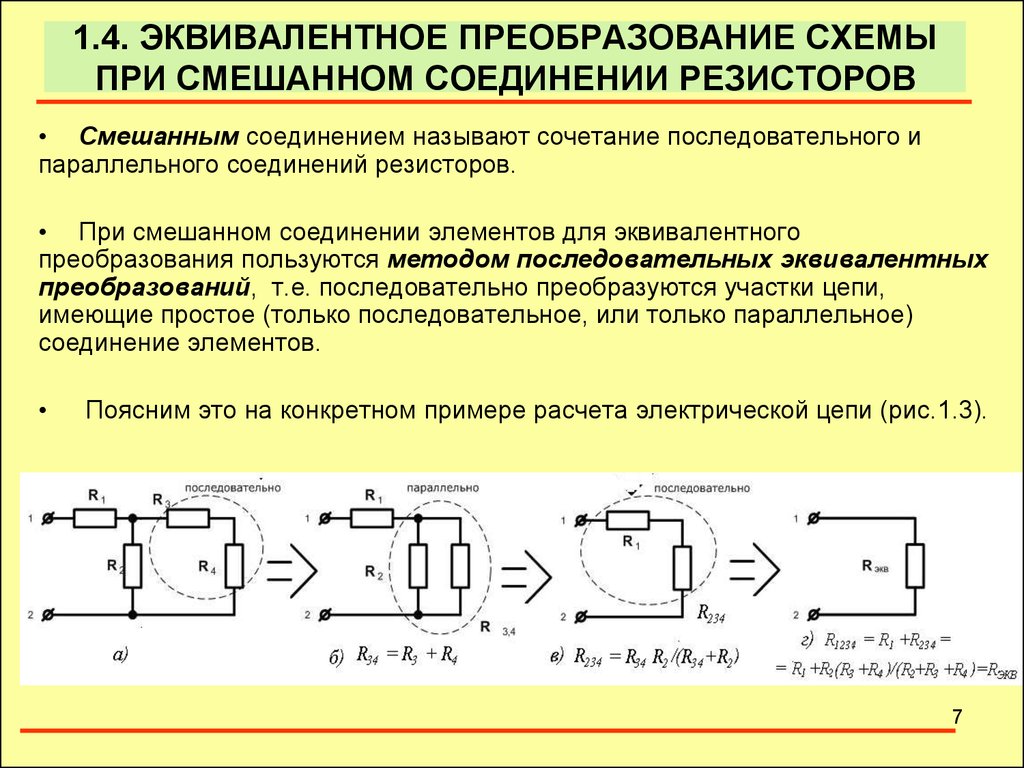 Для этого мы просто делим оба
стороны на 𝐼, что оставляет нам уравнение 𝑉 над 𝐼 равно 𝑅. Нам дана ячейка, которая
обеспечивает разность потенциалов 18 вольт в цепи. И нам также дано, что
полный ток в цепи 0,36 ампер. Эти значения совпадают через
резистор 𝑅 общ. Итак, подставив значения
разность потенциалов и ток, мы можем использовать закон Ома, чтобы найти, что сумма 𝑅 равна 18
вольт разделить на 0,36 ампера, что равно 50 Ом.
Для этого мы просто делим оба
стороны на 𝐼, что оставляет нам уравнение 𝑉 над 𝐼 равно 𝑅. Нам дана ячейка, которая
обеспечивает разность потенциалов 18 вольт в цепи. И нам также дано, что
полный ток в цепи 0,36 ампер. Эти значения совпадают через
резистор 𝑅 общ. Итак, подставив значения
разность потенциалов и ток, мы можем использовать закон Ома, чтобы найти, что сумма 𝑅 равна 18
вольт разделить на 0,36 ампера, что равно 50 Ом.
Теперь у нас есть два выражения для 𝑅
общий. 𝑅 в сумме равно 50 Ом, а 𝑅
итого равно трем 𝑅 один разделить на пять. Приравнивая эти два выражения, мы
найдите, что три 𝑅 один разделить на пять равно 50 Ом. Умножая обе части на пять и
разделив обе части на три, мы находим, что 𝑅 один равен 50 Ом, умноженный на пять третей,
что 250 разделить на три Ома или 83,333 и так далее Ом.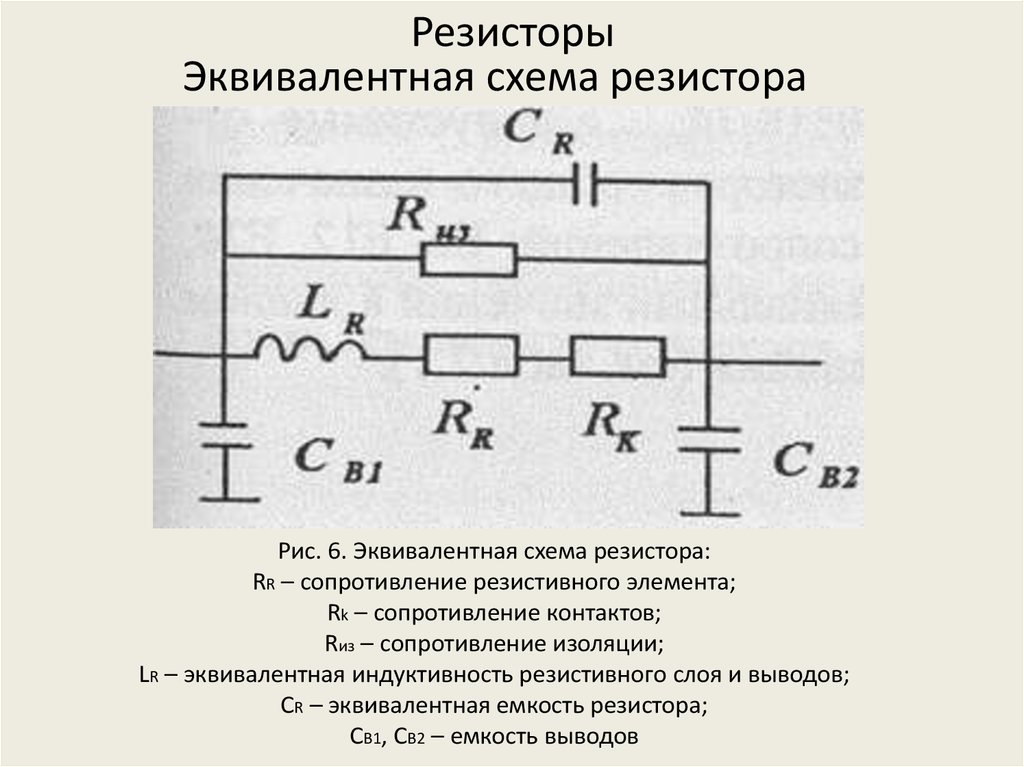

 2)
2) 9)
9) 10)
10)