Электроемкость. Конденсаторы
Что такое электроемкость проводников
Если у нас есть два проводника, изолированных друг от друга, которым мы сообщаем некоторые заряды (обозначим их соответственно q1 и q2), то между ними возникнет определенная разность потенциалов. Ее величина будет зависеть от формы проводников, а также от исходных величин зарядов. Обозначим такую разность Δφ. Если мы говорим о разности, возникающей в электрическом поле между двумя точками, то ее обычно обозначают U.
В рамках темы данной статьи нам больше всего интересна такая разность потенциалов между проводниками, когда их заряды противоположны по знаку, но равны друг другу по модулю. В таком случае мы можем ввести новое понятие – электрическая емкость (электроемкость).
Определение 1Электрической емкостью системы, состоящей из двух проводников, называется отношение заряда одного проводника (q) к разности потенциалов между этими двумя проводниками.
В виде формулы это записывается так: C=q∆φ=qU.
Для измерения электрической емкости применяется единица, называемая фарад. Она обозначается буквой Ф.
1Φ=1 Кл1 В.
Конфигурации и размеры проводников, а также свойства диэлектрика определяют величину электроемкости заданной системы. Наибольший интерес для нас представляют проводники особой формы, называемые конденсаторами.
Определение 2Конденсатор – это проводник, конфигурация которого позволяет локализовать (сосредотачивать) электрическое поле в одной выделенной части пространства. Проводники, составляющие конденсатор, называются обкладками.
Определение 3Если мы возьмем две плоские пластины из проводящего материала, расположим их на небольшом расстоянии друг от друга и проложим между ними слой диэлектрика, то мы получим простейший конденсатор, называемый плоским. При его работе электрическое поле будет располагаться преимущественно в промежутке между пластинами, но небольшая часть этого поля будет рассеиваться вокруг них.
Часть электрического поля вблизи конденсатора называется полем рассеяния.
Иногда в задачах мы можем не учитывать его и работать только с той частью электрического поля, которое расположено между обкладками. Однако пренебрегать полем рассеяния допустимо далеко не всегда, поскольку это может привести к ошибочным расчетам из-за нарушения потенциального характера электрического поля.
Рисунок 1.6.1. Электрическое поле в плоском конденсаторе.
Рисунок 1.6.2. Электрическое поле конденсатора без учета поля рассеяния, не обладающее потенциальностью.
Модуль напряженности электрического поля, которое создает каждая обкладка в плоском конденсаторе, выражается соотношением следующего вида:
E1=σ2ε0.
Исходя из принципа суперпозиции, можно утверждать, что напряженность E→ поля, которое создают обе пластины конденсатора, будет равна сумме напряженностей E+→ и E-→ полей каждой пластины, то есть E→=E+→+E-→.
Векторы напряженностей обеих пластин во внутренней части конденсатора будут параллельны друг другу. Значит, мы можем выразить модуль напряженности их суммарного поля в виде формулы E=2E1=σε0.
Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!
Описать заданиеКак рассчитать электроемкость конденсатора
Вне пластин векторы напряженности будут направлены в противоположные друг от друга стороны, значит, E будет равно нулю. Если мы обозначим заряд каждой обкладки как q, а ее площадь как S, то соотношение qS даст нам представление о поверхностной плотности. Умножив E на расстояние между обкладками (d), мы получим разность потенциалов между пластинами в однородном электрическом поле. Теперь возьмем оба этих соотношения и выведем из них формулу, по которой может быть рассчитана электрическая емкость конденсатора.
C=q∆φ=σ·SE·d=ε0Sd.
Определение 5Электрическая емкость плоского конденсатора – величина, обратно пропорциональная расстоянию между обкладками и прямо пропорциональная их площади.
Заполнение пространства между проводниками диэлектрическим материалом может увеличить электроемкость плоского конденсатора в число раз, кратное undefined.
Определение 6Введем обозначение емкости в виде буквы С и запишем это в виде формулы:
C=εε0Sd.
Данная формула называется формулой электроемкости плоского конденсатора.
Конденсаторы бывают не только плоскими. Возможны и другие конфигурации, также обладающие специфическими свойствами.
Сферическим конденсатором называется система из 2-х концентрических сфер, сделанных из проводящего материала, радиусы которых равны R1 и R2 соответственно.
Определение 8Цилиндрическим конденсатором называется системы из двух проводников цилиндрической формы, длина которых равна L, а радиусы R1 и R2.
Обозначим проницаемость диэлектрического материала как ε и запишем формулы, по которым можно найти электрическую емкость конденсаторов:
- C=4πε0εR1R2R2-R1(сферический конденсатор),
- C=2πε0εLlnR2R1(цилиндрический конденсатор).

Как рассчитать электроемкость батареи конденсаторов
Определение 9Если мы соединим несколько проводников между собой, то мы получим конструкцию, называемую батареей.
Способы соединения могут быть разными. Если соединение будет параллельным, то напряжение всех конденсаторов в системе будет одинаково: U1=U2 =U, а заряды можно найти по формулам q1=С1U и q2=C2U. При таком соединении вся система может считаться одним конденсатором, электроемкость которого равна C, заряд – q=q1+q2, а напряжение – U. В виде формулы это выглядит так:
С=q1+q2U или C=C1+C2
Определение 10Если в батарее конденсаторов элементы соединены параллельно, то для нахождения общей электроемкости нам нужно сложить емкости ее отдельных элементов.
Рисунок 1.6.3. Конденсаторы, соединенные параллельно. C=C1+C2
Рисунок 1.6.4. Конденсаторы, соединенные последовательно: 1C=1C1+1C2
Если же батарея состоит из двух последовательно соединенных конденсаторов, то заряды обоих будут одинаковы: q1=q2=q. Найти их напряжения можно так: U1=qC1 и U2=qC2. Такую систему тоже можно считать одним конденсатором, заряд которого равен q, а напряжение U=U1+U2.
Найти их напряжения можно так: U1=qC1 и U2=qC2. Такую систему тоже можно считать одним конденсатором, заряд которого равен q, а напряжение U=U1+U2.
C=qU1+U2 или 1C=1C1+1C2
Определение 11Если конденсаторы в батарее соединены последовательно, то для нахождения общей электроемкости нам нужно сложить величины, обратные емкостям каждого из них.
Справедливость обеих формул, приведенных выше, не зависит от количества конденсаторов в батарее.
Рисунок 1.6.5. Смоделированное электрическое поле плоского конденсатора.
Презентация к уроку физики в 8 классе по теме «Конденсаторы»
Муниципальное автономное общеобразовательное учреждение
«Лицей № 7» г. Бердск
Конденсаторы
8 класс
Учитель физики
И.В.Торопчина
Конденсатор
Конденсатор- это устройство, предназначенное для накопления электрического заряда и энергии электрического поля.
Конденсатор
Конденсатор представляет собой два
проводника (обкладки), разделенных слоем
диэлектрика, толщина которого мала по
сравнению с размерами проводников.
Все электрическое поле сосредоточено внутри конденсатора и однородно.
Заряд конденсатора — это абсолютное значение заряда одной из обкладок конденсатора.
Зарядка конденсатора от электрофорной машины
Различные типы конденсаторов
— по виду диэлектрика : воздушные,
слюдяные, керамические,
электролитические. — по форме обкладок : плоские,
сферические, цилиндрические. — по величине емкости:
постоянные, переменные.
Различные типы конденсаторов
- В зависимости от назначения конденсаторы имеют различное устройство.

Различные типы конденсаторов
- Обычный технический бумажный конденсатор состоит из двух полосок алюминиевой фольги, изолированных друг от друга и от металлического корпуса бумажными лентами, пропитанными парафином. Полоски и ленты туго свернуты в пакет небольшого размера
Различные типы конденсаторов
Конденсаторы переменной электроемкости
Обозначение конденсаторов
Конденсатор постоянной ёмкости
Конденсатор переменной ёмкости
Электроемкость
Физическая величина, характеризующая способность двух проводников накапливать электрический заряд называется электроёмкостью, или ёмкостью.
При увеличении заряда в 2, 3, 4 раза соответственно в 2, 3, 4
раза увеличатся показания электрометра, т. е. увеличится
напряжение между пластинами конденсатора.
Отношение заряда к напряжению будет оставаться
постоянным:
Электроёмкость конденсатора
- Величина, измеряемая отношением заряда ( q) одной из пластин конденсатора к напряжению ( U) между пластинами, называется электроёмкостью конденсатора .
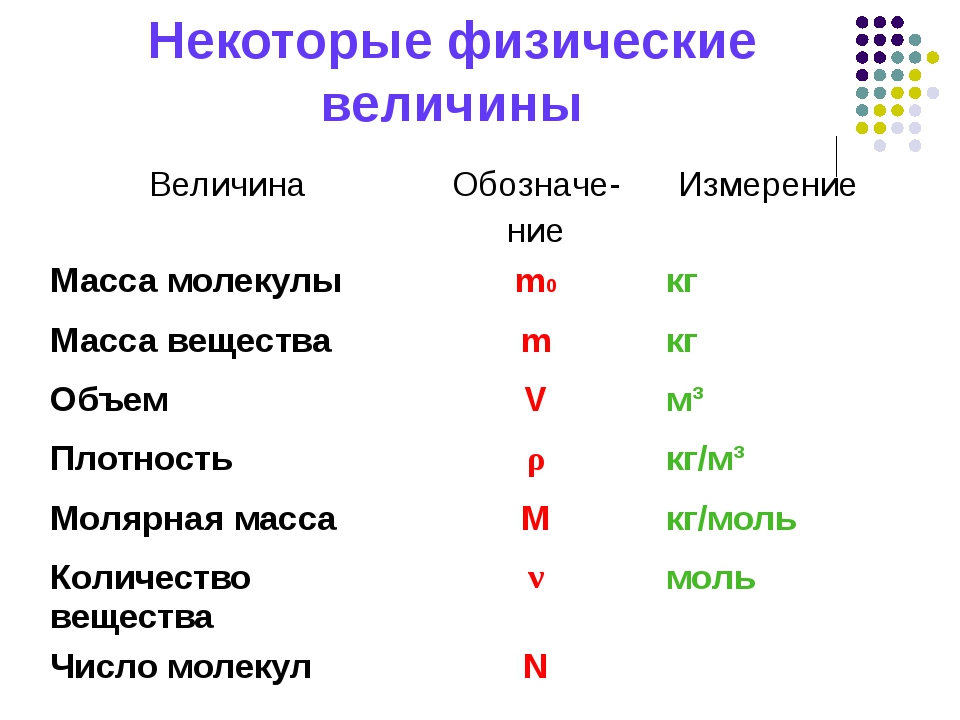
- Электроёмкость конденсатора вычисляется по формуле:
C = q / U
Единицы электроемкости
Электроемкость измеряется в фарадах(Ф)
[ С ] = 1Ф (фарад)
Электроемкость двух проводников численно
равна единице, если при сообщении им зарядов
+1 Кл и -1 Кл между ними возникает разность
потенциалов 1В
1Ф = 1Кл/В
Единицы электроемкости
1 мкФ (микрофарад)=10 -6 Ф
1 нФ ( нанофарад)=10 -9 Ф
1 пФ ( пикофарад)=10 -12 Ф
От чего зависит электроемкость конденсатора?
От чего зависит электроемкость конденсатора?
- Чем больше площадь пластин, тем больше ёмкость конденсатора.
- При уменьшении расстояния между пластинами конденсатора при неизменном заряде ёмкость конденсатора увеличивается.

- При внесении диэлектрика ёмкость конденсатора увеличивается.
Емкость конденсатора зависит от площади пластин, расстояния между пластинами, от свойств внесённого диэлектрика.
Электроемкость
от геометрических
размеров проводников
Зависит
от формы проводников и
их взаимного расположения
от электрических свойств
среды между проводниками
Энергия конденсатора
- Для того чтобы зарядить конденсатор, нужно совершить работу по разделению положительных и отрицательных зарядов. В соответствии с законом сохранения энергии, совершённая работа А равна энергии конденсатора Е, т. е
А = Е,
где Е — энергия конденсатора.
- Работу электрическое поле конденсатора, можно найти по формуле: А = qU cp ,
где U ср — это среднее значение напряжения.
U ср = U/2; тогда А = qU ср = qU/2, так как q = CU, то А = CU 2 /2.
- Энергия конденсатора ёмкостью С равна:
W = CU 2 /2
Применение конденсаторов
- Конденсаторы могут длительное время накапливать энергию, а при разрядке они отдают её почти мгновенно.
- Свойство конденсатора накапливать и быстро отдавать электрическую энергию широко используется в электротехнических и электронных устройствах, в медицинской технике (рентгеновская техника, устройства электротерапии), при изготовлении дозиметров, аэрофотосъёмке.
Применение конденсаторов
- Лампа-вспышка питается электрическим током разрядки конденсатора.
- Газоразрядные трубки зажигаются при разрядки батареи конденсаторов.
- Радиотехника .
Историческая справка
Первый конденсатор был изобретен в 1745 г. немецким юристом и учёным Эвальд Юрген фон Клейстом
немецким юристом и учёным Эвальд Юрген фон Клейстом
Первый конденсатор: одна обкладка-ртуть, другая обкладка- рука экспериментатора, державшая банку.
Историческая справка
- Почти такой же опыт и почти в то же время был поставлен в голландском городе Лейдене профессором университета Питером ван Мушенбруком.
- Зарядив воду и взяв банку в одну руку, он прикоснулся другой рукой к металлическому стержню, служившему для подвода заряда к воде. При этом Мушенбрук ощутил такой сильный удар в руки, плечи и грудь, что потерял сознание, и два дня приходил в себя.
- Эксперимент ван Мушенбрука получил большую известность, поэтому конденсатор стал известен как «лейденская банка».
Домашнее задание
§ 54, Упражнение 38
Конденсатор. Энергия электрического поля — материалы для подготовки к ЕГЭ по Физике
Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: электрическая ёмкость, конденсатор, энергия электрического поля конденсатора.
Предыдущие две статьи были посвящены отдельному рассмотрению того, каким образом ведут себя в электрическом поле проводники и каким образом — диэлектрики. Сейчас нам понадобится объединить эти знания. Дело в том, что большое практическое значение имеет совместное использование проводников и диэлектриков в специальных устройствах — конденсаторах.
Но прежде введём понятие электрической ёмкости.
Ёмкость уединённого проводника
Предположим, что заряженный проводник расположен настолько далеко от всех остальных тел, что взаимодействие зарядов проводника с окружающими телами можно не принимать во внимание. В таком случае проводник называется уединённым.
Потенциал всех точек нашего проводника, как мы знаем, имеет одно и то же значение , которое называется потенциалом проводника. Оказывается, что потенциал уединённого проводника прямо пропорционален его заряду. Коэффициент пропорциональности принято обозначать , так что
Величина называется электрической ёмкостью проводника и равна отношению заряда проводника к его потенциалу:
(1)
Например, потенциал уединённого шара в вакууме равен:
где — заряд шара, — его радиус. Отсюда ёмкость шара:
Отсюда ёмкость шара:
(2)
Если шар окружён средой-диэлектриком с диэлектрической проницаемостью , то его потенциал уменьшается в раз:
Соответственно, ёмкость шара в раз увеличивается:
(3)
Увеличение ёмкости при наличии диэлектрика — важнейший факт. Мы ещё встретимся с ним при рассмотрении конденсаторов.
Из формул (2) и (3) мы видим, что ёмкость шара зависит только от его радиуса и диэлектрической проницаемости окружающей среды. То же самое будет и в общем случае: ёмкость уединённого проводника не зависит от его заряда; она определяется лишь размерами и формой проводника, а также диэлектрической проницаемостью среды, окружающей проводник. От вещества проводника ёмкость также не зависит.
В чём смысл понятия ёмкости? Ёмкость показывает, какой заряд нужно сообщить проводнику, чтобы увеличить его потенциал на В. Чем больше ёмкость — тем, соответственно, больший заряд требуется поместить для этого на проводник.
Единицей измерения ёмкости служит фарад (Ф). Из определения ёмкости (1) видно, что Ф = Кл/В.
Давайте ради интереса вычислим ёмкость земного шара (он является проводником!). Радиус считаем приближённо равным км.
мкФ.
Как видите, Ф — это очень большая ёмкость.
Единица измерения ёмкости полезна ещё и тем, что позволяет сильно сэкономить на обозначении размерности диэлектрической постоянной . В самом деле, выразим из формулы (2):
Следовательно, диэлектрическая постоянная может измеряться в Ф/м:
Ф.
Так легче запомнить, не правда ли?
Ёмкость плоского конденсатора
Ёмкость уединённого проводника на практике используется редко. В обычных ситуациях проводники не являются уединёнными. Заряженный проводник взаимодействует с окружающими телами и наводит на них заряды, а потенциал поля этих индуцированных зарядов (по принципу суперпозиции!) изменяет потенциал самого проводника. В таком случае уже нельзя утверждать, что потенциал проводника будет прямо пропорционален его заряду, и понятие ёмкости проводника самого по себе фактически утрачивает смысл.
В таком случае уже нельзя утверждать, что потенциал проводника будет прямо пропорционален его заряду, и понятие ёмкости проводника самого по себе фактически утрачивает смысл.
Можно, однако, создать систему заряженных проводников, которая даже при накоплении на них значительного заряда почти не взаимодействует с окружающими телами. Тогда мы сможем снова говорить о ёмкости — но на сей раз о ёмкости этой системы проводников.
Наиболее простым и важным примером такой системы является плоский конденсатор. Он состоит из двух параллельных металлических пластин (называемых обкладками), разделённых слоем диэлектрика. При этом расстояние между пластинами много меньше их собственных размеров.
Для начала рассмотрим воздушный конденсатор, у которого между обкладками находится воздух
Пусть заряды обкладок равны и . Именно так и бывает в реальных электрических схемах: заряды обкладок равны по модулю и противоположны по знаку. Величина — заряд положительной обкладки — называется зарядом конденсатора.
Пусть — площадь каждой обкладки. Найдём поле, создаваемое обкладками в окружающем пространстве.
Поскольку размеры обкладок велики по сравнению с расстоянием между ними, поле каждой обкладки вдали от её краёв можно считать однородным полем бесконечной заряженной плоскости:
Здесь — напряжённость поля положительной обкладки, — напряженность поля отрицательной обкладки, — поверхностная плотность зарядов на обкладке:
На рис. 1 (слева) изображены векторы напряжённости поля каждой обкладки в трёх областях: слева от конденсатора, внутри конденсатора и справа от конденсатора.
Рис. 1. Электрическое поле плоского конденсатора
Согласно принципу суперпозиции, для результирующего поля имеем:
Нетрудно видеть, что слева и справа от конденсатора поле обращается в нуль (поля обкладок погашают друг друга):
Внутри конденсатора поле удваивается:
или
(4)
Результирующее поле обкладок плоского конденсатора изображено на рис. 1 справа. Итак:
1 справа. Итак:
Внутри плоского конденсатора создаётся однородное электрическое поле, напряжённость которого находится по формуле (4). Снаружи конденсатора поле равно нулю, так что конденсатор не взаимодействует с окружающими телами.
Не будем забывать, однако, что данное утверждение выведено из предположения, будто обкладки являются бесконечными плоскостями. На самом деле их размеры конечны, и вблизи краёв обкладок возникают так называемые краевые эффекты: поле отличается от однородного и проникает в наружное пространство конденсатора. Но в большинстве ситуаций (и уж тем более в задачах ЕГЭ по физике) краевыми эффектами можно пренебречь и действовать так, словно утверждение, выделенное курсивом, является верным без всяких оговорок.
Пусть расстояние между обкладками конденсатора равно . Поскольку поле внутри конденсатора является однородным, разность потенциалов между обкладками равна произведению на (вспомните связь напряжения и напряжённости в однородном поле!):
(5)
Разность потенциалов между обкладками конденсатора, как видим, прямо пропорциональна заряду конденсатора. Данное утверждение аналогично утверждению «потенциал уединённого проводника прямо пропорционален заряду проводника», с которого и начался весь разговор о ёмкости. Продолжая эту аналогию, определяем ёмкость конденсатора как отношение заряда конденсатора к разности потенциалов между его обкладками:
Данное утверждение аналогично утверждению «потенциал уединённого проводника прямо пропорционален заряду проводника», с которого и начался весь разговор о ёмкости. Продолжая эту аналогию, определяем ёмкость конденсатора как отношение заряда конденсатора к разности потенциалов между его обкладками:
(6)
Ёмкость конденсатора показывает, какой заряд ему нужно сообщить, чтобы разность потенциалов между его обкладками увеличилась на В. Формула (6), таким образом, является модификацией формулы (1) для случая системы двух проводников — конденсатора.
Из формул (6) и (5) легко находим ёмкость плоского воздушного конденсатора:
(7)
Она зависит только от геометрических характеристик конденсатора: площади обкладок и расстояния между ними.
Предположим теперь, что пространство между обкладками заполнено диэлектриком с диэлектрической проницаемостью . Как изменится ёмкость конденсатора?
Напряжённость поля внутри конденсатора уменьшится в раз, так что вместо формулы (4) теперь имеем:
(8)
Соответственно, напряжение на конденсаторе:
(9)
Отсюда ёмкость плоского конденсатора с диэлектриком:
(10)
Она зависит от геометрических характеристик конденсатора (площади обкладок и расстояния между ними) и от диэлектрической проницаемости диэлектрика, заполняющего конденсатор.
Важное следствие формулы (10): заполнение конденсатора диэлектриком увеличивает его ёмкость.
Энергия заряженного конденсатора
Заряженный конденсатор обладает энергией. В этом можно убедиться на опыте. Если зарядить конденсатор и замкнуть его на лампочку, то (при условии, что ёмкость конденсатора достаточно велика) лампочка ненадолго загорится.
Следовательно, в заряженном конденсаторе запасена энергия, которая и выделяется при его разрядке. Нетрудно понять, что этой энергией является потенциальная энергия взаимодействия обкладок конденсатора — ведь обкладки, будучи заряжены разноимённо, притягиваются друг к другу.
Мы сейчас вычислим эту энергию, а затем увидим, что существует и более глубокое понимание происхождения энергии заряженного конденсатора.
Начнём с плоского воздушного конденсатора. Ответим на такой вопрос: какова сила притяжения его обкладок друг к другу? Величины используем те же: заряд конденсатора , площадь обкладок .
Возьмём на второй обкладке настолько маленькую площадку, что заряд этой площадки можно считать точечным. Данный заряд притягивается к первой обкладке с силой
Данный заряд притягивается к первой обкладке с силой
где — напряжённость поля первой обкладки:
Следовательно,
Направлена эта сила параллельно линиям поля (т. е. перпендикулярно пластинам).
Результирующая сила притяжения второй обкладки к первой складывается из всех этих сил , с которыми притягиваются к первой обкладке всевозможные маленькие заряды второй обкладки. При этом суммировании постоянный множитель вынесется за скобку, а в скобке просуммируются все и дадут . В результате получим:
(11)
Предположим теперь, что расстояние между обкладками изменилось от начальной величины до конечной величины . Сила притяжения пластин совершает при этом работу:
Знак правильный: если пластины сближаются , то сила совершает положительную работу, так как пластины притягиваются друг к другу. Наоборот, если удалять пластины , то работа силы притяжения получается отрицательной, как и должно быть.
С учётом формул (11) и (7) имеем:
где
Это можно переписать следующим образом:
где
(12)
Работа потенциальной силы притяжения обкладок оказалась равна изменению со знаком минус величины . Это как раз и означает, что — потенциальная энергия взаимодействия обкладок, или энергия заряженного конденсатора.
Используя соотношение , из формулы (12) можно получить ещё две формулы для энергии конденсатора (убедитесь в этом самостоятельно!):
(13)
(14)
Особенно полезными являются формулы (12) и (14).
Допустим теперь, что конденсатор заполнен диэлектриком с диэлектрической проницаемостью . Сила притяжения обкладок уменьшится в раз, и вместо (11) получим:
При вычислении работы силы , как нетрудно видеть, величина войдёт в ёмкость , и формулы (12) — (14) останутся неизменными. Ёмкость конденсатора в них теперь будет выражаться по формуле (10).
Итак, формулы (12) — (14) универсальны: они справедливы как для воздушного конденсатора, так и для конденсатора с диэлектриком.
Энергия электрического поля
Мы обещали, что после вычисления энергии конденсатора дадим более глубокое истолкование происхождения этой энергии. Что ж, приступим.
Рассмотрим воздушный конденсатор и преобразуем формулу (14) для его энергии:
Но — объём конденсатора. Получаем:
(15)
Посмотрите внимательно на эту формулу. Она уже не содержит ничего, что являлось бы специфическим для конденсатора! Мы видим энергию электрического поля , сосредоточенного в некотором объёме .
Энергия конденсатора есть не что иное, как энергия заключённого внутри него электрического поля.
Итак, электрическое поле само по себе обладает энергией. Ничего удивительного для нас тут нет. Радиоволны, солнечный свет — это примеры распространения энергии, переносимой в пространстве электромагнитными волнами.
Величина — энергия единицы объёма поля — называется объёмной плотностью энергии. Из формулы (15) получим:
(16)
В этой формуле не осталось вообще никаких геометрических величин. Она даёт максимально чистую связь энергии электрического поля и его напряжённости.
Если конденсатор заполнен диэлектриком, то его ёмкость увеличивается в раз, и вместо формул (15) и (16) будем иметь:
(17)
(18)
Как видим, энергия электрического поля зависит ещё и от диэлектрической проницаемости среды, в которой поле находится.
Замечательно, что полученные формулы для энергии и плотности энергии выходят далеко за пределы электростатики: они справедливы не только для электростатического поля, но и для электрических полей, меняющихся во времени.
Виды конденсаторов и их применение презентация. Презентация по физике на тему «Конденсаторы. Электроемкость». Конденсаторы переменной электроемкости
Сформировать понятие электроемкости; Ввести новую характеристику – электроемкость конденсатора, и ее единицу измерения. Рассмотреть виды конденсаторов и где они применяются
Повторим… 1 вариант 1) Кем и когда была создана теория электромагнитного поля и в чем заключается ее суть. 2) Перечислите виды электромагнитных волн. Инфракрасное излучение, его свойства и влияние на организм человека. 2 вариант 1) Что называют электромагнитной волной?. Какими основными свойствами обладает электромагнитная волна? 2) Перечислите виды электромагнитных волн. Рентгенвоское излучение, его свойства и влияние на организм человека.
Конденсатор представляет собой два проводника, разделенные слоем диэлектрика, толщина которого мала по сравнению с размерами проводников. Электроемкость конденсатора равна где q – заряд положительной обкладки, U – напряжение между обкладками. Электроемкость конденсатора зависит от его геометрической конструкции и электрической проницаемости заполняющего его диэлектрика и не зависит от заряда обкладок. Конденсатор
Электроёмкостью двух проводников называют отношение заряда одного из проводников к разности потенциалов между этим проводником и соседним. Единица измерения ёмкости – фарад – [ Ф ] Это надо знать:
Электроемкость плоского конденсатора равна где S– площадь каждой из обкладок, d– расстояние между ними, ε – диэлектрическая проницаемость вещества между обкладками. При этом предполагается, что геометрические размеры пластин велики по сравнению с расстоянием между ними. Запомните, что…
В настоящее время широко применяются бумажные конденсаторы для напряжений в несколько сот вольт и ёмкостью в несколько микрофарад. В таких конденсаторах обкладками служат две длинные ленты тонкой металлической фольги, а изолирующей прокладкой между ними – несколько более широкая бумажная лента, пропитанная парафином. Бумажной лентой покрывается одна из обкладок, затем ленты туго свёртываются в рулон и укладываются в специальный корпус. Такой конденсатор, имея размеры спичечного коробка, обладает ёмкостью 10мкФ (металлический шар такой ёмкости имел бы радиус 90км). Бумажный конденсатор
Керамический конденсатор В радиотехнике применяют керамические конденсаторы. Диэлектриком в них служит специальная керамика. Обкладки керамических конденсаторов изготавливаются в виде слоя серебра, нанесённого на поверхность керамики и защищённого слоем лака. Керамические конденсаторы изготавливаются на ёмкости о единиц до сотен пикофарад и на напряжения от сотен до тысяч вольт.
Запишите какова их электроемкость.
Слайд 14
Какова электроемкость конденсатора, если заряд конденсатора 10 нКл, а разность потенциалов 20 кВ. А теперь задача…
Слайд 15
Конденсатору емкостью 10 мкФ сообщили заряд 4 мкКл. Какова энергия заряженного конденсатора. А теперь задача…
Муниципальное автономное общеобразовательное учреждение
«Лицей № 7» г. Бердск
Конденсаторы
8 класс
Учитель физики
И.В.Торопчина
Конденсатор
Конденсатор- это устройство, предназначенное для накопления электрического заряда и энергии электрического поля.
Конденсатор
Конденсатор представляет собой два
проводника (обкладки), разделенных слоем
диэлектрика, толщина которого мала по
сравнению с размерами проводников.
Все электрическое поле сосредоточено внутри конденсатора и однородно.
Заряд конденсатора — это абсолютное значение заряда одной из обкладок конденсатора.
— по виду диэлектрика : воздушные,
слюдяные, керамические,
электролитические. — по форме обкладок : плоские,
сферические, цилиндрические. — по величине емкости:
постоянные, переменные.
- В зависимости от назначения конденсаторы имеют различное устройство.
- Обычный технический бумажный конденсатор состоит из двух полосок алюминиевой фольги, изолированных друг от друга и от металлического корпуса бумажными лентами, пропитанными парафином. Полоски и ленты туго свернуты в пакет небольшого размера
Конденсаторы переменной электроемкости
Обозначение конденсаторов
Конденсатор постоянной ёмкости
Конденсатор переменной ёмкости
Электроемкость
Физическая величина, характеризующая способность двух проводников накапливать электрический заряд называется электроёмкостью, или ёмкостью.
При увеличении заряда в 2, 3, 4 раза соответственно в 2, 3, 4
раза увеличатся показания электрометра, т. е. увеличится
напряжение между пластинами конденсатора.
Отношение заряда к напряжению будет оставаться
постоянным:
Электроёмкость конденсатора
- Величина, измеряемая отношением заряда ( q) одной из пластин конденсатора к напряжению ( U) между пластинами, называется электроёмкостью конденсатора .
- Электроёмкость конденсатора вычисляется по формуле:
C = q / U
Единицы электроемкости
Электроемкость измеряется в фарадах(Ф)
[ С ] = 1Ф (фарад)
Электроемкость двух проводников численно
равна единице, если при сообщении им зарядов
+1 Кл и -1 Кл между ними возникает разность
потенциалов 1В
1Ф = 1Кл/В
Единицы электроемкости
1 мкФ (микрофарад)=10 -6 Ф
1 нФ (нанофарад)=10 -9 Ф
1 пФ (пикофарад)=10 -12 Ф
- Чем больше площадь пластин, тем больше ёмкость конденсатора.
- При уменьшении расстояния между пластинами конденсатора при неизменном заряде ёмкость конденсатора увеличивается.
- При внесении диэлектрика ёмкость конденсатора увеличивается.
Емкость конденсатора зависит от площади пластин, расстояния между пластинами, от свойств внесённого диэлектрика.
Электроемкость
от геометрических
размеров проводников
Зависит
от формы проводников и
их взаимного расположения
от электрических свойств
среды между проводниками
Энергия конденсатора
- Для того чтобы зарядить конденсатор, нужно совершить работу по разделению положительных и отрицательных зарядов. В соответствии с законом сохранения энергии, совершённая работа А равна энергии конденсатора Е, т. е
А = Е,
где Е — энергия конденсатора.
- Работу электрическое поле конденсатора, можно найти по формуле: А = qU cp ,
где U ср — это среднее значение напряжения.
U ср = U/2; тогда А = qU ср = qU/2, так как q = CU, то А = CU 2 /2.
- Энергия конденсатора ёмкостью С равна:
W = CU 2 /2
- Конденсаторы могут длительное время накапливать энергию, а при разрядке они отдают её почти мгновенно.
- Свойство конденсатора накапливать и быстро отдавать электрическую энергию широко используется в электротехнических и электронных устройствах, в медицинской технике (рентгеновская техника, устройства электротерапии), при изготовлении дозиметров, аэрофотосъёмке.
- Лампа-вспышка питается электрическим током разрядки конденсатора.
- Газоразрядные трубки зажигаются при разрядки батареи конденсаторов.
- Радиотехника .
Первый конденсатор был изобретен в 1745 г. немецким юристом и учёным Эвальд Юрген фон Клейстом
Первый конденсатор: одна обкладка-ртуть, другая обкладка- рука экспериментатора, державшая банку.
- Почти такой же опыт и почти в то же время был поставлен в голландском городе Лейдене профессором университета Питером ван Мушенбруком.
- Зарядив воду и взяв банку в одну руку, он прикоснулся другой рукой к металлическому стержню, служившему для подвода заряда к воде. При этом Мушенбрук ощутил такой сильный удар в руки, плечи и грудь, что потерял сознание, и два дня приходил в себя.
- Эксперимент ван Мушенбрука получил большую известность, поэтому конденсатор стал известен как «лейденская банка».
Домашнее задание
§ 54, Упражнение 38
«Конденсатор физика» — Виды конденсаторов. — Бумажный конденсатор — слюдяной конденсатор электролитический конденсатор. Воздушный конденсатор. Соединения конденсаторов. — Воздушный конденсатор. Определение конденсатора. При подключении электролитического конденсатора необходимо соблюдать полярность. Назначение конденсаторов.
«Использование конденсаторов» — Опыты с конденсатором. Конденсатор используется в схемах зажигания. Формулы энергии. Применение конденсаторов. Особенности применения конденсаторов. Конденсатор используется в медицине. Светильники с разрядными лампами. Емкостная клавиатура. Конденсатор. Мобильные телефоны. Применяется в телефонии и телеграфии.
«Электроемкость и конденсаторы» — В клавиатуре компьютера. Конденсатор переменной емкости. Соединение конденсаторов. Электроемкость. Последовательное. Фотовспышки. Схемы соединения конденсаторов. Обозначение на электрических схемах: Конденсаторы. Электроемкость плоского конденсатора. Все электрическое поле сосредоточено внутри конденсатора.
«Применение конденсаторов» — Для аккумуляторов последних время регенерации принципиально важно. Полимерные конденсаторы с твёрдым электролитом на чипсете. Схема телефонного «жучка». Схема выпрямителя тока. Конденсатор CTEALTG STC — 1001. Микрофон конденсаторный. Удачная ассоциация есть на сайте Sciencentral. Студийный конденсаторный направленный микрофон широкого применения.
«Конденсатор» — Емкость конденсатора. Отношение заряда. Энергия конденсатора. Конденсатор переменной емкости. Бумажный конденсатор. Площадь. Конденсатор. Применение конденсаторов. Урок физики в 9 классе
Cлайд 1
Выполнил: Каретко Дима, ученик 10 «А» Руководитель: Попова Ирина Александровна, учитель физики Белово 2011 Муниципальное общеобразовательное учреждение «Средняя общеобразовательная школа № 30 г. Белово» Конденсаторы Миипроект по физикеCлайд 2
План Введение Конденсаторы Основные параметры конденсатора Классификация конденсаторов Применение конденсаторов Вывод ЛитератураCлайд 3
Введение Систему проводников очень большой электроемкости вы можете обнаружить в любом радиоприемнике или купить в магазине. Называется она конденсатором. Сейчас вы узнаете, как устроены подобные системы и от чего зависит их электроемкость.Cлайд 4
Конденсаторы Конденсатор — двухполюсник с определённым значением ёмкости и малой омической проводимостью; устройство для накопления энергии электрического поля.Cлайд 5
Основные параметры конденсатора: 1)Ёмкость: в обозначении конденсатора фигурирует ёмкости, в то время как реальная ёмкость может значительно меняться в зависимости от многих факторов. Реальная ёмкость- определяет по электрическим свойствам. 2)Удельною емкостью называют отношением ёмкости к объёму (или массе) диэлектрика. 3) Номинальное напряжение — значение напряжения, обозначенное на конденсаторе, при котором он может работать в заданных условиях в течение срока службы с сохранением параметров в допустимых пределах. 4)Полярность: многие конденсаторы с оксидным диэлектриком (электролитические) функционируют только при корректной полярности напряжения из-за химических особенностей взаимодействия электролита с диэлектриком.Cлайд 6
Классификация конденсаторов Конденсаторы вакуумные (обкладки без диэлектрика находятся в вакууме). Конденсаторы с газообразным диэлектриком. Конденсаторы с жидким диэлектриком. Конденсаторы с твёрдым неорганическим диэлектриком: стеклянные (стеклоэмалевые, стеклокерамические), слюдяные, тонкослойные из неорганических плёнок. Конденсаторы с твёрдым органическим диэлектриком: бумажные, металлобумажные, плёночные. Электролитические и оксидно-полупроводниковые конденсаторы (Такие конденсаторы отличаются от всех прочих типов прежде всего своей огромной удельной ёмкостью). Постоянные конденсаторы — основной класс конденсаторов, не меняющие своей ёмкости. Переменные конденсаторы — конденсаторы, которые допускают изменение ёмкости. Подстроечные конденсаторы — конденсаторы, ёмкость которых изменяется при разовой или периодической регулировке.Cлайд 7
Применение конденсаторов Конденсаторы используются для построения различных цепей с частотно-зависимыми свойствами При быстром разряде конденсатора можно получить импульс большой мощности, например, в фотовспышках. Так как конденсатор способен длительное время сохранять заряд, то его можно использовать в качестве элемента памяти или устройства хранения электрической энергии. В промышленной электротехнике конденсаторы используются для компенсации реактивной мощности и в фильтрах высших гармоник. Измерительный преобразователь (ИП) малых перемещений: малое изменение расстояния между обкладками очень заметно сказывается на ёмкости конденсатора. ИП влажности воздуха (изменение состава диэлектрика приводит к изменению емкости) ИП влажности древесины В схемах РЗиА конденсаторы используются для реализации логики работы некоторых защит.Формулы конденсатора
Формулы емкости конденсаторов
Для любого конденсатора справедлива формула:
где C – емкость конденсатора; q – величина заряда одной из обкладок конденсатора; – разность потенциалов между его обкладками.
Емкость конденсатора, между пластинами которого находится диэлектрик (C) (диэлектрическая проницаемость которого равна в раз больше, чем емкость такого же воздушного конденсатора ():
Для расчета емкости плоского конденсатора применяют формулу:
где – электрическая постоянная; S – площадь каждой (или наименьшей) пластины; d – расстояние между пластинами.
Емкость плоского конденсатора, содержащего N слоев диэлектрика (толщина i-го слоя равна , диэлектрическая проницаемость i-го слоя , определяется как:
Электрическая емкость цилиндрического конденсатора вычисляют как:
где l – высота цилиндров; – радиус внешней обкладки; – радиус внутренней обкладки.
Емкость сферического (шарового) конденсатора находят по формуле:
где – радиусы обкладок конденсатора.
Формулы для расчета емкости соединения конденсаторов
При параллельном соединении конденсаторов суммарная емкость батареи (C) равна сумме емкостей отдельных конденсаторов (), ее составляющих:
Электрическая емкость последовательного соединения конденсаторов может быть вычислена по формуле:
Если последовательно соединены N конденсаторов, с емкостями то емкость батареи вычислим как:
Сопротивление конденсатора
При включении конденсатора в цепь с постоянным током сопротивление конденсатора считают бесконечно большим.
Если конденсатор включен в цепь переменного тока, то его сопротивление называют емкостным и вычисляют при помощи формулы:
где – частота переменного тока; – угловая частота тока; C – емкость конденсатора.
Формула энергии поля конденсатора
где –энергия поля конденсатора; q – заряд конденсатора; C – емкость конденсатора; – разность потенциалов между обкладками конденсатора.
Энергия поля плоского конденсатора:
Примеры решения задач по теме «Конденсатор»
Фарад (единица измерения) — это… Что такое Фарад (единица измерения)?
- Фарад (единица измерения)
-
Фара́д (обозначение: Ф, F) — единица измерения электрической ёмкости в системе СИ (ранее называлась фара́да).
1 фарад равен электрической ёмкости конденсатора, при которой заряд 1 кулон создаёт между обкладками конденсатора напряжение 1 вольт.
- Ф = Кл/В = A·c/B
Единица названа в честь английского физика Майкла Фарадея
Фарад — очень большая ёмкость. Емкостью 1Ф обладал бы уединенный шар, радиус которого был бы равен 13 радиусам Солнца. Для сравнения, ёмкость Земли (шара размером с Землю, как уединенного проводника) составляет всего около 700 микрофарад.
Промышленно выпускаемые конденсаторы обычно имеют номиналы измеряемые в нано- и пикофарадах.
Впрочем, ёмкость т. н. ионисторов (конденсаторов с двойным электрическим слоем) может достигать нескольких килофарад.Кратные и дольные единицы
Десятичные кратные и дольные единицы образуют с помощью стандартных приставок СИ.
Кратные Дольные величина название обозначение величина название обозначение 101 Ф декафарад даФ daF 10−1 Ф децифарад дФ dF 102 Ф гектофарад гФ hF 10−2 Ф сантифарад сФ cF 103 Ф килофарад кФ kF 10−3 Ф миллифарад мФ mF 106 Ф мегафарад МФ MF 10−6 Ф микрофарад мкФ µF 109 Ф гигафарад ГФ GF 10−9 Ф нанофарад нФ nF 1012 Ф терафарад ТФ TF 10−12 Ф пикофарад пФ pF 1015 Ф петафарад ПФ PF 10−15 Ф фемтофарад фФ fF 1018 Ф эксафарад ЭФ EF 10−18 Ф аттофарад аФ aF 1021 Ф зеттафарад ЗФ ZF 10−21 Ф зептофарад зФ zF 1024 Ф йоттафарад ИФ YF 10−24 Ф йоктофарад иФ yF применять не рекомендуется - Также не рекомендуется употреблять миллифарад и нанофарад.
См также
Wikimedia Foundation. 2010.
- Фара Диба
- Фарадей (единица кол-ва электричества)
Смотреть что такое «Фарад (единица измерения)» в других словарях:
Единица измерения Сименс — Сименс (обозначение: См, S) единица измерения электрической проводимости в системе СИ, величина обратная ому. До Второй мировой войны (в СССР до 1960 х годов) сименсом называлась единица электрического сопротивления, соответсвующая сопротивлению … Википедия
Зиверт (единица измерения) — Зиверт (обозначение: Зв, Sv) единица измерения эффективной и эквивалентной доз ионизирующего излучения в Международной системе единиц (СИ), используется с 1979 г. 1 зиверт это количество энергии, поглощённое килограммом… … Википедия
Беккерель (единица измерения) — У этого термина существуют и другие значения, см. Беккерель. Беккерель (обозначение: Бк, Bq) единица измерения активности радиоактивного источника в Международной системе единиц (СИ). Один беккерель определяется как активность источника, в… … Википедия
Ньютон (единица измерения) — У этого термина существуют и другие значения, см. Ньютон. Ньютон (обозначение: Н) единица измерения силы в Международной системе единиц (СИ). Принятое международное название newton (обозначение: N). Ньютон производная единица. Исходя из второго… … Википедия
Сименс (единица измерения) — У этого термина существуют и другие значения, см. Сименс. Сименс (русское обозначение: См; международное обозначение: S) единица измерения электрической проводимости в Международной системе единиц (СИ), величина обратная ому. Через другие… … Википедия
Тесла (единица измерения) — У этого термина существуют и другие значения, см. Тесла. Тесла (русское обозначение: Тл; международное обозначение: T) единица измерения индукции магнитного поля в Международной системе единиц (СИ), численно равная индукции такого… … Википедия
Паскаль (единица измерения) — У этого термина существуют и другие значения, см. Паскаль (значения). Паскаль (обозначение: Па, международное: Pa) единица измерения давления (механического напряжения) в Международной системе единиц (СИ). Паскаль равен давлению… … Википедия
Грей (единица измерения) — У этого термина существуют и другие значения, см. Грей. Грей (обозначение: Гр, Gy) единица измерения поглощённой дозы ионизирующего излучения в Международной системе единиц (СИ). Поглощённая доза равна одному грею, если в результате… … Википедия
Вебер (единица измерения) — У этого термина существуют и другие значения, см. Вебер. Вебер (обозначение: Вб, Wb) единица измерения магнитного потока в системе СИ. По определению, изменение магнитного потока через замкнутый контур со скоростью один вебер в секунду наводит в… … Википедия
Генри (единица измерения) — У этого термина существуют и другие значения, см. Генри. Генри (русское обозначение: Гн; международное: H) единица измерения индуктивности в Международной системе единиц (СИ). Цепь имеет индуктивность один генри, если изменение тока со скоростью… … Википедия
В чем измеряются единицы емкости конденсаторов
Конденсатор представляет собой электрическое устройство, которое обладает возможностью накапливать заряд, состоит из обкладок и слоя диэлектрика между ними. Одной из важнейших характеристик прибора является ёмкость.
Конденсатор
Единица измерения емкости
В Международной системе СИ за единицу измерения ёмкости конденсатора принимают фарад:
[C] = Ф, где С – обозначение ёмкости устройства.
Международное обозначение – F. Названа в честь английского физика М.Фарадея и используется в Международной системе СИ с 1960г.
Формула для расчёта электроёмкости записывается следующим образом:
С = Dq / U (1), где:
- Dq – заряд (измеряется в кулонах, или Кл),
- U – разность потенциалов между обкладками (измеряется в вольтах или В).
Следовательно, 1Ф = 1Кл / 1В.
То есть конденсатор ёмкостью в 1 фарад накапливает на обкладках заряд, равный 1 кулон, создавая напряжение между ними, равное 1 вольт.
В фарадах измеряются электроёмкости проводников и конденсаторов.
Согласно правилам написания, принятых в СИ, если название происходит от фамилии учёного, то полное её название «фарад» пишется с маленькой (строчной) буквы, а её сокращённое название «Ф» – с прописной.
Единица измерения электроёмкости в других системах
Помимо СИ, есть ещё устаревшая система СГС, которой пользовались ранее. Первые три символа в названии обозначают:
- С – сантиметр,
- Г – грамм,
- С – секунда.
Существует две разновидности системы: СГСЭ и СГСМ. Символ Э в СГСЭ обозначает электростатическую систему, а символ М – магнитную. В системе СГСЭ емкость конденсатора измеряется в сантиметрах, или см. Для пересчёта используют соотношение:
- 1см » 1,1126 · 10-12Ф,
- 1Ф » 8,99 · 1011 статФ.
Сантиметр по-другому может называться статфарад, или статФ.
В системе СГСМ единицей измерения является абфарад, или абФ. Абфарад связан с фарадом следующим образом:
1абф = 1·109 Ф = 1ГФ.
Для перевода из СГСЭ и СГСМ в СИ в сети Интернет имеются специальные сервисы, которые позволяют автоматизировать эти действия.
Онлайн переводчик из СГС в СИ
Фарады через основные единицы системы СИ
Для выражения фарады через основные единицы СИ воспользуемся следующими формулами.
Единица измерения заряда вычисляется как:
Dq = I · Dt (2), где:
- I – сила тока (измеряется в амперах или А),
- Dt – время прохождения заряда (измеряется в секундах или с).
В свою очередь, напряжение определяется как работа, которую нужно выполнить для перемещения заряда в электростатическом поле:
U = А / Dq (3), где А – работа по перемещению заряда, определяется в джоулях, или Дж.
Из механики известно, что:
А = F · s = m · a · s (4), где:
- m – масса, измеряется в килограммах, или кг,
- s – перемещение, рассчитывается в метрах, или м,
- a – ускорение, определяется в м/с2.
Из формул 1-4 имеем:
Таким образом, 1 фарад через единицы СИ определяется как:
Кратные единицы ёмкости
При покупке радиодеталей невозможно купить конденсатор с электроёмкостью даже в несколько единиц фарад. Они выпускаются с гораздо меньшими параметрами. Это объясняется тем, что ёмкость в 1 фарад является очень большой величиной. Например, такую электроёмкость может иметь изолированный проводник в форме шара с радиусом в 13 раз больше радиуса Солнца.
Именно по этой причине для характеристики емкостных устройств применяют дольные единицы, которые рассчитываются как доля от определённого числа фарад. Для обозначения используют приставки, которые применяются для сокращения длины записываемого числа.
Таблица перевода дольных единиц
| Приставка | Обозначение | Множитель | |
|---|---|---|---|
| деци | дФ | dF | 10^-1 |
| санти | сФ | sF | 10^-2 |
| милли | мФ | mF | 10^-3 |
| микро | мкФ | F или uF | 10^-6 |
| нано | нФ | nF | 10^-9 |
| пико | пФ | pF, mmF, uuF | 10^-12 |
| фемто | фФ | fF | 10^-15 |
| атто | аФ | aF | 10^-18 |
| зепто | зФ | zF | 10^-21 |
| йокто | иФ | yF | 10^-24 |
Таким образом, если параметр указывается равным 5 uF, то для перевода в фарады необходимо умножить цифру 5 на соответствующий множитель. Получаем 5 uF = 5 · 10-6 F.
В радиотехнике наиболее популярны модели, ёмкость которых измеряется в микрофарадах, нанофарадах (микромикрофарадах) или пикофарадах.
Также промышленность выпускает устройства ионисторы, которые представляют собой конденсаторы, имеющие двойной электрический слой. У некоторых ионисторов ёмкость может измеряться в килофарадах.
Ионистор с характеристикой в 1F
Маркировка конденсаторов в зависимости от ёмкости
Кодировка маленьких по размерам устройств
Существует специальная цифровая кодировка. Её используют для маркировки маленьких по размерам приборов. Кодировка электроёмкости выполняется согласно стандарту EIA.
Внимание! Ёмкость небольших конденсаторов, например, керамических или танталовых, обычно измеряется в пикофарадах, а больших, например, алюминиевых электролитических, в микрофарадах.
Существует специальная таблица таких обозначений, с помощью которой можно быстро подобрать такую же или аналогичную радиодеталь по соответствующему коду. Её можно свободно найти в Интернете.
В старых маркировках использовалась следующая кодировка. Если нанесено целое двузначное число, значит, значение ёмкость измеряется в пикофарадах, а если нанесена десятичная дробь, значит, параметр определяется в микрофарадах.
Например, радиодеталь с параметром 1000 nF =1 uF будет иметь маркировку 105, с параметрами 820 nF = 0, 82 uF – маркировку 824, а 0,27 uF = 270nF будет обозначено кодом 274.
В настоящее время, если на устройстве нанесено значение, не содержащее буквы, то оно обозначает ёмкость в пикофарадах. Если перед цифрами или после них стоит символ «н» («n»), то это означает, что значение даётся в нанофарадах, если «мк» («m», «u») – микрофарадах. В том случае, когда символ располагается перед числом, цифры в нём обозначают сотые доли. Например, n61 расшифровывается как 0,61нФ. Если символ располагается посередине значения, то на место символа нужно поставить запятую. Сам символ покажет единицы измерения. Например, 5u2 обозначает 5,2 мкФ.
Также в настоящее время используется цифровая кодировка, содержащая три числа. Первые две цифры являются числовыми характеристиками ёмкости. Параметр при этом измеряется в пикофарадах. Если значение меньше 1, то первая цифра – 0. Третья цифра определяет множитель, на который нужно умножить число, получаемое из первых двух цифр.
В случае, когда последнее число находится в диапазоне от 0 до 6, к значению дописывают количество нулей, равное третьей цифре. Например, если указано число 270, то устройство имеет параметр 27 пФ, если 271 – то на 270 пФ.
Трёхзначная кодировка
Если число равно 8, то в этом случае множитель равен 0,01. То есть если указано число 278, то ёмкость будет равна 27 · 10-2 = 0,27. Когда третье число равно 9, то множитель будет 0,1. Например, маркировка 109 указывает на электроёмкость в 1 пФ.
Если в кодировке присутствует символ «R», то параметр указывается в пикофарадах, а символ показывает место расположения запятой. Например, 4R1 расшифровывается как 4,1пФ.
Кодировка больших по размерам устройств
На больших по габаритным размерам конденсаторах маркировка наносится сверху на корпус, причём в данном случае будет присутствовать полная информация о параметрах устройства.
В обозначениях может встречаться значение MF. В приставках Международной системы единиц СИ если перед единицей измерения располагается большая буква М, то это обозначает, что должен использоваться множитель 106. В случае с конденсатором это всё равно будет обозначать микрофарады.
Также может встречаться обозначение МFD или mfd. В данном случае сочетание символов «fd» обозначает farad. Таким образом, если на корпусе написано 5 mfd, то значит, что конденсатор используется на 5 микрофарад.
Маркировка больших по размерам конденсаторов
Таким образом, при ремонте электросхемы, содержащей конденсатор, нужно правильно читать маркировку устройства и соответственно информации подбирать нужный прибор.
Видео
Оцените статью:| символ | количество | символ | шт. |
|---|---|---|---|
| r , r | положение, разделение, радиус, радиус кривизны | кв.м | метр |
| с , с | перемещение, расстояние | кв.м | метр |
| θ , φ , |
угол, угловое перемещение, угловое разделение, угол поворота | рад | радиан |
| x , y , z | декартовы координаты | кв.м | метр |
| до , ĵ , k̂ | декартовых единичных векторов | безразмерный | |
| r , θ, φ | сферические координаты | м, |
метр, радиан |
| r̂, θ̂, φ̂ | сферические единичные векторы | безразмерный | |
| ρ, φ, z | цилиндрические координаты | м, |
метр, радиан |
| ρ̂, φ̂, ẑ | цилиндрические единичные векторы | безразмерный | |
| № | нормальный единичный вектор | безразмерный | |
| т | тангенциальный единичный вектор | безразмерный | |
| ч | высота, глубина | кв.м | метр |
| ℓ, л | длина | кв.м | метр |
| г | расстояние, отрыв, толщина | кв.м | метр |
| т | толщина | кв.м | метр |
| Д | диаметр | кв.м | метр |
| К | окружность | кв.м | метр |
| А , А | площадь, площадь поперечного сечения, площадь проекции, площадь поверхности | м 2 | квадратных метров |
| В | том | м 3 | куб.м |
| т | раз, продолжительность | с | второй |
| т | Период, периодическое время | с | второй |
| τ | постоянная времени | с | второй |
| f | частота | Гц | герц |
| ω | угловая частота | рад / с | радиан в секунду |
| символ | количество | символ | шт. |
| в , в | скорость, скорость | м / с | метр в секунду |
| а , а | разгон | м / с 2 | метр в секунду в квадрате |
| a c , a c | центростремительное ускорение, центробежное ускорение | м / с 2 | метр в секунду в квадрате |
| г , г | гравитационное поле, ускорение свободного падения | м / с 2 | метр в секунду в квадрате |
| м | масса | кг | килограмм |
| F , F | сила | N | ньютон |
| F г , |
сила тяжести, вес | N | ньютон |
| F n , |
нормальная сила, нормальная | N | ньютон |
| F f , |
Сила трения (статическая, кинетическая) | N | ньютон |
| μ с , μ k | коэффициент трения (статический, кинетический) | безразмерный | |
| p , p | импульс | кг м / с | килограмм-метр в секунду |
| Дж , Дж | импульс | Н с | ньютон секунда |
| Вт | работа | Дж | джоуль |
| E | энергия, общая энергия | Дж | джоуль |
| K , |
кинетическая энергия (поступательная, вращательная) | Дж | джоуль |
| U , |
потенциальная энергия (гравитационная, пружинная) | Дж | джоуль |
| V г | гравитационный потенциал | Дж / кг | джоуль на килограмм |
| η | КПД | безразмерный | |
| п. | мощность | Вт | ватт |
| ω , ω | скорость вращения, частота вращения | рад / с | радиан в секунду |
| α , α | ускорение вращения | рад / с 2 | радиан на секунду в квадрате |
| τ , τ | крутящий момент | Н м | Ньютон-метр |
| I | момент инерции | кг м 2 | килограмм метр в квадрате |
| л , л | Угловой момент | кг · м 2 / с | килограмм-метр в секунду |
| H , H | угловой импульс | Н м | ньютон-метр секунда |
| к | жесткость пружины | Н / м | ньютон на метр |
| п. | давление | Па | паскаль |
| σ | нормальное напряжение | Па | паскаль |
| τ | напряжение сдвига | Па | паскаль |
| ρ | плотность, объемно-массовая плотность | кг / м 3 | килограмм на кубический метр |
| σ | удельная масса поверхности, поверхностная плотность массы | кг / м 2 | килограмм на квадратный метр |
| λ | линейная массовая плотность | кг / м | килограмм на метр |
| F B , |
Плавучесть, подъемная сила | N | ньютон |
| q м | массовый расход | кг / с | килограмм в секунду |
| q V | объемный расход | м 3 / с | кубометров в секунду |
| F D , |
сопротивление, аэродинамическое сопротивление, сопротивление воздуха | N | ньютон |
| C , C D | Коэффициент аэродинамического сопротивления, коэффициент аэродинамического сопротивления | безразмерный | |
| η | Вязкость, динамическая вязкость | Па · с | паскаль секунды |
| ν | кинематическая вязкость | м 2 / с | квадратных метров в секунду |
| млн лет | Машинный номер | безразмерный | |
| Re | число Рейнольдса | безразмерный | |
| Fr | номер модели | безразмерный | |
| E | Модуль Юнга, модуль упругости | Па | паскаль |
| G | Модуль сдвига, модуль жесткости | Па | паскаль |
| К | Модуль объемной упругости, модуль сжатия | Па | паскаль |
| ε | линейная деформация | безразмерный | |
| γ | деформация сдвига | безразмерный | |
| θ | объемная деформация | безразмерный | |
| γ | поверхностное натяжение | Н / м | ньютон на метр |
| символ | количество | символ | шт. |
| т | температура | К | кельвин |
| α | линейное расширение, коэффициент линейного теплового расширения | К -1 | обратный кельвин |
| β | объемное расширение, коэффициент объемного теплового расширения | К -1 | обратный кельвин |
| Q | тепло | Дж | джоуль |
| в | удельная теплоемкость, удельная теплоемкость | Дж / кг K | джоуль на килограмм кельвина |
| л | скрытая теплота, удельная скрытая теплота | Дж / кг | джоуль на килограмм |
| n | количество вещества | моль | |
| N | количество частиц | безразмерный | |
| п. | тепловой поток | Вт | ватт |
| к | теплопроводность | Вт / м K | ватт на метр кельвина |
| ε | излучательная способность | безразмерный | |
| U | внутренняя энергия | Дж | джоуль |
| S | энтропия | Дж / К | джоуль на кельвин |
| w | путей, количество одинаковых микросостояний | безразмерный | |
| COP | коэффициент полезного действия | безразмерный | |
| символ | количество | символ | шт. |
| q , Q | заряд, электрический заряд | С | кулон |
| ρ | Плотность заряда, объемная плотность заряда | С / м 3 | кулонов на кубический метр |
| σ | поверхностная плотность заряда, поверхностная плотность заряда | С / м 2 | кулонов на квадратный метр |
| λ | линейная плотность заряда | С / м | кулонов на метр |
| F E , F E | электрическая сила, электростатическая сила | N | ньютон |
| E , E | электрическое поле | Н / К, В / м | ньютон на кулон, вольт на метр |
| Φ E | электрический поток | Н · м 2 / C, В · м | Ньютон-метр в квадрате на кулон, вольтметр |
| U , U E | потенциальная энергия, электрическая потенциальная энергия | Дж | джоуль |
| В, В E | напряжение, потенциал, электрический потенциал | В | вольт |
| ℰ | Электродвижущая сила, ЭДС | В | вольт |
| К | емкость | F | фарад |
| κ | диэлектрическая проницаемость | безразмерный | |
| I | ток, электрический ток | А | ампер |
| R , R | сопротивление, электрическое сопротивление, внутреннее сопротивление | Ом | Ом |
| ρ | удельное сопротивление | Ом · м | омметр |
| G | проводимость | S | сименс |
| σ | проводимость | См / м | сименс на метр |
| F B , F B | магнитная сила | N | ньютон |
| B , B | магнитное поле | т | тесла |
| Φ B | магнитный поток | Вт | Вебер |
| N | количество витков | безразмерный | |
| n | витков на единицу длины, плотность витков | м −1 | обратный счетчик |
| η | плотность энергии | Дж / м 3 | джоуль на кубический метр |
| S , S | вектор пойнтинга, интенсивность | Вт / м 2 | ватт на квадратный метр |
| символ | описание | ||
| + | плюс, сложение, плюс | ||
| – | минус, вычесть, минус | ||
| ± | неопределенность, погрешность, плюс-минус | ||
| · | умножение, точка, скалярное произведение, скалярное произведение | ||
| × | умножение, крест, векторное произведение, векторное произведение | ||
| ÷, / | делить | ||
| x 2 | квадрат | ||
| x 3 | куб | ||
| √ | корень квадратный, корень, корень | ||
| ∛ | кубический корень | ||
| 1 x , x −1 | обратное, обратное | ||
| = | равно, равенство | ||
| ≈ | примерно равно | ||
| ∝ | пропорционально | ||
| ≠ | не равно, неравенство | ||
| ~ | на заказ, тильда | ||
| < | менее | ||
| > | больше | ||
| ≤ | меньше или равно | ||
| ≥ | больше или равно | ||
| ⇒, | логическое следствие | ||
| ⇔ | логическая эквивалентность | ||
| … | и так далее, многоточие | ||
| ∴ | следовательно | ||
| f ( x ) | (функция | )||
| грех | синус | ||
| cos | косинус | ||
| желто-коричневый | касательная | ||
| синх | гиперболический синус | ||
| cosh | гиперболический косинус | ||
| танх | гиперболический тангенс | ||
| x̂ | единичный вектор, шляпа, циркумфлекс | ||
| ∥ | параллельно | ||
| ⟂ | перпендикуляр | ||
| x | среднее, среднее, античастица, черта, черта | ||
| x | медиана, суперсимметричная частица, тильда | ||
| ⟨⟩ | среднее по времени, среднее по ансамблю, брекет | ||
| p ( x ) | Распределение вероятностей, функция плотности вероятности | ||
| ∆ | приращение, изменение, дельта | ||
| г | дифференциал, d | ||
| ∂ | частичный дифференциал, d частичный | ||
| ∇ | градиент, дель | ||
| · | расхождение, деление, точка | ||
| ∇ × | локон, дель-крест | ||
| ∇ 2 | лапласиан, дель-квадрат | ||
| ∑ | суммирование, сигма | ||
| ∫ | интегральный | ||
| ∬ | двойной интеграл | ||
| ∭ | тройной интеграл | ||
| ∮ | контур интегральный | ||
| ∯ | поверхность интегральная | ||
| ∰ | интегральный объем | ||
| ∞ | бесконечность | ||
| ℵ 0 | Трансфинитное число, алеф ноль |
% PDF-1.3 % ReportLab Созданный PDF-документ http://www.reportlab.com % ‘BasicFonts’: класс PDFDictionary 1 0 obj % Стандартный словарь шрифтов > эндобдж % ‘F3’: класс PDFType1Font 2 0 obj % Шрифт Times-Roman > эндобдж % ‘FormXob.4cbe102a2c6b956e23357d257fe5910e’: класс PDFImageXObject 3 0 obj > поток Gb «0M; $ qh- $ j4l5s3O. & 6Zd’W, \` $ uS @!) ROhg’6’Pd # BX1V! U` конечный поток эндобдж % ‘Annot.NUMBER1’: класс PDFDictionary 4 0 объект > / Граница [0 0 0] / Rect [99. 676,7102 113,2369 688.7102] / Подтип / Ссылка / Тип / Аннотация >> эндобдж % ‘Annot.NUMBER2’: класс PDFDictionary 5 0 obj > / Граница [0 0 0] / Rect [99. 658,7102 181,2369 670.7102] / Подтип / Ссылка / Тип / Аннотация >> эндобдж % ‘Annot.NUMBER3’: класс PDFDictionary 6 0 obj > / Граница [0 0 0] / Rect [59.69291 640,7102 93, 652.=> 1Y, a8 # \ A-DandQS? A_nN2V # s_ + b ~> конечный поток эндобдж % ‘FormXob.146b44ab55072f5521b9ee801672d1ba’: класс PDFImageXObject 8 0 объект > поток Gb «0K9 + CqV # QiA`s.PoB5X- \ g, poqLL [> p! 6U! QD0! 4SWTS4% a / WDB & \ _ K`fendstream эндобдж % ‘Annot.NUMBER4’: класс PDFDictionary 9 0 объект > / Граница [0 0 0] / Rect [99. 600,7102 169,2449 612.7102] / Подтип / Ссылка / Тип / Аннотация >> эндобдж % ‘Annot.NUMBER5 ‘: класс PDFDictionary 10 0 obj > / Граница [0 0 0] / Rect [350.6582] 600,7102 367,3222 612.7102] / Подтип / Ссылка / Тип / Аннотация >> эндобдж % ‘Annot.NUMBER6’: класс PDFDictionary 11 0 объект > / Граница [0 0 0] / Rect [350.6582] 588,7102 372.2022 600.7102] / Подтип / Ссылка / Тип / Аннотация >> эндобдж % ‘Annot.NUMBER7’: класс PDFDictionary 12 0 объект > / Граница [0 0 0] / Rect [384.HQ $$] kck ~> конечный поток эндобдж % ‘Annot.NUMBER8’: класс PDFDictionary 14 0 объект > / Граница [0 0 0] / Rect [99. 570,7102 137,2289 582.7102] / Подтип / Ссылка / Тип / Аннотация >> эндобдж % ‘Annot.NUMBER9’: класс PDFDictionary 15 0 объект > / Граница [0 0 0] / Rect [99. 552,7102 141.9009 564.7102] / Подтип / Ссылка / Тип / Аннотация >> эндобдж % ‘Annot.НОМЕР10 ‘: класс PDFDictionary 16 0 объект > / Граница [0 0 0] / Rect [99. 534,7102 171,9089 546.7102] / Подтип / Ссылка / Тип / Аннотация >> эндобдж % ‘FormXob.9f68d9c70322413c8b1b554a517
eoNTB) ~> конечный поток эндобдж % ‘Annot.NUMBER53’: класс PDFDictionary 84 0 объект > / Граница [0 0 0] / Rect [99. 482,7169 163,6929 494.7169] / Подтип / Ссылка / Тип / Аннотация >> эндобдж % ‘Annot.NUMBER54’: класс PDFDictionary 85 0 объект > / Граница [0 0 0] / Rect [99. 7? +.SW3M’3, NgB «G1A3alt’7ODE` / + MfR2PTq / = m4tAi1 ~> endstream эндобдж % ‘Annot.NUMBER56’: класс PDFDictionary 88 0 объект > / Граница [0 0 0] / Rect [99. 428,7169 134,5729 440.7169] / Подтип / Ссылка / Тип / Аннотация >> эндобдж % ‘Annot.NUMBER57’: класс PDFDictionary 89 0 объект > / Граница [0 0 0] / Rect [350.6582] 428,7169 370,8742 440.7169] / Подтип / Ссылка / Тип / Аннотация >> эндобдж % ‘Annot.NUMBER58 ‘: класс PDFDictionary 90 0 объект > / Граница [0 0 0] / Rect [99. 410,7169 134,1489 422.7169] / Подтип / Ссылка / Тип / Аннотация >> эндобдж % ‘Annot.NUMBER59’: класс PDFDictionary 91 0 объект > / Граница [0 0 0] / Rect [99. 392,7169 162,3569 404.7169] / Подтип / Ссылка / Тип / Аннотация >> эндобдж % ‘FormXob.261b2046e5624d8
конечный поток эндобдж % ‘Annot.NUMBER175’: класс PDFDictionary 262 0 объект > / Граница [0 0 0] / Rect [153.2798 643,7102 290,5758 655.7102] / Подтип / Ссылка / Тип / Аннотация >> эндобдж % ‘FormXob.77e9d93dcd08ec9732ec565e4aa’: класс PDFImageXObject 263 0 объект > поток Gb «/ cgMR *: $ q0pkO%, BQWChas @ s \ 2’ot30JbMb # .hCFj`V, Ca! RT6 # WpZF% i [n3aoi0ATGB, TC * dt6 = CZ.IsR-p /; [9p-Mm% qc2iKbdh6W ]? 9eSroIpn-VXn> J] mcF / [B @ $ EiETA] PV4ghGkqpTF (7AlgJ.D3DB + a% 37r # Qo) h \ a * 6 \ a`) $ 5ihSL)! ICl, 2P * 1ZUFNfuB_R @ ‘D: «! Endstream эндобдж % ‘Annot.NUMBER176’: класс PDFDictionary 264 0 объект > / Граница [0 0 0] / Rect [296,5858 642,2202 353,0178 654.2202] / Подтип / Ссылка / Тип / Аннотация >> эндобдж % ‘Page5’: класс PDFPage 265 0 объект % Стр. Словарь > >> / Повернуть 0 / Транс> / Тип / Страница >> эндобдж % ‘Annot.NUMBER177’: класс PDFDictionary 266 0 объект > / Граница [0 0 0] / Rect [62.k`tjdoPԊN% N u0 ؾ wb * gO & v ~ b {#czrhGM 옚 = y # Fe4aBL s «xy م (PZBΌ } #
Для
простота понимания и удобство, даны 22 производные единицы СИ
специальные имена и символы, как показано в таблице 3.
Примечание о градусах Цельсия. Производная единица в таблице 3 со специальным названием градус Цельсия и специальный символ ° C заслуживает комментария. Из-за температуры шкалы, которые раньше определялись, остается обычной практикой выражать термодинамические температура, условное обозначение T , в части отличия от эталонной температура Т 0 = 273,15 К, ледяная точка. Эта температура разница называется температурой Цельсия, символ t , и составляет определяется количественным уравнением т = т — т 0 . Единицей измерения температуры по Цельсию является градус Цельсия, символ ° C. В числовое значение температуры Цельсия t , выраженное в градусах Цельсия — t / ° C = T / K — 273,15. Из определения t следует, что градус Цельсия равен
по величине до кельвина, что, в свою очередь, означает, что числовой
значение заданной разницы температур или температурного интервала,
значение выражается в единицах градуса Цельсия (° C) равно
числовое значение той же разницы или интервала, когда его значение равно
выражается в единицах кельвина (К).Таким образом, перепады температур или температура
интервалы могут быть выражены либо в градусах Цельсия, либо в кельвинах.
используя то же числовое значение. Например, температура по Цельсию
разница т
и термодинамический перепад температур T
между точкой плавления галлия и тройной точкой воды может
можно записать как t
= 29,7546 ° C = T
= 29,7546 К. Специальные названия и символы 22 производных единиц СИ со специальными названиями и символами приведенные в таблице 3, сами могут быть включены в названия и символы другие производные единицы СИ, как показано в таблице 4.
Продолжить до префиксов SI |
||||
|
|
|
Определение удельной теплоемкости
Определение удельной теплоемкости
Удельная теплоемкость — это количество тепловой энергии, необходимое для повышения температуры вещества на единицу массы.Удельная теплоемкость материала — это физическое свойство. Это также пример обширного свойства, поскольку его значение пропорционально размеру исследуемой системы.
Ключевые выводы: удельная теплоемкость
- Удельная теплоемкость — это количество тепла, необходимое для повышения температуры на единицу массы.
- Обычно это тепло в Джоулях, необходимое для повышения температуры 1 грамма образца на 1 градус Кельвина или 1 градус Цельсия.
- Вода имеет чрезвычайно высокую удельную теплоемкость, что делает ее удобной для регулирования температуры.
В единицах СИ удельная теплоемкость (обозначение: c) — это количество тепла в джоулях, необходимое для поднятия 1 грамма вещества на 1 градус Кельвина. Его также можно выразить как Дж / кг · К. Удельная теплоемкость также может быть выражена в калориях на грамм-градус Цельсия. Связанные значения — молярная теплоемкость, выраженная в Дж / моль · K, и объемная теплоемкость, выраженная в Дж / м 3 · K.
Теплоемкость определяется как отношение количества энергии, переданной материалу, к произведенному изменению температуры:
С = Q / ΔT
где C — теплоемкость, Q — энергия (обычно выражается в джоулях), а ΔT — изменение температуры (обычно в градусах Цельсия или Кельвинах).В качестве альтернативы уравнение можно записать:
Q = CmΔT
Удельная теплоемкость и теплоемкость связаны по массе:
С = м * S
Где C — теплоемкость, m — масса материала, а S — удельная теплоемкость. Обратите внимание, что, поскольку удельная теплоемкость рассчитана на единицу массы, ее значение не меняется, независимо от размера образца. Итак, удельная теплоемкость галлона воды такая же, как удельная теплоемкость капли воды.
Важно отметить, что взаимосвязь между добавленным теплом, удельной теплотой, массой и изменением температуры не применяется во время фазового перехода .Причина этого в том, что тепло, которое добавляется или удаляется при фазовом переходе, не изменяет температуру.
Также известен как: удельная теплоемкость, удельная теплоемкость по массе, теплоемкость.
Вода имеет удельную теплоемкость 4,18 Дж (или 1 калорию на грамм ° C). Это намного более высокое значение, чем у большинства других веществ, что делает воду исключительно хорошей при регулировании температуры. В отличие от меди, удельная теплоемкость составляет 0,39 Дж.
Таблица общих значений удельной теплоемкости и теплоемкости
Эта таблица значений удельной теплоемкости и теплоемкости должна помочь вам лучше понять типы материалов, которые легко проводят тепло, по сравнению с теми, которые этого не делают.Как и следовало ожидать, металлы имеют относительно низкую удельную теплоемкость.
| Материал | Удельная теплоемкость (Дж / г ° C) |
Теплоемкость (Дж / ° C на 100 г) |
| золото | 0,129 | 12,9 |
| ртуть | 0,140 | 14,0 |
| медь | 0,385 | 38,5 |
| утюг | 0.450 | 45,0 |
| соль (Nacl) | 0,864 | 86,4 |
| алюминий | 0,902 | 90,2 |
| воздух | 1.01 | 101 |
| лед | 2,03 | 203 |
| вода | 4,179 | 417,9 |
Источники
- Холлидей, Дэвид; Резник, Роберт (2013). Основы физики . Вайли. п. 524.
- Киттель, Чарльз (2005). Введение в физику твердого тела (8-е изд.). Хобокен, Нью-Джерси, США: John Wiley & Sons. п. 141. ISBN 0-471-41526-X.
- Лейдер, Кейт Дж. (1993). Мир физической химии . Издательство Оксфордского университета. ISBN 0-19-855919-4.
- необычный A. Cengel и Michael A. Boles (2010). Термодинамика: инженерный подход (7-е издание).Макгроу-Хилл. ISBN 007-352932-X.
| любой символ ¯ любой символ ¯ размер 12 {{overline {«any» `» symbol «}}} {} | средняя (обозначается полосой над символом, например, v¯v¯ size 12 {{overline {v}}} {} — средняя скорость) |
| ° C ° C размер 12 {° C} {} | градусов Цельсия |
| ° F ° F размер 12 {° F} {} | градусов по Фаренгейту |
| //// размер 12 {«//»} {} | параллельно |
| ⊥⊥ размер 12 {орто} {} | перпендикуляр |
| ∝∝ размер 12 {prop} {} | пропорционально |
| ± ± размер 12 {+ — {}} {} | плюс-минус |
| 00 размер 12 {{} rSub {размер 8 {0}}} {} | ноль в качестве нижнего индекса обозначает начальное значение |
| αα размер 12 {α} {} | альфа-лучи |
| αα размер 12 {α} {} | угловое ускорение |
| αα размер 12 {α} {} | температурный коэффициент (ы) удельного сопротивления |
| ββ размер 12 {β} {} | бета-лучи |
| ββ размер 12 {β} {} | уровень звука |
| ββ размер 12 {β} {} | объемный коэффициент расширения |
| β − β− размер 12 {β rSup {размер 8 {- {}}}} {} | электрон испускается при бета-распаде ядра |
| β + β + размер 12 {β rSup {размер 8 {+ {}}}} {} | распад позитрона |
| γγ размер 12 {γ} {} | гамма-лучи |
| γγ размер 12 {γ} {} | поверхностное натяжение |
| γ = 1/1 − v2 / c2γ = 1/1 − v2 / c2 размер 12 {γ = {1} косая черта {sqrt {1 — {v rSup {размер 8 {2}}} косая черта {c rSup {размер 8 { 2}}}}}} {} | константа, используемая в теории относительности |
| ΔΔ размер 12 {Δ} {} | изменение любого количества, следующего за |
| δδ размер 12 {δ} {} | неопределенность в любой величине, следующей за |
| ΔEΔE размер 12 {ΔE} {} | изменение энергии между начальной и конечной орбитами электрона в атоме |
| ΔEΔE размер 12 {ΔE} {} | Неуверенность в энергии |
| ΔmΔm размер 12 {Δm} {} | разница в массе между исходным и конечным продуктом |
| ΔNΔN размер 12 {ΔN} {} | Количество распадов |
| ΔpΔp размер 12 {Δp} {} | изменение импульса |
| ΔpΔp размер 12 {Δp} {} | Неопределенность импульса |
| ΔPEgΔPEg размер 12 {Δ «PE» rSub {размер 8 {g}}} {} | изменение гравитационной потенциальной энергии |
| ΔθΔθ размер 12 {Δθ} {} | угол поворота |
| ΔsΔs размер 12 {Δs} {} | пройденное расстояние по круговой траектории |
| ΔtΔt размер 12 {Δt} {} | неопределенность во времени |
| Δt0Δt0 размер 12 {Δt rSub {размер 8 {0}}} {} | собственное время, измеренное наблюдателем в состоянии покоя относительно процесса |
| ΔVΔV размер 12 {ΔV} {} | разность потенциалов |
| ΔxΔx размер 12 {Δx} {} | неопределенность положения |
| ε0ε0 размер 12 {ε rSub {размер 8 {0}}} {} | диэлектрическая проницаемость свободного пространства |
| ηη размер 12 {η} {} | вязкость |
| θθ размер 12 {θ} {} | Угол между вектором силы и вектором смещения |
| θθ размер 12 {θ} {} | угол между двумя линиями |
| θθ размер 12 {θ} {} | угол контакта |
| θθ размер 12 {θ} {} | направление результирующего |
| θbθb размер 12 {θ rSub {size 8 {b}}} {} | Угол Брюстера |
| θcθc размер 12 {θ rSub {size 8 {c}}} {} | критический угол |
| κκ размер 12 {κ} {} | диэлектрическая проницаемость |
| λλ размер 12 {λ} {} | константа распада нуклида |
| λλ размер 12 {λ} {} | длина волны |
| λnλn размер 12 {λ rSub {размер 8 {n}}} {} | длина волны в среде |
| μ0μ0 размер 12 {μ rSub {размер 8 {0}}} {} | проницаемость свободного пространства |
| μkμk размер 12 {μ rSub {размер 8 {k}}} {} | коэффициент кинетического трения |
| мкс мкс размер 12 {μ rSub {размер 8 {s}}} {} | коэффициент трения покоя |
| veve размер 12 {v rSub {размер 8 {e}}} {} | электронное нейтрино |
| π + π + размер 12 {π rSup {размер 8 {+ {}}}} {} | положительный пион |
| π − π− размер 12 {π rSup {размер 8 {- {}}}} {} | отрицательный пион |
| π0π0 размер 12 {π rSup {размер 8 {0}}} {} | нейтральный пион |
| ρρ размер 12 {ρ} {} | плотность |
| ρcρc размер 12 {ρ rSub {размер 8 {c}}} {} | критическая плотность, плотность, необходимая только для остановки универсального расширения |
| ρflρfl размер 12 {ρ rSub {размер 8 {«fl»}}} {} | плотность жидкости |
| ρ¯objρ¯obj size 12 {{overline {ρ}} rSub {size 8 {«obj»}}} {} | средняя плотность объекта |
| ρ / ρwρ / ρw размер 12 {{ρ} косая черта {ρ rSub {размер 8 {w}}}} {} | удельный вес |
| ττ размер 12 {τ} {} | характеристическая постоянная времени для сопротивления и индуктивности (RL) (RL) размера 12 {\ (ital «RL» \)} {} или сопротивления и емкости (RC) (RC) размера 12 {\ (ital «RC» \) } {} схема |
| ττ размер 12 {τ} {} | характеристическое время для резистора и конденсатора (RC) (RC) габарита 12 {\ (ital «RC» \)} {} цепи |
| ττ размер 12 {τ} {} | крутящий момент |
| ΥΥ размер 12 {Υ} {} | ипсилон-мезон |
| ΦΦ размер 12 {Φ} {} | магнитный поток |
| ϕϕ размер 12 {ϕ} {} | фазовый угол |
| ΩΩ размер 12 {% OMEGA} {} | Ом (единица) |
| ωω размер 12 {ω} {} | угловая скорость |
| Размер AA 12 {A} {} | ампер (текущая единица) |
| Размер AA 12 {A} {} | площадь |
| Размер AA 12 {A} {} | площадь поперечного сечения |
| Размер AA 12 {A} {} | общее количество нуклонов |
| aa размер 12 {a} {} | разгон |
| aBaB размер 12 {a rSub {размер 8 {B}}} {} | Боровский радиус |
| acac размер 12 {a rSub {размер 8 {c}}} {} | центростремительное ускорение |
| atat size 12 {a rSub {size 8 {t}}} {} | тангенциальное ускорение |
| ACAC размер 12 {«AC»} {} | переменного тока |
| AMAM размер 12 {«AM»} {} | амплитудная модуляция |
| атм. размер 12 {«атм»} {} | атмосфера |
| BB размер 12 {B} {} | барионное число |
| BB размер 12 {B} {} | синий кварк цвет |
| B¯B¯ размер 12 {{overline {B}}} {} | антисиний (желтый) цвет антикварк |
| bb размер 12 {b} {} | творожный аромат снизу или красотка |
| BB размер 12 {B} {} | Модуль объемной упругости |
| BB размер 12 {B} {} | Напряженность магнитного поля |
| BintBint размером 12 {B rSub {size 8 {«int»}}} {} | Собственное магнитное поле электрона |
| BorbBorb размер 12 {B rSub {размер 8 {«orb»}}} {} | Орбитальное магнитное поле |
| BEBE размер 12 {«BE»} {} | энергия связи ядра — это энергия, необходимая для полного разложения его на отдельные протоны и нейтроны |
| BE / ABE / A размер 12 {{«BE»} косая черта {A}} {} | энергия связи на нуклон |
| Размер 12 БкБк {«Бк»} {} | беккерель — один распад в секунду |
| Размер CC 12 {C} {} | Емкость (количество накопленного заряда на вольт) |
| Размер CC 12 {C} {} | кулон (основная единица заряда в системе СИ) |
| CpCp, размер 12 {C rSub {size 8 {p}}} {} | общая емкость параллельно |
| CsCs размер 12 {C rSub {размер 8 {s}}} {} | общая емкость в серии |
| CGCG размер 12 {«CG»} {} | центр тяжести |
| CMCM размер 12 {«CM»} {} | центр масс |
| куб.см размер 12 {c} {} | Подвеска со вкусом творога |
| куб.см размер 12 {c} {} | удельная теплоемкость |
| кубический размер 12 {c} {} | скорость света |
| CalCal size 12 {«Cal»} {} | килокалорий |
| размер известкового налета 12 {«cal»} {} | калорий |
| COPhpCOPhp, размер 12 {ital «COP» rSub {size 8 {«hp»}}} {} | КПД теплового насоса |
| COPrefCOPref размер 12 {ital «COP» rSub {size 8 {«ref»}}} {} | КПД холодильников и кондиционеров |
| cosθcosθ размер 12 {«cos» θ} {} | косинус |
| cotθcotθ size 12 {«детская кроватка» θ} {} | котангенс |
| cscθcscθ размер 12 {«csc» θ} {} | косеканс |
| DD размер 12 {D} {} | постоянная диффузии |
| dd размер 12 {d} {} | рабочий объем |
| dd размер 12 {d} {} | творожный ароматный пух |
| дБдБ, размер 12 {«дБ»} {} | децибел |
| диди размер 12 {d rSub {размер 8 {i}}} {} | расстояние изображения от центра линзы |
| дронт размером 12 {d rSub {размер 8 {o}}} {} | расстояние объекта от центра линзы |
| DCDC размер 12 {«DC»} {} | постоянный ток |
| EE размер 12 {E} {} | Напряженность электрического поля |
| εε размер 12 {ε} {} | ЭДС (напряжение) или электродвижущая сила Холла |
| emfemf размер 12 {«emf»} {} | электродвижущая сила |
| EE размер 12 {E} {} | энергия одиночного фотона |
| EE размер 12 {E} {} | энергия ядерной реакции |
| EE размер 12 {E} {} | полная релятивистская энергия |
| EE размер 12 {E} {} | общая энергия |
| E0E0 размер 12 {E rSub {размер 8 {0}}} {} | Энергия основного состояния для водорода |
| E0E0 размер 12 {E rSub {размер 8 {0}}} {} | энергия покоя |
| ECEC размер 12 {«EC»} {} | захват электронов |
| EcapEcap размер 12 {E rSub {размер 8 {«cap»}}} {} | энергия, запасенная в конденсаторе |
| EffEff, размер 12 {ital «Eff»} {} | КПД— полезная работа, деленная на затраченную энергию |
| EffCEffC, размер 12 {ital «Eff» rSub {size 8 {C}}} {} | КПД Карно |
| EinEin размер 12 {E rSub {размер 8 {«in»}}} {} | потребляемая энергия (пища, усваиваемая человеком) |
| EindEind размер 12 {E rSub {size 8 {«ind»}}} {} | Энергия, запасенная в индукторе |
| EoutEout размер 12 {E rSub {размер 8 {«out»}}} {} | выход энергии |
| ее размер 12 {e} {} | излучательная способность объекта |
| e + e + размер 12 {e rSup {размер 8 {+ {}}}} {} | антиэлектрон или позитрон |
| размер 12 эВэВ {«эВ»} {} | электрон-вольт |
| FF, размер 12 {F} {} | фарад (единица емкости, кулон на вольт) |
| FF, размер 12 {F} {} | фокус объектива |
| FF, размер 12 {F} {} | сила |
| FF, размер 12 {F} {} | величина силы |
| FF, размер 12 {F} {} | восстанавливающая сила |
| FBFB размер 12 {F rSub {размер 8 {B}}} {} | подъемная сила |
| FcFc размер 12 {F rSub {размер 8 {c}}} {} | центростремительная сила |
| FiFi, размер 12 {F rSub {size 8 {i}}} {} | усилие |
| FnetFnet размер 12 {F rSub {размер 8 {«net»}}} {} | чистая сила |
| FoFo размер 12 {F rSub {размер 8 {o}}} {} | выходное усилие |
| FMFM размер 12 {«FM»} {} | частотная модуляция |
| ff размер 12 {f} {} | фокусное расстояние |
| ff размер 12 {f} {} | частота |
| f0f0 размер 12 {f rSub {размер 8 {0}}} {} | Резонансная частота сопротивления, индуктивности и емкости (RLC) (RLC) размер 12 {\ (ital «RLC» \)} {} последовательная цепь |
| f0f0 размер 12 {f rSub {размер 8 {0}}} {} | пороговая частота для конкретного материала (фотоэффект) |
| f1f1 размер 12 {f rSub {размер 8 {1}}} {} | основной |
| f2f2 размер 12 {f rSub {размер 8 {2}}} {} | первый обертон |
| f3f3 размер 12 {f rSub {размер 8 {3}}} {} | второй обертон |
| fBfB размер 12 {f rSub {размер 8 {B}}} {} | частота ударов |
| fkfk размер 12 {f rSub {размер 8 {k}}} {} | Величина кинетического трения |
| fsfs размер 12 {f rSub {размер 8 {s}}} {} | величина статического трения |
| GG размер 12 {G} {} | гравитационная постоянная |
| GG размер 12 {G} {} | зеленый кварк цвет |
| G¯G¯ размер 12 {{overline {G}}} {} | антизеленый (пурпурный) цвет антикварк |
| gg размер 12 {g} {} | ускорение свободного падения |
| gg размер 12 {g} {} | глюонов (частицы-носители для сильного ядерного взаимодействия) |
| hh размер 12 {h} {} | изменение вертикального положения |
| hh размер 12 {h} {} | высота над некоторой точкой отсчета |
| hh размер 12 {h} {} | Максимальная высота снаряда |
| hh размер 12 {h} {} | Постоянная Планка |
| hfhf размер 12 {ital «hf»} {} | энергия фотона |
| hihi размер 12 {h rSub {размер 8 {i}}} {} | высота изображения |
| hoho размер 12 {h rSub {размер 8 {o}}} {} | высота объекта |
| II размер 12 {I} {} | электрический ток |
| II размер 12 {I} {} | интенсивность |
| II размер 12 {I} {} | Интенсивность прошедшей волны |
| II размер 12 {I} {} | момент инерции (также называемый инерцией вращения) |
| I0I0 размер 12 {I rSub {размер 8 {0}}} {} | Интенсивность поляризованной волны до прохождения через фильтр |
| IaveIave размер 12 {I rSub {size 8 {«ave»}}} {} | Средняя интенсивность непрерывной синусоидальной электромагнитной волны |
| IrmsIrms, размер 12 {I rSub {size 8 {«rms»}}} {} | средний текущий |
| JJ размер 12 {J} {} | джоуль |
| J / ΨJ / Ψ размер 12 {{J} косая черта {Ψ}} {} | Джоуль / пси-мезон |
| KK размер 12 {K} {} | кельвин |
| кк размер 12 {к} {} | Постоянная Больцмана |
| кк размер 12 {к} {} | силовая постоянная пружины |
| KαKα размер 12 {K rSub {размер 8 {α}}} {} | рентгеновских лучей, создаваемых, когда электрон попадает в вакансию оболочки n = 1n = 1 размером 12 {n = 1} {} из n = 3n = 3 размер 12 {n = 3} {} оболочки |
| KβKβ размер 12 {K rSub {размер 8 {β}}} {} | рентгеновских лучей, создаваемых, когда электрон попадает в вакансию оболочки n = 2n = 2 размера 12 {n = 2} {} из n = 3n = 3 размер 12 {n = 3} {} оболочки |
| ккалкал 12 {«ккал»} {} | килокалорий |
| KEKE размер 12 {«KE»} {} | поступательная кинетическая энергия |
| KE + PEKE + PE размер 12 {«KE» + «PE»} {} | механическая энергия |
| KEeKEe размер 12 {«KE» rSub {размер 8 {e}}} {} | кинетическая энергия выброшенного электрона |
| KErelKErel размер 12 {«KE» rSub {size 8 {«rel»}}} {} | релятивистская кинетическая энергия |
| KErotKrot размер 12 {«KE» rSub {размер 8 {«rot»}}} {} | кинетическая энергия вращения |
| KE¯KE¯ размер 12 {{overline {«KE»}}} {} | тепловая энергия |
| кгкг размер 12 {«кг»} {} | килограмм (основная единица массы в системе СИ) |
| LL, размер 12 {L} {} | Угловой момент |
| LL, размер 12 {L} {} | литр |
| LL, размер 12 {L} {} | Величина углового момента |
| LL, размер 12 {L} {} | самоиндуктивность |
| ℓℓ размер 12 {ℓ} {} | Квантовое число углового момента|
| LαLα размер 12 {L rSub {размер 8 {α}}} {} | рентгеновских лучей, создаваемых, когда электрон попадает в оболочку n = 2n = 2 размера 12 {n = 2} {} из оболочки n = 3n = 3 размера 12 {n = 3} {} |
| LeLe размер 12 {L rSub {размер 8 {e}}} {} | электрон общее семейное число |
| LμLμ размер 12 {L rSub {размер 8 {μ}}} {} | Общее количество семейства мюонов |
| LτLτ размер 12 {L rSub {размер 8 {τ}}} {} | семья тау всего |
| LfLf размер 12 {L rSub {размер 8 {f}}} {} | теплота плавления |
| Lf andLvLf andLv размер 12 {L rSub {размер 8 {f}} «и» `L rSub {размер 8 {v}}} {} | Коэффициенты скрытой теплоты |
| LorbLorb размер 12 {L rSub {размер 8 {«orb»}}} {} | Орбитальный угловой момент |
| LsLs размер 12 {L rSub {размер 8 {s}}} {} | теплота сублимации |
| LvLv размер 12 {L rSub {размер 8 {v}}} {} | теплота испарения |
| LzLz размер 12 {L rSub {размер 8 {z}}} {} | z — составляющая момента количества движения |
| Размер мм 12 {M} {} | угловое увеличение |
| Размер мм 12 {M} {} | взаимная индуктивность |
| размер 12 мм {} | указывает на метастабильное состояние |
| размер 12 мм {} | увеличение |
| размер 12 мм {} | масса |
| размер 12 мм {} | Масса объекта, измеренная человеком в состоянии покоя относительно объекта |
| размер 12 мм {} | метр (основная единица измерения длины в системе СИ) |
| размер 12 мм {} | порядок вмешательства |
| размер 12 мм {} | общее увеличение (произведение отдельных увеличений) |
| mAXmAX, размер 12 {м слева («» lSup {размер 8 {A}} X справа)} {} | атомная масса нуклида |
| MAMA размер 12 {«MA»} {} | механическое преимущество |
| мем размером 12 {m rSub {size 8 {e}}} {} | Увеличение окуляра |
| мем размером 12 {m rSub {size 8 {e}}} {} | масса электрона |
| мℓмℓ размер 12 {м rSub {размер 8 {ℓ}}} {} | Квантовое число проекции углового момента|
| mnmn размер 12 {m rSub {size 8 {n}}} {} | масса нейтрона |
| momo размер 12 {м rSub {размер 8 {o}}} {} | Увеличение линзы объектива |
| размер мольмоль 12 {«моль»} {} | моль |
| MPMP размер 12 {m rSub {размер 8 {p}}} {} | Масса протона |
| MSMS размер 12 {м rSub {размер 8 {s}}} {} | квантовое число проекции спина |
| NN размер 12 {N} {} | Величина нормальной силы |
| NN размер 12 {N} {} | ньютон |
| NN размер 12 {N} {} | нормальная сила |
| NN размер 12 {N} {} | количество нейтронов |
| nn размер 12 {n} {} | показатель преломления |
| nn размер 12 {n} {} | количество бесплатных начислений на единицу объема |
| NANA размер 12 {N rSub {размер 8 {A}}} {} | Число Авогадро |
| NrNr размер 12 {N rSub {size 8 {r}}} {} | Число Рейнольдса |
| НмН⋅м, размер 12 {N cdot m} {} | ньютон-метр (единица работы-энергии) |
| НмН⋅м, размер 12 {N cdot m} {} | Ньютон на метр (единица измерения крутящего момента в системе СИ) |
| OEOE размер 12 {«OE»} {} | другая энергия |
| ПП размер 12 {P} {} | мощность |
| ПП размер 12 {P} {} | оптика линзы |
| ПП размер 12 {P} {} | давление |
| размер страницы 12 {p} {} | импульс |
| размер страницы 12 {p} {} | импульсная величина |
| размер страницы 12 {p} {} | релятивистский импульс |
| ptotptot size 12 {p rSub {size 8 {«tot»}}} {} | общий импульс |
| ptot’ptot ‘размер 12 {{{p}} sup {‘} rSub {size 8 {`» tot «}}} {} | общий импульс некоторое время спустя |
| PabsPabs размер 12 {P rSub {size 8 {«abs»}}} {} | абсолютное давление |
| PatmPatm размер 12 {P rSub {size 8 {«atm»}}} {} | атмосферное давление |
| PatmPatm размер 12 {P rSub {size 8 {«atm»}}} {} | стандартное атмосферное давление |
| PEPE размер 12 {«PE»} {} | потенциальная энергия |
| PEELPEel размер 12 {«PE» rSub {size 8 {«el»}}} {} | Упругая потенциальная энергия |
| PEelecPEelec размер 12 {«PE» rSub {size 8 {«elec»}}} {} | электрическая потенциальная энергия |
| PEsPEs размер 12 {«PE» rSub {size 8 {s}}} {} | потенциальная энергия пружины |
| PgPg размер 12 {P rSub {size 8 {g}}} {} | избыточное давление |
| PinPin, размер 12 {P rSub {size 8 {«in»}}} {} | потребляемая мощность или потребляемая мощность |
| PoutPout размер 12 {P rSub {size 8 {«out»}}} {} | полезная выходная мощность, переходящая в полезную работу или желаемую форму энергии |
| QQ размер 12 {Q} {} | скрытое тепло |
| QQ размер 12 {Q} {} | чистое тепло передано в систему |
| QQ размер 12 {Q} {} | расход — объем в единицу времени, проходящий мимо точки |
| + Q + Q размер 12 {+ Q} {} | положительный заряд |
| −Q − Q размер 12 {- Q} {} | отрицательный заряд |
| qq размер 12 {q} {} | заряд электрона |
| qpqp размер 12 {q rSub {размер 8 {p}}} {} | заряд протона |
| qq размер 12 {q} {} | пробный заряд |
| QFQF размер 12 {«QF»} {} | добротность |
| Размер RR 12 {R} {} | Активность, скорость распада |
| Размер RR 12 {R} {} | радиус кривизны сферического зеркала |
| Размер RR 12 {R} {} | красный кварк цвет |
| R¯R¯ размер 12 {{overline {R}}} {} | антикрасный (голубой) кварк, цвет |
| Размер RR 12 {R} {} | сопротивление |
| Размер RR 12 {R} {} | результирующее или полное смещение |
| Размер RR 12 {R} {} | Постоянная Ридберга |
| Размер RR 12 {R} {} | универсальная газовая постоянная |
| rr размер 12 {r} {} | расстояние от точки поворота до точки приложения силы |
| rr размер 12 {r} {} | внутреннее сопротивление |
| r⊥r⊥ размер 12 {r rSub {размер 8 {ortho}}} {} | Плечо перпендикулярного рычага |
| rr размер 12 {r} {} | радиус ядра |
| rr размер 12 {r} {} | радиус закругления |
| rr размер 12 {r} {} | удельное сопротивление |
| r или radr или rad размер 12 {«r or rad»} {} | единица дозы облучения |
| remrem размер 12 {«rem»} {} | человек в рентгеновском эквиваленте |
| радрад размер 12 {«рад»} {} | радиан |
| RBERBE размер 12 {«RBE»} {} | Относительная биологическая эффективность |
| RCRC размер 12 {ital «RC»} {} | Цепь резистора и конденсатора|
| rmsrms размер 12 {«rms»} {} | Среднеквадратичное значение |
| rnrn размер 12 {r rSub {размер 8 {n}}} {} | радиус n -й орбиты H-атома |
| RpRp размер 12 {R rSub {размер 8 {p}}} {} | полное сопротивление параллельного соединения |
| RsRs размер 12 {R rSub {size 8 {s}}} {} | полное сопротивление последовательного соединения |
| RsRs размер 12 {R rSub {size 8 {s}}} {} | Радиус Шварцшильда |
| SS размер 12 {S} {} | энтропия |
| Размер SS 12 {S} {} | Собственный спин (собственный угловой момент) |
| Размер SS 12 {S} {} | Величина собственного (внутреннего) спинового углового момента |
| Размер SS 12 {S} {} | Модуль сдвига |
| Размер SS 12 {S} {} | квантовое число странности |
| ss размер 12 {s} {} | творожный вкус странный |
| ss размер 12 {s} {} | секунда (основная единица времени в системе СИ) |
| ss размер 12 {s} {} | спиновое квантовое число |
| ss размер 12 {s} {} | полный рабочий объем |
| secθsecθ размер 12 {«sec» θ} {} | секущая |
| sinθsinθ размер 12 {«sin» θ} {} | синус |
| szsz размер 12 {s rSub {размер 8 {z}}} {} | z -компонента спинового углового момента |
| Размер ТТ 12 {T} {} | Период— время завершения одного колебания |
| Размер ТТ 12 {T} {} | температура |
| TcTc размер 12 {T rSub {размер 8 {c}}} {} | критическая температура — температура, ниже которой материал становится сверхпроводником |
| Размер ТТ 12 {T} {} | напряжение |
| Размер ТТ 12 {T} {} | тесла (напряженность магнитного поля B ) |
| тт размер 12 {т} {} | верх со вкусом творога или правда |
| тт размер 12 {т} {} | время |
| t1 / 2t1 / 2 размер 12 {t rSub {size 8 {{1} косая черта {2}}}} {} | Период полураспада— время, за которое половина исходных ядер распадается. |
| tanθtanθ размер 12 {«tan» θ} {} | касательная |
| UU размер 12 {U} {} | внутренняя энергия |
| uu размер 12 {u} {} | творожный аромат до |
| uu размер 12 {u} {} | единая атомная единица массы |
| uu размер 12 {u} {} | Скорость объекта относительно наблюдателя |
| u’u ‘размер 12 {{{u}} sup {‘}} {} | Скорость относительно другого наблюдателя |
| VV размер 12 {V} {} | электрический потенциал |
| VV размер 12 {V} {} | напряжение на клеммах |
| VV размер 12 {V} {} | вольт (единица) |
| VV размер 12 {V} {} | том |
| vv размер 12 {v} {} | относительная скорость между двумя наблюдателями |
| vv размер 12 {v} {} | скорость света в материале |
| vv размер 12 {v} {} | скорость |
| v¯v¯ размер 12 {{overline {v}}} {} | средняя скорость жидкости |
| VB − VAVB − VA, размер 12 {V rSub {размер 8 {B}} — V rSub {размер 8 {A}}} {} | изменение потенциала |
| vdvd размер 12 {v rSub {размер 8 {d}}} {} | скорость дрейфа |
| Впвп, размер 12 {V rSub {размер 8 {p}}} {} | входное напряжение трансформатора |
| VrmsVrms, размер 12 {V rSub {size 8 {«rms»}}} {} | действующее напряжение |
| VsVs размер 12 {V rSub {size 8 {s}}} {} | Выходное напряжение трансформатора |
| vtotvtot размер 12 {v rSub {size 8 {«tot»}}} {} | общая скорость |
| vwvw размер 12 {v rSub {размер 8 {w}}} {} | скорость распространения звука или другой волны |
| vwvw размер 12 {v rSub {размер 8 {w}}} {} | скорость волны |
| WW, размер 12 {W} {} | работа |
| WW, размер 12 {W} {} | чистая работа, выполненная системой |
| WW, размер 12 {W} {} | ватт |
| ww размер 12 {w} {} | вес |
| wflwfl размер 12 {w rSub {размер 8 {«fl»}}} {} | Вес жидкости, вытесненной предметом |
| Туалет, размер 12 {W rSub {размер 8 {c}}} {} | всего работы, проделанной всеми консервативными силами |
| WncWnc размер 12 {W rSub {размер 8 {«nc»}}} {} | общая работа, проделанная всеми неконсервативными силами |
| WoutWout размер 12 {W rSub {размер 8 {«out»}}} {} | объем полезной работы |
| XX размер 12 {X} {} | амплитуда |
| XX размер 12 {X} {} | Обозначениедля элемента |
| ZAXNZAXN размер 12 {«» lSub {размер 8 {Z}} lSup {размер 8 {A}} X rSub {размер 8 {N}}} {} | Обозначениедля конкретного нуклида |
| xx размер 12 {x} {} | Деформация или смещение от равновесия |
| xx размер 12 {x} {} | Смещение пружины из недеформированного положения |
| xx размер 12 {x} {} | горизонтальная ось |
| XCXC размер 12 {X rSub {размер 8 {C}}} {} | емкостное сопротивление |
| XLXL, размер 12 {X rSub {размер 8 {L}}} {} | индуктивное сопротивление |
| xrmsxrms размер 12 {x rSub {размер 8 {«rms»}}} {} | Среднеквадратичное расстояние диффузии |
| yy размер 12 {y} {} | вертикальная ось |
| YY размер 12 {Y} {} | Модуль упругостиили модуль Юнга |
| ZZ размер 12 {Z} {} | Атомный номер(количество протонов в ядре) |
| ZZ размер 12 {Z} {} | сопротивление |
термодинамика — Как выразить теплоемкость через тепло?
Я не виню вас за то, что вы сбиты с толку, потому что запись, в которой часто пишется первый закон термодинамики ($ \ mathrm {d} U = \ mathrm {d} Q — \ mathrm {d} W $), на самом деле довольно противоречиво.В ваших обозначениях удельная теплоемкость будет
$$ C_V = \ biggl (\ frac {\ omega_q} {\ mathrm {d} T} \ biggr) _V $$
Обычно $ \ omega_q $ записывают как $ \ mathrm {d} Q $ (или $ \ partial Q $), чтобы указать, что оно бесконечно малой величины.
Что касается более глубокого объяснения: фундаментальная проблема заключается в том, что дифференциальная величина $ \ mathrm {d} x $ для некоторого $ x $ не должна быть представлена как изменение некоторой функции. На самом деле он представляет собой «бесконечно малую величину», которая представляет собой некоторую величину, связанную с бесконечно малым продвижением по пути, который система проходит через свое пространство состояний.
Например, в термодинамической системе пространство состояний может быть параметризовано координатами $ (N, P, V) $. Любой термодинамический процесс, через который проходит эта система, можно представить как однопараметрический путь через пространство состояний. Теперь представьте, что путь разбит на сегменты бесконечно малой длины. Вы можете сделать это, разделив время, в течение которого происходит процесс, на бесконечно малые приращения $ \ mathrm {d} t $, но вам не нужно использовать время; вы можете использовать любой параметр, который не повторяет значения.
В данном сегменте $ \ mathrm {d} X $ для любого $ X $ представляет некоторую сумму $ X $, связанную с этим сегментом. Иногда $ \ mathrm {d} X $ — это реальное изменение; например, $ \ mathrm {d} P $ — это изменение давления от начала сегмента до конца, или $ \ mathrm {d} U $ — это изменение внутренней энергии от начала до конца. Но иначе нельзя выразить разницу начальной и конечной сумм. Например, $ \ mathrm {d} Q $ (ваш $ \ omega_q $) — это количество тепла, полученное системой в течение этого сегмента , или, точнее, $ \ mathrm {d} Q $ — это количество энергии получаемые системой через механизм теплопередачи.Точно так же $ \ mathrm {d} W $ — это количество энергии, теряемой системой из-за механизма механической работы.
Очевидно, что механизм передачи энергии не имеет смысла, когда энергия фактически не передается. Таким образом, вы можете сделать это разделение на работу и тепло только для изменений энергии вашей системы, а не для количества энергии. Поэтому нет государственной функции по теплу или по индивидуальной работе. Однако, если вы проигнорируете разделение между различными способами , по которым передается энергия, и рассмотрите только общее количество энергии, проблем не будет: энергия сохраняется, поэтому начальное количество энергии плюс изменение энергии равно конечное количество энергии.Итак, когда вы объединяете изменение из-за тепла и изменение из-за работы, вы получаете что-то ($ \ mathrm {d} U $), которое действительно соответствует изменению в функции состояния.
Между прочим, это то же самое, что происходит с консервативными и неконсервативными силами в механике Ньютона. Так же, как я описал выше для термодинамических систем, вы можете отслеживать путь, который механическая система проходит через физическое пространство, разбивать этот путь на небольшие сегменты и вычислять различные величины для каждого сегмента.
Иногда эти сегменты соответствуют изменениям в некоторой функции положения. Например, если вы вычислите работу, проделанную гравитацией во время сегмента, $ \ mathrm {d} W_g = -mg \ mathrm {d} y $, вы обнаружите, что она не зависит от пути, и затем вы можете определить функцию состояния $ U_g $ для него, $ \ mathrm {d} W_g = — \ mathrm {d} U_g $. Потенциальные энергии — это функции состояния ньютоновской механики.
Но если вы вычислите работу, проделанную трением во время сегмента, $ \ mathrm {d} W_f = -F_f \ mathrm {d} s $, вы не сможете выразить это как изменение какой-либо функции состояния.Соответственно трение — неконсервативная сила.
В некотором смысле, вы можете думать о тепле и работе как о неконсервативных «силах» термодинамики. В частности, $ \ mathrm {d} Q $ и $ \ mathrm {d} W $ (ваш $ \ omega _ {{w, q}} $) выполняют ту же роль в термодинамике, что и $ \ mathrm {d} W_f $ и т. Д. залить механику. Конечно, $ \ mathrm {d} Q $ и $ \ mathrm {d} W $ случайно объединяются таким образом, что создают функцию состояния; Я не знаю, есть ли у этого общего эквивалента в механике.

