Как рассчитать общую емкость при последовательном и параллельном соединении конденсаторов. Какие формулы использовать для вычисления результирующей емкости. Как распределяется напряжение и заряд в цепи из нескольких конденсаторов. Когда применяют различные схемы соединения конденсаторов на практике.
Основные способы соединения конденсаторов
В электронике существует два основных способа соединения конденсаторов:
- Параллельное соединение
- Последовательное соединение
Также возможно комбинированное (смешанное) соединение, сочетающее оба способа. Выбор схемы соединения зависит от требуемых параметров результирующей емкости.
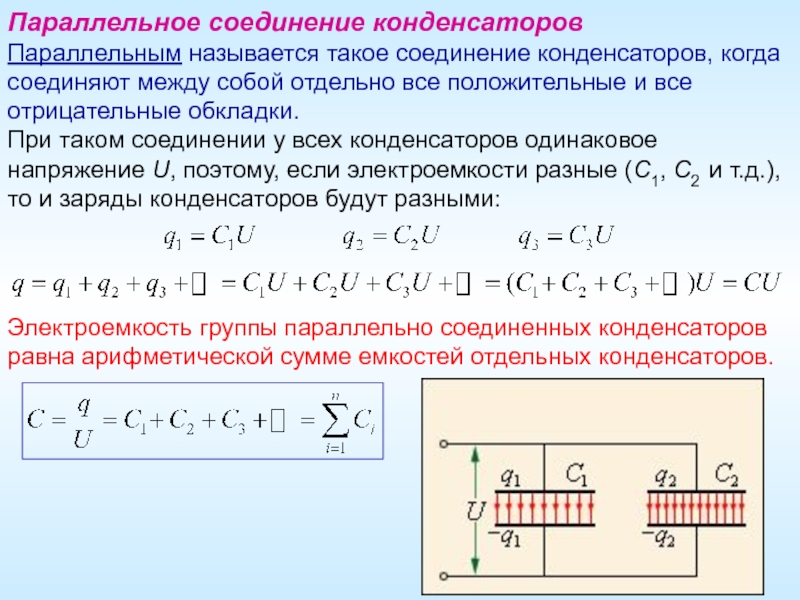
Параллельное соединение конденсаторов
При параллельном соединении конденсаторы подключаются одноименными выводами. Схематически это выглядит следующим образом:
[Схема параллельного соединения конденсаторов]
Основные характеристики параллельного соединения:
- Общая емкость равна сумме емкостей отдельных конденсаторов
- Заряд распределяется между конденсаторами пропорционально их емкостям
Формула расчета общей емкости при параллельном соединении
Для расчета общей емкости при параллельном соединении используется следующая формула:
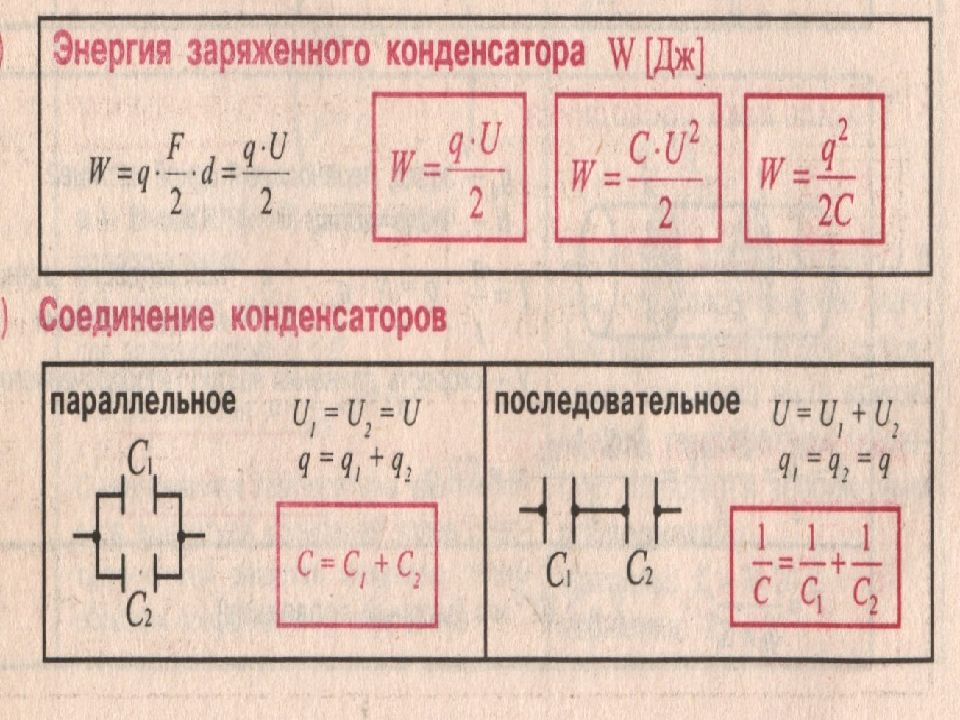
C = C1 + C2 + C3 + … + Cn
где C — общая емкость, C1, C2, C3, …, Cn — емкости отдельных конденсаторов.
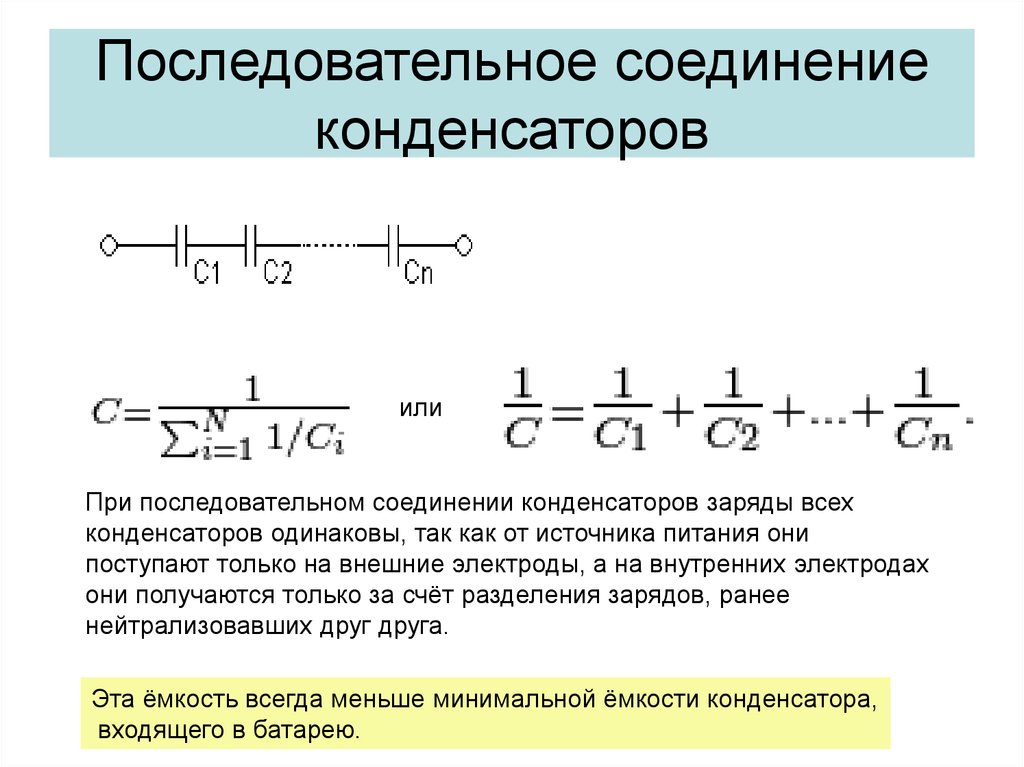
Последовательное соединение конденсаторов
При последовательном соединении конденсаторы подключаются «цепочкой» — положительный вывод одного к отрицательному выводу другого. Схема выглядит так:
[Схема последовательного соединения конденсаторов]
Основные характеристики последовательного соединения:
- Общая емкость меньше емкости наименьшего из конденсаторов
- Напряжение распределяется между конденсаторами обратно пропорционально их емкостям
- Заряд на всех конденсаторах одинаковый
Формула расчета общей емкости при последовательном соединении
Общая емкость при последовательном соединении рассчитывается по формуле:1/C = 1/C1 + 1/C2 + 1/C3 + … + 1/Cn
где C — общая емкость, C1, C2, C3, …, Cn — емкости отдельных конденсаторов.
Распределение напряжения в цепи из конденсаторов
Как распределяется напряжение между конденсаторами в цепи? Это зависит от способа их соединения:
При параллельном соединении:
Напряжение на всех конденсаторах одинаковое и равно общему приложенному напряжению:
U = U1 = U2 = U3 = … = Un
При последовательном соединении:
Напряжение распределяется обратно пропорционально емкостям конденсаторов:
U1/C1 = U2/C2 = U3/C3 = … = Un/Cn
где U1, U2, U3, …, Un — напряжения на отдельных конденсаторах.
Распределение заряда в цепи из конденсаторов
Распределение заряда между конденсаторами также зависит от схемы их соединения:
При параллельном соединении:
Заряд распределяется между конденсаторами пропорционально их емкостям:
q1/C1 = q2/C2 = q3/C3 = … = qn/Cn
где q1, q2, q3, …, qn — заряды на отдельных конденсаторах.
При последовательном соединении:
Заряд на всех конденсаторах одинаковый и равен общему заряду цепи:
q = q1 = q2 = q3 = … = qn
Практическое применение различных схем соединения конденсаторов
На практике различные схемы соединения конденсаторов применяются в следующих случаях:
Параллельное соединение используется для:
- Увеличения общей емкости
- Снижения эквивалентного последовательного сопротивления (ESR)
- Увеличения максимального тока пульсаций
Последовательное соединение применяется для:
- Увеличения максимального рабочего напряжения
- Уменьшения общей емкости
- Создания емкостных делителей напряжения
Выбор конкретной схемы зависит от требуемых параметров и имеющихся в наличии компонентов.
Пример расчета емкости при смешанном соединении конденсаторов
Рассмотрим пример расчета общей емкости для смешанной схемы соединения конденсаторов:
[Схема смешанного соединения конденсаторов]
Дано: C1 = 10 мкФ, C2 = 20 мкФ, C3 = 30 мкФ, C4 = 40 мкФ
Решение:
- Рассчитаем емкость параллельной ветви C2 и C3: C23 = C2 + C3 = 20 + 30 = 50 мкФ
- Теперь имеем последовательное соединение C1, C23 и C4. Используем формулу для последовательного соединения: 1/C = 1/C1 + 1/C23 + 1/C4 1/C = 1/10 + 1/50 + 1/40 = 0.1 + 0.02 + 0.025 = 0.145
- Общая емкость: C = 1/0.145 ≈ 6.9 мкФ
Таким образом, общая емкость данной смешанной схемы составляет примерно 6.9 мкФ.
Основные правила при соединении конденсаторов
При соединении конденсаторов важно соблюдать следующие правила:
- Учитывать полярность электролитических конденсаторов
- Не превышать максимальное рабочее напряжение конденсаторов
- По возможности использовать конденсаторы одного типа и номинала
- Учитывать паразитные параметры реальных конденсаторов
- При необходимости использовать балансировочные резисторы в последовательных цепях
Соблюдение этих правил позволит создать надежную и эффективную схему с нужными параметрами.
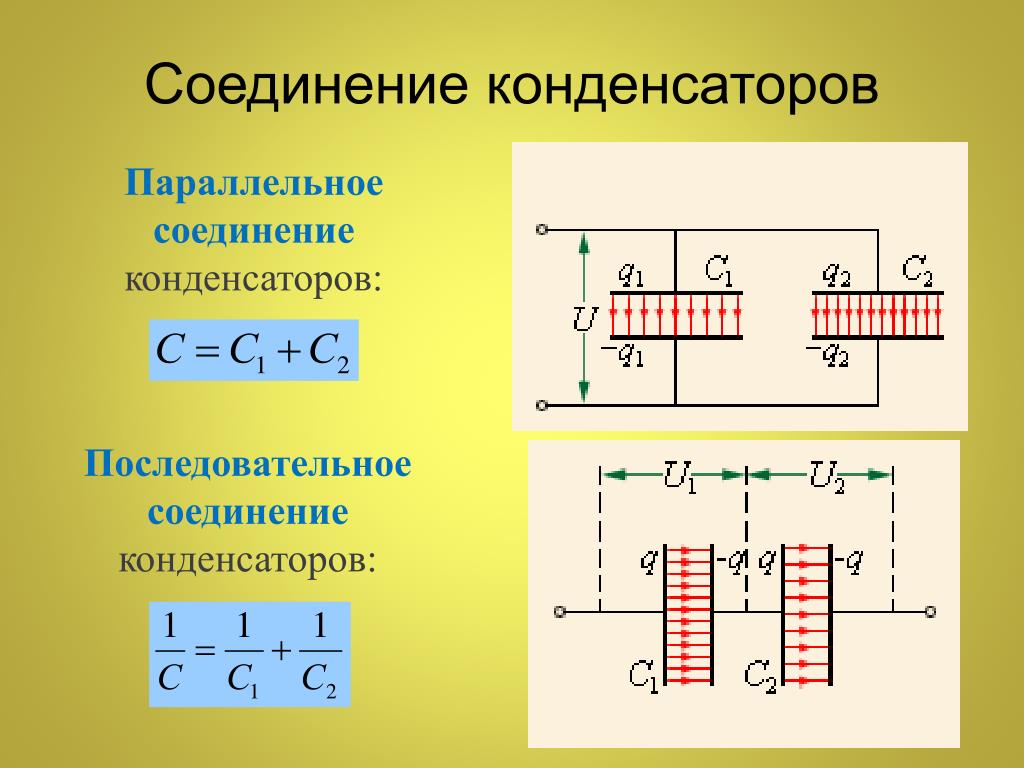
Последовательное и параллельное соединение конденсаторов
Соединение конденсаторов в электрической цепи может быть последовательным, параллельным и последовательно-пареллельным (смешанным).
Если провести аналогию между соединением конденсаторов и соединением резисторов , то стоит отметить, что формулы расчета общей емкости и общего сопротивления идентичны, только между разными типами соединений:
Формула Cобщ при параллельном соединении конденсаторов = формула Rобщ при последовательном соединении резисторов.
Формула Cобщ при последовательном соединении конденсаторов = формула R общ при параллельном соединении резисторов.
- Cобщ — общая емкость
- Rобщ — общее сопротивление
Параллельное соединение конденсаторов
Параллельное соединение конденсаторов — это соединение при котором конденсаторы соединяются собой обоими контактами. В результате к одной точке может быть присоединено несколько конденсаторов.
При параллельном соединении формируется один большой конденсатор с площадью обкладок, равной сумме площадей обкладок всех отдельных компонентов. Поскольку емкость конденсаторов прямо пропорциональна площади обкладок, общая емкость Собщ при параллельном соединении равняется сумме емкостей всех конденсаторов в цепи.
Параллельное соединение конденсаторов
Напряжение при параллельном соединении
На все параллельно соединенные конденсаторы падает одинаковое напряжение. Так происходит, потому что существует всего лишь две точки, между которыми может быть разность потенциалов (напряжение). Другими словами, можно сказать что при параллельном соединении все конденсаторы подключены к одному источнику напряжения.
Падение напряжения при параллельном соединении
Ток при параллельном соединении
Ток конденсатора во время переходного периода зависит от его емкости и изменения напряжения:
- ic — ток конденсатора
- C — Емкость конденсатора
- ΔVC/Δt – Скорость изменения напряжения
При параллельном соединении через каждый конденсатор потечет одельный ток, в зависимости от емкости конденсатора:
Ток при параллельном соединении
Последовательное соединение конденсаторов
Последовательное соединение конденсаторов – это соединение двух или более конденсаторов в форме цепи, в которой каждый отдельный конденсатор соединяется с другим отдельным конденсатором только в одной точке.
Последовательное соединение конденсаторов
Ток при последовательном соединении
Ток (iC), заряжающий последовательную цепь конденсаторов, будет одинаковым для всех конденсаторов, поскольку у него есть только один возможный путь прохождения:
Вследствие того что через все последовательно соединенные конденсаторы течет одинаковый ток, количество накопленого электрического заряда для каждого конденсатора будет одинаковым, независимо от его емкости. Так происходит, потому что электрический заряд, накапливаемый на обкладке любого конденсатора, должен прийти с обкладки примыкающего конденсатора.
Таким образом, последовательно соединенные конденсаторы имеют одинаковый электрический заряд:
Посмотрим на последовательную цепь из трех конденсаторов на рисунке выше. Правая обкладка первого конденсатора С1 соединяется с левой второго конденсатора С2, у которого правая обкладка соединяется с левой третьего конденсатора С3. Это означает, что в режиме постоянного тока конденсатор С2 электрически изолирован от общей цепи.
В итогое эффективная площадь обкладок уменьшается до площади обкладок самого маленького конденсатора. Это объясняется тем, что как только обкладки наименшей площади заполнятся электрическим зарядом, данный конденсатор перестанет пропускать ток. В результате ток прекратиться во всей цепи, и процесс зарядки остальных конденсаторов также прекратится.
При последовательном соединении общее расстояние между обкладками увеличивается до суммы расстояний между обкладками всех конденсаторов.
Таким образом, последовательная цепь формирует один большой конденсатор с площадью обкладок элемента с наименьшей емкостью, и расстоянием между обкладками, равному сумме всех расстояний в цепи.
Площадь и расстояние между обкладками при последовательном соединении
Падение напряжения и общая емкость при последовательном соединении
На каждый отдельный конденсатор в последовательной цепи падает разное напряжение. Поскольку емкость обратно пропрциональна напряжению (С = Q/V), то чем меньше емкость конденсатора, тем большее напряжение на него упадет.
Применим закон Кирхгофа для напряжения в последовательной цепи из трех конденсаторов:
Падение напряжения при последовательном соединении
Емкость конденсатора прямо пропорциональна его заряду и обратно пропорциональна его напряжению — C = Q/V. Как уже упоминалось выше, последовательно соединенные конденсаторы имеют одинаковый электрический заряд — Qобщ = Q1 = Q2 = Q3.
Следовательно:
Разделив все выражение на Qобщ мы получим уравнение для общей емкости при последовательном соединении:
Из данного уравнения можно легко вывести формулу общей емкости для любого частного случая последовательного соединения.
Например, общая емкость для трех конденсаторов:
Общая емкость для двух конденсаторов:
Смешанное соединение конденсаторов
Если в цепи есть и последовательное и параллельное соединение, то такую цепь называют смешанной или последовательно-параллельной. Тем не менее, смешанное соединение может иметь как последовательный, так и параллельный характер.
Смешанное соединение конденсаторов
Общая емкость смешанного соединения конденсаторов
Чтобы посчитать общую емкость смешанного соединения конденсаторов, следуют такому же алгоритму, как и при расчете общего сопротивления смешанного соединения резисторов.
- Цепь разбивают на участки с только пареллельным или только последовательным соединением
- Вычисляют общую емкость для каждого отдельного участка.
- Вычисляют общую емкость для всей цепи смешанного соединения.
Так это будет выглядеть для схемы 2:
Преобразование смешанного соединения в параллельное
Зачем все это нужно?
Вполне справедливым может оказаться вопрос, для чего надо соединять конденсаторы последовательно, если общая емкость будет меньше? Скорее всего, первым что приходит в голову — это чтобы получить новый эквивалентный конденсатор с меньшей емкостью. Но в производстве микросхем вряд ли будут делать подобное, поскольку, во -первых, обычно нужно экономить место на печатной плате, а во-вторых, нет смысла тратить деньги на два компонента или больше, если можно купить один с требуемой емкостью.
Но если в параллельном или последовательном соединении конденсаторов еще есть хоть какая-то логика, то кому вообще нужно смешанное?
Дело в том, что емкостью, то есть способностью накапливать электрический заряд, обладает любое тело в природе, даже человеческое. Если мы говорим о электрической цепи, то все ее элементы на практике обладают емкостью, и их можно представить как конденсаторы. Часто такую емкость еще называют паразитической, потому как она создает разного рода помехи.
Например, у нас есть какая-то электронная цепь с множеством различных компонентов, которая принимает сигнал, обрабатывает его определенным образом и выдает на выход результат. Известно, что время задержки сигнала, в основном, зависит от паразитической емкости электронных компонентов схемы. Поскольку должно пройти время зарядки паразитической емкости, прежде чем она начнет пропускать сигнал. Если мы хотим узнать время задержки, нужно посчитать общую емкость всех компонентов, конвертировав их в цепь из конденсаторов.
Соединение конденсаторов.
Как правильно соединять конденсаторы?
У многих начинающих любителей электроники в процессе сборки самодельного устройства возникает вопрос: “Как правильно соединять конденсаторы?”
Казалось бы, зачем это надо, ведь если на принципиальной схеме указано, что в данном месте схемы должен быть установлен конденсатор на 47 микрофарад, значит, берём и ставим. Но, согласитесь, что в мастерской даже заядлого электронщика может не оказаться конденсатора с необходимым номиналом!
Похожая ситуация может возникнуть и при ремонте какого-либо прибора. Например, необходим электролитический конденсатор ёмкостью 1000 микрофарад, а под рукой лишь два-три на 470 микрофарад. Ставить 470 микрофарад, вместо положенных 1000? Нет, это допустимо не всегда. Так как же быть? Ехать на радиорынок за несколько десятков километров и покупать недостающую деталь?
Как выйти из сложившейся ситуации? Можно соединить несколько конденсаторов и в результате получить необходимую нам ёмкость. В электронике существует два способа соединения конденсаторов: параллельное и последовательное.
В реальности это выглядит так:
Параллельное соединение
Принципиальная схема параллельного соединения
Последовательное соединение
Принципиальная схема последовательного соединения
Также можно комбинировать параллельное и последовательное соединение. Но на практике вам вряд ли это пригодиться.
Как рассчитать общую ёмкость соединённых конденсаторов?
Помогут нам в этом несколько простых формул. Не сомневайтесь, если вы будете заниматься электроникой, то эти простые формулы рано или поздно вас выручат.
Общая ёмкость параллельно соединённых конденсаторов:
С1 – ёмкость первого;
С2 – ёмкость второго;
С3 – ёмкость третьего;
СN – ёмкость N-ого конденсатора;
Cобщ – суммарная ёмкость составного конденсатора.
Как видим, при параллельном соединении ёмкости нужно всего-навсего сложить!
Внимание! Все расчёты необходимо производить в одних единицах. Если выполняем расчёты в микрофарадах, то нужно указывать ёмкость C1, C2 в микрофарадах. Результат также получим в микрофарадах. Это правило стоит соблюдать, иначе ошибки не избежать!
Чтобы не допустить ошибку при переводе микрофарад в пикофарады, а нанофарад в микрофарады, необходимо знать сокращённую запись численных величин. Также в этом вам поможет таблица. В ней указаны приставки, используемые для краткой записи и множители, с помощью которых можно производить пересчёт. Подробнее об этом читайте здесь.
Ёмкость двух последовательно соединённых конденсаторов можно рассчитать по другой формуле. Она будет чуть сложнее:
Внимание! Данная формула справедлива только для двух конденсаторов! Если их больше, то потребуется другая формула. Она более запутанная, да и на деле не всегда пригождается .
Или то же самое, но более понятно:
Если вы проведёте несколько расчётов, то увидите, что при последовательном соединении результирующая ёмкость будет всегда меньше наименьшей, включённой в данную цепочку. Что это значить? А это значит, что если соединить последовательно конденсаторы ёмкостью 5, 100 и 35 пикофарад, то общая ёмкость будет меньше 5.
В том случае, если для последовательного соединения применены конденсаторы одинаковой ёмкости, эта громоздкая формула волшебным образом упрощается и принимает вид:
Здесь, вместо буквы M ставиться количество конденсаторов, а C1 – его ёмкость.
Стоит также запомнить простое правило:
При последовательном соединении двух конденсаторов с одинаковой ёмкостью результирующая ёмкость будет в два раза меньше ёмкости каждого из них.
Таким образом, если вы последовательно соедините два конденсатора, ёмкость каждого из которых 10 нанофарад, то в результате она составит 5 нанофарад.
Не будем пускать слов по ветру, а проверим конденсатор, замерив ёмкость, и на практике подтвердим правильность показанных здесь формул.
Возьмём два плёночных конденсатора. Один на 15 нанофарад (0,015 мкф.),а другой на 10 нанофарад (0,01 мкф.) Соединим их последовательно. Теперь возьмём мультиметр Victor VC9805+ и замерим суммарную ёмкость двух конденсаторов. Вот что мы получим (см. фото).
Замер ёмкости при последовательном соединении
Ёмкость составного конденсатора составила 6 нанофарад (0,006 мкф.)
А теперь проделаем то же самое, но для параллельного соединения. Проверим результат с помощью того же тестера (см. фото).
Измерение ёмкости при параллельном соединении
Как видим, при параллельном соединении ёмкость двух конденсаторов сложилась и составляет 25 нанофарад (0,025 мкф.).
Что ещё необходимо знать, чтобы правильно соединять конденсаторы?
Во-первых, не стоит забывать, что есть ещё один немаловажный параметр, как номинальное напряжение.
При последовательном соединении конденсаторов напряжение между ними распределяется обратно пропорционально их ёмкостям. Поэтому, есть смысл при последовательном соединении применять конденсаторы с номинальным напряжением равным тому, которое имеет конденсатор, взамен которого мы ставим составной.
Если же используются конденсаторы с одинаковой ёмкостью, то напряжение между ними разделится поровну.
Для электролитических конденсаторов.
При соединении электролитических конденсаторов (электролитов) строго соблюдайте полярность! При параллельном соединении всегда подключайте минусовой вывод одного конденсатора к минусовому выводу другого,а плюсовой вывод с плюсовым.
Параллельное соединение электролитов
Схема параллельного соединения
В последовательном соединении электролитов ситуация обратная. Необходимо подключать плюсовой вывод к минусовому. Получается что-то вроде последовательного соединения батареек.
Последовательное соединение электролитов
Схема последовательного соединения
Также не забывайте про номинальное напряжение. При параллельном соединении каждый из задействованных конденсаторов должен иметь то номинальное напряжение, как если бы мы ставили в схему один конденсатор. То есть если в схему нужно установить конденсатор с номинальным напряжением на 35 вольт и ёмкостью, например, 200 микрофарад, то взамен его можно параллельно соединить два конденсатора на 100 микрофарад и 35 вольт. Если хоть один из них будет иметь меньшее номинальное напряжение (например, 25 вольт), то он вскоре выйдет из строя.
Желательно, чтобы для составного конденсатора подбирались конденсаторы одного типа (плёночные, керамические, слюдяные, металлобумажные). Лучше всего будет, если они взяты из одной партии, так как в таком случае разброс параметров у них будет небольшой.
Конечно, возможно и смешанное (комбинированное) соединение, но в практике оно не применяется (я не видел ). Расчёт ёмкости при смешанном соединении обычно достаётся тем, кто решает задачи по физике или сдаёт экзамены 🙂
Тем же, кто не на шутку увлёкся электроникой непременно надо знать, как правильно соединять резисторы и рассчитывать их общее сопротивление!
Главная » Радиоэлектроника для начинающих » Текущая страница
Также Вам будет интересно узнать:
Параллельное и последовательное соединение конденсаторов
Иногда в наличии нет конденсатора с нужными параметрами. В таком случае, можно соединить несколько конденсаторов так, чтобы полученная система обладала необходимой электрической емкостью. Существуют два основных способа соединений:
- параллельный;
- последовательный;
Комбинируя эти способы, можно получить смешанное соединение.
Для каждого способа применяют специальные формулы, описывающие распределение заряда и напряжения на конденсаторах, а, так же, получаемую итоговую электроемкость системы.
Параллельное соединение
Этот способ соединения получаем, соединяя каждый вывод одного прибора с соответствующим ему выводом другого (рис. 1).
Рис. 1. Параллельный способ соединения
Емкость для параллельного включения можно определить так:
\[\large \boxed { C_{1} + C_{2} = C_{\text{общ}} } \]
При этом, общая \(\large C_{\text{Общ}} \) электроемкость получится больше самой большой емкости, входящей в соединение.
\(\large C_{1}, C_{2} \left( \text{Ф} \right) \) – электроемкости конденсаторов.
Общая электроемкость включенных параллельно конденсаторов больше емкости большего из них.
Напряжение на конденсаторах
Напряжения, приложенные к параллельно подключенным обкладкам, равны.
\[\large \boxed { U_{1} = U_{2} = U_{\text{общ}} } \]
\(\large U_{1}, U_{2}\left( B\right) \) – напряжения на обкладках.
Рис. 2. Равенство напряжений на параллельно соединенных обкладках
Правило для зарядов
Общий заряд системы разделится на части. Каждая из параллельно соединенных емкостей получит свой заряд.
\[\large \boxed { q_{1} + q_{2} = q_{\text{общ}} } \]
\(\large q_{1}, q_{2}\left( \text{Кл} \right) \) – заряды на конденсаторах.
Рис. 3. Заряды, содержащиеся на каждом параллельно включенном элементе, складываются
При этом, из формулы емкости (ссылка), связывающей ее с напряжением на обкладках и зарядом, следует (рис. 4):
При параллельном соединении меньшая емкость содержит меньший заряд.
Рис. 4. Пример распределения зарядов на конденсаторах при их параллельном включении
Из рисунка 4 следует, в параллельной части цепи конденсатор с наименьшей (0,1 Ф) электроемкостью накапливает меньший (1 Кулон) заряд. А набиольший заряд 4 Кулона содержится на приборе, обладающем максимальной емкостью 0,4 Ф.
Последовательное соединение
Для такого способа соединения складываются величины, обратные емкостям.
\[\large \boxed { \frac {1}{C_{1}} + \frac {1}{C_{2}} = \frac {1}{C_{\text{общ}}} } \]
Примечание: Величина, обратно пропорциональная емкости, измеряется в обратных Фарадах.
\(\large \displaystyle \frac {1}{C} \left( \frac {1}{\text{Ф}} \right) \) – величину, обратную электроемкости в некоторых источниках называют электрической эластичностью (эластансом).
\(\large C_{1}, C_{2}\left( \text{Ф}\right) \) – емкости конденсаторов.
При последовательном включении общая \(\large C_{\text{Общ}} \) электроемкость цепочки окажется меньше самой маленькой емкости включенной в цепочку.
Рис. 5. Последовательный способ соединения емкостей
Общая емкость системы меньше меньшей из включенных последовательно емкостей.
Правило для напряжений
Приложенное к концам последовательной цепочки напряжение распределится между элементами.
\[\large \boxed { U_{1} + U_{2} = U_{\text{общ}} } \]
где \(\large U_{1}, U_{2}\left( B\right) \) — это напряжения на обкладках.
Чем больше емкость конденсатора, тем меньшее напряжение будет наблюдаться на его обкладках при последовательном соединении.
Рис. 6. Способ определить общее напряжение на последовательно включенных емкостях
Общее напряжение разделится на части. Большее напряжение будет на конденсаторе с меньшей электроемкостью.
На рисунке 7 представлена цепочка, состоящая из 4-ех емкостей, соединенных последовательно. На конденсаторе с наименьшей емкостью 0,3 Ф напряжение составляет 4 Вольта.
Рис. 7. Пример распределения напряжений на элементах последовательной цепи
А наименьшее напряжение 1 Вольт, находится на обкладках конденсатора с наибольшей емкостью 1,2 Ф. Общее напряжение на концах цепочки равняется 10-и Вольтам.
Заряд на конденсаторах
Зарядив одну из обкладок конденсатора, мы получим на второй его обкладке такой же (по модулю) заряд противоположного знака. Поэтому, все конденсаторы, соединенные последовательно, будут иметь одинаковые заряды на обкладках.
\[\large \boxed { q_{1} = q_{2} = q_{\text{общ}} } \]
где \(\large q_{1}, q_{2}\left( \text{Кл} \right) \) – заряды, накопленные конденсаторами.
В последовательно включенной цепочке все конденсаторы обладают равными зарядами.
Рис. 8. Равенство зарядов на обкладках последовательно включенных емкостей
Выводы
- Правила, приведенные в статье, будут справедливы не только для двух, но и для любого количества включенных конденсаторов.
- Связывающие напряжения и заряды формулы для последовательно и параллельно включенных элементов, можно получить из принципа сложения емкостей и обратных емкостей, а, так же, отношения между приложенным напряжением и зарядом.
Рис. 9. Основные формулы для различных способов соединения
Формула расчета последовательного соединения конденсатора
У многих радиолюбителей, особенно приступающих впервые к конструированию электросхем, возникает вопрос, как надо подключить конденсатор требуемой ёмкости? Когда, к примеру, в каком-то месте схемы нужен конденсатор ёмкостью 470 мкФ, и такой элемент есть в наличии, то проблемы не возникнет. Но когда требуется поставить конденсатор на 1000 мкФ, а присутствуют только элементы неподходящей емкости, на помощь приходят схемы из нескольких конденсаторов, соединённых вместе. Соединять элементы можно, применяя параллельное и последовательное соединение конденсаторов по отдельности или по комбинированному принципу.
Последовательное соединение конденсаторов
Схема последовательного соединения
Когда применяется схема последовательного соединения конденсаторов, заряд каждой детали эквивалентен. С источником соединены только внешние пластины, другие – заряжаются перераспределением электрозарядов между ними. Все конденсаторы сохраняют аналогичное количество заряда на своих обкладках. Это объясняется тем, что на каждый последующий элемент поступает заряд от соседнего. Вследствие этого справедливо уравнение:
q = q1 = q2 = q3 = …
Известно, что при последовательном соединении резисторных элементов их сопротивления суммируются, но емкость конденсатора, включенного в такую электроцепь, рассчитывается по-другому.
Падение напряжения на отдельном конденсаторном элементе зависит от его емкости. Если в последовательной электроцепи имеется три конденсаторных элемента, составляется выражение для напряжения U на основании закона Кирхгофа:
U = U1 + U2 + U3,
при этом U= q/C, U1 = q/C1, U2 = q/C2, U3 = q/C3.
Подставляя значения для напряжений в обе части уравнения, получается:
q/C = q/C1 + q/C2 + q/C3.
Так как электрозаряд q – величина одинаковая, на нее можно поделить все части полученного выражения.
Результирующая формула для емкостей конденсаторов:
1/С = 1/С1 + 1/С2 + 1/С3.
Важно! Если конденсаторы подключаются в последовательную электроцепь, показатель, обратный результирующей емкости, равен совокупности обратных значений единичных емкостей.
Особенности последовательного соединения
Пример. Три конденсаторных элемента подключены в последовательную цепь и обладают емкостями: С1 = 0,05 мкф, С2 = 0,2 мкФ, С3 = 0,4 мкФ. Рассчитать общую емкостную величину:
- 1/С = 1/0,05 + 1/0,2 + 1/0,4 = 27,5;
- С = 1/27,5 = 0,036 мкФ.
Важно! Когда конденсаторные элементы включены в последовательную электроцепь, общее емкостное значение не превышает наименьшей емкости отдельного элемента.
Если цепь состоит всего из двух компонентов, формула переписывается в таком виде:
С = (С1 х С2)/(С1 + С2).
В случае создания цепи из двух конденсаторов с идентичным емкостным значением:
С = (С х С)/(2 х С) = С/2.
Последовательно включенные конденсаторы имеют реактивное сопротивление, зависящее от частоты протекающего тока. На каждом конденсаторе напряжение падает из-за наличия этого сопротивления, поэтому на основе такой схемы создается емкостной делитель напряжения.
Емкостной делитель напряжения
Формула для емкостного делителя напряжения:
U1 = U x C/C1, U2 = U x C/C2, где:
- U – напряжение питания схемы;
- U1, U2 – падение напряжения на каждом элементе;
- С – итоговая емкость схемы;
- С1, С2 – емкостные показатели единичных элементов.
Вычисление падений напряжения на конденсаторах
К примеру, имеются сеть переменного тока 12 В и две альтернативных электроцепи подсоединения последовательных конденсаторных элементов:
- первая – для подключения одного конденсатора С1 = 0,1 мкФ, другого С2 = 0,5 мкФ;
- вторая – С1 = С2 = 400 нФ.
Первый вариант
- Итоговая емкость электросхемы С = (С1 х С2)/(С1 + С2) = 0,1 х 0,5/(0,1 + 0,5) = 0,083 мкФ;
- Падение напряжения на одном конденсаторе: U1 = U x C/C1 = 12 x 0,083/0,1 = 9,9 В
- На втором конденсаторе: U2 = U x C/C2 = 12 х 0,083/0,5 = 1,992 В.
Второй вариант
- Результирующая емкость С = 400 х 400/(400 + 400) = 200 нФ;
- Падение напряжения U1 = U2 = 12 x 200/400 = 6 В.
Согласно расчетам, можно сделать выводы, что если подключаются конденсаторы равных емкостей, вольтаж делится поровну на обоих элементах, а когда емкостные значения различаются, то на конденсаторе с меньшей емкостной величиной напряжение увеличивается, и наоборот.
Параллельное и комбинированное соединение
Параллельное соединение конденсаторов представляется иным уравнением. Для определения общего емкостного значения надо просто найти совокупность всех величин по отдельности:
С = С1 + С2 + С3 + …
Напряжение к каждому элементу будет прикладываться идентичное. Следовательно, для усиления емкости надо соединить несколько деталей параллельно.
Если соединения смешанные, последовательно-параллельные, то для таких контуров применяют эквивалентные, или упрощенные, электросхемы. Каждую область цепи рассчитывают отдельно, а затем, представляя их вычисленными емкостями, объединяют в простую цепь.
Варианты получения эквивалентных схем
Особенности замены конденсаторов
К примеру, в наличии сеть переменного тока 12 В и две альтернативных группы последовательных конденсаторных элементов.
Конденсаторы подсоединяются в последовательный контур для увеличения напряжения, под которым они остаются работоспособными, но их общая емкость падает в соответствии с формулой для ее расчета.
Часто применяется смешанное соединение конденсаторов, чтобы создать нужную емкостную величину и увеличить напряжение, которое детали способны выдержать.
Можно привести вариант, как соединить несколько компонентов, чтобы выйти на нужные параметры. Если требуется конденсаторный элемент 80 мкФ при напряжении 50 В, но есть только конденсаторы 40 мкФ на 25 В, необходимо образовать следующую комбинацию:
- Два конденсатора 40 мкФ/25 В подсоединить последовательно, что позволит иметь в общей сложности 20 мкФ /50 В;
- Теперь вступает в действие параллельное включение конденсаторов. Пара конденсаторных групп, включенных последовательно, созданных на первом этапе, соединяются параллельно, получится 40 мкФ / 50 В;
- Две собранные в итоге группы соединить параллельно, в результате получим 80 мкФ/50 В.
Важно! Для того чтобы усилить конденсаторы по напряжению, возможно их объединить в последовательную электросхему. Увеличение общей емкостной величины достигается параллельным подключением.
Что необходимо учитывать при создании последовательной цепи:
- При соединениях конденсаторов оптимальный вариант – брать элементы с мало различающимися или с одинаковыми параметрами, вследствие большой разницы в напряжениях разряда;
- Для баланса токов утечки на каждый конденсаторный элемент (в параллель) включается уравнительное сопротивление.
Получение неполярного конденсатора
Включение в последовательную цепь всегда должно происходить с соблюдением «плюса» и «минуса» конденсаторов. Если их соединить одноименными полюсами, то такое сочетание уже теряет поляризованность. При этом емкость созданной группы будет равна половине от емкостного значения одной из деталей. Такие конденсаторы возможно применять в качестве пусковых на электромоторах.
Видео
Оцените статью:Электричество и магнетизм
Решение. Емкость прежнего конденсатора, чьими обкладками были сферы радиусами дается формулой (2.18):
Как видно из рисунка, новый конденсатор представляет собой последовательное соединение двух сферических конденсаторов: образованного сферами радиусами (его емкость обозначим как ) и (его емкость будет ). Имеем по той же формуле:
|
(2.30) |
Для емкости последовательно соединенных конденсаторов получаем теперь
Емкость нового конденсатора оказалась больше емкости первоначального.
Аналитическая формула для емкости такой батареи имеет вид:
|
(2.31) |
При бесконечно тонкой внутренней сфере заряды на ее поверхностях скомпенсируют друг друга, и мы должны получить формулу для емкости конденсатора без внутренней оболочки. Так оно и следует из формулы (2.31) при . В обратном предельном случае, когда стенки внутренней оболочки близки к обкладкам первоначального конденсатора, получается формула для емкости двух последовательно соединенных плоских конденсаторов.
Конденсаторы нашли широкое практическое применение, особенно в радиотехнике. Некоторые типы конденсаторов показаны на рис. 2.18.
Рис. 2.18. Различные типы конденсаторов, применяемых в технике: 1 — конденсаторы постоянной емкости; 2 — конденсатор переменной емкости
Дополнительная информация
http://www.elektropolus.com/condensator/type.php — типы конденсаторов;
http://gete.ru/post_1212414212.html — классификация и маркировка конденсаторов;
http://www.chipdip.ru/video.aspx?vid=ID000274696&tag=dielectric — видео «Конструкция электролитического алюминиевого конденсатора»;
http://www.symmetron.ru/articles/tantalum_replacement.shtml — керамические конденсаторы большой емкости;
http://radiobooka.ru/radio_nach/kak_sdelat_kondensator.phtml — как сделать конденсатор своими руками;
http://chipinfo.ru/literature/radio/194701/p54-57.html — статья «Переменные конденсаторы»;
http://www.eham.net/articles/5217 — переменный конденсатор своими руками;
http://www.kpsec.freeuk.com/components/capac.htm — коденсаторы, переменные конденсаторы;
http://qrx.narod.ru/arhn/e_d.htm — бесконтактные емкостные датчики;
http://www.lionprecision.com/capacitive-sensors/index.html — обзор емкостных датчиков;
http://pda-reader.ru/93 — принципы работы сенсорных экранов;
http://pcavto.ru/kak-eto-rabotaet/printscipyi-rabotyi-sensornyix-ekranov-touch-screen.html — как работают сенсорные экраны разных типов.
Последовательное и параллельное соединение конденсаторов (ёмкостей)
Практически ни одно электронное устройство не обходится без конденсатора. Он может стоять на входе или выходе устройства, перед или после некоторых элементов. Применяется последовательное и параллельное соединение конденсаторов. Как и для чего их подключать тем или иным способом и будем обсуждать.
Содержание статьи
Что такое конденсатор и его основные характеристики
Конденсатор — это радиодеталь, которая работает как накопитель электрической энергии. Чтобы понятнее было, как он работает, его можно представить как своего рода небольшой аккумулятор. Обозначается двумя параллельными чёрточками.
Обозначения различных типов конденсаторов на схемах. Чаще всего из строя выходят электролитические конденсаторы, так что стоит запомнить их обозначение
Основная характеристика конденсатора любого типа — ёмкость. Это то количество заряда, которое он в состоянии накопить. Измеряется в Фарадах (сокращенно просто буква F или Ф), а вернее, в более «мелких» единицах:
- микрофарадах — мкФ это 10-6 фарада,
- нанофарадах — нФ это 10-9 фарада;
- пикофарадах — пФ это 10-12 фарада.
Вторая важная характеристика — номинальное напряжение. Это то напряжение, при котором гарантирована длительная безотказная работа. Например, 4700 мкФ 35 В, где 35 В — это номинальное напряжение 35 вольт.
У крупных по размеру конденсаторов, ёмкость и напряжение указаны на корпусе
Нельзя ставить конденсатор в цепь с более высоким напряжением чем то, которое на нём указано. В противном случае он быстро выйдет из строя.
Можно использовать конденсаторы на 50 вольт вместо конденсаторов на 25 вольт. Но это порой нецелесообразно, так как те, которые рассчитаны на более высокое напряжение, дороже, да и габариты у них больше.
Что он из себя представляет и как работает
В самом простейшем случае конденсатор состоит из двух токопроводящих пластин (обкладок), разделённых слоем диэлектрика.
Между обкладками находится слой диэлектрика — материала плохо проводящего электрический ток
На пластины подаётся постоянный или переменный ток. Вначале, пока энергия накапливается, потребление энергии конденсатором высокое. По мере «наполнения» ёмкости оно снижается. Когда заряд набран полностью, токопотребления вообще нет, источник питания как бы отключается. В это время конденсатор сам начинает отдавать накопленный заряд. То есть, он на время становится своеобразным источником питания. Поэтому его и сравнивают с аккумулятором.
Где и для чего используются
Как уже говорили, сложно найти схему без конденсаторов. Их применяют для решения самых разных задач:
- Для сглаживания скачков сетевого напряжения. В таком случае их ставят на входе устройств, перед микросхемами, которые требовательны к параметрам питания.
- Для стабилизации выходного напряжения блоков питания. В таком случае надо искать их перед выходом.
Часто можно увидеть электролитические цилиндрические конденсаторы
- Датчик прикосновения (тач-пады). В таких устройствах оной из «пластин» конденсаторов является человек. Вернее, его палец. Наше тело обладает определённой проводимостью. Это и используется в датчиках прикосновения.
- Для задания необходимого ритма работы. Время заряда конденсаторов разной ёмкости отличается. При этом цикл заряд/разряд конденсатора остаётся величиной постоянной. Это и используется в цепях, где надо задавать определённый ритм работы.
- Ячейки памяти. Память компьютеров, телефонов и других устройств — это огромное количество маленьких конденсаторов. Если он заряжен — это единица, разряжен — ноль.
- Есть стартовые конденсаторы, которые помогают «разогнать» двигатель. Они накапливают заряд, потом резко его отдают, создавая требуемый «толчок» для разгона мотора.
- В фотовспышках. Принцип тот же. Сначала накапливается заряд, затем выдаётся, но преобразуется в свет.
Конденсаторы встречаются часто и область их применения широка. Но надо знать как правильно их подключить.
Как подключать конденсаторы
В электротехнике есть два основных вида соединения деталей — параллельное и последовательное. Конденсаторы также можно подключать по любому из указанных способов. Есть ещё особая — мостовая схема. Она имеет собственную область использования.
В схеме может быть последовательное и параллельное соединение конденсаторов
Параллельное подключение конденсаторов
При параллельном соединении все конденсаторы объединены двумя узлами. Чтобы параллельно подключить конденсаторы, скручиваем попарно их ножки, обжимаем пассатижами, потом пропаиваем. У некоторых конденсаторов большие корпуса (банки), а выводы маленькие. В таком случае используем провода (как на рисунке ниже).
Так физически выглядит параллельное подключение конденсаторов
Если конденсаторы электролитические, следите за полярностью. На них должны стоять «+» или «-«. При их параллельном подключении соединяем одноимённые выводы — плюс к плюсу, минус — к минусу.
Расчёт суммарной ёмкости
При параллельном подключении конденсаторов их номинальная ёмкость складывается. Просто суммируете номиналы всех подключённых элементов, сколько бы их ни было. Два, три, пять, тридцать. Просто складываем. Но следите, чтобы размерность совпадала. Например, складывать будем в микрофарадах. Значит, все значения переводим в микрофарады и только после этого суммируем.
Расчёт ёмкости при параллельном подключении конденсаторов
Когда на практике применяют параллельное соединение конденсаторов? Например, тогда, когда надо заменить «пересохший» или сгоревший, а нужного номинала нет и бежать в магазин некогда или нет возможности. В таком случае подбираем из имеющихся в наличии. В сумме они должны дать требуемое значение. Все их проверяем на работоспособность и соединяем по приведенному выше принципу.
Пример расчёта
Например, включили параллельно два конденсатора — 8 мкФ и 12 мкФ. Следуя формуле, их номиналы просто складываем. Получаем 8 мкФ + 12 мкФ = 20 мкФ. Это и будет суммарная ёмкость в данном случае.
Пример расчёта конденсаторов при параллельном подключении
Последовательное соединение
Последовательным называется соединение, когда выход одного элемента соединяется со входом другого. Сравнить можно с вагонами или цепочкой из лампочек. По такому же принципу последовательно соединяют и конденсаторы.
Вот что значит последовательно соединить конденсаторы
При подключении полярных электролитических «кондеров» надо следить за соблюдением полярности. Плюс первого конденсатора подаете на минус второго и так далее. Выстраиваете цепочку.
Существуют неполярные (биполярные) электролитические конденсаторы. При их соединении нет необходимости соблюдать полярность.
Как определить ёмкость последовательно соединенных конденсаторов
При последовательном соединении конденсаторов суммарная ёмкость элементов будет меньше самого маленького номинала в цепочке. То есть, ёмкость последовательно соединённых конденсаторов уменьшается. Это также может пригодиться при ремонте техники — замена конденсатора требуется часто.
Последовательно соединённые конденсаторы
Использовать формулу расчёта приведённую выше не очень удобно, поэтому её обычно используют в преобразованном виде:
Формула расчёта ёмкости при последовательном соединении
Это формула для двух элементов. При увеличении их количества она становится значительно сложнее. Хотя, редко можно встретить больше двух последовательных конденсаторов.
Пример расчёта
Какая суммарная ёмкость будет если конденсаторы на 12 мкФ и 8 мкФ соединить последовательно? Считаем: 12*8 / (12+8) = 96 / 20 = 4,8 мкФ. То есть, такая цепочка соответствует номиналу 4,8 мкФ.
Пример расчета ёмкости при последовательном подключении конденсаторов
Как видите, значение меньше чем самый маленький номинал в последовательности. А если подключить таким образом два одинаковых конденсатора, то результат будет вполовину меньше номинала. Например, рассчитаем для двух ёмкостей по 12 мкФ. Получим: 12*12 / (12 + 12) = 144 / 24 = 6 мкФ. Проверим для 8 мкФ. Считаем: 8*8 / (8+8) = 64 / 16 = 4 мкФ. Закономерность подтвердилась. Это правило можно использовать при подборе номинала.
Почему электролитические конденсаторы выходят из строя и что делать
Зачастую, чтобы отремонтировать вышедшую из строя электронную технику, достаточно найти и заменить вздувшиеся конденсаторы. Дело в том, что срок жизни их небольшой — 1000-2000 тысячи рабочих часов. Потом он обычно выходит из строя и требуется его замена. И это при нормальном напряжении не выше номинального. Так происходит потому, что диэлектрик в конденсаторах, чаще всего, жидкий. Жидкость понемногу испаряется, меняются параметры и, рано или поздно, конденсатор вздувается.
Электролитические конденсаторы имеют специальные насечки на верхушке корпуса, чтобы при выходе из строя избежать взрыва
Высыхает электролит не только во время работы. Даже просто «от времени». Это конструктивная особенность электролитических конденсаторов. Поэтому не стоит ставить выпаянные из старых схем конденсаторы или те, которые несколько лет (или десятков лет) хранятся в мастерской. Лучше купить «свежий», но проверьте дату производства.
Можно ли продлить срок эксплуатации конденсаторов? Можно. Надо улучшить теплоотвод. Чем меньше греется электролит, тем медленнее высыхает. Поэтому не стоит ставить аппаратуру вблизи отопительных приборов.
Для улучшения отвода тепла ставят радиаторы
Второе — надо следить за тем, чтобы хорошо работали кулера. Третье — если рядом стоят детали, которые активно греются во время работы, надо конденсаторы каким-то образом от температуры защитить.
Как подобрать замену
Если часто приходится менять один и тот же конденсатор, его лучше заменить на более «мощный» — той же ёмкости, но на большее напряжение. Например, вместо конденсатора на 25 вольт, поставить конденсатор на 35 вольт. Только надо иметь в виду, что более мощные конденсаторы имеют большие размеры. Не всякая плата позволяет сделать такую замену.
Конденсатор той же ёмкости, но рассчитанный на большее напряжение, имеет больший размер
Можно поставить параллельно несколько конденсаторов с тем же напряжением, подобрав номиналы так, чтобы получить требуемую ёмкость. Что это даст? Лучшую переносимость пульсаций тока, меньший нагрев и, как следствие, более продолжительный срок службы.
Что будет, если поставить конденсатор большей ёмкости?
Часто приходит в голову идея поставить вместо сгоревшего или вздувшегося конденсатор большей ёмкости. Ведь он должен меньше греться. Так, во всяком случае, кажется. Ёмкость практически никак не связана со степенью нагрева корпуса. И в этом выигрыша не будет.
Устройство электролитического конденсатора
По нормативным документам отклонение номинала конденсаторов допускается в пределах 20%. Вот на эту цифру можете спокойно ставить больше/меньше. Но это может привести к изменениям в работе устройства. Так что лучше найти «родной» номинал. И учтите, что не всегда можно ставить большую ёмкость. Можно если конденсатор стоит на входе и сглаживает скачки питания. Вот тут большая ёмкость уместна, если для её установки достаточно места. Это точно нельзя делать там, где конденсатор работает как фильтр, отсекающий заданные частоты.
Можно менять на ту же ёмкость, но чуть более высокое напряжение. Это имеет смысл. Но размеры такого конденсатора будут намного больше. Не в любую плату получится его установить. И учтите, что корпус его не должен соприкасаться с другими деталями.
Параллельное и последовательное соединение конденсаторов, схемы, расчет
Радиоэлементы можно соединить между собой тремя способами. Существует параллельное и последовательное соединение конденсаторов, а также смешанный тип. Всегда можно точно определить емкость равноценного конденсатора по этому показателю. Его можно поменять на ряд соединенных в цепь других, более мелких по емкости конденсаторов. Для равнозначного конденсаторы должно быть выполнено некоторое условие, а именно подключенное напряжение к конденсатору равно напряжению на зажимах этой группы этих.
Таким же образом подключается все радиоэлементы, существующие на данный момент. Главным образом используются параллельное и последовательное соединение конденсаторов. В данной статьи рассмотрены все типы соединений конденсаторов. В качестве бонуса. в статье есть видеоролик и статья, посвященные этой теме.
Виды соединения конденсаторов в обмотке.
Последовательное и параллельное соединение конденсаторов
Соединение конденсаторов в электрической цепи может быть последовательным, параллельным и последовательно-пареллельным (смешанным). Если провести аналогию между соединением конденсаторов и соединением резисторов, то стоит отметить, что формулы расчета общей емкости и общего сопротивления идентичны, только между разными типами соединений: Формула Cобщ при параллельном соединении конденсаторов = формула Rобщ при последовательном соединении резисторов.
- Cобщ — общая емкость.
- Rобщ — общее сопротивление.
При последовательном соединении конденсаторов (рис. 3) на обкладках отдельных конденсаторов электрические заряды по величине равны: Q1 = Q2 = Q3 = Q. Действительно, от источника питания заряды поступают лишь на внешние обкладки цепи конденсаторов, а на соединенных между собой внутренних обкладках смежных конденсаторов происходит лишь перенос такого же по величине заряда с одной обкладки на другую (наблюдается электростатическая индукция), поэтому и на них по- являются равные и разноименые электрические заряды.
Соединения конденсаторов.
Напряжения между обкладками отдельных конденсаторов при их последовательном соединении зависят от емкостей отдельных конденсаторов: U1 = Q/C1, U1 = Q/C2, U1 = Q/C3, а общее напряжение U = U1 + U2 + U3. Общая емкость равнозначного (эквивалентного) конденсатора C = Q / U = Q / (U1 + U2 + U3), т. е. при последовательном соединении конденсаторов величина, обратная общей емкости, равна сумме обратных величин емкостей отдельных конденсаторов. Формулы эквивалентных емкостей аналогичны формулам эквивалентных проводимостей.
Материал в тему: все о переменном конденсаторе.
Параллельное соединение конденсаторов
Параллельное соединение конденсаторов — это соединение при котором конденсаторы соединяются собой обоими контактами. В результате к одной точке может быть присоединено несколько конденсаторов. При параллельном соединении формируется один большой конденсатор с площадью обкладок, равной сумме площадей обкладок всех отдельных компонентов. Поскольку емкость конденсаторов прямо пропорциональна площади обкладок, общая емкость Собщ при параллельном соединении равняется сумме емкостей всех конденсаторов в цепи.
Напряжение при параллельном соединении
На все параллельно соединенные конденсаторы падает одинаковое напряжение. Так происходит, потому что существует всего лишь две точки, между которыми может быть разность потенциалов (напряжение). Другими словами, можно сказать что при параллельном соединении все конденсаторы подключены к одному источнику напряжения. Ток конденсатора во время переходного периода зависит от его емкости и изменения напряжения:
- ic — ток конденсатора
- C — Емкость конденсатора
- ΔVC/Δt – Скорость изменения напряжения
При параллельном соединении через каждый конденсатор потечет одельный ток, в зависимости от емкости конденсатора:
Последовательное соединение конденсаторов
Если же соединение конденсаторов в батарею производится в виде цепочки и к точкам включения в цепь непосредственно присоединены пластины только первого и последнего конденсаторов, то такое соединение конденсаторов называется последовательным. При последовательном соединении все конденсаторы заряжаются одинаковым количеством электричества, так как непосредственно от источника тока заряжаются только крайние пластины, а остальные пластины заряжаются через влияние. При этом заряд пластины будет равен по величине и противоположен по знаку заряду пластины 1, заряд пластины 3 будет равен по величине и противоположен по знаку заряду пластины 2 и т. д.
Напряжения на различных конденсаторах будут, вообще говоря, различными, так как для заряда одним и тем же количеством электричества конденсаторов различной емкости всегда требуются различные напряжения.
Типы соединений конденсаторов.
Чем меньше емкость конденсатора, тем большее напряжение необходимо для того, чтобы зарядить этот конденсатор требуемым количеством электричества, и наоборот.
Таким образом, при заряде группы конденсаторов, соединенных последовательно, на конденсаторах малой емкости напряжения будут больше, а на конденсаторах большой емкости — меньше.
Аналогично предыдущему случаю можно рассматривать всю группу конденсаторов, соединенных последовательно, как один эквивалентный конденсатор, между пластинами которого существует напряжение, равное сумме напряжений на всех конденсаторах группы, а заряд которого равен заряду любого из конденсаторов группы. Возьмем самый маленький конденсатор в группе. На нем должно быть самое большое напряжение. Но напряжение на этом конденсаторе составляет только часть общего напряжения, существующего на всей группе конденсаторов. Напряжение на всей группе больше напряжения на конденсаторе, имеющем самую малую емкость. А отсюда непосредственно следует, что общая емкость группы конденсаторов, соединенных последовательно, меньше емкости самого малого конденсатора в группе.
Последовательное соединение конденсаторов – это соединение двух или более конденсаторов в форме цепи, в которой каждый отдельный конденсатор соединяется с другим отдельным конденсатором только в одной точке. Ток (iC), заряжающий последовательную цепь конденсаторов, будет одинаковым для всех конденсаторов, поскольку у него есть только один возможный путь прохождения.
Вследствие того что через все последовательно соединенные конденсаторы течет одинаковый ток, количество накопленого электрического заряда для каждого конденсатора будет одинаковым, независимо от его емкости. Так происходит, потому что электрический заряд, накапливаемый на обкладке любого конденсатора, должен прийти с обкладки примыкающего конденсатора. Таким образом, последовательно соединенные конденсаторы имеют одинаковый электрический заряд.
Стоит почитать: все об электолитических конденсаторах.
Правая обкладка первого конденсатора С1 соединяется с левой второго конденсатора С2, у которого правая обкладка соединяется с левой третьего конденсатора С3. Это означает, что в режиме постоянного тока конденсатор С2 электрически изолирован от общей цепи. В итогое эффективная площадь обкладок уменьшается до площади обкладок самого маленького конденсатора. Это объясняется тем, что как только обкладки наименшей площади заполнятся электрическим зарядом, данный конденсатор перестанет пропускать ток. В результате ток прекратиться во всей цепи, и процесс зарядки остальных конденсаторов также прекратится. При последовательном соединении общее расстояние между обкладками увеличивается до суммы расстояний между обкладками всех конденсаторов.
Таким образом, последовательная цепь формирует один большой конденсатор с площадью обкладок элемента с наименьшей емкостью, и расстоянием между обкладками, равному сумме всех расстояний в цепи. На каждый отдельный конденсатор в последовательной цепи падает разное напряжение. Поскольку емкость обратно пропрциональна напряжению (С = Q/V), то чем меньше емкость конденсатора, тем большее напряжение на него упадет. Применим закон Кирхгофа для напряжения в последовательной цепи из трех конденсаторов.
Емкость конденсатора прямо пропорциональна его заряду и обратно пропорциональна его напряжению — C = Q/V. Как уже упоминалось выше, последовательно соединенные конденсаторы имеют одинаковый электрический заряд — Qобщ = Q1 = Q2 = Q3. Из данного уравнения можно легко вывести формулу общей емкости для любого частного случая последовательного соединения.
Интересно почитать: принцип действия и основные характеристики варисторов.
Если в цепи есть и последовательное и параллельное соединение, то такую цепь называют смешанной или последовательно-параллельной. Тем не менее, смешанное соединение может иметь как последовательный, так и параллельный характер.
Типы соединений конденсаторов.
Общая емкость смешанного соединения конденсаторов
Чтобы посчитать общую емкость смешанного соединения конденсаторов, следуют такому же алгоритму, как и при расчете общего сопротивления смешанного соединения резисторов.
- Цепь разбивают на участки с только пареллельным или только последовательным соединением
- Вычисляют общую емкость для каждого отдельного участка.
- Вычисляют общую емкость для всей цепи смешанного соединения.
Вполне справедливым может оказаться вопрос, для чего надо соединять конденсаторы последовательно, если общая емкость будет меньше? Скорее всего, первым что приходит в голову — это чтобы получить новый эквивалентный конденсатор с меньшей емкостью. Но в производстве микросхем вряд ли будут делать подобное, поскольку, во -первых, обычно нужно экономить место на печатной плате, а во-вторых, нет смысла тратить деньги на два компонента или больше, если можно купить один с требуемой емкостью.
Но если в параллельном или последовательном соединении конденсаторов еще есть хоть какая-то логика, то кому вообще нужно смешанное? Дело в том, что емкостью, то есть способностью накапливать электрический заряд, обладает любое тело в природе, даже человеческое.
Если мы говорим о электрической цепи, то все ее элементы на практике обладают емкостью, и их можно представить, как конденсаторы. Часто такую емкость еще называют паразитической, потому как она создает разного рода помехи.
Например, у нас есть какая-то электронная цепь с множеством различных компонентов, которая принимает сигнал, обрабатывает его определенным образом и выдает на выход результат. Известно, что время задержки сигнала, в основном, зависит от паразитической емкости электронных компонентов схемы. Поскольку должно пройти время зарядки паразитической емкости, прежде чем она начнет пропускать сигнал. Если мы хотим узнать время задержки, нужно посчитать общую емкость всех компонентов, конвертировав их в цепь из конденсаторов.
Материал в тему: описание и область применения подстроечного резистора.
Последовательное и параллельное соединение конденсаторов
Последовательное и параллельное соединение конденсаторов применяют в зависимости от поставленной цели. При последовательном соединении конденсаторов уменьшается общая емкость и увеличивается общее напряжение конденсаторов. А общее напряжение будет равняться сумме напряжений всех конденсаторов. Например: мы имеем три конденсатора по 30 мкФ x 100 В каждый. При их последовательном соединении общий конденсатор будет иметь следующие данные: 10 мкФ x 300 В.
При параллельном соединении общая емкость конденсаторов складывается, а допустимое напряжение всего набора будет равно напряжению конденсатора, имеющего самое низкое значение допустимого напряжения из всего набора. C = C1 + C2 + C3 + C4 + …Например: мы имеем три конденсатора 30 мкФ x 100 В, соединённые параллельно. Параметры всего набора конденсаторов в этом случае будут следующие: 90 мкФ x 100 В.
Соединение более двух конденсаторов последовательно редко встречается в реальных схемах. Хотя для увеличения общего напряжения такой набор может встретиться в высоковольтных источниках питания. А вот в низковольтных источниках довольно часто встречается параллельное соединение нескольких конденсаторов для сглаживания пульсаций после выпрямления при больших токах потребления. Обратите внимание, формулы вычисления емкости последовательного и параллельного соединения конденсаторов в точности обратным формулам вычисления сопротивления при последовательном и параллельном соединении резисторов.
Более подробно о типах подключения конденсаторов можно узнать прочитав статью подключения конденсаторов. Если у вас остались вопросы, можно задать их в комментариях на сайте. Также в нашей группе ВК можно задавать вопросы и получать на них подробные ответы от профессионалов.
Чтобы подписаться на группу, вам необходимо будет перейти по следующей ссылке: https://vк.coм/еlеctroinfonеt. В завершение статьи хочу выразить благодарность источникам, откуда мы черпали информацию:
www.electricalschool.info
www.sxemotehnika.ru
www.katod-anod.ru
www.hightolow.ru
Предыдущая
КонденсаторыКонденсатор — простыми словами о сложном
СледующаяКонденсаторыКак обозначаются конденсаторы на схеме?
факторов, влияющих на емкость | Конденсаторы
Существует три основных фактора конструкции конденсатора, определяющих величину создаваемой емкости. Все эти факторы определяют емкость, влияя на то, какой поток электрического поля (относительная разница электронов между пластинами) будет развиваться для данной величины силы электрического поля (напряжения между двумя пластинами):
ПЛОЩАДЬ ПЛАСТИНЫ : При прочих равных условиях большая площадь пластины дает большую емкость; меньшая площадь пластины дает меньшую емкость.
Пояснение: Большая площадь пластины приводит к большему потоку поля (заряд, накопленный на пластинах) для данной силы поля (напряжение на пластинах).
РАССТОЯНИЕ ПЛАСТИН : При прочих равных условиях большее расстояние между пластинами дает меньшую емкость; меньшее расстояние между пластинами дает большую емкость.
Пояснение: Более близкое расстояние приводит к большей силе поля (напряжение на конденсаторе, деленное на расстояние между пластинами), что приводит к большему потоку поля (заряд, накопленный на пластинах) для любого заданного напряжения, приложенного к пластинам.
ДИЭЛЕКТРИЧЕСКИЙ МАТЕРИАЛ : При прочих равных условиях большая диэлектрическая проницаемость диэлектрика дает большую емкость; меньшая диэлектрическая проницаемость диэлектрика дает меньшую емкость.
Пояснение: Хотя это сложно объяснить, некоторые материалы предлагают меньшее сопротивление потоку поля для данной величины силы поля. Материалы с большей диэлектрической проницаемостью допускают больший поток поля (предлагают меньшее сопротивление) и, следовательно, больший накопленный заряд для любой заданной величины силы поля (приложенного напряжения).
«Относительная» диэлектрическая проницаемость означает диэлектрическую проницаемость материала относительно диэлектрической проницаемости чистого вакуума. Чем больше число, тем больше диэлектрическая проницаемость материала. Стекло, например, с относительной диэлектрической проницаемостью 7, имеет в семь раз большую диэлектрическую проницаемость, чем чистый вакуум, и, следовательно, позволяет создать поток электрического поля, в семь раз более сильный, чем у вакуума, при прочих равных условиях. В следующей таблице перечислены относительные диэлектрические проницаемости (также известные как «диэлектрическая проницаемость») различных распространенных веществ:
|
Материал |
Относительная диэлектрическая проницаемость (диэлектрическая проницаемость) |
|---|---|
| Вакуум | 1.0000 |
| Воздух | 1.0006 |
| PTFE, FEP («тефлон») | 2,0 |
| Полипропилен | от 2,20 до 2,28 |
| Смола АБС | от 2,4 до 3,2 |
| Полистирол | от 2,45 до 4,0 |
| Вощеная бумага | 2,5 |
| Масло трансформаторное | 2,5 до 4 |
| Твердая резина | 2.От 5 до 4,80 |
| Дерево (Дуб) | 3,3 |
| Силиконы | от 3,4 до 4,3 |
| Бакелит | от 3,5 до 6,0 |
| Кварц плавленый | 3,8 |
| Дерево (клен) | 4,4 |
| Стекло | от 4,9 до 7,5 |
| Касторовое масло | 5,0 |
| Дерево (береза) | 5,2 |
| Слюда, мусковит | 5.От 0 до 8,7 |
| Стекловолоконная слюда | от 6,3 до 9,3 |
| Фарфор, стеатит | 6,5 |
| Глинозем | от 8,0 до 10,0 |
| Вода дистиллированная | 80,0 |
| Барий-стронций-титанит | 7500 |
Приблизительное значение емкости для любой пары разделенных проводов можно найти по следующей формуле:
Конденсатор можно сделать переменным, а не фиксированным, путем изменения любого из физических факторов, определяющих емкость.Один относительно простой фактор, который можно изменить в конструкции конденсатора, — это площадь пластины или, точнее, величина перекрытия пластин.
На следующей фотографии показан пример переменного конденсатора, использующего набор чередующихся металлических пластин и воздушный зазор в качестве диэлектрического материала:
При вращении вала степень перекрытия наборов пластин будет изменяться, изменяя эффективную площадь пластин, между которыми может быть установлено концентрированное электрическое поле.Этот конкретный конденсатор имеет емкость в пикофарадном диапазоне и находит применение в радиосхемах.
СВЯЗАННЫЕ РАБОЧИЕ ЛИСТЫ:
конденсаторов параллельно | Приложения
Конденсаторы, как и другие электрические элементы, могут подключаться к другим элементам последовательно или параллельно. Иногда бывает полезно подключить несколько конденсаторов параллельно, чтобы получился функциональный блок, подобный показанному на рисунке. В таких случаях важно знать эквивалентную емкость блока параллельного подключения.В этой статье основное внимание будет уделено анализу параллельного соединения конденсаторов и возможному применению таких схем.
Анализ
Все конденсаторы в параллельном соединении имеют одинаковое напряжение на них, что означает:
, где от V 1 до V n представляют напряжение на каждом соответствующем конденсаторе. Это напряжение равно напряжению, приложенному к параллельному соединению конденсаторов через входные провода.Однако количество заряда, накопленного на каждом конденсаторе, не одинаково и зависит от емкости каждого конденсатора по формуле:
, где Q n — это количество заряда, накопленного на конденсаторе, C n — это емкость конденсатора, а V n — это напряжение, приложенное к конденсатору, которое равно напряжению, приложенному ко всей параллельной блок подключения. Общее количество заряда, которое хранится в блоке конденсаторов, обозначается Q и делится между всеми конденсаторами, присутствующими в этой цепи.Это представлено:
Следующее уравнение используется для определения эквивалентной емкости для параллельного соединения нескольких конденсаторов:
, где C eq — эквивалентная емкость при параллельном соединении конденсаторов, V — напряжение, приложенное к конденсаторам через входные провода, а Q 1 — Q n представляют собой заряды, накопленные на каждом соответствующем конденсаторе. Это подводит нас к важному выводу, что:
, что означает, что эквивалентная емкость при параллельном соединении конденсаторов равна сумме индивидуальных емкостей.Этот результат также интуитивно понятен — конденсаторы, включенные параллельно, можно рассматривать как один конденсатор, площадь пластин которого равна сумме площадей пластин отдельных конденсаторов.
Приложения
Конденсаторы — это устройства, предназначенные для хранения электрической энергии в виде электрического заряда. При параллельном подключении нескольких конденсаторов полученная схема может хранить больше энергии, поскольку эквивалентная емкость является суммой отдельных емкостей всех задействованных конденсаторов.Этот эффект используется в некоторых приложениях.
Источники питания постоянного тока
Одним из примеров являются источники постоянного тока, которые иногда используют несколько параллельных конденсаторов, чтобы лучше фильтровать выходной сигнал и устранять пульсации переменного тока. Используя этот подход, можно использовать конденсаторы меньшего размера, которые имеют превосходные характеристики пульсации, при этом получая более высокие значения емкости.
Более высокие значения емкости
В некоторых приложениях просто требуется, чтобы значения емкости были намного выше, чем могут предложить коммерчески доступные конденсаторы.В таких приложениях используются конденсаторные батареи. Одним из примеров являются конденсаторные батареи, используемые для коррекции коэффициента мощности с индуктивными нагрузками. Другим примером являются батареи накопителей энергии, которые заявлены для использования в автомобильной промышленности, а именно KERS (система рекуперации кинетической энергии), используемая для рекуперативного торможения в больших транспортных средствах, таких как трамваи, а также в гибридных автомобилях.
Импульсные нагрузки
Одна лаборатория с сильным магнитным полем приводит в действие самый мощный в мире магнит, способный создавать магнитное поле почти 100 тесла за счет накопления энергии в конденсаторной батарее.Сохраненная энергия высвобождается через магнитную катушку за очень короткий промежуток времени, создавая очень мощное магнитное поле.
В любом случае конденсаторные батареи могут достигать очень высоких значений емкости. При использовании нескольких суперконденсаторов, соединенных параллельно, возможны емкости в несколько десятков килофарад, особенно с учетом того, что суперконденсаторы способны достигать значений емкости более 2000 фарад.
Ограничения по конструкции
При параллельном подключении конденсаторов следует помнить о некоторых моментах.Во-первых, максимальное номинальное напряжение при параллельном соединении конденсаторов равно минимальному номинальному напряжению всех конденсаторов, используемых в системе. Таким образом, если несколько конденсаторов номиналом 500 В подключены параллельно конденсатору на 100 В, максимальное номинальное напряжение всей системы составляет всего 100 В, поскольку на все конденсаторы в параллельной цепи подается одинаковое напряжение.
Безопасность
Еще один момент, о котором следует помнить, заключается в том, что батареи конденсаторов могут быть опасными из-за количества хранимой энергии и того факта, что конденсаторы могут высвобождать накопленную энергию за очень короткий промежуток времени.Эта накопленная энергия иногда может вызвать серьезные травмы или повреждение электропроводки и устройств в случае случайного короткого замыкания.
конденсаторов последовательно и параллельно
конденсаторов последовательно и параллельноДалее: Энергия, запасаемая конденсаторами Up: Емкость Предыдущая: Диэлектрики Конденсаторы — один из стандартных компонентов электронных схем. Кроме того, часто встречаются сложные комбинации конденсаторов. в практических схемах.Это, поэтому полезно иметь набор правил для определения эквивалентной емкости некоторого общего расположения конденсаторов. Оказывается, всегда можно найти эквивалентная емкость при повторном применение двух простых правил . Эти правила относятся к подключенным конденсаторам. последовательно и параллельно.
| (113) |
давая
| (114) |
Здесь мы воспользовались тем фактом, что напряжение является общим для всех трех конденсаторы.Таким образом, правило таково:
Эквивалентная емкость двух конденсаторов, соединенных параллельно представляет собой сумму отдельных емкостей.Для конденсаторов, соединенных параллельно, уравнение. (114) обобщает на .
| (115) |
давая
| (116) |
Здесь мы воспользовались тем фактом, что заряд является общим для всех трех конденсаторы. Следовательно, правило таково:
Величина, обратная эквивалентной емкости двух конденсаторов, подключенных в серия — это сумма обратных величин отдельных емкостей.Для конденсаторов, соединенных последовательно, уравнение.(116) обобщает на
Далее: Энергия, запасаемая конденсаторами Up: Емкость Предыдущая: Диэлектрики Ричард Фицпатрик 2007-07-14
8.3: Последовательные и параллельные конденсаторы
Несколько конденсаторов могут быть соединены вместе для использования в различных приложениях. Несколько подключений конденсаторов ведут себя как один эквивалентный конденсатор. Общая емкость этого эквивалентного одиночного конденсатора зависит как от отдельных конденсаторов, так и от способа их подключения.Конденсаторы могут быть объединены в два простых и распространенных типа соединений, известных как серии и параллельно , для которых мы можем легко вычислить общую емкость. Эти две основные комбинации, последовательная и параллельная, также могут использоваться как часть более сложных соединений.
Серия конденсаторов
На рисунке \ (\ PageIndex {1} \) показано последовательное сочетание трех конденсаторов, расположенных в ряд внутри схемы. Как и в случае любого конденсатора, емкость комбинации связана как с зарядом, так и с напряжением:
\ [C = \ dfrac {Q} {V}.\]
Когда эта последовательная комбинация подключена к батарее с напряжением В , каждый из конденсаторов получает идентичный заряд Q . Чтобы объяснить, сначала обратите внимание, что заряд на пластине, подключенной к положительной клемме батареи, равен \ (+ Q \), а заряд на пластине, подключенной к отрицательной клемме, равен \ (- Q \). Затем на других пластинах индуцируются заряды, так что сумма зарядов на всех пластинах и сумма зарядов на любой паре пластин конденсатора равна нулю.Однако падение потенциала \ (V_1 = Q / C_1 \) на одном конденсаторе может отличаться от падения потенциала \ (V_2 = Q / C_2 \) на другом конденсаторе, потому что, как правило, конденсаторы могут иметь разные емкости. Последовательная комбинация двух или трех конденсаторов напоминает один конденсатор с меньшей емкостью. Как правило, любое количество последовательно соединенных конденсаторов эквивалентно одному конденсатору, емкость которого (называемая эквивалентной емкостью ) меньше наименьшей из емкостей в последовательной комбинации.Заряд этого эквивалентного конденсатора такой же, как заряд любого конденсатора в последовательной комбинации: то есть все конденсаторы последовательной комбинации имеют одинаковый заряд . Это происходит из-за сохранения заряда в цепи. Когда заряд Q в последовательной цепи удаляется с пластины первого конденсатора (который мы обозначаем как \ (- Q \)), он должен быть помещен на пластину второго конденсатора (который мы обозначаем как \ ( + Q \)) и т. Д.
Рисунок \ (\ PageIndex {1} \): (a) Три конденсатора соединены последовательно.Величина заряда на каждой пластине равна Q. (b) Сеть конденсаторов на (a) эквивалентна одному конденсатору, который имеет меньшую емкость, чем любая из отдельных емкостей на (a), а заряд на его пластинах равен Q.Мы можем найти выражение для полной (эквивалентной) емкости, рассматривая напряжения на отдельных конденсаторах. Потенциалы на конденсаторах 1, 2 и 3 равны, соответственно, \ (V_1 = Q / C_1 \), \ (V_2 = Q / C_2 \) и \ (V_3 = Q / C_3 \). Эти потенциалы должны в сумме равняться напряжению батареи, давая следующий баланс потенциалов:
\ [V = V_1 + V_2 + V_3.\]
Потенциал \ (V \) измеряется на эквивалентном конденсаторе, который держит заряд \ (Q \) и имеет эквивалентную емкость \ (C_S \). Вводя выражения для \ (V_1 \), \ (V_2 \) и \ (V_3 \), получаем
\ [\ dfrac {Q} {C_S} = \ dfrac {Q} {C_1} + \ dfrac {Q} {C_2} + \ dfrac {Q} {C_3}. \]
Отменяя заряд Q , мы получаем выражение, содержащее эквивалентную емкость \ (C_S \) трех последовательно соединенных конденсаторов:
\ [\ dfrac {1} {C_S} = \ dfrac {1} {C_1} + \ dfrac {1} {C_2} + \ dfrac {1} {C_3}.\]
Это выражение можно обобщить на любое количество конденсаторов в последовательной сети.
Комбинация серии
Для конденсаторов, соединенных последовательно, эквивалентная емкость, обратная величине, равна сумме обратных величин индивидуальных емкостей:
\ [\ dfrac {1} {C_S} = \ dfrac {1} {C_1} + \ dfrac {1} {C_2} + \ dfrac {1} {C_3} + \ dots \ label {capseries} \]
Пример \ (\ PageIndex {1} \): эквивалентная емкость последовательной сети
Найдите общую емкость для трех последовательно соединенных конденсаторов, учитывая, что их отдельные емкости равны \ (1.000 мкФ \), \ (5.000 мкФ \) и \ (8.000 мкФ \).
Стратегия
Поскольку в этой сети всего три конденсатора, мы можем найти эквивалентную емкость, используя уравнение \ ref {capseries} с тремя членами.
Решение
Вводим указанные емкости в уравнение \ ref {capseries}:
\ [\ begin {align *} \ dfrac {1} {C_S} & = \ dfrac {1} {C_1} + \ dfrac {1} {C_2} + \ dfrac {1} {C_3} \\ [4pt] & = \ dfrac {1} {1.000 \ mu F} + \ dfrac {1} {5.000 \ mu F} + \ dfrac {1} {8.000 \ mu F} \\ [4pt] & = \ dfrac {1.325} {\ mu F}. \ End {align *} \]
Теперь инвертируем этот результат и получаем
\ [\ begin {align *} C_S & = \ dfrac {\ mu F} {1.325} \\ [4pt] & = 0.755 \ mu F. \ end {align *} \ nonumber \]
Значение
Обратите внимание, что в последовательной сети конденсаторов эквивалентная емкость всегда меньше наименьшей отдельной емкости в сети.
Параллельная комбинация конденсаторов
Параллельная комбинация трех конденсаторов, одна пластина каждого конденсатора подключена к одной стороне цепи, а другая пластина подключена к другой стороне, показана на рисунке \ (\ PageIndex {2a} \).Поскольку конденсаторы соединены параллельно, все они имеют одинаковое напряжение V на своих пластинах . Однако каждый конденсатор в параллельной сети может накапливать свой заряд. Чтобы найти эквивалентную емкость \ (C_p \) параллельной сети, отметим, что общий заряд Q , хранящийся в сети, представляет собой сумму всех отдельных зарядов:
\ [Q = Q_1 + Q_2 + Q_3. \]
В левой части этого уравнения используется соотношение \ (Q = C_pV \), которое выполняется для всей сети.В правой части уравнения мы используем соотношения \ (Q_1 = C_1 V \), \ (Q_2 = C_2V \) и \ (Q_3 = C_3V \) для трех конденсаторов в сети. Таким образом получаем
\ [C_pV = C_1V + C_2V + C_3V. \]
Это уравнение в упрощенном виде представляет собой выражение для эквивалентной емкости параллельной сети из трех конденсаторов:
\ [C_p = C_1 + C_2 + C_3. \]
Это выражение легко обобщается на любое количество конденсаторов, включенных параллельно в сеть.
Параллельная комбинация
Для конденсаторов, соединенных параллельно, эквивалентная (полезная) емкость представляет собой сумму всех индивидуальных емкостей в сети,
\ [C_p = C_1 + C_2 + C_3 + … \ label {capparallel} \]
Рисунок \ (\ PageIndex {2} \): (a) Три конденсатора подключены параллельно. Каждый конденсатор подключен напрямую к батарее. (b) Заряд эквивалентного конденсатора представляет собой сумму зарядов отдельных конденсаторов.Пример \ (\ PageIndex {2} \): эквивалентная емкость параллельной сети
Найдите полезную емкость для трех конденсаторов, соединенных параллельно, учитывая, что их индивидуальные емкости равны \ (1.0 \ mu F \), \ (5.0 \ mu F \) и \ (8.0 \ mu F \).
Стратегия
Поскольку в этой сети всего три конденсатора, мы можем найти эквивалентную емкость, используя уравнение \ ref {capparallel} с тремя членами.
Решение
Ввод заданных емкостей в уравнение \ ref {capparallel} дает
\ [\ begin {align *} C_p & = C_1 + C_2 + C_3 \\ [4pt] & = 1.0 \ mu F + 5.0 \ mu F + 8.0 \ mu F \\ [4pt] & = 14.0 \ mu F.\ end {align *} \]
Значение
Обратите внимание, что в параллельной сети конденсаторов эквивалентная емкость всегда больше, чем любая из отдельных емкостей в сети.
Конденсаторные сети обычно представляют собой комбинацию последовательных и параллельных соединений, как показано на Рисунке \ (\ PageIndex {3} \). Чтобы найти чистую емкость таких комбинаций, мы определяем части, которые содержат только последовательные или только параллельные соединения, и находим их эквивалентные емкости.Мы повторяем этот процесс, пока не сможем определить эквивалентную емкость всей сети. Следующий пример иллюстрирует этот процесс.
Рисунок \ (\ PageIndex {3} \): (a) Эта схема содержит как последовательные, так и параллельные соединения конденсаторов. (b) \ (C_1 \) и \ (C_2 \) идут последовательно; их эквивалентная емкость \ (C_S \) c) Эквивалентная емкость \ (C_S \) подключена параллельно с \ (C_3 \). Таким образом, эквивалентная емкость всей сети является суммой \ (C_S \) и \ (C_3 \).Пример \ (\ PageIndex {3} \): эквивалентная емкость сети
Найдите общую емкость комбинации конденсаторов, показанной на рисунке \ (\ PageIndex {3} \). Предположим, что емкости известны с точностью до трех десятичных знаков (\ (C_1 = 1.000 мкФ, C_2 = 5.000 мкФ, C_3 = 8.000 мкФ \)). Округлите ответ до трех десятичных знаков.
Стратегия
Сначала мы определяем, какие конденсаторы включены последовательно, а какие — параллельно. Конденсаторы \ (C_1 \) и \ (C_2 \) включены последовательно.Их комбинация, обозначенная \ (C_S \), параллельна \ (C_3 \).
Решение
Поскольку \ (C_1 \) и \ (C_2 \) включены последовательно, их эквивалентная емкость \ (C_S \) получается с помощью уравнения \ ref {capseries}:
\ [\ begin {align *} \ dfrac {1} {C_S} & = \ dfrac {1} {C_1} + \ dfrac {1} {C_2} \\ [4pt] & = \ dfrac {1} {1.000 \ mu F} + \ dfrac {1} {5.000 \ mu F} \\ [4pt] & = \ dfrac {1.200} {\ mu F} \ end {align *} \]
Для этого
\ [C_S = 0,833 \ mu F. \ nonumber \]
Емкость \ (C_S \) соединена параллельно с третьей емкостью \ (C_3 \), поэтому мы используем уравнение \ ref {capparallel}, чтобы найти эквивалентную емкость C всей сети:
\ [\ begin {align *} C & = C_S + C_3 \\ [4pt] & = 0.833 \ mu F + 8.000 \ mu F \\ [4pt] & = 8.833 \ mu F. \ end {align *} \]
Сеть конденсаторов
Определите чистую емкость C комбинации конденсаторов, показанной на рисунке \ (\ PageIndex {4} \), когда емкости равны \ (C_1 = 12,0 мкФ, C_2 = 2,0 мкФ \) и \ (C_3 = 4,0 мкФ \). Когда на комбинации поддерживается разность потенциалов 12,0 В, найдите заряд и напряжение на каждом конденсаторе.
Рисунок \ (\ PageIndex {4} \): (a) Комбинация конденсаторов.(b) Эквивалентная комбинация из двух конденсаторов. СтратегияСначала мы вычисляем чистую емкость \ (C_ {23} \) параллельного соединения \ (C_2 \) и \ (C_3 \). Тогда C — это чистая емкость последовательного соединения \ (C_1 \) и \ (C_ {23} \). Мы используем соотношение \ (C = Q / V \), чтобы найти заряды \ (Q_1, Q_2 \) и \ (Q_3 \), а также напряжения \ (V_1, V_2 \) и \ (V_3 \) на конденсаторы 1, 2 и 3 соответственно.
Решение Эквивалентная емкость для \ (C_2 \) и \ (C_3 \) составляет
\ [C_ {23} = C_2 + C_3 = 2.0 мк F + 4,0 мк F = 6,0 мк F. \]
Вся комбинация из трех конденсаторов эквивалентна двум последовательно включенным конденсаторам,
\ [\ dfrac {1} {C} = \ dfrac {1} {12.0 \ mu F} + \ dfrac {1} {6.0 \ mu F} = \ dfrac {1} {4.0 \ mu F} \ Rightarrow C = 4,0 мкм F. \]
Рассмотрим эквивалентную комбинацию из двух конденсаторов на рисунке \ (\ PageIndex {2b} \). Поскольку конденсаторы включены последовательно, они имеют одинаковый заряд, \ (Q_1 = Q_ {23} \). Кроме того, конденсаторы разделяют разность потенциалов 12,0 В, поэтому
\ [12.0 V = V_1 + V_ {23} = \ dfrac {Q_1} {C_1} + \ dfrac {Q_ {23}} {C_ {23}} = \ dfrac {Q_1} {12.0 \ mu F} + \ dfrac {Q_1 } {6.0 \ mu F} \ Rightarrow Q_1 = 48.0 \ mu C. \]
Теперь разность потенциалов на конденсаторе 1 равна
.\ [V_1 = \ dfrac {Q_1} {C_1} = \ dfrac {48.0 \ mu C} {12.0 \ mu F} = 4.0 V. \]
Поскольку конденсаторы 2 и 3 подключены параллельно, они имеют одинаковую разность потенциалов:
\ [V_2 = V_3 = 12,0 В — 4,0 В = 8,0 В. \]
Следовательно, заряды на этих двух конденсаторах равны, соответственно,
\ [Q_2 = C_2V_2 = (2.0 мкФ) (8,0 В) = 16,0 мкФ, \]
\ [Q_3 = C_3V_3 = (4,0 мкФ) (8,0 В) = 32,0 мкФ \]
Значимость Как и ожидалось, чистая плата за параллельную комбинацию \ (C_2 \) и \ (C_3 \) составляет \ (Q_ {23} = Q_2 + Q_3 = 48,0 \ mu C. \)
Упражнение \ (\ PageIndex {1} \)
Определите чистую емкость C каждой сети конденсаторов, показанной ниже. Предположим, что \ (C_1 = 1,0 пФ, C_2 = 2,0 пФ, C_3 = 4,0 пФ \) и \ (C_4 = 5,0 пФ \). Найдите заряд на каждом конденсаторе, предполагая, что разность потенциалов равна 12.0 В в каждой сети.
- Ответьте на
-
\ (C = 0,86 пФ, Q_1 = 10 пКл, Q_2 = 3,4 пКл, Q_3 = 6,8 пКл \)
- Ответ б
-
\ (C = 2,3 пФ, Q_1 = 12 пКл, Q_2 = Q_3 = 16 пКл \)
- Ответ c
-
\ (C = 2,3 пФ, Q_1 = 9,0 пКл, Q_2 = 18 пКл, Q_3 = 12 пКл, Q_4 = 15 пКл \)
Этот калькулятор параллельных конденсаторов позволяет оценить итоговую емкость цепи.Вы можете смоделировать параллельную установку до 10 отдельных конденсаторов. Кроме того, мы также предоставляем формулу для параллельных конденсаторов, а также объясняем, откуда она взялась. Мы также предоставим вам объяснение различий между конденсаторами, включенными последовательно и параллельно, и их соответствие формулам для резисторов.
Добавление конденсаторов параллельно
Конденсатор — один из важнейших электронных компонентов. Он действует как место, где может храниться некоторый электрический заряд.Конденсаторы можно объединять как последовательно, так и параллельно. Возникает вопрос: Какова результирующая емкость для цепи, полностью состоящей из конденсаторов, включенных параллельно? Давайте вместе разберемся, на примере конденсаторов с параллельными пластинами!
Когда конденсаторы расположены параллельно в системе с источником напряжения В , , напряжения на каждом элементе равны и равны исходному конденсатору:
V₁ = V₂ = ... = V .
Общая формула заряда, Q i , хранящегося в конденсаторе, C i :
Q i = V i * C i
Если мы хотим заменить все элементы замещающей емкостью, C , нам нужно понять, что общий заряд, Q , является суммой всех зарядов :
Q = Q₁ + Q₂ + ... ,
, которое также можно записать как:
В * C = V * C₁ + V * C₂ +... .
Разделив обе стороны на В , получим формулу выходной мощности:
C = C₁ + C₂ + ... .
Как видите, формула подключения конденсаторов точно такая же, как и для последовательных резисторов, которая представляет собой просто сумму всех отдельных компонентов. Оказывается, уравнение для конденсаторов, включенных последовательно, похоже на уравнение для параллельных резисторов, а также для параллельных катушек индуктивности.
В общем, если мы хотим построить систему с более высокой емкостью, мы должны размещать конденсаторы параллельно.С другой стороны, если конденсаторы включены последовательно, результирующая емкость ниже, чем у любого из отдельных компонентов.
Как использовать параллельный калькулятор конденсаторов?
Давайте подключим несколько конденсаторов параллельно и найдем результирующую емкость. Пусковой комплект состоит из следующих конденсаторов: C₁ = 30 мФ , C₂ = 500 мкФ , C₃ = 6 мФ , C₄ = 750 мкФ .
-
Чтобы облегчить нашу жизнь, переведите единицы измерения, чтобы они были одинаковыми, например.грамм.
мФ:C₁ = 30 мФ,C₂ = 0,5 мФ,C₃ = 6 мФ,C₄ = 0,75 мФ -
Суммируйте все значения:
C₁ + C₂ + C₃ + C₄ = 30 мФ + 0,5 мФ + 6 мФ + 0,75 мФ = 37,25 мФ -
Мы можем записать результат для конденсаторов, подключенных параллельно, в другой форме, используя научную запись:
C = 3,725 · 10⁻² F
Хотя оценка не является сложной, мы рекомендуем вам использовать наш параллельный калькулятор конденсаторов, чтобы проверить правильность ваших расчетов!
Цепи конденсаторов сериии параллельные
Разница между Кулоном и Фарадом
Раньше переходя к последовательным и параллельным цепям конденсаторов, сначала посмотрите на разница между кулоном и фарадом, потому что многие люди запутаться в определении разницы между кулоном и Фарад.
Электрический заряд измеряется в кулонах. Один кулон (1С) равен равно количеству заряда, передаваемого за одну секунду Текущий одного Ампера (1А).
Емкость является способность тела или устройства накапливать электрический заряд. Емкость измеряется в фарадах (Ф). Устройство с большим Емкость (96F) сохранит большой заряд.Точно так же устройство с малой емкостью (1F) будет хранить небольшая сумма заряда.
серии конденсаторная цепь
А последовательный конденсатор схема — это электронная схема, в которой все конденсаторы подключаются друг за другом по одному и тому же пути, поэтому что к каждому конденсатору протекает одинаковый заряд или ток.
общая емкость цепи последовательного конденсатора получается как сложение обратных величин (1 / C) значений емкости отдельных конденсаторов, а затем взяв обратную величину Общая.
Для Например, если три конденсатора соединены последовательно. Тогда общая емкость цепи
Все ток или заряд, протекающий через первый конденсатор, другого пути нет.Следовательно, он также должен проходить через второй конденсатор, третий конденсатор, четвертый конденсатор и т. д. на.
Пример:
А
Схема последовательного конденсатора показана на рисунке ниже. В
схема состоит из трех конденсаторов, которые включены в
последовательный и источник постоянного напряжения.
емкости из трех конденсаторов: C 1 = 2F, C 2 = 4F, C 3 = 6F и постоянное напряжение = 10 В.
Как как показано на рисунке, положительный полюс батареи постоянного тока подключается к правой боковой пластине конденсатора С 3 отрицательная клемма батареи постоянного тока подключена к Левая боковая пластина конденсатора С 1 .
Когда а напряжение приложено к цепи, отрицательные заряды в правой боковой пластине конденсатора С 3 находятся притянул к плюсовой клемме аккума.Это вызывает Недостаток отрицательных зарядов в правой боковой пластине C 3 . В итоге правая боковая пластина конденсатора С 3 заряжен положительно.
Аналогично, в положительные заряды в левой боковой пластине конденсатора С 1 притягиваются к отрицательной клемме аккумулятора. Этот вызывает нехватку положительных зарядов в левой боковой пластине из C 1 .В результате левая боковая пластина Конденсатор C 1 заряжен отрицательно.
отрицательные заряды в левой боковой пластине конденсатора С 1 отталкивать отрицательные заряды в правой боковой пластине конденсатор С 1 . Это вызывает отрицательные заряды. сток с правой боковой пластины конденсатора С 1 к левой боковой пластине конденсатора С 2 .Как В результате правая боковая пластина конденсатора С 1 оказывается положительно заряжена и левая боковая пластина конденсатора С 2 заряжен отрицательно.
отрицательные заряды в левой боковой пластине конденсатора С 2 отталкивать отрицательные заряды в правой боковой пластине конденсатор С 2 .Это вызывает отрицательные заряды. сток с правой боковой пластины конденсатора С 2 к левой боковой пластине конденсатора С 3 . Как В результате правая боковая пластина конденсатора С 2 оказывается положительно заряжена и левая боковая пластина конденсатора С 3 заряжен отрицательно.
Таким образом, все три конденсатора заряжаются.
ср знайте, что ток означает поток заряда. Так как же ток течет через все три конденсатора, поэтому каждый конденсатор будет держать такой же заряд. Это означает, что если один конденсатор держит заряд 2C, тогда остальные конденсаторы тоже держит такой же заряд 2С.
Так если вы обнаружите заряд на одном из конденсаторов, у вас нашел заряд на всех оставшихся конденсаторах.
В чтобы найти заряд на каждом конденсаторе, сначала нам нужно найти общую емкость или эквивалентную емкость.
общая емкость эквивалентного конденсатора
Автор используя формулу C = Q / V, легко найти заряд хранится на эквивалентном конденсаторе.
Начисление на каждого физ. конденсаторы, подключенные последовательно, такие же, как заряд на эквиваленте конденсатор.
Итак, так как заряд на эквивалент конденсатор был 10,91 кулонов, заряд на каждой из отдельные конденсаторы, включенные последовательно, будут иметь 10,91 кулонов.
Следовательно,
Плата за C 1 = 10.91 C
Заряд на C 2 = 10.91 C
Заряд на C 3 = 10.91 С
Однако в цепи последовательного конденсатора напряжение на каждом индивидуальный конденсатор разный.
ср легко найти напряжение на каждом отдельном конденсаторе по формуле C = Q / V
емкость и заряд на каждом отдельном конденсаторе известны. Итак, мы нужно найти неизвестное напряжение.
В = Q / C
напряжение на конденсаторе (C 1 ) составляет V 1 = Q / C 1 = 10,91 / 2 = 5,455 В
напряжение на конденсаторе (C 2 ) составляет V 2 = Q / C 2 = 10,91 / 4 = 2,727 В
напряжение на конденсаторе (C 3 ) составляет V 3 = Q / С 3 = 10.91/6 = 1,818 В
полное напряжение в цепи последовательного конденсатора равно сумма всех отдельных напряжений, сложенных вместе.
Т.е. V = V 1 + V 2 + V 3 = 5,455 + 2,727 + 1,818 = 10 В
Параллельно конденсаторная цепь
А параллельная конденсаторная схема — это электронная схема, в которой все конденсаторы подключены бок о бок в разных пути, чтобы тот же заряд или ток не проходили через каждый конденсатор.
Когда на параллельную цепь подается напряжение, каждый конденсатор получит другой заряд. Конденсатор с высоким емкость получит больший заряд, тогда как конденсатор с чем меньше емкость, тем меньше будет заряда. Например, восьмерка Фарадный конденсатор (8F) получит больше заряда, чем четыре фарада конденсатор (4Ф) попадает.
Путь конденсаторы параллельно будет увеличиваться размер пластин конденсатора без увеличения расстояния между ними. Итак, общая емкость параллельной конденсаторной цепи получается просто суммируя значения емкости отдельных конденсаторы.
Пример:
А
Схема параллельного конденсатора показана на рисунке ниже.В
схема состоит из трех конденсаторов, которые включены в
параллельный и источник постоянного напряжения.
Если Значения трех конденсаторов: C 1 = 8F, C 2 = 4F, C 3 = 2F и батарея постоянного тока = 10 В, тогда
общая емкость составляет C T = C 1 + C 2 + C 3 = 8 + 4 + 2 = 14F
В Принципиальная схема, нижние обкладки трех конденсаторов напрямую подключены к положительной клемме аккумулятора а верхние обкладки трех конденсаторов непосредственно подключен к отрицательной клемме аккумуляторной батареи.Следовательно, напряжение на всех трех конденсаторах одинаковое, что составляет равно напряжению АКБ постоянного тока (10 В).
Однако
в параллельной цепи конденсаторов заряд сохраняется на каждом
конденсатор будет другим.
Автор используя формулу емкости, легко найти заряд хранится на каждом конденсаторе.
И.е. C = Q / V
Q = C × V
заряд, накопленный на конденсаторе (C 1 ), составляет Q 1 = С 1 × V = 8 × 10 = 80 С
заряд, накопленный на конденсаторе (C 2 ), составляет Q 2 = С 2 × V = 4 × 10 = 40 С
Заряд, накопленный на конденсаторе (C 3 ), составляет Q 3 = C 3 × V = 2 × 10 = 20 С
Общий заряд, хранящийся в параллельном конденсаторная цепь равна сумме всех отдельных заряды конденсатора складываются.
Т.е. Q T = Q 1 + Q 2 + Q 3 = 80 + 40 + 20 = 140 C
Серия
и калькулятор параллельной емкости — Apogeeweb
Часто задаваемые вопросы
1.Как рассчитать параллельную емкость?
Общее значение емкости конденсаторов, соединенных параллельно, фактически вычисляется путем сложения площадей пластин. Другими словами, общая емкость равна сумме всех отдельных емкостей, включенных параллельно.
2. Как отличить последовательный конденсатор от параллельного?
Когда разность потенциалов на пластинах одинакова, они параллельны. Когда ток через них равен, они включены последовательно.
3. Зачем нужно последовательно включать конденсаторы?
Причина, по которой вы можете соединять конденсаторы последовательно, заключается в том, чтобы увеличить эффективное управление напряжением цепи. Конденсаторы имеют номинальное напряжение пробоя, превышение которого значительно увеличивает вероятность отказа. Два одинаковых конденсатора будут иметь половину напряжения на каждом.
4. Последовательные или параллельные конденсаторы накапливают больше энергии?
Энергия, запасенная в конденсаторе, является функцией напряжения на конденсаторе.Напряжение будет выше, когда они подключены параллельно, поэтому при параллельном подключении сохраняется больше энергии.
5. Какова основная функция конденсатора?
Конденсатор — это электронный компонент, который накапливает и выделяет электричество в цепи. Он также пропускает переменный ток, не пропуская постоянный ток. Конденсатор является неотъемлемой частью электронного оборудования и поэтому почти всегда используется в электронных схемах.
6.В чем разница между последовательной и параллельной схемой?
В последовательной цепи сумма напряжений, потребляемых каждым отдельным сопротивлением, равна напряжению источника. Компоненты, соединенные параллельно, соединяются несколькими путями, так что ток может разделяться; одинаковое напряжение приложено к каждому компоненту.
7. Почему последовательно подключенные конденсаторы уменьшают емкость?
Полное сопротивление двух последовательно соединенных конденсаторов равно сумме индивидуальных сопротивлений двух конденсаторов.Поскольку импеданс пропорционален обратной величине емкости, больший импеданс последовательной цепи означает меньшую емкость.
8. Что произойдет, если резистор и конденсатор соединить параллельно?
Когда резисторы и конденсаторы смешиваются вместе в параллельных цепях (так же, как в последовательных цепях), общий импеданс будет иметь фазовый угол где-то между 0 ° и -90 °. Ток в цепи будет иметь фазовый угол от 0 ° до + 90 °.
9. Как узнать, включен ли последовательный конденсатор параллельно?
Если у каждого конденсатора ОБЕ клеммы подключены к ОБЕИМ клеммам других, то они включены параллельно. Если у каждого конденсатора только одна клемма, подключенная к одной клемме другого конденсатора, они подключены последовательно.
10. Почему последовательно подключенные конденсаторы уменьшают емкость?
Полное сопротивление двух последовательно соединенных конденсаторов равно сумме индивидуальных сопротивлений двух конденсаторов.Поскольку импеданс пропорционален обратной величине емкости, больший импеданс последовательной цепи означает меньшую емкость.
11. Как соединить параллельно конденсаторы и резисторы?
Детальная операция начинается с 1:42.
12. Почему мы используем конденсаторы в цепях постоянного тока?
При использовании в цепи постоянного или постоянного тока конденсатор заряжается до напряжения питания, но блокирует прохождение тока через него, потому что диэлектрик конденсатора непроводящий и в основном является изолятором.
13. Преобразует ли конденсатор переменный ток в постоянный?
Конденсатор не может самостоятельно преобразовывать переменный ток в постоянный, но хороший синхронизированный переключатель, который пропускает выбранные пики и отклоняет части формы волны переменного тока, сделает это.
14. Что происходит, когда конденсатор подключен к постоянному току?
Когда конденсаторы подключаются к источнику постоянного напряжения постоянного тока, они становятся заряженными до значения приложенного напряжения, действуя как устройства временного хранения и сохраняя или удерживая этот заряд неопределенно долго, пока присутствует напряжение питания.
15. Есть ли у конденсаторов положительная и отрицательная сторона?
Большинство электролитических конденсаторов поляризованного типа, то есть напряжение, подключенное к клеммам конденсатора, должно иметь правильную полярность, то есть положительную полярность и отрицательную отрицательную.
16. Как решить проблемы, связанные с подключением конденсаторов последовательно и параллельно?
На видео ниже показано, как рассчитать емкость в последовательной и параллельной цепях, а также на лабораторном примере показано, как работает математика.
Серия Подключение конденсаторов
На рис. 1 (а) показано, что два конденсатора соединены последовательно. Для каждого конденсатора он имеет одинаковый ток, а соотношение тока и напряжения соответствует
.«
(а) (б)
Рисунок 1. Последовательное соединение
Итак, два конденсатора соединены последовательно, эквивалентная емкость составляет
.
Эквивалентная схема показана на рисунке 1 (б).При последовательном соединении конденсаторов напряжение на каждом конденсаторе соответствует
.
Параллельное соединение конденсаторов
На рис. 2 (а) показано, что два конденсатора подключены параллельно. Для каждого конденсатора оно имеет одинаковое напряжение, а соотношение тока и напряжения соответствует
.
Рисунок 2. Cicuit параллельных конденсаторов
Два конденсатора подключены параллельно, эквивалентная емкость
Эквивалентная схема показана на рисунке 2 (б).При параллельном соединении конденсаторов ток на каждом конденсаторе соответствует
.
Разница между последовательными конденсаторами и параллельными конденсаторами
При последовательном соединении конденсаторов емкость уменьшается (для расчета общей емкости после последовательного соединения см. Метод параллельного подключения резисторов), а выдерживаемое напряжение увеличивается.
Конденсаторы подключаются параллельно, емкость увеличивается (добавление каждой емкости), а выдерживаемое напряжение наименьшее.Последовательный конденсатор: чем больше число последовательно, тем меньше емкость, но выше выдерживаемое напряжение. Отношение емкости: 1 / C = 1 / C1 + 1 / C2 + 1 / C3 Параллельная емкость: чем больше параллельное соединение, тем больше емкость, но выдерживаемое напряжение не изменяется, его отношение емкости: C = C1 + C2 + C3
См. Более подробную информацию о конденсаторах, включенных последовательно и параллельно. Кликните сюда!
.
