Емкости конденсаторов. Как соединять конденсаторы для изменения емкости: параллельное и последовательное подключение

Как увеличить или уменьшить емкость конденсаторов путем их соединения. Какие формулы использовать для расчета общей емкости при параллельном и последовательном подключении. Когда применять различные способы соединения конденсаторов.

Способы соединения конденсаторов для изменения емкости

При ремонте электронной техники или создании радиотехнических схем часто возникает необходимость получить конденсатор с нестандартной емкостью. В таких случаях используют соединение нескольких конденсаторов для получения требуемого номинала. Существует два основных способа соединения конденсаторов:

• Параллельное
• Последовательное

Каждый из этих способов позволяет по-разному изменять результирующую емкость. Рассмотрим подробнее особенности и формулы расчета для каждого варианта.

Параллельное соединение конденсаторов

При параллельном соединении конденсаторов их общая емкость увеличивается. Это наиболее распространенный способ, позволяющий получить большую емкость.

Как соединить конденсаторы параллельно?

Для параллельного соединения нужно объединить все выводы конденсаторов одной полярности вместе, а выводы другой полярности — между собой. То есть создаются две группы выводов:

• Все положительные выводы соединяются в одну точку
• Все отрицательные выводы соединяются во вторую точку

Формула расчета емкости при параллельном соединении

При параллельном подключении общая емкость равна сумме емкостей всех конденсаторов:

C = C1 + C2 + C3 + … + Cn

где C — общая емкость, C1, C2, C3 и т.д. — емкости отдельных конденсаторов.

Пример расчета

Допустим, нужно соединить параллельно три конденсатора с емкостями 100 мкФ, 220 мкФ и 470 мкФ. Рассчитаем общую емкость:

C = 100 мкФ + 220 мкФ + 470 мкФ = 790 мкФ

Таким образом, при параллельном соединении этих трех конденсаторов получим общую емкость 790 мкФ.

Последовательное соединение конденсаторов

При последовательном соединении конденсаторов их общая емкость уменьшается. Этот способ применяется реже, в основном когда нужно увеличить рабочее напряжение.

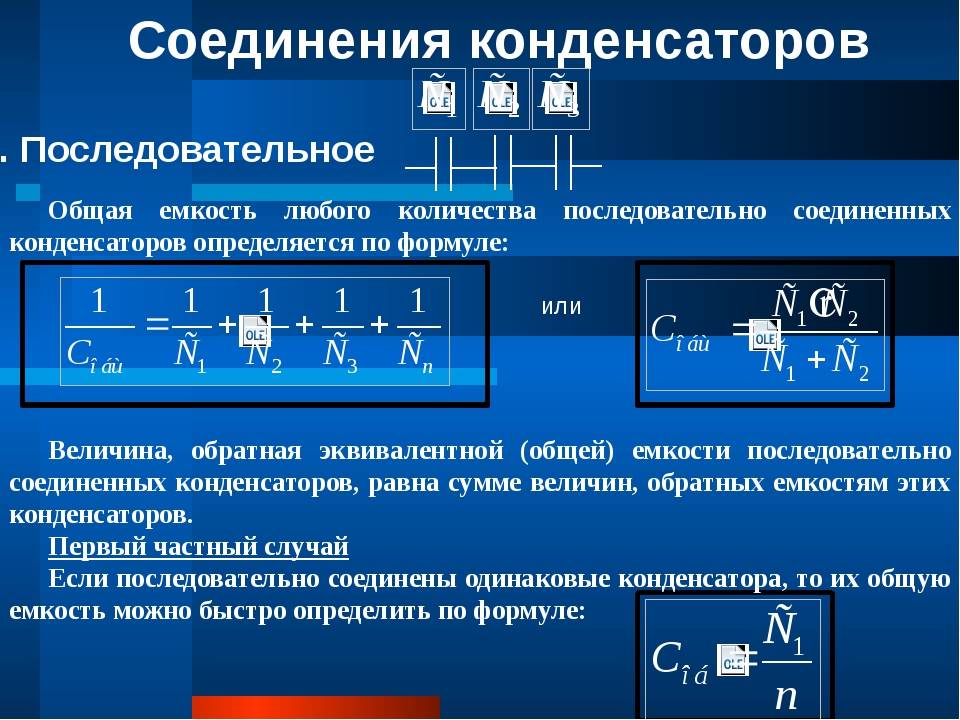
Как соединить конденсаторы последовательно?

Для последовательного соединения нужно соединить конденсаторы «цепочкой»:

• Положительный вывод первого конденсатора соединяется с отрицательным второго
• Положительный вывод второго — с отрицательным третьего
• И так далее по цепочке

Формула расчета емкости при последовательном соединении

При последовательном подключении общая емкость рассчитывается по формуле:

1/C = 1/C1 + 1/C2 + 1/C3 + … + 1/Cn

где C — общая емкость, C1, C2, C3 и т.д. — емкости отдельных конденсаторов.

Пример расчета

Рассчитаем общую емкость при последовательном соединении трех конденсаторов: 100 мкФ, 220 мкФ и 470 мкФ.

1/C = 1/100 + 1/220 + 1/470 = 0.01 + 0.00454 + 0.00213 = 0.01667

C = 1 / 0.01667 ≈ 60 мкФ

Таким образом, при последовательном соединении этих трех конденсаторов получим общую емкость около 60 мкФ, что меньше емкости самого маленького конденсатора в цепочке.

Когда применять разные способы соединения конденсаторов?

Выбор способа соединения конденсаторов зависит от поставленной задачи:

• Параллельное соединение применяют, когда нужно увеличить емкость. Это наиболее распространенный способ в бытовой электронике.
• Последовательное соединение используют, когда требуется уменьшить емкость или увеличить рабочее напряжение конденсатора. Применяется реже, в основном в специфических задачах.

Также возможно комбинированное (смешанное) соединение, сочетающее оба способа. Оно позволяет более гибко подбирать нужную емкость и напряжение.

Практические рекомендации по соединению конденсаторов

При соединении конденсаторов важно учитывать следующие моменты:

• Для получения точного номинала лучше использовать конденсаторы одного типа и производителя.
• При параллельном соединении электролитических конденсаторов нужно соблюдать полярность.
• Общее рабочее напряжение при параллельном соединении равно минимальному среди всех конденсаторов.
• При последовательном соединении напряжения на конденсаторах складываются, но распределяются неравномерно.

Измерение емкости соединенных конденсаторов

После соединения конденсаторов рекомендуется проверить полученную емкость. Как измерить емкость конденсатора?

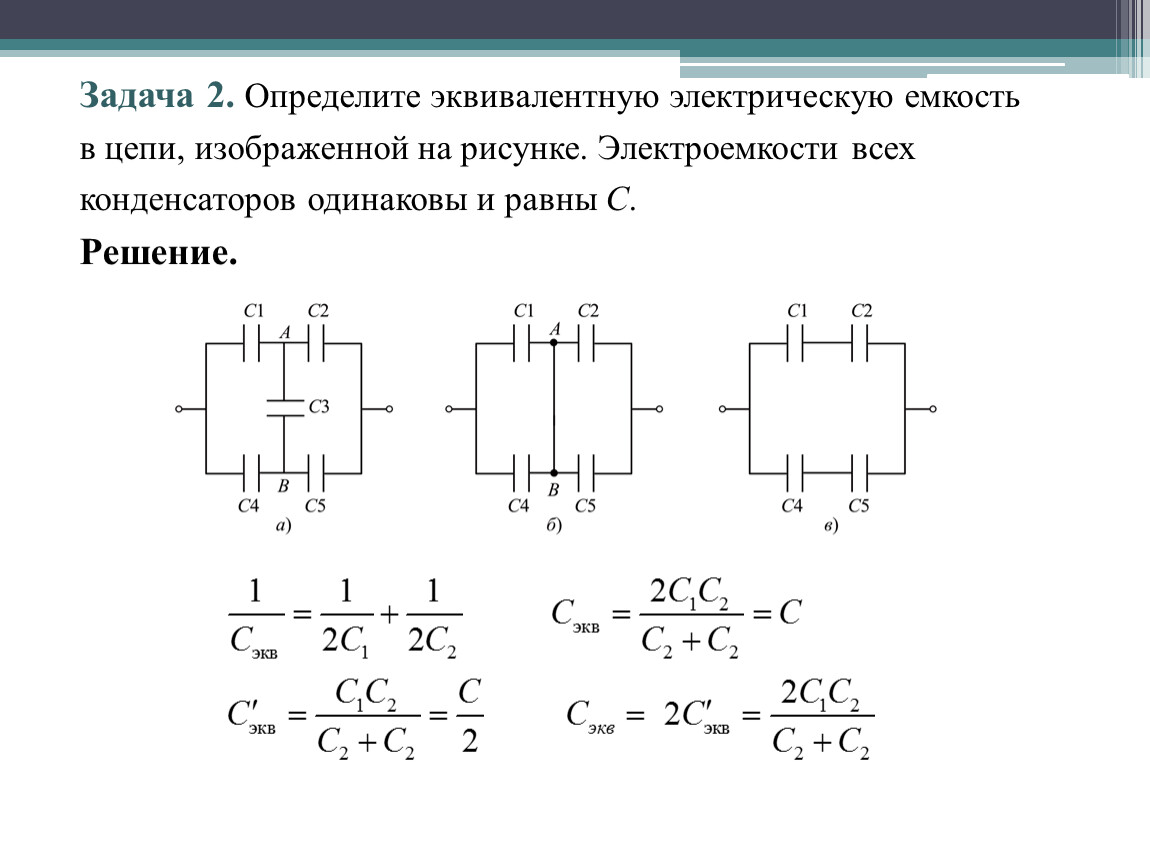
• Можно использовать мультиметр с функцией измерения емкости.
• Для более точных измерений применяют специальные измерители емкости (RLC-метры).
• При отсутствии приборов можно воспользоваться косвенными методами, например, через измерение постоянной времени RC-цепи.

Измерение позволит убедиться, что реальная емкость соответствует расчетной, и при необходимости скорректировать схему соединения.

Заключение

Соединение конденсаторов — простой и эффективный способ получить нужную емкость при отсутствии подходящего номинала. Зная формулы и особенности параллельного и последовательного соединения, можно легко подобрать нужную конфигурацию. Главное — правильно рассчитать и измерить результат, чтобы убедиться в соответствии полученной емкости требуемой.

В чем измеряются единицы емкости конденсаторов

Конденсатор представляет собой электрическое устройство, которое обладает возможностью накапливать заряд, состоит из обкладок и слоя диэлектрика между ними. Одной из важнейших характеристик прибора является ёмкость.

Конденсатор

Единица измерения емкости

В Международной системе СИ за единицу измерения ёмкости конденсатора принимают фарад:

[C] = Ф, где С – обозначение ёмкости устройства.

Международное обозначение – F. Названа в честь английского физика М.Фарадея и используется в Международной системе СИ с 1960г.

Формула для расчёта электроёмкости записывается следующим образом:

С = Dq / U (1), где:

• Dq – заряд (измеряется в кулонах, или Кл),
• U – разность потенциалов между обкладками (измеряется в вольтах или В).

Следовательно, 1Ф = 1Кл / 1В.

То есть конденсатор ёмкостью в 1 фарад накапливает на обкладках заряд, равный 1 кулон, создавая напряжение между ними, равное 1 вольт.

В фарадах измеряются электроёмкости проводников и конденсаторов.

Согласно правилам написания, принятых в СИ, если название происходит от фамилии учёного, то полное её название «фарад» пишется с маленькой (строчной) буквы, а её сокращённое название «Ф» – с прописной.

Единица измерения электроёмкости в других системах

Помимо СИ, есть ещё устаревшая система СГС, которой пользовались ранее. Первые три символа в названии обозначают:

• С – сантиметр,
• Г – грамм,
• С – секунда.

Существует две разновидности системы: СГСЭ и СГСМ. Символ Э в СГСЭ обозначает электростатическую систему, а символ М – магнитную. В системе СГСЭ емкость конденсатора измеряется в сантиметрах, или см. Для пересчёта используют соотношение:

• 1см » 1,1126 · 10-12Ф,
• 1Ф » 8,99 · 1011 статФ.

Сантиметр по-другому может называться статфарад, или статФ.

В системе СГСМ единицей измерения является абфарад, или абФ. Абфарад связан с фарадом следующим образом:

1абф = 1·109 Ф = 1ГФ.

Для перевода из СГСЭ и СГСМ в СИ в сети Интернет имеются специальные сервисы, которые позволяют автоматизировать эти действия.

Онлайн переводчик из СГС в СИ

Фарады через основные единицы системы СИ

Для выражения фарады через основные единицы СИ воспользуемся следующими формулами.

Единица измерения заряда вычисляется как:

Dq = I · Dt (2), где:

• I – сила тока (измеряется в амперах или А),
• Dt – время прохождения заряда (измеряется в секундах или с).

В свою очередь, напряжение определяется как работа, которую нужно выполнить для перемещения заряда в электростатическом поле:

U = А / Dq (3), где А – работа по перемещению заряда, определяется в джоулях, или Дж.

Из механики известно, что:

А = F · s = m · a · s (4), где:

• m – масса, измеряется в килограммах, или кг,
• s – перемещение, рассчитывается в метрах, или м,
• a – ускорение, определяется в м/с2.

Из формул 1-4 имеем:

Таким образом, 1 фарад через единицы СИ определяется как:

Кратные единицы ёмкости

При покупке радиодеталей невозможно купить конденсатор с электроёмкостью даже в несколько единиц фарад. Они выпускаются с гораздо меньшими параметрами. Это объясняется тем, что ёмкость в 1 фарад является очень большой величиной. Например, такую электроёмкость может иметь изолированный проводник в форме шара с радиусом в 13 раз больше радиуса Солнца.

Именно по этой причине для характеристики емкостных устройств применяют дольные единицы, которые рассчитываются как доля от определённого числа фарад. Для обозначения используют приставки, которые применяются для сокращения длины записываемого числа.

Таблица перевода дольных единиц

Приставка	Обозначение		Множитель
деци	дФ	dF	10^-1
санти	сФ	sF	10^-2
милли	мФ	mF	10^-3
микро	мкФ	F или uF	10^-6
нано	нФ	nF	10^-9
пико	пФ	pF, mmF, uuF	10^-12
фемто	фФ	fF	10^-15
атто	аФ	aF	10^-18
зепто	зФ	zF	10^-21
йокто	иФ	yF	10^-24

Таким образом, если параметр указывается равным 5 uF, то для перевода в фарады необходимо умножить цифру 5 на соответствующий множитель. Получаем 5 uF = 5 · 10-6 F.

В радиотехнике наиболее популярны модели, ёмкость которых измеряется в микрофарадах, нанофарадах (микромикрофарадах) или пикофарадах.

Также промышленность выпускает устройства ионисторы, которые представляют собой конденсаторы, имеющие двойной электрический слой. У некоторых ионисторов ёмкость может измеряться в килофарадах.

Ионистор с характеристикой в 1F

Маркировка конденсаторов в зависимости от ёмкости

Кодировка маленьких по размерам устройств

Существует специальная цифровая кодировка. Её используют для маркировки маленьких по размерам приборов. Кодировка электроёмкости выполняется согласно стандарту EIA.

Внимание! Ёмкость небольших конденсаторов, например, керамических или танталовых, обычно измеряется в пикофарадах, а больших, например, алюминиевых электролитических, в микрофарадах.

Существует специальная таблица таких обозначений, с помощью которой можно быстро подобрать такую же или аналогичную радиодеталь по соответствующему коду. Её можно свободно найти в Интернете.

В старых маркировках использовалась следующая кодировка. Если нанесено целое двузначное число, значит, значение ёмкость измеряется в пикофарадах, а если нанесена десятичная дробь, значит, параметр определяется в микрофарадах.

Например, радиодеталь с параметром 1000 nF =1 uF будет иметь маркировку 105, с параметрами 820 nF = 0, 82 uF – маркировку 824, а 0,27 uF = 270nF будет обозначено кодом 274.

В настоящее время, если на устройстве нанесено значение, не содержащее буквы, то оно обозначает ёмкость в пикофарадах. Если перед цифрами или после них стоит символ «н» («n»), то это означает, что значение даётся в нанофарадах, если «мк» («m», «u») – микрофарадах. В том случае, когда символ располагается перед числом, цифры в нём обозначают сотые доли. Например, n61 расшифровывается как 0,61нФ. Если символ располагается посередине значения, то на место символа нужно поставить запятую. Сам символ покажет единицы измерения. Например, 5u2 обозначает 5,2 мкФ.

Также в настоящее время используется цифровая кодировка, содержащая три числа. Первые две цифры являются числовыми характеристиками ёмкости. Параметр при этом измеряется в пикофарадах. Если значение меньше 1, то первая цифра – 0. Третья цифра определяет множитель, на который нужно умножить число, получаемое из первых двух цифр.

В случае, когда последнее число находится в диапазоне от 0 до 6, к значению дописывают количество нулей, равное третьей цифре. Например, если указано число 270, то устройство имеет параметр 27 пФ, если 271 – то на 270 пФ.

Трёхзначная кодировка

Если число равно 8, то в этом случае множитель равен 0,01. То есть если указано число 278, то ёмкость будет равна 27 · 10-2 = 0,27. Когда третье число равно 9, то множитель будет 0,1. Например, маркировка 109 указывает на электроёмкость в 1 пФ.

Если в кодировке присутствует символ «R», то параметр указывается в пикофарадах, а символ показывает место расположения запятой. Например, 4R1 расшифровывается как 4,1пФ.

Кодировка больших по размерам устройств

На больших по габаритным размерам конденсаторах маркировка наносится сверху на корпус, причём в данном случае будет присутствовать полная информация о параметрах устройства.

В обозначениях может встречаться значение MF. В приставках Международной системы единиц СИ если перед единицей измерения располагается большая буква М, то это обозначает, что должен использоваться множитель 106. В случае с конденсатором это всё равно будет обозначать микрофарады.

Также может встречаться обозначение МFD или mfd. В данном случае сочетание символов «fd» обозначает farad. Таким образом, если на корпусе написано 5 mfd, то значит, что конденсатор используется на 5 микрофарад.

Маркировка больших по размерам конденсаторов

Таким образом, при ремонте электросхемы, содержащей конденсатор, нужно правильно читать маркировку устройства и соответственно информации подбирать нужный прибор.

Видео

Оцените статью:

единица измерения, как измерить мультиметром

Ёмкость — это мера способности конденсатора накапливать заряды. Ёмкость измеряется в фарадах, по имени почетного члена Петербургского университета английского физика Майкла Фарадея.

Что такое емкость?

Если удалить одиночный электропроводник бесконечно далеко, исключить влияние заряженных тел друг на друга, то потенциал удаленного проводника станет пропорционален заряду. Но у отличающихся по размеру проводников потенциалы не совпадают.

Единицей емкости конденсатора в СИ является фарад. Коэффициент пропорциональности обозначают буквой С — это емкость, на которую влияет размер и внешняя структура проводника. Материал, фазовое состояние вещества электрода роли не играют — заряды распределяются на поверхности. Поэтому в международных правилах СГС ёмкость измеряется не в фарадах, а в сантиметрах.

Уединенный шар радиусом 9 млн км (1400 радиусов Земли) содержит 1 фарад. Отдельный проводящий элемент удерживает заряды в недостаточных для применения в технике количествах. По технологиям XXI в. создается ёмкость конденсаторов с единицами измерений выше 1 фарада.

Накапливать требуемое для работы электронных схем количество электричества способна структура из минимум 2 электродов и разделяющего диэлектрика. В такой конструкции положительные и отрицательные частицы взаимно притягиваются и сами себя держат. Диэлектрик между электронно-позитронной парой не допускает аннигиляции. Подобное состояние зарядов называется связанным.

Раньше для измерения электрических величин применяли громоздкое оборудование, не отличающееся точностью. Теперь, как измерить ёмкость тестером, знает даже начинающий радиолюбитель.

Маркировка на конденсаторах

Знать характеристики электронных приборов требуется для точной и безопасной работы.

Определение ёмкости конденсатора включает измерение величины приборами и чтение маркировки на корпусе. Обозначенные значения и полученные при измерениях отличаются. Это вызвано несовершенством производственных технологий и эксплуатационным разбросом параметров (износ, влияние температур).

На корпусе указана номинальная емкость и параметры допустимых отклонений. В бытовых устройствах используют приборы с отклонением до 20%. В космической отрасли, военном оборудовании и в автоматике опасных объектов разрешают разброс характеристик в 5-10%. Рабочие схемы не содержат значений допусков.

Номинальная емкость кодируется по стандартам IEC — Международной электротехнической комиссии, которая объединяет национальные организации по стандартам 60 стран.

Стандарт IEC использует обозначения:

1. Кодировка из 3 цифр. 2 знака в начале — количество пФ, третий — число нулей, 9 в конце — номинал меньше 10 пФ, 0 спереди — не больше 1 пФ. Код 689 — 6,8 пФ, 152 — 1500 пФ, 333 — 33000 пФ или 33 нФ, или 0,033 мкФ. Для облегчения чтения десятичная запятая в коде заменяется буквой «R». R8=0,8 пФ, 2R5 — 2,5 пФ.
2. 4 цифры в маркировке. Последняя — число нулей. 3 первых — величина в пФ. 3353 — 335000 пФ, 335 нФ или 0,335 мкФ.
3. Использование букв в коде. Буква µ — мкФ, n — нанофарад, p — пФ. 34p5 — 34,5 пФ, 1µ5 — 1,5 мкФ.
4. Планерные керамические изделия кодируют буквами A-Z в 2 регистрах и цифрой, обозначающей степень числа 10. K3 — 2400 пФ.
5. Электролитические SMD приборы маркируются 2 способами: цифры — номинальная емкость в пФ и рядом или во 2 строчке при наличии места — значение номинального напряжения; буква, кодирующая напряжение и рядом 3 цифры, 2 определяют емкость, а последняя — количество нулей. А205 значит 10 В и 2 мкФ.
6. Изделия для поверхностного монтажа маркируются кодом из букв и чисел: СА7 — 10 мкФ и 16 В.
7. Кодировки — цветом корпуса.

Маркировка IEC, национальные обозначения и кодировки брендов делают запоминание кодов бессмысленным. Разработчикам аппаратуры и мастерам-ремонтникам требуются справочные источники.

Вычисление с помощью формул

Вычисление номинальной емкости элемента требуется в 2 случаях:

1. Конструкторы электронной аппаратуры рассчитывают параметр при создании схем.
2. Мастера при отсутствии конденсаторов подходящей мощности и емкости используют расчет элемента для подбора из доступных деталей.

RC цепи рассчитывают с применением величины импеданса — комплексного сопротивления (Z). Rа — потери тока на нагревание участников цепи. Ri и Rе — учитывают влияние индуктивности и ёмкости элементов. На выводах резистора в RC цепи напряжение Uр обратно пропорционально Z.

Тепловое сопротивление увеличивает потенциал на нагрузке, а реактивное уменьшает. Работа конденсатора на частотах выше резонансных, когда растет реактивная составляющая комплексного сопротивления, приводит к потерям напряжения.

Частота резонанса обратно пропорциональна способности накапливать заряд. Из формулы для определения Fр вычисляют, какие значения Ск (емкости конденсатора) требуются для работы цепи.

Для расчета импульсных схем используют постоянную времени цепи, определяющую воздействие RC на структуру импульса. Если знают сопротивление цепи и время заряда конденсатора, по формуле постоянной времени вычисляют емкость. На истинность результата влияет человеческий фактор.

Мастера используют параллельные и последовательные соединения конденсаторов. Формулы расчета обратны формулам для резисторов.

Последовательное соединение делает емкость меньше меньшей в соединении элементов, параллельная схема суммирует величины.

Как измерить ёмкость конденсатора мультиметром?

Измеряя параметры, конденсатор предварительно разряжают, замкнув выводы между собой отверткой с изоляцией на ручке. Если этого не сделать, маломощный мультиметр выйдет из строя.

Ответ на вопрос, как проверить емкость конденсатора мультиметром с режимом «Сх» такой:

1. Включить режим «Сх» и подобрать предел замера — 2000 пФ — 20 мкФ в стандартном приборе;
2. Вставить конденсатор в гнезда в приборе или приложить щупы к выводам конденсатора и посмотреть значение на шкале прибора.

Амперовольтметром или мультиметром определяют наличие внутри корпуса короткого замыкания или обрыва.

Полярный конденсатор включают в цепь прибора с учетом направления тока. Электроды изделия производители маркируют. Конденсатор, рассчитанный для напряжения 1-3 В, при обратном токе выше нормы выйдет из строя.

Перед тем как измерить характеристики, полярный электролитический конденсатор выпаивают из платы. Включают мультиметр в режим измерения сопротивления или проверки полупроводников. Прикладывают щупы к электродам полярного конденсатора — плюс к плюсу, минус к минусу. Исправная емкость покажет плавный рост сопротивления. По мере заряда ток уменьшается, ЭДС растет и достигает напряжения источника питания.

Обрыв в конденсаторе будет выглядеть на мультиметре как бесконечное сопротивление. Прибор не отреагирует или стрелка на аналоговом экземпляре едва шевельнется.

При пробое элемента измеряемый параметр не соответствует номинальному значению в меньшую сторону, пропорционально величине пробоя.

Если задаться вопросом, как измерить мультиметром комплексное или эквивалентное последовательное сопротивление (ESR конденсатора), то без приставки сделать это проблематично. Реактивные свойства конденсатор проявляет при высокочастотном токе.

Прочие способы измерения

Измеритель емкости конденсаторов своими руками собирают по схемам импульсных устройств. Последовательности RC цепей с переменными резисторами создают на выходе изделия серии сигналов со ступенчатым изменением частоты. Для наладки устройства используют мультиметр, с которым будет применяться приставка.

Набор проверенных конденсаторов поочередно подключают к конструкции и настраивают точность работы в каждом поддиапазоне.

Измеритель ёмкости полярных электролитических элементов своими руками схематически реализуется и настраивается, как часть приставки без колебательного контура. На выходе вместо импульсного — постоянное напряжение.

В цифровых измерителях ёмкости источник питания — высокостабильный. «Плавающие» параметры элементов, из которых собирается схема, дадут неприемлемую для точности измерений погрешность.

На логических элементах создаются источники переменного импульсного тока для замеров ESR.

Недорогие приборы для измерения емкости конденсатора, типа мостовых RLC устройств с дополнительной функцией проверки SMD сопротивлений, сетевой зарядкой и жидкокристаллическим дисплеем, сами размером с палец. Выполняют функции профессионального метрологического комплекса. Способны выступать в роли измерителя емкости электролитических конденсаторов, как полярных, так и переменных.

Электрическая емкость. Конденсаторы. Емкость конденсатора.

Электрическая емкость. Конденсаторы.
Емкость уединенного проводника. Уединенным будем называть проводник, размеры которого много меньше расстояний до окружающих тел. Пусть это будет шар радиусом r. Если потенциал на бесконечности принять за 0, то потенциал заряженного уединенного шара равен:  , где e — диэлектрическая проницаемость окружающей среды.  Следовательно:  эта величина не зависит ни от заряда, ни от потенциала и определяется только размерами шара (радиусом) и диэлектрической проницаемостью среды. Этот вывод справедлив для проводника любой формы.
Электрической емкостью проводника наз. отношение заряда проводника к его потенциалу: .
Емкость определяется геометрической формой, размерами проводника и свойствами среды (от материала проводника не зависит). Чем больше емкость проводника, тем меньше меняется потенциал при изменении заряда.	Емкость шара в СИ:   —
Единицы емкости. Емкостью 1Ф (фарад) обладает такой проводник, у которого потенциал возрастает на 1 В при сообщении ему заряда в 1 Кл. Емкостью 1Ф  обладал бы уединенный шар, радиус которого был бы равен 13 радиусам Солнца. Емкость Земли  700 мкФ Если проводник не уединенный, то потенциалы складываются по правилу суперпозиции и емкость проводника меняется.	1 мкФ=10-6Ф 1нФ=10-9Ф 1пФ=10-12Ф
Конденсаторы (condensare — сгущение) . Можно создать систему проводников, емкость которой не зависит от окружающих тел. Первые конденсаторы — лейденская банка (Мушенбрук, сер. XVII в.).
Конденсатор представляет собой систему из двух проводников, разделенных слоем диэлектрика, толщина которого мала по сравнению с размерами проводников.  Проводники наз.  обкладками  конденсатора. Если заряды пластин конденсатора одинаковы по модулю и противоположны по знаку, то  под зарядом конденсатора понимают абсолютное значение заряда одной из его обкладок.
На рисунке — плоский и сферический конденсаторы. Поле плоского конденсатора почти все сосредоточено внутри (у идеального — все). Усферического — все поле сосредоточено между обкладками.
Электроемкостью конденсатора называют отношение заряда конденсатора к разности потенциалов между обкладками: .
При подключении конденсатора к батарее аккумуляторов происходит поляризация диэлектрика внутри конденсатора и на обкладках появляютсязаряды — конденсатор заряжается. Электрические поля окружающих тел почти не проникают через металлические обкладки и не влияют на разность потенциалов между ними.
Емкость плоского конденсатора. , т.о. емкость плоского конденсатора зависит только от его размеров, формы и диэлектрической проницаемости. Для создания конденсатора большой емкости необходимо увеличить площадь пластин и уменьшить толщину слоя диэлектрика.
Емкость сферического конденсатора . Если зазор между обкладками мал по сравнению с радиусами, то формула переходит в формулу емкости плоского конденсатора.
Виды конденсаторов
При подключении электролитического конденсатора необходимо соблюдать полярность.
Назначение конденсаторов Накапливать на короткое время заряд или энергию для быстрого изменения потенциала. Не пропускать постоянный ток. В радиотехнике: колебательный контур, выпрямитель. Фотовспышка.

проверенный способ соединения, формула, типы подключений

Если нужно срочно отремонтировать технику, а нужного конденсатора нет, то можно увеличить емкость конденсатора, как известно из школьной программы, соединив несколько приборов в одну цепь.

Такая проблема может также возникнуть, если, например, нужного номинала нет в продаже, то есть для нестандартных подключений, например, в радиотехнических опытах.

Электрическая емкость

При соединении приборов для конденсации заряда, как правило, техника интересует электрическая емкость, которая получится в итоге.

Электроемкость показывает способность двухполюсника накапливать в себе заряд и измеряется в фарадах. Может показаться, что чем выше это значение, тем лучше, но на практике не существует возможности создать все возможные на свете емкости, более того, часто это и не нужно, так как во всех приборах, использующихся повседневно,

применяются стандартные приборы для конденсации.

Можно соединить несколько приборов для конденсации в цепь, создав одну конденсирующую емкость, при этом значение характерной величины будет зависеть от типа подключения, и для его расчета есть давно известные формулы.

Параллельное соединение

Существует два типа подключения приборов в цепь: последовательное и параллельное. Каждый из них обладает своими свойствами, но, как правило, используется параллельное соединение конденсаторов.

Параллельное соединение обладает такими свойствами:

1. Емкость составного двухполюсника увеличивается по сравнению с каждым отдельным прибором.
2. Напряжение в сети не изменяется.

Соединить конденсаторы для увеличения емкости, как показывают свойства, лучше этим способом. Для этого нужно соединить выводы с каждого двухполюсника по группам: у каждого из них два вывода. Нужно создать две группы: в одну соединить все конденсаторы с одного вывода, а во вторую с оставшегося.

При таком соединении приборы для конденсации образуют одну емкость, поэтому верна такая формула: С=С1+С2+…СN, где N — количество конденсаторов в цепи.

Например, если имеются номинальные значения 50мкф, 100мкф и 150мкф, то при последовательном подключении общее значение в цепи будет 300мкф.

В жизни это подключение используют довольно часто, например, если при расчетах оказалось, что требуется такой двухполюсник, которого в продаже точно не найти. С помощью этого способа можно варьировать емкость конденсатора так, как это потребуется, при этом не изменяя напряжение в сети.

Последовательное включение конденсаторов

Свойства последовательного включения конденсаторов:

1. Емкость последовательно соединенных приборов для конденсации заряда в отличие от емкости параллельно соединенных конденсаторов уменьшается.
2. Напряжение на приборах растет.

Для такого подключения нужно просто соединять выводы двухполюсников один с другим, образуя цепочку: вывод первого будет соединен с выводом второго, оставшийся вывод второго с выводом третьего и так далее.

Формула подключения: 1/(1/С1+1/С2+…+1/СN), где N — это количество приборов в соединении.

Например, есть три конденсатора по 100мкф. 1/100+1/100+1/100=0,03мкф. 1/0,03=33мкф.

Заряды распределятся с чередующимся знаком, а емкостное значение будет ограничено только им же для самого слабого звена в цепи. Как только он получит свой заряд, передача тока в цепи прекратится.

Для чего тогда нужен подобный способ подключения? Такая цепь более устойчива и может выдержать большее напряжение при подключении в схему при меньшем емкостном номинале конденсатора. Однако в продаже имеются приборы, которые и без того обладают нужными свойствами, поэтому-то такое подключение в жизни практически не используется, а если используется, то для специфических задач.

Смешанный способ

Сочетает в себе параллельное и последовательное подключения.

При этом для участков с последовательным соединением характерны свойства последовательного соединения, а для участков с параллельным — свойства параллельного.

Оно используется, когда ни электроемкость, ни номинальное напряжение приборов, имеющихся в продаже, не подходят для задачи. Обычно такая проблема возникает в радиотехнике.

Чтобы определить общее значение электроемкости, нужно будет сначала определить это же значение для параллельно соединенных двухполюсников, а потом для их последовательного соединения.

Сравнение различных вариантов

	Емкость	Напряжение
Параллельное	Увеличивается	Не изменяется
Последовательное	Уменьшается	Увеличивается
Смешанное	Изменяется	Увеличивается

Для выбора соединения можно воспользоваться такой таблицей. Слева тип соединения приборов, сверху свойства прибора для конденсации заряда.

Если требуется увеличить емкость, то нужно использовать параллельное соединение, а если увеличить напряжение — то последовательное. Если же требуется и то, и то, то нужно будет рассчитывать смешанное подключение конденсаторов в цепь.

ТОЧНОЕ ИЗМЕРЕНИЕ ЕМКОСТИ КОНДЕНСАТОРА

Сейчас практически каждый универсальный мультиметр имеет возможность измерения емкости конденсаторов. Это особенно полезно, когда имеем дело с конденсаторами, маркировка которых нечитаема или отсутствует. В этом случае достаточно измерения с точностью до нескольких процентов, потому что во-первых, сами конденсаторы не так точны, а во-вторых, для устройств этого хватает. Но иногда необходимо знать точное значение емкости конденсатора. Ведь прецизионные конденсаторы труднодоступны и довольно дороги. Поэтому просто берем упаковку одинаковых и подбираем подходящий. Так как точно измеряется емкость конденсатора? Есть несколько способов сделать это.

Метод 1: мост Вина

Это один из первых методов точного измерения емкости, изобретенный Максом Вином в 1891 году. С помощью моста Вина можно точно измерить как емкость, так и сопротивление. А после преобразования в мост Максвелла еще и индуктивность. Все аналоговые мосты RLC основаны на принципе этой схемы.

Вход Uwe подключен к генератору синусоидальной волны с фиксированной или регулируемой частотой. К Uwy подключен вольтметр. Rx и Cx — искомые сопротивление и емкость. R3 и C2 известны и постоянны. R2 и R4 — потенциометры, снабженные шкалами, с которых считываются значения Rx и Cx. Эти потенциометры регулируются до тех пор, пока мост не будет сбалансирован и вольтметр не покажет ноль. Тогда удовлетворяются две зависимости:

     

Точность измерения зависит от стабильности генератора питающего мост, и знания номинала резисторов и емкости C2. Используя известные значения Rx и Cx, его можно откалибровать.

Метод 2: измерение частоты LC-генератора

В схеме использован простой LC-генератор с компаратором. В резонансном контуре работают известная емкость и известная индуктивность. Дополнительная, подключаемая к реле, позволяет рассчитать точные значения L и C используемых компонентов. Во время измерения добавленная внешняя емкость или индуктивность изменяет частоту колебаний генератора и это изменение позволяет рассчитать измеренное значение.

Эта схема существует в нескольких вариантах, часто с использованием встроенных в микроконтроллер компараторов. Точность расчетов в исходной версии — 0,1%. Точность калибровки зависит от точности калибровочного конденсатора.

Метод 3: измерение ёмкости с помощью CTMU

CTMU или блок измерения времени зарядки — это модуль имеющийся во многих микроконтроллерах PIC, предназначенный в основном для управления клавиатурами и сенсорными интерфейсами. Модуль также позволяет точно измерять емкость, измеряя напряжение на тестируемом конденсаторе, питаемом от источника тока в течение определенного периода времени. В основе работы системы лежит формула заряда:

Поскольку нам известны ток I и время t, и можем измерить напряжение V, то чтоб вычислить значение C. Метод работы показан на рисунке ниже из документации к AN1375. Тут видно, как откалибровать и измерить емкость.

Предпосылками для точного измерения абсолютного значения емкости являются точная калибровка источника тока, относительно точный таймер микроконтроллера и хороший источник опорного сигнала для АЦП. Источник тока можно легко откалибровать — просто подсоедините внешний точный резистор и измерьте приложенное к нему напряжение. Кстати, прецизионные резисторы найти легче, чем прецизионные конденсаторы.

Но прямое измерение емкости имеет еще один недостаток — вся схема нагружена различными паразитными емкостями. Поэтому рекомендуется постоянно подключать конденсатор параллельно измерительному входу, проводить измерения и использовать это значение как «ноль».

Последовательность шагов:

1. Сформировать и откалибровать источник тока, используя вход ANx и резистор.
2. Переключение на вход ANy и разряд емкости контура.
3. Таймер запускает текущую операцию источника, измеряет заданное время и останавливает источник. АЦП выполняет измерение.
4. Подключается внешний конденсатор, шаги второй и третий повторяются.
5. Если значение АЦП близко к нулю, повторим все измерение с более высоким током или более длительным временем. Когда значение близко к максимальному значению, время измерения сокращается.
6. Результаты обоих измерений конвертируются в значения пикофарад.
7. Результат первого измерения вычитается из результата второго, чтобы вычесть паразитные емкости схемы.
8. Результат форматируется и отображается на дисплее.

Источник тока CTMU имеет четыре возможных значения: 0,55 мкА, 5,5 мкА, 55 мкА и 550 мкА и регулируется в диапазоне 0,341 мкА для основного диапазона с шагом 0,011 мкА. Для измерения большой емкости потребуется увеличенное время зарядки источника, но такой измеритель должен иметь приличную точность 0,1% и диапазон измерения от единиц пикофарад до тысяч микрофарад. При измерении больших емкостей может потребоваться добавить внешний транзистор для разряда емкости, поскольку внутренний транзистор может не выдержать больших токов.

Метод 4: измерение ёмкости с помощью внешнего источника тока

Для этого метода требуются три PNP-транзистора, согласованные по Vbe и усилению, соединенные вместе для термостатики, и несколько резисторов с точностью 0,1%. Посмотрим на схему:

Резисторы R1-R3 и транзисторы Q1-Q3 образуют токовое зеркало. Резисторы R4 — R8 подключены к цифровым выходам микроконтроллера. Установив низкое состояние на одном из них, в то время как остальные находятся в состоянии высокого сопротивления, можно выбрать одно из пяти значений тока: 1 мкА, 10 мкА, 100 мкА, 1 мА и 10 мА. В свою очередь, установка низкого состояния на одном из выходов, подключенных к R9, R10 или R11, позволяет измерять ток, генерируемый источником, путем измерения напряжения на соответствующем резисторе.

Q4 и R12 используются для разряда емкости между измерениями. Измерение точно такое же, как и для метода CTMU. Подбираем зарядный ток, замеряем заданное время, останавливаем ток, измеряем напряжение на конденсаторе. При необходимости меняем время зарядки или ток зарядки.

Измерения этим методом ограничиваются только разрешающей способностью АЦП, стабильностью опорного напряжения и точностью резисторов. Подключив мультиметр вместо Cx, можно предварительно откалибровать все диапазоны. Большинство недорогих мультиметров имеют довольно точные диапазоны тока, хотя измерение напряжения на резисторах R9-R11 может быть более точным.

Метод 5: измерение ёмкости с помощью модуля CVD

Модуль CVD, емкостной делитель напряжения, можно найти в некоторых микроконтроллерах PIC. Это еще одна идея Microchip для создания сенсорных клавиатур, например в семействе PIC18FQ41.

Интересно, что измерение с помощью этого метода может выполняться без этого модуля, манипулируя битами конфигурации порта микроконтроллера и его модуля АЦП, соответственно.

Предположим, имеется конденсатор емкостью 1 нФ, заряженный напряжением 5 В. Подключим к нему второй конденсатор емкостью 1 нФ. Какое напряжение будет у обоих? Правильный ответ — 2,5 В. Теперь возьмем два других конденсатора: 10 нФ и 22 нФ. Первый заряжен на 5 В, второй замкнут на массу. Затем соединяем их обоих вместе. Какое будет напряжение? 1,5625 В. Теперь зарядим второй конденсатор до 5 В, разрядим первый и подключим два. Какое будет напряжение? 3,4375 В. Модуль CVD выполняет именно это измерение, при этом конденсатор выборки АЦП (плюс дополнительно подключенные емкости внутри микроконтроллера) действует как первый конденсатор, а все что подключено к выводу АЦП, на котором выполняется измерение, как конденсатор 2.

Модуль CVD сначала автоматически загружает внутреннюю емкость, подключает внешнюю емкость и измеряет ее, затем разряжает внутреннюю емкость, заряжает внешнюю емкость и выполняет второе измерение. Результаты автоматически вычитаются друг из друга, а полученное значение сравнивается с заданным пороговым значением — таким образом, модуль в основном используется для управления сенсорными кнопками, но вы также можете измерить значение присоединенной внешней емкости как изменение в дифференциальное напряжение. Но тут измерение будет менее точным, чем измерение CTMU.

Метод 6: измерение ёмкости RC-генератором

Этот метод частично относится к методу номер 2. Основа — RC-генератор, у которого значение R ровно 10 кОм. RC-генератор настроен на непрерывную работу и генерирует сигнал в диапазоне 1 / 3–2 / 3 напряжения питания. Схема всего прибора выглядит так:

Основа — PIC16F628 (A) с кварцем 16 МГц, что означает внутренний таймер имеет частоту 4 МГц. Во время измерения модуль Capture / Compare / PWM (CCP1) подсчитывает значения модуля Timer1 для каждого переднего фронта сигнала от компаратора. Программа подсчитывает и суммирует значения таймера и количество подсчитанных передних фронтов, пока не наберет значение более 2 миллионов отсчетов, то есть >0,5 секунды. Этот результат увеличивается в тысячу раз, а затем делится на количество измеренных наклонов. Результат преобразуется и отображается как значение емкости в пико-, нано- или микрофарадах: Диапазоны 0,00-18000,00 пФ; 18,000-999,000 нФ; 1,0000-50,0000 мкФ. Разрешение измерений намного выше, чем у других любительских решений. По тестам точность измерения лучше 0,2%. В схеме есть возможность сброса и режим относительного измерения для сравнения конденсаторов. Так что методов измерения ёмкости есть несколько — просто выбираем самый подходящий для своих целей и собираем С-метр.

   Форум

   Форум по обсуждению материала ТОЧНОЕ ИЗМЕРЕНИЕ ЕМКОСТИ КОНДЕНСАТОРА

Плавное регулирование емкости конденсаторов

Введение

Регулирование емкости конденсаторов требуется как в электротехнических, так и в радиотехнических устройствах. В радиотехнических устройствах, например в параметрических усилителях, регулирование емкости конденсатора, представляющего собой полупроводниковый переход, смещенный в обратном направлении, осуществляется регулированием напряжения смещения [1]. Небольшая емкость перехода на радиочастотах оказывается вполне достаточной.

В электротехнике регулирование емкости возбуждающих конденсаторов асинхронного генератора используется, например, для регулирования его выходного напряжения [2]. Поскольку частоты генерируемых напряжений на много порядков ниже, чем в радиотехнике, емкость полупроводникового перехода оказывается ничтожно малой по сравнению с необходимой емкостью. Поэтому используются нелинейные конденсаторы (вариконды) [2]. Их емкость изменяется в зависимости от приложенного напряжения благодаря особым свойствам диэлектрика.

В электротехнике широко применяются импульсные методы регулирования не только величин токов и напряжения, но даже их частоты. Последнее время благодаря успехам в силовой электронике и микропроцессорной технике импульсные методы регулирования применяются уже в устройствах, мощность которых достигает десятков мегаватт. Это наводит на мысль об импульсном регулировании параметров элементов электротехнических устройств, например емкости конденсаторов.

 

Идея импульсного регулирования емкости конденсатора

Рассмотрим конденсатор постоянной емкости, к которому с помощью ключа К параллельно можно подключать другой конденсатор, как показано на рис. 1а.

При разомкнутом ключе К емкость на зажимах a и b равна С₁, а при замкнутом ключе К эта емкость равна сумме С₁+С₂. Можно предположить, что переключение К из положения «1» в положение «2» с высокой частотой позволит регулировать емкость между зажимами a и b. Чем больше часть периода, в течение которой ключ К находится в положении «1», тем больше величина эквивалентной емкости С_экв. Очевидно, что при изменении времени от 0 до Т, а g = t/T от 0 до 1, С_экв будет изменяться в пределах от С₁ до С₁+С₂.

Рассмотрим вначале идеальный случай, когда ключ К обладает нулевым сопротивлением (r = 0) в замкнутом состоянии и бесконечным сопротивлением (R = ∞) в разомкнутом состоянии. Кроме того, положим, что существует устройство, не показанное на рис. 1а, поддерживающее при разомкнутом ключе К напряжение на конденсаторе С₂ равным напряжению на С₁. Благодаря этому в момент замыкания ключа К никаких токов между конденсаторами С₁ и С₂, выравнивающих их напряжения, не возникает.

На временном интервале t_n< t< t_n+t ветвь ab описывается уравнением

откуда следует:

Аналогично на интервале t_n+t< t< t_n+1 = t_n+Т получаем:

Средняя скорость изменения напряжения и_ab(t) на интервале t_n< t< t_n+1 равна

Если i(t) = I = const, то напряжение и_ab(t) будет изменяться по закону ломаной линии с чередующимися прямолинейными отрезками (рис. 1б). С уменьшением периода T ломаная линия все меньше будет отличаться от прямой (рис. 1б), имеющей наклон, равный средней скорости изменения напряжения и_ab(t):

Очевидно, что прямолинейный закон изменения, к которому реальный закон изменения напряжения и_ab(t) неограниченно приближается при T→0, имеет место при одном эквивалентном конденсаторе емкостью:

Таким образом, в идеальном случае при достаточно высокой частоте коммутации ключа К можно плавно изменять эквивалентную емкость на зажимах ab, изменяя относительную продолжительность подключения конденсатора С₂–g = t/Т. Эквивалентная емкость изменяется при этом в пределах от С₁ при g = 0 до С₁+С₂ при g = 1.

В реальных условиях ключ К, реализованный на MOSFET или IGBT, имеет конечные сопротивления r ≠ 0 в открытом состоянии и R ≠ ∞ в закрытом состоянии. Использование устройства, поддерживающего при разомкнутом ключе К напряжение на конденсаторе С₂ равным напряжению на конденсаторе С₁, несколько уменьшает привлекательность рассматриваемого метода. Кроме того, при достаточно высокой частоте коммутации различие напряжений на конденсаторах С₁ и С₂ в момент замыкания ключа К может оказаться вполне допустимым с точки зрения ограничения уравнительного тока.

 

Анализ упрощенной схемы импульсного регулирования емкости конденсаторов

На временном интервале t_n< t< t_n+t эквивалентная схема, представленная на рис. 2а, описывается системой уравнений:

Приведение системы уравнений (5) к нормальной форме дает:

В векторно-матричной форме уравнения (6) записываются в виде:

где

Аналогично на временном интервале t_n+t< t< t_n+1 = t_n+Т эквивалентная схема, представленная на рис. 2б, описывается системой дифференциальных уравнений (ДУ) в нормальной форме:

или в векторно-матричной форме:

где

Согласно основам теории систем с периодическим высокочастотным изменением структуры [3] предельная непрерывная модель системы описывается векторно-матричным уравнением:

где

Полученное описание предельной непрерывной модели системы (8) позволяет изобразить ее электрическую схему (рис. 2в). Таким образом, очевидно, что без поддержания при разомкнутом ключе К напряжения на конденсаторе С₂ равным напряжению на конденсаторе С₁, за счет изменения g изменяется только величина эквивалентного сопротивления r_экв = r/g. Поэтому при реально малой величине сопротивления r замкнутого ключа К и величине g, заметно превышающей нулевое значение, ветвь ав в цепи с сопротивлением, многократно превышающим сопротивление замкнутого ключа К, что всегда имеет место на практике, ведет себя практически как конденсатор емкостью С₁+С₂. Экспериментально этот вывод подтверждается исследованием процесса подключения ветви ав через сопротивление R, всего на два порядка превышающее сопротивление замкнутого ключа r, к источнику постоянного напряжения. Ток в цепи уменьшался практически по экспоненте с постоянной времени, равной R(С₁+С₂). Физически это объясняется тем, что увеличение напряжения на конденсаторе С₁, при разомкнутом ключе К происходящее с большей скоростью, компенсируется уменьшением его за счет выравнивания напряжений при подключении конденсатора С₂ в момент замыкания ключа К.

Таким образом, без поддержания напряжения на конденсаторе С₂ равным при разомкнутом ключе К напряжению на конденсаторе С₁эффективное импульсное управление величиной емкости осуществить невозможно. Следовательно, введение устройства, поддерживающего при разомкнутом ключе К напряжение на отключенном конденсаторе С₂ равным напряжению на включенном конденсаторе С₁, необходимо. Не останавливаясь на технической его реализации, имеющей очевидно множество вариантов, рассмотрим схему с управляемым генератором тока (ГТ), представленную на рис. 3а.

 

Предельная непрерывная модель схемы импульсного регулирования емкости конденсаторов

На первой части периода переключений К и К₁t_n< t< t_n+t схема описывается уравнением (6а). Во второй части периода t_n+t< t< t_n+1 = = t_n+Т справедлива система ДУ:

где k_i — коэффициент преобразования ГТ [k_i] =А/В = Ом^-1.

В векторно-матричной форме эта система уравнений имеет вид:

где

Предельная непрерывная модель схемы рис. 3а описывается уравнением:

где

Система ДУ предельной непрерывной модели системы имеет вид:

Подставляя (u_C1–u_C2), выраженное из второго уравнения, в первое и учтя, что u_C1 ~ u_C2, с хорошей точностью получаем:

 

где

 

При k_ir = 1 получаем

С_экв = С₁+ gС₂. (12а)

Переходя к изображениям по Лапласу в векторно-матричном уравнении (10) при нулевых начальных условиях, получаем:

U_ab(p) = U_C1(p) = c^T[pE – A]^-1hI(p),

где U_ab(p) = U_C1(p) = L{u_C1(t)}, I(p) = L{i(t)}— преобразование Лапласа u_C1(t) и i(t) соответственно, Е — единичная 2×2 матрица, c^T = [1,0] — вектор-строка.

Из последнего уравнения получаем передаточную функцию предельной непрерывной модели цепи рис. 3а:

Разложение W(p) на сумму двух простейших дробей дает:

где

Согласно (14) можно построить эквивалентную электрическую схему предельной непрерывной модели, представленную на рис. 3б:

Переходя к изображениям по Лапласу, получаем:

Сравнение выражений (14) и (15) дает:

 

Экспериментальная проверка полученных теоретических результатов

С целью экспериментальной проверки полученных теоретически результатов моделировалось подключение RC-цепи к генератору синусоидального напряжения частотой f = 50 Гц, амплитудой U_m = 100 В и нулевой начальной фазой j = 0. Принято R = 10 Ом, а величина Сустанавливалась равной 1,2×10^-4 и 1,8×10^-4 Ф путем импульсного регулирования по схеме рис. 3а. При этом С₁ = С₂ =1×10^-4 Ф, T = 10^-5 с, r = 0,1 Ом, k_ir = 1. В соответствии с формулой (12а) величина g принималась равной 0,2 и 0,8 соответственно при С_экв = 1,2×10^-4 и 1,8×10^-4Ф.

Одновременно моделировалось подключение к тому же напряжению RC-цепи, в которой импульсно регулируемый конденсатор представлялся его предельной моделью рис. 3б. Схема, построенная в системе моделирования MATLAB 6.5 Simulink 5 Sim Power System, изображена на рис. 4.

Рис. 4. Схема моделирования в системе MATLAB 6.5 Simulink 5 Sim Power System

Результаты моделирования представлены на рис. 5а, б. На временных диаграммах i — ток RC-цепи с регулированием емкости конденсатора, i_М — ток RC-цепи, в которой регулируемый конденсатор представлен его предельной непрерывной моделью, Di = i_М – i.

Рис. 5. Временные диаграммы токов в реальной схеме и в ее предельной непрерывной модели (i и iM) и их разности, увеличенной в 100 раз: а) Сэкв = 1,2×10-4 Ф; б) Сэкв = 1,8×10-4 Ф

Моделирование проводилось методом ode15s при ограничении максимального шага интегрирования величиной 10^-6.

Анализ результатов моделирования показывает очень хорошее приближение предельно непрерывной модели к реальному импульсно регулируемому конденсатору. Увеличение T снижает точность приближения. Следует подчеркнуть, что рассмотренный способ регулирования емкости конденсаторов представляет собой схемное решение. Емкости конденсаторов в действительности не изменяются. В момент уменьшения емкости ветви ab (в момент отключения С₂) напряжение на ветви не изменяется, хотя при мгновенном уменьшении емкости конденсатора напряжение на нем (u_C = q/C) возрастает.

 

Выводы

• Изменение относительной продолжительности периодического подключения дополнительного конденсатора параллельно основному при поддержании на отключенном конденсаторе напряжения, равного напряжению на основном конденсаторе, позволяет плавно регулировать эквивалентную емкость.
• При достаточно высокой частоте переключений схему регулирования емкости можно с необходимой точностью заменить ее эквивалентной предельной непрерывной моделью.

Литература

1. Баскаков С. И. Радиотехнические цепи и сигналы. М: Высшая школа. 2003.
2. Торопцев Н. Д. Авиационные асинхронные генераторы. М: Транспорт. 1970.
3. Коршунов А. И. Предельная непрерывная модель системы с высокочастотным периодическим изменением структуры // Изв. вузов. Приборостроение. 2009. Т. 52, № 9.

Все о конденсаторах

Конденсатор — двухполюсник с постоянным или переменным значением ёмкости и малой проводимостью; устройство для накопления заряда и энергии электрического поля.

Во всех радиотехнических и электронных устройствах кроме транзисторов и микросхем применяются конденсаторы. В одних схемах их больше, в других меньше, но совсем без конденсаторов не бывает практически ни одной электронной схемы.

При этом конденсаторы могут выполнять в устройствах самые разные задачи. Прежде всего, это емкости в фильтрах выпрямителей и стабилизаторов. С помощью конденсаторов передается сигнал между усилительными каскадами, строятся фильтры низких и высоких частот, задаются временные интервалы в выдержках времени и подбирается частота колебаний в различных генераторах.

Свою родословную конденсаторы ведут от лейденской банки, которую в середине XVIII века в своих опытах использовал голландский ученый Питер ван Мушенбрук. Жил он в городе Лейдене, так что нетрудно догадаться, почему так называлась эта банка.

Собственно это и была обыкновенная стеклянная банка, выложенная внутри и снаружи оловянной фольгой – станиолем. Использовалась она в тех же целях, как и современная алюминиевая, но тогда алюминий открыт еще не был.

Единственным источником электричества в те времена была электрофорная машина, способная развивать напряжение до нескольких сотен киловольт. Вот от нее и заряжали лейденскую банку. В учебниках физики описан случай, когда Мушенбрук разрядил свою банку через цепь из десяти гвардейцев взявшихся за руки.

В то время никто не знал, что последствия могут быть трагическими. Удар получился достаточно чувствительным, но не смертельным. До этого не дошло, ведь емкость лейденской банки была незначительной, импульс получился очень кратковременным, поэтому мощность разряда была невелика.

Как устроен конденсатор

Устройство конденсатора практически ничем не отличается от лейденской банки: все те же две обкладки, разделенные диэлектриком. Именно так на современных электрических схемах изображаются конденсаторы. На рисунке 1 показано схематичное устройство плоского конденсатора и формула для его расчета.

Рисунок 1. Устройство плоского конденсатора

Здесь S – площадь пластин в квадратных метрах, d – расстояние между пластинами в метрах, C — емкость в фарадах, ε – диэлектрическая проницаемость среды. Все величины, входящие в формулу, указаны в системе СИ. Эта формула справедлива для простейшего плоского конденсатора: можно просто расположить рядом две металлические пластины, от которых сделаны выводы. Диэлектриком может служить воздух.

Из этой формулы можно понять, что емкость конденсатора тем больше, чем больше площадь пластин и чем меньше расстояние между ними. Для конденсаторов с другой геометрией формула может быть иной, например, для емкости одиночного проводника или электрического кабеля. Но зависимость емкости от площади пластин и расстояния между ними та же, что и у плоского конденсатора: чем больше площадь и чем меньше расстояние, тем больше емкость.

На самом деле пластины не всегда делаются плоскими. У многих конденсаторов, например металлобумажных, обкладки представляют собой алюминиевую фольгу свернутую вместе с бумажным диэлектриком в плотный клубок, по форме металлического корпуса.

Для увеличения электрической прочности тонкая конденсаторная бумага пропитывается изолирующими составами, чаще всего трансформаторным маслом. Такая конструкция позволяет делать конденсаторы с емкостью до нескольких сотен микрофарад. Примерно так же устроены конденсаторы и с другими диэлектриками.

Формула не содержит никаких ограничений на площадь пластин S и расстояние между пластинами d. Если предположить, что пластины можно развести очень далеко, и при этом площадь пластин сделать совсем незначительной, то какая-то емкость, пусть небольшая, все равно останется. Подобное рассуждение говорит о том, что даже просто два проводника, расположенные по соседству, обладают электрической емкостью.

Этим обстоятельством широко пользуются в высокочастотной технике: в некоторых случаях конденсаторы делаются просто в виде дорожек печатного монтажа, а то и просто двух скрученных вместе проводков в полиэтиленовой изоляции. Обычный провод–лапша или кабель также обладают емкостью, причем с увеличением длины она увеличивается.

Кроме емкости C, любой кабель обладает еще и сопротивлением R. Оба этих физических свойства распределены по длине кабеля, и при передаче импульсных сигналов работают как интегрирующая RC – цепочка, показанная на рисунке 2.

Рисунок 2.

На рисунке все просто: вот схема, вот входной сигнал, а вот он же на выходе. Импульс искажается до неузнаваемости, но это сделано специально, для чего и собрана схема. Пока же речь идет о влиянии емкости кабеля на импульсный сигнал. Вместо импульса на другом конце кабеля появится вот такой «колокол», а если импульс короткий, то он может и вовсе не дойти до другого конца кабеля, вовсе пропасть.

Исторический факт

Здесь вполне уместно вспомнить историю о том, как прокладывали трансатлантический кабель. Первая попытка в 1857 году потерпела неудачу: телеграфные точки – тире (прямоугольные импульсы) искажались так, что на другом конце линии длиной 4000 км разобрать ничего не удалось.

Вторая попытка была предпринята в 1865 году. К этому времени английский физик У. Томпсон разработал теорию передачи данных по длинным линиям. В свете этой теории прокладка кабеля оказалась более удачной, сигналы принять удалось.

За этот научный подвиг королева Виктория пожаловала ученого рыцарством и титулом лорда Кельвина. Именно так назывался небольшой город на побережье Ирландии, где начиналась прокладка кабеля. Но это просто к слову, а теперь вернемся к последней букве в формуле, а именно, к диэлектрической проницаемости среды ε.

Немножко о диэлектриках

Эта ε стоит в знаменателе формулы, следовательно, ее увеличение повлечет за собой возрастание емкости. Для большинства используемых диэлектриков, таких как воздух, лавсан, полиэтилен, фторопласт эта константа практически такая же, как у вакуума. Но вместе с тем существует много веществ, диэлектрическая проницаемость которых намного выше. Если воздушный конденсатор залить ацетоном или спиртом, то его емкость возрастет раз в 15…20.

Но подобные вещества обладают кроме высокой ε еще и достаточно высокой проводимостью, поэтому такой конденсатор заряд держать будет плохо, он быстро разрядится сам через себя. Это вредное явление называется током утечки. Поэтому для диэлектриков разрабатываются специальные материалы, которые позволяют при высокой удельной емкости конденсаторов обеспечивать приемлемые токи утечки. Именно этим и объясняется такое разнообразие видов и типов конденсаторов, каждый из которых предназначен для конкретных условий.

Электролитический конденсатор

Наибольшей удельной емкостью (соотношение емкость / объем) обладают электролитические конденсаторы. Емкость «электролитов» достигает до 100 000 мкФ, рабочее напряжение до 600В. Такие конденсаторы работают хорошо только на низких частотах, чаще всего в фильтрах источников питания. Электролитические конденсаторы включаются с соблюдением полярности.

Электродами в таких конденсаторах является тонкая пленка из оксида металлов, поэтому часто эти конденсаторы называют оксидными. Тонкий слой воздуха между такими электродами не очень надежный изолятор, поэтому между оксидными обкладками вводится слой электролита. Чаще всего это концентрированные растворы кислот или щелочей.

На рисунке 3 показан один из таких конденсаторов.

Рисунок 3. Электролитический конденсатор

Чтобы оценить размеры конденсатора рядом с ним сфотографировался простой спичечный коробок. Кроме достаточно большой емкости на рисунке можно разглядеть еще и допуск в процентах: ни много ни мало 70% от номинальной.

В те времена, когда компьютеры были большими и назывались ЭВМ, такие конденсаторы стояли в дисководах (по-современному HDD). Информационная емкость таких накопителей теперь может вызвать лишь улыбку: на двух дисках диаметром 350 мм хранилось 5 мегабайт информации, а само устройство весило 54 кг.

Основным назначением показанных на рисунке суперконденсаторов был вывод магнитных головок из рабочей зоны диска при внезапном отключении электроэнергии. Такие конденсаторы могли хранить заряд несколько лет, что было проверено на практике.

Чуть ниже с электролитическими конденсаторами будет предложено проделать несколько простых опытов, чтобы понять, что может делать конденсатор.

Для работы в цепях переменного тока выпускаются неполярные электролитические конденсаторы, вот только достать их почему-то очень непросто. Чтобы как-то эту проблему обойти, обычные полярные «электролиты» включают встречно-последовательно: плюс-минус-минус-плюс.

Если полярный электролитический конденсатор включить в цепь переменного тока, то сначала он будет греться, а потом раздастся взрыв. Отечественные старые конденсаторы разлетались во все стороны, импортные же имеют специальное приспособление, позволяющее избежать громких выстрелов. Это, как правило, либо крестовая насечка на донышке конденсатора, либо отверстие с резиновой пробкой, расположенное там же.

Очень не любят электролитические конденсаторы повышенного напряжения, даже если полярность соблюдена. Поэтому никогда не надо ставить «электролиты» в цепь, где предвидится напряжение близкое к максимальному для данного конденсатора.

Иногда в некоторых, даже солидных форумах, начинающие задают вопрос: «На схеме означен конденсатор 470µF * 16V, а у меня есть 470µF * 50V, можно ли его поставить?». Да, конечно можно, вот обратная замена недопустима.

Конденсатор может накапливать энергию

Разобраться с этим утверждением поможет простая схема, показанная на рисунке 4.

Рисунок 4. Схема с конденсатором

Главным действующим лицом этой схемы является электролитический конденсатор C достаточно большой емкости, чтобы процессы заряда – разряда протекали медленно, и даже очень наглядно. Это дает возможность наблюдать работу схемы визуально с помощью обычной лампочки от карманного фонаря. Фонари эти давно уступили место современным светодиодным, но лампочки для них продаются до сих пор. Поэтому, собрать схему и провести простые опыты очень даже просто.

Может быть, кто-то скажет: «А зачем? Ведь и так все очевидно, да если еще и описание почитать…». Возразить тут, вроде, нечего, но любая, даже самая простая вещь остается в голове надолго, если ее понимание пришло через руки.

Итак, схема собрана. Как она работает?

В положении переключателя SA, показанном на схеме, конденсатор C заряжается от источника питания GB через резистор R по цепи: +GB __ R __ SA __ C __ -GB. Зарядный ток на схеме показан стрелкой с индексом iз. Процесс заряда конденсатора показан на рисунке 5.

Рисунок 5. Процесс заряда конденсатора

На рисунке видно, что напряжение на конденсаторе возрастает по кривой линии, в математике называемой экспонентой. Ток заряда прямо-таки зеркально отражает напряжение заряда. По мере того, как напряжение на конденсаторе растет, ток заряда становится все меньше. И только в начальный момент соответствует формуле, показанной на рисунке.

Через некоторое время конденсатор зарядится от 0В до напряжения источника питания, в нашей схеме до 4,5В. Весь вопрос в том, как это время определить, сколько ждать, когда же конденсатор зарядится?

Постоянная времени «тау» τ = R*C

В этой формуле просто перемножаются сопротивление и емкость последовательно соединенных резистора и конденсатора. Если, не пренебрегая системой СИ, подставить сопротивление в Омах, емкость в Фарадах, то результат получится в секундах. Именно это время необходимо для того, чтобы конденсатор зарядился до 36,8% напряжения источника питания. Соответственно для заряда практически до 100% потребуется время 5* τ.

Часто, пренебрегая системой СИ, подставляют в формулу сопротивление в Омах, а емкость в микрофарадах, тогда время получится в микросекундах. В нашем случае результат удобнее получить в секундах, для чего придется микросекунды просто умножить на миллион, а проще говоря, переместить запятую на шесть знаков влево.

Для схемы, показанной на рисунке 4, при емкости конденсатора 2000мкФ и сопротивлении резистора 500Ω постоянная времени получится τ = R*C = 500 * 2000 = 1000000 микросекунд или ровно одна секунда. Таким образом, придется подождать приблизительно 5 секунд, пока конденсатор зарядится полностью.

Если по истечении указанного времени переключатель SA перевести в правое положение, то конденсатор C разрядится через лампочку EL. В этот момент получится короткая вспышка, конденсатор разрядится и лампочка погаснет. Направление разряда конденсатора показано стрелкой с индексом iр. Время разряда также определяется постоянной времени τ. График разряда показан на рисунке 6.

Рисунок 6. График разряда конденсатора

Конденсатор не пропускает постоянный ток

Убедиться в этом утверждении поможет еще более простая схема, показанная на рисунке 7.

Рисунок 7. Схема с конденсатором в цепи постоянного тока

Если замкнуть переключатель SA, то последует кратковременная вспышка лампочки, что свидетельствует о том, что конденсатор C зарядился через лампочку. Здесь же показан и график заряда: в момент замыкания переключателя ток максимальный, по мере заряда конденсатора уменьшается, а через некоторое время прекращается совсем.

Если конденсатор хорошего качества, т.е. с малым током утечки (саморазряда) повторное замыкание выключателя к вспышке не приведет. Для получения еще одной вспышки конденсатор придется разрядить.

Конденсатор в фильтрах питания

Конденсатор ставится, как правило, после выпрямителя. Чаще всего выпрямители делаются двухполупериодными. Наиболее распространенные схемы выпрямителей показаны на рисунке 8.

Рисунок 8. Схемы выпрямителей

Однополупериодные выпрямители также применяются достаточно часто, как правило, в тех случаях, когда мощность нагрузки незначительна. Самым ценным качеством таких выпрямителей является простота: всего один диод и обмотка трансформатора.

Для двухполупериодного выпрямителя емкость конденсатора фильтра можно рассчитать по формуле

C = 1000000 * Po / 2*U*f*dU, где C емкость конденсатора мкФ, Po мощность нагрузки Вт, U напряжение на выходе выпрямителя В, f частота переменного напряжения Гц, dU амплитуда пульсаций В.

Большое число в числителе 1000000 переводит емкость конденсатора из системных Фарад в микрофарады. Двойка в знаменателе представляет собой число полупериодов выпрямителя: для однополупериодного на ее месте появится единица

C = 1000000 * Po / U*f*dU,

а для трехфазного выпрямителя формула примет вид C = 1000000 * Po / 3*U*f*dU.

Суперконденсатор – ионистор

В последнее время появился новый класс электролитических конденсаторов, так называемый ионистор. По своим свойствам он похож на аккумулятор, правда, с несколькими ограничениями.

Заряд ионистора до номинального напряжения происходит в течение короткого времени, буквально за несколько минут, поэтому его целесообразно использовать в качестве резервного источника питания. По сути ионистор прибор неполярный, единственное, чем определяется его полярность это зарядкой на заводе – изготовителе. Чтобы в дальнейшем эту полярность не перепутать она указывается знаком +.

Большую роль играют условия эксплуатации ионисторов. При температуре 70˚C при напряжении 0,8 от номинального гарантированная долговечность не более 500 часов. Если же прибор будет работать при напряжении 0,6 от номинального, а температура не превысит 40 градусов, то исправная работа возможна в течение 40 000 часов и более.

Наиболее распространенное применение ионистора это источники резервного питания. В основном это микросхемы памяти или электронные часы. В этом случае основным параметром ионистора является малый ток утечки, его саморазряд.

Достаточно перспективным является использование ионисторов совместно с солнечными батареями. Здесь также сказывается некритичность к условию заряда и практически неограниченное число циклов заряд-разряд. Еще одно ценное свойство в том, что ионистор не нуждается в обслуживании.

Пока получилось рассказать, как и где работают электролитические конденсаторы, причем, в основном в цепях постоянного тока.

Ранее ЭлектроВести писали, что в новом исследовании ученые создали микропленочный ультратонкий конденсатор для накопления энергии, который может приклеиваться к поверхности как стикер. Батарея прикрепляется с помощью ультракоротких лазерных импульсов, которые частично расплавляют ее, позволяя удерживаться почти на любой поверхности.

По материалам: electrik.info.

8.1 Конденсаторы и емкость — University Physics Volume 2

Цели обучения

К концу этого раздела вы сможете:

• Объясните понятие конденсатора и его емкости
• Опишите, как оценить емкость системы проводов

Конденсатор — это устройство, используемое для хранения электрического заряда и электрической энергии. Конденсаторы обычно состоят из двух электрических проводников, разделенных расстоянием.(Обратите внимание, что такие электрические проводники иногда называют «электродами», но, точнее, это «обкладки конденсатора».) Пространство между конденсаторами может быть просто вакуумом, и в этом случае конденсатор будет известен как «Вакуумный конденсатор». Однако пространство обычно заполняется изолирующим материалом, известным как диэлектрик. (Вы узнаете больше о диэлектриках в разделах, посвященных диэлектрикам, далее в этой главе.) Объем накопителя в конденсаторе определяется свойством, называемым емкостью , , о котором вы узнаете больше чуть позже в этом разделе.

Конденсаторы

могут применяться в самых разных областях — от фильтрации статического электричества от радиоприема до накопления энергии в дефибрилляторах сердца. Обычно в промышленных конденсаторах две токопроводящие части расположены близко друг к другу, но не соприкасаются, как на рис. 8.2. В большинстве случаев между двумя пластинами используется диэлектрик. Когда клеммы батареи подключены к первоначально незаряженному конденсатору, потенциал батареи перемещает небольшое количество заряда величиной Q с положительной пластины на отрицательную.Конденсатор в целом остается нейтральным, но с зарядами + Q + Q и −Q − Q, находящимися на противоположных пластинах.

Фигура 8,2 Оба конденсатора, показанные здесь, были изначально разряжены перед подключением к батарее. Теперь у них на пластинах есть заряды + Q + Q и −Q − Q (соответственно). (a) Конденсатор с параллельными пластинами состоит из двух пластин противоположного заряда с площадью A, , разделенных расстоянием d . (b) Катаный конденсатор имеет диэлектрический материал между двумя проводящими листами (пластинами).

Система, состоящая из двух идентичных параллельно проводящих пластин, разделенных расстоянием, называется конденсатором с параллельными пластинами (рис. 8.3). Величина электрического поля в пространстве между параллельными пластинами равна E = σ / ε0E = σ / ε0, где σσ обозначает поверхностную плотность заряда на одной пластине (напомним, что σσ — это заряд Q на площадь поверхности A ). Таким образом, величина поля прямо пропорциональна Q .

Фигура 8,3 Разделение зарядов в конденсаторе показывает, что заряды остаются на поверхности пластин конденсатора.Линии электрического поля в конденсаторе с параллельными пластинами начинаются с положительных зарядов и заканчиваются отрицательными зарядами. Величина электрического поля в пространстве между пластинами прямо пропорциональна количеству заряда на конденсаторе.

Конденсаторы с разными физическими характеристиками (такими как форма и размер пластин) накапливают разное количество заряда для одного и того же приложенного напряжения В на своих пластинах. Емкость C конденсатора определяется как отношение максимального заряда Q , который может храниться в конденсаторе, к приложенному напряжению В, на его пластинах.Другими словами, емкость — это наибольшая величина заряда на вольт, которая может храниться на устройстве:

Единица измерения емкости в системе СИ — фарад (Ф), названная в честь Майкла Фарадея (1791–1867). Поскольку емкость — это заряд на единицу напряжения, один фарад равен одному кулону на один вольт, или

.

По определению, конденсатор емкостью 1,0 мкФ может сохранять заряд 1,0 К (очень большой заряд), когда разность потенциалов между его пластинами составляет всего 1,0 В. Следовательно, один фарад является очень большой емкостью.Типичные значения емкости варьируются от пикофарад (1пФ = 10−12Ф) (1пФ = 10−12Ф) до миллифарадов (1мФ = 10−3Ф) (1мФ = 10−3Ф), что также включает микрофарады (1мкФ = 10−6F1мкФ = 10− 6F). Конденсаторы могут быть разных форм и размеров (рис. 8.4).

Фигура 8,4 Это некоторые типичные конденсаторы, используемые в электронных устройствах. Размер конденсатора не обязательно зависит от его емкости. (Источник: Windell Oskay)

Расчет емкости

Мы можем рассчитать емкость пары проводов с помощью следующего стандартного подхода.

Стратегия решения проблем

Расчет емкости

1. Предположим, что конденсатор имеет заряд Q .
2. Определить электрическое поле E → E → между проводниками. Если в расположении проводников присутствует симметрия, вы можете использовать закон Гаусса для этого расчета.
3. Найдите разность потенциалов между проводниками из VB − VA = −ABE → · dl →, VB − VA = −ABE → · dl →,

   8,2

   где путь интегрирования ведет от одного проводника к другому.Тогда величина разности потенциалов равна V = | VB-VA | V = | VB-VA |.
4. Зная В, , определите емкость непосредственно из уравнения 8.1.

Чтобы показать, как работает эта процедура, мы теперь вычисляем емкости параллельных пластин, сферических и цилиндрических конденсаторов. Во всех случаях мы предполагаем вакуумные конденсаторы (пустые конденсаторы) без диэлектрического вещества в пространстве между проводниками.

Конденсатор с параллельными пластинами

Конденсатор с параллельными пластинами (рисунок 8.5) имеет две идентичные токопроводящие пластины, каждая с площадью поверхности A, , разделенными расстоянием d . Когда на конденсатор подается напряжение В, , он сохраняет заряд Q , как показано. Мы можем увидеть, как его емкость может зависеть от A и d , рассматривая характеристики кулоновской силы. Мы знаем, что сила между зарядами увеличивается с увеличением заряда и уменьшается с расстоянием между ними. Следует ожидать, что чем больше пластины, тем больше заряда они могут хранить.Таким образом, C должно быть больше для большего значения A . Точно так же, чем ближе пластины расположены друг к другу, тем сильнее на них притяжение противоположных зарядов. Следовательно, C должно быть больше для меньшего d .

Фигура 8,5 В конденсаторе с параллельными пластинами, разделенными пластинами на расстояние d , каждая пластина имеет одинаковую площадь поверхности A, .

Определим плотность поверхностного заряда σσ на пластинах как

Из предыдущих глав мы знаем, что когда d мало, электрическое поле между пластинами довольно однородно (без учета краевых эффектов) и что его величина определяется как

.

где постоянная ε0ε0 — диэлектрическая проницаемость свободного пространства, ε0 = 8.85 × 10–12Ф / м. Ε0 = 8,85 × 10–12Ф / м. Единица СИ в Ф / м эквивалентна C2 / N · m2.C2 / N · m2. Поскольку электрическое поле E → E → между пластинами однородно, разность потенциалов между пластинами составляет

V = Ed = σdε0 = Qdε0A.V = Ed = σdε0 = Qdε0A.

Следовательно, уравнение 8.1 дает емкость конденсатора с параллельными пластинами как

C = QV = QQd / ε0A = ε0Ad.C = QV = QQd / ε0A = ε0Ad.

8,3

Обратите внимание на это уравнение, что емкость является функцией только геометрии и того, какой материал заполняет пространство между пластинами (в данном случае вакуум) этого конденсатора.Фактически, это верно не только для конденсатора с параллельными пластинами, но и для всех конденсаторов: емкость не зависит от Q или В . При изменении заряда соответственно изменяется и потенциал, так что Q / V остается постоянным.

Пример 8.1

Емкость и заряд в конденсаторе с параллельными пластинами

(а) Какова емкость пустого конденсатора с параллельными пластинами с металлическими пластинами, каждая из которых имеет площадь 1?00м21.00м2, расстояние между которыми составляет 1,00 мм? (b) Сколько заряда хранится в этом конденсаторе, если к нему приложено напряжение 3,00 × 103 В3,00 × 103 В?

Стратегия

Определение емкости C представляет собой прямое применение уравнения 8.3. Найдя C , мы сможем найти накопленный заряд, используя уравнение 8.1.

Решение

1. Ввод заданных значений в уравнение 8.3 дает C = ε0Ad = (8,85 × 10−12Fm) 1,00м21,00 × 10−3м = 8,85 × 10−9F = 8,85nF.C = ε0Ad = (8,85 × 10−12Fm) 1,00м21.00 × 10−3m = 8,85 × 10−9F = 8,85 нФ. Это небольшое значение емкости указывает на то, насколько сложно изготовить устройство с большой емкостью.
2. Обращение уравнения 8.1 и ввод известных значений в это уравнение дает Q = CV = (8,85 × 10–9F) (3,00 × 103 В) = 26,6 мкКл. Q = CV = (8,85 × 10–9F) (3,00 × 103 В) = 26,6 мкКл.

Значение

Этот заряд лишь немного больше, чем в типичных приложениях для статического электричества. Поскольку воздух разрушается (становится проводящим) при напряженности электрического поля около 3.0 МВ / м, на этом конденсаторе больше нельзя накапливать заряд при увеличении напряжения.

Пример 8,2

Конденсатор с параллельными пластинами, 1 Ф

Предположим, вы хотите сконструировать конденсатор с параллельными пластинами емкостью 1,0 F. Какую площадь вы должны использовать для каждой пластины, если пластины разделены на 1,0 мм?

Решение

Преобразуя уравнение 8.3, получаем A = Cdε0 = (1.0F) (1.0 × 10−3m) 8.85 × 10−12F / m = 1.1 × 108m2 A = Cdε0 = (1.0F) (1.0 × 10−3m) 8,85 × 10−12F / m = 1,1 × 108 м2.

Каждая квадратная пластина должна быть 10 км в поперечнике.Раньше было обычным розыгрышем — попросить студента пойти в склад лаборатории и попросить конденсатор с параллельными пластинами 1F, пока обслуживающий персонал не устанет от этой шутки.

Проверьте свое понимание 8.1

Проверьте свое понимание Емкость конденсатора с параллельными пластинами составляет 2,0 пФ. Если площадь каждой пластины составляет 2,4 см 22,4 см2, каково расстояние между пластинами?

Проверьте свое понимание 8,2

Проверьте свое понимание Убедитесь, что σ / Vσ / V и ε0 / dε0 / d имеют одинаковые физические единицы.

Сферический конденсатор

Сферический конденсатор — это еще один набор проводников, емкость которых можно легко определить (рис. 8.6). Он состоит из двух концентрических проводящих сферических оболочек радиусов R1R1 (внутренняя оболочка) и R2R2 (внешняя оболочка). Оболочкам приписываются равные и противоположные заряды + Q + Q и −Q − Q соответственно. Из-за симметрии электрическое поле между оболочками направлено радиально наружу. Мы можем получить величину поля, применив закон Гаусса к сферической гауссовой поверхности радиусом r , концентричной оболочкам.dr) = Q4πε0∫R1R2drr2 = Q4πε0 (1R1−1R2).

В этом уравнении разность потенциалов между пластинами равна V = — (V2 − V1) = V1 − V2V = — (V2 − V1) = V1 − V2. Мы подставляем этот результат в уравнение 8.1, чтобы найти емкость сферического конденсатора:

C = QV = 4πε0R1R2R2 − R1.C = QV = 4πε0R1R2R2 − R1.

8,4

Фигура 8,6 Сферический конденсатор состоит из двух концентрических проводящих сфер. Обратите внимание, что заряды на проводнике находятся на его поверхности.

Пример 8.3

Емкость изолированной сферы

Вычислите емкость одиночной изолированной проводящей сферы радиуса R1R1 и сравните ее с уравнением 8.4 в пределе R2 → ∞R2 → ∞.

Стратегия

Мы предполагаем, что заряд на сфере равен Q , и поэтому следуем четырем шагам, описанным ранее. Мы также предполагаем, что другой проводник представляет собой концентрическую полую сферу бесконечного радиуса.

Решение

На внешней стороне изолированной проводящей сферы электрическое поле задается уравнением 8.dr) = Q4πε0∫R1 + ∞drr2 = 14πε0QR1.

Таким образом, емкость изолированной сферы равна

. C = QV = Q4πε0R1Q = 4πε0R1.C = QV = Q4πε0R1Q = 4πε0R1.

Значение

Тот же результат можно получить, взяв предел уравнения 8.4 при R2 → ∞R2 → ∞. Таким образом, одиночная изолированная сфера эквивалентна сферическому конденсатору, внешняя оболочка которого имеет бесконечно большой радиус.

Проверьте свое понимание 8,3

Проверьте свое понимание Радиус внешней сферы сферического конденсатора в пять раз больше радиуса его внутренней оболочки.Каковы размеры этого конденсатора, если его емкость 5,00 пФ?

Цилиндрический конденсатор

Цилиндрический конденсатор состоит из двух концентрических проводящих цилиндров (рисунок 8.7). Внутренний цилиндр радиуса R1R1 может быть либо оболочкой, либо полностью твердым. Внешний цилиндр представляет собой оболочку внутреннего радиуса R2R2. Мы предполагаем, что длина каждого цилиндра составляет l и что избыточные заряды + Q + Q и -Q − Q находятся на внутреннем и внешнем цилиндрах соответственно.

Фигура 8,7 Цилиндрический конденсатор состоит из двух концентрических проводящих цилиндров. Здесь заряд на внешней поверхности внутреннего цилиндра положительный (обозначен ++), а заряд на внутренней поверхности внешнего цилиндра отрицательный (обозначен −−).

Без учета краевых эффектов электрическое поле между проводниками направлено радиально наружу от общей оси цилиндров. Используя гауссову поверхность, показанную на рисунке 8. dA = E (2πrl) = Qε0.dr) = Q2πε0l∫R1R2drr = Q2πε0llnr | R1R2 = Q2πε0llnR2R1.

Таким образом, емкость цилиндрического конденсатора

C = QV = 2πε0lln (R2 / R1). C = QV = 2πε0lln (R2 / R1).

8,6

Как и в других случаях, эта емкость зависит только от геометрии расположения проводников. Важным применением уравнения 8.6 является определение емкости на единицу длины коаксиального кабеля , который обычно используется для передачи изменяющихся во времени электрических сигналов. Коаксиальный кабель состоит из двух концентрических цилиндрических проводников, разделенных изоляционным материалом.(Здесь мы предполагаем наличие вакуума между проводниками, но физика качественно почти такая же, когда пространство между проводниками заполнено диэлектриком.) Эта конфигурация экранирует электрический сигнал, распространяющийся по внутреннему проводнику, от паразитных электрических полей, внешних по отношению к проводнику. кабель. Ток течет в противоположных направлениях во внутреннем и внешнем проводниках, при этом внешний провод обычно заземлен. Теперь из уравнения 8.6 емкость коаксиального кабеля на единицу длины равна

. Cl = 2πε0ln (R2 / R1).Cl = 2πε0ln (R2 / R1).

В практических приложениях важно выбирать конкретные значения C / l . Это может быть достигнуто за счет соответствующего выбора радиусов проводников и изоляционного материала между ними.

Проверьте свое понимание 8,4

Проверьте свое понимание Когда цилиндрический конденсатор получает заряд 0,500 нКл, между цилиндрами измеряется разность потенциалов 20,0 В. а) Какова емкость этой системы? (b) Если цилиндры 1.Длина 0 м, каково соотношение их радиусов?

Несколько типов конденсаторов, которые можно использовать на практике, показаны на рис. 8.4. Обычные конденсаторы часто состоят из двух небольших кусочков металлической фольги, разделенных двумя небольшими кусочками изоляции (см. Рисунок 8.2 (b)). Металлическая фольга и изоляция покрыты защитным покрытием, а два металлических вывода используются для подключения фольги к внешней цепи. Некоторые распространенные изоляционные материалы — это слюда, керамика, бумага и антипригарное покрытие Teflon ™.

Другой популярный тип конденсатора — электролитический конденсатор.Он состоит из окисленного металла в проводящей пасте. Основным преимуществом электролитического конденсатора является его высокая емкость по сравнению с другими распространенными типами конденсаторов. Например, емкость одного типа алюминиевого электролитического конденсатора может достигать 1,0 F. Однако вы должны быть осторожны при использовании электролитического конденсатора в цепи, потому что он работает правильно только тогда, когда металлическая фольга находится под более высоким потенциалом, чем проводящая паста. Когда возникает обратная поляризация, электролитическое действие разрушает оксидную пленку.Этот тип конденсатора не может быть подключен к источнику переменного тока, потому что в половине случаев переменное напряжение будет иметь неправильную полярность, поскольку переменный ток меняет свою полярность (см. Схемы переменного тока в цепях переменного тока).

Конденсатор переменного тока (рисунок 8.8) имеет два набора параллельных пластин. Один набор пластин закреплен (обозначен как «статор»), а другой набор пластин прикреплен к валу, который может вращаться (обозначается как «ротор»). Поворачивая вал, можно изменять площадь поперечного сечения в перекрытии пластин; следовательно, емкость этой системы может быть настроена на желаемое значение.Настройка конденсатора может применяться в любом типе радиопередачи и при приеме радиосигналов от электронных устройств. Каждый раз, когда вы настраиваете автомобильное радио на любимую станцию, думайте о емкости.

Фигура 8,8 В переменном воздушном конденсаторе емкость можно регулировать, изменяя эффективную площадь пластин. (кредит: модификация работы Робби Спрула)

Символы, показанные на рисунке 8.9, представляют собой схемные изображения различных типов конденсаторов.Обычно мы используем символ, показанный на рис. 8.9 (а). Символ на Рисунке 8.9 (c) представляет конденсатор переменной емкости. Обратите внимание на сходство этих символов с симметрией конденсатора с параллельными пластинами. Электролитический конденсатор представлен символом на рис. 8.9 (b), где изогнутая пластина обозначает отрицательный вывод.

Фигура 8.9 Здесь показаны три различных схемных представления конденсаторов. Символ в (а) является наиболее часто используемым.Символ в (b) представляет собой электролитический конденсатор. Символ в (c) представляет конденсатор переменной емкости.

Интересный прикладной пример модели конденсатора взят из клеточной биологии и имеет дело с электрическим потенциалом в плазматической мембране живой клетки (рис. 8.10). Клеточные мембраны отделяют клетки от их окружения, но позволяют некоторым отобранным ионам проходить внутрь или из клетки. Разность потенциалов на мембране составляет около 70 мВ. Клеточная мембрана может иметь толщину от 7 до 10 нм.Рассматривая клеточную мембрану как наноразмерный конденсатор, оценка наименьшей напряженности электрического поля на ее « пластинах » дает значение E = Vd = 70 × 10−3V10 × 10−9m = 7 × 106V / m> 3MV / mE. = Vd = 70 × 10−3V10 × 10−9m = 7 × 106V / m> 3MV / m.

Этой величины электрического поля достаточно, чтобы вызвать электрическую искру в воздухе.

Фигура 8.10 Полупроницаемая мембрана биологической клетки имеет разные концентрации ионов на внутренней поверхности, чем на внешней.Диффузия перемещает ионы K + K + (калий) и Cl – Cl– (хлорид) в показанных направлениях, пока кулоновская сила не остановит дальнейший перенос. Таким образом, внешняя поверхность мембраны приобретает положительный заряд, а ее внутренняя поверхность приобретает отрицательный заряд, создавая разность потенциалов на мембране. Мембрана обычно непроницаема для Na + (ионов натрия).

конденсаторов последовательно и параллельно

Цели обучения

К концу этого раздела вы сможете:

• Выведите выражения для полной емкости последовательно и параллельно.
• Обозначает последовательные и параллельные части при соединении конденсаторов.
• Рассчитайте эффективную емкость последовательно и параллельно с учетом индивидуальных емкостей.

Несколько конденсаторов могут быть соединены вместе в различных приложениях. Несколько подключений конденсаторов действуют как один эквивалентный конденсатор. Общая емкость этого эквивалентного одиночного конденсатора зависит как от отдельных конденсаторов, так и от способа их подключения.Существует два простых и распространенных типа соединений, которые называются серии и параллельно , для которых мы можем легко вычислить общую емкость. Некоторые более сложные соединения также могут быть связаны с комбинациями последовательного и параллельного.

Емкость серии

На рисунке 1а показано последовательное соединение трех конденсаторов с приложенным напряжением. Как и для любого конденсатора, емкость комбинации связана с зарядом и напряжением [латекс] C = \ frac {Q} {V} \\ [/ latex].

Обратите внимание на рисунок 1, что противоположные заряды величиной Q протекают по обе стороны от первоначально незаряженной комбинации конденсаторов при приложении напряжения В . Для сохранения заряда необходимо, чтобы на пластинах отдельных конденсаторов создавались заряды одинаковой величины, поскольку заряд разделяется только в этих изначально нейтральных устройствах. Конечным результатом является то, что комбинация напоминает одиночный конденсатор с большим эффективным разделением пластин, чем у отдельных конденсаторов.(См. Рисунок 1b.) Чем больше расстояние между пластинами, тем меньше емкость. Общей особенностью последовательного соединения конденсаторов является то, что общая емкость меньше любой из отдельных емкостей.

Рис. 1. (a) Конденсаторы, подключенные последовательно. Величина заряда на каждой пластине равна Q. (b) Эквивалентный конденсатор имеет большее расстояние между пластинами d. При последовательном соединении общая емкость меньше, чем у любого из отдельных конденсаторов.

Мы можем найти выражение для общей емкости, рассматривая напряжение на отдельных конденсаторах, показанных на рисунке 1.Решение [latex] C = \ frac {Q} {V} \\ [/ latex] для V дает [latex] V = \ frac {Q} {C} \\ [/ latex]. Таким образом, напряжения на отдельных конденсаторах равны [латексному] V_1 = \ frac {Q} {C_1}, V_2 = \ frac {Q} {C_2}, \ text {и} V_3 = \ frac {Q} {C_3} \\ [/латекс].

Общее напряжение складывается из отдельных напряжений:

V = V ₁ + V ₂ + V ₃ .

Теперь, называя общую емкость C _S последовательной емкостью, считайте, что

[латекс] V = \ frac {Q} {C _ {\ text {S}}} = V_1 + V_2 + V_3 \\ [/ latex].

Вводя выражения для V ₁ , V ₂ и V ₃ , получаем

[латекс] \ frac {Q} {C _ {\ text {S}}} = \ frac {Q} {C_ {1}} + \ frac {Q} {C_ {2}} + \ frac {Q} { C_ {3}} \\ [/ латекс].

Отменяя Q s, мы получаем уравнение для полной емкости в серии C _S , равной

[латекс] \ frac {1} {C _ {\ text {S}}} = \ frac {1} {C_ {1}} + \ frac {1} {C_ {2}} + \ frac {1} { C_ {3}} + \ точки, \\ [/ latex]

, где «…» означает, что выражение действительно для любого количества конденсаторов, соединенных последовательно.Выражение этой формы всегда приводит к общей емкости C _S , которая меньше любой из отдельных емкостей C ₁ , C ₂ ,…, как показано в примере 1.

Общая емкость в серии,

C _с

Общая емкость в серии:

[латекс] \ frac {1} {C _ {\ text {S}}} = \ frac {1} {C_ {1}} + \ frac {1} {C_ {2}} + \ frac {1} { C_ {3}} + \ dots \\ [/ latex]

Пример 1. Что такое серийная емкость?

Найдите общую емкость для трех последовательно соединенных конденсаторов, учитывая, что их отдельные емкости равны 1.000, 5.000 и 8.000 мкФ.

Стратегия

Имея данную информацию, общую емкость можно найти, используя уравнение для емкости в серии.

Решение

Ввод заданных емкостей в выражение для [latex] \ frac {1} {C _ {\ text {S}}} \\ [/ latex] дает [latex] \ frac {1} {C _ {\ text {S} }} = \ frac {1} {C_ {1}} + \ frac {1} {C_ {2}} + \ frac {1} {C_ {3}} \\ [/ latex].

[латекс] \ frac {1} {C _ {\ text {S}}} = \ frac {1} {1.000 \ mu \ text {F}} + \ frac {1} {5.000 \ mu \ text {F} } + \ frac {1} {8.000 \ mu \ text {F}} = \ frac {1.325} {\ mu \ text {F}} \\ [/ latex]

Преобразование для нахождения C _S дает [латекс] C _ {\ text {S}} = \ frac {1.325} {\ mu \ text {F}} = 0,755 \ mu \ text {F} \\ [/ латекс].

Обсуждение

Общая последовательная емкость C _с меньше наименьшей индивидуальной емкости, как было обещано. При последовательном соединении конденсаторов сумма меньше деталей. На самом деле это меньше, чем у любого человека. Обратите внимание, что иногда возможно и более удобно решить уравнение, подобное приведенному выше, путем нахождения наименьшего общего знаменателя, который в данном случае (показаны только вычисления целых чисел) равен 40.Таким образом,

[латекс] \ frac {1} {C _ {\ text {S}}} = \ frac {40} {40 \ mu \ text {F}} + \ frac {8} {40 \ mu \ text {F} } + \ frac {5} {40 \ mu \ text {F}} = \ frac {53} {40 \ mu \ text {F}} \\ [/ latex]

, так что

[латекс] C _ {\ text {S}} = \ frac {40 \ mu \ text {F}} {53} = 0,755 \ mu \ text {F} \\ [/ latex]

Параллельные конденсаторы

На рис. 2а показано параллельное соединение трех конденсаторов с приложенным напряжением. Здесь общую емкость найти легче, чем в последовательном случае. Чтобы найти эквивалентную общую емкость C _p , сначала отметим, что напряжение на каждом конденсаторе составляет В, , то же самое, что и у источника, поскольку они подключены к нему напрямую через проводник.(Проводники являются эквипотенциальными, поэтому напряжение на конденсаторах такое же, как и на источнике напряжения.) Таким образом, конденсаторы имеют такой же заряд, как и при индивидуальном подключении к источнику напряжения. Общая сумма начислений Q представляет собой сумму отдельных сборов: Q = Q ₁ + Q ₂ + Q ₃ .

Рис. 2. (a) Конденсаторы, включенные параллельно. Каждый из них подключен непосредственно к источнику напряжения, как если бы он был полностью один, поэтому общая параллельная емкость — это просто сумма отдельных емкостей.(b) Эквивалентный конденсатор имеет большую площадь пластины и поэтому может удерживать больше заряда, чем отдельные конденсаторы.

Используя соотношение Q = CV , мы видим, что общий заряд равен Q = C _p V , а индивидуальные расходы равны Q ₁ = C ₁ V , Q ₂ = C ₂ V , и Q ₃ = C ₃ V .Ввод их в предыдущее уравнение дает

C _p V = C ₁ V + C ₂ V + C ₃ V .

Исключая из уравнения В , получаем уравнение для полной емкости параллельно

C _p : C _p = C ₁ + C ₂ + C ₃ +….

Общая емкость при параллельном подключении — это просто сумма отдельных емкостей. (И снова «… » указывает на то, что выражение действительно для любого количества конденсаторов, подключенных параллельно.) Так, например, если конденсаторы в Примере 1 были подключены параллельно, их емкость была бы

C _p = 1.000 мкФ + 5.000 мкФ + 8.000 мкФ = 14000 мкФ.

Эквивалентный конденсатор для параллельного соединения имеет значительно большую площадь пластины и, следовательно, большую емкость, как показано на рисунке 2b.

Общая емкость параллельно,

C _p

Общая емкость параллельно C _p = C ₁ + C ₂ + C ₃ +…

Более сложные соединения конденсаторов иногда могут быть последовательными и параллельными. (См. Рис. 3.) Чтобы найти общую емкость таких комбинаций, мы идентифицируем последовательные и параллельные части, вычисляем их емкости, а затем находим общую.

Рис. 3. (a) Эта схема содержит как последовательные, так и параллельные соединения конденсаторов. См. Пример 2 для расчета общей емкости цепи. (b) C ₁ и C ₂ идут последовательно; их эквивалентная емкость C _S меньше, чем у любого из них. (c) Обратите внимание, что C _S находится параллельно с C ₃ . Таким образом, общая емкость равна сумме C _S и C ₃ .

Пример 2. Смесь последовательной и параллельной емкостей

Найдите общую емкость комбинации конденсаторов, показанной на рисунке 3. Предположим, что емкости на рисунке 3 известны с точностью до трех десятичных знаков ( C ₁ = 1.000 мкФ, C ₂ = 3.000 мкФ и C ₃ = 8.000 мкФ) и округлите ответ до трех десятичных знаков.

Стратегия

Чтобы определить общую емкость, мы сначала определяем, какие конденсаторы включены последовательно, а какие — параллельно.Конденсаторы C ₁ и C ₂ идут последовательно. Их комбинация, обозначенная на рисунке C _S , параллельна C ₃ .

Решение

Поскольку C ₁ и C ₂ включены последовательно, их общая емкость определяется как [латекс] \ frac {1} {C _ {\ text {S}}} = \ frac {1} { C_ {1}} + \ frac {1} {C_ {2}} + \ frac {1} {C_ {3}} \\ [/ latex]. Ввод их значений в уравнение дает

[латекс] \ frac {1} {C _ {\ text {S}}} = \ frac {1} {C_ {1}} + \ frac {1} {C_ {2}} = \ frac {1} { 1.000 \ mu \ text {F}} + \ frac {1} {5.000 \ mu \ text {F}} = \ frac {1.200} {\ mu \ text {F}} \\ [/ latex].

Инвертирование дает C _S = 0,833 мкФ.

Эта эквивалентная последовательная емкость подключена параллельно третьему конденсатору; Таким образом, общая сумма составляет

[латекс] \ begin {array} {lll} C _ {\ text {tot}} & = & C _ {\ text {S}} + C _ {\ text {S}} \\\ text {} & = & 0.833 \ mu \ text {F} +8.000 \ mu \ text {F} \\\ text {} & = & 8.833 \ mu \ text {F} \ end {array} \\ [/ latex]

Обсуждение

Этот метод анализа комбинаций конденсаторов по частям, пока не будет получена общая сумма, может быть применен к более крупным комбинациям конденсаторов.

Сводка раздела

• Общая емкость последовательно [латекс] \ frac {1} {C _ {\ text {S}}} = \ frac {1} {C_ {1}} + \ frac {1} {C_ {2}} + \ гидроразрыв {1} {C_ {3}} + \ dots \\ [/ latex]
• Общая емкость параллельно C _p = C ₁ + C ₂ + C ₃ +…
• Если схема содержит комбинацию конденсаторов, включенных последовательно и параллельно, определите последовательную и параллельную части, вычислите их емкости, а затем найдите общую сумму.

Концептуальные вопросы

1. Если вы хотите хранить большое количество энергии в конденсаторной батарее, подключите ли вы конденсаторы последовательно или параллельно? Объяснять.

Задачи и упражнения

1. Найдите общую емкость комбинации конденсаторов на Рисунке 4.

   Рисунок 4. Комбинация последовательного и параллельного подключения конденсаторов.

2. Предположим, вам нужна конденсаторная батарея с общей емкостью 0.750 Ф, и у вас есть множество конденсаторов емкостью 1,50 мФ. Какое наименьшее число вы могли бы связать вместе, чтобы достичь своей цели, и как бы вы их связали?
3. Какую общую емкость можно получить, соединив вместе конденсатор 5,00 мкФ и конденсатор 8,00 мкФ?
4. Найдите общую емкость комбинации конденсаторов, показанной на рисунке 5.

   Рисунок 5. Комбинация последовательного и параллельного подключения конденсаторов.

5. Найдите общую емкость комбинации конденсаторов, показанной на рисунке 6.

   Рисунок 6. Комбинация последовательного и параллельного подключения конденсаторов.

6. Необоснованные результаты. (a) Конденсатор емкостью 8,00 мкФ подключен параллельно другому конденсатору, что дает общую емкость 5,00 мкФ. Какая емкость у второго конденсатора? б) Что неразумного в этом результате? (c) Какие предположения необоснованны или непоследовательны?

Избранные решения проблем и упражнения

1. 0,293 мкФ

3.3,08 мкФ в последовательном соединении, 13,0 мкФ в параллельном соединении

4. 2,79 мкФ

6. (a) –3,00 мкФ; (б) У вас не может быть отрицательного значения емкости; (c) Предположение, что конденсаторы были подключены параллельно, а не последовательно, было неверным. Параллельное соединение всегда дает большую емкость, в то время как здесь предполагалась меньшая емкость. Это могло произойти, только если конденсаторы подключены последовательно.

Конденсаторы

и формулы для расчета емкости

Конденсаторы — это пассивные устройства. в электронных схемах для хранения энергии в виде электрического поля.Они комплимент индукторы, хранящие энергию в виде магнитного поля. Идеальный конденсатор является эквивалентом разомкнутой цепи (бесконечное сопротивление) для постоянного тока (DC) и представляет собой импеданс (реактивное сопротивление) для переменные токи (AC), зависящие от частоты тока (или напряжения). Реактивное сопротивление (сопротивление току расход) конденсатора обратно пропорционален частоте сигнала, воздействующего на него. Конденсаторы изначально были называемые «конденсаторами» по причине, восходящей к временам Лейденской банки, когда считалось, что электрические заряды накапливаться на пластинах в результате конденсации.

Свойство емкости, которая препятствует изменению напряжения, используется для передачи сигналов с компонент с более высокой частотой, предотвращая прохождение сигналов компонентов с более низкой частотой. Обычное применение конденсатор в РЧ (радиочастотной) цепи — это место, где есть напряжение смещения постоянного тока, которое необходимо заблокировать от присутствия в цепи, позволяя РЧ-сигналу проходить. Источники питания постоянного тока используют большие значения емкости параллельно с выходом. клеммы для сглаживания низкочастотных пульсаций из-за выпрямления и / или переключения форм сигналов.

При использовании последовательно (левый рисунок) или параллельно (правый рисунок) с его комплемент схемы, индуктор, комбинация индуктор-конденсатор образует контур, который резонирует на определенной частоте это зависит от значений каждого компонента. В последовательной цепи сопротивление протеканию тока на резонансной частоте равен нулю с идеальными компонентами. В параллельной цепи (справа) сопротивление протеканию тока бесконечно с идеальными компонентами.

Реальные конденсаторы, состоящие из физических компонентов, демонстрируют больше, чем просто емкость, когда присутствует в цепи переменного тока.Слева показана модель симулятора общей схемы. Он включает в себя собственно идеальный конденсатор с параллельным резистивным подключением. компонент («Утечка»), реагирующий на переменный ток. Эквивалентный резистивный компонент постоянного тока (‘ESR’) последовательно с идеальным конденсатором и эквивалентной последовательной индуктивной составляющей. («ESL») присутствует из-за металлических выводов (если они есть) и характеристик поверхностей пластин. Эта индуктивность в сочетании с емкостью создает резонансную частоту, на которой конденсатор выглядит как чистое сопротивление.

Когда рабочая частота увеличивается за пределы резонанса (также известного как собственная резонансная частота или SRF), схема ведет себя как индуктивность, а не как емкость. Следовательно, требуется тщательное рассмотрение SRF, когда выбор конденсаторов. Симуляторы типа SPICE используют эту или даже более сложную модель для облегчения более точных расчетов. в широком диапазоне частот.

Уравнения для последовательного и параллельного объединения конденсаторов приведены ниже.Для конденсаторов приведены дополнительные уравнения. различной конфигурации. Как показывают эти цифры и формулы, емкость — это мера способности двух поверхностей. для хранения электрического заряда. Разделенный и изолированный диэлектриком (изолятором), чистый положительный заряд накапливается на одна поверхность и чистый отрицательный заряд хранится на другой поверхности. В идеальном конденсаторе заряд будет храниться бесконечно; однако реальные конденсаторы постепенно теряют заряд из-за токов утечки через неидеальный диэлектрик.

Общая емкость последовательно соединенных конденсаторов равна обратной величине сумма обратных величин индивидуальных емкостей. Держите единицы постоянными. Емкость (C в фарадах) двух параллельных пластин равной площади равна произведению площади (A, в метрах) одной пластины, расстояние (d, в метрах), разделяющее пластины, и диэлектрическая проницаемость (ε, в Фарадах на метр) пространства. разделение пластин.ε, полная диэлектрическая проницаемость, является произведением диэлектрической проницаемости свободного пространства, ε 0 , и относительная диэлектрическая проницаемость материала ε r . Обратите внимание, что единицы измерения длины и площади могут быть метрическими. или английский, если они согласованы. Коэффициент рассеяния (DF), также известный как тангенс потерь (tan δ), взаимозаменяемо определяется как величина, обратная коэффициенту качества (QF) или отношению эквивалентного последовательного сопротивления (ESR) и емкостного реактивного сопротивления (X C ).Это показатель степени потери накопленного заряда. DF обычно используется в низкочастотных приложениях, в то время как tan δ чаще используется в высокочастотных приложениях.

Общая емкость параллельно соединенных конденсаторов равна сумме индивидуальных емкости. Держите единицы постоянными. Следующие физические константы и механические размерные переменные применимы к уравнениям на этой странице.Единицы для уравнений показаны в скобках в конце уравнений; например, означает, что длина дана в дюймах, а индуктивность — в единицах Генри. Если единицы не указаны, то можно использовать любые, если они согласованы для всех объектов; т.е. все измерители, все мкФ, пр. C = емкость L = индуктивность W = энергия ε r = относительная диэлектрическая проницаемость (безразмерная) ε 0 = 8,85 x 10 -12 Ф / м (диэлектрическая проницаемость свободного пространства) µ r = Относительная проницаемость (безразмерная) µ 0 = 4π x 10 -7 Гн / м (проницаемость свободного пространства) 1 метр = 3.2808 футов <—> 1 фут = 0,3048 метра 1 мм = 0,03937 дюйма <—> 1 дюйм = 25,4 мм Кроме того, точки (не путать с десятичными знаками) используются для обозначения умножения. во избежание двусмысленности. Емкостное реактивное сопротивление (X C , в Ω) обратно пропорциональна частоте (ω в радианах / сек или f в Гц) и емкости (C в фарадах).Чистая емкость имеет фазовый угол -90 ° (напряжение отстает от тока с фазовым углом 90 °). Заряд (Q, в кулонах) конденсатора Пластины — это произведение емкости (C в фарадах) и напряжения (V в вольтах) на устройстве. Энергия (Вт, в Джоулях) хранится в конденсаторе представляет собой половину произведения емкости (C в фарадах) на напряжение (V в вольтах) на устройстве. Ток действительно течет «через» идеальный конденсатор. Напротив, заряд, накопленный на его пластинах, передается в подключенную цепь, тем самым облегчая ток. поток. И наоборот, сетевое напряжение, приложенное к пластинам, вызывает протекание тока в подключенной цепи по мере накопления заряда. на тарелках. Добротность безразмерная. отношение реактивного сопротивления к сопротивлению в конденсаторе.

Связанные страницы RF Cafe
— Конденсаторы и Расчет емкости
— Конденсатор Цветовые коды
— Преобразование емкости
— Конденсатор Диэлектрики
— Стандартные значения конденсаторов
— Поставщики конденсаторов
— Благородное искусство разъединения

Емкость

• • Что такое емкость?
• • Диэлектрик.
• • диэлектрическая проницаемость.
• • Диэлектрическая прочность и максимальное рабочее напряжение.
• • Расчет заряда конденсатора.

Емкость

Количество энергии, которое может хранить конденсатор, зависит от величины или ЕМКОСТИ конденсатора. Емкость (символ C) измеряется в базовой единице FARAD (символ F). Один фарад — это величина емкости, которая может хранить 1 кулон (6.24 x 10 ¹⁸ электронов) при зарядке до напряжения 1 вольт. Однако Фарада слишком большая единица для использования в электронике, поэтому следующие единицы емкости более полезны.

Дополнительный блок	Сокращение	Стандартное обозначение
мкФ	мкФ	х 10 -6
нано Фарады	нФ	х 10 -9
пико Фарадс	пФ	х 10 -12

Однако помните, что при решении задач, связанных с емкостью, формулы и используемые значения должны быть в основных единицах измерения: фарадах, вольтах и ​​т. Д.Поэтому при вводе значения 0,47 нФ, например, в формулу (или ваш калькулятор), его следует вводить в фарадах, используя версию стандартной формы для технических обозначений: 0,47 x 10 ^-9 (Загрузите буклет «Советы по математике», чтобы узнать больше Информация).

Емкость зависит от четырех вещей;

1. Площадь пластин

2. Расстояние между пластинами

3. Тип диэлектрического материала

4. Температура

Из этих четырех наименьшее влияние на большинство конденсаторов оказывает температура.Стоимость большинства конденсаторов довольно стабильна в «нормальном» диапазоне температур.

Значения конденсатора могут быть фиксированными или переменными. Большинство переменных конденсаторов имеют очень маленькое значение (несколько десятков или сотен пФ). Значение может быть изменено на:

.

• • Изменение площади пластин.
• • Изменение толщины диэлектрика.

Емкость (C) ПРЯМО ПРОПОРЦИОНАЛЬНА ПЛОЩАДИ ДВУХ ПЛАСТИН , которые непосредственно перекрывают друг друга, чем больше площадь перекрытия, тем больше емкость.

Емкость ОБРАТНО ПРОПОРЦИОНАЛЬНО РАССТОЯНИЮ МЕЖДУ ПЛАСТИНАМИ. т.е. если пластины раздвигаются, емкость уменьшается.

Диэлектрик

Электроны на одной пластине конденсатора воздействуют на электроны на другой пластине, вызывая искажение орбит электронов в диэлектрическом материале (изолирующем слое между пластинами). Величина искажения зависит от природы диэлектрического материала и измеряется диэлектрической проницаемостью материала.

Разрешающая способность

Проницаемость указывается для любого конкретного материала как ОТНОСИТЕЛЬНАЯ ДОПУСТИМОСТЬ, которая является мерой эффективности диэлектрического материала. Это число без единиц измерения, которое указывает, насколько диэлектрическая проницаемость материала больше, чем диэлектрическая проницаемость воздуха (или вакуума), для которого задана диэлектрическая проницаемость 1 (единица). Например, если диэлектрический материал, такой как слюда, имеет относительную диэлектрическую проницаемость 6, это означает, что конденсатор будет иметь диэлектрическую проницаемость, а значит, и емкость, в шесть раз больше, чем у конденсатора с такими же размерами, но диэлектриком которого является воздух.

Диэлектрическая прочность

Другой важный аспект диэлектрика — ДИЭЛЕКТРИЧЕСКАЯ ПРОЧНОСТЬ. это указывает на способность диэлектрика выдерживать напряжение, приложенное к нему, когда конденсатор заряжен. В идеале диэлектрик должен быть как можно более тонким, чтобы обеспечить максимальную емкость для данного размера компонента. Однако чем тоньше диэлектрический слой, тем легче разрушаются его изоляционные свойства. Таким образом, диэлектрическая прочность определяет максимальное рабочее напряжение конденсатора.

Максимальное рабочее напряжение (VDCwkg max)

При использовании конденсаторов очень важно, чтобы максимальное рабочее напряжение, указанное производителем, не превышалось. В противном случае существует большая опасность внезапного пробоя изоляции внутри конденсатора. Поскольку в это время на конденсаторе существует максимальное напряжение (отсюда и пробой), большие токи будут протекать с реальным риском возгорания или взрыва в некоторых цепях.

Заряд конденсатора.

Заряд (Q) конденсатора зависит от комбинации вышеперечисленных факторов, которые можно представить вместе как емкость (C) и приложенное напряжение (V). Для компонента данной емкости соотношение между напряжением и зарядом является постоянным. Увеличение приложенного напряжения приводит к пропорциональному увеличению заряда. Эту связь можно выразить формулой;

Q = CV

или

C = Q / V

или

V = Q / C

Где V — приложенное напряжение в вольтах.

C — емкость в Фарадах.

Q — количество заряда в кулонах.

Итак, любое из этих количеств может быть найдено, если известны два других. Формулы можно легко переставить, используя простой треугольник, аналогичный тому, который используется для расчета закона Ома при проведении расчетов резисторов.

Конденсаторы

и емкость

Различные типы конденсаторов

Конденсатор — электронное устройство для накопления заряда.Конденсаторы можно найти почти во всех электронных схемах, кроме самых простых. Есть много разных типов конденсаторов, но все они работают одинаково. Упрощенный вид конденсатора представляет собой пару металлических пластин, разделенных зазором, в котором находится изолирующий материал, известный как диэлектрик. Этот упрощенный конденсатор также выбран, поскольку символ электронной схемы для конденсатора представляет собой пару параллельных пластин, как показано на рисунке 1.

Рис. 1. Символ неполяризованного конденсатора.

Обычно электроны не могут войти в проводник, если не существует пути для выхода равного количества электронов. Однако лишние электроны могут быть «втиснуты» в проводник без пути для выхода, если электрическое поле может развиваться в пространстве относительно другого проводника. Количество дополнительных свободных электронов, добавленных к проводнику (или отнятых свободных электронов), прямо пропорционально величине потока поля между двумя проводниками.

В этом упрощенном конденсаторе диэлектрик — воздух.Когда на клеммы конденсатора подается напряжение В , электроны перетекают на одну из пластин и уносятся с другой пластины. Общее количество электронов в конденсаторе остается прежним. На одной отрицательной пластине их больше, а на положительной — меньше.

Рисунок 2. Зарядка конденсатора от аккумулятора

Если бы напряжение было увеличено, увеличившаяся разность потенциалов между пластинами подтолкнула бы больше электронов к отрицательно заряженной пластине.Мы могли измерить заряд, накопленный на пластине, в зависимости от различных приложенных напряжений.

При нулевом напряжении пластины конденсатора нейтральны, поэтому заряд не сохраняется. (мы предполагаем, что мы начали с полностью разряженного конденсатора), при напряжении V заряд на пластинах равен Q, а при удвоенном напряжении заряд удваивается. Мы обнаруживаем, что с увеличением напряжения заряд увеличивается линейно. Мы можем построить это как прямую линию.

Предположим, что мы уходим, проводим некоторые исследования и возвращаемся с лучшим конденсатором, который хранит больше заряда для данного напряжения, мы можем построить график зависимости сохраненного заряда от приложенного напряжения.

Это можно было бы представить как другую линию с более крутым уклоном.Если бы мы построили много графиков для разных конденсаторов, мы получили бы много прямых линий. Мы можем сказать, что мера емкости — это то, сколько заряда сохраняется при заданном напряжении. Иногда это выражается как Q = CV .

Конечно, при зарядке конденсатора должна выполняться работа по перемещению заряда. Следовательно, энергия должна подаваться, и эта энергия доступна, когда конденсатор разряжен.

Проделанная работа определяется как W = qV .Первоначально заряд легко перемещается на пластины конденсатора, однако по мере того, как больше заряда перемещается на пластины конденсатора, сила отталкивания между зарядами затрудняет добавление заряда, когда сила отталкивания зарядов равна мощности батареи, больше нельзя перемещать заряд на пластины. Следовательно, средняя работа составляет 1/2 qV . Если мы посмотрим на наш график зависимости заряда от напряжения, то увидим, что это то же самое, что и площадь под кривой. В общем, проделанная работа равна переданной энергии.Математически,

Факторы, влияющие на емкость

Как увеличить емкость конденсатора с параллельными пластинами? На емкость конденсатора с параллельными пластинами влияют три фактора.

Площадь

Конденсатор переменной емкости

Увеличивая площадь пластин, мы можем поместить на пластины больше заряда, прежде чем силы отталкивания станут проблемой. Следовательно, емкость пропорциональна площади перекрытия пластин.В переменном конденсаторе площадь перекрытия может быть увеличена или уменьшена путем вращения взаимопроникающих пластин, таким образом увеличивая или уменьшая емкость. Пластины электролитических конденсаторов протравлены для получения шероховатой поверхности, которая еще больше увеличивает площадь поверхности.

Отделение

Уменьшение расстояния между пластинами снижает напряжение конденсатора, поскольку электрическое поле не зависит от расстояния между пластинами. Напряжение на конденсаторе В = Ед.Следовательно, напряжение увеличивается. Для постоянного заряда Q , C = Q / V = ​​Q / Ed.

Диэлектрическая проницаемость

Емкость конденсатора с параллельными пластинами определяется как C = ε _r A / d , где A — площадь пластин, d — расстояние между пластинами, а ε _r — площадь пластин. относительная проницаемость диэлектрика между пластинами. Относительная проницаемость — это некоторый коэффициент, K , умножающий допустимость свободного пространства ε ₀ .ε ₀ имеет значение 8,85×10 ^-12 F.m ^-1 .

Полный список относительных допусков можно найти практически для любого диэлектрического материала. Чем больше относительная проницаемость, тем больше емкость конденсатора. Хорошие материалы — слюда, полистирол, масло.

ε _r = K ε ₀

Конденсаторные сети

Рисунок 3. Последовательные и параллельные сети конденсаторов

серии

Рассмотрим последовательную сеть конденсаторов, показанную на рисунке 3a.где положительная пластина соединена с отрицательной пластиной следующего. Какова эквивалентная емкость сети? Посмотрите на пластины посередине, эти пластины физически отключены от цепи, поэтому общий заряд на них должен оставаться постоянным. Следовательно, когда на оба конденсатора подается напряжение, заряд + Q на положительной пластине конденсатора C ₁ должен уравновешиваться зарядом — Q на отрицательной пластине конденсатора C. ₂ .В результате оба конденсатора обладают одинаковым зарядом Q. Падения потенциала В ₁ и В ₂ на двух конденсаторах в целом различаются. Однако сумма этих падений равна общему падению потенциала В , приложенному к входным и выходным проводам. В = В ₁ + В ₂ . Эквивалентная емкость пары снова составляет C _T = Q / V .Таким образом, 1/ C _T = V / Q = ( V ₁ + V ₂ ) / Q = V ₁ / Q + V ₂ / Q подача

Как правило, для конденсаторов Н, соединенных последовательно , это

Соединяя конденсаторы в сериях, вы сохраняете меньше заряда, поэтому есть ли смысл подключать конденсаторы последовательно? Иногда это делается потому, что конденсаторы имеют максимальное рабочее напряжение, и, если последовательно соединить два конденсатора с максимальным напряжением 900 вольт, вы можете увеличить рабочее напряжение до 1800 вольт.

Параллельный

Для параллельной схемы, такой как на рисунке 3b. напряжения одинаковы для всех компонентов. Однако общий заряд делится между двумя конденсаторами, поскольку он должен распределяться таким образом, чтобы напряжение на них было одинаковым. Кроме того, поскольку конденсаторы могут иметь разные емкости C ₁ и C ₂ , заряды Q ₁ и Q ₂ также должны быть разными.Эквивалентная емкость C _T пары конденсаторов — это просто отношение Q / V , где Q = Q ₁ + Q ₂ — это общий накопленный заряд. Отсюда следует, что C _T = Q / V = (Q ₁ + Q ₂ ) / V = Q ₁ / V + Q ₂ / В подача

Из предыдущего обсуждения довольно очевидно, что для конденсаторов Н , включенных параллельно, общая емкость составляет

Общая емкость увеличивается за счет параллельного соединения конденсаторов, поэтому мы получаем большую емкость, чем это возможно при использовании одного конденсатора.В лабораториях физики высоких энергий часто есть большие батареи конденсаторов, которые могут накапливать большое количество энергии, которая высвобождается за очень короткое время. Самая большая батарея конденсаторов в 2006 году может хранить 50 МДж энергии.

Конденсаторы зарядные и разрядные

Цепь, состоящая из батареи, переключателя, резистора и конденсатора в последовательном контуре, называется RC-цепью. Закон Кирхгофа по напряжению для этой схемы имеет вид

V = IR + Q / C .Если выразить чисто в терминах заряда, это становится

V = dQ / dt R + Q / C .

Это дифференциальное уравнение, решение которого является экспоненциальной функцией. Когда переключатель замкнут, конденсатор со временем заряжается:

Q = Q _f (1 — e ^{-t / RC} ),

, где Q — это заряд в момент времени t , а Q _f — последний заряд конденсатора.Обратите внимание, что Q никогда не равно Q _f , но поскольку t становится чрезвычайно большим, Q становится произвольно близким к Q _f . Произведение RC называется постоянной времени RC и является характеристической величиной RC цепи. Когда t = RC , конденсатор заряжен до доли (1 — 1/ e , около 63%) от своего окончательного значения. Необходимо использовать постоянную времени, а не какое-то конечное время, поскольку процесс асимптотический.Его значение — произвольный выбор; мы, естественно, выбираем значение в терминах экспоненциального основания (когда показатель отрицательный).

Мигающая анимация 1. Измените значения резистора и конденсатора, чтобы увидеть влияние на время достижения конденсатором пикового напряжения.

Flash Animation 2. Зарядите конденсатор, пока он не достигнет пика, а затем разрядите его. Как значения R и C влияют на процессы?

Типы конденсаторов

Конденсаторы электролитические

Алюминиевые электролитические конденсаторы изготавливаются путем наложения электролитической бумаги между анодной и катодной фольгами и последующего наматывания результата.Процесс изготовления электрода, обращенного к поверхности протравленной анодной фольги, чрезвычайно сложен. Следовательно, противоположный электрод создается путем заполнения конструкции электролитом. Благодаря этому процессу электролит по существу выполняет роль катода.

Электролитические конденсаторы пропитаны жидкостью или бумагой, пропитанной жидкостью, которая не является диэлектриком, но при приложении напряжения создает слой оксида алюминия, который действует как диэлектрик. Реакция зависит от полярности приложенного напряжения.Если полярность поменять, конденсатор будет выделять газ и, вероятно, взорвется или лопнет из-за давления внутри, поэтому он не подходит для применения с переменным током.

MEMs Конденсаторы

Микро-электромеханические системы (MEM) — это небольшие устройства, изготовленные из кремния. Пластинчатые конденсаторы могут быть изготовлены с небольшими изменениями емкости при увеличении или уменьшении расстояния между пластинами. Небольшие устройства можно использовать как датчики и гироскопы.

Распространенными типами устройств являются конденсаторы с параллельными пластинами для определения положения. Кроме того, взаимопроникающие гребенчатые конструкции, в которых емкость может быть изменена с использованием перемещения одной гребенки относительно другой, либо в поперечном направлении, либо в продольном направлении. Из-за их небольшого размера изменение емкости очень мало, порядка 10 ^-15 Ф (фемто-Фарад).

Конденсаторы танталовые

Танталовые конденсаторы поляризованы и имеют низкое напряжение, как электролитические конденсаторы.Они дороги, но очень малы, поэтому используются там, где требуется большая емкость в небольших размерах, например, в мобильных телефонах или портативных компьютерах. Эти конденсаторы становятся все более важными, поскольку растет спрос на все меньшие электронные устройства. Колумбит-танталит — колтан , сокращенно руда, из которой очищается тантал, добывается в Австралии, г. Егпыт. Высокий спрос на руду также финансировал гражданские войны в Демократической Республике Конго. В докладе Совета безопасности ООН утверждается, что большая часть руды добывается незаконно и переправляется через восточные границы страны вооруженными формированиями из соседних Уганды, Бурунди и Руанды, обеспечивая доход для финансирования военной оккупации Конго.

Суперконденсаторы

Суперконденсаторы — это конденсаторы, которые способны накапливать большие количества заряда и, следовательно, энергии в очень небольшом объеме. Накопление энергии происходит за счет статического заряда, а не электрохимического процесса, присущего батарее. Применение разности напряжений на положительной и отрицательной пластинах заряжает суперконденсатор. Эта концепция похожа на электрический заряд, который накапливается при ходьбе по ковру. Впервые суперконденсатор был задуман в 1957 году, но теперь исследования сосредоточены на их использовании в качестве легких источников питания в качестве альтернативы батареям.суперконденсатор переходит в аккумуляторную технологию благодаря использованию специальных электродов и небольшого количества электролита. Суперконденсаторы могут найти применение в таких случаях, как временные резервные источники питания в электросети или обеспечение первоначального всплеска энергии для движения электромобилей.

Сводка

Конденсаторы

обладают способностью заряжать и высвобождать накопленный заряд очень быстро, что позволяет им функционировать разными способами. Они занимают важное место во всем: от схем стабилизации напряжения в чувствительной электронике до помощи в преобразовании мощности переменного тока в постоянный для зарядки аккумуляторов во всем, от мобильных скутеров до портативных компьютеров.

Конденсаторы — это устройства, накапливающие заряд. Емкость определяется как отношение накопленного заряда к единице напряжения. C = Q / V

Емкость конденсатора с параллельными пластинами определяется как C = ε _r A / d .

Энергия, запасенная в конденсаторе, рассчитывается по работе, совершаемой при перемещении заряда по пластинам. dW = V dq . Накопитель энергии — это область под графиком заряда / напряжения. 1 / 2QV или из C = Q / V, 1 / 2CV ² = 2Q ² / C.

Изменение емкости и изменение емкости конденсаторов

ВЛАЖНОСТЬ

Всякий раз, когда пары влаги проникают в диэлектрик конденсатора, емкость несколько увеличивается в зависимости от величины и эффективности проникновения, процента от общего расстояния между электродами, представленного воздухом, и процента воздуха, который находится в воздухе. насыщенный или, по сути, замененный влагой.

Для наглядности предположим следующее:

На этой иллюстрации мы видим увеличение емкости приблизительно на 27% из-за влажности.

Конечно, вы обычно не увидите такого грубого проникновения влаги, но — увеличение до 5% не является редкостью для негерметично закрытых коммерческих единиц при испытании на ускоренные тесты влажности MIL-STD.

НАПРЯЖЕНИЕ

За исключением керамики общего назначения (с высоким K), напряжение очень незначительно влияет на K стандартных диэлектрических материалов. В случае керамики с высоким содержанием K напряжение переменного тока вызовет увеличение K, в то время как напряжение постоянного тока вызовет уменьшение K.Величина заряда будет зависеть от исходного значения K для данной керамической смеси.

Например, для смеси K = 1200 нередко можно увидеть изменения, составляющие примерно + 20% при подаче 20 В переменного тока (RMS) и -30% при подаче 200 В постоянного тока.

ЧАСТОТА

Что касается нашей основной области применения, мы в основном занимаемся низкочастотным диапазоном от 0 до 30 кГц. В этой области K слюды, стекла, тефлона, полистирола и керамических диэлектриков типа N PO не показывает никаких измеримых изменений.Пленка из поликарбоната покажет небольшое снижение K примерно на 0,4% при 30 кГц. Падение содержания майлара составляет от 1,5 до 2,0%, керамики с высоким содержанием K (1200) — примерно от 2,0 до 2,5%, а для блоков, пропитанных бумагой, — от 3,0 до 6,0%, в зависимости от пропитки. Эталонная частота измерения здесь составляет 1000 Гц.

ТЕМПЕРАТУРА

Температура влияет на K всех стандартных диэлектрических материалов. Этот эффект будет довольно небольшим для одних диэлектриков и весьма значительным для других.

На следующих диаграммах сравниваются средние кривые различных диэлектриков в зависимости от изменения емкости в зависимости от температуры. Для некоторого изменения этих кривых можно использовать специальную обработку и другие факторы.

Рисунок 1 Рисунок 2 Рисунок 3

Рисунок 1 основан на единицах пленки «сухого» типа; то есть пропитки не использовались. На самом деле пленки не пропитываются, но использование пропиток в качестве «наполнителя» довольно распространено для достижения определенных результатов. Когда это будет сделано, кривые могут измениться.

На рис. 2 наглядно показано влияние различных пропиточных материалов на результирующий K материала между электродами. И, что еще больше усложняет картину, использование различных добавок к пропиточному материалу может значительно изменить даже эти кривые.

На рис. 3 показаны относительные кривые для других распространенных диэлектриков.

Для керамических конденсаторов построение «типичной» кривой зависимости емкости от температуры невозможно, так как эти блоки могут иметь практически любую желаемую характеристику в зависимости от используемой диэлектрической смеси, обработки, метода сборки и методы стабилизации, используемые после изготовления.

В этой статье мы увидели, как внешние напряжения, приложенные к конденсатору, вызывают изменение емкости. В следующих статьях будет обсуждаться, как эти же напряжения влияют на другие параметры.

Емкость | Electronics Club

Емкость | Клуб электроники

Емкость | Зарядка и энергия | Реактивное сопротивление | Последовательный и параллельный | Зарядка | Постоянная времени | Разрядка | Использует | Конденсаторная муфта

Следующая страница: Импеданс и реактивное сопротивление

См. Также: Конденсаторы | Блоки питания

Емкость

Емкость (символ C) — это мера способности конденсатора накапливать заряд .Большая емкость означает, что можно хранить больше заряда. Емкость измеряется в фарадах, символ F, но 1F очень большой, поэтому для отображения меньших значений используются префиксы (множители):

• мкФ (микро) означает 10 ^-6 (миллионная), поэтому 1000000 мкФ = 1F
• n (нано) означает 10 ^-9 (миллиардная), поэтому 1000 нФ = 1 мкФ
• p (пико) означает 10 ^-12 (миллионно-миллионная), поэтому 1000 пФ = 1 нФ

неполяризованный конденсатор

поляризованный конденсатор

Rapid Electronics: Конденсаторы

---

Заряд и накопленная энергия

Количество заряда (Q), сохраняемого конденсатором, определяется как:

Заряд, Q = C × V

Когда они накапливают заряд, конденсаторы также накапливают энергию (E):

Энергия, E = ½QV = ½CV²

Q = заряд в кулонах (Кл)
C = емкость в фарадах (Ф)
В = напряжение в вольтах (В)
E = энергия в джоулях (Дж) )

Конденсаторы возвращают накопленную энергию в цепь

Обратите внимание, что конденсаторы возвращают накопленную энергию в схему.Они не расходуют электрическую энергию преобразовывая его в тепло, как это делает резистор.

Энергия, запасаемая конденсатором, намного меньше, чем энергия, хранящаяся в батарее, поэтому они не могут использоваться в качестве источника энергии для большинства целей.

---

Емкостное реактивное сопротивление Xc

Емкостное реактивное сопротивление (Xc) — это мера сопротивления конденсатора переменному току (переменному току). Как и сопротивление, он измеряется в Ом () но реактивное сопротивление сложнее, чем сопротивление, потому что его значение зависит от частоты (f) электрического сигнала, проходящего через конденсатор, а также емкости (C).

Емкостное реактивное сопротивление, Xc =	1
	2fC

Xc = реактивное сопротивление в Ом ()
f = частота в герцах (Гц)
C = емкость в фарадах (F)

Реактивное сопротивление велико на низких частотах и ​​мало на высоких частотах. Для постоянного постоянного тока, который является нулевой частотой, Xc бесконечно (полное противодействие), отсюда правило, что Конденсаторы пропускают переменный ток, но блокируют постоянный ток .

Например, конденсатор 1 мкФ имеет реактивное сопротивление 3,2 кГц для сигнала 50 Гц, но когда частота выше 10 кГц, его реактивное сопротивление составляет только 16.

Емкостное и индуктивное сопротивление

Символ Xc используется для отличия емкостного реактивного сопротивления от индуктивного X _L что является свойством индукторов.

Различие важно, потому что X _L увеличивается с частотой (противоположно Xc) и если в цепи присутствуют оба X _L и Xc, то комбинированное реактивное сопротивление (X) равно разнице между ними .

Для получения дополнительной информации см. Страницу Импеданс.

---

---

Последовательные и параллельные конденсаторы

Суммарная емкость (C) конденсаторов, подключенных в серии , определяется по формуле:

1	=	1	+	1	+	1	+…
C		C1		C2		C3

Суммарная емкость (C) конденсаторов, подключенных параллельно , составляет

C = C1 + C2 + C3 + …

Два или более конденсатора редко намеренно соединяются последовательно в реальных цепях, но может быть полезно подключить конденсаторы параллельно, чтобы получить очень большую емкость, например, чтобы сгладить питание.

Обратите внимание, что эти уравнения обратны для резисторы последовательно и параллельно.

---

Зарядка конденсатора

Конденсатор (C) на принципиальной схеме заряжается от напряжения питания (Vs) с током проходящий через резистор (R). Напряжение на конденсаторе (Vc) изначально равно нулю, но увеличивается. по мере заряда конденсатора. Конденсатор полностью заряжен, когда Vc = Vs.

Зарядный ток (I) определяется напряжением на резисторе (Vs — Vc):

Зарядный ток, I = (Vs — Vc) / R

Сначала Vc = 0V, поэтому:

Начальный ток, Io = Vs / R

Vc увеличивается, как только заряд (Q) начинает накапливаться (Vc = Q / C), это снижает напряжение на резисторе и, следовательно, снижает ток зарядки.Это означает, что скорость зарядки постепенно снижается.

---

Постоянная времени (RC)

Постоянная времени — это мера того, насколько медленно конденсатор заряжается током, протекающим через резистор. Большая постоянная времени означает, что конденсатор заряжается медленно. Обратите внимание, что постоянная времени является свойством схема , содержащая конденсатор и резистор, не является свойством только конденсатора.

Постоянная времени (RC) — это время, необходимое для того, чтобы зарядный (или разрядный) ток (I) упал до ¹ / е от исходного значения (Io).’е’ — важное число в математике (нравиться ). e = 2,71828 (до 6 значащих цифр), поэтому мы можем грубо сказать, что постоянная времени — это время, необходимое для того, чтобы ток упал до ¹ / ₃ от его начального значения.

После каждой постоянной времени ток падает на ¹ / e (около ¹ / ₃ ). После 5 постоянных времени (5RC) ток упал до менее 1% от своего начального значения, и мы можем разумно говорят, что конденсатор полностью заряжен , а на самом деле конденсатор требует вечной зарядки полностью!

Нижний график показывает, как напряжение (В) увеличивается по мере заряда конденсатора.Сначала напряжение быстро меняется из-за большого тока; но по мере уменьшения тока заряд нарастает медленнее, а напряжение увеличивается медленнее.

Время	Напряжение	Заряд
0RC	0,0 В	0%
1RC
1RC		5,7 В V	86%
3RC	8.6 В	95%
4RC	8,8 В	98%
5RC	8,9 В	99%

Зарядка конденсатора
постоянная времени = RC

После 5 постоянных времени (5RC) конденсатор почти полностью заряжен, а его напряжение почти равно напряжение питания. Можно с полным основанием сказать, что конденсатор полностью заряжен после 5RC, хотя реально заряжается продолжается вечно (или до тех пор, пока схема не будет изменена).

---

---

Разряд конденсатора

Верхний график показывает, как ток (I) уменьшается по мере разряда конденсатора. Начальный ток (Io) определяется начальным напряжением на конденсаторе (Vo) и сопротивлением (R):

Начальный ток, Io = Vs / R

Обратите внимание, что графики тока имеют одинаковую форму как для зарядки, так и для разрядки конденсатора. Этот тип графика является примером экспоненциального убывания.

Нижний график показывает, как напряжение (В) уменьшается по мере разряда конденсатора.

Время	Напряжение	Заряд
0RC	9,0 В	100%
1RC
1RC	3,3 V	14%
3RC	0,4 ​​V	5%
4RC	0.2 В	2%
5RC	0,1 В	1%

Разрядка конденсатора
постоянная времени = RC

Сначала ток большой из-за большого напряжения, поэтому заряд быстро теряется и напряжение быстро уменьшается. По мере того, как заряд теряется, напряжение уменьшается, уменьшая ток, поэтому скорость разрядки становится все медленнее.

После 5 постоянных времени (5RC) напряжение на конденсаторе почти равно нулю, и мы можем с полным основанием сказать, что конденсатор полностью разряжен, хотя реально разряд продолжается вечно (или пока не поменяют схему).

---

Применение конденсаторов

Конденсаторы

используются в нескольких целях:

---

Конденсаторная муфта (CR-муфта)

Секции электронных схем могут быть связаны с конденсатором, потому что конденсаторы проходят переменный ток (изменяющиеся) сигналы, но блокируют DC (постоянные) сигналы. Это называется конденсаторной связью или CR-связью .

Он используется между ступенями аудиосистемы для передачи аудиосигнала (переменного тока) без постоянного напряжения (постоянного тока). которые могут присутствовать, например, для подключения громкоговорителя.Он также используется для установки переключателя «AC» на осциллографе.

Точное поведение конденсаторной связи определяется ее постоянной времени (RC). Обратите внимание, что сопротивление (R) может быть внутри следующего участка цепи, а не отдельного резистора.

Для успешной связи конденсаторов в аудиосистеме сигналы должны проходить через с небольшим искажением или без него. Это достигается, если постоянная времени (RC) больше, чем период времени (T) аудиосигналов самой низкой частоты требуется (обычно 20 Гц, T = 50 мс).

• Выход при RC >> T
  Когда постоянная времени намного больше, чем период времени входного сигнала конденсатор не успевает существенно зарядиться или разрядиться, поэтому сигнал проходит с незначительными искажениями.
• Выход при RC = T
  Когда постоянная времени равна периоду времени, вы можете видеть, что конденсатор успевает частично зарядиться и разрядиться до изменения сигнала. В результате есть значительное искажение сигнала при прохождении через CR-муфту.Обратите внимание, как внезапные изменения входного сигнала проходят прямо через конденсатор на выход.
• Выход при RC << T
  Когда постоянная времени намного меньше периода времени, конденсатор успевает для полной зарядки или разрядки после каждого резкого изменения входного сигнала. Фактически только внезапные изменения передаются на выходе, и они выглядят как «всплески», попеременно положительный и отрицательный. Это может быть полезно в системе, которая должна определять, когда сигнал меняется внезапно, но игнорируйте медленные изменения.

---

Следующая страница: Импеданс и реактивное сопротивление | Исследование

---

Политика конфиденциальности и файлы cookie

Этот сайт не собирает личную информацию. Если вы отправите электронное письмо, ваш адрес электронной почты и любая личная информация будет используется только для ответа на ваше сообщение, оно не будет передано никому. На этом веб-сайте отображается реклама, если вы нажмете на рекламодатель может знать, что вы пришли с этого сайта, и я могу быть вознагражден. Рекламодателям не передается никакая личная информация.Этот веб-сайт использует некоторые файлы cookie, которые классифицируются как «строго необходимые», они необходимы для работы веб-сайта и не могут быть отклонены, но они не содержат никакой личной информации.