Что такое фильтр низких частот и как он работает. Какие бывают виды ФНЧ. Где применяются фильтры нижних частот. Как рассчитать частоту среза ФНЧ. Какие преимущества у активных фильтров.
Что такое фильтр низких частот (ФНЧ)
Фильтр низких частот (ФНЧ) — это электронная схема, которая пропускает сигналы с частотой ниже определенного порогового значения (частоты среза) и ослабляет сигналы с частотой выше этого значения. Основная функция ФНЧ — подавление высокочастотных составляющих сигнала.
Принцип работы ФНЧ основан на зависимости сопротивления конденсатора или катушки индуктивности от частоты сигнала. С увеличением частоты сопротивление конденсатора уменьшается, а катушки — увеличивается.
Основные виды фильтров нижних частот
Существует несколько основных типов ФНЧ:
- Пассивные RC-фильтры — состоят только из резисторов и конденсаторов
- Пассивные LC-фильтры — используют катушки индуктивности и конденсаторы
- Активные фильтры — содержат операционные усилители и пассивные компоненты
- Цифровые фильтры — реализуются программно на микроконтроллерах или сигнальных процессорах
Как работает пассивный RC-фильтр нижних частот
Простейший пассивный ФНЧ состоит из резистора и конденсатора. На низких частотах конденсатор имеет большое сопротивление и не пропускает сигнал. На высоких частотах сопротивление конденсатора падает, он шунтирует сигнал на землю. В результате высокие частоты подавляются.

Частота среза RC-фильтра рассчитывается по формуле:
fc = 1 / (2πRC)
где R — сопротивление резистора, C — емкость конденсатора.
Принцип работы активного фильтра низких частот
Активные ФНЧ строятся на основе операционных усилителей. Наиболее распространенная топология — фильтр Саллена-Ки. Он состоит из двух резисторов, двух конденсаторов и ОУ. На низких частотах схема работает как повторитель напряжения. На высоких частотах конденсаторы шунтируют сигнал на землю.
Преимущества активных фильтров:
- Возможность получить крутизну спада АЧХ более 6 дБ/октаву
- Не требуют катушек индуктивности
- Легко каскадируются для увеличения порядка фильтра
- Имеют низкий выходной импеданс
Где применяются фильтры нижних частот
Основные области применения ФНЧ:
- Подавление высокочастотных помех в аудиосистемах
- Сглаживание пульсаций в источниках питания
- Ограничение полосы в системах связи
- Удаление шумов в измерительных системах
- Фильтрация в аналого-цифровых преобразователях
- Формирование сигналов в синтезаторах частот
Как рассчитать частоту среза фильтра нижних частот
Частота среза — это частота, на которой коэффициент передачи фильтра уменьшается на 3 дБ относительно полосы пропускания. Для фильтра Саллена-Ки частота среза вычисляется по формуле:
fc = 1 / (2π√(R1R2C1C2))
где R1, R2 — сопротивления резисторов, C1, C2 — емкости конденсаторов.
Влияние ФНЧ на различные типы сигналов
Фильтр нижних частот по-разному воздействует на сигналы различной формы:
- Синусоидальный сигнал — уменьшается амплитуда высокочастотных составляющих
- Прямоугольный сигнал — сглаживаются фронты, скругляются углы
- Пилообразный сигнал — сглаживаются острые кромки
Степень влияния ФНЧ зависит от соотношения частоты сигнала и частоты среза фильтра.
Преимущества активных фильтров перед пассивными
Активные фильтры имеют ряд преимуществ по сравнению с пассивными RC и LC-фильтрами:
- Возможность получить большую крутизну спада АЧХ
- Не требуют громоздких и дорогих катушек индуктивности
- Легко перестраиваются и каскадируются
- Имеют низкий выходной импеданс
- Могут обеспечивать усиление сигнала
Поэтому в современной электронике активные фильтры используются гораздо чаще пассивных, особенно на низких частотах.
Проектирование фильтра нижних частот
При проектировании ФНЧ необходимо выполнить следующие шаги:
- Определить требуемую частоту среза и порядок фильтра
- Выбрать тип аппроксимации (Баттерворта, Чебышева и др.)
- Рассчитать номиналы компонентов по формулам или с помощью специальных программ
- Провести моделирование схемы в программе типа LTspice
- Собрать макет и измерить реальные характеристики фильтра
Для расчета активных фильтров удобно использовать онлайн-калькуляторы или специализированное ПО.
RC-фильтры
Фильтры — это схемы, которые пропускают без затухания (ослабления) определенную полосу частот и подавляют все остальные частоты. Частота, на которой начинается подавление, называется частотой среза f
Рис. 28.1. Частотная характеристика фильтра нижних (а) и верхних (б) частот.
Влияние фильтра на прямоугольный сигнал
Как уже говорилось в гл. 3, прямоугольный сигнал представляет собой сложное колебание, состоящее из основной гармоники и бесконечного количества нечетных гармоник. Низкочастотные составляющие формируют основание и плоскую вершину импульса, а высокочастотные — его фронт и срез.
Когда прямоугольный сигнал проходит через фильтр, его форма искажается. Фильтр нижних частот (ФНЧ) будет искажать главным образом Фронты и срезы, делая их менее крутыми и скругляя углы, как показано на рис. 28.7(б). ФНЧ оказывает на прямоугольный сигнал такое же Действие, как усилители с недостаточной шириной полосы пропускания. Фильтр верхних частот (ФВЧ), наоборот, искажает плоскую вершину и снование прямоугольного сигнала (рис. 28.5(б)).
RC— фильтры
Простейшим среди фильтров является RC-фильтр. Принцип его работы основан на том, что при изменении частоты реактивное сопротивление конденсатора изменяется обратно пропорционально частоте, а сопротивление резистора остается неизменным. На схеме рис. 28.2 конденсатор соединен последовательно с резистором. При подаче на вход такого фильтра низкочастотного сигнала реактивное сопротивление конденсатора С будет гораздо больше, чем сопротивление резистора R. В результате падение напряжения Vc на конденсаторе будет большим, а на резисторе Vr — малым. При подаче на вход этого фильтра высокочастотного сигнала картина будет обратная: Vc будет малым, а Vr — большим. Если теперь представить эту схему, как на рис. 28.3(б), где падение напряжения на конденсаторе является выходным, то в выходном сигнале будут преобладать НЧ-составляющие, а высокочастотные будут сильно ослабляться. Другими словами, мы получили фильтр нижних частот. И наоборот, если выходное напряжение снимать с резистора (рис. 28.3(а)), то получим фильтр верхних частот. Значения
Дифференциатор
Дифференциатор — это фильтр верхних частот. Если на вход дифференциатора подать последовательность прямоугольных импульсов, то на выходе будут получаться высокочастотные всплески, или «пички». На рис. 28.4 изображен RC-дифференциатор. Конденсатор С беспрепятственно пропускает ВЧ-составляющие входного сигнала, образующие фронт импульса АВ, а затем начинает заряжаться до 10 В.
Если постоянная времени (произведение RC) мала в сравнении с периодом входных импульсов, конденсатор успеет полностью зарядиться до 10 В, прежде чем придет следующая ВЧ-составляющая импульса — срез CD (рис. 28.5(а)). Когда конденсатор полностью зарядится, ток прекращается и падение напряжения на резисторе, т. е. на выходе, равно нулю. Срез CD представляет собой перепад напряжения 10 В и состоит из ВЧ-компонент. Поэтому он свободно пройдет через конденсатор и напряжение на выходе скачком упадет до –10 В. После этого конденсатор начнет перезаряжаться до –10 В, и, если постоянная времени мала, он успеет полностью зарядиться до этого напряжения. При этом выходное напряжение спадет до нуля и будет оставаться таким до прихода следующего фронта и т. д. Если постоянная времени больше, чем период входных импульсов, то выходной сигнал будет иметь форму, как на рис. 28.5(б).
Рис. 28.4. RC-дифференциатор.
Рис. 28.5. Сигнал на выходе дифференциатора,
изображенного на рис. 28.4, при малой (а) и большой (б) постоянной времени.
Интегрирующая
Интегрирующая RC-цепь (интегратор) является фильтром нижних частот (ФНЧ) и при подаче на его вход прямоугольного сигнала выдает на выходе сигнал треугольной (пилообразной) формы. На рис. 28.6 изображен RC-интегратор. При подаче на его вход фронта прямоугольного импульса (рис. 28.7) конденсатор начинает заряжаться до напряжения +10 В. Еслизадать постоянную времени RC, большую в сравнении с периодом входного сигнала, то срез CD импульса поступит прежде, чем конденсатор успеет полностью зарядиться (рис. 28.7(а)). После этого конденсатор начинает заряжаться в обратном направлении. И опять в связи с большой постоянной времени фронт FE следующего импульса придет прежде, чем конденсатор успеет полностью зарядиться в отрицательном направлении и т.д. В результате на выходе получается сигнал треугольной формы, амплитуда которого меньше, чем амплитуда входного сигнала.
Если постоянная времени мала в сравнении с периодом входного сигнала, то выходной сигнал будет иметь вид, как на рис. 28.7(б). Обратите внимание, что и в интеграторе, и в дифференциаторе постоянная времени всегда сравнивается с периодом входного сигнала. Например, постоянная времени 100 мкс является большой по сравнению с периодом, скажем, 5 мкс (частота входного сигнала 200 кГц), но малой в сравнении с периодом 5 мс (частота входного сигнала 200 Гц).
Влияние RC-цети на синусоидальный сигнал
Синусоидальный сигнал является простым гармоническим колебанием и не содержит высших гармоник, поэтому при подаче такого сигнала на фильтр любого типа его форма не изменяется. Амплитуда выходного синусоидального сигнала может уменьшиться в зависимости от того, находится его частота в пределах полосы пропускания или нет. В первом случае синусоидальный сигнал претерпевает очень малое затухание, во втором случае затухание может быть очень большим.
Воздействие RC
Интегратор скругляет острые кромки пилообразного сигнала (рис. 28.8). Степень скругления определяется постоянной времени схемы. При очень большой постоянной времени выходной сигнал будет иметь вид, как на рис.28.8(б).
Рис. 28.8. Влияние интегрирующей цепочки
на форму пилообразного напряжения.
Рис. 28.9. Влияние дифференцирующей цепочки
на форму пилообразного напряжения.
На рис. 28.9 показано воздействие дифференциатора на сигнал пилообразной формы. При очень малой постоянной времени выходной сигнал получается в виде импульсов (пичков) (рис. 28.9(б)).
В этом видео рассказывается о полосовых фильтрах:
Добавить комментарий
Фильтр низких частот (ФНЧ) | Типы фильтра нижних частот
СОДЕРЖАНИЕ
- Определение фильтра низких частот
- Схема
- Активный и пассивный фильтр нижних частот
- Что делает LPF? Как это работает?
- операция
- Частотный отклик
- Передаточная функция ФНЧ
- Проектирование ФНЧ
- Угловая частота фильтра нижних частот
- Идеальный и настоящий фильтр
- Фильтр низких частот против фильтра высоких частот
- Преимущества ФНЧ
- Каковы применения фильтра нижних частот
- Часто задаваемые вопросы
«Фильтр нижних частот передает сигналы более низкой частоты с меньшим сопротивлением и имеет постоянное выходное усиление от нуля до частоты среза».
Как правило, фильтр нижних частот ослабляет частоты выше пороговых значений.
Принципиальная схема фильтра нижних частот:Существует два типа активных фильтров:
- Активный фильтр низких частот — состоит в основном из активных компонентов, таких как операционный усилитель, транзистор.
- Пассивный фильтр нижних частот — состоит в основном из пассивных компонентов, таких как конденсаторы, резисторы и т. Д.
На рисунке 1.1 это обычно используемый активный фильтр нижних частот.
Фильтрация обычно выполняется RC-цепью, а операционный усилитель используется как усилитель с единичным усилением. Резистор RF(= R) включено для смещения постоянного тока.
При постоянном токе емкостное реактивное сопротивление бесконечно, и резистивный путь постоянного тока к земле для обоих выводов должен быть одинаковым.
Здесь все напряжения Vi, Vx, Vy, V0 измеряются относительно земли.
Входное сопротивление операционного усилителя всегда бесконечно; ток на входные клеммы не поступает.
Согласно правилу делителя напряжения, напряжение на конденсаторе
Поскольку коэффициент усиления операционного усилителя бесконечен,
Где,
= усиление полосы пропускания фильтра
f = частота входного сигнала
= частота среза сигнала
AcL
= коэффициент усиления фильтра с обратной связью как функция частоты.
Величина прироста,
И фазовый угол (в градусах),
Работа фильтра нижних частот:Работу фильтра нижних частот можно проверить из уравнения величины усиления следующим образом:
На очень низких частотах, т.е. f >> fc,
При f = fc,
При f> fc,
|AcL| <АF
Таким образом, фильтр имеет постоянное усиление AF от 0 Гц до частоты среза fc. На fc, рост 0.707AF, а после fc, она уменьшается с постоянной скоростью с увеличением частоты.
Здесь фактический отклик отклоняется от приближения линейной пунктирной линии в окрестности ‘fc».
Частотная характеристика фильтра низких частот:Характеристики фильтра нижних частотКонструкция фильтра нижних частот:Значение частоты среза ωc выбран.
Емкость C выбирается с определенным значением; обычно значение составляет от 0.001 до 0.1 мкФ. Для лучшей производительности рекомендуются майларовые или танталовые конденсаторы.
Значение R рассчитывается из соотношения,
Fc = частота среза в герцах
Ωc = частота среза в радианах секундах.
C = в Фараде
Наконец, значения R1 и RF выбираются в зависимости от желаемого усиления полосы пропускания с помощью соотношения,
Масштабирование частоты: — После разработки фильтра может возникнуть необходимость изменить его частоту среза. Метод преобразования исходной частоты среза fc к новой частоте среза называется «масштабированием частоты».
Чтобы изменить частоту среза, умножьте R или C, но не оба, на соотношение: —
Угловая частота и частота среза фильтра низких частот:Переход фильтра нижних частот всегда происходит быстро и плавно. полоса пропускания в непропускания. Кроме того, частота среза не является параметром для измерения качества или недостатка в диапазоне частот. Частота среза более точно называется частотой -3 дБ, т. Е. Это частота, при которой амплитуда отклика на 3 дБ ниже значения при 0 Гц.
Что такое Pass-Band?«Полоса пропускания — это конкретный диапазон частот, через который проходит фильтр внутри него».
Для фильтров нижних частот частоты, которые движутся к концу полосы пропускания, не могут иметь значительного усиления или внимания.
Что такое Stopband?«Фильтр всегда содержит фильтры в пределах заданного диапазона и отклоняет частоты, находящиеся ниже заданного диапазона. Этот конкретный диапазон известен как полоса задерживания ».
Поскольку ограничения существуют для фильтров нижних частот, полоса задерживания ослабляется на определенной частоте, которая приближается к частоте среза ближе к 0 Гц.
Передаточная функция фильтра низких частот:Что такое передаточная функция?Передаточная функция — это комплексное число, которое имеет как величину, так и фазу. В случае фильтров передаточная функция помогает ввести разность фаз между входом и выходом.«.
Поскольку фильтр нижних частот пропускает низкочастотные сигналы переменного тока, выходной сигнал ослабляется. Мы используем разные активные и пассивные компоненты для создания фильтра, который в конечном итоге имеет другие характеристики. Передаточная функция сообщает нам, как один вход связан с выходом в зависимости от характеристик компонента. Передаточную функцию легко определить по графику выходного сигнала на различных частотах. Мы также можем вычислить передаточную функцию, используя законы Кирхгофа, чтобы получить дифференциальное уравнение фильтра.
По мере прохождения через него большего количества сигнала фильтр будет применять фазовый сдвиг к выходному сигналу для входного сигнала. Следовательно, передаточная функция фильтра является сложной функцией частоты. Он также содержит всю важную информацию, необходимую для определения величины выходного сигнала и его фазы.
Идеальный фильтр и настоящий фильтр:Иногда в целях упрощения мы часто используем активные фильтры для приблизительного определения путей. Мы модернизируем их до идеальной теоретической модели, которая называется «Идеальный фильтр».
Использование этих стандартов недостаточно, что приводит к ошибкам; тогда фильтр следует рассматривать на основе точного реального поведения, т. е. как «настоящий фильтр».
Основные ключевые термины идеального фильтра:- Единица усиления
- Полная деградация входного сигнала по диапазонам.
- Переход реакции из одной зоны в другую довольно резкий.
- Он не создает никаких искажений при прохождении сигнала через транзитную зону.
- Фильтры нижних частот могут легко удалить эффекты наложения спектров из схемы, что обеспечивает плавную работу схемы.
- Низкочастотные фильтры экономичны, поэтому их можно легко использовать.
- Фильтры нижних частот имеют низкий выходной импеданс; таким образом, он предотвращает влияние нагрузки на частоту среза фильтров.
- В фильтрах «шипения» используется фильтр нижних частот.
- LPF используется в аудиоколонках для уменьшения высоких частот.
- LPF можно использовать как усилитель звука и эквалайзер.
- В аналого-цифровом преобразователе LPF используется в качестве фильтров сглаживания для управляющих сигналов.
- LPF используется для сглаживания изображения, размытия изображения.
- LPF также используется в радиопередатчиках для блокировки излучения гармоник.
- Эти фильтры используются в музыкальных системах для фильтрации высокочастотных звуков, вызывая эхо на более высоких звуках.
Ø
Что такое пассивный фильтр нижних частот?Пассивный фильтр нижних частот — это фильтр, состоящий из всех пассивных компонентов, таких как конденсаторы, резисторы и т. Д. Он вызывает меньший выходной уровень по сравнению с входным уровнем.
Ø
Что такое RC-схема низких частот?RC-цепь нижних частот состоит только из резисторов и конденсаторов, как следует из названия. Это также важный пассивный фильтр. В этом фильтре реактивное сопротивление конденсатора изменяется обратно пропорционально частоте, а значение резистора остается постоянным при изменении частоты.
Ø
Что такое фильтр нижних частот Баттерворта?A Фильтр Баттерворта — это тот тип фильтра, в котором частотная характеристика плоская по всей полосе пропускания. Фильтр Баттерворта низких частот обеспечивает постоянный выходной сигнал от источника постоянного тока до определенной частоты среза и отклоняет частоты более высокого уровня.
Ø
Как можно построить фильтр нижних частот второго порядка?Мы знаем, что фильтр нижних частот первого порядка можно создать, подключив один резистор и конденсатор, один полюс которых может дать нам крутизну спада -20 дБ / декаду. Чтобы создать пассивный фильтр нижних частот второго порядка, мы соединяем или каскадируем два пассивных фильтра (первого порядка). Это тоже двухполюсная сеть.
Ø
Запишите угловую частоту фильтра второго порядка.В фильтре нижних частот второго порядка мы наблюдаем точку угловой частоты -3 дБ, и, следовательно, частота полосы пропускания изменяется от своего первоначального значения, рассчитанного по формуле:
Узнать больше об электронике нажмите сюда
О Сумали Бхаттачарье
В настоящее время я инвестирую в сферу электроники и связи.
Мои статьи сосредоточены на основных областях базовой электроники с использованием очень простого, но информативного подхода.
Я хорошо учусь и стараюсь быть в курсе всех последних технологий в области электроники.
Подключимся через LinkedIn —
https://www.linkedin.com/in/soumali-bhattacharya-34833a18b/
Активные фильтры: теория и практика
Аудио-фильтры на пассивных компонентах в наши дни используют редко. RC-фильтры не могут обеспечить крутизны АЧХ больше 6 дБ на октаву. Этого недостатка лишены LC-фильтры. Однако на частотах 0-20 кГц им требуются катушки индуктивности на десятки-сотни миллигенри. Такие катушки делают, но они сравнительно дороги, а выбор номиналов ограничен. Поэтому обычно используют активные фильтры, речь о которых и пойдет далее.
Теория: простые фильтры
Активные фильтры, как несложно догадаться, используют активные компоненты. Обычно это операционные усилители. Для примера рассмотрим простой фильтр нижних частот. Его можно сделать, добавив конденсатор в обычную неинвертирующую схему включения операционного усилителя:
Без C1 схема просто увеличивает амплитуду сигнала в 1 + R2 / R1 раз, что в нашем случае соответствует:
>>> from math import log10
>>> 20*log10(1+10/5.1)
9.428135423904662
… примерно 9.5 дБ. На низких частотах C1 ничего не делает, и схема работает как обычно. Но чем выше частота, тем большая часть сигнала обходит R2 через C1, и тем меньше усиление. Получаем ни что иное, как фильтр нижних частот.
Рассчитаем АЧХ этого фильтра с помощью LTspice:
Аналогично можно сделать фильтр высоких частот, соединив конденсатор параллельно с R1. Фильтры на основе инвертирующей схемы включения ОУ делаются по тому же принципу. Но инвертирующая схема неудобна тем, что имеет низкий входной импеданс, а неинвертирующая схема имеет минимальное усиление 0 дБ. Не во всех задачах нужно, чтобы фильтр усиливал сигнал.
Теория: топология Саллена-Ки
Поэтому были придуманы другие топологии активных фильтров. О них хорошо рассказано в статье об активных фильтрах на Википедии и далее по ссылкам. Мы рассмотрим лишь самую популярную, топологию Саллена-Ки (Sallen–Key topology).
Так выглядит схема фильтра нижних частот:
На низких частотах C1 и C2 имеют высокий импеданс. В результате схема превращается в повторитель напряжения (буфер). С ростом частоты импеданс C1 падает, и все меньшая часть сигнала попадает на неинвертирующий вход операционного усилителя. Как следствие, падает уровень выходного сигнала. Теперь C2 почти что подключен к земле. В итоге схема работает, как два последовательно соединенных RC-фильтра, и достигает крутизны АЧХ в 12 дБ на октаву.
А почему бы просто не использовать два RC-фильтра? Так иногда делают, но у этого подхода есть проблема. Первый RC-фильтр в цепочке видит второй фильтр, как нагрузку, соединенную параллельно с конденсатором. Поэтому второй фильтр должен иметь высокий импеданс, а его нагрузка — еще более высокий. Активные фильтры не накладывают таких ограничений.
Вернемся к нашему фильтру. Его частота среза приходится:
>>> from math import pi, sqrt
>>> R1 = 1000
>>> R2 = R1
>>> C1 = 15/1000/1000/1000
>>> C2 = 47/1000/1000/1000
>>> 1/(2*pi*sqrt(R1*R2*C1*C2))
5994.121932819674
… приблизительно на 6 кГц:
Можно заметить, что на некоторых частотах в полосе пропускания фильтр имеет небольшое усиление. Насколько будет гладкой АЧХ в полосе пропускания определяется величиной Q. Она также вычисляется из R1, R2, C1 и C2:
>>> sqrt(R1*R2*C1*C2)/((R1+R2)*C1)
0.8850612031567836
Чем больше Q, тем больше пик при переходе от полосы пропускания к полосе подавления.
Топология и принцип работы фильтра высоких частот аналогичны, только R и C меняются местами:
Частота среза определяется по той же формуле:
>>> C1 = 100/1000/1000/1000/1000
>>> C2 = C1
>>> R1 = 220*1000
>>> R2 = 470*1000
>>> 1/(2*pi*sqrt(R1*R2*C1*C2))
4949.483288837733
Q вычисляется немного иначе:
>>> sqrt(R1*R2*C1*C2)/((C1+C2)*R1)
0.7308152359460695
Фильтр обладает следующей АЧХ:
Q получился меньше, чем в прошлый раз. Теперь никакого усиления в полосе пропускания не наблюдается.
Практика
Все три приведенных фильтра были спаяны на макетной печатной плате:
Здесь использованы операционные усилители LM741 (даташит [PDF]). Выбор ОУ не принципиален. LM741 можно заменить на TL081. Он менее шумный (Vn = 18 nV/√Hz против 28 nV/√Hz), имеет большую частоту единичного усиления (3 МГц против 1.5 МГц), может работать при меньшем напряжении питания, а также стоит дешевле. LM741 и TL081 имеют одинаковую распиновку. Существуют аналогичные чипы TL082 и TL084. Они содержат два и четыре ОУ в одном корпусе соответственно. Ранее использованные нами NE5532 и LM358 тоже подойдут.
Если раньше вы не использовали LM741, у вас может возникнуть вопрос, к чему подключать выходы offset null, пины 1 и 5. В приведенных схемах, да и в целом при работе с AC-сигналами, эти пины не используются и ни к чему не подключаются. Они нужны при работе с DC-сигналами, и то не во всех схемах. Дело в том, что при равности напряжений на инвертирующем и неинвертирующем входах выход ОУ должен быть нулевым. Но поскольку транзисторы в ОУ не идеальны, это свойство нарушается. LM741 можно подстроить, включив потенциометр между пинами 1 и 5.
Фильтры были проверены при помощи осциллографа Rigol DS1054Z и генератора сигналов MHS-5200A. Их поведение соответствует моделям с точностью до погрешности в номиналах компонентов.
Заключение
Само собой разумеется, все варианты активных фильтров в рамках одного поста рассмотреть невозможно. При проектировании нового фильтра помогают LTspice, а также различные калькуляторы фильтров. Например, есть онлайн-калькулятор от компании Analog Devices. Также калькулятор активных фильтров есть в открытом приложении Qucs. Читателям, которые хотят больше углубиться в теорию, можно порекомендовать книгу Op Amp Applications Handbook.
Все модели, использованные в статье, вы найдете в этом архиве. А доводилось ли вам делать активные фильтры? В каких задачах вы их использовали и каким образом рассчитывали?
Дополнение: Измеренная АЧХ фильтра нижних частот приводится в обзоре генератора сигналов и частотомера Rigol DG4162. Еще один фильтр вы найдете в статье Активный фильтр для приема телеграфа.
Метки: Аудио, Электроника.
3. Фильтры верхних частот | 8. Фильтры | Часть2
3. Фильтры верхних частот
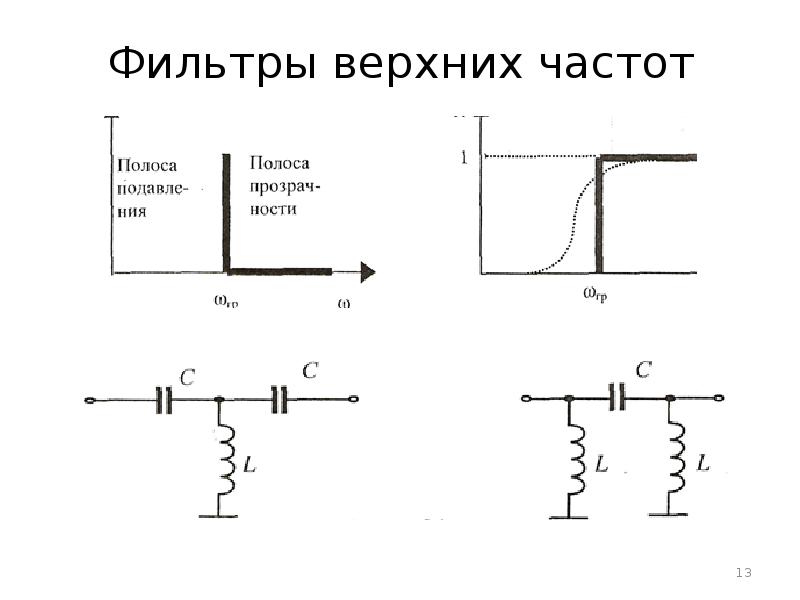
Фильтры верхних частот
Принцип работы фильтров верхних частот противоположен принципу работы фильтров нижних частот: они эффективно пропускают частотный спектр сигнала выше некоторой частоты (частоты среза), и уменьшают (подавляют) частоты сигнала ниже этой частоты. Исходя из вышесказанного, можно сделать вывод, что конструкции индуктивного и емкостного фильтров верхних частот противоположны соответствующим конструкциям фильтров нижних частот:
Емкостной фильтр верхних частот
С уменьшением частоты импеданс конденсатора возрастает. Этот высокий импеданс, при последовательном включении, блокирует низкочастотные сигналы от поступления на нагрузку. Проверить данное утверждение можно при помощи SPICE анализа:
capacitive highpass filter v1 1 0 ac 1 sin c1 1 2 0.5u rload 2 0 1k .ac lin 20 1 200 .plot ac v(2) .end
Индуктивный фильтр верхних частот
С уменьшением частоты импеданс катушки индуктивности уменьшается. Этот низкий импеданс, при параллельном включении с сопротивлением нагрузки, имеет тенденцию «закорачивать» низкочастотные сигналы, пропуская большую часть напряжения через последовательный резистор R1.
inductive highpass filter v1 1 0 ac 1 sin r1 1 2 200 l1 2 0 100m rload 2 0 1k .ac lin 20 1 200 .plot ac v(2) .end
На этот раз конструкция емкостного фильтра верхних частот является самой простой, для ее изготовления нужен всего один компонент — конденсатор. И опять же, конденсаторы являются более «чистыми» реактивными компонентами, чем катушки индуктивности, а следовательно, их использование в конструкции фильтров предпочтительнее. Применение индуктивных фильтров верхних частот может создать дополнительные проблемы, поскольку высокие частоты иногда способствуют не совсем адекватному поведению катушек индуктивности (благодаря скин-эффекту и электромагнитным потерям в сердечнике).
Фильтры верхних частот, как и фильтры нижних частот, имеют номинальную частоту среза, при превышении которой величина выходного напряжения увеличивается выше 70,7% по отношению к входному напряжению. Рассчитать частоту среза простого емкостного фильтра верхних частот можно по той же формуле, по которой рассчитывается частота среза простого емкостного фильтра нижних частот:
На приведенной в примере схеме нет никакого сопротивления кроме сопротивления нагрузки. Именно это сопротивление мы и будем подставлять в формулу вместо значения R.
Давайте в качестве примера рассмотрим стереосистему. В этой системе конденсатор, соединенный последовательно с высокочастотным динамиком (твиттером), будет служить фильтром верхних частот, налагающим высокий импеданс на низкочастотные сигналы (басы), тем самым предотвращая их поступление на динамик, неэффективный для воспроизведение таких звуков. Катушка индуктивности, соединенная последовательно с низкочастотным динамиком, будет служить фильтром нижних частот, предотвращающим поступление высоких частот на этот динамик. На среднечастотный динамик будет поступать весь спектр частот, производимых стереосистемой. В реальной аппаратуре могут использоваться более сложные схемы фильтров, но для ознакомительных целей изложенного материала вам будет достаточно. Так же примите во внимание, что мы показали вам только один канал стереосистемы (левый или правый). Реальная стереосистема содержит 6 динамиков: 2 НЧ-динамика, 2 СЧ-динамика и 2 ВЧ-динамика.
В целях повышения производительности нам неплохо было бы иметь фильтр, способный пропускать на СЧ-динамик все частоты, кроме высоких и низких. Такой фильтр называется полосовым, и его мы рассмотрим в следующей статье.
1.19. RC-фильтры
ОСНОВЫ ЭЛЕКТРОНИКИ
Полное и реактивное сопротивление
Благодаря тому что импеданс конденсатора, равный Zc = -j/ωС, зависит от частоты, с помощью конденсаторов и резисторов можно строить частотно-зависимые делители напряжения, которые будут пропускать только сигналы нужной частоты, а все остальные подавлять. В этом разделе вы познакомитесь с примерами простейших RС-фильтров, к которым мы будем неоднократно обращаться в дальнейшем. В гл. 5 описаны более сложные фильтры.
Рис. 1.52. Фильтр высоких частот.
Фильтры высоких частот. На рис. 1.52 показан делитель напряжения, состоящий из конденсатора и резистора. Согласно закону Ома для комплексных величин,
I = Uвх/Zполн = Uвх/R — (j/ωC) = Uвх[R + j/ωC)]/R2 + 1/ω2C2.
(Окончательный результат получек после умножения числителя и знаменателя на комплексное число, сопряженное знаменателю.) Итак, напряжение на резисторе R равно
Uвых = IZR = IR = Uвх[R + (j/ωС)R]/R2+1/ω2C2.
Чаще всего нас интересует не фаза, а амплитуда Uвых:
Uвых = (UвыхUвых*)1/2 = UвхR/[R2 + (1/ω2C2)]1/2.
Сравните полученный результат с выражением для резистивного делителя:
Uвых = UвхR1/(R1 + R2).
Векторное представление импеданса RС — цепи (рис. 1.53) показано на рис. 1.54.
Рис. 1.53.
Рис. 1.54.
Итак, если не принимать во внимание сдвиг фаз, а рассматривать только модули комплексных амплитуд, то «отклик» схемы будет определяться следующим образом:
Uвых = UвхR/[R2 + (1/ω2C2)]1/2 = Uвх2πƒRC/[1 + (2πƒRC)]1/2.
График этой зависимости представлен на рис. 1.55. Такой же результат мы бы получили, если бы определили отношение модулей импедансов как в упражнении 1.17 и в примере перед этим упражнением; числитель представляет собой модуль импеданса нижнего плеча делителя R, а знаменатель — модуль импеданса последовательного соединения R и С.
Рис. 1.55. Частотная характеристика фильтра высоких частот.
Как вы видите, на высоких частотах выходное напряжение приблизительно равно входному (ω > 1/RC), а на низких частотах выходное напряжение уменьшается до нуля. Мы пришли к важному результату, запомните его. Подобная схема, по понятным причинам, называется фильтром высоких частот. На практике ее используют очень широко. Например, в осциллографе предусмотрена возможность связи по переменному току между исследуемой схемой и входом осциллографа. Эта связь обеспечивается с помощью фильтра высоких частот, имеющего перегиб характеристики в области 10 Гц (связь по переменному току используют для того, чтобы рассмотреть небольшой сигнал на фоне большого напряжения постоянного тока). Инженеры часто пользуются понятием «точки излома» -3 дБ для фильтра (или любой другой схемы, которая ведет себя как фильтр)! В случае простого RC — фильтра высоких частот точка излома -3 дБ определяется выражением:
ƒ3дб = 1/2πRC.
Обратите внимание, что конденсатор не пропускает ток (ƒ = 0). Самый распространенный пример использования конденсатора-это использование его в качестве блокирующего конденсатора постоянного тока. Если возникает необходимость обеспечить связь между усилителями, то почти всегда прибегают к помощи конденсатора. Например, у любого усилителя звуковой частоты высокого класса все входы имеют емкостную связь, так как заранее не известно, какой уровень постоянного тока будут иметь входные сигналы. Для обеспечения связи необходимо подобрать R и С таким образом, чтобы все нужные частоты (в данном случае 20 Гц — 20 кГц) поступали на вход без потерь (без деления на входе).
Рис. 1.56. а — Изменение реактивного сопротивления индуктивностей и конденсаторов в зависимости от частоты. Все декады одинаковы и отличаются лишь масштабом. б — Увеличенное изображение одной декады из графика А. график построен для стандартных компонентов, имеющих точность 20%.
В качестве примера рассмотрим фильтр, показанный на рис. 1.57. Это фильтр высоких частот с точкой перегиба 3 дБ на частоте 15,9 кГц. Импеданс нагрузки, подключаемой к фильтру, должен быть значительно больше 1 кОм. иначе нагрузка будет искажать выходное напряжение фильтра. Источник сигнала должен обеспечивать возможность подключения нагрузки 1 кОм без значительной аттенюапии (потери амплитуды сигнала), иначе фильтр будет искажать выход источника сигнала.
Рис. 1.57. Рис. 1.58. Фильтр низких частот.
Фильтры низких частот. Если поменять местами R и С (рис. 1.58), то фильтр будет вести себя противоположным образом в отношении частоты. Можно показать, что Uвых = [1/1 + ω2R2С2)1/2] Uвх. График этой зависимости представлен на рис. 1.59. Такой фильтр называют фильтром низких частот. Точка -3 дБ на характеристике фильтра находится на частоте ƒ = 1/2πRC. Фильтры низких частот находят очень широкое применение. Например, их используют для устранения влияния близлежащих радио — и телевизионных станций (550 кГц — 800 МГц), на работу усилителей звуковых частот и других чувствительных электронных приборов.
Рис. 1.59 Частотная характеристика фильтра низких частот.
Упражнение 1.21. Докажите справедливость выражения для выходного напряжения фильтра низких частот.
Выход фильтра низких частот можно рассматривать в качестве самостоятельного источника сигналов. При использовании идеального источника напряжения переменного тока (с нулевым импедансом) фильтр со стороны выхода низких частот имеет сопротивление R (при расчетах полных сопротивлений идеальный источник сигналов можно заменить коротким замыканием, т.е. его нулевым импедансом для малого сигнала). В выходном импедансе фильтра преобладает емкостная составляюшая. и на высоких частотах он становится равным нулю. Для входного сигнала фильтр представляет собой нагрузку, состоящую на низких частотах из сопротивления R и сопротивления нагрузки, а на высоких частотах — нагрузку, равную просто сопротивлению R.
Рис. 1.60. Фазочастотная и амплитудно-частотная характеристики фильтра низких частот, изображенные в логарифмическом масштабе. В точке 3 дБ фазовый сдвиг составляет 45° и в пределах декады изменения частоты лежит в пределах 6° от асимптотическою значения.
На рис. 1.60 изображена также частотная характеристика фильтра низких частот, но в более общепринятом виде для вертикальной и горизонтальной осей использован логарифмический масштаб. Можно считать, что по вертикальной оси откладываются децибелы, а по горизонтальной — октавы (или декады). На таком графике равные расстояния соответствуют равным отношениям величин. В виде графика изображен также фазовый сдвиг, при этом для вертикальной оси (градусы) использован линейный масштаб, а для оси частот-логарифмический. Такой график удобен для анализа частотной характеристики даже в случае значительной аттенюации (справа): целый ряд таких графиков представлен в гл. 5, посвященной изучению активных фильтров. Отметим, что при значительной аттенюации изображенная на графике кривая вырождается в прямую линию с наклоном -20 дБ/декада (инженеры предпочитают выражение « -6 дБ/октава»). Отметим также, что фазовый сдвиг плавно изменяется от 0° (на частотах ниже точки перегиба) до 90° (на частотах существенно выше точки перегиба), а в точке -3 дБ составляет 45°. Практическое правило для односекционных RС — фильтров говорит о том. что фазовый сдвиг составляет ≈6° от асимптот в точках 0.1ƒ3дБ и 10ƒ3дБ.
Упражнение 1.22. Докажите последнее утверждение.
Возникает интересный вопрос: можно ли сделать фильтр с какой-либо другой заданной амплитудной характеристикой и какой-либо другой заданной фазовой характеристикой. Пусть вас это не удивляет, но ответить можно только отрицательно — нельзя. Фазовая и амплитудная характеристики для всех возможных фильтров подчиняются законам причинной связи (т.е. характеристика является следствием определенных свойств, но не их причиной).
Частотные характеристики дифференцирующих и интегрирующих RС — цепей. Схема дифференцирующей RС — цепи, которую мы рассмотрели в разд. 1.14, имеет такой же вид, как и схема фильтра высоких частот, приведенная в настоящем разделе. Чем же считать такую схему, зависит от того, что вас больше интересует: преобразование сигналов во времени или частотная характеристика. Полученное ранее временное условие правильной работы схемы (Uвых « Uвх) можно сформулировать иначе, применительно к частотной характеристике: для того чтобы выходной сигнал был небольшим по сравнению с входным, частота должна быть значительно ниже, чем в точке -3 дБ. В этом легко убедиться. Допустим, что входной сигнал равен Uвх = sinωt. Воспользуемся уравнением, которое мы получили ранее для выхода дифференциатора:
Uвх = RC d/dt sinωt = ωRCcosωt.
Отсюда Uвых « Uвх, если ωRC « 1, т.е. RC « 1/ω. Если входной сигнал содержит некоторый диапазон частот, то условие должно выполняться для самых высоких частот входного диапазона.
Схема интегрирующей RC — цепи (разд. 1.15) имеет такой же вид, как и схема фильтра низких частот: аналогично в хорошем интеграторе самые низкие частоты входного сигнала должны существенно превышать частоту в точке -ЗдБ.
Индуктивности и конденсаторы. Индуктивности, также как и конденсаторы, в сочетании с резисторами образуют схемы фильтров низких (или высоких) частот. Однако на практике RL — фильтры низких и высоких частот встречаются редко. Это связано с тем, что индуктивности более громоздки и дороги, а работают хуже, чем конденсаторы (их характеристики более существенно отличаются от идеальных). Если есть возможность выбора, то предпочтение лучше отдать конденсатору. Исключением из этой общей рекомендации являются ферритовые бусины (маленькие торроидальные сердечники) и дроссели в высокочастотных схемах. Несколько бусин нанизывают на провод, благодаря этому соединение, выполненное с помощью провода, становится в некоторой степени индуктивным; импеданс на высоких частотах увеличивается и предотвращает «колебания» в схеме, при этом в отличие от RС — фильтра активное сопротивление схемы не увеличивается. Радиочастотный дроссель — это катушка, состоящая из нескольких витков провода и ферритового сердечника и используемая с той же целью в радиочастотных схемах.
Диоды и диодные схемы
что такое Low-Pass фильтр и как им пользоваться
Фильтры низких частот — простые инструменты с огромным влиянием на общее звучание микса. При правильном использовании Low-Pass фильтр превращает сырые исходники в отполированные треки, а плоские звуки — в глубокие и богатые сигналы. Вместе с тем бесконтрольная фильтрация низких частот вымывает из композиции яркость, создавая мутную и мямлющую картину.
Продолжая серию материалов об эквализации, редакция SAMESOUND.RU приводит адаптированный перевод заметки из блога компании iZotope, посвящённой возможностям низкочастотных фильтров. Из этого текста вы узнаете, что такое Low-Pass фильтры, а также посмотрите на несколько вариантов использования фильтра, которые доказывают, что их возможности значительно шире обычного ограничения сигнала.
Что такое Low-Pass фильтр
Low-Pass фильтр, низкочастотный пропускной фильтр или фильтр низких частот (ФНЧ) — инструмент, отрезающий все высокие частоты после определённой отметки, называемой частотой среза (точка обрезки). Во время работы фильтр устраняет всё, что выходит за выбранную точку обрезки, но не затрагивает сигнал ниже.
Low-Pass фильтр — один из самых простых, но вместе с тем действенных и даже деструктивных методов использования эквалайзера. С его помощью звукорежиссёр может оставить в сигнале только низкие частоты до определённой отметки — фильтр отсечёт все, что живёт выше выбранной точки.
Фильтр — простейший инструмент, управляемый только параметром частоты среза, однако его влияние на звучание микса велико.
Основное предназначение низкочастотных фильтров — ограничить высокочастотный контент, который не нужен миксу. Для настройки параметров работы используется всего лишь один параметр — точка обрезки, задающий конкретную границу спектра, после которой происходит отсечение частот. К примеру, применив низкочастотную фильтрацию к бас-бочке и выбрав точку обрезки в районе 5 кГц, мы можем устранить весь частотный контент выше заданной отметки. Чаще всего низкочастотным фильтром устраняют шумы и различные высокочастотные наводки, незначительные артефакты, а также убирают лишний верх у синтезаторов, ударных, вокала и других инструментов.
Как низкочастотная фильтрация влияет на сигнал
Как и в случае с другими инструментами, используемыми при сведении музыки, Low-Pass фильтр нужно применять осторожно (особенно, если вы новичок). Главное здесь — вовремя остановиться и не зафильтровать всё напрочь.
Чтобы оценить влияние низкочастотного фильтра на сигнал, проведём небольшой эксперимент. Поместите фильтр на мастер-канал DAW и установите достаточно высокую частоту обрезки — 10 кГц или выше. По мере понижения точки фильтрации микс постепенно превратится в низкочастотное мутное месиво (особенно явно потеря верха проявится, если обрезка перевалит ниже 7 кГц). Теперь постепенно повысим точку фильтрации (двигайте фильтр вправо, выше по спектру). Повышение порога срабатывания фильтра постепенно вернёт миксу яркость и полноту звука.
Такой пример отлично демонстрирует деструктивную суть фильтрации — перестараетесь, и музыка перестанет быть музыкой.
Конечно, вряд ли кто-то в здравом уме будет так активно использовать фильтр на основном выходе проекта. Так или иначе, но при работе с отдельными дорожками ситуация практически не отличается от нашего эксперимента — сильные ограничения убивают полноту и естественность звука.
Даже при аккуратной работе с фильтром его деструктивная природа может привести к смерти микса от нехватки высоких частот. Человеческий слух более восприимчив к средним и высоким частотам, во время сведения чувствительность ушей быстро снижается. Так как работа в студии обычно связана с постоянным прослушиванием микса в течение длительного времени, звукорежиссёры и музыканты подвержены риску не заметить, что Low-Pass фильтр отрезал лишнее. Как только в миксе активнее появляются высокие частоты, слух воспринимает их как слишком резкие звуки и стремится «задавить» их куда подальше, а то и вырезать напрочь. В итоге уставшие уши не слышат реальную звуковую картину, что приводит к появлению искалеченных миксов с частотным дисбалансом.
Чтобы понять важность аккуратной фильтрации, послушайте пример ниже. Синтезаторный бас звучит вместе с барабанным лупом и разными настройками фильтра низких частот.
- Эксперимент с низкочастотной фильтрацией 0:30
В первой части аудиофайла частота среза слишком высока — бас звучит очень ярко и в отрыве от ударных. Во второй части примера фильтрация менее активна, бас звучит округло и плотно, но потерял резкость оригинального сигнала. В третьей части мы слышим сбалансированное звучание: бас звучит округло, не мешает ударным, но и не лишён нужной яркости.
Как использовать Low-Pass фильтр при сведении музыки
Самое частое применение фильтра — обрезка высоких частот. Благодаря этому сигнал становится чище, а в верхнем диапазоне частот микса появляется дополнительное пространство для инструментов. Тем не менее возможности низкочастотного фильтра не ограничиваются простой чисткой спектра, ведь фильтр может работать не только как корректирующий, но и как креативный инструмент обработки.
1 Устранение немузыкальных элементов
Как гул и мутность, мешающие частотам в нижнем низе прорваться через микс, шипящие и резкие звуки в районе 10 кГц отвлекают внимание от более важной высокочастотной информации в других точках частотного спектра. В зависимости от инструмента, различные немузыкальные звуки могут жить ниже 10 кГц.
Использование фильтра низких частот для устранения шума из сигнала басаНа скриншоте выше мы видим басовую линию с активированным эквалайзером Neutron. В этом конкретном случае интерес вызывает то, что происходит ниже 2 кГц. Обратите внимание на шумы, попавшие в сигнал во время записи — их наличие делает сигнал баса излишне активным в общем миксе. Когда мы повышаем громкость баса, существование таких помех становится критичным: шум усиливается вместе с сигналом и даже маскирует за собой другие инструменты.
Слушателю незачем слышать шум, ему не нужно знать, откуда он взялся и что вообще присутствует в сигнале. Задача звукорежиссера в том, чтобы скрыть подобный контент от ушей посторонних и переключить внимание людей на то, что реально важно — звук баса. Здесь-то и нужен Low-Pass фильтр: наведя точку обрезки на место, где шум исчезает, мы скроем его в миксе. Главное не отфильтровать лишнего, иначе сигнал баса исказится и потеряет в естественности.
При фильтрации всегда соблюдайте баланс. Фильтр должен отрезать лишнее, но не изменить сам сигнал.
2 Придание глубины
Глубина микса — важный фактор качественной записи. Благодаря ей мы можем почувствовать, что инструменты на переднем и заднем плане звуковой картины находятся на разном расстоянии. Обычно на переднем плане оставляют голос и вокал, ударные и гитары. На задний план отодвигают перкуссию, пэды и клавишные.
Мы привыкли, что в повседневной жизни объекты, находящиеся далеко от нас, звучат более тихо и менее ярко. Когда мы идём по улице, то двигатели и сигналы автомобилей звучат достаточно глухо. Несмотря на то, что в звуке двигателя преобладают низкие частоты, а в сигнале клаксона — высокие, когда мы находимся на некотором удалении от этих источников звука сигналы сливаются между собой в единую глухую картинку.
Какими бы высокими не был звуки, по мере удаления от слушателя они обязательно сливаются в единую монолитную массу. Вспомните, как обычно звучит шумная улица, когда вы находитесь где-то далеко — все звуки неразборчивы и звучат единым фронтом.Этот принцип работает и при сведении музыки. Фильтруя верхний верх и снижая уровень инструментов, мы отодвигаем их на задний план микса.
Положение инструмента в миксе можно автоматизировать. Для этого достаточно активировать на дорожке Low-Pass фильтр и запрограммировать его так, чтобы в нужные моменты микса (например, в припеве) он отодвигал точку обрезки и выдвигал сигнал вперёд. Затем фильтр можно вернуть обратно, чтобы инструмент снова переехал на задний план. Благодаря автоматизации, о которой мы подробно рассказывали здесь, фильтр превращается из ограничивающего в креативный инструмент.
3 Устранение сталкивающихся частот у инструментов со схожим звучанием
Фильтрация полезна при создании пространства для разных сигналов. С помощью Low-Pass фильтра звукорежиссёр может выборочно удалить высокие частоты, чтобы дать больше свободы звучащим высоко инструментам.
Представим, что в вашем проекте присутствует множество слоев вокала и ярких синтезаторов. Из-за того, что вокал и синтезаторы живут в одних и тех же (или очень близких) частотных диапазонах, их звук становится зажатым — сигналам попросту тесно вместе. В попытках исправить эту ситуацию начинающие звукорежиссеры обычно усиливают верхний верх у вокала так, чтобы он выделился на фоне остальных сигналов. Ход логичный, но неправильный: проблема тесноты только усиливается, микс становится ярким до боли в ушах .
На деле же решение значительно проще: отфильтровать частоты в районе верхнего верха в тех сигналах, которым они не нужны. По итогам фильтрации мы получим вместо излишне накаченного энергией звука более аккуратный и отполированный саунд. Посмотрите на свои синтезаторы: если тело их звука присутствует только в среднем диапазоне, отсеките верх — так вы освободите место вокалу. Яркий звук снейра (с характерным хрустящим призвуком) также может мешать вокалу, поэтому лёгкое «помутнение» звука точно пойдет на пользу миксу.
Мы постоянно слышим советы усилить в миксе то или это. Но не менее важен другой совет: в первую очередь думайте не об усилении, а о том, что можно ослабить или вовсе убрать в миксе.
Выявить частотный дисбаланс помогает модуль Tonal Balance Control, входящий в iZotope Neutron и Ozone. Для пущей простоты сравните свой микс с референс-треком, чтобы понять, где наблюдается перекос по частотам в вашем треке. При сравнении синими областями модуль показывает расхождение вашего микса с референс-треком: синие области — количество частот в вашем миксе, белые линии — уровень частот в референс-треке.
Модуль Tonal Balance Control от iZotope. Синие регионы — количество частотных диапазонов в миксе, белые линии — количество частот в референс-треке.Если средние и высокие частоты выходят за верхнюю границу области, яркие элементы микса нужно откатить назад — отфильтровать сильнее. Если же эти частоты выходят за нижнюю границу или находятся около неё, то фильтрацию нужно ослабить — слишком активное ограничение не нужно.
4 Создание баланса между основным и бэк-вокалом
Чем больше вокальных дорожек в проекте, тем активнее частоты накладываются друг на друга и тем тяжелее что-либо разобрать в миксе. Пожалуй, самым мощным столкновением частот становится борьба добра со злом — основного и бэк-вокала.
Бэк-вокал всегда работает фоном и не должен конкурировать с основной вокальной партией за внимание слушателя. Чтобы освободить место основному вокалу, отфильтруйте Low-Pass фильтром бэк-вокал так, чтобы он стал похож на тень ведущего голоса. Скорее всего понадобится сделать ещё несколько подрезок в спектре, чтобы гармонично склеить две дорожки (это тема для отдельной статьи, которую мы обязательно напишем).
Если сбалансировать основной и бэк-вокал никак не получается, действуйте методом «от противного» — уменьшите количество вокальных дорожек в проекте. Слишком много однотипных треков с легкостью разрушает баланс микса, нарушает динамику и уменьшает доступный запас хедрума. Поэтому перед фильтрацией в первую очередь оцените, насколько вам нужно десять бэк-вокальных линий — правило «меньше — лучше» никто не отменял.
5 Выделение частот
Итак, мы знаем, что Low-Pass фильтр применяется для устранения частот. Тем не менее ему по силам не только устранять частоты, но и усиливать их в определённых границах. Благодаря этому можно аккуратно приручить инструменты в миксе, улучшив не только общую картину, но и подчеркнув интересные стороны их звучания.
Допустим, в сигнале присутствуют интересные верхние обертона, которые звучат слишком тихо. Поместив Low-Pass фильтр на дорожке и настроив точку обрезки на место, где обертона теряют энергию, мы можем без лишних проблем усилить их небольшим подъёмом. Активное задирание фильтра здесь не к чему: переусердствуете — середина станет звучать картонно, верх обязательно зашипит.
Усиление в районе обрезкиЧтобы избежать картонности и шипения, полагайтесь на буст широкой области частот вместо узкого точечного усиления. Широкий подъём усилит сигнал более естественно, а также минимизирует возможные искажения сигнала.
Тот же самый приём можно провести на другом конце спектра с помощью High-Pass фильтра. В этом случае речь идёт о подчеркивании гармоник и обертонов в низких частотах.
What’s Your Reaction?
Фильтр нижних частот.
Фильтр нижних частот первого порядка на ОУ и его АЧХ. Если объединить схему инвертирующего усилителя со схемой интегратора, образуется схема фильтра нижних частот первого порядка, которая показана ниже. Амплитудно-частотная характеристика – зависимость амплитуды сигнала на выходе устройства от частоты при постоянной амплитуде на входе этого устройства – представлена ниже.
Такой фильтр представляет собой инвертирующий усилитель, обладающий постоянным коэффициентом усиления в полосе прозрачности от постоянного тока до граничной частоты fср. Частотную характеристику такого фильтра можно охарактеризовать формулой (0 ≤ f ≤ fср).
Видно, что в пределах полосы пропускания, пока емкостное сопротивление конденсатора достаточно велико, коэффициент усиления схемы совпадает с коэффициентом усиления инвертирующего усилителя (см. выражение (1)).
Частота среза этого фильтра определяется элементами цепи обратной связи в соответствии с выражением (2).
В полосе затухания выше частоты среза fср усиление уменьшается с интенсивностью 20 дБ/декада (или 6 дБ/октава), что означает уменьшение коэффициента усиления по напряжению в 10 раз при увеличении частоты также в 10 раз или уменьшение коэффициента усиления в два раза при каждом удвоении частоты.
Фильтр нижних частот второго порядка на ОУ. Если такой крутизны наклона амплитудно-частотной характеристики в полосе затухания недостаточно, можно использовать фильтр нижних частот второго порядка, схема которого показана ниже.
Коэффициент усиления фильтра нижних частот второго порядка такой же, как у фильтра первого порядка, в связи с тем, что суммарное сопротивление резисторов в цепи инверсного входа, как и ранее, выражается согласно формуле (1).
АЧХ этого фильтра отличается повышенной крутизной наклона, которая составляет 12 дБ/октава. Таким образом, в полосе затухания при увеличении частоты вдвое напряжение сигнала на выходе фильтра уменьшается в четыре раза.
4. Описание и классификация активных фильтров. Фильтр верхних частот. Описание и классификация активных фильтров.
Активный фильтр – аналоговый электронный фильтр, в котором присутствует один или несколько активных компонентов.
При использовании в качестве элемента схемы фильтра операционного усилителя (ОУ) можно синтезировать характеристику любого LC-фильтра без применения катушек индуктивности. В отличие от пассивных RC-фильтров, активные обеспечивают более качественное разделение полос пропускания и затухания. В схемы активных фильтров помимо пассивных компонентов (резисторов, конденсаторов и катушек индуктивности) входят такие активные изделия, как транзисторы или интегральные микросхемы.
Активные резисторно-конденсаторные фильтры имеют огромное преимущество перед их пассивными аналогами, особенно на частотах ниже 10 кГц. Пассивные фильтры для низких частот должны содержать катушки большой индуктивности и конденсаторы большой емкости. Поэтому они получаются громоздкими, дорогостоящими, а их характеристики оказываются далеко не идеальными.
Схемы дифференциатора (см. рис. а) и интегратора (см. рис. б), построенные с применением операционных усилителей, представляют собой простейшие активные фильтры. При выборе элементов схемы в определенной зависимости от частоты дифференциатор становится фильтром верхних частот, а интегратор — фильтром нижних частот.
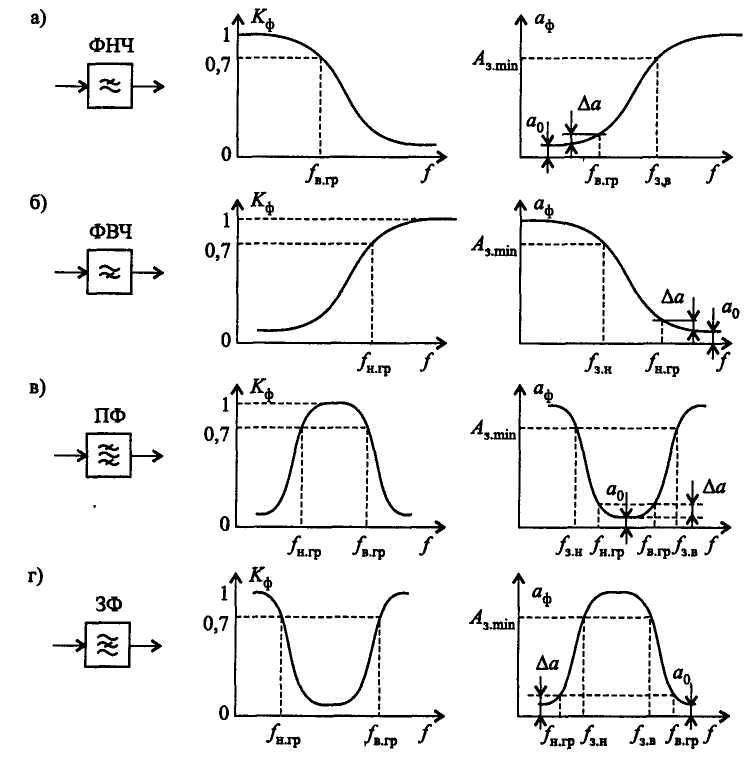
Активные фильтры можно разделить на группы по различным признакам: назначению, полосе пропускаемых частот, типу усилительных элементов, виду обратных связей и др. По полосе пропускаемых частот фильтры делятся на четыре основные группы: нижних частот, верхних частот, полосовые и заграждающие.
По назначению фильтры делятся на сглаживающие фильтры источников питания, заграждающие фильтры помех, фильтры для селективных усилителей низкой или высокой частоты и др.
По типу усилительных элементов можно выделить транзисторные фильтры, фильтры на усилителях с ограниченным усилением, на операционных усилителях, на повторителях напряжения и др. Все рассмотренные фильтры могут иметь одну цепь обратной связи или несколько. В связи с этим различают фильтры с одноконтурной и с многоконтурной обратной связью. Кроме этого, различают фильтры по числу полюсов на частотной характеристике – фильтры первого порядка, второго и более высоких порядков. Фильтры высоких порядков имеют более крутые границы полос пропускания и затухания и более плоскую характеристику в области полосы пропускания, что естественно улучшает качество фильтра.
Широкие возможности активных RC-фильтров связаны с использованием в них активных элементов. Цепи, содержащие только сопротивления и емкости, имеют полюсы передаточной функции на отрицательной действительной полуоси комплексной плоскости p=σ+iω, что ограничивает возможности создания фильтров. В отличие от пассивных, активные RC-фильтры (ARС-фильтры) могут иметь полюсы в любой части комплексной плоскости. Однако схемы с полюсами в правой полуплоскости неустойчивы, поэтому в активных фильтрах используются только те схемы, полюсы передаточной функции которых располагаются в левой полуплоскости или на оси jω.
При проектировании активных фильтров фильтр заданного порядка разбивается на звенья первого и второго порядка. Результирующая АЧХ получится перемножением характеристик всех звеньев. Применение активных элементов (транзисторов, операционных усилителей) позволяет исключить влияние звеньев друг на друга и проектировать их независимо. Это обстоятельство значительно упрощает и удешевляет проектирование и настройку активных фильтров.
Принцип работы фильтра низких и высоких частот
Индуктивность и емкость весьма полезны в электронных схемах. Одним из примеров такой полезности является фильтр. Фильтр — это схема, разделяющая определенные частоты.
Существует множество конструкций фильтров. Например, фильтры могут быть разработаны для пропускания низких частот и подавления высоких частот; для отклонения низких частот и пропускания высоких частот либо для пропуска или отклонения определенных частотных диапазонов.
Каждый тип фильтра назван в соответствии с его функцией.Существует четыре основных типа фильтров:
- нижних частот,
- верхних частот,
- полосовых и
- полосовых.
Фильтры также используются для регулировки пульсирующего тока, исходящего от выпрямителя. Выпрямитель — это устройство, преобразующее переменный ток в пульсирующий постоянный ток. Поскольку для большинства электронных схем требуется чистый постоянный ток, необходимо регулировать постоянный ток. Эта схема фильтра выравнивает пики и спады тока.
Действие фильтрации
При изучении действия фильтрации следует учитывать следующие моменты:
- Конденсатор блокирует постоянный ток, но пропускает переменный ток.
- Проводник может пропускать ток, который имеет как постоянную, так и переменную составляющую. На графике в части A Рисунок 1 показан постоянный постоянный ток напряжением 10 вольт. В части B рисунка показано напряжение переменного тока, пиковое значение которого составляет 10 вольт. В части C рисунка показаны эти два напряжения вместе. Эта волна изображает сумму двух волн.
Обратите внимание на новую ось переменного напряжения. Теперь он изменяется выше и ниже уровня 10 В постоянного тока. Поскольку ось поднята постоянным напряжением, переменное напряжение больше не меняет полярность.Этот ток представляет собой переменный постоянный ток.
Рисунок 1. A — Установившийся постоянный ток. B –пиковый переменный ток 10 В. C — Комбинированный источник постоянного и переменного тока.
Амплитуда тока колеблется от нуля до 20 вольт. Когда этот переменный постоянный ток подключается к цепи, конденсатор C немедленно заряжается до среднего уровня постоянного напряжения. В данном случае этот уровень составляет 10 вольт.
Когда входящее напряжение повышается до 20 вольт, ток течет через резистор R и заряжает конденсатор C.В следующем полупериоде входящее напряжение падает до нуля, и конденсатор C разряжается до нуля через R.
Рисунок 2. Генератор переменного тока и источник постоянного тока подключены последовательно к RC-цепи.
Обратите внимание, что напряжение появляется на R из-за заряда и разряда C. Выход этой схемы, взятый через R, представляет только переменную составляющую напряжения входящего сигнала. См. Рисунок 3 .
Постоянный ток блокируется конденсатором C.Между входной и выходной волнами существует небольшой фазовый сдвиг, потому что значение R выбирается в десять или более раз больше значения реактивного сопротивления C на частоте входного напряжения. Когда это соотношение сопротивления к реактивному сопротивлению сохраняется, фазовый сдвиг не влияет на волны.
Рисунок 3. Напряжение на R является результатом тока заряда-разряда и представляет собой переменную составляющую сигнала.
Шунтирование
Иногда необходимо создавать падение напряжения на резисторе, возникающее только из-за постоянной составляющей напряжения сигнала.Это делается путем обхода сигнала переменного тока или напряжения вокруг сопротивления. Это шунтирование может быть выполнено с помощью конденсатора.
Часть A из На рис. 4 показаны два резистора на 1500 Ом, подключенные к источнику 10 В постоянного тока. Общее сопротивление равно R1 + R2, или 3000 Ом. Ток в цепи:
\ [I = \ frac {E} {R} = \ frac {10V} {3000 \ Omega} = 3,3 мА \]
Падение напряжения на каждом резисторе:
$ \ begin {align} & {{E} _ {{{R} _ {1}}}} = I * R = 0.0033A * 1500 \ Omega = 5V \\ & {{E} _ {{{R} _ {2}}}} = I * R = 0.0033A * 1500 \ Omega = 5V \\\ end {align} $
Рис. 4. Напряжение постоянного тока A – A вызывает одинаковые падения на R 1 и R 2 . B — Падение напряжения на R 2 поддерживается постоянным за счет обхода составляющей переменного тока.
- Подключите 10-вольтный источник переменного тока, и переменное напряжение появится на обоих резисторах. Но мы хотим обойти эту составляющую переменного тока около 2 рэнд. Для этого подключите конденсатор с низким реактивным сопротивлением к переменному напряжению параллельно с R 2 .
- Если реактивное сопротивление C составляет одну десятую сопротивления R, большая часть переменного тока будет протекать через C, а не через R. Используйте значения, указанные в части B на рисунке 4. C имеет реактивное сопротивление 150 Ом для частота переменного тока. Это реактивное сопротивление составляет одну десятую значения 1500 Ом для R 2 . По большей части импеданс R 2 || X C (R 2 и X C параллельно) может быть задано как значение 150 Ом. Распределение напряжения в этой цепи можно измерить или вычислить.
- Суммарное сопротивление для всей цепи равно 1 + (R 2 || X C ) или 1650 Ом. R 2 || X C представляет собой одну одиннадцатую от общего сопротивления переменному току.
- Поскольку падение напряжения является функцией сопротивления, десять одиннадцатых напряжения появляется на R 1 и только одна одиннадцатая — на R 2 || Х С . Приложенное переменное напряжение составляет 10 вольт, поэтому:
$ \ begin {align} & {{E} _ {{{R} _ {1}}}} = 9.1 В \\ & и \\ & {{E} _ {{{R} _ {2}}}} = 0,9 В \\\ end {align} $
- Если напряжение постоянного тока 10 В подключено последовательно при 10-вольтовом переменном напряжении для объединенного входного напряжения постоянное напряжение будет делиться поровну между 1 и 2 рэнд. Напряжение постоянного тока на каждом резисторе упадет на пять вольт. C — обрыв цепи для постоянного тока.
- Переменное напряжение делится в рассчитанном ранее соотношении. Большая часть этого напряжения возникает на R 1 . Напряжение на R 2 остается довольно постоянным из-за действия шунтирующего конденсатора.
Подводя итог, выберите конденсатор, который будет образовывать путь с низким реактивным сопротивлением вокруг резистора для токов выбранных частот. Это создает почти полностью постоянное напряжение на одном резисторе.
Рабочие фильтры нижних частот
Иногда требуется фильтр, который пропускает низкие частоты, но снижает токи высоких частот. Этот фильтр называется фильтром нижних частот .
Схема фильтра нижних частот всегда имеет сопротивление или катушку индуктивности, включенную последовательно с напряжением входящего сигнала.Он также имеет конденсатор в шунте или поперек линии, Рисунок 5.
Рисунок 5. Схема фильтра нижних частот.
- По мере увеличения частоты реактивное сопротивление L увеличивается, так что большее количество напряжения появляется на L.
- Также с увеличением частоты реактивное сопротивление C уменьшается. Таким образом, конденсатор обеспечивает байпас для токов более высокой частоты вокруг сопротивления нагрузки R.
- Из-за повышенного реактивного сопротивления катушки индуктивности и уменьшенного реактивного сопротивления конденсатора на высоких частотах более высокие частоты появляются только в небольших количествах на нагрузке.
- Низкие частоты создают более высокие напряжения в нагрузке. Низкие частоты пропускаются, высокие отбрасываются.
Рабочие фильтры верхних частот
Противоположным фильтру нижних частот является фильтр верхних частот . Фильтры верхних частот пропускают выбранный высокочастотный ток и отклоняют низкочастотные токи.
Схема фильтра включает конденсатор, включенный последовательно с напряжением входящего сигнала, и шунт индуктивности через линию, Рисунок 6 .
- По мере увеличения частоты X L увеличивается, и более высокое напряжение развивается параллельно L и R.
- По мере увеличения частоты X C уменьшается, обеспечивая путь с низким реактивным сопротивлением для высокочастотных сигналов.
- Низкие частоты шунтируются или обходятся вокруг нагрузки R из-за низкого реактивного сопротивления L на низких частотах.
Рисунок 6. Схема фильтра верхних частот.
Для улучшения фильтрующего действия как нижних, так и верхних частот, две или более секции часто объединяются.Эти секции названы в соответствии с составом схемы. Рисунок 7 иллюстрирует схематические рисунки и названия нескольких типов фильтров.
Рис. 7. Цепям фильтра можно дать имя в соответствии с конфигурацией цепи.
Фильтры настроенных цепей
Последовательные и параллельные резонансные цепи называются приемными или отклоняющими цепями. Эти настроенные схемы можно использовать в качестве фильтров, поскольку они способны давать максимальный отклик на настроенной резонансной частоте.
В рис. 8 в качестве полосового фильтра используется последовательный резонансный контур. Полосовой фильтр принимает только токи, близкие к его резонансной частоте.
В рис. 9 последовательный резонансный контур шунтируется поперек нагрузки или параллельно ей. Это обеспечивает путь с низким импедансом вокруг токов на резонансных частотах (в обход нагрузки). В этом случае фильтр будет реагировать как фильтр с отклонением полосы. Фильтры отклонения полосы пропускают определенную полосу частот.
Рисунок 8. Последовательно настроенная схема, используемая в качестве полосового фильтра.
Рис. 9. Последовательно настроенная схема, выполненная как режекторный фильтр.
В схемах на рис. 10 используется параллельная настроенная схема. Эффект параллельной настроенной схемы противоположен последовательной настроенной цепи.
Когда контур резервуара включен последовательно с входящими токами, он обеспечивает максимальное сопротивление и отклоняет частоты вокруг своей резонансной частоты.
Когда контур резервуара шунтируется на через нагрузку, это вызывает максимальный отклик через нагрузку при резонансе. Частоты, отличные от резонанса, пропускаются из-за пониженного импеданса цепи настроенного резервуара.
Рисунок 10. A — Параллельно настроенная схема в качестве режекторного фильтра. B — Параллельно настроенная схема в качестве полосового фильтра.
Комбинации последовательно и параллельно настроенных цепей могут использоваться для обеспечения более резкой отсечки и большего затухания.
Фильтр низких частот — Учебное пособие по пассивному RC-фильтру
Другими словами, они «отфильтровывают» нежелательные сигналы, и идеальный фильтр будет отделять и пропускать синусоидальные входные сигналы в зависимости от их частоты. В низкочастотных приложениях (до 100 кГц) пассивные фильтры обычно создаются с использованием простых цепей RC (резистор-конденсатор), тогда как фильтры более высоких частот (выше 100 кГц) обычно изготавливаются из компонентов RLC (резистор-индуктор-конденсатор).
Пассивные фильтры состоят из пассивных компонентов, таких как резисторы, конденсаторы и катушки индуктивности, и не имеют усилительных элементов (транзисторов, операционных усилителей и т. Д.), Поэтому не имеют усиления сигнала, поэтому их выходной уровень всегда меньше входного.
Фильтры названы так в соответствии с частотным диапазоном сигналов, которые они позволяют проходить через них, блокируя или «ослабляя» остальные. Наиболее часто используемые конструкции фильтров:
- Фильтр нижних частот — фильтр нижних частот пропускает только низкочастотные сигналы от 0 Гц до его частоты среза, точка c, но блокирует те, что выше.
- Фильтр верхних частот — фильтр верхних частот пропускает только высокочастотные сигналы с частотой среза, ƒc и выше до бесконечности, блокируя при этом более низкие.
- Полосовой фильтр — полосовой фильтр пропускает сигналы, попадающие в определенную полосу частот между двумя точками, при этом блокируя как нижние, так и верхние частоты по обе стороны от этой полосы частот.
Простые пассивные фильтры первого порядка (1-го порядка) могут быть изготовлены путем последовательного соединения одного резистора и одного конденсатора через входной сигнал (V IN ) с выходом фильтра (V OUT ) взятый из стыка этих двух компонентов.
В зависимости от того, каким образом мы подключаем резистор и конденсатор относительно выходного сигнала, определяется тип конструкции фильтра, в результате чего получается либо фильтр нижних частот , либо фильтр верхних частот .
Поскольку функция любого фильтра состоит в том, чтобы позволить сигналам данной полосы частот проходить без изменений, ослабляя или ослабляя все остальные, которые не нужны, мы можем определить характеристики амплитудной характеристики идеального фильтра, используя идеальную кривую частотной характеристики четыре основных типа фильтров, как показано.
Кривые идеального отклика фильтра
Фильтры можно разделить на два различных типа: активные фильтры и пассивные фильтры. Активные фильтры содержат усилительные устройства для увеличения мощности сигнала, а пассивные не содержат усилительных устройств для усиления сигнала. Поскольку в конструкции пассивного фильтра есть два пассивных компонента, выходной сигнал имеет меньшую амплитуду, чем соответствующий входной сигнал, поэтому пассивные RC-фильтры ослабляют сигнал и имеют коэффициент усиления менее единицы (единицы).
Фильтр нижних частот может представлять собой комбинацию емкости, индуктивности или сопротивления, предназначенную для обеспечения высокого затухания выше указанной частоты и небольшого затухания или отсутствия затухания ниже этой частоты. Частота, с которой происходит переход, называется «граничной» или «угловой» частотой.
Простейшие фильтры нижних частот состоят из резистора и конденсатора, но более сложные фильтры нижних частот имеют комбинацию последовательных катушек индуктивности и параллельных конденсаторов. В этом уроке мы рассмотрим простейший тип — пассивный двухкомпонентный RC-фильтр нижних частот.
Фильтр низких частот
Простой пассивный фильтр нижних частот RC или LPF может быть легко изготовлен путем последовательного соединения одного резистора с одним конденсатором, как показано ниже. В этом типе конфигурации фильтра входной сигнал (V IN ) применяется к последовательной комбинации (как резистор, так и конденсатор вместе), но выходной сигнал (V OUT ) проходит только через конденсатор.
Этот тип фильтра обычно известен как «фильтр первого порядка» или «однополюсный фильтр», почему первый порядок или однополюсный ?, потому что он имеет только «один» реактивный компонент, конденсатор, в цепи .
RC Цепь фильтра нижних частот
Как упоминалось ранее в руководстве по емкостному реактивному сопротивлению, реактивное сопротивление конденсатора изменяется обратно пропорционально частоте, в то время как значение резистора остается постоянным при изменении частоты. На низких частотах емкостное реактивное сопротивление (X C ) конденсатора будет очень большим по сравнению с сопротивлением резистора R.
Это означает, что потенциал напряжения V C на конденсаторе будет намного больше, чем падение напряжения V R , возникающее на резисторе.На высоких частотах верно обратное: V C мало, а V R велико из-за изменения значения емкостного реактивного сопротивления.
Хотя приведенная выше схема является схемой RC-фильтра нижних частот, ее также можно рассматривать как схему частотно-зависимого переменного делителя потенциала, аналогичную той, которую мы рассматривали в руководстве по резисторам. В этом руководстве мы использовали следующее уравнение для расчета выходного напряжения для двух отдельных резисторов, соединенных последовательно.
Мы также знаем, что емкостное реактивное сопротивление конденсатора в цепи переменного тока определяется как:
Противодействие протеканию тока в цепи переменного тока называется сопротивлением , , символ Z, а для последовательной цепи, состоящей из одного резистора, соединенного последовательно с одним конденсатором, полное сопротивление цепи рассчитывается как:
Затем, подставив наше уравнение для импеданса выше в уравнение резистивного делителя потенциала, мы получим:
Уравнение делителя потенциала RC
Итак, используя уравнение делителя потенциала двух последовательно соединенных резисторов и подставляя импеданс, мы можем вычислить выходное напряжение RC-фильтра для любой заданной частоты.
Фильтр низких частот Пример №1
Фильтр нижних частот Схема , состоящая из резистора 4 к7 Ом, соединенного последовательно с конденсатором 47 нФ, подключена к источнику синусоидального напряжения 10 В. Рассчитайте выходное напряжение (V OUT ) на частоте 100 Гц и снова на частоте 10 000 Гц или 10 кГц.
Выходное напряжение с частотой 100 Гц.
Выходное напряжение с частотой 10 000 Гц (10 кГц).
Частотная характеристика
Из результатов выше видно, что по мере того, как частота, подаваемая на RC-сеть, увеличивается со 100 Гц до 10 кГц, напряжение на конденсаторе падает, и, следовательно, выходное напряжение (V OUT ) из схемы уменьшается с 9,9 В до 0,718. v.
Построив график зависимости выходного напряжения сети от различных значений входной частоты, можно найти функцию Frequency Response Curve или Bode Plot схемы фильтра нижних частот, как показано ниже.
Частотная характеристика фильтра нижних частот 1-го порядка
График Боде показывает, что частотная характеристика фильтра почти плоская для низких частот, и весь входной сигнал передается непосредственно на выход, что приводит к усилению почти 1, называемому единицей, до тех пор, пока он не достигнет значения среза . -off Частота точек (ƒc). Это связано с тем, что реактивное сопротивление конденсатора высокое на низких частотах и блокирует любой ток, протекающий через конденсатор.
После этой точки отсечки частота отклика схемы уменьшается до нуля с наклоном -20 дБ / декада или (-6 дБ / октава) «спад». Обратите внимание, что угол наклона, этот спад -20 дБ / декада всегда будет одинаковым для любой комбинации RC.
Любые высокочастотные сигналы, подаваемые на схему фильтра нижних частот выше этой точки среза частоты, будут сильно ослаблены, то есть они быстро уменьшатся. Это происходит потому, что на очень высоких частотах реактивное сопротивление конденсатора становится настолько низким, что возникает эффект короткого замыкания на выходных клеммах, что приводит к нулевому выходу.
Затем, тщательно выбрав правильную комбинацию резистора и конденсатора, мы можем создать RC-цепь, которая позволяет диапазону частот ниже определенного значения проходить через цепь без изменений, в то время как любые частоты, подаваемые на схему выше этой точки отсечки, будут ослаблены. , создавая то, что обычно называют фильтром нижних частот .
Для этого типа схемы «Фильтр нижних частот» все частоты ниже этой точки отсечки, ƒc, которые не изменяются с небольшим ослаблением или без него и считаются находящимися в зоне полосы пропускания фильтров .Эта зона полосы пропускания также представляет ширину полосы фильтра. Любые частоты сигнала выше этой точки отсечки обычно считаются находящимися в зоне полосы заграждения фильтров , и они будут значительно ослаблены.
Эта частота «отсечки», «угла» или «точки останова» определяется как точка частоты, в которой емкостное реактивное сопротивление и сопротивление равны, R = Xc = 4k7Ω. Когда это происходит, выходной сигнал ослабляется до 70,7% значения входного сигнала или -3 дБ (20 log (Vout / Vin)) входного.Хотя R = Xc, выходной сигнал составляет , а не половину входного сигнала. Это потому, что он равен векторной сумме двух и, следовательно, составляет 0,707 входных данных.
Поскольку фильтр содержит конденсатор, фазовый угол (Φ) выходного сигнала LAGS отстает от входного и на частоте среза -3 дБ (c) сдвинут по фазе -45 o . Это связано с тем, что для зарядки пластин конденсатора требуется время, когда изменяется входное напряжение, в результате чего выходное напряжение (напряжение на конденсаторе) «отстает» от входного сигнала.Чем выше входная частота, приложенная к фильтру, тем сильнее запаздывает конденсатор, и схема становится все более и более «не в фазе».
Точка отсечки частоты и угол сдвига фаз могут быть найдены с помощью следующего уравнения:
Частота отсечки и фазовый сдвиг
Тогда для нашего простого примера схемы « Low Pass Filter », приведенной выше, частота среза (c) задается как 720 Гц с выходным напряжением 70,7% от значения входного напряжения и углом сдвига фазы -45. или .
Фильтр нижних частот второго порядка
До сих пор мы видели, что простые RC-фильтры нижних частот первого порядка могут быть изготовлены путем последовательного соединения одного резистора с одним конденсатором. Эта однополюсная схема дает нам крутизну спада -20 дБ / декаду для частот выше точки отсечки на -3 дБ . Однако иногда в схемах фильтров этого угла наклона -20 дБ / декада (-6 дБ / октава) может быть недостаточно для удаления нежелательного сигнала, тогда можно использовать два этапа фильтрации, как показано.
Фильтр нижних частот второго порядка
В приведенной выше схеме используются два пассивных фильтра нижних частот первого порядка, соединенные или «каскадно соединенные» вместе, чтобы сформировать сеть фильтров второго порядка или двухполюсную сеть. Таким образом, мы можем видеть, что фильтр нижних частот первого порядка можно преобразовать в фильтр второго порядка, просто добавив к нему дополнительную RC-цепь, и чем больше RC-каскадов мы добавляем, тем выше становится порядок фильтра.
Если несколько (n) таких RC-каскадов соединены каскадом вместе, результирующая схема RC-фильтра будет известна как фильтр «n th -order» с крутизной спада «n x -20 дБ / декада».
Так, например, фильтр второго порядка будет иметь наклон -40 дБ / декаду (-12 дБ / октава), фильтр четвертого порядка будет иметь наклон -80 дБ / декаду (-24 дБ / октава) и так далее. Это означает, что по мере увеличения порядка фильтра крутизна спада становится более крутой, и фактическая характеристика полосы задерживания фильтра приближается к его идеальным характеристикам полосы задерживания.
Фильтры второго порядка важны и широко используются в конструкциях фильтров, потому что в сочетании с фильтрами первого порядка любые фильтры более высокого порядка со значениями n и могут быть разработаны с их использованием.Например, фильтр нижних частот третьего порядка формируется путем последовательного или каскадного соединения фильтров нижних частот первого и второго порядка.
Но есть и обратная сторона — каскадирование вместе ступеней RC-фильтров. Несмотря на то, что порядок фильтра, который может быть сформирован, не ограничен, по мере увеличения порядка коэффициент усиления и точность окончательного фильтра снижаются.
Когда идентичные каскады RC-фильтра соединены каскадом, выходное усиление на требуемой частоте среза (c) уменьшается (ослабляется) на величину по отношению к количеству используемых каскадов фильтра по мере увеличения крутизны спада.Мы можем определить величину ослабления на выбранной частоте среза, используя следующую формулу.
Усиление пассивного фильтра нижних частот при c
, где «n» — количество ступеней фильтрации.
Таким образом, для пассивного фильтра нижних частот второго порядка коэффициент усиления на частоте излома ƒc будет равен 0,7071 x 0,7071 = 0,5Vin (-6 дБ), пассивный фильтр нижних частот третьего порядка будет равен 0,353Vin (-9 дБ). ), четвертого порядка будет 0,25Vin (-12 дБ) и так далее. Граничная частота ƒc для пассивного фильтра нижних частот второго порядка определяется комбинацией резистор / конденсатор (RC) и обозначается как.
Угловая частота фильтра 2-го порядка
В действительности, когда каскад фильтра и, следовательно, его крутизна спада увеличивается, точка излома фильтра нижних частот -3 дБ и, следовательно, его частота полосы пропускания изменяется от своего исходного вычисленного значения выше на величину, определяемую следующим уравнением.
Фильтр нижних частот 2-го порядка -3 дБ Частота
, где ƒc — вычисленная частота среза, n — порядок фильтрации, а ƒ -3 дБ — новая частота полосы пропускания -3 дБ в результате увеличения порядка фильтров.
Тогда частотная характеристика (график Боде) для фильтра нижних частот второго порядка, предполагающая ту же точку отсечки -3 дБ, будет выглядеть так:
Частотная характеристика фильтра нижних частот 2-го порядка
На практике, каскадирование пассивных фильтров вместе для создания фильтров большего порядка трудно реализовать точно, поскольку динамический импеданс каждого порядка фильтров влияет на соседнюю сеть. Однако, чтобы уменьшить эффект нагрузки, мы можем сделать импеданс каждого следующего каскада в 10 раз больше, чем у предыдущего каскада, так что R2 = 10 x R1 и C2 = 1/10 C1.Сети фильтров второго порядка и выше обычно используются в цепях обратной связи операционных усилителей, создавая так называемые активные фильтры или сеть с фазовым сдвигом в цепях RC-генератора.
Сводка по фильтру нижних частот
Итак, чтобы подвести итог, фильтр нижних частот имеет постоянное выходное напряжение от постоянного тока (0 Гц) до заданной частоты среза ( C ). Эта точка отсечки частоты составляет 0,707 или -3 дБ (дБ = –20log * V OUT / IN ) допустимого усиления напряжения.
Частотный диапазон «ниже» этой точки отсечки ƒ C обычно известен как полоса пропускания , поскольку входной сигнал может проходить через фильтр. Частотный диапазон «выше» этой точки отсечки обычно известен как полоса заграждения , поскольку входной сигнал блокируется или не проходит через него.
Простой фильтр нижних частот 1-го порядка может быть выполнен с использованием одного резистора, подключенного последовательно с одним неполяризованным конденсатором (или любым отдельным реактивным компонентом) на входном сигнале Vin, в то время как выходной сигнал Vout берется через конденсатор.
Частоту среза или точку -3 дБ можно найти по стандартной формуле ƒc = 1 / (2πRC). Фазовый угол выходного сигнала при c и составляет -45 o для фильтра нижних частот.
Коэффициент усиления фильтра или любого другого фильтра в этом отношении обычно выражается в децибелах и является функцией выходного значения, деленного на его соответствующее входное значение, и дается как:
Пассивные фильтры нижних частот применяются в аудиоусилителях и акустических системах для направления низкочастотных басовых сигналов на большие низкочастотные динамики или для уменьшения высокочастотного шума или искажения типа «шипение».При использовании подобным образом в аудиоприложениях фильтр нижних частот иногда называют фильтром «среза высоких» или «среза высоких частот».
Если бы мы поменяли местами резистор и конденсатор в цепи так, чтобы выходное напряжение теперь снималось с резистора, у нас была бы схема, которая дает кривую выходной частотной характеристики, аналогичную кривой фильтра высоких частот, и это обсуждается в следующем уроке.
Постоянная времени
До сих пор нас интересовала частотная характеристика фильтра нижних частот при воздействии синусоидальной формы волны.Мы также видели, что частота среза фильтров (ƒc) является произведением сопротивления (R) и емкости (C) в цепи относительно некоторой заданной точки частоты, и что при изменении любого из двух компонентов изменяется эту точку отсечки частоты, увеличивая или уменьшая ее.
Мы также знаем, что фазовый сдвиг схемы отстает от фазового сдвига входного сигнала из-за времени, необходимого для зарядки, а затем разрядки конденсатора по мере изменения синусоидальной волны.Эта комбинация R и C производит эффект заряда и разряда на конденсаторе, известный как его постоянная времени (τ) схемы, как показано в учебных пособиях по RC-цепи, давая фильтру отклик во временной области.
Постоянная времени tau (τ) связана с частотой среза ƒc следующим образом:
или выражается через частоту среза, ƒc как:
Выходное напряжение, В OUT зависит от постоянной времени и частоты входного сигнала.С синусоидальным сигналом, который плавно изменяется во времени, схема ведет себя как простой фильтр нижних частот 1-го порядка, как мы видели выше.
Но что, если бы мы изменили входной сигнал на сигнал типа «ВКЛ / ВЫКЛ» в форме «прямоугольной волны», который имеет почти вертикальный ступенчатый вход, что бы сейчас случилось с нашей схемой фильтра. Выходной отклик схемы резко изменится и создаст схему другого типа, обычно называемую интегратором .
RC-интегратор
Интегратор в основном представляет собой схему фильтра нижних частот, работающую во временной области, которая преобразует входной сигнал прямоугольной волны «ступенчатого» отклика в выходной сигнал треугольной формы по мере того, как конденсатор заряжается и разряжается.Треугольный сигнал состоит из чередующихся, но равных, положительных и отрицательных пилообразных изменений.
Как показано ниже, если постоянная времени RC длинна по сравнению с периодом времени входного сигнала, результирующая выходная форма волны будет треугольной по форме, и чем выше входная частота, тем ниже будет выходная амплитуда по сравнению с входной.
Цепь интегратора RC
Это делает схему этого типа идеальной для преобразования одного типа электронного сигнала в другой для использования в схемах генерации или формирования волны.
Что такое фильтр низких частот? Учебное пособие по основам пассивных фильтров RC
Что такое фильтрация? Узнайте, что такое резисторно-конденсаторные (RC) фильтры нижних частот и где их можно использовать.
Эта статья знакомит с концепцией фильтрации и подробно объясняет назначение и характеристики резистивно-конденсаторных (RC) фильтров нижних частот.
Временная и частотная области
Когда вы смотрите на электрический сигнал на осциллографе, вы видите линию, которая представляет изменения напряжения во времени. В любой конкретный момент времени сигнал имеет только одно значение напряжения. То, что вы видите на осциллографе, — это представление сигнала во временной области.
Типичная осциллограмма осциллографа проста и интуитивно понятна, но она также несколько ограничительна, потому что она не показывает напрямую частотную составляющую сигнала.В отличие от представления во временной области, в котором один момент времени соответствует только одному значению напряжения, представление в частотной области (также называемое спектром ) передает информацию о сигнале путем идентификации различных частотных компонентов , которые являются одновременно присутствует .
Представления во временной области синусоиды (вверху) и прямоугольной волны (внизу).
Представления синусоиды (вверху) и прямоугольной волны (внизу) в частотной области.
Что такое фильтр?
Фильтр — это схема, которая удаляет или «отфильтровывает» определенный диапазон частотных составляющих. Другими словами, он разделяет спектр сигнала на частотные составляющие, которые будут переданы , и частотные составляющие, которые будут заблокированы .
Если у вас нет большого опыта в анализе частотной области, вы все равно можете не знать, что это за частотные компоненты и как они сосуществуют в сигнале, который не может иметь несколько значений напряжения одновременно.Давайте рассмотрим краткий пример, который поможет прояснить эту концепцию.
Давайте представим, что у нас есть аудиосигнал, состоящий из идеальной синусоидальной волны 5 кГц. Мы знаем, как выглядит синусоидальная волна во временной области, а в частотной области мы не увидим ничего, кроме частотного «всплеска» на 5 кГц. Теперь предположим, что мы активируем генератор с частотой 500 кГц, который вносит высокочастотный шум в звуковой сигнал.
Сигнал, видимый на осциллографе, по-прежнему будет представлять собой только одну последовательность напряжений с одним значением в момент времени, но сигнал будет выглядеть по-другому, потому что его изменения во временной области теперь должны отражать как синусоидальную волну 5 кГц, так и высокий уровень сигнала. частота шумовых колебаний.
Однако в частотной области синусоидальная волна и шум представляют собой отдельные частотные компоненты, которые одновременно присутствуют в этом одном сигнале. Синусоидальная волна и шум занимают разные части представления сигнала в частотной области (как показано на диаграмме ниже), и это означает, что мы можем отфильтровать шум, направляя сигнал через схему, которая пропускает низкие частоты и блокирует высокие частоты.
Типы фильтров
Фильтры можно разделить на широкие категории, которые соответствуют общим характеристикам частотной характеристики фильтра .Если фильтр пропускает низкие частоты и блокирует высокие частоты, он называется фильтром нижних частот. Если он блокирует низкие частоты и пропускает высокие частоты, это фильтр высоких частот. Существуют также полосовые фильтры, которые пропускают только относительно узкий диапазон частот, и полосовые фильтры, которые блокируют только относительно узкий диапазон частот.
Фильтры
также можно классифицировать по типам компонентов, которые используются для реализации схемы.В пассивных фильтрах используются резисторы, конденсаторы и катушки индуктивности; эти компоненты не обладают способностью обеспечивать усиление, и, следовательно, пассивный фильтр может только поддерживать или уменьшать амплитуду входного сигнала. С другой стороны, активный фильтр может как фильтровать сигнал, так и применять усиление, поскольку он включает в себя активный компонент, такой как транзистор или операционный усилитель.
Этот активный фильтр нижних частот основан на популярной топологии Саллена – Ки.
В этой статье исследуется анализ и конструкция пассивных фильтров нижних частот. Эти схемы играют важную роль в самых разных системах и приложениях.
RC-фильтр нижних частот
Чтобы создать пассивный фильтр нижних частот, нам нужно объединить резистивный элемент с реактивным элементом. Другими словами, нам нужна схема, состоящая из резистора и конденсатора или катушки индуктивности. Теоретически топология нижних частот резистор-индуктор (RL) эквивалентна с точки зрения фильтрующей способности топологии нижних частот резистор-конденсатор (RC).Однако на практике гораздо более распространена версия резистора-конденсатора, и, следовательно, остальная часть этой статьи будет сосредоточена на RC-фильтре нижних частот.
RC-фильтр нижних частот.
Как вы можете видеть на диаграмме, низкочастотный отклик RC создается путем размещения резистора последовательно с трактом прохождения сигнала и конденсатора параллельно нагрузке. На схеме нагрузка представляет собой отдельный компонент, но в реальной схеме это может быть что-то гораздо более сложное, например аналого-цифровой преобразователь, усилитель или входной каскад осциллографа, который вы используете для измерения. ответ фильтра.
Мы можем интуитивно проанализировать фильтрующее действие RC-топологии нижних частот, если мы узнаем, что резистор и конденсатор образуют частотно-зависимый делитель напряжения.
RC-фильтр нижних частот перерисован так, чтобы он выглядел как делитель напряжения.
Когда частота входного сигнала низкая, сопротивление конденсатора высокое по сравнению с сопротивлением резистора; таким образом, большая часть входного напряжения падает на конденсатор (и на нагрузку, которая параллельна конденсатору).Когда входная частота высока, сопротивление конденсатора низкое по сравнению с сопротивлением резистора, что означает, что на резисторе падает большее напряжение и меньше передается на нагрузку. Таким образом, низкие частоты пропускаются, а высокие частоты блокируются.
Это качественное объяснение функциональности RC-низкочастотного диапазона является важным первым шагом, но оно не очень полезно, когда нам действительно нужно спроектировать схему, потому что термины «высокая частота» и «низкая частота» чрезвычайно расплывчаты.Инженерам необходимо создавать схемы, которые пропускают и блокируют определенные частоты. Например, в аудиосистеме, описанной выше, мы хотим сохранить сигнал 5 кГц и подавить сигнал 500 кГц. Это означает, что нам нужен фильтр, который переходит от прохода к блокировке где-то между 5 кГц и 500 кГц.
Частота среза
Диапазон частот, для которых фильтр не вызывает значительного затухания, называется полосой пропускания , а диапазон частот, для которых фильтр действительно вызывает значительное затухание, называется полосой задерживания .Аналоговые фильтры, такие как RC-фильтр нижних частот, всегда постепенно переходят от полосы пропускания к полосе задерживания. Это означает, что невозможно определить одну частоту, на которой фильтр перестает пропускать сигналы и начинает блокировать сигналы. Однако инженерам нужен способ удобного и лаконичного резюмирования частотной характеристики фильтра, и именно здесь в игру вступает концепция частоты среза .
Когда вы посмотрите на график частотной характеристики RC-фильтра, вы заметите, что термин «частота среза» не очень точен.Изображение спектра сигнала, «разрезанного» на две половины, одна из которых сохраняется, а другая отбрасывается, неприменимо, потому что затухание постепенно увеличивается по мере того, как частоты перемещаются от нижнего предела к верхнему пределу среза.
Частота среза RC-фильтра нижних частот — это фактически частота, на которой амплитуда входного сигнала уменьшается на 3 дБ (это значение было выбрано, потому что уменьшение амплитуды на 3 дБ соответствует снижению мощности на 50%). Таким образом, частота среза также называется –3 дБ, частота , и на самом деле это название более точное и информативное.Термин полоса пропускания относится к ширине полосы пропускания фильтра, а в случае фильтра нижних частот полоса пропускания равна частоте –3 дБ (как показано на диаграмме ниже).
Эта диаграмма передает общие характеристики частотной характеристики RC-фильтра нижних частот. Полоса пропускания равна частоте –3 дБ.
Как объяснено выше, поведение фильтра нижних частот RC-фильтра вызвано взаимодействием между частотно-независимым импедансом резистора и частотно-зависимым импедансом конденсатора.Чтобы определить детали частотной характеристики фильтра, нам необходимо математически проанализировать взаимосвязь между сопротивлением (R) и емкостью (C), а также мы можем манипулировать этими значениями, чтобы разработать фильтр, который соответствует точным спецификациям. Частота среза (f C ) RC-фильтра нижних частот рассчитывается следующим образом:
Давайте посмотрим на простой пример дизайна. Значения конденсатора более строгие, чем значения резистора, поэтому мы начнем с обычного значения емкости (например, 10 нФ), а затем воспользуемся уравнением для определения требуемого значения сопротивления.Цель состоит в том, чтобы разработать фильтр, который сохранит звуковую волну 5 кГц и отклонит шумовую волну 500 кГц. Мы попробуем установить частоту среза 100 кГц, а позже в статье мы более тщательно проанализируем влияние этого фильтра на две частотные составляющие.
Таким образом, резистор на 160 Ом в сочетании с конденсатором 10 нФ даст нам фильтр, который точно соответствует желаемой частотной характеристике.
Расчет чувствительности фильтра
Мы можем рассчитать теоретическое поведение фильтра нижних частот, используя частотно-зависимую версию типичного расчета делителя напряжения.Выход резистивного делителя напряжения выражается следующим образом:
В RC-фильтре используется эквивалентная структура, но вместо R 2 используется конденсатор. Сначала заменяем R 2 (в числителе) на реактивное сопротивление конденсатора (X C ). Затем нам нужно рассчитать величину полного импеданса и поместить ее в знаменатель. Таким образом, имеем
Реактивное сопротивление конденсатора указывает величину сопротивления протеканию тока, но, в отличие от сопротивления, величина сопротивления зависит от частоты сигнала, проходящего через конденсатор.Таким образом, мы должны рассчитать реактивное сопротивление на конкретной частоте , и уравнение, которое мы используем для этого, выглядит следующим образом:
В приведенном выше примере конструкции R ≈ 160 Ом и C = 10 нФ. Предположим, что амплитуда V IN равна 1 В, так что мы можем просто исключить V IN из расчета. Сначала давайте вычислим амплитуду V OUT на частоте синусоиды:
Амплитуда синусоиды практически не изменилась.Это хорошо, поскольку мы стремились сохранить синусоидальную волну при подавлении шума. Этот результат неудивителен, поскольку мы выбрали частоту среза (100 кГц), которая намного выше, чем частота синусоидальной волны (5 кГц).
Теперь посмотрим, насколько успешно фильтр подавляет шумовую составляющую.
Амплитуда шума составляет всего около 20% от первоначального значения.
Визуализация отклика фильтра
Самый удобный способ оценить влияние фильтра на сигнал — это изучить график частотной характеристики фильтра.Эти графики, часто называемые графиками Боде , имеют величину (в децибелах) по вертикальной оси и частоту по горизонтальной оси; горизонтальная ось обычно имеет логарифмический масштаб, так что физическое расстояние между 1 Гц и 10 Гц совпадает с физическим расстоянием между 10 Гц и 100 Гц, между 100 Гц и 1 кГц и так далее. Эта конфигурация позволяет нам быстро и точно оценить поведение фильтра в очень большом диапазоне частот.
Пример графика частотной характеристики.
Каждая точка на кривой указывает величину выходного сигнала, если входной сигнал имеет амплитуду 1 В и частоту, равную соответствующему значению на горизонтальной оси. Например, когда входная частота равна 1 МГц, выходная амплитуда (при условии, что входная амплитуда 1 В) будет 0,1 В (поскольку –20 дБ соответствует уменьшению в десять раз).
Общая форма этой кривой частотной характеристики станет вам очень знакомой, если вы будете уделять больше времени схемам фильтров.Кривая в полосе пропускания почти идеально плоская, а затем она начинает падать быстрее, когда входная частота приближается к частоте среза. В конечном итоге скорость изменения затухания, называемая спадом, стабилизируется на уровне 20 дБ / декаду, то есть величина выходного сигнала уменьшается на 20 дБ для каждого десятикратного увеличения входной частоты.
Оценка производительности фильтра нижних частот
Если мы внимательно построим график частотной характеристики фильтра, который мы разработали ранее в этой статье, мы увидим, что амплитудная характеристика на частоте 5 кГц по существу равна 0 дБ (т.е.е., почти нулевое затухание), а амплитуда отклика на частоте 500 кГц составляет приблизительно –14 дБ (что соответствует усилению 0,2). Эти значения согласуются с результатами расчетов, которые мы выполнили в предыдущем разделе.
Поскольку RC-фильтры всегда имеют постепенный переход от полосы пропускания к полосе задерживания и поскольку затухание никогда не достигает бесконечности, мы не можем разработать «идеальный» фильтр, то есть фильтр, который не влияет на синусоидальную волну и полностью устраняет шум.Вместо этого мы всегда идем на компромисс. Если мы переместим частоту среза ближе к 5 кГц, у нас будет большее ослабление шума, но также большее ослабление синусоидальной волны, которую мы хотим отправить в динамик. Если мы переместим частоту среза ближе к 500 кГц, мы получим меньшее затухание на частоте синусоидальной волны, но также меньшее затухание на частоте шума.
Фазовый сдвиг фильтра нижних частот
До сих пор мы обсуждали способ, которым фильтр изменяет амплитуду различных частотных компонентов в сигнале.Однако реактивные элементы схемы всегда вносят фазовый сдвиг в дополнение к эффектам амплитуды.
Понятие фазы относится к значению периодического сигнала в определенный момент в пределах цикла. Таким образом, когда мы говорим, что схема вызывает фазовый сдвиг, мы имеем в виду, что она создает рассогласование между входным и выходным сигналами: входные и выходные сигналы больше не начинают и заканчивают свои циклы в один и тот же момент времени. Значение фазового сдвига, например 45 ° или 90 °, указывает, насколько сильно возникло рассогласование.
Каждый реактивный элемент в цепи вносит фазовый сдвиг на 90 °, но этот фазовый сдвиг не происходит сразу. Фаза выходного сигнала, как и величина выходного сигнала, постепенно изменяется с увеличением входной частоты. В RC-фильтре нижних частот у нас есть один реактивный элемент (конденсатор), и, следовательно, схема в конечном итоге внесет фазовый сдвиг на 90 °.
Как и в случае с амплитудной характеристикой, фазовую характеристику легче всего оценить, исследуя график, на котором горизонтальная ось указывает логарифмическую частоту.Описание ниже передает общую картину, а затем вы можете заполнить детали, исследуя сюжет.
- Фазовый сдвиг изначально равен 0 °.
- Постепенно увеличивается, пока не достигнет 45 ° на частоте среза; во время этой части ответа скорость изменения увеличивается.
- После частоты среза фазовый сдвиг продолжает увеличиваться, но скорость изменения уменьшается.
- Скорость изменения становится очень малой, когда фазовый сдвиг асимптотически приближается к 90 °.
Сплошная линия — это характеристика амплитуды, а пунктирная линия — фазовая характеристика. Частота среза 100 кГц. Обратите внимание, что фазовый сдвиг составляет 45 ° на частоте среза.
Фильтры нижних частот второго порядка
До сих пор мы предполагали, что RC-фильтр нижних частот состоит из одного резистора и одного конденсатора. Эта конфигурация представляет собой фильтр первого порядка .
«Порядок» пассивного фильтра определяется количеством реактивных элементов — т.е.е., конденсаторы или катушки индуктивности, которые присутствуют в цепи. Фильтр более высокого порядка имеет больше реактивных элементов, и это приводит к большему фазовому сдвигу и более крутому спаду. Эта вторая характеристика является основной мотивацией для увеличения порядка фильтра.
Добавляя один реактивный элемент к фильтру — например, переходя от первого порядка ко второму или от второго порядка к третьему — мы увеличиваем максимальный спад на 20 дБ / декаду. Более крутой спад приводит к более быстрому переходу от низкого затухания к высокому затуханию, и это может привести к улучшенным характеристикам, когда сигнал не имеет широкой полосы частот, которая отделяет желаемые частотные компоненты от шумовых компонентов.
Фильтры второго порядка обычно строятся вокруг резонансного контура, состоящего из катушки индуктивности и конденсатора (эта топология называется «RLC» для обозначения резистор-индуктор-конденсатор). Однако также возможно создание RC-фильтров второго порядка. Как показано на диаграмме ниже, все, что нам нужно сделать, это каскадировать два RC-фильтра первого порядка.
Хотя эта топология определенно создает отклик второго порядка, она широко не используется — как мы увидим в следующем разделе, частотная характеристика часто уступает таковой у активного фильтра второго порядка или RLC второго порядка. фильтр.
Частотная характеристика RC-фильтра второго порядка
Мы можем попытаться создать RC-фильтр нижних частот второго порядка, спроектировав фильтр первого порядка в соответствии с желаемой частотой среза и затем соединив два из этих каскадов первого порядка последовательно. В результате получается фильтр с аналогичной общей частотной характеристикой и максимальным спадом 40 дБ / декада вместо 20 дБ / декада.
Однако, если мы посмотрим на отклик более внимательно, мы увидим, что частота –3 дБ уменьшилась.RC-фильтр второго порядка ведет себя не так, как ожидалось, потому что два каскада не являются независимыми — мы не можем просто соединить эти два каскада вместе и проанализировать схему как фильтр нижних частот первого порядка, за которым следует идентичный фильтр нижних частот первого порядка. фильтр.
Кроме того, даже если мы вставим буфер между двумя каскадами, чтобы первый RC-каскад и второй RC-каскад могли функционировать как независимые фильтры, затухание на исходной частоте среза будет 6 дБ вместо 3 дБ.Это происходит точно , потому что два каскада работают независимо — первый фильтр имеет ослабление 3 дБ на частоте среза, а второй фильтр добавляет еще 3 дБ ослабления.
Основным ограничением RC-фильтра нижних частот второго порядка является то, что разработчик не может точно настроить переход от полосы пропускания к полосе задерживания, регулируя коэффициент добротности фильтра; этот параметр указывает, насколько затухает частотная характеристика.Если вы каскадируете два идентичных RC-фильтра нижних частот, общая передаточная функция соответствует ответу второго порядка, но коэффициент добротности всегда равен 0,5. Когда Q = 0,5, фильтр находится на границе чрезмерного демпфирования, и это приводит к «проседанию» частотной характеристики в переходной области. Активные фильтры второго порядка и фильтры на основе резонанса второго порядка не имеют этого ограничения; разработчик может управлять коэффициентом добротности и тем самым точно настраивать частотную характеристику в переходной области.
Сводка
- Все электрические сигналы содержат смесь желаемых частотных составляющих и нежелательных частотных составляющих. Нежелательные частотные составляющие обычно вызваны шумом и помехами, а в некоторых ситуациях они могут отрицательно повлиять на производительность системы.
- Фильтр — это схема, которая по-разному реагирует на разные части спектра сигнала. Фильтр нижних частот предназначен для пропускания низкочастотных компонентов и блокировки высокочастотных компонентов.
- Частота среза фильтра нижних частот указывает частотную область, в которой фильтр переходит от низкого затухания к значительному.
- Выходное напряжение RC-фильтра нижних частот можно рассчитать, рассматривая схему как делитель напряжения, состоящий из (частотно-независимого) сопротивления и (частотно-зависимого) реактивного сопротивления.
- График зависимости амплитуды (в дБ по вертикальной оси) от логарифмической частоты (в герцах по горизонтальной оси) — удобный и эффективный способ изучить теоретическое поведение фильтра.Вы также можете использовать график зависимости фазы от логарифмической частоты, чтобы определить величину сдвига фазы, которая будет применена к входному сигналу.
- Фильтр второго порядка обеспечивает более крутой спад; этот ответ второго порядка полезен, когда сигнал не обеспечивает широкой полосы разделения между желательными частотными компонентами и нежелательными частотными компонентами.
- Вы можете создать RC-фильтр нижних частот второго порядка, построив два идентичных RC-фильтра нижних частот первого порядка, а затем подключив выход одного к входу другого.Общая частота –3 дБ будет ниже ожидаемой.
Схема, типы, калькуляторы и их применение
В электронных устройствах фильтры — это схемы, которые позволяют задавать частотные компоненты и блокируют все остальные частотные компоненты сигнала. Например, в радио или телевидении схема настраивающего фильтра отклоняет нежелательные частоты, разрешая только желаемый канал. Цепи фильтров делятся на четыре типа в зависимости от диапазона частот, который позволяет схема при блокировании всех остальных частот.Это фильтры нижних частот, фильтры верхних частот, полосовые фильтры и полосовые фильтры. Эти типы цепей фильтров подпадают под категорию пассивных фильтров, потому что в цепи используются резистор пассивных элементов, конденсатор и катушки индуктивности. В этой статье описывается фильтр нижних частот, использующий операционный усилитель (активный элемент), который также называют активным ФНЧ.
Что такое фильтр низких частот?
Определение: Схема фильтра, которая допускает только низкочастотные компоненты и блокирует все другие высокочастотные компоненты, называется фильтром нижних частот.Само название LPF указывает на частоту нижнего диапазона.
Этот тип схемы фильтра позволяет использовать частотные составляющие сигнала меньше, чем вырезка частотного диапазона сигнала. Коэффициент усиления фильтра нижних частот обратно пропорционален частоте. Если частота входного сигнала увеличивается, коэффициент усиления схемы уменьшается и также становится равным нулю на конечной стадии переходной полосы. Таким образом, пропускная способность также ограничена. Но на практике LPF позволяет использовать низкочастотные компоненты сигнала, даже если он достигает частоты среза.
Цепь фильтра нижних частот
Схема цепи фильтра нижних частот показана ниже. Он содержит пассивные элементы, резистор и конденсатор, соединенные последовательно с приложенным входным напряжением на резисторе, а его выходное напряжение получается на конденсаторе.
Схема фильтра нижних частот
ФНЧ первого порядка
Фильтр нижних частот первого порядка бывает двух типов. Это
Индуктивный тип LPF
Этот тип представляет собой простую цепь RL, как показано ниже.Когда частота сигнала увеличивается, сопротивление катушки индуктивности увеличивается. Это приводит к блокировке высокочастотных сигналов и пропускает только низкие частоты сигнала через цепь.
Индуктивный LPF
Емкостный LPF
Этот тип представляет собой простую RC-цепочку LPF, как показано на рисунке выше. Ее также называют простой схемой фильтра нижних частот. Когда частота сигнала увеличивается, тогда сопротивление конденсатора уменьшается, что приводит к блокировке высоких частот сигнала и пропускает только низкие частоты сигнала через цепь.
ФНЧ второго порядка
Схема фильтра нижних частот второго порядка представляет собой схему RLC, как показано на диаграмме ниже. Выходное напряжение получается на конденсаторе. Этот тип LPF работает более эффективно, чем LPF первого порядка, потому что два пассивных элемента, индуктор и конденсатор, используются для блокировки высоких частот входного сигнала.
Фильтр нижних частот второго порядка
Фильтр нижних частот с ОУ
ФНЧ с ОУ называется активным фильтром нижних частот.Очень легко спроектировать схему фильтра нижних частот с использованием операционного усилителя без использования электрических компонентов, таких как индуктор, который очень сложно спроектировать, а также является дорогостоящим. Операционные усилители (операционные усилители) используются в схемах фильтров для усиления сигнала, а также для управления усилением. Операционные усилители изменяют частотную характеристику и обеспечивают лучшее усиление напряжения в своей обратной связи. Он также имеет более высокий входной импеданс, более низкий выходной импеданс, низкий уровень шума и высокий уровень производительности.
Фильтр нижних частот с использованием операционного усилителя
Работа базовой схемы LPF (пассивного фильтра) и фильтра нижних частот с использованием операционного усилителя (активного фильтра) одинакова, за исключением того, что операционный усилитель подключен к цепи RC-фильтра. .Это может быть инвертирующий или неинвертирующий операционный усилитель. Принципиальная схема фильтра нижних частот с использованием операционного усилителя показана ниже.
Схема активного LPF первого порядка с ОУ
Активная схема LPC первого порядка спроектирована с конденсатором, резистором и операционным усилителем, как показано ниже. Инвертирующий или неинвертирующий операционный усилитель подключается к RC-цепи, чтобы получить активную схему LPF. Амплитуда выходного сигнала, полученного от схемы RC-фильтра нижних частот, меньше амплитуды входного сигнала.Этот низкочастотный сигнал RC-цепи LPF подается на операционный усилитель в качестве входа для достижения усиления, высокого коэффициента усиления и стабильности фильтра. Здесь операционный усилитель действует как буферная схема, как повторитель напряжения с коэффициентом усиления постоянного тока = 1.
Активный ФНЧ первого порядка
По мере увеличения частоты входного сигнала он проходит через конденсатор, увеличивая амплитуду выходного сигнала для усиление, связанное с усилением полосы пропускания. На низких частотах выходной сигнал RC-цепи проходит непосредственно через операционный усилитель для усиления.
Коэффициент усиления по напряжению определяется как DC = 1 + R2 / R1
Схема активного LPF второго порядка с ОУ
Схема активного LPF второго порядка спроектирована путем каскадирования двух RC цепей фильтра нижних частот с операционный усилитель. Здесь операционный усилитель действует как усилитель источника с управляемым напряжением. Частотная характеристика такая же, как у активного ФНЧ первого порядка, за исключением того, что усиление полосы задерживания в два раза больше, чем у активного ФНЧ первого порядка, то есть 40 дБ / декаду. Каскадирование цепей фильтров формирует фильтры более высокого порядка, усиление которых является произведением каждой RC-цепи LPF.
Активный фильтр нижних частот второго порядка
Мы знаем, что усиление активного ФНЧ первого порядка составляет -3 дБ на частоте среза. Таким образом, усиление активного ФНЧ второго порядка составляет -6 дБ на частоте среза, то есть усиление увеличилось вдвое.
Коэффициент усиления рассчитывается как
Av = Av1 x Av2
Общий коэффициент усиления в дБ
Av = Av1 + Av2
Принципиальная схема активного ФНЧ второго порядка показана ниже.
Калькулятор ФНЧ
Калькулятор фильтра нижних частот предназначен для вычисления частоты среза, усиления по напряжению и фазового сдвига цепи ФНЧ.
Из принципиальной схемы LPF (RC-цепи) мы можем заметить, что Vi — это приложенное входное напряжение
Vo — выходное напряжение
Используя передаточную функцию схемы, мы получаем
H ( s) = V₀ (s) / Vᵢ (s) = (1 / sC) / (R + (1 / sC))
Так как Vo (s) = 1 / sC
Vi (s) = R + 1 / с
H (s) = 1 / (1 + sCR)
Пусть s = jω
Тогда приведенное выше уравнение принимает вид
H (jω) = 1 / (1 + jωCR)
Мы можем вычислить величину передаточной функции из приведенного выше уравнения. 2]
Поскольку общее усиление напряжения равно,
Av = 20log10 (Vout / Vin) в дБ
Рассмотрим f = рабочая частота и fc = частота среза
Фазовый сдвиг цепи LPF составляет
Φ = tan⁻¹ (ω / ωc)
Отсечка частота цепи ФНЧ,
fc = 1 / 2πRC
Следовательно,
Сдвиг фазы равен, 90 005
Φ ⁼ tan⁻¹ (2πfRC)
Уравнение емкостного реактивного сопротивления в омах цепи LPF дается как
Xc = 1 / 2πfC
Где C = емкость в фарадах
f = рабочая частота в Гц
Характеристики частотной характеристики представлены между усилением (дБ) и частотой (Гц).
Частотная характеристика
На низких частотах усиление LPF выше, чем усиление полосы пропускания фильтра
На высоких частотах усиление LPF меньше, чем его усиление полосы пропускания, и оно падает до -20 дБ
По мере увеличения частоты выходное напряжение падает на 70,71% ниже входного.
Приложения
Приложения с фильтром нижних частот включают следующее.
- Используется для удаления шума высокочастотных сигналов
- Используется в аудиоприложениях
- Используется в биомедицинских приложениях
- Используется в электронных приложениях, таких как громкоговорители, сабвуферы и т. Д.
- Используется в цифро-аналоговых преобразователях
- Используется как анти -анализирующие фильтры
- Используются в анализаторах волн, усилителях звука и эквалайзерах.
Таким образом, это все о обзоре схемы фильтра нижних частот с использованием операционного усилителя, базовой схемы LPF, активного LPF первого порядка, активного LPF второго порядка, вычислителя фильтра нижних частот и приложений. Назначение LPF — пропускать только низкочастотные сигналы и блокировать высокочастотные сигналы. Вот несколько вопросов для вас: Каковы преимущества LPF с ОУ? Что такое полосовой стоп-фильтр?
Фильтр низких частот (ФНЧ) | Типы фильтра низких частот
СОДЕРЖАНИЕ
- Определение фильтра низких частот
- Принципиальная схема
- Активный и пассивный фильтр низких частот
0
- Что делает a ФНЧ делать? Как это работает?
- Эксплуатация
- Частотная характеристика
- Передаточная функция ФНЧ
- Проектирование ФНЧ
- Частотный фильтр нижних частот
- Идеальный и реальный фильтр
- Фильтр низких частот и фильтр высоких частот
- Преимущества LPF
- Каковы применения фильтра низких частот
- FAQs
Определение LPF:
«Фильтр нижних частот передает низкочастотные сигналы с меньшим сопротивлением и имеет постоянное усиление на выходе от нуля до частоты среза.”
Обычно фильтр нижних частот ослабляет частоты выше пороговых значений.
Принципиальная схема фильтра нижних частот :
Существует два типа активных фильтров:
- Активный фильтр нижних частот — состоит в основном из активных компонентов, таких как операционный усилитель и транзистор.
- Пассивный фильтр нижних частот — состоит в основном из пассивных компонентов, таких как конденсаторы, резисторы и т. Д.
Что делает фильтр нижних частот?
На рисунке 1.1 это обычно используемый активный фильтр нижних частот.
Фильтрация обычно выполняется RC-цепью, а операционный усилитель используется как усилитель с единичным усилением. Резистор R F (= R) включен для смещения постоянного тока.
При постоянном токе емкостное реактивное сопротивление бесконечно, и резистивный путь постоянного тока к земле для обоих выводов должен быть одинаковым.
Здесь все напряжения V i , V x , V y , V 0 измеряются относительно земли.
Входное сопротивление операционного усилителя всегда бесконечно; ток не будет течь на входные клеммы.
В соответствии с правилом делителя напряжения, напряжение на конденсаторе,
Поскольку коэффициент усиления операционного усилителя бесконечен,
Где,
= усиление полосы пропускания фильтра
f = частота входного сигнала
= частота среза сигнала
A cL
= коэффициент усиления фильтра с обратной связью в зависимости от частоты.
Величина усиления,
И фазовый угол (в градусах),
Работа фильтра нижних частот:
Работу фильтра нижних частот можно проверить по величине усиления уравнение:
При очень низких частотах, т.е. f >> f c ,
При f = f c ,
При f> f c ,
| A cL | F
Таким образом, фильтр имеет постоянное усиление A F от 0 Гц до частоты среза f c .При f c рост составляет 0,707A F , а после f c он уменьшается с постоянной скоростью с увеличением частоты.
Здесь фактическая характеристика отклоняется от аппроксимации линейной пунктирной линией в окрестности f c .
Частотная характеристика фильтра нижних частот: Характеристики фильтра нижних частот
Конструкция фильтра нижних частот:
Выбрано значение частоты среза ω c .
Емкость C выбирается с определенным значением; обычно значение находится в диапазоне от 0.001 и 0,1 мкФ. Для повышения производительности рекомендуются майларовые или танталовые конденсаторы.
Значение R рассчитывается по соотношению:
F c = частота среза в герцах
Ом c = частота среза в радианах секундах.
C = в фарадах
Наконец, значения R 1 и R F выбираются в зависимости от желаемого усиления полосы пропускания с помощью отношения
Масштабирование частоты: — Один раз Фильтр разработан, возможно, потребуется изменить его частоту среза.Метод преобразования исходной частоты среза f c в новую частоту среза называется «масштабированием частоты».
Чтобы изменить частоту среза, умножьте R или C, но не оба на коэффициент : —
Угловая частота и частота среза фильтра нижних частот:
Переход фильтра нижних частот всегда быстрый и плавный от полосы пропускания к полосе задерживания . Кроме того, частота среза не является каким-либо параметром для измерения качества или недостатка в диапазоне частот.Частота среза более точно называется частотой -3 дБ, то есть это частота, при которой амплитуда отклика на 3 дБ ниже значения при 0 Гц.
Что такое полоса пропускания?
«Полоса пропускания — это конкретный диапазон частот, через который проходит фильтр внутри него».
Для фильтров нижних частот частоты, которые движутся к концу полосы пропускания, не могут иметь значительного усиления или внимания.
Что такое полоса задерживания?
«Фильтр всегда переносит фильтры в пределах заданного диапазона и отклоняет частоты, которые находятся ниже заданного диапазона.Этот конкретный диапазон известен как полоса задерживания ».
Поскольку существуют ограничения для фильтров нижних частот, полоса задерживания затухает на определенной частоте, которая приближается к частоте среза ближе к 0 Гц.
Передаточная функция фильтра нижних частот:
Что такое передаточная функция?
“ Передаточная функция — это комплексное число, которое имеет как величину, так и фазу. В случае фильтров передаточная функция помогает ввести разность фаз между входом и выходом .”
Поскольку фильтр нижних частот пропускает через себя низкочастотные сигналы переменного тока, выходной сигнал ослабляется. Мы используем разные активные и пассивные компоненты для создания фильтра, который в конечном итоге имеет другие характеристики. Передаточная функция сообщает нам, как один вход соотносится с выходом в зависимости от характеристик компонента. Передаточную функцию легко определить по графику выходного сигнала на различных частотах. Мы также можем рассчитать передаточную функцию, используя законы Кирхгофа, чтобы вывести дифференциальное уравнение фильтра.
По мере прохождения через него большего количества сигналов фильтр применяет фазовый сдвиг к выходному сигналу для входного сигнала. Следовательно, передаточная функция фильтра является сложной функцией частоты. Он также содержит всю важную информацию, необходимую для определения величины выходного сигнала и его фазы.
Идеальный фильтр и реальный фильтр:
Иногда, для упрощения, мы часто используем активные фильтры для приблизительного определения способов. Мы модернизируем их до идеальной теоретической модели, которая называется «Идеальный фильтр».’
Эти стандарты используются недостаточно, что приводит к ошибкам; тогда фильтр следует рассматривать на основе точного реального поведения, т. е. как «настоящий фильтр».
Основными ключевыми условиями идеального фильтра являются
- Блок усиления
- Полная деградация входного сигнала по диапазонам.
- Переход реакции из одной зоны в другую довольно резкий.
- Не создает искажений при прохождении сигнала через транзитную зону.
В чем разница между фильтром низких частот и фильтром высоких частот?
Каковы преимущества фильтра нижних частот?
- Фильтры нижних частот могут легко удалить эффекты наложения спектров из схемы, что обеспечивает плавную работу схемы.
- Фильтры низких частот экономичны, поэтому их можно легко использовать.
- Фильтры нижних частот имеют низкий выходной импеданс; таким образом, это предотвращает влияние нагрузки на частоту среза фильтров.
- В фильтрах «шипения» используется фильтр нижних частот.
- LPF используется в аудиоколонках для снижения высоких частот.
- LPF можно использовать как усилитель звука и эквалайзер.
- В аналого-цифровом преобразователе LPF используется в качестве фильтров сглаживания для управляющих сигналов.
- LPF используется для сглаживания изображения, размытия изображения.
- LPF также используется в радиопередатчиках для блокировки излучения гармоник.
- Эти фильтры используются в музыкальных системах для фильтрации высокочастотных звуков, вызывая эхо на более высоких звуках.
Ø
Что такое пассивный фильтр нижних частот?Пассивный фильтр нижних частот — это фильтр, состоящий из всех пассивных компонентов, таких как конденсаторы, резисторы и т. Д.Это вызывает меньший выходной уровень по сравнению с входным.
Ø
Что такое RC-цепь низких частот?RC-цепь нижних частот состоит только из резисторов и конденсаторов, как следует из названия. Это также важный пассивный фильтр. В этом фильтре реактивное сопротивление конденсатора изменяется обратно пропорционально частоте, а значение резистора остается постоянным при изменении частоты.
Ø
Что такое фильтр нижних частот Баттерворта?Фильтр Баттерворта — это фильтр того типа, в котором частотная характеристика является ровной в области полосы пропускания.Фильтр Баттерворта нижних частот обеспечивает постоянный выходной сигнал от источника постоянного тока до определенной частоты среза и отклоняет частоты более высокого уровня.
Ø
Как можно построить фильтр нижних частот второго порядка?Мы знаем, что фильтр нижних частот первого порядка может быть изготовлен путем соединения одного резистора и конденсатора, один полюс которого может дать нам крутизну спада -20 дБ / декаду. Чтобы создать пассивный фильтр нижних частот второго порядка, мы соединяем или каскадируем два пассивных фильтра (первого порядка).Это тоже двухполюсная сеть.
Ø
Запишите угловую частоту фильтра второго порядка.В фильтре нижних частот второго порядка мы наблюдаем точку угловой частоты -3 дБ, и, следовательно, частота полосы пропускания изменяется от исходного значения, рассчитанного по формуле:
Чтобы узнать больше об электронике , щелкните здесь
О Сумали Бхаттачарья
В настоящее время я инвестирую в сферу электроники и связи.
Мои статьи сосредоточены на основных областях базовой электроники с очень простым, но информативным подходом.
Я хорошо учусь и стараюсь быть в курсе всех последних технологий в области электроники.
Давайте подключимся через LinkedIn —
https://www.linkedin.com/in/soumali-bhattacharya-34833a18b/
Что такое схема фильтра нижних частот?
Активные фильтры нижних частот рассматриваются в этой презентации.Для тех, кто никогда не работал с фильтрами, краткий обзор терминологии, относящейся к характеристикам фильтров и терминологии, предшествует фактическому обсуждению. Обсуждаются топология Саллена-Ки и фильтр нижних частот Баттерворта , рабочие параметры рассчитываются и затем проверяются экспериментально.
Каталог
Ⅰ Введение
Фильтр нижних частот — это разновидность фильтрующих устройств.В частности, фильтр нижних частот — это фильтр , который пропускает сигналы с частотой ниже выбранной частоты среза и ослабляет сигналы с частотами выше частоты среза. Точная частотная характеристика фильтра зависит от конструкции фильтра. Его правило — низкочастотный сигнал может проходить нормально, но высокочастотный сигнал, превышающий установленный порог, блокируется и ослабляется. Однако величина блокировки и затухания будет варьироваться в зависимости от частоты и различных процедур фильтрации (другими словами, различных целей фильтрации).Кроме того, это иногда называют высокочастотной фильтрацией удаления или фильтрацией максимального удаления.
Фильтр нижних частот
Ⅱ Терминология
2.1 Низк. — -проходная фильтрация
Фильтр нижних частот можно просто подумать: установка точки частоты, когда частота сигнала выше чем эта частота, она не может пройти. В цифровом сигнале эта частотная точка также называется частотой среза.Когда частотная область выше, чем частота среза, тогда всем присваивается 0. Поскольку низкочастотный сигнал проходит через весь этот процесс, это называется фильтрацией нижних частот.
Концепция фильтрации нижних частот существует во множестве различных областей, таких как электронные схемы, сглаживание данных, акустическая блокировка, размытие изображения и так далее. Например, в области цифровой обработки изображений фильтрация нижних частот может сглаживать и устранять шум в изображении.
2.2 C utoff Частота фильтра нижних частот
В электронике частота среза — это частота, при которой мощность выходного сигнала схемы (например, провода, усилителя, электронного фильтра) превышает или падает ниже проводимая частота.
Когда частота сигнала ниже частоты среза, сигнал проходит; когда частота сигнала выше, чем частота среза, выходной сигнал значительно ослабляется. Эта частота среза определяется как граница между полосой пропускания и полосой задерживания.
Формула расчета частоты среза:
2.3 Принцип работы
Используйте принцип конденсаторов для передачи высокой частоты и блокировки низкой частоты, прохождения низкой частоты и блокировки высокой частоты с эффектом индуктивности. Для высокой частоты, которую необходимо отсечь, она блокируется методом емкостного поглощения и индуктивного преграды; для требуемой низкой частоты он должен пропускать высокое сопротивление с помощью конденсаторов и проходить через низкое сопротивление с помощью катушки индуктивности.
Ⅲ Фильтр нижних частот
Для разных фильтров затухание сигнала на каждой частоте разное. При использовании в аудиоприложениях его иногда называют высокочастотным или высокочастотным фильтром.
Концепция фильтра нижних частот имеет множество различных форм, в том числе электронные схемы (такие как хаос-фильтр, используемый в звуковом оборудовании, цифровые алгоритмы сглаживания данных, акустические барьеры, размытие изображения и т. Д.) А устранение краткосрочных колебаний и сохранение долгосрочных трендов обеспечивает плавную форму сигнала.
Роль фильтра нижних частот в обработке сигналов эквивалентна скользящей средней в финансовой области. Существует много типов фильтров нижних частот, среди которых наиболее распространены фильтры Баттерворта и фильтры Чебышева.
Ⅳ Низкий P ass F ilter ing C ir circuit
Фильтр нижних частот представляет собой схему, пропускающую сигналов низкой частоты через автомобильный усилитель без прохождения средних и высокочастотных сигналов.Его функция состоит в том, чтобы отфильтровать средне- и высокочастотные компоненты аудиосигнала и усилить низкочастотную составляющую для управления низкочастотным динамиком динамика. Поскольку часть автомобильного усиления мощности является полнополосным усилителем мощности, обычно принимается конструкция усиления класса AB, и потери мощности относительно велики. Таким образом, фильтрация сигнала низкочастотного диапазона делает средне- и высокочастотный динамик лучшим выбором для экономии энергии и обеспечения качества звука.
Идеальный фильтр нижних частот , который позволяет низкочастотным сигналам проходить через фильтр без потерь.Когда частота сигнала превышает частоту среза, сигнал затухает до бесконечности.
Схема активного фильтра нижних частот первого порядка является простейшей схемой фильтра, а также наименьшим блоком, составляющим схему активного фильтра нижних частот второго порядка или высокого порядка .
Электрические схемы: общий контур низкочастотной фильтрации
Фильтр первого порядка снижает интенсивность сигнала наполовину (примерно -6 дБ), когда частота увеличивается вдвое (увеличивая октаву).График Боде амплитуды фильтра первого порядка представляет собой горизонтальную линию ниже частоты среза и диагональную линию выше частоты среза. На границе между двумя прямыми линиями также имеется «изгиб колена».
Фильтр второго порядка может играть более важную роль в уменьшении высокочастотных сигналов. График Боде этого типа фильтра аналогичен графику фильтра первого порядка, но его скорость спада выше. Например, фильтр Баттерворта второго порядка (который представляет собой схему RLC с критическим затуханием без пиков) снижает уровень сигнала до начальной четверти (12 дБ на удвоение частоты), когда частота удваивается.Начальная скорость спада других фильтров второго порядка может зависеть от их добротности, но конечная скорость составляет -12 дБ на удвоение частоты.
Фильтры третьего и высшего порядка аналогичны. Одним словом, скорость спада последнего фильтра n-го порядка составляет 6 дБ на октаву.
Ⅴ Рекомендации по технике
5.1 Схема фильтрации
Обычно используемые схемы фильтров — это пассивная фильтрация и активная фильтрация .Если компонент схемы фильтрации состоит только из пассивных компонентов (резисторов, конденсаторов, катушек индуктивности), это называется схемой пассивного фильтра. Основными формами пассивной фильтрации являются конденсаторный фильтр, фильтр индуктивности и комплексный фильтр (включая инвертированный L-тип, LC-фильтр, LCπ-фильтр и RCπ-фильтр и т. Д.). Если схема фильтра состоит не только из пассивных компонентов, но и из активных компонентов (биполярных, монопольных и интегрированных операционных усилителей), она называется схемой активного фильтра. Основная форма активной фильтрации — это активная RC-фильтрация, также известная как электронные фильтры.
1. Схема пассивного фильтра
Схема пассивного фильтра имеет простую структуру и удобна в проектировании, но ее коэффициент усиления полосы пропускания и частота среза зависят от нагрузки, поэтому она не подходит для приложений, где требуется высокая обработка сигналов. Цепи пассивных фильтров обычно используются в цепях питания, таких как выпрямление источника постоянного тока или фильтрация цепей LC (индуктор, конденсатор) для сильноточных нагрузок.
2. Схема активного фильтра
Нагрузка схемы активного фильтра не влияет на характеристики фильтра, поэтому она часто используется в приложениях, где требуется высокая степень обработки сигнала.Схема активного фильтра обычно состоит из RC-цепи и интегрированного операционного усилителя и должна использоваться с подходящим источником питания постоянного тока, а также может быть усилена. Но состав и конструкция схемы также более сложны. Цепи активных фильтров не подходят для высоковольтных и сильноточных приложений и подходят только для обработки сигналов.
В соответствии с характеристиками фильтра, амплитудно-частотная характеристика его усиления по напряжению может точно описать, принадлежит ли схема к фильтру нижних, верхних, полосовых или полосовых, поэтому, если полоса пропускания и полоса задерживания можно качественно проанализировать в полосе частот, можно определить тип фильтра.
5.2 Методы идентификации фильтра нижних частот
Если частота сигнала стремится к ноль , существует определенный коэффициент усиления напряжения, а когда частота сигнала стремится к бесконечности, коэффициент усиления напряжения стремится к нулю, что является фильтр нижних частот; наоборот, если частота сигнала стремится к бесконечности, существует определенный коэффициент усиления напряжения. А когда частота сигнала стремится к нулю, коэффициент усиления напряжения стремится к нулю, что является фильтром верхних частот; если частота сигнала стремится к нулю и бесконечности, коэффициент усиления напряжения стремится к нулю, то это полосовой фильтр; в противном случае, если частота сигнала при напряжении равна нулю и бесконечности, усиление напряжения имеет такое же определенное значение, а коэффициент усиления напряжения стремится к нулю в определенном диапазоне частот, который является полосовым фильтром.
Ⅵ Функции фильтра нижних частот
1. Фильтр нижних частот представляет собой компонент или комбинацию электронных схем, которые пропускают сигналы, которые проходят ниже частоты среза, а сигналы, которые выше частоты среза не может пройти.
2. Когда фильтр нижних частот используется в сплиттере динамика, басы в сигнале можно отделить и установить отдельный усилитель, позволяющий работать сабвуферу.
3.В радиопередатчиках можно использовать фильтр нижних частот, чтобы блокировать выбросы гармоник, которые могут создавать помехи другим каналам связи.
4. При сетевой передаче разветвитель DSL использует фильтр нижних и верхних частот для разделения сигналов DSL и POTS, которые совместно используют витую пару.
5. В электронном аналоговом музыкальном устройстве, музыкальном аналоговом синтезаторе, работает фильтр нижних частот.
Пример :
PWM имитирует ЦАП через фильтр нижних частот RC
Когда схема требует ЦАП, а микроконтроллер не имеет периферийного ЦАП , ШИМ может использоваться для имитации функции ЦАП через RC-фильтр нижних частот.
При использовании фильтра нижних частот для имитации ЦАП частота ШИМ должна быть намного больше, чем частота среза схемы RC фильтра нижних частот fc = 1/2 πRC (более чем в 10 раз). Выходное напряжение Vout = Vcc * Duty.
Примечание:
1. При нормальных условиях , когда емкость C мала, а сопротивление R велико, потери выходного напряжения малы и пульсации большие; когда емкость C велика, а сопротивление R мало, потери выходного напряжения велики, а пульсации малы.Следовательно, чтобы получить точное DA-преобразование с более высокой линейностью, обычно используется конденсатор меньшего размера, а электролитический конденсатор не используется в максимально возможной степени.
2. Чтобы улучшить управляемость выхода, после RC-фильтра нижних частот обычно добавляется высокопроизводительный повторитель напряжения, а к выходу повторителя добавляется электролитический конденсатор фильтра для дальнейшего увеличения выходное напряжение плавно. Однако следует отметить, что выходное напряжение в это время может содержать больше гармонических составляющих переменного тока.При неправильном обращении повторитель напряжения может быть поврежден. Решение состоит в использовании небольшого танталового конденсатора. Более того, порядок расположения конденсаторов здесь должен быть таким, чтобы электролитический конденсатор находился спереди, а танталовый конденсатор — сзади.
3. Если требования к точности выходного напряжения и линейности невысокие, но требования к пульсации высоки, или когда напряжение относительно фиксировано, можно использовать более крупную комбинацию фильтров. Хотя потери постоянного тока в больших конденсаторах велики, мы можем достичь необходимого выходного напряжения, регулируя рабочий цикл ШИМ, или добиться точного фиксированного выходного напряжения за счет обратной связи первичного аналого-цифрового преобразования.Необходимо только добавить повторитель напряжения, чтобы облегчить использование схемы сбора данных после каскада, и точка сбора данных AD помещается на выходе повторителя.
4. Если первичный RC-фильтр нижних частот не работает, можно использовать многоступенчатый RC-фильтр нижних частот для дальнейшего улучшения плавности вывода.
Пассивный фильтр нижних частот
Ⅶ Конструкция фильтра низких частот
7.1 Конструкция КИХ-фильтра
Конструкция КИХ-фильтра относительно проста, то есть разработать цифровой фильтр, близкий к идеальному низкочастотному. пройти фильтр.Обычно этот идеальный фильтр нижних частот представляет собой прямоугольное окно в частотной области. Согласно преобразованию Фурье, мы можем видеть, что эта функция является функцией дискретизации во временной области, в общем, выражение этой функции: sa (n) = sin (n∩) / n∏.
Эта последовательность выборки бесконечна и не может быть рассчитана компьютером. Следовательно, нам нужно усечь эту функцию выборки. То есть добавить оконную функцию, другими словами, легендарное окно. Это означает, что последовательность выборки во временной области умножается на оконную функцию, а бесконечная последовательность выборки во временной области сокращается до конечного значения последовательности.Однако с помощью оконной функции также затрагивается частотная область последовательности выборок: частотная область в это время представляет собой не идеальное прямоугольное окно, а фильтр нижних частот с полосой перехода и рябью. Как правило, в зависимости от добавленной оконной функции после выборки окна затухание в полосе задерживания фильтра нижних частот, полученное в частотной области, также различается. Обычно мы выбираем подходящую оконную функцию на основе этого затухания в полосе задерживания, такую как прямоугольное окно, окно Ханнинга, окно Хэмминга, окно BLACKMAN, окно Цезаря и так далее.После выбора конкретной оконной функции требуемый порядок и выражение этой оконной функции вычисляются в соответствии с параметрами разработанного фильтра, затем используйте эту оконную функцию для умножения последовательности выборок, чтобы получить импульсную характеристику фактического фильтра.
7.2 Дизайн БИХ-фильтра (метод билинейного преобразования)
Концепция дизайна БИХ-фильтра заключается в следующем: передаточная функция аналогового фильтра определяется в соответствии с параметрами проектируемого фильтра, а затем — в соответствии с конструкцией цифрового фильтра. выполняется билинейным преобразованием или инвариантностью импульсного отклика согласно передаточной функции.Его конструкция более сложна, и сложность заключается в определении передаточной функции аналогового фильтра H (s), но это может быть сделано программно. Конкретные этапы его реализации: Сначала вам нужно определить, какой тип фильтра вам нужен, тип Баттерворта, тип Чебышева или любой другой тип фильтра. При выборе модели можно определить порядок и выражение передаточной функции на основе параметров конструкции и формулы расчета для этого фильтра. Обычно в этом процессе возникает проблема предыскажения (это только проблема, на которую нужно обратить внимание методом билинейного преобразования, тогда как метод инварианта импульсной характеристики не имеет такой проблемы).После определения H (S) разностное уравнение его цифровой области может быть получено с помощью билинейного преобразования.
7.3 Сравнение IIR и FIR
С точки зрения производительности, передаточная функция IIR-фильтра включает два набора регулируемых коэффициентов, нулевой и полюсный, и единственное ограничение на полюсе находится в единичной окружности. Следовательно, высокая селективность может быть получена с меньшим порядковым номером, меньшим количеством ячеек памяти, меньшим объемом вычислений и более высокой эффективностью. Но такой высокий КПД достигается за счет фазовой нелинейности.Чем выше селективность, тем сильнее фазовая нелинейность. Полюс передаточной функции КИХ-фильтра зафиксирован в начале координат и неподвижен. Он может изменить свои характеристики, только изменив нулевое положение. Следовательно, для достижения высокой селективности необходимо использовать более высокий порядок; для того же индекса конструкции фильтра порядок, требуемый КИХ-фильтром, может быть в 5-10 раз выше, чем БИХ-фильтр. В результате стоимость выше, а сигнал выше. Задержка тоже большая; если требуется линейная фаза, БИХ-фильтр должен быть добавлен к многопроходной сети для фазовой коррекции, что также значительно увеличивает порядок и сложность фильтра, и КИХ-фильтр может получить строго линейную фазу.
Структурно БИХ-фильтр должен использовать рекурсивную структуру для настройки полюсов и обеспечения того, чтобы полюса находились в единичной окружности. Из-за эффекта конечной длины слова коэффициенты округляются во время операции, вызывая смещение полюсов. Эта ситуация иногда вызывает проблемы со стабильностью и даже паразитные колебания. Напротив, до тех пор, пока КИХ-фильтр принимает нерекурсивную структуру, нет проблем со стабильностью как в теоретических, так и в практических операциях с конечной точностью, и, следовательно, погрешность частоты также мала.Кроме того, КИХ-фильтр может использовать алгоритм быстрого преобразования Фурье, и скорость работы может быть намного выше при том же порядке.
Кроме того, следует отметить, что, хотя конструкция БИХ-фильтра проста, он по-прежнему спроектирован как обычный фильтр с сегментацией с постоянными характеристиками , такими как низкие, высокие, полосовые и полосовые. -стоп, который часто нельзя отделить от формы аналогового фильтра. КИХ-фильтр гораздо более гибок, особенно потому, что его легко адаптировать к определенным специальным приложениям, таким как формирование цифрового дифференциатора или преобразователя Хиллера, поэтому он имеет большую адаптируемость и широкий спектр приложений.
Из упомянутого выше сравнения мы видим, что БИХ-фильтры и КИХ-фильтры имеют свои сильные стороны, поэтому в практических приложениях нам следует выбирать из многих аспектов. С точки зрения требований к использованию, в случае нечувствительности к фазовым требованиям, таким как языковая коммуникация, более целесообразно использовать IIR, чтобы он мог полностью использовать свои экономичные и эффективные функции; для обработки сигналов изображения, передачи данных и других систем, передающих информацию по форме волны, требуется, чтобы линейная фаза была выше.По возможности лучше использовать КИХ-фильтр. Конечно, в практических приложениях можно учитывать и другие факторы.
Независимо от IIR и FIR, чем выше порядок , тем больше задержка сигнала. Между тем, в БИХ-фильтре, чем выше порядок, тем выше требования к точности коэффициента, в противном случае легко вызвать ошибку конечной длины слова, чтобы переместить полюс к блоку за пределами поля. Поэтому при выборе заказа он учитывается всесторонне.
Часто задаваемые вопросы о работе фильтра низких частот
1. Для чего нужен фильтр нижних частот?
Фильтры нижних частот используются для фильтрации шума в цепи. «Шум» — это высокочастотный сигнал. При прохождении через фильтр нижних частот большая часть шума удаляется, и получается чистый звук.
2. Когда бы вы использовали фильтр нижних частот?
Фильтр нижних частот можно очень эффективно использовать для имитации ощущения, что один сигнал находится дальше от слушателя, чем другой (нефильтрованный) сигнал.Эту технику можно очень быстро и легко использовать для установления пространственного контраста между двумя сигналами, особенно если они разделены в стереополе.
3. Как работают фильтры нижних частот?
Фильтр нижних частот (LPF) ослабляет содержимое, превышающее частоту среза, позволяя более низким частотам проходить через фильтр. Например, фильтр нижних частот используется в синтезаторах для ослабления высоких гармоник и делает звуки «темнее» или «плавнее» по тембру.
4.Почему идеальный фильтр нижних частот невозможен?
Это бесконечно не причинно:
Если импульсная характеристика обозначена как h (t), выходной сигнал y (t), соответствующий входному сигналу x (t), определяется следующим образом: Значение y при любом t зависит от значений x полностью до, если h (t) продолжается до. Таким образом, реализация идеального фильтра нижних частот в реальном времени невозможна.
5. Какая частота среза фильтра нижних частот?
Частота среза фильтра нижних частот — это частота, при которой выходное напряжение (нагрузочное) равно 70.7% от входного (исходного) напряжения. Выше частоты среза выходное напряжение ниже 70,7% входного, и наоборот.
Вам также может понравиться
Полное введение и классификация фильтров и приложений
Важные меры по предотвращению электромагнитных помех — технология фильтрации
Принцип и принцип действия фильтра
Общие области применения фильтра
Альтернативные модели
| Часть | Сравнить | Производители | Категория | Описание | |
| ПроизводительНомер детали: DAC5675IPHP | Сравнить: Текущая часть | Производитель: TI | Категория: Цифро-аналоговый | Описание: Цифро-аналоговый преобразователь TEXAS INSTRUMENTS DAC5675IPHP, 14 бит, 400 MSPS, параллельный, 3.От 15 В до 3,6 В, QFP, 48 контактов | |
| Производитель Номер детали: DAC5675IPHPR | Сравнить: DAC5675IPHP VS DAC5675IPHPR | Производитель: TI | Категория: Цифро-аналоговый | Описание: 14-битный цифро-аналоговый преобразователь (ЦАП) 400MSPS 48-HTQFP -40–85 ℃ | |
| Mfr.Номер детали: DAC5675IPHPG4 | Сравнить: DAC5675IPHP против DAC5675IPHPG4 | Производитель: TI | Категория: Цифро-аналоговый | Описание: 14-битный, 400MSPS ЦАП с LVDS, лучшая производительность ЦАП в отрасли 48-HTQFP -40 ℃ до 85 ℃ | |
| Mfr.Номер детали: DAC5675IPHPRG4 | Сравнить: DAC5675IPHP VS DAC5675IPHPRG4 | Производитель: TI | Категория: Цифро-аналоговый | Описание: 14-битный цифро-аналоговый преобразователь (ЦАП) 400MSPS 48-HTQFP -40–85 ℃ |
Схема и применение активного фильтра нижних частот
В предыдущем уроке мы узнали о активных фильтрах верхних частот , где фильтр верхних частот разработан с использованием пассивного RC-фильтра вместе со схемой операционного усилителя.В этом руководстве мы узнаем об активном фильтре низких частот и поймем, что переход от фильтра низких частот к фильтру высоких частот — это просто замена компонентов R и C.
Если вы ищете информацию о пассивных фильтрах, ознакомьтесь со следующими руководствами: «Пассивные RC-фильтры нижних частот» и «Пассивные RC-фильтры верхних частот» .
Введение
Фильтр нижних частот — это фильтр, который пропускает все частоты от постоянного тока до верхней частоты среза fH и отклоняет любые сигналы выше этой частоты.
В идеальном случае кривая АЧХ падает на частоте среза. На практике сигнал не падает внезапно, а постепенно падает от переходной области к области стоп-зоны.
Частота среза означает точку, в которой отклик падает на -3 дБ или 70,7% от полосы пропускания. Переходная область означает область, где происходит спад.
Область полосы заграждения означает область, где затухание происходит в основном для входных сигналов. Таким образом, этот фильтр также называется фильтром высоких частот или фильтром, отсекающим высокие частоты.Идеальный ответ показан ниже.
Вместо использования только пассивных компонентов, активный фильтр нижних частот состоит из активных компонентов, таких как операционные усилители, полевые транзисторы и транзисторы, в сочетании с пассивными компонентами. Эти фильтры очень эффективны по сравнению с пассивными фильтрами. Активные фильтры вводятся для устранения недостатков пассивных фильтров.
Простой активный фильтр нижних частот сформирован с использованием операционного усилителя. Операционный усилитель принимает сигнал с высоким импедансом в качестве входа и выдает сигнал с низким сопротивлением в качестве выхода.Компонент усилителя в этой схеме фильтра увеличивает амплитуду выходного сигнала.
Благодаря этому действию усилителя выходной сигнал станет шире или уже. Максимальная частотная характеристика фильтра зависит от усилителя, используемого в схемотехнике.
Цепь активного фильтра нижних частот
Ослабление сигнала, т.е. амплитуда выходного сигнала меньше амплитуды входного сигнала в пассивной цепи. Чтобы преодолеть этот недостаток пассивного фильтра, разработан активный фильтр.Пассивный фильтр нижних частот, подключенный к инвертирующему или неинвертирующему операционному усилителю, дает нам простой активный фильтр нижних частот.
Активный фильтр первого порядка образован одним операционным усилителем с RC-цепью. Ниже показан простой RC-пассивный фильтр, подключенный к неинвертирующему выводу операционного усилителя.
Эта RC-цепь обеспечивает низкочастотный тракт ко входу усилителя. Усилитель действует как буферная схема, обеспечивающая выход с единичным усилением. Эта схема имеет большее значение входного импеданса.Несмотря на то, что входное сопротивление операционных усилителей значительно ниже частоты среза, это входное сопротивление ограничено последовательным импедансом, равным R + 1⁄jωC.
Выходное сопротивление операционного усилителя, подключенного к цепи, всегда низкое. Эта схема обеспечивает высокую стабильность фильтра. Главный недостаток такой конфигурации — коэффициент усиления по напряжению равен единице. Даже для этой схемы выходная мощность также высока, поскольку входное сопротивление низкое.
Активный фильтр нижних частот с усилением высокого напряжения
Вышеупомянутая активная схема фильтра нижних частот не обеспечивает усиление более единицы.Таким образом, мы используем приведенную ниже схему, чтобы обеспечить высокий коэффициент усиления по напряжению.
Когда входные сигналы имеют низкие частоты, сигналы будут проходить через схему усиления напрямую, но если входная частота высока, сигналы проходят через конденсатор C1. С помощью этой схемы фильтра амплитуда выходного сигнала увеличивается на коэффициент усиления полосы пропускания фильтра.
Мы знаем, что для схемы неинвертирующего усилителя величина усиления по напряжению получается путем деления его резистора обратной связи R 2 на соответствующий входной резистор R 3 .2)
Где
- A макс. = усиление полосы пропускания = 1 + R_2⁄R_3
- f = рабочая частота.
- f c = частота среза.
- В выход = Выходное напряжение.
- В в = Входное напряжение.
Когда частота увеличивается, усиление уменьшается на 20 дБ на каждые 10 временных приращений частоты. Эта операция наблюдается как ниже
На низких частотах, то есть когда рабочая частота f меньше частоты среза, тогда
В выход / В дюйм = A макс
Когда рабочая частота равна частоте среза, тогда
В выход / В дюйм = А макс / √2 = 0.707 А макс
Когда рабочая частота меньше частоты среза, тогда
В на выходе / В на дюйм макс.
С помощью этих уравнений можно сказать, что на низких частотах коэффициент усиления схемы равен максимальному усилению, а на высоких частотах коэффициент усиления схемы меньше максимального усиления A max .
Когда фактическая частота равна частоте среза, тогда коэффициент усиления равен 70.7% от A макс . Этим мы можем сказать, что для каждого десятикратного (декадного) увеличения частоты коэффициент усиления напряжения делится на 10.
Величина усиления напряжения (дБ): A макс. = 20 log 10 (В на выходе / В на )
На частоте -3 дБ коэффициент усиления определяется как:
3 дБ A макс. = 20 log 10 {0,707 (В на выходе / В на )}
Пример активного фильтра нижних частот
Давайте рассмотрим неинвертирующий активный фильтр нижних частот с частотой среза 160 Гц и входным сопротивлением 15 кОм.Предположим, что на низких частотах эта схема имеет коэффициент усиления по напряжению 10.
Коэффициент усиления в дБ определяется как 20log (A макс. ) = 20log (10) = 20 дБ
Мы знаем, что коэффициент усиления по напряжению определяется как:
A макс. = 10 = 1 + ( 2 / 1 )
Пусть резистор R 1 равен 1,2 кОм
R 2 = 9R 1 = 9 x 1,2k = 10,8 кОм
Следовательно, полученное R 2 составляет 10,8 кОм. Так как этого значения не существует, мы можем рассматривать ближайшее предпочтительное стандартное значение как 11 кОм.
Рассматривая уравнение частоты среза, мы можем получить значение конденсатора.
f C = 1 / 2πRC
Считая C основным, мы можем записать приведенное выше уравнение следующим образом:
C = 1 / 2πf C R
Замените значение входного сопротивления как 15 кОм, значение f_C как 160 Гц.
Следовательно, C = 0,068 мкФ.
Из полученных значений можно получить активный фильтр нижних частот:
Частотная характеристика
Отклик активного фильтра показан на рисунке ниже.
Активный фильтр нижних частот второго порядка
Просто добавив дополнительную RC-цепь к фильтру нижних частот первого порядка, схема ведет себя как фильтр второго порядка. Схема фильтра второго порядка показана выше.
Коэффициент усиления приведенной выше схемы составляет макс. = 1 + ( 2 / 1 )
Частота среза фильтра нижних частот второго порядка f c = 1 / 2π√ (C 1 C 2 R 3 R 4 )
Частотная характеристика и этапы проектирования фильтра второго порядка и фильтра первого порядка почти одинаковы, за исключением спада полосы заграждения.Значение спада фильтра второго порядка вдвое больше, чем у фильтра первого порядка, которое составляет 40 дБ / декаду или 12 дБ / октаву. Эти фильтры задерживают более крутые высокочастотные сигналы.
Применение активных фильтров нижних частот
- В электронике эти фильтры широко используются во многих приложениях. Эти фильтры используются в качестве фильтров шипения в аудиоколонках, чтобы уменьшить высокочастотное шипение, производимое в системе, и они используются в качестве входов для сабвуферов.

