Фильтры низких частот: принцип работы, виды и применение

Что такое фильтр низких частот. Как работают аналоговые и цифровые ФНЧ. Какие бывают виды ФНЧ первого и высших порядков. Где применяются фильтры низких частот.

Что такое фильтр низких частот и как он работает

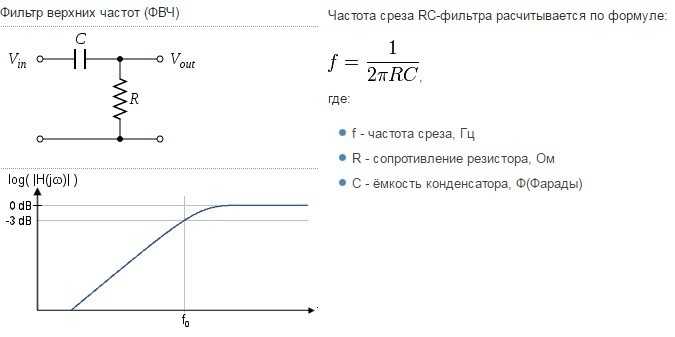
Фильтр низких частот (ФНЧ) — это устройство или алгоритм, которые пропускают сигналы низких частот и ослабляют сигналы высоких частот выше определенной частоты среза. Принцип работы ФНЧ заключается в следующем:

• Пропускает сигналы с частотой ниже частоты среза практически без ослабления
• Значительно ослабляет или полностью подавляет сигналы с частотой выше частоты среза
• В области частоты среза происходит плавный переход между зоной пропускания и зоной подавления

Частота среза является ключевым параметром ФНЧ и определяет границу между пропускаемыми и подавляемыми частотами. Чем круче спад амплитудно-частотной характеристики (АЧХ) в области среза, тем эффективнее фильтрация.

Основные виды фильтров низких частот

Существует два основных типа фильтров низких частот:

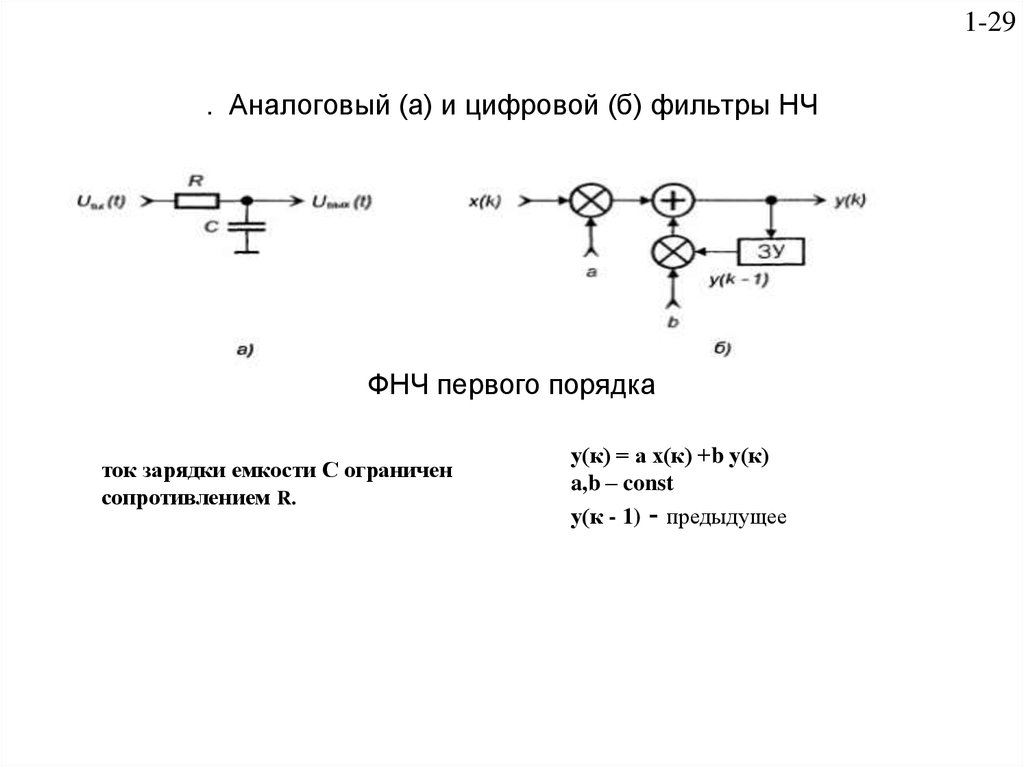
1. Аналоговые ФНЧ

Реализуются на пассивных или активных электронных компонентах:

• RC-фильтры на резисторах и конденсаторах
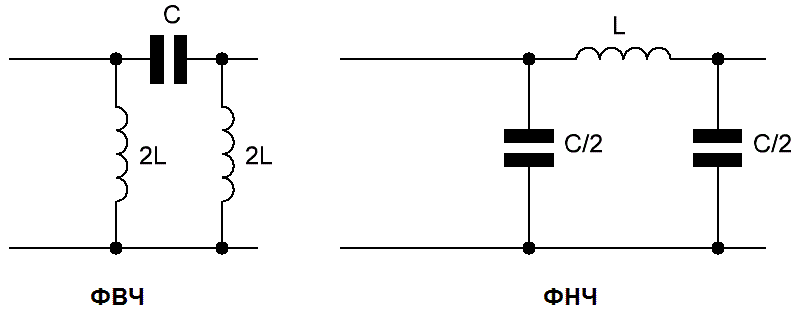
• LC-фильтры на катушках индуктивности и конденсаторах
• Активные фильтры на операционных усилителях

2. Цифровые ФНЧ

Реализуются программно или на цифровых сигнальных процессорах:

• КИХ-фильтры (с конечной импульсной характеристикой)
• БИХ-фильтры (с бесконечной импульсной характеристикой)

Цифровые фильтры позволяют точнее задавать АЧХ и легко перестраивать их параметры.

Фильтры низких частот первого порядка

Простейшим ФНЧ является фильтр первого порядка, который содержит один реактивный элемент (конденсатор или катушку индуктивности). Рассмотрим основные схемы:

Пассивный RC-фильтр первого порядка

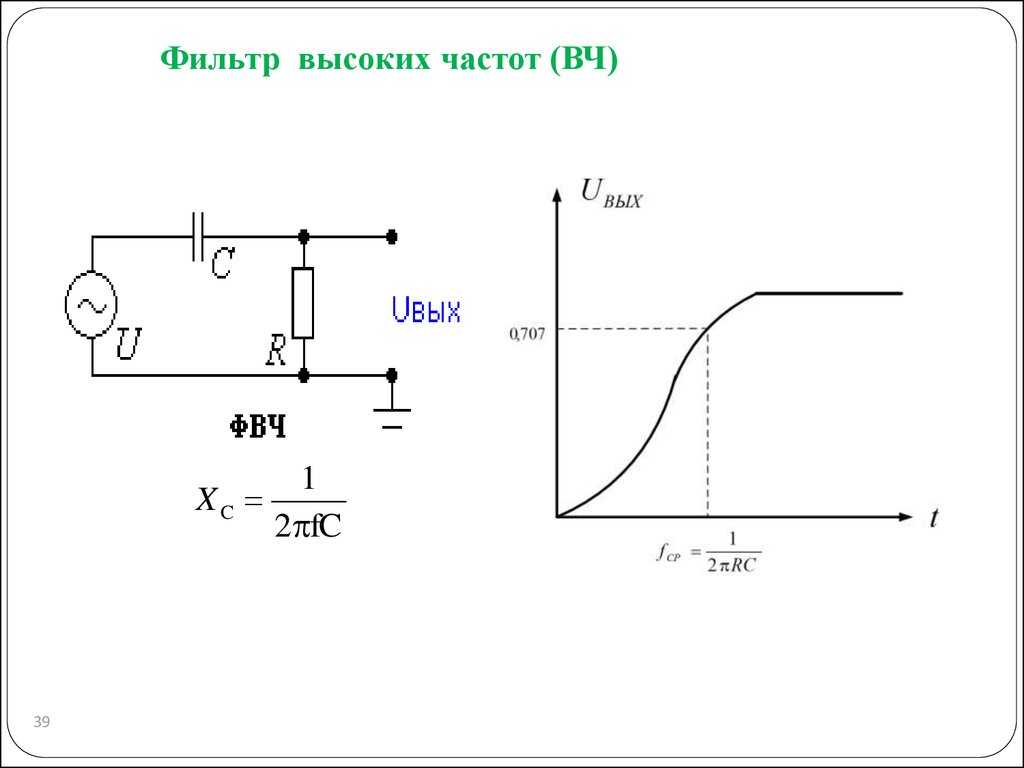
Состоит из резистора R и конденсатора C, соединенных последовательно. Частота среза определяется формулой:

f_c = 1 / (2π * R * C)

Спад АЧХ составляет -20 дБ/декаду или -6 дБ/октаву выше частоты среза.

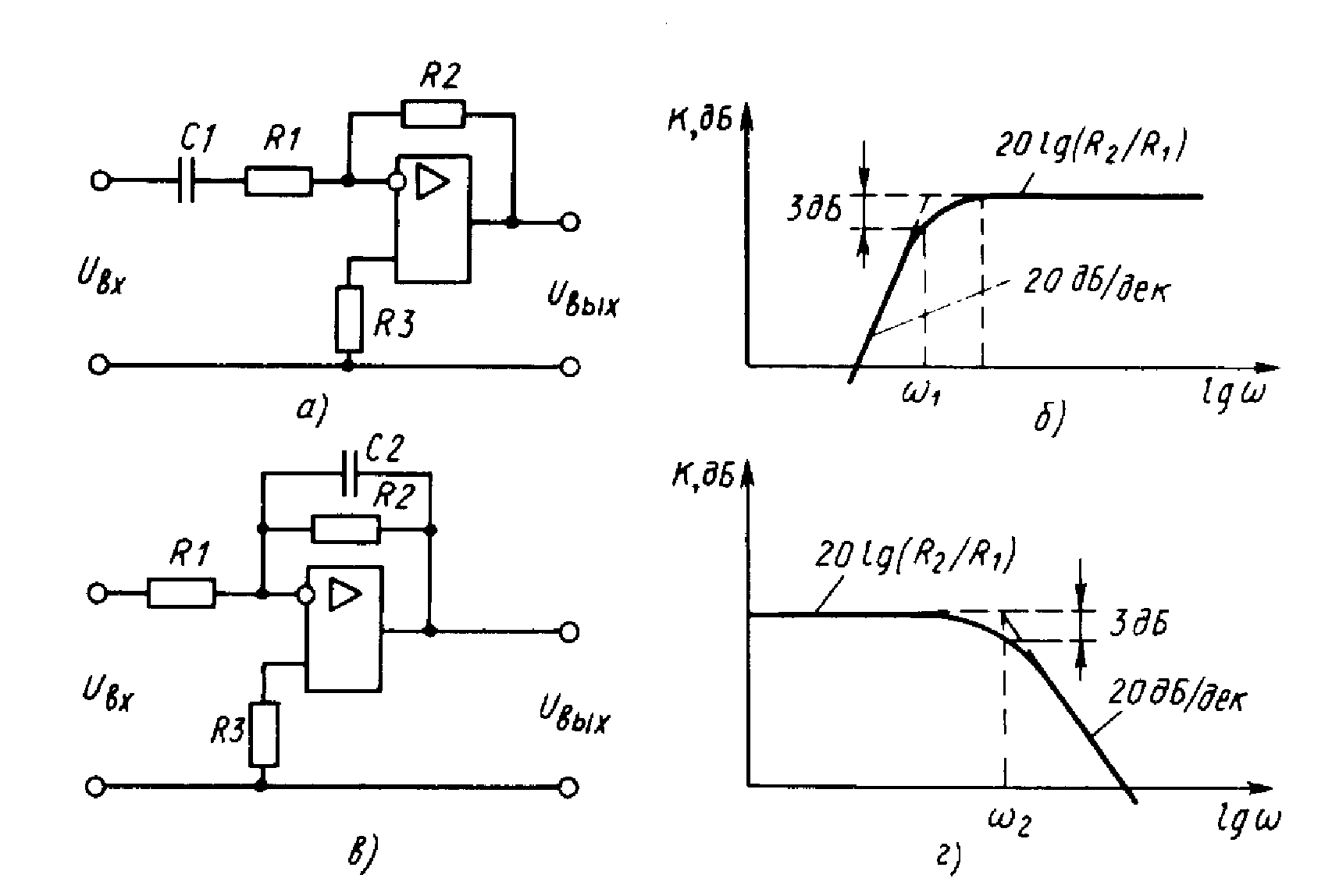
Активный ФНЧ первого порядка

Строится на основе операционного усилителя и RC-цепи в цепи обратной связи. Позволяет получить единичное усиление в полосе пропускания и более крутой спад АЧХ.

Фильтры низких частот второго и высших порядков

Для получения более крутого спада АЧХ и лучшего подавления высоких частот применяют ФНЧ второго и более высоких порядков.

Пассивный LC-фильтр второго порядка

Содержит катушку индуктивности L и конденсатор C. Обеспечивает спад АЧХ -40 дБ/декаду выше частоты среза. Частота среза определяется формулой:

f_c = 1 / (2π * √(L * C))

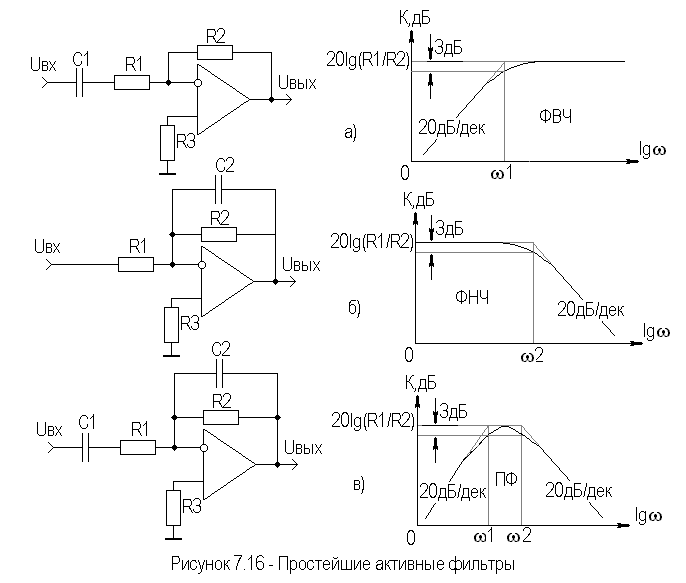
Активный ФНЧ второго порядка

Реализуется на операционном усилителе с двумя конденсаторами в цепи обратной связи. Позволяет получить различные виды АЧХ — Баттерворта, Чебышева, Бесселя.

ФНЧ высших порядков

Строятся каскадным включением звеньев первого и второго порядков. Обеспечивают очень крутой спад АЧХ за счет увеличения порядка фильтра. Широко применяются в радиотехнике для эффективного подавления высокочастотных помех.

Применение фильтров низких частот

Фильтры низких частот находят широкое применение в различных областях:

• Подавление высокочастотных шумов и помех в аудиосистемах
• Выделение низкочастотной составляющей сигнала в измерительной технике
• Сглаживание пульсаций в источниках питания
• Ограничение полосы частот в системах связи
• Подавление зеркального канала в радиоприемниках
• Фильтрация видеосигнала в телевизионной технике

Правильный выбор типа и параметров ФНЧ позволяет эффективно решать задачи фильтрации сигналов в самых разных приложениях.

Преимущества и недостатки ФНЧ различных типов

Рассмотрим основные достоинства и ограничения фильтров низких частот разных видов:

Пассивные RC-фильтры:

Преимущества:

• Простота и дешевизна
• Не требуют питания
• Высокая надежность

Недостатки:

• Низкая крутизна спада АЧХ
• Сложность перестройки параметров

Активные фильтры на ОУ:

Преимущества:

• Высокая крутизна спада АЧХ
• Возможность реализации различных видов АЧХ
• Легкость каскадирования

Недостатки:

• Требуют источника питания
• Ограничены полосой пропускания ОУ

Цифровые фильтры:

Преимущества:

• Высокая точность и стабильность параметров
• Гибкая перестройка характеристик
• Возможность реализации сложных АЧХ

Недостатки:

• Требуют АЦП и ЦАП для работы с аналоговыми сигналами
• Ограничены быстродействием процессора

Выбор оптимального типа ФНЧ зависит от конкретной задачи и требований к характеристикам фильтрации.

Методы расчета и проектирования ФНЧ

При разработке фильтров низких частот используются следующие основные подходы:

Аналитический расчет

Применяется для простых фильтров первого и второго порядков. Параметры рассчитываются по формулам на основе заданной частоты среза и требуемой АЧХ.

Табличный метод

Используются справочные таблицы с нормированными значениями элементов для различных видов АЧХ (Баттерворта, Чебышева и др.). Реальные номиналы получают масштабированием табличных значений.

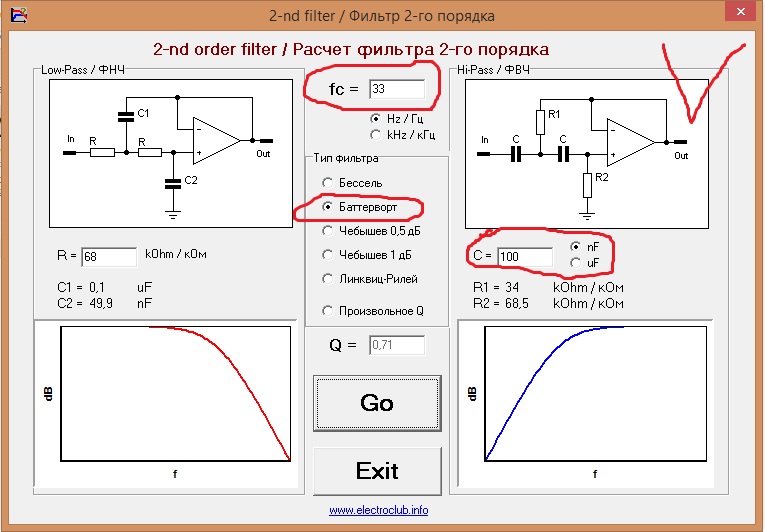
Компьютерное моделирование

Применяются специализированные САПР для расчета и оптимизации параметров сложных фильтров. Позволяет учесть реальные характеристики компонентов.

Синтез цифровых фильтров

Используются алгоритмы синтеза КИХ и БИХ-фильтров на основе заданных требований к АЧХ. Реализуется программно или на сигнальных процессорах.

Правильный выбор метода расчета позволяет получить оптимальные характеристики ФНЧ для конкретного применения.

Разработка и исследование микрополосковых фильтров низких частот с высокой крутизной склона АЧХ и влияние электромагнитного окружения на основные параметры фильтров

Ю.А. Ламанов, Т.О. Кудрявцева, Н.Б. Дроботун

Введение 

Частотно-селективные устройства СВЧ-диапазона, в частности полосно-пропускающие фильтры (ППФ) и фильтры низких частот (ФНЧ), в последнее время являются наиболее востребованными устройствами среди разработчиков радиоаппаратуры различного назначения. Они применяются при разработке систем связи, радиолокационных и радионавигационных устройств, а также в различной измерительной и специальной радиоаппаратуре. Стремительное развитие современных средств связи делает крайне актуальной разработку ППФ с широкой полосой и высокой крутизной, однако в решении задач подавления зеркальной частоты в высокочастотном тракте приемников и измерительной аппаратуре (векторные анализаторы цепей) активно применяются ФНЧ [1,2]. Их повсеместное использование обусловлено высокой избирательностью, малыми потерями в полосе пропускания и технологичностью производства при низкой стоимости.

В по­следние годы активно разрабатываются и исследу­ются разнообразные конструкции ФНЧ в микрополосковом исполнении [3–6]. Для улучшения их характеристик, как правило, используется большой набор различных резонаторов, который формирует полосу пропускания и полосу заграждения, а также позволяет увеличить крутизну склона АЧХ и расширить диапазон полосы заграждения и пропускания.      

На сегодняшний день среди множества топологий фильтров ФНЧ с распределенными параметрами являются наиболее простыми как в расчете, так и в производстве. Примером такого фильтра является гребешковый и полосковый фильтр [7, 8]. Несмотря на вышеперечисленные достоинства у таких фильтров существует ряд существенных недостатков, например, сравнительно низкая собственная добротность и, как следствие, высокие потери в полосе пропускания.

Относительно низкие потери в полосе пропускания имеют двумерные конструкции ФНЧ на микрополосковых резонаторах [9]. К основным недостаткам таких конструкций относятся их большой размер и сравнительно малый уровень подавления помех в полосе заграждения. Этот недостаток можно скомпенсировать конструкцией ФНЧ с двусторонним рисунком или дополнительными вырезами на тыльной стороне диэлектрической подложки, подвешенной в металлическом корпусе [10, 11].

В настоящей работе, вопреки всем достоинствам фильтров с двусторонним рисунком, разрабатывается и исследуется ФНЧ с двумерной конструкцией. Выбор данной топологии обусловлен несколькими причинами. Во-первых, данные фильтры будут устанавливаться на печатную плату с помощью токопроводящего клея EPO-TEK, полимеризующегося при высокой температуре. Во-вторых, установка фильтров на плате позволяет существенно сэкономить место в устройстве, так как не придется выносить фильтр отдельным блоком. Компактное расположение элементов на плате дает возможность освободить больше пространства для подложки фильтра, что необходимо для ФНЧ, топология которых занимает большую площадь.

В-третьих, производство таких фильтров существенно дешевле, а размещение их на плате не сложнее установки в блоке.

Расчет фильтра на основе чередующихся резонаторов с низким и высоким сопротивлением

Исходя из требований технического задания по обеспечению равномерной АЧХ в полосе пропускания, в качестве фильтра прототипа использовался фильтр Баттерворта 16-ого порядка с максимально плоской характеристикой. При аппроксимации с помощью гладкой кривой частотная характеристика фильтра-прототипа НЧ описывается формулой (1)

Производные функции L_Б начиная от первой и кончая (2N − 1)-ой равны нулю при x = 0. Таким образом, функция L_Б является максимально плоской при x = 0  [12].

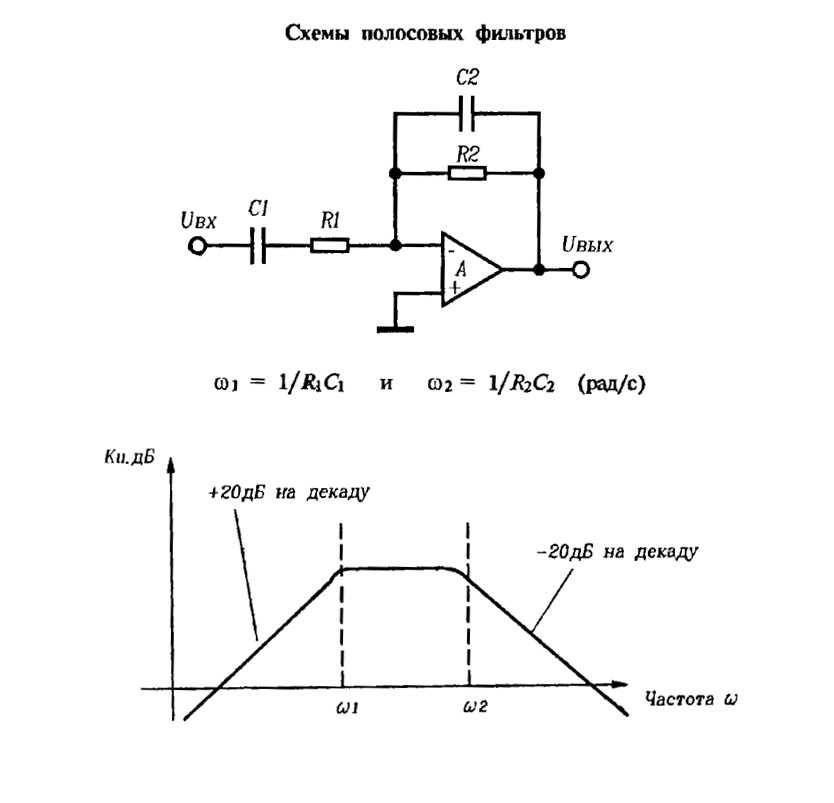
На рисунке 1 приведена схема нормированного фильтра прототипа нижних частот с сосредоточенными параметрами для нечетного числа элементов.

Рис. 1.  Схема нормированного фильтра прототипа нижних частот

Количество элементов в схеме показывает степень N в функции L_Б. Для обеспечения низкого уровня подавления установлен большой порядок фильтра, число элементов в нем равно 33.

Коэффициент передачи, соответствующий максимально плоской частотной характеристики фильтра прототипа, может быть реализован с помощью схемы, изображенной на рисунке 1, при определенном подборе ее нормированных параметров g.

Значения параметров g определяется по формуле Беннета (2) [12]:

В таблице 1 приведены значения для фильтра НЧ Баттерворта с 33-мя элементами.

Таблица 1

Значение парметров g фильтра Баттерворта

gk	значение	gk	значение	gk	значение
g1	0. 095	g12	1.778	g23	1.683
g2	0.285	g13	1.857	g24	1.572
g3	0.472	g14	1.919	g25	1.447
g4	0.654	g15	1.964	g26	1.31
g5	0.831	g16	1.991	g27	1. 16
g6	1	g17	2	g28	1
g7	1.16	g18	1.991	g29	0.831
g8	1.31	g19	1.964	g30	0.654
g9	1.447	g20	1.919	g31	0.472
g10	1.572	g21	1. 857	g32	0.285
g11	1.683	g22	1.778	g33	0.095

  Для перехода от схемы фильтра-прототипа к эквивалентной схеме проектируемого фильтра, представленной на рисунке 2, были рассчитаны значения элементов при заданных ω_с = 2πf, частоте среза f = 6 ГГц, волновом сопротивлении Z_{в= 50  по формулам (3) (для k-нечетных) и (4) (для k-нечетных) [12]:}

Рис. 2. Эквивалентная схема ФНЧ

Рассчитанные значения сосредоточенных элементов L и C показаны в таблице 2.

Таблица 2

Значение схемы ФНЧ

k	Элементы
	Индуктивность L, нГн	Емкость C, пФ
1	-	0. 05049
2	0.3775	-
3	-	0.2501
4	0.8676	-
5	-	0.4408
6	1.326	-
7	-	0.6155
8	1.737	-
9	-	0.7679
10	2.085	-
11	-	0. 8926
12	2.358	-
13	-	0.985
14	2.545	-
15	-	1.042
16	2.641	-
17	-	1.061
18	2.641	-
19	-	1.042
20	2.545	-
21	-	0. 985
22	2.358	-
23	-	0.8926
24	2.085	-
25	-	0.7679
26	1.737	-
27	-	0.6155
28	1.326	-
29	-	0.4408
30	0.8676	-
31	-	0. 2501
32	0.3775	-
33	-	0.05049

Далее были найдены длины и ширины отрезков линий, реализующих индуктивности и емкости. Длина волны в линии λ_g. = λ_gL = λ_gC (формула 5) [13]_.

Были рассчитаны волновые сопротивления несимметричной полосковой линии (рисунок 3).

Рис. 3. Несимметричная полосковая линия передачи

  

Параметры индуктивности технологически были ограничены шириной, она не должна быть меньше 20 мкм. Также ширина не должна превышать 200 мкм, так как это значение близко к значению регулярной линии передач. Диапазон ширин составляет от 40 мкм до 180 мкм.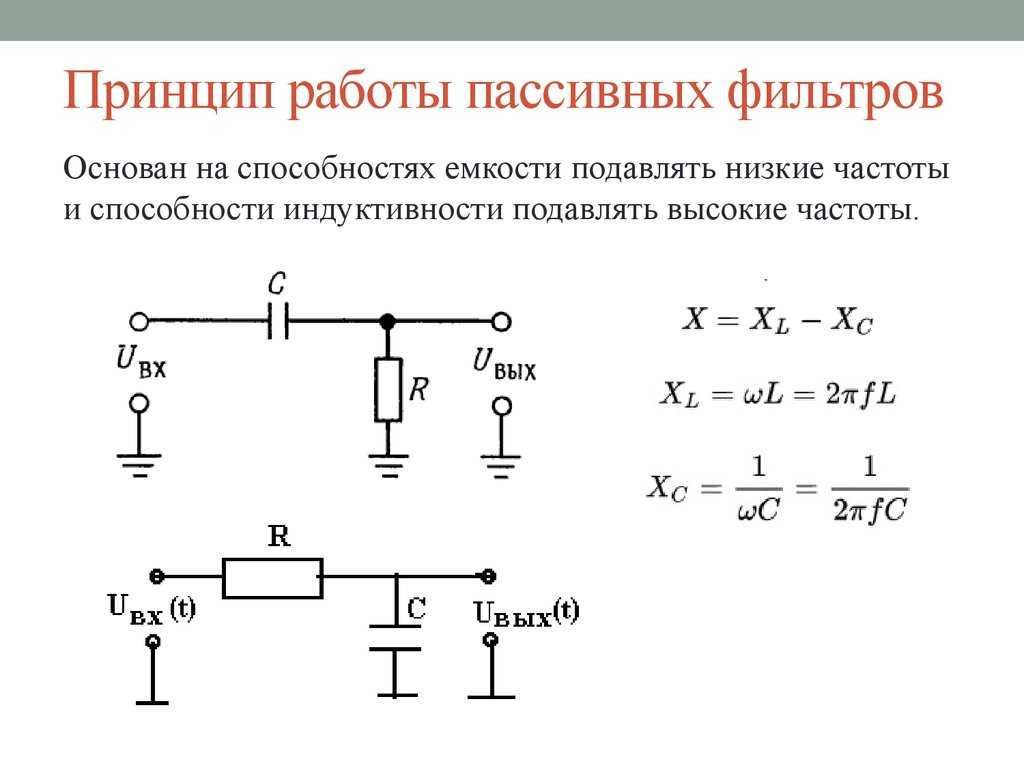

Ширины, выбранные для расчета, представлены в таблице 3.

Таблица 3

Ширины отрезков линий, реализующих индуктивные элементы

№	b, мкм
1	40
2	60
3	80
4	100
5	120
6	140
7	160
8	180

Волновое сопротивление индуктивности рассчитано по формуле (6), при b/d < 2 [14]:

где d = 254 мкм; t = 3 мкм.

Для обеспечения так называемого «скачка сопротивлений» при переходе от индуктивного элемента к емкостному было необходимо обеспечить разницу волновых сопротивлений этих элементов не менее чем в 3 раза.

После того, как были найдены средние значения волновых сопротивлений, были рассчитаны длины отрезков, реализующих индуктивности и емкости, по приведённым формулам 7-8 [13].

Таблица 4

Значения длин отрезков линий, реализующих индуктивности и емкости

Индуктивность L, нГн	Длина  lL, мм	Емкость C, пФ	Длина lC, мм
0.3775	0.518	0.05049	0. 109
0.8676	1.233	0.2501	0.542
1.326	2.026	0.4408	0.972
1.737	3.149	0.6155	1.396
2.085	4.114	0.7679	1.807
2.358	4.318	0.8926	2.195
2.545	4.448	0.985	2.539
2.641	4. 511	1.042	2.796
		1.061	2.896

Из диапазона 40-180 мкм было выбрано среднее значение ширины индуктивного элемента. Ширина емкостного элемента была рассчитана по формуле (9), при b/d > 2 [14].

В таблицы 5 представлены расчётные значения длин отрезков микрополосковых линий.

Таблица 5

Средние значения длин микрополосковых линий, реализующих индуктивные и емкостные элементы  

	Индуктивность	Емкость
Среднее значения волнового сопротивления, Ом	69	23
Среднее значение длин отрезков, мм	2,64	1,695
Среднее значение ширин отрезков, мм	0,110	1,64

По данным из таблицы 5 в САПР Advanced Design System (ADS) была реализована модель ФНЧ с двумерной конструкцией (рисунок 4), в которой реализуется дополнительная электромагнитная связь между несмежными резонаторами. Такая перекрестная связь позволяет существенно увеличить крутизну склона АЧХ [15].

Рис. 4. Топология фильтра нижних частот

Синтез топологии фильтра в САПР

Согласно требованиям технического задания разрабатываемый фильтр планируется применять как дополнительное частотно-селективное звено совместно с ППФ диапазона 5…6 ГГц для подавления побочных полос пропускания ППФ. Таким образом, было принято решение оптимизировать предложенную топологию под требуемый частотный диапазон. В качестве целей оптимизации были установлены: возвратные потери в полосе частот 5…6 ГГц не хуже −20 дБ, потери в полосе не более −3 дБ. Сама оптимизация проводилась в несколько этапов. На первом этапе были получены желаемые характеристики в полосе. Целью второго этапа было увеличение крутизны частоты среза. Для этого потребовалось увеличить перекрёстную связь между звеньями фильтра, что было достигнуто за счёт добавления в топологию коротких меандровых элементов.

В качестве материала подложки был выбран поликор. Фильтр 16-го порядка был расположен на подложке с диэлектрической проницаемостью ε = 10,3 и толщиной d = 0,25 мм. Рассматриваемая топология симметрична относительно центрального емкостного элемента. Финальный рисунок топологии фильтра после программной оптимизации представлен на рисунке 5.

Рис. 5. Топология измененного ФНЧ с двумерной конструкцией

Рис. 6. Амплитудно-частотные характеристики фильтра нижних частот с двумерной конструкцией. Сплошная – FEM, точки – Momentum Microware

На рисунке 6 представлены результаты моделирования в САПР ADS двумя методами расчета (Momentum Microware и FEM): АЧХ прямых потерь S₂₁ и возвратных потерь S₁₁ фильтра нижних частот с полосой пропускания 5…6 ГГц и полосой затухания 7…8 ГГц. 

Зависимости на рисунке 6 показывают высокую крутизну склона АЧХ.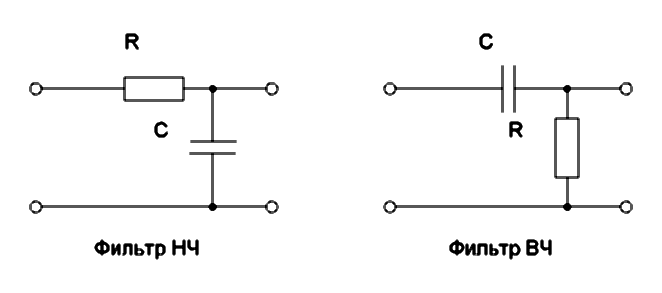 Однако видно, что при расчете разными методами, характеристика смещается, в данном случае на 0,3 ГГц.

Исследование изготовленных опытных образцов фильтров

Для проведения исследований топологии в коаксиальном тракте разработанный фильтр 16-го порядка на подложке из поликора устанавливался на печатную плату с помощью токопроводящего клея EPO-TEK (рисунок 7). Размеры подложки — 36 × 7,1 мм. Подводящие отрезки на печатной плате выполнены в виде копланарных линий с волновым сопротивлением 50 Ом.

Рис. 7. Конструкция фильтра нижних частот

На рисунке 8 показано сравнение расчетных данных с экспериментальными. По результатам измерения видно, что подавление в полосе заграждения, по сравнению с расчетным, выше на 20 дБ, крутизна склона по экспериментальным данным увеличилась.

Рис. 8. Амплитудно-частотные характеристики измеренного фильтра нижних частот.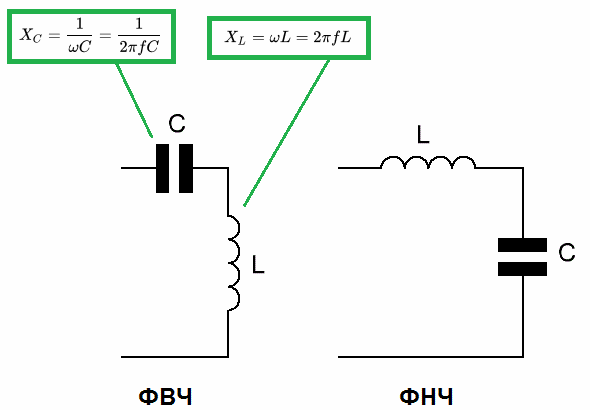 Сплошная – измеренные, точки – Momentum Microware, пунктир – FEM

Для проверки параметров фильтра  в условиях, приближенных к реальным (фильтры предполагается устанавливать во фрезерованный паз глубиной 3 мм и накрывать сверху крышкой) на него была установлена конструкция, имитирующая указанное реальное электромагнитное окружение (рисунок 9). Другими словами, фильтр находился в прямоугольном волноводе, широкая стенка а которого равна 10 мм, узкая­ b — 3 мм. Расстояние от платы до крышки составило 3 мм. Помимо конструктивных особенностей данная сборка обеспечивает ЭМС фильтра с другими элементами системы, в которой данный фильтр будет использован.

Однако данная конструкция не должна оказывать существенного влияния на характеристики фильтра. Для этого не должно выполняться условие (10), при котором длина волны в волноводе меньше критической. Критическая длина волны волновода, рассчитанная по формуле (11) на основном типе волны H₁₀, равна 20 мм, тогда как длина волны на частоте среза равна 50 мм.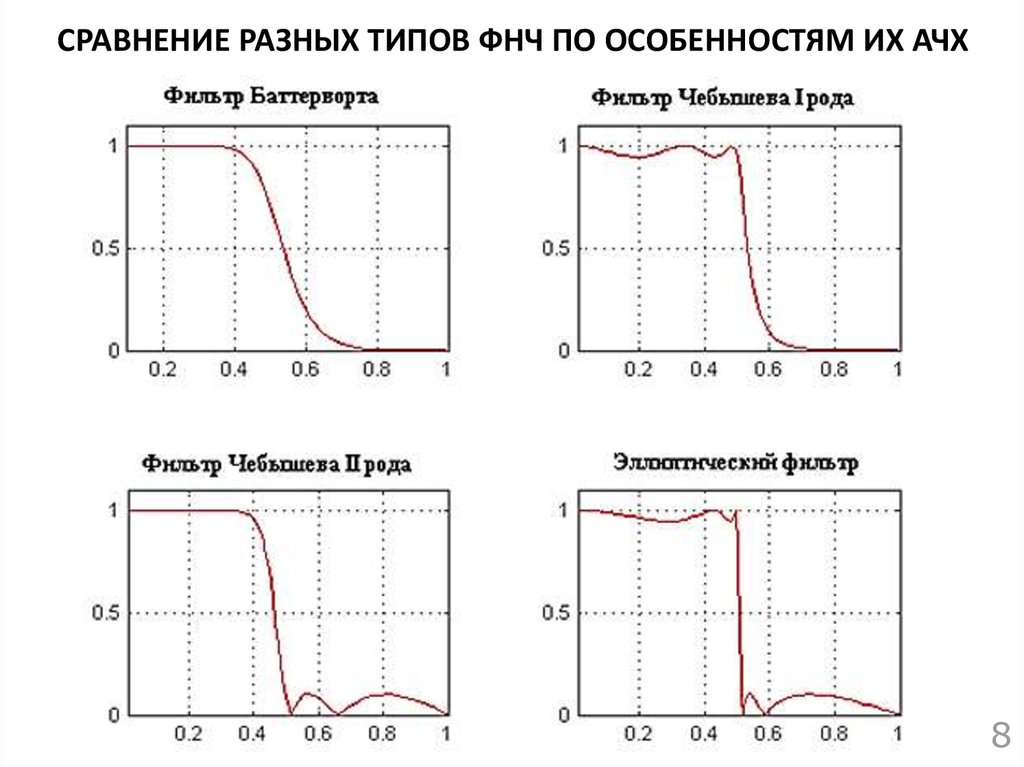 Следовательно, условие не выполняется, волновод не работает в диапазоне частот 5…6 ГГц и никак не влияет на работу фильтра нижних частот [14].

Рис. 9. Конструкция фильтра нижних частот с крышкой

На рисунке 10 сравниваются АЧХ фильтра с крышкой и без. С крышкой возвратные потери увеличиваются, это происходит из-за переотражения волн. Данная проблема решается с помощью поглотителя ЗИПСИЛ КЛ РПМ-01 ТУ 2541-004-24624998-2014, графики сравнения представлены на рисунке 11.

Рис. 10. Амплитудно-частотные характеристики измеренного фильтра нижних частот. Сплошная – без крышки, точки – с крышкой

Рис. 11. Амплитудно-частотные характеристики измеренного фильтра нижних частот. Сплошная – без крышки, точки – с крышкой, пунктир – с крышкой и поглотителем ЗИПСИЛ

Благодаря простоте изготовления и высоким частотно-селективным свойствам, фильтры такого типа весьма перспективны для применения в СВЧ-устройствах.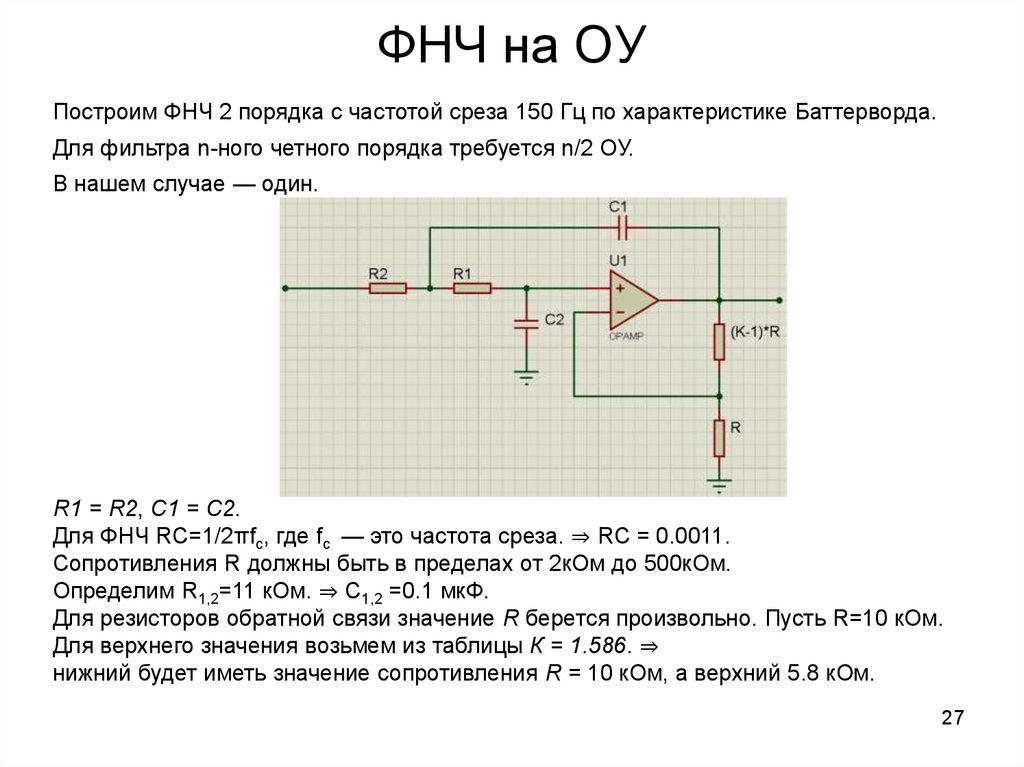 В качестве продолжения эксперимента по предложенной методике был рассчитан, изготовлен и измерен фильтр аналогичной конструкции, но оптимизированный для полосы пропускания 6-7 ГГц. Конструкция фильтра и его характеристики представлены на рисунке 12.

Рис.12. Фильтр нижних частот (6…7 ГГц)

Рис. 13. Амплитудно-частотные характеристики фильтра нижних частот (6-7 ГГц) с двумерной конструкцией. Сплошная – S₂₁, точки – S₁₁. Сверху фото образца фильтра

Заключение

Изготовленная конструкция на микрополосковых резонаторах обладает большой крутизной и высокими амплитудно-частотными характеристиками. Благодаря свернутой форме образуются дополнительные связи, с помощью которых существенно увеличивается крутизна склона АЧХ. Такой фильтр прост в изготовлении, а установка на плате существенно экономит место в приборе. При этом численный электродинамический расчет хорошо согласуется с экспериментом, что позволяет без кардинальных изменений проводить синтез устройств с заданными характеристиками.

В ходе работы было экспериментально исследовано влияние электромагнитного окружения (фрезерованный канал и заполнение его поглощающим материалом) на топологию фильтра.

Литература

1.     Morgan M. A. Reflectionless Filters. In: Artech House Microwave Library. Boston; L., 2017. 258 p.

2.     Hunter I. C. Theory and Design of Microwave Filters. IET Electromagnetic Waves Series. Cambridge: Cam­bridge Univ. Press, 2006. V. 48. 353 p.

3.     Li K., Zhao M., Fan Yo., Zhu Z., Cui W. With Parallel Open-Ended Stubusing Novel Double-Folded SCMRC Structurecompact Lowpass Filter with Wide Stop­band // Progress in Electromagn. Res. Lett. 2013. V. 36. P. 77–86.

4.     Hayati M., Shama F. A Compact Lowpass Filter with Ultra Wide Stopband Using Stepped Impedance Resonator // Radioengineering. 2017. V. 26. № 1. P. 269– 274.

5.     Kumarand D., De A. Compact Ultra Wide Band Filter Using Triangular Patch Resonators // Radioelectronics and Communs Syst. 2015. V. 58. № 4. P. 151–156.

6.     Hayati M., Asadbeigi H., Sheikhi A. Microstrip Lowpass Flter with High and Wide Rejection Band // Electron­ics Lett. 2012. V. 48. № 19. P. 1217–1219.

7.     Arfiya K., Pramod K., Kumaraswamy H., Jayaraj N. Design and Simulation of Printed micro strip Low pass Filter based on the Electromagnetic models 18GHz printed microstrip Lowpass Filter using x-models // International Journal of Research in Engineering and Technology. 2014. № 3. P. 312–318.

8.     Hong J., Liu Y., Wang B., Mei K. A Novel Differential Equation Model for a Microstrip Lowpass Filter // Microwave and Optical Technology Letters. 2002. V. 35. № 5. P. 368–370.

9.     Беляев Б. А., Ходенков С. А., Галеев Р. Г., Шабанов В. Ф. Фильтр нижних частот на двумерном микрополосковом электромагнитном кристалле // Доклады академии наук. 2019. Т. 485. № 1. С. 27–32.

10. Беляев Б.А., Сержантов А.М., Лексиков Ан. А., Бальва Я.Ф., Грушевский Е.О., Ходенков С.А. Высокоселективный полосковый фильтр нижних частот с уровнем заграждения более 100 dB в широкой полосе // Письма в ЖТФ. 2020. Т. 46. № 8. С. 10–13.

11. Abid A., Zhirun H. Sharp cut-off, Miniaturized Metamaterial Binomial Microstrip Low-pass Filter // Microwave and Optical Technology Letters. 2007. V/ 49. № 10. P. 2406–2409.

12. Неганов В.А., Клюев Д.С., Табаков Д.П. Устройства СВЧ и антенны Ч.1 // Под ред. В.А. Неганова. Изд. Стереотип. М.: ЛЕНАНД, 2016 – 608 с.

13. Вольман А.А., Муравцова А.Д. СВЧ цепи Анализ и автоматизированное проектирование // пер. с англ. Под ред. В.И. Вольмана – М.: Радио и связь, 1990. 288 с.

14. Гошин Г.Г. Антенны и фидеры. Сборник задач с формулами и решениями // Учебное пособие. – Томск, ТУСУР, 2012. – 236 с.

15. Belyaev B. A., Serzhantov A. M., Bal’va Y.F., Ty­urnev V. V., Leksikov A. A., Galeev R. G. Implementa­tions of Cross Couplings in Microwave Bandpass Fil­ters // Microwave and Optical Technol.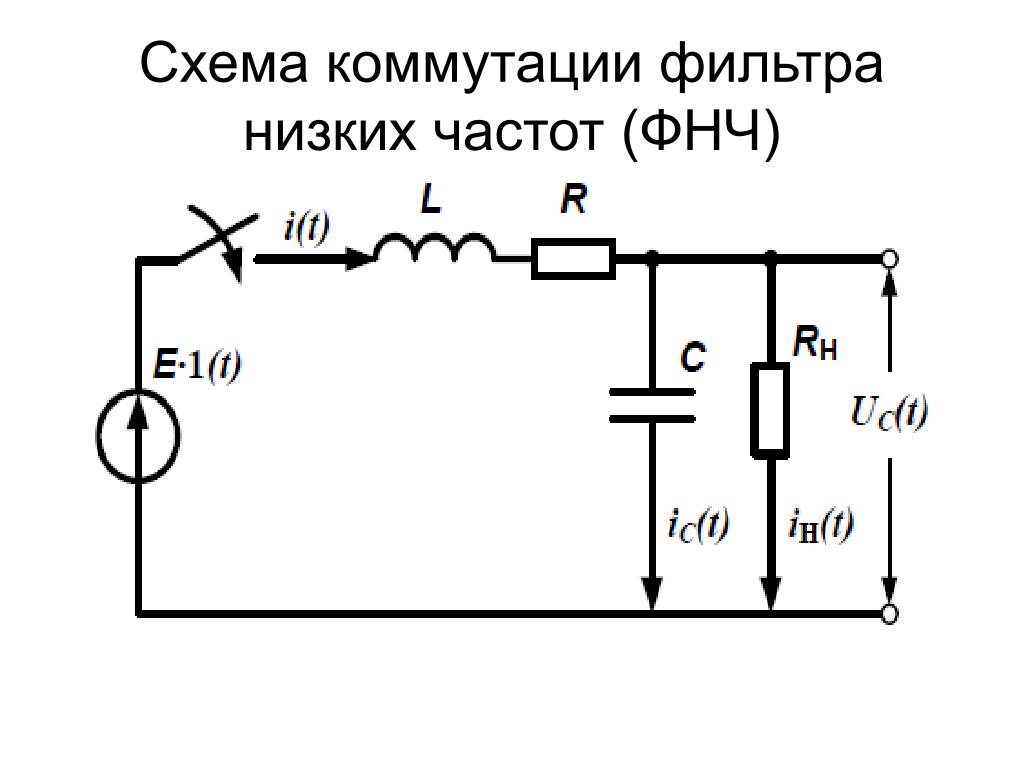 Lett. 2014. V. 56. № 9. P. 2021–2025.

Фильтр низких частот — frwiki.wiki

Изображение, к которому был применен фильтр нижних частот (результат справа)

Фильтр низких частот представляет собой фильтр , который проходит низкие частоты и ослабляет высокие частоты , то есть частоты выше частоты среза . Его также можно было бы назвать фильтром высоких частот. Фильтр нижних частот является инверсией фильтра верхних частот, и эти два фильтра вместе образуют полосовой фильтр .

Концепция фильтра нижних частот — это математическое преобразование, применяемое к данным (сигналу). Фильтр нижних частот можно реализовать в цифровом виде или с помощью электронных компонентов. Функция этого преобразования состоит в том, чтобы ослабить частоты выше его частоты среза , чтобы сохранить только низкие частоты. Частота среза фильтра — это частота, разделяющая два идеальных режима работы фильтра: прохождение или блокирование. жпротив{\ displaystyle f_ {c}}

Резюме

• 1 Идеальный фильтр
• 2 Аналоговый фильтр нижних частот
  • 2. 1 Фильтр нижних частот первого порядка
    • 2.1.1 Пассивная схема
    • 2.1.2 Активная цепь
  • 2.2 Фильтр нижних частот второго порядка
    • 2.2.1 Пассивная схема
    • 2.2.2 Активная цепь
  • 2.3 Фильтр высшего порядка
• 3 Цифровой фильтр нижних частот
• 4 См. Также
  • 4.1 Связанные статьи

Идеальный фильтр

Идеальный фильтр нижних частот имеет постоянное усиление в полосе пропускания и нулевое усиление в полосе среза. Переход между двумя состояниями происходит мгновенно. Математически это может быть достигнуто путем умножения сигнала на прямоугольное окно в частотной области или путем свертки с кардинальным синусом (sinc) во временной области. Этот тип фильтра на инженерном жаргоне называется «кирпичной стеной».

Конечно, идеальный фильтр вряд ли возможен, поскольку кардинальный синус — бесконечная функция. Таким образом, фильтр должен предсказывать будущее и иметь бесконечное знание прошлого, чтобы выполнить свертку и достичь желаемого эффекта. Этот фильтр можно очень точно аппроксимировать в цифровом виде, когда есть предварительно записанный сигнал (путем добавления нулей на обоих концах серии выборок) или для периодического сигнала.

В реальном времени цифровые фильтры могут аппроксимировать этот фильтр, вставляя преднамеренную задержку в сигнал, что позволяет «узнать будущее сигнала». Эта операция создает фазовый сдвиг между выходом и входом, и, естественно, чем дольше вставленная задержка, тем больше фильтр будет приближаться к идеальному фильтру.

Аналоговый фильтр нижних частот

Фильтр нижних частот может быть реализован аналогично электронным компонентам. Таким образом, этот вид фильтра применяется к непрерывным сигналам в реальном времени. Компоненты и конфигурация схемы фиксируют различные характеристики фильтра , такие как порядок, частота среза и его диаграмма Боде . Обычные аналоговые фильтры бывают первого или второго порядка. Существует несколько семейств аналоговых фильтров: Баттерворта , Чебышева , Бесселя , эллиптические и др. Реализация фильтров одного и того же семейства обычно выполняется с использованием одной и той же конфигурации схемы, и они имеют одинаковую форму передаточной функции , но меняются ее параметры, а следовательно, и значение компонентов электрической схемы.

Фильтр нижних частот первого порядка

Фильтр нижних частот первого порядка характеризуется частотой среза . Передаточная функция фильтра получается денормализацией нормализованного фильтра нижних частот путем замены на , что дает следующую передаточную функцию : жпротив{\ displaystyle f_ {c}}ωнет{\ displaystyle \ omega _ {n}}ω/ωпротив{\ displaystyle \ omega / \ omega _ {c}}

ЧАС(jω)знак равноvоvязнак равноK1+jωωпротив{\ displaystyle H (j \ omega) = {\ frac {v_ {o}} {v_ {i}}} = {\ frac {K} {1 + j {\ frac {\ omega} {\ omega _ {c }}}}}}

или же

vя{\ displaystyle v_ {i}} входной сигнал vо{\ displaystyle v_ {o}} выходной сигналωзнак равно2πж{\ displaystyle \ displaystyle \ omega = 2 \ pi f}ωпротивзнак равно2πжпротив{\ displaystyle \ displaystyle \ omega _ {c} = 2 \ pi f_ {c}}

Модуль и фаза передаточной функции равны:

|ЧАС(ω)|знак равно|vоvя|знак равноK1+(ωωпротив)2{\ displaystyle | H (\ omega) | = \ left | {\ frac {v_ {o}} {v_ {i}}} \ right | = {\ frac {K} {\ sqrt {1 + {\ big ( } {\ frac {\ omega} {\ omega _ {c}}} {\ big)} ^ {2}}}}}ϕ(ω)знак равноаргумент⁡ЧАС(jω)знак равно-аргумент⁡(1+jωωпротив)знак равно-арктан⁡(ωωпротив){\ displaystyle \ phi (\ omega) = \ arg H (j \ omega) = — \ arg \ left (1 + j {\ frac {\ omega} {\ omega _ {c}}} \ right) = — \ arctan \ left ({\ frac {\ omega} {\ omega _ {c}}} \ right)}

Есть несколько способов реализовать этот фильтр. Здесь представлены активная реализация и пассивная реализация. K — коэффициент усиления фильтра.

Пассивная схема

Самый простой способ получить этот фильтр физически — использовать RC-цепь . Как следует из названия, эта схема состоит из резистора и конденсаторного конденсатора . Эти два элемента размещены последовательно с источником сигнала. Выходной сигнал восстанавливается на выводах конденсатора. Несмотря на то, что сопротивление постоянно независимо от частоты, оно не одинаково для конденсатора; чем выше частота, тем меньше времени у конденсатора для заряда / разряда. Когда частота стремится к бесконечности, конденсатор ведет себя как короткое замыкание (шунт). Когда частота стремится к 0, это ведет себя как разомкнутая цепь. В каком-то смысле это переменный резистор, зависящий от частоты. Чтобы найти передаточную функцию этого фильтра, необходимо работать в области Лапласа, используя импедансы элементов. С помощью этой техники схема становится простым делителем напряжения , и мы получаем: р{\ displaystyle R}ПРОТИВ{\ displaystyle C}vя{\ displaystyle v_ {i}}vо{\ displaystyle v_ {o}}

ЧАС(jω)знак равноvоvязнак равно11+jрПРОТИВω{\ displaystyle H (j \ omega) = {\ frac {v_ {o}} {v_ {i}}} = {\ frac {1} {1 + jRC \ omega}}}

В этом уравнении — комплексное число (j такое, что j² = -1) и представляет собой пульсацию цепи или радиальную частоту, выраженную в рад / с. Поскольку частота среза RC-цепи равна: j{\ displaystyle j}ω{\ displaystyle \ omega}

Аналоговый фильтр нижних частот первого порядка на RC-цепи.

жпротивзнак равно12πрПРОТИВ{\ displaystyle f_ {c} = {\ frac {1} {2 \ pi RC}}} или же ωпротивзнак равно1рПРОТИВ{\ displaystyle \ omega _ {c} = {\ frac {1} {RC}}}

Здесь пульсация отсечки также является собственной пульсацией контура. Это также величина, обратная постоянной времени цепи (увеличенной на константу ). Таким образом, действительно получается типичная передаточная функция фильтра нижних частот первого порядка. ωпротив{\ displaystyle \ omega _ {c}}ωо{\ displaystyle \ omega _ {o}}τ{\ Displaystyle \ тау}2π{\ displaystyle 2 \ pi}

С помощью этой передаточной функции мы можем получить диаграммы Боде  :

• Прирост в децибелах  :

граммdB(ω)знак равно20⋅бревно⁡|ЧАС(ω)|знак равно-10⋅бревно⁡(1+(ωрПРОТИВ)2){\ Displaystyle G_ {дБ} (\ omega) = 20 \ cdot \ log | H (\ omega) | = -10 \ cdot \ log \ left (1 + {\ big (} \ omega RC) ^ {2} \ верно)}

• Фаза в радианах  :

ϕ(ω)знак равно-арктан⁡(ωрПРОТИВ){\ displaystyle \ phi (\ omega) = — \ arctan {\ big (} \ omega RC)}

Тогда мы можем выделить две идеальные ситуации:

Расположение Боде пассивного фильтра нижних частот первого порядка

• Когда у нас есть:ω≪ωпротив{\ displaystyle \ omega \ ll \ omega _ {c}}

граммdB≃0{\ Displaystyle G_ {дБ} \ simeq 0} а также ϕ≃0{\ displaystyle \ phi \ simeq 0}(фильтр проходит)

• Когда у нас есть:ω≫ωпротив{\ displaystyle \ omega \ gg \ omega _ {c}}

граммdB∼-20⋅бревно⁡(ωωпротив){\ Displaystyle G_ {дБ} \ sim -20 \ cdot \ log \ left ({\ frac {\ omega} {\ omega _ {c}}} \ right)} а также ϕ≃-90{\ displaystyle \ phi \ simeq -90}(затем сигнал фильтруется)

Обратите внимание, что для , у нас = -3 дБ. ωзнак равноωпротив{\ displaystyle \ omega = \ omega _ {c}}граммdB{\ displaystyle G_ {дБ}}

Активная схема

Также возможно реализовать фильтр нижних частот с активной схемой. Эта опция позволяет добавить усиление к выходному сигналу, то есть получить амплитуду более 0 дБ в полосе пропускания. Несколько конфигураций позволяют реализовать этот вид фильтра.

Активный фильтр нижних частот

В представленной здесь конфигурации частота среза определяется следующим образом:

жпротивзнак равно12πр2ПРОТИВ{\ displaystyle f_ {c} = {1 \ более 2 \ pi R_ {2} C}} или же ωпротивзнак равно1р2ПРОТИВ{\ displaystyle \ omega _ {\ mathrm {c}} = {\ frac {1} {R_ {2} C}}}

Используя свойства операционных усилителей и импедансы элементов, мы получаем следующую передаточную функцию:

ЧАС(jω)знак равноvоvязнак равно-р2р1⋅11+jр2ПРОТИВω{\ displaystyle H (j \ omega) = {\ frac {v_ {o}} {v_ {i}}} = {\ frac {-R_ {2}} {R_ {1}}} \ cdot {\ frac { 1} {1 + jR_ {2} C \ omega}}}

На низкой частоте конденсатор действует как разомкнутая цепь , что подтверждается тем фактом, что правый член предыдущего уравнения стремится к 1. Полученная таким образом упрощенная формула дает нам коэффициент усиления в полосе пропускания:

ЧАС(ω)ω≪ωпротивзнак равноvоvязнак равно-р2р1{\ displaystyle H (\ omega) _ {\ omega \ ll \ omega _ {c}} = {\ frac {v_ {o}} {v_ {i}}} = {\ frac {-R_ {2}} { R_ {1}}}}

На высокой частоте конденсатор действует как замкнутая цепь, и член справа стремится к нулю, что заставляет формулу стремиться к нулю.

ЧАС(ω)ω≫ωпротивзнак равноvоvя≃0{\ displaystyle H (\ omega) _ {\ omega \ gg \ omega _ {c}} = {\ frac {v_ {o}} {v_ {i}}} \ simeq 0}

С помощью передаточной функции можно продемонстрировать, что затухание в отклоненной полосе составляет 20 дБ / декаду или 6 дБ на октаву, как ожидается для фильтра первого порядка.

Часто можно увидеть схему усиления или ослабления, преобразованную в фильтр нижних частот путем добавления конденсатора C. Это уменьшает отклик высокочастотной схемы и помогает уменьшить колебания в усилителе. Например, аудиоусилитель может быть активным фильтром нижних частот с частотой среза порядка 100  кГц для уменьшения усиления на частотах, которые в противном случае будут колебаться.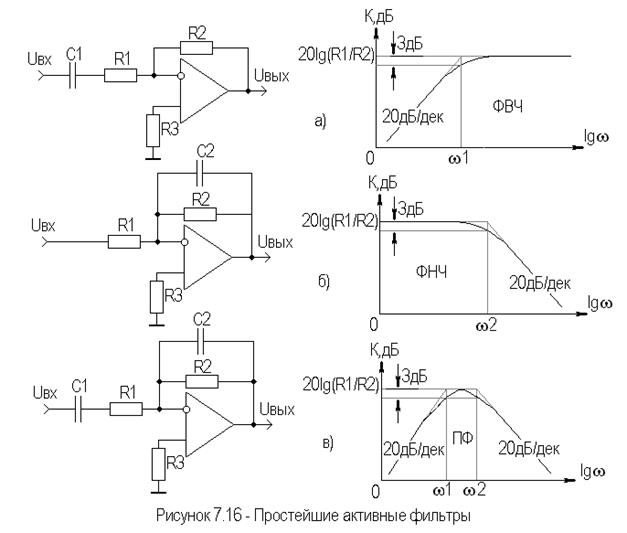 {2}}} \ right)}

Активная схема

Для создания активного фильтра второго порядка существует несколько типов фильтров. Наиболее популярны конструкции MFB и VCVS.

Фильтр высшего порядка

Фильтры более высокого порядка обычно состоят из фильтров первого и второго порядка в каскаде. Например, реализация фильтра 5-го порядка осуществляется путем размещения двух фильтров 2-го порядка и фильтра 1-го порядка. Можно было бы напрямую реализовать фильтр 5-го порядка, но сложность конструкции значительно возрастет. Также следует знать, что любой фильтр порядка больше 2 может быть разложен на продукт (каскад) фильтров порядка 1 и 2, благодаря свойствам полиномов (любой полином порядка больше 2 может быть разложен на произведение многочленов степени меньше или равной 2). Это объясняет, почему бесполезно напрямую разрабатывать фильтр 5-го порядка, когда мы можем получить точно такой же результат с каскадом из двух фильтров 2-го и 1-го порядка. Однако концепция фильтра более высокого порядка является ошибкой. Практика, которая существовала, в основном, на заре электроники, когда активные компоненты были относительно дорогими. Фильтр пятого порядка, разработанный как таковой, действительно требует только одного активного компонента, тогда как каскад из трех фильтров потребует трех.

Цифровой фильтр нижних частот

См. Цифровой фильтр .

Смотрите также

Статьи по Теме

• Режекторный фильтр
• Полосовой фильтр
• Фильтр высоких частот
• Фильтр (электронный)
• Пространственная фильтрация с помощью оптической , более конкретно к очистке лазера .

Фильтры
Типы фильтров	Фильтр низких частот  · High Pass Filter  · полосовой фильтр  · режекторный фильтр
линейные фильтры	Фильтр Бесселя  · Фильтр Баттерворта  · Фильтр Чебышева  · Фильтр эллиптический
цифровые фильтры	Конечная импульсная характеристика  · фильтр бесконечной импульсной характеристики

<img src=»https://fr. wikipedia.org/wiki/Special:CentralAutoLogin/start?type=1×1″ alt=»» title=»»>

RC Пассивный фильтр нижних частот — фильтры

Фильтры

Фильтр нижних частот пропускает частоты ниже определенной частоты среза. и ослабляет те, что выше этой частоты.

RC Фильтр нижних частот.

Первая схема, которую мы будем анализировать, представляет собой RC-фильтр нижних частот, как показано на рисунке. на рисунке выше. Прежде чем приступить к математическому анализу, мы можем сделать вывод о некоторых электрических свойствах путем визуального осмотра цепи.

Если приложенное напряжение имеет очень низкую частоту, реактивное сопротивление С будет очень высоким по сравнению с R и C можно считать открытая цепь. Поэтому на низких частотах входное напряжение В _в будут появляться практически без затухания на выходе. Отсюда и название фильтра нижних частот. По мере увеличения входной частоты реактивное сопротивление X _C становится меньше, в результате чего вход быть все более ослабленным.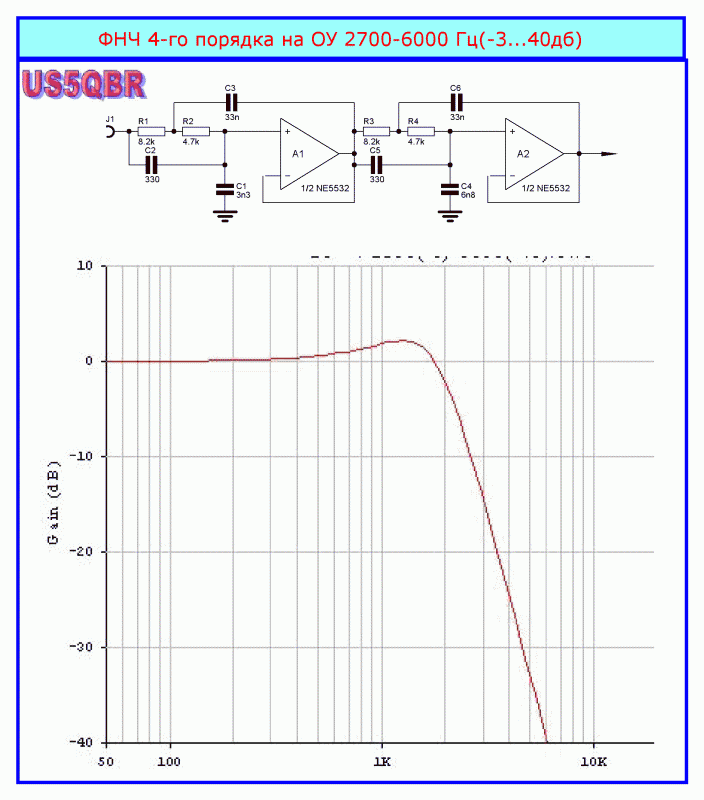 На бесконечно высокой частоте Х _С = 0 и, следовательно, выходное напряжение В _вых = 0.

Для математического анализа схемы мы будем использовать делитель напряжения отношения и написать

Мы, однако, решим отношение В _из к V _в , так как обычно мы хотим выразить усиления или потери фильтра. Это отношение называется передаточной функцией . Тогда в качестве передаточной функции имеем

где ω _C = 1/ RC – характеристическая частота .

Передаточная функция может быть выражена в полярной форме

Частотная характеристика

Наиболее полезное средство отображения частотных характеристик фильтра. заключается в построении величины передаточной функции (амплитудной характеристики) от частоты на одну кривую и фазовую характеристику на отдельную кривой, но с той же осью частот.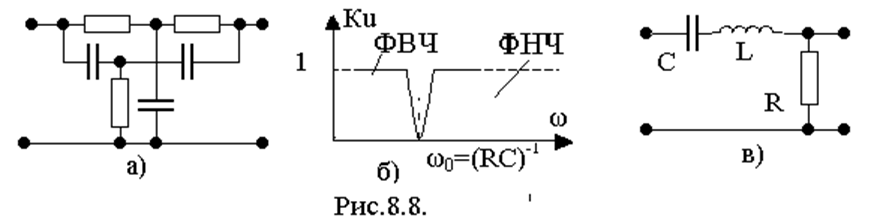 Амплитудная характеристика, которая может изменяться в широких пределах, удобно изображать в децибелах. Кривые с этим типом отображения известны как Графики Боде и находят широкое применение при анализе цепей переменного тока.

Амплитудная характеристика

Сначала рассмотрим амплитудную характеристику (спектр), соответствующую уравнение выше. Это абсолютное значение (величина) передаточной функции или

В децибелах это становится

Давайте рассмотрим приведенное выше уравнение для очень низких и для очень высоких частот. Для низких частот имеем

Таким образом, низкочастотное поведение практически не зависит от частоты и может быть представлен горизонтальной прямой линией на уровне 0 дБ, как показано на рисунке ниже. Реальная амплитудная характеристика, заданная передаточной функцией, имеет вид асимптотик этой прямой при малых ω .

Ломаная аппроксимация и фактическая характеристика амплитудного спектра фильтра RC.

Для другой крайности имеем

Это форма Г _дБ = -20 х , где x = log ₁₀ ( ω / ω _C ). Определенная таким образом прямая линия является высокочастотной асимптотой фактического характеристика. Наклон асимптоты равен dG _дБ / dx = -20; то есть, когда x увеличивается на одну единицу, G _дБ уменьшается на 20 дБ. Но

и так ω / ω _С должно увеличиться в множитель 10 или один десятичный , чтобы увеличить x на одну единицу. Следовательно, наклон высокочастотной асимптоты составляет -20 дБ за декаду. Некоторые люди предпочитают использовать октаву (отношение частот 2:1). соответствующий наклон составляет -6 дБ на октаву. Две прямолинейные асимптоты пересекаются в точке ω / ω _C = 1, тогда амплитудная характеристика имеет нулевое значение. показаны две асимптоты пунктиром на рисунке выше. Их точка пересечения, ω = ω _C , помимо того, что называется характерная частота цепи, также называемая точкой разрыва , или частота среза . Вместе две асимптоты образуют ломаную линию. приближение к реальной характеристике. В зависимости от желаемой точности ни одна из линий не может быть достаточно хорошим приближением к фактическому характеристика в окрестности ω = ω _C . Можно показать, что максимальная ошибка возникает при ω / ω _C = 1 и составляет примерно 3 дБ. Более того, в октаве от этой точки (при ω / ω _С = 0,5 и ω / ω _С = 2) ошибка составляет примерно 1 дБ. Отсюда легко сделать набросок фактического амплитудная характеристика с приемлемой точностью. Фактическая характеристика показано сплошной линией на рисунке выше. Низкочастотный характеристика цепи хорошо видна на этом рисунке.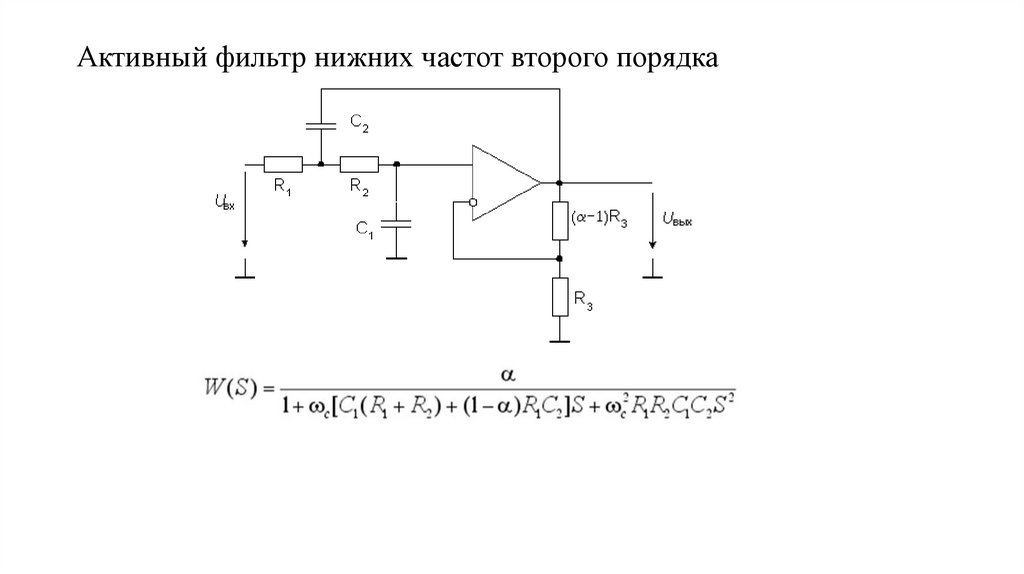

Фазовая характеристика

Рассмотрим теперь угол передаточной функции фильтра (иногда его называют фазовым спектром), который

Фазовый угол начинается с нуля для ω = 0 и приближается к -π/2. радианы в целом ω . Фазовая характеристика может быть аппроксимирована достаточно хорошо тремя прямолинейными отрезками, как показано на рисунке внизу: низкочастотная аппроксимация при 0 радианах, высокочастотная приближение при -π/2 радианах и приближение промежуточной частоты которая касается кривой на уровне -π/4 радиан. Можно показать, что средний сегмент пересекает низкочастотное приближение при ω / ω _C = 1/4,81 и пересекает высокочастотное приближение при ω / ω _C = 4,81. Фактическая характеристика показана сплошной линией на рисунке.

Ломаная аппроксимация и фактическая характеристика фазового спектра фильтра RC.

Фильтр нижних частот — MATLAB & Simulink

Фильтр нижних частот — это фильтр, пропускающий сигналы ниже частоты среза (известный как полоса пропускания) и ослабляющий сигналы выше частоты среза (известный как полоса задерживания).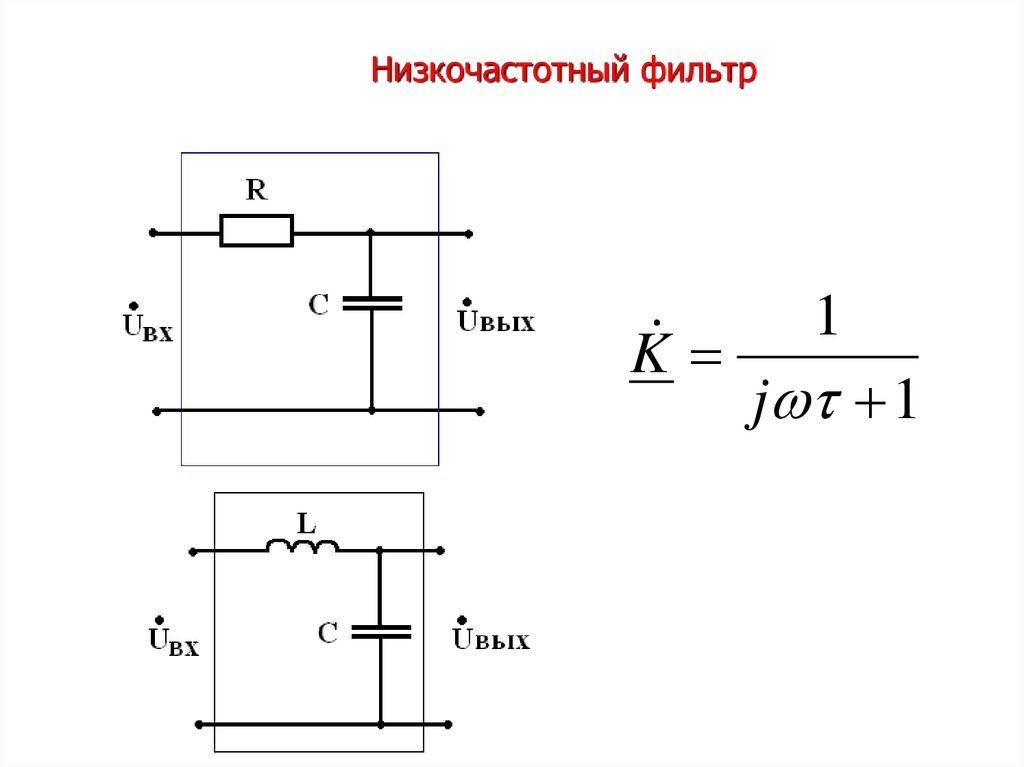

Фильтры нижних частот, особенно фильтры скользящего среднего или фильтры Савицкого-Голея, часто используются для очистки сигналов, удаления шума, создания эффекта сглаживания, выполнения усреднения данных и разработки дециматоров и интерполяторов. Фильтры нижних частот производят медленные изменения выходных значений, чтобы было легче увидеть тенденции и повысить общее отношение сигнал/шум с минимальным ухудшением сигнала.

Сглаживание сигналов с использованием фильтра Савицкого-Голея и фильтра скользящего среднего.

Вы можете использовать MATLAB ^® для проектирования фильтров на основе конечной импульсной характеристики (FIR) и бесконечной импульсной характеристики (IIR), двух распространенных методов фильтрации нижних частот.

КИХ-фильтры очень привлекательны, поскольку они по своей природе стабильны. Они могут иметь линейную фазу, которая вносит задержку в отфильтрованный сигнал при сохранении формы сигнала. Тем не менее, эти фильтры могут иметь длительные переходные характеристики и могут оказаться дорогостоящими в вычислительном отношении в некоторых приложениях.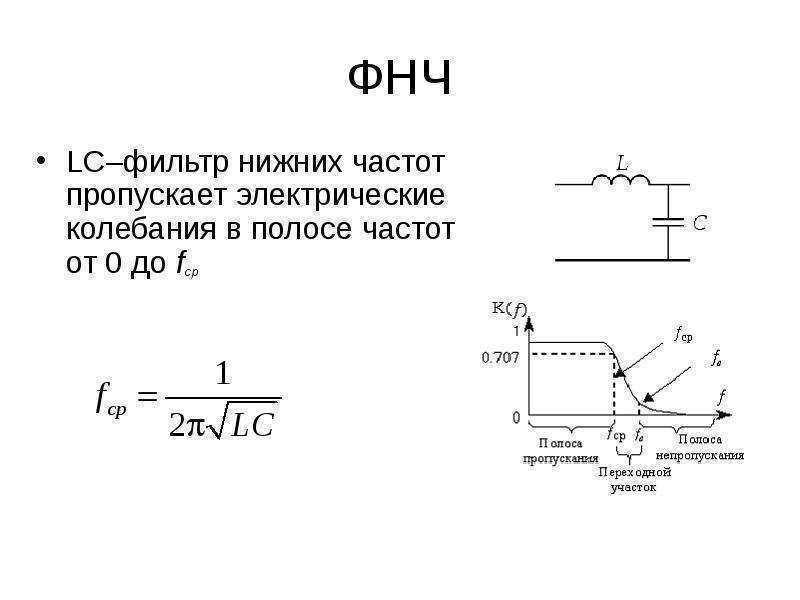 КИХ-фильтры полезны в аудио, биомедицинских, радиолокационных и других приложениях, где форма сигнала предоставляет полезную информацию. Общие методы проектирования низкочастотных КИХ-фильтров включают окно Кайзера, метод наименьших квадратов и аппаратную рябь.

Технические характеристики проекта и отклик низкочастотного КИХ-фильтра Кайзера в MATLAB.

БИХ-фильтры полезны, когда вычислительные ресурсы ограничены. Однако стабильные причинно-следственные БИХ-фильтры не имеют идеально линейной фазы.   БИХ-фильтры обычно используются для выравнивания звука, обработки сигналов биомедицинских датчиков, интеллектуальных датчиков IoT/IIoT и высокоскоростных телекоммуникационных/радиочастотных приложений. Методы проектирования фильтров на основе БИХ включают фильтры Баттерворта, Чебышева (тип I и тип II) и эллиптические.

Технические характеристики конструкции и характеристика фильтра нижних частот Чебышева типа I IIR в MATLAB.

Функция lowpass в Signal Processing Toolbox™ особенно полезна для быстрой фильтрации сигналов.