Что такое делитель напряжения. Как рассчитать делитель напряжения. Для чего используется делитель напряжения в электронных схемах. Какие бывают типы делителей напряжения. Как работает резистивный делитель напряжения.
Что такое делитель напряжения и как он работает
Делитель напряжения — это простая электрическая цепь, состоящая из двух или более последовательно соединенных резисторов, которая позволяет получить часть входного напряжения на выходе. Принцип работы делителя напряжения основан на том, что при последовательном соединении резисторов напряжение распределяется между ними пропорционально их сопротивлениям.
Базовая схема делителя напряжения включает два резистора R1 и R2, соединенных последовательно:
- На вход подается напряжение Vin
- Выходное напряжение Vout снимается с резистора R2
- Величина выходного напряжения зависит от соотношения сопротивлений R1 и R2
Формула для расчета выходного напряжения делителя:
Vout = Vin * R2 / (R1 + R2)
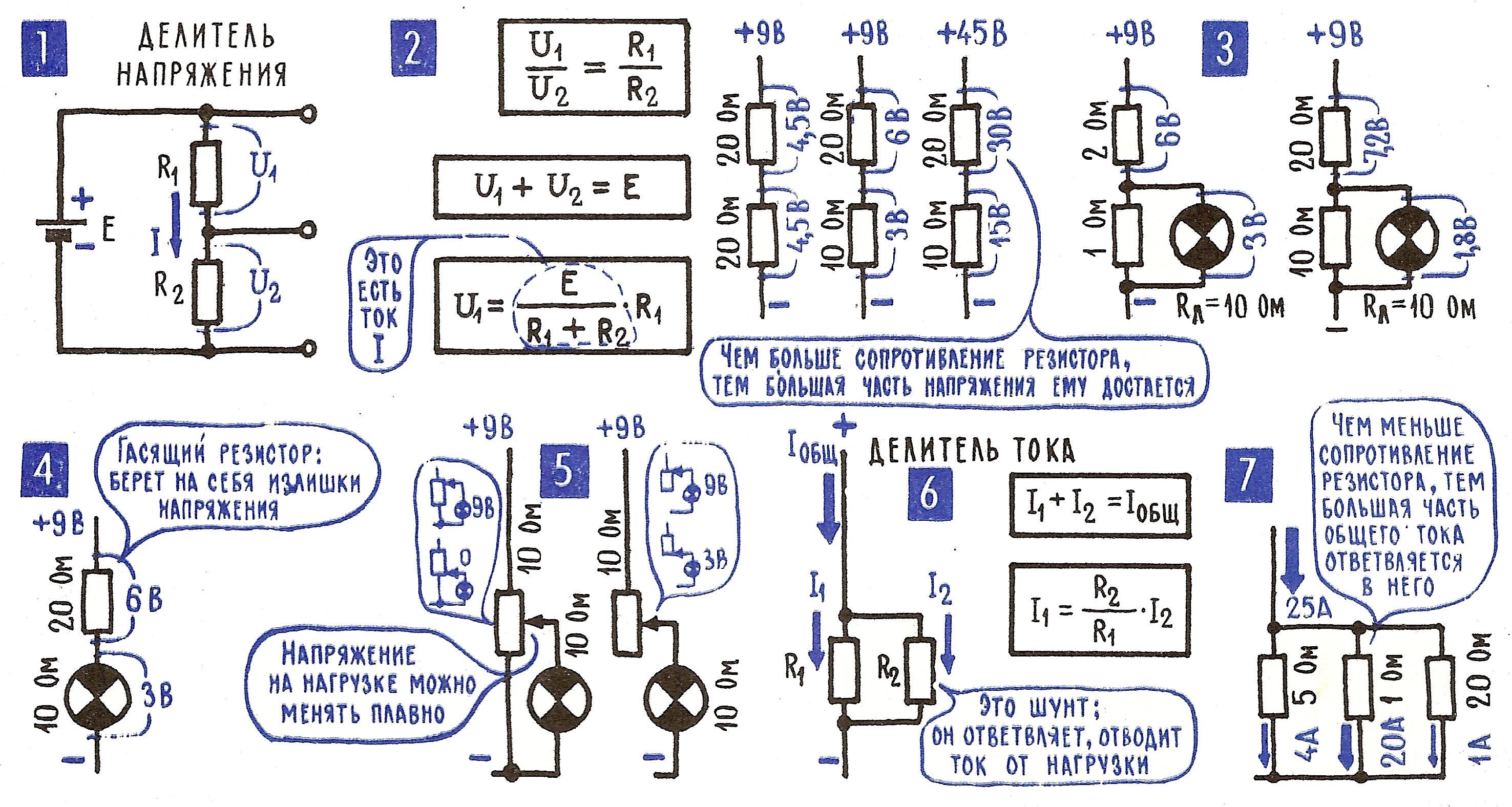
Таким образом, изменяя номиналы резисторов, можно получить требуемую часть входного напряжения на выходе делителя.
Основные формулы для расчета делителя напряжения
Для расчета делителя напряжения используются следующие основные формулы:
- Выходное напряжение: Vout = Vin * R2 / (R1 + R2)
- Ток через делитель: I = Vin / (R1 + R2)
- Мощность, рассеиваемая на резисторах: P1 = I^2 * R1 P2 = I^2 * R2
- Входное сопротивление делителя: Rin = R1 + R2
- Выходное сопротивление делителя: Rout = R1 * R2 / (R1 + R2)
Используя эти формулы, можно рассчитать все параметры делителя напряжения для конкретной схемы.
Типы делителей напряжения
Существует несколько основных типов делителей напряжения:
1. Резистивный делитель напряжения
Простейший и наиболее распространенный тип делителя. Состоит из двух или более резисторов, соединенных последовательно. Применяется для получения постоянного опорного напряжения.
2. Емкостный делитель напряжения
Использует последовательно соединенные конденсаторы для деления переменного напряжения. Применяется в высоковольтных цепях для снижения напряжения.

3. Индуктивный делитель напряжения
Состоит из катушек индуктивности, соединенных последовательно. Используется для деления переменного напряжения в силовых цепях.
4. Трансформаторный делитель напряжения
Использует трансформатор с отводами от вторичной обмотки для получения нескольких уровней напряжения. Применяется в источниках питания.
Применение делителей напряжения в электронике
Делители напряжения широко используются в электронных схемах для различных целей:
- Получение опорного напряжения для питания микросхем и других устройств
- Смещение рабочей точки транзисторов и других активных элементов
- Преобразование уровней сигналов
- Измерение напряжения в высоковольтных цепях
- Формирование шкалы аналоговых измерительных приборов
- Создание многоуровневых источников питания
- Регулировка громкости в аудиотехнике
Благодаря простоте и универсальности, делители напряжения являются одним из базовых элементов при проектировании электронных устройств.
Расчет резистивного делителя напряжения
Рассмотрим пример расчета простого резистивного делителя напряжения:

Дано: Входное напряжение Vin = 12 В Требуемое выходное напряжение Vout = 5 В Ток нагрузки Iн = 10 мА
Необходимо рассчитать номиналы резисторов R1 и R2.
Решение:
- Определим соотношение резисторов из формулы делителя: R2 / (R1 + R2) = Vout / Vin = 5 / 12 = 0.417
- Выберем R2 = 1 кОм. Тогда R1 можно найти: R1 = R2 * (Vin / Vout — 1) = 1000 * (12 / 5 — 1) = 1400 Ом
- Проверим ток через делитель: I = Vin / (R1 + R2) = 12 / (1400 + 1000) = 5 мА
- Этот ток должен быть больше тока нагрузки в 5-10 раз. В нашем случае 5 мА > 10 мА, поэтому уменьшим сопротивления: R1 = 470 Ом, R2 = 330 Ом
- Проверим выходное напряжение: Vout = 12 * 330 / (470 + 330) = 5.025 В
Таким образом, для получения напряжения 5 В из 12 В при токе нагрузки 10 мА подойдет делитель с резисторами R1 = 470 Ом и R2 = 330 Ом.
Преимущества и недостатки делителей напряжения
Делители напряжения обладают рядом преимуществ:
- Простота конструкции
- Низкая стоимость
- Отсутствие активных элементов
- Высокая надежность
- Линейность характеристик
Однако у делителей напряжения есть и недостатки:

- Низкий КПД из-за постоянного тока через резисторы
- Зависимость выходного напряжения от тока нагрузки
- Ограниченная нагрузочная способность
- Возможность самовозбуждения при емкостной нагрузке
Поэтому при проектировании электронных устройств необходимо учитывать особенности делителей напряжения и при необходимости применять дополнительные схемы стабилизации.
Практические рекомендации по применению делителей напряжения
При использовании делителей напряжения в электронных схемах следует учитывать следующие рекомендации:
- Ток через делитель должен быть в 5-10 раз больше тока нагрузки для обеспечения стабильности выходного напряжения.
- Для уменьшения влияния температуры используйте резисторы с малым температурным коэффициентом сопротивления.
- При работе с высокими напряжениями учитывайте максимально допустимое напряжение на резисторах.
- Для повышения точности используйте прецизионные резисторы с малым допуском.
- При емкостной нагрузке добавляйте шунтирующий конденсатор параллельно нижнему резистору для предотвращения самовозбуждения.
- Для регулируемых делителей используйте переменные резисторы или потенциометры.
- При необходимости добавляйте буферный усилитель на выходе делителя для увеличения нагрузочной способности.
Соблюдение этих рекомендаций позволит создавать надежные и эффективные схемы на основе делителей напряжения.
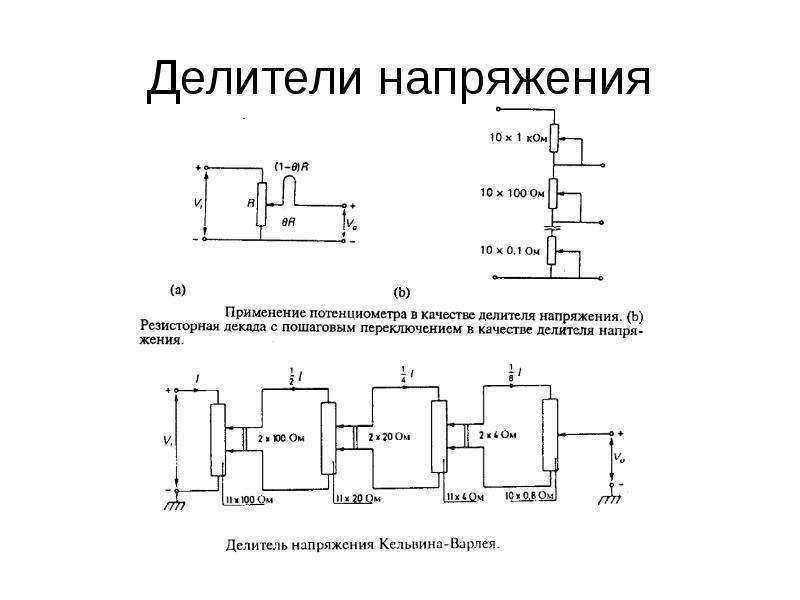
Делитель напряжения | Расчет делителя напряжения
Делитель напряжения – это это цепь, состоящая из двух и более пассивных радиоэлементов, которые соединены последовательно.
Делитель напряжения на резисторах
Давайте разберем самый простой делитель напряжения, состоящий из двух резисторов. Эти два резистора соединим последовательно и подадим на них напряжение. Напряжение может быть как постоянное, так и переменное.
Подавая напряжение на эту цепь, состоящую из двух резисторов, у нас получается, что цепь становится замкнутой, и в цепи начинает течь электрический ток с какой-то определенной силой тока, которая зависит от номиналов резисторов.
Итак, мы знаем, что при последовательном соединении сила тока в цепи одинакова. То есть какая сила тока протекает через резистор R1, такая же сила тока течет и через резистор R2. Как же вычислить эту силу тока? Оказывается, достаточно просто, используя закон Ома: I=U/R.
Так как наши резисторы соединены последовательно, то и их общее сопротивление будет выражаться формулой
То есть в нашем случае мы можем записать, что
Как найти напряжение, которое падает на резисторе R2?
Так как ток для обоих резисторов общий, то согласно закону Ома
Подставляем вместо I формулу
и получаем в итоге
Для другого резистора ситуация аналогичная.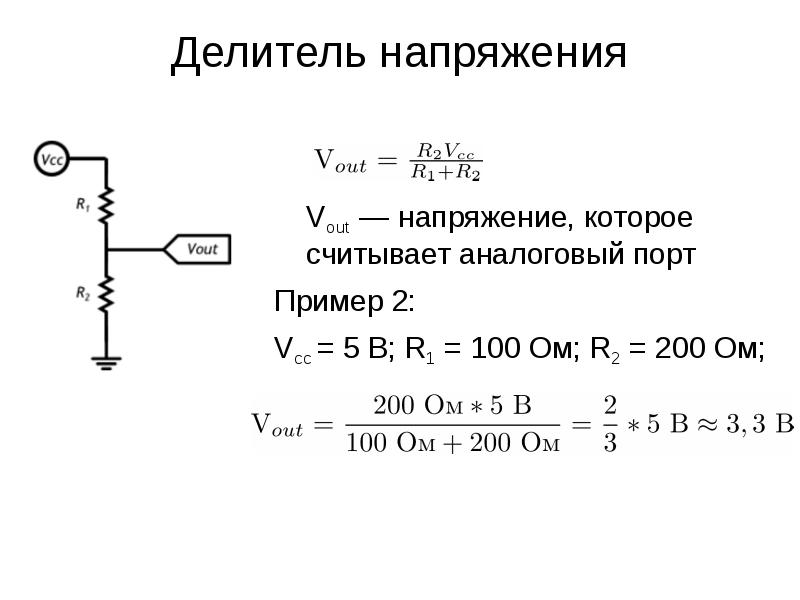 На нем падает напряжение
На нем падает напряжение
Для него формула запишется
Давайте докажем, что сумма падений напряжений на резисторах равняется напряжению питания, то есть нам надо доказать, что U=UR1 +UR2 . Подставляем значения и смотрим.
что и требовалось доказать.
Эта формула также работает и для большого количества резисторов.
На схеме выше мы видим резисторы, которые соединены последовательно. Чему будет равняться Uобщ ? Так как резисторы соединены последовательно, следовательно, на каждом резисторе падает какое-то напряжение. Сумма падений напряжения на всех резисторах будет равняться Uобщ . В нашем случае формула запишется как
Как работает делитель напряжения на практике
Итак у нас имеются вот такие два резистора и наш любимый мультиметр:
Замеряем сопротивление маленького резистора, R1=109,7 Ом.
Замеряем сопротивление большого резистора R2=52,8 Ом.
Выставляем на блоке питания ровно 10 Вольт. Замер напряжения производим с помощью мультиметра.
Цепляемся блоком питания за эти два резистора, запаянные последовательно. Напомню, что на блоке ровно 10 Вольт. Показания амперметра на блоке питания тоже немного неточны. Силу тока мы будем замерять в дальнейшем также с помощью мультиметра.
Замеряем падение напряжения на большом резисторе, который обладает номиналом в 52,8 Ом. Мультиметр намерял 3,21 Вольта.
Замеряем напряжение на маленьком резисторе номиналом в 109,7 Ом. На нем падает напряжение 6,77 Вольт.
Ну что, с математикой, думаю, у всех в порядке. Складываем эти два значения напряжения. 3,21+6,77 = 9,98 Вольт. А куда делись еще 0,02 Вольта? Спишем на погрешность щупов и средств измерений. Вот наглядный пример того, что мы смогли разделить напряжение на два разных напряжения. Мы еще раз убедились, что сумма падений напряжений на каждом резистора равняется напряжению питания, которое подается на эту цепь.
Сила тока в цепи при последовательном соединении резисторов
Давайте убедимся, что сила тока при последовательном соединении резисторов везде одинакова. Как измерить силу тока постоянного напряжения, я писал здесь. Как видим, мультиметр показал значение 0,04 А или 40 мА в начале цепи, в середине цепи и даже в конце цепи. Где бы мы не обрывали нашу цепь, везде одно и то же значение силы тока.
Переменный резистор в роли делителя напряжения
Для того, чтобы плавно регулировать выходное напряжение, у нас есть переменный резистор в роли делителя напряжения. Его еще также называют
Его обозначение на схеме выглядит вот так:
Принцип работы такой: между двумя крайними контактами постоянное сопротивление. Сопротивление относительно среднего контакта по отношению к крайним может меняться в зависимости от того, куда мы будем крутить крутилку этого переменного резистора. Этот резистор рассчитан на мощность 1Вт и имеет полное сопротивление 330 Ом. Давайте посмотрим, как он будет делить напряжение.
Этот резистор рассчитан на мощность 1Вт и имеет полное сопротивление 330 Ом. Давайте посмотрим, как он будет делить напряжение.
Так как мощность небольшая, всего 1 Вт, то мы не будем нагружать его большим напряжением. Мощность, выделяемая на каком-либо резисторе рассчитывается по формуле P=I2R. Значит, этот переменный резистор может делить только маленькое напряжение при маленьком сопротивлении нагрузки и наоборот. Главное, чтобы значение мощности этого резистора не вышло за грани. Поэтому я буду делить напряжение в 1 Вольт.
Для этого выставляем на блоке напряжение в 1 Вольт и цепляемся к нашему резистору по двум крайним контактам.
Крутим крутилку в каком-нибудь произвольном направлении и останавливаем ее. Замеряем напряжение между левым и средним контактом и получаем 0,34 Вольта.
Замеряем напряжение между средним и правым контактом и получаем 0,64 Вольта
Суммируем напряжение и получаем 0,34+0,64=0,98 Вольт. 0,02 Вольта опять где-то затерялись. Скорее всего на щупах, так как они тоже обладают сопротивлением. Как вы видите, простой переменный резистор мы можем использовать в роли простейшего делителя напряжения.
0,02 Вольта опять где-то затерялись. Скорее всего на щупах, так как они тоже обладают сопротивлением. Как вы видите, простой переменный резистор мы можем использовать в роли простейшего делителя напряжения.
Похожие статьи по теме “делитель напряжения”
Делитель тока
Что такое резистор
Что такое напряжение
Блок питания
Делитель тока
В этой статье расскажем о делители тока, где он применяется и примеры решения задач.
Представьте, что течёт река, и вдруг ширина её русла резко уменьшается, через некоторое расстояние ширина русла снова увеличивается. Что же происходит в том месте, где русло узкое? Скорость потока воды резко возрастает, вода пытается расширить русло реки, происходит разрушение берегов и углубление русла. Для того, чтобы скорость потока упала, достаточно прорыть дополнительный параллельный канал, по которому пустить часть потока. При этом, этот искусственный канал можно использовать в своих целях, например крутить водяное колесо (по современному — гидроэлектростанцию). Как правило, сначала делают «колесо», а потом перекрывают основное русло реки. Другими словами — поток воды делят на два потока, которые потом всё равно объединяются, но при этом один из потоков используют в своих определённых целях. В частности, на гидроэлектростанциях всегда имеется два потока — один используется для вращения турбин электростанции, а другой в зависимости от полноводности реки — «сброс», или дополнительный канал отвода воды — водосливную плотину, предназначенную для регулирования уровня воды перед плотиной ГЭС.
Как правило, сначала делают «колесо», а потом перекрывают основное русло реки. Другими словами — поток воды делят на два потока, которые потом всё равно объединяются, но при этом один из потоков используют в своих определённых целях. В частности, на гидроэлектростанциях всегда имеется два потока — один используется для вращения турбин электростанции, а другой в зависимости от полноводности реки — «сброс», или дополнительный канал отвода воды — водосливную плотину, предназначенную для регулирования уровня воды перед плотиной ГЭС.
Делитель тока на резисторах предназначен для того, чтобы, не изменяя общего тока протекающего через электрическую цепь, часть его направить в другое плечо делителя, а после выполнения определённой функции вернуть эту часть обратно.
Где применяется делитель тока? Делитель тока применяется в измерительных приборах, когда необходимо измерить большой ток (единицы, или сотни Ампер) прибором, рассчитанным на маленький ток (миллиамперы или даже микроамперы). В этом случае, внутреннее сопротивление измерительного прибора выступает в качестве одного из резисторов, а второй резистор в таком случае называют «шунтом», так как он шунтирует проходящий ток (основная часть тока бежит через него). Шунт в схеме измерения имеет сопротивление, которое намного меньше внутреннего сопротивления измерительного прибора. Кроме того, делитель тока применяется в различных схемах автоматического регулирования, использующих в качестве контролируемого параметра — ток, проходящий через электрическую цепь. Делитель тока может применяться в различных каскадах передачи, или усиления тока, когда один пассивный, или усилительный элемент по своим электрическим параметрам не способен обеспечить прохождение через него большого тока. В этом случае их подключают параллельно, разделяя ток на равные доли (пополам). Наглядным примером использования делителя тока является его применение в цепи автоматического регулирования и измерения в Универсальном зарядном устройстве, или в цепи контроля схемы защиты от перегрузки по току и удвоения мощности выходных транзисторов в Универсальном блоке стабилизированного питания.
В этом случае, внутреннее сопротивление измерительного прибора выступает в качестве одного из резисторов, а второй резистор в таком случае называют «шунтом», так как он шунтирует проходящий ток (основная часть тока бежит через него). Шунт в схеме измерения имеет сопротивление, которое намного меньше внутреннего сопротивления измерительного прибора. Кроме того, делитель тока применяется в различных схемах автоматического регулирования, использующих в качестве контролируемого параметра — ток, проходящий через электрическую цепь. Делитель тока может применяться в различных каскадах передачи, или усиления тока, когда один пассивный, или усилительный элемент по своим электрическим параметрам не способен обеспечить прохождение через него большого тока. В этом случае их подключают параллельно, разделяя ток на равные доли (пополам). Наглядным примером использования делителя тока является его применение в цепи автоматического регулирования и измерения в Универсальном зарядном устройстве, или в цепи контроля схемы защиты от перегрузки по току и удвоения мощности выходных транзисторов в Универсальном блоке стабилизированного питания.
Изобразим цепь делителя тока:
На рисунке видно, что общий входящий ток делится на два, и проходя цепь, снова объединяется в один.
Расчёт делителя тока на резисторах основывается на законе Ома, правиле сложения токов (законе Кирхгофа) и формуле параллельного соединения резисторов:
(14)
(15)
(16)
Выведем закон Ома для этой цепи. Его можно записать в следующем виде:
(17)
Преобразовывая указанные формулы так, как нам удобно, мы можем определить:
1. Определить ток I1 и I2 в плечах резисторов R1, R2 по известным значениям общего тока Iобщ и сопротивлений резисторов R1, R2 :
(18)
Делитель напряжения
Делитель напряжения применяют с целью получения части напряжения, для отдельных компонентов схемы, используя всего один источник питания.
Принципиальная схема делителя напряжения до элементарного проста и состоит всего из двух резисторов.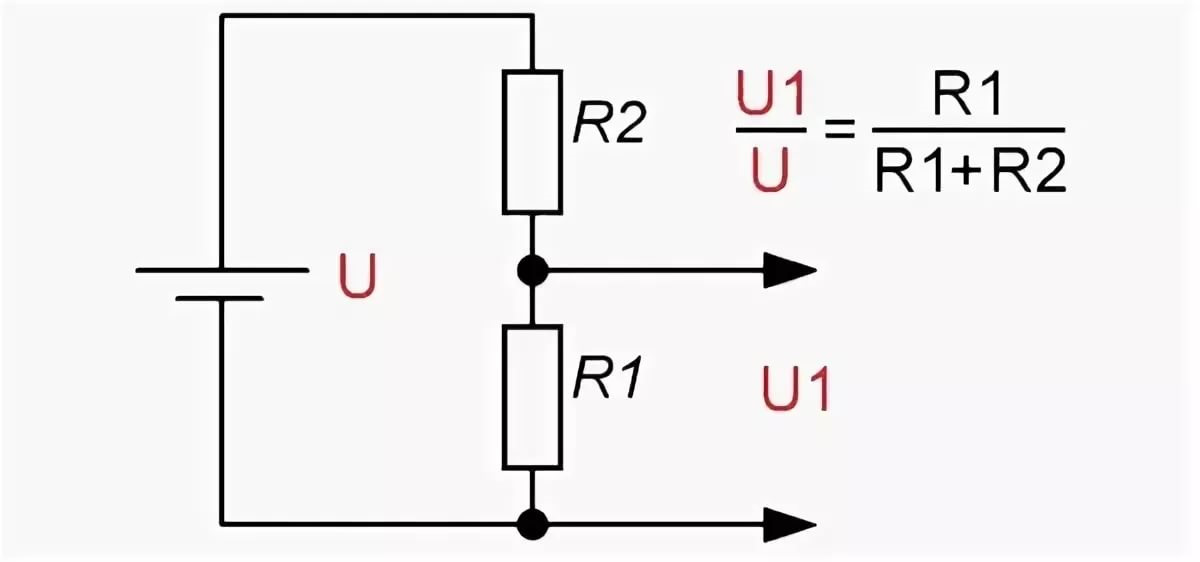 Главным в ее сборке остается правильный расчет сопротивления резисторов, необходимый для получения конкретного напряжения, и мощности, проходящей через них.
Главным в ее сборке остается правильный расчет сопротивления резисторов, необходимый для получения конкретного напряжения, и мощности, проходящей через них.
К примеру, для делителя напряжения возьмем сопротивлением исходя из расчетов:
Расчет резисторов для делителя напряжения происходит с конца схемы, а именно имеем изначальные данные: Нагрузка устройства (части компонентов на схеме), для которого рассчитываем делитель напряжения (I) – 20 mA; необходимо получить ток (Uout) – 5 v.
R2 = Uout / I = 5 v / 0.02A = 250 Om;
Зная сопротивление резистора R2, можем найти сопротивление резистора R1:
R1 = Uin / I – R2 = 12 v / 0.02A – 250 Om = 350 Om;
Расчет делителя напряжения окончен, но не все на практике так хорошо, как в теории. Так как нагрузка на выходе делителя напряжения имеет свое сопротивление, расчет необходимо производить с поправкой на это.
Помним, что нагрузка у нас составляет 20 mA, исходя из этого, по закону Ома, рассчитываем сопротивление нагрузки:
Rнагр = U / I = 5 v / 0.02 A = 250 Om;
Как видно, данный расчет мы уже производили выше для резистора R2 делителя напряжения.
В данном случае нагрузка служит параллельным сопротивлением резистору R2, и все расчеты следует поправить, иначе мы потеряем почти 2v:
Rобщ(Rнагр и R2) = Rнагр * R2 / (Rнагр + R2) = 250 * 250 / 250 + 250 = 125 Om;
Uout = Uin ( Rобщ / (R1 + Rобщ ) ) = 12 v ( 125 Om / ( 350 Om + 125 Om) ) = 3,16 v;
Исходя из этого, сопротивление резистора R1 необходимо рассчитывать по формуле:
R1 = Uin / Uout * Rобщ – Rобщ = 12 v / 5 v * 125 Om – 125 Om = 175 Om;
Делаем проверку:
Uout = Uin ( Rобщ / (R1 + Rобщ ) ) = 12 v ( 125 Om / ( 175 Om + 125 Om) ) = 5 v;
Расчет резисторов необходимых для нашего делителя напряжения закончен, осталось выяснить тип резистора, способный выдержать нагрузку. Рассчитываем мощность, проходящую через резистор делителя напряжения:
Рассчитываем мощность, проходящую через резистор делителя напряжения:
P = Uin2 / R1 = 12 v * 12 v / 175 Om ≈ 0,823 Watt;
Делаем вывод, что нам подойдут резисторы, например МЛТ-1 – мощностью не менее 1 Watt.
Применять такого типа делители напряжения можно, только если подключаемая нагрузка потребляет от долей до нескольких десятков миллиампер тока. Данный делитель напряжения никак нельзя использовать для питания мощных приборов, таких как ламп, двигателей и т.д.
Также в качестве эксперимента можно произвести масштабируемость сопротивлений делителя напряжения. Но помните, что чем меньше сопротивление в резисторах делителя напряжения, тем больше на них нагрузка и больше расход энергии.
Делители напряжения удачно подходят для преобразования сигнала с датчиков на основе резисторов. Такие резисторы как фоторезисторы, терморезисторы, тензорезисторы и т.д. способны изменять свое сопротивление в ходе воздействия на них окружающей среды. Подключение такого сенсора к выходу делителя напряжения или вместо одного из резисторов R1 и R2 и вольтметра к точке Uout можно снимать показания.
Подключение такого сенсора к выходу делителя напряжения или вместо одного из резисторов R1 и R2 и вольтметра к точке Uout можно снимать показания.
, примеры и его применение
В электронике правило делителя напряжения — это простая и наиболее важная электронная схема, которая используется для преобразования большого напряжения в малое. Используя только напряжение i / p и два последовательных резистора, мы можем получить напряжение o / p. Здесь выходное напряжение является частью напряжения i / p. Лучший пример делителя напряжения — два последовательно соединенных резистора. Когда напряжение i / p приложено к паре резисторов, напряжение o / p появится из соединения между ними.Как правило, эти разделители используются для уменьшения величины напряжения или для создания опорного напряжения, а также используются на низких частотах в качестве сигнала аттенюатора. Для постоянного тока и относительно низких частот делитель напряжения может быть подходящим вариантом, если он состоит только из резисторов; где частотная характеристика требуется в широком диапазоне.
Что такое правило делителя напряжения?
Определение: В области электроники делитель напряжения представляет собой базовую схему, используемую для генерации части входного напряжения, например выходного.Эта схема может быть сконструирована с двумя резисторами или любыми пассивными компонентами вместе с источником напряжения. Резисторы в цепи могут быть подключены последовательно, в то время как источник напряжения подключен к этим резисторам. Эту схему еще называют делителем потенциала. Входное напряжение может передаваться между двумя резисторами в цепи, так что происходит разделение напряжения.
Когда использовать правило делителя напряжения?
Правило делителя напряжения используется для решения схем, чтобы упростить решение.Применение этого правила также может полностью решить простые схемы. Основная идея этого правила делителя напряжения заключается в том, что «напряжение делится между двумя резисторами, которые соединены последовательно, прямо пропорционально их сопротивлению.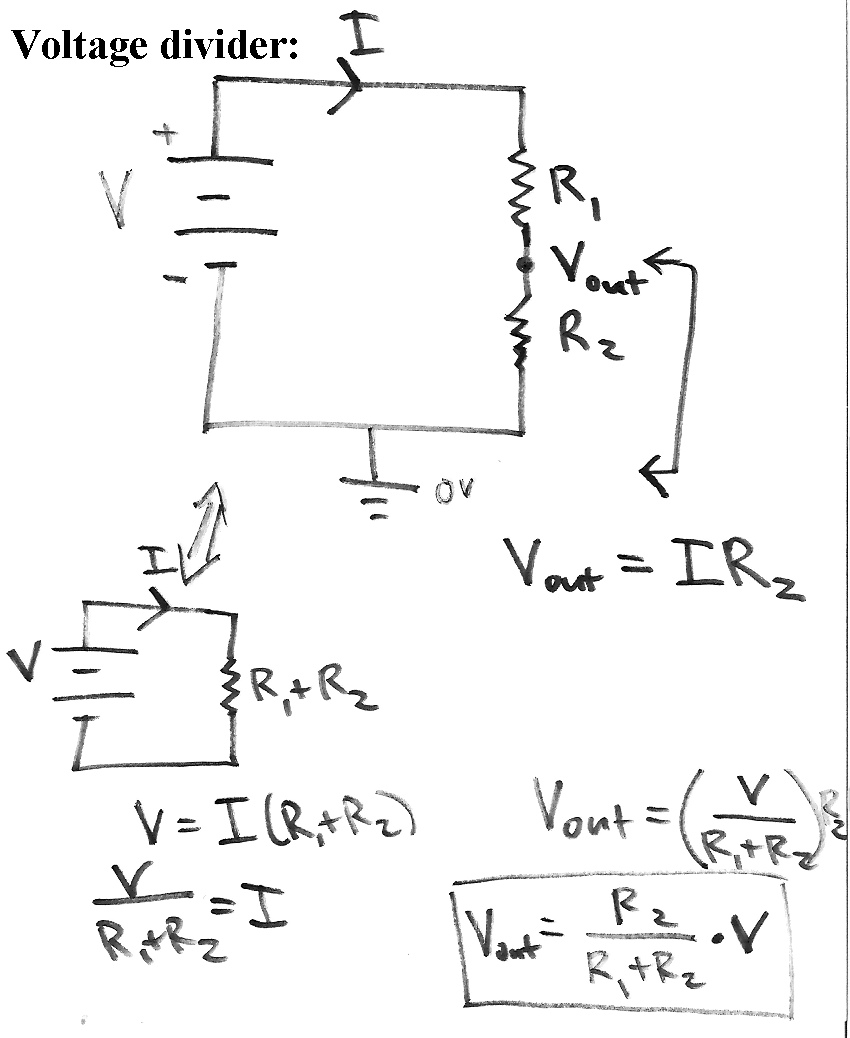 Делитель напряжения состоит из двух важных частей: схемы и уравнения.
Делитель напряжения состоит из двух важных частей: схемы и уравнения.
Различные схемы делителя напряжения
Делитель напряжения включает в себя источник напряжения, подключенный к серии из двух резисторов. Вы можете увидеть различные схемы напряжения, нарисованные по-разному, как показано ниже.Но эти разные схемы всегда должны быть одинаковыми. Схема делителя напряжения
В приведенных выше схемах делителя напряжения резистор R1 находится ближе всего к входному напряжению Vin, а резистор R2 находится ближе всего к клемме заземления. Падение напряжения на резисторе R2 называется Vout, которое представляет собой разделенное напряжение цепи.
Расчет делителя напряжения
Рассмотрим следующую схему, подключенную с помощью двух резисторов R1 и R2. Где переменный резистор включен между источником напряжения.В приведенной ниже схеме R1 — это сопротивление между скользящим контактом переменной и отрицательной клеммой. R2 — сопротивление между положительной клеммой и скользящим контактом.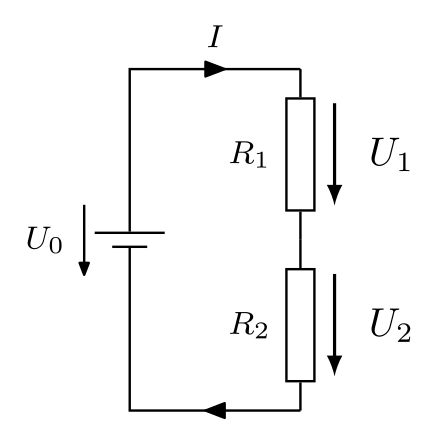 Это означает, что два резистора R1 и R2 включены последовательно.
Это означает, что два резистора R1 и R2 включены последовательно.
Правило делителя напряжения с использованием двух резисторов
Закон Ома гласит, что V = IR
Из приведенного выше уравнения мы можем получить следующие уравнения
V1 (t) = R1i (t) …………… (I)
V2 (t) = R2i (t) …………… (II)
Применение закона Кирхгофа
KVL утверждает, что когда алгебраическая сумма напряжений вокруг замкнутого контура в цепи равна нулю.
-V (t) + v1 (t) + v2 (t) = 0
V (t) = V1 (t) + v2 (t)
Следовательно,
V (t) = R1i (t) + R2i (t) = i (t) (R1 + R2)
Следовательно,
i (t) = v (t) / R1 + R2 ……………. (III)
Подставляя III в уравнения I и II
V1 (t) = R1 (v (t) / R1 + R2)
V (t) (R1 / R1 + R2)
V2 (t) = R2 (v (t) / R1 + R2)
V (t) (R2 / R1 + R2)
На приведенной выше схеме показан делитель напряжения между двумя резисторами, который прямо пропорционален их сопротивлению. Это правило делителя напряжения можно распространить на схемы, в которых используется более двух резисторов.
Это правило делителя напряжения можно распространить на схемы, в которых используется более двух резисторов.
Правило деления напряжения для цепи с двумя резисторами
V1 (t) = V (t) R1 / R1 + R2 + R3 + R4
V2 (t) = V (t) R2 / R1 + R2 + R3 + R4
V3 (t) = V (t) R3 / R1 + R2 + R3 + R4
V4 (t) = V (t) R4 / R1 + R2 + R3 + R4
Делитель напряжения Уравнение
Уравнение правила делителя напряжения принимает, когда вы знаете три значения в приведенной выше схеме, это входное напряжение и два значения резистора.Используя следующее уравнение, мы можем найти выходное напряжение.
Vout = Vin. R2 / R1 + R2
В приведенном выше уравнении указано, что Vout (напряжение o / p) прямо пропорционально Vin (входное напряжение) и соотношению двух резисторов R1 и R2.
Резистивный делитель напряжения
Это очень легкая и простая схема для разработки и понимания.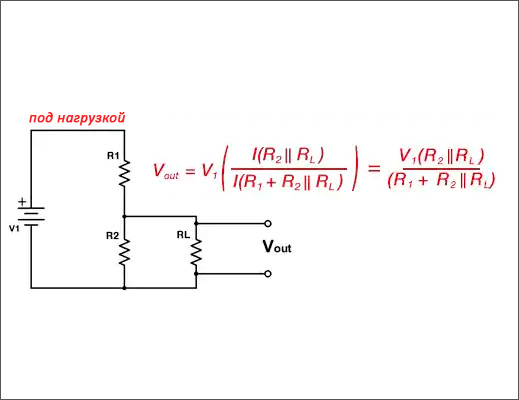 Основной тип схемы пассивного делителя напряжения может состоять из двух последовательно соединенных резисторов.Эта схема использует правило делителя напряжения для измерения падения напряжения на каждом последовательном резисторе. Схема резистивного делителя напряжения показана ниже.
Основной тип схемы пассивного делителя напряжения может состоять из двух последовательно соединенных резисторов.Эта схема использует правило делителя напряжения для измерения падения напряжения на каждом последовательном резисторе. Схема резистивного делителя напряжения показана ниже.
В схеме резистивного делителя два резистора, такие как R1 и R2, соединены последовательно. Таким образом, ток в этих резисторах будет одинаковым. Следовательно, он обеспечивает падение напряжения (I * R) на каждом резисторе.
Резистивный типС помощью источника напряжения на эту цепь подается напряжение. Применяя к этой схеме закон КВЛ и Ома, мы можем измерить падение напряжения на резисторе.Таким образом, поток тока в цепи может быть задан как
Применяя KVL
VS = VR1 + VR2
Согласно закону Ома
VR1 = I x R1
VR2 = I x R2
VS = I x R1 + I x R2 = I (R1 + R2)
I = VS / R1 + R2
Протекание тока через последовательную цепь составляет I = V / R по Ому. Закон. Таким образом, ток в обоих резисторах одинаков. Итак, теперь можно рассчитать падение напряжения на резисторе R2 в цепи
Закон. Таким образом, ток в обоих резисторах одинаков. Итак, теперь можно рассчитать падение напряжения на резисторе R2 в цепи
IR2 = VR2 / R2
Vs / (R1 + R2)
VR2 = Vs (R2 / R1 + R2)
Точно так же падение напряжения на резисторе R1 можно рассчитать как
IR1 = VR1 / R1
Vs / (R1 + R2)
VR1 = Vs (R1 / R1 + R2)
Емкостный Делители напряжения
Схема емкостного делителя напряжения генерирует падение напряжения на конденсаторах, которые подключены последовательно к источнику переменного тока.Обычно они используются для снижения чрезвычайно высокого напряжения для обеспечения сигнала низкого выходного напряжения. В настоящее время эти разделители применимы в планшетах с сенсорным экраном, мобильных телефонах и устройствах отображения.
В отличие от схем резистивного делителя напряжения, емкостные делители напряжения работают с синусоидальным источником переменного тока, поскольку деление напряжения между конденсаторами можно рассчитать с помощью реактивного сопротивления конденсаторов (X C ), которое зависит от частоты источника переменного тока.
Формула емкостного реактивного сопротивления может быть получена как
Xc = 1 / 2πfc
Где:
Xc = емкостное реактивное сопротивление (Ом)
π = 3.142 (числовая константа)
ƒ = Частота, измеренная в Герцах (Гц)
C = Емкость, измеренная в Фарадах (Ф)
Реактивное сопротивление каждого конденсатора может быть измерено напряжением, а также частотой источника переменного тока и заменителя их в приведенном выше уравнении, чтобы получить эквивалентное падение напряжения на каждом конденсаторе. Схема емкостного делителя напряжения показана ниже.
Используя эти конденсаторы, которые соединены последовательно, мы можем определить среднеквадратичное падение напряжения на каждом конденсаторе с точки зрения их реактивного сопротивления после их подключения к источнику напряжения.
Xc1 = 1 / 2πfc1 & Xc2 = 1 / 2πfc2
X CT = X C1 + X C2
V C1 = X CT )
V C2 = Vs (X C2 / X CT )
Емкостные делители не допускают ввода постоянного тока.
Простое емкостное уравнение для входа переменного тока:
Vout = (C1 / C1 + C2) .Vin
Индуктивные делители напряжения
Индуктивные делители напряжения будут создавать перепады напряжения на катушках, в противном случае индукторы подключаются последовательно через Источник переменного тока.Он состоит из катушки, иначе одиночной обмотки, которая разделена на две части, где бы ни поступало напряжение o / p с одной из частей.
Лучшим примером этого индуктивного делителя напряжения является автотрансформатор, имеющий несколько точек отвода с вторичной обмоткой. Индуктивный делитель напряжения между двумя катушками индуктивности можно измерить с помощью реактивного сопротивления катушки индуктивности, обозначенной XL.
Индуктивный типФормула индуктивного реактивного сопротивления может быть получена как
XL = 1 / 2πfL
«XL» — это индуктивное реактивное сопротивление, измеренное в Ом (Ом)
π = 3.142 (числовая константа)
» — частота, измеренная в герцах (Гц)
‘L’ — индуктивность, измеренная в Генри (Г)
Реактивное сопротивление двух катушек индуктивности может быть вычислено, если мы знаем частоту и напряжение источника переменного тока и использовать их с помощью закона делителя напряжения, чтобы получить падение напряжения на каждой катушке индуктивности, как показано ниже.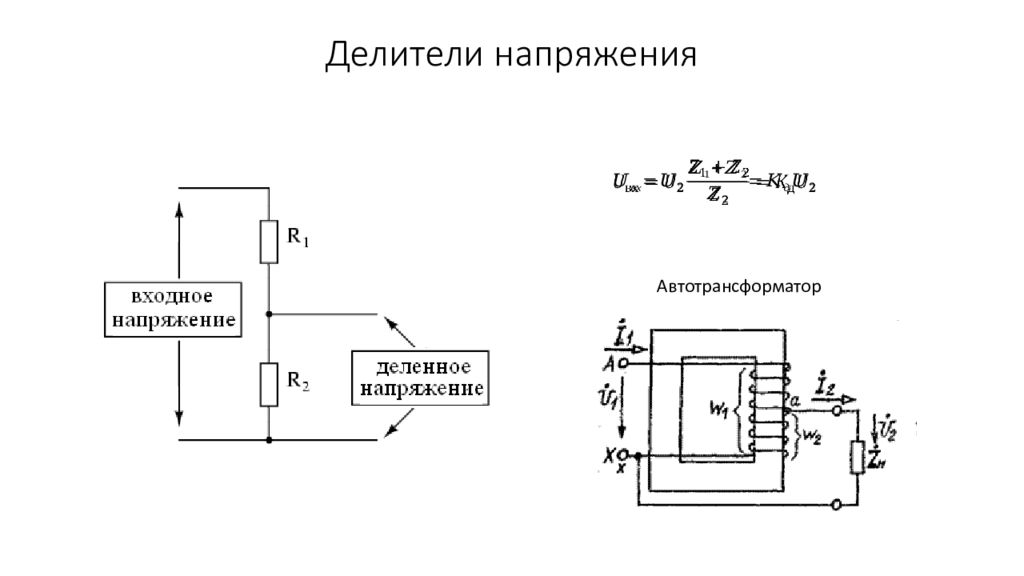 Схема индуктивного делителя напряжения показана ниже.
Схема индуктивного делителя напряжения показана ниже.
Используя две катушки индуктивности, которые соединены последовательно в цепи, мы можем измерить среднеквадратичные падения напряжения на каждом конденсаторе с точки зрения их реактивного сопротивления после их подключения к источнику напряжения.
X L1 = 2πfL1 и X L2 = 2πfL2
X LT = X L1 + X L2
L1 L1 / X LT )V L2 = Vs ( X L2 / X LT )
Вход переменного тока может быть разделен индуктивными делителями в зависимости от индуктивности: : Vout = (L2 / L1 + L2) * Vin Это уравнение предназначено для катушек индуктивности, которые не взаимодействуют, и взаимная индуктивность в автотрансформаторе изменит результаты. Проблемы с примером делителя напряжения могут быть решены с помощью вышеуказанных резистивных, емкостных и индуктивных цепей. 1). Предположим, полное сопротивление переменного резистора составляет 12 Ом. Скользящий контакт расположен в точке, где сопротивление делится на 4 Ом и 8 Ом. Переменный резистор подключен к батарее 2,5 В.Давайте посмотрим, какое напряжение появляется на вольтметре, подключенном к 4-омному участку переменного резистора. Согласно правилу делителя напряжения, падение напряжения будет, Vout = 2,5 В x 4 Ом / 12 Ом = 0,83 В 2). Когда два конденсатора C1-8uF и C2-20uF соединены последовательно в цепи, среднеквадратичные падения напряжения могут быть рассчитаны на каждом конденсаторе, когда они подключены к источнику питания 80 Гц RMS и напряжению 80 В. Xc1 = 1 / 2πfc1 1/2 × 3.14x80x8x10-6 = 1 / 4019,2 × 10-6 = 248,8 Ом Xc2 = 1 / 2πfc2 1/2 × 3,14x80x20x10-6 = 1/10048 x10-6 = 99,52 Ом XCT = XC1 + XC2 = 248,8 + 99,52 = 348,32 VC1 = Vs (XC1 / XCT) 80 (248,8 / 348,32) = 57,142 VC2 = Vs (XC2 / XCT) 80 (99,52 / 348,32) 3). Когда две катушки индуктивности L1-8 мГн и L2-15 мГн соединены последовательно, мы можем вычислить среднеквадратичное падение напряжения на каждом конденсаторе, которое можно рассчитать, когда они подключены к источнику питания 40 В, 100 Гц. XL1 = 2πfL1 = 2 × 3,14x100x8x10-3 = 5,024 Ом XL2 = 2πfL2 = 2 × 3,14x100x15x10-3 9,42 Ом XLT = XL1 + XL2  Вход постоянного тока может быть разделен на основе сопротивления элементов в соответствии с правилом резистивного делителя.
Вход постоянного тока может быть разделен на основе сопротивления элементов в соответствии с правилом резистивного делителя. Примеры проблем с делителем напряжения

XLT = XL1 + XL2
Vs (XL1 / XLT)= 40 (5,024 / 14,444) = 13,91 вольт
VL2 = Vs (XL2 / XLT)
= 40 (9,42 / 14,444) = 26,08 вольт
Точки отвода напряжения в сети делителя
Когда количество резисторов подключено последовательно к источнику напряжения Vs в цепи, то различные точки отвода напряжения можно рассматривать как A, B, C, D и E
Общее сопротивление в цепи можно рассчитать, добавив все значения сопротивления вроде 8 + 6 + 3 + 2 = 19 кОм.Это значение сопротивления ограничит ток, протекающий по цепи, которая генерирует напряжение питания (VS).
Для расчета падения напряжения на резисторах используются следующие уравнения: VR1 = VAB,
VR2 = VBC, VR3 = VCD и VR4 = VDE.
Уровни напряжения в каждой точке ответвления рассчитываются относительно клеммы GND (0 В). Следовательно, уровень напряжения в точке «D» будет эквивалентен VDE, тогда как уровень напряжения в точке «C» будет эквивалентен VCD + VDE.Здесь уровень напряжения в точке «C» — это величина двух падений напряжения на двух резисторах R3 и R4.
Итак, выбрав соответствующий набор номиналов резистора, мы можем сделать серию падений напряжения. Эти падения напряжения будут иметь относительное значение напряжения, которое достигается только за счет напряжения. В приведенном выше примере каждое значение напряжения o / p является положительным, поскольку отрицательная клемма источника напряжения (VS) подключена к клемме заземления.
Применения делителя напряжения
К числу применений делителя напряжения относятся следующие.
- Делитель напряжения используется только там, где напряжение регулируется путем снижения определенного напряжения в цепи. Он в основном используется в таких системах, где энергоэффективность не обязательно должна рассматриваться серьезно.
- В нашей повседневной жизни делитель напряжения чаще всего используется в потенциометрах. Лучшими примерами потенциометров являются ручки регулировки громкости, прикрепленные к нашим музыкальным системам, радиотранзисторам и т. Д. Базовая конструкция потенциометра включает три контакта, которые показаны выше.При этом два контакта подключены к резистору, который находится внутри потенциометра, а оставшийся контакт подключен к очищающему контакту, который скользит по резистору. Когда кто-то меняет ручку на потенциометре, то напряжение будет появляться на стабильных контактах и очищающем контакте в соответствии с правилом делителя напряжения.
- Делители напряжения используются для регулировки уровня сигнала, для измерения напряжения и смещения активных устройств в усилителях. Мультиметр и мост Уитстона включают делители напряжения.
- Делители напряжения можно использовать для измерения сопротивления датчика. Чтобы сформировать делитель напряжения, датчик подключается последовательно с известным сопротивлением, и известное напряжение подается на делитель. Аналого-цифровой преобразователь микроконтроллера подключен к центральному отводу делителя, чтобы можно было измерить напряжение отвода. Используя известное сопротивление, можно рассчитать измеренное сопротивление датчика напряжения.
- Делители напряжения используются для измерения датчика, напряжения, сдвига логического уровня и регулировки уровня сигнала.
- Как правило, правило резисторного делителя в основном используется для создания опорных напряжений, иначе величина напряжения уменьшается, так что измерения очень просты. Дополнительно; они работают как аттенюаторы сигнала на низкой частоте.
- Он используется в случае чрезвычайно меньшего количества частот и DC
- Емкостный делитель напряжения, используемый при передаче энергии для компенсации емкости нагрузки и измерения высокого напряжения.
Это все о правиле деления напряжения для цепей, это правило применимо как для источников напряжения переменного, так и постоянного тока.Кроме того, любые сомнения относительно этой концепции или проектов электроники и электротехники, пожалуйста, дайте свой отзыв, комментируя в разделе комментариев ниже. Вот вам вопрос, какова основная функция правила делителя напряжения?
Делитель напряжения Формула
Предположим, у вас есть источник напряжения (входное напряжение), соединенный последовательно с n импедансами. Чтобы узнать выходное напряжение по общему импедансу, используется закон Ома:
выходное напряжение = (общий импеданс / сумма от первого до n-го импеданса цепи) * входное напряжение.
Уравнение записано
У нас:
В выход = выходное напряжение.
Z i = общий импеданс.
= сумма от первого до n-го импеданса цепи.
В в = входное напряжение.
Формула делителя напряжения Вопросы.
1) У нас есть цепь с двумя резисторами, первый 3 Ом и второй 5 Ом, подключенные последовательно, напряжение источника имеет значение 12 В, рассчитайте напряжение деления после первого сопротивления.
Ответ:
Прежде всего, следует отметить, что это схема резистивного делителя, поэтому значения импедансов совпадают со значениями сопротивлений.Импеданс Z i принимает значение 3 Ом. Теперь добавим импедансы цепи, чтобы получить делитель напряжения, это
= 3 Ом + 5 Ом = 8 Ом.
Затем мы делим значение второго импеданса на сумму импедансов и умножаем его на значение входного напряжения, чтобы получить делитель напряжения,
В выход = (5 Ом / 8 Ом) * 12 В = 0,625 * 12 В = 7,824 В
В выход = 7,824 В.
2) Рассчитайте делитель напряжения для двух последовательно соединенных конденсаторов, имеющих значения емкости 10 мкФ и 22 мкФ соответственно.Здесь напряжение в цепи составляет 10 В при частоте 40 Гц.
Ответ:
Прежде всего необходимо получить значение импеданса каждого конденсатора.
Z = 1 / (2 * π * f * C)
Z 1 = 1 / (2 * π * 40 Гц * 10 * 10 -6 F) = 400 Ом.
Z 2 = 1 / (2 * π * 40 Гц * 22 * 10 -6 F) = 180 Ом.
Затем,
В выход = = 10 В = 0,31 * 10 В = 3,1 В
В выход = 3.1 В.
Правило делителя напряжения— калькулятор, решаемые примеры и приложения
Схема делителя напряжения— калькулятор VDR, примеры и приложения
Схема делителя напряжения
Схема делителя напряжения использует резисторы для понижения напряжения и самая распространенная схема, применяемая в электронике. Делитель напряжения может использоваться, чтобы сделать много вещей, как создать схему управления громкостью или генерировать опорного напряжения и многое другое. Делители напряжения также используются в аналоговых схемах для получения выходов переменного напряжения.Эта схема отлично работает как с переменным, так и с постоянным входным напряжением, при этом значение входного напряжения преобразуется в другое значение напряжения.
Примечание: Значение выходного напряжения схемы делителя напряжения всегда меньше, чем значение входного напряжения.
В схеме делителя напряжения выходное напряжение всегда зависит от пропорции величины сопротивления. Например, если вы взяли два одинаковых резистора, вы получите на выходе ровно половину входного напряжения.
Электрическая эквивалентная схема делителя напряжения приведена ниже:
Как видите, схема делителя напряжения состоит из двух последовательно соединенных резисторов с отводом напряжения между ними. Входное напряжение прикладывается к резистору R 1 и R 2 . Следовательно, мы можем наблюдать, что выходное напряжение — это падение напряжения на резисторе R 2 . Напряжение на R 1 и R 2 будет равно значению входного напряжения, приложенного к схеме делителя напряжения.
Формула уравнения делителя напряжения для нахождения значения выходного напряжения будет выражена как:
Где,
В в = Входное напряжение
В выход = Выходное напряжение
R 1 = резистор, подключенный к источнику
R 2 = резистор, подключенный к земле
Формула доказательства делителя напряжения
Теперь мы объясним вам математическое объяснение приведенной выше формулы.Итак, согласно закону Ома, разность потенциалов на идеальном проводнике будет равна току, протекающему по нему.
V = IR
Где V, I и R — напряжение, ток и сопротивление соответственно.
Таким образом, напряжение на вышеуказанной цепи будет равно произведению тока в цепи и полного сопротивления.
Общее сопротивление цепи в цепи делителя напряжения составляет
R T = R 1 + R 2
Vin = IR T
Vin = I (R 1 + R 2 )
При решении,
I = V in / (R 1 + R 2 )
Здесь выходное напряжение снимается через сопротивление R 2 , поэтому V out будет выражен как:
Vout = IR 2
Теперь поместите значение I из приведенного выше уравнения,
Теперь мы объясним вам, как работает делитель напряжения, и как вы даже можете найти значение сопротивления, чтобы получить желаемое значение напряжения.
Напряжение Делитель Схема — пример
Как показано выше, схема делителя напряжения состоит из двух резисторов (R 1 и R 2 ), и выход будет проходить через резистор Р 2 . Единственное, о чем нужно позаботиться, — это номинальная мощность резисторов. Потому что, если мы не выберем правильную номинальную мощность резистора, резисторы будут перегреваться или также могут сгореть. Вы можете рассчитать номинальную мощность, если знаете значение I (в зависимости от нагрузки), используя уравнение степенного закона (P = VI).
Вещи, необходимые для разработки схемы делителя напряжения:
- Резисторы (10 кОм, 47 кОм)
- Входное питание (9 В)
- Макетная плата
- Мультиметр (для измерения)
Теперь мы продемонстрирует вам выход схемы делителя напряжения практически и теоретически.
Здесь, в эту схему, мы подключили входное напряжение 9 В и резисторы R 1 и R 2 (47 кОм и 10 кОм соответственно). После снятия выходного сигнала схемы делителя напряжения с мультиметра получаем 1.49В .
Теперь мы вычислим выходное напряжение вышеуказанной схемы теоретически,
Здесь V в = 9 В, R 1 = 47 кОм и R 2 = 10 кОм
Итак, используя уравнение делителя напряжения
У нас есть
В выход = (9 × 10) / (47 + 10)
В выход = 1,5789
Следовательно, вы можете увидеть разницу Между практическим и теоретическим значением, поскольку напряжение батареи не совсем 9 В.Кроме того, вы можете найти номинал резистора в соответствии с желаемым выходным напряжением, используя приведенную выше формулу.
Связанное сообщение: Требуемое значение резистора для калькулятора цепи светодиода
Калькулятор правил делителя напряжения
Вы также можете использовать калькулятор делителя напряжения для расчета выхода делителя напряжения или даже значения резисторов в соответствии с желаемым входом и выходные значения.
Введите любые три из следующих значений и нажмите кнопку «Рассчитать».Результат отобразит требуемое значение.
Примечание. Формулы и уравнения для этого калькулятора приведены ниже (после калькулятора). Также не забудьте поделиться и предложить своим друзьям. Кроме того, если вы хотите увидеть другие электрические и электронные калькуляторы в прямом эфире в нашем блоге, укажите это в поле для комментариев ниже. Благодарю.
Формула для калькулятора VDR
V OUT = V IN x (R 2 / (R 1 + R 2 ))
Где
Где
IN = Входное напряжение питания
R 1 + R 2 = Значения резисторов
В OUT = Выходное напряжение
Связанное сообщение: Калькулятор ближайшего значения стандартного резистора
Преимущества схемы делителя напряжения
У схемы делителя напряжения есть некоторые преимущества и недостатки, которые указаны ниже:
Преимущества схемы делителя напряжения
- Простой и удобный метод измерения высокого напряжения (до 100 кВ)
- Простой метод смещения уровня напряжения.
- Помогает в установке выходного напряжения регуляторов (например, LM317)
Недостатки схемы делителя напряжения
- Неэффективно использовать для источников питания.
- Резисторы делителей напряжения вносят небольшие потери мощности.
- Иногда сопротивление вольтметра влияет на соотношение резисторов.
Применение схемы делителя напряжения
Теперь, как мы знаем, существует ряд применений схемы делителя напряжения.Некоторые из приложений упомянуты ниже:
Потенциометры
Потенциометр — это трехконтактный переменный резистор, с его помощью можно создать регулируемый делитель напряжения. Если вы будете использовать только два контакта потенциометра (один должен быть регулируемым), он будет работать как реостат. Но если вы используете все клеммы и пропускаете выход через регулируемый вывод, здесь он работает как делитель напряжения.
Аналогичным образом, потенциометры имеют много применений, она также используется в джойстиков и для создания опорного напряжения.
Чтение резистивных датчиков
Большинство датчиков представляют собой просто резистивные устройства, такие как LDR (светозависимый резистор), сопротивление которого изменяется в зависимости от интенсивности падающего на него света. Подобно LDR, существует ряд датчиков, которые делают то же самое в отношении сопротивления, таких как датчик изгиба, датчик силы и термисторы.
Здесь схема делителя напряжения используется для расчета сопротивления датчика. Заменив резистор R 2 (согласно принципиальной схеме) резистивным датчиком, мы можем рассчитать его сопротивление по следующей формуле
R2 = (Vout x R1) / (Vin — Vout)
Где , R 2 — резистивный датчик
Сдвиг уровня
При взаимодействии с микроконтроллером не все датчики работают при стандартном значении напряжения (5 В), есть несколько датчиков, которые работают при относительно низком напряжении.Здесь возникает проблема смещения уровня, поэтому, чтобы понизить напряжение интерфейса, мы используем схемы делителя напряжения, чтобы получить определенное напряжение.
Измерение высокого напряжения
Когда трудно измерить значение высокого напряжения, снова применяется делитель напряжения. Делитель напряжения уменьшает очень высокое напряжение, поэтому его легко измерить с помощью вольтметров.
Проще говоря, высокое напряжение подается на вход делителя напряжения, а его выход (установлен ниже, чем макс.диапазон) измеряется вольтметром. В вольтметрах специально разработаны зонды с высоковольтным резистором, чтобы выдерживать приходящее высокое входное напряжение и получать точные результаты при измерении высокого напряжения. Используя эту схему делителя напряжения, мы можем измерить напряжение до 100 кВ. Схема конденсаторного делителя используется для измерения значения напряжения более 100 кВ.
Связанный пост: Калькулятор параллельного резистора
Делитель напряжения для переменного источника питания
Предположим, у нас есть батарея 9 В, и вам нужно значение выходного напряжения от 1 В до 8 В.Как упоминалось выше, регулируя потенциометр, подключенный к батарее 9 В, мы можем получить выходное напряжение от 1 В до 8 В.
Подключите аккумулятор в соответствии со схемой ниже:
Примечание: Использование схемы делителя напряжения для источника питания может вызвать эффект нагрузки . Кроме того, это неэффективный способ управления напряжением питания, поскольку мощность рассеивается в резисторе R 1 без полезного усиления.
Таким образом, потенциометр может выдавать переменное выходное напряжение.
Теперь предположим, что вам нужно фиксированное напряжение питания для любого конкретного устройства или контроллера, что вы будете делать? Для этого вам нужно точное значение резистора вместо потенциометра, чтобы получить желаемый выход.
Как нам нужен выход 5 В от батареи 9 В (без учета тока нагрузочного резистора)
Переставив формулу делителя напряжения, вы можете найти значения резистора, который вам нужен для любого конкретного выходного значения. В противном случае вы можете использовать наш калькулятор делителя напряжения для того же.
Во-первых, вы должны выбрать значение входного напряжения и любое значение резистора (R 1 или R 2 ). Итак, если вы зафиксировали значение R 1 и теперь вам нужно найти значение R 2 , используйте следующую формулу:
Если вы зафиксировали значение R 2 и вам нужно найдите значение R 1 , затем используйте приведенную ниже формулу:
Здесь мне нужно 5 В на выходе из входного напряжения 9 В,
Итак,
В в = 9 В
В из = 5V
R 1 = 8k (постоянный резистор)
R 2 =?
Используя формулу для R 2
Мы имеем,
R 2 = (5 x 8) / (9-5)
R 2 = 40/4
R 2 = 10
Следовательно, если вы возьмете R 2 из 10 кОм и R 1 из 8 кОм с входным напряжением 9 В, выходное напряжение будет равно 5 В.
Связанные сообщения:
Схема цепи делителя потенциала или напряженияи формула
Цепь делителя напряжения или напряжения обычно используется в электронике, где входное напряжение должно быть преобразовано в другое напряжение, меньшее, чем исходное. Это очень полезно для всех аналоговых схем, где требуются переменные напряжения, поэтому важно понимать, как эта схема работает и как рассчитать значения резисторов, необходимых для того, чтобы схема делала напряжение для вывода желаемого напряжения.
Необходимые материалы
- Резистор (1 кОм — 1 шт., 10 кОм — 1 шт.)
- Батарея — 9В
- Мультиметр
- Соединительные провода
- Макет
Принципиальная схема
Схема делителя напряжения — очень простая схема, состоящая всего из двух резисторов (R1 и R2), как показано выше на принципиальных схемах. Требуемое выходное напряжение (V OUT ) может быть получено на резисторе R2.Используя эти два резистора, мы можем преобразовать входное напряжение в любое необходимое выходное напряжение.
ПРИМЕЧАНИЕ: Выходное напряжение (V OUT ) всегда меньше входного напряжения (V IN )
Формула делителя напряжения
Предположим, что если ток (I) в выходном проводе равен нулю, то соотношение между входным напряжением (V IN ) и выходным напряжением (V из ) определяется как:
V OUT = (V IN * R 2 ) / (R 1 + R 2 )….(Уравнение делителя напряжения)
Где,
В ВЫХ = Выходное напряжение
В IN = Входное напряжение
R 1 = верхний резистор
R 2 = Нижний резистор
Доказательство формулы потенциального делителя
Согласно закону Ома, напряжение через идеальный проводник равно току, протекающему через него.
Напряжение = ток * сопротивление
В = ИК
Теперь по схеме
V IN = I * (R 1 + R 2 ) I = V IN / (R 1 + R 2 )… уравнение (1) V OUT = I * R 2 … уравнение (2)
Если подставить значение « I » из уравнения (1) в уравнение (2), мы получим
V OUT = (V IN * R 2 ) / (R 1 + R 2 )
О чем следует помнить
- Если значение R1 равно R2, то значение выходного напряжения составляет половину входного значения.
- Если значение R1 намного меньше, чем R2, то значение выходного напряжения будет примерно равно входному напряжению.
- Если значение R1 намного больше, чем R2, то значение выходного напряжения будет примерно равно нулю.
Работа цепи делителя напряжения
Согласно схеме делителя напряжения, которую мы использовали здесь, мы взяли 9 В в качестве входного напряжения, а значение сопротивления R 1 и R 2 равно 1 кОм и 10 кОм соответственно.Практически мы получаем 8.16V в качестве выходного напряжения, как показано на изображении выше.
Попробуем теоретически,
В IN = 9 В, R1 = 1 кОм и R2 = 10 кОм . Vout = (9 × 10000) / (1000 + 10000) Vout = () / (11000)
Vout = 8.1818V
Существует очень небольшая разница между практическим и теоретическим значением, потому что батарея не обеспечивает точное 9В.
Еще одним важным фактором, который следует учитывать при выборе номиналов резистора, является его номинальная мощность (P) . Когда вы знаете значения I (в зависимости от нагрузки), V IN , R 1 и R 2 , сложите R 1 и R 2 вместе, чтобы получить R ИТОГО и использовать закон Ома. калькулятор, чтобы узнать номинальную мощность (Вт), необходимую для резисторов. Или просто используйте формулы P = VI , чтобы определить номинальную мощность вашего резистора.Если не выбрана правильная номинальная мощность, резистор будет перегреваться и также может сгореть.
Калькулятор делителя напряжения
Вы можете напрямую использовать Калькулятор делителя напряжения ниже, чтобы вычислить любое из значений, упомянутых в формулах делителя напряжения .
Применение схемы делителя напряжения
Цепи делителя напряжения или потенциала часто используются в различных проектах и приложениях.Ниже приведены некоторые примеры схем, в которых используется концепция делителя потенциала:
Правило разделения тока и напряжения
Правило разделения тока
Параллельная цепь действует как делитель тока, поскольку ток делится во всех ветвях параллельной цепи, а напряжение на них остается неизменным. Правило деления тока определяет ток через полное сопротивление цепи. Текущее деление объясняется с помощью схемы, показанной ниже:
Ток I разделен на I 1 и I 2 на две параллельные ветви с сопротивлением R 1 и R 2 , а V — падение напряжения на сопротивлении R 1 и R 2 .
Как известно,
В = ИК …… .. (1)
Тогда уравнение тока запишется как:
Пусть полное сопротивление цепи равно R и определяется уравнением, показанным ниже:
Уравнение (1) также можно записать как:
I = V / R ………. (3)
Теперь, подставив значение R из уравнения (2) в уравнение (3), мы получим
Но
Положив значение V = I 1 R 1 из уравнения (5) в уравнение (4), мы в итоге получим уравнение:
А теперь, учитывая V = I 2 R 2 , уравнение будет:
Таким образом, из уравнений (6) и (7) значение тока I 1 и I 2 соответственно определяется уравнением ниже:
Таким образом, в правиле деления тока сказано, что ток в любой из параллельных ветвей равен отношению сопротивления противоположной ветви к общему сопротивлению, умноженному на общий ток.
Правило разделения напряжения
Правило деления напряжения можно понять, рассмотрев последовательную схему, показанную ниже. В последовательной цепи напряжение делится, а ток остается прежним.
Рассмотрим источник напряжения E с последовательно включенными сопротивлениями r 1 и r 2 .
Как известно,
I = V / R или можно сказать I = E / R
Следовательно, ток (i) в контуре ABCD будет:
Помещая значение I из уравнения (8) в уравнение (9), напряжение на сопротивлении r 1 и r 2 соответственно определяется уравнением, показанным ниже, как:
Таким образом, напряжение на резисторе в последовательной цепи равно значению этого резистора, умноженному на общее приложенное напряжение на последовательных элементах, деленное на общее сопротивление последовательных элементов.
Делители напряжения | Книга Ultimate Electronics
Ultimate Electronics: Практическое проектирование и анализ схем
Чрезвычайно распространенная конфигурация резисторов 2+. Приближения, рекомендации по проектированию. Пример светодиодного регулятора тока. Читать 22 мин
Делители напряжения — это просто определенные комбинации резисторов, последовательно подключенных к идеальным источникам напряжения и тока.
В то время как математика решения этих схем была рассмотрена в предыдущих разделах, делители напряжения заслужили свое собственное имя, потому что они появляются достаточно часто, чтобы быть полезным сокращением при анализе многих более крупных схем.(Поскольку более сложные подсхемы могут быть аппроксимированы как один резистор, термин и методы здесь также могут применяться в более широком смысле, помимо резисторов.) Мы начнем с идеального случая, рассмотрим неидеальный случай, а затем покажем, когда приближения полезны при проектировании и анализе.
Когда вы видите, как опытный инженер-электрик бросает быстрый взгляд на аналоговую схему и быстро определяет, что происходит, он, скорее всего, делает приближения делителя напряжения в своей голове — иногда даже не осознавая этого!
Идеальный делитель напряжения состоит из двух последовательно соединенных резисторов.Физически это иногда реализуется как потенциометр, который разделяет один физический резистор на два с помощью физически подвижного проводящего центрального контакта. Но чаще всего это два дискретных постоянных резистора.
Когда на пару подается напряжение, выходное напряжение составляет некоторую часть входного напряжения:
Exercise Щелкните, чтобы открыть и смоделировать схему выше. Измените сопротивления и посмотрите, как изменяется выходное напряжение в ответ.
Это можно увидеть, используя закон Кирхгофа и закон Ома, чтобы записать сумму разностей напряжений вокруг контура:
vin-iR1-iR2 = 0вин = i (R1 + R2) vinR1 + R2 = i
Теперь мы можем написать закон Ома для R2, vout = iR2 (поскольку другой конец R2 заземлен) и подставляем в наше выражение для тока контура i выше:
vout = vin (R2R1 + R2)
Для удобства выделим дробь f , коэффициент делителя напряжения :
f = R2R1 + R2
где vout = vin⋅f .Поскольку сопротивления не могут быть отрицательными, 0≤f≤1 .
Есть несколько особых случаев, о которых следует подумать:
- В относительно частом частном случае двух равных сопротивлений R1 = R2 , отношение f = 12 .
- Если R1≫R2 отношение f → 0 .
- Если R1≪R2 отношение f → 1 .
Эти приближения невероятно полезны, и более подробные версии разработаны в Алгебраических приближениях.
Делитель напряжения всегда выдает уменьшенную версию входного напряжения.Вот пример с делителем напряжения, управляемым синусоидой от функционального генератора:
Exercise Щелкните, чтобы открыть и смоделировать схему выше и посмотреть на взаимосвязь между входными и выходными сигналами.
Поскольку делитель напряжения выводит масштабированную мультипликативно версию входного сигнала, если мы возьмем логарифм обеих сторон (по любой базе), мы обнаружим, что коэффициент делителя напряжения превращается в аддитивную константу:
vout = vin⋅flog (vout) = журнал (vin) + журнал (f)
As f≤1 , всегда будет так, что log (f) ≤0 .
Вот пример с функциональным генератором, управляющим делителем напряжения, где мы отображаем напряжения в логарифмической шкале:
Exercise Щелкните, чтобы открыть и смоделировать схему выше. Обратите внимание на то, как в логарифмическом масштабе две кривые кажутся просто сдвинутыми по вертикали на постоянное смещение. В разделе «Advanced Graphing» измените его обратно на линейный масштаб, чтобы увидеть исходный сигнал.
В этом примере мы особо позаботились о том, чтобы наш входной сигнал оставался строго положительным, но вы также можете применить ту же логику к амплитуде сигнала, который со временем становится как положительным, так и отрицательным.В этом случае делитель напряжения производит сдвиг амплитудного графика в частотной области:
Exercise Щелкните, чтобы открыть и смоделировать схему выше.
При запуске этого моделирования графики входного и выходного напряжений с уровнем −6 дБ. сдвиг между входной и выходной амплитудой. Это −6 дБ потому что амплитуда напряжения уменьшается вдвое. См. Дополнительные сведения в разделах «Порядок величин, логарифмические шкалы и децибелы».
Делители напряжения могут быть выполнены с N резисторы серии N − 1 узлы между ними.Пока нет тока, входящего или выходящего из цепи делителя напряжения, с точки зрения любого конкретного ответвления, резисторы «вверху» можно объединить в один, а резисторы «внизу» можно объединить в другой.
Это позволяет легко создавать большое количество соотношений напряжений для одного входа. Например:
Exercise Щелкните, чтобы открыть и смоделировать схему выше.
На схеме выше используются пять последовательно соединенных резисторов. Он превращает 12-вольтный вход в четыре разных выхода, которые могут быть полезны в блоке питания компьютера.
Поскольку это последовательная схема, существует только один ток, и его легко определить, рассматривая последовательно включенные резисторы:
итотал = vin∑R
Падение напряжения на любом резисторе равно:
.
