Как рассчитать общее сопротивление при параллельном соединении резисторов. Почему суммируются обратные величины сопротивлений. В чем преимущества параллельного соединения резисторов.
Что такое параллельное соединение резисторов
Параллельное соединение резисторов — это способ подключения нескольких резисторов, при котором все они присоединяются к одним и тем же двум точкам электрической цепи. При таком соединении напряжение на всех резисторах одинаково, а общий ток разветвляется между ними.
Основные особенности параллельного соединения резисторов:
- Напряжение на всех резисторах одинаково и равно напряжению источника
- Общий ток равен сумме токов через отдельные резисторы
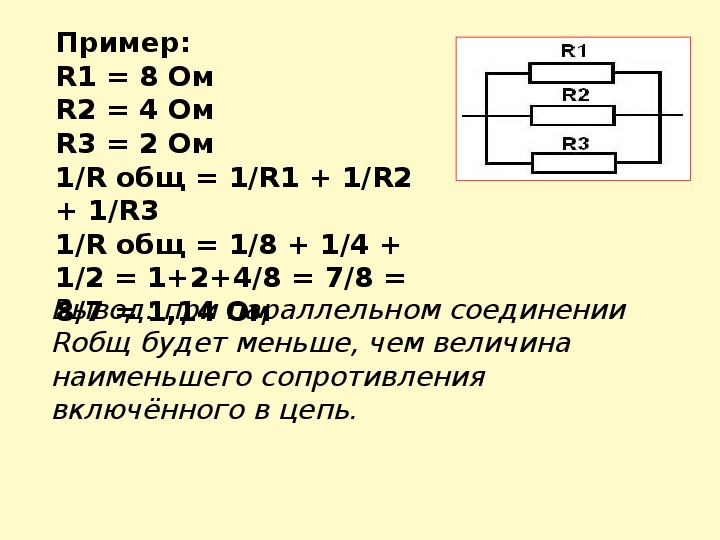
- Общее сопротивление всегда меньше сопротивления самого маленького резистора в цепи
Формула для расчета общего сопротивления при параллельном соединении
Для расчета общего сопротивления при параллельном соединении резисторов используется следующая формула:
1/R = 1/R1 + 1/R2 + 1/R3 + …
Где R — общее сопротивление, а R1, R2, R3 и т.д. — сопротивления отдельных резисторов.
Почему используется именно такая формула? Это связано с тем, что при параллельном соединении складываются не сами сопротивления, а величины, обратные сопротивлениям. Эти обратные величины называются проводимостями.
Физический смысл формулы параллельного соединения
Чтобы понять физический смысл формулы параллельного соединения, рассмотрим следующую аналогию:
Представьте, что у вас есть несколько труб разного диаметра, по которым течет вода. Если соединить эти трубы параллельно, то общий поток воды будет равен сумме потоков через каждую трубу. Чем больше труб и чем они шире, тем больше общий поток.
Аналогично в электрической цепи — чем больше параллельных «путей» для тока и чем меньше их сопротивление, тем больше общая проводимость цепи. А проводимость — это величина, обратная сопротивлению.
Примеры расчета параллельного соединения резисторов
Рассмотрим несколько примеров расчета общего сопротивления при параллельном соединении резисторов:
Пример 1: Два резистора
Даны два резистора: R1 = 10 Ом, R2 = 20 Ом
1/R = 1/10 + 1/20 = 0.1 + 0.05 = 0.15
R = 1/0.15 ≈ 6.67 Ом
Пример 2: Три резистора
Даны три резистора: R1 = 6 Ом, R2 = 12 Ом, R3 = 4 Ом
1/R = 1/6 + 1/12 + 1/4 = 0.167 + 0.083 + 0.25 = 0.5
R = 1/0.5 = 2 Ом
Преимущества параллельного соединения резисторов
Параллельное соединение резисторов имеет ряд преимуществ в электрических схемах:
- Уменьшение общего сопротивления цепи
- Увеличение максимально допустимого тока
- Возможность получить нестандартное значение сопротивления
- Повышение надежности цепи (при выходе из строя одного резистора цепь продолжит работать)
Применение параллельного соединения резисторов
Параллельное соединение резисторов широко применяется в электронике и электротехнике. Вот несколько примеров:
- Делители напряжения
- Схемы согласования импедансов
- Шунты для измерительных приборов
- Балластные резисторы в осветительных приборах
- Схемы защиты от перенапряжения
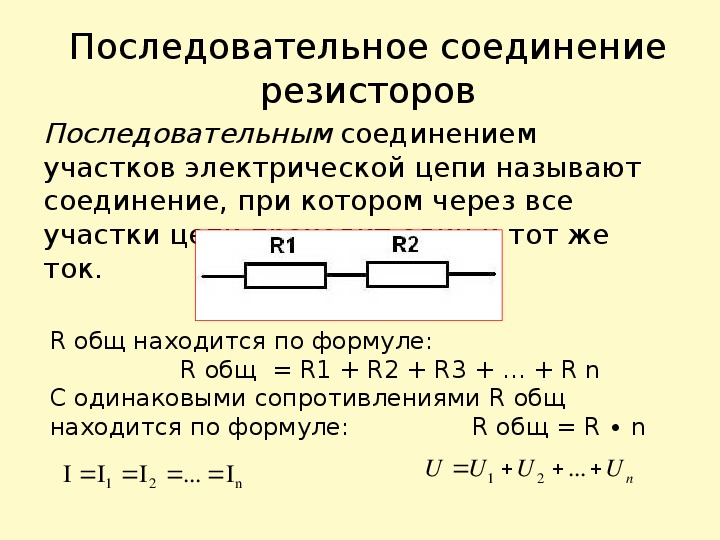
Особенности параллельного соединения в сравнении с последовательным
Как параллельное соединение резисторов отличается от последовательного? Рассмотрим основные различия:
| Параметр | Параллельное соединение | Последовательное соединение |
|---|---|---|
| Напряжение | Одинаково на всех элементах | Сумма напряжений на элементах |
| Ток | Сумма токов через элементы | Одинаков во всех элементах |
| Общее сопротивление | Меньше наименьшего | Сумма сопротивлений |
Ошибки при расчете параллельного соединения резисторов
При расчете параллельного соединения резисторов часто допускаются следующие ошибки:
- Попытка просто сложить сопротивления (как при последовательном соединении)
- Забывание про необходимость взять обратное значение в конце расчета
- Неправильное округление промежуточных результатов, что приводит к значительной погрешности
Чтобы избежать этих ошибок, важно внимательно следовать формуле и перепроверять свои расчеты.
Практические советы по работе с параллельным соединением резисторов
При работе с параллельным соединением резисторов полезно помнить следующее:
- Общее сопротивление всегда меньше сопротивления самого маленького резистора в цепи
- Добавление дополнительных параллельных резисторов всегда уменьшает общее сопротивление
- При параллельном соединении одинаковых резисторов общее сопротивление равно сопротивлению одного резистора, деленному на их количество
- Для быстрой оценки можно использовать правило: общее сопротивление чуть меньше половины меньшего из двух параллельных резисторов
Эти правила помогут вам быстро оценивать схемы и проверять правильность ваших расчетов.
электрического тока — Что скрывается за суммой обратных значений резисторов в параллельной цепи?
$\begingroup$
Я хочу понять в области параллельных цепей почему работает эта формула: $$\frac{1}{R_T} = \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} + \cdot\cdot\cdot+$$
в частности в чем смысл $\frac{1}{R_x}$. Я понимаю, что это происходит от \начать{выравнивать} I_T &= I_1 + I_2 + I_3 \\ \frac{V}{R_{t}} &= \frac{V}{R_1} + \frac{V}{R_2} + \frac{V}{R_3} \\ \frac{V}{R_{t}} &= V \left(\frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3}\right) \end{выравнивание} и так я знаю как это работает. Но я пытаюсь интуитивно понять, что означает сумма обратных номиналов отдельных резисторов в параллельной цепи. Я не ищу математического объяснения.
- электрические цепи
- электрические токовые
- электрические сопротивления
- напряжения
$\endgroup$
0
$\begingroup$
Сопротивление $R = \frac{U}{I}$.
Обратное сопротивление $G = \frac{1}{R} = \frac{I}{U}$ представляет собой электрическую проводимость .
Сопротивления складываются в последовательных сценариях, так как напряжения при одном и том же токе складываются.
$$R_\mathrm{T} = \frac{U_\mathrm{T}}{I} = \frac {U_1 + U_2 + U_3}{I} = \frac{U_1}{I} + \frac{ U_2}{I} + \frac{U_3}{I} = R_1 + R_2 + R_3$$
В параллельных сценариях проводимости аддитивны, так как аддитивны токи при одном и том же напряжении. 9{n} \frac{1}{R_i} }$$
Это справедливо даже для других пассивных компонентов, таких как конденсаторы и катушки индуктивности, если задействованы соответствующие комплексные арифметические и обобщенные величины импеданса (комплексного сопротивления) и полной проводимости (комплексной проводимости). .
Несколько аналогий:
- Представьте, что в топливном баке вашего автомобиля есть негерметичное отверстие с некоторым сопротивлением потоку, и бензин вытекает из бака. Помогает ли это замедлить утечку, если вы пробьете много других отверстий?
- Если вышеуказанный резервуар протекает в одном месте, помогает ли это полностью остановить течь, если в других местах течи нет вообще?
- Изолированный провод — это параллельное соединение провода и его изоляции.
Если бы их сопротивление было аддитивным, вы не могли бы использовать изолированные провода для проведения электричества.
$\endgroup$
3
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью GoogleЗарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.Ветви, узлы и циклы с последовательностью и параллельностью
Опубликовано
Каждый шаг в процессе обучения необходим для создания основы для следующего шага. В некоторых случаях это более верно, чем в других случаях. В данном случае это вдвойне верно, так как многие вещи, которые мы обсуждаем сегодня, не будут напрямую применимы к решению схем, но будут абсолютно фундаментальными для понимания структуры схем, что, возможно, является первым шагом в решении схемы. Так что, возможно, я противоречу себе. Но со временем это станет настолько естественным, что даже не будет осознанным шагом.
Первая часть схемы, которую мы собираемся обсудить, — это ответвления. Ответвление — это общий термин, обозначающий один элемент в цепи. Это может быть источник напряжения, резистор, конденсатор, катушка индуктивности или что-то еще. Он охватывает любой двухполюсник. Более сложные устройства, такие как операционные усилители или микроконтроллеры, не подходят под термин «ветвь», но ничего страшного, мы пока не будем иметь дело с чем-то настолько сложным.
Второй частью цепи является узел. Это точка соединения между двумя или более ветвями. Хорошим способом думать об этом может быть соединение, где токи втекают и вытекают в зависимости от разных ветвей. Узлы являются важной частью анализа и проектирования схем, поэтому давайте рассмотрим пару примеров того, что такое узлы:
Наконец, последняя часть цепи, которая важна для нас в данный момент, — это петля. Петля — это замкнутый путь в цепи. Замкнутый путь означает, что он начинается в узле, проходит через другие узлы и заканчивается в том же узле, не проходя через какой-либо другой узел дважды. Обратите внимание, что определение является гибким в том смысле, что вы можете включать больше узлов или исключать узлы, если вы не проходите через один и тот же узел дважды, кроме начального/конечного узла. Давайте посмотрим на пример одной и той же цепи и двух разных петель, которые перекрываются.
Это важно, потому что при анализе цепей у вас есть преимущество в том, что вы можете выбирать циклы, которые наилучшим образом соответствуют ситуации, но есть недостаток, заключающийся в том, что они немного сложнее, поскольку вам нужно убедиться, что ваши циклы имеют математический смысл. и в сочетании друг с другом. С большой гибкостью приходит большая ответственность.
Теперь, когда мы рассмотрели эти термины и, в частности, узнали, что такое узлы, мы можем поговорить о последовательных и параллельных ответвлениях и в чем их отличия.
Последовательное и параллельное
Ответвление или элемент с двумя выводами соединены последовательно с одним или несколькими другими ответвлениями, если они используют только один узел и пропускают одинаковую величину тока. Обычно они выглядят так, как будто они соединены последовательно, один за другим, как цепочка. Лучший способ описать это, вероятно, с помощью нескольких изображений. В качестве примера мы будем использовать резисторы, которыми славится наш друг из CircuitBread, компания Ohmite.
Как вы можете видеть на первом изображении, есть две ветви, обе резисторы, и между ними есть узел, который является исключительным для этих двух ветвей. Таким образом, любой ток, протекающий через один резистор, будет протекать через другой.
На втором изображении есть три ответвления, два резистора сверху и один резистор снизу. Это более сложный пример, поскольку есть один узел, к которому подключены все три ветви. Если посмотреть на это с одной стороны, сгруппировав два верхних резистора, то два верхних резистора включены последовательно с нижним резистором. Любой ток, протекающий через эти верхние резисторы, будет протекать через нижний резистор, поэтому оба этих верхних резистора включены последовательно с нижним резистором. Важно отметить, что только один из этих резисторов наверху имеет номинал 9.0116, а не
последовательно с нижним резистором, это то, что оба из этих резисторов наверху последовательно соединены с одним резистором внизу.Ветки параллельны, когда два или более двухполюсных элемента подключены к одним и тем же двум узлам. В этом случае не имеет значения, подключены ли другие вещи к любому из этих узлов — пока оба элемента двухполюсника подключены к одним и тем же узлам, они параллельны. В то время как последовательные устройства имеют одинаковый ток через них, параллельные устройства имеют одинаковое напряжение на них. Еще раз, некоторые изображения, надеюсь, помогут.
Как вы можете легко видеть на первом и втором изображениях, эти ветви, снова представленные резисторами, имеют обе стороны своих узлов. На втором изображении, несмотря на то, что ветвей больше, все они имеют одни и те же два узла, поэтому все они параллельны. Однако третье изображение немного усложняет ситуацию. Есть два последовательно соединенных резистора, и эти два последовательно соединенных резистора параллельны одному резистору. Иногда сложные массивы резисторов или любые другие ответвления можно легко упростить, если вы можете распознавать такие вещи.
Прежде чем мы будем слишком взволнованы, мы должны помнить, что не все последовательно или параллельно, но это происходит достаточно часто, так что вы не только должны, но и почти наверняка станете естественным в идентификации и получении информации из последовательностей и параллельных схемы.
Помимо знания того, что последовательные ветви имеют общий ток, а параллельные ветви имеют одинаковое напряжение на них, одна из важных причин важности параллельных и последовательных компонентов заключается в том, что их обычно можно упростить. Давайте рассмотрим, как это сделать, и я хотел бы отметить, что это применимо только к резисторам, хотя позже принципы будут довольно хорошо перенесены на другие компоненты.
Чтобы упростить последовательные резисторы, просто сложите их вместе. Это очень просто и безболезненно. Это также имеет смысл — если электричество должно сначала пройти через один резистор, а затем через другой, оно должно пробиться через сопротивление обоих из них. Давайте посмотрим на несколько очень быстрых примеров.
Мы всегда рекомендуем проводить практические эксперименты во время обучения, так как это помогает усвоить информацию. Компания Ohmite известна своими мощными резисторами, которые определенно являются излишними для этих примеров (хотя их интересно проверить!), но вы можете получить некоторые из них. Маленькие резисторы Rebel, которые являются отличными резисторами, но намного, намного дешевле, чем резисторы большой мощности. Если вы можете, я рекомендую выбрать несколько разных значений и попробовать эти схемы с помощью недорогого мультиметра или омметра.
Упрощение параллельных резисторов немного сложнее, но все же просто, и есть даже случаи, когда шаги можно упростить еще больше. В общем случае, чтобы рассчитать эквивалентное сопротивление параллельных резисторов, вы просто используете это уравнение:
Little Rebel Resistors
Высококачественные, но недорогие резисторы от Ohmite, которые можно использовать для проверки этих концепций на макетной плате.
Купить онлайн
ОТ Ohmite
Это очень просто, если у вас есть калькулятор, а у нас есть инструмент, который делает это еще проще. уравнение. Убедитесь, что вы не пропустите этот шаг! Тем не менее, самое главное — получить интуитивное представление об этом. Одна вещь, которую вы должны понимать, заключается в том, что резисторы, соединенные параллельно, будут создавать эквивалентное сопротивление, меньшее, чем сопротивление наименьшего резистора. И чем больше резисторов вы соедините параллельно, тем меньше будет общее сопротивление.
Есть два случая, когда это уравнение можно упростить. Дело в том, что у вас всего два резистора. Тогда уравнение упрощается до:
В последнем случае, если два резистора имеют одинаковое сопротивление, то эквивалентное сопротивление составляет половину двух резисторов. Вы можете подставить любое число в любое уравнение и доказать это себе, если вы недоверчивый тип.
Краткое описание ветвей, узлов и контуров с последовательными и параллельными компонентами
Теперь мы на один шаг ближе к тому, чтобы анализировать существующие схемы и разрабатывать собственные! Мы узнали несколько важных терминов об электронных схемах и теперь можем идентифицировать ветви, узлы и петли. Мы использовали наши знания о ветвях и узлах, чтобы узнать о последовательных и параллельных цепях, как их идентифицировать и как их упростить. Мы скоро воспользуемся нашими знаниями о петлях, когда узнаем о законах тока и напряжения Кирхгофа (KCL и KVL соответственно), двух больших частях анализа цепей, которые откроют огромный сундук с инструментами для вашего электронного арсенала. Однако, прежде чем мы узнаем о KCL и KVL, осталось узнать о различных источниках питания в нашем следующем руководстве.
Автор:
Джош Бишоп
Интересуясь встраиваемыми системами, туризмом, кулинарией и чтением, Джош получил степень бакалавра электротехники в Университете штата Бойсе. Проработав несколько лет офицером CEC (Seabee) в ВМС США, Джош уволился и в конце концов начал работать над CircuitBread с кучей замечательных людей. В настоящее время Джош живет на юге Айдахо с женой и четырьмя детьми.
Создано с нашим другом:
Компания Ohmite является ведущим поставщиком резистивных изделий для сильноточных, высоковольтных и высокоэнергетических приложений .
