Формула последовательного соединения резисторов. Последовательное и параллельное соединение резисторов: формулы, правила и примеры

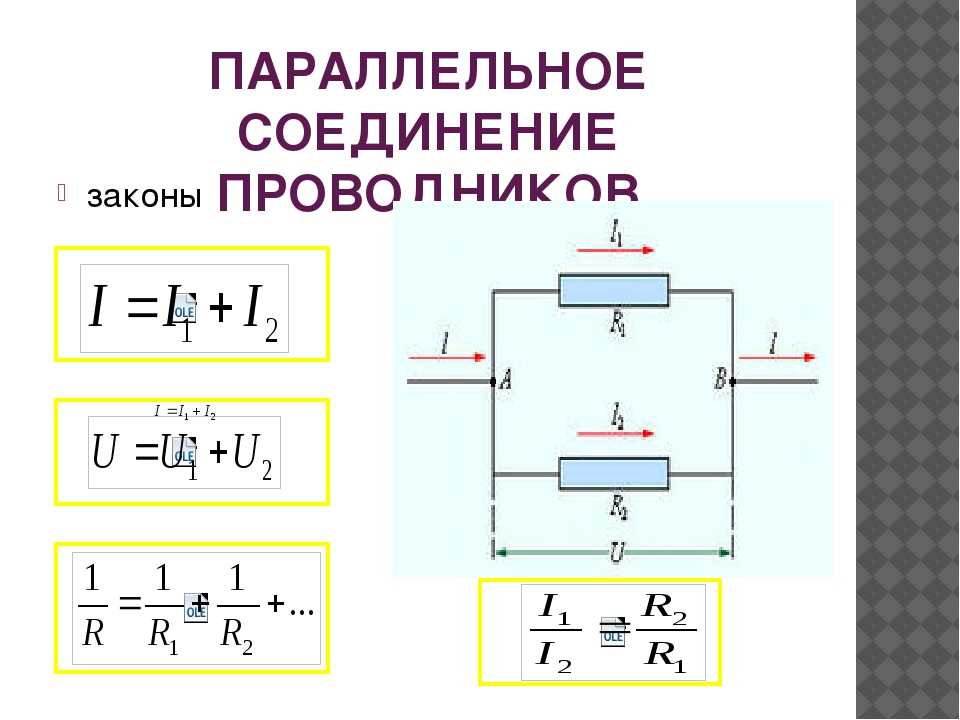
Как рассчитать общее сопротивление при последовательном и параллельном соединении резисторов. Какие основные правила и формулы нужно знать. Как ток и напряжение распределяются в цепи при разных типах соединений. Какие есть практические примеры расчетов.

Последовательное соединение резисторов

При последовательном соединении резисторы подключаются один за другим, образуя единую цепь. Основные характеристики такого соединения:

• Общее сопротивление равно сумме сопротивлений всех резисторов
• Ток через все резисторы одинаковый
• Напряжение на резисторах различное и пропорционально их сопротивлению

Формула для расчета общего сопротивления при последовательном соединении:

R = R1 + R2 + R3 + … + Rn

Где R — общее сопротивление, R1, R2, R3 и т.д. — сопротивления отдельных резисторов.

Параллельное соединение резисторов

При параллельном соединении резисторы подключаются между одними и теми же точками цепи. Основные характеристики:

• Общее сопротивление меньше сопротивления любого из резисторов
• Напряжение на всех резисторах одинаковое
• Ток через резисторы различный и обратно пропорционален их сопротивлению

Формула для расчета общего сопротивления при параллельном соединении:

1/R = 1/R1 + 1/R2 + 1/R3 + … + 1/Rn

Где R — общее сопротивление, R1, R2, R3 и т.д. — сопротивления отдельных резисторов.

Распределение тока и напряжения в цепях

Как распределяются ток и напряжение при разных типах соединений резисторов:

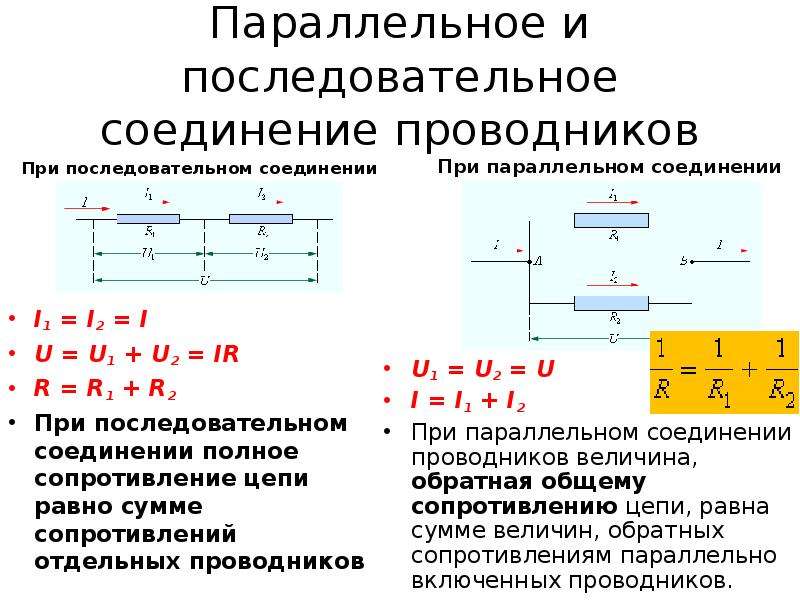
Последовательное соединение:

• Ток через все резисторы одинаковый: I = I1 = I2 = I3 …
• Общее напряжение равно сумме напряжений на резисторах: U = U1 + U2 + U3 …

Параллельное соединение:

• Напряжение на всех резисторах одинаковое: U = U1 = U2 = U3 …
• Общий ток равен сумме токов через резисторы: I = I1 + I2 + I3 …

Практические примеры расчетов

Рассмотрим несколько примеров расчета общего сопротивления при различных соединениях резисторов.

Пример 1: Последовательное соединение

Дано: 3 резистора соединены последовательно, R1 = 10 Ом, R2 = 20 Ом, R3 = 30 Ом.

Решение: R = R1 + R2 + R3 = 10 + 20 + 30 = 60 Ом

Ответ: Общее сопротивление цепи равно 60 Ом.

Пример 2: Параллельное соединение

Дано: 2 резистора соединены параллельно, R1 = 100 Ом, R2 = 200 Ом.

Решение: 1/R = 1/R1 + 1/R2 = 1/100 + 1/200 = 0.015

R = 1/0.015 = 66.7 Ом

Ответ: Общее сопротивление цепи равно 66.7 Ом.

Применение законов соединения резисторов

Знание законов последовательного и параллельного соединения резисторов важно для:

• Проектирования электрических цепей
• Расчета параметров электрических схем
• Анализа работы электронных устройств
• Выбора номиналов компонентов при разработке

Правильное применение этих законов позволяет создавать эффективные и надежные электрические схемы.

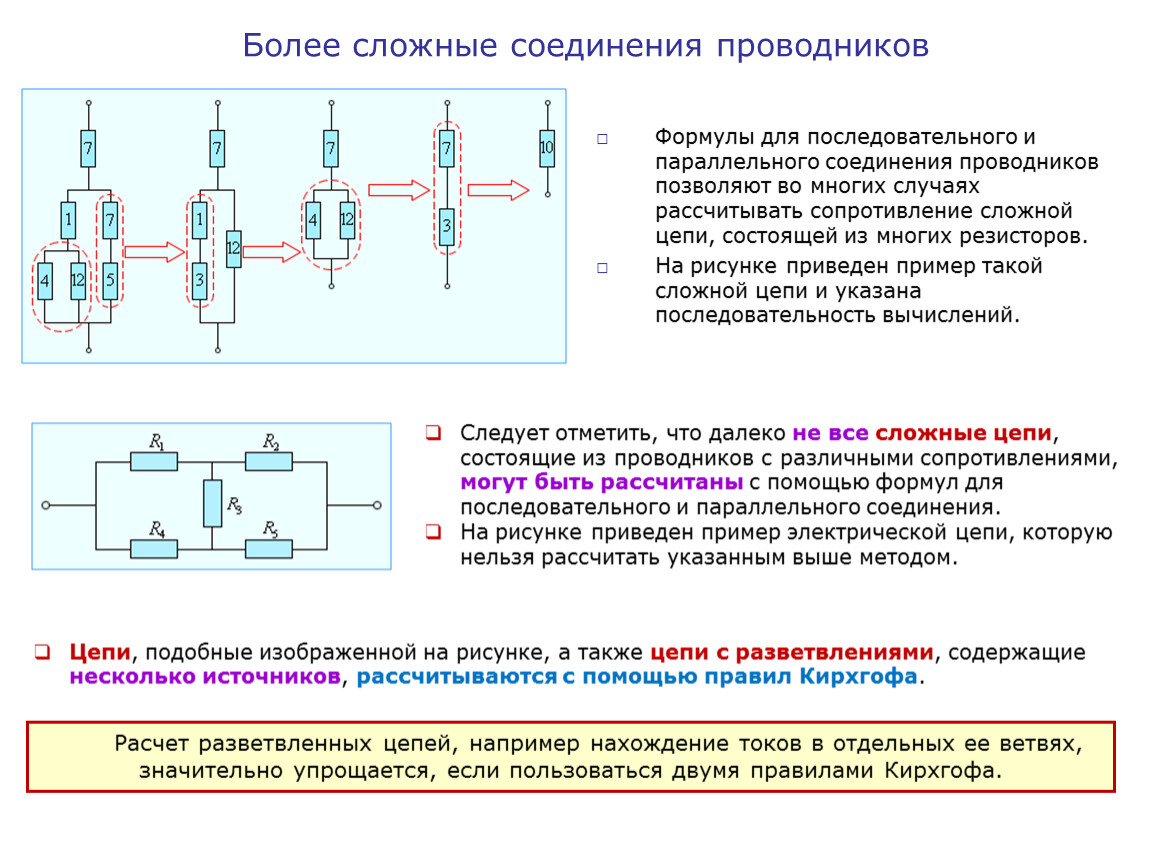
Смешанное соединение резисторов

В реальных электрических схемах часто встречается смешанное (последовательно-параллельное) соединение резисторов. В этом случае расчет общего сопротивления проводится поэтапно:

1. Выделяются группы резисторов, соединенных последовательно или параллельно
2. Рассчитывается эквивалентное сопротивление для каждой группы
3. Полученные эквивалентные сопротивления рассматриваются как отдельные резисторы
4. Процесс повторяется, пока не будет получено общее сопротивление всей цепи

Такой подход позволяет анализировать сложные электрические схемы, разбивая их на более простые элементы.

Особенности выбора типа соединения резисторов

При проектировании электрических схем выбор типа соединения резисторов зависит от требуемых характеристик цепи:

• Последовательное соединение используется, когда нужно увеличить общее сопротивление или разделить напряжение
• Параллельное соединение применяется для уменьшения общего сопротивления или разделения тока
• Смешанное соединение позволяет достичь более точной настройки параметров цепи

Правильный выбор типа соединения резисторов позволяет оптимизировать работу электрической схемы и добиться требуемых характеристик.

Заключение

Понимание принципов последовательного и параллельного соединения резисторов является фундаментальным для работы с электрическими цепями. Эти знания позволяют:

• Рассчитывать параметры сложных электрических схем
• Проектировать эффективные электронные устройства
• Анализировать работу существующих электрических цепей
• Находить неисправности в электронном оборудовании

Применение этих принципов на практике открывает широкие возможности в области электроники и электротехники.

Последовательное соединение резисторов

Физика > Последовательное соединение резисторов

 

Узнайте, чему равно сопротивление резисторов при последовательном соединении: общее сопротивление цепи, схема последовательного соединения, формула закона Ома.

В цепочке последовательной связи резисторов полное сопротивление равняется сумме отдельных.

Задача обучения

• Вывести общее сопротивление цепочки.

Основные пункты

• Одинаковый поток протекает сквозь каждый резистор последовательно.
• Индивидуальные резисторы не получают общее напряжение, но разделяют его.
• Общее сопротивление в последовательной цепи равно сумме отдельных: RN _{(последовательно)} = R₁ + R₂ + R₃ + … + R_N.

Термины

• Серии – несколько элементов, следующих один за другим или связанных последовательно.
• Сопротивление – противодействие поступлению электрического тока.

Обзор

Многие схемы электрических цепей размещают больше одного резистора, ограничивающего поток заряда в цепи. Мера предела потока – сопротивление. Простейшими резисторными комбинациями выступают последовательные и параллельные соединения. Полное сопротивление зависит от индивидуальных значений и метода связи.

Последовательное соединение

Резисторы пребывают в последовательном соединении, если поток заряда или тока проходит сквозь составляющие последовательно.

Эти 4 резистора находятся в последовательном подключении, потому что если на одном конце подать ток, то он пройдет по всем резисторам по очереди до второго конца

Полное сопротивление в последовательном соединении резисторов электрической цепи приравнивается к сумме отдельных сопротивлений, потому что ток должен пройти сквозь каждый по очереди.

Три резистора объединены последовательно с батареей (слева) и эквивалентным однократным сопротивлением (справа)

Закон Ома в расчете изменения напряжения в последовательном подключении

В законе Ома падение напряжения (V) вычисляется формулой: V = IR (I – ток в амперах, а R – сопротивление в Ом).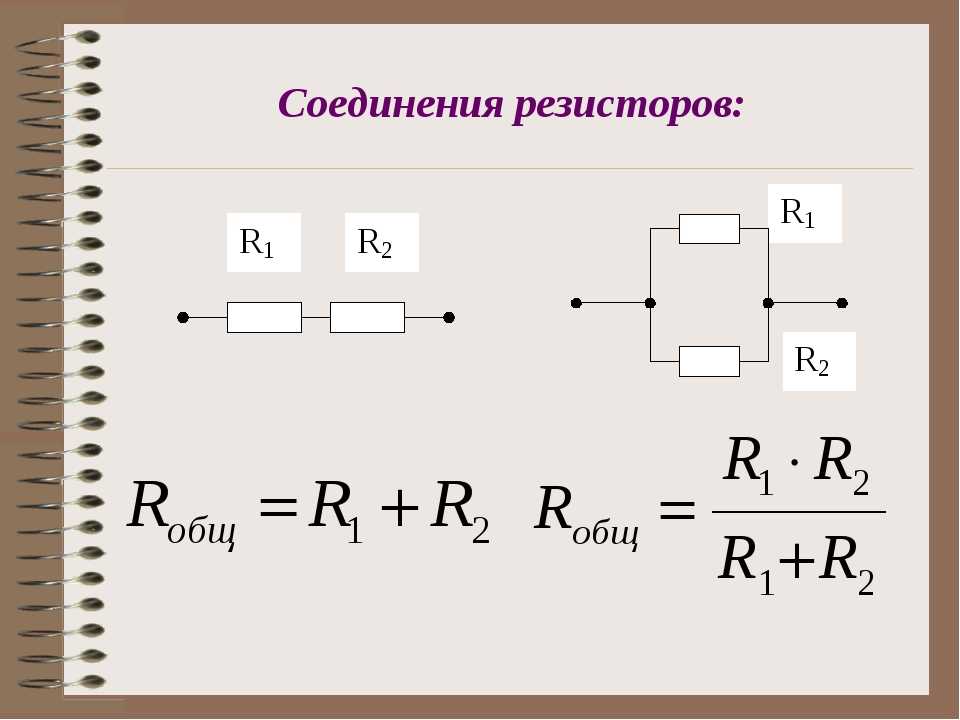 В итоге, падение напряжения равно:

V₁ = IR₁

V₂ = IR₂

V₃ = IR₃.

Сумма напряжений: V = V₁ + V₂ + V₃, основываясь на сохранении энергии и заряда. Если подставить значения для отдельных напряжений:

V = IR₁ + IR₂ + IR₃ или V = I (R₁ + R₂ + R₃).

То есть, общее сопротивление в ряду равно сумме отдельных. Поэтому для каждой схемы с N числом резисторов, соединенных последовательно: RN _{(последовательно)}

= R₁ + R₂ + R₃ + … R_N.

Весь ток должен пройти через каждый резистор, поэтому сопротивления добавляются. Напряжение и сопротивления обладают обратной зависимостью, поэтому отдельные резисторы не получают общее напряжение, а разделяют его. Допустим, у нас есть простая схема с батарей 1.5 В и лампочкой, чье напряжение составляет 1.5 В. Но, если подключить последовательно две лампочки, то каждая имела бы 0. 75 В (1.5В/2). Это было бы заметно по яркости сияния.

---

Последовательное соединение резисторов

При последовательном соединении резисторов, на этом участке цепи ток будет все время одинаковым.

Формула расчета простая — Суммарное сопротивление на участке цепи будет равна сумме значений сопротивлений всех резисторов, включенных в цепь. Вид формулы следующий

Rсум=∑R

, где R – значение каждого из резисторов в цепи

т. е. Вам надо сложить сопротивление всех резисторов в цепи и их сумма покажет общее сопротивление.

Давайте сделаем шаг в сторону, чтобы проще было понять смысл суммарного сопротивления.

Ток течет по цепи, и визуально его можно представит, как поток воды, который течет сквозь трубу.

Трубы меньшего диаметра — по сути, являются резисторами, которые затрудняют проток и делают его меньше. Например, вы когда-нибудь пробовали потянуть напиток из кружки через очень очень узкую трубочку? Усилий можно делать много, но поток в рот будет все равно слишком маленьким. И чем больше таких разных сужений будет, тем сложнее вам будет тянуть напиток через трубочку. По такому же принципу работают резисторы, уменьшая ток.

Закон Ома гласит, что ток равен напряжению, деленному на сопротивление.

I=U/R

Давайте рассмотрим примеры использования формулы, а заодно изучим понятие падения напряжения.

Пример №1

Дана схема цепи с последовательным сопротивлением трех резисторов.

Источник постоянного тока с напряжением на входе 24 V

Три резистора, соединенных последовательно, с сопротивлениями, 6,3 и 3 Ом соответственно. Т.е. R1=6 Ом, R2=3 Ом, R3=3 Ом

Cхема простейшей цепи постоянного тока с последовательным соединением Резисторов

Определим суммарное сопротивление этой простой цепи:

Согласно нашей формуле, суммарное сопротивление последовательно соединенных транзисторов будет равно сумме всех сопротивлений:

Rсум=6Ом+3Ом+3Ом=12 Ом

Давайте определим ток на участке по формуле выше:

I=Uвх/Rсум

I=24В/12Ом=2А

Таким образом, мы определили, что ток на всем участке будет равен 2 амперам.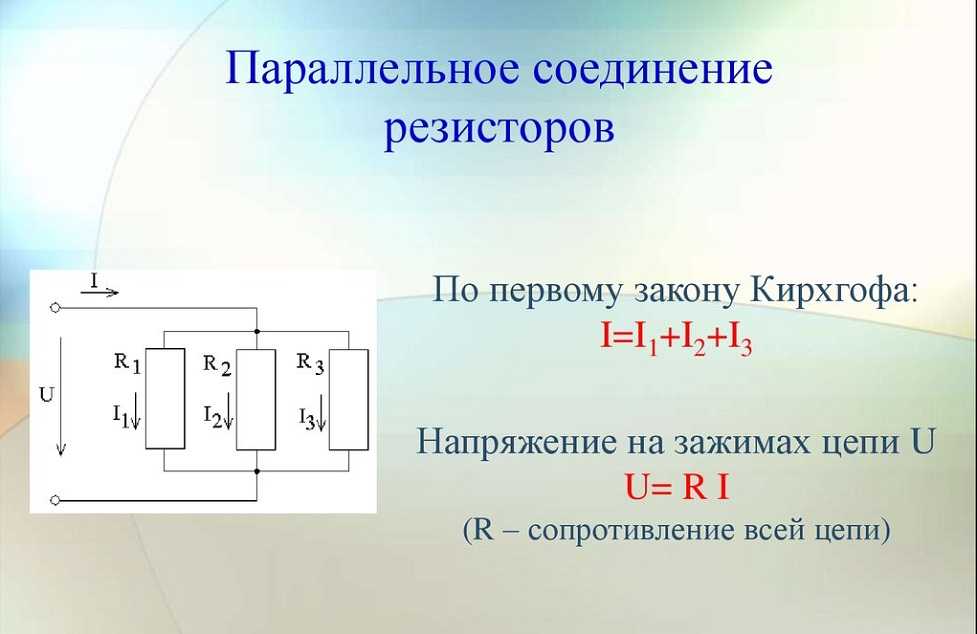

Давайте определим падение напряжения на каждом элементе нашей цепи.

Еще небольшое отступление. Каждый резистор будет как бы забирать часть напряжения на себя, и чем выше его сопротивление, тем больше напряжения будет на нем «падать».

В любом замкнутом контуре, сумма напряжений равна нулю. Таким образом, в нашем случае справедлива формула Uвх=Ur1+ Ur2+ Ur3

А как определить эти значения? Очень просто. Мы знаем, что ток везде одинаковый, и знаем значения каждого отдельного сопротивления R1,R2,R3.

Тогда Ur1= R1*I=6Ом*2А=12В

Ur2= R2*I=3Ом*2А=6В

Ur3= R3*I=3Ом*2А=6В

Пример №2

Схема цепи с последовательным сопротивлением двух резисторов.

Схема с двумя резисторами, подключенными последовательно

Источник постоянного тока с напряжением на входе 12 V

Два резистора, соединенных последовательно, с сопротивлениями, 2,1 Ом соответственно. Т.е. R1=2 Ом, R2=1 Ом

Далее все расчеты аналогичны.

Шаг первый — определяем суммарное значение сопротивления: Rсум=2Ом+1Ом=3Ом

Шаг второй — определяем ток в этом участке цепи: I=12В/3Ом=4А

Шаг третий — считаем падения напряжения на каждом элементе цепи с последовательным сопротивлением двух резисторов:

Ur1= R1*I=2Ом*4А=8В

Ur2= R2*I=1Ом*4А=4В

Как и в прошлом расчете, сумма падений напряжений (8+4) будет равна входному напряжению.

Обратите внимание, что в случае последовательного соединения резисторов, суммарное сопротивление всегда будет больше любого отдельно взятого резистора в этой цепи.

Надеюсь, что это поможет вам в понимании. Если есть какие-то вопросы по написанному материалу, то пишите в комментах.

резисторов, соединенных последовательно и параллельно: формула

Слово «сопротивление» имеет много разных значений: сопротивление воздуха — это сила, которая замедляет объекты, движущиеся по воздуху, ваше тело обладает устойчивостью ко многим болезням благодаря вашей иммунной системе, а группа людей может сформировать сопротивление политическому режиму. В случае электрических цепей сопротивление является сопротивлением протеканию тока. Сопротивление цепи можно увеличить или уменьшить, добавив компоненты цепи, называемые резисторами. Они могут быть добавлены либо в последовательном соединении, либо в параллельном соединении. В этой статье мы рассмотрим оба этих типа соединений и их последствия в электрических цепях.

Добавление резисторов последовательно и параллельно

Схемы, которые мы будем рассматривать в этой статье, будут содержать только батареи, провода и резисторы. Батареи — это источник питания, который пропускает ток по цепи, а резисторы обеспечивают сопротивление этому току.

Электрическое сопротивление — это мера сопротивления электрического компонента протеканию тока. Измеряется в Омах, \(\mathrm\Omega\).

Обозначение цепи для резистора показано на рис. 1. На самом деле это называется фиксированный резистор и существуют различные другие типы резисторов. Общее сопротивление цепи зависит от того, как различные резисторы соединены вместе.

Рис. 1 — Схема резистора.

Резисторы могут быть объединены в серии , то есть когда они добавляются друг за другом — они находятся на одной ветви цепи. В этой настройке мы говорим, что они используют только один узел.

Узел — это область на цепи между двумя элементами схемы.

Рис. 2 — Резисторы последовательно соединены на одной ветви.

Резисторы также могут быть добавлены в параллельно , когда они добавляются друг напротив друга — они находятся на разных ветвях цепи. В этом случае резисторы имеют общие узлы на обоих концах.

Рис, 3 — Параллельно резисторы находятся на разных ветвях, но имеют одни и те же узлы.

Напряжение на резисторах, соединенных последовательно и параллельно

Мы можем узнать больше о резисторах, соединенных последовательно и параллельно, рассматривая падение напряжения на них при протекании тока.

Напряжение — энергия, передаваемая на единицу проходящего заряда.

Общее падение напряжения на последовательно соединенных резисторах равно сумме падений напряжения на каждом резисторе. Например, рассмотрим цепь с батареей и двумя резисторами одинакового сопротивления \(R\), соединенными последовательно. Если напряжение, подаваемое батареей, равно \( V \), то падение напряжения на каждом резисторе будет \( \frac V2 \).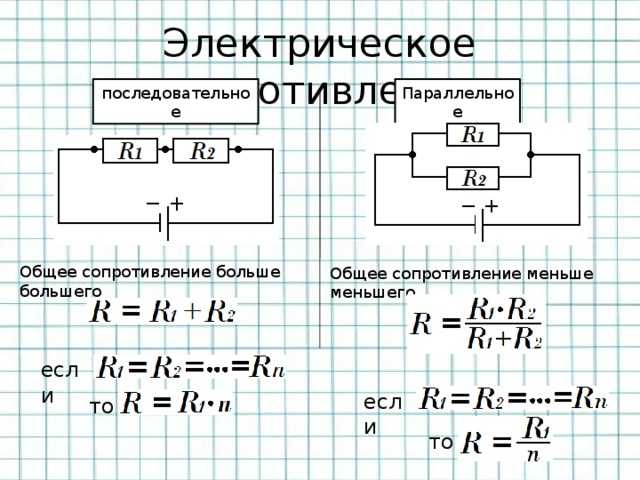

Рис. 4. Общее падение напряжения на последовательно соединенных резисторах равно сумме падений напряжения на каждом резисторе. Падение напряжения можно измерить с помощью вольтметра.

С другой стороны, одинаковое напряжение будет подаваться на каждый резистор для цепи с батареей и двумя резисторами, соединенными параллельно. Если напряжение батареи равно \(V\), то падение напряжения на каждом резисторе также будет \(V\).

Рис. 5 — Все резисторы в параллельном соединении получают все напряжение от батареи.

Эти два случая легко обобщаются на любое количество резисторов. Для последовательно соединенных резисторов подаваемое напряжение определяется как

$$V=V_1+V_2+…+V_N,$$

, где нижние индексы указывают резистор. Для резисторов, включенных параллельно:

$$V=V_1=V_2=…=V_N.$$

Ток через резисторы, включенные последовательно и параллельно

Величина тока, протекающего через резисторы, отличается, когда они соединены последовательно и когда они соединены параллельно.

Поток носителей заряда в электрической цепи называется током . Он измеряется в амперах, \(\mathrm A \).

Для резисторов, соединенных последовательно, через все резисторы протекает один и тот же ток, поскольку между резисторами нет соединений, в которых ток может разделяться.

$$I=I_1=I_2=…=I_N.$$

При параллельном соединении резисторов ток распределяется между ними. Для \( N \) резисторов, включенных параллельно, общий ток через них определяется как

$$I=I_1+I_2+…+I_N.$$

Резисторы в последовательном и параллельном соединении Формулы

Чтобы найти формулы для сопротивления резисторов, включенных последовательно и параллельно, нам нужно использовать закон Ома, который гласит, что для омического проводника соотношение между его напряжением, током и сопротивлением равно

$$V=IR.$$

Постоянные резисторы являются омическими проводниками и подчиняются закону Ома. Для резисторов, соединенных последовательно, подводимое напряжение определяется падением напряжения на резисторах по

$$V=V_1+V_2+.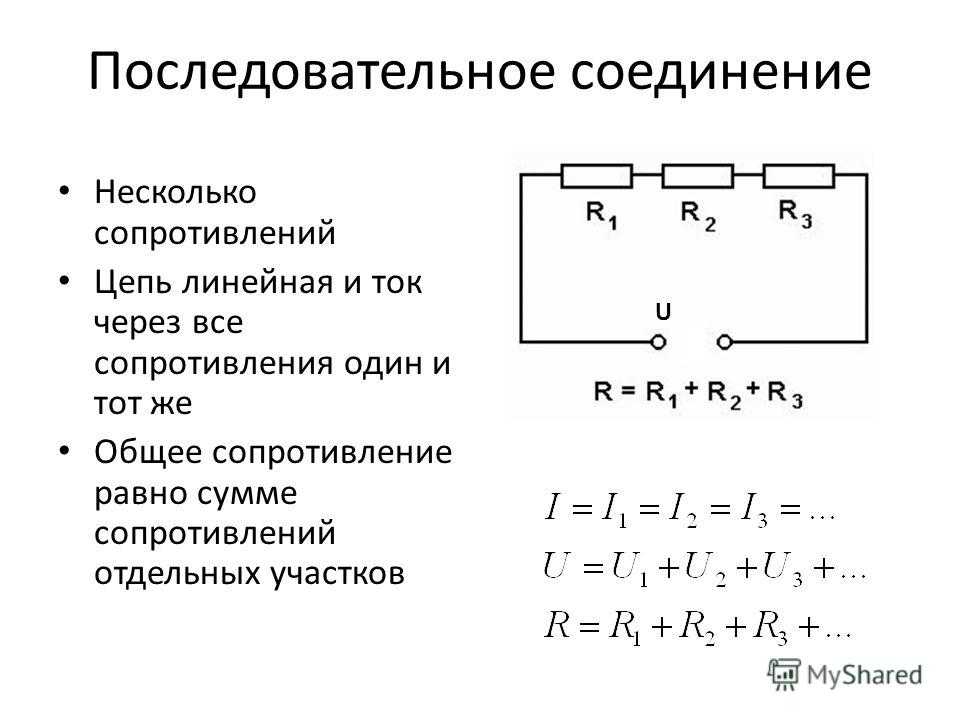 ..+V_N.$$

Общее сопротивление резисторов определяется измененная версия закона Ома:

$$R_T=\frac VI.$$

Ток одинаков через каждый резистор для последовательной комбинации, поэтому

$$R_T=\frac{V_1}{I}+\ frac{V_2}{I}+…\frac{V_N}{I}.$$

Каждый член представляет собой просто сопротивление каждого резистора, поэтому общее сопротивление последовательного соединения равно сумме сопротивлений резисторов!

$$R_T=R_1+R_2+…R_N.$$ Тот же процесс можно повторить, чтобы найти общее сопротивление параллельной комбинации. Для резисторов, включенных параллельно, ток распределяется между ними, и общий ток равен

$$I=I_1+I_2+…+I_N.$$

Общий ток будет равен подаваемому напряжению, деленному на общее сопротивление:

$$I=\frac {V}{R_T}.$$

Падение напряжения на каждом резисторе равно \( V \), поэтому ток через каждый резистор можно выразить аналогичным образом. Например, для первого резистора:

$$I_1=\frac{V}{R_1},$$

можно записать следующее выражение (оба слагаемых равны полному току):

$$\frac {V}{R_T}=\frac{V}{R_1}+\frac{V}{R_2}+.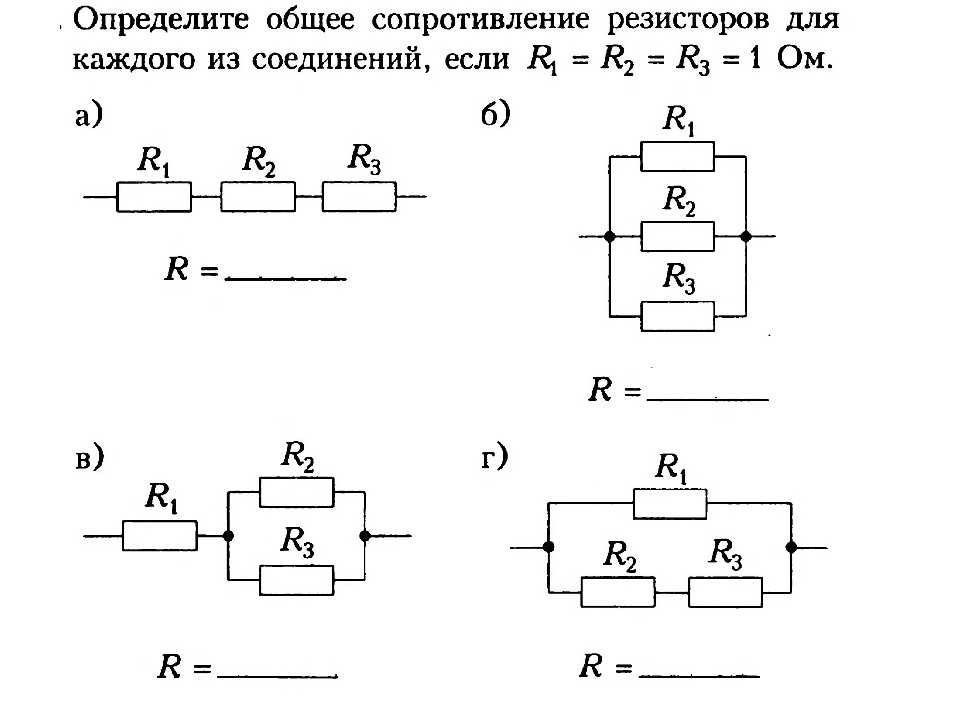 ..+\frac{V}{R_N}.$$

\( V \) на любой сторона компенсируется и оставляет уравнение для сопротивления комбинации параллельных резисторов.

$$\frac 1{R_T}=\frac{1}{R_1}+\frac{1}{R_2}+…+\frac{1}{R_N}.$$

Разница между резисторами в Последовательное и параллельное

Существует несколько основных различий между резисторами при параллельном и последовательном соединении:

• Общее падение напряжения при последовательном соединении равно сумме падений отдельных напряжений. Падение напряжения на каждом резисторе при параллельном соединении одинаково.
• Ток через все резисторы при последовательном соединении одинаков. Ток распределяется между резисторами при параллельном соединении.
• Последовательное добавление резисторов увеличивает общее сопротивление, поскольку ток должен проходить через каждый резистор. Добавление большего количества резисторов параллельно уменьшает общее сопротивление, потому что есть больше путей для прохождения тока.

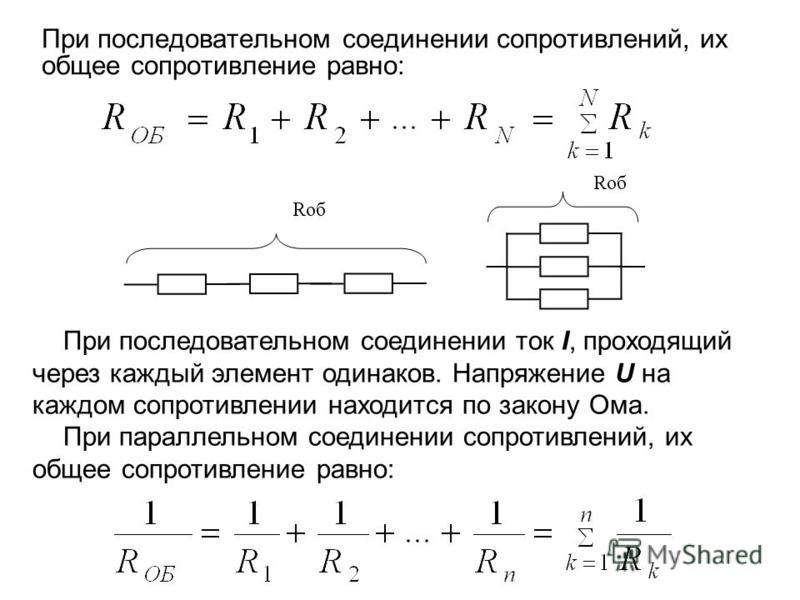
Правила для резисторов в последовательном и параллельном соединении

Правила для резисторов в последовательном и параллельном соединении приведены в таблице ниже, и их следует помнить.

Серия	Параллельный
Общее сопротивление равно \( R_T=R_1+R_2+…R_N \).	Суммарное сопротивление равно \( \frac 1{R_T}=\frac{1}{R_1}+\frac{1}{R_2}+…+\frac{1}{R_N} \).
Ток через резисторы одинаковый.	Ток распределяется между резисторами.
Падение напряжения представляет собой сумму падений напряжения на резисторах.	Падение напряжения на каждом резисторе одинаково.
Добавление дополнительных резисторов увеличивает сопротивление.	Добавление дополнительных резисторов уменьшает сопротивление.

Эквивалентные резисторы, включенные последовательно и параллельно

Рассмотрим два параллельно включенных резистора, каждый из которых имеет сопротивление \(2R\), как показано на схеме ниже.

Рис. 6 — Два резистора \(2R\), помещенные параллельно, имеют такое же сопротивление, как один резистор сопротивления \(R\).

Общее сопротивление комбинации можно рассчитать по формуле параллельных резисторов с \( N=2 \):

$$\frac 1{R_T}=\frac{1}{R_1}+\frac{1}{R_2}.$$

Оба сопротивления равны \( R \), поэтому получается

$$ \frac 1{R_T}=\frac{1}{2R}+\frac{1}{2R}=\frac 2R.$$

Преобразование этого выражения дает общее сопротивление как \( R_T=R \). Это показывает, что два резистора с сопротивлением \(2R\), соединенные параллельно, имеют такое же общее сопротивление, как и один резистор с сопротивлением \(R\).

Примеры резисторов, соединенных последовательно и параллельно

Формулы для резисторов, соединенных последовательно и параллельно, могут быть полезны при решении практических задач. В следующих практических задачах сопротивление батареи предполагается пренебрежимо малым.

Аккумулятор подает напряжение \( 6\,\mathrm V \) в цепь с резистором \( 5\,\mathrm\Omega \) и резистором неизвестного сопротивления.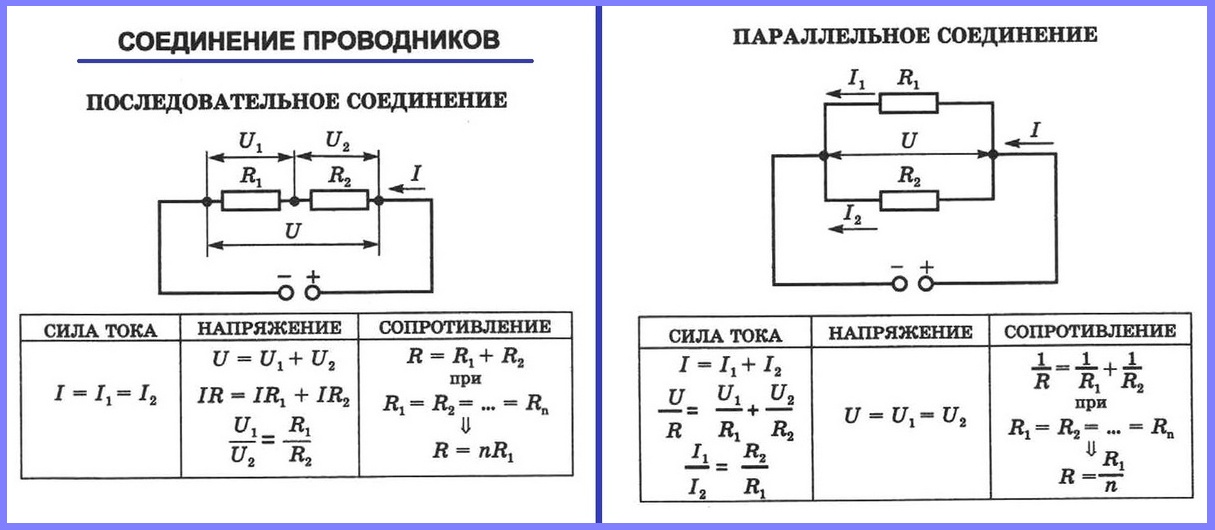 Схема показана ниже. Если ток, протекающий по цепи, равен \(1\,\mathrm A\), каково сопротивление второго резистора?

Рис. 7 — Ток измеряется амперметром в цепи с резистором неизвестного сопротивления.

Мы можем найти полное сопротивление цепи, используя закон Ома,

$$V=IR,$$

, которое можно преобразовать в

$$R=\frac VI.$$

Напряжение, выдаваемое батареей, равно \( 6\,\mathrm V \), а ток в цепи равен \( 3\, \mathrm A \), поэтому общее сопротивление равно

$$R=\frac{6\,\mathrm V}{1\,\mathrm A}=6\,\mathrm\Omega.$$

Имеем узнал, что общее сопротивление резисторов, соединенных последовательно, равно сумме их сопротивлений, поэтому неизвестное сопротивление будет равно сумме минус другое сопротивление:

$$6\,\mathrm\Omega-5\,\mathrm\Omega= 1\,\mathrm\Омега.$$

Два резистора в цепи снова соединены параллельно друг другу. Каков ток через каждый резистор? Чему равно полное сопротивление в цепи?

Рис. 8. Ток через каждый резистор изменяется при их параллельном соединении.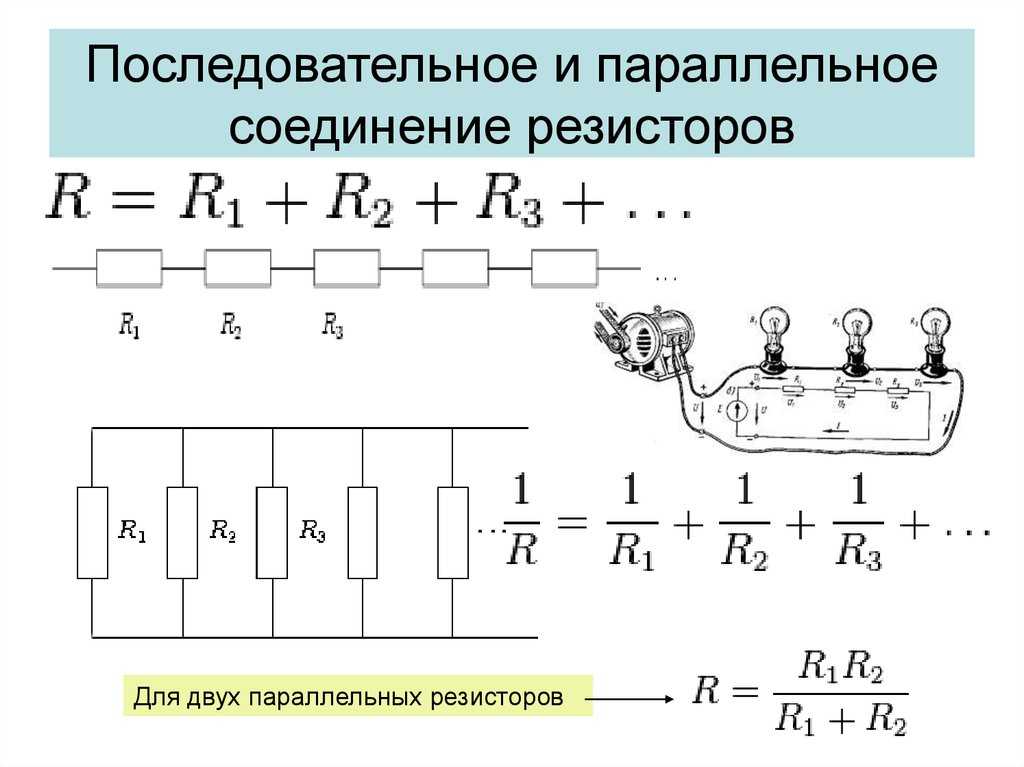

В параллельных цепях каждая ветвь получает все напряжение от батареи. Закон Ома, преобразованный для тока, равен

$$I=\frac VR.$$

Напряжение на обоих резисторах равно \( 6\,\mathrm V \), поэтому ток через \( 5\,\mathrm\ Омега \) резистор 9{-1}}=0,83\,\mathrm\Omega.$$

Это значение также можно получить, разделив напряжение батареи на общий ток. Полный ток равен сумме токов в ветвях

$$I=1.2\,\mathrm A+6\,\mathrm A=7.2\,\mathrm A$$

и, следовательно,

$$ R_T=\frac VI=\frac{6\,\mathrm V}{7.2\,\mathrm A}=0,83\,\mathrm\Omega.$$

Объединение резисторов последовательно и параллельно

В этой статье может показаться, что мы предполагали наличие одного резистора на каждой ветви в параллельных комбинациях. Однако, даже если их несколько, формулу последовательного соединения можно использовать для определения общего сопротивления нескольких резисторов на ответвлении, чтобы их можно было рассматривать как один резистор при использовании формулы параллельного резистора.

Рассчитайте общее сопротивление цепи на рис. 9.

Рис. 9 — Резисторы можно соединять параллельно и последовательно с другими резисторами.

В первой ветви схемы резистор \( 4\,\mathrm\Omega\) и резистор \( 6\,\mathrm\Omega \) соединены параллельно. Мы можем использовать формулу параллельных резисторов, чтобы найти их общее сопротивление:

$$\frac 1{R_T}=\frac 1{R_1}+\frac 1{R_2}.$$

Назовем общее сопротивление этих резисторов \( Р_П \).

$$\frac1{R_P}=\frac 1{4\,\mathrm\Omega}+\frac 1{6\,\mathrm\Omega}=\frac5{12\,\mathrm\Omega}$$

и

$$R_P=\frac{12}{5}\,\mathrm\Omega=2.4\,\mathrm\Omega.$$

Сопротивление первой ветви, \( R_{B1} \) , равно этому, добавленному к сопротивлению другого сопротивления на ветви, которое равно \( 2\,\mathrm\Omega \), поэтому

$$R_{B1}=2,4\,\mathrm\Omega+2 \,\mathrm\Omega=4.4\,\mathrm\Omega.$$

Суммарное сопротивление второй ветви равно \( 5\,\mathrm\Omega \). Мы можем найти полное сопротивление цепи \(R_C\) по формуле для параллельных резисторов:

$$\frac 1{R_C}=\frac 1{4. 4\,\mathrm\Omega}+\frac 1{5\,\mathrm\Omega}=0.43\,\mathrm\Omega,$$

который ведет к

$$R_C=\frac{1}{0,43}\,\mathrm\Omega=2.3\,\mathrm\Omega.$$

Резисторы в последовательном и параллельном соединении – основные выводы

• Электрическое сопротивление – это мера сопротивления электрического компонента протеканию тока. Измеряется в Омах, \(\mathrm\Omega\).
• Резисторы последовательно добавляются в цепь один за другим и имеют только один общий узел.
• Параллельные резисторы добавляются в цепь друг напротив друга и используют оба узла совместно.
• Узел — это область цепи между двумя элементами цепи.
• Последовательно соединенные резисторы пропускают через себя одинаковый ток.
• Резисторы, включенные параллельно, имеют одинаковое падение напряжения на них.
• Последовательное добавление резисторов увеличивает общее сопротивление.
• Параллельное добавление дополнительных резисторов уменьшает общее сопротивление.

---

Каталожные номера

1. Рис. 1 — «Схема резисторов», StudySmarter Originals
2. Рис. 2 — «Последовательно соединенные резисторы», StudySmarter Originals
3. Рис. 3 — «Параллельные резисторы», StudySmarter Originals Fig
4. 4 — «Схема с последовательными резисторами», StudySmarter Originals
5. Рис. 5 — «Схема с параллельными резисторами», StudySmarter Originals
6. Рис. 6 — «Пример схемы с параллельными резисторами», StudySmarter Originals
7. Рис. 7 — «Схема с последовательными резисторами». пример», StudySmarter Originals
8. Рис. 8 — «Схема параллельных резисторов с амперметрами», StudySmarter Originals
9. Рис. 9 — «Схема с параллельными и последовательными резисторами», StudySmarter Originals

Пример последовательного резистора

4 июля 2022 г.

0 26 мая 2018 г. , автор: Michal

Электрические компоненты можно соединять двумя способами: последовательно или параллельно. Оба типа соединений имеют свои преимущества и применение. Начнем с рассмотрения последовательного соединения. Используйте резистор в последовательном калькуляторе, чтобы ускорить расчет.

Серия Соединение резисторов:

Два компонента будут вызываться последовательно, если к узлу, к которому они подключены, не подключен другой компонент.

• 7 Меры предосторожности при ремонте электрооборудования в домашних условиях
• Краткое руководство по электронным генераторам и их различным типам

Предположим, два резистора подключены в точке b, а головка второго резистора соединена с хвостом первого резистора. Резисторы обычно не имеют головы и хвоста. Но когда течет ток, вы можете назначить им головы и хвосты, назначив положительные и отрицательные знаки в зависимости от падения напряжения, как показано.

Последовательная цепь обеспечивает только один путь для тока.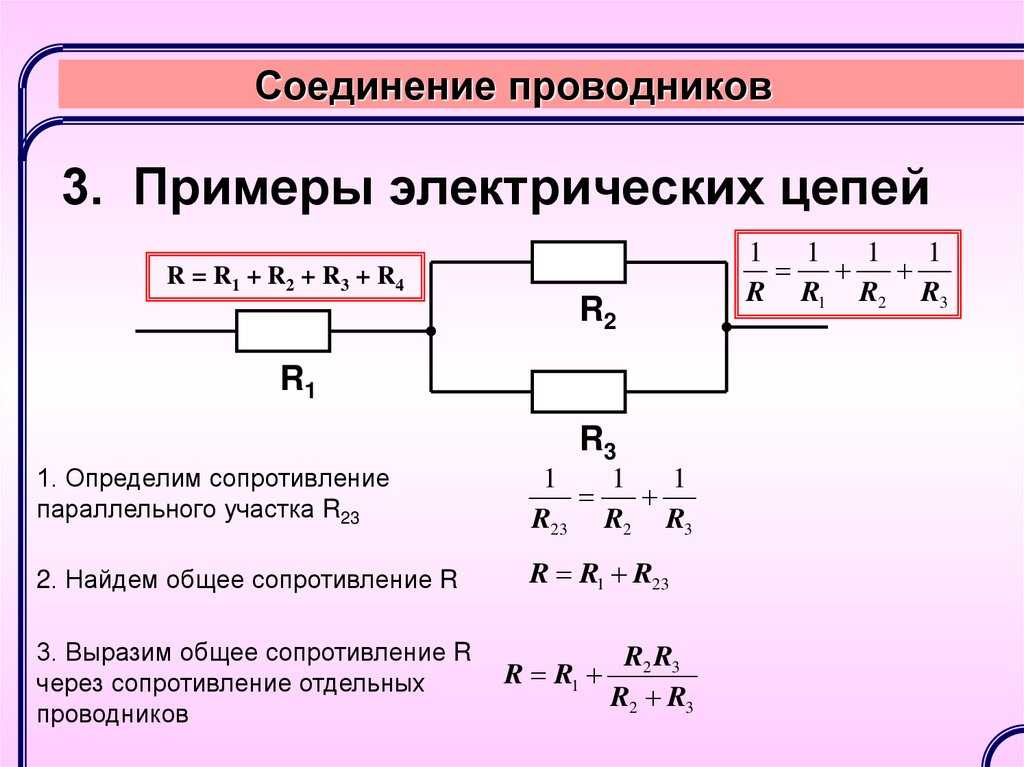

Обратите внимание, что ток может течь только по одному пути. Положительная клемма R ₂ соединена с отрицательной клеммой R ₁ , и к этой точке не подключен ни один элемент цепи, исходя из предположения, что ток течет из точки a в точку c. Если к точке b подключен какой-либо третий компонент цепи (источник или резистор), R ₁ и R ₂ больше не будут последовательно друг с другом.

Резистор в калькуляторе серии:

R ₁

R ₂

R ₃

R _{ЭКАКАВАЛЬНЫЙ}

В СЕРИОНЕ СКРИОВА. определили и попытались определить тип цепи. Следующий шаг — узнать, как найти эквивалентное сопротивление в сложной цепи? Предположим, у нас есть следующая сложная схема, и нас интересуют ответы на следующие вопросы.

Какой общий ток обеспечивает источник?

Чтобы узнать общий ток источника, во-первых, нам нужно знать, какое сопротивление испытывает источник? Общее сопротивление мы можем рассчитать по следующей формуле или использовать резистор в последовательном калькуляторе.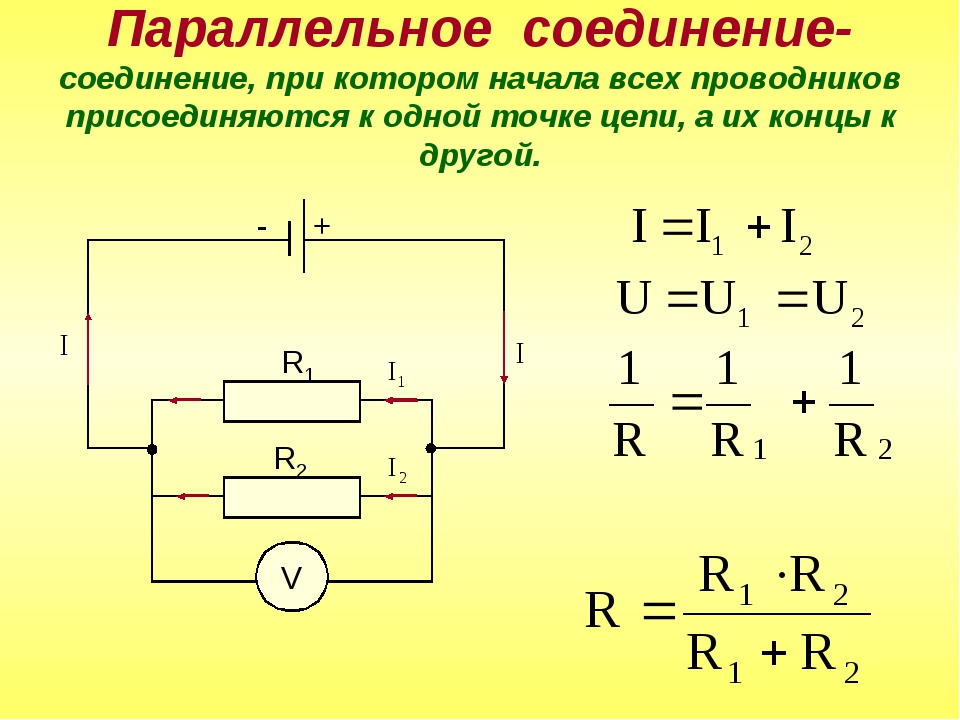 Здесь «n» — это общее количество резисторов, соединенных последовательно, в нашем случае n=3.

$R_{эквивалент}=R_{1}+R_{2}+\ldots +R_{n} $
$R_{Eq}=R_{1}+R_{2}+R_{3}$

Предположим  $R_{1} R_{2}$ и $R_{3}$ равны 20, 40 и 10 $ \Omega $ соответственно. Подставляя значения в приведенную выше формулу, мы получаем:

$R_{Eq}=20\Omega +40\Omega +10\Omega $
$R_{Eq}=70\Omega $

После нахождения эквивалентного сопротивления схему можно свести к следующей схеме и найти общий ток.

• Как рассчитать KVA трансформатора: калькулятор KVA трансформатора
• Классификация трансформаторов тока на основе четырех параметров

$I_{T}=\frac{V}{R_{Eq}}$

$=\frac {140 В}{70 \Омега} $
$I_{T}=2 A$

Какова сила тока в каждом резисторе?

Для всех резисторов в последовательной цепи всегда есть только один путь для протекания тока. Из-за того, что они находятся на одном пути, ток всегда одинаков для всех последовательно соединенных резисторов, как показано в следующем уравнении.

$I_{T}=I_{1}=I_{2}=\ldots =I_{n} $

Здесь I ₁ , I _2, и I _n — ток резистора R1, R2 и Rn соответственно, а n представляет собой общее количество резисторов. В нашем случае ток для R1, R2 и R3 равен I1, а I ₂ и I ₃ 2 ампера.
I _T = 2 А
I ₁ = 2 А,
I ₂ = 2 А,
I ₃ = 2 А

Какое напряжение на последовательном резисторе?

Это несложно, и закон Ома — лучший инструмент для этого, потому что у нас есть сопротивление и ток каждого резистора, поэтому мы можем легко найти соответствующее напряжение.

В ₁ = I ₁ R ₁ = 2 А x 20 Ом = 40 В
В ₂ = I ₂ R ₂ = 2 А x 40 Ом = 80 В
В ₃ = I ₃ R ₃ = 2 В x 10 Ом = 20 _ 900 вольт 3 V_{1}+V_{2}+V_{3} $
$V_{T}=40 В+80 В+20 В$
$V_{T}=120 В $

Обратите внимание, что полное падение напряжения на цепь точно равна приложенному к цепи напряжению.