Как рассчитать мощность резистора по формуле. Какие формулы используются для расчета сопротивления, тока и напряжения резистора. От чего зависит мощность резистора и как ее определить.
Основные формулы для расчета параметров резистора
Резисторы являются одними из самых распространенных компонентов в электронных схемах. Для правильного выбора и использования резисторов необходимо уметь рассчитывать их основные параметры. Рассмотрим ключевые формулы для расчета резисторов:
- Закон Ома: U = I * R, где U — напряжение, I — ток, R — сопротивление
- Мощность резистора: P = U * I или P = I^2 * R или P = U^2 / R
- Сопротивление: R = U / I
- Ток: I = U / R
- Напряжение: U = I * R
Эти базовые формулы позволяют рассчитать любой параметр резистора, зная два других. Например, зная напряжение и ток, можно определить сопротивление и мощность резистора.
Как рассчитать мощность резистора
Мощность является одним из важнейших параметров резистора, определяющим его способность рассеивать тепло. Для расчета мощности резистора используются следующие формулы:
- P = U * I — зная напряжение и ток
- P = I^2 * R — зная ток и сопротивление
- P = U^2 / R — зная напряжение и сопротивление
При выборе резистора его номинальная мощность должна быть больше расчетной с запасом 20-50%. Это обеспечит надежную работу и длительный срок службы компонента.
Пример расчета мощности резистора
Рассчитаем мощность резистора сопротивлением 100 Ом, через который протекает ток 0.1 А:
- Находим напряжение: U = I * R = 0.1 А * 100 Ом = 10 В
- Рассчитываем мощность: P = U * I = 10 В * 0.1 А = 1 Вт
Таким образом, для данной схемы необходимо выбрать резистор мощностью не менее 1.2-1.5 Вт.
От чего зависит мощность резистора
Мощность, рассеиваемая резистором, зависит от следующих факторов:
- Величина протекающего тока — чем больше ток, тем выше мощность
- Сопротивление резистора — при одинаковом токе мощность выше на резисторах с большим сопротивлением
- Приложенное напряжение — повышение напряжения увеличивает мощность
- Температура окружающей среды — при повышении температуры снижается допустимая мощность
- Способ охлаждения — лучший теплоотвод позволяет рассеивать большую мощность
Учет этих факторов позволяет правильно выбрать резистор для конкретной схемы и обеспечить его надежную работу.
Расчет сопротивления резистора
Сопротивление является основным параметром резистора. Для его расчета используются следующие формулы:
- R = U / I — по закону Ома, зная напряжение и ток
- R = U^2 / P — зная напряжение и мощность
- R = P / I^2 — зная мощность и ток
При последовательном соединении резисторов их сопротивления складываются: R = R1 + R2 + R3 + …
При параллельном соединении общее сопротивление рассчитывается по формуле:
1/R = 1/R1 + 1/R2 + 1/R3 + …
Пример расчета сопротивления резистора
Определим сопротивление резистора, если известно, что при напряжении 12 В он рассеивает мощность 3 Вт.
- Используем формулу: R = U^2 / P
- Подставляем значения: R = 12^2 / 3 = 144 / 3 = 48 Ом
Таким образом, сопротивление резистора составляет 48 Ом.
Расчет тока через резистор
Для определения тока, протекающего через резистор, используются следующие формулы:
- I = U / R — по закону Ома, зная напряжение и сопротивление
- I = sqrt(P / R) — зная мощность и сопротивление
- I = P / U — зная мощность и напряжение
Зная ток через резистор, можно рассчитать падение напряжения на нем и рассеиваемую мощность.
Пример расчета тока через резистор
Рассчитаем ток через резистор 220 Ом при напряжении 5 В:
- Используем формулу I = U / R
- Подставляем значения: I = 5 В / 220 Ом = 0.0227 А = 22.7 мА
Итак, через резистор протекает ток 22.7 мА.
Как рассчитать напряжение на резисторе
Для расчета напряжения на резисторе применяются формулы:
- U = I * R — по закону Ома, зная ток и сопротивление
- U = sqrt(P * R) — зная мощность и сопротивление
- U = P / I — зная мощность и ток
Падение напряжения на резисторе позволяет определить его влияние на работу схемы.
Пример расчета напряжения на резисторе
Определим напряжение на резисторе 1 кОм, если через него протекает ток 5 мА:
- Используем формулу U = I * R
- Подставляем значения: U = 0.005 А * 1000 Ом = 5 В
Таким образом, падение напряжения на резисторе составляет 5 В.
Особенности расчета мощных резисторов
При расчете мощных резисторов необходимо учитывать следующие факторы:
- Температурный коэффициент сопротивления — при нагреве сопротивление может значительно изменяться
- Способ охлаждения — для мощных резисторов критически важен эффективный теплоотвод
- Импульсный режим работы — допустимая импульсная мощность может в несколько раз превышать номинальную
- Конструкция резистора — проволочные и композитные резисторы имеют разные характеристики
Для ответственных применений рекомендуется выбирать резисторы с запасом по мощности 50-100% от расчетной.

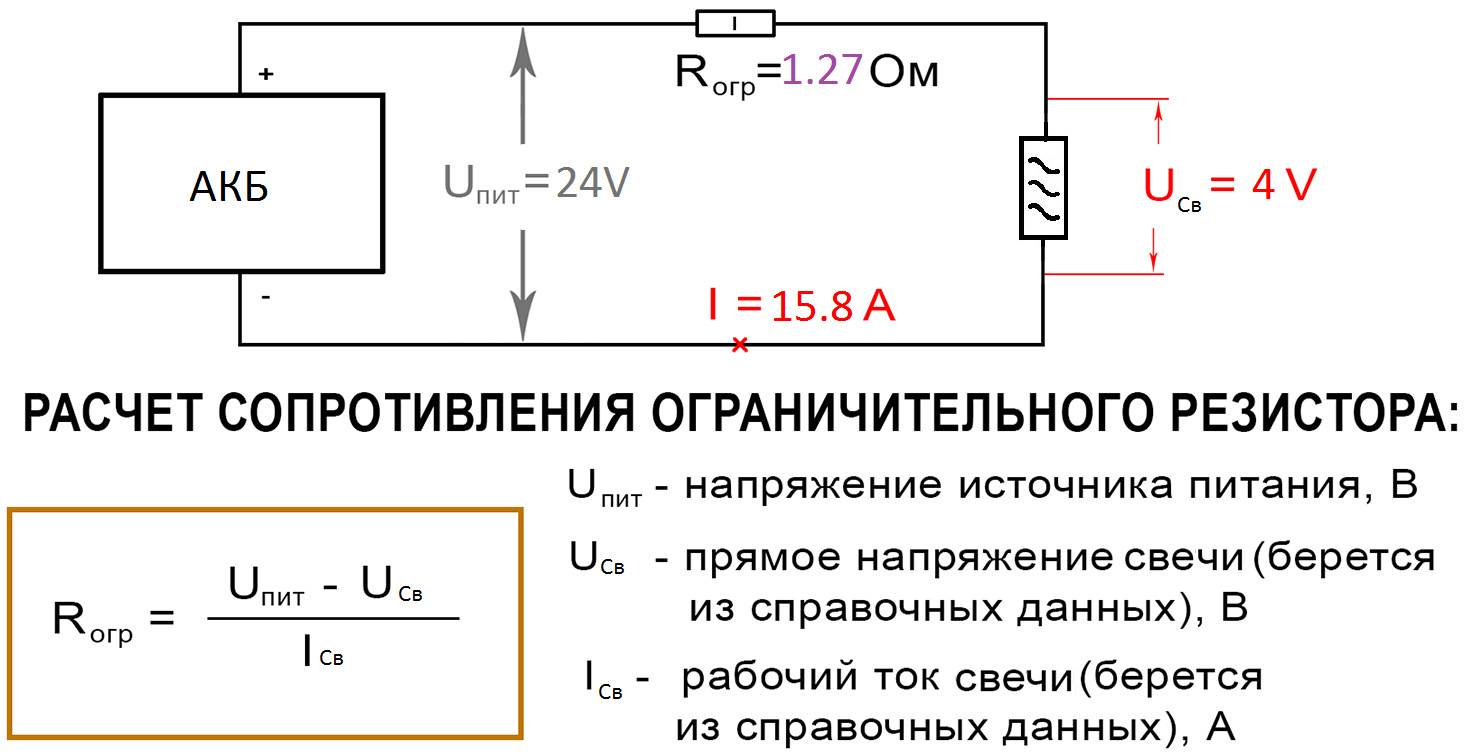
Расчет резисторов для светодиодов
Светодиоды требуют ограничения тока с помощью резисторов. Для расчета сопротивления токоограничивающего резистора используется формула:
R = (U — Uсд) / I
Где:
- U — напряжение питания
- Uсд — прямое падение напряжения на светодиоде
- I — номинальный ток светодиода
Мощность резистора рассчитывается по формуле:
P = (U — Uсд) * I
Пример расчета резистора для светодиода
Рассчитаем резистор для светодиода с Uсд = 2В и I = 20 мА при напряжении питания 5В:
- Сопротивление: R = (5В — 2В) / 0.02А = 150 Ом
- Мощность: P = (5В — 2В) * 0.02А = 0.06 Вт
Выбираем резистор 150 Ом мощностью 0.125 Вт.
Заключение
Правильный расчет параметров резисторов критически важен для создания надежных электронных устройств. Используя приведенные формулы, можно легко определить необходимое сопротивление, допустимую мощность и другие характеристики резисторов для конкретной схемы. При этом всегда следует учитывать реальные условия эксплуатации и выбирать компоненты с запасом по основным параметрам.
Какой формулой рассчитать мощность резисторов
Резисторы применяются практически во всех электросхемах. Это наиболее простой компонент, в основном, служащий для ограничения или регулирования тока, благодаря наличию сопротивления при его протекании.
Резисторы
Виды резисторов
Внутреннее устройство детали может быть различным, но преимущественно это изолятор цилиндрической формы, с нанесённым на его внешнюю поверхность слоем либо несколькими витками тонкой проволоки, проводящими ток и рассчитанными на заданное значение сопротивления, измеряемое в омах.
Существующие разновидности резисторов:
- Постоянные. Имеют неизменное сопротивление. Применяются, когда определенный участок электроцепи требует установки заданного уровня по току или напряжению. Такие компоненты необходимо рассчитывать и подбирать по параметрам;
- Переменные. Оснащены несколькими выводными контактами. Их сопротивление поддается регулировке, которая может быть плавной и ступенчатой. Пример использования – контроль громкости в аудиоаппаратуре;
- Подстроечные – представляют собой вариант переменных. Разница в том, что регулировка подстроечных резисторов производится очень редко;
- Есть еще резисторы с нелинейными характеристиками – варисторы, терморезисторы, фоторезисторы, сопротивление которых меняется под воздействием освещения, температурных колебаний, механического давления.
Важно! Материалом для изготовления практически всех нелинейных деталей, кроме угольных варисторов, применяемых в стабилизаторах напряжения, являются полупроводники.
Параметры резисторного элемента
- Для резисторов применяется понятие мощности. При прохождении через них электротока происходит выделение тепловой энергии, рассеиваемой в окружающее пространство. Мощность детали является параметром, который показывает, сколько энергии она может выделить в виде тепла, оставаясь работоспособной. Мощность зависит от габаритов детали, поэтому у маленьких зарубежных резисторов ее определяют на глаз, сравнивая с российскими, технические характеристики которых известны;
Важно! Импортные резисторные элементы идентичной мощности имеют несколько меньшие размеры, так как российские производятся с некоторым запасом по этому показателю.
На схеме мощность показана следующим образом.
Условное обозначение мощности
- Второй параметр – сопротивление элемента. На российских деталях типа МЛТ и крупных импортных образцах оба параметра указываются на корпусе (мощность – Вт, сопротивление – Ом, кОм, мОм). Для визуального определения сопротивления миниатюрных импортных элементов применяется система условных обозначений с помощью цветных полосок;
Цветовая маркировка резисторов
- Допуски. Невозможно изготовить деталь с номинальным сопротивлением, в точности соответствующим заявленному значению. Поэтому всегда указываются границы погрешности, называемые допуском. Его величина – 0,5-20%;
- ТКС – коэффициент температуры. Показывает, как варьируется сопротивление при изменении внешней температуры на 1°С. Желательно, но не обязательно подбирать элементы с близким или идентичным значением этого показателя для одной цепи.
Расчет резисторов
Для расчета сопротивления резистора формула применяемая в первую очередь – это закон Ома:
I = U/R.
Исходя из этой формулы, можно вывести выражение для сопротивления:
R = U/I,
где U – разность потенциалов на выводных контактах резистора.
Пример. Необходимо провести зарядку аккумулятора 2,4 В зарядным током 50 мА от автомобильной 12-вольтовой батареи. Прямое соединение сделать нельзя из-за слишком высоких показателей по току и напряжению. Но возможно поставить в схему сопротивление, которое обеспечит нужные параметры.
Предварительно нужно рассчитать резистор:
- Расчет начинается с определения падения напряжения, которое должен обеспечить резисторный элемент:
U = 12-2,4 = 9,6 B
- Протекающий по детали ток – 50 мА. Следовательно, R = 9,6/0,05 = 192 Ом
Теперь можно уже подобрать нужный резистор по одному показателю.
Если рассчитанной детали не нашлось, можно применить соединение из нескольких резисторных элементов, установив их последовательно или параллельно. Расчет сопротивлений при этом имеет свои особенности.
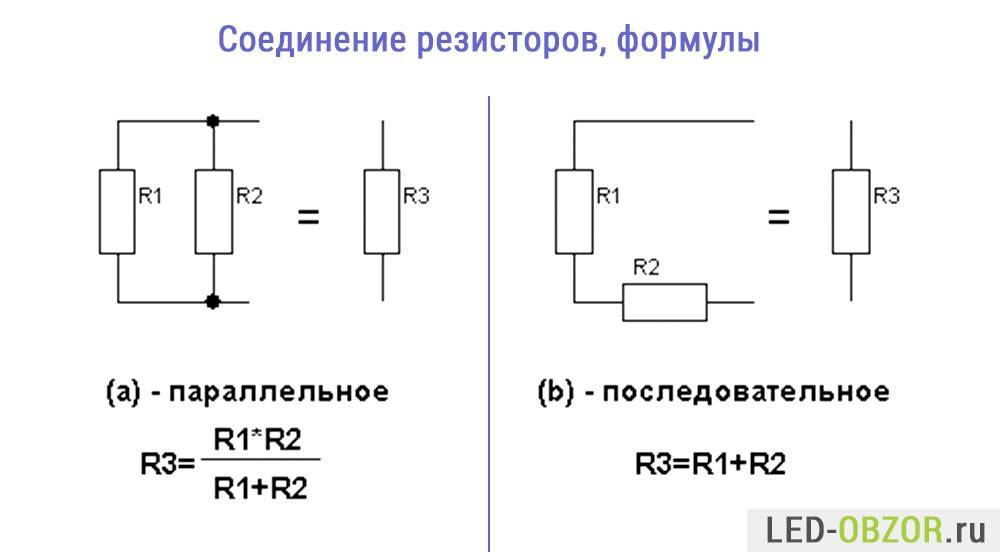
Последовательное соединение
Последовательно соединенные сопротивления складываются:
R = R1+ R2.
Если нужно получить общий результат 200 Ом, и имеется один резистор на 120 Ом, то расчет другого:
R2 = R-R1 = 200-120 = 80 Ом.
Последовательное соединение
Параллельное соединение
При параллельной схеме другая зависимость:
1/R = 1/R1 + 1/R2.
Или преобразованный вариант:
R = (R1 x R2)/ (R1 + R2).
Важно! Параллельное соединение можно использовать, когда в наличии детали с большим сопротивлением, чем требуется, последовательное наоборот.
Пример. Необходимо сопротивление 200 Ом. Имеется деталь R2 на 360 Ом. Какое сопротивление подобрать еще? R1 = R2/(R2/R-1) = 360/(360/200-1) = 450 Ом.
Параллельное соединение
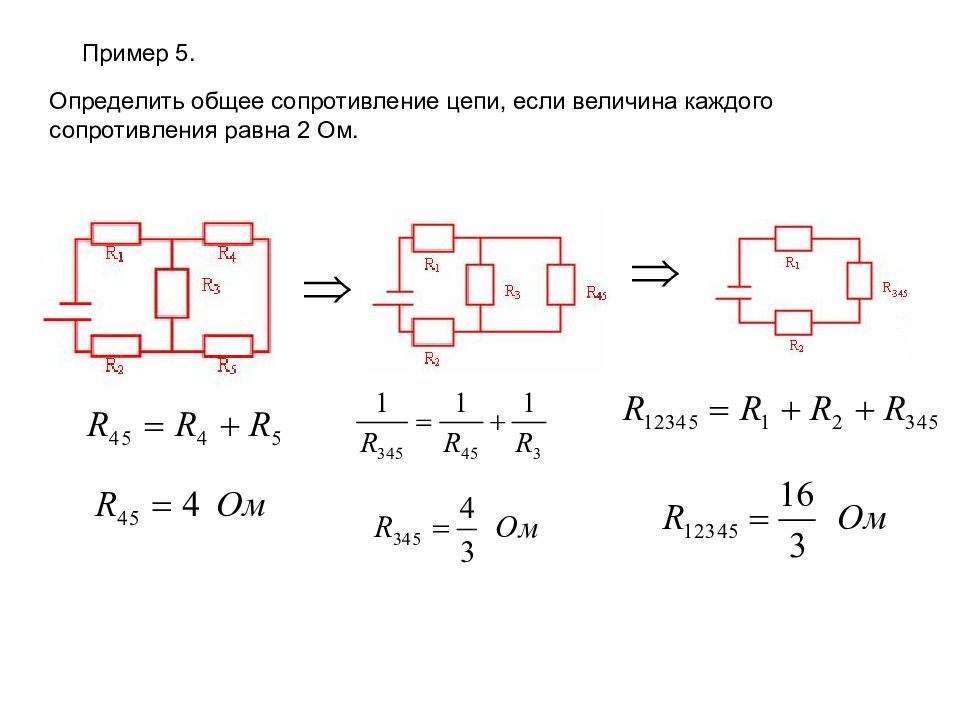
Смешанное соединение
В смешанных схемах присутствуют последовательно-параллельные комбинации. Расчет таких схем сводится к их упрощению путем преобразований. На рисунке ниже представлено, как упростить схему, рассчитывая общий показатель для шести резисторов с учетом их соединения.
Расчет сопротивления в смешанной схеме
Мощность
Определив сопротивление, еще нельзя выбрать деталь. Чтобы обеспечить надежную работу схемы, необходимо найти и другой параметр – мощность. Для этого надо знать, как рассчитать мощность резисторного элемента.
Формулы, по которым можно рассчитать мощность резистора:
Пример. I = 50 мА; R = 200 Ом. Тогда P = I² x R = 0,05² x 200 = 0,5 Вт.
Если не учитывать значение тока, расчет мощности резистора ведется по другой формуле.
Пример. U = 9,6 В, R = 200 Ом. P = U²/R = 9,6²/200 = 0,46 Вт. Получился тот же результат.
Теперь, зная точные параметры рассчитываемого резисторного элемента, подберем радиодеталь.
Важно! При выборе деталей возможно их заменить на резисторы с мощностью, больше рассчитанной, но обратный вариант не подходит.
Это основные формулы для расчета резисторных деталей, на основании которых производится анализ узлов схемы, где главным является определение токов и напряжений, протекающих через конкретный элемент.
Видео
Оцените статью:в чем измеряется, от чего зависит
Автор Aluarius На чтение 7 мин. Просмотров 371 Опубликовано
В чем измеряется сопротивление резистора
Чтобы ответить на вопрос в чем измеряется сопротивление резистора, нужно обратиться к стандартизации и наукам об измерениях. Международная и общепринятая схема цветовых кодов резисторов была разработана много лет назад как простой и быстрый способ определения омического значения резистора независимо от его размера или состояния. Он состоит из набора отдельных цветных колец или полос в спектральном порядке, представляющих каждую цифру значения резисторов. Сила сопротивления определеяет качество резистора.
Цветовая маркировка резистора всегда считывается по одной полосе за раз, начиная слева направо, с большей полосой допуска ширины, ориентированной на правую сторону, что указывает на ее допуск. Путем сопоставления цвета первой полосы с соответствующим номером в столбце цифр цветовой диаграммы под первой цифрой идентифицируется, и это представляет первую цифру значения сопротивления.
Опять же, сопоставляя цвет второй полосы с соответствующим номером в столбце цифр цветовой диаграммы, мы получаем вторую цифру значения сопротивления и так далее. Затем цветовой код резистора читается слева направо, как показано ниже:

Это система маркировки. Резисторы бывают разных размеров и значений сопротивления, а чтобы вычислить нужный, и существуют формулы расчета. Резисторы изготавливаются по определенной стандартной сетке, которая подходит для большинства целей. Чтобы не быть голословными, нужно приложить цветовую таблицу.
Вместо последовательных значений сопротивления от 1 Ом (базовая единица измерений) и выше, определенные значения резисторов существуют в определенных пределах допуска. Допуск резистора представляет собой максимальную разницу между его фактическим значением и требуемым значением и обычно выражается как зависимость положительного или отрицательного значения в процентах. Например, резистор с допуском 1 кОм ± 20% может иметь максимальное и минимальное значение сопротивления:
Максимальное значение сопротивления
- 1 кОм или 1000 Ом + 20% = 1200 Ом
Минимальное значение сопротивления
- 1 кОм или 1000 Ом – 20% = 800 Ом
От чего зависит сопротивление резистора
Температура и последовательность включения – два главных фактора, которые определяют сопротивление в цепи. Но помимо этих показателей есть и допуски. Как же измерять? В большинстве электрических или электронных цепей большой 20% -ный допуск на один и тот же резистор, как правило, не является проблемой, но если для высокоточных цепей, таких как фильтры, генераторы или усилители и т. д., требуются резисторы с малым допуском, то необходимо использовать резистор с правильным допуском. Так как резистор с допуском 20% обычно не может использоваться для замены типа допуска 2% или даже 1%.
Цветовой код пяти- и шестиполосного резистора чаще всего ассоциируется с высокопрецизионными типами пленок 1% и 2%, в то время как универсальные садовые разновидности 5% и 10% общего назначения обычно используют четырехполосный цветовой код резистора. Резисторы имеют различные допуски, но наиболее распространенными являются E12 и E24 .
Е12 серия поставляется в двенадцати значений сопротивления за десятилетие (А десятилетие , представляющее кратные 10, то есть 10, 100, 1000 и т.д.), в то время как Е24 серия приходит в двадцать четыре значений за десятилетие и E96 серии девяносто шесть значений за десятилетие. Серия E192 с очень высокой точностью теперь доступна с допусками до ± 0,1%, что дает массивные 192 значения отдельных резисторов за десятилетие.

Как зависит от температуры
Чем выше температура, тем выше сопротивление. Это связано с быстрой скоростью движения атомов внутри твердого тела. Обратное явление – сверхпроводимость при низких температурах. Опять же, не забываем про погрешность.
От других параметров
Если резистор подключен в сложную цепь с множеством преобразующих, защитных, трансформирующих, компрессирующих устройств, то он будет иметь другое, отличное от стандартного, сопротивление, так как часть напряжения все равно будет проходить через него в нескомпрессированном виде, что не позволит ему отработать как следует. Чтобы более точно узнать удельный ток и сопротивление, показатель, полученный в расчетах, нужно уменьшить или увеличить на заданную величину.
Как найти сопротивление резистора в цепи
Система цветового кода резистора хороша, но нам нужно понять, как ее применять, чтобы получить правильное значение резистора. «Левая» или наиболее значимая цветная полоса – это полоса, ближайшая к соединительному выводу, полосы с цветовой кодировкой читаются слева направо следующим образом:
Цифра, цифра, множитель = цвет, цвет х 10 цветов в омах (Ω)
Например, резистор имеет следующие схемы маркировки;
Желтый Фиолетовый Красный = 4 7 2 = 4 7 x 10 2 = 4700 Ом или 4 кОм Ом.
Типичные допуски на резисторы для пленочных резисторов варьируются от 1% до 10%, в то время как для углеродных резисторов допуски составляют до 20%. Резисторы с допусками ниже 2% называются прецизионными, а резисторы с более низким допуском более дорогими. Само напряжение играет малую роль.
Большинство пятиполосных резисторов являются прецизионными резисторами с допусками 1% или 2%, в то время как большинство четырехполосных резисторов имеют допуски 5%, 10% и 20%. Цветовой код, используемый для обозначения номинального допуска резистора, имеет вид:
Коричневый = 1%, красный = 2%, золото = 5%, серебро = 10%
При параллельном соединении
Как находить сопротивление при параллельном соединении? По формуле: 1 / Rобщ = (1 / R1) + (1 / R2) + … + (1 / Rn).
При последовательном соединении
Общее сопротивление цепи при последовательном соединении в электрической цепи равно сумме сопротивлений отдельных проводников (или отдельных участков цепи): R = R 1 + R 2.
Могут ли быть погрешности и какие
Если резистор не имеет четвертой полосы допусков, тогда допуск по умолчанию будет обозначаться 20% . Остальной ток будет рассеиваться.
Иногда проще запомнить цветовой код резистора, используя короткие, легко запоминающиеся предложения в форме выражений, рифм и фраз, называемых акростихами , в которых есть отдельное слово в предложении для представления каждого из десяти + двух цветов.
Полученная мнемоника сопоставляет первую букву каждого слова каждому цвету, который составляет цветовой код резисторов в порядке возрастания величины, и есть много разных мнемонических фраз, которые можно использовать. Однако эти высказывания часто бывают очень грубыми, но тем не менее эффективными для запоминания цветов резисторов, но все же помогают определить сопротивление.
Таблица погрешнойстей для более точного определения сопротивления
| Коды допусков для резисторов (±) |
| B = 0,1% |
| С = 0,25% |
| D = 0,5% |
| F = 1% |
| G = 2% |
| J = 5% |
| К = 10% |
| М = 20% |
Кроме того, при чтении этих письменных кодов соблюдайте осторожность, чтобы не перепутать букву сопротивления k для килограммов с буквой допуска K для допуска 10% или буквой сопротивления M для мегаом с буквой допуска M для допуска 20%.
Как использовать на практике
Существует множество различных типов резисторов, которые можно использовать как в электрических, так и в электронных цепях для управления током или для падения напряжения различными способами. Но для того, чтобы сделать это, реальный резистор должен иметь некоторую форму «резистивного» или «резистивного» значения. Резисторы доступны в диапазоне различных значений сопротивления от долей Ом ( Ом ) до миллионов Ом.
Очевидно, что было бы нецелесообразно иметь в наличии резисторов каждого возможного значения , например, 1 Ом , 2 Ом , 3Ω , 4Ω и т.д., потому что буквально десятки сотен тысяч, если не десятки миллионов различных резисторов должны существовать , чтобы покрыть все возможные значения. Вместо этого резисторы изготавливаются в так называемых «предпочтительных значениях», а их значения сопротивления печатаются на корпусе цветными чернилами.
Значение сопротивления, допуск и номинальная мощность обычно печатаются на корпусе резистора в виде цифр или букв, когда корпус резистора достаточно большой, чтобы считывать отпечаток, например, большие силовые резисторы. Но когда резистор маленький, такой как углеродный или пленочный тип на 1/4 Вт, эти характеристики должны быть показаны другим способом, так как отпечаток будет слишком маленьким для чтения. Подача большого напряжения нагреет краску и расплавит надписи.
Таким образом, чтобы преодолеть это, маленькие резисторы используют цветные окрашенные полосы, чтобы указать как их значение сопротивления, так и их допуск с физическим размером резистора, указывающим его номинальную мощность. Эти цветные окрашенные полосы производят систему идентификации, обычно известную как цветовой код резисторов.

10 формул по физике
Доброго дня уважаемые радиолюбители!
Приветствую вас на сайте “Радиолюбитель“
Формулы составляют скелет науки об электронике. Вместо того, чтобы сваливать на стол целую кучу радиоэлементов, а потом переподключать их между собой, пытаясь выяснить, что же появится на свет в результате, опытные специалисты сразу строят новые схемы на основе известных математических и физических законов. Именно формулы помогают определять конкретные значения номиналов электронных компонентов и рабочих параметров схем.
Точно так же эффективно использовать формулы для модернизации уже готовых схем. К примеру, для того, чтобы выбрать правильный резистор в схеме с лампочкой, можно применить базовый закон Ома для постоянного тока (о нем можно будет прочесть в разделе “Соотношения закона Ома” сразу после нашего лирического вступления). Лампочку можно заставить, таким образом, светить более ярко или, наоборот — притушить.
В этой главе будут приведены многие основные формулы физики, с которыми рано или поздно приходится сталкиваться в процессе работы в электронике. Некоторые из них известны уже столетия, но мы до сих пор продолжаем ими успешно пользоваться, как будут пользоваться и наши внуки.
Соотношения закона Ома
Закон Ома представляет собой взаимное соотношение между напряжением, током, сопротивлением и мощностью. Все выводимые формулы для расчета каждой из указанных величин представлены в таблице:
| Искомая величина | Формула |
| Напряжение, В | U=I*R |
| Ток, А | I=U/R |
| Сопротивление, Ом | R=U/I |
| Мощность, Вт | P=U*I |
В этой таблице используются следующие общепринятые обозначения физических величин:
U — напряжение (В),
I — ток (А),
Р — мощность (Вт),
R — сопротивление (Ом),
Потренируемся на следующем примере: пусть нужно найти мощность схемы. Известно, что напряжение на ее выводах составляет 100 В, а ток— 10 А. Тогда мощность согласно закону Ома будет равна 100 х 10 = 1000 Вт. Полученное значение можно использовать для расчета, скажем, номинала предохранителя, который нужно ввести в устройство, или, к примеру, для оценки счета за электричество, который вам лично принесет электрик из ЖЭК в конце месяца.
А вот другой пример: пусть нужно узнать номинал резистора в цепи с лампочкой, если известно, какой ток мы хотим пропускать через эту цепь. По закону Ома ток равен:
I = U / R
Схема, состоящая из лампочки, резистора и источника питания (батареи) показана на рисунке. Используя приведенную формулу, вычислить искомое сопротивление сможет даже школьник.
Что же в этой формуле есть что? Рассмотрим переменные подробнее.
> U пит (иногда также обозначается как V или Е): напряжение питания. Вследствие того, что при прохождении тока через лампочку на ней падает какое-то напряжение, величину этого падения (обычно рабочее напряжение лампочки, в нашем случае 3,5 В) нужно вычесть из напряжения источника питания. К примеру, если Uпит = 12 В, то U = 8,5 В при условии, что на лампочке падает 3,5 В.
> I: ток (измеряется в амперах), который планируется пропустить через лампочку. В нашем случае – 50 мА. Так как в формуле ток указывается в амперах, то 50 миллиампер составляет лишь малую его часть: 0,050 А.
> R: искомое сопротивление токоограничивающего резистора, в омах.
В продолжение, можно проставить в формулу расчета сопротивления реальные цифры вместо U, I и R:
R = U/I = 8,5 В / 0,050 А= 170 Ом
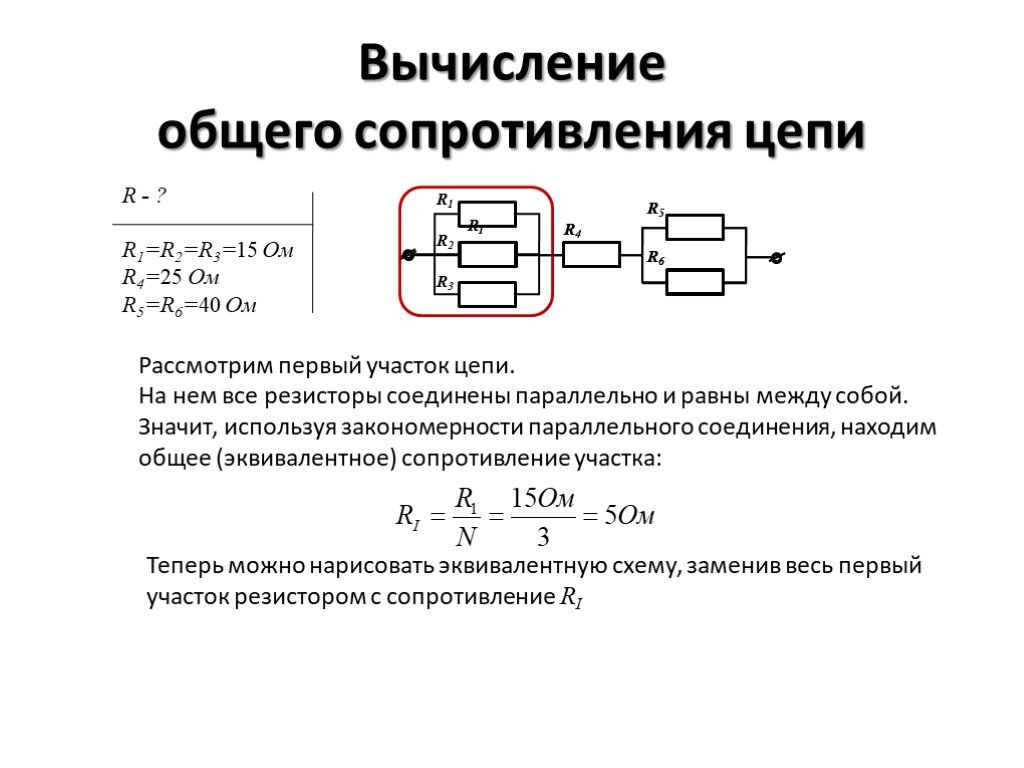
Расчёты сопротивления
Рассчитать сопротивление одного резистора в простой цепи достаточно просто. Однако с добавлением в нее других резисторов, параллельно или последовательно, общее сопротивление цепи также изменяется. Суммарное сопротивление нескольких соединенных последовательно резисторов равно сумме отдельных сопротивлений каждого из них. Для параллельного же соединения все немного сложнее.
Почему нужно обращать внимание на способ соединения компонентов между собой? На то есть сразу несколько причин.
> Сопротивления резисторов составляют только некоторый фиксированный ряд номиналов. В некоторых схемах значение сопротивления должно быть рассчитано точно, но, поскольку резистор именно такого номинала может и не существовать вообще, то приходится соединять несколько элементов последовательно или параллельно.
> Резисторы — не единственные компоненты, которые имеют сопротивление. К примеру, витки обмотки электромотора также обладают некоторым сопротивлением току. Во многих практических задачах приходится рассчитывать суммарное сопротивление всей цепи.
Расчет сопротивления последовательных резисторов
Формула для вычисления суммарного сопротивления резисторов, соединенных между собой последовательно, проста до неприличия. Нужно просто сложить все сопротивления:
Rобщ = Rl + R2 + R3 + … (столько раз, сколько есть элементов)
В данном случае величины Rl, R2, R3 и так далее — сопротивления отдельных резисторов или других компонентов цепи, а Rобщ — результирующая величина.
Так, к примеру, если имеется цепь из двух соединенных последовательно резисторов с номиналами 1,2 и 2,2 кОм, то суммарное сопротивление этого участка схемы будет равно 3,4 кОм.
Расчет сопротивления параллельных резисторов
Все немного усложняется, если требуется вычислить сопротивление цепи, состоящей из параллельных резисторов. Формула приобретает вид:
R общ = R1 * R2 / (R1 + R2)
где R1 и R2 — сопротивления отдельных резисторов или других элементов цепи, а Rобщ -результирующая величина. Так, если взять те же самые резисторы с номиналами 1,2 и 2,2 кОм, но соединенные параллельно, получим
776,47 = 2640000 / 3400
Для расчета результирующего сопротивления электрической цепи из трех и более резисторов используется следующая формула:
Здесь снова величины Rl, R2, R3 и так далее — сопротивления отдельных резисторов, a Rобщ — суммарная величина.
Расчёты ёмкости
Формулы, приведенные выше, справедливы и для расчета емкостей, только с точностью до наоборот. Так же, как и для резисторов, их можно расширить для любого количества компонентов в цепи.
Расчет емкости параллельных конденсаторов
Если нужно вычислить емкость цепи, состоящей из параллельных конденсаторов, необходимо просто сложить их номиналы:
Собщ = CI + С2 + СЗ + …
В этой формуле CI, С2 и СЗ — емкости отдельных конденсаторов, а Собщ суммирующая величина.
Расчет емкости последовательных конденсаторов
Для вычисления общей емкости пары связанных последовательно конденсаторов применяется следующая формула:
Собщ = С1 * С2 /( С1+С2)
где С1 и С2 — значения емкости каждого из конденсаторов, а Собщ — общая емкость цепи
Расчет емкости трех и более последовательно соединенных конденсаторов
В схеме имеются конденсаторы? Много? Ничего страшного: даже если все они связаны последовательно, всегда можно найти результирующую емкость этой цепи:
И здесь опять величины C1, С2, СЗ и так далее — емкости отдельных конденсаторов, а Собщ. — суммарная величина.
Так зачем же вязать последовательно сразу несколько конденсаторов, когда могло хватить одного? Одним из логических объяснений этому факту служит необходимость получения конкретного номинала емкости цепи, аналога которому в стандартном ряду номиналов не существует. Иногда приходится идти и по более тернистому пути, особенно в чувствительных схемах, как, например, радиоприемники.
Расчёт энергетических уравнений
Наиболее широко на практике применяют такую единицу измерения энергии, как киловатт-часы или, если это касается электроники, ватт-часы. Рассчитать затраченную схемой энергию можно, зная длительность времени, на протяжении которого устройство включено. Формула для расчета такова:
ватт-часы = Р х Т
В этой формуле литера Р обозначает мощность потребления, выраженную в ваттах, а Т — время работы в часах. В физике принято выражать количество затраченной энергии в ватт-секундах, или Джоулях. Для расчета энергии в этих единицах ватт-часы делят на 3600.
Расчёт постоянной ёмкости RC-цепочки
В электронных схемах часто используются RC-цепочки для обеспечения временных задержек или удлинения импульсных сигналов. Самые простые цепочки состоят всего лишь из резистора и конденсатора (отсюда и происхождение термина RC-цепочка).
Принцип работы RC-цепочки состоит в том, что заряженный конденсатор разряжается через резистор не мгновенно, а на протяжении некоторого интервала времени. Чем больше сопротивление резистора и/или конденсатора, тем дольше будет разряжаться емкость. Разработчики схем очень часто применяют RC-цепочки для создания простых таймеров и осцилляторов или изменения формы сигналов.
Каким же образом можно рассчитать постоянную времени RC-цепочки? Поскольку эта схема состоит из резистора и конденсатора, в уравнении используются значения сопротивления и емкости. Типичные конденсаторы имеют емкость порядка микрофарад и даже меньше, а системными единицами являются фарады, поэтому формула оперирует дробными числами.
T = RC
В этом уравнении литера Т служит для обозначения времени в секундах, R — сопротивления в омах, и С — емкости в фарадах.
Пусть, к примеру, имеется резистор 2000 Ом, подключенный к конденсатору 0,1 мкФ. Постоянная времени этой цепочки будет равна 0,002 с, или 2 мс.
Для того чтобы на первых порах облегчить вам перевод сверхмалых единиц емкостей в фарады, мы составили таблицу:
| Значение емкости конденсатора, мкФ | Емкость конденсатора для расчета |
| 10 | 0,000 01 |
| 1 | 0,000 001 |
| 0,1 | 0,000 000 1 |
| 0,01 | 0,000 000 01 |
Расчёты частоты и длины волны
Частота сигнала является величиной, обратно пропорциональной его длине волны, как будет видно из формул чуть ниже. Эти формулы особенно полезны при работе с радиоэлектроникой, к примеру, для оценки длины куска провода, который планируется использовать в качестве антенны. Во всех следующих формулах длина волны выражается в метрах, а частота — в килогерцах.
Расчет частоты сигнала
Предположим, вы хотите изучать электронику для того, чтобы, собрав свой собственный приемопередатчик, поболтать с такими же энтузиастами из другой части света по аматорской радиосети. Частоты радиоволн и их длина стоят в формулах бок о бок. В радиолюбительских сетях часто можно услышать высказывания о том, что оператор работает на такой-то и такой длине волны. Вот как рассчитать частоту радиосигнала, зная длину волны:
Частота = 300000 / длина волны
Длина волны в данной формуле выражается в миллиметрах, а не в футах, аршинах или попугаях. Частота же дана в мегагерцах.
Расчет длины волны сигнала
Ту же самую формулу можно использовать и для вычисления длины волны радиосигнала, если известна его частота:
Длина волны = 300000 / Частота
Результат будет выражен в миллиметрах, а частота сигнала указывается в мегагерцах.
Приведем пример расчета. Пусть радиолюбитель общается со своим другом на частоте 50 МГц (50 миллионов периодов в секунду). Подставив эти цифры в приведенную выше формулу, получим:
6000 миллиметров = 300000 / 50 МГц
Однако чаще пользуются системными единицами длины — метрами, поэтому для завершения расчета нам остается перевести длину волны в более понятную величину. Так как в 1 метре 1000 миллиметров, то в результате получим 6 м. Оказывается, радиолюбитель настроил свою радиостанцию на длину волны 6 метров. Прикольно!
Формула электрического сопротивления от А до Я
В моей практике много случаев, когда электрик тратит лишнее время на правильный подбор деталей при ремонте оборудования. А решить эту проблему довольно просто: достаточно представлять принцип его работы.
Формула электрического сопротивления, выраженная разными способами для цепей постоянного или переменного тока, позволяет правильно выполнить расчет под исходные данные действующей схемы.
При этом соотношение проходящей через нее мощности, создающей нагрев, должно соответствовать условиям теплоотвода. Выполняя эти требования, вы будете работать быстрее, повысите свой авторитет в глазах окружающих.
Для начинающих электриков я подготовил небольшой теоретический материал про физические процессы, происходящие с электричеством.
Вы же можете сразу перейти к вычислениям, щелкнув по второму подзаголовку из содержания по формулам или третьему через онлайн калькулятор удельного сопротивления.
Содержание статьи
Что надо знать про электрические процессы
Если говорить простым языком, то под сопротивлением принято понимать свойство среды, по которой протекает электрический ток, снижающее его величину.
Так работают провода и изоляторы высоковольтной линии электропередач, показанные на верхней картинке, да и любое вещество.
Изоляторы обладают очень высокими диэлектрическими свойствами, изолируют высоковольтное напряжение, присутствующее на токоведущих шинах от контура земли. Это их основное назначение.
Провода же должны максимально эффективно передавать транслируемые по ним мощности. Их создают так, чтобы они обладали минимальным электрическим сопротивлением, работали с наименьшими потерями энергии на нагрев.
В этом случае передача электричества от источника напряжения к потребителю на любое расстояние будет проходить эффективно.
Приведу для примера картинку из предыдущей моей статьи.
Ее, как и верхнюю, можно представить таким обобщенным видом.
На внешнем участке цепи токоведущие жилы отделены друг от друга воздушной средой и слоем изоляции с высокими диэлектрическими свойствами.
Хорошей проводимостью обладают токоведущие жилы. Подключенный к ним электрический прибор функционирует оптимально.
Как работает резистор
Ток в металлах проходит под действием приложенного напряжения за счет направленного движения электронов. При этом они соударяются, встречаются с положительно и отрицательно заряженными ионами.
Такие столкновения повышают температуру среды, уменьшают силу тока.
За направление электрического тока в электротехнике принято движение заряженных частиц от плюса к минусу. Электроны же движутся от катода к аноду.
Электрическое сопротивление металла зависит от его структуры и геометрических размеров.
Аналогичные процессы протекают в любой другой токопроводящей среде, включая газы или жидкости.
Какие существуют виды сопротивлений
В домашних электрических приборах используется большое разнообразие резисторов с постоянной или регулируемой величиной.
Они ограничивают величину тока всех бытовых устройств, а в наиболее сложных модулях их количество может достигать тысячи или более. Резисторы работают практически во всех схемах.
При использовании в цепях переменного тока они обладают активным сопротивлением, а конденсаторы и дроссели — реактивным.
Причем, на конденсаторах создается емкостное сопротивление, а у дросселей — индуктивное.
Реактивная составляющая на конденсаторах и дросселях сильно зависит от частоты электромагнитного колебания.
2 Шутки электриков о токах через конденсатор и дроссель
Их я привожу потому, что они позволяют запомнить характер прохождения тока через реактивные элементы.
Шутка №1 о емкости
В домашней сети и внутри многих приборов работают переменный и постоянный токи. Они по-разному ведут себя, если встречают на своем пути конденсатор.
Поскольку он состоит из двух токопроводящих пластин, разделенных слоем диэлектрика, то его обозначают на схемах двумя жирными черточками, расположенными параллельно. К их серединам подключены провода, нарисованные перпендикулярными линиями.
Переменный ток имеет форму гармоничной синусоиды, состоящей из двух симметричных половинок.
Такая гармоника движется от начала координат, встречает на своем пути обкладки, переваливается через них и, скатившись, начинает обгонять приложенное напряжение.
Постоянный ток таким свойством не обладает. Его тупой конец просто упирается в обкладку и останавливается. Пройти через конденсатор он не может. Это для него непреодолимое препятствие.
Шутка №2 о дросселе
Индуктивность выполнена витками изолированного провода. Любой ток проходит по нему. Но синусоида своими волнами путается в витках катушки, начинает отставать от напряжения.
Постоянка же спокойно перемещается внутри провода дросселя без ощущения какого-либо значительного противодействия. Поэтому постоянное напряжение может своим током спалить дроссель, созданный для работы на переменке.
Что же это за зверь: сверхпроводимость
Сто лет назад выявлена способность определенных металлов полностью терять свое сопротивление электрическому току при сверхнизких температурах. Выглядит этот процесс следующим образом.
Со сверхпроводниками домашний мастер не работает. Но на верхнюю часть приведенного графика рекомендую обратить внимание: нагрев металла повышает его электрическое сопротивление.
При электротехнических расчетах, требующих получения точного результата, необходимо учитывать температурный коэффициент, взятый из справочников.
Как просто вычислить сопротивление по закону Ома из электрических величин
Шутки и их разъяснения закончились, хотя они приведены для объяснения поведения токов внутри индуктивностей и емкостей. Пора переходить к расчетам.
Его позволяет выполнить одна из формул, приведенных в шпаргалке электрика. Для этого достаточно знать два из трех электрических параметров: ток I, мощность P или напряжение U.
Если же вам лениво вычислять цифры, то можете спокойно использовать онлайн калькулятор закона Ома. Он избавит вас от сложных арифметических действий.
Формула электрического сопротивления по свойствам среды: научный подход
Электротехника давно использует термин: удельное сопротивление. Он учитывает свойства материала токопроводящей среды с ее размерами: длиной и поперечным сечением, через которое протекает электрический ток.
Все данные для него получены в результате многочисленных исследований и сведены в таблицы. Для бытовых вычислений достаточно следующих сведений.
Таблица характеристик металлов, используемых в быту
| Металл провода | Удельное сопротивление (Ом∙мм.кв/м) |
| Медь техническая | 0,017 |
| Алюминий | 0,028 |
| Стальные сплавы | 0,11 |
| Свинец | 0,21 |
| Сплавы нихрома | 1,11 |
На основе этих данных удобно подбирать провода, детали, вычислять их сопротивление R либо определять другие параметры.
Например, нас интересует сопротивление проволоки нихрома диаметром 1 мм, при температуре 20 градусов.
Определяем площадь поперечного сечения через площадь круга.
S = 3.14 x 1 x 1 / 4 = 0,785 мм кв.
Делаем расчет на основе приведенной формулы.
R = 1,1 х 5 / 0,785 = 7 Ом
Простой онлайн калькулятор сопротивления проводов
Его назначение — облегчить работу с формулами и арифметическими действиями. Он позволяет решать одну из двух часто встречающихся задач:
- Определение сопротивления провода.
- Расчет его длины.
Достаточно заполнить исходные данные в соответствующей размерности и нажать кнопку “Рассчитать”.
Формулы расчета электрического сопротивления для переменного тока простыми словами
Переменное напряжение наводится вращением рамки (ротора генератора) в магнитном поле (создается обмоткой или магнитами статора).
Ток потребителя, подключенного к выводам генератора, по-разному ведет себя на резисторе, индуктивности и конденсаторе.
Формула активного сопротивления
Резисторы изготавливают из металлов с повышенными удельными характеристиками для ограничения силы тока без изменения его направления.
Синусоиды токов и напряжений на резисторе совпадают по времени. В векторном выражении они обладают одинаковым направлением.
Активное сопротивление переменному току вычисляется по закону Ома так же, как и при постоянной форме напряжения.
Формула индуктивного сопротивления
В обмотках катушек электромагнитов, дросселей, трансформаторов наводится электродвижущая сила индукции. Она взаимодействует с приложенным переменным напряжением. В результате происходит сдвиг фазы тока относительно направления вращения электромагнитного поля (ротора генератора).
Формула индуктивного сопротивления XL сильно зависит от частоты тока f и индуктивности L.
Ток в такой цепи сдвигается от напряжения и отстает от него на 90 угловых градусов.
Число ∏ в формуле отображает отношение длины окружности к ее диаметру (3,14).
Формула емкостного сопротивления ХС
Конденсатор состоит из двух токопроводящих пластин, отделенных слоем диэлектрика. При появлении на них напряжения они накапливают электрический заряд.
Его энергия постоянно взаимодействует с приложенным переменным напряжением. Поэтому в цепи создается ток, зависящий от частоты электромагнитного сигнала и емкости конденсатора.
Он сдвигается вперед от вектора напряжения по направлению вращения поля.
Формула полного сопротивления
Электротехника, как и сама жизнь, описывает явления, переплетенные между собой, а не в чистом виде.
Электрическая энергия, поступающая к нам в квартиру по проводам и кабелям от трансформаторной подстанции, преодолевает:
- активное сопротивление токоведущих шин;
- емкость кабельных линий;
- индуктивное противодействие обмоток трансформаторов.
Поэтому для расчетов применяют метод полного сопротивления, выражаемый законом прямоугольного треугольника.
Каждая его сторона отображает определенную характеристику сопротивления:
- гипотенуза — суммарную, полную величину Z:
- прилегающий катет — активную составляющую R;
- противолежащий — реактивную X, представленную геометрической суммой емкостного XL и индуктивного сопротивления XC.
Точно так же каждая сторона этого треугольника создает определенную величину затраченной мощности электрической энергии.
На активном участке создается мощность, совершающая полезную для нас работу, обеспечивающую вращение роторов электродвигателей, свечение осветительных приборов, нагрев обогревателей и другие нужные действия.
Полная мощность, расходуемая всеми видами потребителей, состоит из полезной активной и потерь, создающих индуктивными и емкостными составляющими. Они снижают эффективность работы электрической системы. Поэтому с ними борются.
Запомнить роль реактивной мощности помогает простая и наглядная картинка, естественно, выраженная в шутливой форме.
Однако стоит понимать, что угол φ, образованный между гипотенузой и прилегающим к нему катетом, характеризует величину реактивной части, создающей бесполезные потери энергии. Ее всегда стремятся снизить.
Что такое вольтамперная характеристика
Металлы в обычном состоянии формируют электрический ток строго по прямолинейной характеристике в зависимости от величины приложенного напряжения.
У других сложных веществ и индуктивностей этот принцип не соблюдается. Зависимость выражается кривыми линиями и называется вольтамперной характеристикой.
ВАХ индуктивностей
Характер протекания тока зависит от величины индуктивности. Если в рабочей обмотке возникает пробой изоляции, приводящий к образованию короткозамкнутого витка, то вольтамперная характеристика резко изменяет свой вид: падает.
За счет уменьшения индуктивного сопротивления при меньшем значении величины приложенного напряжения в обмотке начинают протекать бОльшие токи.
Они свидетельствуют о возникновении неисправности, требующей немедленного устранения. Поэтому снятие ВАХ является обязательным элементом проверки исправности обмоток всех видов трансформаторов или дросселей.
Она выполняется различными методами с определением состояния точки перегиба характеристики.
ВАХ полупроводникового прибора
На правой картинке показан один из примеров работы нелинейного элемента — диода.
В первой четверти квадранта проходит прямой участок характеристики, а у третьей — обратный.
На прямом участке повышение напряжения выше точки перегиба ведет к открытию переходного полупроводникового слоя и пропусканию через него тока практически по прямой линейной характеристике.
Такие же действия на обратном участке ведут к потере диодом своих свойств.
Закон Шварцнегера или как надо обеспечивать надежную работу резистора под нагрузкой
Знаменитый на весь мир атлет Арнольд постоянно тренировался по методике нашего советского силача Юрия Власова. Он брал его опыт за основу и даже приезжал в Россию погостить к своему кумиру.
В основе метода постоянных результативных тренировок положен принцип не столько полноценного питания и отдыха, сколько подбор правильных нагрузок, которые должен преодолевать организм.
Все это полностью соответствует законам электротехники, применяется в работе любого электрического сопротивления. Рассмотрим его на примере резистора: так проще для понимания.
Его металл не только пропускает электрический ток, но и нагревается, выделяя тепло. Нагрев увеличивается с повышением тока. При этом температура может снижаться за счет теплоотвода в окружающую среду или увеличиваться в герметичном, не теплопроводящем объеме.
Так работает электропроводка, выполненная одним и тем же кабелем, проложенным открыто по стенам или спрятанным в штробах.
В первом случае от нагревающегося током кабеля тепло отводится в окружающий воздух за счет его естественной циркуляции, а во втором нагрев идет более интенсивно.
Однако повышать температуру жил можно только до определенной величины. За ее рабочим диапазоном вначале происходит разрушение слоя изоляции, а потом — простое перегорание металла, когда проводка сгорает.
На этом примере я попытался показать, что любой резистор обладает запасом тепловой мощности, за который его нельзя переводить.
Для облегчения работы электриков всем видам резисторов введен термин мощности теплового рассеивания. Она указывается в технической документации или прямо на корпусе, измеряется ваттами. Ее же показывают на электрических схемах.
Как выбрать резистор по тепловой нагрузке за 2 шага
Действуют по следующему алгоритму:
- Вначале определяют мощность, которая будет проходить через искомый резистор. Достаточно перемножить величину номинального тока на напряжение, выразить полученное значение в ваттах.
- Под эту величину из всего многообразия элементов подбирают тот, который соответствует по значению сопротивления и обладает мощностью теплового рассеивания не меньшего номинала.
Желательно брать его с небольшим резервом. Он не будет лишним для работы в критических ситуациях электрической схемы, но повлияет на габариты устройства.
Полезные примеры из жизни
Как продлить ресурс лампы накаливания
В пожарном депо Ливермоля (Калифорния) зарегистрирован рекорд рабочего режима осветительной лампы: 117 лет. Она практически непрерывно выполняет свою задачу с 1901 года по настоящее время.
Такой ресурс обеспечен за счет:
- правильного выбора сопротивления, ограничивающего ток через нить накала и создания экономного режима освещения;
- беспрерывной работы, исключающей переходные процессы при включениях/выключениях, сопровождаемые бросками токов;
- надежной конструкции.
Как регулировать токи от 100 ампер в силовой цепи
Этот случай я привожу не для повторения, а с целью расширения кругозора и лучшего уяснения процессов, происходящих в электричестве.
Ни один обычный резистор не способен длительно выдерживать токи такой величины. Он просто сгорит. Однако при наладке промышленных генераторов требуется иметь устройство, справляющееся с подобными мощностями.
Это водяной реостат, состоящий из металлического корпуса — ведра прямоугольной формы, служащего одним из контактов для подключения провода от нагрузки.
Второй контакт составляет металлический нож, подключаемый через изоляторы.
Внутрь ведра наливают воду и засыпают соль: создают электролит, хорошо проводящий большие токи.
Перемещение ножа в электролите меняет сопротивление среды и обеспечивает регулировку высоких токов. Проводимость можно изменять концентрацией соли в растворе.
Напоминаю: подобное устройство нельзя использовать в бытовых цепях: оно не отвечает требованиям безопасности.
Таким образом, под каждый конкретный случай расчета используется своя формула электрического сопротивления, которой следует внимательно пользоваться. Исключить ошибки в расчетах помогает специализированный онлайн калькулятор.
По этой теме рекомендую посмотреть видеоролик Владимира Романова.
Если хотите задать вопрос или дополнить информацию, то воспользуйтесь разделом комментариев.
Сопротивление тока: формула нахождения сопротивления электротока
Сопротивление – способность материала препятствовать направленному движению заряженных частиц. Определяется величина согласно закону Ома. Точные значения параметра требуются во многих сферах, включая электронику и радиодетали. Определенным уровнем сопротивления обладает каждый материал на планете, вне зависимости от агрегатной формы. Некоторые вещества имеют настолько высокое сопротивление, что проведение через них электрического тока практически невозможно.
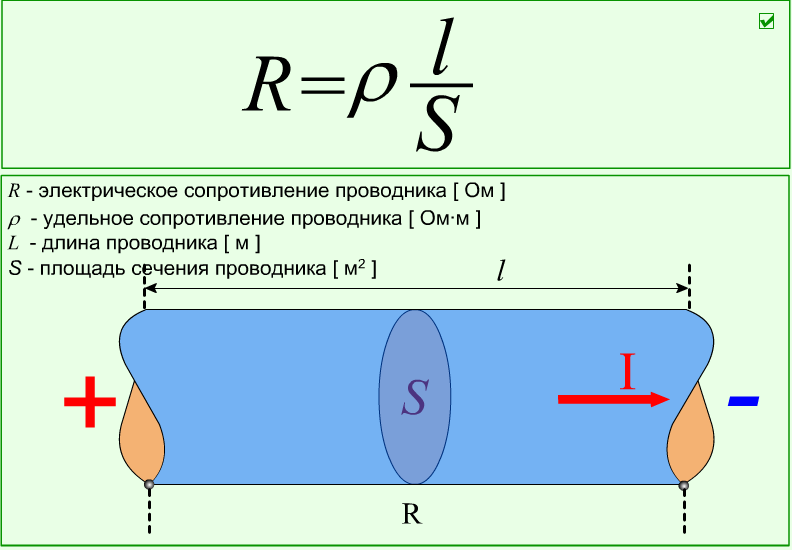
Формула удельного сопротивления
Формулировка закона Ома
Закон Ома имеет следующую формулировку. Чтобы рассчитать сопротивления, нужно напряжение разделить на силу тока в электрической цепи. Физическая величина обуславливается количеством свободных заряженных частиц в материале.
Какой буквой обозначается сопротивление? В системе измерений СИ на конгрессе ООН символом для записи физического явления была избрана латинская R (от английского resistance).
Отличные степени величины присущи каждому материалу из-за разной концентрации носителей электрического тока. Наибольшая концентрация присуща металлам, поэтому именно они являются лучшими проводниками. Особенность заключается в максимальном количестве проводящих электронов, представляющих собой заряженные частицы, не принадлежащие ни одной элементарной частице в металле или другом сырье. Возникновение тока и как следствие движение заряженных частиц возникают под действием внешних электрических полей.
Определение единицы сопротивления – Ом
Как обозначается сопротивление? Величина измеряется в Омах (русское обозначение), в то время как в других странах символ для маркировки – омега (Ω). Единица представляет собой значение силы препятствия прохождению электрического тока проводника, по которому течет напряжение в 1В с силой постоянного электрического тока в 1А.
Единица измерения была введена в 1960 году, вместе с принятием международной системы величин в целом. Существующая величина имеет обратное значение в виде проводимости электрического тока, которая измеряется в сименсах.
Расчет сопротивления последовательных резисторов
При последовательном сопротивлении нескольких резисторов соответственно увеличивается эквивалентная величина. Расчет сопротивления нескольких элементов, соединенных между собой последовательно, проводится за счет суммирования номиналов каждого элемента. Например, при соединении нескольких элементов, которые соединены в одну цепь последовательно, величина электрического сопротивления будет равной сумме уровня противодействия каждого из резисторов. Формула имеет одинаковый вид для любого количества резисторов.
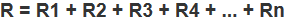
Как найти сопротивление формула для последовательной цепи
Если заменить в последовательной цепи один из элементов, то соответственно изменится уровень противодействия направленному движению частиц в этой цепи. Это также повлечет изменение силы тока.

Резистор
Расчет сопротивления параллельных резисторов
Сопротивление формула для параллельного соединения имеет несколько другой вид.
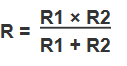
Формула
Относительно большого количества последовательных элементов при увеличении количества резисторов в цепи соответственно возрастает сложность проведения расчета. Удельное сопротивление буква, которая ему соответствует, – латинская ρ.
Использование параллельного соединения оправдано в цепях, в которых требуется высокая величина параметра. Тогда применяются радиоэлементы с одинаковым параметром мощности и сопротивления. Например, 10 элементов, обладающих уровнем сопротивления 1000 Ом, которые объединены в единую цепь с параллельным соединением, на выходе будут иметь величину препятствия движению заряженных частиц в 100 Ом.
Удельное электрическое сопротивление
Удельное сопротивление представляет собой параметр, который определяет уровень препятствия движению электрического тока через проводник определенной длины. Зависит от параметра конкретного вещества, от длины. Для материала с однородными свойствами и известной величиной сопротивления и длиной проводника расчет удельного параметра идет по формуле ниже.
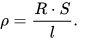
Расчет удельного объемного электрического сопротивления
Фактически смысл уравнение имеет следующий. Удельное сопротивление – величина сопротивления при прохождении через проводник определенной длины, с одинаковой площадью поперечного сечения на протяжении всего маршрута.
Параметр измеряется в Ом*метр. Таким образом, один Ом*метр равняется уровню препятствия направленному движению заряженных частиц через однородную проводящую среду с длиной в 100 см и площадью сечения в 1 квадратный метр.
Значение сопротивления
Таблица параметров для различных проводников
| Название | Величина удельного сопротивления |
|---|---|
| Провод из алюминия | 2.7•10^-8 |
| Вольфрам | 5.5•10^-8 |
| Графит | 8.0•10^-6 |
| Чистое железо | 2.2•10^-8 |
| Золото | 2.2•10^-8 |
| Иридий | 4.74•10^-8 |
| Сталь | 1.3•10^-7 |
| Магний | 4.4•10^-8 |
| Медь | 1.72•10^-8 |
| Никель | 8.7•10^-8 |
| Платина | 1.07•10^-7 |
| Ртуть | 9.6•10^-7 |
| Свинец | 2.08•10^-7 |
| Серебро | 1.6•10^-8 |
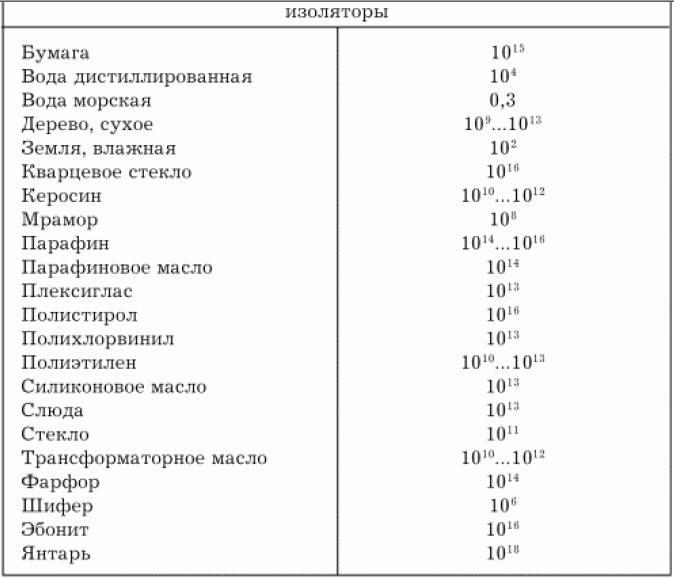
Величины сопротивлений для некоторых диэлектриков
Показатели для жидких проводников
Жидкими проводниками электричества чаще всего выступают расплавленные металлы и другие электролиты (кислоты и щелочи). Обычно температура плавления жидких проводников достаточно высока, исключая ртуть. Поэтому в нормальных условиях примерами жидкого вещества, проводящего электрический ток, могут быть только ртуть и галлий.
Величины удельного препятствия направленному движению заряженных частиц у растворенных электролитов (солей и кислот) являются динамическими характеристиками. На величину влияют концентрация активного проводящего вещества и температура. Влияние последней противоположно металлам. Во время нагрева жидких проводников соответственно снижается уровень сопротивления. И, наоборот, при существенных снижениях температуры проводимость падает. При переходе жидких проводников в твердое агрегатное состояние проводимость электрического тока снижается до нуля.
Явным примером последнего является влияние температуры на автомобильные аккумуляторные батареи во время сильного мороза. При этом жидкость, проводящая электрический ток (раствор сернистой кислоты), замерзает, из-за чего сопротивление внутреннего контура аккумулятора возрастает до максимума, и питание стартера и электроники не представляется возможным.
Катушка индуктивности
Катушки индуктивности представляет собой устройство, главной частью которого является проводящий металл, скрученный в некое подобие колец либо обернутый вокруг диэлектрического сердечника. Если через такое устройство проходит электрический ток, то формируется местное магнитное поле. Это происходит из-за концентрации переменного магнитного поля.
Для вычислительной техники используется дроссель, который применяется для питания различного высокоточного оборудования. Устройство требуется для снижения колебаний переменного напряжения. С добавлением частоты сопротивление соответственно увеличивается. Технические параметры дросселя зависят от площади поперечного сечения проводящего материала, числа витков вокруг сердечника из диэлектрика.

Катушка индуктивности
Пример из практики
Последовательно с источником освещения включен тестер. Напряжение осветительного прибора = 220 Вольт. Мощность неизвестна. На показателе амперметра указано 276 миллиампер тока. Какая величина у спирали лампы при последовательном включении в схему резисторов?
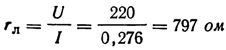
Формула нахождения сопротивления спирали
Электросопротивление представляет собой физическую величину, которая соответствует степени препятствия движению электрических частиц у каждого материала. Возможно измерить уровень величины мультиметром. В таком случае придется находить значение по формуле. Для предотвращения попадания электрического тока на непредназначенные для этого участки желательно заземлять линии передачи. Данная физическая величина используется во многих радиодеталях, например, светодиодах. В электрической цепи, чтобы узнать величину, требуется подключить к вольтметру фазу и ноль при известной силе тока, затем рассчитать по закону Ома.
Видео
Расчет полного сопротивления в цепи переменного тока — импеданс
Понятие импеданса используется в разных сферах науки. Существуют разные его формы: гидродинамический, артериальный (медицинский термин, состоит из статического и кинетического компонентов), используемый при измерении гидростатического давления. Есть и электрический импеданс, описывающий полное сопротивление цепного фрагмента. Электрику необходимо знать, от чего зависит и как вычисляется эта величина в однофазных и трехфазных цепях с трансформаторами тока и иными компонентами.

Импеданс описывает сопротивление всей цепи
Что такое импеданс
Это понятие описывает комплексное сопротивление цепи или ее межузлового участка. Оно было введено лондонским инженером и физиком О. Хевисайдом в 1886 году. В состав полного сопротивления цепи входят активная и реактивная компоненты. Фазовый сдвиг и само значение импенданса при электротоке, чья кривая имеет форму синусоиды, могут быть рассчитаны с ориентиром на то, каким образом соединены входящие в цепь компоненты.
Аналогия с электрическим сопротивлением проводника на примере резистора
Чтобы суметь рассчитать импеданс цепи, нужно представлять, как себя ведут различные входящие в нее элементы: катушки индуктивности, резисторные и емкостные детали, с точки зрения вклада в составляющие общей резистивности цепи.
Активное сопротивление
Резистор относится к числу пассивных деталей цепи, не содержащих внутренних источников электроэнергии, при этом почти все создаваемое им противодействие приходится на активную компоненту. Реактивная составляющая если и присутствует, то настолько мала, что ею зачастую принято пренебрегать. Это связано с тем, что отношение напряжения на деталь и электротока, проходящего через нее, не зависит от их частоты. Когда к резисторной детали присоединяют источник напряжения (обозначим его U), через нее будет идти электроток значением I. Если к концам радиодетали подсоединяют источник тока, равного I, между ними будет иметь место падение напряжения U.
Важно! Выражение для сопротивления резистора можно записать так: R=U/I.

Резисторы – источники активного сопротивления
Реактивное сопротивление
К основным компонентам электроцепей, несущим такую нагрузку, относятся дроссели (и подобные им индуктивные элементы) и конденсаторы. При достижении резонанса наблюдается наименьшее значение общего противодействия подключенных последовательно конденсатора и дросселя и наибольшее – включенных параллельно.
Индуктивная нагрузка
Если индуктивный дроссель подключить к постоянному току, на нем будут наблюдаться следующие эффекты: резистивность будет приближаться к нулевому значению, а при пропускании электротока через катушечный элемент падение напряжения будет отсутствовать, независимо от токовой величины:
R=U/I=0/I=0.
Такие цифры справедливы для идеального дросселя, на практике они все же несколько отклоняются от нуля. Если к детали будет приложен переменный ток, напряжение между катушечными выводами будет отличным от нуля.

Катушка индуктивности
Емкостная нагрузка
При включении идеального конденсаторного элемента в сеть с постоянным напряжением его резистивность будет иметь очень большую величину, стремящуюся к бесконечной. Когда к радиодетали прикладывают такое напряжение, проходящий через нее ток будет равен нулю. Если к выводам конденсатора подсоединить источник переменного напряжения, ток будет ненулевым.

Детали, обладающие емкостью
Данные эффекты, наблюдаемые на емкостных радиодеталях и катушках, нельзя описывать в категориях активного противодействия в условиях константного электротока, так как последнее подразумевает стабильное, независимое от условий и не изменяющееся во времени отношение электротока и напряжения и исключает явление сдвига фаз между этими величинами. Таким образом, становится целесообразным введение для реактивных деталей характеристики, связывающей электроток и напряжение так, как это делает активное противодействие в омовском законе для константного тока.
Важно! При рассмотрении поведения катушек и конденсаторов под действием гармонических сигналов обнаруживается, что токовая сила и напряжение могут быть связаны константной величиной, которую также называют импедансом. При ее изучении применяется понятие о гармонических сигналах, учитывающее как их амплитудные характеристики, так и особенности, связанные с фазами.
Такое значение импеданса можно определить как частное комплексной амплитуды, которой обладает напряжение приложенного к двухполюсному элементу сигнала, и комплексной амплитуды идущего через элемент электротока. В отношении пассивных электроцепей со стабильными показателями в устоявшемся режиме стоит сказать, что импедансный показатель у них не будет привязанным к течению времени. Если временной параметр при формульной записи не сокращается, то категория импеданса для рассматриваемого двухполюсника окажется неприменимой.
Расчет эквивалентного сопротивления элементов цепи
Определение общего цепного сопротивления будет зависеть от того, какого типа конфигурацию составляют компоненты цепи. Для параллельного и последовательного подключений правила расчета будут неодинаковыми. Опираться при вычислениях нужно на закон Ома.
Согласно ему, у всех последовательно соединенных деталей, подключенных в цепь переменного тока, будет одно и то же значение электротока:
I=U/Z, где Z – общий импеданс цепи.
Напряжения будут различаться и окажутся привязанными к сопротивлениям деталей: на концах резистора его значение будет равно UR = IR (здесь R – активная резистивность элемента), для дросселя – UL = IXL, для емкостного элемента – UC = IXC (XL и XC – реактивные показатели соответствующих устройств). Так как векторы напряженности катушки и конденсатора имеют противоположные направления, суммарный показатель на реактивных деталях будет равен: UX = UL – UC . Противодействие будет равно: X = XL – XC.
Напряжения (общее, реактивное и активное) могут быть представлены в виде прямоугольного треугольника. Из него получается, что U² = UR² + UX². Поскольку противодействия входящих в цепь компонентов пропорциональны напряжениям, имеем Z2=R2+X2=R2+(XL – XC)2.
Для параллельного соединения принято выводить значения импеданса из проводимостей элементов, которые обратны их сопротивлениям. Отсюда 1/z2 = 1/R2 + 1/X2. Таким образом, выходит следующая формула:
Z2=1/(1/R2+(1/ XL – 1/ XC)2).
Общее сопротивление определяется компонентным составом цепи и характером соединения ее элементов. При расчетах показателей используется закон Ома.
Видео
Физическая формула расчета эквивалентного сопротивления в цепи
Расчёт электрических схем, содержащих несколько сопротивлений (резисторов), при нахождении силы тока в цепи, напряжения или мощности, производится с использованием метода свёртывания. Метод заключается в том, чтобы найти эквивалентное сопротивление выделенных участков цепи. Основная задача – замена резисторов, имеющих различное подключение относительно друг друга, на эквивалент (Rэкв.).

Эквивалентное сопротивление резисторов
Определение эквивалентного сопротивления
При рассмотрении схем любых электрических или электронных устройств можно увидеть, что такие компоненты, как резисторы, имеют разные типы соединений между собой. Чтобы определить эквивалентное соединение, необходимо рассматривать два элемента, включенных в определённом порядке. Несмотря на то, что на чертеже их может быть несколько десятков, и соединены они по-разному, есть только два типа включения их друг с другом: последовательное и параллельное. Остальные конфигурации – это лишь их вариации.
Последовательное соединение элементов
Подобное включение подразумевает комбинацию деталей в прямой последовательности. Выход одного сопротивления подключается к входу другого. При этом отсутствуют какие-либо ответвления на участке. Величина тока, который проходит через все соединённые последовательно компоненты, будет одна и та же.
Внимание! Снижение потенциала на каждом резистивном элементе в сумме даст полное напряжение, приложенное к последовательной цепи.
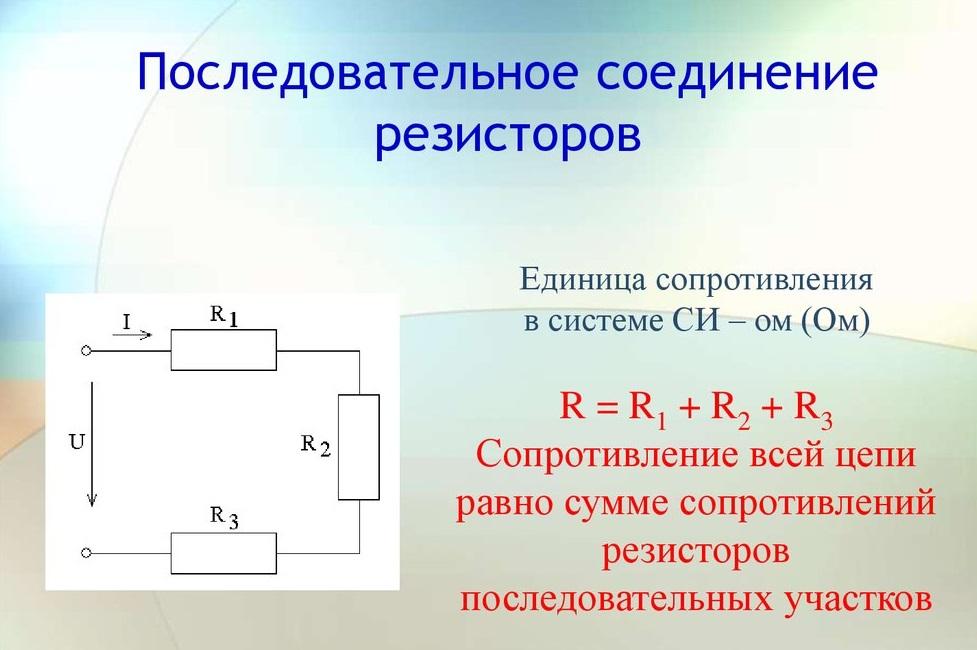
Последовательное включение резисторов
В случае постоянного тока формула закона Ома для отрезка цепи имеет вид:
I = U/R.
Сила тока зависит от приложенного напряжения и оказанного ему сопротивления. Если выразить R, его формула:
R = U/I.
Параметры последовательной цепи, включающей n соединённых друг с другом элементов, имеют свои особенности.
Проходящий по цепи ток везде одинаковый:
I = I1= I2= … = In.
Прикладываемое напряжение является суммой напряжений на каждом резисторе:
U = U1 + U2+ … + Un.
Следовательно, рассчитать можно общее:
Rэкв.= U1/I + U2/I + … +Un/I) = R1 + R2 + … +Rn.
Важно! Последовательная цепь, имеющая в своём составе N резисторов равного номинала, имеет эквивалентное сопротивление Rэкв. = N*R.
Параллельное соединение
Когда условные выходы деталей имеют общий контакт в одной точке (узле) схемы, а условные входы так же объединены во второй, говорят о параллельном соединении. Узел на чертеже обозначается графической точкой. Это место, где происходят разветвления цепей в схемах. Такой вариант подключения резисторов обеспечивает одинаковое падение напряжения U для всех параллельных элементов. Ток в этой позиции будет равен сумме токов, идущих по каждому компоненту.
Когда в параллельное подключение входит n резистивных элементов, то разность потенциалов, ток и общее сопротивление будут иметь следующие выражения:
- общий ток: I = I1 + I2 + … + In;
- общее напряжение: U = U1 = U2 = … = Un;
- Rобщ. = Rэкв. = U/I1 + U/I2 + …+ U/In) = 1/R1 + 1/R2 +…+ 1/Rn.
Величину, обратно пропорциональную сопротивлению 1/R, называют проводимостью.
Если n равных по номиналу сопротивлений включить параллельно, то Rэкв. = (R*R)/n*R = R/n. Формула подходит и для индуктивных сопротивлений проволочных катушек и ёмкостных сопротивлений конденсаторов.
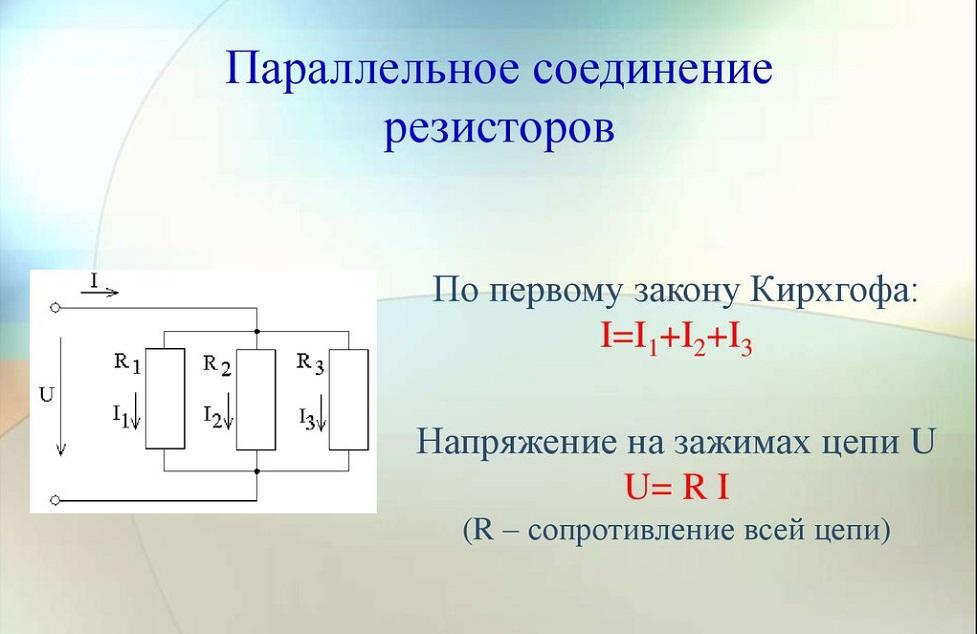
Параллельное включение резисторов
Расчёт при смешанном соединении устройств
Произвести расчет сопротивления цепи, когда она разветвлена и наполнена разными видами резистивных соединений, просто не получится. Затрудняет решение задачи множество участков, где детали подключены друг другу в разных комбинациях. В таких обстоятельствах желательно выполнять ряд преобразований, добиваясь упрощения схемы вводом отдельных эквивалентных элементов. Выявляют при этом подходящие контуры последовательных и параллельных присоединений.
Например, выискав некоторое количество последовательных подключений резисторов, заменяют их на один эквивалентный компонент. Определив элементы, соединённые последовательно, также рисуют вместо него эквивалент. Вновь начинают искать подобные простые соединения.
Метод называют «методом свёртывания». Схему упрощают до тех пор, пока в ней не останется одно Rэкв.
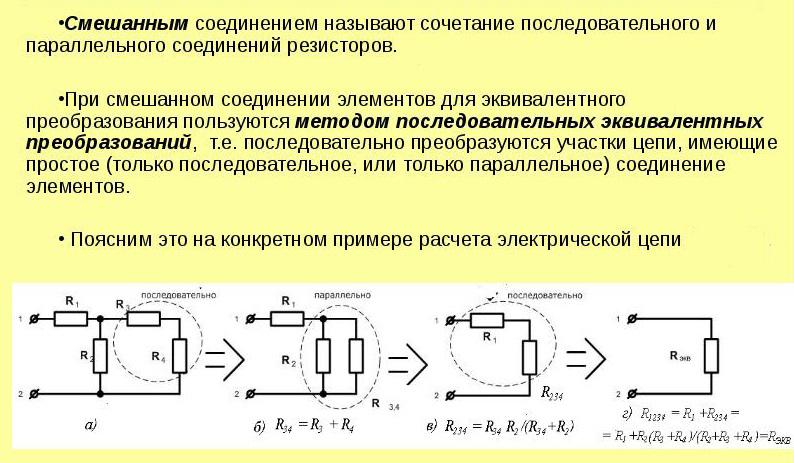
Способ расчёта при смешанном соединении
Важно! Метод эквивалентных преобразований применяется тогда, когда питание рассматриваемого участка цепи осуществляется от одного источника электрического тока, а также при определении Rэкв. в замкнутом контуре с одной ЭДС.
Такой относительный способ определения Rэкв используют и для изучения зависимости токов в некоторой цепи от значения R нагрузки. Это метод эквивалентного генератора, при котором сложный двухполюсник, являющийся активным, представляют эквивалентным генератором. При этом считают, что ЭДС его соответствует Uх.х. (холостого хода) на зажимах, R внутреннее соответствует R входному двухполюсника пассивного на тех же зажимах. Для такого определения источники тока разъединяют, а канал ЭДС закорачивают.
Физические формулы и примеры вычислений
Формулы для эквивалентных сопротивлений цепи, состоящей из пары резисторов R1 и R2, можно выделить в определённый ряд:
- параллельное присоединение определяют по формуле Rэкв. = (R1*R2)/R1+R2;
- последовательное включение вычисляют, определяя его сумму Rэкв. = R1+R2.
У смешанного соединения резистивных элементов нет конкретной формулы. Чтобы не запутаться при длительных преобразованиях, здесь допустимо воспользоваться специальной программой из интернета. Это сервис «онлайн-калькулятор». Он поможет разобраться со сложными схемами соединения, будь то треугольник, квадрат, пятиугольник или иная схематичная фигура, образованная резистивными элементами.
Понять, как работают все формулы и методы, можно на конкретной задаче. На представленном первом рисунке – смешанная электрическая схема. Она включает в себя 10 резисторов. Элементы представлены в следующих номиналах:
- R1 = 1 Ом;
- R2 = 2 Ом;
- R3 = 3 Ом;
- R4 = 6 Ом;
- R5 = 9 Ом;
- R6 = 18 Ом;
- R7 = 2Ом;
- R8 = 2Ом;
- R9 = 8 Ом;
- R10 = 4 Ом.
Напряжение, поданное на схему:
U = 24 В.
Требуется рассчитать токи на всех резистивных элементах.
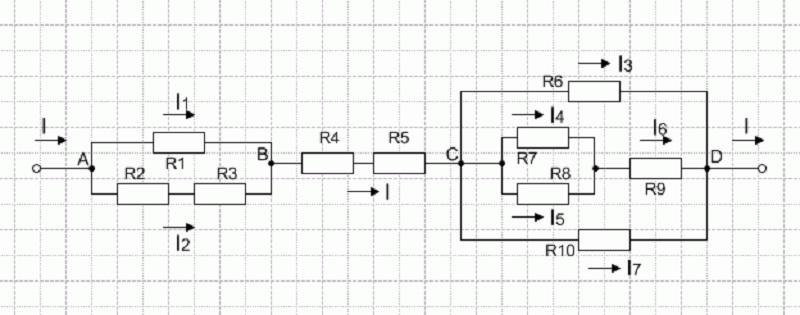
Исходная цепь
Для расчётов применяется закон Ома:
I = U/R, подставляя вместо R эквивалентное сопротивление.
Внимание! Для решения этой задачи сначала вычисляют общее (эквивалентное) R, после чего уже рассчитывают ток в цепи и напряжение на каждом резистивном компоненте.
Вычисляя Rэкв., разделяют заданную цепь на звенья, вмещающие в себя параллельные и последовательные включения. Делают расчёты для каждого такого звена, после – всей цепи целиком.
На рисунке выше изображено смешанное соединение сопротивлений. Его можно разбить на три участка:
- АВ – участок, имеющий две параллельных ветви;
- ВС – отрезок, вмещающий в себя последовательное сопряжение;
- CD – отрезок схемы с расположением трёх параллельных цепочек.
Сопротивления R2 и R3, образующие нижнюю ветку отрезка АВ, соединены последовательно, что учитывается при расчёте.
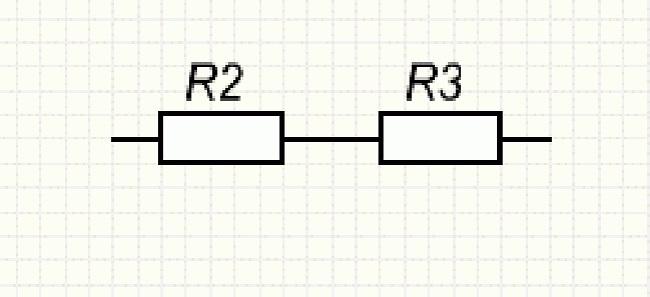
Последовательно соединённые резисторы R2 и R3
Если посмотреть на участок СD, то можно отметить смешанное включение резистивных элементов.
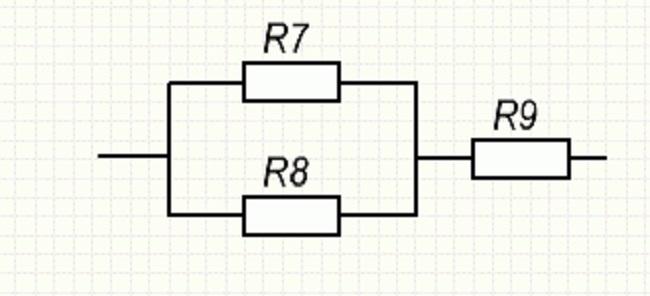
Смешанное включение на участке CD
Начало расчётов состоит в определении эквивалентных сопротивлений для этих смешанных фрагментов. Выполняют это в следующем порядке:
- Rэкв.2,3 = R2+R3=2 + 3 = 5 Ом;
- Rэкв.7,8 = (R7*R8)/R7 + R8 = (2*2)/2 + 2 = 1 Ом;
- Rэкв.7,8,9 = Rэкв.7,8 + R9 = 1 + 8 = 9 Ом.
Зная значения полученных эквивалентов, упрощают первоначальную схему. Она будет иметь вид, представленный на рисунке ниже.
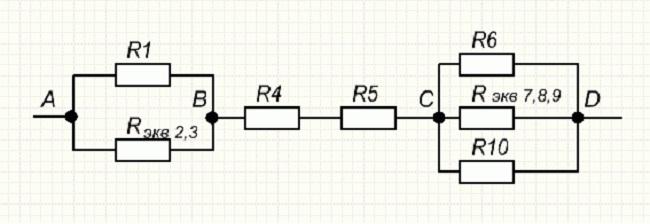
Результат первого свёртывания
Далее можно уже определить Rэкв. для участков AB, BC, CD, по формулам:
- Rэкв.AB = (R1*Rэкв 2,3)/R1 + Rэкв 2,3 = (1*5)/1 + 5 = 0,83 Ом;
- Rэкв.BC = R4 + R5 = 6 + 9 = 15 Ом;
- 1/Rэкв.CD = 1/R6 + 1/Rэкв.7,8,9 + 1/R10 = 1/18 + 1/9 + 1/4 = 0,05 + 0,11 + 0,25 = 0,41 Ом.
В результате выполненных вычислений получается эквивалентная схема, в которую входят три Rэкв. сопротивления. Она имеет вид, показанный на рисунке ниже.
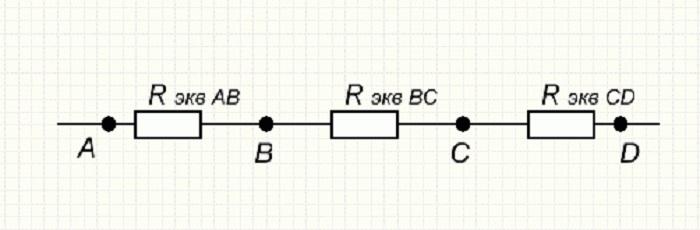
Результат последующего свёртывания
Теперь можно определить эквивалентное сопротивление всей первоначальной схемы, сложив эквивалентные значения всех трёх участков:
Rэкв. = Rэкв.AB + Rэкв.BC + Rэкв.CD = 0,83 + 15 + 0,41 = 56,83 Ом.
Далее, используя закон Ома, находят ток в последнем последовательном участке:
I = U/ Rэкв. = 24/56,83 = 0,42 А.
Зная силу тока, можно найти, какое падение напряжения на рассмотренных участках AB, BC, CD. Это выполняется следующим образом:
- UAB = I* Rэкв.AB= 0,42*0,83 = 0,35 В;
- UBC = I* Rэкв.BC= 0,42*15 = 6,3В;
- UCD = I* Rэкв.CD = 0,42*0,41 = 0,17 В.
Следующим шагом станет определение токов на параллельных отрезках AB и CD:
- I1 = UAB/R1 = 0,35/1 = 0,35 А;
- I2 = UAB/Rэкв.2,3 = 0,35/5 = 0,07 А;
- I3 = UCD/R6 = 0,17/18 = 0,009 А;
- I6 = UCD/Rэкв.7,8,9= 0,17/9 = 0,02 А;
- I7 = UCD/R10 = 0,17/4 = 0,04 А.
Далее, чтобы найти значения токов, проходящих через R7 и R8, нужно рассчитать напряжение на этих двух резисторах. Предварительно находят падение напряжения на R9.
U9 = R9*I6 = 8*0,02 = 0,16 В.
Теперь напряжение, падающее на Rэкв.7,8, будет разностью между U CD и U9.
U7,8 = UCD – U9= 0,17 – 0,16 = 1 В.
После этого можно уже узнать значение токов, движущихся по резисторам R7 и R8, используя формулы:
- I4 = U7,8/R7 = 1/2 = 0,5 A;
- I5 = U7,8/R8 = 1/2 = 0,5 A.
Стоит заметить! Ток, протекающий через R4 и R5, по своему значению равен току на отрезке, не имеющем разветвления.
Рассчитывая схемы и решая задачи по нахождению значений электрических параметров, необходимо использовать эквивалентные сопротивления. С помощью такой замены сложные построения превращаются в элементарные цепи, которые сводятся к параллельным и последовательным соединениям резистивных элементов.
Видео
Этот калькулятор может решать другие математические задачи. Этот калькулятор можно использовать для рабочих задач. Например, «А» может покрасить комнату за 5 часов, а «Б» покрасить комнату за 6 часов. Если они оба работают вместе, сколько времени займет работа? Введите 5 и 6 просто как если бы они были резисторами и получите ответ. Этот калькулятор можно использовать для задач «заполнения». Например, одна труба может заполнить воду бак за 5 часов, в то время как другая труба может заполнить тот же бак за 6 часов. Если обе трубы работают одновременно …….. хммм кажется жутко знакомым к другой проблеме, не так ли? Удачи тебе с математическими задачами. Числа отображаются в экспоненциальном представлении с указанием количества значащие цифры, которые вы указываете. Для удобства чтения числа от 0,001 до 1000. будет не в экспоненциальной нотации, но все равно будет иметь ту же точность. Вы можете изменить количество значащих цифр, отображаемых изменение числа в поле выше. Большинство браузеров будут отображать ответы правильно, но если вы вообще не видите ответов, введите ноль в поле выше, что приведет к устраните все форматирование, но по крайней мере вы увидите ответы. Вернуться на главную страницу Авторские права © 1999 — 1728 Программные системы |
||
Мощность и энергия
- Изучив этот раздел, вы сможете:
- Выполнять расчеты мощности, напряжения, тока и сопротивления.
- • с использованием соответствующих единиц и подразделов.
- Различайте мощность и энергию в электрических цепях.
Мощность резисторов
Когда через резистор протекает ток, электрическая энергия преобразуется в ТЕПЛОВУЮ энергию.Тепло, генерируемое в компонентах цепи, каждый из которых обладает хотя бы некоторым сопротивлением, рассеивается в воздухе вокруг компонентов. Скорость рассеивания тепла называется МОЩНОСТЬЮ, обозначается буквой P и измеряется в ваттах (Вт).
Количество рассеиваемой мощности может быть определено с использованием любых двух величин, используемых в расчетах по закону Ома. Помните, как и в любой формуле, в формуле должны использоваться ОСНОВНЫЕ КОЛИЧЕСТВА, то есть ВОЛЬТЫ, ОМЫ и АМПЕРЫ (не милли, мег и т. Д.).
Чтобы найти мощность P, используя V и I
Чтобы найти мощность P, используя V и R
Чтобы найти мощность P, используя I и R
Перед тем, как начать, подумайте об этих нескольких советах, они облегчат задачу, если следовать им.
1. Найдите ответы карандашом и бумагой; в противном случае легко запутаться на полпути и получить неправильный ответ.
2.Конечно, ответ — это не просто число, это будет определенное количество ватт (или несколько или несколько единиц ватт). Не забудьте указать правильную единицу измерения (например, Вт или мВт и т. Д.), А также число, иначе ответ не имеет смысла.
3. Преобразуйте все вспомогательные единицы, такие как мВ или кОм, в ватты, указав их в соответствующей формуле. Ошибка здесь даст действительно глупые ответы, в тысячи раз слишком большие или слишком маленькие.
4. Хотя структура этих формул мощности кажется очень похожей на формулы закона Ома, есть небольшое различие — они содержат некоторые квадраты (I 2 и V 2 ).Будьте очень осторожны при использовании трюка с треугольником для транспонирования этих формул. Если вам нужно связать мощность с сопротивлением, то I или V необходимо возвести в квадрат (умножить на себя). Однако вы можете построить треугольник, который соответствует любой из формул для получения R, как показано ниже.
Не забудьте загрузить нашу брошюру «Советы по математике», в которой показано, как использовать калькулятор с показателями степени и инженерной нотацией, чтобы работать с этими частями и каждый раз получать правильный ответ.
Нет научного калькулятора? Буклет «Подсказки по математике» объясняет, что вам нужно (и что вам не нужно, чтобы не тратить деньги без надобности). Если вы не хотите покупать научный калькулятор, вы всегда можете получить его бесплатно в сети. Пользователи ПК могут попробовать Calc98 на сайте www.calculator.org/download.html. Какой бы калькулятор вы ни выбрали, прочтите инструкции, чтобы ознакомиться с методами работы, которые вам следует использовать, поскольку они варьируются от калькулятора к калькулятору.
Важно знать о влиянии рассеивания мощности в компонентах: чем больше мощность, тем больше тепла должно рассеиваться компонентом. Обычно это означает, что компоненты, рассеивающие большое количество энергии, нагреваются, а также они будут значительно больше по размеру, чем типы с низким энергопотреблением. Если компоненту требуется рассеивать больше энергии, чем он предназначен, он не сможет достаточно быстро избавиться от выделяемого тепла. Его температура повысится, и перегрев может вызвать полный выход из строя компонента и, возможно, повреждение других компонентов и самой печатной платы (PCB).В качестве меры предосторожности резисторы большой мощности часто устанавливают вне печатной платы с помощью более длинных выводных проводов, заключенных в керамические гильзы. Резисторы с проволочной обмоткой большой мощности могут даже быть заключены в металлический радиатор и прикреплены болтами к большой металлической поверхности, например к корпусу оборудования, чтобы избавиться от нежелательного тепла. Примеры резисторов большой мощности показаны на странице конструкции резистора.
Такие компоненты, как резисторы, имеют конкретную номинальную мощность, указанную производителем (в ваттах или милливаттах).Этот рейтинг (параметр) необходимо проверить при замене компонента, чтобы не произошло завышения рейтинга. Это важный фактор безопасности при обслуживании электронного оборудования.
НАКОНЕЧНИК
Тепло, выделяемое резисторами большой мощности, является основной причиной преждевременного выхода из строя многих цепей. Либо сам резистор выходит из строя из-за «разомкнутой цепи», особенно в резисторах с проволочной обмоткой. В резисторах из углеродного состава перегрев в течение длительного периода может вызвать изменение значения. Это может увеличиваться в типах с высоким сопротивлением или более опасно уменьшаться (позволяя увеличить ток) в типах с низким сопротивлением.Увеличение тока, вызванное уменьшением сопротивления, только ускоряет процесс, и в конечном итоге резистор (а иногда и другие связанные компоненты) сгорает!
Энергия в резисторах
Если определенное количество мощности рассеивается в течение заданного времени, то рассеивается ЭНЕРГИЯ. Энергия (мощность x время) измеряется в Джоулях, и, включив время (t) в формулы мощности, можно рассчитать энергию, рассеиваемую компонентом или схемой.
Рассеиваемая энергия = Pt или VIt или V 2 t / R или даже I 2 Rt Джоули
Обратите внимание, что в формулах для энергии такие величины, как мощность, время, сопротивление, ток и напряжение, должны быть преобразованы в их основные единицы, например.грамм. Ватты, секунды, Ом, Амперы, Вольт и т. Д. Никаких дополнительных единиц или нескольких единиц! Как описано в буклете «Советы по математике».
Все вышеперечисленные единицы являются частью интегрированной системы международно стандартизированных единиц; Система S.I. (Système International d´Unités). Эта система устанавливает основные единицы для любых электрических, механических и физических свойств и их отношения друг к другу. Он также включает стандартную форму кратных и долей кратных, описанную в буклете «Подсказки по математике».
.
Что такое шунтирующий резистор? — Определение и формула
Определение: Резистор с очень низким значением сопротивления такого типа резистора называется шунтирующим сопротивлением. Шунтирующий резистор в основном изготавливается из материала, имеющего низкотемпературный коэффициент сопротивления. Он подключается параллельно амперметру, диапазон которого должен быть расширен. Он также подключен последовательно с нагрузкой, ток которой необходимо измерить.
Допустим, амперметр имеет сопротивление R м и измеряет только небольшой ток I м .Шунтирующий резистор R s размещен параллельно с амперметром для увеличения их диапазона.
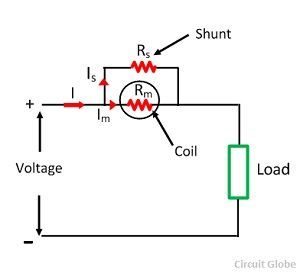
Let, R с = сопротивление шунта
I с = ток шунта
I = общий измеряемый ток нагрузки или цепи
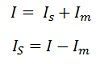
Поскольку шунт включен параллельно амперметру, 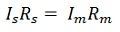
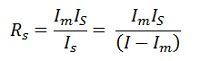
Из приведенного выше уравнения получаем,
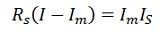
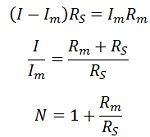
Где N — отношение полного измеряемого тока (I) к току полного отклонения I м известно как умножающая способность шунта.
Шунт используется в гальванометре для измерения большого тока. Он подключен параллельно цепи гальванометра. Гальванометр — это устройство для измерения тока. Направление протекания тока внутри цепи определяется стрелкой гальванометра.
.Шунтирующие резисторы< Шунтирующие резисторы считывания тока >
Что такое шунтирующий резистор (шунтирующий резистор для измерения тока)?
Раньше резистор, подключенный параллельно амперметру в качестве шунта для расширения диапазона измерения тока, назывался шунтирующими резисторами, но в последние годы резисторы, используемые для определения тока в цепи, все вместе называются шунтирующими резисторами (шунтирующий резистор для измерения тока ).
Шунтирующие резисторы (делитель)
Слово «шунт», которое имеет различные значения, включая «отклонять», «избегать» и «разделять», обычно относится к резистору, помещенному параллельно с амперметром для шунтирования тока.
Чтобы расширить диапазон измерения амперметра, параллельно установлен резистор, который шунтирует ток, и измеряется общий ток, протекающий в цепи.
[Делитель потока] Im: Полный контур, протекающий в контур
Ir: Ток, протекающий через амперметр
r: Внутреннее электрическое сопротивление амперметра
R: Шунтирующее (делительное) сопротивление
Например, полный ток (Im), протекающий в верхнюю цепь, можно выразить следующим уравнением.
Im = Ir + Ir (r / R) = Ir (1 + r / R)
В результате, отношение полного тока, протекающего по цепи, к току, протекающему через амперметр
Im / Ir = (1 + r / R)
будет.
То есть, (1 + r / R), в раз больше отображаемого на измерителе тока (Ir: ток, протекающий через амперметр), представляет собой общий ток, протекающий через цепь.
Шунтирующие резисторы (серия)
В цепи, в которой резисторы соединены последовательно, определяется разность потенциалов (падение напряжения) на резисторе, и ток, протекающий в цепи, измеряется с использованием закона Ома.
[Схема обнаружения] I: Ток, протекающий в цепи
R: Шунтирующее сопротивление
В: Разница потенциалов на резисторе
Например, при протекании тока (I) на резисторе создается разность потенциалов (V).
Эту разность потенциалов можно рассчитать с помощью закона Ома.
В = I × R (закон Ома)
Ток, протекающий по цепи, можно измерить, определив напряжение (В) с помощью цепи обнаружения.
Поскольку ток (I) и напряжение (V) пропорциональны друг другу, фактическое изменение значения тока (I) может использоваться как изменение обнаруженного напряжения (V) и использоваться для управления обратной связью и контроля пороговых значений.
[Пример контроля обратной связи] [Пример контроля пороговых значений]Шунтирующие резисторы (резисторы определения тока) на страницу продукта
Шунтирующие резисторы ROHM (Current Sense Shunt Resistors) были разработаны с использованием технологии обработки металлических материалов, культивируемой на протяжении многих лет, для обеспечения совместимости с широким спектром приложений, от портативных устройств, таких как смартфоны, до автомобильных и промышленных систем, требующих большей степени надежности.Шунтирующие резисторы
(шунтирующие резисторы для измерения тока) широко используются на автомобильном и промышленном рынках для определения тока в установках большой мощности. В автомобильной сфере переход к компьютеризации и электромеханическим системам, вызванный необходимостью обеспечения большей безопасности и эффективности наряду с появлением электромобилей, привел к увеличению количества требуемых небольших двигателей и ЭБУ, что привело к спросу на компактные шунтирующие резисторы.


