Формула сопротивления при параллельном соединении резисторов. Последовательное и параллельное соединение проводников: формулы, расчеты, примеры — Производство и поставка электростанций, Бензиновые и дизельные генераторы от 1 до 100 кВт. Мини ТЭЦ на базе двигателя Стирлинга.

Как рассчитать общее сопротивление при последовательном и параллельном соединении проводников. Какие формулы используются для вычисления токов и напряжений в электрических цепях. Какие особенности имеют различные схемы соединения резисторов.

Содержание

Основные виды соединения проводников в электрических цепях

В электротехнике выделяют три основных способа соединения проводников:

Последовательное соединение
Параллельное соединение
Смешанное соединение

Каждый из этих видов соединения имеет свои особенности и применяется для решения различных задач. Рассмотрим подробнее последовательное и параллельное соединения, а также формулы для их расчета.

Последовательное соединение проводников

При последовательном соединении проводники соединяются друг за другом, образуя единую неразветвленную цепь. Главные особенности такого соединения:

Сила тока одинакова во всех участках цепи
Общее напряжение равно сумме напряжений на отдельных участках
Общее сопротивление равно сумме сопротивлений отдельных проводников

Формулы для расчета последовательного соединения

Основные формулы для расчета параметров цепи при последовательном соединении:

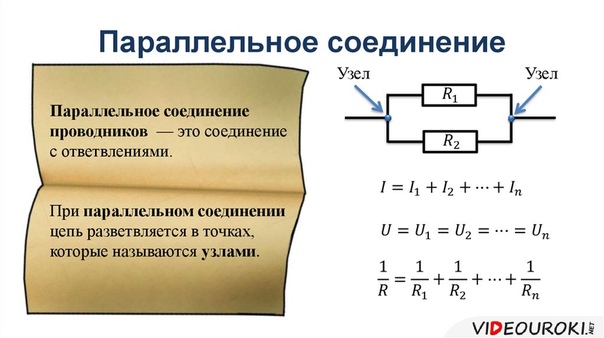
I = I1 = I2 = … = In
U = U1 + U2 + … + Un
R = R1 + R2 + … + Rn

Где I — сила тока, U — напряжение, R — сопротивление.

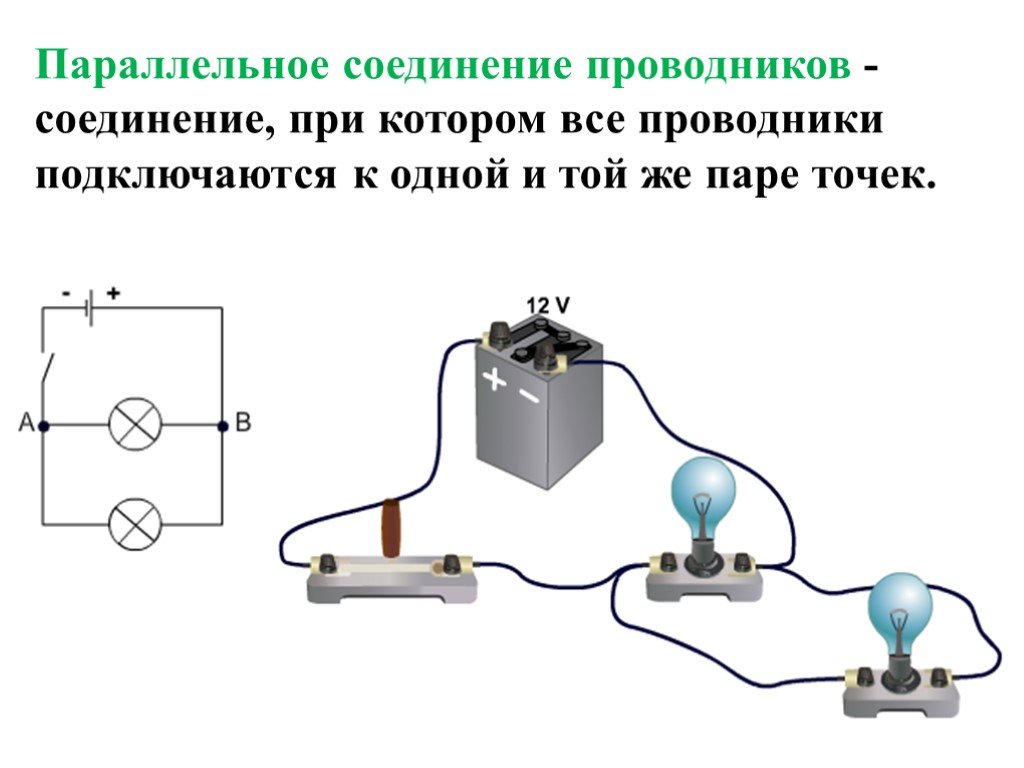
Параллельное соединение проводников

При параллельном соединении все проводники подключаются к одним и тем же точкам цепи. Основные свойства:

Напряжение на всех участках одинаково
Общий ток равен сумме токов в отдельных ветвях
Общее сопротивление меньше сопротивления любого из проводников

Формулы для расчета параллельного соединения

Ключевые формулы для параллельного соединения:

U = U1 = U2 = … = Un
I = I1 + I2 + … + In
1/R = 1/R1 + 1/R2 + … + 1/Rn

Расчет сопротивления при параллельном соединении

Расчет общего сопротивления при параллельном соединении имеет некоторые особенности. Рассмотрим это на примере.

Пример расчета параллельного соединения

Дано: три резистора сопротивлением 6 Ом, 12 Ом и 4 Ом соединены параллельно. Необходимо найти общее сопротивление.

Решение:

Используем формулу: 1/R = 1/R1 + 1/R2 + 1/R3
Подставляем значения: 1/R = 1/6 + 1/12 + 1/4
Приводим к общему знаменателю: 1/R = 2/12 + 1/12 + 3/12 = 6/12 = 1/2
Окончательный результат: R = 2 Ом

Таким образом, общее сопротивление параллельно соединенных резисторов составляет 2 Ом.

Применение различных схем соединения проводников

Выбор схемы соединения проводников зависит от конкретной задачи:

Последовательное соединение применяется, когда необходимо увеличить общее сопротивление цепи
Параллельное соединение используется для уменьшения общего сопротивления
Смешанное соединение позволяет комбинировать свойства обоих типов

Первый закон Кирхгофа и его применение

Первый закон Кирхгофа играет важную роль при анализе электрических цепей. Он гласит: алгебраическая сумма токов в узле равна нулю.

Математическая запись закона Кирхгофа

Формула первого закона Кирхгофа:

∑I = 0

Где ∑ обозначает алгебраическую сумму, а I — сила тока в ветвях, сходящихся в узле.

Применение закона Кирхгофа на практике

Закон Кирхгофа позволяет:

Рассчитывать токи в сложных разветвленных цепях
Анализировать распределение токов в параллельных соединениях
Проверять правильность расчетов электрических схем

Особенности расчета сложных электрических цепей

При расчете сложных цепей со смешанным соединением проводников следует придерживаться определенного алгоритма:

Разбить схему на простые участки с последовательным или параллельным соединением
Рассчитать сопротивление каждого участка
Заменить участки эквивалентными сопротивлениями
Повторять процесс, пока схема не упростится до одного эквивалентного сопротивления

Зависимость сопротивления проводника от различных факторов

На величину сопротивления проводника влияют следующие факторы:

Материал проводника
Длина проводника
Площадь поперечного сечения
Температура

Формула зависимости сопротивления от параметров проводника

Сопротивление проводника можно рассчитать по формуле:

R = ρ * L / S

Где ρ — удельное сопротивление материала, L — длина проводника, S — площадь поперечного сечения.

Практическое применение знаний о соединении проводников

Понимание принципов соединения проводников важно во многих областях:

Проектирование электрических схем
Расчет и монтаж электропроводки
Диагностика и ремонт электрооборудования
Разработка электронных устройств

Грамотное применение различных схем соединения позволяет оптимизировать работу электрических цепей и повысить их эффективность.

Последовательное и параллельное соединение проводников — урок. Физика, 8 класс.

В быту и в промышленности в электрическую цепь соединяются сразу несколько потребителей электрической энергии. Различают три вида соединения сопротивлений (резисторов):

последовательное соединение проводников
параллельное соединение проводников
смешанное соединение проводников

Последовательное соединение проводников

Схема соединения выглядит следующим образом:

Обрати внимание!

При последовательном соединении все входящие в него проводники соединяются друг за другом, т.е. конец первого проводника соединяется с началом второго.

Опыт показывает:

Сила тока в любых частях цепи одна и та же (об этом свидетельствуют показания амперметров): I=I1=I2.

Если выкрутить одну лампу, то цепь разомкнётся, а другая лампа тоже погаснет.

Опыт показывает следующее:

При последовательном соединении сопротивлений результирующее напряжение равно сумме напряжений на участках: U=U1+U2.

Результирующее сопротивление последовательно соединённых потребителей равно сумме сопротивлений потребителей: R=R1+R2.

Для проверки данного утверждения можно использовать омметр. При подключении омметра ключ должен быть разомкнут!

Омметр подключают по очереди к каждому потребителю, а потом к обоим одновременно.

Сопротивление цепи \(R\), состоящей из \(n\) одинаковых ламп, сопротивлением R1 каждая, в \(n\) раз больше сопротивления одной лампы: \(R\) = R1* \(n\).

Параллельное соединение проводников

Схема соединения выглядит следующим образом:

Обрати внимание!

При параллельном соединении все входящие в него проводники одним своим концом присоединяются к одной точке цепи А, а вторым концом — к другой точке В.

Опыт доказывает:

Сила тока в неразветвлённой части цепи равна сумме сил тока в отдельных параллельно соединённых проводниках.

Об этом свидетельствуют показания амперметров: I=I1+I2.

Если выкрутить одну лампу, то другая лампа продолжает гореть. Это свойство используют для подключения бытовых приборов в помещении.

Опыт свидетельствует, что:

Напряжение на участке цепи АВ и на концах всех параллельно соединённых проводников одно и то же.

Об этом свидетельствуют показания вольтметров:

U=U1=U2.

Общее сопротивление цепи при параллельном соединении проводников определяется по формуле:

1R=1R1+1R2.

Обратное значение общего сопротивления равно сумме обратных значений сопротивлений отдельных проводников.

Для проверки формулы можно использовать омметр. При подключении омметра ключ должен быть разомкнут!

Сопротивление цепи \(R\), состоящей из \(n\) одинаковых ламп, сопротивлением R1 каждая, в \(n\) раз меньше сопротивления одной лампы: \(R\) = R1/ \(n\).

Источники:

http://files.school-collection.edu.ru/dlrstore/669ba073-e921-11dc-95ff-0800200c9a66/3_17.swf
http://files.school-collection.edu.ru/dlrstore/669ba074-e921-11dc-95ff-0800200c9a66/3_18.swf

http://class-fizika.narod.ru/8_33.htm

Параллельная схема: характеристики, преимущества и недостатки

Параллельное соединение проводников

Параллельным соединением проводников называется такое соединение, когда начала всех проводников соединены в одну точку, а концы проводников – в другую точку (рисунок 4). Начало цепи присоединяется к одному полюсу источника напряжения, а конец цепи – к другому полюсу.

Рисунок 4. Схема параллельного соединения проводников

Из рисунка видно, что при параллельном соединении проводников для прохождения тока имеется несколько путей. Ток, протекая к точке разветвления А, растекается далее по трем сопротивлениям и равен сумме токов, уходящих от этой точки:

I = I₁ + I₂ + I₃.

Если токи, приходящие к точке разветвления, считать положительными, а уходящие – отрицательными, то для точки разветвления можно написать:

то есть алгебраическая сумма токов для любой узловой точки цепи всегда равна нулю. Это соотношение, связывающее токи в любой точке разветвления цепи, называется первым законом Кирхгофа. Определение первого закона Кирхгофа может звучать и в другой формулировке, а именно: сумма токов втекающих в узел электрической цепи равна сумме токов вытекающих из этого узла.

Видео 2. Первый закон Кирхгофа

Обычно при расчете электрических цепей направление токов в ветвях, присоединенных к какой либо точке разветвления, неизвестны. Поэтому для возможности самой записи уравнения первого закона Кирхгофа нужно перед началом расчета цепи произвольно выбрать так называемые положительные направления токов во всех ее ветвях и обозначить их стрелками на схеме.

Пользуясь законом Ома, можно вывести формулу для подсчета общего сопротивления при параллельном соединении потребителей.

Общий ток, приходящий к точке А, равен:

Токи в каждой из ветвей имеют значения:

По формуле первого закона Кирхгофа

I = I₁ + I₂ + I₃

или

Вынося U в правой части равенства за скобки, получим:

Сокращая обе части равенства на U, получим формулу подсчета общей проводимости:

или

g = g₁ + g₂ + g₃.

Таким образом, при параллельном соединении увеличивается не сопротивление, а проводимость.

Пример 3. Определить общее сопротивление трех параллельно включенных сопротивлений, если r₁ = 2 Ом, r₂ = 3 Ом, r₃ = 4 Ом.

откуда

Пример 4. Пять сопротивлений 20, 30 ,15, 40 и 60 Ом включены параллельно в сеть. Определить общее сопротивление:

откуда

Следует заметить, что при подсчете общего сопротивления разветвления оно получается всегда меньше, чем самое меньшее сопротивление, входящее в разветвление.

Если сопротивления, включенные параллельно, равны между собой, то общее сопротивление r цепи равно сопротивлению одной ветви r₁, деленному на число ветвей n:

Пример 5. Определить общее сопротивление четырех параллельно включенных сопротивлений по 20 Ом каждое:

Для проверки попробуем найти сопротивление разветвления по формуле:

откуда

Как видим, ответ получается тот же.

Пример 6. Пусть требуется определить токи в каждой ветви при параллельном их соединении, изображенном на рисунке 5, а.

Рисунок 5. К примеру 6

Найдем общее сопротивление цепи:

откуда

Теперь все разветвления мы можем изобразить упрощенно как одно сопротивление (рисунок 5, б).

Падение напряжения на участке между точками А и Б будет:

U = I × r = 22 × 1,09 = 24 В.

Возвращаясь снова к рисунку 5, а видим, что все три сопротивления окажутся под напряжением 24 В, так как они включены между точками А и Б.

Рассматривая первую ветвь разветвления с сопротивлением r₁, мы видим, что напряжение на этом участке 24 В, сопротивление участка 2 Ом. По закону Ома для участка цепи ток на этом участке будет:

Ток второй ветви

Ток третьей ветви

Проверим по первому закону Кирхгофа

I = I₁ + I₂ + I₃ = 12 + 6 + 4 = 22 А.

Следовательно, задача решена верно.

Обратим внимание на то, как распределяются токи в ветвях нашего параллельного соединения. Первая ветвь: r1 = 2 Ом, I1 = 12 А

Вторая ветвь: r2 = 4 Ом, I2 = 6 А. Третья ветвь: r3 = 6 Ом, I3 = 4 А

Первая ветвь: r₁ = 2 Ом, I₁ = 12 А. Вторая ветвь: r₂ = 4 Ом, I₂ = 6 А. Третья ветвь: r₃ = 6 Ом, I₃ = 4 А.

Как видим, сопротивление первой ветви в два раза меньше сопротивление второй ветви, а ток первой ветви в два раза больше тока второй ветви. Сопротивление третьей ветви в три раза больше сопротивления первой ветви, а ток третьей ветви в три раза меньше тока первой ветви. Отсюда можно сделать вывод, что токи в ветвях при параллельном соединении распределяются обратно пропорционально сопротивлениям этих ветвей. Таким образом, по ветви с большим сопротивлением потечет ток меньший, чем по ветви с малым сопротивлением.

Для двух параллельных ветвей можно также, конечно, пользоваться данной выше формулой.

Однако общее сопротивление проводника при параллельном соединении в этом случае легче подсчитать по формуле:

или окончательно:

Последовательное соединение ламп накаливания.

Последовательное соединение ламп накаливания в домашнем быту используется редко. В свое время я подключал две лампы последовательно у себя в подъезде, но это был единичный случай.

Тут ситуация была такая, что подъездная лампа перегорала с периодичностью в один месяц, и надо было что-то делать.

Обычно, в таких случаях лампу включают через диод, чтобы она питалась пониженным напряжением 110В и долго служила. Вариант проверенный, но при этом сама лампа мерцает, да и светит в полнакала.

Когда же стоят две последовательно, то они так же питаются пониженным напряжением 110В, не мерцают, долго служат, светят и потребляют энергии как одна. Причем их можно развести по разным углам помещения, что тоже плюс.Но повторюсь – это редкий случай.

Посмотрите на рисунок ниже. Здесь изображены две схемы последовательного соединения ламп накаливания. В верхней части рисунка показана принципиальная схема, а в нижней части – монтажная. Причем для лучшего восприятия, монтажная схема показана с реальным изображением ламп и двужильного провода.

Здесь в линии коричневого цвета, лампы HL1 и HL2 соединены последовательно – одна за другой. Поэтому такое соединение называют последовательным.

Если подать напряжение питания 220В на концы L и N, то загорятся обе лампы, но гореть они будут не в полную силу, а в половину накала. Так как сопротивление нитей ламп рассчитано на питающее напряжение 220В, и когда они стоят в цепи последовательно, одна за другой, то за счет добавления сопротивления нити накала следующей лампы, общее сопротивление цепи будет увеличиваться, а значит, для следующей лампы напряжение всегда будет меньше согласно закону Ома.

Поэтому при последовательном соединении двух ламп напряжение 220В будет делиться пополам, и составит 110В для каждой.

На следующем рисунке показаны три лампы соединенные последовательно.

На этой схеме напряжение на каждой лампе составит около 73 Вольт, так как будет делиться уже между тремя лампами.

Так же примером последовательного соединения могут служить новогодние гирлянды. Здесь из миниатюрных лампочек с низким питанием создается одна лампа на напряжение 220В.

Например, берем лампочки, рассчитанные на 6,3 Вольта и делим их на 220 Вольт. Получается 35 штук. То есть, чтобы сделать одну лампу на напряжение 220В, нам нужно соединить последовательно 35 штук с напряжением питания 6,3 Вольта.

P.S. Так как напряжение в сети не постоянно, то расчет лучше производить исходя из 245 – 250 Вольт.

Как Вы знаете, у гирлянд есть один недостаток. Перегорает одна из ламп, например, канала зеленого цвета, значит, не горит канал зеленого цвета. Тогда мы идем на базар, покупаем лампочки зеленого цвета, а потом дома по одной вынимаем, вставляем новую, и пока не заработает канал, перебираем его весь.

Вывод:

Недостатком последовательного соединения является то, что если выйдет из строя хоть одна из ламп, гореть не будут все, так как нарушается электрическая цепь.

А вторым недостатком, как Вы уже догадались, является слабое свечение. Поэтому последовательное соединение ламп накаливания на напряжение 220В в домашних условиях практически не применяется.

Первый закон Кирхгофа

Как я уже упоминал, законы Кирхгофа вместе с законом Ома являются основными при анализе и расчётах электрических цепей. Закон Ома был подробно рассмотрен в двух предыдущих статьях, теперь настала очередь для законов Кирхгофа. Их всего два, первый описывает соотношения токов в электрических цепях, а второй – соотношение ЭДС и напряжениями в контуре. Начнём с первого.

Первый закон Кирхгофа гласит, что алгебраическая сумма токов в узле равна нулю. Описывается это следующим выражением

где ∑ — обозначает алгебраическую сумму.

Слово «алгебраическая» означает, что токи необходимо брать с учётом знака, то есть направления втекания. Таким образом, всем токам, которые втекают в узел, присваивается положительный знак, а которые вытекают из узла – соответственно отрицательный. Рисунок ниже иллюстрирует первый закон Кирхгофа

На рисунке изображен узел, в который со стороны сопротивления R1 втекает ток, а со стороны сопротивлений R2, R3, R4 соответственно вытекает ток, тогда уравнение токов для данного участка цепи будет иметь вид

Первый закон Кирхгофа применяется не только к узлам, но и к любому контуру или части электрической цепи. Например, когда я говорил о параллельном соединении приемников энергии, где сумма токов через R1, R2 и R3 равна втекающему току I.

Примеры использования

Батареи гальванических элементов или аккумуляторов, в которых отдельные химические источники тока соединены последовательно (для увеличения напряжения) или параллельно (для увеличения тока).
Регулировка мощности электрического устройства, состоящего из нескольких одинаковых потребителей электроэнергии, путём их переключения с параллельного на последовательное соединение. Таким способом регулируется мощность конфорки электрической плиты, состоящей из нескольких спиралей; мощность (скорость движения) электровоза, имеющего несколько тяговых двигателей.
Делитель напряжения
Балласт
Шунт

Какой способ лучше?

Метод «шлейфов» не слишком удобен только тем, что любой потребитель по цепи зависит от предыдущего. Например, если произойдёт обрыв провода на второй розетке, то третья и четвёртая также останутся без напряжения. Но при этом нельзя не выделить экономию проводника при начальном монтаже электропроводки.

Рисунок 3: Комбинированное соединение розеток

К тому же, «шлейфом» очень удобно проводить линии, когда необходимо минимизировать количество штроб в стенах. А делают это при монтаже проводки по полу или потолку, в специальной гофрированной трубе. Тогда остаётся провести только основные штробы к розеткам и между ними.

Вывод: прокладка электропроводки «шлейфом» удобна и экономична, не занимает много времени в процессе монтажа, имеет длительный эксплуатационный срок и совсем незначительные недостатки, которые можно оставить без внимания.

Последовательное соединение ламп накаливания.

На следующем рисунке показаны три лампы соединенные последовательно.

P.S. Так как напряжение в сети не постоянно, то расчет лучше производить исходя из 245 – 250 Вольт.

Вывод:

Как выглядит формула Георга Ома

Примером такого типа подключения резисторов может быть соединение цепи потребителей электроэнергии в многоквартирном доме. Так, светодиоды, отопительный радиатор, микроволновка и другие приборы установлены в цепи параллельно.

Вольтметр, который подключают в цепь, будет показывать напряжение на всех резисторах. Тогда оно везде будет равным и формулу можно записать как:

U1 = U2 = U.

Схема параллельного соединения

Когда образуются ветви при подключении, то часть общего напряжения проходит через первый резистор, а часть — через второй и так далее. Поэтому при таком виде соединения резисторов Fтока в неразветвлённой точке будет равняться суммарной Fтока в отдельных резисторах и записывается как:

I = I1 + I2.

Расчет силы тока при помощи закона Ома записывается как:

I = U/R;

I1 = U1/R1;

I2 = U2/R2.

Из формулы следует:

U/R = U1/R1 + U2/R2;

U = U1 = U2;

1/R = 1/R1 + 1/R2.

Дословно правило звучит так: число, обратное общему сопротивлению при параллельном подключении, будет суммарно равно числу обратного сопротивления.

Зависимость сопротивления

Значение электропроводимости зависит от нескольких факторов, которые необходимо учитывать при расчетах, изготовлении элементов резистивной нагрузки (резисторов), ремонте и проектировании устройств. К этим факторам необходимо отнести следующие:

Температура окружающей среды и материала.
Электрические величины.
Геометрические свойства вещества.
Тип материала, из которого изготовлен проводник (полупроводник).

Электрические величины

Зависимость величины электропроводимости от параметров электричества определяется законом Ома. Существует две формулировки: одна — для участка, а другая — для полной цепи. В первом случае соотношение определяются, исходя из значений силы тока (I) и напряжения (U) простой формулой: I = U / R. Из соотношения видна прямо пропорциональная зависимость тока от величины напряжения, а также обратно пропорциональная от сопротивления. Можно выразить R: R = U / I.

Для расчета электропроводимости всего участка следует воспользоваться соотношением между ЭДС (e), силой тока (i), а также внутренним сопротивлением источника питания (Rвн): i = e / (R+Rвн). В этом случае величина R вычисляется по формуле: R = (e / i) — Rвн. Однако при выполнении расчетов необходимо учитывать также геометрические параметры и тип проводника, поскольку они могут существенно повлиять на вычисления.

Тип и геометрические параметры

Свойство вещества к проводимости электричества определяется структурой кристаллической решетки, а также количеством свободных носителей. Исходя из этого, тип вещества является ключевым фактором, который определяет величину электропроводимости. В науке коэффициент, определяющий тип вещества, обозначается литерой «р» и называется удельным сопротивлением. Его значение для различных материалов (при температуре +20 градусов по Цельсию) можно найти в специальных таблицах.

Иногда для удобства расчетов используется обратная величина, которая называется удельной проводимостью (σ). Она связана с удельным сопротивлением следующим соотношением: p = 1 / σ. Площадь поперечного сечения (S) влияет на электрическое сопротивление. С физической точки зрения, зависимость можно понять следующим образом: при малом сечении происходят более частые взаимодействия частиц электрического тока с узлами кристаллической решетки. Поперечное сечение можно вычислить по специальному алгоритму:

Измерение геометрических параметров проводника (диаметр или длину сторон) при помощи штангенциркуля.
Визуально определить форму материала.
Вычислить площадь поперечного сечения по формуле, найденной в справочнике или интернете.

В случае когда проводник имеет сложную структуру, необходимо вычислить величину S одного элемента, а затем умножить результат на количество элементов, входящих в его состав. Например, если провод является многожильным, то следует вычислить S для одной жилы. После этого нужно умножить, полученную величину S, на количество жил. Зависимость R от вышеперечисленных величин можно записать в виде соотношения: R = p * L / S. Литера «L» является длиной проводника. Однако для получения точных расчетов необходимо учитывать температурные показатели внешней среды и проводника.

Температурные показатели

Существует доказательство зависимости удельного сопротивления материала от температуры, основанное на физическом эксперименте. Для проведения опыта нужно собрать электрическую цепь, состоящую из следующих элементов: источника питания, нихромовой спирали, соединительных проводов амперметра и вольтметра. Приборы нужны для измерения значений силы тока и напряжения соответственно. При протекании электричества происходит нагревание нихромовой пружины. По мере ее нагревания, показания амперметра уменьшаются. При этом происходит существенное падение напряжения на участке цепи, о котором свидетельствуют показания вольтметра.

В радиотехнике уменьшение величины напряжение называется просадкой или падением. Формула зависимости р от температуры имеет следующий вид: p = p0 * . Значение p0 — удельное сопротивление материала, взятого из таблицы, а литера «t» — температура проводника.

Температурный коэффициент «а» принимает следующие значения: для металлов — a>0, а для электролитических растворов — a<0. Для получения формулы, определяющей все зависимости, необходимо подставить все соотношения в общую формулу зависимости R от типа материала, температуры, длины и сечения: R = p0 * * L / S. Формулы используются только для расчетов и изготовления резисторов. Для быстрого измерения величины сопротивления применяется омметр.

Формула параллельного соединения резисторов

Общее сопротивление нескольких резисторов соединенных параллельно определяется по следующей формуле:

Ток, протекающий через отдельно взятый резистор, согласно закону Ома, можно найти по формуле:

Пример №1

При разработке устройства, возникла необходимость установить резистор с сопротивлением 8 Ом. Если мы просмотрим весь номинальный ряд стандартных значений резисторов, то мы увидим, что резистора с сопротивлением в 8 Ом в нем нет.

Выходом из данной ситуации будет использование двух параллельно соединенных резисторов. Эквивалентное значение сопротивления для двух резисторов соединенных параллельно рассчитывается следующим образом:

Данное уравнение показывает, что если R1 равен R2, то сопротивление R составляет половину сопротивления одного из двух резисторов. При R = 8 Ом, R1 и R2 должны, следовательно, иметь значение 2 × 8 = 16 Ом.
Теперь проведем проверку, рассчитав общее сопротивление двух резисторов:

Таким образом, мы получили необходимое сопротивление 8 Ом, соединив параллельно два резистора по 16 Ом.

Пример расчета №2

Найти общее сопротивление R из трех параллельно соединенных резисторов:

Общее сопротивление R рассчитывается по формуле:

Этот метод расчета может быть использованы для расчета любого количества отдельных сопротивлений соединенных параллельно.

Один важный момент, который необходимо запомнить при расчете параллельно соединенных резисторов – это то, что общее сопротивление всегда будет меньше, чем значение наименьшего сопротивления в этой комбинации.

Как рассчитать сложные схемы соединения резисторов

Более сложные соединения резисторов могут быть рассчитаны путем систематической группировки резисторов. На рисунке ниже необходимо посчитать общее сопротивление цепи, состоящей из трех резисторов:

Резисторы R2 и R3 соединены последовательно (группа 2). Они в свою очередь соединены параллельно с резистором R1 (группа 1).

Последовательное соединение резисторов группы 2 вычисляется как сумма сопротивлений R2 и R3:

В результате мы упрощаем схему в виде двух параллельных резисторов. Теперь общее сопротивление всей схемы можно посчитать следующим образом:

Расчет более сложных соединений резисторов можно выполнить используя законы Кирхгофа.

Ток, протекающий в цепи параллельно соединенных резисторах

Общий ток I протекающий в цепи параллельных резисторов равняется сумме отдельных токов, протекающих во всех параллельных ветвях, причем ток в отдельно взятой ветви не обязательно должен быть равен току в соседних ветвях.

Несмотря на параллельное соединение, к каждому резистору приложено одно и то же напряжение. А поскольку величина сопротивлений в параллельной цепи может быть разной, то и величина протекающего тока через каждый резистор тоже будет отличаться (по определению закона Ома).

Рассмотрим это на примере двух параллельно соединенных резисторов. Ток, который течет через каждый из резисторов ( I1 и I2 ) будет отличаться друг от друга поскольку сопротивления резисторов R1 и R2 не равны.
Однако мы знаем, что ток, который поступает в цепь в точке «А» должен выйти из цепи в точке «B» .

Первое правило Кирхгофа гласит: «Общий ток, выходящий из цепи равен току входящий в цепь».

Таким образом, протекающий общий ток в цепи можно определить как:
I = I1 + I2
Затем с помощью закона Ома можно вычислить ток, который протекает через каждый резистор:
Ток, протекающий в R1 = U ÷ R1 = 12 ÷ 22 кОм = 0,545 мА
Ток, протекающий в R 2 = U ÷ R2 = 12 ÷ 47 кОм = 0,255 мА
Таким образом, общий ток будет равен:
I = 0,545 мА + 0,255 мА = 0,8 мА
Это также можно проверить, используя закон Ома:
I = U ÷ R = 12 В ÷ 15 кОм = 0,8 мА (то же самое)
где 15кОм — это общее сопротивление двух параллельно соединенных резисторов (22 кОм и 47 кОм)
И в завершении хочется отметить, что большинство современных резисторов маркируются цветными полосками и назначение ее можно узнать здесь.

Параллельное соединение резисторов — онлайн калькулятор

Чтобы быстро вычислить общее сопротивление двух и более резисторов, соединенных параллельно, вы можете воспользоваться следующим онлайн калькулятором:

Подведем итог

Когда два или более резистора соединены так, что оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов, то говорят, что они соединены между собой параллельно. Напряжение на каждом резисторе внутри параллельной комбинации одинаковое, но токи, протекающие через них, могут отличаться друг от друга, в зависимости от величины сопротивлений каждого резистора.

Эквивалентное или полное сопротивление параллельной комбинации всегда будет меньше минимального сопротивления резистора входящего в параллельное соединение.

Последовательное соединение источников питания

Теперь давайте представим вот такую ситуацию. Что будет, если в нашей обрезанной водобашне полной воды добавим еще одну такую же сверху полную воды? Схематически это будет выглядеть примерно вот так:

Как вы думаете, уменьшится давление на землю, или увеличится? Понятное дело, что увеличится! Да еще и ровно в два раза! Почему так произошло? Уровень воды стал выше, следовательно, давление на дно увеличилось.

Если “минус” одной батарейки соединить с “плюсом” другой батарейки, то их общее напряжение суммируется.

Полностью заряженная батарейка будет выглядеть как башня, полностью залитая водой с учетом того, что работает насос автоматической подачи воды. По аналогии, насос – это ЭДС.

Наполовину разряженная батарейка будет уже выглядеть примерно вот так:

Можно сказать, насос уже не справляется.

Батарейка посаженная в “ноль” будет выглядеть вот так:

Насос автоматической подачи воды сломался.

Естественно, что если вы соедините полностью заряженную и наполовину дохлую батарейку последовательно, то их общее напряжение будет выглядеть примерно вот так:

Давайте все это продемонстрируем на практике. Итак, у нас есть 2 литий-ионных аккумулятора. Я их пометил цифрами 1 и 2. С плюса каждого аккумулятора я вывел красный провод, а с минуса – черный.

Давайте замеряем напряжение аккумулятора под №1 с помощью мультиметра. Как это сделать, я еще писал в статье Как измерить ток и напряжение мультиметром.

На первом аккумуляторе у нас напряжение 3,66 Вольт. Это типичное значение литий-ионного аккумулятора.

Таким же способом замеряем напряжение на аккумуляторе №2

О, как совпало). Те же самые 3,66 Вольт.

Для того, чтобы соединить последовательно эти аккумуляторы, нам надо сделать что-то подобное:

Также как и в башнях, нам надо соединить основание одной башни с верхушкой другой башни. В источниках питания, типа аккумуляторов или батареек, нам надо соединить минус одной батарейки с плюсом другой. Так мы и сделаем. Соединяем плюс одной батарейки с минусом другой и получаем… сумму напряжений каждой батарейки! Как вы помните, на первой батарейке у нас было напряжение 3,66 В, на второй тоже 3,66 В. 3,66+3,6=7,32 В.

Мультиметр показывает 7,33 В. 0,01В спишем на погрешность измерений.

Это свойство прокатывает не только с двумя аккумуляторами, но также с их бесконечным множеством. Думаю, не стоит говорить, что если выставить в ряд штук 100 таких аккумуляторов, соединить последовательно и коснуться крайних полюсов голыми руками, то все это может завершиться даже летальным исходом.

Оцените статью:

формула расчета общего сопротивления. Примеры параллельного соединения проводников

Резистор — это элемент электрической схемы, который обладает сопротивлением электрическому току. Классифицируют два типа резисторов: постоянные и переменные (подстроечные). При моделировании той или иной электрической схемы, а также при ремонте электронных изделий, возникает необходимость использовать резистор определенного номинала. Хотя и существует множество различных номиналов постоянных резисторов, в данный момент под рукой может не оказаться требуемого, либо резистора с таким номиналом не существует. Чтобы выйти из такой ситуации, можно использовать как последовательное так и параллельное соединение резисторов. О том, как правильно произвести расчет и подбор различных номиналов сопротивлений, будет рассказано в этой статье.

Последовательное соединение резисторов — это самая элементарная схема сборки радиодеталей, оно применяется для увеличения общего сопротивления цепи. При последовательном соединении, сопротивление используемых резисторов просто складывается, а вот при параллельном соединении необходимо производить расчет по нижеописанным формулам. Параллельное соединение необходимо для снижения результирующего сопротивления, а также для увеличения мощности, несколько параллельно подключенных резисторов имеют большую мощность, чем у одного.

На фотографии можно увидеть параллельное подключение резисторов.

Ниже представлена принципиальная схема параллельного соединения резисторов.

Общее номинальное сопротивление необходимо рассчитывать по следующей схеме:

R(общ)=1/(1/R1+1/R2+1/R3+1/R n).

R1, R2, R3 и Rn — параллельно подключенные резисторы.

Когда параллельное соединение резисторов состоит всего из двух элементов, в таком случае общее номинальное сопротивление можно высчитать по следующей формуле:

R(общ)=R1*R2/R1+R2.

R(общ) — общее сопротивление;

R1, R2 — параллельно подключенные резисторы.

В радиотехнике существует следующее правило: если параллельное подключение резисторов состоит из элементов одного номинала, то результирующее сопротивление можно высчитать, разделив номинал резистора на количество соединенных резисторов:

R(общ) — общее сопротивление;

R — номинал параллельно подключенного резистора;

N — количество соединенных элементов.

Важно учитывать, что при параллельном соединении результирующее сопротивление всегда будет ниже, чем сопротивление самого малого по номиналу резистора.

Приведем практический пример: возьмем три резистора, со следующими значениями номинального сопротивления: 100 Ом, 150 Ом и 30 Ом. Проведем расчет общего сопротивления, по первой формуле:

R(общ)=1/(1/100+1/150+1/30)=1/(0,01+0,007+0,03)=1/0,047=21,28Ом.

После расчета формулы мы видим, что параллельное соединение резисторов, состоящее из трех элементов, с наименьшим номиналом 30 Ом, в результате дает общее сопротивление в электрической цепи 21,28 Ом, что ниже наименьшего номинального сопротивления в цепи почти на 30 процентов.

Параллельное соединение резисторов чаще всего используют в тех случаях, когда необходимо получить сопротивление с большей мощностью. В таком случае необходимо взять резисторы одинаковой мощности и с одинаковым сопротивлением. Результирующая мощность в таком случае рассчитывается путем умножения мощности одного элемента сопротивления на общее количество параллельно подключенных резисторов в цепи.

Например: пять резисторов с номиналом в 100 Ом и с мощностью 1 Вт в каждом, подключенные параллельно, имеют общее сопротивление 20 Ом и мощность 5 Вт.

При последовательном подключении тех же резисторов (мощность так же складывается), получим результирующую мощность 5 Вт, общее сопротивление составит 500 Ом.

Проверим справедливость показанных здесь формул на простом эксперименте.

Возьмём два резистора МЛТ-2 на 3 и 47 Ом и соединим их последовательно. Затем измерим общее сопротивление получившейся цепи цифровым мультиметром. Как видим оно равно сумме сопротивлений резисторов, входящих в эту цепочку.

Замер общего сопротивления при последовательном соединении

Теперь соединим наши резисторы параллельно и замерим их общее сопротивление.

Измерение сопротивления при параллельном соединении

Как видим, результирующее сопротивление (2,9 Ом) меньше самого меньшего (3 Ом), входящего в цепочку. Отсюда вытекает ещё одно известное правило, которое можно применять на практике:

При параллельном соединении резисторов общее сопротивление цепи будет меньше наименьшего сопротивления, входящего в эту цепь.

Что ещё нужно учитывать при соединении резисторов?

Во-первых, обязательно учитывается их номинальная мощность. Например, нам нужно подобрать замену резистору на 100 Ом и мощностью 1 Вт . Возьмём два резистора по 50 Ом каждый и соединим их последовательно. На какую мощность рассеяния должны быть рассчитаны эти два резистора?

Поскольку через последовательно соединённые резисторы течёт один и тот же постоянный ток (допустим 0,1 А ), а сопротивление каждого из них равно 50 Ом , тогда мощность рассеивания каждого из них должна быть не менее 0,5 Вт . В результате на каждом из них выделится по 0,5 Вт мощности. В сумме это и будет тот самый 1 Вт .

Данный пример достаточно грубоват. Поэтому, если есть сомнения, стоит брать резисторы с запасом по мощности.

Подробнее о мощности рассеивания резистора читайте .

Во-вторых, при соединении стоит использовать однотипные резисторы, например, серии МЛТ. Конечно, нет ничего плохого в том, чтобы брать разные. Это лишь рекомендация.

На практике нередко встречается задача нахождения сопротивления проводников и резисторов при различных способах соединения. В статье рассмотрено, как рассчитывается сопротивление при параллельном соединении проводников и некоторые другие технические вопросы.

Сопротивление проводника

Все проводники имеют свойство препятствовать течению электрического тока, его принято называть электрическим сопротивлением R, оно измеряется в омах. Это основное свойство проводниковых материалов.

Для ведения электротехнических расчётов применяется удельное сопротивление — ρ Ом·м/мм 2 . Все металлы — хорошие проводники, наибольшее применение получили медь и алюминий, гораздо реже применяется железо. Лучший проводник — серебро, оно применяется в электротехнической и электронной промышленности. Широко распространены сплавы с высоким

При расчёте сопротивления используется известная из школьного курса физики формула:

R = ρ · l/S, S — площадь сечения; l — длина.

Если взять два проводника, то их сопротивление при параллельном соединении станет меньше из-за увеличения общего сечения.

и нагрев проводника

Для практических расчётов режимов работы проводников применяется понятие плотности тока — δ А/мм 2 , она вычисляется по формуле:

δ = I/S, I — ток, S — сечение.

Ток, проходя по проводнику, нагревает его. Чем больше δ, тем сильнее нагревается проводник. Для проводов и кабелей разработаны нормы допустимой плотности, которые приводятся в Для проводников нагревательных устройств существуют свои нормы плотности тока.

Если плотность δ выше допустимой, может произойти разрушение проводника, например, при перегреве кабеля у него разрушается изоляция.

Правилами регламентируется производить расчёт проводников на нагрев.

Способы соединения проводников

Любой проводник гораздо удобнее изображать на схемах как электрическое сопротивление R, тогда их легко читать и анализировать. Существует всего три способа соединения сопротивлений. Первый способ самый простой — последовательное соединение.

На фото видно, что полное сопротивление равно: R = R 1 + R 2 + R 3 .

Второй способ более сложный — параллельное соединение. Расчёт сопротивления при параллельном соединении выполняется поэтапно. Рассчитывается полная проводимость G = 1/R, а затем полное сопротивление R = 1/G.

Можно поступить и по-другому, прежде рассчитать общее сопротивление при R1 и R2, после этого повторить операцию и найти R.

Третий способ соединения наиболее сложный — смешанное соединение, то есть присутствуют все рассмотренные варианты. Схема приведена на фото.

Для расчёта этой схемы её следует упростить, для этого заменяют резисторы R2 и R3 одним R2,3. Получается несложная схема.

R2,3,4 = R2,3 · R4/(R2,3 + R4).

Схема становится ещё проще, в ней остаются резисторы, имеющие последовательное соединение. В более сложных ситуациях используется этот же метод преобразования.

Виды проводников

В электронной технике, при производстве проводники представляют собою тонкие полоски медной фольги. Ввиду малой длины сопротивление у них незначительно, им во многих случаях можно пренебречь. Для этих проводников сопротивление при параллельном соединении уменьшается вследствие увеличения сечения.

Большой раздел проводников представляют обмоточные провода. Они выпускаются разных диаметров — от 0,02 до 5,6 миллиметра. Для мощных трансформаторов и электродвигателей выпускаются медные шинки прямоугольного сечения. Иногда при ремонте заменяют провод большого диаметра на несколько параллельно соединённых меньшего размера.

Особый раздел проводников представляют провода и кабели, промышленность предоставляет широчайший выбор марок для самых различных нужд. Нередко приходится заменять один кабель на несколько, меньшего сечения. Причины этого бывают самые различные, например, кабель сечением 240 мм 2 очень трудно прокладывать по трассе с крутыми изгибами. Его заменяют на 2×120 мм 2 , и проблема решена.

Расчёт проводов на нагрев

Проводник нагревается протекающим током, если его температура превысит допустимую, наступает разрушение изоляции. ПУЭ предусматривает расчёт проводников на нагрев, исходными данными для него являются сила тока и условия внешней среды, в которой проложен проводник. По этим данным из таблиц в ПУЭ выбирается рекомендуемое проводника сечение (провода или кабеля).

На практике встречаются ситуации, когда нагрузка на действующий кабель сильно возросла. Существует два выхода ‒ заменить кабель на другой, это бывает дорого, или параллельно ему проложить ещё один, чтобы разгрузить основной кабель. В этом случае сопротивление проводника при параллельном соединении уменьшается, следовательно падает выделение тепла.

Чтобы правильно выбрать сечение второго кабеля, пользуются таблицами ПУЭ, важно при этом не ошибиться с определением его рабочего тока. В этой ситуации охлаждение кабелей будет даже лучше, чем у одного. Рекомендуется рассчитать сопротивление при двух кабелей, чтобы точнее определить их тепловыделение.

Расчёт проводников на потерю напряжения

При расположении потребителя R н на большом расстоянии L от источника энергии U 1 возникает довольно большое падение напряжения на проводах линии. К потребителю R н поступает напряжение U 2 значительно ниже начального U 1 . Практически в качестве нагрузки выступает различное электрооборудование, подключаемое к линии параллельно.

Для решения проблемы производят расчет сопротивления при параллельном соединении всего оборудования, так находится сопротивление нагрузки R н. Далее следует определить сопротивление проводов линии.

R л = ρ · 2L/S,

Здесь S — сечение провода линии, мм 2 .

Параллельное соединение резисторов. При параллельном соединении резисторов нескольких приемников они включаются между двумя точками электрической цепи, образуя параллельные ветви (рис. 26, а). Заменяя

лампы резисторами с сопротивлениями R1, R2, R3, получим схему, показанную на рис. 26, б.
При параллельном соединении ко всем резисторам приложено одинаковое напряжение U. Поэтому согласно закону Ома:

I 1 =U/R 1 ; I 2 =U/R 2 ; I 3 =U/R 3 .

Ток в неразветвленной части цепи согласно первому закону Кирхгофа I = I 1 +I 2 +I 3 , или

I = U / R 1 + U / R 2 + U / R 3 = U (1/R 1 + 1/R 2 + 1/R 3) = U / R эк (23)

Следовательно, эквивалентное сопротивление рассматриваемой цепи при параллельном соединении трех резисторов определяется формулой

1/R эк = 1/R 1 + 1/R 2 + 1/R 3 (24)

Вводя в формулу (24) вместо значений 1/R эк, 1/R 1 , 1/R 2 и 1/R 3 соответствующие проводимости G эк, G 1 , G 2 и G 3 , получим: эквивалентная проводимость параллельной цепи равна сумме проводимостей параллельно соединенных резисторов :

G эк = G 1 + G 2 +G 3 (25)

Таким образом, при увеличении числа параллельно включаемых резисторов результирующая проводимость электрической цепи увеличивается, а результирующее сопротивление уменьшается.
Из приведенных формул следует, что токи распределяются между параллельными ветвями обратно пропорционально их электрическим сопротивлениям или прямо пропорционально их проводимостям. Например, при трех ветвях

I 1: I 2: I 3 = 1/R 1: 1/R 2: 1/R 3 = G 1 + G 2 + G 3 (26)

В этом отношении имеет место полная аналогия между распределением токов по отдельным ветвям и распределением потоков воды по трубам.
Приведенные формулы дают возможность определить эквивалентное сопротивление цепи для различных конкретных случаев. Например, при двух параллельно включенных резисторах результирующее сопротивление цепи

R эк =R 1 R 2 /(R 1 +R 2)

при трех параллельно включенных резисторах

R эк =R 1 R 2 R 3 /(R 1 R 2 +R 2 R 3 +R 1 R 3)

При параллельном соединении нескольких, например n, резисторов с одинаковым сопротивлением R1 результирующее сопротивление цепи Rэк будет в n раз меньше сопротивления R1, т.е.

R эк = R1 / n (27)

Проходящий по каждой ветви ток I1, в этом случае будет в п раз меньше общего тока:

I1 = I / n (28)

При параллельном соединении приемников, все они находятся под одним и тем же напряжением, и режим работы каждого из них не зависит от остальных. Это означает, что ток, проходящий по какому-либо из приемников, не будет оказывать существенного влияния на другие приемники. При всяком выключении или выходе из строя любого приемника остальные приемники остаются включенными. Поэтому параллельное соединение имеет существенные преимущества перед последовательным, вследствие чего оно получило наиболее широкое распространение. В частности, электрические лампы и двигатели, предназначенные для работы при определенном (номинальном) напряжении, всегда включают параллельно.
На электровозах постоянного тока и некоторых тепловозах тяговые двигатели в процессе регулирования скорости движения нужно включать под различные напряжения, поэтому они в процессе разгона переключаются с последовательного соединения на параллельное.

Возьмем три постоянных сопротивления R1, R2 и R3 и включим их в цепь так, чтобы конец первого сопротивления R1 был соединен с началом второго сопротивления R 2, конец второго — с началом третьего R 3, а к началу первого сопротивления и к концу третьего подведем проводники от источника тока (рис. 1 ).

Такое соединение сопротивлений называется последовательным. Очевидно, что ток в такой цепи будет во всех ее точках один и тот же.

Рис 1

Как определить общее сопротивление цепи, если все включенные в нее последовательно сопротивления мы уже знаем? Используя положение, что напряжение U на зажимах источника тока равно сумме падений напряжений на участках цепи, мы можем написать:

U = U1 + U2 + U3

где

U1 = IR1 U2 = IR2 и U3 = IR3

или

IR = IR1 + IR2 + IR3

Вынеся в правой части равенства I за скобки, получим IR = I(R1 + R2 + R3) .

Поделив теперь обе части равенства на I , будем окончательно иметь R = R1 + R2 + R3

Таким образом, мы пришли к выводу, что при последовательном соединении сопротивлений общее сопротивление всей цепи равно сумме сопротивлений отдельных участков.

Проверим этот вывод на следующем примере. Возьмем три постоянных сопротивления, величины которых известны (например, R1 == 10 Ом, R 2 = 20 Ом и R 3 = 50 Ом). Соединим их последовательно (рис. 2 ) и подключим к источнику тока, ЭДС которого равна 60 В ( пренебрегаем).

Рис. 2. Пример последовательного соединения трех сопротивлений

Подсчитаем, какие показания должны дать приборы, включенные, как показано на схеме, если замкнуть цепь. Определим внешнее сопротивление цепи: R = 10 + 20 + 50 = 80 Ом.

Найдем ток в цепи : 60 / 80 = 0 ,75 А

Зная ток в цепи и сопротивления ее участков, определим падение напряжения на каждое участке цепи U 1 = 0,75х 10 = 7,5 В, U 2 = 0,75 х 20=15 В, U3 = 0,75 х 50 = 37,5 В.

Зная падение напряжений на участках, определим общее падение напряжения во внешней цепи, т. е. напряжение на зажимах источника тока U = 7,5+15 + 37,5 = 60 В.

Мы получили таким образом, что U = 60 В, т. е. несуществующее равенство ЭДС источника тока и его напряжения. Объясняется это тем, что мы пренебрегли внутренним сопротивлением источника тока.

Замкнув теперь ключ выключатель К, можно убедиться по приборам, что наши подсчеты примерно верны.

Возьмем два постоянных сопротивления R1 и R2 и соединим их так, чтобы начала этих сопротивлений были включены в одну общую точку а, а концы — в другую общую точку б. Соединив затем точки а и б с источником тока, получим замкнутую электрическую цепь. Такое соединение сопротивлений называется параллельным соединением.

Рис 3. Параллельное соединение сопротивлений

Проследим течение тока в этой цепи. От положительного полюса источника тока по соединительному проводнику ток дойдет до точки а. В точке а он разветвится, так как здесь сама цепь разветвляется на две отдельные ветви: первую ветвь с сопротивлением R1 и вторую — с сопротивлением R2. Обозначим токи в этих ветвях соответственно через I1 и I 2. Каждый из этих токов пойдет по своей ветви до точки б. В этой точке произойдет слияние токов в один общий ток, который и придет к отрицательному полюсу источника тока.

Таким образом, при параллельном соединении сопротивлений получается разветвленная цепь. Посмотрим, какое же будет соотношение между токами в составленной нами цепи.

Включим амперметр между положительным полюсом источника тока (+) и точкой а и заметим его показания. Включив затем амперметр (показанный «а рисунке пунктиром) в провод, соединяющий точку б с отрицательным полюсом источника тока (-), заметим, что прибор покажет ту же величину силы тока.

Значит, до ее разветвления (до точки а) равна силе тока после разветвления цепи (после точки б).

Будем теперь включать амперметр поочередно в каждую ветвь цепи, запоминая показания прибора. Пусть в первой ветви амперметр покажет силу тока I1 , а во второй — I 2. Сложив эти два показания амперметра, мы получим суммарный ток, по величине равный току I до разветвления (до точки а).

Следовательно, сила тока, протекающего до точки разветвления, равна сумме сил токов, утекающих от этой точки. I = I1 + I2 Выражая это формулой, получим

Это соотношение, имеющее большое практическое значение, носит название закона разветвленной цепи .

Рассмотрим теперь, каково будет соотношение между токами в ветвях.

Включим между точками а и б вольтметр и посмотрим, что он нам покажет. Во-первых, вольтметр покажет напряжение источника тока, так как он подключен, как это видно из рис. 3 , непосредственно к зажимам источника тока. Во-вторых, вольтметр покажет падения напряжений U1 и U2 на сопротивлениях R1 и R2, так как он соединен с началом и концом каждого сопротивления.

Следовательно, при параллельном соединении сопротивлений напряжение на зажимах источника тока равно падению напряжения на каждом сопротивлении.

Это дает нам право написать, что U = U1 = U2 ,

где U — напряжение на зажимах источника тока; U1 — падение напряжения на сопротивлении R1 , U2 — падение напряжения на сопротивлении R2. Вспомним, что падение напряжения на участке цепи численно равно произведению силы тока, протекающего через этот участок, на сопротивление участка U = IR .

Поэтому для каждой ветви можно написать: U1 = I1R1 и U2 = I2R2 , но так как U1 = U2, то и I1R1 = I2R2 .

Применяя к этому выражению правило пропорции, получим I1/ I2 = U2 / U1 т. е. ток в первой ветви будет во столько раз больше (или меньше) тока во второй ветви, во сколько раз сопротивление первой ветви меньше (или больше) сопротивления второй ветви.

Итак, мы пришли к важному выводу, заключающемуся в том, что при параллельном соединении сопротивлений общий ток цепи разветвляется на токи, обратно пропорциональные величинам сопротивлении параллельных ветвей. Иначе говоря, чем больше сопротивление ветви, тем меньший ток потечет через нее, и, наоборот, чем меньше сопротивление ветви, тем больший ток потечет через эту ветвь.

Убедимся в правильности этой зависимости на следующем примере. Соберем схему, состоящую из двух параллельно соединенных сопротивлений R1 и R 2, подключенных к источнику тока. Пусть R1 = 10 Ом, R2 = 20 Ом и U = 3 В.

Подсчитаем сначала, что покажет нам амперметр, включенный в каждую ветвь:

I1 = U / R1 = 3 / 10 = 0 ,3 А = 300 мА

I 2 = U / R 2 = 3 / 20 = 0,15 А = 150 мА

Общий ток в цепи I = I1 +I2 = 300 + 150 = 450 мА

Проделанный нами расчет подтверждает, что при параллельном соединении сопротивлений ток в цепи разветвляется обратно пропорционально сопротивлениям.

Действительно, R1 == 10 Ом вдвое меньше R 2 = 20 Ом, при этом I1 = 300 мА вдвое больше I2 = 150 мА. Общий ток в цепи I = 450 мА разветвился на две части так, что большая его часть (I1 = 300 мА) пошла через меньшее сопротивление (R1 = 10 Ом), а меньшая часть (R2 = 150 мА) -через большее сопротивление (R 2 = 20 Ом).

Такое разветвление тока в параллельных ветвях сходно с течением жидкости по трубам. Представьте себе трубу А, которая в каком-то месте разветвляется на две трубы Б и В различного диаметра (рис. 4). Так как диаметр трубы Б больше диаметра трубок В, то через трубу Б в одно и то же время пройдет больше воды, чем через трубу В, которая оказывает потоку воды большее сопротивление.

Рис. 4

Рассмотрим теперь, чему будет равно общее сопротивление внешней цепи, состоящей из двух параллельно соединенных сопротивлений.

Под этим общим сопротивлением внешней цепи надо понимать такое сопротивление, которым можно было бы заменить при данном напряжении цепи оба параллельно включенных сопротивления, не изменяя при этом тока до разветвления. Такое сопротивление называется эквивалентным сопротивлением.

Вернемся к цепи, показанной на рис. 3, и посмотрим, чему будет равно эквивалентное сопротивление двух параллельно соединенных сопротивлений. Применяя к этой цепи закон Ома, мы можем написать: I = U/R , где I — ток во внешней цепи (до точки разветвления), U — напряжение внешней цепи, R — сопротивление внешней цепи, т. е. эквивалентное сопротивление.

Точно так же для каждой ветви I1 = U1 / R1 , I2 = U2 / R2 , где I1 и I 2 — токи в ветвях; U1 и U2 — напряжение на ветвях; R1 и R2 — сопротивления ветвей.

По закону разветвленной цепи: I = I1 + I2

Подставляя значения токов, получим U / R = U1 / R1 + U2 / R2

Так как при параллельном соединении U = U1 = U2 , то можем написать U / R = U / R1 + U / R2

Вынеся U в правой части равенства за скобки, получим U / R = U (1 / R1 + 1 / R2 )

Разделив теперь обе части равенства на U , будем окончательно иметь 1 / R = 1 / R1 + 1 / R2

Помня, что проводимостью называется величина, обратная сопротивлению , мы можем сказать, что в полученной формуле 1 / R — проводимость внешней цепи; 1 / R1 проводимость первой ветви; 1 / R2- проводимость второй ветви.

На основании этой формулы делаем вывод: при параллельном соединении проводимость внешней цепи равна сумме проводимостей отдельных ветвей.

Следовательно, чтобы определить эквивалентное сопротивление включенных параллельно сопротивлений, надо определить проводимость цепи и взять величину, ей обратную.

Из формулы также следует, что проводимость цепи больше проводимости каждой ветви, а это значит, что эквивалентное сопротивление внешней цепи меньше наименьшего из включенных параллельно сопротивлений.

Рассматривая случай параллельного соединения сопротивлений, мы взяли наиболее простую цепь, состоящую из двух ветвей. Однако на практике могут встретиться случаи, когда цепь состоит из трех и более параллельных ветвей. Как же поступать в этих случаях?

Оказывается, все полученные нами соотношения остаются справедливыми и для цепи, состоящей из любого числа параллельно соединенных сопротивлений.

Чтобы убедиться в этом, рассмотрим следующий пример.

Возьмем три сопротивления R1 = 10 Ом, R2 = 20 Ом и R3 = 60 Ом и соединим их параллельно. Определим эквивалентное сопротивление цепи (рис. 5 ).

Рис. 5. Цепь с тремя параллельно соединенными сопротивлениями

Применяя для этой цепи формулу 1 / R = 1 / R1 + 1 / R2 , можем написать 1 / R = 1 / R1 + 1 / R2 + 1 / R3 и, подставляя известные величины, получим 1 / R = 1 / 10 + 1 / 20 + 1 / 60

Сложим эта дроби: 1/R = 10 / 60 = 1 / 6, т. е.. проводимость цепи 1 / R = 1 / 6 Следовательно, эквивалентное сопротивление R = 6 Ом.

Таким образом, эквивалентное сопротивление меньше наименьшего из включенных параллельно в цепь сопротивлений , т. е. меньше сопротивления R1.

Посмотрим теперь, действительно ли это сопротивление является эквивалентным, т. е. таким, которое могло бы заменить включенные параллельно сопротивления в 10, 20 и 60 Ом, не изменяя при этом силы тока до разветвления цепи.

Допустим, что напряжение внешней цепи, а следовательно, и напряжение на сопротивлениях R1, R2, R3 равно 12 В. Тогда сила токов в ветвях будет: I1 = U/R1 = 12 / 10 = 1 ,2 А I 2 = U/R 2 = 12 / 20 = 1 ,6 А I 3 = U/R1 = 12 / 60 = 0,2 А

Общий ток в цепи получим, пользуясь формулой I = I1 + I2 + I3 =1,2 + 0,6 + 0,2 = 2 А.

Проверим по формуле закона Ома, получится ли в цепи ток силой 2 А, если вместо трех параллельно включенных известных нам сопротивлений включено одно эквивалентное им сопротивление 6 Ом.

I = U / R = 12 / 6 = 2 А

Как видим, найденное нами сопротивление R = 6 Ом действительно является для данной цепи эквивалентным.

В этом можно убедиться и на измерительных приборах, если собрать схему с взятыми нами сопротивлениями, измерить ток во внешней цепи (до разветвления), затем заменить параллельно включенные сопротивления одним сопротивлением 6 Ом и снова измерить ток. Показания амперметра и в том и в другом случае будут примерно одинаковыми.

На практике могут встретиться также параллельные соединения, для которых рассчитать эквивалентное сопротивление можно проще, т. е. не определяя предварительно проводимостей, сразу найти сопротивление.

Например, если соединены параллельно два сопротивления R1 и R2 , то формулу 1 / R = 1 / R1 + 1 / R2 можно преобразовать так: 1/R = (R2 + R1) / R1 R2 и, решая равенство относительно R, получить R = R1 х R2 / (R1 + R2 ), т. е. при параллельном соединении двух сопротивлений эквивалентное сопротивление цепи равно произведению включенных параллельно сопротивлений, деленному на их сумму.

Напряжение и сопротивление при последовательном соединении

Сопротивление проводников. Параллельное и последовательное соединение проводников.

Электри́ческое сопротивле́ние — физическая величина, характеризующая свойства проводника препятствовать прохождению электрического тока и равная отношениюнапряжения на концах проводника к силе тока, протекающего по нему [1] . Сопротивление для цепей переменного тока и для переменных электромагнитных полей описывается понятиями импеданса и волнового сопротивления. Сопротивлением (резистором) также называют радиодеталь, предназначенную для введения в электрические цепи активного сопротивления.

Сопротивление (часто обозначается буквой R или r) считается, в определённых пределах, постоянной величиной для данного проводника; её можно рассчитать как

U — разность электрических потенциалов (напряжение) на концах проводника;

I — сила тока, протекающего между концами проводника под действием разности потенциалов.

При последовательном соединении проводников (рис. 1.9.1) сила тока во всех проводниках одинакова:

Последовательное соединение проводников

По закону Ома, напряжения U₁ и U₂ на проводниках равны

Общее напряжение U на обоих проводниках равно сумме напряжений U₁ и U₂:

где R – электрическое сопротивление всей цепи. Отсюда следует:

При последовательном соединении полное сопротивление цепи равно сумме сопротивлений отдельных проводников.

Этот результат справедлив для любого числа последовательно соединенных проводников.

При параллельном соединении (рис. 1.9.2) напряжения U₁ и U₂ на обоих проводниках одинаковы:

Сумма токов I₁ + I₂, протекающих по обоим проводникам, равна току в неразветвленной цепи:

Этот результат следует из того, что в точках разветвления токов (узлы A и B) в цепи постоянного тока не могут накапливаться заряды. Например, к узлу A за время Δt подтекает заряд IΔt, а утекает от узла за то же время заряд I₁Δt + I₂Δt. Следовательно,I = I₁ + I₂.

Параллельное соединение проводников

Записывая на основании закона Ома

где R – электрическое сопротивление всей цепи, получим

При параллельном соединении проводников величина, обратная общему сопротивлению цепи, равна сумме величин, обратных сопротивлениям параллельно включенных проводников.

Этот результат справедлив для любого числа параллельно включенных проводников.

Формулы для последовательного и параллельного соединения проводников позволяют во многих случаях рассчитывать сопротивление сложной цепи, состоящей из многих резисторов. На рис. 1.9.3 приведен пример такой сложной цепи и указана последовательность вычислений.

Расчет сопротивления сложной цепи. Сопротивления всех проводников указаны вомах (Ом)

Следует отметить, что далеко не все сложные цепи, состоящие из проводников с различными сопротивлениями, могут быть рассчитаны с помощью формул для последовательного и параллельного соединения. На рис. 1.9.4 приведен пример электрической цепи, которую нельзя рассчитать указанным выше методом.

Пример электрической цепи, которая не сводится к комбинации последовательно и параллельно соединенных проводников

Во всех электрических схемах используются резисторы, представляющие собой элементы, с точно установленным значением сопротивления. Благодаря специфическим качествам этих устройств, становится возможной регулировка напряжения и силы тока на любых участках схемы. Данные свойства лежат в основе работы практически всех электронных приборов и оборудования. Так, напряжение при параллельном и последовательном соединении резисторов будет отличаться. Поэтому каждый вид соединения может применяться только в определенных условиях, чтобы та или иная электрическая схема могла в полном объеме выполнять свои функции.

Напряжение при последовательном соединении

При последовательном соединении два резистора и более соединяются в общую цепь таким образом, что каждый из них имеет контакт с другим устройством только в одной точке. Иначе говоря, конец первого резистора соединяется с началом второго, а конец второго – с началом третьего и т.д.

Особенностью данной схемы является прохождение через все подключенные резисторы одного и того же значения электрического тока. С возрастанием количества элементов на рассматриваемом участке цепи, течение электрического тока становится все более затрудненным. Это происходит из-за увеличения общего сопротивления резисторов при их последовательном соединении. Данное свойство отражается формулой: R_общ = R₁ + R₂.

Распределение напряжения, в соответствии с законом Ома, осуществляется на каждый резистор по формуле: V_Rn = I_Rn x R_n. Таким образом, при увеличении сопротивления резистора, возрастает и падающее на него напряжение.

Напряжение при параллельном соединении

При параллельном соединении, включение резисторов в электрическую цепь выполняется таким образом, что все элементы сопротивлений подключаются друг к другу сразу обоими контактами. Одна точка, представляющая собой электрический узел, может соединять одновременно несколько резисторов.

Такое соединение предполагает течение отдельного тока в каждом резисторе. Сила этого тока находится в обратно пропорциональной зависимости с сопротивлением резистора. В результате, происходит увеличение общей проводимости данного участка цепи, при общем уменьшении сопротивления. В случае параллельного соединения резисторов с различным сопротивлением, значение общего сопротивления на этом участке всегда будет ниже самого маленького сопротивления отдельно взятого резистора.

На представленной схеме, напряжение между точками А и В представляет собой не только общее напряжение для всего участка, но и напряжение, поступающее к каждому отдельно взятому резистору. Таким образом, в случае параллельного соединения, напряжение, подаваемое ко всем резисторам, будет одинаковым.

В результате, напряжение при параллельном и последовательном соединении будет отличаться в каждом случае. Благодаря этому свойству, имеется реальная возможность отрегулировать данную величину на любом участке цепи.

Последовательное соединение резисторов

Последовательное соединение – это соединение двух или более резисторов в форме цепи, в которой каждый отдельный резистор соединяется с другим отдельным резистором только в одной точке.

Общее сопротивление R

_общ

При таком соединении, через все резисторы проходит один и тот же электрический ток. Чем больше элементов на данном участке электрической цепи, тем «труднее» току протекать через него. Следовательно, при последовательном соединении резисторов их общее сопротивление увеличивается, и оно равно сумме всех сопротивлений.

Напряжение при последовательном соединении

Напряжение при последовательном соединении распределяется на каждый резистор согласно закону Ома:

Т.е чем большее сопротивление резистора, тем большее напряжение на него падает.

Параллельное соединение резисторов

Параллельное соединение – это соединение, при котором резисторы соединяются между собой обоими контактами. В результате к одной точке (электрическому узлу) может быть присоединено несколько резисторов.

Общее сопротивление R

_общ

При таком соединении, через каждый резистор потечет отдельный ток. Сила данного тока будет обратно пропорциональна сопротивлению резистора. В результате общая проводимость такого участка электрической цепи увеличивается, а общее сопротивление в свою очередь уменьшается.

Таким образом, при параллельном подсоединении резисторов с разным сопротивлением, общее сопротивление будет всегда меньше значения самого маленького отдельного резистора.

Формула общей проводимости при параллельном соединении резисторов:

Формула эквивалентного общего сопротивления при параллельном соединении резисторов:

Для двух одинаковых резисторов общее сопротивление будет равно половине одного отдельного резистора:

Соответственно, для n одинаковых резисторов общее сопротивление будет равно значению одного резистора, разделенного на n.

Напряжение при параллельном соединении

Напряжение между точками A и B является как общим напряжением для всего участка цепи, так и напряжением, падающим на каждый резистор в отдельности. Поэтому при параллельном соединении на все резисторы упадет одинаковое напряжение.

Электрический ток при параллельном соединении

Через каждый резистор течет ток, сила которого обратно пропорциональна сопротивлению резистора. Для того чтобы узнать какой ток течет через определенный резистор, можно воспользоваться законом Ома:

Смешанное соединение резисторов

Смешанным соединением называют участок цепи, где часть резисторов соединяются между собой последовательно, а часть параллельно. В свою очередь, смешанное соединение бывает последовательного и параллельного типов.

Общее сопротивление R

_общ

Для того чтобы посчитать общее сопротивление смешанного соединения:

Цепь разбивают на участки с только пареллельным или только последовательным соединением.
Вычисляют общее сопротивление для каждого отдельного участка.
Вычисляют общее сопротивление для всей цепи смешанного соединения.

Так это будет выглядеть для схемы 1:

Также существует более быстрый способ расчета общего сопротивления для смешанного соединения. Можно, в соответствии схеме, сразу записывать формулу следующим образом:

Если резисторы соединяются последоватеьно — складывать.
Если резисторы соединяются параллельно — использовать условное обозначение «||».
Подставлять формулу для параллельного соединения где стоит символ «||».

Так это будет выглядеть для схемы 1:

После подстановки формулы параллельного соединения вместо «||»:

Расчет сопротивления двух параллельно соединенных резисторов. Последовательное и параллельное соединение резисторов. Формула для расчета параллельного соединения сопротивлений

В каждой электрической схеме присутствует резистор, имеющий сопротивление электрическому току. Резисторы бывают двух типов: постоянные и переменные. Во время разработки любой электрической схемы и ремонта электронных изделий часто приходится применять резистор, обладающий необходимым номиналом.

Несмотря на то что для резисторов предусмотрены различные номиналы , может случиться так, что не будет возможности найти необходимый или же вообще ни один элемент не сможет обеспечить требуемый показатель.

Рассчитать производительность и работу

Угол сдвига фаз вычисляется по изображению указателя. Чтобы иметь возможность определять мощности, поглощаемые схемой, предыдущие формулы используются снова. Для определения работы используются следующие формулы.

Дальнейший интересный контент по теме

Резисторы переменного тока представляют собой омические, индуктивные и емкостные резисторы. Для параллельного подключения таких резисторов в цепи переменного тока применяются разные законы, чем для сопротивлений в цепи постоянного тока. Учитывая это, например, катушку: настоящая катушка имеет как индуктивное, так и омическое сопротивление и поэтому может рассматриваться как последовательная связь чисто индуктивного и чисто омического резистора.

Решением этой проблемы может стать применение последовательного и параллельного соединения. Ознакомившись с этой статьей, вы узнаете об особенностях выполнения расчета и подбора различных номиналов сопротивлений.

Часто при изготовлении какого-либо устройства используют резисторы, которые соединяются в соответствии с последовательной схемой. Эффект от применения такого варианта сборки сводится к увеличению общего сопротивления цепи. Для данного варианта соединения элементов создаваемое ими сопротивление рассчитывается как сумма номиналов. Если же сборка деталей выполняется по параллельной схеме, то здесь потребуется рассчитать сопротивление , используя нижеописанные формулы.

Примеры параллельного соединения проводников

Мы рассматриваем только индуктивную составляющую резистора, т.е. катушку как чисто индуктивный резистор. Аналогично, используется омическое сопротивление и емкостное сопротивление, поскольку омическое сопротивление также может иметь индуктивный компонент. В то время как в случае сопротивления проволоки витки, подобные виткам, видны напрямую, это обычно скрыто в резисторах слоя. Фактически, проводящий слой наносят на носитель, из которого материал, проводящий материал, удаляется с помощью процесса спирально-циркулирующего фрезерования, так что остается спирально циркулирующий слой.

К схеме параллельного соединения прибегают в ситуации, когда стоит задача по снижению суммарного сопротивления, а, помимо этого, увеличения мощности для группы элементов, подключенных по параллельной схеме, которое должно быть больше, чем при их отдельном подключении.

Таким образом генерируется требуемое значение сопротивления. Сразу видно, что эта катушечная структура приводит к индуктивному компоненту. Однако это обычно настолько мало, что его можно пренебречь. Общая обработка взаимосвязи любых резисторов переменного тока невозможна и не требуется с помощью математических знаний, доступных в школе.

Объяснение Подключение серии и параллельное соединение

Ниже приведен упрощенный случай параллельной схемы чисто омического, индуктивного и емкостного резисторов. В этой статье мы рассмотрим параллельное соединение и последовательное соединение резисторов. Давайте сначала уточним, что такое последовательное соединение и что такое параллельное соединение, и где разница между последовательным соединением и параллельным соединением. В последовательной цепи мы имеем два или более сопротивления последовательно. Тот же ток протекает через все резисторы.

Расчет сопротивления

В случае подключения деталей друг с другом, с применением параллельной схемы для расчета суммарного сопротивления, будет использоваться следующая формула:

R(общ)=1/(1/R1+1/R2+1/R3+1/Rn).

R1- R3 и Rn – резисторы, подсоединенные по параллельной схеме.

Причем, если цепь создается на основе только двух элементов, то для определения суммарного номинального сопротивления следует использовать такую формулу:

Универсальная схема расчета

На следующем графике показаны резисторы последовательно, два резистора, индивидуально нарисованные в начале, и три резистора под электрической цепью. Напротив, существует параллельное соединение резисторов. Что такое параллельная схема? Теперь, в параллельной цепи, линия распадается, и, следовательно, и ток разлагается. В случае параллельного подключения резисторов во многих случаях впервые рассматривается параллельное соединение двух резисторов. Это выглядит следующим образом, включая формулу для расчета.

R(общ)=R1*R2/R1+R2.

R(общ) – суммарное сопротивление;
R1 и R2 – резисторы, подсоединенные по параллельной схеме.

Универсальная схема расчета

Применительно к радиотехнике следует уделить внимание одному важному правилу: если подключаемые друг к другу элементы по параллельной схеме имеют одинаковый показатель , то для расчета суммарного номинала необходимо общее значение разделить на число подключенных узлов:

Для трех резисторов в параллельной схеме это будет выглядеть на следующем графике, включая формулу для расчета. Разностное соединение и параллельное соединение. В случае последовательной цепи все резисторы подключаются по одной линии за другой. В случае параллельной схемы, с другой стороны, линия расщепляется, резисторы лежат в отдельных линиях. В последовательной цепи тот же ток протекает через все резисторы, а в случае параллельной цепи ток расщепляется. В случае параллельной схемы одно и то же напряжение подается на каждый резистор, но не в последовательной цепи. Другое примечание: смесь последовательной цепи и параллельной схемы называется групповой схемой.

R(общ) – суммарное значение сопротивления;
R – номинал резистора, подсоединенного по параллельной схеме;
n – число подключенных узлов.

Особое внимание следует обратить на то, что конечный показатель сопротивления в случае использования параллельной схемы подключения обязательно будет меньше по сравнению с номиналом любого элемента, подключаемого в цепь.

Примеры Подключение серий и параллельное соединение

В следующих примерах мы увидим, как рассчитать смесь схемы параллельной цепи и серии. В этой области шаг за шагом должен быть рассчитан набор последовательных схем и параллельных схем. На следующем графике показана смесь последовательного соединения и параллельного соединения. Каково общее сопротивление?

Сначала мы суммируем 20 Ом и 30 Ом, так как здесь имеется параллельная схема. Таким образом, схема выглядит следующим образом. Теперь добавим эту схему, добавив резисторы для вычисления общего сопротивления. Вычислите общее сопротивление следующего контура.

Пример расчета

Для большей наглядности можно рассмотреть следующий пример: допустим, у нас есть три резистора, чьи номиналы соответственно равны 100, 150 и 30 Ом. Если воспользоваться первой формулой для определения общего номинала, то получим следующее:

Прежде всего, вы должны увидеть, что есть короткое замыкание на резисторе с 95 Ом. Поэтому ток течет практически полностью по линии ниже, а 95 Ом не учитывается при расчете полного сопротивления. В противном случае у нас есть сочетание последовательной цепи и параллельной схемы.

Комбинированные последовательные и параллельные схемы

Вам нужно знать, как рассчитать резисторы последовательно, параллельно и комбинацию резисторов параллельно и последовательно? Если вы не хотите жарить свою печатную плату, вы это делаете! Эта статья покажет вам, как это сделать за несколько простых шагов. Это просто образный способ говорить, чтобы понятий было легко понять.

Некоторые факты, которые вы должны учитывать

Любой материал, который проводит электрический ток, имеет удельное сопротивление, которое представляет собой сопротивление материала при прохождении электрического тока.

Понять понятие сопротивления.
Единицей измерения резисторов является Ом.

Параллельное соединение резисторов характеризуется тем, что входные клеммы каждого из резисторов соединены друг с другом.

R(общ)=1/(1/100+1/150+1/30)=1/(0,01+0,007+0,03)=1/0,047=21,28Ом.

Если выполнить несложные расчеты, то можно получить следующее: для цепи, включающей в себя три детали, где наименьший показатель сопротивления составляет 30 Ом, результирующее значение номинала будет равно 21,28 Ом. Этот показатель будет меньше минимального значения номинала в цепи практически на 30%.

Аналогично, в конфигурации параллельного резистора выходные клеммы также соединены друг с другом. Из-за этого все резисторы пропускают одинаковое напряжение, т.е. имеют одинаковое падение напряжения. Это связано с тем, что концы каждого из резисторов соединены с одной и той же точкой в цепи, и поэтому они имеют одинаковое напряжение.

Однако общий ток, протекающий через резисторы параллельно, равен сумме интенсивностей, которые проходят каждый резистор. Дифференциация параллельного соединения из последовательного интерфейса проста. В последовательной конфигурации резистора выходной разъем одного подключается к входному разъему следующего.

Важные нюансы

Обычно для резисторов параллельное соединение применяется тогда, когда стоит задача по созданию сопротивления большей мощности. Для ее решения потребуются резисторы, которые должны иметь равные показатели сопротивления и мощности. При таком варианте определить общую мощность можно следующим образом : мощность одного элемента необходимо перемножить с суммарным числом всех резисторов, из которых состоит цепь, подсоединенных друг с другом в соответствии с параллельной схемой.

Вычисление сопротивлений параллельно: формула

Чтобы вычислить эквивалентное сопротивление нескольких подключенных параллельных резисторов, мы должны применить формулу, указанную выше этих строк. Чтобы избежать ошибок в расчетах, лучше всего разделить формулу на два шага. Сначала мы вычисляем сумму обратного для каждого сопротивления и, когда получаем результат, вычисляем его обратно, чтобы знать эквивалентное сопротивление.

Решенное сопротивление сопротивлениям параллельно

Например, мы вычислим эквивалентное сопротивление конфигурации, аналогичное той, что мы имеем на следующем рисунке. Первый шаг: вычислить сумму обратного каждого сопротивления. Шаг второй: вычислите обратное только что полученное сопротивление.

Вычисление трех резисторов параллельно

Если мы хотим решить предыдущий пример, но используя наш калькулятор из трех резисторов параллельно в сети, просто заполните значение каждого резистора в соответствующем поле. Порядок, в котором вы его пишете, не имеет значения, поэтому вам не нужно его уважать.

Скажем, если нами будут использоваться пять резисторов, чей номинал составляет 100 Ом, а мощность каждого равна 1 Вт, которые присоединены друг к другу в соответствии с параллельной схемой, то суммарный показатель сопротивления будет равен 20 Ом, а мощность составит 5 Вт.

Если взять те же резисторы, но подсоединить их в соответствии с последовательной схемой, то конечная мощность составит 5 Вт, а суммарный номинал будет равен 500 Ом.

Когда вы пишете значение трех резисторов параллельно, просто нажмите кнопку расчета, и вы автоматически получите результат без применения формулы для расчета сопротивления параллельно. С этим вы экономите время и, прежде всего, просчеты. Как мы видели в предыдущих разделах, устройства, которые выступают против прохода электрического тока более выраженным образом, чем обычно, обычно используются в электрических цепях. Эти устройства называются резисторами и могут быть связаны таким образом, что вместе они эквивалентны значению другого сопротивления, называемого эквивалентным сопротивлением.

Заключение

Параллельная схема подключения резисторов очень востребована по той причине, что часто возникает задача по созданию такого номинала, которого невозможно добиться при помощи простого параллельного соединения. При этом процедура расчета этого параметра отличается достаточной сложностью , где необходимо учитывать разные параметры.

Ассоциация резисторов в серии

Он называется полученным сопротивлением или эквивалентом, к значению сопротивления, которое получается путем связывания их набора. В основном резисторы могут быть связаны последовательно, параллельно или комбинацией обоих смешанных вызовов. Когда два или более резисторов последовательно, интенсивность тока, проходящая через каждую из них, одинакова.

Если применить закон Ома к каждому из сопротивлений предыдущего рисунка, мы получим. Если мы сделаем сумму от члена к элементу по трем уравнениям, заметим, что. Таким образом, приведенное выше уравнение, если учесть, что. Итак, если вы понимаете, вы можете видеть, что три предыдущих резистора серии эквивалентны одному резистору, значение которого представляет собой сумму трех предыдущих.

Здесь важная роль отводится не только количеству подключаемых элементов, но и рабочим параметрам резисторов — прежде всего, сопротивлению и мощности. Если один из подключаемых элементов будет иметь неподходящий показатель, то это не позволит эффективно решить задачу по созданию требуемого номинала в цепи.

Ассоциация резисторов в параллельном

Когда два или более резисторов параллельны, они делятся своими концами, как показано на следующем рисунке. Если мы применим закон Ома в каждом из сопротивлений фигуры. Зная, что сумма интенсивностей каждого сопротивления равна интенсивности перед входом и выходом из набора, образованного тремя сопротивлениями.

Ассоциация смешанного сопротивления

Как правило, в электрических цепях они не просто похожи на последовательные или параллельные резисторы, но и на комбинацию обоих. Чтобы лучше понять, как подойти к этим типам ассоциаций, мы проиллюстрируем пример. Представьте себе следующую схему сопротивлений.

Общее сопротивление R общ

Подключение 2 равных громкоговорителей последовательно добавляет импедансы и ватты? Сопротивление добавляется, и общая мощность рассеивания на громкоговоритель уменьшается вдвое. Предположим, что выход 8 вольт и динамик 8 Ом ток, который циркулирует громкоговорителем.

Таким образом, динамик должен будет поддерживать более 8 Вт, чтобы он не был поврежден. Теперь подключите два динамика 8 Ом и 8 Вт последовательно, импеданс обоих составляет 16 Ом. Теперь мы вычисляем ток, протекающий через динамики. С этими данными мы вычисляем мощность в каждом динамике.

Напряжение при последовательном соединении

Напряжение при последовательном соединении распределяется на каждый резистор согласно закону Ома:

Т.е чем большее сопротивление резистора, тем большее напряжение на него падает.

Вывод: динамики работают более сдержанно, но усилитель будет поставлять половину мощности, когда динамик составляет 8 Ом. Разделен ли импеданс и ватт параллельно? Если мы рассмотрим одни и те же ораторы на примере предыдущего вопроса, можно сказать, что общий импеданс уменьшается наполовину и рассчитывается следующим образом.

Для работы с более чем двумя динамиками параллельно необходимо использовать другое уравнение для расчета импеданса. Если мы анализируем отдельно каждого динамика, мы понимаем, что каждый из них ведет себя так же, как в примере 1, когда каждый из них подключен к усилителю, через который они будут циркулировать 1 А, а мощность, подлежащая рассеиванию, будет составлять 8 Вт в каждом динамике.

Общее сопротивление R общ

Формула общей проводимости при параллельном соединении резисторов:

Формула эквивалентного общего сопротивления при параллельном соединении резисторов:

Для двух одинаковых резисторов общее сопротивление будет равно половине одного отдельного резистора:

Напряжение при параллельном соединении

Общее сопротивление R общ

Цепь разбивают на участки с только пареллельным или только последовательным соединением.
Вычисляют общее сопротивление для каждого отдельного участка.
Вычисляют общее сопротивление для всей цепи смешанного соединения.

Если резисторы соединяются последоватеьно — складывать.
Если резисторы соединяются параллельно — использовать условное обозначение «||».
Подставлять формулу для параллельного соединения где стоит символ «||».

Так это будет выглядеть для схемы 1:

Как считать сопротивление при последовательном соединении — MOREREMONTA

Как правильно соединять резисторы?

О том, как соединять конденсаторы и рассчитывать их общую ёмкость уже рассказывалось на страницах сайта. А как соединять резисторы и посчитать их общее сопротивление? Именно об этом и будет рассказано в этой статье.

Резисторы есть в любой электронной схеме, причём их номинальное сопротивление может отличаться не в 2 – 3 раза, а в десятки и сотни раз. Так в схеме можно найти резистор на 1 Ом, и тут же неподалёку на 1000 Ом (1 кОм)!

Поэтому при сборке схемы либо ремонте электронного прибора может потребоваться резистор с определённым номинальным сопротивлением, а под рукой такого нет. В результате быстро найти подходящий резистор с нужным номиналом не всегда удаётся. Это обстоятельство тормозит процесс сборки схемы или ремонта. Выходом из такой ситуации может быть применение составного резистора.

Для того чтобы собрать составной резистор нужно соединить несколько резисторов параллельно или последовательно и тем самым получить нужное нам номинальное сопротивление. На практике это пригождается постоянно. Знания о правильном соединении резисторов и расчёте их общего сопротивления выручают и ремонтников, восстанавливающих неисправную электронику, и радиолюбителей, занятых сборкой своего электронного устройства.

Последовательное соединение резисторов.

В жизни последовательное соединение резисторов имеет вид:

Последовательно соединённые резисторы серии МЛТ

Принципиальная схема последовательного соединения выглядит так:

На схеме видно, что мы заменяем один резистор на несколько, общее сопротивление которых равно тому, который нам необходим.

Подсчитать общее сопротивление при последовательном соединении очень просто. Нужно сложить все номинальные сопротивления резисторов входящих в эту цепь. Взгляните на формулу.

Общее номинальное сопротивление составного резистора обозначено как R_общ.

Номинальные сопротивления резисторов включённых в цепь обозначаются как R₁, R₂, R₃,…R_N.

Применяя последовательное соединение, стоит помнить одно простое правило:

Из всех резисторов, соединённых последовательно главную роль играет тот, у которого самое большое сопротивление. Именно он в значительной степени влияет на общее сопротивление.

Так, например, если мы соединяем три резистора, номинал которых равен 1, 10 и 100 Ом, то в результате мы получим составной на 111 Ом. Если убрать резистор на 100 Ом, то общее сопротивление цепочки резко уменьшиться до 11 Ом! А если убрать, к примеру, резистор на 10 Ом, то сопротивление будет уже 101 Ом. Как видим, резисторы с малыми сопротивлениями в последовательной цепи практически не влияют на общее сопротивление.

Параллельное соединение резисторов.

Можно соединять резисторы и параллельно:

Два резистора МЛТ-2, соединённых параллельно

Принципиальная схема параллельного соединения выглядит следующим образом:

Для того чтобы подсчитать общее сопротивление нескольких параллельно соединённых резисторов понадобиться знание формулы. Выглядит она вот так:

Эту формулу можно существенно упростить, если применять только два резистора. В таком случае формула примет вид:

Есть несколько простых правил, позволяющих без предварительного расчёта узнать, каково должно быть сопротивление двух резисторов, чтобы при их параллельном соединении получить то, которое требуется.

Если параллельно соединены два резистора с одинаковым сопротивлением, то общее сопротивление этих резисторов будет ровно в два раза меньше, чем сопротивление каждого из резисторов, входящих в эту цепочку.

Это правило исходит из простой формулы для расчёта общего сопротивления параллельной цепи, состоящей из резисторов одного номинала. Она очень проста. Нужно разделить номинальное сопротивление одного из резисторов на общее их количество:

Здесь R₁ – номинальное сопротивление резистора. N – количество резисторов с одинаковым номинальным сопротивлением.

Ознакомившись с приведёнными формулами, вы скажите, что все они справедливы для расчёта ёмкости параллельно и последовательно соединённых конденсаторов. Да, только в отношении конденсаторов всё действует с точностью до «наоборот”. Узнать подробнее о соединении конденсаторов можно здесь.

Проверим справедливость показанных здесь формул на простом эксперименте.

Замер общего сопротивления при последовательном соединении

Теперь соединим наши резисторы параллельно и замерим их общее сопротивление.

Измерение сопротивления при параллельном соединении

Что ещё нужно учитывать при соединении резисторов?

Во-первых, обязательно учитывается их номинальная мощность. Например, нам нужно подобрать замену резистору на 100 Ом и мощностью 1 Вт. Возьмём два резистора по 50 Ом каждый и соединим их последовательно. На какую мощность рассеяния должны быть рассчитаны эти два резистора?

Поскольку через последовательно соединённые резисторы течёт один и тот же постоянный ток (допустим 0,1 А), а сопротивление каждого из них равно 50 Ом, тогда мощность рассеивания каждого из них должна быть не менее 0,5 Вт. В результате на каждом из них выделится по 0,5 Вт мощности. В сумме это и будет тот самый 1 Вт.

Данный пример достаточно грубоват. Поэтому, если есть сомнения, стоит брать резисторы с запасом по мощности.

Подробнее о мощности рассеивания резистора читайте тут.

Последовательное соединение резисторов

Общее сопротивление R

_общ

Напряжение при последовательном соединении

Напряжение при последовательном соединении распределяется на каждый резистор согласно закону Ома:

Т.е чем большее сопротивление резистора, тем большее напряжение на него падает.

Параллельное соединение резисторов

Общее сопротивление R

_общ

Формула общей проводимости при параллельном соединении резисторов:

Формула эквивалентного общего сопротивления при параллельном соединении резисторов:

Для двух одинаковых резисторов общее сопротивление будет равно половине одного отдельного резистора:

Напряжение при параллельном соединении

Электрический ток при параллельном соединении

Смешанное соединение резисторов

Общее сопротивление R

_общ

Для того чтобы посчитать общее сопротивление смешанного соединения:

Цепь разбивают на участки с только пареллельным или только последовательным соединением.
Вычисляют общее сопротивление для каждого отдельного участка.
Вычисляют общее сопротивление для всей цепи смешанного соединения.

Так это будет выглядеть для схемы 1:

Если резисторы соединяются последоватеьно — складывать.
Если резисторы соединяются параллельно — использовать условное обозначение «||».
Подставлять формулу для параллельного соединения где стоит символ «||».

Так это будет выглядеть для схемы 1:

После подстановки формулы параллельного соединения вместо «||»:

Параллельное соединение резисторов — одно из двух видов электрических соединений, когда оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов. Зачастую резисторы соединяют последовательно или параллельно для того, чтобы создать более сложные электронные схемы.

Схема параллельного соединения резисторов показан на рисунке ниже. При параллельном соединении резисторов, напряжение на всех резисторах будет одинаковым, а протекающий через них ток будет пропорционален их сопротивлению:

Формула параллельного соединения резисторов

Общее сопротивление нескольких резисторов соединенных параллельно определяется по следующей формуле:

Ток, протекающий через отдельно взятый резистор, согласно закону Ома, можно найти по формуле:

Параллельное соединение резисторов — расчет

Пример №1

Таким образом, мы получили необходимое сопротивление 8 Ом, соединив параллельно два резистора по 16 Ом.

Пример расчета №2

Найти общее сопротивление R из трех параллельно соединенных резисторов:

Общее сопротивление R рассчитывается по формуле:

Один важный момент, который необходимо запомнить при расчете параллельно соединенных резисторов – это то, что общее сопротивление всегда будет меньше, чем значение наименьшего сопротивления в этой комбинации.

Как рассчитать сложные схемы соединения резисторов

Для простоты расчета, сначала сгруппируем резисторы по параллельному и последовательному типу соединения.
Резисторы R2 и R3 соединены последовательно (группа 2). Они в свою очередь соединены параллельно с резистором R1 (группа 1).

Последовательное соединение резисторов группы 2 вычисляется как сумма сопротивлений R2 и R3:

Расчет более сложных соединений резисторов можно выполнить используя законы Кирхгофа.

Ток, протекающий в цепи параллельно соединенных резисторах

Первое правило Кирхгофа гласит: «Общий ток, выходящий из цепи равен току входящий в цепь».

Таким образом, протекающий общий ток в цепи можно определить как:

Затем с помощью закона Ома можно вычислить ток, который протекает через каждый резистор:

Ток, протекающий в R1 = U ÷ R1 = 12 ÷ 22 кОм = 0,545 мА

Ток, протекающий в R 2 = U ÷ R2 = 12 ÷ 47 кОм = 0,255 мА

Таким образом, общий ток будет равен:

I = 0,545 мА + 0,255 мА = 0,8 мА

Это также можно проверить, используя закон Ома:

I = U ÷ R = 12 В ÷ 15 кОм = 0,8 мА (то же самое)

где 15кОм — это общее сопротивление двух параллельно соединенных резисторов (22 кОм и 47 кОм)

И в завершении хочется отметить, что большинство современных резисторов маркируются цветными полосками и назначение ее можно узнать здесь.

Параллельное соединение резисторов — онлайн калькулятор

Подведем итог

При последовательном соединении сопротивление равно. Параллельное соединение сопротивлениий (резисторов)

Последовательное, параллельное и смешанное соединения резисторов. Значительное число приемников, включенных в электрическую цепь (электрические лампы, электронагревательные приборы и др.), можно рассматривать как некоторые элементы, имеющие определенное сопротивление. Это обстоятельство дает нам возможность при составлении и изучении электрических схем заменять конкретные приемники резисторами с определенными сопротивлениями. Различают следующие способы соединения резисторов (приемников электрической энергии): последовательное, параллельное и смешанное.

Последовательное соединение резисторов . При последовательном соединении нескольких резисторов конец первого резистора соединяют с началом второго, конец второго — с началом третьего и т. д. При таком соединении по всем элементам последовательной цепи проходит
один и тот же ток I.
Последовательное соединение приемников поясняет рис. 25, а.
.Заменяя лампы резисторами с сопротивлениями R1, R2 и R3, получим схему, показанную на рис. 25, б.
Если принять, что в источнике Ro = 0, то для трех последовательно соединенных резисторов согласно второму закону Кирхгофа можно написать:

E = IR 1 + IR 2 + IR 3 = I(R 1 + R 2 + R 3) = IR эк (19)

где R эк = R 1 + R 2 + R 3 .
Следовательно, эквивалентное сопротивление последовательной цепи равно сумме сопротивлений всех последовательно соединенных резисторов.Так как напряжения на отдельных участках цепи согласно закону Ома: U 1 =IR 1 ; U 2 = IR 2 , U 3 = IR з и в данном случае E = U, то длярассматриваемой цепи

U = U 1 + U 2 +U 3 (20)

Следовательно, напряжение U на зажимах источника равно сумме напряжений на каждом из последовательно включенных резисторов.
Из указанных формул следует также, что напряжения распределяются между последовательно соединенными резисторами пропорционально их сопротивлениям:

U 1: U 2: U 3 = R 1: R 2: R 3 (21)

т. е. чем больше сопротивление какого-либо приемника в последовательной цепи, тем больше приложенное к нему напряжение.

В случае если последовательно соединяются несколько, например п, резисторов с одинаковым сопротивлением R1, эквивалентное сопротивление цепи Rэк будет в п раз больше сопротивления R1, т. е. Rэк = nR1. Напряжение U1 на каждом резисторе в этом случае в п раз меньше общего напряжения U:

При последовательном соединении приемников изменение сопротивления одного из них тотчас же влечет за собой изменение напряжения на других связанных с ним приемниках. При выключении или обрыве электрической цепи в одном из приемников и в остальных приемниках прекращается ток. Поэтому последовательное соединение приемников применяют редко — только в том случае, когда напряжение источника электрической энергии больше номинального напряжения, на которое рассчитан потребитель. Например, напряжение в электрической сети, от которой питаются вагоны метрополитена, составляет 825 В, номинальное же напряжение электрических ламп, применяемых в этих вагонах, 55 В. Поэтому в вагонах метрополитена электрические лампы включают последовательно по 15 ламп в каждой цепи.
Параллельное соединение резисторов . При параллельном соединении нескольких приемников они включаются между двумя точками электрической цепи, образуя параллельные ветви (рис. 26, а). Заменяя

I 1 =U/R 1 ; I 2 =U/R 2 ; I 3 =U/R 3 .

Ток в неразветвленной части цепи согласно первому закону Кирхгофа I = I 1 +I 2 +I 3 , или

I = U / R 1 + U / R 2 + U / R 3 = U (1/R 1 + 1/R 2 + 1/R 3) = U / R эк (23)

1/R эк = 1/R 1 + 1/R 2 + 1/R 3 (24)

G эк = G 1 + G 2 +G 3 (25)

I 1: I 2: I 3 = 1/R 1: 1/R 2: 1/R 3 = G 1 + G 2 + G 3 (26)

R эк =R 1 R 2 /(R 1 +R 2)

при трех параллельно включенных резисторах

R эк =R 1 R 2 R 3 /(R 1 R 2 +R 2 R 3 +R 1 R 3)

R эк = R1 / n (27)

Проходящий по каждой ветви ток I1, в этом случае будет в п раз меньше общего тока:

I1 = I / n (28)

ченными. Поэтому параллельное соединение имеет существенные преимущества перед последовательным, вследствие чего оно получило наиболее широкое распространение. В частности, электрические лампы и двигатели, предназначенные для работы при определенном (номинальном) напряжении, всегда включают параллельно.
На электровозах постоянного тока и некоторых тепловозах тяговые двигатели в процессе регулирования скорости движения нужно включать под различные напряжения, поэтому они в процессе разгона переключаются с последовательного соединения на параллельное.

Смешанное соединение резисторов . Смешанным соединением называется такое соединение, при котором часть резисторов включается последовательно, а часть — параллельно. Например, в схеме рис. 27, а имеются два последовательно включенных резистора сопротивлениями R1 и R2, параллельно им включен резистор сопротивлением Rз, а резистор сопротивлением R4 включен последовательно с группой резисторов сопротивлениями R1, R2 и R3.
Эквивалентное сопротивление цепи при смешанном соединении обычно определяют методом преобразования, при котором сложную цепь последовательными этапами преобразовывают в простейшую. Например, для схемы рис. 27, а вначале определяют эквивалентное сопротивление R12 последовательно включенных резисторов с сопротивлениями R1 и R2: R12 = R1 + R2. При этом схема рис. 27, а заменяется эквивалентной схемой рис. 27, б. Затем определяют эквивалентное сопротивление R123 параллельно включенных сопротивлений и R3 по формуле

R 123 =R 12 R 3 /(R 12 +R 3)=(R 1 +R 2)R 3 /(R 1 +R 2 +R 3).

При этом схема рис. 27, б заменяется эквивалентной схемой рис. 27, в. После этого находят эквивалентное сопротивление всей цепи суммированием сопротивления R123 и последовательно включенного с ним сопротивления R4:

R эк = R 123 + R 4 = (R 1 + R 2) R 3 / (R 1 + R 2 + R 3) + R 4

Последовательное, параллельное и смешанное соединения широко применяют для изменения сопротивления пусковых реостатов при пуске э. п. с. постоянного тока.

1. При последовательном соединении проводников

1. Сила тока во всех проводниках одинакова :

I 1 = I 2 = I

2. Общее напряжение U на обоих проводниках равно сумме напряжений U 1 и U 2 на каждом проводнике :

U = U 1 + U 2

3. По закону Ома, напряжения U 1 и U 2 на проводниках равны U 1 = IR 1 , U 2 = IR 2 а общее напряжение U = IR где R – электрическое сопротивление всей цепи, тогда IR = IR 1 + I R 2. Отсюда следует

R = R 1 + R 2

Этот результат справедлив для любого числа последовательно соединенных проводников.

2. При параллельном соединении проводников

1. Напряжения U 1 и U 2 на обоих проводниках одинаковы

U 1 = U 2 = U

2. Сумма токов I 1 + I 2 , протекающих по обоим проводникам, равна току в неразветвленной цепи :

I = I 1 + I 2

Этот результат следует из того, что в точках разветвления токов (узлы A и B ) в цепи постоянного тока не могут накапливаться заряды. Например, к узлу A за время Δt подтекает заряд I Δt , а утекает от узла за то же время заряд I 1 Δt + I 2 Δt . Следовательно, I = I 1 + I 2 .

3. Записывая на основании закона Ома

где R – электрическое сопротивление всей цепи, получим

Этот результат справедлив для любого числа параллельно включенных проводников.

Формулы для последовательного и параллельного соединения проводников позволяют во многих случаях рассчитывать сопротивление сложной цепи, состоящей из многих резисторов. На рисунке приведен пример такой сложной цепи и указана последовательность вычислений. Сопротивления всех проводников указаны в омах (Ом).

На пракутике одного источника тока в цепи бывает недостаточно, и тогда источники тока тоже соединяют между собой для питания цепи. Соединение источников в батарею может быть последовательным и параллельным.

При последовательном соединении два соседних источника соединяются разноименными полюсами.

Т.е., для последовательного соединения аккумуляторов, к ″плюсу″ электрической схемы подключают положительную клемму первого аккумулятора. К его отрицательной клемме подключают положительную клемму второго аккумулятора и т.д. Отрицательную клемму последнего аккумулятора подключают к ″минусу″ электрической схемы.

Получившаяся при последовательном соединении аккумуляторная батарея имеет ту же емкость, что и у одиночного аккумулятора, а напряжение такой аккумуляторной батареи равно сумме напряжений входящих в нее аккумуляторов. Т.е. если аккумуляторы имеют одинаковые напряжения, то напряжение батареи равно напряжению одного аккумулятора, умноженному на количество аккумуляторов в аккумуляторной батарее.

1. ЭДС батареи равна сумме ЭДС отдельных источников ε= ε 1 + ε 2 + ε 3

2 . Общее сопротивление батареи источников равно сумме внутренних сопротивлений отдельных источников r батареи = r 1 + r 2 + r 3

Если в батарею соединены n одинаковых источников, то ЭДС батареи ε= nε 1, а сопротивление r батареи = nr 1

При параллельном соединении соединяют между собой все положительные и все отрицательные полюсы двух или n источников.

Т.е., при параллельном соединении, аккумуляторы соединяют так, чтобы положительные клеммы всех аккумуляторов были подключены к одной точке электрической схемы (″плюсу″), а отрицательные клеммы всех аккумуляторов были подключены к другой точке схемы (″минусу″).

Параллельно соединяют только источники с одинаковой ЭДС . Получившаяся при параллельном соединении аккумуляторная батарея имеет то же напряжение, что и у одиночного аккумулятора, а емкость такой аккумуляторной батареи равна сумме емкостей входящих в нее аккумуляторов. Т.е. если аккумуляторы имеют одинаковые емкости, то емкость аккумуляторной батареи равна емкости одного аккумулятора, умноженной на количество аккумуляторов в батарее.

1. ЭДС батареи одинаковых источников равна ЭДС одного источника. ε= ε 1 = ε 2 = ε 3

2. Сопротивление батареи меньше, чем сопротивление одного источника r батареи = r 1 /n
3. Сила тока в такой цепи по закону Ома

Электрическая энергия, накопленная в аккумуляторной батарее равна сумме энергий отдельных аккумуляторов (произведению энергий отдельных аккумуляторов, если аккумуляторы одинаковые), независимо от того, как соединены аккумуляторы — параллельно или последовательно.

Внутреннее сопротивление аккумуляторов, изготовленных по одной технологии, примерно обратно пропорционально емкости аккумулятора. Поэтому т.к.при параллельном соединении емкость аккумуляторной батареи равна сумме емкостей входящих в нее аккумуляторов, т.е увеличивается, то внутреннее сопротивление уменьшается.

Параллельным соединением сопротивлений называется такое соединение, когда начала сопротивлений соединены в одну общую точку, а концы — в другую.

Для параллельного соединения сопротивлений характерны следующие свойства:

Напряжения на зажимах всех сопротивлений одинаковы:

U 1 = U 2 =U 3 =U ;

Проводимость всех параллельно соединённых сопротивлений равна сумме проводимостей отдельных сопротивлений:

1/R = 1/R 1 + 1/R 2 + 1/R 3 = R 1 R 2 + R 1 R 3 + R 2 R 3 /R 1 R 2 R 3 ,

где R — эквивалентное (равнодействующее) сопротивление трёх сопротивлений (в данном случае R 1 , R 2 и R 3 ) .

Чтобы получить сопротивление такой цепи, надо перевернуть дробь, определяющую величину её проводимости. Следовательно, сопротивление параллельного разветвления из трёх резисторов:

R = R 1 R 2 R 3 /R 1 R 2 + R 2 R 3 + R 1 R 3 .

Эквивалентным сопротивлением называется такое сопротивление, которым можно заменить несколько сопротивлений (включенных параллельно или последовательно), не изменяя величины тока в цепи.

Чтобы найти эквивалентное сопротивление при параллельном соединении, необходимо сложить проводимости всех отдельных участков, т.е. найти общую проводимость. Величина, обратная общей проводимости, и является общим сопротивлением.

При параллельном соединении эквивалентная проводимость равна сумме проводимостей отдельных ветвей, следовательно, эквивалентное сопротивление в этом случае всегда меньше наименьшего из параллельно включенных сопротивлений.

На практике могут быть случаи, когда цепь состоит из более, чем трёх параллельных ветвей. Все полученные соотношения остаются справедливыми и для цепей, состоящих из любого числа параллельно соединённых резисторов.

Найдём эквивалентное сопротивление двух параллельно включенных сопротивлений R 1 и R 2 (см. рис.). Проводимость первой ветви равна 1/R 1 , проводимость второй ветви — 1/R 2 . Общая проводимость:

1/R = 1/R 1 + 1/R 2 .

Приведём к общему знаменателю:

1/R = R 2 + R 1 /R 1 R 2 ,

отсюда эквивалентное сопротивление

R = R 1 R 2 /R 1 + R 2 .

Эта формула и служит для расчётов общего сопротивления цепи, состоящей из двух параллельно включенных сопротивлений.

Таким образом, эквивалентное сопротивление двух параллельно включенных сопротивлений равно произведению этих сопротивлений, делённому на их сумму.

При параллельном соединении n равных сопротивлений R 1 эквивалентное сопротивление их будет в n раз меньше, т.е.

R = R 1 /n .

На схеме, изображённой на последнем рисунке, включено пять сопротивлений R 1 по 30 Ом каждое. Следовательно, общее сопротивление R будет

R = R 1 /5 = 30/5 = 6 Ом.

Можно сказать, что сумма токов, подходящих к узловой точке А (на первом рисунке), равна сумме токов, от неё отходящих:

I = I 1 + I 2 + I 3 .

Рассмотрим, как происходит разветвление тока в цепях с сопротивлениями R 1 и R 2 (второй рисунок). Так как напряжение на зажимах этих сопротивлений одинаково, то

U = I 1 R 1 и U = I 2 R 2 .

Левые части этих равенств одинаковы, следовательно, равны и правые части:

I 1 R 1 = I 2 R 2 ,

или

I 1 /I 2 = R 2 /R 1 ,

Т.е. ток при параллельном соединении сопротивлений разветвляется обратно пропорционально сопротивлениям ветвей (или прямо пропорционально их проводимостям). Чем больше сопротивление ветви, тем меньше ток в ней, и наоборот.

Таким образом, из нескольких одинаковых резисторов можно получить общий резистор с бОльшей мощностью рассеивания.

При параллельном соединении неодинаковых резисторов в наиболее высокоомном резисторе выделяется наибольшая мощность.

Пример 1. Имеются два сопротивления, включенных параллельно. Сопротивление R 1 = 25 Ом, а R 2 = 50 Ом. Определить общее сопротивление цепи R общ .

Решение. R общ = R 1 R 2 /R 1 + R 2 = 25 . 50 / 25 + 50 ≈ 16, 6 Ом.

Пример 2. В ламповом усилителе имеются три лампы, нити накала которых включены параллельно. Ток накала первой лампы I 1 = 1 ампер, второй I 2 = 1, 5 ампера и третьей I 3 = 2, 5 ампера. Определить общий ток цепи накала ламп усилителя I общ .

Решение. I общ = I 1 + I 2 + I 3 = 1 + 1, 5 + 2, 5 = 5 ампер.

Параллельное соединение резисторов часто встречается в радиотехнической аппаратуре. Два или более резисторов включается параллельно в тех случаях, когда ток в цепи слишком большой и может вызвать чрезмерный нагрев резистора.

Примером параллельного соединения потребителей электрической энергии может служить включение электрических ламп обычной осветительной сети, которые соединяются параллельно. Достоинство параллельного соединения потребителей заключается в том, что выключение одного из них не влияет на работу других.

Резисторы серии
и параллельные [Analog Devices Wiki]
Цель:
Целью этой лабораторной работы является исследование последовательно и параллельно соединенных резисторов.
Серия
и параллельные схемы
Простые схемы, состоящие всего из нескольких компонентов, обычно просты для понимания новичками. Но все усложняется, когда в смесь входит большее количество компонентов.Куда идет ток? Что делают узловые напряжения? Можно ли упростить схему и облегчить понимание? Следующая информация должна помочь.
В этой лабораторной работе мы сначала обсудим разницу между последовательными цепями и параллельными цепями, используя цепи, содержащие самые основные компоненты, резисторы и батареи (или источники напряжения), чтобы показать разницу между двумя конфигурациями.
Прежде чем мы углубимся в объяснение, нам нужно определить, что такое узел схемы.Узел в цепи — это не что иное, как электрическое соединение между двумя или более компонентами. Когда схема изображена на схеме, такой как рисунок 1, узлы представлены проводами (линиями) между компонентами.
Рисунок 1, Пример схемы узла
На схеме изображена схема с 4 резисторами и источником напряжения. Также есть четыре уникальных узла. Цветные узлы (линии) Красный соединяет (+) конец источника напряжения с резистором R ₁, оранжевый соединяет R ₁ и R ₂ вместе, синий соединяет R ₂ с R ₃ и R ₄ и зеленый соединяет (-) конец источника напряжения с R ₃ и R ₄.Обратите внимание, что мы обычно определяем один узел как общий узел, на который ссылаются все остальные узлы, в данном случае это зеленый наземный узел.
Нам также необходимо понять, как ток течет по цепи. Обычный ток течет от более высокого или более положительного напряжения к более низкому или менее положительному напряжению в цепи. Некоторое количество тока будет проходить по каждому пути, который может пройти, чтобы добраться до точки с наименьшим напряжением, обычно называемой землей (0 вольт). Используя приведенную выше схему в качестве примера, вот как будет течь ток, когда он проходит от положительной клеммы источника напряжения к отрицательной клемме.
Обратите внимание, что в некоторых узлах (например, между R ₁ и R ₂) ток на входе такой же, как на выходе. В других узлах (в частности, трехсторонний переход между R ₂, R ₃ и R ₄) основной (красный) ток разделяется на два разных: фиолетовый ток, текущий в R ₃ и оранжевый ток протекает в R ₄. Также обратите внимание, что токи I _R3 и I _R4 рекомбинируют как зеленый ток.Это подчеркивает ключевое различие между последовательным и параллельным подключением.
Определение схем серии
Когда резисторы подключаются последовательно (как показано на рисунке 2), вывод одного резистора подключается непосредственно к выводу следующего резистора, без каких-либо других возможных путей, так что весь ток в одном резисторе должен течь в следующий и скоро.
Когда резисторы включены последовательно, они могут быть объединены или объединены в один эквивалентный резистор с сопротивлением, равным сумме последовательных сопротивлений, i.е. , г.
Рисунок 2: Последовательные резисторы, R _СЕРИЯ = R ₁ + R ₂ + R ₃ +…
Почему это правда? Закон Ома говорит нам, что напряжение на резисторе равно току через резистор, умноженному на сопротивление. Итак, для приведенной выше последовательной схемы:
Мы знаем, что все резисторы имеют одинаковый ток I _S.
Аналогично для остальных трех резисторов так:
Или за вычетом I _S:
Таким образом, полное эквивалентное сопротивление — это просто сумма их значений.
Определение параллельных цепей
Когда резисторы включены параллельно (как показано на рисунке 3), все их первые выводы соединены вместе, а все их вторые выводы соединены вместе.
Когда резисторы включены параллельно, они могут быть объединены или объединены в один эквивалентный одиночный резистор, значение которого определяется следующим уравнением:
Для двух параллельно подключенных резисторов это упрощает:
Рисунок 3: Параллельные резисторы
Почему это правда? Закон Ома говорит нам, что напряжение на резисторе равно току через резистор, умноженному на сопротивление.Итак, для вышеуказанной параллельной схемы:
Мы знаем, что все резисторы имеют одинаковое напряжение В _S.
Ток, подаваемый источником напряжения В _S, является суммой токов в резисторах.
Подставляя четыре резистора, получаем:
Или вычтем V _S:
Переставляя сопротивление, получаем полное эквивалентное сопротивление:
Эксперименты
Материалы:
Аппаратный модуль ADALM1000
Макетная плата без пайки и перемычки
Резисторы 3–100 Ом
Резисторы 3–470 Ом
Резисторов в серии:
Поместите три резистора 100 Ом последовательно на беспаечную макетную плату, как показано на рисунке 4.Подключите с помощью перемычек вход CH A к левой стороне первого резистора, а вход CH B к правой стороне того же резистора.
Рисунок 4, последовательно соединенные резисторы
Запустите прибор ALICE M1K Ohm Meter. Здесь показан экран. Программное обеспечение использует известный резистор для проверки неизвестного резистора. ADALM1000 имеет встроенный резистор 50 Ом, который можно использовать для этого. Убедитесь, что выбран параметр Int. Уровень напряжения, который используется для измерения резистора, может быть установлен.Тестирование при максимальном напряжении 5,0 В дает наилучшие результаты для большинства номиналов резисторов. Нажмите Run, и вы должны увидеть что-то подобное с единственным резистором 100 Ом.
Переместите перемычку CH B к правому концу второго резистора, как показано ниже.
Рисунок 5, два резистора последовательно
Омметр должен теперь показать значение для двух последовательно соединенных резисторов или около 200 Ом. Теперь переместите перемычку CH B к правому концу третьего резистора, как показано ниже.
Рисунок 6, три резистора последовательно
Омметр должен теперь показать значение трех последовательно соединенных резисторов или около 300 Ом.
Сопротивление параллельно:
Теперь замените резисторы 100 Ом на резисторы 470 Ом, как показано на рисунке 7.
Измерение одного резистора 470 Ом
Омметр должен теперь показать значение одиночного резистора или около 470 Ом. Переместите средний резистор 470 Ом так, чтобы он был параллелен резистору справа, как показано ниже.
Измерение двух резисторов 470 Ом, включенных параллельно
Омметр должен теперь показать значение для двух резисторов 470 Ом, включенных параллельно. Соответствует ли измеренное значение формуле для параллельных резисторов?
Переместите третий резистор 470 Ом так, чтобы он был параллелен двум другим резисторам справа, как показано ниже.
Измерение трех резисторов 470 Ом, включенных параллельно
Омметр должен теперь показать значение для трех резисторов 470 Ом, включенных параллельно.Соответствует ли измеренное значение формуле для параллельных резисторов?
Поэкспериментируйте с другими комбинациями резисторов и номиналов, чтобы убедиться, что формулы верны для любого номинала резистора.
Комбинированные схемы
Более сложные соединения резисторов обычно представляют собой просто комбинации последовательного и параллельного соединения. Это часто встречается, особенно если учитывать сопротивление проводов. В этом случае сопротивление провода включено последовательно с другими сопротивлениями, включенными параллельно.
Комбинированная схема может быть разбита на аналогичные части, которые являются последовательными или параллельными, как показано на рисунке 7. На рисунке общее сопротивление может быть вычислено путем соединения трех резисторов друг с другом последовательно или параллельно.
Комбинированные последовательные и параллельные резисторы
R ₂ и R ₃ соединены параллельно друг другу, поэтому мы знаем, что для этих двух резисторов эквивалентное сопротивление будет:
Комбинированное сопротивление R ₂ и R ₃ последовательно с R1, поэтому общее эквивалентное сопротивление будет:
Для более сложных комбинированных схем различные части могут быть идентифицированы как последовательные или параллельные, уменьшены до их эквивалентов, а затем уменьшены до тех пор, пока не останется единственное сопротивление.
Для дальнейшего изучения:
Академия Хана — схемы резисторов
Безграничная физика
Последовательные и параллельные схемы (по физике)
Вернуться к разделу «Введение в деятельность электротехнической лаборатории» Содержание
Последовательные и параллельные резисторы · Физика
Последовательные и параллельные резисторы · Физика
Нарисуйте цепь с резисторами, включенными параллельно и последовательно.
Рассчитайте падение напряжения тока на резисторе, используя закон Ома.
Contrast Способ расчета общего сопротивления для резисторов, включенных последовательно и параллельно.
Объясните, почему полное сопротивление параллельной цепи меньше наименьшего сопротивления любого из резисторов в этой цепи.
Рассчитайте общее сопротивление цепи, которая содержит смесь резисторов, включенных последовательно и параллельно.
Большинство схем имеет более одного компонента, называемого резистором , который ограничивает поток заряда в цепи.Мера этого предела расхода заряда называется сопротивлением . Простейшие комбинации резисторов — это последовательное и параллельное соединение, показанное в [ссылка]. Общее сопротивление комбинации резисторов зависит как от их индивидуальных значений, так и от способа их подключения.
Резисторы
серии
Когда резисторы в серии ? Резисторы включены последовательно всякий раз, когда поток заряда, называемый током , должен проходить через устройства последовательно.Например, если ток течет через человека, держащего отвертку, и попадает в Землю, тогда R1 размер 12 {R rSub {размер 8 {1}}} {}
дюйма [ссылка] (а) может соответствовать сопротивлению вала отвертки R2, размер 12 {R rSub {размер 8 {2}}} {}
сопротивление его ручки, R3 размер 12 {R rSub {размер 8 {3}}} {}
сопротивление тела человека и R4 размер 12 {R rSub {размер 8 {4}}} {}
сопротивление ее обуви.
[ссылка] показывает резисторы, последовательно подключенные к источнику напряжения .Кажется разумным, что полное сопротивление является суммой отдельных сопротивлений, учитывая, что ток должен проходить через каждый резистор последовательно. (Этот факт был бы преимуществом для человека, желающего избежать поражения электрическим током, который мог бы уменьшить ток, надев обувь с высоким сопротивлением на резиновой подошве. Это могло бы стать недостатком, если бы одним из сопротивлений был неисправный шнур с высоким сопротивлением. прибор, уменьшающий рабочий ток.)
Чтобы убедиться, что последовательно соединенные сопротивления действительно складываются, давайте рассмотрим потерю электроэнергии, называемую падением напряжения , в каждом резисторе в [ссылка].
Согласно закону Ома , падение напряжения, В, величина 12 {V} {}
, через резистор, когда через него протекает ток, рассчитывается по формуле V = размер IR 12 {V = курсив «IR»} {}
, где I размер 12 {I} {}
соответствует току в амперах (A), а размер R 12 {R} {}
— это сопротивление в Ом. Ω размер 12 {слева (% OMEGA справа)} {}
. Другой способ думать об этом: размер V 12 {V} {}
— это напряжение, необходимое для создания тока I размера 12 {I} {}
протекает через сопротивление R размер 12 {R} {}
.
Итак, падение напряжения на R1 размером 12 {R rSub {size 8 {1}}} {}
— это V1 = IR1, размер 12 {V rSub {size 8 {1}} = ital «IR» rSub {size 8 {1}}} {}
, что для R2 размера 12 {R rSub {size 8 {2}}} {}
— это V2 = IR2, размер 12 {V rSub {size 8 {2}} = ital «IR» rSub {size 8 {2}}} {}
и R3 размера 12 {R rSub {size 8 {3}}} {}
— это V3 = IR3 размер 12 {V rSub {size 8 {3}} = ital «IR» rSub {size 8 {3}}} {}
.Сумма этих напряжений равна выходному напряжению источника; то есть
V = V1 + V2 + V3. размер 12 {V = V rSub {размер 8 {1}} + V rSub {размер 8 {2}} + V rSub {размер 8 {3}}} {}
Это уравнение основано на сохранении энергии и сохранении заряда. Электрическая потенциальная энергия может быть описана уравнением PE = qV размер 12 {ital «PE» = ital «qV»} {}
, где q размер 12 {q} {}
— это электрический заряд и V размер 12 {V} {}
— это напряжение. Таким образом, энергия, поставляемая источником, равна qV size 12 {ital «qV»} {}
, а рассеиваемая на резисторах —
qV1 + qV2 + qV3.размер 12 {ital «qV» rSub {size 8 {1}} + ital «qV» rSub {size 8 {2}} + ital «qV» rSub {size 8 {3}}} {}
Связи: законы сохранения
Вывод выражений для последовательного и параллельного сопротивления основан на законах сохранения энергии и сохранения заряда, которые гласят, что общий заряд и полная энергия постоянны в любом процессе. Эти два закона непосредственно участвуют во всех электрических явлениях и будут многократно использоваться для объяснения как конкретных эффектов, так и общего поведения электричества.
Эти энергии должны быть равны, потому что в цепи нет другого источника и другого назначения для энергии. Таким образом, qV = qV1 + qV2 + qV3 размер 12 {ital «qV» = ital «qV» rSub {size 8 {1}} + ital «qV» rSub {size 8 {2}} + ital «qV» rSub {size 8 {3}}} {}
. Размер заряда q 12 {q} {}
отменяется, давая V = V1 + V2 + V3 размер 12 {V = V rSub {размер 8 {1}} + V rSub {размер 8 {2}} + V rSub {размер 8 {3}}} {}
, как указано. (Обратите внимание, что одинаковое количество заряда проходит через батарею и каждый резистор за заданный промежуток времени, поскольку нет емкости для хранения заряда, нет места для утечки заряда и заряд сохраняется.)
Теперь подстановка значений отдельных напряжений дает
V = IR1 + IR2 + IR3 = I (R1 + R2 + R3). размер 12 {V = ital «IR» rSub {size 8 {1}} + ital «IR» rSub {size 8 {2}} + ital «IR» rSub {size 8 {3}} = I \ (R rSub { размер 8 {1}} + R rSub {размер 8 {2}} + R rSub {размер 8 {3}} \)} {}
Обратите внимание, что для эквивалентного сопротивления одиночной серии
рупий
, у нас
V = IR.
Это означает, что полное или эквивалентное последовательное сопротивление
рупий.
из трех резисторов: Rs = R1 + R2 + R3 размер 12 {R rSub {размер 8 {s}} = R rSub {размер 8 {1}} + R rSub {размер 8 {2}} + R rSub {размер 8 {3}}} {}
.
Эта логика действительна в общем для любого количества резисторов, включенных последовательно; таким образом, общее сопротивление
рупий.
последовательного подключения —
Rs = R1 + R2 + R3 + …, размер 12 {R rSub {размер 8 {s}} = R rSub {размер 8 {1}} + R rSub {размер 8 {2}} + R rSub {размер 8 { 3}} + «.» «.» «.» } {}
, как предлагается. Поскольку весь ток должен проходить через каждый резистор, он испытывает сопротивление каждого, а последовательно соединенные сопротивления просто складываются.
Расчет сопротивления, тока, падения напряжения и рассеиваемой мощности: анализ последовательной цепи
Предположим, что выходное напряжение батареи в [ссылка] равно 12.0V размер 12 {«12» «.» 0`V} {}
, а сопротивления равны R1 = 1,00 Ом размер 12 {R rSub {размер 8 {1}} = 1 «.» «00»% OMEGA} {}
, R2 = 6,00 Ом, размер 12 {R rSub {размер 8 {2}} = 6 «.» «00»% OMEGA} {}
, и R3 = 13,0 Ом, размер 12 {R rSub {size 8 {3}} = «13» «.» 0% OMEGA} {}
. а) Каково полное сопротивление? (б) Найдите ток. (c) Вычислите падение напряжения на каждом резисторе и покажите, как они складываются, чтобы равняться выходному напряжению источника. (d) Рассчитайте мощность, рассеиваемую каждым резистором.(e) Найдите выходную мощность источника и покажите, что она равна общей мощности, рассеиваемой резисторами.
Стратегия и решение для (а)
Общее сопротивление — это просто сумма отдельных сопротивлений, определяемая следующим уравнением:
Rs = R1 + R2 + R3 = 1,00 Ом + 6,00 Ом + 13,0 Ом = 20,0 Ом.
Стратегия и решение для (b)
Ток определяется по закону Ома, V = размер IR 12 {V = ital «IR»} {}
.Ввод значения приложенного напряжения и общего сопротивления дает ток для цепи:
I = VRs = 12,0 В 20,0 Ом = 0,600 A. Размер 12 {I = {{V} больше {R rSub {size 8 {s}}}} = {{«12» «.» 0 «V»} больше {«20» «.» «0»% OMEGA}} = 0 «.» «600» «A»} {}
Стратегия и решение для (c)
Напряжение или размер ИК 12 {ital «IR»} {}
капля — в резисторе по закону Ома. Ввод тока и значения первого сопротивления дает
. V1 = IR1 = (0.600 A) (1,0 Ом) = 0,600 В. размер 12 {V rSub {size 8 {1}} = ital «IR» rSub {size 8 {1}} = \ (0 «.» «600» «A» \ ) \ (1 «.» 0% OMEGA \) = 0 «.» «600» «V»} {}
Аналогично
V2 = IR2 = (0,600 A) (6,0 Ом) = 3,60 В, размер 12 {V rSub {size 8 {2}} = ital «IR» rSub {size 8 {2}} = \ (0 «.» «600» «A» \) \ (6 «.» 0% OMEGA \) = 3 «.» «60» «V»} {}
и
V3 = IR3 = (0,600 A) (13,0 Ом) = 7,80 В. размер 12 {V rSub {size 8 {3}} = ital «IR» rSub {size 8 {3}} = \ (0 «.» «600 «» A «\) \ (» 13 «». «0% OMEGA \) = 7″.»» 80 «» V «} {}
Обсуждение для (c)
Три размера IR 12 {ital «IR»} {}
капли прибавляют к 12,0 В для размера 12 {«12» «». 0`V} {}
, как и прогнозировалось:
V1 + V2 + V3 = (0,600 + 3,60 + 7,80) V = 12,0 В. размер 12 {V rSub {размер 8 {1}} + V rSub {размер 8 {2}} + V rSub {размер 8 {3}} = \ (0 «.» «600» +3 «.» «60» +7 «.» «80» \) «V» = «12» «.» 0 «V»} {}
Стратегия и решение для (d)
Самый простой способ рассчитать мощность в ваттах (Вт), рассеиваемую резистором в цепи постоянного тока, — это использовать закон Джоуля , P = IV размер 12 {P = курсив «IV»} {}
, где P размер 12 {P} {}
— электрическая.В этом случае через каждый резистор протекает одинаковый полный ток. Подставляя закон Ома V = IR, размер 12 {V = ital «IR»} {}
в закон Джоуля, мы получаем мощность, рассеиваемую первым резистором, как
P1 = I2R1 = (0,600 A) 2 (1,00 Ом) = 0,360 Вт. Размер 12 {P rSub {размер 8 {1}} = I rSup {размер 8 {2}} R rSub {размер 8 {1}} = \ (0 «.» «600» «A» \) rSup {size 8 {2}} \ (1 «.» «00»% OMEGA \) = 0 «.» «360» «W»} {}
Аналогично
P2 = I2R2 = (0,600 A) 2 (6,00 Ом) = 2,16 Вт, размер 12 {P rSub {размер 8 {2}} = I rSup {размер 8 {2}} R rSub {размер 8 {2}} = \ ( 0 «.»» 600 «» A «\) rSup {размер 8 {2}} \ (6». «» 00 «% OMEGA \) = 2». «» 16 «» W «} {}
и
P3 = I2R3 = (0,600 A) 2 (13,0 Ом) = 4,68 Вт. Размер 12 {P rSub {размер 8 {3}} = I rSup {размер 8 {2}} R rSub {размер 8 {3}} = \ (0 «.» «600» «A» \) rSup {size 8 {2}} \ («13» «.» 0% OMEGA \) = 4 «.». «68» «W»} {}
Обсуждение для (д)
Мощность также можно рассчитать, используя либо P = IV, размер 12 {P = ital «IV»} {}
или P = V2R размер 12 {P = {{V rSup {размер 8 {2}}} больше {R}}} {}
, где V размер 12 {V} {}
— это падение напряжения на резисторе (а не полное напряжение источника).Получатся те же значения.
Стратегия и решение для (e)
Самый простой способ рассчитать выходную мощность источника — использовать P = IV размер 12 {P = ital «IV»} {}
, где V размер 12 {V} {}
— напряжение источника. Это дает
P = (0,600 A) (12,0 В) = 7,20 Вт. Размер 12 {P = \ (0 «.» «600» «A» \) \ («12» «.» 0 «V» \) = 7 » . » «20» «W»} {}
Обсуждение для (e)
Обратите внимание, что по совпадению общая мощность, рассеиваемая резисторами, также равна 7.20 Вт, столько же, сколько мощность, выдаваемая источником. То есть
P1 + P2 + P3 = (0,360 + 2,16 + 4,68) W = 7,20 W. размер 12 {P rSub {размер 8 {1}} + P rSub {размер 8 {2}} + P rSub {размер 8 {3}} = \ (0 «.» «360» +2 «.» «16» +4 «.» «68» \) «W» = 7 «.» «20» «W»} {}
Мощность — это энергия в единицу времени (ватты), поэтому для сохранения энергии требуется, чтобы выходная мощность источника была равна общей мощности, рассеиваемой резисторами.
Основные характеристики последовательно соединенных резисторов
Сопротивления серии добавляют: Rs = R1 + R2 + R3 +…. размер 12 {R rSub {размер 8 {s}} = R rSub {размер 8 {1}} + R rSub {размер 8 {2}} + R rSub {размер 8 {3}} + «.» «.» «.» «.» } {}
Одинаковый ток протекает последовательно через каждый резистор.
Отдельные последовательно включенные резисторы не получают полное напряжение источника, а делят его.
Параллельные резисторы
[ссылка] показывает резисторы параллельно , подключенные к источнику напряжения. Резисторы включены параллельно, когда каждый резистор подключен непосредственно к источнику напряжения с помощью соединительных проводов с незначительным сопротивлением.Таким образом, к каждому резистору приложено полное напряжение источника.
Каждый резистор потребляет такой же ток, как если бы он один был подключен к источнику напряжения (при условии, что источник напряжения не перегружен). Например, автомобильные фары, радио и т. Д. Подключены параллельно, так что они используют полное напряжение источника и могут работать полностью независимо. То же самое и в вашем доме, или в любом другом здании. (См. [Ссылка] (b).)
Чтобы найти выражение для эквивалентного параллельного сопротивления Rp размером 12 {R rSub {size 8 {p}}} {}
, давайте рассмотрим протекающие токи и их отношение к сопротивлению.Поскольку каждый резистор в цепи имеет полное напряжение, токи, протекающие через отдельные резисторы, равны I1 = VR1 размер 12 {I rSub {размер 8 {1}} = {{V} сверх {R rSub {размер 8 {1}} }}} {}
, I2 = VR2 размер 12 {I rSub {размер 8 {2}} = {{V} больше {R rSub {size 8 {2}}}}} {}
, и I3 = VR3 размер 12 {I rSub {размер 8 {3}} = {{V} больше {R rSub {size 8 {3}}}}} {}
. Сохранение заряда подразумевает, что общий ток I размера 12 {I} {}
, произведенное источником, является суммой этих токов:
Я = I1 + I2 + I3.размер 12 {I = I rSub {размер 8 {1}} + I rSub {размер 8 {2}} + I rSub {размер 8 {3}}} {}
Подстановка выражений для отдельных токов дает
Я = VR1 + VR2 + VR3 = V1R1 + 1R2 + 1R3. размер 12 {I = {{V} больше {R rSub {размер 8 {1}}}} + {{V} больше {R rSub {размер 8 {2}}}} + {{V} больше {R rSub { размер 8 {3}}}} = V слева ({{1} больше {R rSub {размер 8 {1}}}} + {{1} больше {R rSub {размер 8 {2}}}} + {{ 1} больше {R rSub {size 8 {3}}}} вправо)} {}
Обратите внимание, что закон Ома для эквивалентного одиночного сопротивления дает
I = VRp = V1Rp.размер 12 {I = {{V} над {R rSub {размер 8 {p}}}} = V слева ({{1} над {R rSub {размер 8 {p}}}} справа)} {}
Члены в круглых скобках в последних двух уравнениях должны быть равны. Обобщая на любое количество резисторов, общее сопротивление Rp размером 12 {R rSub {size 8 {p}}} {}
параллельного соединения связано с отдельными сопротивлениями на
1Rp = 1R1 + 1R2 + 1R.3 + …. размер 12 {{{1} больше {R rSub {size 8 {p}}}} = {{1} больше {R rSub {размер 8 {1}} }} + {{1} больше {R rSub {размер 8 {2}}}} + {{1} больше {R rSub {размер 8 {«.»3}}}} +». «». «». «». «} {}
Это соотношение приводит к общему сопротивлению Rp размером 12 {R rSub {size 8 {p}}} {}
, что меньше наименьшего из отдельных сопротивлений. (Это видно в следующем примере.) При параллельном подключении резисторов от источника течет больше тока, чем протекает по любому из них по отдельности, поэтому общее сопротивление ниже.
Расчет сопротивления, тока, рассеиваемой мощности и выходной мощности: анализ параллельной цепи
Пусть выходное напряжение батареи и сопротивления в параллельном соединении в [link] будут такими же, как в ранее рассмотренном последовательном соединении: V = 12.0 В, размер 12 {V = «12» «.» 0 «V»} {}
, R1 = 1,00 Ом, размер 12 {R rSub {размер 8 {1}} = 1 «.» «00»% OMEGA} {}
, R2 = 6,00 Ом, размер 12 {R rSub {размер 8 {2}} = 6 «.» «00»% OMEGA} {}
, и R3 = 13,0 Ом, размер 12 {R rSub {size 8 {3}} = «13» «.» 0% OMEGA} {}
. а) Каково полное сопротивление? (б) Найдите полный ток. (c) Рассчитайте токи в каждом резисторе и покажите, как они складываются, чтобы равняться общему выходному току источника. (d) Рассчитайте мощность, рассеиваемую каждым резистором.(e) Найдите выходную мощность источника и покажите, что она равна общей мощности, рассеиваемой резисторами.
Стратегия и решение для (а)
Общее сопротивление для параллельной комбинации резисторов находится с помощью следующего уравнения. Ввод известных значений дает
1Rp = 1R1 + 1R2 + 1R3 = 11,00 Ом + 16,00 Ом + 113,0 Ом. размер 12 {{{1} больше {R rSub {размер 8 {p}}}} = {{1} больше {R rSub {размер 8 {1}}}} + {{1} больше {R rSub {размер 8 {2}}}} + {{1} больше {R rSub {size 8 {3}}}} = {{1} больше {1 «.»» 00 «% OMEGA}} + {{1} более {6». «» 00 «% OMEGA}} + {{1} более {» 13 «». «0% OMEGA}}} {}
Таким образом,
1Rp = 1,00 Ом + 0,1667 Ом + 0,07692 Ом = 1,2436 Ом. размер 12 {{{1} больше {R rSub {size 8 {p}}}} = {{1 «.» «00»} больше {% OMEGA}} + {{0 «.» «167»} больше {% OMEGA}} + {{0 «.» «0769»} более {% OMEGA}} = {{1 «.» «244»} больше {% OMEGA}}} {}
(Обратите внимание, что в этих расчетах каждый промежуточный ответ отображается с дополнительной цифрой.)
Мы должны перевернуть это, чтобы найти полное сопротивление Rp размером 12 {R rSub {size 8 {p}}} {}
.Это дает
Rp = 11,2436 Ом = 0,8041 Ом. размер 12 {R rSub {размер 8 {p}} = {{1} более {1 «.» «2436»}}% OMEGA = 0 «.» «8041»% OMEGA} {}
Общее сопротивление с правильным количеством значащих цифр Rp = 0,804 Ом. размер 12 {R rSub {размер 8 {p}} = 0 «.» «804»% OMEGA} {}
Обсуждение для (а)
Rp
, как и предполагалось, меньше минимального индивидуального сопротивления.
Стратегия и решение для (b)
Полный ток можно найти из закона Ома, заменив Rp размер 12 {R rSub {размер 8 {p}}} {}
для общего сопротивления.Это дает
I = VRp = 12,0 V0,8041 Ом = 14,92 A. размер 12 {I = {{V} over {R rSub {size 8 {p}}}} = {{«12» «.» 0 «V»} больше {0 «.» «804»% OMEGA}} = «14» «.» «92» «A»} {}
Обсуждение для (б)
Текущий размер I 12 {I} {}
для каждого устройства намного больше, чем для тех же устройств, подключенных последовательно (см. Предыдущий пример). Схема с параллельным соединением имеет меньшее общее сопротивление, чем резисторы, включенные последовательно.
Стратегия и решение для (c)
Отдельные токи легко вычислить по закону Ома, поскольку каждый резистор получает полное напряжение.Таким образом,
I1 = VR1 = 12,0 В, 1,00 Ом = 12,0 А. размер 12 {I rSub {размер 8 {1}} = {{V} больше {R rSub {размер 8 {1}}}} = {{«12″ » . » 0 «V»} больше {1 «.» «00»% OMEGA}} = «12» «.» 0 «А»} {}
Аналогично
I2 = VR2 = 12,0 В 6,00 Ом = 2,00 А размер 12 {I rSub {размер 8 {2}} = {{V} больше {R rSub {размер 8 {2}}}} = {{«12» «. » 0 «V»} больше {6 «.» «00»% OMEGA}} = 2 «.» «00» «A»} {}
и
I3 = VR3 = 12,0 В 13,0 Ом = 0,92 А. размер 12 {I rSub {размер 8 {3}} = {{V} больше {R rSub {размер 8 {3}}}} = {{«12″ » .»0″ V «} больше {» 13 «». «» 0 «% OMEGA}} = 0». «» 92 «» A «} {}
Обсуждение для (c)
Общий ток складывается из отдельных токов:
I1 + I2 + I3 = 14,92 A. размер 12 {I rSub {размер 8 {1}} + I rSub {размер 8 {2}} + I rSub {размер 8 {3}} = «14» «.» «92» «A»} {}
Это соответствует сохранению заряда.
Стратегия и решение для (d)
Мощность, рассеиваемую каждым резистором, можно найти с помощью любого из уравнений, связывающих мощность с током, напряжением и сопротивлением, поскольку все три известны.Давайте использовать P = V2R размер 12 {P = {{V rSup {size 8 {2}}} вместо {R}}} {}
, так как каждый резистор получает полное напряжение. Таким образом,
P1 = V2R1 = (12,0 В) 21,00 Ом = 144 Вт. Размер 12 {P rSub {размер 8 {1}} = {{V rSup {размер 8 {2}}} больше {R rSub {размер 8 {1}}) }} = {{\ («12» «.» 0 «V» \) rSup {size 8 {2}}} больше {1 «.» «00»% OMEGA}} = «144» «W»} {}
Аналогично
P2 = V2R2 = (12,0 В) 26,00 Ом = 24,0 Вт размер 12 {P rSub {размер 8 {2}} = {{V rSup {размер 8 {2}}} больше {R rSub {размер 8 {2}}} } = {{\ («12» «.»0» V «\) rSup {size 8 {2}}} больше {6». «» 00 «% OMEGA}} =» 24 «». «0» W «} {}
и
P3 = V2R3 = (12,0 В) 213,0 Ом = 11,1 Вт. Размер 12 {P rSub {размер 8 {3}} = {{V rSup {размер 8 {2}}} больше {R rSub {размер 8 {3}}) }} = {{\ («12» «.» 0 «V» \) rSup {size 8 {2}}} больше {«13» «.» «0»% OMEGA}} = «11» «.» 1 «Вт»} {}
Обсуждение для (д)
Мощность, рассеиваемая каждым резистором при параллельном подключении, значительно выше, чем при последовательном подключении к тому же источнику напряжения.
Стратегия и решение для (e)
Общую мощность также можно рассчитать несколькими способами. Выбираем P = IV размер 12 {P = ital «IV»} {}
, а ввод полного тока дает
P = IV = (14,92 A) (12,0 В) = 179 Вт. Размер 12 {P = ital «IV» = \ («14» «.» «92» «A» \) \ («12» «.». » 0 «V» \) = «179» «.» 1 «Вт»} {}
Обсуждение для (e)
Общая мощность, рассеиваемая резисторами, также составляет 179 Вт:
P1 + P2 + P3 = 144 Вт + 24.0 Вт + 11,1 Вт = 179 Вт. размер 12 {P rSub {размер 8 {1}} + P rSub {размер 8 {2}} + P rSub {размер 8 {3}} = «144» «W» + «24» «.» 0 «W» + «11» «.» 1 «W» = «179» «W»} {}
Это соответствует закону сохранения энергии.
Общее обсуждение
Обратите внимание, что как токи, так и мощность при параллельном подключении больше, чем для тех же устройств, подключенных последовательно.
Основные характеристики параллельных резисторов
Параллельное сопротивление находится от 1Rp = 1R1 + 1R2 + 1R3 +… размер 12 {{{1} больше {R rSub {размер 8 {p}}}} = {{1} больше {R rSub {размер 8 {1}}}} + {{1} больше {R rSub { размер 8 {2}}}} + {{1} больше {R rSub {size 8 {3}}}} + «.» «.» «.» } {}
, и это меньше, чем любое отдельное сопротивление в комбинации.
Каждый резистор, включенный параллельно, имеет то же полное напряжение, что и источник. (В системах распределения электроэнергии чаще всего используются параллельные соединения для питания бесчисленных устройств, обслуживаемых одним и тем же напряжением, и для того, чтобы они могли работать независимо.)
Параллельные резисторы не получают суммарный ток каждый; они делят это.
Сочетания последовательного и параллельного
Более сложные соединения резисторов иногда представляют собой просто комбинации последовательного и параллельного. Они часто встречаются, особенно если учитывать сопротивление провода. В этом случае сопротивление провода включено последовательно с другими сопротивлениями, включенными параллельно.
Комбинации последовательного и параллельного подключения можно уменьшить до одного эквивалентного сопротивления, используя метод, показанный в [ссылка].Различные части идентифицируются как последовательные или параллельные, уменьшаются до их эквивалентов и далее уменьшаются до тех пор, пока не останется единственное сопротивление. Процесс занимает больше времени, чем труден.
Простейшая комбинация последовательного и параллельного сопротивления, показанная в [ссылка], также является наиболее поучительной, поскольку она используется во многих приложениях. Например, размер R1 12 {R rSub {размер 8 {1}}} {}
может быть сопротивлением проводов от автомобильного аккумулятора к его электрическим устройствам, которые соединены параллельно.R2 размер 12 {R rSub {размер 8 {1}}} {}
и R3 размер 12 {R rSub {размер 8 {1}}} {}
мог быть стартером и светом салона. Ранее мы предполагали, что сопротивление провода незначительно, но, когда это не так, оно имеет важные последствия, как показывает следующий пример.
Расчет сопротивления, Размер ИК 12 {ital «IR»} {} Падение, ток и рассеяние мощности: объединение последовательных и параллельных цепей
[ссылка] показывает резисторы из двух предыдущих примеров, подключенные другим способом — комбинацией последовательного и параллельного.Мы можем рассмотреть R1 размера 12 {R rSub {size 8 {1}}} {}
— сопротивление проводов, ведущих к R2 размером 12 {R rSub {размер 8 {2}}} {}
и R3 размер 12 {R rSub {размер 8 {3}}} {}
. (а) Найдите полное сопротивление. (б) Что такое ИК-размер 12 {итал. «ИК»} {}
капля R1 размер 12 {R rSub {размер 8 {1}}} {}
? (c) Найдите текущий размер I2 12 {I rSub {size 8 {2}}} {}
С
по R2 размер 12 {R rSub {размер 8 {2}}} {}
.(d) Какая мощность рассеивается R2 размером 12 {R rSub {размер 8 {2}}} {}
?
Стратегия и решение для (а)
Чтобы найти полное сопротивление, отметим, что R2 размер 12 {R rSub {размер 8 {2}}} {}
и R3 размер 12 {R rSub {размер 8 {3}}} {}
параллельно и их комбинация Rp размер 12 {R rSub {size 8 {p}}} {}
входит в серию с R1 размером 12 {R rSub {размер 8 {1}}} {}
.Таким образом, полное (эквивалентное) сопротивление этой комбинации составляет
. Rtot = R1 + Rp. размер 12 {R rSub {размер 8 {«tot»}} = R rSub {размер 8 {1}} + R rSub {размер 8 {p}}} {}
Сначала находим Rp size 12 {R rSub {size 8 {p}}} {}
, используя уравнение для параллельных резисторов и вводя известные значения:
1Rp = 1R2 + 1R3 = 16,00 Ом + 113,0 Ом = 0,2436 Ом. размер 12 {{{1} больше {R rSub {размер 8 {p}}}} = {{1} больше {R rSub {размер 8 {2}}}} + {{1} больше {R rSub {размер 8 {3}}}} = {{1} более {6 «.»» 00 «% OMEGA}} + {{1} более {» 13 «». «0% OMEGA}} = {{0». «» 2436 «} более {% OMEGA}}} {}
Инвертирование дает
Rp = 10,2436 Ом = 4,11 Ом. размер 12 {R rSub {размер 8 {p}} = {{1} более {0 «.» «2436»}}% OMEGA = 4 «.» «11»% OMEGA} {}
Таким образом, общее сопротивление равно
. Rtot = R1 + Rp = 1,00 Ом + 4,11 Ом = 5,11 Ом. размер 12 {R rSub {размер 8 {«tot»}} = R rSub {размер 8 {1}} + R rSub {размер 8 {p}} = 1 «.» «00»% OMEGA +4 «.» «11»% OMEGA = 5 «.» «11»% OMEGA} {}
Обсуждение для (а)
Общее сопротивление этой комбинации является промежуточным между значениями чистой серии и чистой параллели (20.0 Ом
и 0,804 Ом
соответственно), найденные для тех же резисторов в двух предыдущих примерах.
Стратегия и решение для (b)
Чтобы найти ИК-размер 12 {ital «IR»} {}
капля R1 размер 12 {R rSub {размер 8 {1}}} {}
, отметим, что полный ток I размера 12 {I} {}
проходит через размер R1 12 {R rSub {размер 8 {1}}} {}
. Таким образом, его размер IR 12 {ital «IR»} {}
дроп — это
V1 = IR1.размер 12 {V rSub {размер 8 {1}} = ital «IR» rSub {size 8 {1}}} {}
Мы должны найти I размер 12 {I} {}
, прежде чем мы сможем вычислить размер V1 12 {V rSub {size 8 {1}}} {}
. Суммарный ток I размера 12 {I} {}
находится с помощью закона Ома для схемы. То есть
I = VRtot = 12,0 В 5,11 Ом = 2,35 А. размер 12 {I = {{V} больше {R rSub {size 8 {«tot»}}}} = {{«12» «.» 0 «V»} больше {5 «.» «11»% OMEGA}} = 2 «.» «35» «A»} {}
Вводя это в выражение выше, мы получаем
V1 = IR1 = (2.35 A) (1,00 Ом) = 2,35 В. размер 12 {V rSub {size 8 {1}} = ital «IR» rSub {size 8 {1}} = \ (2 «.» «35» «A» \ ) \ (1 «.» «00»% OMEGA \) = 2 «.» «35» «V»} {}
Обсуждение для (б)
Напряжение, приложенное к R2 типоразмера 12 {R rSub {размер 8 {2}}} {}
и R3 размер 12 {R rSub {размер 8 {3}}} {}
меньше общего напряжения на величину V1 размер 12 {V rSub {размер 8 {1}}} {}
. Большое сопротивление провода может существенно повлиять на работу устройств, представленных R2 размером 12 {R rSub {размер 8 {2}}} {}
и R3 размер 12 {R rSub {размер 8 {3}}} {}
.
Стратегия и решение для (c)
Чтобы найти ток через R2 размер 12 {R rSub {размер 8 {2}}} {}
, мы должны сначала найти приложенное к нему напряжение. Мы называем это напряжение Vp размером 12 {V rSub {size 8 {p}}} {}
, потому что применяется к параллельной комбинации резисторов. Напряжение, приложенное к обоим R2 типоразмера 12 {R rSub {размер 8 {2}}} {}
и R3 размер 12 {R rSub {размер 8 {3}}} {}
уменьшается на размер V1 12 {V rSub {size 8 {1}}} {}
, так что это
Vp = V − V1 = 12.0 В − 2,35 В = 9,65 В. Размер 12 {V rSub {размер 8 {p}} = V — V rSub {размер 8 {1}} = «12» «.» 0 «В» — 2 «.» «35» «V» = 9 «.» «65» «V»} {}
Теперь текущий размер I2 12 {I rSub {размер 8 {2}}} {}
через сопротивление R2 размер 12 {R rSub {размер 8 {2}}} {}
находится по закону Ома:
I2 = VpR2 = 9,65 V6,00 Ом = 1,61 A. размер 12 {I rSub {размер 8 {2}} = {{V rSub {размер 8 {p}}} больше {R rSub {размер 8 {2}}} } = {{9 «.» «65 В»} более {6 «.» «00»% OMEGA}} = 1 «.» «61» «A»} {}
Обсуждение для (c)
Ток меньше 2.00 A, который прошел через R2 размера 12 {R rSub {размер 8 {2}}} {}
, когда он был подключен параллельно к батарее в предыдущем примере параллельной схемы.
Стратегия и решение для (d)
Мощность, рассеиваемая R2 размером 12 {R rSub {размер 8 {2}}} {}
выдается
P2 = (I2) 2R2 = (1,61 A) 2 (6,00 Ом) = 15,5 Вт. Размер 12 {P rSub {размер 8 {2}} = \ (I rSub {размер 8 {2}} \) rSup {размер 8 {2}} R rSub {размер 8 {2}} = \ (1 «.» «61» «A» \) rSup {размер 8 {2}} \ (6 «.»» 00 «% OMEGA \) =» 15 «». «5» W «} {}
Обсуждение для (д)
Мощность меньше 24,0 Вт, рассеиваемых этим резистором при параллельном подключении к источнику 12,0 В.
Практическое применение
Одним из следствий этого последнего примера является то, что сопротивление в проводах снижает ток и мощность, подаваемую на резистор. Если сопротивление провода относительно велико, как в изношенном (или очень длинном) удлинителе, то эти потери могут быть значительными. Если потребляется большой ток, размер IR 12 {ital «IR»} {}
Падение
в проводах также может быть значительным.
Например, когда вы роетесь в холодильнике и включается мотор, свет холодильника на мгновение гаснет. Точно так же вы можете увидеть тусклый свет в салоне, когда вы запускаете двигатель вашего автомобиля (хотя это может быть связано с сопротивлением внутри самой батареи).
Что происходит в этих сильноточных ситуациях, показано в [ссылка]. Устройство представлено размером R3 12 {R rSub {размер 8 {3}}} {}
имеет очень низкое сопротивление, поэтому при включении протекает большой ток.Этот увеличенный ток приводит к увеличению размера IR 12 {ital «IR»} {}
Падение
в проводах, представленное R1 размером 12 {R rSub {размер 8 {1}}} {}
, уменьшая напряжение на лампочке (это R2 размер 12 {R rSub {размер 8 {2}}} {}
), который затем заметно тускнеет.
Проверьте свое понимание
Можно ли любую произвольную комбинацию резисторов разбить на последовательную и параллельную? Посмотрите, сможете ли вы нарисовать принципиальную схему резисторов, которые нельзя разбить на комбинации последовательно и параллельно.
Нет, есть много способов подключения резисторов, которые не являются комбинациями последовательного и параллельного, включая петли и переходы. В таких случаях правила Кирхгофа, которые будут включены в Правила Кирхгофа, позволят вам проанализировать схему.
Стратегии решения проблем для последовательных и параллельных резисторов
Нарисуйте четкую принципиальную схему, пометив все резисторы и источники напряжения. Этот шаг включает список известных проблем, поскольку они отмечены на вашей принципиальной схеме.
Определите, что именно необходимо определить в проблеме (определите неизвестные). Письменный список полезен.
Определите, включены ли резисторы последовательно, параллельно или в комбинации последовательно и параллельно. Изучите принципиальную схему, чтобы сделать эту оценку. Резисторы включены последовательно, если через них должен последовательно проходить один и тот же ток.
Используйте соответствующий список основных функций для последовательных или параллельных подключений, чтобы найти неизвестные.Есть один список для серий, а другой — для параллелей. Если ваша проблема представляет собой комбинацию последовательного и параллельного соединения, уменьшайте ее поэтапно, рассматривая отдельные группы последовательных или параллельных соединений, как это сделано в этом модуле и примерах. Особое примечание: при нахождении Rp, размер 12 {R «» lSub {size 8 {p}}} {}
, с обратным следует обращаться осторожно.
Проверьте, являются ли ответы разумными и последовательными. Единицы и числовые результаты должны быть разумными.Общее последовательное сопротивление должно быть больше, а общее параллельное сопротивление, например, должно быть меньше. Мощность должна быть больше для одних и тех же устройств, подключенных параллельно, по сравнению с последовательными и т. Д.
Сводка раздела
Полное сопротивление электрической цепи с последовательно включенными резисторами является суммой отдельных сопротивлений: Rs = R1 + R2 + R3 + …. размер 12 {R rSub {размер 8 {s}} = R rSub {размер 8 {1}} + R rSub {размер 8 {2}} + R rSub {размер 8 { 3}} + «.»». «». «». «} {}
Каждый резистор в последовательной цепи имеет одинаковое количество тока, протекающего через него.
Падение напряжения или рассеиваемая мощность на каждом отдельном резисторе в серии различаются, и их общая сумма складывается с входом источника питания.
Общее сопротивление электрической цепи с резисторами, подключенными параллельно, меньше наименьшего сопротивления любого из компонентов и может быть определено по формуле: 1Rp = 1R1 + 1R2 + 1R3 +…. размер 12 {{{1} больше {R rSub {размер 8 {p}}}} = {{1} больше {R rSub {размер 8 {1}}}} + {{1} больше {R rSub {размер 8 {2}}}} + {{1} больше {R rSub {size 8 {3}}}} + «.» «.» «.» «.» } {}
Каждый резистор в параллельной цепи имеет одинаковое полное напряжение источника.
Ток, протекающий через каждый резистор в параллельной цепи, различается в зависимости от сопротивления.
Если более сложное соединение резисторов представляет собой комбинацию последовательного и параллельного соединения, оно может быть уменьшено до одного эквивалентного сопротивления, идентифицируя его различные части как последовательные или параллельные, уменьшая каждую до своего эквивалента и продолжая до тех пор, пока в конечном итоге не будет достигнуто единое сопротивление. .
Концептуальные вопросы
Переключатель имеет переменное сопротивление, близкое к нулю в замкнутом состоянии и очень большое в разомкнутом, и он подключается последовательно с устройством, которым он управляет. Объясните влияние переключателя в [ссылка] на ток в разомкнутом и замкнутом состоянии.
Какое напряжение на разомкнутом переключателе в [ссылка]?
Есть напряжение на разомкнутом переключателе, например, в [ссылка]. Почему же тогда мощность, рассеиваемая разомкнутым переключателем, мала?
Почему мощность, рассеиваемая замкнутым переключателем, например в [link], мала?
Студент в физической лаборатории по ошибке подключил электрическую лампочку, батарею и выключатель, как показано на [ссылка].Объясните, почему лампочка горит, когда переключатель разомкнут, и гаснет, когда переключатель замкнут. (Не пытайтесь — батарея сильно разряжается!)
Зная, что сила удара зависит от величины тока, протекающего через ваше тело, вы бы предпочли, чтобы он был включен последовательно или параллельно с сопротивлением, таким как нагревательный элемент тостера, если он поражен им? Объяснять.
Были бы ваши фары тусклыми при запуске двигателя автомобиля, если бы провода в вашем автомобиле были сверхпроводниками? (Не пренебрегайте внутренним сопротивлением батареи.) Объяснять.
Некоторые гирлянды праздничных огней соединены последовательно для экономии затрат на проводку. В старой версии использовались лампочки, которые при перегорании прерывали электрическое соединение, как открытый выключатель. Если одна такая лампочка перегорит, что случится с остальными? Если такая цепочка работает от 120 В и имеет 40 одинаковых лампочек, каково нормальное рабочее напряжение каждой? В более новых версиях используются лампы, которые при перегорании замыкаются накоротко, как замкнутый выключатель. Если одна такая лампочка перегорит, что случится с остальными? Если такая цепочка работает от 120 В и в ней осталось 39 идентичных лампочек, каково тогда рабочее напряжение каждой?
Если две бытовые лампочки мощностью 60 и 100 Вт подключить последовательно к бытовой электросети, какая из них будет ярче? Объяснять.
Предположим, вы проводите физическую лабораторию, в которой вас просят вставить резистор в схему, но все прилагаемые резисторы имеют большее сопротивление, чем запрошенное значение. Как бы вы соединили доступные сопротивления, чтобы попытаться получить меньшее запрошенное значение?
Перед Второй мировой войной некоторые радиостанции получали питание через «шнур сопротивления», который имел значительное сопротивление. Такой резистивный шнур снижает напряжение до желаемого уровня для ламп радиоприемника и т.п., и это экономит расходы на трансформатор.Объясните, почему шнуры сопротивления нагреваются и тратят энергию при включенном радио.
У некоторых лампочек есть три уровня мощности (не включая ноль), получаемые от нескольких нитей накала, которые индивидуально переключаются и соединяются параллельно. Какое минимальное количество нитей необходимо для трех режимов мощности?
Проблемные упражнения
Примечание. Можно считать, что данные, взятые из цифр, имеют точность до трех значащих цифр.
(a) Каково сопротивление десяти 275-омных размеров 12 {«275» -% OMEGA} {}
резистора соединены последовательно? (б) Параллельно?
(а) 2.75 кОм размер 12 {2 «.» «75» «k»% OMEGA} {}
(b) 27,5 Ом, размер 12 {«27» «.» 5% ОМЕГА} {}
(a) Каково сопротивление 1,00 × 102 Ом
, 2,50 кОм
и 4,00 кОм размером 12 {4 «.» «00» «- k»% OMEGA} {}
резистор соединен последовательно? (б) Параллельно?
Какое наибольшее и наименьшее сопротивление можно получить, подключив 36,0 Ом
, размер 50,0 Ом 12 {«50» «.» 0-% OMEGA} {}
и размер 700 Ом 12 {«700» -% OMEGA} {}
резистор вместе?
(a) 786 Ом, размер 12 {«786″% OMEGA} {}
(б) 20.3Ω размер 12 {«20» «.» 3% ОМЕГА} {}
Тостер на 1800 Вт, электрическая сковорода на 1400 Вт и лампа на 75 Вт подключены к одной розетке в цепи 15 А, 120 В. (Три устройства работают параллельно, если подключены к одной розетке.) а) Какой ток потребляет каждое устройство? (b) Перегорит ли эта комбинация предохранитель на 15 А?
Фара мощностью 30,0 Вт и стартер мощностью 2,40 кВт обычно подключаются параллельно в систему на 12,0 В. Какую мощность потребляли бы одна фара и стартер при последовательном подключении к 12.0-вольтовый аккумулятор? (Не обращайте внимания на любое другое сопротивление в цепи и любое изменение сопротивления в двух устройствах.)
29,6 Вт, размер 12 {«29» «.» 6 «Вт»} {}
(a) Учитывая батарею на 48,0 В и номинальное сопротивление 24,0 Ом 12 {«24» «.» 0-% OMEGA} {}
и 96,0 Ом, размер 12 {«96» «». 0-% OMEGA} {}
резистора, найдите ток и мощность для каждого при последовательном соединении. (b) Повторите, когда сопротивления включены параллельно.
Ссылаясь на пример комбинирования последовательных и параллельных цепей и [ссылка], вычислите размер I3 12 {I rSub {размер 8 {3}}} {}
двумя следующими способами: (a) из известных значений I размера 12 {I} {}
и I2 размер 12 {I rSub {размер 8 {2}}} {}
; (б) используя закон Ома для R3 размера 12 {R rSub {size 8 {3}}} {}
.В обеих частях явно показано, как вы выполняете шаги, указанные в Стратегиях решения проблем для последовательных и параллельных резисторов.
Ссылаясь на [ссылку]: (a) Рассчитайте размер P3 12 {P rSub {size 8 {3}}} {}
и обратите внимание на его сравнение с размером P3 12 {P rSub {size 8 {3}}} {}
обнаружил в первых двух примерах проблем в этом модуле. (b) Найдите полную мощность, отдаваемую источником, и сравните ее с суммой мощностей, рассеиваемых резисторами.
См. [Ссылка] и обсуждение затемнения света при включении тяжелого прибора. (a) Если источник напряжения составляет 120 В, сопротивление провода составляет 0,400 Ом размером 12 {0 «.» «800»% OMEGA} {}
, а номинальная мощность лампы составляет 75,0 Вт, какая мощность будет рассеиваться лампой, если при включении двигателя по проводам пройдет в общей сложности 15,0 А? Предположите незначительное изменение сопротивления лампы. б) Какая мощность потребляет двигатель?
ЛЭП 240 кВ по 5.00 × 102A
подвешен на заземленных металлических опорах с помощью керамических изоляторов, каждая из которых имеет размер 1,00 × 109 Ом 12 {1 «». «00» ´ «10» rSup {размер 8 {9}} -% OMEGA} {}
сопротивление. [ссылка на сайт]. а) Какое сопротивление относительно земли у 100 изоляторов? (b) Рассчитайте мощность, рассеиваемую 100 из них. (c) Какая доля мощности, переносимой линией, составляет это? Ясно покажите, как вы выполняете шаги, указанные в Стратегиях решения проблем для последовательных и параллельных резисторов.
Покажите, что если два резистора R1 размером 12 {R rSub {размер 8 {1}}} {}
и R2 размер 12 {R rSub {размер 8 {2}}} {}
объединены, и один намного больше другого (R1 >> R2 размер 12 {R rSub {размер 8 {1}} «>>» R rSub {размер 8 {2}}} {}
): (a) Их последовательное сопротивление почти равно большему сопротивлению R1 размера 12 {R rSub {size 8 {1}}} {}
.(b) Их параллельное сопротивление почти равно меньшему сопротивлению R2 размера 12 {R rSub {размер 8 {2}}} {}
.
(a) Rs = R1 + R2⇒Rs≈R1R1 >> R2alignl {стек {размер 12 {R rSub {размер 8 {s}} = R rSub {размер 8 {1}} + R rSub {размер 8 {2}) }} {} # drarrow R rSub {размер 8 {s}} »R rSub {размер 8 {1}} слева (R rSub {размер 8 {1}}» >> «R rSub {размер 8 {2}} справа ) {}}} {}
(b) 1Rp = 1R1 + 1R2 = R1 + R2R1R2 размер 12 {{{1} больше {R rSub {размер 8 {p}}}}} = {{1} больше {R rSub {размер 8 {1}}} } + {{1} больше {R rSub {размер 8 {2}}}} = {{R rSub {размер 8 {1}} + R rSub {размер 8 {2}}} больше {R rSub {размер 8 { 1}} R rSub {размер 8 {2}}}}} {}
,
так что
Rp = R1R2R1 + R2≈R1R2R1 = R2R1 >> R2.выровняйте {стек {размер 12 {R rSub {размер 8 {p}} = {{R rSub {размер 8 {1}} R rSub {размер 8 {2}}} больше {R rSub {размер 8 {1}} + R rSub {размер 8 {2}}}} »{{R rSub {размер 8 {1}} R rSub {размер 8 {2}}} больше {R rSub {размер 8 {1}}}}} {} # = R rSub {размер 8 {2}} слева (R rSub {размер 8 {1}} «>>» R rSub {размер 8 {2}} справа) «.» {}}} {}
Необоснованные результаты
Два резистора, один с сопротивлением 145 Ом, размер 12 {1 «45»% OMEGA} {}
, соединены параллельно для создания общего сопротивления 150 Ом, размер 12 {150% OMEGA} {}
.а) Каково значение второго сопротивления? б) Что неразумного в этом результате? (c) Какие предположения необоснованны или непоследовательны?
Необоснованные результаты
Два резистора, один с сопротивлением 900 кОм, размер 12 {9 «00 к»% OMEGA} {}
, соединены последовательно для создания общего сопротивления 0,500 МОм размером 12 {0 «.» «500 M»% OMEGA} {}
. а) Каково значение второго сопротивления? б) Что неразумного в этом результате? (c) Какие предположения необоснованны или непоследовательны?
(a) -400 кОм размер 12 {+ — «400 кОм»% OMEGA} {}
(b) Сопротивление не может быть отрицательным.
(c) Считается, что последовательное сопротивление меньше, чем у одного из резисторов, но должно быть больше, чем у любого из резисторов.
Глоссарий
серия
последовательность резисторов или других компонентов, включенных в цепь один за другим
резистор
компонент, обеспечивающий сопротивление току, протекающему через электрическую цепь
сопротивление
вызывает потерю электроэнергии в цепи
Закон Ома
взаимосвязь между током, напряжением и сопротивлением в электрической цепи: V = размер IR 12 {V = курсив «IR»} {}
напряжение
электрическая потенциальная энергия на единицу заряда; электрическое давление, создаваемое источником питания, например аккумулятором
падение напряжения
потеря электроэнергии при прохождении тока через резистор, провод или другой компонент
текущий
поток заряда через электрическую цепь мимо заданной точки измерения
Закон Джоуля
взаимосвязь между потенциальной электрической мощностью, напряжением и сопротивлением в электрической цепи, определяемая по формуле: Pe = IV размер 12 {P rSub {size 8 {e}} = ital «IV»} {}
параллельно
разводку резисторов или других компонентов в электрической цепи, так что каждый компонент получает одинаковое напряжение от источника питания; часто изображается на диаграмме в виде лестницы, где каждый компонент находится на ступеньке лестницы

Эта работа находится под лицензией Creative Commons Attribution 4.0 Международная лицензия.
Вы также можете бесплатно скачать по адресу http://cnx.org/contents/[email protected]
Атрибуция:
Параллельные резисторы | Электрические цепи
17,5 Резисторы параллельные (ЭСАФК)
Когда мы добавляем резисторы параллельно цепи:
Имеется больше путей для прохождения тока, что обеспечивает разделение тока по различным путям .
Напряжение на резисторах то же .Напряжение на батарее в цепи равно напряжению на каждом из параллельных резисторов:
\ [{V} _ {\ text {battery}} = {V} _ {1} = {V} _ {2} = {V} _ {3} \ ldots \]
Сопротивление току уменьшается . Общее сопротивление \ ({R} _ {P} \) дается выражением:
\ [\ frac {1} {{R} _ {P}} = \ frac {1} {{R} _ {1}} + \ frac {1} {{R} _ {2}} + \ ldots \ ]
При параллельном подключении резисторов начальная и конечная точки для всех резисторов одинаковы.Эти точки имеют одинаковую потенциальную энергию, поэтому разность потенциалов между ними одинакова, независимо от того, что между ними вставлено. Между двумя точками может быть один, два или несколько резисторов, разность потенциалов не изменится. Вы можете игнорировать любые компоненты, находящиеся между двумя точками в цепи, при вычислении разницы между двумя точками.
Посмотрите на следующие принципиальные схемы. Батарея во всех случаях одна и та же, меняется только добавление резисторов между точками, отмеченными черными точками.Если бы мы измерили разность потенциалов между двумя точками в этих схемах, мы бы получили одинаковый ответ для всех трех случаев.
Давайте посмотрим на два параллельно подключенных резистора более внимательно. Когда вы строите схему, вы используете провода, и вы можете подумать, что измерение напряжения в разных местах на проводах будет иметь значение. Это неправда. Измерение разности потенциалов или напряжения будет отличаться только в том случае, если вы измеряете другой набор компонентов. Все точки на проводах, между которыми нет компонентов схемы, дадут вам одинаковые измерения.
Все три измерения, показанные на рисунке ниже (т. Е. A – B, C – D и E – F), дадут вам одинаковое напряжение. Различные точки измерения слева не имеют компонентов между собой, поэтому нет изменений в потенциальной энергии. То же самое относится и к разным точкам справа. Когда вы измеряете разность потенциалов между точками слева и справа, вы получите одинаковый ответ.
Рабочий пример 7: Напряжения I
Рассмотрим эту принципиальную схему:
Какое напряжение на резисторе в показанной цепи?
Проверьте, что у вас есть и единицы
У нас есть схема с батареей и одним резистором.Нам известно напряжение на батарее. Мы хотим найти это напряжение на резисторе.
\ [{V} _ {\ text {battery}} = \ text {2} \ text {V} \]
Применимые принципы
Мы знаем, что напряжение на батарее должно быть равно общему напряжению на всех других компонентах схемы.
\ [{V} _ {\ text {battery}} = {V} _ {\ text {total}} \]
Есть только один другой компонент схемы — резистор.
\ [{V} _ {\ text {total}} = {V} _ {1} \]
Это означает, что напряжение на батарее такое же, как и на резисторе.
\ begin {align *} {V} _ {\ text {battery}} & = {V} _ {\ text {total}} = {V} _ {1} \\ {V} _ {1} & = \ text {2} \ text {V} \ end {align *}
Рабочий пример 8: Напряжения II
Рассмотрим эту схему:
Какое напряжение на неизвестном резисторе в показанной цепи?
Проверьте, что у вас есть и единицы
У нас есть схема с батареей и двумя резисторами. Нам известно напряжение на батарее и на одном из резисторов.Мы хотим найти это напряжение на резисторе.
\ begin {align *} {V} _ {\ text {battery}} & = \ text {2} \ text {V} \\ {V} _ {B} & = \ text {1} \ text {V} \ end {align *}
Применимые принципы
Мы знаем, что напряжение на батарее должно быть равно общему напряжению на всех других компонентах схемы, которые включены последовательно.
\ [{V} _ {\ text {battery}} = {V} _ {\ text {total}} \]
Общее напряжение в цепи — это сумма напряжений на отдельных резисторах
\ [{V} _ {\ text {total}} = {V} _ {A} + {V} _ {B} \]
Использование зависимости между напряжением на батарее и общим напряжением на резисторах
\ begin {align *} {V} _ {\ text {battery}} & = {V} _ {\ text {total}} \\\\ {V} _ {\ text {battery}} & = {V} _ {1} + {V} _ {\ text {resistor}} \\ \ text {2} \ text {V} & = {V} _ {1} + \ text {1} \ text {V} \\ {V} _ {1} & = \ text {1} \ text {V} \ end {align *}
Рабочий пример 9: Напряжения III
Рассмотрим принципиальную схему:
Какое напряжение на неизвестном резисторе в показанной цепи?
Проверьте, что у вас есть и единицы
У нас есть схема с батареей и тремя резисторами.Нам известно напряжение на батарее и двух резисторах. Мы хотим найти это напряжение на неизвестном резисторе.
\ begin {align *} {V} _ {\ text {battery}} & = \ text {7} \ text {V} \\ {V} _ {\ text {известное}} & = {V} _ {A} + {V} _ {C} \\ & = \ текст {1} \ текст {V} + \ текст {4} \ текст {V} \ end {align *}
Применимые принципы
Мы знаем, что напряжение на батарее должно быть равно общему напряжению на всех других компонентах схемы, которые включены последовательно.
\ [{V} _ {\ text {battery}} = {V} _ {\ text {total}} \]
Общее напряжение в цепи — это сумма напряжений на отдельных резисторах
\ [{V} _ {\ text {total}} = {V} _ {B} + {V} _ {\ text {known}} \]
Использование зависимости между напряжением на батарее и общим напряжением на резисторах
\ begin {align *} {V} _ {\ text {battery}} & = {V} _ {\ text {total}} \\ {V} _ {\ text {battery}} & = {V} _ {B} + {V} _ {\ text {known}} \\ \ text {7} \ text {V} & = {V} _ {B} + \ text {5} \ text {V} \\ {V} _ {B} & = \ text {2} \ text {V} \ end {align *}
Рабочий пример 10: Напряжения IV
Рассмотрим принципиальную схему:
Какое напряжение на параллельной комбинации резисторов в показанной цепи? Подсказка: остальная часть схемы такая же, как и в предыдущей задаче.
Быстрый ответ
Схема такая же, как и в предыдущем примере, и мы знаем, что разница напряжений между двумя точками в цепи не зависит от того, что между ними, поэтому ответ такой же, как указано выше \ ({V} _ {\ text {parallel }} = \ текст {2} \ текст {V} \).
Проверьте, что у вас есть и единицы — длинный ответ
У нас есть схема с батареей и пятью резисторами (два последовательно и три параллельно). Нам известно напряжение на батарее и двух резисторах.Мы хотим найти это напряжение на параллельных резисторах \ ({V} _ {\ text {parallel}} \).
\ begin {align *} {V} _ {\ text {battery}} = \ text {7} \ text {V} \\ {V} _ {\ text {известное}} = \ text {1} \ text {V} + \ text {4} \ text {V} \ end {align *}
Применимые принципы
Мы знаем, что напряжение на батарее должно быть равно общему напряжению на всех других компонентах схемы.
\ [{V} _ {\ text {battery}} = {V} _ {\ text {total}} \]
Напряжения складываются только алгебраически для последовательно соединенных компонентов.Параллельно подключенные резисторы можно рассматривать как единый компонент, который включен последовательно с другими компонентами, а затем можно складывать напряжения.
\ [{V} _ {\ text {total}} = {V} _ {\ text {parallel}} + {V} _ {\ text {известное}} \]
Использование зависимости между напряжением на батарее и общим напряжением на резисторах
\ begin {align *} {V} _ {\ text {battery}} & = {V} _ {\ text {total}} \\ {V} _ {\ text {battery}} & = {V} _ {\ text {parallel}} + {V} _ {\ text {known}} \\ \ text {7} \ text {V} & = {V} _ {\ text {parallel}} + \ text {5} \ text {V} \\ {V} _ {\ text {parallel}} & = \ text {2} \ text {V} \ end {align *}
В отличие от последовательного случая, когда мы добавляем резисторы параллельно, мы создаем еще пути , по которым может течь ток.Делая это, мы уменьшаем полное сопротивление цепи!
Взгляните на диаграмму ниже. Слева у нас та же схема, что и в предыдущем разделе, с батареей и резистором. Амперметр показывает ток \ (\ text {1} \) \ (\ text {A} \). Справа мы добавили второй резистор параллельно первому. Это увеличило количество путей (ответвлений), по которым заряд может проходить через цепь — общее сопротивление уменьшилось. Вы можете видеть, что ток в цепи увеличился.Также обратите внимание, что ток в разных ветвях может быть разным.
Общее сопротивление ряда параллельных резисторов НЕ является суммой отдельных сопротивлений, так как общее сопротивление уменьшается с увеличением количества путей прохождения тока. Общее сопротивление для параллельных резисторов равно:
\ [\ frac {1} {{R} _ {P}} = \ frac {1} {{R} _ {1}} + \ frac {1} {{R} _ {2}} + \ ldots \ ]
Давайте рассмотрим случай, когда у нас есть два резистора параллельно, и выясним, каким будет конечное сопротивление.Эта ситуация показана на диаграмме ниже:
Применяя формулу для общего сопротивления, получаем:
\ begin {align *} \ frac {1} {{R} _ {P}} & = \ frac {1} {{R} _ {1}} + \ frac {1} {{R} _ {2}} + \ ldots \\ & \ text {Резисторов всего два} \\ \ frac {1} {{R} _ {P}} & = \ frac {1} {{R} _ {1}} + \ frac {1} {{R} _ {2}} \\ & \ text {Добавить дроби} \\ \ frac {1} {{R} _ {P}} & = \ frac {1} {{R} _ {1}} \ times \ frac {{R} _ {2}} {{R} _ {2 }} + \ frac {1} {{R} _ {2}} \ times \ frac {{R} _ {1}} {{R} _ {1}} \\ \ frac {1} {{R} _ {P}} & = \ frac {{R} _ {2}} {{R} _ {1} {R} _ {2}} + \ frac {{R} _ {1}} {{R} _ {1} {R} _ {2}} \\ & \ text {Переставить} \\ \ frac {1} {{R} _ {P}} & = \ frac {{R} _ {2} + {R} _ {1}} {{R} _ {1} {R} _ {2} } \\ \ frac {1} {{R} _ {P}} & = \ frac {{R} _ {1} + {R} _ {2}} {{R} _ {1} {R} _ {2} } \\ {R} _ {P} & = \ frac {{R} _ {1} {R} _ {2}} {{R} _ {1} + {R} _ {2}} \ end {выровнять *}
Для любых двух параллельно подключенных резисторов мы теперь знаем, что
\ [{R} _ {P} = \ frac {\ text {произведение сопротивлений}} {\ text {сумма сопротивлений}} = \ frac {{R} _ {1} {R} _ {2}} { {R} _ {1} + {R} _ {2}} \]
Делители тока
Цель
Проверьте, что происходит с током и напряжением в последовательных цепях при добавлении дополнительных резисторов.
Аппарат
Аккумулятор
Вольтметр
Амперметр
Провода
Резисторы
Метод
Подключите каждую цепь, показанную ниже
Измерьте напряжение на каждом резисторе в цепи.
Измерьте ток до и после каждого резистора в цепи, а также до и после параллельных ветвей.
Результаты и выводы
Сравните токи через отдельные резисторы друг с другом.
Сравните сумму токов через отдельные резисторы с током до параллельных ветвей.
Сравните различные измерения напряжения на параллельных резисторах.
Рабочий пример 11: Параллельные резисторы I
А цепь содержит два параллельно включенных резистора. Резисторы имеют значения сопротивления \ (\ text {15} \) \ (\ text {Ω} \) и \ (\ text {7} \) \ (\ text {Ω} \).
Какое полное сопротивление в цепи?
Проанализировать вопрос
Нам говорят, что резисторы в цепи включены в параллельную цепь и что нам нужно рассчитать общее сопротивление.Значения двух резисторов указаны в правильных единицах, Ом.
Применять соответствующие принципы
Было показано, что полное сопротивление резисторов, включенных параллельно, является произведением сопротивлений, разделенных на сумму. Мы можем использовать
\ [{R} _ {P} = \ frac {{R} _ {1} {R} _ {2}} {{R} _ {1} + {R} _ {2}} \]
У нас всего два резистора, и теперь мы резисторы. В данном случае это:
\ begin {align *} {R} _ {P} & = \ frac {{R} _ {1} {R} _ {2}} {{R} _ {1} + {R} _ {2}} \\ & = \ frac {\ left (\ text {15} \ text {Ω} \ right) \ left (\ text {7} \ text {Ω} \ right)} {\ text {15} \ text {Ω} + \ text {7} \ text {Ω}} \\ & = \ frac {105 {\ Omega} ^ {2}} {\ text {22} \ text {Ω}} \\ & = \ текст {4,77} \ текст {Ω} \ end {align *}
Цитировать окончательный результат
Общее сопротивление параллельно включенных резисторов \ (\ text {4,77} \) \ (\ text {Ω} \)
Рабочий пример 12: Параллельные резисторы II
Мы добавляем третий параллельный резистор в конфигурацию (настройку) в предыдущем примере.Дополнительный резистор имеет сопротивление \ (\ text {3} \) \ (\ text {Ω} \).
Какое полное сопротивление в цепи?
Проанализировать вопрос
Нам говорят, что резисторы в цепи включены в параллельную цепь и что нам нужно рассчитать общее сопротивление. Значение дополнительного резистора указано в правильных единицах, Ом.
Применять соответствующие принципы
Общее сопротивление резисторов, включенных параллельно, было задано как
. \ [\ frac {1} {{R} _ {P}} = \ frac {1} {{R} _ {1}} + \ frac {1} {{R} _ {2}} + \ ldots \ ]
У нас есть три резистора, и теперь мы резисторы.В данном случае это:
\ begin {align *} \ frac {1} {{R} _ {P}} & = \ frac {1} {{R} _ {1}} + \ frac {1} {{R} _ {2}} + \ ldots \\ & \ text {есть три резистора} \\ \ frac {1} {{R} _ {P}} & = \ frac {1} {{R} _ {1}} + \ frac {1} {{R} _ {2}} + \ frac {1 } {{R} _ {3}} \\ & \ text {добавить дроби} \\ \ frac {1} {{R} _ {P}} & = \ frac {1} {{R} _ {1}} \ times \ frac {{R} _ {2} {R} _ {3}} {{R} _ {2} {R} _ {3}} + \ frac {1} {{R} _ {2}} \ times \ frac {{R} _ {1} {R} _ {3} } {{R} _ {1} {R} _ {3}} + \ frac {1} {{R} _ {3}} \ times \ frac {{R} _ {1} {R} _ {2 }} {{R} _ {1} {R} _ {2}} \\ \ frac {1} {{R} _ {P}} & = \ frac {{R} _ {2} {R} _ {3}} {{R} _ {1} {R} _ {2} { R} _ {3}} + \ frac {{R} _ {1} {R} _ {3}} {{R} _ {1} {R} _ {2} {R} _ {3}} + \ frac {{R} _ {1} {R} _ {2}} {{R} _ {1} {R} _ {2} {R} _ {3}} \\ & \ text {переставить} \\ \ frac {1} {{R} _ {P}} & = \ frac {{R} _ {2} {R} _ {3} + {R} _ {1} {R} _ {3} + { R} _ {2} {R} _ {3}} {{R} _ {1} {R} _ {2} {R} _ {3}} \\ {R} _ {P} & = \ frac {{R} _ {1} {R} _ {2} {R} _ {3}} {{R} _ {2} {R} _ {3} + {R} _ {1} {R} _ {3} + {R} _ {2} {R} _ {3}} \\ {R} _ {P} & = \ frac {\ left (\ text {15} \ text {Ω} \ right) \ left (\ text {7} \ text {Ω} \ right) \ left (\ text { 3} \ text {Ω} \ right)} {\ left (\ text {7} \ text {Ω} \ right) \ left (\ text {3} \ text {Ω} \ right) + \ left (\ text {15} \ text {Ω} \ right) \ left (\ text {3} \ text {Ω} \ right) + \ left (\ text {7} \ text {Ω} \ right) \ left (\ text { 15} \ text {Ω} \ right)} \\ {R} _ {P} & = \ frac {315 {\ Omega} ^ {3}} {21 {\ Omega} ^ {2} + 45 {\ Omega} ^ {2} + 105 {\ Omega} ^ { 2}} \\ {R} _ {P} & = \ frac {315 {\ Omega} ^ {3}} {171 {\ Omega} ^ {2}} \\ {R} _ {P} & = \ text {1,84} \ text {Ω} \ end {align *}
Цитировать окончательный результат
Полное сопротивление параллельно включенных резисторов \ (\ text {1,84} \) \ (\ text {Ω} \)
При расчете сопротивления для сложных конфигураций резисторов вы можете начать с любой комбинации двух резисторов (последовательно или параллельно) и рассчитать их общее сопротивление.Затем вы можете заменить их одним резистором с рассчитанным вами общим сопротивлением. Теперь используйте этот новый резистор в сочетании с любым другим резистором и повторяйте процесс, пока не останется только один резистор. В приведенном выше примере мы могли бы просто использовать ответ из первого примера параллельно с новым резистором, и мы получили бы тот же ответ.
Рабочий пример 13: Параллельные резисторы III
Мы добавляем третий параллельный резистор к первой конфигурации (настройке), работающей параллельно.Дополнительный резистор имеет сопротивление \ (\ text {3} \) \ (\ text {Ω} \)
Какое полное сопротивление в цепи?
Проанализировать вопрос
Нам говорят, что резисторы в цепи включены в параллельную цепь и что нам нужно рассчитать общее сопротивление. Значение дополнительного резистора указано в правильных единицах, Ом.
Применять соответствующие принципы
Мы можем поменять местами резисторы, не меняя схему:
Мы уже рассчитали, что полное сопротивление двух резисторов в пунктирной рамке равно \ (\ text {4,77} \) \ (\ text {Ω} \). {2}} {\ text {11,77} \ Omega} \\ & = \ текст {1,84} \ текст {Ω} \ end {align *}
Цитировать окончательный результат
Общее сопротивление параллельно включенных резисторов составляет \ (\ text {1,84} \) \ (\ text {Ω} \).Это тот же результат, что и при одновременном сложении всех трех резисторов.
Высокие оценки в науке — залог вашего успеха и будущих планов. Проверьте себя и узнайте больше о практике Сиявулы.
Зарегистрируйтесь и проверьте себя
Resistance
Exercise 17.1
Как называется единица сопротивления и каков ее символ?
Решение пока недоступно
Объясните, что происходит с общим сопротивлением цепи, когда резисторы добавляются последовательно?
Решение пока недоступно
Объясните, что происходит с общим сопротивлением цепи, когда резисторы добавляются параллельно?
Решение пока недоступно
Почему батарейки разряжаются?
Решение пока недоступно
21.1 Последовательные и параллельные резисторы — Главы физики колледжа 1-17
На рисунке 3 показаны резисторы параллельно , подключенные к источнику напряжения. Резисторы включены параллельно, когда каждый резистор подключен непосредственно к источнику напряжения с помощью соединительных проводов с незначительным сопротивлением. Таким образом, к каждому резистору приложено полное напряжение источника.
Каждый резистор потребляет такой же ток, как если бы он один был подключен к источнику напряжения (при условии, что источник напряжения не перегружен).Например, автомобильные фары, радио и т. Д. Подключены параллельно, так что они используют полное напряжение источника и могут работать полностью независимо. То же самое и в вашем доме, или в любом другом здании. (См. Рис. 3 (b).)
Чтобы найти выражение для эквивалентного параллельного сопротивления [латекс] \ boldsymbol {R _ {\ textbf {p}}} [/ latex], давайте рассмотрим протекающие токи и их связаны с сопротивлением. Поскольку каждый резистор в цепи имеет полное напряжение, токи, протекающие через отдельные резисторы, составляют [латекс] \ boldsymbol {I_1 = \ frac {V} {R_1}} [/ latex], [латекс] \ boldsymbol {I_2 = \ frac {V} {R_2}} [/ latex] и [latex] \ boldsymbol {I_3 = \ frac {V} {R_3}} [/ latex].Сохранение заряда подразумевает, что общий ток [латекс] \ boldsymbol {I} [/ latex], производимый источником, является суммой этих токов:
[латекс] \ boldsymbol {I =} [/ латекс] [латекс] \ boldsymbol {\ frac {V} {R_1}} [/ latex] [латекс] \ boldsymbol {+} [/ latex] [латекс] \ boldsymbol {\ frac {V} {R_2}} [/ latex] [латекс] \ boldsymbol {+} [/ latex] [латекс] \ boldsymbol {\ frac {V} {R_3}} [/ latex] [латекс] \ boldsymbol {= V} [/ latex] [латекс] \ boldsymbol {(\ frac { 1} {R_1}} [/ latex] [латекс] \ boldsymbol {+} [/ latex] [латекс] \ boldsymbol {\ frac {1} {R_2}} [/ latex] [латекс] \ boldsymbol {+} [ / latex] [латекс] \ boldsymbol {\ frac {1} {R_3})}.[/ latex]
[латекс] \ boldsymbol {I =} [/ latex] [латекс] \ boldsymbol {\ frac {V} {R_p}} [/ latex] [латекс] \ boldsymbol {= V} [/ латекс ] [latex] \ boldsymbol {(\ frac {1} {R_p})}. [/ latex]
Члены в скобках в последних двух уравнениях должны быть равны. Обобщая для любого количества резисторов, общее сопротивление [латекс] \ boldsymbol {R_p} [/ latex] параллельного соединения связано с отдельными сопротивлениями соотношением
[латекс] \ boldsymbol {\ frac {1} {R_p}} [/ latex] [латекс] \ boldsymbol {=} [/ latex] [латекс] \ boldsymbol {\ frac {1} {R_1}} [/ latex] [латекс] \ boldsymbol {+} [/ latex] [латекс] \ boldsymbol {\ frac {1} {R_2}} [/ latex] [латекс] \ boldsymbol {+} [/ latex] [латекс] \ boldsymbol {\ frac {1} {R_3}} [/ latex] [латекс] \ boldsymbol {+ \ cdots} [/ latex]
Это соотношение приводит к общему сопротивлению [латекс] \ boldsymbol {R_p} [/ latex], которое меньше наименьшего из отдельных сопротивлений.(Это видно в следующем примере.) При параллельном подключении резисторов от источника течет больше тока, чем протекает по любому из них по отдельности, поэтому общее сопротивление ниже.
Пример 2: Расчет сопротивления, тока, рассеиваемой мощности и выходной мощности: анализ параллельной цепи
Пусть выходное напряжение батареи и сопротивления в параллельном соединении на Рисунке 3 будут такими же, как и в ранее рассмотренном последовательном соединении: [latex] \ boldsymbol {V = 12.0 \; \ textbf {V}} [/ latex], [latex] \ boldsymbol {R_1 = 1.00 \; \ Omega} [/ latex], [latex] \ boldsymbol {R_2 = 6.00 \; \ Omega} [/ латекс ] и [латекс] \ boldsymbol {R_3 = 13.0 \; \ Omega} [/ latex]. а) Каково полное сопротивление? (б) Найдите полный ток. (c) Рассчитайте токи в каждом резисторе и покажите, как они складываются, чтобы равняться общему выходному току источника. (d) Рассчитайте мощность, рассеиваемую каждым резистором. (e) Найдите выходную мощность источника и покажите, что она равна общей мощности, рассеиваемой резисторами.
Стратегия и решение для (а)
Общее сопротивление для параллельной комбинации резисторов находится с помощью следующего уравнения. Ввод известных значений дает
[латекс] \ boldsymbol {\ frac {1} {R_p}} [/ latex] [латекс] \ boldsymbol {=} [/ latex] [латекс] \ boldsymbol {\ frac {1} {R_1}} [/ латекс ] [латекс] \ boldsymbol {+} [/ латекс] [латекс] \ boldsymbol {\ frac {1} {R_2}} [/ latex] [латекс] \ boldsymbol {+} [/ латекс] [латекс] \ boldsymbol { \ frac {1} {R_3}} [/ latex] [latex] \ boldsymbol {=} [/ latex] [latex] \ boldsymbol {\ frac {1} {1.00 \; \ Omega}} [/ latex] [латекс] \ boldsymbol {+} [/ latex] [latex] \ boldsymbol {\ frac {1} {6.00 \; \ Omega}} [/ latex] [латекс] \ boldsymbol {+} [/ latex] [латекс] \ boldsymbol {\ frac {1} {13.0 \; \ Omega}}. [/ latex]
Таким образом,
[латекс] \ boldsymbol {\ frac {1} {R_p}} [/ latex] [латекс] \ boldsymbol {=} [/ латекс] [латекс] \ boldsymbol {\ frac {1.00} {\ Omega}} [/ латекс] [латекс] \ boldsymbol {+} [/ латекс] [латекс] \ boldsymbol {\ frac {0.1667} {\ Omega}} [/ латекс] [латекс] \ boldsymbol {+} [/ латекс] [латекс] \ boldsymbol {\ frac {0.07692} {\ Omega}} [/ latex] [латекс] \ boldsymbol {=} [/ latex] [латекс] \ boldsymbol {\ frac {1.2436} {\ Omega}} [/ латекс]
(Обратите внимание, что в этих расчетах каждый промежуточный ответ отображается с дополнительной цифрой.)
Мы должны инвертировать это, чтобы найти полное сопротивление [латекс] \ boldsymbol {R_p} [/ latex]. Это дает
[латекс] \ boldsymbol {R_p =} [/ latex] [латекс] \ boldsymbol {\ frac {1} {1.2436}} [/ latex] [латекс] \ boldsymbol {\ Omega = 0.8041 \; \ Omega}. [ / латекс]
Общее сопротивление с правильным количеством значащих цифр составляет [латекс] \ boldsymbol {R_p = 0.804 \; \ Omega} [/ latex]
Обсуждение для (а)
[латекс] \ boldsymbol {R_p} [/ latex], как и предполагалось, меньше наименьшего индивидуального сопротивления.
Стратегия и решение для (b)
Полный ток можно найти из закона Ома, заменив полное сопротивление [латекс] \ boldsymbol {R_p} [/ latex]. Это дает
[латекс] \ boldsymbol {I =} [/ latex] [латекс] \ boldsymbol {\ frac {V} {R_p}} [/ latex] [латекс] \ boldsymbol {=} [/ latex] [латекс] \ boldsymbol {\ frac {12.0 \; \ textbf {V}} {0.8041 \; \ Omega}} [/ latex] [latex] \ boldsymbol {= 14.92 \; \ textbf {A}} [/ latex]
Обсуждение для (б)
Ток [latex] \ boldsymbol {I} [/ latex] для каждого устройства намного больше, чем для тех же устройств, подключенных последовательно (см. Предыдущий пример).Схема с параллельным соединением имеет меньшее общее сопротивление, чем резисторы, включенные последовательно.
Стратегия и решение для (c)
Отдельные токи легко вычислить по закону Ома, поскольку каждый резистор получает полное напряжение. Таким образом,
[латекс] \ boldsymbol {I_1 =} [/ latex] [латекс] \ boldsymbol {\ frac {V} {R_1}} [/ latex] [латекс] \ boldsymbol {=} [/ latex] [латекс] \ boldsymbol {\ frac {12.0 \; \ textbf {V}} {1.00 \; \ Omega}} [/ latex] [latex] \ boldsymbol {= 12.0 \; \ textbf {A}}. [/ Latex]
Аналогично
[латекс] \ boldsymbol {I_2 =} [/ latex] [латекс] \ boldsymbol {\ frac {V} {R_2}} [/ latex] [латекс] \ boldsymbol {=} [/ latex] [латекс] \ boldsymbol {\ frac {12.0 \; \ textbf {V}} {6.00 \; \ Omega}} [/ latex] [latex] \ boldsymbol {= 2.00 \; \ textbf {A}} [/ latex]
и
[латекс] \ boldsymbol {I_3 =} [/ latex] [латекс] \ boldsymbol {\ frac {V} {R_3}} [/ latex] [латекс] \ boldsymbol {=} [/ latex] [латекс] \ boldsymbol {\ frac {12.0 \; \ textbf {V}} {13.0 \; \ Omega}} [/ latex] [latex] \ boldsymbol {= 0.92 \; \ textbf {A}}. [/ Latex]
Обсуждение для (c)
Общий ток складывается из отдельных токов:
[латекс] \ boldsymbol {I_1 + I_2 + I_3 = 14.92 \; \ textbf {A}}. [/ Latex]
Это соответствует сохранению заряда.
Стратегия и решение для (d)
Мощность, рассеиваемую каждым резистором, можно найти с помощью любого из уравнений, связывающих мощность с током, напряжением и сопротивлением, поскольку все три известны.2} {13.0 \; \ Omega}} [/ latex] [latex] \ boldsymbol {= 11.1 \; \ textbf {W}}. [/ Latex]
Обсуждение для (д)
Мощность, рассеиваемая каждым резистором при параллельном подключении, значительно выше, чем при последовательном подключении к тому же источнику напряжения.
Стратегия и решение для (e)
Общую мощность также можно рассчитать несколькими способами. Выбирая [латекс] \ boldsymbol {P = IV} [/ latex] и вводя общий ток, получаем
[латекс] \ boldsymbol {P = IV = (14.92 \; \ textbf {A}) (12.0 \; \ textbf {V}) = 179 \; \ textbf {W}}. [/ Latex]
Обсуждение для (e)
Общая мощность, рассеиваемая резисторами, также составляет 179 Вт:
[латекс] \ boldsymbol {P_1 + P_2 + P_3 = 144 \; \ textbf {W} + 24.0 \; \ textbf {W} + 11.1 \; \ textbf {W} = 179 \; \ textbf {W}}. [/ латекс]
Это соответствует закону сохранения энергии.
Общее обсуждение
Обратите внимание, что как токи, так и мощность при параллельном подключении больше, чем для тех же устройств, подключенных последовательно.
Цепь параллельных резисторов
и простая схема делителя тока
Формула для параллельного резистора будет нашим основным фокусом здесь. После обсуждения последовательного резистора и делителя напряжения давайте узнаем о параллельных резисторах и делении тока. Параллельный резистор относится к одному из пассивных элементов.
Вы узнаете, включены ли резисторы параллельно или последовательно, просто по их клеммному соединению. Мы называем резисторы подключенными параллельно, если их выводы соединены вместе, соответственно, от резистора к резистору.
Определение параллельной цепи
Этот параллельный резистор отличается от последовательного резистора, у которого есть только один прямой путь, проходящий через резисторы. В параллельном резисторе будет много путей от головы к голове и от хвоста к хвосту. Исходя из этого термина, параллельный резистор используется как делитель тока, а последовательный резистор — как делитель напряжения.
Поскольку ток разделен на несколько путей или ответвлений, ток для каждой ветви может отличаться друг от друга.Но падение напряжения на каждом резисторе будет одинаковым. Отсюда следует, что для резисторов, включенных параллельно, они могут иметь разный ток через каждый из них, но всегда иметь одинаковое падение напряжения на каждом из них.
Зачем нам нужно изучать формулу для параллельного резистора? Вы должны знать, прочитав этот пост, пока не закончите.
Определение параллельных резисторов — это резистивная цепь, в которой резисторы подключены вместе к одним и тем же узлам и образуют более одного пути тока, подключенного к одному источнику напряжения.Если вы все еще не понимаете, как мы делаем параллельную резистивную схему, мы можем найти ее ниже.
Схема параллельной цепи
Пример ниже представляет собой простой параллельный резистор в цепи. Мы используем три резистора R ₁, R ₂ и R ₃. Из объяснения выше, падение напряжения на резисторах при параллельном подключении будет одинаковым для друг друга и равным источнику напряжения.
Следовательно,
Все три резистора соединены между собой между A и B.
В отличие от последовательных резистивных цепей, где эквивалентное сопротивление является суммой всех резисторов, параллельный резистор рассчитывается по-другому. Мы используем величину, обратную сопротивлению (1 / R) для каждого сложенного резистора.
Формула для параллельного резистора
Как мы уже упоминали выше, эквивалентное сопротивление параллельных резисторов является суммой, обратной величине каждого резистора. Если резисторы, соединенные параллельно, имеют одинаковое значение, это будет очень просто.
Как мы уже упоминали выше, мы можем посмотреть на пример ниже:
Если два резистора, подключенных параллельно, имеют одинаковое сопротивление, то эквивалентное сопротивление, R _T — это половина сопротивления одного резистора. резистор. Следовательно, эквивалентное сопротивление двух резисторов, соединенных параллельно, если они имеют одинаковое сопротивление, равно R / 2. Если параллельно подключено три резистора, эквивалентное сопротивление равно R / 3 и так далее.

Помимо последовательных резисторов, этот тип цепи является наиболее распространенным типом электрических цепей.Для анализа схемы параллельного резистора мы можем использовать тот же метод для последовательного резистора, используя законы Кирхгофа и закон Ома.

Рассмотрим схему на рисунке. (1),
Рисунок 1. Параллельное подключение резистора
, где два резистора подключены параллельно и, следовательно, имеют одинаковое напряжение на них.
Из закона Ома
(1)

Применение KCL в узле a дает общий ток i как
(2)

Подстановка уравнения.(1) в (2), имеем
(3)
, где R _eq — эквивалентное сопротивление резисторов, включенных параллельно:
(4)
или
(5)
Следовательно ,
Эквивалентное сопротивление двух параллельных резисторов равно произведению их сопротивлений на их сумму.
Выше приведено простейшее уравнение параллельного резистора, которое мы можем использовать каждый раз, когда оно нам нужно.
Следует отметить, что уравнение.(5) работает только для двух параллельно подключенных резисторов.
Мы можем расширить уравнение параллельного резистора в уравнении (4) до общего случая схемы с N резисторами, включенными параллельно. Эквивалентное сопротивление составляет
(6)
Обратите внимание, что R _eq всегда меньше, чем сопротивление наименьшего резистора в параллельном соединении. Если R ₁ = R ₂ =… = R _N = R , то
(7)
Например, если 4 резистора с сопротивлением 100 Ом подключены параллельно, их эквивалентное сопротивление составляет 25 Ом.
Имейте в виду, что
Эквивалентное сопротивление параллельных резисторов всегда меньше, чем сопротивление наименьшего резистора, подключенного к этой сети. Следовательно, эквивалентное сопротивление RT будет уменьшаться каждый раз, когда у нас есть дополнительные параллельные резисторы.
Формула проводимости для параллельной цепи
Из-за этого простого, но сложного уравнения параллельного резистора для эквивалентного сопротивления мы узнаем о новом значении, известном как проводимость (G), измеренном в Сименсах (S).Проводимость обратно пропорциональна сопротивлению, где G = 1 / R. После того, как мы получим проводимость, мы преобразуем ее обратно обратно, чтобы получить эквивалентное сопротивление R _T параллельных резисторов.
При параллельном подключении резисторов легче использовать проводимость, чем сопротивление.

Из уравнения (6) эквивалентная проводимость для резисторов N составляет
(8)
, где:
Уравнение.(8) указывает:
Эквивалентная проводимость резисторов, соединенных параллельно, является суммой их индивидуальных проводимостей.
Это означает, что мы можем перерисовать рисунок (1) на (2), где мы заменим сопротивления на проводимости.

Эквивалентные сопротивления параллельных резисторов получаются таким же образом, как эквивалентные сопротивления последовательных резисторов.
Напротив, эквивалентные проводимости последовательных резисторов получаются таким же образом, как эквивалентные сопротивления параллельных резисторов.
Рисунок 2. Эквивалентное сопротивление или проводимость
Следовательно, эквивалентная проводимость G _eq последовательно соединенных резисторов N составляет
(9)
Учитывая полный ток i, входящий в узел a на рисунке. (1) с одинаковые значения напряжения, получаем
(10)
Мы определяем параллельные резисторы как резисторы, соединенные между собой между двумя одинаковыми точками. Сам параллельный резистор имеет различные схемы.
Как найти ток в параллельной цепи
Поскольку ток в параллельной цепи зависит от ее сопротивления, теперь мы узнаем, как найти ток в параллельной цепи.Токи I ₁, I ₂,…, I _n , входящие в параллельный путь резисторов, зависят от сопротивления этой ветви. Общий ток I _T представляет собой сумму токов в параллельных ветвях. Если сопротивление между ветвями равно, то токи также будут разделены поровну.
Если R ₁ = R ₂, то I ₁ = I ₂ = 0.5 Я _Т . Это означает, что общий ток I _T делится поровну на две ветви. Если R ₁ имеет другое сопротивление, чем R ₂, тогда нам нужно рассчитать I ₁ и I ₂ по-разному. Даже если напряжения на ветвях равны, ток может отличаться по закону Ома.
Для примера параллельной схемы давайте посмотрим на схему ниже и попытаемся найти все токи,
Так как R ₁ и R ₂ имеют разные значения, тогда токи I ₁ и I ₂ гарантированно имеют разные значения.Помните один из законов Кирхгофа?

Текущие законы Кирхгофа гласят:
Общий ток, выходящий из узла, равен току, входящему в тот же самый узел.
Следовательно,
Полный ток в цепи может быть выражен как:
После этого мы будем использовать закон Ома для расчета тока, поступающего в каждую ветвь через резисторы. I ₁ — это текущий ввод R ₁, а I ₂ — текущий ввод R ₂.Источник напряжения В _с имеет 12 В, и мы получаем:
И получаем полный ток,
Чтобы прояснить это, мы используем закон Ома для вычисления I _T из В _s и R _T .
Общее сопротивление R _T составляет
Тогда полный ток I _T равен
Следовательно, это проясняет наши расчеты.
Мы заключаем, что
Уравнение делителя тока
Комбинируя уравнения. (1) и (10) мы получаем уравнение текущего делителя.
(11)
, который показывает, что полный ток i распределяется между резисторами обратно пропорционально их сопротивлениям.
Это известно как принцип деления тока , а схема на рисунке (1) известна как делитель тока .
Обратите внимание, что больший ток проходит через меньшее сопротивление.
Рисунок 3. Короткое замыкание и разрыв в параллельном соединении
Предположим, что один из резисторов на рисунке (1) равен нулю, скажем, R ₂ = 0; поэтому R ₂ — это короткое замыкание, как видно на рисунке. (3a).
Из уравнения (11) R ₂ = 0 означает, что i ₁ = 0, i ₂ = i . Это означает, что весь ток i обходит R ₁ и протекает через короткое замыкание R ₂ = 0, путь с наименьшим сопротивлением.
При коротком замыкании цепи, как показано на рисунке (3a), обратите внимание, что:
Эквивалентное сопротивление R _экв = 0
Весь ток протекает через короткое замыкание.
Для другого крайнего примера, где R ₂ = ∞, то есть R ₂ — это разомкнутая цепь, как видно на рисунке. (3b).
Ток по-прежнему течет по пути с наименьшим сопротивлением, R ₁.
Уравнение (11) преобразуется в
(12)
В общем, если у делителя тока есть N проводников, параллельно с током источника i , N -й проводник будет иметь ток
(13)
Очень удобно комбинировать резисторы последовательно и параллельно в одно эквивалентное сопротивление R _eq .
Такое эквивалентное сопротивление должно иметь те же значения тока и напряжения, что и исходная сеть на выводе.
Примеры параллельного резистора
Давайте рассмотрим приведенный ниже пример для лучшего понимания
Найдите R _экв для схемы на рисунке. (4)
Рисунок 4. Пример параллельного резистора
6 Ом и 3 Ом в параллельно
1 Ом и 5 Ом последовательно
2 Ом и 2 Ом последовательно
6 Ом и 4 Ом параллельно
Три резистора последовательно
Резисторы в Схемы — Практика — Физика Гипертекст
Давайте начнем процесс с объединения резисторов.В этой схеме четыре последовательных пары.
осталось
R _с = 3 Ом + 1 Ом
R _с = 4 Ом
R _с = 4 Ом + 2 Ом
R _с = 6 Ом
справа
R _с = 2 Ом + 3 Ом
R _с = 5 Ом
R _с = 1 Ом + 4 Ом
R _с = 5 Ом
Эти пары образуют две параллельные цепи, одну слева и одну справа.
осталось
1 = 1 + 1
R _p 4 Ом 6 Ом
R _p = 12 Ом = 2.4 Ом
5
справа
1 = 1 + 1
R _p 5 Ом 5 Ом
R _p = 5 Ом = 2.5 Ом
2
Каждый набор из четырех резисторов включен последовательно с другим.
осталось
R _с = 2,4 Ом + 0,6 Ом
R _с = 3 Ом
справа
R _с = 2,5 Ом + 0,5 Ом
R _с = 3 Ом
Левая и правая половины цепи параллельны друг другу и батарее.
1 = 1 + 1 = 2
R _p 3 Ом 3 Ом 3 Ом
R _p = 3 Ом = 1.5 Ом
2
Теперь, когда у нас есть эффективное сопротивление всей цепи, давайте определим ток от источника питания, используя закон Ома.
I _всего = V _всего + 24 В = 16 А
R _Всего 1.5 Ом
Теперь пройдите по трассе (конечно, не буквально). На каждом соединении ток будет делиться: больше по пути с меньшим сопротивлением и меньше по пути с большим сопротивлением. Поскольку заряд не протекает нигде в полной цепи, ток будет одинаковым для всех элементов, последовательно соединенных друг с другом.
Левая и правая половины схемы идентичны по общему сопротивлению, что означает, что ток будет равномерно делиться между ними.

8 A для резистора 0,6 Ом
на слева .

8 A для резистора 0,5 Ом
на правой стороне .
С каждой стороны ток снова делится на две параллельные ветви.
Ветви на слева имеют сопротивления в соотношении…
R _{1 и 3} = 4 Ом + 2
R _{2 и 4} 6 Ом 3

что означает, что токи разделятся в соотношении…
для резисторов 1 Ом и 3 Ом
на слева .
для резисторов 2 Ом и 4 Ом
на слева .
Ветви на правом идентичны, поэтому ток разделяется на две равные половины.
☟
☟
☟
☟
☟
для резисторов 2 Ом и 3 Ом
на правой стороне .
для резисторов 1 Ом и 4 Ом
на правой стороне .
резисторов, включенных последовательно и параллельно | Комбинации резисторов
Результаты обучения
Рассчитайте общее сопротивление различных комбинаций резисторов, т. Е. Последовательных, параллельных и последовательно-параллельных.
Покажите, как резисторы используются в качестве делителей напряжения и тока.
Рассчитайте сопротивление и значение мощности для последовательного резистора, понижающего напряжение.
Отдельные резисторы могут быть соединены вместе последовательно, параллельно или в комбинации последовательно и параллельно. Это приводит к более сложной схеме, полное сопротивление которой представляет собой комбинацию отдельных резисторов.
Комбинация резисторов серии

Для подключения резисторов серии , они соединяются встык вместе в одну линию, как показано, если Рисунок 1 .Характеристики последовательно соединенных резисторов можно резюмировать следующим образом:
Общее сопротивление цепи ( R _T ) увеличивается, если дополнительные резисторы соединены последовательно, и уменьшается, если резисторы удалены.
Чтобы определить общее сопротивление цепи, просто найдите сумму отдельных сопротивлений нагрузок.
В этом примере, если резисторы имеют маркировку R ₁, R ₂ и R ₃, то общее сопротивление R _T рассчитывается по формуле
Рисунок 1 Резисторы, подключенные последовательно.
ПРИМЕР 1
Проблема: Три резистора, R ₁ (4 Ом), R ₂ (50 Ом) и R ₃ (75 Ом) подключены последовательно, как показано на Рисунок 2 . Определите значение общего сопротивления комбинированной цепи.
Рисунок 2 Схема для примера 1.
Решение:
Резисторы, соединенные последовательно, используются как делители напряжения , , как показано на схеме , Рисунок 3 .Делители напряжения широко используются в цепях, где один источник напряжения должен обеспечивать несколько разных значений напряжения для разных частей цепи.
Характеристики схемы последовательного делителя напряжения можно резюмировать следующим образом:
Через каждый резистор проходит одинаковый ток.
Входное напряжение делится пропорционально между последовательно соединенными резисторами.
Падение напряжения на резисторе в последовательной цепи прямо пропорционально сопротивлению резистора.
Чем выше значение сопротивления, тем больше падение напряжения.
Рисунок 3 Схема делителя напряжения.
Для схемы делителя напряжения падение напряжения на каждом резисторе обычно является фактором, который необходимо определить. Падение напряжения на любом резисторе пропорционально отношению его сопротивления к общему сопротивлению цепи.
Формула для делителя напряжения позволяет рассчитать падение напряжения на любом из последовательно соединенных резисторов без необходимости сначала рассчитывать значение тока цепи.Заявлено в виде формулы:
ПРИМЕР 2
Резисторы R ₁ (5 кОм), R ₂ (3 кОм) и R ₃ (2 кОм) ) соединены последовательно, образуя делитель напряжения, как показано на рис. 4 . Если на схему подается входное напряжение 9 вольт, рассчитайте значение падения напряжения на каждом из резисторов, используя формулу делителя напряжения.
Рисунок 4 Цепь для примера 2.
Решение:
ПРИМЕР 3
У вас есть источник на 120 В и вы хотите использовать последовательно понижающий резистор в сочетании с контрольной лампой 6 В при 150 мА для индикации подачи питания ( Рисунок 5 ). Определите значение сопротивления падения серии и требуемую мощность.
Рисунок 5 Схема для примера 3.
Решение:
Параллельная комбинация резисторов
Резисторы соединены параллельно путем соединения бок о бок как показано на рис. 6 .Обратите внимание, что два конца резисторов подключены к одним и тем же двум точкам.
Характеристики параллельно включенных резисторов можно резюмировать следующим образом:
Общее сопротивление (R _T) сформированной цепи на меньше, чем на , чем сопротивление самого низкого значения сопротивления, присутствующего в любой из ветвей.
Каждый резистор обеспечивает отдельный параллельный путь для прохождения тока.
Если у вас есть несколько резисторов одинакового номинала, подключенных параллельно, то общее сопротивление легче всего найти, разделив общее значение сопротивления на количество подключенных резисторов.Для трех резисторов по 150 Ом, включенных параллельно, общее сопротивление составляет
Рисунок 6 Резисторы , подключенные параллельно.
Чтобы найти полное сопротивление двух неравных значений резисторов, соединенных параллельно (очень распространенное использование), используется формула произведения на сумму. Эта формула:
ПРИМЕР 4
Проблема: Резистор 60 Ом подключен параллельно с резистором 40 Ом, как показано на Рисунок 7 .Определите значение общего комбинированного сопротивления двух компонентов, используя формулу «произведение на сумму».
Рисунок 7 Схема для примера 4.
Решение:
Формула произведения на сумму лучше всего работает для двух резисторов, включенных параллельно. Если параллельно подключено более двух резисторов, использование становится труднее и менее практичным. Для более чем двух резисторов разных номиналов, соединенных параллельно, используется общая формула для полного сопротивления параллельной цепи.Эта формула:
ПРИМЕР 5
Проблема: Три резистора, R ₁ (120 Ом), R ₂ (60 Ом) и R ₃ ( 40 Ом) подключены параллельно, как показано на рис. 8 . Определите значение общего сопротивления комбинированной цепи.
Рисунок 8 Схема для примера 5.
Решение:
Параллельные резистивные цепи можно рассматривать как делители тока , потому что ток делится или делится между различными резисторами, как показано на рисунке 9 .
Характеристики схемы параллельного делителя тока можно резюмировать следующим образом:
Ток, протекающий через каждый резистор ответвления, обратно пропорционален его значению сопротивления.
Чем меньше значение сопротивления, тем больше ток, и наоборот.
Резисторы с одинаковым сопротивлением пропускают через них одинаковое количество тока.
Формула, описывающая делитель тока, аналогична формуле для делителя напряжения и может быть выражена следующим образом:
Рисунок 9 Схема делителя тока.
ПРИМЕР 6
Проблема: Резисторы R ₁ R ₂ и R ₃ (2 Ом, 3 Ом и 6 Ом соответственно) подключены параллельно, как показано на Рисунок 10 . Используйте формулу делителя тока, чтобы вычислить значение тока, протекающего через каждый из нагрузочных резисторов, если общий ток, протекающий в цепи, составляет 10 ампер.
Рисунок 10 Цепь для примера 6.
Решение:
ПРИМЕР 7
Проблема: При параллельном подключении дополнительных нагрузок общее сопротивление цепи уменьшается. Для цепи, показанной на рис. 11 , определите полное сопротивление цепи при каждом из следующих условий эксплуатации:
Переключатели 1 и 2 замкнуты.
Переключатели 1, 2 и 3 замкнуты.
Рисунок 11 Цепь для примера 7.
Решение:
Последовательно-параллельная комбинация резисторов
Комбинированные резистивные цепи, также известные как последовательно-параллельные резистивные цепи , объединяют резисторы последовательно с резисторами, включенными параллельно, как показано на рисунке 12 .
Правила, регулирующие эти цепи, такие же, как и правила, разработанные для последовательных и параллельных цепей. Сначала определяется сопротивление совокупного полного сопротивления параллельной части.Затем общее сопротивление параллельной части добавляется к любому последовательному сопротивлению, чтобы найти общее сопротивление последовательно-параллельной комбинированной цепи.
Рисунок 12 Последовательно-параллельное соединение резисторов.
ПРИМЕР 8
Проблема: Резистор 9 Ом, R ₁, и резистор 60 Ом, R ₂, подключены параллельно друг другу и последовательно с резистор 40 Ом, R ₃, как показано на Рис.13 .Определите общее сопротивление этой последовательно-параллельной комбинации резисторов.
Рисунок 13 Цепь для примера 8.
Решение:
ПРИМЕР 9
Проблема: Показания сопротивления можно использовать для проверки цепей на наличие неисправностей. Как определено в предыдущем примере, нормальное полное сопротивление этой последовательно-параллельной схемы схемы , рис. 14, составляет 60 Ом.
Найдите новое значение R _T , если резистор R ₁ будет поврежден разомкнут , в то время как значения сопротивления R ₂ и R ₃ останутся одно и тоже.
Аналогичным образом найдите новое значение R _T , если резистор R ₃ будет поврежден закорочен , в то время как значения сопротивления R ₁ и R ₂ остаются тоже самое.
Рисунок 14 Цепь для примера 9.
Решение:
При разомкнутом отказе R ₁ цепь будет состоять из ₃ R последовательно с R ₂ и всего сопротивление будет:
При коротком замыкании R ₃ цепь будет состоять из R ₁ параллельно с R ₂, а общее сопротивление будет:
Контрольные вопросы
Рассчитайте общее сопротивление для каждой из следующих цепей резисторов:
Последовательная цепь: R1 = 40 Ом, R2 = 75 Ом
Параллельная цепь: R1 = 200 Ом, R2 = 200 Ом, R3 = 200 Ом
Последовательная цепь: R1 = 2000 Ом, R2 = 6000 Ом, R3 = 2200 Ом
Параллельная цепь: R1 = 14 Ом, R2 = 32 Ом
Последовательная цепь: R1 = 4700 Ом, R2 = 800 Ом, R3 = 200 Ом
Параллельная цепь: R1 = 60 Ом, R2 = 30 Ом, R3 = 15 Ом
9 0257 Резисторы R ₁, R ₂ и R ₃ (50 Ом, 30 Ом и 20 Ом соответственно) подключены последовательно через приложенное напряжение 200 В, чтобы сформировать делитель напряжения.Используя формулу делителя напряжения, рассчитайте напряжения E ₁, E ₂ и E ₃.
Суммарный ток на два параллельно соединенных резистора составляет 3 А. Сопротивление R ₁ составляет 10 Ом, а сопротивление R ₂ равно 40 Ом. Используя формулу делителя тока, рассчитайте токи I ₁ и I ₂.
Резистор 5 Ом, R ₁, и резистор 20 Ом, R ₂, подключены параллельно друг другу и последовательно с резистором 6 Ом, R ₃.Вычислите полное сопротивление этой последовательно-параллельной цепи.
Вам даны три резистора по 100 Ом, которые нужно соединить вместе. Опишите три возможные конфигурации цепей и вычислите их значения общего сопротивления.
Контрольные вопросы — ответы
(а) 115 Ом, (б) 66,7 Ом, (в) 10200 Ом, (г) 9,74 Ом, (д) 5700 Ом, (е) 8,57 Ом
E ₁ = 100 В, E ₂ = 60 В, E ₃ = 40 В
I ₁ = 2.