Как рассчитать общее сопротивление при последовательном соединении проводников. Какова формула для параллельного соединения резисторов. Чем отличаются эти два типа соединений с точки зрения электрических характеристик. Как решать задачи на расчет эквивалентного сопротивления цепи.
Последовательное соединение проводников: основные принципы
При последовательном соединении проводники соединяются один за другим, образуя единую цепь. Ключевые особенности такого соединения:
- Ток через все элементы одинаков
- Общее напряжение равно сумме напряжений на отдельных элементах
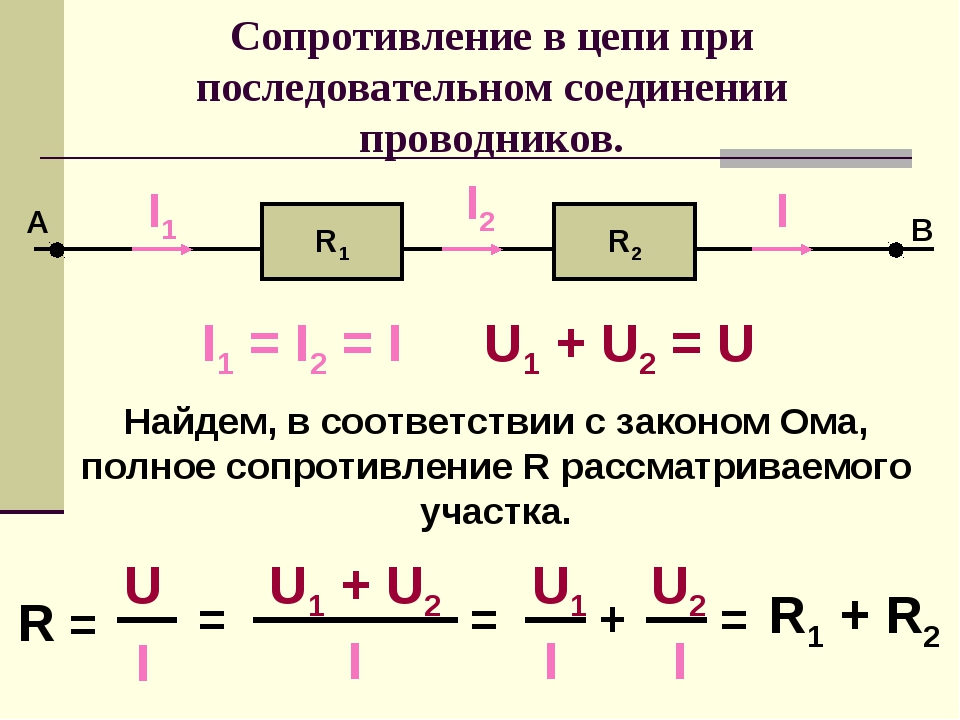
- Общее сопротивление равно сумме сопротивлений отдельных элементов
Формула для расчета общего сопротивления при последовательном соединении:
R = R1 + R2 + R3 + … + Rn
где R — общее сопротивление, R1, R2, R3 и т.д. — сопротивления отдельных элементов.
Параллельное соединение проводников: ключевые характеристики
При параллельном соединении все элементы подключаются к одним и тем же точкам цепи. Основные свойства:
- Напряжение на всех элементах одинаково
- Общий ток равен сумме токов через отдельные элементы
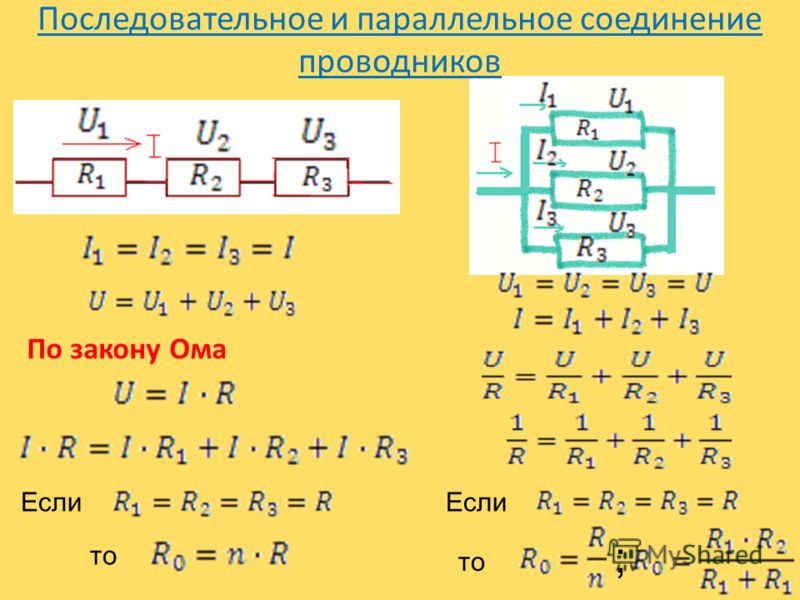
- Обратная величина общего сопротивления равна сумме обратных величин сопротивлений элементов
Формула для расчета общего сопротивления при параллельном соединении:
1/R = 1/R1 + 1/R2 + 1/R3 + … + 1/Rn
где R — общее сопротивление, R1, R2, R3 и т.д. — сопротивления отдельных элементов.
Сравнение последовательного и параллельного соединения
Чем отличаются эти два типа соединений с точки зрения электрических характеристик?
- При последовательном соединении общее сопротивление всегда больше сопротивления любого отдельного элемента
- При параллельном соединении общее сопротивление всегда меньше сопротивления любого отдельного элемента
- Последовательное соединение используется для увеличения общего сопротивления цепи
- Параллельное соединение применяется для уменьшения общего сопротивления
Решение задач на расчет эквивалентного сопротивления
Как применять формулы на практике? Рассмотрим пример:
Задача: Найти эквивалентное сопротивление цепи, состоящей из трех резисторов 10 Ом, 20 Ом и 30 Ом, соединенных последовательно.
Решение:
- Применяем формулу для последовательного соединения: R = R1 + R2 + R3
- Подставляем значения: R = 10 + 20 + 30
- Вычисляем: R = 60 Ом
Ответ: Эквивалентное сопротивление цепи равно 60 Ом.
Применение формул сопротивления в электротехнике
Знание формул расчета сопротивления при различных соединениях проводников критически важно для:
- Проектирования электрических цепей
- Расчета параметров электронных устройств
- Диагностики неисправностей в электрооборудовании
- Оптимизации энергопотребления систем
Как эти формулы применяются на практике? Например, при разработке делителей напряжения, согласовании импедансов в радиотехнике или расчете нагрузочной способности источников питания.
Влияние типа соединения на характеристики электрической цепи
Выбор типа соединения элементов может существенно повлиять на работу электрической цепи. Рассмотрим основные эффекты:
- Последовательное соединение увеличивает общее сопротивление, что может использоваться для ограничения тока
- Параллельное соединение уменьшает общее сопротивление, позволяя увеличить общий ток в цепи
- При последовательном соединении выход из строя одного элемента приводит к разрыву всей цепи
- При параллельном соединении выход из строя одного элемента не нарушает работу остальных
Как это применяется на практике? Например, в системах резервирования часто используют параллельное соединение для повышения надежности.
Комбинированные схемы: сочетание последовательного и параллельного соединения
В реальных электрических цепях часто встречаются комбинации последовательного и параллельного соединения. Как рассчитывать сопротивление в таких случаях?
- Разбить схему на участки с однотипным соединением
- Рассчитать эквивалентное сопротивление для каждого участка
- Объединить полученные значения, используя соответствующие формулы
Пример: Цепь состоит из двух параллельных ветвей, в каждой из которых последовательно соединены два резистора. Как найти общее сопротивление?
- Рассчитать сопротивление каждой ветви по формуле последовательного соединения
- Применить формулу параллельного соединения к полученным значениям
Факторы, влияющие на сопротивление проводников
При расчете сопротивления цепей важно учитывать факторы, влияющие на сопротивление отдельных проводников:
- Материал проводника (удельное сопротивление)
- Длина проводника
- Площадь поперечного сечения
- Температура
Как эти факторы учитываются в расчетах? Например, при повышении температуры сопротивление металлических проводников увеличивается, что может потребовать корректировки расчетов для обеспечения стабильной работы устройства.
Последовательно и параллельно
Хорошо, если у установщика есть возможность применить схему поканального усиления. Однако в большинстве случаев это считается непозволительной роскошью, и в процессе инсталляции аудиосистемы в девяти случаях из десяти возникает потребность нагрузить, к примеру, двухканальный аппарат четырьмя динамиками или четырехканальный — восемью.
Собственно, страшного в этом ничего нет. Важно только держать в памяти несколько основных способов соединения громкоговорителей. Даже не несколько, а всего-то два: последовательный и параллельный. Третий — последовательно-параллельный — производная из двух перечисленных. Другими словами, если у вас имеется больше одного динамика на канал усиления и вы знаете с какими нагрузками может справиться аппарат, то выбрать одну, наиболее приемлемую схему из трех возможных не так уж и сложно.
Последовательное соединение динамиков
Понятно, что когда драйверы соединены в последовательную цепочку, возрастает сопротивление нагрузки.
Также понятно, что с увеличением количества звеньев оно растет. Обычно потребность увеличения сопротивления возникает для снижения выходных показателей акустики. В частности, при установке тыловой подзвучки или динамика центрального канала, которые в основном выполняют вспомогательную роль, и значительных мощностей от усилителя им не требуется. В принципе последовательно можно соединить сколько угодно динамиков, однако их общее сопротивление не должно превышать 16 Ом: усилителей, работающих с более высокими нагрузками, немного.
Положительный выходной разъем канала усилителя соединяется с плюсовой клеммой динамика А, а «минус» того же драйвера — с «плюсом» динамика В. После чего минусовая клемма динамика В подключается к отрицательному выходу того же канала усиления. По той же схеме строится и второй канал.
Это два динамика. Если требуется последовательно соединить, скажем, четыре громкоговорителя, то метод аналогичный. «Минус» динамика В вместо того, чтобы подключаться к выходу усилителя, соединяется с «плюсом» С.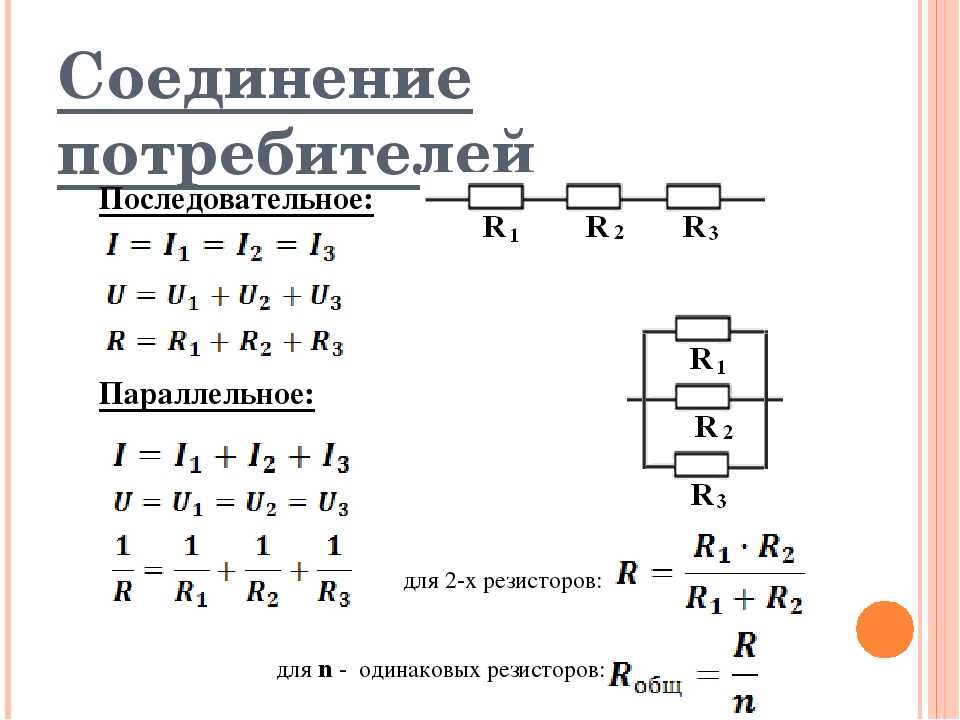
Дальше от минусовой клеммы C бросается провод на «плюс» D, а уже от «минуса» D происходит соединение с отрицательным выходным разъемом усилителя.
Вычисление эквивалентного сопротивления нагрузке канала усиления, на который нагружена цепочка последовательно соединенных динамиков, производится простым сложением по следующей формуле: Zt = Za + Zb, где Zt — эквивалентное сопротивление нагрузке, а Za и Zb соответственно сопротивление динамиков А и В. К примеру, имеется у вас четыре 12-дюймовых сабвуферных головки сопротивлением в 4 ома и один-единственный стереоусилитель 2 х 100 Вт, не терпящий низкоомных (2 Ом и меньше) нагрузок. В этом случае последовательное соединение НЧ-динамиков — единственно возможный вариант. Каждый канал усиления при этом обслуживает пару головок с общим сопротивлением 8 Ом, что легко вписывается в указанные выше 16-омные рамки. Тогда как параллельное включение динамиков (о нем позже) приведет к недопустимому (меньше 2 Ом) снижению сопротивления нагрузки обоих каналов и в результате выходу из строя усилителя.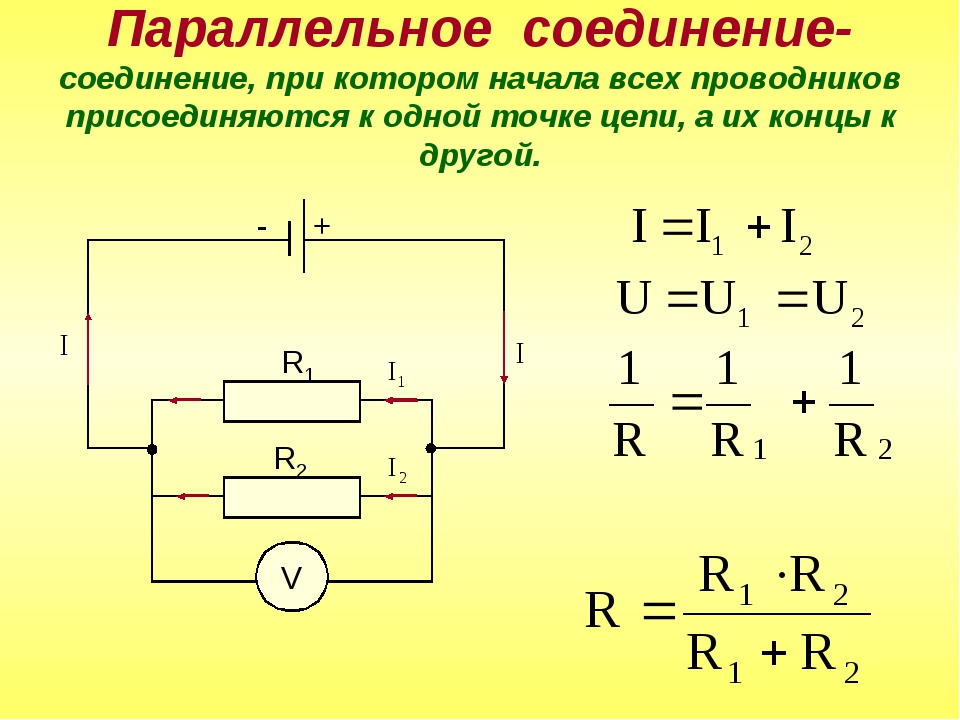
Когда к одному каналу усиления последовательно подключается более одного динамика, это неизбежно отражается на выходной мощности. Вернемся к примеру с двумя соединенными последовательно 12-дюймовыми головками и одним 200-ваттным стереоусилителем, минимальное сопротивление нагрузки которого 4 Ом. Чтобы выяснить, сколько ватт при таких условиях сможет отдать динамикам усилитель, нужно решить еще одно несложное уравнение: Po = Pr x (Zr/Zt), где Po — подводимая мощность, Pr — измеренная мощность усилителя, Zr — сопротивление нагрузке, при котором проводились измерения реальной мощности усилителя, Zt — суммарное сопротивление динамиков, нагруженных на данный канал. В нашем случае получается: Po = 100 x (4/8). То есть 50 ватт. Динамиков у нас два, поэтому «полтинник» делится на два. В итоге каждая головка получит по 25 ватт.
Параллельное соединение динамиков
Здесь все в точности до наоборот: при параллельном соединении сопротивление нагрузке падает пропорционально количеству динамиков.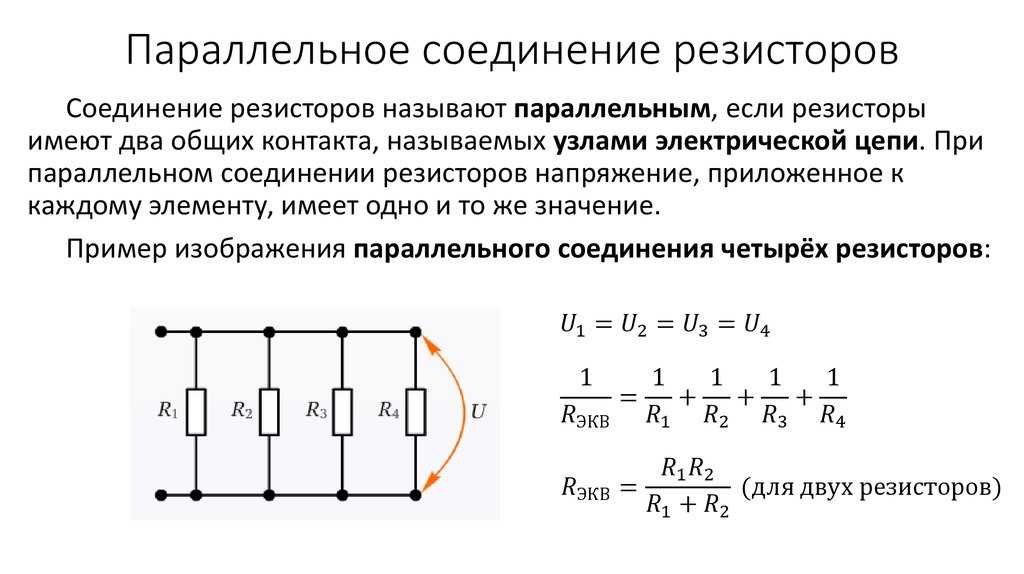
Соответственно вырастает выходная мощность. Число громкоговорителей ограничено способностью усилителя работать на низких нагрузках и мощностными пределами самих динамиков, включенных параллельно. В большинстве случаев усилители вполне справляются с нагрузками в 2 ома, реже в 1 ом. Существуют аппараты, которым по зубам и 0,5 ома, но это уже действительно большая редкость. Что касается современных громкоговорителей, то здесь разброс мощностных параметров от десятков до сотен ватт.
Провод от плюсового выходного разъема соединяется с положительными клеммами динамиков А и В (проще всего соединить сначала выход усилителя с «плюсом» динамика А, а затем уже от него тянуть провод к динамику В). По той же схеме соединяются минусовой вывод усилителя с «минусами» обоих динамиков.
Вычисление эквивалентного сопротивления нагрузке канала усиления при параллельном соединении динамиков несколько сложнее. Формула такая: Zt = (Za x Zb) / (Za + Zb), где Zt — эквивалентное сопротивление нагрузке, a Za и Zb — сопротивление динамиков.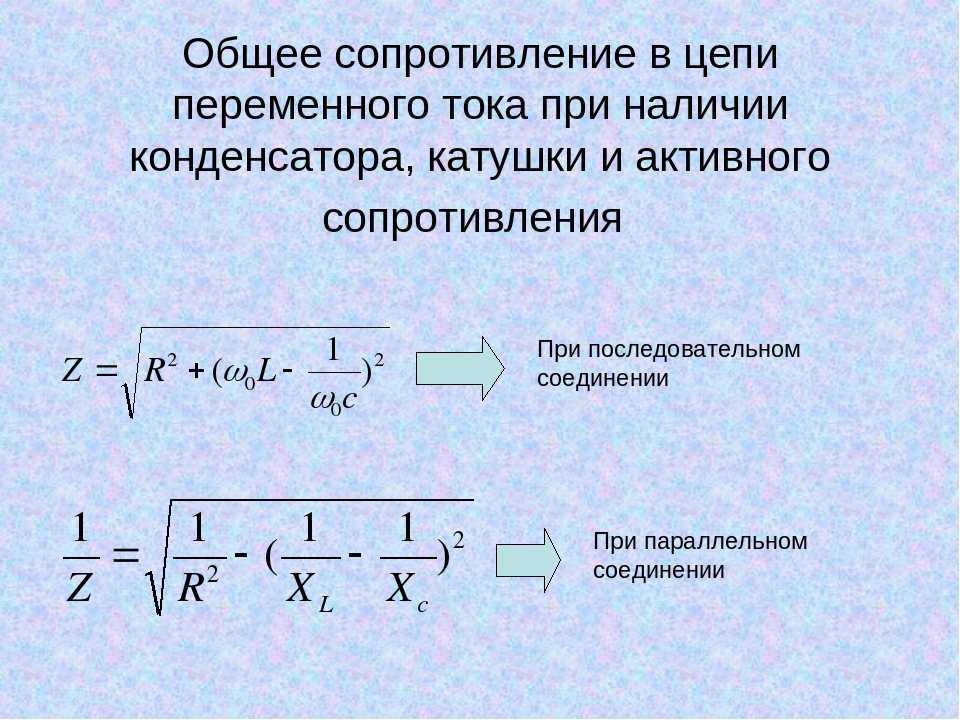
Теперь представим, что на низкочастотное звено в системе отводится опять-таки 2-канальный аппарат (2 х 100 Вт на нагрузку 4 Ом), но стабильно работающий при 2 омах. Включение двух 4-омных сабвуферных головок в параллель позволит значительно увеличить выходную мощность, поскольку сопротивление нагрузке канала усиления сократиться вдвое. По нашей формуле получаем: Zt = (4 + 4) / (4 + 4). В результате имеем 2 Ом, что при условии хорошего запаса по току у усилителя даст 4-кратный прирост мощности на канал: Po = 100 x (4/2). Или 200 ватт на канал вместо 50, полученных при последовательном соединении динамиков.
Последовательно-параллельное соединение динамиков
Обычно эта схема применяется для увеличения количества динамиков на борту транспортного средства с тем, чтобы добиться повышения суммарной мощности аудиосистемы при сохранении адекватного сопротивления нагрузке. То есть на один канал усиления можно задействовать сколько угодно динамиков, если их суммарное сопротивление находится в уже обозначенных нами пределах от 2 до 16 Ом.
Подключение, к примеру, 4 динамиков по этому способу производится следующим образом. Кабель от положительного выходного разъема усилителя соединяется с плюсовыми клеммами динамиков А и С. Затем «минуса» A и C подключаются к «плюсам» громкоговорителей B и D соответственно. Наконец, кабель от отрицательного выхода усилителя соединяется с минусовыми клеммами динамиков B и D.
Для вычисления суммарного сопротивления нагрузке канала усиления, который работает с четырьмя головками, соединенными по комбинаторному способу, применяется следующая формула: Zt = (Zab x Zcd) / (Zab x Zcd), где Zab — суммарное сопротивление динамиков А и В, а Zcd — суммарное сопротивление динамиков C и D (между собой они соединены последовательно, поэтому сопротивление суммируется).
Возьмем все тот же пример с 2-канальным усилителем, стабильно функционирующим при 2 омах. Только на этот раз два 4-омных сабвуфера, включенных параллельно, нас уже не устраивают, и мы хотим подключить к одному каналу усиления 4 НЧ-головки (тоже 4-омные).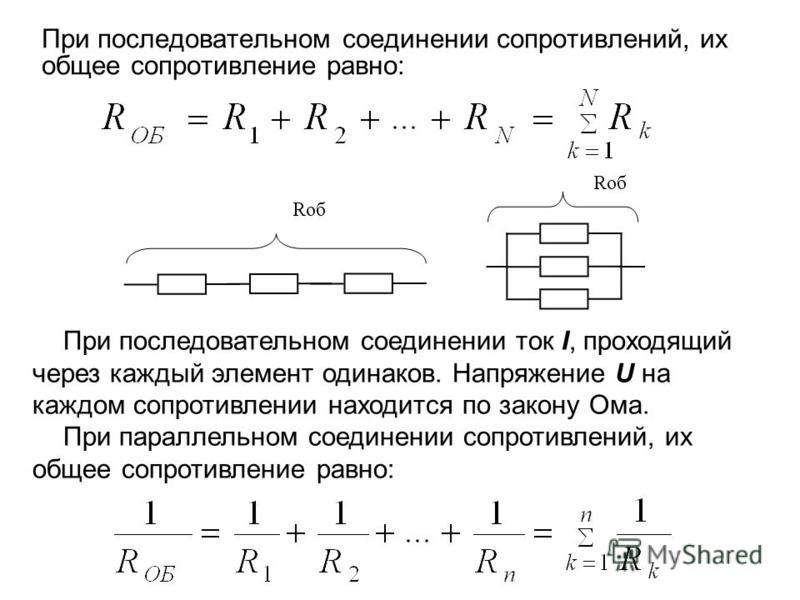
Для этого нам нужно знать, выдержит ли аппарат такую нагрузку. При последовательном соединении суммарное сопротивление будет равно 16 Ом, что никого не устраивает. При параллельном — 1 Ом, что уже не вписывается в параметры усилителя. Остается последовательно-параллельная схема. Простые подсчеты показывают, что в нашем случае один канал усиления будет нагружен стандартными 4 омами, раскачивая при этом сразу четыре саба. Поскольку 4 Ом — нагрузка стандартная для любого автомобильного усилителя мощности, то никаких потерь и приростов мощностных показателей в данном случае не произойдет. В нашем случае — это 100 ватт на канал, поровну поделенные на четыре 4-омных динамика.
Подводим итоги. Главное при построении подобных схем — не переусердствовать. Прежде всего в том, что касается минимальной нагрузки усилителя. Большинство современных аппаратов вполне справляются с 2-омными нагрузками. Однако это совсем не значит, что они будут работать и при 1 оме. Кроме того, на низких нагрузках снижается способность усилителя контролировать движение диффузора динамика, что чаще всего результируется в «размытом» басе.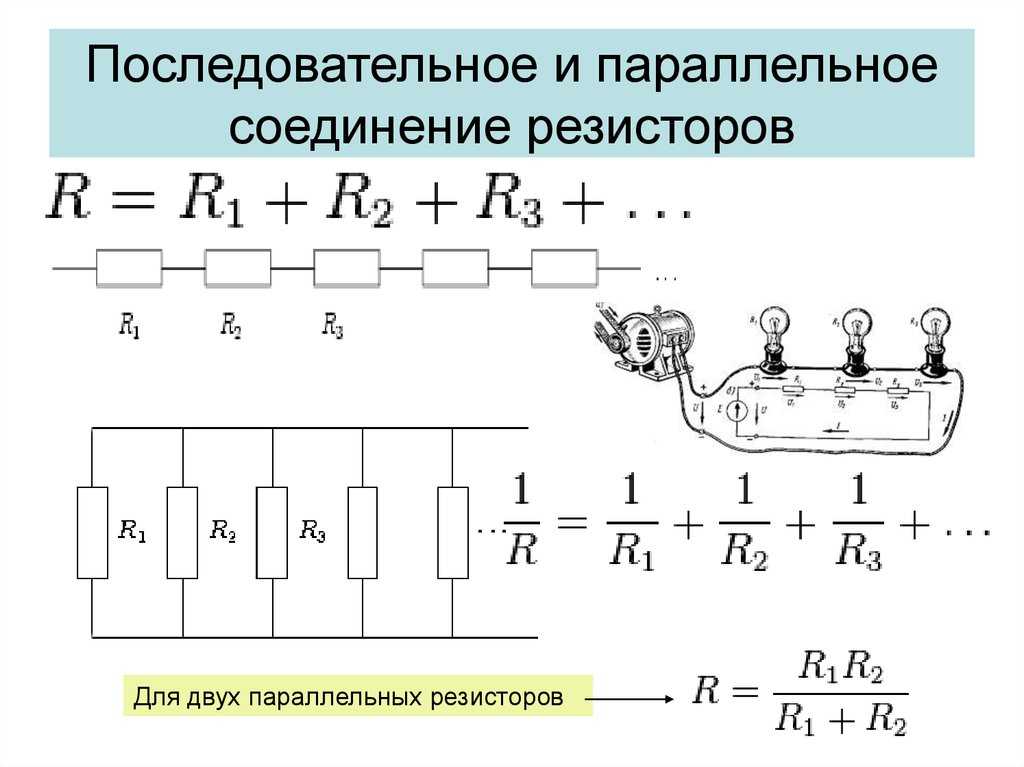
Все три приведенных выше примера касались исключительно низкочастотного звена аудиокомплекса. С другой стороны, теоретически на одном двухканальном аппарате можно построить всю акустическую систему в автомобиле с мид-басами, среднечастотниками и твитерами. То есть с динамиками, играющими в разных областях частотного спектра. Следовательно придется задействовать пассивные кроссоверы. Здесь важно помнить, что их элементы — конденсаторы и индуктивности — должны быть согласованы с эквивалентным сопротивлением нагрузке данного канала усиления. Кроме того, фильтры сами привносят сопротивление. При этом чем дальше сигнал от полосы пропускания фильтров, тем больше сопротивление.
Последовательное соединение сопротивления, индуктивности, емкости
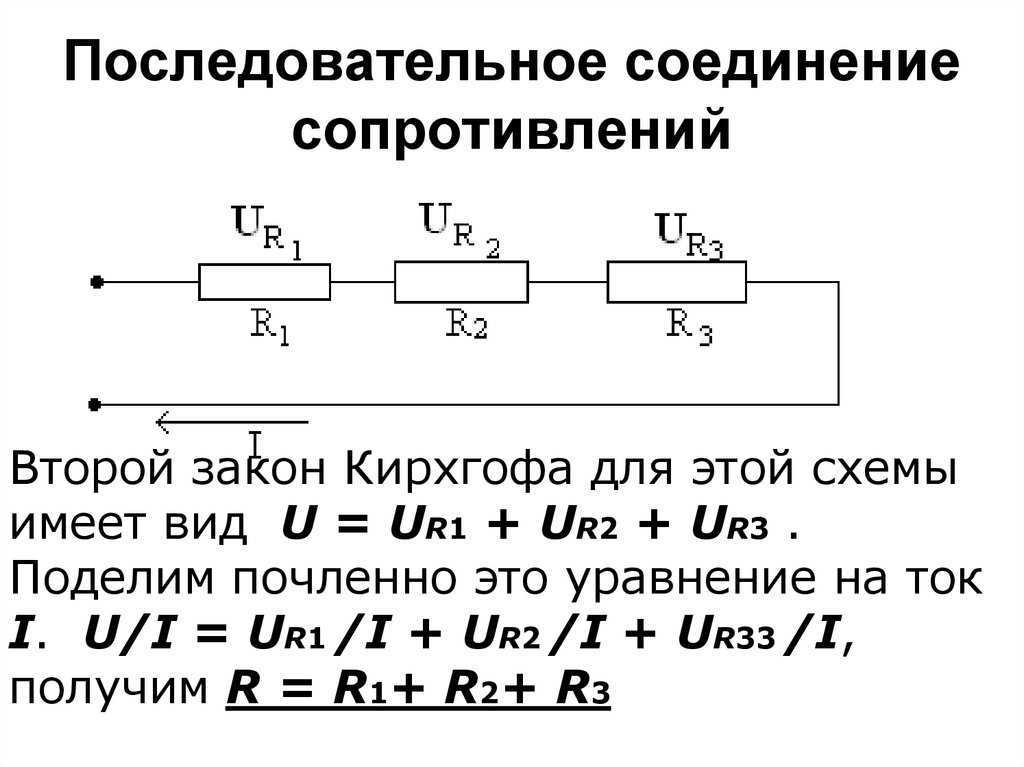
В схеме, состоящей из последовательно соединенных активного сопротивления,
индуктивности и емкости (рис. 22.1), заданы приложенное напряжение U, частота f и числовые значения
параметров R, L и С.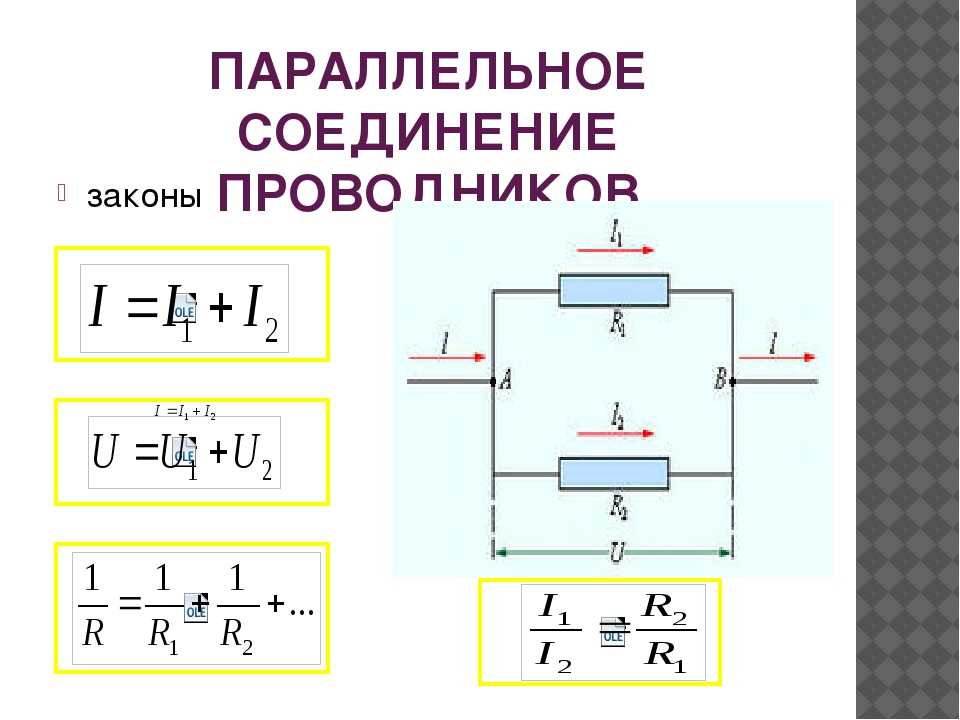
Требуется найти ток и напряжения на элементах.
При анализе электрических цепей синусоидального тока типична ситуация, когда метод решения незнакомой задачи неизвестен. Во многих случаях помогает следующий подход. По установленным ранее правилам строится векторная диаграмма, из анализа которой выводятся необходимые расчетные формулы. Так же поступим сейчас и мы.
В последовательной цепи общим для всех элементов является протекающий по ним ток, поэтому именно с него начинаем построение векторной диаграммы. Проводим его изображение горизонтально (рис. 22.2).
Вообще, направление первого вектора при построении диаграмм произвольно. Оно
диктуется соображениями удобства. Дальше мы должны показать векторы напряжений на всех элементах и в
соответствии со вторым законом Кирхгофа в векторной форме U=UR+UL+UC получить вектор входного
напряжения. Сложение векторов можно выполнять по правилу параллелограмма, однако удобнее применять
правило многоугольника, когда каждый последующий вектор пристраивается к концу предыдущего.
Нам известно, что напряжение на активном сопротивлении совпадает по фазе с током, поэтому вектор UR мы направляем по вектору I. К его концу пристраиваем вектор UL и направляем его вверх, так как напряжение на индуктивности опережает ток на 90°. Напряжение UС находится в противофазе с UL, т.е. отстает от тока на тот же угол 90°, поэтому вектор UС, пристроенный к концу вектора UL, направлен вниз. Векторная сумма UR, UL и UС дает вектор приложеного напряжения U.
Величины напряжений на отдельных элементах цепи нам известны:
Из треугольника oab (рис. 22.2) по теореме Пифагора находим:
Вынося из под знака радикала, записываем последнее выражение в виде: U=I*z; где,z — полное сопротивление.
В последней формуле разность индуктивного и емкостного сопротивлений мы обозначили
буквой х. Это общее реактивное сопротивление цепи: х = хL – xC. Сами индуктивность и емкость называются
реактивными элементами, и их сопротивления хL и xC тоже носят названия реактивных.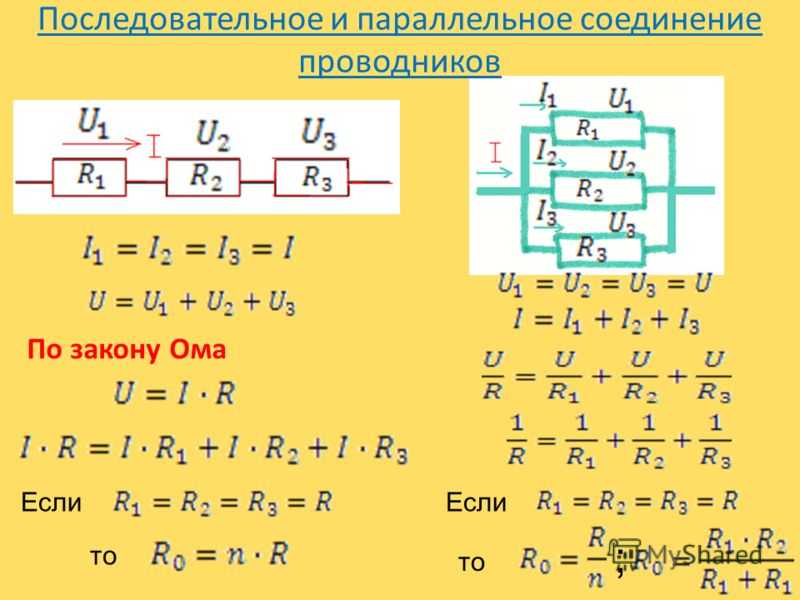
Выражение U=Iz называется законом Ома для всей цепи. Оно может быть записано и так: I=U/z=Uy.
где, y– полная проводимость цепи, представляющая величину, обратную полному сопротивлению 1/z
Если необходимо определить угол сдвига фаз между напряжением и током, то это можно сделать из треугольника напряжений oab (рис. 22.2):
Векторная диаграмма на рис. 22.2 построена для случая, когда UL>UC, что имеет место при XL>XC, когда в цепи преобладает индуктивность, и цепь носит активно-индуктивный характер. Общий ток отстает по фазе от входного напряжения.
Возможны также режимы, когда ULC и UL=UC
СерияСопротивление
Доля
Доля
Доля
Доля
Серийное сопротивление (Rs) и его коэффициенты Три различных фактора вызывают последовательное сопротивление в солнечных элементах: — Прохождение тока через эмиттер и основание солнечного элемента — Контактное сопротивление между кремнием и металлическим контактом — Сопротивление задних и верхних металлических контактов.
Очевидным методом оценки Rs солнечного элемента является нахождение наклона ВАХ в точке напряжения холостого хода. Уравнение для коэффициента заполнения как функции Rs может быть представлено с учетом того, что для нормальных значений последовательного сопротивления , максимальная мощность может быть аппроксимирована как мощность при отсутствии последовательного сопротивления минус потерянная мощность в последовательном сопротивлении. Уравнение максимальной мощности солнечной батареи: P’ MP ≈ V MP I MP – I 2 MP /R S
FF .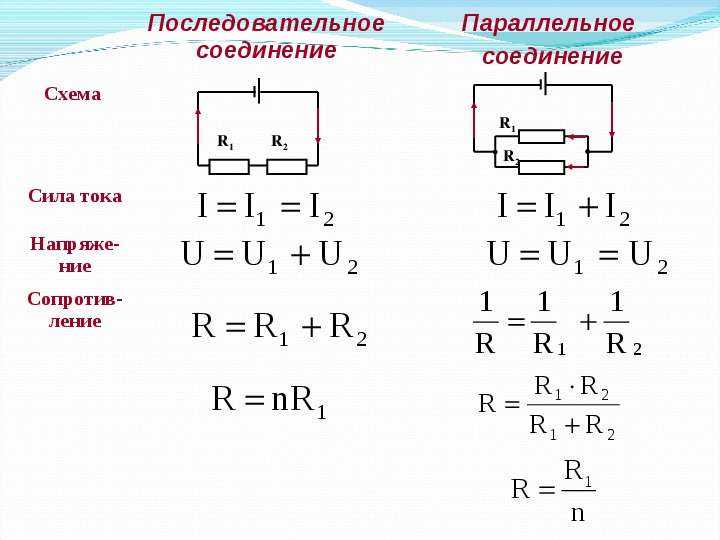
Тогда уравнение будет таким: =FF 0 (1–1,1 r S ) + R S 2 / 5,4 Это действительно для R S Менее 0,4 и V OC больше 10 . потери от последовательного сопротивления.
Формула эквивалентного сопротивления — GeeksforGeeks
Эквивалентное сопротивление определяется как общее сопротивление цепи для резисторов, соединенных последовательно или параллельно. Резисторы — это электрические устройства, которые ограничивают ток в цепи и подчиняются закону Ома, V = IR. В цепи может быть более одного резистора, из-за которого необходимо оценить эквивалентное сопротивление. Значение тока и напряжения зависит от ориентации резисторов в цепи. Эквивалентное сопротивление можно интерпретировать как сумму отдельных сопротивлений каждого резистора. Обозначается символом R экв. . Его единицей измерения является ом (Ом), а размерная формула определяется как [M 1 L 2 A −2 T −3 ].
Формула эквивалентного сопротивления для последовательного соединения
В последовательной цепи резисторов n резисторов (n > 1) соединены рядом в одну линию (один за другим) так, что совокупность этих резисторов может быть заменена один эквивалентный резистор, чтобы дать такое же значение сопротивления. Здесь сумма отдельных сопротивлений будет эквивалентным сопротивлением ряда резисторов. Ток через каждый резистор одинаков, но напряжение делится на n частей между резисторами.
R Уравнение = R 1 + R 2 + R 3 +… .. + R N
, где
R EQVIVELANCE, Equivivels .
R 1 — сопротивление первого резистора,
R 2 — сопротивление второго резистора,
R 3 — сопротивление третьего резистора и так далее.
Формула эквивалентного сопротивления для параллельного соединения
В параллельной цепи резисторов n резисторов (n > 1) соединены параллельно проводами, начинающимися из общей точки.
Здесь сумма обратных величин отдельных сопротивлений равна обратной величине эквивалентного сопротивления. Напряжение на каждом резисторе одинаково, но ток делится на n частей между резисторами.
Примеры задач1/R экв. = 1/R 1 + 1/R 2 + 1/R 3 + ….. + 1/R n
где,
R eq эквивалентное сопротивление,
R 1 сопротивление первого резистора,
R 2 сопротивление первого резистора,
R 2 сопротивление 3 — сопротивление третьего резистора и так далее.
Задача 1. Найдите эквивалентное сопротивление, если три сопротивления 4 Ом, 2 Ом и 5 Ом соединены последовательно.
Решение:
Мы имеем,
R 1 = 4 ω
R 2 = 2 Ом
R 3 = 5 ω
Использование.
R eq = R 1 + R 2 + R 3
= 4 + 2 + 5
= 11 Ом
R eq = R 1 + R 2 + R 3 920016. 1 Ом и 12 Ом соединены последовательно.
Решение:
Мы имеем,
R 1 = 6 ω
R 2 = 1 Ом
R 3 = 12 ω
Используя Formula We Get,
3 = 12 ω, используя Formula We Get,
3 3 3 = 12 ω
. eq = R 1 + R 2 + R 3
= 6 + 1 + 12
= 19 Ом
и x Ом соединены последовательно, чтобы получить эквивалентное сопротивление 10 Ом.
Решение:
Мы имеем,
R 1 = 2 ω
R 2 = 5 Ом
R EQ = 10 0004
Использование. R eq = R 1 + R 2 + R 3
=> 10 = 2 + 5 + x
=> 10 = 7 + x
7 0 4 9 0 0 4 = 9 0 0 3 Задача 4.Решение:
Мы имеем,
R 1 = 7 ω
R 2 = 3 ОД
R EQ = 15 ω
Использование. R Уравнение = R 1 + R 2 + R 3
=> 15 = 7 + 3 + x
=> 15 = 10 + x
=> x = 5 Ом
Задача 5. Найдите эквивалентное сопротивление, если три сопротивления 6 Ом, 3 Ом и 8 Ом соединены параллельно.
Solution:
We have,
R 1 = 6 Ω
R 2 = 3 Ω
R 3 = 8 Ω
Using the formula we get,
1/R экв. = 1/R 1 + 1/R 2 + 1/R 3
1/R экв. = 1/6 + 1/3 + 1/8
4 1/8
4 /R eq = 1/1,6
R eq = 1,6 Ом
Задача 6.
Solution:
We have,
R 1 = 2 Ω
R 2 = 5 Ω
R 3 = 1 Ω
Using the formula we get,
1/R экв. = 1/R 1 + 1/R 2 + 1/R 3
1/R экв. = 1/2 + 1/5 + 1/1
4 /R
eq = 1/0,59R eq = 0,59 Ом
эквивалентное сопротивление 0,5 Ом.
Решение:
Мы имеем,
R 1 = 4 ω
R 2 = 2 ~
R 3 = 1 ω
R EQ 3 = 1 ω
R EQ 3 = 1 ω
R EQ 3 = 1 ω
1 2 r 3 = 1 ω
1 2 r 3 = 1.Используя формулу получаем,
1/R eq = 1/R 1 + 1/R 2 + 1/R 3 + 1/R 4
4 = > 5
4.
Найдите неизвестное сопротивление, если три сопротивления 7 Ом, 3 Ом и x Ом соединены последовательно, чтобы получить эквивалентное сопротивление 15 Ом. 
Найдите эквивалентное сопротивление, если три сопротивления 2 Ом, 5 Ом и 1 Ом соединены параллельно. 
