Формула токов в параллельных ветвях: Формула разброса | Электрикам

2.2. Параллельное соединение элементов электрических цепей

На рис. 2.2 показана электрическая цепь с параллельным соединением сопротивлений.

Рис. 2.2

Токи в параллельных ветвях определяются по формулам:

      В соответствии с первым законом Кирхгофа, ток в неразветвленной части схемы равен сумме токов в параллельных ветвях.

        где

     Эквивалентная проводимость электрической цепи, состоящей из n параллельно включенных элементов, равна сумме проводимостей параллельно включенных элементов. Эквивалентным сопротивлением цепи называется величина, обратная эквивалентной проводимости

  Пусть электрическая схема содержит три параллельно включенных сопротивления. Эквивалентная проводимость

  Эквивалентное сопротивление схемы, состоящей из n одинаковых элементов, в n раз меньше сопротивлений R одного элемента

Возьмем схему, состоящую из двух параллельно включенных сопротивлений (рис.

2.3). Известны величины сопротивлений и ток в неразветвленной части схемы. Необходимо определить токи в параллельных ветвях.

Рис. 2.3 Эквивалентная проводимость схемы

,

    а эквивалентное сопротивление

Напряжение на входе схемы

Токи в параллельных ветвях

Аналогично

Ток в параллельной ветви равен току в неразветвленной части схемы, умноженному на сопротивление противолежащей, чужой параллельной ветви и деленному на сумму сопротивлений чужой и своей параллельно включенных ветвей.

2.3.Преобразование треугольника сопротивлений в эквивалентную звезду

Встречаются схемы, в которых отсутствуют сопротивления, включенные последовательно или параллельно, например, мостовая схема, изображенная на рис. 2.4. Определить эквивалентное сопротивление этой схемы относительно ветви с источником ЭДС описанными выше методами нельзя. Если же заменить треугольник сопротивлений R1-R2-R3, включенных между узлами 1-2-3, трехлучевой звездой сопротивлений, лучи которой расходятся из точки 0 в те же узлы 1-2-3, эквивалентное сопротивление полученной схемы легко определяется.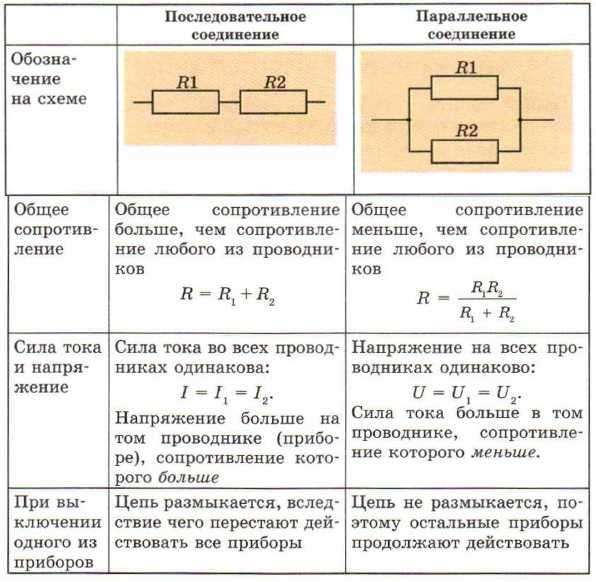

Рис. 2.4 Сопротивление луча эквивалентной звезды сопротивлений равно произведению сопротивлений прилегающих сторон треугольника, деленному на сумму сопротивлений всех сторон треугольника. В соответствии с указанным правилом, сопротивления лучей звезды определяются по формулам:

Эквивалентное соединение полученной схемы определяется по формуле

2.4.Преобразование звезды сопротивлений в эквивалентный треугольник

Иногда для упрощения схемы полезно преобразовать звезду сопротивлений в эквивалентный треугольник. Рассмотрим схему на рис. 2.5. Заменим звезду сопротивлений R1-R2-R3 эквивалентным треугольником сопротивлений R?1-R?2-R?3, включенных между узлами 1-2-3.

2.5. Преобразование звезды сопротивлений в эквивалентный треугольник

Сопротивление стороны эквивалентного треугольника сопротивлений равно сумме сопротивлений двух прилегающих лучей звезды плюс произведение этих же сопротивлений, деленное на сопротивление оставшегося (противолежащего) луча.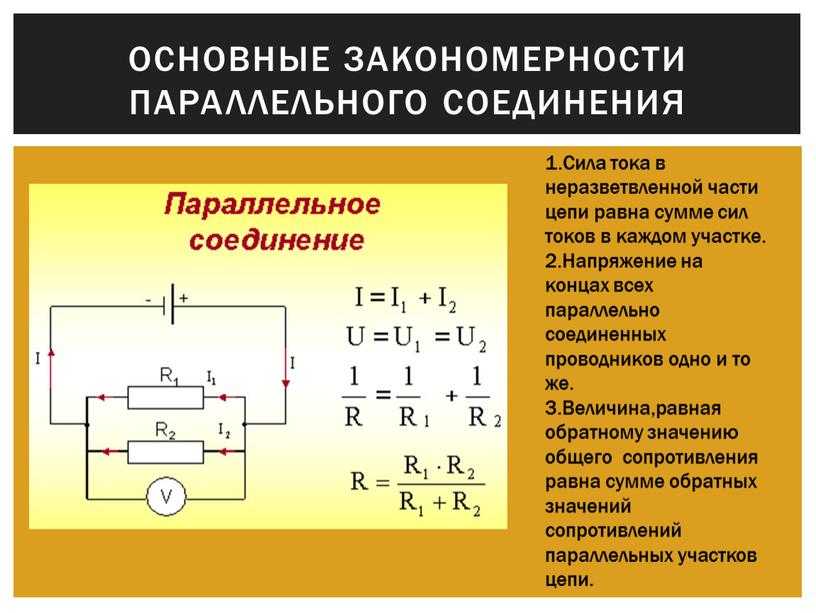 Сопротивления сторон треугольника определяются по формулам:

      Эквивалентное сопротивление преобразованной схемы равно

3. Анализ электрических цепей постоянного тока с одним источником энергии

3.1. Расчет электрических цепей постоянного тока с одним источником методом свертывания

    В соответствии с методом свертывания, отдельные участки схемы упрощают и постепенным преобразованием приводят схему к одному эквивалентному (входному) сопротивлению, включенному к зажимам источника. Схема упрощается с помощью замены группы последовательно или параллельно соединенных сопротивлений одним, эквивалентным по сопротивлению. Определяют ток в упрощенной схеме, затем возвращаются к исходной схеме и определяют в ней токи. Рассмотрим схему на рис. 3.1. Пусть известны величины сопротивлений R1, R2, R3, R4, R5, R6, ЭДС Е. Необходимо определить токи в ветвях схемы. .

Рис. 3.1 Рис. 3.2 Сопротивления R4 и R5 соединены последовательно, а сопротивление R6 — параллельно с ними, поэтому их эквивалентное сопротивление

      После проведенных преобразований схема принимает вид, показанный на рис.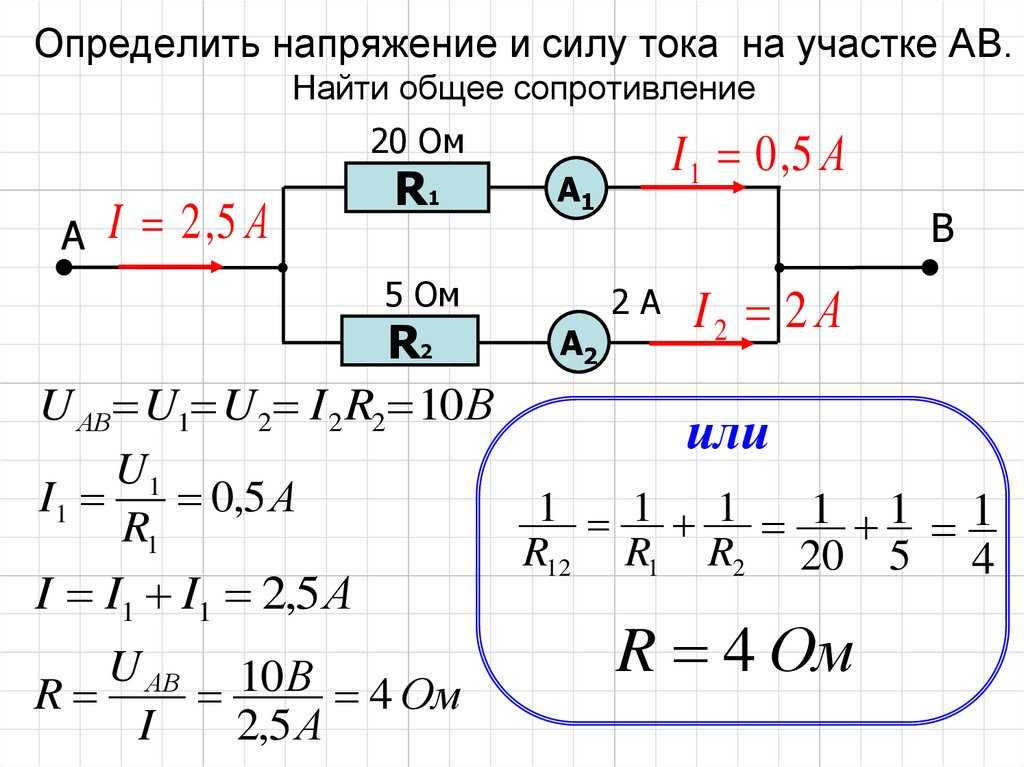 3.2, а эквивалентное сопротивление всей цепи

Ток I1 в неразветвленной части схемы определяется по формуле:

     Найдем токи I2 и I3 в схеме на рис. 3.2 по формулам:

  I3 = I1 — I2 — формула получается из уравнения, составленного по первому закону Кирхгофа:

I₁— I₂

— I₃= 0.

    Переходим к исходной схеме на рис. 3.1 и определим токи в ней по формулам:

        I6 = I3 — I4 (в соответствии с первым законом Кирхгофа I3 — I4 — I6 =0).

Формула чужого сопротивления | FaultAn.ru

Формула «чужого» сопротивления позволяет определить токи в параллельных ветвях при известном токе в ветви, подходящей к данным ветвям.

Воспользуйтесь программой онлайн-расчёта электрических цепей. Программа позволяет рассчитывать электрические цепи по закону Ома, по законам Кирхгофа, по методам контурных токов, узловых потенциалов и эквивалентного генератора, а также рассчитывать эквивалентное сопротивление цепи относительно источника питания.

Рассмотрим схему, представленную на рис. 1.

Рис. 1. Схема для определения токов в ветвях по формуле «чужого» сопротивления

Для данной схемы токи $ \underline{I}_{1} $ и $ \underline{I}_{2} $ будут определяться по формулам

$$ {{\underline{I}}_{1}}=\underline{I}\cdot \frac{{{\underline{Z}}_{2}}}{{{\underline{Z}}_{1}}+{{\underline{Z}}_{2}}}, $$

$$ {{\underline{I}}_{2}}=\underline{I}\cdot \frac{{{\underline{Z}}_{1}}}{{{\underline{Z}}_{1}}+{{\underline{Z}}_{2}}}, $$

т.е. ток в одной из параллельных ветвей равен току, подводимому к параллельным ветвям, умноженному на сопротивление «чужой» ветви, и поделённому на сумму сопротивлений параллельных ветвей.

Для более сложного случая, когда в параллельных ветвях имеются источники ЭДС (рис. 2), формула чужого сопротивления будет записываться в следующем виде:

$$ {{\underline{I}}_{1}}=\frac{\underline{I}\cdot {{\underline{Z}}_{2}}+{{\underline{E}}_{1}}-{{\underline{E}}_{2}}}{{{\underline{Z}}_{1}}+{{\underline{Z}}_{2}}}, $$

$$ {{\underline{I}}_{2}}=\frac{\underline{I}\cdot {{\underline{Z}}_{1}}+{{\underline{E}}_{2}}-{{\underline{E}}_{1}}}{{{\underline{Z}}_{1}}+{{\underline{Z}}_{2}}}, $$

т.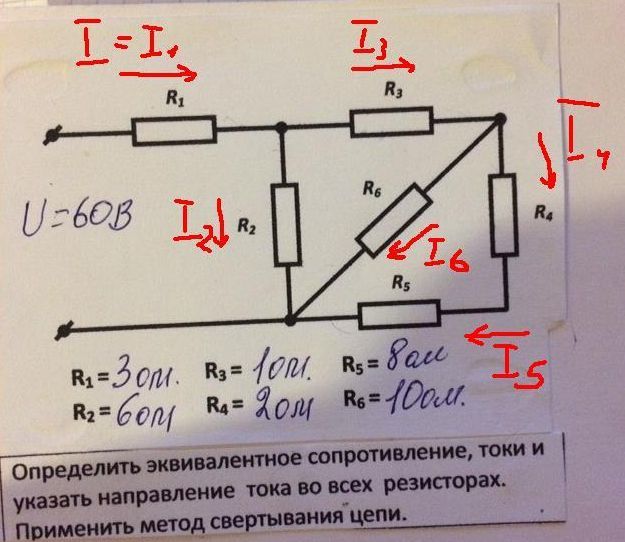 е. дополнительно учитываются источники ЭДС, расположенные в данных ветвях. Формула справедлива при указанных на рис. 2 направлениях ЭДС.

Рис. 2. Схема для определения токов в ветвях по формуле чужого сопротивления при наличии ЭДС

Вывод формул

Выведем формулу чужого сопротивления для схемы по рис. 1.

По закону Ома с учётом параллельного соединения ветвей ток $ \underline{I} $ будет определяться по формуле

$$ \underline{I}=\frac{\underline{U}}{\frac{{{\underline{Z}}_{1}}\cdot {{\underline{Z}}_{2}}}{{{\underline{Z}}_{1}}+{{\underline{Z}}_{2}}}}=\frac{\underline{U}\left( {{\underline{Z}}_{1}}+{{\underline{Z}}_{2}} \right)}{{{\underline{Z}}_{1}}\cdot {{\underline{Z}}_{2}}}. $$

Также по закону Ома

$$ {{\underline{I}}_{1}}=\frac{\underline{U}}{{{\underline{Z}}_{1}}}. $$

Разделим $ \underline{I}_{1} $ на $ \underline{I} $ и получим

$$ \frac{{{\underline{I}}_{1}}}{\underline{I}}=\frac{\frac{\underline{U}}{{{\underline{Z}}_{1}}}}{\frac{\underline{U}\left( {{\underline{Z}}_{1}}+{{\underline{Z}}_{2}} \right)}{{{\underline{Z}}_{1}}\cdot {{\underline{Z}}_{2}}}}=\frac{{{\underline{Z}}_{2}}}{{{\underline{Z}}_{1}}+{{\underline{Z}}_{2}}}, $$

откуда

$$ {{\underline{I}}_{1}}=\underline{I}\frac{{{\underline{Z}}_{2}}}{{{\underline{Z}}_{1}}+{{\underline{Z}}_{2}}}. $$

Формула для тока $ \underline{I}_{2} $ выводится аналогично.

Выведем формулу чужого сопротивления для схемы по рис. 2.

При выбранных по рис. 2 положительных направлениях тока составим уравнение по первому закону Кирхгофа для узла

$$ \underline{I}={{\underline{I}}_{1}}+{{\underline{I}}_{2}}. $$

По второму закону Кирхгофа

$$ {{\underline{I}}_{2}}\cdot {{\underline{Z}}_{2}}-{{\underline{I}}_{1}}\cdot {{\underline{Z}}_{1}}={{\underline{E}}_{2}}-{{\underline{E}}_{1}}, $$

откуда

$$ {{\underline{I}}_{2}}=\frac{{{\underline{E}}_{2}}-{{\underline{E}}_{1}}+{{\underline{I}}_{1}}\cdot {{\underline{Z}}_{1}}}{{{Z}_{2}}}. $$

Разделим $ \underline{I}_{1} $ на $ \underline{I} $ и получим

$$ \frac{{{\underline{I}}_{1}}}{\underline{I}}=\frac{{{\underline{I}}_{1}}}{{{\underline{I}}_{1}}+{{\underline{I}}_{2}}}=\frac{{{\underline{I}}_{1}}}{{{\underline{I}}_{1}}+\frac{{{\underline{E}}_{2}}-{{\underline{E}}_{1}}+{{\underline{I}}_{1}}\cdot {{\underline{Z}}_{1}}}{{{Z}_{2}}}}=\frac{{{\underline{I}}_{1}}\cdot {{Z}_{2}}}{{{\underline{I}}_{1}}\cdot {{Z}_{2}}+{{\underline{E}}_{2}}-{{\underline{E}}_{1}}+{{\underline{I}}_{1}}\cdot {{\underline{Z}}_{1}}}. $$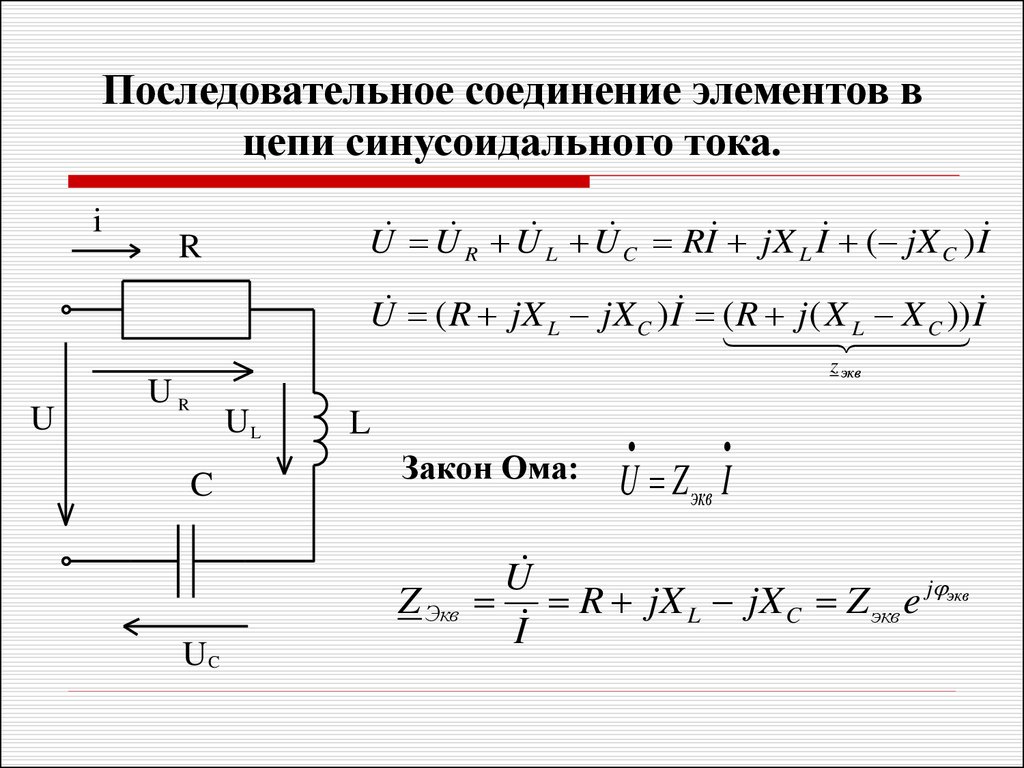

Произведём преобразования, сократив $ \underline{I}_{1} $ в левой и правой частях, и приведём к следующему виду

$$ {{\underline{I}}_{1}}\cdot {{Z}_{2}}+{{\underline{E}}_{2}}-{{\underline{E}}_{1}}+{{\underline{I}}_{1}}\cdot {{\underline{Z}}_{1}}=\underline{I}\cdot {{Z}_{2}}. $$

Отсюда

$$ {{\underline{I}}_{1}}=\frac{\underline{I}\cdot {{\underline{Z}}_{2}}+{{\underline{E}}_{1}}-{{\underline{E}}_{2}}}{{{\underline{Z}}_{1}}+{{\underline{Z}}_{2}}}. $$

Формула для тока $ \underline{I}_{2} $ выводится аналогично.

5.3: Цепи делителя тока и формула делителя тока

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

17336

• Tony R. Kuphaldt
• Schweitzer Engineering Laboratories via All About Circuits

Параллельную цепь часто называют делителем тока за ее способность пропорционировать или делить общий ток на дробные части

Чтобы понять, что это значит, давайте сначала проанализируем простую параллельную цепь, определяя токи ветвей через отдельные резисторы. :

Зная, что напряжения на всех компонентах в параллельной цепи одинаковы, мы можем заполнить нашу таблицу напряжение/ток/сопротивление 6 вольтами в верхней строке:

Используя закон Ома (I=E/R), мы можем рассчитать ток каждой ветви:

Зная, что сумма токов ветвей в параллельных цепях равна общему току, мы можем получить общий ток, суммируя 6 мА. , 2 мА и 3 мА:

Последним шагом, конечно же, является вычисление полного сопротивления. Это можно сделать с помощью закона Ома (R=E/I) в столбце «сумма» или с помощью формулы параллельного сопротивления для отдельных сопротивлений.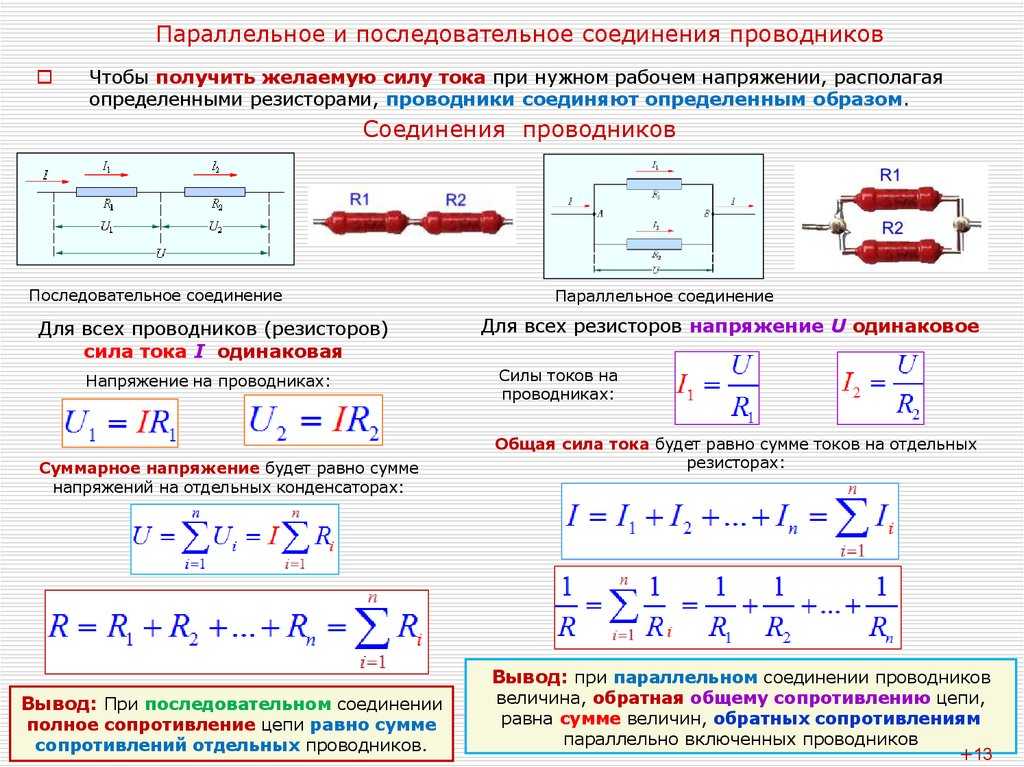 В любом случае, мы получим тот же ответ:

Опять же, должно быть очевидно, что ток через каждый резистор связан с его сопротивлением, учитывая, что напряжение на всех резисторах одинаково. Здесь зависимость не прямо пропорциональна, а обратно пропорциональна. Например, ток через R

1 в два раза больше, чем ток через R ₃ , который имеет вдвое большее сопротивление, чем R ₁ .

Если бы мы изменили напряжение питания этой схемы, мы обнаружили бы, что (сюрприз!) эти пропорциональные отношения не меняются:

Ток через R ₁ по-прежнему ровно вдвое больше, чем через R ₃ , несмотря на то, что напряжение источника изменилось. Пропорциональность между токами различных ветвей строго зависит от сопротивления.

О делителях напряжения также напоминает тот факт, что токи ветвей являются фиксированными пропорциями общего тока. Несмотря на четырехкратное увеличение напряжения питания, отношение тока любой ветви к общему току остается неизменным:

Теперь мы можем сами убедиться в том, что мы сделали в начале этой страницы: параллельную цепь часто называют делителем тока

за ее способность пропорционировать или делить общий ток на дробные части.

Формула делителя тока

Приложив немного алгебры, мы можем вывести формулу для определения тока параллельного резистора, учитывая только общий ток, отдельное сопротивление и общее сопротивление:

Отношение общего сопротивления к индивидуальному сопротивлению такое же, как отношение тока отдельного (ветви) к общему току. Это известно как формула делителя тока , и это быстрый метод определения токов ветвей в параллельной цепи, когда известен общий ток.

Пример формулы делителя тока

Используя исходную параллельную цепь в качестве примера, мы можем пересчитать токи ветвей, используя эту формулу, если мы начнем со знания общего тока и общего сопротивления:

Если вы уделите время сравнению двух формул делителя, вы увидите, что они удивительно похожи. Обратите внимание, однако, что отношение в формуле делителя напряжения равно R _n (индивидуальное сопротивление), деленное на R _Total , и как отношение в формуле делителя тока равно R _Total , деленное на R _n :

Формула делителя тока и формула делителя напряжения

Довольно легко спутать эти два уравнения, получая соотношения сопротивлений наоборот. Один из способов помочь запомнить правильную форму — помнить, что оба отношения в уравнениях делителя напряжения и тока должны быть меньше единицы. Ведь это делителя уравнений, а не множителя уравнений! Если дробь перевернута, она даст отношение больше единицы, что неверно.

Зная, что общее сопротивление в последовательной цепи (делитель напряжения) всегда больше, чем любое из отдельных сопротивлений, мы знаем, что дробь для этой формулы должна быть R _n над R _Total . И наоборот, зная, что общее сопротивление в параллельной цепи (делитель тока) всегда меньше, чем любое из отдельных сопротивлений, мы знаем, что дробь для этой формулы должна быть R _Итого сверх R _n .

Схема делителя тока Пример применения: Цепь электрического счетчика

Цепи делителя тока находят применение в цепях электрических счетчиков, где требуется провести часть измеренного тока через чувствительное устройство обнаружения. Используя формулу делителя тока, можно выбрать правильный шунтирующий резистор, чтобы пропорционально распределить ток, необходимый для устройства в любом конкретном случае:

Обзор схемы делителя тока:

• Параллельные цепи пропорциональны или «делят» общий ток цепи между токами отдельных ветвей, пропорции строго зависят от сопротивлений: I _n = I _Total (R _Total / R _n )

---

Эта страница под названием 5. 3: Current Divider Circuits и Current Divider Formula распространяется под лицензией GNU Free Documentation License 1.3 и была создана, изменена и/или курирована Тони Р. Купхалдтом (Все о цепях) через исходный контент, который был отредактировано в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.

1. Наверх

• Была ли эта статья полезной?

1. Тип изделия

   Раздел или Страница

   Автор

   Тони Р. Купхалдт

   Лицензия

   ГНУ ФДЛ

   Версия лицензии

   1,3

   Показать оглавление

   нет

   Включено

   да

2. Теги

   1. источник@https://www. allaboutcircuits.com/textbook
   2. источник[1]-рабочая сила-723

led — Как рассчитать ток в параллельных ветвях?

спросил 12 лет, 2 месяца назад

Изменено 8 лет, 4 месяца назад

Просмотрено 3к раз

\$\начало группы\$

Я уже некоторое время играю с Arduino, и хотя я знаю достаточно о простых схемах, чтобы запускать и запускать небольшие проекты, я все еще недостаточно знаю, чтобы понять, что происходит во всем, кроме простейшая из схем.

Я прочитал несколько книг по электронике и несколько статей в Интернете, и хотя я думаю, что понимаю, как работают напряжение, ток, резисторы, конденсаторы и другие компоненты; когда я вижу схему с их большим количеством, я не знаю, что и где происходит.

Немного погодя, чтобы, наконец, разобраться с этим, я купил набор для проектирования электроники 300-в-1, однако он, похоже, перескакивает с «Вот схема с двумя параллельными резисторами» на более сложные вещи, не объясняя, как это сделать. оно работает.

Например, здесь показана простая схема батарея->резистор->светодиод, но показано, что если подключить кнопку параллельно светодиоду, нажатие кнопки выключит светодиод.

Я понимаю, что ток должен проходить по пути наименьшего сопротивления, но я не понимаю , почему он не проходит через оба .

Меня учили, что параллельное соединение двух резисторов приводит к тому, что ток течет через оба, и поэтому в цепи течет больший ток. Я также попытался заменить кнопку в приведенной выше схеме резисторами разного номинала, и, как я и подозревал, резистор с большим значением вообще не влияет на лампочку, но при более низких значениях лампочка начинает тускнеть.

Я не уверен, как применить уравнение E = IR ко всему этому.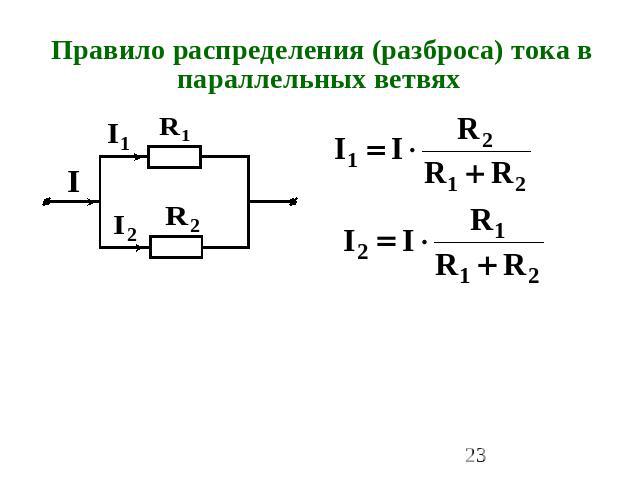

Кроме того, какое сопротивление имеет светодиод? Я попытался измерить его мультиметром, но он не дал показаний.

Извините, если я много болтаю здесь, но я пытаюсь нарисовать картину того, что, как мне кажется, я понимаю и что я хочу понять. Не уверен, что я достиг этого!

О да, и ожидайте еще многого, когда я углублюсь в свой проектный комплект 300-в-1!

• светодиод
• диоды
• сопротивление
• параллельный

\$\конечная группа\$

4

\$\начало группы\$

Ну, я сейчас учусь на электротехнику и могу вам сказать, что такие прыжки, как вы описали, занимают около двух лет лекций в моем университете.

Прежде всего важно знать, какие элементы пассивны, а какие активны. Затем вам нужно знать, какие элементы являются линейными, а какие нет.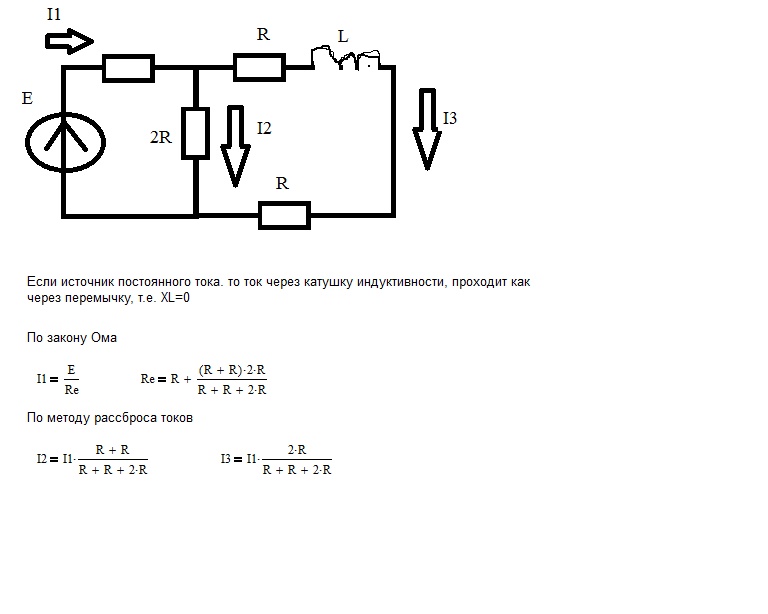 Следующий шаг — получить эквивалентные схемы для имеющихся у вас элементов и посмотреть, как они себя ведут.

Возьмем, к примеру, выключатель. В выключенном состоянии он работает как разомкнутая цепь, а во включенном состоянии — как короткое замыкание. Затем, если у вас есть чувствительное оборудование, вы сможете заметить, что переключатель на самом деле не короткое замыкание, потому что у него есть некоторое сопротивление, но оно очень низкое. Теперь займемся диодом. Диод не является линейным компонентом, поэтому у него нет сопротивления в классическом смысле, в котором, например, есть резисторы. Вместо этого есть кривая V-I диода. Для резистора это линейная функция, и мы можем использовать сопротивление как его характеристику, но для диода она выглядит экспоненциальной.

Как видно из изображения, для правильной работы диода требуется определенное напряжение, и когда вы нажимаете переключатель, это напряжение исчезает. Это означает, что «сопротивление» диода просто стало огромным.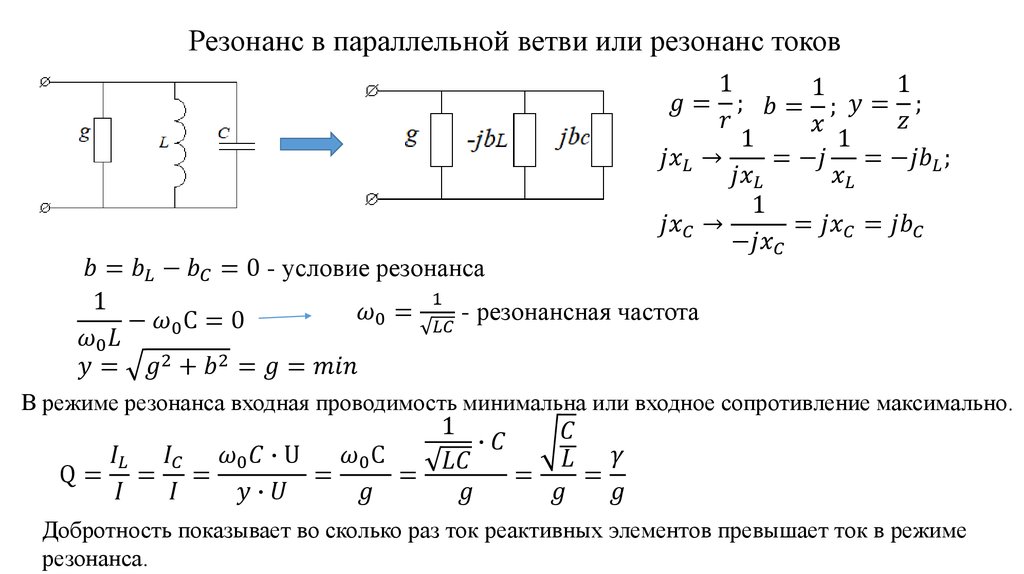 Чтобы понять это, используйте параллельный расчет резистора, скажем, для резистора 1 мОм и резистора 1 МОм и посмотрите, какой ток проходит через каждый из них. Именно так ведет себя схема, которую вы упомянули.

\$\конечная группа\$

3

\$\начало группы\$

Вы не можете напрямую применить E=IR к этому, потому что светодиод — это диод, который является нелинейным устройством.

Упрощенно: диод не будет проводить ток, если на его клеммах нет достаточного напряжения правильной полярности для прямого смещения.

Сопротивление переключателя, закорачивающего диод, очень мало, поэтому напряжение, генерируемое на нем, также очень мало, определенно на много порядков меньше, чем прямое смещение диода.

Если заменить переключатель резистором, все может измениться. Представьте, что светодиод выпал из цепи. Если резистор ограничивает ток в достаточной степени, чтобы создать падение напряжения на нем, равное или превышающее требование прямого смещения светодиода, как только вы включите светодиод в цепь, вы увидите, что светодиод будет гореть тускло, когда вы наблюдаемый.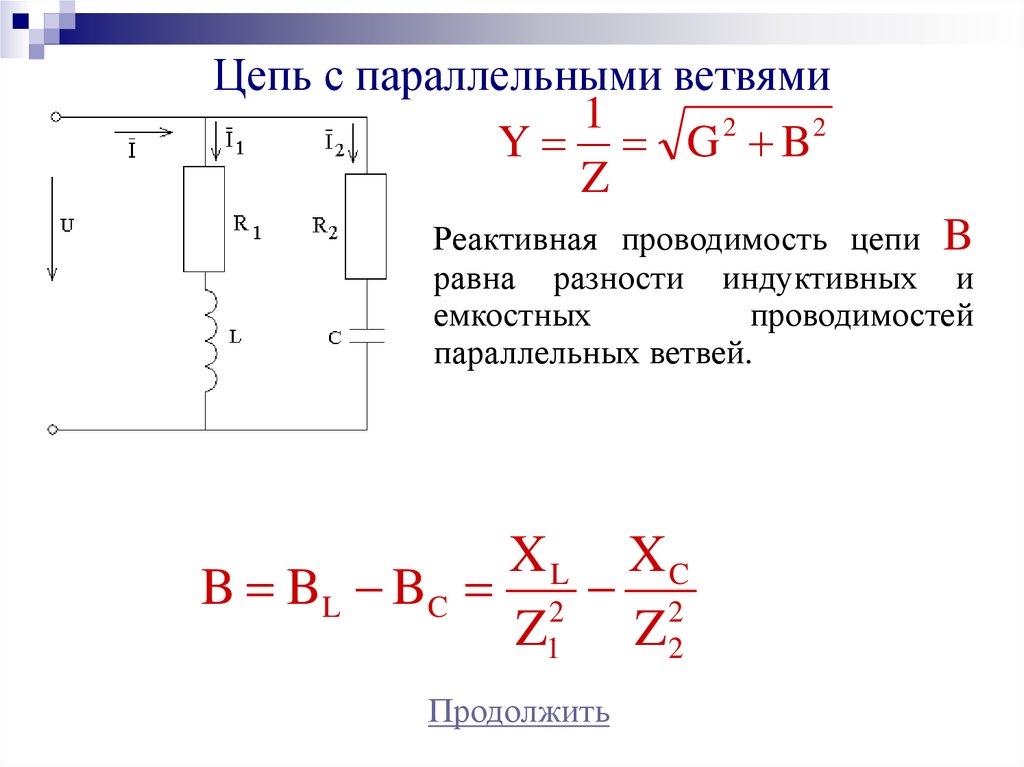 Светодиод и резистор «разделяют» ток — вы заметите, что напряжение на резисторе, параллельном диоду, «зажимается» диодом.

Диоды не являются внутренне резистивными, как резисторы. Их сопротивление чрезвычайно мало, поэтому в цепи светодиодов требуется последовательный резистор, чтобы обеспечить сопротивление, ограничивающее ток и защищающее диод от выхода из строя.

См. статью в Википедии о диодах.

\$\конечная группа\$

\$\начало группы\$

Обычные резисторы являются линейными устройствами; если 10 В через резистор дают ток 1 мА, то 20 В дадут вам 2 мА. Это достаточно просто, но немногие компоненты настолько просты.
Например, светодиод (или любой другой диод) ведет себя иначе.

Если подать низкое напряжение, например 100 мВ, на диод, то вряд ли будет какой-либо ток. Если вы медленно увеличиваете напряжение, вы увидите, что около 0,7 В начинает течь ток, который очень скоро достигает высокого значения, см. график. Мы видим, что напряжение на диоде более или менее постоянно. 0,7 В для обычного кремниевого диода, для светодиодов это напряжение будет выше, в основном в зависимости от цвета, но график в основном такой же. Поскольку ток резко увеличится до значения, которое разрушит светодиод, вам придется использовать токоограничивающий резистор. Увеличение тока будет внезапным, но не немедленным; линия на графике не совсем вертикальная. Это потому, что светодиод также имеет небольшое сопротивление, но оно слишком мало, чтобы ограничить ток до безопасного значения. Итак, что это означает в схеме?

Две основные вещи в цепях (помимо закона Ома) — это законы Кирхгофа, есть закон Кирхгофа о напряжении, также известный как KVL, и закон Кирхгофа о токе (KCL). Мы на мгновение забываем о KCL и смотрим на KVL, закон напряжения. Это говорит о том, что сумма напряжений в любом замкнутом контуре равна нулю. Вы выбираете направление, в котором будете проходить петлю. Выбираем по часовой стрелке. Напряжение источника питания обычно выбирается положительным, двигаясь по часовой стрелке от отрицательного к положительному. Тогда напряжения на резисторе и светодиоде будут отрицательными, потому что сначала мы встречаем положительное. Тогда Кирхгоф говорит: \$V_{BAT} — V_{R} — V_{LED} = 0\$, или \$V_{BAT} = V_{R} + V_{LED}\$. Предположим, что светодиод имеет напряжение 2 В. Тогда мы можем вычислить \$V_{R} = V_{BAT} — V_{LED} = 6V — 2V = 4V\$, а ток через цепь \$I = \frac{V_{R}}{R} = \frac{4V}{330 \Omega} = 12 мА\$.

Что произойдет, если мы поместим переключатель параллельно светодиоду? Если переключатель замкнут, он имеет нулевое сопротивление, и, согласно закону Ома, на нем будет нулевое напряжение. И все же согласно Ому нулевое напряжение на любом сопротивлении означает нулевой ток, поэтому при заданном сопротивлении светодиода через него не будет течь ток.

\$\конечная группа\$

1

\$\начало группы\$

Диод не характеризуется импедансом, в то время как резисторы, конденсаторы и катушки индуктивности могут быть отлиты в одной и той же электрической форме, причем каждый из них имеет «сопротивление» (которое потенциально варьируется в зависимости от «частоты» приложенного сигнала напряжения) .

Диод, с другой стороны, потребляет величину тока, которая нелинейно зависит от напряжения, приложенного к его выводам. Переключатель, включенный параллельно с ним, в закрытом состоянии фактически делает падение напряжения на нем равным нулю, и поэтому он не проводит ток.

Кстати, и по другой причине, вы бы наблюдали подобное явление, если бы заменили светодиод резистором. Нажатие переключателя равносильно включению резистора 0 Ом (или очень маленького) параллельно ему. Почти весь ток будет протекать через короткое замыкание. 9—-+ —> i_2 Delta_V = i_1 * R_1 Delta_V = i_2 * R_2 поэтому: i_1 * R_1 = i_2 * R_2 эквивалентно: i_2 = i_1 * R_1 / R_2 эквивалентно: i_1 = i_2 * R_2 / R_1 эквивалентно: i_1 / i_2 = R_2 / R_1

То есть ток распределяется между параллельными резисторами обратно пропорционально их относительному сопротивлению. Таким образом, если один резистор R_1 в три раза меньше , чем R_2, то он будет потреблять в три раза больше тока, чем R_2.