Что такое закон Ома для полной цепи. Как применяется формула на практике. Примеры решения задач на расчет параметров электрической цепи. Особенности использования закона Ома в различных ситуациях.
Что такое закон Ома для полной цепи
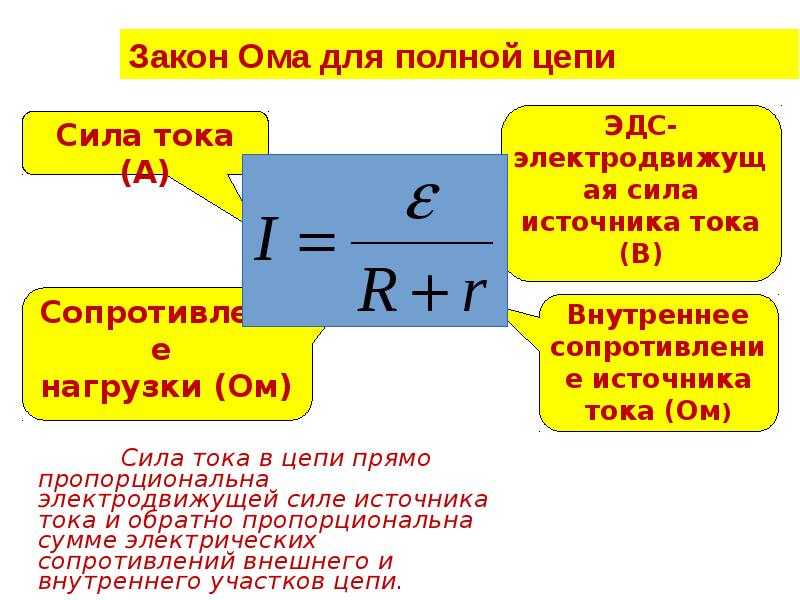
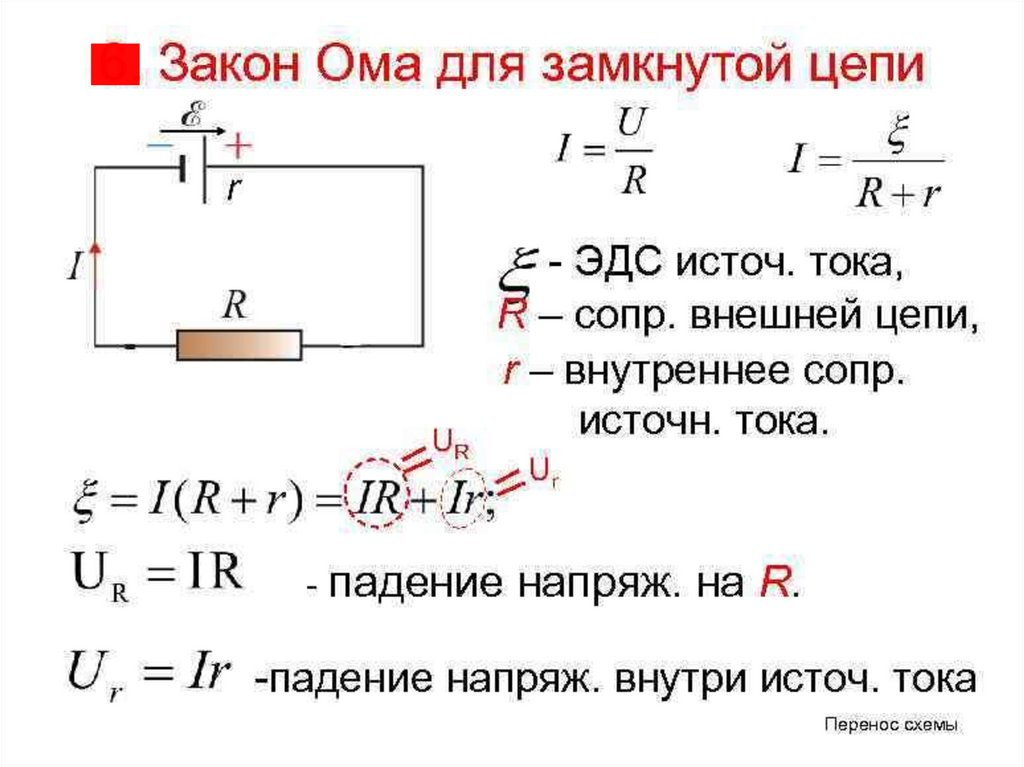
Закон Ома для полной цепи устанавливает связь между электродвижущей силой (ЭДС) источника тока, силой тока в цепи и полным сопротивлением цепи. Он позволяет рассчитывать параметры замкнутой электрической цепи, содержащей источник тока.
Формула закона Ома для полной цепи выглядит следующим образом:
I = ε / (R + r)
где:
- I — сила тока в цепи
- ε — ЭДС источника тока
- R — сопротивление внешней цепи
- r — внутреннее сопротивление источника тока
Физический смысл закона Ома для полной цепи
Закон Ома для полной цепи показывает, что сила тока в замкнутой цепи прямо пропорциональна ЭДС источника и обратно пропорциональна полному сопротивлению цепи, которое складывается из сопротивления внешней цепи и внутреннего сопротивления источника.
Чем больше ЭДС источника, тем больший ток будет протекать по цепи при неизменном сопротивлении. И наоборот, увеличение сопротивления цепи приводит к уменьшению силы тока.
Как применять закон Ома для полной цепи на практике
Закон Ома для полной цепи позволяет решать три основных типа задач:
- Расчет силы тока в цепи при известных ЭДС и сопротивлениях.
- Определение ЭДС источника по известным значениям тока и сопротивлений.
- Нахождение сопротивления участка цепи, зная ЭДС, силу тока и другие сопротивления.
Рассмотрим примеры применения закона Ома для полной цепи в каждом из этих случаев.
Пример расчета силы тока
Дано: ЭДС источника ε = 12 В, сопротивление внешней цепи R = 5 Ом, внутреннее сопротивление источника r = 1 Ом.
Требуется найти силу тока в цепи.
Решение:
Подставляем значения в формулу закона Ома для полной цепи:
I = ε / (R + r) = 12 / (5 + 1) = 12 / 6 = 2 А
Ответ: сила тока в цепи равна 2 А.
Пример определения ЭДС источника
Дано: сила тока в цепи I = 0,5 А, сопротивление внешней цепи R = 9 Ом, внутреннее сопротивление источника r = 1 Ом.
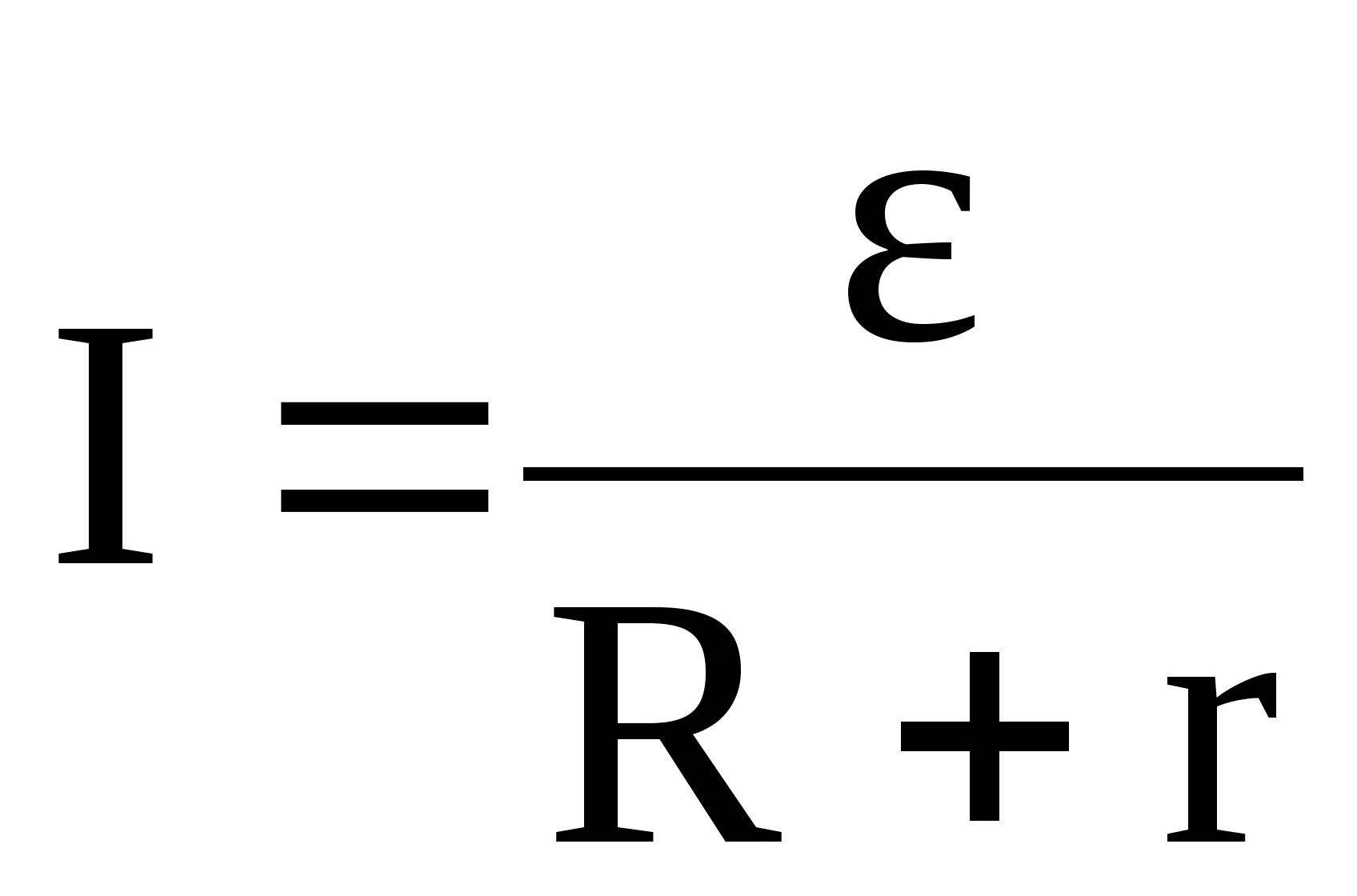
Требуется найти ЭДС источника тока.
Решение:
Преобразуем формулу закона Ома для полной цепи:
ε = I * (R + r)
Подставляем значения:
ε = 0,5 * (9 + 1) = 0,5 * 10 = 5 В
Ответ: ЭДС источника равна 5 В.
Пример расчета сопротивления участка цепи
Дано: ЭДС источника ε = 24 В, сила тока в цепи I = 2 А, внутреннее сопротивление источника r = 2 Ом.
Требуется найти сопротивление внешней цепи.
Решение:
Преобразуем формулу закона Ома для полной цепи:
R = ε / I — r
Подставляем значения:
R = 24 / 2 — 2 = 12 — 2 = 10 Ом
Ответ: сопротивление внешней цепи равно 10 Ом.
Особенности применения закона Ома для полной цепи
- Закон применим только для замкнутых цепей постоянного тока.
- Необходимо учитывать внутреннее сопротивление источника тока.
- При последовательном соединении нескольких источников их ЭДС суммируются.
- Для сложных цепей с несколькими источниками используются правила Кирхгофа.
Значение закона Ома для полной цепи в электротехнике
Закон Ома для полной цепи имеет большое практическое значение в электротехнике. Он позволяет:
- Рассчитывать параметры электрических цепей
- Подбирать оптимальные режимы работы источников тока
- Анализировать эффективность передачи электроэнергии
- Проектировать электрические системы и устройства
Сравнение с законом Ома для участка цепи
Закон Ома для полной цепи является обобщением закона Ома для участка цепи. Основные отличия:
- Учитывает ЭДС источника и его внутреннее сопротивление
- Применяется ко всей замкнутой цепи, а не к отдельному участку
- Позволяет рассчитывать параметры источника тока
Ограничения закона Ома для полной цепи
Несмотря на широкое применение, закон Ома для полной цепи имеет ряд ограничений:
- Не применим для цепей переменного тока
- Не учитывает нелинейные элементы (диоды, транзисторы)
- Нарушается в сверхпроводниках
- Не работает для очень сильных токов и напряжений
Часто задаваемые вопросы
В чем измеряется ЭДС источника тока?
ЭДС источника тока измеряется в вольтах (В), так же как и напряжение.
Что такое внутреннее сопротивление источника?
Внутреннее сопротивление — это сопротивление, которое оказывает прохождению тока сам источник. Оно обусловлено конструкцией источника и его физическими свойствами.

Как закон Ома связан с мощностью электрического тока?
Зная силу тока и напряжение, можно рассчитать мощность по формуле P = I * U. Таким образом, закон Ома позволяет определить мощность в электрической цепи.
Заключение
Закон Ома для полной цепи — фундаментальный закон электротехники, позволяющий анализировать и рассчитывать параметры замкнутых электрических цепей. Его понимание и правильное применение необходимо для эффективной работы с электрическими системами и устройствами.
Закон ома для полной цепи: формула для расчета
В электрике и электронике действует несколько основных физических законов, объясняющих и регулирующих все текущие процессы. К наиболее значимым относится закон Ома для полной цепи, описывающий взаимодействия меду током, напряжением и сопротивлением. Эти положения широко применяются на практике при расчетах всевозможных электронных схем.
Содержание
Отдельный участок и полная электрическая цепь
Закон Ома, применительно к участку или всей цепи, может рассматриваться в двух вариантах расчетов:
- Отдельный краткий участок. Является частью схемы без источника ЭДС.
- Полная цепь, состоящая из одного или нескольких участков. Сюда же входит источник ЭДС со своим внутренним сопротивлением.
Расчет тока участка электрической схемы
В этом случае применяется основная формула I = U/R, в которой I является силой тока, U – напряжением, R – сопротивлением. По ней можно сформулировать общепринятую трактовку закона Ома:
Электрический ток, проходящий через некоторый участок цепи, находится в прямой пропорции с приложенным напряжением, и в обратной пропорции – с сопротивлением.
Данная формулировка является основой для многих других формул, представленных на так называемой «ромашке» в графическом исполнении. В секторе Р – определяется мощность, в секторах I, U и R – проводятся действия, связанные с силой тока, напряжением и сопротивлением.
Каждое выражение – и основное и дополнительные, позволяют рассчитать точные параметры элементов, предназначенных для использования в схеме.
Специалисты, работающие с электрическими цепями, выполняют быстрое определение любого из параметров по методике треугольников, изображенных на рисунке.
В расчетах следует учитывать сопротивление проводников, соединяющих между собой элементы участка. Поскольку они изготавливаются из разных материалов, данный параметр будет отличаться в каждом случае. Если же потребуется сформировать полную схему, то основная формула дополняется параметрами источника напряжения, например, аккумуляторной батареи.
Вариант расчета для полной цепи
Полная цепь состоит из отдельно взятых участков, объединенных в единое целое вместе с источником напряжения (ЭДС). Таким образом, существующее сопротивление участков дополняется внутренним сопротивлением подключенного источника. Следовательно, основная трактовка, рассмотренная ранее, будет читаться следующим образом: I = U / (R + r). Здесь уже добавлен резистивный показатель (r) источника ЭДС.
Таким образом, существующее сопротивление участков дополняется внутренним сопротивлением подключенного источника. Следовательно, основная трактовка, рассмотренная ранее, будет читаться следующим образом: I = U / (R + r). Здесь уже добавлен резистивный показатель (r) источника ЭДС.
С точки зрения чистой физики этот показатель считается очень малой величиной. Однако, на практике, рассчитывая сложные схемы и цепи, специалисты вынуждены его учитывать, поскольку дополнительное сопротивление оказывает влияние на точность работы. Кроме того, структура каждого источника очень разнородная, в результате, сопротивление в отдельных случаях может выражаться достаточно высокими показателями.
Приведенные расчеты выполняются применительно к цепям постоянного тока. Действия и расчеты с переменным током производятся уже по другой схеме.
Действие закона к переменной величине
При переменном токе сопротивление цепи будет представлять из себя так называемый импеданс, состоящий из активного сопротивления и реактивной резистивной нагрузки. Это объясняется наличием элементов с индуктивными свойствами и синусоидальной величиной тока. Напряжение также является переменной величиной, действующей по своим коммутационным законам.
Это объясняется наличием элементов с индуктивными свойствами и синусоидальной величиной тока. Напряжение также является переменной величиной, действующей по своим коммутационным законам.
Следовательно, схема цепи переменного тока по закону Ома рассчитывается с учетом специфических эффектов: опережения или отставания величины тока от напряжения, а также наличия активной и реактивной мощности. В свою очередь, реактивное сопротивление включает в себя индуктивную или емкостную составляющие.
Все этим явлениям будет соответствовать формула Z = U / I или Z = R + J * (XL – XC), в которой Z является импедансом; R – активной нагрузкой; XL , XC – индуктивной и емкостной нагрузками; J – поправочный коэффициент.
Последовательное и параллельное включение элементов
Элементы полной цепи или участка цепи могут соединяться последовательно или параллельно. Для каждого варианта действие тока и напряжения будет разным, поэтому закон Ома для замкнутой цепи в обоих случаях тоже отличается. Данный физические свойства комбинированно используются в различных электрических схемах.
Данный физические свойства комбинированно используются в различных электрических схемах.
Цепь последовательно включенных резистивных элементов
Если в качестве примера взять два элемента на отдельном участке, то поведение основных величин можно записать в следующем виде:
- I = I1= I2 (силы токов равны)
- U = U1+ U2 (общее напряжение состоит из суммы напряжений)
- R = R1+ R2 (общее сопротивление также является суммой двух сопротивлений)
Отсюда можно сделать вывод, что вне зависимости от количества резистивных элементов 1, 2 или 3, соединенных последовательно, сила тока на участке остается неизменной. Общее значение напряжения эквивалентно источнику ЭДС, а для каждого компонента определяется основной формулой закона Ома.
Цепь параллельно включенных резистивных элементов
При параллельном подключении действие закона Ома происходит несколько иначе:
- I = I1+ I2 … (силы токов, проходящих через элементы, складываются)
- U = U1= U2 … (все напряжения равны между собой)
- 1 / R = 1 / R1+ 1 / R2 + … (сопротивление суммируется по отдельной схеме)
Довольно часто используются смешанные схемы подключения, в которых используются оба варианта, объединенные в замкнутый контур. В этом случае сначала рассчитывается общий резистивный номинал на участке с параллельным подключением, после чего к полученному результату добавляется значение резистора на последовательном соединении.
В этом случае сначала рассчитывается общий резистивный номинал на участке с параллельным подключением, после чего к полученному результату добавляется значение резистора на последовательном соединении.
Интегральная и дифференциальная формы закона
Все варианты, рассмотренные выше, подходят ближе к идеальным условиям, где каждый элемент имеет свой постоянный показатель. В том числе и в проводниках рассматривается однородная структура, хотя на практике такое встречается очень редко. Большинство схем состоят из множества участков, на которых используются разные проводники, отличающиеся материалом и сечением.
Интегральная форма расчетов практически совпадает с действием закона Ома для полной цепи и других его производных. Следовательно, сила тока, протекающего в проводнике, будет зависеть от разности потенциалов на его концах и его полного сопротивления. То есть, напряжение можно определить: I * R = φ1 – φ2 + έ или же U=I x R.
Дифференциальная форма используется в основном для изучения и теоретических расчетов бесконечно малых проводников на ничтожно малом участке цепи. Коротко это можно написать в таком виде:
Коротко это можно написать в таком виде:
- ej = aE
В этом выражении А является удельной теплопроводностью, E – напряженностью электрического поля, j – плотностью потока частиц с электрическим зарядом. Следовательно, произведение ej будет плотностью электрического тока. Поскольку Закон Ома в данном случае касается лишь одной точки, поэтому он и получил название дифференциальной формы.
Выводы
В данной статье мы постарались дать простое объяснение закона Ома для полной цепи. Знание этих на первый взгляд простых вещей может сослужить Вам неплохую службу на экзамене. Специалисты в области электрики и электроники в своей работе постоянно используют закон Ома для полной электрической цепи и ее отдельных участков.
Видеоинструкция
Закон Ома для полной цепи
1.
 Источник тока
Источник токаПри прохождении тока в проводнике выделяется некоторое количество теплоты. Согласно закону сохранения энергии при этом в электрическую цепь должна поступать энергия.
Может ли источником этой энергии быть электростатическое поле? Нет, не может, потому что при перемещении заряда вдоль всей цепи, то есть по замкнутой траектории, работа электростатического поля равна кулю.
Следовательно, для существования тока в замкнутой цепи в ней должен быть участок, на котором свободные заряды движутся против сил электростатического поля. Таким участком цепи является источник тока (рис. 59.1).
В источнике тока на свободные заряды действуют силы, которые имеют не электростатическую природу. Их называют сторонними силами. В результате действия сторонних сил происходит разделение зарядов: на одном полюсе источника тока накапливается положительный заряд, а на другом – отрицательный. Вследствие этого возникает электростатическое поле, которое движет свободные заряды в электрической цепи вне источника тока, то есть во внешней цепи.
В химических источниках тока сторонние силы имеют химическую природу. Например, если погрузить цинковый и медный электроды в серную кислоту, то положительные ионы цинка будут чаще покидать электрод, чем положительные ионы меди. В результате между медным и цинковым электродами возникнет разность потенциалов: потенциал медного электрода будет больше, чем цинкового. Медный электрод станет положительным полюсом источника тока, а цинковый – отрицательным.
В генераторах электростанций сторонними силами являются силы, действующие на свободные электроны в металле со стороны вихревого электрического поля, порождаемого переменным магнитным полем. Работа вихревого электрического поля по перемещению заряда вдоль замкнутого контура не равна нулю. Действие генераторов тока мы рассмотрим в курсе физики 11-го класса.
Электродвижущая сила источника тока
В источнике тока сторонние силы, перемещая свободные заряды против действия сил электростатического поля, совершают работу, которую мы обозначим Aстор.
Эта работа пропорциональна заряду q, который перемещается вдоль цепи за данный промежуток времени. Поэтому отношение работы сторонних сил к величине заряда не зависит ни от Aстор, ни от q. Следовательно, оно является характеристикой источника тока. Это отношение называют электродвижущей силой источника (ЭДС) и обозначают ξ:
ξ = Aстор/q. (1)
(Это название не совсем удачно, потому что ЭДС – не «сила» в механическом смысле, а энергетическая характеристика источника.)
ЭДС, как и напряжение, измеряют в вольтах. Например, ЭДС батарейки составляет несколько вольт.
2. Закон Ома для полной цепи
Если сила тока в цепи равна I, то за время t по цепи проходит заряд q = It. Поэтому формулу (1) можно записать в виде
Aстор = ξIt. (2)
При этом во внешней цепи сопротивлением R выделяется количество теплоты
Qвнеш = I2Rt, (3)
а внутри источника тока выделяется количество теплоты
Qвнутр = I2rt, (4)
где r – сопротивление источника, которое называют его внутренним сопротивлением.
Из закона сохранения энергии следует, что
Qвнеш + Qвнутр = Aстор. (5)
? 1. Докажите, что из формул (2) – (5) следует:
I = ξ / (R + r). (6)
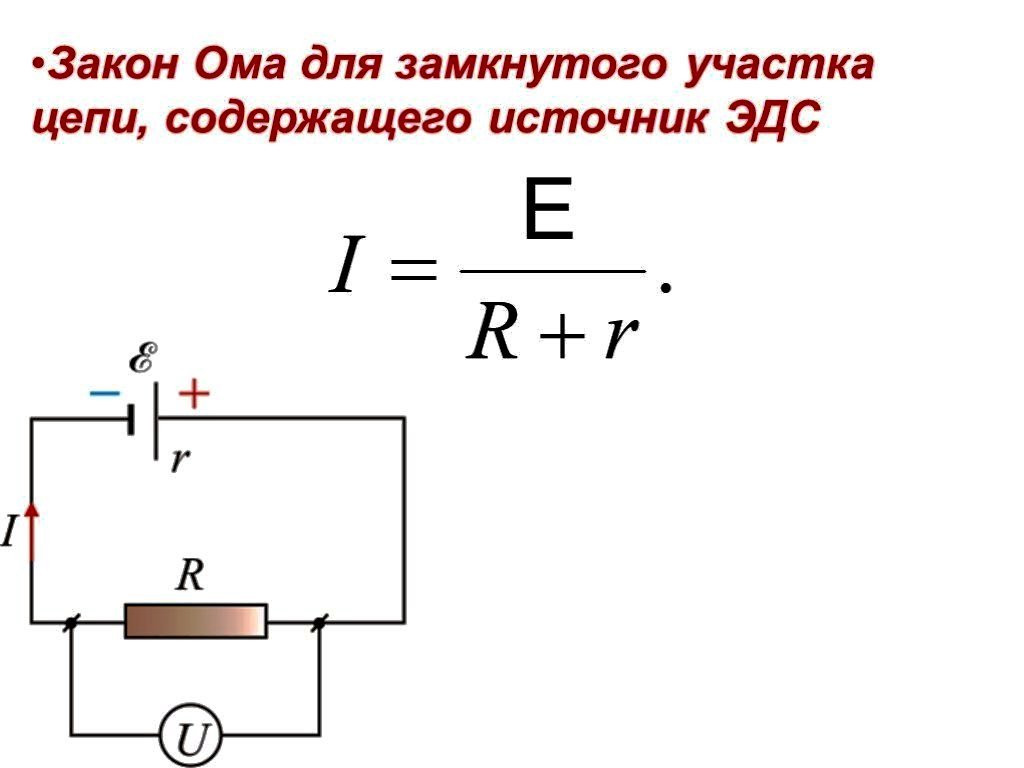
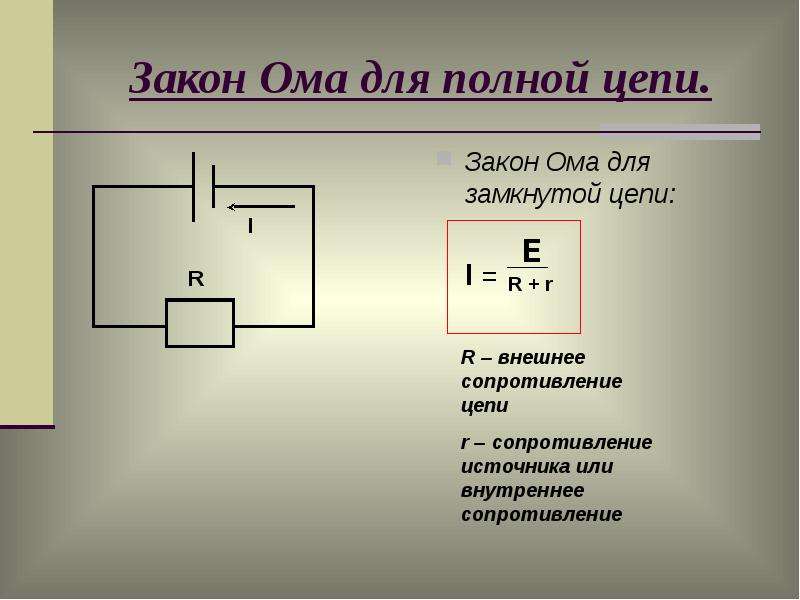
Это соотношение называют законом Ома для полной цепи.
Сумму сопротивлений R + r называют полным сопротивлением цепи.
? 2. ЭДС источника тока 12 В, а его внутреннее сопротивление равно 2 Ом.
а) Чему равна сила тока в цепи, если сопротивление внешней цепи равно 4 Ом?
б) Какова максимально возможная сила тока в цепи? При каком сопротивлении внешней цепи это имеет место?
? 3. При внешнем сопротивлении 2 Ом сила тока в цепи равна 1,5 А, а при внешнем сопротивлении 4 Ом сила тока равна 1 А.
а) Чему равно внутреннее сопротивление источника?
б) Чему равна ЭДС источника?
Напряжение на полюсах источника
Закон Ома для полной цепи можно записать в виде
ξ = IR + Ir. (7)
Первое слагаемое в этой формуле согласно закону Ома для участка цепи равно напряжению U на полюсах источника тока:
IR = U.
Поэтому формулу (7) можно записать в виде
U = ξ – Ir. (8)
Формула (8) выражает зависимость напряжения U на полюсах источника тока от силы тока I в цепи.
Поставим опыт
Зависимость U(I) можно измерить на опыте, изменяя силу тока в цепи с помощью реостата (рис. 59.2, а, б). Красная пунктирная линия на схеме 59.2, б показывает, как идет ток в реостате. Например, если ползунок реостата, изображенного на рисунке 59,2, а, сдвинуть вправо, то сопротивление реостата увеличится, потому что увеличится длина обмотки, по которой идет ток.
? 4. На рисунке 59.3 изображен график зависимости U(I) для некоторого источника тока.
а) Чему равна ЭДС этого источника тока?
б) Чему равна наибольшая сила тока?
в) Чему равно внутреннее сопротивление источника тока?
г) Чему равно внешнее сопротивление, когда сила тока равна нулю?
д) Чему равно внешнее сопротивление, когда сила тока максимальна?
е) Чему равно внешнее сопротивление при I = 1,5 А?
Максимальное напряжение на полюсах источника равно ξ. Это имеет место при I = 0. Сила тока равна нулю, когда полюса источника разомкнуты (в этом случае внешнее сопротивление цепи является бесконечно большим).
Это имеет место при I = 0. Сила тока равна нулю, когда полюса источника разомкнуты (в этом случае внешнее сопротивление цепи является бесконечно большим).
Следовательно, напряжение между разомкнутыми полюсами источника тока равно ЭДС этого источника.
Минимальное же напряжение между полюсами источника равно нулю. Это имеет место при коротком замыкании, когда внешнее сопротивление R = 0. В этом случае сила тока максимальна. Ее называют силой тока короткого замыкания.
? 5. Покажите, что сила тока короткого замыкания выражается формулой
Iка = ξ/r. (9)
Подсказка. Воспользуйтесь законом Ома для полной цепи.
Из формулы (9) видно, что при очень малом внутреннем сопротивлении источника (как, например, у автомобильного аккумулятора) сила тока короткого замыкания будет очень большой, что может вывести источник тока из строя.
? 6. Сила тока при коротком замыкании батарейки равна 2 А. Когда к батарейке подключили резистор сопротивлением 4 Ом, сила тока стала равной 1 А.
а) Как изменилось полное сопротивление цепи?
б) Чему равно внутреннее сопротивление батарейки?
Измерив напряжение на полюсах источника и силу тока в цепи при двух различных значениях сопротивления внешней цепи, можно найти ЭДС ξ и внутреннее сопротивление r источника тока. Это можно сделать графически и аналитически.
? 7. При силе тока в цепи 2 А напряжение на полюсах источника равно 8 В, а при силе тока 4 А напряжение на полюсах равно 4 В.
а) Постройте систему координат I, U и нанесите две точки графика зависимости U(I) согласно приведенным данным.
б) Проведите прямую через эти точки и отметьте точки пересечения этой прямой с осями координат. Используя этот график, найдите, чему равны ЭДС, сила тока короткого замыкания и внутреннее сопротивление источника тока.
в) Используя уравнение (8), составьте систему двух уравнений с двумя неизвестными ξ и r и решите ее.
3. КПД источника тока
Работу тока во внешней цепи называют полезной работой. Обозначим ее Aпол. Используя формулу для работы тока, получаем:
Используя формулу для работы тока, получаем:
Aпол = I2Rt.
Поскольку источник обладает внутренним сопротивлением, полезная работа меньше работы сторонних сил, потому что часть работы сторонних сил расходуется на выделение в источнике тока количества теплоты I2rt. Поскольку
Aстор = I2Rt + I2rt,
получаем для отношения полезной работы к работе сторонних сил:
η = Aпол / Aстор = (I2Rt) / (I2Rt + I2rt) = R / (R + r).
Это отношение, выраженное в процентах, называют КПД источника тока.
? 8. При каком отношении внешнего сопротивления к внутреннему сопротивлению КПД источника тока равен: 50 %; 80 %? Почему случай, когда КПД источника тока равен 100 %, не представляет практического интереса?
Дополнительные вопросы и задания
9. На рисунке 59.4 изображена схема измерения зависимости напряжения U на полюсах источника тока от силы тока I.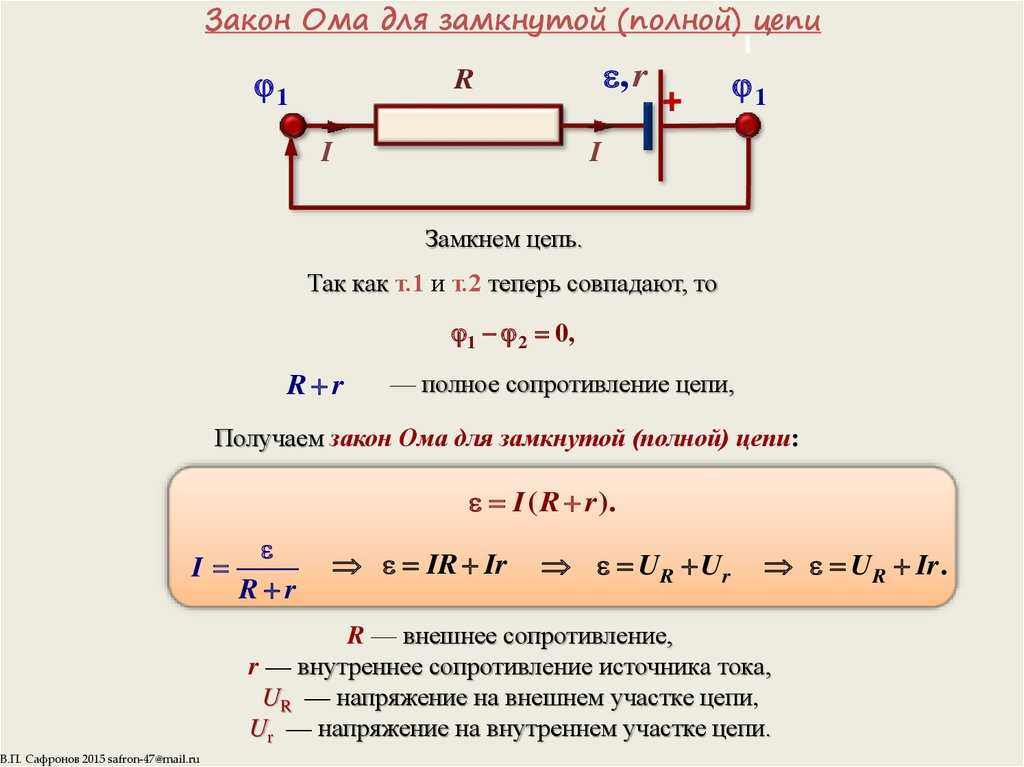 Амперметр и вольтметр считайте идеальными. Сопротивление всей обмотки реостата 16 Ом. При первом положении ползунка реостата показания приборов 3 А и 8 В, а при втором положении – 2 А и 12 В.
Амперметр и вольтметр считайте идеальными. Сопротивление всей обмотки реостата 16 Ом. При первом положении ползунка реостата показания приборов 3 А и 8 В, а при втором положении – 2 А и 12 В.
а) Как сдвинули ползунок реостата между первым и вторым измерениями – влево или вправо?
б) Чему равны ЭДС источника тока и его внутреннее сопротивление?
в) Каковы будут показания приборов, если ползунок реостата передвинуть в крайнее левое положение? в крайнее правое?
10. При силе тока 6 А мощность тока во внешней цепи равна 90 Вт, а при силе тока 2 А она равна 60 Вт.
а) Чему равна ЭДС источника тока?
б) Чему равно внутреннее сопротивление источника тока?
в) Чему равно напряжение на полюсах источника в первом и втором случаях?
г) Чему равен КПД источника тока в первом и втором случаях?
Закон Ома для полной цепи – формула, определение
4.6
Средняя оценка: 4.6
Всего получено оценок: 151.
4.6
Средняя оценка: 4.6
Всего получено оценок: 151.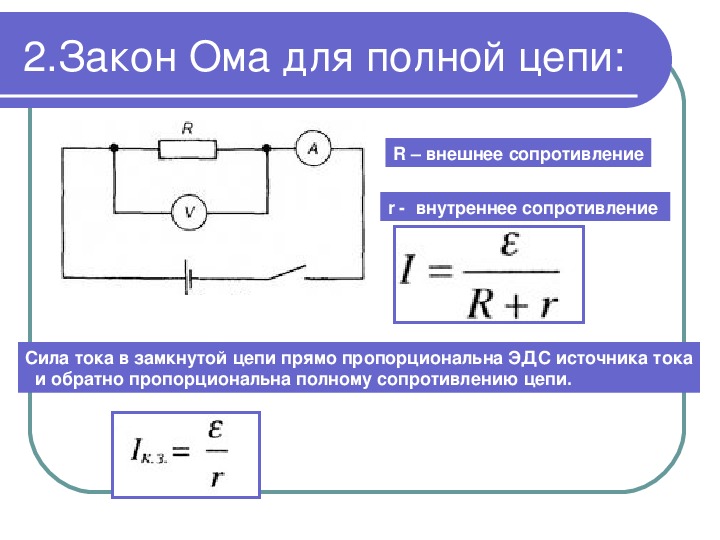
Закон Ома связывает в одной формуле электрические параметры, с помощью которых можно определить токи и напряжения на каждом элементе цепи. Данный закон можно распространить на всю электрическую цепь. Рассмотрим, как это происходит.
Источник ЭДС в полной цепи
Для возникновения электрического тока в замкнутой цепи, эта цепь должна содержать хотя бы один особый элемент, в котором будет происходить работа по переносу зарядов между его полюсами. Силы, переносящие заряды внутри этого элемента, делают это против электрического поля, а значит, их природа должна быть отлична от электрической. Поэтому такие силы называются сторонними.
Рис. 1. Сторонние силы в физике.Элемент электрической цепи, в котором происходит работа сторонних сил по переносу зарядов против действия электрического поля, называется источником тока. Главная его характеристика – это величина сторонних сил. Для ее характеристики вводится специальная мера – Электродвижущая Сила (ЭДС), она обозначается буквой $\mathscr{E}$.
Значение ЭДС источника тока равно отношению сторонних сил по переносу заряда к величине этого заряда:
$$\mathscr{E}={A_{ст}\over q}$$
Поскольку смысл ЭДС очень близок к смыслу электрического напряжения (напомним, напряжение – это отношение работы, совершаемой электрическим полем, переносящим заряд, к величине этого заряда), то ЭДС так же, как и напряжение, измеряется в Вольтах:
$$1В={Дж\overКл}$$
Второй важнейшей электрической характеристикой реального источника тока является его внутреннее сопротивление. При переносе зарядов между клеммами происходит их взаимодействие с веществом источника ЭДС, а поэтому, источник для электрического тока также представляет некоторое сопротивление. Внутреннее сопротивление, как и обычное сопротивление, измеряется в Омах, но обозначается малой латинской буквой $r$.
Рис. 2. Примеры источников тока.Закон Ома для полной цепи
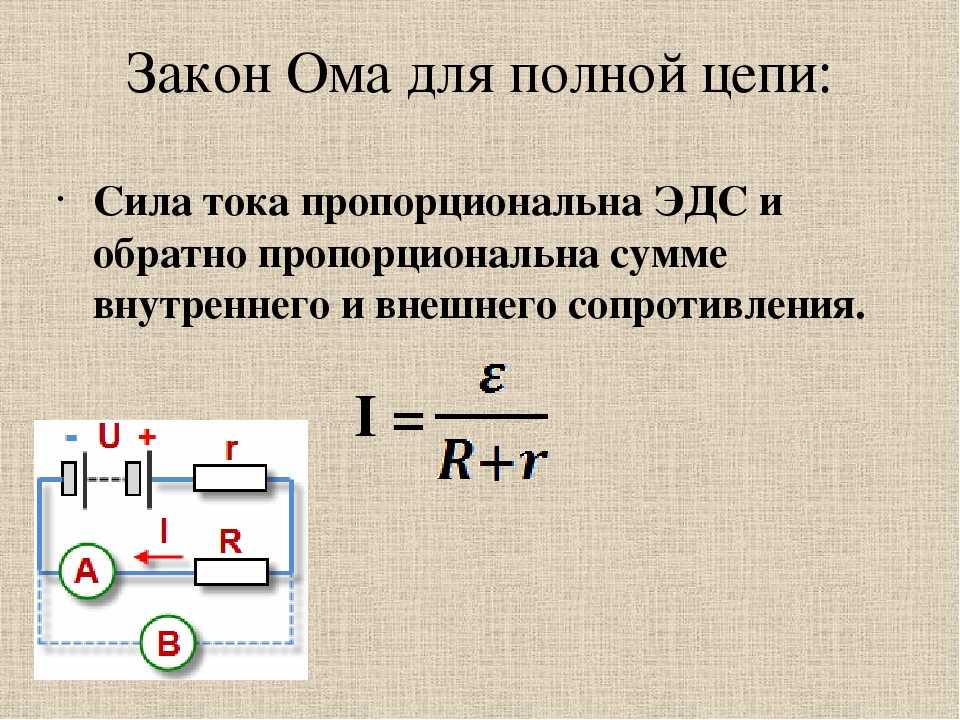
Когда в полной электрической цепи имеется источник ЭДС, в цепи возникает ток. Его величину можно найти, используя закон сохранения энергии и закон Джоуля-Ленца, выражающий энергию, выделяемую на электрическом элементе при прохождении по нему тока.
Сокращая и перенося значение тока влево, окончательно получаем формулу Закона Ома для полной цепи:
$$I={\mathscr{E}\over R+r}$$
Сила тока в замкнутой цепи равна отношению ЭДС источника тока к сумме сопротивления цепи и внутреннего сопротивления источника.
Внутреннее сопротивление реальных источников тока очень невелико (доли ома), поэтому для небольших мощностей оно почти не оказывает влияния на электрическую цепь. Однако, если мощность цепи велика, то пренебрегать этим сопротивлением нельзя, на нем может выделяться заметное количество тепла.
Сложные цепи с несколькими источниками тока
В замкнутой цепи может быть не один источник тока.
В этом случае полная ЭДС цепи равна алгебраической сумме ЭДС источников. В цепи произвольно выбирается направление обхода, и если источник вызывает ток в этом направлении, его ЭДС считается положительной, а иначе – отрицательной. Сопротивление не имеет направления, а поэтому внешние и внутренние сопротивления всегда суммируются.
В реальных сложных электрических цепях может быть много разветвлений и контуров, причем, источники тока могут находиться в различных местах. Для определения токов на всех ветвях цепи используются системы уравнений, построенные на основе специальных правил (законов) Кирхгофа.
Рис. 3. Сложные цепи и законы Кирхгофа.Что мы узнали?
Реальные источники тока обладают внутренним сопротивлением. Согласно Закону Ома для полной цепи, ток в замкнутой цепи равен отношению ЭДС источника тока к сумме сопротивления цепи и внутреннего сопротивления источника. Если в простой цепи несколько источников ЭДС, то общая ЭДС равна алгебраической сумме ЭДС источников. Для сложных цепей используются системы уравнений на основе правил Кирхгофа.
Тест по теме
Доска почёта
Чтобы попасть сюда — пройдите тест.
Пока никого нет. Будьте первым!
Оценка доклада
4.6
Средняя оценка: 4. 6
6
Всего получено оценок: 151.
А какая ваша оценка?
Закон Ома: Полное руководство
На этой странице:
Закон Ома является одним из наиболее важных и фундаментальных законов, когда речь идет об управлении электрическими цепями и системами. Кто-то может возразить, что закон Ома так же важен для студентов-электриков и проектирования электротехники, как законы Эйнштейна для физиков.
Закон Ома связывает ток, сопротивление и напряжение в простом уравнении. Если мы знаем любую из двух основных величин (напряжение, ток или сопротивление), мы можем использовать закон Ома для расчета третьей. В этой статье мы рассмотрим, что такое закон Ома, как мы используем различные формулы, а также ответим на некоторые из наиболее часто задаваемых вопросов о нем.
Что такое закон Ома?
Закон Ома — это расчет, который используется для определения и определения взаимосвязи между напряжением, током и сопротивлением в электрической цепи. Закон Ома гласит, что ток в проводнике между двумя разными точками пропорционален величине напряжения на проводнике. точки.
Закон Ома гласит, что ток в проводнике между двумя разными точками пропорционален величине напряжения на проводнике. точки.
Закон Ома, названный в честь немецкого физика Георга Ома, рассматривает и принимает во внимание ключевые величины, которые используются и обнаруживаются в электрических цепях. Ключевыми величинами в электрической цепи являются напряжение (В), ток (I) и сопротивление (Ом). Если какая-либо из двух ключевых величин известна, вы можете применить закон Ома для определения недостающей величины с помощью треугольника закона Ома (подробнее об этом позже).
Это привело к открытию уравнений закона Ома V=IR или I=V/R или R=V/I. Мы подробно рассмотрим все уравнения ниже, но давайте начнем с основ.
Кто открыл закон Ома?
Георг Ом Георг Саймон Ом открыл закон Ома , когда он описал математическую зависимость между напряжением, током и сопротивлением в электрических цепях. Закон Ома был назван в честь немецкого физика Георга Ома. Георг Ом жил с 1789 г.-1854. Она была опубликована в его статье 1827 года, которая называлась «Математическое исследование гальванической цепи».
Георг Ом жил с 1789 г.-1854. Она была опубликована в его статье 1827 года, которая называлась «Математическое исследование гальванической цепи».
Уравнение закона Ома
Уравнение закона Ома использует основные величины, которые находятся в электрической цепи или системе. Как мы уже говорили ранее, мы должны знать любую из двух-трех величин, чтобы использовать закон Ома. Тремя основными величинами являются напряжение, ток и сопротивление. В законе Ома используется простой треугольник, чтобы упростить использование уравнения.
Формулы для закона Ома выглядят так:
I = V/R или V = IR или R = V/I
- I = ток
- V = напряжение
- R = Сопротивление

Ниже мы рассмотрим несколько примеров того, как использовать треугольник закона Ома при расчете напряжения, тока и сопротивления.
Чтобы найти уровень напряжения с помощью треугольника закона Ома
Треугольник закона Ома для расчета напряженияВольт (В) = Ампер (I) x Сопротивление (Ом) используйте значения тока и сопротивления в приведенной выше формуле.
Чтобы найти напряжение (В), используя закон Ома, мы используем формулу – Напряжение (В) = ток (I) x сопротивление (Ом)
Чтобы найти уровень тока, используя треугольник закона Ома
Треугольник закона Ома для рассчитать токАмпер (I) = Напряжение (В) ÷ Сопротивление (Ом)
Если мы не знаем значение тока, мы можем использовать значения напряжения и сопротивления в приведенной выше формуле.
Чтобы найти ток (I), используя закон Ома, мы используем формулу – Ток (I) = Напряжение (В) ÷ Сопротивление (Ом)
Чтобы найти уровень сопротивления, используя треугольник закона Ома
Треугольник закона Ома для расчета сопротивленияСопротивление (Ом) = Напряжение (В) ÷ Ампер (I)
Если мы не знаем значения сопротивления, мы можем использовать значения напряжения и тока в приведенной выше формуле.
Чтобы найти Сопротивление (Ом) по закону Ома, мы используем формулу – Сопротивление (Ом) = Напряжение (В) ÷ Ток (I) ) может быть выражен как E — это потому, что некоторые люди используют E для обозначения напряжения на источнике питания, таком как батареи или электрические генераторы.
Если какое-либо из двух значений известно, вы можете использовать приведенные выше уравнения, чтобы узнать третье значение.
Теперь мы применим формулы на практике и используем их в примерах ниже, чтобы найти значения.
Несколько примеров использования закона Ома
Ниже мы рассмотрим несколько примеров использования закона Ома на ряде электрических цепей с отсутствующим значением ключа. Применим формулу закона Ома для расчета недостающих значений.
Для расчета напряжения (В)
Используя треугольник закона Ом, мы видим, что нам нужно выполнить расчет:
В или E = I X R
В или E = 4 A X 14 Ом = 56 В
56 В = 4 A x 14 Ом
Ответ: 56 Вольт
Для расчета силы тока (А)
Используя треугольник закона Ом, мы видим, что нам нужно выполнить расчет:
I = V или E ÷ R
I = 12 В ÷ 6 Ом = 2 А
2 А = 12 В ÷ 6 Ом
Ответ: 2 Ампера
Для расчета сопротивления (Ом)
Используя треугольник закона Ом, мы видим, что нам нужно выполнить расчет:
R = V или E ÷ I
R = 48 В ÷ 10 А = 4,8 Ом
4,8 Ом = 48 В ÷ 10 А
Ответ: 4,8 Ом
Почему напряжение обозначается буквой Е в законе Ома?
Буква E в законе Ома означает электромагнитную силу или по-немецки «Elektromotorische Kraft». Это связано с тем, что термин «напряжение» не использовался, поскольку вольт не был общепризнанной единицей измерения примерно до 1881 года.0003
Это связано с тем, что термин «напряжение» не использовался, поскольку вольт не был общепризнанной единицей измерения примерно до 1881 года.0003
Вольт был назван в честь Алессандро Вольта, итальянского физика, который изобрел батарею.
Почему ток обозначен буквой I в законе Ома?
I в законе Ома на самом деле происходит от немецкого слова «Intensität», которое в переводе с немецкого означает интенсивность. Это на самом деле имеет большой смысл, когда Георг Ом разработал закон Ома в 1827 году, он заявил, что ток зависит от его потока или интенсивности.
Буква А использовалась в 1820 году для обозначения тока, когда французский физик Андре-Мари Ампер разработал закон Ампера.
Применение закона Ома
Закон Ома используется для определения ряда вещей, которые вы будете использовать или видеть вокруг себя в повседневной жизни. Ниже мы приведем несколько примеров использования формул Георга Ома.
- Бытовые электрические вентиляторы – скорость электрического вентилятора регулируется поворотным переключателем на стене или нажатием кнопки скорости.
 Это означает, что ток контролируется путем регулирования или регулировки сопротивления через устройство регулятора, которое затем отправляется на выходную клемму, чтобы сообщить двигателю, на какой скорости работать. Вы можете рассчитать значение входа здесь, взяв любое из двух фиксированных показаний — сопротивление, ток или напряжение.
Это означает, что ток контролируется путем регулирования или регулировки сопротивления через устройство регулятора, которое затем отправляется на выходную клемму, чтобы сообщить двигателю, на какой скорости работать. Вы можете рассчитать значение входа здесь, взяв любое из двух фиксированных показаний — сопротивление, ток или напряжение. - Электронные схемы – в электронных схемах применяется закон Ома для преднамеренного падения напряжения. Падение напряжения требуется в электронных схемах, чтобы обеспечить определенный уровень напряжения для различных компонентов в цепи.
- Чайники и утюги – резисторы используются в электрических чайниках и утюгах. Работа резистора состоит в том, чтобы ограничить количество тока, протекающего через них, чтобы дать прибору требуемый/правильный уровень тепла. Чтобы решить, какой размер резистора требуется, используется закон Ома.
- Конструкция плавких предохранителей – плавкий предохранитель представляет собой тип защитного устройства, используемого в электрических системах для ограничения величины тока, протекающего по цепи, и надлежащего уровня напряжения.
 Закон Ома применяется, чтобы решить, какой размер резисторов используется в предохранителях.
Закон Ома применяется, чтобы решить, какой размер резисторов используется в предохранителях.
Закон Ома и электрическая формула PIR
Используя тот же метод треугольника Ома, мы можем использовать следующее колесо для расчета мощности (Вт), напряжения (В), тока (I) и сопротивления (R). . 92 x R
Что такое I в законе Ома?
I обозначает ток по закону Ома, который измеряется в амперах.
Что такое V в законе Ома?
В обозначает напряжение по закону Ома, которое измеряется в вольтах.
Что такое R в законе Ома?
R обозначает сопротивление по закону Ома, которое измеряется в Омах.
Можно ли применить закон Ома к любой электрической цепи?
Нет, закон Ома нельзя применить к каждой электрической цепи, так как он имеет некоторые ограничения. Чтобы понять эти ограничения, ознакомьтесь с нашей статьей здесь.
Лиам Коуп
Привет, меня зовут Лиам. Я основал Engineer Fix с целью предоставить студентам, инженерам и людям, которые могут быть любопытны, онлайн-ресурс, который может упростить проектирование.
Я работал на различных инженерных должностях, выполняя бесчисленное количество часов механических и электрических работ/проектов. Я также прошел 6-летнее обучение, которое включало повышение квалификации и получение степени HNC в области электротехники.
Закон Ома: сопротивление и простые схемы | Физика |
Цели обучения
К концу этого раздела вы сможете:
- Объяснить происхождение закона Ома.
- Расчет напряжения, тока или сопротивления по закону Ома.
- Объясните, что такое омический материал.
- Опишите простую схему.
Что движет током? Мы можем думать о различных устройствах, таких как батареи, генераторы, настенные розетки и т. д., которые необходимы для поддержания тока. Все такие устройства создают разность потенциалов и в широком смысле называются источниками напряжения. Когда источник напряжения подключен к проводнику, он создает разность потенциалов  Электрическое поле, в свою очередь, воздействует на заряды, вызывая ток.
Электрическое поле, в свою очередь, воздействует на заряды, вызывая ток.
Закон Ома
Ток, протекающий через большинство веществ, прямо пропорционален приложенному к нему напряжению В . Немецкий физик Георг Симон Ом (1787–1854) первым экспериментально продемонстрировал, что ток в металлическом проводе прямо пропорционален приложенному напряжению :
I∝VI\propto{V}\\I∝V
. Это важное соотношение известно как закон Ома . Его можно рассматривать как причинно-следственную связь, где напряжение является причиной, а ток — следствием. Это эмпирический закон, аналогичный закону трения — экспериментально наблюдаемому явлению. Такая линейная зависимость не всегда имеет место.
Сопротивление и простые схемы
Если напряжение управляет током, что ему препятствует? Электрическое свойство, препятствующее току (грубо похожее на трение и сопротивление воздуха), называется 9. 0251 сопротивление R . Столкновения движущихся зарядов с атомами и молекулами в веществе передают энергию веществу и ограничивают ток. Сопротивление определяется как обратно пропорциональное току, или
0251 сопротивление R . Столкновения движущихся зарядов с атомами и молекулами в веществе передают энергию веществу и ограничивают ток. Сопротивление определяется как обратно пропорциональное току, или
I∝1RI\propto \frac{1}{R}\\I∝R1
. Так, например, ток уменьшается вдвое, если сопротивление удваивается. Сочетание отношений тока к напряжению и тока к сопротивлению дает
I=VRI=\frac{V}{R}\\I=RV
.
Эту зависимость также называют законом Ома. Закон Ома в этой форме действительно определяет сопротивление для определенных материалов. Закон Ома (как и закон Гука) не является универсальным. Многие вещества, для которых выполняется закон Ома, называются омический . К ним относятся хорошие проводники, такие как медь и алюминий, и некоторые плохие проводники при определенных обстоятельствах. Омические материалы имеют сопротивление Ом , которое не зависит от напряжения В и тока I .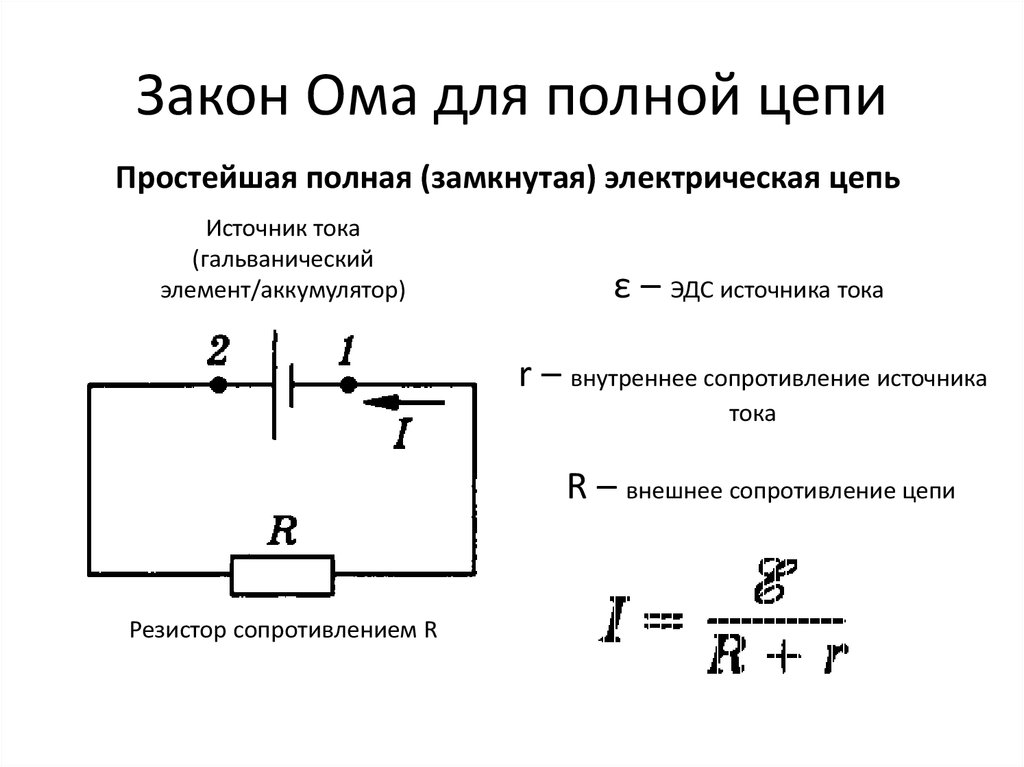 Объект, имеющий простое сопротивление, называется резистором , даже если его сопротивление невелико. Единицей измерения сопротивления является Ом и обозначается символом Ω (греческая омега в верхнем регистре). Перестановка I = V/R дает R = V/I , поэтому единицами сопротивления являются 1 Ом = 1 вольт на ампер:
Объект, имеющий простое сопротивление, называется резистором , даже если его сопротивление невелико. Единицей измерения сопротивления является Ом и обозначается символом Ω (греческая омега в верхнем регистре). Перестановка I = V/R дает R = V/I , поэтому единицами сопротивления являются 1 Ом = 1 вольт на ампер:
1Ω=1VA1 \Omega=1\frac{V}{A}\\1Ω= 1АВ
. На рис. 1 показана схема простой цепи. Простая схема имеет один источник напряжения и один резистор. Провода, соединяющие источник напряжения с резистором, можно считать имеющими пренебрежимо малое сопротивление, или их сопротивление можно включить в R .
Рис. 1. Простая электрическая цепь, в которой замкнутый путь для протекания тока обеспечивается проводниками (обычно металлическими проводами), соединяющими нагрузку с клеммами батареи, представленными красными параллельными линиями. Зигзагообразный символ представляет одиночный резистор и включает любое сопротивление в соединениях с источником напряжения.
Зигзагообразный символ представляет одиночный резистор и включает любое сопротивление в соединениях с источником напряжения.
Пример 1. Расчет сопротивления: автомобильная фара
Каково сопротивление автомобильной фары, через которую протекает ток 2,50 А при подаче на нее напряжения 12,0 В?
СтратегияМы можем преобразовать закон Ома в формулу I = V/R и использовать его для определения сопротивления.
РастворПреобразование I = V/R и подстановка известных значений дает
R=VI=12,0V2,50A=4,80ΩR=\frac{V}{I}=\frac{12\text{}.{}\text{ }0 В{}}{2\text{}.{}\text{}50 A{}}=\text{}4{}\text{}.{}\text{}80 \Omega {}\\ R=IV=2.50A12.0V=4.80Ω
.
Обсуждение Это относительно небольшое сопротивление, но оно больше холодового сопротивления фары. Как мы увидим в разделе «Сопротивление и удельное сопротивление», сопротивление обычно увеличивается с температурой, поэтому лампочка имеет более низкое сопротивление при первом включении и будет потреблять значительно больший ток в течение короткого периода прогрева.
Как мы увидим в разделе «Сопротивление и удельное сопротивление», сопротивление обычно увеличивается с температурой, поэтому лампочка имеет более низкое сопротивление при первом включении и будет потреблять значительно больший ток в течение короткого периода прогрева.
Сопротивления колеблются в пределах многих порядков. Некоторые керамические изоляторы, например те, которые используются для поддержки линий электропередач, имеют сопротивление 10 12 Ом или больше. У сухого человека сопротивление между руками и ногами может составлять 10 5 Ом, тогда как сопротивление человеческого сердца составляет около 10 3 Ом. Метровый отрезок медного провода большого диаметра может иметь сопротивление 10 −5 Ом, а сверхпроводники вообще не имеют сопротивления (они неомические). Сопротивление связано с формой объекта и материалом, из которого он состоит, как будет показано в разделе «Сопротивление и удельное сопротивление». Дополнительную информацию можно получить, решив I = V/R для V , что дает
Дополнительную информацию можно получить, решив I = V/R для V , что дает
V = IR
Это выражение для V можно интерпретировать как падение напряжения на резисторе, вызванное протеканием тока I . Для этого напряжения часто используется фраза IR drop . Например, фара в примере 1 выше имеет падение IR 12,0 В. Если напряжение измеряется в различных точках цепи, будет видно, что оно увеличивается на источнике напряжения и уменьшается на резисторе. Напряжение аналогично давлению жидкости. Источник напряжения подобен насосу, создающему перепад давления, вызывающему ток — поток заряда. Резистор подобен трубе, которая снижает давление и ограничивает поток из-за своего сопротивления. Сохранение энергии имеет здесь важные последствия. Источник напряжения поставляет энергию (вызывая электрическое поле и ток), а резистор преобразует ее в другую форму (например, в тепловую энергию). В простой цепи (с одним простым резистором) напряжение, подаваемое источником, равно падению напряжения на резисторе, поскольку PE = q Δ V , и через каждый протекает один и тот же q . Таким образом, энергия, подаваемая источником напряжения, и энергия, преобразуемая резистором, равны. (См. рис. 2.)
В простой цепи (с одним простым резистором) напряжение, подаваемое источником, равно падению напряжения на резисторе, поскольку PE = q Δ V , и через каждый протекает один и тот же q . Таким образом, энергия, подаваемая источником напряжения, и энергия, преобразуемая резистором, равны. (См. рис. 2.)
Рис. 2. Падение напряжения на резисторе в простой цепи равно выходному напряжению батареи.
Соединения: сохранение энергииВ простой электрической цепи единственный резистор преобразует энергию, поступающую от источника, в другую форму. О сохранении энергии здесь свидетельствует тот факт, что вся энергия, подаваемая источником, преобразуется в другую форму одним только резистором. Мы обнаружим, что закон сохранения энергии имеет и другие важные применения в цепях и является мощным инструментом анализа цепей.
Исследования PhET: Закон Ома Посмотрите, как формула закона Ома соотносится с простой цепью. Отрегулируйте напряжение и сопротивление и посмотрите, как изменится ток в соответствии с законом Ома. Размеры символов в уравнении изменяются в соответствии с принципиальной схемой.
Отрегулируйте напряжение и сопротивление и посмотрите, как изменится ток в соответствии с законом Ома. Размеры символов в уравнении изменяются в соответствии с принципиальной схемой.
Нажмите, чтобы запустить моделирование.
Резюме раздела
Концептуальные вопросы
- Падение IR на резисторе означает, что на резисторе есть изменение потенциала или напряжения. Изменяется ли ток при прохождении через резистор? Объяснять.
- Чем падение давления на резисторе IR похоже на падение давления в жидкости, протекающей по трубе?
Задачи и упражнения
1. Какой ток протекает через лампу фонарика на 3,00 В, если его сопротивление в горячем состоянии равно 3,60 Ом?
2. Рассчитайте эффективное сопротивление карманного калькулятора с батареей на 1,35 В, через который протекает ток 0,200 мА.
3. Каково эффективное сопротивление стартера автомобиля, когда через него протекает ток 150 А, когда автомобильный аккумулятор подает на двигатель напряжение 11,0 В?
Каково эффективное сопротивление стартера автомобиля, когда через него протекает ток 150 А, когда автомобильный аккумулятор подает на двигатель напряжение 11,0 В?
4. Сколько вольт подается на световой индикатор DVD-проигрывателя с сопротивлением 140 Ом, если через него проходит 25,0 мА?
5. а) Найдите падение напряжения в удлинителе с сопротивлением 0,0600 Ом, по которому протекает ток 5,00 А. (b) Более дешевый шнур использует более тонкую проволоку и имеет сопротивление 0,300 Ом. Каково падение напряжения в нем при протекании 5,00 А? в) Почему напряжение любого используемого электроприбора уменьшается на эту величину? Каково влияние на прибор?
6. Линия электропередачи подвешена к металлическим опорам со стеклянными изоляторами сопротивлением 1,00×10 9 Ом. Какой ток протекает через изолятор, если напряжение равно 200 кВ? (Некоторые высоковольтные линии постоянного тока. )
)
Глоссарий
- Закон Ома:
- эмпирическое соотношение, утверждающее, что ток I пропорционален разности потенциалов В , ∝ В ; его часто записывают как I = V/R , где R сопротивление
- сопротивление:
- электрическое свойство, препятствующее току; для омических материалов это отношение напряжения к току, R = V/I
- ом:
- единица сопротивления, определяемая как 1 Ом = 1 В/А
- омическое: a 1 тип материала, для которого справедлив закон Ома
- простая цепь:
- цепь с одним источником напряжения и одним резистором
Избранные решения задач и упражнений
1. 0,833 A
3. 7,33 × 10 −2 Ом
5. (a) 0,300 В
(b) 1,50 В
(c) Напряжение, подаваемое на любой используемый прибор, уменьшается, поскольку общее падение напряжения от стены до конечного выхода прибора фиксируется. Таким образом, если падение напряжения на удлинителе велико, падение напряжения на устройстве значительно уменьшается, поэтому выходная мощность устройства может быть значительно снижена, что снижает способность устройства работать должным образом.
Таким образом, если падение напряжения на удлинителе велико, падение напряжения на устройстве значительно уменьшается, поэтому выходная мощность устройства может быть значительно снижена, что снижает способность устройства работать должным образом.
Лицензии и ссылки
Контент по лицензии CC, совместно используемый ранее
- College Physics. Автор : Колледж OpenStax. Расположен по адресу : https://openstax.org/books/college-physics/pages/1-introduction-to-science-and-the-realm-of-physics-physical-quantities-and-units. Лицензия : CC BY: Attribution . Условия лицензии : Лицензия
- Интерактивное моделирование PhET . Автор: : http://phet.colorado.edu. Лицензия : CC BY: Атрибуция
19.1 Закон Ома — Физика
Раздел Цели обучения
К концу этого раздела вы сможете делать следующее:
- Описывать, как ток связан с зарядом и временем, и различать постоянный и переменный ток
- Дайте определение сопротивлению и устно опишите закон Ома
- Расчет силы тока и решение задач на закон Ома
Поддержка учителей
Поддержка учителей
Цели обучения в этом разделе помогут вашим учащимся освоить следующие стандарты:
- (5) Научные концепции.
 Учащийся знает природу сил в физическом мире. Ожидается, что студент:
Учащийся знает природу сил в физическом мире. Ожидается, что студент:- (F) проектировать, конструировать и рассчитывать сквозной ток, разность потенциалов, сопротивление и мощность, используемую элементами электрической цепи, соединенными как последовательно, так и параллельно.
Кроме того, в Руководстве по физике для средней школы рассматривается содержание этого раздела лабораторной работы под названием Закон Ома, а также следующие стандарты:
- (5) Учащийся знает природу сил в физическом мире. Ожидается, что студент:
- (Ф) проектировать, конструировать и рассчитывать с точки зрения сквозного тока, разности потенциалов, сопротивления и мощности, используемой элементами электрической цепи, соединенными как последовательно, так и параллельно.
Основные термины раздела
| переменный ток | ампер | обычный ток | постоянный ток | электрический ток |
| неомический | омический | Закон Ома | сопротивление |
Постоянный и переменный ток
Подобно тому, как вода течет с большой высоты на низкую, электроны, которые могут свободно двигаться, будут перемещаться из места с низким потенциалом в место с высоким потенциалом. Аккумулятор имеет две клеммы с разным потенциалом. Если клеммы соединить токопроводящим проводом, будет протекать электрический ток (заряды), как показано на рисунке 19..2. Затем электроны будут двигаться от клеммы батареи с низким потенциалом (отрицательный конец ) по проводу и войдут в клемму батареи с высоким потенциалом (положительный конец ).
Аккумулятор имеет две клеммы с разным потенциалом. Если клеммы соединить токопроводящим проводом, будет протекать электрический ток (заряды), как показано на рисунке 19..2. Затем электроны будут двигаться от клеммы батареи с низким потенциалом (отрицательный конец ) по проводу и войдут в клемму батареи с высоким потенциалом (положительный конец ).
Рисунок 19.2 У батареи есть провод, соединяющий положительные и отрицательные клеммы, что позволяет электронам перемещаться от отрицательной клеммы к положительной клемме.
Поддержка учителей
Поддержка учителей
Подчеркните, что электроны движутся от отрицательного вывода к положительному, потому что они несут отрицательный заряд, поэтому они отталкиваются кулоновской силой от отрицательного вывода.
Электрический ток — это скорость, с которой движется электрический заряд. Большой ток, например, используемый для запуска двигателя грузовика, очень быстро перемещает большое количество заряда, в то время как слабый ток, например, используемый для работы ручного калькулятора, перемещает небольшое количество заряда медленнее. В форме уравнения электрический ток I определяется как
В форме уравнения электрический ток I определяется как
I=ΔQΔtI=ΔQΔt
, где ΔQΔQ — количество заряда, протекающего мимо данной области, а ΔtΔt — время, за которое заряд проходит мимо этой области. Единица СИ для электрического тока — ампер (А), названная в честь французского физика Андре-Мари Ампера (1775–1836). Один ампер равен одному кулону в секунду, или
1A=1C/с. 1A=1C/с.
Электрический ток, движущийся по проводу, во многом подобен водяному току, движущемуся по трубе. Чтобы определить поток воды через трубу, мы можем подсчитать количество молекул воды, протекающих через данный участок трубы. Как показано на рис. 19.3, электрический ток очень похож. Мы подсчитываем количество электрических зарядов, протекающих по сечению проводника; в данном случае проволока.
Рисунок
19,3
Электрический ток, протекающий по этому проводу, равен заряду, прошедшему через поперечное сечение А, деленному на время, за которое этот заряд пройдет сечение А .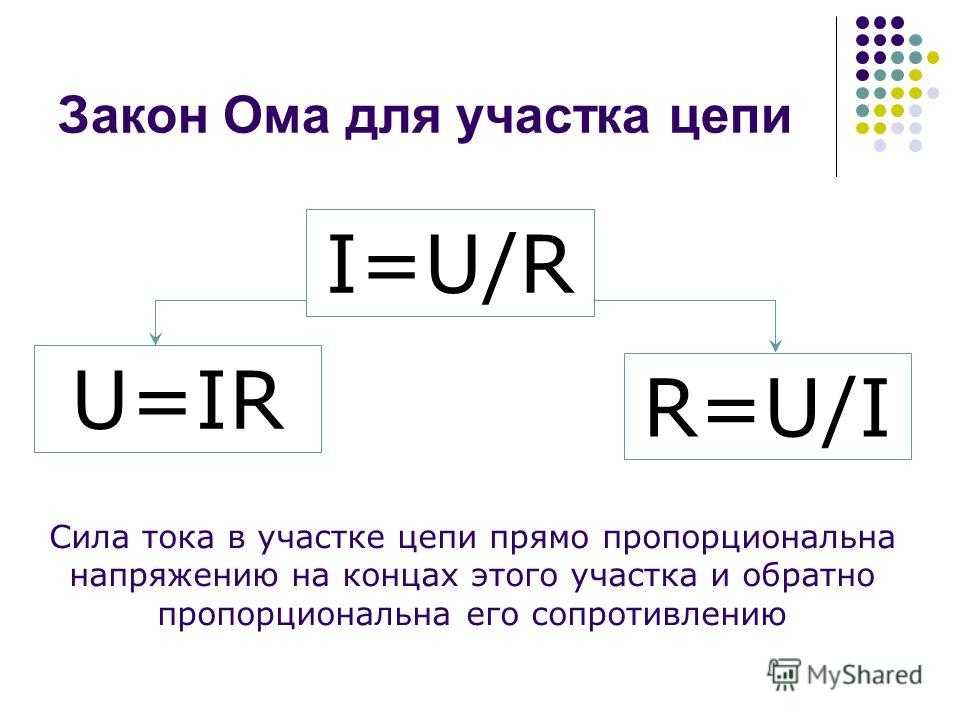
Поддержка учителей
Поддержка учителей
Обратите внимание, что носители заряда на этом рисунке положительны, поэтому они движутся в том же направлении, что и электрический ток.
Предположим, что каждая частица q на рис. 19.3 несет заряд q=1nCq=1nC, и в этом случае показанный общий заряд будет ΔQ=5q=5nC ΔQ=5q=5nC . Если эти заряды пролетят площадь А за время Δt=1нс Δt=1нс, то ток будет
I=ΔQΔt=5nC1ns=5A.I=ΔQΔt=5nC1ns=5A.
19.1
Обратите внимание, что мы приписали положительный заряд зарядам на рис. 19.3. Обычно отрицательные заряды — электроны — представляют собой подвижный заряд в проводах, как показано на рис. 19.2. Положительные заряды обычно застревают в твердых телах и не могут свободно перемещаться. Однако, поскольку положительный ток, движущийся вправо, аналогичен отрицательному току равной величины, движущемуся влево, как показано на рис. 19.4, мы определяем обычный ток как текущий в том же направлении, в котором протекал бы положительный заряд, если бы он мог двигаться. . Таким образом, если не указано иное, предполагается, что электрический ток состоит из положительных зарядов.
19.4, мы определяем обычный ток как текущий в том же направлении, в котором протекал бы положительный заряд, если бы он мог двигаться. . Таким образом, если не указано иное, предполагается, что электрический ток состоит из положительных зарядов.
Также обратите внимание, что один кулон — это значительное количество электрического заряда, поэтому 5 А — это очень большой ток. Чаще всего вы увидите ток порядка миллиампер (мА).
Рисунок 19,4 а) Электрическое поле направлено вправо, ток движется вправо, положительные заряды движутся вправо. (b) Эквивалентная ситуация, но с отрицательными зарядами, движущимися влево. Электрическое поле и ток по-прежнему находятся справа.
Поддержка учителей
Поддержка учителей
Укажите, что электрическое поле одинаково в обоих случаях и что ток течет в направлении электрического поля.
Предупреждение о заблуждении
Убедитесь, что учащиеся понимают, что ток определяется как направление, в котором будет течь положительный заряд, даже если электроны чаще всего являются подвижными носителями заряда. Математически результат будет одинаковым независимо от того, предположим ли мы, что положительный заряд течет в одну сторону, или отрицательный — в противоположную. Однако физически ситуация совершенно иная (хотя разница уменьшается после определения дырок).
Математически результат будет одинаковым независимо от того, предположим ли мы, что положительный заряд течет в одну сторону, или отрицательный — в противоположную. Однако физически ситуация совершенно иная (хотя разница уменьшается после определения дырок).
Снап Лаборатория
Овощной ток
Эта лабораторная работа помогает учащимся понять, как работает ток. Учитывая, что частицы, заключенные в трубе, не могут занимать одно и то же пространство, вталкивание большего количества частиц в один конец трубы вытеснит такое же количество частиц из противоположного конца. Это создает поток частиц.
Найдите соломинку и сушеный горох, которые могут свободно перемещаться в соломе. Положите соломинку на стол и наполните ее горошком. Когда вы вставляете одну горошину с одного конца, с другого конца должна выйти другая горошина. Эта демонстрация является моделью электрического тока. Определите часть модели, которая представляет электроны, и часть модели, которая представляет подачу электроэнергии. За 30 с посчитайте, сколько горошин вы можете протолкнуть через соломинку. Когда закончите, посчитайте горошин ток путем деления количества горошин на время в секундах.
За 30 с посчитайте, сколько горошин вы можете протолкнуть через соломинку. Когда закончите, посчитайте горошин ток путем деления количества горошин на время в секундах.
Обратите внимание, что движение гороха основано на физическом столкновении горошин друг с другом; электроны толкают друг друга за счет взаимно отталкивающих электростатических сил.
Предположим, у вас есть резервуар с горохом, каждый из которых заряжен до 1 нКл. Если вы пропускаете горох через соломинку со скоростью четыре горошинки в секунду, как вы вычислите электрический ток, переносимый вашими заряженными горошинами?
Измерьте длину соломинки, затем разделите на скорость потока горошин и умножьте на стоимость одной горошинки.
Умножьте расход гороха на стоимость гороха.

Измерьте длину соломинки, затем умножьте на скорость потока горошин и разделите на стоимость горошин.
Разделить расход гороха на стоимость гороха.
Направление обычного тока — это направление, в котором будет течь положительный заряд . В зависимости от ситуации могут перемещаться положительные заряды, отрицательные заряды или и то, и другое. В металлических проводах, как мы видели, ток переносится электронами, поэтому движутся отрицательные заряды. В ионных растворах, таких как соленая вода, движутся как положительно заряженные, так и отрицательно заряженные ионы. Это верно и для нервных клеток. Чисто положительные токи относительно редки, но встречаются. История приписывает американскому политику и ученому Бенджамину Франклину описание тока как направления, в котором положительные заряды текут по проводу. Он назвал тип заряда, связанного с электронами, отрицательным задолго до того, как стало известно, что они несут ток во многих ситуациях.
История приписывает американскому политику и ученому Бенджамину Франклину описание тока как направления, в котором положительные заряды текут по проводу. Он назвал тип заряда, связанного с электронами, отрицательным задолго до того, как стало известно, что они несут ток во многих ситуациях.
Когда электроны движутся по металлической проволоке, они сталкиваются с препятствиями, такими как другие электроны, атомы, примеси и т. д. Электроны рассеиваются от этих препятствий, как показано на рис. 19.5. Обычно электроны теряют энергию при каждом взаимодействии. 1 Таким образом, чтобы поддерживать движение электронов, требуется сила, которая обеспечивается электрическим полем. Электрическое поле в проводе направлено от конца провода с более высоким потенциалом к концу провода с более низким потенциалом. Электроны, несущие отрицательный заряд, движутся в среднем (или на дрейфует ) в направлении, противоположном электрическому полю, как показано на рис. 19.5.
19.5.
Рисунок 19,5 Свободные электроны, движущиеся в проводнике, совершают много столкновений с другими электронами и атомами. Показан путь одного электрона. Средняя скорость свободных электронов направлена против электрического поля. Столкновения обычно передают энергию проводнику, поэтому для поддержания постоянного тока требуется постоянная подача энергии.
До сих пор мы обсуждали ток, который постоянно движется в одном направлении. Это называется постоянным током, потому что электрический заряд течет только в одном направлении. Постоянный ток часто называют DC ток.
Многие источники электроэнергии, такие как гидроэлектростанция, показанная в начале этой главы, производят переменный ток, в котором направление тока меняется вперед и назад. Переменный ток часто называют , переменный ток . Переменный ток движется вперед и назад через равные промежутки времени, как показано на рис.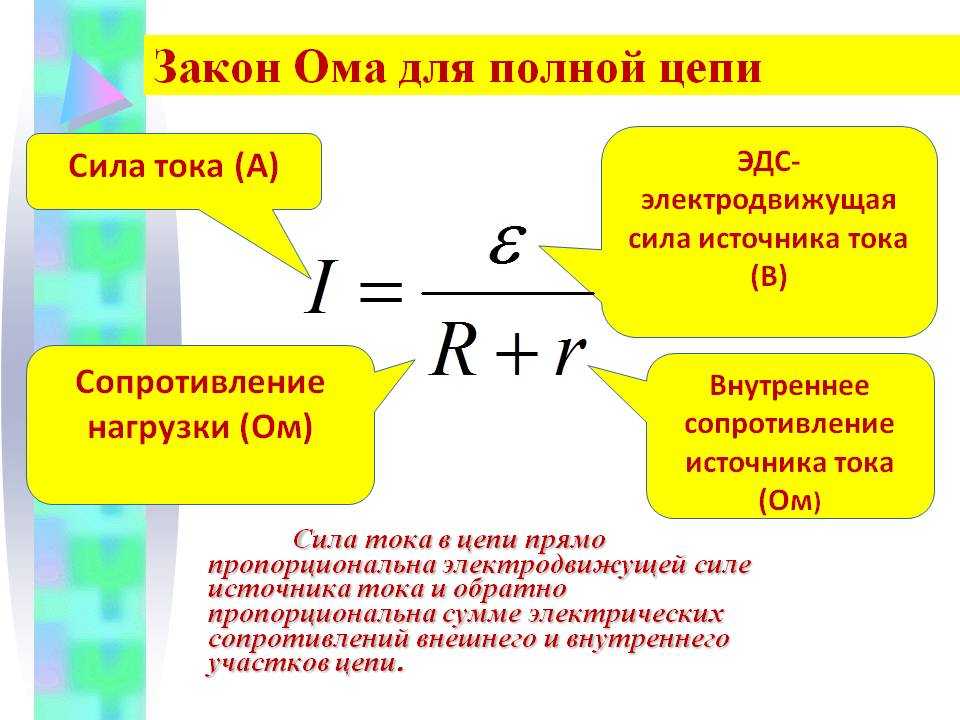 19.6. Переменный ток, поступающий из обычной настенной розетки, не меняет направление внезапно. Скорее, он плавно увеличивается до максимального тока, а затем плавно уменьшается до нуля. Затем он снова растет, но в противоположном направлении, пока не достигнет того же максимального значения. После этого она плавно уменьшается до нуля, и цикл начинается заново.
19.6. Переменный ток, поступающий из обычной настенной розетки, не меняет направление внезапно. Скорее, он плавно увеличивается до максимального тока, а затем плавно уменьшается до нуля. Затем он снова растет, но в противоположном направлении, пока не достигнет того же максимального значения. После этого она плавно уменьшается до нуля, и цикл начинается заново.
Рисунок 19,6 При переменном токе направление тока меняется на противоположное через равные промежутки времени. На графике вверху показана зависимость тока от времени. Отрицательные максимумы соответствуют току, движущемуся влево. Положительные максимумы соответствуют току, движущемуся вправо. Между этими двумя максимумами ток регулярно и плавно чередуется.
Поддержка учителей
Поддержка учителей
Помогите учащимся интерпретировать график, подчеркнув, что ток не меняет направление мгновенно, а плавно переходит от одного максимума к противоположному максимуму и обратно. Объясните, что четыре изображения внизу показывают ток в соответствующих максимумах. Обратите внимание, что для упрощения интерпретации операторы мобильной связи на изображении считаются положительными.
Объясните, что четыре изображения внизу показывают ток в соответствующих максимумах. Обратите внимание, что для упрощения интерпретации операторы мобильной связи на изображении считаются положительными.
К устройствам, использующим переменный ток, относятся пылесосы, вентиляторы, электроинструменты, фены и многие другие. Эти устройства получают необходимую им мощность, когда вы подключаете их к сетевой розетке. Настенная розетка подключена к электросети, которая обеспечивает переменный потенциал (потенциал переменного тока). Когда ваше устройство подключено к сети, потенциал переменного тока перемещает заряды вперед и назад в цепи устройства, создавая переменный ток.
Однако многие устройства используют постоянный ток, например компьютеры, сотовые телефоны, фонарики и автомобили. Одним из источников постоянного тока является батарея, которая обеспечивает постоянный потенциал (потенциал постоянного тока) между своими клеммами. Когда ваше устройство подключено к аккумулятору, потенциал постоянного тока перемещает заряд в одном направлении по цепи вашего устройства, создавая постоянный ток. Другой способ получения постоянного тока — использование трансформатора, который преобразует переменный потенциал в постоянный. Небольшие трансформаторы, которые можно подключить к настенной розетке, используются для зарядки ноутбука, мобильного телефона или другого электронного устройства. Люди обычно называют это зарядное устройство или аккумулятор , но это трансформатор, который преобразует переменное напряжение в постоянное напряжение. В следующий раз, когда кто-то попросит одолжить ваше зарядное устройство для ноутбука, скажите им, что у вас нет зарядного устройства для ноутбука, но они могут одолжить ваш переходник.
Другой способ получения постоянного тока — использование трансформатора, который преобразует переменный потенциал в постоянный. Небольшие трансформаторы, которые можно подключить к настенной розетке, используются для зарядки ноутбука, мобильного телефона или другого электронного устройства. Люди обычно называют это зарядное устройство или аккумулятор , но это трансформатор, который преобразует переменное напряжение в постоянное напряжение. В следующий раз, когда кто-то попросит одолжить ваше зарядное устройство для ноутбука, скажите им, что у вас нет зарядного устройства для ноутбука, но они могут одолжить ваш переходник.
Рабочий пример
Ток при ударе молнии
Удар молнии может передать до 10201020 электронов из облака на землю. Если удар длится 2 мс, какова средняя сила тока в молнии?
Стратегия
Используйте определение тока I=ΔQΔtI=ΔQΔt . Заряд ΔQΔQ
из 10201020 электронов составляет ΔQ=neΔQ=ne, где n=1020n=1020 — число электронов, а e=−1,60×10−19Ce=−1,60×10−19C — заряд электрона. Это дает
Заряд ΔQΔQ
из 10201020 электронов составляет ΔQ=neΔQ=ne, где n=1020n=1020 — число электронов, а e=−1,60×10−19Ce=−1,60×10−19C — заряд электрона. Это дает
ΔQ=1020×(-1,60×10-19C)=-16,0C. ΔQ=1020×(-1,60×10-19C)=-16,0C.
19,2
Время Δt=2×10-3 с Δt=2×10-3 с – это продолжительность удара молнии.
Решение
Сила тока при ударе молнии
I=ΔQΔt=-16,0C2×10-3с=-8кА.I=ΔQΔt=-16,0C2×10-3с=-8кА.
19.3
Обсуждение
Знак минус отражает тот факт, что электроны несут отрицательный заряд. Таким образом, хотя электроны текут от облака к земле, положительный ток определяется как течет от земли к облаку.
Рабочий пример
Средний ток для зарядки конденсатора
В цепи, содержащей конденсатор и резистор, требуется 1 мин для зарядки конденсатора емкостью 16 мкФ с помощью 9-В батарея. Какова средняя сила тока за это время?
Стратегия
Мы можем определить заряд конденсатора, используя определение емкости: C=QVC=QV .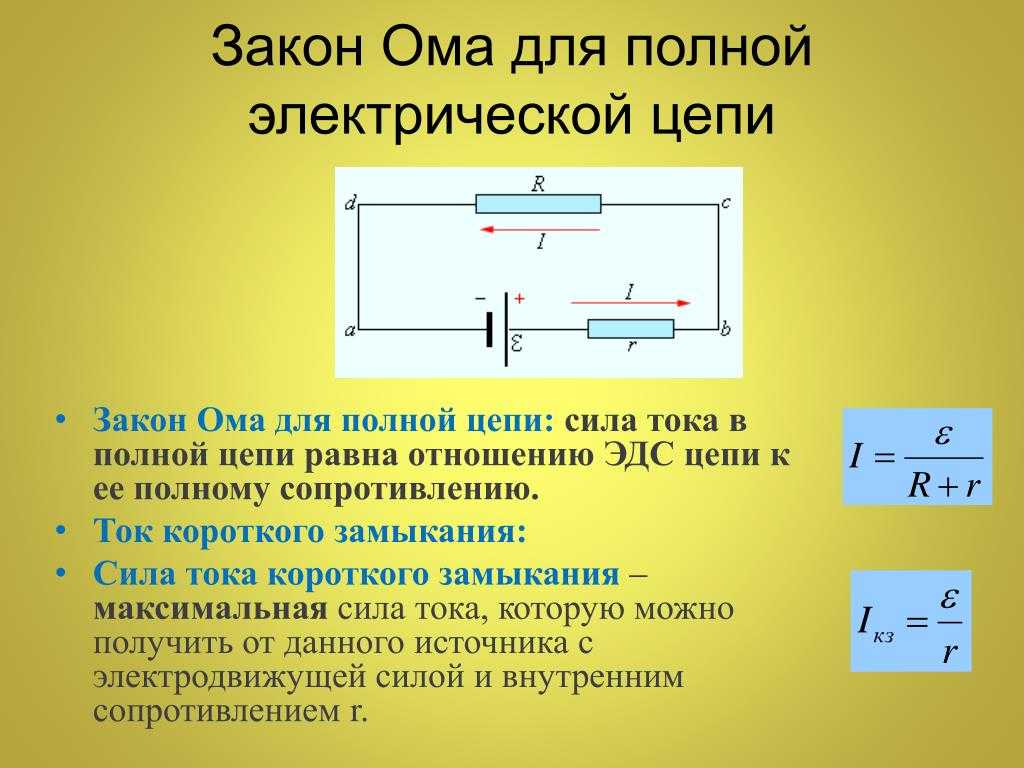 Когда конденсатор заряжается от 9-вольтовой батареи, напряжение на конденсаторе будет V=9VV=9V. Это дает заряд
Когда конденсатор заряжается от 9-вольтовой батареи, напряжение на конденсаторе будет V=9VV=9V. Это дает заряд
C=QVQ=CV.C=QVQ=CV.
19,4
Подставляя это выражение для заряда в уравнение для тока I=ΔQΔtI=ΔQΔt, мы можем найти средний ток.
Решение
Средний ток
I=ΔQΔt=CVΔt=(16×10−6F)(9V)60s=2,4×10−6A=2,4 мкA.I=ΔQΔt=CVΔt=(16×10−6F) (9 В) 60 с = 2,4 × 10–6 А = 2,4 мкА.
19,5
Обсуждение
Этот малый ток типичен для тока, встречающегося в цепях, подобных этой.
Практические задачи
1.
Заряд 10 нКл проходит по цепи за 3,0 × 10 −6 с. Какой ток в это время?
- Ток, протекающий по цепи, равен 3,3·10 −3 А.
- По цепи проходит ток 30 А.
- По цепи проходит ток 33 А.
- Ток, проходящий через цепь, составляет 0,3 А.

2.
Сколько времени потребуется току 10\text{-мА} для зарядки конденсатора с 5,0\,\text{мКл}?
0,50\,\текст{с}
5\,\text{ns}
0,50\,\text{ns}
50\,\мю\текст{с}
Сопротивление и закон Ома
Как упоминалось ранее, электрический ток в проводе во многом подобен воде, протекающей по трубе. На поток воды, который может течь по трубе, влияют препятствия в трубе, такие как засоры и узкие участки трубы. Эти препятствия замедляют течение тока по трубе. Точно так же электрический ток в проводе может быть замедлен многими факторами, включая примеси в металле провода или столкновения между зарядами в материале. Эти факторы создают сопротивление электрическому току. Сопротивление — это описание того, насколько провод или другой электрический компонент сопротивляется потоку заряда через него.
В 19XX века немецкий физик Георг Симон Ом (1787–1854) экспериментально установил, что сила тока в проводнике пропорциональна падению напряжения на проводнике с током.
На поток воды, который может течь по трубе, влияют препятствия в трубе, такие как засоры и узкие участки трубы. Эти препятствия замедляют течение тока по трубе. Точно так же электрический ток в проводе может быть замедлен многими факторами, включая примеси в металле провода или столкновения между зарядами в материале. Эти факторы создают сопротивление электрическому току. Сопротивление — это описание того, насколько провод или другой электрический компонент сопротивляется потоку заряда через него.
В 19XX века немецкий физик Георг Симон Ом (1787–1854) экспериментально установил, что сила тока в проводнике пропорциональна падению напряжения на проводнике с током.
И∝ВИ∝В
Константой пропорциональности является сопротивление R материала, что приводит к
В=ИК(1,3).В=ИК(1,3).
Это соотношение называется законом Ома. Его можно рассматривать как причинно-следственную связь, где напряжение является причиной, а ток — следствием. Закон Ома — это эмпирический закон, подобный закону трения, а это означает, что это экспериментально наблюдаемое явление. Единицами сопротивления являются вольты на ампер или В/А. Мы называем V / A ом , что обозначается заглавной греческой буквой омега (ΩΩ). Таким образом,
Закон Ома — это эмпирический закон, подобный закону трения, а это означает, что это экспериментально наблюдаемое явление. Единицами сопротивления являются вольты на ампер или В/А. Мы называем V / A ом , что обозначается заглавной греческой буквой омега (ΩΩ). Таким образом,
1Ом=1В/А(1.4).1Ом=1В/А(1.4).
Закон Ома выполняется для большинства материалов и при обычных температурах. При очень низких температурах сопротивление может упасть до нуля (сверхпроводимость). При очень высоких температурах тепловое движение атомов в материале препятствует потоку электронов, увеличивая сопротивление. Многие вещества, для которых выполняется закон Ома, называются омическими. К омическим материалам относятся хорошие проводники, такие как медь, алюминий и серебро, а также некоторые плохие проводники при определенных обстоятельствах. Сопротивление омических материалов остается практически одинаковым в широком диапазоне напряжений и токов.
Смотреть физику
Введение в электричество, цепи, ток и сопротивление
В этом видео представлен закон Ома и показана простая электрическая цепь.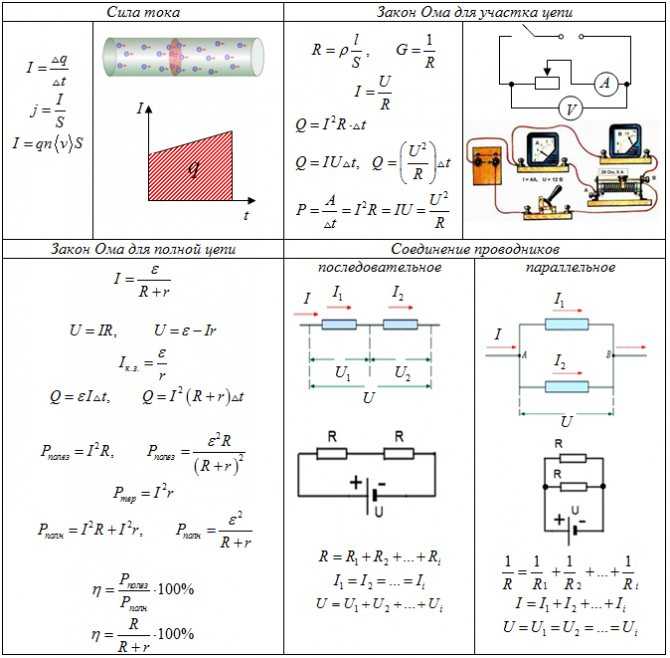 Спикер использует аналогию с давлением, чтобы описать, как электрический потенциал заставляет двигаться заряд. Он называет электрический потенциал , электрическое давление . Другой способ представления об электрическом потенциале — представить, что множество частиц одного знака скопилось в небольшом ограниченном пространстве. Поскольку эти заряды имеют одинаковый знак (все они положительные или все отрицательные), каждый заряд отталкивает окружающие его заряды. Это означает, что множество зарядов постоянно выталкивается за пределы пространства. Полная электрическая цепь подобна открытию двери в маленьком пространстве: какие бы частицы ни подтолкнули к двери, теперь у них есть способ убежать. Чем выше электрический потенциал, тем сильнее каждая частица давит на другую.
Спикер использует аналогию с давлением, чтобы описать, как электрический потенциал заставляет двигаться заряд. Он называет электрический потенциал , электрическое давление . Другой способ представления об электрическом потенциале — представить, что множество частиц одного знака скопилось в небольшом ограниченном пространстве. Поскольку эти заряды имеют одинаковый знак (все они положительные или все отрицательные), каждый заряд отталкивает окружающие его заряды. Это означает, что множество зарядов постоянно выталкивается за пределы пространства. Полная электрическая цепь подобна открытию двери в маленьком пространстве: какие бы частицы ни подтолкнули к двери, теперь у них есть способ убежать. Чем выше электрический потенциал, тем сильнее каждая частица давит на другую.
Если на принципиальной схеме, показанной на видео, вместо одного резистора R начертить два резистора сопротивлением R каждый, что можно сказать о токе через цепь?
Количество тока в цепи должно уменьшиться вдвое.
Количество тока в цепи должно увеличиться вдвое.
Ток в цепи должен оставаться одинаковым.
Количество тока в цепи удвоится.
Виртуальная физика
Закон Ома
Эта симуляция имитирует простую схему с батареями, обеспечивающими источник напряжения, и резистором, подключенным параллельно батареям. Посмотрите, как на ток влияет изменение сопротивления и/или напряжения. Обратите внимание, что сопротивление моделируется как элемент, содержащий небольшие центров рассеяния .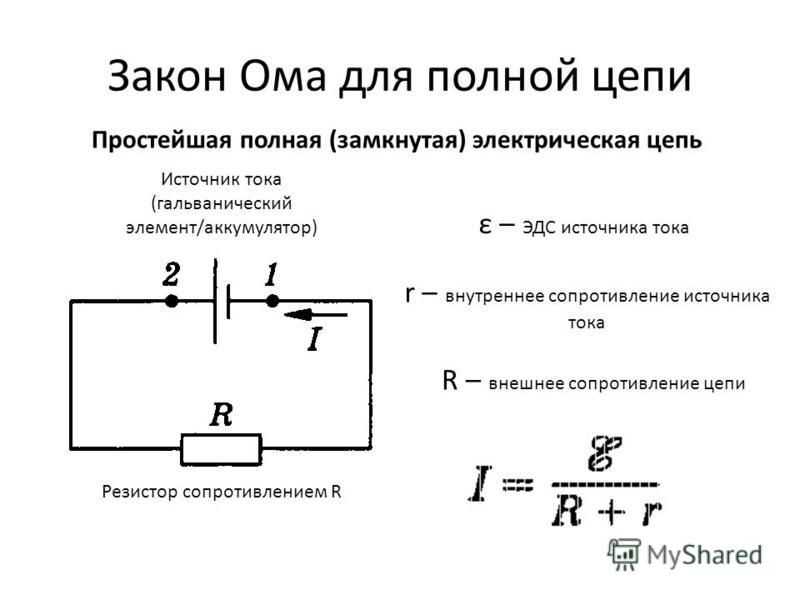 Они представляют собой примеси или другие препятствия, препятствующие прохождению тока.
Они представляют собой примеси или другие препятствия, препятствующие прохождению тока.
PhET Исследования: Закон Ома. Посмотрите, как форма уравнения закона Ома соотносится с простой цепью. Отрегулируйте напряжение и сопротивление и посмотрите, как изменится ток в соответствии с законом Ома. Размеры символов в уравнении изменяются в соответствии с принципиальной схемой.
Нажмите, чтобы просмотреть содержимое
В цепи, если сопротивление оставить постоянным, а напряжение удвоить (например, с 3\,\text{В} до 6\,\text{В}), как изменится ток? Соответствует ли это закону Ома?
Ток удвоится. Это соответствует закону Ома, поскольку ток пропорционален напряжению.
Ток удвоится.
 Это не соответствует закону Ома, поскольку ток пропорционален напряжению.
Это не соответствует закону Ома, поскольку ток пропорционален напряжению.Ток увеличится вдвое. Это соответствует закону Ома, поскольку ток пропорционален напряжению.
Ток уменьшится вдвое. Это не соответствует закону Ома, поскольку ток пропорционален напряжению.
Рабочий пример
Сопротивление фары
Каково сопротивление автомобильной фары, через которую протекает ток 2,50 А при подаче на нее напряжения 12,0 В?
Стратегия
Закон Ома говорит нам, что Vheadlight=IRheadlightVheadlight=IRheadlight . Падение напряжения при прохождении через фару — это просто повышение напряжения, обеспечиваемое аккумулятором, Vheadlight=VbatteryVheadlight=Vbattery. Мы можем использовать это уравнение и изменить закон Ома, чтобы найти сопротивление RheadlightRheadlight фары.
Мы можем использовать это уравнение и изменить закон Ома, чтобы найти сопротивление RheadlightRheadlight фары.
Решение
Решая закон Ома для сопротивления фары, получаем
19.6
Обсуждение
Это относительно небольшое сопротивление. Как мы увидим ниже, сопротивления в цепях обычно измеряются в кВт или МВт.
Рабочий пример
Определите сопротивление по графику ток-напряжение
Предположим, вы прикладываете к цепи несколько разных напряжений и измеряете ток, протекающий по цепи. График ваших результатов показан на рис. 19.7. Каково сопротивление цепи?
Рисунок 19,7 Линия показывает ток как функцию напряжения. Обратите внимание, что сила тока указана в миллиамперах. Например, при 3 В ток равен 0,003 А или 3 мА.
Стратегия
График показывает, что ток пропорционален напряжению, что соответствует закону Ома. По закону Ома (V=IRV=IR) константа пропорциональности равна сопротивлению Р . Поскольку на графике ток показан как функция напряжения, мы должны преобразовать закон Ома в следующую форму: I=VR=1R×VI=VR=1R×V. Это показывает, что наклон линии I по сравнению с V составляет 1R1R. Таким образом, если мы найдем наклон линии на рисунке 19.7, мы можем вычислить сопротивление R .
По закону Ома (V=IRV=IR) константа пропорциональности равна сопротивлению Р . Поскольку на графике ток показан как функция напряжения, мы должны преобразовать закон Ома в следующую форму: I=VR=1R×VI=VR=1R×V. Это показывает, что наклон линии I по сравнению с V составляет 1R1R. Таким образом, если мы найдем наклон линии на рисунке 19.7, мы можем вычислить сопротивление R .
Решение
Наклон линии равен подъему , деленному на пробег . Глядя на нижний левый квадрат сетки, мы видим, что линия увеличивается на 1 мА (0,001 А) и проходит при напряжении 1 В. Таким образом, наклон линии равен
наклон=0,001A1V.наклон=0,001A1V.
19,7
Приравнивание наклона с 1R1R и решением для r дает
1R = 0,001A1R = 1V0,001A = 1000 Ом1R = 0,001A1R = 1V0,001A = 1000 Ом
9,8
или 1V0,001A = 1000 Ом
или 1-е. .
.
Обсуждение
Это сопротивление больше, чем то, что мы нашли в предыдущем примере. Сопротивления, подобные этому, распространены в электрических цепях, как мы узнаем в следующем разделе. Обратите внимание, что если линия на рис. 19.7 не были прямыми, тогда материал не был бы омическим, и мы не могли бы использовать закон Ома. Материалы, которые не подчиняются закону Ома, называются неомическими.
Практические задачи
3.
Если удвоить напряжение на омическом резисторе, как изменится ток через резистор?
Ток удвоится.
Ток увеличится вдвое.
Ток уменьшится вдвое.

Ток уменьшится в два раза.
4.
Ток через резистор равен 0,025\,\text{A}. Чему равно падение напряжения на резисторе?
2,5\,\текст{мВ}
0,25\,\текст{В}
2.5\,\текст{В}
0,25\,\текст{мВ}
Проверьте свое понимание
5.
Что такое электрический ток?
Электрический ток – это электрический заряд, находящийся в состоянии покоя.
Электрический ток — это движущийся электрический заряд.
Электрический ток — это электрический заряд, который перемещается только от положительного полюса батареи к отрицательному полюсу.
Электрический ток — это электрический заряд, который перемещается только из области с более низким потенциалом в область с более высоким потенциалом.

6.
Что такое омический материал?
Омический материал — это материал, подчиняющийся закону Ома.
Омический материал — это материал, который не подчиняется закону Ома.
Омический материал — это материал с высоким сопротивлением.
Омический материал — это материал с низким сопротивлением.
7.