Как рассчитать сопротивление катушки индуктивности. Какие формулы используются для расчета. Как работает онлайн калькулятор для расчета сопротивления катушки. Какие параметры влияют на сопротивление катушки индуктивности.
Что такое катушка индуктивности и ее основные параметры
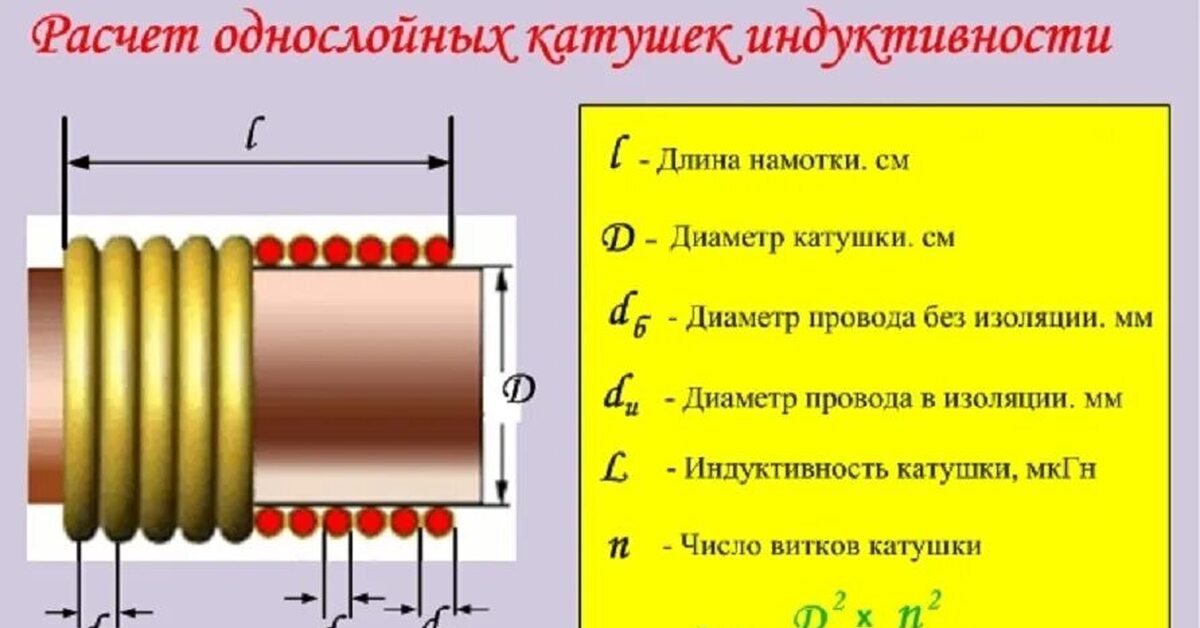
Катушка индуктивности представляет собой один из базовых элементов электрических и электронных схем. Это проводник, намотанный в виде спирали на каркас определенной формы. Основные параметры катушки индуктивности:
- Индуктивность (L) — способность катушки накапливать энергию магнитного поля. Измеряется в Генри (Гн).
- Активное сопротивление (R) — сопротивление провода катушки постоянному току. Измеряется в Омах (Ом).
- Реактивное сопротивление (XL) — сопротивление катушки переменному току. Измеряется в Омах (Ом).
- Добротность (Q) — отношение реактивного сопротивления к активному.
Сопротивление катушки индуктивности зависит от ее конструкции и параметров протекающего тока. Рассмотрим подробнее, как рассчитать различные виды сопротивления катушки.

Формулы для расчета сопротивления катушки индуктивности
Для расчета сопротивления катушки индуктивности используются следующие основные формулы:
Активное сопротивление катушки
Активное сопротивление R определяется длиной и сечением провода:
R = ρ * l / S
где:
- ρ — удельное сопротивление материала провода
- l — длина провода
- S — площадь поперечного сечения провода
Индуктивное сопротивление катушки
Индуктивное сопротивление XL зависит от индуктивности и частоты тока:
XL = 2πfL
где:
- f — частота переменного тока
- L — индуктивность катушки
Полное сопротивление катушки
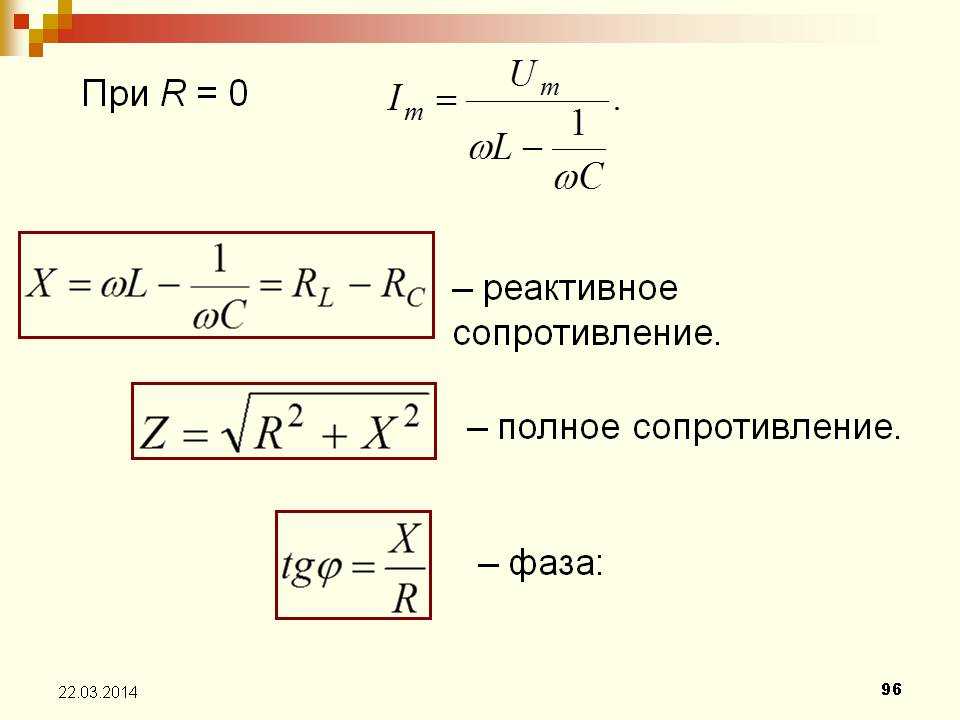
Полное или импедансное сопротивление Z учитывает активную и реактивную составляющие:
Z = √(R^2 + XL^2)
Данные формулы позволяют рассчитать различные виды сопротивления катушки индуктивности при известных параметрах.
Онлайн калькулятор для расчета сопротивления катушки
Для упрощения расчетов можно воспользоваться онлайн калькулятором сопротивления катушки индуктивности. Типичный калькулятор включает следующие поля для ввода:
- Индуктивность катушки (мкГн, мГн или Гн)
- Частота тока (Гц, кГц или МГц)
- Активное сопротивление провода (Ом)
После ввода параметров калькулятор автоматически рассчитает:
- Индуктивное сопротивление XL (Ом)
- Полное сопротивление Z (Ом)
- Добротность катушки Q
Использование онлайн калькулятора значительно ускоряет и упрощает расчеты, позволяя быстро определить сопротивление катушки при различных параметрах.
Факторы, влияющие на сопротивление катушки индуктивности
На сопротивление катушки индуктивности оказывают влияние следующие основные факторы:
Геометрические параметры катушки
- Длина намотки
- Диаметр катушки
- Количество витков
- Шаг намотки
Характеристики провода
- Материал провода
- Диаметр провода
- Длина провода
Параметры сердечника
- Наличие или отсутствие сердечника
- Материал сердечника
- Форма сердечника
Характеристики тока
- Частота тока
- Амплитуда тока
Учет всех этих факторов позволяет точно рассчитать сопротивление катушки индуктивности для конкретных условий применения.
Практическое применение расчета сопротивления катушки
Расчет сопротивления катушки индуктивности имеет важное практическое значение в различных областях электротехники и электроники:

- Проектирование фильтров и колебательных контуров
- Расчет импедансов в радиочастотных цепях
- Согласование импедансов в линиях передачи
- Определение добротности катушек
- Расчет потерь в магнитных компонентах
Точное знание сопротивления катушки позволяет оптимизировать ее параметры и характеристики для конкретного применения.
Типичные ошибки при расчете сопротивления катушки
При расчете сопротивления катушки индуктивности следует избегать следующих распространенных ошибок:
- Игнорирование частотной зависимости сопротивления
- Неучет активных потерь в катушке
- Пренебрежение влиянием сердечника на индуктивность
- Ошибки в расчете длины провода катушки
- Использование неверных единиц измерения
Внимательность к деталям и правильное применение формул позволит избежать ошибок и получить корректные результаты расчетов.
Особенности расчета сопротивления многослойных катушек
Расчет сопротивления многослойных катушек имеет свои особенности:
- Необходимо учитывать взаимную индуктивность слоев
- Важно правильно рассчитать общую длину провода
- Следует учитывать неравномерность распределения тока по слоям
- Требуется принимать во внимание емкость между слоями
Для точного расчета многослойных катушек часто используются специализированные программы моделирования.
Измерение сопротивления катушки индуктивности
Помимо расчетов, сопротивление катушки индуктивности можно измерить экспериментально. Основные методы измерения:
- Измерение активного сопротивления омметром на постоянном токе
- Измерение импеданса RLC-метром на переменном токе
- Определение добротности методом резонанса
- Измерение параметров катушки анализатором импеданса
Сравнение расчетных и измеренных значений позволяет оценить точность расчетов и выявить возможные отклонения реальных параметров катушки от расчетных.
Расчет сопротивления катушки индуктивности
Рубрика: Коммуникации и связь. Скачать файл: referat. Краткое описание работы: Обзор конструкций типичных катушек индуктивности. Расчет глубины проникновения тока, величины индуктивности, числа витков и длины однослойной обмотки, оптимального диаметра провода, сопротивления потерь в диэлектрике каркаса и добротности катушки.
Поиск данных по Вашему запросу:
Расчет сопротивления катушки индуктивности
Схемы, справочники, даташиты:
Прайс-листы, цены:
Обсуждения, статьи, мануалы:
Дождитесь окончания поиска во всех базах.
По завершению появится ссылка для доступа к найденным материалам.
Содержание:
- Индуктивное сопротивление
- Расчет катушки индуктивности
- Расчет катушки индуктивности
- Катушка индуктивности в цепи постоянного и переменного тока
- Калькулятор расчета многослойной катушки индуктивности
- Расчет катушек индуктивности без сердечника
- Катушка индуктивности в цепи переменного тока – принцип действия и значение
- Конвертер величин
ПОСМОТРИТЕ ВИДЕО ПО ТЕМЕ: Лекция 116. Энергия катушки индуктивности
Энергия катушки индуктивности
Индуктивное сопротивление
Катушки индуктивности и расчеты. Катушки индуктивности, в отличии от проводников, не обладают стабильным сопротивлением. Однако, для них существует определенная математическая зависимость между напряжением и током :. Как видите, эта формула похожа на аналогичную формулу «Закона Ома» для конденсатора. Она связывает одну переменную в нашем случае напряжение на катушке индуктивности со скоростью изменения другой переменной тока через катушку. Поведение катушки индуктивности по аналогии с конденсатором тесно связано с переменной времени.
Если не учитывать внутреннее сопротивление катушки индуктивности ради чистоты эксперимента мы принимаем его равным нулю , то напряжение на ее выводах будет зависеть от изменения тока во времени. Давайте предположим, что мы подключили идеальную катушку индуктивности имеющую нулевое сопротивление провода к цепи, позволяющей измерить ток через эту катушку при помощи потенциометра:.
Если механизм потенциометра находится в одном положении ползунок неподвижен , то соединенный последовательно с ним амперметр зарегистрирует постоянный неизменный ток, а подключенный к катушке индуктивности вольтметр покажет 0 вольт.
С точки зрения физики, если ток будет постоянным неизменным , то постоянным будет и произведенное катушкой индуктивности магнитное поле.
Ток в цепи при этом будет возрастать, что можно увидеть по медленному отклонению стрелки амперметра:. Это значение, умноженное на индуктивность так же имеющую фиксированную величину , даст нам постоянное напряжение некоторой величины.
С точки зрения физики, постепенное увеличение тока приведет к росту магнитного поля. Это напряжение принимает такую полярность, которая пытается противодействовать изменению тока. Другими словами, полярность напряжения, индуцированного в результате увеличения тока, будет ориентирована против направления этого тока, чтобы сохранить его величину на прежнем уровне. Это явление демонстрирует более общий принцип физики, известный как Правило Ленца , который гласит : Индукционный ток всегда имеет такое направление, что он ослабляет действие причины, возбуждающей этот ток.
В этом случае катушка индуктивности выступает в качестве нагрузки. Если мы будем двигать ползунок потенциометра в том же направлении, но с различной скоростью, то получим следующий график:. Когда линия тока на графике растёт быстро крутой подъем , напряжение имеет большое значение.
Когда линия тока растет медленно пологий подъем , напряжение имеет маленькое значение. В одном месте графика можно увидеть строго горизонтальный отрезок линии тока нулевой наклон, представляющий период времени, когда ползунок потенциометра не двигался вообще , при котором напряжение упало до нулевой отметки. Катушка индуктивности всегда выступает против любого изменения тока, полярность индуцированного ей напряжения будет противоположна направлению этого изменения:.
Величина производимого катушкой индуктивности напряжения конечно же зависит от скорости уменьшения тока. Как гласит Закон Ленца, индуцированное напряжение будет противоположно изменению тока. При уменьшении тока полярность напряжения будет ориентирована таким образом, чтобы попытаться сохранить величину этого тока на прежнем уровне.
В данном случае катушка выступает в качестве источника. Чем быстрее уменьшается ток, тем больше напряжения будет производить катушка индуктивности за счет высвобождения накопленной энергии. Если ток через катушку индуктивности изменяется очень быстро , то она произведет очень высокое напряжение. В качестве примера давайте рассмотрим следующую схему :.
В этой схеме лампа подключена параллельно катушке индуктивности. Переключатель используется для управления током в цепи , а питание подается от 6 -вольтовой батареи.
При включении выключателя, катушка индуктивности окажет кратковременное сопротивление изменению тока от нуля до некоторой величины, на ее выводах сгенерируется небольшое напряжение.
Так как для ионизации газа внутри неоновой лампы необходимо напряжение порядка 70 вольт, шести вольт источника питания, а тем более низкого мгновенного напряжения катушки индуктивности в момент включения выключателя будет явно недостаточно, чтобы зажечь эту лампу:. Если выключатель разомкнуть, то в цепи мгновенно возникнет очень высокое сопротивление сопротивление воздушного зазора между контактами.
Это сопротивление спровоцирует почти мгновенное уменьшение тока. Такое быстрое изменение тока с некоторой величины до нуля, в короткий промежуток времени приведет к возникновению очень высокого напряжения на катушке индуктивности пытающегося противодействовать понижению тока. Этого напряжения , как правило, более чем достаточно чтобы зажечь неоновую лампу , хотя бы на короткое время , пока ток не упадет до нуля :. Для достижения максимального эффекта , индуктивность катушки должна быть как можно больше по крайней мере один Генри.
Катушки индуктивности 2. Катушки индуктивности и расчеты Катушки индуктивности, в отличии от проводников, не обладают стабильным сопротивлением. Последние новости 6. Мера стабилизации трансформатора.
Конфигурации обмоток трансформаторов. Фазировка в трансформаторах. Электрическая изоляция. Повышающие и понижающие трансформаторы.
Взаимоиндукция — основа работы трансформаторов. Резонансные фильтры. Полосно-заграждающие режекторные фильтры. Полосовые фильтры. Фильтры верхних частот. Фильтры нижних частот. Что такое фильтр? Популярное Неисправности телевизоров из практики ремонта Что такое напряжение и ток Расчет блоков питания 6. Температурный коэффициент сопротивления Подключение джойстиков от игровых приставок к шине USB 6. Добротность и полоса пропускания резонансной цепи.
Полосовые фильтры. Фильтры верхних частот. Фильтры нижних частот. Что такое фильтр? Популярное Неисправности телевизоров из практики ремонта Что такое напряжение и ток Расчет блоков питания 6. Температурный коэффициент сопротивления Подключение джойстиков от игровых приставок к шине USB 6. Добротность и полоса пропускания резонансной цепи.
Расчет катушки индуктивности
Онлайн расчет многослойной катушки. Калькулятор считает по алгоритму с применением эллиптических интегралов Максвелла. Катушка индуктивности — винтовая, спиральная или винтоспиральная катушка из свёрнутого изолированного проводника, обладающая значительной индуктивностью при относительно малой ёмкости и малом активном сопротивлении. Индуктивность катушки зависит от ее геометрических размеров, числа витков и способа намотки катушки. Чем больше диаметр, длина намотки и число витков катушки, тем больше ее индуктивность. Все калькуляторы. Конвертеры Обратная связь Приложения.
Многослойная катушка индуктивности он лайн расчет **Под сопротивлением катушки имеется ввиду сопротивление катушки.
Расчет катушки индуктивности
Катушкой индуктивности — это элемент электрической цепи с высоким значением индуктивности, при этом низкими емкостью и активным сопротивлением. Их используют:. Катушка представляет собой намотанную на каркасе проволоку в виде спирали, а намотка может быть однослойной или многослойной, виток к витку или с расстоянием. Они бывают различных типов и форм, например, без сердечника обладают небольшой индуктивностью, а с сердечником она значительно увеличивается. Это обусловлено магнитной проницаемостью материала. Форма сердечника может быть разной, выделяют броневые, стержневые и тороидальные. Для улучшения массогабаритных параметров катушки наматывают на ферритовом кольце — такой вариант называется тороидальным способом намотки. Как рассчитать катушку в онлайн калькуляторе и вручную? На её параметры влияет количество витков длина провода , наличие и материал сердечника.
Катушка индуктивности в цепи постоянного и переменного тока
Катушка индуктивности представляет собой электрическую сборную конструкцию, которая может изготавливаться в следующих исполнениях:. Особенностью этого электротехнического компонента является наличие у него значительной по величине индуктивности при относительно малой емкостной составляющей и низком активном сопротивлении. Это приводит к тому, что при протекании переменного тока она проявляет себя как элемент, обладающий большой инерционностью. Обратите внимание: Благодаря этой особенности катушки текущий по ней ток отстает от приложенного напряжения на определенный угол 90 градусов. Для того, чтобы получить точные значения индуктивности катушки заданной формы, следует ввести ее основные параметры в онлайн-калькулятор.
Особенностью этого электротехнического компонента является наличие у него значительной по величине индуктивности при относительно малой емкостной составляющей и низком активном сопротивлении. Это приводит к тому, что при протекании переменного тока она проявляет себя как элемент, обладающий большой инерционностью. Обратите внимание: Благодаря этой особенности катушки текущий по ней ток отстает от приложенного напряжения на определенный угол 90 градусов. Для того, чтобы получить точные значения индуктивности катушки заданной формы, следует ввести ее основные параметры в онлайн-калькулятор.
Random converter.
Калькулятор расчета многослойной катушки индуктивности
Код для вставки без рекламы с прямой ссылкой на сайт. Код для вставки с рекламой без прямой ссылки на сайт. Скопируйте и вставьте этот код на свою страничку в то место, где хотите, чтобы отобразился калькулятор. Калькулятор справочный портал. Избранные сервисы. Кликните, чтобы добавить в избранные сервисы.
Расчет катушек индуктивности без сердечника
Катушкой индуктивности — это элемент электрической цепи с высоким значением индуктивности, при этом низкими емкостью и активным сопротивлением. Их используют:. Катушка представляет собой намотанную на каркасе проволоку в виде спирали, а намотка может быть однослойной или многослойной, виток к витку или с расстоянием. Они бывают различных типов и форм, например, без сердечника обладают небольшой индуктивностью, а с сердечником она значительно увеличивается. Это обусловлено магнитной проницаемостью материала. Форма сердечника может быть разной, выделяют броневые, стержневые и тороидальные. Для улучшения массогабаритных параметров катушки наматывают на ферритовом кольце — такой вариант называется тороидальным способом намотки. Как рассчитать катушку в онлайн калькуляторе и вручную?
Их используют:. Катушка представляет собой намотанную на каркасе проволоку в виде спирали, а намотка может быть однослойной или многослойной, виток к витку или с расстоянием. Они бывают различных типов и форм, например, без сердечника обладают небольшой индуктивностью, а с сердечником она значительно увеличивается. Это обусловлено магнитной проницаемостью материала. Форма сердечника может быть разной, выделяют броневые, стержневые и тороидальные. Для улучшения массогабаритных параметров катушки наматывают на ферритовом кольце — такой вариант называется тороидальным способом намотки. Как рассчитать катушку в онлайн калькуляторе и вручную?
Калькулятор расчета индуктивности катушки производит расчет **Под сопротивлением катушки имеется ввиду сопротивление катушки постоянному.
Катушка индуктивности в цепи переменного тока – принцип действия и значение
Расчет сопротивления катушки индуктивности
Сегодня нами будет рассмотрена катушка индуктивности в цепи переменного тока, узнаем, в чем бы была разница, если бы цепь питалась от постоянного тока, а также много интересных особенностей этого простого, но очень важного радиоэлемента. Для начала давайте определим назначение этой детали, а также основные понятия и термины, связанные с ней. Катушка индуктивности — это радиоэлемент, применяющийся в разных схемах для следующего:. Представляет собой данный элемент спиральную, винтовую или винтоспиральную катушку, сделанную из изолированного проводника.
Для начала давайте определим назначение этой детали, а также основные понятия и термины, связанные с ней. Катушка индуктивности — это радиоэлемент, применяющийся в разных схемах для следующего:. Представляет собой данный элемент спиральную, винтовую или винтоспиральную катушку, сделанную из изолированного проводника.
Конвертер величин
ВИДЕО ПО ТЕМЕ: Катушки индуктивности
На практике нередко случаются ситуации, когда при выходе со строя катушки индуктивности, ее необходимо восстановить — намотать новую проволоку взамен старой. При этом вам уже известны геометрические параметры катушки, но требуется узнать, сколько сделать витков, слоев, их толщину и длину необходимого для этого провода. Стоит отметить, что при намотке витки должны ложиться вплотную без зазора. Тогда, зная общее число витков и принимая, что d — это усредненное значение диаметра для всех витков, длина всего провода будет определяться по формуле:. Через сопротивление провода можно определить его диаметр, для чего понадобится выразить сопротивление через геометрические параметры устройства.
Через сопротивление провода можно определить его диаметр, для чего понадобится выразить сопротивление через геометрические параметры устройства.
Для работы калькулятора необходимо включить JavaScript в вашем браузере! Имя обязательное.
Если подключить катушку индуктивности в цепь электротока переменного типа, то этот ток будет изменяться под влиянием непрерывного изменения электронапряжения. Такие изменения являются генераторами магнитного поля, которое убывает и возрастает периодами. Магнитное поле влияет на катушку, которая создает встречное электронапряжение, что препятствует изменению тока. Соответственно, ток протекает по цепи с постоянным противодействием, которое называется индуктивным сопротивлением. Такое сопротивление напрямую зависит от значения индуктивности и частоты приложенного электрического напряжения.
В цепь переменного электрического тока входят активные содержащие внутренние источники энергии и пассивные элементы потребители энергии. К пассивным элементам относят резисторы и реактивные устройства. В электротехнике рассматривают два типа резисторов: активное и реактивное сопротивление. Активным — обладают приборы, в которых энергия электрического тока преобразуется в тепловую.
В электротехнике рассматривают два типа резисторов: активное и реактивное сопротивление. Активным — обладают приборы, в которых энергия электрического тока преобразуется в тепловую.
Активное сопротивление катушки: что это, формула, расчеты
Конденсатор в цепи переменного тока
Ну а теперь давайте вместо резистора поставим конденсатор.
Смотрим осциллограммы:
Как вы видите, конденсатор обладает сопротивлением, так как сила тока в цепи значительно уменьшилась
Но обратите внимание, что произошел сдвиг желтой осциллограммы, то бишь осциллограммы силы тока
Вспоминаем алгебру старшие классы. Итак, полный период T – это 2П
Теперь давайте прикинем, какой сдвиг фаз у нас получился на графике:
Где-то примерно П/2 или 90 градусов.
Почему так произошло? Во всем виновато физическое свойство конденсатора. В самые первые доли секунд, конденсатор ведет себя как проводник с очень малым сопротивлением, поэтому сила тока в этот момент будет максимальна. В этом можно легко убедиться, если резко подать на конденсатор напряжение и в начальный момент времени посмотреть, что происходит с силой тока
В этом можно легко убедиться, если резко подать на конденсатор напряжение и в начальный момент времени посмотреть, что происходит с силой тока
Красная осциллограмма – это напряжение, которое мы подаем на конденсатор, а желтая – это сила тока в цепи конденсатора. По мере заряда конденсатора сила тока падает и достигает нуля при полном заряде конденсатора.
К чему приведет дальнейшее увеличение частоты? Давайте посмотрим:
50 Герц.
100 Герц
200 Герц
Как вы видите, с увеличением частоты, у нас сила тока в цепи с конденсатором возрастает.
Реактивное сопротивление катушки индуктивности
Поскольку в первую половину периода энергия электрического тока запасается в магнитном поле катушки, а во вторую — возвращается в цепь, то в среднем работа электрического тока равна по модулю работе ЭДС самоиндукции, но имеет противоположный знак:
$$e_i =-u$$
Однако амплитудные значения напряжения и тока на катушке индуктивности достигаются неодновременно.
Мгновенное значение тока:
$$i =I_msin \omega t$$
Мгновенное значение напряжения:
$$u =L\omega I_m cos \omega t$$
Учитывая, что максимальная амплитуда напряжения $U_m$ равна $ L\omega I_m $, и приводя к синусу, получаем:
$$u =U_m sin(\omega t+{\pi \over 2})$$
Таким образом, колебания силы тока в катушке индуктивности отстают от колебаний напряжения на четверть периода
В этом важное отличие реактивного сопротивления от активного, где отставания между током и напряжения нет
Рис. 2. Графики тока и напряжения для индуктивности.
Амплитуда силы тока в катушке равна:
$$I_m={U_m\over \omega L}$$
Сравним эту формулу с законом Ома, который используется для определения силы тока в цепи:
$$I={U\over R}$$
Можно видеть, что эти формулы аналогичны, и величина $ \omega L$ играет роль сопротивления. То есть реактивное сопротивление катушки индуктивности (индуктивное сопротивление) равно:
$$X_L= \omega L$$
Отметим, что реактивное сопротивление катушки прямо пропорционально циклической частоте переменного тока. Чем она больше, тем больше сопротивление.
Чем она больше, тем больше сопротивление.
Поскольку любой проводник обладает некоторой индуктивностью, то на очень высоких частотах даже эта малая индуктивность обычных проводников достаточно сильно влияет на сигнал. Поэтому приходится применять специальные меры для ее компенсации. Например, применять вместо проводов волноводы — пустотелые металлические конструкции:
Рис. 3. Волноводы.
Мощность в цепи с реактивными радиоэлементами
При подключении таких элементов в цепь в четных четвертях периода мощность будет иметь отрицательное значение (в это время компонент направляет накопленную энергию в источник напряжения). В итоге использование энергии элементом за весь цикл оказывается равным нулю. Это означает, что на нем не происходит выделения энергии, так что на электросхемах такие детали изображаются холодными. На деле положение вещей может быть немного иным (это зависит от параметров конкретного элемента), бывает, что небольшие тепловые потери на конденсаторе или соленоиде все-таки имеют место. Но они не будут значительными, измеряющимися в кв.
Но они не будут значительными, измеряющимися в кв.
Импеданс элемента
Общее сопротивление конденсатора (импеданс) переменному сигналу складывается из трёх составляющих: ёмкостного, резистивного и индуктивного сопротивления. Все эти величины при конструировании схем, содержащих накопительный элемент, необходимо учитывать. В ином случае в электрической цепи, при соответствующей обвязке, конденсатор может вести себя как дроссель и находится в резонансе.
Из всех трёх величин наиболее значимой является ёмкостное сопротивление конденсатора, но при определённых обстоятельствах индуктивное тоже оказывает влияние. Часто при расчётах паразитные значения вроде индуктивности или активного сопротивления принимаются ничтожно малыми, а конденсатор в этом случае называется идеальным.
Полное сопротивление элемента выражается в формуле Z = (R2 + (Xl-Xc) 2 ) ½, где
- Xl — индуктивность;
- Xс — ёмкость;
- R — активная составляющая.
Последняя возникает из-за появления электродвижущей силы (ЭДС) самоиндукции. Непостоянство тока приводит к изменению магнитного потока, поддерживающего ток ЭДС самоиндукции постоянным. Это значение определяется индуктивностью L и частотой протекающих зарядов W. Xl = wL = 2*p*f*L. Xc — ёмкостное сопротивление, зависящее от ёмкости накопителя C и частоты тока f. Xc = 1/wC = ½*p*f*C, где w — круговая частота.
Непостоянство тока приводит к изменению магнитного потока, поддерживающего ток ЭДС самоиндукции постоянным. Это значение определяется индуктивностью L и частотой протекающих зарядов W. Xl = wL = 2*p*f*L. Xc — ёмкостное сопротивление, зависящее от ёмкости накопителя C и частоты тока f. Xc = 1/wC = ½*p*f*C, где w — круговая частота.
Разница между ёмкостным и индуктивным значениями называется реактивным сопротивлением конденсатора: X = Xl-Xc. По формулам можно увидеть, что при увеличении частоты f сигнала начинает преобладать индуктивное значение, при уменьшении — ёмкостное. Поэтому если:
- X > 0, в элементе проявляются индуктивные свойства;
- X = 0, в ёмкости присутствует только активная величина;
- X
Активное сопротивление R связывается с потерями мощности, превращением её электрической энергии в тепловую. Реактивное – с обменом энергии между переменным током и электромагнитным полем. Таким образом, полное сопротивление можно найти, используя формулу Z = R +j*X, где j — мнимая единица.
Импеданс элемента.
Какие существуют виды сопротивлений
Их немного, одно из которых мы уже разобрали:
- омическое;
- активное;
- индуктивное;
- ёмкостное.
Формулы расчёта электрического сопротивления для переменного тока простыми словами.
К сожалению, наш друг-физик решил не идти нам навстречу и вывел несколько формул по нахождению всех трёх величин. Электрическое сопротивление обозначается буквой R.
Но перед тем как пойти дальше, совет: всегда придумывайте какие-нибудь ассоциации, чтобы запомнилось на всю жизнь, например:
- R (сопротивление). Можете запомнить что R, как рюмка. Нужно сопротивляться, чтобы не выпить ещё одну рюмку.
- I (сила тока). Латинская «I», как проводок, по которому идёт ток.
- U (напряжение). Эта буква, как дуга. И напряжение разносится с одного конца на другой по дуге.
Ну и, конечно, формула закона Ома для участка цепи.
- R=U/I т.е., чтобы найти сопротивление(рюмку) надо напряжение (дугу) разделить на ток (проводок).

- U=IR, хотите найти напряжение (дугу), умножьте проводок на рюмку.
- I=U/R чтобы найти чему равен проводок, нужно напряжение разделить на сопротивление.
Ну а теперь главное, для чего мы все здесь собрались: «Зачем нужен этот закон? Что он даёт?»
Также не забывате, если вдруг вас спросят от чего зависит сопротивление — отвечайте: » От напряжения и мощности».
Формула активного сопротивления
Ну что сказать? Придется запастись терпением и потратить время на все эти законы и определения.
Но к счастью, активное сопротивление, так и осталось большой буквой R. Просто немного поменялась формула и ее предназначение.
Подключим к нашей цепи проводник. Проводником может выступать лампа.
Понятно, что по нему тоже будет проходить ток. Это как танец «волна». Все 5 человек берутся за руки и начинают по очереди создавать колебания. Сопротивление уже известно на всех. Так же и здесь.
Если посмотреть, то можно найти сходство танца «волны» с этой буквой. Так и запомните.
Так и запомните.
Формула, как рассчитать силу тока:
I=U/Z
О том, как найти общее сопротивление мы поговорим ниже.
Формула индуктивного сопротивления
Боюсь, что когда вы увидите данную формулу, то она вам точно не понравится. Но нет слова «не хочу», есть слово «надо».
Начнем с обозначения:
- XL (индуктивное сопротивление). Прямо как размер в одежде. Но почему именно так? L — это цепь переменного тока;
- f — частота, в Гц;
- сопротивление с частотой взаимосвязаны, так, если возрастает одно — увеличивается и другое;
- единица СИ индуктивного сопротивления: = Ом;
- запомните, что индуктивное сопротивление отличается от омического тем, что у первого нет потери мощности;
- XL=2π×f×L;
- формула расчета мощности по напряжению: P = U×I;
- мощность электрического тока вычисляется в Ватах.
Формула ёмкостного сопротивления Xc
Ёмкостное сопротивление — это проводник, который подключен к цепи. Он не имеет сопротивление, но есть ёмкость. Обозначается это ёмкостное сопротивление буквами Xc.
Он не имеет сопротивление, но есть ёмкость. Обозначается это ёмкостное сопротивление буквами Xc.
- Xc = 1/ωC;
- ω — циклическая частота;
- С — ёмкость.
Формула полного сопротивления
Как говорилось выше — полное сопротиление что-то на подобии танца «волны». Нужно узнать R (сопротивление) всех.
Чтобы определить полное сопротивление цепи:
R = R1 +R2 (проводников может быть несколько).
Теперь, если у вас спросят как определить общее сопротивление цепи, вы знаете что делать.
Свойства ёмкостей
Основное свойство состоит в их способности накапливать и отдавать электрический заряд. Оба этих процесса происходят не мгновенно, а за вполне определённый период, который поддаётся расчету. Данное свойство используется для создания различных времязадающих RC цепей. Если зарядить конденсатор до некоторого значения, то время его разряда через резистор R будет зависеть от ёмкости C. RC цепь Ещё одно распространённое свойство конденсаторов – это возможность ограничивать переменный ток. Вызвана она реактивом этих элементов. Ёмкость, включенная в цепь переменного тока, ограничивает его до значения I = 2pfCU.
Вызвана она реактивом этих элементов. Ёмкость, включенная в цепь переменного тока, ограничивает его до значения I = 2pfCU.
Свойства ёмкостей.
Здесь U – напряжение источника питания. Дополнительная информация. Ёмкость, подключенная параллельно с катушкой, имеющей индуктивный характер сопротивления, называется колебательным контуром. Данная цепь обладает высокой амплитудой колебаний на резонансной частоте. Она применяется для выделения из множества окружающих радиосигналов именно того, на который требуется настроить приём.
Сопротивление – это одна их характеристик конденсатора, подключенного к цепи переменного тока. Понимание процессов, происходящих с этим элементом в подобных схемах, существенно расширяет сферу его использования. Реактивное сопротивление конденсаторов учитывается как в простых бытовых электроприборах, так и в сложной вычислительной технике.
Резистор обладает активным (омическим) сопротивлением. Катушка индуктивности и конденсатор обладают реактивным сопротивлением. В цепи переменного тока на конденсаторе ток опережает напряжение на 90 градусов, а на катушке ток отстает от напряжения на 90 градусов. Сопротивление катушки вычисляется по формуле. Сопротивление конденсатора вычисляется по формуле:
В цепи переменного тока на конденсаторе ток опережает напряжение на 90 градусов, а на катушке ток отстает от напряжения на 90 градусов. Сопротивление катушки вычисляется по формуле. Сопротивление конденсатора вычисляется по формуле:
Расчет сопротивления.
В цепи переменного тока на идеальном реактивном сопротивлении не выделяется мощность.
Будет интересно Сколько стоят керамические конденсаторы?
Z = R + i X , где Z – импеданс, R – величина активного сопротивления , X – величина реактивного сопротивления, i – мнимая единица . В зависимости от величины X какого-либо элемента электрической цепи, говорят о трёх случаях:
- X > 0 – элемент проявляет свойства индуктивности .
- X = 0 – элемент имеет чисто активное сопротивление .
- X < 0 – элемент проявляет ёмкостные свойства.
Величина реактивного сопротивления может быть выражена через величины индуктивного и ёмкостного сопротивлений.
Индуктивное сопротивление (X L ) обусловлено возникновением ЭДС самоиндукции . Электрический ток создает магнитное поле. Изменение тока, и как следствие изменение магнитного поля, вызывает ЭДС самоиндукции, которая препятствует изменению тока. Величина индуктивного сопротивления зависит от индуктивности элемента и частоты протекающего тока. Ёмкостное сопротивление (X C ). Величина ёмкостного сопротивления зависит от ёмкости элемента С и также частоты протекающего тока.
Электрический ток создает магнитное поле. Изменение тока, и как следствие изменение магнитного поля, вызывает ЭДС самоиндукции, которая препятствует изменению тока. Величина индуктивного сопротивления зависит от индуктивности элемента и частоты протекающего тока. Ёмкостное сопротивление (X C ). Величина ёмкостного сопротивления зависит от ёмкости элемента С и также частоты протекающего тока.
Вам интересно?
Сегодня очень много учёных, интересующихся магнетизмом и магнитными явлениями. Они изучают как магнитную, так и электрическую стороны веществ, пытаясь выявить закономерности и синтезировать мощные магниты с определёнными нужными свойствами: например, с высокой температурой плавления или сверхпроводимостью. Все эти материалы могут быть использованы в огромном количестве отраслей.
Приведём пример с аэрокосмической отраслью: перспективными для дальних межзвёздных перелётов являются ракеты с ионными двигателями, которые создают тягу посредством выброса ионизированного газа из сопла. Сила толчка в таком двигателе зависит от температуры газа и скорости его движения. Соответственно, чтобы придать газу максимальную силу для разгона, нам требуется очень сильный магнит, разгоняющий заряженные частицы и к тому же имеющий очень высокую температуру плавления для того, чтобы не расплавиться при выходе газов из сопла.
Сила толчка в таком двигателе зависит от температуры газа и скорости его движения. Соответственно, чтобы придать газу максимальную силу для разгона, нам требуется очень сильный магнит, разгоняющий заряженные частицы и к тому же имеющий очень высокую температуру плавления для того, чтобы не расплавиться при выходе газов из сопла.
Где применяется катушка индуктивности
Свойства индуктивной катушки своеобразные, небольшая доработка добавляет ей новые свойства, что делает ее весьма востребованной. Рассмотрим лишь некоторые области, где она с успехом нашла свое применение:
- 1. Конечно, это сама электротехника. Сочетания катушки с резистором или конденсатором делает ее способной задерживать или пропускать определенные частоты.
- 2. В импульсной технике катушка индуктивности выступает в качестве накопителя энергии.
- 3. Соединенные определенным образом катушки образуют различные по назначению трансформаторы.
- 4. Катушка индуктивности дает возможность повышать напряжение постоянного тока.
- 5. Электромагнит – еще одно применение катушки.
- 6. Используются для выплавки металла в доменных печах.
- 7. Особенно в старых приемниках катушка часто выступала в качестве антенны.
- 8. Современные индукционные плиты никак не могут работать без катушки индуктивности.
- 9. Если сердечник катушки соединить с подвижным механизмом – получится отличный датчик движения.
- 10. Индукционные магнитометры имеют основным элементом катушку индуктивности.
- 11. Для ускорения частиц в лабораториях также применяют своеобразную катушку.
- 12. Специальные накопителя энергии не могут обойтись без этого элемента.
Это лишь основные области применения, но уже по этому списку видно, что катушка – хороший труженик. Рассмотрим некоторые области применения более подробно.
Катушка как электромагнит
Для получения электромагнита используют сердечник из магнитомягкого материала. Для этого подходят:
- металлы: сталь, чугун;
- сплавы железа с никелем или кобальтом.

| Интересно. Если магнитопровод сделать цельным, тогда у него будут большие потери, поэтому его собирают из отдельных листов. |
Электромагниты могут работать как от постоянного, так и переменного тока. Причем электромагнит постоянного тока может быть нейтральным, когда притягивающая сила образуется независимо от направления движения тока, и поляризованным. В этом случае используется две обмотки: основная и поляризующая. Основная создает магнитный поток, а вторая направляет его в нужном направлении.
Электромагниты, работающие на переменном токе, вырабатывают переменное магнитное поле, но на сердечник оно действует в одном направлении. Однако сила притяжения меняется от нуля до максимума. Частота притяжения вдвое выше частоты тока.
Катушка как источник ЭДС
Эта особенность используется в индукционных плитах. Катушка, расположенная прямо под плитой, при работе создает вокруг себя электромагнитные волны. Эти волны, воздействуя на материал кухонной посуды, нагревают ее. Причем сама плита остается достаточно холодной, нагревается лишь от самой посуды. Такие плиты перестают работать, если посуды на ней нет, что делает их безопасными в пожарном отношении.
Причем сама плита остается достаточно холодной, нагревается лишь от самой посуды. Такие плиты перестают работать, если посуды на ней нет, что делает их безопасными в пожарном отношении.
Более мощные устройства используются на сталелитейных заводах. Доменную печь делают круглой и обвивают ее толстыми, обычно медными проводами. Когда по проводу пропускают ток большой мощности и частоты, создается мощное электромагнитное поле, воздействующее на металл, находящийся в печи. От действия этого поля металл нагревается и плавится.
Это же устройство, но меньшего размера используется, когда необходимо нагреть небольшой кусок металла, например, для ковки.
Катушки индуктивности в качестве трансформатора
В первых двух вариантах обычно используется одна катушка, но если соединить две и более катушки и по одной из них пропустить ток, то получится интересный момент. В этой катушке появится наведенная ЭДС. Она окутает все находящиеся в ее поле другие катушки и в них появится ток. Но это еще не все.
Но это еще не все.
Регулируя число витков в других катушках, можно подобрать необходимое напряжение. То есть, число витков может увеличивать или уменьшать напряжение относительно напряжения, проходящего по рабочей катушке. Чтобы такая передача была более продуктивной, используют один из видов сердечника:
- стержневой;
- броневой;
- тороидальный.
Конструкция сердечника особого влияния на трансформатор не оказывает, это больше предпочтение производителя. Осталось рассмотреть еще одну удивительную особенность катушки индуктивности – способность генерации.
Принцип работы катушки зажигания
Катушку зажигания на простом языке можно назвать обычным повышающим напряжение трансформатором. Её задача преобразовать низковольтное напряжение (6-15В) в высокое (20-30кВ). Она, как и трансформатор, состоит из двух обмоток — первичной и вторичной. Первичная низковольтная катушка состоит из небольшого количества витков, а вторичная из большего.
Но есть ещё один нюанс. Витки в катушке расположены определённым образом, что позволяет катушке, кроме индуктивности, иметь ещё и ёмкость. То есть, своего рода — колебательный контур.
Витки в катушке расположены определённым образом, что позволяет катушке, кроме индуктивности, иметь ещё и ёмкость. То есть, своего рода — колебательный контур.
При подаче тока в первичную обмотку в катушке генерируется магнитное поле. Наведенное напряжение генерируется в катушке путем самоиндукции. В момент воспламенения ток в катушке прерывается выходным каскадом (в старых системах — контактами прерывателя). Мгновенно сворачивающееся магнитное поле генерирует высокое индукционное напряжение в первичной обмотке. Оно трансформируется на вторичной обмотке катушки и преобразуется в соотношении — количество витков вторичной обмотки отнесенное к количеству витков первичной обмотки. В свече зажигания происходит высоковольтный разряд с ионизацией искрового промежутка и прохождением тока. Это продолжается, пока накопленная энергия не будет истрачена.
Эти все физические явления, наверное, мало кому интересны, поэтому давайте отвлечёмся и посчитаем, на мой взгляд, интересные факты. Сколько раз свеча зажигания «производит» искру за свой срок службы?
Сколько раз свеча зажигания «производит» искру за свой срок службы?
Количество искрообразований = «об/мин» умножить на «количество цилиндров» и всё это разделить на 2. Возьмём обычный 4-цилиндровый 4-тактный двигатель. Допустим, обороты двигателя составляют 3000 об/мин. Значит количество искрообразований = 3000 х 4/2 = 6000 искр / мин!
Свечи я меняю раз в 30000 км.
Если пройденное расстояние составляет 30 000 км со средней частотой вращения коленчатого вала двигателя 3000 об/мин при средней скорости 60 км/ч, то количество искрообразований составляет 45 000 000 на каждую свечу зажигания! Во как трудится катушка зажигания! Как Золушка, прям
Поэтому катушка зажигания вполне заслуженно может когда-нибудь устать и молча выйти из строя.
Что такое индуктивность
Что такое индуктивность — это физическая величина, которая рассказывает нам о магнитных свойствах электрической цепи. Индуктивность измеряют в Гн (Генри). Если вы вообще не понимаете о чём речь, то советую ознакомиться сначала с вот с этой статьей.
В электрических схемах например, нам встречаются какие-то непонятные катушки, дроссели и многие даже не знают их функциональную роль. В этой статье я постараюсь доступным языком рассказать, что такое индуктивность и как это явление применить на своей любимой работе.
Давайте посмотрим на рисунок
Давайте начнём движение проводника в магнитном поле таким образом, чтобы он пересек силовые линии постоянного магнита. Если это условие выполняется, то тогда в нашем проводнике появляется электродвижущая сила (ЭДС). Или наоборот проводник остаётся на месте, а магнит передвигают таким образом, чтобы силовые линии магнита пересекали проводник. Сейчас был пример электромагнитной индукции. Значение индуцированной электродвижущей силы в проводнике прямо пропорциональна магнитной индукции поля, скорости перемещения и длине проводника
Направление возникшей электродвижущей силы в проводнике определяют через правило правой руки.
Правая рука находится в таком положении чтобы силовые линии магнита заходили в ладонь. Следовательно, большой палец показывает нам направление перемещения проводника, а остальные пальцы покажут нам направление возникшей электродвижущей силы.
Следовательно, большой палец показывает нам направление перемещения проводника, а остальные пальцы покажут нам направление возникшей электродвижущей силы.
Для усиления электродвижущей силы индукции применяют электрические катушки
А если подать напряжение на катушку, то по её виткам потечёт ток, который создаёт своё магнитное поле.
Свойства катушки индуктивности
Катушка индуктивности в электрической цепи хорошо проводит постоянный ток и в то же время оказывает сопротивление переменному току , поскольку при изменении тока в катушке возникает ЭДС самоиндукции , препятствующая этому изменению.
Катушка индуктивности обладает реактивным сопротивлением величина которого равна: , где- индуктивность катушки,-циклическая частота протекающего тока. Соответственно, чем больше частота тока, протекающего через катушку, тем больше её сопротивление.
При протекании тока катушка запасает энергию, равную работе, которую необходимо совершить для установления текущего тока . Величина этой энергии равна
Величина этой энергии равна
При изменении тока в катушке возникает ЭДС самоиндукции, значение которой
Катушка индуктивности в цепи переменного тока
В цепи переменного тока в катушке индуктивности происходит следующий процесс:
- ток возбуждает в катушке электромагнитное поле. Поскольку он переменный, то и параметры электромагнитного поля во времени меняются, то есть оно тоже переменное;
- переменное магнитное поле в соответствии с законом электромагнитной индукции возбуждает в самой катушке ЭДС. Ее так и называют — ЭДС самоиндукции. Она всегда идет против направления изменения силы тока. Следовательно, в первой половине полупериода, когда сила тока возрастает, катушка это нарастание сдерживает. При этом часть энергии электричества накапливается в формируемом катушкой магнитном поле;
- во второй половине полупериода, катушка, наоборот, противостоит снижению силы тока, возвращая в цепь накопленную в виде магнитного поля энергию.
Таким образом, катушка индукции оказывает сопротивление источнику переменного тока. Это сопротивление имеет иную природу, нежели активное, преобразующее электрическую энергию в тепло.
Это сопротивление имеет иную природу, нежели активное, преобразующее электрическую энергию в тепло.
Сопротивление катушки энергию не потребляет, а лишь аккумулирует ее и затем снова возвращает в цепь, меняя характер протекания в ней тока. Его называют индуктивным. В противоположность активному, оно, как и емкостное сопротивление конденсатора, является реактивным.
Эффект проявляется тем сильнее, чем выше частота переменного тока, то подтверждается формулой расчета индуктивного сопротивления: XL = w*L = 2 π * f * L, где:
- XL — индуктивное сопротивление, Ом;
- W — круговая частота переменного тока, рад/с;
- F — частота переменного тока, Гц;
- L — индуктивность катушки, Гн.
Индуктивное сопротивление, несмотря на иной принцип действия, измеряется в тех же единицах, что и активное — Омах. Таким образом, в цепях переменного тока катушка индуктивности выступает ограничителем силы тока и нагрузку, в отличие от цепи постоянного, вводить не требуется.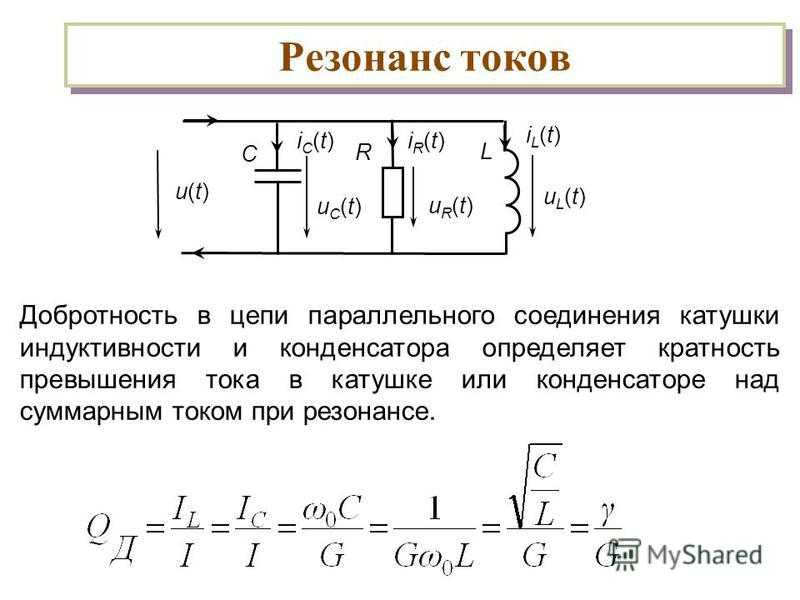
Зависимость индуктивного сопротивления катушки от частоты тока позволяет использовать данный элемент помимо прочего, для фильтрации высокочастотных помех или сигналов. Например, при установке его в схеме динамика, последний воспроизводит только низкие частоты, то есть играет роль сабвуфера.
На преодоление индуктивного сопротивления источник расходует часть мощности — это реактивная мощность (Wр). Остальное называют активной или полезной мощностью (Wа) — она производит полезную работу. Вместе реактивная и активная мощности образуют полную: Wр + Wа = Wпол.
График происходящих процессов в катушке индуктивности
Доля активной мощности характеризуется параметром cosϕ: cosϕ = Wа / W пол. Полную мощность принято измерять в вольт-амперах (ВА). Именно эти единицы указываются в характеристике источников бесперебойного питания (ИБП) и дизельных электрогенераторов. Активная мощность измеряется в привычных ваттах (Вт).
Все сказанное имеет отношение к потребителям с электродвигателями и трансформаторами, поскольку обмотки этих элементов по сути, являются катушками индуктивности. То есть если на шильдике импульсного блока питания компьютера указано, что его мощность составляет 400 Вт и cosϕ = 0,7, то от «бесперебойника» данное устройство потянет мощность Wпол = Wа / cosϕ = 400 0,7 = 571,4 ВА.
То есть если на шильдике импульсного блока питания компьютера указано, что его мощность составляет 400 Вт и cosϕ = 0,7, то от «бесперебойника» данное устройство потянет мощность Wпол = Wа / cosϕ = 400 0,7 = 571,4 ВА.
Формула расчета реактивного сопротивления
В общем случае для деталей катушечного типа применяются выражения:
X = L*w = 2* π*f*L.
Для конденсаторов применяют формулы:
X = 1/(w*C)= 1/(2* π*f*C).
Для конкретного элемента, нужные параметры которого известны, величина может быть вычислена с использованием онлайн калькулятора. В форму потребуется ввести нужные данные и нажать на кнопку, инициирующую расчеты.
Умение рассчитывать данную составляющую сопротивляемости поможет узнать величину тепловых потерь на используемых нагрузках. При параллельном подсоединении конденсатора с подходящей емкостью можно решить проблему энергетических потерь на индуктивных нагрузках.
О реальном конденсаторе
Реальный конденсатор имеет одновременно два сопротивления: активное и емкостное. Их следует считать включенными последовательно.
Их следует считать включенными последовательно.
Напряжение приложенное генератором к активному сопротивлению и ток идущий по активному сопротивлению совпадают по фазе.
Советуем изучить Плотность энергии магнитного поля
Напряжение приложенное генератором к емкостному сопротивлению и ток идущий по емкостному сопротивлению сдвинуты по фазе на 90 . Результирующее напряжение приложенное генератором к конденсатору можно определить по правилу параллелограмма.
На активном сопротивлении напряжение Uакт и ток I совпадают по фазе. На емкостном сопротивлении напряжение Uc отстает от тока I на 90 . Результирующее напряжение приложенное генератором к конденсатору определяется по правилу параллелограмма. Это результирующее напряжение отстает от тока I на какой то угол φ всегда меньший 90 .
Магнитное поле
Это словосочетание знакомо нам со школьной скамьи. Но многие уже забыли о том, что оно означает. Хотя каждый из нас помнит, что магнитное поле способно воздействовать на предметы, притягивая или отталкивая их. Но, помимо этого, у него есть и другие особенности: например, магнитное поле может воздействовать на электрически заряженные объекты, а это значит, что электричество и магнетизм тесно связаны между собой, и одно явление может плавно перетекать в другое. Учёные поняли это достаточно давно и поэтому стали называть все эти процессы вместе одним словом — «электромагнитные явления». На самом деле электромагнетизм — довольно интересная и ещё не до конца изученная область физики. Она очень обширна, и те знания, что мы можем здесь изложить вам, — это очень малая часть того, что известно человечеству о магнетизме сегодня.
Но, помимо этого, у него есть и другие особенности: например, магнитное поле может воздействовать на электрически заряженные объекты, а это значит, что электричество и магнетизм тесно связаны между собой, и одно явление может плавно перетекать в другое. Учёные поняли это достаточно давно и поэтому стали называть все эти процессы вместе одним словом — «электромагнитные явления». На самом деле электромагнетизм — довольно интересная и ещё не до конца изученная область физики. Она очень обширна, и те знания, что мы можем здесь изложить вам, — это очень малая часть того, что известно человечеству о магнетизме сегодня.
А сейчас перейдём непосредственно к предмету нашей статьи. Следующий раздел будет посвящён рассмотрению непосредственно устройства катушки индуктивности.
Расчет эквивалентного сопротивления элементов цепи
Определение общего цепного сопротивления будет зависеть от того, какого типа конфигурацию составляют компоненты цепи. Для параллельного и последовательного подключений правила расчета будут неодинаковыми. Опираться при вычислениях нужно на закон Ома.
Опираться при вычислениях нужно на закон Ома.
Согласно ему, у всех последовательно соединенных деталей, подключенных в цепь переменного тока, будет одно и то же значение электротока:
I=U/Z, где Z – общий импеданс цепи.
Напряжения будут различаться и окажутся привязанными к сопротивлениям деталей: на концах резистора его значение будет равно UR = IR (здесь R – активная резистивность элемента), для дросселя – UL = IXL, для емкостного элемента – UC = IXC (XL и XC – реактивные показатели соответствующих устройств). Так как векторы напряженности катушки и конденсатора имеют противоположные направления, суммарный показатель на реактивных деталях будет равен: UX = UL – UC . Противодействие будет равно: X = XL – XC.
Напряжения (общее, реактивное и активное) могут быть представлены в виде прямоугольного треугольника. Из него получается, что U² = UR² + UX². Поскольку противодействия входящих в цепь компонентов пропорциональны напряжениям, имеем Z2=R2+X2=R2+(XL – XC)2.
Для параллельного соединения принято выводить значения импеданса из проводимостей элементов, которые обратны их сопротивлениям. Отсюда 1/z2 = 1/R2 + 1/X2. Таким образом, выходит следующая формула:
Отсюда 1/z2 = 1/R2 + 1/X2. Таким образом, выходит следующая формула:
Z2=1/(1/R2+(1/ XL – 1/ XC)2).
Общее сопротивление определяется компонентным составом цепи и характером соединения ее элементов. При расчетах показателей используется закон Ома.
Реактивное сопротивление
При прохождении переменного тока через реактивные элементы возникает реактивное сопротивление. Оно обусловлено в первую очередь ёмкостями и индуктивностями.
Индуктивностью в цепи переменного тока обладает катушка индуктивности, причём в идеальном случае, активным сопротивлением её обмотки пренебрегают. Реактивное сопротивление катушки переменному току создаётся благодаря её ЭДС самоиндукции. Причем с ростом частоты тока, сопротивление также растёт.
Реактивное сопротивление катушки зависит от частоты тока и индуктивности катушки
Конденсатор обладает реактивным сопротивлением благодаря своей ёмкости. Его сопротивление с увеличением частоты тока уменьшается, что позволяет его активно использовать в электронике в качестве шунта переменной составляющей тока.
Сопротивление конденсатора можно рассчитать по формуле
От каких факторов зависит сопротивление
Изменение силы тока создает электромагнитное поле переменной интенсивности. Результатом его воздействия на проводник является противодействие происходящему изменению тока.
Это противодействие называется реактивным сопротивлением. Существуют две его разновидности: индуктивная и емкостная. Первая создается при наличии в схеме индуктивного элемента, вторая — конденсатора.
В ситуации, когда в цепи присутствует катушка, ее реакция усиливается по мере увеличения частоты.
Цепь, в которой возникает индукция
В случае, когда ее индуктивность уменьшается, то противодействующая сила также становится меньше. При увеличении она возрастает.
Индуктивное сопротивление существенно связано с тем, какую форму принимает проводник. Оно имеется также и у отдельного провода, лежащего прямо. Однако если рядом будет еще один, то он будет оказывать воздействие дополнительно, что повлияет на рассматриваемую величину.
Вам это будет интересно Особенности свободной энергии
Рассматриваемую характеристику отдельного провода можно определять в зависимости от его толщины, но оно никак не связано с его сечением.
Принцип действия электродвижущей силы
Как смотреть силу тока в цепи через осциллограф
Чем же резистор отличается от катушки индуктивности и конденсатора? Понятное дело, что выполняемыми функциями, но этим все не ограничивается. Итак, давайте рассмотрим самую простую схемку во всей электронике:
На схеме мы видим генератор частоты и резистор.
Давайте визуально посмотрим, что у нас творится в этой схеме. Для этого, как я уже сказал, нам понадобится генератор частоты
А также цифровой осциллограф:
С помощью него мы будем смотреть напряжение и силу тока .
Что?
Силу тока?
Но ведь осциллограф предназначен для того, чтобы рассматривать форму сигнала напряжения? Как же мы будем рассматривать форму сигнала силы тока? А все оказывается просто). Для этого достаточно вспомнить правило шунта.
Для этого достаточно вспомнить правило шунта.
Кто не помнит – напомню. Имеем обыкновенный резистор:
Что будет, если через него прогнать электрический ток?
На концах резистора у нас будет падение напряжения. То есть, если замерить с помощью мультиметра напряжение на его концах, мультиметр покажет какое-то значение в Вольтах
И теперь главный вопрос: от чего зависит падение напряжения на резисторе? В дело опять же вступает закон Ома для участка цепи: I=U/R. Отсюда U=IR. Мы видим зависимость от номинала самого резистора и от силы тока, текущей в данный момент в цепи. Слышите? От СИЛЫ ТОКА! Так почему бы нам не воспользоваться таким замечательным свойством и не глянуть силу тока через падение напряжения на самом резисторе? Ведь номинал резистора у нас постоянный и почти не изменяется с изменением силы тока
Как рассчитать сердечник и витки самодельных катушек индуктивности
Содержание
- Как определить эффективную магнитную проницаемость сердечника с зазором
- Самоиндукция
- Что такое электрический дроссель?
- Особенности применения дросселей в схемах
- Изготовление дросселя
- Реактивное сопротивление катушки индуктивности.

- Расчёт катушки с броневым сердечником
- Изготовление дросселя
- Плагин Ferrite: Расчет индуктивности на ферритовом стержне
Как определить эффективную магнитную проницаемость сердечника с зазором
Эффективная магнитная проницаемость сердечника с зазором μе связанная c таким понятием, как сопротивление магнитному потоку Rm, которое имеет сходство с электрическим сопротивлением в том плане, что зависит от длины и сечения магнитопровода (электросопротивление зависит от длины и сечения электрического проводника). Сопротивление магнитному потоку определяется следующим выражением
Из данного выражения можно сделать вывод, что чем меньше магнитная проницаемость материала, тем выше магнитное сопротивление. Не трудно заметить, что с учетом относительной магнитной проницаемости вещества сердечника (порядка нескольких тысяч) и воздуха (примерно равно единице), магнитное сопротивление сердечника с зазором будет, в значительной степени, определятся размерами воздушного зазора.
Таким образом, полное магнитное сопротивление сердечника с зазором RO будет состоять из последовательных магнитных сопротивлений сердечника RC и магнитного сопротивления зазора RЗ. С учётом того что относительная магнитная проницаемость воздуха примерно равна единице μr = 1, то получим следующее выражение
где μ – магнитная постоянная, μ0 = 4π*10-7,
μе – эквивалентная магнитная проницаемость сердечника с зазором,
μr – абсолютная магнитная проницаемость вещества сердечника,
Se – эффективная площадь поперечного сечения сердечника,
le – эффективный путь магнитной линии сердечника,
l – длина магнитной силовой линии сердечника с зазором,
δ – длина воздушного зазора.
После преобразования получим
Так как длина зазора меньше чем длина магнитной линии сердечника (δ << le), то из данного выражения можно получить выражение для эффективной магнитной проницаемости сердечника с зазором
где μе – эквивалентная магнитная проницаемость сердечника с зазором,
μr – абсолютная магнитная проницаемость вещества сердечника,
le – эффективный путь магнитной линии сердечника,
δ – длина воздушного зазора.
Данное выражение показывает, что эффективная магнитная проницаемость сердечника с зазором, а, следовательно, и индуктивность катушки про прочих постоянных параметрах уменьшается при увеличении величины зазора.
Самоиндукция
Катушка индуктивности обладает также очень интересным свойством. При подаче на катушку постоянного напряжения, в катушке возникает на короткий промежуток времени противоположное напряжение.
Это противоположное напряжение называется ЭДС самоиндукции. Эта ЭДС зависит от значения индуктивности катушки. Поэтому, в момент подачи напряжения на катушку сила тока в течение долей секунд плавно меняет свое значение от 0 до некоторого значения, потому что напряжение, в момент подачи электрического тока, также меняет свое значение от ноля и до установившегося значения. Согласно Закону Ома:
где
I – сила тока в катушке , А
U – напряжение в катушке, В
R – сопротивление катушки, Ом
Как мы видим по формуле, напряжение меняется от нуля и до напряжения, подаваемого в катушку, следовательно и ток тоже будет меняться от нуля и до какого то значения. Сопротивление катушки для постоянного тока также постоянное.
Сопротивление катушки для постоянного тока также постоянное.
И второй феномен в катушке индуктивности заключается в том, что если мы разомкнем цепь катушка индуктивности – источник тока, то у нас ЭДС самоиндукции будет суммироваться к напряжению, которое мы уже подали на катушку.
То есть как только мы разрываем цепь, на катушке напряжение в этот момент может быть в разы больше, чем было до размыкания цепи, а сила тока в цепи катушки будет тихонько падать, так как ЭДС самоиндукции будет поддерживать убывающее напряжение.
Сделаем первые выводы о работе катушки индуктивности при подаче на нее постоянного тока. При подаче на катушку электрического тока, сила тока будет плавно увеличиваться, а при снятии электрического тока с катушки, сила тока будет плавно убывать до нуля. Короче говоря, сила тока в катушке мгновенно измениться не может.
Что такое электрический дроссель?
Дросселем, в общем случае, называют катушку индуктивности, чаще всего с сердечником, которая служит для устранения или уменьшения переменного (импульсного) тока, разделения или ограничения сигналов различной частоты. Исходя из этого, дроссели условно можно разделить на следующие типы:
Исходя из этого, дроссели условно можно разделить на следующие типы:
— сглаживающие дроссели, предназначены для ослабления переменной составляющей постоянного тока или напряжения различной частоты, то есть сглаживания пульсаций, на выходе и входе силовых преобразователей или выпрямителей;
— дроссели переменного тока, предназначены для ограничения электрического тока, при резких изменениях нагрузки, например, при пуске электродвигателей или источников питания;
— дроссели насыщения, или управляемые дроссели, предназначенные для регулирования индуктивного сопротивления за счёт изменения тока подмагничивания.
Дроссели, как и любая другая катушка индуктивности, может быть без сердечника, с замкнутым сердечником, с сердечником, имеющим малый зазор и с сердечником, имеющим большой зазор или разомкнутым сердечником. Поэтому в независимости от назначения дросселя его принцип действия основан на электромагнитных свойствах катушки индуктивности и сердечника, на котором она выполнена.
Особенности применения дросселей в схемах
Дроссели можно соединять последовательно и параллельно.
[Индуктивность последовательно соединенных дросселей] = [Индуктивность первого дросселя] + [Индуктивность второго дросселя]
[Индуктивность параллельно соединенных дросселей] = 1 / (1 / [Индуктивность первого дросселя] + 1 / [Индуктивность второго дросселя])
На рисунке приведены типовые схемы на катушках индуктивности. (А) — Индуктивный делитель переменного напряжения. [Напряжение на нижнем дросселе] = [Входное напряжение] * [индуктивность нижнего дросселя] / ([индуктивность нижнего дросселя] + [индуктивность верхнего дросселя]) (Б) — Фильтр высших частот. (В) — Фильтр низших частот.
(читать дальше…) :: (в начало статьи)
| 1 | 2 | 3 |
:: ПоискТехника безопасности :: Помощь
К сожалению в статьях периодически встречаются ошибки, они исправляются, статьи дополняются, развиваются, готовятся новые. Подпишитесь, на новости, чтобы быть в курсе.
Подпишитесь, на новости, чтобы быть в курсе.
Если что-то непонятно, обязательно спросите!Задать вопрос. Обсуждение статьи. сообщений.
Вот одна формула = * * / / , по которой получается, что чем больше ток через дроссель, тем больше получается число витков — что в корне противоречит теории — чем нужен больший ток, тем должно быть меньше число витков (ЭТО Читать ответ…
А что такое E в первой формуле, прямо таки получается огромная величина индуктивности.
В первой формуле правдоподобно, если индуктивность в микрогенри
Если я правильно понял, то, например, E-3 означает 0.001? Читать ответ…
Как рассчитать и изготовить самому дроссель ВЧ, индуктивностью 5мкГн, на ток 3-4А ? Читать ответ…
Еще статьи
Силовой мощный импульсный трансформатор, дроссель. Намотка. Изготовить…
Приемы намотки импульсного дросселя / трансформатора….
Инвертор, преобразователь, чистая синусоида, синус…
Как получить чистую синусоиду 220 вольт от автомобильного аккумулятора, чтобы за…
Преобразователь однофазного в трехфазное. Конвертер одной фазы в три. …
Конвертер одной фазы в три. …
Схема преобразователя однофазного напряжения в трехфазное….
Резонансный инвертор, преобразователь напряжения повышающий. Схема, ко…
Инвертор 12/24 в 300. Резонансная схема….
Простой импульсный прямоходовый преобразователь напряжения. 5 — 12 вол…
Схема простого преобразователя напряжения для питания операционного усилителя….
Диодные схемы. Схемные решения. Схемотехника. Частота, мощность, шумы….
Классификация, типы полупроводниковых диодов. Схемы, схемные решения на диодах. …
Понижающий импульсный источник питания. Онлайн расчет. Форма. Подавлен…
Как рассчитать понижающий импульсный преобразователь напряжения. Как подавить пу…
Проверка электронных элементов, радиодеталей. Проверить исправность, р…
Как проверить исправность детали. Методика испытаний. Какие детали можно использ…
Изготовление дросселя
Для изготовления дросселя нужно выбрать подходящий каркас — в нашем случае это резистор определенной мощности и соответственно габаритов. Ниже приведены фото отечественных и зарубежных резисторов с обозначением их мощности.
Ниже приведены фото отечественных и зарубежных резисторов с обозначением их мощности.
Рис. 2. Резисторы МЛТ и зарубежные резисторы по мощности.
Рис. 3. Пример намотки дросселя на резисторе МЛТ-0,5.
Для намотки дросселя подойдут резисторы с высоким сопротивлением, например: 100кОм, 200кОм и т.д
Важно чтобы сопротивление резистора было большим, иначе добротность вашего самодельного дросселя может получиться плохой
Пример намотки равномерными слоями приведен на рисунке 3.
Для намотки можно использовать тонкий эмалированный провод (ПЭТВ) или же провод в шелковой изоляции (ПЭЛШО) диаметром 0,1-0,2мм, важно чтобы все витки намотанные таким проводом вместились на нашем каркасе из резистора. После намотки каждый из концов провода припаивают к выводам резистора, а на катушку сверху можно капнуть немножко клея чтобы витки потом не расползались
После намотки каждый из концов провода припаивают к выводам резистора, а на катушку сверху можно капнуть немножко клея чтобы витки потом не расползались.
Реактивное сопротивление катушки индуктивности.
При протекании переменного тока I в катушке, магнитное поле создаёт в её витках ЭДС, которая препятствует изменению тока.
При увеличении тока, ЭДС отрицательна и препятствует нарастанию тока, при уменьшении — положительна и препятствует его убыванию,
оказывая таким образом сопротивление изменению тока на протяжении всего периода.
В результате созданного противодействия, на выводах катушки индуктивности в противофазе формируется напряжение U, подавляющее ЭДС,
равное ей по амплитуде и противоположное по знаку.
При прохождении тока через нуль, амплитуда ЭДС достигает максимального значения,
что образует расхождение во времени тока и напряжения в 1/4 периода.
Если приложить к выводам катушки индуктивности напряжение U, ток не может начаться мгновенно по причине противодействия ЭДС,
равного -U, поэтому ток в индуктивности всегда будет отставать от напряжения на угол 90°. Сдвиг при отстающем токе называют положительным.
Сдвиг при отстающем токе называют положительным.
Запишем выражение мгновенного значения напряжения u исходя из ЭДС (ε), которая
пропорциональна индуктивности L и скорости изменения тока: u = -ε = L(di/dt).
Отсюда выразим синусоидальный ток .
Интегралом функции sin(t) будет -соs(t), либо равная ей функция sin(t-π/2).
Дифференциал dt функции sin(ωt) выйдет из под знака интеграла множителем 1/ω.
В результате получим выражение мгновенного значения тока со
сдвигом от функции напряжения на угол π/2 (90°).
Для среднеквадратичных значений U и I в таком случае можно записать .
В итоге имеем зависимость синусоидального тока от напряжения согласно Закону Ома,
где в знаменателе вместо R выражение ωL, которое и является реактивным сопротивлением:
Реактивное сопротивлениие индуктивностей называют индуктивным.
Расчёт катушки с броневым сердечником
Броневые сердечники представляют собой сборную конструкцию, состоящую из двух чашеобразных частей. В центре каждой чашки имеется центральный керн, в большинстве случаев имеющий осевое отверстие, используемое для подстройки величины индуктивности.
В центре каждой чашки имеется центральный керн, в большинстве случаев имеющий осевое отверстие, используемое для подстройки величины индуктивности.
Такие сердечники имеют универсальное применение благодаря высокой добротности в заданной полосе частот, низким искажениям, отсутствие полей рассеяния и небольшими габаритами.
Расчёт постоянных С1 и С2 данного типа сердечника выполняется по аналогии с предыдущими типами, но в связи с формой броневого сердечника имеются свои особенности. Рассмотрим сечение броневого сердечника
Разделим данный сердечник на простейшие линейные и угловые участки с различным сечением: линейные – l1, l2, l3 и угловые – l4, l5, так же выделим соответствующие им поперечные сечения: S1, S2, S3, S4, S5. Длины линейных участков достаточно просто определить, для нахождения длины угловых участков и сечений на всех участках можно используя следующие выражения
Таким образом, вычислив длину и площадь поперечного сечения отдельных участков, можно вычислить постоянные для данного типа сердечников
Данные выражения определяют параметры сердечника без технологических пазов и вырезов. При желании их учитывать необходимо, внести следующие поправки
При желании их учитывать необходимо, внести следующие поправки
где n – число пазов,
g – ширина паза.
Пример. В качестве примера рассчитаем индуктивность дросселя выполненного на броневом сердечнике, состоящем из двух чашек типа Ч22 из феррита марки 50ВН (μr = 50), количество витков ω = 100.
123412
С учётом конструктивных особенностей выразим величины заложенные в требуемые нам выражения:
Найдем длины и сечение участков магнитопровода. Расчёт будем вести без учёта технологических пазов и вырезов.
С учётом рассчитанных выше значений определим индуктивность исходного дросселя
На этом можно и остановиться с расчётами индуктивных элементов с замкнутыми сердечниками. В следующей статье я рассмотрю индуктивные элементы на разомкнутых сердечниках.
Изготовление дросселя
Для изготовления дросселя нужно выбрать подходящий каркас — в нашем случае это резистор определенной мощности и соответственно габаритов. Ниже приведены фото отечественных и зарубежных резисторов с обозначением их мощности.
Ниже приведены фото отечественных и зарубежных резисторов с обозначением их мощности.
Рис. 2. Резисторы МЛТ и зарубежные резисторы по мощности.
Рис. 3. Пример намотки дросселя на резисторе МЛТ-0,5.
Для намотки дросселя подойдут резисторы с высоким сопротивлением, например: 100кОм, 200кОм и т.д
Важно чтобы сопротивление резистора было большим, иначе добротность вашего самодельного дросселя может получиться плохой
Пример намотки равномерными слоями приведен на рисунке 3.
Для намотки можно использовать тонкий эмалированный провод (ПЭТВ) или же провод в шелковой изоляции (ПЭЛШО) диаметром 0,1-0,2мм, важно чтобы все витки намотанные таким проводом вместились на нашем каркасе из резистора. После намотки каждый из концов провода припаивают к выводам резистора, а на катушку сверху можно капнуть немножко клея чтобы витки потом не расползались
После намотки каждый из концов провода припаивают к выводам резистора, а на катушку сверху можно капнуть немножко клея чтобы витки потом не расползались.
Плагин Ferrite: Расчет индуктивности на ферритовом стержне
В отличии от тороидальной индуктивности на ферритовом кольце, магнитный поток катушки на ферритовом стержне не замкнут целиком внутри феррита и каждая силовая линия проходит и по ферритовому стержню и по воздуху, поэтому расчет такой катушки представляет довольно сложную задачу. Индуктивность зависит от:
- магнитной проницаемости ферритового стержня и его размеров;
- размеров самой катушки;
- взаимного соотношения размеров катушки и стержня;
- положения катушки относительно центра стержня.
Расчет индуктивности катушки на ферритовом стержне основан на определении относительной эффективной проницаемости стержня. Другими словами, нам нужно определить насколько возрастет индуктивность катушки с «воздушным сердечником» если внутрь нее вставить ферритовый стержень. Основная формула выглядит вот так:
,где Lf / Lair — отношение индуктивности катушки с ферритом к индуктивности той же катушки без феррита, а коэффициенты x, k и μfe вычисляются по следующему алгоритму:
- l’ = lc + 0.
 45 dc;
45 dc; - φ_φmax ≈ 1 / [ 1 + { ( ( lf — lc ) / df )1.4 } / ( 5 μ ) ];
- Canf = 0.5 π ε ( lf — lc ) / [ ln { 2 ( lf + df) / df } — 1 ];
- k = [ (φ_φmax Canf / ε ) + 2 df ] / 2 dc
- x = 5.1 [ l’ / dc ] / [1+ 2.8 ( dc / l’ )];
- μfe = ( μ -1) ( df /dc)2 +1;
где ε = 8,8542*10-12 Ф/м — электрическая постоянная, μ — начальная магнитная проницаемость материала стержня. Основные размеры в метрах, обозначения понятны из рисунка:
Немного теории обосновывающей этот алгоритм.
- Можно считать что воздушная катушка имеет магнитную цепь состоящую из двух частей. Снаружи катушки и внутри нее. Они отличаются плотностью силовых линий и . Если магнитное сопротивление внутренней части магнитной цепи выше, чем наружной части (а это так, поскольку ее площадь поперечного сечения намного меньше), тогда применение феррита уменьшает это сопротивление и имеет эффект увеличения индуктивности.
 Это отношение двух частей магнитных сопротивлений магнитной цепи воздушной катушки обозначено в основной формуле как x и вычисляется на 5-ом шагу алгоритма.
Это отношение двух частей магнитных сопротивлений магнитной цепи воздушной катушки обозначено в основной формуле как x и вычисляется на 5-ом шагу алгоритма. - Параметр μfe учитывает случай, когда обмотка не плотно прилегает к стержню, т.е. между стержнем и обмоткой существует радиальный зазор.
- Параметр Canf учитывает влияние частей стержня, которые выступают за пределы катушки. Эти части уменьшают магнитное сопротивление внешней части магнитной цепи и также увеличивают индуктивность.
- Параметр φ_φmax учитывает конечное магнитное сопротивление феррита. Этот параметр, наряду с параметром Canf используется для расчета коэффициента k из основного уравнения
При смещении катушки относительно стержня индуктивность катушки уменьшается, это обстоятельство учитывается с помощью поправочного коэффициента K:
,где
sh — относительное смещение = смещение s деленное на половину длины сердечника [sh = s / ( lf / 2 )].
Эта формула получена методом регрессионного анализа и справедлива при s = 0,05 — 0,75
В итоге индуктивность катушки на ферритовом стержне определяется по следующей формуле:
Индуктивность катушки «воздушным» сердечником Lair рассчитывается по алгоритму расчета однослойной катушки с учетом шага намотки. Длину намотки можно определить по следующей формуле:
,где
- N — число витков.
- dw — диаметр провода.
- p — шаг намотки.
Алгоритм имеет следующие ограничения в расчетах:
- шаг намотки не может превышать удвоенного диаметра провода;
- диаметр катушки не может быть больше удвоенного диаметра стержня;
- длина намотки должна быть меньше 3/4 длины стержня;
- длина стержня должна быть не менее чем в 12 раз больше его диаметра;
- при смещении катушки она не должна доходить до края стержня на 1/8 его длины;
- начальная магнитная проницаемость стержня должна быть больше 100;
Также как и в дросселе на ферритовом кольце с немагнитным зазором, при больших значениях начальной магнитной проницаемости стержня его эффективная магнитная проницаемость слабо зависит от начальной и составляет величину не более нескольких десятков.
Кроме того, вы можете воспользоваться онлайн-калькулятором катушки на ферритовом стержне.
Особая благодарность за конструктивную помощь и соавторство в разработке методики расчета.
Tags: амплитуда, бра, вид, дом, е, знак, импульсный, как, кт, магнит, магнитный, мощность, напряжение, принцип, провод, пуск, р, размер, расчет, резистор, ряд, сопротивление, схема, тип, ток, трансформатор, ук, фото, эффект
2.5: Относительно практических индукторов — технические библиотеки LibreTexts
-
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 25241
- Джеймс М. Фиоре
- Муниципальный колледж Mohawk Valley
До сих пор катушки индуктивности считались идеальными компонентами, то есть чистой индуктивностью. На самом деле все катушки индуктивности имеют определенное сопротивление, связанное с сопротивлением провода, из которого изготовлена катушка. Это называется ESR или эквивалентным последовательным сопротивлением. Он также обозначается как \(R_{катушка}\). В идеале это сопротивление должно быть достаточно малым, чтобы им можно было пренебречь, но в конечном итоге оно наложит ограничение на производительность любой схемы, в которой используется индуктор.
На самом деле все катушки индуктивности имеют определенное сопротивление, связанное с сопротивлением провода, из которого изготовлена катушка. Это называется ESR или эквивалентным последовательным сопротивлением. Он также обозначается как \(R_{катушка}\). В идеале это сопротивление должно быть достаточно малым, чтобы им можно было пренебречь, но в конечном итоге оно наложит ограничение на производительность любой схемы, в которой используется индуктор.
Хотя сопротивление катушки индуктивности можно измерить с помощью цифрового мультиметра, это не даст точного значения на всех частотах. На самом деле с увеличением частоты будет увеличиваться и СОЭ. Это связано со скин-эффектом. При более высоких частотах ток распределяется неравномерно по всему поперечному сечению проводника. На самом деле он стремится «обнять» внешнюю поверхность или «кожу» проводника. Это уменьшает эффективную площадь поперечного сечения и тем самым увеличивает сопротивление 1 . В общем, с ростом частоты растет и \(R_{катушка}\). 2R\). Ток обязательно одинаков как для реактивной, так и для резистивной составляющих, поэтому \(Q\) катушки равно отношению ее реактивного сопротивления к ее сопротивлению на интересующей частоте.
2R\). Ток обязательно одинаков как для реактивной, так и для резистивной составляющих, поэтому \(Q\) катушки равно отношению ее реактивного сопротивления к ее сопротивлению на интересующей частоте.
\[Q_{катушка} = \frac{X_L}{R_{катушка}} \label{2.4} \]
Где
\(Q_{coil}\) — добротность катушки индуктивности,
\(X_L\) — величина индуктивного сопротивления на интересующей частоте,
\(R_{coil}\) — сопротивление катушки индуктивности на интересующей частоте.
В целом, чем выше \(Q_{coil}\), тем лучше. Как видно на рисунке \(\PageIndex{1}\), \(Q_{coil}\) не является константой. Действительно, он увеличивается с частотой, пока не будет достигнут пик, после чего он начинает падать.
При работе с практическими катушками индуктивности эффективную \(Q_{coil}\) можно определить по графику, если известна рабочая частота. Как только \(Q_{катушка}\) найдена, действующее значение \(Q_{катушка}\) может быть найдено из уравнения \ref{2.4}.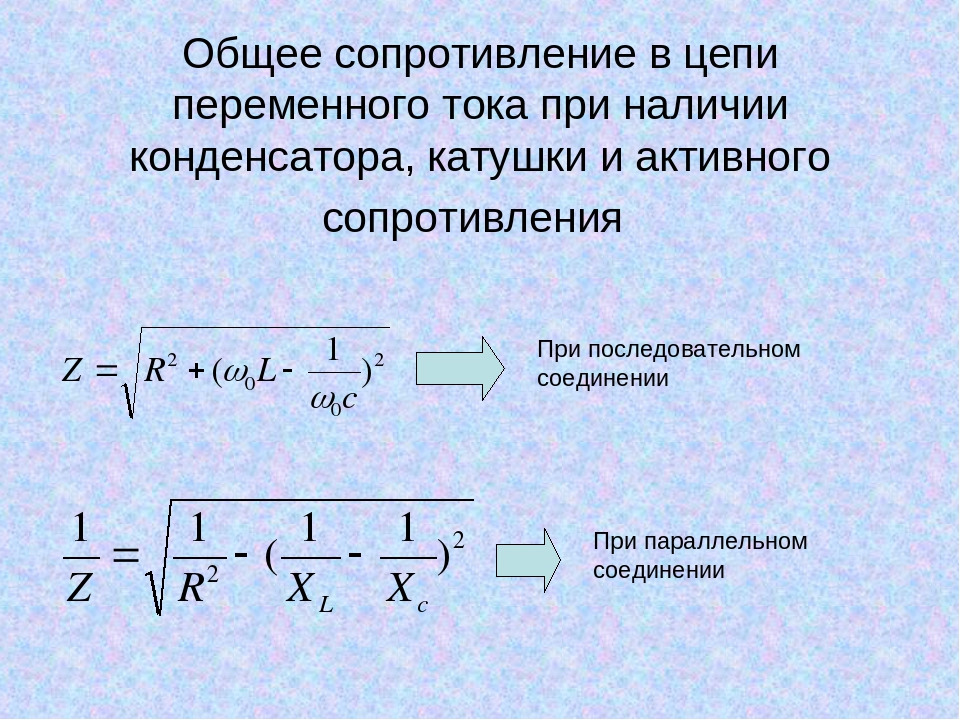 Затем это значение может быть помещено последовательно с идеальной катушкой индуктивности для получения более точного результата. Для анализа эту пару иногда рисуют с рамкой вокруг нее, чтобы обозначить, что \(Q_{катушка}\) не является отдельным физическим резистором, а является эффективным сопротивлением катушки индуктивности. 9{\circ}\) от пика до пика на частоте 20 кГц. \(L\) равно 10 мГн, \(Q_{катушка}\) равно 50, а \(R_1\) равно \(600 \Омега\).
Затем это значение может быть помещено последовательно с идеальной катушкой индуктивности для получения более точного результата. Для анализа эту пару иногда рисуют с рамкой вокруг нее, чтобы обозначить, что \(Q_{катушка}\) не является отдельным физическим резистором, а является эффективным сопротивлением катушки индуктивности. 9{\circ}\) от пика до пика на частоте 20 кГц. \(L\) равно 10 мГн, \(Q_{катушка}\) равно 50, а \(R_1\) равно \(600 \Омега\).
Помните, что индуктор состоит из обоих элементов в пунктирной рамке. Сначала найдите величину индуктивного сопротивления.
\[| Х_Л | = 2\pi f L \номер\]
\[| Х_Л | = 2\pi 20 кГц 10 мГн \номер \]
\[| Х_Л | = 1257 \Omega \nonumber \]
Теперь мы можем найти \(R_{катушка}\) по уравнению \ref{2.4}: 9{\circ}\). Это небольшое, но измеримое отклонение.
1 Напомним, что \(R = \rho l / A\). Уменьшение площади \(A\) приводит к увеличению сопротивления \(R\).
Эта страница под названием 2.5: О практических индукторах распространяется под лицензией CC BY-NC-SA 4.0 и была создана, изменена и/или курирована Джеймсом М. Фиоре с помощью исходного контента, который был отредактирован в соответствии со стилем и стандартами Платформа LibreTexts; подробная история редактирования доступна по запросу.
- Наверх
-
- Была ли эта статья полезной?
-
- Тип изделия
- Раздел или Страница
- Автор
- Джеймс М. Фиоре
- Лицензия
- CC BY-NC-SA
- Версия лицензии
- 4,0
- Показать оглавление
- нет
-
- Теги
-
- source@http://www.
 dissidents.com/resources/ACElectricalCircuitAnalysis.pdf
dissidents.com/resources/ACElectricalCircuitAnalysis.pdf
- source@http://www.
Реактивное сопротивление, индуктивное и емкостное | Физика II |
Цели обучения
К концу этого раздела вы сможете:
- Схема зависимости напряжения и тока от времени в простых индуктивных, емкостных и резистивных цепях.
- Рассчитать индуктивное и емкостное сопротивление.
- Расчет тока и/или напряжения в простых индуктивных, емкостных и резистивных цепях.
Многие схемы также содержат конденсаторы и катушки индуктивности в дополнение к резисторам и источнику переменного напряжения. Мы видели, как конденсаторы и катушки индуктивности реагируют на постоянное напряжение при его включении и выключении. Теперь мы рассмотрим, как катушки индуктивности и конденсаторы реагируют на синусоидальное переменное напряжение.
Катушки индуктивности и индуктивное сопротивление
Предположим, что катушка индуктивности подключена непосредственно к источнику переменного напряжения, как показано на рис. 1. Разумно предположить пренебрежимо малое сопротивление, так как на практике мы можем сделать сопротивление катушки индуктивности настолько малым, что оно окажет незначительное влияние на цепь. Также показан график зависимости напряжения и тока от времени.
1. Разумно предположить пренебрежимо малое сопротивление, так как на практике мы можем сделать сопротивление катушки индуктивности настолько малым, что оно окажет незначительное влияние на цепь. Также показан график зависимости напряжения и тока от времени.
Рис. 1. (a) Источник переменного напряжения, включенный последовательно с катушкой индуктивности, сопротивление которой пренебрежимо мало. (б) График тока и напряжения на катушке индуктивности в зависимости от времени.
График на рисунке 1(b) начинается с максимального напряжения. Обратите внимание, что ток начинается с нуля и достигает своего пика 90 180 после 90 181 управляющего им напряжения, как это было в случае, когда в предыдущем разделе было включено постоянное напряжение. Когда напряжение в точке а становится отрицательным, ток начинает уменьшаться; он становится равным нулю в точке b, где напряжение является самым отрицательным. Затем ток становится отрицательным, снова следуя за напряжением. Напряжение становится положительным в точке с и начинает делать ток менее отрицательным. В точке d ток проходит через нуль как раз в тот момент, когда напряжение достигает своего положительного пика, чтобы начать новый цикл. Это поведение резюмируется следующим образом:
Напряжение становится положительным в точке с и начинает делать ток менее отрицательным. В точке d ток проходит через нуль как раз в тот момент, когда напряжение достигает своего положительного пика, чтобы начать новый цикл. Это поведение резюмируется следующим образом:
Напряжение переменного тока в катушке индуктивности
Когда к катушке индуктивности приложено синусоидальное напряжение, оно опережает ток на одну четвертую периода или на фазовый угол 90º.
Ток отстает от напряжения, так как катушки индуктивности препятствуют изменению тока. Изменение тока индуцирует противо-ЭДС В = − L (Δ I / Δ t ). Это считается эффективным сопротивлением катушки индуктивности переменному току. Действующее значение тока I через дроссель L дается вариантом закона Ома:
I=VXLI=\frac{V}{{X}_{L}}\\I=XLV
, где В — среднеквадратичное напряжение на катушке индуктивности, а X L определяется как
XL=2πfL{X}_{L}=2\pi{fL}\\XL=2πfL
,
где f частота источника переменного напряжения в герцах (анализ цепи с использованием правила контура Кирхгофа и исчисления фактически дает это выражение).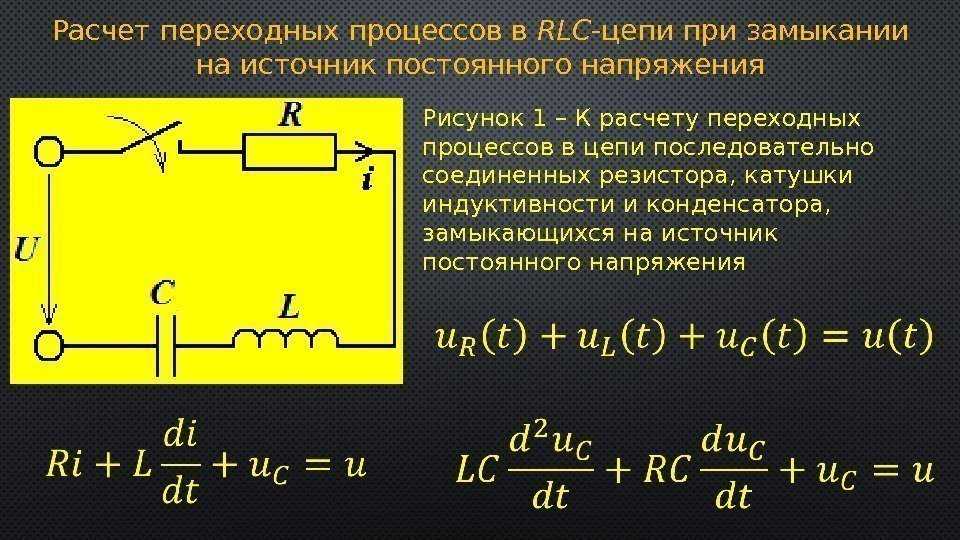 Х Д называется индуктивным сопротивлением , потому что индуктор реагирует на сопротивление току. X L измеряется в омах (1 Гн = 1 Ом ⋅ с, так что частота, умноженная на индуктивность, выражается в единицах (циклов/с) (Ом ⋅ с) = Ом)), что соответствует его роли в качестве эффективное сопротивление. Имеет смысл, что X L пропорционально L , поскольку чем больше индукция, тем больше ее сопротивление изменению. Также разумно, что X L пропорционально частоте f , так как большая частота означает большее изменение тока. То есть Δ I /Δ t велико для больших частот (большие f , малые Δ t ). Чем больше изменение, тем больше сопротивление индуктора.
Х Д называется индуктивным сопротивлением , потому что индуктор реагирует на сопротивление току. X L измеряется в омах (1 Гн = 1 Ом ⋅ с, так что частота, умноженная на индуктивность, выражается в единицах (циклов/с) (Ом ⋅ с) = Ом)), что соответствует его роли в качестве эффективное сопротивление. Имеет смысл, что X L пропорционально L , поскольку чем больше индукция, тем больше ее сопротивление изменению. Также разумно, что X L пропорционально частоте f , так как большая частота означает большее изменение тока. То есть Δ I /Δ t велико для больших частот (большие f , малые Δ t ). Чем больше изменение, тем больше сопротивление индуктора.
Пример 1. Расчет индуктивного сопротивления, а затем тока
(a) Рассчитайте индуктивное сопротивление катушки индуктивности 3,00 мГн при подаче переменного напряжения частотой 60,0 Гц и 10,0 кГц. б) Чему равно среднеквадратичное значение тока на каждой частоте, если приложенное среднеквадратичное напряжение равно 120 В?
б) Чему равно среднеквадратичное значение тока на каждой частоте, если приложенное среднеквадратичное напряжение равно 120 В?
Стратегия
Индуктивное сопротивление находится непосредственно из выражения X L = 2πf L . После того, как X L найдено на каждой частоте, можно использовать закон Ома, как указано в уравнении I = V / X L , чтобы найти ток на каждой частоте.
Решение для (а)
Ввод частоты и индуктивности в уравнение x L = 2πf L дает
x L = 2πf L = (60,0/с.).
Аналогично, на частоте 10 кГц
X L = 2πf L = 6,28 (1,00 × 10 4 /с) (3,00 мГн) при 180 кОм.
Решение для (b)
Среднеквадратичное значение тока теперь находится с использованием версии закона Ома в уравнении 9.0180 I = В / X L , учитывая приложенное среднеквадратичное значение напряжения 120 В. Для первой частоты это дает
I=VXL=120 В1,13 Ом=106 А при =\frac{V}{{X}_{L}}=\frac{120\text{ V}}{1.13\text{ }\Omega}=106\text{ A при } 60\text{ Гц}\ \I=XLV=1,13 Ом, 120 В=106 A при 60 Гц
. Точно так же на частоте 10 кГц
I=VXL=120 V188 Ω=0,637 A на частоте 10 кГц I=\frac{V}{{X}_{L}}=\frac{120\text{V}}{188\ text{ }\Omega}=0,637\text { A при } 10 кГц}\\I=XLV=188 Ω120 В=0,637 A при 10 кГц
.
Обсуждение
Индуктор реагирует очень по-разному на двух разных частотах. На более высокой частоте его реактивное сопротивление велико, а ток мал, что соответствует тому, как индуктор препятствует быстрому изменению. Таким образом, высокие частоты препятствуют больше всего. Индукторы можно использовать для фильтрации высоких частот; например, большой индуктор можно включить последовательно с системой воспроизведения звука или последовательно с вашим домашним компьютером, чтобы уменьшить высокочастотный звук, выходящий из ваших динамиков, или высокочастотные скачки мощности в вашем компьютере.
Таким образом, высокие частоты препятствуют больше всего. Индукторы можно использовать для фильтрации высоких частот; например, большой индуктор можно включить последовательно с системой воспроизведения звука или последовательно с вашим домашним компьютером, чтобы уменьшить высокочастотный звук, выходящий из ваших динамиков, или высокочастотные скачки мощности в вашем компьютере.
Обратите внимание, что хотя сопротивление в рассматриваемой цепи незначительно, переменный ток не очень велик, поскольку индуктивное сопротивление препятствует его протеканию. При переменном токе нет времени для того, чтобы ток стал чрезвычайно большим.
Конденсаторы и емкостные реактивные сопротивления
Рассмотрим конденсатор, подключенный непосредственно к источнику переменного напряжения, как показано на рис. 2. Сопротивление такой цепи можно сделать настолько малым, что оно оказывает незначительное влияние по сравнению с конденсатором, поэтому мы можем предположить пренебрежимо малое сопротивление. Напряжение на конденсаторе и ток представлены на рисунке как функции времени.
Напряжение на конденсаторе и ток представлены на рисунке как функции времени.
Рис. 2. (a) Источник переменного напряжения, включенный последовательно с конденсатором C, сопротивление которого пренебрежимо мало. (б) График тока и напряжения на конденсаторе в зависимости от времени.
График на рисунке 2 начинается с максимального напряжения на конденсаторе. В этот момент ток равен нулю, потому что конденсатор полностью заряжен и останавливает поток. Затем напряжение падает, а ток становится отрицательным по мере разряда конденсатора. В точке а конденсатор полностью разряжен ( Q = 0 на нем) и напряжение на нем равно нулю. Ток между точками a и b остается отрицательным, что приводит к изменению напряжения на конденсаторе. Это завершается в точке b, где ток равен нулю, а напряжение имеет самое отрицательное значение. Ток становится положительным после точки b, нейтрализуя заряд конденсатора и сводя напряжение к нулю в точке c, что позволяет току достигать своего максимума.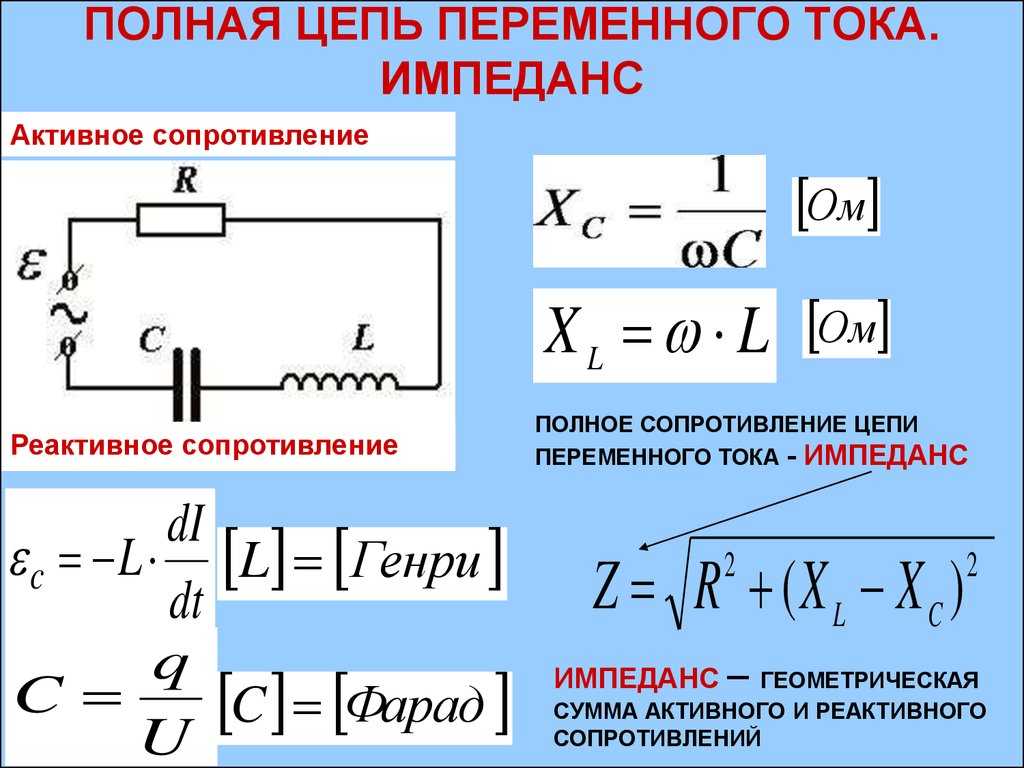 Между точками c и d ток падает до нуля, когда напряжение достигает своего пика, и процесс начинает повторяться. На протяжении всего цикла напряжение следует за током на одну четвертую цикла:
Между точками c и d ток падает до нуля, когда напряжение достигает своего пика, и процесс начинает повторяться. На протяжении всего цикла напряжение следует за током на одну четвертую цикла:
Напряжение переменного тока в конденсаторе
Когда к конденсатору прикладывается синусоидальное напряжение, напряжение следует за током на одну четвертую периода или на фазовый угол 90º.
Конденсатор влияет на ток, имея возможность полностью остановить его при полной зарядке. Поскольку применяется переменное напряжение, существует среднеквадратичное значение тока, но оно ограничено конденсатором. Это считается эффективным сопротивлением конденсатора переменному току, поэтому среднеквадратичное значение тока I в цепи, содержащей только конденсатор C по другой версии закона Ома определяется как
I=VXCI=\frac{V}{{X}_{C}}\\I=XCV
, where V is the rms voltage and X C is defined (As with X L , this expression for X C results from an analysis of the circuit using правила Кирхгофа и исчисление) равным
XC=12πfC{X}_{C}=\frac{1}{2\pi fC}\\XC=2πfC1
,
где X C называется емкостным реактивным сопротивлением , потому что конденсатор реагирует на сопротивление току. X C измеряется в омах (проверка оставлена читателю в качестве упражнения). X C обратно пропорциональна емкости C ; чем больше конденсатор, тем больший заряд он может хранить и тем больший ток может протекать. Он также обратно пропорционален частоте ф ; чем больше частота, тем меньше времени остается для полной зарядки конденсатора, и поэтому он меньше препятствует току.
X C измеряется в омах (проверка оставлена читателю в качестве упражнения). X C обратно пропорциональна емкости C ; чем больше конденсатор, тем больший заряд он может хранить и тем больший ток может протекать. Он также обратно пропорционален частоте ф ; чем больше частота, тем меньше времени остается для полной зарядки конденсатора, и поэтому он меньше препятствует току.
Пример 2. Расчет емкостного реактивного сопротивления, а затем тока
(a) Рассчитайте емкостное реактивное сопротивление конденсатора емкостью 5,00 мФ при подаче переменного напряжения частотой 60,0 Гц и 10,0 кГц. б) Чему равно среднеквадратичное значение тока, если приложенное среднеквадратичное напряжение равно 120 В?
Стратегия
Емкостное сопротивление находится непосредственно из выражения в
XC=12πfC{X}_{C}=\frac{1}{2\pi fC}\\XC=2πfC1
. После того, как X C найдено на каждой частоте, можно использовать закон Ома, сформулированный как I = V / X C тока на каждой частоте.
После того, как X C найдено на каждой частоте, можно использовать закон Ома, сформулированный как I = V / X C тока на каждой частоте.
Решение для (а)
Ввод частоты и емкости в
XC=12πfC{X}_{C}=\frac{1}{2\pi fC}\\XC=2πfC1
дает
XC=12πfC=16,28(60,0 /с)(5,00 мкФ)=531 Ом при 60 Гц\begin{array}{lll}{X}_{C}& =& \frac{1}{2\pi fC}\\ & =& \frac{ 1}{6.28\left(60.0/\text{s}\right)\left(5.00\text{ }\mu\text{F}\right)}=531\text{ }\Omega\text{ в }60 \text{ Гц}\end{массив}\\XC==2πfC16,28(60,0/с)(5,00 мкФ)1=531 Ом при 60 Гц 9{4}/\text{s}\right)\left(5.00\mu\text{F}\right)}\\ & =& 3.18\text{ }\Omega\text{ при }10 \text{ кГц} \end{массив}\\XC==2πfC1=6,28(1,00×104/с)(5,00 мкФ)13,18 Ом при 10 кГц
.
Решение для (b)
Среднеквадратичное значение тока теперь находится с использованием версии закона Ома в I = В / X C , учитывая приложенное среднеквадратичное напряжение 120 В. Для первой частоты это дает
Для первой частоты это дает
I= VXC=120 V531 Ом=0,226 A при 60 ГцI=\frac{V}{{X}_{C}}=\frac{120 \text{ V}}{531\text{ }\Omega}=0,226 \text { A при }60\text{ Гц}\\I=XCV=531 Ω120 В=0,226 A при 60 Гц
. Аналогично, при 10 кГц
I=VXC=120 V3,18 Ом=3,37 A при 10 Гц I=\frac{V}{{X}_{C}}=\frac{120 \text{V}}{ 3,18\text{ }\Omega}=3,37 \text{ A при }10 \text{ Гц}\\I=XCV=3,18 Ω120 В=3,37 A при 10 Гц
.
Обсуждение
Конденсатор реагирует совершенно по-разному на двух разных частотах, и совершенно противоположным образом реагирует катушка индуктивности. На более высокой частоте его реактивное сопротивление мало, а ток велик. Конденсаторы способствуют изменениям, тогда как индукторы сопротивляются изменениям. Конденсаторы больше всего препятствуют низким частотам, поскольку низкая частота дает им время зарядиться и остановить ток. Конденсаторы можно использовать для фильтрации низких частот. Например, конденсатор, включенный последовательно со звуковоспроизводящей системой, избавляет ее от гула частотой 60 Гц.
Например, конденсатор, включенный последовательно со звуковоспроизводящей системой, избавляет ее от гула частотой 60 Гц.
Хотя конденсатор в основном представляет собой разомкнутую цепь, в цепи с переменным напряжением, приложенным к конденсатору, существует среднеквадратичное значение тока. Это связано с тем, что напряжение постоянно меняется, заряжая и разряжая конденсатор. Если частота стремится к нулю (постоянный ток), X C стремится к бесконечности, а ток равен нулю после зарядки конденсатора. На очень высоких частотах реактивное сопротивление конденсатора стремится к нулю — он имеет пренебрежимо малое реактивное сопротивление и не препятствует протеканию тока (он действует как простой провод). Конденсаторы оказывают на цепи переменного тока противоположное действие катушек индуктивности .
Резисторы в цепи переменного тока
В качестве напоминания рассмотрим рисунок 3, на котором показано напряжение переменного тока, приложенное к резистору, и график зависимости напряжения и тока от времени.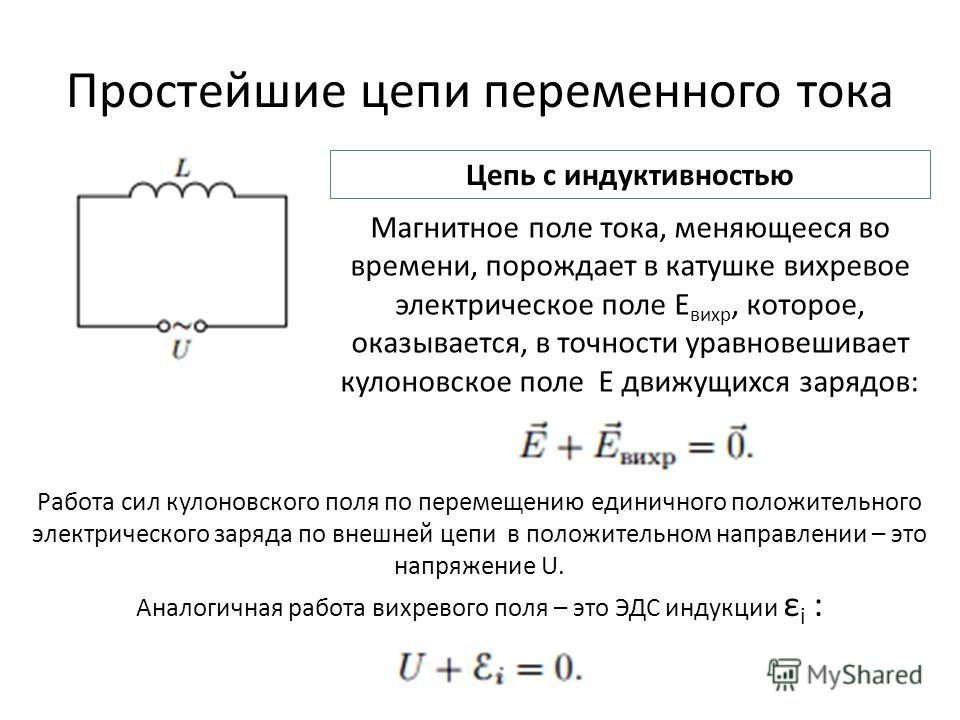 Напряжение и ток равны в фазе в резисторе. Поведение простого сопротивления в цепи не зависит от частоты:
Напряжение и ток равны в фазе в резисторе. Поведение простого сопротивления в цепи не зависит от частоты:
Рис. 3. (a) Источник переменного напряжения, включенный последовательно с резистором. (b) График зависимости тока и напряжения на резисторе от времени, показывающий, что они точно совпадают по фазе.
Переменное напряжение в резисторе
Когда на резистор подается синусоидальное напряжение, оно точно совпадает по фазе с током — фазовый угол равен 0º.
Резюме раздела
- Для катушек индуктивности в цепях переменного тока мы обнаружили, что когда к катушке индуктивности прикладывается синусоидальное напряжение, напряжение опережает ток на одну четвертую периода или на фазовый угол 90º.
- Противодействие катушки индуктивности изменению тока выражается как вид сопротивления переменному току.
- Закон Ома для индуктора:
I=VXLI=\frac{V}{{X}_{L}}\\I=XLV
,
где В — среднеквадратичное напряжение на катушке индуктивности.
- X L определяется как индуктивное сопротивление, определяемое как
XL=2πfL{X}_{L}=2\pi fL\\XL=2πfL
,
с f частота источника переменного напряжения в герцах. - Индуктивное сопротивление X L выражается в омах и имеет наибольшее значение на высоких частотах.
- Для конденсаторов мы обнаружили, что когда к конденсатору прикладывается синусоидальное напряжение, напряжение следует за током на одну четвертую периода или на фазовый угол 90º.
- Поскольку конденсатор может останавливать ток при полной зарядке, он ограничивает ток и предлагает другую форму сопротивления переменному току; Закон Ома для конденсатора:
I=VXCI=\frac{V}{{X}_{C}}\\I=XCV
,
где В — среднеквадратичное напряжение на конденсаторе. - Х С определяется как емкостное реактивное сопротивление, определяемое как
XC=12πfC{X}_{C}=\frac{1}{2\pi fC}\\XC=2πfC1
.

- X C измеряется в омах и максимальна на низких частотах.
Концептуальные вопросы
1. Пресбиакузис — возрастная потеря слуха, которая постепенно влияет на более высокие частоты. Усилитель слухового аппарата предназначен для одинакового усиления всех частот. Чтобы настроить его выход на пресбиакузис, вы бы включили конденсатор последовательно или параллельно с динамиком слухового аппарата? Объяснять.
2. Будете ли вы использовать большую индуктивность или большую емкость последовательно с системой для фильтрации низких частот, таких как фон 100 Гц в звуковой системе? Объяснять.
3. Высокочастотный шум в сети переменного тока может повредить компьютеры. Использует ли сменный блок, предназначенный для предотвращения этого повреждения, большую индуктивность или большую емкость (последовательно с компьютером) для фильтрации таких высоких частот? Объяснять.
4. Зависит ли индуктивность от тока, частоты или от того и другого? А индуктивное сопротивление?
5. Объясните, почему конденсатор на рис. 4(а) действует как фильтр низких частот между двумя цепями, а конденсатор на рис. 4(б) действует как фильтр высоких частот.
Рис. 4. Конденсаторы и катушки индуктивности. Конденсатор с высокой частотой и низкой частотой.
6. Если конденсаторы на рисунке 4 заменить катушками индуктивности, что будет работать как фильтр низких частот, а что как фильтр высоких частот?
Задачи и упражнения
1. При какой частоте дроссель 30,0 мГн будет иметь реактивное сопротивление 100 Ом?
2. Какое значение индуктивности следует использовать, если требуется реактивное сопротивление 20,0 кОм на частоте 500 Гц?
3. Какую емкость следует использовать для получения реактивного сопротивления 2,00 МОм при частоте 60,0 Гц?
Какую емкость следует использовать для получения реактивного сопротивления 2,00 МОм при частоте 60,0 Гц?
4. При какой частоте конденсатор емкостью 80,0 мФ будет иметь реактивное сопротивление 0,250 Ом?
5. (a) Найдите ток через катушку индуктивности 0,500 Гн, подключенную к источнику переменного тока с частотой 60,0 Гц и напряжением 480 В. б) Какой будет сила тока на частоте 100 кГц?
6. (a) Какой ток протекает, когда источник переменного тока с частотой 60,0 Гц, 480 В подключен к конденсатору 0,250 мкФ? б) Какой будет сила тока на частоте 25,0 кГц?
7. Источник 20,0 кГц, 16,0 В, подключенный к катушке индуктивности, создает ток силой 2,00 А. Индуктивность какая?
8. Источник 20,0 Гц, 16,0 В производит ток силой 2,00 мА при подключении к конденсатору. Какова емкость?
9. (а) Катушка индуктивности, предназначенная для фильтрации высокочастотных помех от питания, подаваемого на персональный компьютер, включена последовательно с компьютером. Какая минимальная индуктивность должна быть у него, чтобы создать реактивное сопротивление 2,00 кОм для шума 15,0 кГц? б) Каково его реактивное сопротивление при частоте 60,0 Гц?
(а) Катушка индуктивности, предназначенная для фильтрации высокочастотных помех от питания, подаваемого на персональный компьютер, включена последовательно с компьютером. Какая минимальная индуктивность должна быть у него, чтобы создать реактивное сопротивление 2,00 кОм для шума 15,0 кГц? б) Каково его реактивное сопротивление при частоте 60,0 Гц?
10. Конденсатор на рис. 4(а) предназначен для фильтрации низкочастотных сигналов, препятствуя их передаче между цепями. (а) Какая емкость необходима для создания реактивного сопротивления 100 кОм на частоте 120 Гц? б) Каким будет его реактивное сопротивление на частоте 1,00 МГц? (c) Обсудите последствия ваших ответов на вопросы (a) и (b).
11. Конденсатор на рис. 4(b) фильтрует высокочастотные сигналы, замыкая их на землю. а) Какая емкость необходима, чтобы получить реактивное сопротивление
10,0 мОм 10,0 м\Омега 10,0 мОм
для сигнала 5,00 кГц? б) Каким будет его реактивное сопротивление при частоте 3,00 Гц? (c) Обсудите последствия ваших ответов на вопросы (a) и (b).
12. Необоснованные результаты При записи напряжений, вызванных мозговой активностью (ЭЭГ), сигнал 10,0 мВ с частотой 0,500 Гц подается на конденсатор, производящий ток 100 мА. Сопротивление незначительно. а) Чему равна емкость? б) Что неразумного в этом результате? (c) Какое предположение или предпосылка являются ответственными?
13. Создайте свою собственную задачу Рассмотрим использование катушки индуктивности последовательно с компьютером, работающим от электричества 60 Гц. Постройте задачу, в которой вы вычисляете относительное снижение напряжения входящего высокочастотного шума по сравнению с напряжением 60 Гц. Среди вещей, которые следует учитывать, — приемлемое последовательное реактивное сопротивление катушки индуктивности для мощности 60 Гц и вероятные частоты шума, проходящего через линии электропередач.
Глоссарий
- индуктивное реактивное сопротивление:
- противодействие катушки индуктивности изменению тока; рассчитывается как X л = 2π фл
- емкостное реактивное сопротивление:
- сопротивление конденсатора изменению тока; рассчитано по формуле
XC=12πfC{X}_{C}=\frac{1}{2\pi fC}\\XC=2πfC1
Избранные решения задач и упражнений
1. 531 Гц
531 Гц
3. 1,33 нФ
5. (а) 2,55 А (б) 1,53 мА
7. 63,7 мкГн 9. (а) 21,2 мГн (б) 8,00 Ом
Лицензии и ссылки
Контент по лицензии CC, совместно используемый ранее
- College Physics. Автор : Колледж OpenStax. Расположен по адресу : https://openstax.org/books/college-physics/pages/1-introduction-to-science-and-the-realm-of-physics-physical-quantities-and-units. Лицензия : CC BY: Attribution . Условия лицензии : Находится в лицензии
Что такое DCR в индукторах и как это влияет на вашу схему
Катушки индуктивности широко используются в электронике после резисторов и конденсаторов. Идеальная катушка индуктивности накапливает энергию в магнитном поле и подает плавный выходной ток на нагрузку. Но в практической схеме индуктор также имеет небольшое сопротивление, связанное с его свойством индуктивности. Во время подачи постоянного тока или, если быть точнее, на частоте 0 Гц, катушки индуктивности оказывают сопротивление потоку тока. Это сопротивление постоянному току называется DCR, что означает сопротивление постоянному току. В этом уроке мы узнаем больше о DCR и о том, как он влияет на производительность схемы. Мы также узнаем , как измерить значение DCR индуктора и , как уменьшить значение DCR индуктора при его изготовлении.
Во время подачи постоянного тока или, если быть точнее, на частоте 0 Гц, катушки индуктивности оказывают сопротивление потоку тока. Это сопротивление постоянному току называется DCR, что означает сопротивление постоянному току. В этом уроке мы узнаем больше о DCR и о том, как он влияет на производительность схемы. Мы также узнаем , как измерить значение DCR индуктора и , как уменьшить значение DCR индуктора при его изготовлении.
Подобно DCR для индукторов, конденсаторы также имеют некоторые неидеальные параметры, связанные с ним, называемые эквивалентным последовательным сопротивлением (ESR) и эквивалентной последовательной индуктивностью (ESL). Вы можете прочитать статью об ESR и ESL в конденсаторах, чтобы узнать больше об этом. и их значение в схемотехнике.
Что такое DCR в катушках индуктивности?
Термин DCR означает Сопротивление постоянному току . Это значение представляет собой 90 184 величину сопротивления, которое может оказать катушка индуктивности, когда через нее проходит сигнал постоянного тока частотой 0 Гц 90 185 . На практике все катушки индуктивности будут иметь небольшое значение DCR, связанное с этим.
На практике все катушки индуктивности будут иметь небольшое значение DCR, связанное с этим.
На приведенном ниже изображении показан практичный индуктор с фактической индуктивностью, включенной последовательно с небольшим сопротивлением постоянному току (DCR). Символ индуктора здесь представляет индуктивность, а последовательно с ним резистор представляет собой сопротивление индуктора постоянному току. В принципе катушки индуктивности обеспечивают очень низкое сопротивление для постоянного тока с низкой частотой и обеспечивают высокое сопротивление для высокочастотных входов.
DCR индуктора обусловлен сопротивлением катушки , из которой изготовлен индуктор. Сопротивление катушки пропорционально длине провода, используемого для формирования катушки, а длина катушки также пропорциональна значению индуктивности индуктора. Следовательно, катушки индуктивности с более высоким значением обеспечивают высокое сопротивление, а катушки индуктивности с низким значением обеспечивают низкое сопротивление. Большое значение индуктивности требует большего количества обмоток, чем катушки индуктивности с низким значением, что увеличивает длину медного провода. DCR катушек индуктивности обычно колеблется от гораздо менее 1 Ом до 3-4 Ом.
Большое значение индуктивности требует большего количества обмоток, чем катушки индуктивности с низким значением, что увеличивает длину медного провода. DCR катушек индуктивности обычно колеблется от гораздо менее 1 Ом до 3-4 Ом.
Практическое значение DCR
Теперь мы знаем, что катушки индуктивности имеют небольшое значение сопротивления, но в чем проблема? Почему важно учитывать это небольшое значение сопротивления при разработке нашей схемы?
DCR, являющийся резистором , рассеивает тепло и снижает эффективность , как и любой другой резистор с падением напряжения на нем. Эффективность измеряется по приведенной ниже формуле
Q = w (L/R)
Где Q называется Q-фактором . L — индуктивный реактор, а R — сопротивление индуктора на определенной частоте. Отношение индуктивного сопротивления к сопротивлению на данной частоте называется добротностью. Эта добротность имеет важное значение в различных приложениях. Чем выше добротность, тем выше КПД. Если теоретически рассчитать, идеальная катушка индуктивности имеет более высокую добротность по сравнению с реальной. В реальных индукторах эта добротность надежна в DCR.
Эта добротность имеет важное значение в различных приложениях. Чем выше добротность, тем выше КПД. Если теоретически рассчитать, идеальная катушка индуктивности имеет более высокую добротность по сравнению с реальной. В реальных индукторах эта добротность надежна в DCR.
Индуктивность с высокой добротностью используется в радиочастотных цепях, где конденсатор используется параллельно для формирования резонансного контура. В таком случае высокое значение добротности индуктора помогает сбалансировать верхнюю и нижнюю частоты резонансного контура, работающего в непрерывной полосе частот.
В приложениях, связанных с силовой электроникой, низкое значение DCR важно для меньшего рассеивания мощности, а также для небольших размеров корпуса. Индуктор с low DCR будет иметь более низкий форм-фактор , чем индукторы с высоким значением DCR. Основным эффектом DCR катушки индуктивности является рассеивание мощности из-за сопротивления катушки. Рассеиваемая мощность может быть рассчитана по степенному закону P = I 2 R, где R эквивалентно сопротивлению индуктора постоянному току, а I — току, протекающему через него.
Как измерить DCR катушки индуктивности?
Большинство людей измеряют сопротивление постоянному току (DCR) катушки индуктивности, подключая стандартный мультиметр к проводам катушки индуктивности для измерения сопротивления медного провода. Это может работать достаточно хорошо для больших катушек индуктивности, потому что медный провод там достаточно большой, чтобы получить высокое значение DCR, которое можно измерить с типичным мультиметровым разрешением.
Но для катушки индуктивности меньшего значения значение сопротивления постоянному току слишком мало (обычно в диапазоне миллиомов) для измерения стандартными недорогими мультиметрами. Кроме того, провода датчика мультиметра также имеют сопротивление постоянному току, которое в сумме увеличивает значение DCR, что приводит к ошибочным показаниям. Таким образом, в измерении DCR индуктора возникает общая проблема.
Фактический способ измерения значения DCR катушки индуктивности заключается в использовании измерительного пути по шкале Кельвина между выводами и подаче тока на катушку индуктивности. Поскольку DCR индуктора представляет собой сопротивление медного провода постоянному току, оно будет создавать напряжение на выводе индуктора в соответствии с законом Ома, В = I x R. Это напряжение можно измерить с помощью мультиметра. Очевидно, что этот метод измерения имеет ограничения. Прежде чем проводить измерения, необходимо знать о нескольких вещах, которые перечислены ниже.
Поскольку DCR индуктора представляет собой сопротивление медного провода постоянному току, оно будет создавать напряжение на выводе индуктора в соответствии с законом Ома, В = I x R. Это напряжение можно измерить с помощью мультиметра. Очевидно, что этот метод измерения имеет ограничения. Прежде чем проводить измерения, необходимо знать о нескольких вещах, которые перечислены ниже.
- Максимальный номинальный ток катушек индуктивности. Ток не должен превышать максимальный номинальный ток, указанный в паспорте индуктора.
- Макет не подходит для измерения DCR индукторов, так как соединение с макетом также способствует шуму и сопротивлению.
- Рекомендуется использовать подходящую печатную плату только с контрольными точками, входными и выходными разъемами тока и держателем компонента, чтобы избежать пайки.
На изображении ниже показана схема для измерения значения DCR катушки индуктивности. Показанная здесь катушка индуктивности является идеальной катушкой индуктивности, а сопротивление постоянному току является эквивалентным последовательным сопротивлением. Смысловая линия – это смысловая линия Кельвина.
Смысловая линия – это смысловая линия Кельвина.
Предположим, что используемый здесь индуктор имеет номинальный постоянный ток 1 А. Таким образом, входной ток здесь будет 1А. Чем выше значение входного тока, тем выше будет разрешение измеренного значения DCR, но если ваша катушка индуктивности не может работать с большим током, можно также использовать токи с низким значением.
После прохождения тока необходимо измерить падение напряжения на выводах катушки индуктивности. Предположим, что падение напряжения на катушке индуктивности составляет примерно 50 мВ. Тогда DCR этого индуктора можно рассчитать как
. В = I x R Р = В/Я R = 0,05/1 R = 0,05 Ом
Как уменьшить DCR при конструировании индуктора
Значение DCR индуктора не имеет значительного преимущества, поэтому всегда лучше выбирать индуктор с низким значением DCR.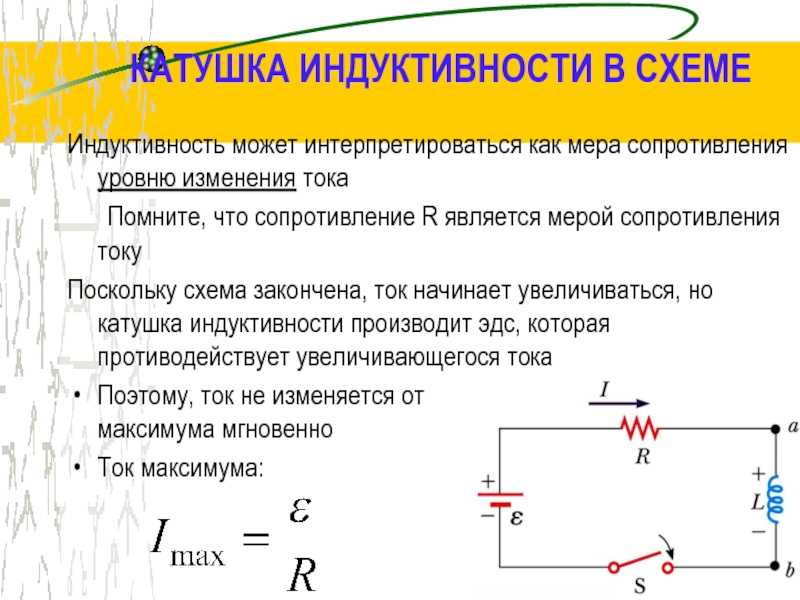 Обычно, когда индукторы строятся или проектируются, также учитывается параметр DCR. DCR индуктора должен быть очень низким, чтобы индуктор не блокировал протекание постоянного тока. Следующие методы используются для уменьшения значения DCR катушки индуктивности 9.0032
Обычно, когда индукторы строятся или проектируются, также учитывается параметр DCR. DCR индуктора должен быть очень низким, чтобы индуктор не блокировал протекание постоянного тока. Следующие методы используются для уменьшения значения DCR катушки индуктивности 9.0032
1. Сопротивление зависит от длины и толщины медного провода. Чтобы снизить сопротивление индуктора постоянному току, вместо одного провода можно намотать параллельно несколько проводов . Благодаря такому соединению результирующее сопротивление становится меньше. Рассмотрим один медный провод с некоторым значением сопротивления x. Если несколько таких проводов соединены параллельно, эквивалентное сопротивление будет уменьшено, поскольку параллельные резисторы будут иметь низкое эквивалентное сопротивление на выходе.
2. Увеличение площади поперечного сечения медного провода снижает сопротивление индукторов постоянному току. Следовательно, более толстые провода выгодны для снижения DCR.
3. Другой метод заключается в использовании плоского медного провода вместо круглых медных проводов. Плоские провода имеют большую площадь по сравнению с круглыми проводами. Это также полезно для снижения общего сопротивления.
На изображении ниже показана катушка индуктивности, изготовленная из плоского провода. Производитель Wurth Electronics, номер детали 7443641000. Согласно техническому описанию, катушка индуктивности имеет индуктивность 10 мкГн и сопротивление постоянному току 2,4 мОм при 20 градусах Цельсия.
4. В техническом описании катушки индуктивности указаны номинальные характеристики катушки индуктивности, где указано максимальное значение DCR. Это значение варьируется в зависимости от температуры. Рекомендуется использовать индуктор в заданных условиях температуры окружающей среды , чтобы эксплуатировать их в области минимального значения DCR.
Таким образом, постоянный ток катушки индуктивности является важным фактором, который следует учитывать при проектировании любой схемы.

