Формула закона ома для участка цепи. Закон Ома и закон Ватта в электрических цепях: основы для специалистов по ОВКВ — Производство и поставка электростанций, Бензиновые и дизельные генераторы от 1 до 100 кВт. Мини ТЭЦ на базе двигателя Стирлинга.

Что такое закон Ома и закон Ватта. Как они связаны с электрическими цепями. Почему эти законы важны для специалистов по отоплению, вентиляции и кондиционированию воздуха. Как применять эти законы на практике при работе с электрооборудованием ОВКВ.

Содержание

Ключевые электрические термины и определения

Прежде чем углубиться в законы Ома и Ватта, важно понять несколько ключевых электрических терминов:

Напряжение (В) — электрический потенциал или разность потенциалов, измеряемая в вольтах. Это «давление», толкающее электроны по цепи.
Ток (I) — поток электронов через проводник, измеряемый в амперах. Это количество электричества, проходящего через точку цепи за единицу времени.
Сопротивление (R) — противодействие потоку электронов, измеряемое в омах. Чем выше сопротивление, тем труднее току протекать.
Мощность (P) — скорость выполнения работы или преобразования энергии, измеряемая в ваттах.

Закон Ома: фундаментальная связь напряжения, тока и сопротивления

Закон Ома, сформулированный немецким физиком Георгом Омом, описывает фундаментальную связь между напряжением, током и сопротивлением в электрической цепи. Он выражается формулой:

I = V / R

Где:

I — ток в амперах (А)
V — напряжение в вольтах (В)
R — сопротивление в омах (Ω)

Этот закон показывает, что:

Ток прямо пропорционален напряжению — при увеличении напряжения ток также увеличивается.
Ток обратно пропорционален сопротивлению — при увеличении сопротивления ток уменьшается.

Практическое применение закона Ома в ОВКВ

Для специалистов по отоплению, вентиляции и кондиционированию воздуха понимание закона Ома критически важно по нескольким причинам:

Расчет параметров электрических нагревателей: Зная требуемую мощность нагревателя и напряжение сети, можно рассчитать ток и подобрать провода нужного сечения.

Проектирование систем управления: При разработке схем управления важно учитывать сопротивление проводов и компонентов для обеспечения корректной работы.
Диагностика неисправностей: Измеряя напряжение и ток в различных точках цепи, можно выявить аномальное сопротивление и локализовать проблему.
Выбор предохранителей и автоматов: Зная максимальный рабочий ток оборудования, можно правильно подобрать защитные устройства.

Закон Ватта: связь мощности с напряжением и током

Закон Ватта, названный в честь шотландского инженера Джеймса Ватта, описывает связь между электрической мощностью, напряжением и током. Он выражается формулой:

P = V * I

Где:

P — мощность в ваттах (Вт)
V — напряжение в вольтах (В)

I — ток в амперах (А)

Этот закон показывает, что электрическая мощность прямо пропорциональна как напряжению, так и току.

Применение закона Ватта в системах ОВКВ

Закон Ватта имеет множество практических применений в области ОВКВ:

Расчет энергопотребления: Зная напряжение и ток, потребляемые оборудованием, можно рассчитать его мощность и оценить затраты на электроэнергию.
Подбор оборудования: При проектировании систем важно учитывать мощность всех компонентов для правильного выбора источника питания и проводки.
Оценка эффективности: Сравнивая потребляемую электрическую мощность с полезной мощностью оборудования, можно оценить его КПД.
Диагностика перегрузок: Аномально высокая потребляемая мощность может указывать на проблемы в работе оборудования.

Взаимосвязь законов Ома и Ватта

Законы Ома и Ватта тесно связаны между собой. Комбинируя эти законы, можно получить дополнительные полезные формулы:

P = I^2 * R — мощность, выделяемая на сопротивлении
P = V^2 / R — мощность через напряжение и сопротивление

Эти формулы особенно полезны при расчете тепловыделения в электрических компонентах систем ОВКВ.

Практические примеры применения законов Ома и Ватта в ОВКВ

Рассмотрим несколько конкретных примеров использования этих законов в работе специалиста по ОВКВ:

Расчет тока для электрического нагревателя:
Допустим, нужно установить электрический нагреватель мощностью 5 кВт в сеть 220 В. Используя закон Ватта, можно рассчитать ток:
I = P / V = 5000 Вт / 220 В ≈ 22.7 А
Зная ток, можно правильно подобрать сечение проводов и номинал защитного автомата.
Определение сопротивления обмотки двигателя вентилятора:
Если известно, что при напряжении 220 В через обмотку двигателя протекает ток 2 А, то по закону Ома можно найти сопротивление обмотки:
R = V / I = 220 В / 2 А = 110 Ом
Это значение может быть полезно при диагностике состояния двигателя.
Расчет падения напряжения на длинной линии:
Предположим, кондиционер потребляет ток 10 А, а сопротивление проводки от щита до кондиционера составляет 0.5 Ом. Падение напряжения на этом участке будет:

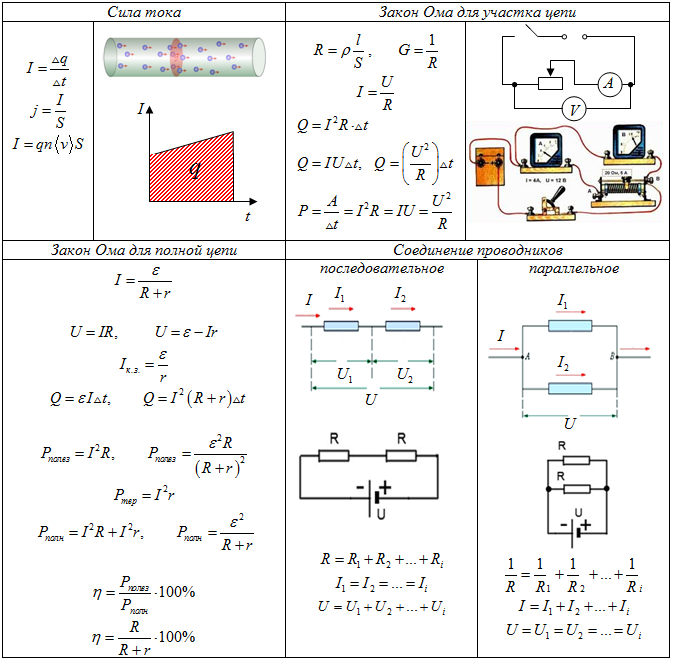
V = I * R = 10 А * 0.5 Ом = 5 В
Это позволяет оценить, не будет ли напряжение на кондиционере слишком низким для его нормальной работы.

Заключение: важность понимания электрических законов в ОВКВ

Глубокое понимание законов Ома и Ватта критически важно для специалистов по отоплению, вентиляции и кондиционированию воздуха. Эти фундаментальные принципы лежат в основе проектирования, монтажа, эксплуатации и диагностики электрических компонентов систем ОВКВ. Они позволяют:

Правильно рассчитывать параметры электрических цепей
Обеспечивать безопасность и эффективность работы оборудования
Быстро и точно диагностировать неисправности
Оптимизировать энергопотребление систем

Постоянное применение этих законов на практике и совершенствование навыков их использования позволит специалистам по ОВКВ повысить качество своей работы и стать более ценными профессионалами в своей области.

Закон Ома для участка цепи с источником ЭДС. (Лекция N 5)

Возьмем два участка цепи a—bи c—d (см. рис. 1) и составим для них уравнения в комплексной форме с учетом указанных на рис. 1 положительных направлений напряжений и токов.

Объединяя оба случая, получим

(1)

или для постоянного тока

(2)

Формулы (1) и (2) являются аналитическим выражением закона Ома для участка цепи с источником ЭДС, согласно которому ток на участке цепи с источником ЭДС равен алгебраической сумме напряжения на зажимах участка цепи и ЭДС, деленной на сопротивление участка. В случае переменного тока все указанные величины суть комплексы. При этом ЭДС и напряжение берут со знаком “+”, если их направление совпадает с выбранным направлением тока, и со знаком “-”, если их направление противоположно направлению тока.

Основы символического метода расчета цепей
синусоидального тока

Расчет цепей переменного синусоидального тока может производиться не только путем построения векторных диаграмм, но и аналитически – путем операций с комплексами, символически изображающими синусоидальные ЭДС, напряжения и токи. Достоинством векторных диаграмм является их наглядность, недостатком – малая точность графических построений. Применение символического метода позволяет производить расчеты цепей с большой степенью точности.

Символический метод расчета цепей синусоидального тока основан на законах Кирхгофа и законе Ома в комплексной форме.

Уравнения, выражающие законы Кирхгофа в комплексной форме, имеют совершенно такой же вид, как и соответствующие уравнения для цепей постоянного тока. Только токи, ЭДС, напряжения и сопротивления входят в уравнение в виде комплексных величин.

1. Первый закон Кирхгофа в комплексной форме:

(3)

2. Второй закон Кирхгофа в комплексной форме:

(4)

или применительно к схемам замещения с источниками ЭДС

(5)

3. Соответственно матричная запись законов Кирхгофа в комплексной форме имеет вид:

§ первый закон Кирхгофа:

. ;

(6)

§ второй закон Кирхгофа

(7)

Пример.

Дано:

Рис. 2

Определить:
1) полное комплексное сопротивление цепи ;
2) токи

Решение:

1. .

2. .

4. Принимая начальную фазу напряжения за нуль, запишем:

Тогда

5. Поскольку ток распределяется обратно пропорционально сопротивлению ветвей (это вытекает из закона Ома), то

6. .

7. Аналогичный результат можно получить, составив для данной схемы уравнения по законам Кирхгофа в комплексной форме

или после подстановки численных значений параметров схемы

Специальные методы расчета

Режим работы любой цепи полностью характеризуется уравнениями, составленными на основании законов Кирхгофа. При этом необходимо составить и решить систему с n неизвестными, что может оказаться весьма трудоемкой задачей при большом числе n ветвей схемы. Однако, число уравнений, подлежащих решению, может быть сокращено, если воспользоваться специальными методами расчета, к которым относятся методы контурных токов и узловых потенциалов.

Метод контурных токов

Идея метода контурных токов: уравнения составляются только по второму закону Кирхгофа, но не для действительных, а для воображаемых токов, циркулирующих по замкнутым контурам, т.е. в случае выбора главных контуров равных токам ветвей связи. Число уравнений равно числу независимых контуров, т.е. числу ветвей связи графа

. Первый закон Кирхгофа выполняется автоматически. Контуры можно выбирать произвольно, лишь бы их число было равно и чтобы каждый новый контур содержал хотя бы одну ветвь, не входящую в предыдущие.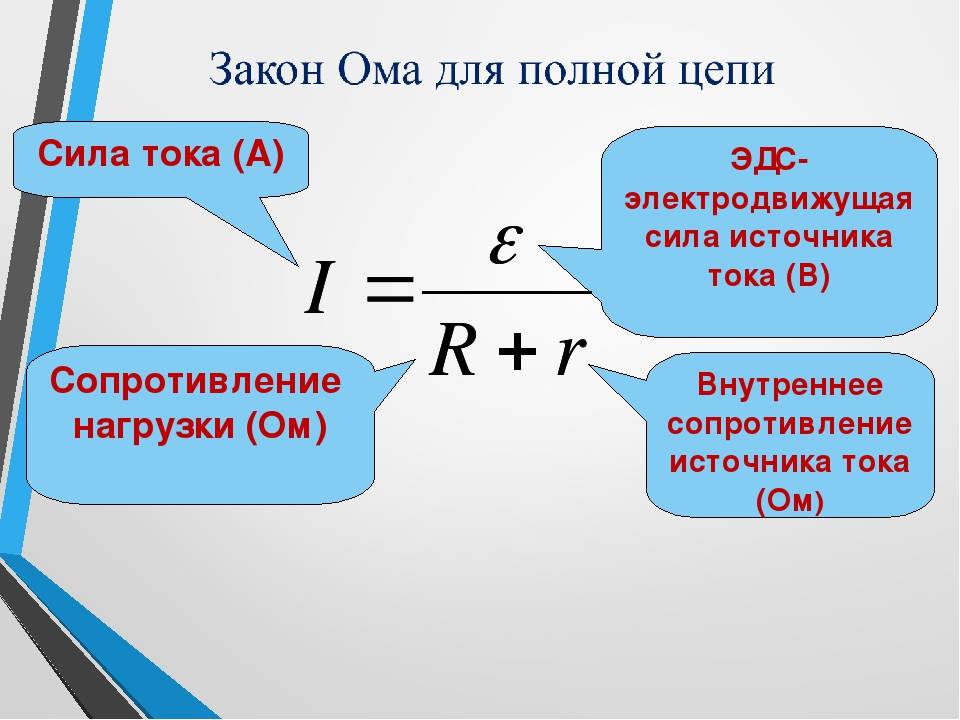

Такие контуры называются независимыми. Их выбор облегчает использование топологических понятий дерева и ветвей связи.

Направления истинных и контурных токов выбираются произвольно. Выбор положительных направлений перед началом расчета может не определять действительные направления токов в цепи. Если в результате расчета какой-либо из токов, как и при использовании уравнений по законам Кирхгофа, получится со знаком “-”, это означает, что его истинное направление противоположно.

Пусть имеем схему по рис. 3.

Выразим токи ветвей через контурные токи:

;

; ;

; .

Обойдя контур aeda, по второму закону Кирхгофа имеем

Поскольку ,

то

Таким образом, получили уравнение для первого контура относительно контурных токов. Аналогично можно составить уравнения для второго, третьего и четвертого контуров:

совместно с первым решить их относительно контурных токов и затем по уравнениям, связывающим контурные токи и токи ветвей, найти последние.

Однако данная система уравнений может быть составлена формальным путем:

При составлении уравнений необходимо помнить следующее:

— сумма сопротивлений, входящих в i-й контур;

— сумма сопротивлений, общих для i-го и k-го контуров, причем ;

члены на главной диагонали всегда пишутся со знаком “+”;

знак “+” перед остальными членами ставится в случае, если через общее сопротивление i-й и k- й контурные токи проходят в одном направлении, в противном случае ставится знак “-”;

если i-й и k- й контуры не имеют общих сопротивлений, то ;

в правой части уравнений записывается алгебраическая сумма ЭДС, входящих в контур: со знаком “+”, если направление ЭДС совпадает с выбранным направлением контурного тока, и “-”, если не совпадает.

В нашем случае, для первого уравнения системы, имеем:

Следует обратить внимание на то, что, поскольку , коэффициенты контурных уравнений всегда симметричны относительно главной диагонали.

Если в цепи содержатся помимо источников ЭДС источники тока, то они учитываются в левых частях уравнений как известные контурные токи: k- й контурный ток, проходящий через ветвь с k- м источником тока равен этому току .

Метод узловых потенциалов

Данный метод вытекает из первого закона Кирхгофа. В качестве неизвестных принимаются потенциалы узлов, по найденным значениям которых с помощью закона Ома для участка цепи с источником ЭДС затем находят токи в ветвях. Поскольку потенциал – величина относительная, потенциал одного из узлов (любого) принимается равным нулю. Таким образом, число неизвестных потенциалов, а следовательно, и число уравнений равно , т.е. числу ветвей дерева .

Пусть имеем схему по рис. 4, в которой примем .

Допустим, что и известны. Тогда значения токов на основании закона Ома для участка цепи с источником ЭДС

Запишем уравнение по первому закону Кирхгофа для узла а:

и подставим значения входящих в него токов, определенных выше:

Сгруппировав соответствующие члены, получим:

Аналогично можно записать для узла b:

Как и по методу контурных токов, система уравнений по методу узловых потенциалов может быть составлена формальным путем. При этом необходимо руководствоваться следующими правилами:

1. В левой части i-го уравнения записывается со знаком “+”потенциал i-го узла, для которого составляется данное i-е уравнение, умноженный на сумму проводимостей ветвей, присоединенных к данному i-му узлу, и со знаком “-”потенциал соседних узлов, каждый из которых умножен на сумму проводимостей ветвей, присоединенных к i-му и k-му узлам.

Из сказанного следует, что все члены , стоящие на главной диагонали в левой части системы уравнений, записываются со знаком “+”, а все остальные – со знаком “-”, причем .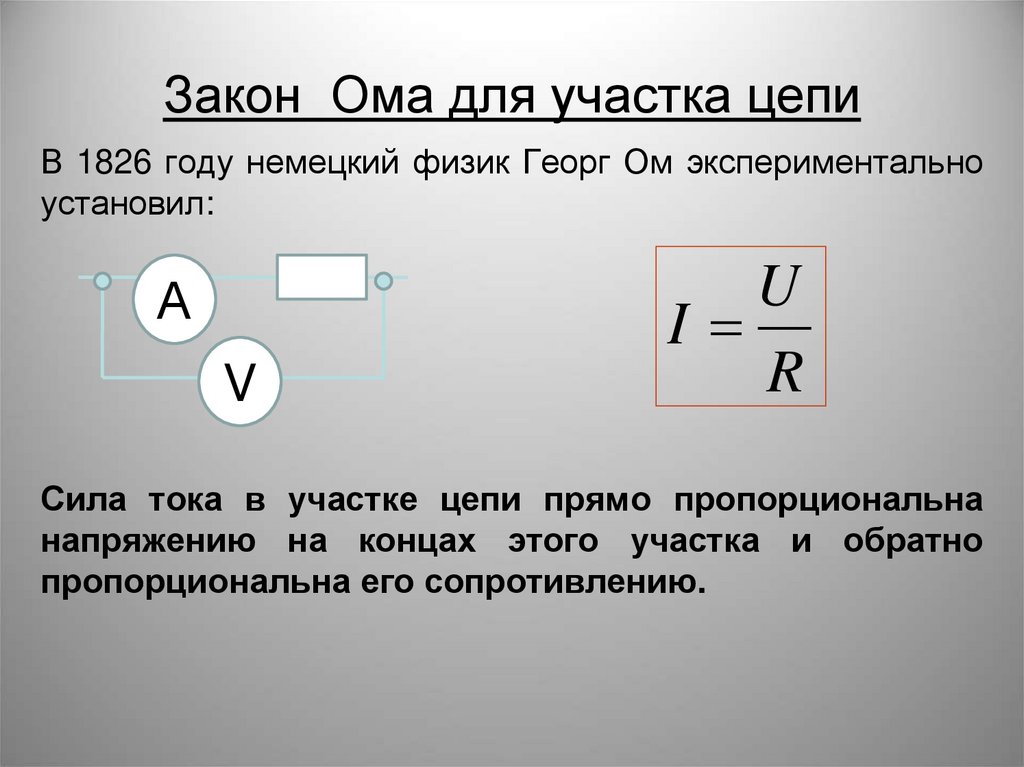 Последнее равенство по аналогии с методом контурных токов обеспечивает симметрию коэффициентов уравнений относительно главной диагонали.

2. В правой части i-го уравнения записывается так называемый узловой ток , равный сумме произведений ЭДС ветвей, подходящих к i-му узлу, и проводимостей этих ветвей. При этом член суммы записывается со знаком “+”, если соответствующая ЭДС направлена к i-му узлу, в противном случае ставится знак “-”. Если в подходящих к i-му узлу ветвях содержатся источники тока, то знаки токов источников токов, входящих в узловой ток простыми слагаемыми, определяются аналогично.

В заключение отметим, что выбор того или иного из рассмотренных методов определяется тем, что следует найти, а также тем, какой из них обеспечивает меньший порядок системы уравнений. При расчете токов при одинаковом числе уравнений предпочтительнее использовать метод контурных токов, так как он не требует дополнительных вычислений с использованием закона Ома. Метод узловых потенциалов очень удобен при расчетах многофазных цепей, но не удобен при расчете цепей со взаимной индуктивностью.

Литература

1. Основы теории цепей: Учеб.для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с.

2. Бессонов Л.А. Теоретические основы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с

Контрольные вопросы и задачи

1. В ветви на рис. 1 . Определить ток .

Ответ: .

2. В чем заключается сущность символического метода расчета цепей синусоидального тока?

3. В чем состоит сущность метода контурных токов?

4. В чем состоит сущность метода узловых потенциалов?

5. В цепи на рис. 5 ; ;

; . Методом контурных токов определить комплексы действующих значений токов ветвей.
Ответ: ; ; .
6. В цепи на рис. 6 . Рассчитать токи в ветвях, используя метод узловых потенциалов.
Ответ: ; ; ; ; ; ; .
Закон Ома для участка цепи с ЭДС
Для однозначного определения потенциала любой точки электрической цепи необходимо задать (произвольно) потенциал какой-нибудь одной точки. Выберем для схемы, представленной на рис. 1. 7, а,
. По определению потенциал точки 3 больше φ₂ на значение ЭДС:
Ток I во внешней части простейшей электрической цепи, а в общем случае в любом пассивном элементе цепи, а значит, и схемы, направлен, как указывалось, от точки с более высоким потенциалом (3) к точке с более низким (1). Поэтому потенциал φ₃ больше потенциала φ₁:
Из (1.9) и (1.10) имеем
Аналогично можно написать формулу для тока участка сложной электрической схемы, состоящего из любого числа последовательно соединенных источников, представленных схемами замещения на рис. 1.7, и приемников при заданной разности потенциалов на концах этого участка (рис. 1.9). Ток I на участке схемы, содержащем источники ЭДС, может быть направлен от точки а к точке b или наоборот. Если направление тока заранее не известно, то для составления выражений, подобных (1.11), нужно выбрать направление тока произвольно. Такое произвольно выбранное направление тока условились называть положительным направлением и обозначать (как и выше действительное направление) стрелкой с просветом или отмечать индексами у буквы I.
Если принять за положительное направление тока I направление от точки а к точке b, то потенциал φ_b определяется через потенциал φ_a выражением
Из этого равенства следует
где
— суммарное сопротивление участка схемы; — разность потенциалов или напряжение между выводами рассматриваемого участка, взятые по выбранному направлению тока;
— алгебраическая сумма ЭДС, действующих на том же участке, причем каждая ЭДС, направление действия которой совпадает с положительным направлением тока, записывается с положительным знаком, а в противном случае — с отрицательным.
Формула (1.12а) представляет собой закон Ома для участка цепи (схемы) с ЭДС (обобщенный закон Ома).
Если в результате расчета по (1.12а) для тока получается отрицательное значение, то это значит, что действительное направление тока не совпадает с выбранным положительным направлением (противоположно произвольно выбранному направлению).
Для напряжения между любыми точками цепи также может быть произвольно выбрано положительное направление. Положительное направление напряжения указывается индексами у буквы U или обозначается на схемах стрелкой, которую, например, для напряжения будем в дальнейшем ставить от точки а к точке b. Таким образом, напряжение, как и ток, при расчетах надо рассматривать как алгебраическую величину.
Для ЭДС источников напряжения и токов источников тока, если их действительные направления не известны, также выбираются произвольные положительные направления, которые указывают двойными индексами или обозначают стрелками.
На участках схемы с пассивными элементами положительные направления напряжения и тока будем всегда выбирать совпадающими. В этом случае отдельную стрелку для напряжения можно и не ставить.
Закон Ома: сопротивление и простые цепи
Цели обучения
К концу этого раздела вы сможете:
Объяснить происхождение закона Ома.
Расчет напряжения, тока или сопротивления по закону Ома.
Объясните, что такое омический материал.
Опишите простую схему.
Что движет током? Мы можем думать о различных устройствах, таких как батареи, генераторы, настенные розетки и т. д., которые необходимы для поддержания тока. Все такие устройства создают разность потенциалов и в широком смысле называются источниками напряжения. Когда источник напряжения подключен к проводнику, он создает разность потенциалов V , создающий электрическое поле. Электрическое поле, в свою очередь, воздействует на заряды, вызывая ток.
Закон Ома
Ток, протекающий через большинство веществ, прямо пропорционален приложенному к нему напряжению В . Немецкий физик Георг Симон Ом (1787–1854) первым экспериментально продемонстрировал, что ток в металлической проволоке прямо пропорционален приложенному напряжению :
[латекс]I\propto{V}\\[/latex ].
Это важное соотношение известно как закон Ома . Его можно рассматривать как причинно-следственную связь, где напряжение является причиной, а ток — следствием. Это эмпирический закон, аналогичный закону трения — экспериментально наблюдаемому явлению. Такая линейная зависимость не всегда имеет место.
Сопротивление и простые схемы
Если напряжение управляет током, что этому препятствует? Электрическое свойство, препятствующее току (грубо похожее на трение и сопротивление воздуха), называется 9.0017 сопротивление R . Столкновения движущихся зарядов с атомами и молекулами в веществе передают энергию веществу и ограничивают ток. Сопротивление определяется как обратно пропорциональное току, или
[латекс]I\propto \frac{1}{R}\\[/латекс].
Так, например, ток уменьшается вдвое, если сопротивление удваивается. Сочетание отношений тока к напряжению и тока к сопротивлению дает
[латекс]I=\frac{V}{R}\\[/латекс].
Это соотношение также называют законом Ома. Закон Ома в этой форме действительно определяет сопротивление для определенных материалов. Закон Ома (как и закон Гука) не является универсальным. Многие вещества, для которых выполняется закон Ома, называются омический . К ним относятся хорошие проводники, такие как медь и алюминий, и некоторые плохие проводники при определенных обстоятельствах. Омические материалы имеют сопротивление Ом , которое не зависит от напряжения В и тока I . Объект, имеющий простое сопротивление, называется резистором , даже если его сопротивление невелико. Единицей измерения сопротивления является Ом и обозначается символом Ω (греческая омега в верхнем регистре). Перестановка I = V/R дает R = V/I , поэтому единицами сопротивления являются 1 Ом = 1 вольт на ампер:
[латекс]1 \Omega=1\frac{V}{A}\\[ /латекс].
На рис. 1 показана схема простой цепи. Простая схема имеет один источник напряжения и один резистор. Провода, соединяющие источник напряжения с резистором, можно считать имеющими пренебрежимо малое сопротивление, или их сопротивление можно включить в R .
Рисунок 1. Простая электрическая цепь, в которой замкнутый путь для протекания тока обеспечивается проводниками (обычно металлическими проводами), соединяющими нагрузку с клеммами батареи, представленными красными параллельными линиями. Зигзагообразный символ представляет одиночный резистор и включает любое сопротивление в соединениях с источником напряжения.
Пример 1. Расчет сопротивления: автомобильная фара
Каково сопротивление автомобильной фары, через которую протекает ток 2,50 А при подаче на нее напряжения 12,0 В?
Стратегия
Мы можем преобразовать закон Ома в соответствии с формулой I = V/R и использовать его для нахождения сопротивления.
Решение
Перестановка I = V/R и подстановка известных значений дает
[латекс]R=\frac{V}{I}=\frac{\text{12}\text{.}\ text{0 V}}{2\text{.}\text{50 A}}=\text{4}\text{.}\text{80 \Omega }\\[/latex].
Обсуждение
Это относительно небольшое сопротивление, но оно больше морозостойкости фары. Как мы увидим в разделе «Сопротивление и удельное сопротивление», сопротивление обычно увеличивается с температурой, поэтому лампочка имеет более низкое сопротивление при первом включении и будет потреблять значительно больший ток в течение короткого периода прогрева.
Диапазон сопротивлений превышает многие порядки. Некоторые керамические изоляторы, например те, которые используются для поддержки линий электропередач, имеют сопротивление 10 ¹² Ом или больше. У сухого человека сопротивление руки к ноге может составлять 10 ⁵ Ом, тогда как сопротивление человеческого сердца составляет около 10 ³ Ом. Метровый отрезок медного провода большого диаметра может иметь сопротивление 10 ⁻⁵ Ом, а сверхпроводники вообще не имеют сопротивления (они неомические). Сопротивление связано с формой объекта и материалом, из которого он состоит, как будет показано в разделе «Сопротивление и удельное сопротивление». Дополнительную информацию можно получить, решив I = V/R для В , что дает
В = IR
Это выражение для В можно интерпретировать как падение напряжения на резисторе, создаваемое протеканием тока I . Для этого напряжения часто используется фраза IR drop . Например, фара в Примере 1 выше имеет падение IR 12,0 В. Если измерить напряжение в различных точках цепи, будет видно, что оно увеличивается на источнике напряжения и уменьшается на резисторе. Напряжение аналогично давлению жидкости. Источник напряжения подобен насосу, создающему перепад давления, вызывающему ток — поток заряда. Резистор подобен трубе, которая снижает давление и ограничивает поток из-за своего сопротивления. Сохранение энергии имеет здесь важные последствия. Источник напряжения поставляет энергию (вызывая электрическое поле и ток), а резистор преобразует ее в другую форму (например, в тепловую энергию). В простой цепи (с одним простым резистором) напряжение, подаваемое источником, равно падению напряжения на резисторе, поскольку PE = q Δ V , и через каждый протекает тот же самый q . Таким образом, энергия, подаваемая источником напряжения, и энергия, преобразуемая резистором, равны. (См. рис. 2.)
Рис. 2. Падение напряжения на резисторе в простой цепи равно выходному напряжению батареи.
Соединения: сохранение энергии
В простой электрической цепи единственный резистор преобразует энергию, поступающую от источника, в другую форму. О сохранении энергии здесь свидетельствует тот факт, что вся энергия, подаваемая источником, преобразуется в другую форму одним только резистором. Мы обнаружим, что закон сохранения энергии имеет и другие важные применения в цепях и является мощным инструментом анализа цепей.
Исследования PhET: Закон Ома
Посмотрите, как формула закона Ома соотносится с простой цепью. Отрегулируйте напряжение и сопротивление и посмотрите, как изменится ток в соответствии с законом Ома. Размеры символов в уравнении изменяются в соответствии с принципиальной схемой.
Нажмите, чтобы запустить симуляцию.
Резюме раздела
Простая цепь — это цепь, в которой есть один источник напряжения и одно сопротивление.
Одно из утверждений закона Ома дает отношение между током I , напряжением В и сопротивлением R в простой цепи [латекс]I=\frac{V}{R}\\[/latex] .
Сопротивление выражается в омах (Ом) и относится к вольтам и амперам как 1 Ом = 1 В/А.
Падение напряжения или IR на резисторе, вызванное протеканием через него тока, определяется как В = IR .
Концептуальные вопросы
Падение IR на резисторе означает, что на резисторе произошло изменение потенциала или напряжения. Изменяется ли ток при прохождении через резистор? Объяснять.
Чем падение IR на резисторе похоже на падение давления в жидкости, протекающей по трубе?
Задачи и упражнения
1. Какой ток протекает через лампу фонарика на 3,00 В, если ее сопротивление в горячем состоянии равно 3,60 Ом?
2. Рассчитайте эффективное сопротивление карманного калькулятора с батареей на 1,35 В, через который протекает ток 0,200 мА.
3. Каково эффективное сопротивление стартера автомобиля, когда через него протекает ток 150 А, когда автомобильный аккумулятор подает на двигатель напряжение 11,0 В?
4. Какое напряжение подается на световой индикатор DVD-плеера с сопротивлением 140 Ом, если через него проходит ток 25,0 мА?
5. а) Найдите падение напряжения в удлинителе с сопротивлением 0,0600 Ом, по которому протекает ток 5,00 А. (b) Более дешевый шнур использует более тонкую проволоку и имеет сопротивление 0,300 Ом. Каково падение напряжения в нем при протекании 5,00 А? в) Почему напряжение любого используемого электроприбора уменьшается на эту величину? Каково влияние на прибор?
6. Линия электропередачи подвешена к металлическим опорам со стеклянными изоляторами сопротивлением 1,00×10 ⁹ Ом. Какой ток протекает через изолятор, если напряжение равно 200 кВ? (Некоторые высоковольтные линии постоянного тока.)
Глоссарий
Закон Ома:
эмпирическое соотношение, утверждающее, что ток I пропорционален разности потенциалов В , ∝ В ; его часто записывают как I = V/R , где R это сопротивление
сопротивление:
электрическое свойство, препятствующее току; для омических материалов это отношение напряжения к току, R = V/I
Ом:
единица сопротивления, определяемая как 1 Ом = 1 В/А
омический:
тип материала, для которого действует закон Ома
простая схема:
схема с одним источником напряжения и одним резистором
Выбранные решения проблем и упражнений
1. 0,833 A
3. 7,33 × 10 ⁻² ω
5. (a) 0,300 В
(b) 1,50 V
независимо от того, какой прибор используется, уменьшается, потому что общее падение напряжения от стены до конечного выхода устройства является фиксированным. Таким образом, если падение напряжения на удлинителе велико, падение напряжения на устройстве значительно уменьшается, поэтому выходная мощность устройства может быть значительно снижена, что снижает способность устройства работать должным образом.
Закон Ома и закон Ватта – основы ОВКВ
Электрические термины и определения
Нажмите кнопку воспроизведения в следующем аудиоплеере, чтобы слушать, пока вы читаете этот раздел.
В этом разделе дается краткое описание двух наиболее фундаментальных электрических отношений: , описывающего протекание тока в электрических цепях, и , описывающего, как рассеивается мощность.
Объединение элементов , и , Джордж Ом разработал следующую формулу:
[латекс]\текст{I}=\dfrac{\текст{E}}{\текст{R}}[/латекс]
Где:
E = Напряжение в вольтах
I = ток в амперах
R = сопротивление в омах
Это называется законом Ома.
Предположим, например, что у нас есть цепь с потенциалом 1 вольт, током 1 ампер и сопротивлением 1 Ом. Используя закон Ома, мы можем сказать:
[латекс]1\текст{А}=\dfrac{1\текст{В}}{1\текст{Ом}}[/латекс]
Допустим, это бак с широким шлангом. Количество воды в баке определяется как 1 вольт, а «узость» (сопротивление течению) шланга определяется как 1 Ом. Используя закон Ома, это дает нам поток (ток) в 1 ампер.
Используя эту аналогию, давайте теперь посмотрим на бак с узким шлангом. Поскольку шланг уже, его сопротивление потоку выше. Определим это сопротивление как 2 Ом. Количество воды в баке такое же, как и в другом баке, поэтому, используя закон Ома, наше уравнение для бака с узким шлангом:
[латекс]?=\dfrac{1\text{V}}{2\text{Ом}}[/latex]
Но какой ток? Поскольку сопротивление больше, а напряжение такое же, это дает нам значение тока 0,5 ампер:
[латекс]0,5\текст{А}=\dfrac{1\текст{В}}{2\текст{Ом}}[/латекс]
Объединяя элементы , и , названные в честь Джеймса Уатта, закон Уатта определяется как следующая формула:
[латекс]\текст{P}=\текст{E} * \текст{I}[/латекс]
Где:
P = мощность в ваттах
E = напряжение в вольтах
I = ток в амперах
Электрический — скорость передачи энергии.