Как работает гасящий конденсатор в цепи переменного тока. Как рассчитать емкость гасящего конденсатора. Для чего применяются гасящие конденсаторы. Какие преимущества и недостатки у схем с гасящими конденсаторами.
Принцип работы гасящего конденсатора в цепи переменного тока
Гасящий конденсатор в цепи переменного тока используется для снижения напряжения без значительных потерь мощности. Принцип его работы основан на реактивном сопротивлении конденсатора, которое зависит от частоты переменного тока:
Xc = 1 / (2πfC)
где:
- Xc — реактивное сопротивление конденсатора
- f — частота переменного тока
- C — емкость конденсатора
При прохождении переменного тока через конденсатор происходит сдвиг фаз между током и напряжением на 90°. Это позволяет снизить напряжение на нагрузке без заметного нагрева конденсатора.
Расчет емкости гасящего конденсатора
Для расчета емкости гасящего конденсатора используется следующая формула:
C = I / (2πfU)
где:
- C — необходимая емкость конденсатора
- I — требуемый ток через нагрузку
- f — частота сети (обычно 50 Гц)
- U — напряжение сети (обычно 220 В)
Например, для питания лампы мощностью 100 Вт и напряжением 36 В от сети 220 В емкость гасящего конденсатора составит:
C = 2.77 A / (2π * 50 Гц * 220 В) ≈ 4 мкФ
Области применения гасящих конденсаторов
Гасящие конденсаторы применяются в следующих случаях:
- Питание маломощных устройств от сети 220 В
- Снижение напряжения для светодиодных ламп
- Управление яркостью ламп накаливания
- Питание электродвигателей малой мощности
- Простые источники питания без трансформатора
Преимущества схем с гасящими конденсаторами
Основные преимущества использования гасящих конденсаторов:
- Простота конструкции
- Малые габариты и вес
- Высокий КПД (до 95%)
- Низкое тепловыделение
- Невысокая стоимость
Недостатки и ограничения гасящих конденсаторов
К недостаткам схем с гасящими конденсаторами можно отнести:
- Опасность поражения электрическим током
- Зависимость от частоты сети
- Чувствительность к перепадам напряжения
- Ограниченная мощность (до 100-200 Вт)
- Возможные помехи в сети
Особенности выбора гасящего конденсатора
При выборе гасящего конденсатора необходимо учитывать следующие факторы:
- Рабочее напряжение конденсатора должно быть не менее 400 В
- Желательно использовать специальные конденсаторы класса X2
- Емкость конденсатора нужно выбирать с запасом 20-30%
- Для защиты от перенапряжений рекомендуется параллельно ставить варистор
- Необходимо обеспечить надежную изоляцию конденсатора
Схемы включения гасящих конденсаторов
Рассмотрим основные схемы включения гасящих конденсаторов:
Простейшая схема
Самая простая схема состоит из гасящего конденсатора, включенного последовательно с нагрузкой:
«` «`Эта схема проста, но не обеспечивает защиты от перенапряжений и имеет высокое выходное сопротивление.
Схема с защитным резистором
Для ограничения пускового тока и защиты конденсатора последовательно с ним включают резистор небольшого номинала:
«` «`Эта схема более надежна, но имеет несколько меньший КПД из-за потерь на резисторе R1.
Расчет мощности нагрузки при использовании гасящего конденсатора
Мощность нагрузки, питаемой через гасящий конденсатор, можно рассчитать по формуле:
P = U * I * cos φ
где:
- P — мощность нагрузки
- U — напряжение на нагрузке
- I — ток через нагрузку
- cos φ — коэффициент мощности нагрузки
Для активной нагрузки cos φ = 1, поэтому расчет упрощается до P = U * I.
Меры безопасности при работе с гасящими конденсаторами
При использовании схем с гасящими конденсаторами необходимо соблюдать следующие меры безопасности:
- Использовать конденсаторы с напряжением не менее 400 В
- Обеспечить надежную изоляцию всех токоведущих частей
- Не прикасаться к схеме во время работы
- Устанавливать предохранитель для защиты от короткого замыкания
- После отключения дать конденсатору разрядиться
Помните, что даже после отключения от сети на конденсаторе может сохраняться опасное напряжение!
Альтернативы гасящим конденсаторам
Вместо гасящих конденсаторов для снижения напряжения можно использовать:
- Понижающие трансформаторы
- Импульсные преобразователи напряжения
- Линейные стабилизаторы напряжения
- Тиристорные регуляторы
Каждый из этих способов имеет свои преимущества и недостатки по сравнению с гасящими конденсаторами.
Заключение
Гасящие конденсаторы представляют собой простой и эффективный способ снижения напряжения в цепях переменного тока. При правильном расчете и соблюдении мер безопасности они позволяют создавать компактные и недорогие источники питания. Однако необходимо помнить об ограничениях и потенциальной опасности таких схем.
Расчет понижающего конденсатора
|
|
|
|||||||||||||||||||||||||||||||||||||
334146654694E-5 Фарад 
Угол между ними.
Матрица смежности онлайнКонденсатор в цепи переменного тока
- Details
- 16 April 2017
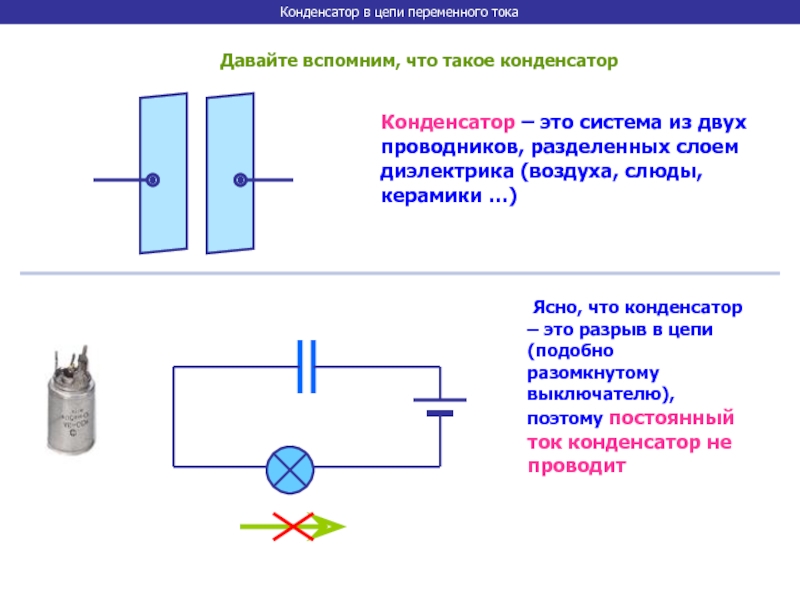
Господа, в сегодняшней статье я хотел бы рассмотреть такой интересный вопрос, как конденсатор в цепи переменного тока.
Эта тема весьма важна в электричестве, поскольку на практике конденсаторы повсеместно присутствуют в цепях с переменным током и, в связи с этим, весьма полезно иметь четкое представление, по каким законам изменяются в этом случае сигналы. Эти законы мы сегодня и рассмотрим, а в конце решим одну практическую задачу определения тока через конденсатор.
Господа, сейчас для нас наиболее интересным моментом является то, как связаны между собой напряжение на конденсаторе и ток через конденсатор для случая, когда конденсатор находится в цепи переменного сигнала.
Почему сразу переменного? Да просто потому, что конденсатор в цепи постоянного тока ничем не примечателен. Через него течет ток только в первый момент, пока конденсатор разряжен. Потом конденсатор заряжается и все, тока нет (да-да, слышу, уже начали кричать, что заряд конденсатора теоретически длится бесконечно долгое время, да еще у него может быть сопротивление утечки, но пока что мы этим пренебрегаем).
Заряженный конденсатор для постоянного тока – это как разрыв цепи. Когда же у нас случай переменного тока – тут все намного интереснее. Оказывается, в этом случае через конденсатор может протекать ток и конденсатор в этом случае как бы эквивалентен резистору с некоторым вполне определенным сопротивлением (если пока забить забыть про всякие там сдвиги фазы, об этом ниже). Нам надо каким-нибудь образом получить связь между током и напряжением на конденсаторе.
Пока мы будем исходить из того, что в цепи переменного тока находится только конденсатор и все. Без каких-либо других компонентов типа резисторов или индуктивностей. Напомню, что в случае, когда у нас в цепи находится исключительно одни только резисторы, подобная задача решается очень просто: ток и напряжения оказываются связанными между собой через закон Ома. Мы про это уже не один раз говорили. Там все очень просто: делим напряжение на сопротивление и получаем ток. А как же быть в случае конденсатора? Ведь конденсатор-то это не резистор.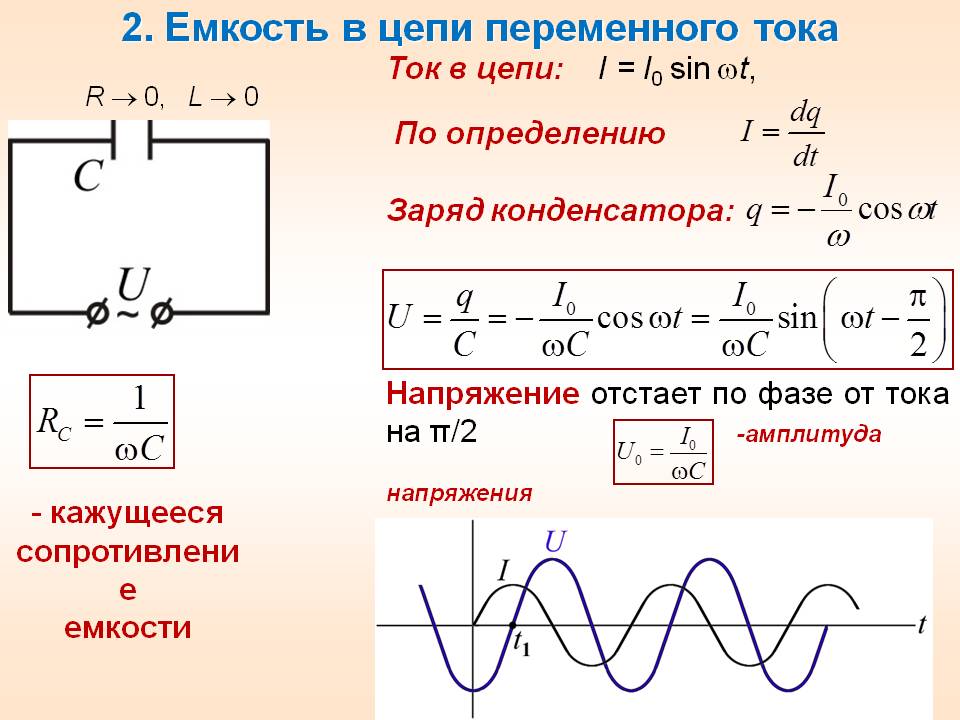
Там совсем иная физика протекания процессов, поэтому вот так вот с наскока не получится просто связать между собой ток и напряжение. Тем не менее, сделать это надо, поэтому давайте попробуем порассуждать.
Сперва давайте вернемся назад. Далеко назад. Даже очень далеко. К самой-самой первой моей статье на этом сайте. Старожилы должно быть помнят, что это была статья про силу тока. Вот в этой самой статье было одно интересное выражение, которое связывало между собой силу тока и заряд, протекающий через сечение проводника. Вот это самое выражение
Кто-нибудь может возразить, что в той статье про силу тока запись была через Δq и Δt – некоторые весьма малые величины заряда и времени, за которое этот заряд проходит через сечение проводника. Однако здесь мы будем применять запись через dq и dt – через дифференциалы. Такое представление нам потребуется в дальнейшем. Если не лезть глубоко в дебри матана, то по сути dq и dt здесь особо ничем не отличаются от Δq и Δt.
Безусловно, глубоко сведущие в высшей математике люди могут поспорить с этим утверждением, но да сейчас я не хочу концентрировать внимание на данных вещах.
Итак, выражение для силы тока мы вспомнили. Давайте теперь вспомним, как связаны между собой емкость конденсатора С, заряд q, который он в себе накопил, и напряжение U на конденсаторе, которое при этом образовалось. Ну, мы же помним, что если конденсатор накопил в себе какой-то заряд, то на его обкладках неизбежно возникнет напряжение. Про это все мы тоже говорили раньше, вот в этой вот статье. Нам будет нужна вот эта формула, которая как раз и связывает заряд с напряжением
Давайте-ка выразим из этой формулы заряд конденсатора:
А теперь есть очень большой соблазн подставить это выражение для заряда конденсатора в предыдущую формулу для силы тока. Приглядитесь-ка повнимательнее – у нас ведь тогда окажутся связанными между собой сила тока, емкость конденсатора и напряжение на конденсаторе! Сделаем эту подстановку без промедлений:
Емкость конденсатора у нас является величиной постоянной.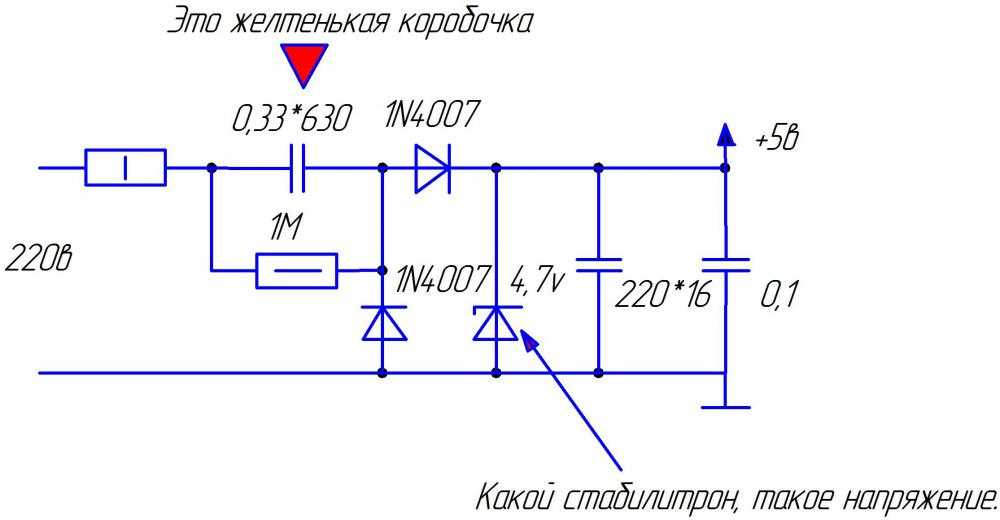
Она определяется исключительно самим конденсатором, его внутренним устройством, типом диэлектрика и всем таким прочим. Про все это подробно мы говорили в одной из прошлых статей. Следовательно, емкость С конденсатора, поскольку это константа, можно смело вынести за знак дифференциала (такие вот правила работы с этими самыми дифференциалами). А вот с напряжением U нельзя так поступить! Напряжение на конденсаторе будет изменяться со временем. Почему это происходит? Ответ элементарный: по мере протекания тока на обкладках конденсатора, очевидно, заряд будет изменяться. А изменение заряда непременно приведет к изменению напряжения на конденсаторе. Поэтому напряжение можно рассматривать как некоторую функцию времени и его нельзя выносить из-под дифференциала. Итак, проведя оговоренные выше преобразования, получаем вот такую вот запись:
Господа, спешу вас поздравить – только что мы получили полезнейшее выражение, которое связывает между собой напряжение, приложенное к конденсатору, и ток, который течет через него.
Таким образом, если мы знаем закон изменения напряжения, мы легко сможем найти закон изменения тока через конденсатор путем простого нахождения производной.
А как быть в обратном случае? Допустим, нам известен закон изменения тока через конденсатор и мы хотим найти закон изменения напряжения на нем. Читатели, сведущие в математике, наверняка уже догадались, что для решения этой задачи достаточно просто проинтегрировать написанное выше выражение. То есть, результат будет выглядеть как-то так:
По сути оба этих выражений про одно и тоже. Просто первое применяется в случае, когда нам известен закон изменения напряжения на конденсаторе и мы хотим найти закон изменения тока через него, а второе – когда нам известно, каким образом меняется ток через конденсатор и мы хотим найти закон изменения напряжения. Для лучшего запоминания всего этого дела, господа, я приготовил для вас поясняющую картинку. Она изображена на рисунке 1.
Рисунок 1 – Поясняющая картинка
На ней, по сути, в сжатой форме изображены выводы, которые хорошо бы запомнить.
Господа, обратите внимание – полученные выражения справедливы для любого закона изменения тока и напряжения. Здесь не обязательно должен быть синус, косинус, меандр или что-то другое. Если у вас есть какой-то совершенно произвольный, пусть даже совершенно дикий, не описанный ни в какой литературе, закон изменения напряжения U(t), поданного на конденсатор, вы, путем его дифференцирования можете определить закон изменения тока через конденсатор. И аналогично если вы знаете закон изменения тока через конденсатор I(t) то, найдя интеграл, сможете найти, каким же образом будет меняться напряжение.
Итак, мы выяснили как связать между собой ток и напряжение для абсолютно любых, даже самых безумных вариантов их изменения. Но не менее интересны и некоторые частные случаи. Например, случай успевшего уже нам всем полюбиться синусоидального тока. Давайте теперь разбираться с ним.
Пусть напряжение на конденсаторе емкостью C изменяется по закону синуса вот таким вот образом
Какая физическая величина стоит за каждой буковкой в этом выражении мы подробно разбирали чуть раньше.
Как же в таком случае будет меняться ток? Используя уже полученные знания, давайте просто тупо подставим это выражение в нашу общую формулу и найдем производную
Или можно записать вот так
Господа, хочу вам напомнить, что синус ведь только тем и отличается от косинуса, что один сдвинут относительно другого по фазе на 90 градусов. Ну, или, если выражаться на языке математики, то . Не понятно, откуда взялось это выражение? Погуглите формулы приведения . Штука полезная, знать не помешает. А еще лучше, если вы хорошо знакомы с тригонометрическим кругом, на нем все это видно очень наглядно.
Господа, отмечу сразу один момент. В своих статьях я не буду рассказывать про правила нахождения производных и взятия интегралов. Надеюсь, хотя бы общее понимание этих моментов у вас есть. Однако даже если вы не знаете, как это делать, я буду стараться излагать материал таким образом, чтобы суть вещей была понятна и без этих промежуточных выкладок.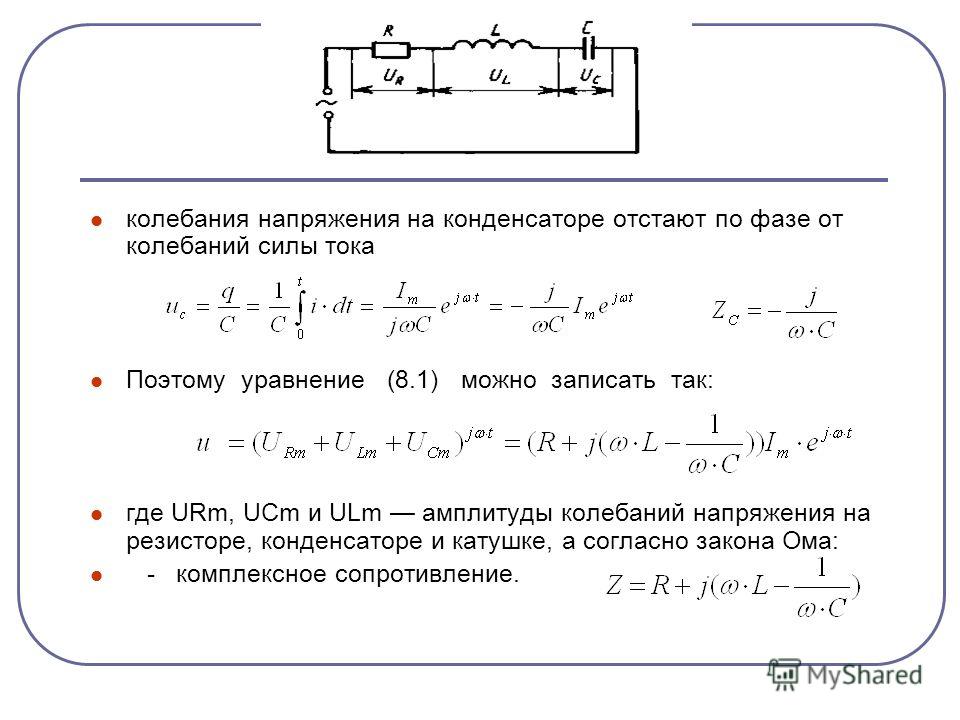
Итак, сейчас мы получили немаловажный вывод – если напряжение на конденсаторе изменяется по закону синуса, то ток через него будет изменяться по закону косинуса. То есть ток и напряжение на конденсаторе сдвинуты друг относительно друга по фазе на 90 градусов. Кроме того, мы можем относительно легко найти и амплитудное значение тока (это множители, которые стоят перед синусом). Ну то есть тот пик, тот максимум, которого ток достигает. Как видим, оно зависит от емкости C конденсатора, амплитуды приложенного к нему напряжения Um и частоты ω. То есть чем больше приложенное напряжение, чем больше емкость конденсатора и чем больше частота изменения напряжения, тем большей амплитуды достигает ток через конденсатор. Давайте построим график, изобразив на одном поле ток через конденсатор и напряжение на конденсаторе. Пока без конкретных цифр, просто покажем качественный характер. Этот график представлен на рисунке 2 (картинка кликабельна).
Рисунок 2 – Ток через конденсатор и напряжение на конденсаторе
На рисунке 2 синий график – это синусоидальный ток через конденсатор, а красный – синусоидальное напряжение на конденсаторе.
По этому рисунку как раз очень хорошо видно, что ток опережает напряжение (пики синусоиды тока находятся левее соответствующих пиков синусоиды напряжения, то есть наступают раньше).
Давайте теперь проделаем работу наоборот. Пусть нам известен закон изменения тока I(t) через конденсатор емкостью C. И закон этот пусть тоже будет синусоидальным
Давайте определим, как в таком случае будет меняться напряжение на конденсаторе. Воспользуемся нашей общей формулой с интегральчиком:
По абсолютнейшей аналогии с уже написанными выкладками, напряжение можно представить вот таким вот образом
Здесь мы снова воспользовались интересными сведениями из тригонометрии, что . И снова формулы приведения придут вам на помощь, если не понятно, почему получилось именно так.
Какой же вывод мы можем сделать из данных расчетов? А вывод все тот же самый, какой уже был сделан: ток через конденсатор и напряжение на конденсаторе сдвинуты по фазе друг относительно друга на 90 градусов.
Более того, они не просто так сдвинуты. Ток опережает напряжение. Почему это так? Какая за этим стоит физика процесса? Давайте разберемся.
Представим, что незаряженный конденсатор мы подсоединили к источнику напряжения. В первый момент никаких зарядов в конденсаторе вообще нет: он же разряжен. А раз нет зарядов, то нет и напряжения. Зато ток есть, он возникает сразу при подсоединении конденсатора к источнику. Замечаете, господа? Напряжения еще нет (оно не успело нарасти), а ток уже есть. И кроме того, в этот самый момент подключения ток в цепи максимален (разряженный конденсатор ведь по сути эквивалентен короткому замыканию цепи). Вот вам и отставание напряжения от тока. По мере протекания тока, на обкладках конденсатора начинает накапливаться заряд, то есть напряжение начинает расти а ток постепенно уменьшаться. И через некоторое время накопится столько заряда на обкладках, что напряжение на конденсаторе сравняется с напряжением источника и ток в цепи совсем прекратится.
Теперь давайте этот самый заряженный конденсатор отцепим от источника и закоротим накоротко. Что получим? А практически то же самое. В самый первый момент ток будет максимален, а напряжение на конденсаторе останется таким же, какое оно и было без изменений. То есть снова ток впереди, а напряжение изменяется вслед за ним. По мере протекания тока напряжение начнет постепенно уменьшаться и когда ток совсем прекратится, оно тоже станет равным нулю.
Для лучшего понимания физики протекающих процессов можно в который раз уже использовать водопроводную аналогию. Представим себе, что заряженный конденсатор – это некоторый бачок, полный воды. У этого бачка есть внизу краник, через который можно спустить воду. Давайте этот краник откроем. Как только мы его откроем, вода потечет сразу же. А давление в бачке будет падать постепенно, по мере того, как вода будет вытекать. То есть, грубо говоря, ручеек воды из краника опережает изменение давления, подобно тому, как ток в конденсаторе опережает изменение напряжения на нем.
Подобные рассуждения можно провести и для синусоидального сигнала, когда ток и напряжения меняются по закону синуса, да и вообще для любого. Суть, надеюсь, понятна.
Давайте проведем небольшой практический расчет переменного тока через конденсатор и построим графики.
Пусть у нас имеется источник синусоидального напряжения, действующее значение равно 220 В, а частота 50 Гц. Ну, то есть все ровно так же, как у нас в розетках. К этому напряжению подключают конденсатор емкостью 1 мкФ. Например, пленочный конденсатор К73-17, рассчитанный на максимальное напряжение 400 В (а на меньшее напряжение конденсаторы ни в коем случае нельзя подключать в сети 220 В), выпускается с емкостью 1 мкФ. Чтобы вы имели представление, с чем мы имеем дело, на рисунке 3 я разместил фотографию этого зверька (спасибо Diamond за фото )
Рисунок 3 – Ищем ток через этот конденсатор
Требуется определить, какая амплитуда тока будет протекать через этот конденсатор и построить графики тока и напряжения.
Сперва нам надо записать закон изменения напряжения в розетке. Если вы помните, амплитудное значение напряжения в этом случае равно около 311 В. Почему это так, откуда получилось, и как записать закон изменения напряжения в розетке, можно прочитать вот в этой статье. Мы же сразу приведем результат. Итак, напряжение в розетке будет изменяться по закону
Теперь мы можем воспользоваться полученной ранее формулой, которая свяжет напряжение в розетке с током через конденсатор. Выглядеть результат будет так
Мы просто подставили в общую формулу емкость конденсатора, заданную в условии, амплитудное значение напряжения и круговую частоту напряжения сети. В результате после перемножения всех множителей имеем вот такой вот закон изменения тока
Вот так вот, господа. Получается, что амплитудное значение тока через конденсатор чуть меньше 100 мА. Много это или мало? Вопрос нельзя назвать корректным. По меркам промышленной техники, где фигурируют сотни ампер тока, очень мало.
Да и для бытовых приборов, где десятки ампер не редкость – тоже. Однако для человека даже такой ток представляет большую опасность! Отсюда следует вывод, что хвататься за такой конденсатор, подключенный к сети 220 В не следует . Однако на этом принципе возможно изготовление так называемых источников питания с гасящим конденсатором. Ну да это тема для отдельной статьи и здесь мы не будем ее затрагивать.
Все это хорошо, но мы чуть не забыли про графики, которые должны построить. Надо срочно исправляться! Итак, они представлены на рисунке 4 и рисунке 5. На рисунке 4 вы можете наблюдать график напряжения в розетке, а на рисунке 5 – закон изменения тока через конденсатор, включенный в такую розетку.
Рисунок 4 – График напряжения в розетке
Рисунок 5 – График тока через конденсатор
Как мы можем видеть из этих рисунков, ток и напряжение сдвинуты на 90 градусов, как и должно быть.
И, возможно, у читателя возникла мысль – если через конденсатор течет ток и на нем падает какое-то напряжение, вероятно, на нем должна выделяться и некоторая мощность. Однако спешу предупредить вас – для конденсатора дело обстоит совершенно не так. Если рассматривать идеальный конденсатор, то мощность на нем не будет вообще выделяться, даже при протекании тока и падении на нем напряжения. Почему? Как же так? Об этом – в будущих статьях. А на сегодня все. Спасибо что читали, удачи, и до новых встреч!
Вступайте в нашу группу Вконтакте
Вопросы и предложения админу: This email address is being protected from spambots. You need JavaScript enabled to view it.
Social button for Joomla
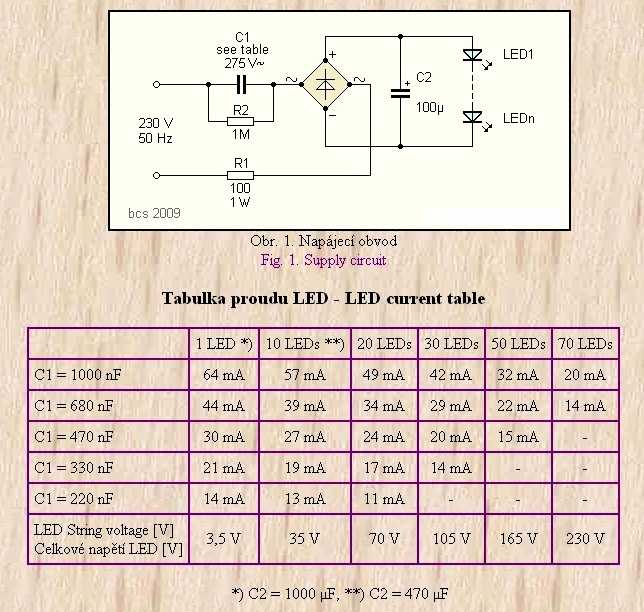
Как рассчитать и подобрать гасящий конденсатор
В самом начале темы, что касается подбора гасящего конденсатора, рассмотрим схему, состоящую из резистора и конденсатора, соединенных последовательно в сеть.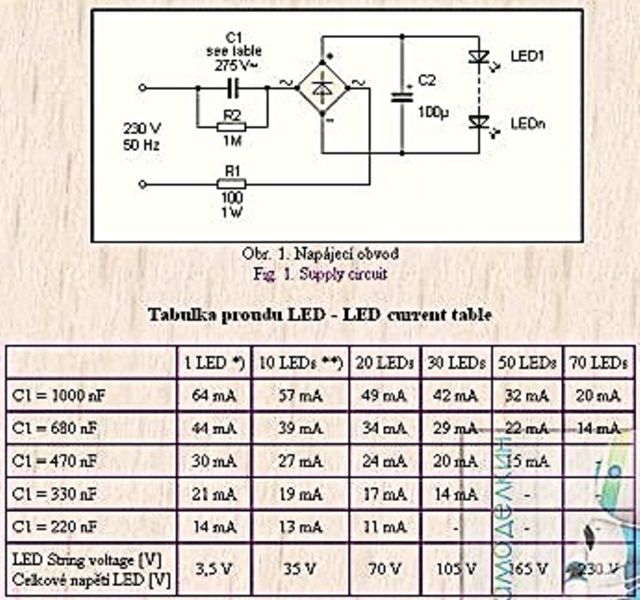
Полное сопротивление такой цепи будет равно:
Действующее значение тока соответственно находится по закону Ома, напряжение сети деленное на полное сопротивление цепи:
В итоге для нагрузки ток и входное и выходное напряжения, получаем следующее соотношение:
А если выходное напряжение достаточно мало, то мы вправе считать действующее значение тока примерно равным:
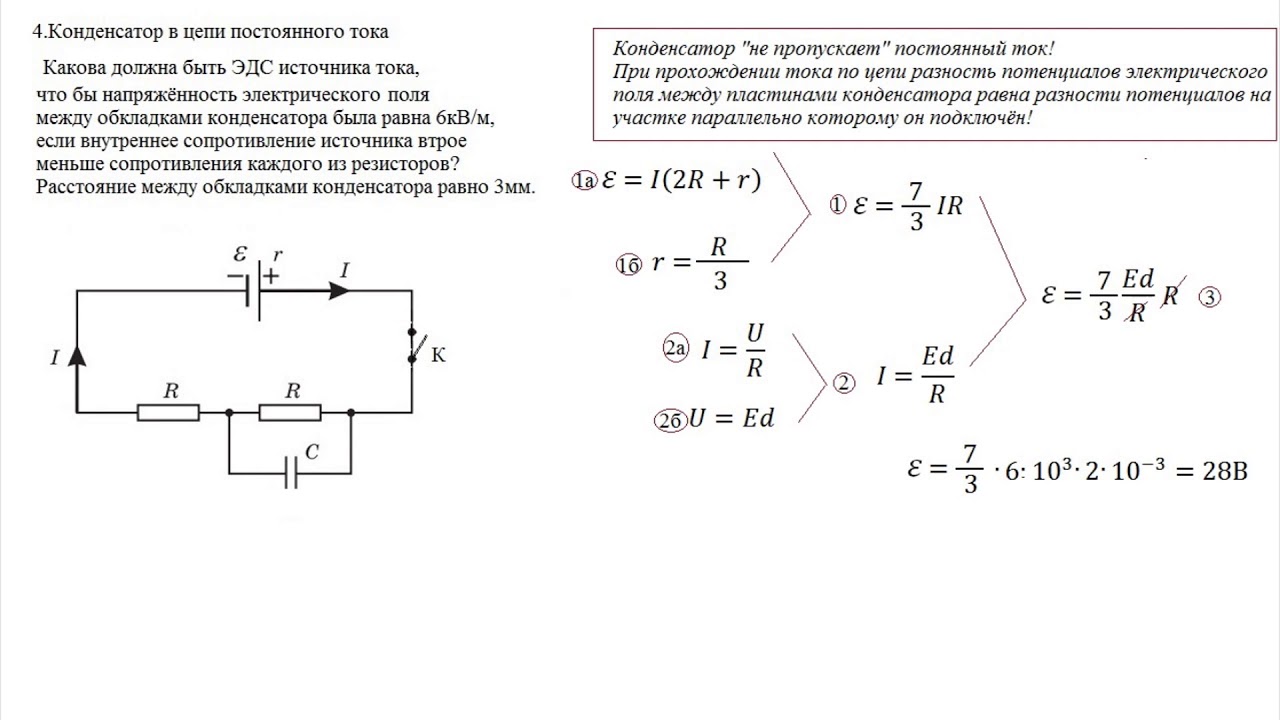
Однако рассмотрим с практической точки зрения вопрос выбора гасящего конденсатора для включения в Сеть переменного тока нагрузки рассчитана на напряжение ниже стандартного напряжения сети.
Предположим, у нас есть лампа накаливания мощностью 100 Вт, рассчитанная на напряжение 36 вольт, и по какой-то невероятной причине нам необходимо запитать ее от бытовой сети 220 вольт. Лампе нужен эффективный ток, равный:
Тогда емкость необходимого гасящего конденсатора будет равна:
Имея такой конденсатор, мы обретаем надежду получить нормальное свечение лампы, надеемся, что она хотя бы не перегорит.
Такой подход, если исходить из действующего значения тока, приемлем для активных нагрузок, таких как лампа или обогреватель.
А если нагрузка нелинейная и включена через диодный мост? Предположим, вам нужно зарядить свинцово-кислотный аккумулятор. Что тогда? Тогда зарядный ток для аккумулятора будет пульсирующим, и его значение будет меньше действующего значения:
Иногда радиоисточнику может пригодиться источник питания, в котором гасящий конденсатор включен последовательно с диодным мостом, выходом которого, в свою очередь, является фильтрующий конденсатор значительной емкости, к которому подключена нагрузка постоянного тока. Получается эдакий бестрансформаторный источник питания с конденсатором вместо понижающего трансформатора:
Здесь нагрузка в целом будет нелинейной, а ток станет далеко не синусоидальным, и надо будет проводить расчеты немного по-другому. Дело в том, что сглаживающий конденсатор с диодным мостом и нагрузкой внешне будет проявлять себя как симметричный стабилитрон, т.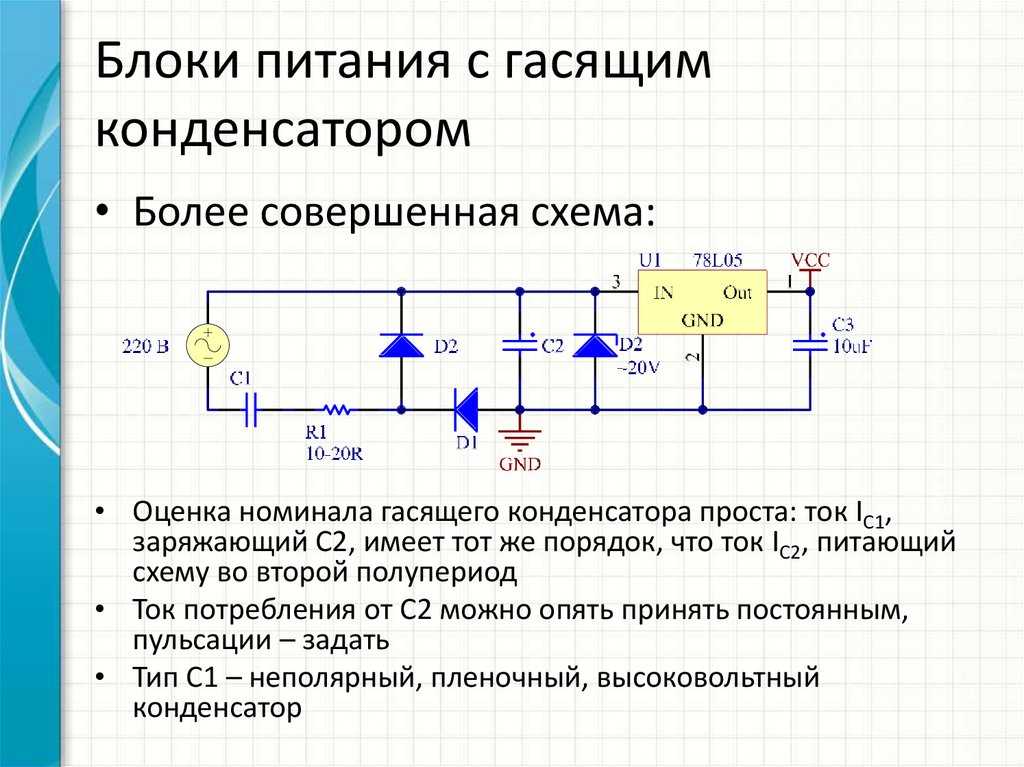
к. пульсации при значительной емкости фильтра станут незначительными.
При напряжении на конденсаторе меньше некоторого значения мост закроется, а если выше — ток пойдет, но напряжение на выходе моста не увеличится. Рассмотрим процесс подробнее с графиками:
В момент времени t1 напряжение сети достигло амплитуды, конденсатор С1 в этот момент также заряжается до максимально возможного значения за вычетом падения напряжения на мосту, которое будет примерно равно выходному Напряжение. Ток через конденсатор С1 в этот момент равен нулю. Далее напряжение в сети стало уменьшаться, напряжение на мосту тоже, но на конденсаторе С1 оно еще не изменилось, и ток через конденсатор С1 по-прежнему равен нулю.
Далее напряжение на мосту меняет знак, стремясь упасть до минус Uвх, и в этот момент ток мчится через конденсатор С1 и через диодный мост. Далее напряжение на выходе моста не меняется, а ток в последовательной цепи зависит от скорости изменения напряжения питания, как если бы к сети был подключен только конденсатор С1.
Когда синусоида сети достигает противоположной амплитуды, ток через С1 снова становится равным нулю и процесс идет по кругу, повторяясь каждые полпериода. Очевидно, что ток через диодный мост течет только в промежутке между t2 и t3, и среднее значение тока можно рассчитать, определив площадь закрашенной фигуры под синусоидой, которая будет равна:
Если выходное напряжение схемы достаточно мало, то эта формула приближается к значению, полученному ранее. Если выходной ток установить равным нулю, то получим:
То есть при обрыве нагрузки выходное напряжение станет равным напряжению сети!!! Поэтому в схеме следует использовать такие компоненты, чтобы каждый из них выдерживал амплитуду питающего напряжения.
Кстати, при уменьшении тока нагрузки на 10% выражение в скобках уменьшится на 10%, то есть выходное напряжение увеличится примерно на 30 вольт, если изначально иметь дело, скажем, с 220 вольтами при на входе и 10 вольт на выходе. Таким образом, использование стабилитрона параллельно нагрузке строго необходимо!!!
А если выпрямитель однополупериодный? Тогда ток необходимо рассчитать по следующей формуле:
При малых значениях выходного напряжения ток нагрузки станет вдвое меньше, чем при выпрямлении полным мостом.
А напряжение на выходе без нагрузки будет в два раза больше, так как здесь мы имеем дело с удвоителем напряжения.
Итак, блок питания с гасящим конденсатором рассчитывается в следующем порядке:
Прежде всего, выберите, каким будет выходное напряжение.
Затем определите максимальный и минимальный токи нагрузки.
Далее определите максимальное и минимальное напряжение питания.
Если предполагается, что ток нагрузки нестабилен, необходим стабилитрон параллельно нагрузке!
Наконец, вычисляется емкость гасящего конденсатора.
Для схемы с однополупериодным выпрямлением, для частоты сети 50 Гц емкость находится по следующей формуле:
Полученный по формуле результат округляют в сторону большей номинальной емкости (желательно не более 10%).
Следующим шагом является нахождение тока стабилизации стабилитрона при максимальном напряжении питания и минимальном токе потребления:
Для однополупериодной схемы выпрямления гасящий конденсатор и максимальный ток стабилитрона рассчитываются по следующим формулам:
При выборе гасящего конденсатора лучше ориентироваться на пленочные и бумажные конденсаторы.
Пленочные конденсаторы небольшой емкости — до 2,2 мкФ на рабочее напряжение 250 вольт хорошо работают в этих схемах при питании от сети 220 вольт. Если вам нужна большая емкость (более 10 мкФ) — лучше выбрать конденсатор на рабочее напряжение 500 вольт.
Калькулятор емкостного реактивного сопротивления
Автор Wojciech Sas, PhD
Отзыв Стивена Вудинга
Последнее обновление: 13 февраля 2023 г.
Содержание:- Что такое емкостное реактивное сопротивление?
- Как рассчитать емкостное сопротивление? Формула емкостного сопротивления
- Как пользоваться калькулятором емкостного сопротивления?
Это калькулятор емкостного реактивного сопротивления — отличный инструмент, который поможет вам оценить так называемое сопротивление конденсатора в электрической цепи. Вы можете найти формула емкостного реактивного сопротивления в тексте ниже, и мы объясним, почему реактивное сопротивление возникает для переменного тока, а не для постоянного тока.
Если вы ищете формулу для расчета емкости, воспользуйтесь нашим калькулятором емкости, но если вы хотите узнать, как рассчитать реактивную емкость, вы попали в нужное место – вперед!
Что такое емкостное сопротивление?
Реактивное сопротивление — это свойство элемента электрической цепи противодействовать протеканию тока . Используя это определение, мы можем сказать, что емкостное сопротивление подобно сопротивлению конденсатора . Даже единица измерения реактивного сопротивления такая же, как и сопротивление — Ом ( Ом ). Обычно мы обозначаем реактивное сопротивление как 90 108 X 90 109 .
Хотя реактивное сопротивление ( X ) и сопротивление ( R ) имеют тенденцию быть одним и тем же в цепи, между ними есть определенное различие. Реактивное сопротивление влияет на переменный ток (AC), а сопротивление влияет на постоянный ток (DC) . В общем случае они являются составляющими импеданса Z , комплексной величины, определяющей полное сопротивление цепи протеканию тока: 1 — мнимое число (квадратный корень из отрицательного числа).
Емкостное реактивное сопротивление является свойством конденсатора . Точно так же индуктивное сопротивление является свойством катушки индуктивности — проверьте калькулятор индуктивного сопротивления для более подробного объяснения и формул. Идеальный резистор имеет нулевое реактивное сопротивление, хотя это чисто резистивный элемент. Наоборот, 9Совершенные конденсаторы 0096 и катушки индуктивности имеют нулевое сопротивление .
Итак, строго говоря, сопротивления конденсатора не существует. Обычно мы относимся к этой фразе как к мысленному сокращению емкостного реактивного сопротивления.
Как рассчитать емкостное реактивное сопротивление? Формула емкостного реактивного сопротивления
Как мы упоминали в предыдущем разделе, емкостное реактивное сопротивление — это свойство конденсатора, противодействующее переменному току. То же самое верно для любого набора конденсаторов, которые мы можем расположить последовательно или параллельно.
Одним из важнейших свойств переменного тока является его частота f . Мы можем вычислить емкостное реактивное сопротивление X конденсатора C , используя следующее уравнение:
X = 1 / (2 × π × f × C) .
В качестве альтернативы мы можем записать формулу емкостного реактивного сопротивления как:
X = 1 / (ω × C) ,
, где ω = 2 × π × f — угловая частота тока.
🙋 Вы всегда можете узнать емкость, проверив код конденсатора и воспользовавшись калькулятором конденсатора Omni.
Как видите, чем выше частота емкости, тем ниже реактивное сопротивление . Имеет ли это смысл?
Абсолютно! Помните, что конденсатор хранит электрическую энергию. Во время зарядки похоже, что конденсатор почти свободно пропускает ток. Чем больше он может поглощать (чем выше емкость), тем меньше он сопротивляется пропусканию тока. Кроме того, когда частота переменного тока становится выше, конденсатору требуется меньше времени для полной зарядки.
В случае постоянного тока ( f = 0 ), конденсатор сначала заряжается, но затем (в равновесном состоянии) действует как разомкнутая цепь.
Как пользоваться калькулятором емкостного сопротивления?
Нет ничего сложного в оценке емкостного реактивного сопротивления любого конденсатора. Попрактикуемся в вычислениях на примере.
Допустим, у нас есть схема со сферическим конденсатором емкостью Кл = 30 нФ . Подаем источник напряжения, чередующийся с частотой f = 60 Гц . Чему равно емкостное сопротивление этой цепи?
Перевести единицы измерения емкости в фарады. Мы можем использовать экспоненциальную запись, чтобы компактно записать значения:
С = 30 нФ = 3×10⁻⁸ Ф .
Вычислите произведение всех значений в знаменателе из формулы емкостного реактивного сопротивления:
2 × π × f × C знак равно 2 × π × 60 × 3×10⁻⁸ = 1,131×10⁻⁵ .
