Индуктивное сопротивление формула. Индуктивное сопротивление: формула, расчет и примеры

Что такое индуктивное сопротивление. Как рассчитать индуктивное сопротивление катушки. Какова зависимость индуктивного сопротивления от частоты тока. Чем отличается индуктивное сопротивление от активного.

Что такое индуктивное сопротивление

Индуктивное сопротивление — это параметр, характеризующий противодействие катушки индуктивности прохождению переменного электрического тока. В отличие от активного сопротивления, индуктивное сопротивление не вызывает потерь электрической энергии, а лишь создает сдвиг фаз между током и напряжением.

Индуктивное сопротивление обозначается X_L и измеряется в омах (Ом). Оно зависит от индуктивности катушки L и частоты переменного тока f.

Формула индуктивного сопротивления

Формула для расчета индуктивного сопротивления:

X_L = ωL = 2πfL

где:

• X_L — индуктивное сопротивление, Ом
• ω — угловая частота, рад/с
• f — частота переменного тока, Гц
• L — индуктивность катушки, Гн

Зависимость индуктивного сопротивления от частоты

Из формулы видно, что индуктивное сопротивление прямо пропорционально частоте переменного тока. При увеличении частоты индуктивное сопротивление возрастает.

Это объясняется тем, что при более высокой частоте скорость изменения тока больше, а значит, в катушке индуктивности возникает большая ЭДС самоиндукции, препятствующая изменению тока.

Расчет индуктивного сопротивления

Рассмотрим пример расчета индуктивного сопротивления катушки.

Дано: L = 0,1 Гн f = 50 Гц

Решение: X_L = 2πfL = 2 * 3,14 * 50 * 0,1 = 31,4 Ом

Таким образом, индуктивное сопротивление данной катушки при частоте 50 Гц составляет 31,4 Ом.

Отличие индуктивного сопротивления от активного

Основные отличия индуктивного сопротивления от активного:

• Индуктивное сопротивление не вызывает потерь энергии, а лишь создает сдвиг фаз между током и напряжением
• Индуктивное сопротивление зависит от частоты тока, а активное — нет
• На постоянном токе индуктивное сопротивление равно нулю
• Индуктивное сопротивление измеряется в реактивных омах, а не в обычных

Применение индуктивного сопротивления

Знание индуктивного сопротивления необходимо при:

• Расчете электрических цепей переменного тока
• Проектировании фильтров, дросселей, трансформаторов
• Согласовании нагрузок в радиотехнике
• Компенсации реактивной мощности

Таким образом, индуктивное сопротивление играет важную роль во многих областях электротехники и электроники, связанных с переменным током.

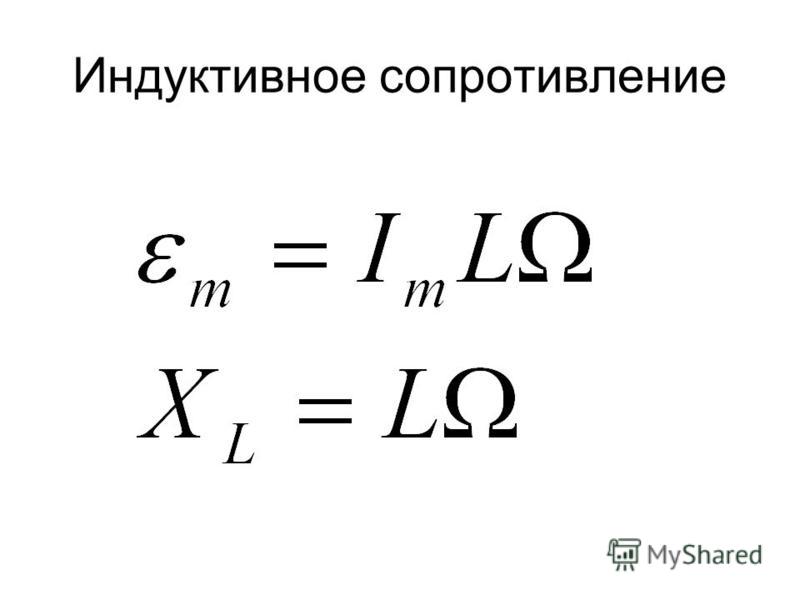
Вопросы по индуктивному сопротивлению

От чего зависит индуктивное сопротивление катушки?

Индуктивное сопротивление катушки зависит от двух основных параметров:

1. Индуктивности катушки L. Чем больше индуктивность, тем выше индуктивное сопротивление.
2. Частоты переменного тока f. При увеличении частоты индуктивное сопротивление возрастает.

Эта зависимость отражена в формуле индуктивного сопротивления: X_L = 2πfL

Как изменится индуктивное сопротивление при увеличении частоты в 2 раза?

При увеличении частоты в 2 раза индуктивное сопротивление также увеличится в 2 раза. Это следует из прямой пропорциональной зависимости X_L от f в формуле X_L = 2πfL.

Например, если при частоте 50 Гц индуктивное сопротивление составляло 100 Ом, то при увеличении частоты до 100 Гц оно станет равным 200 Ом.

Чему равно индуктивное сопротивление на постоянном токе?

На постоянном токе индуктивное сопротивление равно нулю. Это объясняется тем, что:

• Частота постоянного тока f = 0
• Подставляя f = 0 в формулу X_L = 2πfL, получаем X_L = 0

Таким образом, на постоянном токе катушка индуктивности ведет себя как простой проводник с очень малым активным сопротивлением.

Практическое применение индуктивного сопротивления

Понимание концепции индуктивного сопротивления важно для многих практических применений в электротехнике и электронике:

1. Фильтрация сигналов

Катушки индуктивности часто используются в фильтрах для подавления высокочастотных составляющих сигнала. С ростом частоты индуктивное сопротивление увеличивается, что позволяет эффективно блокировать высокие частоты.

2. Компенсация реактивной мощности

В электроэнергетике индуктивное сопротивление играет важную роль при компенсации реактивной мощности. Используя катушки индуктивности, можно снизить реактивную составляющую тока в сети.

3. Импедансное согласование

В радиотехнике индуктивное сопротивление используется для согласования импедансов различных участков схемы, что позволяет минимизировать потери и улучшить передачу сигнала.

4. Электромагнитные реле

Принцип работы электромагнитных реле основан на индуктивном сопротивлении катушки. При подаче переменного напряжения индуктивное сопротивление ограничивает ток через катушку.

Заключение

Индуктивное сопротивление является важным параметром в электрических цепях переменного тока. Оно характеризует способность катушки индуктивности противодействовать изменениям тока. Основные особенности индуктивного сопротивления:

• Зависит от индуктивности катушки и частоты тока
• Не вызывает потерь энергии
• Создает сдвиг фаз между током и напряжением
• Равно нулю на постоянном токе

Понимание индуктивного сопротивления необходимо для расчета и проектирования различных электротехнических устройств и систем.

Индуктивное сопротивление: обозначение, формула сопротивления катушки

Когда в цепи присутствует катушка, ее отклик увеличивается с ростом частоты.

Когда к катушке прикладывается переменное напряжение, ток, протекающий через катушку, изменяется в зависимости от приложенного напряжения. Это вызывает изменение магнитного поля, которое создает электродвижущую силу.

Диаграмма измерений

В такой цепи существует два типа электрической зависимости: обычная и индуктивная. Они обозначаются R и XL соответственно.

К обычным относится производство электроэнергии. Однако на реактивных элементах он равен нулю. Это происходит из-за постоянного изменения направления переменного тока.

За один период колебаний энергия дважды закачивается в катушку и столько же раз возвращается к источнику.

Определение индуктивности

Еще одно применение электромагнитов в быту – индукционные плиты. Катушка индуцирует высокочастотный переменный ток в металлическом поддоне. Это, в свою очередь, нагревает кастрюлю за счет теплового воздействия. В промышленности нечто подобное используется для нагрева и плавления металлов. Только в этом случае используются на порядки более высокие мощности и другие частоты тока.

Содержание

Формулы, соотношения и виды индуктивности

Электрическая индуктивность L – это величина, равная отношению тока I, протекающего в замкнутом контуре, к создаваемому им магнитному потоку, иначе называемому током обмотки катушки Y:

Если к клеммам катушки на некоторое время приложить напряжение, в катушке потечет ток I и возникнет магнитное поле. Чем меньше индуктивность L, тем быстрее происходит этот процесс. В результате рассматриваемый биполяр будет накапливать некоторую потенциальную энергию. При отключении электричества он, как правило, выдает себя. В результате на выводах катушки возникает самоиндуцированная ЭДС E, во много раз превышающая первоначально приложенное напряжение. Подобная технология ранее использовалась в магнето зажигания в двигателях внутреннего сгорания, а теперь широко применяется в повышающих DC-DC преобразователях.

Катушка (также известная как дроссель) является радиоэлементом с ярко выраженной индуктивностью – она была разработана именно для этой цели. Однако практически все элементы обладают этим свойством. Например, конденсатор, резистор, кабель, кусок провода и даже человеческое тело также обладают определенной индуктивностью. Это необходимо учитывать при расчете ВЧ цепей.

Важно! При измерении индуктивности с помощью специализированного измерительного прибора стоит помнить, что нельзя держать оба провода руками. В противном случае показания могут измениться и быть неверными. Это связано с включением человеческого тела с его собственной индуктивностью в измеряемую цепь.

Рассчитайте индуктивность катушки для заданной частоты по формуле

сопротивление индуктивности катушки

Поскольку индуктивность препятствует быстрому изменению тока в цепи, она представляет собой особый тип сопротивления для переменного тока, называемый чистое индуктивное сопротивление.

Чисто индуктивное сопротивление отличается от обычного (омического) сопротивления тем, что при протекании через него переменного тока не происходит потери энергии.

На странице чистое индуктивное сопротивление мы понимаем сопротивление переменному току через катушку, проводник которой вообще не имеет омического сопротивления. Фактически, каждая катушка имеет некоторое омическое сопротивление. Однако, если это сопротивление мало по сравнению с индуктивным сопротивлением, им можно пренебречь.

Наблюдается следующее явление: в одну четверть периода, когда ток увеличивается, магнитное поле забирает энергию из контура, а в следующую четверть периода, когда ток уменьшается, оно отдает энергию обратно в контур. Поэтому в среднем периоде в индуктивном резисторе не рассеивается мощность. Именно поэтому индуктивное сопротивление называется реактивным сопротивлением (ранее неправильно называлось безваттным сопротивлением).

Индуктивное сопротивление одной и той же катушки будет разным для токов разной частоты. Чем выше частота переменного тока, тем большую роль играет индуктивность и тем больше будет индуктивное сопротивление данной катушки. И наоборот, чем ниже частота тока, тем меньше индуктивность катушки. При частоте, равной нулю (установившийся постоянный ток), индуктивное сопротивление также равно нулю.

Рисунок 1. Зависимость индуктивного сопротивления катушки от частоты переменного тока. Реактивное сопротивление катушки увеличивается с ростом частоты тока.

Индуктивное сопротивление обозначается как X_L и измеряется в омах.

Рассчитайте индуктивное сопротивление катушки для переменного тока заданной частоты по формуле

X_L=2π- f -L

где X_L – индуктивность в омах; f – частота переменного тока в гц; L – индуктивность катушки в гн

Известно, что 2π- f называется круговой частотой и обозначается буквой ω (омега). Таким образом, приведенная выше формула может быть представлена следующим образом:

Из этого следует, что для постоянного тока (ω = 0) индуктивное сопротивление равно нулю. Поэтому, когда необходимо пропустить постоянный ток через цепь с одновременной задержкой переменного тока, в цепь последовательно включается индукционная катушка.

Для того чтобы преградить путь токам с низкими звуковыми частотами, вставляются катушки с железным сердечником, так называемый “железный сердечник”. низкочастотные дроссели, а для более высоких радиочастот – катушки без железного сердечника, которые называются высокочастотными дросселями.

ПОНРАВИЛАСЬ ЛИ ВАМ ЭТА СТАТЬЯ? ПОДЕЛИТЕСЬ ИМ СО СВОИМИ ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!

Циклическая частота может быть определена выражением

Чтобы получить доступ к этому и другим видеоурокам набора, добавьте его в свой личный кабинет, купив в каталоге.

Получите удивительные возможности

Конспект урока “Емкостное сопротивление.

Индуктивное сопротивление”

Физика – что такое емкость – слово,

Физика для нас не просто звук,

Физика является основой и фундаментом

Всех наук без исключения!

Проблема 1. В цепи переменного тока с частотой 50 Гц при напряжении 220 В возникает ток силой 4 А. Известно, что эта цепь содержит катушку с пренебрежимо малым активным сопротивлением. Какова индуктивность этой катушки?

Индуктивное сопротивление задается формулой

Циклическая частота может быть рассчитана с помощью выражения

Запишите закон Ома для участка цепи

Приравняйте две последние формулы для расчета индуктивного сопротивления и выразите индуктивность катушки

Ответ175 MH.

Проблема 2. . После увеличения частоты с 50 до 60 Гц емкость фиксированного конденсатора уменьшилась на 10 Ом. Найдите емкость конденсатора.

Емкость задается формулой

Циклическая частота может быть определена выражением

Тогда емкостное сопротивление

Давайте применим эту формулу к двум значениям частоты

Изменение емкости конденсатора дается следующим образом

Тогда емкость конденсатора

Ответ53 мкФ.

Проблема 3. Известно, что через катушку, подключенную к цепи переменного тока с частотой 200 Гц, протекает ток не более 3 А. Найдите напряжение на катушке в момент времени t = 0,2 мс, если он максимален в начале. Индуктивность катушки равна 5 мГн.

Это следует из закона Ома для данного участка цепи

Индуктивная реактивность задается формулой

Напряжение от пика до пика рассчитывается по формуле

Запишем уравнение гармонического напряжения

Циклическая частота составляет

Тогда уравнение гармонического напряжения будет выглядеть следующим образом

Затем в момент t = 0,2 мс напряжение будет равно

Ответ следующий: 18,3 В.

Проблема 4. Докажите, что если частота переменного тока равна собственной частоте колебаний, то через индуктор и конденсатор будет протекать одинаковый ток, а к индуктору и конденсатору будет приложено одинаковое напряжение.

Собственная циклическая частота в колебательном контуре равна

По определению, собственная частота – это частота свободных колебаний (т.е. колебаний в отсутствие активного сопротивления).

Поэтому возможны два случая: либо катушка и конденсатор соединены параллельно, либо они соединены последовательно. Активного сопротивления нет.

Из приведенного выше уравнения следует, что амплитуда напряжения U_m = ωLI_m. Сравнивая это выражение с законом Ома U_m = RI_mмы видим, что величина ωL играет роль сопротивления.

Индуктивное сопротивление

Индуктивность L в электрической цепи вызывает задержку тока (см. самоиндукция). В результате ток достигает своего максимального значения I_m позже, чем напряжение. Если R = 0, то приложенное напряжение противоположно индуцированному:

Между напряжением и током существует разность фаз (сдвиг фаз) +π/2.

В цепи переменного тока, содержащей только индуктивность, напряжение проводит ток на π/2 (или T/4).

Из приведенного выше уравнения следует, что амплитуда напряжения U_m = ωLI_m. Сравнивая это выражение с законом Ома U_m = RI_mмы видим, что величина ωL играет роль сопротивления.

Цепь переменного тока, содержащая индуктивность L, имеет сопротивление переменному току; это называется индуктивное сопротивление X_L.

Единица СИ индуктивного сопротивления: [X_L] = Ом.

XL	индуктивное сопротивление цепи переменного тока,	Ом
L	индуктивность контура,	Генри
ω = 2πf	круговая частота переменного тока,	Радиан/секунда

Индуктивная реактивность X_L Для постоянного тока (f = 0) этот показатель равен нулю.

Если цепь имеет только индуктивное сопротивление, то ток задается выражением

Емкостные токи оказывают значительное влияние на работу линий напряжением 110 кВ и выше, а также в сильноточных линиях, проложенных идентичными проводниками выше 10 кВ.

Емкостная проводимость

Одним из показателей эффективности остается этот параметр, определяющий емкость между проводниками и землей и аналогичный параметр между самими проводниками.

Для его определения в трехфазной воздушной линии используется выражение:

Наблюдается прямая зависимость между рабочей емкостью и уменьшением расстояния между кабелями и их сечением. Поэтому для линий низкого напряжения это значение всегда будет выше, чем для линий высокого напряжения.

Проводимость этого типа в воздушных линиях одноцепной конструкции рассчитывается следующим образом: Емкостные токи оказывают существенное влияние на работу линий с пакетными характеристиками рабочего напряжения 110 кВ и выше, а также в магистральных линиях, проложенных идентичными проводами выше 10 кВ.

Попытка применить этот конкретный метод для отдельного применения была бы очень сложной задачей, поскольку в этом случае возникают различные конструктивные нюансы, такие как геометрические характеристики, диэлектрическая проницаемость изоляционного слоя и многие другие факторы. Поэтому лучшим решением является информация, содержащаяся в таблицах, разработанных производителями для данной марки кабеля. В каталогах все данные приводятся с учетом номинального напряжения для каждой модификации.

В начале линии, когда речь идет о токе холостого хода, емкостной ток определяется следующим образом:

Это значение является объективным только при полном отключении потребителей электроэнергии от напряжения.

Указанная емкость в любой рассматриваемой конструкции имеет большое значение для точного выполнения предварительных расчетов для устройств компонентов защиты и заземляющих элементов.

Для воздушных линий применяется следующая формула:

Для кабельных сетей:

Читайте далее:

• Урок 7 Свободные и вынужденные электромагнитные колебания. колебательный контур – физика – 11 класс – Русская электронная школа.
• Лекции по ТЭ – #27 Явление резонанса в электрических цепях.
• Механические колебания и волны; FIZI4KA.
• Форум RadioCat; Просмотр темы – Измерение индуктивности простыми методами.
• Полное сопротивление цепи переменного тока – Основы электроники.
• 1 Понятие электромагнитного поля и его различные проявления. Материальность – Работа в школе.
• Урок 28 Электрическая емкость. Конденсатор – Физика – 10 класс – Российская электронная школа.

5.7. Активное и внутреннее индуктивное сопротивление проводов

Активное и внутреннее индуктивное сопротивление проводников можно определить с помощью теоремы Умова – Пойнтинга в комплексной форме.

Перед тем, как записать теорему Умова – Пойнтинга 4.8) в комплексной форме, рассмотрим вопрос о полной мощности в цепи синусоидального тока. Полная мощность

Здесь – сопряженное значение комплекса тока .

Пусть цепь синусоидального тока содержит последовательно соединенные активные сопротивления R, индуктивность L и емкость С.

Тогда реактивная мощность

Здесь и где U_c – напряжение на конденсаторе.

Таким образом, реактивная мощность Q равна разности между магнитной W_М и электрической W_Э энергиями цепи, умноженной на 2w.

Введем также в рассмотрение комплексный вектор Пойнтинга

Последнее выражение отличается от мгновенного значения вектора Пойнтинга тем, что здесь комплексная величина вектора напряженности электрического поля умножается на сопряженное значение вектора напряженности магнитного поля.

С учетом этого, теорему Умова – Пойнтинга (4.8) можно переписать в следующем виде:

Первое слагаемое правой части данного выражения представляет собой активную мощность, второе – реактивную. Таким образом, теорему Умова – Пойнтинга можно записать еще следующим образом:

В таком виде ее и используют для определения активного и внутреннего индуктивного сопротивления проводников на переменном токе. С этой целью подсчитывают поток вектора Пойнтинга через боковую поверхность проводника на необходимой длине (например, 1 м) и делят его на квадрат тока, протекающего по проводнику, в результате чего и получают комплексное сопротивление проводника на этой длине

В качестве примера определим активное и внутреннее индуктивное сопротивление цилиндрического провода (см. рис. 5.11) на длине l:

(5.14)

Здесь d – радиус ( новое обозначение введено, чтобы отличать от сопротивления) проводника; и — комплексная амплитуда напряженности электрического поля и сопряженное значение комплексной амплитуды напряженности магнитного поля на поверхности проводника.

Используя формулу

а также выражения (5.11), (5.12) и (5.13), преобразуем уравнение (5.14) к следующему виду:

Если рассчитать сопротивление данного провода на длине l постоянному току, то оно будет равно 1.273?10^-3l. Таким образом,

Отсюда видно, что активное сопротивление провода почти в четыре раза превышает сопротивление провода постоянному току.

Отметим, что если поле обладает цилиндрической симметрией, как в случае прямолинейного одиночного провода (обратный провод находится достаточно далеко) или в случае прямолинейного цилиндрического кабеля, то выражение для определения активного и внутреннего индуктивного сопротивления провода можно получить и иным путем

.

(5.15)

Здесь — комплексное значение падения напряжения на длине l провода.

Формула (5.15) просто получается и из выражения (5.14), если в нем заменить квадрат тока его значением, определенным с помощью закона полного тока

23.2: Реактивное, индуктивное и емкостное сопротивление

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

2717

• OpenStax
• OpenStax

Цели обучения

К концу этого раздела вы сможете:

• Зарисовывать зависимость напряжения и тока от времени в простых индуктивных, емкостных и резистивных цепях.
• Рассчитать индуктивное и емкостное сопротивление.
• Расчет тока и/или напряжения в простых индуктивных, емкостных и резистивных цепях.

Многие схемы также содержат конденсаторы и катушки индуктивности в дополнение к резисторам и источнику переменного напряжения. Мы видели, как конденсаторы и катушки индуктивности реагируют на постоянное напряжение при его включении и выключении. Теперь мы рассмотрим, как катушки индуктивности и конденсаторы реагируют на синусоидальное переменное напряжение.

Катушки индуктивности и индуктивное реактивное сопротивление

Предположим, что катушка индуктивности подключена непосредственно к источнику переменного напряжения, как показано на рисунке. Разумно предположить пренебрежимо малое сопротивление, так как на практике мы можем сделать сопротивление катушки индуктивности настолько малым, что оно окажет незначительное влияние на цепь. Также показан график зависимости напряжения и тока от времени.

Рисунок \(\PageIndex{1}\): (a) Источник переменного напряжения последовательно соединен с катушкой индуктивности, сопротивление которой пренебрежимо мало. (б) График тока и напряжения на катушке индуктивности в зависимости от времени.

График на рисунке (b) начинается с максимального напряжения. Обратите внимание, что ток начинается с нуля и достигает своего пика 90 050 после 90 051 напряжения, управляющего им, точно так же, как это было в случае, когда напряжение постоянного тока было включено в предыдущем разделе. Когда напряжение в точке а становится отрицательным, ток начинает уменьшаться; он становится равным нулю в точке b, где напряжение является самым отрицательным. Затем ток становится отрицательным, снова следуя за напряжением. Напряжение становится положительным в точке с и начинает делать ток менее отрицательным. В точке d ток проходит через нуль как раз в тот момент, когда напряжение достигает своего положительного пика, чтобы начать новый цикл. Это поведение резюмируется следующим образом: 9о\) фазовый угол.

Ток отстает от напряжения, так как катушки индуктивности препятствуют изменению тока. Изменение тока индуцирует противо-ЭДС \(V = -L(\Delta I/\Delta t)\). Это считается эффективным сопротивлением катушки индуктивности переменному току. Действующее значение тока \(I\) через катушку индуктивности \(L\) определяется версией закона Ома: vo

\[I = \dfrac{V}{X_L},\], где \(V\) равно среднеквадратичное напряжение на катушке индуктивности и \(X_L\) определяется как \[X_L = 2\pi fL,\] с \(f\) частотой источника переменного напряжения в герцах (анализ схемы с использованием метода Кирхгофа). правило цикла и исчисление фактически производят это выражение). \(X_L\) называется индуктивным реактивным сопротивлением, потому что индуктор реагирует, препятствуя току. \(X_L\) имеет единицы измерения в омах (\(1 \, H = 1 \, \Omega \cdot s\), так что частота, умноженная на индуктивность, имеет единицы (циклы/с)\((\Omega \cdot s) = \Омега\)), в соответствии с его ролью эффективного сопротивления. Имеет смысл, что \(X_L\) пропорциональна \(L\), поскольку чем больше индукция, тем больше ее сопротивление изменению. Также разумно, что \(X_L\) пропорциональна частоте \(f\), поскольку большая частота означает большее изменение тока. То есть \(\Delta I/\Delta t\) велико для больших частот (больших \(f\), малых \(\Delta t\)). Чем больше изменение, тем больше сопротивление индуктора.

Пример \(\PageIndex{1}\): расчет индуктивного сопротивления, а затем тока

(a) Рассчитайте индуктивное сопротивление катушки индуктивности 3,00 мГн при подаче переменного напряжения частотой 60,0 Гц и 10,0 кГц. б) Чему равно среднеквадратичное значение тока на каждой частоте, если приложенное среднеквадратичное напряжение равно 120 В?

Стратегия

Индуктивное сопротивление находится непосредственно из выражения \(X_L = 2\pi fL\). Как только \(X_L\) найдено на каждой частоте, можно использовать закон Ома, как указано в уравнении \(I = V/X_L\), чтобы найти ток на каждой частоте. 94/с)(3,00 мкГн) = 188 л, \Омега \, при \, 10 мкГц.\]

Решение задачи (б) закона в уравнении \(I = V/X_L\), при условии, что приложенное среднеквадратичное напряжение равно 120 В. Для первой частоты это дает

\[I = \dfrac{V}{X_L} = \dfrac{120 \, V}{1,13 \, \Omega} = 106 \, A \, при \, 60 \, Гц. \]

Аналогично, при 10 кГц,

\[I = \dfrac{V}{X_L} = \ dfrac{120 \, V}{188 \, \Omega} = 0,637 \, A \, at \, 10 \, кГц.\]

Обсуждение

Катушка индуктивности очень по-разному реагирует на двух разных частотах. На более высокой частоте его реактивное сопротивление велико, а ток мал, что соответствует тому, как индуктор препятствует быстрому изменению. Таким образом, высокие частоты препятствуют больше всего. Индукторы можно использовать для фильтрации высоких частот; например, большой индуктор можно включить последовательно с системой воспроизведения звука или последовательно с вашим домашним компьютером, чтобы уменьшить высокочастотный звук, выходящий из ваших динамиков, или высокочастотные скачки мощности в вашем компьютере.

Обратите внимание, что хотя сопротивление в рассматриваемой цепи незначительно, переменный ток не очень велик, поскольку индуктивное сопротивление препятствует его протеканию. При переменном токе нет времени для того, чтобы ток стал чрезвычайно большим.

Конденсаторы и емкостное реактивное сопротивление

Рассмотрим конденсатор, подключенный непосредственно к источнику переменного напряжения, как показано на рисунке. Сопротивление такой цепи можно сделать настолько малым, что оно оказывает незначительное влияние по сравнению с конденсатором, и поэтому мы можем предположить пренебрежимо малое сопротивление. Напряжение на конденсаторе и ток представлены на рисунке как функции времени.

Рисунок \(\PageIndex{2}\): (a) Источник переменного напряжения последовательно соединен с конденсатором C, имеющим незначительное сопротивление. (б) График тока и напряжения на конденсаторе в зависимости от времени.

График на рисунке начинается с максимального напряжения на конденсаторе. В этот момент ток равен нулю, потому что конденсатор полностью заряжен и останавливает поток. Затем напряжение падает, а ток становится отрицательным по мере разряда конденсатора. В точке а конденсатор полностью разряжен (на нем \(Q = 0\)) и напряжение на нем равно нулю. Ток между точками a и b остается отрицательным, что приводит к изменению напряжения на конденсаторе. Это завершается в точке b, где ток равен нулю, а напряжение имеет самое отрицательное значение. Ток становится положительным после точки b, нейтрализуя заряд конденсатора и сводя напряжение к нулю в точке c, что позволяет току достигать своего максимума. Между точками c и d ток падает до нуля, когда напряжение достигает своего пика, и процесс начинает повторяться. На протяжении всего цикла напряжение следует за током на одну четвертую цикла:

Напряжение переменного тока в конденсаторе

Когда к конденсатору прикладывается синусоидальное напряжение, напряжение следует за током на одну четвертую периода или на фазовый угол.

Конденсатор влияет на ток, имея возможность полностью остановить его при полной зарядке. Поскольку применяется переменное напряжение, существует среднеквадратичное значение тока, но оно ограничено конденсатором. Это считается эффективным сопротивлением конденсатора переменному току, поэтому среднеквадратичное значение тока в цепи, содержащей только конденсатор \(I\), согласно другой версии закона Ома, равно

\[I = \dfrac{V}{X_C},\], где \(V\) — среднеквадратичное значение напряжения, а \(X_C\) определяется (как и в случае \(X_L\), это выражение для \(X_C \) получается в результате анализа схемы с использованием правил и исчисления Кирхгофа) как

\[X_C = \dfrac{1}{2\pi fC},\], где \(X_C\) называется емкостным сопротивлением, потому что конденсатор реагирует на сопротивление току. \(X_C\) измеряется в омах (проверка оставлена ​​читателю в качестве упражнения). \(X_C\) обратно пропорциональна емкости \(C\), чем больше конденсатор, тем больший заряд он может хранить и тем больший ток может протекать. Он также обратно пропорционален частоте \(f\), чем больше частота, тем меньше времени остается для полной зарядки конденсатора, и поэтому он меньше препятствует току.

Пример \(\PageIndex{2}\): расчет емкостного реактивного сопротивления, а затем тока

(a) Рассчитайте емкостное реактивное сопротивление конденсатора емкостью 5,00 мФ при подаче переменного напряжения частотой 60,0 Гц и 10,0 кГц. б) Чему равно среднеквадратичное значение тока, если приложенное среднеквадратичное напряжение равно 120 В?

Стратегия

Емкостное реактивное сопротивление находится непосредственно из выражения \(X_C = \frac{1}{2\pi fC}\). Как только \(X_C\) найдено на каждой частоте, закон Ома формулируется как \(I = V/X_C\) 94/с)(5,00 мкФ)}. \]

\[= 3,18 мк, \Омега \, при \, 10 мкГц\]

Решение для (б)

Среднеквадратичное значение ток теперь находится с использованием версии закона Ома в \(I = V/X_C\), учитывая приложенное среднеквадратичное напряжение 120 В. Для первой частоты это дает

\[I = \dfrac{V}{X_C } = \dfrac{120 \, V}{531 \, \Omega} = 0,226 \, A \, при \, 60 \, Гц.\]

Аналогично, при 10 кГц,

\[I = \dfrac {V}{X_C} = \dfrac{120 \, V}{3,18 \, \Omega} = 37,7 \, A \, at \, 10 \, кГц.\]

Обсуждение

Конденсатор очень по-разному реагирует на двух разных частотах, и совершенно противоположным образом реагирует индуктор. На более высокой частоте его реактивное сопротивление мало, а ток велик. Конденсаторы способствуют изменениям, тогда как индукторы сопротивляются изменениям. Конденсаторы больше всего препятствуют низким частотам, поскольку низкая частота дает им время зарядиться и остановить ток. Конденсаторы можно использовать для фильтрации низких частот. Например, конденсатор, включенный последовательно со звуковоспроизводящей системой, избавляет ее от гула частотой 60 Гц.

Хотя конденсатор в основном представляет собой разомкнутую цепь, в цепи с переменным напряжением, приложенным к конденсатору, существует среднеквадратичное значение тока. Это связано с тем, что напряжение постоянно меняется, заряжая и разряжая конденсатор. Если частота стремится к нулю (DC), \(X_C\) стремится к бесконечности, а ток равен нулю после зарядки конденсатора. На очень высоких частотах реактивное сопротивление конденсатора стремится к нулю — он имеет пренебрежимо малое реактивное сопротивление и не препятствует протеканию тока (он действует как простой провод). Конденсаторы действуют на цепи переменного тока противоположно действию катушек индуктивности .

Резисторы в цепи переменного тока

В качестве напоминания рассмотрите рисунок, на котором показано напряжение переменного тока, приложенное к резистору, и график зависимости напряжения и тока от времени. Напряжение и ток равны в фазе в резисторе. Поведение простого сопротивления в цепи не зависит от частоты:

Рисунок \(\PageIndex{3}\): (a) Источник переменного напряжения последовательно с резистором. (b) График зависимости тока и напряжения на резисторе от времени, показывающий, что они точно совпадают по фазе. 9о\) фазовый угол.

Противодействие катушки индуктивности изменению тока выражается как вид сопротивления переменному току.

Закон Ома для катушки индуктивности: \[ I = \dfrac{V}{X_L},\], где \(V\) — среднеквадратичное напряжение на катушке индуктивности.

\(X_L\) определяется как индуктивное сопротивление, определяемое как \[X_L = 2\pi fL,\] с \(f\) частотой источника переменного напряжения в герцах.

Индуктивное сопротивление \(X_L\) измеряется в омах и имеет наибольшее значение на высоких частотах. 9о\) фазовый угол.

Поскольку конденсатор может останавливать ток при полной зарядке, он ограничивает ток и предлагает другую форму сопротивления переменному току; Закон Ома для конденсатора: \[I = \dfrac{V}{X_C},\], где \(V\) — среднеквадратичное напряжение на конденсаторе.

\(X_C\) определяется как емкостное реактивное сопротивление, определяемое как \[X_C = \dfrac{1}{2\pi fC}.\]

\(X_C\) измеряется в омах и максимален на низких частотах.

Глоссарий

индуктивное реактивное сопротивление

противодействие катушки индуктивности изменению тока; рассчитывается как \(X_L = 2\pi fL\)

емкостное реактивное сопротивление

сопротивление конденсатора изменению тока; рассчитывается как \(X_C = \frac{1}{2\pi fC}\)

Авторы

Пол Питер Урон (почетный профессор Калифорнийского государственного университета, Сакраменто) и Роджер Хинрихс (Государственный университет Нью-Йорка, Колледж в Освего) с соавторами: Ким Диркс (Оклендский университет) и Манджула Шарма (Сиднейский университет) ). Эта работа находится под лицензией OpenStax University Physics в соответствии с лицензией Creative Commons Attribution License (4. 0).

---

Эта страница под названием 23.2: Reactance, Inductive and Capacitive распространяется под лицензией CC BY 4.0 и была создана, изменена и/или курирована OpenStax с использованием исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.

1. Наверх

• Была ли эта статья полезной?

1. Тип изделия

   Раздел или Страница

   Автор

   ОпенСтакс

   Лицензия

   СС BY

   Версия лицензии

   4,0

   Программа OER или Publisher

   ОпенСтакс

   Показать оглавление

   нет

2. Теги

   1. емкостный
   2. емкостное реактивное сопротивление
   3. Индуктивный
   4. индуктивное сопротивление
   5. Реактивное сопротивление
   6. источник@https://openstax. org/details/books/college-physics

Расчет индуктивного сопротивления

Google Ads

• Изучив этот раздел, вы сможете описать:
• • Расчет индуктивного сопротивления.
• • Многоэтапные расчеты.

Для расчетов, основанных на индуктивном реактивном сопротивлении, вам в первую очередь нужно подумать об информации о реактивном сопротивлении во введении к этому модулю, чтобы узнать о различиях между реактивным сопротивлением и сопротивлением. Для расчетов вы можете выбрать, какую формулу использовать для индуктивного сопротивления, либо 2πƒL, либо ωL, но чаще используется 2πƒL (одна из причин заключается в том, что в научных калькуляторах в основном есть клавиша π, но нет клавиши ω!).

Помните, что некоторые проблемы, которые вам могут понадобиться для решения, не обязательно будут иметь очевидное решение, например, просто вычисление реактивного сопротивления компонента. Например, если вас просят рассчитать напряжение питания, необходимое для получения определенного протекающего тока, или напряжения на компоненте, могут потребоваться два или более шагов, используя ответ из одного расчета, чтобы предоставить информацию для второго расчета, прежде чем достичь окончательный ответ.

Прежде чем начать, подумайте о следующих советах. Они облегчат вам задачу, если вы будете им следовать.

1. Подготовьте ответы с помощью карандаша и бумаги; перерисуйте схему, над которой вы работаете.

2. Перечислите информацию, которую вы получили, и то, что вам нужно найти для ответа. Это поможет вам решить, можно ли найти ответ за один шаг или вам понадобится промежуточный ответ.

3. После того, как вы перечислите информацию на шаге 2 (выше), вам нужно будет решить, какую подходящую формулу (или формулы) использовать. Запишите и это.

4. Конечно, ответ — это не просто число, если вы вычисляете X _L , это будет определенное количество Ом, не забудьте указать правильную единицу измерения (например, Ом, кОм или МОм) или твой ответ бессмыслен.

5. При вводе значений в калькулятор конвертируйте все значения кОм или МОм в омы с помощью клавиши EXP. Если вы ошибетесь здесь, вы получите действительно глупые ответы, в тысячи раз слишком большие или слишком маленькие.

Все эти шаги поначалу кажутся трудоемкими, но привыкните, и они облегчат ваши расчеты, потому что вы будете следовать знакомому методу. Они также будут более надежными, потому что, когда вам нужно выполнить многоэтапные вычисления, вам нужно быть организованным. Так легко ошибиться на полпути к своей работе, потому что вы забыли, где именно вы находитесь в расчетах. Однако, если вы записали каждую проблему, это позволит вам вернуться и увидеть, где вы ошиблись, чтобы вы не повторяли одни и те же ошибки. См. рабочий пример ниже.

Зачем лезть во все эти хлопоты, когда в Интернете полно калькуляторов, которые сделают расчеты за вас?

Многие электронные и веб-калькуляторы превосходны, просто введите данные и нажмите, чтобы получить ответ. Но вам все равно нужно инстинктивно знать, какую формулу использовать, когда и почему. Чтобы быть достаточно знакомым, чтобы сделать это хорошо, вам нужно знать, как работают различные формулы. Лучший способ сделать это — начать с решения некоторых задач вручную, тогда вы найдете многие калькуляторы, предлагаемые на веб-сайтах, гораздо более полезными.

Чтобы помочь вам на правильном пути, почему бы не загрузить нашу брошюру «Советы по математике», в которой показано, как использовать калькулятор с показателями степени и техническими обозначениями для работы с этими единицами и каждый раз получать правильный ответ.

Нет научного калькулятора? В буклете «Советы по математике» объясняется, что вам нужно (и что вам не нужно, чтобы не тратить деньги напрасно). Если вы не хотите покупать научный калькулятор, вы всегда можете взять его бесплатно на сайте www.calculator.org/download.html. Пользователи ПК могут попробовать Calc98.

Какой бы калькулятор вы ни выбрали, помните, что вы должны прочитать инструкции, чтобы ознакомиться с методами работы, которые вы должны использовать, поскольку они различаются от калькулятора к калькулятору.

Итак, вы прочитали эти инструкции и готовы начать. Вот способ решить типичную проблему на бумаге, чтобы (с практикой) вы не запутались.

Вопрос:

Рассчитайте напряжение питания (V _S ), необходимое для того, чтобы ток 10 мА протекал через дроссель 15 мГн при частоте питания 400 Гц.

1. Начертите схему и перечислите значения:

L = 15 мГн

ƒ = 400 Гц

I = 10 мА

2. Перечислите необходимые формулы.

Напряжение питания V _S = IX _L

Индуктивная реактивная реакция x _L = 2πƒL

3. Рассчитайте X _L

X _{. Ω}

4. Используйте X _L для расчета V _S

V _S = IX _L = 10exp ^-3 x 37,7 = 0,377

5. Дайте ответ в соответствующей форме (Используйте клавишу калькулятора ENG для преобразования между В, мВ, мкВ и т. д., чтобы числовой ответ оставался между 1 и 999)

Ответ: V

_S = 377 мВ

Примечание: При ответе на подобные задачи обычно следует округлять десятичные дроби до двух знаков после запятой.