Что такое индуктивное сопротивление. Как оно влияет на ток в цепи переменного тока. Какие факторы определяют величину индуктивного сопротивления. Как рассчитать индуктивное сопротивление катушки. Какое значение имеет индуктивное сопротивление в электротехнике.
Что такое индуктивное сопротивление
Индуктивное сопротивление — это противодействие катушки индуктивности протеканию переменного тока. В отличие от активного сопротивления, индуктивное сопротивление возникает только в цепях переменного тока и зависит от частоты тока.
Причина возникновения индуктивного сопротивления заключается в явлении самоиндукции — возникновении ЭДС в катушке при изменении протекающего через нее тока. Эта ЭДС направлена против изменения тока и препятствует его нарастанию или убыванию.
Физическая сущность индуктивного сопротивления
При протекании переменного тока через катушку индуктивности в ней возникает переменное магнитное поле. Изменяющееся магнитное поле наводит в витках катушки ЭДС самоиндукции, которая согласно правилу Ленца препятствует изменению тока. Чем быстрее изменяется ток, тем большая ЭДС самоиндукции возникает.
Таким образом, катушка индуктивности как бы «сопротивляется» изменению тока, что и обуславливает наличие индуктивного сопротивления. При этом энергия не рассеивается в виде тепла, как в случае с активным сопротивлением, а периодически запасается в магнитном поле катушки и возвращается в цепь.
Формула для расчета индуктивного сопротивления
Индуктивное сопротивление катушки рассчитывается по формуле:
XL = ωL = 2πfL
где:
- XL — индуктивное сопротивление (Ом)
- ω — угловая частота тока (рад/с)
- f — частота тока (Гц)
- L — индуктивность катушки (Гн)
Из формулы видно, что индуктивное сопротивление:
- прямо пропорционально частоте тока
- прямо пропорционально индуктивности катушки
Факторы, влияющие на величину индуктивного сопротивления
Основными факторами, определяющими величину индуктивного сопротивления катушки, являются:
- Частота переменного тока — чем выше частота, тем больше индуктивное сопротивление.
- Индуктивность катушки — зависит от числа витков, геометрических размеров и наличия сердечника.
- Материал сердечника катушки — ферромагнитный сердечник увеличивает индуктивность.
- Конструкция катушки — влияет на ее индуктивность.
Влияние индуктивного сопротивления на ток в цепи
Индуктивное сопротивление оказывает следующее влияние на ток в цепи переменного тока:
- Уменьшает амплитуду тока по сравнению с цепью постоянного тока
- Создает сдвиг фаз между током и напряжением — ток отстает от напряжения на 90°
- Потребляет реактивную мощность, которая не преобразуется в другие виды энергии
Чем больше индуктивное сопротивление, тем сильнее его влияние на ток в цепи.
Применение индуктивного сопротивления в электротехнике
Явление индуктивного сопротивления широко используется в различных электротехнических устройствах:
- Дроссели — для сглаживания пульсаций тока
- Трансформаторы — для передачи электроэнергии
- Электрические фильтры — для выделения сигналов определенной частоты
- Катушки зажигания — для создания высоковольтных импульсов
- Электродвигатели — для создания вращающегося магнитного поля
Понимание природы и свойств индуктивного сопротивления необходимо для эффективного проектирования и эксплуатации электрических устройств и систем.
Сравнение индуктивного и емкостного сопротивлений
Индуктивное и емкостное сопротивления имеют ряд схожих и отличительных черт:
- Оба являются реактивными сопротивлениями и не потребляют активной мощности
- Индуктивное сопротивление растет с увеличением частоты, а емкостное — уменьшается
- Ток через индуктивность отстает от напряжения на 90°, через емкость — опережает на 90°
- Индуктивность накапливает энергию в магнитном поле, емкость — в электрическом
Эти различия позволяют использовать индуктивные и емкостные элементы для создания различных фильтров и резонансных контуров.
Расчет индуктивного сопротивления на практике
Рассмотрим пример расчета индуктивного сопротивления катушки:
Дано: катушка индуктивностью L = 0,1 Гн, частота тока f = 50 Гц.
Решение:
- Находим угловую частоту: ω = 2πf = 2 × 3,14 × 50 = 314 рад/с
- Рассчитываем индуктивное сопротивление: XL = ωL = 314 × 0,1 = 31,4 Ом
Таким образом, при частоте 50 Гц катушка будет иметь индуктивное сопротивление 31,4 Ом.
Индуктивное сопротивление в сложных цепях
В реальных электрических цепях индуктивное сопротивление часто сочетается с активным сопротивлением и емкостным сопротивлением. В таких случаях для анализа цепи используют метод комплексных чисел, где:
- Активное сопротивление представляет действительную часть
- Индуктивное сопротивление — положительную мнимую часть
- Емкостное сопротивление — отрицательную мнимую часть
Это позволяет рассчитывать сложные цепи переменного тока, учитывая взаимодействие различных типов сопротивлений.
Сопротивление в цепи переменного тока. (11 класс)
Похожие презентации:
Влияния состава и размера зерна аустенита на температуру фазового превращения и физико-механические свойства сплавов
Газовая хроматография
Геофизические исследования скважин
Искусственные алмазы
Трансформаторы тока и напряжения
Транзисторы
Воздушные и кабельные линии электропередач
Создание транспортно-энергетического модуля на основе ядерной энергодвигательной установки мегаваттного класса
Магнитные аномалии
Нанотехнологии
1. АКТИВНОЕ, ЕМКОСТНОЕ И ИНДУКТИВНОЕ СОПРОТИВЛЕНИЯ В ЦЕПИ ПЕРЕМЕННОГО ТОКА 11 класс
НАГРУЗКА В ЦЕПИ ПЕРЕМЕННОГОТОКА
РЕАКТИВНАЯ
Индуктивная
АКТИВНАЯ
Емкостная
3. АКТИВНОЕ СОПРОТИВЛЕНИЕ В ЦЕПИ ПЕРЕМЕННОГО ТОКА
• Электрические устройства, преобразующиеэлектрическую энергию во внутреннюю,
называются активными сопротивлениями.
15 Ом
4.
АКТИВНОЕ СОПРОТИВЛЕНИЕ В ЦЕПИ ПЕРЕМЕННОГО ТОКА• От чего зависит активное сопротивлениепроводника?
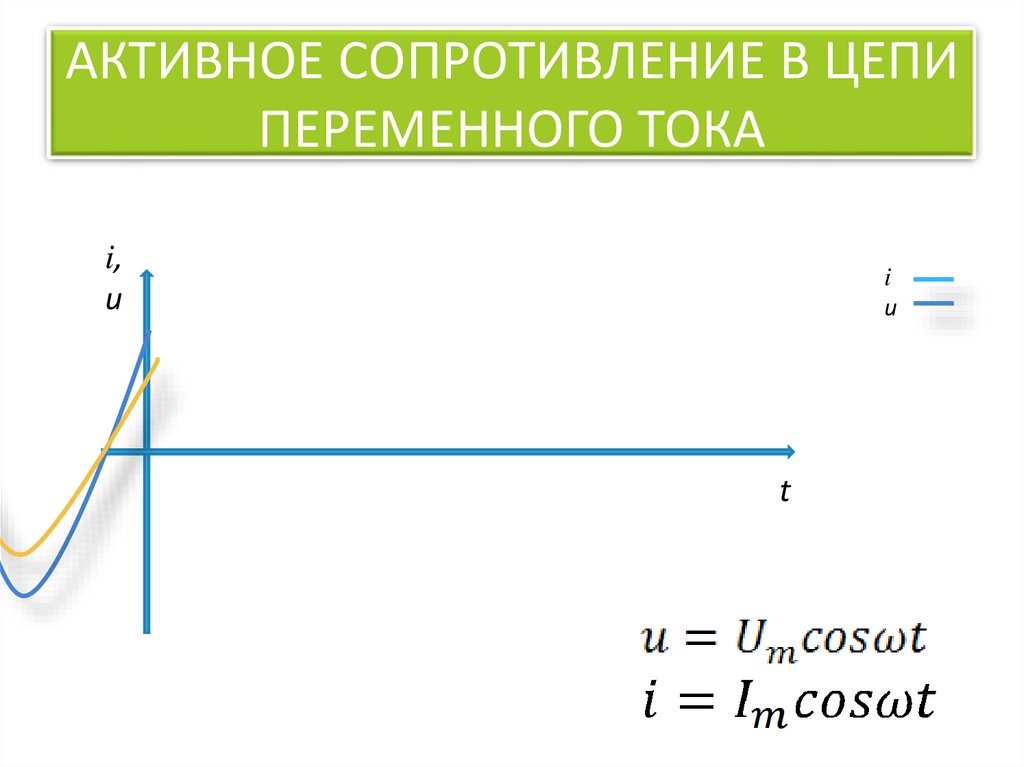
5. АКТИВНОЕ СОПРОТИВЛЕНИЕ В ЦЕПИ ПЕРЕМЕННОГО ТОКА
Рассмотрим сначала цепь, состоящую из одного лишь
сопротивления , подключённого к синусоидальной ЭДС:
• Из второго правила Кирхгофа для такой цепи
можно сделать следующие три вывода:
• 1) ток через сопротивление совершает гармонические колебания в
одной фазе с напряжением;
• 2) максимальная сила тока (достигается при значении синуса,
равном единице) ;
• 3) связь амплитуд силы тока и напряжения на сопротивлении
формально совпадает с законом Ома для участка цепи с постоянным
током.
6. АКТИВНОЕ СОПРОТИВЛЕНИЕ В ЦЕПИ ПЕРЕМЕННОГО ТОКА
iu
R
7. ЕМКОСТНОЕ СОПРОТИВЛЕНИЕ В ЦЕПИ ПЕРЕМЕННОГО ТОКА
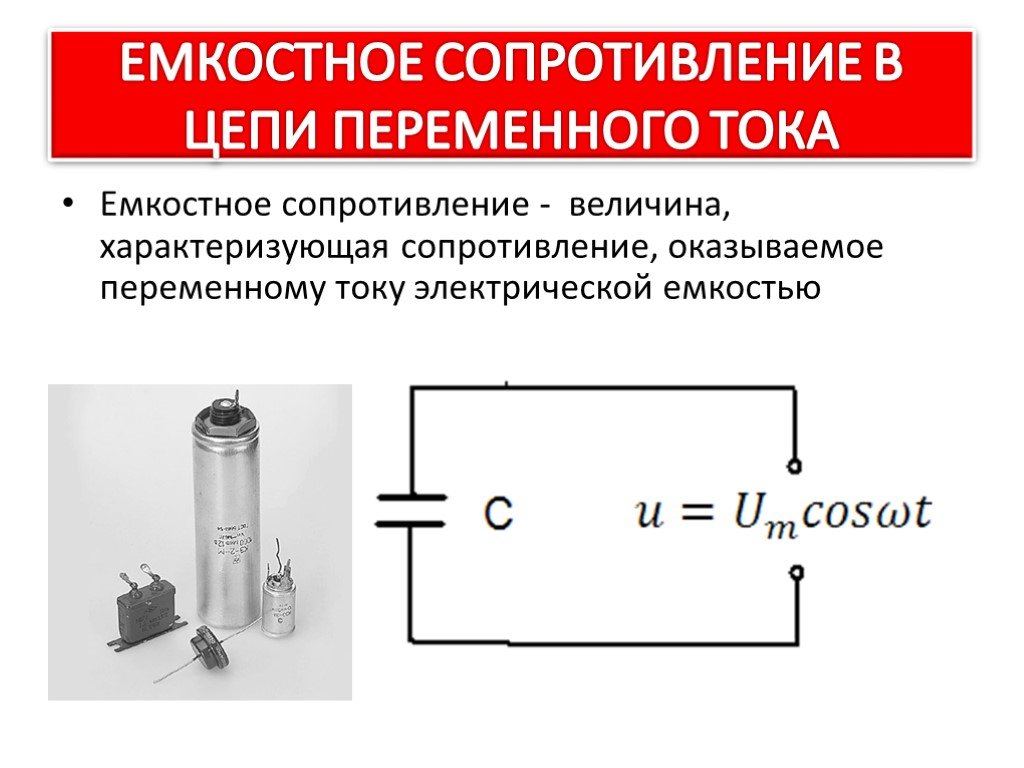
• Емкостное сопротивление — величина,характеризующая сопротивление, оказываемое
переменному току электрической емкостью
8. ЕМКОСТНОЕ СОПРОТИВЛЕНИЕ В ЦЕПИ ПЕРЕМЕННОГО ТОКА
9.
ЕМКОСТНОЕ СОПРОТИВЛЕНИЕ В ЦЕПИ ПЕРЕМЕННОГО ТОКАРассмотрим цепь, состоящую из одной лишь ёмкости , подключенной ксинусоидальной ЭДС. Второе правило Кирхгофа для такой цепи
Тогда сила тока .
Величина
называется ёмкостным сопротивлением.
Можно сделать следующие три вывода:
1) ток в цепи совершает гармонические колебания, опережая по фазе
напряжение на
;
2) максимальная сила тока
;
3) связь амплитуд силы тока и напряжения на конденсаторе формально
совпадает с законом Ома для участка цепи в случае постоянных токов.
10. ЕМКОСТНОЕ СОПРОТИВЛЕНИЕ В ЦЕПИ ПЕРЕМЕННОГО ТОКА
Почему конденсатор оказывает конечноесопротивление переменному току? Ведь между
обкладками конденсатора – диэлектрик, а
значит, цепь разомкнута, и её сопротивление
должно быть очень большим. Этот факт имеет
простое объяснение. Переменный
электрический ток не проходит сквозь
конденсатор, а представляет собой
периодически повторяющийся процесс
зарядки и разрядки конденсатора.
11. ЕМКОСТНОЕ СОПРОТИВЛЕНИЕ В ЦЕПИ ПЕРЕМЕННОГО ТОКА
i,u
i
u
t
0
Uc
Ic
12. ИНДУКТИВНОЕ СОПРОТИВЛЕНИЕ В ЦЕПИ ПЕРЕМЕННОГО ТОКА
Индуктивное сопротивление- величина,характеризующее сопротивление, оказываемое
переменному току индуктивностью цепи
13. ИНДУКТИВНОЕ СОПРОТИВЛЕНИЕ В ЦЕПИ ПЕРЕМЕННОГО ТОКА
14. ИНДУКТИВНОЕ СОПРОТИВЛЕНИЕ В ЦЕПИ ПЕРЕМЕННОГО ТОКА
Рассмотрим цепь, состоящую из одной лишь катушки индуктивности ,присоединённой к синусоидальной ЭДС. Второе правило Кирхгофа для
такой цепи
Интегрируя, получаем:
Величина
называется индуктивным сопротивлением.
Можно сделать следующие три вывода:
1) ток через индуктивность совершает гармонические колебания и отстаёт
от напряжения по фазе на
;
2) максимальная сила тока
;
3) связь амплитуд силы тока и напряжения на индуктивности формально
совпадает с законом Ома для участка цепи в случае постоянных токов.
15.
ИНДУКТИВНОЕ СОПРОТИВЛЕНИЕ В ЦЕПИ ПЕРЕМЕННОГО ТОКАi,u
i
u
t
U
0
16. ИНДУКТИВНОЕ СОПРОТИВЛЕНИЕ В ЦЕПИ ПЕРЕМЕННОГО ТОКА
17. Сравнить накал лампочек, подключённых к синусоидальному и постоянному напряжениям. Накал лампочек для рисунка (а) одинаков.
Одинаковый накал лампочек на рис (а)означает, что напряжения источника
постоянного тока равно эффективному
напряжению источника переменного тока
Если в обе цепи включить конденсатор
достаточно большой ёмкости (б), то лампочка в
цепи источника переменного тока будет попрежнему гореть ярко, поскольку ёмкостное
сопротивление переменному току обратно
пропорционально ёмкости и, следовательно,
будет мало. В цепи постоянного тока накал
отсутствует, поскольку между обкладками
конденсатора диэлектрик, и цепь разомкнута.
анализируя формулу
.
Постоянный ток означает, что циклическая частота
,
и, значит,
.
Если в обе цепи включить катушку достаточно большой индуктивности, то ток в цепи источника
переменного тока будет мал из-за большого индуктивного сопротивления, лампочка погаснет, а в цепи
источника постоянного тока лампочка по-прежнему будет гореть ярко, поскольку индуктивное
сопротивление постоянному току равно нулю.
Действительно, в случае постоянного тока,и
индуктивное сопротивление
.
18. Метод векторных диаграмм
1) Векторнаправлен вдоль оси 0x
так как напряжение на активном
сопротивлении колеблется в одной фазе
с током.
U 0 U 0 R U 0 L U 0C
2) напряжение на индуктивности
опережает ток по фазе на
, вектор
повёрнут относительно оси 0x на угол
против часовой стрелки, т.е. направлен
вдоль положительного направления оси
0y.
3) напряжение на ёмкости отстаёт от
тока по фазе на
, вектор
повёрнут относительно оси 0x на угол
по часовой стрелке, т.е. направлен
вдоль отрицательного направления
оси 0y.
Сначала удобно сложить противоположно направленные вектора
и
сумма равна вектору, направленному вдоль оси 0y и по величине равному
. Их
,
где реактивное сопротивление цепи. Далее по теореме Пифагора
находим величину результирующего вектора
Величина
называется полным
сопротивлением цепи.
20. закон Ома для переменного тока
21. Пример Рассчитать допустимую амплитуду напряжения генератора в электрической цепи на рис, если пробой конденсатора наступает
при напряжении U=500 В.Параметры схемы: C=10 мкФ, L= 1Гн, R=3 Ом, частота
генератора 50 Гц.
22. Cдвиг фаз между током в цепи и суммарным напряжением на концах цепи
• Сдвиг фаз равен углумежду векторами
и . Из
прямоугольного
треугольника
1
L
I0 X X
C
tg
I0R R
R
English Русский Правила
PhysBook:Электронный учебник физики — PhysBook
Содержание
- 1 Учебники
-
2 Механика
- 2.1 Кинематика
- 2.2 Динамика
-
2.
3 Законы сохранения
- 2.4 Статика
- 2.5 Механические колебания и волны
-
3 Термодинамика и МКТ
- 3.1 МКТ
- 3.2 Термодинамика
-
4 Электродинамика
- 4.1 Электростатика
- 4.2 Электрический ток
-
4. 3 Магнетизм
- 4.4 Электромагнитные колебания и волны
-
5 Оптика. СТО
- 5.1 Геометрическая оптика
- 5.2 Волновая оптика
- 5.3 Фотометрия
- 5.4 Квантовая оптика
- 5.5 Излучение и спектры
- 5.6 СТО
-
6 Атомная и ядерная
-
6. 1 Атомная физика. Квантовая теория
- 6.2 Ядерная физика
-
6.
- 7 Общие темы
- 8 Новые страницы
3 Законы сохранения
3 Магнетизм
1 Атомная физика. Квантовая теория
Здесь размещена информация по школьной физике:
- материалы из учебников, лекций, рефератов, журналов;
- разработки уроков, тем;
- flash-анимации, фотографии, рисунки различных физических процессов;
- ссылки на другие сайты
и многое другое.
Каждый зарегистрированный пользователь сайта имеет возможность выкладывать свои материалы (см. справку), обсуждать уже созданные.
Учебники
Формулы по физике – 7 класс – 8 класс – 9 класс – 10 класс – 11 класс –
Механика
Кинематика
Основные понятия кинематики – Прямолинейное движение – Криволинейное движение – Движение в пространстве
Динамика
Законы Ньютона – Силы в механике – Движение под действием нескольких сил
Законы сохранения
Закон сохранения импульса – Закон сохранения энергии
Статика
Статика твердых тел – Динамика твердых тел – Гидростатика – Гидродинамика
Механические колебания и волны
Механические колебания – Механические волны
Термодинамика и МКТ
МКТ
Основы МКТ – Газовые законы – МКТ идеального газа
Термодинамика
Первый закон термодинамики – Второй закон термодинамики – Жидкость-газ – Поверхностное натяжение – Твердые тела – Тепловое расширение
Электродинамика
Электростатика
Электрическое поле и его параметры – Электроемкость
Электрический ток
Постоянный электрический ток – Электрический ток в металлах – Электрический ток в жидкостях – Электрический ток в газах – Электрический ток в вакууме – Электрический ток в полупроводниках
Магнетизм
Магнитное поле – Электромагнитная индукция
Электромагнитные колебания и волны
Электромагнитные колебания – Производство и передача электроэнергии – Электромагнитные волны
Оптика.
СТОГеометрическая оптика
Прямолинейное распространение света. Отражение света – Преломление света – Линзы
Волновая оптика
Свет как электромагнитная волна – Интерференция света – Дифракция света
Фотометрия
Фотометрия
Квантовая оптика
Квантовая оптика
Излучение и спектры
Излучение и спектры
СТО
СТО
Атомная и ядерная
Атомная физика. Квантовая теория
Строение атома – Квантовая теория – Излучение атома
Ядерная физика
Атомное ядро – Радиоактивность – Ядерные реакции – Элементарные частицы
Общие темы
Измерения – Методы решения – Развитие науки- Статья- Как писать введение в реферате- Подготовка к ЕГЭ — Репетитор по физике
Новые страницы
Запрос не дал результатов.
Индуктивные цепи переменного тока
Катушка индуктивности обычно представляет собой катушку из проволоки, которая создает вокруг себя переменное магнитное поле, когда через нее протекает переменный ток.
Индуктивность — это свойство катушки индуктивности, противодействующее изменению тока. Измеряется в Генри. Из-за этой индуктивности в катушке индуцируется противо-ЭДС, когда она подвергается воздействию переменного тока.
[adsense1]
Согласно закону Ленца, эта ЭДС противодействует изменению тока. Следовательно, приложенное напряжение должно преодолевать только эту противо-ЭДС, потому что в цепи нет сопротивления. Таким образом, приложенное напряжение и обратная ЭДС должны быть равны и противоположны, чтобы поддерживать ток, протекающий через цепь.
Поведение цепи переменного тока с катушкой индуктивности полностью отличается от цепи постоянного тока. При этом ток, протекающий через катушку, зависит не только от индуктивности, но и от частоты переменного источника. Кратко обсудим поведение цепи переменного тока с индуктивной нагрузкой.
Схема
Переменный ток, приложенный к чистому индуктору
Чистый индуктор не имеет сопротивления в обмотке катушки, но имеет только индуктивность.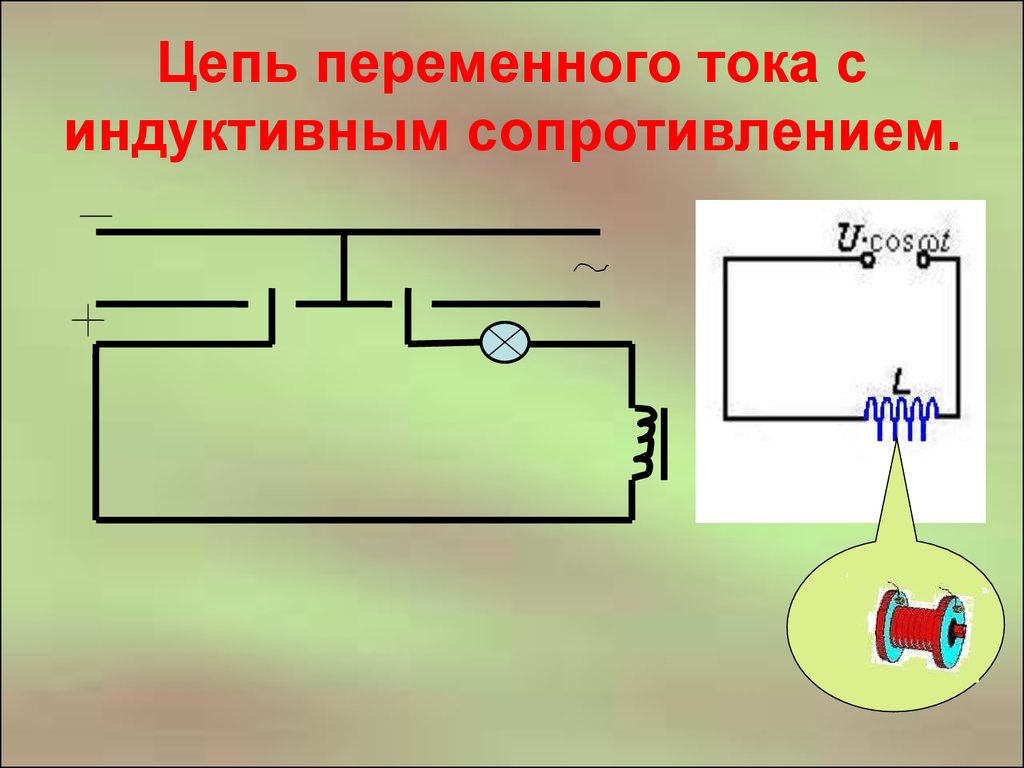
Это свойство индуктивности проявляют все двигатели, трансформаторы и генераторы (с некоторым сопротивлением в катушке). На рисунке ниже показана чисто индуктивная цепь с источником переменного напряжения и соответствующие формы сигналов.
[adsense2]
Пусть приложенное напряжение, v = V м sin ωt. Как указано выше, индуцированная ЭДС равна и противоположна приложенному напряжению, т. е. v = – e
Где e – противо-ЭДС, равная –L di/dt
Подставляя выражение ЭДС, получаем
v = L di/dt
V м sin ωt = L di/dt
di = (V м / L) sin ωt dt
Интегрируя обе стороны, получаем
i = (V м / L) ∫ sin ωt dt
= (V м / ωL) (– cos ωt)
i = (V м / wL) (sin ωt – π/2 )
Когда (sin ωt – π/2) равно единице, ток, протекающий по цепи, будет максимальным. Таким образом,
im = (V м / ωL)
Тогда текущее уравнение принимает вид / ωL)
Из приведенных выше выражений тока и напряжения видно, что ток отстает от напряжения на 900.
Следовательно, в чисто индуктивной цепи ток находится в квадратуре с напряжением, как показано на осциллограммах на приведенном выше рисунке.
Это означает, что при максимальном изменении тока (при прохождении тока через ноль) напряжение, индуцированное на катушке индуктивности, максимально. Точно так же при максимальных значениях тока, когда ток не изменяется, индуцированное напряжение на катушке индуктивности будет равно нулю.
Таким образом, напряжение на индукторе опережает ток через этот индуктор на ¼ (четверть) цикла. Векторная диаграмма чисто индуктивной цепи переменного тока приведена ниже.
Inductive Reactance
From the above derivation, the maximum current equation is given as
i m = (V m / ωL)
ωL = V m / i m
Это отношение напряжения к току представляет собой сопротивление, предлагаемое индуктивной цепью протеканию тока. Эта величина wL называется индуктивным реактивным сопротивлением и обозначается как XL, измеряется в Омах.
Индуктивное сопротивление цепи переменного тока можно представить как
XL = ωL = 2ΠfL (поскольку ω = 2Πf)
Где XL — индуктивное сопротивление в Омах
f — частота питающего напряжения
L — индуктивность катушки в Генри
Приведенное выше уравнение что, когда частота входного источника питания увеличивается, скорость изменения тока также меняется. Следовательно, ЭДС индукции (или реактивное напряжение) на катушке индуктивности будет увеличиваться.
В результате чистый ток, протекающий через индуктор, уменьшится. Следует сделать вывод, что реактивное сопротивление катушки индуктивности зависит от частоты питания линейно, как показано на рисунке.
Мощность и коэффициент мощности в индуктивной цепи переменного тока
Мощность в цепи переменного тока является произведением мгновенного напряжения и тока. Это можно представить как
P = v × i
P = V м sin ωt × I м sin (ωt – 90)
Интегрируя по циклу, мы получаем,
P = V м sin ?0022 SIN (ωt — 90) DωT)
= (V M I M / 2π) (∫ 0 2π SIN ωt × ( — COS ωt) DWT)
= (V M 2222222222222222222222222222222222222222222222222222222222222221.
I м / 2π) (∫ 0 2π (– sin 2 ωt)/2 dwt)
= (V м I м = / 8π) (cos 4π – 9000 03) (V м I м / 8π) (1 – 1)
P =0
Средняя мощность в чистом индукторе всегда равна нулю, поскольку количество энергии, полученное от источника за полупериод, возвращается к источник в следующем полупериоде.
На приведенном ниже рисунке показана кривая мощности индуктивной цепи переменного тока, в которой положительная мощность равна отрицательной мощности, поэтому результирующая мощность за цикл равна нулю. Это ясно объясняет, что чистая индуктивность не потребляет никакой энергии.
В этой цепи ток также синусоидальный, но отстает от напряжения на 900. Поскольку ток отстает от напряжения на 90 0 , разность фаз θ равна 90 0 . Тогда
Коэффициент мощности, cos 90 = 0
Коэффициент мощности в чисто индуктивной цепи равен нулю, т. е. чисто отстающий коэффициент мощности.
Цепь серии RL
Как мы знаем, не существует чисто индуктивной физической цепи, поскольку каждая катушка имеет некоторое сопротивление обмотки наряду с индуктивностью. В такой цепи сопротивление рассматривается как последовательный элемент по отношению к индуктору.
Рассмотрим приведенный ниже рисунок, на котором чистое сопротивление соединено последовательно с чистой индуктивностью. Эта последовательная комбинация подключена к источнику переменного тока с напряжением v = V м sin ωt.
В последовательной цепи R L напряжение на катушке индуктивности не совпадает по фазе с током, протекающим через цепь, и напряжением на сопротивлении, как показано на рисунке выше. Индуцированное напряжение в катушке индуктивности противодействует протеканию тока, поэтому V L опережает ток I и падение сопротивления V R на 90 0 .
Пусть I будет током, протекающим по цепи, В L и В R — падение напряжения на индуктивности и сопротивлении соответственно.
Напряжение на резисторе, В R = I R
Напряжение на дросселе, В L = I × XL (где XL = 2πfL)
В=
, √ (V R 2 + V L 2 ) = √ (IR) 2 + (I XL) 2 )= I √ (r 2 + + x. 2
= I √ (r 2 + + x. + x = I √ (r 2 + + x = I √ (r 2 + + x = I √ (r 2 + x = I √ (r 2 )= I √ (I XL) 2 ) ) = I Z
Где Z — полное сопротивление в последовательной цепи R L , равное √ (R 2 + XL 2 ).
Треугольник импеданса
Противодействие цепи переменного тока протеканию синусоидального тока называется импедансом. Его также можно определить как отношение синусоидального напряжения к току. Обозначается буквой Z и измеряется в Омах.
Из векторной диаграммы серии RL,
tan ϕ = V L / V R = XL / R
cos ϕ = V R / V = R / Z
sin ϕ = V L / V = XL / Z
Если все стороны треугольника получены в X L Последовательная цепь делится по току, мы получаем треугольник импеданса, как показано на рисунке.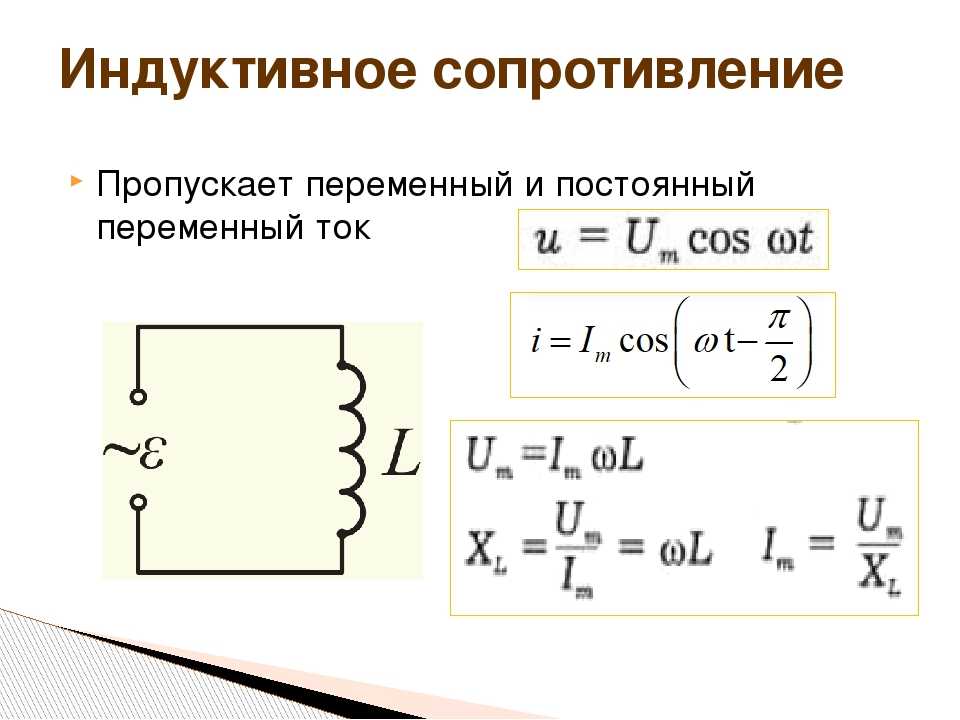
Из этого треугольника компоненты R, X L и Z можно выразить как
R = Z cos ϕ
XL = Z sin ϕ
Z = √ (R 2 + XL 2 )
= загар-1 (XL/R)
Пример
Найдите выражение для тока, а также рассчитайте мощность последовательной цепи RL с сопротивлением R = 50 Ом и L = 0,159 Гн, возбуждаемой напряжением v = 283 sin 100πt.
Индуктивное сопротивление, XL = 2πfL = 100π × 0,159
= 49,95 Ом
Z = R + j XL = 50 + j49,95
Переводя в полярную форму, получаем Z = 70,60 Ом ∠ 39,95 i = v/ Z = (283 sin (100πt – 44,97))/ 70,675
i = 4 sin (100πt – π/4) A
P = VI cos θ
= (283/√2) (4/√2) cos 44,97
= 400,43 А
Индуктивность и реактивное сопротивление переменного тока видно, что поведение резистора одинаково в режиме постоянного или переменного тока при нормальных частотах. Однако другие основные электрические компоненты, такие как индуктор
, , сильно зависят от частоты сигнала переменного тока.
Представление концепции индуктивности дано в первом разделе для того, чтобы понять явления, определяющие работу катушки индуктивности. Описание катушек индуктивности также дано позже в этом же разделе. Мы также объясним, почему определенные типы катушек индуктивности лучше подходят для высокочастотных применений.
Во втором разделе выделены зависимости с частотой наблюдаемой в них индуктивности и фазового сдвига.
Наконец, последний раздел посвящен соединению резистора и катушки индуктивности для создания цепей фильтрации.
Представление
Индуктивность
Индуктивность — это свойство электрического компонента, состоящее в создании сопротивления изменению тока, когда на его выводы подается переменное напряжение. Это замедление тока можно объяснить электромагнитный закон индукции , подробно описанный в руководстве по сопротивлению переменному току.
Чтобы лучше понять это определение, давайте рассмотрим цепь, состоящую из источника переменного тока и никаких других компонентов, кроме проводника длиной l , закорачивающего источник, как показано на рис.
1 ниже:
Петля тока, образованная цепью, создает магнитное поле B , когда в него втекает ток I , генерируемый источником переменного тока. Круг с крестом означает, что при протекании тока I, как показано на рис. 1 , магнитное поле направлено вниз.
Согласно закону Ленца, если ток имеет форму переменного тока, B также является переменным, что создает индукционный ток I i , создаваемый электродвижущей силой E , чтобы смягчить изменение магнитного поля с индуцированным полем Б и . Когда ток I i протекает так, как показано на рис. 1 , индуцированное магнитное поле направлено вверх, что обозначено кружком с точкой.
Выражение магнитного поля B определяется следующим уравнением 1 :
уравнение 1 : Выражение магнитного поля в пределах одного провода Где μ 0 =4π×10 -7 Гн/м есть магнитная проницаемость вакуума .
Таким образом, магнитный поток равен Φ=B×A , где A — поперечное сечение проволочной петли. Наконец, индуктивность L задается уравнением 2 ниже:
Таким образом, индуктивность зависит только от геометрии, а не от источника (напряжения или тока). ) и выражается в Генри (H). Чтобы лучше понять, что представляет собой эта величина, стоит привести выражение электродвижущей силы Е в уравнении 3 :
уравнение 3 : Выражение электродвижущей силыЕсли мы изолируем L в этом уравнении, мы понимаем, что 1 Генри представляет собой индуктивность цепи, в которой индуцируется электродвижущая сила в 1 вольт, когда ток, переменный со скоростью 1 Ампер в секунду течет в него.
Катушки индуктивности
Чтобы значительно увеличить индуктивность провода, было бы очень сложно работать только с геометрическими параметрами A и l .
На практике компоненты индуктивности называют индукторы , которые представляют собой провода с определенным количеством витков вокруг оси и представлены в виде электрического компонента, такого как показано на рисунке 2 :
Если мы рассмотрим количество N обмоток , Уравнение 2 изменяется на Уравнение 4 :
уравнение 4 : Выражение индуктивности катушки индуктивностиИндуктивность витков катушки индуктивности увеличивается, следовательно, в раз.N 2 в сравнении с таким же проводом, представленным в Рисунок 1 .
Существует еще одна модификация катушек индуктивности для увеличения их индуктивности: добавить сердечник . Сердечник представляет собой центральную область индуктора, окруженную проволокой.
Он может быть изготовлен из немагнитного материала, такого как пластик, керамика или даже воздух, который по своим магнитным свойствам подобен вакууму.
Катушки индуктивности этого типа известны как .Катушки индуктивности с воздушным сердечником и представленные символически, например, на рис. 2 , имеют меньшую индуктивность, но лучшие частотные характеристики.
Другим типом являются катушки индуктивности с ферромагнитным сердечником , их сердечник изготовлен из магнитного материала, повышающего общую магнитную проницаемость. Катушки индуктивности с ферромагнитным сердечником имеют гораздо более высокую индуктивность, чем катушки индуктивности с воздушным сердечником, потому что они могут лучше концентрировать магнитное поле. Однако они менее подходят для высокочастотных применений из-за важного присутствия Вихревые токи в сердечнике при повышении частоты приводят к потерям тепла.
Катушки индуктивности с ферромагнитным сердечником могут быть представлены, как показано ниже:
рис. 3: Изображение катушки индуктивности с ферромагнитным сердечникомЧастотная характеристика
Реактивное сопротивление
Довольно неоднозначно говорить об «индуктивности переменного тока», поскольку понятие индуктивности справедливо только в режиме переменного тока.
Действительно, учитывая уравнение 3 и то, что было сказано в предыдущем разделе, можно понять, что электродвижущая сила, индуцированный ток и магнитное поле существуют только в присутствии источника переменного тока. По сути, в режиме постоянного тока катушка индуктивности рассматривается просто как простой провод, закорачивающий часть цепи.
Полное сопротивление катушки индуктивности можно определить как сопротивление току, создаваемому индуктивным компонентом. Импедансы, описанные в другом учебном пособии, представляют собой комплексные числа, действительная часть которых представляет сопротивление , а мнимая часть представляет собой реактивное сопротивление .
Для катушки индуктивности реактивное сопротивление X L представляет сопротивление компонента изменению тока. Импеданс катушки индуктивности является чисто мнимым числом, что означает, что сопротивление не учитывается, а его реактивное сопротивление определяется по следующей формуле:
eq 5 : Реактивное сопротивление катушки индуктивности Таким образом, сопротивление переменному току увеличивается линейно с частотой.
При f=0 Гц (режим постоянного тока) индуктор, как было сказано ранее, действует как короткое замыкание, а когда f→+∞ – как разомкнутая цепь.
Фазовый сдвиг
Полное сопротивление катушки индуктивности определяется просто как Z L = jX L . Фазовый сдвиг φ между током на катушке индуктивности и напряжением, генерируемым на ее клеммах (электродвижущая сила), постоянен и определяется выражением Arg(Z L )=arctan(y) с y→+∞, что дает φ=+π/2 рад или 90° .
Это конкретное значение фазового сдвига, как подчеркивается в руководстве по фазовращателям, называется квадратурным фазовым сдвигом и проиллюстрировано на Рис. 3 :
рис. 3 : Иллюстрация квадратурного фазового сдвига в дросселе. Построено с помощью MatLab® Если амплитуда (относительно пика) тока определяется как I max , амплитуда электродвижущей силы равна В макс =I макс ×X L .
Индукционные явления
Когда частота источника переменного тока увеличивается, внутри индукторов происходят подобные явления, которые уже были подробно описаны в руководстве по сопротивлению переменному току.
Первый – это скин-эффект , он вызван перераспределением тока вблизи границы провода, из которого состоит индуктор. Такая высокая концентрация тока в небольшой области увеличивает сопротивление индуктора, что, как следствие, приводит к тепловым потерям.
Эффект близости также присутствует в катушках индуктивности. Действительно, каждый виток провода индуцирует вихревые токи в пограничной области соседних проводов. Например, для скин-эффекта это имеет тенденцию уменьшать эффективное поперечное сечение для тока, что увеличивает сопротивление.
Фильтры RL
В этом руководстве мы увидели, что катушки индуктивности очень чувствительны к частоте, а резисторы — нет. Поэтому возникает естественный вопрос: что произойдет, если мы объединим эти компоненты в одной цепи?
Рассмотрим цепь RL, входное напряжение которой обозначено как V в , а выходное напряжение V out :
рис.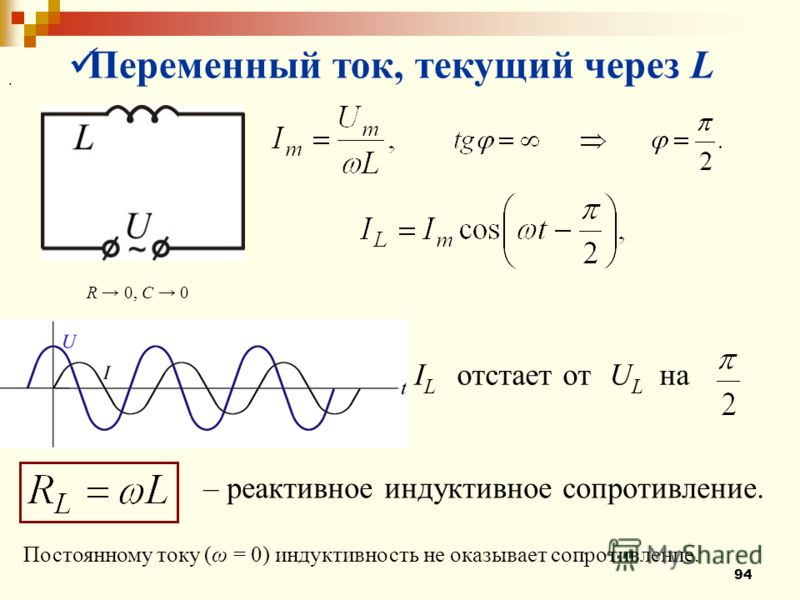
которое определяется отношением V из /V из . Чтобы найти выражение T V , мы можем просто посмотреть на схему как на делитель напряжения. В итоге имеем: eq 6 : Выражение передаточной функции цепи RLЭта функция интересна тем, что она дает нам одновременно коэффициент усиления по напряжению и фазовый сдвиг цепи для любой частоты.
Коэффициент усиления определяется модулем T V , а фазовый сдвиг Φ – его аргументом, оба значения приведены в уравнении 7 ниже. Рекомендуем читателю обратиться к учебнику по комплексным числам, чтобы узнать, как определить модуль и аргумент комплексной дроби.
eq 7 : Коэффициент усиления и фазовый сдвиг цепи RL Возьмем R = 1 кОм и L = 100 мГн и построим две величины, представленные в уравнении 7 , в логарифмическом масштабе для частоты. Полученный график широко известен как диаграмма Боде и показан на поглощается сопротивлением и не поглощается индуктивностью.
В режиме постоянного тока наблюдается квадратурный фазовый сдвиг.
На высокой частоте преобладает импеданс индуктивности, поэтому падение напряжения поглощается индуктивностью, что дает коэффициент усиления, стремящийся к 1. Фазовый сдвиг стремится к нулю при увеличении частоты.
В заключение можно сказать, что RL-схема действует как фильтр верхних частот , так как низкие частоты не передаются.
Заключение
Как было показано в этом руководстве, катушки индуктивности ведут себя иначе, чем резисторы при изменении частоты.
Прежде всего, было дано представление о концепции индуктивности. Индуктивность является важным фактором для понимания закона индукции, она описывает, насколько сильно компонент будет реагировать на изменение тока в цепи. Позже, при представлении катушек индуктивности, мы увидели, что индуктивность можно увеличить с помощью обмоток и наличия магнитопровода.
Во втором разделе мы более подробно рассмотрели частотные характеристики катушек индуктивности.
