Как проявляется индуктивное сопротивление в цепях постоянного и переменного тока. Почему в цепи постоянного тока индуктивное сопротивление равно нулю. Как рассчитывается индуктивное сопротивление в цепи переменного тока. Какие факторы влияют на величину индуктивного сопротивления.
Индуктивное сопротивление в цепи постоянного тока
В цепи постоянного тока индуктивное сопротивление катушки индуктивности равно нулю. Это связано с тем, что в установившемся режиме ток через катушку не изменяется со временем. Рассмотрим подробнее, почему это происходит:
- При включении цепи постоянного тока в катушке индуктивности возникает ЭДС самоиндукции, которая препятствует нарастанию тока.
- По мере нарастания тока ЭДС самоиндукции уменьшается.
- В установившемся режиме ток через катушку постоянен, его производная по времени равна нулю.
- Следовательно, ЭДС самоиндукции также становится равной нулю.
- Катушка индуктивности в этом случае ведет себя как короткозамкнутый участок цепи.
Таким образом, в цепи постоянного тока индуктивное сопротивление проявляется только в переходных процессах при включении или выключении цепи. В установившемся режиме оно равно нулю.
Индуктивное сопротивление в цепи переменного тока
В цепи переменного тока ситуация принципиально иная. Здесь ток через катушку индуктивности постоянно изменяется, что приводит к появлению индуктивного сопротивления. Рассмотрим основные особенности:
- В катушке индуктивности постоянно возникает ЭДС самоиндукции, противодействующая изменению тока.
- Эта ЭДС пропорциональна скорости изменения тока и индуктивности катушки.
- Индуктивное сопротивление зависит от частоты переменного тока и индуктивности катушки.
- Оно рассчитывается по формуле: XL = 2πfL, где f — частота, L — индуктивность.
- Индуктивное сопротивление вызывает сдвиг фаз между током и напряжением на 90°.
Расчет индуктивного сопротивления
Для расчета индуктивного сопротивления катушки в цепи переменного тока используется следующая формула:
XL = 2πfL
Где:
- XL — индуктивное сопротивление (Ом)
- π — число пи (≈3.14)
- f — частота переменного тока (Гц)
- L — индуктивность катушки (Гн)
Из формулы видно, что индуктивное сопротивление:
- Прямо пропорционально частоте переменного тока
- Прямо пропорционально индуктивности катушки
- Измеряется в Омах, как и активное сопротивление
Факторы, влияющие на индуктивное сопротивление
На величину индуктивного сопротивления катушки в цепи переменного тока влияют следующие основные факторы:

- Частота переменного тока — чем выше частота, тем больше индуктивное сопротивление
- Индуктивность катушки — зависит от числа витков, размеров катушки, наличия сердечника
- Магнитная проницаемость сердечника катушки (если он есть)
- Конструкция и материал обмотки катушки
При проектировании электрических цепей важно учитывать эти факторы для правильного расчета индуктивного сопротивления катушек.
Сравнение индуктивного сопротивления в цепях постоянного и переменного тока
Рассмотрим основные различия в проявлении индуктивного сопротивления в цепях постоянного и переменного тока:
| Характеристика | Постоянный ток | Переменный ток |
|---|---|---|
| Величина в установившемся режиме | Равно нулю | Отлично от нуля |
| Зависимость от частоты | Отсутствует | Прямо пропорциональная |
| Сдвиг фаз | Отсутствует | 90 градусов |
| Влияние на ток в цепи | Только в переходных процессах | Постоянное |
Практическое применение индуктивного сопротивления
Знание особенностей индуктивного сопротивления важно для многих практических применений:

- Проектирование фильтров и частотно-зависимых цепей
- Расчет параметров трансформаторов и дросселей
- Создание резонансных контуров в радиотехнике
- Компенсация реактивной мощности в электроэнергетике
- Разработка импульсных источников питания
Понимание природы и особенностей индуктивного сопротивления позволяет эффективно использовать катушки индуктивности в различных электротехнических и электронных устройствах.
Методы измерения индуктивного сопротивления
Существует несколько методов измерения индуктивного сопротивления катушек:
- Метод вольтметра-амперметра на переменном токе
- Мостовой метод (мост Максвелла-Вина)
- Резонансный метод
- Использование специализированных измерителей импеданса
Выбор конкретного метода зависит от требуемой точности, диапазона измерений и доступного оборудования.
Заключение
Индуктивное сопротивление играет важную роль в цепях переменного тока, существенно влияя на их характеристики. В то же время, в цепях постоянного тока оно проявляется только в переходных процессах. Понимание природы и особенностей индуктивного сопротивления необходимо для эффективного проектирования и анализа электрических цепей и устройств.
чем это может быть полезно?
1) Сопротивление катушки постоянному току обозначается буквой R.
Re — фактическое сопротивление катушки постоянному току. Именно это сопротивление увидит усилитель в двух случаях: когда катушка вне магнитного поля, когда катушка в состоянии покоя(не подведен ток, заклинила и т.п.). То есть, знать Re нужно только для этих вот случаев.
Измерить можно обычным мультиметром, но хороших их мало, а значит измерение в большинстве случаев будет совсем не точным. Правильно взять батарейку, на короткое время подключить к ней катушку и измерить силу тока+напряжение, а затем рассчитать Re как U/I.
Rnom — номинальное сопротивление катушки постоянному току.
Когда в любой заявке, будь то сопротивление, или мощность, или давление, или что-угодно еще, вы видите слово «номинальное» — знайте, это НЕ измеренный параметр, а приведенный, назначенный. Так, Rnom — часто это банально округленный в бОльшую сторону Re. То есть, заявка Rnom 2+2Ом на деле может означать и 1. 1+1.1, и 1.9+1.9, и 1.1+1.9 Ом.
1+1.1, и 1.9+1.9, и 1.1+1.9 Ом.
В хороших случаях, не лишенных смысла, и редких, Rnom = Zmin. Как вы понимаете, в остальных случаях знание Re или Rnom для не профессионала, в общем-то, бесполезно. Заявляя Rnom, подавляющее большинство производителей, с одной стороны, бережет вас от поломок, а с другой — вынуждает приобретать более дорогие усилители.
2) Индуктивное сопротивление обозначается буквой Z. В народе такое сопротивление называют «импеданс» («импеданс» в переводе с англ и значит «сопротивление»).
Во всех прочих случаях, кроме описанных выше, усилитель видит Z, а не R. Z — гораздо более сложный, комплексный параметр, который изменяется в зависимости от многих факторов. Однако, Z не бывает ниже Re, а выше — бывает почти всегда.
Zmin и Zmax — минимальное и максимальное сопротивление, которое увидит усилитель. Оба прямо или косвенно зависят от частоты, от хода, от мощности, от характера акустической нагрузки(и корпуса, и салона), от температуры, от конструкции динамика. ..
..
Имеет смысл измерять Z как для динамика вне оформления, так и в полностью готовой, законченной системе. Измерения проще всего выполнить путем измерения силы тока и напряжения, а затем вычислить Z через U\I.
Оформление не может сделать Zmin ниже, чем то, что измерено на динамике вне оформления.
В ситуации, когда катушка стремится покинуть зазор, оба эти сопротивления устремляются к Re. Зная это, возможно определять и так контролировать величину хода, что полезно во множестве случаев.
Нет никаких вариантов «предположить» Z без фактических измерений — импеданс от системы к системе сильно отличается. Вопрос «а можно ли подключать пару DD812 в 0.25» звучит глупо и без измерений не имеет ответа.
Znom или номинальный импеданс — это очередная «заявка», сделанная с теми или иными целями. Иногда Znom=Zmin*1,15, в других случаях Znom=Zmin*1,3, ну а во многих случаях — от балды.
Z-характеристика.
Если измерить импеданс на каждой частоте, то на выходе получим «Z-характеристику динамика» или «Z-кривую» или «импедансную кривую». Зная Z-кривую, можно выяснить множество моментов, полезных для проектирования системы, от подбора усилителей и до проектирования корпуса. Дайте знать если вам интересно — сделаем отдельный пост.
Зная Z-кривую, можно выяснить множество моментов, полезных для проектирования системы, от подбора усилителей и до проектирования корпуса. Дайте знать если вам интересно — сделаем отдельный пост.
Обратите внимание на комментарии к иллюстрациям.
3) Z и усилитель.
Взяли вы в руки динамик, измерили Zmin, и теперь подбираете к нему усилитель.
Мощность, как известно, является произведением силы тока на напряжение. Напряжение ведет к клипу, а ток ведет к перегреву — и то, и другое в перспективе плохо.
Т.к. напряжение и сила тока — оба описывают один и тот же процесс и не существуют друг без друга, то выбор усилителя достаточно прост. За одни и те же деньги вы выберете или надежность+меньшую мощность, или риск+большую мощность. Тут нет никаких иных вариантов, никаких чудодейственных иноземных рецептов.
Имея некий Z на частоте настройки ФИ, мы видим огромный рост ниже и выше, за которыми следуют глубокие спады. Кроссоверы сверх-высоких порядков что-то обрежут, а 1-4 порядки — нет. Поэтому, бюджетные усилители следует подбирать, ориентируясь на Zmin динамика вне оформления, а топовые модели с большим запасом в БП — ориентируясь на Z, найденный на частоте настройки.
Поэтому, бюджетные усилители следует подбирать, ориентируясь на Zmin динамика вне оформления, а топовые модели с большим запасом в БП — ориентируясь на Z, найденный на частоте настройки.
Как мы можем менять Z? С одной стороны, можем выбирать сопротивление катушек, для того они и сделаны разными, с другой стороны — использовать один мощный или мост более слабых усилителей (в т.ч. «бразилию»).
Измерение Re — только 2 из 5 моих мультиметров показывают более-менее верное значение. Оба они стоят не 100р, да и то измеряют не сразу — приходится некоторое время ждать.
0.387/0.78 = 0.496 Ом. Вот так гораздо лучше. Для замера сгодится и пара мультиков за 100р каждый — дешево и сердито. Ну и попутно выяснили, что заявка катушек(Rnom) 1+1Ом — это именно Re. Честный Re, и, тем не менее, не Zmin.
Re этого динамика равен 0.5Ом. Посмотрите, как растет и как меняется импеданс на разной подведенной мощности на одной и той же частоте — от 2.8 и до 1. 8Ом. И это не предел, тк динамик вытерпит гораздо больше.
8Ом. И это не предел, тк динамик вытерпит гораздо больше.
Этот же разброс увидит и ваш усилитель. То есть, ориентироваться на маломощные измерения (а именно такие регламентированы большинством стандартов), определенно, не следует.
Современные теории, учитывающие реальную картину, сложны и не популярны, понятны лишь узкому кругу специалистов, как правило, занятых профессиональной разработкой АС. Если вы не один из них — проще измерьте Z-кривую своей системы сразу на максимальном используемом ходе\мощности и по полученным цифрам делайте выводы.
А это замер Z-кривой динамика в реальном оформлении. Тут, как видим, Z на частоте настройки(33Гц) равен 2.7Ом, а Zmin приходится на 63Гц и равен 2.1Ом.
Если выбирать усилитель в эту систему, то в случае с DD DM серией ориентироваться следует на Z@63Гц, а в случае с DD M — на Z@33Гц. То есть, с выбором в пользу DD M, получим либо серьезный запас в надежности, либо существенно больше мощности при равной надежности — и то, и другое очень неплохо! Ну а с выбором DD DM — неплохо сэкономим!
Если рассматриваете другие усилители, не DD, то картина в целом будет такой же — усилитель, который не боится больших токов, всегда надежнее. Усилитель с минимальной заявкой 2 Ом сработает тут на пределе своих возможностей, тогда как усилитель с заявкой 1Ом покажет очень большой запас.
Усилитель с минимальной заявкой 2 Ом сработает тут на пределе своих возможностей, тогда как усилитель с заявкой 1Ом покажет очень большой запас.
К тому же, если фильтрами высоких порядков обрезать диапазон, к примеру, 30-50Гц, то и динамику, и усилителю будет работать гораздо проще, а значит и нагрузить оба можно больше при необходимости. От ящика к ящику такой диапазон будет меняться.
Пример Z-кривой для динамика вне оформления. Zmin — сопротивление, ниже которого усилитель видеть не будет.
То есть, пара таких динамиков и один усилитель, либо мост усилителей на один динамик — прям то, что доктор прописал))
И соответствующим образом планируем настройку оформления + фильтров. Zmax — на этой частоте ход максимален и получится ранний клип, Zmin — там катушка получит максимум тепла. Хорошо бы если оформление превратит слабые стороны в сильные 😉
|
Заглавная страница
КАТЕГОРИИ: Археология Религия Социология Технологии Физика Философия Финансы Химия Экология ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрации Техника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ? Влияние общества на человека Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. |
⇐ ПредыдущаяСтр 6 из 59Следующая ⇒
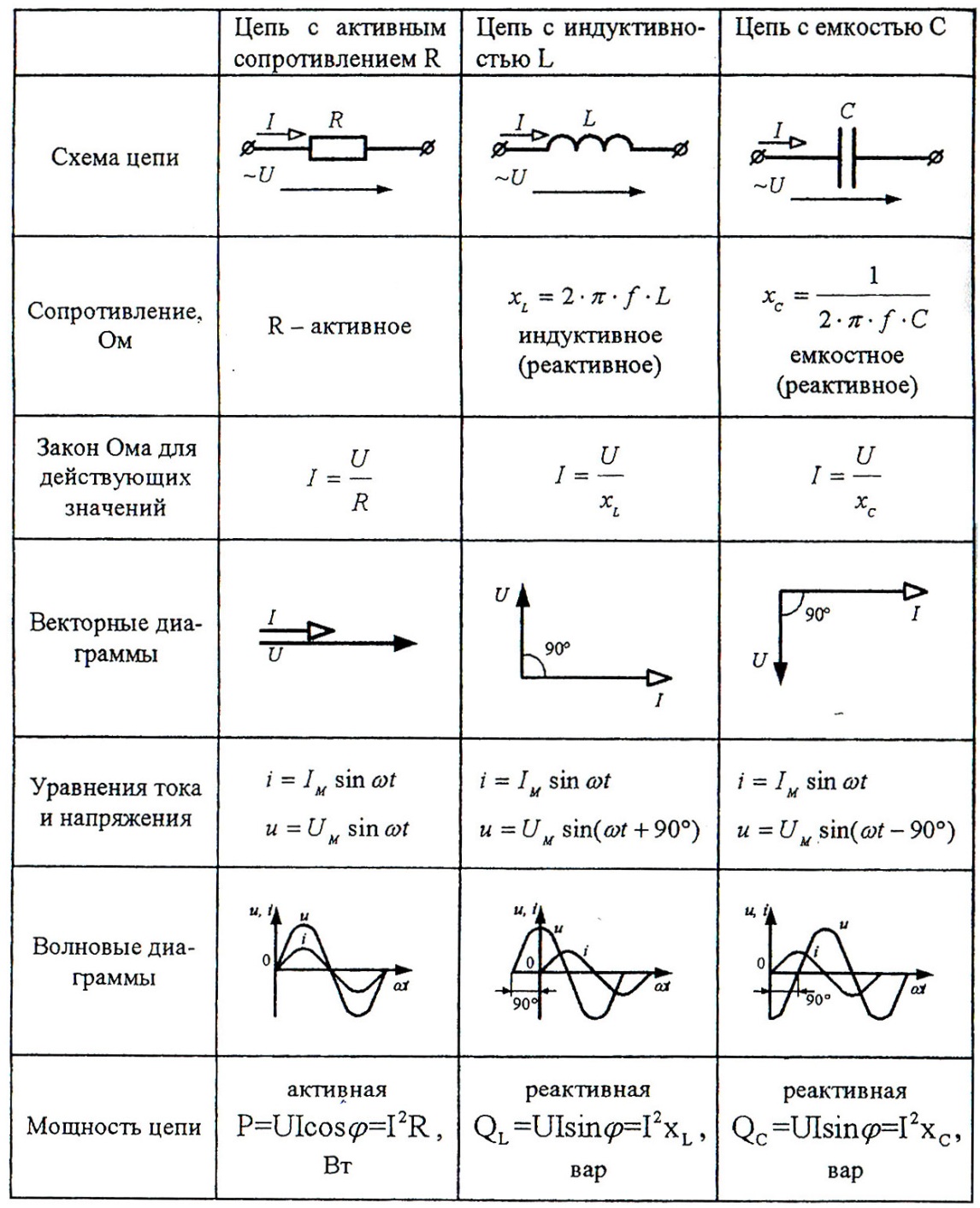
Это зависит от вида тока. Для постоянного‑ тока идеальный конденсатор представляет собой сопротивление (активное) R = , не позволяющее протекать постоянному току. На переменном токе с частотой f реактивное сопротивление конденсатора С или емкостное сопротивление выражается формулой Хс = 1/2πfС . Если перейти от частоты f к ω , то Хс = 1/ωС . Из этой зависимости следует, что емкостное сопротивление убывает с ростом частоты тока. На очень высоких частотах емкостное сопротивление стремится к нулю. Как уже указывалось, реактивность вызывает сдвиг фазы между током и напряжением (рис. 2.1). В результате этого сдвига (для конденсатора) ток опережает напряжение на 90°.
Рис. 2.1. Сдвиг фазы между током и напряжением на емкости
Какое электрическое сопротивление имеет катушка индуктивности?
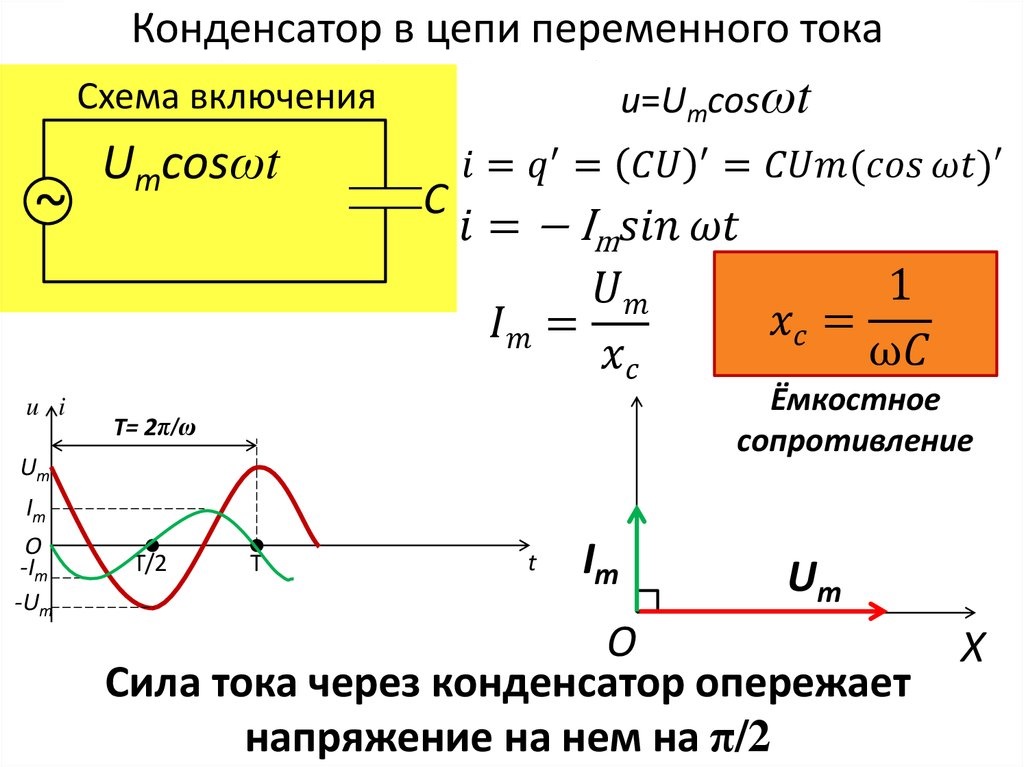
Для постоянного тока идеальная индуктивность обладает нулевым сопротивлением Фазовый сдвиг, вызываемый индуктивностью, таков, что напряжение опережает ток на 90° (рис. 2.2).
Рис. 2.2. Сдвиг фазы между током и напряжением на индуктивности
Из каких элементов состоят электрические цепи?
Элементы электронных схем можно разделить на две группы: активные и пассивные. Активными называют такие элементы, которые могут увеличивать энергию подводимого сигнала (транзисторы и лампы).
Резистор как элемент схемы
Резистор – элемент схемы, вносящий в цепь определенное постоянное или переменное (регулируемое) сопротивление. Элементы с постоянным сопротивлением чаще всего изготавливают в виде проволочных и пленочных резисторов. Проволочные резисторы выполняют путем навивки провода с высоким сопротивлением на керамический корпус, а пленочные – посредством напыления соответствующих металлических сплавов на керамические столбики (цилиндрики) или трубки. Резистор (рис. 2.3) характеризуют в основном следующие параметры: сопротивление и его допуск; допустимая мощность (рассеяния).
Рис. 2.3. Графическое изображение постоянного (а ) и переменного (б ) резисторов
Основной единицей сопротивления является ом (Ом]. В СССР и ПНР в крупносерийном производстве находятся резисторы с допусками на номинальное значение ±30, ±20, ±10, ±5 % и менее. Для каждого допуска существует подобранный ряд номинальных сопротивлений. Так, для допуска ± 20 % выпускают резисторы с сопротивлениями 10, 15, 22, 33, 47, 68 Ом и сопротивлениями, полученными путем умножения этих номиналов на 0,1, 10, 100, 1000 и более. Для допусков ± 10 % ряд номинальных сопротивлений в 2 раза больше. Аналогично стандартизованы номинальные значения максимально допустимой мощности резисторов, связанные с допустимой рабочей температурой. Различают резисторы, для которых максимальная выделяющаяся мощность при температуре окружающей среды 20 °C может иметь значения: 0,125, 0,25, 0,5, 1, 2, 3 Вт и более. Выделяющаяся мощность в резисторе, работающем в цепи, рассматривается обычно по току, протекающему в ней (Р = I 2R ). Помимо резисторов с постоянным сопротивлением существуют переменные или регулируемые резисторы (потенциометры). Они допускают плавную регулировку сопротивления путем вращения оси, связанном с движком, скользящим по поверхности, покрытой резистивным слоем. Изменения сопротивления в зависимости от угла поворота могут происходить по линейному, логарифмическому или экспоненциальному закону. Переменные, так же как и постоянные, резисторы могут быть выполнены проволочными или пленочными. Реальные резисторы помимо чисто активного сопротивления обладают также некоторой собственной емкостью и индуктивностью, которые образуют паразитные реактивности. Определение результирующего сопротивления при последовательном и параллельном соединении резисторов поясняется на рис. 2.4.
Рис. 2.4. Определение результирующего сопротивления при последовательном (а ) и параллельном (б ) соединении резисторов
⇐ Предыдущая12345678910Следующая ⇒ Читайте также: Где возникла философия и почему? Относительная высота сжатой зоны бетона Сущность проекции Гаусса-Крюгера и использование ее в геодезии Тарифы на перевозку пассажиров |
|
Последнее изменение этой страницы: 2021-01-14; просмотров: 94; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia. |
Индуктивное реактивное сопротивление
Если к одной и той же цепи, в которой катушка индуктивности включена последовательно с нагрузкой, приложены равные значения постоянного и переменного напряжения, в цепи постоянного тока будет протекать больший ток, чем в цепи переменного тока.
[adsense1]
Это связано с тем, что только индуцированное напряжение противодействует протеканию тока в цепи постоянного тока, когда ток приближается к своему максимальному значению, и как только он достигает установившегося значения, индуктивного эффекта больше не будет.
В цепях переменного тока ток постоянно меняется, поэтому индуктивный эффект присутствует постоянно. Рассмотрим следующие цепи постоянного и переменного тока, чтобы понять эту концепцию.
Схема
Индуктивная цепь постоянного тока
На приведенном выше рисунке, если переключатель работает от узла A к узлу B и сразу от узла B к узлу A, изменение тока протекает через цепь.
Это изменение тока индуцирует ЭДС в катушке индуктивности, пропорциональную скорости изменения тока, и эта ЭДС противодействует приложенному напряжению (что является причиной возникновения тока). Это называется самоиндукцией.
Как только ток достигнет установившегося значения, в катушке индуктивности не будет самоиндукции и, следовательно, не будет противодействия току.
[adsense2]
Индуктивная цепь переменного тока
Мы знаем, что, когда в цепь подается переменный ток, ток непрерывно изменяется с частотой сети, и, следовательно, противо-ЭДС будет соответственно изменяться.
Эта противо-ЭДС противодействует напряжению питания и, следовательно, ограничивает протекание тока. Следовательно, фактическое противодействие току, создаваемому катушкой индуктивности в цепи переменного тока, называется индуктивным реактивным сопротивлением.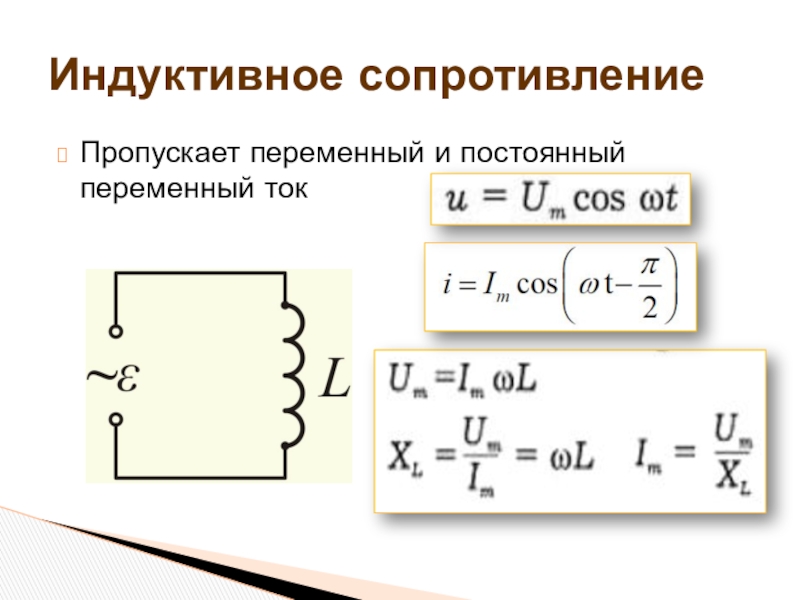
Индуктивное сопротивление в индукторе
В индуктивной цепи, наблюдая за собственной индуктивностью и ее влиянием на цепь, мы можем определить индуктивное сопротивление. Магнитное поле индуцирует в индукторе напряжение, всегда противоположное по полярности напряжению, которое его создает, т. е. приложенному напряжению.
Это противоположное напряжение ограничивает ток, протекающий через катушку индуктивности, и называется реактивным сопротивлением (X). Поскольку это реактивное сопротивление обусловлено индуктивностью, оно называется индуктивным реактивным сопротивлением (X L ). Измеряется в Омах.
Величина индуктивного сопротивления катушки индуктивности пропорциональна индуктивности и частоте приложенного напряжения. Это реактивное сопротивление можно определить по следующей формуле.
X L = 2 π fL
Где X L = индуктивное сопротивление в омах
π = 3,14
f = частота в герцах (Гц) по закону Ома индуктивное сопротивление прямо пропорционально приложенному напряжению и обратно пропорционально току. Это может быть выражено как
Это может быть выражено как
I = V/X L
Из приведенного выше уравнения видно, что увеличение напряжения или уменьшение индуктивного сопротивления вызывает увеличение тока. Точно так же ток уменьшается с увеличением индуктивного сопротивления и уменьшением напряжения.
Любая практическая катушка индуктивности должна быть изготовлена из намотанной проволоки, состоящей из некоторого сопротивления, поэтому невозможно получить чисто индуктивную катушку.
Таким образом, есть два фактора, которые препятствуют протеканию тока в индукторе, а именно сопротивление, связанное с катушкой (которая рассматривается как отдельный резистор R, включенный последовательно с индуктором), и индуктивное реактивное сопротивление, обеспечиваемое свойством индуктивности.
Таким образом, свойство ограничения полного тока катушки индуктивности в цепи переменного тока представляет собой комбинацию сопротивления и реактивного сопротивления, которая называется импедансом Z.
Это значение импеданса рассчитывается по закону Ома и выражается как
Где Z = полное сопротивление катушки индуктивности протекающему току, в омах
V = приложенное напряжение
I = ток, протекающий по цепи
Треугольник импеданса
метод, когда известны значения индуктивного сопротивления и сопротивления. На приведенной ниже диаграмме показан треугольник импеданса, который состоит из векторов сопротивления и реактивного сопротивления.
На приведенном выше рисунке вектор сопротивления расположен вдоль горизонтальной линии (поскольку сопротивление не дает фазового сдвига), а вектор индуктивного сопротивления — вдоль вертикальной линии (поскольку чистая индуктивность дает фазовый сдвиг 90 0 ).
Соединив концы этих двух векторов, получим импеданс Z. Следовательно, полное сопротивление току или импедансу можно рассчитать как
Z = √[(R) 2 +(X L ) 2 ]
, где
z = импеданс в OHMS
R = сопротивление в OHMS
x L = индуктивное реактивное сопротивление в OHMS
Также, с вышеупомянутой диаграммы,
Tan∅ = X L /R
SEN ∅= X L /R
cos∅= R/Z
Влияние частоты или индуктивности на индуктивное сопротивление
Как обсуждалось выше, индуктивное сопротивление определяется по формуле
X L = 2 л л
В данном уравнении значение индуктивного сопротивления пропорционально индуктивности и частоте.
Индуктивное сопротивление увеличивается либо с увеличением индуктивности, либо с увеличением частоты. Следовательно, индуктивное сопротивление линейно зависит от индуктивности и частоты.
Таким образом, сопротивление току увеличивается с увеличением индуктивности или частоты. Рассмотрим приведенные ниже графики для четкого понимания этой взаимосвязи.
Рассмотрим приведенный выше рисунок, на котором показана зависимость индуктивного сопротивления от частоты при фиксированной индуктивности. При нулевой частоте индуктивное сопротивление равно нулю, а по мере увеличения частоты индуктивное сопротивление увеличивается соответствующим образом.
Рассмотрим приведенный выше рисунок, на котором показана зависимость индуктивного сопротивления от индуктивности при фиксированной частоте. Можно предположить, что по мере увеличения индуктивности индуктора увеличивается и индуктивное реактивное сопротивление.
Пример индуктивного реактивного сопротивления
Рассмотрим дроссель с индуктивностью (L) 100 мкГн при рабочей частоте (f) 1 МГц. Затем индуктивная индуктивность рассчитывается следующим образом:
Затем индуктивная индуктивность рассчитывается следующим образом:
X л = 2πfL=2π×1 МГц×100 мкГн
X л = 628 Ом
RL Цепи и индуктивное сопротивление
На рисунке ниже показано соотношение между приложенным напряжением и током через индуктивную цепь. В чисто индуктивной цепи ток отстает от напряжения источника на 900. Можно также утверждать, что напряжение источника опережает ток на 90 0 в индуктивной цепи.
Когда катушка индуктивности соединена последовательно с резистором RL, получается последовательная цепь, как показано ниже. Это также можно рассматривать как индуктивность, состоящую из некоторого сопротивления (которое считается последовательным сопротивлением), поскольку оно сделано из провода.
Таким образом, ток и напряжение не точно поддерживают фазовый сдвиг 90 0 , но меньше, чем в чисто индуктивном случае, как показано ниже.
На рисунке ниже показана векторная диаграмма последовательной цепи RL, состоящая из векторов падения напряжения на резисторе и катушке индуктивности. AE представляет текущую опорную линию. AB представляет собой падение напряжения на сопротивлении, которое находится в фазе с линией тока.
AE представляет текущую опорную линию. AB представляет собой падение напряжения на сопротивлении, которое находится в фазе с линией тока.
AD представляет индуктивное падение напряжения, которое опережает ток на 90 0 . Результат этих векторов дает общее напряжение в цепи.
, применив теорему Pythagoras к треугольнику выше, мы получаем
V Всего = √ (V L 2 +V R 2 )
TAN∅ = V 2 )
7 8 2 ) 8 2 ) 8 2 ) /V RМы знаем, что V R =I×R и V L =I×X L
С помощью этих уравнений мы можем переписать V в сумме как
V всего = √((I×R) 2 +(I×X L ) 2 )
I = V/ √((R) 2 8 3 +(X 3 ) 2 ) = V/Z (А)
электрических цепей — Индуктивное реактивное сопротивление 0 для постоянного тока?
спросил
Изменено 2 года, 9 месяцев назад
Просмотрено 1к раз
$\begingroup$
Индуктивное реактивное сопротивление:
$$X_L=\omega L=2\pi f L$$
является противодействием протеканию тока индуктором.
Частота $f$ равна $0$ для постоянного тока, индуктивное сопротивление также равно $0$. Но разве обратная ЭДС, возникающая при включении выключателя, не противостоит и постоянному току? Не будет ли это считаться оппозицией?
- электрические цепи
- электрические токовые
- электромагнитные индукционные
$\endgroup$
1
$\begingroup$
Когда вы включаете выключатель, вы запускаете ток. Вы можете проанализировать ток Фурье и найти множество различных частот, для которых может быть индуктивное сопротивление. Если цепь устанавливается на постоянном токе, вы правы в том, что индуктивного сопротивления нет.
$\endgroup$
2
9{\circ}$ не совпадает по фазе с этим током, если нет других импедансов:
$$i_l=I_{max}\sin(\omega t + \phi_o)\ \to\ v_{L}=\omega LI_{max}\cos(\omega t + \phi_o). $$
$$
Когда вы замкнуть электрический переключатель, чтобы подать постоянное напряжение на индуктор, наклон тока через индуктор огромен, хотя сам ток должен начинаться с нуля. То же самое, когда вы открываете переключатель: наклон тока (уменьшение) огромен.
Как отметили @RossMillikan и комментаторы, это внезапное изменение тока можно смоделировать, удвоив разложение Фурье шага фронта прямоугольной волны. Вы получите много разных частот, поэтому у вас будет сумма реактивных сопротивлений, которая приведет к большой обратной ЭДС.
$\endgroup$
$\begingroup$
Не обязательно, если в пределах постоянной времени цепи вы меняете параметры цепи, так как при подсчете обмоток вы можете иметь постоянную индуктивность. поскольку отношение магнитного потока к току изменяется по мере добавления или вычитания обмоток, что в соответствии с законом Ленца будет противодействовать, поэтому у вас есть изменение тока, которое подпадает под действие индуктивного реактивного сопротивления.


 Определение реакций опор и моментов защемления
Определение реакций опор и моментов защемления

 Пассивные элементы не дают увеличения мощности. К ним относятся резисторы, конденсаторы, катушки индуктивности, трансформаторы, диоды[4], переключатели и т. п.
Пассивные элементы не дают увеличения мощности. К ним относятся резисторы, конденсаторы, катушки индуктивности, трансформаторы, диоды[4], переключатели и т. п.
 В случае, если в цепи течет только переменный ток, учитывается его действующее значение, а при протекании постоянного и переменного тока значение тока, требующееся для определения мощности, выделяемой в резисторе в виде тепла, определяют с учетом постоянной составляющей тока и действующего значения переменной составляющей[5]. Допустимое значение тока при определенной мощности резистора при заданной температуре окружающей среды можно рассчитать по закону Ома.
В случае, если в цепи течет только переменный ток, учитывается его действующее значение, а при протекании постоянного и переменного тока значение тока, требующееся для определения мощности, выделяемой в резисторе в виде тепла, определяют с учетом постоянной составляющей тока и действующего значения переменной составляющей[5]. Допустимое значение тока при определенной мощности резистора при заданной температуре окружающей среды можно рассчитать по закону Ома.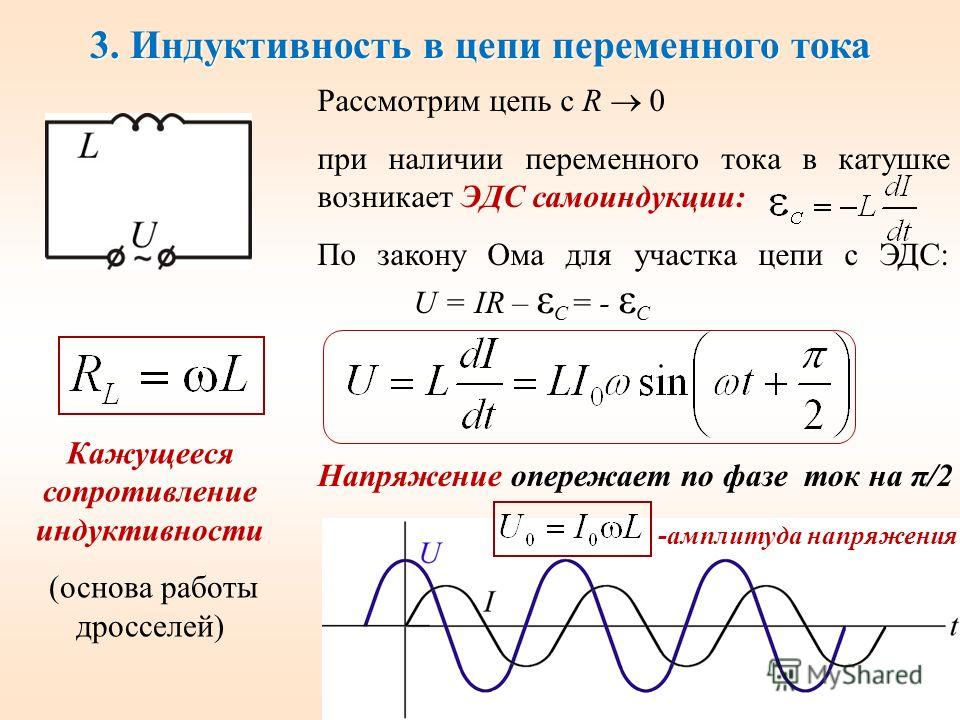 Особенно это относится к проволочным элементам. Во многих случаях применения существование реактивностей крайне нежелательно.
Особенно это относится к проволочным элементам. Во многих случаях применения существование реактивностей крайне нежелательно.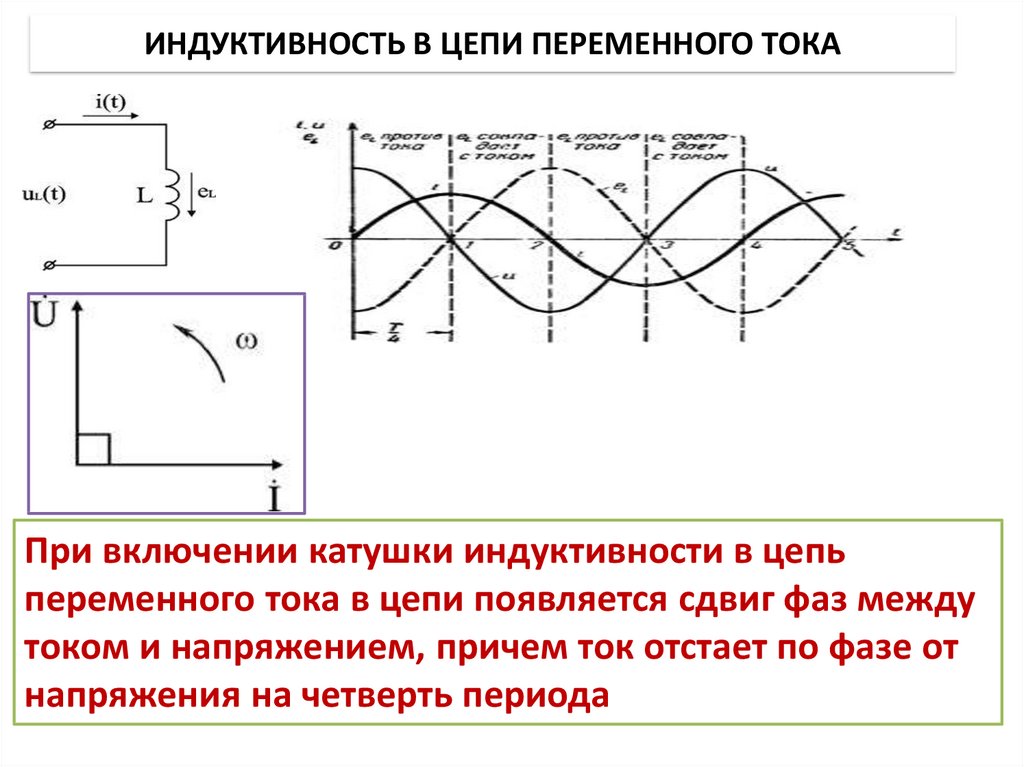 su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 161.97.168.212 (0.004 с.)
su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 161.97.168.212 (0.004 с.) 