Индуктивность как найти. Индуктивность катушки: расчет, формулы, примеры

Что такое индуктивность катушки. Как рассчитать индуктивность соленоида. Какие факторы влияют на величину индуктивности. Формулы для расчета энергии магнитного поля катушки. Примеры решения задач на индуктивность.

Что такое индуктивность катушки

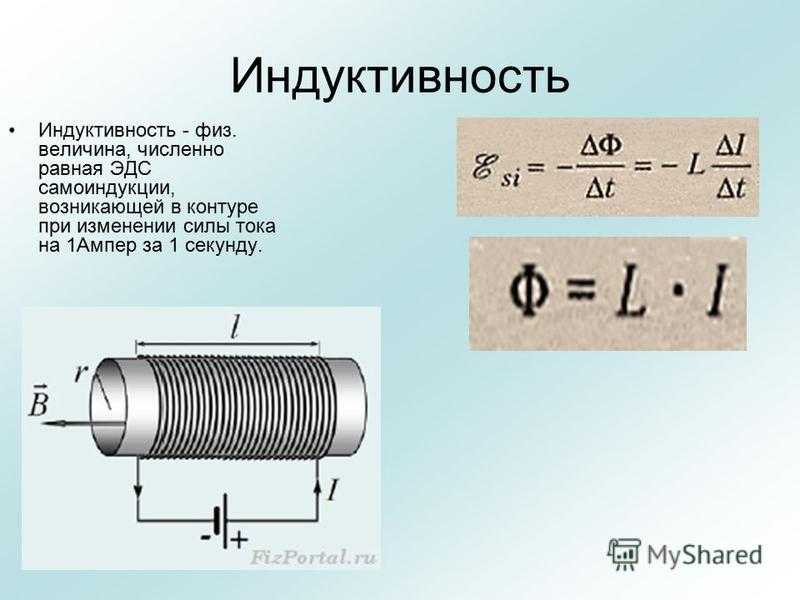
Индуктивность — это физическая величина, характеризующая способность проводника создавать магнитное поле при протекании через него электрического тока. Индуктивность обозначается буквой L и измеряется в генри (Гн).

Основные свойства индуктивности:

• Чем больше индуктивность катушки, тем сильнее она препятствует изменению тока в цепи
• При изменении тока в катушке возникает ЭДС самоиндукции, препятствующая этому изменению
• В катушке с индуктивностью накапливается энергия магнитного поля

Формула для расчета ЭДС самоиндукции:

[латекс]e = -L\frac{dI}{dt}[/латекс]

где L — индуктивность катушки, dI/dt — скорость изменения тока.

Факторы, влияющие на индуктивность катушки

Величина индуктивности катушки зависит от следующих параметров:

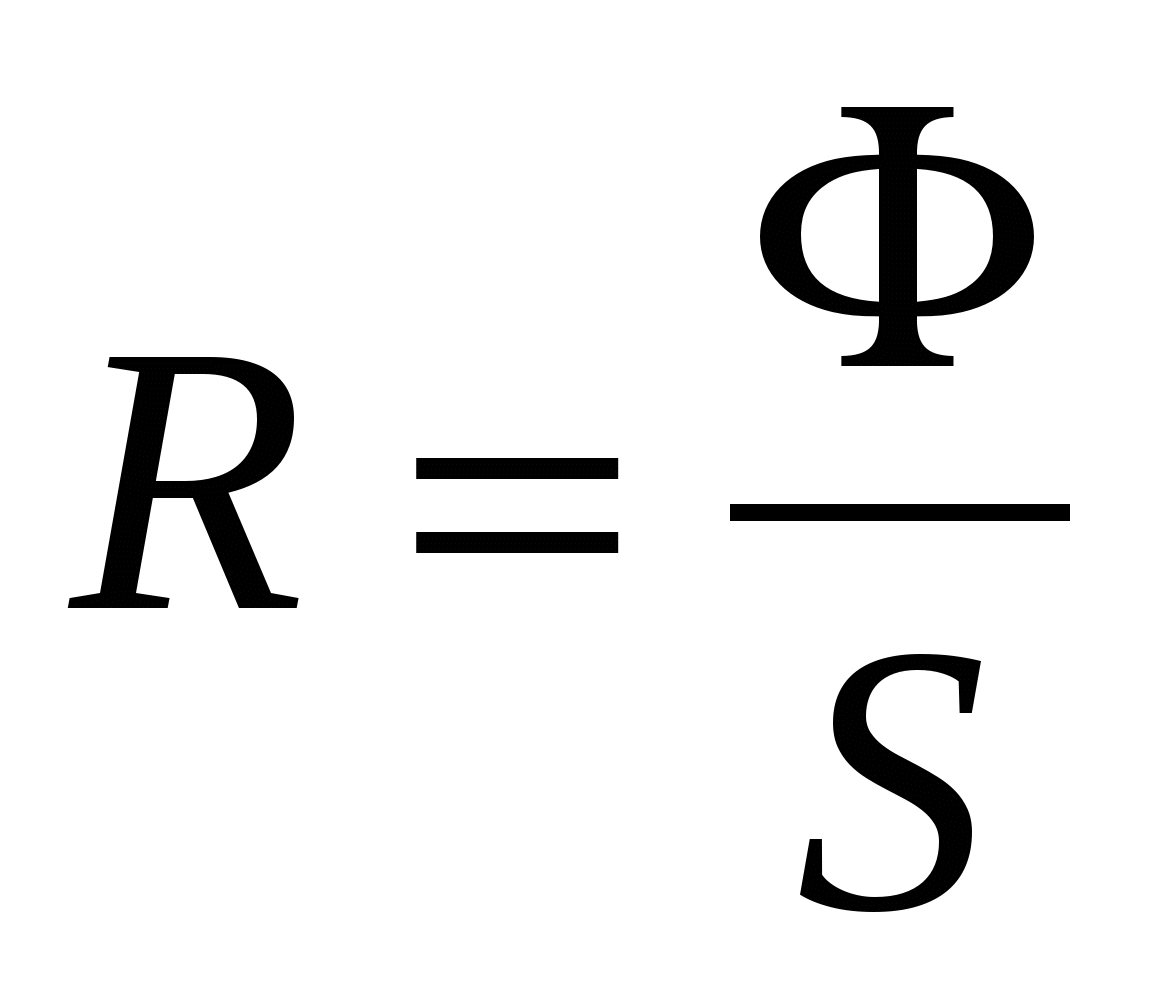
• Количество витков — чем больше витков, тем выше индуктивность
• Площадь поперечного сечения катушки — при увеличении площади индуктивность возрастает
• Длина катушки — чем короче катушка, тем выше ее индуктивность
• Наличие сердечника — ферромагнитный сердечник значительно увеличивает индуктивность
• Форма катушки — тороидальная катушка имеет большую индуктивность, чем цилиндрическая

Расчет индуктивности соленоида

Для длинного соленоида без сердечника индуктивность можно рассчитать по формуле:

[латекс]L = \frac{\mu_0 N^2 A}{l}[/латекс]

где:

• μ0 = 4π × 10^-7 Гн/м — магнитная постоянная
• N — число витков катушки
• A — площадь поперечного сечения катушки
• l — длина катушки

Энергия магнитного поля катушки

Энергия, запасенная в магнитном поле катушки с индуктивностью L при протекании тока I:

[латекс]W = \frac{1}{2}LI^2[/латекс]

Эта энергия может быть преобразована в другие виды энергии, например, в электрическую при резком отключении тока.

Примеры расчета индуктивности

Рассмотрим несколько примеров решения задач на расчет индуктивности катушек.

Пример 1

Задача: Рассчитать индуктивность соленоида длиной 20 см и диаметром 4 см, если он содержит 400 витков.

Решение:

1. Находим площадь поперечного сечения: [латекс]A = \pi r^2 = \pi (0.02 \text{ м})^2 = 1.26 \times 10^{-3} \text{ м}^2[/латекс]
2. Подставляем значения в формулу: [латекс]L = \frac{4\pi \times 10^{-7} \times 400^2 \times 1.26 \times 10^{-3}}{0.2} = 5.05 \text{ мГн}[/латекс]

Ответ: Индуктивность соленоида равна 5.05 мГн.

Пример 2

Задача: В катушке индуктивностью 0.5 Гн сила тока равномерно возрастает от 0 до 5 А за 0.1 с. Определить ЭДС самоиндукции.

Решение:

1. Находим скорость изменения тока: [латекс]\frac{dI}{dt} = \frac{5 \text{ А} — 0 \text{ А}}{0.1 \text{ с}} = 50 \text{ А/с}[/латекс]
2. Подставляем в формулу ЭДС самоиндукции: [латекс]e = -L\frac{dI}{dt} = -0.5 \text{ Гн} \times 50 \text{ А/с} = -25 \text{ В}[/латекс]

Ответ: ЭДС самоиндукции равна 25 В и направлена против изменения тока.

Применение индуктивности в технике

Катушки индуктивности широко применяются в различных областях техники:

• В электрических фильтрах для разделения сигналов разной частоты
• В колебательных контурах радиоприемников и передатчиков
• В импульсных источниках питания для накопления энергии
• В системах зажигания автомобилей для создания высоковольтных импульсов
• В электромагнитных реле для создания магнитного поля

Взаимная индуктивность катушек

При расположении двух катушек рядом друг с другом возникает явление взаимной индукции. Изменение тока в одной катушке вызывает ЭДС индукции в другой катушке.

Взаимная индуктивность M определяется по формуле:

[латекс]e_2 = -M\frac{dI_1}{dt}[/латекс]

где e2 — ЭДС, индуцируемая во второй катушке, dI1/dt — скорость изменения тока в первой катушке.

Взаимная индуктивность зависит от взаимного расположения катушек, их размеров и формы. Она используется в трансформаторах для передачи энергии между обмотками.

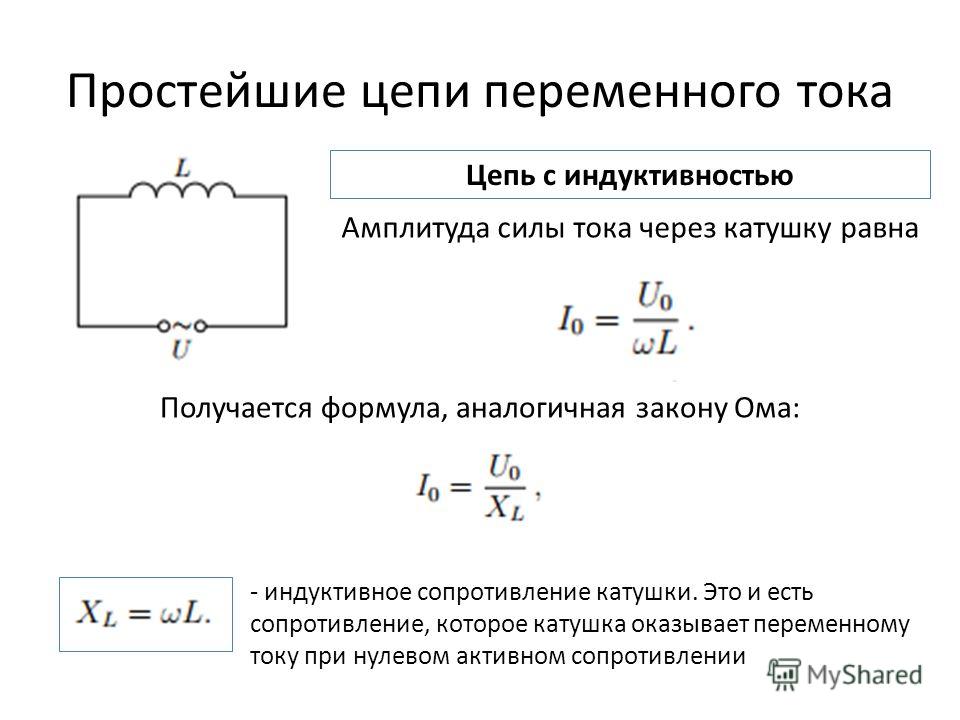
Индуктивность в цепях переменного тока

В цепях переменного тока катушка индуктивности создает индуктивное сопротивление:

[латекс]X_L = \omega L = 2\pi f L[/латекс]

где ω — угловая частота, f — частота переменного тока.

Индуктивное сопротивление приводит к сдвигу фаз между током и напряжением. Ток в цепи с индуктивностью отстает по фазе от напряжения на 90°.

Заключение

Индуктивность — важная характеристика электрических цепей, особенно в цепях переменного тока и импульсных устройствах. Понимание свойств индуктивности необходимо для расчета и проектирования различных электротехнических устройств.

Основные формулы для расчета индуктивности и связанных с ней величин:

• Индуктивность соленоида: [латекс]L = \frac{\mu_0 N^2 A}{l}[/латекс]
• ЭДС самоиндукции: [латекс]e = -L\frac{dI}{dt}[/латекс]
• Энергия магнитного поля: [латекс]W = \frac{1}{2}LI^2[/латекс]
• Индуктивное сопротивление: [латекс]X_L = 2\pi f L[/латекс]

Эти соотношения позволяют рассчитывать параметры катушек индуктивности и анализировать их поведение в электрических цепях.

Индуктивность | Страница 2 из 3 | Electronov.net

Индуктивность обладает комплексным импедансом (сопротивлением):

где:

j — мнимая единица;

ω — циклическая частота (рад/с) протекающего синусоидального тока;

f — частота в Гц;

L — индуктивность катушки (Генри).

Комплексный импеданс в общем случае записывается как сумма активного и реактивного сопротивлений:

Отсюда следует, что активное сопротивление идеальной индуктивности равно нулю, а реактивное сопротивление равно: Для постоянного тока частота равна нулю, следовательно, реактивное сопротивление равно нулю. Индуктивность по определению численно равна отношению создаваемого током потока магнитного поля, пронизывающего катушку, к силе протекающего тока. Отсюда следует, что применять катушки индуктивности имеет смысл только в цепях переменного тока.

Если Вы не привыкли слепо доверять формулам, то следующий абзац для Вас:

Спойлер

Чтобы разобраться, почему с ростом частоты тока у индуктивности растет реактивное сопротивление, необходимо вспомнить явление самоиндукции, которое можно сформулировать в 2 эквивалентных вариантах:

• Возникновение магнитного потока самоиндукции при протекании по цепи тока;
• Возникновение ЭДС индукции в том контуре, по которому протекает переменный ток.

По Закону электромагнитной индукции Фарадея, ЭДС индукции можно записать как:

где:

ε_i — величина ЭДС индукции;

Φ — величина магнитного потока.

В случае контура, содержащего N витков, используется понятие потокосцепления Ψ_s самоиндукции (Ψ_s = NΦ_s).

С учетом данных формул, можно записать ЭДС и ток самоиндукции:

Знак минуса показывает, что направление тока самоиндукции противоположно направлению основного тока.

Из этих формул следует, что любые изменения тока в цепи тормозятся, и тем сильнее, чем больше индуктивность цепи и меньше ее сопротивление.

Если сформулировать по научному:

Правило Ленца для явления самоиндукции – ток самоиндукции препятствует любым изменениям основного тока, текущего по цепи.

Можно также сказать, что индуктивность цепи является мерой ее электрической инертности, подобно тому, как масса в механике является мерой инертности тела при его поступательном движении.

И как Вы уже наверняка догадались, природа реактивного сопротивления индуктивности заключена в явлении ЭДС и тока самоиндукции, а скорость изменения величины тока – это его частота.

Схема замещения не идеальной (реальной) индуктивности:Рисунок 1 — Схема замещения неидеальной (реальной) индуктивности.

Сопротивление потерь:

В катушках индуктивности помимо основного эффекта взаимодействия тока и магнитного поля, наблюдаются паразитные эффекты, вследствие которых импеданс катушки не является чисто реактивным. Наличие паразитных эффектов ведет к появлению потерь в катушке, оцениваемых сопротивлением потерь:

где:

R_CL – диэлектрические потери;

R_L – индуктивные потери.

Диэлектрические потери вызваны магнитными свойствами диэлектрика, а также паразитной емкости, которая образуется между витками, вследствие наличия изоляции обмоточного провода, и соответственно появляются межвитковые утечки и прочие потери, характерные для диэлектриков конденсаторов. Однако для современных катушек общего применения эти потери пренебрежимо малы.

Индуктивные потери складываются из следующих составляющих:

• Потери в проводах:

В свою очередь, потери в проводах вызваны тремя причинами:

• Провода обмотки обладают омическим (активным) сопротивлением.
• Сопротивление провода обмотки возрастает с ростом частоты, что обусловлено поверхностным эффектом (скин-эффектом). Суть эффекта состоит в вытеснении тока в поверхностные слои провода. Как следствие, уменьшается полезное сечение проводника и растет сопротивление. Подробнее о поверхностном эффекте можно прочитать [гиперссылка]здесь[/гиперссылка].
• В проводах обмотки, свитой в спираль, проявляется эффект близости (англ. proximity effect), суть которого состоит в вытеснении тока под воздействием вихревых токов и магнитного поля, которые появляются из-за явления взаимной индуктивности, к периферии намотки. В результате сечение, по которому протекает ток, принимает серповидную форму, что ведет к дополнительному возрастанию сопротивления провода. Подробнее о эффекте близости можно прочитать [гиперссылка]здесь[/гиперссылка].

• Потери на перемагничивание ферромагнитного сердечника:

Данные потери связаны с эффектом гистерезиса в ферромагнетиках.

• Потери на вихревые токи (токи Фуко):

Переменное магнитное поле индуцирует вихревые ЭДС в окружающих проводниках, т.е. витках и сердечнике. При этом возникают вихревые (т.е. замкнутые в кольце) токи — токи Фуко, которые по физической природе ничем не отличаются от индукционных токов, возникающих в линейных проводах. Помимо электрических потерь, вихревые токи также разогревают каркас и обмотку катушки.

Резонансная частота индуктивности:

При f > f_р катушка индуктивности в цепи переменного тока ведет себя как конденсатор. Следовательно, индуктивность целесообразно использовать лишь на частотах f < f_p, на которых ее сопротивление носит индуктивный характер. Обычно максимальная рабочая частота индуктивности примерно в 2—3 раза ниже резонансной.

Добротность:

Добротность катушки индуктивности определяется отношением между ее реактивным и активным сопротивлениями:

Повышение добротности достигается оптимальным выбором диаметра провода, увеличением размеров катушки индуктивности и применением сердечников с высокой магнитной проницаемостью и малыми потерями, намоткой вида «универсаль», применением посеребренного провода, применением многожильного провода вида «литцендрат» для снижения потерь, вызванных скин-эффектом. Подробнее о проводе вида «литцендрат» можно прочитать [гиперссылка]здесь[/гиперссылка].

Страниц: 1 2 3

Электромагнитная индукция | Формулы по физике

Индуктивные электродвижущая сила (ЭДС)

Найти

  Известно, что:

     ΕΦt =   

Вычислить ‘Ε’

Индуктивные электродвижущая сила (ЭДС)

Найти

  Известно, что:

     ΕΦNt =   

Вычислить ‘Ε’

Индуктивные электродвижущая сила (ЭДС) в прямолинейном проводнике, движущемся в поле

Найти

  Известно, что:

     ΕvBla =   

Вычислить ‘Ε’

Магнитный поток и индуктивность

Найти

  Известно, что:

     ΦLI =   

Вычислить ‘Φ’

Электродвижущая сила самоиндукции

Найти

  Известно, что:

     ΕLIt =   

Вычислить ‘Ε’

Индуктивность соленоида

Найти

  Известно, что:

     Lμμ0SNl =   

Вычислить ‘L’

Индуктивность соленоида

Найти

  Известно, что:

     Lμμ0nSl =   

Вычислить ‘L’

Индуктивность соленоида

Найти

  Известно, что:

     Lμμ0nV =   

Вычислить ‘L’

Энергия магнитного поля соленоида

Найти

  Известно, что:

     WLI =   

Вычислить ‘W’

Энергия магнитного поля соленоида

Найти

  Известно, что:

     Wμμ0SNl =   

Вычислить ‘W’

Энергия магнитного поля соленоида

Найти

  Известно, что:

     Wμμ0nlV =   

Вычислить ‘W’

Энергия магнитного поля соленоида

Найти

  Известно, что:

     Wμμ0HSl =   

Вычислить ‘W’

Энергия магнитного поля соленоида

Найти

  Известно, что:

     Wμμ0HV =   

Вычислить ‘W’

Энергия магнитного поля соленоида

Найти

  Известно, что:

     WBVμμ0 =   

Вычислить ‘W’

Энергия магнитного поля соленоида

Найти

  Известно, что:

     WBHV =   

Вычислить ‘W’

Объемная плотность электромагнитной энергии

Найти

  Известно, что:

     Wε0εEBμμ0 =   

Вычислить ‘W’

23.

9 Индуктивность – Колледж физики

Резюме

• Рассчитать индуктивность катушки индуктивности.
• Рассчитайте энергию, запасенную в катушке индуктивности.
• Рассчитайте ЭДС, создаваемую катушкой индуктивности.

Индукция – это процесс, при котором ЭДС индуцируется изменением магнитного потока. До сих пор обсуждалось множество примеров, некоторые из которых более эффективны, чем другие. Трансформаторы, например, спроектированы таким образом, чтобы быть особенно эффективными при наведении желаемого напряжения и тока с очень небольшой потерей энергии в другие формы. Существует ли полезная физическая величина, связанная с тем, насколько «эффективно» данное устройство? Ответ положительный, и эта физическая величина называется 9.0013 индуктивность .

Взаимная индуктивность — это действие закона индукции Фарадея для одного устройства на другое, например, первичная катушка при передаче энергии вторичной обмотке в трансформаторе. См. рис. 1, где простые катушки наводят друг в друге ЭДС.

Рисунок 1. Эти катушки могут индуцировать ЭДС друг в друге, как неэффективный трансформатор. Их взаимная индуктивность М указывает на эффективность связи между ними. Здесь видно, что изменение тока в катушке 1 индуцирует ЭДС в катушке 2. (Обратите внимание, что « E ₂ индуцируется» представляет собой ЭДС индукции в катушке 2.)

Во многих случаях, когда геометрия устройств фиксирована, поток изменяется при изменении тока. Поэтому мы сосредоточимся на скорости изменения тока, [латекс]\жирныйсимвол{\Delta I / \Delta t}[/латекс], как на причине индукции. Изменение тока [latex]\boldsymbol{I_1}[/latex] в одном устройстве, катушка 1 на рисунке, индуцирует [latex]\boldsymbol{\textbf{emf}_2}[/latex] в другом. Выразим это в виде уравнения как

[латекс]\boldsymbol{\textbf{emf}_2 = -M}[/латекс] [латекс]\boldsymbol{\frac{\Delta I_1}{\Delta t}}[/латекс],

, где [латекс]\boldsymbol{M}[/латекс] определяется как взаимная индуктивность между двумя устройствами. Знак минус является выражением закона Ленца. Чем больше взаимная индуктивность [латекс]\boldsymbol{M}[/латекс], тем эффективнее связь. Например, катушки на рисунке 1 имеют маленький [латекс]\жирныйсимвол{M}[/латекс] по сравнению с катушками трансформатора в главе 23.7. Рисунок 3. Единицы для [латекс]\жирныйсимвол{М}[/латекс] равны [ латекс]\boldsymbol{(\textbf{V} \cdot \;\textbf{s})/ \textbf{A} = \Omega \cdot \;\textbf{s}}[/latex], который называется Генри (H), в честь Джозефа Генри. То есть [латекс]\boldsymbol{1 \;\textbf{H} = 1 \Omega \cdot \;\textbf{s}}[/latex].

Природа здесь симметрична. Если мы изменим ток [latex]\boldsymbol{I_2}[/latex] в катушке 2, мы индуцируем [latex]\boldsymbol{\textbf{emf}_1}[/latex] в катушке 1, которая определяется как

[латекс]\boldsymbol{\textbf{emf}_1 = -M}[/латекс] [латекс]\boldsymbol{\frac{\Delta I_2}{\Delta t}}[/латекс],

, где [латекс]\жирный символ{М}[/латекс] — то же, что и для обратного процесса. Трансформаторы работают в обратном направлении с той же эффективностью или взаимной индуктивностью [латекс]\boldsymbol{M}[/латекс] .

Большая взаимная индуктивность [латекс]\boldsymbol{M}[/латекс] может быть или не быть желательной. Мы хотим, чтобы трансформатор имел большую взаимную индуктивность. Но такой прибор, как электрическая сушилка для белья, может индуцировать на своем корпусе опасную ЭДС, если взаимная индуктивность между его катушками и корпусом велика. Один из способов уменьшить взаимную индуктивность [латекс]\boldsymbol{M}[/латекс] – это встречная обмотка катушек, чтобы нейтрализовать создаваемое магнитное поле. (См. рис. 2.)

Рисунок 2. Нагревательные спирали электрической сушилки для белья могут быть встречно намотаны, так что их магнитные поля компенсируют друг друга, что значительно снижает взаимную индуктивность с корпусом сушилки.

Самоиндукция , действие закона Фарадея об индукции устройства на себя, также существует. Когда, например, ток через катушку увеличивается, магнитное поле и поток также увеличиваются, индуцируя противо-ЭДС, как того требует закон Ленца. И наоборот, если ток уменьшается, индуцируется ЭДС, препятствующая уменьшению. Большинство устройств имеют фиксированную геометрию, поэтому изменение потока полностью связано с изменением тока [латекс]\boldsymbol{\Delta I}[/латекс] через устройство. ЭДС индукции связана с физической геометрией устройства и скоростью изменения тока. Это дается

[латекс]\boldsymbol{\textbf{emf}= -L}[/латекс] [латекс]\boldsymbol{\frac{\Delta I}{\Delta t}}[/латекс],

, где [latex]\boldsymbol{L}[/latex] – собственная индуктивность устройства. Устройство, обладающее значительной собственной индуктивностью, называется катушкой индуктивности и обозначено символом на рисунке 3.

Рис. 3.

Знак минус является выражением закона Ленца, указывающим, что ЭДС противодействует изменению тока. Единицами самоиндукции являются генри (Гн), как и для взаимной индуктивности. Чем больше собственная индуктивность [латекс]\boldsymbol{L}[/латекс] устройства, тем больше его сопротивление любому изменению тока через него. Например, большая катушка с большим количеством витков и железным сердечником имеет большой [латекс]\жирныйсимвол{L}[/латекс] и не позволит току быстро измениться. Чтобы избежать этого эффекта, необходимо добиться небольшого [латекса]\жирного символа{L}[/латекса], например, путем встречной намотки катушек, как показано на рис. 2.9.0015

Катушка индуктивности 1 Гн представляет собой большую катушку индуктивности. Чтобы проиллюстрировать это, рассмотрим устройство с [латекс]\boldsymbol{L = 1,0 \;\textbf{H}}[/латекс], через которое протекает ток 10 А. Что произойдет, если мы попытаемся отключить ток быстро, возможно, всего за 1,0 мс? ЭДС, заданная формулой [латекс]\жирныйсимвол{\текстбф{ЭДС} = -L(\Delta I/\Delta t)}[/латекс], будет препятствовать изменению. Таким образом, ЭДС будет индуцироваться следующим образом: A})/(1,0 \;\textbf{ms})]=10 000 \;\textbf{V}}[/latex]. Положительный знак означает, что это большое напряжение направлено в том же направлении, что и ток, противодействуя его уменьшению. Такие большие ЭДС могут вызывать искрение, повреждая коммутационное оборудование, поэтому может потребоваться более медленное изменение тока.

Для такого большого наведенного напряжения есть применение. Вспышки камеры используют батарею, две катушки индуктивности, которые функционируют как трансформатор, и систему переключения или осциллятор для создания больших напряжений. (Помните, что нам нужно изменяющееся магнитное поле, вызванное изменяющимся током, чтобы индуцировать напряжение в другой катушке.) Система генератора будет делать это много раз, когда напряжение батареи увеличится до более чем одной тысячи вольт. (Вы можете услышать пронзительный вой трансформатора во время зарядки конденсатора.) Конденсатор сохраняет высокое напряжение для последующего использования при питании вспышки. (См. рис. 4.)

Рисунок 4. Благодаря быстрому переключению катушки индуктивности батареи напряжением 1,5 В можно использовать для наведения ЭДС в несколько тысяч вольт.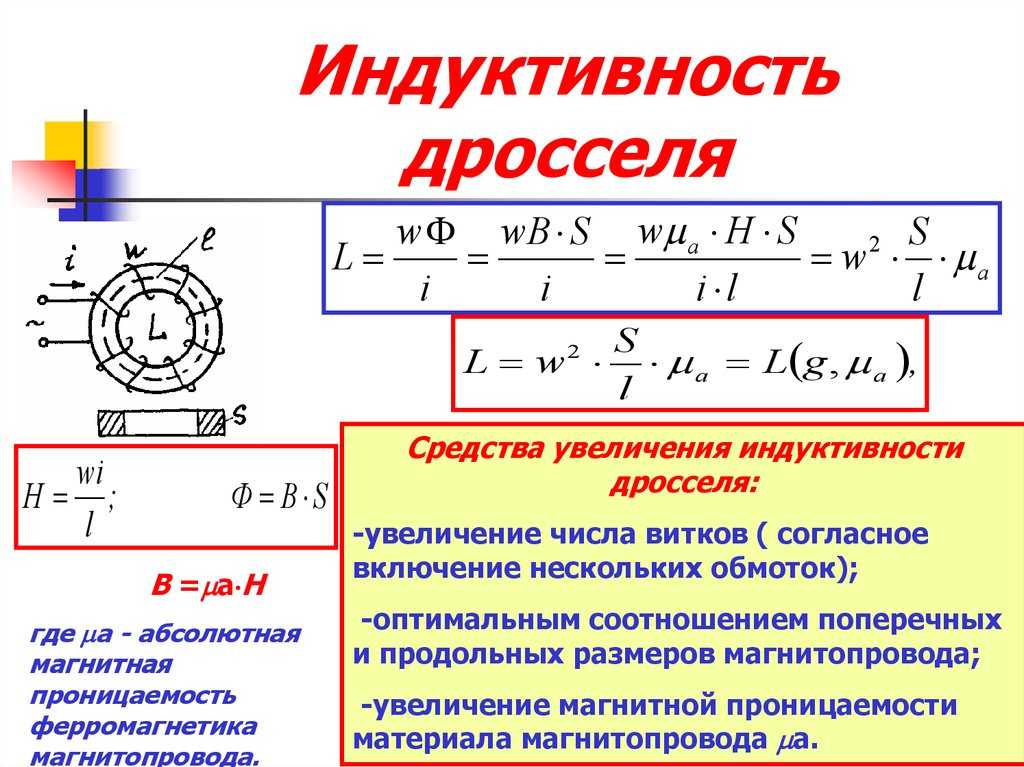 Это напряжение можно использовать для хранения заряда в конденсаторе для последующего использования, например, во вспышке фотоаппарата.

Можно рассчитать [латекс]\boldsymbol{L}[/латекс] для индуктора, зная его геометрию (размер и форму) и зная создаваемое им магнитное поле. В большинстве случаев это сложно из-за сложности создаваемого поля. Итак, в этом тексте индуктивность [латекс]\жирный символ{L}[/латекс] обычно является заданной величиной. Единственным исключением является соленоид, потому что он имеет очень однородное поле внутри, почти нулевое поле снаружи и простую форму. Поучительно вывести уравнение для его индуктивности. Начнем с того, что заметим, что ЭДС индукции задается законом индукции Фарадея как собственной индуктивности, как [латекс]\boldsymbol{\textbf{ЭДС}=-L(\Delta I/ \Delta t)}[/latex]. Приравнивая эти выходы

[латекс]\boldsymbol{\textbf{emf} = -N}[/латекс] [латекс]\boldsymbol{\frac{\Delta \phi}{\Delta t}}[/латекс] [латекс]\boldsymbol{ = -L}[/latex] [латекс]\boldsymbol{\frac{\Delta I}{\Delta t}}[/latex].

Решение для [латекс]\boldsymbol{L}[/латекс] дает

[латекс]\boldsymbol{L = N}[/латекс] [латекс]\boldsymbol{\frac{\Delta \phi}{\Delta I}}[/latex].

Это уравнение для собственной индуктивности [латекс]\boldsymbol{L}[/латекс] устройства всегда справедливо. Это означает, что самоиндукция [латекс]\boldsymbol{L}[/латекс] зависит от того, насколько эффективен ток в создании потока; чем эффективнее, тем больше [латекс]\boldsymbol{\Delta \phi \Delta I}[/latex].

Воспользуемся этим последним уравнением, чтобы найти выражение для индуктивности соленоида. Поскольку площадь [латекс]\жирныйсимвол{А}[/латекс] соленоида фиксирована, изменение потока составляет [латекс]\жирныйсимвол{\Дельта \фи = \Дельта (ВА) = А \Дельта В}[/ латекс]. Чтобы найти [латекс]\boldsymbol{\Delta B}[/латекс], заметим, что магнитное поле соленоида определяется выражением [латекс]\жирный символ{В = \mu _0 nI = \mu 0 \frac{NI} {\ell}}[/латекс]. (Здесь [латекс]\boldsymbol{n = N/ \ell}[/latex], где [латекс]\boldsymbol{N}[/латекс] — количество витков, а [латекс]\boldsymbol{\ell}[/ латекс] — длина соленоида. ) Изменяется только ток, так что [латекс]\жирныйсимвол{\Delta \phi = A \Delta B = \mu_0 NA \frac{\Delta I}{\ell}}[/latex] . Замена [латекс]\boldsymbol{\Delta \phi}[/latex] на [латекс]\boldsymbol{L = N \frac{\Delta \phi}{\Delta I}}[/latex] дает 92A}{\ell}}[/latex][latex]\boldsymbol{(\textbf{соленоид})}.[/latex]

Это собственная индуктивность соленоида с площадью поперечного сечения [латекс]\boldsymbol{A}[/латекс] и длиной [латекс]\boldsymbol{\ell}[/латекс]. Обратите внимание, что индуктивность зависит только от физических характеристик соленоида, соответствующих его определению.

Пример 1. Расчет собственной индуктивности соленоида среднего размера

Рассчитайте собственную индуктивность соленоида длиной 10,0 см и диаметром 4,00 см с 200 витками. 92) {0,100 \;\textbf{м}} \\[1em] & \boldsymbol{0,632 \;\textbf{мГн}} \end{массив}[/latex].

Обсуждение

Этот соленоид средних размеров. Его индуктивность около миллигенри также считается умеренной.

Одно из распространенных применений индуктивности используется в светофорах, которые могут определять, когда транспортные средства ожидают на перекрестке. Электрическая цепь с индуктором размещена на дороге под местом остановки ожидающего автомобиля. Кузов автомобиля увеличивает индуктивность, и схема меняется, посылая сигнал светофору изменить цвет. Точно так же металлоискатели, используемые для обеспечения безопасности в аэропортах, используют ту же технику. Катушка или индуктор в корпусе металлоискателя действует как передатчик и приемник. Импульсный сигнал в катушке передатчика индуцирует сигнал в приемнике. На самоиндукцию цепи влияет любой металлический предмет на пути. Такие детекторы могут быть настроены на чувствительность, а также могут указывать примерное местонахождение обнаруженного на человеке металла. (Но они не смогут обнаружить пластиковую взрывчатку, подобную той, что была обнаружена на «подрывнике в нижнем белье».) См. рис. 5.

Рисунок 5 Знакомые ворота безопасности в аэропорту могут не только обнаруживать металлы, но и указывать их приблизительную высоту над полом. (кредит: Alexbuirds, Wikimedia Commons)

Из закона Ленца мы знаем, что индуктивности противодействуют изменениям тока. Есть альтернативный взгляд на эту оппозицию, основанный на энергии. Энергия хранится в магнитном поле. Требуется время, чтобы накопить энергию, и также нужно время, чтобы истощить энергию; следовательно, существует оппозиция быстрым изменениям. В индукторе магнитное поле прямо пропорционально току и индуктивности устройства. Можно показать, что 92 = 0,284 \;\textbf{J}}. \end{array}[/latex]

Обсуждение

Этого количества энергии определенно достаточно, чтобы вызвать искру, если ток внезапно отключится. Он не может быть построен мгновенно, если только потребляемая мощность не бесконечна.

• Индуктивность — это свойство устройства, которое показывает, насколько эффективно оно индуцирует ЭДС в другом устройстве.
• Взаимная индуктивность — это действие двух устройств, индуцирующих ЭДС друг в друге.
• Изменение тока [латекс]\boldsymbol{\Delta I_1 / \Delta t}[/латекс] в одном индуцирует ЭДС [латекс]\boldsymbol{\textbf{ЭДС}_2}[/латекс] во втором:

  [латекс]\boldsymbol{\textbf{emf}_2 = — M}[/latex][латекс]\boldsymbol{\frac{\Delta I_1}{\Delta t}}[/latex],

  , где [латекс]\жирныйсимвол{М}[/латекс] определяется как взаимная индуктивность между двумя устройствами, а знак минус соответствует закону Ленца.

• Симметрично, изменение тока [латекс]\boldsymbol{\Delta I_2/ \Delta t}[/латекс] через второе устройство индуцирует ЭДС [латекс]\boldsymbol{\textbf{ЭДС}_1[/латекс] в первое:

  [латекс]\boldsymbol{\textbf{emf}_1 = — M}[/latex][латекс]\boldsymbol{\frac{\Delta I_2}{\Delta t}}[/latex] ,

  , где [латекс]\boldsymbol{M}[/латекс] — та же взаимная индуктивность, что и в обратном процессе.

• Текущие изменения в устройстве индуцируют ЭДС в самом устройстве.
• Самоиндукция — это эффект устройства, индуцирующего ЭДС само по себе.
• Прибор называется индуктором, а ЭДС, индуцируемая в нем изменением тока через него, равна

  [латекс]\boldsymbol{ЭДС = -L}[/латекс][латекс]\boldsymbol{\frac{\Delta I}{\Delta t}}[/latex],

  , где [latex]\boldsymbol{L}[/latex] — собственная индуктивность катушки индуктивности, а [latex]\boldsymbol{\Delta I / \Delta t}[/latex] — скорость изменения тока через Это. Знак минус указывает на то, что ЭДС противодействует изменению тока, как того требует закон Ленца.

• Единицей собственной и взаимной индуктивности является генри (H), где [latex]\boldsymbol{1 \;\textbf{H} = 1 \Omega \cdot \;\textbf{s}}[/latex].
• Самоиндукция [латекс]\boldsymbol{L}[/латекс] катушки индуктивности пропорциональна тому, насколько поток изменяется с током. Для [латексного]\boldsymbol{N}[/латексного]-виткового индуктора

  [латекс]\boldsymbol{L = N}[/латекс][латекс]\boldsymbol{\frac{\Delta \phi}{\Delta T}}[/latex]

• Самоиндукция соленоида 92}[/латекс].

Задачи и упражнения

1: Две катушки расположены близко друг к другу в физической лаборатории, чтобы продемонстрировать закон индукции Фарадея. Ток 5,00 А в одном отключается за 1,00 мс, индуцируя ЭДС 9,00 В в другом. Чему равна их взаимная индуктивность?

2: Если две катушки, расположенные рядом, имеют взаимную индуктивность 5,00 мГн, какое напряжение индуцируется в одной, когда ток 2,00 А в другой отключается через 30,0 мс?

3: Ток 4,00 А через катушку индуктивности 7,50 мГн отключается за 8,33 мс. Какая ЭДС индуцирует противодействие этому?

4: Устройство включено, и через него через 0,100 мс проходит ток 3,00 А. Чему равна собственная индуктивность прибора, если ей противодействует ЭДС наведенного напряжения 150 В?

5: Начиная с [латекс]\boldsymbol{\textbf{эдс}_2 = -M \frac{\Delta I_1}{\Delta t}}[/latex], покажите, что единицами измерения индуктивности являются [латекс ]\boldsymbol{(\textbf{V} \cdot \;\textbf{s})/ \textbf{A} = \Omega \cdot \;\textbf{s}}[/latex].

6: Фотовспышки заряжают конденсатор до высокого напряжения, быстро включая и выключая ток через катушку индуктивности. За какое время необходимо включить или выключить ток 0,100 А через катушку индуктивности 2,00 мГн, чтобы индуцировать ЭДС 500 В?

7: Большой исследовательский соленоид имеет собственную индуктивность 25,0 Гн. а) Какая ЭДС наведения препятствует его отключению, если ток 100 А через него отключается за 80,0 мс? б) Сколько энергии запасается в катушке индуктивности при полном токе? в) С какой скоростью в ваттах должна рассеиваться энергия, чтобы ток выключился за 80,0 мс? (d) Принимая во внимание ответ на последнюю часть, удивительно ли, что так быстро закрыть его сложно?

8: (a) Рассчитайте собственную индуктивность соленоида длиной 50 см и диаметром 10 см, имеющего 1000 витков. б) Сколько энергии запасается в этом индукторе при протекании через него тока силой 20,0 А? в) Как быстро его можно выключить, если ЭДС индукции не может превышать 3,00 В?

9: Прецизионный лабораторный резистор изготовлен из витка проволоки диаметром 1,50 см и длиной 4,00 см и имеет 500 витков. а) Чему равна его собственная индуктивность? б) Какая средняя ЭДС индуцируется, если ток 12,0 А через него включается за 5,00 мс (одна четвертая периода для переменного тока частотой 50 Гц)? в) Какова его индуктивность, если его укоротить наполовину и намотать встречно (два слоя по 250 витков в противоположных направлениях)?

10: Нагревательные спирали в фене имеют диаметр 0,800 см, общую длину 1,00 м и 400 витков. а) Какова их полная собственная индуктивность, если предположить, что они действуют как одиночный соленоид? б) Сколько энергии запасается в них при токе 6,00 А? (c) Какая средняя ЭДС препятствует их отключению, если это делается за 5,00 мс (одна четвертая часть цикла для переменного тока с частотой 50 Гц)?

11: Когда ток 20,0 А через индуктор отключается за 1,50 мс, индуцируется ЭДС 800 В, противодействующая изменению. Каково значение собственной индуктивности?

12: Как быстро может быть отключен ток 150 А через дроссель 0,250 Гн, если ЭДС индукции не может превышать 75,0 В?

13: Integrated Concepts

Очень большой сверхпроводящий соленоид, например, используемый в МРТ, сохраняет 1,00 МДж энергии в своем магнитном поле при токе 100 А. а) Найдите его индуктивность. (б) Если катушки «идут нормально», они приобретают сопротивление и начинают рассеивать тепловую энергию. Какое повышение температуры произойдет, если вся запасенная энергия пойдет на нагрев магнита массой 1000 кг, если его средняя удельная теплоемкость равна 9{\circ} \textbf{C}}[/латекс]?

14: необоснованные результаты

Катушка индуктивности 25,0 Гн отключает ток 100 А за 1,00 мс. а) Какое напряжение индуцируется, чтобы противостоять этому? б) Что неразумного в этом результате? (c) Какое предположение или предпосылка являются ответственными?

индуктивность

свойство устройства, описывающее, насколько эффективно оно создает ЭДС в другом устройстве

взаимная индуктивность

насколько эффективно пара устройств индуцирует ЭДС друг в друге

Генри

единица индуктивности; [латекс]\boldsymbol{1 \;\textbf{H} = 1 \;\Omega \cdot \;\textbf{s}}[/latex]

самоиндукция

насколько эффективно устройство создает ЭДС само по себе

индуктор

устройство со значительной собственной индуктивностью

энергия, запасенная в катушке индуктивности

не требует пояснений; рассчитано по формуле [латекс]\жирныйсимвол{Е_{\текстбф{инд}} = \фракция{1}{2} LI^2}[/латекс]

 

23.

9 Индуктивность – College Physics

Глава 23 Электромагнитная индукция, цепи переменного тока и электрические технологии

Резюме

• Рассчитать индуктивность катушки индуктивности.
• Рассчитайте энергию, запасенную в катушке индуктивности.
• Рассчитайте ЭДС, создаваемую катушкой индуктивности.

Индукция – это процесс, при котором ЭДС индуцируется изменением магнитного потока. До сих пор обсуждалось множество примеров, некоторые из которых более эффективны, чем другие. Трансформаторы, например, спроектированы таким образом, чтобы быть особенно эффективными при наведении желаемого напряжения и тока с очень небольшой потерей энергии в другие формы. Существует ли полезная физическая величина, связанная с тем, насколько «эффективно» данное устройство? Ответ положительный, и эта физическая величина называется 9.0013 индуктивность .

Взаимная индуктивность — это действие закона индукции Фарадея для одного устройства на другое, например, первичная катушка при передаче энергии вторичной обмотке в трансформаторе. См. рис. 1, где простые катушки наводят друг в друге ЭДС.

Рисунок 1. Эти катушки могут индуцировать ЭДС друг в друге, как неэффективный трансформатор. Их взаимная индуктивность М указывает на эффективность связи между ними. Здесь видно, что изменение тока в катушке 1 индуцирует ЭДС в катушке 2. (Обратите внимание, что « E ₂ индуцируется» представляет ЭДС индукции в катушке 2.)

Во многих случаях, когда геометрия устройств фиксирована, поток изменяется при изменении тока. Поэтому мы сосредоточимся на скорости изменения тока [латекс] {\ дельта I / \ дельта t} [/ латекс] как на причине индукции. Изменение тока [латекс]{I_1}[/латекс] в одном устройстве, катушка 1 на рисунке, индуцирует [латекс]{\текст{ЭДС}_2}[/латекс] в другом. Мы выражаем это в форме уравнения как

[латекс] {\ текст {ЭДС} _2 = -M} [/ латекс] [латекс] {\ гидроразрыва {\ Delta I_1} {\ Delta t}} [/ латекс],

, где [латекс]{М}[/латекс] определяется как взаимная индуктивность между двумя устройствами. Знак минус является выражением закона Ленца. Чем больше взаимная индуктивность [латекс]{М}[/латекс], тем эффективнее связь. Например, катушки на рисунке 1 имеют небольшой [латекс]{M}[/латекс] по сравнению с катушками трансформатора в главе 23.7. Рисунок 3. Единицами для [латекс]{М}[/латекс] являются [латекс]{( \text{V} \cdot \;\text{s})/ \text{A} = \Omega \cdot \;\text{s}}[/latex], который называется Генри (H), в честь Джозефа Генри. То есть [латекс]{1 \;\text{H} = 1 \Omega \cdot \;\text{s}}[/latex].

Природа здесь симметрична. Если мы изменим ток [латекс]{I_2}[/латекс] в катушке 2, мы индуцируем [латекс]{\текст{ЭДС}_1}[/латекс] в катушке 1, которая определяется как

[латекс] {\ текст {ЭДС} _1 = -M} [/ латекс] [латекс] {\ гидроразрыва {\ Delta I_2} {\ Delta t}} [/ латекс],

, где [латекс]{М}[/латекс] такой же, как и для обратного процесса. Трансформаторы работают в обратном направлении с той же эффективностью или взаимной индуктивностью [латекс]{М}[/латекс] .

Большая взаимная индуктивность [латекс]{M}[/латекс] может быть желательной, а может и нежелательной. Мы хотим, чтобы трансформатор имел большую взаимную индуктивность. Но такой прибор, как электрическая сушилка для белья, может индуцировать на своем корпусе опасную ЭДС, если взаимная индуктивность между его катушками и корпусом велика. Один из способов уменьшить взаимную индуктивность [латекс]{M}[/латекс] – это встречные катушки, чтобы нейтрализовать создаваемое магнитное поле. (См. рис. 2.)

Рисунок 2. Нагревательные спирали электрической сушилки для белья могут быть встречно намотаны, так что их магнитные поля компенсируют друг друга, что значительно снижает взаимную индуктивность с корпусом сушилки.

Самоиндукция , действие закона Фарадея об индукции устройства на себя, также существует. Когда, например, ток через катушку увеличивается, магнитное поле и поток также увеличиваются, индуцируя противо-ЭДС, как того требует закон Ленца. И наоборот, если ток уменьшается, индуцируется ЭДС, препятствующая уменьшению. Большинство устройств имеют фиксированную геометрию, поэтому изменение потока полностью связано с изменением тока [латекс] {\ дельта I} [/латекс], проходящего через устройство. ЭДС индукции связана с физической геометрией устройства и скоростью изменения тока. Это дается

[латекс] {\ текст {ЭДС} = -L} [/ латекс] [латекс] {\ гидроразрыва {\ Delta I} {\ Delta t}} [/ латекс],

, где [латекс]{L}[/латекс] — собственная индуктивность устройства. Устройство, обладающее значительной собственной индуктивностью, называется катушкой индуктивности и обозначено символом на рисунке 3.

Рис. 3.

Знак минус является выражением закона Ленца, указывающим, что ЭДС противодействует изменению тока. Единицами самоиндукции являются генри (Гн), как и для взаимной индуктивности. Чем больше собственная индуктивность [латекс]{L}[/латекс] устройства, тем больше его сопротивление любому изменению тока через него. Например, большая катушка с большим количеством витков и железным сердечником имеет большой [латекс]{L}[/латекс] и не позволяет току быстро изменяться. Чтобы избежать этого эффекта, необходимо добиться малого [латекса]{L}[/латекса], например, за счет встречной намотки катушек, как показано на рис. 2.9.0015

Катушка индуктивности 1 Гн представляет собой большую катушку индуктивности. Чтобы проиллюстрировать это, рассмотрим устройство с [латексом]{L = 1,0 \;\text{H}}[/латекс], через которое протекает ток 10 А. Что произойдет, если мы попытаемся отключить ток быстро, возможно, всего за 1,0 мс? ЭДС, заданная как [латекс] {\ текст {ЭДС} = -L (\ Delta I / \ Delta t)} [/ латекс], будет препятствовать изменению. Таким образом, ЭДС будет индуцироваться по формуле )/(1,0 \;\text{ms})]=10 000 \;\text{V}}[/latex]. Положительный знак означает, что это большое напряжение направлено в том же направлении, что и ток, противодействуя его уменьшению. Такие большие ЭДС могут вызывать искрение, повреждая коммутационное оборудование, поэтому может потребоваться более медленное изменение тока.

Для такого большого наведенного напряжения есть применение. Вспышки камеры используют батарею, две катушки индуктивности, которые функционируют как трансформатор, и систему переключения или осциллятор для создания больших напряжений. (Помните, что нам нужно изменяющееся магнитное поле, вызванное изменяющимся током, чтобы индуцировать напряжение в другой катушке.) Система генератора будет делать это много раз, когда напряжение батареи увеличится до более чем одной тысячи вольт. (Вы можете услышать пронзительный вой трансформатора во время зарядки конденсатора.) Конденсатор сохраняет высокое напряжение для последующего использования при питании вспышки. (См. рис. 4.)

Рисунок 4. Благодаря быстрому переключению катушки индуктивности батареи напряжением 1,5 В можно использовать для наведения ЭДС в несколько тысяч вольт. Это напряжение можно использовать для хранения заряда в конденсаторе для последующего использования, например, во вспышке фотоаппарата.

Можно рассчитать [латекс]{L}[/латекс] для индуктора, зная его геометрию (размер и форму) и зная создаваемое им магнитное поле. В большинстве случаев это сложно из-за сложности создаваемого поля. Итак, в этом тексте индуктивность [латекс]{L}[/латекс] обычно является заданной величиной. Единственным исключением является соленоид, потому что он имеет очень однородное поле внутри, почти нулевое поле снаружи и простую форму. Поучительно вывести уравнение для его индуктивности. Начнем с того, что заметим, что ЭДС индукции определяется законом индукции Фарадея как [латекс] {\ текст {ЭДС} = -N (\ Delta \ phi/ \ Delta t)} [/ латекс] -индуктивность, как [латекс] {\ текст {ЭДС} = -L (\ Delta I / \ Delta t)} [/ латекс]. Приравнивая эти выходы

[латекс] {\ текст {ЭДС} = -N} [/ латекс] [латекс] {\ гидроразрыва {\ Delta \ phi} {\ Delta t}} [/латекс] [латекс] {= -L} [/ латекс] [латекс] {\ гидроразрыва {\ Delta I} {\ Delta t}} [/латекс].

Решение для [латекс]{L}[/латекс] дает

[латекс] {L = N} [/латекс] [латекс] {\ гидроразрыва {\ Delta \ phi} {\ Delta I}} [/ латекс].

Это уравнение для собственной индуктивности [латекс]{L}[/латекс] устройства всегда справедливо. Это означает, что самоиндукция [латекс]{L}[/латекс] зависит от того, насколько эффективен ток в создании потока; чем эффективнее, тем больше [латекс] {\ дельта \ фи \ дельта I} [/ латекс].

Воспользуемся этим последним уравнением, чтобы найти выражение для индуктивности соленоида. Поскольку площадь [латекс] {А} [/латекс] соленоида фиксирована, изменение потока равно [латекс] {\ Дельта \ фи = \ Дельта (ВА) = А \ Дельта В} [/латекс]. Чтобы найти [латекс]{\Delta B}[/латекс], заметим, что магнитное поле соленоида определяется выражением [латекс]{В = \mu _0 nI = \mu 0 \frac{NI}{\ell} }[/латекс]. (Здесь [латекс]{n = N/ \ell}[/латекс], где [латекс]{N}[/латекс] – количество витков, а [латекс]{\ell}[/латекс] – длина соленоида. .) Изменяется только ток, так что [латекс]{\Delta \phi = A \Delta B = \mu_0 NA \frac{\Delta I}{\ell}}[/latex]. Замена [латекс]{\Delta \phi}[/latex] на [латекс]{L = N \frac{\Delta \phi}{\Delta I}}[/latex] дает 92A}{\ell}}[/латекс] [латекс]{(\текст{соленоид})}.[/латекс]

Это собственная индуктивность соленоида с площадью поперечного сечения [латекс]{А}[/латекс] и длиной [латекс]{\ell}[/латекс]. Обратите внимание, что индуктивность зависит только от физических характеристик соленоида, соответствующих его определению.

Пример 1. Расчет собственной индуктивности соленоида среднего размера

Рассчитайте собственную индуктивность соленоида длиной 10,0 см и диаметром 4,00 см с 200 витками. 92) {0,100 \;\text{m}} \\[1em] \;= & {0,632 \;\text{mH}} \end{array}[/latex].

Обсуждение

Этот соленоид средних размеров. Его индуктивность около миллигенри также считается умеренной.

Одно из распространенных применений индуктивности используется в светофорах, которые могут определять, когда транспортные средства ожидают на перекрестке. Электрическая цепь с индуктором размещена на дороге под местом остановки ожидающего автомобиля. Кузов автомобиля увеличивает индуктивность, и схема меняется, посылая сигнал светофору изменить цвет. Точно так же металлоискатели, используемые для обеспечения безопасности в аэропортах, используют ту же технику. Катушка или индуктор в корпусе металлоискателя действует как передатчик и приемник. Импульсный сигнал в катушке передатчика индуцирует сигнал в приемнике. На самоиндукцию цепи влияет любой металлический предмет на пути. Такие детекторы могут быть настроены на чувствительность, а также могут указывать примерное местонахождение обнаруженного на человеке металла. (Но они не смогут обнаружить пластиковую взрывчатку, подобную той, что была обнаружена на «подрывнике в нижнем белье».) См. рис. 5.

Рисунок 5 Знакомые ворота безопасности в аэропорту могут не только обнаруживать металлы, но и указывать их приблизительную высоту над полом. (кредит: Alexbuirds, Wikimedia Commons)

Из закона Ленца мы знаем, что индуктивности противодействуют изменениям тока. Есть альтернативный взгляд на эту оппозицию, основанный на энергии. Энергия хранится в магнитном поле. Требуется время, чтобы накопить энергию, и также нужно время, чтобы истощить энергию; следовательно, существует оппозиция быстрым изменениям. В индукторе магнитное поле прямо пропорционально току и индуктивности устройства. Можно показать, что 92 = 0,284 \;\text{J}}. \end{array}[/latex]

Обсуждение

Этого количества энергии определенно достаточно, чтобы вызвать искру, если ток внезапно отключится. Он не может быть построен мгновенно, если только потребляемая мощность не бесконечна.

• Индуктивность — это свойство устройства, которое показывает, насколько эффективно оно индуцирует ЭДС в другом устройстве.
• Взаимная индуктивность — это действие двух устройств, индуцирующих ЭДС друг в друге.
• Изменение тока [латекс]{\Delta I_1 / \Delta t}[/латекс] в одном индуцирует ЭДС [латекс]{\текст{ЭДС}_2}[/латекс] во втором:

  [латекс] {\ текст {ЭДС} _2 = — M} [/ латекс] [латекс] {\ гидроразрыва {\ Delta I_1} {\ Delta t}} [/ латекс],

  , где [латекс]{М}[/латекс] определяется как взаимная индуктивность между двумя устройствами, а знак минус соответствует закону Ленца.

• Симметрично изменение тока [латекс]{\Delta I_2/\Delta t}[/латекс] через второе устройство индуцирует ЭДС [латекс]{\текст{ЭДС}_1}[/латекс] в первом:

  [латекс] {\ текст {ЭДС} _1 = — М} [/ латекс] [латекс] {\ гидроразрыва {\ Delta I_2} {\ Delta t}} [/ латекс],

  , где [латекс]{М}[/латекс] — та же взаимная индуктивность, что и в обратном процессе.

• Текущие изменения в устройстве индуцируют ЭДС в самом устройстве.
• Самоиндукция — это эффект устройства, индуцирующего ЭДС само по себе.
• Прибор называется индуктором, а ЭДС, индуцируемая в нем изменением тока через него, равна

  [латекс] {ЭДС = -L} [/ латекс] [латекс] {\ гидроразрыва {\ Delta I} {\ Delta t}} [/ латекс],

  , где [латекс]{L}[/латекс] — собственная индуктивность индуктора, а [латекс] {\Delta I / \Delta t}[/латекс] — скорость изменения тока через него. Знак минус указывает на то, что ЭДС противодействует изменению тока, как того требует закон Ленца. 92}[/латекс].

Задачи и упражнения

1: Две катушки расположены близко друг к другу в физической лаборатории, чтобы продемонстрировать закон индукции Фарадея. Ток 5,00 А в одном отключается за 1,00 мс, индуцируя ЭДС 9,00 В в другом. Чему равна их взаимная индуктивность?

2: Если две катушки, расположенные рядом, имеют взаимную индуктивность 5,00 мГн, какое напряжение индуцируется в одной, когда ток 2,00 А в другой отключается через 30,0 мс?

3: Ток 4,00 А через катушку индуктивности 7,50 мГн отключается за 8,33 мс. Какая ЭДС индуцирует противодействие этому?

4: Устройство включено, и через него через 0,100 мс проходит ток 3,00 А. Чему равна собственная индуктивность прибора, если ей противодействует ЭДС наведенного напряжения 150 В?

5: Начиная с [латекс]{\текст{ЭДС}_2 = -M \frac{\Delta I_1}{\Delta t}}[/латекс], покажите, что единицами измерения индуктивности являются [латекс]{ (\text{V} \cdot \;\text{s})/ \text{A} = \Omega \cdot \;\text{s}}[/latex].

6: Фотовспышки заряжают конденсатор до высокого напряжения, быстро включая и выключая ток через катушку индуктивности. За какое время необходимо включить или выключить ток 0,100 А через катушку индуктивности 2,00 мГн, чтобы индуцировать ЭДС 500 В?

7: Большой исследовательский соленоид имеет собственную индуктивность 25,0 Гн. а) Какая ЭДС наведения препятствует его отключению, если ток 100 А через него отключается за 80,0 мс? б) Сколько энергии запасается в катушке индуктивности при полном токе? в) С какой скоростью в ваттах должна рассеиваться энергия, чтобы ток выключился за 80,0 мс? (d) Принимая во внимание ответ на последнюю часть, удивительно ли, что так быстро закрыть его сложно?

8: (a) Рассчитайте собственную индуктивность соленоида длиной 50 см и диаметром 10 см, имеющего 1000 витков. б) Сколько энергии запасается в этом индукторе при протекании через него тока силой 20,0 А? в) Как быстро его можно выключить, если ЭДС индукции не может превышать 3,00 В?

9: Прецизионный лабораторный резистор изготовлен из витка проволоки диаметром 1,50 см и длиной 4,00 см и имеет 500 витков. а) Чему равна его собственная индуктивность? б) Какая средняя ЭДС индуцируется, если ток 12,0 А через него включается за 5,00 мс (одна четвертая периода для переменного тока частотой 50 Гц)? в) Какова его индуктивность, если его укоротить наполовину и намотать встречно (два слоя по 250 витков в противоположных направлениях)?

10: Нагревательные спирали в фене имеют диаметр 0,800 см, общую длину 1,00 м и 400 витков. а) Какова их полная собственная индуктивность, если предположить, что они действуют как одиночный соленоид? б) Сколько энергии запасается в них при токе 6,00 А? (c) Какая средняя ЭДС препятствует их отключению, если это делается за 5,00 мс (одна четвертая часть цикла для переменного тока с частотой 50 Гц)?

11: Когда ток 20,0 А через индуктор отключается за 1,50 мс, индуцируется ЭДС 800 В, противодействующая изменению. Каково значение собственной индуктивности?

12: Как быстро может быть отключен ток 150 А через дроссель 0,250 Гн, если ЭДС индукции не может превышать 75,0 В?

13: Integrated Concepts

Очень большой сверхпроводящий соленоид, например, используемый в МРТ, сохраняет 1,00 МДж энергии в своем магнитном поле при токе 100 А.