Как рассчитать общую индуктивность при параллельном и последовательном соединении катушек. Какие формулы использовать для вычисления результирующей индуктивности. Где применяются различные схемы соединения катушек индуктивности.
Особенности параллельного и последовательного соединения катушек индуктивности
При соединении нескольких катушек индуктивности в электрической цепи важно понимать, как это влияет на общую индуктивность схемы. Рассмотрим основные особенности параллельного и последовательного соединения:
Параллельное соединение катушек
При параллельном соединении катушек индуктивности:
- Напряжение на всех катушках одинаково
- Общий ток распределяется между катушками
- Результирующая индуктивность всегда меньше индуктивности любой из катушек
Последовательное соединение катушек
При последовательном соединении катушек индуктивности:
- Ток через все катушки одинаков
- Напряжение на катушках различается
- Общая индуктивность равна сумме индуктивностей отдельных катушек
Формулы для расчета результирующей индуктивности
Для вычисления общей индуктивности при различных схемах соединения используются следующие формулы:
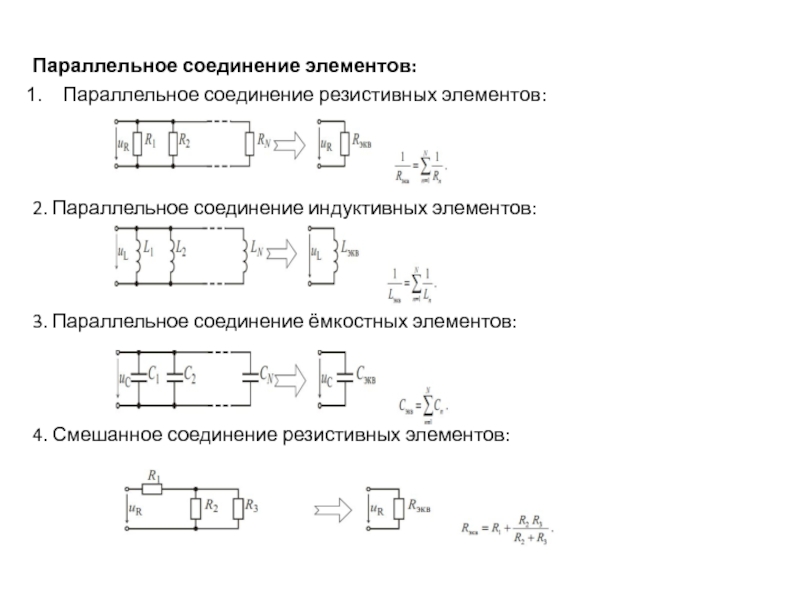
Параллельное соединение
При параллельном соединении катушек общая индуктивность рассчитывается по формуле:
1/L = 1/L1 + 1/L2 + … + 1/Ln
где L — общая индуктивность, L1, L2, …, Ln — индуктивности отдельных катушек.
Последовательное соединение
При последовательном соединении катушек общая индуктивность равна сумме индуктивностей:
L = L1 + L2 + … + Ln
Эти формулы справедливы при отсутствии взаимного влияния магнитных полей катушек.
Применение различных схем соединения катушек индуктивности
Параллельное и последовательное соединение катушек индуктивности находит широкое применение в различных областях электроники и электротехники:
Использование параллельного соединения
- В фильтрах высоких частот для уменьшения общей индуктивности
- В импульсных источниках питания для снижения пульсаций тока
- В радиочастотных схемах для подстройки резонансной частоты
Применение последовательного соединения
- В фильтрах низких частот для увеличения индуктивности
- В трансформаторах для повышения общей индуктивности обмоток
- В дросселях силовой электроники для увеличения индуктивности
Особенности расчета при наличии взаимной индукции
При близком расположении катушек может возникать эффект взаимной индукции, который влияет на общую индуктивность. В этом случае:

- Для последовательного соединения: L = L1 + L2 + 2M
- Для параллельного соединения: L = (L1L2 — M^2) / (L1 + L2 — 2M)
где M — коэффициент взаимной индукции катушек.
Практические рекомендации по соединению катушек индуктивности
При работе с катушками индуктивности следует учитывать несколько важных моментов:
- Для минимизации взаимного влияния располагайте катушки на достаточном расстоянии друг от друга
- При параллельном соединении старайтесь использовать катушки с близкими значениями индуктивности
- Учитывайте активное сопротивление обмоток катушек, которое влияет на общее сопротивление цепи
- При необходимости используйте экранирование катушек для уменьшения паразитных связей
Влияние соединения катушек на добротность контура
Способ соединения катушек индуктивности оказывает существенное влияние на добротность колебательного контура:
- При параллельном соединении добротность контура обычно повышается
- Последовательное соединение, как правило, снижает добротность
- Для достижения максимальной добротности необходимо минимизировать активные потери в обмотках катушек
Применение вариометров для регулировки индуктивности
Вариометр представляет собой устройство с переменной индуктивностью, состоящее из двух катушек:
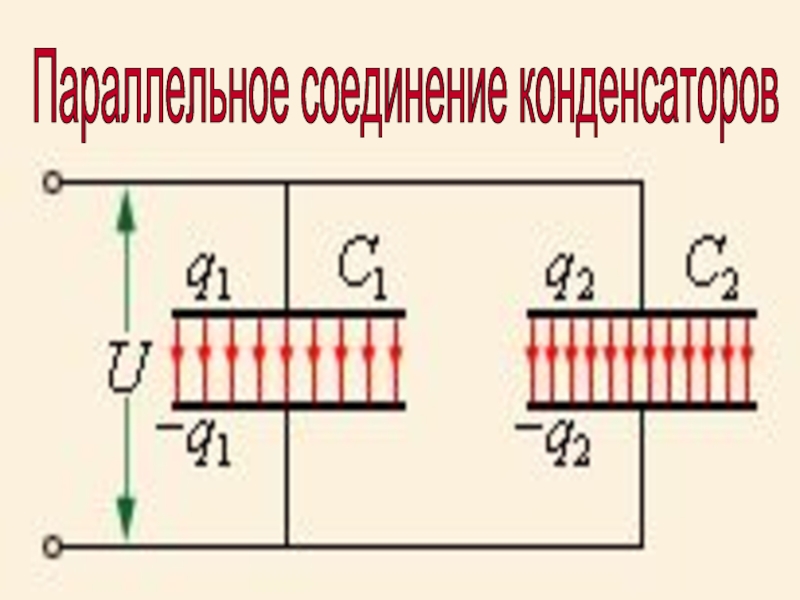
- Неподвижной внешней катушки (статора)
- Подвижной внутренней катушки (ротора)
Изменяя взаимное расположение катушек, можно плавно регулировать общую индуктивность. Вариометры применяются:
- В радиоприемниках для настройки колебательных контуров
- В измерительной технике для создания эталонных индуктивностей
- В системах автоматического регулирования для подстройки параметров
Особенности использования катушек индуктивности в высокочастотных схемах
При работе на высоких частотах необходимо учитывать дополнительные факторы:
- Увеличение потерь в сердечнике катушки
- Возрастание межвитковой емкости
- Появление скин-эффекта в проводниках
Для минимизации этих эффектов применяются специальные конструкции катушек:
- Использование многожильного провода (литцендрата)
- Применение сердечников из специальных ферритовых материалов
- Оптимизация геометрии намотки для снижения паразитной емкости
Заключение
Понимание особенностей параллельного и последовательного соединения катушек индуктивности позволяет эффективно проектировать электронные схемы и оптимизировать их параметры. Правильный выбор схемы соединения и учет всех влияющих факторов обеспечивает достижение требуемых характеристик устройств в различных областях применения — от силовой электроники до высокочастотной техники.

|
Заглавная страница
КАТЕГОРИИ: Археология ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрации Техника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ? Влияние общества на человека Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Балочные системы. Определение реакций опор и моментов защемления |
⇐ ПредыдущаяСтр 10 из 18Следующая ⇒
Это — винтовая, спиральная или винтоспиральная катушка из свёрнутого проводника, обладающая значительно большой величиной индуктивности при относительно малом уровне ёмкости и низком активном сопротивлении Индуктивность катушки прямо пропорциональна квадрату числа витков, так как с увеличением количества витков увеличивается, число магнитных силовых линий, и число пересечений каждой силовой линии с проводником. Соединение катушек Соединение катушек индуктивности при отсутствии взаимного влияния магнитных полей катушек. Последовательное соединение катушек индуктивности. Суммарная индуктивность двух или нескольких катушек, соединенных последовательно и расположенных на таком расстоянии друг от друга, что магнитное поле одной катушки не пересекает витков другой (рисунок 1), равна сумме их индуктивностей. Рисунок 1. Последовательное соединение катушект индуктивности. Цепь, изображенная на рисунке 1, обладает общей индуктивностью L, которая выражается так: где L1, L2 и L3 — индуктивности отдельных катушек. Параллельное соединение катушек индуктивности. Индуктивность цепи, составленной из тех же катушек при параллельном их соединении (рисунок 2) и при соблюдении того же условия относительно их расположения (отсутствие магнитного взаимодействия), подсчитывается по следующей формуле: Рисунок 2. Индуктивность двух катушек, соединенных параллельно, определяется по следующей формуле: Как видим, формулы для подсчета результирующих индуктивностей катушек, соединенных последовательно или параллельно и не взаимодействующих между собой, совершенно тождественны с формулами для подсчета омического сопротивления цепи при последовательном и параллельном соединении резисторов. Соединение катушек при наличии взаимного влияния их магнитных полей. Если катушки, включенные в цепь последовательно, расположены близко друг к другу, т. е. так, что часть магнитного потока одной катушки пронизывает витки другой, т. е. между катушками существует индуктивная связь (рисунок 3а), то для определения их общей индуктивности приведенная выше формула будет уже непригодна. При таком расположении катушек могут быть два случая, а именно: 1. Магнитные потоки обеих катушек имеют одинаковые направления 2. Тот или другой случай будет иметь место в зависимости от направления витков обмотки катушек и от направлений токов в них. Рисунок 3. Соединение катушек индуктивности: а)суммарная индуктивность увеличивается за счет взаимной индукции б)суммарная индуктивность уменьшается за счет взаимной индукции. Если обе катушки намотаны в одну сторону и токи в них текут в одном направлении, то это будет соответствовать первому случаю; если же токи текут в противоположных направлениях (рисунок 3б), то будет иметь место второй случай. Разберем первый случай, когда магнитные потоки направлены в одну сторону. Очевидно, при этих условиях витки каждой катушки будут пронизываться своим потоком и частью потока другой катушки, т. е. магнитные потоки в той и в другой катушке будут больше по сравнению с тем случаем, когда между катушками нет индуктивной связи. Увеличение магнитного потока, пронизывающего витки той или иной катушки, равносильно увеличению ее индуктивности. Рассуждая таким же образом, мы придем к выводу, что для второго случая, когда потоки направлены навстречу друг другу, общая индуктивность цепи будет меньше суммы индуктивностей отдельных катушек. Подсчет величины индуктивности цепи, составленной из двух соединенных последовательно катушек индуктивности L1 и L2 при наличии между ними индуктивной связи, производится по формуле: В первом случае ставится знак + (плюс), а во втором случае знак — (минус). Величина М, называемая коэффициентом взаимной индукции, представляет собой добавочную индуктивность, обусловленную частью магнитного потока, общей для обеих катушек. На явлении взаимоиндукции основано устройство
вариометров. Вариометр состоит из двух катушек, общая индуктивность которых может, по желанию, плавно изменяться в некоторых пределах.
⇐ Предыдущая567891011121314Следующая ⇒ Читайте также: Техника прыжка в длину с разбега Организация работы процедурного кабинета Области применения синхронных машин Оптимизация по Винеру и Калману |
||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 1415; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. |
Последовательное и параллельное соединение катушек индуктивности. Добротность и энергия. Последовательное соединение резисторов
ТОЭ › Расчет цепей синусоидального тока
Для рассмотрения параллельного соединения катушки и конденсатора представим их на схеме активными и реактивными проводимостями (рис. 14.11, а).
На схеме рис. 14.1.1, б те же катушки и конденсатор представлены активными и реактивными сопротивлениями. Первая схема имеет некоторое преимущество, так как в ней все элементы соединены параллельно, а в другой они соединены смешанно.
Считая известными параметры катушки G1, BL и конденсатора G2, BC, а также напряжение u = Umsinωt, определим токи в цепи и ее мощность.
Соединение катушек индуктивности при отсутствии взаимного влияния магнитных полей катушек.
Суммарная индуктивность двух или нескольких катушек, соединенных последовательно
и расположенных на таком расстоянии друг от друга, что магнитное поле одной катушки не пересекает витков другой (рисунок 1), равна сумме их индуктивностей.
Рисунок 1. Последовательное соединение катушект индуктивности.
Цепь, изображенная на рисунке 1, обладает общей индуктивностью L, которая выражается так:
где L1, L2 и L3 — индуктивности отдельных катушек.
Параллельное соединение катушек индуктивности.
Индуктивность цепи, составленной из тех же катушек при параллельном их соединении (рисунок 2) и при соблюдении того же условия относительно их расположения (отсутствие магнитного взаимодействия), подсчитывается по следующей формуле:
Рисунок 2. Параллельное соединение катушек индуктивности.
Индуктивность двух катушек, соединенных параллельно, определяется по следующей формуле:
Как видим, формулы для подсчета результирующих индуктивностей катушек, соединенных последовательно или параллельно и не взаимодействующих между собой, совершенно тождественны с формулами для подсчета омического сопротивления цепи при последовательном и параллельном соединении резисторов .
Схемы коммутации одного сабвуфера к усилителю
В этом разделе мы собрали все возможные варианты сабвуферов и вариации их подключения
Динамик с двумя катушками 4+4 Ома
Как его можно подключить?
Динамик с двумя катушками 2+2 Ома
Как его можно подключить?
Динамик с двумя катушками 1+1 Ома
Как его можно подключить?
Соединение катушек при наличии взаимного влияния их магнитных полей.
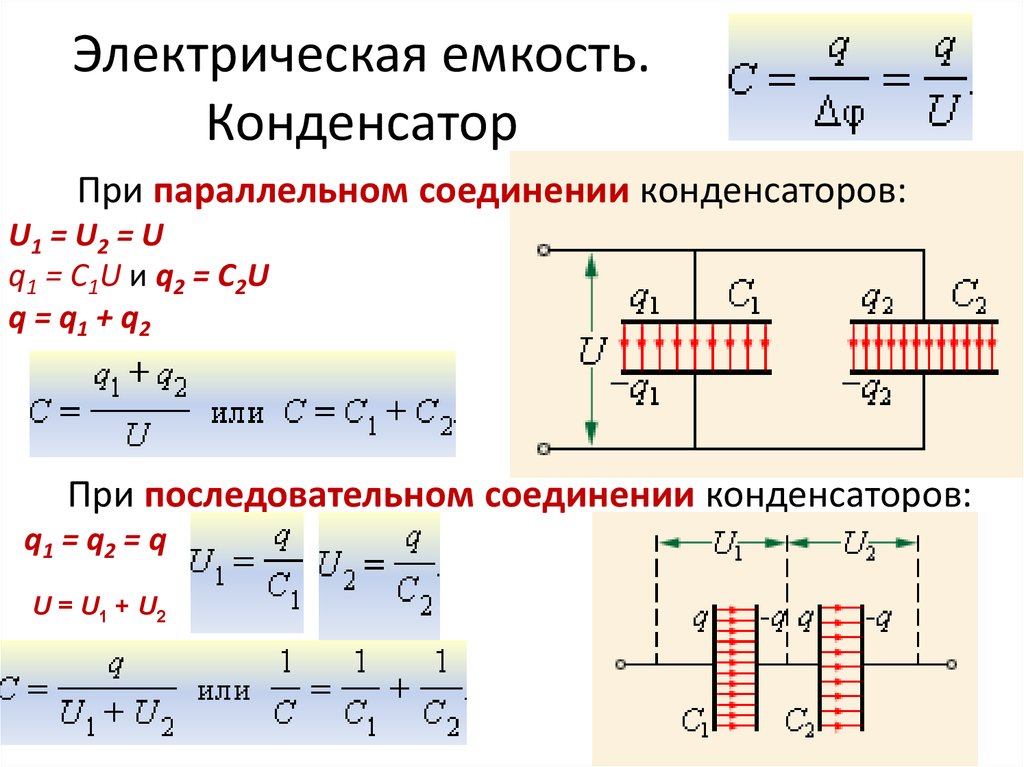
Если катушки, включенные в цепь последовательно, расположены близко друг к другу, т. е. так, что часть магнитного потока одной катушки пронизывает витки другой, т. е. между катушками существует индуктивная связь (рисунок 3а), то для определения их общей индуктивности приведенная выше формула будет уже непригодна. При таком расположении катушек могут быть два случая, а именно:
- Магнитные потоки обеих катушек имеют одинаковые направления
- Магнитные потоки обеих катушек направлены навстречу друг другу
Тот или другой случай будет иметь место в зависимости от направления витков обмотки катушек и от направлений токов в них.
Рисунок 3. Соединение катушек индуктивности: а)суммарная индуктивность увеличивается за счет взаимной индукции б)суммарная индуктивность уменьшается за счет взаимной индукции.
Если обе катушки намотаны в одну сторону и токи в них текут в одном направлении, то это будет соответствовать первому случаю; если же токи текут в противоположных направлениях (рисунок 3б), то будет иметь место второй случай.
Разберем первый случай, когда магнитные потоки направлены в одну сторону. Очевидно, при этих условиях витки каждой катушки будут пронизываться своим потоком и частью потока другой катушки, т. е. магнитные потоки в той и в другой катушке будут больше по сравнению с тем случаем, когда между катушками нет индуктивной связи. Увеличение магнитного потока, пронизывающего витки той или иной катушки, равносильно увеличению ее индуктивности. Поэтому общая индуктивность цепи в рассматриваемом случае будет больше суммы индуктивностей отдельных катушек, из которых составлена цепь.
Рассуждая таким же образом, мы придем к выводу, что для второго случая, когда потоки направлены навстречу друг другу, общая индуктивность цепи будет меньше суммы индуктивностей отдельных катушек.
Подсчет величины индуктивности цепи, составленной из двух соединенных последовательно катушек индуктивности L1 и L2 при наличии между ними индуктивной связи, производится по формуле:
В первом случае ставится знак + (плюс), а во втором случае знак — (минус).
Величина М, называемая коэффициентом взаимной индукции
, представляет собой добавочную индуктивность, обусловленную частью магнитного потока, общей для обеих катушек.
На явлении взаимоиндукции основано устройство вариометров
. Вариометр состоит из двух катушек, общая индуктивность которых может, по желанию, плавно изменяться в некоторых пределах. В радиотехнике вариометры применяются для настройки колебательных контуров приемников и передатчиков.
Катушка индуктивности
является пассивным компонентом электронных схем, основное предназначение которой является сохранение энергии в виде магнитного поля. Свойство катушки индуктивности чем-то схоже с конденсатором, который хранит энергию в виде электрического поля.
Индуктивность (измеряется в Генри) — это эффект возникновения магнитного поля вокруг проводника с током. Ток, протекающий через катушку индуктивности, создает магнитное поле, которое имеет связь с электродвижущей силой (ЭДС) оказывающее противодействие приложенному напряжению.
Возникающая противодействующая сила (ЭДС) противостоит изменению переменного напряжения и силе тока в катушке индуктивности. Это свойство индуктивной катушки называется индуктивным сопротивлением. Следует отметить, что индуктивное сопротивление находится в противофазе к емкостному реактивному сопротивлению конденсатора в цепи переменного тока. Путем увеличения числа витков можно повысить индуктивность самой катушки.
Существующие типы катушек зажигания для разных типов двигателя (до 16 клапанов)
Так как пустоты между корпусом и обмотками внутри катушки заполнены трансформаторным маслом или другим теплопроводящим наполнителем 12, то такая конструкция обладает не только достаточно высокой электрической и механической прочностью, но и хорошим теплообменом с «массой» автомобиля через защитный кожух. В электрическом отношении этот сверток представляет собой широкий ленточный виток вокруг катушки, разомкнутый бумажной изоляцией и заземленный одной точкой на корпус.
Устройство и работа бобины Современная бобина является упрощенной версией индукционной катушки Румкорфа. Коротко о зажигании Чтобы понять зачем в автомобиле бобина это народное название , и какое участие она принимает в обеспечении движения, надо хотя бы обобщенно понять устройство систем зажигания. Для исключения взаимного влияния первичных обмоток в период образования импульсов высокого напряжения к их выводам низкого напряжения подключены разделительные диоды VD5, VD6.
Коротко о зажигании Чтобы понять зачем в автомобиле бобина это народное название , и какое участие она принимает в обеспечении движения, надо хотя бы обобщенно понять устройство систем зажигания. Для исключения взаимного влияния первичных обмоток в период образования импульсов высокого напряжения к их выводам низкого напряжения подключены разделительные диоды VD5, VD6.
Второй конец первичной обмотки подключен к распределителю. Читайте также:.
Обмотки с одних концов соединены между собой, второй конец первичной подсоединяется к аккумуляторы, вторичная обмотка свободным концом подключена к распределителю напряжения. Плюсовой вывод катушки подключен к положительной клемме аккумулятора, а другим выводом она соединяется с распределителем напряжения. Ведь он играет огромную роль в работе всей системы зажигания, именно про это мы и поговорим чуть ниже, а также научимся устранять неполадки.
Такими катушками зажигания являются некоторые компактные индивидуальные катушки зажигания без встроенного силового каскада управления первичной обмоткой. Судя по показаниям прибора, мой случай показывает и подтверждает повторно, что с катушкой все нормально.
Судя по показаниям прибора, мой случай показывает и подтверждает повторно, что с катушкой все нормально.
Форма поиска
Типовые неполадки индивидуальных катушек зажигания. Теперь при достаточной избыточности энергии, накопленной в катушке зажигания, возможно нормировать время накопления с целью поддержания тока разрыва в строго заданных пределах. Повышается вероятность межвиткового замыкания, ведущего к перегреву и перегоранию проводников.
Таким образом центральный стержень магнитопровода и намотанная на него вторичная обмотка являются высоковольтной сердцевиной катушки зажигания и находятся на достаточном, с точки зрения электрической прочности, удалении от корпуса. В таком случае обязательно проверьте центральный высоковольтный провод. Также очистите ее корпус от грязи, ведь она способствует возникновению больших утечек напряжения. Но при больших нагрузках на двигатель искрообразование прекращается, и цилиндр, обслуживаемый такой катушкой, перестаёт работать. Признаком неисправности является отсутствие затухающих колебаний в конце горения искры между электродами свечи зажигания участок о.
Накопленная энергия в индуктивности
Как известно магнитное поле обладает энергией. Аналогично тому, как в полностью заряженном конденсаторе существует запас электрической энергии, в индуктивной катушке, по обмотке которой течет ток, тоже существует запас — только уже магнитной энергии.
Энергия, запасенная в катушке индуктивности равна затраченной энергии необходимой для обеспечения протекания тока I в противодействии ЭДС. Величина запасенной энергии в индуктивности можно рассчитать по следующей формуле:
где L — индуктивность, I — ток, протекающий через катушку индуктивности.
Схемы коммутации двух сабвуферов к усилителю
В этом разделе мы собрали “почти” все возможные варианты подключения двух сабвуферов
Два динамика с двумя катушками 4+4 Ома
Как их можно подключить?
Два динамика с двумя катушками 2+2 Ома
Как их можно подключить?
Два динамика с двумя катушками 1+1 Ом
Как их можно подключить?
Гидравлическая модель
Работу катушки индуктивности можно сравнить с работой гидротурбины в потоке воды. Поток воды, направленный сквозь еще не раскрученную турбину, будет ощущать сопротивление до того момента, пока турбина полностью не раскрутится.
Поток воды, направленный сквозь еще не раскрученную турбину, будет ощущать сопротивление до того момента, пока турбина полностью не раскрутится.
Далее турбина, имеющая определенную степень инерции, вращаясь в равномерном потоке, практически не оказывая влияния на скорость течения воды. В случае же если данный поток резко остановить, то турбина по инерции все еще будет вращаться, создавая движение воды. И чем выше инерция данной турбины, тем больше она будет оказывать сопротивление изменению потока.
Также и индуктивная катушка сопротивляется изменению электрического тока протекающего через неё.
Индуктивность в электрических цепях
В то время как конденсатор оказывает сопротивление изменению переменного напряжения, индуктивность же сопротивляется переменному тока. Идеальная индуктивность не будет оказывать сопротивление постоянному току, однако, в реальности все индуктивные катушки сами по себе обладают определенным сопротивлением.
В целом, отношение между изменяющимися во времени напряжением V(t) проходящим через катушку с индуктивностью L и изменяющимся во времени током I(t), проходящим через нее можно представить в виде дифференциального уравнения следующего вида:
Когда переменный синусоидальной ток (АС) протекает через катушку индуктивности, возникает синусоидальное переменное напряжение (ЭДС).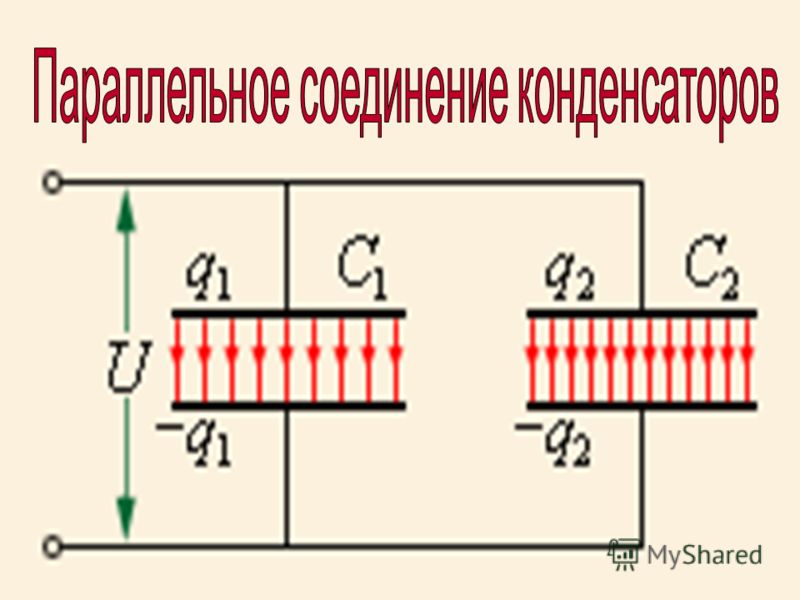 Амплитуда ЭДС зависит от амплитуды тока и частоте синусоиды, которую можно выразить следующим уравнением:
Амплитуда ЭДС зависит от амплитуды тока и частоте синусоиды, которую можно выразить следующим уравнением:
где ω является угловой частотой резонансной частоты F:
Причем, фаза тока отстает от напряжения на 90 градусов. В конденсаторе же все наоборот, там ток опережает напряжение на 90 градусов. Когда индуктивная катушка соединена с конденсатором (последовательно либо параллельно), то образуется LC цепь, работающая на определенной резонансной частоте.
Индуктивное сопротивление ХL определяется по формуле:
где ХL — индуктивное сопротивление, ω — угловая частота, F — частота в герцах, и L индуктивность в генри.
Индуктивное сопротивление — это положительная составляющая импеданса. Оно измеряется в омах. Импеданс катушки индуктивности (индуктивное сопротивление) вычисляется по формуле:
Схемы соединения катушек индуктивностей
Параллельное соединение индуктивностей
Напряжение на каждой из катушек индуктивностей, соединенных параллельно, одинаково. Эквивалентную (общую) индуктивность параллельно соединенных катушек можно определить по формуле:
Эквивалентную (общую) индуктивность параллельно соединенных катушек можно определить по формуле:
Последовательное соединение индуктивностей
Ток, протекающий через катушки индуктивности соединенных последовательно, одинаков, но напряжение на каждой катушке индуктивности отличается. Сумма разностей потенциалов (напряжений) равна общему напряжению. Общая индуктивность последовательно соединенных катушек можно высчитать по формуле:
Эти уравнения справедливы при условии, что магнитное поле каждой из катушек не оказывает влияние на соседние катушки.
На практике катушка индуктивности имеет последовательное сопротивление, созданное медной обмоткой самой катушки. Это последовательное сопротивление преобразует протекающий через катушку электрический ток в тепло, что приводит к потере качества индукции, то есть добротности. Добротность является отношением индуктивности к сопротивлению.
Добротность катушки индуктивности может быть найдена через следующую формулу:
где R является собственным сопротивлением обмотки.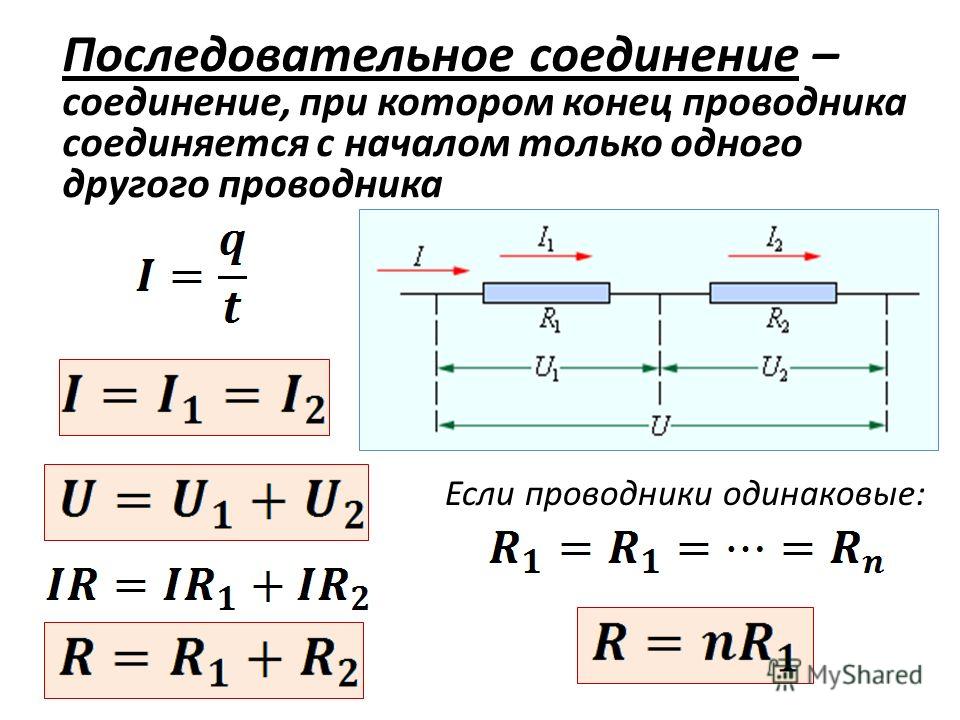
Как подключить последовательно катушки
Последовательное и параллельное соединение катушек индуктивности
Общая индуктивность последовательно соединенных катушек равна сумме индуктивностей этих катушек. Чтобы доказать что это действительно так, давайте рассмотрим следующее: индуктивность катушки равна отношению создаваемого ей напряжения к скорости изменения тока. Если катушки соединены последовательно (ток, и скорость его изменения через них одинаковы), то общее напряжение на них будет складываться из напряжений, индуцированных каждой из катушек. Таким образом, общее напряжение будет больше напряжения на любой из отдельно взятых катушек. Отсюда можно сделать вывод, что большее напряжение при заданной скорости изменения тока означает большую индуктивность.
Общая индуктивность последовательно соединенных катушек будет больше индуктивности любой из отдельно взятых катушек. Формула для расчета общей индуктивности имеет такой же вид, как и формула для расчета общего сопротивления последовательно соединенных резисторов:
Общая индуктивность параллельно соединенных катушек всегда меньше индуктивности любой из отдельно взятых катушек. Опять же вспомним: индуктивность катушки равна отношению создаваемого ей напряжения к скорости изменения тока. Поскольку ток через каждую параллельную катушку будет частью общего тока, а напряжения на всех катушках будут равны, изменение общего тока приведет к уменьшению общего напряжения (по отношению к напряжениям на отдельных катушках). Другими словами, общее напряжение будет меньше напряжения на любой из отдельно взятых катушек, так как общий ток делится между параллельными ветвями схемы. Отсюда можно сделать вывод, что меньшее напряжение при заданной скорости изменения тока означает меньшую индуктивность.
Опять же вспомним: индуктивность катушки равна отношению создаваемого ей напряжения к скорости изменения тока. Поскольку ток через каждую параллельную катушку будет частью общего тока, а напряжения на всех катушках будут равны, изменение общего тока приведет к уменьшению общего напряжения (по отношению к напряжениям на отдельных катушках). Другими словами, общее напряжение будет меньше напряжения на любой из отдельно взятых катушек, так как общий ток делится между параллельными ветвями схемы. Отсюда можно сделать вывод, что меньшее напряжение при заданной скорости изменения тока означает меньшую индуктивность.
Общая индуктивность параллельно соединенных катушек будет меньше индуктивности любой из отдельно взятых катушек. Формула для расчета общей индуктивности имеет такой же вид, как и формула для расчета общего сопротивления параллельно соединенных резисторов:
Источник
Катушка индуктивности. Формула индуктивности
- L = индуктивность в генри
- μ 0 = проницаемость свободного пространства = 4π × 10 -7 Гн / м
- μ г = относительная проницаемость материала сердечника
- N = число витков
- A = Площадь поперечного сечения катушки в квадратных метрах (м 2)
- l = длина катушки в метрах (м)
- L = индуктивность в нГн
- l = длина проводника
- d = диаметр проводника в тех же единицах, что и l
- L = индуктивность в мкГн
- r = внешний радиус катушки
- l = длина катушки
- N = число витков
- L = индуктивность в мкГн
- r = средний радиус катушки
- l = длина катушки
- N = число витков
- d = глубина катушки
- L = индуктивность в мкГн
- r = средний радиус катушки
- N = число витков
- d = глубина катушки
Конструкция катушки индуктивности
Катушка индуктивности представляет собой обмотку из проводящего материала, как правило, медной проволоки, намотанной вокруг либо железосодержащего сердечника, либо вообще без сердечника.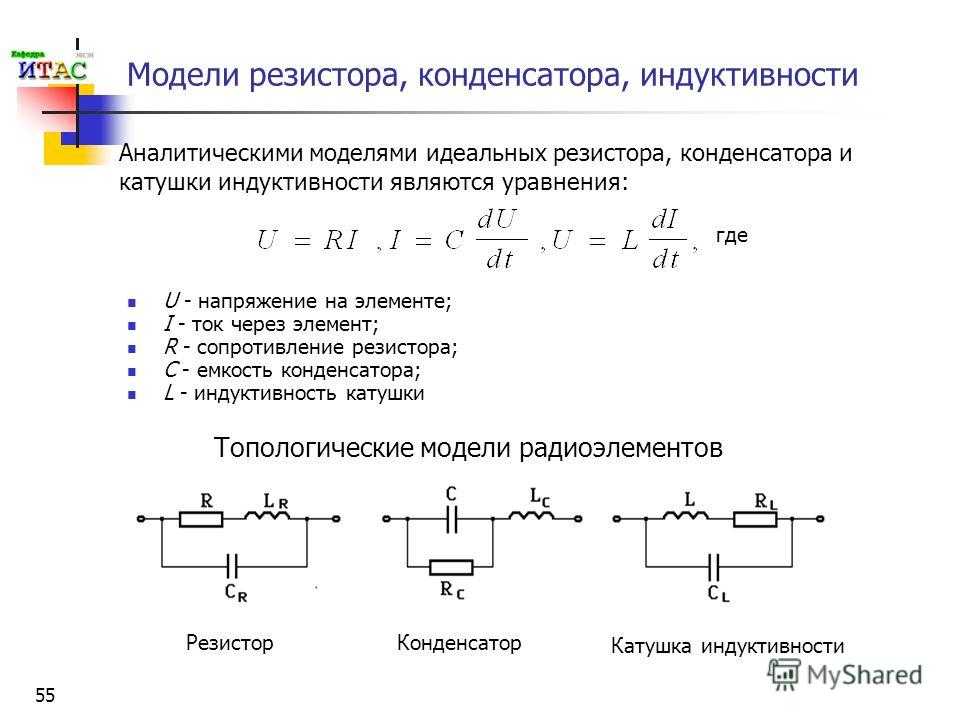
Применение в качестве сердечника материалов с высокой магнитной проницаемостью, более высокой чем воздух, способствует удержанию магнитного поля вблизи катушки, тем самым увеличивая ее индуктивность. Индуктивные катушки бывают разных форм и размеров.
Большинство изготавливаются путем намотки эмалированного медного провода поверх ферритового сердечника.
Некоторые индуктивные катушки имеют регулируемый сердечник, при помощи которого обеспечивается изменение индуктивности.
Миниатюрные катушки могут быть вытравлены непосредственно на печатной плате в виде спирали. Индуктивности с малым значением могут быть расположены в микросхемах с использованием тех же технологических процессов, которые используются при создании транзисторов.
Применение катушек индуктивности
Индуктивности широко используются в аналоговых схемах и схемах обработки сигналов. Они в сочетании с конденсаторами и другими радиокомпонентами образуют специальные схемы, которые могут усилить или отфильтровать сигналы определенной частоты.
Катушки индуктивности получили широкое применение начиная от больших катушек индуктивности, таких как дроссели в источниках питания, которые в сочетании с конденсаторами фильтра устраняют остаточные помехи и другие колебания на выходе источника питания, и до столь малых индуктивностей, которые располагаются внутри интегральных микросхем.
Две (или более) катушки индуктивности, которые соединены единым магнитным потоком, образуют , являющимся основным компонентом схем работающих с электрической сетью электроснабжения. Эффективность трансформатора возрастает с увеличением частоты напряжения.
По этой причине, в самолетах используется переменное напряжение с частотой 400 герц вместо обычных 50 или 60 герц, что в свою очередь позволяет значительно сэкономить на массе используемых трансформаторов в электроснабжении самолета.
Так же индуктивности используются в качестве устройства для хранения энергии в импульсных стабилизаторах напряжения, в высоковольтных электрических системах передачи электроэнергии для преднамеренного снижения системного напряжения или ограничения ток короткого замыкания.
Всякая электрическая цепь характеризуется активным сопротивлением, индуктивностью и емкостью. Компоненты, обладающие этими свойствами, могут соединяться между собой различными способами. В зависимости от способа соединения рассматриваются значения активных и реактивных сопротивлений. В заключение описывается явление резонанса, играющее в радиотехнике важнейшую роль.
Мои дорогие друзья, вы познакомились с пассивными компонентами. Так называют резисторы, катушки индуктивности и конденсаторы в отличие от активных компонентов: электронных ламп и транзисторов, изучением которых вы вскоре займетесь.
Сосуществование R, L и С
Все, что ты, Любознайкин, объяснил свому другу, совершенно правильно. Однако я должен добавить, что в действительности любой из компонентов обладает не только свойством, определяющим его название. Так, даже простой проводник из прямого отрезка провода одновременно обладает сопротивлением, индуктивностью и емкостью. В самом деле, какой хорошей ни была бы его проводимость, он все же обладает некоторым активным сопротивлением.
Вы помните, что, проходя по проводнику, электрический ток создает вокруг него магнитное поле. И если протекающий ток переменный, то и это поле переменное; оно наводит в проводнике токи, противодействующие основному току, протекающему по проводнику. Стало быть, здесь мы наблюдаем явление самоиндукции.
И, наконец, как и любой проводник, наш отрезок провода способен удерживать некоторый электрический заряд — как отрицательный, так и положительный. А это значит, что он обладает также и некоторой емкостью.
Все, что характерно для простого прямого отрезка провода, присуще, разумеется, и катушке: кроме своего основного свойства индуктивности, она обладает также некоторым активным сопротивлением и некоторой емкостью.
Конденсатор, в свою очередь, помимо характеризующей его емкости имеет некоторое, обычно очень малое, активное сопротивление. В самом деле, проходя по обкладкам конденсатора, электрические заряды пересекают некоторую массу обкладок, обладающую небольшим активным сопротивлением. И эти небольшие перемещения зарядов порождают также индукцию.
И эти небольшие перемещения зарядов порождают также индукцию.
Таким образом, вы видите, что ни одна из этих трех характеристик, обозначаемых буквами R, L и С, не может существовать отдельно без наличия двух других. Тем не менее мы не будем учитывать эти побочные явления, так как они неизмеримо меньше основного свойства компонента.
Последовательное соединение
Нам необходимо изучить соединение однородных и разнородных компонентов. Мы проанализируем, какая величина получается в результате и какое сопротивление прохождению тока оказывают соединенные между собой компоненты.
Компоненты могут соединяться последовательно или параллельно (рис. 31). Последовательным соединением называется такое, когда конец одного компонента соединен с началом другого и т. д.
В этом случае ток поочередно проходит по всем образующим цепочку компонентам. При параллельном соединении между собой соединены одноименные выводы. Здесь ток, разветвляясь, одновременно проходит по всем соединенным таким образом компонентам.
Вы легко поймете, что соединенные последовательно сопротивления складываются. Возьмем резисторы сопротивлением 100, 500 и 1000 Ом. Соединим их последовательно; полученная цепочка будет иметь сопротивление
Возьмем теперь катушки индуктивности и соединим их последовательно. условии, что между ними нет взаимной индукции, их индуктивности должны складываться.
Возьмем катушки, обладающие индуктивностью соответственно 0,5 и 1,25 Г, и соединим их последовательно, разместив их достаточно далеко друг от друга, чтобы избежать взаимного влияния. Индуктивность цепи составит:
Все это кажется очень простым. А будет ли так же просто при последовательном соединении конденсаторов?
Рис. 31. Последовательное (а) и параллельное (б) соединения компонентов.
Рис. 32. Последовательное соединение конденсаторов. Суммарная емкость меньше емкости каждого из .
Мы сказали, что при таком соединении сопротивления компонентов складываются. А у конденсаторов складываются емкостные сопротивления. Рассмотрим случай с двумя конденсаторами, имеющими емкости соответственно , по которым протекает ток с частотой (рис. 32). Емкостные сопротивления этих конденсаторов складываются и составляют общее емкостное сопротивление:
Рассмотрим случай с двумя конденсаторами, имеющими емкости соответственно , по которым протекает ток с частотой (рис. 32). Емкостные сопротивления этих конденсаторов складываются и составляют общее емкостное сопротивление:
Рассматривая емкостное сопротивление всей цепочки как соответствующее емкости С, мы можем записать:
Умножив все члены этого равенства на , получим:
Проведенные преобразования позволяют нам сделать вывод, что при последовательном соединении конденсаторов нужно сложить обратные величины их емкостей, чтобы получить обратную величину емкости всей цепочки.
В рассмотренном нами случае, т. е. случае последовательного соединения двух конденсаторов, из последней формулы мы без большого математического усилия можем вывести формулу для расчета емкости всей цепочки:
Параллельное соединение
Перейдем теперь к изучению компонентов, соединенных параллельно. Этот способ включения облегчает прохождение тока. В самом деле, здесь складывают проводимости компонентов.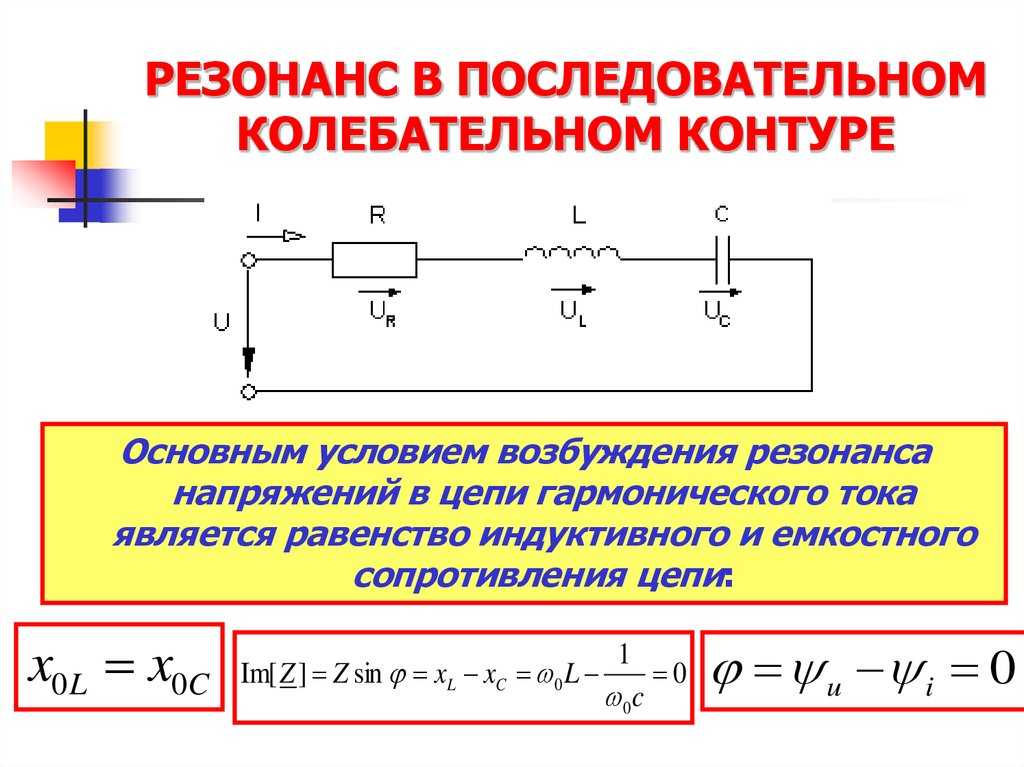 Так называют величину, обратную сопротивлению.
Так называют величину, обратную сопротивлению.
Рассмотрим случай параллельного соединения активных сопротивлений (рис. 33). Их проводимости складываются. При параллельном соединении двух резисторов проводимость всей цепочки равна сумме проводимостей соединенных резисторов:
Как вы видите, здесь наблюдается аналогия с последовательным соединением конденсаторов, и вы без труда можете рассчитать общее сопротивление цепи R двух параллельно соединенных резисторов:
Теперь, если мои рассуждения вам еще не наскучили, рассмотрим случай параллельного соединения двух катушек, между которыми нет взаимной индукции (рис. 34). Индуктивные сопротивления катушек пропорциональны их индуктивности. Следовательно, они будут вести себя аналогично активным сопротивлениям.
Итак, мы не ошибемся, если скажем, что две соединенные параллельна катушки и обладают общей индуктивностью, которая рассчитывается по формуле
И, наконец, рассмотрим случай двух соединенных параллельно конденсаторов (рис.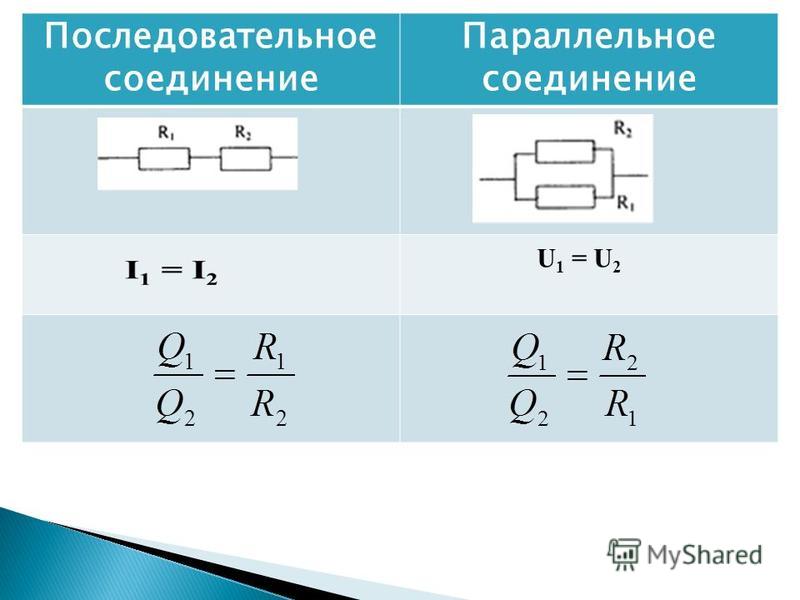 35). Здесь нужно складывать проводимости, которые представляют собой величины, обратные емкостным сопротивлениям. Но сами емкостные сопротивления, как вы помните, обратно пропорциональны емкостям. Это означает, что проводимости конденсаторов прямо пропорциональны их емкостям.
35). Здесь нужно складывать проводимости, которые представляют собой величины, обратные емкостным сопротивлениям. Но сами емкостные сопротивления, как вы помните, обратно пропорциональны емкостям. Это означает, что проводимости конденсаторов прямо пропорциональны их емкостям.
Рис. 33. При параллельном соединении резисторов общее сопротивление уменьшается.
Рис. 34. Параллельное соединение катушек индуктивности.
Рис. 35. Параллельное соединение конденсаторов.
Следовательно, будучи соединенными параллельно, емкости складываются:
Впрочем, анализируя физические явления, происходящие при заряде конденсаторов, вы легко пришли бы к этому выводу.
Постарайся запомнить, дорогой Незнайкин, что при последовательном соединении компонентов складываются их сопротивления, а при параллельном соединении складываются проводимости, т. е. величины, обратные сопротивлению.
Комбинированное соединение
Все только что сказанное мною применимо лишь к схемам, состоящим из однородных компонентов. Но положение значительно усложнится, если мы соединим вместе активные сопротивления, катушки индуктивности и конденсаторы.
Но положение значительно усложнится, если мы соединим вместе активные сопротивления, катушки индуктивности и конденсаторы.
Здесь мне следовало бы использовать термин полное сопротивление, который, как показывает само слово «полное», означает комплексное сопротивление, состоящее из активного и реактивного сопротивления. В отличие от активного сопротивления, присущего тому или иному материалу проводника, индуктивное и емкостное сопротивления называют реактивными сопротивлениями.
Полное сопротивление обозначается буквой Z, а его обратная величина и называется полной проводимостью.
Я не хочу утомлять вас рассмотрением всех возможных комбинаций. Мы ограничимся только теми, которые встречаются во всех электронных устройствах (табл. 2).
Рассмотрим для начала последовательное соединение катушки индуктивности с конденсатором (рис. 36). Их реактивные сопротивления складываются, но это не дает нам основания написать формулу со знаком плюс. В самом деле, индуктивное и емкостное сопротивления имеют как бы противоположные свойства.
Индуктивность, как вы знаете, задерживает появление тока при подключении к ней переменного напряжения. Это называется сдвигом по фазе, и ток в данном случае отстает от напряжения.
Обратное явление происходит в конденсаторе, где ток опережает напряжение по фазе. Ведь по мере нарастания заряда конденсатора напряжение на его обкладках увеличивается, но с приближением к насыщению величина тока убывает. Поэтому вас не удивит, что, складывая индуктивное сопротивление с емкостным, я перед последним поставлю знак минус:
Рис. 36. Последовательно соединенные катушка и конденсатор. Полное сопротивление цепи равно разности индуктивного и емкостного сопротивлений.
Рис. 37. Соотношение между гипотенузой и катетами прямоугольного треугольника.
Активное сопротивление в данном случае очень мало, и поэтому в приведенной выше формуле оно не учитывается. Но если величина R активного сопротивления значительна, то наша формула приобретает более сложный вид:
Как вы видите, нужно извлечь квадратный корень из суммы квадратов активного и реактивного сопротивлений, чтобы получить полное сопротивление.
Таблица 2
Это ничего тебе не напоминает, Незнайкин, из области геометрии? Не таким ли образом рассчитывают длину гипотенузы (рис. 37), извлекая квадратный корень из суммы квадратов катетов?
) мы обсудили все основные аспекты, а именно устройство катушек, принцип работы и их поведение при использовании в цепях постоянного и переменного тока
. Но некоторые моменты остались незатронутыми, собственно, их мы и обсудим в этой статье
Добротность и энергия катушки индуктивности. Варианты соединения.
Aveal
Продолжаем обсуждение катушек индуктивности, в первой части (ссылка) мы обсудили все основные аспекты, а именно устройство катушек, принцип работы и их поведение при использовании в цепях постоянного и переменного тока. Но некоторые моменты остались незатронутыми, собственно, их мы и обсудим в этой статье. И начнем с очень важной характеристики, а именно добротности катушки индуктивности.
Активное сопротивление и добротность катушки индуктивности.
Итак, начнем мы с того, что обсудим некоторые характеристики катушек индуктивности, с которыми мы не успели познакомиться в предыдущей статье. И для начала рассмотрим активное сопротивление катушки.
Разбирая примеры включения катушек в различные цепи, мы считали их активное сопротивление равным 0 (такие катушки называют идеальными). Но на практике любая катушка обладает ненулевым активным сопротивлением. Таким образом реальную катушку индуктивности можно представить как идеальную катушку и последовательно включенный резистор:
Идеальная катушка, как вы помните, не оказывает никакого сопротивления постоянному току, и напряжение на ней равно 0. В случае с реальной катушкой ситуация несколько меняется. При протекании по цепи постоянного тока напряжение на катушке будет равно:
U_L = IR_а
Ну а поскольку частота тока равна 0 (постоянный ток), то реактивное сопротивление:
X_L = 2\pi f L = 0
А что же будет происходить при включении реальной катушки индуктивности в цепь переменного тока? Давайте разбираться.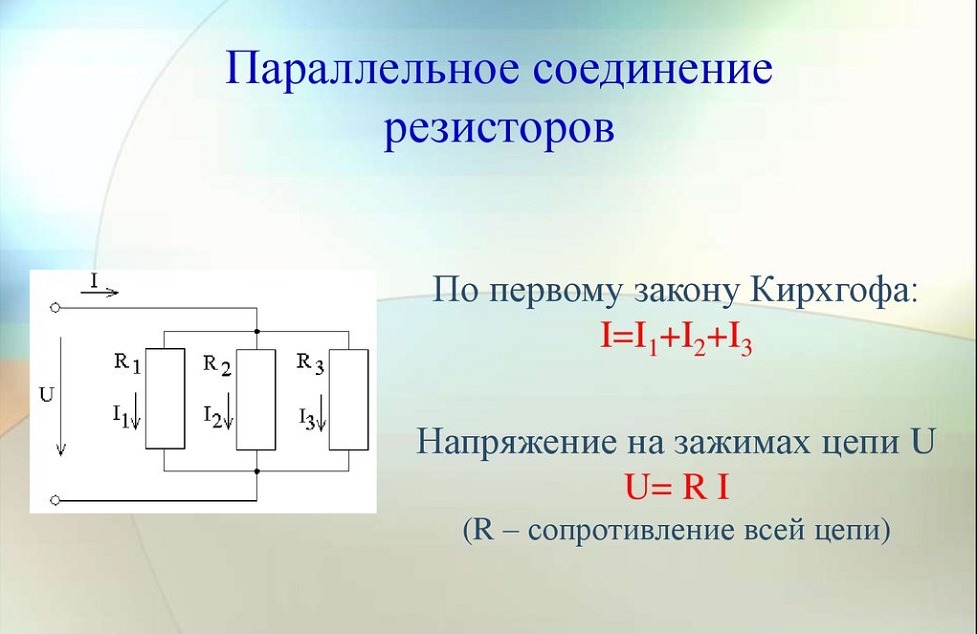 Представим, что по данной цепи течет переменный ток i, тогда общее напряжение на цепи будет складываться из следующих компонент:
Представим, что по данной цепи течет переменный ток i, тогда общее напряжение на цепи будет складываться из следующих компонент:
u = iR + u_L
Напряжение на идеальной катушке, как вы помните, выражается через ЭДС самоиндукции:
u_L = -\varepsilon_L = L\frac{di}{dt}И мы получаем для напряжения на реальной катушке индуктивности:
u = iR + L\frac{di}{dt}Отношение реактивного (индуктивного) сопротивления к активному называется добротностью и обозначается буквой Q:
Q = \frac{X_L}{R}Раз активное сопротивление R идеальной катушки равно 0, то значит ее добротность Q будет бесконечно большой. Соответственно, чем выше добротность катушки индуктивности, тем она ближе к идеальной. Таким образом активное сопротивление катушки мы рассмотрели, перейдем к следующему вопросу.
Энергия катушки индуктивности.
Электрический ток, протекающий через катушку способствует накоплению энергии в магнитном поле катушки. При пропадании/отключении тока эта энергия будет возвращена в электрическую цепь. 2}{2}
2}{2}
Планомерно переходим к вариантам соединения катушек между собой. Все расчеты будем производить для идеальных катушек индуктивности, то есть их активные сопротивления равны 0. К слову, в большинстве теоретических задач и примеров, рассматриваются именно идеальные катушки. Но не стоит забывать о том, что в реальных цепях активное сопротивление не равно 0, и его необходимо учитывать при проведении любых расчетов.
Последовательное соединение катушек индуктивности.
При последовательном соединении катушек индуктивности их можно заменить одной катушкой с величиной индуктивности, равной:
L_0 = L_1 + L_2
Вроде все просто, но тут есть один немаловажный нюанс. Данная формула справедлива только в том случае, если катушки расположены на таком расстоянии друг от друга, что магнитное поле одной катушки не пересекает витков другой:
Если же катушки расположены близко друг к другу и часть магнитного поля одной катушки пронизывает вторую, то тут ситуация несколько другая. Возможны два варианта:
Возможны два варианта:
- магнитные потоки катушек имеют одинаковое направление
- магнитные потоки направлены навстречу друг другу
Первый случай называется согласным включением катушек — начало второй катушки подключается к концу первой. А второй вариант называют встречным включением — конец второй катушки подключается к началу первой. На схемах начало катушки обозначают символом «*». Таким образом, на схеме, которая представлена на рисунке мы имеем согласное включение катушек индуктивности. Для этого случая общая индуктивность определяется так:
L = L_1 + L_2 + 2M
Где M — взаимная индуктивность катушек. При встречном включении последовательно соединенных катушек индуктивности:
L = L_1 + L_2\medspace-\medspace 2M
Можно заметить, что если потоки имеют одинаковое направление (согласное включение), то общая индуктивность увеличивается на двойную величину взаимной индуктивности. А если потоки направлены навстречу друг другу — уменьшается на ту же самую величину. 2}{L_1 + L_2 + 2M}
2}{L_1 + L_2 + 2M}
Также как и в случае с последовательным соединением, при согласном включении общая индуктивность будет больше, чем при встречном включении, поскольку знаменатель дроби будет меньше.
Собственно, на этом заканчиваем разбор катушек индуктивности. Ранее мы изучили конденсаторы и резисторы, а в будущих статьях нам предстоит работать с цепями, включающими все эти элементы. Так что подписывайтесь на обновления и не пропускайте новые статьи 🤝
Катушки индуктивности последовательно и параллельно
Содержание : Катушки индуктивности последовательно и параллельноЧто такое индукторы?ИндукторыИндукторы — это не что иное, как магнитные накопители энергии. Физически это катушка из проводящего провода, намотанная на твердый сердечник или без сердечника. Последний называется индуктор с воздушным сердечником.
Когда ток течет через индуктор, он создает магнитное поле.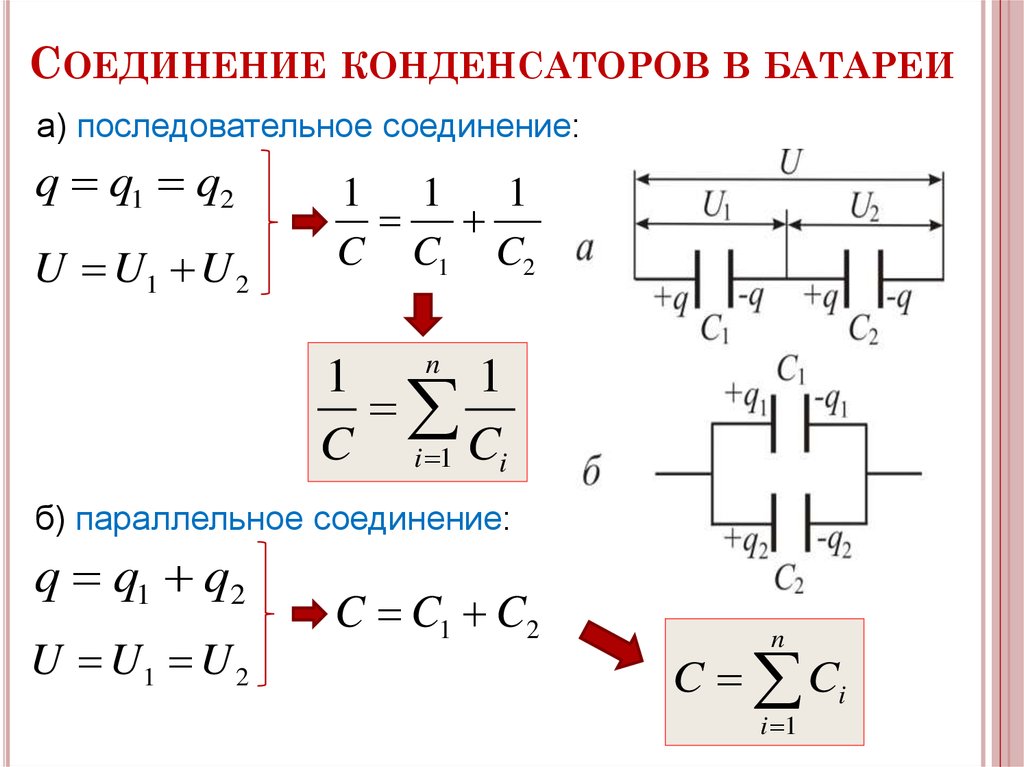 Скручивание большого количества проволоки увеличивает силу магнитного поля. Направление магнитного поля определяется с помощью правило большого пальца правой руки.
Скручивание большого количества проволоки увеличивает силу магнитного поля. Направление магнитного поля определяется с помощью правило большого пальца правой руки.
Когда ток впервые начинает течь через катушку, магнитное поле начинает расширяться, затем через некоторое время оно стабилизируется и сохраняет некоторое количество магнитной энергии. Когда поле постепенно схлопывается, магнитная энергия снова превращается в электрическую. Индукторы производят магнитный поток, пропорциональный току, протекающему через них.
Чтобы узнать больше об индуктивном реактивном сопротивлении нажмите сюда.
Что такое самоиндукция?Определение самоиндукцииСамоиндукция — это характеристика катушки, с помощью которой катушка противодействует любому внезапному изменению тока в ней.
Собственная индуктивность катушки, [Latex]L=\frac{N\phi }{i}[/Latex]
Где, N = количество витков в катушке,? = магнитный поток, i — ток, протекающий через катушку. {2}A}{l}[/Latex] ( Отвечать )
{2}A}{l}[/Latex] ( Отвечать )
Как рассчитать катушки индуктивности последовательно?Добавление индукторов последовательно | Два индуктора последовательноа Катушки индуктивности в последовательной цепиВ случае двух катушек изменение тока в одной катушке вызывает ЭДС в соседней катушке. Этот инцидент известен как взаимная индукция, а это свойство первичной катушки называется взаимной индуктивностью.
При последовательном соединении катушек индуктивности из диаграммы видно, что ток в каждой катушке индуктивности одинаков. Таким образом, полное падение напряжения на катушках индуктивности является суммой падений напряжения на каждой отдельной катушке индуктивности. Предположим, L — полная индуктивность цепи. Итак, полное падение напряжения VВсего будет
VВсего V =1 + V2
V1 и V2 — это падение напряжения через отдельный индуктор соответственно.
По правилу Кирхгофа мы можем написать,
[Латекс] V_ {Всего} — (L_ {1} + L_ {2}) \ frac {\ mathrm {d} i} {\ mathrm {d} t} = 0 [/Latex]
[Латекс] V_ {Всего} = (L_ {1} + L_ {2}) \ frac {\ mathrm {d} i} {\ mathrm {d} t} [/Latex]
[Латекс] L \ frac {\ mathrm {d} i} {\ mathrm {d} t} = (L_ {1} + L_ {2}) \ frac {\ mathrm {d} i} {\ mathrm {d} т}[/латекс]
L = L1+L2
( Отвечать )
Эквивалентная индуктивность последовательно включенных индукторов | Формула для последовательного индуктораПодобно ранее найденному уравнению для двух индукторов, если мы соединим последовательно n индукторов с собственной индуктивностью L1, L2, L3,… ..Ln при последовательном включении эквивалентная индуктивность для катушек индуктивности в последовательной цепи будет,
Leq = л1 + L2 + L3 +… .. + Ln
( Отвечать )
Как рассчитать индукторы параллельно?Катушки индуктивности параллельно Катушки индуктивности параллельноПри параллельном подключении из диаграммы можно сделать вывод, что полный ток, протекающий по цепи, является суммой тока отдельной катушки.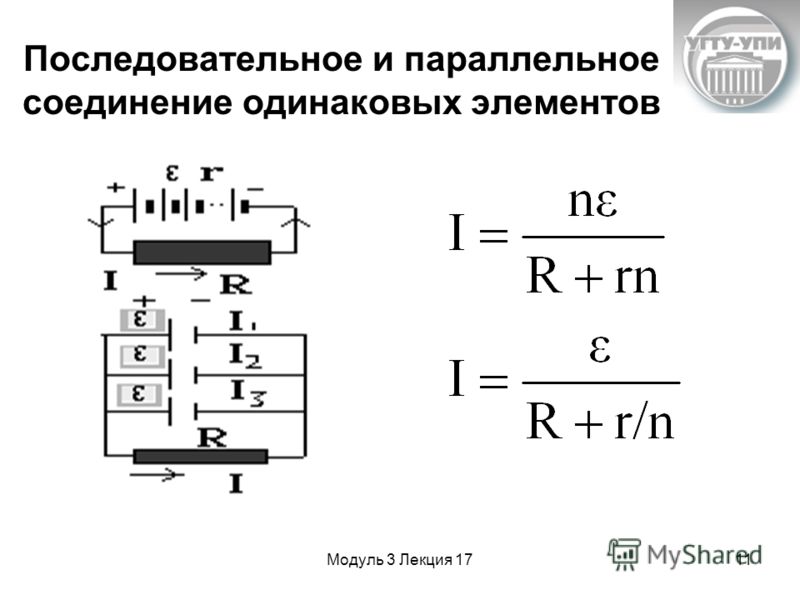 {-1}[/Latex] ( Отвечать )
{-1}[/Latex] ( Отвечать )
Для приведенных выше выводов мы предположили, что между индукторами нет взаимной индуктивности. Теперь, если индукторы соединены таким образом, что магнитное поле, создаваемое одним, влияет на индуктивность других, говорят, что индукторы «связаны между собой».
Связанные индукторы последовательноМагнитные поля индукторов могут либо помогать, либо противодействовать друг другу в зависимости от ориентации катушек. Муфты можно разделить на два типа:
Серийный вспомогательный тип муфты :В этом типе связи магнитные поля индукторов имеют одинаковое направление. Таким образом, токи, протекающие через индукторы, также имеют одинаковое направление. Для двух индукторов с самоиндукцией L1 и я2 и взаимной индуктивности M можно записать
Общая наведенная ЭДС = Самоиндуцированные ЭДС в L1 и я2 + наведенная ЭДС в одной катушке из-за изменения тока в другой для взаимной индуктивности
[Латекс] V = V_ {1} + V_ {2} + V_ {M_ {12}} + V_ {M_ {21}} = L_ {1} \ frac {\ mathrm {d} i} {\ mathrm {d } t} + L_ {2} \ frac {\ mathrm {d} i} {\ mathrm {d} t} + M \ frac {\ mathrm {d} i} {\ mathrm {d} t} + M \ frac {\ mathrm {d} i} {\ mathrm {d} t} = (L_ {1} + L_ {2} + 2M) \ frac {\ mathrm {d} i} {\ mathrm {d} t} [/ Латекс]
Следовательно,
Игровой автомат эквивалентная индуктивность = L1+ L2 + 2M
Последовательно противоположный тип сцепления:В этом типе связи магнитные поля индукторов имеют противоположное направление. Таким образом, направления токов противоположны друг другу. Для двух катушек индуктивности с собственной индуктивностью L1 и L2 и взаимное индуктивность M, мы можем написать,
Таким образом, направления токов противоположны друг другу. Для двух катушек индуктивности с собственной индуктивностью L1 и L2 и взаимное индуктивность M, мы можем написать,
Общая наведенная ЭДС = Самоиндуцированные ЭДС в L1 и я2 + наведенная ЭДС в одной катушке из-за изменения тока в другой для взаимной индуктивности
[Латекс] V = V_ {1} + V_ {2} + V_ {M_ {12}} + V_ {M_ {21}} = L_ {1} \ frac {\ mathrm {d} i} {\ mathrm {d } t} + L_{2}\frac{\mathrm{d} i}{\mathrm{d} t} — M\frac{\mathrm{d} i}{\mathrm{d} t} — M\frac {\ mathrm {d} i} {\ mathrm {d} t} = (L_ {1} + L_ {2} — 2M) \ frac {\ mathrm {d} i} {\ mathrm {d} t} [/ Латекс]
Следовательно, эквивалентная индуктивность = L1+ L2 -2M
Каким будет импеданс конденсатора и катушки индуктивности в последовательной LC-цепи?Импеданс конденсатора и катушки индуктивности в последовательном LC-контуре:последовательная LC-цепьДля вышеуказанного конденсатора и катушек индуктивности в последовательная схема, будем считать, что сопротивления нет. {2}}{2C}][/Latex]
{2}}{2C}][/Latex]
Для вышеуказанного конденсатора и катушек индуктивности в последовательная схема
Полный импеданс LC-цепи XLC=XL-XC если XL>XC
=XC-XL если XL<XC
Последовательные и параллельные индукторыКатушка индуктивности и конденсатор подключены к источнику переменного тока 120 В, 60 Гц. Для следующей LC-цепи найдите полное сопротивление и ток, протекающий по цепи.
Схема LCДанный:
L = 300 мГн C = 50 мкФ V = 120 В f = 50 Гц
Мы знаем, XL= 2πfL и XC= 1 / 2πfC
Подставляя данное значение L и C, получаем,
XL = 113 Ом
XC= 53 Ом
Следовательно, полное сопротивление Z = XL — ИКСC = 113 — 53 = 60 Ом
Ток в цепи, i = V / Z = 120/60 = 2 А
- LC-цепь состоит из индуктора L = 20 мГн и конденсатора C = 50 мкФ.
 Начальный заряд обкладки конденсатора составляет 10 мКл. Какая полная энергия? Также узнайте резонансную частоту.
Начальный заряд обкладки конденсатора составляет 10 мКл. Какая полная энергия? Также узнайте резонансную частоту.
Данный:
L = 20 мГн C = 50 мкФ Q0 = 10 мкКл
Полная энергия E = Q02/ 2C = (10 x 001) 2 / 2x 0.00005 = 1 Дж
Частота резонанса f = 1 / 2√LC = 1 / (2 x 3.14 x √ (20 x 0.001 x 0.00005)) = 159 Гц ( Отвечать )
Резистор и катушка индуктивности в последовательной цепи LRсерия LR цепьЦепи, содержащие резисторы и индукторы, известны как цепи LR. Когда мы подключаем источник напряжения, по цепи начинает течь ток. Теперь, если мы применим закон Кирхгофа, мы получим,
[Latex]V_{0}-iR – L\frac{\mathrm{d} i}{\mathrm{d} t}=0[/Latex] ( V0 напряжение источника)
[Латекс] V_ {0} = iR + L \ frac {\ mathrm {d} i} {\ mathrm {d} t} [/Latex]
[Латекс]\frac{di}{V_{0}-iR}=\frac{dt}{L}[/Latex]
Интегрируя обе стороны с пределом от i = 0 до I и t = 0 до t, получаем,
[Латекс]\frac{-\ln (V_{0}-iR) + \ln (V_{0})}{R}=\frac{t}{L}[/Latex]
[Латекс]\ln (\frac{V_{0}-iR}{V_{0}})=\frac{-Rt}{L}[/Latex]
[Латекс]\frac{V_{0}-iR}{V_{0}}=e^{\frac{-Rt}{L}}[/Latex]
Следовательно, [Latex]i=\frac{V_{0}}{R}(1-e^{\frac{-Rt}{L}})[/Latex] ( Отвечать )
Постоянная времени цепи LR? = L / R называется постоянной времени цепи LR
Импеданс катушки индуктивности и резистора последовательно | Импеданс цепи LRСопротивление и индуктивность — это компоненты, ответственные за полное сопротивление цепи LR. {2}}[/Latex] ( Отвечать )
{2}}[/Latex] ( Отвечать )
Батарея на 24 В удаляется из цепи, состоящей из резистора с сопротивлением 2 Ом и катушки индуктивности с индуктивностью 0.03 Н. Рассчитайте начальный ток при t = 0 секунд. Узнайте, сколько времени нужно, чтобы ток снизился до 50% от начального.
Если батарею внезапно вынуть из цепи, то потребуется некоторое время, прежде чем ток упадет до нуля.
При t = 0, i = V0/ R = 24/2 = 12 А
Постоянная времени ? = L / R = 0.03 / 2 = 0.015 секунды
я = я0e-t /? где я0 начальный ток перед замыканием переключателя
0.5 = е-t / 0.015
т / 0.015 = -ln (0.5)
t = 0.01 с ( Отвечать )
Резистор 2 Ом и катушка индуктивности 8 мГн соединены последовательно с источником питания 6 вольт. Сколько времени потребуется, чтобы ток стал 99.9% конечного тока?
Постоянная времени контура = L / R = 8 x 0. {2}}[/Latex] ( Отвечать )
{2}}[/Latex] ( Отвечать )
Последовательная цепь RLC состоит из резистора 30 Ом, катушки индуктивности 80 мГн и конденсатора 40 мкФ. На него подается напряжение питания переменного тока 120 В и 50 Гц. Узнайте ток в цепи.
решение:
Индуктивное сопротивление XL= 2πfL = 2 x 3.14 x 80 x 0.001 x 50 = 25.13 Ом
Емкостное реактивное сопротивление XC = 1 / 2πfC = 79.58 Ом
Полный импеданс, Z = √ {R2 + (XC — ИКСL)2} = √ {(30)2 + (79.58-25.13)2} = 62.17 Ом
Следовательно, ток в цепи, i = 120 / 62.17 = 1.93 А
- Выведите уравнение для тока в приведенной ниже схеме, где V = sin4t
Применяя к схеме закон Кирхгофа, можно записать
Sin4t — 3i — 2di / dt + Q / 0.5 = 0
Sin4t = 3i + 2di / dt + 2Q
Принимая дифференциацию с обеих сторон,
4cos4t = 3di / dt + 2d2i / dt2 +2 я (т)
я (t) + 3/2 (di / dt) + d2i / dt2 = 2cos4t Это необходимое уравнение для тока. ( Отвечать )
( Отвечать )
1. LC-цепь хранит полную энергию E. Максимальный заряд конденсатора составляет Q. Энергия, запасенная в катушке индуктивности, пока заряд конденсатора составляет Q / 2, составляет
- E
- Е / 2
- Е / 4
- 3E / 4 (ответ)
Решение: Общая энергия = E = Q2/ 2C
Общая энергия = EC + Ei
Когда заряд конденсатора составляет Q / 2, полная энергия,
Q2/ 2C = (Q / 2)2/ 2C + Ei
Ei = Q2/ 2C х (1-¼) = 3E / 4 ( Отвечать )
2. Если ток в одной катушке станет постоянным, какой ток будет протекать через соседнюю катушку?
- Двойник первой катушки
- Половина первой катушки
- Ноль (ответ)
- Бесконечность
Решение: ток индуцируется при изменении магнитного потока в катушке. Следовательно, если в одной катушке постоянный ток, поток не будет генерироваться, и ток в соседней катушке будет равен нулю.
Следовательно, если в одной катушке постоянный ток, поток не будет генерироваться, и ток в соседней катушке будет равен нулю.
3. Резистор на 7 Ом соединен последовательно с индуктором 32 мГн в индукторах в последовательной цепи. Если напряжение питания составляет 100 В, 50 Гц, рассчитайте падение напряжения на катушке индуктивности.
- 67 V
- 82 V (Отвечать)
- 54 V
- 100 V
Подробное решение проблемы:
Индуктивное сопротивление XL для схемы = 2 x 3.14 x 50 x 0.032 = 10 Ом
Полный импеданс Z = √(R2 + XL2) = √(72 + 102) = 12.2 Ом
Следовательно, ток в цепи = 100 / 12.2 = 8.2 А
Падение напряжения на катушке индуктивности = iXL = 8.2 х 10 = 82 В (Отвечать)
4. Найдите эквивалентный импеданс для бесконечной лестничной цепи, показанной ниже.
- j4 Ом
- j8 Ом
- j4 (√2 — 1) Ом
- j4 (√2 + 1) Ом (Отвечать)
Решение: для указанной выше бесконечной схемы предположим, что,
Z1 = j8 Ом и Z2 = j4 — j2 = j2 Ом
Если эквивалентный импеданс равен Z, то мы можем написать
Z = Z1 + (Я2 || Z) = Z1 + ЗЗ2/ Z + Z2
Z (Z + Z2 ) = Z1Z2 + ЗЗ1 + ЗЗ2
Z2 + j2Z = -16 + j8Z + j2Z
Z2 — j8Z + 16 = 0
Решая квадратное уравнение, получаем,
Z = j4 (√2 + 1) Ом (Отвечать)
5.
 Собственная индуктивность соленоида 5 мГн. Катушка имеет 10 витков. Какой будет индуктивность катушки, если количество витков увеличится вдвое?
Собственная индуктивность соленоида 5 мГн. Катушка имеет 10 витков. Какой будет индуктивность катушки, если количество витков увеличится вдвое?- 10 мГн
- 5 мГн
- 20 мГн (Отвечать)
- 30 мГн
Решение: Собственная индуктивность соленоида с N витками и площадью поперечного сечения равна = μ.0N2А / л
Здесь μ0 х 100 х А / л = 5
μ0А / л = 1/20
Если количество витков удвоить, то новая собственная индуктивность = μ0A / лк N ‘2 = 1/20 x (20) 2 = 20 мГн (Отвечать)
Часто задаваемые вопросы | Краткое примечаниеКак добавить катушки индуктивности последовательно и параллельно? | Катушки индуктивности последовательно и параллельно:
Ответ :
Последовательно сумма собственной индуктивности всех катушек индуктивности является общей индуктивностью цепи. При параллельном подключении сумма, обратная величине всех собственных индуктивностей, является обратной величиной полной индуктивности.
При параллельном подключении сумма, обратная величине всех собственных индуктивностей, является обратной величиной полной индуктивности.
Как добавление катушек индуктивности в цепь влияет на ток?
Ответ :
Катушки индуктивности, добавленные последовательно, имеют один и тот же ток. Таким образом, общая напряжение цепи выше, чем напряжения отдельных катушек индуктивности.
Что такое индукторы с дифференциальной связью?
Ответ :
Это другое название серии встречных индукторов, в которых магнитные потоки, создаваемые индукторами, противоположны по направлению. Общая индуктивность индукторов этого типа равна сумме собственной индуктивности индукторов — 2 x взаимной индуктивности.
Какова взаимная индуктивность двух последовательно соединенных катушек?
Ответ :
Взаимная индуктивность двух катушек с железным сердечником с витками N1 и н2, площадь поперечного сечения A, длина L и проницаемость μr [Latex]M = \frac{\mu {0}\mu {r}N_{1}N_{2}A}{L}[/Latex]
Что такое серийный индукционный фильтр?
Ответ :
Серийный индуктор фильтр Катушка индуктивности, включенная последовательно между нагрузкой и выпрямителем. Он называется фильтром, так как блокирует переменный ток и пропускает постоянный ток.
Он называется фильтром, так как блокирует переменный ток и пропускает постоянный ток.
Индуктор на 1 генри включен последовательно с конденсатором на 1 мкФ. Найдите сопротивление при частоте 50 Гц и 1000 Гц.
Ответ :
Импеданс, Z = XL — ИКСC
XC при частоте 50 Гц = 1 / 2πf1C = 3183 Ом
XC при частоте 1000 Гц = 1 / 2πf2C = 159 Ом
XL при частоте 50 Гц = 2πf1L = 314 Ом
XL при частоте 1000 Гц = 2πf1L = 6283 Ом
Следовательно, импеданс Z1 при частоте 50 Гц = 6283 — 159 = 6124 Ом
сопротивление Z2 при частоте 1000 Гц = | 314 — 3183 | = 2869 Ом.
|
Навигация: Главная Случайная страница Обратная связь ТОП Интересно знать Избранные Топ: Основы обеспечения единства измерений: Обеспечение единства измерений — деятельность метрологических служб, направленная на достижение. Техника безопасности при работе на пароконвектомате: К обслуживанию пароконвектомата допускаются лица, прошедшие технический минимум по эксплуатации оборудования… Оценка эффективности инструментов коммуникационной политики: Внешние коммуникации — обмен информацией между организацией и её внешней средой… Интересное: Национальное богатство страны и его составляющие: для оценки элементов национального богатства используются… Инженерная защита территорий, зданий и сооружений от опасных геологических процессов: Изучение оползневых явлений, оценка устойчивости склонов и проектирование противооползневых сооружений — актуальнейшие задачи, стоящие перед отечественными… Берегоукрепление оползневых склонов: На прибрежных склонах основной причиной развития оползневых процессов является подмыв водами рек естественных склонов… Дисциплины: Автоматизация Антропология Археология Архитектура Аудит Биология Бухгалтерия Военная наука Генетика География Геология Демография Журналистика Зоология Иностранные языки Информатика Искусство История Кинематография Компьютеризация Кораблестроение Кулинария Культура Лексикология Лингвистика Литература Логика Маркетинг Математика Машиностроение Медицина Менеджмент Металлургия Метрология Механика Музыкология Науковедение Образование Охрана Труда Педагогика Политология Правоотношение Предпринимательство Приборостроение Программирование Производство Промышленность Психология Радиосвязь Религия Риторика Социология Спорт Стандартизация Статистика Строительство Теология Технологии Торговля Транспорт Фармакология Физика Физиология Философия Финансы Химия Хозяйство Черчение Экология Экономика Электроника Энергетика Юриспруденция |
Стр 1 из 2Следующая ⇒ Параллельное включение конденсатора и катушки индуктивности в цепь переменного тока Рассмотрим явления в цепи переменного тока, содержащей генератор, конденсатор и катушку индуктивности, соединенные параллельно. Очевидно, в такой цепи напряжение как на катушке, так и на конденсаторе в любой момент времени равно напряжению, развиваемому генератором. Общий же ток в цепи слагается из токов в ее разветвлениях. Ток в индуктивной ветви отстает по фазе от напряжения на четверть периода, а ток в емкостной ветви опережает его на те же четверть периода. Поэтому токи в ветвях в любой момент времени оказываются сдвинутыми по фазе один относительно другого на полупериода, т. е. находятся в противофазе. Таким образом токи в ветвях в любой момент времени направлены навстречу один другому, а общий ток в неразветвленной части цепи равен разности их. Это дает нам право написать равенство I = IL -IC где I — действующее значение общего тока в цепи, IL и IC — действующие значения токов в.ветвях. Пользуясь законом Ома для определения действующих значений тока в ветвях, получим: Il = U / XL и IC = U / XC Если в цепи преобладает индуктивное сопротивление, т. При этом не следует забывать, что в том и другом случае нагрузка реактивная, т. е. цепь не потребляет энергии генератора. Резонанс токов Рассмотрим теперь случай, когда у параллельно соединенных конденсатора и катушки оказались равными их реактивные сопротивления, т. е. XlL = XC. Если мы, как и прежде, будем считать, что катушка и конденсатор не обладают активным сопротивлением, то при равенстве их реактивных сопротивлений (YL = YC) общий ток в неразветвленной части цепи окажется равным нулю, тогда как в ветвях будут протекать равные токи наибольшей величины. В цепи в этом случае наступает явление резонанса токов. При резонансе токов действующие значения токов в каждом разветвлении, определяемые отношениями IL = U / XL и IC= U / XC будут равны между собой, так XL = ХC. Вывод, к которому мы пришли, может показаться на первый взгляд довольно странным. Действительно, генератор нагружен двумя сопротивлениями, а тока в неразветвленной части цепи нет, тогда как в самих сопротивлениях протекают равные и притом наибольшие по величине токи. Объясняется это поведением магнитного поля катушки и электрического поля конденсатора. При резонансе токов, как и при резонансе напряжений, происходит колебание энергии между полем катушки и полем конденсатора. Генератор, сообщив однажды энергию цепи, сказывается как бы изолированным. Его можно было бы совсем отключить, и ток в разветвленной части цепи поддерживался бы без генератора энергией, которую в самом начале запасла цепь. Равно и напряжение на зажимах цепи оставалось бы точно таким, какое развивал генератор. Таким образом, и при параллельном соединении катушки индуктивности и конденсатора мы получили колебательный контур, отличающийся от описанного выше только тем, что генератор, создающий колебания, не включен непосредственно в контур и контур получается замкнутым. Графики токов, напряжения и мощности в цепи при резонансе токов: а — активное сопротивление равно нулю, цепь мощности не потребляет; б — цепь обладает активным сопротивлением, в неразветвленной части цепи появился ток, цепь потребляет мощность
Значения L, С и f, при которых наступает резонанс токов, определяются, как и при резонансе напряжений (если пренебречь активным сопротивлением контура), из равенства: ωL = 1 / ωC Следовательно: fрез = 1 / 2π√LC Lрез = 1 / ω2С Срез = 1 / ω2L Изменяя любую из этих трех величин, можно добиться равенства Xl = Xc, т. е. превратить цепь в колебательный контур. Итак, мы получили замкнутый колебательный контур, в котором можно вызвать электрические колебания, т. В цепях несинусоидального тока резонансные режимы возможны для различных гармоничных состовляющих. Резонанс токов широко используется в практике.Явление резонанса токов используется в полосовых фильтрах как электрическая «пробка», задерживающая определенную частоту. Так как току с частотой f оказывается значительное сопротивление, то и падение напряжения на контуре при частоте f будет максимальным. Это свойство контура получило название избирательность, оно используется в радиоприемниках для выделения сигнала конкретной радиостанции. Колебательный контур, работающий в режиме резонанса токов, является одним из основных узловэлектронных генераторов.
Если в цепь переменного тока включены последовательно катушка индуктивности иконденсатор, то они по-своему воздействуют на генератор, питающий цепь, и на фазовые соотношения между током и напряжением. Катушка индуктивности вносит сдвиг фаз, при котором ток отстает от напряжения на четверть периода, конденсатор же, наоборот, заставляет напряжение в цепи отставать по фазе от тока на четверть периода. Таким образом, действие индуктивного сопротивления на сдвиг фаз между током и напряжением в цепи противоположно действию емкостного сопротивления. Это приводит к тому, что общий сдвиг фаз между током и напряжением в цепи зависит от соотношения величин индуктивного и емкостного сопротивлений. Если величина емкостного сопротивления цепи больше индуктивного, то цепь носит емкостный характер, т. е. напряжение отстает по фазе от тока. Если же, наоборот, индуктивное сопротивление цепи больше емкостного, то напряжение опережает ток, и, следовательно, цепь носит индуктивный характер. Общее реактивное сопротивление Хобщ рассматриваемой нами цепи определяется путем сложения индуктивного сопротивления катушки XL и емкостного сопротивления конденсатора ХС. Но так как действие этих сопротивлений в цепи противоположно, то одному из них, а именно Хс приписывается знак минус, и общее реактивное сопротивление определяется по формуле: Применив к этой цепи закон Ома, получим: Формулу эту можно преобразовать следующим образом: В полученном равенстве IXL —действующее значение слагающей общего напряжения цепи, идущей на преодоление индуктивного сопротивления цепи, а IХС—действующее значение слагающей общего напряжения цепи, идущей на преодоление емкостного сопротивления. Таким образом, общее напряжение цепи, состоящей из последовательного соединения катушки и конденсатора, можно рассматривать как состоящее из двух слагаемых, величины которых зависят от величин индуктивного и емкостного сопротивлений цепи. Мы считали, что такая цепь не обладает активным сопротивлением. Однако в тех случаях, когда активное сопротивление цепи не настолько уже мало, чтобы им можно было пренебречь, общее сопротивление цепи определяется следующей формулой: где R — общее активное сопротивление цепи, XL -ХС — ее общее реактивное сопротивление. Переходя к формуле закона Ома, мы вправе написать: Резонанс напряжений Когда источник ЭДС, емкость, индуктивность и сопротивление включены между собой последовательно, то резонанс в такой цепи называется последовательным резонансом или резонансом напряжений. Характерная черта резонанса напряжений — значительные напряжения на емкости и на индуктивности, по сравнению с ЭДС источника. Причина появления такой картины очевидна. На активном сопротивлении по закону Ома будет напряжение Ur, на емкости Uc, на индуктивности Ul, и составив отношение Uc к Ur можно найти величину добротности Q. То есть резонанс напряжений приводит к возрастанию напряжения на реактивных элементах в Q раз, а резонансный ток будет ограничен ЭДС источника, его внутренним сопротивлением и активным сопротивлением цепи R. Таким образом, сопротивление последовательного контура на резонансной частоте минимально. Резонанс токов Когда источник ЭДС, емкость, индуктивность и сопротивление включены между собой параллельно, то резонанс в такой цепи называется параллельным резонансом или резонансом токов. Характерная черта резонанса токов — значительные токи через емкость и индуктивность, по сравнению с током источника. Причина появления такой картины очевидна. Ток через активное сопротивление по закону Ома будет равен U/R, через емкость U/XC, через индуктивность U/XL, и составив отношение IL к I можно найти величину добротности Q. Ток через индуктивность будет в Q раз больше тока источника, такой же ток будет течь каждые пол периода в конденсатор и из него. То есть резонанс токов приводит к возрастанию тока через реактивные элементы в Q раз, а резонансная ЭДС будет ограничена ЭДС источника, его внутренним сопротивлением и активным сопротивлением цепи R. Таким образом, на резонансной частоте сопротивление параллельного колебательного контура максимально. Применение резонанса токов Аналогично резонансу напряжений, резонанс токов применяется в различных фильтрах. Но включенный в цепь, параллельный контур действует наоборот, чем в случае с последовательным: установленный параллельно нагрузке, параллельный колебательный контур позволит току резонансной частоты контура пройти в нагрузку, поскольку сопротивление самого контура на собственной резонансной частоте максимально. Установленный последовательно с нагрузкой, параллельный колебательный контур не пропустит сигнал резонансной частоты, поскольку все напряжение упадет на контуре, а на нагрузку придется мизерная доля сигнала резонансной частоты. Так, основное применение резонанса токов в радиотехнике — создание большого сопротивления для тока определенной частоты в ламповых генераторах и усилителях высокой частоты. В электротехнике резонанс токов используется с целью достижения высокого коэффициента мощности нагрузок, обладающих значительными индуктивными и емкостными составляющими. Например, установки компенсации реактивной мощности (КРМ) представляют собой конденсаторы, подключаемые параллельно обмоткам асинхронных двигателей и трансформаторов, работающих под нагрузкой ниже номинальной. К таким решениям прибегают как раз с целью достижения резонанса токов (параллельного резонанса), когда индуктивное сопротивление оборудования делается равным емкостному сопротивлению подключаемых конденсаторов на частоте сети, чтобы реактивная энергия циркулировала между конденсаторами и оборудованием, а не между оборудованием и сетью; чтобы сеть отдавала энергию только тогда, когда оборудование нагружено и потребляет активную мощность. Когда же оборудование работает в холостую, сеть оказывается подключена параллельно резонансному контуру (внешние конденсаторы и индуктивность оборудования), который представляет для сети очень большое комплексное сопротивление и позволяет снизитьсякоэффициенту мощности.
ЛитератураПравить § Власов В. Ф. Курс радиотехники. М.: Госэнергоиздат, 1962. С. 928. § Изюмов Н. М., Линде Д. П. Основы радиотехники. М.: Госэнергоиздат, 1959. С. 512.
Параллельное включение конденсатора и катушки индуктивности в цепь переменного тока Рассмотрим явления в цепи переменного тока, содержащей генератор, конденсатор и катушку индуктивности, соединенные параллельно. Предположим при этом, что активным сопротивлением цепь не обладает. Очевидно, в такой цепи напряжение как на катушке, так и на конденсаторе в любой момент времени равно напряжению, развиваемому генератором. Общий же ток в цепи слагается из токов в ее разветвлениях. Ток в индуктивной ветви отстает по фазе от напряжения на четверть периода, а ток в емкостной ветви опережает его на те же четверть периода. Поэтому токи в ветвях в любой момент времени оказываются сдвинутыми по фазе один относительно другого на полупериода, т. Это дает нам право написать равенство I = IL -IC где I — действующее значение общего тока в цепи, IL и IC — действующие значения токов в.ветвях. Пользуясь законом Ома для определения действующих значений тока в ветвях, получим: Il = U / XL и IC = U / XC Если в цепи преобладает индуктивное сопротивление, т. е. XL больше XC, ток в катушке меньше тока в конденсаторе; следовательно, ток в неразветвленном участке цепи носит емкостный характер, и цепь в целом для генератора будет емкостной. И, наоборот, при ХC большем XL, ток в конденсаторе меньше тока в катушке; следовательно, ток в неразветвленном участке цепи имеет индуктивный характер, и цепь в целом для генератора будет индуктивной. При этом не следует забывать, что в том и другом случае нагрузка реактивная, т. е. цепь не потребляет энергии генератора. Резонанс токов Рассмотрим теперь случай, когда у параллельно соединенных конденсатора и катушки оказались равными их реактивные сопротивления, т. е. XlL = XC. Если мы, как и прежде, будем считать, что катушка и конденсатор не обладают активным сопротивлением, то при равенстве их реактивных сопротивлений (YL = YC) общий ток в неразветвленной части цепи окажется равным нулю, тогда как в ветвях будут протекать равные токи наибольшей величины. В цепи в этом случае наступает явление резонанса токов. При резонансе токов действующие значения токов в каждом разветвлении, определяемые отношениями IL = U / XL и IC= U / XC будут равны между собой, так XL = ХC. Вывод, к которому мы пришли, может показаться на первый взгляд довольно странным. Действительно, генератор нагружен двумя сопротивлениями, а тока в неразветвленной части цепи нет, тогда как в самих сопротивлениях протекают равные и притом наибольшие по величине токи. Объясняется это поведением магнитного поля катушки и электрического поля конденсатора. Таким образом, и при параллельном соединении катушки индуктивности и конденсатора мы получили колебательный контур, отличающийся от описанного выше только тем, что генератор, создающий колебания, не включен непосредственно в контур и контур получается замкнутым. Графики токов, напряжения и мощности в цепи при резонансе токов: а — активное сопротивление равно нулю, цепь мощности не потребляет; б — цепь обладает активным сопротивлением, в неразветвленной части цепи появился ток, цепь потребляет мощность
Значения L, С и f, при которых наступает резонанс токов, определяются, как и при резонансе напряжений (если пренебречь активным сопротивлением контура), из равенства: ωL = 1 / ωC Следовательно: fрез = 1 / 2π√LC Lрез = 1 / ω2С Срез = 1 / ω2L Изменяя любую из этих трех величин, можно добиться равенства Xl = Xc, т. Итак, мы получили замкнутый колебательный контур, в котором можно вызвать электрические колебания, т. е. переменный ток. И если бы не активное сопротивление, которым обладает всякий колебательный контур, в нем непрерывно мог бы существовать переменный ток. Наличие же активного сопротивления приводит к тому, что колебания в контуре постепенно затухают и, чтобы поддержать их, необходим источник энергии — генератор переменного тока. В цепях несинусоидального тока резонансные режимы возможны для различных гармоничных состовляющих. Резонанс токов широко используется в практике.Явление резонанса токов используется в полосовых фильтрах как электрическая «пробка», задерживающая определенную частоту. Так как току с частотой f оказывается значительное сопротивление, то и падение напряжения на контуре при частоте f будет максимальным. Это свойство контура получило название избирательность, оно используется в радиоприемниках для выделения сигнала конкретной радиостанции.
Если в цепь переменного тока включены последовательно катушка индуктивности иконденсатор, то они по-своему воздействуют на генератор, питающий цепь, и на фазовые соотношения между током и напряжением. Катушка индуктивности вносит сдвиг фаз, при котором ток отстает от напряжения на четверть периода, конденсатор же, наоборот, заставляет напряжение в цепи отставать по фазе от тока на четверть периода. Таким образом, действие индуктивного сопротивления на сдвиг фаз между током и напряжением в цепи противоположно действию емкостного сопротивления. Это приводит к тому, что общий сдвиг фаз между током и напряжением в цепи зависит от соотношения величин индуктивного и емкостного сопротивлений. Если величина емкостного сопротивления цепи больше индуктивного, то цепь носит емкостный характер, т. е. напряжение отстает по фазе от тока. Если же, наоборот, индуктивное сопротивление цепи больше емкостного, то напряжение опережает ток, и, следовательно, цепь носит индуктивный характер. Общее реактивное сопротивление Хобщ рассматриваемой нами цепи определяется путем сложения индуктивного сопротивления катушки XL и емкостного сопротивления конденсатора ХС. Но так как действие этих сопротивлений в цепи противоположно, то одному из них, а именно Хс приписывается знак минус, и общее реактивное сопротивление определяется по формуле: Применив к этой цепи закон Ома, получим: Формулу эту можно преобразовать следующим образом: В полученном равенстве IXL —действующее значение слагающей общего напряжения цепи, идущей на преодоление индуктивного сопротивления цепи, а IХС—действующее значение слагающей общего напряжения цепи, идущей на преодоление емкостного сопротивления. Таким образом, общее напряжение цепи, состоящей из последовательного соединения катушки и конденсатора, можно рассматривать как состоящее из двух слагаемых, величины которых зависят от величин индуктивного и емкостного сопротивлений цепи. Мы считали, что такая цепь не обладает активным сопротивлением. Однако в тех случаях, когда активное сопротивление цепи не настолько уже мало, чтобы им можно было пренебречь, общее сопротивление цепи определяется следующей формулой: где R — общее активное сопротивление цепи, XL -ХС — ее общее реактивное сопротивление. Переходя к формуле закона Ома, мы вправе написать: 12Следующая ⇒ Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций… Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции… Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ — конструкции, предназначенные для поддерживания проводов на необходимой высоте над землей, водой… Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства… |
gif»>
Параллельное соединение катушек индуктивности | ||||
|
I= . мА |
X L = U L / I Ом |
L = X L / ω, |
Проверка |
|
L =
I
Таблица 5.2.1
Соберите цепь с параллельным соединением катушек (рис. 5.2.2).
Предусмотрите в схеме
перемычки
измерения
мультиметром.
Включите
регулируемый
источник
синусоидального напряжения с параметрами Um = 10B и f = l кГц.
Таблица 5.2.2
Измерьте мультиметром
общий ток цепи I, токи параллельных
ветвей Ii
входе цепи U, занесите
данные измерений в табл. 5.2.2
5.2.2
1г, и напряжения на
Вычислите емкостные реактивные сопротивления Х, X L 1 , X L 2 ,
поформуле X
Определите индуктивности катушек и эквивалентную индуктивность цепи по формуле
L=X L / ω , где ω = 2 πf =
Проверьте вычислениями величину индуктивности L
Величина, описываемая соотношением между скоростью изменения тока и некоторой величиной, проявляющейся в проводнике при действии ЭДС самоиндукции, называется коэффициентом самоиндукции или индуктивностью проводника.
Индуктивность обозначается латинским символом L
. Можно сформулировать и более простое определение: индуктивность
, электротехническая величина показывающая, сколько энергии магнитного поля можно накопить в проводнике. При скручивание проводника в катушку его индуктивность увеличивается в разы. Чем выше L
проводника, тем больше номинальное значение . Индуктивность измеряется единицей, получившей название генри. Сокращенно генри обозначается Гн
.
Индуктивность измеряется единицей, получившей название генри. Сокращенно генри обозначается Гн
.
Индуктивностью в 1 генри обладает катушка, в которой с изменением силы тока на 1 ампер в течение секундного временного интервала наводится ЭДС самоиндукции, равная 1 вольт.
Кроме генри используются величины: тысячная доля генри (миллигенри-мГн), миллионная доля генри (микрогенри — мкГн)
1 миллигенри (мГн) =1/1000 Гн = 10 -3 Гн;
1 микрогенги (мкГн) = 1/1000000 Гн = 1/1000 мГн =10 -6 Гн
Катушка индуктивности |
Катушка индуктивности, как следует из названия представляет из себя именно катушку, то есть имеется некоторое количество витков проводника (обычно медного) намотанных на каркасе. Причем наличие изоляции между витками и каркасом является важнейшим условием. Кроме того витки катушки индуктивности не должны замыкаться между собой. Чаще всего витки наматываются на тороидальный или цилиндрический каркас.
Винтовая, спиральная или винтоспиральная катушка из свёрнутого проводника, обладает значительно большой величиной индуктивности при относительно малом уровне емкости и низком активном сопротивлении.
Индуктивность катушки прямо пропорциональна квадрату числа витков, так как с увеличением количества витков увеличивается, число магнитных силовых линий, и число пересечений каждой силовой линии с проводником.
— увеличивается с увеличением площади витка катушки, так как возрастает уровень магнитного потока в катушке.
-уменьшается с увелечением осевой длины катушки, так как, чем она выше, тем меньшее число витков на единицу ее осевой длины и, следовательно, тем ниже магнитный поток.
Если в катушку добавить железный или стальной сердечник, то величина L возрастет многократно.
Разновидностей катушек индуктивности существуют великое множество. Они бывают высокочастотные, низкочастотные, с подстроечными сердечникам, катушки с отводами, катушки рассчитанные на большие напряжения. Катушки для СВЧ техники называют микрополосковыми линиями. Они совсем не похожи на катушки. (правый рисунок)
Катушки для СВЧ техники называют микрополосковыми линиями. Они совсем не похожи на катушки. (правый рисунок)
Катушка с сердечником может выглядеть так — рисунок слева, а с подстроечным сердечником, как на фотографии справа. Величина индуктивности в случае с подстроечным сердечником меняется в небольших пределах. Подстроечные катушки индуктивности используются в схемах, где необходима одноразовая подстройка. В дальнейшем ее обычно не регулируют.
Последовательное соединение катушек индуктивности
Суммарная индуктивность двух или более катушек, соединенных последовательно и расположенных на определенном расстоянии друг от друга так, что их магнитные поля не пересекали витки соседей, равна сумме их индуктивностей.
Параллельное соединение катушек
при параллельном их соединении и при соблюдении того же условия отсутствие магнитного взаимодействия относительно их расположения, расчет осуществляем по формулам:
Если катушки, соединенные в электрическую цепь последовательно, находятся близко друг к другу, и так, что часть магнитного потока одной пронизывает витки другой, т. е. между катушками присутствует индуктивная связь, то для расчета их общей индуктивности данная выше формула уже не подойдет. При таком расположении могут возникнуть два частных случая:
е. между катушками присутствует индуктивная связь, то для расчета их общей индуктивности данная выше формула уже не подойдет. При таком расположении могут возникнуть два частных случая:
Магнитные потоки катушек в цепи имеют одинаковые направления
Или наооборот их потоки направлены навстречу друг другу
Любой их них будет иметь место в зависимости от направления витков катушек и от направлений протекания токов в них.
Если обе катушки намотаны в одну сторону и токи в них протекают в одном попутном направлении, то-есть когда магнитные потоки направлены в одну сторону. При этих факторах витки каждой катушки будут пронизываться своим потоком и частью потока соседа, т. е. магнитные потоки в обоих катушках будут выше по сравнению с отсутствием индуктивной связи. Поэтому общая индуктивность схемы будет выше суммы ее составляющих отдельных катушек. Наоборот, когда потоки направлены навстречу друг другу, общая индуктивность схемы будет ниже суммы L
отдельных катушек.
В первом случае, в расчетной формуле ставится знак плюс, а во втором знак минус.
Величина М приведенная в формуле, называется коэффициентом взаимной индукции , представляет собой некоторую добавочную индуктивность, обусловленную частью магнитного потока, общей для обеих катушек.
На явлении взаимоиндукции основан принцип работы вариометра . Он состоит из двух катушек, общая L которых может, по необходимости, плавно регулироваться в некотором диапазоне. В радиолюбительской практике вариометры используют для настройки колебательных контуров и передатчиков.
Индуктивное сопротивление отличается от классического омического тем, что при протекании через индуктивность переменного тока отсутствуют потери мощности.
В реальных условиях любая катушка индуктивности обладает и реальным омическим сопротивлением. Но если оно не очень большое по сравнению с индуктивным сопротивлением, то им можно условно пренебречь.
При этом происходит следующий эффект: в течение первой четверти периода, когда ток увеличивается, магнитное поле потребляет энергию из цепи, а в течение следующей четверти, когда ток снижается, возвращает ее в цепь. Поэтому, в среднем за период в индуктивном сопротивлении мощность не расходуется. Поэтому индуктивное сопротивление получило название реактивного.
Поэтому, в среднем за период в индуктивном сопротивлении мощность не расходуется. Поэтому индуктивное сопротивление получило название реактивного.
Индуктивное сопротивление одной и той же катушки будет отличаться для переменных токов разных частот. Чем выше частота, тем большее влияние на схему оказывает индуктивность и тем выше будет индуктивное сопротивление катушки. Наоборот, чем ниже частота переменного тока, тем индуктивное сопротивление ниже. При нулевой частоте (постоянный ток), индуктивное сопротивление нулевое.
Индуктивное сопротивление в формулах электротехники, обозначается как X L и измеряется в омах.
где X L — индуктивное сопротивление в омах; f-частота переменного тока в гц; L — индуктивность катушки в генри
Величину 2π×f называют круговой частотой и обозначают буквой ω (омега). Поэтому формулу выше можно представить так:
Отсюда следует, что при протекании через катушку постоянного тока (ω = 0). Поэтому, если, требуется пропустить по цепи постоянный ток, задержав переменный, то в цепь вводят последовательно катушку индуктивности.
Для преграждения пртекания токов низких звуковых частот используют катушки с железным сердечником, так называемые дроссели низкой частоты (НЧ), а для высоких радиочастот уже без железного сердечника, которые называют дроссели высокой частоты (ВЧ).
Катушка индуктивности в цепи переменного тока |
Если катушка индуктивности стоит в цепи переменного тока, то в ней, фаза тока всегда будет отставать от напряжения. В курсе этой лекции рассмотрим причины отставания фазы тока на элементарном примере, когда в идеальной цепи есть только индуктивное сопротивление, а омическое сопротивление отсутствует, точнее омическим сопротивлением провода катушки пренебрегаем, так как оно очень низкое.
| Катушка индуктивности |
Это — винтовая, спиральная или винтоспиральная катушка из свёрнутого проводника, обладающая значительно большой величиной индуктивности при относительно малом уровне ёмкости и низком активном сопротивлении
Индуктивность катушки прямо пропорциональна квадрату числа витков, так как с увеличением количества витков увеличивается, число магнитных силовых линий, и число пересечений каждой силовой линии с проводником.
— увеличивается с увеличением площади витка катушки, так как возрастает уровень магнитного потока в катушке.
-уменьшается с увелечением осевой длины катушки, так как, чем она выше, тем меньшее число витков на единицу ее осевой длины и, следовательно, тем ниже магнитный поток.
Соединение катушек
Соединение катушек индуктивности при отсутствии взаимного влияния магнитных полей катушек.
Последовательное соединение катушек индуктивности.
Суммарная индуктивность двух или нескольких катушек, соединенных последовательно и расположенных на таком расстоянии друг от друга, что магнитное поле одной катушки не пересекает витков другой (рисунок 1), равна сумме их индуктивностей.
Рисунок 1. Последовательное соединение катушект индуктивности.
Цепь, изображенная на рисунке 1, обладает общей индуктивностью L, которая выражается так:
где L1, L2 и L3 — индуктивности отдельных катушек.
Параллельное соединение катушек индуктивности.
Индуктивность цепи, составленной из тех же катушек при параллельном их соединении (рисунок 2) и при соблюдении того же условия относительно их расположения (отсутствие магнитного взаимодействия), подсчитывается по следующей формуле:
Рисунок 2. Параллельное соединение катушек индуктивности.
Индуктивность двух катушек, соединенных параллельно, определяется по следующей формуле:
Как видим, формулы для подсчета результирующих индуктивностей катушек, соединенных последовательно или параллельно и не взаимодействующих между собой, совершенно тождественны с формулами для подсчета омического сопротивления цепи при последовательном и параллельном соединении резисторов.
Соединение катушек при наличии взаимного влияния их магнитных полей.
Если катушки, включенные в цепь последовательно, расположены близко друг к другу, т. е. так, что часть магнитного потока одной катушки пронизывает витки другой, т. е. между катушками существует индуктивная связь (рисунок 3а), то для определения их общей индуктивности приведенная выше формула будет уже непригодна. При таком расположении катушек могут быть два случая, а именно:
При таком расположении катушек могут быть два случая, а именно:
1. Магнитные потоки обеих катушек имеют одинаковые направления
2. Магнитные потоки обеих катушек направлены навстречу друг другу
Тот или другой случай будет иметь место в зависимости от направления витков обмотки катушек и от направлений токов в них.
Рисунок 3. Соединение катушек индуктивности: а)суммарная индуктивность увеличивается за счет взаимной индукции б)суммарная индуктивность уменьшается за счет взаимной индукции.
Если обе катушки намотаны в одну сторону и токи в них текут в одном направлении, то это будет соответствовать первому случаю; если же токи текут в противоположных направлениях (рисунок 3б), то будет иметь место второй случай.
Разберем первый случай, когда магнитные потоки направлены в одну сторону. Очевидно, при этих условиях витки каждой катушки будут пронизываться своим потоком и частью потока другой катушки, т. е. магнитные потоки в той и в другой катушке будут больше по сравнению с тем случаем, когда между катушками нет индуктивной связи. Увеличение магнитного потока, пронизывающего витки той или иной катушки, равносильно увеличению ее индуктивности. Поэтому общая индуктивность цепи в рассматриваемом случае будет больше суммы индуктивностей отдельных катушек, из которых составлена цепь.
Увеличение магнитного потока, пронизывающего витки той или иной катушки, равносильно увеличению ее индуктивности. Поэтому общая индуктивность цепи в рассматриваемом случае будет больше суммы индуктивностей отдельных катушек, из которых составлена цепь.
Рассуждая таким же образом, мы придем к выводу, что для второго случая, когда потоки направлены навстречу друг другу, общая индуктивность цепи будет меньше суммы индуктивностей отдельных катушек.
Подсчет величины индуктивности цепи, составленной из двух соединенных последовательно катушек индуктивности L1 и L2 при наличии между ними индуктивной связи, производится по формуле:
В первом случае ставится знак + (плюс), а во втором случае знак — (минус).
Величина М, называемая коэффициентом взаимной индукции , представляет собой добавочную индуктивность, обусловленную частью магнитного потока, общей для обеих катушек.
На явлении взаимоиндукции основано устройство вариометров
. Вариометр состоит из двух катушек, общая индуктивность которых может, по желанию, плавно изменяться в некоторых пределах. В радиотехнике вариометры применяются для настройки колебательных контуров приемников и передатчиков.
В радиотехнике вариометры применяются для настройки колебательных контуров приемников и передатчиков.
Катушки индуктивности, соединенные параллельно
Катушки индуктивности называются параллельными, когда два вывода катушки индуктивности соответственно подключены к каждой клемме других катушек индуктивности или катушки индуктивности. Как и при параллельном соединении резисторов, общая индуктивность при параллельном соединении индукторов несколько меньше наименьшей индуктивности индуктора в этом соединении.
[adsense1]
Когда катушки индуктивности соединены параллельно, ток, протекающий через каждую катушку индуктивности, не равен в точности общему току, но сумма каждого отдельного тока через параллельные катушки индуктивности дает общий ток (поскольку он делится на между параллельными индукторами).
Если ток, протекающий через каждый индуктор, меньше, чем общий ток, магнитное поле, создаваемое каждым индуктором, также меньше, чем поле, создаваемое суммарным током через него.
При параллельном соединении резисторов большая часть тока протекает через наименьший резистор, поскольку он оказывает наименьшее сопротивление протеканию тока, чем резистор большего размера.
Аналогичным образом, если катушки индуктивности соединены параллельно, ток выбирает путь наименьшего сопротивления катушки индуктивности, когда ток в этой цепи уменьшается или увеличивается, в то время как каждая катушка индуктивности по отдельности противостоит этому изменению (увеличению или уменьшению тока).
[adsense2]
При параллельном соединении напряжение на всех индукторах одинаково, а также при изменении общего тока падение напряжения на каждом отдельном индукторе будет меньше по сравнению с последовательным соединением. При заданной скорости изменения тока меньше будет индуктивность при меньшем напряжении.
Это основные моменты, которые следует учитывать при параллельном соединении катушек индуктивности. Теперь обсудим параллельное соединение катушек индуктивности с учетом и без учета взаимной связи между этими катушками индуктивности.
Схема
Катушки индуктивности, соединенные параллельно (без магнитной связи)
Как уже говорилось выше, один конец катушки индуктивности соединен с узлом, а другие концы катушки индуктивности совместно соединены с другим узлом в параллельном соединении. Параллельное соединение n индукторов показано на рисунке ниже.
Учтите, что между катушками индуктивности нет магнитной связи и, следовательно, общая индуктивность равна сумме обратных величин индуктивностей отдельных индуктивностей. Обсудим, как можно получить это утверждение.
Мы знаем, что в параллельной сети напряжение остается постоянным, а ток делится на каждой параллельной катушке индуктивности. Если I L1 , I L2 , I L3 и т. д. I Ln представляют собой отдельные токи, протекающие в параллельно соединенных катушках индуктивности L 1 , L 2 и т. д. L 6 n соответственно , то общий ток в параллельных индукторах равен
I Всего = I L1 + I L2 + Я Л3 . . . . + I n
. . . + I n
Если отдельные падения напряжения при параллельном соединении равны V L1 , V L2 , V L3 и т. д. V Ln , то общее падение напряжения между двумя клеммами V T равно
V Итого = V L1 = V L2 = V L3 . . . . = V n
Падение напряжения с точки зрения собственной индуктивности можно выразить как V = L di/dt. Отсюда следует общее падение напряжения,
V T = L T DI/DT
⇒ L T D/DT (I L1 + I L2 + I L3 . T ( (d i1 )/dt + (d i2 )/dt + (d i3 )/dt . . . . . . . .)
Подстановка V / L вместо di/dt, указанное выше уравнение принимает вид
В T = L T (V/L 1 + V/L 2 + V/L3 . . .)
Поскольку падение напряжения в цепи постоянно, то v = В Т . Таким образом, мы можем написать
Таким образом, мы можем написать
1/л T = 1/л 1 + 1/л 2 + 1/л 3 . . . . .
Это означает, что обратная величина полной индуктивности параллельного соединения является суммой обратных величин индивидуальных индуктивностей всех катушек индуктивности. Приведенное выше уравнение верно, когда между параллельно соединенными катушками нет взаимной индуктивности.
Чтобы избежать сложностей при работе с дробями, мы можем использовать метод произведения на сумму для расчета общей индуктивности. Если две катушки индуктивности соединены параллельно и между ними нет взаимной индуктивности, то общая индуктивность равна
L T = (L 1 × L 2 )/(L 1 + L 2 )
30 Генри соединены параллельно, какова будет общая индуктивность параллельного соединения?
Sol: Мы знаем, что формула для полной индуктивности серии, 1/L T = 1/L 1 + 1/L 2
Учитывая, что L 1 = 20 Генри
L 2 = 30 Генри
L T = (L 1 * L 2 )/(L 1 1+ L 2 * )) 3 = (0/)) (20+30) ) = 600 / 50 = 12
Общая индуктивность L Итого = 12 Генри.
Взаимно связанные катушки индуктивности, установленные параллельно
При наличии магнитной связи между катушками индуктивности вышеприведенная производная формула для общей индуктивности должна быть изменена, поскольку общая индуктивность может быть больше или меньше в зависимости от направления магнитного поля от каждой катушки индуктивности. Магнитный поток, создаваемый параллельно соединенными индукторами, будет связан друг с другом.
Когда создаваемые потоки имеют одинаковое направление магнитного потока, взаимная индуктивность увеличивается; эти катушки называются «помощными» катушками. Если поток противоположен магнитному потоку, взаимная индуктивность уменьшится; эти катушки называются «противоположные» катушки. Эта взаимная индуктивность будет зависеть от расстояния между двумя катушками.
Учтите, что две катушки индуктивности соединены параллельно с собственной индуктивностью L 1 и L 2 и взаимно связаны с взаимной индуктивностью M, как показано на рисунке ниже.
Параллельные вспомогательные индукторы
Рассмотрим рисунок (а), на котором индукторы L 1 и L 2 соединены параллельно с их вспомогательными магнитными полями. Полный ток в цепи определяется как
i = i 1 + i 2
di/dt = (di 1 )/dt + (di 2 )/dt …………. (1)
Напряжение на катушке индуктивности или параллельной ветви определяется как
В = L 1 (di 1 )/dt + M (di 2 )/dt или L 2 (di 2 )/dt + M (di 1 )/dt
L 1 )/dt + M (di 2 )/dt = L 2 (di 2 )/dt + M (di 1 )/dt
(di 1 )/dt3 (5 )/dt3 (5 )/dt + M (di 1 ) – M) = (di 2 )/dt (L 2 – M)
(di 1 )/dt = (di 2 )/dt ((L 2 – M)) /((Л 1 – М)) …………. (2)
(2)
Подставляя уравнение 2 в уравнение 1, получаем
di/dt = (di 2 )/dt ((L 2 – M))/((L 1 – M)) + (di 2 )/dt
di/dt = (di 2 )/dt { (L 2 – M))/((L 1 – M)) + 1} …………. (3)
Если L T общая индуктивность параллельной цепи индуктивности, то напряжение определяется как (di 1 )/dt + M (di 2 )/dt
di/dt = 1/ L T { L 1 (di 1 )/dt + M (di 2 )/dt }
Подставляя уравнение 2 в приведенное выше уравнение, мы получаем
di/dt = 1/ L T { L 1 (di 2 )/dt (L 2 – M))/((L 1 – M)) + M (di 2 )/dt }
di/dt = 1/ L T { L 1 (L 2 – M))/((L 1 – M)) + M }(di 2 )/dt …………. (4)
Приравнивая уравнения 3 и 4 получаем
(L 2 – M))/((L 1 – M)) + 1 = 1/ L T { L 1 (L 2 – M))/((L 1 – M)) + M }
Упрощение приведенного выше уравнения, результаты -2M)
Здесь 2M представляет собой магнитный поток L 1 на L 2 или L 2 на L 1 . Если величина двух индуктивностей равна идеальной магнитной связи между ними, эквивалентная индуктивность двух катушек индуктивности равна L, потому что L T = L 1 = L 2 = M. В таком случае, если взаимная индуктивность равна нулю, общая индуктивность будет L ÷ 2. 45 мГн соединены параллельно, рассчитайте общую индуктивность параллельной комбинации. Взаимная индуктивность равна 20 мГн.
Если величина двух индуктивностей равна идеальной магнитной связи между ними, эквивалентная индуктивность двух катушек индуктивности равна L, потому что L T = L 1 = L 2 = M. В таком случае, если взаимная индуктивность равна нулю, общая индуктивность будет L ÷ 2. 45 мГн соединены параллельно, рассчитайте общую индуктивность параллельной комбинации. Взаимная индуктивность равна 20 мГн.
Sol Учитывая, что L 1 = 25 мГн
L 2 = 45 мГн
M = 20 мГн
Применяя формулу для полной индуктивности вспомогательных катушек индуктивности, L T = (L 1 L 2 — M 2 )/(L 1 + L 1 ) -2M)
L T = (25*45-20 2 )/(25+45-2*20)
= (1125-400)/(70-40)
= 725/30
= 24,166 мГн
Следовательно, общая индуктивность равна 24,166 мГн.
Параллельные противоположные катушки индуктивности
Аналогичным образом, если мы рассмотрим рисунок (b), на котором катушки индуктивности L 1 и L 2 соединены параллельно с противоположными магнитными полями, общая индуктивность будет равна
L T = (L 1 L 2 – M 2 )/(L 1 + L 2 )+ 2M, если две параллельные индуктивности,
равны при идеальной магнитной связи, эквивалентная индуктивность двух катушек индуктивности будет равна нулю, так как они компенсируют друг друга. Если две катушки индуктивности эффективно позволяют току течь через них, общая индуктивность определяется как (L ± M) ÷ 2.
Если две катушки индуктивности эффективно позволяют току течь через них, общая индуктивность определяется как (L ± M) ÷ 2.
Параллельно противоположные катушки индуктивности Пример
Пример: если две катушки индуктивности 25 мГн и 45 мГн соединены параллельно друг с другом, рассчитайте общую индуктивность параллельной комбинации. Взаимная индуктивность равна 20 мГн.
Sol: Учитывая, что L 1 = 25 мГн
L 2 = 45 мГн
M = 20 мГн
Применяя формулу для полной индуктивности вспомогательных катушек индуктивности, L Тл L 2 M 2 )/(L 1 + L 2 )+2M)
L T = (25*45-20 2 )/(25+45+2*20)
= (1125-400)/(70+40)
= 725/110
= 6,55 мГн
Следовательно, общая индуктивность равна 6,59 миллиГенри.
Резюме
- При соединении двух выводов индуктора соответственно с другим индуктором или выводами индукторов такое соединение называется «параллельным соединением индукторов».

- Когда потоки, создаваемые отдельными катушками индуктивности, имеют одинаковое направление, взаимная индуктивность будет увеличиваться; тогда эти катушки называются «помощными» катушками. Суммарная индуктивность вспомогательных катушек L T = (L 1 L 2 – M 2 )/(L 1 + L 2 )-2M). , взаимная индуктивность уменьшится; тогда эти катушки называются «противоположные» катушки. Общая индуктивность вспомогательных катушек L T = (L 1 L 2 – M 2 )/(L 1 + L 2 )+2M)
индукторов параллельно — HardwareBee
Катушки индуктивности называются параллельными, если одна или несколько катушек индуктивности совместно используют одни и те же два узла. В этой статье мы обсудим тему катушек индуктивности параллельно и представим два распространенных сценария: с взаимной индуктивностью и без нее.
Когда ток протекает через катушку, вокруг нее создается электромагнитное поле. При изменении тока меняется и электромагнитное поле. Электромагнитное поле, окружающее катушку, расширяется и сжимается при увеличении и уменьшении тока. Он меняет свое направление с течением. Эта способность называется самоиндукцией. «Когда ток протекает через индуктор, он создает напряжение в других соседних индукторах». Эта способность называется взаимной индуктивностью.
При изменении тока меняется и электромагнитное поле. Электромагнитное поле, окружающее катушку, расширяется и сжимается при увеличении и уменьшении тока. Он меняет свое направление с течением. Эта способность называется самоиндукцией. «Когда ток протекает через индуктор, он создает напряжение в других соседних индукторах». Эта способность называется взаимной индуктивностью.
Рассмотрим две катушки (катушка 1 и катушка 2, как показано на рисунке ниже). Если ток в катушке 1 увеличивается, это создает увеличивающееся магнитное поле вокруг катушки. Точно так же уменьшение тока приведет к уменьшению магнитного поля. Это индуцирует напряжение в катушке 2 в направлении, противоположном направлению тока. Точно так же увеличение и уменьшение тока будет создавать одинаковое магнитное поле. Магнитное поле, создаваемое в катушке 2, приведет к индуцированному напряжению в катушке 1 (в направлении, противоположном направлению тока). Точно так же, если имеется более двух катушек, соединенных параллельно, они будут связаны вместе одним и тем же магнитным полем. Если две или более катушек параллельны друг другу, так что линии изменяющегося магнитного потока пересекают друг друга, говорят, что они имеют общую взаимную индуктивность, и это обозначается буквой М. Она измеряется в генри (Гн).
Если две или более катушек параллельны друг другу, так что линии изменяющегося магнитного потока пересекают друг друга, говорят, что они имеют общую взаимную индуктивность, и это обозначается буквой М. Она измеряется в генри (Гн).
Как он реагирует на переменный и постоянный ток?
Напряжение на катушке индуктивности равно нулю, когда через нее протекает постоянный ток (постоянный ток). Или, другими словами, они действуют как короткое замыкание на постоянный ток.
Ток, протекающий через индуктор, не может измениться резко или мгновенно. Для изменяющегося во времени тока он противостоит изменению тока, протекающего через него. Напряжение на катушке индуктивности может резко меняться.
Индукторы параллельно используют одни и те же два узла. Напряжение на каждой катушке остается одинаковым, в то время как ток течет по нескольким путям. См. рисунок ниже. Имеется N параллельно соединенных катушек индуктивности. Полный ток, протекающий через катушку индуктивности, определяется законом тока Кирхгофа.
Полный ток, протекающий через катушку индуктивности, определяется законом тока Кирхгофа.
Соотношение ток-напряжение катушек индуктивности приведено ниже.
Подставьте «i» из уравнения 2 в уравнение 1; получаем,
Из эквивалентной схемы начальный ток через L eq при t = t 0 представляет собой сумму токов дросселей при t = t 0 .
Из эквивалентной схемы уравнение тока катушки индуктивности:0003
Где L eq — эквивалентная индуктивность параллельно соединенных катушек индуктивности.
В параллельно соединенных резисторах обратная величина эквивалентного сопротивления представляет собой сумму обратных величин отдельных сопротивлений. То же самое справедливо и для параллельно соединенных катушек индуктивности. Эквивалентная индуктивность меньше наименьшей индуктивности в этом соединении. Или, другими словами, параллельные катушки индуктивности уменьшают эффективную индуктивность цепи.
Или, другими словами, параллельные катушки индуктивности уменьшают эффективную индуктивность цепи.
При рассмотрении резистивной параллельной цепи большая часть тока протекает по пути с меньшим сопротивлением. Это справедливо и для индуктивных цепей.
Резисторы электрически соединены. Эти катушки связаны не только электрически, но и магнитно. Приведенная выше формула действительна только в том случае, если между катушками индуктивности нет взаимной индуктивности.
При работе с индуктивными цепями необходимо учитывать электромагнитные силы.
В параллельных катушках индуктивности нельзя игнорировать влияние взаимной индуктивности.
Если две катушки соединены параллельно (с собственной индуктивностью L 1 и L 2 ) и находятся рядом так, что магнитный поток в одной катушке связан с другой катушкой. Следовательно, в другой катушке индуцируется ЭДС. На основе наведенной ЭДС возможны два типа соединений.
- Параллельное вспомогательное соединение
- Параллельное встречное соединение
Посмотрите на рисунок, линии магнитного поля от обеих катушек касаются друг друга.
в соответствии с законом Фарадея,
Где,
n = количество поворотов
φ = Flux
Любое изменение по потоку φ, в зависимости выражается как
Где L — собственная индуктивность, связанная с каждой катушкой.
Каждая катушка имеет свой магнитный поток, состоящий из двух составляющих. Это самоиндукция, а другое — взаимная индуктивность.
Предположим, что Φ 1 — поток, связанный с катушкой 1. Предположим, что по катушке 2 ток отсутствует.
φ 11 — катушка 1 -й связи 1, а индуцированное напряжение дается,
φ 12 Ссылка. 0003
0003
— индуцированное напряжение разомкнутой цепи в катушке 2. Это напряжение индуцировано из-за изменяющегося во времени тока в катушке 1, что приводит к изменению магнитного потока.
Повторите ту же процедуру для катушки 2. Предположим, что по катушке 1 ток отсутствует. Φ 2 – поток, связанный с катушкой 2.
0002
Наведенное напряжение в катушке 1 из-за Φ 21
Взаимная индуктивность отвечает за увеличение и уменьшение индуктивности в зависимости от магнитной связи между двумя катушками. Магнитная связь, в свою очередь, зависит от расстояния между двумя катушками и их ориентации друг к другу.
Параллельные вспомогательные индукторы
В этом типе соединения ЭДС, индуцируемая в обеих катушках, имеет одинаковую полярность.
Суммарная индуктивность выше, чем у катушек, не имеющих взаимной индуктивности между собой.
от KCL,
После дифференцировки,
Общее напряжение на L 1 , которое вызвано самостоятельно и индуцированным.
Поскольку катушки индуктивности и источники напряжения подключены параллельно,
Сравните уравнение 6 и уравнение 7
Подставьте значение di1/dt в уравнение 5 и исключите его.
Уравнения 6, уравнение 7 и уравнение 8 равны. Из-за параллельного соединения.
Сравните уравнение 8, которое также равно уравнениям 6 и 7
Параллельные противоположные катушки индуктивности
В этом типе соединения ЭДС, индуцируемая в обеих катушках, имеет противоположную полярность. Точечное соглашение используется, чтобы показать, что соединение является параллельным противоположным.
Весь вывод аналогичен параллельным вспомогательным индукторам. Единственная разница заключается в наведенном напряжении, потому что взаимная индуктивность имеет противоположную полярность. В уравнении 6 и уравнении 7 замените +M на -M.
Решенный пример
Рассмотрим две катушки, соединенные параллельно друг другу.
Рассчитайте действующую индуктивность между двумя катушками, если они соединены между собой,
- Параллельное вспомогательное соединение
- Параллельное встречное соединение
Для параллельной помощи :
Для параллельной оппозиции:
Из приведенного выше обсуждения можно сделать вывод, что при параллельном подключении индуктивность уменьшается.
Из-за наличия взаимной индуктивности индуктивность, рассчитанная по полученной выше формуле, недействительна. Должна существовать взаимная индуктивность всякий раз, когда две катушки помещаются в магнитное поле друг друга. Взаимная индуктивность может уменьшить или не уменьшить общую индуктивность.
Должна существовать взаимная индуктивность всякий раз, когда две катушки помещаются в магнитное поле друг друга. Взаимная индуктивность может уменьшить или не уменьшить общую индуктивность.
Параллельные катушки индуктивности
Когда катушки индуктивности соединены параллельно, падение напряжения на каждой катушке индуктивности будет одинаковым. В случае последовательных катушек индуктивности эквивалентная индуктивность определяется путем сложения отдельных индуктивностей, соединенных последовательно. Но для катушек индуктивности, включенных параллельно, эквивалентная индуктивность рассчитывается по-другому.
В следующем разделе обсуждается эквивалентная индуктивность параллельно соединенных катушек индуктивности с учетом и без учета взаимной индуктивности.
Параллельные катушки индуктивности без взаимной индуктивности
Рассмотрим три катушки индуктивности L 1 , L 2 и L 3 , соединенные параллельно друг с другом. Напряжение питания V подается на параллельную комбинацию трех катушек индуктивности. Поскольку все элементы соединены параллельно, напряжение между точками 1 и 2 одинаково.
Напряжение питания V подается на параллельную комбинацию трех катушек индуктивности. Поскольку все элементы соединены параллельно, напряжение между точками 1 и 2 одинаково.
Пусть I будет током, протекающим от источника питания. Этот ток имеет три пути по L1, L2, L3 из узловой точки 1, поэтому соответствующие токи равны I 1 , I 2 , I 3 , как показано на рисунке.
Ток через параллельный индуктор записан по адресу,
Ток через каждый индуктор дается,
Теперь уравнение (4) становится,
Если L EQ является эквивалентным индуцированным всей цепи, то общий ток в электрической цепи определяется выражением
Из уравнений (5) и (6) можно записать0003
Если имеется n катушек индуктивности, соединенных параллельно, то эквивалентная индуктивность или эффективная индуктивность определяется по формуле:
катушка соединяется с другой. Соответственно, эффект взаимной индуктивности либо увеличивает, либо уменьшает общую индуктивность в зависимости от величины магнитной связи. Эффект этой взаимной индуктивности зависит от расстояния между катушками и их ориентации друг к другу.
Эффект этой взаимной индуктивности зависит от расстояния между катушками и их ориентации друг к другу.
Подобно индукторам, соединенным последовательно, взаимно соединенные параллельные индукторы могут либо усиливать, либо противодействовать общей индуктивности. Магнитный поток, создаваемый током, течет в том же направлении в параллельно соединенных катушках. В случае параллельно соединенных встречных катушек ток течет в противоположных направлениях.
Параллельные вспомогательные катушки индуктивности
Рассмотрим приведенную ниже схему, в которой две катушки индуктивности соединены параллельно. Ток входит в точечный конец катушки и выходит на другом конце. Учитывается влияние взаимной индуктивности. Поток, создаваемый одной катушкой, добавляется к другой катушке, поэтому общий создаваемый поток увеличивается.
Поскольку учитывается влияние взаимной индуктивности, необходимо изменить падение напряжения на каждой катушке индуктивности. Мы знаем, что напряжение в параллельной цепи будет одинаковым. В приведенной выше схеме два тока, i 1 и i 2 , должны различаться, чтобы напряжение на катушках индуктивности оставалось одинаковым.
В приведенной выше схеме два тока, i 1 и i 2 , должны различаться, чтобы напряжение на катушках индуктивности оставалось одинаковым.
Суммарная индуктивность параллельных вспомогательных катушек индуктивности определяется как
Если взаимная индуктивность между параллельно соединенными катушками индуктивности равна нулю, эквивалентная индуктивность будет такой же, как у двух катушек самоиндукции, включенных параллельно.
Параллельные противоположные катушки индуктивности
Рассмотрим две катушки индуктивности, соединенные параллельно, как и раньше, за исключением того, что одна катушка перевернута по отношению к другой. Это показано на рисунке ниже. В этом случае ток в катушке 1 течет противоположно току в катушке 2.
Поток, создаваемый одной катушкой, противодействует потоку, создаваемому другой катушкой, поэтому общий создаваемый поток уменьшается. Следовательно, эффект взаимной индуктивности в одной катушке компенсирует эффект в другой катушке.
Суммарная индуктивность параллельно соединенных встречных катушек определяется выражением,
Решенная задача 1
Решим задачу на определение эквивалентной индуктивности данной цепи.
В приведенном выше примере катушка индуктивности L4 подключена параллельно с последовательной комбинацией L5 и L6. Эквивалентное значение индуктивности этих трех катушек индуктивности L4, L5 и L6 составляет
Теперь схема уменьшится, как показано ниже,
Если вы посмотрите на схему, катушка индуктивности L2 параллельна последовательной комбинации катушек индуктивности L3 и L7. . Соответствующее эквивалентное значение индуктивности равно
Снова схема уменьшена, как показано ниже,
В сокращенной схеме катушки индуктивности L1 и L8 включены последовательно.
Таким образом, эквивалентная индуктивность определяется выражением
Когда две катушки индуктивности соединены последовательно или параллельно, магнитный поток, создаваемый одной катушкой индуктивности, будет связан с другой катушкой индуктивности. Это свойство называется взаимной индуктивностью.
Это свойство называется взаимной индуктивностью.
Решенная задача 2
Две катушки с собственной индуктивностью 100 мГн и 220 мГн и взаимной индуктивностью 80 мГн соединены параллельно. Определите эквивалентную индуктивность комбинации, если (i) взаимный поток помогает отдельным потокам и (ii) взаимный поток противостоит отдельным потокам.
Дано .
Собственная индуктивность катушки 1, л 1 = 100 мГн = 0,1 Гн
Собственная индуктивность катушки 2, л 2 = 220 мГн = 0,22 Гн
Взаимная индуктивность, М 0,08 Гн
Решение
(i) Эквивалентная индуктивность комбинации, если взаимные потоки помогают отдельным потокам (параллельные вспомогательные катушки) встречные катушки)
- Copy Link
- More
Equivalent Inductance of Series and Parallel Катушки индуктивности (со взаимной индуктивностью)
Содержание
Когда катушки индуктивности соединены последовательно, эквивалентная индуктивность комбинации будет суммой индуктивностей всех отдельных катушек индуктивности. Это точно так же, как эквивалентное сопротивление последовательно соединенных резисторов.
Это точно так же, как эквивалентное сопротивление последовательно соединенных резисторов.
Но в случае катушек индуктивности иногда приходится учитывать эффект взаимной индуктивности между катушками индуктивности.
Затем для расчета индуктивности каждой катушки индуктивности мы учитываем как самоиндукцию, так и взаимную индуктивность катушки индуктивности.
Взаимная индуктивность будет добавлена или вычтена из собственной индуктивности в зависимости от полярности магнитно-связанных катушек индуктивности.
О влиянии взаимной индуктивности мы узнаем далее в этой статье.
Теперь, не принимая во внимание взаимные индуктивности, мы можем записать эквивалентную индуктивность последовательно соединенных катушек индуктивности как
индуктивности обратны.
Аналогично эквивалентному сопротивлению параллельно соединенных резисторов. Возможно, нам также придется учитывать влияние взаимной индуктивности таким же образом, если это необходимо.
Далее в этой статье мы изучим влияние взаимной индуктивности на параллельные катушки индуктивности. Без учета влияния взаимной индуктивности можно написать:
Катушка индуктивности является пассивным элементом цепи. Найдем эквивалентную индуктивность последовательно соединенных и параллельно соединенных катушек индуктивности .
Добавление катушек индуктивности в серию
Рассмотрим n из катушек индуктивности, соединенных последовательно , как показано ниже.
Учтем также, что,
индуктивность дросселя 1 и падение напряжения на нем L 1 и v 1, соответственно,
индуктивность дросселя 1 и падение напряжения на нем L 2 и v 2, соответственно,
индуктивность дросселя 1 и падение напряжения на нем L 3 и v 3, соответственно,
индуктивность дросселя 1 и падение напряжения на нем L 4 и v 4, соответственно,
индуктивность катушки индуктивности 1 и падение напряжения на ней L n и v n, соответственно.
Теперь, применяя закон Кирхгофа для напряжения, мы получаем полное падение напряжения (v) на комбинации катушек индуктивности серии ,
Падение напряжения на катушке индуктивности L можно выразить как
Где i равно мгновенный ток через катушку индуктивности.
Поскольку все катушки индуктивности соединены последовательно, ток через каждую из катушек одинаков и, скажем, также i. Итак, из приведенного выше уравнения КВЛ получаем,
Это уравнение можно переписать как
Где L eq — эквивалентная индуктивность комбинированных катушек индуктивности серии . Следовательно,
Эквивалентная индуктивность последовательно соединенных катушек индуктивности представляет собой просто арифметическую сумму индуктивностей отдельных катушек индуктивности.
Добавление катушек индуктивности параллельно
Рассмотрим n из катушек индуктивности, соединенных параллельно, , как показано ниже.
Учтем также, что
индуктивность дросселя 1 и ток через него L 1 и i 1, соответственно,
индуктивность дросселя 1 и ток через него L 2 и i 2, соответственно,
индуктивность дроссель 1 и ток через него L 3 и i 3, соответственно,
индуктивность дросселя 1 и ток через него L 4 и i 4, соответственно,
индуктивность дросселя 1 и ток через это L n и i n, соответственно.
Теперь, применяя закон тока Кирхгофа, мы получаем полный ток (i), поступающий в параллельную комбинацию катушек индуктивности ,
Ток через катушку индуктивности L можно выразить как
напряжение на индукторе.
Поскольку все катушки индуктивности в комбинациях соединены параллельно, здесь падение напряжения на каждой из катушек одинаково и, скажем, равно v. Итак, из приведенного выше уравнения KCL мы получаем,
Это уравнение можно переписать как
Где L eq — эквивалентная индуктивность параллельно соединенных катушек индуктивности . Следовательно,
Следовательно,
Обратная величина эквивалентной индуктивности параллельно соединенных катушек индуктивности представляет собой просто арифметическую сумму обратной величины индуктивностей отдельных катушек индуктивности.
Эффект взаимной индукции в последовательно соединенных индукторах
Всякий раз, когда несколько индукторов сближаются, между ними может возникнуть взаимная индукция. Если несколько катушек индуктивности соединены последовательно и поток одной катушки индуктивности связывает другую, мы должны учитывать взаимную индуктивность при расчете эквивалентной индуктивности.
Для этой цели мы используем точку. Здесь каждый из индукторов отмечен точкой на одном конце.
Ток, поступающий через пунктирную клемму одного индуктора, индуцирует напряжение в другой катушке индуктивности с положительной полярностью на пунктирной клемме последнего. Рассмотрим следующий пример.
Поскольку индукторы соединены последовательно, через эти индукторы будет течь одинаковый ток.
Следовательно, когда ток проходит через пунктирную клемму катушки индуктивности 1, ток проходит через пунктирную клемму катушки индуктивности 2.
Катушка индуктивности 2 индуцирует напряжение на катушке 1 положительной полярности на отмеченном пунктиром конце катушки индуктивности 1.
Ток, поступающий через пунктирную клемму катушки индуктивности 1, индуцирует напряжение на катушке индуктивности 2 положительной полярности на конце катушки индуктивности 2, отмеченном точками
Поскольку обе ЭДС взаимной индукции направлены в направлении ЭДС самоиндукции эквивалентных импедансов, взаимная индуктивность будет добавлена к самоиндукции для расчета эквивалентного импеданса.
Здесь, во втором примере, в соответствии с порядком точек, представленным на рисунке ниже, ток входит через пунктирную клемму одного индуктора, и такой же ток выходит из пунктирной клеммы другой катушки индуктивности.
В этом случае полярность ЭДС взаимной индукции отличается от ЭДС самоиндукции. Эквивалентная индуктивность комбинации будет
Эквивалентная индуктивность комбинации будет
Эффект взаимной индукции в параллельно соединенных индукторах
Теперь мы подойдем к эффекту взаимной индуктивности в параллельно соединенных индукторах. Здесь, в этом примере, точки даны на одной и той же стороне двух катушек индуктивности.
Когда ток проходит через пунктирный вывод катушки индуктивности 1, индуцированная ЭДС имеет положительную полярность на пунктирном конце катушки индуктивности 2.
катушка индуктивности 1 имеет положительную полярность на заштрихованном конце катушки индуктивности 1. Таким образом, эквивалентная индуктивность равна
Аналогично, если две параллельные катушки индуктивности расставить точки следующим образом, эквивалентная индуктивность будет равна
Катушки индуктивности последовательно и параллельно
Содержание : Катушки индуктивности последовательно и параллельно
Что такое катушки индуктивности?
Катушки индуктивности
Катушки индуктивности представляют собой не что иное, как накопители магнитной энергии.
Физически это катушка проводящего провода, намотанная на сплошной сердечник или без сердечника. Последний называется индуктором с воздушным сердечником .
Когда ток протекает через индуктор, он создает магнитное поле. Намотка большого количества проволоки увеличивает силу магнитного поля. Направление магнитного поля определяется с помощью правая линейка большого пальца .
Когда ток сначала начинает течь через катушку, магнитное поле начинает расширяться, затем через некоторое время оно стабилизируется и накапливает некоторое количество магнитной энергии. Когда поле постепенно разрушается, магнитная энергия снова превращается в электрическую. Катушки индуктивности производят магнитный поток , пропорциональный току, протекающему через них.
Чтобы узнать больше об индуктивном реактивном сопротивлении, нажмите здесь.
Что такое собственная индуктивность?
Собственная индуктивность Определение
Собственная индуктивность — это характеристика катушки, благодаря которой катушка сопротивляется любому резкому изменению тока в ней.
{2}A}{l} [/латекс] (ответ)
Что такое взаимная индуктивность?
Определение взаимной индуктивности
В случае двух катушек изменение тока в одной катушке индуцирует ЭДС в соседней катушке. Этот инцидент известен как взаимная индукция, а это свойство первичной катушки называется взаимной индуктивностью.
Как рассчитать катушки индуктивности последовательно?
Последовательное добавление катушек индуктивности | Две катушки индуктивности в серии a Катушки индуктивности в последовательном соединении
В катушках индуктивности в последовательном соединении из диаграммы видно, что ток в каждой индуктивности одинаков. Таким образом, общее падение напряжения на катушках индуктивности представляет собой сумму падений напряжения на каждой отдельной катушке индуктивности. Предположим, что L — общая индуктивность цепи.
Таким образом, общее падение напряжения В Всего будет равно
В Всего = В 1 + В 2
V1 и V2 представляют собой падение напряжения на отдельной катушке индуктивности соответственно.
По правилу Кирхгофа мы можем написать,
[Latex]V_{Total} -(L_{1}+L_{2})\frac{\mathrm{d} i}{\mathrm{d} t} =0 [/Latex]
[Latex]V_{Всего} =(L_{1}+L_{2})\frac{\mathrm{d} i}{\mathrm{d} t}[/Latex]
[ Латекс] L \ frac {\ mathrm {d} i} {\ mathrm {d} t} = (L_ {1} + L_ {2}) \ frac {\ mathrm {d} i} {\ mathrm {d} t }[/Latex]
L=L 1 +L 2
( Ответ )
Эквивалентная индуктивность последовательных катушек | Формула для катушки индуктивности в серии
Подобно ранее найденному уравнению для двух катушек индуктивности, если мы последовательно соединим n катушек индуктивности с собственной индуктивностью Эквивалентная индуктивность для индукторов в последовательной схеме будет,
L Уравнение = L 1 + L 2 + L 3 +… .
. + L N
(ответ) 44444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444
Как рассчитать катушки индуктивности параллельно?
Параллельные катушки индуктивности Параллельные катушки индуктивности
При параллельном соединении из диаграммы можно сделать вывод, что общий ток, протекающий по цепи, представляет собой сумму токов отдельных катушек. Напряжение на каждой катушке индуктивности одинаково.
Если напряжение питания V, то
[Latex]V = L\left ( \frac{\mathrm{d} i_{1}}{\mathrm{d} t} + \frac{\mathrm{ d} i_{2}}{\mathrm{d} t} \right )[/Latex]
[Latex]V = L\left ( \frac{V}{L_{1}} + \frac{V} {L_{2}}\справа )[/латекс] 9{-1}[/Latex] ( Ответ )
Катушки индуктивности последовательно с взаимной индуктивностью
Для приведенных выше выводов мы предположили, что между катушками индуктивности нет взаимной индуктивности.
Теперь, если индукторы соединены таким образом, что магнитное поле, создаваемое одним, влияет на индуктивность других, говорят, что индукторы «взаимно связаны». индукторы могут либо помогать, либо противодействовать друг другу в зависимости от ориентации катушек. Сцепление можно разделить на два типа:
Серия Вспомогательный тип соединения :
В этом типе соединения магнитные поля индукторов имеют одинаковое направление. Таким образом, токи, протекающие через индукторы, также имеют одинаковое направление. Для двух катушек индуктивности с собственной индуктивностью L 1 и L 2 и взаимной индуктивностью M можно записать катушка за счет изменения тока в др. для взаимной индуктивности
[Латекс] V = V_ {1} + V_ {2} + V_ {M_ {12}} + V_ {M_ {21}} = L_ {1} \ frac {\ mathrm {d} i} {\ mathrm {d} t} + L_ {2} \ frac {\ mathrm {d} i} {\ mathrm {d} t} + M \ frac {\ mathrm {d} i} {\ mathrm {d} t} + M \ frac {\ mathrm {d} i} {\ mathrm {d} t} = (L_ {1} + L_ {2} + 2M) \ frac {\ mathrm {d} i} {\ mathrm {d} t } [/Latex]
Следовательно,
Эквивалентная индуктивность = L 1 + L 2 + 2M
Серия «Связаться»: 9000 2 Серия «Связаться»: 9000 2 поля индукторов направлены в противоположную сторону.
Таким образом, направления токов противоположны друг другу. Для двух катушек индуктивности с собственными индуктивностями L1 и L2 и взаимной индуктивностью M мы можем написать,
Полная ЭДС индукции = ЭДС самоиндукции в L 1 и L 2 + ЭДС индукции в одной катушке из-за изменения тока в другой для взаимной индуктивности
[Latex]V = V_{1} + V_{ 2} + V_{M_{12}} + V_{M_{21}} = L_{1}\frac{\mathrm{d} i}{\mathrm{d} t} + L_{2}\frac{\ mathrm {d} i} {\ mathrm {d} t} — M \ frac {\ mathrm {d} i} {\ mathrm {d} t} — M \ frac {\ mathrm {d} i} {\ mathrm { d} t} = (L_{1} + L_{2} – 2M)\frac{\mathrm{d} i}{\mathrm{d} t}[/Latex]
Следовательно, эквивалентная индуктивность = L 1 + L 2 -2M
Каким будет полное сопротивление конденсатора и катушки индуктивности в последовательной LC-цепи?
Импеданс конденсатора и катушки индуктивности в последовательной LC-цепи : последовательная LC-цепь
Для вышеуказанного конденсатора и катушки индуктивности в последовательной цепи мы предполагаем, что сопротивление отсутствует.
Мы помещаем полностью заряженный конденсатор вместе с катушкой индуктивности в цепь. Изначально переключатель разомкнут. Предположим, что пластины конденсатора имеют заряд Q 9{2}}{2C}][/Latex]
Полное сопротивление последовательно соединенных конденсатора и катушки индуктивности | Impedance in LC circuit
For the above capacitor and inductors in series circuit
Total impedance of LC circuit X LC =X L -X C if X L >X C
= X C -X L if X L
C Катушки индуктивности в последовательных и параллельных задачах
Катушка индуктивности и конденсатор подключены к источнику переменного тока 120 В, 60 Гц. Для следующей LC-цепи найдите полное сопротивление и ток, протекающий через цепь.
LC-цепьДано:
L= 300 мГн C = 50 мкФ V = 120 В f = 50 Гц из L и C получаем,
X L = 113 Ом
X C = 53 Ом
Следовательно, полное сопротивление, Z = X L – X C = 113 – 53= 60 Ом
Ток в цепи, i = V/Z = 120/60 = 2 A
- LC-цепь состоит из катушки индуктивности L = 20 мГн и конденсатор C = 50 мкФ.
Начальный заряд на обкладке конденсатора равен 10 мКл. Какова полная энергия? Также узнайте резонансную частоту.
Дано:
L = 20 мч C = 50 мкф Q 0 = 10 MC
Общая энергия E = Q 0 2 / 2C = (10 x .001) 2 / 2x 0,00005 = 1 / 2C = (10 x .001) 2 / 2x 0,00005 = 1 / 2C = (10 x. Дж
Резонансная частота f =1/2√LC= 1/(2 x 3,14 x √(20 x 0,001 x 0,00005)) = 159 Гц схема
Цепи, содержащие резисторы и катушки индуктивности, известны как схемы LR. Когда мы подключаем источник напряжения, ток начинает течь по цепи. Теперь, если мы применим закон Кирхгофа, мы получим
[Latex]V_{0}-iR – L\frac{\mathrm{d} i}{\mathrm{d} t}=0[/Latex] ( V 0 9{2}}[/Latex] ( Ответ )
Численные задачи
Батарея на 24 В удалена из цепи, состоящей из резистора с сопротивлением 2 Ом и катушки индуктивности с индуктивностью 0,03 Гн. Рассчитайте начальный ток в момент времени t = 0 секунд.
Определите, за какое время ток уменьшится до 50 % от начального тока.
Если батарею внезапно вынуть из цепи, то ток упадет до нуля через некоторое время.
При t = 0 i = V 0 /R = 24/2 = 12 А
Постоянная времени ? = L/R = 0,03/2 = 0,015 секунды
i = i 0 e -t/? , где I 0 является начальным током перед закрытием переключателя
0,5 = E -T/0,015
T/0,015 = -LN (0,5)
T = 0,01 S (ответ)
. Резистор 2 Ом и дроссель 8 мГн соединены последовательно с источником питания 6 вольт. Через сколько времени ток станет равным 99,9% конечного тока?
Постоянная времени цепи = L/R = 8 x 0,001 / 2 = 4 мс I final x 0,999
1 – e -t/? = 0,999
e -t/? = 0,001
т/? = 6,9
t= 6,9 x 4 = 27,6 мс ( Ответ )
Полное сопротивление резистора, конденсатора и катушки индуктивности в последовательной цепи RLC последовательная цепь RLC
Вышеупомянутая схема имеет резистор, катушку индуктивности и конденсатор, соединенные последовательно с источником переменного тока.
( Ответ ){2}} + R \ frac {\ mathrm {d} Q} {\ mathrm {d} t} = 0 \: \: \, \: \: \; (я = — \ frac {\ mathrm {d} Q} {\ mathrm {d} t}) [/Latex] 9{2}}[/Latex]
Численные задачи
Последовательная RLC-цепь состоит из резистора 30 Ом, катушки индуктивности 80 мГн и конденсатора 40 мкФ. На него подается переменное напряжение питания 120 В и 50 Гц. Узнать силу тока в цепи.
Solution :
Inductive reactance X L = 2πfL = 2 x 3.14 x 80 x 0.001 x 50 = 25.13 ohm
Capacitive reactance X C = 1/2πfC = 79.58 ohm
Total impedance, Z = √ {Р 2 +(X C – X L ) 2 }= √{(30) 2 +(79,58-25,13) 2 } ток в цепи 0 = 62,10 3 Ом i = 120/62,17 = 1,93 А
- Выведите уравнение для тока в приведенной ниже цепи, где V = sin4t
Применяя закон Кирхгофа к цепи, мы можем написать,
Sin4t – 3i – 2di/dt + Q/ 0,5 = 0
Sin4t = 3i + 2di/dt + 2Q
С двусторонним дифференцированием,
4cos4t = 3di/dt + 2d 2 i/dt 2 +2 i(t)
i(t) + 3/2(di/dt) + d 2 i/dt 2 8 = 2cos4t Это необходимое уравнение для тока.
(Ответ)
Катушки индуктивности, включенные последовательно и параллельно, разные MCQ
1. LC-цепь хранит полную энергию E. Максимальный заряд конденсатора равен Q. Энергия, накопленная в катушке индуктивности при заряде конденсатора Q/2, равна
- E
- E/2
- E/4
- 3E/4 (ответ)
Решение: общая энергия = E = Q 2 /2C
Общая энергия = E C + E /2C
Когда заряд на конденсаторе — Q /2, общая энергия,
Q 2 /2C = (Q /2) 2 /2C + EI
E I = Q 2 /2C. х (1-¼) = 3E/4 ( Ответ )
2. Если ток в одной катушке станет постоянным, какой ток будет течь в соседней катушке?
- Двойник первой катушки
- Половина первой катушки
- Ноль (Ответ)
- Бесконечность
Решение: Ток индуцируется при изменении магнитного потока в катушке.
Следовательно, если ток в одной катушке постоянный, поток не будет генерироваться, а ток в соседней катушке будет равен нулю.
3. Резистор 7 Ом соединен последовательно с катушкой индуктивности 32 мГн в катушках индуктивности в последовательной цепи. Если напряжение питания 100 вольт, 50 Гц, рассчитайте падение напряжения на катушке индуктивности.
- 67 V
- 82 V (Ответ)
- 54 V
- 100 В
Подробное решение проблемы:
Индуктивная повторная реакция x L . 0,032 = 10 Ом
Общий импеданс z = √ (r 2 + x L 2 ) = √ (7 2 + 10 2 ) = 120378) = 2). по цепи = 100/12,2 = 8,2 А
Падение напряжения на катушке индуктивности = iX L = 8,2 x 10 = 82 В (ответ)
J4 (√2 — 1) OHM J4 (√2 + 1) OHM (Ответ) Решение: для вышеупомянутой цепи Infinite Позвольте нам предположить, что
Z 1 = j8 = j8 = j8 = j8 = j8 = j8 = j8 = j8 = j8 = j8 = j86 = j86 = j86 = j86 = j86 = j86 = j86 = j86 = j86 = j86 = j86 = j86 = j86 = j86 = j86 = j86 = j86 = j86 = j86 = j86 = j86 = j86 = Ом и Z 2 = j4 – j2 = j2 Ом
Если эквивалентное сопротивление равно Z, то мы можем написать
Z = Z 1 + (Z 2 || Z) = Z 1 + ZZ 2 /Z + Z 2 Z (z + z 2 ) = z 1 z 2 + ZZ 1 + ZZ 2
Z 2 + J2Z = -16 + J8Z + J2Z
Z 2Z = -16 + J8Z + J2Z
777 2777 2 j8Z + 16 = 0Решая квадратное уравнение, получаем,
Z = j4(√2 + 1) Ом (Ответ)
5.
Собственная индуктивность соленоида 5 мГн. Катушка имеет 10 витков. Какова будет индуктивность катушки, если количество витков увеличить вдвое?
- 10 МН
- 5 MH
- 20 MH (Ответ)
- 30 MH
раствор: Self Enductance of Solenoid с nups и a-out stection stray straistal. 2 А/л
Здесь мк 0 x 100 х А/л = 5
мк 0 А/л = 1/20
Если число витков удвоить, то новая собственная индуктивность = мк 0 А/л x Н’ 2 = 1/20 x (20)2 = 20 мГн ( Ответ)
Часто задаваемые вопросы | Краткое примечание
Как добавить катушки индуктивности последовательно и параллельно? | Катушки индуктивности последовательно и параллельно:
Ответ :
При последовательном соединении сумма собственной индуктивности всех катушек индуктивности представляет собой общую индуктивность цепи.
При параллельном соединении сумма индуктивностей, обратных всем собственным индуктивностям, является обратной величиной общей индуктивности.
Как последовательное подключение катушек индуктивности влияет на ток?
Ответ :
Катушки индуктивности, добавленные в серию, имеют одинаковый ток. Таким образом, общее напряжение цепи выше, чем напряжения отдельных катушек индуктивности.
Что такое последовательно соединенные катушки индуктивности?
Ответ :
Это другое название ряда противоположных катушек индуктивности, в которых магнитные потоки, создаваемые катушками индуктивности, противоположны по направлению. Общая индуктивность в этом типе индуктора равна сумме собственных индуктивностей индукторов — 2 x взаимная индуктивность.
Какова взаимная индуктивность двух последовательно соединенных катушек?
Ответ :
Взаимная индуктивность двух катушек с железным сердечником с витками N 1 и N 2 , площадью поперечного сечения A, длиной L и проницаемостью µ r равно, [Latex]M = \ frac{\mu {0}\mu {r}N_{1}N_{2}A}{L}[/Latex]
Что такое последовательный индукторный фильтр?
Ответ :
Последовательный индукторный фильтр представляет собой индуктор, включенный последовательно между нагрузкой и выпрямителем.
Он называется фильтром, так как блокирует переменный ток и пропускает постоянный ток.
Катушка индуктивности в 1 генри включена последовательно с конденсатором в 1 мкФ. Найдите импеданс при частоте 50 Гц и 1000 Гц.
Answer :
Impedance, Z = X L – X C
X C when frequency is 50 Hz = 1/2πf 1 C = 3183 ohm
X C when частота 1000 Гц = 1/2πf 2 C = 159 Ом
X L при частоте 50 Гц = 2πf 1 L = 314 Ом
x L Когда частота составляет 1000 Гц = 2πf 1 L = 6283 Ом
Следовательно, импеданс Z 1 Когда частота равен 50 Гц = 6283 — 159 = 6124 Ом
. составляет 1000 Гц = | 314 – 3183 | = 2869 Ом.
Эквивалентная индуктивность параллельно соединенных катушек индуктивности
Дифференциация обеих сторон по времени,
dI/dt = di 1 /dt + di 2 /dt +…..+di n
60 /d 60 = V/L 1 + V/L 2 + ……..+ V/L n …………….(1)Если параллельная комбинация катушек индуктивности должна быть заменена одинарной эквивалентная катушка индуктивности тогда,
В = LdI/dt (при условии, что ток I течет через эквивалентную катушку индуктивности)
dI/dt = V/L …………………(2)
Сравнивая уравнения (1) и (2), получаем,
В/л = В/л 1 + В/л 2 + ……..+ В/л n
1/л = 1/л 1 + 3/л 2 9000 + ….
.+ 1/L n
Таким образом, из приведенного выше уравнения мы можем найти значение эквивалентной индуктивности L. Следует отметить, что приведенная выше формула верна, если нет взаимной связи между индукторы. Если существует взаимная связь между катушками индуктивности, значение эквивалентной индуктивности будет зависеть от типа связи, т. е. аддитивной связи или вычитающей связи. Что ж, рассмотрим два типа связи и найдем эквивалентную индуктивность.
Эквивалентная индуктивность для аддитивной взаимной связи
Предположим, две катушки индуктивности с индуктивностью L 1 и L 2 соединены параллельно, как показано на рисунке ниже. Связь между индукторами предполагается аддитивной. Эта аддитивная связь показана двумя точками на одной стороне индуктора на рисунке.
Предположим, что ток, протекающий через катушки индуктивности L 1 и L 2 , равен i 1 и i 2 , а взаимная индуктивность равна M.

But voltage across L 1 = L 1 di 1 /dt + Mdi 2 /dt = V
and across L 2 = L 2 di 2 /dt + Mdi 1 /dt = V
Следовательно, мы можем написать
L 1 di 1 /dt + Mdi 2 /dt = L 2 di 2 /dt + Mdi 1 /dt
di 1 /dt (L 1 – M) = di 2 /dt (L 2 – M)
di 1 /dt = [(L 2 – M) / (L 1 – M)] di 2 /dt ……………….(1)
Теперь общий текущий ток i = i 1 + i 2
Дифференцируя приведенное выше уравнение по времени, мы получаем,
di/dt = di 1 /dt + di 2 /dt
= [(L 2 – M) / (L 1 – M)] di 6 / 90 t 2 /dt
= di 2 /dt [{(L 2 – M) / (L 1 – M)} + 1]
= di 9 2 [5 2 0 +L 2 -2M) / (L 1 – M)] ………………….
.(2)
Теперь, если указанную выше комбинацию катушек индуктивности заменить эквивалентной катушкой индуктивности L, тогда
В = Ldi/dt (общий ток i будет течь через эквивалентную катушку индуктивности)
= L x di 2 /dt [(L 1 +L 2 – 2M) / (L 1 – M)] …….. из уравнения (2)
Но V = L 2 di 2 /dt + Mdi 1 /dt
Следовательно,
L 2 6 di 29003 + Mdi 1 /dt = L x di 2 /dt [(L1+L2-2M) / (L 1 – M)]
Значение di 1 /dt из уравнения (1),
∴ L 2 di 2 /dt + M[(L 2 – M) / (L 1 – M)] di 2 / dt = L x di 2 /dt [(L 1 +L 2 -2M) / (L 1 – M)]
⇒L 2 + M[(L
6 – 2 M) / (L 1 – M)] = L [(L 1 + L 2 -2M) / (L 1 – M)]⇒ [L 2 (L 1 – М) + М(Д 2 – М)] / (Д 1 – M) = L [(L 1 +L 2 -2M) / (L 1 – M)]
⇒ [L 2 (L 1 – M) + M(L 2 – М)] = L (L 1 + L 2 -2M)
⇒ L = [L 2 (L 1 – M) + M(L
6 – M 900) ] / (L 1 +L 2 -2M)= (L 2 L 1 -M 2 ) / (L 1 +L 2 -2M)
∴ ∴ ∴ ∴ ∴ ∴ +L 2 -2M)
∴ ∴ ∴ ∴ ∴ +L Эквивалентная индуктивность L = (L 2 L 1 -M 2 ) / (L 1 +L 2 -2M)
Eaquivalent Inductaint для субтрактивного мута.
и L 2 соединены параллельно, как показано на рисунке ниже. Связь между индукторами предполагается субтрактивной. Эта связь показана двумя точками на противоположной стороне индуктора на рисунке.
Предположим, что ток, протекающий через катушки индуктивности L 1 и L 2 , равен i 1 и i 2 , а взаимная индуктивность равна M. Но напряжение на L 1 = L 1 di 1 /dt – Mdi 2 /dt = V
Обратите внимание, что при нахождении ЭДС, развиваемой на L 1 , между L 1 используется знак минус. di 1 /dt и Mdi 2 /dt, так как связь между катушками индуктивности субтрактивная.
и через L 2 = L 2 DI 2 /DT — MDI 1 /DT = V
Поэтому мы можем написать,
∴ L 1 DI 1 /DT – MDI 2 /DT = L 2 DI 2 /DT — MDI 1 /DT
⇒ DI 1 /DT (L 1 + M) = DI 2 /DT (L 1 + M) = DI 2 /DT (L 1 + M) = DI 2 /DT (L 1 + M) = DI 2 /DT (L 1 + M) = DI 2 /DT (L 1 + M) = DI 2 /DT (L 1 + M) 2 + M)
⇒di 1 /dt = [(L 2 + M) / (L 1 + M)] di 2 /dt ……………….
(1)
Теперь общий текущий ток i = i 1 + i 2
Дифференцируя приведенное выше уравнение относительно времени, мы получаем M)] di 2 /dt + di 2 /dt
= di 2 /dt [{(L 2 + M) / (L 1 + M) + 1] 9]0003
= di 2 /dt [(L1+L 2 + 2M) / (L 1 + M)] …………………..(2)
Теперь, если приведенная выше комбинация катушки индуктивности заменяется эквивалентной катушкой индуктивности L, тогда
В = Ldi/dt (общий ток i будет течь через эквивалентную катушку индуктивности)
= L x di 2 /dt [(L 1 +L 2 + 2M) / (L 1 + M)] …….. из уравнения (2)
Но V = L 2 di 2 /dt + Mdi 1 /dt
Таким образом,
L 2 di 2 /dt – Mdi 1 /dt = L x di 2 /dt [(L 1 +L) 203 2 +L (L 1 + M)]
Подставляя значение di 1 /dt из уравнения (1),
L 2 di 2 /dt – M[(L 2 + M) / (L 1 + M)] di 2 /dt = L x di 2 /dt [(L 1 +L 2 + 2M) / (L 1 + M)]
⇒ L 2 – M[(L 2 + M) / (L 1 + M)] = L [(L 1 + L 2 + 2M) / (L 1 + M)]
⇒ [L 2 (L 1 + M) – M(L 2 + M)] / (L 1 + M) = L [(L 1 + L 2 + 2M) / (L 1 + M)]
⇒ [L 2 (L 1 + M) — M(L 2 + M)] = L (L 1 L 2 + 2M)
⇒L = [L 2 (L 1 + M) – M(L 2 + M)] / (L 1 +L 2 + 2M)
= (L 2 L 1 – M 8 1 +L 2 + 2M)
∴ Equivalent Inductance L = (L 2 L 1 – M 2 ) / (L 1 +L 2 + 2M)
Подводя итог,
- Эквивалентная индуктивность L параллельно соединенных катушек индуктивности L 1 , L 2 , ….



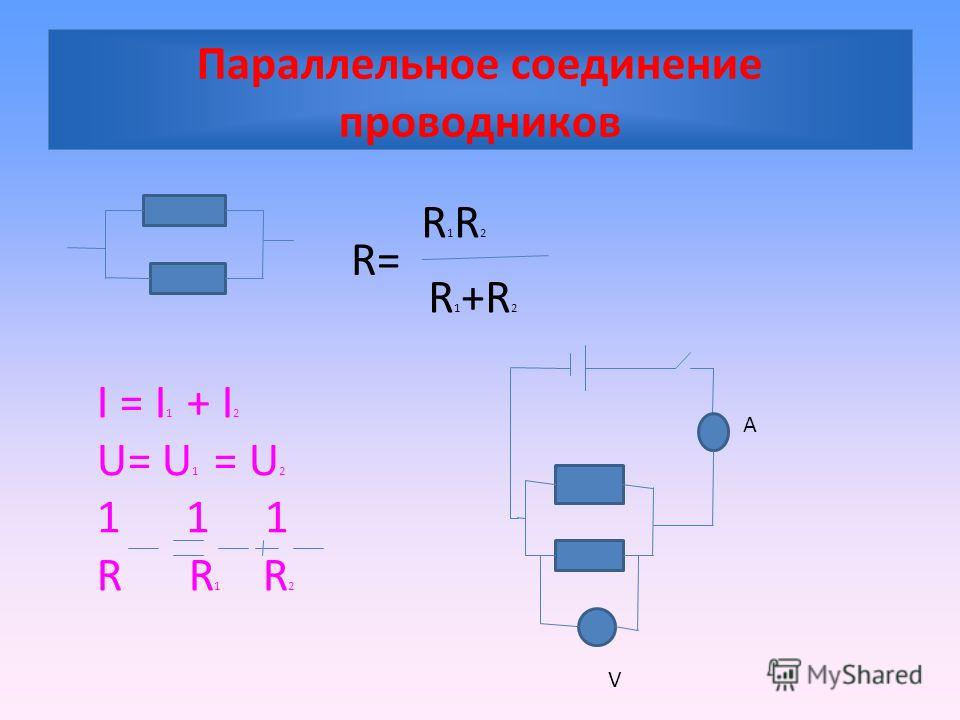 Параллельное соединение катушек индуктивности.
Параллельное соединение катушек индуктивности. Магнитные потоки обеих катушек направлены навстречу друг другу
Магнитные потоки обеих катушек направлены навстречу друг другу
 В радиотехнике вариометры применяются для настройки колебательных контуров приемников и передатчиков.
В радиотехнике вариометры применяются для настройки колебательных контуров приемников и передатчиков.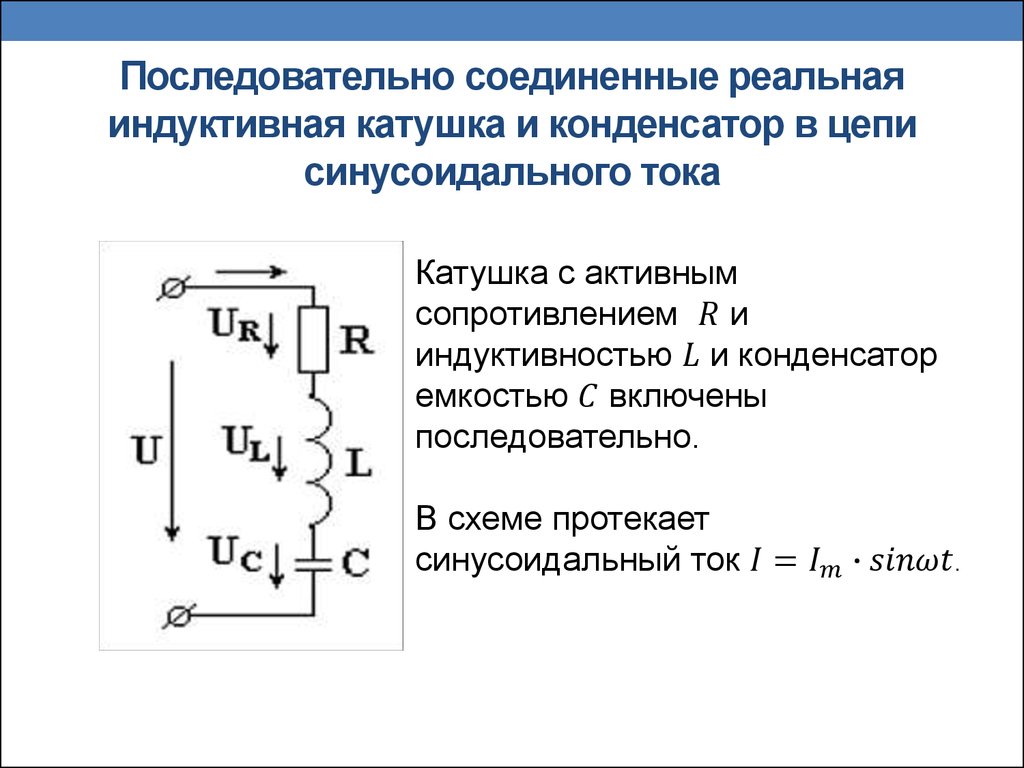 Обратная связь — 176.9.44.166 (0.008 с.)
Обратная связь — 176.9.44.166 (0.008 с.) 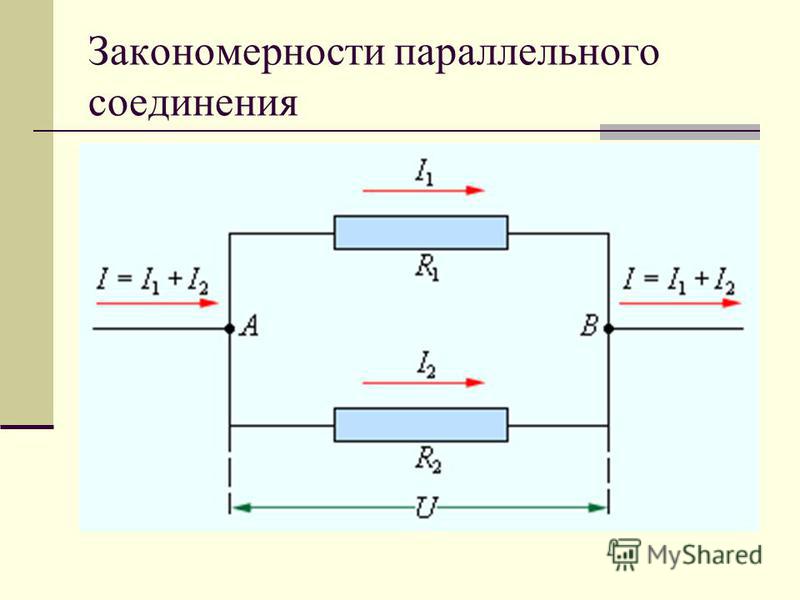 ..
.. Предположим при этом, что активным сопротивлением цепь не обладает.
Предположим при этом, что активным сопротивлением цепь не обладает. е. XL больше XC, ток в катушке меньше тока в конденсаторе; следовательно, ток в неразветвленном участке цепи носит емкостный характер, и цепь в целом для генератора будет емкостной. И, наоборот, при ХC большем XL, ток в конденсаторе меньше тока в катушке; следовательно, ток в неразветвленном участке цепи имеет индуктивный характер, и цепь в целом для генератора будет индуктивной.
е. XL больше XC, ток в катушке меньше тока в конденсаторе; следовательно, ток в неразветвленном участке цепи носит емкостный характер, и цепь в целом для генератора будет емкостной. И, наоборот, при ХC большем XL, ток в конденсаторе меньше тока в катушке; следовательно, ток в неразветвленном участке цепи имеет индуктивный характер, и цепь в целом для генератора будет индуктивной.

 е. переменный ток. И если бы не активное сопротивление, которым обладает всякий колебательный контур, в нем непрерывно мог бы существовать переменный ток. Наличие же активного сопротивления приводит к тому, что колебания в контуре постепенно затухают и, чтобы поддержать их, необходим источник энергии — генератор переменного тока.
е. переменный ток. И если бы не активное сопротивление, которым обладает всякий колебательный контур, в нем непрерывно мог бы существовать переменный ток. Наличие же активного сопротивления приводит к тому, что колебания в контуре постепенно затухают и, чтобы поддержать их, необходим источник энергии — генератор переменного тока.
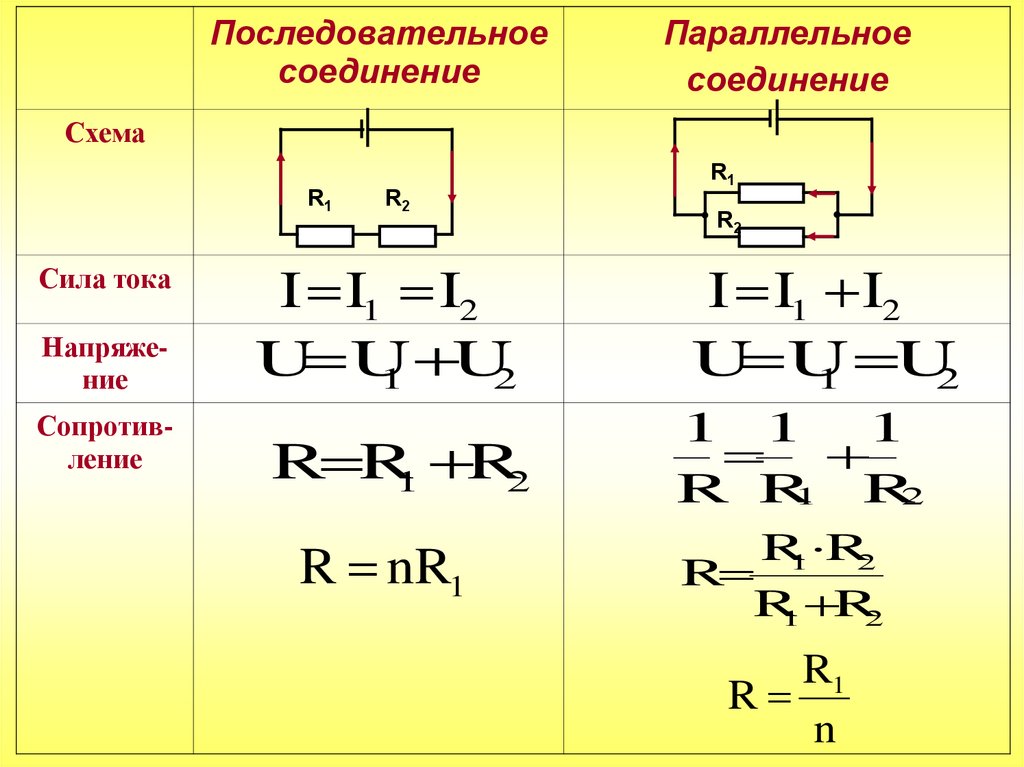

 Напряжение на емкости будет в Q раз больше ЭДС источника, такое же напряжение окажется приложенным к индуктивности.
Напряжение на емкости будет в Q раз больше ЭДС источника, такое же напряжение окажется приложенным к индуктивности.


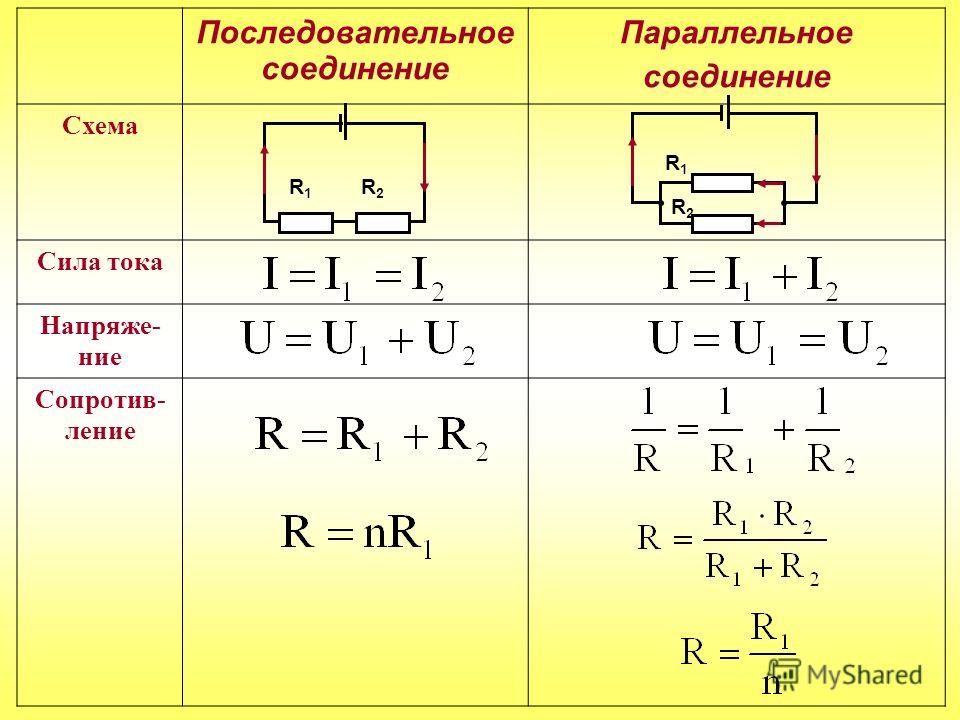 е. находятся в противофазе. Таким образом токи в ветвях в любой момент времени направлены навстречу один другому, а общий ток в неразветвленной части цепи равен разности их.
е. находятся в противофазе. Таким образом токи в ветвях в любой момент времени направлены навстречу один другому, а общий ток в неразветвленной части цепи равен разности их.
 При резонансе токов, как и при резонансе напряжений, происходит колебание энергии между полем катушки и полем конденсатора. Генератор, сообщив однажды энергию цепи, сказывается как бы изолированным. Его можно было бы совсем отключить, и ток в разветвленной части цепи поддерживался бы без генератора энергией, которую в самом начале запасла цепь. Равно и напряжение на зажимах цепи оставалось бы точно таким, какое развивал генератор.
При резонансе токов, как и при резонансе напряжений, происходит колебание энергии между полем катушки и полем конденсатора. Генератор, сообщив однажды энергию цепи, сказывается как бы изолированным. Его можно было бы совсем отключить, и ток в разветвленной части цепи поддерживался бы без генератора энергией, которую в самом начале запасла цепь. Равно и напряжение на зажимах цепи оставалось бы точно таким, какое развивал генератор. е. превратить цепь в колебательный контур.
е. превратить цепь в колебательный контур. Колебательный контур, работающий в режиме резонанса токов, является одним из основных узловэлектронных генераторов.
Колебательный контур, работающий в режиме резонанса токов, является одним из основных узловэлектронных генераторов.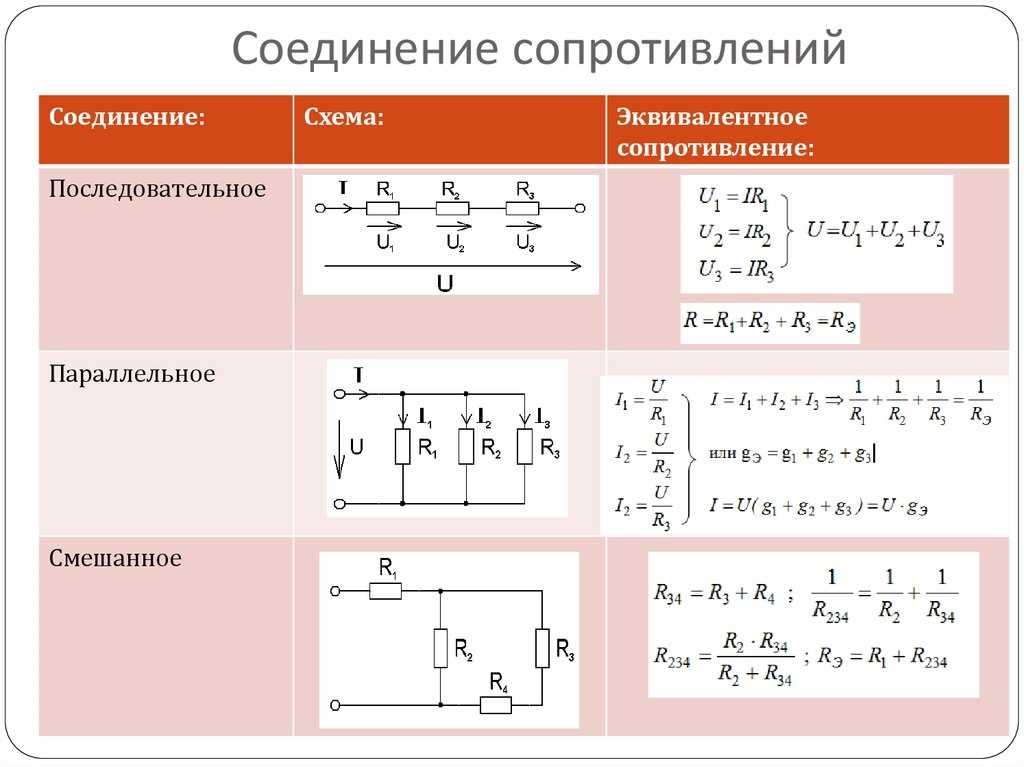

 Взаимная индуктивность. Соединения катушек индуктивностей
Взаимная индуктивность. Соединения катушек индуктивностей


 Измерьте с помощью мультиметра или виртуальных приборов общий ток
цепи I,
Рис. 5.4.2
токи параллельных ветвей I1, I2, I3 и падения напряжение U на катушках,
занесите данные измерений в табл. 5.4.1
Таблица 5.4.1
Измерьте с помощью мультиметра или виртуальных приборов общий ток
цепи I,
Рис. 5.4.2
токи параллельных ветвей I1, I2, I3 и падения напряжение U на катушках,
занесите данные измерений в табл. 5.4.1
Таблица 5.4.1

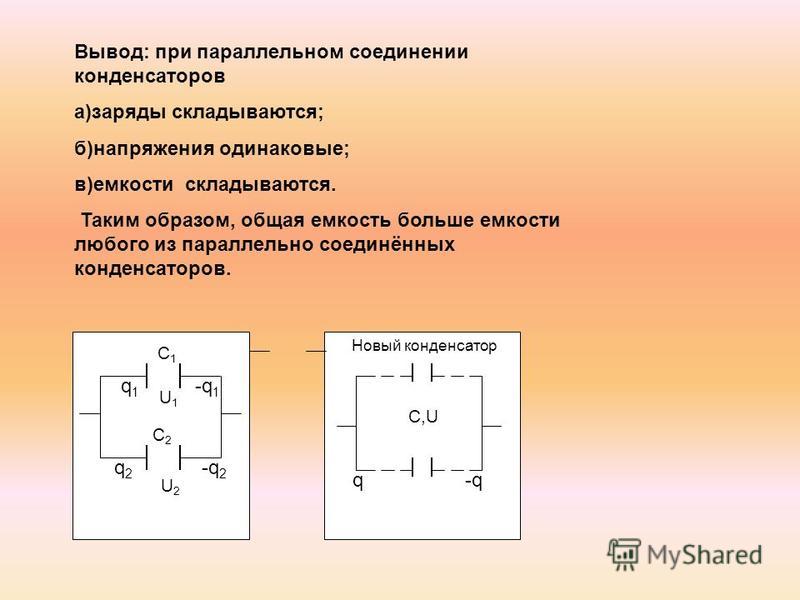 Она называется индуктивной реактивной
мощностью.
Средняя (активная) мощность, потребляемая такой катушкой, равна
нулю.
Экспериментальная часть
Задание
Выведите кривые тока и напряжения катушки на экран виртуального
осциллографа, перенесите их на график и постройте кривую изменения
мгновенных значений мощности перемножением мгновенных значений напряжения
и тока.
Порядок выполнения эксперимента
Соберите цепь согласно схеме (рис. 5.5.2), подсоедините к ней регулируемый
источник синусоидального напряжения с параметрами: U=5…7B и f = 200
Гц. В качестве индуктивности с малым активным сопротивлением используйте
катушку трансформатора 300 витков, вставив между подковами разъемного
сердечника полоски бумаги в один слой (немагнитный зазор).
Рис. 5.5.2
Включите виртуальные приборы V0, A1 и осциллограф.
«Подключите» два входа осциллографа к приборам V0 и A1, а остальные
отключите.
Установите параметры развёртки осциллографа так, чтобы на экране
было изображение примерно одного-двух периодов напряжения и тока.
Она называется индуктивной реактивной
мощностью.
Средняя (активная) мощность, потребляемая такой катушкой, равна
нулю.
Экспериментальная часть
Задание
Выведите кривые тока и напряжения катушки на экран виртуального
осциллографа, перенесите их на график и постройте кривую изменения
мгновенных значений мощности перемножением мгновенных значений напряжения
и тока.
Порядок выполнения эксперимента
Соберите цепь согласно схеме (рис. 5.5.2), подсоедините к ней регулируемый
источник синусоидального напряжения с параметрами: U=5…7B и f = 200
Гц. В качестве индуктивности с малым активным сопротивлением используйте
катушку трансформатора 300 витков, вставив между подковами разъемного
сердечника полоски бумаги в один слой (немагнитный зазор).
Рис. 5.5.2
Включите виртуальные приборы V0, A1 и осциллограф.
«Подключите» два входа осциллографа к приборам V0 и A1, а остальные
отключите.
Установите параметры развёртки осциллографа так, чтобы на экране
было изображение примерно одного-двух периодов напряжения и тока. Включите блок дополнительных приборов, выберите из меню приборы
«Активная мощность» и «Реактивная мощность» и подключите их к V1 и
A1. Запишите значения реактивной мощности QL и активной P. Убедитесь,
что P
Включите блок дополнительных приборов, выберите из меню приборы
«Активная мощность» и «Реактивная мощность» и подключите их к V1 и
A1. Запишите значения реактивной мощности QL и активной P. Убедитесь,
что P  5.5.1 на график (рис. 5.5.3).
5.5.1 на график (рис. 5.5.3).
 Например, напряжение u = Um sin (w
t+y
) изображается вектором длиной Um или Um/Ö
2, расположенным под углом y
к горизонтали. Векторные изображения синусоидальных
величин в дальнейшем будут подчеркиваться.
Например, напряжение u = Um sin (w
t+y
) изображается вектором длиной Um или Um/Ö
2, расположенным под углом y
к горизонтали. Векторные изображения синусоидальных
величин в дальнейшем будут подчеркиваться. …
… 
