Что такое исключающее ИЛИ (XOR). Как работает логический оператор XOR. Какие свойства имеет исключающее ИЛИ. Где применяется XOR в программировании и электронике. Примеры использования исключающего ИЛИ.
Что такое исключающее ИЛИ (XOR)
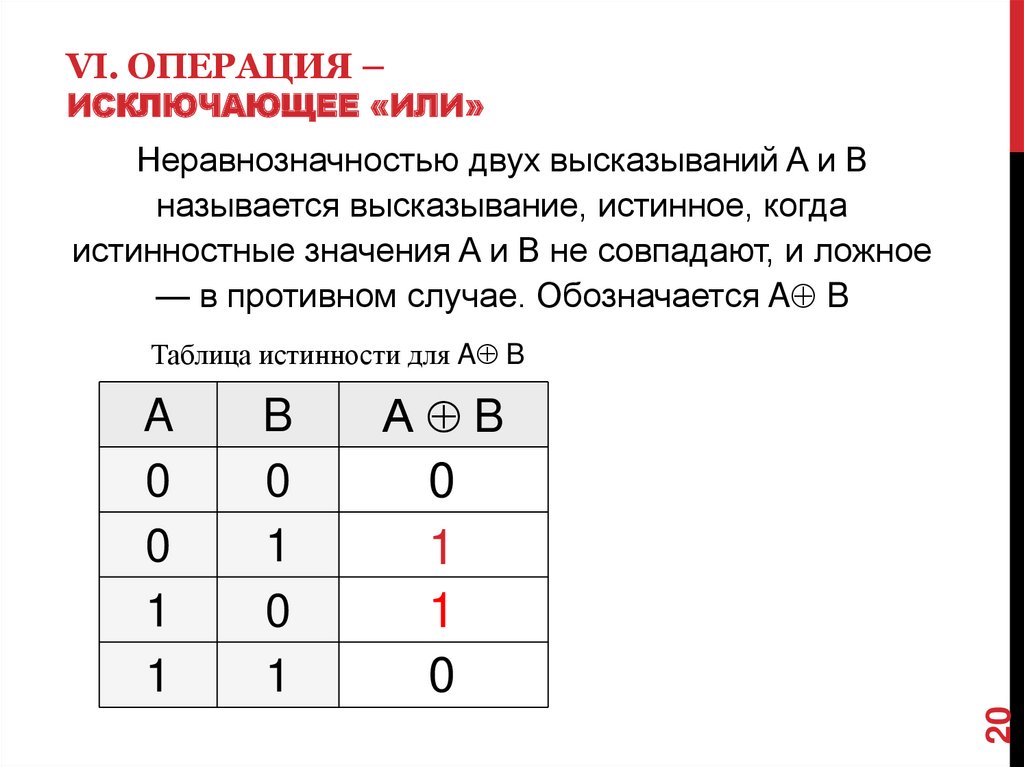
Исключающее ИЛИ (XOR) — это логическая операция, которая возвращает истинное значение тогда и только тогда, когда количество истинных входов нечетно. Другими словами, XOR истинно, если один и только один из входов истинен.
Основные свойства операции XOR:
- Коммутативность: A XOR B = B XOR A
- Ассоциативность: A XOR (B XOR C) = (A XOR B) XOR C
- Свойство нуля: A XOR 0 = A
- Свойство единицы: A XOR 1 = NOT A
- Самоинверсия: A XOR A = 0
Таблица истинности для XOR
Таблица истинности для операции XOR выглядит следующим образом:
| A | B | A XOR B |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Применение XOR в программировании
Операция XOR имеет множество полезных применений в программировании и работе с битами:
- Обмен значений переменных без использования временной переменной
- Шифрование данных
- Обнаружение изменений в данных
- Вычисление контрольной суммы
- Реализация некоторых алгоритмов сжатия данных
Обмен значений переменных с помощью XOR
Одно из интересных применений XOR — обмен значений двух переменных без использования третьей временной переменной:
a = a XOR b
b = a XOR b
a = a XOR b
После выполнения этих операций значения a и b будут обменены. Как это работает?
- a = a XOR b — сохраняем в a информацию о различиях между a и b
- b = a XOR b — восстанавливаем исходное значение a в b
- a = a XOR b — восстанавливаем исходное значение b в a
XOR в криптографии
Операция XOR активно используется в криптографических алгоритмах благодаря следующим свойствам:
- XOR обратимо: (A XOR B) XOR B = A
- XOR между случайным ключом и данными дает случайный результат
- XOR не требует сложных вычислений
Простейший пример шифрования с XOR:
Открытый текст: 1010 1111 0011
Ключ: 1100 0101 1010
----------------------------
Шифротекст: 0110 1010 1001
Для расшифровки достаточно выполнить XOR между шифротекстом и тем же ключом.
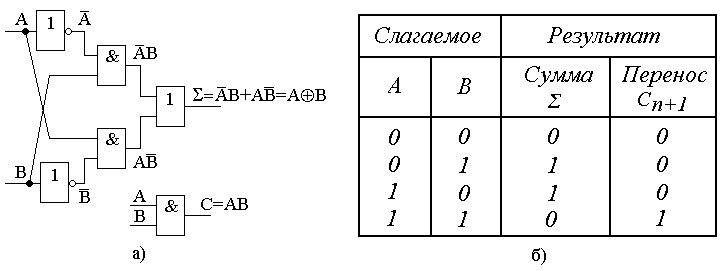
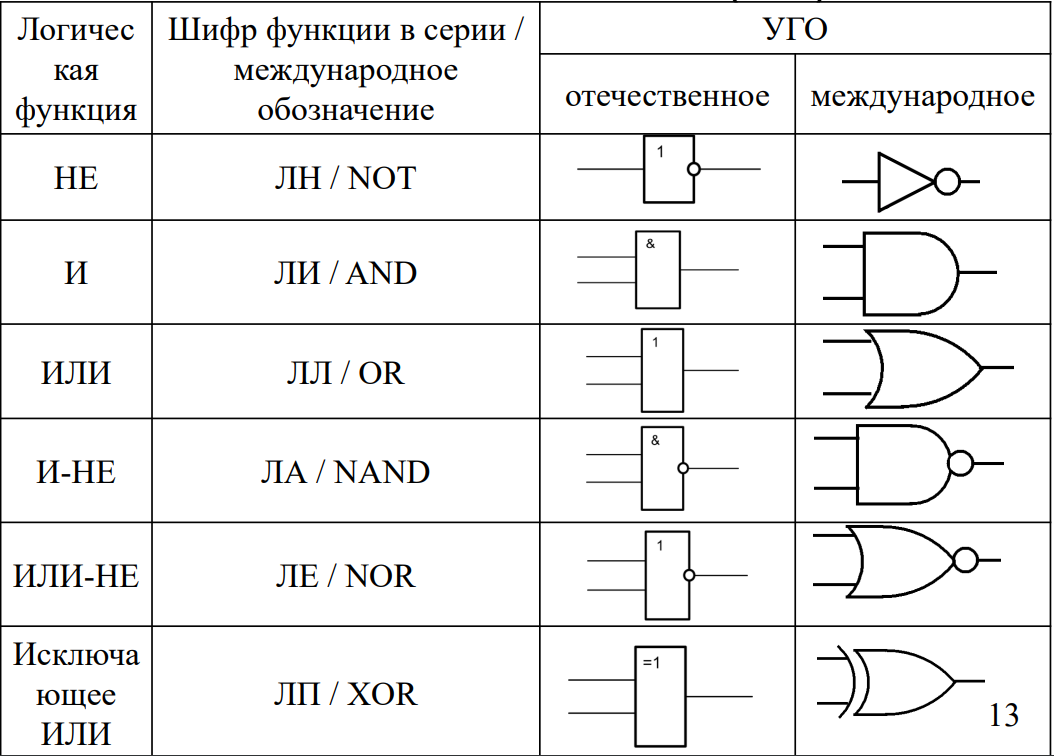
Применение XOR в электронике
В электронных схемах XOR реализуется с помощью логических вентилей. Вентиль XOR используется для построения:
- Схем сравнения
- Сумматоров
- Схем контроля четности
- Мультиплексоров
Как работает вентиль XOR?
Логический вентиль XOR имеет два входа A и B и один выход Y. Выход Y будет иметь высокий уровень (логическая 1) тогда и только тогда, когда уровни сигналов на входах A и B различаются.
XOR в языках программирования
Большинство языков программирования поддерживают операцию XOR. Вот несколько примеров:
XOR в Python
a = 5 # 101 в двоичной системе
b = 3 # 011 в двоичной системе
c = a ^ b # XOR
print(c) # Выведет 6 (110 в двоичной системе)
XOR в Java
int a = 5; // 101 в двоичной системе
int b = 3; // 011 в двоичной системе
int c = a ^ b; // XOR
System.out.println(c); // Выведет 6 (110 в двоичной системе)
XOR в C++
int a = 5; // 101 в двоичной системе
int b = 3; // 011 в двоичной системе
int c = a ^ b; // XOR
std::cout << c << std::endl; // Выведет 6 (110 в двоичной системе)
Полезные свойства XOR для программистов
При работе с битовыми операциями полезно помнить следующие свойства XOR:
- x ^ 0 = x - XOR с нулем не меняет значение
- x ^ x = 0 - XOR числа с самим собой дает ноль
- x ^ y ^ x = y - повторное применение XOR с тем же числом восстанавливает исходное значение
- (x ^ y) ^ z = x ^ (y ^ z) - ассоциативность позволяет группировать операции произвольным образом
Задачи на применение XOR
Операция XOR часто используется для решения алгоритмических задач. Вот несколько примеров:
Поиск одиночного элемента
Задача: дан массив чисел, в котором все элементы встречаются четное число раз, кроме одного. Найти этот элемент.
Решение: XOR всех элементов массива. Все парные элементы "обнулятся", останется только искомый элемент.
def find_single(arr):
result = 0
for num in arr:
result ^= num
return result
print(find_single([1, 2, 1, 3, 2, 5, 3])) # Выведет 5
Обнаружение дублирующегося числа
Задача: в массиве от 1 до n есть одно повторяющееся число. Найти его, используя только O(1) дополнительной памяти.
Решение: XOR всех чисел от 1 до n, затем XOR результата со всеми элементами массива. Останется только дублирующееся число.
def find_duplicate(arr):
n = len(arr) - 1
result = 0
# XOR всех чисел от 1 до n
for i in range(1, n + 1):
result ^= i
# XOR со всеми элементами массива
for num in arr:
result ^= num
return result
print(find_duplicate([3, 1, 2, 5, 4, 2])) # Выведет 2
XOR в реальных приложениях
Операция XOR находит применение во многих областях компьютерных технологий:
Графические редакторы
XOR используется для реализации режима "инвертирования" при рисовании. Это позволяет временно отображать линии или фигуры, не повреждая фоновое изображение.
Сетевые протоколы
XOR применяется в некоторых алгоритмах обнаружения ошибок при передаче данных, например, в CRC (циклическом избыточном коде).
Сжатие данных
Некоторые алгоритмы сжатия без потерь, такие как DEFLATE (используемый в ZIP), применяют XOR для улучшения степени сжатия.
Генераторы псевдослучайных чисел
XOR является компонентом некоторых алгоритмов генерации псевдослучайных чисел, например, в линейном конгруэнтном генераторе.
Заключение
Исключающее ИЛИ (XOR) - это мощная и универсальная операция, которая находит применение во многих областях программирования и компьютерных технологий. От простых битовых манипуляций до сложных криптографических алгоритмов, XOR доказывает свою полезность благодаря уникальным математическим свойствам.
Глубокое понимание операции XOR и ее свойств может значительно расширить арсенал программиста, позволяя находить элегантные и эффективные решения для широкого спектра задач.
⊻ - Исключающее ИЛИ: U+22BB veebar
U+22BB
Нажмите, чтобы скопировать и вставить символ
Техническая информация
| Название в Юникоде | Xor |
| Номер в Юникоде | U+22BB |
| HTML-код | ⊻ |
| CSS-код | \22BB |
| Мнемоника | ⊻ |
| Раздел | Математические операторы |
| Версия Юникода: | 1. 1 (1993) |
Значение символа
Исключающее ИЛИ. Математические операторы.
Символ «Исключающее ИЛИ» был утвержден как часть Юникода версии 1.1 в 1993 г.
Свойства
| Версия | 1.1 |
| Блок | Математические операторы |
| Тип парной зеркальной скобки (bidi) | Нет |
| Композиционное исключение | Нет |
| Изменение регистра | 22BB |
| Простое изменение регистра | 22BB |
Кодировка
| Кодировка | hex | dec (bytes) | dec | binary |
|---|---|---|---|---|
| UTF-8 | E2 8A BB | 226 138 187 | 14846651 | 11100010 10001010 10111011 |
| UTF-16BE | 22 BB | 34 187 | 8891 | 00100010 10111011 |
| UTF-16LE | BB 22 | 47906 | 10111011 00100010 | |
| UTF-32BE | 00 00 22 BB | 0 0 34 187 | 8891 | 00000000 00000000 00100010 10111011 |
| UTF-32LE | BB 22 00 00 | 187 34 0 0 | 3139567616 | 10111011 00100010 00000000 00000000 |
Наборы с этим символом:
- ∑
Математические знаки
Исключительная функция ИЛИ - frwiki.
wikiВ этой статье есть пароним, см. Exclusive Us .
Для одноименных статей см. XOR (значения) .
| Диаграмма Венна изВ⊕B{\ displaystyle \ scriptstyle A \ oplus B} не давая |
| Диаграмма Венна изВ⊕B⊕ПРОТИВ{\ displaystyle \ scriptstyle A \ oplus B \ oplus C} ⊕ {\ displaystyle ~ \ oplus ~} ⇔ {\ displaystyle ~ \ Leftrightarrow ~} |
Функция исключающего ИЛИ, часто называют исключающей ИЛИ (е х CLUSIVE ИЛИ ) или дизъюнкции исключительной или ⊻ в реляционной алгебре, является логическим оператором из булевой алгебры . С двумя операндами, каждый из которых может иметь значение ИСТИНА или ЛОЖЬ, он связывает результат, который сам имеет значение ИСТИНА, только если два операнда имеют разные значения.
Этот оператор широко используется в электронике, информатике, а также в криптографии из-за его интересных свойств.
Его символом традиционно является знак плюса в круге: «⊕».
Резюме
- 1 Определение
- 2 Эквивалентность, введение и исключение
- 3 Некоторые математические свойства
- 4 Пример использования в криптографии
- 4.1 Иллюстрация
- 4.2 История
- 5 Другие приложения в криптографии
- 6 Применение в электронике
- 7 Компьютерные приложения
- 8 Применение в бытовой электросети
- 9 См. Также
Определение
Назовем A и B двумя рассматриваемыми операндами. Согласимся представлять их стоимость следующим образом:
- 1 = ИСТИНА
- 0 = ЛОЖЬ
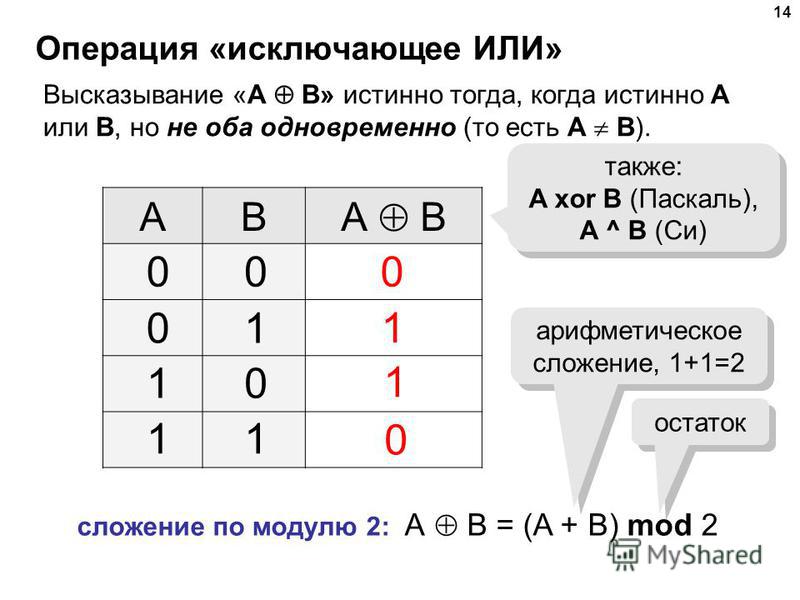
Оператор XOR определяется его таблицей истинности, которая указывает для всех возможных значений A и B значение результата R:
| Таблица истинности XOR | ||
| В | B | R = A ⊕ B |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Как мы видим, логический оператор XOR, или исключающее ИЛИ, может быть определен следующим предложением:
- Результат - ИСТИНА, если один и только один из операндов А и В ИСТИНА.
или же
- Результат будет ИСТИНА, если два операнда A и B имеют разные значения.
или же
- Результат - ИСТИНА, если нечетное количество входов истинно (это особенно применимо, когда два или более логических оператора XOR соединены каскадом (генераторы битов четности )
Он отличается от включающего оператора ИЛИ, потому что дает ЛОЖНЫЙ результат, когда А и В одновременно ИСТИНА. Его символ также отличается от включающего оператора ИЛИ, символ которого представляет собой просто «ПЛЮС»: «+».
В информатике этот оператор может использоваться для объединения двух битов, каждый из которых имеет значение 0 или 1, путем применения правил, определенных в предыдущей таблице, при этом сам результат является значением бита .
С логическими элементами И / ИЛИ A XOR B = (A AND не B) OR (не A AND B).
Функция XOR является примером функции четности .
Эквивалентность, введение и устранение
Исключительная дизъюнкция, или J pq, может быть выражена в терминах конъюнкции («и логического», ), дизъюнкции («или логического», ) и логического отрицания ( ) следующим образом: п⊕q{\ displaystyle p \ oplus q}∧{\ Displaystyle \ клин}∨{\ displaystyle \ lor}¬{\ Displaystyle \ lnot}
Исключительную дизъюнкцию также можно сформулировать следующим образом: п⊕q{\ displaystyle p \ oplus q}
- п⊕qзнак равно(п∧¬q)∨(¬п∧q){\ displaystyle {\ begin {matrix} p \ oplus q & = & (p \ land \ lnot q) \ lor (\ lnot p \ land q) \ end {matrix}}}
Такое представление XOR может быть полезно при построении схемы или сети, потому что оно имеет только одну операцию и небольшое количество операций и .
- п⊕qзнак равно(п∧¬q)∨(¬п∧q)знак равно((п∧¬q)∨¬п)∧((п∧¬q)∨q)знак равно((п∨¬п)∧(¬q∨¬п))∧((п∨q)∧(¬q∨q))знак равно(¬п∨¬q)∧(п∨q)знак равно¬(п∧q)∧(п∨q){\ displaystyle {\ begin {matrix} p \ oplus q & = & (p \ land \ lnot q) & \ lor & (\ lnot p \ land q) \\ [3pt] & = & ((p \ land \ lnot q) \ lor \ lnot p) & \ land & ((p \ land \ lnot q) \ lor q) \\ [3pt] & = & ((p \ lor \ lnot p) \ land (\ lnot q \ lor \ lnot p)) & \ land & ((p \ lor q) \ land (\ lnot q \ lor q)) \\ [3pt] & = & (\ lnot p \ lor \ lnot q) & \ land & (p \ lor q) \\ [3pt] & = & \ lnot (p \ land q) & \ land & (p \ lor q) \ end {matrix}}}Иногда полезно отметить следующее:п⊕q{\ displaystyle p \ oplus q}
- п⊕qзнак равно¬((п∧q)∨(¬п∧¬q)){\ displaystyle {\ begin {matrix} p \ oplus q & = & \ lnot ((p \ land q) \ lor (\ lnot p \ land \ lnot q)) \ end {matrix}}}
или же:
- п⊕qзнак равно(п∨q)∧(¬п∨¬q){\ displaystyle {\ begin {matrix} p \ oplus q & = & (p \ lor q) \ land (\ lnot p \ lor \ lnot q) \ end {matrix}}}
Эту эквивалентность можно установить , дважды применяя законы Де Моргана к четвертой строке приведенного выше доказательства.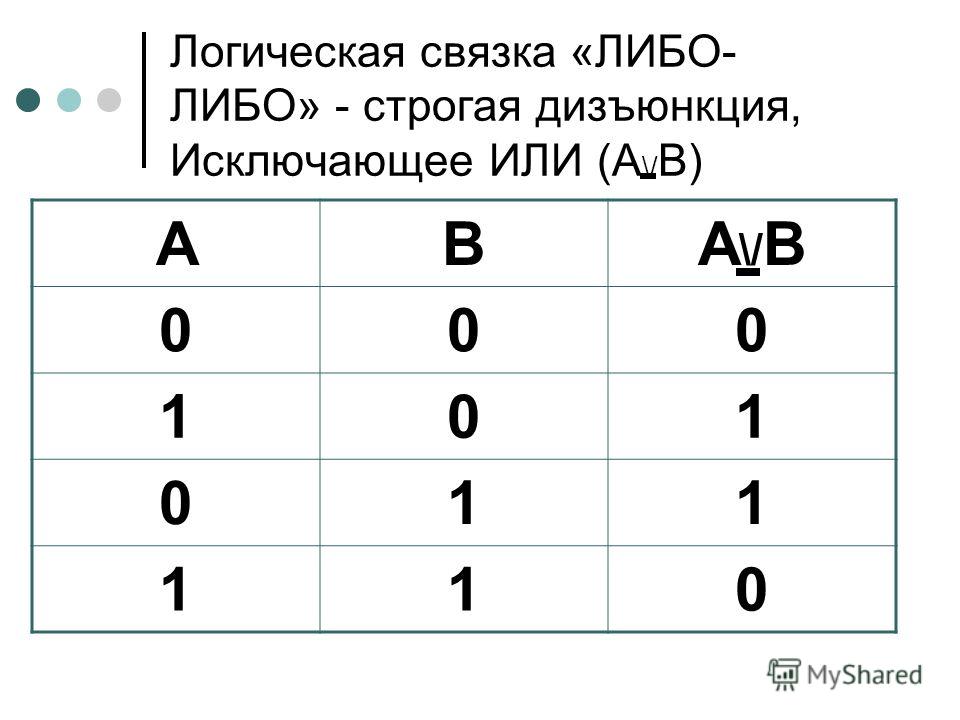
Исключающее или также эквивалентно отрицанию логической эквивалентности по правилам материальной импликации.
Таким образом, мы имеем:
- п⊕qзнак равно(п∧¬q)∨(¬п∧q)знак равнопq¯+п¯qзнак равно(п∨q)∧(¬п∨¬q)знак равно(п+q)(п¯+q¯)знак равно(п∨q)∧¬(п∧q)знак равно(п+q)(пq¯){\ displaystyle {\ begin {matrix} p \ oplus q & = & (p \ land \ lnot q) & \ lor & (\ lnot p \ land q) & = & p {\ overline {q}} + {\ overline {p}} q \\ [3pt] & = & (p \ lor q) & \ land & (\ lnot p \ lor \ lnot q) & = & (p + q) ({\ overline {p}} + {\ overline {q}}) \\ [3pt] & = & (p \ lor q) & \ land & \ lnot (p \ land q) & = & (p + q) ({\ overline {pq} }) \ end {matrix}}}
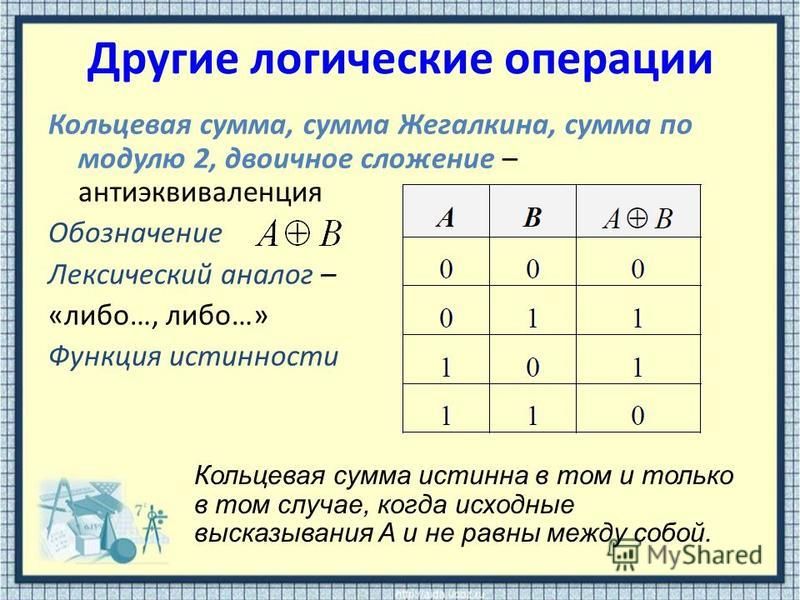
Некоторые математические свойства
- В⊕Взнак равно0{\ Displaystyle A \ oplus A = 0}(легко проверить по таблице 2 возможных значения A )
- В⊕0знак равноВ{\ displaystyle A \ oplus 0 = A}
- В⊕1знак равноВ¯{\ displaystyle A \ oplus 1 = {\ bar {A}}}
- В⊕В¯знак равно1{\ displaystyle A \ oplus {\ bar {A}} = 1}
- Коммутативность В⊕Bзнак равноB⊕В{\ Displaystyle A \ oplus B = B \ oplus A}
- Ассоциативность где - функция совпадения. В⊕(B⊕ПРОТИВ)знак равно(В⊕B)⊕ПРОТИВзнак равноВ⊙(B⊙ПРОТИВ)знак равно(В⊙B)⊙ПРОТИВ{\ Displaystyle A \ oplus (B \ oplus C) = (A \ oplus B) \ oplus C = A \ odot (B \ odot C) = (A \ odot B) \ odot C}⊙{\ displaystyle \ odot}
- В⊕Bзнак равно(В+B)⊕В⋅B{\ Displaystyle A \ oplus B = (A + B) \ oplus A \ cdot B}
- В⊕Bзнак равно0{\ displaystyle A \ oplus B = 0}если и только если (в некотором смысле, это немедленно, в другом, используя свойство ассоциативности и владение: )Взнак равноB{\ displaystyle A = B}В⊕0знак равноВ{\ displaystyle A \ oplus 0 = A}
- В⊕Bзнак равноВ¯⋅B+В⋅B¯{\ displaystyle A \ oplus B = {\ bar {A}} \ cdot B + A \ cdot {\ bar {B}}}Мы выводим из этого свойства: или даже снова: и даже снова:В⊕B¯знак равноВ⋅B+В¯⋅B¯{\ displaystyle {\ overline {A \ oplus B}} = A \ cdot B + {\ bar {A}} \ cdot {\ bar {B}}}В⊕B¯знак равноВ¯⊕Bзнак равноВ⊕B¯{\ displaystyle {\ overline {A \ oplus B}} = {\ overline {A}} \ oplus B = A \ oplus {\ overline {B}}}В⊕Bзнак равноВ¯⊕B¯{\ displaystyle A \ oplus B = {\ overline {A}} \ oplus {\ overline {B}}}
- В⊕Bзнак равноПРОТИВ{\ Displaystyle A \ oplus B = C}так иПРОТИВ⊕Bзнак равноВ{\ Displaystyle C \ oplus B = A}В⊕ПРОТИВзнак равноB{\ Displaystyle A \ oplus C = B}
- (В⊕B)⊕Bзнак равноВ{\ Displaystyle (A \ oplus B) \ oplus B = A} (Следствие первых двух свойств и ассоциативности - полезно в криптографии (см. Ниже))
- Набор {0; 1} с двумя законами внутренней композиции, исключающим ИЛИ и И, является конечным полем .
В⊕(B⊕ПРОТИВ)знак равно(В⊕B)⊕ПРОТИВзнак равноВ⊙(B⊙ПРОТИВ)знак равно(В⊙B)⊙ПРОТИВ{\ Displaystyle A \ oplus (B \ oplus C) = (A \ oplus B) \ oplus C = A \ odot (B \ odot C) = (A \ odot B) \ odot C}⊙{\ displaystyle \ odot}
Ниже))Пример использования в криптографии
Считайте цифровой документ зашифрованным, он состоит из ряда битов . В методе потокового шифрования также должна быть последовательность битов одинаковой длины, полностью случайная, которая называется ключом шифрования . Биты документа обрабатываются один за другим, комбинируя его с битом того же ранга ключа шифрования.
Назовем собой четкий бит и B бит того же ранга случайной последовательности.
Шифрование для вычисления битов C с помощью C = A ⊕ B . С представляет собой зашифрованы .
Для расшифровки С еще раз, используя бит B случайной последовательности и рассчитывается следующим образом : C ⊕ B .
Результатом будет A, бит очистки, потому что C ⊕ B = A ⊕ B ⊕ B = A ⊕ 0 = A, используя первые два свойства выше.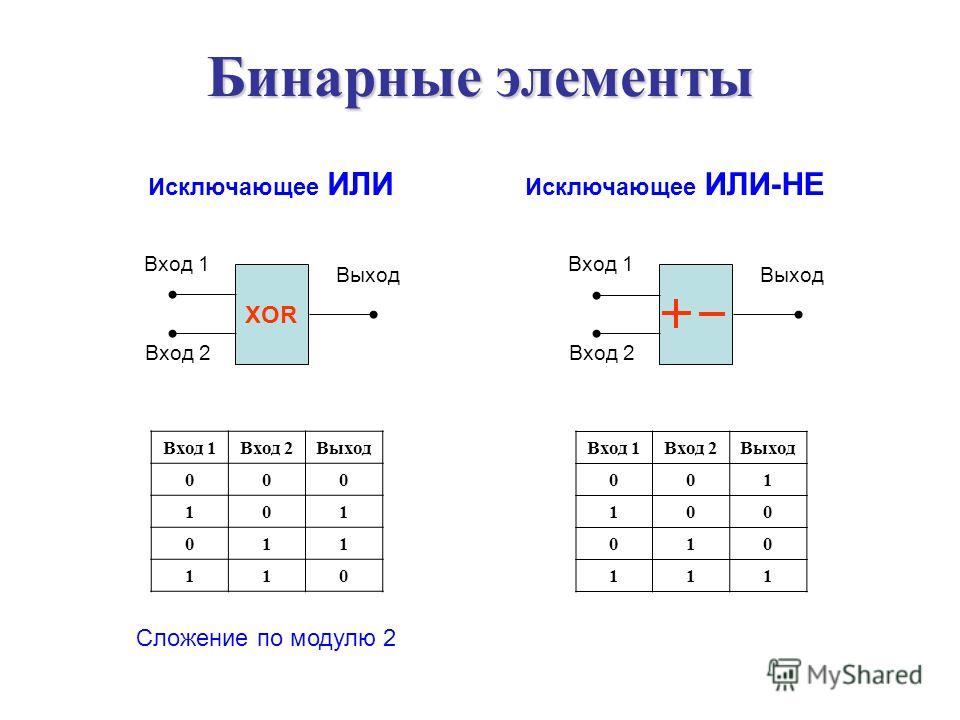
Этот метод является одним из способов выполнения симметричного шифрования, когда один и тот же ключ используется для шифрования и дешифрования.
Эта система, хотя и очень проста в принципе, может оказаться неприкосновенной, если последовательность битов ключа действительно случайна. Последнюю тоже нужно использовать только один раз (мы говорим об одноразовой маске или даже «одноразовой подушечке»). В этом предложении наиболее трудным для реализации оказывается, прежде всего, слово «случайный». Но когда ключ действительно случайный (технически он нарисован в соответствии с равномерным распределением среди всех возможных последовательностей этой длины), эта система совершенно безопасна в том смысле, который строго определил Клод Шеннон в 1949 году в статье основатель "Коммуникационная теория секретных систем". Следует добавить, что это единственное шифрование, которое теоретически обеспечивает абсолютную безопасность.
Смотрите также статью: одноразовая маска
Рисунок
Вот числовой пример предыдущего метода:
M = 0110101011010100 (обычное сообщение)
K = 0101011011100110 (ключ; конечно, держать в секрете)
Согласимся, что символ ⊕ здесь представляет приложение оператора XOR к каждому из битов
Для шифрования вы должны использовать таблицу истинности: «M» - ваше сообщение, а «K» - секретный ключ.
Итак: M ⊕ K = C. "C" представляет зашифрованное сообщение:
Шифрование: C = M ⊕ K = 0011110000110010 (зашифрованное сообщение)
Расшифровка: M = C ⊕ K = 0110101011010100 (расшифрованное сообщение)
История
Эта система шифрования использовалась для красного телефона, фактически телекса, напрямую соединяющего Кремль с Белым домом, а ключи затем проходили через дипломатические сумки . Система одноразовых масок также использовалась советскими шпионами. Некоторые маски использовались более одного раза (иногда с интервалом в несколько лет), что позволяло английским службам шифрования расшифровать определенные сообщения.
Другие приложения в криптографии
Все симметричные шифры используют оператор XOR. Симметричный алгоритм шифрования с высокой степенью защиты AES ( Rijndael ), в частности, использует очень большое их количество.
Применение в электронике
Пример использования: интегральная схема 7486 TTL или интегральная схема CMOS 4070 объединяет четыре логических элемента типа исключающее ИЛИ.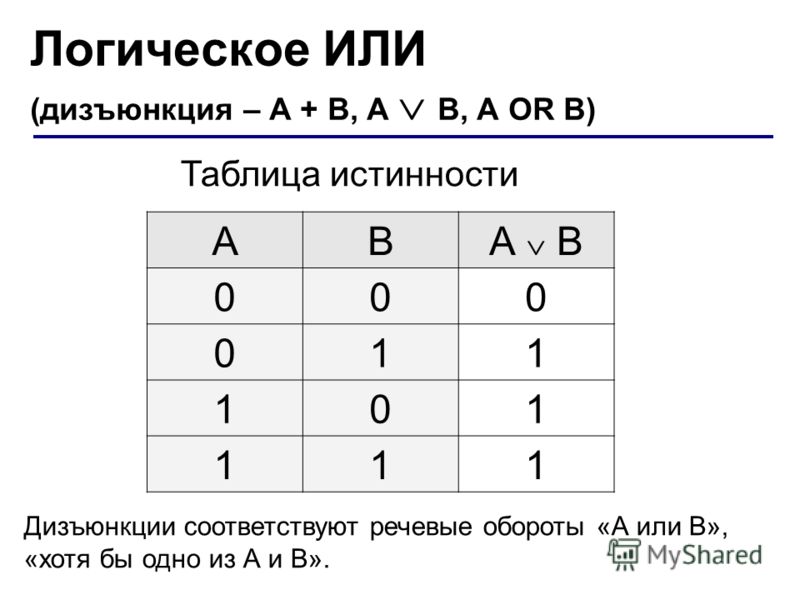
Иллюстрация: Пример: лампа загорается только при нажатии «a» или «b», но не при одновременном нажатии «a» и «b».
- Диаграмма
- Уравнение
- Lзнак равнов⊕б{\ Displaystyle L = а \ oplus b}
- Lзнак равно(в¯.б)+(в.б¯){\ displaystyle L = ({\ bar {a}}. b) + (a. {\ bar {b}})}
- Хронограмма
- Символ IEC
- Символ ANSI (также называемый военным)
Компьютерные приложения
Помимо использования, связанного с криптографией, функция исключающего ИЛИ позволяет быстро сбросить значение переменной (часто регистра ) до нуля.
Возьмем, например, ассемблерный код, который использует исключающее ИЛИ для сброса значения регистра eax до нуля:
xor eax, eax
На процессорах типа x86 эта инструкция короче (по количеству байтов), чем следующий интуитивно понятный код:
mov eax, 0
Он также позволяет обнулить переменную, когда условия не позволяют использовать байт 0x00 в двоичном коде ( шеллкоде ).
Вы также можете использовать исключающее ИЛИ для обмена двумя переменными без использования временной переменной .
Применение в бытовом электричестве
Одно приложение, используемое оператором исключающего ИЛИ в бытовом электричестве, - это помещения, где лампочка может быть включена или выключена двумя переключателями, расположенными рядом с двумя входами. Каждый из двух переключателей может включать или выключать лампочку независимо от положения другого переключателя. Чтобы получить такую функциональность, мы должны соединить два переключателя, чтобы сформировать оператор XOR. Это так называемая сборка « туда-сюда ».
Смотрите также
- Логическая функция
- ДА функция
- Не работает
- И функция
- Функция ИЛИ
- Функция И-НЕ
- Функция ИЛИ
- Функция совпадения
<img src="//fr.wikipedia.org/wiki/Special:CentralAutoLogin/start?type=1x1" alt="" title="">
Логический оператор, который возвращает значение true, только если один из аргументов имеет значение true, а один из аргументов — значение false.
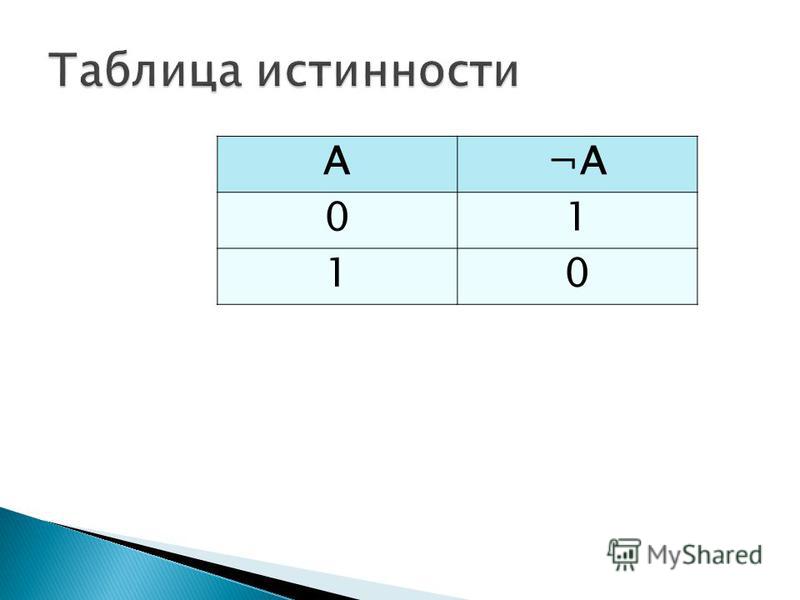
Произношение: /ɪkˈsklusɪv ɔr/ Объяснение
Исключительное или логическое операция который возвращает true, только если один операнд верно, а другое ложно. Для предложений и и b , исключающее или истинно, если либо a , либо b истинны, но не оба. Таблица 1 является таблицей истинности для исключающего или. Эксклюзив или также может быть называется эксклюзивной дизъюнктией. При написании термин «исключающее или» иногда сокращается как «исключающее»; который произносится как «экс-или». 9). В электроника, эксклюзив или гейт рисуется как:
.
| Рисунок 1: Диаграмма Венна для A xor B . |
Свойства эксклюзивных или
| Свойства Использование слов | Свойство Использование символов | Описание |
|---|---|---|
| A XOR FALES | a ⊕ ложь = и | |
| a xor true = not a | а ⊕ правда = ¬ а | |
| a xor a = false | a ⊕ a = ложь | Определение исключающего или подразумевает, что если оба операнда
истинны, или оба операнда ложны, то исключает или возвращает ложь. и ≠ и , и xor и всегда должны быть ложными. |
| a xor not a = true | a ⊕ ¬ a = правда | Определение исключающего или гласит, что если два операнда не равны, исключительный или возвращает true. Начиная с , ≠ ¬ , xor не всегда верно. |
| a xor b = b xor a | а ⊕ б = б ⊕ а | Эксклюзивное или коммутативное. |
| a xor ( b xor c ) = ( a xor b ) xor c | а ⊕ ( б ⊕ в ) = (а⊕б)⊕ в | Эксклюзивное или ассоциативное. |
| a xor b = не a xor не b | а ⊕ б = ¬ а ⊕ ¬ б | Если значение истинности обоих операндов поменяно местами, исключающее или
по-прежнему возвращает то же значение. |
| нет ( a xor b ) = не a xor б = a xили не b | ¬( a ⊕ b ) = ¬ a ⊕ б = а ⊕ ¬ б | Логическое отрицание исключающего или результата — одно и то же как отрицание одного из операндов исключающего или. |
| a xor b = ( a , а не b ) или (не a и b ) | a ⊕ b = ( a ∧ ¬ b ) ∨ (¬ а ∧ б ) | Это переформулировка определения исключительного или: исключительное или операция истинна, только если один из аргументов истинен, а другой ложен. |
| a xor b = ( a или b ) и (не а или не б ) | а ⊕ б = ( а ∨ б ) ∧ (¬ а ∨ ¬ б ) | Это снова переформулировка определения исключающего или. Первый срок
( a или b ) истинно, если либо a или b верно. Второй срок
(не a или не b ) истинно, если либо a и b неверно. С союзом все выражение равно
верно, если либо a или b верны. |
| a xor b = ( a или b ) и не ( а и б ) | a ⊕ b = ( a ∨ b ) ∧ ¬( a ∧ b ) | Это еще одно переформулирование определения исключающего или. |
| Таблица 2: Свойства Exclusive Or. | ||
Побитовое исключающее ИЛИ
В логике операнды исключающего или должны быть значением истинности, должны быть либо
истинное из ложного. В компьютерах операндами исключающего или являются двоичные числа.
Исключающее или применяется к соответствующим битам операндов:
0 xor 0 = 0
0 исключающее ИЛИ 1 = 1
1 исключающее или 0 = 1
1 исключающее ИЛИ 1 = 0
1001 xor 1100 = 0101
Ссылки
- МакАдамс, Дэвид Э. . Словарь всех математических слов, эксклюзивный или . Издание 2-го класса 20150108-4799968. стр. 75. Life is a Story Problem LLC. 8 января 2015. Купить книгу
- xили . www.merriam-webster.com. Британская энциклопедия. Мерриам-Вебстер. Последний доступ 09.07.2018. http://www.merriam-webster.com/dictionary/XOR?db=luna. Купить книгу
- Буль, Джордж; фон Куфнер, Мориц. Математический анализ логики: эссе по исчислению дедуктивных рассуждений . стр. 52-59. www.archive.org. Макмиллан, Барклай и Макмиллан. 1847. Последний доступ 9 июля 2018 г. http://www.archive.org/stream/mathematicalanal00booluoft#page/52/mode/1up/search/exclusive. Купить книгу
. Словарь всех математических слов, эксклюзивный или . Издание 2-го класса 20150108-4799968. стр. 75. Life is a Story Problem LLC. 8 января 2015. Купить книгуЦитируйте эту статью как:
МакАдамс, Дэвид Э. Эксклюзив или . 20.04.2019. Вся энциклопедия математических слов. ООО «Жизнь — это проблема истории». https://www.allmathwords.org/en/e/exclusiveor.
html.
Авторы изображений
- Все изображения и манипуляции сделаны Дэвидом МакАдамсом, если не указано иное. Все изображения Дэвида МакАдамса защищены авторским правом © Life is a Story Problem LLC и находятся под лицензией Creative Commons Attribution-ShareAlike 4.0 International License.
История изменений
20.04.2019:
Обновлены выражения и уравнения для соответствия новому формату.
(МакАдамс, Дэвид Э.)
21.12.2018:
Пересмотрено и исправлено произношение МФА.
(МакАдамс, Дэвид Э.)
05.07.2018:
Удалены битые ссылки, обновлена лицензия, реализована новая разметка, реализован новый протокол Geogebra.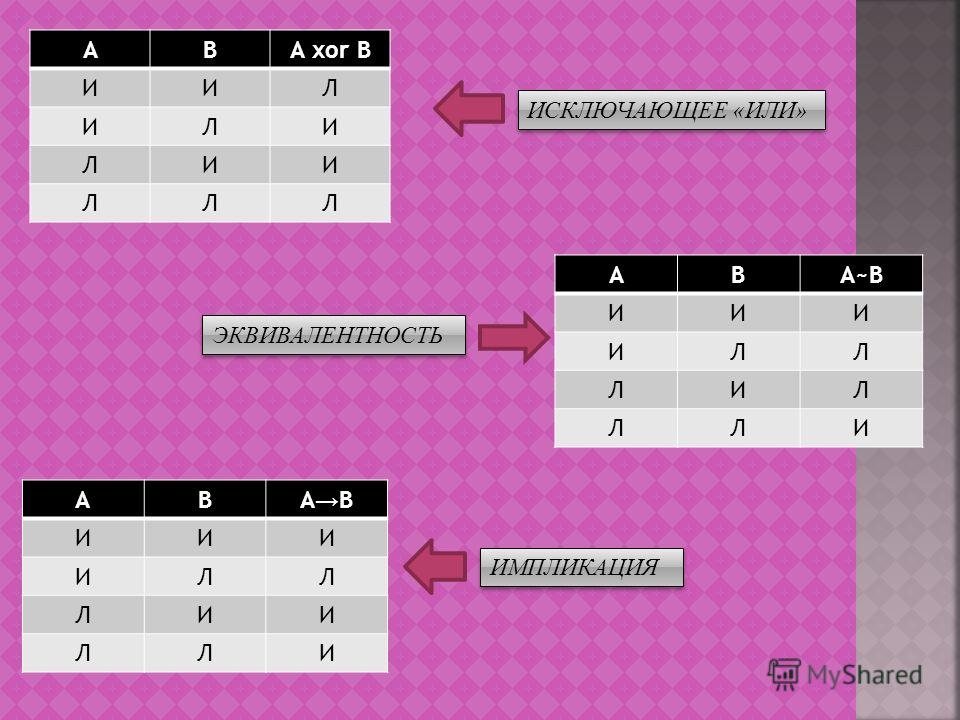
(МакАдамс, Дэвид Э.)
01.02.2010:
Добавлен раздел «Справочники».
(МакАдамс, Дэвид Э.)
18.04.2009:
Исправлено обсуждение xor a.
(МакАдамс, Дэвид Э.)
08.01.2009:
Первоначальная версия.
(МакАдамс, Дэвид Э.)
Функция исключающего ИЛИ — служба поддержки Майкрософт
Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 для Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel для Mac 2011 Дополнительно... Меньше
Функция XOR возвращает логическое исключающее ИЛИ всех аргументов.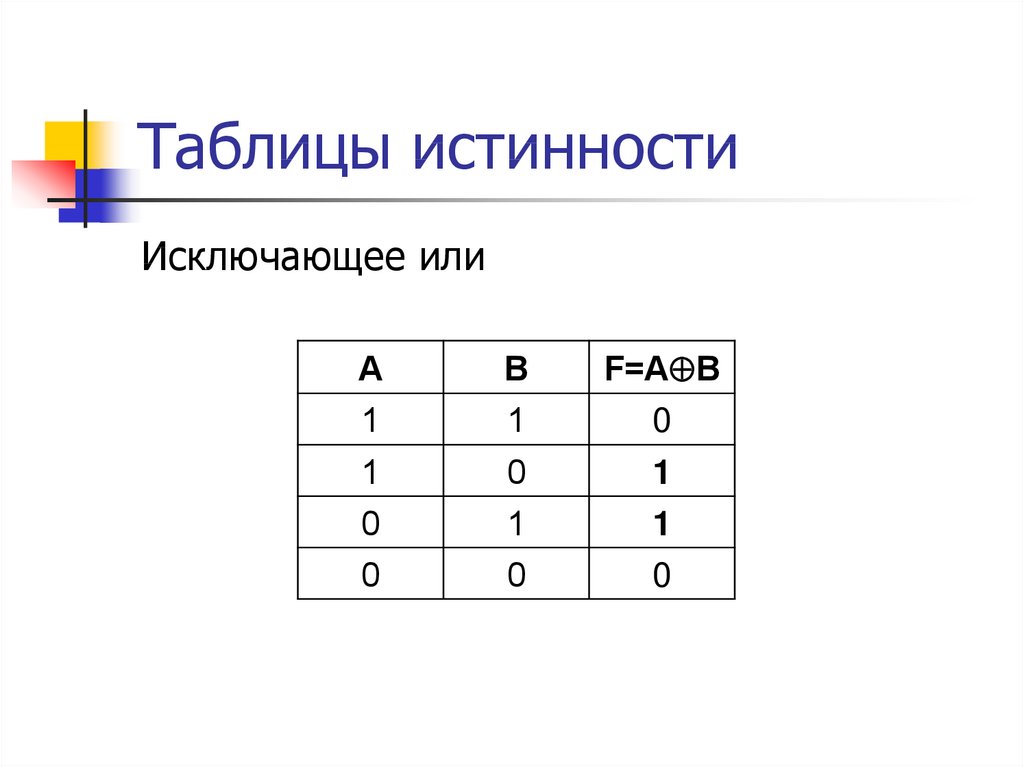
Синтаксис
XOR(логический1, [логический2],…)
Синтаксис функции XOR имеет следующие аргументы.
Логический1, логический2,… Требуется логический 1, последующие логические значения необязательны. От 1 до 254 условий, которые вы хотите проверить, которые могут быть либо ИСТИНА, либо ЛОЖЬ, и могут быть логическими значениями, массивами или ссылками.
Замечания
Аргументы должны давать логические значения, такие как ИСТИНА или ЛОЖЬ, или в массивах или ссылках, содержащих логические значения.
Если указанный диапазон не содержит логических значений, XOR возвращает #VALUE! значение ошибки.
Вы можете использовать формулу массива XOR, чтобы увидеть, встречается ли значение в массиве.
Примечание. Если у вас установлена текущая версия Microsoft 365, вы можете просто ввести формулу в верхнюю левую ячейку выходного диапазона, а затем нажать ENTER , чтобы подтвердить формулу как формулу динамического массива. В противном случае формулу необходимо ввести как устаревшую формулу массива, сначала выбрав выходной диапазон, введя формулу в верхнюю левую ячейку выходного диапазона, а затем нажав 9.
0039 CTRL+SHIFT+ENTER для подтверждения. Excel вставляет фигурные скобки в начале и в конце формулы. Дополнительные сведения о формулах массива см. в разделе Рекомендации и примеры формул массива.Результатом операции XOR является ИСТИНА, если количество входов ИСТИНА нечетное, и ЛОЖЬ, если количество входов ИСТИНА четное.
org/ListItem">Если аргумент массива или ссылки содержит текст или пустые ячейки, эти значения игнорируются.
0039 CTRL+SHIFT+ENTER для подтверждения. Excel вставляет фигурные скобки в начале и в конце формулы. Дополнительные сведения о формулах массива см. в разделе Рекомендации и примеры формул массива.Пример
Скопируйте данные примера из следующей таблицы и вставьте их в ячейку A1 нового рабочего листа Excel. Чтобы формулы отображали результаты, выберите их, нажмите F2, а затем нажмите клавишу ВВОД.
Формула | Описание | Результат |
|---|---|---|
=Исключающее ИЛИ(3>0,2<9) | Поскольку оба теста оцениваются как ИСТИНА, возвращается ЛОЖЬ. Похожие записи |
