Как найти общее напряжение в цепи. Последовательное и параллельное соединение проводников: ключевые особенности и расчет параметров

Как рассчитать общее сопротивление при последовательном и параллельном соединении проводников. Чем отличается распределение тока и напряжения в последовательной и параллельной цепи. Какие формулы используются для расчета параметров электрической цепи при разных типах соединения.

Основные принципы последовательного соединения проводников

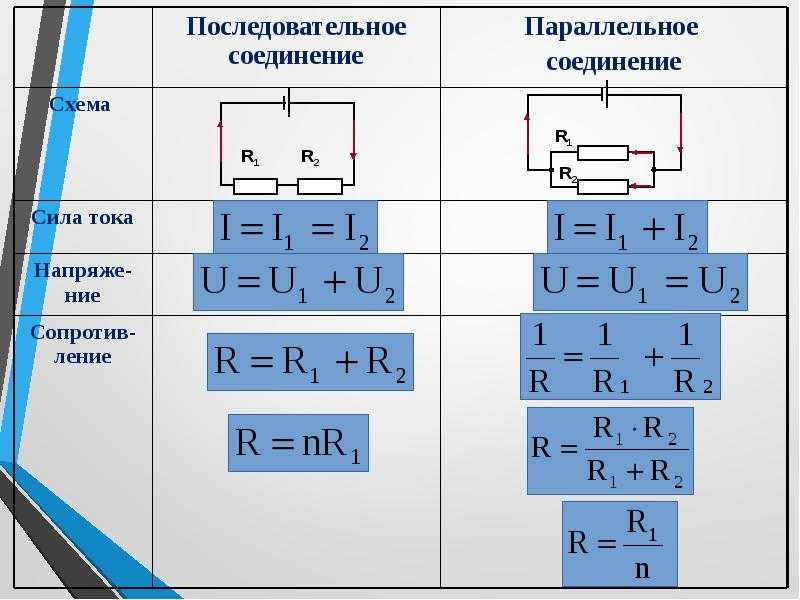
При последовательном соединении проводники подключаются один за другим, образуя единую неразветвленную цепь. Такой тип соединения обладает рядом важных особенностей:

• Сила тока одинакова во всех элементах цепи
• Общее напряжение равно сумме напряжений на отдельных участках
• Общее сопротивление цепи равно сумме сопротивлений всех проводников

Рассмотрим подробнее, как рассчитываются основные параметры последовательной цепи.

Расчет общего сопротивления

При последовательном соединении n проводников общее сопротивление цепи определяется по формуле:

R = R1 + R2 + … + Rn

То есть сопротивления просто складываются. Это объясняется тем, что при последовательном соединении общая длина проводника увеличивается.

Распределение напряжения

Общее напряжение в последовательной цепи распределяется между отдельными проводниками согласно формуле:

U = U1 + U2 + … + Un

При этом падение напряжения на каждом проводнике пропорционально его сопротивлению:

U1 : U2 : … : Un = R1 : R2 : … : Rn

Особенности параллельного соединения проводников

При параллельном соединении все проводники подключаются к одним и тем же точкам цепи. Такая схема имеет свои характерные свойства:

• Напряжение одинаково на всех параллельных участках
• Общий ток равен сумме токов в отдельных ветвях
• Обратная величина общего сопротивления равна сумме обратных величин сопротивлений ветвей

Расчет общего сопротивления параллельной цепи

Для параллельного соединения n проводников общее сопротивление рассчитывается по формуле:

1/R = 1/R1 + 1/R2 + … + 1/Rn

Отсюда следует, что общее сопротивление параллельной цепи всегда меньше сопротивления любого из параллельно соединенных проводников.

Распределение тока в параллельной цепи

Общий ток в неразветвленной части цепи равен сумме токов в параллельных ветвях:

I = I1 + I2 + … + In

При этом сила тока в каждой ветви обратно пропорциональна ее сопротивлению:

I1 : I2 : … : In = 1/R1 : 1/R2 : … : 1/Rn

Сравнение последовательного и параллельного соединения

Рассмотрим основные различия между двумя типами соединения проводников:

Параметр	Последовательное соединение	Параллельное соединение
Сила тока	Одинакова на всех участках	Различна в разных ветвях
Напряжение	Различно на разных участках	Одинаково на всех ветвях
Общее сопротивление	Больше сопротивления любого участка	Меньше сопротивления любой ветви

Применение последовательного и параллельного соединения

Оба типа соединения широко используются в электротехнике и электронике:

Последовательное соединение

• Делители напряжения
• Предохранители и выключатели в цепях
• Соединение элементов питания для увеличения напряжения

Параллельное соединение

• Подключение бытовых электроприборов к сети
• Шунты в измерительных приборах
• Соединение аккумуляторов для увеличения емкости

Смешанное соединение проводников

На практике часто встречаются цепи со смешанным соединением, сочетающим последовательные и параллельные участки. Для расчета таких цепей применяют следующий алгоритм:

1. Разбивают схему на группы последовательно и параллельно соединенных элементов
2. Рассчитывают эквивалентное сопротивление для каждой группы
3. Заменяют группы их эквивалентными сопротивлениями
4. Повторяют процесс, пока вся схема не сведется к одному эквивалентному сопротивлению

Особенности расчета реальных электрических цепей

При анализе реальных цепей следует учитывать ряд факторов, усложняющих расчеты:

• Внутреннее сопротивление источников питания
• Сопротивление соединительных проводов
• Нелинейность характеристик некоторых элементов
• Паразитные емкости и индуктивности

Для точных расчетов сложных цепей применяют специальные методы, такие как метод контурных токов или метод узловых потенциалов.

Практические рекомендации по работе с электрическими цепями

При проектировании и анализе электрических схем полезно помнить следующие правила:

• Всегда проверяйте правильность соединений перед включением схемы
• Используйте предохранители для защиты от коротких замыканий
• Учитывайте допустимую мощность рассеяния на элементах
• При параллельном соединении следите за равномерностью распределения тока
• Для увеличения точности измерений применяйте четырехпроводную схему подключения

Понимание принципов последовательного и параллельного соединения проводников — ключ к успешной работе с электрическими цепями. Эти знания позволяют грамотно проектировать схемы, анализировать их работу и находить неисправности.

Закон Ома для участка цепи. Последовательное и параллельное соединение проводников. 10 класс. Физика. — Объяснение нового материала.

Комментарии преподавателя

Закон Ома для участка цепи

Сила тока на участке цепи прямо пропорциональна напряжению на этом участке и обратно пропорциональна сопротивлению участка.

Закон Ома оказался справедливым не только для металлов, но и для растворов электролитов. Сформулированный закон имеет место для так называемого однородного участка цепи – участка, не содержащего источников тока.

Математическая запись закона Ома проста, как и его формулировка, но экспериментально подтвердить эту зависимость очень трудно. Сила тока, протекающая по участку цепи, мала. Поэтому используют достаточно чувствительные приборы. Г. Ом изготовил чувствительный прибор для измерения силы тока, а в качестве источника тока использовал термопару. Действие амперметра и вольтметра основано на применение закона Ома для участка цепи. Угол поворота стрелки прибора пропорционален силе тока.

Из математической записи закона Ома:

 

можно выразить напряжение :

и сопротивление проводника:

.

Таким образом, закон Ома связывает три параметра, характеризующих постоянный электрический ток, проходящий по проводнику, и позволяет находить любой из них, если известны два других.

Закон Ома имеет границы применимости и выполняется только в том случае, когда при прохождении тока температура заметно не меняется. На вольт–амперной характеристике лампы накаливания видно, что график сильно искривляется при напряжении выше 10В, значит, закон Ома выше этого напряжения применять нельзя.

Также нельзя говорить, что сопротивление проводника зависит от напряжения и силы тока в цепи. Сопротивление участка цепи зависит от свойств проводника: длины, площади поперечного сечения и материала, из которого состоит проводник.

где l-длина проводника, s-его площадь поперечного сечения.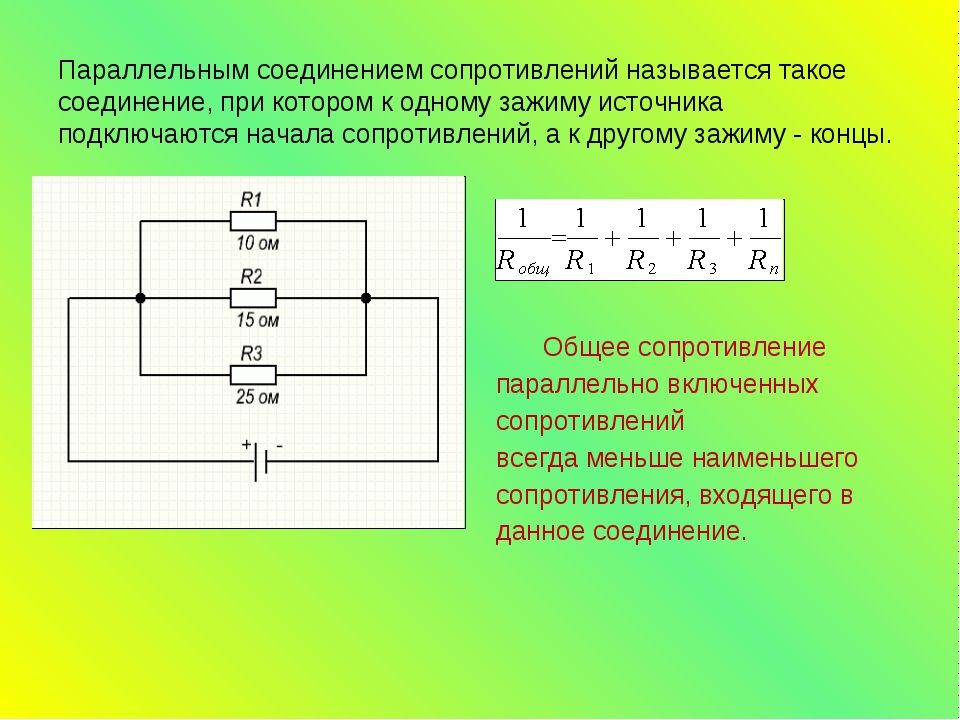

ρ –удельное сопротивление проводника – это физическая величина, характеризующая зависимость сопротивления проводника от материала, из которого он изготовлен.

Удельное сопротивление показывает, каким сопротивлением обладает сделанный из этого вещества проводник длиной 1м и площадью поперечного сечения 1м2 .

Из формулы видно, что единицей измерения в системе СИ является Ом·м. Но так как площадь поперечного сечения проводника достаточно мала, используют единицы измерения

при вычислении площадь поперечного сечения проводника следует выражать в мм2.

В заключении хочется заметить, что Ом начал свои опыты, когда был учителем физики в гимназии. В своих экспериментах Ом брал куски проволоки одинакового диаметра, но разного материала и изменял их длину таким образом, чтобы в цепи сила тока имела одинаковое значение. Находящаяся рядом магнитная стрелка отклонялась при прохождении тока в цепи. Установив связь между напряжением и силой тока, Г. Ом вывел один из основных законов постоянного тока.

Последовательное соединение проводников

Электрические цепи, с которыми приходится иметь дело на практике, обычно состоят не из одного приёмника электрического тока, а из нескольких различных, которые могут быть соединены между собой по-разному. Зная сопротивление каждого и способ их соединения, можно рассчитать общее сопротивление цепи.

На рисунке а изображена цепь последовательного соединения двух электрических ламп, а на рисунке б — схема такого соединения. Если выключать одну лампу, то цепь разомкнётся и другая лампа погаснет.

Рис. Последовательное включение лампочек и источников питания

Мы уже знаем, что при последовательном соединении сила тока в любых частях цепи одна и та же, т. е.

I = I1 = I2

А чему равно сопротивление последовательно соединённых проводников?

Соединяя проводники последовательно, мы как бы увеличиваем длину проводника.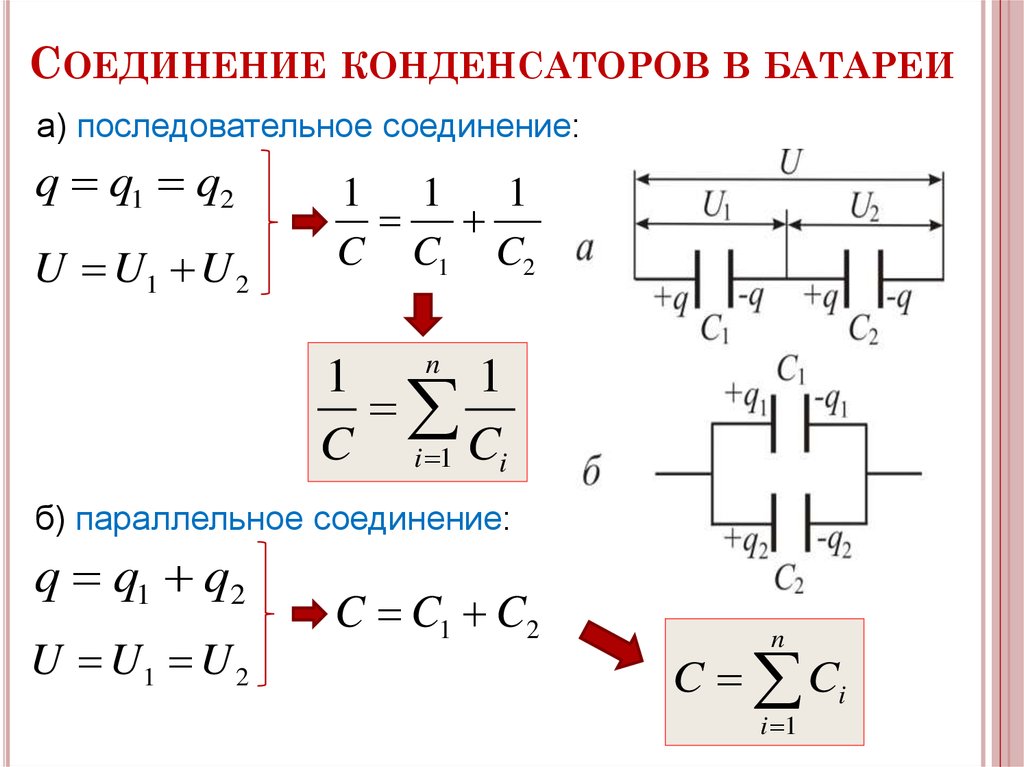 Поэтому сопротивление цепи становится больше сопротивления одного проводника.

Последовательное соединение проводников

Общее сопротивление цепи при последовательном соединении равно сумме сопротивлений отдельных проводников (или отдельных участков цепи):

R = R1 + R2

Напряжение на концах отдельных участков цепи рассчитывается на основе закона Ома:

U1 = IR1, U2 = IR2.

Из приведённых равенств видно, что напряжение будет большим на проводнике с наибольшим сопротивлением, так как сила тока везде одинакова.

Полное напряжение в цепи при последовательном соединении, или напряжение на полюсах источника тока, равно сумме напряжений на отдельных участках цепи:

U = U1 + U2.

Это равенство вытекает из закона сохранения энергии. Электрическое напряжение на участке цепи измеряется работой электрического тока, совершающейся при прохождении по участку цепи электрического заряда в 1 Кл. Эта работа совершается за счёт энергии электрического поля, и энергия, израсходованная на всём участке цепи, равна сумме энергий, которые расходуются на отдельных проводниках, составляющих участок этой цепи.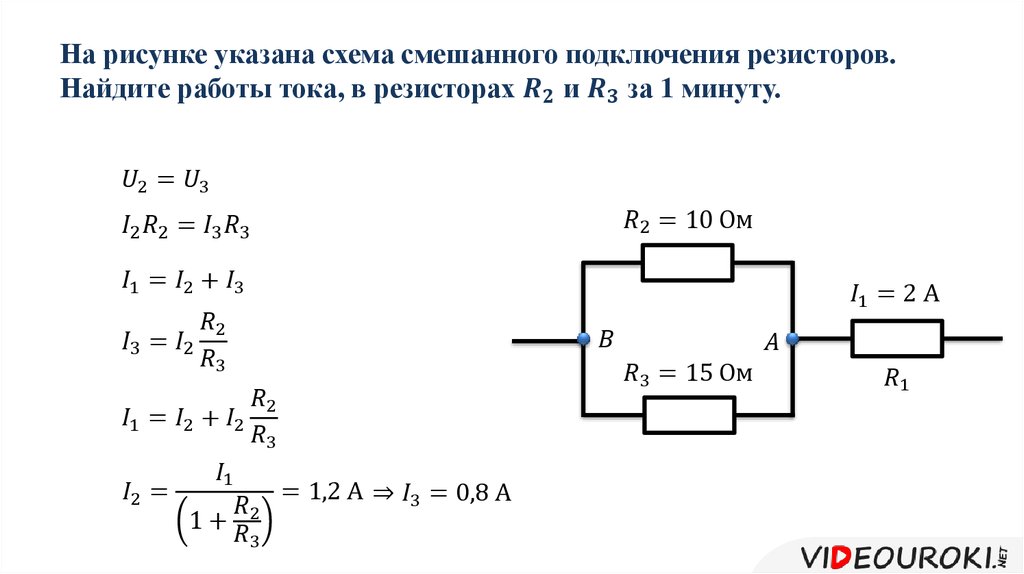

Все приведённые закономерности справедливы для любого числа последовательно соединённых проводников.

Пример 1. Два проводника сопротивлением R1 = 2 Ом, R2 = 3 Ом соединены последовательно. Сила тока в цепи I = 1 А. Определить сопротивление цепи, напряжение на каждом проводнике и полное напряжение всего участка цепи.

Запишем условие задачи и решим её.

ПАРАЛЛЕЛЬНОЕ СОЕДИНЕНИЕ

 

Расчет параметров электрической цепи
при параллельном соединении сопротивлений:

1. сила тока в неразветвленном участке цепи равна сумме сил токов
во всех параллельно соединенных участках

2. напряжение на всех параллельно соединенных участках цепи одинаково

3. при параллельном соединении сопротивлений складываются величины, обратные сопротивлению :

( R — сопротивление проводника,
1/R — электрическая проводимость проводника)

Если в цепь включены параллельно только два сопротивления, то:

( при параллельном соединении общее сопротивление цепи меньше меньшего из включенных сопротивлений )

4. работа электрического тока в цепи, состоящей из параллельно соединенных участков,
равна сумме работ на отдельных участках:

A=A1+A2

5. мощность электрического тока в цепи, состоящей из параллельно соединенных участков,
равна сумме мощностей на отдельных участках:

P=P1+P2

Для двух сопротивлений:

т.е. чем больше сопротивление, тем меньше в нём сила тока.

Домашняя работа.

Задание 1. Ответить на вопросы.

1. Какое соединение проводников называют последовательным? Изобразите его на схеме.
2. Какая электрическая величина одинакова для всех проводников, соединённых последовательно?
3. Как найти общее сопротивление цепи, зная сопротивление отдельных проводников, при последовательном соединении?
4. Как найти напряжение участка цепи, состоящего из последовательно соединённых проводников, зная напряжение на каждом?
5. Какое соединение проводников называют параллельным? Изобразите его на схеме.
6. Какая из электрических величин одинакова для всех проводников, соединённых параллельно?
7. Как выражается сила тока в цепи до её разветвления через силы токов в отдельных ветвях разветвления?
8. Как изменяется общее сопротивление разветвления после увеличения числа проводников в разветвлении?
9. Какое соединение проводников применяется в жилых помещениях? Какие напряжения используются для бытовых нужд?

Задание 2.Решите задачи.

1. Две лампочки соединены последовательно. Сила тока на первой лампочке 2А. Найдите общее напряжение и напряжение на каждой из ламп, если сопротивление на первой лампе 3Ом, а на второй 4Ом.

2. Две лампочки соединены параллельно. Напряжение на второй лампочке10В. Найдите силу тока в цепи и на каждой из ламп, если сопротивление на первой лампе 1Ом, а на второй 2Ом.

К занятию прикреплен файл  «Это интересно». Вы можете скачать файл в любое удобное для вас время.

Использованные источники:

• http://www.tepka.ru/
• http://class-fizika.narod.ru
• http://www.youtube.com/watch?v=cVKE9NItreo
• http://znaika.ru/catalog/10-klass/physics/
• http://www.youtube.com/watch?v=NB7hOVYe7h0
• https://www.youtube.com/watch?v=cVKE9NItreo
• https://www.youtube.com/watch?v=0hFWeR8ybxs
• http://www.youtube.com/watch?v=EDI8DzWSSWY
• http://www.youtube.com/watch?v=bH_-qGnjJqc
   

 

 

 

Постоянно ли напряжение в последовательном соединении: 3 важных пояснения

Напряжение на каждом резисторе в последовательной цепи различается в зависимости от значения сопротивления. Таким образом, последовательное напряжение не является постоянным. Только резисторы одинакового номинала могут дать такое же падение напряжения.

Мы используем слово «константа», чтобы указать фиксированное значение количества, которое остается неизменным. Напряжение никогда не может быть постоянным параметром в любой электрической цепи. У каждого резистора в последовательной комбинации разное падение напряжения. Следовательно, напряжение в последовательных цепях не является ни одинаковым, ни постоянным. 

Что такое последовательная схема? Объясните ток и эквивалентное сопротивление в последовательных цепях.

Когда мы соединяем несколько резисторов или параметров импеданса в линию один за другим, это называется последовательной схемой. Последовательная комбинация имеет одинаковый ток повсюду в цепи.

Эквивалентное сопротивление в последовательной схеме — это сумма всех индивидуальных сопротивлений. Падения напряжения на всех резисторах в сумме составляют общее напряжение. Падение напряжения на каждом компоненте в цепи разное. Эти падения напряжения рассчитываются путем умножения общего тока на номинал резистора.

Rузнать больше о… функциях цепи .series

Как рассчитать напряжение в последовательной цепи? Объясните числовым примером.

Вышеупомянутая схема представляет собой простую последовательную схему с тремя резисторами по 5 Ом, 10 Ом и 20 Ом. Наша цель — найти через них падения напряжения. Сначала мы выясним эквивалентное сопротивление.

Эквивалентное сопротивление R = R₁+R₂+R₃= 5 + 20 + 10 = 35 Ом

Итак, общий ток = общее напряжение / эквивалентное сопротивление = 10/35 = 0.29 ампер.

Напряжение через резистор 5 Ом = 5 * 0.29 = 1.45 Вольт

Напряжение через резистор 10 Ом = 10 * 0.29 = 2.9 Вольт

Напряжение через резистор 20 Ом = 20 * 0.29 = 5.8 Вольт

Постоянно ли напряжение в серии — FAQs

Как напряжение влияет на ток в последовательных цепях?

Каждый резистор в последовательной цепи получает одинаковый ток при последовательном включении. Рассчитываем падение напряжения на них по известным номиналам резисторов. 

Последовательная цепь представляет собой соединение нескольких элементов полного сопротивления. Таким образом, если цепь в любой момент разомкнется, произойдет сбой всей цепи, и ток не будет протекать. Очень распространенный пример — последовательное соединение лампочек разной яркости. Если мы продолжим добавлять лампы, яркость в конечном итоге снизится.

Рассчитайте полное напряжение V в последовательной цепи, показанной ниже.

Схема, изображенная выше, представляет собой четыре последовательно соединенных резистора. В цепи присутствует аккумулятор с неизвестным напряжением В. Ток составляет 0.25 А. Мы должны выяснить ценность V.

Падение напряжения через резистор 6 Ом = 6 * 0.25 = 1.5 Вольт

Падение напряжения через резистор 8 Ом = 8 * 0.25 = 2 Вольт

Падение напряжения через резистор 10 Ом = 10 * 0.25 = 2.5 Вольт

Падение напряжения через резистор 12 Ом = 12 * 0.25 = 3 Вольт

Следовательно, общее напряжение АКБ = В = 1.5 + 2 + 2.5 + 3 = 9 Вольт.

Каковы применения последовательного напряжения?

Последовательные и параллельные цепи считаются строительными блоками схемотехники. Они обычно используются для многих приложений с ограничением тока, таких как деление напряжения, смещение транзистора и т. Д.

Напряжение в последовательной цепи может быть различным. Некоторые распространенные применения последовательного напряжения:

1. Цепи делителя напряжения
2. Батарейки для пульта ТВ
3. Пожарная тревога
4. Аналоговые фильтры
5. Резонансные схемы
6. Сетевые фильтры
7. Гирлянды светодиодных ламп
8. Внутренние компоненты автомобильной техники

Как найти отдельные напряжения в последовательной цепи?

Отдельные напряжения резисторов в последовательной цепи получают из общего тока, умноженного на номинал резистора. 

Допустим, есть два резистора R₁ и R₂ соединены последовательно с батареей V. Следовательно, эквивалентное сопротивление R_eq R₁+R₂. Итак, напряжение на любом резисторе = значение резистора x общий ток.

Напряжение на R₁ V =₁ = VR₁ / Р₁+R₂ Вольт

Напряжение на R₂ V =₂ = VR₂ / Р₁+R₂ Вольт

Последовательно ли напряжение одинаково?

Напряжение в последовательной цепи не является ни одинаковым, ни постоянным. Падение напряжения на каждом резисторе во всех случаях разное, кроме одного, когда все резисторы в последовательной сети имеют одинаковое значение.

Когда резисторы в цепи равны, то только падения напряжения будут одинаковыми для всех резисторов. Предположим, что в схеме, содержащей три резистора, все резисторы имеют сопротивление R Ом. Эквивалентное значение сопротивления = R + R + R = 3R. Напряжение на любом резисторе = V * R / 3R = V / 3 вольта.

Последовательно объясните напряжение на практическом примере.

Один очень интересный пример последовательной схемы в практической жизни — это классическое освещение рождественской елки.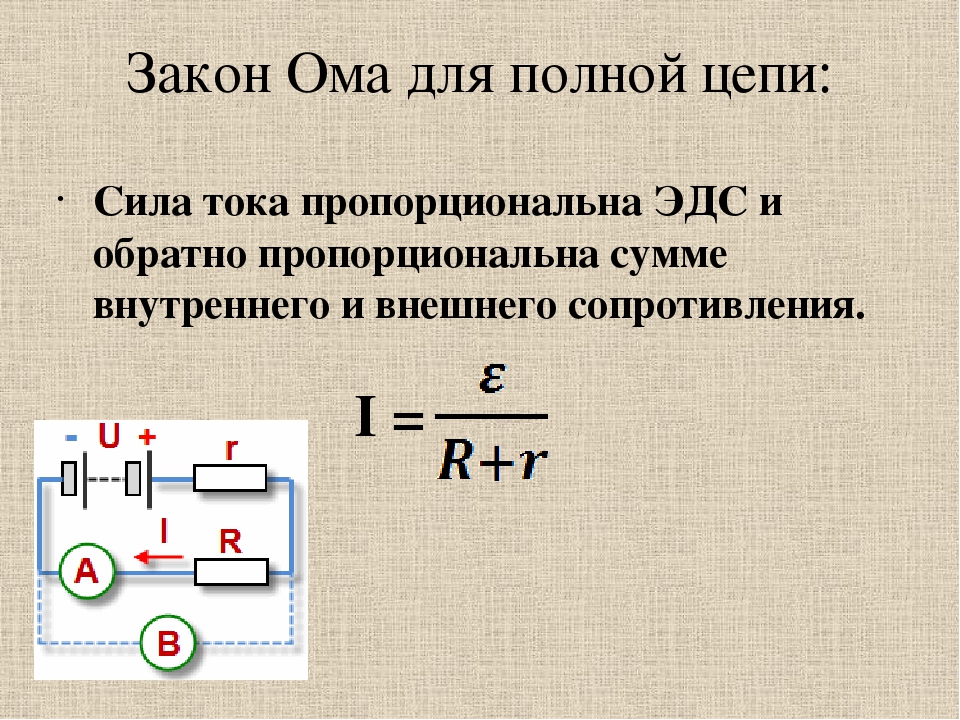 В этом освещении многие крошечные лампочки соединены последовательно.

Мы используем эти лампочки годами. Мы видим, что определенная часть света не работает. Это связано с последовательным подключением. Светильники представляют собой комбинацию множества таких последовательно соединенных струн. Таким образом, даже если одна лампочка в сети выходит из строя, вся ее часть перестает работать.

«Это сезон» by ДонкерДинк под лицензией CC BY-NC-ND 2.0

thevenin — Как найти полное напряжение в двухконтурной цепи

Задать вопрос

спросил 2 года, 7 месяцев назад

Изменено 2 года, 7 месяцев назад

Просмотрено 259 раз

\$\начало группы\$

Я просматривал учебник по теории постоянного тока от NJATC, чтобы изучить основы электроники и получить больше удовольствия от игры на гитаре.

Но я также хочу иметь возможность ремонтировать или, может быть, даже создавать педали эффектов и усилители. Поэтому я пытаюсь понять все, что встречается на моем пути.

Эта книга посвящена теореме о суперпозиции, которая хороша для нахождения токов. Но затем он переходит к нахождению полного напряжения для двухконтурной цепи, и в этот момент он либо пропускает важный шаг, либо вводит неверное значение, после чего оно просто бесполезно, потому что я не могу воспроизвести их результаты, не зная, как это получить. значение (которое они не объясняют).

Мои вопросы:

1. «Как мне получить значение в I1?»

2. «Какое правильное значение в I1, чтобы я мог проверить свою работу?»

Вот схема:

Вот страница (рис. 22-6), где они вводят, казалось бы, произвольное значение для источника тока I1, равное 0,4 А, где обычно используется батарея 24 В. Это значение неоднократно используется для получения общего напряжения цепи на следующих страницах.

(На самом деле они используют вставленное значение 0,4 (стр. 263) для получения значений, которые в сумме составляют 0,4 (стр. 265). (Прекрасный пример кругового рассуждения и плохого редактирования.)

Значения, полученные I для комбинированной схемы, следующие: положительное число обозначает поток со стороны 48-вольтовой батареи (справа), а отрицательное число обозначает поток со стороны 24-вольтовой батареи (слева). R3 имеет оба потока, движущихся вместе в одном направлении.

Суммарные значения: E, I, R

• R1: 28,17 В, 0,031 А, 900 Ом
• R2: -4,17 В, -0,002 А, 2400 Ом
• R3: 19,83 В, 0,033 А, 600 Ом

Вот остальные страницы, чтобы показать, чему пытается научить книга: \$\конечная группа\$

1

\$\начало группы\$

Я также получил такие же значения напряжения и тока для R3, так что ваши расчеты верны для первого изображения.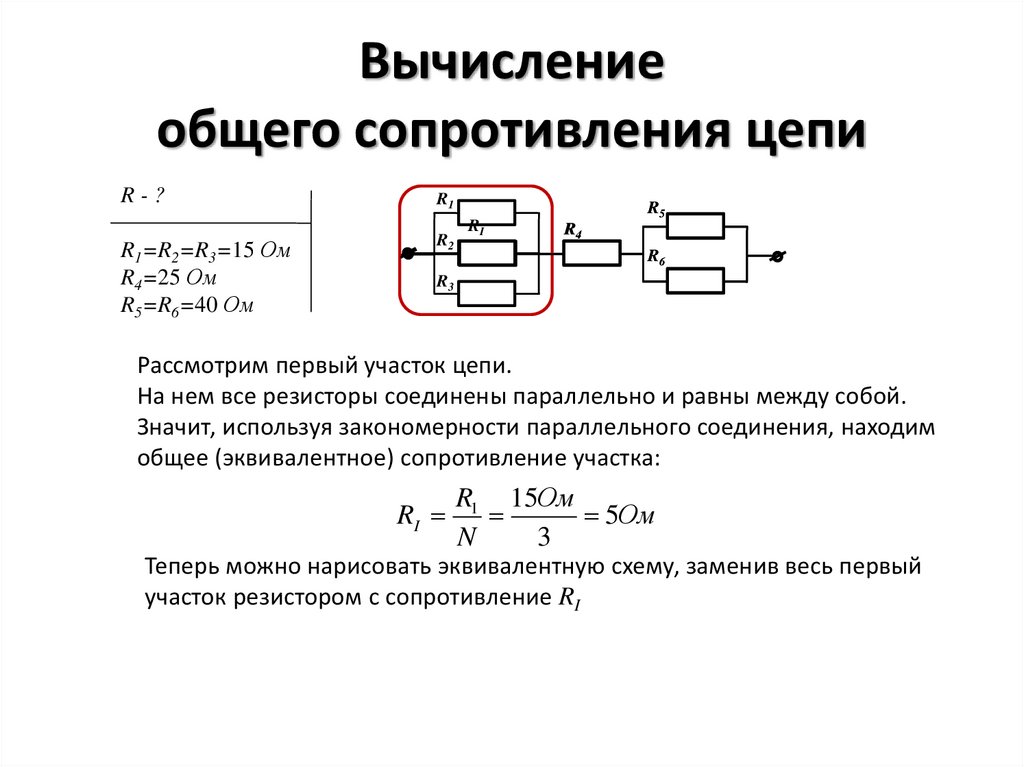

Вторая картинка с текущим источником — это совсем другой пример, не имеющий ничего общего с первым примером. Поскольку в этом примере есть текущий источник, для его решения используется другой подход.

\$\конечная группа\$

5

\$\начало группы\$

1. «Как получить значение в I1?»

Не уверен, в чем смысл замены источника напряжения \$V_2\$ на источник тока \$I_1\$, но чтобы обе цепи имели одинаковые токи и напряжения в узлах, вам потребуется \$I_1 \$ будет текущим, входящим в \$V_2\$

2. «Каково правильное значение I1, чтобы я мог проверить свою работу?»

С помощью симулятора я получил, что \$I_1=-1,739 мА\$, поэтому источник питания \$V_2\$ выдает ток, обратите внимание, что я имею в виду не ток через резистор \$R_1\$, а значение, которое будет работать, если вы сделаете упомянутую вами замену (что, я думаю, является дополнительной работой и не поможет решить систему).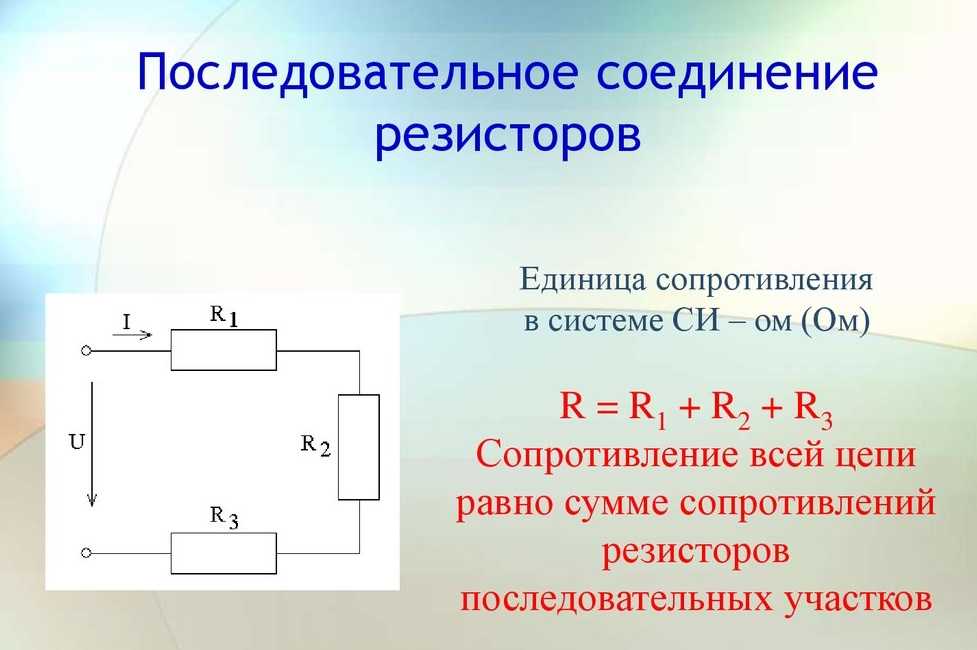

Чтобы решить эту проблему с помощью суперпозиции, проигнорируйте эту замену предложения и сделайте это

Чтобы использовать суперпозицию в этом случае, вы должны решить две одиночные цепи питания и просто сложить их токи.

^{имитация этой схемы – схема создана с помощью CircuitLab}

^{имитация этой схемы \$\конечная группа\$}

3

\$\начало группы\$

Я полагаю, вы читали об эквивалентных схемах Thevenin, использующих делитель напряжения от источника напряжения и преобразующих его в эквивалентное напряжение и ток короткого замыкания с помощью параллельного сопротивления.

Кроме того, я предполагаю, что вы можете вычислить простой коэффициент делителя напряжения \$V_3=R_3/(R_3+R_2)*V_2\$ и параллельный \$R_{eq} = 1/(1/R_1+1/R_2)\ $

Для левой стороны \$I_1\$:

Шаг 1. Вычислите эквивалент нагрузки правой стороны и напряжения для суперпозиции позже.

Шаг 2. Затем соедините и вычислите \$I_1 = — I_2\$ для показанных направлений амперметра.

Интерактивное моделирование с пробником напряжения и амперметром.

В этой книге есть недостатки. У меня в профиле есть несколько руководств.

\$\конечная группа\$

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

.

Резисторы последовательно и параллельно

4 февраля 2013 г. · 19:24

В предыдущем посте мы видели, что для многих материалов электрический ток I через устройство пропорционален приложенному к нему напряжению В , и обратно пропорционально его сопротивлению, т.е. I = V/R (закон Ома). При наличии в цепи более одного устройства (или резистора ) ток через каждое зависит еще и от того, как соединены резисторы, т. е. соединены ли они в серии или параллельно .

В схеме серии (ниже) резисторы соединены один за другим ( так же, как в сериале, смотрят одну серию за другой) . Через каждое устройство проходит один и тот же ток, так как нет альтернативного пути или ответвления, т. е. I = I1 = I2 . Из В = IR мы видим, что напряжение на каждом устройстве будет разным; на самом деле, самое большое падение напряжения будет на самом большом сопротивлении (так же, как самое большое падение энергии происходит на самом большом водопаде в реке). Общее напряжение в последовательной цепи представляет собой сумму отдельных напряжений, т.е. V = V1+V2. Как и следовало ожидать, общее сопротивление (или нагрузка ) цепи представляет собой просто сумму отдельных сопротивлений, R = R1 + R2.

Последовательная цепь: ток в каждой лампе одинаков, а падение напряжения на каждой из них может быть разным (V = V1+V2 +V3)

С другой стороны, резисторы в цепи могут быть подключен в параллельно (см. ниже). В этом случае каждое устройство подключается непосредственно к клеммам источника напряжения и, следовательно, испытывает одинаковое напряжение (V = V1 = V2). С I = V/R , через каждое устройство будет проходить разный ток (если только они не будут иметь одинаковое сопротивление) . Общий ток в параллельной цепи представляет собой сумму отдельных токов, т. е. I = I1+I2. Странным аспектом параллельных цепей является то, что общее сопротивление цепи снижается по мере добавления дополнительных устройств (1/R = 1/r1 + 1/r2). Физическая причина в том, что вы увеличиваете количество альтернативных путей, по которым может идти ток.

Параллельное соединение: напряжение на каждой лампе одинаковое, но токи могут быть разными (I = I1+I2)

Запутались? Простое правило состоит в том, что в цепи серии ток везде одинаков, потому что нет ветвей. С другой стороны, устройства, подключенные в параллельно , видят одинаковое напряжение. В повседневных цепях электрические устройства, такие как чайники, телевизоры и компьютеры, подключаются параллельно друг другу, потому что безопаснее, если каждое устройство видит один и тот же источник напряжения; он также оказывается более эффективным с точки зрения энергопотребления (используется переменное напряжение, об этом позже).

В лаборатории схемы часто содержат одни устройства, соединенные последовательно, а другие — параллельно. Чтобы рассчитать ток через данное устройство, перерисуйте цепь, заменив любые параллельные резисторы эквивалентным сопротивлением последовательно, и проанализируйте полученную последовательную цепь.