Как обозначается реактивное емкостное сопротивление. Реактивное емкостное сопротивление: формулы, особенности и применение в электротехнике — Производство и поставка электростанций, Бензиновые и дизельные генераторы от 1 до 100 кВт. Мини ТЭЦ на базе двигателя Стирлинга.

Что такое реактивное емкостное сопротивление. Как рассчитывается емкостное сопротивление. Какие особенности имеет реактивное емкостное сопротивление в электрических цепях. Где применяется емкостное сопротивление в электротехнике.

Содержание

Что такое реактивное емкостное сопротивление

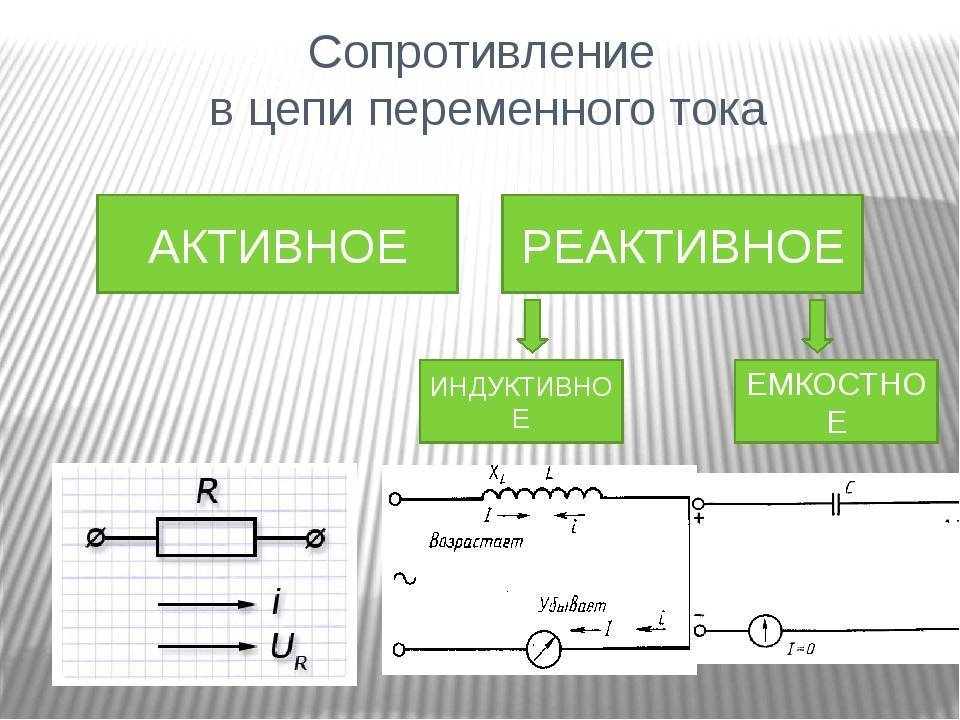
Реактивное емкостное сопротивление — это сопротивление, которое оказывает конденсатор переменному току. В отличие от активного сопротивления, емкостное сопротивление не приводит к потере энергии, а лишь создает сдвиг фаз между током и напряжением.

Основные особенности емкостного сопротивления:

Измеряется в омах (Ом)
Обозначается Xc
Зависит от частоты переменного тока и емкости конденсатора
Уменьшается с ростом частоты и емкости
Создает опережение тока относительно напряжения на 90°

Формула для расчета емкостного сопротивления

Реактивное емкостное сопротивление рассчитывается по формуле:

Xc = 1 / (2πfC)

где:

Xc — емкостное сопротивление, Ом
π — математическая константа пи (≈3,14)

f — частота переменного тока, Гц
C — емкость конденсатора, Ф

Как видно из формулы, емкостное сопротивление обратно пропорционально частоте и емкости. То есть при увеличении частоты или емкости сопротивление конденсатора уменьшается.

Особенности емкостного сопротивления в электрических цепях

Реактивное емкостное сопротивление имеет ряд важных особенностей в электрических цепях переменного тока:

Создает сдвиг фаз между током и напряжением на 90°. Ток опережает напряжение.
Не потребляет активную мощность, а лишь обменивается реактивной энергией с источником.
При последовательном соединении с индуктивностью может вызывать резонанс напряжений.
При параллельном соединении с индуктивностью может вызывать резонанс токов.
Уменьшает полное сопротивление цепи при увеличении частоты.

Где применяется емкостное сопротивление в электротехнике

Реактивное емкостное сопротивление широко используется в различных областях электротехники и электроники:

В фильтрах для разделения сигналов разных частот
В колебательных контурах для создания резонанса
В цепях компенсации реактивной мощности
В импульсных источниках питания
В схемах запуска электродвигателей
В устройствах связи для согласования сопротивлений

Сравнение емкостного и индуктивного сопротивлений

Емкостное и индуктивное сопротивления имеют ряд схожих и отличительных черт:

Параметр	Емкостное сопротивление	Индуктивное сопротивление
Обозначение	Xc	XL
Зависимость от частоты	Обратно пропорциональная	Прямо пропорциональная
Сдвиг фаз	Ток опережает напряжение на 90°	Ток отстает от напряжения на 90°
Формула	Xc = 1 / (2πfC)	XL = 2πfL

Расчет полного сопротивления цепи с емкостью

При наличии в цепи емкостного и активного сопротивлений полное сопротивление рассчитывается по формуле:

Z = √(R² + Xc²)

где:

Z — полное сопротивление цепи, Ом
R — активное сопротивление, Ом
Xc — емкостное сопротивление, Ом

Угол сдвига фаз между током и напряжением определяется как:

φ = arctg(Xc / R)

Влияние емкостного сопротивления на мощность в цепи

Наличие емкостного сопротивления в цепи переменного тока приводит к появлению реактивной мощности. При этом:

Активная мощность P = I²R не зависит от емкостного сопротивления
Реактивная мощность Q = I²Xc определяется емкостным сопротивлением
Полная мощность S = √(P² + Q²) зависит от емкостного сопротивления

Коэффициент мощности цепи с емкостью определяется как:

cos φ = P / S = R / Z

Способы изменения емкостного сопротивления

Емкостное сопротивление в цепи можно изменять следующими способами:

Изменением емкости конденсатора
Изменением частоты переменного тока
Последовательным или параллельным соединением конденсаторов
Применением конденсаторов переменной емкости

При необходимости уменьшить емкостное сопротивление можно увеличить емкость или частоту. Для увеличения сопротивления нужно уменьшить эти параметры.

Практическое применение емкостного сопротивления

Рассмотрим несколько примеров практического использования емкостного сопротивления в электротехнике:

1. Фильтры высоких и низких частот

Емкостное сопротивление используется для создания простейших RC-фильтров. Фильтр низких частот образуется при последовательном включении резистора и конденсатора. Фильтр высоких частот — при параллельном соединении.

2. Компенсация реактивной мощности

Конденсаторные батареи применяются для компенсации индуктивной составляющей нагрузки и повышения коэффициента мощности в электрических сетях.

3. Запуск однофазных двигателей

Пусковой конденсатор создает сдвиг фаз между обмотками, необходимый для запуска однофазного асинхронного двигателя.

Заключение

Реактивное емкостное сопротивление играет важную роль в цепях переменного тока. Понимание его свойств и особенностей позволяет эффективно использовать конденсаторы в различных электротехнических устройствах и системах. При проектировании электрических цепей необходимо учитывать влияние емкостного сопротивления на токи, напряжения и мощности.

Reactance

http://en.wikipedia.org Wikipedia, свободная энциклопедия

Реактивное сопротивление — это мнимая часть импеданса (импедансом называется полное (комплексное) сопротивление цепи переменного тока), которая показывает меру противодействия синусоидальному переменному току. Реактивное сопротивление возникает в присутствии индуктивности и ёмкости в цепи, и обозначается символом X; единица СИ — Ом.

(В этом разделе знак тильда (~) будет использован для обозначения векторов или комплексных величин, а буквы без дополнительных знаков обозначают модули векторов соответствующих величин, а также скалярные величины.)

Для определения импеданса требуется как реактивное сопротивление X, так и резистивное (активное) сопротивление R. Несмотря на то, что в некоторых обстоятельствах реактивное сопротивление может доминировать, требуется хотя-бы приблизительное знание активного сопротивления для определения импеданса.

Как модуль, так и фаза импеданса зависят от обоих сопротивлений – и от активного и от реактивного:

Модуль импеданса — это отношение амплитуд напряжения и тока, тогда как фаза - это разница между фазами напряжения и тока.

Если X>0 говорят, что реактивное сопротивление является индуктивным
Если X=0 говорят, что импеданс чисто резистивный (активный)
Если X<0 говорят, что реактивное сопротивление является ёмкостным

Физическое значение

Определение соотношений между током и напряжением требует знания, как активного, так и реактивного сопротивлений. Реактивное сопротивление само по себе даёт только ограниченную физическую информацию об электрическом устройстве или электрической цепи:

Величина реактивного сопротивления показывает меру противодействия цепи только переменному току, и зависит от частоты переменного тока.
Положительное реактивное сопротивление подразумевает, что фаза напряжения опережает фазу тока, в то время как отрицательное реактивное сопротивление подразумевает, что фаза напряжения отстаёт от фазы тока.
Нулевое реактивное сопротивление подразумевает, что ток и напряжение совпадают по фазе и наоборот, если реактивное сопротивление не равно нулю, тогда существует разность фаз между напряжением и током.

Есть случаи, когда в цепи есть реактивные элементы, но результируюшее реактивное сопротивление цепи равно нулю, для примера: резонанс в RLC-цепи случается, когда реактивные импедансы Z_C и Z_L взаимоуничтожаются. Это значит, что импеданс имеет фазу, равную нулю (специфический пример нулевого реактивного сопротивления для случая 3. выше).

Ёмкостное реактивное сопротивление

Ёмкостное реактивное сопротивление Xc обратнопропорционально частоте сигнала и ёмкости C.

Ёмкостной элемент называется конденсатором. Конденсатор состоит из двух проводников, отделённых друг от друга изолятором, тоесть диэлектриком.

При низких частотах или в цепи постоянного тока конденсатор разрывает (размыкает) цепь, так как ток не может течь через диэлектрик. Если к изначально разряженному конденсатору прикладывают постоянное напряжение – в начальный момент на обкладках конденсатора индуцируются заряды, электрическое поле котрых противоположно полю внешнего источника напряжения. Поэтому ток в этот начальный момент в цепи максимален. Затем потенциалы источника питания и конденсатора точно уравниваются, и ток в цепи прекращается.

Конденсатор, включённый в цепь переменного тока, будет успевать накапливать только ограниченный заряд перед тем, как разность потенциалов изменит знак на противоположный. Тоесть ток не будет успевать упасть до нуля, как в случае цепи постоянного тока. Чем выше частота, тем меньший заряд будет аккумулироваться в конденсаторе, и тем меньше конденсатор будет противодействовать внешнему току (сопротивление уменьшается).

Индуктивное реактивное сопротивление

Индуктивное реактивное сопротивление X_Lпрямопропорционально частоте сигнала и индуктивности L.

Индуктивный элемент представляет собой катушку индуктивности, тоесть длинный проводник, например проволока, намотанный в виде катушки. Изнутри катушка может быть пустая или содержать магнетик. Закон электромагнитной индукции Фарадея устанавливает, что ЭДС электромагнитной индукции в замкнутом контуре численно равна и противоположна по знаку скорости изменения магнитного потока через поверхность, ограниченную этим контуром. Эта ЭДС часто называется противо-ЭДС.

Если индуктивность представляет собой катушку содержащую N витков.

В общем случае ЭДС является следствием изменения магнитного потока в контуре. Но это изменение магнитного потока может иметь разные причины: движение магнита, движение другой катушки с током, изменение собственного тока контура. Последний случай носит название – явление самоиндукции, которое и лежит в основе индуктивного реактивного сопротивления.

В свою очередь противо-ЭДС вызывает в контуре индукционный ток, который направлен противоположно току источника питания. Точная форма правила Ленца: индукционный ток в контуре имеет такое направление, что созданный им магнитный поток, через контур, препятствует изменению магнитного потока, вызвавшего этот ток.

Если к изначально неподключенной катушке индуктивности подключают источник постоянного тока – в начальный момент в катушке начинает течь ток от внешнего источника. Он вызывает изменение магнитного потока. Изменение магнитного потока порождает противо-ЭДС. Противо-ЭДС вызывает противоток. Этот противоток в начальный момент равен току источника.

При низких частотах или в цепи постоянного тока катушка индуктивности проводит электрический ток беспрепятственно, и может рассматриваться как короткозамкнутый участок цепи, тоесть проводник с низким сопротивлением. Если к изначально неподключенной катушке индуктивности подключают источник постоянного тока – в начальный момент в катушке возникает противоток, равный току внешнего источника. Поэтому для идуктивного элемента в этот начальный момент результирующий ток равен нулю, а напряжение максимально. Затем токи источника и индуктивного элемента уравниваются и напряжение на индуктивном элементе становится равным нулю.

Ток в катушке индуктивности, включённой в цепь переменного тока, будет успевать возрасти только до определённого значения перед тем, как ток источника питания изменит знак на противоположный. Тоесть напряжение (на выводах катушки индуктивности) не будет успевать упасть до нуля, как в случае цепи постоянного тока. Чем выше частота, тем выше напряжение на выводах катушки индуктивности (сопротивление увеличивается).

Фазные соотношения

Фаза напряжения приложенного к чисто реактивному устройству (устройству с нулевым активным сопротивлением) отстаёт от фазы тока на Pi/2 для ёмкости и опережает фазу тока на Pi/2 для индуктивности. Необходимо отметить, что для определения соотношений между током и напряжением необходимо знать как активное, так и реактивное сопротивление.

Причина различных знаков ёмкостного и индуктивного сопротивлений заключается в определении фазной переменной импеданса.

Для реактивного элемента цепи синусоидальное напряжение на элементе сдвинуто по фазе на 90 градусов (Pi/2 радиан) относительно тока. Элемент поочерёдно то поглащает энергию из сети, то затем возвращает энергию обратно в сеть, поэтому чисто реактивное сопротивление не поглащает энергию.

Реактивное емкостное сопротивление — Большая Энциклопедия Нефти и Газа, статья, страница 1

Реактивное емкостное сопротивление

Cтраница 1

Реактивное емкостное сопротивление и положительное активное сопротивление элементов этой цепочки могут компенсировать связь через пространственный заряд в узком диапазоне частот. Для этого контур сигнальной сетки настраивают на частоту гетеродина и параметры компенсирующей цепи R и С подбирают так, чтобы на сигнальной сетке не появлялось заметное напряжение гетеродина. [2]

Как и активное, реактивное емкостное сопротивление оценивают в омах. Значение его зависит от емкости и частоты: чем больше емкость и частота, тем меньше сопротивление. Катушка индуктивности, включенная в цепь переменного тока, тоже обладает реактивным сопротивлением XL: ( uL2n L. Катушка с конденсатором образует колебательный контур. [3]

Сопротивление Хс называется реактивным емкостным сопротивлением. Оно отличается от активного сопротивления R, в котором вся мощность, отдаваемая источником тока, превращается в тепло и расходуется на нагревание сопротивления. В случае же емкостного реактивного сопротивления Хс вся работа, совершаемая источником тока при заряде конденсатора, преобразуется в энергию электрического поля, а при разряде вся энергия без остатка возвращается в источник. Потому сопротивление и называют реактивным. [4]

В диэлектрическом усилителе преобразование энергии источника питания в энергию усиливаемого сигнала производится нелинейным реактивным емкостным сопротивлением, роль которого играет конденсатор с сегнетодиэлектриком. [5]

При необходимости длину сварочной цепи можно нарастить, однако стабильность процесса в этом случае ухудшается ввиду увеличения активного, реактивного и емкостного сопротивления сварочной цепи и снижения возможностей источника питания по отработке возмущений, связанных с изменением вылета электрода и длины дуги. Сварочные кабели запрещено при работе укладывать в бухты или наматывать на вьюшки вследствие значительного увеличения индуктивного сопротивления сварочной цепи. [6]

Это происходит в том случае, когда в одних ветвях преобладает реактивное индуктивное сопротивление, а в других — реактивное емкостное сопротивление. [7]

При последовательной схеме замещения измеряемое сопротивление РК ( активная составляющая Ra) равно сумме первого и второго членов правой части выражения (3.24), третий член определяет реактивное емкостное сопротивление. [9]

В электрических цепях переменного тока при параллельном соединении реактивных сопротивлений может возникать резонанс токов. Это происходит в том случае, когда в одних ветвях преобладает реактивное индуктивное сопротивление, а в других — реактивное емкостное сопротивление. [10]

Практически о величине емкости конденсатора ( действующей емкости) мы судим по величине тока, потребляемого конденсатором. Наличие индуктивностиЬв конденсаторе дает увеличение его действующей емкости с ростом частоты ( рис. 30), так как ток будет возрастать за счет компенсации реактивного емкостного сопротивления индуктивным сопротивлением. [12]

В простейшем случае резонанс напряжений может быть получен в электрической цепи переменного тока при последовательном включении катушки индуктивности и конденсаторов. При этом, изменяя емкость конденсаторов при постоянных параметрах катушки, получают резонанс напряжений при неизменных значениях напряжения и индуктивности, частоты и активного сопротивления цепи. При изменении емкости С конденсаторов происходит изменение реактивного емкостного сопротивления. При этом полное сопротивление цепи также изменяется, следовательно, изменяются ток, коэффициент мощности, напряжения на катушке индуктивности, конденсаторах и активном сопротивлении катушки и активная, реактивная и полная мощности электрической цепи. [13]

Страницы: 1

Электрическое реактивное сопротивление — Electrical reactance

«Реактивность (физика)» перенаправляется сюда. Чтобы узнать о других значениях, см. Реактивность .

В электрических и электронных системах реактивное сопротивление — это сопротивление элемента схемы протеканию тока из-за индуктивности или емкости этого элемента . Большее реактивное сопротивление приводит к меньшим токам при одинаковом приложенном напряжении . Реактивное сопротивление аналогично электрическому сопротивлению в этом отношении, но отличается тем, что реактивное сопротивление не приводит к рассеиванию электрической энергии в виде тепла. Вместо этого энергия накапливается в реактивном сопротивлении и позже возвращается в цепь, в то время как сопротивление постоянно теряет энергию.

Реактивное используется для вычисления амплитуды и фазы изменения синусоидального переменного тока ( AC ) , проходящей через элемент цепи. Обозначается символом . Идеальный резистор имеет нулевое реактивное сопротивление, тогда как идеальные катушки индуктивности и конденсаторы имеют нулевое сопротивление, то есть реагируют на ток только реактивным сопротивлением. С увеличением частоты увеличивается индуктивное реактивное сопротивление и уменьшается емкостное реактивное сопротивление. Икс {\ displaystyle \ scriptstyle {X}}

Сравнение с сопротивлением

Реактивное сопротивление похоже на сопротивление в том смысле, что большее реактивное сопротивление приводит к меньшим токам при одинаковом приложенном напряжении. Кроме того, цепь, полностью состоящую из элементов, которые имеют только реактивное сопротивление (но не сопротивление), может рассматриваться так же, как цепь, полностью состоящая из элементов без реактивного сопротивления (чистое сопротивление). Эти же методы можно использовать для комбинирования элементов с реактивным сопротивлением и элементов с сопротивлением, но обычно требуются комплексные числа . Это рассматривается ниже в разделе об импедансе .

Однако есть несколько важных различий между реактивным сопротивлением и сопротивлением. Во-первых, реактивное сопротивление изменяет фазу, так что ток через элемент смещается на четверть цикла относительно напряжения, приложенного к элементу. Во-вторых, мощность не рассеивается в чисто реактивном элементе, а накапливается. В-третьих, реактивные сопротивления могут быть отрицательными, так что они могут «компенсировать» друг друга. Наконец, элементы главной цепи, которые имеют реактивное сопротивление (конденсаторы и катушки индуктивности), имеют частотно-зависимое реактивное сопротивление, в отличие от резисторов, которые обычно имеют одинаковое сопротивление для всех частот.

Термин реактивное сопротивление впервые был предложен французским инженером М. Госпитальером в L’Industrie Electrique 10 мая 1893 года. Он был официально принят Американским институтом инженеров-электриков в мае 1894 года.

Емкостное реактивное сопротивление

Конденсатор состоит из двух проводников, разделенных изолятором , также известным как диэлектрик .

Емкостное реактивное сопротивление — это противодействие изменению напряжения на элементе. Емкостное реактивное является обратно пропорциональной к сигналу частоты (или угловой частоты & omega ; ) и емкости . Икс C {\ displaystyle \ scriptstyle {X_ {C}}} ж {\ displaystyle \ scriptstyle {f}} C {\ displaystyle \ scriptstyle {C}}

В литературе есть два варианта определения реактивного сопротивления конденсатора. Один из них — использовать единообразное понятие реактивного сопротивления как мнимой части импеданса, и в этом случае реактивное сопротивление конденсатора является отрицательным числом,

Икс C знак равно — 1 ω C знак равно — 1 2 π ж C {\ displaystyle X_ {C} = — {\ frac {1} {\ omega C}} = — {\ frac {1} {2 \ pi fC}}} .

Другой вариант — определить емкостное реактивное сопротивление как положительное число,

Икс C знак равно 1 ω C знак равно 1 2 π ж C {\ displaystyle X_ {C} = {\ frac {1} {\ omega C}} = {\ frac {1} {2 \ pi fC}}}

Однако в этом случае нужно помнить , чтобы добавить отрицательный знак для импеданса конденсатора, то есть . Z c знак равно — j Икс c {\ displaystyle Z_ {c} = — jX_ {c}}

На низких частотах конденсатор представляет собой разомкнутую цепь, поэтому в диэлектрике не течет ток .

Постоянное напряжение , подаваемое через конденсатор вызывает положительный заряд накапливаться на одной стороне и отрицательный заряде накапливаться на другой стороне; электрическое поле за счет накопленного заряда является источником оппозиции к току. Когда потенциал, связанный с зарядом, точно уравновешивает приложенное напряжение, ток стремится к нулю.

Управляемый источником переменного тока (идеальный источник переменного тока), конденсатор будет накапливать только ограниченное количество заряда, прежде чем разность потенциалов изменит полярность и заряд вернется к источнику. Чем выше частота, тем меньше заряда будет накапливаться и меньше противодействие току.

Индуктивное реактивное сопротивление

Индуктивное реактивное сопротивление — это свойство индуктора, а индуктивное реактивное сопротивление существует на основе того факта, что электрический ток создает вокруг него магнитное поле. В контексте цепи переменного тока (хотя эта концепция применяется в любое время, когда изменяется ток), это магнитное поле постоянно изменяется в результате колебания тока взад и вперед. Именно это изменение магнитного поля заставляет другой электрический ток течь по тому же проводу (противо-ЭДС) в таком направлении, чтобы противодействовать потоку тока, изначально ответственного за создание магнитного поля (известному как закон Ленца). Следовательно, индуктивное реактивное сопротивление является противодействием изменению тока через элемент.

Для идеальной катушки индуктивности в цепи переменного тока ингибирующее действие на изменение тока приводит к задержке или фазовому сдвигу переменного тока по отношению к переменному напряжению. В частности, идеальная катушка индуктивности (без сопротивления) заставит ток отставать от напряжения на четверть цикла или 90 °.

В электроэнергетических системах индуктивное реактивное сопротивление (и емкостное реактивное сопротивление, однако индуктивное реактивное сопротивление является более распространенным) может ограничивать мощность линии передачи переменного тока, поскольку мощность не передается полностью, когда напряжение и ток не совпадают по фазе (подробно описано выше). . То есть ток будет течь для системы, не совпадающей по фазе, однако реальная мощность в определенные моменты времени не будет передаваться, потому что будут точки, в течение которых мгновенный ток будет положительным, а мгновенное напряжение — отрицательным, или наоборот, подразумевая отрицательную мощность. передача. Следовательно, реальная работа не выполняется, когда передача мощности «отрицательная». Тем не менее, ток все еще течет, даже когда система находится в противофазе, что вызывает нагрев линий передачи из-за протекания тока. Следовательно, линии электропередачи могут нагреваться только настолько (иначе они будут физически слишком сильно провисать из-за тепла, расширяющего металлические линии электропередачи), поэтому операторы линий электропередачи имеют «потолок» на количество тока, который может протекать через данной линии, и чрезмерное индуктивное реактивное сопротивление может ограничить мощность линии. Поставщики электроэнергии используют конденсаторы для сдвига фазы и минимизации потерь в зависимости от характера использования.

Индуктивное сопротивление является пропорционально синусоидальным сигналом частоты и индуктивность , которая зависит от физической формы индуктора. Икс L {\ displaystyle \ scriptstyle {X_ {L}}} ж {\ displaystyle \ scriptstyle {f}} L {\ displaystyle \ scriptstyle {L}}

Икс L знак равно ω L знак равно 2 π ж L {\ Displaystyle X_ {L} = \ омега L = 2 \ pi fL}

Средний ток, протекающий через индуктивность, последовательно соединенную с источником синусоидального переменного напряжения со среднеквадратичной амплитудой и частотой , равен: L {\ displaystyle \ scriptstyle {L}} А {\ displaystyle \ scriptstyle {A}} ж {\ displaystyle \ scriptstyle {f}}

я L знак равно А ω L знак равно А 2 π ж L .

{2} \ over 8 \ omega L} = {A \ pi \ over 16fL}}

создается впечатление, что индуктивное сопротивление для прямоугольной волны было примерно на 19% меньше, чем реактивное сопротивление для синусоидальной волны переменного тока: Икс L знак равно 16 π ж L {\ displaystyle X_ {L} = {16 \ over \ pi} fL}

Любой проводник конечных размеров имеет индуктивность; индуктивность увеличивается за счет нескольких витков в электромагнитной катушке . Закон электромагнитной индукции Фарадея дает противоэдс (напряжение, противодействующее току) из-за скорости изменения плотности магнитного потока через токовую петлю. E {\ displaystyle \ scriptstyle {\ mathcal {E}}} B {\ displaystyle \ scriptstyle {B}}

E знак равно — d Φ B d т {\ displaystyle {\ mathcal {E}} = — {{d \ Phi _ {B}} \ over dt}}

Для индуктора, состоящего из катушки с петлями, это дает. N {\ displaystyle \ scriptstyle N}

E знак равно — N d Φ B d т {\ displaystyle {\ mathcal {E}} = — N {d \ Phi _ {B} \ over dt}}

Противо-ЭДС является источником противодействия току. Постоянный постоянный ток имеет нулевую скорость изменения и рассматривает индуктор как короткое замыкание (обычно он изготовлен из материала с низким удельным сопротивлением ). Переменный ток имеет по скорости изменения усредненных по времени, которое пропорционально частоте, это приводит к увеличению индуктивного сопротивления с частотой.

Импеданс

И реактивное сопротивление, и сопротивление являются составляющими импеданса . Икс {\ displaystyle {X}} р {\ displaystyle {R}} Z {\ displaystyle {\ mathbf {Z}}}

Z знак равно р + j Икс {\ Displaystyle \ mathbf {Z} = R + \ mathbf {j} X}

куда:

Когда конденсатор и катушка индуктивности включены в цепь последовательно, их вклады в полное сопротивление цепи противоположны. Емкостное реактивное сопротивление и индуктивное реактивное сопротивление вносят вклад в общее реактивное сопротивление следующим образом. Икс C {\ displaystyle \ scriptstyle {X_ {C}}} Икс L {\ displaystyle \ scriptstyle {X_ {L}}} Икс {\ displaystyle \ scriptstyle {X}}

Икс знак равно Икс L + Икс C знак равно ω L — 1 ω C {\ displaystyle {X = X_ {L} + X_ {C} = \ omega L — {\ frac {1} {\ omega C}}}}

куда:

Икс L {\ displaystyle \ scriptstyle {X_ {L}}} — индуктивное реактивное сопротивление, измеренное в Ом;
Икс C {\ displaystyle \ scriptstyle {X_ {C}}} — емкостное реактивное сопротивление, измеренное в Ом;
ω {\ displaystyle \ omega} — угловая частота, умноженная на частоту в Гц. 2 π {\ displaystyle 2 \ pi}

Следовательно:

если , полное реактивное сопротивление считается индуктивным; Икс > 0 {\ displaystyle \ scriptstyle X> 0}
если , то сопротивление чисто резистивное; Икс знак равно 0 {\ displaystyle \ scriptstyle X = 0}
если полное реактивное сопротивление называется емкостным. Икс < 0 {\ displaystyle \ scriptstyle X <0}

Однако обратите внимание, что если и предполагаются как положительные по определению, тогда промежуточная формула изменяется на разницу: Икс L {\ displaystyle \ scriptstyle {X_ {L}}} Икс C {\ displaystyle \ scriptstyle {X_ {C}}}

Икс знак равно Икс L — Икс C знак равно ω L — 1 ω C {\ displaystyle {X = X_ {L} -X_ {C} = \ omega L — {\ frac {1} {\ omega C}}}}

но конечная ценность такая же.

Фазовое соотношение

Фаза напряжения на чисто реактивном устройстве (то есть с нулевым паразитным сопротивлением ) отстает от тока на радианы для емкостного реактивного сопротивления и опережает ток на радианы для индуктивного реактивного сопротивления. { \ mathbf {j} {\ pi \ over 2}} = \ mathbf {j} \ omega L = \ mathbf {j} X_ {L} \ quad \ end {align}}}

Для реактивного компонента синусоидальное напряжение на компоненте находится в квадратуре ( разность фаз) с синусоидальным током, протекающим через компонент. Компонент попеременно поглощает энергию из цепи, а затем возвращает энергию в цепь, таким образом, чистое реактивное сопротивление не рассеивает мощность. π 2 {\ displaystyle {\ frac {\ pi} {2}}}

Смотрите также

внешняя ссылка

Активное и реактивное сопротивление

В электротехнике понятие сопротивления представляет собой величину, за счет которой определенная часть цепи может противодействовать электрическому току. Она образуется за счет изменения и перехода электроэнергии в другое энергетическое состояние. Данное явление присуще только переменному току, когда в сети образуется активное и реактивное сопротивление, выражающееся в необратимом изменении энергии или передаче этой энергии между отдельными компонентами электрической цепи. В случае необратимых изменений электроэнергии сопротивление будет считаться активным, а при наличии обменных процессов – реактивным.

Основные различия между активным и реактивным сопротивлением

Когда электрический ток проходит через элементы с активным сопротивлением, происходят необратимые потери выделяемой мощности. Типичным примером служит электрическая плита, где в процессе работы происходят необратимые превращения электричества в тепловую энергию. То же самое происходит с резистором, в котором тепло выделяется, но обратно в электроэнергию не превращается.

Помимо резисторов, свойствами активного сопротивления обладают приборы освещения, электродвигатели, трансформаторные обмотки, провода и кабели и т.д.

Характерной особенностью элементов с активным сопротивлением являются напряжение и ток, совпадающие по фазе. Рассчитать этот параметр можно по формуле: r = U/I. На показатели активного сопротивления оказывают влияние физические свойства проводника – сечение, длина, материал, температура. Эти качества позволяют различать реактивное и активное сопротивление и применять их на практике.

Реактивное сопротивление возникает в тех случаях, когда переменный ток проходит через так называемые реактивные элементы, обладающие индуктивностью и емкостью. Первое свойство характерно для катушки индуктивности без учета активного сопротивления ее обмотки. В данном случае причиной появления реактивного сопротивления считается ЭДС самоиндукции. В зависимости от частоты тока, при ее возрастании, наблюдается и одновременный рост сопротивления, что отражается в формуле xl = wL.

Реактивное сопротивление конденсатора зависит от емкости. Оно будет уменьшаться при увеличении частоты тока, поэтому данное свойство широко используется в электронике для выполнения регулировочных функций. В этом случае для расчетов используется формула xc = 1/wC.

В электронике существует не только активное и реактивное, но и полное сопротивление цепи, представляющее собой сумму квадратов обоих сопротивлений. Этот параметр обозначается символом Z и отображается в виде формулы:

В графике это выражение выглядит в виде треугольника сопротивлений, где реактивное и активное сопротивление соответствуют катетам, а полное сопротивление или импеданс – гипотенузе.

Индуктивное сопротивление

Реактивное сопротивление подразделяется на два основных вида – индуктивное и емкостное.

При рассмотрении первого варианта следует отметить возникновение в индуктивной обмотке магнитного поля под действием переменного тока. В результате, в ней образуется ЭДС самоиндукции, направленной против движения тока при его росте, и по ходу движения при его уменьшении. Таким образом, при всех изменениях тока и наличии взаимосвязей, ЭДС оказывает на него противоположное действие и приводит к созданию индуктивного сопротивления катушки.

Под влиянием ЭДС самоиндукции энергия магнитного поля обмотки возвращается в электрическую цепь. То есть, между источником питания и обмоткой происходит своеобразный обмен энергией.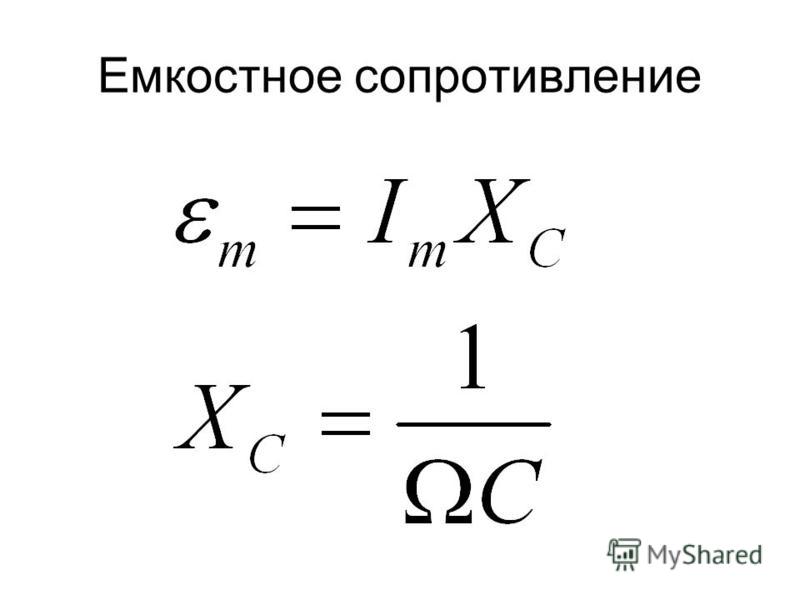 Это дает основание полагать, что катушка индуктивности обладает реактивным сопротивлением.

В качестве типичного примера можно рассмотреть действие реактивного сопротивления в трансформаторе. Данное устройство имеет общий магнитопровод, с расположенными на нем двумя обмотками или более, имеющими общую зависимость. На одну из них поступает электроэнергия из внешнего источника, а из другой выходит уже трансформированный ток.

Под действием первичного тока, проходящего по катушке, в магнитопроводе и вокруг него происходит наведение магнитного потока. В результате пересечения витков вторичной обмотки, в ней формируется вторичный ток. При невозможности создания идеальной конструкции трансформатора, магнитный поток будет частично уходить в окружающую среду, что приведет к возникновению потерь. От них зависит величина реактивного сопротивления рассеяния, которая совместно с активной составляющей образуют комплексное сопротивление, называемое электрическим импедансом трансформатора.

Емкостное сопротивление

В цепи, содержащей емкость и источник переменного тока происходят изменения заряда. Такой емкостью обладают конденсаторы, обладающие максимальной энергией при полном заряде. Напряжение емкости создает сопротивление, противодействующее течению переменного тока, которое считается реактивным. В результате взаимодействия, конденсатор и источник тока постоянно обмениваются энергией.

В конструкцию конденсатора входят токопроводящие пластины в количестве двух и более штук, разделенных слоями диэлектрика. Такое разделение не позволяет постоянному току проходить через конденсатор. Переменный ток может проходить через емкостное устройство, отклоняясь при этом от своей первоначальной величины.

Изменения переменного тока происходят под влиянием емкостного сопротивления. Чтобы лучше понять схему работы, найдем и рассмотрим принцип действия данного явления. Переменное напряжение, приложенное к конденсатору, изменяется в форме синусоиды. Под его воздействием на обкладках наблюдается всплеск, одновременно здесь накапливаются заряды электроэнергии с противоположными знаками. Их общее количество ограничено емкостью устройства и его габаритами. Чем выше емкость устройства, тем больше времени требуется на зарядку.

В момент изменения полупериода колебания, напряжение на обкладках конденсатора меняет свою полярность на противоположное значение, потенциалы также изменяются, а заряды пластин перезаряжаются. За счет этого удается создать течение первичного тока и находить способ противодействовать его прохождению, при уменьшении величины и сдвиге угла. Зарядка обкладок позволяет току, проходящему через конденсатор, опережать напряжение на 90^.

Компенсация реактивной мощности

С помощью электрических сетей осуществляется передача электроэнергии на значительные расстояния. В большинстве случаев она используется для питания электродвигателей, имеющих высокое индуктивное сопротивление и большое количество резистивных элементов. К потребителям поступает полная мощность, которая делится на активную и реактивную. В первом случае с помощью активной мощности совершается полезная работа, а во втором – происходит нагрев трансформаторных обмоток и электродвигателей.

Под действием реактивной составляющей, возникающей на индуктивных сопротивлениях, существенно понижается качество электроэнергии. Противостоять ее вредному воздействию помогает комплекс мероприятий по компенсации с использованием конденсаторных батарей. За счет емкостного сопротивления удается понизить косинус угла φ.

Компенсирующие устройства применяются на подстанциях, от которых электричество поступает к проблемным потребителям. Этот способ дает положительные результаты не только в промышленности, но и на бытовых объектах, снижая нагрузку на оборудование.

Глава 17. Резонансные цепи . Введение в электронику

ЦЕЛИ

После изучения этой главы студент должен быть в состоянии:

• Написать формулы для определения емкостного и индуктивного сопротивления.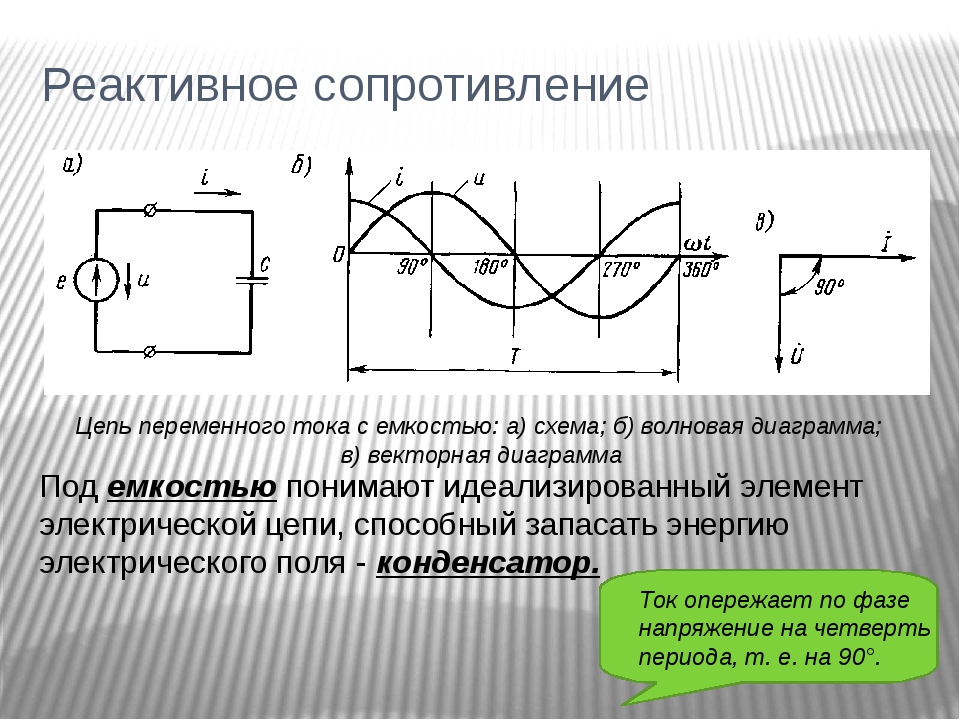

• Описать, как реагируют на переменный ток и напряжение конденсаторы и катушки индуктивности.

• Дать определение реактивного сопротивления последовательной цепи и уметь определить характер цепи (индуктивный или емкостный).

• Дать определение термина импеданс.

• Уметь вычислять импеданс, который содержит как резистивную, так и емкостную или индуктивную составляющие.

• Объяснить, как должен быть модифицирован закон Ома перед использованием его для цепей переменного тока.

• Уметь вычислять Х_с, X_L, X, Z и I_т в последовательных RLC цепях.

• Уметь вычислять I_c, I_L, I_x, I_R и I_z в параллельных RLC цепях.

В предыдущих главах сопротивление, емкость и индуктивность в цепях переменного тока рассматривались по отдельности.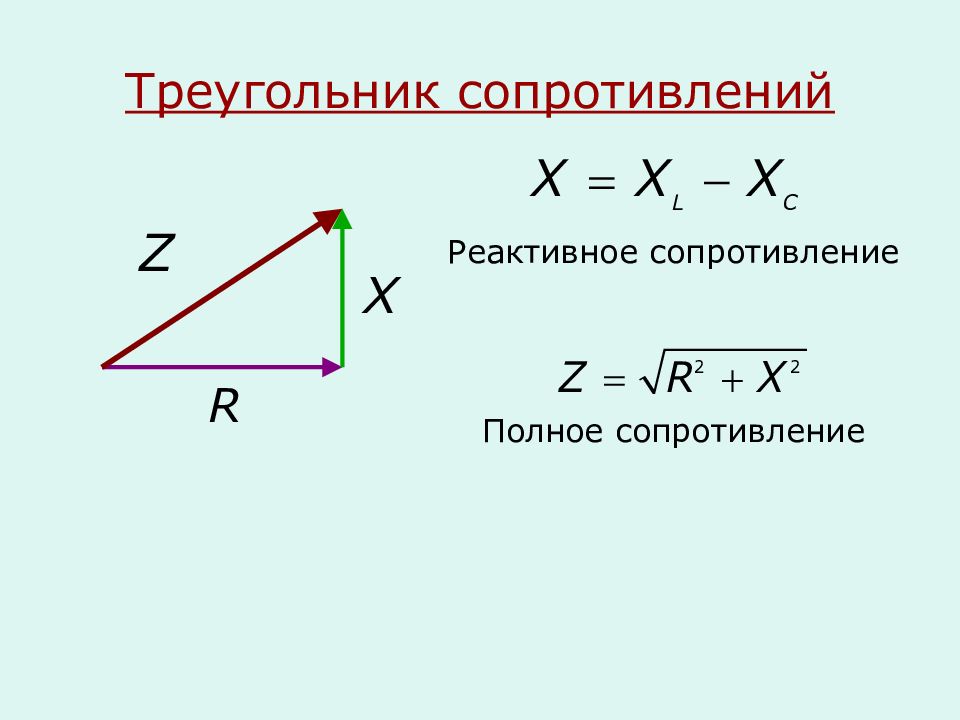 В этой главе исследуется комбинация сопротивления, емкости и индуктивности в цепи переменного тока. Рассматриваемые вопросы не являются новым материалом, но применяют все изложенные ранее принципы.

Когда реактивное сопротивление катушки индуктивности равно реактивному сопротивлению конденсатора в цепи, возникает резонанс. Резонансные цепи широко используются в электронике.

17-1. РЕАКТИВНОЕ СОПРОТИВЛЕНИЕ

Емкостное реактивное сопротивление — это противодействие, которое конденсатор оказывает переменному току. Оно измеряется в омах и обозначается символом Х_с. Емкостное реактивное сопротивление вычисляется по формуле:

Х_с = 1/2πfC

Заметим, что при использовании этой формулы емкость должна быть выражена в фарадах (а не в долях фарады).

Индуктивное реактивное сопротивление — это противодействие, которое катушка индуктивности оказывает переменному току. Оно измеряется в омах и обозначается символом X_L. Индуктивное реактивное сопротивление вычисляется по формуле:

X_L = 2πfL.

Заметим, что при использовании этой формулы индуктивность должна быть выражена в генри (а не в долях генри).

Емкостное реактивное сопротивление служит причиной того, что ток опережает по фазе напряжение. Индуктивное реактивное сопротивление служит причиной того, что ток отстает по фазе от напряжения. Емкостное и индуктивное реактивные сопротивления прямо противоположны по создаваемым эффектам и, следовательно, когда в цепи присутствуют и индуктивность и емкость, общий эффект определяется разностью их значений. Эта разность называется реактивным сопротивлением и обозначается символом X. Реактивное сопротивление может быть выражено следующими формулами:

X = Х_с — X_L или X = X_L — Х_с.

_{ПРИМЕР: Чему равно реактивное сопротивление цепи, содержащей конденсатор емкостью 1 мкФ, соединенный последовательно с индуктивностью 10 генри (рис. 17-1), работающей на частоте 60 герц?}

_{Рис. 17-1}

_Дано:

_{f = 60 Гц; L = 10 Гн; С = 1 мкФ}

_{Х =?}

_{Решение:}

_{Хс = 1/2πfC}

_{Хс =1/(6,28)(60)(0,000001)}

_{Хс =2654 Ом}

_{XL = 2πfL}

_{XL = (6,28)(60)(10)}

_{XL = 3768 Ом}

_{X = XL- XC = 3768–2654}

_{X = 1114 Ом (индуктивное).}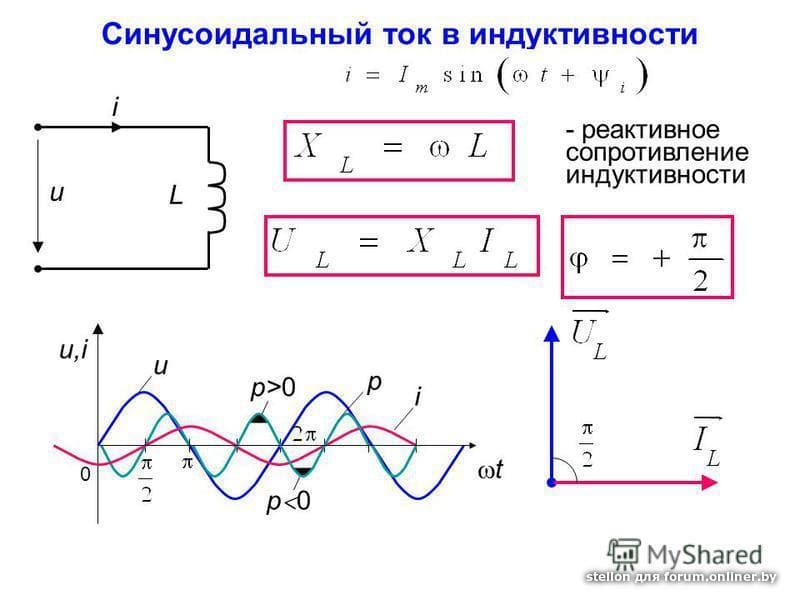

_{ПРИМЕР: Чему равно реактивное сопротивление цепи, содержащей конденсатор емкостью 1 мкФ, соединенный последовательно с индуктивностью 1 генри (рис. 17-2), работающей на частоте 60 герц?}

_{Рис. 17-2}

_Дано:

_{f = 60 Гц; L = 1 Гн; С = 1 мкФ}

_{Х =?}

_{Решение:}

_{Хс = 1/2πfC}

_{Хс = 1/(6,28)(60)(0,000001)}

_{Хс =2654 Ом}

_{XL = 2πfL}

_{XL = (6,28)(60)(1)}

_{XL = 376,8 Ом}

_{X = XC — XL = 2654 — 376,8}

_{X = 2277,2 Ом (емкостное).}

Эти примеры иллюстрируют важный момент. Когда емкостное и индуктивное реактивные сопротивления соединены последовательно, меньшее значение всегда вычитается из большего. Получающееся в результате реактивное сопротивление характеризуется большим значением.

17-1. Вопросы

1. Каково фазовое соотношение между током и напряжением на конденсаторе?

2. Каково фазовое соотношение между током и напряжением на катушке индуктивности?

3. По какой формуле определяется полное реактивное сопротивление последовательной цепи, когда известны значения Х_с и X_L?

4. Какова величина полного реактивного сопротивления (X) последовательной цепи, содержащей Х_с = 50 ом и X_L = 20 ом? Укажите, является X емкостным или индуктивным.

17-2. ИМПЕДАНС

Реактивное сопротивление, как емкостное, так и индуктивное, противодействует протеканию тока в цепях переменного тока. Активное сопротивление также препятствует протеканию тока в цепи. Комбинированное противодействие реактивного и активного сопротивлений называется импедансом и обозначается символом Z.

И активное, и реактивное сопротивления измеряются в омах. Следовательно, кажется логичным сложить эти сопротивления для того, чтобы получить импеданс. Однако этого делать нельзя, поскольку активное и реактивное сопротивления — величины векторные. В цепях переменного тока, содержащих только активное сопротивление, ток и напряжение находятся в фазе. И ток, и напряжение достигают своих максимальных значений одновременно.

Как упоминалось ранее, в цепях переменного тока, содержащих только реактивные сопротивления, ток будет либо опережать, либо отставать от напряжения на 90 градусов. Следовательно, напряжение в чисто реактивной цепи будет отличаться по фазе на 90 градусов от напряжения в чисто резистивной цепи.

Когда цепь содержит и активное, и реактивное сопротивление, импеданс будет больше любого их них. Кроме того, ток в такой цепи будет не в фазе с напряжением. Сдвиг по фазе будет в пределах от нуля до 90 градусов.

Для того чтобы найти импеданс, используется векторная диаграмма — прямоугольный треугольник сопротивлений. Это может быть сделано потому, что ток через резистор находится в фазе с напряжением на нем, а ток через реактивную нагрузку сдвинут по фазе на 90 градусов относительно напряжения на ней. Они находятся под прямым углом друг к другу.

ПРИМЕР: Чему равен импеданс последовательно соединенных резистора сопротивлением 150 ом и индуктивного реактивного сопротивления 100 ом?

В качестве первого шага нарисуем основание треугольника, представляющее резистор 150 ом. Далее нарисуем линию под углом 90 градусов к основанию, представляющую индуктивное сопротивление 100 ом. После этого соединим концы линий, образуя гипотенузу треугольника. Гипотенуза представляет импеданс цепи (рис. 17-3).

Рис. 17-3. Векторная диаграмма.

Теорема Пифагора утверждает:

с² = а² + Ь²,

где с — гипотенуза, а и b — катеты.

Графически это представлено на рис. 17-4.

Рис. 17-4. Векторная диаграмма, показывающая связь активного сопротивления, реактивного индуктивного сопротивления и импеданса в последовательной цепи.

Если импеданс, активное и реактивное сопротивления заменить соответствующими символами, то формула будет выглядеть следующим образом:

Z² = R² + X².

Вернемся к определению импеданса последовательной комбинации резистора 150 ом и индуктивного сопротивления 100 ом.

Дано:

R = 150 Ом; X_L = 100 Ом.

Решение:

Z² = R² + X²

Z² =(150)² + (100)² = 32500

Z = √(32500) = 180,28 Ом.

Если вместо индуктивного в цепи находится емкостное сопротивление, то линию, представляющую емкостное сопротивление, обычно рисуют направленной вниз. Это показывает, что оно действует в направлении противоположном индуктивному сопротивлению, которое рисуют направленным вверх.

В последовательной цепи с емкостным реактивным сопротивлением формула для вычисления импеданса будет выглядеть следующим образом:

Z² = R² + Х²_С.

_{ПРИМЕР: Чему равен импеданс цепи, содержащей резистор сопротивлением 220 ом, соединенный последовательно с конденсатором, имеющим емкостное реактивное сопротивление 270 ом?}

_Дано:

_{R = 220 Ом; Xc = 270 Ом.}

_{Решение:}

_{Z² = R² + X²c}

_{Z² = (220)² + (270)² = 121300}

_{Z = √(121300) = 348,28 Oм.}

_{Z = 348,28 Ом.}

_{Если последовательная цепь содержит индуктивное и емкостное реактивные сопротивления, а также активное сопротивление, необходимо найти полное реактивное сопротивление (X). Реактивное сопротивление может быть либо индуктивным, либо емкостным. Следовательно, может быть использована одна из следующих формул:}

_{Z² = R² + X²L;}

_{Z² = R² + Х²с.}

17-2. Вопросы

1. Как называется полное противодействие в цепи переменного тока?

2. Какая формула используется для вычисления величины полного противодействия в последовательной цепи?

3. Чему равно значение Z в последовательной цепи переменного тока, где Х_с = 3 Ом, X_L = 6 Ом, a R = 4 Ом?

17-3 ЗАКОН ОМА

Закон Ома не может быть применен в цепях переменного тока потому, что он не учитывает реактивное сопротивление. Модифицируя закон Ома путем учета импеданса, можно получить общий закон, который применим к цепям переменного тока.

I = E/R преобразуется в I = E/Z

Эта формула применима к переменному току, текущему в любой цепи.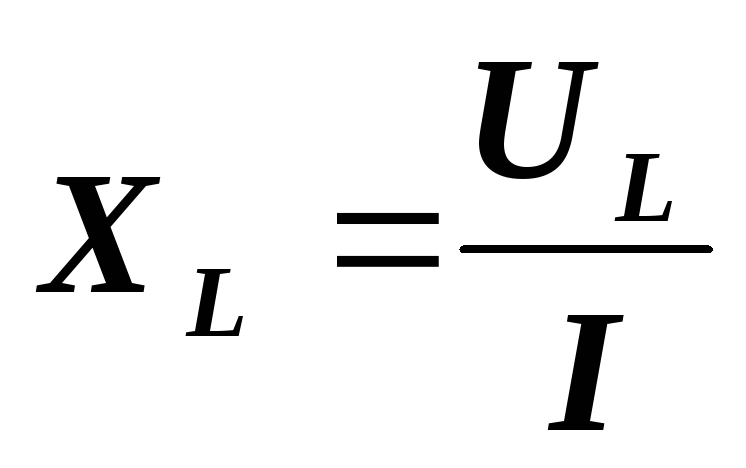

_{ПРИМЕР: Последовательная цепь содержит резистор сопротивлением 510 ом, индуктивное сопротивление 250 ом и емкостное сопротивление 150 ом. Какой ток течет по цепи, если к ней приложено напряжение 120 вольт?}

_Дано:

_{R = 510 Ом; XL = 250 Ом; Xc = 150 Ом; E = 120 В}

_{Решение:}

_{X = ХL + Хc}_{= 250–150}

_{X = 100 Ом (индуктивное)}

_{Z² = R² + X²}

_{Z² =(510)² +(100)²}

_{Z = √(270100)}

_{Z = 519,71 Ом}

_{I = E/Z = 120/519,71}

_{I = 0,23 А или 230 мА.}

17-3. Вопросы

1. Каким образом модифицируется закон Ома, чтобы его можно было применить к цепям переменного тока для определения напряжения и тока?

2. Последовательная цепь содержит резистор сопротивлением 510 ом, индуктивное сопротивление 300 ом и емкостное сопротивление 375 ом. Какой ток течет по цепи, если к ней приложено напряжение 120 вольт?

17-4. ЦЕПИ RLC

Материал, изложенный до сих пор, применим ко всем цепям переменного тока. В приведенных примерах рассматривались последовательные цепи. Понятия, рассмотренные в этом параграфе, не содержат нового материала, но используют все принципы, изложенные ранее.

_{ПРИМЕР: На рис. 17-5 показана последовательная RLC цепь. Необходимо вычислить Хс, XL, X, Z и IT.}

_{Рис. 17-5. Последовательная цепь RLC.}

_{Сначала вычислим Хс, XL и X.}

_Дано:

_{f = 60 Гц; С = 470 мкФ; L = 27 мГн.}

_{Решение:}

_{Xc = 1/2πfC}

_{Xc = 1/(6,28)(60)(0,000470)}

_{XC = 5,65 Ом}

_{XL = 2πfL}

_{XL = (6,28)(60)(0,027)}

_{XL = 10,17 Ом}

_{X = XL — Xc = 10,17 — 5,65}

_{X = 4,52 Ом (индуктивное).}

_{Используем значение X для вычисления Z.}

_Дано:

_{X = 4,52 Ом; R = 10 Ом.}

_{Решение:}

_{Z² = R² + X²}

_{Z² = (10)² + (4,52)² = 120,43}

_{Z = √(120,43) = 10,97 Ом.}

_{Это значение Z может быть использовано для вычисления полного тока (IT).}

_Дано:

_{Z = 10,97 Ом; E = 120 В.}

_{Решение:}

_{IT = E/Z = 120/10,97}

_{IT = 10,94 A.}

Помните, что во всех частях последовательной цепи течет один и тот же ток.

Если элементы в цепях соединены параллельно, то следует учесть одно главное различие между последовательными и параллельными цепями. При последовательном соединении по всей цепи течет один и тот же ток, а в параллельной цепи к каждой ветви приложено одинаковое напряжение. Вследствие этой разницы полный импеданс параллельной цепи должен вычисляться на основе тока в цепи.

В последовательной цепи RLC для вычисления реактивного сопротивления и импеданса используются следующие формулы:

X = Х_с — X_L или X = X_L — Х_с, Z² = R² + X².

В случае параллельных цепей должны использоваться следующие формулы:

I_X = I_с — I_L или I_X = I_L — I_X; I²_Z = (I_R)² + (I_X)²

Импеданс параллельной цепи находится с помощью формулы:

I_Z = E/Z

Замечание: Если неизвестно напряжение (Е), приложенное к цепи, то для вычисления I_c, I_L, I_x, I_R и I_Z можно использовать любое значение Е.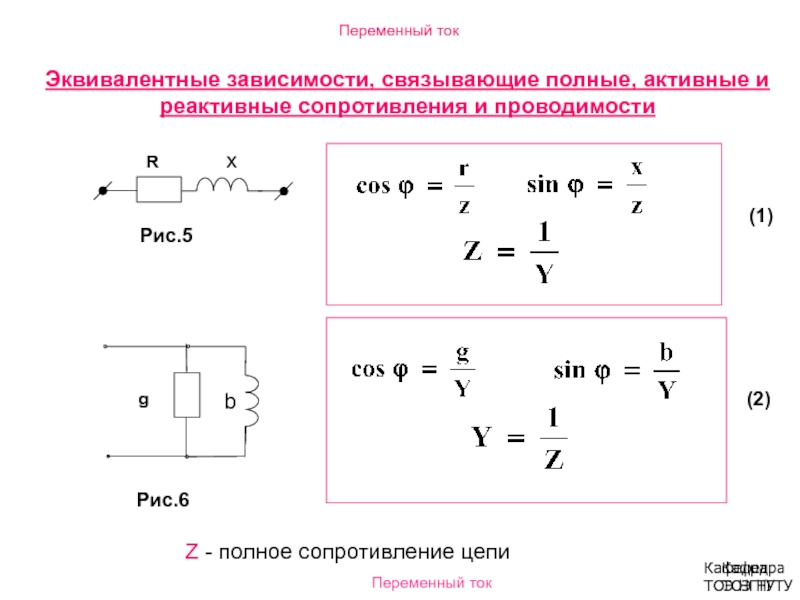 То же значение напряжения должно использоваться для вычисления импеданса.

_{ПРИМЕР: Найти значение Z для цепи, показанной на рис. 17-6.}

_{Рис. 17-6. Параллельная цепь RLC.}

_Дано:

_{Е = 120 В; R = 60 Ом; Хс = 75 Ом; XL = 50 Ом.}

_{Решение:}

_{Первым шагом в вычислении Z является вычисление токов отдельных ветвей.}

_{IR = E/R = 120/60 = 2 A}

_{Ix = E/Xc = 120/75 = 1,6 A}

_{IL = E/XL = 120/50 = 2,4 A}

_{Используя значения IR, Ic, IL, вычислим Ix и Iz}

_{IX = IL — Ic = 2,4 – 1,6}

_{Ix = 0,8 А (индуктивный)}

_{I²z = (IR)^{2 +}(Ix)²}

_{I²z = (2)² + (0,8)² = 4,64}

_{Iz = √(4,64) = 2,15 A.}

_{Используя значение Iz, вычислим Z.}

_{Iz = E/Z}

_{2,15 = 120/Z}

_{Z = 120/2,15 = 55,8 Ом}

В завершение этой главы отметим, что мы рассмотрели все блоки, из которых строятся электрические цепи. При изложении материала использовались ранее изученные понятия и соотношения.

17-4. Вопрос

1. Чем отличаются вычисления импеданса для последовательной цепи переменного тока и для параллельной цепи?

РЕЗЮМЕ

• Конденсатор в цепи переменного тока оказывает противодействие любому изменению напряжения, так же как он это делает в цепи постоянного тока.

• Ток опережает по фазе напряжение на конденсаторе на 90 градусов.

• Противодействие, оказываемое конденсатором переменному току, называется емкостным реактивным сопротивлением. Оно обозначается Х_с и вычисляется по формуле:

X_C = 1/2πfC

• Катушка индуктивности в цепи переменного тока противодействует любому изменению тока, так же как она это делает в цепи постоянного тока.

• На катушке индуктивности ток отстает по фазе от напряжения на 90 градусов.

• Противодействие, оказываемое катушкой индуктивности переменному току, называется индуктивным реактивным сопротивлением. Оно обозначается X_L и вычисляется по формуле

X_L = 2πfL.

• Полное реактивное сопротивление последовательной цепи переменного тока определяется формулами X = X_C — X_L или X = X_L — X_C.

• Полное реактивное сопротивление последовательной цепи переменного тока является либо емкостным, либо индуктивным, в зависимости от того, какая величина больше, Х_C или X_L.

• В параллельной цепи реактивное сопротивление определяется с помощью формул

I_Z = E/Z

где I_z определяется формулой I_z² = (I_R)² + (I_X)², а I_х вычисляется по формуле I_X = I_C — I_L или I_X = I_L — I_C.

• Реактивное сопротивление параллельной цепи также может быть емкостным или индуктивным, в зависимости то того, какая величина больше I_C или I_L.

• Полное сопротивление цепи переменного тока называется импедансом. Он обозначается символом Z. В последовательной цепи Z² = R² + X². В параллельной цепи I²_Z = (I_R)² + (I_X)² и

I_Z = E/Z

• Получена формула для закона Ома, который можно применять для пеней переменного тока:

I = E/Z

Глава 17. САМОПРОВЕРКА

1. Чему равны значения Х_С, X_L, X, Z и I_T для цепи, изображенной на рис. 17-7?

Рис. 17-7. Последовательная цепь RLC.

2. Чему равны значения I_C, I_L, I_X, I_R и I_Z для цепи, изображенной на рис. 17-8?

Рис. 17-8. Параллельная цепь RLC.

Активное емкостное индуктивное реактивное полное сопротивления

Активное сопротивление

, где — импеданс, — величина активного сопротивления, — величина реактивного сопротивления, — мнимая единица.

Активное сопротивление — сопротивление электрической цепи или её участка, обусловленное необратимыми превращениями электрической энергии в другие виды энергии (в тепловую).

Реактивное сопротивление

Реактивное сопротивление — электрическое сопротивление, обусловленное передачей энергии переменным током электрическому илимагнитному полю (и обратно).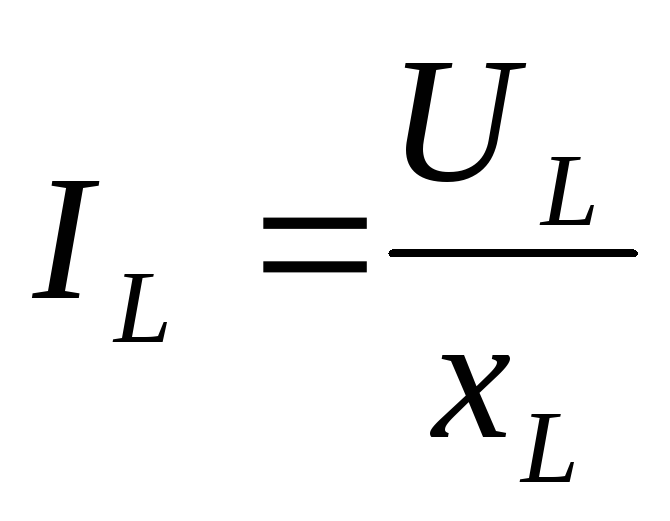

Реактивное сопротивление определяет мнимую часть импеданса:

В зависимости от знака величины какого-либо элемента электрической цепи говорят о трёх случаях:

— элемент проявляет свойства индуктивности.

— элемент имеет чисто активное сопротивление.

— элемент проявляет ёмкостные свойства.

Величина реактивного сопротивления может быть выражена через величины индуктивного и ёмкостного сопротивлений:

Индуктивное сопротивление ( ) обусловлено возникновением ЭДС самоиндукции в элементе электрической цепи. Изменение тока и, как следствие, изменение его магнитного поля вызывает препятствующее изменению этого тока ЭДС самоиндукции. Величина индуктивного сопротивления зависит от индуктивности элемента и частоты протекающего тока:

Ёмкостное сопротивление ( ). Величина ёмкостного сопротивления зависит от ёмкости элемента и также частоты протекающего тока :

Здесь — циклическая частота, равная .

Прямая и обратная зависимость этих сопротивлений от частоты тока приводит к тому, что с увеличением частоты всё бо?льшую роль начинает играть индуктивное сопротивление и всё меньшую ёмкостное.

Полное сопротивление

Полное сопротивление (z) — это векторная сумма всех сопротивлений: активного, емкостного и индуктивного.

Треугольники сопротивлений

Если стороны треугольника напряжений (155, а) разделить на ток I (.155, б), то углы треугольника от этого не изменятся, и мы получим новый треугольник, подобный первому — треугольник сопротивлений (155, в).

В треугольнике сопротивления, показанном на рис, все стороны обозначают сопротивления, причем гипотенуза его является полным или кажущимся сопротивлением цепи.

Из треугольника сопротивлений видно, что полное или кажущееся сопротивление Z равно геометрической сумме активного R и индуктивного X_l сопротивлений.

Применяя теорему Пифагора к треугольнику сопротивлений, получаем:

Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: Да какие ж вы математики, если запаролиться нормально не можете. 8459 — | 7349 — или читать все.

91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.

Отключите adBlock!
и обновите страницу (F5)
очень нужно

Активное сопротивление

Пусть источник переменного тока включен в цепь, в которой индуктивностью и емкостью можно пренебречь. Переменный ток изменяется в соответствии с законом:

Тогда, если применить к участку цепи ($а R в$) (рис.1) закон Ома получим:

где $U$ — напряжение на концах участка. Разность фаз между током и напряжением равна нулю. Амплитудное значение напряжения ($U_m$) равно:

где коэффициент $R$ — называется активным сопротивлением. Наличие активного сопротивления в цепи всегда приводит к выделению тепла.

Ёмкостное сопротивление

Допустим, что в участок цепи включен конденсатор емкости $С$, а $R=0$ и $L=0$. Будем считать силу тока ($I$) положительной, если она имеет направление, которое указано на рис. 2. Пусть заряд на конденсаторе равен $q$.

Мы можем использовать следующие соотношения:

Попробуй обратиться за помощью к преподавателям

Если $I(t)$ определена уравнением (1), то заряд выражен как:

где $q_0$ произвольный постоянный заряд конденсатора, который не связан с колебаниями тока, поэтому можем допустить, что $q_0=0.$ Получим напряжение равно:

Формула (6) показывает, что на конденсаторе колебания напряжения отстают от колебаний силы тока по фазе на $frac<pi ><2>.$ Амплитуда напряжения на емкости равна:

Величину $X_C=frac<1><omega C>$ называют реактивным емкостным сопротивлением (емкостным сопротивлением, кажущимся сопротивлением емкости). Если ток постоянный, то $X_C=infty $. Это значит, что постоянный ток не течет через конденсатор. Из определения емкостного сопротивления видно, что при больших частотах колебаний, малые емкости являются небольшими сопротивлениями переменного тока.

Индуктивное сопротивление

Пусть участок цепи имеет только индуктивность (рис.3). Будем считать $I>0$, если ток направлен от $а$ к $в$.

Задай вопрос специалистам и получи
ответ уже через 15 минут!

Если в катушке течет ток, то в индуктивности появляется ЭДС самоиндукции, следовательно, закон Ома примет вид:

По условию $R=0. mathcal E$ самоиндукции можно выразить как:

Из выражений (8), (9) следует, что:

Амплитуда напряжения в данном случае равна:

где $X_L- $индуктивное сопротивление (кажущееся сопротивление индуктивности).

Закон Ома для цепей переменного тока

называют полным электросопротивлением, или импедансом, иногда называют законом Ома для переменного тока. Однако необходимо помнить, что формула (12) относится к амплитудам тока и напряжения, а не мгновенным их значениям.

Задание: Чему равно действующее значение силы тока в цепи. Цепь переменного тока состоит из последовательно соединенных: конденсатора емкостью $C$, катушки индуктивности $L$, активного сопротивления $R$. На зажимы цепи подается напряжение действующее напряжение $U$ частота которого $
u$.

Решение:

Так как все элементы цепи соединены последовательно, то сила тока во всех элементах одинакова.

Амплитудное значение силы тока выражается «законом Ома для переменного тока»:

оно связано с действующим значением силы тока как:

В условиях задачи мы имеем действующее значение напряжения $U$, нам в формуле (1.1) требуется амплитуда напряжения, используя формулу:

Подставим в формулу (1.2) формулы (1.1) и (1.3), получим:

где $omega =2pi
u .$

Задание: Используя условия задачи в первом примере, найдите действующие значения напряжений на катушке индуктивности ($U_L$), сопротивлении ($U_R$), конденсаторе ($U_C$).

Решение:

Используем результат примера 1. Напряжение на катушке индуктивности выражается формулой:

Напряжение на активном сопротивлении ($U_R$) равно:

Напряжение на конденсаторе ($U_C$) определяется как:

Так и не нашли ответ
на свой вопрос?

Просто напиши с чем тебе
нужна помощь

В данной статье мы подробно поговорим про индуктивное сопротивление, реактивное сопротивление и треугольники напряжения, сопротивления и силы.

Введение

Итак, мы рассмотрели поведение индукторов, подключенных к источникам постоянного тока, и, надеюсь, теперь мы знаем, что когда на индуктор подается постоянное напряжение, рост тока через него происходит не мгновенно, а определяется индуктором, индуцированным самим индуктором или обратным значением ЭДС.

Также мы видели, что ток индукторов продолжает расти, пока не достигнет своего максимального установившегося состояния после пяти постоянных времени. Максимальный ток, текущий через индукционную катушку ограничиваются только резистивной частью катушек обмотки в омах, и как мы знаем из закона Ома, это определяется отношением напряжения к току V / R .

Когда переменное напряжение подается на катушку индуктивности, поток тока через него ведет себя совершенно иначе, чем при приложении постоянного напряжения. Эффект синусоидального питания приводит к разности фаз между напряжением и формами тока. Теперь в цепи переменного тока противодействие току, протекающему через обмотки катушек, зависит не только от индуктивности катушки, но и от частоты сигнала переменного тока.

Сопротивление току, протекающему через катушку в цепи переменного тока, определяется сопротивлением переменного тока, более известным как полное сопротивление (Z) цепи. Но сопротивление всегда связано с цепями постоянного тока, поэтому, чтобы отличить сопротивление постоянного тока от сопротивления переменного тока, обычно используется термин «реактивное сопротивление» .

Как и сопротивление, значение реактивного сопротивления также измеряется в омах, но ему присваивается символ X (заглавная буква «X»), чтобы отличить его от чисто резистивного значения.

Поскольку интересующий нас компонент является индуктором, реактивное сопротивление индуктора поэтому называется «Индуктивное реактивное сопротивление». Другими словами, электрическое сопротивление индуктивности при использовании в цепи переменного тока называется индуктивным сопротивлением .

Индуктивное сопротивление, которому дается символ X _L , является свойством в цепи переменного тока, которое противодействует изменению тока. В наших уроках о конденсаторах в цепях переменного тока мы видели, что в чисто емкостной цепи ток I _C «опережает» напряжение на 90 o . В чисто индуктивной цепи переменного тока верно обратное: ток I _L отстает от напряжения на 90 o или (π / 2 рад).

Схема индуктивности переменного тока

В приведенной выше чисто индуктивной цепи индуктор подключен непосредственно через напряжение питания переменного тока. Когда напряжение питания увеличивается и уменьшается с частотой, самоиндуцированная обратная ЭДС также увеличивается и уменьшается в катушке по отношению к этому изменению.

Мы знаем, что эта самоиндуцированная ЭДС прямо пропорциональна скорости изменения тока через катушку и имеет наибольшее значение при переходе напряжения питания от положительного полупериода к отрицательному полупериоду или наоборот в точках 0 о и 180 о вдоль синусоиды.

Следовательно, минимальная скорость изменения напряжения возникает, когда синусоида переменного тока пересекается при своем максимальном или минимальном пиковом уровне напряжения. В этих положениях в цикле максимальный или минимальный токи протекают через цепь индуктора, и это показано ниже.

Векторная диаграмма индуктора переменного тока

Эти формы напряжения и тока показывают, что для чисто индуктивной цепи ток отстает от напряжения на 90 o . Также можно сказать, что напряжение опережает ток на 90 o . В любом случае общее выражение заключается в том, что ток отстает, как показано на векторной диаграмме. Здесь вектор тока и вектор напряжения показаны смещенными на 90 o . Ток отстает от напряжения .

Мы можем также написать это заявление как, V _L= 0 ö и I _L= -90 о по отношению к напряжению, V _L . Если форма волны напряжения классифицируется как синусоида, то ток I _L можно классифицировать как отрицательный косинус, и мы можем определить значение тока в любой момент времени как:

Поскольку ток всегда отстает от напряжения на 90 o в чисто индуктивной цепи, мы можем найти фазу тока, зная фазу напряжения или наоборот. Так что если мы знаем значение V _L , то I _L должно отставать на 90 o . Аналогичным образом, если мы знаем значение I _L, то V _L, следовательно, должно опережать на 90 o . Затем это отношение напряжения к току в индуктивном контуре будет производить уравнение, определяющее индуктивное сопротивление Х _L катушки.

Мы можем переписать уравнение для индуктивного сопротивления в более привычную форму, которая использует обычную частоту питания вместо угловой частоты в радианах ω и это будет выглядеть так:

Из приведенного выше уравнения для индуктивного реактивного сопротивления можно видеть, что, если увеличить частоту, либо индуктивность, общее значение индуктивного реактивного сопротивления также увеличится. Когда частота приближается к бесконечности, реактивное сопротивление индукторов также увеличивается до бесконечности, действуя как разомкнутая цепь.

Однако, когда частота приближается к нулю или постоянному току, реактивное сопротивление индукторов будет уменьшаться до нуля, действуя как короткое замыкание. Это означает, что индуктивное сопротивление «пропорционально» частоте.

Другими словами, индуктивное реактивное сопротивление увеличивается с частотой, в результате чего X _L будет небольшим на низких частотах, а X _L будет высоким на высоких частотах, что продемонстрировано на графике ниже.

Индуктивное сопротивление от частоты

Затем мы видим, что при постоянном токе индуктор имеет нулевое реактивное сопротивление (короткое замыкание), на высоких частотах индуктор имеет бесконечное реактивное сопротивление (разомкнутая цепь).

Питание от сети переменного тока серии LR

До сих пор мы рассматривали чисто индуктивную катушку, но невозможно иметь чистую индуктивность, поскольку все катушки, реле или соленоиды будут иметь определенное сопротивление, независимо от того, насколько мало связано с витками используемого провода. Тогда мы можем рассматривать нашу простую катушку как последовательное сопротивление с индуктивностью (LR).

В цепи переменного тока, которая содержит как индуктивность L и сопротивление R, напряжение V будет векторная сумма двух компонентов напряжения, V _Rи V _L . Это означает, что ток, протекающий через катушку еще будет отставать от напряжения, но на величину меньше чем 90 ö в зависимости от значений V _Rи V _L .

Новый фазовый угол между напряжением и током известен как фазовый угол цепи и обозначается греческим символом фи, Φ .

Чтобы получить векторную диаграмму зависимости между напряжением и током, необходимо найти эталонный или общий компонент. В последовательно соединенной цепи RL ток является общим, так как один и тот же ток течет через каждый компонент. Вектор этой эталонной величины обычно рисуется горизонтально слева направо.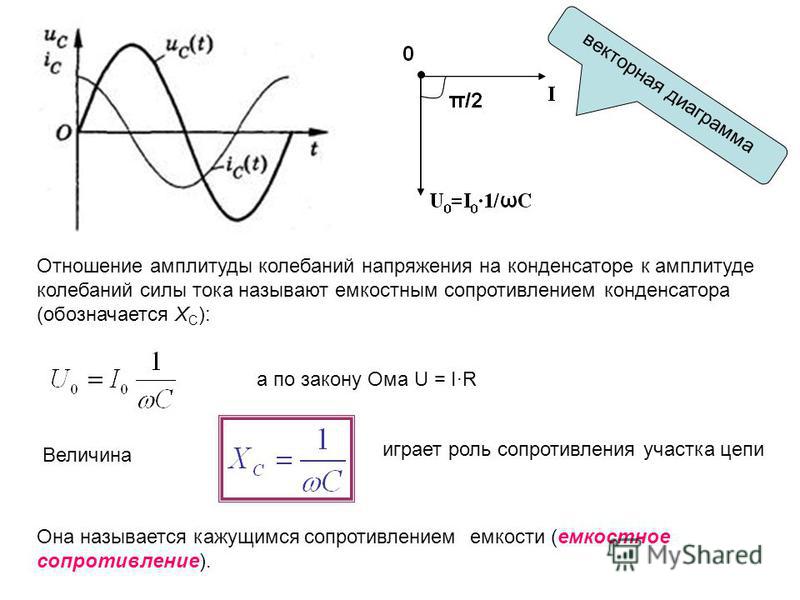

Из наших руководств о резисторах и конденсаторах, мы знаем, что ток и напряжение в цепи переменного резистивного тока, оба «в фазе» и, следовательно, вектор V _R рисуется с наложением на текущую или контрольную линию.

Из вышесказанного также известно, что ток «отстает» от напряжения в чисто индуктивной цепи и, следовательно, вектор V _L отображается на 90 o перед опорным током и в том же масштабе, что и V _R, это показано ниже.

Цепь переменного тока серии LR

На приведенной выше векторной диаграмме видно, что луч OB представляет текущую опорную линию, луч OA — это напряжение резистивного компонента, которое в фазе с током, луч OC показывает индуктивное напряжение, которое составляет 90 o перед током, поэтому видно, что ток отстает от напряжения на 90 o , луч OD дает нам результирующее или питающее напряжение в цепи. Треугольник напряжения выводится из теоремы Пифагора и имеет вид:

Треугольник сопротивления

В цепи постоянного тока отношение напряжения к току называется сопротивлением. Однако в цепи переменного тока это отношение известно как полное сопротивление Z с единицами измерения в омах. Полное сопротивление — это полное сопротивление току в «цепи переменного тока», содержащее как сопротивление, так и индуктивное сопротивление.

Если мы разделим стороны треугольника напряжения выше на ток, получим еще один треугольник, стороны которого представляют сопротивление, реактивное сопротивление и полное сопротивление катушки. Этот новый треугольник называется «Треугольник сопротивления».

Силовой треугольник индуктора переменного тока

Существует еще один тип конфигурации треугольника, который мы можем использовать для индуктивной цепи, и это «силовой треугольник». Мощность в индуктивной цепи называется реактивной мощностью или вольт-амперной реактивной, символ Var, который измеряется в вольт-амперах. В цепи переменного тока серии RL ток отстает от напряжения питания на угол Φ o .

В чисто индуктивной цепи переменного тока ток будет сдвинут по фазе на 90 o к напряжению питания. Таким образом, общая реактивная мощность, потребляемая катушкой, будет равна нулю, так как любая потребляемая мощность компенсируется генерируемой самоиндуцированной ЭДС-мощностью. Другими словами, полезная мощность в ваттах, потребляемая чистым индуктором в конце одного полного цикла, равна нулю, так как энергия берется из источника и возвращается к нему.

Реактивная мощность ( Q ) катушки может быть задана как: I 2 x X _L (аналогично I 2 R в цепи постоянного тока). Затем три стороны силового треугольника в цепи переменного тока представлены кажущейся мощностью ( S ), реальной мощностью ( P ) и реактивной мощностью ( Q ), как показано.

Обратите внимание, что данный индуктор или катушка будет потреблять мощность в ваттах из — за сопротивления обмоток, создающих сопротивление Z.

Тимеркаев Борис — 68-летний доктор физико-математических наук, профессор из России. Он является заведующим кафедрой общей физики в Казанском национальном исследовательском техническом университете имени А. Н. ТУПОЛЕВА — КАИ

Что такое активное сопротивление. Активное, реактивное и полное сопротивление цепи

Полное сопротивление, или импеданс, характеризует сопротивление цепи переменному электрическому току. Данная величина измеряется в омах. Для вычисления полного сопротивления цепи необходимо знать значения всех активных сопротивлений (резисторов) и импеданс всех катушек индуктивности и конденсаторов, входящих в данную цепь, причем их величины меняются в зависимости от того, как меняется проходящий через цепь ток. Импеданс можно рассчитать при помощи простой формулы.

Формулы

Полное сопротивление Z = R или X L или X C (если присутствует что-то одно)
Полное сопротивление (последовательное соединение) Z = √(R 2 + X 2) (если присутствуют R и один тип X)
Полное сопротивление (последовательное соединение) Z = √(R 2 + (|X L — X C |) 2) (если присутствуют R, X L , X C)
Полное сопротивление (любое соединение) = R + jX (j – мнимое число √(-1))
Сопротивление R = I / ΔV
Индуктивное сопротивление X L = 2πƒL = ωL
Емкостное сопротивление X C = 1 / 2πƒL = 1 / ωL

Шаги

Часть 1

Вычисление активного и реактивного сопротивлений

Импеданс обозначается символом Z и измеряется в омах (Ом). Вы можете измерить импеданс электрической цепи или отдельного элемента. Импеданс характеризует сопротивление цепи переменному электрическому току. Есть два типа сопротивления, которые вносят вклад в импеданс:

Активное сопротивление (R) зависит от материала и формы элемента. Наибольшим активным сопротивлением обладают резисторы, но и другие элементы цепи обладают небольшим активным сопротивлением.
Реактивное сопротивление (X) зависит от величины электромагнитного поля. Наибольшим реактивным сопротивлением обладают катушки индуктивности и конденсаторы.

Сопротивление – это фундаментальная физическая величина, описываемая законом Ома: ΔV = I * R. Эта формула позволит вам вычислить любую из трех величин, если вы знаете две другие. Например, чтобы вычислить сопротивление, перепишите формулу так: R = I / ΔV. Вы также можете при помощи мультиметра.

ΔV – это напряжение (разность потенциалов), измеряемое в вольтах (В).
I – сила тока, измеряемая в амперах (А).
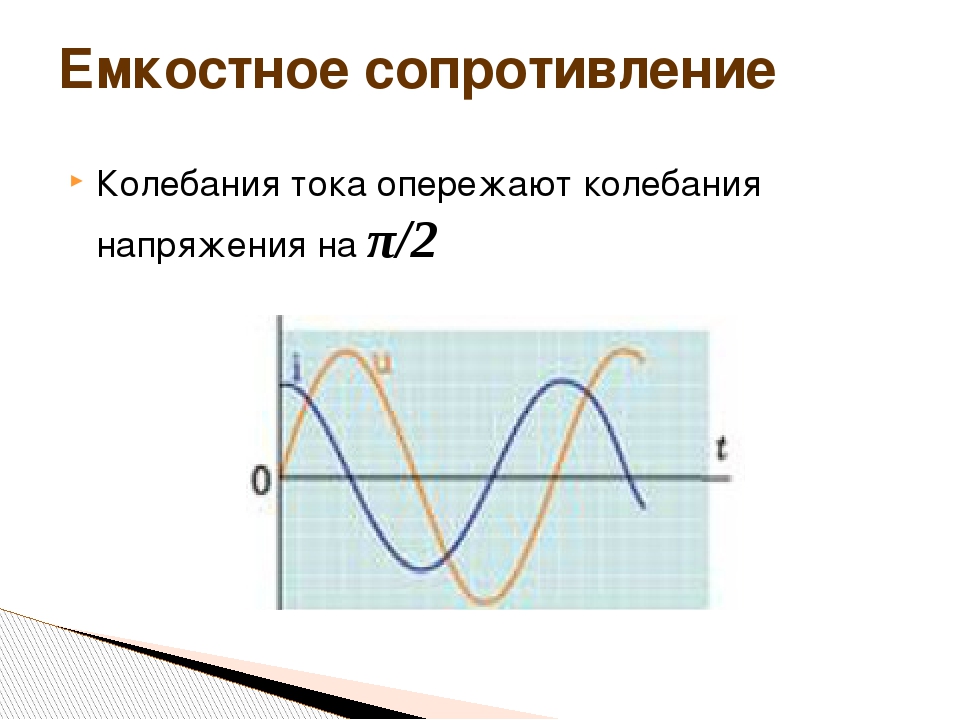
R – это сопротивление, измеряемое в омах (Ом).

Реактивное сопротивление имеет место только в цепях переменного тока. Как и активное сопротивление, реактивное сопротивление измеряется в омах (Ом). Есть два типа реактивного сопротивления:

Вычислите индуктивное сопротивление. Это сопротивление прямо пропорционально быстроте изменения направления тока, то есть частоты тока. Эта частота обозначается символом ƒ и измеряется в герцах (Гц). Формула для расчета индуктивного сопротивления: X L = 2πƒL , где L – индуктивность, измеряемая в генри (Гн).

Вычислите емкостное сопротивление. Это сопротивление обратно пропорционально быстроте изменения направления тока, то есть частоты тока. Формула для вычисления емкостного сопротивления: X C = 1 / 2πƒC . С – это емкость конденсатора, измеряемая в фарадах (Ф).

Вы можете .
Эту формулу можно переписать так: X C = 1 / ωL (объяснения см. выше).

Часть 2

Вычисление полного сопротивления

Если цепь состоит исключительно из резисторов, то импеданс вычисляется следующим образом. Сначала измерьте сопротивление каждого резистора или посмотрите значения сопротивления на схеме цепи.
- Если резисторы соединены последовательно, то полное сопротивление R = R 1 + R 2 + R 3 …
- Если резисторы соединены параллельно, то полное сопротивление R = 1 / R 1 + 1 / R 2 + 1 / R 3 …
Сложите одинаковые реактивные сопротивления. Если в цепи присутствуют исключительно катушки индуктивности или исключительно конденсаторы, то полное сопротивление равно сумме реактивных сопротивлений. Вычислите его следующим образом:

Активное сопротивление зависит от материала, сечения и температуры. Активное сопротивление обусловливает тепловые потери проводов и кабелей. Определяется материалом токоведущих проводников и площадью их сечения.

Различают сопротивление проводника постоянному току (омическое) и переменному току (активное). Активное сопротивление больше активного (R а > R ом) из-за поверхностного эффекта. Переменное магнитное поле внутри проводника вызывает противоэлектродвижущую силу, благодаря которой происходит перераспределение тока по сечению проводника. Ток из центральной его части вытесняется к поверхности. Таким образом, ток в центральной части провода меньше, чем у поверхности, то есть сопротивление провода возрастает по сравнению с омическим. Поверхностный эффект резко проявляется при токах высокой частоты, а также в стальных проводах (из-за высокой магнитной проницаемости стали).

Для ЛЭП, выполненных из цветного металла, поверхностный эффект на промышленных частотах незначителен. Следовательно, R а ≈ R ом.

Обычно влиянием колебания температуры на R а проводника в расчётах пренебрегают. Исключение составляют тепловые расчеты проводников. Пересчет величины сопротивления выполняют по формуле:

где R 20 – активное сопротивление при температуре 20 о;

текущее значение температуры.

Активное сопротивление зависит от материала проводника и сечения:

где ρ –удельное сопротивление, Ом мм 2 /км;

l – длина проводника, км;

F – сечение проводника, мм 2 .

Сопротивление одного километра проводника называют погонным сопротивлением:

где удельная проводимость материала проводника, км См/мм 2 .

Для меди γ Cu =53×10 -3 км См/мм2 , для алюминия γ Al =31.7×10 -3 км См/мм2 .

На практике значение r 0 определяют по соответствующим таблицам, где они указаны для t 0 =20 0 С.

Величина активного сопротивления участка сети рассчитывается:

R = r 0 ×l .

Активное сопротивление стальных проводов намного больше омического из-за поверхностного эффекта и наличия дополнительных потерь на гистерезис (перемагничивание) и от вихревых токов в стали:

r 0 = r 0пост + r 0доп,

где r 0пост – омическое сопротивление одного километра провода;

r 0доп – активное сопротивление, которое определяется переменным магнитным полем внутри проводника, r 0доп = r 0поверх. эф + r 0гистер. + r 0вихр.

Изменение активного сопротивления стальных проводников показано на рисунке 4.1.

При малых величинах тока индукция прямо пропорциональна току. Следовательно, r 0 увеличивается. Затем наступает магнитное насыщение: индукция и r 0 практически не изменяются. При дальнейшем увеличении тока r 0 уменьшается из-за снижения магнитной проницаемости стали (m ).

Сопротивление, оказываемое проводником проходящему на нему переменному току, называется активным сопротивлением .

Если какой-либо потребитель не содержит в себе индуктивности и емкости (лампочка накаливания, нагревательный прибор), то он будет являться для переменного тока также активным сопротивлением.

Активное сопротивление зависит от частоты переменного тока, возрастая с ее увеличением.

Однако многие потребители обладают индуктивными и емкостными свойствами при прохождении через них переменного тока. К таким потребителям относятся трансформаторы, дроссели, электромагниты, конденсаторы, различного рода провода и многие другие.

При прохождении через них переменного тока необходимо учитывать не только активное, но и реактивное сопротивление , обусловленное наличием, в потребителе индуктивных и емкостных свойств его.

Активное сопротивление определяет действительную часть импеданса:

Где — импеданс, — величина активного сопротивления, — величина реактивного сопротивления, — мнимая единица.

Реакти́вное сопротивле́ние — электрическое сопротивление, обусловленное передачей энергии переменным током электрическому или магнитному полю (и обратно).

Величина полного реактивного сопротивления

Индуктивное сопротивление () обусловлено возникновением ЭДС самоиндукции в элементе электрической цепи.

Ёмкостное сопротивление ().

Здесь — циклическая частота

Полное сопротивление цепи при переменном токе:

z =

√

r 2 + x 2

√

r 2 +(x L −x C) 2

Билет №12.

1. 1) Согласование генератора с нагрузкой — обеспечение требуемой величины активного эквивалентного сопротивления нагрузки генераторной лампы, R э, при всех возможных значениях входного сопротивления антенного фидера, которое зависит от его волнового сопротивления и коэффициента бегущей волны (КБВ)

Согласование (в электронике) сводится к правильному выбору сопротивлений генератора (источника), линии передачи и приёмника (нагрузки). Идеального Согласование (в электронике) между линией и нагрузкой можно достичь при равенстве волнового сопротивления линии r полному сопротивлению нагрузки Zh = RH + j ХН, или при RH= r и XH= 0, где RH -активная часть полного сопротивления, XH — его реактивная часть. В этом случае в передающей линии устанавливается режим бегущих волн и характеризующий их коэффициент стоячей волны (КСВ) равен 1. Для линии с пренебрежимо малыми потерями электрической энергии Согласование и, благодаря ему, максимально эффективная передача энергии из генератора в нагрузку достигаются при условии, что полные сопротивления генератора Zr и нагрузки ZH являются комплексно-сопряжёнными, т. е. Zr = Z*H, или Rr = r = R Н =Xr- XH. В этом случае реактивное сопротивление цепи равно нулю, и соблюдаются условия резонанса, способствующие повышению эффективности работы радиотехнических систем (улучшается использование частотных диапазонов, повышается помехозащищенность, снижаются частотные искажения радиосигналов и т.п.). Оценку качества Согласование (в электронике) производят, измеряя коэффициент отражения и КСВ. Практически Согласование (в электронике) считают оптимальным, если в рабочей полосе частот КСВ не превышает 1,2-1,3 (в измерительных приборах 1,05). В отдельных случаях косвенными показателями Согласование (в электронике) могут служить реакции параметров генератора (частоты, мощности, уровня шумов) на изменение нагрузки, наличие электрических пробоев в линии, разогрев отдельных участков линии.

При таком режиме работы в приёмнике выделяется наибольшая мощность, равная половине мощности источника. В этом случае К.П.Д. =0,5. Такой режим используется в измерительных цепях, устройствах средств связи.

При передаче больших мощностей, например по высоковольтным линиям электропередач, работа в согласованном режиме, как правило, недопустима.

Сопротивление одного и того же проводника для переменного тока будет больше, чем для постоянного.

Это объясняется явлением так называемого поверхностного эффекта, заключающегося в том, что переменный ток вытесняется от центральной части проводника к периферийным слоям. В результате плотность тока во внутренних слоях будет меньше, чем в наружных. Таким образом, при переменном токе сечение проводника используется как бы не полностью. Однако при частоте 50 Гц различие в сопротивлениях постоянному и переменному токам незначительно и практически им можно пренебречь.

Сопротивление проводника постоянному току называют омическим, а переменному току –активным сопротивлением.

Омическое и активное сопротивление зависят от материала (внутренней структуры), геометрических размеров и температуры проводника. Кроме того, в катушках со стальным сердечником на величину активного сопротивления влияют потери в стали (далее для самоподготовки).

К активным сопротивлениям относят электрические лампы накаливания, электрические печи сопротивления, различные нагревательные приборы, реостаты и провода, где электрическая энергия практически почти целиком превращается в тепловую.

Если цепь переменного тока содержит только резистор R лампа накаливания, электронагревательный прибор и т. д.), к которому приложено переменное синусоидальное напряжение и (рис. 1-5, а):

то ток i в цепи будет определяться значением этого сопротивления:

где — амплитуда тока; при этом ток i и напряжение и совпадают по фазе. Обе эти величины, как видно, можно изобразить на временной (рис. 1-5, б) и векторной (1-5, в) диаграммах. Теперь установим, как изменяется мощность в любой момент времени — мгновенная мощность, характеризующая собой скорость преобразования электрической энергии в другие виды энергии в данный момент времени

где IU — произведение действующих значений тока и напряжения.

Из полученного следует, что мощность в течение периода остается положительной и пульсирует с удвоенной частотой. Графически это можно представить так, как показано на рисунке 1-6. В этом случае электрическая энергия превращается необратимо, например, в теплоту независимо от направления тока в цепи.

Кроме мгновенного значения мощности различают еще среднюю мощность за период:

но так как второй интеграл равен нулю, то окончательно имеем:

Средняя за период мощность переменного тока называется активной мощностью, а соответствующее ей сопротивление — активным.

Средняя мощность и активное сопротивление связаны с безвозвратным преобразованием электрической энергии в другие виды энергии. Активное сопротивление электрической цепи не сводится только к

сопротивлению проводников, в которых электрическая энергия превращается в теплоту. Это понятие значительно шире, так как средняя мощность электрической цепи равна сумме мощностей всех видов энергии, полученной из электрической, на всех участках цепи (теплота, механическая и др. ).

Из полученных соотношений следует, что

которое является математической записью закона Ома для цепи переменного тока с активным сопротивлением.

Реактивное сопротивление, индуктивное и емкостное | Физика

Цели обучения

К концу этого раздела вы сможете:

Зависимость напряжения и тока от времени в простых индуктивных, емкостных и резистивных цепях.
Рассчитайте индуктивное и емкостное сопротивление.
Рассчитывайте ток и / или напряжение в простых индуктивных, емкостных и резистивных цепях.

Многие цепи также содержат конденсаторы и катушки индуктивности в дополнение к резисторам и источнику переменного напряжения.Мы видели, как конденсаторы и катушки индуктивности реагируют на постоянное напряжение при его включении и выключении. Теперь мы исследуем, как катушки индуктивности и конденсаторы реагируют на синусоидальное переменное напряжение.

Катушки индуктивности и индуктивное сопротивление

Предположим, индуктор подключен непосредственно к источнику переменного напряжения, как показано на рисунке 1. Разумно предположить, что сопротивление пренебрежимо мало, поскольку на практике мы можем сделать сопротивление индуктора настолько малым, что оно окажет незначительное влияние на схему.Также показан график зависимости напряжения и тока от времени.

Рис. 1. (a) Источник переменного напряжения, включенный последовательно с катушкой индуктивности, имеющей незначительное сопротивление. (б) График зависимости тока и напряжения на катушке индуктивности от времени.

График на Рисунке 1 (b) начинается с максимального напряжения. Обратите внимание, что ток начинается с нуля и повышается до своего пика после напряжения, которое им управляет, точно так же, как это было в случае, когда напряжение постоянного тока было включено в предыдущем разделе.Когда напряжение становится отрицательным в точке а, ток начинает уменьшаться; оно становится нулевым в точке b, где напряжение является самым отрицательным. Затем ток становится отрицательным, снова вслед за напряжением. Напряжение становится положительным в точке c и начинает делать ток менее отрицательным. В точке d ток проходит через ноль, когда напряжение достигает своего положительного пика, чтобы начать следующий цикл. Кратко это поведение можно описать следующим образом:

Напряжение переменного тока в индукторе

Когда на катушку индуктивности подается синусоидальное напряжение, оно опережает ток на одну четверть цикла или на фазовый угол 90º.

Ток отстает от напряжения, поскольку индукторы препятствуют изменению тока. Изменение тока индуцирует обратную ЭДС В = — L (Δ I / Δ t ). Это считается эффективным сопротивлением катушки индуктивности переменному току. Среднеквадратичный ток I через катушку индуктивности L определяется версией закона Ома:

[латекс] I = \ frac {V} {{X} _ {L}} \\ [/ latex],

, где В, — среднеквадратичное значение напряжения на катушке индуктивности, а X _L определяется как

[латекс] {X} _ {L} = 2 \ pi {fL} \\ [/ латекс],

с f частота источника переменного напряжения в герцах (анализ схемы с использованием правила петли Кирхгофа и вычислений фактически дает это выражение). X _L называется индуктивным реактивным сопротивлением , потому что катушка индуктивности препятствует прохождению тока. X _L имеет единицы измерения Ом (1 Гн = 1 Ом с, так что частота, умноженная на индуктивность, имеет единицы (циклы / с) (Ом ⋅ с) = Ом)), что соответствует его роли в качестве эффективное сопротивление. Логично, что X _L пропорционально L , поскольку чем больше индукция, тем больше его сопротивление изменению.Также разумно, что X _L пропорционально частоте f , поскольку большая частота означает большее изменение тока. То есть Δ I / Δ t является большим для больших частот (большие f , маленькие Δ t ).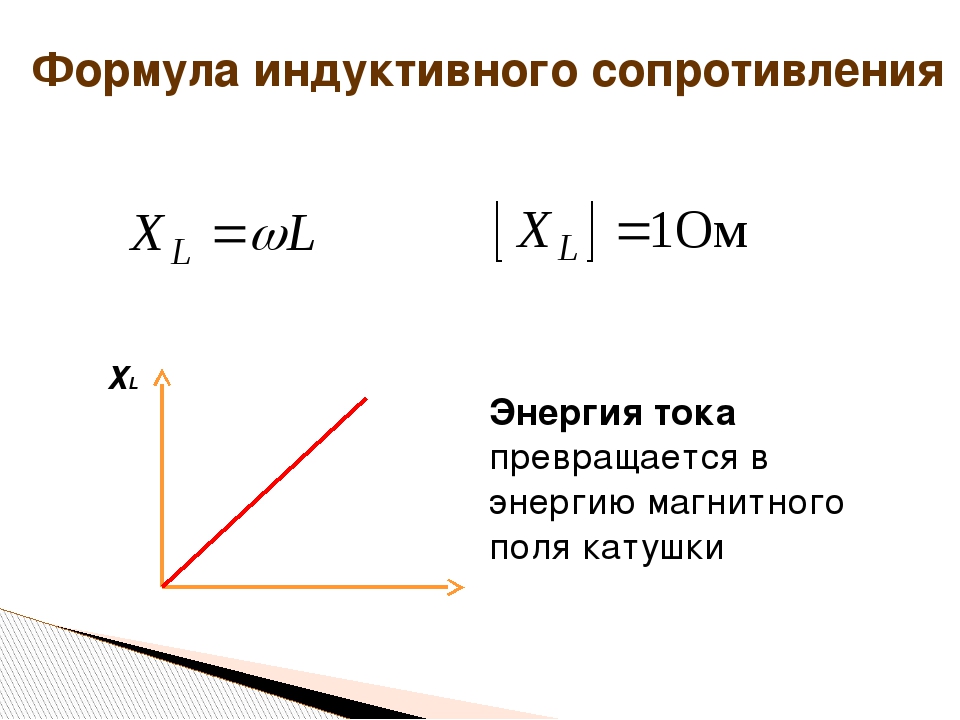 Чем больше изменение, тем больше сопротивление катушки индуктивности.

Пример 1. Расчет индуктивного сопротивления, а затем тока

(a) Вычислите индуктивное реактивное сопротивление 3.Индуктор 00 мГн при подаче переменного напряжения 60,0 Гц и 10,0 кГц. (b) Каков среднеквадратичный ток на каждой частоте, если приложенное действующее напряжение составляет 120 В?

Стратегия

Индуктивное реактивное сопротивление находится непосредственно из выражения X _L = 2πf L . Как только X _L было найдено на каждой частоте, закон Ома, как указано в уравнении I = В / X _L, может быть использован для определения тока на каждой частоте.

Решение для (а)

Ввод частоты и индуктивности в уравнение X _L = 2πf L дает

X _L = 2πf L = 6,28 (60,0 / с) (3,00 мГн) = 1,13 Ом при 60 Гц.

Аналогично, на 10 кГц,

X _L = 2πf L = 6,28 (1,00 × 10 ⁴ / с) (3,00 мГн) = 188 Ом при 10 кГц.

Решение для (b)

Среднеквадратичное значение тока теперь определяется с использованием версии закона Ома в уравнении I = В / X _L, при условии, что приложенное действующее напряжение составляет 120 В.Для первой частоты это дает

[латекс] I = \ frac {V} {{X} _ {L}} = \ frac {120 \ text {V}} {1.13 \ text {} \ Omega} = 106 \ text {A at} 60 \ текст {Hz} \\ [/ latex].

Аналогично, на 10 кГц,

[латекс] I = \ frac {V} {{X} _ {L}} = \ frac {120 \ text {V}} {188 \ text {} \ Omega} = 0,637 \ text {A at} 10 \ текст {кГц} \\ [/ latex].

Обсуждение

Катушка индуктивности по-разному реагирует на двух разных частотах. На более высокой частоте его реактивное сопротивление велико, а ток невелик, что соответствует тому, как катушка индуктивности препятствует быстрому изменению. Таким образом, наиболее затруднены высокие частоты. Индукторы могут использоваться для фильтрации высоких частот; например, большую катушку индуктивности можно включить последовательно с системой воспроизведения звука или последовательно с вашим домашним компьютером, чтобы уменьшить высокочастотный звук, выводимый из ваших динамиков или высокочастотные всплески мощности на ваш компьютер.

Обратите внимание, что, хотя сопротивлением в рассматриваемой цепи можно пренебречь, переменный ток не очень велик, потому что индуктивное реактивное сопротивление препятствует его протеканию.С переменным током нет времени, чтобы ток стал слишком большим.

Конденсаторы и емкостное сопротивление

Рассмотрим конденсатор, подключенный непосредственно к источнику переменного напряжения, как показано на рисунке 2. Сопротивление такой цепи можно сделать настолько малым, что оно окажет незначительное влияние по сравнению с конденсатором, поэтому мы можем предположить, что сопротивление незначительно. Напряжение на конденсаторе и ток показаны на рисунке как функции времени.

Рисунок 2.(а) Источник переменного напряжения, включенный последовательно с конденсатором С, имеющим незначительное сопротивление. (б) График зависимости тока и напряжения на конденсаторе от времени.

График на Рисунке 2 начинается с максимального напряжения на конденсаторе. В этот момент ток равен нулю, потому что конденсатор полностью заряжен и останавливает поток. Затем напряжение падает, а ток становится отрицательным по мере разряда конденсатора. В точке а конденсатор полностью разряжен (на нем Q = 0 ) и напряжение на нем равно нулю.Ток остается отрицательным между точками a и b, вызывая обратное напряжение на конденсаторе. Это завершается в точке b, где ток равен нулю, а напряжение имеет самое отрицательное значение. Ток становится положительным после точки b, нейтрализуя заряд конденсатора и доводя напряжение до нуля в точке c, что позволяет току достичь своего максимума. Между точками c и d ток падает до нуля, когда напряжение достигает своего пика, и процесс начинает повторяться. На протяжении всего цикла напряжение соответствует тому, что делает ток, на четверть цикла:

Напряжение переменного тока в конденсаторе

Когда на конденсатор подается синусоидальное напряжение, оно следует за током на одну четверть цикла или на фазовый угол 90º.

Конденсатор влияет на ток, имея возможность полностью его отключить, когда он полностью заряжен. Поскольку применяется переменное напряжение, возникает среднеквадратичный ток, но он ограничивается конденсатором. Это считается эффективным сопротивлением конденсатора переменному току, поэтому среднеквадратичный ток I в цепи, содержащей только конденсатор C , определяется другой версией закона Ома как

[латекс] I = \ frac {V} {{X} _ {C}} \\ [/ latex],

, где В, — среднеквадратичное значение напряжения, а X _C определяется (Как и в случае с X _L, это выражение для X _C является результатом анализа цепи используя правила и исчисление Кирхгофа) равным

[латекс] {X} _ {C} = \ frac {1} {2 \ pi fC} \\ [/ latex],

, где X _C называется емкостным реактивным сопротивлением , потому что конденсатор препятствует прохождению тока. X _C имеет единицы измерения Ом (проверка оставлена в качестве упражнения для читателя). X _C обратно пропорциональна емкости C ; Чем больше конденсатор, тем больший заряд он может накапливать и тем больше может протекать ток. Она также обратно пропорциональна частоте f ; чем выше частота, тем меньше времени остается для полной зарядки конденсатора, и поэтому он меньше препятствует току.

Пример 2. Расчет емкостного реактивного сопротивления, а затем тока

(a) Рассчитайте емкостное реактивное сопротивление конденсатора 5,00 мФ при приложении переменного напряжения 60,0 Гц и 10,0 кГц. (b) Каков среднеквадратичный ток, если приложенное действующее напряжение составляет 120 В?

Стратегия

Емкостное реактивное сопротивление находится непосредственно из выражения в [latex] {X} _ {C} = \ frac {1} {2 \ pi fC} \\ [/ latex]. После того, как X _C было обнаружено на каждой частоте, закон Ома, сформулированный как I = В, / X _C, можно использовать для определения тока на каждой частоте.

Решение для (а)

Ввод частоты и емкости в [латекс] {X} _ {C} = \ frac {1} {2 \ pi fC} \\ [/ latex] дает

[латекс] \ begin {array} {lll} {X} _ {C} & = & \ frac {1} {2 \ pi fC} \\ & = & \ frac {1} {6.28 \ left (60.0 / \ text {s} \ right) \ left (5.00 \ text {} \ mu \ text {F} \ right)} = 531 \ text {} \ Omega \ text {at} 60 \ text {Hz} \ end {массив }\\[/латекс].

Аналогично, на 10 кГц,

[латекс] \ begin {array} {lll} {X} _ {C} & = & \ frac {1} {2 \ pi fC} = \ frac {1} {6.{4} / \ text {s} \ right) \ left (5,00 \ mu \ text {F} \ right)} \\ & = & 3,18 \ text {} \ Omega \ text {at} 10 \ text {кГц} \ end {array} \\ [/ latex].

Решение для (b)

Среднеквадратичное значение тока теперь определяется с использованием версии закона Ома в I = В / X _C, учитывая приложенное действующее напряжение 120 В. Для первой частоты это дает

[латекс] I = \ frac {V} {{X} _ {C}} = \ frac {120 \ text {V}} {531 \ text {} \ Omega} = 0,226 \ text {A at} 60 \ текст {Hz} \\ [/ latex].

Аналогично, на 10 кГц,

[латекс] I = \ frac {V} {{X} _ {C}} = \ frac {120 \ text {V}} {3.18 \ text {} \ Omega} = 3.37 \ text {A at} 10 \ текст {Hz} \\ [/ latex].

Обсуждение

Конденсатор очень по-разному реагирует на двух разных частотах, а индуктор реагирует прямо противоположным образом. На более высокой частоте его реактивное сопротивление мало, а ток велик. Конденсаторы одобряют изменения, а индукторы — противодействуют. Конденсаторы больше всего препятствуют низким частотам, так как низкая частота позволяет им успеть зарядиться и остановить ток.Конденсаторы можно использовать для фильтрации низких частот. Например, конденсатор, включенный последовательно с системой воспроизведения звука, избавляет ее от гула 60 Гц.

Хотя конденсатор в основном представляет собой разомкнутую цепь, в цепи с напряжением переменного тока, приложенным к конденсатору, присутствует среднеквадратичный ток. Это связано с тем, что напряжение постоянно меняет направление, заряжая и разряжая конденсатор. Если частота стремится к нулю (постоянный ток), X _C стремится к бесконечности, и ток равен нулю, когда конденсатор заряжен.На очень высоких частотах реактивное сопротивление конденсатора стремится к нулю — он имеет незначительное реактивное сопротивление и не препятствует току (действует как простой провод). Конденсаторы оказывают противоположное влияние на цепи переменного тока, чем индукторы .

Резисторы в цепи переменного тока

В качестве напоминания рассмотрим Рисунок 3, на котором показано напряжение переменного тока, приложенное к резистору, и график зависимости напряжения и тока от времени. Напряжение и ток равны точно в фазе в резисторе.Отсутствует частотная зависимость поведения простого сопротивления в цепи:

Рис. 3. (a) Источник переменного напряжения, включенный последовательно с резистором. (b) График зависимости тока и напряжения на резисторе от времени, показывающий, что они точно совпадают по фазе.

Напряжение переменного тока в резисторе

Когда на резистор подается синусоидальное напряжение, напряжение точно совпадает по фазе с током — они имеют фазовый угол 0 °.

Сводка раздела

Для катушек индуктивности в цепях переменного тока мы обнаруживаем, что когда на катушку подается синусоидальное напряжение, напряжение опережает ток на одну четверть цикла или на фазовый угол 90 °.
Противодействие катушки индуктивности изменению тока выражается как сопротивление переменному току.
Закон Ома для катушки индуктивности
[латекс] I = \ frac {V} {{X} _ {L}} \\ [/ latex],
, где В, — действующее значение напряжения на катушке индуктивности.
X _L определяется как индуктивное реактивное сопротивление, определяемое по формуле
[латекс] {X} _ {L} = 2 \ pi fL \\ [/ латекс],
с f частота источника переменного напряжения в герцах.
Индуктивное реактивное сопротивление X _L выражается в единицах Ом и имеет наибольшее значение на высоких частотах.
Для конденсаторов мы обнаруживаем, что когда на конденсатор подается синусоидальное напряжение, напряжение следует за током на одну четверть цикла или на фазовый угол 90º.
Поскольку конденсатор может останавливать ток при полной зарядке, он ограничивает ток и предлагает другую форму сопротивления переменному току; Закон Ома для конденсатора
[латекс] I = \ frac {V} {{X} _ {C}} \\ [/ latex],
, где В, — среднеквадратичное значение напряжения на конденсаторе.
X _C определяется как емкостное реактивное сопротивление, определяемое по формуле
[латекс] {X} _ {C} = \ frac {1} {2 \ pi fC} \\ [/ latex].
X _C имеет единицы измерения Ом и имеет наибольшее значение на низких частотах.

Концептуальные вопросы

1. Пресбиакузис — это возрастная потеря слуха, которая постепенно влияет на высокие частоты. Усилитель слухового аппарата предназначен для равномерного усиления всех частот. Чтобы отрегулировать его мощность на пресбиакузис, включите ли вы конденсатор последовательно или параллельно динамику слухового аппарата? Объяснять.

2. Будете ли вы использовать большую индуктивность или большую емкость последовательно с системой для фильтрации низких частот, таких как гул 100 Гц в звуковой системе? Объяснять.

3. Высокочастотный шум в сети переменного тока может повредить компьютеры. Использует ли съемный блок, предназначенный для предотвращения этого повреждения, большую индуктивность или большую емкость (последовательно с компьютером) для фильтрации таких высоких частот? Объяснять.

4. Зависит ли индуктивность от тока, частоты или и того, и другого? А как насчет индуктивного сопротивления?

5. Объясните, почему конденсатор на рисунке 4 (a) действует как фильтр низких частот между двумя цепями, тогда как конденсатор на рисунке 4 (b) действует как фильтр высоких частот.

Рисунок 4. Конденсаторы и катушки индуктивности. Конденсатор с высокой и низкой частотой.

6. Если конденсаторы на рис. 4 заменить катушками индуктивности, что будет действовать как фильтр низких частот, а какой — как фильтр высоких частот?

Задачи и упражнения

1. На какой частоте индуктор 30,0 мГн будет иметь реактивное сопротивление 100 Ом?

2. Какое значение индуктивности следует использовать, если требуется реактивное сопротивление 20,0 кОм при частоте 500 Гц?

3.Какую емкость следует использовать для получения реактивного сопротивления 2,00 МОм при 60,0 Гц?

4. На какой частоте конденсатор 80,0 мФ будет иметь реактивное сопротивление 0,250 Ом?

5. (a) Найдите ток через катушку индуктивности 0,500 H, подключенную к источнику переменного тока 60,0 Гц, 480 В. (б) Каким будет ток на частоте 100 кГц?

6. (a) Какой ток протекает, когда источник переменного тока 60,0 Гц, 480 В подключен к конденсатору 0,250 мкФ? (b) Каким будет ток на частоте 25,0 кГц?

7. А 20.Источник 0 кГц, 16,0 В, подключенный к катушке индуктивности, вырабатывает ток 2,00 А. Что такое индуктивность?

8. Источник 20,0 Гц, 16,0 В вырабатывает ток 2,00 мА при подключении к конденсатору. Какая емкость?

9. (a) Катушка индуктивности, предназначенная для фильтрации высокочастотного шума от энергии, подаваемой на персональный компьютер, включается последовательно с компьютером. Какая минимальная индуктивность должна обеспечивать реактивное сопротивление 2,00 кОм для шума 15,0 кГц? (б) Каково его реактивное сопротивление при 60?0 Гц?

10. Конденсатор на рисунке 4 (а) предназначен для фильтрации низкочастотных сигналов, препятствуя их передаче между цепями. (а) Какая емкость необходима для создания реактивного сопротивления 100 кОм при частоте 120 Гц? (б) Каким было бы его реактивное сопротивление на частоте 1,00 МГц? (c) Обсудите значение ваших ответов на (a) и (b).

11. Конденсатор на Рисунке 4 (b) будет фильтровать высокочастотные сигналы, замыкая их на землю / землю. (a) Какая емкость необходима для получения реактивного сопротивления [латекса] \ text {10.0 м \ Omega} [/ latex] для сигнала 5,00 кГц? (б) Каким будет его реактивное сопротивление при 3,00 Гц? (c) Обсудите значение ваших ответов на (a) и (b).

12. Необоснованные результаты При регистрации напряжений, обусловленных мозговой активностью (ЭЭГ), сигнал 10,0 мВ с частотой 0,500 Гц подается на конденсатор, создавая ток 100 мА. Сопротивление незначительное. а) Какая емкость? б) Что неразумного в этом результате? (c) Какое предположение или предпосылка ответственны?

13. Создайте свою проблему Рассмотрите возможность использования индуктора последовательно с компьютером, работающим от электричества 60 Гц. Постройте задачу, в которой вы вычисляете относительное снижение напряжения входящего высокочастотного шума по сравнению с напряжением 60 Гц. Среди вещей, которые следует учитывать, — допустимое последовательное реактивное сопротивление катушки индуктивности для мощности 60 Гц и вероятные частоты шума, проходящего через линии электропередач.

Глоссарий

индуктивное реактивное сопротивление:: противодействие катушки индуктивности изменению тока; рассчитывается по X _L = 2π fL

емкостное реактивное сопротивление:: сопротивление конденсатора изменению тока; рассчитывается по [latex] {X} _ {C} = \ frac {1} {2 \ pi fC} \\ [/ latex]

Избранные решения проблем и упражнения

1.531 Гц

3. 1,33 нФ

5. (а) 2,55 А (б) 1,53 мА

7. 63,7 мкГн

9. (а) 21,2 мГн (б) 8,00 Ом

Сопротивление, реактивное сопротивление и импеданс |

Х. Марк Бауэрс

Одним из моих рождественских подарков в декабре прошлого года была книга «Забытый гений Оливера Хевисайда — независимого представителя электротехники». Оливер Хевисайд был англичанином (1850–1925) и провел большую часть своей жизни, развивая свои теории в одиночку — настоящий гений-затворник.Я никогда не слышал о нем, но, похоже, он заслуживает гораздо большего признания, потому что он разработал многие теоретические концепции, которые мы сейчас принимаем как должное. В одной из своих ранее опубликованных статей Хевисайд переформулировал теорию электромагнетизма Максвелла (первоначально 12 уравнений, которые сбивали с толку большинство ученых его времени) в четыре уравнения Максвелла, теперь знакомые всем инженерам-электрикам. В той же статье, опубликованной в 1885 году, Хевисайд разработал формулу для потока энергии через электромагнитное поле, которая продемонстрировала, что электрическая энергия течет не по проводу, а скорее в пространстве рядом с ним.Большая часть работы Хевисайда собрана в пять томов, общий объем которых превышает 2500 страниц!

Цель этой и некоторых будущих статей — рассмотреть некоторые из этих основ, которым многих из нас учили на раннем этапе, но которые сейчас используются редко. Здесь я начну с сопротивления, реактивного сопротивления и импеданса. Кроме того, позвольте мне заявить очевидное: этот столбец позволит только поверхностно изучить эти концепции, потому что пространство не позволяет провести полный анализ.

Сопротивление

Сопротивление согласно определению закона Ома — это «характеристика цепи, ограничивающая ток.Сопротивление может возникать из-за дискретного компонента, такого как резистор, или может представлять совокупное сопротивление току в проводе (-ах), кабеле (-ах) или линии (-ях) передачи, включая коаксиальный кабель. Сопротивление, по определению, дает значение в омах при нулевой частоте (постоянный ток или постоянный ток).

См. Рис. 1, где показаны зависимости по закону Ома между током, напряжением, сопротивлением и мощностью.

При работе с частотами больше нуля (переменный ток или переменный ток) мы обнаруживаем, что одного сопротивления недостаточно для правильной количественной оценки общего сопротивления току, протекающему в цепи.Это приводит нас к реактивному сопротивлению.

Реактивное сопротивление

Реактивное сопротивление (X) определяется как «часть общего сопротивления току в цепи переменного тока из-за емкости, индуктивности или того и другого, и выражается в омах». Реактивное сопротивление имеет как величину, так и фазу и далее разделяется на индуктивную и емкостную составляющие.

Индуктивное сопротивление

Индуктивное реактивное сопротивление (X _L) — это часть общего реактивного сопротивления цепи, вносимая катушками, дросселями и обмотками трансформатора.Любое устройство, в котором провод намотан по кругу, является индуктором. Катушки индуктивности имеют тенденцию противодействовать любому изменению тока с течением времени. Это связано с тем, что ток, протекающий через катушку индуктивности, создает магнитное поле. В цепи постоянного тока напряженность и направление магнитного поля остаются постоянными. В результате ток легко протекает через индуктор, поскольку он выглядит просто как кусок провода. Магнитные поля по своей природе сопротивляются изменениям и противодействуют любому изменению тока. В цепи переменного тока магнитное поле должно постоянно меняться при изменении величины и направления тока.Таким образом, катушка индуктивности легче пропускает низкие частоты, чем более высокие частоты. Это сопротивление изменению протекания тока является индуктивным реактивным сопротивлением и определяется формулой:

, где X _L — индуктивное реактивное сопротивление в Ом, π — 3,14159 (…), F — частота в герцах, L — индуктивность в генри.

Емкостное реактивное сопротивление

Емкостное реактивное сопротивление (X _C) — это часть полного реактивного сопротивления цепи, обусловленная емкостью. Емкость возникает, когда две проводящие поверхности параллельны друг другу и разделены небольшим расстоянием с непроводящим веществом (диэлектриком).Примером может служить компонент дискретной схемы, называемый конденсатором. Конденсаторы являются устройствами ограничения напряжения, поскольку они имеют тенденцию противодействовать изменению напряжения с течением времени.

Когда на конденсатор подается постоянное напряжение, конденсатор потребляет ток и заряжается до значения приложенного напряжения. В цепи переменного тока, чем ниже частота приложенного напряжения, тем больше времени требуется конденсатору для зарядки, прежде чем напряжение изменит полярность и конденсатор начнет разряжаться. Следовательно, конденсатор тратит больше времени на полную зарядку и пропускает меньший ток, что приводит к меньшему протеканию тока (более высокому реактивному сопротивлению) на низких частотах.По мере увеличения частоты конденсатор переходит от зарядки к разрядке быстрее, позволяя протекать большему току (более низкое реактивное сопротивление). Поэтому емкостное реактивное сопротивление уменьшается с увеличением частоты. Фактическое значение X _C обратно пропорционально значению емкости и частоты, как показано в формуле:

, где X _C — емкостное сопротивление в омах, π — 3,14159 (…), F — частота в герцах, а C — емкость в фарадах.

Импеданс

Импеданс (Z) — это полное сопротивление току в цепи переменного тока, которая содержит сопротивление и реактивное сопротивление, и вот что интересно.Если бы цепь, например, была чисто индуктивной (без сопротивления), X _L представляла бы полное сопротивление протеканию тока. В этом примере Z и X _L идентичны и представлены значением некоторой величины с фазовым углом -90 ° (или тета). Если бы цепь была чисто емкостной, то было бы то же самое, за исключением того, что ɵ сдвигается на + 90 °. Фаза тока всегда указывается относительно напряжения (опережающая или запаздывающая). Сети переменного тока обычно содержат элементы сопротивления, индуктивности и емкости, и поэтому импеданс должен быть комплексным значением с величиной и фазой (вектор).Величину Z в цепи можно вычислить, как показано в следующих формулах.

Импеданс последовательной цепи рассчитывается по

, где X _T = X _L — X _C (X _T — реактивное сопротивление комбинированной цепи).

Импеданс параллельной цепи рассчитывается по

где

Теперь рассмотрим схему на Рисунке 2, которая содержит комбинацию сопротивления и емкости (без индуктивности, чтобы не усложнять задачу).Обратите внимание, что резистивные и реактивные токи не суммируются численно, как можно было бы ожидать; 1,0 ампер резистивный ток плюс 1,0 ампер реактивный ток равны 1,414 ампера полного тока. Это сбивает с толку, пока мы не рассмотрим рисунок 3.

На рисунке 3 изображен текущий треугольник в качестве наглядного пособия для иллюстрации величины и фазы. Он показывает соотношение между резистивным, реактивным и полным токами, протекающими в нашей примерной схеме. Если мы построим резистивный ток в 1 ампер по оси x (0 ° тета) и реактивный ток в 1 ампер по оси y (+ 90 ° тета), общий ток будет представлен длиной гипотенузы в 1.414 ампер с опережающим фазовым углом 45 °.

Теперь очевидно, что импеданс и мощность в этой цепи также должны быть комплексными (векторами), и это действительно так. Использование формулы для Z (показанной ранее) для параллельной цепи дает 70,7 Ом для этой RC-цепи, но не обеспечивает фазовый угол. Треугольник импеданса может быть построен аналогично рисунку 3 (не показан). Однако для Z этот процесс непрост, так как сначала мы должны вычислить эквивалентную последовательную схему, а затем построить треугольник.Когда мы это делаем, результат дает комплексное Z 70,7 Ом с тета + 45 °.

В треугольнике мощности (также не показан) по горизонтальной оси отложена истинная мощность (резистивная, 100 Вт), реактивная мощность по вертикальной оси (100 ВА), а гипотенуза равна кажущейся мощности 141,4 вольт-ампера. Кроме того, косинус фазового угла 45 ° равен 0,707, что равно коэффициенту мощности (pf) в этой цепи. Коэффициент мощности — важное понятие в распределительных сетях электроэнергетики и, на мой взгляд, более простой способ концептуализации и расчета реактивных токов и мощности.

Подробную статью, включающую треугольники импеданса и мощности, см. На странице загрузок моего веб-сайта www.cablesoftengineering.com. Мы продолжим этот обзор в моей следующей колонке, когда перейдем к параметрам, относящимся к коаксиальному кабелю.

–

Рисунок 1. График закона Ома

Рисунок 2. Схема RC

Рисунок 3. Текущий треугольник

H.Марк Бауэрс,
Cablesoft Engineering, Inc.

[email protected]

Марк — вице-президент по инженерным вопросам в Cablesoft Engineering, Inc. Он занимается телефонией с 1968 года и кабельной промышленностью с 1973 года. Его последняя должность в отрасли была вице-президентом по корпоративному проектированию в Warner Cable Communications в Дублине, штат Огайо. Образование Марка включает в себя Школу ядерной инженерии ВМС США и степени бакалавра и магистра в области управления технологиями. Марк является членом SCTE • ISBE, IEEE, а также старшим членом и лицензированным главным инженером по телекоммуникациям в iNARTE.

Основы реактивного сопротивления проводника и падения напряжения — Часть 1

Переменный ток создает индуктивность, емкость и связанные с ними свойства индуктивного и емкостного реактивного сопротивления. Несмотря на отсутствие потерь энергии, которые напрямую связаны с этими свойствами, необходимо подавать напряжение и ток, сдвинутые по фазе на 90 градусов, чтобы создаваемые магнитные и электрические поля могли поддерживаться. В результате произойдет небольшое увеличение потерь в проводнике I ² R.

Конечно, есть и другие реактивные сопротивления, не связанные с проводниками, которые составляют всего реактивного сопротивления системы , такие как реактивные сопротивления утечки оборудования и степень контроля коэффициента мощности. Мы ограничим наше обсуждение реактивным сопротивлением проводника.

Индуктивное емкостное сопротивление

Это мера способности индуктора, аналогично резистору противодействовать току . Это выражается следующим уравнением:

X _L = 2ϖfL (Уравнение 1)

Где X _L — индуктивное сопротивление (в омах), f — частота (в герцах), а L — индуктивность (в единицах Генри).

Обратите внимание, что индуктивное реактивное сопротивление прямо пропорционально частоте. С увеличением частоты увеличивается индуктивное реактивное сопротивление. Вы должны знать, что индуктивное реактивное сопротивление заставляет ток отставать от напряжения на 90 градусов.

Емкостное реактивное сопротивление — это мера способности конденсатора, аналогично способности резистора или катушки индуктивности, также противодействовать току. Это выражается следующим уравнением:

X _C = 1 ÷ (2ϖfC) (Уравнение 2)

Где X _C — емкостное реактивное сопротивление (в омах), а C — емкость (в фарадах).

Обратите внимание, что емкостное реактивное сопротивление обратно пропорционально частоте. Следовательно, с увеличением частоты емкостное реактивное сопротивление уменьшается. Следует также отметить, что емкостное реактивное сопротивление приведет к тому, что ток будет опережать напряжение на 90 градусов.

Геометрия проводника

Индуктивность и, как следствие, индуктивное реактивное сопротивление кабеля зависят от его геометрии и физического отношения к другим кабелям. Большинство инженеров и производителей кабелей используют очень сложные серии уравнений для расчета индуктивного сопротивления кабелей.Однако вы можете использовать следующее упрощенное уравнение:

X _L = 2ϖf × [(0,1404 × log ₁₀ (S ÷ r)) + 0,0153] × 10 ^-3 (Уравнение 3)

где X _L — индуктивное реактивное сопротивление (в омах на 100 футов относительно нейтрали), f — частота (в герцах), S — расстояние между центрами одножильных кабелей (в дюймах), а r — радиус одножильного кабеля (в дюймах).

Вы также можете использовать следующее уравнение:

X _L =.023 × [(log _e 2 × (S ÷ d)) + K] (Уравнение 4)

Где d — диаметр одиночного проводника (в дюймах), а K равно 0,25 для кабеля со скручиванием класса B.

Вы можете применить уравнение 3 или 4 к кабелям с разомкнутой оболочкой и к одножильным кабелям с произвольной прокладкой внутри дорожек качения.

Чтобы упростить вам задачу, производители предоставляют номограммы для расчета реактивного сопротивления, которые позволяют определять реактивные сопротивления в зависимости от толщины изоляции и размера проводника для проводников с различным шагом, образец которого показан на рисунке Рисунок (щелкните здесь, чтобы увидеть рисунок ).

(Номограмма — это графическое вычислительное устройство и двухмерная диаграмма, предназначенная для приблизительного графического вычисления функции. Обычно она имеет три шкалы: две шкалы представляют известные значения, а одна — шкала, на которой считывается результат. известные шкалы размещаются снаружи (т. е. шкала результатов находится в центре). Каждое известное значение расчета отмечается на внешних шкалах, и между каждой меткой проводится линия. Место пересечения линии и внутренней шкалы обозначается результат.Эти значения реактивного сопротивления получены из уравнения 3. В зависимости от конструкции проводника и / или кабеля вы должны применить поправочные коэффициенты, показанные в таблице , к любым полученным значениям реактивного сопротивления.

Поскольку результирующие значения реактивного сопротивления равны в омах относительно нейтрали , вам необходимо предпринять дополнительный шаг, чтобы найти межфазное реактивное сопротивление . Для трехфазной системы реактивное сопротивление фаза-фаза равно 1,732-кратному значению фаза-нейтраль. Для однофазной системы полное реактивное сопротивление в два раза превышает реактивное сопротивление фаза-нейтраль.

Примеры проблем с индуктивным реактивным сопротивлением

Задача 1 . Предположим, у вас есть 3-жильный кабель на 500 км / мил, 600 В с гальванизированной сблокированной броней на 3-фазной 3-проводной цепи фидера с частотой 60 Гц. Каждый проводник имеет изоляцию 65 мил. Какое межфазное реактивное сопротивление кабеля?

Поскольку у вас есть одиночные провода на 600 В в трехжильном кабеле, каждый отдельный провод имеет – разделительных лент, полупроводниковых лент, экранов или других покрытий. Таким образом, вы можете обратиться к таблицам реактивного сопротивления и напрямую использовать значение реактивного сопротивления, указанное в столбце «65 мил», для 500кмил, что равно 0.0251 Ом на 1000 футов до нейтрали.

Поскольку стальная броня многожильного кабеля с блокировкой похожа на магнитную связку, вам необходимо умножить это значение на соответствующий поправочный коэффициент, указанный в таблице, который в данном случае равен 1,122. Итак, X _L равно 0,0251 умноженному на 1,122, или 0,0282 Ом на 1000 футов до нейтрали.

Междуфазное реактивное сопротивление для этой цепи равно 0,0282 умножить на 1,732, или 0,0488 Ом на 1000 футов.

Задача 2 .Предположим, у вас есть фидер на 15 кВ, состоящий из трех, произвольной прокладки, 350 км / мил, 100% уровня изоляции, одиночных проводов, каждый с концентрическими экранами из жил в гальванизированном стальном кабелепроводе. У каждого дирижера есть внешний диаметр. 1,34 дюйма

Поскольку конструкция на 15 кВ включает разделительную ленту, полукруглую ленту, концентрическую скрученную проволоку и оболочку, вы не можете просто использовать толщину изоляции, обычно указываемую для 100% уровня изоляции, которая обычно составляет 175 мил. Чтобы быть более точным, вам необходимо рассчитать толщину изоляции, используя следующее уравнение:

Толщина = [(однопроводной О.D. Внешний диаметр неизолированного провода 2) ÷ 2]

Итак, вы знаете, дирижер О.Д. составляет 1,34 дюйма. Из литературы по проводам и кабелям вы можете найти, что 37-жильный неизолированный провод класса B, 350 тыс. Куб. М имеет номинальный внешний диаметр. 0,681 дюйма. Таким образом, толщина изоляции равна 1,34 дюйма минус 0,681 дюйма, разделенному на 2, или 0,33 дюйма (330 мил). Согласно таблицам реактивного сопротивления, значение реактивного сопротивления составляет 0,0373.

Поскольку проводники находятся в магнитопроводе, необходимо умножить это значение на 1,50 (увеличение на 50%).Следовательно, индуктивное сопротивление нейтрали при 6 Гц в омах на 100 футов (X _L) равно 0,0373 умножить на 1,50 или 0,0560. Междуфазное реактивное сопротивление составляет 0,0560 умножить на 1,732, или 0,097 Ом на 1000 футов.

В следующем месяце мы поговорим о том, как рассчитать индуктивное сопротивление в случаях, когда кабели не соприкасаются, но имеют определенную геометрическую конфигурацию.

1.5: Реактивное сопротивление и импеданс — Engineering LibreTexts

В отличие от резистора, напряжение и ток не будут совпадать по фазе для идеального конденсатора или идеальной катушки индуктивности.Для конденсатора ток опережает напряжение на конденсаторе на 90 градусов. Напомним, что напряжение на конденсаторе не может измениться мгновенно, \ (i = C \, dv / dt \). Для индуктора напряжение опережает ток на 90 градусов. Точно так же ток через индуктор не может мгновенно измениться из-за \ (v = L \, di / dt \). Хотя идеальные конденсаторы и катушки индуктивности не обладают сопротивлением, напряжение действительно реагирует на ток. Неудивительно, что мы называем это характеристическим реактивным сопротивлением и обозначаем его буквой \ (X \).{\ circ} \), или, что более удобно, мы просто добавляем \ (- j \), как в \ (X_C = −j75 \ Omega \).

Корпус для индуктора аналогичен и оставлен в качестве упражнения. Индуктивное реактивное сопротивление \ (X_L \) можно найти по формуле:

\ [X_L = + j 2 \ pi f L \ label {1.9} \]

Примером может быть \ (X_L = j68 \ Omega \). Как уже говорилось, хотя сопротивление не может быть добавлено непосредственно к реактивному сопротивлению, реактивные сопротивления можно складывать вместе, если мы прислушиваемся к знакам. Например, если у нас есть емкостное реактивное сопротивление \ (- j60 \ Omega \) последовательно с индуктивным реактивным сопротивлением \ (j100 \ Omega \), результатом будет \ (j40 \ Omega \).Это связано с тем, что эти два элемента не совпадают по фазе на 180 градусов друг с другом, поэтому они частично отменяются. Помните, всегда добавляйте или вычитайте одинаковые предметы: реальное (сопротивление) к реальному и мнимое (реактивное сопротивление) к мнимому.

Уравнения \ ref {1.8} и \ ref {1.9} примечательны тем, что реактивное сопротивление является не только функцией емкости или индуктивности, но также функцией частоты. Реактивное сопротивление катушки индуктивности прямо пропорционально частоте, а реактивное сопротивление конденсатора обратно пропорционально частоте.Омические вариации резистора \ (20 \ Omega \), конденсатора 500 \ (\ mu \) F и катушки индуктивности 500 \ (\ mu \) H по частоте показаны на рисунке \ (\ PageIndex {1} \). .

Мы можем видеть, что значение сопротивления не меняется с частотой, в то время как индуктивное реактивное сопротивление увеличивается с частотой, а емкостное реактивное сопротивление уменьшается.

Рисунок \ (\ PageIndex {1} \): Сопротивление и реактивное сопротивление в зависимости от частоты (линейная ось).

Линейная шкала частоты затрудняет отображение изменения конденсатора.Если это построить снова, но с использованием логарифмической шкалы частот, как на рисунке \ (\ PageIndex {2} \), симметрия станет очевидной.

Рисунок \ (\ PageIndex {2} \): Сопротивление и реактивное сопротивление в зависимости от частоты (логарифмическая ось).

Влияние размера и частоты конденсатора показано на рисунке \ (\ PageIndex {3} \) с использованием логарифмической оси частот: чем меньше конденсатор, тем больше емкостное реактивное сопротивление на любой конкретной частоте.

Рисунок \ (\ PageIndex {3} \): Изменение емкостного реактивного сопротивления в зависимости от емкости и частоты.

Аналогичным образом влияние размера и частоты индуктора показано на рисунке \ (\ PageIndex {4} \) с использованием линейной оси частот: чем больше индуктор, тем больше индуктивное реактивное сопротивление на любой заданной частоте.

Рисунок \ (\ PageIndex {4} \): Изменение индуктивного реактивного сопротивления в зависимости от индуктивности и частоты.

Стоит отметить, что графики на рисунках \ (\ PageIndex {3} \) и \ (\ PageIndex {4} \) предназначены для идеальных компонентов. В действительности все компоненты проявляют некоторые резистивные, емкостные и индуктивные эффекты из-за своей конструкции.Например, в конечном итоге индуктивные и резистивные эффекты приведут к тому, что кривые емкостного реактивного сопротивления на рисунке \ (\ PageIndex {3} \) начнут расти на высоких частотах. Точно так же резистивные и емкостные эффекты заставят кривые Рис. \ (\ PageIndex {4} \) сглаживаться на очень низких и очень высоких частотах.

Следует запомнить интересное наблюдение: конденсаторы и катушки индуктивности немного похожи на химеру. То есть, для разных источников они выглядят как разные вещи, смешанные одновременно.Было бы неправильно думать, скажем, о конкретной катушке индуктивности как о «таком большом количестве Ом». Если исходный сигнал состоит из нескольких синусоидальных волн, таких как прямоугольная волна или музыкальный сигнал, индуктор «выглядит» как разное омическое значение для каждой из различных частотных составляющих одновременно. Это важная концепция, и мы можем воспользоваться ее преимуществами, например, при разработке схем фильтров.

1.5.1: Импеданс

Теперь мы подошли к импедансу. Импеданс представляет собой смесь сопротивления и реактивного сопротивления и обозначается \ (Z \).{\ circ} \ Omega \), то есть величина 600 Ом, которая включает сопротивление и индуктивное реактивное сопротивление (это должно быть индуктивное реактивное сопротивление, а не емкостное реактивное сопротивление, поскольку знак угла положительный).

Чтобы завершить эту систему, у нас есть прием и прием. Восприимчивость, \ (S \), является обратной величиной реактивного сопротивления. Полная проводимость, \ (Y \), является обратной величиной импеданса. Они аналогичны соотношению между проводимостью и сопротивлением и удобны для комбинаций параллельных цепей.

Пример \ (\ PageIndex {1} \)

Определите реактивные сопротивления катушки индуктивности 1 мГн и конденсатора 2 \ (\ mu \) F на синусоидальную волну 2 кГц. Повторите для частоты 50 кГц.

Используйте уравнения \ ref {1.8} и \ ref {1.9}. Для конденсатора на 2 кГц имеем:

\ [X_C = — j \ frac {1} {2 \ pi f C} \ nonumber \]

\ [X_C = — j \ frac {1} {2 \ pi 1 кГц 2 \ mu F} \ nonumber \]

\ [X_C = — j 79.6 \ Omega \ nonumber \]

Для второго источника 50 кГц в 25 раз больше исходного, а емкостное реактивное сопротивление обратно пропорционально частоте.Следовательно, \ (X_C \) в 25 раз меньше, или \ (- j3.18 \ Omega \).

Для индуктора на 2 кГц,

\ [X_L = + j 2 \ pi f L \ nonumber \]

\ [X_L = + j 2 \ pi 2 кГц 1 мГн \ nonumber \]

\ [X L = + j 12,57 \ Omega \ nonumber \]

Индуктивное реактивное сопротивление прямо пропорционально частоте. Таким образом, увеличение f в 25 раз увеличивает \ (X_L \) в том же раз, что приводит к \ (j314.2 \ Omega \).

Пример \ (\ PageIndex {2} \)

Определите чувствительность катушки индуктивности, реактивное сопротивление которой равно \ (j400 \ Omega \).Кроме того, если этот индуктор включен последовательно с резистором \ (1000 \ Омега \), определите результирующий импеданс в полярной форме, а также полную проводимость.

Подвеска — величина, обратная реактивному сопротивлению.

\ [S_L = \ frac {1} {X_L} \ nonumber \]

\ [S_L = \ frac {1} {j 400 \ Omega} \ nonumber \]

\ [S_L = — j 2.5 \ text {миллисименс} \ nonumber \]

Импеданс \ (Z \) — это векторная сумма, или \ (1000 + j400 \ Omega \). {- 1} \ left (\ frac {400} {1000} \ right) \ nonumber \]

\ [\ theta = 21.{\ circ} \ mu S \).

ОМSLAWFORAC

OHMSLAWFORAC ЗАКОН ОМА ДЛЯ ЦЕПЕЙ ПЕРЕМЕННОГО ТОКА
Правила и уравнения для цепей постоянного тока применяются к цепям переменного тока только тогда, когда цепи содержат только сопротивление, как в случае с лампами и обогревом. элементы. Чтобы использовать действующие значения напряжения и тока в переменном токе цепи, влияние индуктивности и емкости с сопротивлением должно быть на рассмотрении.
Комбинированный эффект сопротивления, индуктивного реактивного сопротивления и емкостной реактивное сопротивление составляет полное противодействие протеканию тока в цепи переменного тока.Это полное сопротивление называется импедансом и обозначается буквой «Z.» Единицей измерения импеданса является ом.
Цепи переменного тока серии
Если цепь переменного тока состоит только из сопротивления, значение импеданса совпадает с сопротивлением, а закон Ома для переменного тока Схема I = E / Z точно такая же, как и для цепи постоянного тока. На рисунке 8-188 последовательная цепь, содержащая лампу с сопротивлением 11 Ом, подключенную через источник иллюстрирован.Чтобы узнать, сколько тока будет протекать, если 110 вольт приложен постоянный ток и сколько тока будет протекать, если приложить переменный ток 110 вольт, решены следующие примеры:
Когда цепи переменного тока содержат сопротивление или индуктивность или емкости, полное сопротивление Z не совпадает с сопротивлением R. Импеданс цепи — это полное сопротивление цепи потоку. тока.В цепи переменного тока это противостояние состоит из сопротивления и реактивное сопротивление, индуктивное или емкостное, либо их элементы.
Сопротивление и реактивное сопротивление нельзя сложить напрямую, но их можно учитывать. как две силы, действующие под прямым углом друг к другу. Таким образом, соотношение между сопротивлением, реактивным сопротивлением и импедансом можно проиллюстрировать правой треугольник, как показано на рисунке 8-189.

Поскольку эти величины могут быть связаны со сторонами прямоугольного треугольника, формула для нахождения импеданса или полного противодействия току в цепи переменного тока можно найти, используя закон прямоугольных треугольников.Этот Теорема, называемая теоремой Пифагора, применима к любому прямоугольному треугольнику. В нем говорится, что квадрат гипотенузы равен сумме квадраты двух других сторон. Таким образом, ценность любой стороны права треугольник можно найти, если известны две другие стороны. Если цепь переменного тока содержит сопротивление и индуктивность, как показано на рисунке 8-190, соотношение между сторонами можно записать как: Квадратный корень из обеих частей уравнения дает
Эту формулу можно использовать для определения импеданса, когда значения индуктивного реактивного сопротивления и сопротивления.Его можно изменить на решить для импеданса в цепях, содержащих емкостное реактивное сопротивление и сопротивление заменив XC в формуле на XL. В схемах, содержащих сопротивление с индуктивным и емкостным сопротивлением, реактивные сопротивления можно комбинировать, но поскольку их эффекты в схеме прямо противоположны, они объединяются вычитанием: X = XL — XC или X = XC — XL (меньшее число всегда вычитается из большего). В рисунок 8-190, последовательная цепь, состоящая из сопротивления и индуктивности последовательно подключен к источнику 110 вольт на 60 циклов в секунду.Резистивным элементом является лампа с сопротивлением 6 Ом, а индуктивный элемент представляет собой катушку с индуктивностью 0,021 Генри. Какие это значение импеданса и тока через лампу и катушка?
Решение:
Сначала вычисляется индуктивное реактивное сопротивление катушки:
XL = 2 ш x ш x д
XL = 6,28 x 60 x 0,021
XL = индуктивное сопротивление 8 Ом.
Затем вычисляется полное сопротивление:
Z = квадратный корень из R2 + XL2
Z = квадратный корень из 62 + 82
Z = квадратный корень из 36 + 64
Z = квадратный корень из 100
Z = сопротивление 10 Ом.
Тогда текущий поток,
Падение напряжения на сопротивлении (ER) равно
ER = I x R
ER = 11 x 6 = 66 вольт.
Падение напряжения на индуктивности (EXL) равно
EXL = I x XL
EXL = 11 x 8 = 88 вольт.
Сумма двух напряжений больше приложенного напряжения. Этот возникает из-за того, что два напряжения не совпадают по фазе и, как таковые, представляют максимальное напряжение.Если напряжение в цепи измеряется по вольтметру будет примерно 110 вольт, приложенное напряжение. Это можно доказать уравнением
На рисунке 8-191 показана последовательная цепь, в которой конденсатор 200 мФ подключен последовательно с лампой на 10 Ом. Какая ценность импеданса, тока и падения напряжения на лампе?

Решение:
Сначала емкость изменяется с микрофарад на фарады.С 1 миллион микрофарад равен 1 фараду, тогда
Чтобы найти сопротивление,
Чтобы найти ток,
Падение напряжения на лампе (ER) составляет
ER = 6,7 x 10
ER = 67 вольт
Падение напряжения на конденсаторе (EXC) равно
Сумма этих двух напряжений не равна приложенному напряжению, так как ток опережает напряжение.Чтобы найти приложенное напряжение, формула ET = используется квадратный корень из (ER) 2 + (EXC) 2.
Когда цепь содержит сопротивление, индуктивность и емкость, уравнение
Z = квадратный корень из R2 + (XL — XC) 2
используется для определения импеданса.
Пример:
Каково полное сопротивление последовательной цепи (рисунок 8-192), состоящей из конденсатора с реактивным сопротивлением 7 Ом, катушки индуктивности с реактивным сопротивлением 10 Ом, а резистор сопротивлением 4 Ом?
Решение:
Предполагая, что реактивное сопротивление конденсатора составляет 10 Ом, а реактивное сопротивление индуктивности 7 Ом, то XC больше XL.Таким образом,

Параллельные цепи переменного тока
Методы, используемые при решении задач параллельных цепей переменного тока в основном такие же, как и те, которые используются для последовательных цепей переменного тока. Не в фазе напряжения и токи можно сложить, используя закон прямоугольных треугольников, но при решении схемных проблем токи через ветви добавлено, так как падение напряжения на разных ветвях одинаковое и равны приложенному напряжению.На рисунке 8-193 параллельная цепь переменного тока схематически показан содержащий индуктивность и сопротивление. Электрический ток протекающая через индуктивность IL составляет 0,0584 ампера, а протекающий ток через сопротивление составляет 0,11 ампер. Каков общий ток в схема?
Решение:
Поскольку индуктивное реактивное сопротивление приводит к тому, что напряжение опережает ток, общее ток, который содержит составляющую индуктивного тока, отстает от приложенного Напряжение.Если на графике нанесены ток и напряжения, угол между два, называемые фазовым углом, показывают, насколько ток отстает от Напряжение.
На рисунке 8-194 генератор на 110 В подключен к нагрузке, состоящей из емкости 2 и параллельное сопротивление 10000 Ом. Какое значение импеданса и общий ток?
Решение:
Сначала найдите емкостное сопротивление цепи:
Замена 2 на фарады и ввод значений в приведенную формулу:
Чтобы найти импеданс, формула импеданса используется в последовательной цепи переменного тока. должны быть изменены, чтобы соответствовать параллельной цепи:
Чтобы найти ток через емкость:
Чтобы найти ток, протекающий через сопротивление:
Чтобы найти ток, протекающий через сопротивление:
Чтобы найти полный ток в цепи:
Резонанс
Было показано, что оба индуктивных реактивного сопротивления (XL = 2 f L) и емкостное сопротивление
— функции частоты переменного тока.Уменьшение частоты уменьшает омическое значение индуктивного сопротивления, но уменьшает частота увеличивает емкостное реактивное сопротивление. На определенной частоте известная как резонансная частота, реактивные эффекты конденсатора и индуктор будет равен. Поскольку эти эффекты противоположны одному другой, они отменит, оставив только омическое значение сопротивления противодействовать протеканию тока в цепи. Если значение сопротивления невелико или состоит только из сопротивления в проводниках, величина тока расход может стать очень большим.
В цепи, где катушка индуктивности и конденсатор включены последовательно, а частота — это резонансная частота или частота резонанса, контур называется «резонансным» и называется последовательным резонансным контуром. Обозначение резонансной частоты — Fn.
Если на частоте резонанса индуктивное сопротивление равно к емкостному сопротивлению, то
Разделив обе стороны на 2 fL,
Извлечение квадратного корня из обеих частей дает
Где Fn — резонансная частота в циклах в секунду, C — емкость. в фарадах, а L — индуктивность в генри.По этой формуле частота при котором конденсатор и катушка индуктивности будут резонансными, можно определить.
Чтобы найти индуктивное сопротивление цепи, используйте
Формулу импеданса, используемую в последовательной цепи переменного тока, необходимо изменить на поместите параллельную схему.
Для поиска параллельных цепей индуктивных и емкостных реакторов. использовать
Для поиска параллельных сетей с емкостным сопротивлением и индуктивностью использовать:
Поскольку на резонансной частоте XL отменяет XC, ток может стать равным очень большой, в зависимости от величины сопротивления.В таких случаях напряжение падение на катушке индуктивности или конденсаторе часто будет выше, чем применяемое Напряжение.
В параллельном резонансном контуре (рисунок 8-195) реактивные сопротивления равные и равные токи будут течь через катушку и конденсатор.
Поскольку индуктивное реактивное сопротивление приводит к тому, что ток через катушку отставание напряжения на 90 °, а емкостное реактивное сопротивление вызывает ток через конденсатор, чтобы провести напряжение на 90 °, два тока сдвинуты по фазе на 180 °.Эффект подавления таких токов будет означают, что ток не будет течь от генератора и параллельной комбинации индуктивности и конденсатора будет выглядеть как бесконечный импеданс. На практике такая схема невозможна, так как некоторое значение сопротивления всегда присутствует, и параллельный контур, иногда называемый контуром резервуара, действует как очень высокий импеданс. Его еще называют антирезонансной схемой, поскольку его действие в цепи противоположно действию последовательного резонансного цепь, в которой сопротивление очень низкое.
Питание в цепях переменного тока
В цепи постоянного тока мощность определяется по уравнению P = EI (ватт равен вольты на амперы). Таким образом, если в цепи протекает ток 1 ампер при напряжение 200 вольт, мощность 200 ватт. Произведение вольт а амперы — это истинная мощность в цепи.
В цепи переменного тока вольтметр показывает эффективное напряжение и амперметр показывает действующий ток.Произведение этих двух чтений называется кажущейся мощностью. Только когда цепь переменного тока состоит из чистых сопротивление — полная мощность, равная истинной мощности (рисунок 8-196).
Когда в цепи присутствует емкость или индуктивность, ток и напряжение не точно совпадают по фазе, и истинная мощность меньше, чем полная мощность. Истинная мощность определяется показаниями ваттметра. В отношение истинной мощности к полной мощности называется коэффициентом мощности. и обычно выражается в процентах.В форме уравнения соотношение является:

Проблема:
Двигатель переменного тока 220 вольт отнимает от сети 50 ампер, но ваттметр в строке видно, что на двигатель потребляется всего 9350 Вт. Что такое полная мощность и коэффициент мощности?
Решение:
Влияние частоты на индуктивное сопротивление
Влияние частоты на индуктивное сопротивление
В а.c. цепь индуктивности создает индуктивное реактивное сопротивление, которое вызывает ток отставать по напряжению на 90 градусов. Поскольку индуктор «реагирует» на изменение ток, он известен как реактивный компонент. Противодействие, которое индуктор представляет переменный ток называется индуктивным реактивным сопротивлением (X _L). Это противодействие вызвано индуктор «реагирует» на изменение тока переменного тока. источник. Оба индуктивность и частота определяют величину этого реактивного сопротивления.Эти отношения определяется формулой:
Как показано в уравнении, любое увеличение частоты или «f» вызовет соответствующее увеличение индуктивного сопротивления, или «X _L». Следовательно, ИНДУКТИВНАЯ РЕАКТИВНОСТЬ НАПРЯМУЮ ОТ ЧАСТОТЫ. Как видите, чем выше частота, тем больше индуктивное сопротивление; чем ниже частота, тем меньше индуктивное сопротивление для данной катушки индуктивности.Эта взаимосвязь проиллюстрирована на рисунке 1-2. Возрастающие значения X _L нанесены на график с точки зрения увеличения частоты. Запуск в нижнем левом углу с нулевой частотой индуктивное сопротивление равно нулю. Как частота увеличивается (чтение справа), индуктивное реактивное сопротивление отображается равным увеличение прямо пропорционально.
Рисунок 1-2. — Влияние частоты на индуктивное сопротивление.
Влияние частоты на емкостное сопротивление
В а.c. В цепи конденсатор создает реактивное сопротивление, которое заставляет ток напряжение на 90 градусов. Поскольку конденсатор «реагирует» на изменение напряжения, он известен как реактивный компонент. Сопротивление конденсатора переменному току. называется емкостное реактивное сопротивление (X _C). Противодействие вызвано конденсатором «реагируя» на изменение напряжения переменного тока. источник. Формула для емкостное сопротивление:
В отличие от индуктивного реактивного сопротивления, это уравнение показывает, что ЕМКОСТЬ РЕАКТИВНОСТЬ ЗАМЕНЯЕТСЯ ОТ ЧАСТОТЫ.Когда f = 0, X _C бесконечно и уменьшается с увеличением частоты. То есть чем ниже частота, тем больше емкостное реактивное сопротивление; чем выше частота, тем меньше реактивное сопротивление для данного конденсатор.
Как показано на рисунке 1-3, влияние емкости противоположно влиянию индуктивности. Помните, что емкость заставляет ток опережать напряжение на 90 градусов, в то время как индуктивность заставляет ток отставать от напряжения на 90 градусов.
Рисунок 1-3. — Влияние частоты на емкостное сопротивление.
Влияние частоты на сопротивление
В выражении для индуктивного реактивного сопротивления X _L = 2pfL, а в выражении для емкостного реактивного сопротивления —
оба содержат «f» (частота). Любое изменение частоты изменяет реактивное сопротивление. компонентов схемы, как уже объяснялось.Пока ничего не сказано о влияние частоты на сопротивление. В соотношении по закону Ома, например, R = E / I нет «f» задействовано. Таким образом, для всех практических целей изменение частоты не влияет на сопротивление цепи. Если 60-герцовый переменный ток напряжение вызывает 20 миллиампер тока в резистивной цепи, то такое же напряжение на частоте 2000 Гц, для Например, все равно будет течь 20 миллиампер.
ПРИМЕЧАНИЕ: Помните, что полная оппозиция к.c. называется импедансом (Z). Импеданс сочетание индуктивного реактивного сопротивления (X _L), емкостного реактивного сопротивления (X _C), и сопротивление (R). При работе с переменным током цепей, импеданс — это коэффициент с что вы в конечном итоге будете обеспокоены. Но, как вам только что было показано, сопротивление (R) не зависит от частоты. Таким образом, оставшаяся часть обсуждения переменного тока схемы будут касаться только реактивного сопротивления катушек индуктивности и конденсаторов и будут игнорировать сопротивление.
г. Цепи, содержащие как индуктивное, так и емкостное сопротивление
г. схемы, содержащие как индуктор, так и конденсатор, имеют интересные характеристики из-за противоположного воздействия L и C. X _L и X _C можно рассматривать как реакторы, сдвинутые по фазе на 180 градусов. Как показано на рисунке 1-2, вектор для X _L должен быть нанесен над базовой линией; вектор для X _C, рисунок 1-3 должен быть нанесен ниже базовой линии.В последовательной схеме эффективный реактивное сопротивление, или то, что называется РЕЗУЛЬТАТИВНОЙ РЕАКТИВНОСТЬЮ, — это разница между индивидуальные реактивные сопротивления. Результирующее реактивное сопротивление в виде уравнения:
X = X _L — X _C
Предположим, что переменный ток Схема содержит X _L на 300 Ом и X _C на 250 Ом. Результирующее реактивное сопротивление:
X = X _L — X _C = 300 — 250 = 50 Ом (индуктивное)
В некоторых случаях X _C может быть больше, чем X _L.Если X _L = 1200 Ом и X _C = 4000 Ом, разница составляет: X = X _L — X _C = 1200 — 4000 = -2800 Ом (емкостный). Сумма отмечена знаком (+ или -) большее число (коэффициент).
Q.1 Какова взаимосвязь между частотой и значениями (a) X _L, (b) X _C и (c) R?
Q.2 В переменном токе схема, содержащая как индуктор, так и конденсатор, какой термин используется для разницы между индивидуальными реактивными сопротивлениями?
Определение емкостного реактивного сопротивления и частоты

Емкостное реактивное сопротивление — это противодействие току, протекающему через конденсатор переменного тока.Емкостное реактивное сопротивление обратно пропорционально подаваемой частоте. Изменению напряжения противодействуют конденсаторы с потоком электронов на пластину конденсатора. Поток электронов прямо пропорционален скорости изменения напряжения на пластине конденсатора, когда он заряжается и разряжается. В резисторе противодействие протеканию тока является фактическим сопротивлением; реактивное сопротивление — это противодействие протеканию тока в конденсаторе.
Реактивное сопротивление измеряется в Ом, как и сопротивление, но ему присвоен символ, чтобы отличить его от значения сопротивления.Реактивное сопротивление конденсатора определяется как емкостное реактивное сопротивление, которое измеряется в Ом.
Заряд и разряд конденсатора прямо пропорциональны скорости изменения напряжения на них. Когда напряжение изменяется быстрее, в цепь будет течь больше тока. Протекание тока будет меньше, если изменение напряжения будет медленнее.
Выражение для емкостного реактивного сопротивления имеет следующий вид:

Здесь емкостное реактивное сопротивление в Омах равно, частота в герцах равно, а емкость в Фарадах i.
Емкостное реактивное сопротивление обратно пропорционально частоте и емкости цепи. Увеличение любого из них приведет к увеличению емкостного реактивного сопротивления. Когда частота приближается к нулевому значению, емкостное реактивное сопротивление увеличивается до бесконечности. Емкостное реактивное сопротивление высокое на низкой частоте и низкое на высокой.
Емкостное реактивное сопротивление также может быть определено угловой частотой.
Выражение для емкостного реактивного сопротивления через угловую частоту имеет следующий вид:

Здесь угловая частота равна.
Емкостное реактивное сопротивление обратно пропорционально угловой частоте. Увеличение угловой частоты приведет к уменьшению емкостного реактивного сопротивления.
Вопрос:
Какая связь между частотой и емкостным реактивным сопротивлением?
Ответ:
Определение:
Мера сопротивления конденсатора переменному току (AC) определяется как емкостное реактивное сопротивление. Обозначается символом. Оно измеряется в Ом как сопротивление.Реактивное сопротивление более сложное, поскольку оно зависит от частоты сигнала, проходящего через конденсатор.
Выражение для емкостного реактивного сопротивления имеет следующий вид:

Здесь емкостное реактивное сопротивление в Омах равно, частота в герцах равно, а емкость в Фарадах равна.
Емкостное реактивное сопротивление обратно пропорционально частоте и емкости цепи. Увеличение любого из них приведет к увеличению емкостного реактивного сопротивления. Когда частота приближается к нулевому значению, емкостное реактивное сопротивление увеличивается до бесконечности.Емкостное реактивное сопротивление высокое на низкой частоте и низкое на высокой. Емкостное реактивное сопротивление будет меньше на любой частоте для конденсатора с большей емкостью. Конденсаторы будут иметь бесконечно высокие значения при нулевой частоте. Емкостное реактивное сопротивление падает до низкого уровня, если частота в больших конденсаторах ниже. Конденсаторы большего размера предпочтительны для приложений на низкой частоте. Конденсатор действует как разомкнутая цепь для более низкой частоты. Он действует как замкнутая цепь для более высокой частоты.
Вопрос:
Почему индуктивное или емкостное сопротивление включено в импеданс как мнимая составляющая?
Ответ:
Поведение основных компонентов, таких как резистор, катушка индуктивности и конденсатор, определяется следующим образом:
Для резистора напряжение и ток всегда совпадают по фазе. Работа, совершаемая резистором, является реальной, он преобразует электрическую энергию в тепловую. Для индуктора ток отстает от напряжения на
. В индукторе противоположное магнитное поле создается с изменением тока, которое генерирует ток в противоположном направлении по отношению к исходному току, что заставляет ток отставать от напряжения.Противодействием изменению тока является сопротивление катушки индуктивности переменному току. Для конденсатора напряжение отстает от тока на. Это требуется для тока, необходимого для создания электростатического разделения заряда на пластинах. Противодействием изменению напряжения является сопротивление конденсатора переменному току.
Из-за «полевой постройки» возникли задержки. Резисторы не создают поля. Работы конденсатора и индуктора ненастоящие.
Разность фаз не работает со скалярным представлением.Для представления их в векторном представлении и векторной записи угол обозначается буквой «j».
Для индуктивной цепи напряжение задается следующим образом:

Это означает, что напряжение изменилось в направлении против часовой стрелки.
Для емкостной цепи напряжение задается следующим образом:

Это означает, что напряжение изменилось по часовой стрелке относительно тока.
Вопрос:
Что такое индуктивное и емкостное сопротивление?
Ответ:
Противодействие току, протекающему через катушку индуктивности, называется индуктивным реактивным сопротивлением.Это зависит от угловой частоты и индуктивности.
Противодействие току, протекающему через конденсатор, называется емкостным реактивным сопротивлением. Это зависит от угловой частоты и емкости.
Емкостное реактивное сопротивление — это мера сопротивления конденсатора переменному току. Реактивное сопротивление сложнее сопротивления, потому что значение реактивного сопротивления зависит от частоты электрического сигнала, проходящего через конденсатор.
Индуктивное реактивное сопротивление — это сопротивление протеканию переменного тока в катушке индуктивности.
Индуктивность — это пассивный электрический компонент. Он состоит из мотка проволоки. Он использует взаимосвязь между магнетизмом и электричеством. Это приводит к прохождению электрического тока через катушку.
Выражение для индуктивного реактивного сопротивления выглядит следующим образом:

Здесь — индуктивное реактивное сопротивление, — частота и — индуктивность.
Индуктивность — это пассивный электрический компонент. Он состоит из мотка проволоки. Он использует взаимосвязь между магнетизмом и электричеством.Это приводит к прохождению электрического тока через катушку.
Если внутренним сопротивлением индуктора можно пренебречь, он будет чистым индуктором.

Что такое реактивное емкостное сопротивление

Формула для расчета емкостного сопротивления

Особенности емкостного сопротивления в электрических цепях

Где применяется емкостное сопротивление в электротехнике

Сравнение емкостного и индуктивного сопротивлений

Расчет полного сопротивления цепи с емкостью

Влияние емкостного сопротивления на мощность в цепи

Способы изменения емкостного сопротивления

Практическое применение емкостного сопротивления

1. Фильтры высоких и низких частот

2. Компенсация реактивной мощности

3. Запуск однофазных двигателей

Заключение

Reactance

http://en.wikipedia.org Wikipedia, свободная энциклопедия

Физическое значение

Ёмкостное реактивное сопротивление

Индуктивное реактивное сопротивление

Фазные соотношения

Реактивное емкостное сопротивление — Большая Энциклопедия Нефти и Газа, статья, страница 1

Реактивное емкостное сопротивление

Электрическое реактивное сопротивление — Electrical reactance

Сравнение с сопротивлением

Емкостное реактивное сопротивление

Индуктивное реактивное сопротивление

Импеданс

Фазовое соотношение

Смотрите также

Рекомендации

внешняя ссылка

Активное и реактивное сопротивление

Основные различия между активным и реактивным сопротивлением

Индуктивное сопротивление

Емкостное сопротивление

Компенсация реактивной мощности

Глава 17. Резонансные цепи . Введение в электронику

Активное емкостное индуктивное реактивное полное сопротивления

Активное сопротивление

Ёмкостное сопротивление

Индуктивное сопротивление

Закон Ома для цепей переменного тока

Введение

Схема индуктивности переменного тока

Векторная диаграмма индуктора переменного тока

Индуктивное сопротивление от частоты

Питание от сети переменного тока серии LR

Цепь переменного тока серии LR

Треугольник сопротивления

Силовой треугольник индуктора переменного тока

Что такое активное сопротивление. Активное, реактивное и полное сопротивление цепи

Формулы

Шаги

Реактивное сопротивление, индуктивное и емкостное | Физика

Цели обучения

Катушки индуктивности и индуктивное сопротивление

Пример 1. Расчет индуктивного сопротивления, а затем тока

Конденсаторы и емкостное сопротивление

Пример 2. Расчет емкостного реактивного сопротивления, а затем тока

Резисторы в цепи переменного тока

Сводка раздела

Концептуальные вопросы

Задачи и упражнения

Глоссарий

Избранные решения проблем и упражнения

Сопротивление, реактивное сопротивление и импеданс |

Основы реактивного сопротивления проводника и падения напряжения — Часть 1

Индуктивное емкостное сопротивление

Геометрия проводника

Примеры проблем с индуктивным реактивным сопротивлением

1.5: Реактивное сопротивление и импеданс — Engineering LibreTexts

1.5.1: Импеданс

ОМSLAWFORAC

Влияние частоты на индуктивное сопротивление

Определение емкостного реактивного сопротивления и частоты

Похожие записи

Особенности питания кормящей мамы: что можно и нельзя есть при грудном вскармливании

Новорожденный какает слизью: причины появления слизи в кале грудничка

Гемангиома у новорожденных: причины, виды, лечение и профилактика

Добавить комментарий Отменить ответ