Как посчитать сопротивление провода. Расчет сопротивления провода: формулы, факторы влияния и практическое применение

Как рассчитать сопротивление электрического провода. Какие факторы влияют на сопротивление проводника. Для чего нужно знать сопротивление провода. Как измерить сопротивление на практике.

Что такое электрическое сопротивление провода

Электрическое сопротивление — это свойство проводника препятствовать прохождению электрического тока. Оно измеряется в омах (Ом) и обозначается буквой R. Любой металлический провод обладает определенным сопротивлением, величина которого зависит от нескольких факторов.

Формула для расчета сопротивления провода

Сопротивление провода можно рассчитать по следующей формуле:

R = ρ * L / S

где:

• R — сопротивление провода (Ом)
• ρ (ро) — удельное сопротивление материала провода (Ом*мм²/м)
• L — длина провода (м)
• S — площадь поперечного сечения провода (мм²)

Основные факторы, влияющие на сопротивление провода

На величину сопротивления провода влияют следующие ключевые факторы:

1. Материал провода

Удельное сопротивление ρ зависит от материала, из которого изготовлен провод. Например:

• Медь: ρ = 0,0175 Ом*мм²/м
• Алюминий: ρ = 0,028 Ом*мм²/м
• Сталь: ρ = 0,13 Ом*мм²/м

2. Длина провода

Чем длиннее провод, тем больше его сопротивление. Зависимость прямо пропорциональная — при увеличении длины в 2 раза, сопротивление также возрастает в 2 раза.

3. Площадь поперечного сечения

Чем больше сечение провода, тем меньше его сопротивление. Зависимость обратно пропорциональная — при увеличении площади сечения в 2 раза, сопротивление уменьшается в 2 раза.

4. Температура

С повышением температуры сопротивление металлических проводов увеличивается. Это связано с усилением колебаний атомов в кристаллической решетке металла, что создает дополнительные препятствия для движения электронов.

Как измерить сопротивление провода на практике

Измерить сопротивление провода можно с помощью специальных приборов:

1. Мультиметр (тестер) — самый распространенный прибор для измерения сопротивления. Нужно выбрать режим измерения сопротивления (Ω) и подключить щупы к концам провода.
2. Омметр — прибор, предназначенный только для измерения сопротивления.
3. Микроомметр — используется для измерения очень малых сопротивлений (менее 1 Ом).

При измерении важно помнить:

• Измеряемый участок цепи должен быть обесточен
• Провод должен быть отключен от других элементов схемы
• Для точного измерения нужно учитывать температуру окружающей среды

Практическое применение расчета сопротивления провода

Знание сопротивления провода необходимо во многих практических задачах:

Расчет падения напряжения

Падение напряжения на участке цепи можно рассчитать по закону Ома: U = I * R, где I — сила тока. Зная сопротивление провода, можно определить потери напряжения на линии электропередачи.

Выбор сечения провода

При проектировании электрических сетей важно правильно подобрать сечение провода, чтобы минимизировать потери энергии. Чем меньше сопротивление, тем меньше потери.

Расчет нагрева провода

Мощность тепловых потерь в проводе равна P = I² * R. Зная сопротивление, можно рассчитать, насколько сильно будет нагреваться провод при определенном токе.

Сопротивление проводов в различных электрических схемах

При расчете сложных электрических цепей важно учитывать, как соединены проводники:

Последовательное соединение

При последовательном соединении проводов их сопротивления складываются: R = R1 + R2 + R3 + …

Параллельное соединение

При параллельном соединении общее сопротивление рассчитывается по формуле:

1/R = 1/R1 + 1/R2 + 1/R3 + …

Общее сопротивление всегда меньше сопротивления самого маленького резистора в цепи.

Как уменьшить сопротивление провода

Если необходимо снизить сопротивление провода, можно использовать следующие методы:

1. Увеличить площадь поперечного сечения провода
2. Уменьшить длину провода
3. Использовать материал с меньшим удельным сопротивлением (например, заменить алюминий на медь)
4. Охлаждать провод для снижения температуры
5. Использовать параллельное соединение нескольких проводов

Сопротивление провода в цепях переменного тока

В цепях переменного тока помимо активного сопротивления провода нужно учитывать реактивное сопротивление:

• Индуктивное сопротивление XL = 2πfL, где f — частота тока, L — индуктивность провода
• Емкостное сопротивление XC = 1/(2πfC), где C — емкость между проводами

Полное сопротивление провода в цепи переменного тока (импеданс) рассчитывается по формуле:

Z = √(R² + (XL — XC)²)

где R — активное сопротивление провода.

Влияние сопротивления провода на эффективность электрических устройств

Сопротивление проводов может существенно влиять на работу электрических приборов и систем:

• В системах электроснабжения высокое сопротивление проводов приводит к потерям энергии и падению напряжения у потребителей
• В аудиосистемах сопротивление кабелей может искажать звуковой сигнал
• В компьютерных сетях высокое сопротивление кабелей ограничивает скорость передачи данных
• В силовой электронике сопротивление проводников влияет на КПД устройств

Поэтому при проектировании электрических систем важно правильно рассчитывать и учитывать сопротивление всех проводников.

Сопротивление проволоки, как узнать электрическое сопротивление провода, шнура, кабеля. « ЭлектроХобби

В области электротехники, электроники понятие электрического сопротивления является фундаментальным. Оно относится к основным электрическим величинам, которое повсеместно используется как в теории, так и на практике. Любой электрический проводник имеет свое определенное сопротивление, которое во многом зависит от таких основных факторов: материала проводника, его размер (длина и сечение), температура. Помимо этого стоит учитывать, что сопротивление может быть активным и реактивным.

Электрическое сопротивление провода можно вычислить по следующей простой формуле, в которой присутствуют такие величины: удельное сопротивление материала, из которого сделан провод, его сечение и длина:

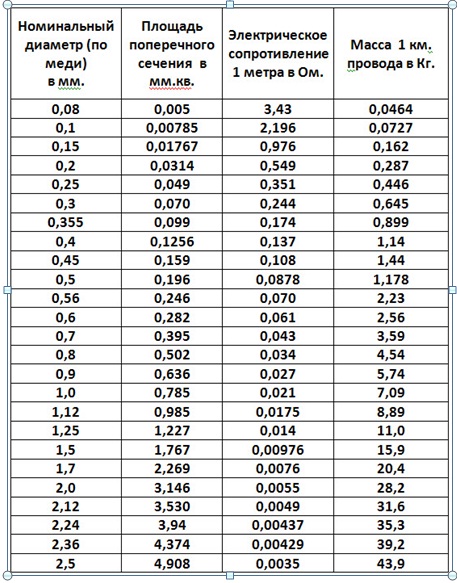
Есть такое понятие как удельное сопротивление материала (вещества). У каждого проводника, сделанного из того или иного материала свое удельное сопротивление. Это обуславливается особенностями внутренней структуры (на атомном уровне) самого вещества. То есть, у каждого отдельно взятого материала (проводника тока) при одних и тех же размерах и условиях будет различное сопротивление. Это удельное сопротивление выражается как Ом на метр (при сечении 1 миллиметр квадратный). Удельное сопротивление каждого отдельного материала проводника нужно смотреть в специальной таблице (в справочниках, интернете).

Нахождением сопротивления по формуле имеет смысл при теоретических расчетах, на практике же намного проще воспользоваться обычным измерителем (электронным тестером, мультиметром, омметром). Стоит учитывать, что измерения электрического сопротивления должны производиться при отключенном электропитании схемы, участка цепи, провода. Если на схеме (измеряемом проводе) будет присутствовать хоть какое-то напряжение, то в лучшем случае это повлечет за собой неверные результаты измерения, ну, а в худшем может выйти из строя и сам измерительный прибор.

Само же измерение электрического сопротивления мультиметром сводится к его включению и выбору на нём определённого диапазона измерения (Ом, килоОм, мегаОм). Наиболее малым сопротивлением является Ом. 1000 Ом, это 1 кОм (килоом). 1000 000 Ом или 1000 кОм, это 1 мОм (мегаом). В обычных проводах (шнуры питания, небольшие куски кабеля и проводов) сопротивление будет примерно до десятков Ом. Сопротивление от десятков и до тысяч Ом уже можно встретить к примеру у обмоток трансформатора, катушек электромагнита, звонка и т.д. Ну, а мегаомным сопротивлением уже обладает электрическая изоляция кабелей и проводов.

В электротехнике в большинстве случаев в роли электрического проводника используют медь. Именно она имеет достаточно хорошую электрическую проводимость при относительно низкой цене (если сравнивать с серебром, золотом). В линиях электропередач и на отдельных участках бытовой электросети также широко применяют алюминий, хотя его электрическая проводимость хуже, чем у меди, зато стоит меньше. И медь и алюминий (если говорить о сопротивлении небольших участков электрической сети, кабеля и шнуры питания) имеет электрическое сопротивление в пределах единиц и десятков Ом. Ну, естественно, чем длиннее и тоньше будет проводник, тем сопротивление будет увеличиваться (допустим у трансформаторной первичной обмотки на 220 вольт сопротивление уже от десятков до нескольких тысяч Ом, в зависимости от мощности транса).

Для чего может, собственно, пригодится известная величина электрического сопротивления? Наиболее используемой в электрике и электронике является формула закона Ома. Она гласит, что сила тока равна электрическое напряжение разделенное на сопротивление. Следовательно, зная любые две величины из трех (тока, напряжения и сопротивления) можно всегда найти одну неизвестную. К примеру, нам нужно узнать, какой ток будет протекать по спирали нагревателя. Нам известно, что этот нагреватель рассчитан на напряжение 220 вольт. Берём мультиметр и измеряем его сопротивление (допустим это 100 Ом). Используя формулу закона Ома мы легко вычислим силу тока: 220 вольт / 100 Ом = 2,2 ампера.

P.S. При нахождении электрического сопротивления через формулу учитывайте, что реальные величины могут слегка отличаться от теоретических (по причине материальных факторов, условий окружающей среды и т. д.). При нахождении сопротивления путем простого измерения учитывайте, что измерительные приборы имеют свою погрешность (хоть она и достаточно мала, но всё же есть).

Решение задач на расчет сопротивления | 8 класс

Содержание

Сила тока в цепи определяется электрическим зарядом, проходящим через поперечное сечение проводника за единицу времени: $I = \frac{q}{t}$.

Электрическое напряжение — это еще одна физическая величина, характеризующая электрическое поле. Она равна отношению работы тока на данном участке к электрическому заряду, прошедшему по этому участку: $U = \frac{A}{q}$.

Электрическое сопротивление — величина, зависящая от свойств проводника. На значение сопротивления не влияет ни значение силы тока в проводнике, ни значение напряжения на его концах. Его можно рассчитать по формуле $R = \frac{\rho l}{S}$, где $\rho$ — удельное сопротивление проводника,  $l$ — длина проводника, $S$ — площадь его поперечного сечения. Значение удельного сопротивления для определенного вещества можно посмотреть в таблице 1 в уроке «Расчет сопротивления проводника. 2}{м}$

$U — ?$

Решение:

Если в условии задачи сказано, что проводник включен в цепь аккумулятора, это означает, что напряжение на полюсах аккумулятора будет равно напряжению на концах проволоки.

Почему? Взгляните на такую электрическую цепь (рисунок 1). Она состоит только из проводника и аккумулятора.

Рисунок 1. Проводник, подключенный к аккумулятору

Если мы захотим измерить напряжение на полюсах аккумулятора c помощью вольтметра, то параллельно подключим его в эту цепь (рисунок 2). А если захотим измерить напряжение на концах проводника? Мы подключим вольтметр точно так же. Получается, что вольтметр подключен параллельно одновременно и к источнику тока, и к проводнику. Поэтому напряжение на концах проводника — это то же самое напряжение на полюсах аккумулятора.

Рисунок 2. Измерение напряжения вольтметром на полюсах источника тока и на концах проводника

Запишем закон Ома:
$I = \frac{U}{R}$.

Выразим из него напряжение, которое нужно найти:
$U = IR$. 2} = \frac{3.44 \space Ом}{0.8} = 4.3 \space Ом$.

Теперь мы можем рассчитать напряжение:
$U = 0.3 \space А \cdot 4.3 \space Ом = 1.29 \space В \approx 1.3 \space В$.

Ответ: $U \approx 1.3 \space В$.

Упражнения

Упражнение №1

Длина одного провода $20 \space см$, другого — $1.6 \space м$. Площадь сечения и материал проводов одинаковы. У какого провода сопротивление больше и во сколько раз?

Обратите внимание, что если материал проводников один и тот же, то одинаковы и значения удельных сопротивлений $\rho$ для этих проводников.

Дано:
$l_1 = 20 \space см$
$l_2 = 1.6 \space м$
$S_1 = S_2 = S$
$\rho_1 = \rho_2 = \rho$

СИ:
$l_1 = 0.2 \space м$

$\frac{R_2}{R_1} — ?$

Показать решение и ответ

Скрыть

Решение:
Сопротивление проводника рассчитывается по формуле $R = \frac{\rho \cdot l}{S}$.

Сопротивление первого провода:
$R_1 = \frac{\rho_1 l_1}{S_1} = \frac{\rho l_1}{S}$. 2} = \frac{0.015 \space Ом}{0.02} = 0.75 \space Ом$.

Теперь мы можем рассчитать напряжение на концах проводника:
$U = 0.25 \space А \cdot 0.75 \space Ом \approx 0.2 \space В$.

Ответ: $U \approx 0.2 \space В$.

Объяснение сопротивления проволоки

Новости и блоги

Резистивная проволока — это проволока из сплава, обладающая определенным уровнем сопротивления электрическому току.

Это сопротивление можно использовать по многим причинам, в том числе для контроля величины тока в цепи, а также в качестве нагревательного элемента. Сопротивление провода прохождению электрического тока может генерировать тепло, которое используется в различных продуктах, таких как обогреватели, тостеры и фены.

Прочие бытовые применения провода сопротивления, кроме того, включают пульты дистанционного управления, лампочки и зарядные устройства для телефонов.

Факторы, влияющие на сопротивление

На сопротивление провода влияют четыре основных фактора; все это следует учитывать при расчете общего сопротивления провода. Факторы сопротивления включают:

Материал – естественное сопротивление материала влияет на общее сопротивление. Например, медь обладает большей проводимостью, чем сталь, поэтому имеет низкое сопротивление электрическому току.

Длина – более длинные провода обладают повышенным сопротивлением электрическому току по сравнению с более короткими проводами; это известно как пропорциональное отношение, поскольку сопротивление увеличивается с увеличением длины. Это связано с тем, что электроны, несущие электрический ток по проводу, сталкиваются с большим количеством ионов, чем длиннее провод, что затрудняет протекание тока.

Толщина – толщина или калибр, также известный как диаметр или поперечное сечение провода, имеет обратно пропорциональную зависимость от сопротивления. Чем тоньше провод, тем большее сопротивление он имеет; это связано с тем, что в более тонком проводе меньше электронов для передачи электрического тока.

Температура – нагревание провода также увеличивает сопротивление провода.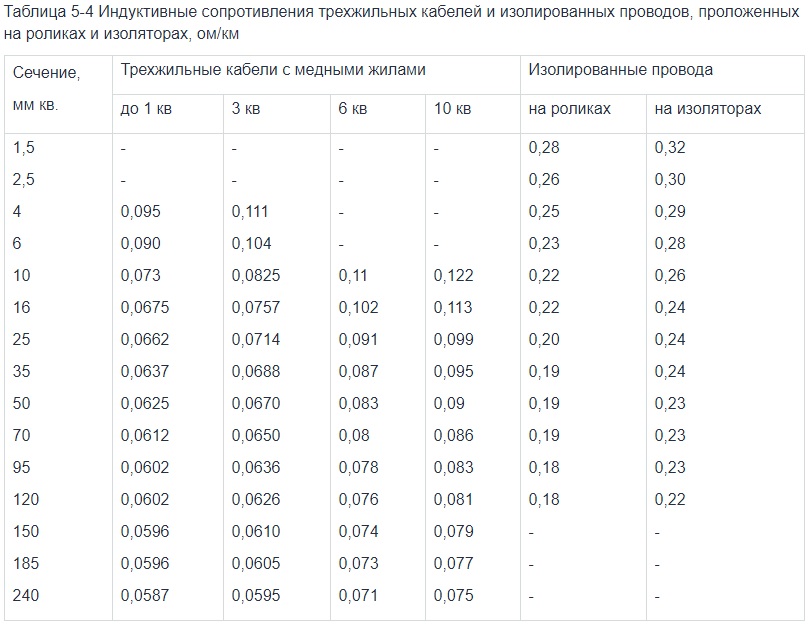 Более горячая проволока будет иметь повышенную вибрацию, из-за чего электронам будет труднее переносить электрический ток, не прерываясь атомами.

Типы проводов сопротивления

Типы проводов сопротивления относятся к комбинациям металлов в проводе, образующих сплав. Наиболее распространенным типом проволоки сопротивления является сплав никеля и хрома, который используется в системах отопления. Другие распространенные типы включают константан (сплав меди и никеля), который легко паяется, и сплав меди, марганца и никеля.

Компания Scott Precision Wire предлагает несколько типов резистивных проводов, соответствующих всем промышленным требованиям. Наш ассортимент проводов сопротивления включает в себя:

Медь Магний: 0,2%; высокопрочный сплав
Медные и никелевые сплавы: создан для нагрева при низких и средних температурах, с хорошей коррозионной стойкостью
Cromaloy 1: для хорошей коррозионной стойкости и применения при высоких температурах
Cromaloy 5: хорошая стойкость к оксидному образованию и подходит для различных применений от промышленных печей до бытовых тостеров
Cromaloy A: отлично подходит для применения при высоких температурах с хорошей стойкостью к серной коррозии


Cumin 11:  сплав на основе меди с марганцем и никелем, подходящий для цепей постоянного тока
Cupronic 2. 5:  сплав на основе меди с низким удельным сопротивлением, подходящий для применения при низких температурах
Kutherm 3 & 10: проволока сопротивления на основе меди с повышенной коррозионной стойкостью и термостойкостью
Никель 205: подходит для применения при высоких температурах
Никель Железные сплавы: саморегулирующаяся нагревательная проволока для повышенного температурного контроля
Нержавеющая сталь 304L: Низкотемпературная резистивная проволока с высокой прочностью

Для получения дополнительной информации о типах резистивной проволоки Scott Precision Wire обратитесь к нашим файлам для загрузки технических данных или обратитесь непосредственно к эксперту из нашей команды.

Сопротивление провода и падение напряжения

Полли Френдшух, инструктор отдела строительства и обслуживания электрооборудования Технологического колледжа Данвуди, объясняет, как рассчитать сопротивление провода и падение напряжения в электрической цепи в этих двух видеороликах. Полли учит принципу электрического сопротивления и факторам, которые могут влиять на сопротивление, шаг за шагом, приводя примеры.

В первом видео вы бы поняли расчет формулы сопротивления,

Сопротивление (Ом) = (K x L) / CM , где;

1. K (постоянный ток)
   1. Температура: удельное сопротивление металла увеличивается с повышением температуры медь) ; K=21,2 (для алюминия)
       
2. L (Длина провода в футах)
   1. Удельное сопротивление увеличивается с увеличением расстояния
       
3. CM (Circular Mil, размер поперечного сечения провода) 908G: Американский размер провода ) определяет значение СМ.
4. Чем меньше значение CM, тем тоньше проволока и выше номер калибра.
5. Пожалуйста, посмотрите на таблицу внизу этой статьи.