Как рассчитать индуктивность: Расчет катушки индуктивности | Онлайн калькулятор

Катушка индуктивности. Описание, характеристики, формула расчета

Главная » Справочник » Катушка индуктивности. Описание, характеристики, формула расчета

Катушка индуктивности является пассивным компонентом электронных схем, основное предназначение которой является сохранение энергии в виде магнитного поля. Свойство катушки индуктивности чем-то схоже с конденсатором, который хранит энергию в виде электрического поля.

Индуктивность (измеряется в Генри) — это эффект возникновения магнитного поля вокруг проводника с током. Ток, протекающий через катушку индуктивности, создает магнитное поле, которое имеет связь с электродвижущей силой (ЭДС) оказывающее противодействие приложенному напряжению.

Возникающая противодействующая сила (ЭДС) противостоит изменению переменного напряжения и силе тока в катушке индуктивности. Это свойство индуктивной катушки называется индуктивным сопротивлением. Следует отметить, что индуктивное сопротивление находится в противофазе к емкостному реактивному сопротивлению конденсатора в цепи переменного тока. Путем увеличения числа витков можно повысить индуктивность самой катушки.

Накопленная энергия в индуктивности

Как известно магнитное поле обладает энергией. Аналогично тому, как в полностью заряженном конденсаторе существует запас электрической энергии, в индуктивной катушке, по обмотке которой течет ток, тоже существует запас — только уже магнитной энергии.

Энергия, запасенная в катушке индуктивности равна затраченной энергии необходимой для обеспечения протекания тока I в противодействии ЭДС. Величина запасенной энергии в индуктивности можно рассчитать по следующей формуле:

где L — индуктивность, I — ток, протекающий через катушку индуктивности.

Гидравлическая модель

Работу катушки индуктивности можно сравнить с работой гидротурбины в потоке воды. Поток воды, направленный сквозь еще не раскрученную турбину, будет ощущать сопротивление до того момента, пока турбина полностью не раскрутится.

Далее турбина, имеющая определенную степень инерции, вращаясь в равномерном потоке, практически не оказывая влияния на скорость течения воды. В случае же если данный поток резко остановить, то турбина по инерции все еще будет вращаться, создавая движение воды. И чем выше инерция данной турбины, тем больше она будет оказывать сопротивление изменению потока.

Также и индуктивная катушка сопротивляется изменению электрического тока протекающего через неё.

Индуктивность в электрических цепях

В то время как конденсатор оказывает сопротивление изменению переменного напряжения, индуктивность же сопротивляется переменному тока. Идеальная индуктивность не будет оказывать сопротивление постоянному току, однако, в реальности все индуктивные катушки сами по себе обладают определенным сопротивлением.

Блок питания 0…30В/3A

Набор для сборки регулируемого блока питания…

Подробнее

В целом, отношение между изменяющимися во времени напряжением V(t) проходящим через катушку с индуктивностью L и изменяющимся во времени током I(t), проходящим через нее можно представить в виде дифференциального уравнения следующего вида:

Когда переменный синусоидальной ток (АС) протекает через катушку индуктивности, возникает синусоидальное переменное напряжение (ЭДС).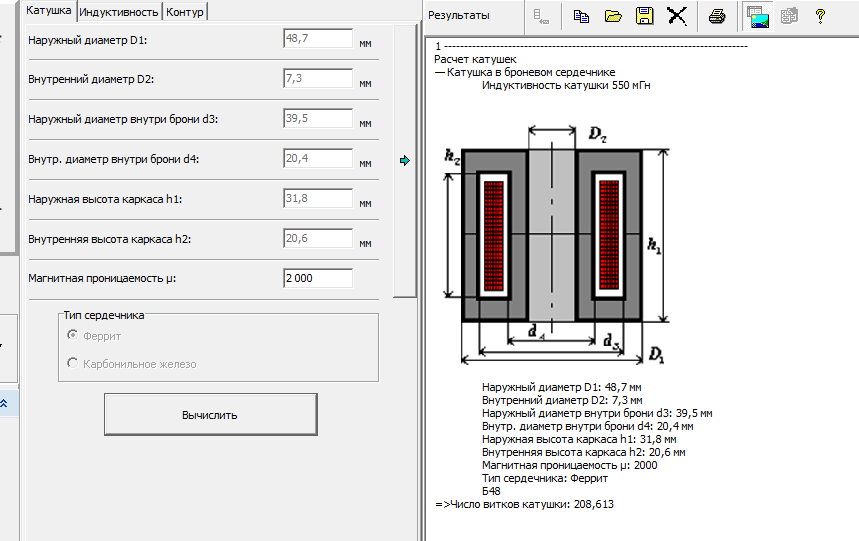 Амплитуда ЭДС зависит от амплитуды тока и частоте синусоиды, которую можно выразить следующим уравнением:

где ω является угловой частотой резонансной частоты F:

Причем, фаза тока отстает от напряжения на 90 градусов. В конденсаторе же все наоборот, там ток опережает напряжение на 90 градусов. Когда индуктивная катушка соединена с конденсатором (последовательно либо параллельно), то образуется LC цепь, работающая на определенной резонансной частоте.

 Индуктивное сопротивление ХL определяется по формуле:

где ХL — индуктивное сопротивление, ω — угловая частота, F — частота в герцах, и L индуктивность в генри.

Индуктивное сопротивление — это положительная составляющая импеданса. Оно измеряется в омах. Импеданс катушки индуктивности (индуктивное сопротивление) вычисляется по формуле:

Схемы соединения катушек индуктивностей

Параллельное соединение индуктивностей

Напряжение на каждой из катушек индуктивностей, соединенных параллельно, одинаково. Эквивалентную (общую) индуктивность параллельно соединенных катушек можно определить по формуле:

Последовательное соединение индуктивностей

Ток, протекающий через катушки индуктивности соединенных последовательно, одинаков, но напряжение на каждой катушке индуктивности отличается. Сумма разностей потенциалов (напряжений) равна общему напряжению. Общая индуктивность последовательно соединенных катушек можно высчитать по формуле:

Эти уравнения справедливы при условии, что магнитное поле каждой из катушек не оказывает влияние на соседние катушки.

Добротность катушки индуктивности

На практике катушка индуктивности имеет последовательное сопротивление, созданное медной обмоткой самой катушки. Это последовательное сопротивление преобразует протекающий через катушку электрический ток  в тепло, что приводит к потере качества индукции, то есть добротности. Добротность является отношением индуктивности к сопротивлению.

Добротность катушки индуктивности может быть найдена через следующую формулу:

 где R является собственным сопротивлением обмотки.

Катушка индуктивности. Формула индуктивности

Базовая формула индуктивности катушки:

• L = индуктивность в генри
• μ 0 = проницаемость свободного пространства = 4π × 10 -7 Гн / м
• μ г = относительная проницаемость материала сердечника
• N = число витков
• A = Площадь поперечного сечения катушки в квадратных метрах (м 2 )
• l = длина катушки в метрах (м)

Индуктивность прямого проводника:

• L = индуктивность в нГн
• l = длина проводника
• d = диаметр проводника в тех же единицах, что и l

Индуктивность катушки с воздушным сердечником:

• L = индуктивность в мкГн
• r = внешний радиус катушки
• l = длина катушки
• N = число витков

Индуктивность многослойной катушки с воздушным сердечником:

• L = индуктивность в мкГн
• r = средний радиус катушки
• l = длина катушки
• N = число витков
• d = глубина катушки

Индуктивность плоской катушки:

• L = индуктивность в мкГн
• r = средний радиус катушки
• N = число витков
• d = глубина катушки

Конструкция катушки индуктивности

Катушка индуктивности представляет собой обмотку из проводящего материала, как правило, медной проволоки, намотанной вокруг либо железосодержащего сердечника, либо вообще без сердечника.

Применение в качестве сердечника материалов с высокой магнитной проницаемостью, более высокой чем воздух, способствует удержанию магнитного поля вблизи катушки, тем самым увеличивая ее индуктивность. Индуктивные катушки бывают разных форм и размеров.

Большинство изготавливаются путем намотки эмалированного медного провода поверх ферритового сердечника.

Некоторые индуктивные катушки имеют регулируемый сердечник, при помощи которого обеспечивается изменение индуктивности.

Миниатюрные катушки могут быть вытравлены непосредственно на печатной плате в виде спирали. Индуктивности с малым значением могут быть расположены в микросхемах с использованием тех же технологических процессов, которые используются при создании транзисторов.

Применение катушек индуктивности

Индуктивности широко используются в аналоговых схемах и схемах обработки сигналов. Они в сочетании с конденсаторами и другими радиокомпонентами образуют специальные схемы, которые могут усилить или отфильтровать сигналы определенной частоты.

Катушки индуктивности получили широкое применение начиная от больших катушек индуктивности, таких как дроссели в источниках питания, которые в сочетании с конденсаторами фильтра устраняют остаточные помехи и другие колебания на выходе источника питания, и до столь малых индуктивностей, которые располагаются внутри интегральных микросхем.

Две (или более) катушки индуктивности, которые соединены единым магнитным потоком, образуют трансформатор, являющимся основным компонентом схем работающих с электрической сетью электроснабжения. Эффективность трансформатора возрастает с увеличением частоты напряжения.

По этой причине, в самолетах используется переменное напряжение с частотой 400 герц вместо обычных 50 или 60 герц, что в свою очередь позволяет значительно сэкономить на массе используемых трансформаторов в электроснабжении самолета.

Так же индуктивности используются в качестве устройства для хранения энергии в импульсных стабилизаторах напряжения, в высоковольтных электрических системах передачи электроэнергии для преднамеренного снижения системного напряжения или ограничения ток короткого замыкания.

Счетчик Гейгера

Высококачественный счетчик Гейгера с высокой чувствительностью для обнаружен…

Подробнее

Как рассчитать индуктивность катушек с замкнутыми сердечниками?

Всем доброго времени суток. В прошлых статьях (часть 1, часть 2, часть 3) я рассказал о расчёте индуктивности индуктивных элементов без сердечников. Однако их применение ограниченно, вследствие, больших габаритных размеров. Поэтому для увеличения индуктивности и уменьшения размеров и улучшения других показателей индуктивные элементы устанавливают на сердечники из материалов с различными магнитными свойствами.

Для сборки радиоэлектронного устройства можно преобрески DIY KIT набор по ссылке.

Особенности расчёта индуктивных элементов с сердечниками

В отличие от индуктивных элементов без сердечников, при расчёте которых учитывался магнитный поток пронизывающий только проводник с током, магнитный поток индуктивных элементов с сердечниками практически полностью замыкается на сердечники. Поэтому при расчёте индуктивности таких элементов необходимо учитывать размеры сердечника и материал, из которого он изготовлен, то есть его магнитную проницаемость.

Обобщённую формулу для расчёта индуктивных элементов с сердечниками можно выразит с помощью следующего выражения

где ω – количество витков катушки,

R_M – сопротивление магнитной цепи,

μ_а – абсолютная магнитная проницаемость вещества, из которого изготовлен сердечник,

S_M – площадь поперечного сечения сердечника,

l_M – длина средней магнитной силовой линии,

Таким образом, зная размеры сердечника можно достаточно просто вычислить индуктивность. Однако в связи с такой простотой выражения и разбросом магнитной проницаемости материала сердечника, погрешность в расчёте индуктивности составит 25 %.

Для сердечников, имеющих сложную конструктивную конфигурацию, вводится понятие эффективных (эквивалентных) размеров, которые учитывают особенности формы сердечников: эффективный путь магнитной линии l_e и эффективная площадь поперечного сечения S_e сердечника. Тогда индуктивность катушки с сердечником будет вычисляться по формуле

где ω – количество витков катушки,

μ₀ – магнитная постоянная, μ₀ = 4π*10^-7,

μ_r – относительная магнитная проницаемость вещества,

S_e – эффективная площадь поперечного сечения сердечника,

l_e – эффективный путь магнитной линии сердечника.

Таким образом, расчёт индуктивности индуктивных элементов с сердечниками сводится к нахождению эффективных размеров сердечника. Для упрощения нахождения данных размеров сердечника ввели вспомогательные величины, называемые постоянные сердечников:

С₁ – первая постоянная сердечника, которая равна сумме отношений длины однородных по сечению участков сердечника к поперечного сечения сердечника, измеряется в мм^-1;

С₂ – вторая постоянная сердечника, которая равна сумме отношений длин однородных по сечению участков сердечника к квадрату своего сечения, измеряется в мм^-3;

где N – количество разнородных участков сердечника,

l_N – длина N – го участка сердечника,

S_N – площадь N – го участка сердечника.

Тогда величины S_e и l_e определятся из следующих выражений

Кроме индуктивности с помощью постоянных С₁ и С­₂ определяют эффективный объём V_e, который требуется для определения параметоров силовых индуктивных элементов – трансформаторов и дросселей. Если же есть необходимость рассчитать только индуктивность L, то используют только постоянную С₁ по следующему выражению

где ω – количество витков катушки,

μ₀ – магнитная постоянная, μ₀ = 4π*10^-7,

μ_r – относительная магнитная проницаемость вещества,

С₁ – первая постоянная сердечника, которая равна сумме отношений длины однородных по сечению участков сердечника к поперечного сечения сердечника.

Несмотря на довольно сложные формулировки и формулы, вычисление индуктивности по ним достаточно простое.

Выпускается достаточно много типов сердечников, которые обладают различными конструктивными особенностями и свойствами, рассмотрим некоторые из них.

Расчёт катушки с тороидальным сердечником

Тороидальные (кольцевые) сердечники, благодаря своей простоте изготовления находят широкое применение в различных импульсных трансформаторах, фильтрах и дросселях и обеспечивают небольшую потребляемую мощность при минимальных потерях.

Тороидальный сердечник.

Для расчёта индуктивности достаточно знать три конструктивных параметра такого магнитопровода: D₁ – внешний диаметр, D₂ – внутренний диаметр, h – высота сердечника.

Расчёт эффективных параметров сердечника, как сказано выше, основан на двух величинах С₁ и С₂, которые составляют

где h_e – эффективная высота сердечника,

D₁ – внешний диаметр сердечника,

D₂ – внутренний диаметр сердечника.

Расчёт эффективной высоты h_e сердечника зависит от конструктивных особенностей.

Расчёт эквивалентной высоты тороидального сердечника: прямоугольное сечение (вверху) и трапецеидальное сечение (снизу).

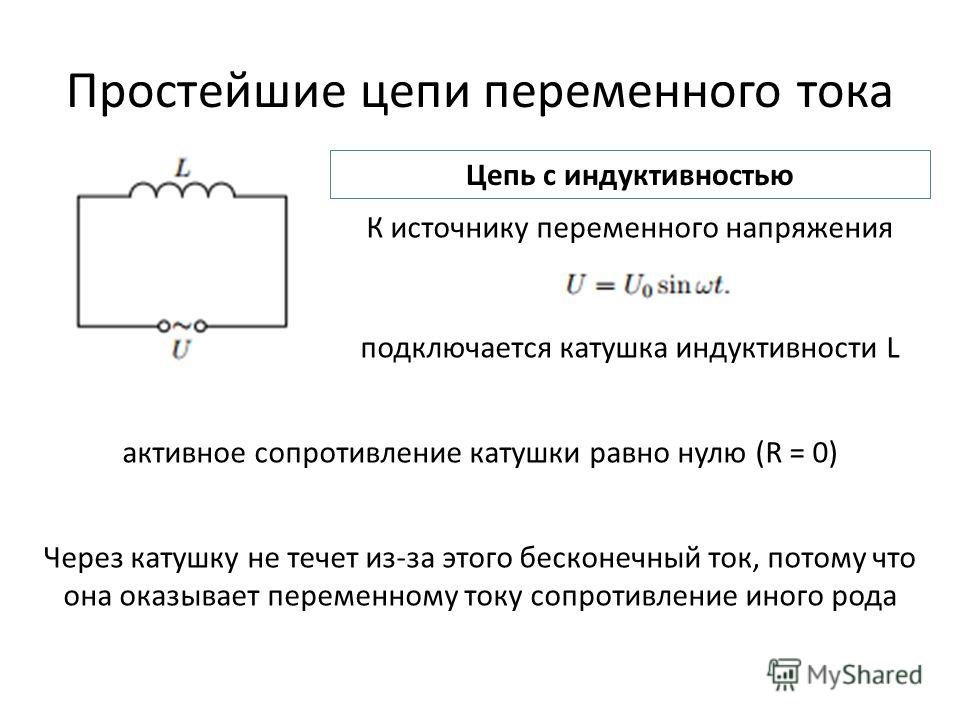
Рассмотрим несколько случаев:

а) прямоугольное поперечное сечение с острыми кромками

б) прямоугольное поперечное сечение со скруглёнными кромками и радиусом скругления r_s

в) трапецеидальное поперечное сечение с острыми кромками

г) трапецеидальное поперечное сечение со скруглёнными кромками

Пример. В качестве примера рассчитаем индуктивность тороидальной катушки, имеющий ω = 50 витков, намотанных на равномерно на магнитопровод со следующими размерами D₁ = 20 мм, D₂ = 10 мм, h = 7 мм, сечение магнитопровода прямоугольное со скруглёнными кромками, радиус скругления r_s = 0,5 мм, относительная магнитная проницаемость материала сердечника μ_r = 1000.

Так как рассчитываем только индуктивность, то в расчёте коэффициента С₂ нет необходимости

Расчёт катушки с П–образным сердечником прямоугольного сечения

В отличие от тороидальных сердечников, П – образные сердечники выполняются разборными и состоят из двух частей. Существует две модификации таких сердечников: состоящие из двух П – образных частей и из П – образной и прямоугольной замыкающей пластины.

Такие сердечники применяются в импульсных трансформаторах и трансформаторах строчной развертки и, обладая большой магнитной проницаемостью, обеспечивают малую потребляемую мощность.

П-образный сердечник с прямоугольным сечением: из двух П-образных частей (слева) и П-образной части с замыкающей прямоугольной пластиной (справа).

Для расчёта параметров сердечника рассмотрим сечение замкнутого П-образного сердечника

Сечение П-образного прямоугольного сердечника.

Данный сердечник состоит из нескольких участков l₁, l₂, l₃, l₄, l₅ имеющих различное сечение S₁, S₂, S₃, S₄, S₅,. Тогда коэффициенты С₁ и С₂ составят

Неизвестные величины можно найти следующим образом

Пример. Необходимо рассчитать индуктивность обмотки трансформатора, выполненного на П-образном сердечнике фирмы Epcos типа UU93/152/16, выполненного из двух П-образных половинок, материал сердечника N87 μ

r = 1950, количество витков ω = 150.

 

Сердечник Epcos U93/76/16.

Таким образом, расчётные параметры сердечника составят

Таким образом коэффициент С1 и индуктивность L составят

Расчёт катушки с П-образным сердечником круглого сечения

Кроме П-образных катушек с прямоугольным сечение, широко применяются П-образные катушки с круговым сечением. Они также состоят из двух П-образных частей

П-образный сердечник с круговым сечением.

Для расчёта рассмотрим сечение замкнутого сердечника состоящего из двух пловинок.

Сечение П-образного сердечника с круговым сечением.

Аналогично сердечнику с прямоугольным сечением выделим пять участков длины сердечника с различным сечением и расчёт соответственно тоже. Площадь круговых участков считается по известной формуле для площади круга, влиянием технологических пазов и отверстий можно пренебречь

Пример. В качестве примера рассчитаем индуктивность катушки, выполненной на сердечнике. Сердечник из двух частей типа SDMR 40 UY20 (μ_r = 2500), количество витков ω = 60.

Сердечник типа SDMR 40 UY20.

Параметры сердечника для расчёта составят

Таким образом коэффициент С1 и индуктивность L составят

На сегодня всё. Продолжение смотри в следующей статье.

Теория это хорошо, но необходимо отрабатывать это всё практически ПОПРОБЫВАТЬ МОЖНО ЗДЕСЬ

Как рассчитать сердечник и витки самодельных катушек индуктивности

Содержание

• 1 Конструкция катушки
• 2 Расчет параметров катушки индуктивности
  • 2.1 Расчёт индуктивности прямого провода
  • 2.2 Расчёт однослойной намотки
  • 2.3 Дроссель с сердечником
  • 2.4 Многослойная намотка
• 3 Видео

Катушки индуктивности предназначены для фильтрации токов высокой частоты. Они устанавливаются в колебательных контурах и используются для других целей в электрических и электронных схемах. Готовое устройство заводского изготовления надёжнее в работе, но дороже, чем изготовленное своими руками. Кроме того, не всегда удаётся приобрести элемент с необходимыми характеристиками. В этом случае расчёт катушки  индуктивности и само устройство можно сделать самостоятельно.

Устройство катушки индуктивности

Конструкция катушки

Каркас устройства изготавливается из диэлектрика. Это может быть тонкий (нефольгированный) гетинакс, текстолит, а на тороидальных сердечниках –просто обмотка из лакоткани или аналогичного материала.

Обмотка выполняется из одножильного или многожильного изолированного провода.

Внутрь обмотки вставляется сердечник. Он изготавливается из железа, трансформаторной стали, феррита и других материалов. Он может быть замкнутым, тороидальным (бублик), квадратным или незамкнутым (стержень). Выбор материала зависит от условий работы: частоты, магнитного потока и других параметров.

Кроме того, есть приборы, в которых сердечник отсутствует. Они характеризуются большой линейностью импеданса, но при намотке тороидальной формы обладают паразитной ёмкостью.

Расчет параметров катушки индуктивности

Протекающий по проводу электрический ток создаёт вокруг него электромагнитное поле. Соотношение величины поля к силе тока называется индуктивностью. Если провод свернуть кольцом или намотать на каркас, то получится катушка индуктивности. Её параметры рассчитывают по определённым формулам.

Расчёт индуктивности прямого провода

Индуктивность: формула

Индуктивность прямого стержня – 1-2мкГн на метр. Она зависит от его диаметра. Точнее можно рассчитать по формуле:

L=0.2l(logl/d-1), где:

• d – диаметр провода,
• l – длина провода.

Эти величины нужно измерять в метрах (м). При этом результат будет иметь размерность микрогенри (мкГн). Вместо натурального логарифма ln допустимо использовать десятичный lg, который в 2,3 раза меньше.

Предположим, что какая-то деталь подключена проводами длиной 4 см и диаметром 0,4 мм. Произведя при помощи калькулятора расчет по выше приведённой формуле, получаем, что индуктивность каждого из этих проводов составит (округлённо) 0,03 мкГн, а двух – 0,06 мкГн.

Ёмкость монтажа составляет порядка 4,5пФ. При этом резонансная частота получившегося контура составит 300 МГц. Это диапазон УКВ.

Важно! Поэтому при монтаже устройств, работающих в частотах УКВ, длину выводов деталей нужно делать минимальной.

Расчёт однослойной намотки

Для увеличения индуктивности провод сворачивается кольцом. Величина магнитного потока внутри кольца выше примерно в три раза. Рассчитать её можно при помощи следующего выражения:

L = 0,27D(ln8D/d-2), где D – диаметр кольца, измеренный в метрах.

При увеличении количества витков индуктивность продолжает расти. При этом индукция отдельных витков влияет на соседние, поэтому получившиеся параметры пропорциональны не количеству витков N, а их квадрату.

Однослойная намотка

Дроссель с сердечником

Параметры обмотки, намотанной на каркас, диаметром намного меньше длины рассчитывается по формуле:

L=*0*N2*S.

Она справедлива для устройства большой длины или большого тора.

Размерность в ней дана в метрах (м) и генри (Гн). Здесь:

• 0 = 4•10-7 Гн/м – магнитная константа,
• S = D2/4 – площадь поперечного сечения обмотки, магнитная проницаемость магнитопровода, которая меньше проницаемости самого материала и учитывает длину сердечника; в разомкнутой конструкции она намного меньше, чем у материала.

Например, если стержень антенны изготовить из феррита с проницаемостью 600 (марки 600НН), то у получившегося изделия она будет равна 150. При отсутствии магнитного сердечника = 1.

Для того чтобы использовать это выражение для расчёта обмоток, намотанных на тороидальном сердечнике, его необходимо измерять по средней линии «бублика». При расчёте обмоток, намотанных на железе Ш-образной формы без воздушного зазора, длину пути магнитного потока измеряют по средней линии сердечника.

Катушка с Ш-образным сердечником

В расчёте диаметр провода не учитывается, поэтому в низкочастотных конструкциях сечение провода выбирается по таблицам, исходя из допустимого нагрева проводника.

В высокочастотных устройствах, так же как и в остальных, стремятся свести омическое сопротивление к минимуму для достижения максимальной добротности прибора. Простое повышение сечения провода не помогает. Это приводит к необходимости наматывать обмотку в несколько слоёв. Но ток ВЧ идёт преимущественно по поверхности, что приводит к увеличению сопротивления. Добротность в высокочастотных элементах растёт вместе с увеличением всех размеров: длины и диаметров обмотки и провода.

Максимальная добротность получается в короткой обмотке большого диаметра, с соотношением диаметр/длина, равным 2,5. Параметры такого устройства вычисляются по формуле:

L=0.08D2N2/(3D+9b+10c).

В этой формуле все параметры измеряются в сантиметрах (см), а результат получается в микрогенри (мкГн).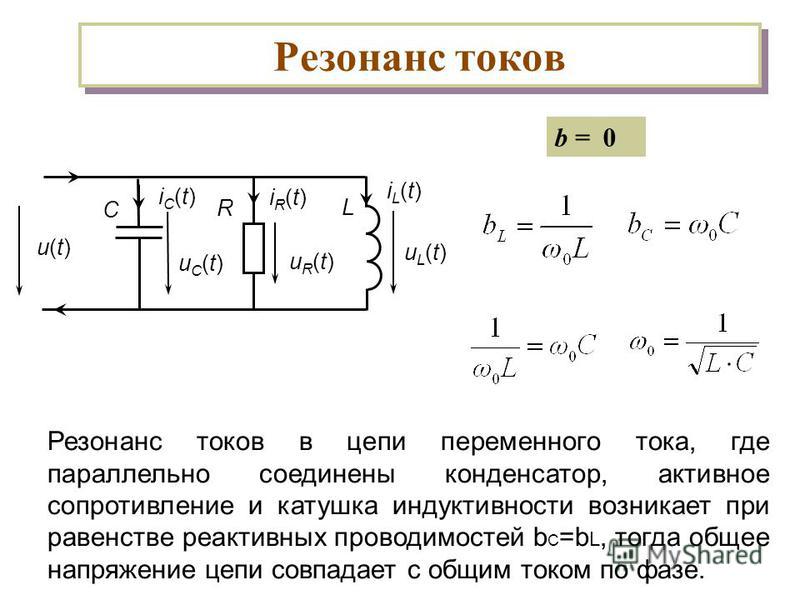

По этой формуле рассчитывается также плоская катушка. Диаметр «D» измеряется по среднему витку, а длина «l» по ширине:

l=Dmax-Dmin.

Плоская катушка

Многослойная намотка

Многослойная намотка без сердечника вычисляется по формуле:

L=0.08D2N2/(3D+9b+10c).

Размеры здесь измеряются в сантиметрах (см), а результат получается в микрогенри (мкГн).

Добротность такого устройства зависит от способа намотки:

• обычная плотная намотка – самая плохая, не более 30-50;
• внавал и универсал;
• «сотовая».

Многослойная катушка

Для увеличения добротности при частоте до 10 мГц вместо обычного, одножильного провода, можно взять литцендрат или посеребренный проводник.

Справка. Литцендрат – это провод, скрученный из большого количества тонких изолированных друг от друга жил.

Литцендрат имеет большую поверхность, по сравнению с одножильным проводником того же сечения, поэтому на высоких частотах его сопротивление ниже.

Использование сердечника в высокочастотных устройствах повышает индуктивность и добротность катушки. Особенно большой эффект даёт использование замкнутых сердечников. При этом добротность дросселя зависит не от активного сопротивления провода, а от проницаемости магнитопровода. Рассчитывается такой прибор по обычным формулам для низкочастотных устройств.

Сделать катушку или дроссель можно самостоятельно. Перед тем, как её изготавливать, необходимо рассчитать индуктивность катушки по формулам или при помощи онлайн-калькулятора.

Видео

Мультипекарь Redmond RMB-611

2172 ₽ Подробнее

Мультипекарь Redmond RMB-611

2172 ₽ Подробнее

Лучшие двухкамерные холодильники

Оцените статью:

что это, как рассчитать, формулы и примеры

Автор Andrey Ku На чтение 4 мин Опубликовано 20. 10.2021

Трансформатор, как элемент радиотехники и электротехники, работает на основе электромагнитной индукции. Говоря об индуктивности трансформатора, имеют в виду индуктивность обмоток и взаимоиндукцию между ними.

Каждая из обмоток представляет некоторое количество витков провода, намотанных на ферромагнитный сердечник, то есть обыкновенную катушку индуктивности.

Трудность в определении параметров катушки заключается в том, что они изменяются в зависимости от нескольких параметров и их сочетания:

• токи в обмотках;
• уровень намагниченности магнитопровода;
• магнитные характеристики сердечника;
• взаимодействие между соседними обмотками;
• наличия постоянной составляющей тока.

Содержание

1. Конструкция и принцип действия силового трансформатора
2. Физическое понятие индуктивности обмоток
3. Формулы и измерение
4. Как измерить в домашних условиях
5. Пример расчета

Конструкция и принцип действия силового трансформатора

В основе конструкции любого трансформатора находятся следующие элементы:

1. Сердечник из ферромагнитного материала.
2. Первичная и вторичные обмотки. В случае автотрансформатора одна обмотка выполняет обе функции.

В сетях переменного тока промышленной частоты (50 или 60Гц) в качестве ферромагнитного материала используется сталь, обработанная по специальной технологии. На высоких частотах часто делаются трансформаторы без сердечника, поскольку для нормальной работы достаточно взаимосвязи межу катушками.

Принцип работы:

• в первичной обмотке, подключенной в цепь питания, создается переменное электрическое поле;
• под действием поля первичной катушки в сердечнике создается переменное магнитное поле;
• в силу электромагнитной индукции во всех обмотках наблюдается ЭДС индукции.

ЭДС индукции в первичной обмотке направлена противоположно поданному напряжению, поэтому они взаимно компенсируются. В результате, при отсутствии нагрузки через первичную обмотку протекает сравнительно небольшой ток холостого хода.

Наличие тока вторичной цепи аналогично вызывает дополнительный магнитный поток, а он – ЭДС самоиндукции в первичное катушке.

В результате компенсация первичного напряжения снижается и растет ток в первичной цепи.

Физическое понятие индуктивности обмоток

Индуктивность представляет собой коэффициент пропорциональности между током, создаваемым замкнутым электрическим контуром, и магнитным потоком, который создается этим контуром.

Более понятной формулировкой будет та, которая говорит о величине ЭДС самоиндукции в замкнутом контуре, которая возникает при изменении силы тока за единицу времени. То есть, понятие индуктивности справедливо для изменяющегося тока.

При постоянном токе говорить об индуктивности бессмысленно.

В идеальном трансформаторе все электромагнитное поле, создаваемое обмотками, замкнуто в магнитном сердечнике. В реальных конструкциях существует поле рассеяния, величина которого зависит от способа выполнения катушки и конструктивных особенностей сердечника. Чем больше толщина намотки, тем большая часть электромагнитного поля замыкается вне магнитопровода.

Этому способствует также качество сборки магнитопровода. Зазоры между пластинами способствуют резкому увеличению рассеивания. В связи с этим наилучшими свойствами обладают О-образные сердечники.

Формулы и измерение

Формулы для расчета индуктивности катушек довольно сложны и имеет различный вид для различных типов исполнения обмоток:

• линейный проводник;
• одновитковая катушка;
• плоская катушка;
• соленоидальная обмотка;
• тороидальная форма.

Наибольшие сложности возникают при расчетах многовитковых многослойных катушек, то есть тех, которые составляют обмотку трансформаторов.

В подавляющем большинстве случаев точный расчет невозможен, поэтому приходится использовать примерные данные и уточнять их после проведения измерений.

Формулы  для расчета индуктивности трансформатора основаны на расчетах соленоида:

L=µ₀µN²S/l, где

µ0 – магнитная постоянная;

µ – магнитная проницаемость сердечника;

N – количество витков;

S – площадь одного витка;

l – длина обмотки.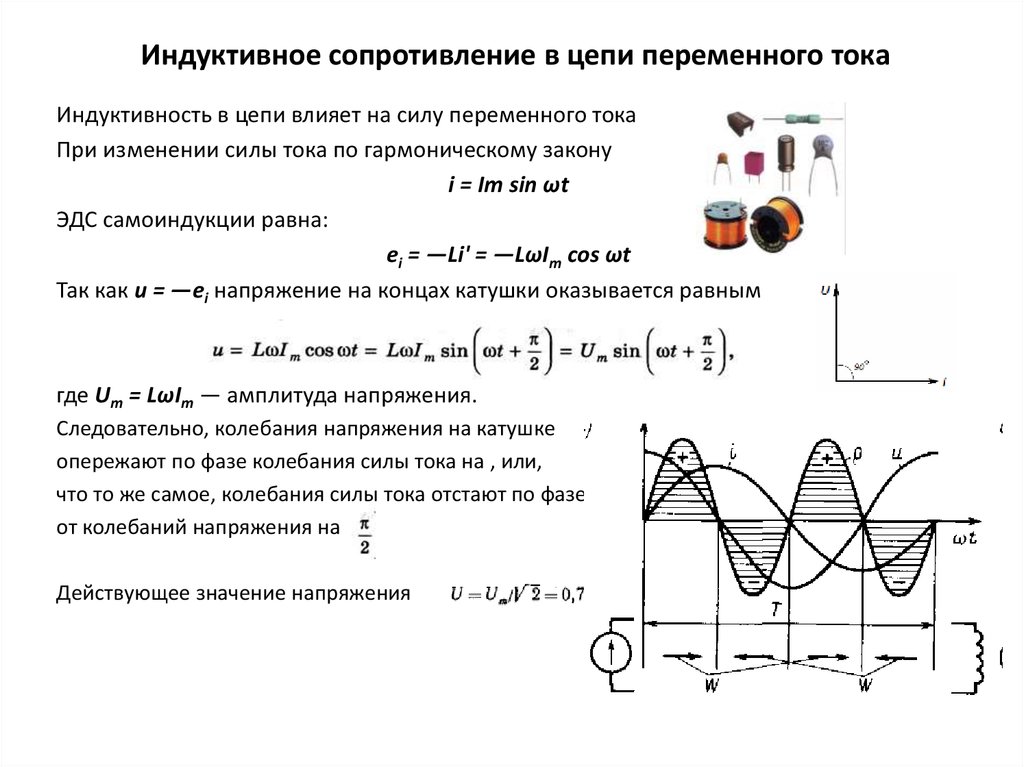

Для измерения индуктивности существует несколько методик и приборов, созданных на их основе. В большинстве случаев измерение производится путем вычислений индуктивного сопротивления катушки при подаче образцового напряжения заданной частоты и измеренного значения тока через обмотку.

В специализированных приборах вычисления производятся автоматически, и пользователь только считывает показания шкалы прибора, выраженные в единицах индуктивности – Гн, мГн или мкГн.

Как измерить в домашних условиях

Приборы для непосредственного измерения индуктивности имеют высокую стоимость и редко используются в домашних условиях. С приемлемой точностью результаты можно получить, используя обычные приборы для измерения переменного тока: амперметр и вольтметр. Также необходим омметр.

Порядок действий следующий:

1. При помощи омметра определяют активное сопротивление обмотки R.
2. Подключают трансформатор последовательно с амперметром в сеть.
3. Параллельно обмотке подключают вольтметр.
4. По показаниям приборов определяют полное сопротивление трансформатора: Z=U/I
5. Индуктивное сопротивление находят, вычитая из полного сопротивления активное: X_L=Z-R
6. Индуктивность определяется по формуле: L=X_L/(2πf), где π – число пи 3.14, f – частота измерений.

Как правило, активное сопротивление намотки значительно (на несколько порядков) меньше индуктивного, поэтому можно его не учитывать. Именно поэтому, включение трансформатора в цепь постоянного напряжения вызывает короткое  замыкание. Ток обмотки при этом будет ограничиваться только активным сопротивлением.

Пример расчета

К примеру, требуется рассчитать индуктивность первичной обмотки трансформатора питания. Путем измерений определено:

1. Сопротивление обмотки 3 Ом.
2. Напряжение сети 220 В.
3. Частота питающего напряжения 50 Гц.
4. Ток холостого хода 05 А.

Полное сопротивление:

Z=U/I=220/0. 05=4400 Ом

Активное сопротивление меньше полного в 10000 раз и его можно не учитывать.

Определяем индуктивность:

L=X_L/(2πf) =4400/ (2∙3.14∙50) =14 Гн.

формула. Измерение индуктивности. Индуктивность контура

ГлавнаяРазноеФормула расчета катушки индуктивности

формула. Измерение индуктивности. Индуктивность контура

Кто в школе не изучал физику? Для кого-то она была интересна и понятна, а кто-то корпел над учебниками, пытаясь выучить наизусть сложные понятия. Но каждый из нас запомнил, что мир основан на физических знаниях. Сегодня мы поговорим о таких понятиях, как индуктивность тока, индуктивность контура, и узнаем, какие бывают конденсаторы и что такое соленоид.

Электрическая цепь и индуктивность

Индуктивность служит для характеристики магнитных свойств электрической цепи. Ее определяют как коэффициент пропорциональности между текущим электрическим током и магнитным потоком в замкнутом контуре. Поток создается этим током через поверхность контура.

Еще одно определение гласит, что индуктивность является параметром электрической цепи и определяет ЭДС самоиндукции. Термин применяется для указания элемента цепи и приходится характеристикой эффекта самоиндукции, который был открыт Д. Генри и М. Фарадеем независимо друг от друга. Индуктивность связана с формой, размером контура и значением магнитной проницаемости окружающей среды. В единице измерения СИ эта величина измеряется в генри и обозначается как L.

Самоиндукция и измерение индуктивности

Индуктивностью называется величина, которая равна отношению магнитного потока, проходящего по всем виткам контура к силе тока:

Индуктивность контура находится в зависимости от формы, размеров контура и от магнитных свойств среды, в которой он находится. Если в замкнутом контуре протекает электрический ток, то возникает изменяющееся магнитное поле. Это впоследствии приведет к возникновению ЭДС. Рождение индукционного тока в замкнутом контуре носит название «самоиндукция».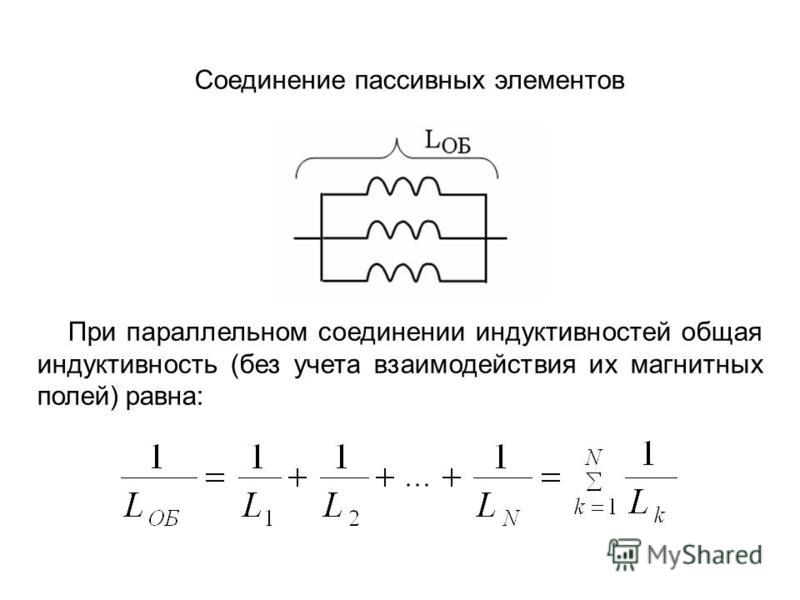 По правилу Ленца величина не дает изменяться току в контуре. Если обнаруживается самоиндукция, то можно применять электрическую цепь, в которой параллельно включены резистор и катушка с железным сердечником. Последовательно с ними подсоединены и электрические лампы. В этом случае сопротивление резистора равно сопротивлению на постоянном токе катушки. Результатом будет яркое горение ламп. Явление самоиндукции занимает одно из главных мест в радиотехнике и электротехнике.

Как найти индуктивность

Формула, которая является простейшей для нахождения величины, следующая:

где F – магнитный поток, I – ток в контуре.

Через индуктивность можно выразить ЭДС самоиндукции:

Из формулы напрашивается вывод о численном равенстве индукции с ЭДС, которое возникает в контуре при изменении силы тока на один амперметр за одну секунду.

Переменная индуктивность дает возможность найти и энергию магнитного поля:

«Катушка ниток»

Катушка индуктивности представляет собой намотанную изолированную медную проволоку на твердое основание. Что касается изоляции, то выбор материала широк – это и лак, и проводная изоляция, и ткань. Величина магнитного потока зависит от площади цилиндра. Если увеличить ток в катушке, то магнитное поле будет становиться все больше и наоборот.

Если подать электрический ток на катушку, то в ней возникнет напряжение, противоположное напряжению тока, но оно внезапно исчезает. Такого рода напряжение называется электродвижущей силой самоиндукции. В момент включения напряжения на катушку сила тока меняет свое значение от 0 до некоего числа. Напряжение в этот момент тоже меняет значение, согласно закону Ома:

где I характеризует силу тока, U – показывает напряжение, R – сопротивление катушки.

Еще одной особенной чертой катушки является следующий факт: если разомкнуть цепь «катушка – источник тока», то ЭДС добавится к напряжению. Ток тоже вначале вырастет, а потом пойдет на спад. Отсюда вытекает первый закон коммутации, в котором говорится, что сила тока в катушке индуктивности мгновенно не меняется.

Катушку можно разделить на два вида:

1. С магнитным наконечником. В роли материала сердца выступают ферриты и железо. Сердечники служат для повышения индуктивности.
2. С немагнитным. Используются в случаях, когда индуктивность не больше пяти миллиГенри.

Устройства различаются и по внешнему виду, и внутреннему строению. В зависимости от таких параметров находится индуктивность катушки. Формула в каждом случае разная. Например, для однослойной катушки индуктивность будет равна:

• L = 10µ0ΠN2R2 : 9R + 10l.

А вот уже для многослойной другая формула:

• L= µ0N2R2 :2Π(6R + 9l + 10w).

Основные выводы, связанные с работой катушек:

1. На цилиндрическом феррите самая большая индуктивность возникает в середине.
2. Для получения максимальной индуктивности необходимо близко наматывать витки на катушку.
3. Индуктивность тем меньше, чем меньше количество витков.
4. В тороидальном сердечнике расстояние между витками не играет роли катушки.
5. Значение индуктивности зависит от «витков в квадрате».
6. Если последовательно соединить индуктивности, то их общее значение равно сумме индуктивностей.
7. При параллельном соединении нужно следить, чтобы индуктивности были разнесены на плате. В противном случае их показания будут неправильными за счет взаимного влияния магнитных полей.

Соленоид

Под этим понятием понимается цилиндрическая обмотка из провода, который может быть намотан в один или несколько слоев. Длина цилиндра значительно больше диаметра. За счет такой особенности при подаче электрического тока в полости соленоида рождается магнитное поле. Скорость изменения магнитного потока пропорциональна изменению тока. Индуктивность соленоида в этом случае рассчитывается следующим образом:

Еще эту разновидность катушек называют электромеханическим исполнительным механизмом с втягиваемым сердечником. В данном случае соленоид снабжается внешним ферромагнитным магнитопроводом – ярмом.

В наше время устройство может соединять в себе гидравлику и электронику. На этой основе созданы четыре модели:

• Первая способна контролировать линейное давление.
• Вторая модель отличается от других принудительным управлением блокировки муфты в гидротрансформаторах.
• Третья модель содержит в своем составе регуляторы давления, отвечающие за работу переключения скоростей.
• Четвертая управляется гидравлическим способом или клапанами.

Необходимые формулы для расчетов

Чтобы найти индуктивность соленоида, формула применяется следующая:

где µ0 показывает магнитную проницаемость вакуума, n – это число витков, V – объем соленоида.

Также провести расчет индуктивности соленоида можно и с помощью еще одной формулы:

где S – это площадь поперечного сечения, а l – длина соленоида.

Чтобы найти индуктивность соленоида, формула применяется любая, которая подходит по решению к данной задаче.

Работа на постоянном и переменном токе

Магнитное поле, которое создается внутри катушки, направлено вдоль оси, и равно:

где µ0 – это магнитная проницаемость вакуума, n – это число витков, а I – значение тока.

Когда ток движется по соленоиду, то катушка запасает энергию, которая равна работе, необходимая для установления тока. Чтобы вычислить в этом случае индуктивность, формула используется следующая:

где L показывает значение индуктивности, а E – запасающую энергию.

ЭДС самоиндукции возникает при изменении тока в соленоиде.

В случае работы на переменном токе появляется переменное магнитное поле. Направление силы притяжения может изменяться, а может оставаться неизменным. Первый случай возникает при использовании соленоида как электромагнита. А второй, когда якорь сделан из магнитомягкого материала. Соленоид на переменном токе имеет комплексное сопротивление, в которое включаются сопротивление обмотки и ее индуктивность.

Самое распространенное применение соленоидов первого типа (постоянного тока) — это в роли поступательного силового электропривода. Сила зависит от строения сердечника и корпуса. Примерами использования являются работа ножниц при отрезании чеков в кассовых аппаратах, клапаны в двигателях и гидравлических системах, язычки замков. Соленоиды второго типа применяются как индукторы для индукционного нагрева в тигельных печах.

Колебательные контуры

Простейшей резонансной цепью является последовательный колебательный контур, состоящий из включенных катушек индуктивности и конденсатора, через которые протекает переменный ток. Чтобы определить индуктивность катушки, формула используется следующая:

где XL показывает реактивное сопротивление катушки, а W — круговая частота.

Если используется реактивное сопротивление конденсатора, то формула будет выглядеть следующим образом:

Xc = 1 : W х C.

Важными характеристиками колебательного контура являются резонансная частота, волновое сопротивление и добротность контура. Первая характеризует частоту, где сопротивление контура имеет активный характер. Вторая показывает, как проходит реактивное сопротивление на резонансной частоте между такими величинами, как емкость и индуктивность колебательного контура. Третья характеристика определяет амплитуду и ширину амплитудно-частотных характеристик (АЧХ) резонанса и показывает размеры запаса энергии в контуре по сравнению с потерями энергии за один период колебаний. В технике частотные свойства цепей оцениваются при помощи АЧХ. В этом случае цепь рассматривается как четырехполюсник. При изображении графиков используется значение коэффициента передачи цепи по напряжению (К). Эта величина показывает отношение выходного напряжения к входному. Для цепей, которые не содержат источников энергии и различных усилительных элементов, значение коэффициента не больше единицы. Оно стремится к нулю, когда на частотах, отличающихся от резонансной, сопротивление контура имеет высокое значение. Если же величина сопротивления минимальна, то коэффициент близок к единице.

При параллельном колебательном контуре включены два реактивных элемента с разной силой реактивности. Использование такого вида контура подразумевает знание, что при параллельном включении элементов нужно складывать только их проводимости, но не сопротивления. На резонансной частоте суммарная проводимость контура равна нулю, что говорит о бесконечно большом сопротивлении переменному току. Для контура, в котором параллельно включены емкость (C), сопротивление (R) и индуктивность, формула, объединяющая их и добротность (Q), следующая:

При работе параллельного контура за один период колебаний дважды происходит энергетический обмен между конденсатором и катушкой. В этом случае появляется контурный ток, который значительно больше значения тока во внешней цепи.

Работа конденсатора

Устройство представляет собой двухполюсник малой проводимости и с переменным или постоянным значением емкости. Когда конденсатор не заряжен, сопротивление его близко к нулю, в противном случае оно равно бесконечности. Если источник тока отсоединить от данного элемента, то он становится этим источником до своей разрядки. Использование конденсатора в электронике заключается в роли фильтров, которые удаляют помехи. Данное устройство в блоках питания на силовых цепях применяются для подпитки системы при больших нагрузках. Это основано на способности элемента пропускать переменную составляющую, но непостоянный ток. Чем выше частота составляющей, тем меньше у конденсатора сопротивление. В результате через конденсатор глушатся все помехи, которые идут поверх постоянного напряжения.

Сопротивление элемента зависит от емкости. Исходя из этого, правильнее будет ставить конденсаторы с различным объемом, чтобы улавливать разного рода помехи. Благодаря способности устройства пропускать постоянный ток только в период заряда его используют как времязадающий элемент в генераторах или как формирующее звено импульса.

Конденсаторы бывают многих типов. В основном используется классификация по типу диэлектрика, так как этот параметр определяет стабильность емкости, сопротивление изоляции и так далее. Систематизация по данной величине следующая:

1. Конденсаторы с газообразным диэлектриком.
2. Вакуумные.
3. С жидким диэлектриком.
4. С твердым неорганическим диэлектриком.
5. С твердым органическим диэлектриком.
6. Твердотельные.
7. Электролитические.

Существует классификация конденсаторов по назначению (общий или специальный), по характеру защиты от внешних факторов (защищенные и незащищенные, изолированные и неизолированные, уплотненные и герметизированные), по технике монтажа (для навесного, печатного, поверхностного, с выводами под винт, с защелкивающимися выводами). Также устройства можно различить по способности к изменению емкости:

1. Постоянные конденсаторы, то есть у которых емкость остается всегда постоянной.
2. Подстроечные. У них емкость не меняется при работе аппаратуры, но можно ее регулировать разово или периодически.
3. Переменные. Это конденсаторы, которые допускают в процессе функционирования аппаратуры изменение ее емкости.

Индуктивность и конденсатор

Токоведущие элементы устройства способны создавать его собственную индуктивность. Это такие конструктивные части, как кладки, соединительные шины, токоотводы, выводы и предохранители. Можно создать дополнительную индуктивность конденсатора путем присоединения шин. Режим работы электрической цепи зависит от индуктивности, емкости и активного сопротивления. Формула расчета индуктивности, которая возникает при приближении к резонансной частоте, следующая:

где Ce определяет эффективную емкость конденсатора, C показывает действительную емкость, f – это частота, L – индуктивность.

Значение индуктивности всегда должно учитываться при работе с силовыми конденсаторами. Для импульсных конденсаторов наиболее важна величина собственной индуктивности.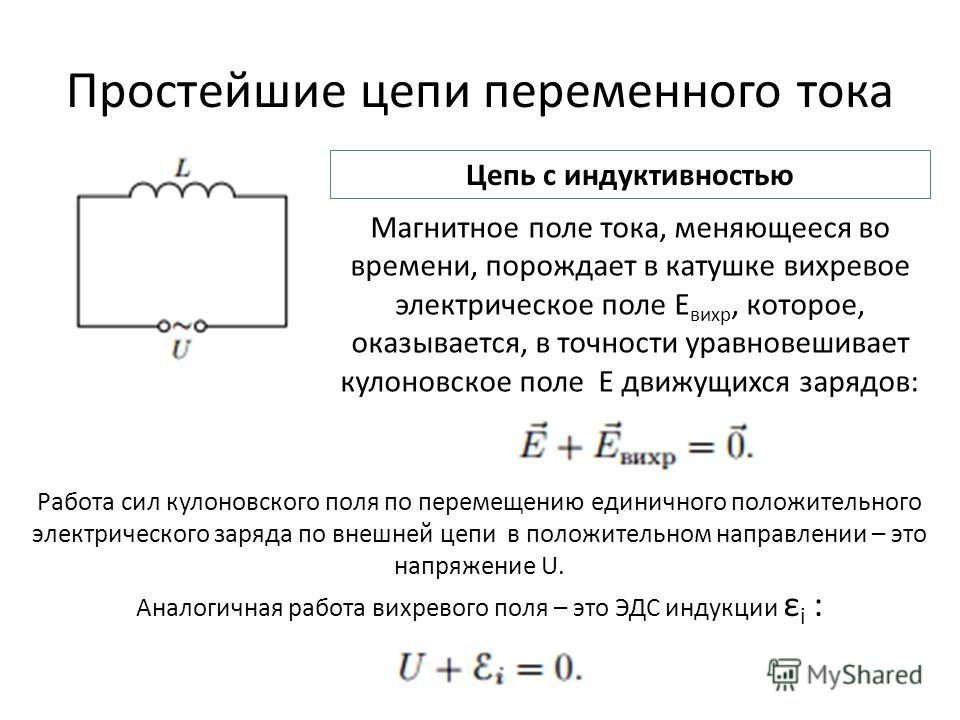 Их разряд приходится на индуктивный контур и имеет два вида – апериодический и колебательный.

Индуктивность в конденсаторе находится в зависимости от схемы соединения элементов в нем. Например, при параллельном соединении секций и шин эта величина равна сумме индуктивностей пакета главных шин и выводов. Чтобы найти такого рода индуктивность, формула следующая:

где Lk показывает индуктивность устройства, Lp –пакета, Lm – главных шин, а Lb – индуктивность выводов.

Если при параллельном соединении ток шины меняется по ее длине, то тогда эквивалентная индуктивность определяется так:

• Lk = Lc : n + µ0 l х d : (3b) + Lb,

где l – длина шин, b – ее ширина, а d – расстояние между шинами.

Чтобы снизить индуктивность устройства, необходимо токоведущие части конденсатора расположить так, чтобы взаимно компенсировались их магнитные поля. Иными словами, токоведущие части с одинаковым движением тока нужно удалять друг от друга как можно дальше, а с противоположным направлением сближать. При совмещении токоотводов с уменьшением толщины диэлектрика можно снизить индуктивность секции. Этого можно достигнуть еще путем деления одной секции с большим объемом на несколько с более мелкой емкостью.

fb.ru

Как рассчитать индуктивность катушек с замкнутыми сердечниками?

Всем доброго времени суток. В прошлых статьях (часть 1, часть 2, часть 3) я рассказал о расчёте индуктивности индуктивных элементов без сердечников. Однако их применение ограниченно, вследствие, больших габаритных размеров. Поэтому для увеличения индуктивности и уменьшения размеров и улучшения других показателей индуктивные элементы устанавливают на сердечники из материалов с различными магнитными свойствами.

Особенности расчёта индуктивных элементов с сердечниками

В отличие от индуктивных элементов без сердечников, при расчёте которых учитывался магнитный поток пронизывающий только проводник с током, магнитный поток индуктивных элементов с сердечниками практически полностью замыкается на сердечники. Поэтому при расчёте индуктивности таких элементов необходимо учитывать размеры сердечника и материал, из которого он изготовлен, то есть его магнитную проницаемость.

Обобщённую формулу для расчёта индуктивных элементов с сердечниками можно выразит с помощью следующего выражения

где ω – количество витков катушки,

RM – сопротивление магнитной цепи,

μа – абсолютная магнитная проницаемость вещества, из которого изготовлен сердечник,

SM – площадь поперечного сечения сердечника,

lM – длина средней магнитной силовой линии,

Таким образом, зная размеры сердечника можно достаточно просто вычислить индуктивность. Однако в связи с такой простотой выражения и разбросом магнитной проницаемости материала сердечника, погрешность в расчёте индуктивности составит 25 %.

Для сердечников, имеющих сложную конструктивную конфигурацию, вводится понятие эффективных (эквивалентных) размеров, которые учитывают особенности формы сердечников: эффективный путь магнитной линии le и эффективная площадь поперечного сечения Se сердечника. Тогда индуктивность катушки с сердечником будет вычисляться по формуле

где ω – количество витков катушки,

μ0 – магнитная постоянная, μ0 = 4π*10-7,

μr – относительная магнитная проницаемость вещества,

Se – эффективная площадь поперечного сечения сердечника,

le – эффективный путь магнитной линии сердечника.

Таким образом, расчёт индуктивности индуктивных элементов с сердечниками сводится к нахождению эффективных размеров сердечника. Для упрощения нахождения данных размеров сердечника ввели вспомогательные величины, называемые постоянные сердечников:

С1 – первая постоянная сердечника, которая равна сумме отношений длины однородных по сечению участков сердечника к поперечного сечения сердечника, измеряется в мм-1;

С2 – вторая постоянная сердечника, которая равна сумме отношений длин однородных по сечению участков сердечника к квадрату своего сечения, измеряется в мм-3;

где N – количество разнородных участков сердечника,

lN – длина N – го участка сердечника,

SN – площадь N – го участка сердечника.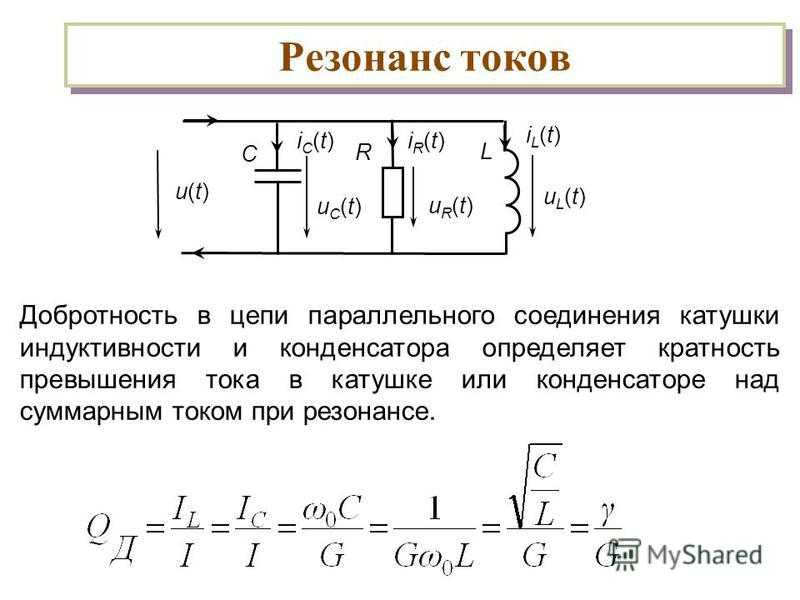

Тогда величины Se и le определятся из следующих выражений

Кроме индуктивности с помощью постоянных С1 и С­2 определяют эффективный объём Ve, который требуется для определения параметоров силовых индуктивных элементов – трансформаторов и дросселей. Если же есть необходимость рассчитать только индуктивность L, то используют только постоянную С1 по следующему выражению

где ω – количество витков катушки,

μ0 – магнитная постоянная, μ0 = 4π*10-7,

μr – относительная магнитная проницаемость вещества,

С1 – первая постоянная сердечника, которая равна сумме отношений длины однородных по сечению участков сердечника к поперечного сечения сердечника.

Несмотря на довольно сложные формулировки и формулы, вычисление индуктивности по ним достаточно простое.

Выпускается достаточно много типов сердечников, которые обладают различными конструктивными особенностями и свойствами, рассмотрим некоторые из них.

Расчёт катушки с тороидальным сердечником

Тороидальные (кольцевые) сердечники, благодаря своей простоте изготовления находят широкое применение в различных импульсных трансформаторах, фильтрах и дросселях и обеспечивают небольшую потребляемую мощность при минимальных потерях.

Тороидальный сердечник.

Для расчёта индуктивности достаточно знать три конструктивных параметра такого магнитопровода: D1 – внешний диаметр, D2 – внутренний диаметр, h – высота сердечника.

Расчёт эффективных параметров сердечника, как сказано выше, основан на двух величинах С1 и С2, которые составляют

где he – эффективная высота сердечника,

D1 – внешний диаметр сердечника,

D2 – внутренний диаметр сердечника.

Расчёт эффективной высоты he сердечника зависит от конструктивных особенностей.

Расчёт эквивалентной высоты тороидального сердечника: прямоугольное сечение (вверху) и трапецеидальное сечение (снизу).

Рассмотрим несколько случаев:

а) прямоугольное поперечное сечение с острыми кромками

б) прямоугольное поперечное сечение со скруглёнными кромками и радиусом скругления rs

в) трапецеидальное поперечное сечение с острыми кромками

г) трапецеидальное поперечное сечение со скруглёнными кромками

Пример. В качестве примера рассчитаем индуктивность тороидальной катушки, имеющий ω = 50 витков, намотанных на равномерно на магнитопровод со следующими размерами D1 = 20 мм, D2 = 10 мм, h = 7 мм, сечение магнитопровода прямоугольное со скруглёнными кромками, радиус скругления rs = 0,5 мм, относительная магнитная проницаемость материала сердечника μr = 1000.

Так как рассчитываем только индуктивность, то в расчёте коэффициента С2 нет необходимости

Расчёт катушки с П–образным сердечником прямоугольного сечения

В отличие от тороидальных сердечников, П – образные сердечники выполняются разборными и состоят из двух частей. Существует две модификации таких сердечников: состоящие из двух П – образных частей и из П – образной и прямоугольной замыкающей пластины.

Такие сердечники применяются в импульсных трансформаторах и трансформаторах строчной развертки и, обладая большой магнитной проницаемостью, обеспечивают малую потребляемую мощность.

П-образный сердечник с прямоугольным сечением: из двух П-образных частей (слева) и П-образной части с замыкающей прямоугольной пластиной (справа).

Для расчёта параметров сердечника рассмотрим сечение замкнутого П-образного сердечника

Сечение П-образного прямоугольного сердечника. Данный сердечник состоит из нескольких участков l1, l2, l3, l4, l5 имеющих различное сечение S1, S2, S3, S4, S5,. Тогда коэффициенты С1 и С2 составят

Неизвестные величины можно найти следующим образом

Пример. Необходимо рассчитать индуктивность обмотки трансформатора, выполненного на П-образном сердечнике фирмы Epcos типа UU93/152/16, выполненного из двух П-образных половинок, материал сердечника N87 μr = 1950, количество витков ω = 150.

 

Сердечник Epcos U93/76/16.

Таким образом, расчётные параметры сердечника составят

Таким образом коэффициент С1 и индуктивность L составят

Расчёт катушки с П-образным сердечником круглого сечения

Кроме П-образных катушек с прямоугольным сечение, широко применяются П-образные катушки с круговым сечением. Они также состоят из двух П-образных частей

П-образный сердечник с круговым сечением.

Для расчёта рассмотрим сечение замкнутого сердечника состоящего из двух пловинок.

Сечение П-образного сердечника с круговым сечением.

Аналогично сердечнику с прямоугольным сечением выделим пять участков длины сердечника с различным сечением и расчёт соответственно тоже. Площадь круговых участков считается по известной формуле для площади круга, влиянием технологических пазов и отверстий можно пренебречь

Пример. В качестве примера рассчитаем индуктивность катушки, выполненной на сердечнике. Сердечник из двух частей типа SDMR 40 UY20 (μr = 2500), количество витков ω = 60.

Сердечник типа SDMR 40 UY20.

Параметры сердечника для расчёта составят

Таким образом коэффициент С1 и индуктивность L составят

На сегодня всё. Продолжение смотри в следующей статье.

Теория это хорошо, но теория без практики — это просто сотрясание воздуха. Перейдя по ссылке всё это можно сделать своими руками

Скажи спасибо автору нажми на кнопку социальной сети

www. electronicsblog.ru

Расчёт индуктивности. Часть 1 | HomeElectronics

Всем доброго времени суток! В прошлой статье я рассказывал о таком явлении как электромагнитная индукция и ЭДС возникающая при самоиндукции и взаимной индукции. Устройства, в основе которых лежат данные явления и процессы, называются индуктивными элементами (катушки колебательных контуров, трансформаторы, дроссели, реакторы). В качестве одного из основных параметров данных элементов выступает индуктивность L(также имеет название коэффициента самоиндукции). О том, как рассчитать данный параметр пойдёт речь в данной статье.

Методы расчёта индуктивностей

Индуктивностью (обозначается L) или коэффициентом самоиндукции называется коэффициент пропорциональности между потокосцеплением (обозначается Ψ­L) и электрическим током, который возбуждает данное потокосцепление.

В простых случаях индуктивность можно рассчитать, применяя формулы для вычисления магнитной индукции B0 (закон Био-Савара-Лапласа), магнитного потока Φ и потокосцепления Ψ­L

где S – площадь поверхности ограниченная контуром, который создает магнитную индукцию;

n – количество контуров с током, которые пронизывает магнитный поток.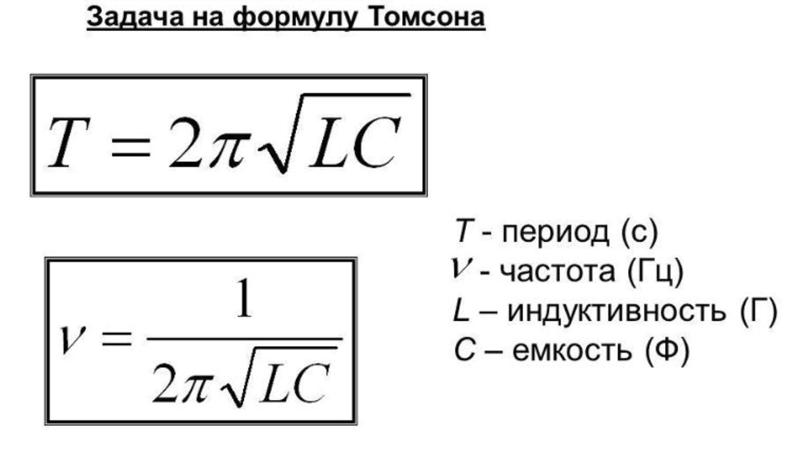

Однако это в идеальном случае, в реальности говоря о токе I, который протекает по проводнику, необходимо отметить, что его распределение по сечению проводника не всегда равномерно, вследствие возникновения скин-эффекта при переменном токе. В результате этого эффекта плотность электрического тока распределяется неравномерно, происходит её уменьшение от внешнего слоя проводника к его центру. Уменьшение плотности тока также происходит неравномерно и зависит от частоты переменного тока. Для оценки скин-эффекта ввели понятие толщины скин-слоя ∆, которая показывает, на каком расстоянии от поверхности проводника плотность тока падает в е = 2,718 раз. Толщину скин-слоя можно вычислить по выражению

где δ – глубина проникновения переменного тока или толщина скин-слоя;

μ – магнитная проницаемость вещества;

γ – удельная электрическая проводимость материала проводника;

ω – круговая частота переменного тока, ω = 2πf.

Поэтому непосредственный способ вычисления индуктивности практически не применяется.

На практике применяется выражения для индуктивности, выведенные с некоторыми допущениями, погрешности вычисления индуктивности по этим выражениями составляет порядка нескольких процентов.

Так как индуктивные элементы довольно разнообразны, их можно разделить на три группы:

индуктивные элементы без сердечников;

индуктивные элементы с замкнутыми сердечниками;

индуктивные элементы с сердечниками, имеющие воздушный зазор.

Самые простые по конструкции являются индуктивные элементы без сердечников, поэтому рассмотрим их в первую очередь. Простейшим из таких элементов является прямой провод.

Индуктивность прямолинейного провода круглого сечения

При расчёте индуктивности необходимо разделять индуктивность на постоянном токе и индуктивность на высокой частоте. Под высокой частотой следует понимать такую частоту, на которой толщина скин-слоя меньше размеров поперечного сечения провода. В случае если толщина скин-слоя больше поперечных размеров провода, то можно вести расчёт для постоянного тока.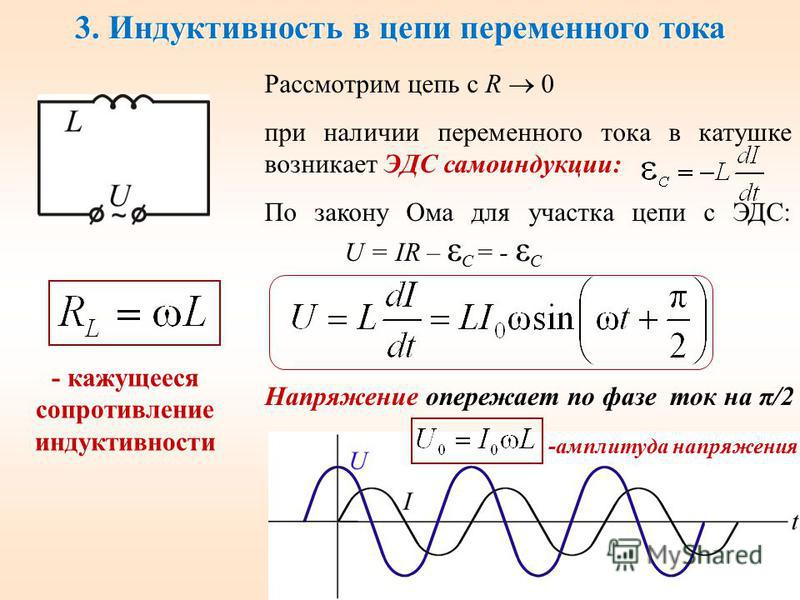

Определение индуктивности прямого провода. l – это длина проводника, d = 2r – диаметр проводника.

В случае постоянного тока или тока низкой частоты индуктивность составит

где μ0 – магнитная постоянная, μ0 = 4π•10-7 Гн/м;

l – длина провода, м;

d – диаметр провода, м.

Как я уже говорил, на величину индуктивности влияет частота переменного тока, поэтому в случае необходимости рассчитать индуктивность на любой частоте применяется следующее выражение

где ξ – коэффициент, вносящий поправку на распространение переменного тока по сечению провода. Данный коэффициент зависит от величины k*r, где

d = 2r – диаметр поперечного сечения провода, м.

где ω – угловая частота переменного тока, ω = 2πf;

μ0 – магнитная постоянная, μ0 = 4π•10-7 Гн/м;

γ – удельная проводимость вещества проводника.

Тогда если k*r < 3, то

если k*r > 3, то

где

Пример. Необходимо рассчитать индуктивность прямолинейного провода круглого сечения из меди (γ = 5,81*107 См/м) диаметром d = 2 мм и длиной l = 4 м, при постоянном токе и токе частотой f = 50 кГц.

На постоянном токе

На частоте 50 кГц

Индуктивность кругового кольца круглого сечения

Теперь рассмотрим, какова будет индуктивность если провод свернуть в кольцо. Такой индуктивный элемент будет иметь вид

Определение индуктивности кругового витка. D – диаметр кольца (витка), d – диаметр провода, из которого сделано кольцо (виток).

При этом его индуктивность можно вычислить по следующему выражению

для  постоянного тока

где R – радиус витка, м, R = D/2;

r – радиус провода, м, r = d/2;

μ0 – магнитная постоянная, μ0 = 4π•10-7 Гн/м.

Так же как и для проводника существует выражение для индуктивности кругового витка на любой частоте

где ξ – коэффициент, вносящий поправку на распространение переменного тока по сечению провода. Определяется также как и для прямого проводника.

Пример. В качестве примера рассчитаем индуктивность такого же провода, как и в первом примере, только свёрнутом в кольцо. В этом случае диаметр провода d = 2 мм, а диаметр кольца D = l/π = 4/3,142 ≈ 1,273 м, провод выполнен из меди (γ = 5,81*107 См/м).

Для постоянного тока индуктивность составит

На частоте 50 кГц

В следующей части я продолжу рассмотрение расчётов индуктивности для различных индуктивных элементов.

Теория это хорошо, но теория без практики — это просто сотрясание воздуха. Перейдя по ссылке всё это можно сделать своими руками

Скажи спасибо автору нажми на кнопку социальной сети

www.electronicsblog.ru

Coil32 — Методы расчета индуктивности катушки.

Методы расчета индуктивностей

Наиболее полно теоретические основы методов расчета индуктивностей изложены в справочной книге: «Расчет индуктивностей. П.Л.Калантаров Л.А.Цейтлин». Здесь же хотелось бы немного систематизировать подходы к расчету индуктивностей.

Прежде всего отметим, что расчет индуктивности можно вести двумя способами:

∙ Численный метод с различной степенью упрощения задачи

∙ Расчет по упрощенным эмпирическим формулам

Эмпирический подход предполагает подбор (подгонку) относительно несложных аппроксимирующих формул по результатам измерений индуктивности реальных катушек. Расчет по упрощенным эмпирическим формулам имеет ограничения в точности и применим только к катушкам с определенной геометрией намотки. Большинство таких формул можно найти здесь. Несмотря на невысокую точность, такой расчет чаще всего вполне достаточен в радиолюбительской практике.

Численные методы основываются на реальных физических моделях катушек индуктивности и их, в свою очередь, можно разбить на две категории:

1. Расчет в программах основанных на фундаментальных законах классической электродинамики, так называемых электромагнитных симуляторах. К ним можно отнести COMSOL Multiphysics, FEMM, ANSYS, GAL-ANA и т.п. Эти программы используют специальные численные методы, такие как метод моментов и метод конечных элементов. Расчет в таких программах довольно точен, позволяет учесть множество нюансов, рассчитать катушку произвольной формы, однако требует огромных ресурсов компьютера. Применяется при научном анализе или если катушка работает в режиме, когда ее нельзя представлять как сосредоточенный элемент [пример]
2. Численные методы расчета, основанные на фундаментальных формулах физики, применимых к круговым проводникам, выведенных в XIX веке Д. К.Максвеллом. Позволяют провести расчет более точно, чем по эмпирическим формулам, но не требуют запредельных аппаратных ресурсов компьютера. На них следует остановится подробнее, т.к их и использует Coil32…

Расчет индуктивности в программе Coil32 основан на модели Максвелла, в которой катушка представляется как множество соосных бесконечно тонких круговых проводников.Из Теоремы Гаусса следует, что силовые линии магнитного поля всегда замкнуты. Из этого следует, что магнитный поток порожденный круговым контуром с током весь проходит через поверхность, ограниченную этим контуром. Это обстоятельство отражено в следующей формуле:

Из этой формулы можно вывести определение для собственной индуктивности кругового проводника через двойной контурный интеграл Ф.Е.Неймана для взаимоиндукции [вывод здесь]:

Как показал Д.К.Максвелл, для двух бесконечно тонких круговых соосных проводников этот интеграл имеет однозначное решение, которое выглядит следующим образом:

, где:

• M — взаимоиндукция;
• r1, r2 — радиусы двух бесконечно тонких круговых проводников;
• x — расстояние между центрами кругов, ограниченных этими проводниками;
• K,E — эллиптические интегралы, соответственно первого и второго рода;

Численный метод расчета по формуле Максвелла сводится к численным методам решения эллиптических интегралов.

По формуле Максвелла можно рассчитывать как индуктивность многослойных и однослойных катушек, так и взаимную индуктивность двух отдельных катушек. Погрешности модели, связанные с допущением, что провод бесконечно тонкий и представляет собой набор круговых проводников (хотя на самом деле — это спираль), можно уменьшить с помощью соответствующих поправок.

Рассчитывая взаимоиндукцию проводника «самого на себя», т.е. его самоиндукцию (собственную индуктивность), Максвелл использует понятие — «среднее геометрическое расстояние» — GDM (g), для круглого провода:

g = e0.25*rw, где rw — радиус провода.

Очень важен следующий момент. Вся вышеприведенная логика рассуждений и вывода формул, начиная от формулы Неймана, справедлива в случае равномерного распределения плотности тока вдоль катушки. В подавляющем большинстве практических случаев так и есть. Однако если катушка работает вблизи частот собственного резонанса, начинает проявляться неравномерность распределения плотности тока по проводнику! Другими словами, начинает проявляться зависимость индуктивности от частоты, которая в наших расчетах не учитывается. Поэтому индуктивность катушки можно рассчитать корректно только на частотах не превышающих 60-70% от частоты ее собственного резонанса. Таким образом Coil32 не годится для точных расчетов, например, катушек Тесла или спиральных резонаторов. В этом случае и в случае если катушка работает в режиме выше частоты собственного резонанса — ее нужно представлять только в виде модели длинной линии и рассчитывать в программах-электромагнитных симуляторах, либо пользоваться специальными эмпирическими формулами.

Ссылки:

1. An introduction to the art of Solenoid Inductance Calculation D W Knight 2013
2. Numerical Methods for Inductance Calculation Robert Weaver 2012
3. Inductance Calculation Techniques — Part II: Approximations and Handbook Methods Marc T. Thompson 1999
4. A new method for inductance calculation M.A.Bueno A K T Assis 1995

coil32.ru

Расчёт катушки индуктивности под динамик – ldsound.ru

Данный расчет является примером для определения данных катушки индуктивности на воздушном сердечнике, нагруженной динамиком. В этом примере выбрана катушка без сердечника во избежание искажений, обусловленных перемагничиванием сердечника.

На рисунке показана оптимальная катушка индуктивности в смысле отношения индуктивности катушки и ее активному сопротивлению. Конструкция получается, когда внутренний диаметр цилиндрического слоя обмотки вдвое больше его высоты, а внешний диаметр в четыре раза больше высоты и в два раза больше внутреннего диаметра.

высота 1 см; внутренний диаметр 2 см; внешний диаметр 4 см.

Пример расчета

Современные программы по расчету пассивных фильтров для акустики, дают значение катушек индуктивности в мГн, здесь нужно перевести в мкГн, т.е. умножить на 1000.

Определим данные катушки с индуктивностью 1,25 мГн (или 1250 мкГн) разделительного фильтра, нагруженного динамиком сопротивлением 4 Ом. Активное сопротивление рассчитываемой катушки должно составлять 5% сопротивления динамика. Это соотношение можно считать вполне приемлемым. Активное сопротивление катушки: R = 0,05 х 4 = 0,2 Ом.

1. откуда: L/R = 1250 / 0,2 = 6250 мкГн/Ом;
2. далее имеем: h = √ ((L/R) / 8,6) = √ (6250 / 8,6) = 26,96 мм;
3. длинна жилы: l = 187,3 х √ (L х h) = 187,3 х √ (1250 х 26,96) = 34383 мм = 34,3 м;
4. количество витков: ω = 19,88 √(L / h) = 19,88 х √ (1250 / 26,96) = 135,36 витков;
5. диаметр жилы: d =0,84h / √ω = 0,84 х 26,96 / √ 135,36 = 1,95 мм;
6. масса намотки: m = (h5 х 10-3) / 21,4 = (26,963 х 10-3) / 21,4 = (19595,65 х 0,001) / 21,4= 0,9 кг.

Полученные значения должны быть округлены (в первую очередь диаметр жилы) до ближайшего стандартизированного. Окончательные значения индуктивности подгоняют путем отматывания нескольких витков обмотки, намотанной с некоторым превышением числа витков сравнительно с рассчитанным.

Итак имеем данные, которые понадобятся для расчета будущей катушки:

1. высота намотки h = 26,96 мм;
2. значит внутренний диаметр a = 53,92 мм;
3. соответственно внешний: b = 107,84 мм;
4. длинна жилы: 34,3 м;
5. количество витков: 135;
6. диаметр жилы, соответствует стандартизированному: 1,95 мм (по меди).

Статья специально подготовлена для сайта ldsound.ru

ldsound.ru

Как произвести расчет катушек индуктивности (однослойных, цилиндрических без сердечника)

Как произвести расчет катушек индуктивности (однослойных, цилиндрических без сердечника)

Индуктивность катушки зависит от ее геометрических размеров, числа витков и способа намотки катушки. Чем больше диаметр, длина намотки и число витков катушки, тем больше ее индуктивность.

Если катушка наматывается плотно виток к витку, то индуктивность ее будет больше по сравнению с катушкой, намотанной неплотно, с промежутками между витками. Когда требуется намотать катушку по заданным размерам и нет провода нужного диаметра, то при намотке ее более толстым проводом надо несколько увеличить, а тонким — уменьшить число витков катушки, чтобы получить необходимую индуктивность.

Все приведенные выше соображения справедливы при намотке катушек без ферритовых сердечников.

Расчет однослойных цилиндрических катушек производится по формуле

где L — индуктивность катушки, мкГн; D — диаметр катушки, см; l — длина намотки катушки, см; n—число витков катушки.

При расчете катушки могут встретиться два случая:

а) по заданным геометрическим размерам необходимо определить индуктивность катушки;

б) при известной индуктивности определить число витков и диаметр провода катушки.

В первом случае все исходные данные, входящие в формулу, известны, и расчет не представляет затруднений.

Пример. Определим индуктивность катушки, изображенной на рис. 97; для этого подставим в формулу все необходимые величины:

Во втором случае известны диаметр катушки и длина намотки, которая, в свою очередь, зависит от числа витков и диаметра провода. Поэтому расчет рекомендуется вести в следующей последовательности. Исходя из конструктивных соображений определяют размеры катушки, диаметр и

длину намотки, а затем рассчитывают число витков по формуле

После того как будет найдено число витков, определяют диаметр провода с изоляцией по формуле

где d— диаметр провода, мм, l — длина обмотки, мм, п — число витков.

Пример. Нужно изготовить катушку диаметром 1 см при длине намотки 2 см, имеющую индуктивность 0,8 мкГн. Намотка рядовая виток к витку.

Подставив в последнюю формулу заданные величины,

получим:

Диаметр провода

Если эту катушку наматывать проводом меньшего диаметра, то нужно полученные расчетным путем 14 витков разместить по всей длине катушки (20 мм) с равными промежутками между витками, т. е. с шагом намотки. Индуктивность данной катушки будет на 1—2% меньше номинальной, что следует учитывать при изготовлении таких катушек. При намотке в случае необходимости более толстым проводом, чем 1,43 мм, следует сделать новый расчет, увеличив диаметр или длину намотки катушки. Возможно, также придется увеличить и то и другое одновременно, пока не будут получены необходимые габариты катушки, соответствующие заданной индуктивности.

Следует заметить, что по приведенным выше формулам рекомендуется рассчитывать такие катушки, у которых длина намотки l равна или больше половины диаметра. Если же длина намотки меньше половины диаметра D/2 , то более точные результаты можно получить по формулам

В.Г.Бастанов, «300 практических советов»

www.radio-schemy.ru

Расчет индуктивности катушек: формула :: ashanet.ru

У каждого из нас бывали проблемы с предметами в школе. У кого-то были проблемы с химией, у кого-то — с физикой. Но даже если с этими предметами у вас всё всегда было хорошо, вы наверняка не помните всех тем, что вам давали в школе. Одной из таких тем является электромагнетизм в целом и расчёт индуктивности катушек в частности.

Для начала окунёмся немного в историю такого явления, как магнетизм.

История

Магнетизм начинает свою историю ещё с Древнего Китая и Древней Греции. Открытый в Китае магнитный железняк использовался тогда в качестве стрелки компаса, указывающей на север. Есть упоминания, что китайский император использовал его во время битвы.

Однако вплоть до 1820 года магнетизм рассматривался лишь как явление. Всё его практическое применение было заключено в указании стрелки компаса на север. Однако в 1820 году Эрстед провёл свой опыт с магнитной стрелкой, показывающий влияние электрического поля на магнит. Этот опыт послужил толчком для некоторых учёных, взявшихся за это всерьёз, чтобы разработать теорию магнитного поля.

Спустя всего 11 лет, в 1831 году, Фарадей открыл закон электромагнитной индукции и ввёл в обиход физиков понятие «магнитное поле». Именно этот закон послужил основой для создания катушек индуктивности, о которых сегодня и пойдёт речь.

А прежде чем приступить к рассмотрению самого устройства этих катушек, освежим в голове понятие магнитного поля.

Магнитное поле

Это словосочетание знакомо нам со школьной скамьи. Но многие уже забыли о том, что оно означает. Хотя каждый из нас помнит, что магнитное поле способно воздействовать на предметы, притягивая или отталкивая их. Но, помимо этого, у него есть и другие особенности: например, магнитное поле может воздействовать на электрически заряженные объекты, а это значит, что электричество и магнетизм тесно связаны между собой, и одно явление может плавно перетекать в другое. Учёные поняли это достаточно давно и поэтому стали называть все эти процессы вместе одним словом — «электромагнитные явления». На самом деле электромагнетизм — довольно интересная и ещё не до конца изученная область физики. Она очень обширна, и те знания, что мы можем здесь изложить вам, — это очень малая часть того, что известно человечеству о магнетизме сегодня.

А сейчас перейдём непосредственно к предмету нашей статьи. Следующий раздел будет посвящён рассмотрению непосредственно устройства катушки индуктивности.

Что такое катушка индуктивности?

Мы сталкиваемся с этими предметами постоянно, но вряд ли придаём им какое-то особое значение. Это для нас обыденность. На самом деле катушки индуктивности встречаются сегодня практически в каждом приборе, но наиболее яркий пример их использования — трансформаторы. Если вы думаете, что трансформаторы бывают только на энергетических подстанциях, то вы сильно ошибаетесь: ваше зарядное устройство от ноутбука или смартфона — тоже своего рода трансформатор, только меньшего размера, чем те, что используются на электростанциях и распределительных подстанциях.

Любая катушка индуктивности состоит из сердечника и обмотки. Сердечник представляет собой стержень из диэлектрического или ферромагнитного материала, на который наматывается обмотка. Последняя делается чаще всего из медной проволоки. Количество витков обмотки напрямую связано с величиной магнитной индукции полученной катушки.

Теперь, прежде чем рассмотреть расчет индуктивности катушек и формулы, необходимые для него, поговорим о том, какие параметры и свойства мы будем вычислять.

Какие параметры есть у катушки?

Катушка обладает несколькими физическими характеристиками, отражающими её качество и пригодность для той или иной работы. Одной из них является индуктивность. Она численно равна отношению потока магнитного поля, создаваемого катушкой, к величине этого тока. Индуктивность измеряется в Генри (Гн) и в большинстве случаев принимает значения от единиц микрогенри до десятков Генри.

Индуктивность является, пожалуй, самым важным параметром катушки. Поэтому неудивительно, что большинство людей даже не думают о том, что существуют другие величины, способные описывать поведение катушки и отражать её пригодность для того или иного применения.

При выборе катушки индуктивности профессионалы также обращают внимание на сопротивление потерь. Как можно понять из этого словосочетания, оно отражает величину потерь электроэнергии, происходящих вследствие паразитных эффектов, таких как, например, нагревание проводов, происходящее по закону Джоуля-Ленца. Нетрудно понять, что чем ниже это значение для катушки, тем она лучше.

Ещё один параметр, который необходимо учитывать, — добротность контура. Она тесно связана с предыдущим параметром и представляет собой отношение реактивного сопротивления к активному (сопротивлению потерь). Соответственно, чем выше добротность — тем лучше. Её повышение достигается за счёт выбора оптимального диаметра провода, материала и диаметра сердечника, числа обмоток.

Сейчас рассмотрим подробнее самый важный и наиболее волнующий нас параметр — индуктивность катушки.

Немного больше про индуктивность

Мы уже разобрали это понятие, и теперь осталось поговорить о нём немного подробнее. Зачем? Нам ведь предстоит расчет индуктивности катушек, а значит, необходимо понимать, что это такое и зачем нам её рассчитывать.

Катушка индуктивности предназначена для создания магнитного поля, а значит, имеет параметры, которые описывают его силу. Таким параметром является магнитный поток. Но разные катушки имеют разные потери при прохождении через них тока и, соответственно, разный КПД. В зависимости от диаметра проводов и количества витков катушка может давать разное по величине магнитное поле. Значит, необходимо ввести такую величину, которая бы отражала зависимость между величиной магнитного потока и силой тока, пропускаемой через катушку. Таким параметром и является индуктивность.

Зачем нужен расчёт индуктивности?

Катушек разных видов в мире достаточно много. Они отличаются между собой свойствами, а значит, и применениями. Одни используются в трансформаторах, другие, соленоиды, выполняют роль электромагнитов большой силы. Кроме этих, применений у катушек индуктивности найдётся предостаточно. И для всех них необходимы разные типы катушек. Они отличаются по своим свойствам. Но большую часть этих свойств можно объединить с помощью понятия индуктивности.

Мы уже близко подошли к объяснению того, что включает в себя формула расчета индуктивности катушки. Но стоит оговориться, что речь пойдёт не о «формуле», а о «формулах», так как все катушки можно разделить на несколько больших групп, для каждой из которых своя отдельная формула.

Виды катушек

По функциональности различают контурные катушки, находящие применение в радиофизике, катушки связи, используемые в трансформаторах, и вариометры, то есть катушки, показатели которых можно варьировать изменением взаимного расположения катушек.

Также существует такой вид катушек, как дроссели. Внутри этого класса также есть деление на обычные и сдвоенные. Они имеют высокое сопротивление переменному току и очень низкое — постоянному, благодаря чему могут служить хорошим фильтром, пропускающим постоянный ток и задерживающим переменный. Сдвоенные дроссели отличаются большей эффективностью при больших токах и частотах по сравнению с обычными.

Формулы расчёта

Пришла пора нам перейти к основной теме статьи. Начнём мы с того, что расскажем о том, как произвести расчет индуктивности катушки без сердечника. Это самый простой вид расчёта. Но тут тоже есть свои тонкости. Возьмём, для простоты, катушку, обмотка которой лежит одним слоем. Для неё справедлив расчет однослойной катушки индуктивности:

L=D2*n2/(45D+100l).

Здесь L — индуктивность, D — диаметр катушки в сантиметрах, n — число витков, l — длина намотки в сантиметрах. Однослойная катушка предполагает то, что толщина намотки будет не больше одного слоя, а значит, для неё справедлив расчет плоской катушки индуктивности. В целом большинство формул для расчётов индуктивностей очень похожи: существенные различия только в коэффициентах при переменных в числителе и знаменателе. Самым простым тут является расчет индуктивности катушки без сердечника.

Представляет интерес также формула расчета индуктивности катушки с большим числом витков:

L=0,08*D2*n2/(3*D+9*b+10*c).

Здесь b — ширина провода, c — его высота. Такая формула эффективна для того, чтобы произвести расчет многослойной катушки индуктивности. Применяется она на практике чуть менее часто, чем та, о которой пойдёт речь ниже.

Самым актуальным, пожалуй, будет расчет индуктивности катушки с сердечником. Есть специальная формула, которая показывает, что эта индуктивность определяется материалом, из которого сделан сердечник, а точнее — его магнитной проницаемостью. Выглядит эта формула так:

L=m*m0*n2*S/l,где m — магнитная проницаемость материала сердечника, m0 — магнитная постоянная (она равна 12,56·10-7 Гн/м), S — площадь поперечного сечения катушки, l — длина намотки.

Расчет витков катушки индуктивности производится очень просто: это число намотанных на сердечник слоёв проводника.

Мы разобрались с формулами, а теперь немного о том, где же конкретно эти формулы и расчёты могут нам пригодиться.

Практическое применение

Эти формулы имеют очень широкое применение ввиду повсеместного распространения катушек индуктивности. Как мы уже выяснили, бывают разные виды катушек, каждый из которых соответствует своему применению. В связи с этим становится необходимым как-то разделять их по характеристикам, ведь для каждой отрасли необходима своя определённая индуктивность и добротность.

В основном расчет индуктивности катушек применяется на производстве и в электротехнике. Каждый радиолюбитель должен знать, как производить расчет индуктивности, иначе как ему определить, какая катушка из огромного множества подойдёт для его цели, а какая — нет.

Вам интересно?

Сегодня очень много учёных, интересующихся магнетизмом и магнитными явлениями. Они изучают как магнитную, так и электрическую стороны веществ, пытаясь выявить закономерности и синтезировать мощные магниты с определёнными нужными свойствами: например, с высокой температурой плавления или сверхпроводимостью. Все эти материалы могут быть использованы в огромном количестве отраслей.

Приведём пример с аэрокосмической отраслью: перспективными для дальних межзвёздных перелётов являются ракеты с ионными двигателями, которые создают тягу посредством выброса ионизированного газа из сопла. Сила толчка в таком двигателе зависит от температуры газа и скорости его движения. Соответственно, чтобы придать газу максимальную силу для разгона, нам требуется очень сильный магнит, разгоняющий заряженные частицы и к тому же имеющий очень высокую температуру плавления для того, чтобы не расплавиться при выходе газов из сопла.

Заключение

Знание никогда не бывает лишним и всегда где-нибудь, да пригодится. Теперь, если вам попадётся программа расчета индуктивности катушки, вы без труда сможете сказать, почему там именно такие формулы и какие переменные в них что означают. Эта статья предназначена лишь для вашего ознакомления, и если вы хотите знать больше, стоит почитать специализированную литературу (благо за много лет изучения магнитных явлений её накопилось очень много).

ashanet.ru

---

• Посудомоечная машина для дома
• Сварочный инвертор своими руками схемы
• Как делают подсветку где потолок
• Что такое варистор и для чего он нужен
• Как сделать напольный торшер своими руками фото
• Реверсивное подключение трехфазного двигателя
• Освещение теплицы
• Отличие многожильного кабеля от одножильного
• Уличный щиток для электросчетчика и автоматов
• Лампочки с цветами
• Напряжения линейные

Вычисление и использование частичной индуктивности в COMSOL®

Версия 6.0 программного обеспечения COMSOL Multiphysics® расширяет функциональные возможности интерфейса Magnetic Fields, Currents Only в модуле «AC/DC» для вычисления стационарных и частотно-зависимых матриц индуктивности и сопротивлений в AC-режиме для электрических систем, состоящих из немагнитных материалов. Данные инструменты полезны для анализа печатных плат и систем токопроводящих шин питания. 2. Квадратная петля с длиной стороны 2 см из провода диаметром 1 мм обладает общей индуктивностью порядка 50.6 нГ.

Квадратная петля из проволоки, расположенная внутри сферической области с внешними условиями, которые имитируют свободное пространство типа Infinite Element Domain. Для такой системы определена общая или полная индуктивность.

В этой модели используется сферическая область с внешним слоем, в котором задано условие Infinite Element Domain для имитации открытых границ. Общий подход к моделированию такой системы очень похож на приведенную в Галерее моделей и приложений демомодель катушки Гельмгольца. В этом примере используются как интерфейс Magnetic Fields, Currents Only, так и интерфейс Magnetic Fields, и демонстрируется, что обе эти формулировки дают идентичные результаты.

Хотя для указанной постановки можно использовать либо интерфейс Magnetic Fields, Currents Only, либо интерфейс Magnetic Fields, но в общем случае между этими двумя формулировками существует ряд различий.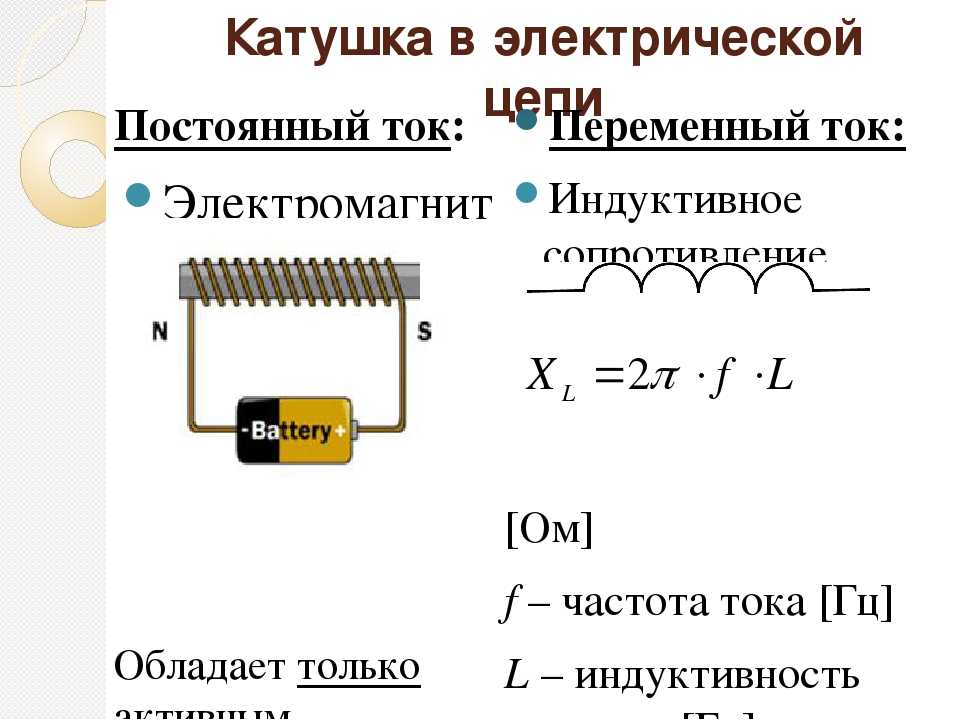 В рамках данной заметки мы сосредоточимся только на трех аспектах, которые уникальны для интерфейса Magnetic Fields, Currents Only:

1. Требуется, чтобы в системе не было магнитных материалов, таких как сердечники или магнитопроводы.
2. Требуется, чтобы все проводники были объёмными.
3. На выходе расчёта доступна не только общая индуктивность, но и матрица частичных индуктивностей.

Наша модель петли из провода круглого сечения с воздушным сердечником явно удовлетворяет первым двум требованиям, поэтому давайте сосредоточимся на третьем пункте: вычислении частичных индуктивностей.

В то время как концепция полной индуктивности всегда требует полного и замкнутого контура тока, концепция частичной индуктивности заключается в разделении общего контура на несколько частей, каждая из которых вносит свой вклад в частичную собственную индуктивность и частичную взаимную индуктивность. Суперпозиция этих вкладов дает общую полную индуктивность исходного замкнутого контура. Как с теоретической, так и с точки зрения моделирования, у нас есть полная свобода в выборе формата разделения, и мы можем сделать все, что наилучшим образом соответствует нашим инженерным целям.

Разделение одного индуктора на 4 части с 4 частичными собственными индуктивностями и 12 частичными взаимными индуктивностями. По соображениям симметрии на схеме указано только 6 из 12 частичных индуктивностей.

В таблице ниже показано несколько различных вариантов проводящего контура. Что касается моделирования, то для каждой из этих областей мы будем использовать отдельный узел Conductor с граничными условиями Terminal и Ground, выбранными и размещенными таким образом, чтобы ток всегда протекал в одном и том же направлении по контуру. Результат, который мы получим, будет представлять собой матрицу частичных индуктивностей. Давайте проанализируем числовые значения элементов этой матрицы. Будем называть члены на диагонали матрицы частичными собственными индуктивностями (partial self-inductances), а недиагональные члены – частичными взаимными индуктивностями (partial mutual inductances).

Тип разделения катушки	Матрица частичной индуктивности (nH)
	\begin {bmatrix}11.84 & 0.85 & -0.89 & 0.85\\ 0.85 & 11.84 & 0.85 & -0.89\\ -0.89 & 0.85 & 11.84 & 0.85\\ 0.85 & -0.89 & 0.85 & 11.84\\\end{bmatrix}
	\begin {bmatrix}14.0 & 0.2 & -1.75 & 0.2\\ 0.2 & 14.0 & 0.2 & -1.75\\ -1.75 & 0.2 & 14.0 & 0.2\\ 0.2 & -1.75 & 2& 14.0\\\end{bmatrix}
	\begin {bmatrix}25.38 & -0.08\\ -0.08 & 25.38\\\end{bmatrix}
	\begin {bmatrix}38.4 & -1.3\\ -1.3 & 14.8\\\end{bmatrix}
	\begin {bmatrix}49.3 & 0.5\\ 0.5 & 0.3\\\end{bmatrix}

Таблица матриц частичной индуктивности для различных вариантов разделения контура с током. {tot} = \sum_ {i,j} L_ {ij}. Это справедливо независимо от того, как разделена катушка. Однако при различных вариантах разделения в матрице частичных индуктивностей может в большей степени преобладать собственная индуктивность.

Наблюдение о том, что определенные разделения катушки приводят к более диагонально доминирующей матрице частичных индуктивностей, оправдывает нашу следующую манипуляцию – построении подмодели только из одной секции катушки в свободном пространстве, как показано на рисунке ниже. Это соответствует первому разделению, указанному в таблице выше. В этой модели мы используем один узел Conductor с граничными условиями Terminal и Ground на обоих концах. На выходе расчета мы получим только одну сосредоточенную величину: частичную собственную индуктивность равную 11.84 нГ. Это значение коррелирует с диагональными членами ранее вычисленной матрицы частичной индуктивности.

Модель с одной четвертью квадратного контура позволяет рассчитать частичную собственную индуктивность, что дает хорошую оценку для общей индуктивности в этом случае. Интерфейс Magnetic Fields, Currents Only поддерживает расчёт катушек, которые незамкнуты в пространстве, при задании условий Terminal и Ground.

Со стороны может показаться, что наша модель «создает» и «уничтожает» ток на концах провода (где применяются граничные условия Terminal и Ground), но этот факт как раз является отличительной особенностью интерфейса Magnetic Fields, Currents Only: он позволяет вычислять частичную собственную индуктивность (и частичную взаимную индуктивность) для любого набора проводящих доменов, даже для тех, которые не соединены в замкнутый контур.

В качестве еще одного примера давайте обсудим второе разделение катушки. Фактически мы рассмотрим отдельный короткий прямой отрезок круглого провода — этот случай представляет особый интерес, поскольку для него существуют опубликованные решения, представленные в таблице ниже. В этом случае мы оценим индуктивность и сопротивление переменному току в диапазоне частот, начиная с низких частот, где глубина скин-слоя намного больше диаметра, и заканчивая высокими частотами, где глубина скин-слоя намного меньше. 2)} Длина: \ell, радиус: r, электрическая проводимость: \sigma, толщина скин-слоя: \delta =\sqrt{ \frac {2} {\omega \mu_0\sigma}}

Полученные в такой модели результаты показывают точное соответствие для сопротивления в DC-режиме и близкое соответствие (в пределах 1%) для низкочастотной индуктивности. Небольшое расхождение в области низких частот связано с краевыми эффектами; соответствие между числовой моделью и справочным значением для прямого провода становится лучше при увеличении длины анализируемого провода.

Крупный план внутренней части провода. На распределении магнитного поля заметны краевые эффекты около торца провода.

Для сопротивления в AC-режиме также получается хорошее соответствие в широком частотном диапазоне, но на очень высоких частотах наблюдается заметное отклонение, что соответствует случаю глубины скин-слоя намного меньшего диаметра провода. Это отклонение связано уже с другой проблемой: на таких высоких частотах нам понадобилась бы очень подробная погранслойная сетка для разрешения скин-эффекта.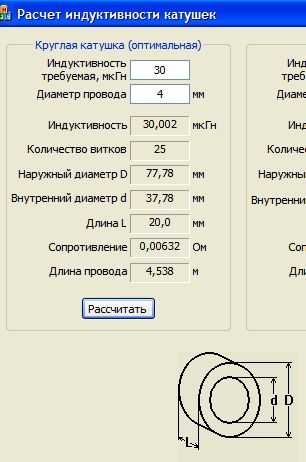

Расчётное сопротивление в AC-режиме для прямого провода и его сравнение с справочными выражениями на основе толщины скин-слоя. На очень высоких частотах потребуется очень подробная сетка, кроме того предположение о незначительных токах смещения в этом диапазоне больше не выполняется.

На таких очень высоких частотах возникает еще одна проблема: предположение о том, что близлежащие диэлектрики можно проигнорировать, больше не действует. Другими словами, токи смещения начинают становиться значимыми. В этой ситуации нам следует перейти к формулировке Magnetic Fields, которая позволяет моделировать токи, протекающие по поверхностям проводников, вместо того, чтобы искать поля внутри объема. В интерфейсе Magnetic Fields также учитываются токи смещения, как и токи проводимости и индуктивные наводки. Формулировки же интерфейса Magnetic Fields, Currents Only пренебрегают всеми токами смещения и учитывают только токи проводимости и индукционные наводки внутри самих проводящих областей.

Вычисленная частичная собственная индуктивность прямого провода и его сравнение со справочными формулами низко- и высокочастотных кабелей, в которых пренебрегают краевыми эффектами.

Итак, теперь, когда мы понимаем, как вычислить частичную индуктивность, и области применимости этой формулировки, как мы можем эффективно использовать этот интерфейс? Важно отметить, что мы никогда не сможем измерить ни одну из этих частичных индуктивностей, поскольку измерима только общая индуктивность замкнутого контура. Но, предположив, что у нас есть большая комплексная система, тогда мы, скорее всего, окажемся в ситуации, когда вычисление общей индуктивности довольно вычислительно сложно и затратно.

В случае, когда мы заинтересованы только в перепроектировании одной небольшой подсистемы, мы может сделать два предположения:

1. Частичные взаимные индуктивности между моделируемыми и немоделируемыми компонентами оказывают относительно небольшое влияние на общую индуктивность.
2. Частичная собственная индуктивность компонентов, которые не моделируются, остается относительно постоянной.

Если эти предположения верны, то разумно смоделировать только эту одну часть (или всего несколько частей) системы. Хотя мы, возможно, никогда не захотим вычислять общую индуктивность, в этой подмодели все еще может быть прогностическая ценность, если будут учтены вышеуказанные предположения и сама концепция частичных индуктивностей, являющихся вкладами в общую индуктивность.

Теперь давайте рассмотрим несколько типовых примеров применения рассмотренного интерфейса.

Типовые области применения интерфейса Magnetic Fields, Currents Only

Ситуации, в которых будет полезен интерфейс Magnetic Fields, Currents Only, включают:

• Вычисление частичных индуктивностей компонентов печатной платы
• Моделирование систем токопроводящих шин питания
• Моделирование кабелей и коннекторов
• Расчёт биполярных транзисторов с изолированным затвором (IGBT)
• Исследование характеристик катушек в случае отсутствия магнитных материалов в их окрестности

Одним из таких примеров является печатная плата с несколькими индукторами (с воздушными сердечниками), как показано ниже. Обладая накопленными знаниями, мы теперь можем уверенно строить модели, которые позволяют извлечь частичную собственную индуктивность одного индуктора или частичную собственную индуктивность и частичную взаимную индуктивность между несколькими близко расположенными индукторами. Рекомендую соответствующий демопример – расчет матрицы индуктивности массива катушек на печатной плате.

Электрический компонент, содержащий множество катушек индуктивности с воздушным сердечником. С помощью интерфейса Magnetic Fields, Currents Only можно вычислить сопротивления в AC-режиме и матрицы частичной индуктивности только для нескольких из этих катушек индуктивности.

Заключительные замечания

В данной статье мы представили интерфейс Magnetic Fields, Currents Only, который эффективен для вычисления полной и частичной индуктивности и сопротивления в AC-режиме. Мы сопоставили его использование с другими подходами и удостоверились в корректности расчёта общей индуктивности.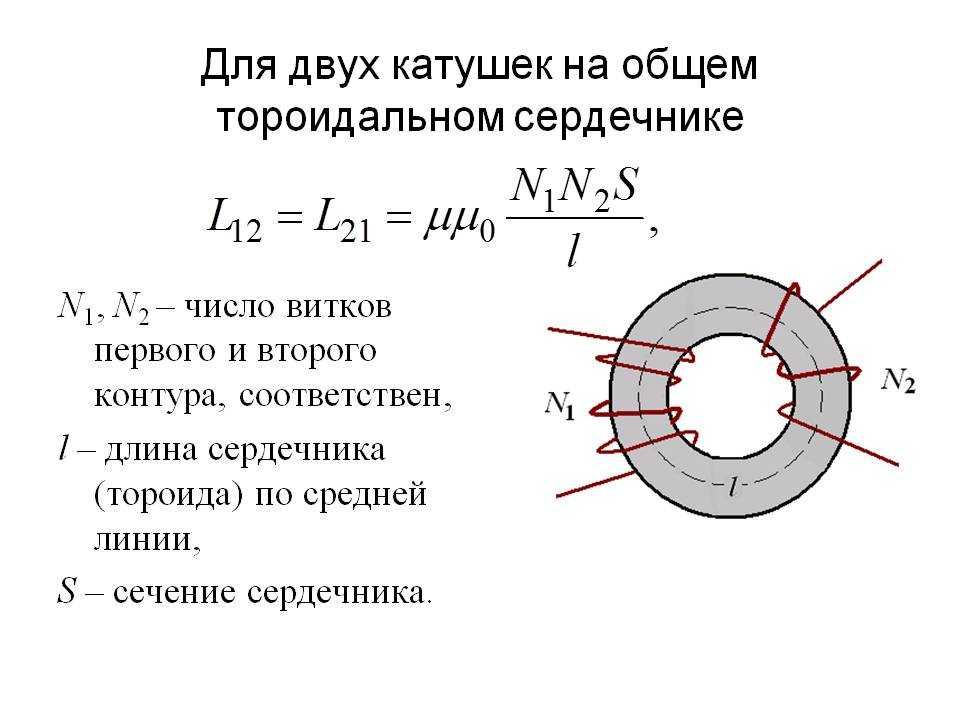 Затем мы обсудили концепцию частичной индуктивности и то, как связаны частичная и полная индуктивности. Мы также рассмотрели вычисление сопротивления в AC-режиме, что помогло нам определить область применимости интерфейса Magnetic Fields, Currents Only при исследованиях в частотной области. Обладая этой информацией, мы теперь определённо готовы решать подобные задачи!

Вы всегда можете узнать дополнительную техническую информацию о модуле «AC/DC» или связаться с нами для получения более информации о других аспектах использования нашей программы.

Свяжитесь с COMSOL

Inductance Formula — GeeksforGeeks

Индуктивность — это термин, с которым должен быть знаком каждый студент-физик. Он имеет собственную формулу и часто комбинируется с сопротивлением и емкостью. Оливер Хевисайд впервые придумал эту фразу в 1886 году. Кроме того, мы используем букву L для обозначения катушек индуктивности на принципиальных схемах и индуктивности в уравнениях в честь выдающегося физика Генриха. Давайте узнаем о формуле индуктивности и о том, как ее использовать для определения индуктивности. любой предмет.

Индуктивность

Индуктивность — это свойство электрического проводника, которое заставляет его сопротивляться изменениям проходящего через него электрического тока. Поток электрического тока создает вокруг проводника магнитное поле. Напряженность поля пропорциональна величине тока и не зависит от колебаний тока. Согласно закону индукции Фарадея, любое изменение магнитного поля в цепи создает электродвижущую силу (ЭДС) (напряжение) в проводниках, процесс, известный как электромагнитная индукция.

Индуктивность присутствует во многих электрических и электронных системах, а также в цепях. Шестерни доступны в различных формах и размерах, а также различных названиях. Примеры включают катушки, дроссели, трансформаторы, катушки индуктивности и другие детали.

Единицей индуктивности в СИ является генри (Гн) , что может быть представлено в скорости изменения тока и напряжения.

Формула индуктивности

• Ниже приведена формула индуктивности,

L = мкН ² А/л

Где,

• L = индуктивность (Гн),
• мк = магнитная проницаемость (Вб/ампер),
• 7 90 витков18
• Н = катушка A = Окружность рулона,
• l = Длина рулона (м).

Вывод перепишите приведенное выше уравнение,

E = -N(dϕ/dt)

Предыдущее уравнение изменено для вычисления значения индуктивности.

E = -N(dϕ/dt)

∴ E = -L(di/dt)

N = dΦ = L di

NΦ = Li

Следовательно,

Плотность потока обозначена B, площадь катушки обозначена A.

Li = NΦ = NBA

Hl = Ni

Намагничивающая сила магнитного потока обозначена H.

B = µH

Li = NBA

L = NBA / я = N ² BA/Ni

N ² BA/Hl = N ² μHA/Hl

∴ L = μN ² A/l 

• With an inductance of L, the voltage induced в катушке (В) равно,

В = L × (di/dt)

Где,

• В = напряжение (вольт),
• L = значение индуктивности (Гн),
• i = Ток (А),
• t = Затраченное время (с).

• Реактивное сопротивление индуктивности рассчитывается следующим образом,

X = 2πfL

Где,

• X = реактивное сопротивление (Ом),
• f = частота (Гц),
• L = индуктивность (Гн).

• Если индуктивность последовательно

L = L ₁ + L ₂ + L ₃ . . . . + L _n

• Если индуктивность параллельна

1/L = 1/L ₁ + 1/L _{2 10149 +0147 3} . . . . + 1/L _n

Примеры вопросов

Вопрос 1: Определение индуктивности.

Ответ :

Индуктивность — это свойство электрического проводника, которое заставляет его сопротивляться изменениям проходящего через него электрического тока. Поскольку индуктивность имеет N в формуле, это означает, что количество витков в проводнике прямо пропорционально присутствующей индуктивности. Однако интересным фактом является то, что даже прямые проводники несут индуктивность очень мало, чтобы быть значительной.

Вопрос 2: Что такое единица индуктивности в системе СИ?

Ответ:

Единицей индуктивности в системе СИ является генри (Гн). Открытие индуктивности приписывают Фарадею, однако введение собственной индуктивности для одиночной цепи было впервые введено Генри. Поэтому единица индуктивности посвящена имени ученого.

Вопрос 3: Определите самоиндукцию 210-виткового соленоида с площадью поперечного сечения 17 см ² и длиной 66,2 см.

Решение:

Дано: μ = 4π × 10 ^-7 N/A ² , n = 210 поворотов, A = 17 × 100023 -4 M ² , L = 66,2 × 10 ^-2 м

Т. к. -4 ))/(66,2 × 10 ^-2 )

∴ L = 0,0001422

∴ L = 14,22 × 10 ^-5 H

Вопрос 4: Каково соответствующее сопротивление при последовательном соединении катушек индуктивности 16H, 10H и 21H?

Решение :

Дано: L ₁ = 16 H, L ₂ = 10 H, L ₃ = 21 H

С.

L ₁ + L _{+ L + L + L + L + L + L + L + L + L + L}

+ L + L

+

. 2 + L ₃ 

∴ L = 16 + 10 + 21

∴ L = 47 Гн

при условии. рассчитать реактивное сопротивление?

Решение:

Дано: F = 240 Гц, L = 61 H

,

x = 2πfl

∴ x = 2 × 3,14 × 240 × 61

∴ x = 91939 o

Вопрос 6: Каково соответствующее сопротивление при параллельном соединении катушек индуктивности 26H, 16H, 21H и 30H?

Решение:

Дано: L ₁ = 26 H, L ₂ = 16 H, L ₃ = 21 H, L ₄ = 30 H

Поскольку,

1/л = 1/л ₁ + 1/л ₂ + 1/л ₃ + 1/л 4

 1/26 + 1/16 + 1/21 + 1/30

∴ 1/л = 0,03 + 0,06 + 0,04 + 0,03

∴ 1/л = 0,16 Гн

∴ Дл = 6,204 00012 Гн Катушка индуктивности и индуктивность — формулы и уравнения

Следующие формулы и уравнения можно использовать для расчета индуктивности и связанных с ней величин различных форм катушек индуктивности следующим образом.

СОДЕРЖАНИЕ

Индуктивность индуктора:

Индуктивность индуктора из базовой формулы индуктора:

Напряжение по всему индуктору:

9003 1111111111111111111111111111111111111111111111.

Где

• В — напряжение на катушке индуктивности
• L — индуктивность катушки индуктивности в Генри
• Di/dt — мгновенная скорость изменения тока через индуктор.
• i от _до = ток в момент времени t = 0.

Реактивное сопротивление катушки индуктивности:

Реактивное сопротивление катушки индуктивности – это сопротивление катушки индуктивности переменному току переменного тока, которое зависит от ее частоты f и измеряется в Омах так же, как сопротивление. Индуктивное сопротивление рассчитывается по формуле:

X _L = ωL = 2π f L

Где

• X _L — индуктивное реактивное сопротивление

  .

• ф — применяемая частота
• L — индуктивность в Генри

Качественный коэффициент индуктора:

Эффективность индуктора известна как коэффициент качества, и он измерен:

QF = x _L /ESR

, где

• x L

  , где

  • x
    . Индуктивное сопротивление
  • ESR — эквивалентное последовательное сопротивление цепи.
  Коэффициент рассеяния катушки индуктивности:

  Является обратным значением добротности и показывает мощность, рассеиваемую внутри индуктора, и определяется по формуле:

  DF = tan δ = ESR/X _L

  Где

  • DF — коэффициент рассеяния
  • δ — угол между емкостным реактивным сопротивлением и отрицательной осью.
  • X _C — емкостное реактивное сопротивление
  .
  • ESR — эквивалентное последовательное сопротивление цепи.
  Энергия, запасенная в индукторе:

  Энергия E, запасенная в катушке индуктивности, определяется по формуле:

  E = ½ Li ²

  Где

  • E – энергия в джоулях
  • L — индуктивность в Генри
  • i — сила тока в амперах

  Related Posts:

  • Что такое соленоид и магнитное поле соленоида
  • Символы индуктора — символы соленоида, блока и катушек
  Средняя мощность индуктора

  Средняя мощность индуктора определяется по формуле:

  P _av  = Li ²  / 2t

  Где

  •  – время в секундах.
  Ток катушки индуктивности во время заряда/разряда:

  Как и конденсатору, катушке индуктивности требуется до 5 постоянных времени для полной зарядки или разрядки, в течение этого времени ток можно рассчитать по формуле:

  Во время зарядки:

  Мгновенный ток катушки индуктивности во время зарядки определяется по формуле:

  Во время разрядки:

  Ток во время разрядки в любое время t определяется как:

  Где

  • I

    C ток катушки индуктивности

  • I ₀  ток в момент времени t=0
  • t — время, прошедшее после подачи тока.
  • τ = L/R — постоянная времени цепи RL

  Related Posts:

  • Калькулятор индуктивности индуктора с воздушным сердечником
  • Калькулятор индуктивности прямого провода и электрода
  Формулы индуктивности
  Индуктивность спиральной катушки «Формула Уилера»

  Где:

  • L – индуктивность
  • R это радиус
  • n — количество витков
  • ч это высота
  Формула индуктивности спиральной катушки

  Где:

  • ИЛИ — внешний радиус в дюймах
  • IR — самый внутренний радиус в дюймах
  Спиральная катушка Формула
  Формула индуктивности конической катушки

  Где:

  • θ — угол за пределами конуса, (предполагайте θ ≈ 15 °)

  Связанные формулы и уравнения Сообщения:

  • Сопротивление, емкость и индуктивность в последовательно-параллельном соединении – уравнения и формулы
  • Основные формулы и уравнения электротехники
  • Основные формулы электрических величин
  • Формулы мощности в однофазных и трехфазных цепях постоянного и переменного тока
  • Потери в электрических машинах – формулы и уравнения
  • Формулы и уравнения генератора постоянного тока
  • Уравнение мощности, напряжения и ЭДС двигателя постоянного тока – формулы
  • Формулы и уравнения синхронного генератора и генератора переменного тока
  • Формулы и уравнения для синхронных, шаговых и двигателей переменного тока
  • Асинхронный двигатель и линейные асинхронные двигатели Формулы и уравнения
  • Трансформаторные формулы и уравнения
  • Формулы и уравнения в области электротехники и электроники
  • Электрические и электронные элементы и символы

  Показать полную статью

  Связанные статьи

  Кнопка «Вернуться к началу»

  Катушка индуктивности i-v уравнение в действии

  Катушка индуктивности является одним из идеальных элементов цепи. Мы узнаем больше о том, как ведет себя индуктор, внимательно изучив его уравнение $i$-$v$.

  Автор Вилли Макаллистер.

  ---

  Содержание

  • Уравнения индуктора $i$-$v$
  • Напряжение дросселя пропорционально скорости изменения тока
  • Катушка индуктивности и источник тока
    • Имитационная модель
    • Иногда катушка индуктивности «выглядит» короткой
  • Катушка индуктивности и источник напряжения
    • Имитационная модель
  • Пример
    9{\,T} v\,\text dt + i_0$

    Это производная и интегральная формы уравнений индуктора.

    $\text L$ индуктивность , физическое свойство катушки индуктивности.
    $\text L$ — масштабный коэффициент между $v$ и $di/dt$.
    $\text L$ показывает, сколько $v$ генерируется для заданного количества $di/dt$.
    $i_0$ — начальный ток, протекающий в катушке индуктивности при $t=0$.

    обозначение исчисления: $di/dt$

    $v = \text L\,\dfrac{di}{dt}$

    9{\,T} v\,\text dt + i_0$

    Зацикленный символ $\int$ тоже из исчисления. Это интегральный признак. Его значение аналогично символу суммирования $\Sigma$. В уравнении индуктора знак интеграла представляет собой бегущую сумму произведения $v\,\times \,dt$, начиная с момента времени $t=0$ и заканчивая моментом времени $t=T$. Интегрирование противоположно взятию производной.

    Напряжение на дросселе пропорционально

    скорости изменения тока

    Когда мы узнали о резисторах, закон Ома сказал нам, что напряжение на резисторе пропорционально току через резистор: $v = \text R\,i$ .

    Теперь у нас есть индуктор с уравнением $i$-$v$: $v = \text L\,\dfrac{di}{dt}$.

    Это говорит нам о том, что напряжение на катушке индуктивности пропорционально не току, а скорее скорости изменения тока через катушку индуктивности. Вот что означает $di/dt$.

    Для реальных резисторов мы должны позаботиться о том, чтобы напряжение и ток не становились слишком большими для резистора. Для реальных катушек индуктивности мы должны быть осторожны со скоростью изменения тока . 0401 не слишком велик для катушки индуктивности. Это может быть сложно. Очень легко создать большое изменение тока при размыкании или замыкании переключателя. В статье об отдаче индуктора мы разрабатываем для этой ситуации.

    Катушка индуктивности и источник тока

    Теперь мы рассмотрим несколько различных простых схем, чтобы понять, что означают уравнения $i$-$v$ для катушки индуктивности. По пути мы увидим, как уравнения учат нас некоторым простым практическим правилам относительно катушки индуктивности.

    Первый пример — катушка индуктивности, подключенная к идеальному источнику тока.

    Источник тока подает постоянный ток на катушку индуктивности, $i = \text I$.
    Например, пусть $i = 2 \,\text{mA}$.

    Какое напряжение на дросселе?

    Уравнение индуктора говорит нам:

    $v = \text L\,\dfrac{di}{dt}$

    Источник тока обеспечивает постоянный ток $2\,\text{мА}$. Это интересно, но что нам действительно нужно знать, так это скорость изменения тока?

    $\dfrac{di}{dt} = \dfrac{d2}{dt} = 0\qquad$ (все знают, что $2$ не меняется со временем)

    Следовательно, напряжение на индукторе равно:

    $v = \text L\cdot 0 = 0$

    Если ток в индукторе постоянный, то $v = \text L\,di/dt = 0$ . На катушке индуктивности появляется ноль вольт. Это верно для любого значения тока и любого значения индуктора.

    Имитационная модель

    Вот имитационная модель катушки индуктивности $5\,\mu\text H$ с постоянным источником тока $2\,\text{мА}$. Откройте ссылку и нажмите TRANS в верхней строке меню, чтобы запустить переходную симуляцию. Результат довольно скучный. Напряжение на катушке индуктивности равно $0$. Измените катушку индуктивности или ток на что угодно, ответ всегда будет $0$.

    Иногда индуктор «выглядит как» короткий

    Очень популярно рисовать мысленные образы индуктора, говоря, что он «похож» на что-то. Вот наш первый пример.

    При постоянном токе разность потенциалов между концами катушки индуктивности составляет $0\,\text V$. В этом состоянии индуктор ведет себя как идеальный провод. (Идеальный провод имеет $0\,\text V$ между концами, несмотря ни на что.)

    Катушка индуктивности «выглядит» как короткое замыкание, когда ток в ней постоянный. {-3}} = 300 \,\text{ампер}/\text{сек}$

    Это означает, что ток через индуктор будет иметь крутизну нарастания $300\,\text{ампер}/\text{секунда}$.

    Удивительно, но именно это и предсказывает уравнение. Излишне говорить, что это не практическая схема. Мы просто хотим посмотреть, что происходит с постоянным напряжением. Если мы построим эту схему, ток будет увеличиваться до тех пор, пока наш реальный источник напряжения не сможет удовлетворить потребность в большем токе. Но в течение короткого промежутка времени именно так работают настоящие катушки индуктивности.

    Имитационная модель

    Вот имитационная модель катушки индуктивности со схемой источника напряжения. Откройте ссылку и нажмите TRANS в верхнем меню, чтобы запустить переходную симуляцию.

    Пример

    На самом деле мы можем придумать что-то более полезное, чем линейно возрастающее линейное изменение тока. Если мы изменим источник напряжения так, чтобы он время от времени менял направление, мы получим более интересную и потенциально полезную схему.

    Вот вам задание: предположим, что амплитуда прямоугольного сигнала равна $\pm1\,\text V$, а частота равна $1\,\text{MHz}$ $($имеет период $1\,\mu \текст{сек})$.

    Нарисуйте форму текущего сигнала и найдите пиковые значения.

    Посмотрите, сможете ли вы это сделать, прежде чем смотреть на ответ или имитационную модель.

    Подсказка: Рассчитайте $di/dt$ для двух различных состояний входного напряжения.

    показать ответ

    Форма волны тока представляет собой треугольную волну, нарастающую при положительном напряжении и убывающую при отрицательном напряжении.

    Мы решим это по частям. Сначала определите ток при напряжении $+1\,\text V$, 9{+6} \,\text{ампер}/\text{сек}$

    Нарастание тока составляет $200{,}000\,\text{ампер}/\text{секунда}$.
    То же, что и $200\,\text{мА}/\мю\текст{сек}$.

    Напряжение меняется с $+1\,\text V$ на $-1\,\text V$ каждые $0,5\,\mu\text{сек}$.

    Насколько сильно возрастает ток на участке $v = +1\,\text V$ прямоугольной волны?

    $i_{\text{+peak}} = 200\,\text{мА}/\mu\text{сек} \times 0,5\,\mu\text{сек} = 100\,\text{мА}$

    Максимальное значение тока достигает $100\,\text{мА}$.

    Когда напряжение падает, весь процесс меняется на противоположный. Для части $v = -1\,\text V$ вы можете снова выполнить математику с $-1\,\text V$ в уравнении наклона. Текущий наклон вниз с отрицательным наклоном той же величины. В конце отрицательного напряжения ток вернется к $0$.

    $i_{\text{-пик}} = 0\,\text{мА}$.

    Ток будет зигзагами между двумя пиками с прямыми линиями между ними. Откройте ссылку на симуляцию ниже и запустите симуляцию переходного процесса, чтобы посмотреть, что произойдет.

    Имитационная модель

    Имитационная модель схемы источника импульсного напряжения. Откройте ссылку и нажмите TRANS, чтобы запустить переходную симуляцию.

    Катушка индуктивности «интегрирует» напряжение по времени, на что указывает значение тока в любой момент. Это точный «двойник» конденсатора, интегрирующий ток.

    Исследовать

    Что произойдет с током, если вы…?

    • Изменить значение индуктора на немного $(2\times)$ и на много $(100\times)$.
    • Изменить амплитуду или частоту источника напряжения.
    • Измените уровни напряжения, чтобы они не были симметричными.
    • Измените рабочий цикл напряжения с $50\%$ на другое значение, например $40\%$.
    что означает «рабочий цикл»?

    Рабочий цикл описывает импульсный сигнал. Это относится к проценту времени, в течение которого напряжение находится в высоком состоянии. Если рабочий цикл равен $25\%$, напряжение равно $+1\,\text V$ в течение четверти времени цикла. Если рабочий цикл составляет $50\%$, напряжение симметрично, проводя половину времени высоким и половину времени низким. Рабочий цикл может варьироваться от $0\%$ до $100\%$.

    Аналогия с массой

    Это самый полезный мысленный образ при взгляде на индуктор.

    Индуктивность, $\text L$, аналогична массе или инерции в механической системе. Энергия магнитного поля катушки индуктивности не позволяет току изменяться мгновенно, точно так же, как тяжелая масса автомобиля имеет тенденцию сопротивляться изменению скорости. Автомобиль не может завестись или остановиться мгновенно. Требуется время, чтобы разогнаться или затормозить. Катушка индуктивности представляет собой электрическую версию первого закона движения Ньютона (также называемого законом инерции): движущееся тело имеет тенденцию оставаться в движении. Для катушки индуктивности это выглядит так: движущийся ток имеет тенденцию оставаться в движении.

    Ток в катушке индуктивности не изменяется (не будет) мгновенно.

    Резюме

    Ток в катушке индуктивности не изменяется мгновенно.

    При постоянном токе индуктор выглядит как короткое замыкание.

    Будьте осторожны при включении катушек индуктивности. Внезапное изменение тока, например размыкание выключателя, прерывающее путь тока, означает, что производная тока, $di/dt$, может стать очень большой. Уравнение индуктора говорит нам, что на индукторе может быть большое напряжение.

    Один из способов справиться с потенциально разрушительным напряжением катушки индуктивности — спроектировать путь для тока, чтобы не было больших $di/dt$. Мы показали, как добавить диод, чтобы обеспечить путь тока и зафиксировать напряжение катушки индуктивности до приемлемого значения, когда переключатель был разомкнут.

    Формула индуктивности катушки индуктивности

    Формула индуктивности очень похожа на формулу сопротивления. То, как мы рассчитываем индуктивность одиночного индуктора и сопротивление одного резистора, зависит от площади поперечного сечения и материала.

    Мало того, мы также можем легко рассчитать последовательные и параллельные катушки индуктивности, как мы это делаем с последовательными и параллельными резисторами.

    Здесь мы будем часто упоминать как индукторы, так и катушки, но не запутайтесь. Оба они по-прежнему имеют одно и то же уравнение и формулу.

    Что такое индуктор

    Катушка индуктивности — один из самых популярных пассивных элементов электрической цепи. Почему он называется пассивным элементом, а не пассивным компонентом? Потому что катушка индуктивности обеспечивает индуктивность в цепи, но индуктивность может быть создана без одной катушки индуктивности в цепи.

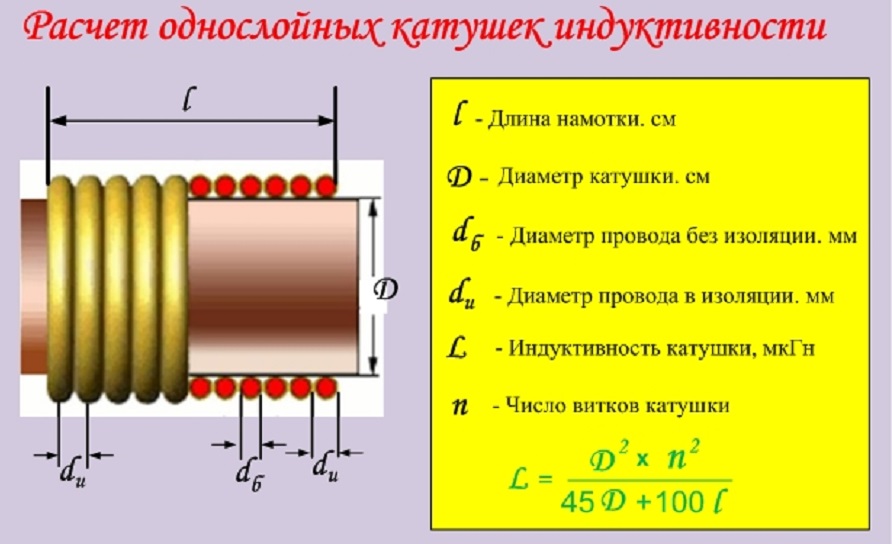
    Имейте в виду, индуктивность может быть обнаружена в одном проводнике, особенно если он соединен с сердечником, таким как катушка. Каждая катушка, скорее всего, будет создавать индуктивность в цепи. Токопроводящий провод создает магнитное поле, когда через него проходит электрический ток.

    Катушки индуктивности производят ЭДС самоиндукции противоположной полярности, когда через них протекает ток (поэтому ЭДС известна как обратная ЭДС). Индуктор будет иметь изменяющееся магнитное поле, пока через него протекает ток.

    Когда ЭДС индуцируется в электрической цепи, где используется индуктор, это называется самоиндукцией (L). Самоиндукция может быть обнаружена в катушке индуктивности, используемой в электрической цепи, где нет катушки индуктивности, используемой в том же магнитном поле.

    Когда ЭДС индуцируется в соседней паре катушек индуктивности, помещенных в одно и то же магнитное поле, это называется взаимной индукцией (В). Взаимная индукция в основном встречается в трансформаторе, реле, электродвигателе и во всем, что имеет пару катушек, намотанных вместе.

    Индуктивность, о которой мы говорили до сих пор, является самоиндукцией. О взаимной индуктивности поговорим позже.

    Что такое индуктивность

    Если резистор обеспечивает сопротивление току в цепи, катушки индуктивности очень похожи на резисторы.

    Катушка индуктивности представляет собой проводник, намотанный на сердечник. Это может быть воздух, феррит и т. д. Конечно, в качестве индуктора рассматривается и катушка из токопроводящего провода.

    Катушка индуктивности представляет собой пассивный элемент, сохраняющий энергию в виде магнитного поля и практически повсеместно встречающийся в электронных схемах, цепях электропитания, системах связи и особенно в трансформаторах.

    Катушка индуктивности обеспечивает индуктивность в цепи. Любой проводник, обладающий индуктивностью в цепи, также считается катушкой индуктивности.

    Что такое индуктивность?

    Индуктивность – это скорость сопротивления изменению тока катушкой индуктивности, когда через нее протекает ток.

    На приведенном выше рисунке индуктивность рассчитывается по длине, площади поперечного сечения, материалу сердечника и количеству витков.

    Математически мы можем использовать уравнение:

       

    Где:

    L = индуктивность, измеренная в Генри (Гн)
    N = число витков
    μ = магнитная проницаемость сердечника
    A = площадь поперечного сечения
    l = длина индуктора

    Судя по приведенному выше уравнению, материал сердечника, обладающий удельной проницаемостью, играет ключевую роль в значении индуктивности. Там будут разные значения для воздушного сердечника и ферритового сердечника.

    Единица измерения Генри (Гн) для индуктивности взята у Джозефа Генри, американского физика, который внес большой вклад в электромагниты. Другой единицей измерения индуктивности является Вебер на Ампер, и он равен Генри, 1 Гн равен 1 Вб/А.

    Индуктивность катушки индуктивности

    Почему ЭДС, создаваемая собственной индуктивностью, называется обратной ЭДС? Мы можем ответить на это из закона Ленца.

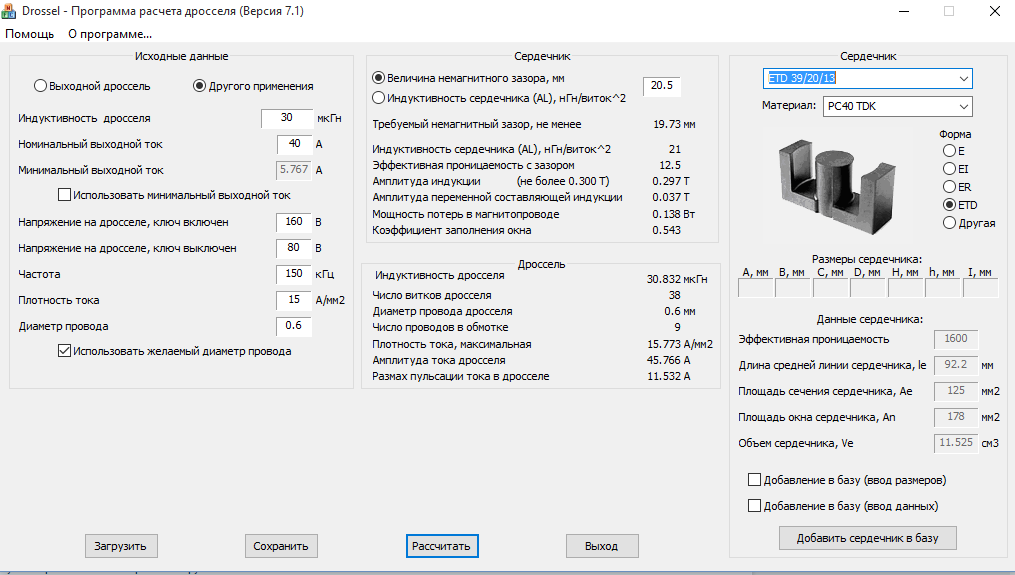
    Согласно закону Ленца:

    Направление электрического тока, индуцированного в проводнике изменяющимся магнитным полем, таково, что магнитное поле, создаваемое индуцированным током, противодействует изменяющемуся первоначальному магнитному полю.

    Кроме того, мы можем определить, что:

    Один Генри будет генерироваться одной катушкой, когда ЭДС создается в результате одного вольта, наведенного в катушке, где изменение силы тока 1 Ампер в секунду протекает через эту катушку .

    Суммарно,

    Создается индуктивность (L) в один Генри при протекании через него тока 1 А/с. Это изменение тока индуцирует напряжение (VL) в один вольт.

    Математически изменение тока катушки за время равно

       

    Где:
    di = изменение тока (А)
    dt = время, необходимое для достижения di, измеряемое в секундах

    В сочетании с индуктивностью (L ) и напряжение (В) получаем,

       

    Где:
    В = индуктивное напряжение в катушке (В)
    L = индуктивность (Гн)

    Небольшое перемещение и получаем,

       

    Где:
    L = индуктивность (Генри)
    В = напряжение индуктор (В)
    di/dt = изменение тока в секунду (А/с)

    Так же, как резистор, который «сопротивляется» току в цепи, индуктор «сопротивляется» изменению тока в цепи. Чем больше Генри, тем меньше изменение текущей ставки, и наоборот.

    Самоиндукция индуктора Формула

    Можно сказать, что индуктор представляет собой петлевой проводник, намотанный на сердечник. Это устройство может хранить энергию в виде магнитного поля. Мы можем увеличить индуктивность, увеличив ее петли или витки провода для катушки или индуктора.

    Если индуктивность увеличивается, магнитный поток также увеличивается при той же величине тока.

    Обратите внимание на приведенное ниже уравнение самоиндукции:

       

    Где:
    L = индуктивность (Гн)
    Н = число витков
    Φ = магнитный поток
    I = ток (А) катушки (NΦ/I).

    Давайте рассмотрим простой пример катушки индуктивности с собственной индуктивностью ниже:

    Предположим, что у нас есть катушка индуктивности с воздушным сердечником:

    • 100 витков медного провода.
    • 5 мВб магнитного потока.
    • Через него протекает постоянный ток 2 ампера.

    Затем, используя собственную индуктивность

       

    Подставив известную переменную в уравнение, получим: Мы найдем его шаг за шагом, чтобы убедиться, что вы понимаете, откуда он взялся (даже это не так важно для большинства из нас, которым нужно только знать, как правильно его использовать).

    Магнитный поток, который мы использовали ранее, определяется конструкцией и характеристикой катушки или индуктора. Конструкция строится из длины индуктора, размера, количества витков, материалов, сердечников и т. д.

    Среди всех факторов ключевыми здесь будут проницаемость сердечника и количество витков. Использование другого сердечника изменит размер катушки, особенно количество витков.

    Сердечник с высокой магнитной проницаемостью и большим числом витков обеспечивает высокий коэффициент самоиндукции катушки индуктивности.

    Магнитный поток, создаваемый его сердечником, равен плотности потока и площади поперечного сечения.

       

    Где:
    Φ = магнитный поток
    B = плотность потока
    А = площадь поперечного сечения

    Если углубиться, то плотность потока зависит от проницаемости сердечника, количества витков, протекающего тока и его длины.

         

    Подстановка плотности потока в формулу индуктивности, которую мы знали ранее, дает:

       

    Упрощение приведенного выше уравнения в формулу индуктивности состоит из материала сердечника, числа витков, площади поперечного сечения и длины.

       

    Где:
    L = индуктивность (Гн)
    µ = магнитная проницаемость сердечника
    N = количество витков
    A = площадь поперечного сечения
    l = длина катушки индуктивности

    Резюме формулы индуктивности

    Прежде чем завершить наше исследование, давайте упомянем некоторые важные вещи. :

    1. Так же, как в приведенной выше формуле индуктивности, где она зависит от скорости изменения тока.

       

    2. Значение v будет равно нулю, если ток установится. Это означает, что поскольку напряжение равно нулю, индуктор действует как короткое замыкание в цепи постоянного тока.

    3. Не допускается мгновенное изменение тока. Это означает, что внезапный скачок тока не может быть правильно рассчитан. А вот для его напряжения возможно обратное поведение.

    4. Идеальный индуктор не рассеивает энергию.

    5. Катушки индуктивности накапливают энергию, забирая энергию из цепи.

    6. Катушки индуктивности возвращают энергию при подаче питания в цепь.

    7. Реальные индукторы имеют резистивный элемент, поскольку они сделаны из проводников, таких как медная проволока. 92 А / л

    Где L — индуктивность, μ — магнитная проницаемость, N — число витков, A — площадь поперечного сечения, а I — ток.

    Что такое N в формуле индуктивности?

    Н в формуле индуктивности указывает количество витков катушки индуктивности или катушки, а l — длину катушки или катушки индуктивности.

    Что такое единица индуктивности?

    Индуктивность измеряется в Генри в честь Джозефа Генри. Один Генри — это значение собственной индуктивности катушки или индуктора, в которой один вольт вырабатывается путем наведения одного ампера в секунду.

    Почему L используется для обозначения индуктивности?

    L используется в честь Генриха Ленца, который ввел электромагнетизм.

    Что такое символ индуктивности?

    Индуктивность представлена ​​символом L (Lenz), а ее единицей измерения является H (Henry).

    [PDF] Методы расчета индуктивности — Часть II: Приближения и методы справочника

    • ID корпуса: 10212100

      title={Методы расчета индуктивности --- Часть II: приближения и методы из справочника},
      автор = {Марк Т. Томпсон},
      год = {1991}
    } 

    • M. T. Thompson
    • Опубликовано в 1991 г.
    • Физика

    ИНДЕКС СИМВОЛОВ A Площадь, окруженная катушкой a Средний радиус катушки b Осевая толщина катушки c Радиальная толщина катушки D Длина стороны квадратной катушки d Расстояние между проводами K Константа катушки Нагоака l Длина катушки p Периметр, охватываемый катушкой P, F Константы катушки диска Гровера R Радиус окружности провода s Длина стороны общего многоугольника w Ширина следа x, y Средние длины сторон прямоугольной катушки μo Магнитная проницаемость свободного пространства 4π×10 Гн /м

    classictesla. com

    Исследование методов расчета индуктивности спиральных катушек в условиях высокой частоты

    В этой статье проводится глубокий анализ моделирования и имитационного моделирования для расчета достаточно точного значения индуктивности катушки в условиях высокой частоты с использованием промышленности Стандартное моделирование Максвелла в ANSYS…

    Модель схемы для связи полевой проволокой электрически малых нерегулярных проволочных структур

    В этой статье предлагается общая модель схемы для эффекта связи с индукторной связью электрически малых нерегулярных проволочных структур различной геометрии. Формулы для элементов схемы…

    Анализ цепей магнитных связей между круговым витком и спиральной катушкой

    • M. Wciślik, T. Kwaśniewski

    • Физика

    • 2014

    В работе рассматривается магнитная связь между спиральными витками, моделирование концентрически расположенных спиральных катушек. на плоскости и одиночный форсированный разворот. Витки организованы осесимметрично…

    Моделирование магнитной муфты на основе одно- и двухслойных прямоугольных плоских катушек с плоскостной несоосностью для беспроводной передачи энергии

    • Франциско Хавьер Лопес-Алколеа, Хавьер Васкес дель Реал, П. Ронсеро-Санчес, А. Торрес

    • Физика

      IEEE Transactions on Power Electronics

    • 2020

      9 расчеты самоиндукции и взаимной индуктивности двух взаимно связанных прямоугольных, плоских и спиральных катушек с воздушным сердечником,…

      Влияние насыщения на величину индуктивности цилиндрического реактора

      В статье представлена ​​методика расчета индуктивности цилиндрического реактора с разъемным магнитопроводом. Расчеты проверены и соотнесены с лабораторными измерениями и подтверждены МКЭ…

      СРАВНИТЕЛЬНОЕ ИССЛЕДОВАНИЕ ВЛИЯНИЯ СТРУКТУРЫ ПЛОСКОЙ СПИРАЛЬНОЙ КРУГЛОЙ КАТУШКИ НА МАГНИТНО-РЕЗОНАНСНУЮ ПРОИЗВОДИТЕЛЬНОСТЬ БЕСПРОВОДНОЙ ПЕРЕДАЧИ ЭНЕРГИИ

      • Н. Мохдеб

      • Электромагнитные исследования3

        Инжиниринг, Физика

        М

      • 2020

      —Беспроводная передача энергии (БПЭ) посредством связанного магнитного резонанса — перспективная технология для применения во многих областях. В данной статье метод с использованием спиральной индукторной структуры с круглой катушкой…

      Анализ формул для расчета индуктивности переменного тока различных конфигураций немагнитных круглых проводников

      • F. Capelli, J. Riba

      • Физика

      • 2017

      Индуктивность одножильных и многожильных проводов, предназначенных для электронных устройств, передачи и распределения электроэнергии или систем заземления, молнии и соединения, в значительной степени зависит от конкретного…

      Optimization of foil conductor layout in inductive power transfer system resonators

      • M. Etemadrezaei, S. Lukic

      • Physics, Engineering

        2014 IEEE Energy Conversion Congress and Exposition (ECCE)

      • 2014

      Proper use площади намотки и расположения проводников в резонирующих катушках систем индуктивной передачи мощности (IPT) имеет большое значение для достижения высокоэффективных систем. В этой статье простой…

      Модели электродинамического магнитного подвеса, законы масштабирования и экспериментальные результаты

      • М. Т. Томпсон

      • Физика, инженерия

        IEEE Trans. Образовательный

      • 2000

      Описан простой эксперимент, иллюстрирующий принципы электродинамического магнитного подвеса, и разработан закон магнитного масштабирования, который показывает, что большие магнитные структуры более эффективны в преобразовании энергии, чем маленькие.

      Разработка и сравнение прямоугольных, квадратных и шестиугольных РЧ-катушек для МРТ-системы 1,5 Тл

      • Никет Угле, Тапас К. Бхуйя, Радхика Дапкар, Д. М. Шинде, С. Багчи

      • Физика

        9-я Международная конференция по компьютерным, коммуникационным и сетевым технологиям (ICCCNT), 2018 г. 60003

      • 2018 В этой статье Показана конструкция прямоугольных, квадратных и шестигранных катушек для систем МРТ мощностью 1,5 Тл, а результаты моделирования катушек сравниваются друг с другом.

        ПОКАЗЫВАЮТСЯ 1-10 ИЗ 25 ССЫЛОК

        СОРТИРОВАТЬ ПОРелевантностьНаиболее влиятельные документыНедавность

        Конструкция плоских прямоугольных катушек индуктивности для микроэлектроники

        • H. Теплица

        • Физика

        • 1974

        Отрицательная взаимная индуктивность возникает в результате связи между двумя проводниками с противоположными направлениями тока. Как величина в электронных схемах, отрицательная взаимная индуктивность обычно такова…

        Формулы для скин-эффекта

        На радиочастотах проникновение токов и магнитных полей в поверхность проводников определяется скин-эффектом. Многие формулы упрощаются, если их выражать в терминах «глубины…

        Индуктор Брукса: исследование оптимальных сечений соленоида индуктивность с данным отрезком провода. Простая процедура, представленная графически и…

        Расчет индуктивности: рабочие формулы и таблицы

        • F. Grover

        • Инженерное дело

        • 1981

        Этот авторитетный сборник формул и таблиц упрощает проектирование катушек индуктивности для инженеров-электриков. Он имеет единую простую формулу практически для каждого типа катушки индуктивности, вместе… исследована статическая индуктивность тонкопленочной спиральной катушки; расчеты выполняются с применением основного поля…

        Статическое и динамическое электричество

        • Г. Темпл

        • Физика

          Природа

        • 1940

        В течение некоторого времени существует острая потребность в стандартном учебнике по электромагнитной теории

        Конструкция соленоидного магнита

        • D. Melville

        • Art

        • 1970

        D B Montgomery Chichester: John Wiley 1969 pp xii + 312 цена 6 фунтов 11 шиллингов В своем предисловии д-р Монтгомери указывает, что это личная книга, основанная на областях дизайна, которые непосредственно касались его…

        VI ССЫЛКИ

        • Медицина

        • 1961

        Предлагается метод оценки центральной остроты зрения сетчатки и зрительного пути.

        Справочник радиоинженеров

        • Ф. Э. Терман

        • Машиностроение

        • 1943

        Электрические катушки и проводники

        Пример расчета индуктивности

        Индуктивность Пример расчета

        David Meeker

        [email protected]

        Companion File: Induct1a.fem

        Введение

        . Расчет индуктивности катушки индуктивности с зазором. Хотя индуктивность можно оценить с помощью простого магнитного теории схем схемный подход обычно игнорирует утечку потока и окантовочные эффекты. Чтобы решить эти неидеальные эффекты более подробно анализ конечных элементов может быть занят. Цель настоящего Например, чтобы показать, как рассчитывается индуктивность в моделировании FEMM, и чтобы сравните этот результат с приближением, полученным с помощью магнитной цепи подход.

         

         

        Пример геометрии

         

        Пример геометрии состоит из слоистого EI с зазорами сердечник с поперечным сечением, как показано на рисунке 1. Сердечник E с центральным полюсом шириной 0,5 дюйма и внешними полюсами Ширина 0,25 дюйма отделена от I-образного обратного пути воздушным зазором.

         

         

        Рис. 1. Пример геометрии

         

        витки провода 18 AWG с толстой изоляцией, для примерно 66% меди заполнить фракцию в окне катушки. это предполагается, что сердцевина простирается на 1 дюйм в направлении страницы. Для целей этой модели материал предполагается, что это линейный ферромагнитный материал с относительной магнитной проницаемостью из 2500.

         

         

        Теория цепей Индуктивность

         

        Для грубой аппроксимации индуктивности можно предположить, что нет утечки и окантовки, и что вклад железа сечения на сопротивление магнитной цепи тривиально по сравнению с взносы из воздуха. Затем, поток, текущий в магнитопроводе, получается путем решения уравнения цепи:

         

         

        для f , итого поток, соединенный катушкой. R представляет сопротивление магнитной цепи, которое при наших предположениях можно записать как:

         

         

        где g = 0,025 дюйма , a _полюс = 0,5 в ² и м _o = 4 p (10 ^-7 ) ч/м. Так как общий поток, связывающий катушку, равен:

         

         

        и полная собственная индуктивность равна произведению потока на Общее количество поворотов:

        , так что самоуниверситет:

        С тех пор, в нашем случае, 66 ходов. получается:

         

        L = 1,39 мГн

         

        Мы ожидаем, что индуктивность получена из конечного элемента вычислений, чтобы быть в окрестности 1,39мГн.

         

         

        Индуктивность конечного элемента (I)

         

        В целях создания конечно-элементного решения Катушка индуктивности помещается в центр коробки размером 2 на 2,5 дюйма. На границах домена есть граница условие A=0 определено. Для Для выполнения конечно-элементного анализа ток 1 А несколько произвольно применяется к катушкам. Довольно грубая плотность сетки с ограничением размера сетки больше 0,05 дюйма определяется везде. Сетчатая проблемная область изображена на рисунке 2.9.0003

         

         

        Рис. 2. Проблемная область, нарисованная в FEMM.

         

        После выполнения анализа и запуска постпроцессора индуктивность можно получить, нажав кнопку Свойства цепи в окне постпроцессор:
        Появится диалоговое окно с рядом свойств обмотки, если смотреть с клемм обмотки. Диалоговое окно «Свойства цепи» для этого примера показано ниже на рис. 3.

         

         

        Рисунок 3: Цепь Диалог результатов свойств.

         

        При отсутствии постоянных магнитов или других катушек, Результат потока/тока можно интерпретировать непосредственно как собственную индуктивность:

         

        L = 1,73 мГн

         

        Этот результат выше, чем 1,39 мГн, предсказанный простой подход теории цепей, потому что эффекты утечки и интерференции которыми пренебрегают в схемном подходе, имеют тенденцию немного повышать индуктивность.

         

        Индуктивность конечных элементов (II)

         

        Альтернативным подходом является получение энергии через Интеграл «Энергия магнитного поля». Для этого подхода энергия получается через:

         

         

        где этот интеграл берется по всей задаче домен, а не только над катушками. Чтобы выполнить эту интеграцию в постпроцессор, переключитесь в блочный интегральный режим, нажав кнопку на панели задач. Затем выберите каждый регион в проблеме с помощью щелчки левой кнопки мыши. Когда выбрана вся проблемная область, нажмите кнопку Integral и выберите Интеграл энергии магнитного поля из выпадающего списка объемных интегралов. Если Вт представляет результат интеграла, результирующая индуктивность:

         

        интеграция:

         

        Вт = 0,000865042 Дж

         

        Что при подстановке в формулу дает то же самое результат метода (I):

         

        L = 1,73 мГн

         

        Выводы

         

        Был представлен простой пример, демонстрирующий, как FEMM можно использовать для получения индуктивности. Была рассмотрена двумерная плоская задача, и индуктивность получается из двух методы сравнивались друг с другом и с «проверкой работоспособности» оценка индуктивности из теории магнитной цепи.

         

        Хотя результаты двух подходов конечных элементов чтобы получить индуктивность в этом случае идентичны, обычно лучше использовать метод (I). Причина в том, что некоторые граничные условия ( т.е. асимптотическое граничное условие, используемое для аппроксимация задачи с «открытой границей») предполагают, что некоторая энергия хранится вне смоделированной проблемной области. Внутри FEMM рассчитывает поток связь с использованием метода, учитывающего эту дополнительную энергию, тогда как интегрирование B*H по всем элементам — нет.

         

        Строго говоря, один коэффициент индуктивности подразумевает линейная зависимость между приложенным током и результирующим потоком. По этой причине пример проблемы с рассматривались только линейные материалы.

         

        Если в задаче есть нелинейные материалы и есть значительное насыщение, больше нет линейной зависимости между ток и поток. Однако есть много ситуаций, в которых применяется синусоидальный ток, и хотелось бы знать амплитуду основной гармоники потока, соответствующую приложенному Текущий.