Как рассчитать катушку индуктивности. Расчет и оптимизация катушек индуктивности: основные параметры и методы

Как рассчитать индуктивность катушки. Какие факторы влияют на добротность катушки индуктивности. Как оптимизировать параметры катушки для получения максимальной добротности. Какие существуют методы расчета катушек индуктивности.

Основные параметры катушек индуктивности

Катушка индуктивности является одним из базовых элементов электронных схем. К ее ключевым параметрам относятся:

• Индуктивность (L) — способность катушки накапливать энергию магнитного поля. Измеряется в Генри (Гн).
• Добротность (Q) — отношение запасенной энергии к рассеиваемой за период колебаний. Безразмерная величина.
• Собственная резонансная частота (f_рез) — частота, на которой катушка ведет себя как параллельный колебательный контур.
• Активное сопротивление (R) — сопротивление провода катушки постоянному току.

Как эти параметры связаны между собой? Добротность катушки можно выразить через формулу:

Q = 2πfL / R

Где f — рабочая частота, L — индуктивность, R — активное сопротивление.

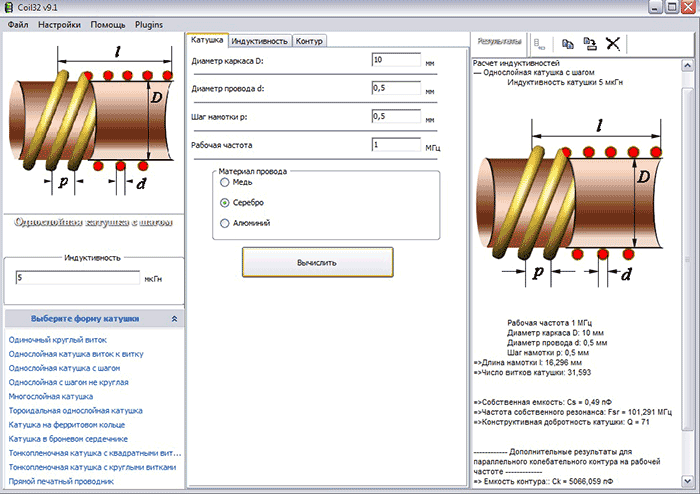
Факторы, влияющие на добротность катушки

Добротность является одним из важнейших параметров катушки индуктивности. От нее зависит качество работы колебательных контуров и фильтров. На добротность влияют следующие факторы:

• Диаметр провода — чем толще провод, тем меньше его сопротивление и выше добротность.
• Диаметр каркаса — большой диаметр позволяет достичь требуемой индуктивности меньшим числом витков.
• Длина намотки — оптимальное соотношение длины к диаметру около 1:1.
• Шаг намотки — оптимальный шаг примерно 2.4 диаметра провода.
• Материал каркаса — керамические и воздушные каркасы обеспечивают меньшие потери.

Какая добротность считается высокой? Для радиочастотных катушек хорошим показателем является Q > 100-200.

Методы расчета катушек индуктивности

Существуют различные подходы к расчету параметров катушек индуктивности:

1. Использование эмпирических формул (например, формула Уиллера для однослойных катушек).
2. Применение точных формул, основанных на решении уравнений Максвелла.
3. Компьютерное моделирование методом конечных элементов.
4. Использование онлайн-калькуляторов и специализированного ПО.

Какой метод выбрать? Для простых однослойных катушек достаточно эмпирических формул. Для сложных конструкций лучше применять компьютерное моделирование.

Оптимизация параметров катушки

Для получения максимальной добротности катушки рекомендуется:

• Использовать провод максимально возможного диаметра.
• Выбирать оптимальное соотношение длины намотки к диаметру (около 1:1).
• Применять керамические каркасы или бескаркасную намотку.
• Обеспечивать равномерный шаг намотки (около 2.4 диаметра провода).
• Минимизировать паразитную емкость между витками.

Какую индуктивность выбрать для максимальной добротности? Оптимальное значение зависит от рабочей частоты. Например, для диапазона 3-30 МГц рекомендуется L = 1-10 мкГн.

Практические рекомендации по изготовлению катушек

При самостоятельном изготовлении катушек индуктивности следует учитывать:

• Использовать провод с качественной изоляцией для уменьшения паразитной емкости.
• Обеспечивать надежное крепление выводов катушки.
• Применять пропитку (например, парафином) для защиты от влаги.
• Экранировать катушку для уменьшения влияния внешних полей.

Какие инструменты потребуются? Намоточный станок или оправка, измеритель индуктивности, паяльник.

Измерение параметров катушек индуктивности

Для контроля качества изготовленных катушек необходимо измерять их параметры:

• Индуктивность — с помощью RLC-метра или измерителя иммитанса.
• Добротность — методом последовательного резонанса.
• Собственную резонансную частоту — с помощью ВЧ генератора и осциллографа.

Какая точность измерений требуется? Для большинства практических применений достаточно погрешности 5-10%.

Применение катушек индуктивности

Катушки индуктивности широко используются в различных областях электроники:

• Колебательные контуры радиоприемников и передатчиков.
• Фильтры верхних и нижних частот.
• Импульсные источники питания.
• Трансформаторы и дроссели.
• Антенные согласующие устройства.

Какие требования предъявляются к катушкам в разных применениях? Для радиочастотных схем критична высокая добротность, для силовой электроники важна большая индуктивность и допустимый ток.

Добротность катушки индуктивности, как изготовить высокодобротную катушку, выбор каркаса и диаметра провода

Это нужно знать Весь перечень знаний находится на этой странице

Необузданные гонки за всё более высокими параметрами добротности колебательных контуров не так просты, как могли бы показаться на первый взгляд. На предыдущей странице, мы определились, что добротность контура в первую очередь определяется добротностью катушки индуктивности, а она в свою очередь напрямую связана с сопротивлением потерь и описывается формулой Q=2πfL/Rпот. Сопротивление потерь — это параметр, связанный не только с потерями в проводах, но и учитывающий потери в диэлектрике, сердечнике и экране. — Потери в сердечнике складываются из потерь на вихревые токи и потерь на гистерезис, связанных с перемагничивание материала в течение периода. — Потери в диэлектрике обусловлены как паразитной межвитковой ёмкостью между соседними витками катушки, так и магнитными свойствами диэлектрика каркаса катушки (эти потери аналогичны потерям в сердечнике). — Потери в экране вызываются индуцированием переменным магнитным полем вихревых ЭДС в окружающих проводниках. Точный расчёт всех перечисленных параметров — дело весьма затруднительное, поэтому, с целью упрощения задачи, обычно учитываются только потери в проводах, как вносящие основной вклад в общую сумму потерь. При этом применяются специальные меры по минимизации неучтённых потерь – керамические, или ребристые каркасы, бескаркасные катушки (с «воздушным» каркасом), отказ от использования сердечника. А теперь, что касается выбора параметра индуктивности катушки для достижения максимальной добротности. Глядя на формулу, описывающую величину добротности Q=2πfL/Rпот, а так же приведённую на рисунке, можно сделать преждевременный вывод — добротность катушки линейно растёт с ростом частоты и достигает максимума на частоте собственного резонанса, когда С минимальна и равна собственной паразитной ёмкости катушки и паразитных емкостей источника, нагрузки и монтажа. Однако, не всё так просто! Оказывается, что для достижения максимальной добротности на определённой частоте существует оптимальная величина индуктивности катушки. При понижении частоты добротность уменьшается, но не линейно, а несколько медленнее, за счёт снижения влияния действия скин эффекта, гуляющего внутри провода, а при повышении — тоже плавно уменьшается из-за проявляющейся зависимости совокупных паразитных ёмкостей от частоты (варикапный эффект). К тому же эти паразитные ёмкости начинают доминировать в общей ёмкости колебательного контура, а образованный ими конденсатор, как известно, обладает далеко не самым выдающимся параметром добротности. И в заключение нашего теоретического экскурса, всё же не воздержусь и приведу основные факторы, определяющие сопротивление потерь в проводах катушек на высоких частотах: 1. Омическое (активное) сопротивление проводника постоянному току — классика жанра, рассчитать можно по длине и диаметру провода на странице    ссылка на страницу. 2. Поверхностный эффект, скин-эффект — эффект роста сопротивления провода с ростом частоты. Суть эффекта состоит в вытеснении тока в поверхностные слои провода, в связи с чем уменьшается полезное сечение проводника и, как следствие, растёт его сопротивление. 3. Эффект близости, суть которого состоит в вытеснении тока под воздействием вихревых токов и магнитного поля к части провода, прилегающей к каркасу. В результате сечение, по которому протекает ток, принимает серповидную форму, что ведёт к дополнительному возрастанию сопротивления проводника. Думаю, на этом хватит! Переходим к опытно-практической части дипломной работы: Приготовим закуски и коктейли, накроем стол… Итак, какой должна быть высокодобротная катушка? 1. Очевидно, что из металла! Ладно, посмеялись — и будет. Нам нужен металл с минимальным удельным сопротивлением и с максимально возможным (в пределах разумного) диаметром проводника. На начальном уровне — медь, на продвинутом — медь с серебряным напылением. 2. Катушка должна быть большой! Опять же, как и в первом пункте — излишний фанатизм не приветствуется. Однако, помимо размеров катушки, пристальное внимание следует обратить и на форм-фактор — отношение длины к диаметру металлоизделия. Опытными мотальщиками было продемонстрировано, что оптимальная по добротности катушка имеет отношение длины к диаметру L/D ≈ 1, причём изменение этого отношения в пару раз в ту, или иную сторону — к существенному изменению добротности не приводит. 3. Желание минимизировать эффект близости и уменьшить собственную ёмкость катушки сподвигло специалистов к следующему постулату: оптимальное отношение шага намотки (расстояние между центрами соседних витков) к диаметру провода равно ≈2. 4. И вот теперь главный вопрос радиолюбительства: Сколько мотать витков в оптимизированной катушке для достижения максимальной добротности? На вопрос викторины отвечает М. Филатов, досконально изучивший этот предмет в 1976 г. на кафедре конструирования РЭА ФРиС РПИ.    Диапазон       Параметры катушки       D каркаса       L, мкГн       расчётные       20 мм       30 мм       40 мм      10 м   1,5   L нам. (мм)   10   15   20   n (вит.)   8,5   7   6   d пров.(мм)   0,84   1,5   2,4   Q   472   708   945   14 м   2,0   L нам. (мм)   12   18   24   n (вит.)   10,3   8,4   7,3   d пров.(мм)   0,8   1,46   2,2   Q   439   660   879   20 м   3,0   L нам. (мм)   12   18   24   n (вит.)   18,7   10,3   9   d пров.(мм)   0,67   1,2   1,8   Q   359   538   718   40 м   6,0   L нам. (мм)   14   21   28   n (вит.)   18,7   15,2   13,2   d пров.(мм)   0,53   0,66   1,46   Q   270   406   542   80 м   12,0   L нам. (мм)   14   21   28   n (вит.)   26,4   21,5   18,6   d пров.(мм)   0,37   0,66   1,0   Q   191   287   382   160 м   24,0   L нам. (мм)   16   24   32   n (вит.)   39   32   27,5   d пров.(мм)   0,31   0,53   0,8   Q   144   216   288 Данная таблица дошла до наших взоров благодаря стараниям латвийского радиолюбителя Юрия Балтина (YL2DX), опубликовавшим её в далёком 2003 году на своём сайте http://dx. ardi.lv, за что ему большое человеческое спасибо! Таблица эта — не догма и не абсолютная истина в последней инстанции, однако она позволяет достаточно наглядно пронаблюдать зависимость параметра добротности катушки индуктивности от диаметра каркаса и толщины провода, а заодно и оценить оптимальное значение индуктивности для того или иного частотного диапазона. Поэтому, если Вы всё-таки озадачились намоткой высокодобротного изделия, вооружайтесь информацией, изложенной на этой странице, доступным каркасом, или оправкой для бескаркасной катушки и бодро шагайте на сайт coil32.ru, где вы найдёте бесплатную, но очень хорошую программу для расчёта катушек индуктивности, а заодно и массу полезной теоретической информации по всему, что касается разнообразных намоточных изделий. А на следующей странице будем мотать высокодобротные катушки на ферритовых кольцах, а также на кольцах из распылённого железа.

Расчёт катушки индуктивности без сердечника

Всем доброго времени суток. В прошлых статьях часть 1, часть 2, часть 3 я рассказал о расчёте индуктивности индуктивных элементов без сердечников. Однако их применение ограниченно, вследствие, больших габаритных размеров. Поэтому для увеличения индуктивности и уменьшения размеров и улучшения других показателей индуктивные элементы устанавливают на сердечники из материалов с различными магнитными свойствами. В отличие от индуктивных элементов без сердечников, при расчёте которых учитывался магнитный поток пронизывающий только проводник с током, магнитный поток индуктивных элементов с сердечниками практически полностью замыкается на сердечники. Поэтому при расчёте индуктивности таких элементов необходимо учитывать размеры сердечника и материал, из которого он изготовлен, то есть его магнитную проницаемость.

Поиск данных по Вашему запросу:

Схемы, справочники, даташиты:

Прайс-листы, цены:

Обсуждения, статьи, мануалы:

Дождитесь окончания поиска во всех базах.

По завершению появится ссылка для доступа к найденным материалам.

Содержание:

• Конвертер величин
• Онлайн-расчет катушки индуктивности
• Конвертер величин
• Расчет индуктивности катушек (однослойных)
• Расчет катушек индуктивности без сердечника
• Расчет катушки индуктивности
• Как произвести расчёт катушек индуктивности (однослойных, цилиндрических без сердечника)
• Расчет индуктивности катушки без сердечника
• Катушка индуктивности

ПОСМОТРИТЕ ВИДЕО ПО ТЕМЕ: КАК СДЕЛАТЬ КАТУШКУ ИНДУКТИВНОСТИ СВОИМИ РУКАМИ

Конвертер величин

Катушкой индуктивности — это элемент электрической цепи с высоким значением индуктивности, при этом низкими емкостью и активным сопротивлением. Их используют:. Катушка представляет собой намотанную на каркасе проволоку в виде спирали, а намотка может быть однослойной или многослойной, виток к витку или с расстоянием.

Они бывают различных типов и форм, например, без сердечника обладают небольшой индуктивностью, а с сердечником она значительно увеличивается. Это обусловлено магнитной проницаемостью материала. Форма сердечника может быть разной, выделяют броневые, стержневые и тороидальные. Для улучшения массогабаритных параметров катушки наматывают на ферритовом кольце — такой вариант называется тороидальным способом намотки.

Как рассчитать катушку в онлайн калькуляторе и вручную? На её параметры влияет количество витков длина провода , наличие и материал сердечника. Форма последнего выбирается исходя из других требований, таких как размеры — они влияют на возможность расположения элемента в корпусе. Но вы можете сделать это и своими руками.

Воспользовавшись формулой для расчёта, зная индуктивность катушки:. Преимущества онлайн калькулятора перед этой формулой — быстрый и простой расчет. Нужно внести необходимую индуктивность, диаметр каркаса и длину намотки. После этого вы должны определится с тем, какой у вас есть провод, измерить диаметр его жилы и, если он изолирован, внешний диаметр по изоляции.

Ваш e-mail не будет опубликован. Вы здесь: Главная Калькуляторы. Автор: Александр Мясоедов. Калькулятор для расчета катушки индуктивности. Опубликовано: Их используют: В фильтрах частот, например, в акустических системах для разделения сигнала по частотам для воспроизведения на соответствующих динамиках, или фильтрации электромагнитных помех. В источниках питания, например, для включения светодиодов от одного элемента питания, где она используется в качестве накопителя энергии и повышения понижения напряжения.

В таком случае этот источник называется импульсным бестрансформаторным преобразователем напряжения. В радиопередающих устройствах, в качестве элемента колебательного контура, настроенного на нужную частоту и в других устройствах.

При этом вы можете подобрать соответствующий частоте конденсатор. Требуемая индуктивность L. Добавить комментарий Отменить ответ Ваш e-mail не будет опубликован.

Другие статьи по теме Калькулятор для расчета плавкой вставки предохранителя.

Онлайн-расчет катушки индуктивности

Индуктивность катушки зависит от ее геометрических размеров, числа витков и способа намотки. Чем больше диаметр, длина намотки и число витков тем больше индуктивность. При плотной намотке витков катушки, ее индуктивность будет больше чем катушка намотанная не плотно. Если необходимо намотать катушку индуктивность которой известна, а так же дано число витков и диаметр провода, но нет провода нужного диаметра, то при более толстом проводе можно увеличить число витков, а при меньшем диаметре провода уменьшить кол-во витков, в итоге можно получить примерно заданную индуктивность катушки.

Калькулятор для расчета катушки индуктивности Катушкой индуктивности — это элемент электрической цепи с высоким значением индуктивности, при.

Конвертер величин

Катушкой индуктивности — это элемент электрической цепи с высоким значением индуктивности, при этом низкими емкостью и активным сопротивлением. Их используют:. Катушка представляет собой намотанную на каркасе проволоку в виде спирали, а намотка может быть однослойной или многослойной, виток к витку или с расстоянием. Они бывают различных типов и форм, например, без сердечника обладают небольшой индуктивностью, а с сердечником она значительно увеличивается. Это обусловлено магнитной проницаемостью материала. Форма сердечника может быть разной, выделяют броневые, стержневые и тороидальные. Для улучшения массогабаритных параметров катушки наматывают на ферритовом кольце — такой вариант называется тороидальным способом намотки.

Расчет индуктивности катушек (однослойных)

Катушки индуктивности являются неотъемлемым элементом различных радиоэлектронных схем. Основным её свойством является наличие большой индуктивности при малой емкости и низком активном сопротивлении. Для автоматического расчета наиболее часто используется программа Coil Её можно бесплатно скопировать с одноименного сайта либо воспользоваться онлайн калькулятором.

Катушки индуктивности являются неотъемлемым элементом различных радиоэлектронных схем.

Расчет катушек индуктивности без сердечника

Индуктивность катушки зависит от её геометрических размеров, числа витков и способа намотки катушки. Чем больше диаметр, длина намотки и число витков катушки, тем больше её индуктивность. Если катушка наматывается плотно виток к витку, то индуктивность её будет больше по сравнению с катушкой, намотанной неплотно, с промежутками между витками. Когда требуется намотать катушку по заданным размерам и нет провода нужного диаметра, то при намотке её более толстым проводом надо несколько увеличить, а тонким — уменьшить число витков катушки, чтобы получить необходимую индуктивность. При расчёте катушки могут встретиться два случая:. В первом случае все исходные данные, входящие в формулу, известны, и расчёт не представляет затруднений.

Расчет катушки индуктивности

Катушкой индуктивности — это элемент электрической цепи с высоким значением индуктивности, при этом низкими емкостью и активным сопротивлением. Их используют:. Катушка представляет собой намотанную на каркасе проволоку в виде спирали, а намотка может быть однослойной или многослойной, виток к витку или с расстоянием. Они бывают различных типов и форм, например, без сердечника обладают небольшой индуктивностью, а с сердечником она значительно увеличивается. Это обусловлено магнитной проницаемостью материала. Форма сердечника может быть разной, выделяют броневые, стержневые и тороидальные.

On-line калькулятор, расчет однослойной катушки индуктивности. катушки индуктивности. Однослойная катушка индуктивности онлайн расчет. ВВЕСТИ ДАННЫЕ: мм, Диаметр провода без изоляции. k,.

Как произвести расчёт катушек индуктивности (однослойных, цилиндрических без сердечника)

Катушкой индуктивности — это элемент электрической цепи с высоким значением индуктивности, при этом низкими емкостью и активным сопротивлением. Их используют:. Катушка представляет собой намотанную на каркасе проволоку в виде спирали, а намотка может быть однослойной или многослойной, виток к витку или с расстоянием. Они бывают различных типов и форм, например, без сердечника обладают небольшой индуктивностью, а с сердечником она значительно увеличивается.

Расчет индуктивности катушки без сердечника

ВИДЕО ПО ТЕМЕ: Урок №8. Катушка индуктивности

Random converter. Калькулятор определяет индуктивность однослойной катушки. Пример: рассчитать индуктивность однослойной катушки без сердечника, состоящей из 10 витков на цилиндрическом каркасе диаметром 2 см; длина катушки 1 см. Введите диаметр каркаса катушки, число витков и длину катушки, выберите единицы и нажмите кнопку Рассчитать. Пример: рассчитать число витков и длину намотки катушки 10 мкГн, намотанной эмалированным проводом 0,65 мм диаметр с изоляцией 0,7 мм на оправке 2 см.

Онлайн расчет многослойной катушки. Калькулятор считает по алгоритму с применением эллиптических интегралов Максвелла.

Катушка индуктивности

При заданной индуктивности, диаметре каркаса катушки и толщины намотки можно рассчитать число витков катушки, а так же определить диаметр провода и число слоев намотки. Следующая форма расчета позволит рассчитать кол-во витков катушки в зависимости от диаметра провода имеющегося у Вас в наличии. Для отправки комментария вам необходимо авторизоваться. Ваш IP: Расчет числа витков многослойной катушки без сердечника. Радиотехнические калькуляторы Все размеры выражены в миллиметрах, а индуктивность в мкГн.

Катушка индуктивности является неотъемлемым элементом большинства современных приборов. При этом она используется для различных целей в работе электрических цепей. В случае необходимости замены можно использовать как заводскую, так и изготовленную самостоятельно катушку. Но при этом необходимо учитывать ее основной параметр — индуктивность.

boost — Расчет количества витков для моей катушки индуктивности

спросил 2 года, 6 месяцев назад

Изменено 2 года, 6 месяцев назад

Просмотрено 1к раз

\$\начало группы\$

, поэтому я подсчитал, что мне нужна индуктивность 0,150 мГн для моего индуктора. Тем не менее, я пытаюсь выяснить, сколько оборотов мне нужно для этого. # У меня есть ответ из 24 ходов, но мне это кажется неправильным. Кто-нибудь может перепроверить мои расчеты?

ниже приведена таблица данных для тора, который я использовал, а также график (из таблицы данных), который я использовал. ***Техническое описание ТОРОИДА (с использованием 3C90)

Если кому интересно, чем я руководствовался в своих расчетах.

Большое спасибо!

• индуктор
• усиление
• индуктивность
• тороид

\$\конечная группа\$

2 92\$, индуктивность 673,92 мкГн.

Не выводите это самостоятельно, потому что в техническом описании номера указаны непосредственно «внутри» \$A_L\$.

Если вам нужно 150 мкГн, вам потребуется около 11 витков (141,6 мкГн)

Если вы работаете ближе к насыщению (как вы говорите), тогда \$A_L\$ уменьшается пропорционально проницаемости. Так, при H-поле 60 Ат/м относительная проницаемость упала с 2300 до 1000, следовательно, \$A_L\$ падает на ту же величину с 1170 до 507.

Теперь, если используются 24 витка, я вычисляю индуктивность 293 мкГн (все еще выше, чем ваши расчеты). По моим оценкам, для получения 146,5 мкГн потребуется 17 витков.

Тем не менее, для меня более важным вопросом является то, почему вы используете этот тор для создания повышающего преобразователя.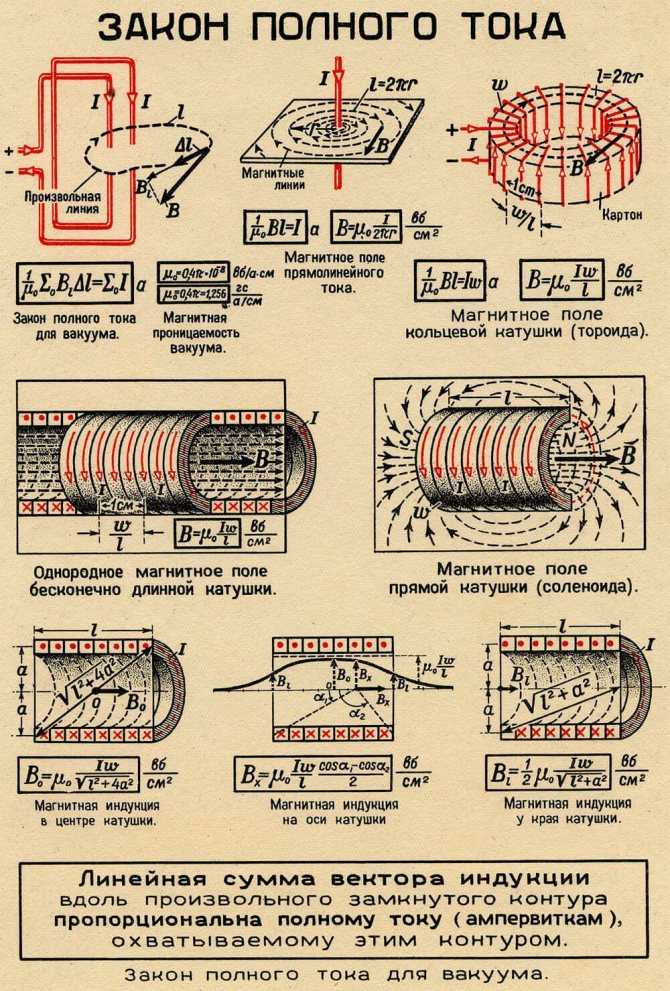 При H-поле 60 Ач/м и эффективной длине сердечника 30,1 мм (см. выше) МДС (магнитодвижущая сила) становится равной 60 x 0,0301 = 1,806 ампер-витков И, учитывая, что у вас есть возможные 17 витков, максимальная ток, который вы можете пропустить через тороид (для разумной эффективной работы), составляет 106 мА, и, по моему скромному мнению, это довольно маломощный повышающий преобразователь.

\$\конечная группа\$

1

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

.

Постоянная времени катушки индуктивности

• Изучив этот раздел, вы сможете описать:
• • Постоянная времени цепи LR.
• …и выполнять расчеты с использованием
• • Постоянные времени в простой цепи LR.

Рис. 4.5.1 Постоянная времени LR.

Когда ток подается на индуктор, требуется некоторое время, чтобы ток достиг своего максимального значения, после чего он останется в «устойчивом состоянии», пока какое-либо другое событие не вызовет изменение входа. Время, необходимое для того, чтобы ток нарастал до установившегося значения в цепи LR, зависит от:

• Сопротивление (R)

Это общее сопротивление цепи, которое включает сопротивление постоянному току самой катушки индуктивности (R _L ), а также любое внешнее сопротивление цепи.

• Индуктивность L

Которая пропорциональна квадрату числа витков, площади поперечного сечения катушки и проницаемости сердечника.

Индуктор препятствует ИЗМЕНЕНИЮ тока

Рис. 4.5.1 Постоянная времени LR

Когда схема на рис. 4.5.1 включена, ток быстро изменяется от нуля, это внезапное изменение создает быстро расширяющееся магнитное поле вокруг катушек индуктивности и при этом индуцирует напряжение обратно в катушку. Это индуцированное напряжение (называемое обратной ЭДС) создает ток (зеленая стрелка на принципиальной схеме), текущий в ПРОТИВОПОЛОЖНОМ направлении по отношению к исходному току (синяя стрелка на принципиальной схеме), подаваемому батареей.

См. изменение тока противо-ЭДС и тока питания в течение времени, показанного на видео на рис. 4.5.1. Результатом внезапного изменения напряжения при включении цепи является то, что скорость изменения тока цепи вместо увеличение тока от 0 В до максимального тока увеличивается медленнее, чем в полностью резистивной цепи.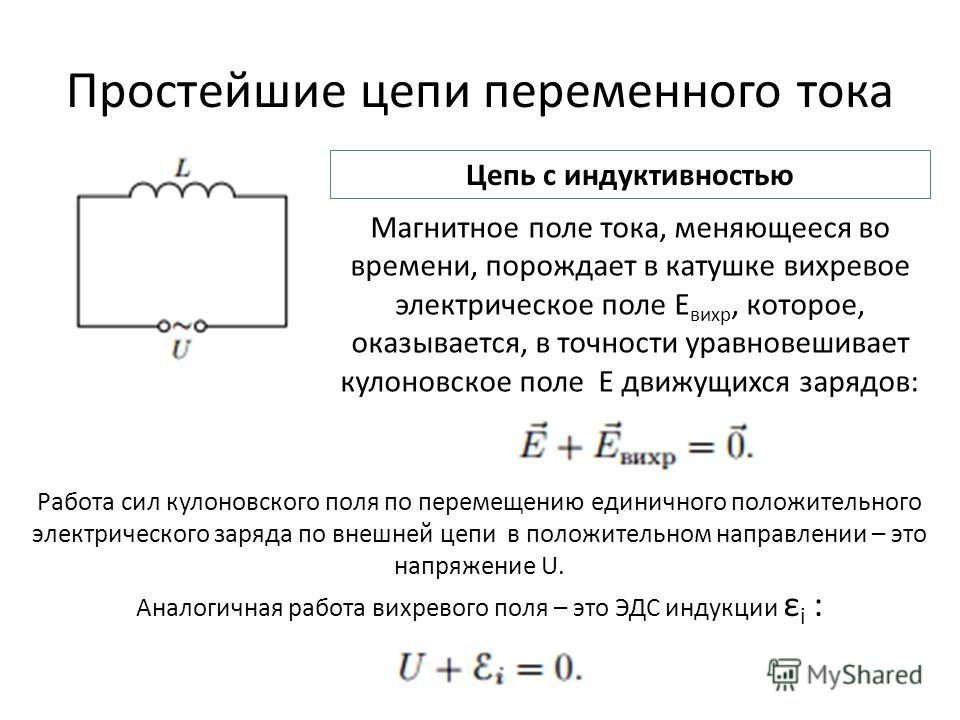 Если бы начальная скорость изменения тока в цепи LR продолжалась линейно, ток достиг бы своего максимального или установившегося «значения состояния» за время (T), определяемое как:

T = L/R секунд.

• T – ПОСТОЯННАЯ ВРЕМЕНИ, измеряется в секундах
• L — это ИНДУКТИВНОСТЬ, измеряется в Генри
.
• R — ОБЩЕЕ СОПРОТИВЛЕНИЕ ЦЕПИ, измеряется в Омах.

Секунды и Генри обычно слишком велики для большинства измерений в электронике, обычно используются милли- и микроединицы, но не забывайте при расчетах преобразовывать любую из этих единиц в секунды или Генри для использования в формулах.

Однако рост тока не является линейным, а следует криволинейной «экспоненциальной» траектории, и за одну постоянную времени (обозначенную на рис. 4.5.1 вертикальной пунктирной линией) ток (обозначенный горизонтальной пунктирной линией) будет только поднялась до 63,2% от своего максимального (установившегося) значения. После двух постоянных времени он достигнет 86,5 %, после 3 постоянных времени 95 % и так далее, пока не достигнет 99,5 %, что считается его максимальным значением после 5 постоянных времени.

Разрядка

Если цепь выключается, ток теперь не сразу падает до нуля, он снова падает экспоненциально, и через один период постоянной времени достигнет 36,8% от предыдущего установившегося значения (т.е. стационарное значение — 63,2%). Считается, что он достигает нуля за пять периодов постоянной времени.

Экспоненциальная кривая

Изменение тока в катушке индуктивности в ответ на ступенчатое изменение входного сигнала является экспоненциальным. В течение серии равных периодов времени ток заряжает катушку индуктивности до ее максимального значения в процентах от оставшейся разницы между текущим и максимальным значениями. Таким образом, хотя эта разница продолжает сокращаться, дополнительная плата, накапливаемая в течение каждого периода времени, также сокращается. Результатом этого является то, что ток никогда не может достичь максимума!

Почему 63,2%?

Если ток никогда не достигает установившегося значения, возникает проблема измерения времени, необходимого для полной зарядки.