Как правильно рассчитать падение напряжения на резисторе. Какие формулы использовать для расчета. Как подобрать номинал резистора для нужного падения напряжения. Как измерить падение напряжения на практике.
Что такое падение напряжения на резисторе
Падение напряжения на резисторе — это разность потенциалов между его выводами, возникающая при протекании через него электрического тока. Другими словами, это та часть общего напряжения цепи, которая «теряется» на конкретном резисторе.
Падение напряжения на резисторе зависит от двух основных факторов:
- Величины сопротивления резистора
- Силы тока, протекающего через резистор
Чем больше сопротивление и сила тока, тем больше будет падение напряжения на резисторе. Этот принцип лежит в основе расчета падения напряжения.
Закон Ома для участка цепи
Основной формулой для расчета падения напряжения на резисторе является закон Ома для участка цепи:
U = I * R
где:
- U — падение напряжения на резисторе (В)
- I — сила тока через резистор (А)
- R — сопротивление резистора (Ом)
Зная любые две величины из этой формулы, можно легко рассчитать третью. Например:
- Падение напряжения: U = I * R
- Сила тока: I = U / R
- Сопротивление: R = U / I
Как рассчитать падение напряжения на резисторе
Для расчета падения напряжения на резисторе нужно выполнить следующие шаги:
- Определить сопротивление резистора (R)
- Измерить или рассчитать силу тока через резистор (I)
- Подставить значения в формулу U = I * R
- Вычислить падение напряжения U
Рассмотрим простой пример:
Дано: резистор 100 Ом, ток через него 0,1 А.
Расчет: U = 0,1 А * 100 Ом = 10 В
Ответ: падение напряжения на резисторе составляет 10 вольт.
Расчет падения напряжения в сложных цепях
В более сложных электрических схемах с несколькими резисторами расчет падения напряжения выполняется по следующему алгоритму:
- Определить общее сопротивление цепи
- Рассчитать общий ток в цепи
- Рассчитать падение напряжения на каждом резисторе по формуле U = I * R
При последовательном соединении резисторов:
- Общее сопротивление: R = R1 + R2 + R3 + …
- Ток через все резисторы одинаковый
- Общее напряжение: U = U1 + U2 + U3 + …
При параллельном соединении:
- Общее сопротивление: 1/R = 1/R1 + 1/R2 + 1/R3 + …
- Напряжение на всех резисторах одинаковое
- Общий ток: I = I1 + I2 + I3 + …
Как подобрать резистор для нужного падения напряжения
При проектировании электрических схем часто нужно подобрать резистор для получения определенного падения напряжения. Для этого:
- Определите требуемое падение напряжения (U)
- Рассчитайте необходимое сопротивление по формуле: R = U / I
- Выберите ближайший номинал резистора из стандартного ряда
Например, нужно получить падение 5 В при токе 20 мА:
R = 5 В / 0,02 А = 250 Ом
Ближайший стандартный номинал — 240 Ом или 270 Ом.
Измерение падения напряжения на практике
Для измерения реального падения напряжения на резисторе используется вольтметр:
- Подключите щупы вольтметра параллельно резистору
- Установите предел измерения больше ожидаемого напряжения
- Включите питание схемы
- Считайте показания вольтметра
Важно: при измерении не размыкайте цепь и соблюдайте технику безопасности!

Факторы, влияющие на падение напряжения
На реальное падение напряжения на резисторе могут влиять следующие факторы:
- Точность номинала резистора (погрешность)
- Температурный коэффициент сопротивления
- Нагрев резистора при протекании тока
- Паразитные емкости и индуктивности
- Нелинейность характеристик при больших токах
Учет этих факторов важен при прецизионных измерениях и расчетах.
Применение расчета падения напряжения
Умение рассчитывать падение напряжения на резисторах используется во многих областях электроники:
- Проектирование делителей напряжения
- Подбор защитных и токоограничивающих резисторов
- Расчет схем стабилизации напряжения
- Измерение тока с помощью шунта
- Анализ работы электрических схем
- Диагностика неисправностей электрооборудования
Понимание принципов расчета падения напряжения — важный навык для любого радиолюбителя и инженера-электронщика.
Типичные ошибки при расчете падения напряжения
При расчетах падения напряжения на резисторах следует избегать следующих распространенных ошибок:

- Неправильное определение направления тока
- Путаница с единицами измерения (вольты, миллиамперы и т.д.)
- Неучет внутреннего сопротивления источника питания
- Игнорирование падения напряжения на проводах
- Ошибки в расчетах при смешанном соединении резисторов
Внимательность и перепроверка расчетов помогут избежать этих ошибок.
Заключение
Расчет падения напряжения на резисторе — базовый навык в электротехнике. Зная закон Ома и правила расчета электрических цепей, можно легко определить распределение напряжения в схеме. Это позволяет грамотно проектировать электронные устройства и анализировать их работу.
Регулярная практика в расчетах и измерениях поможет освоить этот важный навык и применять его для решения различных задач в электронике.
Как рассчитать падение напряжения на резисторах? Показываю на примерах | Будни радиолюбителя
Картинка для карточки. Источник PixabayКартинка для карточки. Источник Pixabay
Простая электрическая цепь состоит из источника питания, проводников и сопротивлений. На практике же электроцепи редко бывают простыми и включают в себя несколько различных ответвлений и повторных соединений.
В больших масштабах в роли сопротивлений может выступать бытовая техника, осветительные приборы и другие потребители. Давайте разберемся, что происходит с током и напряжением на каждом таком потребителе или резисторе с точки зрения электротехники.
Основы электротехники
Закон Ома гласит, что напряжение равно силе тока умноженной на сопротивление. Это может относиться к цепи в целом, участку цепи или к конкретному резистору. Самая распространенная форма этого закона записывается:
U=IR
Два типа схем в электротехнике
Последовательная цепьЗдесь ток протекает по одному проводнику. Независимо от того, какие сопротивления встречаются на его пути, просто суммируйте их, чтобы получить общее сопротивление цепи в целом:
Независимо от того, какие сопротивления встречаются на его пути, просто суммируйте их, чтобы получить общее сопротивление цепи в целом:
Rобщй = R1 + R2 + … + RN (последовательная цепь)
Последовательная цепь. Источник: Нарисовал самПоследовательная цепь. Источник: Нарисовал сам
Параллельная цепьВ этом случае проводник разветвляется на два или более других проводника, на каждом из которых имеется своё сопротивление. В этом случае полное сопротивление определяется как:
1/Rобщ = 1/R1 + 1/R2 + … + 1/R N (параллельная цепь)й
Параллельная цепь. Источник: Собственный рисунокПараллельная цепь. Источник: Собственный рисунок
Если взглянуть на эту формулу, можно сделать вывод, что добавляя сопротивления одинаковой величины, вы уменьшаете сопротивление цепи в целом. Согласно закону Ома это фактически увеличивает ток!
Если это кажется нелогичным, представьте себе поток автомобилей, которые выезжают с парковки через один шлагбаум и тот же самый поток который выезжает со стоянки, которая имеет несколько выездов. Несколько выездов явно увеличит поток покидающих стоянку машин.
Несколько выездов явно увеличит поток покидающих стоянку машин.
Падение напряжения в последовательной цепи
Если вы хотите найти падение напряжения на отдельных резисторах в цепи, выполните следующие действия:
- Рассчитайте общее сопротивление, сложив отдельные значения R.
- Рассчитайте ток в цепи, который одинаков для каждого резистора, поскольку в цепи только один проводник.
- Рассчитайте падение напряжения на каждом резисторе, используя закон Ома.
Пример: источник питания 24 В и три резистора подключены последовательно, где R1 = 4 Ом, R2 = 2 Ом и R3 = 6 Ом. Чему равно падение напряжения на каждом резисторе?
Схема для решения задачи на последовательно подключенное сопротивление. Источник: Собственный рисунокСхема для решения задачи на последовательно подключенное сопротивление. Источник: Собственный рисунок
- Сначала рассчитаем общее сопротивление: 4 + 2 + 6 = 12 Ом.
- Далее рассчитываем ток: 24 В / 12 Ом = 2 А
- Теперь используем ток, чтобы вычислить падение напряжения на каждом резисторе.
 Используя Закон Ома (U = IR) для каждого резистора, получим значения R1, R2 и R3 равными 8 В, 4 В и 12 В соответственно.
Используя Закон Ома (U = IR) для каждого резистора, получим значения R1, R2 и R3 равными 8 В, 4 В и 12 В соответственно.
Падение напряжения в параллельной цепи
Пример: источник питания 24 В и три резистора подключены параллельно, где R1 = 4 Ом, R2 = 2 Ом и R3 = 6 Ом, как и в предыдущей схеме. Чему будет равно падение напряжения на каждом резисторе?
Схема для решения задачи на паралельно подключенное сопротивление. Источник: Собственный рисунокСхема для решения задачи на паралельно подключенное сопротивление. Источник: Собственный рисунок
В этом случае все проще: независимо от значения сопротивления, падение напряжения на каждом резисторе одинаково. Это означает, что падение напряжения на каждом из них — это просто общее напряжение цепи, деленное на количество резисторов в цепи, или 24 В / 3 = 8 В.
Применяя эти несложные правила вы сможете рассчитать падение напряжения даже в сложной цепи, достаточно лишь разделить её на простые участки.
Источником публикации является наш сайт milliamper. ru
ru
Расчет падения напряжения на транзисторе
Во-первых: ток течет в базу, через излучатель. во-вторых, ток течет через коллектор и выходит из излучателя. Суммарный ток через излучатель равен току через основание плюс ток через коллектор.
Вам потребуется таблица данных, чтобы определить точное падение напряжения. Однако также следует помнить, что нет двух идентичных транзисторов.
Таблица данных будет содержать графики, которые вы можете использовать для поиска ожидаемых значений. Для некоторых вычислений полезно предположить, что Vbe обычно составляет около 0,7v. Соединение база-эмиттер по сути является диодом, поэтому оно зажимает напряжение на себе примерно до 0,7 В. Используя этот факт, легко вычислить ток, поступающий в базу: напряжение на R составляет приблизительно 5-0,7 = 4,3 В. Таким образом, ток, идущий в базу, должен быть примерно:
I = V / R = 4,3 / R
Так что, если вы знаете R, вы можете приблизить ток, текущий в базу.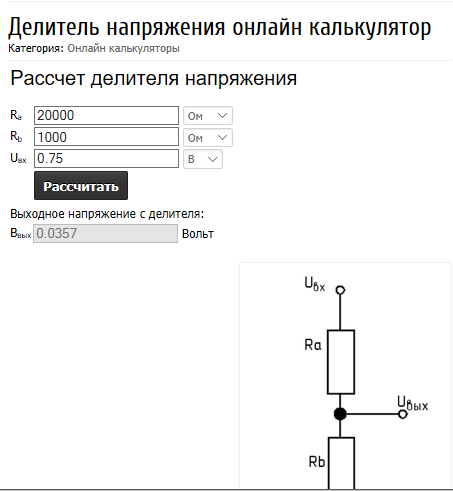 Это даст вам один фактор, который поможет вам прочитать графики из таблицы данных транзистора. Скажем, R составляет 10 кОм, ток, протекающий в базу, будет приблизительно 0,43 мА.
Это даст вам один фактор, который поможет вам прочитать графики из таблицы данных транзистора. Скажем, R составляет 10 кОм, ток, протекающий в базу, будет приблизительно 0,43 мА.
Теперь с этим базовым током вы можете рассчитать ток, протекающий через коллектор — просто умножьте его на коэффициент усиления тока транзистора. Но имейте в виду, что они могут сильно различаться в первую очередь между транзисторами одной модели, а также при разных условиях работы этой модели. Скажем, если 50, то ток, протекающий через коллектор, будет приблизительно 22,5 мА.
Используя приведенную выше схему, предположим, что падение напряжения на светодиоде составляет 2 В при 22,5 мА, что означает, что значение Vbe должно составлять 5-2 = 3 В. Однако, опять же, падение напряжения светодиода при данном токе будет незначительно отличаться между светодиодами одной и той же модели, и некоторые светодиоды, такие как белые светодиоды, имеют тенденцию иметь более высокое падение напряжения, например, 4v.
Чтобы попытаться получить точное значение Vbe, есть формула, которую вы можете использовать, однако, учитывая различия между отдельными транзисторами, гораздо проще просто использовать графики. Поскольку вы знаете приблизительное напряжение Vce и приблизительный базовый ток Ib, вы можете посмотреть Vbe на графике.
И учитывая диапазон возможных значений hfe, указанных в таблице, (обычно они предоставляют три значения: минимальное, типичное и максимальное). Используя верхнюю и нижнюю границы hfe, вы можете рассчитать верхнюю и нижнюю границы тока, который будет проходить через коллектор. Исходя из этого и таблицы данных светодиода, вы можете рассчитать верхнюю и нижнюю границу Vce. Это значение будет полезно при уточнении возможных значений Vbe, поскольку часто Vbe существенно зависит от Vce и Ice; это может иметь значение +/- 0,2 В или около того.
Другие соображения, которые также могут быть весьма значительными, это температура перехода транзистора. Итак, сколько энергии протекает через него, как долго, а также насколько хорошо он отдает тепло в окружающую среду, и температура этой среды будет определять температуру перехода транзистора, что, в свою очередь, повлияет на такие значения, как hfe, Vbe и так далее.
Для вашей схемы выше, вы можете использовать транзистор, такой как NP54 BC547, который является BJT NPN транзистором общего назначения. Эта таблица должна быть достаточной для того, чтобы вы могли понять, как она будет себя вести. Значения hfe, которые я изложил выше, будут разными в BC547; в техническом описании указано минимальное значение 110, максимальное — 800. Таким образом, ваша схема даст очень широкий диапазон значений потенциального льда, поэтому будьте осторожны, чтобы не перегореть светодиод. Вы можете определить hfe любого отдельного транзистора, подав небольшой ток через базу, и измерить ток через коллектор; затем разделите Ic на Ib, и это то, что нужно для этой ситуации. (Если транзистор не «насыщен», то есть светодиод или что-то на его месте в вашей цепи имеет почти 5 В через него, что означает, что транзистор не может еще больше увеличить Ic, поскольку он уже действует как короткое замыкание.) чтобы рассчитать hfe одного конкретного BC547, можно предположить, что он не будет иметь hfe меньше 110, а затем рассчитать резистор для замены R и светодиода (назовем его Rled) на. (Vbe / kt) -1) не применяется, когда транзистор насыщен , поскольку Ie будет ограничено. (Смотри ниже). Во-вторых, решение включает в себя построение пересечения двух графиков: напряжение на R против Ir в соответствии с законом Ома и Vbe против Ib с уравнением Эберса-Молла, решение, где Ir и Ib равны. Ir против Vr будет прямой линией, а Ib против Vbe будет экспоненциальной.
(Vbe / kt) -1) не применяется, когда транзистор насыщен , поскольку Ie будет ограничено. (Смотри ниже). Во-вторых, решение включает в себя построение пересечения двух графиков: напряжение на R против Ir в соответствии с законом Ома и Vbe против Ib с уравнением Эберса-Молла, решение, где Ir и Ib равны. Ir против Vr будет прямой линией, а Ib против Vbe будет экспоненциальной.
График в вашем ответе выглядит правильно, если предположить, что он взят из схемы, которую вы разместили в своем вопросе? (То есть со светодиодом?) Причина, по которой он может перестать быть линейным, заключается в том, что напряжение на светодиоде становится близким к 5 В, что означает, что транзистор насыщается. Таким образом, больший базовый ток приводит лишь к немного большему току, проходящему через светодиод, из-за немного уменьшенных насыщенных значений Vce. Это отражается в следующем:
Если вы посмотрите на эту таблицу данных для 2N3904 , она сведет в таблицу эти два значения:
VBE (sat) Напряжение насыщения базового излучателя:
- С IC = 10 мА и IB = 1,0 мА, тогда Vbe = 0,65
- При IC = 50 мА и IB = 5,0 мА, тогда Vbe = 0,85
Основы измерения тока: Токоизмерительные резисторы.
 Часть 1
Часть 1 Начинаем публикацию статьи, состоящей из трех частей, в которой рассматриваются недооцениваемые особенности чувствительности при измерении тока. В первой части статьи обсуждаются общие настройки, выбор и реализация токоизмерительного резистора. Во
второй части будут рассматриваться действующие совместно схемы, такие как необходимый аналоговый усилительный интерфейс (analog front-end (AFE)) и измерительный усилитель. В третьей части обсуждается использование усилителей при измерении тока в тех случаях, когда нагрузка находится под более высокими напряжениями.Основы измерения тока
Сила тока является одним из наиболее распространенных параметров, используемых для оценки, контроля и диагностики эффективности работы электронных систем. Поскольку это широко распространенное измерение, разработчики часто сталкиваются с проблемами, если недооценивают особенности точного измерения силы тока.
Наиболее распространенным чувствительным элементом, используемым для регистрации тока, является прецизионный низкоомный резистор, устанавливаемый в разрыв цепи тока.
Таким образом, общая конфигурация сигнальной цепи для контроля тока включает аналоговый усилитель (AFE) падающего на шунтовом резисторе напряжения, АЦП для преобразования усиленного напряжения в цифровое представление и системный контроллер (рис. 1).
Рис. 1. Самый простой способ измерения протекающего тока связан с использованием шунтового резистора (крайний слева), на котором падает напряжение, пропорциональное протекающему через него току. Усилитель AFE усиливает низкое напряжение на шунтовом резисторе, чтобы использовать полный диапазон измерений АЦП.
В качестве усилителя AFE обычно используется операционный усилитель или специализированный токовый усилитель, который преобразует небольшое, падающее на шунтовом резисторе дифференциальное напряжение, в повышенное выходное напряжение, которое использует в АЦП полный измерительный диапазон. АЦП, который может быть автономным устройством или встроенным блоком в микроконтроллере или системе на кристалле (SoC), оцифровывает сигнал напряжения и передает полученную информацию управляющему процессору. Системный контроллер использует оцифрованное измерение силы тока, чтобы оптимизировать характеристики системы или внедрить протоколы безопасности, чтобы предотвратить повреждение системы, если ток превышает заданный предел.
Поскольку для преобразования тока в напряжение использован сенсорный компонент в цепи, все физические характеристики резистора (сопротивление, допуск величины, мощность, тепловой коэффициент и тепловая ЭДС) влияют на точность. Следовательно, выбор подходящего шунтового резистора имеет решающее значение для оптимизации измерения тока.
Величина шунтового резистора и падающее на нем напряжение оказывают воздействие на систему. Например, шунтовый резистор со слишком большим сопротивлением может вызвать ненужные потери и понизить напряжение на нагрузке.
Например, при измерении тока, протекающего через обмотку двигателя, пониженное напряжение уменьшает доступную для двигателя электрическую мощность, влияет на его эффективность и/или крутящий момент. Кроме того, большие токи (десятки или сотни ампер), протекающие через шунтовый резистор, приводят к тому, что на резисторе рассеивается значительная энергия в виде выделяемого тепла, понижая точность и эффективность измерения. По этим причинам сопротивление шунта должно быть как можно меньше.
Выбор шунтового резистора для измерения тока
Тот факт, что на шунтовых резисторах рассеивается мощность при протекании через них тока нагрузки, требует минимального значения их сопротивления. Кроме того, для стабильности измерения токоизмерительные резисторы также должны иметь очень низкий температурный коэффициент сопротивления (ТКС). Малый ТКС приведет к высокой точности измерения при низкой зависимости от температуры.
Малый ТКС приведет к высокой точности измерения при низкой зависимости от температуры.
Тепловая ЭДС токочувствительного резистора является еще одной важной характеристикой. Токовые шунтовые резисторы должны работать в широком диапазоне токов. Когда ток низкий, например, в приборе с батарейным питанием в режиме сна или ожидания, тепловая ЭДС шунта добавляет измерительную ошибку к напряжению, создаваемому протекающим через резистор током. Это напряжение ошибки должно быть значительно меньше, чем наименьшее ожидаемое напряжение, создаваемое протекающим через шунтовый резистор током, сводя к минимуму ошибку измерения.
Шунтовые резисторы для датчиков тока доступны с двумя или четырьмя контактами. Шунтовый резистор с двумя контактами является наиболее простым случаем для понимания, поскольку он работает так же, как и любой двухконтактный резистор. При протекании тока через двухконтактный шунтовый резистор на его контактах появляется напряжение, пропорциональное протекающему через него току.
Примерами двухконтактных шунтовых резисторов является серия шунтовых резисторов Bourns CSS2 и серия шунтовых резисторов Vishay WSLP. Серия Bourns CSS2 включает шунтовые резисторы с номинальной мощностью от 2 до 15 Вт, сопротивлением от 0,2 до 5 мОм и с максимальным диапазоном тока от 140 до 273 ампер. Типичный резистор из этих серий, CSS2H-2512R-L500F, поставляется в корпусе для поверхностного монтажа 2512, имеет сопротивление 0,5 мОм и номинальную мощность 6 Вт.
Семейство шунтовых резисторов Vishay WSLP включает устройства в нескольких типах корпусов для поверхностного монтажа в диапазоне размеров от 0603 до 2512, с допустимой мощностью от 0,4 до 3 Вт, с сопротивлениями от 0,5 мОм до 0,1 Ом, при допуске 0,5% или 1%. Типичным шунтовым токовым резистором Vishay является WSLP1206R0200FEA, который поставляется в корпусе 1206 с сопротивлением 20 мОм, допуском 1% и номинальной мощностью 1 Вт.
Обратите внимание, что эти токовые шунтовые резисторы для поверхностного монтажа (SMD) имеют незначительные размеры и занимают очень мало места на плате, но поскольку они могут рассеивать значительное количество тепла, их следует размещать достаточно далеко от чувствительных к нагреву компонентов.
Три сопротивления в одном шунтовом резисторе
Несмотря на их внешний вид, современные шунтовые резисторы не так просты, как кажутся. В частности, сопротивление шунтового резистора фактически состоит из трех частей (рис. 2). Во-первых, есть сопротивление самого шунтового резистора. Затем, есть сопротивления выводов этого резистора и дорожек на печатной плате, подключаемых к шунтовому резистору. Обычно сопротивления выводов и дорожек незначительные, но и сами шунтовые резисторы обычно имеют очень низкие значения сопротивления. При измерениях больших токов даже небольшие сопротивления выводов вносят в результаты измерения погрешность, поскольку они не учтены производителем в спецификациях шунтового резистора.
Рис. 2. Токовый шунтовый резистор с двумя контактами фактически состоит из трех последовательно соединенных сопротивлений: сопротивление самого шунтового резистора (Rshunt), сопротивление двух выводов резистора (Rlead) и сопротивление подводящих дорожек на плате, подключенных к резистору (не показано). Сопротивление выводов может вызвать ошибку измерений для большого тока.
Сопротивление выводов может вызвать ошибку измерений для большого тока.
Одним из способов, позволяющих избежать ошибок измерения, вносимых внешними сопротивлениями выводов, является создание соединения Кельвина, выполнив раздельные токоизмерительные дорожки к двухконтактному шунтовому резистору (рис. 3).
Рис. 3. Соединение Кельвина с двухконтактным токочувствительным резистором уменьшает погрешность измерения, вызываемую сопротивлением выводов резистора и дорожек печатной платы. Пример изображения двухконтактных токовых шунтовых резисторов показан справа.
В этой конфигурации ток, протекающий через резистор токового шунта, проходит через широкие подводящие дорожки на печатной плате. Гораздо более узкие дорожки, которые находятся не в основном канале протекающего тока, но расположены непосредственно рядом с резистивным элементом шунтового резистора, снимают падающее на нем напряжение и передают его на вход AFE. Разделение токоведущих и токочувствительных контактов характеризует соединение Кельвина.
Полученное в результате схематическое представление соединения Кельвина с использованием двухконтактного шунтирующего резистора показано на рис. 4.
Рис. 4. Использование соединения Кельвина с двухконтактным шунтовым резистором выводит линии измерения напряжения из основной цепи тока, что приводит к более точному измерению напряжения на шунтовом резисторе
Очень малый ток протекает через два токочувствительных резистора (Rsense), показанных на рис. 4, потому что они подключены к имеющим высокий импеданс входам усилителя либо АЦП, что делает их сопротивления намного менее критичными, чем значения сопротивления выводов, через которые протекает большой ток шунтового резистора. Следовательно, падение напряжения на резисторах Rsense довольно небольшое и не является значительным источником ошибки при измерении тока.
Что лучше, два вывода или четыре?
Как видно из монтажной схемы печатной платы на рис. 3, невозможно полностью исключить сопротивления выводов в двухконтактном шунтовом резисторе даже при использовании соединения Кельвина. Должен быть определен некоторый допуск для размещения печатной площадки, чтобы учесть ошибку позиционирования, когда шунтовый резистор устанавливается для впаивания на печатную плату.
Кроме того, ТКС медных дорожек печатной платы (3900 м.д. (миллионных долей)/ ?C) намного выше, чем ТКС резистивного элемента шунтового резистора (часто менее 50 м.д./ ?C). Эти параметрические различия приводят к тому, что изменение сопротивления в дорожках печатной платы намного больше, чем в токочувствительном резисторе, что дает более высокую температурную зависимость токочувствительной цепи.
При использовании двухконтактного шунтового резистора с соединением Кельвина, часто уровень точности для чувствительности по току может оказаться недостаточным во многих случаях с очень высоким током. Для таких случаев производители предлагают шунтовые резисторы с четырьмя контактами, в которых соединение Кельвина реализовано внутри резистора. Таким образом, производитель может полностью контролировать все допуски и температурные коэффициенты, относящиеся к соединению Кельвина (рис. 5).
| High Current Trace – Цепь для мощного тока Current Sensing Trace – Токочувствительная цепь Current Sensing Resistor – Токочувствительный резистор Copper Trace – Медная дорожка |
|
| Рис. 5. Четырехконтактный шунтовый резистор обеспечивает высокоточное соединение Кельвина с токочувствительными соединениями, расположенными рядом с шунтовым резистором. Пример изображения токового четырех контактного шунтового резистора представлен справа. | |
Токочувствительный резистор с четырьмя контактами, использующий соединение Кельвина, имеет отдельные выводы для протекающего через резистор большого тока и для измерения напряжения, что помогает повысить точность измерений. Кроме того, использование четырехконтактного шунтового резистора с соответствующим соединением Кельвина снижает влияние ТКС, обеспечивая улучшенную температурную стабильность, по сравнению с двухконтактным шунтовым резистором, использующим компоновку печатной платы для реализации соединения Кельвина.
Bourns предлагает несколько четырехконтактных шунтовых резисторов из серии для поверхностного монтажа CSS4 (рис. 6).
Рис. 6. Шунтовые резисторы Bourns CSS4 для поверхностного монтажа используют четырехконтактное соединение Кельвина для максимальной точности измерения тока.
В состав серии Bourns CSS4 входят шунтовые резисторы CSS4J-4026R-L500F 0,5 мОм, 1%, 5 Вт, и CSS4J-4026K-2L00F 2 мОм, 1%, 4 Вт. Оба эти шунта имеют низкий ТКС, низкую тепловую ЭДС и занимают на плате площадку не более 10 мм × 7 мм.
Заключение
Первым шагом в процессе измерения тока является преобразование электрического тока в более легко измеряемый параметр – напряжение. Токовые шунтовые резисторы являются недорогими компонентами, которые выполняют эту задачу. Однако, как показано в статье, номинальное значение шунтового резистора должно быть низким, чтобы минимизировать его влияние на цепь и рассеиваемую мощность на самом резисторе.
К другим важным параметрам для токовых шунтовых резисторов относятся ТКС и тепловая ЭДС, которые могут значительно повлиять на точность измерения тока.
Наконец, для того, чтобы максимизировать точность измерения, крайне важно не допустить ограничения силы тока, протекающего через шунт, минуя токочувствительный тракт либо с помощью специальной компоновки печатной платы, которая создает соединение Кельвина для двухконтактного шунта, либо с помощью четырехконтактного шунтового резистора.
Поскольку низкое значение сопротивления подразумевает, что падение напряжения на токочувствительном резисторе будет небольшим, во второй части этой статьи будут обсуждаться соображения по проектированию AFE, который усиливает низкое напряжение, упрощая процесс измерения с помощью АЦП.
Делитель напряжения — Вольтик.ру
Перед схемотехниками нередко стоит задача получения пониженного напряжения из высокого напряжения. Это можно сделать с помощью делителя напряжения – простой схемы с использованием двух резисторов. С их помощью можно создать выходное напряжение в несколько раз меньшее, чем входное напряжение.
Простота и надежность делителя напряжения сделали его схему фундаментальной в схемотехнике. При ее внедрении необходимо уделить максимум внимания непосредственно схеме и точности расчета напряжения по специальной формуле.
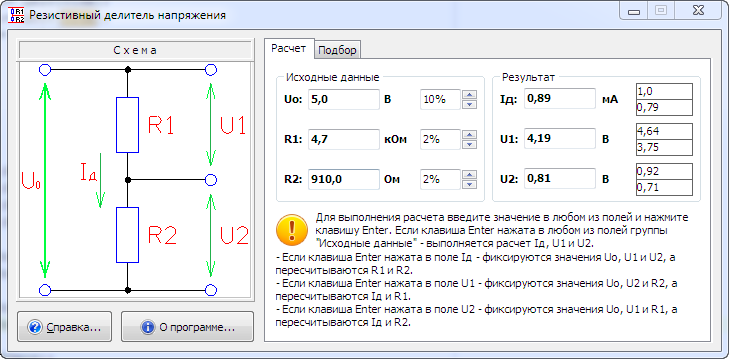
Существует несколько вариантов схем делителя напряжения, с которыми можно будет познакомиться ниже. Особенностью каждой из них является наличие двух резисторов и входного напряжения. Резистор, расположенный у плюса входного напряжения, обозначен на схемах R1, расположенный у минуса – R2. Падение напряжения у второго резистора обозначается Uout. Оно и является результатом работы схемы делителя напряжения.
Чтобы произвести расчет напряжения делителя нужно знать значения следующих величин: сопротивление первого и второго резистора (R1, R2) и входное напряжение Uin. Для расчета используется следующая формула:
Знакомые со школьным курсом физики без труда смогут определить, что в основе этого уравнения лежит закон Ома. Для определения напряжения на выходе делителя выводится формула с использованием силы тока I1 и I2, протекающего через резисторы R1, R2:
Используя закон Ома, мы получаем следующую формулу для Uout:
В этом уравнении для нас остается неизвестной величина I2, но если предположить, что она равна I1, то наша схема приобретет следующий вид:
В этой схеме неизвестным остается Uin – сопротивление на обоих резисторах R1, R2. Так как они соединены последовательно, то их совместное сопротивление суммируется:
В итоге схема делителя напряжения упрощается:
Исходя из школьной формулы U=I*R и помня, что суммарное сопротивление равно R1 + R2, записываем закон Ома в следующем виде:
Так как мы приняли I1=I2, то получаем уравнение, которое нам наглядно демонстрирует, что выходное напряжение будет прямо пропорциональным отношению сопротивлений и входному напряжению.
Делитель напряжения широко используется в радиоэлектронике, приведем несколько примеров:
- потенциометры;
- резистивные датчики;
- фоторезисторы.
Расчёт шунтирующего сопротивления амперметра. Супер онлайн калькулятор. :: АвтоМотоГараж
Для контроля величины тока применяется прибор называемый амперметром. Из практики могу сказать, что не всегда под рукой оказывается прибор с нужным диапазоном измерения. Как правило, диапазон либо мал, либо велик. Здесь мы разберем, как изменить рабочий диапазон амперметра. Амперметры на большие токи от 20 ампер и выше имеют в своём составе внешний шунтирующий резистор. Он подключается параллельно амперметру. На рисунке 1 приведена схема включения амперметра с шунтирующем резистором.
В качестве примера в экспериментах будет использован амперметр M367 со шкалой до 150 ампер, соответственно при таком токе амперметр используется с внешним шунтирующим сопротивлением.
Если убрать шунтирующий резистор, то амперметр станет миллиамперметром с максимальным током отклонения стрелки 30 мА (далее будет пояснение, откуда это значение взялось). Таким образом, используя разные шунтирующие сопротивления можно сделать амперметр практически с любым диапазоном измерения.
Рассмотрим подробнее имеющийся измерительный прибор. Из его маркировок можно узнать следующее. Маркировка в верхнем правом углу (цифра 1 на изображении). Модель измерительной головки М367. Сделан на краснодарском заводе измерительных приборов (это можно определить по ромбику с буковками ЗИП). Год выпуска 1973. Серийный номер 165266.
Маркировка в нижнем левом углу (цифра 2 на изображении). Слева на право. Прибор предназначен для измерения постоянного тока. Магнитоэлектрический прибор с подвижной рамкой. Напряжение между корпусом и мангнитоэлектрической системой не должно превышать 2 КВ. Рабочее положение шкалы прибора вертикальное. Класс точности прибора в процентах 1,5. ГОСТ8711-60. Измерительная головка рассчитана на измерения силы тока до 150 ампер с использованием внешнего шунтирующего сопротивления рассчитанного на падение на нём напряжения номиналом в 75 милливольт.
Итак, это максимум что удалось узнать из маркировки амперметра. Теперь перейдём к расчетам. Сопротивление шунта определяется по формуле:
где :
Rш — сопротивление шунтирующего резистора;
Rприб — внутреннее сопротивление амперметра;
Iприб — максимально измеримый ток амперметром без шунта;
Iраб — максимально измеримый ток с шунтом (требуемое значение)
Если все данные для расчёта имеются, то можно приступать к самому расчёту. Для упрощения можно воспользоваться онлайн калькулятором ниже:
В нашем случае из формулы видно, что данных не достаточно. Нам известен только максимальный измеряемый ток с шунтом. То есть, то, что мы хотим видеть в случае максимального отклонения стрелки амперметра.
Из маркировки прибора удалось узнать падение напряжения на шунтирующем сопротивлении. И это уже что-то. Из этого параметра ясно, что при подаче на прибор напряжения номиналом 0,075 вольт (75мВ) стрелка отклониться до крайнего значения на шкале 150 ампер. Таким образом, получается, что максимальное отклонение стрелки прибора достигается подачей напряжения 75 мВ. Вроде как данных для расчета по-прежнему не хватает. Необходимо узнать сопротивление прибора и ток, при котором стрелка откланяется до максимального значения без шунтирующего резистора. Далее предлагаю несколько способов для определения нужных параметров и решения задачи.
Способ первый. При помощи блока питания выясняем максимальное отклонение стрелки по току и напряжению без шунта. В нашем случае напряжение уже известно. Его замерять не будем. Измеряем ток и отклонение стрелки. Так как блока питания под рукой не оказалось, то пришлось воспользоваться очень разряженой батарейкой типа АА. Ток, который батарейка могла ещё отдать, составил 12 мА (по показаниям мультиметра). При этом токе стрелка прибора отклонилась до значения на циферблате 60А. Далее определяем цену деления и рассчитываем полное (максимальное) отклонение стрелки. Поскольку шкала циферблата амперметра размечена равномерно, то не составит труда узнать (рассчитать) ток максимального отклонения стрелки.
Цена деления прибора рассчитывается по формуле:
где:
х1 – меньшее значение,
х2 – большее значение,
n – количество промежутков (отрезков) между значениями
Для упрощения можно воспользоваться онлайн калькулятором ниже:
Расчёт показал, что цена деления прибора штатной шкалы составляет 5 ампер. При токе 12 мА стрелка отклонялась до показания 60А. Таким образом, цена одного деления без шунта составляет 1 мА. Всего делений 30, соответственно максимальное отклонение стрелки до значения 150А без шунта составляет 30 мА.
Далее при помощи закона Ома находим сопротивление прибора. 0,075/0,03=2,5 Ом
Расчёт:
Rш=Rприб*Iприб/(Iраб-Iприб)=2,5*0,03/(10-0,03)=0,00752 Ом для шкалы 10А мах
Rш=Rприб*Iприб/(Iраб-Iприб)=2,5*0,03/(5-0,03)=0,01509 Ом для шкалы 5А мах
Rш=Rприб*Iприб/(Iраб-Iприб)=2,5*0,03/(3-0,03)=0,02525 Ом для шкалы 3А мах
Для упрощения можно воспользоваться онлайн калькулятором расчёта сопротивления шунтирующего сопротивления выше.
Второй вариант. При помощи прецизионного мультиметра замеряем сопротивление амперметра и далее при помощи закона Ома (зная напряжение максимального отклонения стрелки) находим ток максимального отклонения стрелки. Измерения выполнялись прецизионными мультиметрами Mastech MS8218 и Uni-t UT71E. При измерении сопротивления амперметра значение составило 2,50-2,52 Ом прибором UT71E и 2,52-2,53 прибором MS8218.
Формула для расчёта тока отклонения стрелки до максимального значения:
Расчёт: 0.075/2.52=0.02976А
Для упрощения вычислений максимального тока отклонения стрелки амперметра можно воспользоваться калькулятором ниже:
Далее, как и в первом варианте выполняем расчёт сопротивления шунтирующего резистора (калькулятор выше). Для расчёта было принято среднее показание измеренного сопротивления амперметра двумя мультиметрами Rприб = 2,52Ом
Расчёт:
Rш=Rприб*Iприб/(Iраб-Iприб)=2,52*0,02976/(10-0,02976)=0,00752 Ом для шкалы 10А мах
Rш=Rприб*Iприб/(Iраб-Iприб)=2,52*0,02976/(5-0,02976)=0,01508 Ом для шкалы 5А мах
Rш=Rприб*Iприб/(Iраб-Iприб)=2,52*0,02976/(3-0,02976)=0,02524 Ом для шкалы 3А мах
Если сравнить расчёты двух методик между собой, то получились совпадение данных до четвёртого знака после запятой, а в некоторых случаях даже до пяти знаков.
О тонкостях изготовления шунтирующего сопротивления расскажу в следующей статье: Как сделать шунт (шунтирующий резистор) для амперметра. Самый простой метод подбора.
И ещё одно продолжение этой тематики: Как изменить предел измерения амперметра. Как переделать амперметр постоянного тока на переменный.
Стабилитроны
Если подключить диод и резистор последовательно с источником постоянного напряжения , так что диод вперед предвзятым, падение напряжения на диоде будет оставаться довольно постоянным в широком диапазоне напряжений питания как показано на рисунке ниже (а).
В соответствии с «диодного уравнения» здесь , ток через PN перехода вперед предвзятым пропорциональна е , возведенное в силе прямого падения напряжения. Поскольку это является экспоненциальной функцией, ток возрастает достаточно быстро для умеренного повышения падения напряжения. Другой способ рассмотрения этого сказать, что падение напряжения через переднюю предвзятым диода меняется мало для больших вариаций тока диода. В схеме , показанной на рисунке ниже (а), ток диода ограничен напряжением источника питания, последовательный резистор, и падение напряжения диода, который , как мы знаем , не сильно отличается от 0,7 вольт. Если напряжение питания должны были быть увеличены, падение напряжения на резисторе увеличился бы почти такое же количество, и падение напряжения диода только немного. И наоборот, уменьшение напряжения питания приведет к почти равное уменьшению перепада напряжения резистор, только с небольшим количеством уменьшения перепада напряжения на диоде. Одним словом, мы могли бы суммировать это поведение, говоря , что диод регулирует падение напряжения на примерно 0,7 вольт.
Регулирование напряжения является полезным диодный свойство для использования. Предположим, что мы строим какие-то схемы, которые не могут терпеть изменения в напряжении питания, но необходимо питание от химической батареи, напряжение которого изменяется в течение всего срока службы. Мы могли бы сформировать схему, как показано и подключить цепь, когда требуется постоянное напряжение через диод, где он будет получать неизменные 0,7 вольт.
Это, конечно, работать, но большинство практических схем любого рода требуют напряжения питания свыше 0,7 вольт, чтобы правильно функционировать. Один из способов, мы могли бы увеличить напряжение в точке регулирования будет подключить несколько диодов в серии, так что их отдельные капли прямого напряжения 0,7 вольт каждый бы добавить, чтобы создать большую сумму. Например, если бы мы имели десять диодов в серии, регулируемое напряжение было бы в десять раз 0,7 или 7 вольт на рисунке ниже (б).
Форвард предвзятым Si ссылка: (а) одиночный диод, 0.7В, (б) 10-диодов в серии 7.0V.
До тех пор пока напряжение батареи никогда не просели ниже 7 вольт, там всегда будет около 7 вольт упал через десять-диод «стек».
Если большие регулируемые напряжения необходимо, мы могли бы использовать либо более диодов в серии (в безвкусный вариант, на мой взгляд), или попробовать принципиально иной подход. Известно , что диод прямого напряжения является достаточно постоянной фигурой в широком диапазоне условий, но так обратное напряжение пробоя, и напряжение пробоя , как правило, намного больше , чем прямое напряжение. Если обратная полярность диода в нашем регулятора одного диода схемы и увеличение напряжения питания до точки, где диод «сломалась» (больше не мог выдержать напряжения обратного смещения впечатлил через него), диод будет аналогично регулировать напряжение в этой точке пробоя, не позволяя ей увеличить дальше , как на рисунке ниже (а).
(а) смещен в обратном направлении диод Si малосигнальная ломается при температуре около 100В. (б) Символ для стабилитрона.
К сожалению, когда нормальные выпрямляющие диоды «ломаются», они обычно делают это деструктивно. Тем не менее, можно создать специальный тип диода, который может работать без сбоев пробой полностью. Этот тип диода называется стабилитрон, и его символ выглядит как показано на рисунке выше (б).
Когда вперед предвзятым, стабилитроны ведут себя так же, как стандартные выпрямительные диоды: они имеют прямое падение напряжения, которое следует за «Диод уравнение» и составляет около 0,7 вольт. В режиме обратного смещения, они не проводят , пока приложенное напряжение не достигает или превышает так называемую стабилитрон напряжение, и в этот момент диод способен проводить значительный ток, и при этом будет пытаться ограничить напряжение падает на него , чтобы что точка стабилитроны напряжения. До тех пор пока рассеиваемая мощность этого обратного тока не превышает допустимые пределы перегрева диода, диод не будет нанесен ущерб.
Стабилитроны выпускаются с стабилитроны напряжения в диапазоне от нескольких вольт до сотен вольт. Это стабилитрон напряжение незначительно изменяется с температурой, и, как общие ценности резистор углерода состав, может составлять от 5 до 10 процентов в погрешности от спецификации изготовителя. Тем не менее, эта стабильность и точность , как правило , достаточно для стабилитрон для использования в качестве регулятора напряжения устройства в общей цепи питания на рисунке ниже .
Стабилитрон Регулятор диод цепь, стабилитрон напряжение = 12.6V).
Пожалуйста , обратите внимание ориентации стабилитрона в приведенной выше схеме: диод смещен в обратном направлении, и преднамеренно так. Если бы мы ориентировали диод в «нормальном» пути, с тем, чтобы быть смещенным вперед, было бы только падение 0,7 вольт, так же, как обычный выпрямительный диод. Если мы хотим использовать обратные свойства пробоя этого диода, мы должны работать его в режиме обратного смещения. До тех пор пока остается напряжение питания выше напряжения стабилитрона (12,6 вольт, в этом примере), то падение напряжения через стабилитрон останется примерно 12,6 вольт.
Как и любой полупроводниковый прибор, стабилитрон чувствителен к температуре. Слишком высокая температура уничтожит стабилитрон, и потому, что как падает напряжение и проводит ток, она производит свои собственные тепло в соответствии с законом Джоуля (P = IE). Поэтому, нужно быть осторожным, чтобы разработать схему регулятора таким образом, что рейтинг рассеиваемая мощность диода не превышается. Интересно, что когда стабилитроны не из — за чрезмерной рассеиваемой мощности, они обычно не замкнуты , а не открытым. Диод не удалось таким образом легко обнаруживается: она падает почти до нуля, когда напряжение предвзятым в любом случае, как кусок проволоки.
Рассмотрим регулирующую цепь стабилитрона математически, определения всех напряжений, токов и рассеиваемой мощности. Принимая ту же форму схемы , показанной ранее, мы будем выполнять вычисления , предполагая напряжение стабилитрона 12,6 вольт, напряжение питания 45 вольт, а значение серии резистор 1000 Ом (мы будем рассматривать напряжение стабилитрона быть точно 12,6 вольт , с тем , чтобы избежать того , чтобы квалифицировать все цифры как «приблизительно» на рисунке ниже (а)
Если напряжение стабилитрона составляет 12,6 вольт и напряжение на источник питания составляет 45 вольт, то будет 32,4 вольт сброшенные через резистор (45 вольт — 12,6 вольт = 32,4 вольт). 32.4 вольт падает на 1000 Ω дает 32,4 мА тока в цепи. (Рисунок ниже (б))
(а) регулятор напряжения стабилитрон с 1000 Ом резистор. (б) Расчет падения напряжения и тока.
Мощность рассчитывается путем умножения тока на напряжение (P = IE), так что мы можем вычислить рассеиваемой мощности как для резистора и стабилитрона довольно легко:
Стабилитрон с номинальной мощностью 0,5 Вт будет достаточно, так как бы резистор рассчитан на 1,5 или 2 Вт рассеиваемой.
Если чрезмерное рассеивание мощности вредно, то почему бы не разработать схему для наименьшее количество диссипации возможно? Почему не только размер резистор для очень высокое значение сопротивления, тем самым серьезно ограничивает ток и сохраняя показатели рассеиваемой мощности очень низкая? Возьмем эту схему, например, с 100 кОм вместо 1 кОм. Следует отметить , что как напряжение питания и напряжение зенеровский диода на рисунке ниже идентичны последнему примеру:
Регулятор стабилитрон 100 кОм.
С только 1/100 тока мы имели раньше (324 мкА вместо 32,4 мА), оба показателя рассеиваемой мощности должно быть в 100 раз меньше:
Кажется идеальным, не так ли? Меньше рассеиваемой мощности означает более низкие рабочие температуры, как для диода и резистора, а также меньше потери энергии в системе, не так ли? Более высокое значение сопротивления действительно уменьшает уровень рассеиваемой мощности в цепи, но , к сожалению , представляет еще одну проблему. Следует помнить , что цель цепи регулятора является обеспечение стабильного напряжения для другой схемы. Другими словами, мы в конечном итоге будет к власти что-то с 12,6 вольт, и это что-то будет иметь текущий розыгрыш самостоятельно. Рассмотрим нашу первую схему регулятора, на этот раз с 500 Ω нагрузки , подключенной параллельно с стабилитрона на рисунке ниже .
Регулятор стабилитрон с 1000 резистором Ом и 500 Ом нагрузки.
Если 12,6 вольт поддерживается на нагрузке 500 Ω, нагрузка будет рисовать 25,2 мА тока. Для того, чтобы серии 1 кОм «сбросив» резистор падение 32,4 вольт (уменьшение напряжения блока питания в 45 вольт до 12,6 через стабилитроны), он все равно должен проводить 32,4 мА тока. Это оставляет 7,2 мА тока через стабилитрон.
Теперь рассмотрим «энергосберегающий» регулятор цепи с 100 кОм сбросив резистор, подачи мощности в той же 500 Ом нагрузки. Что предполагается сделать, это сохранить 12,6 вольт на нагрузке, так же, как последний контур. Тем не менее, как мы увидим, он не может выполнить эту задачу. (Рисунок ниже )
ZENER не-регулятор с 100 кОм резистором 500 Ω нагрузки.>
При большем значении падения резистора на месте, там будет только около 224 мВ напряжения через 500 Ω нагрузки, гораздо меньше, чем ожидаемое значение 12,6 вольт! Почему это? Если мы на самом деле было 12,6 вольт на нагрузке, она будет опираться на 25,2 мА тока, как и раньше. Этот ток нагрузки должен был бы пройти через капельную резистор серии, как это было раньше, но с новым (намного больше!) Сбросив резистор в месте, напряжение падает на этот резистор с 25,2 мА тока происходит через него будет 2,520 вольт! Так как мы, очевидно, не имеют такого большого напряжения, подаваемого от батареи, это не может произойти.
Ситуация легче понять , если мы временно удалить стабилитрон из схемы и анализировать поведение двух резисторов в одиночку на рисунке ниже .
Non-регулятор с Зинером удален.
Оба 100 кОм сбрасывают резистор и сопротивление нагрузки 500 Ω соединены последовательно друг с другом, что дает общее сопротивление цепи 100,5 кОм. С общим напряжением 45 вольт и суммарным сопротивлением 100,5 кОм, Закон Ома (I = E / R) говорит нам о том, что ток будет 447.76 мкА. Выяснение падения напряжения на обоих резисторов (E = IR), мы приходим к 44.776 вольт и 224 мВ, соответственно. Если бы мы должны были повторно установить стабилитрон на данный момент, это будет «видеть» 224 мВ через него, а также, будучи параллельно с сопротивлением нагрузки. Это гораздо ниже напряжения пробоя стабилитрона диода и поэтому он не будет «ломаться» и проводить ток. В этом отношении, при таком низком напряжении диод не будет проводить, даже если это были вперед-предвзятым! Таким образом, диод перестает регулировать напряжение. По крайней мере, 12,6 вольт должен быть отброшен через к «активировать» его.
Аналитический метод удаления стабилитрон из схемы и видим ли присутствует или нет, чтобы сделать его достаточно провести напряжение звук один. Просто потому, что стабилитрон случается быть подключен в цепи не гарантирует, что полное напряжение стабилитрона будет всегда падает на него! Помните , что стабилитроны работу путем ограничения напряжения до некоторого максимального уровня; они не могут компенсировать отсутствие напряжения.
Таким образом, любой стабилитрон регулирующий контур будет функционировать до тех пор, как сопротивление от нагрузки равна или больше некоторого минимального значения. Если сопротивление нагрузки слишком низкое, то будет использовать слишком много тока, сбросив слишком много напряжения на серии капельной резисторе, оставляя недостаточное напряжение на стабилитроне, чтобы сделать его проведение. Когда стабилитрон прекращает проведение тока, он больше не может регулировать напряжение и напряжение нагрузки упадет ниже точки регулирования.
Наш регулятор цепи с 100 кОм капельной резистора должно быть хорошо для некоторого значения сопротивления нагрузки, тем не менее. Чтобы найти это приемлемое значение сопротивления нагрузки, мы можем использовать таблицу для расчета сопротивления в цепи серии два резистора (без диода), вставки известных значений полного напряжения и понижая сопротивление резистора, и вычисления для ожидаемого напряжения нагрузки 12,6 вольт :
С 45 вольт полного напряжения и 12,6 вольт на нагрузке, мы должны иметь 32,4 вольт на R сбрасывания:
32,4 вольт через капельную резистор и 100 кОм на сумму сопротивления в нем, ток через него будет 324 мкА:
Будучи последовательной цепи, ток равен через все компоненты в любой момент времени:
Расчет сопротивления нагрузки теперь простой вопрос закона Ома (R = E / I), что дает нам 38.889 кОм:
Таким образом, если сопротивление нагрузки точно 38,889 кОм, то будет 12,6 вольт на него, диод или нет диода. Любое сопротивление нагрузки меньше, чем 38.889 кОм приведет к напряжению нагрузки меньше, чем 12,6 вольт, диод или нет диода. С помощью диода в месте, нагрузочное напряжение будет регулироваться до максимум 12,6 вольт для любого сопротивления нагрузки , превышающей 38.889 кОм.
С первоначальным значением 1 кОм для капельной резистора, наш регулятор схема способна адекватно регулировать напряжение даже при сопротивлении нагрузки столь же низко как 500 Ом. То, что мы видим, это компромисс между рассеиваемой мощности и допустимого сопротивления нагрузки. Чем выше значение капельной резистор дал нам меньше рассеиваемой мощности, за счет повышения допустимого минимального значения сопротивления нагрузки. Если мы хотим, чтобы регулировать напряжение для нагрузочных сопротивлений малоценных, схема должна быть готова справиться с более высокой рассеиваемой мощности.
Стабилитроны регулируют напряжение, действуя в качестве дополнительных нагрузок, используя более или менее тока по мере необходимости, чтобы обеспечить постоянное падение напряжения на нагрузке. Это аналогично тому, регулируя скорость автомобиля при торможении, а не путем изменения положения дроссельной заслонки: она не только расточительно, но тормоза должны быть построены, чтобы обрабатывать всю мощность двигателя, когда условия движения не требуют его. Несмотря на эту фундаментальную неэффективность конструкции, схемы регулятора стабилитрон широко используются из-за их явной простоты. В мощных приложениях, где неэффективность было бы неприемлемо, другие методы напряжения для регулирования применяются. Но даже тогда, маленькие схемы стабилитроны на основе часто используются для обеспечения «опорного» напряжение для управления более эффективной схемы усилителя управления основной мощности.
Стабилитроны выпускаются в стандартных рейтингах напряжения , перечисленных в таблице ниже . В таблице «Общие стабилитрон напряжения» перечислены общие напряжения для 0.3W и 1.3W частей. Потребляемая мощность соответствует умереть и размер пакета, и сила, что диод может рассеять без повреждения.
Общие стабилитрон напряжения
| 0.5W | ||||||
| 2.7V | 3.0V | 3.3V | 3.6V | 3.9V | 4.3V | 4.7V |
| 5.1V | 5.6V | 6.2V | 6,8 В | 7.5V | 8.2V | 9.1V |
| 10V | 11V | 12V | 13V | 15V | 16V | 18V |
| 20V | 24V | 27В | 30V | |||
| 1.3W | ||||||
| 4.7V | 5.1V | 5.6V | 6.2V | 6,8 В | 7.5V | 8.2V |
| 9.1V | 10V | 11V | 12V | 13V | 15V | 16V |
| 18V | 20V | 22V | 24V | 27В | 30V | 33V |
| 36V | 39V | 43V | 47V | 51V | 56V | 62V |
| 68V | 75V | 100V | 200V |
Стабилитрон клипера: вырезку схема , которая отсекает пики сигнала на приблизительно от напряжения Зинера диодов. Схема на рис ниже имеет два Zeners соединенных серии противостоящую симметрично клип сигнала на почти напряжения Зенера. Пределы резистора ток по Zeners до безопасного значения.
* SPICE 03445.eps D1 4 0 диод D2 4 2 диода R1 2 1 1.0k V1 1 0 SIN (0 20 1k) .MODEL диод d = 10 б.в. .tran 0.001 2m .конец |
Стабилитрон машинки для стрижки:
Напряжение пробоя стабилитрона для диодов установлен на 10 В с помощью диодного параметра модели «БВ = 10» в пряность чистого списка на рисунке выше . Это приводит к тому, Zeners клип около 10 В. Диоды спина к спине клип оба пика. Для положительного полупериода, верхний стабилитрон смещен в обратном направлении, разрушение при напряжении стабилитрон 10 В. Чем ниже стабилитрон падает приблизительно 0,7 В, так как он смещен в прямом направлении. Таким образом, более точный уровень отсечения составляет 10 + 0,7 = 10.7V. Подобный отрицательный полупериод отсечение происходит -10.7 В.
(Рисунок ниже ) показывает уровень подрезки на чуть более ± 10 В.
Стабилитрон машинки для стрижки: v (1) вход обрезается сигнала V (2).
- ОБЗОР:
- Стабилитроны предназначены для работы в режиме обратного смещения, что обеспечивает относительно низкую, стабильную пробой или стабилитрон напряжение , при котором они начинают проводить значительный ток обратной.
- Стабилитрон может функционировать в качестве регулятора напряжения, выступая в качестве вспомогательного нагрузку, забирая больше тока от источника, если напряжение слишком велико, и меньше, если оно слишком низкое.
Расчет резистора для понижения напряжения. Делитель напряжения на резисторах. Формула расчета, онлайн калькулятор
Для человека, который знаком с электрооборудованием на уровне простого пользователя (знает, где и как включить/выключить), многие используемые электриками термины кажутся какой-то бессмыслицей. Например, чего только стоит «падение напряжения» или «сборка схемы». Куда и что падает? Кто разобрал схему на детали? На самом же деле, физический смысл происходящих процессов, скрывающийся за большинством этих слов, вполне доступен для понимания даже со школьными знаниями физики.
Чтобы объяснить, что такое падение напряжения, необходимо вспомнить, какие вообще напряжения бывают в (имеется в виду глобальная классификация). Их всего два вида. Первый — это напряжение который подключен к рассматриваемому контуру. Оно может также называться приложенным ко всей цепи. А второй вид — это именно падение напряжения. Может быть рассмотрено как в отношении всего контура, так и любого отдельно взятого элемента.
На практике это выглядит следующим образом. Например, если взять обычную вкрутить ее в патрон, а провода от него подключить в домашнюю сетевую розетку, то приложенное к цепи (источник питания — проводники — нагрузка) напряжение составит 220 Вольт. Но стоит нам с помощью вольтметра замерять его значение на лампе, как станет очевидно, что оно немного меньше, чем 220. Так произошло потому, что возникло падение напряжения на которым обладает лампа.
Пожалуй, нет человека, который не слышал бы о законе Ома. В общем случае формулировка его выглядит так:
где R — активное сопротивление цепи или ее элемента, измеряется в Омах; U — электрическое напряжение, в Вольтах; и, наконец, I — ток в Амперах. Как видно, все три величины непосредственно связаны между собой. Поэтому, зная любые две, можно довольно просто вычислить третью. Конечно, в каждом конкретном случае придется учесть род тока (переменный или постоянный) и некоторые другие уточняющие характеристики, но основа — вышеуказанная формула.
Электрическая энергия — это, фактически, движение по проводнику отрицательно заряженных частиц (электронов). В нашем примере спираль лампы обладает высоким сопротивлением, то есть замедляет перемещающиеся электроны. Благодаря этому возникает видимое свечение, но общая энергия потока частиц снижается. Как видно из формулы, с уменьшением тока уменьшается и напряжение. Именно поэтому результаты замеров у розетки и на лампе различаются. Эта разница и является падением напряжения. Данная величина всегда учитывается, чтобы предотвратить слишком большое снижение на элементах в конце схемы.
Падение напряжения на резисторе зависит от его и силы протекающего по нему тока. Также косвенное влияние оказывают температура и характеристики тока. Если в рассматриваемую цепь включить амперметр, то падение можно определить умножением значения тока на сопротивление лампы.
Но далеко не всегда удается вот так просто с помощью простейшей формулы и измерительного прибора выполнить расчет падения напряжения. В случае параллельно подключенных сопротивлений нахождение величины усложняется. На приходится дополнительно учитывать реактивную составляющую.
Рассмотрим пример с двумя параллельно включенными резисторами R1 и R2. Известно сопротивление провода R3 и источника питания R0. Также дано значение ЭДС — E.
Приводим параллельные ветки к одному числу. Для этой ситуации применяется формула:
R = (R1*R2) / (R1+R2)
Определяем сопротивление всей цепи через сумму R4 = R+R3.
Рассчитываем ток:
Остается узнать значение падение напряжения на выбраном элементе:
Здесь множитель «R5» может быть любым R — от 1 до 4, в зависимости от того, какой именно элемент схемы нужно рассчитать.
Каждый уважающий себя радио-мастер обязан знать формулы для расчета различных электрических величин. Ведь при ремонте электронных устройств или сборке электронных самоделок очень часто приходится проводить подобные расчеты. Не зная таких формул очень сложно и трудоемко, а порой и невозможно справиться с подобного рода задачей!
Первое, что нужно усвоить – ВСЕ ВЕЛЕЧИНЫ В ФОРМУЛАХ УКАЗЫВАЮТЬСЯ В АМПЕРАХ, ВОЛЬТАХ, ОМАХ, МЕТРАХ И КИЛОГЕРЦАХ.
Закон Ома.
Известный из школьного курса физики ЗАКОН ОМА. На нем строится большинство расчетов в радиоэлектронике. Закон Ома выражается в трех формулах:
Где: I – сила тока (А), U – напряжение (В), R– сопротивление, имеющееся в цепи (Ом).
Теперь рассмотрим на практике применение формул в радиолюбительских расчетах.
Сопротивление гасящего резистора рассчитывают по формуле: R= U /I
Где: U – излишек напряжения, который необходимо погасить (В), I – ток потребляемый цепью или устройством (А).
Расчет мощности гасящего резистора проводят по формуле: P=I 2 R
Где I – ток потребляемый цепью или устройством (А), R– сопротивление резистора (Ом).
Напряжение падения на сопротивлении можно рассчитать по формуле: U пад =RI
Где R– сопротивление гасящего резистора (Ом), I– ток потребляемый устройством или цепью (А).
Где P– мощность устройства (Вт), U– напряжение питания устройства (В).
Где I– ток потребляемый устройством (А), U– напряжение питания устройства (В).
Где ƒ-частота в килогерцах ƛ- длинна волны в метрах.
Где ƛ- длинна волны в метрах, ƒ – частота в килогерцах.
Рассчитать номинальную выходную мощность звуковоспроизводящего устройства (усилитель, проигрыватель и т.п.) можно по формуле: P=U 2 вых. / R ном .
Где U 2 – напряжение звуковой частоты на нагрузке, R– номинальное сопротивление нагрузки.
И в завершении еще несколько формул. По этим формулам, ведут расчет сопротивления и емкости резисторов и конденсаторов в тех случаях, когда возникает необходимость в параллельном или последовательном их соединении.
Расчет соединенных параллельно двух резисторов производят по формуле: R=R 1 R 2 /(R 1 +R 2)
Где R 1 и R 2 — сопротивление первого и второго резистора соответственно (Ом).
Расчет сопротивления включенных параллельно более чем двух резисторов проводят по формуле: 1/R=1/R 1 +1/R 2 +1/R n…
Где R 1 , R 2 , R n … — сопротивление первого, второго и последующих резисторов соответственно (Ом).
Расчет емкости соединенных параллельно нескольких конденсаторов проводят по формуле: C=C 1 + C 2 +C n …
Где C 1 , C 2 и C n – емкость первого, второго и последующих конденсаторов соответственно (мФ).
Расчет емкости двух соединенных последовательно конденсаторов проводят по формуле: C=C 1 C 2 /C 1 +C 2
Где C 1 и C 2 – емкость первого и второго конденсаторов соответственно (мФ).
Расчет емкости включенных последовательно более чем двух конденсаторов проводят по формуле :
В электротехнике принято считать, что простая цепь – это цепь, которая сводится к цепи с одним источником и одним эквивалентным сопротивлением. Свернуть цепь можно с помощью эквивалентных преобразований последовательного, параллельного и смешанного соединений. Исключением служат цепи, содержащие более сложные соединения звездой и треугольником. Расчет цепей постоянного тока производится с помощью закона Ома и Кирхгофа.
Пример 1Два резистора подключены к источнику постоянного напряжения 50 В, с внутренним сопротивлением r = 0,5 Ом. Сопротивления резисторов R 1 = 20 и R 2 = 32 Ом. Определить ток в цепи и напряжения на резисторах.
Так как резисторы подключены последовательно, эквивалентное сопротивление будет равно их сумме. Зная его, воспользуемся законом Ома для полной цепи, чтобы найти ток в цепи.
Теперь зная ток в цепи, можно определить падения напряжений на каждом из резисторов.
Проверить правильность решения можно несколькими способами. Например, с помощью закона Кирхгофа, который гласит, что сумма ЭДС в контуре равна сумме напряжений в нем.
Но с помощью закона Кирхгофа удобно проверять простые цепи, имеющие один контур. Более удобным способом проверки является баланс мощностей .
В цепи должен соблюдаться баланс мощностей, то есть энергия отданная источниками должна быть равна энергии полученной приемниками.
Мощность источника определяется как произведение ЭДС на ток, а мощность полученная приемником как произведение падения напряжения на ток.
Преимущество проверки балансом мощностей в том, что не нужно составлять сложных громоздких уравнений на основании законов Кирхгофа, достаточно знать ЭДС, напряжения и токи в цепи.
Пример 2Общий ток цепи, содержащей два соединенных параллельно резистора R 1 =70 Ом и R 2 =90 Ом, равен 500 мА. Определить токи в каждом из резисторов.
Два последовательно соединенных резистора ничто иное, как делитель тока . Определить токи, протекающие через каждый резистор можно с помощью формулы делителя, при этом напряжение в цепи нам не нужно знать, потребуется лишь общий ток и сопротивления резисторов.
Токи в резисторах
В данном случае удобно проверить задачу с помощью первого закона Кирхгофа, согласно которому сумма токов сходящихся, в узле равна нулю.
Если вы не помните формулу делителя тока, то можно решить задачу другим способом. Для этого необходимо найти напряжение в цепи, которое будет общим для обоих резисторов, так как соединение параллельное. Для того чтобы его найти, нужно сначала
Выполняет сразу несколько очень важных задач: служит ограничителем электрического тока в цепи , создает падение напряжения на отдельных ее участках и разделяет пульсирующий ток.
Помимо номинального сопротивления, одним из наиболее важных параметров резистора является рассеиваемая мощность. Она зависима от напряжения и тока. Мощность — это то тепло, которое выделяется на резисторе, когда под воздействием протекающего тока он нагревается. При пропуске тока, превышающего заданное значение мощности, резистор может сгореть.
Мощность постоянного тока может быть рассчитана по простой формуле P(Вт) = U(В) * I(А) ,
- P(Вт) — мощность,
- U(В) — напряжение,
- I(А) — ток.
Чтобы избежать сгорания резистора тока, необходимо учитывать его мощность. Соответственно, если схема указывает на замену резистора с мощностью 0,5 Ватт — 0,5 Ватт в данном случае — минимум.
Мощность резистора может зависеть от его размеров. Как правило, чем меньше резистор — тем меньше мощность его рассеивания. Стандартный ряд мощностей резисторов тока состоит из значений:
- 0.125 Вт
- 0.25 Вт
- 0.5 Вт
- Более 2 Вт
Рассмотрим на примере: номинальное сопротивление нашего резистора тока — 100 Ом. Через него течет ток 0,1 Ампер. Чтобы , на которую рассчитан наш резистор тока, необходимо воспользоваться следующей формулой: P(Вт) = I2(А) * R(Ом),
- P(Вт) — мощность,
- R(Ом) — сопротивление цепи (в данном случае резистора),
- I(А) — ток, протекающий через резистор.
Внимание! При расчётах следует соблюдать размерность. Например, 1 кА= 1000 А. Это же касается и других величин.
Итак, рассчитаем мощность для нашего резистора тока: P(Вт) = 0,12(А) *100 (Ом)= 1(Вт)
Получилось, что минимальная мощность нашего резистора составляет 1 Ватт. Однако в схему следует установить резистор с мощностью в 1,5 — 2 раза выше рассчитанной. Соответственно идеальным для нас будет резистор тока мощностью 2 Вт.
Бывает, что ток, протекающий через резистор неизвестен. Для расчёта мощности в таком случае предусмотрена специальная формула:
Соединение цепи может быть последовательным и параллельным. Однако никакого труда не составляет рассчитать мощность резистора тока как в параллельной, так и в последовательной цепи. Следует учитывать лишь то, что в последовательно цепи через резисторы течет один ток.
Например, нам необходимо произвести замену резистора тока сопротивлением 100 Ом. Ток, протекающий через него — 0,1 Ампер. Соответственно, его мощность — 1 Ватт. Следует рассчитать мощность двух соединенных последовательно резисторов для его замены. Согласно формуле расчёта мощности, мощность рассеивания резистора на 20 Ом — 0,2 Вт, мощность резистора на 80 Ом — 0,8 Вт. Стандартный ряд мощностей поможет выбрать резисторы тока:
R1 — 20 Ом (0.5 Вт)
R2 — 80 Ом (1 Вт)
Из всего вышесказанного можно сделать вывод, что разное сопротивление резисторов гарантирует их разную выделяемую мощность, так как она распределяется между резисторами разных номиналов. Если не учитывать это обстоятельство, то можно столкнуться с большим количеством трудностей. Если один из резисторов выбран неправильно — второй работает в тяжелом температурном режиме. Также присутствует угроза возгорания резистора из-за несоблюдения правил мощности.
Для того, чтобы сэкономить время и не рассчитывать мощность каждого отдельного резистора тока нужно запомнить одно простое правило: мощность заменяемого резистора должна быть равна мощности каждого резистора, составляющего параллельную или последовательную цепь. То есть при замене резистора мощностью 0,5 Вт надо следить за тем, чтобы каждый из резисторов для замены имел мощность не менее 0,5 Вт.
При параллельном соединение резисторов важно помнить, что чем меньше сопротивление резистора, тем больший ток через него протекает, а значит на нем будет рассеяна большая мощность.
Понятия и формулы
На каждом сопротивлении r при прохождении тока I возникает напряжение U=I∙r, которое называется обычно падением напряжения на этом сопротивлении.
Если в электрической цепи только одно сопротивление r, все напряжение источника Uист падает на этом сопротивлении.
Если в цепи имеются два сопротивления r1 и r2, соединенные последовательно, то сумма напряжений на сопротивлениях U1=I∙r1 и U2=I∙r2 т. е. падений напряжения, равна напряжению источника: Uист=U1+U2.
Напряжение источника питания равно сумме падений напряжения в цепи (2-й закон Кирхгофа).
Примеры
1. Какое падение напряжения возникает на нити лампы сопротивлением r=15 Ом при прохождении тока I=0,3 А (рис. 1)?
Рис. 1.
Падение напряжения подсчитывается : U=I∙r=0,3∙15=4,5 В.
Напряжение между точками 1 и 2 лампочки (см. схему) составляет 4,5 В. Лампочка светит нормально, если через нее проходит номинальный ток или если между точками 1 и 2 номинальное напряжение (номинальные ток и напряжение указываются на лампочке).
2. Две одинаковые лампочки на напряжение 2,5 В и ток 0,3 А соединены последовательно и подключены к карманной батарее с напряжением 4,5 В. Какое падение напряжения создается на зажимах отдельных лампочек (рис. 2)?
Рис. 2.
Одинаковые лампочки имеют равные сопротивления r. При последовательном включении через них проходит один и тот же ток I. Из этого следует, что на них будут одинаковые падения напряжения, сумма этих напряжений должна быть равна напряжению источника U=4,5 В. На каждую лампочку приходится напряжение 4,5:2=2,25 В.
Можно решить эту задачу и последовательным расчетом. Сопротивление лампочки рассчитываем по данным: rл=2,5/0,3=8,33 Ом.
Ток в цепи I = U/(2rл)=4,5/16,66=0,27 А.
Падение напряжения на лампочке U=Irл=0,27∙8,33=2,25 В.
3. Напряжение между рельсом и контактным проводом трамвайной линии равно 500 В. Для освещения используются четыре одинаковые лампы, соединенные последовательно. На какое напряжение должна быть выбрана каждая лампа (рис. 3)?
Рис. 3.
Одинаковые лампы имеют равные сопротивления, через которые проходит один и тот же ток. Падения напряжения на лампах будут тоже одинаковыми. Значит, на каждую лампу будет приходиться 500:4=125 В.
4. Две лампы мощностью 40 и 60 Вт с номинальным напряжением 220 В соединены последовательно и включены в сеть с напряжением 220 В. Какое падение напряжения возникает на каждой из них (рис. 4)?
Рис. 4.
Первая лампа имеет сопротивление r1=1210 Ом, а вторая r2=806,6 Ом (в нагретом состоянии). Ток, проходящий через лампы, I=U/(r1+r2)=220/2016,6=0,109 А.
Падение напряжения на первой лампе U1=I∙r1=0,109∙1210=132 В.
Падение напряжения на второй лампе U2=I∙r2=0,109∙806,6=88 В.
На лампе с большим сопротивлением большее падение напряжения, и наоборот. Накал нитей обеих ламп очень слаб, однако у лампы 40 Вт он несколько сильнее, чем у лампы 60 Вт.
5. Чтобы напряжение на электродвигателе Д (рис. 5) было равно 220 В, напряжение в начале длинной линии (на электростанции) должно быть больше 220 В на величину на линии. Чем больше сопротивление линии и ток в ней, тем больше падение напряжения на линии.
Рис. 5.
В нашем примере падение напряжения в каждом проводе линии равно 5 В. Тогда напряжение на шинах электростанции должно быть равно 230 В.
6. От аккумулятора напряжением 80 В потребитель питается током 30 А. Для нормальной работы потребителя допустимо 3% падения напряжения в проводах из алюминия с сечением 16 мм2. Каким может быть максимальное расстояние от аккумулятора до потребителя?
Допустимое падение напряжения в линии U=3/100∙80=2,4 В.
Сопротивление проводов ограничивается допустимым падением напряжения rпр=U/I=2,4/30=0,08 Ом.
По формуле для определения сопротивления подсчитаем длину проводов: r=ρ∙l/S, откуда l=(r∙S)/ρ=(0,08∙16)/0,029=44,1 м.
Если потребитель будет отдален от аккумулятора на 22 м, то напряжение на нем будет меньше 80 В на 3%, т.е. равным 77,6 В.
7. Телеграфная линия длиной 20 км выполнена из стального провода диаметром 3,5 мм. Обратная линия заменена заземлением через металлические шины. Переходное сопротивление между шиной и землей rз=50 Ом. Каким должно быть напряжение батареи в начале линии, если сопротивление реле на конце линии rр=300 Ом, а ток реле I=5 мА?
Рис. 6.
Схема включения показана на рис. 6. При нажатии телеграфного ключа в месте посылки сигнала реле в месте приема на конце линии притягивает якорь К, который в свою очередь включает своим контактом катушку записывающего аппарата. Напряжение источника должно компенсировать падение напряжения в линии, принимающем реле и переходных сопротивлениях заземляющих шин: U=I∙rл+I∙rр+I∙2∙rз; U=I∙(rл+rр+2∙rз).2)/4=9,6 мм2.
Сопротивление линии rл=ρ∙l/S=0,11∙20000/9,6=229,2 Ом.
Результирующее сопротивление r=229,2+300+2∙50=629,2 Ом.
Напряжение источника U=I∙r=0,005∙629,2=3,146 В; U≈3,2 В.
Падение напряжения в линии при прохождении тока I=0,005 А будет: Uл=I∙rл=0,005∙229,2=1,146 В.
Сравнительно малое падение напряжения в линии достигается благодаря малой величине тока (5 мА). Поэтому в месте приема должно быть чувствительное реле (усилитель), которое включается от слабого импульса 5 мА и своим контактом включает другое, более мощное реле.
8. Как велико напряжение на лампах в схеме на рис. 28, когда: а) двигатель не включен; б) двигатель запускается; в) двигатель в работе.
Двигатель и 20 ламп включены в сеть с напряжением 110 В. Лампы рассчитаны на напряжение 110 В и мощность 40 Вт. Пусковой ток двигателя Iп=50 А, а его номинальный ток Iн=30 А.
Подводящий медный провод имеет сечение 16 мм2 и длину 40 м.
Из рис. 7 и условия задачи видно, что ток двигателя и ламп вызывает в линии падение напряжения, поэтому напряжение на нагрузке будет меньше 110 В.
Рис. 7.
U=2∙Uл+Uламп.
Отсюда напряжение на лампах Uламп=U-2∙Uл.
Надо определить падение напряжения в линии при различных токах: Uл=I∙rл.
Сопротивление всей линии
2∙rл=ρ∙(2∙l)/S=0,0178∙(2∙40)/16=0,089 Ом.
Ток, проходящий через все лампы,
20∙Iламп=20∙40/110=7,27 А.
Падение напряжения в линии, когда включены только лампы (без двигателя),
2∙Uл=Iламп∙2∙rл=7,27∙0,089=0,65 В.
Напряжение на лампах в этом случае равно:
Uламп=U-2∙Uл=110-0,65=109,35 В.
При пуске двигателя лампы будут светить слабее, так как падение напряжения в линии больше:
2∙Uл=(Iламп+Iдв)∙2∙rл=(7,27+50)∙0,089=57,27∙0,089=5,1 В.
Минимальное напряжение на лампах при пуске двигателя будет:
Uламп=Uс-2∙Uл=110-5,1=104,9 В.
Когда двигатель работает, падение напряжения в линии меньше, чем при пуске двигателя, но больше, чем при выключенном двигателе:
2∙Uл=(Iламп+Iном)∙2∙rл=(7,27+30)∙0,089=37,27∙0,089=3,32 В.
Напряжение на лампах при нормальной работе двигателя равно:
Uламп=110-3,32=106,68 В.
Даже небольшое снижение напряжения на лампах относительно номинального сильно влияет на яркость освещения.
Ток— Падение напряжения на одном резисторе и на двух резисторах
Сначала я скажу, что вопрос ОП и все ответы здесь (включая последний, сделанный минуту назад) отличные, и я оцениваю их на +1 🙂 Я только дополню их еще несколькими экстравагантными, но «заставляющими задуматься» «соображения …
«Возникает вопрос, почему падение напряжения на резисторах с одинаковым сопротивлением меняется от первой цепи ко второй? Имеет ли это какое-либо отношение к току? Почему это происходит? Я пытаюсь найти интуитивное объяснение: почему это происходит.»
«Что мне действительно нужно, так это ответ на вопрос, почему падение напряжения во второй цепи на каждом резисторе составляет половину, даже если они имеют такое же сопротивление, как и в первой цепи».
Если вы действительно хотите, чтобы падение напряжения на резисторах с одинаковым сопротивлением было одинаковым, я могу предложить вам решение — всего заменить источники напряжения на источники тока . Это не просто шутка, а вполне реальная конфигурация схемы, которую мы можем наблюдать в некоторых хорошо известных электронных схемах (например,например, в так называемом «каскаде с общим эмиттером с вырождением эмиттера» или «фазоделителе»).
Но вернемся к схемам ОП с 1 и 2 резисторами, питаемыми от источников напряжения, и сделаем несколько интересных выводов.
Во-первых, нас может не интересовать ток, протекающий через резисторы, и их сопротивление. В обеих цепях напряжение не зависит ни от тока, ни от сопротивления. Во второй схеме падение напряжения на резисторе зависит только от отношения его сопротивления к общему сопротивлению.
Второй интересный вывод, который мы можем сделать в отношении потенциометра транзистора . Хотя это переменный резистор, когда мы поворачиваем его стеклоочиститель, мы фактически ничего не меняем — ни сопротивление … ни ток … ни напряжение. Мы просто измеряем (выбираем) напряжение в одной точке на его внутреннем резистивном слое … но все остальные точки имеют линейно убывающие напряжения.
Wikimedia Commons
Конечно, мы можем представить, что при вращении стеклоочистителя одно частичное сопротивление увеличивается, когда другое уменьшается, поэтому их сумма остается постоянной… и, как следствие, постоянный ток. Такие «электронные потенциометры» мы можем видеть в каскадах CMOS, усилителях с обратной связью по току (CFA) и т. Д.
Анализ цепи— Определение напряжения на резисторе
Назовем нижний узел «землей» и обозначим его как 0 В. Тогда верхний узел можно назвать напряжением \ $ V_x \ $. Вы знаете, что ток в узле должен быть равен току, текущему обратно (ток не накапливается в узле). Таким образом, должно выполняться следующее:
$$ (1) ~~~~~~~~~~~~ 30 \ textrm {A} = \ frac {V_x} {2.4 \: \ Omega} + \ frac {V_x} {1.6 \: \ Omega + 8 \: \ Omega} $$
На приведенном выше рисунке вы можете видеть два тока ответвления, перечисленные справа, и входящий ток 30 А слева. Они должны быть равны.
Приведенное выше уравнение преобразуется в:
$$ (2) ~~~~~~~~~~~~~~~~~~~~~ V_x = \ frac {30 \ textrm {A}} {\ frac {1} {2.4 \: \ Omega} + \ frac {1} {1.6 \: \ Omega + 8 \: \ Omega}} $$
Но вас не волнует \ $ V_x \ $. Просто нужно выражение, которое является самым правым в первом уравнении, указанном выше, а именно ток через ветвь с двумя резисторами.Таким образом, вы можете подключить один к другому, чтобы получить:
$$ I = \ frac {\ left (\ frac {30 \ textrm {A}} {\ frac {1} {2.4 \: \ Omega} + \ frac {1} {1.6 \: \ Omega + 8 \: \ Omega}} \ right)} {1.6 \: \ Omega + 8 \: \ Omega} = \ frac {30 \ textrm {A}} {\ frac {1.6 \: \ Omega + 8 \: \ Omega} {2.4 \: \ Omega} + 1} = \ frac {30 \ textrm {A}} {\ frac {1.6 \: \ Omega + 8 \: \ Omega + 2.4 \: \ Omega} {2.4 \: \ Omega}} = 30 \ textrm {A} \ frac {2.4 \: \ Omega} {1.6 \: \ Omega + 8 \: \ Omega + 2.4 \: \ Omega} $$
Это просто подтверждает то, что вам уже сказали. Но это не дает интуиции.
В делителе напряжения напряжение на последовательном элементе равно общему напряжению за вычетом всех падений напряжения на других последовательных элементах.n_1 G_i} \ end {align *} $$
Симметрия должна быть очевидной. В вашем случае у вас есть только две проводимости: \ $ G_1 = \ frac {1} {2.4 \: \ Omega} \ $ и \ $ G_2 = \ frac {1} {1.6 \: \ Omega + 8 \: \ Omega } \ $. И в этом случае \ $ G_x = G_2 \ $.
Если вы используете те, которые входят в нижнее уравнение (4), вы получите правильный ответ. Однако это не похоже на то, что написал учитель. Но если вы подключите что-то, вы поймете, почему:
$$ \ begin {align *} (5) ~~~~~~~~~ I_x & = I_T \ cdot \ frac {\ frac {1} {1.6 \: \ Omega + 8 \: \ Omega}} {\ frac {1} {2.4 \: \ Omega} + \ frac {1} {1.6 \: \ Omega + 8 \: \ Omega}} \\ \\ & = I_T \ cdot \ frac {\ frac {1} {1.6 \: \ Omega + 8 \: \ Omega}} {\ frac {2.4 \: \ Omega + 1.6 \: \ Omega + 8 \: \ Omega} { 2.4 \: \ Omega \ cdot \ left (1.6 \: \ Omega + 8 \: \ Omega \ right)}} \\ \\ & = I_T \ cdot \ frac {\ frac {1} {1}} {\ frac {2.4 \: \ Omega + 1.6 \: \ Omega + 8 \: \ Omega} {2.4 \: \ Omega}} = I_T \ cdot \ frac {2.4 \: \ Omega} {2.4 \: \ Omega + 1.6 \: \ Omega + 8 \: \ Omega} \ end {align *} $$
Однако это НЕ общий подход. В этом случае это просто работает. Так что ваша интуиция, возможно, верна, насчет того, что вы запутались в классе.n R_j} \ end {align *} $$
Имейте в виду, что в приведенном выше примере каждый \ $ R_i \ $ равен , а не каждого из ваших резисторов, бесполезно. Эти сопротивления являются эффективными сопротивлениями ветвей. Итак, в одной из ваших веток это значение представляет собой сумму. Не забывай и об этом.
Уравнение (6) намного уродливее, чем вы могли представить, исходя из решения вашего учителя. Но это правильный вариант. Итак, если вы хотите что-то запомнить, используйте метод проводимости. Как видите, использование сопротивлений не сразу интуитивно понятно.
Если вы должны использовать сопротивления в текущем случае ветвления, как это, тогда вы должны следовать (6) выше и НЕ просто пытаться расширить то, что ваш учитель сделал каким-то невежественным образом. Это не сработает.
Это означает, что я не согласен с ответом, предполагающим: «Ваш профессор дал формулу для текущего делителя».
Неправильно!
Обычно люди делают то, что предлагают некоторые другие ответы — вычисляют последовательное и параллельное сопротивление до одного значения (если возможно), а затем вычисляют напряжение.Затем проработайте детали самой ветки, чтобы получить ток. Это в значительной степени то, как большинство подошло бы к этому. (Или используйте узловой анализ, если схема более сложная.)
Формула вашего учителя не является расширяемой формулой . Это как раз то, что выпало в данном случае.
Измерение напряжения на макетной плате
Измерение напряжения на макетной плате
|
Рисунок 1. Измерение падения напряжения на резисторе в цепи. |
Измерение напряжения в цепи аналогично измерению давление в водопроводе. В то время как манометр показывает давление разница между внутренней и внешней стороной трубы, вольтметр указывает «давление» разность между его красным датчиком и черный зонд. Мы называем эту разницу «электрического давления» «Напряжение.»
Каждый резистор в электрической цепи «израсходован» Некоторое напряжение, подаваемое батареей или другим источником.Чтобы измерить это падение напряжения, используйте цифровой мультиметр (DMM), как показано на рисунке, поместив измеритель щупы на каждом конце резистора. См. Рисунок 1.
Ручка цифрового мультиметра должна быть установлена на диапазон постоянного напряжения для измерения постоянного тока. напряжения. Используйте курсор мыши, чтобы щелкнуть и повернуть ручку в желаемый диапазон. На рисунке 2 ручка установлена на « 20 DCV ». Это означает Цифровой мультиметр может отображать измерения 90-100 до 20 вольт. Значит, цифровой мультиметр считывает На рисунке 2 предполагается, что напряжение составляет 5,79 вольт.
|
Рисунок 2. ручка цифрового мультиметра установите диапазон 20 вольт, показав 5,79 вольт. |
Если ручка повернута на «2000 м», цифровой мультиметр может считывать значения от до 2000 милливольт. При этой настройке цифровой мультиметр не будет показывать никаких десятичные разряды. Например, отображение «652» будет понятным как 652 милливольта. Если на дисплее отображается «755» с ручкой, установленной в положение «1000 DCV», что это за измерение? (ответ: 755 вольт!)
Примечание: Будьте осторожны при работе с агрегатами.Большинство формулы, такие как закон Ома, ожидают измерения в вольтах. Но вы часто встретите меры в милливольт (то есть 1/1000 вольт). Итак, вы можете преобразовать меру 652 милливольта в вольты:
Как видите, преобразование милливольт в вольт на самом деле так же просто, как перемещение десятичной запятой на три позиции влево, что приводит к делению числа на 1000.
Основные операции, уход и обслуживание, а также расширенное устранение неисправностей для квалифицированных специалистов
Устранить проблему можно с помощью теста напряжения или сопротивления.Наиболее практично выбрать испытание напряжением. С помощью теста сопротивления вы должны сначала отключить проверяемый компонент от цепи, и, пока вы удаляете проводку, вы можете столкнуть предметы и, возможно, изменить схему, что может временно устранить проблему. Другими словами, вы можете и не найти проблему.
При использовании вольтметра для поиска неисправностей вы обнаружите либо разомкнутый переключатель, либо отказавшую нагрузку. Вы можете сделать это, не перемещая никаких проводов и никоим образом не меняя схему.Затем вы можете снять устройство и дважды проверить его омметром.
Падения напряжения в последовательных цепях
В последовательных цепях полное напряжение является суммой отдельных падений напряжения в цепи, и уравнение E = IR используется для расчета падения напряжения на каждом резисторе. Поскольку ток через каждый резистор одинаков, падение напряжения на каждом резисторе прямо пропорционально значению сопротивления. Другими словами, чем больше номинал резистора в последовательной цепи, тем больше падение напряжения.Рассмотрим простую последовательную схему на рисунке 1.
Рисунок 1 — Последовательная цепь
Из значений, приведенных выше, вы можете легко рассчитать падение напряжения на каждом резисторе по следующей формуле:
E 1 = I 1 × R 1 = 2 A × 40 Ом = 80 В
E 2 = I 2 × R 2 = 2 A × 20 Ом = 40 В
Падение напряжения 80 В на резисторе 40 Ом в два раза превышает падение напряжения на резисторе 20 Ом.
См. Рисунок 2.Если возникает разрыв между резисторами R 1 и R 2 (например, путем отсоединения провода), ток через цепь, конечно, прерывается. Если нет тока, падение напряжения на каждом из резистивных элементов равно нулю (поскольку E = I × R).
Однако разность потенциалов источника все еще существует на открытом воздухе. Если вольтметр подключен через разрыв, показания такие же, как если бы он был подключен непосредственно к клеммам источника питания.
Рисунок 2 — Напряжение в цепи и разрыв цепи
В цепи последовательного освещения вы можете легко определить, какая лампа перегорела, просто измеряя напряжение на клеммах патрона лампы, последовательно, пока не будет измерено полное напряжение источника.
Осторожно! Поскольку напряжение источника все еще присутствует в отверстии в последовательной цепи, это представляет опасность поражения электрическим током. Будьте осторожны, не прикасайтесь к токоведущим частям цепи! Точно так же, если переключатель разомкнут, на контактах переключателя появится полное напряжение источника.Даже если напряжение на нагрузочных устройствах может быть нулевым, если какая-либо из этих нагрузок находится перед переключателем, они будут запитаны с полным напряжением относительно земли.
Напряжение в последовательной цепи
Напряжение в последовательной цепи
Напряжение, падающее на резисторе в цепи, состоящей из одного резистора и источника напряжения, представляет собой полное напряжение в цепи и равно приложенному напряжению.Общее напряжение в последовательной цепи, состоящей из более чем одного резистора, также равно приложенному напряжению, но состоит из суммы падений напряжения отдельных резисторов. В любой последовательной схеме сумма падений напряжения на резисторе должна равняться напряжению источника. Это утверждение может быть подтверждено исследованием схемы, показанной на рисунке 3-17. В этой цепи потенциал источника (E T ) в 20 вольт падает на последовательную цепь, состоящую из двух резисторов сопротивлением 5 Ом. Общее сопротивление цепи (R T ) равно сумме двух отдельных сопротивлений или 10 Ом.Используя закон Ома, ток в цепи можно рассчитать следующим образом:
Рисунок 3-17. — Расчет отдельных падений напряжения в последовательной цепи.
Поскольку известно, что сопротивление каждого резистора составляет 5 Ом, а ток через резисторы составляет 2 ампера, падение напряжения на резисторах может быть рассчитано. Напряжение (E 1 ) на R 1 , таким образом, составляет:
Осмотрев цепь, вы можете увидеть, что R 2 имеет то же омическое значение, что и R 1 , и несет такой же ток.Падение напряжения на R 2 , следовательно, также равно 10 вольт. Если сложить эти два падения по 10 вольт, общее падение составит 20 вольт, что в точности равно приложенному напряжению. Для последовательной схемы:
E T = E 1 = E 2 + E 3 =. . . E n
Пример: последовательная цепь состоит из трех резисторов, имеющих номиналы 20 Ом, 30 Ом и 50 Ом соответственно. Найдите приложенное напряжение, если ток через резистор 30 Ом равен 2 ампера.(Аббревиатура amp обычно используется для обозначения ампер.)
Для решения проблемы сначала рисуется принципиальная схема и маркируется (рис. 3-18).
Рисунок 3-18. — Решение для приложенного напряжения в последовательной цепи.
Подстановка:
ПРИМЕЧАНИЕ. При использовании закона Ома величины для уравнения ДОЛЖНЫ быть взяты из ОДНОЙ части схемы. В приведенном выше примере напряжение на R 2 было вычислено с использованием тока через R 2 и сопротивления R 2 .
Величина падения напряжения на резисторе определяется приложенным напряжением и пропорционально сопротивлению цепи. Падения напряжения, возникающие в последовательной цепи, прямо пропорциональны сопротивлениям. Это результат того, что через каждый резистор протекает одинаковый ток — чем больше сопротивление резистора, тем больше падение напряжения на нем.
Последовательная цепь, состоящая из трех резисторов, имеет ток 3 ампера. Если R 1 = 20 Ом, R 2 = 60 Ом и R 3 = 80 Ом, каковы (а) полное сопротивление и (б) напряжение источника цепи?
Какое напряжение падает на каждом резисторе цепи, описанной в вопросе 17?
Если бы ток был увеличен до 4 ампер, каким было бы падение напряжения на каждом резисторе в цепи, описанной в вопросе 17?
Что нужно сделать со схемой, описанной в вопросе 17, чтобы увеличить ток до 4 ампер?
Основы расчета падения напряжения
Как узнать, обеспечивает ли ваша проводка разумную эффективность работы? Национальный электротехнический кодекс, 210-19 (a) (FPN 4) и 215-2 (b) (FPN 3), рекомендует падение напряжения 5% для фидерных цепей и 3% для ответвленных цепей.Давайте поработаем несколько примеров, используя уравнения на боковой панели (справа). В наших примерах используется медный провод без покрытия в стальном кабелепроводе для ответвлений на 480 В; мы воспользуемся столбцом коэффициента мощности таблицы 9 NEC.
Пример 1: Определение падения напряжения Проложите многожильный провод № 10 на 200 футов при 20 А. Согласно Таблице 9, наше «сопротивление нейтрали на 1000 футов» составляет 1,1 Ом. Чтобы заполнить числитель, умножьте его следующим образом: (2 x 0,866) x 200 футов x 1,1 Ом x 20A = 7620,8 Деление 7621 на 1000 футов дает падение напряжения 7,7 В. Это падение приемлемо для нашей цепи 480 В.№ 12 упадет 11,8 В. Увеличьте длину до 500 футов, и этот № 10 упадет 18 В; № 12 падает 29V.
Пример 2: Определение размера провода Проложите многожильный медный провод на 200 футов при 20 А. Вы можете найти размер провода, алгебраически изменив первое уравнение, или вы можете использовать следующий метод. Чтобы заполнить числитель, умножьте его следующим образом: 1,73 x 212,9 Ом x 200 футов x 20A = 89371,2. Разделив 89371,2 на допустимое падение напряжения 14,4 В, вы получите 6207 круговых милов. Таблица 8 NEC показывает, что No.12-жильный провод соответствует рекомендациям по падению напряжения.
Пример 3: Определение длины провода Проложите многожильный медный провод № 10 для цепи 20 А. Чтобы заполнить числитель, умножьте его следующим образом: 1000 x 14,4 В = 14400 Чтобы заполнить знаменатель, умножьте следующим образом: (2 x 0,866) x 1,1 Ом x 20 A = 38,104 Наконец, разделите числитель на знаменатель следующим образом: 14400 / 38,1044377 футов. Если вы проложили провод № 12 для той же цепи, вы могли бы проложить его на 244 фута.
Пример 4: Определить максимальную нагрузку Выполнить многопроволочный медный провод No.10 проводов для 200-футовой цепи. Чтобы заполнить числитель, умножьте следующим образом: 1000 x 14,4 В = 14400 Чтобы заполнить знаменатель, умножьте следующим образом: (2 x 0,866) x 1,1 Ом x 200 футов = 381,04 Наконец, разделите числитель на знаменатель следующим образом: 14400 / 381.04437A Эта схема может выдерживать ток 37 А на каждом фазном проводе. 200-футовый № 2 мог выдержать 24А.
* Число «0,866» предназначено только для трехфазного тока. Он преобразует число «2» в «1,732» (квадратный корень из 3). Для однофазных цепей не используйте «0.866 «в расчетах. *» CM «обозначает размер провода в круглых милах, как показано в Таблице 8. * Чтобы рассчитать размер провода, используйте 12,9 в качестве K для меди и 21,2 в качестве K для алюминия. *» L «- это односторонняя длина провода в футах. * «R» — это сопротивление на 1000 футов. Используйте таблицу 9 NEC для проводки переменного тока. Если у вас нелинейные нагрузки, используйте столбец, который помогает учесть коэффициент мощности.
Уравнение 1: Расчет фактического падения напряжения в вольтах. Падение вольт = (2 x 0,866) x L x R x Амперы / 1000
Уравнение 2: Расчет сечения провода в круглых миллиметрах CM = 2 x K x L x А / допустимое падение напряжения В качестве альтернативы вы можете алгебраически манипулировать уравнением 1: R410002 Допустимое падение напряжения / 1.732 x L x Ампер, а затем найдите размер провода в соответствии с его сопротивлением переменному току.
Уравнение 3: Расчет длины в футах Длина = 1000 x допустимое падение напряжения / (2 x 0,866) x R x амперы
Уравнение 4: Расчет нагрузки в амперах = 1000 x допустимое падение напряжения / (2 x 0,866) x R x L
2,8: Полярность падений напряжения
-
- Последнее обновление
- Сохранить как PDF
- Обзор
Мы можем проследить направление, в котором электроны будут течь в той же цепи, начав с отрицательной (-) клеммы и пройдя через положительную (+) клемму батареи, единственного источника напряжения в цепи. схема.Из этого мы можем видеть, что электроны движутся против часовой стрелки, от точки 6 к 5, к 4, к 3, к 2, к 1 и снова к 6.
Когда ток достигает сопротивления 5 Ом, на концах резистора падает напряжение. Полярность этого падения напряжения отрицательная (-) в точке 4 по сравнению с положительной (+) в точке 3. Мы можем отметить полярность падения напряжения на резисторе этими отрицательными и положительными символами в соответствии с направлением тока ( на каком бы конце резистора ни был ток , входящий в отрицательный по отношению к концу резистора, он равен на выходе :
Мы могли бы сделать нашу таблицу напряжений немного более полной, указав полярность напряжения для каждой пары точек в этой цепи:
Хотя документировать полярность падения напряжения в этой цепи может показаться немного глупым, это важная концепция, которую нужно освоить.Это будет критически важно при анализе более сложных схем, включающих несколько резисторов и / или батарей.
Следует понимать, что полярность не имеет ничего общего с законом Ома: в уравнения закона Ома никогда не должно входить отрицательное напряжение, ток или сопротивление! Есть и другие математические принципы электричества, которые учитывают полярность с помощью знаков (+ или -), но не закона Ома.

