Как рассчитать общее сопротивление при параллельном и последовательном соединении резисторов. Какие формулы использовать для вычисления эквивалентного сопротивления. Как решать задачи на смешанное соединение резисторов.
Основные принципы соединения резисторов
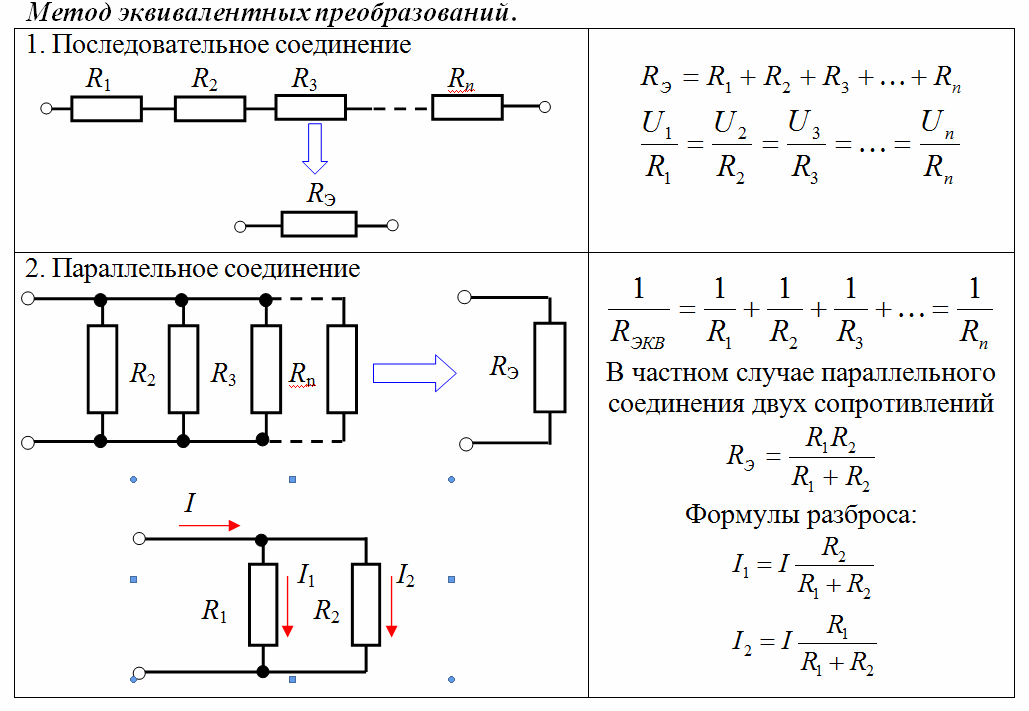
При расчете сопротивления электрических цепей важно понимать принципы последовательного и параллельного соединения резисторов:
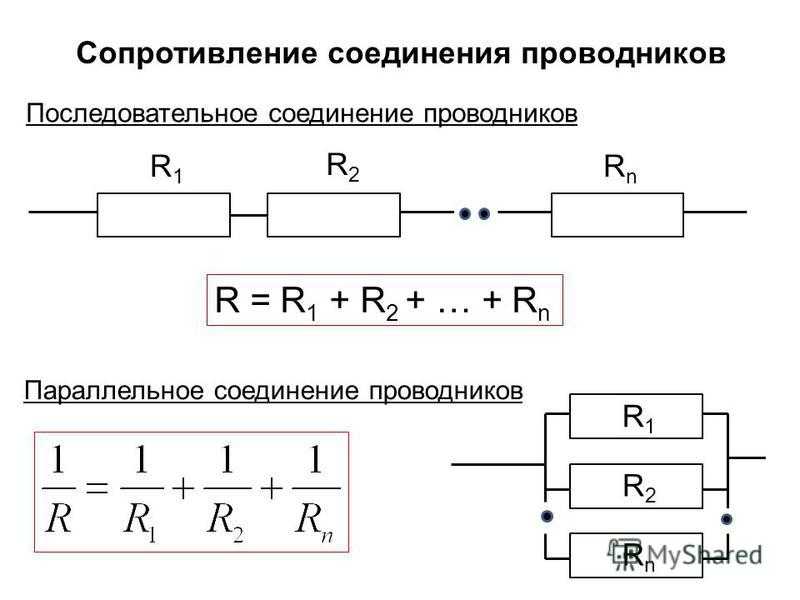
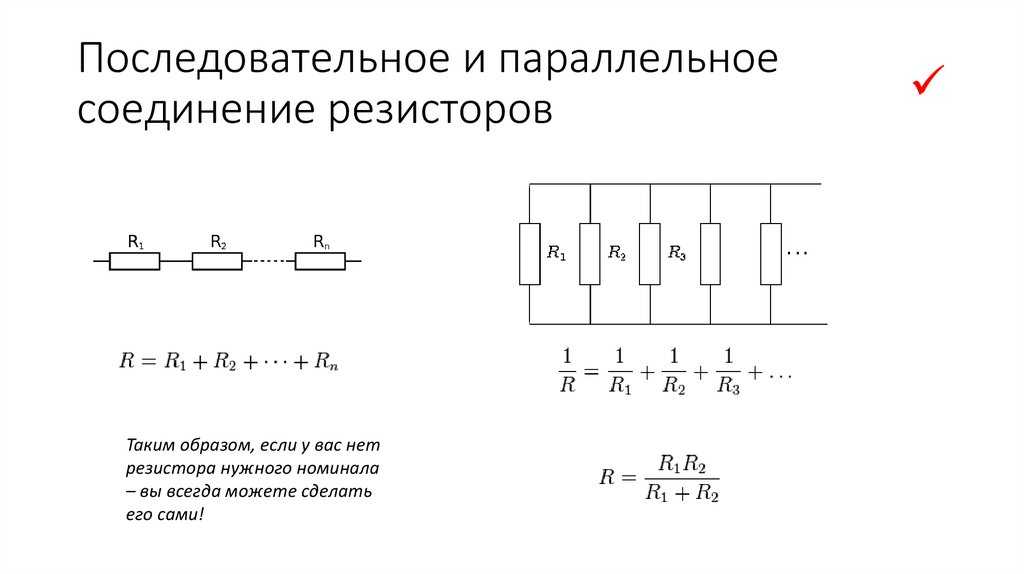
- При последовательном соединении резисторы включаются один за другим. Общее сопротивление равно сумме сопротивлений отдельных резисторов.
- При параллельном соединении все резисторы подключаются к одним и тем же точкам цепи. Общее сопротивление всегда меньше сопротивления любого из параллельно включенных резисторов.
Знание этих принципов позволяет правильно рассчитывать эквивалентное сопротивление в различных схемах.
Формулы для расчета сопротивления при последовательном соединении
При последовательном соединении резисторов используется следующая формула для расчета общего сопротивления:
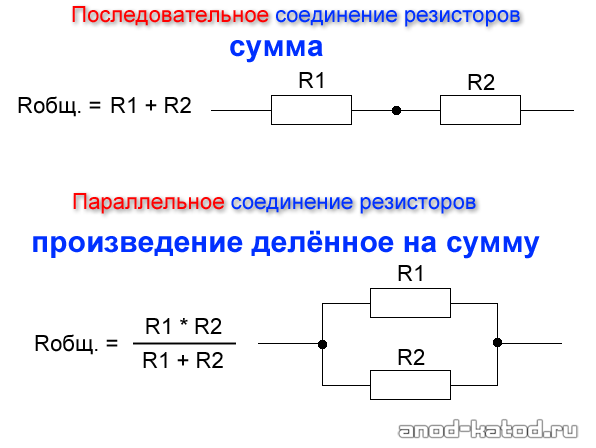
R = R1 + R2 + R3 + … + Rn
где R — общее сопротивление, R1, R2, R3 и т.д. — сопротивления отдельных резисторов.
Эта формула показывает, что общее сопротивление при последовательном соединении всегда больше сопротивления любого из резисторов в цепи. Чем больше резисторов соединено последовательно, тем выше общее сопротивление.
Формулы для расчета сопротивления при параллельном соединении
Для параллельного соединения резисторов применяется другая формула:
1/R = 1/R1 + 1/R2 + 1/R3 + … + 1/Rn
где R — общее сопротивление, R1, R2, R3 и т.д. — сопротивления отдельных резисторов.
Из этой формулы видно, что общее сопротивление при параллельном соединении всегда меньше сопротивления любого из резисторов. При увеличении числа параллельно соединенных резисторов общее сопротивление уменьшается.
Особенности расчета параллельного соединения двух резисторов
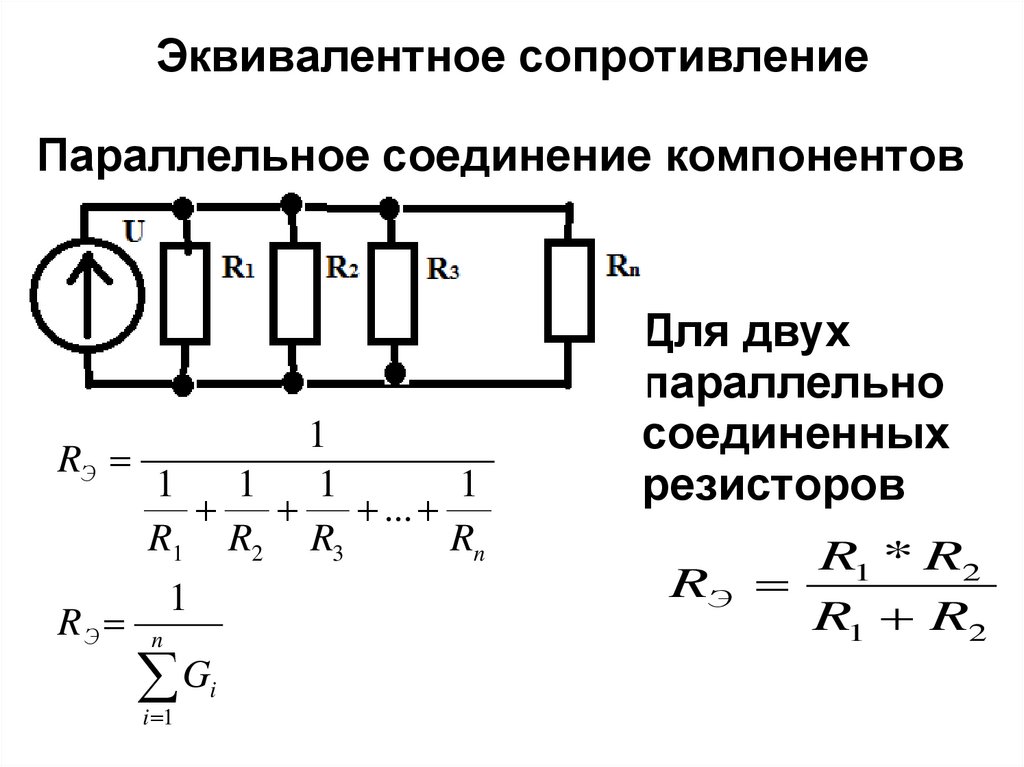
При параллельном соединении только двух резисторов можно использовать упрощенную формулу:
R = (R1 * R2) / (R1 + R2)
Эта формула позволяет быстро рассчитать эквивалентное сопротивление двух параллельно соединенных резисторов без использования обратных величин.

Решение задач на смешанное соединение резисторов
При решении задач на смешанное (последовательно-параллельное) соединение резисторов рекомендуется придерживаться следующего алгоритма:
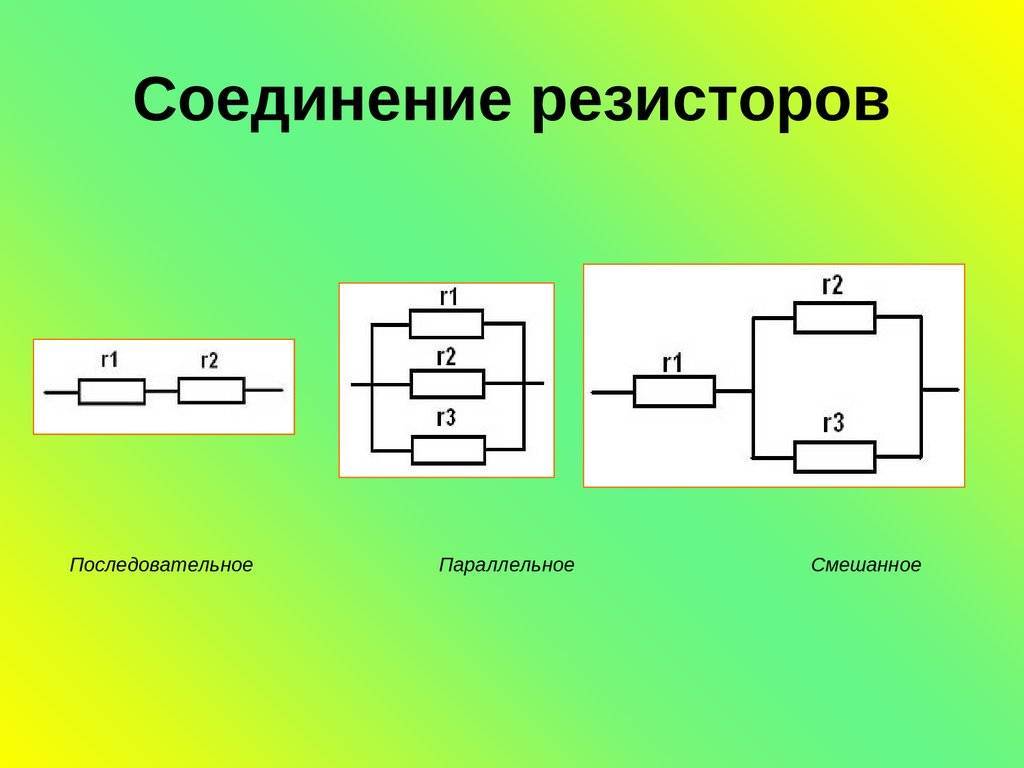
- Разбить схему на участки с последовательным и параллельным соединением.
- Рассчитать эквивалентное сопротивление для каждого участка по соответствующим формулам.
- Заменить рассчитанные участки эквивалентными резисторами.
- Повторять шаги 1-3, пока вся схема не сведется к одному эквивалентному резистору.
Такой пошаговый подход позволяет решать даже сложные задачи на смешанное соединение резисторов.
Примеры расчета сопротивления в различных схемах
Рассмотрим несколько примеров расчета эквивалентного сопротивления:
Пример 1. Последовательное соединение
R = R1 + R2 + R3 = 10 + 20 + 30 = 60 Ом
Пример 2. Параллельное соединение
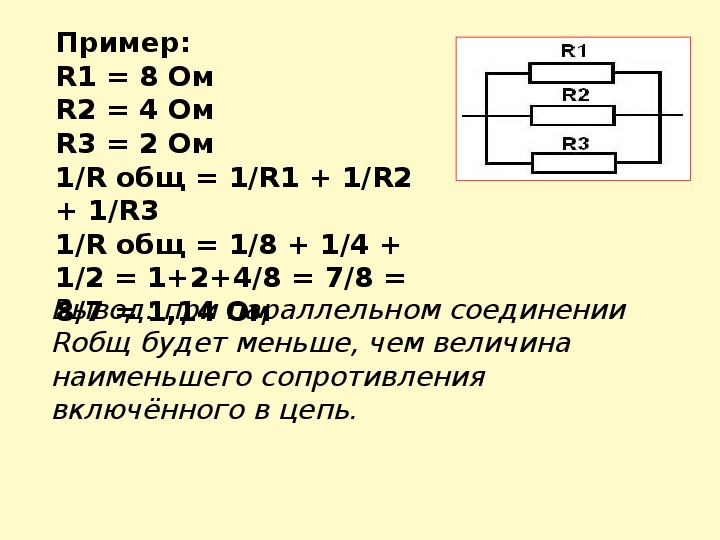
Даны резисторы: R1 = 6 Ом, R2 = 3 Ом
1/R = 1/R1 + 1/R2 = 1/6 + 1/3 = 1/2
R = 1 / (1/2) = 2 Ом
Пример 3. Смешанное соединение
Дана схема: R1 = 10 Ом последовательно с параллельным соединением R2 = 20 Ом и R3 = 30 Ом
1. Рассчитаем параллельное соединение R2 и R3: 1/Rp = 1/20 + 1/30 = 5/60 Rp = 12 Ом
2. Теперь имеем последовательное соединение R1 и Rp: R = R1 + Rp = 10 + 12 = 22 Ом
Эквивалентное сопротивление всей схемы равно 22 Ом.
Практическое применение расчетов сопротивления
Умение рассчитывать эквивалентное сопротивление при различных соединениях резисторов имеет важное практическое значение:
- Проектирование электрических схем с заданными параметрами
- Анализ работы существующих электрических цепей
- Выбор номиналов резисторов для различных устройств
- Расчет токов и напряжений на участках цепи
- Диагностика неисправностей в электрических схемах
Эти навыки необходимы инженерам-электрикам, разработчикам электроники и специалистам по обслуживанию электрооборудования.
Типичные ошибки при расчете сопротивления
При расчете эквивалентного сопротивления часто допускаются следующие ошибки:
- Применение формулы для последовательного соединения к параллельному и наоборот
- Неправильное определение участков с последовательным и параллельным соединением в сложных схемах
- Ошибки в математических вычислениях, особенно при работе с дробями в формуле для параллельного соединения
- Забывание про необходимость находить обратную величину в конце расчета параллельного соединения
- Неучет всех резисторов в схеме
Чтобы избежать этих ошибок, важно внимательно анализировать схему и аккуратно выполнять все расчеты.
Использование компьютерных программ для расчета сопротивления
Для упрощения расчетов сопротивления сложных цепей можно использовать специальные компьютерные программы:
- Онлайн-калькуляторы для расчета параллельного и последовательного соединения резисторов
- Программы схемотехнического моделирования (например, SPICE)
- Специализированные приложения для смартфонов
- Программируемые калькуляторы с функциями расчета электрических цепей
Эти инструменты позволяют быстро и точно рассчитывать эквивалентное сопротивление даже в очень сложных схемах. Однако важно понимать принципы расчета, чтобы правильно интерпретировать результаты, полученные с помощью программ.
Соединение резисторов последовательное, параллельное, смешанное. Пример расчета
Соединение резисторов — это взаимное расположение данных элементов в цепи относительно друг друга и источника питания. Можно по отдельности выделить последовательное и параллельное соединение резисторов. Когда в схеме присутствуют оба варианта, то такое соединение называется смешанным.
Нам известно, что резистор — это электронный компонент, который обладает электрическим сопротивлением и мощностью рассеивания. Если в цепи имеется несколько резисторов, то для получения общего сопротивления прибегают к расчетам по правилам последовательного или параллельного соединения. Помимо общего сопротивления, группы резисторов по закону Ома влияют на напряжение и силу тока на участках цепи. И в данном обзоре будет доступно рассмотрена методика расчета общего сопротивления при различных видах соединения резисторов. Также будет рассмотрен наглядный пример со смешанным соединением резисторов, где помимо сопротивлений будут просчитаны напряжения и сила тока на разных участках.
Стоит сразу отметить, что в данной теме рассеивающая мощность резисторов вынесена за скобки. Мощность важна при подборе и комбинировании резисторов в схеме, но это уже отдельная тема. К тому же все рассмотренные примеры взяты с учетом источника переменного напряжения 220 В. Почему так? Об этом вы узнаете в последнем пункте публикации.
Последовательное соединение резисторов
Последовательное соединение резисторов — это такое взаимное расположение компонентов, при котором ток движется в одном направлении и имеет общее значение для каждого резистора. При таком соединении напряжение на каждом участке будет пропорционально сопротивлению конкретного резистора в цепи.
Принципиальная схема последовательного соединения:
Как видно в цепи последовательно соединено три резистора (их может быть и больше). Сопротивление первого резистора R1 = 20 Ом. Второго R2 = 70 Ом. Третьего R3 = 10 Ом.
Для подсчета общего (эквивалентного) сопротивление при последовательном соединении нужно сложить все номинальные сопротивления резисторов входящих в цепь:
R = R1 + R2 + R3 + … + Rn.
R = 20 + 70 + 10 = 100 Ом.
В представленной схеме для наглядности приведены напряжения на каждом из трех участков. И падение напряжения происходит в зависимости от сопротивления конкретного резистора. Сила тока в цепи общая для всех резисторов (I = I1 = I2 = I3).
I = U / R = U / (R1 + R2 + R3 + … + Rn).
I = 220 / (20 + 70 + 10) = 220 / 100 = 2,2 A.
Формулы нахождения напряжения на участке цепи при известной силе тока (в данном случае I = I1 = I2 = I3 = 2,2 A):
- U1 = I × R1.
- U2 = I × R2.
- U3 = I × R3.
- Un = I × Rn.
Соответственно U1 = 2,2 × 20 = 44 В; U2 = 2,2 × 70 = 154 В; U3 = 2,2 × 10 = 22 В. В итоге сумма разностей потенциалов на резисторах равна общей разности потенциалов всей цепи (220 В).
Рассмотренные три резистора в последовательной цепи можно заменить одним с сопротивлением 100 Ом:
Если можно несколько резисторов заменить одним, то возникает логичный вопрос, зачем применяется такое комбинирование. Простыми словами можно ответить, что иногда невозможно подобрать резистор с требуемыми параметрами или необходимо создать более сложные электронные схемы. В этом случае прибегают к последовательному, параллельному или смешанному соединению в цепи.
В цепи из последовательно соединенных резисторов главную роль играет тот, у которого самое большое сопротивление. Именно он в значительной степени влияет на общее сопротивление. К примеру, если соединить три резистора, номинал которых равен 1, 10 и 100 Ом, то в результате получиться составной с сопротивлением 111 Ом. Если убрать резистор на 100 Ом, то общее сопротивление цепочки резко уменьшиться до 11 Ом. А если убрать резистор на 10 Ом, то сопротивление незначительно уменьшиться до 101 Ом.
Параллельное соединение резисторов
Параллельное соединение резисторов — это такое взаимное соединение компонентов, при котором оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов.
При таком соединении напряжение во всей цепи и на каждом участке одинаково и равно напряжению источника питания U = U1 = U2 = U3 = Un. По каждому резистору течет свой ток. Сумма токов всех резисторов дает общую силу тока цепи: I = I1 + I2 + I3 + … + In. Соответственно общая проводимость параллельной цепи равна сумме ее отдельных проводимостей. Проводимость есть величина, обратная сопротивлению, поэтому эквивалентное сопротивление параллельно соединенных резисторов определяется следующим отношением:
1 / R = 1 / R1 + 1 / R2 + 1 / R3 + … + 1 / Rn. Величина, обратная общему сопротивлению цепи, равна сумме величин, обратных сопротивлениям параллельно включенных проводников.
Рассчитаем общее сопротивление для приведенного выше примера с параллельным соединением резисторов:
1 / R = 1 / 20 + 1 / 70 + 1 / 10 ≈ 0,164.
R ≈ 1 / 0,164 ≈ 6,097 Ом.
Для наглядности смоделируем в программе Electronics Workbench замену трех параллельно соединенных резисторов одним (R = 6,097 Ом):
Как видно, расчет был произведен правильно, так как сила тока в цепи с резистором 6,097 Ом равна силе тока в цепи с параллельным соединением (36,08 A ≈ 36,14 A).
Выделим основные особенности параллельного соединения резисторов:
- Общее сопротивление всегда меньше сопротивления любого параллельно включенного резистора.
- Увеличение числа параллельно соединенных резисторов ведет к уменьшению общего сопротивления и увеличению общей силы тока в цепи.
- Если параллельно соединены два резистора с одинаковым сопротивлением, то общее сопротивление этих резисторов будет ровно в два раза меньше, чем сопротивление каждого из резисторов, входящих в эту цепочку.
- Если в цепи используются резисторы одного номинала, то формула общего сопротивления упрощается и принимает вид R = R1 / N (R1 – номинальное сопротивление резистора; N – количество резисторов с одинаковым номинальным сопротивлением).
Смешанное соединение резисторов
Смешанное соединение резисторов — это комбинация последовательного и параллельного соединения. Иногда такую комбинацию называют последовательно-параллельным соединением.
Пример цепи со смешанным соединением резисторов:
Для расчета эквивалентного сопротивления таких соединений всю цепь разбивают на простейшие участки и придерживаются следующего алгоритма:
| Определяется общее сопротивление участков с параллельным соединением резисторов. | |
| Если эти участки содержат последовательно соединенные резисторы, то сначала вычисляют их общее сопротивление. | |
После промежуточных расчетов схема перерисовывается, и получается цепь из последовательно соединенных эквивалентных сопротивлений. |
|
| Далее рассчитывается сопротивление полученной простой схемы. |
Видео соединение резисторов
Соединение резисторов — пример расчета
В качестве примера смешанного соединения резисторов рассмотрим систему распределения электроэнергии и систему заземления в частном доме. Несмотря на то, что данная схема отношения к электронике не имеет, а в качестве резисторов выступают контуры заземления, все же принципы одни и те же. К тому же, вместо того, чтобы рассматривать произвольную цепь, намного интересней и познавательней дополнительно разобраться в вопросах электричества в быту.
На приведенной выше схеме показана система распределения электроэнергии по системе TN-C-S. Слева направо:
- Источник питания U = 220 В (распределительный трансформатор) с глухозаземленной нейтралью R1 = 2 Ом.
- Далее R2 = 4000 Ом — это имитация прикосновения человека к зануленному корпусу, находящемуся в доме с системой заземления TN-C-S.
- R3 = 30 Ом — повторное заземление в доме с системой TN-C-S.
- R4 = 4 Ом — сопротивление контура заземления (система TT) в соседнем доме.
В доме с системой заземления TT смоделирован пробой фазы на корпус при неработающей автоматике отключения питания. Поэтому потенциал через землю направился к нейтрали трансформатора по трем путям (участок параллельного соединения):
- Через заземление 30 Ом соединенное с нейтралью (рабочий нулевой проводник).
- Через землю — пол — человека — зануленный прибор (4000 Ом).
- Через заземление нейтрали трансформатора 2 Ом.
Получаем параллельное соединение резисторов — R1, R2, R3, и последовательное соединение — R4 и группа с параллельным соединением.
Прежде чем переходить к расчету в цепи со смешанным соединением резисторов, отметим, о чем данная симуляция свидетельствует. Нельзя допускать в одной системе распределения электроэнергии наличия различных систем заземления. Так, согласно приведенной модели, при пробое фазы на корпус в системе TT произошел вынос опасного потенциала 70 В на корпус прибора в соседнем доме с системой заземления TN-C-S.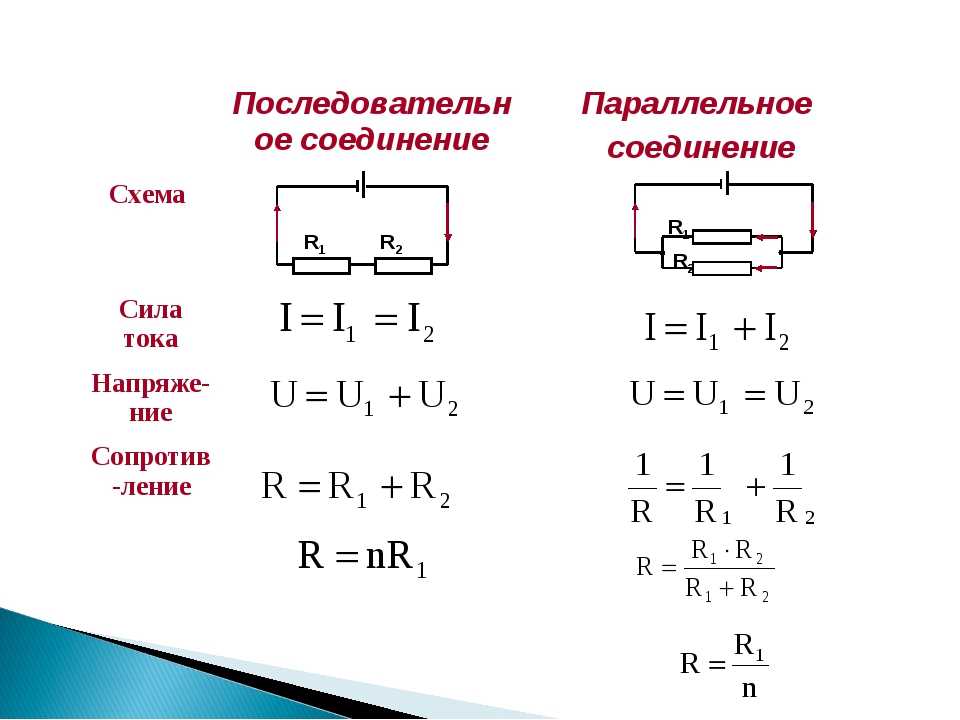 Выносимый потенциал будет снижаться, если в цепи с параллельным соединением будет снижаться общее сопротивление.
Выносимый потенциал будет снижаться, если в цепи с параллельным соединением будет снижаться общее сопротивление.
Рассчитаем, на сколько снизится выносимый потенциал (напряжение), если добавить в участок с параллельным соединением еще 29 домов с системой заземления TN-C-S (сопротивление повторного заземления каждого дома 30 Ом).
Согласно методике расчета в первую очередь определим общее сопротивление на участке с параллельным соединением:
1 / R = 1 / R1 + 1 / R2 + 1 / R3 + 1 / R4 = 1 / 2 + 1 / 4000 + 1 / 30 + 29 / 30 = 1,5 Ом.
R = 1 / 1,5 = 0,67 Ом.
Теперь можно рассмотреть последовательное соединение с резисторами R123(+29 по 30 Ом) = 0,67 Ом и R4 = 4 Ом. R = R123(+29 по 30 Ом) + R4 = 4,67. Зная напряжение, находим силу тока:
I = U / R = 220 / (4 ,67) = 47,1 A.
Зная силу тока, найдем напряжение на участке с параллельным соединением резисторов (где общее сопротивление 0,67 Ом):
U123(+29 по 30 Ом) = R123(+29 по 30 Ом) × I = 0,67 × 47,1 = 31,5 В.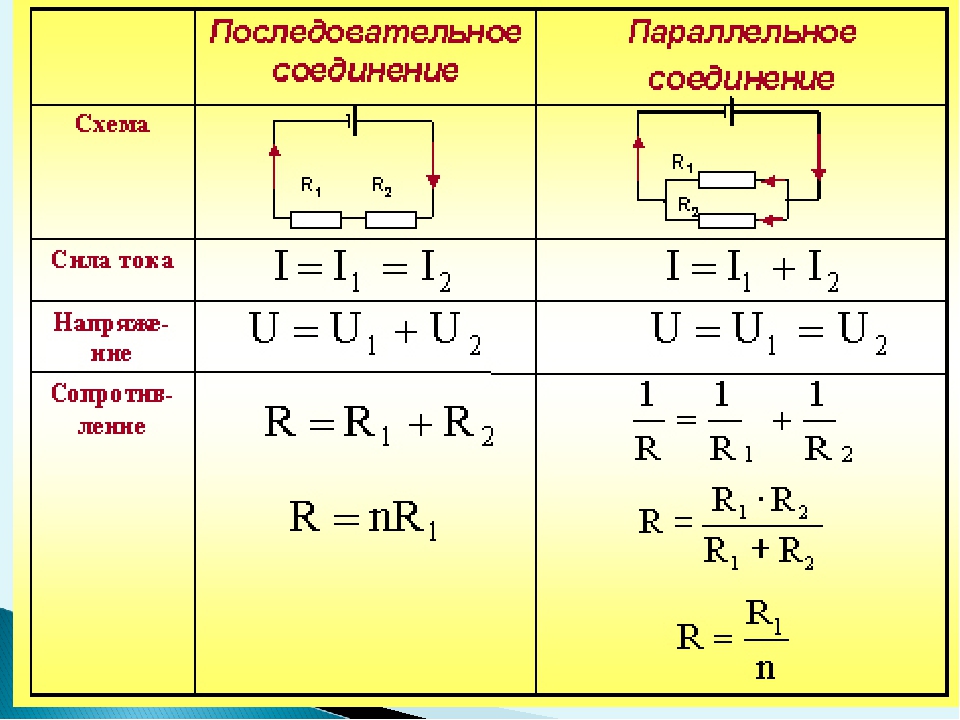
Как видно с добавлением в участок с параллельным соединением 29 дополнительных резисторов с сопротивлением каждого 30 Ом общее сопротивление и напряжение снизились. И, несмотря на то, что ток всей цепи возрос, ток проходящий через человека (R2 = 4000 Ом) значительно снизился за счет снижения напряжения участка цепи. Если посмотреть схему, то изначально через тело человека проходило 17,6 mA. После добавления 29 резисторов это значение снизилось: I2 = U123(+29 по 30 Ом) / R2 = 31,5 / 4000 = 0,0078 A = 7,8 mA.
Подведем итог. При различном соединении резисторов расчет их общих сопротивлений выполняется в соответствии с простыми формулами. И помимо изменения сопротивления в цепи, согласно закону Ома можно проанализировать также такие параметры, как сила тока и напряжение на различных участках.
Расчет общего сопротивления двух последовательно и параллельно соединенных резисторов
Лабораторная работа № 5, 6
Цель:
исследовать закономерности изменения
параметров электрической цепи при
последовательном и параллельном
соединении резисторов и на этой основе
рассчитать общее сопротивление двух
последовательно и параллельно соединенных
резисторов.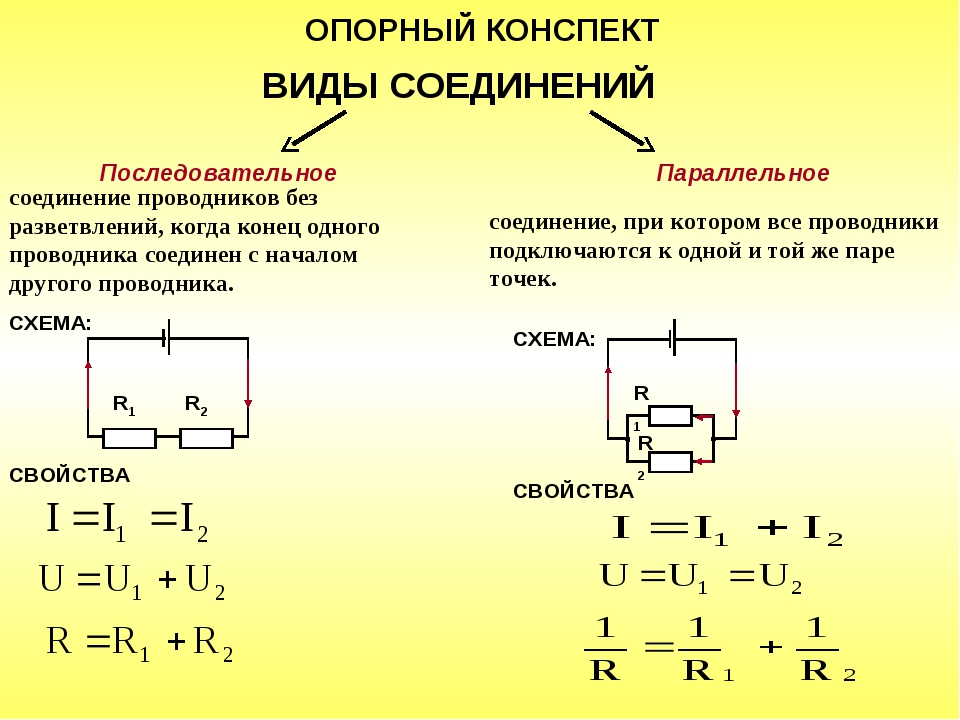
Оборудование: источник тока, ключ, амперметр, вольтметр, два резистора, соединительные провода.
Ход работы:
1. Соберите электрическую цепь по схеме:
2. Замкните цепь ключом и измерьте силу тока I1 и напряжение U1 на концах первого резистора R1:
3. Соберите электрическую цепь по схеме:
4. Замкните цепь и измерьте силу тока I2 и напряжение U2 на концах второго резистора R2. Вычислите сопротивление R2:
5. Соберите электрическую цепь по схеме:
6. Замкните цепь и измерьте силу тока I и напряжение U на концах параллельно соединенных резисторов. Вычислите их общее сопротивление R.
7. Покажите, что
;
;
.
Покажите, что
;
;
.
8. Сделайте вывод.
9. Соберите электрическую цепь по схеме:
10. Замкните цепь ключом и измерьте силу тока I1 и напряжение U1 на концах первого резистора R1. Вычислите сопротивление R1:
11. Соберите электрическую цепь по схеме:
12. Замкните цепь и измерьте силу тока I2 и напряжение U2 на концах второго резистора R2. Вычислите сопротивление R2:
13. Соберите электрическую цепь по схеме:
14. Замкните цепь и измерьте силу тока I и напряжение U на концах параллельно соединенных резисторов. Вычислите их общее сопротивление R.
15. Покажите, что ; ; .
16. Сделайте вывод.
17. Сделайте общий
вывод по лабораторной работе.
Лабораторная работа №7
Цель работы: Опытным путем определить ЭДС и внутреннее сопротивление батареи гальванических элементов.
Оборудование: батарея гальванических элементов, амперметр, вольтметр, реостат, соединительные провода.
Информация к работе.
Закон Ома для всей цепи ε = I(R+r), где
ε – ЭДС источника, I – сила тока в цепи, R – внешнее сопротивление, r – внутреннее сопротивление.
Закон Ома для участка цепи U=I·R
Проектирование эксперимента.
1. Вопросы для обсуждения в группах.
как измерить ЭДС батарейки?
что является внешней (внутренней) частью цепи?
какие величины необходимо измерить?
какие приборы для этого потребуются?
определить цену деления амперметра и вольтметра
как измерить внешнее сопротивление?
как вычислить внутреннее сопротивление источника?
как вычислить среднее значение внутреннего сопротивления?
2. Приготовьте в
тетради таблицу для записи результатов:
Приготовьте в
тетради таблицу для записи результатов:
№ |
ε, В |
I, А |
U, В |
r, Ом |
rсред., Ом |
|
|
|||||
|
|
|||||
|
|
Внутреннее сопротивление источника ,
среднее значение
внутреннего сопротивления
,
где N
– число опытов.
3. Разработайте план (по действиям) выполнения эксперимента.
19.3 Параллельные цепи | Техасский шлюз
Цели обученияПараллельное соединение резисторов. Практические задания. Резисторы, соединенные параллельно. Практические задания. Проверка понимания.
Цели обучения.
| параллельно |
Параллельные резисторы
В предыдущем разделе мы узнали, что последовательно соединенные резисторы — это резисторы, соединенные один за другим. Если вместо этого мы объединим резисторы, соединив их рядом друг с другом, как показано на рис. 19.19, то говорят, что резисторы соединены параллельно . Резисторы параллельны, когда оба конца каждого резистора соединены напрямую друг с другом.
Резисторы параллельны, когда оба конца каждого резистора соединены напрямую друг с другом.
Обратите внимание, что все верхние части резисторов подключены к одному и тому же проводу, поэтому напряжение в верхней части каждого резистора одинаково. Точно так же все основания резисторов подключены к одному и тому же проводу, поэтому напряжение внизу каждого резистора одинаково. Это означает, что падение напряжения на каждом резисторе одинаково. В этом случае падение напряжения соответствует номинальному напряжению В батареи, поскольку верхний и нижний провода подключаются к положительной и отрицательной клеммам батареи соответственно.
Хотя падение напряжения на каждом резисторе одинаково, мы не можем сказать то же самое о токе, протекающем через каждый резистор. Таким образом, I1, I2, и I3I1, I2, и I3 не обязательно одинаковы, поскольку резисторы R1, R2, и R3R1, R2, и R3 не обязательно имеют одинаковое сопротивление.
Обратите внимание, что три резистора на рис. 19.19 обеспечивают три различных пути, по которым может протекать ток. Это означает, что эквивалентное сопротивление этих трех резисторов должно быть меньше наименьшего из трех резисторов. Чтобы понять это, представьте, что наименьший резистор — это единственный путь, по которому может протекать ток. Теперь добавьте альтернативные пути, подключив другие резисторы параллельно. Поскольку у тока больше путей, общее сопротивление (т. Е. Эквивалентное сопротивление) уменьшится. Следовательно, эквивалентное сопротивление должно быть меньше наименьшего сопротивления параллельных резисторов.
19.19 обеспечивают три различных пути, по которым может протекать ток. Это означает, что эквивалентное сопротивление этих трех резисторов должно быть меньше наименьшего из трех резисторов. Чтобы понять это, представьте, что наименьший резистор — это единственный путь, по которому может протекать ток. Теперь добавьте альтернативные пути, подключив другие резисторы параллельно. Поскольку у тока больше путей, общее сопротивление (т. Е. Эквивалентное сопротивление) уменьшится. Следовательно, эквивалентное сопротивление должно быть меньше наименьшего сопротивления параллельных резисторов.
Рис. 19.19 На левой принципиальной схеме показано параллельное подключение трех резисторов. Напряжение В батареи приложено ко всем трем резисторам. Токи, протекающие через каждую ветвь, не обязательно равны. На правой принципиальной схеме показано эквивалентное сопротивление, которое заменяет три параллельных резистора.
Чтобы найти эквивалентное сопротивление RequivRequiv трех резисторов R1, R2, и R3R1, R2, и R3, применим закон Ома к каждому резистору. Так как падение напряжения на каждом резисторе равно В , получаем
Так как падение напряжения на каждом резисторе равно В , получаем
19.21V=I1R1, V=I2R2, V=I3R3V=I1R1, V=I2R2, V=I3R3
или
19.22I1=VR1, I2=VR2, I3=VR3.I1=VR1, I2=VR2, I3=VR3.
Мы также знаем из закона сохранения заряда, что три тока I1, I2, и I3I1, I2, и I3 должны складываться, чтобы получить ток I , который проходит через батарею. Если бы это было не так, ток должен был бы таинственным образом создаваться или уничтожаться где-то в цепи, что физически невозможно. Таким образом, мы имеем
19.23I=I1+I2+I3.I=I1+I2+I3.
Подстановка выражений для I1, I2, и I3I1, I2, и I3 в это уравнение дает
19.24I=VR1+VR2+VR3=V(1R1+1R2+1R3)I=VR1+VR2+VR3=V(1R1+1R2+1R3)
или
19,25 В=I(11/R1+1/R2+1/R3).V=I(11/R1+1/R2+1/R3).
Эта формула представляет собой просто закон Ома, где множитель в скобках означает эквивалентное сопротивление.
19,26 В=I(11/R1+1/R2+1/R3)=IRэкв. V=I(11/R1+1/R2+1/R3)=IRэкв.
V=I(11/R1+1/R2+1/R3)=IRэкв.
Таким образом, эквивалентное сопротивление для трех резисторов, включенных параллельно, равно
19.27Requiv=11/R1+1/R2+1/R3.Requiv=11/R1+1/R2+1/R3.
Та же логика работает для любого количества параллельно соединенных резисторов, поэтому общая форма уравнения, которая дает эквивалентное сопротивление N резисторов, соединенных параллельно, равна
.19,28 Requiv=11/R1+1/R2+⋯+1/RN.Requiv=11/R1+1/R2+⋯+1/RN.
Рабочий пример
Определение тока через параллельные резисторы
Три приведенные ниже схемы эквивалентны. Если номинальное напряжение батареи Vbattery=3 VVbattery=3 V, каково эквивалентное сопротивление цепи и какой ток протекает через цепь?
СТРАТЕГИЯ
Три резистора соединены параллельно, и падение напряжения на них составляет В аккумулятор . Таким образом, мы можем применить уравнение для эквивалентного сопротивления параллельных резисторов, которое принимает вид
19,29Requiv=11/R1+1/R2+1/R3.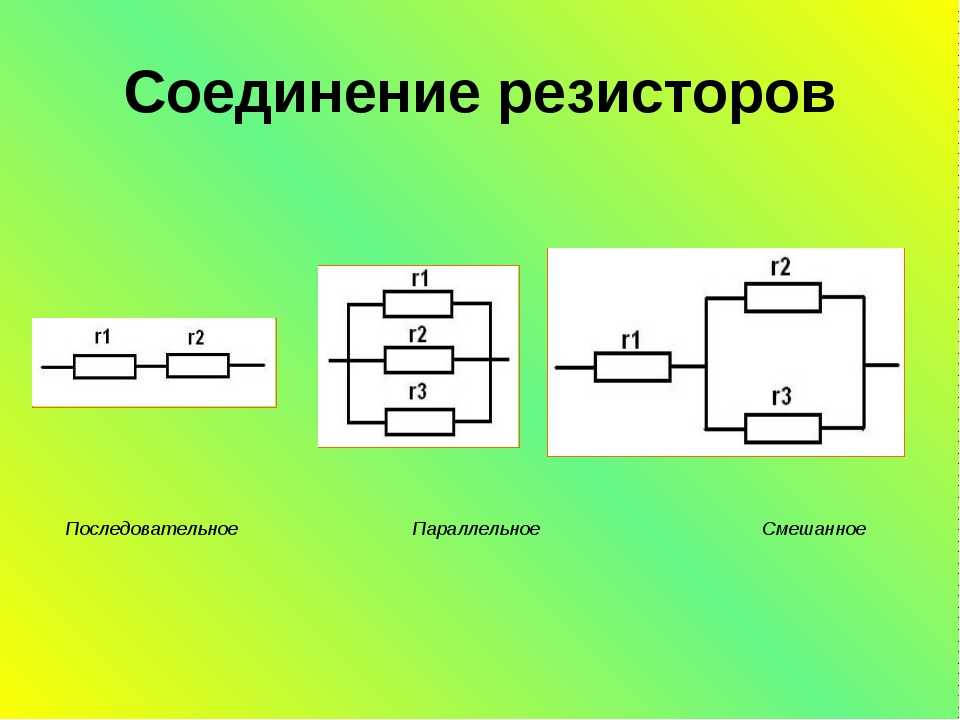 Requiv=11/R1+1/R2+1/R3. .
Requiv=11/R1+1/R2+1/R3. .
Схема с эквивалентным сопротивлением показана ниже. Зная эквивалентное сопротивление, мы можем использовать закон Ома, чтобы найти ток в цепи.
Решение
Подставляя заданные значения сопротивления в уравнение для эквивалентного сопротивления, получаем 4,84 Ом. Requiv=11/R1+1/R2+1/R3=11/10 Ом+1/25 Ом+1/15 Ом=4,84 Ом.
Таким образом, ток в цепи равен
19,31 В=IRI=VR=3 V4,84 Ω=0,62 A.V=IRI=VR=3 V4,84 Ω=0,62 A
Обсуждение
9000 6 Хотя через всей цепи, обратите внимание, что этот ток не протекает через каждый резистор. Однако, поскольку в цепи должен сохраняться электрический заряд, сумма токов, проходящих через каждую ветвь цепи, должна в сумме равняться току, проходящему через батарею. Другими словами, мы не можем волшебным образом создать заряд где-то в цепи и добавить этот новый заряд к току. Давайте проверим это рассуждение, используя закон Ома, чтобы найти ток через каждый резистор.19.32I1=VR1=3 V10 Ω=0,30 AI2=VR2=3 V25 Ω=0,12 AI3=VR3=3 V15 Ω=0,20 AI1=VR1=3 V10 Ω=0,30 AI2=VR2 =3 V25 Ом=0,12 AI3= VR3=3 V15 Ω=0,20 A
Как и ожидалось, эти токи в сумме дают 0,62 A, что является общим найденным током, проходящим через эквивалентный резистор.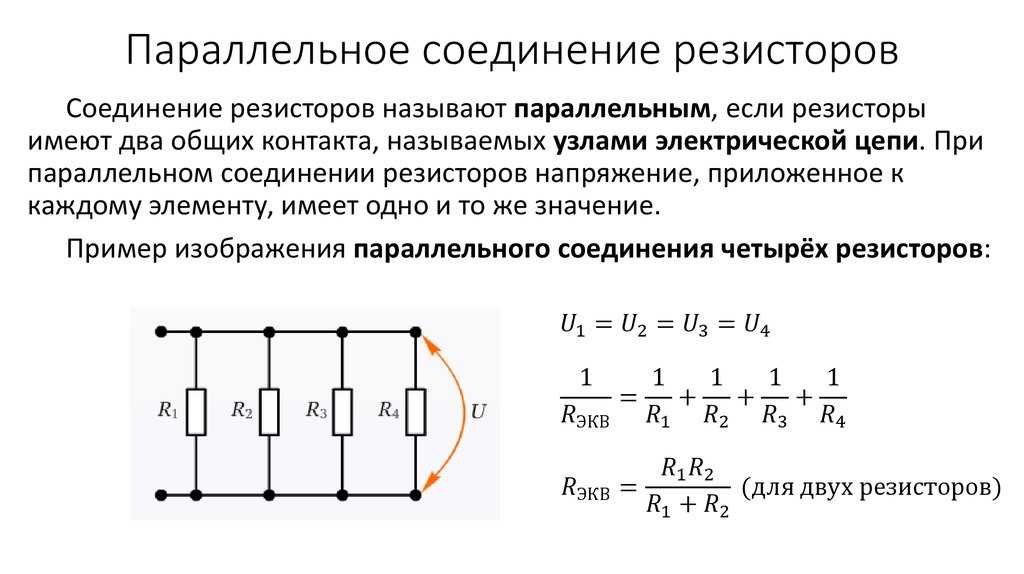 Также обратите внимание, что через самый маленький резистор протекает наибольший ток, и наоборот.
Также обратите внимание, что через самый маленький резистор протекает наибольший ток, и наоборот.
Рабочий пример
Рассуждения с параллельными резисторами
Каково эквивалентное сопротивление трех одинаковых резисторов без каких-либо вычислений R параллельно?
СТРАТЕГИЯ
Три одинаковых резистора R , соединенные параллельно, образуют три одинаковых пути, по которым может протекать ток. Таким образом, току через эти резисторы протекать в три раза легче, чем через один из них.
Раствор
Если протекать через три одинаковых резистора R в три раза легче, чем через один из них, то эквивалентное сопротивление должно быть в три раза меньше: Р /3.
Обсуждение
Проверим наши рассуждения, рассчитав эквивалентное сопротивление трех одинаковых резисторов R , включенных параллельно.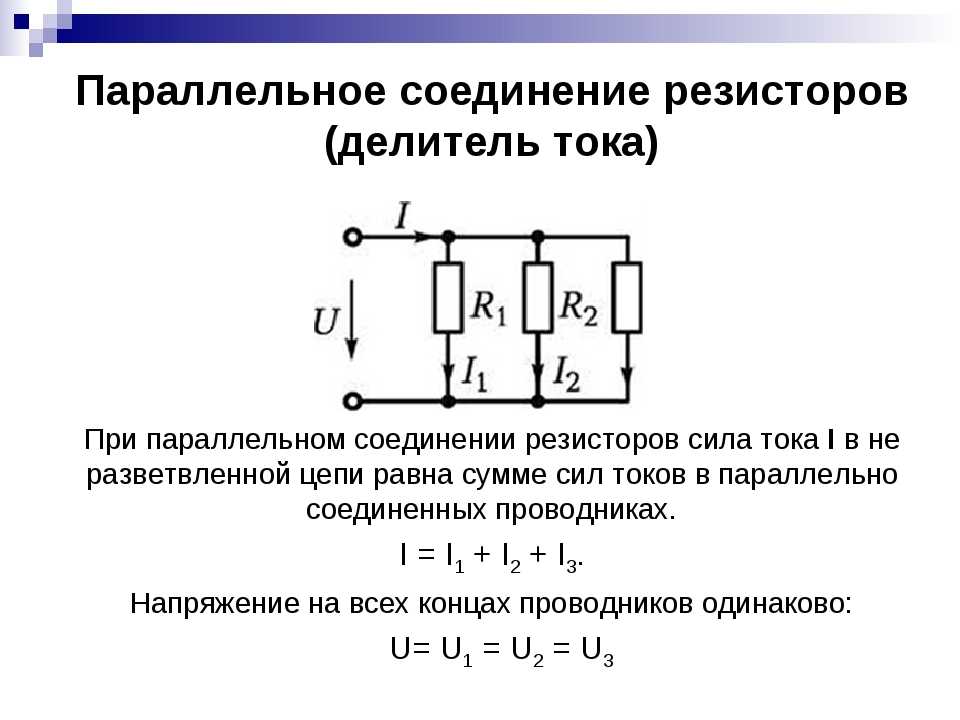 Уравнение для эквивалентного сопротивления параллельных резисторов дает
Уравнение для эквивалентного сопротивления параллельных резисторов дает
19,33Requiv=11/R+1/R+1/R=13/R=R3.Requiv=11/R+1/R+1/R=13/ Р=Р3.
Таким образом, наши рассуждения были верны. В общем, когда доступно больше путей, по которым может протекать ток, эквивалентное сопротивление уменьшается. Например, если у нас есть одинаковые резисторы R параллельно, эквивалентное сопротивление будет R /10.
Практические задачи
Три резистора, 10, 20 и 30 Ом, соединены параллельно. Чему равно сопротивление?
- Эквивалентное сопротивление 5,5 Ом
- Эквивалентное сопротивление 60 Ом
- Эквивалентное сопротивление 6 × 103 Ом
- Эквивалентное сопротивление 6 × 104 Ом
Если на R1 происходит падение напряжения 5 В, а R1 подключен параллельно R2, каково падение напряжения на R2?
- Падение напряжения 0В.
- Падение напряжения на 2,5В.
- Падение напряжения на 5В.
- Падение напряжения на 10В.
Резисторы параллельно и последовательно
Более сложные соединения резисторов иногда представляют собой просто комбинации последовательного и параллельного соединения. Комбинации последовательных и параллельных резисторов можно свести к одному эквивалентному сопротивлению, используя метод, показанный на рисунке 19..20. Различные части идентифицируются как последовательные или параллельные, сокращаются до их эквивалентов и далее сокращаются до тех пор, пока не останется единственное сопротивление. Процесс скорее трудоемкий, чем сложный.
Рисунок 19.20 Эта комбинация семи резисторов имеет как последовательные, так и параллельные части. Каждое идентифицируется и приводится к эквивалентному сопротивлению, а затем они уменьшаются до тех пор, пока не будет достигнуто единственное эквивалентное сопротивление.
Давайте выполним четыре шага, показанные на рис. 19.20, чтобы уменьшить количество семи резисторов до одного эквивалентного резистора. Чтобы не отвлекаться на алгебру, мы будем считать, что сопротивление каждого резистора равно 10 Ом. На шаге 1 мы уменьшаем два набора параллельных резисторов, обведенных синей пунктирной петлей. Верхний набор имеет три параллельных резистора и будет уменьшен до одного эквивалентного резистора RP1RP1. Нижний набор имеет два параллельных резистора и будет уменьшен до одного эквивалентного резистора RP2RP2. Используя уравнение для эквивалентного сопротивления параллельно включенных резисторов, получаем
19.34RP1=11/R2+1/R3+1/R4=11/10 Ом+1/10 Ом+1/10 Ом=103 ОмRP2=11/R5+1/R6=11/10 Ом+1/10 Ом=5 Ом.RP1=11/R2+1/R3+1/R4=11/10 Ом+1/10 Ом+1/10 Ом=103 ОмRP2=11/R5+1/R6=11/10 Ом+ 1/10 Ом=5 Ом.
Эти два эквивалентных сопротивления обведены красной пунктирной петлей после шага 1. Они соединены последовательно, поэтому мы можем использовать уравнение для эквивалентного сопротивления последовательно соединенных резисторов, чтобы свести их к одному эквивалентному сопротивлению RS1RS1.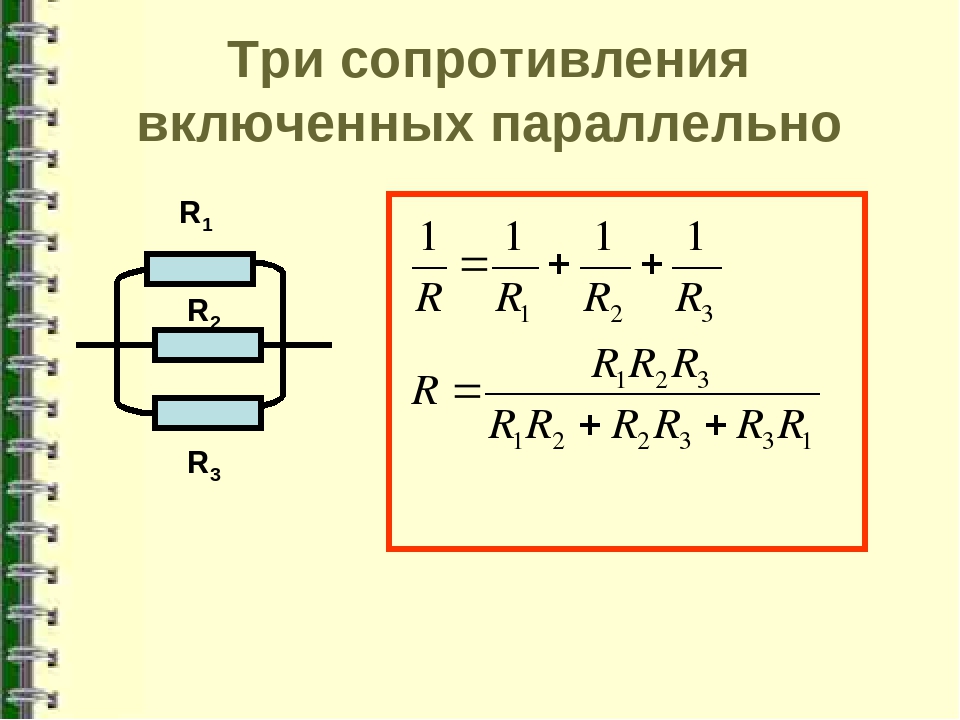 Это делается на шаге 2, в результате получается
Это делается на шаге 2, в результате получается
19.35RS1=RP1+RP2=103 Ом+5 Ом=253 Ом. RS1=RP1+RP2=103 Ом+5 Ом=253 Ом.
Эквивалентный резистор RS1RS1 появляется в зеленой пунктирной петле после шага 2. Этот резистор подключен параллельно резистору R7R7, поэтому пара может быть заменена эквивалентным резистором RP3RP3, который определяется как
.19.36RP3=11/RS1+1/R7=13/25 Ом+1/10 Ом=5011 Ом.RP3=11/RS1+1/R7=13/25 Ом+1/10 Ом=5011 Ом.
Это делается на шаге 3. Резистор RP3RP3 включен последовательно с резистором R1R1, как показано фиолетовым пунктиром после шага 3. Эти два резистора объединяются на последнем шаге, чтобы сформировать окончательный эквивалентный резистор RequivRequiv, который равен
19,37Requiv=R1+RP3=10 Ω+5011 Ω=16011 Ω.Requiv=R1+RP3=10 Ω+5011 Ω=16011 Ω.
Таким образом, всю комбинацию из семи резисторов можно заменить одним резистором с сопротивлением около 14,5 Ом.
Это было много работы, и вы можете спросить, почему мы это делаем.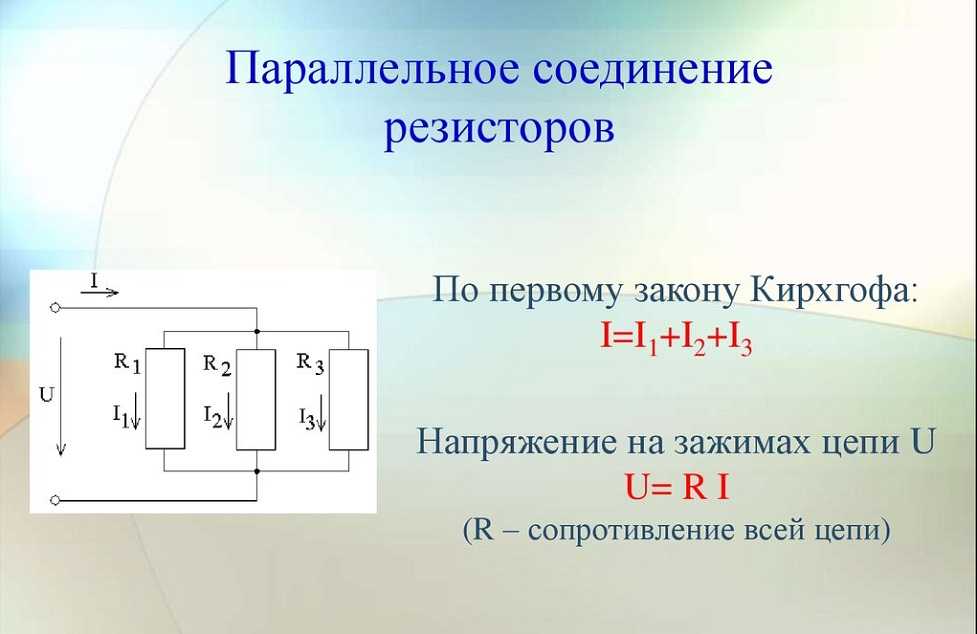 Нам важно знать эквивалентное сопротивление всей цепи, чтобы мы могли рассчитать ток, протекающий по цепи. Закон Ома говорит нам, что ток, протекающий по цепи, зависит от сопротивления цепи и напряжения в цепи. Но чтобы узнать ток, надо сначала узнать эквивалентное сопротивление.
Нам важно знать эквивалентное сопротивление всей цепи, чтобы мы могли рассчитать ток, протекающий по цепи. Закон Ома говорит нам, что ток, протекающий по цепи, зависит от сопротивления цепи и напряжения в цепи. Но чтобы узнать ток, надо сначала узнать эквивалентное сопротивление.
Вот общий подход к поиску эквивалентного резистора для любой произвольной комбинации резисторов:
- Определите группу резисторов, которые включены только параллельно или только последовательно.
- Для резисторов, соединенных последовательно, используйте уравнение для эквивалентного сопротивления последовательно соединенных резисторов, чтобы привести их к одному эквивалентному сопротивлению. Для параллельных резисторов используйте уравнение для эквивалентного сопротивления параллельных резисторов, чтобы привести их к одному эквивалентному сопротивлению.
- Нарисуйте новую принципиальную схему, заменив резисторы из шага 1 эквивалентными им резисторами.
- Если в цепи осталось более одного резистора, вернитесь к шагу 1 и повторите.
 В противном случае вам конец.
В противном случае вам конец.
Веселье в физике
Робот
Роботы захватывают наше коллективное воображение уже более века. Теперь эта мечта о создании умных машин для выполнения нашей грязной работы, а иногда и просто для того, чтобы составить нам компанию, становится реальностью. Робототехника стал огромной областью исследований и разработок, некоторые технологии уже коммерциализированы. Вспомните, например, маленькие автономные пылесосы.
На рис. 19.21 показаны лишь некоторые из множества различных форм, которые могут принимать роботы. Самые продвинутые человекоподобные роботы умеют ходить, разливать напитки, даже танцевать (хотя и не очень грациозно). Другие роботы созданы на основе биологии, например собачий робот , показанный на средней фотографии рис. 19.21. Этот робот может перевозить сотни фунтов груза по пересеченной местности. Фотография справа на рисунке 19. 21 показано внутреннее устройство М-блока , , разработанного Массачусетским технологическим институтом. Эти простые на вид блоки содержат инерционные колеса и электромагниты, которые позволяют им вращаться и подбрасываться в воздух, а также соединяться в различные формы. Общаясь по беспроводной связи между собой, они самособираются в различные формы, такие как столы, стулья, а когда-нибудь, возможно, даже здания.
21 показано внутреннее устройство М-блока , , разработанного Массачусетским технологическим институтом. Эти простые на вид блоки содержат инерционные колеса и электромагниты, которые позволяют им вращаться и подбрасываться в воздух, а также соединяться в различные формы. Общаясь по беспроводной связи между собой, они самособираются в различные формы, такие как столы, стулья, а когда-нибудь, возможно, даже здания.
Все роботы включают в себя огромное количество физики и техники. Роботы освоили простое действие по наливанию напитка лишь недавно, после более чем 30 лет исследований и разработок! Баланс и время, которые мы, люди, считаем само собой разумеющимися, на самом деле являются очень сложными действиями, требующими отличного баланса, ловкости и обратной связи. Чтобы справиться с этим, требуются датчики для определения баланса, вычислительная мощность для анализа данных и передачи соответствующих компенсационных действий, а также соединения и приводы для выполнения необходимых действий.
Помимо определения силы тяжести или ускорения, роботы могут иметь несколько различных датчиков для обнаружения света, звука, температуры, запаха, вкуса и т. д. Все эти устройства основаны на физических принципах, которые вы изучаете в этом тексте. Например, оптика, используемая для роботизированного зрения, аналогична той, что используется в ваших цифровых камерах: пиксельные полупроводниковые детекторы, в которых свет преобразуется в электрические сигналы. Для определения температуры можно использовать простые термисторы, представляющие собой резисторы, сопротивление которых изменяется в зависимости от температуры.
Создание робота сегодня намного проще, чем несколько лет назад. Сейчас многие компании предлагают комплекты для сборки роботов. По сложности они варьируются от подходящих для детей начальной школы до задач, которые могут бросить вызов лучшим профессиональным инженерам. Если интересно, вы можете легко найти их в Интернете и начать делать своего собственного робота уже сегодня.
Рис. 19.21 Роботы бывают разных форм и размеров, от классического гуманоида типа до роботов-собак в маленькие кубики, которые самостоятельно собираются для выполнения различных задач.
Watch Physics
Параллельные резисторы
В этом видео лектор обсуждает простую схему с батареей и парой резисторов, соединенных параллельно. Он подчеркивает, что электроны движутся в направлении, противоположном направлению положительного тока, а также использует тот факт, что напряжение одинаково во всех точках идеального провода. Вывод очень похож на то, что сделано в этом тексте, но лектор хорошо его проходит, объясняя каждый шаг.
Щелкните, чтобы просмотреть содержание
Проверка захвата
Верно или неверно — на принципиальной схеме мы можем предположить, что напряжение одинаково в каждой точке данного провода.
- ложный
- правда
Watch Physics
Резисторы, соединенные последовательно и параллельно
В этом видео показано, как рассчитать эквивалентное сопротивление цепи, содержащей резисторы, соединенные параллельно и последовательно.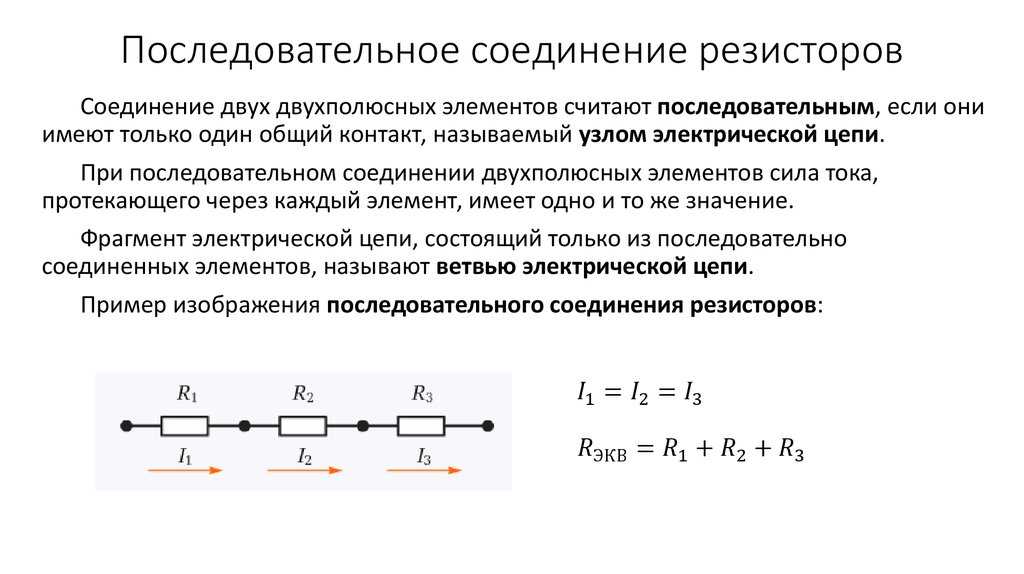 Лектор использует тот же подход, что и изложенный выше, для нахождения эквивалентного сопротивления.
Лектор использует тот же подход, что и изложенный выше, для нахождения эквивалентного сопротивления.
Щелкните, чтобы просмотреть содержание
Проверка захвата
Представьте, что N одинаковых резисторов соединены параллельно. Каждый резистор имеет сопротивление R . Каково эквивалентное сопротивление этой группы параллельных резисторов?
- Эквивалентное сопротивление ( R ) Н .
- Эквивалентное сопротивление NR.
- Эквивалентное сопротивление РН.РН.
- Эквивалентное сопротивление NR.NR.
Рабочий пример
Найдите ток через цепь комплексного резистора
Батарея в схеме ниже имеет номинальное напряжение 10 В. Какой ток течет по цепи и в каком направлении?
СТРАТЕГИЯ
Примените стратегию нахождения эквивалентного сопротивления, заменив все резисторы одним эквивалентным сопротивлением, затем используйте закон Ома, чтобы найти ток через эквивалентный резистор.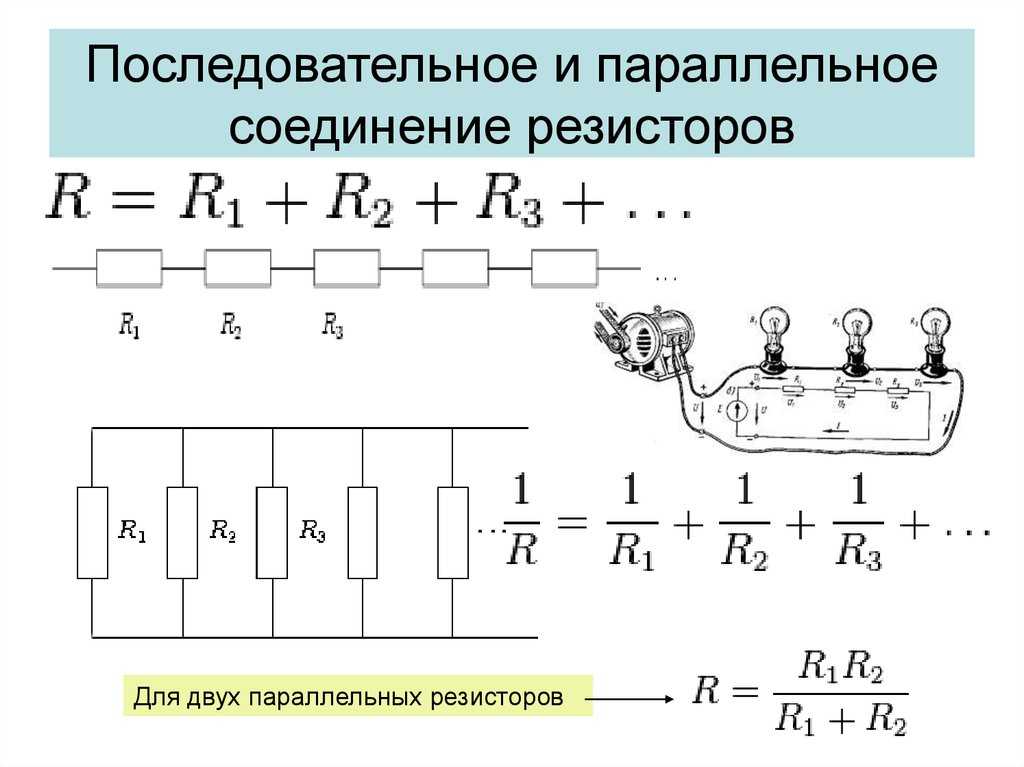
Решение
Комбинация резисторов R4R4 и R5R5 может быть уменьшена до эквивалентного сопротивления 9 Ом.0003
19,38RP1=11/R4+1/R5=11/45 Ω+1/60 Ω=25,71 ΩR.RP1=11/R4+1/R5=11/45 Ω+1/60 Ω=25,71 ΩR.
Замена R4R4 и R5R5 этим эквивалентным сопротивлением дает приведенную ниже схему.
Теперь заменим два верхних резистора R2R2 и R3R3 эквивалентным резистором RS1RS1, а два нижних резистора RP1RP1 и R6R6 эквивалентным резистором RS2RS2. Эти резисторы включены последовательно, поэтому мы складываем их вместе, чтобы найти эквивалентное сопротивление.
19,39RS1=R2+R3=50 Ом+30 Ом=80 ОмRS2=RP1+R6=25,71 Ом+20 Ом=45,71 ОмRS1=R2+R3=50 Ом+30 Ом=80 ОмRS2=RP1+R6=25 0,71 Ом +20 Ом=45,71 Ом
Замена соответствующих резисторов эквивалентными резисторами дает следующую схему.
Теперь замените два резистора RS1 и RS2RS1 и RS2, включенных параллельно, на эквивалентный им резистор RP2RP2. Сопротивление RP2RP2 составляет
19,40RP2=11/RS1+1/RS2=11/80 Ом+1/45,71 Ом=29,09 Ом. RP2=11/RS1+1/RS2=11/80 Ом+1/45,71 Ом =29,09 Ом.
RP2=11/RS1+1/RS2=11/80 Ом+1/45,71 Ом =29,09 Ом.
Обновление электрической схемы путем замены RS1 и RS2RS1 и RS2 этим эквивалентным сопротивлением дает приведенную ниже схему.
Наконец, мы соединяем резисторы R1 и RP2R1 и RP2, которые включены последовательно. Эквивалентное сопротивление: RS3=R1+RP2=75 Ом+29,09 Ом=104,09 Ом. RS3=R1+RP2=75 Ом+29,09 Ом=104,09 Ом. Окончательная схема показана ниже.
Теперь воспользуемся законом Ома, чтобы найти силу тока в цепи.
19,41 В=IRS3I=VRS3=10 V104,09 Ом=0,096 AV=IRS3I=VRS3=10 V104,09 Ом=0,096 A поэтому в этой цепи он течет по часовой стрелке.
Обсуждение
Этот расчет может показаться довольно длинным, но немного потренировавшись, вы сможете комбинировать некоторые шаги. Обратите также внимание на то, что в расчетах учитывались дополнительные значащие цифры. Только в конце окончательный результат округлялся до двух значащих цифр.
Рабочий пример
Странно выглядящие принципиальные схемы
Иногда вы можете столкнуться с не очень аккуратно нарисованными принципиальными схемами, такими как схема, показанная ниже. Эта принципиальная схема больше похожа на то, как реальная схема может выглядеть на лабораторном столе. Каково эквивалентное сопротивление резисторов на этой диаграмме, если предположить, что сопротивление каждого резистора равно 10 Ом, а номинальное напряжение батареи равно 12 В?
Эта принципиальная схема больше похожа на то, как реальная схема может выглядеть на лабораторном столе. Каково эквивалентное сопротивление резисторов на этой диаграмме, если предположить, что сопротивление каждого резистора равно 10 Ом, а номинальное напряжение батареи равно 12 В?
СТРАТЕГИЯ
Давайте перерисуем эту принципиальную схему, чтобы сделать ее более понятной. Затем мы применим описанную выше стратегию для расчета эквивалентного сопротивления.
Решение
Чтобы перерисовать диаграмму, рассмотрите рисунок ниже. В верхней схеме синие резисторы образуют путь от положительной клеммы батареи к отрицательной клемме. Параллельно этой цепи расположены красные резисторы, которые образуют еще один путь от положительного к отрицательному выводу батареи. Синие и красные пути показаны более четко на нижней принципиальной схеме. Обратите внимание, что как на верхней, так и на нижней принципиальных схемах синяя и красная дорожки соединяют положительную клемму батареи с отрицательной клеммой батареи.
Теперь легче увидеть, что R1 и R2 R1 и R2 параллельны, а параллельная комбинация последовательно с R4R4. Эта комбинация, в свою очередь, параллельна последовательной комбинации R3 и R5R3 и R5. Сначала мы вычисляем синюю ветвь, которая содержит R1, R2 и R4, R1, R2 и R4. Эквивалентное сопротивление
19,42Rсиний=11/R1+1/R2+R4=11/10 Ом+1/10 Ом+10 Ом=15 Ом.Rсиний=11/R1+1/R2+R4=11/10 Ом+1/10 Ом+10 Ом=15 Ом.
, где мы показываем вклад от параллельной комбинации резисторов и от последовательной комбинации резисторов. Теперь рассчитаем эквивалентное сопротивление красной ветви, которое равно
19,43Rкрасный=R3+R5=10 Ом+10 Ом=20 Ом.Rкрасный=R3+R5=10 Ом+10 Ом=20 Ом.
Вставка этих эквивалентных резисторов в цепь дает следующую схему.
Эти два резистора соединены параллельно, поэтому их можно заменить одним эквивалентным резистором с сопротивлением
11/Rсиний+1/Rкрасный=11/15 Ом+1/20 Ом=8,6 Ом.
Окончательная эквивалентная схема показана ниже.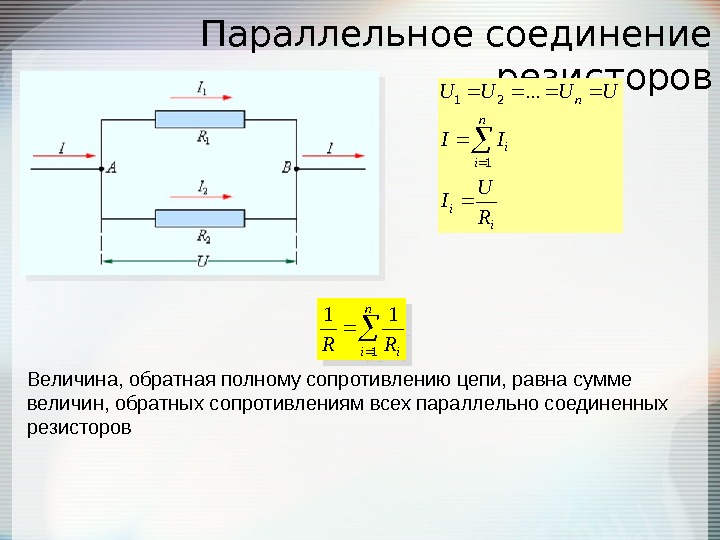
Обсуждение
Найти эквивалентное сопротивление было проще, если была понятная принципиальная схема. Вот почему мы пытаемся сделать четкие принципиальные схемы, где параллельно подключенные резисторы выстроены параллельно друг другу и в одном и том же горизонтальном положении на схеме.
Теперь мы можем использовать закон Ома, чтобы найти ток, проходящий через каждую ветвь этой цепи. Рассмотрим принципиальную схему с RblueRblue и RredRred. Напряжение на каждой из этих ветвей составляет 12 В (т. е. номинальное напряжение батареи). Ток в синей ветви
19,45Iblue=VRblue=12 V15 Ω=0,80 A.Iblue=VRblue=12 V15 Ω=0,80 A
Ток в красной ветви
19,46Ired=VR красный=12 V20 Ω=0,60 A.Ired=VRred=12 V20 Ω=0,60 A
Ток, проходящий через батарею, должен быть суммой этих двух токов (понимаете, почему?), или 1,4 A.
Практические задачи
Какова формула эквивалентного сопротивления двух параллельных резисторов с сопротивлением Ом 1 и Ом 2 ?
- Эквивалентное сопротивление двух параллельных резисторов Reqv=R1+R2Reqv=R1+R2
- Эквивалентное сопротивление двух параллельных резисторов Reqv=R1×R2Reqv=R1×R2
- Эквивалентное сопротивление двух параллельных резисторов Reqv=R1-R2Reqv=R1-R2
- Эквивалентное сопротивление двух параллельных резисторов Reqv=11/R1+1/R2Reqv=11/R1+1/R2
Рисунок 19. 22
22
Каково эквивалентное сопротивление двух показанных ниже резисторов?
- Эквивалентное сопротивление 20 Ом
- Эквивалентное сопротивление 21 Ом
- Эквивалентное сопротивление 90 Ом
- Эквивалентное сопротивление 1925 Ом
Проверьте свое понимание
Упражнение 6
Падение напряжения на параллельных резисторах ________.
- одинаковы для всех резисторов
- больше для больших резисторов
- меньше для больших резисторов
- больше для меньших резисторов
Упражнение 7
Рассмотрим цепь из параллельных резисторов. Минимальный резистор 25 Ом. Каков верхний предел эквивалентного сопротивления?
- Верхний предел эквивалентного сопротивления составляет 2,5 Ом.
- Верхний предел эквивалентного сопротивления составляет 25 Ом.
- Верхний предел эквивалентного сопротивления составляет 100 Ом.

- Нет верхнего предела.
- Печать
- Поделиться
Резисторы последовательно и параллельно
Резисторы последовательно и параллельноСледующая: Правила Кирхгофа Вверх: Электрический ток Предыдущий: ЭДС и внутреннее сопротивление Резисторы, пожалуй, самые распространенные. компоненты в электронных схемах. Практические схемы часто содержат очень сложные комбинации резисторов. Поэтому полезно иметь набор правил для нахождения эквивалента сопротивления некоторого общего расположения резисторов. Оказывается, мы можем всегда находят эквивалентное сопротивление повторным приложением два простых правила . Эти правила относятся к резисторам, соединенным последовательно и в параллели.
Рассмотрим два резистора, соединенных последовательно , как показано на рис. 18.
Ясно, что через оба резистора протекает одинаковый ток.
Ибо, если бы это было не так, заряд накапливался бы в том или ином
резисторов, что не соответствовало бы
стационарная ситуация (тем самым нарушая
основное предположение этого раздела). Предположим, что падение потенциала
из точки в точку есть . Эта капля есть сумма потенциалов
падает и на двух резисторах и соответственно.
Таким образом,
| (135) |
По закону Ома эквивалентное сопротивление между и представляет собой отношение падения потенциала в этих точках и ток, который течет между ними. Таким образом,
| (136) |
давать
| (137) |
Здесь мы воспользовались тем, что ток является общим для все три резистора.
 Следовательно, правило
Следовательно, правило
Эквивалентное сопротивление двух последовательно соединенных резисторов равно сумма индивидуальных сопротивлений.Для резисторов, соединенных последовательно, уравнение (137) обобщает к .
. Рассмотрим два резистора, соединенных в параллельно , как показано на рис. 19. Это
Из рисунка видно, что падение потенциала на двух резисторах равно
такой же. В целом, однако, токи, которые текут
через резисторы и соответственно разные.
По закону Ома эквивалентное сопротивление
между и – отношение падения потенциала
через эти точки и текущий
который течет между ними. Этот ток должен быть равен сумме
токи и протекающие через два резистора, в противном случае
заряд будет накапливаться в одном или обоих соединениях цепи.



