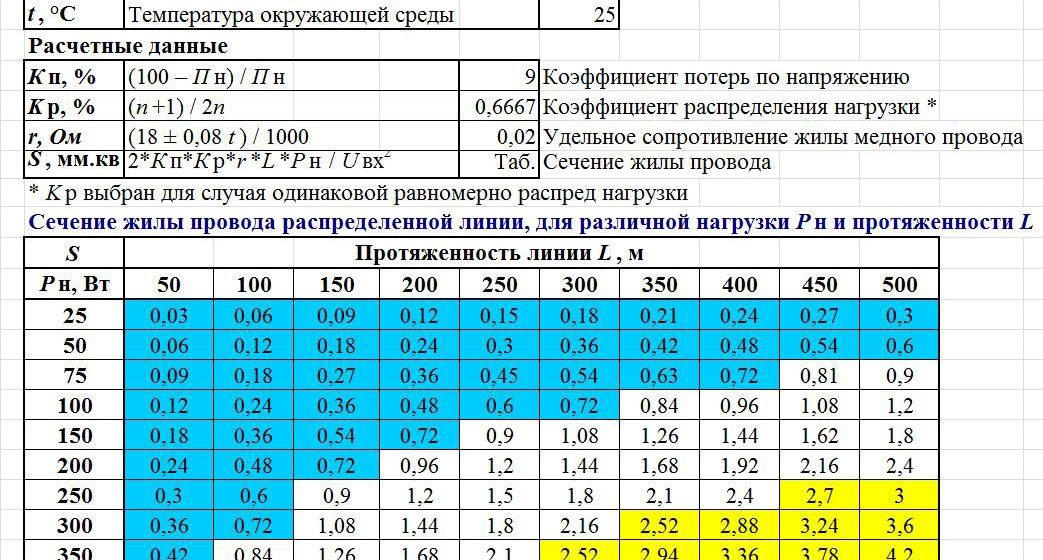
Как рассчитать ток зная сопротивление и напряжение. Расчет тока, сопротивления и напряжения в электрических цепях: закон Ома и методы анализа

Как рассчитать ток в электрической цепи, зная сопротивление и напряжение. Какие формулы используются для расчета сопротивления участка цепи. Как применяется закон Ома для анализа электрических схем. Какие методы используются для расчета сложных электрических цепей.

Закон Ома и основные формулы для расчета тока, напряжения и сопротивления

Закон Ома является фундаментальным законом электротехники, который устанавливает связь между током, напряжением и сопротивлением в электрической цепи. Он позволяет рассчитать любую из этих величин, если известны две другие.

Основная формула закона Ома для участка цепи:

I = U / R

где:

• I — сила тока в амперах (А)
• U — напряжение в вольтах (В)
• R — сопротивление в омах (Ом)

Из этой формулы легко выразить напряжение и сопротивление:

U = I * R

R = U / I

Расчет тока в цепи по известному сопротивлению и напряжению

Чтобы рассчитать ток в цепи, зная сопротивление и напряжение, необходимо использовать формулу:

I = U / R

Например, если напряжение в цепи 12 В, а сопротивление 4 Ом, то ток будет равен:

I = 12 В / 4 Ом = 3 А

Таким образом, зная напряжение и сопротивление, можно легко определить силу тока в любом участке электрической цепи.

Расчет сопротивления участка цепи

Для расчета общего сопротивления участка цепи используются разные формулы в зависимости от типа соединения элементов:

Последовательное соединение

При последовательном соединении общее сопротивление равно сумме сопротивлений всех элементов:

R = R1 + R2 + R3 + …

Параллельное соединение

При параллельном соединении для расчета общего сопротивления используется формула:

1/R = 1/R1 + 1/R2 + 1/R3 + …

Для двух параллельных резисторов можно использовать упрощенную формулу:

R = (R1 * R2) / (R1 + R2)

Применение закона Ома для анализа электрических схем

Закон Ома позволяет анализировать работу электрических схем и рассчитывать параметры их элементов. Основные способы применения:

• Расчет тока в различных участках цепи
• Определение падения напряжения на элементах
• Подбор номиналов резисторов для получения нужных токов и напряжений
• Анализ режимов работы электронных компонентов
• Расчет мощности, выделяемой на элементах

Методы расчета сложных электрических цепей

Для анализа сложных разветвленных цепей используются специальные методы расчета:

Метод контурных токов

Основан на составлении уравнений для независимых контуров цепи. Позволяет уменьшить число уравнений по сравнению с методом узловых потенциалов.

Метод узловых потенциалов

Заключается в составлении уравнений для узлов цепи. Эффективен для цепей с большим числом узлов.

Метод наложения

Основан на принципе суперпозиции — токи в ветвях рассчитываются для каждого источника отдельно, а затем суммируются.

Метод эквивалентного генератора

Позволяет заменить часть сложной цепи эквивалентным активным двухполюсником для упрощения расчетов.

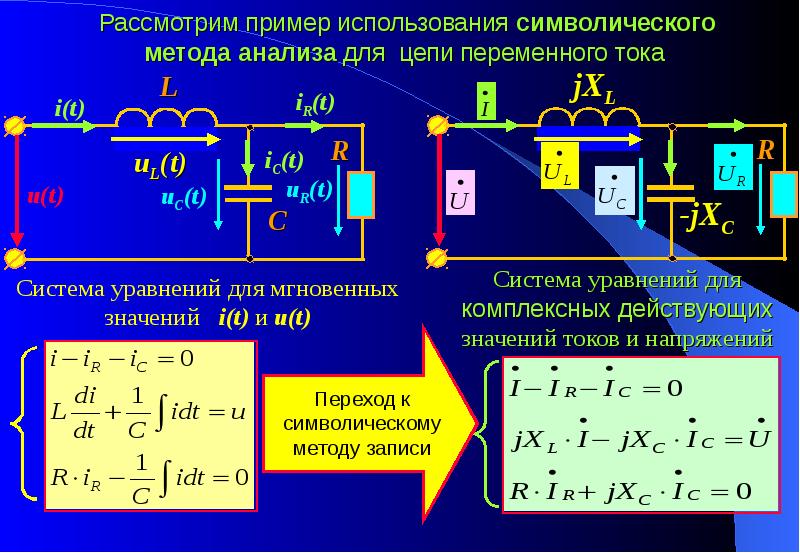
Особенности расчета цепей переменного тока

При расчете цепей переменного тока необходимо учитывать следующие особенности:

• Использование комплексных чисел для учета сдвига фаз
• Применение метода векторных диаграмм
• Учет реактивных сопротивлений катушек индуктивности и конденсаторов
• Расчет полного сопротивления цепи
• Определение активной, реактивной и полной мощности

Практические рекомендации по расчету электрических цепей

При выполнении расчетов электрических цепей рекомендуется придерживаться следующего алгоритма:

1. Составить принципиальную схему цепи
2. Определить исходные данные — напряжения источников, номиналы элементов
3. Выбрать метод расчета в зависимости от сложности цепи
4. Составить систему уравнений
5. Решить систему уравнений аналитически или численными методами
6. Рассчитать искомые токи, напряжения, мощности
7. Проверить правильность расчетов по законам Кирхгофа

Типичные ошибки при расчете электрических цепей

При расчетах электрических цепей часто допускаются следующие ошибки:

• Неправильное определение направлений токов в ветвях
• Ошибки в знаках при составлении уравнений по законам Кирхгофа
• Неучет внутреннего сопротивления источников
• Путаница между действующими и амплитудными значениями в цепях переменного тока
• Ошибки при преобразовании единиц измерения
• Неправильный выбор метода расчета для конкретной схемы

Чтобы избежать этих ошибок, важно внимательно анализировать схему, проверять размерности величин и всегда выполнять проверку результатов.

Компьютерное моделирование электрических цепей

Современные программы позволяют моделировать работу сложных электрических схем. Основные возможности таких программ:

• Построение принципиальных схем
• Задание параметров компонентов
• Расчет токов и напряжений
• Построение графиков и диаграмм
• Анализ переходных процессов
• Частотный анализ
• Оптимизация параметров схемы

Использование программ моделирования позволяет значительно упростить и ускорить расчеты сложных цепей, а также наглядно представить результаты.

Как найти сопротивление силы тока

Здравствуйте. В интернете часто можно встретить вопросы как найти сопротивление тока или найти сопротивление силы тока, но на самом деле это сделать невозможно. Я уже писал в статье про мощность в цепи постоянного тока про закон Ома и три связанные им величины: напряжение, сопротивление и ток. Так вот, ток это —  следствие приложенного напряжения к замкнутой цепи, имеющей сопротивление. Другими словами, у тока нет, и не может быть сопротивления. А вот как найти сопротивление цепи или участка цепи я вам сейчас расскажу.

Как найти сопротивление в цепях постоянного тока

В постоянном токе всё довольно просто. Как правило, сопротивление в таких цепях постоянно, то есть его можно принять за константу (дальше, когда будем рассматривать переменный ток, вы поймёте, про что я говорю). Следовательно, можно выделить два основных способа для вычисления сопротивления: аналитический и физический.

Как найти сопротивление с помощью омметра

Для этого вам потребуется любой прибор, способный измерить сопротивление. Сейчас для этой цели гораздо удобнее использовать мультиметр.

Если значение сопротивления не известно, то надо начинать с самого большого предела мультиметра. Если прибор показывает значение «0», нужно уменьшить предел, пока не появится какое-нибудь сопротивление. В принципе, такие приборы довольно точны и для домашнего применения их более, чем хватает. Если же говорить о точных значениях, то для измерения сопротивления потребуется специальный измерительный мост.

Измерительный мост — это откалиброванное устройство, которое позволяет вычислить значение сопротивления очень точно. Зачастую такие мосты измеряют несколько различных величин.

Аналитический метод поиска сопротивления. Здесь потребуется уже два прибора: амперметр и вольтметр, и чем они будут точнее, тем меньше будет погрешность вычислений.

Какие здесь нюансы? Амперметр всегда включается последовательно в цепь, а вот вольтметр нужно подсоединять как можно ближе к сопротивлению параллельно. Дело в том, что провода тоже имеют сопротивление (об этом расскажу чуть позже). Поэтому, если мы измерим напряжение в источнике питания, то мы получим сопротивление всей цепи, а именно: сопротивление проводов + сопротивление амперметра + само искомое сопротивление. Но даже это ещё не всё. Помните, мы говорили про параллельное и последовательное соединение сопротивлений. Так вот, вольтметр имеет сопротивление, поэтому после измерения напряжения нужно будет узнать сопротивление вольтметра и только тогда, можно точно высчитать номинал сопротивления с учётом места присоединения вольтметра.

Подведём итоги. В постоянном токе гораздо проще сделать вычисления с помощью омметра или функции измерения сопротивления в мультиметре. Если требуется высокая точность, то для вычисления номинала сопротивления нужно использовать измерительный мост.

Как вычислить сопротивление проводника

Как я уже говорил, провод тоже имеет сопротивление, а значит, его можно вычислить. Для этого используется формула:

p- удельное электрическое сопротивление при температуре 20°С, значение которого берётся из таблицы;

l- длина проводника в метрах

S – площадь поперечного сечения (школьный курс геометрии). Если это круг, то , если квадрат или прямоугольник, то одна сторона умножается на другую и т.д. Значение подставляется в мм².

Перейдём к практике. Допустим, у нас есть стальной круглый прут длиной 5 метров и диаметром 5 мм. Посчитаем его сопротивление.  p стали составляет 0,15 Ом·мм²/м, длина известна – 5 метров, площадь поперечного сечения

 

(обратите внимание, что диаметр делим пополам, чтобы получить радиус и только потом вычисляем площадь). Осталось всё это подставить в формулу:

Где можно применить этот расчёт? Например, для изготовления предохранителей, когда нужно из подручных материалов в срочном порядке сделать новый или сделать мощное сопротивление. Под мощным подразумевается способность сопротивления выдерживать большие токи, то есть успевать отдавать тепло в окружающую среду без физического разрушения, а не значение. Таким образом, сопротивление может быть номиналом 1 Ом и мощностью 2000 ватт. Но чаще всего этот расчёт применяют для вычисления потери мощности на линии, однако это тема отдельной статьи, и касаться её мы пока не будем.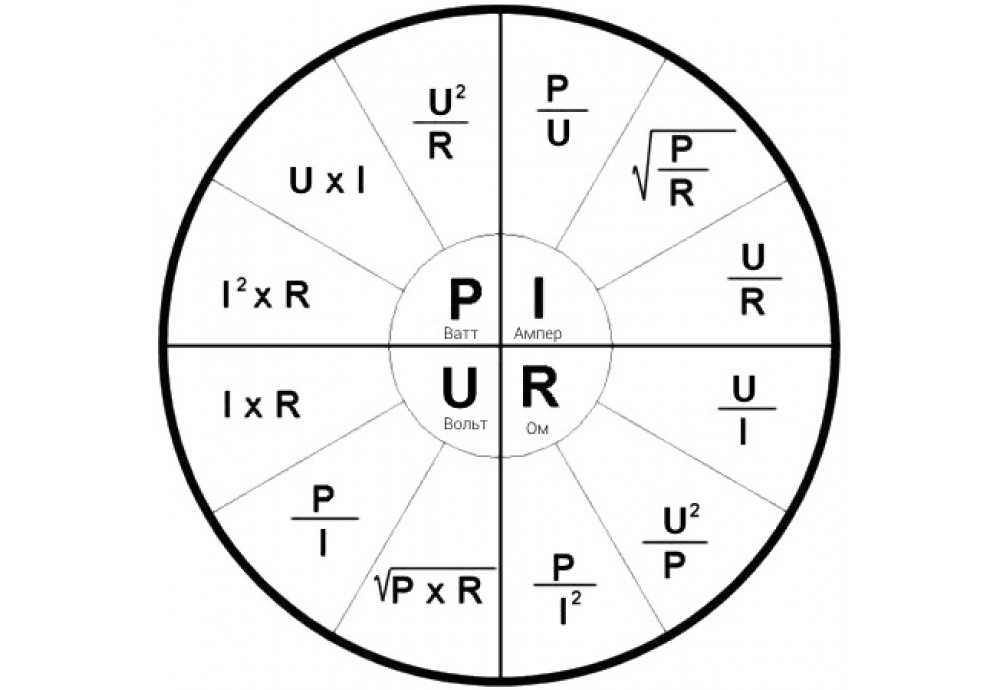 Нужно так же обратить внимание, что при температурных условиях, отличных от 20°С необходимо применять поправочные коэффициенты, если требуется высокая точность.

Как найти сопротивление в цепях переменного тока

Вот здесь, товарищи, будет посложнее. Дело в том, что переменный ток вводит два понятия сопротивления: активное и реактивное. Активное сопротивление не зависит от частоты колебания напряжения, следовательно, и тока, а реактивное, наоборот, очень сильно зависит от этой частоты. Если очень просто, то к активному сопротивлению относят всё то, что не содержит индуктивности или емкости (отдельный провод, лампочка накаливания, спираль электрической плитки (хотя её нельзя назвать исключительно активным сопротивлением, однако реактивная составляющая там очень мала), лист железа и т.д.). Если вы заметили, то я указал отдельный провод, а не двух- и более жильный кабель. По сути, кабель или воздушная линия из нескольких проводов при большой длине превращается в конденсатор, где провода это обкладки конденсатора, а оболочка в кабеле или расстояние между проводами в воздушных линиях электропередачи выступают в роли диэлектрика между обкладками конденсатора. Таким образом, методы вычисления активного сопротивления для переменного и постоянного напряжения одинаковы, в то время, как реактивное сопротивление ведёт себя абсолютно по другому.

В общем, когда мы говорим о сопротивлении в переменном токе или напряжении, то мы говорим о полном электрическом сопротивлении:

Где: R – активное сопротивление;

L – индуктивность в генри;

С – ёмкость в фарадах;

f – частота колебаний сети в герцах.

Давайте посмотрим, почему вычислить сопротивление омметром для индуктивности и ёмкости будет сложнее. Заострим внимание на том, что при измерении сопротивления омметром используется постоянный ток, то есть его частота равна нулю. Смотрим, как меняется сопротивление ёмкости и индуктивности в этом случае:

Почему нельзя делить на ноль? Правильно, потому что получаем бесконечно большое число, то есть бесконечно большое сопротивление. Другими словами, конденсатор в цепи постоянного тока это всё равно, что выключатель. Вроде бы конденсатор в цепи, но он как бы разрывает её.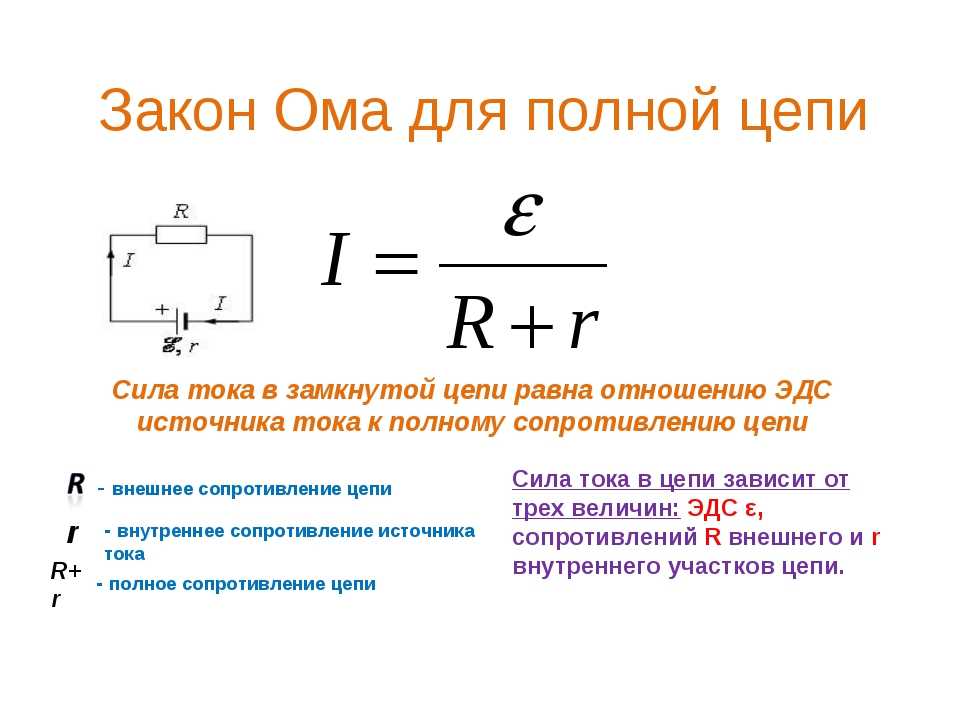

Здесь ситуация другая. Индуктивность в постоянном токе становится просто проводником, а поскольку мы видим из формулы, что полное сопротивление индуктивности это сумма активной и индуктивной (которой, к слову, гораздо больше, чем активной) частей, то мы не учитываем львиную долю сопротивления индуктивности. Именно по этой причине, если включить трансформатор в сеть постоянного напряжения вместо переменного, трансформатор очень быстро нагреется и сгорит – его полное сопротивление уменьшится в разы, а уменьшение сопротивления ведёт к увеличению силы тока, на которую трансформатор не рассчитан.

Где можно использовать эти знания? В основном, эти знания применяются в звукотехнике, где нужно отсечь постоянное напряжение или отсечь определенный звуковой диапазон. Сопротивление конденсатора возрастает с понижением частоты, а сопротивление индуктивности наоборот, с повышением частоты.

Вывод: как найти сопротивление в переменном токе? Для активного сопротивления, так же, как и в постоянном: с помощью омметра или измерительного моста, или амперметра с вольтметром.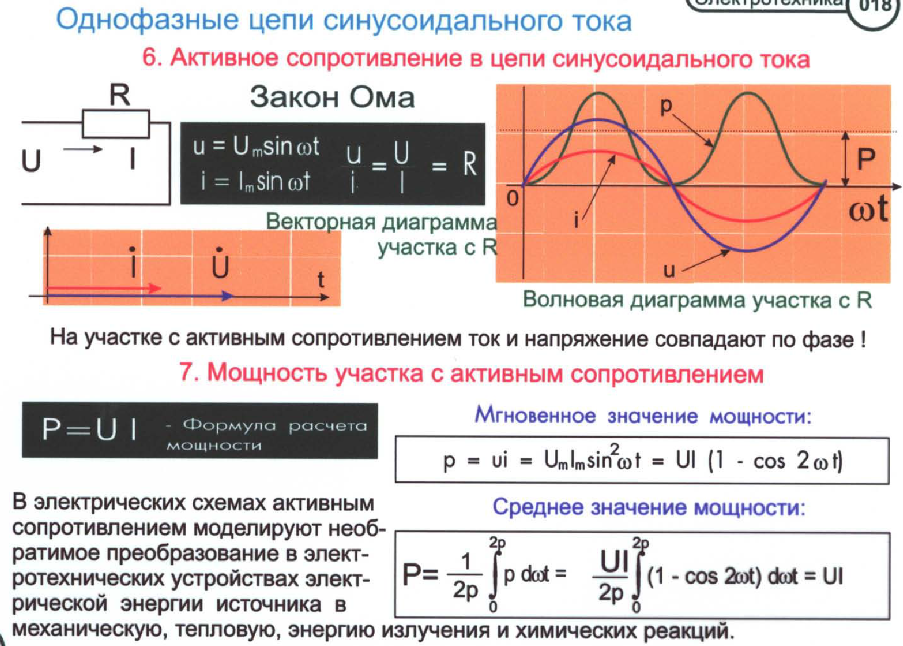 Для реактивного сопротивления использовать измерительные мосты для получения значений индуктивности или ёмкости, затем вычислять их сопротивления с учётом частоты, затем, если это конденсатор, то X_C=R, а индуктивное сопротивление равно X_L+R (то есть, у катушки есть еще активное сопротивление, хоть и небольшое), а затем, если требуется, вычислять полное сопротивление.

На этом можно закончить знакомство с темой, как найти сопротивление тока или как найти сопротивление и вы теперь знаете, что это неправильный вопрос и теперь знаете, что у тока нет сопротивления.

7. Рассчитать действующие значения силы тока в конденсаторе, используя данные;

Ростовский государственный экономический университет (РИНХ)

Елизаров Ю.Д

Электротехника

Методические указания по выполнению практических работ

Ростов-на-Дону

2014 год

Практическая работа №1

Электрические цепи постоянного тока

Цель работы:

-Исследование последовательного и параллельного соединения резисторов;

-Эквивалентная замена двух последовательно включенных источников ЭДС;

-Эквивалентная замена двух параллельно включенных источников ЭДС; -Исследование делителя напряжения;

-Исследование делителя тока.

Краткие сведения из теории

Электрическая цепь обычно состоит из соединительных определенным образом элементов и соединительных проводников. Такими элементами могут быть сопротивления (резисторы), электрические емкости (конденсаторы), индуктивности (катушки индуктивности, реле, обмотки трансформатора и др.) В цепях переменного тока любой элемент цепи обладает сопротивлением, индуктивностью и емкостью, а в цепях постоянного тока имеет значение только сопротивление потребителя энергии, подводящих проводов и измерительных приборов. Поэтому электрическую цепь удобно представить схемой замещения, где каждый из элементов представлен своим сопротивлением.

Закон Ома для замкнутой цепи

I =

Где I – сила тока в цепи, Е-ЭДС источника, R – сопротивление внешней цепи (нагрузки) и внутренней цепи источника.

Напряжение на выходах источника U=E-IRвнутр.

Эквивалентное преобразование участка цепи. Замена является эквивалентной, если ток через заменяемый участок цепи и напряжение на его выводах не изменяется при замене.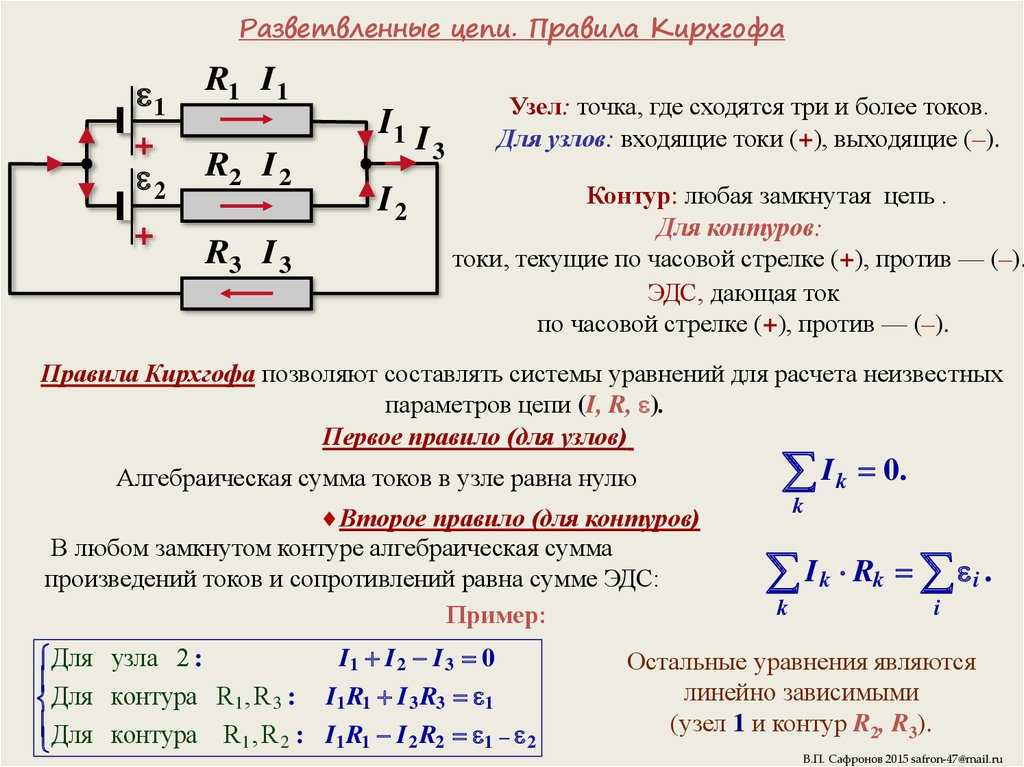

Эквивалентная замена двух последовательно включенных сопротивлений одним Rэ:

Rэ=

Эквивалентная замена двух параллельно включенных сопротивлений одним Rэ:

Rэ =

Замена последовательно включенных источников ЭДС:

Еэ =(сумма алгебраическая, учитывается знак ЭДС)

Делители напряжения предназначены для уменьшения напряжения, подаваемого на участок цепи. Простейший делитель состоит их двух, соединённых последовательно, резисторов; выходное напряжение подают на оба резистора, выходное снимают с одного из них как показано на рисунке 1.1

Рис 1.1 Схема делителя напряжения

Формула для вычисления снимаемого напряжения с плеча делителя

U

Такие делители используются, например, в приборах с несколькими диапазонами измерения. При измерении большего напряжения включается дополнительное сопротивление , а на показывающий прибор подается меньшее, пропорциональное подаваемому, напряжение. Делители тока предназначены для уменьшения тока в цепи. В этом случае два резистора включаются параллельно, и ток измеряется в цепи одного из них (рис 1.2) Так, например, осуществляется шунтирование в измерительных приборах приборов – амперметрах.

Рис 1.2 Схема делителя тока

Формула для вычисления тока через одно из плеч делителя тока (резистор R1) I =

Порядок выполнения работы

1. Изучить основные положения теорем электрических цепей постоянного тока.

2. Рассчитать эквивалентное сопротивление участка электрической цепи из двух последовательно соединённых резисторов .

3. Ознакомиться с вводной частью практикума по «Электротехника». Запустить программу. Найти в «Меню» «Правка» «Описание работ», открыть и выбрать лабораторную работу №1.

4. Открыть файл c1_001 с электрической схемой. Включить мультиметр и измерить сопротивление с заданного участка цепи. Записать полученную величину и сравнить с рассчитанным значением сопротивления.

5. Рассчитать эквивалентное сопротивление участка электрической цепи, состоящего из двух параллельно соединенных резисторов = 12 Ом

6. Открыть файл c1_002. 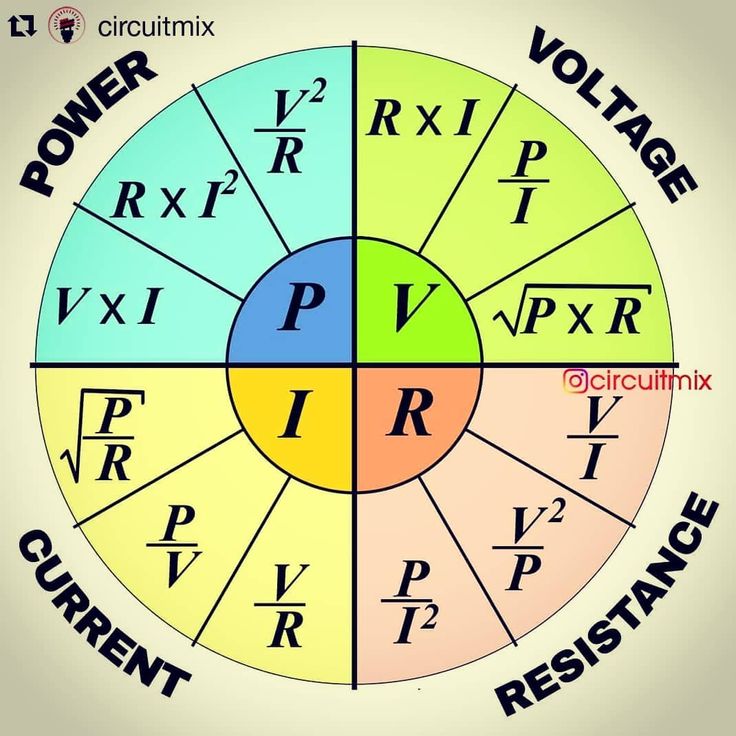Включить мультиметр и измерить сопротивление заданного участка цепи. Записать полученную величину и сравнить с расчётным значение.

7. Рассчитать значение эквивалентной ЭДС для последовательного соединения двух источников ЭДС .

8. Отрыть файл с_003, подключить вольт метр к точкам А и В и проверить условие эквивалентности.

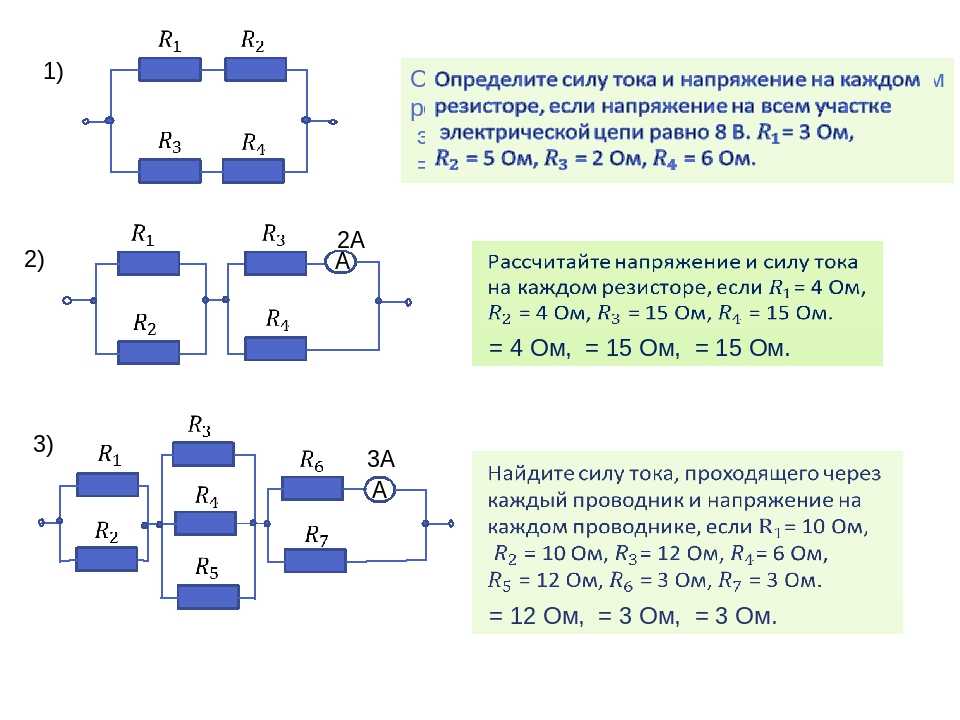
9. Рассчитать напряжение на каждом резисторе делителя напряжения

= 50 Ом = 100 Ом = 15 B

10. Открыть файл с_007. Подключая вольтметр параллельно каждому резистору, проверить правильность расчета.

11. Рассчитать токи через каждый резистор делителя тока — = 5 Ом= 10 ОмI = 6A

12. Откройте файл с_008. Подключая амперметр последовательно с каждым резистором, проверить правильность расчетов.

13. Оформить результат работы отчетом.

Содержание отчета

1. Название. Цель работы.

2. Название эксперимента и исходные данные для расчета.

3. Расчетные формулы, алгоритм вычислений и результаты расчета.

4. Электрическая схема измерений для каждого эксперимента, результаты измерений.

5. Выводы о соответствии расчетных и измерительных электрических величин по каждому эксперименту.

Контрольные вопросы:

1. Сформулируйте закон Ома для замкнутой цепи и для ее участка.

2. В каких единицах выражают ЭДС, напряжение, силу тока, сопротивление.

3. От чего зависит сопротивление однородного металлического проводника?

4. Каково соотношения между ЭДС и напряжением на выводах источника электрической энергии?

5. Как определяется ток при коротком замыкании выводов источника электрической энергии?

6. Почему желательно, чтобы внутреннее сопротивление мощного источника электрической энергии было возможно меньшим?

7. Сформулируйте первый и второй законы Кирхгофа, а также правило знаков для токов и ЭДС.

8. Как определяется общее сопротивление при последовательном, параллельном и смешанном соединении потребителей энергии.

9. Как определяется напряжение в делителе напряжения?

10. Как определяется токи в делителе тока?

Литература, пособия, инструкции:

1. Касаткин А.С., Немцов М.В. «Электротехника». 2008 г, -522е.

2. Синявский Г.П. и др. «Электротехника» Практикум РГЭУ(РИНХ) Ростов-на-Дону 2007г-76с.

Практическая работа №2

Цепи однофазного синусоидального тока.

Цель работы: Исследование амплитудно-фазовых соотношений и мощности для переменного тока и напряжения в резисторе, конденсаторе и катушке индуктивности.

Краткие сведения из теории:

Переменный ток промышленной частоты (f = 50 Гц) имеет синусоидальную форму i – мгновенное (в момент времени t) значение силы тока, Im – амплитуда (максимальное значение) тока, (wt – φi) где i — мгновенное (в момент времени t) значение силы тока, Im – амплитуда (максимальное значение) , (wt – φi) – фаза тока. В выражение для фазы тока входит w – циклическая частота переменного тока, связанные с обычной частатой соотношением w = 2 πf, а так же φ – начальная фаза (в момент времени t = 0).

Соответственно и напряжение в цепи переменного тока имеет синусоидальную форму u = Um sin(wt+ φi), где все величины имеют аналогичный току смысл. Мгновения значения токаи напряжения можно определить амплитудные значения токаи напряжения. Обычно на практике ток и напряжение характеризуют их действующими значениями I и U, которые указывают в паспортах на приборы, на электрической арматуре и т.д. Действующие значения тока и амплитудными значениями соотношениями

I = = 0,707 ; U == 0,707.

В цепи переменного тока с резистором закон Ома выполняется как для амплитудных значений тока напряжения =R, так и для их действующих значений U = IR. Конденсатор в цепи переменного тока имеет емкостное сопротивление

C – величина емкости конденсатора, ƒ – частота переменного тока. Мгновенные значение силы тока в конденсаторе i = (wt – φi), мгновенное значение напряжения на конденсаторе u = (wt – φi).

Начальные фазы связаны соотношением =+ , то есть ток опережает по фазе напряжение на. Закон Ома связывает амплитудные значения тока и напряжения на конденсаторе соотношением=.

Полная мощность двухполюсника определяется произведением действующих значений тока и напряжения (измеряется в ВА) S = =UI Связь полной, активной и реактивной мощностей =+Активную мощность измеряет ваттметрами разного принципа действия. Обычно ваттметр имеет две измерительные цепи, как показано на рис 2.1

рис 2.1

нагрузка

Одна цепь ваттметра включена последовательно нагрузке, ток в ней i равен току нагрузки. Другая цепь включается параллельно и напряжение в ней равно напряжению u нагрузки. В лабораторной работе роль ваттметра выполняет умножитель напряжений.

Порядок выполнения работы:

1. Изучить основные положения теории электрических цепей однофазного синусоидального тока.

2. Ознакомиться с вводной частью работы практикума «Электротехника» [2]. Запустить программу. Найти в меню «Правка» «Описание работ», открыть и выбрать лабораторную работу 2.

3. Рассчитать действующее значение тока в резисторе, используя данные U = 120B, R = 120B, r = 0,01 Oм

4. Открыть файл с2_01.ewb. Подключить амперметр и проверить правильность отчета.

5. Определить фазовые соотношения тока и напряжения.

(Есть ли фазовый сдвиг колебаний тока относительно колебаний подаваемого на резистор напряжения?) Подключить осциллограф и проверить соответствие теории данных эксперимента. Для этого измерить и сравнить периоды колебаний тока и напряжения на осциллограмме, а также сдвиг ∆T.

6. Определить мощность резистора.

Подать сигналы, пропорциональные току и цепи резистора (снимается в виде падения напряжения на вспомогательном резисторе 0,01 Ом) и напряжению на резисторе (снимается с источника ЭДС) на два входа умножителя.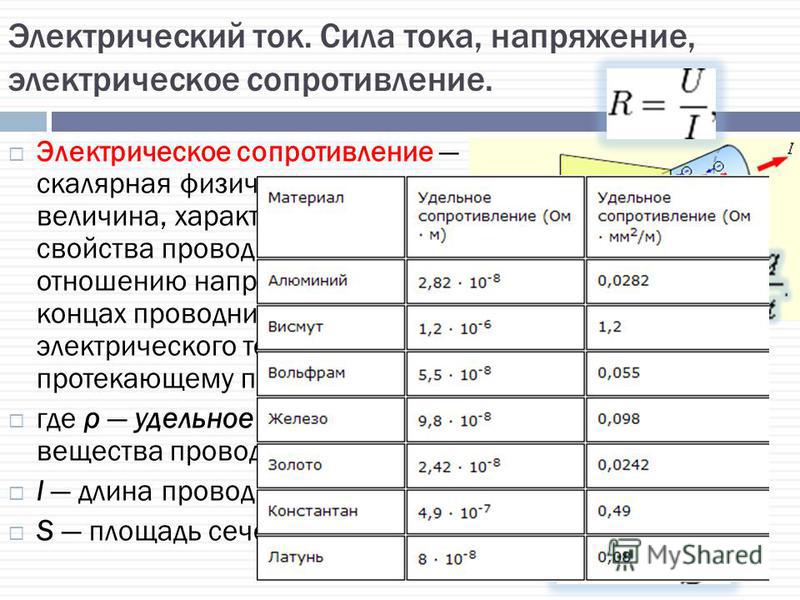 Подключить к выходу умножителя осциллограф в соответствие с электрической схемой рис. 2.1., по осциллограмме определить минимальную и максимальную активную мощность резистора.

Подключив на выход умножителя вольтметр постоянного напряжения, убедиться, что с точностью до некоторого коэффициента он измеряет активную мощность. Определить на опыте этот коэффициент.

u=120 B, f=50 Гц, с=53ϻФ, r=0,01 Oм

8. Открыть файл c2_02.ewb. Подключить амперметр и проверить правильность расчета.

9. Определить фазовые соотношения тока и напряжения на конденсаторе. (Совпадают ли по фазе колебания тока и напряжения в цепи конденсатора?) проверить экспериментально выводы теории. Подключить осциллограф, сравнить осциллограммы тока и напряжения, измерить периоды Т колебаний и сдвиг ∆T. Рассчитать фазовый сдвиг, зная, что периоду соответствует фаза 2π.

10. Измерить мощность конденсатора.

Подать сигналы, пропорциональные току и напряжению, на два входа умножителя подключите на выход умножителя осциллограф. По осциллограмме мощности определить минимальные и максимальные значения реактивной мощности конденсатора.

11. Рассчитать действующую значение тока в катушке индуктивности по данным: u = 120В ƒ =5кГц L = 955,4 Мн r = 0,1Ом

12. Открыть файл с2_03.ewb. Подключить амперметр и проверить правильность расчета.

13. Определить фазовые соотношения тока и напряжения в цепи катушки индуктивности. Подключить осциллограф и проверить соответствие теории экспериментально наблюдаемых соотношений фаз тока и напряжения в цепи катушки индуктивности.

14. Измерение мощности катушки индуктивности. Подайте сигналы, пропорциональные току и напряжению, на два входа умножителя и по осциллограмме мощности. Определить минимальное и максимальное значения реактивной мощности катушки индуктивности.

15. Оформить результаты работы отчётом.

Содержание отчёта:

1.Название, цель работы.

2.Название эксперимента и исходные данные расчета.

3. Расчетные формулы, алгоритм вычислений для расчета.

4. Электрическая схема измерений для каждого эксперимента, результаты измерений.

5. Выводы с соответствием расчетных и измененных электрических величин, а также о соответствии результатов экспериментов теории.

Контрольные вопросы:

1. Каковы основные характеристики синусоидального тока?

2. Какова связь между частотой, периодом и циклической частотой колебаний?

3. Какова связь между действующим, средним и амплитудным значениями синусоидального тока?

4. Как изображаются синусоидальные токи и напряжения с помощью вектора на комплексной плоскости?

5. Как сдвинуты друг относительно друга векторы тока и напряжения резистора, конденсатора, конденсатора, катушки индуктивности?

6. Как преобразуется электрическая энергия источника ЭДС в резисторе, конденсаторе и катушке индуктивности?

Литература, пособия, инструкции:

Касаткин А.С., Немцов М.В. «Электротехника». М.А. «Академия», -2008, 544е.

Синявский Г.П. и др. «Электротехника» Практикум – РГЭУ(РИНХ) г. Ростов-на-Дону, 2007г.,-76с.

Практическая работа №3

Цепи однофазного тока при последовательном включении электроприемников.

Цель работы: Исследование физических процессов, происходящих в установившимся режиме в цепи, содержащий последовательно соединенные активное, индуктивное и емкостное сопротивление.

Краткие сведения из теории.

При последовательном включении элементов схемы силы тока в них одинакова по закону Ома для участка цепи, падение напряжения на резисторе, катушке индуктивности и конденсаторе соответственно пропорционально величине активного тока R, индуктивного Х.

=(1)

==(2)

Полное сопротивление цепи Z определяется по формуле:

Z = (3)

Действующие значение силы тока I, в цепи рассчитывается из выражения

Z = (4)

Где U-напряжение, снимаемое с источника ЭДС.

Полная мощность, потребляемая цепью:

= U; =Z,

Коэффициент мощности можно определить как =,

Цепь потребляет от источника активную мощность :=или=U

Реактивная мощность равна разности индуктивной и емкостной мощностей: =-,

Отметим здесь еще раз смысл коэффициента мощности. Коэффициент мощности равен: =

Полную мощность S можно представить в виде S=, а для цепи содержащей конденсатор и катушку индуктивности,S=.

Тогда для коэффициента мощностей такой цепи справедливо выражение

=

Таким образом, коэффициент мощности представляет собой величину, которая показывает долю активной мощности в общем балансе мощностей, потребляемых электроприемником.

Из анализа последнего выражения можно сделать важные для теории и практики выводы:

1) Если реактивная мощность катушки больше реактивной мощности конденсатора, то цепь потребляет от источника и активную, и реактивную мощность;

2) Если реактивные мощности катушки больше реактивной мощности и конденсатора, то цепь потребляет от источника и активную, реактивную мощность;

3) Если реактивная мощность конденсатора больше реактивной мощности катушки, то цепь потребляет от источника активную мощность и отдает в сеть избыточную реактивную.

Порядок выполнения работы:

1. Изучить основные положения теории электрических цепей однофазного синусоидального тока.

2. Ознакомиться с вводной частью практикума «Электротехника» [2]. Запустить программу. Найти в меню «Правка», «Описание работ», открыть и выбрать в папке Лаб 5 файл 51.ewb.

3. Рассчитать индуктивное, емкостное и полное сопротивление цепи (Ом), используя формулы (1,2,3), при U= 70, 71В., R=10 Ом, =50mГн, С=1mФ;

4. Рассчитать действующее значение силы тока в цепи и падение напряжения в резисторе , катушке индуктивностии конденсаторе.

5. Открыть файл 51.ewb в папке Лаб5. Измерить падение напряжения в резисторе, катушке индуктивности и конденсаторе.

6. Рассчитать катушки, потребляемые цепью: полную, активную и реактивную. Коэффициент катушки.

7. Оформить результаты работы отчетом.

Содержание отчета:

1. Название, цель работы.

2. Исходные данные для расчета.

3. Расчетные формулы, алгоритм вычислений и результаты расчета.

4. Электрическая схема измерений, рисуемых осциллограммы напряжения сети и тока цепи, результаты измерений.

5. Выводы о соответствии расчетный и измерительных электрических величин.

Контрольные вопросы:

1. Как изображается гармоническое колебание с помощью вектора?

2. Как сдвинуты друг относительно друга векторы тока и напряжения для резистора, конденсатора и катушки индуктивности?

3. Как строится векторная диаграмма для последовательного включённых R,L и С?

4. Что такое резонанс напряжений?

5. Какими мощностями характеризуются цепи синусоидального тока?

6. По каким формулам можно рассчитать полную, активную и реактивную мощности?

7. Как измерить активную мощность?

8. Что такое коэффициент мощности, каков смысл?

Литература, пособия, инструкции:

1. Касаткин А.С., Немцов М.В. Электротехника. М: «Академия», 2008г-544с.

2.Синявский Г.П. и др. Электротехника: Практикум-РГЭУ(РИНХ) 2007г.-76с.

Практическая работа №4

Цепи трехфазного тока при соединении электроприемников звездой.

Цель работы: Исследование цепи трехфазного переменного тока в симметрическом режиме и влияния нейтрального провода на величину фазных напряжений электроприемников.

Краткие сведения из теории

В практике передачи и распределения электрической энергии соединяют в одну цепь три цепи синусоидального тока с независимыми источниками энергии. Источником электрической энергии служат три фазных обмотки статора трехфазного генератора переменного тока. При вращении магнитного поля ротора в этих обмотках последовательного тока. При вращении магнитного поля ротора в этих обмотках последовательно индуцируются синусоидальные ЭДС. Сдвинутые на фазный угол (треть периода) относительно друг друга. Цепь каждой обмотки генератора – фазным напряжением источника.

Трехфазную систему получают, соединяя фазы источника энергии и приемники звездой или треугольником. При соединении звездой все концы фазных обмоток генератора соединяются в общий узел, концы фаз приемника тоже образуют узел, а три провода между ними объединяются в один общий нейтральный провод(нейтраль). Начала трех фаз генератора соединяются с фазами приемника тремя линейными проводами. Напряжение между линейными проводами называется линейным напряжением. Действующие значения линейных и фазных напряжений связаны с соотношением UЛ=2UФ*cos30=. Действующие линейные токи равны фазным.

При симметричном режиме цепи, все напряжения источника равны между собой и одинаковы все три сопротивления электроприемника. При соединении в звезду фазные токи равны линейным, а линейные напряжения в раз больше фазных: ==.

Когда электроприемник представляет собой активную нагрузку, то угол сдвига между токами и напряжениями каждой фазной цепи равен 0, а полная мощность электроприемника равна активной, которая складывается из активных мощностей фаз, Вт:

S=P=3=3R.

В общем случае трехфазный электроприемник потребляет от источника активную и реактивную мощность.

Рассчитываются активные мощности каждой фазы, Вт:

= cos φ,

= cosφ,

= cosφ,

Активная мощность электроприемника:

Р=++; при симметрии Р=3.

Рассчитываются реактивные мощности каждой фазы,, вар:

= φ,

= φ,

= φ,

Q = . при симметрииQ = 3.

Коэффициент мощности можно определить:

==

Полная мощность электроприемника, В*А,

S=

Порядок выполнения работы

1. Изучить основные положения теории электрических цепей трехфазного тока.

2. Ознакомиться с вводной частью практикума «Электротехника» [2]. Запустить программу. Найти в меню « Правка» — «Описание работ», открыть и выбрать в папке Лаб8 фаул81.ewb.

3. Рассчитать фазные токи и напряжение в симметрическом режиме, при =50Гц,=100 Ом,=100 Ом,=100 Ом.

4. Открыть файл 81.ewb в папке Лаб8. Измерить замещение фазных токов и напряжений тока, в контрольном проводе. Изменить характер осциллограмм

фазных напряжений.

5. Рассчитать активную, реактивную и полную мощность трехфазной цепи.

6. Оформить результаты работы отчетом.

Содержание отчета:

1. Название, цель работы.

2. Исходные данные для расчета.

3. Расчетные формулы, алгоритм вычислений и результаты расчета.

4. Электрическая схема измерений, рисунок осциллограмм фазных напряжений, результаты измерений.

5. Выводы о соответствии расчетных и измеримых электрических величин.

Контрольные вопросы

1. Что такое трехфазный переменный ток и почему он так называется?

2. Что называется фазой цепи трехфазного тока?

3. Какое соединение обмоток генератора называется соединением «звездой»?

4. При каких условиях можно производить соединение фаз «звездой» без нулевого провода?

5. Что называется линейным напряжением и фазовым напряжением?

6. Каково соотношение между фазовым и линейным напряжениями при соединении «звездой»?

7. К чему приведет обрыв нулевого провода при несимметричной нагрузке?

8. Как измеряют мощность и энергию трехфазной системы при симметричной и несимметричной нагрузках?

Литература, пособия, инструкции:

1. Касаткин А.С., Немцов М.В. Электротехника. М. «Академия»,-2008-544с.

2.Синяковский Г.П. и др. Электротехника: Практикум – РГЭУ(РИНХ) 2007г.76с.

Понимание колеса закона Ома в 2023 году: бесплатный калькулятор закона Ома!

Если вы электрик или специалист по системам вентиляции и кондиционирования , вам необходимо четко понимать закон Ома.

Помогает описать электрические цепи и взаимосвязь между напряжением и током.

Понимание закона Ома позволит вам контролировать ток в цепи и знать, когда добавлять резисторы.

Все равно? Просто нажмите здесь для нашего бесплатного калькулятора колеса закона Ома.   Вот здесь!

✅ Как использовать закон Ома

Закон Ома гласит, что ток между двумя точками прямо пропорционален напряжению в двух точках электрического проводника.

Лучший способ узнать этот закон — использовать круговую диаграмму закона Ома.

В нем используется простая формула с тремя электрическими переменными: напряжением, током и сопротивлением.

R — сопротивление, измеренное в омах, Ом

I — ток, измеренный в амперах или амперах

В измеряется в вольтах = иногда известно как E (вольты)

Представьте себе каждую букву (R, I, V) в углу треугольника с V наверху.

Эта визуализация демонстрирует взаимосвязь между переменными .

Он также может помочь вам определить, сколько ампер будет потреблять цепь, если вы не можете использовать амперметр.

Схема закона Ома

Поместите палец на единицу , которую вы хотите рассчитать, будь то сопротивление, напряжение или ток.

Об остальном позаботится формула закона Ома.

Это потому, что ток через две точки проводника прямо пропорционален его напряжению.

При этом электрический ток обратно пропорционален сопротивлению.

Колесо закона Ома можно представить с помощью следующих математических уравнений:

• I (ток) x R (сопротивление) = V (напряжение)
• В (напряжение) / I (ток) = R ( сопротивление)
• В (напряжение) / R (сопротивление) = I (ток)

Если у вас есть два известных значения, вы можете рассчитать оставшуюся единицу, используя эти формулы.

Сначала подставьте известные значения в формулу.

Во-вторых, умножьте или разделите их (или используйте калькулятор) в зависимости от других значений. Это так просто. 😉

✅

Примеры закона Ома

Мы хотим найти сопротивление электрической цепи, измеренное в омах.

Мы знаем, что напряжение составляет 24 вольта, а сопротивление цепи равно шести омам.

Как рассчитать электрический ток? Поместив известные значения в формулу закона Ома:

• 24 вольта / 6 Ом = 4 ампера

Теперь вы  знаете значение отсутствующей переменной .

Вы можете использовать закон Ома, если в формуле известны две единичные переменные.

Вот еще один пример, в котором у вас есть 200 вольт и 20 ампер:

• 200 вольт / 20 ампер = 10 Ом

✅

ООМ ФОРМУЛА ФОРМУЛА ОХМ ЗАКОН

ООМ ФОРМАЛЬНЫЙ КОЛЕСНЫЙ КОЛЕСКОЙ ДЛЯ ДОЛГОДА: Power (P) измеряется в Watts .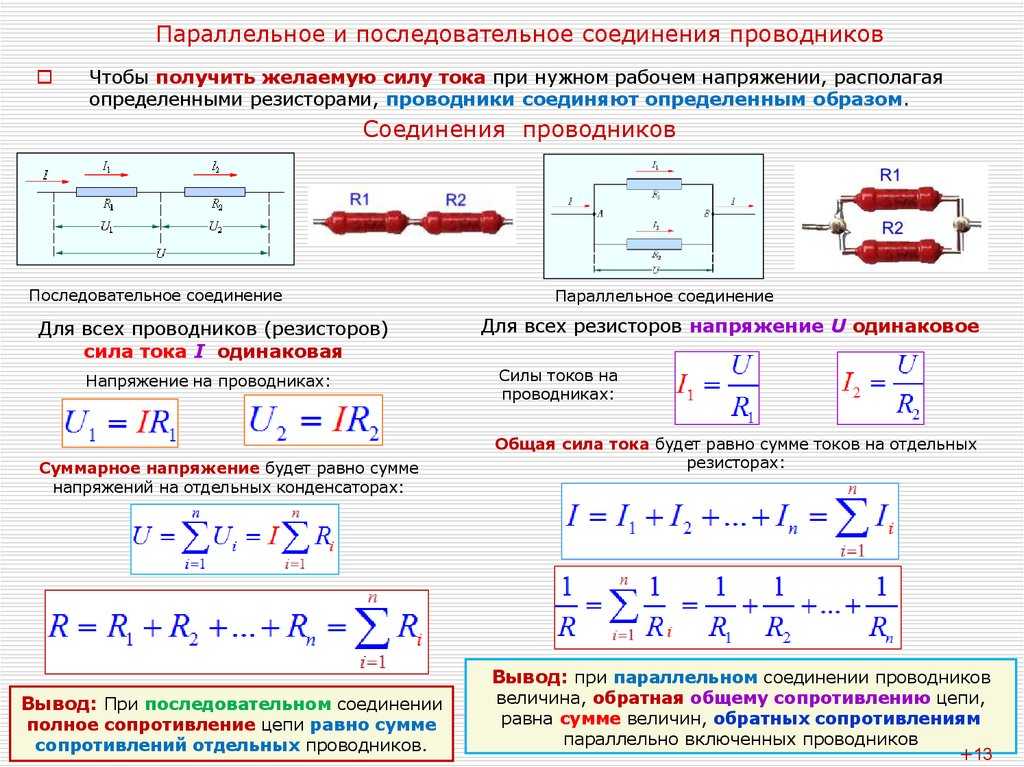

В этом случае мощность определяется как скорость передачи энергии по цепи в единицу времени, выраженная в ваттах.

Колесо формул объединяет круговую диаграмму с законом Ома. Он содержит четыре единицы.

Хотя колесо формул может показаться сложным, им так же легко пользоваться, как круговой диаграммой.

Каждый квадрант диаграммы  содержит формулы, выражающие взаимосвязь между двумя переменными, независимо от того, прямо пропорциональны они или нет.

В каждом квадранте вы найдете по три формулы.

📋

Вот четыре шага, которые необходимо выполнить при использовании колеса закона Ома.

1) Определите, для какой переменной вам нужно найти: мощность (P), сопротивление (R), ампер (I) и вольт (E или V).

2) Определите, какие переменные вы уже знаете: мощность (P), сопротивление (R), амперы (I) и вольты (E или V).

3) Найдите формулу, в которую можно подставить два ваших значения.

4) Решить уравнение.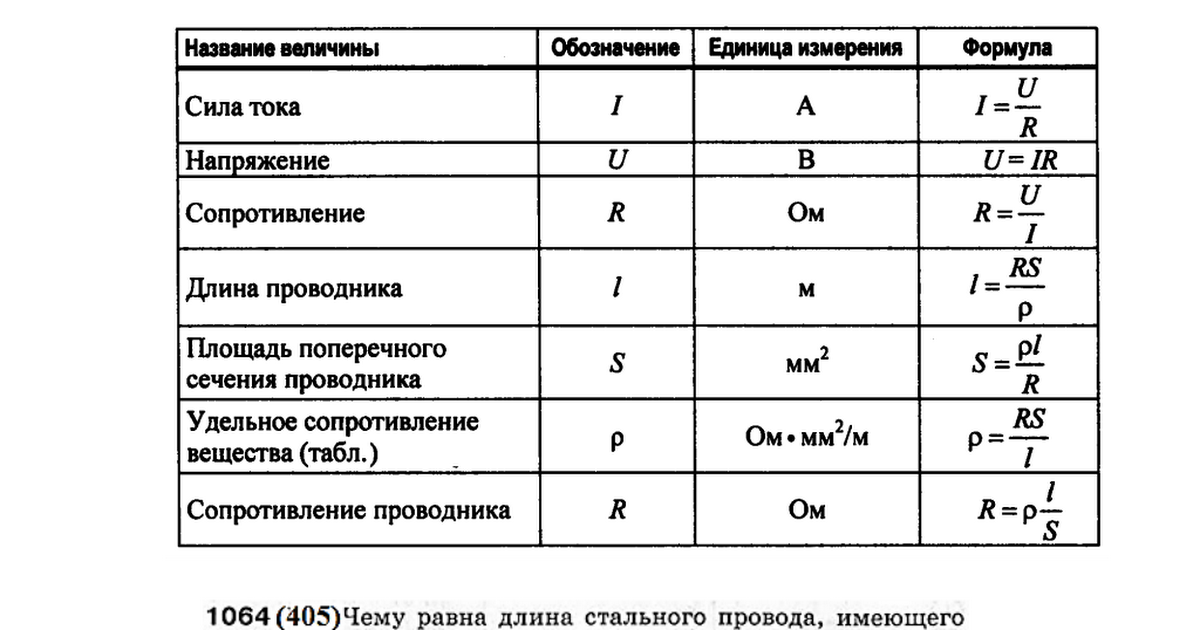

При решении формулы используйте совместимые единицы измерения.  Если вы используете омы и амперы, это нормально, потому что они работают вместе.

Однако, если у вас есть килоомы, вы должны преобразовать число в омы, прежде чем вычислять ответ.

В противном случае вы получите гораздо меньший результат, чем ожидали.

То же самое применимо, если вы используете киловатты вместо ватт или миллиамперы вместо ампер.

✅

Принципы закона Ома

Закон Ома предлагает полезный способ изучения взаимосвязи между переменными.

Все, что вам нужно сделать, это изменить значение одной переменной в формуле.

В результате вы увидите пропорциональное увеличение или уменьшение ответа.

Допустим, вы хотите увеличить сопротивление. Это повлияет на другие компоненты в уравнениях.

Вот три примера, иллюстрирующие эту динамику:

• 240 вольт / 5 Ом = 48 ампер
• 240 вольт / 10 Ом = 24 ампер
• 240 вольт / 20 Ом = 12 ампер

. Эти формируют.

Что происходит в результате?

Напряжение тоже растет, при условии, что сопротивление цепей не меняется.

Давайте попробуем снова этот пример, изменяя напряжение:

• 240 вольт / 10 Ом = 24 ампер
• 480 вольт / 10 Ом = 48 А.
• 960 Вольт / 10 Ом = 96 А.

. Напряжение в этих уравнениях устойчиво увеличивается.

При этом сопротивление остается прежним.

Следовательно, электрическая энергия тока увеличивается пропорционально напряжению.

✅

Когда использовать колесо закона Ома

У закона Ома нет недостатка в реальных приложениях .

Вы можете использовать формулы для решения широкого круга проблем в мире HVAC.

Например, это удобный вариант при работе с рабочей схемой.

Допустим, вы не можете измерить сопротивление рабочей цепи .

Одним из вариантов было бы отключить цепь и таким образом измерить сопротивление.

Однако этот вариант требует ненужного количества времени и усилий.

Колесо закона Ома позволяет рассчитать значение сопротивления в секундах.

Закон Ома также часто сочетается с Законом Джоуля  (в котором используется формула P (мощность) = IV для расчета мощности резистивных элементов, когда переменная неизвестна.

Например, если вы знаете ток (I) и сопротивление (R), но не напряжение, вы можете заменить V в законе Джоуля на закон Ома, чтобы найти мощность в ваттах. Вы получите P = I (IR). постоянное управляющее напряжение или ток .

Цепи постоянного тока (DC) имеют устойчивый поток электричества, который легко измерить.

Если у вас нет этой стабильности, определение напряжения и тока становится сложнее.

Например, вы не можете применять формулы при работе с цепями переменного тока, также известными как изменяющиеся во времени цепи .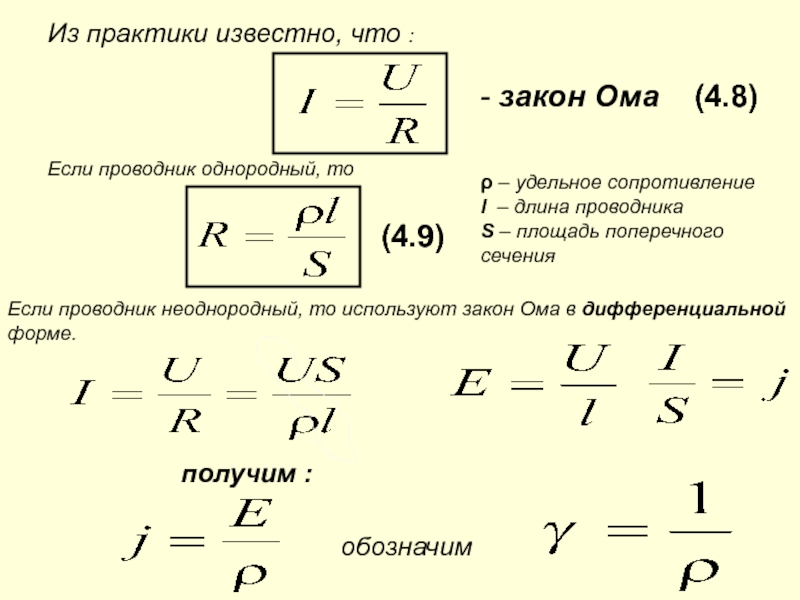

Это потому, что они  не учитывают реактивное сопротивление , которое вы найдете в этом типе схемы.

Обратите внимание, что вы можете настроить формулы для учета импеданса (Z) , но это урок для другой статьи.

✅

Калькулятор закона Ома

Вам нужно рассчитать электрический ток в крайнем случае?  

Мы подготовили для вас калькулятор закона Ома.

Калькулятор может работать с уравнениями, в которых используются мощность, напряжение, ток и сопротивление.

Введите два значения и нажмите «Ввод», чтобы решить формулу.

Хотя этот калькулятор облегчит вашу работу, закон Ома служит основой для работы с электричеством наряду с другими важными формулами.

Независимо от того, являетесь ли вы учеником HVAC или опытным техником, вам необходимо четко понимать эти концепции.

Вы можете  использовать формулы для решения различных задач  при работе с электроэнергией, резистивными элементами, напряжением, током и т. д., и у вас не всегда может быть доступ к калькулятору!

Посетите наш блог, чтобы узнать больше советов, рекомендаций и идей.

Калькулятор закона Ома — Calculator Land

Наш калькулятор закона Ома автоматически рассчитывает напряжение, ток и сопротивление. Также узнайте, что такое закон Ома.

ЯРЛЫКИ:

РАСЧЕТ НАПРЯЖЕНИЯ  | РАССЧИТАТЬ ТЕКУЩУЮ | РАСЧЕТ СОПРОТИВЛЕНИЯ  | ПРОЧИТАЙТЕ СТАТЬЮ

Расчет напряжения

Информация

Как рассчитать напряжение (В), зная сопротивление (R) и ток (I).

Формула: В = R x I

Помните, что:
Напряжение (В) измеряется в вольтах
Сопротивление (R) измеряется в омах
Ток (I) измеряется в амперах

Рассчитайте ток

Информация

Как рассчитать ток (I), зная напряжение (V) и сопротивление (R).

Формула: I = V / R

Помните, что:
Напряжение (В) измеряется в вольтах
Сопротивление (R) измеряется в Омах
Ток (I) измеряется в амперах

Рассчитайте сопротивление

Информация

Как рассчитать сопротивление (R), зная напряжение (V) и ток (I).

Формула: R = V / I

Помните, что:
Напряжение (В) измеряется в Вольтах
Сопротивление (R) измеряется в Омах
Ток (I) измеряется в Амперах

Закон Ома

О чем на самом деле говорит закон Ома? И как мы можем использовать его, чтобы понять электричество и электронику?

Что такое закон Ома?

Закон Ома представляет собой зависимость между напряжением и током. В нем говорится, что количество электрического заряда, проходящего через электрическую цепь в любой момент времени, прямо пропорционально разности потенциалов между двумя точками цепи.

Это можно описать так: если удвоить напряжение на резисторе, то и ток удвоится. Если уменьшить вдвое напряжение на резисторе, то ток уменьшится вдвое. Это означает, что если вы хотите увеличить или уменьшить поток электронов через цепь, вам нужно изменить либо напряжение, либо сопротивление.

Это означает, что пока сопротивление остается постоянным, удвоение или уменьшение вдвое напряжения всегда приводит к удвоению или уменьшению вдвое тока.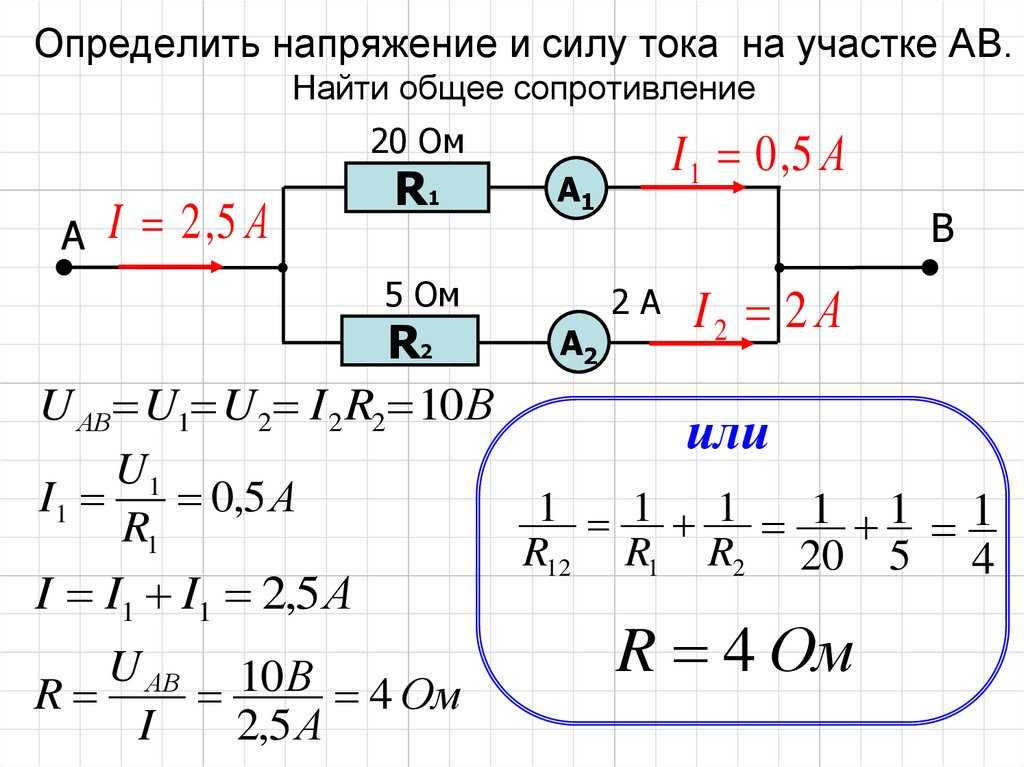

Причина, по которой нас волнует закон Ома, заключается в том, что он рассказывает нам кое-что интересное о том, как электроны движутся в электрической цепи.

Когда мы говорим о силе тока, протекающего по проводу, на самом деле мы имеем в виду количество электронов, протекающих в секунду. Мы называем эту величину текущей.

Пример закона Ома

Но что произойдет, если мы соединим наши провода вместе? Что произойдет, если к одному концу провода подсоединить батарею, а другой конец — к лампочке?

Первое, что происходит, это падение напряжения от положительной клеммы аккумулятора до отрицательной клеммы.

Это означает, что напряжение на отрицательной клемме аккумулятора ниже, чем напряжение на положительной клемме.

Если бы мы нарисовали схему ситуации, то увидели бы, что линия, соединяющая положительные и отрицательные клеммы, разделена на две части. Одна часть идет к положительной стороне батареи, а другая часть идет к отрицательной стороне батареи.

Но что означает, что по проводу течет больший или меньший ток? Ну, это означает, что больше или меньше электронов движется из одной точки в другую в любой конкретный момент. Другими словами, количество электронов, протекающих через провод, меняется со временем.

И когда мы говорим, что количество протекающих электронов изменяется с течением времени, мы говорим, что количество электронов в некоторой точке пространства изменяется с течением времени.

Мы называем это изменением электронной плотности. Итак, когда мы говорим, что ток меняется, мы на самом деле говорим, что меняется плотность электронов.

Теперь здесь вступает в действие закон Ома. Когда мы говорим, что количество или плотность электронов меняется, мы говорим, что существует разница в напряжении между двумя точками в пространстве.

Итак, если представить схему с батареей на одном конце и лампочкой на другом конце, мы увидим градиент напряжения по длине провода.

Теперь давайте подумаем, что произойдет, если последовательно с проводом подключить резистор. Напряжение на резисторе падает пропорционально, а ток не меняется.

Почему бы и нет? Потому что падение напряжения на резисторе точно равно падению напряжения на проводе.

Итак, падение напряжения на всей цепи такое же, как падение напряжения на всем проводе.

Что произойдет, если мы подключим нагрузку параллельно проводу? То есть, если мы вместо батарейки прикрепим к проводу лампочку, то получим другое падение напряжения.

Поскольку электрическое сопротивление лампочки очень велико по сравнению с проводом, большая часть падения напряжения приходится на лампочку.

Итак, теперь падение напряжения как на резисторе, так и на проводе уменьшается на величину, на которую увеличивается падение напряжения на лампочке.

Другими словами, общее падение напряжения в цепи такое же, как и раньше, но падение напряжения на резисторах меньше, а падение напряжения на проводах больше.

Итак, ток в цепи не изменился.

Основная идея закона Ома заключается в том, что сопротивление проводника зависит от силы тока, протекающего по нему.

Итак, если вы знаете ток, протекающий по проводу, вы можете вычислить его сопротивление. А зная сопротивление провода, можно вычислить, какой ток будет течь по нему.

Вот почему так важен закон Ома. Это позволяет нам измерять такие вещи, как рассеивание мощности в цепях.

Для чего можно использовать закон Ома?

Ответ на этот вопрос прост: его можно использовать для расчета сопротивления неизвестной цепи. Закон Ома гласит, что V IR, где R — сопротивление, а I — ток через резистор. Напряжение на любом компоненте всегда будет равно сумме всех токов, втекающих или вытекающих из компонента. Если вы знаете значение тока, вы можете использовать закон Ома, чтобы найти сопротивление компонента. Однако на практике расчет обычно выполняется с помощью мультиметра, а не вручную.

Например, если вы измеряете напряжение на двух резисторах, соединенных последовательно друг с другом, вы можете использовать закон Ома для определения сопротивления обеих частей цепи. Вы делаете это, измеряя разность потенциалов между ними и разделив результат на общий ток, проходящий через цепь.

Что еще?

Итак, что еще нам нужно знать о законе Ома? Ну, нам также нужно знать, что падение напряжения на резисторе пропорционально току, протекающему через него.

Но что это значит? Ну, это просто означает, что зависимость между напряжением и током линейна.

Он линейный, потому что выглядит как прямая линия на графике. Но на самом деле он изогнут.

Он изогнут, потому что зависимость между напряжением и зарядом нелинейна. На самом деле, чем ближе вы смотрите на это, тем сложнее оно становится.

Например, если у вас есть электрическое поле, направленное на заряженную частицу, сила, действующая на частицу, прямо пропорциональна напряженности поля.

Итак, чем сильнее поле, тем больше сила. Но чем слабее поле, тем меньше сила.

Если вы хотите найти потенциальную энергию, связанную с заряженной частицей, вы умножаете силу на расстояние от источника поля.

Но если вы хотите найти кинетическую энергию, связанную с заряженным объектом, вы должны сложить все силы, действующие на объект.

То есть вы должны суммировать силы электрического поля, магнитного поля и любых гравитационных полей.

Суммарная результирующая сила, действующая на объект, всегда равна нулю.

И если результирующая сила равна нулю, скорость объекта постоянна.

Итак, если у меня есть батарея, подключенная к резистору, напряжение на резисторе непостоянно.

Вместо этого она изменяется в зависимости от скорости прохождения зарядов через резистор.

Если резистор велик по сравнению с размером батареи, то изменение напряжения на резисторе мало.

С другой стороны, если резистор мал по сравнению с размером батареи, то разница велика.

Итак, зависимость между напряжением и электрическим зарядом нелинейна, а зависимость между напряжением и электричеством линейна.

Вот почему мы можем использовать, чтобы найти соотношение между напряжением и током.