Как считать сопротивление при параллельном соединении. Параллельное и последовательное соединение проводников: формулы, расчеты, примеры

Как рассчитать сопротивление при параллельном соединении проводников. Какие формулы используются для расчета параллельного соединения емкостей и индуктивностей. Как определить ток и напряжение при параллельном соединении. Где применяется параллельное соединение проводников.

Формулы для расчета параллельного соединения проводников

При параллельном соединении проводников важно уметь правильно рассчитывать общее сопротивление цепи. Существует несколько ключевых формул, которые применяются в зависимости от конкретной ситуации:

• Общая формула для расчета эквивалентного сопротивления при параллельном соединении: 1/R = 1/R1 + 1/R2 + 1/R3 + …
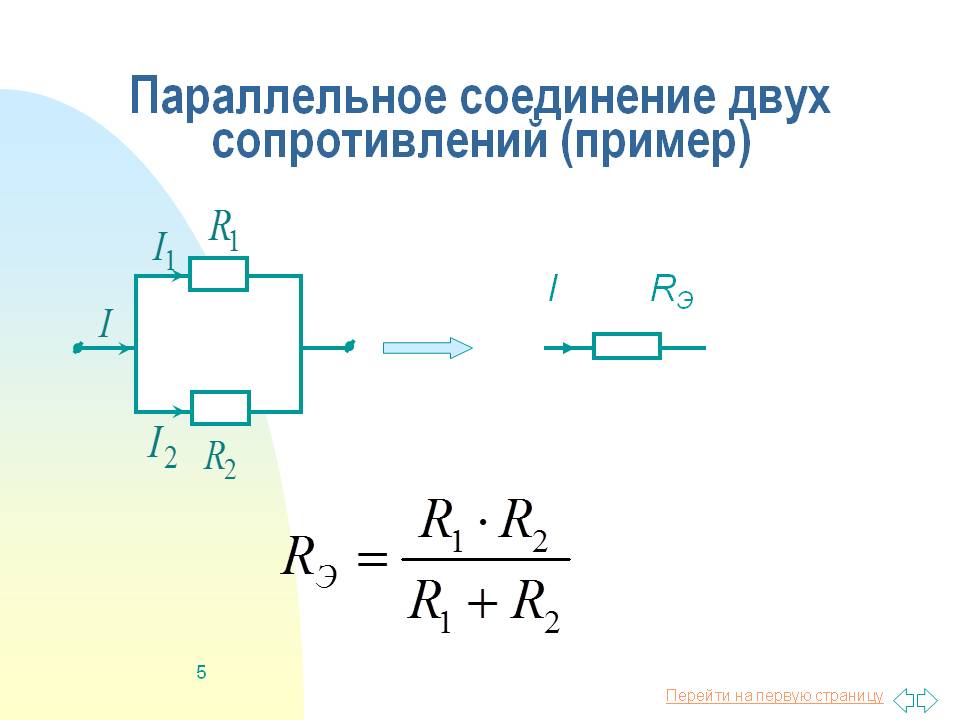
• Формула для двух параллельно соединенных сопротивлений: R = (R1 * R2) / (R1 + R2)
• Формула для n одинаковых параллельно соединенных сопротивлений: R = R1 / n

Эти формулы позволяют быстро и точно определить общее сопротивление цепи при различных вариантах параллельного соединения проводников. Важно помнить, что при параллельном соединении общее сопротивление всегда меньше наименьшего из сопротивлений отдельных проводников.

Особенности расчета параллельного соединения емкостей и индуктивностей

При работе с электрическими цепями часто приходится иметь дело не только с резисторами, но и с конденсаторами и катушками индуктивности. Расчет параллельного соединения этих элементов имеет свои особенности:

• Для параллельного соединения емкостей (конденсаторов) используется формула: C = C1 + C2 + C3 + …
• При параллельном соединении индуктивностей применяется формула: 1/L = 1/L1 + 1/L2 + 1/L3 + …

Обратите внимание, что формула для расчета параллельного соединения индуктивностей аналогична формуле для расчета параллельного соединения сопротивлений. Однако важно учитывать, что в этой формуле не учитываются взаимные индуктивности между катушками, которые могут оказывать существенное влияние на общую индуктивность цепи в некоторых случаях.

Распределение тока и напряжения в параллельных цепях

Для правильного анализа работы электрических схем с параллельным соединением проводников необходимо понимать, как в них распределяются ток и напряжение:

• При параллельном соединении напряжение на всех элементах цепи одинаково и равно напряжению источника питания.
• Ток в каждой ветви параллельной цепи обратно пропорционален сопротивлению этой ветви. Чем меньше сопротивление ветви, тем больший ток через нее протекает.
• Общий ток в цепи равен сумме токов во всех параллельных ветвях: I = I1 + I2 + I3 + …

Эти закономерности позволяют легко анализировать работу параллельных цепей и рассчитывать распределение токов и напряжений в них. Понимание этих принципов особенно важно при проектировании и отладке электронных устройств.

Практическое применение параллельного соединения проводников

Параллельное соединение проводников широко используется в различных областях электротехники и электроники. Вот несколько примеров практического применения:

1. Создание резисторов с нестандартными номиналами. Путем параллельного соединения нескольких стандартных резисторов можно получить требуемое значение сопротивления, которое отсутствует в стандартных рядах.
2. Разработка делителей тока. Параллельное соединение позволяет распределить ток между несколькими потребителями в заданном соотношении.
3. Увеличение мощности нагрузки. При параллельном подключении нескольких потребителей можно увеличить общую мощность нагрузки без превышения допустимого тока через отдельные элементы.
4. Создание батарей конденсаторов. Параллельное соединение конденсаторов позволяет увеличить общую емкость и уменьшить внутреннее сопротивление батареи.

Эти примеры демонстрируют, насколько важно уметь правильно рассчитывать и использовать параллельное соединение проводников в различных электрических схемах.

Методы преобразования сложных электрических цепей

При анализе сложных электрических цепей часто возникает необходимость их упрощения для облегчения расчетов. Существует несколько методов преобразования электрических схем:

• Преобразование треугольника сопротивлений в звезду и обратно. Этот метод позволяет заменить три сопротивления, соединенные треугольником, на три сопротивления, соединенные звездой, что может значительно упростить расчеты.
• Метод эквивалентного генератора. Позволяет заменить часть сложной цепи эквивалентным источником ЭДС и внутренним сопротивлением.
• Метод наложения. Применяется для расчета токов в линейных цепях с несколькими источниками ЭДС.
• Метод контурных токов. Упрощает расчет сложных цепей путем составления уравнений для контурных токов.

Эти методы позволяют значительно упростить анализ сложных электрических цепей и сделать расчеты более наглядными и понятными. Умение применять эти методы на практике — важный навык для специалистов в области электротехники и электроники.

Последовательно-параллельное соединение проводников: особенности расчета

Часто в реальных электрических схемах встречается смешанное, или последовательно-параллельное соединение проводников. Расчет таких цепей требует особого подхода:

1. Схему разбивают на отдельные участки с последовательным или параллельным соединением элементов.
2. Для каждого участка рассчитывают эквивалентное сопротивление, используя соответствующие формулы.
3. Полученные эквивалентные сопротивления объединяют, пока не будет получено общее сопротивление всей цепи.

При расчете смешанных соединений важно правильно определить, какие элементы соединены последовательно, а какие — параллельно. Ошибка на этом этапе может привести к неверному результату всего расчета.

Пример расчета последовательно-параллельного соединения

Рассмотрим схему, где резистор R1 соединен последовательно с параллельным соединением резисторов R2 и R3. Как рассчитать общее сопротивление такой цепи?

1. Сначала находим эквивалентное сопротивление параллельного участка: R23 = (R2 * R3) / (R2 + R3)
2. Затем складываем полученное значение с сопротивлением R1: Rобщ = R1 + R23

Этот пример демонстрирует, как можно поэтапно упростить сложную схему и рассчитать ее общее сопротивление.

Влияние температуры на сопротивление проводников

При расчете электрических цепей важно учитывать, что сопротивление проводников может изменяться в зависимости от температуры. Это особенно важно для устройств, работающих в широком диапазоне температур или с высокими токами.

• Для большинства металлов сопротивление увеличивается с ростом температуры.
• Для некоторых материалов (например, для полупроводников) сопротивление может уменьшаться при нагревании.
• Изменение сопротивления с температурой описывается формулой: R = R0 * (1 + α * (T — T0)), где α — температурный коэффициент сопротивления.

Учет температурной зависимости сопротивления особенно важен при проектировании силовых электрических цепей, где нагрев проводников может быть значительным. Игнорирование этого фактора может привести к неправильной работе устройства или даже к его повреждению.

Практические рекомендации по учету температурной зависимости

Как учесть влияние температуры при расчете электрических цепей? Вот несколько практических советов:

1. Используйте справочные данные о температурных коэффициентах сопротивления для материалов, из которых изготовлены проводники.
2. Оцените максимальную рабочую температуру устройства и рассчитайте изменение сопротивления при этой температуре.
3. При необходимости используйте термокомпенсацию — добавление в схему элементов, компенсирующих изменение сопротивления с температурой.
4. Для точных измерений используйте методы термостатирования — поддержания постоянной температуры измерительных цепей.

Эти рекомендации помогут повысить точность расчетов и обеспечить надежную работу электрических устройств в различных температурных условиях.

Формула для расчета параллельного соединения сопротивлений

При параллельном соединении обратная величина от эквивалентного сопротивления равна сумме обратных величин всех параллельно подключенных сопротивлений. Эквивалентная проводимость равна сумме всех параллельно подключенных проводимостей электрической схемы.

  

Для приведенной выше схемы эквивалентное сопротивление можно рассчитать по формуле:

В частном случае при подключении параллельно двух сопротивлений:

Эквивалентное сопротивление цепи определяется по формуле:

  

 В случае подключения «n» одинаковых сопротивлений, эквивалентное сопротивление можно рассчитать по частной формуле:

  

Формулы для частного рассчета вытекают из основной формулы. 

Формула для расчета параллельного соединения емкостей (конденсаторов)

При параллельном подключении емкостей (конденсаторов) эквивалентная емкость равна сумме параллельно подключенных емкостей:

  

Формула для расчета параллельного соединения индуктивностей

При параллельном подключении индуктивностей, эквивалентная индуктивность рассчитывается так же, как и эквивалентное сопротивление при параллельном соединении: 

  

Необходимо обратить внимание, что в формуле не учтены взаимные индуктивности.

Пример свертывания параллельного сопротивления

Для участка электрической цепи необходимо найти параллельное соединение сопротивлений выполнить их преобразование до одного.

 

Из схемы видно, что параллельно подключены только R2 и R4. R3 не параллельно, т.к. одним концом оно подключено к источнику ЭДС E1. R1 — одним концом подключено к R5, а не к узлу. R5 — одним концом подключено к R1, а не к узлу. Можно так же говорить, что последовательное соединение сопротивлений R1 и R5 подключено параллельно с R2 и R4.

Рассчитать эквивалентное сопротивлений R14 можно по формуле для двух сопротивлений.

Ток при параллельном соединении

При параллельном соединении сопротивлений ток через каждое сопротивление в общем случае разный. Величина тока обратно пропорциональна величине сопротивления.

Напряжение при параллельном соединении

При параллельном соединении разность потенциалов между узлами, объединяющими элементы цепи, одинакова для всех элементов.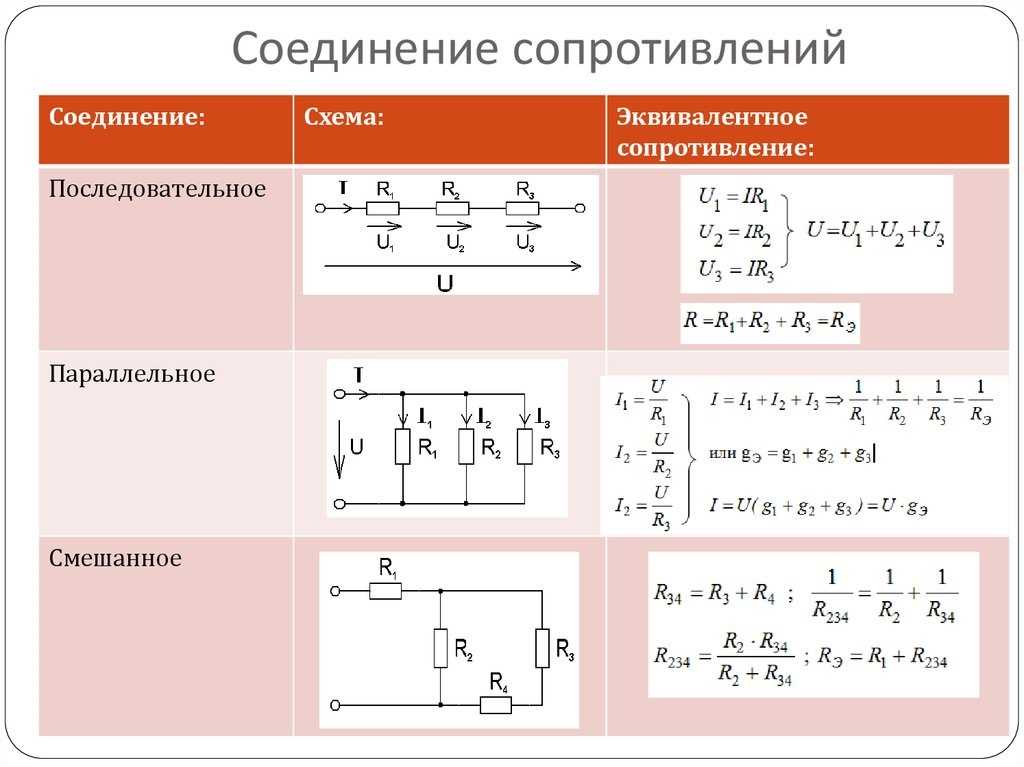

Применение параллельного соединения

1. В промышленности изготавливаются сопротивления определенных величин. Иногда необходимо получить значение сопротивления вне данных рядов. Для этого можно подключить несколько сопротивлений параллельно. Эквивалентное сопротивление всегда будет меньше самого большого номинала сопротивления.

2. Делитель токов

3. Треугольник в звезду

Расчет и исследование сложных электрических цепей во многих случаях можно значительно облегчить и сделать более наглядным путем преобразования электрических схем одного вида в схемы другого вида. Одним из способов является эквивалентное преобразование треугольника в звезду. В этом методе выполняется преобразование пассивной части электрической цепи, т.е. 

приемников электрической энергии.

Определение соединения сопротивлений треугольником

Если три сопротивления соединены так, что образуют собою стороны треугольника, то такое соединение сопротивлений называют треугольником сопротивлений.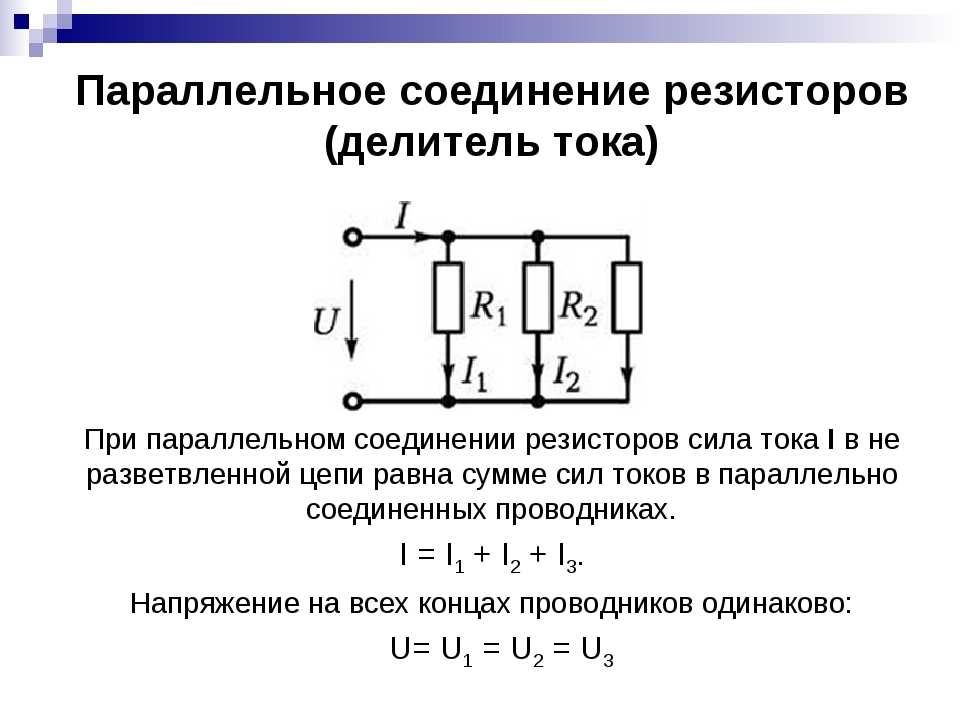

Обычно в курсе электротехники принято элементы рисовать только горизонтально и вертикально. На следующем рисунке так же представлено соединение треугольником.

Определение соединения сопротивлений звездой

Если соединение трех сопротивлений имеет общий узел и имеет внешний вид трехлучевой звезды, то такое соединение сопротивлений называется звездой.

Расчет результирующего сопротивления при последовательно-параллельном соединении

Последовательно-параллельное,
или смешанное, соединение представляет собой сложное соединение трех и
более сопротивлений.
Результирующее сопротивление при смешанном соединении рассчитывается
поэтапно с применением формул расчета сопротивлений при последовательном
и параллельном соединениях. Рассчитать последовательно-параллельное соединение трех сопротивлений по схеме на рисунке. Сначала заменим параллельно соединенные сопротивления r2 и r3 результирующим сопротивление …

Понятия и формулы

Последовательно-параллельное, или смешанное, соединение представляет собой сложное соединение трех и более сопротивлений. Результирующее сопротивление при смешанном соединении рассчитывается поэтапно с применением формул расчета сопротивлений при последовательном и параллельном соединениях.

Примеры

1. Рассчитать последовательно-параллельное соединение трех сопротивлений по схеме на рис. 1.

Сначала заменим параллельно соединенные сопротивления r2 и r3 результирующим сопротивлением r(2-3):

r(2-3)=(r2r3)/(r2+r3 )=(1020)/30=6,6 Ом.

Результирующее сопротивление всей схемы r=r1+r(2-3)=5+6,6=11,6 Ом.

Рис. 1.

2. Какой ток протекает по цепи (рис. 2) в случаях разомкнутого и замкнутого рубильника P? Как изменяется напряжение на сопротивлении r2 в обоих случаях?

Рис. 2.

а) Рубильник разомкнут. Результирующее сопротивление последовательно включенных сопротивлений r1 и r2

r(1-2)=r1+r2=25 Ом.

Ток I(1-2)=U/r(1-2) =100/25=4 А.

Падение напряжения на сопротивлении r2

U2=I(1-2)r2=45=20 В.

б) Рубильник замкнут. Результирующее сопротивление параллельно включенных сопротивлений r1 и r3

r(1-3)=(r1r3)/(r1+r3 )=(2010)/(20+10)=200/30=6,6 Ом.

Общее сопротивление всей схемы r=r(1-3)+r2=6,6+5=11,6 Ом.

Ток I=U/r=100/11,6=8,62 А.

Падение напряжения на сопротивлении r2 в этом случае равно: U2=Ir2=8,625=43,25 В.

Во втором случае ток увеличился в результате подключения параллельного сопротивления R3. Больший ток создает большее падение напряжения на сопротивлении r2.

3. Каким должно быть добавочное сопротивление rд, чтобы две параллельно соединенные лампы на напряжение 120 В и ток 0,2 А могли быть включены в сеть напряжением U=220 В (рис. 3)?

Рис.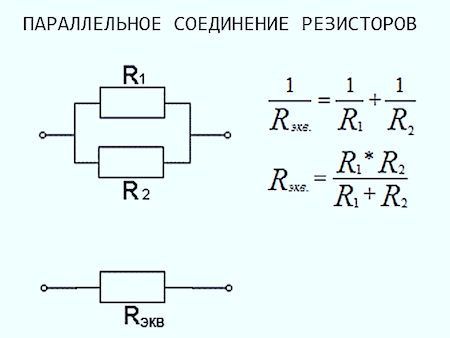 3.

Напряжение на лампах должно быть равно 120 В. Остальное напряжение (100 В) падает на дополнительном сопротивлении rд. Через сопротивление rд проходит ток двух ламп I=0,4 А.

По закону Ома rд=Uд/I=100/0,4=250 Ом.

4. Электронные лампы с напряжением накала 1,2 В и током накала 0,025 и 0,05 А подключены последовательно к источнику постоянного тока напряжением 4,5 В. Какими должны быть добавочное сопротивление rд и параллельное сопротивление (шунт) к лампе, имеющей меньший ток накала (рис. 4)?

Рис. 4.

Сопротивления в схеме должны быть подобраны так, чтобы протекал ток накала второй лампы I=0,05 А. Напряжение на нитях накаливания электронных ламп будет равно 1,2+1,2=2,4 В. Вычтя эту величину из напряжения батареи, получим величину падения напряжения на добавочном сопротивлении rд: Uд=4,5-2,4=2,1 В.

10.12.2016 Без рубрики Нет комментариев

Видео с вопросом: Расчет сопротивления в параллельной цепи

Стенограмма видео

Из приведенной ниже схемы, если показание амперметра три ампера, рассчитайте 𝑅. (A) Девять Ом, (B) три Ом, (C) четыре ома, (D) два ома.

На принципиальной схеме мы Дана ячейка, которая обеспечивает разность потенциалов 18 вольт на схема. Амперметр подключается для измерения ток в цепи. Это дает чтение трех ампер, значит, через часть цепь, содержащая амперметр. Однако, поскольку имеется два резисторы, соединенные параллельно в этой цепи, ток через каждый из параллельные пути будут иметь значение, отличное от трех ампер.

Итак, для расчета сопротивления 𝑅, мы можем заменить два резистора параллельно одним эквивалентным резистором в серия с сопротивлением 𝑅 общ. Делая эту замену, наш эквивалентная схема выглядит так. Напомним, что для ряда компоненты вдоль параллельных путей, полное сопротивление 𝑅 total определяется формула один больше 𝑅 итого равно один больше 𝑅 один плюс один больше 𝑅 два плюс один больше 𝑅 три и так далее. Так как у нас есть два резистора в параллельно, это упрощается до уравнения один на 𝑅 всего равно один на 𝑅 один плюс один на 𝑅 два.

Теперь мы можем заменить два значения для наших резисторов и переставить, чтобы получить общее количество 𝑅. Резистор один имеет сопротивление 𝑅 один равен 𝑅, а резистор два имеет сопротивление 𝑅 два равное двум 𝑅. Итак, это означает, что один закончился 𝑅 сумма равна одному больше 𝑅 плюс одному больше двух 𝑅. Мы можем умножить единицу на 𝑅 член с двумя, разделенными на два, так что оба члена в правой части имеют то же самое знаменателя и могут быть сложены вместе. Складывая вместе эти термины, два больше двух 𝑅 плюс один больше двух 𝑅 равно три больше двух 𝑅. У нас есть то, что больше 𝑅 всего равно трем больше двух 𝑅.

Теперь мы можем взять обратное значение обе части этого уравнения, чтобы получить 𝑅 всего.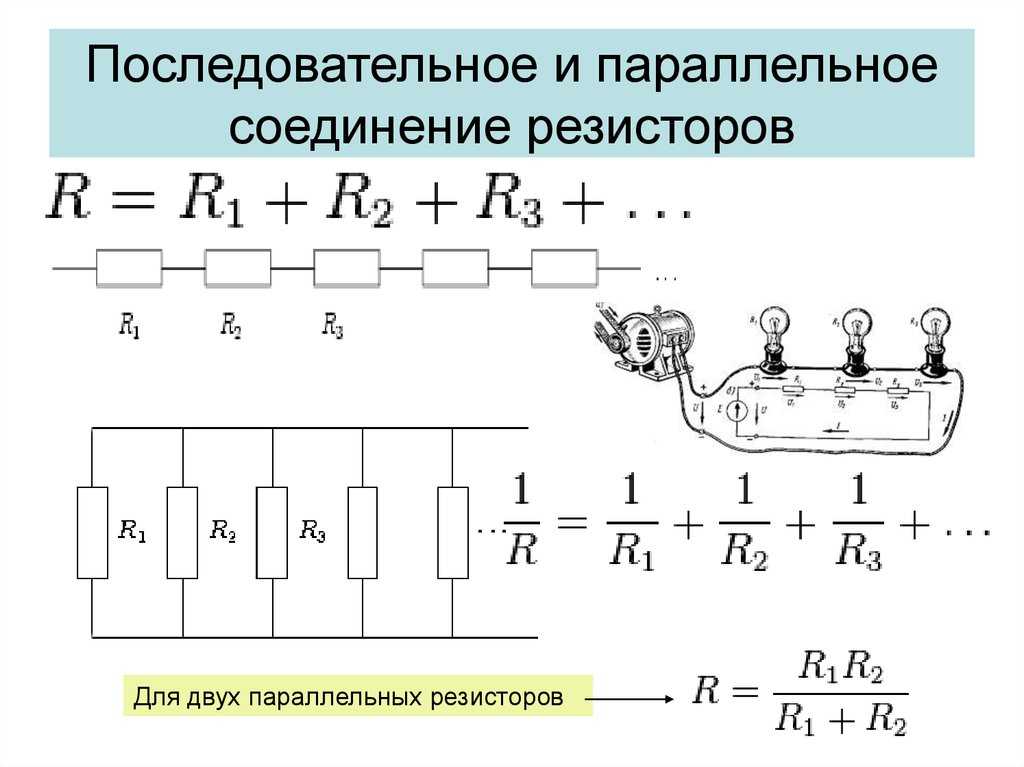 Это дает нам 𝑅 total равно двум 𝑅 разделить на три. Это означает, что у нас сейчас заменил два резистора с сопротивлениями 𝑅 и два 𝑅 параллельно на одинарный резистор сопротивлением два 𝑅 на три. Этот единственный резистор подключен последовательно с ячейкой и амперметром.

Теперь мы можем использовать закон Ома для один резистор, чтобы найти значение 𝑅. Напомним, что закон Ома может быть записывается как 𝑉 равно 𝐼 умноженному на 𝑅, где 𝑉 — разность потенциалов, 𝐼 — ток, а 𝑅 — сопротивление. Подставляя в наши значения, мы имеем 18 вольт равняется трем амперам, умноженным на два 𝑅 на три. Делим обе части на три ампер дает два 𝑅 разделить на три равно 18 вольт разделить на три ампер. 18 вольт более трех ампер работает выходит как шесть Ом. Итак, у нас есть два 𝑅 над тремя равняется шести Ом.