Как записывается закон ома для участка цепи. Закон Ома: формулировка, применение и экспериментальная проверка

Что такое закон Ома и как он связывает напряжение, ток и сопротивление в электрической цепи. Как проверить закон Ома экспериментально. Какие практические применения имеет закон Ома в электротехнике и электронике.

Что такое закон Ома и его математическая формулировка

Закон Ома — это фундаментальный закон электротехники, устанавливающий связь между током, напряжением и сопротивлением в электрической цепи. Он был открыт немецким физиком Георгом Омом в 1826 году и имеет следующую формулировку:

Сила тока в проводнике прямо пропорциональна напряжению на концах проводника и обратно пропорциональна его сопротивлению.

Математически закон Ома выражается формулой:

I = U / R

где:

• I — сила тока, измеряемая в амперах (А)
• U — напряжение, измеряемое в вольтах (В)
• R — сопротивление, измеряемое в омах (Ом)

Из этой формулы также можно выразить напряжение и сопротивление:

U = I * R

R = U / I

Экспериментальная проверка закона Ома

Для экспериментальной проверки закона Ома можно использовать простую электрическую цепь, состоящую из источника питания, резистора с переменным сопротивлением и амперметра. Изменяя сопротивление резистора при постоянном напряжении источника, можно измерять силу тока в цепи.

Типичный порядок действий при проведении эксперимента:

1. Собрать электрическую цепь, включающую источник постоянного напряжения, резистор с переменным сопротивлением и амперметр.
2. Установить постоянное напряжение источника, например 12 В.
3. Изменять сопротивление резистора от 100 Ом до 800 Ом с шагом 100 Ом.
4. Для каждого значения сопротивления измерять силу тока амперметром.
5. Занести полученные данные в таблицу.
6. Построить график зависимости силы тока от сопротивления.
7. Сравнить экспериментальные данные с теоретическими расчетами по формуле закона Ома.

Если закон Ома выполняется, то график зависимости силы тока от сопротивления должен иметь вид гиперболы. При этом произведение силы тока на сопротивление должно быть постоянным и равным напряжению источника.

Применение закона Ома в электротехнике и электронике

Закон Ома имеет множество практических применений в различных областях электротехники и электроники:

• Расчет параметров электрических цепей (токов, напряжений, сопротивлений)
• Проектирование источников питания
• Выбор номиналов резисторов в электронных схемах
• Расчет мощности, выделяемой на элементах цепи
• Анализ работы электрических предохранителей
• Диагностика неисправностей в электрооборудовании
• Расчет потерь в линиях электропередачи

Ограничения применимости закона Ома

Несмотря на широкое применение, закон Ома имеет ряд ограничений:

• Он справедлив только для проводников с линейной вольт-амперной характеристикой (омические проводники).
• Не применим для полупроводниковых приборов (диодов, транзисторов).
• Нарушается при очень сильных токах и напряжениях.
• Не учитывает зависимость сопротивления от температуры.
• Не работает для сверхпроводников.

Поэтому при использовании закона Ома важно учитывать область его применимости и возможные ограничения.

Закон Ома для участка цепи и полной цепи

Различают закон Ома для участка цепи и для полной цепи:

Закон Ома для участка цепи:

I = (U1 — U2) / R

где U1 и U2 — потенциалы начала и конца участка.

Закон Ома для полной цепи:

I = E / (R + r)

где E — ЭДС источника, R — внешнее сопротивление, r — внутреннее сопротивление источника.

Применение закона Ома в цепях постоянного и переменного тока

Закон Ома применим как для цепей постоянного, так и для цепей переменного тока. Однако в цепях переменного тока необходимо учитывать следующие особенности:

• Вместо постоянных значений тока и напряжения используются действующие значения.
• Сопротивление заменяется на полное сопротивление (импеданс), учитывающее активное и реактивное сопротивление.
• Необходимо учитывать сдвиг фаз между током и напряжением.

В этом случае закон Ома записывается в комплексной форме:

I = U / Z

где I и U — комплексные амплитуды тока и напряжения, Z — комплексное сопротивление (импеданс).

Заключение

Закон Ома является одним из основополагающих законов электротехники, устанавливающим связь между основными электрическими величинами — током, напряжением и сопротивлением. Его экспериментальная проверка и практическое применение играют важную роль в понимании принципов работы электрических цепей и электронных устройств. Несмотря на некоторые ограничения, закон Ома остается незаменимым инструментом в расчетах и проектировании электрических и электронных систем.

Лекция № 6 — Закон Ома

        

Георг Симон Ом

    Закон Ома, основанный на опытах, представляет собой в электротехнике основной закон, который устанавливает связь силы электрического тока с сопротивлением и напряжением.

   Закон Ома – полученный экспериментальным путём (эмпирический) закон, который устанавливает связь силы тока в проводнике с напряжением на концах проводника и его сопротивлением, был открыт в 1826 году немецким физиком-экспериментатором Георгом Омом.

   

Закон Ома для участка цепи

 

   Строгая формулировка закона Ома может быть записана так:

      сила тока в проводнике прямо пропорциональна напряжению на его концах (разности потенциалов) и обратно пропорциональна сопротивлению этого проводника.

   Формула закона Ома записывается в следующем виде:

где

I – сила тока в проводнике, единица измерения силы тока — ампер [А];

U – электрическое напряжение (разность потенциалов), единица измерения напряжения- вольт [В];

R – электрическое сопротивление проводника, единица измерения электрического сопротивления — ом [Ом].

    Согласно закону Ома, увеличение напряжения, например, в два раза при фиксированном сопротивлении проводника, приведёт к увеличению силы тока также в два раза

    И напротив, уменьшение тока в два раза при фиксированном напряжении будет означать, что сопротивление увеличилось в два раза.

    Рассмотрим простейший случай применения закона Ома.

    Пусть дан некоторый проводник сопротивлением 3 Ом под напряжением 12 В. Тогда, по определению закона Ома, по данному проводнику течет ток равный:

      Существует мнемоническое правило для запоминания этого закона, которое можно назвать треугольник Ома. Изобразим все три характеристики (напряжение, сила тока и сопротивление) в виде треугольника. В вершине которого находится напряжение, в нижней левой части – сила тока, а в правой – сопротивление.

Правило работы такое: закрываем пальцем величину в треугольнике, которую нужно найти, тогда две оставшиеся дадут верную формулу для поиска закрытой.

Где и когда можно применять закон Ома?

       Закон Ома в упомянутой форме справедлив в достаточно широких пределах для металлов. Он выполняется до тех пор, пока металл не начнет плавиться. Менее широкий диапазон применения у растворов (расплавов) электролитов и в сильно ионизированных газах (плазме).

    Работая с электрическими схемами, иногда требуется определять падение напряжения на определенном элементе. Если это будет резистор с известной величиной сопротивления (она проставляется на корпусе), а также известен проходящий через него ток, узнать напряжение можно с помощью формулы Ома, не подключая вольтметр.

Значение Закона Ома

     Закон Ома определяет силу тока в электрической цепи при заданном напряжении и известном сопротивлении. Он позволяет рассчитать тепловые, химические и магнитные действия тока, так как они зависят от силы тока.

   Закон Ома является чрезвычайно полезным в технике(электронной/электрической), поскольку он касается трех основных электрических величин: тока, напряжения и сопротивления. Он показывает, как эти три величины являются взаимозависимыми на макроскопическом уровне.

    Если бы было можно охарактеризовать закон Ома простыми словами, то наглядно это выглядело бы так:

       Из закона Ома вытекает, что замыкать обычную осветительную сеть проводником малого сопротивления опасно. Сила тока окажется настолько большой, что это может иметь тяжелые последствия.

 

Задача 1.1

  Рассчитать силу тока, проходящую по медному проводу длиной 100 м, площадью поперечного сечения 0,5 мм², если к концам провода приложено напряжение 12 B.

 

  Задачка простая, заключается в нахождении сопротивления медной проволоки с последующим расчетом силы тока по формуле закона Ома для участка цепи. Приступим.

 

Закон Ома для полной цепи 

  Формулировка закона Ома для полной цепи — сила тока прямо пропорциональна сумме ЭДС цепи, и обратно пропорциональна сумме сопротивлений источника и цепи , где E – ЭДС, R- сопротивление цепи, r – внутреннее сопротивление источника.

  Здесь могут возникнуть вопросы. Например, что такое ЭДС?

    Электродвижущая сила — это физическая величина, которая характеризует работу внешних сил в источнике ЭДС. К примеру, в обычной пальчиковой батарейке, ЭДС является химическая реакция, которая заставляет перемещаться заряды от одного полюса к другому. Само слово электродвижущая говорит о том, что эта сила двигает  заряд.

  В каждом источнике присутствует внутреннее сопротивление r, оно зависит от параметров самого источника. В цепи также существует сопротивление R, оно зависит от параметров самой цепи.

  Формулу закона Ома для полной цепи можно представить в другом виде. А именно: ЭДС источника цепи равна сумме падений напряжения на источнике и на внешней цепи.

  

Для закрепления материала, решим две задачи на формулу закона Ома для полной цепи.

Задача 2.1

  Найти силу тока в цепи, если известно что сопротивление цепи 11 Ом, а источник подключенный к ней имеет ЭДС 12 В и внутреннее сопротивление 1 Ом.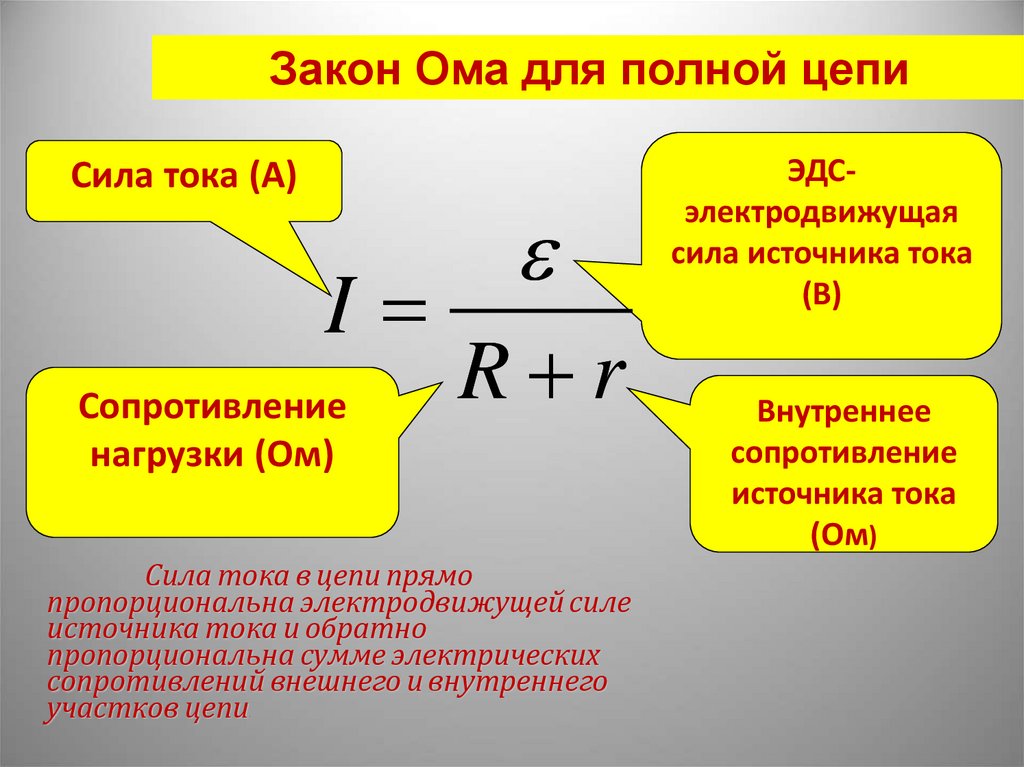

 

  Теперь решим задачу посложнее.

 Задача 2.2

  Источник ЭДС подключен к резистору сопротивлением 10 Ом с помощью медного провода длиной 1 м и площадью поперечного сечения 1 мм². Найти силу тока, зная что ЭДС источника равно 12 В, а внутреннее сопротивление 1,9825 Ом.

Приступим.

 

 

Закон Ома для цепи переменного тока. Мощность

RIR=UR; 1ωCIC=UC; ωLIL=UL.

Указанные выше формулы внешне могут напоминать закон Ома  на участке цепи постоянного тока, но стоит заметить, что в этом случае вместо величин постоянных токов и напряжений на участке цепи, в них входят амплитудные значения напряжений и переменных токов.

Формулы, указанные выше, выражают собой закон Ома для переменного тока, который содержит один из элементов R, L и C.

Определение 1

R – активное сопротивление резистора.

1ωС  – емкостное сопротивление конденсатора.

ωL – индуктивное сопротивление катушки в цепи переменного тока.

Движение переменного тока по участку цепи провоцирует электромагнитное поле выполнять работу, благодаря чему выделяется джоулево тепло.

Определение 2

Мгновенной мощностью в цепи называется произведение мгновенных значений тока и напряжения: p=J·u.

Прикладной интерес у нас вызывает среднее значение мощности за некоторый период переменного тока:

P=Pcα=I0U0cos ωt cos ωt+φ.

В приведенной выше формуле I0 и U0 являются амплитудными значениями тока и напряжения на выбранном участке цепи, а φ – фазовым сдвигом между током и напряжением. Черта же представляет собой символ усреднения. В случае, когда цепь содержит только резистор с сопротивлением R, то фазовый сдвиг φ будет равен нулю: 

PR=IRURcos2ωt=IRUR2=IR2R2.

Действующие значения силы тока и напряжения

Определение 3

По причине необходимости совпадения с уравнением для мощности постоянного тока, нам приходится ввести определения действующих значений силы тока и напряжения: 

IД=l02; UД=U02.

Мощность переменного тока на участке цепи

Определение 4

Средняя величина мощности переменного тока на участке цепи, включающем в себя резистор, равняется: 

PR=IДUД.

Если в цепи содержится лишь конденсатор емкости C, то φ=π2. Отсюда, справедливо следующее выражение:

PC=ICUCcos ωt cosωt+π2=ICUCcos ωt-sin ωt=0.

Таким же способом можно проиллюстрировать, что PL=0.

Исходя из описанного выше получим следующие определение.

Определение 5

Мощность в цепи переменного тока выделяется только на активном сопротивлении, а среднее значение мощности переменного тока на конденсаторе и катушке индуктивности равняется нулю.

Теперь стоит рассмотреть электрическую цепь, включающую последовательно соединенные резистор, конденсатор и катушки, и подключенную к источнику переменного тока некой частоты ω. Следует выделить, что на всех участках цепи, соединенных последовательно, проходит один и тот же ток. Между напряжением внешнего источника e(t) и током J(t) проявляется фазовый сдвиг на определенный угол φ.

Исходя из приведенных выше фактов, мы можем записать:

J(t)=I0cos ωt; e(t)=δ0cos ωt+φ.

Данные формулы мгновенных значений тока и напряжения подходят к построениям, выполненным на векторной диаграмме (рис. 2.3.2).

Рисунок 2.3.2. Гармонические колебания A cos (ωt+φ1), B cos (ωt+φ2) и их суммы C cos (ωt+φ) на векторной диаграмме.

Средняя величина мощности, развиваемой источником переменного тока, может быть найдена из следующего выражения:

P=I0δ0cos ωt cos ωt+φ=I0δ02cos φ=IДδД cos φ.

Исходя из данных векторной диаграммы можно заявить, что UR=δ0·cos φ, следовательно,
P=I0UR2, а вся мощность, которую развивает источник питания, теряется в виде джоулева тепла на резисторе.

В прошлых темах нами было получено выражение, являющееся соотношением амплитуд тока I0 и напряжений δ0 в условиях последовательной RLC-цепи: 

I0=δ0R2+ωL-1ωC2

Определение 6

Z=R2+ωL-1ωC2– это величина, имеющая название полное сопротивление цепи переменного тока.

Определение 7

Связь между амплитудными значениями тока и напряжения в цепи имеет вид:

ZI0=δ0.

Данное выражение представляет собой закон Ома для цепи переменного тока.

Закон Ома в условиях параллельной RLC-цепи

В различных расчетах, связанных с работой над цепями переменного тока, очень важное место занимает понятие полного сопротивления. Для его определения в цепи в большей части случаев практично использовать метод векторных диаграмм. В качестве примера, приведем параллельный подключенный к внешнему источнику переменного тока (рис. 2.4.1) RLC-контур:

Рисунок 2.4.1. Параллельный RLC-контур.

При построении диаграммы важно учесть, что в условиях параллельного соединения напряжение на всех элементах R, C и L идентично и равняется напряжению внешнего источника питания. Ток, текущий в разных ветвях цепи, различается не только по значениям амплитуд, но и по фазовым сдвигам относительно приложенного напряжения. Следовательно, полное сопротивление цепи невозможно вычислить опираясь на законы параллельного соединения цепей постоянного тока.

Векторную диаграмму для параллельного RLC-контура можно увидеть на рис. 2.4.2.

Рисунок 2.4.2. Векторная диаграмма для параллельного RLC-контур.

Исходя из вида диаграммы, следует:

I0=δ01R2+ωL-1ωC2.

Определение 8

Соответственно, полное сопротивление параллельного RLC-контура выражается в виде следующего соотношения:

Z=11R2+ωL-1ωC2.

Определение 9

При параллельном резонансе (ω2=1LC) полное сопротивление цепи принимает свое максимальное значение, которое эквивалентно активному сопротивлению резистора:

Z=Zmax=R.

А значение фазового сдвига φ между током и напряжением при параллельном резонансе равняется нулю.

Учебное пособие по закону Ома | Inspirit

Инструменты для творчества скоро появятся, чтобы вдохновить!

Присоединяйтесь к списку рассылки, чтобы узнать, когда мы запустимся.

Физика

Общая физика

Электрический ток

Учебное пособие по закону Ома

Шринити Махадеван

Чтобы определить закон Ома, он утверждает, что ток, протекающий в проводнике, прямо пропорционален напряжению на проводнике.

ВВЕДЕНИЕ

В современном мире полностью доминирует электричество и наша способность его контролировать. Как часто вы останавливались, чтобы подумать обо всех вещах, которые вы считаете само собой разумеющимися, таких как свет в вашем доме, кондиционер, водонагреватель, тостер и электронные гаджеты? Ничто из этого не работало бы без закона Ома! Этот фундаментальный принцип, открытый около двухсот лет назад, позволил создать машины, которые построили мир, который мы знаем сегодня. Так что же говорит закон Ома? Давай выясним!

Источник

ЧТО ТАКОЕ ЗАКОН ОМА?

Источник

При изучении электрических цепей необходимо знать три важных параметра:

Напряжение (В): Напряжение измеряет разность электрических потенциалов в двух точках. Думайте об этом как об источнике давления в электрической цепи, которая проталкивает электроны (ток) по проводам. Поток электронов выполняет работу, например, зажигает лампочку или запускает двигатель.

Ток (I): Ток измеряет, сколько электронов проходит через данную точку в единицу времени. Думайте о токе как о количестве электронов, протекающих по проводам. Единицей силы тока является ампер (А) или амперы. 1 ампер тока равен 1 кулону (6,24 x 1018) электронов, проходящих через точку за 1 секунду. Это все равно, что измерить, сколько воды вытекает из садового шланга менее чем за 1 секунду.

Сопротивление (R): Проще говоря, сопротивление – это сопротивление провода или проводника току, протекающему в электрической цепи. Медь имеет низкое сопротивление; следовательно, он используется в качестве проводника, тогда как резина обладает таким высоким сопротивлением, что полностью ограничивает протекание тока. Разные материалы имеют разные уровни сопротивления протеканию тока.
Определите закон Ома: этот закон гласит, что ток, протекающий в проводнике, прямо пропорционален напряжению на проводнике. Математически уравнение закона Ома утверждает, что: В ∝ Я Или V=RI

R – константа пропорциональности, которая является сопротивлением. Значение R различно для разных проводников.

Источник

Закон Ома устанавливает зависимость между напряжением, током и сопротивлением. Формулы закона Ома можно использовать для определения тока, протекающего в проводнике, сопротивления или напряжения, если известно какое-либо из двух значений.

НЕКОТОРЫЕ ПРИМЕРЫ ЗАКОНА ОМА:

• Закон Ома лежит в основе работы плавких предохранителей и автоматических выключателей. Предохранители рассчитаны на фиксированный ток и плавятся, когда через них проходит больший ток.
• Дизайн электронных устройств.
• Управление скоростью вращения вентиляторов с помощью потенциометра.
• Функционирование нагревательных элементов.

ЗАКЛЮЧЕНИЕ:

• Закон Ома дает проводнику зависимость между напряжением, током и сопротивлением.
• Напряжение измеряет разность электрических потенциалов в двух точках проводника.
• Ток измеряет, сколько электронов проходит через данную точку в единицу времени.
• Сопротивление — это сопротивление провода или проводника току, протекающему в электрической цепи.

Часто задаваемые вопросы:

1. Что такое закон Ома?

Закон Ома определяет зависимость между напряжением, током и сопротивлением в проводнике. Согласно закону Ома, ток в двух точках проводника прямо пропорционален напряжению в точках.

2. Что такое закон Ома? Напишите формулу?

Ток, текущий в проводнике, прямо пропорционален напряжению на проводнике.

Математически: V=RI

3. Какие три формулы в законе Ома?

V=RI, I=V/R и R=V/I

Мы надеемся, что вам понравился этот урок, и вы узнали что-то интересное о Законе Ома ! Присоединяйтесь к нашему сообществу Discord, чтобы получить ответы на любые вопросы и пообщаться с другими студентами, такими же, как и вы! Не забудьте загрузить наше приложение, чтобы испытать наши веселые классы виртуальной реальности — мы обещаем, это делает учебу намного веселее! 😎

ИСТОЧНИКИ:

1. 20. 10 Закон Ома. https://flexbooks.ck12.org/cbook/ck-12-middle-school-physical-science-flexbook-2.0/section/20.10/primary/lesson/ohms-law-ms-ps/. По состоянию на 28 января 2022 г.
2. Что такое напряжение?. https://www.fluke.com/en-in/learn/blog/electrical/what-is-voltage#:~:text=Voltage%20is%20the%20pressure%20from, измерено%20in%20volts%20(V ). По состоянию на 28 января 2022 г.
3. 20,5 Ток. https://flexbooks.ck12.org/cbook/ck-12-middle-school-physical-science-flexbook-2.0/section/20.5/primary/lesson/electric-current-ms-ps/https://www. fluke.com/en-in/learn/blog/electrical/what-is-resistance. По состоянию на 28 января 2022 г.

Электрические цепи: проверка закона Ома — 2133 слов

Введение

Анализ состоит из трех разделов, где первая часть использовалась для экспериментальной проверки закона Ома. Второй и третий эксперименты были проведены для оценки цепей делителя напряжения и тока. В целом, целью CEN201: Лабораторный эксперимент 1 – Электрические цепи было:

1. Экспериментальная проверка закона Ома путем поддержания постоянного напряжения и изменения сопротивления.
2. Экспериментально проверить формулу делителя напряжения.
3. Для экспериментальной проверки формулы делителя тока.

Теоретическая основа

Закон Ома определяет зависимость между напряжением и током идеального проводника. Эта взаимосвязь была впервые обнаружена немецким физиком Георгом Омом в 1826 году (Engineermaths, nd; University of Kentucky, nd). Закон гласит, что ток, проходящий через электрическую цепь, прямо пропорционален напряжению и обратно пропорционален сопротивлению системы при постоянной температуре (Engineermaths, nd; Technical Books Pdf, nd). Соотношение закона Ома представлено уравнением 1, которое иллюстрирует, что если известны два значения напряжения, тока или сопротивления, можно определить недостающую величину (Технические книги Pdf, n.d). Графическое представление закона Ома называется треугольником закона Ома, показанным на рисунке 1. На рисунке 2 показаны различные комбинации законов Ома, показывающие, как могут быть рассчитаны различные параметры. I = V/R (уравнение 1), где

• I = ток в амперах (А)
• В = напряжение в вольтах (В)
• R = сопротивление в Омах (Ом)

, Различные комбинации законов Ома (Technical Books Pdf, nd).

Закон Ома широко используется в расчетах и ​​проектах электроники. Устройства, которые подчиняются закону Ома, называются омическими, тогда как те, которые не подчиняются, называются неомическими (Университет Кентукки, nd). Резисторы и кабели являются примерами омических устройств, тогда как диоды и транзисторы относятся к категории неомических (Университет Кентукки, nd). Взаимосвязь различных факторов закона Ома может быть установлена ​​экспериментально. В связи с этим первая часть эксперимента заключалась в проверке закона Ома путем определения тока через разное сопротивление при постоянном напряжении. В анализе использовалась простая схема, подобная той, что показана на рис. 3, где график зависимости тока от сопротивления был построен по строгому закону Ома. Второй эксперимент был использован для исследования схемы делителя напряжения и проверки ее формул. Формула делителя напряжения показывает, как напряжение делится между последовательно соединенными резисторами. Рассмотрим схему на рисунке 3, ток, протекающий через цепь, можно рассчитать с помощью уравнения 2. Общее сопротивление цепи будет суммой номиналов резисторов 1 и 2, поскольку они соединены последовательно, как показано в уравнении 2. Напряжение на резисторе 2 можно рассчитать с помощью уравнения 4. Подставив уравнения 2 и 3 в уравнение 4, значение напряжения на резисторе 2 можно рассчитать с помощью выражения 5, которое представляет собой формулу делителя напряжения. Уравнение показывает, что напряжение на последовательных резисторах равно произведению отношения его сопротивления к суммарному значению всех резисторов, умноженному на общее напряжение (Калифорнийский университет, nd). Та же процедура может быть использована для определения напряжения на резисторе 1, которое дано в уравнении 6. Формула делителя напряжения была проверена экспериментально в этом анализе.

Рис. 3. Типичная схема с двумя последовательно соединенными резисторами (Калифорнийский университет, без даты).

I8 = Vs/Req (уравнение 2) Req = R1 + R2 (уравнение 3) V2 = R2I8 (уравнение 4) V2 = R2 / R1+R2 = V8 (уравнение 5) V1 = R1 / R1+R2 = V8 (уравнение 6), где

• i _с = ток, проходящий через цепь
• v _с = напряжение в цепи
• Req = эквивалентное сопротивление сопротивление системы)
• R1 = значение сопротивления резистора 1
• R2 = значение сопротивления резистора 2
• v ₂ = напряжение на резисторе 2
• v ₁ = напряжение на резисторе 1
0 Третий эксперимент 90 был использован для анализа схемы делителя тока и проверки ее формул. Формула делителя тока показывает, как делится ток при прохождении через параллельные резисторы. Рассмотрим схему на рис. 4. Общее сопротивление можно рассчитать по уравнению 7. Напряжение в точках 1 и 2 равно выражению 8. Применив законы Ома к каждому резистору, можно определить ток по уравнению 9.и 10 для резисторов 1 и 2 соответственно (Университет Саймона Фрейзера, nd). Формулы делителя показывают, что ток, проходящий через набор резисторов в параллельной конфигурации, разделяется таким образом, что большее количество течет по пути с меньшим сопротивлением. Если один из резисторов имеет нулевое сопротивление (короткое замыкание), весь ток проходит через другой. Текущая формула делителя была проверена экспериментально в исследовании.
Рис. 4. Типичная схема с двумя резисторами в параллельной конфигурации (Калифорнийский университет, без даты).

Треб. = R1R2 / R1 + R2 (уравнение 7) V12 = I8Req (уравнение 8) I1 = V12/R1 = Треб./R1*I8 = R1 / R1 + R2*I8 (уравнение 9) I2 = V12 / R2 = Req / R2 * I8 = R1 / R1 + R2 * I8 (уравнение 10), где

• i _с = ток, проходящий через цепь
• v _с = напряжение в цепи
• Req = эквивалентное сопротивление (общее сопротивление системы)
• R1 = значение сопротивления резистора 1
• R2 = значение сопротивления резистора 2
• V ₁₂ = напряжение через точки 1 и 2
• I ₁ = ток, проходящий через резистор 1
• I ₂ = текущий прохождение через резистор 2

.

Эксперимент проводился с использованием усовершенствованной электронной экспериментальной платформы, платы электрических сетей и мультиметра, которые представлены на рисунках 5.
, и мультиметр)
1. Усовершенствованная электронная экспериментальная платформа использовалась для питания и обеспечения соединения различных цепей, построенных во время анализа. Он также обеспечивает выход для различных схемных конфигураций.
2. Электрическая сетевая плата представляет собой схемную платформу, которая соединяет различные компоненты цепи, такие как резисторы и кабели.
3. Мультиметр – портативный прибор для измерения тока, напряжения и сопротивления цепи или различных компонентов, используемых в электрической сети.

Процедура

Анализ состоит из трех частей, где первая часть использовалась для проверки закона Ома, а вторая и третья часть экспериментов исследовали цепи делителя напряжения и тока соответственно. Первый эксперимент начался с отключения питания модуля усовершенствованной электронной экспериментальной платформы. Перемычка между розетками 1.6 и 1.7 была подключена. После этого также был подключен лид между 1.10 и 1.12. Мультиметр в режиме постоянного тока был подключен между гнездом 1.13 (плюс) и 1.2 (общий). Схема, рассмотренная для этого эксперимента, представлена ​​на рисунке 6. Значение переменного резистора было установлено на 100 Ом. Был включен модуль питания усовершенствованной электронной экспериментальной платформы. Значение тока было измерено и записано в Таблицу 1. Эксперимент был повторен для различных значений сопротивления (200 Ом, 300 Ом, 400 Ом, 500 Ом, 600 Ом, 700 Ом и 800 Ом).

Рис. 6. Схема по закону Ома, рассматриваемая для данного анализа.

Вторая часть анализа была использована для исследования схемы делителя напряжения и проверки формулы. Эксперимент начался с того, что питание модуля усовершенствованной электронной экспериментальной платформы было отключено. После этого были подключены закорачивающие перемычки между розетками 3.2 и 3.3, а также между розетками 3. 8 и 3.11. Напряжения на резисторах 6 и 7 были рассчитаны с использованием уравнений, аналогичных уравнениям 5 и 6, и записаны в Таблицу 2. Блок питания модуля усовершенствованной электронной экспериментальной платформы был включен, и напряжения на резисторах R6 и R7 были измерены и записаны в Таблицу 2. На Рисунке 7 показана схема делителя напряжения, рассматриваемая при анализе.

Рис. 7. Схема делителя напряжения, рассматриваемая при анализе.

Третий эксперимент был использован для исследования схемы делителя и проверки формулы. Упражнение началось с отключения питания модуля усовершенствованной электронной экспериментальной платформы. Провода между розетками 3.3 и 3.6, 3.5 и 3.13, а также между 3.2 и 3.3 были подключены, как описано в лабораторном руководстве. В анализе использовалась схема делителя тока, представленная на рис. 8. Используя аналогичные уравнения для 9и 10, ток, проходящий через R6 и R8 . После этого был включен источник питания модуля усовершенствованной электронной экспериментальной платформы, а также токи через R6 и R8 с помощью мультиметра в соответствии с подключениями, указанными в лабораторном руководстве. Расчетные и измеренные значения занесены в табл. 3.

Рис. 8. Схема делителя тока, рассматриваемая при анализе.

Результаты

Результаты проверки закона Ома, формулы делителя напряжения и тока были записаны в Таблицы 1, 2 и 3 соответственно. Таблица 1. Результаты эксперимента по проверке Закона Ома

Пример расчета; Учитывая первый эксперимент с сопротивлением 100 Ом. I = V/R

• I = ток
• V = напряжение = 12 В
• R = 100 Ом

I = V/R = 12/100 = 0,12 A = 120 мА Погрешность в процентах = теоретическое значение – экспериментальное значение / теоретическое значение * 100 = 120 – 119,986 / 120 * 100 = 0,012%

Рисунок 9. График зависимости тока от сопротивления.

Таблица 2. Результаты были получены в результате эксперимента с делителем напряжения.

Пример расчета; Расчетное напряжение на R6 V6 = R6 / R7 + R6 * V8 = 1000 / 1000 + 1500 * 12 = 4,8 вольт. Расчетное напряжение на R7 V7 = R7 / R6 + R7 * V8 = 1500 / 1000 + 1500 * 12 = 7,2 В Процентная ошибка = Теоретическое значение — Экспериментальное значение / Теоретическое значение * 100 = 7,200 — 7,257 / 7,200 * 100 = 0,80% для полного напряжения; Процентная ошибка = теоретическое значение — экспериментальное значение / теоретическое значение * 100 = 12,000 — 12,157 / 12,000 * 100 = 1,31% Таблица 3. Результаты, полученные в ходе эксперимента с делителем тока.

Пример расчета; Расчетный ток в R6 I6 = V12 / V6 = 12/100 = 12 мА Погрешность в процентах = теоретическое значение – экспериментальное значение / теоретическое значение * 100 = 12,000 – 12,367 / 12,000 * 100 = 0,031 % Расчетный ток в R7 I8 = V12/R8 = 12 /60 = 17,65 мА Процентная погрешность = Теоретическое значение – Экспериментальное значение / Теоретическое значение * 100 = 17,650 – 18,162 / 17,650 * 100 = 2,90 % Расчетный общий ток; Req = R1R2 / R1+R2 = 1000 * 680 / 1000 + 680 = 404,762 Ом V12 = IsReq = 12 v = Is * 404,762 Ом i _с = 12 В / 404,762 Ом = 29,650 мА Погрешность в процентах = теоретическое значение – экспериментальное значение / теоретическое значение * 100 = 29,650 – 30,503 / 29,650 * 100 = 2,88%

Обсуждение

В первой части эксперимента определяли путем измерения тока через различные сопротивления при постоянном напряжении. Как измеренные, так и расчетные значения показывают, что ток уменьшается с увеличением сопротивления, как показано на рис. 9. Было обнаружено, что между измеренным и расчетным током, проходящим через различные сопротивления, существуют небольшие различия. Измеренный ток оказался выше расчетных значений, что может быть связано с некоторым сопротивлением соединительных кабелей и измерительных устройств, которое предполагается при теоретическом рассмотрении. Второй эксперимент показывает, что напряжение на R7 (7,257 В) было выше по сравнению со значением на R6 (4,9 В).01 вольт). Результаты показывают, что напряжение разделяется в зависимости от значения сопротивления. Чем больше номинал резистора, тем больше напряжение на нем. В третьем эксперименте было обнаружено, что больший ток проходит через R8, который имеет меньшее сопротивление, чем R6. Таким образом, формула делителя тока была проверена экспериментально.

Заключение

Цели анализа были достигнуты, и в первой части эксперимента был сделан вывод, что ток, проходящий через электрическую цепь, обратно пропорционален сопротивлению системы. Формула делителя напряжения была проверена экспериментально, и был сделан вывод, что напряжение делится пропорционально величине сопротивления. В третьем эксперименте было установлено, что ток разделяется таким образом, что большее его количество протекает через путь с меньшим сопротивлением для резисторов, расположенных параллельно в цепи делителя.

Послелабораторные вопросы

• Вопрос 1.1: Сопротивление обратно пропорционально току для источника постоянного напряжения.
• Вопрос 1.2: Ток уменьшится, если напряжение, подаваемое на переменный резистор, уменьшится наполовину, потому что эти два параметра прямо пропорциональны по закону Ома.
• Вопрос 2.1: Напряжение прямо пропорционально номиналу каждого резистора в цепи делителя.
• Вопрос 3.1: В цепи делителя больший ток протекает по пути с меньшим сопротивлением. Через R6 проходит меньший ток по сравнению с R7.

Ссылки

Инженерная математика, (без даты).