Какие электрические цепи называются линейными. Линейные и нелинейные электрические цепи: ключевые отличия и характеристики

Что такое линейные электрические цепи. Какие элементы входят в состав линейных цепей. Чем отличаются нелинейные цепи от линейных. Какие преимущества имеют линейные цепи. В каких случаях используются нелинейные цепи. Как анализировать линейные и нелинейные электрические схемы.

Что такое линейная электрическая цепь

Линейной называется электрическая цепь, параметры которой (сопротивление, индуктивность, емкость) не зависят от величины протекающего тока и приложенного напряжения. В линейных цепях соблюдается принцип суперпозиции — результат воздействия нескольких источников равен сумме результатов воздействия каждого источника в отдельности.

Основные элементы линейных электрических цепей

К линейным элементам относятся:

• Резисторы с постоянным сопротивлением
• Катушки индуктивности без ферромагнитного сердечника
• Конденсаторы с линейной характеристикой
• Идеальные источники ЭДС и тока

Вольт-амперные характеристики линейных элементов представляют собой прямые линии.

Отличия нелинейных цепей от линейных

Нелинейными называются цепи, содержащие хотя бы один нелинейный элемент. Параметры нелинейных элементов зависят от тока и напряжения. Примеры нелинейных элементов:

• Полупроводниковые приборы (диоды, транзисторы)
• Катушки с ферромагнитными сердечниками
• Лампы накаливания
• Варисторы

Вольт-амперные характеристики нелинейных элементов имеют нелинейную форму. В нелинейных цепях не выполняется принцип суперпозиции.

Преимущества линейных электрических цепей

Основные достоинства линейных цепей:

• Простота анализа и расчета
• Возможность использования методов наложения
• Применимость преобразования Лапласа и других математических методов
• Предсказуемое поведение при изменении параметров
• Отсутствие гармонических искажений сигналов

Области применения нелинейных электрических цепей

Несмотря на сложность анализа, нелинейные цепи широко используются в электронике для:

• Преобразования формы сигналов
• Генерации колебаний
• Детектирования сигналов
• Стабилизации напряжения
• Усиления с нелинейными характеристиками
• Создания логических элементов

Методы анализа линейных и нелинейных цепей

Для анализа линейных цепей применяются:

• Методы контурных токов и узловых потенциалов
• Метод наложения
• Метод эквивалентного генератора
• Преобразование Лапласа

Анализ нелинейных цепей выполняется с помощью:

• Графоаналитических методов
• Кусочно-линейной аппроксимации
• Метода гармонической линеаризации
• Численных методов решения нелинейных уравнений

Применение законов Кирхгофа в линейных цепях

Законы Кирхгофа являются основой анализа линейных электрических цепей:

• Первый закон Кирхгофа: алгебраическая сумма токов в узле равна нулю
• Второй закон Кирхгофа: алгебраическая сумма напряжений в замкнутом контуре равна нулю

Эти законы позволяют составить систему уравнений для расчета токов и напряжений в линейных цепях.

Переходные процессы в линейных RLC-цепях

При коммутациях в линейных RLC-цепях возникают переходные процессы. Их анализ выполняется с помощью:

• Классического метода (решение дифференциальных уравнений)
• Операторного метода (с применением преобразования Лапласа)
• Метода переменных состояния

Характер переходного процесса зависит от параметров цепи и может быть апериодическим или колебательным.

Частотные характеристики линейных цепей

Важной характеристикой линейных цепей является их частотный отклик. Для его анализа используются:

• Амплитудно-частотная характеристика (АЧХ)
• Фазо-частотная характеристика (ФЧХ)
• Комплексная частотная характеристика
• Диаграммы Боде

Частотные характеристики позволяют оценить свойства цепей как фильтров, усилителей, корректирующих звеньев.

Моделирование линейных и нелинейных цепей

Для анализа сложных электрических цепей применяется компьютерное моделирование с использованием специализированных программ:

• SPICE и его модификации
• Multisim
• MATLAB/Simulink
• LabVIEW

Эти программы позволяют моделировать как линейные, так и нелинейные цепи, проводить анализ во временной и частотной областях.

Линейные и нелинейные электрические цепи — Мегаобучалка

Ветвь и узел электрической цепи

Электрическая цепь характеризуется совокупностью элементов, из которых она состоит, и способом их соединения. Соединение элементов электрической цепи наглядно отображается ее схемой. В зависимости от особенностей схемы следует применять тот или иной способ расчета электрической цепи. В данном разделе рассмотрим ключевые понятия, которые в дальнейшем будут необходимы для выбора наиболее оптимального и правильного приема решения задач.

Ветвью называется участок электрической цепи, обтекаемый одним и тем же током. Ветвь образуется одним или несколькими последовательно соединенными элементами цепи.

Узел — место соединения трех и более ветвей.

В качестве примера на рисунке изображены схемы двух электрических цепей. Первая из них содержит 6 ветвей и 4 узла. Вторая состоит из 5 ветвей и 3 узлов. В этой схеме обратите внимание на нижний узел. Очень часто допускают ошибку, считая что там 2 узла электрической цепи, мотивируя это наличием на схеме цепи в нижней части 2-х точек соединения проводников. Однако на практике следует считать две и более точки, соединенных между собой проводником, как один узел электрической цепи.

При обходе по соединенным в ветвях цепям можно получить замкнутый контурэлектрической цепи. Каждый контур представляет собой замкнутый путь, проходящий по нескольким ветвям, при этом каждый узел встречается в данном контуре не более одного раза. Ниже приведена электрическая схема, на которой отмечено несколько произвольно выбранных контуров.

Всего для данной цепи можно выделить 6 замкнутых контуров.

Закон Ома

Данный закон очень удобно применять для ветви электрической цепи. Позволяет определить ток ветви при известном напряжении между узлами, к которым данная ветвь подключена. Также позволяет буквально в одно действие рассчитать одноконтурную электрическую цепь.

При применении закона Ома предварительно следует выбрать направление тока в ветви. Выбор направления можно осуществить произвольно. Если при расчете будет получено отрицательное значение, то это значит, что реальное направление тока противоположно выбранному.

Для ветви, состоящей только из резисторов и подключенной к узлам электрической цепиa и b (см. рис.) закон Ома имеет вид:

Соотношение (1.15) написано в предположении, что выбрано направление тока в ветви от узла a к узлу b. Если мы выберем обратное направление, то числитель будет иметь вид: (U_b-U_a). Теперь становится понятно, что если в соотношении (1.15) возникнет ситуация, когда U_b>U_a то получим отрицательное значение тока ветви. Как уже упоминалось выше, это значит, что реальное направление тока противоположно выбранному. Примером практического применения данного частного случая закона Ома при расчетах электрических цепей является соотношение (1. 18) для электрической цепи, изображенной на рисунке.

Для ветви содержащей резисторы и источники электрической энергии закон Ома принимает следующий вид:

Соотношение (1.16) написано в предположении, что предварительно выбрано напавление тока от узла a к узлу b. При расчете алгебраической суммы ЭДС ветви следует знак «+» присваивать тем ЭДС, чье направление совпадает с направлением выбранного тока ветви (направление ЭДС определяется направлением стрелки в обозначении источника электрической энергии). Если направления не совпадают, то ЭДС берется со знаком «-«. На рисунке есть примеры применения данного варианта закона Ома — соотношения (1.17) и (1.19)

Если необходимо рассчитать одноконтурную электрическую цепь с произвольным количеством источников электрической энергии и резисторов, то следует применять соотношение (1.16), имея ввиду что U_a=U_b.

Линейные и нелинейные электрические цепи

Линейной электрической цепью называют такую цепь, все компоненты которой линейны. К линейным компонентам относятся зависимые и независимые идеализированные источники токов и напряжений, резисторы(подчиняющиеся закону Ома), и любые другие компоненты, описываемые линейными дифференциальными уравнениями, наиболее известны электрические конденсаторы и катушки индуктивности. Если цепь содержит отличные от перечисленных компоненты, то она называется нелинейной.

Изображение электрической цепи с помощью условных обозначений называют электрической схемой. Функция зависимости тока, протекающего по двухполюсному компоненту, от напряжения на этом компоненте называется вольт-амперной характеристикой (ВАХ). Часто ВАХ изображают графически в декартовых координатах. При этом по оси абсцисс на графике обычно откладывают напряжение, а по оси ординат — ток.

В частности, омические резисторы, ВАХ которых описывается линейной функцией и на графике ВАХ являются прямыми линиями, называют линейными.

Примерами линейных (как правило, в очень хорошем приближении) цепей являются цепи, содержащие толькорезисторы, конденсаторы и катушки индуктивности без ферромагнитных сердечников.

Некоторые нелинейные цепи можно приближенно описывать как линейные, если изменение приращений токов или напряжений на компоненте мало, при этом нелинейная ВАХ такого компонента заменяется линейной (касательной к ВАХ в рабочей точке). Этот подход называют «линеаризацией». При этом к цепи может быть применён мощный математический аппарат анализа линейных цепей. Примерами таких нелинейных цепей, анализируемых как линейные относятся практически любые электронные устройства, работающие в линейном режиме и содержащие нелинейные активные и пассивные компоненты (усилители, генераторы и др.).

электрическая цепь – это отдельно взятая группа электроприборов (утюги, блоки телевизоры, холодильники и т. д.) совместно с розетками, выключателями, проводами, автоматами и электрической подстанцией (как же без нее получить ток) на данный момент работающих совместно для достижения определенной цели. Ну а вот в зависимости от цели (просмотра любимой передачи, сохранения свежести продуктов или обеспечения стабильности питающих параметров в блоке питания компьютера) электрические цепи подразделяются на простые и сложные, неразветвленные и разветвленные, линейные и нелинейные.

То есть электрическую цепь можно рассматривать как совокупность отдельных электрических устройств, так и совокупность дискретных простейших деталей и связей между ними образующих один из функциональных блоков в электрической схеме какого-то устройства.

Неразветвленныеэлектрические цепи – они же простые – это цепи в которых ток течет не меняя свое значение и по простейшему пути от источника энергии до потребителя. То есть через все элементы этой цепи течет один и тот же ток. Простейшей неразветвленной цепью можно считать цепь освещения одной из комнат в квартире, где используется однорожковая люстра. В данном случае ток течет от источника энергии через автомат, выключатель, лампочку и обратно к источнику энергии.

Разветвленные– это цепи имеющие одно или более ответвленных путей протекания тока. То есть ток начиная свой путь от источника энергии разветвляется на несколько ветвей потребителей, при этом меняя свое значение. Одним из несложных примеров такой цепи является приведенная выше цепь освещения комнаты в квартире, но только с многорожковой люстрой и многоклавишным выключателем.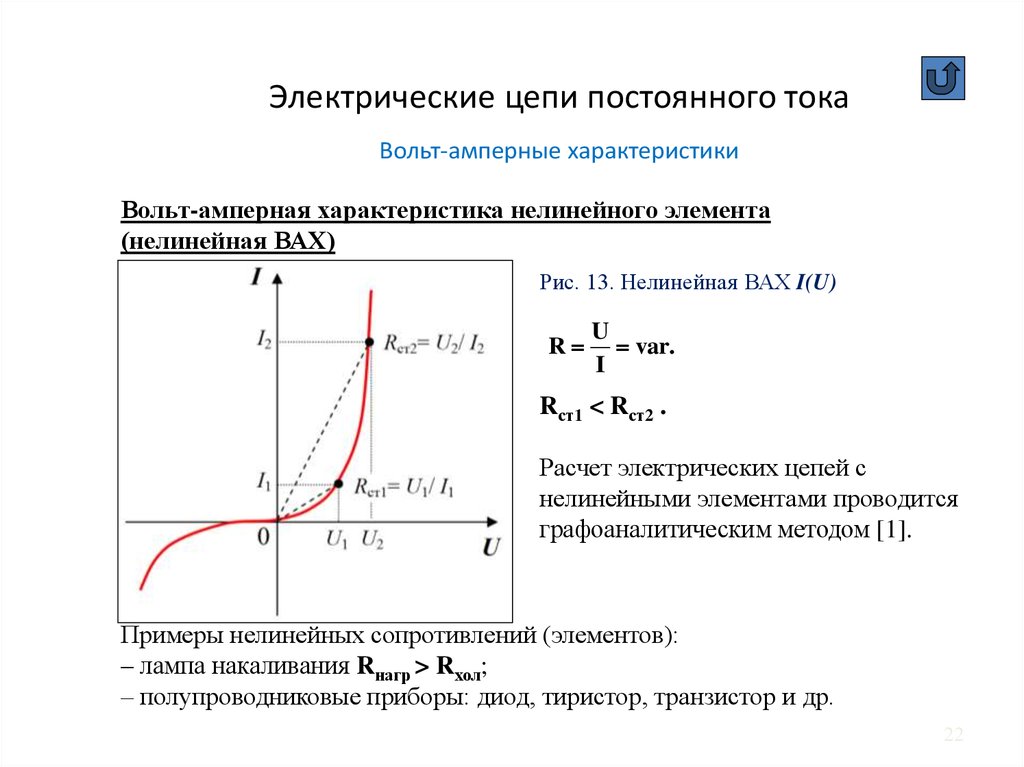 Ток от источника энергии доходит через автомат к многоклавишному выключателю, а дальше разветвляется на несколько ламп люстры, а далее через общий провод обратно к источнику энергии.

Линейной считается такая электрическая цепь, где характеристики всех ее элементов не зависят от величины и характера протекающего тока и приложенного напряжения.

Нелинейной считается цепь содержащая хотя бы один элемент, характеристики которого зависят от протекающего тока и приложенного напряжения.

2. Эквивалентные преобразования в электрических цепях. Определение эквивалентного сопротивления при последовательном, параллельном и смешанном соединении элементов электрических цепей.

При решении задач принято преобразовывать схему, так, чтобы она была как можно проще. Для этого применяют эквивалентные преобразования. Эквивалентными называют такие преобразования части схемы электрической цепи, при которых токи и напряжения в не преобразованной её части остаются неизменными.

Существует четыре основных вида соединения проводников: последовательное, параллельное, смешанное и мостовое.

Последовательное соединение – это такое соединение, при котором сила тока на всем участке цепи одинакова. Ярким примером последовательного соединения является старая елочная гирлянда. Там лампочки подключены последовательно, друг за другом. Теперь представьте, одна лампочка перегорает, цепь нарушена и остальные лампочки гаснут. Выход из строя одного элемента, ведет за собой отключение всех остальных, это является существенным недостатком последовательного соединения.

При последовательном соединении сопротивления элементов суммируются.

Параллельное соединение – это соединение, при котором напряжение на концах участка цепи одинаково. Параллельное соединение наиболее распространено, в основном потому, что все элементы находятся под одним напряжением, сила тока распределена по-разному и при выходе одного из элементов все остальные продолжают свою работу.

При параллельном соединении эквивалентное сопротивление находится как:

В случае двух параллельно соединенных резисторов

 

В случае трех параллельно подключенных резисторов:

Смешанное соединение – соединение, которое является совокупностью последовательных и параллельных соединений. Для нахождения эквивалентного сопротивления нужно, “свернуть” схему поочередным преобразованием параллельных и последовательных участков цепи.

 

Сначала найдем эквивалентное сопротивление для параллельного участка цепи, а затем прибавим к нему оставшееся сопротивление R₃. Следует понимать, что после преобразования эквивалентное сопротивление R₁R₂ и резистор R₃, соединены последовательно.

Итак, остается самое интересное и самое сложное соединение проводников.

Мостовая схема соединения представлена на рисунке ниже.

Для того чтобы свернуть мостовую схему, один из треугольников моста, заменяют эквивалентной звездой.

 

И находят сопротивления R₁, R₂ и R₃.

Затем находят общее эквивалентное сопротивление, учитывая, что резисторы R₃,R₄ и R₅,R₂ соединены между друг другом последовательно, а в парах параллельно.

 

 

Элементы линейных электрических цепей — презентация онлайн

ТЕМА 2.
Элементы линейных электрических
цепей
1. Пассивные элементы
электрической цепи
2. Активные элементы
электрической цепи
3. Внутренние сопротивления
идеальных источников ЭДС и тока
1. Пассивные элементы электрической цепи
Электрическая цепь – это расчетная модель реального
электротехнического устройства. Она строится из
элементов.
Элемент электрической цепи – идеализированный
участок, где генерируется, запасается или преобразуется в
другую форму электрическая энергия. Различают
элементы пассивные и активные.
Элементы, в которых электрическая энергия
запасается или необратимо преобразуется в другую
форму, называются пассивными.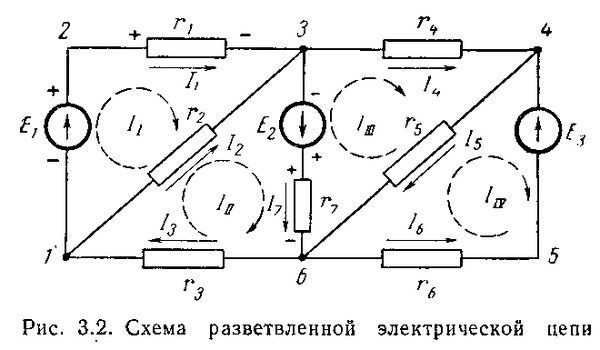
Используемые в теории цепей пассивные элементы
принято делить на три идеализированные группы:
резисторы (сопротивления), индуктивности, емкости.
1. Пассивные элементы электрической цепи
Электрическая цепь (ЭЦ) – это расчетная модель
реального электротехнического устройства. Она строится
из элементов.
Элемент электрической цепи – идеализированный
участок, где генерируется, запасается или преобразуется в
другую форму электрическая энергия. Различают
элементы пассивные и активные.
Элементы, в которых электрическая энергия
запасается или необратимо преобразуется в другую
форму, называются пассивными.
Используемые в теории цепей пассивные элементы
принято делить на три идеализированные группы:
резисторы (сопротивления), индуктивности, емкости.
1. Пассивные элементы электрической цепи
Инженерное воплощение элементов ЭЦ представляют
собой электронные приборы, к которым относят
дискретные элементы и компоненты, а также
интегральные схемы (ИС).
Пассивные дискретные элементы предназначены для
перераспределения электрической энергии:
резисторы, конденсаторы, индуктивности,
трансформаторы, интегральные схемы (ИС) в виде
наборов пассивных элементов.
К активным относят такие компоненты, которые
способны преобразовывать электрические сигналы и
усиливать их мощность. Это диоды, транзисторы,
тиристоры, ИС и т.д.
1. Пассивные элементы электрической цепи
1. Пассивные элементы электрической цепи
1. Пассивные элементы электрической цепи
Резистор – элемент, в котором происходит необратимый процесс
преобразования электрической энергии в тепловую (иногда – в
механическую или химическую).
Резистор – всегда потребитель энергии.
Резистор
При выбранных положительных направлениях ток и напряжение на
резисторе связаны соотношением
Здесь φа, φб – потенциалы точек «а» и «б»; R – сопротивление
резистора.
Если величина R = const (не зависит от протекающего тока либо
приложенного напряжения), то резистор называется линейным. Для
такого резистора при протекании через него переменного тока i(t)
напряжение по форме повторяет ток. Рассмотрим случай, когда
1. Пассивные элементы электрической цепи
В установившемся синусоидальном режиме напряжение и ток в
резисторе по фазе совпадают (одновременно проходят через
ноль, одновременно достигают максимума.
Если ток
То напряжение на резисторе R
Амплитудные значения напряжения и тока в резисторе связаны
соотношением
UmR = RIm
1. Пассивные элементы электрической цепи
Индуктивность– элемент, запасающий электрическую энергию в
магнитном поле. Запасенная энергия при соответствующих условиях
может быть полностью возвращена источнику. Идеальная индуктивность
– только накопитель энергии, свойствами необратимого потребления
энергии не обладает
При выбранных положительных направлениях напряжение и ток в
индуктивности связаны соотношением
т.е. разность потенциалов на индуктивном элементе пропорциональна
быстроте изменения тока во времени.
Величина индуктивности L выступает как коэффициент
пропорциональности между uL и скоростью изменения тока
Если ток в цепи
то
di/dt.
1. Пассивные элементы электрической цепи
Напряжение на индуктивности – гармоническая функция той же частоты, что и
ток. Но фаза синусоидального напряжения на индуктивности превышает
фазу тока на 90°. Кривая напряжения проходит через ноль на четверть
периода раньше.
Амплитуды напряжения и тока в индуктивности связаны соотношением
UmL = ωLIm,
его можно трактовать как закон Ома, причем роль сопротивления выполняет
величина XL = ωL, называемая индуктивным сопротивлением.
Заметим, что наряду с индуктивными свойствами, реальная индуктивность
обладает резистивными потерями. Поэтому простейшая схема замещения
реальной катушки содержит два идеальных элемента: индуктивность и
резистор.
1. Пассивные элементы электрической цепи
Емкость– элемент электрической цепи, запасающий энергию в
электрическом поле. Идеальная емкость только накапливает
энергию и при определенных условиях может вернуть ее
полностью.
При положительных направлениях, напряжение и ток в емкости
связаны соотношением
где С – величина емкости (для линейного элемента С = const).
Продифференцировав обе части последнего уравнения
получим
или
1. Пассивные элементы электрической цепи
Если к обкладкам конденсатора емкостью С приложено переменное
напряжение uc(t) = UmCsin ωt, в его цепи протекает ток
В синусоидальном режиме напряжение и ток в емкости – гармоники одной
частоты, отличающиеся по фазе. Фаза тока в емкости превышает фазу
напряжения на 90°.
Амплитуды напряжения и тока в емкости связаны соотношением
которое также можно трактовать как закон Ома, роль сопротивления
выполняет величина Хс = 1 /(ωС), называемая емкостным сопротивлением.
Заметим, что реальный конденсатор проявляет и резистивные свойства
(главным образом по причине несовершенства изоляции между обкладками).
1. Пассивные элементы электрической цепи
Данные соотношения дают основания полагать, что
Активная мощность выполняет полезную работу и
реализуется только в том случае, когда ток и
напряжение направлены в одном направлении и не
отстают друг от друга, то есть находятся в одной
фазе, что имеет место только на резисторе.
На конденсаторе ток отстает от напряжения на угол φ
= 90°. В результате чего ток и напряжение находятся
в противофазе, поэтому когда ток имеет
максимальное значение напряжение равно нулю, а
произведение этих двух величин дают мощность,
которая в таком случае равна нулю, так как один из
множителей равен нулю.
Следовательно, мощность не потребляется.
Аналогичные процессы протекают и в цепи с
катушкой индуктивности. Разница лишь в том, что на
индуктивности i отстает от u на угол φ = 90°.
Реактивная мощность проявляется только в цепях
переменного тока. Она составляет часть полной
мощности и определяется по формуле:
2. Активные элементы электрической цепи
В теории цепей вводится понятие двух видов
активных элементов, наделенных идеальными
свойствами. Это источники ЭДС и источники
тока (на рис. они изображены в совокупности с
внешней цепью).
Источник ЭДС обеспечивает на своих зажимах напряжение
(разность потенциалов), не зависящее от величины и
направления протекающего через него тока. uаб = φа — φб = Е
Эту величину будем называть интенсивностью источника ЭДС.
Будучи подключенным к внешней цепи, идеальный источник ЭДС
«навязывает», ей свои условия. Поэтому для внешней цепи
должны принять φа — φб = Е.
Если интенсивность источника ЭДС падает до нуля (Е → 0), то
для его внешней цепи это равносильно равенству потенциалов
зажимов «а» и «б» (φа = φб), что соответствует режиму короткого
замыкания – к.з.
2. Активные элементы электрической цепи
Источник тока подает во внешнюю цепь ток i = Iк в направлении,
указанном стрелками, не зависящий от разности потенциалов на
его зажимах. Величину IК будем называть интенсивностью
источника тока.
Таким образом, идеальный источник тока задает ток через все
элементы, включенные с ним последовательно.
В случае, если интенсивность источника тока
падает до нуля Е→0, для внешней цепи это
равносильно обрыву соответствующей ветви, так
как I = IК = 0
Зависимость тока, отдаваемого источником во
внешнюю цепь, от напряжения на его зажимах
называется внешней характеристикой источника.
2. Активные элементы электрической цепи
В общем случае неидеальность реального
источника учитывается при построении его
расчетной модели (эквивалентной схемы
замещения).
Активные
двухполюсники,
изображенные на рис. а, б, обладают
внешними характеристиками такого же вида,
что и прямая 2 (линейный случай).
Действительно, аналитические выражения
внешних характеристик iH (uн) для схем
замещения определяются уравнениями:
Очевидно, для источника с линейной внешней характеристикой (прямая 2)
поэтому для идеальных источников тока и напряжения справедливо:
3. Активные элементы электрической цепи
Если выразить ток ветви «аб» через
напряжение uаб = φб — φа, а также величины
R и Е, очевидно, что точка m разбивает
цепь «аб» на два участка «аm» пассивный, и «mб» — активный.
Для пассивного участка:
Для активного участка Е = φб — φm, или φm=φб — Е.
С учетом последнего получаем
i=(φа – φб + Е)/R=(uaб + Е)/R
Полученное выражение принято называть
обобщенным законом Ома.
В отличие от традиционного закона Ома числитель обобщенного
закона Ома содержит в общем случае алгебраическую сумму
напряжения на участке ua6 и ЭДС Е. Причем эти слагаемые
учитываются с положительными знаками, если их направления
совпадают с положительным направлением тока i .
3. Активные элементы электрической цепи
Электронные цепи, в данной дисциплине,
мы
будем
изучать,
используя
моделирование электронных схем в
программе Multisim 14
3. Активные элементы электрической цепи
Топология электронных цепей
К топологическим элементам относятся ветви, узлы, контуры.
Ветвь – участок, содержащий один или несколько
последовательно включенных элементов (через все элементы
ветви течет один и тот же ток).
Узел – место соединения трех и большего числа ветвей.
Контур – замкнутый путь, проходящий по одной или нескольким
ветвям. Ни один элемент при обходе контура не должен
встречаться дважды.
Независимые контуры – это понятие относится к совокупности
контуров. (каждый следующий контур независим по
отношению к ранее выбранному, если в него входит хотя бы
одна новая ветвь)
3. Активные элементы электрической цепи
Сколько ветвей, узлов и независимых контуров в цепи?
3. Активные элементы электрической цепи
Сколько ветвей, узлов и независимых контуров в цепи?
3. Активные элементы электрической цепи
Если В – число ветвей схемы, У – число узлов. Можно
доказать,что число независимых контуров n = В — (У — 1).
Расчетная модель цепи реального электротехнического
устройства имеет право на существование до тех пор, пока
не нарушаются законы Кирхгофа.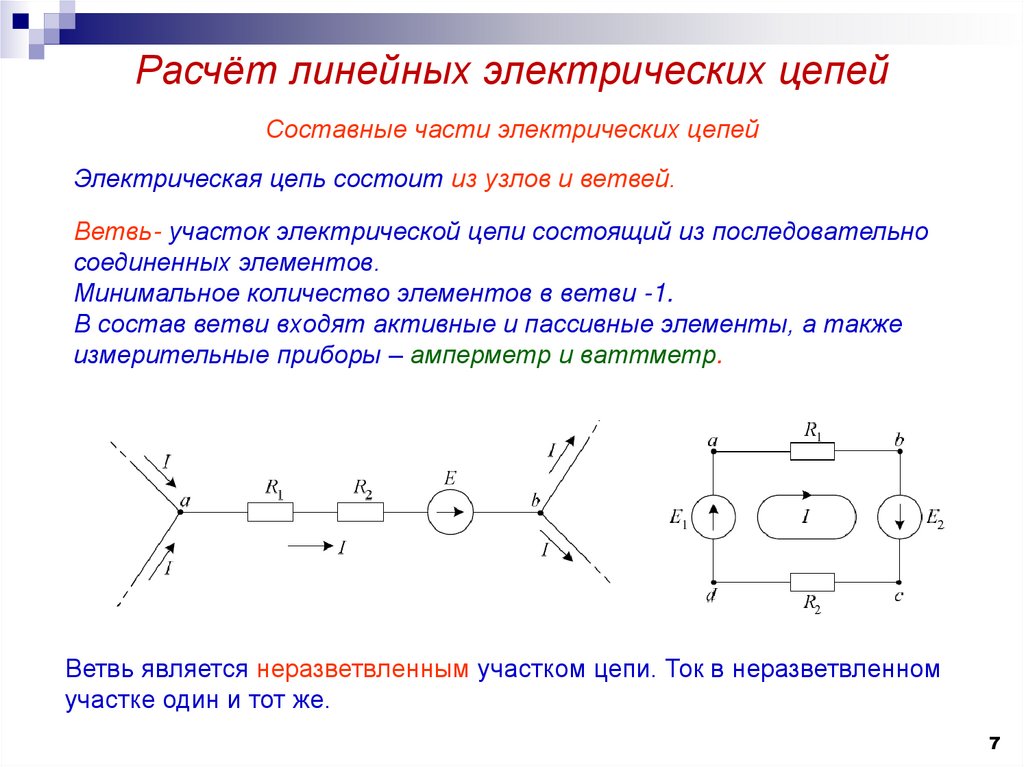 По этой причине
например, недопустим к рассмотрению случай
последовательного включения двух различных по
интенсивности идеальных источников тока (нарушается
первый закон Кирхгофа).
Аналогично мы не можем рассматривать два идеальных
источника ЭДС различной интенсивности, включенных
параллельно (нарушается второй закон Кирхгофа).
Идеальным источником тока (ИТ) называют двухполюсный
элемент, ток которого iо(t) описывается заданной функцией
времени и не зависит от напряжения ИТ.
Идеальным источником напряжения (ИН) называют
двухполюсный элемент, напряжение которого uo(t) является
заданной функцией времени и не зависит от протекающего
через ИН тока
3. Активные элементы электрической цепи
Первый закон Кирхгофа формулируется
следующим образом: алгебраическая
сумма токов в узле электрической цепи
равна нулю.
Подтекающие и оттекающие токи должны
учитываться в алгебраической сумме с
различными знаками. Число
независимых уравнений по первому
закону Кирхгофа на единицу меньше
числа узлов. Например, для узлов 1,2,3
цепи, показанной на рис. при указанных
положительных направлениях токов
уравнения имеют следующий вид:
i1 + i3 – i2 = 0; i6 – i1 – i4 = 0; i4 — i5 — i3 =
0.
Уравнение для четвертого узла
представляет собой линейную
комбинацию записанных трех уравнений
и не является независимым.
Таким образом, для цени, содержащей У
узлов, можно записать У — 1
независимых уравнений по первому
закону Кирхгофа.
3. Активные элементы электрической цепи
Второй закон Кирхгофа формулируется
следующим образом: алгебраическая сумма
ЭДС, действующих в замкнутом контуре
электрической цепи, равна алгебраической
сумме напряжений на всех остальных
элементах контура.
Правило знаков: с положительными знаками
учитывают те ЭДС и те напряжения, которые
направлены согласно с произвольно
выбранным положительным направлением
обхода контура.
Напряжения на пассивных элементах R, L, С в общем случае равны
Они записываются с положительным знаком, если ток в элементе
направлен согласно с обходом контура.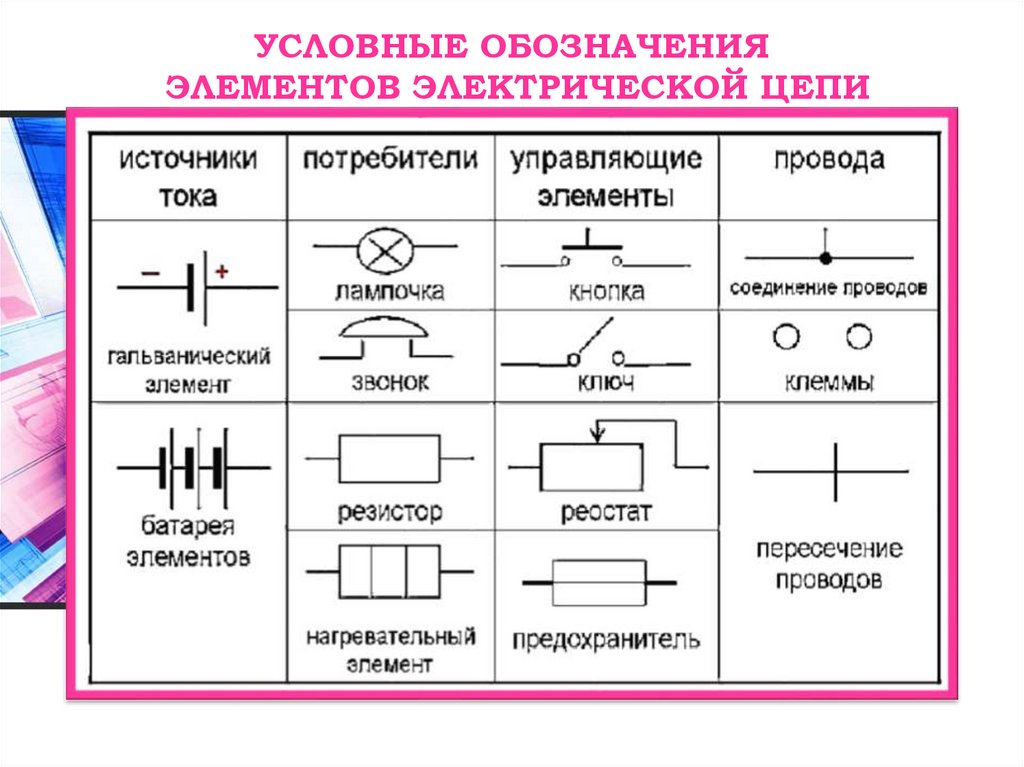
Знак напряжения на источнике тока определяется после выбора
положительного направления для этого напряжения.
Число независимых уравнений по второму
закону Кирхгофа равно числу
независимых контуров. Для контуров I, II,
III при показанном направлении их
обхода уравнения имеют вид
Эти уравнения в
совокупности с
уравнениями 1 закона
представляют собой полную
систему независимых
уравнений по первому и
второму законам Кирхгофа.
Она содержит шесть
уравнений.
В качестве неизвестных в системе уравнений Кирхгофа фигурируют токи в
ветвях, не содержащих источники тока, и напряжения на источниках тока. В
сумме количество названных неизвестных равно числу ветвей схемы.
Следовательно, любая задача по анализу электрической цепи разрешима
однозначно.
Задание на практическое занятие
* ЗАКОН ОМА (по имени немецкого физика Г. Ома (1787-1854)) – единица
электрического сопротивления. Обозначение Ом. Ом
Сопротивление проводника, между концами которого при силе тока 1 А возникает
напряжение 1 В. Определяющее уравнение для электрического сопротивления
R= U / I.
* ЗАКОН ДЖОУЛЯ-ЛЕНЦА (по имени английского физика Дж.П.Джоуля и русского
физика Э.Х.Ленца)
Закон, характеризующий тепловое действие электрического тока.
* ЗАКОНЫ КИРХГОФА (по имени немецкого физика Г.Р.Кирхгофа (1824-1887)) – два
основных закона электрических цепей.
Первый закон устанавливает связь между суммой токов, направленных к узлу
соединения (положительные), и суммой токов, направленных от узла
(отрицательные).
* ЗАКОН ПОЛНОГО ТОКА один из основных законов электромагнитного поля.
Устанавливает взаимосвязь между магнитной силой и величиной тока, проходящего
через поверхность. Намагничивающая сила вдоль контура равна полному току,
проходящему сквозь поверхность, ограниченную этим контуром.
* ЗАКОН ЛЕНЦА — основное правило, позволяющее установить направление
возникающей э.д.с. индукции.
Согласно закону Ленца это направление во всех случаях таково, что ток, созданный
возникшей э. д.с., препятствует тем изменениям, которые вызвали появление э.д.с.
индукции.
* ЗАКОН ЭЛЕКТРОМАГНИТНОЙ ИНДУКЦИИ,
ЭДС электромагнитной индукции в контуре численно равна и противоположна по знаку
скорости изменения магнитного потока сквозь поверхность, ограниченную этим
контуром.

Основная разница между линейной и нелинейной схемой

Содержание

Линейная цепь

Проще говоря, линейная цепь — это электрическая цепь, в которой параметры цепи (сопротивление, индуктивность, емкость, форма волны, частота и т. д.) постоянны. Другими словами, цепь, параметры которой не изменяются в отношении тока и напряжения, называется линейной цепью.

По сути, слово «линейный» буквально означает «вдоль прямой линии». Как следует из названия, линейная цепь означает линейные характеристики между током и напряжением, что означает, что ток, протекающий через цепь, прямо пропорционален приложенному напряжению.

Если мы увеличим приложенное напряжение, то ток, протекающий по цепи, также увеличится, и наоборот. Если мы нарисуем кривую выходной характеристики цепи между током и напряжением, она будет выглядеть как прямая линия (диагональ), как показано на рис. (1).

Обратитесь к закону Ома, где мы признаем, что:

«Если приложенное напряжение увеличивается, то ток также увеличивается (при неизменном сопротивлении)».

Но это не всегда так. Вот почему мы используем P=VxI вместо V=IxR (в Transformer)

Другими словами,

В линейной схеме выходной отклик схемы прямо пропорционален входному. Простое объяснение приведенного выше утверждения:

в электрической цепи, в которой приложенное синусоидальное напряжение с частотой «f», выходной сигнал (ток через компонент или напряжение между двумя точками) этой цепи также является синусоидальным с частотой «f ».

 Нажмите, чтобы увеличить изображение

Линейная цепь и ее характеристическая кривая показаны на рис. (1) ниже.

Примеры линейных цепей и линейных элементов

• Резистивные и резистивные цепи
• Катушка индуктивности и индуктивные цепи
• Конденсатор и емкостные схемы

Нелинейная цепь

Нелинейная цепь представляет собой электрическую цепь, параметры которой варьируются в зависимости от тока и напряжения. Другими словами, электрическая цепь, в которой параметры цепи (сопротивление, индуктивность, емкость, форма волны, частота и т. д.) непостоянны, называется нелинейной цепью.

Если мы нарисуем кривую выходной характеристики цепи между током и напряжением, она будет выглядеть как кривая или изогнутая линия, как показано на рис. (2).

 Нажмите, чтобы увеличить изображение

 

Нелинейная цепь и ее характеристическая кривая показаны на рис. (2) ниже.

Примеры нелинейных схем и нелинейных элементов

• Диод
• Транзистор
• Трансформатор
• Железное ядро ​​
• дроссель (при насыщении сердечника)
• и любая схема, состоящая исключительно из идеальных диодов
• Транзистор
• Трансформатор
• и индуктор с железным сердечником называется нелинейной схемой.

Решение линейных и нелинейных цепей

Решение нелинейных схем немного сложнее, чем линейных схем. Линейную схему можно решить с помощью простых методов и научного калькулятора. При решении нелинейных схем требуется много данных и информации.

Но в настоящее время, благодаря агрессивным технологическим изменениям и модернизации, мы можем очень легко моделировать и анализировать с выходными кривыми как линейные, так и нелинейные схемы с помощью инструментов моделирования цепей, таких как PSpice, MATLAB, Multisim и т. д.

Вы также можете читать:

• Разница между нейтралью, землей и землей
• Разница между сопротивлением постоянному и переменному току и как ее рассчитать
• Разница между односторонними и двусторонними цепями и элементами
• Разница между активными и пассивными компонентами
• Отличие ч/б Электротехника и электроника

Показать полную статью

Связанные статьи

Кнопка «Вернуться к началу»

Что такое линейный компонент в цепи

Линейные электрические цепи и элементы линейных цепей — это такие, в которых сопротивление, емкость и индуктивность не зависят от величины и направления тока или напряжения.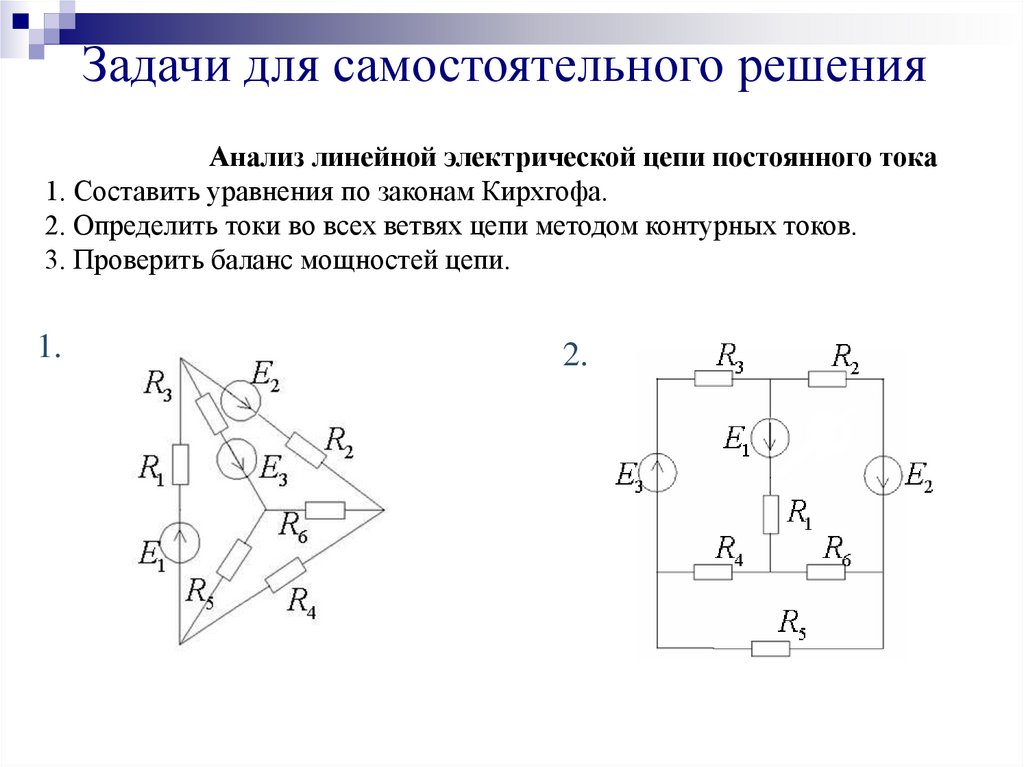

Напряжение и ток определяются линейными алгебраическими или дифференциальными уравнениями.

Например, если r не зависит от тока i или напряжения u , то закон Ома является линейной функцией. То же самое, если емкость C и индуктивность L не зависят от тока i или напряжения u , они определяются линейными дифференциальными уравнениями. Что касается линейных источников и источников напряжения, то источник тока является линейным, когда ток не зависит от падения напряжения на источнике тока; источник напряжения является линейным, если его ЭДС не зависит от тока, протекающего через источник.

К сожалению, настоящие полупроводниковые компоненты не являются линейными устройствами. При протекании тока по проводнику он нагревается, и его сопротивление изменяется. При изменении тока в индукторе с ферромагнитным сердечником изменяется его индуктивность. В зависимости от изолятора его изоляция изменяется в зависимости от заряда, а это означает, что изоляция конденсатора изменяется в зависимости от протекающего тока.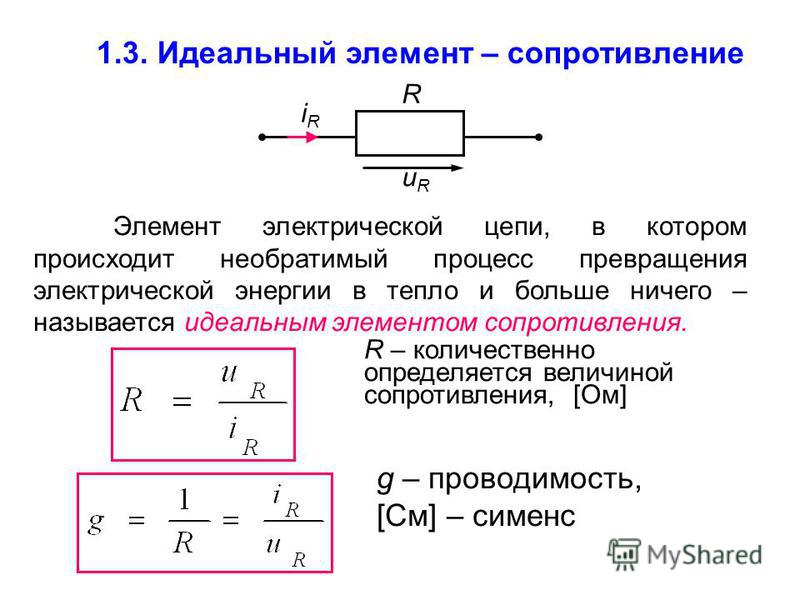

Если в конкретном рабочем диапазоне электронных компонентов ток и напряжение сохраняют свою линейность, они считаются линейными. Линейные цепи легче рассчитать, поэтому, если линейные законы применимы к цепи с некоторой надлежащей близостью, цепи считаются линейными.

В большинстве отделов электронной техники ток и напряжение в цепи называются управляющими сигналами, а ток и напряжение, возникающие в цепи, — выходными сигналами.

В линейной цепи действуют два принципа – принцип наложения и пропорциональности сигналов. Принцип наложения сигналов гласит, что если управляющие сигналы, формируемые в схеме fin1(t) и fin2(t), соответствуют выходным сигналам fout1(t) и fout2(t), то для управляющих сигналов fin1(t)+fin2(t ) соответствует выходному сигналу fout1(t)+fout2(t). Принцип пропорциональности сигналов гласит, что управляющему сигналу Afin(t) соответствует выходной сигнал Afout(t).

Электрическая сеть — графическое изображение электрической цепи. Он показывает, как электрические элементы соединяются друг с другом.