Какое соединение элементов называется последовательным – Какое соединение проводников называется параллельным Какое соединение элементов называется последовательным – Какое соединение проводников называется параллельным Какое соединение проводников называется параллельным Содержание. Последовательное и параллельное соединение проводников: особенности, формулы, применение — Производство и поставка электростанций, Бензиновые и дизельные генераторы от 1 до 100 кВт. Мини ТЭЦ на базе двигателя Стирлинга.

Какие бывают виды соединения проводников в электрической цепи. Каковы основные характеристики последовательного соединения. Каковы особенности параллельного соединения проводников. Как рассчитать общее сопротивление и силу тока при различных соединениях. Где применяются последовательное и параллельное соединения на практике.

Содержание

Виды соединений проводников в электрических цепях

В электротехнике выделяют три основных способа соединения проводников и элементов электрической цепи:

Последовательное соединение
Параллельное соединение
Смешанное (последовательно-параллельное) соединение

Каждый вид соединения имеет свои особенности и характеристики, которые необходимо учитывать при расчете и проектировании электрических схем. Рассмотрим подробнее последовательное и параллельное соединения проводников.

Особенности последовательного соединения проводников

При последовательном соединении проводники подключаются один за другим, образуя единую неразветвленную цепь. Основные характеристики такого соединения:

Сила тока одинакова во всех элементах цепи
Общее напряжение равно сумме напряжений на отдельных участках
Общее сопротивление цепи равно сумме сопротивлений всех элементов

Как рассчитать общее сопротивление при последовательном соединении проводников? Для этого используется формула:

R = R1 + R2 + R3 + … + Rn

где R — общее сопротивление цепи, R1, R2, R3 и т.д. — сопротивления отдельных проводников.

Характеристики параллельного соединения проводников

При параллельном соединении все проводники подключаются к одним и тем же точкам цепи. Особенности такого соединения:

Напряжение одинаково на всех параллельных участках
Общий ток равен сумме токов в отдельных ветвях
Общее сопротивление цепи меньше сопротивления любого из параллельно соединенных проводников

Формула для расчета общего сопротивления при параллельном соединении:

1/R = 1/R1 + 1/R2 + 1/R3 + … + 1/Rn

где R — общее сопротивление, R1, R2, R3 и т.д. — сопротивления параллельных ветвей.

Расчет силы тока при различных соединениях

Как определить силу тока в цепи с последовательным и параллельным соединением проводников?

При последовательном соединении сила тока одинакова во всех элементах и рассчитывается по закону Ома:

I = U / R

где U — общее напряжение в цепи, R — общее сопротивление.

При параллельном соединении общий ток равен сумме токов в отдельных ветвях:

I = I1 + I2 + I3 + … + In

Ток в каждой ветви можно рассчитать по закону Ома, зная напряжение и сопротивление этой ветви.

Применение последовательного соединения на практике

Где используется последовательное соединение проводников? Основные области применения:

Елочные гирлянды

Предохранители в электрических цепях
Добавочные сопротивления в электроизмерительных приборах
Реостаты для регулировки силы тока

Последовательное соединение позволяет увеличить общее сопротивление цепи и уменьшить силу тока. Однако при выходе из строя одного элемента прерывается вся цепь.

Использование параллельного соединения в электротехнике

Параллельное соединение проводников широко применяется в следующих случаях:

Подключение бытовых электроприборов к сети
Соединение аккумуляторов в батареи
Подключение измерительных приборов
Схемы электроснабжения зданий

Преимущество параллельного соединения в том, что при выходе из строя одного элемента остальные продолжают работать. Кроме того, такое соединение позволяет уменьшить общее сопротивление цепи.

Как выбрать оптимальный вид соединения проводников?

При проектировании электрических цепей важно правильно выбрать способ соединения элементов. Какие факторы нужно учитывать?

Требуемые значения силы тока и напряжения
Необходимое общее сопротивление цепи
Надежность работы схемы
Возможность регулировки параметров
Удобство подключения и обслуживания

В сложных схемах часто используется смешанное соединение, сочетающее последовательные и параллельные участки. Это позволяет оптимизировать работу электрической цепи под конкретные задачи.

Сравнение последовательного и параллельного соединений

Чем отличаются последовательное и параллельное соединения проводников? Сравним их основные характеристики:

Параметр	Последовательное соединение	Параллельное соединение
Сила тока	Одинакова во всех элементах	Равна сумме токов в ветвях
Напряжение	Сумма напряжений на элементах	Одинаково на всех ветвях
Сопротивление	Увеличивается	Уменьшается
Надежность	Низкая	Высокая

Как видно из таблицы, каждый вид соединения имеет свои преимущества и недостатки. Выбор зависит от конкретных требований к электрической цепи.

Решение задач на соединение проводников

При решении задач на последовательное и параллельное соединение проводников рекомендуется придерживаться следующего алгоритма:

Определить вид соединения по схеме
Записать формулы для расчета общего сопротивления
Найти общее сопротивление цепи
Рассчитать силу тока по закону Ома
Определить напряжение на отдельных участках

Рассмотрим пример задачи: Три резистора с сопротивлениями 2 Ом, 3 Ом и 6 Ом соединены параллельно. Определите общее сопротивление цепи.

Решение:
1) Используем формулу для параллельного соединения:
1/R = 1/R1 + 1/R2 + 1/R3
2) Подставляем значения:
1/R = 1/2 + 1/3 + 1/6 = 6/12 + 4/12 + 2/12 = 12/12 = 1

3) Получаем: R = 1 Ом

Ответ: Общее сопротивление цепи равно 1 Ом.

Заключение

Последовательное и параллельное соединения проводников — это базовые способы построения электрических цепей. Понимание их особенностей и умение производить расчеты необходимо для успешного изучения электротехники и проектирования электронных устройств. На практике часто используются комбинированные схемы, сочетающие оба вида соединений для достижения оптимальных характеристик электрической цепи.

Какое соединение проводников называется параллельным

Содержание:

Какое соединение называется последовательным
Какое соединение называется параллельным
Видео

Создание электрического тока и его дальнейшая передача потребителям осуществляется с помощью специального комплекса устройств, известного под общим названием электрической цепи. Данные системы связаны между собой разными способами, поэтому часто возникает вопрос, какое соединение проводников называется параллельным, а какое – последовательным. Оба варианта имеют принципиальные отличия, благодаря которым каждая электрическая цепь приобретает собственные индивидуальные свойства. Использование таких соединений на различных участках, позволяет выполнять необходимые регулировки таких значений, как сила тока и напряжение. Смешанные типы соединений успешно применяются в электрических и радиоэлектронных схемах.

Какое соединение называется последовательным

Свойства последовательного соединения лучше всего рассматривать в совокупности с резисторами, у которых может быть одинаковое или разное сопротивление. Последовательным называется такой вид соединения, когда все элементы поочередно соединяются между собой. То есть начало одного резистора подключено к концу второго, а начало второго соединяется к концом третьего и т.д. Правильные расчеты последовательного соединения влияют на количество и характеристики приборов, подключаемых к такой цепи.

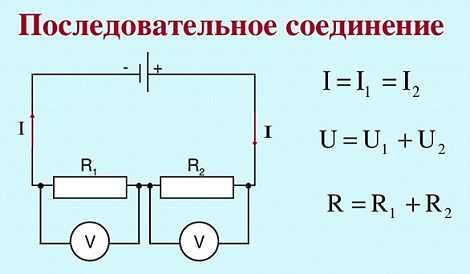
В качестве примера будет рассматриваться электрическая цепь, состоящая из двух потребителей – ламп, обладающих сопротивлением, а также источника питания и ключа для включения и выключения питания.

На схеме № 1 вместо резисторов были включены две лампочки с собственным сопротивлением. Кроме того, в цепь последовательно с нагрузкой включен амперметр, измеряющий силу тока, а к каждой лампе подключены вольтметры для замеров напряжения или падения напряжения. Источник питания обеспечивает цепь электроэнергией, а ключ служит для замыкания и размыкания цепи.

На обоих схемах амперметр расположен в разных местах. Однако при замыкании ключа, его показания остаются одинаковыми в том и другом случае. Следовательно, сила тока в лампах №№ 1 и 2 будет одинаковой. Точно таким же будет и значение тока, протекающего во всей цепи: I = I1 = I2.

После замеров силы тока на каждой лампе измеряется напряжение. Затем этот параметр определяется сразу на двух лампах. В результате измерений общее напряжение, определенное с помощью вольтметра, составит сумму напряжений каждой из ламп: U = U1 + U2. Основным условием данного эксперимента является наличие одинаковых ламп, вольтметров и источников тока.

В завершение остается исследовать характеристики общего сопротивления. На основании полученных результатов измерений силы тока и напряжения, можно сделать следующий вывод: Rобщ = R1 + R2. То есть было фактически было получено эквивалентное сопротивление цепи, в которой все проводники, соединенные последовательно, могут быть заменены аналогичным проводником с таким же сопротивлением. В рассматриваемом случае оно будет равно сопротивлению обеих ламп, имеющихся в цепи.

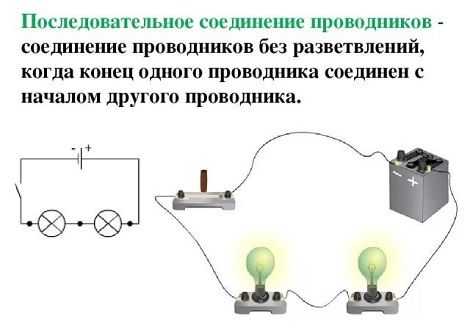
Формула эквивалентного сопротивления была получена на основании закона Ома: I = U/R. После этого получить нужный результат было уже несложно: R = U/I. Как уже было установлено, общее напряжение представляет собой сумму напряжений каждой лампы. При одинаковой силе тока на всех участках, получается следующее равенство: U/I = U1/I1 + U2/I2. В этой формуле каждая дробь является соответствующим сопротивлением – обеих нагрузок и общего. Значение общего сопротивления всегда превышает сопротивление любой из нагрузок, включенных в последовательную цепь.

Следует помнить, что в случае перегорания хотя бы одного прибора, включенного в такую цепь, она разомкнется и все остальные устройства тоже перестанут работать. Наиболее ярким примером служит елочная гирлянда, состоящая из большого количества, последовательно соединенных лампочек.

Какое соединение называется параллельным

Не менее распространенным способом, широко применяющимся в различных схемах, является параллельное соединение проводников. Его также можно рассмотреть на примере двух ламп, с участием измерительных приборов, источника питания и выключателя.

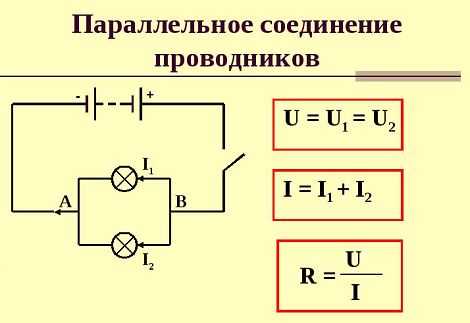
Данный вид соединения предполагает наличие двух точек А и В, объединяющих начала и концы проводников, независимо от их количества. Поэтому общее напряжение цепи и напряжения на концах всех подключенных проводников будет одинаковым: U = U1 = U2. В связи с этим способ параллельного соединения эффективно используется во многих областях. Изготовление потребителей осуществляется из расчета на их работу при одинаковом напряжении. Если выключается какой-либо прибор, то все остальные подключенные устройства продолжают работать, поскольку ток в цепи не прерывается, и она остается в замкнутом состоянии.

Что касается силы тока, то при использовании параллельного соединения, общий ток разветвляется в точке А, после чего, пройдя по отдельным проводникам, вновь соединяется в точке В. Поэтому общая сила тока в неразветвленных частях цепи составляет сумму сил токов в каждом проводнике, соединенном параллельно: I = I1 + I2. При использовании схемы параллельного соединения поперечное сечение проводника условно увеличивает свою площадь. В связи с этим происходит уменьшение общего сопротивления цепи по сравнению с сопротивлением каждого проводника, включенного в цепь. Таким образом Rобщ = R1/2. Значение общего сопротивления может быть выражено и с помощью другой формулы: 1 / R = 1 / R1 + 1 / R2.

Свойства и характеристики параллельного подключения позволяют одновременно использовать в цепи разные приборы и устройства. Например, электродвигатели могут включаться вместе с нагревательными приборами. В жилых домах все потребители, включаемые параллельно, разбиваются на отдельные группы, в зависимости от своего назначения: осветительные приборы, розетки в комнатах, оборудование кухонь и ванных комнат. Все потребители, которые включаются в домашнюю сеть, должны работать от одного и того же напряжения, равного напряжению этой сети.

electric-220.ru

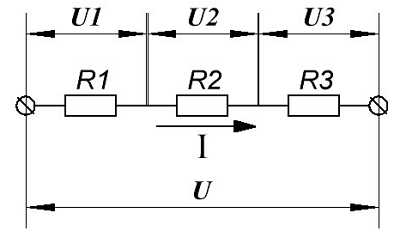
Электрическая цепь с последовательным соединением элементов

Рис. 1.4

Рис. 1.5

Последовательным называют такое соединение элементов цепи, при котором во всех включенных в цепь элементах возникает один и тот же ток I (рис. 1.4).

На основании второго закона Кирхгофа (1.5) общее напряжение U всей цепи равно сумме напряжений на отдельных участках:

U = U₁ + U₂ + U₃ или IR_экв = IR₁ + IR₂ + IR₃,

откуда следует

R_экв = R₁ + R₂ + R₃.

Таким образом, при последовательном соединении элементов цепи общее эквивалентное сопротивление цепи равно арифметической сумме сопротивлений отдельных участков. Следовательно, цепь с любым числом последовательно включенных сопротивлений можно заменить простой цепью с одним эквивалентным сопротивлением R_экв (рис. 1.5). После этого расчет цепи сводится к определению тока I всей цепи по закону Ома

и по вышеприведенным формулам рассчитывают падение напряжений U₁, U₂, U₃ на соответствующих участках электрической цепи (рис. 1.4).

Недостаток последовательного включения элементов заключается в том, что при выходе из строя хотя бы одного элемента, прекращается работа всех остальных элементов цепи.

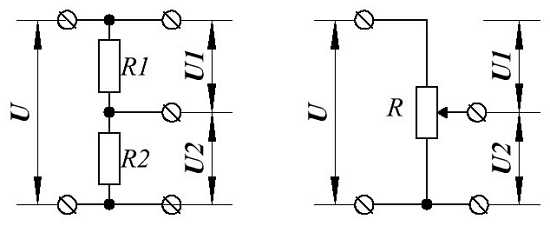
Электрическая цепь с параллельным соединением элементов

Параллельным называют такое соединение, при котором все включенные в цепь потребители электрической энергии, находятся под одним и тем же напряжением (рис. 1.6).

Рис. 1.6

В этом случае они присоединены к двум узлам цепи а и b, и на основании первого закона Кирхгофа можно записать, что общий ток I всей цепи равен алгебраической сумме токов отдельных ветвей:

I = I₁ + I₂ + I₃, т.е.

откуда следует, что

В том случае, когда параллельно включены два сопротивления R₁ и R₂, они заменяются одним эквивалентным сопротивлением

(1.7)

Из соотношения (1.6), следует, что эквивалентная проводимость цепи равна арифметической сумме проводимостей отдельных ветвей:

g_экв = g₁ + g₂ + g₃.

По мере роста числа параллельно включенных потребителей проводимость цепи g_экв возрастает, и наоборот, общее сопротивление R_экв уменьшается.

Напряжения в электрической цепи с параллельно соединенными сопротивлениями (рис. 1.6)

U = IR_экв = I₁R₁ = I₂R₂ = I₃R₃.

Отсюда следует, что

т.е. ток в цепи распределяется между параллельными ветвями обратно пропорционально их сопротивлениям.

По параллельно включенной схеме работают в номинальном режиме потребители любой мощности, рассчитанные на одно и то же напряжение. Причем включение или отключение одного или нескольких потребителей не отражается на работе остальных. Поэтому эта схема является основной схемой подключения потребителей к источнику электрической энергии.

Электрическая цепь со смешанным соединением элементов

Смешанным называется такое соединение, при котором в цепи имеются группы параллельно и последовательно включенных сопротивлений.

Рис. 1.7

Для цепи, представленной на рис. 1.7, расчет эквивалентного сопротивления начинается с конца схемы. Для упрощения расчетов примем, что все сопротивления в этой схеме являются одинаковыми: R₁=R₂=R₃=R₄=R₅=R. Сопротивления R₄ и R₅ включены параллельно, тогда сопротивление участка цепи cd равно:

В этом случае исходную схему (рис. 1.7) можно представить в следующем виде (рис. 1.8):

Рис. 1.8

На схеме (рис. 1.8) сопротивление R₃ и R_cd соединены последовательно, и тогда сопротивление участка цепи ad равно:

Тогда схему (рис. 1.8) можно представить в сокращенном варианте (рис. 1.9):

Рис. 1.9

На схеме (рис. 1.9) сопротивление R₂ и R_ad соединены параллельно, тогда сопротивление участка цепи аb равно

Схему (рис. 1.9) можно представить в упрощенном варианте (рис. 1.10), где сопротивления R₁ и R_ab включены последовательно.

Тогда эквивалентное сопротивление исходной схемы (рис. 1.7) будет равно:

Рис. 1.10

Рис. 1.11

В результате преобразований исходная схема (рис. 1.7) представлена в виде схемы (рис. 1.11) с одним сопротивлением R_экв. Расчет токов и напряжений для всех элементов схемы можно произвести по законам Ома и Кирхгофа.

ЛИНЕЙНЫЕ ЦЕПИ ОДНОФАЗНОГО СИНУСОИДАЛЬНОГО ТОКА.

Получение синусоидальной ЭДС. . Основные характеристики синусоидального тока

Основным преимуществом синусоидальных токов является то, что они позволяют наиболее экономично осуществлять производство, передачу, распределение и использование электрической энергии. Целесообразность их использования обусловлена тем, что коэффициент полезного действия генераторов, электрических двигателей, трансформаторов и линий электропередач в этом случае оказывается наивысшим.

Для получения в линейных цепях синусоидально изменяющихся токов необходимо, чтобы э. д. с. также изменялись по синусоидальному закону. Рассмотрим процесс возникновения синусоидальной ЭДС. Простейшим генератором синусоидальной ЭДС может служить прямоугольная катушка (рамка), равномерно вращающаяся в однородном магнитном поле с угловой скоростью ω (рис. 2.1, б).

Пронизывающий катушку магнитный поток во время вращения катушки abcd наводит (индуцирует) в ней на основании закона электромагнитной индукции ЭДС е. Нагрузку подключают к генератору с помощью щеток 1, прижимающихся к двум контактным кольцам 2, которые, в свою очередь, соединены с катушкой. Значение наведенной в катушке abcd э. д. с. в каждый момент времени пропорционально магнитной индукции В, размеру активной части катушки l = ab + dc и нормальной составляющей скорости перемещения ее относительно поля v_н:

e = Blv_н (2.1)

где В и l — постоянные величины, a v_н — переменная, зависящая от угла α. Выразив скорость v_н через линейную скорость катушки v, получим

e = Blv·sinα (2.2)

В выражении (2.2) произведение Blv = const. Следовательно, э. д. с., индуцируемая в катушке, вращающейся в магнитном поле, является синусоидальной функцией угла α.

Если угол α = π/2, то произведение Blv в формуле (2.2) есть максимальное (амплитудное) значение наведенной э. д. с. E_m = Blv. Поэтому выражение (2.2) можно записать в виде

e = E_msinα (2.3)

Так как α есть угол поворота за время t, то, выразив его через угловую скорость ω, можно записать α = ωt, a формулу (2.3) переписать в виде

e = E_msinωt (2.4)

где е — мгновенное значение э. д. с. в катушке; α = ωt — фаза, характеризующая значение э. д. с. в данный момент времени.

Необходимо отметить, что мгновенную э. д. с. в течение бесконечно малого промежутка времени можно считать величиной постоянной, поэтому для мгновенных значений э. д. с. е, напряжений и и токов i справедливы законы постоянного тока.

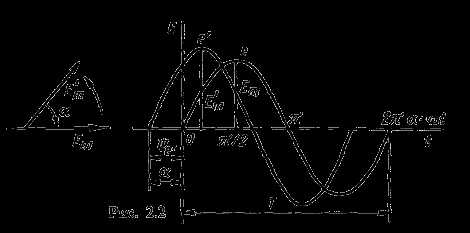
Синусоидальные величины можно графически изображать синусоидами и вращающимися векторами. При изображении их синусоидами на ординате в определенном масштабе откладывают мгновенные значения величин, на абсциссе — время. Если синусоидальную величину изображают вращающимися векторами, то длина вектора в масштабе отражает амплитуду синусоиды, угол, образованный с положительным направлением оси абсцисс, в начальный момент времени равен начальной фазе, а скорость вращения вектора равна угловой частоте. Мгновенные значения синусоидальных величин есть проекции вращающегося вектора на ось ординат. Необходимо отметить, что за положительное направление вращения радиус-вектора принято считать направление вращения против часовой стрелки. На рис. 2.2 построены графики мгновенных значений э. д. с. е и е’.

Если число пар полюсов магнитов p ≠ 1, то за один оборот катушки (см. рис. 2.1) происходит p полных циклов изменения э. д. с. Если угловая частота катушки (ротора) n оборотов в минуту, то период уменьшится в pn раз. Тогда частота э. д. с., т. е. число периодов в секунду,

f = Pn / 60

Из рис. 2.2 видно, что ωТ = 2π, откуда

ω = 2π / T = 2πf (2.5)

Величину ω, пропорциональную частоте f и равную угловой скорости вращения радиус-вектора, называют угловой частотой. Угловую частоту выражают в радианах в секунду (рад/с) или в 1 / с.

Графически изображенные на рис. 2.2 э. д. с. е и е’ можно описать выражениями

e = E_msinωt; e’ = E’_msin(ωt + ψ_e’).

Здесь ωt и ωt + ψ_e’ — фазы, характеризующие значения э. д. с. e и e’ в заданный момент времени; ψ_e’ — начальная фаза, определяющая значение э. д. с. е’ при t = 0. Для э. д. с. е начальная фаза равна нулю (ψ_e = 0). Угол ψ всегда отсчитывают от нулевого значения синусоидальной величины при переходе ее от отрицательных значений к положительным до начала координат (t = 0). При этом положительную начальную фазу ψ (рис. 2.2) откладывают влево от начала координат (в сторону отрицательных значений ωt), а отрицательную фазу — вправо.

Если у двух или нескольких синусоидальных величин, изменяющихся с одинаковой частотой, начала синусоид не совпадают по времени, то они сдвинуты друг относительно друга по фазе, т. е. не совпадают по фазе.

Разность углов φ, равная разности начальных фаз, называют углом сдвига фаз. Сдвиг фаз между одноименными синусоидальными величинами, например между двумя э. д. с. или двумя токами, обозначают α. Угол сдвига фаз между синусоидами тока и напряжения или их максимальными векторами обозначают буквой φ (рис. 2.3).

Когда для синусоидальных величин разность фаз равна ±π, то они противоположны по фазе, если же разность фаз равна ±π/2, то говорят, что они находятся в квадратуре. Если для синусоидальных величин одной частоты начальные фазы одинаковы, то это означает, что они совпадают по фазе.

Синусоидальные напряжение и ток, графики которых представлены на рис. 2.3, описываются следующим образом:

u = U_msin(ωt + ψ_u); i = I_msin(ωt + ψ_i), (2.6)

причем угол сдвига фаз между током и напряжением (см. рис. 2.3) в этом случае φ = ψ_u — ψ_i.

Уравнения (2.6) можно записать иначе:

u = U_msin(ωt + ψ_i + φ); i = I_msin(ωt + ψ_u — φ),

поскольку ψ_u = ψ_i + φ и ψ_i = ψ_u — φ.

Из этих выражений следует, что напряжение опережает по фазе ток на угол φ (или ток отстает по фазе от напряжения на угол φ).

Формы представления синусоидальных электрических величин.

Любая, синусоидально изменяющаяся, электрическая величина (ток, напряжение, ЭДС) может быть представлена в аналитическом, графическом и комплексном видах.

1). Аналитическая форма представления

I = I_m·sin(ω·t + ψ_i), u = U_m·sin(ω·t + ψ_u), e = E_m·sin(ω·t + ψ_e),

где I, u, e – мгновенное значение синусоидального тока, напряжения, ЭДС, т. е. Значения в рассматриваемый момент времени;

I_m, U_m, E_m – амплитуды синусоидального тока, напряжения, ЭДС;

(ω·t + ψ) – фазовый угол, фаза; ω = 2·π/Т – угловая частота, характеризующая скорость изменения фазы;

ψ_i, ψ_u, ψ_e – начальные фазы тока, напряжения, ЭДС отсчитываются от точки перехода синусоидальной функции через нуль к положительному значению до начала отсчета времени (t = 0). Начальная фаза может иметь как положительное так и отрицательное значение.

Графики мгновенных значений тока и напряжения показаны на рис. 2.3

Начальная фаза напряжения сдвинута влево от начала отсчёта и является положительной ψ_u > 0, начальная фаза тока сдвинута вправо от начала отсчёта и является отрицательной ψ_i < 0. Алгебраическая величина, равная разности начальных фаз двух синусоид, называется сдвигом фаз φ. Сдвиг фаз между напряжением и током

φ = ψ_u – ψ_i = ψ_u – ( — ψ_i) = ψ_u + ψ_i.

Применение аналитической формы для расчёта цепей является громоздкой и неудобной.

На практике приходится иметь дело не с мгновенными значениями синусоидальных величин, а с действующими. Все расчёты проводят для действующих значений, в паспортных данных различных электротехнических устройств указаны действующие значения (тока, напряжения), большинство электроизмерительных приборов показывают действующие значения. Действующий ток является эквивалентом постоянного тока, который за одно и то же время выделяет в резисторе такое же количество тепла, как и переменный ток. Действующее значение связано с амплитудным простым соотношением

2). Векторная форма представления синусоидальной электрической величины – это вращающийся в декартовой системе координат вектор с началом в точке 0, длина которого равна амплитуде синусоидальной величины, угол относительно оси х – её начальной фазе, а частота вращения – ω = 2πf. Проекция данного вектора на ось у в любой момент времени определяет мгновенное значение рассматриваемой величины.

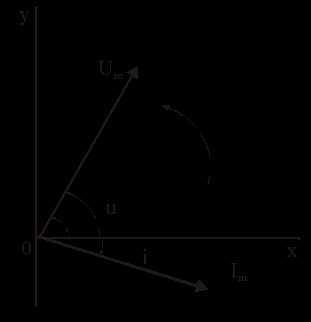Рис. 2.4

Совокупность векторов, изображающих синусоидальные функции, называют векторной диаграммой, рис. 2.4

3). Комплексное представление синусоидальных электрических величин сочетает наглядность векторных диаграмм с проведением точных аналитических расчётов цепей.

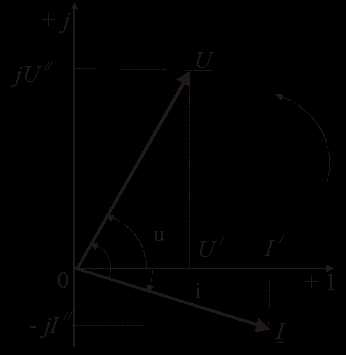Рис. 2.5

Ток и напряжение изобразим в виде векторов на комплексной плоскости, рис.2.5 Ось абсцисс называют осью действительных чисел и обозначают +1, ось ординат называют осью мнимых чисел и обозначают +j. (В некоторых учебниках ось действительных чисел обозначают Re, а ось мнимых – Im). Рассмотрим векторы U и I в момент времени t = 0. Каждому из этих векторов соответствует комплексное число, которое может быть представлено в трех формах:

а). Алгебраической

U = U’+ jU«

I = I’ – jI«,

где U‘, U«, I‘, I» – проекции векторов на оси действительных и мнимых чисел.

б). Показательной

где U, I – модули (длины) векторов; е – основание натурального логарифма; поворотные множители, т. к. умножение на них соответствует повороту векторов относительно положительного направления действительной оси на угол, равный начальной фазе.

в). Тригонометрической

U = U·(cosψ_u + jsinψ_u)

I = I·(cosψ_i – jsinψ_i).

При решении задач в основном применяют алгебраическую форму (для операций сложения и вычитания) и показательную форму (для операций умножения и деления). Связь между ними устанавливается формулой Эйлера

е^j^·ψ= cosψ + jsinψ.

Неразветвлённые электрические цепи

studfiles.net

§ 11. Последовательное, параллельное и смешанное соединения резисторов (приемников электрической энергии)

Последовательное, параллельное и смешанное соединения резисторов. Значительное число приемников, включенных в электрическую цепь (электрические лампы, электронагревательные приборы и др.), можно рассматривать как некоторые элементы, имеющие определенное сопротивление. Это обстоятельство дает нам возможность при составлении и изучении электрических схем заменять конкретные приемники резисторами с определенными сопротивлениями. Различают следующие способы соединения резисторов (приемников электрической энергии): последовательное, параллельное и смешанное.

Рис. 25. Схемы последовательного соединения приемников

Последовательное соединение резисторов. При последовательном соединении нескольких резисторов конец первого резистора соединяют с началом второго, конец второго — с началом третьего и т. д. При таком соединении по всем элементам последовательной цепи проходит
один и тот же ток I.
Последовательное соединение приемников поясняет рис. 25, а.
.Заменяя лампы резисторами с сопротивлениями R1, R2 и R3, получим схему, показанную на рис. 25, б.
Если принять, что в источнике Ro = 0, то для трех последовательно соединенных резисторов согласно второму закону Кирхгофа можно написать:

E = IR₁ + IR₂ + IR₃ = I(R₁ + R₂ + R₃) = IR_эк (19)

где R_эк = R₁ + R₂ + R₃.
Следовательно, эквивалентное сопротивление последовательной цепи равно сумме сопротивлений всех последовательно соединенных резисторов.Так как напряжения на отдельных участках цепи согласно закону Ома: U₁=IR₁; U₂ = IR₂, U₃ = IR_з и в данном случае E = U, то длярассматриваемой цепи

U = U₁ + U₂ +U₃ (20)

Следовательно, напряжение U на зажимах источника равно сумме напряжений на каждом из последовательно включенных резисторов.
Из указанных формул следует также, что напряжения распределяются между последовательно соединенными резисторами пропорционально их сопротивлениям:

U₁ : U₂ : U₃ = R₁ : R₂ : R₃ (21)

т. е. чем больше сопротивление какого-либо приемника в последовательной цепи, тем больше приложенное к нему напряжение.

В случае если последовательно соединяются несколько, например п, резисторов с одинаковым сопротивлением R1, эквивалентное сопротивление цепи Rэк будет в п раз больше сопротивления R1, т. е. Rэк = nR1. Напряжение U1 на каждом резисторе в этом случае в п раз меньше общего напряжения U:

U1 = U/n. (22)

При последовательном соединении приемников изменение сопротивления одного из них тотчас же влечет за собой изменение напряжения на других связанных с ним приемниках. При выключении или обрыве электрической цепи в одном из приемников и в остальных приемниках прекращается ток. Поэтому последовательное соединение приемников применяют редко — только в том случае, когда напряжение источника электрической энергии больше номинального напряжения, на которое рассчитан потребитель. Например, напряжение в электрической сети, от которой питаются вагоны метрополитена, составляет 825 В, номинальное же напряжение электрических ламп, применяемых в этих вагонах, 55 В. Поэтому в вагонах метрополитена электрические лампы включают последовательно по 15 ламп в каждой цепи.
Параллельное соединение резисторов. При параллельном соединении нескольких приемников они включаются между двумя точками электрической цепи, образуя параллельные ветви (рис. 26, а). Заменяя

Рис. 26. Схемы параллельного соединения приемников

лампы резисторами с сопротивлениями R1, R2, R3, получим схему, показанную на рис. 26, б.
При параллельном соединении ко всем резисторам приложено одинаковое напряжение U. Поэтому согласно закону Ома:

I₁=U/R₁; I₂=U/R₂; I₃=U/R₃.

Ток в неразветвленной части цепи согласно первому закону Кирхгофа I = I₁+I₂+I₃, или

I = U / R₁ + U / R₂ + U / R₃ = U (1/R₁ + 1/R₂ + 1/R₃) = U / R_эк (23)

Следовательно, эквивалентное сопротивление рассматриваемой цепи при параллельном соединении трех резисторов определяется формулой

1/R_эк = 1/R₁ + 1/R₂ + 1/R₃ (24)

Вводя в формулу (24) вместо значений 1/R_эк, 1/R₁, 1/R₂ и 1/R₃ соответствующие проводимости G_эк, G₁, G₂ и G₃, получим: эквивалентная проводимость параллельной цепи равна сумме проводимостей параллельно соединенных резисторов:

G_эк = G₁+ G₂ +G₃ (25)

Таким образом, при увеличении числа параллельно включаемых резисторов результирующая проводимость электрической цепи увеличивается, а результирующее сопротивление уменьшается.
Из приведенных формул следует, что токи распределяются между параллельными ветвями обратно пропорционально их электрическим сопротивлениям или прямо пропорционально их проводимостям. Например, при трех ветвях

I₁ : I₂ : I₃ = 1/R₁ : 1/R₂ : 1/R₃ = G₁ + G₂ + G₃ (26)

В этом отношении имеет место полная аналогия между распределением токов по отдельным ветвям и распределением потоков воды по трубам.
Приведенные формулы дают возможность определить эквивалентное сопротивление цепи для различных конкретных случаев. Например, при двух параллельно включенных резисторах результирующее сопротивление цепи

R_эк=R₁R₂/(R₁+R₂)

при трех параллельно включенных резисторах

R_эк=R₁R₂R₃/(R₁R₂+R₂R₃+R₁R₃)

При параллельном соединении нескольких, например n, резисторов с одинаковым сопротивлением R1 результирующее сопротивление цепи Rэк будет в n раз меньше сопротивления R1, т.е.

R_эк = R1 / n (27)

Проходящий по каждой ветви ток I1, в этом случае будет в п раз меньше общего тока:

I1 = I / n (28)

При параллельном соединении приемников, все они находятся под одним и тем же напряжением, и режим работы каждого из них не зависит от остальных. Это означает, что ток, проходящий по какому-либо из приемников, не будет оказывать существенного влияния на другие приемники. При всяком выключении или выходе из строя любого приемника остальные приемники остаются вклю-

Рис. 27. Схемы смешанного соединения приемников

ченными. Поэтому параллельное соединение имеет существенные преимущества перед последовательным, вследствие чего оно получило наиболее широкое распространение. В частности, электрические лампы и двигатели, предназначенные для работы при определенном (номинальном) напряжении, всегда включают параллельно.
На электровозах постоянного тока и некоторых тепловозах тяговые двигатели в процессе регулирования скорости движения нужно включать под различные напряжения, поэтому они в процессе разгона переключаются с последовательного соединения на параллельное.

Смешанное соединение резисторов. Смешанным соединением называется такое соединение, при котором часть резисторов включается последовательно, а часть — параллельно. Например, в схеме рис. 27, а имеются два последовательно включенных резистора сопротивлениями R1 и R2, параллельно им включен резистор сопротивлением Rз, а резистор сопротивлением R4 включен последовательно с группой резисторов сопротивлениями R1, R2 и R3.
Эквивалентное сопротивление цепи при смешанном соединении обычно определяют методом преобразования, при котором сложную цепь последовательными этапами преобразовывают в простейшую. Например, для схемы рис. 27, а вначале определяют эквивалентное сопротивление R12 последовательно включенных резисторов с сопротивлениями R1 и R2: R12 = R1 + R2. При этом схема рис. 27, а заменяется эквивалентной схемой рис. 27, б. Затем определяют эквивалентное сопротивление R123 параллельно включенных сопротивлений и R3 по формуле

R₁₂₃=R₁₂R₃/(R₁₂+R₃)=(R₁+R₂)R₃/(R₁+R₂+R₃).

При этом схема рис. 27, б заменяется эквивалентной схемой рис. 27, в. После этого находят эквивалентное сопротивление всей цепи суммированием сопротивления R123 и последовательно включенного с ним сопротивления R4:

R_эк = R₁₂₃ + R₄ = (R₁ + R₂) R₃ / (R₁ + R₂ + R₃) + R₄

Последовательное, параллельное и смешанное соединения широко применяют для изменения сопротивления пусковых реостатов при пуске э. п. с. постоянного тока.

electrono.ru

Электрическая цепь

Строительные машины и оборудование, справочник

Категория:

Крановщикам и стропальщикам

Публикация:

Электрическая цепь

Читать далее:

Электрическая цепь

Что называется электрической цепью?

Совокупность устройств, предназначенных для создания и прохождения в них электрического тока, называется электрической цепью.

Последовательное и параллельное соединения проводников.

Какое соединение проводников называется последовательным?

Последовательным соединением проводников называется такое соединение, когда условный конец первого проводника соединяется с условным началом второго, конец второго — с условным началом третьего и т. д.

Рис. 1. Параллельное соединение проводников

Причем начало первого и конец последнего проводника подключаются к источнику тока или к каким- либо точкам электрической цепи.

При последовательном соединении проводников сила тока во всех соединенных проводниках одинакова, а напряжения на проводниках пропорциональны их сопротивлениям.

Сопротивление цепи, состоящей из нескольких последовательно соединенных проводников, равно сумме сопротивлений отдельных проводников.

Какое соединение проводников называется параллельным?

Параллельным соединением проводников называется такое Соединение, при котором к одним и тем же двум узлам электрической цепи присоединяют несколько проводников (рис. 1).

При параллельном соединении проводников напряжение на зажимах всех проводников одно и то же, так как они присоединены к одним и тем же узлам, а токи в параллельных ветвях с проводниками распределяются прямо пропорционально проводимостям ветвей или обратно пропорционально их сопротивлениям.

Главная → Справочник → Статьи → Форум

stroy-technics.ru

3624 ТЕОРИЯ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ

Страница 1 из 3

Научиться измерять и рассчитывать входное сопротивление; исследовать распределение токов и напряжений при смешанном соединении элементов; исследовать работу делителя напряжения.

1. Изучить теоретическую часть работы, изложенную в приложении.

2. Для схемы рис.1.1 рассчитать входное сопротивление относительно зажимов источника, напряжения и токи в ветвях схемы. Данные для расчета взять из табл.1.1 в соответствии с номером бригады. Результаты расчетов занести в табл.1.2.

Рис.1.1

Таблица 1.1

Номер бригады	1	2	3	4	5	6	7	8
E, В	12	13	12	13	12	13	12	13
R₁, Ом	150	100	200	120	150	100	100	180
R₂, Ом	200	240	150	180	150	120	150	120
R₃, Ом	750	750	680	560	360	430	680	360

Работа выполняется на стенде, на котором установлены все элементы и приборы, необходимые для выполнения работы. На панели приведены изображения элементов и выведены гнезда, к которым они присоединены. Сама цепь уже почти полностью собрана. Небольшие дополнительные соединения в цепи, а также подключение измерительных приборов проводятся с помощью проводников, которые можно получить у лаборанта перед началом работы.

Собрать цепь по схеме рис. 1.1, измерить напряжения и токи в ветвях. По результатам измерений рассчитать сопротивления R1, R2, R3 и входное сопротивление цепи. Результаты измерений занести в табл.1.2 и сравнить с расчетными.

Таблица 1.2

Величина	U_bc,B	U_bc,B	U_aс,B	I₁, мА	I₂, мА	I₃, мА	R_вх, Ом
Расчет
Эксперимент.

1. Какое соединение элементов называется последовательным, параллельным и смешанным?

2. Записать выражения для входного сопротивления схем, указанных на рис. 1.2, относительно заданных зажимов.

Рис.1.2

Вычислить токи и напряжения в схемах рис. 1.3, если
Е=100 В, R₁=100 Ом, R₂=10 Ом, J=1 A.

Рис. 1.3

4. Для делителя напряжения (рис. 1.4) получить формулу и построить график зависимости напряжения U_н от R_x для R_н=R.

Рис. 1.4

Входным сопротивлением пассивной электрической цепи называется отношение напряжения к току на зажимах этой цепи.

На практике часто возникает задача рассчитать входное сопротивление цепи, когда известны элементы цепи и способ их соединения. Простейшие виды соединений – это последовательное, параллельное и смешанное соединение элементов.

Последовательным называется такое соединение, при котором конец каждого элемента соединен только с началом последующего элемента. При последовательном соединении через все участки цепи проходит один и тот же ток. На рис.1.5 показано последовательное соединение сопротивлений.

Рис. 1.5

Входное сопротивление для этой цепи может быть найдено, если, согласно второму правилу Кирхгофа, входное напряжение заменить суммой падений напряжений на сопротивлениях.

При последовательном соединении больше любого сопротивления, входящего в это соединение.

Напряжение на каждом сопротивлении может быть найдено по закону Ома:

Таким образом, напряжение на каждом сопротивлении меньше, чем на входе. Чем больше сопротивление, тем большая часть входного напряжения падает на нем.

Параллельным называется такое соединение, при котором элементы подключены к одной паре узлов. При параллельном соединении к элементам приложено одно и тоже напряжение. Параллельное соединение сопротивлений показано на рис.1.6.

Рис.1.6

Для параллельного соединения легко находится входная проводимость, которая является обратной величиной для входного сопротивления . Формулу для вычисления можно получить, используя первое правило Кирхгофа и закон Ома:

Эту формулу удобно использовать при большом количестве параллельных сопротивлений. Если параллельно соединены два сопротивления, то для вычисления удобнее использовать следующую формулу: .

При параллельном соединении входное сопротивление меньше любого сопротивления, входящего в соединение.

Если известен ток на входе цепи, то ток в каждом сопротивлении может быть найден следующим образом:.

Смешанным называют такое соединение, при котором имеются только участки с последовательным и параллельным соединением элементов. Для расчета режима в такой цепи можно последовательно преобразовывать схему до неразветвленной, заменяя последовательно и параллельно соединенные сопротивления эквивалентными. После расчета режима в неразветвленной цепи можно легко найти токи
и напряжения во всех ветвях схемы, используя полученные выше формулы.

В качестве примера рассмотрим расчет режима в схеме рис.1.7.

Рис. 1.7

Если заменить последовательно соединенные сопротивления и эквивалентным , а параллельно соединенные сопротивления и эквивалентным сопротивлением , исходная схема преобразуется к виду, показанному на рис.1.8.

Рис. 1.8 Рис.1.9 Рис1.10

Заменяя в ней последовательно соединенные сопротивления и сопротивлением , получим схему рис. 1.9. В этой схеме можно заменить параллельные сопротивления и сопротивлением . В результате этого получим неразветвленную схему, показанную на рис. 1.10, в которой можно найти ток , а затем напряжение . Затем, возвращаясь к схеме рис. 1.9, находятся токи и : , .

По найденному току в схеме рис.1.8 можно найти напряжение , а затем и токи и в схеме рис. 1.7 , .

Экспериментальная проверка принципа наложения. Экспериментальное определение параметров активного двухполюсника, исследование зависимости величины мощности, передаваемой от активного двухполюсника в нагрузку, от значения сопротивления нагрузки.

Изучить рассматриваемые темы по конспекту лекций или литературе[1-3].

Рис.2.1

Для активного двухполюсника, схема которого изображена на рис. 2.1 Рассчитать параметры эквивалентной схемы замещения U_ХХ, I_КЗ и R_ВХ. Данные для расчетов взять из табл.2.1 в соответствии с номером бригады.
Используя найденные параметры активного двухполюсника, рассчитать зависимости и построить графики напряжения и мощности в нагрузке в зависимости от сопротивления нагрузки, изменяя его от нуля до двух килоом.

Таблица 2.1

Номер бригады	1	2	3	4	5	6	7	8
E₁, В	12	13	12	13	12	13	12	13
E₂, В	6	7	6	7	6	7	6	7
R₁, Ом	150	100	200	120	150	100	100	180
R₂, Ом	200	240	150	180	150	120	150	120
R₃, Ом	750	750	680	560	360	430	680	360
R₄, Ом	510	560	470	360	680	510	560	510
R₅, Ом	390	560	470	390	390	430	470	510

В цепях, собранных по рис. 2.2, 2.3 и 2.4, измерить и записать значения токов I₃(1), I₃(2) и I₃. Убедиться в справедливости принципа наложения.

Рис. 2.2 Рис.2.3 Рис.2.4

Для активного двухполюсника, собранного по схеме рис. 2.1, измерить и записать U_ХХ и I_КЗ. По измеренным значениям рассчитать входное сопротивление двухполюсника и сравнить его с расчетным.
Подключить к зажимам активного двухполюсника нагрузку в виде переменного резистора и записать значения U_Н и I_Н при изменении сопротивления от нуля до максимального значения. По результатам измерений рассчитать R_Н и Р_Н. Результаты измерений и расчетов оформить в виде таблицы. Построить экспериментальную зависимость Р_Н(R_Н) на том же чертеже, где построен расчетный график этой зависимости.

1. Какая цепь называется линейной?

2. Как определить токи в ветвях методом наложения?

Какими параметрами характеризуется активный двухполюсник? Изобразить его схемы замещения.
Как экспериментально определить параметры активного двухполюсника?
Каково условие передачи максимальной мощности от генератора в нагрузку?
Каков порядок расчета цепи методом эквивалентного генератора?

metods-rgrtu.ru

Электротехника часть 4. Соединение элементов цепи

Всем доброго времени суток. В прошлой статье я рассмотрел закон Ома, применительно к электрическим цепям, содержащие источники энергии. Но в основе анализа и проектирования электронных схем вместе с законом Ома лежат также законы баланса токов, называемым первым законом Кирхгофа, и баланса напряжения на участках цепи, называемым вторым законом Кирхгофа, которые рассмотрим в данной статье. Но для начала выясним, как соединяются между собой приёмники энергии и какие при этом взаимоотношения между токами, напряжениями и сопротивлениями.

Последовательное соединение приемников энергии

Приемники электрической энергии можно соединить между собой тремя различными способами: последовательно, параллельно или смешано (последовательно — параллельно). Вначале рассмотрим последовательный способ соединения, при котором конец одного приемника соединяют с началом второго приемника, а конец второго приемника – с началом третьего и так далее. На рисунке ниже показано последовательное соединение приемников энергии с их подключением к источнику энергии

Пример последовательного подключения приемников энергии.

В данном случае цепь состоит из трёх последовательных приемников энергии с сопротивлением R1, R2, R3 подсоединенных к источнику энергии с напряжением U. Через цепь протекает электрический ток силой I, то есть, напряжение на каждом сопротивлении будет равняться произведению силы тока и сопротивления

Таким образом, падение напряжения на последовательно соединённых сопротивлениях пропорциональны величинам этих сопротивлений.

Из вышесказанного вытекает правило эквивалентного последовательного сопротивления, которое гласит, что последовательно соединённые сопротивления можно представить эквивалентным последовательным сопротивлением величина, которого равна сумме последовательно соединённых сопротивлений. Это зависимость представлена следующими соотношениями

где R – эквивалентное последовательное сопротивление.

Применение последовательного соединения

Основным назначением последовательного соединения приемников энергии является обеспечение требуемого напряжения меньше, чем напряжение источника энергии. Одними из таких применений является делитель напряжения и потенциометр

Делитель напряжения (слева) и потенциометр (справа).

В качестве делителей напряжения используют последовательно соединённые резисторы, в данном случае R1 и R2, которые делят напряжение источника энергии на две части U1 и U2. Напряжения U1 и U2 можно использовать для работы разных приемников энергии.

Довольно часто используют регулируемый делитель напряжения, в качестве которого применяют переменный резистор R. Суммарное сопротивление, которого делится на две части с помощью подвижного контакта, и таким образом можно плавно изменять напряжение U2 на приемнике энергии.

Параллельное соединение приемников энергии

Ещё одним способом соединения приемников электрической энергии является параллельное соединение, которое характеризуется тем, что к одним и тем же узлам электрической цепи присоединены несколько преемников энергии. Пример такого соединения показан на рисунке ниже

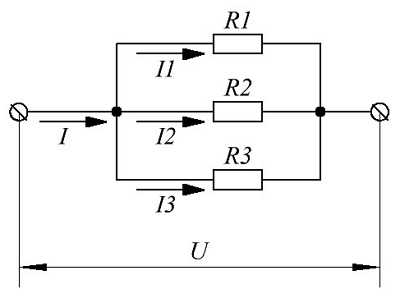
Пример параллельного соединения приемников энергии.

Электрическая цепь на рисунке состоит из трёх параллельных ветвей с сопротивлениями нагрузки R1, R2 и R3. Цепь подключена к источнику энергии с напряжением U, через цепь протекает электрический ток с силой I. Таким образом, через каждую ветвь протекает ток равный отношению напряжения к сопротивлению каждой ветви

Так как все ветви цепи находятся под одним напряжением U, то токи приемников энергии обратно пропорциональны сопротивлениям этих приемников, а следовательно параллельно соединённые приемники энергии можно заметь одним приемником энергии с соответствующим эквивалентным сопротивлением, согласно следующих выражений

Таким образом, при параллельном соединении эквивалентное сопротивление всегда меньше самого малого из параллельно включенных сопротивлений.

Смешанное соединение приемников энергии

Наиболее широко распространено смешанное соединение приемников электрической энергии. Данной соединение представляет собой сочетание последовательно и параллельно соединенных элементов. Общей формулы для расчёта данного вида соединений не существует, поэтому в каждом отдельном случае необходимо выделять участки цепи, где присутствует только лишь один вид соединения приемников – последовательное или параллельное. Затем по формулам эквивалентных сопротивлений постепенно упрощать данные участи и в конечном итоге приводить их к простейшему виду с одним сопротивлением, при этом токи и напряжения вычислять по закону Ома. На рисунке ниже представлен пример смешанного соединения приемников энергии

Пример смешанного соединения приемников энергии.

В качестве примера рассчитаем токи и напряжения на всех участках цепи. Для начала определим эквивалентное сопротивление цепи. Выделим два участка с параллельным соединением приемников энергии. Это R1||R2 и R3||R4||R5. Тогда их эквивалентное сопротивление будет иметь вид

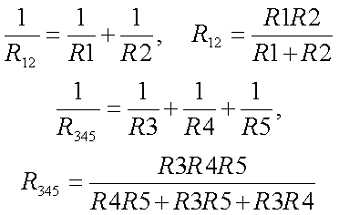
В результате получили цепь из двух последовательных приемников энергии R₁₂R₃₄₅ эквивалентное сопротивление и ток, протекающий через них, составит

Тогда падение напряжения по участкам составит

Тогда токи, протекающие через каждый приемник энергии, составят

Первый закон Кирхгофа

Как я уже упоминал, законы Кирхгофа вместе с законом Ома являются основными при анализе и расчётах электрических цепей. Закон Ома был подробно рассмотрен в двух предыдущих статьях, теперь настала очередь для законов Кирхгофа. Их всего два, первый описывает соотношения токов в электрических цепях, а второй – соотношение ЭДС и напряжениями в контуре. Начнём с первого.

Первый закон Кирхгофа гласит, что алгебраическая сумма токов в узле равна нулю. Описывается это следующим выражением

где ∑ — обозначает алгебраическую сумму.

Слово «алгебраическая» означает, что токи необходимо брать с учётом знака, то есть направления втекания. Таким образом, всем токам, которые втекают в узел, присваивается положительный знак, а которые вытекают из узла – соответственно отрицательный. Рисунок ниже иллюстрирует первый закон Кирхгофа

Изображение первого закона Кирхгофа.

На рисунке изображен узел, в который со стороны сопротивления R1 втекает ток, а со стороны сопротивлений R2, R3, R4 соответственно вытекает ток, тогда уравнение токов для данного участка цепи будет иметь вид

Первый закон Кирхгофа применяется не только к узлам, но и к любому контуру или части электрической цепи. Например, когда я говорил о параллельном соединении приемников энергии, где сумма токов через R1, R2 и R3 равна втекающему току I.

Второй закон Кирхгофа

Как говорилось выше, второй закон Кирхгофа определяет соотношение между ЭДС и напряжениями в замкнутом контуре и звучит следующим образом: алгебраическая сумма ЭДС в любом контуре цепи равна алгебраической сумме падений напряжений на элементах этого контура. Второй закон Кирхгофа определяется следующим выражением

В качестве примера рассмотрим ниже следующую схему, содержащую некоторый контур

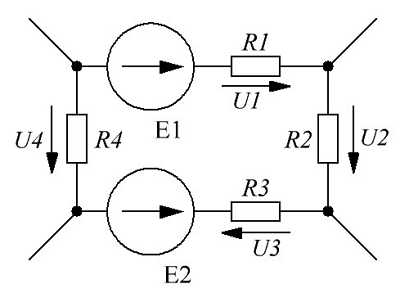
Схема, иллюстрирующая второй закон Кирхгофа.

Для начала необходимо определится с направлением обхода контура. В принципе можно выбрать как по ходу часовой стрелки, так и против хода часовой стрелки. Я выберу первый вариант, то есть элементы будут считаться в следующем порядке E1R1R2R3E2, таким образом, уравнение по второму закону Кирхгофа будет иметь следующий вид

Второй закон Кирхгофа применяется не только к цепям постоянного тока, но и к цепям переменного тока и к нелинейным цепям.
В следующей статье я рассмотрю основные способы расчёта сложных цепей с использованием закона Ома и законов Кирхгофа.

Теория это хорошо, но без практического применения это просто слова.Здесь можно всё сделать своими руками.

Скажи спасибо автору нажми на кнопку социальной сети

www.electronicsblog.ru

📌 Последовательное соединение — это… 🎓 Что такое Последовательное соединение?

Последовательное соединение

Последовательное соединение проводников.

Параллельное соединение проводников.

Последовательное и параллельное соединение в электротехнике — два основных способа соединения элементов электрической цепи. При последовательном соединении все элементы связаны друг с другом так, что включающий их участок цепи не имеет ни одного узла. При параллельном соединении все, входящие в цепь, элементы объединены двумя узлами и не имеют связей с другими узлами. При последовательном соединении проводников сила тока во всех проводниках одинакова.

При параллельном соединении падение напряжения между двумя узлами, объединяющими элементы цепи, одинаково для всех элементов. При этом величина, обратная общему сопротивлению цепи, равна сумме величин, обратных сопротивлениям параллельно включенных проводников.

Последовательное соединение

При последовательном соединении проводников сила тока в любых частях цепи одна и та же: I = I₁ = I₂

Полное напряжение в цепи при последовательном соединении, или напряжение на полюсах источника тока, равно сумме напряжений на отдельных участках цепи: U = U₁ + U₂

Резисторы

Катушка индуктивности

Электрический конденсатор

Мемристоры

Параллельное соединение

Сила тока в неразветвленной части цепи равна сумме сил токов в отдельных параллельно соединенных проводниках: I = I₁ + I₂

Напряжение на участках цепи АВ и на концах всех параллельно соединенных проводников одно и то же: U = U₁ = U₂

Резисторы

Катушка индуктивности

Электрический конденсатор

Мемристоры

См. также

Wikimedia Foundation. 2010.

Последняя фантазия
Последовательности баркера

Смотреть что такое «Последовательное соединение» в других словарях:

последовательное соединение — Электрическое соединение, при котором через рассматриваемые участки электрической цепи возможен только один и тот же электрический ток. [ГОСТ Р 52002 2003] Тематики электротехника, основные понятия Синонимы последовательное соединение участков… … Справочник технического переводчика
ПОСЛЕДОВАТЕЛЬНОЕ СОЕДИНЕНИЕ — в электротехнике 1) соединение двухполюсников, при котором через них проходит один и тот же ток.2) Соединение четырехполюсников, при котором напряжение и ток на выходе предыдущего четырехполюсника равны напряжению и току на входе последующего … Большой Энциклопедический словарь
последовательное соединение — в электротехнике, 1) соединение двухполюсников, при котором через них проходит один и тот же ток. 2) Соединение четырёхполюсников, при котором напряжение и ток на выходе предыдущего четырёхполюсника равны напряжению и току на входе последующего.… … Энциклопедический словарь
последовательное соединение — nuoseklusis jungimas statusas T sritis automatika atitikmenys: angl. connection in series; series connection vok. Reihenschaltung, f; Serienschaltung, f rus. последовательное соединение, n pranc. couplage en série, m; couplage série, m … Automatikos terminų žodynas
последовательное соединение — nuoseklusis jungimas statusas T sritis chemija apibrėžtis Elektrinės grandinės elementų jungimas vienas paskui kitą (kiekviename jų teka tokio pat stiprio srovė). atitikmenys: angl. series connection rus. последовательное соединение … Chemijos terminų aiškinamasis žodynas
последовательное соединение — nuoseklusis jungimas statusas T sritis fizika atitikmenys: angl. connection in series; series connection vok. Reihenschaltung, f; Reihenschluß, m; Serienschaltung, f rus. последовательное соединение, n pranc. connexion en série, f; montage en… … Fizikos terminų žodynas
Последовательное соединение — в электротехнике, 1) соединение Двухполюсников, при котором через них проходит один и тот же ток, т.к. для него имеется один единственный путь. П. с. источников электроэнергии применяется для получения напряжения, превышающего эдс одного… … Большая советская энциклопедия
ПОСЛЕДОВАТЕЛЬНОЕ СОЕДИНЕНИЕ — в электротехнике 1) соединение двухполюсников, при к ром через них проходит один и тот же ток, т. к. для него имеется единств. путь. П. с. источников электроэнергии применяется для получения напряжения, превышающего эдс одного источника. При П. с … Большой энциклопедический политехнический словарь
последовательное соединение — см. в ст. Электрическая цепь. Энциклопедия «Техника». М.: Росмэн. 2006 … Энциклопедия техники
Последовательное соединение элементов системы — [serial linkage] такое соединение элементов в единую систему, при котором выход предыдущего является входом следующего. Таким образом, вход системы совпадает со входом первого звена, а выходом системы служит выход последнего звена. (Рис. П.4).… … Экономико-математический словарь

dic.academic.ru

Виды соединений проводников в электрических цепях

Особенности последовательного соединения проводников

Характеристики параллельного соединения проводников

Расчет силы тока при различных соединениях

Применение последовательного соединения на практике

Использование параллельного соединения в электротехнике

Как выбрать оптимальный вид соединения проводников?

Сравнение последовательного и параллельного соединений

Решение задач на соединение проводников

Заключение

Какое соединение проводников называется параллельным

Какое соединение называется последовательным

Какое соединение называется параллельным

Электрическая цепь с последовательным соединением элементов

Электрическая цепь с параллельным соединением элементов

Электрическая цепь со смешанным соединением элементов

§ 11. Последовательное, параллельное и смешанное соединения резисторов (приемников электрической энергии)

Электрическая цепь

Строительные машины и оборудование, справочник

Реклама:

Главная → Справочник → Статьи → Форум

3624 ТЕОРИЯ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ

Электротехника часть 4. Соединение элементов цепи

Последовательное соединение приемников энергии

Применение последовательного соединения

Параллельное соединение приемников энергии

Смешанное соединение приемников энергии

Первый закон Кирхгофа

Второй закон Кирхгофа

📌 Последовательное соединение — это… 🎓 Что такое Последовательное соединение?

Последовательное соединение

Резисторы

Катушка индуктивности

Электрический конденсатор

Мемристоры

Параллельное соединение

Резисторы

Катушка индуктивности

Электрический конденсатор

Мемристоры

См. также

Смотреть что такое «Последовательное соединение» в других словарях:

Похожие записи

Особенности питания кормящей мамы: что можно и нельзя есть при грудном вскармливании

Новорожденный какает слизью: причины появления слизи в кале грудничка

Гемангиома у новорожденных: причины, виды, лечение и профилактика

Добавить комментарий Отменить ответ