Какое сопротивление называется активным а какое реактивным. Активное и реактивное сопротивление: определение, отличия, формулы расчета

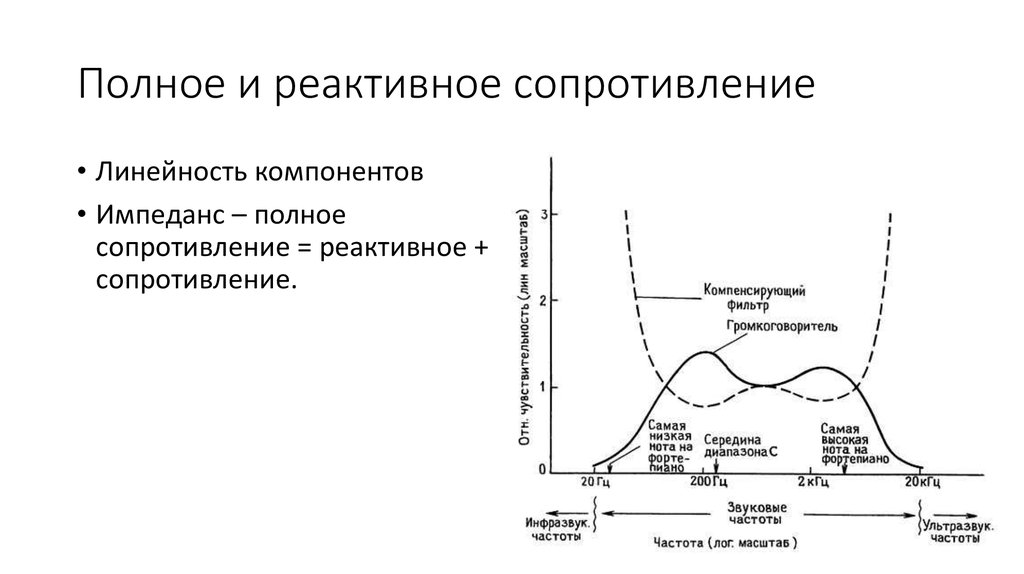
Что такое активное сопротивление. Чем отличается реактивное сопротивление от активного. Как рассчитать активное и реактивное сопротивление. Какие формулы используются для нахождения полного сопротивления цепи.

Что такое активное сопротивление

Активное сопротивление — это свойство проводника препятствовать прохождению электрического тока, при котором электрическая энергия необратимо преобразуется в тепловую. Активное сопротивление обозначается буквой R и измеряется в омах (Ом).

Основные характеристики активного сопротивления:

• Не зависит от частоты переменного тока
• Вызывает необратимые потери энергии в виде тепла
• Ток и напряжение на активном сопротивлении совпадают по фазе
• Определяется материалом, длиной и сечением проводника

Чем отличается реактивное сопротивление от активного

Реактивное сопротивление, в отличие от активного, не преобразует электрическую энергию в тепло, а накапливает ее в магнитном или электрическом поле. Основные отличия реактивного сопротивления:

• Зависит от частоты переменного тока
• Не вызывает необратимых потерь энергии
• Создает сдвиг фаз между током и напряжением
• Характерно для катушек индуктивности и конденсаторов

Таким образом, главное отличие в том, что активное сопротивление рассеивает энергию, а реактивное — запасает ее.

Формулы для расчета активного сопротивления

Основные формулы для расчета активного сопротивления проводников:

1. R = ρ * l / S, где ρ — удельное сопротивление материала, l — длина, S — площадь сечения
2. R = U / I — по закону Ома
3. R = P / I^2 — через мощность и ток

Какую из формул использовать зависит от имеющихся исходных данных. Наиболее универсальна первая формула, позволяющая рассчитать сопротивление по геометрическим параметрам проводника.

Как рассчитать реактивное сопротивление

Реактивное сопротивление бывает двух видов:

• Индуктивное: XL = ωL = 2πfL, где ω — угловая частота, f — частота, L — индуктивность
• Емкостное: XC = 1 / (ωC) = 1 / (2πfC), где C — емкость

Полное реактивное сопротивление цепи:

X = XL — XC

Реактивное сопротивление измеряется в омах, как и активное. При расчетах важно учитывать знак — индуктивное сопротивление считается положительным, а емкостное отрицательным.

Полное сопротивление электрической цепи

Полное сопротивление цепи переменного тока (импеданс) складывается из активного и реактивного сопротивлений. Оно рассчитывается по формуле:

Z = √(R^2 + X^2)

Где Z — полное сопротивление, R — активное, X — реактивное.

Эта формула позволяет найти результирующее сопротивление любой цепи переменного тока, содержащей резисторы, катушки и конденсаторы.

Практическое применение активного и реактивного сопротивления

Понимание природы активного и реактивного сопротивления важно для:

• Расчета электрических цепей
• Проектирования электротехнических устройств
• Оптимизации энергопотребления
• Компенсации реактивной мощности
• Выбора проводников и компонентов

В реальных устройствах всегда присутствуют оба вида сопротивления. Их правильный учет позволяет создавать эффективные и экономичные электрические системы.

Методы измерения активного и реактивного сопротивления

Для измерения активного и реактивного сопротивления применяются различные методы:

• Прямые измерения омметром (только для активного сопротивления)
• Измерение методом вольтметра-амперметра
• Измерительные мосты переменного тока
• Векторные измерители импеданса
• Анализаторы цепей

Выбор метода зависит от требуемой точности, диапазона измерений и типа исследуемой цепи. Современные цифровые приборы позволяют быстро и точно определять как активную, так и реактивную составляющие сопротивления.

Влияние частоты на активное и реактивное сопротивление

Частота переменного тока по-разному влияет на активное и реактивное сопротивление:

• Активное сопротивление практически не зависит от частоты (есть небольшое увеличение на высоких частотах из-за поверхностного эффекта)
• Индуктивное сопротивление прямо пропорционально частоте
• Емкостное сопротивление обратно пропорционально частоте

Это приводит к тому, что соотношение активного и реактивного сопротивления в цепи может сильно меняться при изменении частоты. Учет этой зависимости важен при проектировании устройств, работающих в широком диапазоне частот.

ИМПЕДАНС • Большая российская энциклопедия

Авторы: С. П. Вятчанин

ИМПЕДА́НС (от лат. impedio – пре­пят­ст­во­вать) (ком­плекс­ное со­про­тив­ле­ние), ана­лог элек­трич. со­про­тив­ле­ния для гар­мо­нич. про­цес­сов. Раз­ли­ча­ют И. эле­мен­та це­пи пе­ре­мен­но­го то­ка, вол­но­вой и по­ле­вой И. По­ня­тие И. вве­де­но англ. фи­зи­ка­ми О. Лод­жем и О. Хе­ви­сай­дом, по­ле­во­го И. – С. А. Щел­ку­но­вым (1938).

В тео­рии элек­трич. це­пей для ста­цио­нар­ных гар­мо­нич. про­цес­сов элек­трич. на­пря­же­ние $u$ и ток $j$ че­рез к.-л. эле­мент за­пи­сы­ва­ют в ком­плекс­ном ви­де: $u = U\text{exp}(iωt),\, j = I\text{exp}(iωt)$, где $t$ – вре­мя, $i$ – мни­мая еди­ни­ца, $ω$  – кру­го­вая ча­сто­та. И. $Z$ пас­сив­но­го эле­мен­та (оми­че­ско­го со­про­тив­ле­ния $R$, ка­туш­ки ин­дук­тив­но­сти $L$ или кон­ден­са­то­ра ём­ко­сти $C$) на­зы­ва­ют от­но­ше­ние ком­плекс­ных ам­пли­туд на­пря­же­ния $U$ и то­ка $I: Z(ω ) = U/I$. Ве­ще­ст­вен­ную часть И. $\text{Re}(Z)$ на­зы­ва­ют ак­тив­ным со­про­тив­ле­ни­ем, мни­мую часть – ре­ак­тив­ным со­про­тив­ле­ни­ем или ре­ак­тан­сом. 2/2$. Ре­ак­тив­ное со­про­тив­ле­ние ха­рак­те­ри­зу­ет энер­гию, на­ка­п­ли­вае­мую в эле­мен­те (двух­по­люс­ни­ке) и от­да­вае­мую об­рат­но, ко­то­рая пуль­си­ру­ет с час­то­той $2ω$ и в ср. за пе­ри­од рав­на ну­лю.

Вол­но­вым И. (вол­но­вым со­про­тив­ле­ни­ем) $Z_{\text{в}}$ длин­ной ли­нии на­зы­ва­ют от­но­ше­ние ам­пли­ту­ды гар­мо­нич. вол­ны на­пря­же­ния к ам­пли­ту­де со­от­вет­ст­вую­щей вол­ны то­ка. Для длин­ной ли­нии без потерь вол­но­вой И. ра­вен $Z_{\text{в}}=\sqrt{L_{\text{п}}/C_{\text{п}}}$, где $L_{\text{п}}$ и $C_{\text{п}}$ – по­гон­ные ин­дук­тив­ность и ём­кость.

По­ле­вой И. (вол­но­вое со­про­тив­ле­ние сре­ды) $Z_{\text{п}}$ оп­ре­де­ля­ет­ся для элек­трич. и маг­нит­но­го по­лей пло­ской мо­но­хро­ма­тич. элек­тро­маг­нит­ной вол­ны в сре­де как от­но­ше­ние ам­пли­туд элек­трич. и маг-нит­ной ком­по­нент $Z_{\text{п}}=E/H=\sqrt{μμ_0/εε_0}$ (в СИ). Здесь μ и ε – маг­нит­ная и ди­элек­трич. про­ни­цае­мо­сти сре­ды, μ₀ и ε₀ – маг­нит­ная и ди­элек­трическая про­ни­цае­мо­сти ва­куу­ма.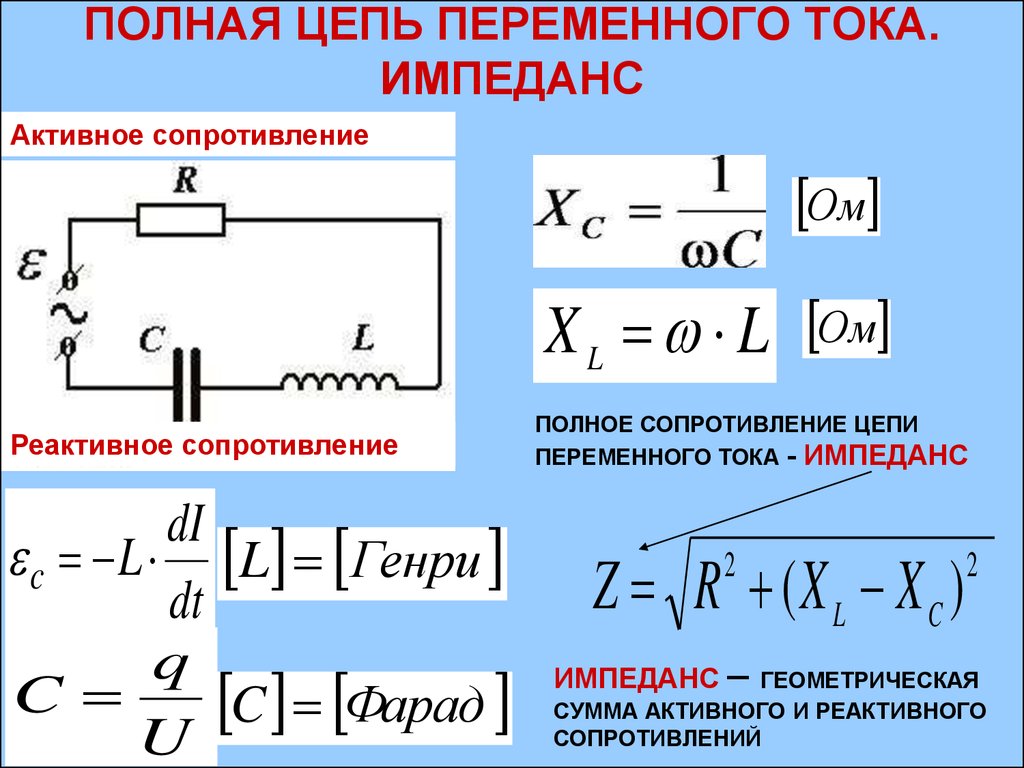 В ва­куу­ме по­ле­вой И. ра­вен $Z_{\text{п}}= 120π$ Ом (в СИ), его так­же на­зы­ва­ют ха­рак­те­ри­сти­че­ским И. ва­куу­ма.

сопротивление электрическое | это… Что такое сопротивление электрическое?

ТолкованиеПеревод

сопротивление электрическое

сопротивле́ние электри́ческое

величина, характеризующая противодействие электрической цепи (или её участка) электрическому току. Электрическое сопротивление обусловлено преобразованием электрической энергии в другие виды энергии; при необратимом преобразовании (преимущественно в теплоту). Электрическое сопротивление называют активным сопротивлением; электрическое сопротивление, обусловленное передачей энергии электрическому или магнитному полю (и обратно), называют реактивным сопротивлением.

* * *

СОПРОТИВЛЕНИЕ ЭЛЕКТРИЧЕСКОЕ

СОПРОТИВЛЕ́НИЕ ЭЛЕКТРИ́ЧЕСКОЕ,
1) Величина, характеризующая противодействие электрической цепи (или ее участка) электрическому току.

При постоянном токе (см. ПОСТОЯННЫЙ ТОК) электрическое сопротивление цепи R можно определить в соответствии с законом Ома (см. ОМА ЗАКОН). Электрическое сопротивление цепи равно отношению приложенного к ней напряжения (см. НАПРЯЖЕНИЕ (электрическое)) U к силе тока (см. СИЛА ТОКА) I, протекающего в ней (при отсутствии в цепи других источников тока или электродвижущей силы (см. ЭЛЕКТРОДВИЖУЩАЯ СИЛА)).
R = U/I.
Такое сопротивление называют омическим или активным сопротивлением (см. АКТИВНОЕ СОПРОТИВЛЕНИЕ). Активное сопротивление элемента электрической цепи зависит как от формы элемента и его размеров, так и от материала, из которого он изготовлен. Для однородного по составу элемента с удельным сопротивлением (см. УДЕЛЬНОЕ СОПРОТИВЛЕНИЕ) , изготовленным в виде бруска, пластины, трубки или проволоки при постоянном его сечении S и длине l, электрическое сопротивление

R = l/S
При очень низких температурах электрическое сопротивление некоторых веществ падает до нуля (см. Сверхпроводники (см. СВЕРХПРОВОДНИКИ)).
Электрическое активное сопротивление обусловлено преобразованием электрической энергии в другие виды энергии (преимущественно в теплоту). Такое преобразование в активных сопротивлениях носит необратимый характер.
Величина электрического сопротивления зависит от температуры. Характер температурной зависимости определяется природой вещества, т. е. механизмом проводимости. Сопротивление металлов при повышении температуры возрастает, а полупроводников и электролитов — падает.
В СИ единицей электрического сопротивления проводников является ом (см. ОМ (единица измерения)) (Ом). Сопротивлением в 1 Ом обладает такой участок цепи, в котором при напряжении 1 В возникает ток силой 1 А.
Электрическое сопротивление, обусловленное передачей энергии электрическому или магнитному полю (и обратно), называется реактивным сопротивлением (см. РЕАКТИВНОЕ СОПРОТИВЛЕНИЕ). В цепи переменного тока (см. ПЕРЕМЕННЫЙ ТОК) проводник помимо активного сопротивления обладает еще и емкостным сопротивлением (см. ЕМКОСТНОЕ СОПРОТИВЛЕНИЕ) и индуктивным сопротивлением (см. ИНДУКТИВНОЕ СОПРОТИВЛЕНИЕ).
Электрическое сопротивление измеряют омметрами или измерительными мостами.
2) Структурный элемент электрической цепи, включаемый в цепь для ограничения или регулирования силы тока.

Энциклопедический словарь. 2009.

Игры ⚽ Поможем написать реферат

• сопротивление материалов
• сопряжённые связи

Полезное

Анализ схемы

— Потребляют ли резисторы реактивную мощность?

спросил 4 года, 4 месяца назад

Изменено 4 года, 4 месяца назад

Просмотрено 2к раз

\$\начало группы\$

Я столкнулся с этой задачей в одной из своих книг, где задача заключалась в том, чтобы найти потери мощности в сердечнике асинхронного двигателя. Я проработал проблему и нашел ток, как на картинке, но до меня дошло, что если я найду мощность на этой нагрузке, а затем найду ток, который проходит через интересующий резистор, и, наконец, умножу ток на напряжение, полученный мощность будет комплексным числом. Но моя интуиция подсказывает мне, что это большое НЕТ. Как известно, резисторы не могут накапливать энергию, поэтому комплексная мощность не имеет особого смысла.

Теперь я обнаружил, что в подобных задачах люди умножают величину вектора каждого компонента, чтобы найти мощность на резисторе, и просто игнорируют фазовый угол, как если бы он имел нулевую фазовую степень. Но я не могу понять, почему они просто предполагают, что фазы не существует.

Кто-нибудь может мне подробно объяснить?

• мощность
• анализ цепей
• переменный ток
• электрическая машина
• стационарное состояние

\$\конечная группа\$

\$\начало группы\$

Нет, резисторы потребляют только активную мощность. Также реактивная мощность не «расходуется» — она запасается или возвращается.

Любой «комплексный ток», протекающий через резистор, создаст напряжение на резисторе, пропорциональное этому току. Мощность, потребляемая резистором, будет равна \$|I|.R\$, где \$|I|\$ — величина тока. Ток, представленный в виде комплексного числа, также предоставляет информацию о фазе тока по отношению к напряжению на частоте, которая не упоминается в вашем примере (она уже используется для определения реактивного сопротивления катушки индуктивности).

Комплексный ток в этом примере должен быть разделен на реальную и реактивную части. Действительная часть проходит через резистор, а реактивная часть через катушку индуктивности.

Это можно объяснить тем, что ток, протекающий через резистор, не имеет фазового сдвига по отношению к напряжению на выводах резистора — а это напряжение и есть само напряжение источника.

Таким образом, мощность, потребляемая резистором, составляет \$63,6405\mathrm{Вт}\$.

Если бы резистор и катушка индуктивности были соединены последовательно, то ток не разделялся бы таким образом, но он по-прежнему имеет ненулевую мнимую часть, поскольку фаза тока будет сдвинута относительно напряжения источника. Резистор потреблял бы столько, сколько указано в первой части этого ответа, т.е. \$1340.60\mathrm{W}\$. На самом деле в этом случае нам нужна только величина тока — его фаза не имеет значения.

Примечание

Можно утверждать, что вопрос сформулирован не полностью, так как мы не знаем, что такое ссылка для тока. Мы предполагаем, что фаза относится к выходному напряжению черного ящика, а не к внутреннему идеальному источнику напряжения черного ящика перед внутренним сопротивлением источника черного ящика (которое само по себе может быть комплексным). Если эталонным является внутреннее напряжение, то нам нужна дополнительная информация о фазе выходного напряжения черного ящика (комплексное напряжение, например, \$5\mathrm{V}+j*.5\mathrm{V}\$).

\$\конечная группа\$

\$\начало группы\$

По KCL часть тока i протекает через резистор, а часть через катушку индуктивности. Вы можете использовать правило делителя тока, чтобы найти ток через резистор. Назовем это \$i_R\$.

Каким бы ни было \$i_R\$, напряжение на резисторе будет \$(435\ \Omega)i_R\$. Если представить \$i_R\$ как \$I\угол\тета\$, то напряжение будет равно \$RI\угол \тета\$.

Таким образом, разность фаз между током и напряжением резисторов будет равна 0.

я заметил, что если я найду мощность на этой нагрузке, а затем найду ток, который проходит через интересующий резистор, и, наконец, умножу ток на напряжение, результирующая мощность будет комплексным числом.

Это непонятно. Как вы использовали мощность в нагрузке, чтобы найти ток через резистор без предварительного разделения резистивной и индуктивной частей? Вы должны были бы предположить, что индуктор отвечает за всю реактивную мощность, а резистор отвечает за всю активную мощность. Тогда, конечно, у вас будет чисто реальная мощность резистора.

\$\конечная группа\$

1

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

.

Знать об активной, реактивной и полной мощности и важности коэффициента мощности на судне

Система переменного тока используется на судне из-за ее гибкости в применении, т. е. легкого преобразования в постоянный ток, изменения напряжения по мере необходимости, меньшего и компактного оборудования для определенной номинальной мощности и т. д.

Основные электротехнические услуги на судне: двигатель, освещение и отопление. Эти услуги также называются нагрузкой для генератора электроэнергии (Generator). Эти нагрузки потребляют электроэнергию через резистор, катушку индуктивности и конденсатор. Это пассивные электрические компоненты из-за их характера акцептора энергии. На самом деле эти компоненты хранят или поддерживают энергию в виде напряжения или тока.

Электрическая мощность (электрическая мощность — это не что иное, как поток электрической энергии) системы переменного тока имеет 2 компонента: активная мощность и реактивная мощность

пассивные компоненты электрической мощности

• резистор: потребляет реальную мощность .
• Индуктор: Потребляет реактивную мощность.
• Конденсатор: Потребляет реактивную мощность.

Примечание. Катушка индуктивности и конденсатор являются компонентами накопителя энергии.

Активная мощность

• Предположим, простая цепь с резистором, питание V (напряжение) и ток I (ток). Осциллограммы напряжения и тока совпадают по фазе, то есть ток и напряжение находятся в одной фазе. И его форма волны мощности (V × I) всегда положительна, т. е. поток мощности всегда положителен. Это означает, что мощность берется из источника питания (источника) и преобразуется в выходную мощность резистором. Эта сила есть не что иное, как Активная Сила.
• Потеря мощности на сопротивлении. Это фактическая мощность, подаваемая на нагрузку.
• Активная мощность течет только в одном направлении и представляет выходную мощность.
• Эта мощность также называется реальной мощностью, фактической мощностью, истинной мощностью, полезной мощностью и полной мощностью в ваттах.
• Его символ (P) и единица измерения (кВт). (1000 Вт = 1 кВт)

Реактивная мощность

• Предположим, что катушка индуктивности находится в цепи с питанием V (напряжение) и потоком I (ток). Здесь формы сигналов напряжения и тока расположены под углом 90° друг к другу, т. е. ток и напряжение не находятся в одной фазе, как поток активной мощности. Его форма волны мощности является как положительной, так и отрицательной. Эта мощность есть не что иное, как реактивная мощность.
• Это потеря мощности на реактивном сопротивлении (реактивное сопротивление = индуктивность + емкость). Эта мощность непрерывно перемещается туда-сюда (т. е. течет между нагрузкой и источником).
• Реактивная мощность меняет направление на противоположное каждые 1/4 ^-го -го цикла и не представляет выходную мощность.
• Во время пуска каждые 1/4 ^-го -го цикла электрический ток передается от источника к нагрузке (элемент накопления энергии) по мере увеличения тока и накопления энергии в магнитном поле/электрическом поле нагрузки. А в следующей 1/4 ^-й -й цикл ток падает до нуля и исчезает магнитное/электрическое поле нагрузки с запасенной в ней энергией. Эта накопленная энергия возвращается к источнику. Снова в следующей 1/4 ^-го -го цикла ток увеличивается и подается на нагрузку, и процесс повторяется.
• Здесь мощность попеременно положительная и отрицательная, поскольку энергия накапливается и разряжается. Таким образом, форма волны мощности сначала положительная, а затем отрицательная.
• Эта мощность также называется бесполезной мощностью и мощностью без ватт.
• Его символ (Q) и единица измерения (кВАр). (1000 ВАр = 1 кВАр)

Суммарная мощность

• Это равнодействующая активной мощности и реактивной мощности.
• Полная мощность = Активная мощность + Реактивная мощность
• Эта мощность также называется полной мощностью.
• Его символ (S) и единица измерения (кВА). (1000 ВА = 1 кВА)

Электрическая мощность в однофазной и трехфазной системе: (для трехфазной системы уравнения мощности умножаются на √3 с уравнениями мощности однофазной системы)

Теперь мы можем понять взаимосвязь между активной мощностью, реактивной мощностью и полной мощностью с помощью треугольника мощности.
Треугольник мощности

Соотношение активной мощности, реактивной мощности и полной мощности можно представить тригонометрически (т. е. с помощью прямоугольного треугольника), и это представление называется треугольником мощности.
Для графического представления предположим, что активная мощность = основание (по горизонтали), реактивная мощность = высота (по вертикали) и полная мощность = гипотенуза, тогда согласно теореме Пифагора: (полная мощность)² = (активная мощность)² + (реактивная мощность)² .
Коэффициент мощности = (активная мощность)/(полная мощность), т. е. Cos ϕ = кВт/кВА

Для более практического понимания рассмотрим две известные аналогии: Аналогия с пивом и Аналогия с пакетом чипсов
Аналогия с пивом

Предположим, что вы в ресторане за пивом, а теперь наблюдайте за стаканом пива и сравните с этой электрической мощностью:
Фактическое количество пива = Активная мощность, Количество пены = Реактивная мощность и Общее количество пива есть не что иное, как (фактическое количество пива + количество пены) и это то же самое, что и полная мощность.
Здесь только фактическое количество пива удовлетворяет нашу потребность или жажду, а не пену. Точно так же только активная мощность удовлетворяет потребность в мощности, а не в реактивной мощности, и поэтому она называется полезной мощностью.

Полная мощность представляет собой сумму активной и реактивной мощностей. Если вы хотите увеличить активную мощность (кВт), вам необходимо уменьшить реактивную мощность (кВАр) для конкретного оборудования. кВА = кВт ↑ + кВАр ↓, Это означает, что для постоянной номинальной мощности (кВА) при увеличении активной мощности реактивная мощность уменьшается.

Аналогия пакета чипов

Рассмотрим пакет чипов и соотнесем его как: фактическое наличие чипов = активная мощность, воздух (пустой) присутствует = реактивная мощность и общая емкость (размер) пакета есть не что иное, как кажущаяся (общая) мощность.
Здесь полезно только фактическое количество микросхем, а не воздух (пустое пространство) и точно так же в системе переменного тока полезна только активная мощность, а не реактивная.

Понятие коэффициента мощности

• Это не что иное, как доля активной мощности в общей мощности. Например: если коэффициент мощности равен 0,8, это означает, что активная мощность составляет 80 % от общей мощности (100 %).
• Измеряет эффективность преобразования общей мощности в выходную мощность (активную мощность).
• Это косинус угла между током и напряжением, т.е. угол отставания тока. Это означает, что диапазон cos представляет собой диапазон коэффициента мощности, т. е. -1 ≤ коэффициент мощности (cos ϕ) ≤ 1
• Cos ϕ = кВт/кВА, Cos ϕ = P/VI, Cos ϕ = сопротивление/импеданс, Cos ϕ = True мощность/Полная мощность
• На корабле предпочтителен коэффициент мощности 0,8, но это не обязательно. В электрической системе всегда присутствуют индуктивные нагрузки, поэтому мы не можем полностью игнорировать реактивную мощность.

Мы хотим, чтобы коэффициент мощности был как можно ближе к 1. Это означает, что активная мощность должна иметь тенденцию к полной мощности, поскольку более высокий коэффициент мощности (т. е. более высокая активная мощность) указывает на меньшие потери, хорошее регулирование напряжения, высокий КПД, уменьшенный размер оборудования. и т. д.

Низкий коэффициент мощности

P = VI Cos ϕ, I = P/(V Cos ϕ), поэтому коэффициент мощности обратно пропорционален току.
Если коэффициент мощности уменьшается, ток увеличивается. А из-за сильного тока возможны следующие возможности:

• Потери будут высокими, а эффективность низкой.
• Для больших токов требуется проводник большего размера, поэтому это дорого.
• Меньший коэффициент мощности означает более высокую номинальную мощность в кВА, больший размер оборудования и, следовательно, более высокую стоимость.
• Более низкий коэффициент мощности означает более высокий ток, что приводит к более высокому падению напряжения. Возникнет дисбаланс в регулировании напряжения.

Повышение коэффициента мощности

Как правило, все нагрузки потребляют как активную, так и реактивную мощность. Но в идеале они должны потреблять активную мощность. Поэтому должна быть система увеличения активной мощности и уменьшения реактивной мощности. И делается это за счет улучшения коэффициента мощности. Улучшение коэффициента мощности означает улучшение распределения активной мощности в полной (полной) мощности. Для улучшения коэффициента мощности нам необходимо увеличить активную мощность или уменьшить реактивную мощность, и это делается следующими способами:

• Использование конденсатора: Уменьшает индуктивную нагрузку, т.е. реактивную мощность, и минимизирует разность фаз между током и напряжением.
• При использовании синхронного конденсатора: Он действует как конденсатор и увеличивает коэффициент мощности. Это дорого в использовании.
• С помощью фазовращателя: Используется в двигателях для возбуждения ампер-витков для улучшения коэффициента мощности. Ускоритель фазы — это просто возбудитель.

Примечание.