Расчет однослойной катушки индуктивности. Расчет индуктивности однослойной катушки: полное руководство

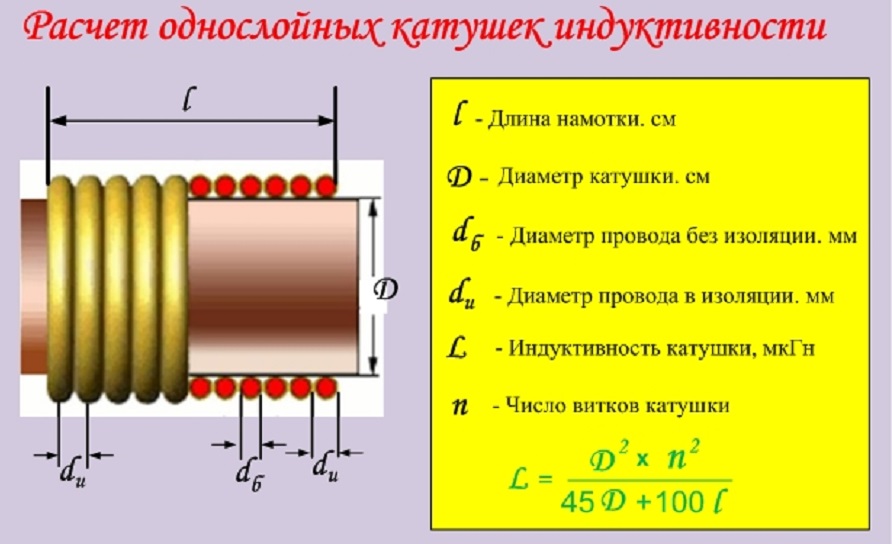
Как рассчитать индуктивность однослойной катушки. Какие параметры влияют на индуктивность. Какие формулы использовать для точного расчета. Как оптимизировать конструкцию катушки.

Что такое однослойная катушка индуктивности

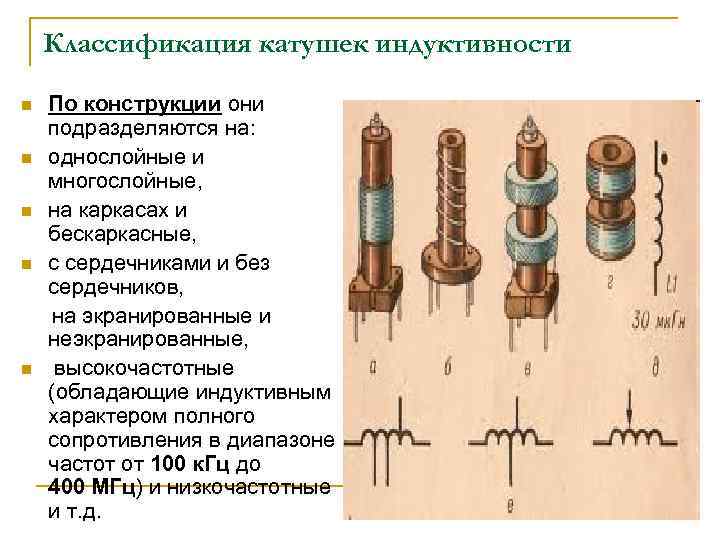
Однослойная катушка индуктивности представляет собой проводник, намотанный в один слой на цилиндрический каркас. Это один из самых распространенных типов катушек, который широко используется в радиотехнике и электронике.

Основные параметры однослойной катушки:

• Диаметр каркаса D
• Длина намотки l
• Число витков N
• Диаметр провода d
• Шаг намотки t

От этих параметров зависит индуктивность катушки — ее главная электрическая характеристика.

Почему важно уметь рассчитывать индуктивность катушки

Точный расчет индуктивности катушки необходим при проектировании различных радиоэлектронных устройств:

• Колебательных контуров
• Фильтров
• Трансформаторов
• Дросселей
• Антенн

Неправильно рассчитанная индуктивность может привести к:

• Ухудшению характеристик устройства
• Нестабильной работе схемы
• Повышенным потерям энергии

Поэтому умение точно рассчитать индуктивность катушки — важный навык для радиоинженера.

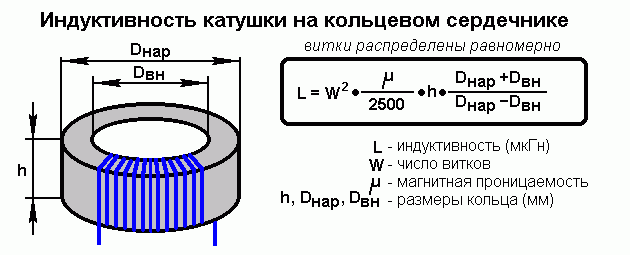
Основные формулы для расчета индуктивности

Существует несколько формул для расчета индуктивности однослойных катушек. Рассмотрим наиболее точные и часто используемые.

Формула Нагаока

Одна из самых точных формул для расчета индуктивности однослойных катушек:

L = μ0 * N^2 * D^2 / (4l) * K

Где:

• L — индуктивность в Генри
• μ0 — магнитная постоянная (4π * 10^-7 Гн/м)
• N — число витков
• D — диаметр катушки в метрах
• l — длина намотки в метрах
• K — поправочный коэффициент Нагаока

Коэффициент K зависит от отношения длины катушки к ее диаметру (l/D) и определяется по специальным таблицам.

Формула Уиллера

Более простая формула, дающая хорошую точность:

L = (N^2 * D^2) / (45.7 * D + 102 * l)

Где L — в микрогенри, D и l — в сантиметрах.

Формула для катушек с большим отношением длины к диаметру

Для длинных катушек (l > 0.8D) можно использовать упрощенную формулу:

L = (μ0 * N^2 * S) / l

Где S — площадь поперечного сечения катушки.

Как правильно выбрать параметры катушки

При проектировании однослойной катушки необходимо учитывать следующие рекомендации:

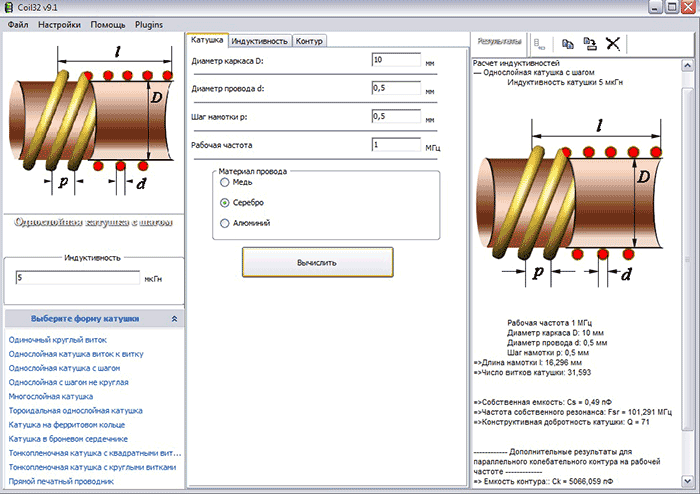
• Оптимальное отношение длины к диаметру l/D = 0.7 — 1
• Шаг намотки t = 1.1 — 1.2 диаметра провода
• Диаметр провода d выбирается из условия минимальных потерь на заданной частоте
• Число витков N рассчитывается по формулам, исходя из требуемой индуктивности

Выбор конкретных размеров катушки зависит от ее назначения, рабочей частоты, требований к добротности и других факторов.

Влияние экрана на индуктивность катушки

При помещении катушки в металлический экран ее индуктивность уменьшается. Это происходит из-за наведения вихревых токов в экране.

Степень уменьшения индуктивности зависит от:

• Размеров экрана
• Расстояния между катушкой и экраном
• Материала экрана

Для минимального влияния экрана рекомендуется:

• Диаметр экрана Dэ ≥ 2D
• Длина экрана lэ ≥ l + D
• Расстояние от катушки до экрана ≥ 0.5D

При необходимости учета влияния экрана в расчетах используются специальные поправочные коэффициенты.

Как измерить индуктивность катушки

Для проверки расчетов индуктивность катушки можно измерить следующими способами:

1. С помощью измерителя RLC. Это наиболее простой и точный метод.
2. Методом резонанса. Катушка включается в колебательный контур с известной емкостью. По частоте резонанса определяется индуктивность.
3. Мостовым методом. Используется мост переменного тока, в одно плечо которого включается измеряемая катушка.

При измерениях важно учитывать влияние паразитных параметров — собственной емкости катушки, сопротивления провода и т.д.

Программы для расчета катушек индуктивности

Для автоматизации расчетов удобно использовать специальные программы:

• Coil32 — простой калькулятор для однослойных катушек
• Coil64 — расширенный калькулятор с возможностью расчета многослойных катушек
• MMANA-GAL — программа для моделирования антенн, включает модуль расчета катушек
• ANSYS Maxwell — профессиональный пакет для электромагнитного моделирования

Эти программы позволяют быстро рассчитать параметры катушек и оптимизировать их конструкцию.

Заключение

Расчет индуктивности однослойных катушек — важная задача при проектировании радиоэлектронной аппаратуры. Используя приведенные формулы и рекомендации, можно с высокой точностью рассчитать параметры катушки под конкретные требования. Для сложных случаев рекомендуется использовать специализированное программное обеспечение.

Расчет катушки индуктивности колебательного контура и обоснование выбора материалов.

Федеральное агентство по образованию

Государственное образовательное учреждение

высшего профессионального образования

САМАРСКИЙ ГОСУДАРСТВЕННЫЙ

АЭРОКОСМИЧЕСКИЙ УНИВЕРСИТЕТ

имени академика С.П. Королёва ( СГАУ )

Факультет инженеров воздушного транспорта

Кафедра электронных систем и устройств

Выполнил студентка: Воробьёва А.Ю.

Группа № 3203

Вариант № 33

Проверил преподаватель:

Макарычев Ю. И.

Самара 2011

1 Задание для расчета	3
2 Расчет	3
2.1 Нахождение индуктивности Lк	3
2.2 Выбор материала каркаса	4
2.3 Выбор размеров каркаса	4
2.4 Расчет индуктивности катушки с учетом сердечника.	5
2. 5 Определение числа витков	6
2.6 Определение оптимального диаметра провода	7
2.7 Учет влияния экрана	9
2.8 Расчет собственной емкости катушки.	10
2.9 Расчет добротности	11
3 Расчет ТКИ и ТКЧ	12
4 Выбор конденсатора контура	13
5 Итог	15
Список используемой литературы	16

1 Задание.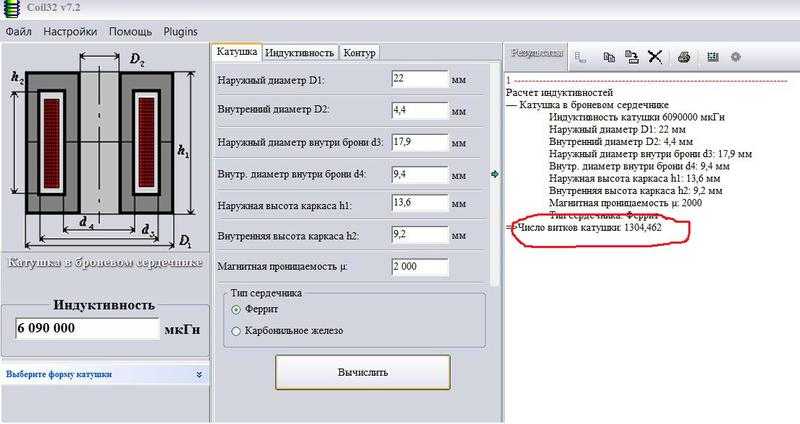

Рассчитать индуктивность колебательного контура на резонансной частоте .При условии, что емкость конденсатора . Тип и материалы сердечников, , и другие необходимые данные для расчета приведены

Материал экрана: алюминий.

Тип и материал сердечника: СЦР-1,Р-20.

Выбрать материал и размеры каркаса, тип намотки. Определить число витков и оптимальный диаметр провода. Вычислить собственную емкость, добротность, температурный коэффициент индуктивности и температурный коэффициент частоты.

Рисунок 1.Колебательный контур.

где С_к – емкость контура;

L_к – индуктивность контура.

2 Расчет

2.1 Нахождение индуктивности контура.

Рисунок 2. Схема замещения катушки идеальными элементами.

где L – идеальная индуктивность катушки;

С₀– собственная емкость катушки;

r_f– сопротивление обмотки катушки;

r_д – сопротивление диэлектрика каркаса за счет поляризации.

Определим индуктивность исходя из формулы

определим L.

,

2.2 Выбор материала каркаса.

Каркас катушки в значительной степени определяет ее стоимость и электрические параметры.

Каркас должен быть удобным для намотки и крепления в приборе, обеспечивать устройство (распайку) выводов обмотки и надежную фиксацию положения построечного элемента. Материал каркаса должен допускать применение прогрессивных технологических методов изготовления, быть дешевым, механически прочным, вносить малые потери, обладать необходимой теплостойкостью, малой влагостойкостью и небольшим коэффициентом линейного расширения и, в ряде случаев, малым значением температурного коэффициента диэлектрической проницаемости.

В достаточной степени этим требованиям отвечают каркасы из полистирола, фенопластов, пресс-материалов типов АГ-4С, ДСВ-2Р-2М и им подобных. На пониженных частотах может оказаться целесообразным применение более дешевых каркасов из бакелизированных трубок.

Для каркасов катушек с высокой стабильностью применяют радиокерамику типа В, радиофарфор, ультрафарфор и высокочастотный стеатитит.

Исходя из заданных параметров наиболее подходящим материалом является

высокочастотный стеатитит.

2.3 Выбор размеров каркаса.

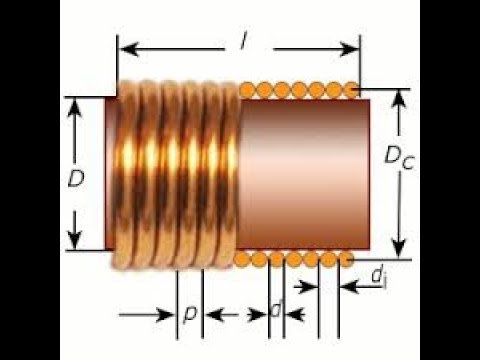
Прежде чем приступить к дальнейшим вычислениям, для удобства, приведем чертеж катушки:

Рисунок 3. Чертеж катушки индуктивности.

где l_c – длина сердечника;

l_к – длина намотки;

D_c – диаметр сердечника;

D_к – диаметр катушки;

d – диаметр провода без изоляции.

По сводным таблицам для СЦР — 1 можно найти D_c=0,6см, l_c=0,9см.

Для цилиндрических сердечников D_k=0,9см и предварительно возьмем l_к=0,9см.

2.4 Расчет индуктивности катушки с учетом сердечника.

где — необходимая величина расчетной индуктивности;

— действующая магнитная проницаемость сердечника.

где — начальная магнитная проницаемость материала сердечника;

— коэффициент использования магнитных свойств;

-поправочный коэффициент.

определяем по графику =f(l_k/ D_c), определяем по графику =f(l_c/ D_c)

(l_k/ D_c)=0,9/0,6=1,5; =0,28.

(l_c/ D_c)=0,9/0,6=1,5; =0,9.

определяем по таблице, исходя из того, что задана марка магнитного материала Р-20.

=10.

Таким образом

2.5 Определение числа витков и типа намотки.

Применяемые виды намотки можно разделить на однослойные и многослойные.

При однослойной намотке витки располагаются на цилиндрической поверхности каркаса в один слой. При плотном расположении витков, разделяемых лишь изоляцией провода, получается сплошная однослойная намотка при расположении витков на некотором расстоянии друг от друга — намотка с шагом.

Однослойные катушки с шагом отличаются высокой добротностью (150 -400) и стабильностью; они в основном применяются в контурах KB и УКВ.

Для повышения точности намотки провода применяются нарезные каркасы, т. е. каркасы, на поверхности которых сделана неглубокая (0,2 — 0,3d) спиральная канавка. Однако погружение провода в диэлектрик каркаса несколько понижает добротность и стабильность катушки.

Для высокостабильных катушек применяются специальные способы изготовления намоток — тугая, горячая и осажденная или нанесенная намотки.

Катушки без каркаса могут быть практически выполнены при числе витков не более трех. Они отличаются несколько более высокой добротностью, но, имеют малую механическую жесткость и пониженную стабильность.

Для катушек индуктивностью выше 15—20 мкГн применяют сплошную однослойную намотку. Целесообразность перехода на сплошную намотку определяется диаметром катушки: чем больше диаметр катушки, тем большая индуктивность может быть получена при применении намотки с шагом.

Катушки со сплошной намоткой также отличаются высокой добротностью (150—250) и стабильностью и широко используются в контурах для коротких, промежуточных и средних волн, если требуется индуктивность не выше 200—500 мкГн.

Для изготовления катушек с индуктивностью выше 200—500 мкГн применяют многослойные намотки.

Целесообразность перехода на многослойную намотку определяется диаметром катушки. Чем больше диаметр катушки, тем при большей индуктивности следует переходить на многослойную намотку.

Многослойные намотки могут быть разделены на простые и сложные.

Широкое применение имеют сложные многослойные намотки, например универсальные.

Катушки, предназначенные для работы в диапазоне частот до 500 кГц, имеют многослойную обмотку. Применяют рядовую многослойную или универсальную намотки, а также намотку «внавал». Катушки для частот выше 1—2 МГц имеют однослойную намотку.

Для намотки катушек применяют провода в эмалевой изоляции марок ПЭЛ, ПЭ, ПЭВ, комбинированной изоляции марок ПШО, ПШД, ПЭЛШО, ПЭШД, а также литцендрат ЛЭШО И ЛЭШД.

Для многослойных катушек с универсальной намоткой применяют обычно провода с волокнистой изоляцией, так как волок­нистая изоляция обеспечивает большее сцепление витков.

Для катушек с шагом применяется неизолированный провод МГМ, покрытый слоем серебра.

В данной работе целесообразно применить однослойную намотку из ПЭЛ.

Для определения числа витков однослойной катушки воспользуемся формулой:

Значение L₀ определяем по графику, L₀=f(l_k/ D_к)

(l_k/ D_к)=1; L₀ =7

Откуда

2. 6 Определение оптимального диаметра провода.

Между сопротивлением провода катушки и его диаметром существует сложная зависимость, так как при этом изменяется проявление поверхностного эффекта и эффекта близости.

Рассмотрим вопрос о влиянии диаметра провода на сопротивление катушки. В случае прямолинейного провода увеличение диаметра вызывает увеличение его периметра, а, следовательно, уменьшение сопротивления току высокой частоты. Зависимость сопротивления отрезка прямолинейного провода от диаметра при некоторой частоте выражается кривой L на рис. 4 (кривая I представляет собой зависимость сопротивления току высокой частоты от диаметра). При свертывании провода в спираль возникает эффект близости, который проявляется тем сильнее, чем больше диаметр провода. Увеличение сопротивления за счет эффекта близости примерно пропорционально диаметру провода и изображается прямой II. Сложив величины, характеризуемые кривыми I и II, получим изменение полного активного сопротивления провода катушки в зависимости от его диаметра; эта зависимость выражается кривой III. Ход кривой III показывает, что при вполне определенном диаметре провода сопротивление катушки имеет минимальное значение. Можно показать, что при этом сопротивление провода катушки (с учетом поверхностного эффекта) равно увеличению сопротивления за счет эффекта близости.

Рис. 4

Оптимальный диаметр провода катушки рассчитывают при помощи вспомогательного коэффициента:

где — вспомогательный параметр;

-поправочный коэффициент.

D_к – диаметр катушки;

N –число витков намотки;

где f ₀ – резонансная частота.

к=f(l/D)

к=4

,т.к. , то ;

0,065см, в целях экономии меди возьмем d_опт = 0,69мм

Используя эмалевую изоляцию провода типа ПЭЛ принимаем диаметр провода равным 0,35

Проведем проверку подобранного диаметра провода:

, следовательно, выбор параметров каркаса сделан правильно.

2.7 Учет влияния экрана.

Для устранения паразитных связей, обусловленных внешним электромагнитным полем катушки, и для устранения влияния внешних полей катушка экранируется, то есть располагается внутри замкнутого, металлического заземленного экрана.

Экранирующее действие характеризуется отношением напряженности внешнего поля катушки при наличии экрана к напряженности поля при его отсутствии. Для экрана среднего качества, выполненного, например, в виде алюминиевого стакана, это отношение равно приблизительно 0,01 — 0,05, что бывает достаточно для большинства практических случаев. Для усиления экранирующего действия применяются двойные и даже тройные экраны.

Под влиянием экрана изменяются основные электрические параметры катушки; уменьшается ее индуктивность, а также увеличиваются сопротивление и собственная емкость. Добротность экранированной катушки оказывается ниже добротности той же катушки при отсутствии экран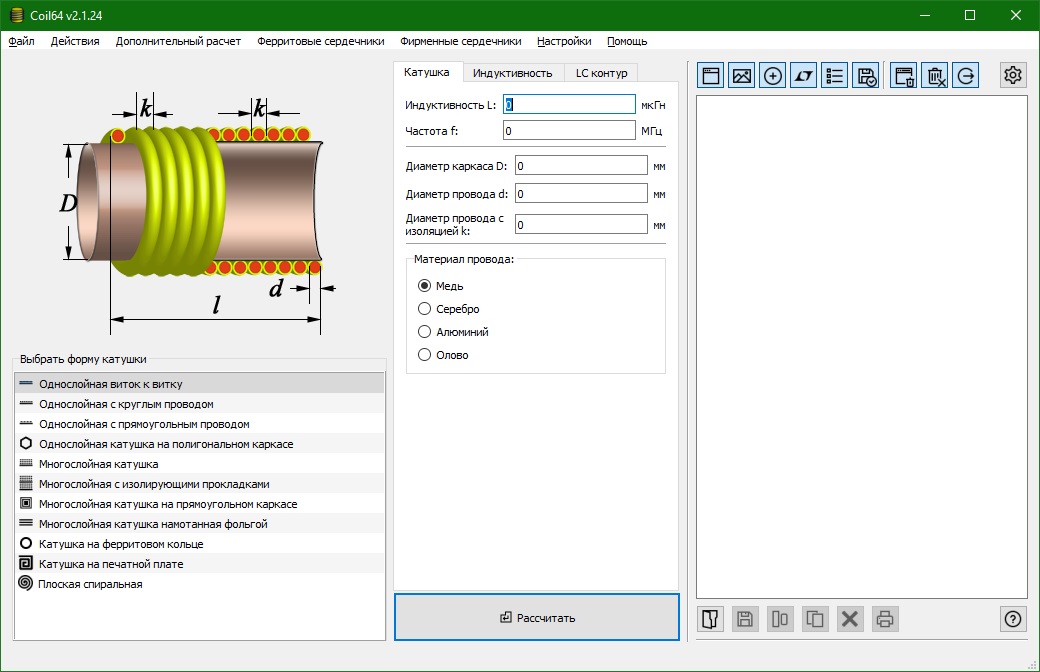а. Изменение параметров катушки зависит от соотношения между ее размерами и размерами экрана.

Для того чтобы индуктивность и добротность падали не более чем на 10%:, рекомендуются следующие соотношения м.д. диаметрами экрана и катушки:[3]

;

где — диаметр экрана.

Выберем диаметр экрана равным 2,3см, высоту равную 1,8см;

При помещении катушки в экран ее индуктивность и добротность уменьшаются. Индуктивность экранированной катушки составляет:

где — индуктивность неэкранированной катушки;

к – коэффициент связи м.д. экраном и катушкой.

Для однослойных катушек:

где — коэффициент зависящий от отношения длины катушки к ее диаметру.

;

Определяем индуктивность экранированной катушки:

Т. к и высота между катушкой и экраном равна высоте катушки, то потери вносимые экраном в К.И. можно определить по формуле:[3]

Где латуни

2.8 Расчет собственной емкости катушки.

В катушке, между отдельными витками и между витками и ближайшими металлическими телами—экранами, шасси прибора и т. п., всегда существует разность потенциалов, которая создает электрическое поле. Влияние этого поля подобно влиянию некоторой емкости, включенной параллельно катушке; эту емкость называют собственной (или распределенной) емкостью катушки. Ее величина зависит от размеров катушки, конструкции обмотки, близости расположения витков со значительной разностью потенциалов, удаленности их от экранов, диэлектрической проницаемости изоляции провода и каркаса, а также ряда других конструктивных факторов. Чем больше диаметр катушки, чем ближе друг к другу расположены витки со значительной разностью потенциалов, чем выше диэлек­трическая проницаемость изоляции провода и материала каркаса, тем больше собственная емкость катушки индуктивности.

Наименьшей собственной емкостью (1—2 пФ) обладают однослойные катушки, намотанные с шагом. Многослойные катушки обладают большей емкостью,- величина которой зависит от способа намотки. Например, емкость катушек с простой универсальной намоткой составляет 5 — 10 пФ, с перекрестной универсальной намоткой 15 — 30 пФ.

Расчет собственной емкости однослойных катушек удобнее производить по эмпирической формуле:

где определяется по графикам.

Тогда

.

2.9 Расчет добротности.

Добротность контура зависит не только от его параметров, но также и от параметров внешней цепи — внутреннего сопротивления источника и сопротивления нагрузки.

Добротность контура определяют по формуле:

Сопротивление току высокой частоты.

Для катушек, работающих на частотах выше 10МГц, сопротивление вычисляется по формуле:

где d – диаметр провода без изоляции;

N – число витков катушки;

D – диаметр катушки;

Ом

Потери вносимые сердечником.

Потери вносимые сердечником могут быть найдены по следующей формуле:

Предположим, что катушка находится в радиоприемнике, тогда Н=0, и тогда

Ом.

Потери в диэлектрике.

Диэлектрические потери возникают в поле собственной емкости катушки через диэлектрик С_ол и зависят от величины этой емкости, качества tgδ материала каркаса и частоты. Потери в диэлектрике обусловлены тем, что между соседними витками катушки существует емкость, имеющая две составляющих — емкость через воздух С_ов и емкость через диэлектрик С_ол.

рис.5

Сопротивление, вносимое диэлектрическими потерями, можно представить включенным параллельно собственной емкости катушки. Величина этого сопротивления равна:[3]

.

Пересчитывая это сопротивление на последовательное, получаем:

Откуда , поэтому добротность контура равна:

Однослойная катушка — Большая Энциклопедия Нефти и Газа, статья, страница 2

Cтраница 2

Плоская однослойная катушка с внутренним радиусом 2 см и внешним радиусом 6 см образована плотной укладкой 100 витков провода по спирали.  [16]

Однослойные катушки главного полюса ( сериесные) являются составной частью катушек крановых машин постоянного тока серии ДП со смешанным возбуждением.  [17]

Если дисковые и однослойные катушки — выполняются из проводников значительных сечений, то многослойная катушка может выполняться из провода любого сечения и любого профиля.  [18]

Геометрическая модель однослойной катушки с квадратным каркасом.  [19]

Индуктивность однослойной катушки, расположенной на каркасе квадратного сечения, приближенно на 20 % больше индуктивности однослойной катушки, расположенной на цилиндрическом каркасе ( рис. 2 — 9), если диаметр цилиндрического каркаса 2г2 равен стороне каркаса с квадратным сечением 2Ь2 и прочие геометрические размеры катушек совпадают.  [20]

Геометрическая модель однослойной тороидальной катушки.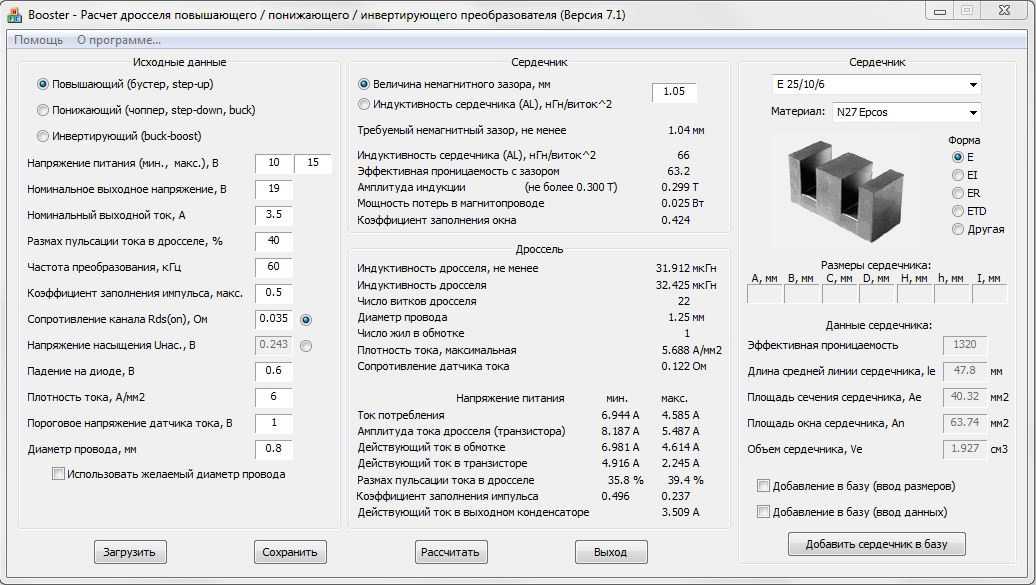  [21]

Индуктивность однослойной катушки, намотанной на каркасе с прямоугольным сечением со сторонами 262 и 26j, приближенно в l 2bj / 62 раза больше индуктивности однослойной катушки, намотанной на цилиндрическом каркасе ( рис. 2 — 9) с радиусом / 1 — & а4 мм, если значения других геометрических размеров катушек совпадают.  [22]

Для однослойных катушек с керамическим, полистироловым каркасом или каркасом из пресс-порошка ТКИ составляет ( 50 ч — 100) X XlO e 1 / С. Для многослойных катушек ТКИ равен ( 100 ч — 200) X X 10 1 / С. Величина нецикличности равна от десятых долей до единиц процента.  [23]

Для однослойных катушек диаметром 20 — — 30 мм оптимальный диаметр провода равен 0 2 — 0 6 мм; для многослойных катушек он не превышает 0 25 — 0 3 мм. Некоторые отступления от оптимальных соотношений сопровождаются лишь незначительным снижением добротности. Следует заметить, что при выборе диаметра провода минимальные потери не являются единственным и самым существенным критерием. Иногда выбор диаметра провода диктуется условиями поставки, необходимой механической прочностью обмотки и прочими факторами.  [24]

Намотка типа уни.  [25]

Добротность однослойной катушки зависит от частоты, диаметра провода, шага намотки и соотношений диаметра катушки к ее длине. Расчет добротности может быть произведен по известным формулам и вспомогательным.  [26]

Для однослойных катушек существует оптимальное отношение — при котором их добротность получается наибольшей. Если необходимо получить нчивыс-шую добротность катушки, следует правильно выбрать диаметр провода.  [27]

У однослойных катушек индуктивности, выполненных из провода без изоляции, стабильность собственной емкости и добротности при воздействии влаги определяется свойствами диэлектрика каркаса; у многослойных катушек, кроме того — свойствами изоляции провода и пропиточных материалов.  [28]

Емкость современных однослойных катушек не превышает обычно 5 пф, а емкость многослойных 8 — 10 пф. При некоторых способах намотки емкость многослойных катушек может достигать 20 — 30 пф.  [29]

Если однослойную катушку намотать на ферритовом сердечнике не виток к витку, а с принудительным шагом, стремясь покрыть обмоткой большую часть длины сердечника, то действующая высота магнитной антенны и, следовательно, ее эффективность несколько увеличиваются. При намотке с шагом от 1 5 — 2 мм и более марка применяемого обмоточного провода практически не оказывает влияния на качество катушки входного контура.  [30]

Страницы:      1    2    3    4

Coil32 — Калькулятор однослойных катушек

Детали

Опубликовано: 07 января 2015 г.

Последнее обновление: 08 января 2023 г.

Просмотров: 21632

Для работы калькулятора на этой странице необходимо включить JavaScript в вашем браузере!

---

Если вам нужно изготовить самодельную катушку индуктивности для согласующей цепи, для усилителя, для магического кристалла и т.д., у вас есть вопрос:

• сколько витков в катушке?
• какой диаметр и длина обмотки?
• какой провод использовать?

Конструкцию обмотки следует выбирать опытным путем, руководствуясь следующими общими советами. Большинство онлайн-калькуляторов позволяют найти индуктивность катушки, зная размеры ее намотки и количество витков. Этот калькулятор поможет вам рассчитать количество витков вашего самовара однослойного Р.Ф. индуктор или дроссель на стадии проектирования. Калькулятор использует уравнение Боба Уивера с поправками на круглую проволоку. Coil32 для Android и кроссплатформенный Coil64 позволяют рассчитать собственную емкость и добротность однослойной катушки.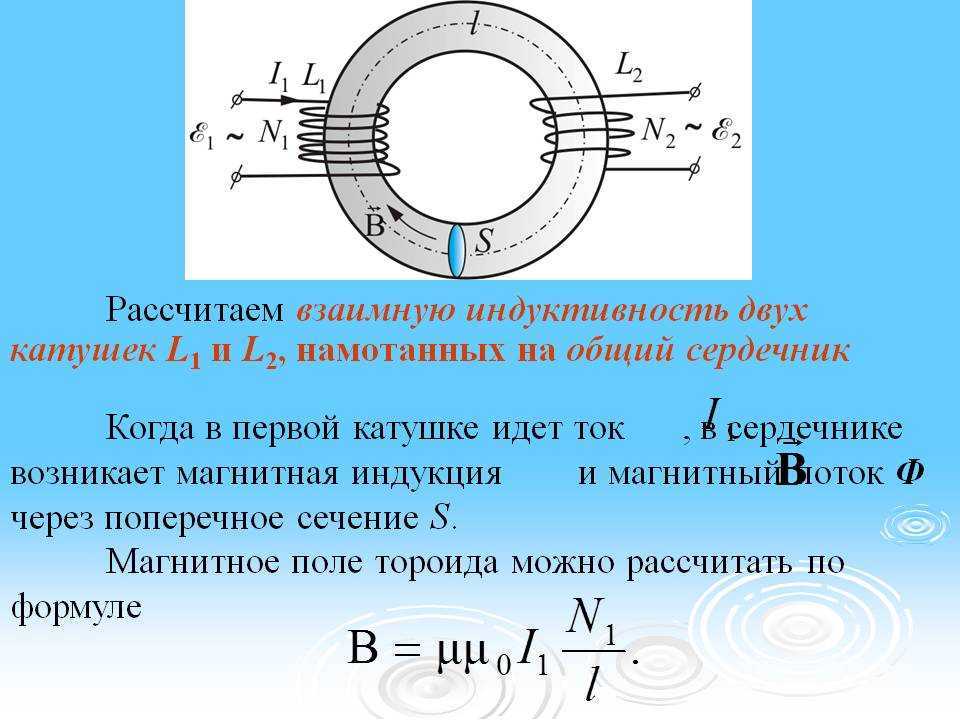

Рассчитать количество витков

ВВЕДИТЕ ВВОДНЫЕ ДАННЫЕ:

---

Выберите единицы измерения:

мм/см мил/дюйм

AWG → 000000000012345678910111213141516171819202122232425262728293031323334353637383940

---

---

л	= мГмГнГн	– Требуемая индуктивность
Д		– Диаметр катушки
д		— Диаметр провода без изоляции
к		— Диаметр провода с изоляцией	Автоматический

---

Вычислить

РЕЗУЛЬТАТ:

---

Н	=	– количество витков
л		– Длина обмотки

Очистить все

 

Рассчитать индуктивность

ВВЕДИТЕ ВВОДНЫЕ ДАННЫЕ:

---

Выберите единицы измерения:

мм/см мил/дюйм

---

---

Н	=	– Количество витков
Д		– Диаметр катушки
л		– Длина обмотки

---

Вычислить

РЕЗУЛЬТАТ:

---

Л

= мГмГнГн

– Индуктивность

Очистить все

 Coil64 также оценивает добротность и собственную емкость однослойной ВЧ-катушки.

Ниже приведены ссылки на лучшие, на мой взгляд, онлайн-калькуляторы, позволяющие найти индуктивность готового индуктора.

---

Каталожные номера:

1. Калькулятор индуктивности однослойной катушки от IN3OTD
2. Калькулятор ВЧ индуктивности от ON4AA
3. Калькулятор индуктивности круглой катушки R.Weaver

 

Электроника | Бесплатный полнотекстовый | Расчет индуктивности однослойной планарной спиральной катушки

1. Введение

Благодаря простоте реализации спиральная катушка нашла широкое применение во многих электромагнитных приложениях, начиная от высокочастотной радиочастотной идентификации (RFID) [1] и заканчивая относительно низкочастотная беспроводная передача энергии [2,3,4]. Для успешного применения в этих приложениях требуется точное моделирование спиральной катушки. Для решения этой проблемы было проделано много работ. Некоторые из них кратко рассмотрены в этой статье.

В [5,6,7] собственная индуктивность плоской спиральной катушки вычисляется путем рассмотрения ее как группы концентрических окружностей. Поэтому всегда существует некоторая погрешность между вычисленным и результатом измерения. Кроме того, для получения собственной индуктивности плоской спиральной катушки требуется вычисление индуктивностей каждой окружности и взаимных индуктивностей между ними. Следовательно, вычислительная сложность увеличивается.

Собственная индуктивность спиральной катушки аппроксимируется с помощью формулы Уилера или ее модифицированной формы [8,9]. Однако в этих формулах не учитывался один из параметров, влияющих на индуктивность: диаметр провода. Поэтому точность формул снижается при изменении диаметра проволоки спирального витка. Более того, точная деталь их вывода не установлена, и вместо аналитического метода индуктивность вычисляется эмпирически.

Программное обеспечение ANSYS Maxwell 3-D — один из лучших методов определения собственной индуктивности спиральной катушки любой формы; однако моделирование требует значительного времени расчета.

Для решения этого вопроса в статье предложено точное выражение собственной индуктивности плоской спиральной катушки, включающее все параметры, влияющие на индуктивность. Кроме того, используя интегральную формулу Неймана, этот метод вычисляет индуктивность плоской спиральной катушки, рассматривая всю спираль, не предполагая ее как группу концентрических окружностей. В результате вычислительная сложность формулы снижается.

Для проверки точности предлагаемого метода результаты расчета сравниваются с результатом моделирования и общепринятыми формулами, которые показывают хорошее совпадение. Для экспериментальной проверки несколько катушек с разными геометрическими параметрами изготавливаются на бобине, специально разработанной с помощью 3D-принтера. Наконец, сравнение результатов расчета и измерений подтверждает точность предложенного метода.

Структура документа следующая: Расчет собственной индуктивности плоской катушки обсуждается в Разделе 2. Раздел 3 проверяет результаты расчета с помощью другого традиционного метода и моделирования с использованием метода конечных элементов (МКЭ). Экспериментальная проверка результата расчета показана в разделе 4. Наконец, в разделе 5 подводятся итоги.

2. Расчет собственной индуктивности плоской спиральной катушки

Самоиндукция круглой плоской спиральной катушки может быть рассчитана путем решения интегральной формулы Неймана для взаимной индуктивности между двумя катушками [10]. Геометрические параметры плоской спирали, лежащие в плоскости x–y, показаны на рис. 1. Предполагается, что по спиральной катушке течет постоянный ток.

На рис. 1 R — внешний радиус спиральной катушки. θ — угол поворота R относительно оси x. w показывает диаметр провода, а s — расстояние между витками.

Внешний радиус R определяется по уравнению плоской спиральной катушки.

где R _i — внутренний радиус катушки, а — коэффициент шага, влияющий на расстояние между каждым витком.

Н – количество витков спиральной катушки.

Когда радиус кривизны спиральной катушки с одинаковой площадью поперечного сечения больше, чем радиус проводника катушки, самоиндукция плоской спиральной катушки будет равна взаимной индуктивности между исходной спиральной катушкой и ее фиктивной катушка размещена на расстоянии среднего геометрического расстояния (GMD) проводника [11]. Среднее геометрическое расстояние для литцендрата круглого сечения приведено в уравнении (4)

г представляет собой среднее геометрическое расстояние, а r представляет собой радиус проводника.

Радиус кривизны (внешний радиус) исходного R ₁ и его фиктивного спирального витка R ₂ показан в уравнениях (5) и (6).

θ ₁ и θ ₂ — угол поворота исходного и его фиктивного спирального витка соответственно.

Интегральная формула Неймана может быть представлена ​​уравнением (7).

где μ ₀ — вакуумная проницаемость, dl ₁ и dl ₂ — составляющие линии, а R — расстояние между dl ₁ и dl ₂ . Индуктивность плоской катушки можно рассчитать, оценив параметры в уравнении (7).

Скалярное произведение между dl ₁ и dl ₂ дано в уравнении (10).

Расстояние R можно представить с помощью формулы косинуса.

Подставив уравнения (10) и (11) в уравнение (7), получим точное уравнение собственной индуктивности плоской спиральной катушки, как показано в уравнении (12)

Уравнение (11) содержит все параметры, влияющие на индуктивность, такие как внутренний и внешний радиус спиральной катушки, число витков, диаметр проволоки и расстояние между витками. Влияние каждого параметра на индуктивность подробно обсуждается в следующих разделах.

3. Сравнение с моделированием и традиционными методами

Для проверки предлагаемого метода индуктивности нескольких спиральных катушек с различными геометрическими параметрами рассчитываются с использованием уравнения (12). Индуктивности также рассчитываются с использованием обычного метода и метода конечных элементов (МКЭ). По отношению к результату моделирования вычисляются погрешность расчета и условные результаты. Ошибка вычисляется как RFem-RcRFem×100, где R _Fem представляет результат моделирования, а R _c показывает расчетный или обычный результат.

Моделирование МКЭ проводится с использованием программного обеспечения ANSYS Maxwell 15. Тип решения — магнетостатический. Сетка назначается как длина на основе катушки и ее границы. Длина элемента является значением по умолчанию. Ток назначается равномерно по поперечному сечению катушки для простоты. Существует множество традиционных методов расчета спиральной катушки [8,9].,12]. В большинстве этих методов использовалась модифицированная формула Уилера для расчета собственной индуктивности спиральной катушки. Некоторые из этих формул были выбраны для сравнения в данной работе и обсуждаются ниже.

В [8] собственная индуктивность спиральной катушки аппроксимирована с использованием понятия среднего диаметра катушки, как показано в уравнении (13).

Собственная индуктивность спиральной катушки определяется исходя из эквивалентных плотностей тока и аппроксимации спирали [9]. Уравнение этого метода аппроксимации индуктивности спиральной катушки приведено в уравнении (16).

C _i – зависимый коэффициент. Для спиральной катушки круглой формы значение C ₁ равно 1, C ₂ равно 2,46, C ₃ равно 0,00 и C ₄ равно 0,20.

Методом приближения Уилера вычисляется собственная индуктивность спиральной катушки [12].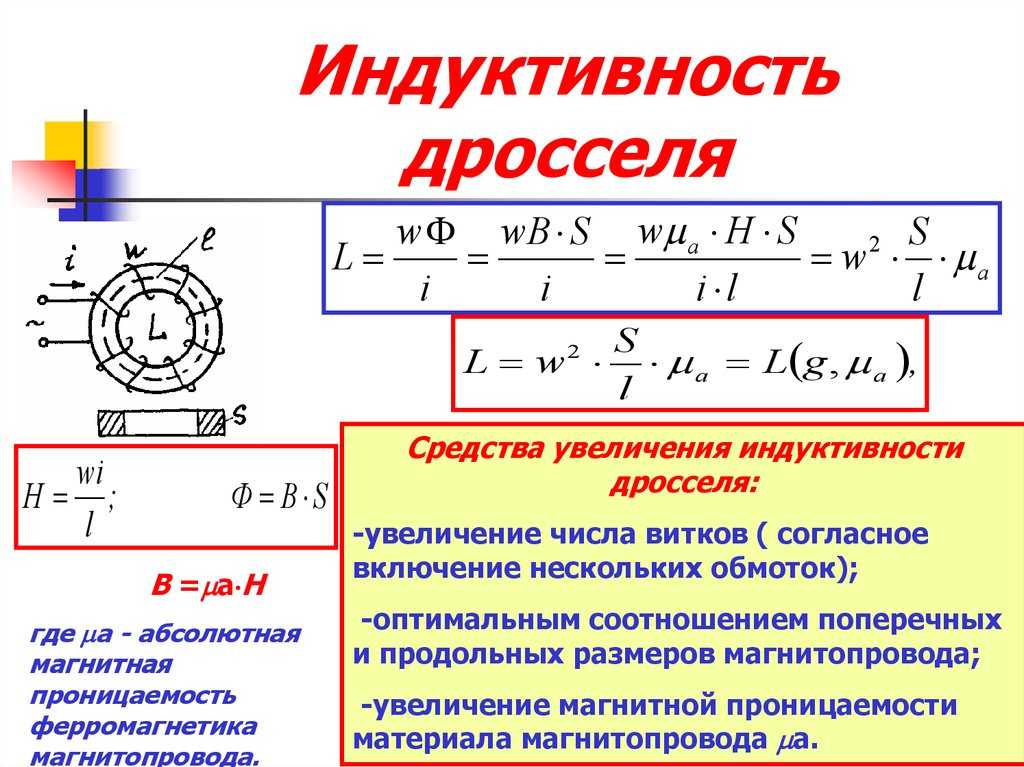 Эта формула недействительна, когда расстояние между витками меньше диаметра проволоки и катушка имеет меньшее количество витков. Эта формула аппроксимации математически обозначена в уравнении (17) и представлена ​​графически на рисунке 2.

Для расчета индуктивности однослойной круглой спиральной катушки в уравнении (18) используется модифицированная формула Гарольда А. Уилера.

где N — общее количество витков, w — диаметр проволоки, s — зазор между витками, а d _в и d _вых — внутренний и наружный диаметр проволоки соответственно.

Уравнения (13), (16)–(18) получены с использованием формулы Уилера или ее модифицированной формы для расчета индуктивности спиральной катушки. Следовательно, собственная индуктивность плоской спиральной катушки будет одинаковой при использовании любой из этих формул, а значит, и их погрешность относительно предлагаемого метода будет одинаковой. Любая из этих формул может быть выбрана для сравнения с предлагаемым методом.

Сравнение индуктивности путем изменения каждого геометрического параметра обсуждается в следующем подразделе.

3.1. Изменение внешнего радиуса

Для различного внешнего радиуса сравнивается поведение самоиндукции спирали для провода радиусом r = 1,8 мм, числом витков N = 10 и зазором между витками s = 4 мм. . Подробное сравнение показано на рисунке 3. На приведенном выше рисунке показано, что индуктивность катушки увеличивается, когда увеличивается внешний радиус или внешний диаметр катушки. Это можно объяснить определением индуктивности катушки.

Одним из факторов, от которых зависит индуктивность, является размер катушки. С увеличением размера катушки увеличивается и индуктивность. Индуктивность, полученная традиционным методом, ниже, чем результат расчета и моделирования. Таким образом, относительно результата моделирования ошибка традиционного метода выше, которая составляет около 16 %, по сравнению с ошибкой результата расчета, которая составляет менее 4 %. Таким образом, предлагаемый метод обеспечивает хорошую точность в отношении изменения внешнего радиуса.

3.2. Изменение диаметра провода

На рис. 4 показано поведение индуктивности для диаметров провода 3 мм и 3,6 мм. Значения остальных параметров такие же, как показано в разделе 3.1. По сравнению с проводом большого диаметра индуктивность катушки меньшего диаметра выше в результате расчета и моделирования. Однако индуктивность остается постоянной при изменении диаметра провода во многих традиционных формулах, потому что эти формулы не учитывают диаметр провода. При использовании обычного метода для расчета индуктивности ошибка составляет менее 17 % для диаметра провода 3,6 мм и 20 % для w = 3,0 мм по сравнению с результатом моделирования, и ошибка увеличивается по мере уменьшения диаметра провода. Однако погрешность результата расчета для всех случаев составляет менее 4%, что подтверждает его точность.

3.3. Изменение числа витков

На рис. 5 показано сравнение расчета собственной индуктивности и обычных результатов при различном числе витков для R _i = 10 мм, s = 4 мм и w = 3,6 мм. При увеличении числа витков катушки индуктивность возрастает. В обычных методах ошибка увеличивается с увеличением числа витков; однако он показал лучшую точность для меньшего количества витков по сравнению с результатом расчета. Можно сделать вывод, что обычная формула подходит для приложений, где требуется катушка с меньшим количеством витков. С другой стороны, погрешность результата расчета относительно результата МКЭ составляет менее 6 %, и точность сохраняется для всех случаев.

3.4. Изменение зазора между витками

На рис. 6 показано поведение индуктивности спиральной катушки при различных зазорах между витками при w = 3,6 мм, R _i = 10 мм и N = 10. Геометрия катушка расходуется с увеличением зазора между витками, увеличивая таким образом индуктивность. Погрешность резко возрастает с увеличением зазора между витками при использовании обычного метода.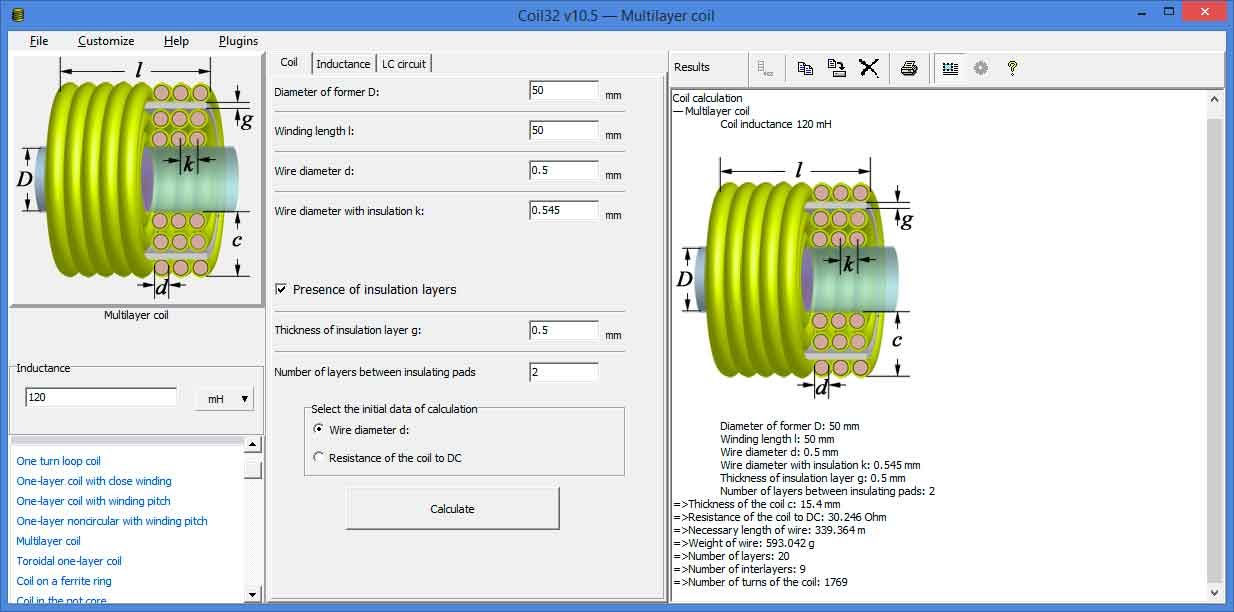 Однако результат расчета имеет погрешность менее 5% для увеличения зазора между витками. Таким образом, эти сравнения подтверждают справедливость результата расчета при различных вариациях геометрического параметра спирального витка.

4. Экспериментальная проверка

Для экспериментальной проверки предложенного метода необходимо рассчитать некоторые параметры изготовления спиральной катушки, такие как длина провода и сопротивления постоянному току. Кроме того, необходимо учитывать тип проволоки, качество пайки и катушку для удержания проволоки. Каждый из этих факторов кратко обсуждается в следующем подразделе.

4.1. Выбор провода

Различные типы проводов используются для изготовления катушки, но в этом исследовании выбран литцендратный провод из-за его огромных преимуществ и многократного использования во многих приложениях, таких как кристаллическое радио, рамочная антенна, высокодобротные катушки, коммутация. электроснабжение и индукционное нагревательное оборудование. Литцендрат изготавливается путем соединения нескольких жил тонкой изолированной проволоки рядом друг с другом. Каждая изолированная жила несет часть тока, уменьшая воздействие на кожу и близость. Благодаря этим эффектам литцендраты уменьшают увеличение сопротивления на более высоких частотах [13]. Этот провод можно использовать примерно до 1 МГц. В этой работе для изготовления спиральных катушек используется 500 прядей литцендрата, каждая прядь диаметром 0,1 мм. Диаметр проволоки составляет около 3,6 мм, что определяется эмпирическим путем по уравнению (19).).

где D _e — расчетный диаметр литцендрата, D _s — диаметр одной жилы, а N _s — общее количество жил.

4.2. Качество пайки

Диаметр провода, который является одним из факторов, влияющих на индуктивность, может быть уменьшен во время пайки. Поэтому для качественной пайки необходимы надлежащий процесс и меры предосторожности. Температура припоя (свинца) должна равномерно распределяться внутри паяльной ванны, при этом лучше выбирать припой с меньшим количеством примесей. Температура пайки зависит от типа и ширины проволоки. Таким образом, температуру следует регулировать и проверять термометром. Наконец, требуется специальное приспособление и соответствующий набор для пайки, как показано на рис. 7.

4.3. Расчет длины провода и сопротивления провода

Длина провода пропорциональна его сопротивлению постоянному току. Поэтому важно рассчитать длину провода и сопротивление. Общая длина и сопротивление провода могут быть рассчитаны по уравнениям (20) и (21). Кроме того, расчетная и фактическая длина и сопротивление постоянному току провода показаны на рис. 8а,б. Сопротивление постоянному току измеряется с помощью Gwinstek LCR-6020.

где l длина провода; σ постоянная, ее значение равно 58 000; n — количество прядей; r — радиус одной нити.

4.4. Бобина

Для крепления проволоки спиральной катушки с помощью 3D-принтера изготавливаются различные бобины с разным диаметром проволоки, количеством витков, расстоянием между витками и внешним радиусом. Нить для печати была PLA (полимолочная кислота). На рис. 9а,б показаны катушка и спиральная катушка с катушкой.

4.5. Экспериментальный результат

Для проверки предлагаемого метода изготавливаются три случайные катушки разных размеров, и их индуктивность измеряется с помощью Gwinstek LCR-6020 m. Частота тестирования для этого измерения составляет 20 кГц. Наконец, результаты измерений сравниваются с результатом расчета, и их результаты представлены в таблице 1. Кроме того, результаты измерений также показаны на рисунке 10.

Из таблицы 1 видно, что результаты расчета хорошо согласуются с результатом измерений. Относительная ошибка составляет менее 5%.

5. Выводы

В этой статье представлен новый способ расчета индуктивности однослойной плоской спирали. Используя принцип среднего геометрического расстояния, предлагаемый метод определяется путем решения формулы Неймана для взаимной индуктивности между двумя катушками. Численно рассчитаны индуктивности различных размеров спиральных катушек с различными внешними радиусами, числом витков, диаметром проволоки и зазором между витками. Результаты расчетов проверяются моделированием, экспериментальными и общепринятыми формулами. Погрешность результатов расчета составляет менее 5 % для всех случаев по сравнению с общепринятой формулой, которая составляла более 20 %. Более того, предлагаемый метод содержит все параметры, влияющие на индуктивность. Однако традиционные формулы не учитывали все параметры, что приводило к ошибочным результатам.

В этом исследовании индуктивность однослойной спиральной катушки рассчитывается для равномерного протекания тока в проводе. Однако индуктивность может быть разной для неоднородных токов. В этом случае она требует дальнейшего исследования и может быть учтена в дальнейшей работе.

Вклад авторов

И.Х. предложил теоретическую модель и провел эксперимент; Д.-К.В. пересмотрела проект и дала указания. Все авторы прочитали и согласились с опубликованной версией рукописи.

Финансирование

Это исследование не получило внешнего финансирования.

Конфликт интересов

Авторы заявляют об отсутствии конфликта интересов.

Ссылки

1. Лю, Ю.; Терри, Т.Ю. Антенна с сопряженной планарной катушкой (CPC) в качестве датчика смещения для меток NFC или HF RFID. В материалах Международной конференции IEEE по RFID (RFID) 2020 г., Орландо, Флорида, США, 5–9 октября 2020 г.; IEEE: Манхэттен, штат Нью-Йорк, США, 2020 г.; стр. 1–6. [Google Scholar]
2. Ифтихар Х.; Ву, Д.-К. Упрощенный расчет взаимной индуктивности плоской спиральной катушки для беспроводных приложений питания. Датчики 2022 , 22, 1537. [Google Scholar] [CrossRef] [PubMed]
3. Шахид, Х. ; Мохамед, А .; Ахмед, К.-Б.Л.; Ким, Ю.К. Весовая схема зарядки с нечеткой логикой для оптимального распределения мощности зарядки между электромобилями на стоянке. Energies 2020 , 13, 3119. [Google Scholar] [CrossRef]
4. Young, D.J. Беспроводное питание и телеметрия данных для биомедицинских имплантатов. В материалах ежегодной международной конференции IEEE Engineering in Medicine and Biology Society 2009 г., Миннеаполис, Миннесота, США, 3–6 сентября 2009 г.; IEEE: Манхэттен, штат Нью-Йорк, США, 2009 г.; стр. 3221–3224. [Google Scholar]
5. Чан, Х.Л.; Ченг, KWE; Сутанто, Д. Упрощенная формула Неймана для расчета индуктивности спиральной катушки. В материалах Восьмой международной конференции 2000 г. по силовой электронике и частотно-регулируемым приводам (публикация IEE Conf. No.475), Лондон, Великобритания, 18–19 сентября 2000 г.; стр. 69–73. [Google Scholar]
6. Рам Рахьяни, А.К.; Шахриар, М .; Mu, C. Проектирование и оптимизация эффективных беспроводных систем подачи энергии на основе резонанса для биомедицинских имплантатов. IEEE транс. Биомед. Цепи Сист. 2010 , 5, 48–63. [Google Scholar] [CrossRef] [PubMed]
7. Li, X.; Ханру, З .; Фей, П.; Ян, Л .; Тяньян, Ю .; Поклон.; Dongming, F. Беспроводная магнитно-резонансная система передачи энергии для микроимплантируемых медицинских датчиков. Датчики 2012 , 12, 10292–10308. [Google Scholar] [CrossRef] [PubMed]
8. Jie, L.; Костинетт, Д. Анализ и разработка последовательной саморезонансной катушки для беспроводной передачи энергии. В материалах конференции и выставки IEEE Applied Power Electronics Conference and Exposition (APEC) 2018 г., Сан-Антонио, Техас, США, 4–8 марта 2018 г.; стр. 1052–1059.. [Google Scholar]
9. Тао, Л.; Вэй, З .; Чи, Х .; Инь, Б. Расчет индуктивности многослойных круглых печатных спиральных катушек. Дж. Физ. конф. сер. 2019 , 1176, 062045. [Google Scholar]
10. Инан, Инженерная электромагнетика США; Pearson Education: Noida, India, 1998. [Google Scholar]
11. Калантаров П.Л. расчет индуктивности; National Power Press: Москва, Россия, 1955. [Google Scholar]
12. Чаттерджи, С.; Айер, А .; Бхаратираджа, К.; Вагасия, И.; Валивети, Р. Оптимизация конструкции эффективной беспроводной системы передачи энергии для электромобилей. Энергетическая процедура 2017 , 117, 1015–1023. [Google Scholar] [CrossRef]
13. Вяйсянен, В.; Хилтунен, Дж.; Нерг, Дж.; Сильвентойнен, П. Методы расчета сопротивления переменному току и практические соображения по проектированию при использовании литцендрата. В материалах IECON 2013—39th Annual Conference of the IEEE Industrial Electronics Society, Вена, Австрия, 10–13 ноября 2013 г.; стр. 368–375. [Google Scholar]

Рисунок 1. Плоская спиральная катушка.

Рис. 1. Плоская спиральная катушка.

Рисунок 2. Поперечный разрез спиральной катушки.

Рис. 2. Поперечный разрез спиральной катушки.

Рисунок 3. Поведение собственной индуктивности спиральной катушки в зависимости от внешнего радиуса.

Рис. 3. Поведение собственной индуктивности спиральной катушки в зависимости от внешнего радиуса.

Рисунок 4. Влияние изменения диаметра проволоки на самоиндукцию спиральной катушки.

Рис. 4. Влияние изменения диаметра проволоки на самоиндукцию спиральной катушки.

Рисунок 5. Влияние изменения числа витков на индуктивность спиральной катушки.

Рис. 5. Влияние изменения числа витков на индуктивность спиральной катушки.

Рисунок 6. Влияние изменения зазора между витками на индуктивность спиральной катушки.

Рис. 6. Влияние изменения зазора между витками на индуктивность спиральной катушки.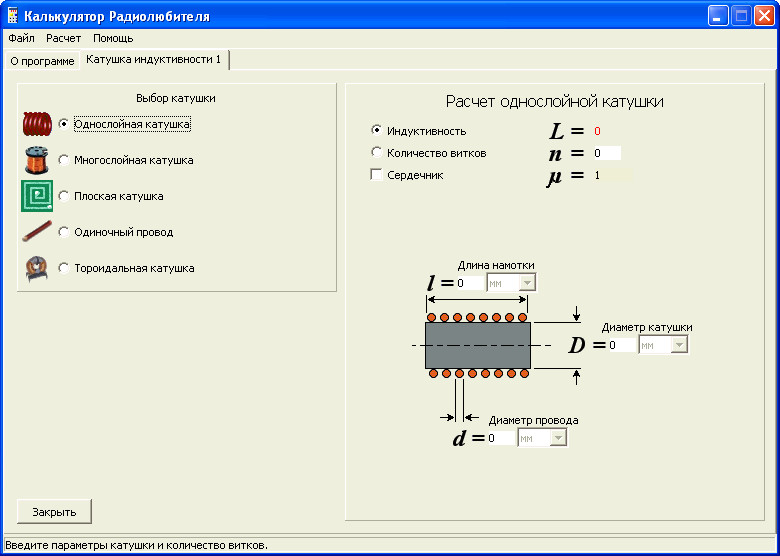

Рисунок 7. Настройка пайки.

Рис. 7. Настройка пайки.

Рисунок 8. Сравнение расчетной и измеренной длины и DCR. ( a ) Сравнение длины. ( b ) Сравнение DCR.

Рис. 8. Сравнение расчетной и измеренной длины и DCR. ( а ) Сравнение длин. ( b ) Сравнение DCR.

Рисунок 9. Спиральная катушка и бобина. ( a ) Шпулька. ( b ) Спиральная катушка, намотанная на бобины.

Рис. 9. Спиральная катушка и бобина. ( a ) Шпулька. ( b ) Спиральная катушка, намотанная на бобины.

Рисунок 10. Измерены индуктивности спиральной катушки разных размеров. ( и ) 7 витков. ( б ) 10 витков. ( c ) 16 витков.

Рис. 10. Измерены индуктивности спиральной катушки разных размеров. ( и ) 7 витков. ( б ) 10 витков. ( c ) 16 витков.

Таблица 1. Сравнение результата расчета и измерения.

Таблица 1. Сравнение результата расчета и измерения.

Параметры					Результаты
N	R i (мм)	с (мм)	W (мм)	R O (MM)	Индуктивность (μh) (CALCUDED) 9069	(μH) (CALCUDED)
. (%)
7	12	4	3.6	40	2. Похожие записи 21.11.2024 0 Особенности питания кормящей мамы: что можно и нельзя есть при грудном вскармливании 19.11.2024 0 Новорожденный какает слизью: причины появления слизи в кале грудничка 19.11.2024 0 Гемангиома у новорожденных: причины, виды, лечение и профилактика Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт