Какие основные виды сигналов используются в электросвязи. Каковы их ключевые характеристики и параметры. Как выглядят спектры различных сигналов электросвязи. Какова ширина спектра основных видов сигналов.
Классификация сигналов в электросвязи
Сигналы в электросвязи можно классифицировать по нескольким основным признакам:
- По характеру изменения во времени:
- Периодические — повторяющиеся через равные промежутки времени
- Непериодические — не имеющие строгой периодичности
- По типу передаваемой информации:
- Речевые (телефонные)
- Музыкальные
- Изображения (факсимильные, телевизионные)
- Данные (телеграфные, компьютерные)
- По способу представления информации:
- Аналоговые — непрерывно изменяющиеся во времени
- Дискретные — принимающие конечное число значений
Рассмотрим подробнее основные виды сигналов, используемых в современных системах электросвязи.
Характеристики речевых (телефонных) сигналов
Речевой сигнал образуется в результате колебаний голосовых связок человека и резонансных явлений в ротовой и носовой полостях. Основные характеристики речевого сигнала:

- Частота основного тона: 50-250 Гц
- Наличие обертонов (гармоник основного тона)
- Формантная структура спектра
- Эффективный частотный диапазон: 300-3400 Гц
Речевой сигнал имеет сложную форму колебаний звукового давления. При преобразовании в электрический сигнал с помощью микрофона сохраняется характер изменения амплитуды во времени.
Особенности сигналов звукового вещания
Сигналы звукового вещания отличаются от телефонных следующими параметрами:
- Более широкий частотный диапазон: 20-20000 Гц
- Выше динамический диапазон (отношение максимальной мощности к минимальной)
- Требования к качеству воспроизведения:
- Первый класс: 50-10000 Гц
- Высший класс: 30-15000 Гц
Расширенный частотный диапазон позволяет более точно передавать тембр музыкальных инструментов и голоса исполнителей.
Специфика факсимильных сигналов
Факсимильные сигналы используются для передачи неподвижных изображений. Их основные характеристики:
- Построчная развертка изображения
- Представление в виде последовательности импульсов
- Ширина спектра зависит от:
- Скорости развертки
- Размера элемента изображения
- Типичная ширина спектра: 1.5-3 кГц
- Для передачи газет: до 180 кГц
Факсимильные сигналы могут содержать как двухградационные (черно-белые), так и полутоновые изображения.
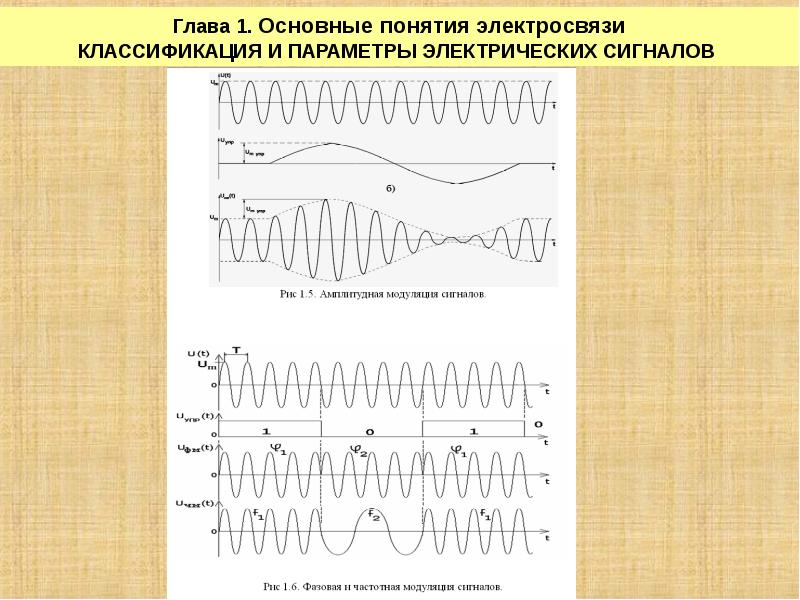
Особенности телевизионных сигналов
Телевизионные сигналы предназначены для передачи движущихся изображений. Их ключевые параметры:
- Частота кадров: 25 Гц
- Число строк: 625
- Число элементов в строке: 833
- Время передачи одного элемента: 80 нс
- Верхняя граница спектра: 6.5 МГц
- Нижняя граница спектра: 50 Гц
Телевизионный сигнал включает в себя сигнал изображения, звукового сопровождения и служебные импульсы синхронизации.
Характеристики телеграфных сигналов и сигналов передачи данных
Телеграфные сигналы и сигналы передачи данных относятся к дискретным сигналам. Их особенности:
- Представление в виде комбинаций импульсов и пауз
- Использование телеграфных кодов (МТК-2 и др.)
- Скорость передачи измеряется в бодах
- Стандартные скорости:
- Телеграфия: 50 Бод
- Передача данных: от 200 до 9600 Бод и выше
- Ширина спектра примерно равна скорости в бодах
Сигналы передачи данных могут использовать более сложные коды для обнаружения и исправления ошибок.
Сравнение спектров различных сигналов электросвязи
Ширина спектра сигнала определяет требования к полосе пропускания канала связи. Сравним спектры основных видов сигналов:
- Телеграфный: 0-100 Гц
- Передача данных (2400 Бод): 0-2400 Гц
- Телефонный: 300-3400 Гц
- Звуковое вещание: 50-10000 Гц
- Факсимильный:
- Стандартный: 0-1465 Гц
- Для передачи газет: 0-180000 Гц
- Телевизионный: 50-6000000 Гц
Как видно, наиболее широкополосным является телевизионный сигнал, а самый узкополосный — телеграфный.
Влияние параметров сигналов на системы электросвязи
Характеристики сигналов оказывают существенное влияние на проектирование и эксплуатацию систем электросвязи:
- Ширина спектра определяет требуемую полосу пропускания каналов
- Динамический диапазон влияет на требования к линейности усилителей
- Скорость передачи данных задает требования к тактовой синхронизации
- Помехоустойчивость сигналов определяет необходимость применения помехоустойчивого кодирования
Учет этих факторов позволяет создавать эффективные системы связи для различных применений.
Характеристики различных сигналов
Все сигналы могут быть подразделены на периодические и непериодические.
Периодическим называется сигнал, значения которого повторяются через определенные равные промежутки времени, называемые периодом повторения сигнала, или просто периодом. Для непериодического сигнала это условие не выполняется.
Простейшим периодическим сигналом является гармоническое колебание.
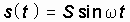 ,
,
где S, w – амплитуда и угловая частота колебания.
Другим примером периодического сигнала является последовательность прямоугольных импульсов (рис. 3.2, а). Как вы думаете, из чего состоит эта последовательность импульсов? Оказывается, из синусоид. Взгляните на рис. 3.2. В качестве исходной синусоиды выберем такую, у которой период колебаний совпадает с периодом T прямоугольных импульсов (рис. 3.2, б)
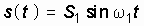 , (3.1)
, (3.1)
где 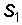 – амплитуда синусоиды, а
– амплитуда синусоиды, а 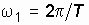 .
.
Колебание (3.2.) заданной частоты  и амплитуды
и амплитуды 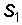 можно представить в виде графика: на оси частот отметить значение
можно представить в виде графика: на оси частот отметить значение 
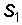 (см. рис. 3.2, б).
(см. рис. 3.2, б).
Следующая синусоида имеет частоту колебаний в 3 раза большую, а амплитуду – в 3 раза меньшую.
Сумма этих двух синусоид  пока еще мало похожа на прямоугольные импульсы (рис. 3.2, в). Но если мы добавим к ним синусоиды с частотами колебаний в 5, 7, 9, 11, и т.д. раз большими, а с амплитудами в 5, 7, 9, 11, и т.д. раз меньшими, то сумма всех этих колебаний:
пока еще мало похожа на прямоугольные импульсы (рис. 3.2, в). Но если мы добавим к ним синусоиды с частотами колебаний в 5, 7, 9, 11, и т.д. раз большими, а с амплитудами в 5, 7, 9, 11, и т.д. раз меньшими, то сумма всех этих колебаний:
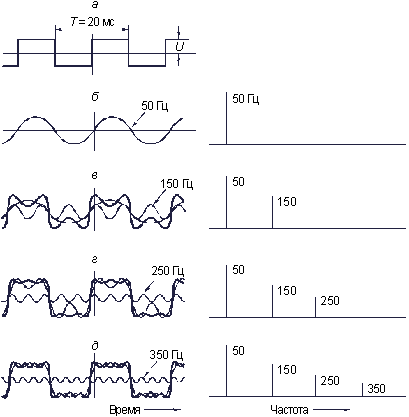
Рис. 3.2. Периодическая последовательность прямоугольных импульсов (а) и формирование ее сигнала (б–д)
где 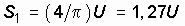 , будет не так уже сильно отличатся от прямоугольных импульсов (рис. 3.2, г и д). Таким образом, степень “прямоугольности” импульсов определяется тем, сколько синусоид со все более высокими частотами колебаний мы будем суммировать.
, будет не так уже сильно отличатся от прямоугольных импульсов (рис. 3.2, г и д). Таким образом, степень “прямоугольности” импульсов определяется тем, сколько синусоид со все более высокими частотами колебаний мы будем суммировать.
Может показаться, что представление прямоугольных импульсов в виде совокупности синусоид есть не более чем математический прием и не имеет никакого отношения к реальности. Однако это не так. Радиоинженерам хорошо знакомы приборы (они называются анализаторами спектров), которые позволяют выделить каждую входящую в сложный сигнал синусоиду.
Тот факт, что сигнал произвольной формы (а не только прямоугольные импульсы) можно “разложить” на сумму обыкновенных синусоид, впервые доказал в 20-х годах прошлого века французский математик Ж. Фурье. Такой набор синусоид получил название
Непериодический сигнал легко получить из периодического, увеличивая период вплоть до 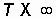 (рис. 3.3, а–г). Спектр амплитуд для сигналов с разными периодами показаны на рис. 3.4, а–в.
(рис. 3.3, а–г). Спектр амплитуд для сигналов с разными периодами показаны на рис. 3.4, а–в.
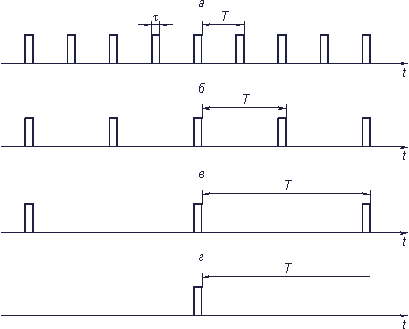
Рис. 3.3. Увеличение периода последовательности прямоугольных импульсов
При увеличении периода сигнала частота первой гармоники 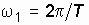
Следовательно, при переходе к непериодическому сигналу (например, к одиночному импульсу) мы получаем в спектре такого сигнала вместо отдельных гармоник бесконечно большое число синусоидальных колебаний с бесконечно близкими частотами, заполняющими всю шкалу частот. Причем амплитуда каждого такого колебания становится исчезающе малой, потому что на его долю приходится бесконечно малая часть энергии сигнала. Другими словами, в любой бесконечно узкой полосе частот мы всегда обнаружим синусоидальное колебание, правда, бесконечно малой амплитуды.
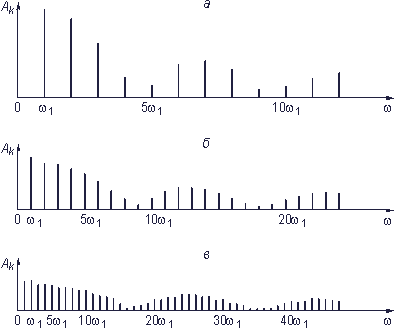
Рис. 3.4. Спектры амплитуд периодических последовательностей импульсов с разными периодами а–в см. в тексте
Поскольку сравнивать между собой бесконечно малые величины неудобно, то вместо амплитуд 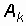 по оси ординат откладывают произведение
по оси ординат откладывают произведение 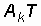 , которое с увеличением периода Т остается постоянным. В новых координатах спектры, показанные на рис. 3.4, а–в, будут выглядеть так, как показано на рис. 3.5, а–г. Понятие спектра амплитуд здесь лишено смысла и заменяется понятием спектральной плотности амплитуд, которая указывает, по сути, на удельный вес бесконечно малой амплитуды синусоидального колебания в любой бесконечно узкой полосе частот. Понятие спектра фаз заменяется понятием спектральной плотности фаз. Таким образом, спектр непериодического сигнала является в общем случае не дискретным, а непрерывным.
, которое с увеличением периода Т остается постоянным. В новых координатах спектры, показанные на рис. 3.4, а–в, будут выглядеть так, как показано на рис. 3.5, а–г. Понятие спектра амплитуд здесь лишено смысла и заменяется понятием спектральной плотности амплитуд, которая указывает, по сути, на удельный вес бесконечно малой амплитуды синусоидального колебания в любой бесконечно узкой полосе частот. Понятие спектра фаз заменяется понятием спектральной плотности фаз. Таким образом, спектр непериодического сигнала является в общем случае не дискретным, а непрерывным.
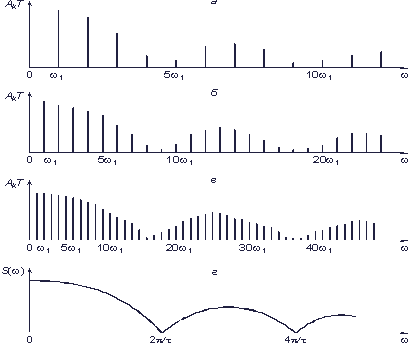
Рис. 3.5. Переход к спектральной плотности (г) одиночного прямоугольного импульса а–в см. в тексте
Уровни сигналов
Для сравнения мощностей сигналов, передаваемых по системе электросвязи, часто пользуются логарифмическими единицами – децибелами. Децибел (русское обознач. ДБ, международное – dB), как показывает приставка “деци”, составляет десятую часть другой, более крупной единицы, названной белом в честь А.Г. Белла – изобретателя телефона. Бел – это десятичный логарифм отношения двух мощностей. Если известны две мощности: Р1 и Р2, то их отношение, выраженное в белах, определяется формулой p=lg(P2/P1).
Для практики бел – слишком крупная величина. Обычно отношение мощностей выражают в децибелах, для чего при расчетах пользуются формулой p=10lg(p2/p1).
Динамический диапазон и пик-фактор сигналов. Мгновенная мощность сигналов связи может принимать различные значения в самых широких пределах. Чтобы охарактеризовать эти пределы, вводят понятия динамического диапазона и пик-фактора сигналов.
Динамический диапазон сигнала, дБ, определяется выражением:
Dc=10lg(Pmax/Pmin),
где Pmax, Pmin – максимальное и минимальное значения мгновенной мощности.
Пик-фактором сигнала называют отношение его максимальной мощности к средней, выраженное в логарифмических единицах:
Q=10lg(Pmax/Pср).
Пример. Пусть имеется периодический прямоугольный сигнал
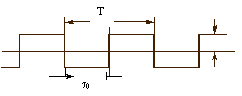
Он может быть разложен на составляющие с частотами f1=1/T, f3=3/T, f5=5/T и т.д. Число составляющих бесконечно, но чем выше частота, тем меньше амплитуда. Следовательно, теоретически полоса частот, которую занимает данный сигнал, стремится к Ґ .
Для передачи такого сигнала требуется канал, имеющий бесконечную полосу пропускания. Во-первых, таких каналов нет, во-вторых, чем шире полоса пропускания канала, тем он дороже. Но т.к. чем выше частота составляющей, тем ниже амплитуда, то составляющими с частотой і fn можно пренебречь.
Возьмём только составляющие f1, f3, f5. Полоса частот, которую занимают эти составляющие, f5 – f1=D fc.
Пусть f1=1000 Гц, f3=3000 Гц, f5=5000 Гц.
Занимаемая этими составляющими, полоса частот:
5000-1000 = 4000 Гц.
Уменьшим длительность единичного элемента в 3 раза, тогда f1=3000 Гц, f3=9000 Гц, f5=15000 Гц и занимаемая полоса 12000 Гц.
Вывод. Чем меньше длительность единичного элемента (t 0), тем шире полоса частот, занимаемая сигналом!
Отсюда следствие: чем больше скорость телеграфирования В, тем шире полоса частот, занимаемая сигналом, и тем шире требуется канал и, следовательно, тем дороже доставка информации.
Сигналы электросвязи и их спектры. Рассмотрим наиболее часто встречающиеся сигналы электросвязи и обсудим их спектры.
Телефонные (речевые) сигналы. Человек набрал в легкие воздух и издал звук. Что же произошло? Воздух, выходя из легких, заставляет вибрировать голосовые связки. От них колебания воздуха передаются через гортань голосовому аппарату, заканчивающемуся ротовой и носовой полостями (рис. 3.6).
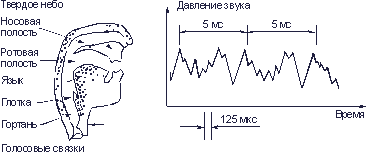
Рис. 3.6. Кривая звукового давления при произнесении звука «а» мужским голосом
Последние выполняют роль резонаторов – они усиливают колебания воздуха, подобно тому, как полый корпус гитары или скрипки, также являясь резонатором, усиливает звуки струн. Колебания воздуха из голосового аппарата человека передаются окружающему воздуху. Возникает звуковая волна. Характер издаваемого звука определяется натяжением голосовых связок, формой ротовой полости, положением языка, губ и т.д.Из описания голосового аппарата человека нетрудно понять, что голосовые связки играют роль своеобразных струн, они создают основной тон и обильное количество обертонов. Частота основного тона речи лежит в пределах от 50…80 Гц (очень низкий голос – бас) до 200…250 Гц (женский и детский голоса). При разговоре частота основного тона меняется в значительных пределах, особенно при переходе от гласных звуков к согласным и наоборот.
В совместном звучании основной тон и обертоны создают соответствующую окраску звука или тембр. Один тембр отличается от другого числом и силой обертонов. При преобладании в человеческом голосе высоких обертонов над низкими мы слышим в нем “звучание металла”. Люди, у которых в голосе преобладают низкие обертоны, говорят мягким, бархатным голосом.
Для получения формы кривой звукового давления, создаваемого речью человека, нужно сложить синусоидальные кривые основного тона и обертонов. Из-за наличия большого числа обертонов форма результирующей кривой будет сложной. На рис. 3.6 показано, какое давление создает звук “а”, произнесенный мужским голосом с частотой основного тона 200 Гц (период основного тона 5 мс). Для передачи звука на расстояние он в телефонном аппарате превращается в сигнал. Для этой цели служит микрофон.
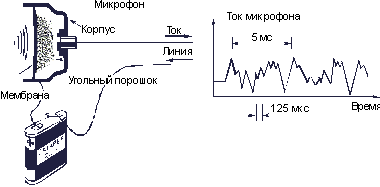
Рис. 3.7. Превращение звука в электрический сигнал с помощью микрофона
Телефон был изобретен А.Г. Беллом, учителем в школе глухонемых в американском городе Бостоне в 1876 г. С тех пор в его конструкцию было внесено много усовершенствований. В частности, в современном телефоне используется чувствительный угольный микрофон (рис. 3.7). В нем мембрана соприкасается с угольным порошком. Пока в микрофон не говорят, сопротивление порошка остается неизменным и через него от батареи в линию (провода) протекает постоянный ток. Стоит произнести в микрофон какое-нибудь слово, порошок под действием колеблющейся мембраны будет то спрессовываться, то разрыхляться. Изменение плотности порошка приводит к изменению его электрического сопротивления, а значит, и к изменению тока, текущего через порошок. В проводах, идущих от микрофона, рождается электрический ток, повторяющий форму звукового давления.
Изучение речи показывает, что речь – это процесс, частотный спектр которого находится в пределах от 50…100 до 8000…10000 Гц. Установлено однако, что качество речи остается вполне удовлетворительным, если ограничить спектр снизу и сверху частотами 300 и 3400 Гц. Эти частоты приняты Международным союзом электросвязи (МСЭ) в качестве границ эффективного спектра речи. При указанной полосе частот сохраняется хорошая разборчивость речи и удовлетворительная натуральность ее звучания.
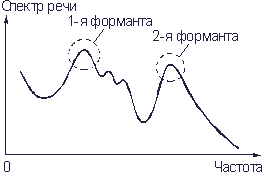
Рис. 3.8. Спектр человеческой речи
На рис. 3.8 показан спектр речи. Как видно из рисунка, некоторые частотные составляющие речи усилены, а другие ослаблены. Усиленные области спектра частот называются формантами. Звуки речи различных людей отличаются числом формант и их расположением в частотном спектре. Отдельные звуки могут иметь до шести формант, из которых только одна или две являются определяющими. Они обязательно находятся в диапазоне частот 300…3400 Гц. Между формантами лежат менее мощные составляющие звуковых частот. Однако именно они придают голосу каждого человека индивидуальность, позволяющую узнавать говорящего.
Сигналы звукового вещания. Источниками звука при передаче программ вещания обычно являются музыкальные инструменты или голос человека. Формирование сигналов звукового вещания и их прием осуществляется так же, как и телефонных сигналов. Используются лишь другие типы микрофонов.
Спектр звукового сигнала занимает полосу частот 20…20000 Гц. Однако в зависимости от требований к качеству воспроизведения ширина спектра сигнала вещания может быть ограничена. Для достаточно высокого качества (каналы вещания первого класса) полоса частот должна составлять 50…10000 Гц, для безукоризненного воспроизведения программ вещания (каналы высшего класса) – 30…15000 Гц.
Факсимильные сигналы. Обратите внимание на то, как вы читаете книгу. Ваши глаза скользят по строке слева направо, затем вы переходите к началу другой строки и т.д. до конца страницы. Словом вы “просматриваете” все элементы строки последовательно. Можно сказать, что при чтении книги происходит построчная развертка текстового изображения.
Именно по такому принципу “просматривается” изображение в современных факсимильных аппаратах, предназначенных для передачи на расстоянии различного рода неподвижных изображений (документов, чертежей, рисунков, фотографий). Для этого с помощью источника света и системы оптических линз формируют световое пятно так, чтобы освещать на передаваемом изображении площадку размером, скажем, 0,2ґ 0,2 мм. Это световое пятно перемещается сначала вдоль одной строки, затем переходит на другую и движется по ней – и так до конца последней строки. Свет, отражаясь от каждой элементарной площадки, попадает на фотоэлемент и вызывает в его цепи ток (рис. 3.9). Значение этого тока зависит от яркости отраженного света, а последняя – от яркости освещенной площадки. Таким образом, при переходе светового пятна на изображении от одной элементарной площадки к другой ток в цепи фотоэлемента меняется пропорционально яркости площадок: мы получаем точную электрическую копию изображения.
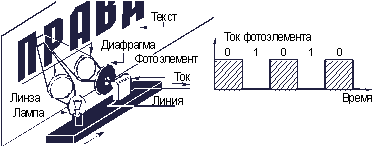
Рис. 3.9. Преобразование изображения в электрический сигнал в факсимильном аппарате
Рассмотрим изображение, состоящее только из двух цветов: черного и белого, например, страницу книги, какой-либо чертеж и т.п. Очевидно, каждый элемент изображения (напомним, что размером он всего 0,2ґ 0,2 мм) будет представлять собой либо черную, либо белую площадку, напоминая чередованием шахматную доску. Черные площадки практически полностью поглощают падающий на них свет. Яркость отраженного ими света при этом настолько ничтожна, что при просмотре черных площадок ток в цепи фотоэлемента не возникает. Наоборот, площадки белого цвета почти полностью отражают падающий на них свет, и при попадании на них светового луча ток в цепи фотоэлемента скачком принимает максимальное значение. Таким образом, перемещая световое пятно, а вслед за ним и фотоэлемент вдоль каждой строки изображения, получаем на выходе фотоэлемента последовательность импульсов (рис. 3.9).
При таком “шахматном” чередовании элементов изображения спектр факсимильного сигнала будет шире, чем для любого другого изображения, поскольку круче фронтов импульсов, чем у прямоугольных, не бывает.
Ширина спектра факсимильного сигнала зависит от скорости развертки изображения и размеров светового пятна.
На стандартном листе бумаги формата А4 в строке помещается примерно 1000 черно-белых элементов изображения при ширине пятна 0,2 мм. Если в факсимильном аппарате скорость развертки составляет 60 строк/мин, т.е. каждая строка считывается за 1 с, то за эту секунду 500 раз будет осуществлен переход с черного на белое, или наоборот. Это означает, что максимальная частота чередования импульсов равна 500 Гц. При ширине светового пятна 0,1 мм в строке будет в 2 раза больше элементов изображения, и максимальная частота чередования импульсов повысится до 1000 Гц. Так как для сохранения хорошей степени “прямоугольности” импульсов нужно передавать кроме основной гармоники еще и несколько высших, то ширина спектра факсимильного сигнала может простираться до 1,5…3,0 кГц.
При увеличении скорости развертки изображения черные и белые площадки будут считываться чаще и, следовательно, спектр факсимильного сигнала будет шире. При передаче изображений с полутонами получается сигнал сложной формы, спектр которого является непрерывным и соединяет все частоты от нуля до максимальной.
Факсимильная связь широко используется для передачи газетных полос (т.е. их изображений) в пункты централизованного печатания. Для передачи газет используют специальные высокоскоростные факсимильные аппараты с шириной светового пятна 0,05 мм. Повышенная скорость развертки позволяет передавать одну газетную полосу за 2–3 минуты. Это приводит к расширению спектра факсимильного сигнала до 180 кГц.
Телевизионные сигналы. Любое подвижное изображение – это, как правило, смена через каждые 40 мс одного неподвижного изображения другим (25 кадров в 1 с). За время между сменой кадров нужно успеть просмотреть все неподвижное изображение, которое содержит полмиллиона элементарных площадок или элементов изображения (625 строк по 833 элемента в строке). Значит, каждый элемент изображения придется рассматривать в течение одной полумиллионной доли от отведенных на весь кадр 40 мс. Это непостижимо короткий отрезок времени – всего две десятимиллиардных доли секунды! Ясно, что ни одно механическое устройство не способно перемещать световое пятно и фотоэлемент по строкам изображения с такой скоростью.
Вы никогда не задумывались над тем, что вы видите на экране телевизора, когда усаживаетесь перед ним в свободный вечер? Изображение? Нет, в действительности на экране никакого изображения нет, абсолютно никакого! Если бы мы сумели открыть глаза на какую-то ничтожную долю секунды (а речь идет о миллионных и даже миллиардных долях), то увидели бы на экране всего одну светящуюся точку. Это она бежит с невероятной скоростью по экрану, оставляя в нашем глазу след (мы видим то, чего уже нет, еще в течение 0,1 с), изменяющийся по яркости.
Что же заставляет светящуюся точку перемещаться с такой головокружительной быстротой? Электронный луч. Это он способен почти мгновенно отклоняться под действием изменяющегося магнитного поля и развертывать “картинки”. Это его можно очень точно сфокусировать с помощью специальных электрических “линз”. Первые опыты с электронным лучом начались в самом начале XX в. Еще в 1907 г. профессор Петербургского технологического института Б.Л. Розинг сконструировал первую электронно-лучевую трубку и получил на ней изображение, правда, невысокого качества. Изобретение в начале 30-х годов этого столетия первых качественных передающих трубок связано с именами советских ученых, пионеров отечественного телевидения С.И. Катаева и П.И. Шмакова.
Как бы не отличались конструкции передающих телевизионных трубок разных лет, все они в чем-то имитируют глаз. Роль хрусталика выполняет объектив, роль зрачка – диафрагма. Имеется в трубке и своя “сетчатка” – пластинка, напоминающая пчелиные соты, в ячейках которых располагаются микроскопические фотоэлементы. Конечно, их намного меньше, чем фоторецепторов в глазу: всего около 0,5 млн. Изображение, которое нужно превратить в серию электрических импульсов, проектируется с помощью объектива на эту искусственную “сетчатку”. Каждый микроскопический фотоэлемент (представляющий собой капельку светочувствительного серебряно-цезиевого сплава) получает свою порцию света и, если его подключить к внешней цепи, создаст ток, пропорциональный освещенности. Что касается электронного луча, то он как раз и подключает поочередно каждый из 500000 фотоэлементов к внешней цепи трубки, причем отводится ему на это всего 40 мс, пока не сменится кадр. Таким образом, на одном элементе изображения луч “задерживается” не более 80 миллиардных долей секунды (т.е. 80 нс). Величина тока во внешней цепи трубки отражает в каждый момент времени яркость соответствующего элемента изображения, спроектированного объективом на “сетчатку” передающей трубки, и является точной электронной копией передаваемого изображения.
Подсчитаем ширину спектра телевизионного сигнала. Пусть и на этот раз чередуются черные и белые площадки (элементы). Всего таких элементов будет 625 строк ґ 833 элемента = 520 625. В секунду меняется 25 кадров, т.е. 25 ґ 520 625 = 133 015 625 элементов. Значит переход с черного на белое, или наоборот, происходит примерно 6500000 раз в 1 с. Максимальная частота повторения импульсов равна 6,5 мГц, что и принято за верхнюю границу ширины спектра телевизионного сигнала. Нижней границей считают 50 Гц (нижняя граница сигнала звукового сопровождения).
Во время смены строк и кадров развертывающий луч приемной трубки должен быть погашен. Кроме того, необходимо синхронизировать лучи приемной и передающей трубок. Таким образом, кроме сигнала изображения необходимо передавать вспомогательные управляющие импульсы (гасящие и синхронизирующие). Электрический сигнал, включающий в себя сигнал изображения и управляющие импульсы, называется полным телевизионным сигналом.
В системах цветного телевидения передаваемое изображение расчленяется с помощью светофильтров на три одноцветных изображения – красное, зеленое и синее. Красные, зеленые и синие лучи попадают каждый на свою телевизионную трубку. В приемном устройстве путем сложения трех одноцветных изображений воспроизводится передаваемое цветное изображение.
Таким образом, спектр телевизионного сигнала простирается от 50 Гц до 6,5 мГц.
Телеграфные сигналы и сигналы передачи данных. Все рассматриваемые до сих пор сообщения и сигналы являются непрерывными. Сообщения и сигналы телеграфии и передачи данных относятся к дискретным.
Устройства преобразования телеграфных сообщений и данных в электрический сигнал представляют каждый знак сообщения (букву, цифру) в виде определенной комбинации импульсов и пауз одинаковой длительности. Импульс соответствует наличию тока на выходе устройства преобразования (например, телеграфного аппарата), пауза – отсутствию тока.
В телеграфии таблица, которая ставит в соответствие буквам, цифрам и другим знакам комбинации импульсов и пауз, называется телеграфным кодом. Если обозначить импульс через 1, а паузу через 0 и воспользоваться международным телеграфным кодом МТК-2, то можно, например, знак А записать в виде 11000, знак В – в виде 10011 и т.д.
Для передачи данных используют более сложные коды, которые позволяют обнаруживать и исправлять ошибки в принятой комбинации импульсов, возникающие от действия помех.
Устройства преобразования сигналов телеграфии и передачи данных в сообщения по принятым комбинациям импульсов и пауз восстанавливают в соответствии с таблицей кода знаки сообщения (буквы, цифры и др.) и выдают их на печатающее устройство либо на экран дисплея.
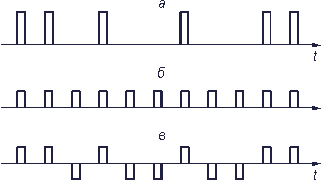
Рис. 3.10. Представление потока импульсов (а) в виде регулярной (б) и случайной (в) составляющих
Заметим, что чем меньше длительность импульсов, отображающих сообщения, тем больше их будет передано в единицу времени. Величина, обратная длительности импульса, называется скоростью телеграфирования: 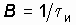 , где
, где 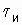 – длительность импульса, с.
– длительность импульса, с.
В честь французского инженера Ж. Бодо единицу скорости телеграфирования назвали бодом. При длительности импульса 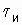 = 1 с скорость В = 1 Бод. В телеграфии используются импульсы длительностью 0,02 с, что соответствует стандартной скорости телеграфирования 50 Бод. Применяются и другие скорости телеграфирования (например, 75 Бод). Скорости передачи данных существенно выше. Существует аппаратура передачи данных со скоростями 200, 600, 1200 Бод и более.
= 1 с скорость В = 1 Бод. В телеграфии используются импульсы длительностью 0,02 с, что соответствует стандартной скорости телеграфирования 50 Бод. Применяются и другие скорости телеграфирования (например, 75 Бод). Скорости передачи данных существенно выше. Существует аппаратура передачи данных со скоростями 200, 600, 1200 Бод и более.
Сигналы телеграфии и передачи данных обычно имеют вид последовательностей прямоугольных импульсов.
Посмотрите внимательно на рис. 3.10. Можно представить (разумеется, чисто условно) поток импульсов в виде суммы двух последовательностей: регулярной и случайной. Спектр регулярной последовательности дискретный и создает нечетные гармоники тактовой частоты (т.е. частоты следования), а случайная последовательность имеет непрерывный заштрихованный спектр. Эти спектры показаны на рис. 3.11.
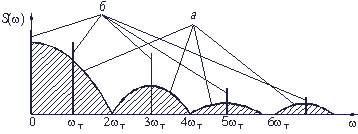
Рис. 3.11. Спектры случайной (а) и регулярной (б) составляющей потока импульсов
При передаче двоичных сигналов (т.е. 0 и 1) нет необходимости восстанавливать в приемнике импульсы без искажений, т.е. сохранять их форму; для восстановления информации достаточно зафиксировать только знак импульса при двуполярном сигнале либо наличие или отсутствие при однополярном сигнале. Расчеты показывают, что импульсы можно уверенно зафиксировать, если для их передачи используется ширина полосы частот, численно равная скорости передачи в бодах. Так, для стандартной скорости телеграфирования 50 Бод ширина спектра телеграфного сигнала составит 50 Гц. При скорости 2400 Бод (среднескоростная система передачи данных) ширина спектра сигнала равна примерно 2400 Гц.
Для удобства спектры основных сигналов электросвязи сведены в табл. 3.1. Даже беглый взгляд на табл. 3.1 позволяет понять, что для передачи разных видов сигналов требуется различная ширина полосы пропускания системы электросвязи.
Таблица 3.1. Ширина спектров сигналов электросвязи
|
Вид сигнала |
Ширина спектра, Гц |
| Телеграфный |
0…100 |
| Передачи данных со скоростью 2 400 Бод |
0…2 400 |
| Телефонный |
300…3 400 |
| Звукового вещания |
50…10 000 |
| Факсимильный – при скорости 120 мин-1 – при передаче газет |
0…1 465 0…180 000 |
| Телевизионный |
50…6 000 000 |
Контрольные вопросы
- На какие простейшие составляющие “раскладывается” периодически повторяющийся прямоугольный импульс?
- Чем отличается спектр периодического сигнала от спектра непериодического сигнала?
- У какого импульса амплитуда спектральных составляющих убывает быстрее: а) более короткого или более длинного? б) с более крутым фронтом или с более пологим? в) повторяющегося чаще или реже?
- Какие частотные диапазоны занимают спектры основных сигналов электросвязи
Список литературы
- Бакалов В.П., Дмитриков В.Ф., Крук Б.И. Основы теории цепей: Учебник для вузов; Под ред. В.П.Бакалова. – М.: Радио и связь, 2000. – 592 с.
- Бакалов В.П., Воробиенко П.П., Крук Б.И. Теория электрических цепей. Учебник для вузов: под ред. В.П. Бакалова – М.: Радио и связь. 1998. – 444 с.
- Бакалов В.П., Журавлева О.Б., Крук Б.И. Анализ линейных электрических цепей: Учебное пособие для дистанционного обучения. – Новосибирск: СибГУТИ. 2001г.
Сигнал — это любая переменная содержащая какой-либо вид информации. Причем эту информацию можно передавать на расстояние, переносить на устройства хранения, выводить на экран и через динамики или совершать с ней подобные действия. Существующие аналоговый и цифровой кардинально отличаются природой происхождения, способом передачи и хранения.


Аналоговый сигнал
Это природный тип сигналов окружает нас повсеместно и постоянно. Звук, изображение, тактильные ощущения, запах, вкус и команды мозга. Все возникающие, во Вселенной без участия человека, сигналы являются аналоговыми.
В электронике, электротехнике и системах связи аналоговую передачу данных применяют со времени изобретения электричества. Характерной особенностью является непрерывность и плавность изменения параметров. Графически сеанс аналоговой связи можно описать как непрерывную кривую, соответствующую величине электрического напряжения в определённый момент времени. Линия изменяется плавно, разрывы возникают только при обрыве связи. В природе и электронике аналоговые данные генерируются и распространяются непрерывно. Отсутствие непрерывного сигнала означает тишину или черный экран.
В непрерывных системах связи аналогом звука, изображения и любых других данных является электрические или электромагнитные импульсы. Например, громкость и тембр голоса передаются от микрофона на динамик посредством электрического сигнала. Громкость зависит от величины, а тембр от частоты напряжения. Поэтому при голосовой связи сначала напряжение становится аналогом звука, а потом звук аналогом напряжения. Таким же образом происходит передача любых данных в аналоговых системах связи.
Что такое дискретный сигнал
В цифровой системе хранения и передачи данных, отсутствие сигнала, также является формой обмена информацией. В какой-то момент времени он равен нулю, в другой принимает какое-либо значение. Поэтому дискретным называют сигнал прерывный, отсюда и название discretus или разделённый. Аналоговые данные разбиваются на отдельные блоки, обрабатываются и передаются в виде цифрового кода.


Дискретность не подразумевает разрыв связи. В цифровых системах широко используется двоичная система обработки и обмена информацией. Двоичная подразумевает кодировку данных с помощью единицы и нулей. В доли секунды сигнал прерывисто принимает значение 1 или 0. Вместо непрерывной кривой имеем отдельные дискретные значения. Определенный набор нулей и единичек уже несёт в себе какую либо информацию. Примитивный набор это бит или двоичный разряд. Сам по себе он ничего не значит. Данные могут кодироваться только при объединении восьми битов в следующую по сложности комбинацию – байт. Чем больше объединённых байтов, тем больше и точнее можно описать передаваемую информацию.
На качество генерируемых данных влияет не только количество объединённых битов, но и скорость передачи. Непрерывная аналоговая кривая должна быть разбита на как много больше мини участков прерывного сигнала. Полученный таким образом звук и цвет будут соответствовать оригиналу. Качественный дискретный сигнал формирует точную копию аналогового. Например, звуковая дорожка MP3 закодированная со скоростью 320 000 бит в секунду (320 kbps) значительно лучше кодированной в 128 kbps. Дорожки скоростью меньше 128 слушать вообще невозможно.
Чем отличается непрерывный сигнал от дискретного
На первый взгляд отличия в сигналах можно не различить. Оба передаются в виде электрических импульсов по проводам или электромагнитными волнами в эфире. Преобразовываются в звук и изображение, выводятся на динамики и экран. Но разница существенна. Отличие аналогового сигнала от цифрового обусловлено особенностями обработки и передачи данных.
Аналоговые данные не кодируются и не шифруются, просто отображаются в электрические или электромагнитные импульсы. Приёмник преобразовывает импульсы в полном соответствии с полученным сигналом. Передаваемый и принимаемый импульс многогранен и характеризуются постоянным плавным изменением с течением времени. Величина и частота определяют параметры информации. Примером может быть соответствие определённого цвета экрана заданному напряжению. С течением времени цвета плавно меняются следуя изменению напряжения.
Казалось бы, природное происхождение, простота генерации, передачи и приёма благоприятствуют использованию аналогового сигнала. Но в дело вмешиваются электрические и электромагнитные помехи. Это могут быть электромагнитные наводки от электрических сетей, работающих механизмов, рельеф местности, грозы, бури на солнце, шумы создаваемые работой передающего и принимающего оборудования, прочие. Они изменяют плавную кривую. На приёмник информация поступает с изменениями. Шипение, хрипы и искаженное изображение обычная история для аналоговой связи.
Цифровая технология использует совсем иной принцип передачи. Аналоговые данные сначала кодируются и только потом передаются. Кодировка заключается в описании непрерывной кривой аналоговой информации. В каждый конкретный момент времени, передаваемый импульс имеет значение единицы или нуля, и определенная последовательность битов отображает всю полноту оригинальной картинки или звука.
Дискретный сигнал как азбука Морзе, только вместо точек и тире — чёткие биты. Ничего более, шумы и помехи им не мешают. Цифровой информации главное дойти до цели. Цифры без примесей передадут данные и без изменений перевоплотятся в звук и цвет. Но слабый сигнал может не донести полную картину. Как пример — пропадание слов или изображения полностью. Поэтому сотовые передатчики, устанавливают как можно ближе друг от друга, также используют повторители.
Примером непрерывных и дискретных сигналов могут служить старая проводная и новая сотовая связь. Через старые АТС иногда невозможно было разговаривать с соседним домом. Шумы и плохое усиление сигнала мешали слышать друг друга. Что бы вести полноценную беседу, приходилось громко кричать самому и прислушиваться к собеседнику. Другое дело сотовая связь основанная на цифровой технологии. Звук закодирован и хорошо передаётся на далёкие расстояния. Отчетливо слышно собеседника даже с другого континента.
Оба вида связи не лишены недостатков, а ключевыми отличиями являются:
- Аналоговый подвержен помехам и поступает с искажениями. В то время как цифровой доходит полностью без искажений или отсутствует вовсе.
- Принять или перехватить аналоговое вещание может любой приёмник такого принципа. Дискретная передача адресована конкретному адресату, кодируется и мало доступна к перехвату.
- Объём передаваемых данных у аналоговой связи конечен, поэтому она практически исчерпала себя в передаче теле сигнала. Напротив с развитием технологии преобразования аналоговой информации в цифровой код растут объемы и качество трансляции. Например, главным отличием цифрового от аналогового телевидения является превосходное качество изображения.
Цифровая технология выигрывает по всем показателям. Споры идут только среди любителей музыки. Многие меломаны и звукорежиссеры утверждают, что могут различить аналоговый оригинал и цифровую копию. Однако большинство слушателей этого сделать не в состоянии. Да и с развитием цифровых систем аналоговые данные кодируются точнее. Оригинальное звучание и цифровая копия делаются практически неразличимым.
Как аналоговый сигнал преобразуется в цифровой и наоборот
Первой в цифровую форму преобразовали математическую, физическую и компьютерную информацию. Описать формулы и расчеты не составило труда. А вот для преображения аналоговой действительности в цифровые массивы уже потребовались специальные устройства. Ими стали аналого-цифровые преобразователи или сокращенно АЦП. Они предназначены для преобразования различных физических величин в цифровые коды. Обратное действие совершают устройства ЦАП.
Любые цифровые передатчики и приёмники оснащены такими преобразователями. Например, сотовому телефону, поступивший звук необходимо обработать и передать в оцифрованном виде. В то же время необходимо принять от другого абонента код, преобразовать и передать напряжение на динамик. Так же и с изображением на смартфонах и в телевизорах. В любом случае первоначальной информацией выступает напряжение.


Существует много видов АЦП, но самыми распространёнными являются следующие:
- параллельного преобразования;
- последовательного приближения;
- дельта-сигма, с балансировкой заряда.
Преобразования в АЦП понятийно связаны с измерением и сравнением. Кодировка, это процесс сравнения полученных от источника данных с эталоном. То есть полученная аналоговая величина сравнивается с эталонной (с заданным напряжением). Эталоном выступает информация о конкретном цвете, звуке и т.п. Она соответствует заложенным в устройство представлениям о преобразуемом сигнале. Потом данные эталонной величины кодируются для передачи. Во время аналого-цифровой обработки физических превращений сигнала не происходит. С аналогового делается цифровой матрица (модель).
Упрощенно работу любого АЦП можно представить так:
- Измерение через определенные интервалы времени амплитуды напряжения.
- Сравнение с эталоном и формирование данных.
- Отгрузка оцифрованных сведений об изменениях амплитуды на передатчик.
Качество передаваемой информации зависит от двух параметров — точности и частоты измерений. Чем точнее измеряется и зашифровывается входящее напряжение, тем качественней передаваемая информация. Поэтому, имеет большое значение, сколько бит может зашифровать преобразователь. Чем плотнее информационный поток, тем точней передача данных. Это выражается в красках экрана, контрастности картинки и чистоте звука. Следующим важным показателем является дискретизация, то есть частота измерений. Чем чаще, тем меньше провалов в измерениях и необходимости сглаживания. В совокупности, чем чаще и точнее преобразователь может измерять и обрабатывать полученное напряжение, тем он лучше.
Как выглядят спектры аналогового и дискретного сигнала
Изображение сигналов можно представить как две функции. На рисунке наглядно представлено, чем отличается непрерывный сигнал от дискретного. Напряжение исходного изменяется плавно, обработанного прерывисто. Спектр дискретного периодически ступенчато совпадает с непрерывным.


Изменения дискретного происходят резко, через определённый период времени. Уровень в цифровой системе зашифровывается и любую величину напряжения описывают двоичным кодом. От частоты измерений зависит сглаженность преобразования и оригинальность передаваемых данных. Чем точнее описан уровень сигнала и чем чаще проводится и обрабатывается измерение, тем точнее совпадает спектр начального и переданного сигналов.


Какие системы связи используют цифровой сигнал а какие аналоговый
Несмотря на архаичность аналоговая технология ещё используется для телефонной и радио связи. Многие проводные сети до сих пор остаются аналоговыми. В основном это традиционные телефонные линии местных операторов. Но, для магистральной передачи данных связи уже повсеместно используют цифровые каналы. Так же аналоговая технология применяется в простых и дешёвых переносных радиостанциях.
Во всех вновь создаваемых системах используют цифровую технологию обработки сигнала. Это оптоволоконные и проводные линии, сигнализация и телеметрия, военная и гражданская промышленная связь. И конечно же на цифровое вещание переходит телевидение. Аналоговый способ передачи данных исчерпал себя. На смену пришла новая высококачественная и защищенная связь.
Список книг помогающих разобраться в аналоговых и цифровых сигналах
Более подробно изучить и сравнить принципы обработки и передачи данных можно прочитав следующую литературу:
- Сато Ю. Обработка сигналов. Первое знакомство. / Пер. с яп.; под ред. Ёсифуми Амэмия. — М: Изд-кий дом «Додэка-XXI», 2002. Книга даёт основы знаний о способах ЦОС. Адресована радиолюбителям, студентам и школьникам, только начинающим изучение систем передачи данных.
- Введение в цифровую фильтрацию /под ред. Р. Богнера и А. Константинидиса; перевод с англ. — М: Изд-во «Мир», 1977. В этой книге популярно и доступно изложена информация о различных системах обработки данных. Сравниваются аналоговая и цифровая системы, описаны плюсы и минусы.
- Основы цифровой обработки сигналов: Курс лекций /Авторы: А.И. Солонина, Д.А. Улахович, С.М. Арбузов, Е.Б. Соловьев, И.И. Гук. — СПб: Изд-во «БХВ-Петербург», 2005. Книга написана по курсу лекций для студентов ГУТ им. Бонч-Бруевича. Изложены теоретические основы обработки данных, описаны дискретные и цифровые системы разных способов преобразования. Предназначена для изучения в вузах и повышения квалификации специалистов.
- Сергиенко А.Б. Цифровая обработка сигналов (второе издание) — СПб: Изд-во «Питер», 2006. Электронный учебно-методический комплекс по дисциплине «Цифровая обработка сигналов». Представлены курс лекций, лабораторный практикум и методические рекомендации по самостоятельной работе. Предназначена для преподавателей и самостоятельного изучения для студентов уровня подготовки бакалавр.
- Лайонс Р. Цифровая обработка сигналов. 2-е изд. Пер. с англ. – М.: ООО «Бином-Пресс», 2006. Книга представляет подробную информацию о ЦОС. Написана понятным языком и снабжена большим количеством иллюстрации. Одна из самых простых и понятных книг на русском языке.
Старая добрая аналоговая связь быстро сдаёт позиции. Несмотря на модернизацию и улучшения, возможность обмена данными достигла предела. К тому же, остались старые болезни – искажения и шумы. В то же время цифровая связь лишена этих недостатков, и передаёт большие объёмы информации быстро, качественно, без ошибок.
INFOблог: Непрерывные и дискретные сигналы
В предыдущем посте мы рассматривали различные определения понятия «информация» и пришли к выводу, что информация может быть определена множеством разных способов в зависимости от выбранного подхода. Но об одном мы можем говорить однозначно: информация — знания, данные, сведения, характеристики, отражения и т.д. — категория нематериальная. Но мы живем в мире материальном. Следовательно, для существования и распространения в нашем мире информация должна быть связана с какой-либо материальной основой. Без нее информация не может передаваться и сохраняться.Тогда материальный объект (или среда), с помощью которого представляется та или иная информация будет являться носителем информации, а изменение какой-либо характеристики носителя мы будем называть сигналом.
Например, представим равномерно горящую лампочку, она не передает никакой информации. Но, если мы будем включать и выключать лампочку (т.е. изменять ее яркость), тогда с помощью чередований вспышек и пауз мы сможем передать какое-нибудь сообщение (например, посредством азбуки Морзе). Аналогично, равномерный гул не дает возможности передать какую-либо информацию, однако, если мы будем изменять высоту и громкость звука, то сможем сформировать некоторое сообщение (что мы и делаем с помощью устной речи).
При этом сигналы могут быть двух видов: непрерывный (или аналоговый) и дискретный.
В учебнике даны следующие определения.
Непрерывный сигнал принимает множество значений из некоторого диапазона. Между значениями, которые он принимает, нет разрывов.
Дискретный сигнал принимает конечное число значений. Все значения дискретного сигнала можно пронумеровать целыми числами.
Немного уточним эти определения.
Сигнал называется непрерывным (или аналоговым), если его параметр может принимать любое значение в пределах некоторого интервала.
Сигнал называется дискретным, если его параметр может принимать конечное число значений в пределах некоторого интервала.
Графики этих сигналов выглядят следующим образом
Примерами непрерывных сигналов могут быть музыка, речь, изображения, показания термометра (высота столба ртути может быть любой и представляет собой ряд непрерывных значений).
Примерами дискретных сигналов могут быть показания механических или электронных часов, тексты в книгах, показания цифровых измерительных приборов и т.д.
Вернемся к примерам, рассмотренным в начале сообщения — мигающая лампочка и человеческая речь. Какой из этих сигналов является непрерывным, а какой дискретным? Ответьте в комментариях и аргументируйте свой ответ. Можно ли непрерывную информацию преобразовать в дискретную? Если да — приведите примеры.
Часто ко мне обращаются люди с вопросами по задачам из области цифровой обработки сигналов (ЦОС). Я подробно рассказываю нюансы, подсказываю нужные источники информации. Но всем слушателям, как показало время, не хватает практических задач и примеров в процессе познания этой области. В связи с этим я решил написать краткий интерактивный курс по цифровой обработке сигналов и выложить его в открытый доступ.
Большая часть обучающего материала для наглядного и интерактивного представления реализована с использованием Jupyter Notebook. Предполагается, что читатель имеет базовые знания из области высшей математики, а также немного владеет языком программирования Python.
Список лекций
Этот курс содержит материалы в виде законченных лекций по разным тематикам из области цифровой обработки сигналов. Материалы представлены с использованием библиотек на языке Python (пакеты numpy, scipy, matplotlib, и т.д.). Основная информация для этого курса взята из моих лекций, которые я, будучи аспирантом, читал студентам Московского Энергетического Института (НИУ МЭИ). Частично информация из этих лекций была использована на обучающих семинарах в Центре Современной Электроники, где я выступал в качестве лектора. Кроме того, в этот материал входит перевод различных научных статей, компиляция информации из достоверных источников и литературы по тематике цифровой обработки сигналов, а также официальная документация по прикладным пакетам и встроенным функциям библиотек scipy и numpy языка Python.
Для пользователей MATLAB (GNU Octave) освоение материала с точки зрения программного кода не составит труда, поскольку основные функции и их атрибуты во многом идентичны и схожи с методами из Python-библиотек.
Все материалы сгруппированы по основным тематикам цифровой обработки сигналов:
- Сигналы: аналоговые, дискретные, цифровые. Z-преобразование,
- Преобразование Фурье: амплитудный и фазовый сигнала, ДПФ и БПФ,
- Свертка и корреляция. Линейная и циклическая свертка. Быстрая свёртка,
- Случайные процессы. Белый шум. Функция плотности вероятностей,
- Детерминированные сигналы. Модуляция: АМ, ЧМ, ФМ, ЛЧМ. Манипуляция,
- Фильтрация сигналов: БИХ, КИХ фильтры,
- Оконные функции в задачах фильтрации. Детектирование слабых сигналов,
- Ресемплинг: децимация и интерполяция. CIC-фильтры, фильтры скользящего среднего,
- Непараметрические методы спектрального анализа,
- Усреднение по частоте и по времени. Полифазный БПФ.
Список лекций — достаточный но, разумеется, неполный для вводного знакомства с областью ЦОС. При наличии свободного времени я планирую поддерживать и развивать этот проект.
Где найти?
Все материалы — абсолютно бесплатны и доступны в виде открытого репозитория на моем гитхабе как opensource проект. Материалы представлены в двух форматах — в виде тетрадок Jupyter Notebook для интерактивной работы, изучения и редактирования, и в виде скомпилированных из этих тетрадок HTML-файлов (после скачивания с гитхаба имеют вполне пригодный формат для чтения и для печати).
Ниже приводится очень краткое описание разделов курса с небольшими пояснениями, терминами и определениями. Основная информация доступна в исходных лекциях, здесь представлен лишь краткий обзор!
Сигналы. Z-преобразование
Вводный раздел, в котором содержится основная информация по типам сигналов. Вводится понятие дискретной последовательности, дельта-функции и функции Хевисайда (единичный скачок).
Все сигналы по способу представления на множестве можно разделить на четыре группы:
- аналоговые — описываются непрерывными во времени функциями,
- дискретные — прерываются во времени с шагом заданным дискретизации,
- квантованные — имеют набор конечных уровней (как правило, по амплитуде),
- цифровые — комбинация свойств дискретных и квантованных сигналов.
Для правильного восстановления аналогового сигнала из цифрового без искажений и потерь используется теорема отсчетов, известная как Теорема Котельникова (Найквиста-Шеннона).
Любой непрерывный сигнал с ограниченным спектром может быть восстановлен однозначно и без потерь по своим дискретным отсчетам, взятым с частотой строго больше удвоенной верхней частоты спектра непрерывного сигнала.
Такая трактовка справедлива при условии, что непрерывная функция времени занимает полосу частот от 0 до значения верхней частоты. Если шаг квантования и дискретизации выбраны неправильно, преобразование сигнала из аналоговой формы в дискретную будет происходить с искажениями.
Также в этом разделе описывается Z-преобразование и его свойства, показывается представление дискретных последовательностей в Z-форме.
Пример конечной дискретной последовательности:
x(nT) = {2, 1, -2, 0, 2, 3, 1, 0}Пример этой же последовательности в Z-форме:
X(z) = 2 + z-1 — 2z-2 + 2z-4 + 3z-5 + 1z-6
Преобразование Фурье. Свойства. ДПФ и БПФ
В этом разделе описывается понятие временной и частотной области сигнала. Вводится определение дискретного преобразования Фурье (ДПФ). Рассмотрены прямое и обратное ДПФ, их основные свойства. Показан переход от ДПФ к алгоритму быстрого преобразования Фурье (БПФ) по основанию 2 (алгоритмы децимации по частоте и по времени). Отражена эффективность БПФ в сравнении с ДПФ.
В частности, в этом разделе описывается Python пакет scipy.ffpack для вычисления различных преобразований Фурье (синусное, косинусное, прямое, обратное, многомерное, вещественное).
Преобразование Фурье позволяет представить любую функцию в виде набора гармонических сигналов! Преобразование Фурье лежит в основе методов свертки и проектировании цифровых корреляторов, активно применяется при спектральном анализе, используется при работе с длинными числами.
Особенности спектров дискретных сигналов:
1. Спектральная плотность дискретного сигнала – периодическая функция с периодом, равным частоте дискретизации.
2. Если дискретная последовательность вещественная, то модуль спектральной плотности такой последовательности есть четная функция, а аргумент – нечетная функция частоты.
Спектр гармонического сигнала:
Сравнение эффективности ДПФ и БПФ
Эффективность алгоритма БПФ и количество выполняемых операций линейно зависит от длины последовательности N:
Как видно, чем больше длина преобразования, тем больше экономия вычислительных ресурсов (по скорости обработки или количеству аппаратных блоков)!
Любой сигнал произвольной формы можно представить в виде набора гармонических сигналов разных частот. Иными словами, сигнал сложной формы во временной области имеет набор комплексных отсчетов в частотной области, которые называются *гармоники*. Эти отсчеты выражают амплитуду и фазу гармонического воздействия на определенной частоте. Чем больше набор гармоник в частотной области, тем точнее представляется сигнал сложной формы.
Свертка и корреляция
В этом разделе вводится понятие корреляции и свертки для дискретных случайных и детерминированных последовательностей. Показана связь автокорреляционной и взаимнокорреляционной функций со сверткой. Описываются свойства свертки, в частности, рассмотрены методы линейной и циклической свертки дискретного сигнала с подробным разбором на примере дискретной последовательности. Кроме того, показан метод вычисления «быстрой» свертки с помощью алгоритмов БПФ.
В реальных задачах часто ставится вопрос о степени похожести одного процесса на другой или же о независимости одного процесса от другого. Иными словами, требуется определить взаимосвязь между сигналами, то есть найти корреляцию. Методы корреляции используются в широком диапазоне задач: поиск сигналов, компьютерное зрение и обработка изображений, в задачах радиолокации для определения характеристик целей и определения расстояния до объекта. Кроме того, с помощью корреляции производится поиск слабых сигналов в шумах.
Свертка описывает взаимодействие сигналов между собой. Если один из сигналов — импульсная характеристика фильтра, то свертка входной последовательности с импульсной характеристикой есть ни что иное, как реакция цепи на входное воздействие. Иными словами, результирующий сигнал отражает прохождение сигнала через фильтр.
Автокорреляционная функция (АКФ) находит применение в кодировании информации. Выбор кодирующей последовательности по параметрам длины, частоты и формы во многом обусловлен корреляционными свойствами этой последовательности. Наилучшая кодовая последовательность обладает наименьшим значением вероятности ложного обнаружения или срабатывания (для детектирования сигналов, для пороговых устройств) или ложной синхронизации (для передачи и приема кодовых последовательностей).
В этом разделе представлена таблица сравнения эффективности быстрой свертки и свертки, вычисляемой по прямой формуле (по числу вещественных умножений).
Как видно, для длин БПФ до 64, быстрая свёртка проигрывает у прямого метода. Однако, при увеличении длины БПФ результаты меняются в обратную сторону — быстрая свертка начинает выигрывать у прямого метода. Очевидно, чем больше длина БПФ, тем лучше выигрыш частотного метода.
Случайные сигналы и шум
В этом разделе вводится понятие случайных сигналов, плотности распределения вероятностей, закона распределения случайной величины. Рассматриваются математические моменты — среднее (математическое ожидание) и дисперсия (или корень этой величины — среднеквадратическое отклонение). Также в этом разделе рассматривается нормальное распределение и связанное с ним понятие белого шума, как основного источника шумов (помех) при обработке сигналов.
Случайным сигналом называют функцию времени, значения которой заранее неизвестны и могут быть предсказаны лишь с некоторой вероятностью. К основным характеристикам случайных сигналов относятся:
- закон распределения (относительное время пребывания значения сигнала в определенном интервале),
- спектральное распределение мощности сигнала.
В задачах ЦОС случайные сигналы делятся на два класса:
- шумы — беспорядочные колебания, состоящие из набора разных частот и амплитуд,
- сигналы, несущие информацию, для обработки которых требуется прибегать к вероятностным методам.
С помощью случайных величин можно моделировать воздействие реальной среды на прохождение сигнала от источника к приёмнику данных. При прохождении сигнала через какое-то шумящее звено, к сигналу добавляется так называемый белый шум. Как правило, спектральная плотность такого шума равномерно (одинаково) распределена на всех частотах, а значения шума во временной области распределены нормально (Гауссовский закон распределения). Поскольку белый шум физически добавляется к амплитудам сигнала в выбранные отсчеты времени, он называется аддитивный белый гауссовский шум (AWGN — Additive white Gaussian noise).
Сигналы, модуляция и манипуляция
В этом разделе показаны основные способы изменения одного или нескольких параметров гармонического сигнала. Вводятся понятия амплитудной, частотной и фазовой модуляции. В частности, выделяется линейная частотная модуляция, применяемая в задачах радиолокации. Показаны основные характеристики сигналов, спектры модулированных сигналов в зависимости от параметров модуляции.
Для удобства на языке Python создан набор функций, осуществляющих перечисленные виды модуляции. Пример реализации ЛЧМ-сигнала:
def signal_chirp(amp=1.0, freq=0.0, beta=0.25, period=100, **kwargs):
"""
Create Chirp signal
Parameters
----------
amp : float
Signal magnitude
beta : float
Modulation bandwidth: beta < N for complex, beta < 0.5N for real
freq : float or int
Linear frequency of signal
period : integer
Number of points for signal (same as period)
kwargs : bool
Complex signal if is_complex = True
Modulated by half-sine wave if is_modsine = True
"""
is_complex = kwargs.get('is_complex', False)
is_modsine = kwargs.get('is_modsine', False)
t = np.linspace(0, 1, period)
tt = np.pi * (freq * t + beta * t ** 2)
if is_complex is True:
res = amp * (np.cos(tt) + 1j * np.sin(tt))
else:
res = amp * np.cos(tt)
if is_modsine is True:
return res * np.sin(np.pi * t)
return res
Также в этом разделе из теории передачи дискретных сообщений описаны виды цифровой модуляции — манипуляции. Как и в случае с аналоговыми сигналами, цифровые гармонические последовательности могут быть манипулированы по амплитуде, фазе и частоте (либо по нескольким параметрам сразу).
Цифровые фильтры — БИХ и КИХ
Достаточно большой раздел, посвященный вопросам цифровой фильтрации дискретных последовательностей. В задачах цифровой обработки сигналов данные проходят через цепи, которые называются фильтрами. Цифровые фильтры, как и аналоговые, обладают различными характеристиками — частотные: АЧХ, ФЧХ, временная: импульсная характеристика, а также передаточная характеристика фильтра. Цифровые фильтры используются в основном для улучшения качества сигнала — для выделения сигнала из последовательности данных, либо для ухудшения нежелательных сигналов — для подавления определенных сигналов в приходящих последовательностях отсчетов.
В разделе перечислены основные преимущества и недостатки цифровых фильтров (в сравнении с аналоговыми). Вводится понятие импульсной и передаточной характеристик фильтра. Рассматривается два класса фильтров — с бесконечной импульсной характеристикой (БИХ) и конечной импульсной характеристикой (КИХ). Показан способ проектирования фильтров по канонической и прямой форме. Для КИХ фильтров рассматривается вопрос о способе перехода к рекурсивной форме.
Для КИХ фильтров показан процесс проектирования фильтра от стадии разработки технического задания (с указанием основных параметров), до программной и аппаратной реализации — поиска коэффициентов фильтра (с учетом формы представления числа, разрядности данных и т.д.). Вводятся определения симметричных КИХ фильтров, линейной ФЧХ и её связи с понятием групповой задержки.
Оконные функции в задачах фильтрации
В задачах цифровой обработки сигналов используются оконные функции различной формы, которые при наложении на сигнал во временной области, позволяют качественно улучшить его спектральные характеристики. Большое количество всевозможных окон обусловлено в первую очередь одной из главных особенностей любого оконного наложения. Эта особенность выражается во взаимосвязи уровня боковых лепестков и ширины центрального лепестка. Правило:
Чем сильнее подавление боковых лепестков спектра, тем шире главный лепесток спектра и наоборот.
Одно из применений оконных функций: обнаружение слабых сигналов на фоне более сильных путём подавления уровня боковых лепестков. Основные оконные функции в задачах ЦОС — **треугольное, синусоидальное, окно Ланцоша, Ханна, Хэмминга, Блэкмана, Харриса, Блэкмана-Харриса, окно с плоской вершиной, окно Наталла, Гаусса, Кайзера** и множество других. Большая часть из них выражена через конечный ряд путём суммирования гармонических сигналов с определенными весовыми коэффициентами. Такие сигналы отлично реализуются на практике на любых аппаратных устройствах (программируемые логические схемы или сигнальные процессоры).
Ресемплинг. Децимация и интерполяция
В этом разделе рассматриваются вопросы многоскоростной обработки сигналов — изменения частоты дискретизации. Многоскоростная обработка сигналов (multirate processing) предполагает, что в процессе линейного преобразования цифровых сигналов возможно изменение частоты дискретизации в сторону уменьшения или увеличения, либо в дробное число раз. Это приводит к более эффективной обработке сигналов, так как открывается возможность использования минимально допустимых частот дискретизации и, как следствие, значительного уменьшения требуемой вычислительной производительности проектируемой цифровой системы.
Децимация (прореживание) – понижение частоты дискретизации. Интерполяция – повышение частоты дискретизации.
Также в разделе рассматривается класс однородных КИХ фильтров, которые называются интегрально-гребенчатыми фильтрами (CIC, Cascaded integrator–comb). Показана реализация, основные свойства и особенности CIC фильтров. В силу линейности математических операций, происходящих в CIC фильтре возможно каскадное соединение нескольких фильтров подряд, что дает пропорциональное уменьшение уровня боковых лепестков, но также увеличивает «завал» главного лепестка амплитудно-частотной характеристики.
График АЧХ фильтра в зависимости от коэффициента децимации:
Также в этом разделе обсуждается вопрос увеличения разрядности данных на выходе CIC фильтра в зависимости от его параметров. Это особенно важно в задачах программной реализации, в частности на ПЛИС.
Для практической реализации CIC фильтров на Python разработан отдельный класс CicFilter, реализующий методы децимации и интерполяции. Также показаны примеры изменения частоты дискретизации с помощью встроенных методов из scipy пакета Python.
Python CicFilter Class for Digital Signal Processingclass CicFilter:
"""
Cascaded Integrator-Comb (CIC) filter is an optimized class of
finite impulse response (FIR) filter.
CIC filter combines an interpolator or decimator, so it has some
parameters:
R - decimation or interpolation ratio,
N - number of stages in filter (or filter order)
M - number of samples per stage (1 or 2)*
* for this realisation of CIC filter just leave M = 1.
CIC filter is used in multi-rate processing. In hardware
applications CIC filter doesn't need multipliers, just only
adders / subtractors and delay lines.
Equation for 1st order CIC filter:
y[n] = x[n] - x[n-RM] + y[n-1].
Parameters
----------
x : np.array
input signal
"""
def __init__(self, x):
self.x = x
def decimator(self, r, n):
"""
CIC decimator: Integrator + Decimator + Comb
Parameters
----------
r : int
decimation rate
n : int
filter order
"""
# integrator
y = self.x[:]
for i in range(n):
y = np.cumsum(y)
# decimator
y = y[::r]
# comb stage
return np.diff(y, n=n, prepend=np.zeros(n))
def interpolator(self, r, n, mode=False):
"""
CIC inteprolator: Comb + Decimator + Integrator
Parameters
----------
r : int
interpolation rate
n : int
filter order
mode : bool
False - zero padding, True - value padding.
"""
# comb stage
y = np.diff(self.x, n=n,
prepend=np.zeros(n), append=np.zeros(n))
# interpolation
if mode:
y = np.repeat(y, r)
else:
y = np.array([i if j == 0 else 0 for i in y for j in range(r)])
# integrator
for i in range(n):
y = np.cumsum(y)
if mode:
return y[1:1 - n * r]
else:
return y[r - 1:-n * r + r - 1]
Наконец, в этом разделе приведен особый класс фильтров — скользящего среднего. Показано три способа реализации: через свертку сигналов, с помощью КИХ-фильтра и БИХ-фильтра.
Заключение
Надеюсь, этот курс лекций в совокупности с моими предыдущими статьями по цифровой обработке сигналов на ПЛИС принесет практическую пользу и поможет читателю лучше понять основы цифровой обработки сигналов. Этот проект будет улучшаться и дополняться новым полезным и не менее интересным материалом. Следите за развитием!
Дополнительно к этому материалу я поддерживаю и развиваю свой проект по основным модулям ЦОС (на языке Python). Он содержит пакет генерации различных сигналов, класс CIC фильтров для задач децимации и интерполяции, алгоритм расчета коэффициентов корректирующего КИХ-фильтра, фильтр скользящего среднего, алгоритм вычисления сверх-длинного БПФ через методы двумерного преобразования (последнее очень пригодилось в работе при аппаратной реализации на ПЛИС).
UPD: 20.04.2020
В курс добавлено две лекции:
- Непараметрические методы спектрального анализа (Владимир Фадеев)
- Усреднение по частоте и по времени. Полифазный БПФ.
TODO:
- Вейвлет анализ
- STFT, мел-спектрограммы, преобразование Гриффина-Лима
Спасибо за внимание!
Попробуем нестандартно в сравнении с книгами по радиоэлектронике и цифровым системам связи, простыми житейскими примерами объяснить суть теоремы Котельникова. Если читатель еще не знаком с теоремой отсчётов, то рекомендуется сначала изучить ее формулировку в деловом официальном стиле. Смотрите, например, прошлую статью.
Аналоговые и дискретные процессы в природе
Абсолютное большинство процессов в природе протекают непрерывно, (изменение температуры воздуха на улице, давления, влажности, изменение скорости ветра, колебание электрического тока в проводнике, сияние Солнца). Почему все эти процессы непрерывны? Нам кажется, что время течет непрерывно, а значит в каждый момент времени должно существовать какое-то значение температуры воздуха или значение силы тока в проводнике, или значение интенсивности света Солнца. Непрерывные процессы, функции или сигналы называют аналоговыми (от слова аналог – нечто сходное, подобное чему-то, т.е. функция как модель является аналогом какому-то физическому процессу). Можно наблюдать множество непрерывных процессов в природе, например, непрерывный поток воды в источнике. Струя воды при падении вниз сужается как раз в силу поддержания непрерывности потока.

Аналоговый сигнал даже на конечном временном промежутке подразумевает набор бесконечного числа значений. Однако регистрирующие устройства, как правило фиксируют конечное число значений, поэтому мы получаем дискретные сигналы (дискретный от лат. discretus означает раздельный, состоящий из отдельных частей).

Представление непрерывного и дискретного сигналов.
Дискретные процессы также многочисленны в природе, как и аналоговые состояния. Дискретные процессы не могут находиться в каком-то промежуточном состоянии между определенными значениями. Придумаем несколько примеров из жизни:
- Из квантовой физики 1-й постулат Бора: электрон в атоме может двигаться только по определенным (можно сказать по дискретным) орбитам, находясь на которых, он не излучает и не поглощает энергию. Электроны в атоме, находясь на определенных стационарных (т.е. дискретных) орбитах, имеет вполне определённые дискретные значения энергии Е1, Е2, Е3 и т.д.
- Если вы играете на пианино, то звучащая музыка во времени представляет собой перескоки с одной дискретной ноты на другую, то есть ноты – это отдельно выбранные дискретные звуки.
- Когда мы поднимаемся по лестнице, ступня в пространстве оси высот находится только на определенной дискретной координате (ступеньке)

Поскольку человек не может оперировать с бесконечными числами и величинами, обычно все округляем до ближайших целых чисел – в результате получаем цифровые сигналы. Например, мы наносим цифровую шкалу на столбик термометра и фиксируем округленное значение температуры. Непрерывное время мы разбиваем на секунды минуты, часы – наносим цифры на циферблат часов. Все символьные и знаковые системы, созданные человечеством для обмена информацией, использует конечное число возможных элементов.
Поскольку все вычислительные информационные устройства могут работать лишь с дискретными символьными системами и с цифровыми сигналами, постоянно возникает необходимость в переходе от существующих в природе непрерывных процессов, к дискретным и цифровым. С развитием цифровой связи и цифровых устройств (микроконтроллеров, компьютеров) постоянно и повсеместно на каждом шагу выполняется аналого-цифровое преобразование сигналов, неотъемлемой частью которого является дискретизация сигналов. Но здесь важно следующее: перейти от непрерывного сигнала к дискретному дело нехитрое – здесь удачно подходит выражение «ломать не строить». По аналогии можно сказать «ломать аналоговый сигнал – не восстанавливать его», здесь все просто реализовать, но главное при этом выполнить дискретизацию правильно. Одно дело просто произвести выборку отдельных значений сигнала, но есть еще другое дело – потом надо будет по этим значениям снова восстановить исходный непрерывный сигнал. Как правильно дискретизировать сигналы говорится в теореме о дискретизации сигналов, или ее можно называть в честь автора – теоремой Котельникова.
Если не знать теорему Котельникова
Итак, мы выяснили, что как и множество процессов в природе, электрические сигналы, используемые во всей электронике и системах связи бывают аналоговые и дискретные. В цифровых системах необходимо переходить от аналоговых сигналов к дискретным, при этом переход должен быть корректным.
Наглядный пример номер раз. Давайте посмотрим на примере двух музыкальных фрагментов, что будет, если осуществлять дискретизацию сигнала некорректно.
Вот что будет при неправильной оцифровке музыки
Исходная музыкальная запись
После неправильной дискретизации
Вот что будет при неправильной оцифровке речи
Исходная запись
После неправильной дискретизации
Наглядный пример № 2. На рисунке ниже представлены 7 сигналов, каждый из которых соответствует своей музыкальной ноте – До, Ре, Ми, Фа, Соль, Ля, Си. Все они оцифрованы с частотой дискретизации 1700 Гц.
Давайте послушаем, что из этого получилось.


Надеюсь, с музыкальным слухом все в порядке и вы услышали, что с последними двумя прозвучавшими нотами что-то не так. Если не знать теорему Котельникова, то будет непонятно, почему звук при дискретизации исказился. Поэтому давайте разбираться в этой теореме.
Наглядное, но нестандартное объяснение теоремы о дискретизации
Представим себе, что мы работники Animal Planet и хотим изучить траекторию движения в джунглях какой-нибудь редкой змейки из красной книги. Назовем, например, изучаемую змею Зигзагусс.

С целью исследования мест обитания змеи и ее повадок цепляем к ее хвосту GPS-датчик, который будет регистрировать ее местоположение в отдельные моменты времени.

Вопрос: как надо запрограммировать датчик, чтобы мы получили точную траекторию движения змейки, т.е. получили самый подробный график траектории движения юркой змейки со всеми ее виляниями и изгибами? Через сколько миллисекунд или секунд датчику необходимо будет записывать и посылать нам очередную координату положения в пространстве?

Допустим, наша змея Зигзагусс ползет гармонично – ее хвост совершает гармонические колебания и ее движения можно описать синусоидальными функциями.

Фото настоящего следа от змеи на песке.
Траектория движения представляет собой колебания с различными частотами. Так вот, по правилам теоремы о дискретизации, чтобы восстановить всю траекторию движения змейки, необходимо найти составляющую колебаний самой высокой частоты.

Если по дискретным точкам мы сможем восстановить составляющую колебаний самой высокой частоты, то мы сможем восстановить всю траекторию змейки. Определим периоды всех колебаний (см. рисунок ниже).

Как видно из рисунка, наименьшим периодом колебаний является период . Следовательно, необходимо подобрать частоту выборки дискретных точек именно для колебания с периодом , тогда и все остальные колебания мы сможем потом восстановить. Другими словами, в соответствии с теоремой о дискретизации (см. формулировку здесь) можно полностью восстановить данную синусоидальную функцию, если брать дискретные точки через интервал времени вдвое меньший длительности периода . Это означает, что необходимо брать точки с таким интервалом, чтобы на период колебания самой высокой частоты приходилось не менее 2-х точек.

В этом случае можно будет с высокой точностью восстановить всю непрерывную траекторию движения исследуемой змеи.
Предположим теперь, что Зигзагусс опьянилась запахом одурманивающего цветка и стала ползти негармонично, несуразно.

В этом случае для определения периода дискретизации нам необходимо самим отыскать гармонию в данной кривой функции, а она есть внутри любого сигнала всегда, что пытался в свое время доказать всем людям французский математик Жан-Батист Фурье. Также как любое тело можно разложить на множество атомов, также и полученную сложную функцию (от траектории змеи), можно разложить на множество гармонических функций. Физические тела разные, потому что они отличаются друг от друга структурой молекул. Например, мы говорим h3O – это вода, что означает: молекула воды состоит из двух атомов водорода H и одного атома кислорода O. Точно также можно сказать, что разные сигналы отличаются разным составом. Например, такой вот сигнал

состоит из двух гармонических функций (синус и косинус) с частотой 1000 Гц и одного синуса с частотой 2000 Гц (2000 Гц означает, что гармоника совершает 2 тысячи колебаний в секунду). В соответствии с условием теоремы Котельникова, о котором мы уже ранее говорили, для такого сигнала временной интервал между дискретными точками необходимо брать таким, чтобы он был меньше половины периода самой высокой частоты. В нашем случае имеется гармоника с максимальной частотой 2 тысячи колебаний в секунду (2000 Гц), значит период сигнала равен 1/2000 = 0.005 секунд и значит период между дискретными точками должен быть менее, чем 0.005/2 = 0.0025 секунды.
Чтобы определить требуемый период между дискретными точками для траектории нашей змейки, необходимо определить из каких гармонических функций она состоит, а точнее нас интересует значение частоты наивысшей гармонической функции (т.е. фиолетовой на рисунке).

Делим период фиолетовой гармоники пополам, и получаем граничное значение для периода дискретизации функции траектории одурманенной змеи. Все, задача решена, можно произвести дискретизацию данного сложного сигнала.
Знаем и соблюдаем условия теоремы Котельникова
Теперь, когда мы знаем теорему Котельникова, давайте еще раз рассмотрим задачу правильного перехода от аналоговых 7 сигналов- музыкальных нот к дискретным. Итак, у нас есть семь гармонических колебаний, с частотами

Для правильной дискретизации, чтобы не было искажений, необходимо взять частоту дискретизации не менее в два раза больше максимальной частоты сигнала. Ранее мы брали частоту 1700 Гц, но как можно посчитать, такая частота подходит для сигналов нот До – Соль (для ноты Соль требуется частота дискретизации 784*2=1568 Гц), а вот для сигналов нот Ля и Си значение 1700 Гц уже не годится.
Еще раз рассмотрим дискретизацию наших сигналов

Как видно из рисунка из-за несоблюдения условий теоремы Котельникова для сигналов Ля и Си с частотами 880 Гц и 988 Гц, через получившиеся дискретные отсчёты можно провести другие гармонические сигналы (красные функции), частоты которых меньше 1700 Гц / 2 = 850 Гц. Произошел эффект, который называют наложение спектров (в англоязычной литературе – aliasing). В рамках данной статьи «для чайников» мы не будем подробно рассматривать этот эффект, поскольку здесь уже требуются знания спектрального анализа сигналов. Этот эффект интересен тем, что объясняет условия теоремы Котельникова с позиций представления сигналов в частотной области (см. рисунок ниже). Если разобраться в этом, то теорема Котельникова и принципы восстановления сигналов станут более понятными. Описание этого эффекта можно найти почти в каждой книге по цифровой обработке сигналов.

Но сейчас новичкам в этой области главное запомнить результат несоблюдения теоремы отсчётов – восстановление сигналов по имеющимся дискретным отсчётам будет неоднозначно. Чтобы такого не происходило, необходимо чтить теорему Котельникова.
Максимальная частота среди наших 7 сигналов 988 Гц (нота Си), следовательно частота дискретизации должна быть больше, чем 2*988=1976 Гц. Важно здесь неуместно отметить, что в 1976 году был создан первый персональный компьютер – начался кустарный выпуск Apple I.
Значит надо выбрать частоту дискретизации больше значения 1976.
Вот как будут звучать семь наших сигналов при частоте дискретизации 2000 Гц.
Задачка для разминки мозгов
Нельзя сказать, что эта задачка очень простая для начинающих и ее решит любой. Новички в этой области не унывайте, если не получится (здесь нужны знания теории сигналов), ну а тот, кто решит, может собой гордиться.
С двух датчиков регистрируются сигналы
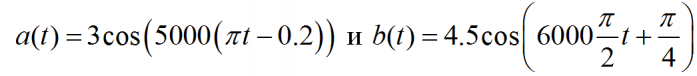

Какой должна быть минимальная частота дискретизации в АЦП по условию теоремы о дискретизации, если К – операция сложения и если К – операция умножения?
1. Преобразование Фурье и спектр сигнала
Во многих случаях задача получения (вычисления) спектра сигнала выглядит следующим образом. Имеется АЦП, который с частотой дискретизации Fd преобразует непрерывный сигнал, поступающий на его вход в течение времени Т, в цифровые отсчеты — N штук. Далее массив отсчетов подается в некую программку, которая выдает N/2 каких-то числовых значений (программист, который
Чтобы проверить, правильно ли работает программа, сформируем массив отсчетов как сумму двух синусоид sin(10*2*pi*x)+0,5*sin(5*2*pi*x) и подсунем программке. Программа нарисовала следующее:
рис.1 График временной функции сигнала
рис.2 График спектра сигнала
На графике спектра имеется две палки (гармоники) 5 Гц с амплитудой 0.5 В и 10 Гц — с амплитудой 1 В, все как в формуле исходного сигнала. Все отлично, программист молодец! Программа работает правильно.
Это значит, что если мы подадим на вход АЦП реальный сигнал из смеси двух синусоид, то мы получим аналогичный спектр, состоящий из двух гармоник.
Итого, наш реальный измеренный сигнал, длительностью 5 сек, оцифрованный АЦП, то есть представленный дискретными отсчетами, имеет дискретный непериодический спектр.
С математической точки зрения — сколько ошибок в этой фразе?
Теперь
рис.3 График функции sin(10*2*pi*x)+0,5*sin(5*2*pi*x) на периоде измерения 0.5 сек
рис.4 Спектр функции
Что-то как бы не то! Гармоника 10 Гц рисуется нормально, а вместо палки на 5 Гц появилось несколько каких-то непонятных гармоник. Смотрим в интернетах, что да как…
Во, говорят, что в конец выборки надо добавить нули и спектр будет рисоваться нормальный.
рис.5 Добили нулей до 5 сек
рис.6 Получили спектр
Все равно не то, что было на 5 секундах. Придется разбираться с теорией. Идем в Википедию — источник знаний.
2. Непрерывная функция и представление её рядом Фурье
Математически наш сигнал длительностью T секунд является некоторой функцией f(x), заданной на отрезке {0, T} (X в данном случае — время). Такую функцию всегда можно представить в виде суммы гармонических функций (синусоид или косинусоид) вида:
(1), где:
k — номер тригонометрической функции ( номер гармонической составляющей, номер гармоники)
T — отрезок, где функция определена (длительность сигнала)
Ak — амплитуда k-ой гармонической составляющей,
θk- начальная фаза k-ой гармонической составляющей
Что значит «представить функцию в виде суммы ряда»? Это значит, что, сложив в каждой точке значения гармонических составляющих ряда Фурье, мы получим значение нашей функции в этой точке.
(Более строго, среднеквадратичное отклонение ряда от функции f(x) будет стремиться к нулю, но несмотря на среднеквадратичную сходимость, ряд Фурье функции, вообще говоря, не обязан сходиться к ней поточечно. См. https://ru.wikipedia.org/wiki/Ряд_Фурье.)
Этот ряд может быть также записан в виде:
(2),
где , k-я комплексная амплитуда.
или
(3)
Связь между коэффициентами (1) и (3) выражается следующими формулами:
и
Отметим, что все эти три представления ряда Фурье совершенно равнозначны. Иногда при работе с рядами Фурье бывает удобнее использовать вместо синусов и косинусов экспоненты мнимого аргумента, то есть использовать преобразование Фурье в комплексной форме. Но нам удобно использовать формулу (1), где ряд Фурье представлен в виде суммы косинусоид с соответствующими амплитудами и фазами. В любом случае неправильно говорить, что результатом преобразования Фурье действительного сигнала будут комплексные амплитуды гармоник. Как правильно говорится в Вики «Преобразование Фурье (ℱ) — операция, сопоставляющая одной функции вещественной переменной другую функцию, также вещественной переменной.»
Итого:
Математической основой спектрального анализа сигналов является преобразование Фурье.
Преобразование Фурье позволяет представить непрерывную функцию f(x) (сигнал), определенную на отрезке {0, T} в виде суммы бесконечного числа (бесконечного ряда) тригонометрических функций (синусоид и\или косинусоид) с определёнными амплитудами и фазами, также рассматриваемых на отрезке {0, T}. Такой ряд называется рядом Фурье.
Отметим еще некоторые моменты, понимание которых требуется для правильного применения преобразования Фурье к анализу сигналов. Если рассмотреть ряд Фурье (сумму синусоид) на всей оси Х, то можно увидеть, что вне отрезка {0, T} функция представленная рядом Фурье будет будет периодически повторять нашу функцию.
Например, на графике рис.7 исходная функция определена на отрезке {-T\2, +T\2}, а ряд Фурье представляет периодическую функцию, определенную на всей оси х.
Это происходит потому, что синусоиды сами являются периодическими функциями, соответственно и их сумма будет периодической функцией.
рис.7 Представление непериодической исходной функции рядом Фурье
Таким образом:
Наша исходная функция — непрерывная, непериодическая, определена на некотором отрезке длиной T.
Спектр этой функции — дискретный, то есть представлен в виде бесконечного ряда гармонических составляющих — ряда Фурье.
По факту, рядом Фурье определяется некоторая периодическая функция, совпадающая с нашей на отрезке {0, T}, но для нас эта периодичность не существенна.
Далее.
Периоды гармонических составляющих кратны величине отрезка {0, T}, на котором определена исходная функция f(x). Другими словами, периоды гармоник кратны длительности измерения сигнала. Например, период первой гармоники ряда Фурье равен интервалу Т, на котором определена функция f(x). Период второй гармоники ряда Фурье равен интервалу Т/2. И так далее (см. рис. 8).
рис.8 Периоды (частоты) гармонических составляющих ряда Фурье (здесь Т=2π)
Соответственно, частоты гармонических составляющих кратны величине 1/Т. То есть частоты гармонических составляющих Fk равны Fk= к\Т, где к пробегает значения от 0 до ∞, например к=0 F0=0; к=1 F1=1\T; к=2 F2=2\T; к=3 F3=3\T;… Fk= к\Т (при нулевой частоте — постоянная составляющая).
Пусть наша исходная функция, представляет собой сигнал, записанный в течение Т=1 сек. Тогда период первой гармоники будет равен длительности нашего сигнала Т1=Т=1 сек и частота гармоники равна 1 Гц. Период второй гармоники будет равен длительности сигнала, деленной на 2 (Т2=Т/2=0,5 сек) и частота равна 2 Гц. Для третьей гармоники Т3=Т/3 сек и частота равна 3 Гц. И так далее.
Шаг между гармониками в этом случае равен 1 Гц.
Таким образом сигнал длительностью 1 сек можно разложить на гармонические составляющие (получить спектр) с разрешением по частоте 1 Гц.
Чтобы увеличить разрешение в 2 раза до 0,5 Гц — надо увеличить длительность измерения в 2 раза — до 2 сек. Сигнал длительностью 10 сек можно разложить на гармонические составляющие (получить спектр) с разрешением по частоте 0,1 Гц. Других способов увеличить разрешение по частоте нет.
Существует способ искусственного увеличения длительности сигнала путем добавления нулей к массиву отсчетов. Но реальную разрешающую способность по частоте он не увеличивает.
3. Дискретные сигналы и дискретное преобразование Фурье
С развитием цифровой техники изменились и способы хранения данных измерений (сигналов). Если раньше сигнал мог записываться на магнитофон и храниться на ленте в аналоговом виде, то сейчас сигналы оцифровываются и хранятся в файлах в памяти компьютера в виде набора чисел (отсчетов).
Обычная схема измерения и оцифровки сигнала выглядит следующим образом.
рис.9 Схема измерительного канала
Сигнал с измерительного преобразователя поступает на АЦП в течение периода времени Т. Полученные за время Т отсчеты сигнала (выборка) передаются в компьютер и сохраняются в памяти.
рис.10 Оцифрованный сигнал — N отсчетов полученных за время Т
Какие требования выдвигаются к параметрам оцифровки сигнала? Устройство, преобразующее входной аналоговый сигнал в дискретный код (цифровой сигнал) называется аналого-цифровой преобразователь (АЦП, англ. Analog-to-digital converter, ADC) ( Wiki).
Одним из основных параметров АЦП является максимальная частота дискретизации (или частота семплирования, англ. sample rate) — частота взятия отсчетов непрерывного во времени сигнала при его дискретизации. Измеряется в герцах. (( Wiki))
Согласно теореме Котельникова, если непрерывный сигнал имеет спектр, ограниченный частотой Fмакс, то он может быть полностью и однозначно восстановлен по его дискретным отсчетам, взятым через интервалы времени , т.е. с частотой Fd ≥ 2*Fмакс, где Fd — частота дискретизации; Fмакс — максимальная частота спектра сигнала. Другими слова частота оцифровки сигнала (частота дискретизации АЦП) должна как минимум в 2 раза превышать максимальную частоту сигнала, который мы хотим измерить.
А что будет, если мы будем брать отсчеты с меньшей частотой, чем требуется по теореме Котельникова?
В этом случае возникает эффект «алиасинга» (он же стробоскопический эффект, муаровый эффект), при котором сигнал высокой частоты после оцифровки превращается в сигнал низкой частоты, которого на самом деле не существует. На рис. 11 красная синусоида высокой частоты — это реальный сигнал. Синяя синусоида более низкой частоты — фиктивный сигнал, возникающий вследствие того, за время взятия отсчета успевает пройти больше, чем пол-периода высокочастотного сигнала.
Рис. 11. Появление ложного сигнала низкой частоты при недостаточно высокой частоте дискретизации
Чтобы избежать эффекта алиасинга перед АЦП ставят специальный антиалиасинговый фильтр — ФНЧ (фильтр нижних частот), который пропускает частоты ниже половины частоты дискретизации АЦП, а более высокие частоты зарезает.
Для того, чтобы вычислить спектр сигнала по его дискретным отсчетам используется дискретное преобразование Фурье (ДПФ). Отметим еще раз, что спектр дискретного сигнала «по определению» ограничен частотой Fмакс, меньшей половине частоты дискретизации Fd. Поэтому спектр дискретного сигнала может быть представлен суммой конечного числа гармоник, в отличие от бесконечной суммы для ряда Фурье непрерывного сигнала, спектр которого может быть неограничен. Согласно теореме Котельникова максимальная частота гармоники должна быть такой, чтобы на нее приходилось как минимум два отсчета, поэтому число гармоник равно половине числа отсчетов дискретного сигнала. То есть если в выборке имеется N отсчетов, то число гармоник в спектре будет равно N/2.
Рассмотрим теперь дискретное преобразование Фурье (ДПФ).
Сравнивая с рядом Фурье
видим, что они совпадают, за исключением того, что время в ДПФ имеет дискретный характер и число гармоник ограничено величиной N/2 — половиной числа отсчетов.
Формулы ДПФ записываются в безразмерных целых переменных k, s, где k – номера отсчетов сигнала, s – номера спектральных составляющих.
Величина s показывает количество полных колебаний гармоники на периоде Т (длительности измерения сигнала). Дискретное преобразование Фурье используется для нахождения амплитуд и фаз гармоник численным методом, т.е. «на компьютере»
Возвращаясь к результатам, полученным в начале. Как уже было сказано выше, при разложении в ряд Фурье непериодической функции (нашего сигнала), полученный ряд Фурье фактически соответствует периодической функции с периодом Т. (рис.12).
рис.12 Периодическая функция f(x) с периодом Т0, с периодом измерения Т>T0
Как видно на рис.12 функция f(x) периодическая с периодом Т0. Однако из-за того, что длительность измерительной выборки Т не совпадает с периодом функции Т0, функция, получаемая как ряд Фурье, имеет разрыв в точке Т. В результате спектр данной функции будет содержать большое количество высокочастотных гармоник. Если бы длительность измерительной выборки Т совпадала с периодом функции Т0, то в полученном после преобразования Фурье спектре присутствовала бы только первая гармоника (синусоида с периодом равным длительности выборки), поскольку функция f(x) представляет собой синусоиду.
Другими словами, программа ДПФ «не знает», что наш сигнал представляет собой «кусок синусоиды», а пытается представить в виде ряда периодическую функцию, которая имеет разрыв из-за нестыковки отдельных кусков синусоиды.
В результате в спектре появляются гармоники, которые должны в сумме изобразить форму функции, включая этот разрыв.
Таким образом, чтобы получить «правильный» спектр сигнала, являющегося суммой нескольких синусоид с разными периодами, необходимо чтобы на периоде измерения сигнала укладывалось целое число периодов каждой синусоиды. На практике это условие можно выполнить при достаточно большой длительности измерения сигнала.
Рис.13 Пример функции и спектра сигнала кинематической погрешности редуктора
При меньшей длительности картина будет выглядеть «хуже»:
Рис.14 Пример функции и спектра сигнала вибрации ротора
На практике бывает сложно понять, где «реальные составляющие», а где «артефакты», вызванные некратностью периодов составляющих и длительности выборки сигнала или «скачками и разрывами» формы сигнала. Конечно слова «реальные составляющие» и «артефакты» не зря взяты в кавычки. Наличие на графике спектра множества гармоник не означает, что наш сигнал в реальности из них «состоит». Это все равно что считать, будто число 7 «состоит» из чисел 3 и 4. Число 7 можно представить в виде суммы чисел 3 и 4 — это правильно.
Так и наш сигнал… а вернее даже не «наш сигнал», а периодическую функцию, составленную путем повторения нашего сигнала (выборки) можно представить в виде суммы гармоник (синусоид) с определенными амплитудами и фазами. Но во многих важных для практики случаях (см. рисунки выше) действительно можно связать полученные в спектре гармоники и с реальными процессами, имеющими циклический характер и вносящими значительный вклад в форму сигнала.
Некоторые итоги
1. Реальный измеренный сигнал, длительностью T сек, оцифрованный АЦП, то есть представленный набором дискретных отсчетов (N штук), имеет дискретный непериодический спектр, представленный набором гармоник (N/2 штук).
2. Сигнал представлен набором действительных значений и его спектр представлен набором действительных значений. Частоты гармоник положительны. То, что математикам бывает удобнее представить спектр в комплексной форме с использованием отрицательных частот не значит, что «так правильно» и «так всегда надо делать».
3. Сигнал, измеренный на отрезке времени Т определен только на отрезке времени Т. Что было до того, как мы начали измерять сигнал, и что будет после того — науке это неизвестно. И в нашем случае — неинтересно. ДПФ ограниченного во времени сигнала дает его «настоящий» спектр, в том смысле, что при определенных условиях позволяет вычислить амплитуду и частоту его составляющих.
Использованные материалы и другие полезные материалы.
FourierScope — программа для построения радио сигналов и их спектрального анализа.
Graph — программа с открытым кодом, предназначенная для построения математических графиков.
ДИСКРЕТНОЕ ПРЕОБРАЗОВАНИЕ ФУРЬЕ – КАК ЭТО ДЕЛАЕТСЯ
Дискретное преобразование Фурье (ДПФ)
2. Сигналы и помехи. Теория передачи сигналов
2.1. Определение и классификация сигналов
2.2. Сигнал как случайный процесс
2.3. Статистические характеристики флуктуационной помехи
2.4. Разложение сигнала на элементарные составляющие
2.5. Спектральное представление сигналов
2.6. Энергетический спектр сигнала
2.7. Временное представление сигналов. Теорема В. А. Котельникова
2.8. Аналитический сигнал
2.9. Линейное и нелинейное преобразования сигналов и помех
2.10. Геометрические представления сигналов
2.11. Различимость сигналов
2.1. Определение и классификация сигналов
Передача и хранение информации, т. е. перенос информации в пространстве и времени, осуществляются с помощью сигналов. В системах управления и связи обычно используются электрические сигналы. Физической величиной, определяющей такой сигнал, является напряжение (или ток), изменяющееся во времени по закону, отображающему передаваемое сообщение.
Сигналы можно классифицировать по ряду признаков. Один из таких признаков мы уже рассмотрели — это дискретность. По этому признаку различают дискретные и непрерывные сигналы, которые, в свою очередь, могут быть детерминированными или случайными. Различают также сигналы простые и сложные.
Сигнал называется детерминированным или регулярным, если его математическим представлением является заданная функция времени. С информационной точки зрения это означает, что под регулярным сигналом понимается такой сигнал, который соответствует известному сообщению. Такие сигналы не несут информации.
Сущность связи состоит в том, чтобы передать получателю не известные ему сведения. Сигналы, несущие такие сведения, на приемном конце заранее также будут неизвестными. Сигналы и тем более помехи для получателя являются случайными (недетермитнированными).
Необходимо подчеркнуть относительность понятия недетерминированности. Сигнал для отправителя на передающем конце детерминирован, так как три заданном способе передачи он определяется известным сообщением. Для получателя тот же сигнал недетерминирован, так как передаваемое сообщение на приемном конце неизвестно. Реальные сигналы, передаваемые по системам связи, как правило, обладают сочетанием свойств детерминированных и недетерминированных сигналов: некоторые параметры
Непрерывный сигнал
Непрерывный сигнал или сигнал с непрерывным временем — это переменная величина (сигнал), чья область, которая часто является временем, является континуумом (например, связанный интервал действительных значений). То есть домен функции — это несчетное множество. Сама функция не должна быть непрерывной. Для сравнения, дискретный сигнал времени имеет счетную область, как натуральные числа.
Сигнал определяется по домену, который может быть или не быть конечным, и существует функциональное сопоставление домена со значением сигнала.Непрерывность временной переменной в связи с законом плотности вещественных чисел означает, что значение сигнала можно найти в любой произвольный момент времени.
Типичный пример сигнала бесконечной длительности:
Конечным аналогом вышеуказанного сигнала может быть:
и f ( т ) = 0 в противном случае.
Значение сигнала конечной (или бесконечной) длительности может быть или не быть конечным. Например,
и f ( т ) = 0 в противном случае,
— сигнал конечной длительности, но он принимает бесконечное значение для.
Во многих дисциплинах принято считать, что непрерывный сигнал всегда должен иметь конечное значение, что имеет больше смысла в случае физических сигналов.
Для некоторых целей допустимы бесконечные особенности, если сигнал интегрируем в любой конечный интервал (например, сигнал t — 1 не является интегрируемым, но t — 2 ).
Любой аналоговый сигнал является непрерывным по своей природе. Дискретные сигналы, используемые в цифровой обработке сигналов, могут быть получены путем дискретизации и квантования непрерывных сигналов.
Непрерывный сигнал также может быть определен по независимой переменной, отличной от времени. Другая очень распространенная независимая переменная — это пространство, которая особенно полезна при обработке изображений, где используются два измерения пространства.
,Цель этого поста — показать, почему непрерывное вейвлет-преобразование является настолько мощным и как использовать его для классификации нескольких нестационарных сигналов и временных рядов.

В эпоху цифровизации и четвертой промышленной революции компании все больше внимания уделяют разработке приложений на основе данных для создания новых бизнес-моделей. Часто необходимым условием для получения новых услуг является запись нестационарных данных или сигналов (данных, которые динамически изменяются во времени) и временных рядов, таких как финансовые тренды или звуки, вибрации, электричество, акселерометр или другие виды сигналов датчиков.Чтобы создать желаемую ценность для бизнеса, эти данные должны обычно обнаруживаться и пониматься этими данными.
Именно здесь вступают в действие машинное и глубокое обучение. Эти математические модели позволяют очень эффективно классифицировать и прогнозировать состояние устройства IoT. К сожалению, часто требуется множество нестационарных сигналов (временных рядов), которые являются очень сложными и подвержены шуму и вводящим в заблуждение значениям. Чтобы повысить точность прогнозирования модели, часто полезно использовать методы цифровой обработки сигналов.Одним из очень мощных методов для этой области является непрерывное вейвлет-преобразование.
Непрерывное вейвлет-преобразование (CWT) очень эффективно при определении коэффициента демпфирования колебательных сигналов (например, идентификация демпфирования в динамических системах). CWT также очень устойчив к шуму в сигнале
Carmen Hurley & Jaden Mclean: Wavelet, Analysis and Methods (2018). Page 73
Ps. В дополнение к CWT существует также дискретное вейвлет-преобразование (DWT), которое я не буду более подробно объяснять в этом посте.
Непонятно, что CWT не очень популярен в науке о данных. По этой причине в следующем посте я хотел бы показать, насколько легко CWT можно использовать для машинного и глубокого обучения (раздел 3). Во-первых, я хотел бы изложить некоторые основные теории, касающиеся CWT (раздел 2).
В этом разделе я хотел бы дать краткий обзор того, почему вейвлет-преобразование так полезно для анализа нестационарных сигналов (раздел 2.1), например, его концепция (раздел 2.2).
Преобразование Фурье (FT) разлагает сигнал на частоты, используя серию синусоидальных волн.Это помогает переходить между временной и частотной областью. Для лучшего понимания FT, я рекомендую это полезное видео.
Чтобы проиллюстрировать ограничение FT, нам нужен очень простой стационарный и нестационарный сигнал. Стационарный сигнал не меняет своего среднего значения, дисперсии и ковариации во времени вместо динамически нестационарного сигнала. В FT мы должны учитывать временную и частотную области. Временная область показывает амплитуду / силу сигнала как функцию времени, которая может быть представлена в виде отдельных изолированных частот в частотной области после FT (рисунок 1).
Рисунок 1. Анализ нестационарных сигналов с использованием FT не дает полной картины его временной и частотной области.Как вы можете видеть (рисунок 1), FT очень хорошо работает для синусоидальных волн, которые генерируются стационарным процессом, потому что сигнал содержит все свои частоты все время (в этом примере только одна частота). Теперь давайте сосредоточимся на всплеске нестационарного сигнала, который может быть своего рода аномалией или характерным паттерном. Как и в случае стационарного процесса, вы также можете идентифицировать частоты с помощью FT, хотя вы не можете определить, какие частоты точно представляют пакет в сигнале.Особенность FT в том, что он разлагает сигнал только в своей частотной области без какой-либо информации о своей временной области. Это объясняет, почему невозможно определить, какие частоты являются частью сигнала в конкретный момент времени или наоборот. Таким образом, с нестационарными сигналами в сочетании с FT вы ограничены либо временной, либо частотной областью, но вы никогда не получите полную картину сигнала. Для интеллектуального решения этой проблемы давайте подробнее рассмотрим непрерывное вейвлет-преобразование в следующем разделе.
Вейвлеты — это математические функции, которые часто называют мини-вейвлетами. В отличие от синусоидальных функций бесконечности (от бесконечности до бесконечности), которые используются для FT, WT содержит:
- Различные семейства и типы вейвлетов с различной компактностью и гладкостью
- , которые имеют нулевое среднее значение и ограничены (конечны) во времени
Различные формы вейвлета позволяют нам выбрать тот, который наилучшим образом соответствует функциям, которые мы ищем в нашем сигнале.Наиболее распространенными вейвлетами для CWT являются вейвлеты «мексиканский, морлетский и гауссовский» (рис. 2). Их также называют «Мать Вейвлеты».
Рисунок 2: Форма мексиканской шляпы, материнских вейвлетов Морле и Гаусса.Ps: Используемый пакет Python «PyWavelets» предоставляет дополнительные материнские вейвлеты, совместимые с CWT. Поэтому, пожалуйста, прочитайте ссылки на API PyWavelets.
На рисунке 2 также показано нулевое среднее и ограничение по времени материнских вейвлетов. Оба эти условия допускают локализацию по времени и частоте одновременно.Кроме того, они обеспечивают необходимое интегрируемое и обратное вейвлет-преобразование. CWT можно описать следующим уравнением:
Следовательно, вейвлет-преобразование использует материнские вейвлеты для разделения временного ряда или изображения от 1D до ND на масштабированные компоненты. В связи с этим преобразование основано на понятиях масштабирования и сдвига.
- Масштабирование: растяжение или сжатие сигнала во времени на коэффициент масштабирования.
- Shifting: перемещение по-разному масштабированных вейвлетов от начала до конца сигнала.
Масштабный коэффициент соответствует тому, насколько масштабируется сигнал во времени и обратно пропорционален частоте. Это означает, что чем выше шкала, тем лучше усмотрение шкалы (Рисунок 3).
Рисунок 3: Демонстрация усадки и растянутого материнского вейвлета Морле во времени. Коэффициент масштабирования обратно пропорционален частоте.Соответственно, это помогает:
- растянутых вейвлетов для захвата медленных изменений; и
- сжимают вейвлеты для захвата резких изменений в сигнале.
Различные вейвлеты в масштабах и во времени сдвигаются по всему сигналу и умножаются на его интервал дискретизации для получения физических значений, что приводит к коэффициентам, которые являются функцией масштабов вейвлетов и параметров сдвига. Например, сигнал с 100 временными шагами, умноженный на 32 (в диапазоне от 1 до 33) шкалы, дает 3200 коэффициентов. Это позволяет лучше характеризовать колебательное поведение в сигналах с CWT.
Если мы применим CWT к нашему нестационарному примеру сигнала и визуализируем результирующие коэффициенты в скалограмме, мы получим следующий результат.
Рисунок 4: Сравнение между нестационарным сигналом с пачкой (временная область) и его CWT (временной и частотной областью) по скейлограммеНа скалогограмме на рисунке 4 показано, где находится большая часть энергии (см. Цветную полосу справа от скалогограммы). ) исходного сигнала содержится во времени и частоте. Кроме того, мы можем видеть, что характеристики сигнала теперь отображаются с высокой разрешающей способностью. Таким образом, вы можете увидеть резкие изменения всплеска, которые обнаруживаются усадочным вейвлетом со шкалой 1 и 2, и медленные изменения синусоидальной волны растянутыми всплесками со шкалой от 15 до 25.
Ps: резкие изменения часто являются наиболее важной частью данных как в ощутимом виде, так и с точки зрения информации, которую они предоставляют.
Такая визуализация коэффициентов CWT, как двумерная скалограмма, может использоваться для улучшения различия между различными типами сигнала. В промышленном контексте это позволяет проводить различие между различными производственными процессами в машине (мониторинг процесса), идентифицировать такие компоненты, как подшипники, а также неисправности станка или инструмента (мониторинг состояния), просто как проблемы качества (мониторинг качества) на основе, например, не -статические сигналы датчика вибрации.Я надеюсь, что это поможет вам лучше понять, насколько мощным CWT может быть анализ данных. Теперь важно увидеть, как вы можете использовать эту технику в машинном и глубоком обучении.
В разделе 2.2 мы видели, что CWT преобразует одномерный временной ряд в двумерные коэффициенты. Таким образом, коэффициенты представляют время, частоту и характеристики сигнала и, следовательно, гораздо больше информации, чем только временной ряд или FT (рисунок 4). Цель этого раздела — использовать эту сгенерированную информацию в качестве основы для классификации с помощью распознавания образов (раздел 3.3) или функция извлечения (раздел 3.4). Ранее я предоставил краткий обзор выбранного примера набора данных (раздел 3.1) и того, как применить CWT к этим данным (раздел 3.2).
В открытом наборе данных HAR содержится датчик смартфона (акселерометр и гироскоп), который измеряет разных людей во время выполнения ими следующих действий:
Имеется 7532 поезда и 2947 тестовых образцов (измерений) с 50% -ным перекрытием между каждым образцом. Каждый образец содержит девять сигналов фиксированного размера со 128 показаниями и временными шагами.
Вы можете скачать и прочитать больше о наборе данных по этой ссылке.
Мы загружаем почти необработанные инерционные сигналы, в которых отфильтрован только гравитационный эффект.
полезная информация: формы (n_samples, n_steps, n_signals) X_train: (7352, 128, 9) и X_test: (2947, 128, 9) все X имеют среднее значение: 0,10 и стандартный вывод: 0,40
Как видите, сигналы практически нормализованы.
Если вы нанесете на график сигналы тела акселерометра и гироскопа тела двух разных видов деятельности, вы увидите динамически изменяющиеся (нестационарные) сигналы для каждого образца (рисунок 5).Для большей наглядности мы не будем строить общие значения акселерометра.
Рисунок 5: Пример визуализации активности при ходьбе и укладке через сигналы акселерометра и смартфона тела смартфона из набора данных HARВ соответствии с динамическим поведением сигналов (рисунок 5) этот набор данных кажется идеальным для применения вейвлет-преобразования.
Как уже упоминалось (раздел 2.2), мы можем различать различные события посредством визуализации коэффициента CWT вручную.Это также возможно для набора данных HAR?
Чтобы выяснить это, мы должны сначала установить пакет PyWavelets Python с «pip install PyWavelets» или «conda install pywavelets», который мы можем использовать для применения вейвлет-преобразования к нашему набору данных.
Во-вторых, мы должны определить удобный материнский вейвлет и масштаб для непрерывной вейвлет-функции pywt.cwt. Что касается этого типа сигнала (рисунок 5), мы выбираем материнский вейвлет Морлет (рисунок 2), основываясь на его наиболее подходящей форме.Чтобы выбрать подходящий диапазон шкал, давайте рассмотрим коэффициенты CWT трех разных диапазонов 32, 64 и 128, представленных в виде скалограммы (рисунок 6).
Рисунок 6: Представление возрастающей информации о поведении сигнала в расширяющемся диапазоне шкал.В целом, меньший размер шкал (в нашем примере 32) позволяет больше сосредоточиться на резких изменениях. Как уже упоминалось, эти внезапные изменения часто являются наиболее важными характеристиками. В противном случае широкий диапазон шкал (в нашем примере 64 или 128) предоставляет больше информации (о медленных изменениях), что может обеспечить лучшую точность классификации.Однако вам понадобится более глубокий CNN для второго варианта.
Для следующей иллюстрации шкала 64 кажется полезным компромиссом для достижения хорошей точности прогнозирования.
Рисунок 7: Различение различных действий HAR на основе визуализации данных датчика с непрерывным вейвлет-преобразованием с помощью скейлограммыКак вы можете видеть (рисунок 7), вручную возможно различать различные действия посредством визуализации коэффициентов CWT. через скалограмму.Пожалуйста, не стесняйтесь выбирать другие сигналы или сэмплы, тогда вы увидите, что каждый сигнал более или менее удобно различать между шестью активностями. Например, вы не достигнете хорошей точности классификации для неподвижных действий, таких как сидя, стоя и лежа, используя только данные общего датчика ускорения в x, y и z.
Я уверен, что вы не хотели бы рассматривать и сравнивать тысячи скалограмм вручную, чтобы определить активность каждого образца. По этой причине мы сначала используем обычную нейронную сеть (раздел 3.3) и второй метод извлечения признаков плюс классификатор (раздел 3.4) для автоматической классификации различных действий набора данных HAR.
CNN — это высокоэффективная программа для изучения характерных шаблонов меток на изображениях. Этот тип нейронной сети также может обрабатывать 2D-коэффициенты CWT, такие как пиксели изображения, для прогнозирования соответствующей активности. Давайте посмотрим, как работает эта комбинация.
Однако, прежде чем мы сможем начать подачу CNN, мы должны:
- преобразовать сигналы набора данных HAR, используя pywt.функция cwt; и ,
- приводят полученные коэффициенты в подходящий формат.
В этом случае мы также выберем материнский вейвлет Морлет и размер шкалы 64 для функции pywt.cwt, как в разделе 3.2. Кроме того, мы изменяем размеры всех матриц коэффициентов (64×128) до квадратной формы (64×64). Этот шаг не является абсолютно необходимым, но сохраняет много параметров и вычислительных ресурсов, и в то же время мы не должны терять слишком много деталей изображений (рисунок 8).
Рисунок 8: Изображение влияния понижающей дискретизации непрерывных вейвлет-преобразованных 2D-коэффициентов с использованием скалогограммВ качестве второго пункта мы все еще должны уточнить, как подавать полученные матрицы коэффициентов CWT в CNN.Здесь наилучшим подходом является размещение 2D-коэффициентов (изображений) девяти сигналов друг на друге, подобно трем каналам красного, зеленого и синего (RGB) цветного изображения. Соответственно, все зависимости между различными данными датчика могут быть учтены одновременно, что очень важно. Обратите внимание: если вы объедините коэффициенты CWT девяти различных сигналов в один массив Numpy (изображение), между ними будут резкие изменения. Это может привести к тому, что CNN фокусируется на границах из-за резких изменений вместо значимых характеристик каждого сигнала.Соответственно, вам потребуется гораздо более глубокий CNN, чтобы игнорировать этот вид шума.
Для иллюстрации мы создаем простую CNN с архитектурой LeNet-5 (рисунок 9) и делаем два улучшения:
.
