Петля гистерезиса что. Петля гистерезиса: механизм возникновения и основные характеристики

Что такое петля гистерезиса. Как формируется петля гистерезиса. Какие основные характеристики можно определить по петле гистерезиса. Чем отличаются петли гистерезиса для различных магнитных материалов.

Что такое петля гистерезиса

Петля гистерезиса — это замкнутая кривая, отображающая зависимость магнитной индукции B от напряженности магнитного поля H при циклическом перемагничивании ферромагнетика. Она наглядно демонстрирует явление магнитного гистерезиса — отставания изменения намагниченности от изменения внешнего магнитного поля.

Основные характеристики, которые можно определить по петле гистерезиса:

• Остаточная индукция Br — значение магнитной индукции при H = 0
• Коэрцитивная сила Hc — значение напряженности поля, необходимое для полного размагничивания образца
• Индукция насыщения Bs — максимальное значение магнитной индукции
• Площадь петли — характеризует потери энергии на перемагничивание

Механизм формирования петли гистерезиса

Процесс формирования петли гистерезиса можно разделить на несколько этапов:

1. Начальное намагничивание из размагниченного состояния до насыщения
2. Уменьшение поля до нуля — формирование остаточной намагниченности
3. Перемагничивание в противоположном направлении до насыщения
4. Повторное уменьшение поля до нуля и намагничивание в исходном направлении

При этом намагниченность отстает от изменения поля из-за необратимых процессов смещения доменных границ. Это и приводит к формированию характерной петлевидной формы кривой намагничивания.

Петли гистерезиса для разных магнитных материалов

Форма и размеры петли гистерезиса существенно различаются для магнитомягких и магнитотвердых материалов:

• Магнитомягкие материалы (электротехническая сталь, пермаллой) имеют узкую петлю с малой коэрцитивной силой
• Магнитотвердые материалы (сплавы AlNiCo, ферриты) характеризуются широкой петлей с большой коэрцитивной силой

Это определяет области применения данных материалов — магнитомягкие используются в трансформаторах и электромашинах, а магнитотвердые — для изготовления постоянных магнитов.

Влияние внешних факторов на петлю гистерезиса

На форму и параметры петли гистерезиса оказывают влияние различные факторы:

• Температура — с ростом температуры петля сужается
• Механические напряжения — приводят к изменению формы петли
• Частота перемагничивания — с ростом частоты петля расширяется
• Форма образца — влияет на размагничивающий фактор

Учет этих факторов важен при проектировании и эксплуатации магнитных устройств.

Методы измерения петли гистерезиса

Существует несколько основных методов экспериментального определения петли гистерезиса:

• Баллистический метод — основан на измерении магнитного потока
• Вибрационный метод — использует явление электромагнитной индукции
• Осциллографический метод — позволяет визуально наблюдать петлю на экране

Каждый метод имеет свои особенности и области применения. Выбор конкретного метода зависит от исследуемого материала и требуемой точности измерений.

Практическое применение петли гистерезиса

Знание характеристик петли гистерезиса важно во многих практических приложениях:

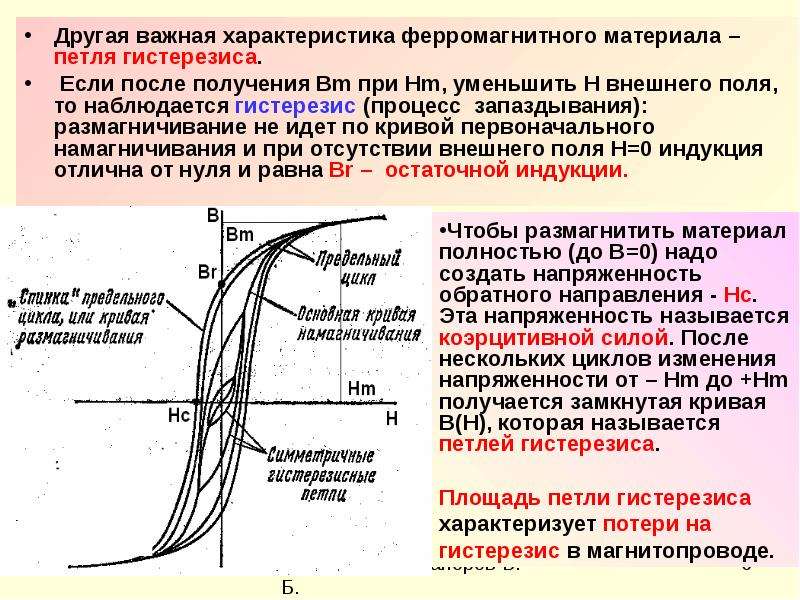
• Разработка электрических машин и трансформаторов
• Создание постоянных магнитов
• Проектирование устройств магнитной записи
• Неразрушающий контроль ферромагнитных изделий

Анализ петли гистерезиса позволяет оценить магнитные свойства материалов и оптимизировать параметры магнитных устройств.

Моделирование петли гистерезиса

Для описания петли гистерезиса используются различные математические модели:

• Модель Прейзаха — основана на статистическом подходе
• Модель Джилса-Атертона — учитывает физические процессы намагничивания
• Феноменологические модели — используют аппроксимирующие функции

Выбор модели зависит от конкретной задачи и требуемой точности. Современные методы компьютерного моделирования позволяют с высокой точностью воспроизводить экспериментальные петли гистерезиса.

Заключение

Петля гистерезиса является важнейшей характеристикой магнитных материалов, отражающей процессы их намагничивания и перемагничивания. Анализ петли гистерезиса позволяет определить ключевые параметры материалов и оптимизировать их применение в различных технических устройствах.

Развитие методов измерения и моделирования петли гистерезиса остается актуальной задачей магнитных исследований, имеющей большое практическое значение для совершенствования магнитных материалов и устройств на их основе.

Что такое петля гистерезиса 🚩 для чего нужна петля эффектов 🚩 Наука 🚩 Другое

Наличие остроугольной петли на графике обусловливается неодинаковостью траекторий между соседними расстояниями, а также эффектом «насыщения». Гистерезис часто путают с инерционностью, однако это не одно и то же. Инерционность – это такая модель поведения, которая обозначает постоянное, однородное и монотонное сопротивление системы изменениям ее состояния.

Гистерезис в физике

В физике это свойство систем представлено тремя основными разновидностями: магнитным, сегнетоэлектрическим и упругим гистерезисом.

Магнитный гистерезис – явление, которое отражает зависимость вектора напряженности магнитного поля и вектора намагничивания в веществе. Причем как от приложенного внешнего поля, так и от предыстории конкретного образца. Существование постоянных магнитов обуславливается именно этим явлением.

Модель петли представляет собой определенный цикл, который некоторые свойства отправляет на повторную проверку и согласование, а некоторые использует дальше. Избирательный характер зависит от свойств конкретной системы.

Сегнетоэлектрический гистерезис – изменяющаяся зависимость поляризации сегнетоэлектриков от циклического изменения внешнего электрического поля.

Упругий гистерезис – поведение упругих материалов, способных сохранять и утрачивать деформацию под воздействием больших давлений. Это явление обуславливает анизотропию механических характеристик и высокие механические качества кованных изделий.

Гистерезис в электронике

В электротехнике и электронике свойством гистерезиса пользуются устройства, которые используют различные магнитные взаимодействия. Например, магнитные носители информации или триггер Шмитта.

Это свойство необходимо знать, чтобы использовать его для подавления шумов в момент переключения определенных логических сигналов (дребезга контактов, быстрых колебаний).

Упругий гистерезис бывает двух видов: динамический и статический. В первом случае график будет изображать постоянно изменяющуюся петлю, во втором – равномерную.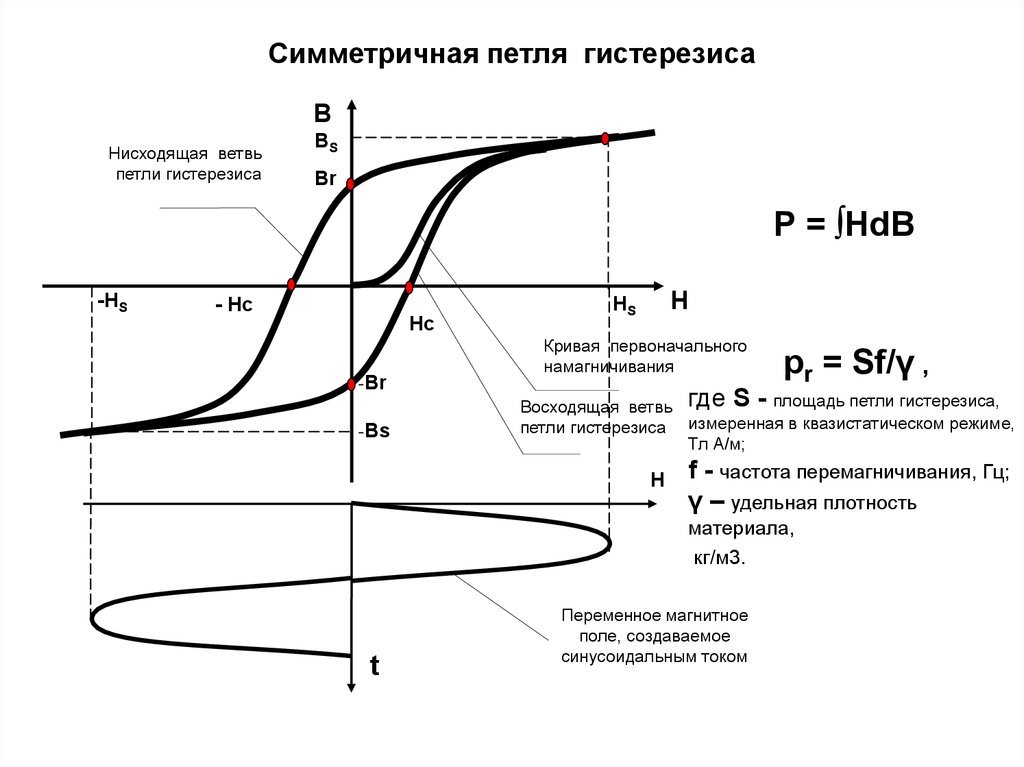

Во всех приборах электронного типа наблюдается тепловой гистерезис. После того как прибор был нагрет, а затем охлажден, его характеристики не принимают прежнего значения.

Это происходит из-за того, что неодинаковое тепловое расширение корпусов микросхем, кристаллодержателей, печатных плат и кристаллов полупроводников вызывает механическое напряжение, сохраняющееся и после охлаждения.

Наиболее заметно это явление в прецизионных источниках опорного напряжения, которые используются в измерительных преобразователях.

Петля гистерезиса, теория и примеры задач

Основные понятия гистерезиса. Петля гистерезиса

Важное свойство сегнетоэлектриков обнаруживается при изучении зависимости электрического смещения (D) от напряженности поля (E). Смещение является не прямо пропорциональным полю. Диэлектрическая проницаемость вещества () зависит от напряженности поля. Кроме того, величина диэлектрического смещения зависит не только от значения напряженности электрического поля в настоящий момент, но и от предыстории состояний поляризации.

Это явление носит название диэлектрического гистерезиса. Зависимость смещения D от напряженности поля E для сегнетоэлектриков графически изображается петлей гистерезиса (рис.1).

Между обкладками плоского конденсатора поместим сегнетоэлектрик. Будем изменять напряженность (E) внешнего электрического поля по гармоническому закону. При этом станем проводить измерение диэлектрической проницаемости сегнетоэлектрика (). При этом используется схема, которая состоит из двух конденсаторов, соединенных последовательно. К крайним клеммам конденсаторов присоединен генератор, который создает разность потенциалов, которая изменяется по гармоническому закону. Один из имеющихся конденсаторов заполнен сегнетоэлектриком (его емкость обозначим C), в другом диэлектрик отсутствует (). Считаем, что площади обкладок конденсаторов равны, расстояния между обкладками – d. Тогда напряженности полей конденсаторов:

   

тогда разности потенциалов между обкладками соответствующих конденсаторов:

   

где – плотность заряда на пластинах конденсатора. Тогда отношение равно:

   

Если напряжение U подают на горизонтальную развертку осциллографа, а напряжение на вертикальную развертку, то на экране осциллографа отобразится, при изменении E, кривая, абсцисса точек которой в некотором масштабе равна , а ордината – . Данная кривая будет петлей гистерезиса (рис.1).

Рис. 1

Стрелки на представленной кривой указывают направления изменения напряженности поля. Отрезок ОВ – отображает величину остаточной поляризации сегнетоэлектрика. Это поляризация диэлектрика при внешнем поле равном нулю. Чем больше отрезок ОВ, тем больше остаточная поляризация. Отрезок ОС отображает величину напряженности, противоположного направления к вектору поляризации, при которой сегнетоэлектрик полностью деполяризован (остаточная поляризация равна нулю). Чем больше длина отрезка ОС, тем лучше остаточную поляризацию удерживает сегнетоэлектрик.

Петлю гистерезиса можно получить, если производить перемагничивание ферромагнетика в периодическом магнитном поле. Кивая зависимости магнитной индукции магнетика от напряженности внешнего магнитного поля (B(H)) будет иметь вид аналогичный рис.1. Демонстрация петли гистерезиса для ферромагнетиков проводится по выше описанной схеме, но при замене конденсаторов на катушки.

Примеры решения задач

Магнитный гистерезис, теория и примеры задач

Основные понятия магнитного гистерезиса

Если взять ферромагнетик в ненамагниченном состоянии, поместить его в магнитное поле, напряженность которого можно постепенно изменять, увеличивать величину H от нуля до некоторого значения . Зависимость (рис.1 (б)) будет отображать отрезок ОА. Потом будем постепенно уменьшать напряженность внешнего магнитного поля. При этом кривая намагничивания пойдет не по тому же пути (AO), что шла наверх, а по кривой, которая на рис. 1(б) обозначена как ACD. Если от величины напряжения изменять магнитное поле снова до H, то кривая намагничивания пройдет ниже и вернется в точку А (см.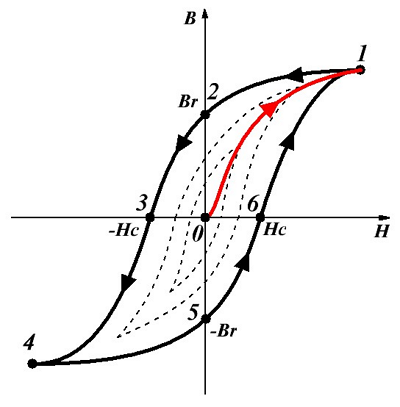 рис.1). Получается замкнутая кривая, которая называется петлей гистерезиса. Из рис.1 видно, что при индукция пол ферромагнетика (и его намагниченность) не становятся равными нулю. Из рис. 1(б) видно, что модуль магнитной индукции равен длине отрезка ОС. Этому отрезку соответствует остаточное намагничивание. С существованием остаточного намагничивания связано наличие постоянных магнитов. Для размагничивания ферромагнетика его следует поместить в обратное магнитное поле, величина которого равна так называемой коэрцитивной силе ферромагнетика ().

Рис. 1(a)

Рис. 1(б)

Петля магнитного гистерезиса

Величины остаточного намагничивания и коэрцитивной силы могут испытывать большие вариации для разных ферромагнетиков. Так, для мягких ферромагнетиков петля гистерезиса узкая, соответственно коэрцитивная сила небольшая. Для материалов, которые применяют при изготовлении постоянных магнитов петля гистерезиса широкая. Петля гистерезиса для зависимости имеет подобную форму (рис. 1 (а)).

Следует отметить, что при увеличении внешнего магнитного поля намагниченность ферромагнетиков растет быстро, затем ее скорость ее роста уменьшается и при некоторой величине, которую называют магнитным насыщением, остается постоянной и не зависит от напряженности внешнего поля. Аналогичный процесс происходит и со связью магнитной индукции ферромагнетика и внешнего магнитного поля. Такую зависимость объясняют тем, что магнитные моменты молекул при увеличении напряженности внешнего поля ориентируются по полю, так растет степень ориентации моментов. Когда неориентированных моментов остается все меньше и меньше, увеличение J прекращается и происходит магнитное насыщение. На рис. 1 точка А – является точкой насыщения.

Мы получили, что величина магнитной индукции (или величина намагниченности) в ферромагнетике определяется не только существующим внешним магнитным полем, но еще зависит от предыдущих состояний намагничивания, при этом происходит некоторое отставание изменения индукции (намагничивания) от изменений напряженности поля.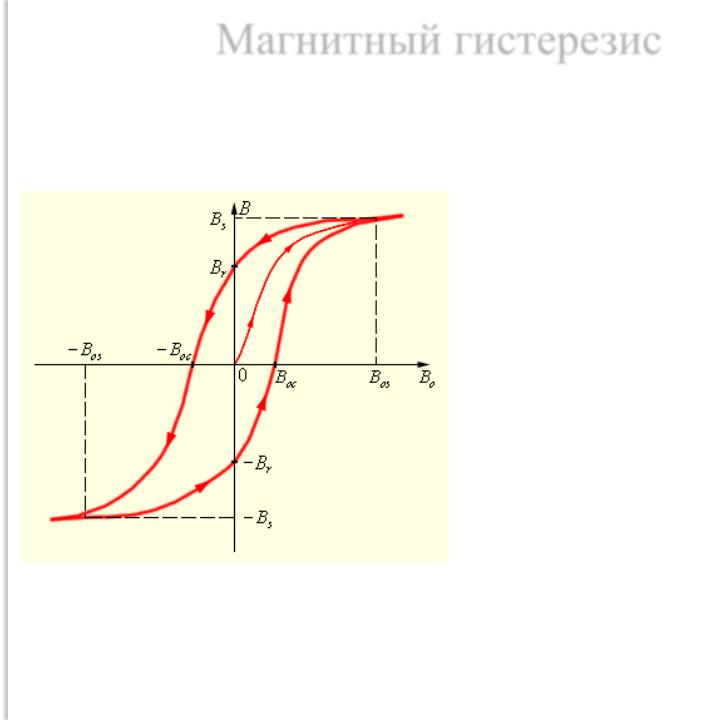 Магнитный гистерезис подобен диэлектрическому гистерезису в сегнетоэлектриках. Гистерезис очень сильно зависит от состава ферромагнетика и способов его обработки.

Примеры решения задач

Понравился сайт? Расскажи друзьям!

Кривая намагничивания и петля гистерезиса — Студопедия

Для характеристики явления намагничивания вещества вводится величина Iназываемая намагниченностью вещества. Намагниченность в СИ определяется формулой

Для ферромагнитных тел намагниченность Iявляется сложной нелинейной функцией B₀. Зависимость I от величины Во/µ₀ называется кривой на­магниченности (рис. 2). Кривая указывает на явление магнитного насыщения: начиная с некоторого значения Во/µ₀= В_0н/µ₀, намагниченность практически остается постоянной, равной Iн(намагниченность насыщения).

Магнитным гистерезисом (От греческого «hysteresis» — отставание следствия от его причины) ферромагнетика называется отставание измене­ния величины намагниченности ферромагнитного вещества от изменения внешнего магнитного поля, в котором находится вещество. Важнейшей причиной магнитного гистерезиса является характерная для ферромагнетика зависимость его магнитных характеристик (µ, I) не только от состояния вещества в данный момент, но и от значений величин µ и I в предыдущие моменты времени. Таким образом, суще­ствует зависимость магнитных свойств от предшествующей намагниченности вещества.

Петлей гистерезиса называется кривая зависимости изменения величины намагниченности ферромагнитного тела, помещенного во внешнее магнитное поле, от изменения индукции этого поля от + Во/µ₀ до — Во/µ₀ и обратно. Значение + Во/µ₀ соответствует намагниченности насыщения I_н. Для того чтобы полностью размагнитить ферромагнитное тело, необходимо изменить на­правление внешнего поля. При некотором зна­чении магнитной индукции — В_{0к ,} которой соот­ветствует величина В_0к/µ₀, называемая коэрцитивной(задерживающей) силoй, намагничен­ность I тела станет равной нулю.

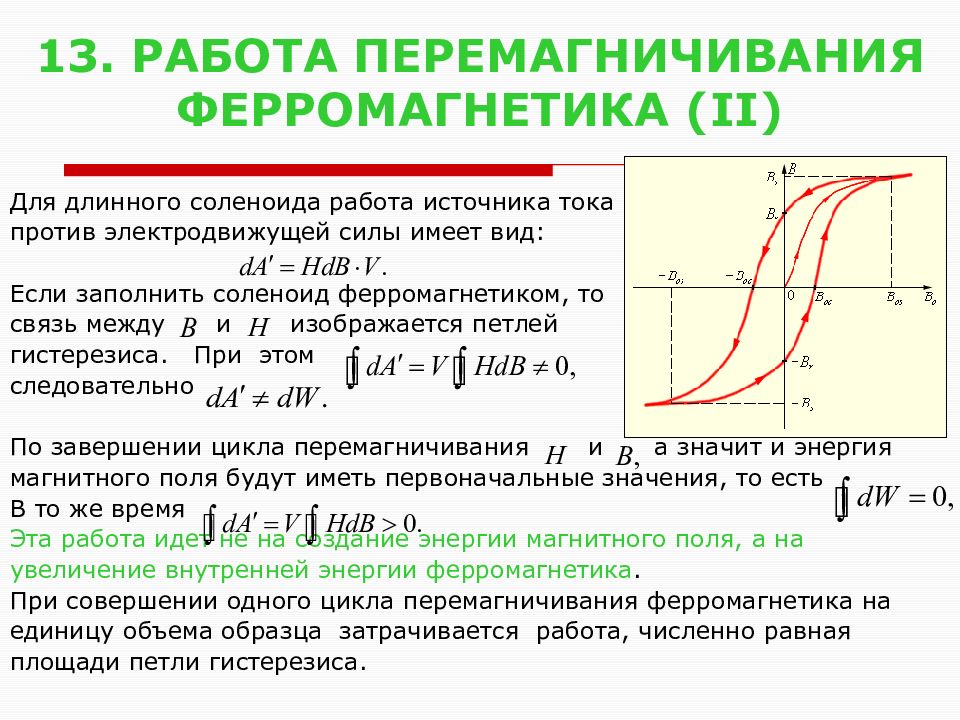
Коэрцитивная сила и форма петли гистерезиса характеризуют свойство ферромагнетика сохранять остаточное намагничивание и определяют использова­ние ферромагнетиков для различных целей. Ферромагнетики с широкой петлей ги­стерезиса называются жесткими магнитными материалами (углеродистые, воль­фрамовые, хромовые, алюминиево-никелевые и другие стали). Они обладают большой коэрцитивной силой и используются для создания постоянных магнитов различной формы (полосовых,подковообразных, магнитных стрелок). К мягким магнитным материалам,обладающим малой коэрцитивной силой и узкой петлей гистерезиса, относятся железо, сплавы железа с никелем. Эти материалы исполь­зуются для изготовления сердечников трансформаторов, генераторов и других устройств, по условиям работы которых происходит перемагничивание в пере­менных магнитных петлях. Перемагничивание ферромагнетика связано с поворотом областей самопроизвольного намагничивания. Работа, необходимая для это­го, совершается за счет энергии внешнего магнитного поля. Количество теплоты, выделяющейся при перемагничивании, пропорционально площади петли гистерезиса.

При температурах меньших точки Кюри любое ферромагнитное тело состоит из доменов — малых областей с линейными размерами порядка 10^-2 -10^-3 см, внутри которых существует наибольшая величина намагниченности, равная намаг­ниченности насыщения. Домены называются иначе областями самопроиз­вольной намагниченности. В отсутствие внешнего магнитного поля векторы магнитных моментов от­дельных доменов ориентированы внутри ферромагнетика совершенно беспорядоч­но, так что суммарный магнитный момент всего тела равен нулю (рис. ). Под влиянием внешнего магнитного поля в ферромагнетиках происходит поворот вдоль поля магнитных моментов не отдельных атомов или молекул, как в парамаг­нетиках, а целых областей самопроизвольной намагниченности — доме­нов. При увеличении внешнего поля размеры доменов, намагни­ченных вдоль внешнего поля, растут за счет уменьшения размеров доменов с дру­гими (не совпадающими с направлением внешнего поля) ориентациями. При достаточно сильном внешнем магнитном поле все ферромагнитное тело оказывается намагниченным. Величина намагничен­ности достигает максимального значения — наступает магнитное насыщение. В отсутствие внешнего поля часть магнитных моментов до­менов остается ориентированной, и этим объясняется существование остаточной намагниченности и возможность создания постоянных магнитов.

Применение ферромагнетиков в технике. Роторы генераторов и электродвигателей; сердечники трансформаторов, электромагнитных реле; в электронно-вычислитель­ных машинах (ЭВМ), телефонах, магнитофонах, на магнитных лентах.

Парамагнитные вещества характеризуются тем, что намагничиваются во внешнем магнитном поле; если же это поле выключить, парамагнетики возвращаются в ненамагниченное состояние. Намагниченность в ферромагнетиках сохраняется и после выключения внешнего поля. На рис. 2 представлена типичная петля гистерезиса для магнитно-твердого (с большими потерями) ферромагнитного материала. Она характеризует неоднозначную зависимость намагниченности магнитоупорядоченного материала от напряженности намагничивающего поля. С увеличением напряженности магнитного поля от исходной (нулевой) точки (1) намагничивание идет по штриховой линии 1-2, причем величина m существенно изменяется по мере того, как возрастает намагниченность образца. В точке 2 достигается насыщение, т.е. при дальнейшем увеличении напряженности намагниченность больше не увеличивается. Если теперь постепенно уменьшать величину H до нуля, то кривая B(H) уже не следует по прежнему пути, а проходит через точку 3, обнаруживая как бы «память» материала о «прошлой истории», откуда и название «гистерезис». Очевидно, что при этом сохраняется некоторая остаточная намагниченность (отрезок 1-3). После изменения направления намагничивающего поля на обратное кривая В (Н) проходит точку 4, причем отрезок (1)-(4) соответствует коэрцитивной силе, препятствующей размагничиванию. Дальнейший рост значений (-H) приводит кривую гистерезиса в третий квадрант — участок 4-5. Следующее за этим уменьшение величины (-H) до нуля и затем возрастание положительных значений H приведет к замыканию петли гистерезиса через точки 6, 7 и 2.

Рис. 2. ТИПИЧНАЯ ПЕТЛЯ ГИСТЕРЕЗИСА для магнитно-твердого ферромагнитного материала. В точке 2 достигается магнитное насыщение. Отрезок 1-3 определяет остаточную магнитную индукцию, а отрезок 1-4 — коэрцитивную силу, характеризующую способность образца противостоять размагничиванию.

Магнитно-твердые материалы характеризуются широкой петлей гистерезиса, охватывающей значительную площадь на диаграмме и потому соответствующей большим значениям остаточной намагниченности (магнитной индукции) и коэрцитивной силы. Узкая петля гистерезиса (рис. 3) характерна для магнитно-мягких материалов — таких, как мягкая сталь и специальные сплавы с большой магнитной проницаемостью. Такие сплавы и были созданы с целью снижения обусловленных гистерезисом энергетических потерь. Большинство подобных специальных сплавов, как и ферриты, обладают высоким электрическим сопротивлением, благодаря чему уменьшаются не только магнитные потери, но и электрические, обусловленные вихревыми токами.

Рис. 3. ТИПИЧНАЯ ПЕТЛЯ ГИСТЕРЕЗИСА для магнитно-мягкого материала (например, железа). Поскольку площадь петли пропорциональна потерям энергии, такие материалы слабо сопротивляются размагничиванию и характеризуются малыми потерями энергии.

Магнитные материалы с высокой проницаемостью изготовляются путем отжига, осуществляемого выдерживанием при температуре около 1000° С, с последующим отпуском (постепенным охлаждением) до комнатной температуры. При этом очень существенны предварительная механическая и термическая обработка, а также отсутствие в образце примесей. Для сердечников трансформаторов в начале 20 в. были разработаны кремнистые стали, величина m которых возрастала с увеличением содержания кремния. Между 1915 и 1920 появились пермаллои (сплавы Ni с Fe) с характерной для них узкой и почти прямоугольной петлей гистерезиса. Особенно высокими значениями магнитной проницаемости m при малых значениях H отличаются сплавы гиперник (50% Ni, 50% Fe) и му-металл (75% Ni, 18% Fe, 5% Cu, 2% Cr), тогда как в перминваре (45% Ni, 30% Fe, 25% Co) величина m практически постоянна в широких пределах изменения напряженности поля. Среди современных магнитных материалов следует упомянуть супермаллой — сплав с наивысшей магнитной проницаемостью (в его состав входит 79% Ni, 15% Fe и 5% Mo).

(взято с http://www.phyzika.ru/Magnitnoe.html)

Гистерезис для инженеров. Петля гистерезиса. Прерванные процессы на петле гистерезиса. Смена направления процесса.

	Навигация по справочнику TehTab. ru:  главная страница  / / Техническая информация / / Инженерные приемы и понятия / / Теория автоматического управления (регулирования). ТАУ  / / Гистерезис для инженеров. Петля гистерезиса. Прерванные процессы на петле гистерезиса. Смена направления процесса. Гистерезис для инженеров. Петля гистерезиса. Прерванные процессы на петле гистерезиса. Смена направления процесса. Гистерезис по определению, это свойство систем, которые не сразу следуют приложенным силам. Реакция этих систем зависит от сил, действовавших ранее, то есть системы зависят от собственной истории. Рисунок 1. Классическая петля гистерезиса. По пунктам: казалось бы, что любая выявленная на широком интервале, аналитическая зависимость физических величин вида Y=f(X) при премещении из точки 0(условный ноль, для удобства) в точку 1 является хорошим описанием процесса но, на самом деле, некоторые процессы всегда в одну сторону идут по одной кривой, а в другую по другой ( сходясь в конечных точках) — напоминает ежедневный путь на работу и обратно верно? эти явления и получили название явлений «классического гистерезиса», к основным из которых относят: магнитный гистерезис сегнетоэлектрический гистерезис упругий гистерезис многие другие мы же рассмотрим и явления классического гистерезиса и огромный класс явлений, которые, на первый взгляд, являются явлениями гистерезиса, но показывают совершенно самостоятельное поведение, назовем их «инженерный гистерезис» подробные описания явлений классического гистерезиса широко доступны и не являются предметом рассмотрения Что такое «инженерный гистерезис»? В отличие от классического гистерезиса «инженерный гистерезис» обусловлен не остаточными явлениями в системе при смене направления процесса, а резким изменением свойств системы в точках начала и конца процесса (например, при срабатывании автоматики, меняющем коммутацию/геометрию/логику и др. внутри системы). Проиллюстрируем разницу. Рисунки 2 и 3 показывают полные кривые гистерезиса для классического и инженерного гистерезисов. При движении из точки 0 в точку 1 при отличий нет. Но! Рассмотрим вопрос о том, как ведет себя система, обладающая гистерезисом по каким-то свойствам (характеристикам) в том случае, если процесс перемещения из точки начала процесса в точку конца будет прерван где-то посередине. Рисунок 2. Классический гистерезис. Смена направления процесса. Рисунок 3. «Инженерный гистерезис». Смена направления процесса. Обратите внимание! В классическом гистерезисе смена направления процесса образует новую петлю гистерезиса. В «инженерном гистерезисе» при недостижении крайних точек процесса ничего подобного не происходит. К чему это приведет? Рисунок 4. Прерваный процесс на петле «инженерного гистерезиса». Контрольный параметр Y для работы автоматики зависит от рабочего параметра Р, и на первый вид эта зависимость — гистерезис, хоть это и не так на самом деле В зависимости от того, на каком из участков процесса находится рабочая точка сейчас эта зависимость носит различный характер При аварии или обрыве питания, в зависимости от настроек работы системы «по умолчанию» для промежуточных точек между уровнями включения и выключения автоматики повторный запуск наверняка приведет к нештатным относительно контрольного параметра значениям рабочего параметра Требуется определенное внимание инженера при перезапуске процесса к тому на каком из этапов процесса произошел сбой Иногда требуются специальные решения для защиты логики системы от неверной интерпретации состояния системы Проблема особенно характерна для систем с дискретным (релейным) регулированием, но не только для них Данный процесс, строго говоря, вообще гистерезисом не является и употребление термина может вызывать недопонимание при общении с другими инженерами и, особенно, с инженерами-учеными другое прочее
Нашли ошибку? Есть дополнения? Напишите нам об этом, указав ссылку на страницу.
TehTab.ru Реклама, сотрудничество: [email protected]	Обращаем ваше внимание на то, что данный интернет-сайт носит исключительно информационный характер. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Все риски за использование информаци с сайта посетители берут на себя. Проект TehTab.ru является некоммерческим, не поддерживается никакими политическими партиями и иностранными организациями.

Петля Гистерезиса

Петля гистерезиса. При циклическом изменении напряженности постоянного магнитного поля от 0 до +Н, от +Н до –Н и снова от –Н до +Н кривая изменения индукции (кривая перемагничивания) имеет форму замкнутой кривой – петли гистерезиса. Для слабых полей петля имеет вид эллипса. При увеличении значения напряженности магнитного поля Н получают серию заключенных одна в другую петель гистерезиса. Когда все векторы намагниченности доменов сориентируются вдоль направления поля, процесс намагничивания закончится состоянием технического насыщения намагниченности материала. Петлю гистерезиса, полученную при условии насыщения намагничивания, называют предельной петлей гистерезиса. Она характеризуется максимально достигнутым значением индукции Bs, называется индукцией насыщения. При уменьшении напряженности магнитного поля от +Н до 0 магнитная индукция сохраняет остаточную индукцию Вс. Чтобы получить остаточную магнитную индукцию, равную 0, необходимо приложить противоположно направленное размагничивающее поле определенной напряженности -Нс. Отрицательная напряженность магнитного поля -Нс называется коэрцитивной силой материала. При достижении напряженности магнитного поля значения –Н, а затем 0 вновь возникает остаточная индукция –Вс. Если повысить напряженность магнитного поля до +Нс, то остаточная магнитная индукция Вс будет равна 0. Площадь гистерезисных петель в промежуточных и предельных состояниях характеризует рассеивание электрической энергии в процессе перемагничивания материала, т.е. потери на гистерезис. Площадь гистерезисной петли зависит от свойств материала, его геометрических размеров и частоты перемагничивания. По предельной петле гистерезиса определяют такие характеристики магнитных материалов, как индукцию насыщения Bs, остаточную индукцию Вс, коэрцитивную силу Нс.

Кривая намагничивания

Кривая намагничивания. Это важнейшая характеристика магнитных материалов, она показывает зависимость намагниченности или магнитной индукции материала от напряженности внешнего поля Н. Магнитная индукция материала Bi измеряется в теслах (Тл) и связана с намагниченностью . Основная (коммутационная) кривая намагничивания представляет собой геометрическое место вершин петель гистерезиса, полученных при циклическом перемагничивании и отражает изменение магнитной индукции В в зависимости от напряженности магнитного поля Н, которое создается в материале при намагничивании.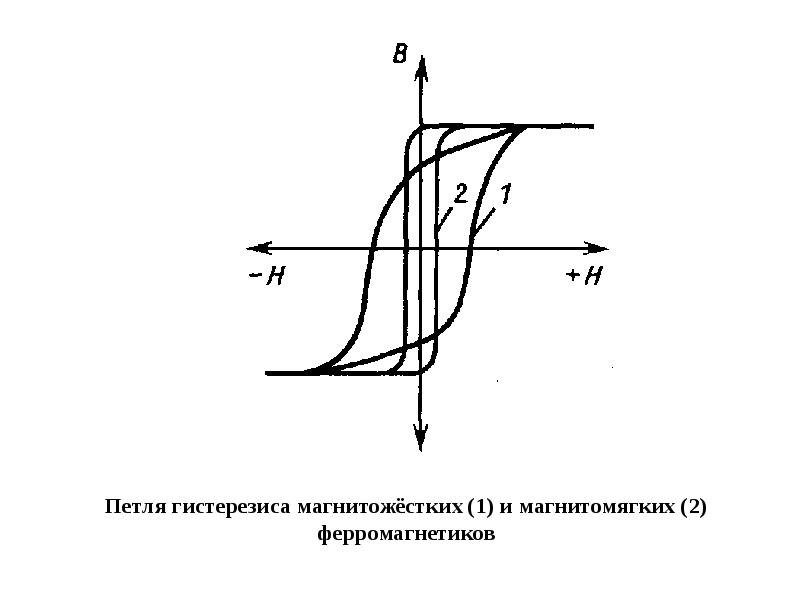 Напряженность магнитного поля в образце в виде тороида, когда магнитная цепь замкнута, равна напряженности внешнего поля Нв. В разомкнутой магнитной цепи на концах образца появляются магнитные полюса, создающие размагничивающее поле Нр. Разница между магнитными напряженностями внешнего и размагничивающего полей определяют внутреннюю магнитную напряженность Hi материала. Основная кривая намагничивания имеет ряд характерных участков, которые можно условно выделить при намагничивании монокристалла ферромагнетика. Первый участок кривой намагничивания соответствует процессу смещения границ менее благоприятно ориентированных доменов. На втором участке происходит поворот векторов намагниченности доменов в направлении внешнего магнитного поля. Третий участок соответствует парапроцессу, т.е. завершающему этапу процесса намагничивания, когда сильное магнитное поле поворачивает в направлении своего действия не сориентированные магнитные моменты доменов ферромагнетика.

Объяснение петли гистерезиса

— База знаний идеальных магнитных решений

Гистерезис означает запаздывание

Гистерезис основан на греческом слове, означающем запаздывание. Итак, магнитный гистерезис — это то, как магнитные свойства материала отстают от силы, создающей эти свойства. Кривая гистерезиса многое говорит нам о реакции материала на магнитное поле, поэтому, если мы знаем, как ее интерпретировать, мы будем много знать и понимать реакцию материала на магнитное поле.

Мы наносим гистерезис материала на график, известный как петля гистерезиса. Другой способ выразить это — сказать, что петля гистерезиса показывает взаимосвязь между внешней силой намагничивания и индуцированной плотностью магнитного потока.

Что такое кривая BH?

График гистерезиса известен как кривая BH, где B (плотность потока материала, измеренная в теслах или мегагауссах) отложена на вертикальной оси, а H (внешняя приложенная сила намагничивания, измеренная в амперах на метр) отложена по горизонтальной оси.Мы также можем изучить ряд других магнитных концепций и принципов, просто изучив подробно петлю гистерезиса.

Кривая магнитного материала B-H. Следуя буквам от a до g, мы генерируем важные магнитные данные о материале, которые помогают нам понять магнитные свойства материала.

Плотность магнитного потока (B) магнитного материала будет увеличиваться — от точки до в исходной точке — в присутствии приложенного магнитного поля (H) до тех пор, пока не достигнет максимума, при котором он больше не реагирует на увеличение магнитного поля. поле точка b .Это точка Положительного насыщения , где любое дальнейшее увеличение внешнего магнитного поля не приведет к дальнейшему увеличению плотности потока материала.

Обнаружение остаточной и коэрцитивной силы в петле гистерезиса

Следующее, что мы делаем, — это возвращаемся влево по горизонтальной оси к началу координат. Мы обнаруживаем, что материал высвобождает часть своего магнетизма, и когда приложенное поле снова достигает нуля (точка c на кривой B-H), материал обретает остаточную магнитную силу, которая называется остаточной магнитной способностью (также известной как удерживающая способность).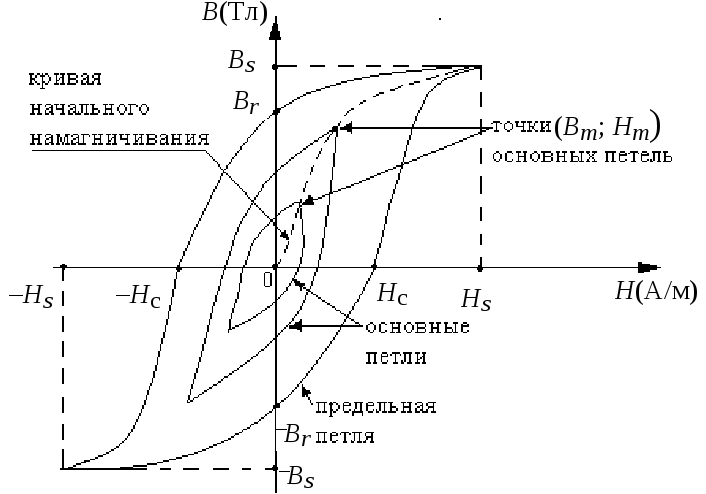

Что такое Remanence?

Остаточная магнитная индукция — это остаточное магнитное поле, обнаруженное в материале после того, как приложенное магнитное поле уменьшится до нуля. Основываясь на исходном значении остаточной намагниченности и форме кривой, которую мы генерируем с приложенным магнитным полем, мы можем определить, является ли исследуемый образец твердым или магнитомягким материалом.

Теперь, когда мы обращаем приложенное магнитное поле (H) и перемещаем его влево, мы видим, что значение B (плотность потока материала) падает до нуля.Мы сейчас в точке d на кривой B-H.

Что такое коэрцитивность?

Количество (H), необходимое для перемещения (B) к нулевой линии, дает нам значение Коэрцитивной силы материала. Коэрцитивная сила, также известная как коэрцитивная сила, — это сопротивление материала изменениям намагниченности. Магнитомягкие материалы имеют низкую коэрцитивную силу, а магнитотвердые материалы — высокую. Независимо от магнитной жесткости или мягкости материала точка d определяет момент потери магнитной силы.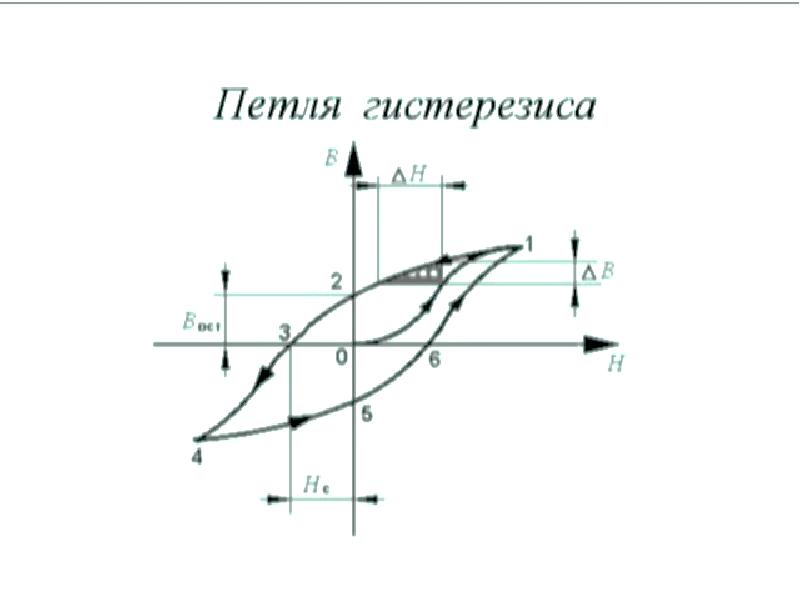

Форма кривой ЧД в твердых и мягких магнитных материалах

Магнитомягкие материалы имеют тонкую кривую гистерезиса, поэтому они широко используются в приложениях, где требуется частое переключение полярности, например, в трансформаторах и т. Д. обмотки двигателя. Как показано ниже, магнитомягкие материалы имеют низкую магнитную индукцию и уже потеряли значительную часть своего магнитного поля к тому времени, когда они пересекают нулевую линию. У них также есть крутой отрицательный наклон размагничивания на нулевой линии.

Магнитомягкие материалы с их низкой коэрцитивной силой могут часто менять полярность и выдерживать относительно небольшие электрические потери. Ширина петли гистерезиса многое говорит нам о потерях. Чем уже кривая, тем меньше потери.

Твердые магнитные материалы имеют очень широкую кривую гистерезиса, что делает их практичными в приложениях, где они воздействуют своим магнитным полем на магнитомягкие материалы. Как видно на рисунке ниже, магнитотвердые материалы обладают высокой остаточной магнитной индукцией и теряют лишь небольшой процент своего магнитного поля к тому времени, когда они пересекают нулевую линию.Их наклон размагничивания на нулевой линии очень пологий и не увеличивается до тех пор, пока не уйдет далеко влево от нулевой линии. Если бы твердые магнитные материалы часто меняли полярность, потери на гистерезис были бы огромными, поэтому они не используются таким образом.

Negative Saturation

Нажимая влево по оси B, мы продолжаем увеличивать магнитное поле в противоположном направлении до тех пор, пока не достигнем точки e — точки отрицательной насыщенности.Эта точка похожа на точку b , но в противоположном направлении. Независимо от того, твердый или мягкий, магнитный материал в нашем исследовании теперь намагничен в направлении, противоположном его намагниченности в точке b .

Если мы продолжим назад к точке точка b от точки точка e , мы просто снова сделаем то же самое, что делали изначально, но в противоположном направлении.

Обращаясь к Рисунку 1, с которого мы начали, мы видим, как мы прошли весь путь по петле гистерезиса.Но нужно отметить еще одну вещь. Из-за Remanence мы никогда не вернемся к точке a, с которой мы начали, потому что точка a была точкой, где материал никогда не подвергался воздействию магнитного поля.

Хотели бы вы изучить этот материал более подробно? Здесь вы найдете очень хороший видеоурок.

Петля гистерезиса

Петля гистерезиса
Далее: Домены Up: Микромагнитные системы Предыдущий: Микромагнитные системы Содержание

Петля гистерезиса

Отличительной чертой магнитной системы является петля гистерезиса .Этот традиционно представляется графически как общая намагниченность образца против некоторого приложенного магнитного поля. Значение приложенное поле, где петля пересекает нулевую намагниченность, известно как коэрцитивное поле или , и, следовательно, представляет величина приложенного поля, необходимого для обратного намагничивания направление магнита. Остаточная намагниченность намагниченность, которая сохраняется, когда приложенное поле уменьшается до нуля. Коэрцитивное поле т.е. приложенное поле где общая намагниченность образца равна нулю Коэрцитивное поле т.е. приложенное поле где общая намагниченность образца равна нулю ( ) Остаточная намагниченность , т.е. величина намагничивание образца при нулевом приложенном магнитном поле

Сравнение петель гистерезиса, показанных на рисунке 2.10, из мягкого и жесткого магнита можно обратите внимание, что более мягкий магнит будет иметь узкую петля гистерезиса, i.е. прикладное поле, необходимое для реверсирования намагниченность относительно низкая, и жесткий магнит будет обладают сравнительно широкой петлей гистерезиса.

Точка, в которой общая намагниченность образца больше не может быть увеличенным (так как вся намагниченность полностью направлена ​​в один направление) — насыщенность точка или — идентифицируется в виде плато на крайних точках приложенного поля в петле гистерезиса. Точка насыщения i.е. величина максимально возможной намагниченности образца

Также следует отметить, что площадь под петлей гистерезиса составляет эквивалентной энергии, которая при изменении поля на противоположное равна превращается в тепло.

Для длительного хранения данных желательно наличие материала с широкой петлей гистерезиса и, следовательно, большим коэрцитивным полем, так как это затрудняет потерю указанного материала состояние намагниченности. Узкая петля гистерезиса — характеристика полезно для таких приложений, как записывающие головки, как в этих временное намагничивание способствует легкому переключению между намагничиванием состояния.Идеальные петли гистерезиса для магнитных сред можно увидеть на рисунке 2.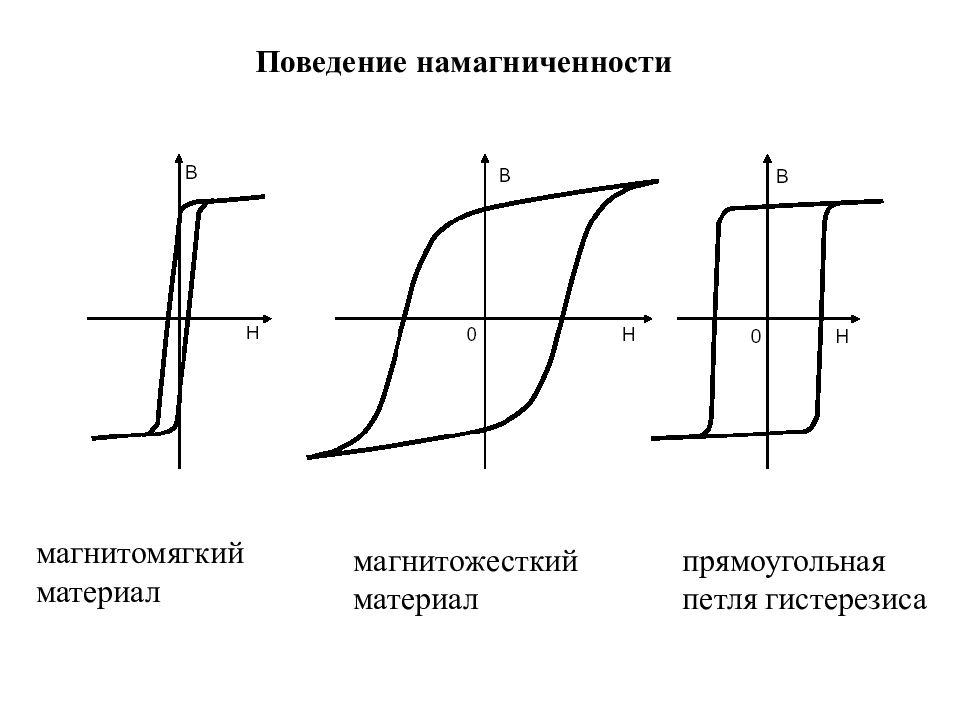 11.

Рисунок 2.10: Две типичные петли гистерезиса — левая петля показывает какой-то постоянный магнитный материал, правая петля — более мягкий магнит. Сплошная синяя линия указывает на уменьшающееся поле, пунктирная красная линия указывает на увеличивающееся поле

Рисунок 2.11: Идеалы магнитной записи. Квадратный цикл с высокой коэрцитивной силой хорош для длительного хранения данных; бесконечно узкая петля с диагональными характеристиками желательна для переключения поля, необходимого для считывающих головок в приложениях с магнитными носителями

---

Далее: Домены Up: Микромагнитные системы Предыдущий: Микромагнитные системы Содержание

Ричард Бордман 2006-11-28

Двойная петля гистерезиса в сегнетоэлектрической керамике на основе BaTiO3

1. Введение

В 1951 году понятие антисегнетоэлектричества, основанное на феноменологической теории, было впервые предложено К. Киттелем (Kittel, 1951), который предсказал существование антисегнетоэлектрических материалов и их некоторых внутренних характеристик. Впоследствии двойная петля гистерезиса (P – E) и фазовый переход сегнетоэлектрик-антисегнетоэлектрик (FE-AFE) наблюдались в PbZrO ₃ (Shirane et al., 1951, 1952) и Pb (Zr, Ti) O ₃ (Sawaguchi, 1953) керамика со структурой перовскита.С тех пор двойная петля гистерезиса, один из важных макроскопических эффектов, рассматривается как типичная характеристика антисегнетоэлектрических материалов. Такое антисегнетоэлектрическое поведение наблюдается также в керамике Pb (Zr, Sn, Ti) O ₃ и Pb (La, Zr, Sn, Ti) O ₃ (Berlincourt, 1963, 1964; Biggers & Schulze, 1974; Gttrttritja et al., 1980; Шебанов и др., 1994).

Интересно, что двойные петли гистерезиса наблюдались в BaTiO ₃ (Merz, 1953), на основе BaTiO ₃ (Ren, 2004; Zhang & Ren, 2005, 2006; Liu et al. , 2006), (Na _0,5 Bi _0,5 ) на основе TiO ₃ (Takenaka, 1991; Sakata & Masuda, 1974; Tu et al., 1994; Sakata et al., 1992), (Ba, Sr ) TiO ₃ (Zhang et al., 2004), KNbO ₃ (Feng & Ren, 2007, 2008), BiFeO ₃ (Yuen et al., 2007) и другой перовскитовой керамике на основе свинца, такой как Pb (Yb _0,5 Ta _0,5 ) O ₃ (Yasuda & Konda, 1993) _, Pb (Fe _2/3 W _1/3 ) O ₃ -Pb (Co _{1 / 2} W _1/2 ) O ₃ (Uchino & Nomura, 1978), Pb (Sc _0.5 Ta _0,5 ) O ₃ (Chu et al., 1993) и Pb (Co _1/2 W _1/2 ) O ₃ (Hachiga et al., 1985) в прошлом десятилетия. Однако наблюдаемые двойные петли гистерезиса имеют разное физическое происхождение.

Что касается физического происхождения двойных петель P-E в материалах со структурой перовскита, их в целом можно разделить на несколько групп ниже: (1) двойные петли P-E являются результатом антисегнетоэлектрических компонентов. т.е. наблюдаемые двойные петли P-E в керамике PbZrO ₃ и Pb (Zr, Ti) O ₃ . (2) двойные петли P-E являются результатом индуцированного электрическим полем фазового перехода из антисегнетоэлектрика в сегнетоэлектрик, как показано в керамике Pb (La, Zr, Sn, Ti) O ₃ . (3) в высокоупорядоченных перовскитных комплексных соединениях на основе свинца и бессвинца часто наблюдаются два последовательных фазовых перехода параэлектрик-антисегнетоэлектрик-сегнетоэлектрик ( PE-AFE-FE ), и ожидается, что это будут сопровождаться двойными петлями PE . фаза перехода.Такие случаи часто встречаются в Pb (Yb _0,5 Ta _0,5 ) O _3, Pb (Fe _2/3 W _1/3 ) O ₃ -Pb (Co _1/2 W _1/2 ) O ₃ , Pb (Sc _0,5 Ta _0,5 ) O ₃ и Pb (Co _1/2 W _1/2 ) O ₃ и (Na _0,5 Bi _0,5 ) Керамика на основе TiO ₃ . (4) эффект старения намного ниже температуры Кюри ( T _c ) может вызвать наблюдение двойных петель PE во многих различных композиционных керамиках, таких как керамика BaTiO ₃ , легированная актором, легированная Mn ( Ba, Sr) TiO ₃ керамика, KNbO _{3 керамика на основе} и керамика BiFeO ₃ .Вызванные старением двойные петли P-E были основными на основании высококачественных публикаций и времени их цитирования. (5) для наблюдаемых двойных петель P-E в кристаллах BaTiO ₃ в точке Кюри, их происхождение не может быть отнесено ни к одной из упомянутых выше групп. Кристаллы BaTiO ₃ переходят из параэлектрического в сегнетоэлектрическое состояние, а керамика (Pb, Ba) ZrO ₃ переходит из антисегнетоэлектрического в сегнетоэлектрическое состояние при приложении электрического поля.Обычно считается, что точка Кюри кристалла BaTiO ₃ смещается в сторону более высокой температуры при приложении постоянного поля смещения. Более подробное обсуждение происхождения двойных петель P-E в кристалле BaTiO ₃ можно найти в предыдущей литературе, озаглавленной «Теория двойного гистерезиса для сегнетоэлектрических кристаллов» (Srivastava, 2006).

После краткого обзора физического происхождения петель двойного гистерезиса в различной структуре перовскита (A ⁺ B ⁵⁺ O ₃ , A ²⁺ B ⁴⁺ O ₃ , AA ‘ BO ₃ , ABB’O ₃ и т. Д.), Эта глава начинается с эффекта старения, а именно постепенного изменения физических свойств с течением времени.Затем следует обсуждение вызванных старением петель двойного гистерезиса в легированной Bi (Ba, Ca) TiO ₃ и легированной Bi (Ba, Sr, Ca) TiO ₃ сегнетоэлектрической керамике. Некоторый акцент будет сделан на роли акцепторного и донорного легирования в понимании физики этих материалов.

2. Методика эксперимента

2.1. Синтез керамики

Для синтеза керамических образцов использовали обычный твердый реакционный путь. Реактивная чистота BaCO ₃ (99.8%), Bi ₂ O ₃ (99,8%), SrCO ₃ (99,8%), CaCO ₃ (99,8%) и TiO ₂ (98%) в качестве сырья взвешивали согласно к составам (Ba _1-x Ca _x ) _1-1,5y Bi _y TiO ₃ (Bi-BCT, x = 0,10, 0,20 и 0,30, y = 0,05) и (Ba _{1- x} Ca _{x /2} Sr _{x /2} ) _{1-1,5 y} Bi _y TiO ₃ (Bi-BCST, x ) 0.10, 0,20 и 0,40, y = 0 и 0,05). (Ba _0,925 Bi _0,05 ) (Ti _0,90 Ca _0,10 ) O ₃ (обозначаемый здесь и далее Bi-BTC) был подготовлен для сравнения эффекта замещения Ca на сайтах Ti в Bi-BCT. После измельчения в шаровой мельнице в спирте в течение 6 часов с использованием агатовых шаров в планетарной мельнице суспензию сушили, а затем прокаливали при 1100 ^o ° C в течение 4-5 часов. Прокаленный порошок измельчали ​​в шаровой мельнице и снова сушили с получением гомогенного порошка. Гранулы диаметром 10 мм и толщиной ~ 1 мм прессовали на связующем ПВА 5%.При медленном нагревании при 500 ° C в течение 3-4 часов связующее выгорело. Образцы спекали при 1240, ^o ° C -1300 ° C на воздухе в течение 3 часов со скоростью нагрева 200 ° C / час. Охлаждение образцов проводилось в печи.

2.2. Характеристики

Фазовые структуры керамики при различных температурах проверяли методом порошковой рентгеновской дифракции (XRD, D / Max2200 RZGAKV: Rigaku Inc., Япония) на автоматическом рентгеновском дифрактометре Rigaku D / max 2400 с вращающимся датчиком. анод с использованием излучения CuK _{.Микроструктуры исследовали с помощью сканирующей электронной микроскопии (SEM, Quanta 200 FEG System: FEI Co., USA) с рентгеновской энергодисперсионной спектроскопией (EDS) для химического анализа. Исследование комбинационного рассеяния света проводили при комнатной температуре с использованием дисперсионного рамановского спектрометра ALMEGA (ALMEGA, Therm Nicolet, Madison, WI).}

2.3. Измерения свойств

После полировки размеры были измерены перед нанесением серебряных электродов на таблетки, затем образцы обжигались при 810 ° C в течение 10 минут.Диэлектрические свойства в диапазоне частот от 0,1 кГц до 100 кГц были измерены с помощью измерителя Agilent 4284A LCR, поскольку образцы нагревали со скоростью 2 ° C / мин от отрицательных 80 до положительных 200 ° C. Петли гистерезиса были измерены в широком диапазоне температур с использованием модифицированной схемы Сойера-Тауэра с компьютерным управлением на частоте 1 Гц. Отношение тока к полю измерялось на автоматической тестовой системе сегнетоэлектрика aixACT TF-ANALY2ER2000. Сигнал приложенного электрического поля имеет треугольную форму, а период времени равен секунде.

3. Результаты и обсуждение

3.1. Структурный анализ

Сообщалось, что предел растворимости Bi составляет около 5 ат. % в BaTiO ₃ (Zhou et al., 1999) и около 10 ат. % в (Ba _0,2 Sr _0,8 ) TiO ₃ (Zhou et al., 2000) соответственно. Причем 5 ат. % легирования Bi может быть полностью включено в решетку перовскита Ba _1-x Sr _x TiO ₃ (x <0,80) (Zhou et al., 2001).Тогда можно предположить, что 5 ат. % легирования Bi может быть полностью включено в решетку перовскита (Ba _{1- x} Ca _x ) TiO ₃ (Bi-BCT, x = 0,10, 0,20 и 0,30) и (Ba _{1- x} Ca _{x /2} Sr _{x /2} ) TiO ₃ (Bi-BSCT, x = 0,10, 0,20 и 0,40). Рентгеноструктурный анализ подтвердил это предположение. На рис. 1 показаны рентгенограммы 5 ат. % легированного Bi (Ba _1-x Ca _x ) TiO ₃ керамика.На рентгенограммах всех составов в основном обнаружена одна фаза перовскита.

Структурная эволюция образцов керамики BCST, легированных Bi, от x = 0,10 до 0,40 показана на рис. 2. Результаты XRD для 5 ат. % Bi-легированного BCST соответствует таковым из (Ba _{1- x} Sr _x ) _{1-1,5 y} Bi _y TiO ₃ (Zhou et al., 2001) и Bi-BCT, показывая, что они однофазные. Кристаллическая симметрия керамики BCST, легированной Bi, является ромбоэдрической при x = 0.40. Однако он заметно стремится к тетрагональному при x = 0,20. Ромбоэдрическая фаза проиллюстрирована увеличенным расщеплением между пиками (021) и (003) в двух-тета около 39 °, в то время как тетрагональная фаза иллюстрируется увеличенным расщеплением между пиками (002) и (200) в двух-тета. около 45 °. Имеются расщепления в пиках, наблюдаемых при двух-тета около 39 ° и 45 ° соответственно, как показано на фиг.3, что указывает на сосуществование тетрагональной и ромбоэдрической фаз Bi-BCST для x = 0.10 и Bi-BCT для x = 0,10 и 0,20.

Рис. 1.

Рентгенограммы керамики Bi-BCT различного состава (x = 0,10, 0,20 и 0,30, y = 0,05).

Рис. 2.

Рентгенограммы керамики Bi-BSCT разного состава (x = 0,10, 0,20 и 0,40, y = 0,05).

Рис. 3.

Увеличенные рентгеновские дифрактограммы керамики Bi-BCT и Bi-BSCT (y = 0,05) с различным составом с двумя значениями тета в диапазоне от 37,5 ° до 46,5 °.

Рис. 4.

Изменения в отражении (002) / (200) рентгенограмм Bi-BCT и Bi-BSCT (x = 0.10, y = 0,05) керамики с разными температурами.

Для проверки симметрии кристалла была проведена порошковая рентгеновская дифракция (XRD) при разных температурах для Bi-BCT и Bi-BSCT (x = 0,10, y = 0,05). На рис. 4 показана форма одного из структурно-чувствительных максимумов на рентгенограммах. По изменению отражения (002) / (200) с температурой установлено, что керамика Bi-BCT имеет тетрагональную структуру во всем диапазоне температур от 280 K до 320 K, тогда как керамика Bi-BSCT имеет тетрагональную структуру во всем диапазоне температур. весь температурный диапазон от 280 К до 300 К.

3.2. Сегнетоэлектрические свойства

На рисунках 5 и 6 показаны графики поляризации P в зависимости от электрического поля E ( PE ) при повышенной температуре для Bi-BCT и Bi-BCST (x = 0,10 и 0,20, y = 0,05) соответственно. Хорошая петля гистерезиса может наблюдаться при 280 K для Bi-BCT (x = 0,10 и 0,20). При повышении температуры двойная петля гистерезиса, типичная для антисегнетоэлектрических материалов, наблюдалась при 300 K для Bi-BCT и при 280 K для Bi-BSCT с почти линейной зависимостью PE в средней части гистерезиса. петля.При дальнейшем повышении температуры гистерезис обнаружить не удалось, петли P-E были тонкими и демонстрировали диэлектрическую квазилинейность в широком диапазоне электрических полей.

Рис. 5.

Зависимость поляризации (P) от электрического поля (E) при повышенной температуре, измеренная при 1 Гц для Bi-BCT и Bi-BSCT (x = 0,10, y = 0,05).

Обратите внимание, что замечательная двойная петля P-E не наблюдается для Bi-BCT (x = 0,30). Однако зависимость E от P и зависимости плотности тока ( J ) (J-E) показали, что для Bi-BCT наблюдаются четыре замечательных пика J (x = 0.30), что не позволяет установить наличие двойной петли P-E для x = 0,30 в Bi-BCT. Говоря о том, что в настоящей главе рассматриваются двойные петли P-E в керамике Bi-BCT и Bi-BSCT, соответствующие данные для отношения J-E здесь не показаны.

Петли P-E преобразуются из нормальной петли гистерезиса в интересную двойную петлю гистерезиса, а затем в почти линейную при повышении температуры. Эти характеристики, полученные из петель при повышенной температуре, позволяют предположить, что в Bi-BCT проявились различные сегнетоэлектрические свойства.Похоже, что в керамике Bi-BCT существуют два последовательных фазовых перехода параэлектрик-антисегнетоэлектрик-сегнетоэлектрик ( PE-AFE-FE ). Напротив, это аналогичное преобразование от нормального к двойному и квазилинейному не может быть обнаружено в керамике Bi-BSCT. Данные о поляризации при более низкой температуре не могут быть получены для керамики Bi-BSCT из-за ограничений существующего измерительного оборудования. Однако можно предположить, что для керамики BCST, легированной Bi, сегнетоэлектрик – антисегнетоэлектрическое преобразование происходит при более низкой температуре (температура менее 280 K).Это предположение нуждается в подтверждении экспериментально. Соответствующие исследования сейчас проводятся.

Рис. 6.

Зависимость поляризации (P) от электрического поля (E) при повышенной температуре, измеренная при 1 Гц для Bi-BCT и Bi-BSCT (x = 0,20, y = 0,05).

Для Bi-BCT и Bi-BSCT наблюдается линейный диэлектрический отклик, то есть соотношение P-E близко к линейному, в отличие от нормальных сегнетоэлектриков и релаксоров на основе свинца. Квазилинейная зависимость P-E выглядит примерно так, как на образце антисегнетоэлектрика.При этом линейная зависимость P-E характерна для антисегнетоэлектрических материалов. Чтобы продемонстрировать, что диэлектрическая квазилинейность в определенном диапазоне электрических полей является типичным антисегнетоэлектрическим поведением или нет, полное исследование, включая индуцированный электрическим полем и температурно-индуцированный фазовый переход структуры, было выполнено в наших предыдущих публикациях.

3.3. Диэлектрические свойства

Температурная зависимость диэлектрической проницаемости и диэлектрических потерь керамики Bi-BCT и Bi-BSCT для разных частот представлена ​​на рис.7 (А) — (Г). Диэлектрическая проницаемость имеет широкий максимум при температуре пика диэлектрической проницаемости (Т _м ). Т _м увеличивается с увеличением частоты. Например, T _m равно 341 K на 1 кГц и 347 K на 1 МГц для Bi-BCT (x = 0,10), соответственно. При понижении температуры величина диэлектрических потерь быстро увеличивается примерно до температуры диэлектрических потерь. С увеличением частоты пик диэлектрической проницаемости уменьшается и T _m смещается в сторону высоких температур.Такие тенденции изменения диэлектрической проницаемости и диэлектрических потерь в зависимости от частоты и температуры являются типом поведения диэлектрической релаксации, о котором подробно сообщалось в учебнике по физике твердого тела.

Возможный механизм наблюдения релаксорного поведения в Bi-легированном SrTiO ₃ (Ang et al., 1998), Bi-легированном Ba _{1- x} Sr _x TiO ₃ (Zhou et al., 2001), SrTiO ₃ , легированный кальцием (Bednorz & Müller, 1984), и KTaO ₃ , легированный литием (Toulouse et al., 1994) подробно обсуждалась в предыдущих публикациях. Широко распространена точка зрения, согласно которой поведение диэлектрической релаксации в этих системах было вызвано случайным электрическим полем, индуцированным доменным состоянием сегнетоэлектрика. Согласно их точке зрения, ионы Bi ³⁺ , которые заменяют ионы A-позиции в керамике BCT и BCST, также могут находиться в нецентральных позициях, и вакансии в A-позиции могут также компенсировать несоответствие зарядов, возникающее из Ионы А-участка замещены ионами Bi ³⁺ .Случайное электрическое поле, образованное нецентральными ионами Bi ³⁺ и диполями Bi ³⁺ –V _A , затем подавило бы сегнетоэлектричество BCT и BCST и привело бы к релаксорному поведению, наблюдаемому для Bi-легированных BCT и BCST . Если ионы Ca ²⁺ могут располагаться в B-узлах, таких как ионы Ti ⁴⁺ , чтобы уравновесить несоответствие заряда, кислород следующего соседа может быть пустым и образовывать нейтральный Ca ²⁺ –V _O . центр. Такие центры Ca ²⁺ –V _O образуют диполи и, таким образом, создают локальные электрические поля, которые подавляют сегнетоэлектричество BCT и BCST и приводят к релаксорному поведению, наблюдаемому в BCT и BCST.

В большинстве случаев сегнетоэлектрического фазового перехода, когда новая упорядоченная фаза возникает в результате структурных изменений, в диэлектрическом спектре будет пик, но не все особенности или пики соответствуют структурному фазовому переходу. Например, все классические релаксоры, такие как Pb (Mg _1/3 Nb _2/3 ) O ₃ (PMN) и low x (1-x) Pb (Mg _1/3 Nb _{2 / 3} ) O ₃ -xPbTiO ₃ (Bokov & Ye, 2006), показывают диэлектрические пики, но не подвергаются сегнетоэлектрическому (или антисегнетоэлектрическому) фазовому переходу.Следовательно, диэлектрический пик может указывать только на возможный фазовый переход. Если переход FE-AFE-PE произошел в Bi-BCT, в диэлектрическом спектре будут два соответствующих диэлектрических пика. Однако диэлектрический спектр Bi-BCT и Bi-BSCT показывает только один пик в диапазоне температур от 190 K до 428 K, как показано на фиг.7.

С другой стороны, нет прямых указаний на появление антисегнетоэлектрических компонентов в (Ba, Ca) TiO ₃ (Han et al., 1987; Чжуанг и др., 1987; Мицуи и Вестфаль, 1961; Баскара и Чанг, 2003). Следовательно, вызванный старением эффект должен быть ответственным за обнаружение двойного сегнетоэлектрического гистерезиса в керамиках Bi-BCT и Bi-BSCT.

Рисунок 7.

Температурная зависимость диэлектрической проницаемости и диэлектрических потерь Bi-BCT и Bi-BSCT для x = 0,10 ((A) и (B)), x = 0,20 ((C) и (D) ) и y = 0,05 при 0,1, 1, 10, 100 кГц (для диэлектрической проницаемости сверху вниз, для диэлектрических потерь снизу вверх).

3.4. Эффект сегнетоэлектрического старения

Интересная двойная петля гистерезиса P-E , вызванная старением, также была обнаружена в различных сегнетоэлектрических системах. Многие механизмы, такие как эффект границ зерен (Karl & Hardtl, 1978), эффект закрепления доменных стенок (Postnikov et al, 1970), эффект объема (Lambeck & Jonker, 1986) и ближнее упорядочение, соответствующее симметрии (SC- SRO) механизм точечных дефектов (Ren, 2004; Zhang & Ren, 2005, 2006; Liu et al., 2006) был предложен для объяснения этого явления.Хотя все эти модели, кажется, могут обеспечить самосогласованное объяснение двойной петли гистерезиса в состаренных сегнетоэлектрических кристаллах, эффект границы зерен не может объяснить идеальную двойную петлю PE , существующую в состаренном монокристаллическом образце, доменную Эффект закрепления стенки не может объяснить восстановление исходного многодоменного состояния из однодоменного, потому что не было бы доменной стенки, которую можно было бы отодвинуть назад, а эффект объема основан на ключевом предположении, что существуют дипольные дефекты и они следуют за спонтанной поляризацией после старения (Zhang & Ren, 2005, 2006).По сравнению со всеми этими моделями механизм SC-SRO, который также является объемным эффектом, дает микроскопическое объяснение происхождения старения и не предполагает никаких предположений. Конформация дефектного диполя со спонтанной поляризацией естественным образом проистекает из свойства соответствия симметрии дефектов. В целом все эти модели согласны с тем, что дефекты играют решающую роль в явлениях, вызванных старением. Однако они сильно различаются движущей силой миграции дефектов.

Рисунок 8.

Петли гистерезиса для свежего и выдержанного Bi-BCT (x = 0.10) керамические образцы при комнатной температуре 300 К. (1 — свежие или деформированные; 2 — более короткий период старения; 3 — более длительный период старения).

Чтобы дополнительно проверить наличие эффекта диффузионного старения, образцы «дегазировали», выдерживая их при 470 К в течение 1 часа, с последующим быстрым охлаждением до комнатной температуры выше температуры Кюри. Одновременно измерялись петли гистерезиса при комнатной температуре. На рис. 8 показаны экспериментальные результаты петель гистерезиса для Bi-BCT в устаревшем (свежем) и состаренном состоянии, соответственно.Образец после старения показывает нормальную петлю гистерезиса, но все образцы после старения демонстрируют интересные двойные петли гистерезиса. Замена одиночных петель P-E в состаренном образце на двойные петли P-E в состаренном образце должна исключить антисегнетоэлектрические компоненты и любой индуцированный электрическим полем фазовый переход PE-FE вблизи температуры Кюри. Это указывает на то, что эффект старения должен быть ответственным за двойные петли P-E , наблюдаемые в Bi-BCT.

3.5. Рамановский анализ

Обычно считается, что эффект старения в сегнетоэлектриках, легированных акцепторами, связан с миграцией кислородных вакансий (которые очень подвижны) во время старения (Ren, 2004; Zhang & Ren, 2005, 2006; Liu et al. ., 2006; Zhang et al., 2004; Feng & Ren, 2007, 2008). Однако вакансии O ^2- в наших образцах Bi-BCT и Bi-BSCT не были образованы искусственно за счет замещения ионов Ti на B-узлах ионами с более низкой валентностью. Чтобы понять эффект старения в Bi-BCT, нам необходимо проанализировать его дефектную структуру.Для легированного Bi BCT и BSCT со структурой первоскита ABO ₃ [(Ba _0,90 Ca _0,10 ) _0,925 Bi _0,05 TiO ₃ и (Ba _0,90 Sr _0,05 Ca ) _0,925 Bi _0,05 TiO ₃ ], возможны две вакансии: во-первых, ионы Bi ³⁺ , замещенные двухвалентными ионами в A-позиции (Ba ²⁺ , Sr ²⁺ или / и Ca ²⁺ ) в BCT и BSCT могут быть расположены в нецентральных положениях A-сайта, так что вакансии A-сайта образуются для компенсации дисбаланса заряда, возникающего в результате замещения, и, во-вторых, что Ca ^{2 Ионы +} замещают ионы Ti ⁴⁺ в BCT и вызывают образование вакансий O ^2– для компенсации несоответствия зарядов.Предыдущие экспериментальные результаты по равновесной электропроводности (Han et al., 1987), сканирующей электрической микроскопии (Zhuang, et al., 1987), дифракции нейтронов (Krishna et al., 1993), комбинационной и диэлектрической спектроскопии (Zhuang, et al. , 1987; Chang & Yu, 2000; Park et al., 1992), показали, что небольшое количество ионов Ca ²⁺ может замещать ион Ti ⁴⁺ , вызывая образование вакансий O ^2–. чтобы уравновесить несоответствие зарядов, хотя ионный радиус и химическая валентность ионов Ca ²⁺ сильно отличаются от таковых для ионов Ti ⁴⁺ .Было обнаружено, что 4 мол.% Ионов Ca ²⁺ замещают ионы Ti ⁴⁺ , даже когда молярное соотношение (Ba + Ca) / Ti было 1 для исходных материалов, используемых Krishna et al. при исследовании образцов Ba _0,88 Ca _0,12 TiO ₃ , полученных методом твердофазной реакции. Следуя вышеупомянутому предположению, кажется, что замещение ионов Ca ²⁺ на ионы Ti ⁴⁺ произошло в керамике Bi-BCT и Bi-BSCT, полученной методом твердотельной реакции.

Поскольку старение контролируется миграцией подвижных кислородных вакансий, экспериментальное исследование образования вакансий O ^2– в Bi-BCT с помощью комбинационного рассеяния света при комнатной температуре было выполнено с результатами, показанными на рис. 9. (Ba0 Керамика .925Bi0.05) (Ti0.90Ca0.10) O2.90 (Bi-BTC) была приготовлена ​​для того, чтобы сравнить эффект замещения Ca в Ti-центрах Bi-BCT. В монокристаллических и керамических образцах BaTiO ₃ почти такие же полосы комбинационного рассеяния, например, при 165 см ^-1 [A (TO)], 173 см ^-1 (смешанные моды), 266 см ^{— 1} [A (TO)], 306 см ^-1 [E (TO)], 470 см ^-1 [E (T) + A (L)], 516 см ^-1 [A (T )] и 712 см ^-1 [A (LO) + E (LO)] (Burns, 1974; Begg et al., 1996). Очень похожие результаты наблюдались также в керамике (Ba _{1- x} Ca _x ) TiO ₃ и BaTi _1-y Ca _y O ₃ (Chang & Yu, 2000) . Для замещения A-узла с увеличением x полосы комбинационного рассеяния, связанные с фононным колебанием связей Ba-O, смещаются в сторону более высоких частот (512 и 719 см ^-1 для x = 0,005, 521 и 730 см ^–1 для x = 0,20), в то время как полосы комбинационного рассеяния, вызванные фононным колебанием связей Ti-O, смещаются в сторону более низкой частоты (259 и 306 см ^-1 для x = 0.005, 248 и 298 см ^–1 для x = 0,20). Для замещения B-сайта связи Ba-O тесно связаны с образованием полос 517 и 718 см ^-1 , а связи Ti-O тесно связаны с образованием полос 257 и 307 см ^-1 в BaTi _1-й Ca _y O ₃ . На фиг.9 показано, что полосы 299, 520 и 723 см ^-1 не зависят от образования Ca _{, Ba} и Ca _{, Ti} в Bi-BCT и Bi-BTC. Из этих результатов можно сделать вывод, что связи Ba-O тесно связаны с образованием полос 520 и 723 см ^-1 , а связи Ti-O — с образованием полос 262 и 299 см ^-1 .Мы также обнаруживаем развитие слабой новой полосы комбинационного рассеяния на 827 см ^-1 для Bi-BTC и Bi-BCT (см. Рис. 9). Почти такие же полосы комбинационного рассеяния (832 см, ^-1 ) наблюдались в Ba (Ti _0,985 Ca _0,005 Nb _0,01 ) O ₃ и BaTi _1-y Ca _y O ₃ (y = 0,005 и 0,015) керамика (Chang & Yu, 2000). Эта более высокочастотная полоса комбинационного рассеяния является результатом образования дефектов Ca _Ti . То есть, в Bi-BCT произошло замещение ионов Ca ²⁺ на ионы Ti ⁴⁺ в B-позиции, и образовались вакансии O ^2-, чтобы компенсировать дисбаланс заряда.Настоящие результаты являются важным доказательством образования вакансий O ^2-.

Рис. 9.

Рамановские спектры керамики Bi-BCT и Bi-BTC при комнатной температуре.

3.6. Происхождение двойных петель P-E в Bi-BCT и Bi-BSCT

Как упоминалось выше, вокруг акцепторного иона Ca ²⁺ есть два типа вакансий, вакансии A-позиции и кислородные вакансии. Учитывая подвижность кислородных вакансий и неподвижность катионных вакансий при обычных температурах, наблюдение двойных петель P-E на рис.8 можно объяснить особым эффектом старения, связанным с симметрией дефекта, определяемой как условная вероятность нахождения вакансий O ^2- в позиции i ( i = 1-6) одиночной ячейки ABO ₃ ( Ren, 2004; Zhang & Ren, 2005, 2006; Liu et al., 2006; Zhang et al., 2004; Feng & Ren, 2007, 2008). На рис. 10 показано, как двойные петли P-E образуются в монокристаллическом зерне состаренного образца Bi-BCT. Высокотемпературное спекание обеспечивает достаточную подвижность кислородных и катионных вакансий.Таким образом, в параэлектрической фазе вероятность обнаружения вакансии O ^2- и вакансии A-узла вокруг акцепторного иона Ca ²⁺ будет иметь кубическую симметрию в соответствии с механизмом точечных дефектов SC-SRO [ Инжир. 10 (d)] (Ren, 2004).

Для разложенных тетрагональных образцов, которые образуются путем немедленного охлаждения из параэлектрического состояния при 470 K до 300 K, SRO-распределение точечных дефектов сохраняет ту же кубическую симметрию, что и в кубической параэлектрической фазе, поскольку бездиффузионная параэлектрическая -сегнетоэлектрический переход не может изменить исходную кубическую SRO-симметрию точечных дефектов (Ren, 2004).В результате деградированное сегнетоэлектрическое состояние имеет тетрагональную симметрию кристалла, но кубическую симметрию дефектов; таким образом, две симметрии не совпадают (см. рис. 10 (а)). Согласно механизму SC-SRO (Ren, 2004; Zhang & Ren, 2005, 2006; Liu et al., 2006; Zhang et al., 2004; Feng & Ren, 2007, 2008) такое состояние [Рис. 10 (а)] нестабильно из-за несоответствия между симметрией дефекта и симметрией кристалла. После старения в течение длительного времени симметрия дефекта в каждом домене соответствует полярной тетрагональной симметрии кристалла и демонстрирует дипольный момент дефекта, соответствующий направлению поляризации остаточного домена.Каждый домен находится в стабильном состоянии, как показано на рис. 10 (b). SRO-симметрия вакансий O ^2- вокруг иона Ca ²⁺ может постепенно изменяться на полярную тетрагональную симметрию (что дает дефектный диполь P _D ) [см. Рис. 10 (b) и 10 (e)] за счет миграции подвижных вакансий O ^2-, что является тем же процессом, что и для случая, легированного акцепторами (Ren, 2004; Zhang & Ren, 2005, 2006; Liu et al., 2006; Zhang et al., 2004; Feng & Ren, 2007, 2008).Однако SRO-симметрия вакансий A-позиции вокруг иона Ca ²⁺ все еще остается кубической, поскольку катионные вакансии неподвижны при таких температурах (Tan et al., 1999) [рис. 10 (b) и 10 (f)]. Когда электрическое поле прикладывается к естественно состаренному тетрагональному образцу Bi-BCT, P _S переключается на направление поля E , а P _D сохраняет свое первоначальное направление во время такого внезапного процесс [Рис. С 10 (b) по 10 (c)].Поэтому после снятия электрического поля [рис. С 10 (c) по 10 (b)], неизменная симметрия дефекта и связанный с ним P _D вызывают обратимое переключение домена. Как следствие, восстанавливается исходный паттерн доменов [Рис. 10 (b)], так что симметрия дефекта и дипольный момент следуют симметрии кристалла в каждой области. Ожидается, что интересная двойная петля гистерезиса в соотношении P-E для Bi-BCT будет сопровождаться

синонимами петли гистерезиса, антонимами петли гистерезиса

Основой для рассмотрения переходных эффектов является анализ изменений петли гистерезиса при циклическом нагружении.где [ФОРМУЛА НЕ ВОСПРОИЗВОДИМА В ASCII] — накопленное усталостное повреждение до зарождения трещины, которое характеризуется шириной петли гистерезиса [ФОРМУЛА НЕ ВОСПРОИЗВОДИМА В ASCII] — накопленное усталостное повреждение до зарождения трещины, которое характеризуется шириной петли гистерезиса [ФОРМУЛА НЕ ВОЗМОЖНА В ASCII] и т.д. FS и RS для C [H.sub.3] N [H.sub.3] Pb [I.sub.3] Film.Rodellar, «Изменение петли гистерезиса с параметрами модели Бук-Вена», Нелинейная динамика, vol.So основные вклады этого статьи заключаются в следующем: (1) предлагается использовать динамически изменяемый размер шага для модификации FOA; (2) обсуждение эффективности MFOA путем тестирования пяти типичных функций; (3) анализ влияния коэффициента вариации h на производительность MFOA; (4) применение MFOA для извлечения параметров петли гистерезиса и анализа результатов моделирования по сравнению с PSO и FOA.Для MoP-CA 2 петли гистерезиса сдвинулись к значениям P / P 0 при 0,4-0,6 с увеличением общего адсорбированного объема, что свидетельствует о существовании мезопор типа чернильниц. Гигроскопическое поведение муки из маниоки из сухой и водной групп. при 25 ° C показало, что обе муки имеют изотермы типа II и петлю гистерезиса типа h4 между изотермами адсорбции и десорбции. (a) Петля гистерезиса, наблюдаемая в центре центральной ветви. Уравнение (3) определяет секущую жесткость, [K.sub.i], каждой петли гистерезиса: По сравнению с нелегированной пленкой ZnO, все пленки ZnO, легированные Ni, показывают отчетливо петли гистерезиса, что указывает на то, что образцы обладают ферромагнетизмом при комнатной температуре.Петля магнитного гистерезиса [Fe.sub.3] [O.sub.4] феррита / нанокомпозита PANI при комнатной температуре изображена на рисунке 4 (b). Модель Бук-Вен уже была проверена, что она адаптивна для описания петля гистерезиса ПЭА [43], где A, [бета], [гамма], n — параметры петли, контролирующие форму и величину петли гистерезиса. свойства одновременно, а именно: напряжение, амплитуда деформации, жесткость, накопленная энергия и энергия потерь, демпфирование материала и циклическая ползучесть, сервогидравлическая испытательная машина (MTS 8100) с цифровым контроллером и пакетом программного обеспечения для оценки гистерезиса В этом исследовании использовалась петля. Доступный программный пакет позволяет оцифровывать петлю гистерезиса материала, которая измеряется непрерывно, а средняя кривая рассчитывается в петле гистерезиса.

hysteresis loop — Перевод на французский — примеры английский

Эти примеры могут содержать грубые слова на основании вашего поиска.

Эти примеры могут содержать разговорные слова, основанные на вашем поиске.

Чтобы определить желаемый предел текучести, через петлю гистерезиса проводится прямая линия .

Pour la détermination de la limit Conventionnelle d’élasticité recherchée, une droite est tracée en travers de la boucle d’Hystérésis .

Идеальный магнитный материал характеризуется идеально прямоугольной петлей гистерезиса , т. Е. Прямоугольностью петли, равной 1, с коэрцитивной силой 25 кА / м или менее и высокой намагниченностью насыщения.

Магнетический материал идеален как образец boucle d’hystérésis parfaitement rectangulaire, c’est-à-dire, un rectangularité de boucle de 1, принудительно де 25kA / m или moins, и еще больше увеличивают насыщенность.

Пленка легко переключается и характеризуется по существу квадратной формой петли гистерезиса .

Ledit film является легко коммутируемым и работает на основе цикла гистерезиса de forme pratiquement carrée.

Использование этой структуры с 7τ-сопряженными органическими молекулами приводит к петле гистерезиса с измерениями тока-напряжения, которые полезны для электронного запоминающего устройства.

Использование этой структуры с органическими молекулами 7T-конъюги для восстановления и удаления цикла гистерезиса avec des mesures courant-stretch ubles pour une mémoire électronique.

Представлены способ и устройство для смещения петли гистерезиса магниторезистивного устройства.

Настоящее изобретение касается одежды и обработки, которая позволяет менять boucle d’hystérèse d’un dispositif magnétorésistif.

дополнительный порог может быть использован для создания петли гистерезиса

Стоунер и Вольфарт рассчитали основную петлю гистерезиса для изотропной системы случайно ориентированных идентичных частиц.

Stoner et Wohlfarth ont Calculé le cycle d’hystérésis принципиально для изотропной системы, составной части идентичности и ориентированной альтернативы.

построение графика зависимости вращательного смещения от силы в декартовой системе координат дает непрерывный, ограниченный, четырехквадрантный контур петля гистерезиса

en reportant les rotations en fonction des force sur un système de correconnées cartésiennes, on obtient une boucle d’hystérèse continue bornée à quatre quadrants

Простая петля гистерезиса — Большая химическая энциклопедия

Кривые стационарного состояния или бифуркационные диаграммы, показанные на рис.1.13 (b) и 1.12 (f), представляют две из простейших возможных моделей монотонного изменения и одну петлю гистерезиса соответственно. Это единственные качественно различные ответы, возможные для кубической автокаталитической стадии сама по себе. Они также обнаруживаются для экзотермической реакции первого порядка в адиабатическом проточном реакторе (см. Главу 6). Имея лишь несколько более сложные химические механизмы, можно найти целый ряд экзотических паттернов, таких как те, что показаны на рис. 1.14. Происхождение этих форм будет определено в главе 4.[Стр.22]

Рис. 6.19. Пять паттернов локусов в стационарном состоянии, обнаруженные при включении в модель некаталитического превращения A в B: (а) уникальное, (б) изола (в) грибовидное соединение (г) одиночная петля гистерезиса (волна разрушения) (д) петля гистерезиса + изола.

С экспоненциальным приближением (y 0) и предположением, что температуры притока и окружающей среды равны, у нас есть уравнение стационарного состояния, которое связывает ass с tres и которое включает два других параметра разворачивания, 0ad и tn.В зависимости от конкретных значений последних двух параметров локус (1 — ass) по сравнению с rres имеет одну из пяти возможных качественных форм. Эти различные модели показаны на рис. 7.4 как уникальная одиночная петля гистерезиса, изола, гриб и петля гистерезиса плюс изола. Пять соответствующих областей на плоскости параметров 0ad-rN показаны на рис. 7.5. Эта плоскость параметров разделена на эти области прямой линией и выступом, которые пересекают друг друга в двух точках. [Стр.193]

модель FONI (а) уникальная (б) одиночная петля гистерезиса или волна обрыва (в) изола (г) изола + петля гистерезиса (д) гриб.При полном законе скорости Аррениуса и предварительном нагреве или охлаждении обнаруживаются две дополнительные модели (f) обратная петля гистерезиса и (g) обратная петля гистерезиса + изола. Также показаны различные вырожденные локусы, соответствующие значениям параметров на границах или особых точках на плоскости параметров (см. Рис. 7.5). [Стр.194]

Это соответствует обычному куспиду с развёртыванием до уникального локуса или единственной петли гистерезиса. [Стр.202]

Рис. 7.8. Полное развертывание локуса стационарного состояния (а), соответствующего сингулярности крылатого каспа, (б) уникальное (в) изола (г) гриб (д) одиночная петля гистерезиса (е) петля гистерезиса + изола (ж) петля обратного гистерезиса (з) обратная петля гистерезиса + изола.

ИНЖИР. 9.6. Пять качественных форм локуса стационарного состояния ass (0) -D для кубического автокатализа с распадом в реакционно-диффузионной ячейке (а) уникальная (б) одиночная петля гистерезиса (в) гриб (г) изола (д) изола + петля гистерезиса, (f) Разделение плоскости параметров Pcx-k2, дающее пять областей, соответствующих формам стационарного состояния на (a) — (e), обратите внимание, что область для отклика (e), показанная на вставке, особенно мала и пока не удалось найти.[Стр.249]

Рис. 12.5. (a) Область многократного стационарного состояния для модели поверхностной реакции Такудиса-Шмидта-Ариса, с = 10 3 и k2 = 2 x 10-3 (b), (c) и (d) показывают, как скорость реакции в стационарном состоянии изменяется в зависимости от давления газовой фазы реагента R для различных значений p, что дает изолу, грибовидную форму и одну петлю гистерезиса соответственно. (Адаптировано и перепечатано с разрешения McKarnin, M. A. et al. (1988). Proc. R. Soc., A415, 363-87.) … [Pg.326]

Рис.4.5-96а, б MHPOBC. D — E петли гистерезиса, полученные из измерений тока переключения. D — электрическое смещение. Толщина образца ceU = 3 мкм. (а) Двойная петля гистерезиса при 2 Гц. (b) Одна петля гистерезиса при 100 Гц … [Pg.935]

Петли гистерезиса M-H были определены для одноатомных монослоев Fe и Ni, которые были получены и измерены в сверхвысоком вакууме. [Pg.725]

TbPc2 SIMM (одноионный молекулярный магнит) и намагничивание Ni на неплоских пленках Ni / Cu (100), (b) Петли гистерезиса с элементным разрешением для Ni (вверху) и Tb (внизу ) для TbPc2 / Ni / Cu (100), измеренного при падении вне плоскости (8 = 0 °) при T = 8K.Единицы измерения … [Pg.268]

После нескольких циклов сжатия и расширения динамическая кривая jc-A становится единственной замкнутой петлей, несколько искаженной по сравнению с настоящим эллипсоидом. Чтобы проанализировать формы петли гистерезиса в стационарных условиях, мы измерили временную диаграмму динамического поверхностного давления после пяти циклов сжатия и расширения, а затем преобразовали ее Фурье в частотную область. Преобразование Фурье было адаптировано для количественной оценки нелинейной вязкоупругости.Подробное теоретическое рассмотрение использования преобразования Фурье для оценки нелинейности содержится в опубликованных статьях [8,43]. [Pg.245]

Как обсуждалось выше, петли гистерезиса могут появляться на изотермах сорбции в результате различных механизмов адсорбции и десорбции, возникающих в отдельных порах. Пористый материал обычно состоит из связанных между собой пор неправильного размера и геометрии. Даже если механизм адсорбции обратим, гистерезис все равно может возникать из-за сетевых эффектов, которые в настоящее время широко принимаются как проблема перколяции [21, 81], связанная со специфической связностью пор.Теория перколяции для описания явлений, связанных со связностью, была впервые представлена ​​Брод-бентом и др. [88]. Следуя этому подходу, Ситон [89] предложил метод определения параметров связности на основе измерений сорбции азота. [Pg.23]

Рис. Похожие записи 21.11.2024 0 Особенности питания кормящей мамы: что можно и нельзя есть при грудном вскармливании 19.11.2024 0 Новорожденный какает слизью: причины появления слизи в кале грудничка 19.11.2024 0 Гемангиома у новорожденных: причины, виды, лечение и профилактика Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт