Что такое закон Ома для участка цепи. Как формулируется и записывается математически. Зависимость силы тока от напряжения и сопротивления. Примеры применения закона Ома.
Что такое закон Ома для участка цепи
Закон Ома для участка цепи — это один из основных законов электродинамики, устанавливающий связь между силой тока, напряжением и сопротивлением на участке электрической цепи. Он был открыт немецким физиком Георгом Омом в 1826 году.
Закон Ома позволяет рассчитать любую из трех величин (силу тока, напряжение или сопротивление), если известны две другие. Это делает его чрезвычайно полезным инструментом в электротехнике и электронике.
Формулировка закона Ома для участка цепи
Закон Ома для участка цепи формулируется следующим образом:
Сила тока в участке цепи прямо пропорциональна напряжению на концах этого участка и обратно пропорциональна его сопротивлению.
Это означает, что:
- При увеличении напряжения сила тока увеличивается (при постоянном сопротивлении)
- При увеличении сопротивления сила тока уменьшается (при постоянном напряжении)
Математическая запись закона Ома
Математически закон Ома для участка цепи записывается следующей формулой:
I = U / R
где:
- I — сила тока (в амперах, А)
- U — напряжение (в вольтах, В)
- R — сопротивление (в омах, Ом)
Из этой формулы легко выразить напряжение и сопротивление:
U = I * R
R = U / I
Зависимость силы тока от напряжения
При постоянном сопротивлении сила тока прямо пропорциональна напряжению. Это означает, что график зависимости I от U представляет собой прямую линию, выходящую из начала координат.
Чем больше угол наклона этой прямой к оси напряжений, тем меньше сопротивление участка цепи.
Как определить сопротивление по графику I(U)?
Сопротивление участка цепи можно определить по графику I(U), взяв любую точку на прямой и разделив соответствующее значение напряжения на значение силы тока:
R = U / I
Зависимость силы тока от сопротивления
При постоянном напряжении сила тока обратно пропорциональна сопротивлению. График зависимости I от R представляет собой гиперболу.
Чем больше сопротивление, тем меньше сила тока в цепи при одном и том же напряжении.
Применение закона Ома для расчетов в электрических цепях
Закон Ома широко применяется для расчетов параметров электрических цепей. Вот несколько примеров:

Расчет силы тока
Задача: Напряжение на участке цепи 220 В, сопротивление 100 Ом. Определить силу тока.
Решение:
I = U / R = 220 В / 100 Ом = 2.2 А
Расчет напряжения
Задача: Сила тока в цепи 0.5 А, сопротивление 400 Ом. Найти напряжение.
Решение:
U = I * R = 0.5 А * 400 Ом = 200 В
Расчет сопротивления
Задача: Напряжение в сети 120 В, сила тока через лампу 0.3 А. Определить сопротивление лампы.
Решение:
R = U / I = 120 В / 0.3 А = 400 Ом
Ограничения применимости закона Ома
Важно понимать, что закон Ома применим не всегда. Он хорошо работает для металлических проводников при не слишком высоких температурах и напряжениях. Однако есть ряд случаев, когда закон Ома не выполняется:
- Для полупроводниковых приборов (диодов, транзисторов)
- Для газоразрядных приборов
- При очень высоких напряжениях и токах
- При быстропеременных токах высокой частоты
В этих случаях зависимость между током и напряжением становится нелинейной, и требуются более сложные модели для описания поведения электрической цепи.

Исторический контекст открытия закона Ома
Георг Ом открыл свой знаменитый закон в 1826 году, проводя эксперименты с электрическими цепями. В то время природа электричества была еще плохо изучена, и работа Ома внесла огромный вклад в понимание электрических явлений.
Интересно, что первоначально научное сообщество скептически отнеслось к открытию Ома. Потребовалось несколько лет, прежде чем значимость его работы была по достоинству оценена. Сегодня закон Ома считается одним из фундаментальных законов электродинамики и широко применяется в электротехнике и электронике.
Проверка понимания закона Ома
Чтобы проверить свое понимание закона Ома, попробуйте ответить на следующие вопросы:
- Как изменится сила тока, если напряжение увеличить в 2 раза при постоянном сопротивлении?
- Как изменится напряжение, если сопротивление уменьшить в 3 раза при постоянной силе тока?
- Почему для параллельного подключения потребителей используются провода с меньшим сопротивлением, чем для последовательного?
- Как изменится яркость лампочки, если последовательно с ней включить резистор?
Если вы можете уверенно ответить на эти вопросы, значит, вы хорошо усвоили закон Ома и его применение в электрических цепях.

Заключение
Закон Ома для участка цепи — это фундаментальный закон электродинамики, устанавливающий связь между силой тока, напряжением и сопротивлением. Его понимание необходимо для анализа и расчета электрических цепей. Несмотря на свою простоту, закон Ома лежит в основе работы многих электрических устройств и систем.
Помните, что хотя закон Ома очень полезен, он имеет свои ограничения. В сложных электронных схемах и при работе с полупроводниками часто требуются более сложные модели. Тем не менее, закон Ома остается незаменимым инструментом для базового анализа электрических цепей и является отправной точкой для более глубокого изучения электродинамики.
Какой закон ома правильный — MOREREMONTA
Закон Ома, основанный на опытах, представляет собой в электротехнике основной закон, который устанавливает связь силы электрического тока с сопротивлением и напряжением.
Появление смартфонов, гаджетов, бытовых приборов и прочей электротехники коренным образом изменило облик современного человека. Приложены огромные усилия, направленные на исследование физических закономерностей для улучшения старой и создания новой техники. Одной из таких зависимостей является закон Ома.
Закон Ома – полученный экспериментальным путём (эмпирический) закон, который устанавливает связь силы тока в проводнике с напряжением на концах проводника и его сопротивлением, был открыт в 1826 году немецким физиком-экспериментатором Георгом Омом.
Строгая формулировка закона Ома может быть записана так: сила тока в проводнике прямо пропорциональна напряжению на его концах (разности потенциалов) и обратно пропорциональна сопротивлению этого проводника.
Формула закона Ома записывается в следующем виде:
U – электрическое напряжение (разность потенциалов), единица измерения напряжения- вольт [В];
Согласно закону Ома, увеличение напряжения, например, в два раза при фиксированном сопротивлении проводника, приведёт к увеличению силы тока также в два раза
И напротив, уменьшение тока в два раза при фиксированном напряжении будет означать, что сопротивление увеличилось в два раза.
Рассмотрим простейший случай применения закона Ома. Пусть дан некоторый проводник сопротивлением 3 Ом под напряжением 12 В. Тогда, по определению закона Ома, по данному проводнику течет ток равный:
Существует мнемоническое правило для запоминания этого закона, которое можно назвать треугольник Ома. Изобразим все три характеристики (напряжение, сила тока и сопротивление) в виде треугольника. В вершине которого находится напряжение, в нижней левой части – сила тока, а в правой – сопротивление.
Правило работы такое: закрываем пальцем величину в треугольнике, которую нужно найти, тогда две оставшиеся дадут верную формулу для поиска закрытой.
Где и когда можно применять закон Ома?
Закон Ома в упомянутой форме справедлив в достаточно широких пределах для металлов. Он выполняется до тех пор, пока металл не начнет плавиться. Менее широкий диапазон применения у растворов (расплавов) электролитов и в сильно ионизированных газах (плазме).
Работая с электрическими схемами, иногда требуется определять падение напряжения на определенном элементе. Если это будет резистор с известной величиной сопротивления (она проставляется на корпусе), а также известен проходящий через него ток, узнать напряжение можно с помощью формулы Ома, не подключая вольтметр.
Значение Закона Ома
Закон Ома определяет силу тока в электрической цепи при заданном напряжении и известном сопротивлении.
Он позволяет рассчитать тепловые, химические и магнитные действия тока, так как они зависят от силы тока.
Закон Ома является чрезвычайно полезным в технике(электронной/электрической), поскольку он касается трех основных электрических величин: тока, напряжения и сопротивления. Он показывает, как эти три величины являются взаимозависимыми на макроскопическом уровне.
Если бы было можно охарактеризовать закон Ома простыми словами, то наглядно это выглядело бы так:
Из закона Ома вытекает, что замыкать обычную осветительную сеть проводником малого сопротивления опасно. Сила тока окажется настолько большой, что это может иметь тяжелые последствия.
Все в этом мире живет и происходит по своим законам. Маугли, писателя Киплинга, жил по закону джунглей, люди живут по своим писаным законам, так и в физике электрического тока существуют свои законы и один из этих законов называется “закон Ома“. Это очень важный закон, один из основополагающих законов в физике электрического тока, и ты обязан его знать и понимать, если хочешь разбираться в электрике и электронике. Я же постараюсь помочь тебе и объясню для тебя,
закон Ома простыми словами.
Впервые, закон открыл и описал в 1826 году немецкий физик Георг Ом, показавший (с помощью гальванометра) количественную связь между электродвижущей силой, электрическим током и свойствами проводника, как пропорциональную зависимость. В честь этого самого Георга Ома и назван закон.
Теперь давай выведем определение закона Ома.
Величина тока на участке цепи, прямо пропорциональна напряжению приложенному к этому участку цепи и обратно пропорциональна его сопротивлению. Теперь разберем эту абракадабру по частям. Часть первая — Величина тока на участке цепи, прямо пропорциональна напряжению приложенному к этому участку цепи.
Формула закона Ома
В этой формуле – I– Сила тока (Ампер), U– Напряжение (Вольт), R– Сопротивление (Ом).
Прикладываю к этому объяснению шуточный рисунок ты мог видеть его и раньше на других сайтах, это очень хороший “рисунок – пример” многие его используют на страницах своих сайтов.
Что можно рассчитать пи помощи этой формулы?
Как найти силу тока, что такое сила тока — это значит, если к концам проводника сопротивлением R = 1 Ом приложено напряжение U = 1 Вольт, тогда величина тока I в проводнике будет равна 1/1 = 1 Ампер.
I=U/R — формула тока
Рассчитать напряжение — если в проводнике, сопротивлением 1 Ом, протекает ток 1 Ампер, значит на концах проводника напряжение 1 Вольт (падение напряжения).
U = IR — формула напряжения
Сопротивление — если на концах проводника есть напряжение 1 Вольт и по нему протекает ток 1 Ампер, значит сопротивление проводника равно 1 Ом.
R = U/I — формула сопротивления
Для удобства пользования формулой можно применить такую “фишку “.
Закрывая пальцем на треугольнике, значение, которое нужно определить, видим действие, которое нужно выполнить. Например — если тебе нужно определить значение сопротивления, закроем – R
Например — если тебе нужно определить значение сопротивления, закроем – R
Теперь ты видишь, какое действие нужно выполнить? Правильно, напряжение U разделить на силу тока I .
Формулы, которые тебе обязательно пригодятся .
Я рассказал тебе очень кратко и простым языком о законе Ома, но этого вполне достаточно, чтобы ты смог самостоятельно на первых парах производить расчеты для своих будущих электронных шедевров!
Говорят: «не знаешь закон Ома – сиди дома». Так давайте же узнаем (вспомним), что это за закон, и смело пойдем гулять.
Основные понятия закона Ома
Как понять закон Ома? Нужно просто разобраться в том, что есть что в его определении. И начать следует с определения силы тока, напряжения и сопротивления.
Сила тока I
Пусть в каком-то проводнике течет ток. То есть, происходит направленное движение заряженных частиц – допустим, это электроны. Каждый электрон обладает элементарным электрическим зарядом (e= -1,60217662 × 10 -19 Кулона). В таком случае через некоторую поверхность за определенный промежуток времени пройдет конкретный электрический заряд, равный сумме всех зарядов протекших электронов.
То есть, происходит направленное движение заряженных частиц – допустим, это электроны. Каждый электрон обладает элементарным электрическим зарядом (e= -1,60217662 × 10 -19 Кулона). В таком случае через некоторую поверхность за определенный промежуток времени пройдет конкретный электрический заряд, равный сумме всех зарядов протекших электронов.
Отношение заряда к времени и называется силой тока. Чем больший заряд проходит через проводник за определенное время, тем больше сила тока. Сила тока измеряется в Амперах.
Напряжение U, или разность потенциалов
Это как раз та штука, которая заставляет электроны двигаться. Электрический потенциал характеризует способность поля совершать работу по переносу заряда из одной точки в другую. Так, между двумя точками проводника существует разность потенциалов, и электрическое поле совершает работу по переносу заряда.
Физическая величина, равная работе эффективного электрического поля при переносе электрического заряда, и называется напряжением. Измеряется в Вольтах. Один Вольт – это напряжение, которое при перемещении заряда в 1 Кл совершает работу, равную 1 Джоуль.
Измеряется в Вольтах. Один Вольт – это напряжение, которое при перемещении заряда в 1 Кл совершает работу, равную 1 Джоуль.
Сопротивление R
Ток, как известно, течет в проводнике. Пусть это будет какой-нибудь провод. Двигаясь по проводу под действием поля, электроны сталкиваются с атомами провода, проводник греется, атомы в кристаллической решетке начинают колебаться, создавая электронам еще больше проблем для передвижения. Именно это явление и называется сопротивлением. Оно зависит от температуры, материала, сечения проводника и измеряется в Омах.
Памятник Георгу Симону Ому
Формулировка и объяснение закона Ома
Закон немецкого учителя Георга Ома очень прост. Он гласит:
Сила тока на участке цепи прямо пропорционально напряжению и обратно пропорциональна сопротивлению.
Георг Ом вывел этот закон экспериментально (эмпирически) в 1826 году. Естественно, чем больше сопротивление участка цепи, тем меньше будет сила тока. Соответственно, чем больше напряжение, тем и ток будет больше.
Естественно, чем больше сопротивление участка цепи, тем меньше будет сила тока. Соответственно, чем больше напряжение, тем и ток будет больше.
Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы
Данная формулировка закона Ома – самая простая и подходит для участка цепи. Говоря «участок цепи» мы подразумеваем, что это однородный участок, на котором нет источников тока с ЭДС. Говоря проще, этот участок содержит какое-то сопротивление, но на нем нет батарейки, обеспечивающей сам ток.
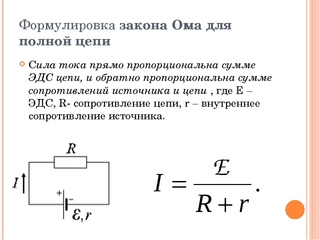
Если рассматривать закон Ома для полной цепи, формулировка его будет немного иной.
Пусть у нас есть цепь, в ней есть источник тока, создающий напряжение, и какое-то сопротивление.
Закон запишется в следующем виде:
Объяснение закона Ома для полой цепи принципиально не отличается от объяснения для участка цепи. Как видим, сопротивление складывается из собственно сопротивления и внутреннего сопротивления источника тока, а вместо напряжения в формуле фигурирует электродвижущая сила источника.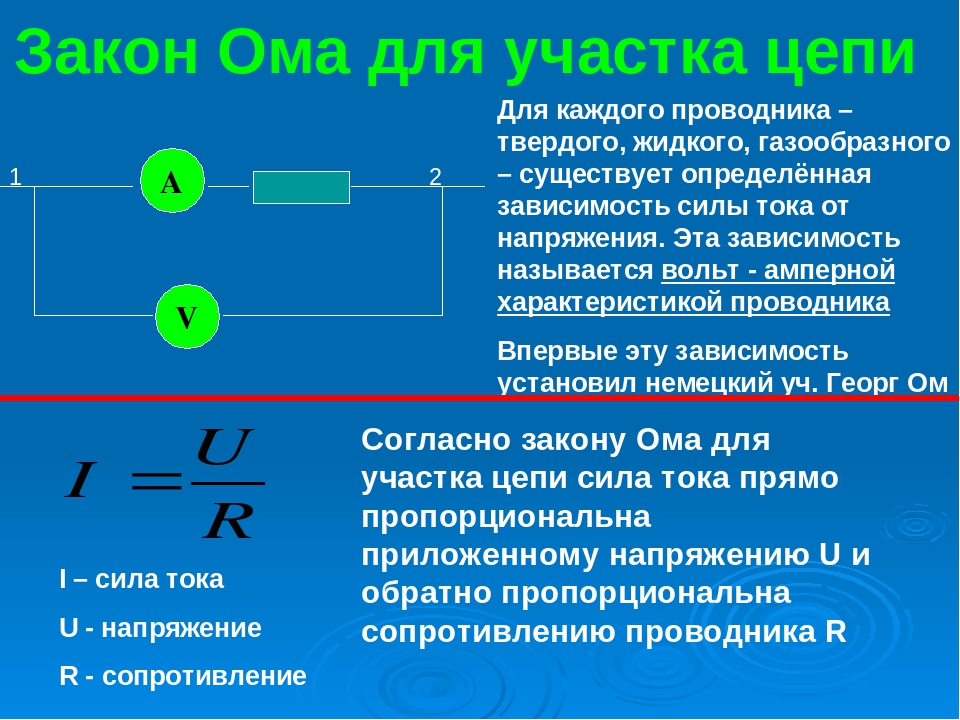
Кстати, о том, что такое что такое ЭДС, читайте в нашей отдельной статье.
Как понять закон Ома?
Чтобы интуитивно понять закон Ома, обратимся к аналогии представления тока в виде жидкости. Именно так думал Георг Ом, когда проводил опыты, благодаря которым был открыт закон, названный его именем.
Представим, что ток – это не движение частиц-носителей заряда в проводнике, а движение потока воды в трубе. Сначала воду насосом поднимают на водокачку, а оттуда, под действием потенциальной энергии, она стремиться вниз и течет по трубе. Причем, чем выше насос закачает воду, тем быстрее она потечет в трубе.
Отсюда следует вывод, что скорость потока воды (сила тока в проводе) будет тем больше, чем больше потенциальная энергия воды (разность потенциалов)
Сила тока прямо пропорциональна напряжению.
Теперь обратимся к сопротивлению. Гидравлическое сопротивление – это сопротивление трубы, обусловленное ее диаметром и шероховатостью стенок. Логично предположить, что чем больше диаметр, тем меньше сопротивление трубы, и тем большее количество воды (больший ток) протечет через ее сечение.
Логично предположить, что чем больше диаметр, тем меньше сопротивление трубы, и тем большее количество воды (больший ток) протечет через ее сечение.
Сила тока обратно пропорциональна сопротивлению.
Такую аналогию можно проводить лишь для принципиального понимания закона Ома, так как его первозданный вид – на самом деле довольно грубое приближение, которое, тем не менее, находит отличное применение на практике.
В действительности, сопротивление вещества обусловлено колебанием атомов кристаллической решетки, а ток – движением свободных носителей заряда. В металлах свободными носителями являются электроны, сорвавшиеся с атомных орбит.
Ток в проводнике
В данной статье мы постарались дать простое объяснение закона Ома. Знание этих на первый взгляд простых вещей может сослужить Вам неплохую службу на экзамене. Конечно, мы привели его простейшую формулировку закона Ома и не будем сейчас лезть в дебри высшей физики, разбираясь с активным и реактивным сопротивлениями и прочими тонкостями.
Если у Вас возникнет такая необходимость, Вам с удовольствием помогут сотрудники нашего студенческого сервиса. А напоследок предлагаем Вам посмотреть интересное видео про закон Ома. Это действительно познавательно!
Закон Ома для участка цепи
Тип урока: Комбинированный.
Вид урока: Изучение нового материала.
Цели урока:
Образовательная: установить зависимость между силой тока, напряжением на однородном участке электрической цепи и сопротивлением этого участка.
Развивающая:
- развивать умения наблюдать, сопоставлять, сравнивать и обобщать результаты экспериментов;
- продолжить формирование умений пользоваться
теоретическими и экспериментальными методами
физической науки для обоснования выводов по
изучаемой теме и для решения задач.

Воспитательная: развивать познавательный интерес к предмету, тренировка рационального метода запоминания формул.
Задачи урока.
- Усвоить, что сила тока прямо пропорциональна напряжению на концах проводника, если при этом сопротивление проводника не меняется;
- Усвоить, что сила в участке цепи обратно пропорциональна его сопротивлению, если при этом напряжение остается постоянным;
- Знать закон Ома для участка цепи;
- Уметь определять силу тока; напряжения по графику зависимости между этими величинами и по нему же – сопротивление проводника;
- Уметь наблюдать, сопоставлять, сравнивать и обобщать результаты демонстрационного эксперимента;
- Уметь применять закон Ома для участка цепи при решении задач;
- Отрабатывать навыки проверки размерности;
- Отрабатывать навыки соотношения полученных
результатов с реальными значениями величин.

Оборудование.
Демонстрационные амперметр и вольтметр, источник тока В-24, ключ, соединительные провода, демонстрационный магазин сопротивления, ТСО, экран, магнитная доска, магниты, портрет Ома, таблицы с формулами.
Ход урока
1. Организационный момент.
Учитель: Здравствуйте, садитесь (дежурный, отсутствующие).
2. Этап актуализации знаний.С целью проверки качества усвоения
знаний проводится дидактическая игра “Проверь
себя!”. Игра состоит из двух частей. В первой
части работы дети выбирают обозначение, формулу,
единицы измерения, прибор для измерения одной из
основных характеристик тока. Во второй части
учащиеся заполняют пропуски в таблице. Класс
делится на три варианта. Каждому варианту дается
определенное задание. Оценивание работ
проводится методом взаимопроверки.
Оценивание работ
проводится методом взаимопроверки.
На предыдущих занятиях мы рассмотрели три величины, с которыми мы имеем дело в любой электрической цепи, – это … (Сила тока, напряжение и сопротивление). Но в жизни и на практике недостаточно знать в отдельности физические величины, характеризующие электрические цепи, их надо рассматривать во взаимозависимости. Вот взаимозависимость мы и будем раскрывать сегодня на уроке.
Запишите тему нашего урока: “Закон Ома для участка цепи”.
О значении исследований Георга Ома
точно сказал профессор физики Мюнхенского
университета Ломмель Эуген Корнелиус Йозеф
при открытии памятника ученому в 1895 году
“Открытие Ома было ярким факелом, осветившим ту
область электричества, которая до него была
окутана мраком. Ом указал единственно правильный
путь через непроходимый лес непонятных фактов.
Замечательные успехи в развитии электротехники,
за которыми мы с удивлением наблюдали в
последние десятилетия, могли быть достигнуты
только на основе открытия Ома. Лишь тот в
состоянии господствовать над силами природы и
управлять ими, кто сумеет разгадать законы
природы. Ом вырвал у природы так долго скрываемую
тайну и передал ее в руки современников”.
Ом указал единственно правильный
путь через непроходимый лес непонятных фактов.
Замечательные успехи в развитии электротехники,
за которыми мы с удивлением наблюдали в
последние десятилетия, могли быть достигнуты
только на основе открытия Ома. Лишь тот в
состоянии господствовать над силами природы и
управлять ими, кто сумеет разгадать законы
природы. Ом вырвал у природы так долго скрываемую
тайну и передал ее в руки современников”.
Вопрос: Какую так долго скрываемую тайну Ом вырвал у природы и передал ее в руки современников? Давайте же выясним это.
4. Этап изучения нового материала.
На сегодняшнем уроке нам необходимо
решить следующую задачу: выяснить, как зависит
сила тока на участке цепи от приложенного
напряжения и величины сопротивления
одновременно. Это является главной целью
нашего урока.
Итак, работу на сегодняшнем уроке будем проводить по этапам.
1) Сначала установим зависимость силы тока от напряжения, запишем математически эту зависимость и проверим на опыте.
2) Установим зависимости между силой тока и сопротивлением, при постоянном напряжении; запишем результаты в таблицу, сделаем вывод о характере этой зависимости.
3) Сделаем общий вывод о том, как зависит сила тока одновременно от напряжения и сопротивления, т.е. решим основную задачу урока.
Этапы:
1. Установим зависимость силы тока от напряжения на опыте.
а) На демонстрационной доске собрана цепь: источник тока, реостат, амперметр, резистор, вольтметр, ключ.
б) Чертим схему цепи на доске.
в) Включаю цепь. Вольтметр показывает
2В. Какую силу тока показывает амперметр? 0,4А.
Вольтметр показывает
2В. Какую силу тока показывает амперметр? 0,4А.
Увеличиваю напряжение до – 3В. Изменились ли показания амперметра? Да, сила тока в цепи 0,6А.
Увеличиваю напряжение до – 4В. Как изменилась сила тока? Увеличилась, сила тока в цепи 0,8А.
Запишем полученные результаты в таблицу и начертим график:
U, В |
2В |
3В |
4В |
I, А |
0,4А |
0,6А |
0,8А |
Увеличивается напряжение, сила тока
тоже увеличивается – I U.
Изменилось ли сопротивление проводника? Нет, оно постоянно: R= cons t.
Вывод 1. При R=const, I ~ U.
2.
Установим зависимость между силой тока и сопротивлением.а) Подумайте и скажите: будет ли одинаковой сила тока в проводнике с большим сопротивлением и в проводнике с маленьким сопротивлением? Сила тока будет разная. А в каком случае сила тока будет меньше? Где больше R.
б) Итак, давайте убедимся в этом на опыте. На столе собрана цепь: источник тока, магазин сопротивлений, амперметр, вольтметр, ключ.
б) Чертим схему цепи на доске.
в) Установим зависимость между I и R, при U=const. Начертим таблицу в тетрадь и будем ее заполнять по ходу опыта.
U, В |
5В |
5В |
5В |
R, Ом |
4Ом |
2Ом |
1Ом |
I, А |
1А |
2А |
4А |
Сейчас общее сопротивление составляет
4 Ом, подано напряжение 5В.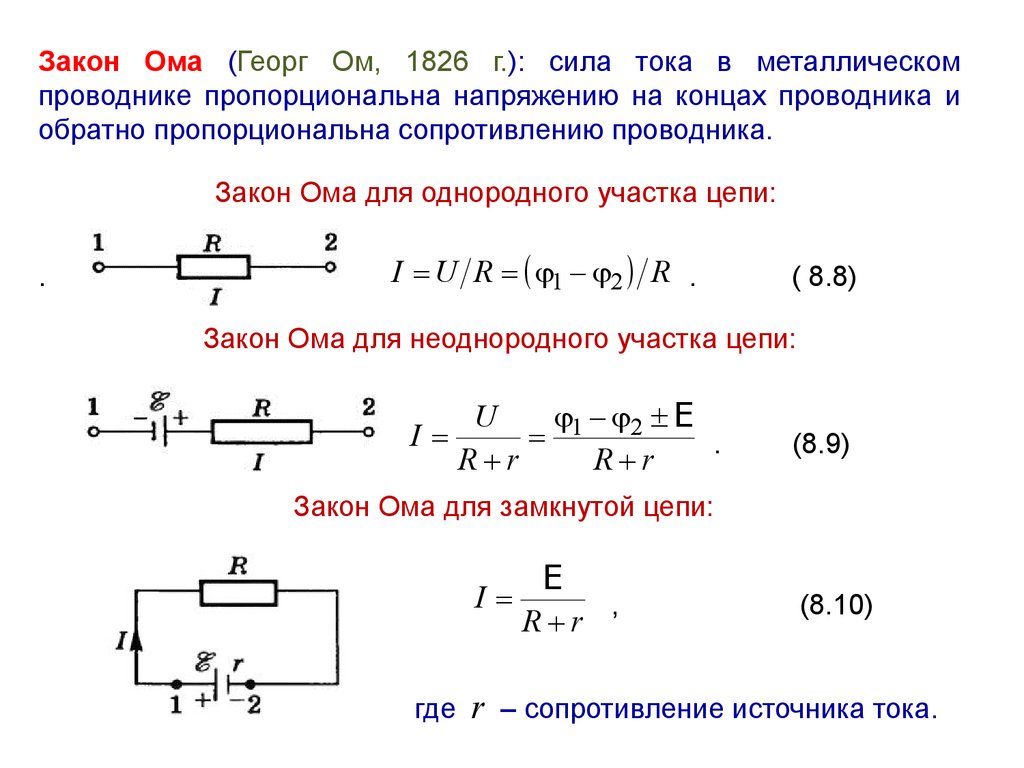 Какой ток в цепи? I
= 1 А
Какой ток в цепи? I
= 1 А
Уменьшаем сопротивление до 2 Ом, не меняя напряжение, какой ток в цепи сейчас? I = 2 А. Теперь сопротивление равно1 Ом, напряжение по прежнему не меняем. Как изменилась сила тока? I = 4 А
Итак, глядя на таблицу, что можно сказать о зависимости между силой тока и сопротивлением? Начертим график.
Вывод 2: При U= const I 1/R
3.
Сделаем общий вывод о том, как зависит сила тока I одновременно от U и R.Мы уже знаем две зависимости. И теперь мы объединим эти зависимости в одну формулу. Мы получим с вами один из основных законов электрического тока, который называется законом Ома:
Сила тока в участке цепи прямо
пропорциональна напряжению на концах этого
участка и обратно пропорциональна сопротивлению
этого же участка.
“Ом вырвал у природы так долго скрываемую тайну и передал ее в руки современников” в 1827 году. Ему было 38 лет.
Пользуясь этим законом, мы можем рассчитать силу тока, зная напряжение и сопротивление, то есть, зная две величины, мы всегда можем найти третью.
5. Этап применения нового знания
Итак, ребята, между какими величинами устанавливает зависимость закон Ома?
- между силой тока, напряжением и сопротивлением.
Как зависит сила тока от напряжения?
- Прямо пропорционально.
Как зависит сила тока от сопротивления?
- обратно пропорционально.
Как формулируется закон Ома?
Давайте решим задачи:
- на графики зависимости;
- комбинированная задача.

1.
2.
6. Первичная проверка полученных знаний
С целью проверки усвоения первичных знаний используются две задачи. Класс делится на два варианта. На доске высвечиваются условия задач. Проверка производится методом взаимопроверки.
7. Домашнее задание:
1. §§43, 44. Прочитать;
2. Упр. 20 (1, 2, 3) стр.88; Упр. 21 (2, 4, 6, 7) стр. 91.
3. Подготовить историческую справку об ученых, чьи имена очень тесно связаны с законом Ома.
Литература:

Презентация
Закон Ома тест (8 класс) по физике с ответами по теме
Сложность: знаток. Последний раз тест пройден 12 часов назад.
Последний раз тест пройден 12 часов назад.
Вопрос 1 из 10
Как сила тока в проводнике зависит от его сопротивления?
- Правильный ответ
- Неправильный ответ
- Вы и еще 60% ответили правильно
- 60% ответили правильно на этот вопрос
В вопросе ошибка?
Следующий вопросОтветитьВопрос 2 из 10
Зависимость силы тока от каких физических величин устанавливает закон Ома?
- Правильный ответ
- Неправильный ответ
- Вы и еще 81% ответили правильно
- 81% ответили правильно на этот вопрос
В вопросе ошибка?
ОтветитьВопрос 3 из 10
Какова формула закона Ома?
- Правильный ответ
- Неправильный ответ
- Вы и еще 91% ответили правильно
- 91% ответили правильно на этот вопрос
В вопросе ошибка?
ОтветитьВопрос 4 из 10
На рисунке представлен график зависимости силы тока в проводнике от напряжения на его концах.
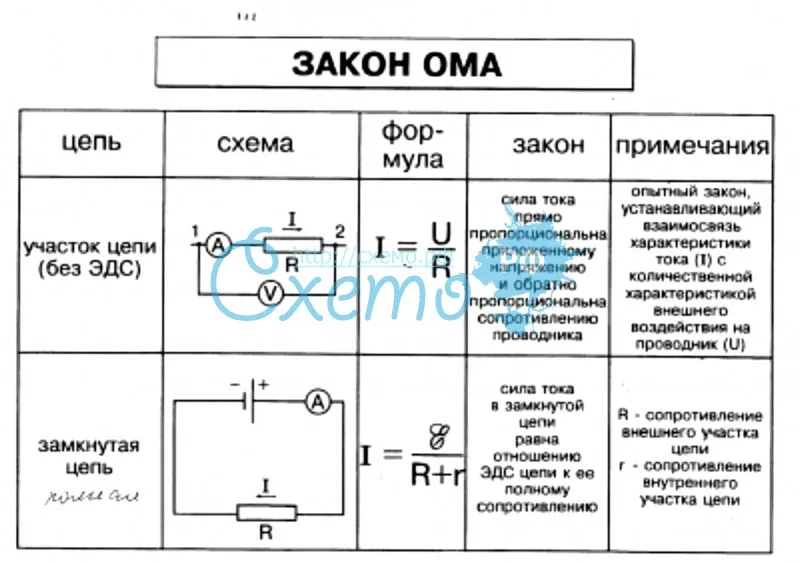 Определите по нему сопротивление проводника
Определите по нему сопротивление проводника - Правильный ответ
- Неправильный ответ
- Вы и еще 57% ответили правильно
- 57% ответили правильно на этот вопрос
В вопросе ошибка?
ОтветитьВопрос 5 из 10
Какой из проводников, для которых графики зависимости силы тока от напряжения показаны на рисунке, обладает наибольшим сопротивлением? Изменится ли оно при возрастании напряжения?
- Правильный ответ
- Неправильный ответ
- Вы и еще 53% ответили правильно
- 53% ответили правильно на этот вопрос
В вопросе ошибка?
ОтветитьВопрос 6 из 10
Сопротивление нагревательного элемента утюга 88 Ом, напряжение в электросети 220 В.
 Какова сила тока в нагревательном элементе?
Какова сила тока в нагревательном элементе?- Правильный ответ
- Неправильный ответ
- Вы и еще 70% ответили правильно
- 70% ответили правильно на этот вопрос
В вопросе ошибка?
ОтветитьВопрос 7 из 10
Сопротивление проводника 70 Ом, сила тока в нем 6 мА. Каково напряжение на его концах?
- Правильный ответ
- Неправильный ответ
- Вы ответили лучше 58% участников
- 42% ответили правильно на этот вопрос
В вопросе ошибка?
ОтветитьВопрос 8 из 10
Найдите сопротивление спирали, сила тока в которой 0,5 А, а напряжение на ее концах 120 В
- Правильный ответ
- Неправильный ответ
- Вы и еще 55% ответили правильно
- 55% ответили правильно на этот вопрос
В вопросе ошибка?
ОтветитьВопрос 9 из 10
Чтобы экспериментально определить сопротивление проводника, включенного в цепь, какие нужно измерить величины? Какими приборами?
- Правильный ответ
- Неправильный ответ
- Вы и еще 78% ответили правильно
- 78% ответили правильно на этот вопрос
В вопросе ошибка?
ОтветитьВопрос 10 из 10
Зависит ли сопротивление проводника от напряжения и силы тока?
- Правильный ответ
- Неправильный ответ
- Вы ответили лучше 66% участников
- 34% ответили правильно на этот вопрос
В вопросе ошибка?
Ответить
Доска почёта
Чтобы попасть сюда — пройдите тест.
-
Ералы Асетулы
10/10
Ольгита Степанова
10/10
Тимур Чередниченко
10/10
Татьяна Засимович
10/10
Каждому, кто задается вопросом, как знать физику на «отлично», окажется полезен тест «Закон Ома» (8 класс) с ответами, ведь такой формат предполагает возможность самоконтроля. Тест содержит десять заданий с выбором правильного ответа; они включают в себя теоретические вопросы по теме, задания на вычисление сопротивления для участка цепи, силы тока по графику и т.п.
Тест по физике «Закон Ома» предназначен для восьмиклассников и их родителей, желающих проверить уровень знаний своего ребенка, но может использоваться также для подготовки к экзаменам или повторения материала.
Рейтинг теста
Средняя оценка: 3.6. Всего получено оценок: 408.
А какую оценку получите вы? Чтобы узнать — пройдите тест.
Тест Закон Ома для участка цепи по физике онлайн
Сложность: знаток.Последний раз тест пройден более 24 часов назад.
Перед прохождением теста рекомендуем прочитать:Вопрос 1 из 10
Георгом Омом было установлено, что:
- Правильный ответ
- Неправильный ответ
- Вы и еще 71% ответили правильно
- 71% ответили правильно на этот вопрос
В вопросе ошибка?
Следующий вопросОтветитьВопрос 2 из 10
Сопротивление цепи зависит от:
- Правильный ответ
- Неправильный ответ
- Вы и еще 69% ответили правильно
- 69% ответили правильно на этот вопрос
В вопросе ошибка?
ОтветитьВопрос 3 из 10
Закон Ома для участка цепи справедлив для:
- Правильный ответ
- Неправильный ответ
- Вы ответили лучше 57% участников
- 43% ответили правильно на этот вопрос
В вопросе ошибка?
ОтветитьВопрос 4 из 10
Закон Ома для участка цепи записывается:
- Правильный ответ
- Неправильный ответ
- Вы и еще 76% ответили правильно
- 76% ответили правильно на этот вопрос
В вопросе ошибка?
ОтветитьВопрос 5 из 10
Падением напряжения называют:
- Правильный ответ
- Неправильный ответ
- Вы ответили лучше 51% участников
- 49% ответили правильно на этот вопрос
В вопросе ошибка?
ОтветитьВопрос 6 из 10
Для более простого запоминания и использования закона Ома придумали:
- Правильный ответ
- Неправильный ответ
- Вы и еще 76% ответили правильно
- 76% ответили правильно на этот вопрос
В вопросе ошибка?
ОтветитьВопрос 7 из 10
Сопротивление проводника – 2 Ом.
 Сила тока – 1 А. Чем равно напряжение на участке цепи?
Сила тока – 1 А. Чем равно напряжение на участке цепи?- Правильный ответ
- Неправильный ответ
- Вы и еще 73% ответили правильно
- 73% ответили правильно на этот вопрос
В вопросе ошибка?
ОтветитьВопрос 8 из 10
Сила тока на участке цепи – 10 А. Падение напряжения – 200 В. Чему равно сопротивление проводника?
- Правильный ответ
- Неправильный ответ
- Вы и еще 80% ответили правильно
- 80% ответили правильно на этот вопрос
В вопросе ошибка?
ОтветитьВопрос 9 из 10
Два резистора соединены параллельно, R1 = 10 Ом, R2 = 20 Ом. К участку цепи подведена разность потенциалов – 100 В.
 Чему равна сила тока на всем участке?
Чему равна сила тока на всем участке?- Правильный ответ
- Неправильный ответ
- Вы и еще 51% ответили правильно
- 51% ответили правильно на этот вопрос
В вопросе ошибка?
ОтветитьВопрос 10 из 10
Три резистора (R1 = 10 Ом, R2 = 30 Ом, R3 = 50 Ом) соединены последовательно. Разность потенциалов на этом участке – 150 В. Чему равна сила тока на каждом из резисторов?
- Правильный ответ
- Неправильный ответ
- Вы ответили лучше 65% участников
- 35% ответили правильно на этот вопрос
В вопросе ошибка?
Ответить
Доска почёта
Чтобы попасть сюда — пройдите тест.
-
Ринат Баишев
10/10
Денис Иванов
9/10
Мария Кшевач
7/10
Рейтинг теста
Средняя оценка: 3. 6. Всего получено оценок: 202.
6. Всего получено оценок: 202.
А какую оценку получите вы? Чтобы узнать — пройдите тест.
Закон ома в природе. Закон Ома для «чайников»: понятие, формула, объяснение
Если изолированный проводник поместить в электрическое поле \(\overrightarrow{E} \), то на свободные заряды \(q\) в проводнике будет действовать сила \(\overrightarrow{F} = q\overrightarrow{E}\) В результате в проводнике возникает кратковременное перемещение свободных зарядов. Этот процесс закончится тогда, когда собственное электрическое поле зарядов, возникших на поверхности проводника, скомпенсирует полностью внешнее поле. Результирующее электростатическое поле внутри проводника будет равно нулю.
Однако, в проводниках при определенных условиях может возникнуть непрерывное упорядоченное движение свободных носителей электрического заряда.
Направленное движение заряженных частиц называется электрическим током.
За направление электрического тока принято направление движения положительных свободных зарядов. Для существования электрического тока в проводнике необходимо создать в нем электрическое поле.
Количественной мерой электрического тока служит сила тока \(I\) — скалярная физическая величина, равная отношению заряда \(\Delta q\), переносимого через поперечное сечение проводника (рис. 1.8.1) за интервал времени \(\Delta t\), к этому интервалу времени:
$$I = \frac{\Delta q}{\Delta t} $$
Если сила тока и его направление не изменяются со временем, то такой ток называется постоянным .
В Международной системе единиц СИ сила тока измеряется в Амперах (А). Единица измерения тока 1 А устанавливается по магнитному взаимодействию двух параллельных проводников с током.
Постоянный электрический ток может быть создан только в замкнутой цепи
, в которой свободные носители заряда циркулируют по замкнутым траекториям. Электрическое поле в разных точках такой цепи неизменно во времени. Следовательно, электрическое поле в цепи постоянного тока имеет характер замороженного электростатического поля. Но при перемещении электрического заряда в электростатическом поле по замкнутой траектории, работа электрических сил равна нулю. Поэтому для существования постоянного тока необходимо наличие в электрической цепи устройства, способного создавать и поддерживать разности потенциалов на участках цепи за счет работы сил неэлектростатического происхождения
. Такие устройства называются источниками постоянного тока
. Силы неэлектростатического происхождения, действующие на свободные носители заряда со стороны источников тока, называются сторонними силами
.
Электрическое поле в разных точках такой цепи неизменно во времени. Следовательно, электрическое поле в цепи постоянного тока имеет характер замороженного электростатического поля. Но при перемещении электрического заряда в электростатическом поле по замкнутой траектории, работа электрических сил равна нулю. Поэтому для существования постоянного тока необходимо наличие в электрической цепи устройства, способного создавать и поддерживать разности потенциалов на участках цепи за счет работы сил неэлектростатического происхождения
. Такие устройства называются источниками постоянного тока
. Силы неэлектростатического происхождения, действующие на свободные носители заряда со стороны источников тока, называются сторонними силами
.
Природа сторонних сил может быть различной. В гальванических элементах или аккумуляторах они возникают в результате электрохимических процессов, в генераторах постоянного тока сторонние силы возникают при движении проводников в магнитном поле. Источник тока в электрической цепи играет ту же роль, что и насос, который необходим для перекачивания жидкости в замкнутой гидравлической системе. Под действием сторонних сил электрические заряды движутся внутри источника тока против
сил электростатического поля, благодаря чему в замкнутой цепи может поддерживаться постоянный электрический ток.
Источник тока в электрической цепи играет ту же роль, что и насос, который необходим для перекачивания жидкости в замкнутой гидравлической системе. Под действием сторонних сил электрические заряды движутся внутри источника тока против
сил электростатического поля, благодаря чему в замкнутой цепи может поддерживаться постоянный электрический ток.
При перемещении электрических зарядов по цепи постоянного тока сторонние силы, действующие внутри источников тока, совершают работу.
Физическая величина, равная отношению работы \(A_{ст}\) сторонних сил при перемещении заряда \(q\) от отрицательного полюса источника тока к положительному к величине этого заряда, называется электродвижущей силой источника (ЭДС):
$$ЭДС=\varepsilon=\frac{A_{ст}}{q}. $$
Таким образом, ЭДС определяется работой, совершаемой сторонними силами при перемещении единичного положительного заряда. Электродвижущая сила, как и разность потенциалов, измеряется в Вольтах (В).
При перемещении единичного положительного заряда по замкнутой цепи постоянного тока работа сторонних сил равна сумме ЭДС, действующих в этой цепи, а работа электростатического поля равна нулю.
Цепь постоянного тока можно разбить на отдельные участки. Те участки, на которых не действуют сторонние силы (т. е. участки, не содержащие источников тока), называются однородными . Участки, включающие источники тока, называются неоднородными .
При перемещении единичного положительного заряда по некоторому участку цепи работу совершают как электростатические (кулоновские), так и сторонние силы. Работа электростатических сил равна разности потенциалов \(\Delta \phi_{12} = \phi_{1} — \phi_{2}\) между начальной (1) и конечной (2) точками неоднородного участка. Работа сторонних сил равна по определению электродвижущей силе \(\mathcal{E}\), действующей на данном участке. Поэтому полная работа равна
$$U_{12} = \phi_{1} — \phi_{2} + \mathcal{E}$$
Величину U
12 принято называть напряжением
на участке цепи 1-2. В случае однородного участка напряжение равно разности потенциалов:
В случае однородного участка напряжение равно разности потенциалов:
$$U_{12} = \phi_{1} — \phi_{2}$$
Немецкий физик Г. Ом в 1826 году экспериментально установил, что сила тока \(I\), текущего по однородному металлическому проводнику (т. е. проводнику, в котором не действуют сторонние силы), пропорциональна напряжению \(U\) на концах проводника:
$$I = \frac{1}{R} U; \: U = IR$$
где \(R\) = const.
Величину R принято называть электрическим сопротивлением . Проводник, обладающий электрическим сопротивлением, называется резистором . Данное соотношение выражает закон Ома для однородного участка цепи: сила тока в проводнике прямо пропорциональна приложенному напряжению и обратно пропорциональна сопротивлению проводника.
В СИ единицей электрического сопротивления проводников служит Ом
(Ом). Сопротивлением в 1 Ом обладает такой участок цепи, в котором при напряжении 1 В возникает ток силой 1 А.
Проводники, подчиняющиеся закону Ома, называются линейными . Графическая зависимость силы тока \(I\) от напряжения \(U\) (такие графики называются вольт-амперными характеристиками , сокращенно ВАХ) изображается прямой линией, проходящей через начало координат. Следует отметить, что существует много материалов и устройств, не подчиняющихся закону Ома, например, полупроводниковый диод или газоразрядная лампа. Даже у металлических проводников при токах достаточно большой силы наблюдается отклонение от линейного закона Ома, так как электрическое сопротивление металлических проводников растет с ростом температуры.
Для участка цепи, содержащего ЭДС, закон Ома записывается в следующей форме:
$$IR = U_{12} = \phi_{1} — \phi_{2} + \mathcal{E} = \Delta \phi_{12} + \mathcal{E}$$
$$\color{blue}{I = \frac{U}{R}}$$
Это соотношение принято называть обобщенным законом Ома или законом Ома для неоднородного участка цепи .
На рис. 1.8.2 изображена замкнутая цепь постоянного тока. Участок цепи (cd
) является однородным.
1.8.2 изображена замкнутая цепь постоянного тока. Участок цепи (cd
) является однородным.
|
Рисунок 1.8.2. Цепь постоянного тока |
По закону Ома
$$IR = \Delta\phi_{cd}$$
Участок (ab ) содержит источник тока с ЭДС, равной \(\mathcal{E}\).
По закону Ома для неоднородного участка,
$$Ir = \Delta \phi_{ab} + \mathcal{E}$$
Сложив оба равенства, получим:
$$I(R+r) = \Delta\phi_{cd} + \Delta \phi_{ab} + \mathcal{E}$$
Но \(\Delta\phi_{cd} = \Delta \phi_{ba} = -\Delta \phi_{ab}\).
$$\color{blue}{I=\frac{\mathcal{E}}{R + r}}$$
Эта формула выражает закон Ома для полной цепи : сила тока в полной цепи равна электродвижущей силе источника, деленной на сумму сопротивлений однородного и неоднородного участков цепи (внутреннего сопротивления источника).
Сопротивление r
неоднородного участка на рис. 1.8.2 можно рассматривать как внутреннее сопротивление источника тока
. В этом случае участок (ab
) на рис. 1.8.2 является внутренним участком источника. Если точки a
и b
замкнуть проводником, сопротивление которого мало по сравнению с внутренним сопротивлением источника (\(R\ \ll r\)), тогда в цепи потечет ток короткого замыкания
1.8.2 можно рассматривать как внутреннее сопротивление источника тока
. В этом случае участок (ab
) на рис. 1.8.2 является внутренним участком источника. Если точки a
и b
замкнуть проводником, сопротивление которого мало по сравнению с внутренним сопротивлением источника (\(R\ \ll r\)), тогда в цепи потечет ток короткого замыкания
$$I_{кз}=\frac{\mathcal{E}}{r}$$
Сила тока короткого замыкания — максимальная сила тока, которую можно получить от данного источника с электродвижущей силой \(\mathcal{E}\) и внутренним сопротивлением \(r\). У источников с малым внутренним сопротивлением ток короткого замыкания может быть очень велик и вызывать разрушение электрической цепи или источника. Например, у свинцовых аккумуляторов, используемых в автомобилях, сила тока короткого замыкания может составлять несколько сотен ампер. Особенно опасны короткие замыкания в осветительных сетях, питаемых от подстанций (тысячи ампер). Чтобы избежать разрушительного действия таких больших токов, в цепь включаются предохранители или специальные автоматы защиты сетей.
В ряде случаев для предотвращения опасных значений силы тока короткого замыкания к источнику последовательно подсоединяется некоторое внешнее сопротивление. Тогда сопротивление r равно сумме внутреннего сопротивления источника и внешнего сопротивления, и при коротком замыкании сила тока не окажется чрезмерно большой.
Если внешняя цепь разомкнута, то \(\Delta \phi_{ba} = -\Delta \phi_{ab} = \mathcal{E}\), т. е. разность потенциалов на полюсах разомкнутой батареи равна ее ЭДС.
Если внешнее нагрузочное сопротивление R включено и через батарею протекает ток I , разность потенциалов на ее полюсах становится равной
$$\Delta \phi_{ba} = \mathcal{E} — Ir$$
На рис. 1.8.3 дано схематическое изображение источника постоянного тока с ЭДС равной \(\mathcal{E}\) и внутренним сопротивлением r
в трех режимах: «холостой ход», работа на нагрузку и режим короткого замыкания (к. з.). Указаны напряженность \(\overrightarrow{E}\) электрического поля внутри батареи и силы, действующие на положительные заряды:\(\overrightarrow{F}_{э}\) — электрическая сила и \(\overrightarrow{F}_{ст}\) — сторонняя сила. В режиме короткого замыкания электрическое поле внутри батареи исчезает.
В режиме короткого замыкания электрическое поле внутри батареи исчезает.
Для измерения напряжений и токов в электрических цепях постоянного тока используются специальные приборы — вольтметры и амперметры .
Вольтметр предназначен для измерения разности потенциалов, приложенной к его клеммам. Он подключается параллельно участку цепи, на котором производится измерение разности потенциалов. Любой вольтметр обладает некоторым внутренним сопротивлением \(R_{В}\). Для того, чтобы вольтметр не вносил заметного перераспределения токов при подключении к измеряемой цепи, его внутреннее сопротивление должно быть велико по сравнению с сопротивлением того участка цепи, к которому он подключен. Для цепи, изображенной на рис. 1.8.4, это условие записывается в виде:
$$R_{В} \gg R_{1}$$
Это условие означает, что ток \(I_{В} = \Delta \phi_{cd} / R_{В}\), протекающий через вольтметр, много меньше тока \(I = \Delta \phi_{cd} / R_{1}\), который протекает по тестируемому участку цепи.
Поскольку внутри вольтметра не действуют сторонние силы, разность потенциалов на его клеммах совпадает по определению с напряжением. Поэтому можно говорить, что вольтметр измеряет напряжение.
Амперметр предназначен для измерения силы тока в цепи. Амперметр включается последовательно в разрыв электрической цепи, чтобы через него проходил весь измеряемый ток. Амперметр также обладает некоторым внутренним сопротивлением \(R_{А}\). В отличие от вольтметра, внутреннее сопротивление амперметра должно быть достаточно малым по сравнению с полным сопротивлением всей цепи. Для цепи на рис. 1.8.4 сопротивление амперметра должно удовлетворять условию
$$R_{А} \ll (r + R_{1} + R{2})$$
чтобы при включении амперметра ток в цепи не изменялся.
Измерительные приборы — вольтметры и амперметры — бывают двух видов: стрелочные (аналоговые) и цифровые. Цифровые электроизмерительные приборы представляют собой сложные электронные устройства. Обычно цифровые приборы обеспечивают более высокую точность измерений.
Георг Симон Ом начал свои исследования вдохновляясь знаменитым трудом Жана Батиста Фурье «Аналитическая теория тепла». В этой работе Фурье представлял тепловой поток между двумя точками как разницу температур, а изменение теплового потока связывал с его прохождением через препятствие неправильной формы из теплоизолирующего материала. Аналогично этому Ом обуславливал возникновение электрического тока разностью потенциалов.
Исходя из этого Ом стал экспериментировать с разными материалами проводника. Для того, чтобы определить их проводимость он подключал их последовательно и подгонял их длину таким образом, чтобы сила тока была одинаковой во всех случаях.
Важно при таких измерениях было подбирать проводники одного и того же диаметра. Ом, замеряя проводимость серебра и золота, получил результаты, которые по современным данным не отличаются точностью. Так, серебряный проводник у Ома проводил меньше электрического тока, чем золотой. Сам Ом объяснял это тем, что его проводник из серебра был покрыт маслом и из-за этого, по всей видимости, опыт не дал точных результатов.
Однако не только с этим были проблемы у физиков, которые в то время занимались подобными экспериментами с электричеством. Большие трудности с добычей чистых материалов без примесей для опытов, затруднения с калибровкой диаметра проводника искажали результаты тестов. Еще большая загвоздка состояла в том, что сила тока постоянно менялась во время испытаний, поскольку источником тока служили переменные химические элементы. В таких условиях Ом вывел логарифмическую зависимость силы тока от сопротивления провода.
Немногим позже немецкий физик Поггендорф, специализировавшийся на электрохимии, предложил Ому заменить химические элементы на термопару из висмута и меди. Ом начал свои эксперименты заново. В этот раз он пользовался термоэлектрическим устройством, работающем на эффекте Зеебека в качестве батареи. К нему он последовательно подключал 8 проводников из меди одного и того же диаметра, но различной длины. Чтобы измерить силу тока Ом подвешивал с помощью металлической нити над проводниками магнитную стрелку. Ток, шедший параллельно этой стрелке, смещал ее в сторону. Когда это происходило физик закручивал нить до тех пор, пока стрелка не возвращалась в исходное положение. Исходя из угла, на который закручивалась нить можно было судить о значении силы тока.
Ток, шедший параллельно этой стрелке, смещал ее в сторону. Когда это происходило физик закручивал нить до тех пор, пока стрелка не возвращалась в исходное положение. Исходя из угла, на который закручивалась нить можно было судить о значении силы тока.
В результате нового эксперимента Ом пришел к формуле:
Х = a / b + lЗдесь X – интенсивность магнитного поля провода, l – длина провода, a – постоянная величина напряжения источника, b – постоянная сопротивления остальных элементов цепи.
Если обратиться к современным терминам для описания данной формулы, то мы получим, что Х – сила тока, а – ЭДС источника, b + l – общее сопротивление цепи .
Закон Ома для участка цепиЗакон Ома для отдельного участка цепи гласит: сила тока на участке цепи увеличивается при возрастании напряжения и уменьшается при возрастании сопротивления этого участка.
I = U / RИсходя из этой формулы, мы можем решить, что сопротивление проводника зависит от разности потенциалов. С точки зрения математики, это правильно, но ложно с точки зрения физики. Эта формула применима только для расчета сопротивления на отдельном участке цепи.
С точки зрения математики, это правильно, но ложно с точки зрения физики. Эта формула применима только для расчета сопротивления на отдельном участке цепи.
Таким образом формула для расчета сопротивления проводника примет вид:
R = p ⋅ l / s Закон Ома для полной цепиОтличие закона Ома для полной цепи от закона Ома для участка цепи заключается в том, что теперь мы должны учитывать два вида сопротивления. Это «R» сопротивление всех компонентов системы и «r» внутреннее сопротивление источника электродвижущей силы. Формула таким образом приобретает вид:
I = U / R + r Закон Ома для переменного токаПеременный ток отличается от постоянного тем, что он изменяется с определенными временными периодами. Конкретно он изменяет свое значение и направление. Чтобы применить закон Ома здесь нужно учитывать, что сопротивление в цепи с постоянным током может отличатся от сопротивления в цепи с током переменным. И отличается оно в том случае если в цепи применены компоненты с реактивным сопротивлением. Реактивное сопротивление может быть индуктивным (катушки, трансформаторы, дроссели) и емкостными (конденсатор).
Реактивное сопротивление может быть индуктивным (катушки, трансформаторы, дроссели) и емкостными (конденсатор).
Попробуем разобраться, в чем реальная разница между реактивным и активным сопротивлением в цепи с переменным током. Вы уже должны были понять, что значение напряжение и силы тока в такой цепи меняется со временем и имеют, грубо говоря, волновую форму.
Если мы схематически представим, как с течением времени меняются эти два значения, у нас получится синусоида. И напряжение, и сила тока от нуля поднимаются до максимального значения, затем, опускаясь, проходят через нулевое значение и достигают максимального отрицательного значения. После этого снова поднимаются через нуль до максимального значения и так далее. Когда говорится, что сила тока или напряжение имеет отрицательное значение, здесь имеется ввиду, что они движутся в обратном направлении.
Весь процесс происходит с определенной периодичностью. Та точка, где значение напряжения или силы тока из минимального значения поднимаясь к максимальному значению проходит через нуль называется фазой.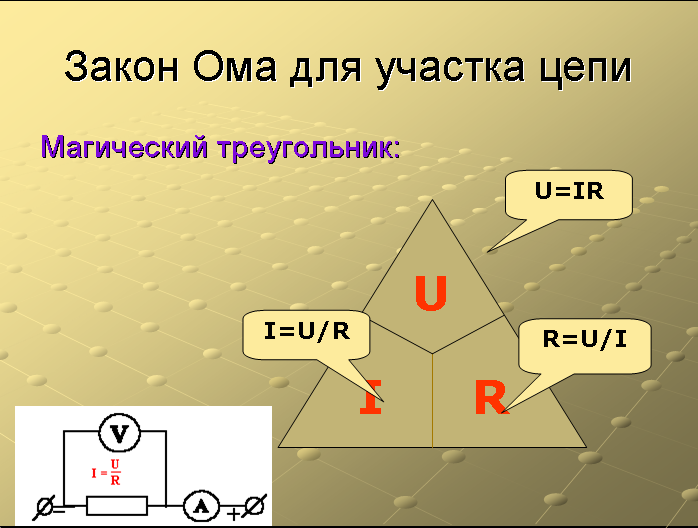
На самом деле, это только предисловие. Вернемся к реактивному и активному сопротивлению. Отличие в том, что в цепи с активным сопротивлением фаза тока совпадает с фазой напряжения. То есть, и значение силы тока, и значение напряжения достигают максимума в одном направлении одновременно. В таком случае наша формула для расчета напряжения, сопротивления или силы тока не меняется.
Если же цепь содержит реактивное сопротивление, фазы тока и напряжения сдвигаются друг от друга на ¼ периода. Это означает, что, когда сила тока достигнет максимального значения, напряжение будет равняться нулю и наоборот. Когда применяется индуктивное сопротивление, фаза напряжения «обгоняет» фазу тока. Когда применяется емкостное сопротивление, фаза тока «обгоняет» фазу напряжения.
Формула для расчета падения напряжения на индуктивном сопротивлении:
U = I ⋅ ωLГде L
– индуктивность реактивного сопротивления, а ω
– угловая частота (производная по времени от фазы колебания).
Формула для расчета падения напряжения на емкостном сопротивлении:
U = I / ω ⋅ С
С – емкость реактивного сопротивления.
Эти две формулы – частные случаи закона Ома для переменных цепей.
Полный же будет выглядеть следующем образом:
I = U / ZЗдесь Z – полное сопротивление переменной цепи известное как импеданс.
Сфера примененияЗакон Ома не является базовым законом в физике, это лишь удобная зависимость одних значений от других, которая подходит почти в любых ситуациях на практике. Поэтому проще будет перечислить ситуации, когда закон может не срабатывать:
- Если есть инерция носителей заряда, например, в некоторых высокочастотных электрических полях;
- В сверхпроводниках;
- Если провод нагревается до такой степени, что вольтамперная характеристика перестает быть линейной. Например, в лампах накаливания;
- В вакуумных и газовых радиолампах;
- В диодах и транзисторах.
Физический закон , определяющий связь (или электрического напряжения) с силой тока , протекающего в проводнике , и сопротивлением проводника. Установлен Георгом Омом в 1826 году и назван в его честь.
Закон Ома для переменного тока
Вышеприведённые соображения о свойствах электрической цепи при использовании источника (генератора) с переменной во времени ЭДС остаются справедливыми. Специальному рассмотрению подлежит лишь учёт специфических свойств потребителя, приводящих к разновремённости достижения напряжением и током своих максимальных значений, то есть учёта фазового сдвига .
Если ток является синусоидальным с циклической частотой ω {\displaystyle \omega } , а цепь содержит не только активные, но и реактивные компоненты (ёмкости , индуктивности), то закон Ома обобщается; величины, входящие в него, становятся комплексными:
U = I ⋅ Z {\displaystyle \mathbb {U} =\mathbb {I} \cdot Z}- U = U 0 e i ωt — напряжение или разность потенциалов,
- I — сила тока,
- Z = Re −i δ — комплексное сопротивление (электрический импеданс),
- R = √ R a 2 + R r 2 — полное сопротивление,
- R r = ωL − 1/(ωC ) — реактивное сопротивление (разность индуктивного и емкостного),
- R а — активное (омическое) сопротивление, не зависящее от частоты,
- δ = − arctg (R r
/R a
)
— сдвиг фаз между напряжением и силой тока.
 {i(\omega t+\varphi)},}
что
Im
U
=
U
.
{\displaystyle \operatorname {Im} \mathbb {U} =U.}
Тогда все значения токов и напряжений в схеме надо считать как
F
=
Im
F
{\displaystyle F=\operatorname {Im} \mathbb {F} }
{i(\omega t+\varphi)},}
что
Im
U
=
U
.
{\displaystyle \operatorname {Im} \mathbb {U} =U.}
Тогда все значения токов и напряжений в схеме надо считать как
F
=
Im
F
{\displaystyle F=\operatorname {Im} \mathbb {F} }
Отправить свою хорошую работу в базу знаний просто. Используйте форму, расположенную ниже
Студенты, аспиранты, молодые ученые, использующие базу знаний в своей учебе и работе, будут вам очень благодарны.
Размещено на http://www.allbest.ru/
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ
Кафедра естественнонаучных дисциплин
Реферат
Закон Ома
Выполнил:
Иванов М. А.
Введение
1. Общий вид закона Ома
2. История открытия закона Ома, краткая биография ученого
3. Виды законов Ома
4. Первые исследования сопротивления проводников
5. Электрические измерения
Заключение
Литература, другие источники информации
Введение
Явления, связанные с электричеством были замечены в древнем Китае, Индии и древней Греции за несколько столетий до начала нашей эры. Около 600 года до н.э., как гласят сохранившиеся предания, древнегреческому философу Фалесу Милетскому было известно свойство янтаря, натертого об шерсть, притягивать легкие предметы. Кстати словом “ электрон” древние греки называли янтарь. От него же пошло и слово “электричество”. Но греки всего лишь наблюдали явления электричества, но не могли объяснить.
XIX век был полон открытий связанных с электричеством. Одно открытие порождало целую цепь открытий в течении нескольких десятилетий. Электричество из предмета исследования начало превращаться в предмет потребления. Началось его широкое внедрение в различные области производства. Были изобретены и созданы электрические двигатели, генераторы, телефон, телеграф, радио. Начинается внедрение электричества в медицину.
Напряжение, сила тока и сопротивление — физические величины, характеризующие явления, происходящие в электрических цепях. Эти величины связаны между собой. Эту связь впервые изучил немецкий физик 0м. Закон Ома был открыт в 1826 .
1. Общий вид закона Ома
Закон Ома звучит так: Сила тока на участке цепи прямо пропорциональна напряжению на этом участке (при заданном сопротивлении) и обратно пропорциональна сопротивлению участка (при заданном напряжении): I = U / R, из формулы следует, что U = IЧR и R = U / I. Так как сопротивление данного проводника не зависит ни от напряжения, ни от силы тока, то последнюю формулу надо читать так: сопротивление данного проводника равно отношению напряжения на его концах к силе протекающего по нему тока. В электрических цепях чаще всего проводники (потребители электрической энергии) соединяются последовательно (например, лампочки в елочных гирляндах) и параллельно (например, домашние электроприборы).
При последовательном соединении сила тока в обоих проводниках (лампочках) одинакова: I = I1 = I2, напряжение на концах рассматриваемого участка цепи складывается из напряжения на первой и второй лампочках: U = U1 + U2. Общее сопротивление участка равно сумме сопротивлений лампочек R = R1 + R2.
При параллельном соединении резисторов напряжение на участке цепи и на концах резисторов одинаково: U = U1 = U2. сила тока в неразветвленной части цепи равна сумме сил токов в отдельных резисторах: I = I1 + I2. Общее сопротивление участка меньше сопротивления каждого резистора.
Если сопротивления резисторов одинаковы (R1 = R2) то общее сопротивление участка Если в цепь включено параллельно три и более резисторов, то общее сопротивление может быть —
найдено по формуле: 1/R = 1/R1 + 1/R2 + … + 1/RN. Параллельно соединяются сетевые потребители, которые рассчитаны на напряжение, равное напряжению сети.
Итак, Закон Ома устанавливает зависимость между силой тока I в проводнике и разностью потенциалов (напряжением) U между двумя фиксированными точками (сечениями) этого проводника:
Коэффициент пропорциональности R , зависящий от геометрических и электрических свойств проводника и от температуры, называется омическим сопротивлением или просто сопротивлением данного участка проводника.
2. История открытия закона Ома, краткая биография ученого
Георг Симон Ом родился 16 марта 1787 года в Эрлангене, в семье потомственного слесаря. После окончания школы Георг поступил в городскую гимназию. Гимназия Эрлангена курировалась университетом. Занятия в гимназии вели четыре профессора. Георг, закончив гимназию, весной 1805 года приступил к изучению математики, физики и философии на философском факультете Эрлангенского университета.
Проучившись три семестра, он принял приглашение занять место учителя математики в частной школе швейцарского городка Готтштадта.
В 1811 году он возвращается в Эрланген, заканчивает университет и получает степень доктора философии. Сразу же по окончании университета ему была предложена должность приват-доцента кафедры математики этого же университета.
В 1812 году Ом был назначен учителем математики и физики школы в Бамберге. В 1817 году он публикует свою первую печатную работу, посвященную методике преподавания «Наиболее оптимальный вариант преподавания геометрии в подготовительных классах». Ом занялся исследованиями электричества. В основу своего электроизмерительного прибора Ом заложил конструкцию крутильных весов Кулона. Результаты своих исследований Ом оформил в виде статьи под названием «Предварительное сообщение о законе, по которому металлы проводят контактное электричество». Статья была опубликована в 1825 году в «Журнале физики и химии», издаваемом Швейггером. Однако выражение, найденное и опубликованное Омом, оказалось неверным, что стало одной из причин его длительного непризнания. Приняв все меры предосторожности, заранее устранив все предполагаемые источники ошибок, Ом приступил к новым измерениям.
Появляется в свет его знаменитая статья «Определение закона, по которому металлы проводят контактное электричество, вместе с наброском теории вольтаического аппарата и мультипликатора Швейггера», вышедшая в 1826 году в «Журнале физики и химии».
В мае 1827 года «Теоретические исследования электрических цепей» объемом в 245 страниц, в которых содержались теперь уже теоретические рассуждения Ома по электрическим цепям. В этой работе ученый предложил характеризовать электрические свойства проводника его сопротивлением и ввел этот термин в научный обиход. Ом нашел более простую формулу для закона участка электрической цепи, не содержащего ЭДС: «Величина тока в гальванической цепи прямо пропорциональна сумме всех напряжений и обратно пропорциональна сумме приведенных длин. При этом общая приведенная длина определяется как сумма всех отдельных приведенных длин для однородных участков, имеющих различную проводимость и различное поперечное сечение».
В 1829 году появляется его статья «Экспериментальное исследование работы электромагнитного мультипликатора», в которой были заложены основы теории электроизмерительных приборов. Здесь же Ом предложил единицу сопротивления, в качестве которой он выбрал сопротивление медной проволоки длиной 1 фут и поперечным сечением в 1 квадратную линию.
В 1830 году появляется новое исследование Ома «Попытка создания приближенной теории униполярной проводимости». Только в 1841 году работа Ома была переведена на английский язык, в 1847 году — на итальянский, в 1860 году — на французский.
16 февраля 1833 года, через семь лет после выхода из печати статьи, в которой было опубликовано его открытие, Ому предложили место профессора физики во вновь организованной политехнической школе Нюрнберга. Ученый приступает к исследованиям в области акустики. Результаты своих акустических исследований Ом сформулировал в виде закона, получившего впоследствии название акустического закона Ома.
Раньше всех из зарубежных ученых закон Ома признали русские физики Ленц и Якоби. Они помогли и его международному признанию. При участии русских физиков, 5 мая 1842 года Лондонское Королевское общество наградило Ома золотой медалью и избрало своим членом.
В 1845 году его избирают действительным членом Баварской академии наук. В 1849 году ученого приглашают в Мюнхенский университет на должность экстраординарного профессора. В этом же году он назначается хранителем государственного собрания физико-математических приборов с одновременным чтением лекций по физике и математике. В 1852 году Ом получил должность ординарного профессора. Ом скончался 6 июля 1854 года. В 1881 году на электротехническом съезде в Париже ученые единогласно утвердили название единицы сопротивления — 1 Ом.
3. Виды законов Ома
Существует несколько видов закона Ома.
Закон Ома для однородного участка цепи (не содержащего источника тока): сила тока в проводнике прямо пропорциональна приложенному напряжению и обратно пропорциональна сопротивлению проводника:
Закон Ома для полной цепи — сила тока в цепи пропорциональна действующей в цепи ЭДС и обратно пропорциональна сумме сопротивлений цепи и внутреннего сопротивления источника.
где I — сила тока
E — электродвижущая сила
R — внешнее сопротивление цепи (т.е. сопротивление той
части цепи, которая находится за пределами источника ЭДС)
ЭДС — работа сторонних сил (т.е. сил неэлектрического происхождения) по перемещению заряда в цепи отнесенная к величине этого заряда.
Единицы измерения:
ЭДС — вольты
Ток — амперы
Сопротивления (R и r) — омы
Применяя основной закон электрической цепи (закон Ома), можно объяснить многие природные явления, которые на первый взгляд кажутся загадочными и парадоксальными. Например, всем известно, что любой контакт человека с электрическими проводами, находящимися под напряжением, является смертельно опасным. Всего лишь одно прикосновение к оборвавшемуся проводу высоковольтной линии способно убить электрическим током человека или животное. Но в то же время, мы постоянно видим, как птицы спокойно усаживаются на высоковольтные провода электропередач, и ничто не угрожает жизни этих живых существ. Тогда как же найти объяснение такому парадоксу?
А объясняется подобное явление довольно просто, если представить, что находящаяся на электрическом проводе птица — это один из участков электрической сети, сопротивление второго значительно превышает сопротивление другого участка той же цепи (то есть небольшого промежутка между лапками птицы). Следовательно, сила электрического тока, воздействующая на первый участок цепи, то есть на тело птицы, будет совершенно безопасной для неё. Однако полная безопасность гарантирована ей только при соприкосновении с участком высоковольтного провода. Но стоит только птице, усевшейся на линию электропередач, задеть крылом или клювом провод или какой-либо предмет, находящийся вблизи от провода (например, телеграфный столб), то птица неминуемо погибнет. Ведь столб непосредственно связан с землёй, и поток электрических зарядов, переходя на тело птицы, способен мгновенно убить её, стремительно двигаясь по направлению к земле. К сожалению, по этой причине в городах гибнет немало птиц.
Для защиты пернатых от губительного воздействия электричества зарубежными учеными были разработаны специальные устройства — насесты для птиц, изолированные от электрического тока. Такие приспособления размещали на высоковольтных линиях электропередач. Птицы, усаживаясь на изолированный насест, могут без всякого риска для жизни прикасаться клювом, крыльями или хвостом к проводам, столбам или кронштейнам. Наибольшим сопротивлением обладает поверхность верхнего, так называемого рогового слоя кожи человека. Сопротивление сухой и неповреждённой кожи может достигать 40 000 — 100 000 Ом. Роговой слой кожи очень незначителен, всего 0,05 — 0,2 мм. и легко пробивается напряжением 250 В. При этом сопротивление уменьшается в сто раз и падает тем скорее, чем дольше действует на тело человека ток. Резко, до 800 — 1000 Ом, уменьшают сопротивление тела человека повышенная потливость кожного покрова, переутомление, нервное возбуждение, опьянение. Этим объясняется, что порой даже небольшое напряжение может вызвать поражение электрическим током. Если, например, сопротивление тела человека равно 700 Ом, то опасным будет напряжение всего в 35 В. Именно поэтому, например, специалисты-электрики даже при работе с напряжением 36 В применяют изолирующие защитные средства — резиновые перчатки или инструмент с изолированными ручками.
Закон Ома выглядит настолько просто, что трудности, которые пришлось преодолеть при его установлении, упускают из виду и забывают. Закон Ома нелегко проверить, и его нельзя рассматривать как очевидную истину; действительно, для многих материалов он не выполняется.
В чем же все-таки заключаются эти трудности? Разве нельзя проверить, что дает изменение числа элементов вольтова столба, определяя ток при разном числе элементов?
Дело в том, что, когда мы берем разное число элементов, мы меняем всю цепь, т.к. дополнительные элементы имеют и дополнительное сопротивление. Поэтому необходимо найти способ изменять напряжение, не меняя самой батареи. Кроме того, разный по величине ток нагревает проволоку до развой температуры, и этот эффект тоже может влиять на силу тока. Ом (1787—1854) преодолел эти трудности, воспользовавшись явлением термоэлектричества, которое открыл Зеебек (1770—1831) в 1822 г.
Таким образом, Ом показал, что ток пропорционален напряжению и обратно пропорционален полному сопротивлению цепи. Это был простой результат для сложного эксперимента. Так по крайней мере должно казаться нам сейчас.
Современники Ома, в особенности его соотечественники, полагали иначе: возможно, именно простота закона Ома вызывала у них подозрение. Ом столкнулся с затруднениями в cлужебной карьере, испытывал нужду; особенно угнетало Ома то, что не признавались его труды. К чести Великобритании, и в особенности Королевского общества, нужно сказать, что работа Ома получила там заслуженное признание. Ом входит в число тех великих людей, имена которых часто встречаются написанными с маленькой буквы: название «ом» было присвоено единице сопротивления.
4. Первые исследования сопротивления проводников
Что такое проводник? Это чисто пассивная составная часть электрической цепи, отвечали первые исследователи. Заниматься его исследованием — значит попросту ломать себе голову над ненужными загадками, т.к. только источник тока представляет собой активный элемент.
Такой взгляд на вещи объясняет нам, почему ученые, по крайней мере до 1840 г., почти не проявляли интереса к тем немногим работам, которые проводились в этом направлении.
Так, на втором съезде итальянских ученых, состоявшемся в Турине в 1840 г. (первый собирался в Пизе в 1839 г. и приобрел даже некое политическое значение), выступая в прениях по докладу, представленному Марианини, Де ла Рив утверждал, что проводимость большинства жидкостей не является абсолютной, «а скорее относительной и изменяется с изменением силы тока». А ведь закон Ома был опубликован за 15 лет до этого!
Среди тех немногих ученых, которые первыми стали заниматься вопросом проводимости проводников после изобретения гальванометра, был Стефано Марианини (1790—1866).
К своему открытию он пришел случайно, изучая напряжение батарей. Он заметил, что с увеличением числа элементов вольтова столба электромагнитное воздействие на стрелку не увеличивается заметным образом. Это заставило Марианини сразу же подумать, что каждый вольтов элемент представляет собой препятствие для прохождения тока. Он делал опыты с парами «активными» и «неактивными» (т. е. состоящими из двух медных пластинок, разделенных влажной прокладкой) и опытным путем нашел отношение, в котором современный читатель узнает частный случай закона Ома, когда сопротивление внешней цепи не принимается во внимание, как это и было в опыте Марианини.
Георг Симон Ом (1789—1854) признавал заслуги Марианини, хотя его труды и не оказали Ому непосредственной помощи в работе. Ом вдохновлялся в своих исследованиях работой («Аналитическая теория тепла», Париж, 1822 г.) Жана Батиста Фурье (1768—1830)—одной из самых значительных научных работ всех времен, очень быстро получившей известность и высокую оценку среди математиков и физиков того времени. Ому пришла мысль, что механизм «теплового потока», о котором говорит Фурье, можно уподобить электрическому току в проводнике. И подобно тому как в теории Фурье тепловой поток между двумя телами или между двумя точками одного и того же тела объясняется разницей температур, точно так же Ом объясняет разницей «электроскопических сил» в двух точках проводника возникновение электрического тока между ними.
Придерживаясь такой аналогии, Ом начал свои экспериментальные исследования с определения относительных величин проводимости различных проводников. Применив метод, который стал теперь классическим, он подключал последовательно между двумя точками цепи тонкие проводники из различных материалов одинакового диаметра и изменял их длину так, чтобы получалась определенная величина тока. Первые результаты, которые ему удалось получить, сегодня кажутся довольно скромными. закон ом электрический гальванометр
Историки поражаются, например, тем, что по измерениям Ома серебро обладает меньшей проводимостью, чем медь и золото, и снисходительно принимают данное впоследствии самим Омом объяснение, согласно которому опыт проводился с серебряной проволокой, покрытой слоем масла, и это вводило в заблуждение относительно точного значения диаметра.
В то время имелось множество источников ошибок при проведении опытов (недостаточная чистота металлов, трудность калибровки проволоки, трудность точных измерений и т. п.). Важнейшим же источником ошибок была поляризация батарей. Постоянные (химические) элементы тогда еще не были известны, так что за время, необходимое для измерений, электродвижущая сила элемента существенно менялась. Именно эти причины, вызывавшие ошибки, привели к тому, что Ом на основании своих опытов пришел к логарифмическому закону зависимости силы тока от сопротивления проводника, включенного между двумя точками цепи. После опубликования первой статьи Ома Поггендорф посоветовал ему отказаться от химических элементов и воспользоваться лучше термопарой медь — висмут, незадолго до этого введенной Зеебеком.
Ом прислушался к этому совету и повторил свои опыты, собрав установку с термоэлектрической батареей, во внешнюю цепь которой включались последовательно восемь медных проволок одинакового диаметра, но разной длины. Силу тока он измерял с помощью своего рода крутильных весов, образуемых магнитной стрелкой, подвешенной на металлической нити. Когда ток, параллельный стрелке, отклонял ее, Ом закручивал нить, на которой она была подвешена, пока стрелка не оказывалась в своем обычном положении;
сила тока считалась пропорциональной углу, на который закручивалась нить. Ом пришел к выводу, что результаты опытов, проведенных с восемью различными проволоками, «могут быть выражены очень хорошо уравнением
где X означает интенсивность магнитного действия проводника, длина которого равна х, а а и b — константы, зависящие соответственно от возбуждающей силы и от сопротивления остальных частей цепи».
Условия опыта менялись: заменялись сопротивления и термоэлектрические пары, но результаты все равно сводились к приведенной выше формуле, которая очень просто переходит в известную нам, если X заменить силой тока, a —электродвижущей силой и b+x,—общим сопротивлением цепи.
Получив эту формулу, Ом пользуется ею для изучения действия мультипликатора Швейггера на отклонение стрелки и для изучения тока, который проходит во внешней цепи батареи элементов, в зависимости от того, как они соединены — последовательно или параллельно. Таким образом он объясняет (как это делается теперь в учебниках), чем определяется внешний ток батареи,— вопрос, который был довольно темным для первых исследователей. Ом надеялся, что его экспериментальные работы откроют ему путь в университет, чего он так желал. Однако статьи прошли незамеченными. Тогда он оставил место преподавателя в кельнской гимназии и отправился в Берлин, чтобы теоретически осмыслить полученные результаты. В 1827 г. в Берлине он опубликовал свой главный труд «Die galvanische Kette, mathe-matisch bearbeitet» («Гальваническая цепь, разработанная математически»).
Эта теория, при разработке которой он вдохновлялся, как мы уже указывали, аналитической теорией теплоты Фурье, вводит понятия и точные определения электродвижущей силы, или «электроскопической силы», как ее называет Ом, электропроводности (Starke der Leitung) и силы тока. Выразив выведенный им закон в дифференциальной форме, приводимой современными авторами, Ом записывает его и в конечных величинах для частных случаев конкретных электрических цепей, из которых особенно важна термоэлектрическая цепь. Исходя из этого, он формулирует известные законы изменения электрического напряжения вдоль цепи.
Но теоретические исследования Ома также остались незамеченными, а если кто-нибудь и писал о них, то лишь для того, чтобы, высмеять «болезненную фантазию, единственной целью которой является стремление принизить достоинство природы». И лишь лет десять спустя его гениальные работы постепенно начали пользоваться должным признанием: в
Германии их оценили Поггендорф и Фехнер, в России — Ленц, в Англии — Уитстон, в Америке — Генри, в Италии — Маттеуччи.
Одновременно с опытами Ома во Франции проводил свои опыты А. Беккерель, а в Англии — Барлоу. Опыты первого особенно замечательны введением дифференциального гальванометра с двойной обмоткой рамки и применением «нулевого» метода измерения. Опыты же Барлоу стоит упомянуть потому, что они экспериментально подтвердили постоянство силы тока во всей цепи. Этот вывод был проверен и распространен на внутренний ток батареи Фехнером в 1831 г., обобщен в 1851 г. Рудольфом Кольраушем
(180Э—1858) на жидкие проводники, а затем еще раз подтвержден тщательными опытами Густава Нидмана (1826—1899).
5. Электрические измерения
Беккерель применил дифференциальный гальванометр для сравнения электрических сопротивлений. На основе проведенных им исследований он сформулировал известный закон зависимости сопротивления проводника от его длины и сечения. Эти работы были продолжены Пуйе и описаны им в последующих изданиях его известных «Elements de
physique experimentale» («Основы экспериментальной физики»), первое издание которых появилось в 1827 г. Сопротивления определялись методом сравнения.
Уже в 1825 г. Марианини показал, что в разветвляющихся цепях электрический ток распределяется по всем проводникам независимо от того, из какого материала они сделаны, вопреки утверждению Вольты, который полагал, что если одна ветвь цепи образуется металлическим проводником, а остальные — жидкими, то весь ток должен проходить по металлическому проводнику. Араго и Пуйе популяризировали во Франции наблюдения Марианини. Не зная еще закона Ома, Пуйе в 1837 г. воспользовался этими наблюдениями и законами Беккереля, чтобы показать, что проводимость цепи, эквивалентной двум
разветвленным цепям, равна сумме проводимостей обеих цепей. Этой работой Пуйе положил начало изучению разветвленных цепей. Пуйе установил для них целый ряд терминов,
которые живы и до сих пор, и некоторые частные законы, обобщенные Кирхгофом в 1845 г. в его известных «принципах»..
Самый большой толчок для проведения электрических измерений, и в частности измерений сопротивления, был дан возросшими потребностями техники, и в первую очередь проблемами, возникшими с появлением электрического телеграфа. Впервые мысль об использовании электричества для передачи сигналов на расстояние родилась еще в XVIII веке. Вольта описал проект телеграфа, а Ампер еще в 1820 г. предлагал использовать электромагнитные явления для передачи сигналов. Идея Ампера была подхвачена многими учеными и техниками: в 1833 г. Гаусс и Вебер построили в Геттингене простейшую телеграфную линию, соединявшую астрономическую обсерваторию и физическую лабораторию. Но практическое применение телеграф получил благодаря американцу Самуэлу Морзе (1791—1872), которому в 1832 г. пришла удачная мысль создать телеграфный алфавит, состоящий всего из двух знаков. После многочисленных попыток Морзе в 1835 г. наконец удалось построить частным образом первую грубую модель телеграфа в Нью-Йоркском университете. В 1839 г. была проведена экспериментальная
линия между Вашингтоном и Балтиморой, а в 1844 г. возникла организованная Морзе первая американская компания по коммерческой эксплуатации нового изобретения. Это было также первое практическое применение результатов научных изысканий в области электричества.
В Англии изучением и усовершенствованием телеграфа занялся Чарльз Уитстон (1802—1875), бывший мастер по изготовлению музыкальных инструментов. Понимая важность
измерений сопротивления, Уитстон стал искать наиболее простые и точные методы таких измерений. Бывший в то время в ходу метод сравнения, как мы видели, давал ненадежные результаты, главным образом из-за отсутствия стабильных источников питания. Уже в 1840 г. Уитстон нашел способ измерения сопротивления независимо от постоянства электродвижущей силы и показал свое устройство Якоби. Однако статья, в которой это устройство описано и которую вполне можно назвать первой работой в области электротехники, появилась лишь в 1843 г. В этой статье дано описание знаменитого «мостика», названного затем в честь Уитстона. Фактически такое устройство было описано —
еще в 1833 г. Гюнтером Кристи и независимо от него в 1840 г. Марианини; оба они предлагали метод сведения к нулю, но их теоретические объяснения, при которых не учитывался закон Ома, оставляли желать лучшего.
Уитстон же был поклонником Ома и очень хорошо знал его закон, так что данная им теория «мостика Уитстона» ничем не отличается от приводимой сейчас в учебниках. Кроме того, Уитстон, чтобы можно было быстро и удобно изменять сопротивление одной стороны мостика для получения нулевой силы тока в гальванометре, включенном в диагональное плечо мостика, сконструировал три типа реостатов (само это слово было предложено им по
аналогии с «реофором», введенным Ампером, в подражание которому Пекле ввел также термин «реометр»). Первый тип реостата с подвижной скобкой, применяемый и сейчас, был создан Уитстоном по аналогии со схожим приспособлением, применявшимся Якоби в 1841 г. Второй тип реостата имел вид деревянного цилиндра, вокруг которого была намотана часть подключенного в цепь провода, который легко перематывался с деревянного цилиндра на бронзовый. Третий тип реостата был похож на «магазин сопротивлений», который Эрнст
Вернер Сименс (1816—1892), ученый и промышленник, в 1860 г. улучшил и широко распространил. «Мостик Уитстона» дал возможность измерять электродвижущие силы и сопротивления.
Создание подводного телеграфа, пожалуй, еще более, нежели воздушного телеграфа, потребовало разработки методов электрических измерений. Опыты с подводным телеграфом начались еще в 1837 г., и одной из первых проблем, которую предстояло разрешить, было определение скорости распространения тока. Еще в 1834 г. Уитстон с помощью вращающихся зеркал, о чем мы уже упоминали в гл. 8, произвел первые измерения этой скорости, но полученные им результаты противоречили результатам Латимера Кларка, а последние в свою очередь не соответствовали более поздним исследованиям других ученых.
В 1855 г. Уильям Томсон (получивший впоследствии титул лорда Кельвина) объяснил причину всех этих расхождений. Согласно Томсону, скорость тока в проводнике не имеет определенной величины. Подобно тому как скорость распространения тепла в стержне зависит от материала, так и скорость тока в проводнике зависит от произведения его сопротивления на электрическую емкость. Следуя этой своей теории, которая в»»его времена
подверглась ожесточенной критике, Томсон занялся проблемами, связанными с подводным телеграфом.
Первый трансатлантический кабель, соединивший Англию и Америку, функционировал около месяца, но затем испортился. Томсон рассчитал новый кабель, провел многочисленные измерения сопротивления и емкости, придумал новые передающие аппараты, из коих следует упомянуть астатический отражательный гальванометр, замененный «сифонным регистратором» его же изобретения. Наконец, в 1866 г. новый трансатлантический кабель успешно вступил в действие. Созданию этого первого большого электротехнического сооружения сопутствовала разработка системы единиц электрических и магнитных измерений.
Основа электромагнитной метрики была заложена Карлом Фридрихом Гауссом (1777—1855) в его знаменитой статье «Intensitas vis magneticae terrestris ad mensuram absolutam revocata» («Величина силы земного магнетизма в абсолютных мерах»), опубликованной в 1832 г. Гаусс заметил, что различные магнитные единицы измерения несоотносимы между
собой, по крайней мере в большей своей части, и поэтому предложил систему абсолютных единиц, основанную на трех основных единицах механики: секунде (единице времени), миллиметре (единице длины) и миллиграмме (единице массы). Через них он выразил все остальные физические единицы и придумал ряд измерительных приборов, в частности магнетометр для измерения в абсолютных единицах земного магнетизма. Работу Гаусса продолжил Вебер, который построил много собственных приборов и приборов, задуманных еще Гауссом. Постепенно, особенно благодаря работам Максвелла, проводившимся в созданной Британской ассоциацией специальной комиссии по измерениям, которая издавала ежегодные отчеты с 1861 по 1867 г., возникла идея создать единые системы мер, в частности систему электромагнитных и электростатических мер.
Мысли о создании таких абсолютных систем единиц были подробно изложены в историческом отчете за 1873 г. второй комиссии Британской ассоциации. Созванный в Париже в 1881 г. Международный конгресс впервые установил международные единицы измерения, присвоив каждой из них название в честь какого-нибудь великого физика. Большая часть этих названий сохраняется до сих пор: вольт, ом, ампер, джоуль и т. д. После
многих перипетий в 1935 г. была введена международная система Джорджи, или MKSQ, которая принимает за основные единицы метр, килограмм-массу, секунду и ом.
С «системами» единиц связаны «формулы размерностей», примененные впервые Фурье в его аналитической теории тепла (1822 г.) и распространенные Максвеллом, которым и установлены применяемые в них обозначения. Метрология прошлого века, основывавшаяся на стремлении объяснить все явления с помощью механических моделей, придавала большое значение формулам размерностей, в которых она хотела видеть не больше и не меньше как ключ к тайнам природы. При этом выдвигался ряд утверждений почти догматического характера. Так, чуть ли не обязательным догматом было требование, чтобы основных величин было непременно три. Но к концу века начали понимать, что формулы размерностей — это чистая условность, вследствие чего интерес к теориям размерностей стал постепенно падать.
Заключение
О значении исследований Ома хорошо сказал профессор физики Мюнхенского университета Е. Ломмель при открытии памятника ученому в 1895 году:
«Открытие Ома было ярким факелом, осветившим ту область электричества, которая до него была окутана мраком. Ом указал единственно правильный путь через непроходимый лес непонятных фактов. Замечательные успехи в развитии электротехники, за которыми мы с удивлением наблюдали в последние десятилетия, могли быть достигнуты только на основе открытия Ома. Лишь тот в состоянии господствовать над силами природы и управлять ими, кто сумеет разгадать законы природы, Ом вырвал у природы так долго скрываемую ею тайну и передал ее в руки современников».
Список используемых источников
Дорфман Я. Г. Всемирная история физики . М., 1979 Ом Г. Определение закона, по которому металлы проводят контактное электричество. — В кн.: Классики физической науки. М., 1989
Энциклопедия Сто человек. Которые изменили мир. Ом.
Прохоров А. М. Физический энциклопедический словарь, М., 1983
Орир Дж. Физика , т. 2. М., 1981
Джанколи Д. Физика , т. 2. М., 1989
http://www.portal-slovo.ru/
http://www.polarcom.ru/~vvtsv/s_doc9c.html)
Размещено на Allbest.ru
Подобные документы
История открытия Исааком Ньютоном «Закона всемирного тяготения», события, предшествующие данному открытию. Суть и границы применения закона. Формулировка законов Кеплера и их применение к движению планет, их естественных и искусственных спутников.
презентация , добавлен 25.07.2010
Изучение движения тела под действием постоянной силы. Уравнение гармонического осциллятора. Описание колебания математического маятника. Движение планет вокруг Солнца. Решение дифференциального уравнения. Применение закона Кеплера, второго закона Ньютона.
реферат , добавлен 24.08.2015
История открытия закона всемирного тяготения. Иоган Кеплер как один из первооткрывателей закона движения планет вокруг солнца. Сущность и особенности эксперимента Кавендиша. Анализ теории силы взаимного притяжения. Основные границы применимости закона.
презентация , добавлен 29.03.2011
Изучение «Закона Архимеда», проведение опытов по определению архимедовой силы. Вывод формул для нахождения массы вытесненной жидкости и расчета плотности. Применение «Закона Архимеда» для жидкостей и газов. Методическая разработка урока по данной теме.
конспект урока , добавлен 27.09.2010
Биографические сведения о Ньютоне — великом английском физике, математике и астрономе, его труды. Исследования и открытия ученого, эксперименты по оптике и теории цвета. Первый вывод Ньютоном скорости звука в газе, основанный на законе Бойля-Мариотта.
презентация , добавлен 26.08.2015
Изучение причины магнитной аномалии. Методы определения горизонтальной составляющей напряженности магнитного поля Земли. Применение закона Био-Савара-Лапласа. Определение причины поворота стрелки после подачи напряжения на катушку тангенс–гальванометра.
контрольная работа , добавлен 25.06.2015
Описание основных законов Ньютона. Характеристика первого закона о сохранении телом состояния покоя или равномерного движения при скомпенсированных действиях на него других тел. Принципы закона ускорения тела. Особенности инерционных систем отсчета.
презентация , добавлен 16.12.2014
Законы движения планет Кеплера, их краткая характеристика. История открытия Закона всемирного тяготения И. Ньютоном. Попытки создания модели Вселенной. Движение тел под действием силы тяжести. Гравитационные силы притяжения. Искусственные спутники Земли.
реферат , добавлен 25.07.2010
Проверка справедливости соотношений при параллельном соединении резисторов и первого закона Кирхгофа. Особенности сопротивления приемников. Методика расчета напряжения и тока для различных соединений. Сущность закона Ома для участка и для всей цепи.
лабораторная работа , добавлен 12.01.2010
Фундаментальные взаимодействия в природе. Взаимодействие электрических зарядов. Свойства электрического заряда. Закон сохранения электрического заряда. Формулировка закона Кулона. Векторная форма и физический смысл закона Кулона. Принцип суперпозиции.
Закон Ома является одним из основных законов электротехники. Он довольно прост и применяется при расчете практически любых электрических цепей. Но данный закон имеет некоторые особенности работы в цепях переменного и постоянного тока при наличии в цепи реактивных элементов. Эти особенности нужно помнить всегда.
Классическая схема закона Ома выглядит так:
А звучит и того проще – ток, протекающей на участке цепи, будет равен отношению напряжения цепи к ее сопротивлению, что выражается формулой:
Но ведь мы знаем, что помимо активного сопротивления R, существует и реактивные сопротивления индуктивности Х L и емкости X C . А ведь согласитесь, что электрические схемы с чисто активным сопротивлением встречаются крайне редко. Давайте рассмотрим схему, в которой последовательно включена катушка индуктивности L, конденсатор С и резистор R:
Помимо чисто активного сопротивления R, индуктивность L и емкость С имеют и реактивные сопротивления Х L и X C , которые выражены формулами:
Где ω это циклическая частота сети, равная ω = 2πf. f – частота сети в Гц.
Для постоянного тока частота равна нулю (f = 0), соответственно реактивное сопротивление индуктивности станет равным нулю (формула (1)), а емкости – бесконечности (2), что приведет к разрыву электрической цепи. Отсюда можно сделать вывод, что реактивное сопротивление элементов в цепях постоянного напряжения отсутствует.
Если рассматривать классическую электрическую цепь и на переменном токе, то она практически ничем не будет отличаться от постоянного тока, только источником напряжения (вместо постоянного — переменное):
Соответственно и формула для такого контура останется прежней:
Но если мы усложним схему и добавим к ней реактивных элементов:
Ситуация изменится кардинально. Теперь f у нас не равна нулю, что сигнализирует о том, что помимо активного, в цепь вводится и реактивное сопротивление, которое также может влиять на величину тока, протекаемого в контуре и . Теперь полное сопротивление контура (обозначается как Z) и оно не равно активному Z ≠ R. Формула примет следующий вид:
Соответственно немного изменится и формула для закона Ома:
Почему это важно?
Знание этих нюансов позволит избежать серьезных проблем, которые могут возникнуть при неправильном подходе к решению некоторых электротехнических задач. Например, в контур переменного напряжения подключена катушка индуктивности со следующими параметрами: f ном = 50 Гц, U ном = 220 В, R = 0,01 Ома, L = 0,03 Гн. Ток, протекающий через данную катушку будет равен.
Почему закон Ома не работает для этой простой схемы?
У меня есть 70W 12V-500V DC преобразователь питания, и что-то на этих фотографиях не складывается.
Я запускаю выход 500 В через высоковольтный резистор 332 кОм .
Теперь, используя левый мультиметр, я отслеживаю ток через цепь, и он работает около 320 мА. Используя правый мультиметр, я сначала проверяю напряжение на проводах блока питания: 511В. (Так что сразу мы знаем, что что-то не так — запас даже не нагревается после нескольких минут тестирования.)
Затем я использую правильный мультиметр, чтобы проверить напряжение на резисторе: 12В!
Я проверил значение резистора с обоими метрами. Если все это верно, то закон Ома предполагает, что либо напряжение на резисторе должно быть 0,320 мА * 332 кОм = 106 кВ, либо ток через цепь должен быть 511 В / 332 кОм = 1,5 мА.
(Конечно, сам правильный мультиметр обеспечивает путь для тока, но его сопротивление должно быть очень высоким. Действительно: когда я удаляю правильный мультиметр из цепи, ток увеличивается только на 2-3 мА.)
Мое лучшее предположение состоит в том, что выходной сигнал преобразователя не очень плавный, или имеет некоторую характеристику, которая приводит к тому, что эти мультиметры дают ошибочные значения. Если да, то, что это может быть характерно, и как я могу приспособиться к нему?
Кстати, вот крупный план преобразователя постоянного тока. Возможно, дизайн будет кому-то знаком.
И в случае, если проводка не ясно из фотографий, вот как это было связано
смоделировать эту схему — схема, созданная с использованием CircuitLab
А вот еще немного информации. Во-первых, чтобы устранить все сомнения, вот после этого измеряется резистор , поэтому он, похоже, не зажегся.
А вот и весь Шебанг. Если амперметру на источнике постоянного тока можно доверять, и этот преобразователь питания не способен вырабатывать энергию из воздуха, то истинный ток цепи составляет менее 3,6 мА. (Это согласуется с тем фактом, что я не наблюдал накопления тепла ни на одном компоненте.) В этом случае возникает вопрос: почему значение Extech составляет ~ 320 мА? Если я переключаю Extech на шкалу µA, это показывает около 3180 (все еще не правильно). Другой мультиметр показывает 0А на всех шкалах, что соответствует падению напряжения на резисторе (что подразумевает истинный ток 36 мкА).
Эпилог: Я открыл мультиметр Extech, чтобы найти его перегоревший предохранитель на 250 мА. Замена на то, что заставило его вести себя нормально. Очевидно, это просто сбивает с толку режим сбоя!
ЗАКОН ОМА ДЛЯ ЗАМКНУТОЙ ЦЕПИ (ф 11)
ЗАКОН ОМА ДЛЯ ЗАМКНУТОЙ ЦЕПИ. (ф 11)
УЭ – 1 Цель: Восприятие и первичное осознание нового материала: ЭДС. Направление тока во внешней цепи. Закон Ома для замкнутой цепи. Сила тока короткого замыкания.
УЭ – 2 Входной контроль (письменно в тетради для контрольных работ)
1 ВАРИАНТ: 1. Что называется электрическим током?
2. Что называют силой тока?
3. Закон Ома для участка цепи
2 ВАРИАНТ: 1. Условия существования электрического тока
2. Формула силы тока
3. Что называют падением напряжения?
Отметка «5» — 3 «4» — 2 «3» — 1
УЭ – 3 ОСУМ
Гальванический элемент – источник постоянного тока, состоит из медной и цинковой пластин, помещённых в раствор серной кислоты (рис. 35 стр. 36 Касьянов В.А.)
ε
– +
A r В
I ↑
R
Направление тока во внешней цепи АВ от плюса к минусу источника тока с внутренним сопротивлением r (эр) и ЭДС – ε
Физическая величина, равная отношению работы сторонних (не кулоновских) сил при перемещении единичного положительного заряда q (ку) от отрицательного полюса источника тока к положительному к величине этого заряда, называется электродвижущей силой источника (ЭДС).
АСТ
ε = ———-
q
Где ε – электродвижущая сила, В (Вольт)
АСТ – сторонние силы (химические, механические, Дж)
q (ку) – заряд, Кл (Кулон)
Напряжение (разность потенциалов) на участке цепи, содержащем источник тока, определяется формулой: U = ε – I · r
Где U(у) – напряжение, В (Вольт)
I – сила тока, А (Ампер)
r (эр) – внутреннее сопротивление источника тока, Ом
Сила тока в полной цепи равна отношению ЭДС цепи к ей полному сопротивлению. ε
I = ———- Закон Ома для полной цепи
R + r
Отсюда: ε = IR + Ir
ЭДС равна сумме падений напряжений на внешнем IR и внутреннем Ir участках замкнутой цепи. ε
При коротком замыкании когда R → 0, тогда IК.З. = ——
r
Сила тока при коротком замыкании возрастает в 1000 раз, что приводит к пожару.
УЭ – 4 Закрепление ОСУМ
ЗАДАЧА: к источнику тока с ε = 12 В и r = 1 Ом подключили резистор R = 9 Ом. Найти разность потенциалов φ1 – φ2 = U между полюсами источника: а) при разомкнутой цепи б) при замкнутой цепи
φ1 – φ2 = ? Решение:
а) φ1 – φ2 = ε = 12 В
ε = 12 В ε 12 B
r = 1 Ом б) I = ———- = ———- = 1,2 А
R = 9 Ом R + r 10 Ом
φ1 – φ2 = ε – I · r = 12 В – 1,2 А · 1 Ом = 10,8 В
Ответы: а) φ1 – φ2 = 12 В б) φ1 – φ2 = 10,8 В
УЭ – 5 Разноуровневая самостоятельная работа № 26 «Закон Ома для полной цепи»
Начальный уровень
1. Какое из приведенных ниже выражений характеризует силу тока в полной цепи? Выберите правильный ответ.
l ε
А. U / R Б. ρ · —- В. ———
S R + r
2. Как называется физическая величина, характеризующая работу сторонних сил по разделению заряда 1 Кл внутри источника тока? Выберите правильный ответ.
А. напряжение Б. сила тока В. электродвижущая сила
3. Какое из приведённых ниже выражений характеризует работу сторонних сил по перемещению заряда внутри источника тока? Выберите правильный ответ.
А. ε q Б. I ∆t В. U / R
4. Какая физическая величина определяется отношением ЭДС в цепи к полному сопротивлению этой цепи? Выберите правильный ответ.
А. напряжение Б. работа электрического тока В. сила тока
5. Какая физическая величина определяется отношением работы, совершаемой сторонними силами при перемещении заряда q по всей замкнутой электрической цепи, к значению этого заряда? Выберите правильный ответ.
А. сила тока Б. электродвижущая сила В. напряжение
6. Режим короткого замыкания в цепи возникает, когда….. Выберите правильное утверждение.
А. внутреннее сопротивление источника тока очень мало
Б. внешнее сопротивление цепи R → 0
В. внешнее сопротивление цепи R → ∞
Средний уровень
1. Аккумулятор мотоцикла имеет ЭДС 6 В и внутреннее сопротивление 0,5 Ом. К нему подключён реостат сопротивлением 5,5 Ом. Найдите силу тока в реостате.
2. ЭДС батарейки карманного фонарика равна 3,7 В, внутреннее сопротивление 1,5 Ом. Батарейка замкнута на сопротивление 11,7 Ом. Каково напряжение на зажимах батарейки?
3. К источнику с ЭДС 12 В и внутренним сопротивлением 1 Ом подключён реостат, сопротивление которого 5 Ом. Найти силу тока в цепи и напряжение на зажимах источника.
4. ЭДС батареи 6 В. Внешнее сопротивление цепи равно 11,5 Ом, а внутреннее – 0,5 Ом. Найти силу тока в цепи и напряжение на зажимах батареи.
Достаточный уровень
1. Определите силу тока при коротком замыкании батарейки с ЭДС 9 В, если при замыкании её на внешнее сопротивление 3 Ом ток в цепи равен 2 А.
2. Источник тока с ЭДС 2 В и внутренним сопротивлением 0,8 Ом замкнут никелиновой проволокой длиной 2,1 м и сечением 0,21 мм2. Определите напряжение на зажимах источника тока.
Отметка «5» 9 – 10 баллов «4» 7 – 8 баллов «3» 5 – 6 баллов
УЭ – 6 Разноуровневое домашнее задание
1 уровень § 11 стр. 35 – 38 до…..замкнутая цепь……. и модуль
2 уровень § 11 вопросы 1 – 5 стр. 40
3 уровень § 11 № 1 – 3 стр. 40
Желающим прочитать § 12, 13
УЭ – 7 Рефлексия. Получили ли удовлетворение собственных познавательных интересов?
ЗаконОма — Университетская физика, том 2
Цели обучения
К концу этого раздела вы сможете:
- Опишите закон Ома
- Распознавать, когда применяется закон Ома, а когда нет.
До сих пор в этой главе мы обсуждали три электрических свойства: ток, напряжение и сопротивление. Оказывается, что многие материалы демонстрируют простую взаимосвязь между значениями этих свойств, известную как закон Ома.Многие другие материалы не демонстрируют эту взаимосвязь, поэтому, несмотря на то, что они называются законом Ома, они не считаются законом природы, как законы Ньютона или законы термодинамики. Но это очень полезно для расчетов с материалами, которые подчиняются закону Ома.
Описание закона Ома
Ток, протекающий через большинство веществ, прямо пропорционален приложенному к нему напряжению В, . Немецкий физик Георг Симон Ом (1787–1854) первым экспериментально продемонстрировал, что ток в металлической проволоке прямо пропорционален приложенному напряжению :
.Это важное соотношение лежит в основе закона Ома.Его можно рассматривать как причинно-следственную связь, в которой напряжение является причиной, а ток — следствием. Это эмпирический закон, который означает, что это экспериментально наблюдаемое явление, подобное трению. Такая линейная зависимость возникает не всегда. Любой материал, компонент или устройство, подчиняющееся закону Ома, где ток, протекающий через устройство, пропорционален приложенному напряжению, известен как омический материал или омический компонент. Любой материал или компонент, который не подчиняется закону Ома, известен как неомический материал или неомный компонент.
Эксперимент Ома
В статье, опубликованной в 1827 году, Георг Ом описал эксперимент, в котором он измерял напряжение и ток через различные простые электрические цепи, содержащие провода различной длины. Аналогичный эксперимент показан на (Рисунок). Этот эксперимент используется для наблюдения за током через резистор, возникающим в результате приложенного напряжения. В этой простой схеме резистор включен последовательно с батареей. Напряжение измеряется вольтметром, который необходимо разместить на резисторе (параллельно резистору).Ток измеряется амперметром, который должен быть на одной линии с резистором (последовательно с резистором).
Экспериментальная установка, используемая для определения того, является ли резистор омическим или неомическим устройством. (а) Когда батарея подключена, ток течет по часовой стрелке, а вольтметр и амперметр показывают положительные значения. (b) Когда выводы батареи переключаются, ток течет против часовой стрелки, а вольтметр и амперметр показывают отрицательные показания.
В этой обновленной версии оригинального эксперимента Ома было выполнено несколько измерений тока для нескольких различных напряжений. Когда батарея была подключена, как показано на (Рисунок) (а), ток протекал по часовой стрелке, и показания вольтметра и амперметра были положительными. Изменится ли поведение тока, если ток течет в обратном направлении? Чтобы заставить ток течь в обратном направлении, выводы батареи можно переключить.При переключении выводов батареи показания вольтметра и амперметра были отрицательными, поскольку ток протекал в обратном направлении, в данном случае против часовой стрелки. Результаты аналогичного эксперимента показаны на (Рисунок).
Резистор вставлен в цепь с батареей. Приложенное напряжение изменяется от -10,00 В до +10,00 В с шагом 1,00 В. На графике показаны значения напряжения в зависимости от тока, типичные для случайного экспериментатора.
В этом эксперименте напряжение, приложенное к резистору, изменяется от -10,00 до +10,00 В с шагом 1,00 В. Измеряются ток через резистор и напряжение на резисторе. Построен график зависимости напряжения от тока, и результат будет приблизительно линейным. Наклон линии — это сопротивление или напряжение, деленное на ток. Этот результат известен как закон Ома:
, где В, — напряжение, измеренное в вольтах на рассматриваемом объекте, I — ток, измеренный через объект в амперах, а R — сопротивление в единицах Ом.Как указывалось ранее, любое устройство, которое показывает линейную зависимость между напряжением и током, известно как омическое устройство. Следовательно, резистор — это омическое устройство.
Проверьте свое понимание Напряжение, подаваемое в ваш дом, изменяется как. Если к этому напряжению подключить резистор, будет ли действовать закон Ома?
Да, закон Ома все еще в силе. В каждый момент времени ток равен, поэтому ток также является функцией времени.
Неомические устройства не показывают линейной зависимости между напряжением и током.Одним из таких устройств является элемент полупроводниковой схемы, известный как диод. Диод — это схемное устройство, которое позволяет току течь только в одном направлении. Схема простой схемы, состоящей из батареи, диода и резистора, показана на (рисунок). Хотя мы не рассматриваем теорию диода в этом разделе, диод можно протестировать, чтобы определить, является ли он омическим или неомическим устройством.
Диод — это полупроводниковое устройство, которое пропускает ток, только если диод смещен в прямом направлении, что означает, что анод положительный, а катод отрицательный.
График зависимости тока от напряжения показан на (Рисунок). Обратите внимание, что поведение диода показано как зависимость тока от напряжения, тогда как работа резистора показана как зависимость напряжения от тока. Диод состоит из анода и катода. Когда анод находится под отрицательным потенциалом, а катод — под положительным потенциалом, как показано в части (а), говорят, что диод имеет обратное смещение. При обратном смещении диод имеет чрезвычайно большое сопротивление, и через диод и резистор протекает очень небольшой ток — практически нулевой ток.По мере увеличения напряжения, приложенного к цепи, ток остается практически нулевым, пока напряжение не достигнет напряжения пробоя и диод не будет проводить ток, как показано на (Рисунок). Когда аккумулятор и потенциал на диоде меняются местами, что делает анод положительным, а катод отрицательным, диод проводит, и ток течет через диод, если напряжение больше 0,7 В. Сопротивление диода близко к нулю. (Это причина наличия резистора в цепи; если бы его не было, ток стал бы очень большим.) Из графика на (Рисунок) видно, что напряжение и ток не имеют линейной зависимости. Таким образом, диод является примером безомного устройства.
Когда напряжение на диоде отрицательное и небольшое, через диод протекает очень небольшой ток. Когда напряжение достигает напряжения пробоя, диод проводит. Когда напряжение на диоде положительное и превышает 0,7 В (фактическое значение напряжения зависит от диода), диод проводит. По мере увеличения приложенного напряжения ток через диод увеличивается, но напряжение на диоде остается приблизительно равным 0.7 В.
Закон Ома обычно формулируется как, но первоначально он был сформулирован как микроскопическое изображение с точки зрения плотности тока, проводимости и электрического поля. Этот микроскопический взгляд предполагает, что пропорциональность обусловлена дрейфовой скоростью свободных электронов в металле, возникающей в результате приложенного электрического поля. Как было сказано ранее, плотность тока пропорциональна приложенному электрическому полю. Переформулировка закона Ома приписывается Густаву Кирхгофу, имя которого мы снова увидим в следующей главе.
Насколько верен закон Ома? : askscience
Закон Ома — это не закон, выводимый из уравнений Максвелла, а скорее просто описание поведения многих материалов, полученное непосредственно из экспериментов. (Хотя для этого есть какое-то оправдание с атомной точки зрения.) Все материалы не будут подчиняться закону Ома после точки их диэлектрического разрыва. Есть также материалы, которые просто не подчиняются закону Ома даже в слабом электрическом поле (например, полупроводники), и говорят, что они неомичны, .
Также обратите внимание, что если вы измеряете сопротивление в лаборатории и не контролируете джоулевое нагревание, вы обнаружите, что В не является линейной функцией I просто потому, что сопротивление (скажем, лампы) увеличивается с температурой. , которое само увеличивается с током. Следовательно, V = I * R ( I ), при этом R является строго возрастающей функцией I (т. Е. Непостоянной). Это не обязательно является нарушением закона Ома, поскольку полное изложение закона Ома содержит оговорку, что оно применяется к элементу цепи в заданном состоянии , в частности, при постоянной температуре.
edit: Здесь необходимы некоторые пояснения, так как многие из комментариев ошибаются, , по-видимому, противоречат мне или просто прямо противоречат мне.
Во многих физических системах у нас есть некоторый набор уравнений, которые выполняются независимо от того, что (например, уравнения Максвелла в классической электродинамике, или уравнение Навье-Стокса в гидродинамике, или уравнения Власова-Максвелла в физике плазмы). Часто наша система уравнений не замкнута , что примерно означает, что у нас больше переменных, чем уравнений.Проблема замыкания особенно известна в физике плазмы. Поэтому нам нужно дополнить наши уравнения так называемыми определяющими соотношениями . Это уравнения, которые справедливы только для определенного материала и только при определенных условиях или приближениях. Они позволяют нам добавить достаточно уравнений к нашей системе уравнений, чтобы сделать ее разрешимой.
Например, в гидродинамике мы можем использовать приближение, согласно которому жидкость является ньютоновской, что дает нам определяющее соотношение для тензора напряжений Коши, тензора вязкости и поля скоростей.(Мы можем даже дополнительно аппроксимировать жидкость как однородную и / или изотропную, что дает нам дополнительное определяющее соотношение, упрощающее форму тензора вязкости.) По-прежнему будет проблема, возможно, закрыть уравнения надлежащим определяющим соотношением для давления.
В электродинамике одним из таких определяющих соотношений, которые мы можем наложить, является закон Ома, который равен J = σ E , где σ — фиксированное число . Это достаточно точное приближение для самых разных сред.Конечно, если вы хотите быть более точным или если вы исследуете режим, в котором закон Ома не верен для материала, для которого он обычно является, мы можем написать, что J = σ . E . Здесь σ — тензор ранга 2, и это более общее определяющее соотношение. (Более подробную информацию см. В сообщении / u / RobusEtCeleritas ниже.)
Конечно, мы всегда можем составить любое определяющее отношение, какое захотим. Но если он дает нам бессмысленные результаты или результаты, которые очень плохо аппроксимируют нашу проблему, он не будет использоваться много, если вообще.Закон Ома является хорошим приближением для многих сред, в частности, для многих простых элементов схемы, для которых температура (и другие параметры состояния) не слишком сильно меняются. Так что закон Ома используется довольно часто.
Некоторая путаница в других комментариях, я думаю, заключается в трактовке (или неправильном обращении) с законом Ома как с определением . Например, мы определяем ньютоновскую жидкость как жидкость, так что τ = µ . ( ∇ **** v ), где µ — это фиксированный тензор 4-го ранга .Но это просто определяющее соотношение, и мы знаем, что не все жидкости будут подчиняться этому уравнению. Точно так же мы, , определяем омической средой как такую среду, что J = σ E , но это справедливо не для всех сред. В этом смысле закон Ома всегда абсолютно верен, потому что это всего лишь определение. Все, что нарушает закон Ома, является просто неомической средой.
Наконец, обратите внимание, что электрическое сопротивление R элемента схемы равно , определенному как как отношение напряжения В и тока I через тот же элемент.Конечно, нет никаких оснований полагать, что R постоянен или даже не зависит от V или I . Таким образом, в этом смысле уравнение V = IR равно всегда , несмотря ни на что. Но это уравнение , а не закон Ома . Закон Ома — это , а именно , утверждение, что R не зависит как от V, , так и от I (но все же может зависеть от других параметров состояния, таких как температура и деформация), т.е. что V и I пропорциональны .Итак, закон Ома категорически не всегда верен.
То же самое происходит и с эластиками. Мы можем определить тело Гука как такое тело, что σ = — k . ε , где k — фиксированный тензор 4-го ранга (здесь σ — тензор напряжений, а ε — тензор деформации). В одном измерении это сводится к F = -kx, где k — постоянная. Это просто обычный закон Гука , который вы изучаете в физике в средней школе.Но никто в здравом уме не скажет что-то вроде «Закон Гука справедлив для всех упругих тел». Это просто абсурд. Это всего лишь конститутивная связь между напряжением и деформацией, которая оказывается хорошим приближением для широкого диапазона материалов.
Закон Ома воспринимается многими по-другому, потому что, честно говоря, я думаю, что они забывают, что уравнение V = IR само по себе является определением R и , а не закона Ома. (Обратите внимание, что закон Гука F = -kx не используется в качестве определения чего-либо, поскольку F и x могут быть определены и определяются полностью независимо от пружин.С другой стороны, электрическое сопротивление необходимо определять с точки зрения элементов схемы.)
Является ли закон Ома «универсальным»? — Профессор Электрон
© 2019 L A Waygood
.Закон Ома — один из самых фундаментальных «законов» в электротехнике, и большинство студентов и электриков считают его «универсальным», т.е. он применяется к ко всем проводникам, цепям и электронным компонентам , а к — ко всем условиям .
На самом деле это НЕ! Закон Ома не «универсален», и существует больше проводников, цепей и электронных компонентов, которые НЕ «подчиняются» закону Ома, чем их количество!
Существует также широко распространенное мнение, что закон Ома можно резюмировать в следующем простом уравнении:
I = UR… где I представляет ток, U представляет разность потенциалов, а R представляет сопротивление.
В более широком смысле, основываясь на этом уравнении, многие считают, что закон Ома может быть выражен как «Ток, проходящий через цепь, прямо пропорционален приложенному напряжению и обратно пропорционален сопротивлению» .
Фактически, приведенное выше определение НЕ является общепринятым определением закона Ома. Фактически, закон Ома вообще не упоминает о сопротивлении !
Закон Ома, таким образом, ни в коем случае не «универсальный» закон! Не многие схемы или электронные компоненты действительно «подчиняются» закону Ома! Описанное выше уравнение не , а не , фактически, представляет закон Ома, а выводится из определения ома! Итак, приведенное выше определение совершенно неверно!
Итак, какое является общепринятым определением закона Ома?
Закон Ома гласит, что «ток, протекающий в проводнике, прямо пропорционален разности потенциалов, приложенной к его концам, при условии, что температура и другие физические характеристики остаются постоянными.’
Объяснение закона Ома
В 19 веке, после проведения множества экспериментов, Райнлендер, учитель Георг Саймон Ом , пришел к выводу, что в строго контролируемых условиях ток, проходящий через металлический проводник, прямо пропорционален напряжению, приложенному к этому проводнику. .
Учитывая, что в те времена не было стандартных измерительных приборов (Ому пришлось разработать свои собственные) и не было единиц измерения для тока или напряжения (в то время не существовало ампер и вольт!) , это был действительно замечательный эксперимент.И сам Ом ввел термин «сопротивление », чтобы описать сопротивление потоку тока.
«Строго контролируемые условия», указанные Омом, включали поддержание постоянной температуры на протяжении всего эксперимента. Но это не ограничивалось только этим; Также было важно, например, не сгибать или иным образом искажать проводники во время эксперимента.
Повторить эксперименты Ома в школьной или университетской лаборатории очень просто, и большинство учеников когда-нибудь проводили это во время уроков естествознания.
Простой эксперимент включает приложение постепенно возрастающих напряжений через проводник (или, чаще, резистор какого-либо типа) и запись результирующего значения тока для каждого приращения. Если результатом этого эксперимента является прямолинейный график (зависимости тока от напряжения), проходящий через начало координат, то закон Ома подтверждается. Прямолинейный график свидетельствует о пропорциональности.
Однако в большинстве случаев результатом будет изогнутая линия .Например, если бы мы использовали вольфрам (металл, из которого изготовлены нити лампы), по мере увеличения приложенного к нему напряжения он нагревается. По мере того, как он нагревается, его сопротивление увеличивается, и результирующий график будет кривой — свидетельство отсутствия пропорциональности , что означает, что закон Ома НЕ применяется!
Те проводники или электронные устройства, которые подчиняются закону Ома, таким образом, описываются как « линейный » или « омический », тогда как те, которые не описываются как « нелинейный » или « не- омический ‘.И есть НАМНОГО больше «нелинейных», чем «линейных».
Чтобы закон Ома был «универсальным», , тогда ток должен, , оставаться пропорциональным напряжению для изменений напряжения . В случае с вольфрамом это явно не так, поэтому вольфрам НЕ «подчиняется» закону Ома.
И это НЕ только вольфрам, который не подчиняется закону Ома. Любой металл , сопротивление которого зависит от температуры, не подчиняется закону Ома! И большинство электронных устройств также не «подчиняются» закону Ома.В качестве крайнего примера возьмем следующую характеристическую кривую (рабочую кривую) для туннельного диода :
Между точками A-B график представляет собой прямую линию , поэтому устройство подчиняется закону Ома (он «омический») на этой части кривой. Но между точками B-C линия изогнута на , поэтому больше не подчиняется закону Ома (он «неомический»). Между точками C-D это не только кривая, но и отрицательная кривая , , поэтому противоречит закону Ома — i.е. когда напряжение увеличивается , соответствующий ток уменьшается ! И, наконец, между точками D-E график представляет собой положительную кривую , поэтому, опять же, не подчиняется закону Ома .
Туннельный диод — довольно яркий пример электронного устройства, не подчиняющегося закону Ома. Но другие электронные устройства, включая простые диоды, также не полностью подчиняются закону Ома.
Итак, закон Ома НЕ является универсальным законом. Это правило , а не , применяется ко всем устройствам и не применяется во всех обстоятельствах.На самом деле, существует гораздо больше проводников и электронных устройств, которые не подчиняются закону Ома , , чем их!
Это привело к тому, что один корреспондент (Гленн Элерт, «Гипертекст по физике», ) написал: «Закон Ома — не очень серьезный закон. Это «переходный путь» физики! Разумные материалы и устройства подчиняются ему, но есть много мошенников, которые этого не делают! »
Конечно, отношение напряжения к току (по крайней мере, для цепи постоянного тока) называется «сопротивление ».Все мы знакомы с уравнением:
R = UIЭто уравнение: всегда истинно , независимо от того, подчиняется ли устройство закону Ома или нет. Но он применяет ТОЛЬКО в любой заданной точке на характеристической кривой устройства. Его нельзя использовать для прогнозирования сопротивления где-либо еще на той же кривой (если, конечно, это прямолинейная кривая).
Итак, пора ли выбросить закон Ома на свалку истории? Возможно. Но пересмотренное определение может сделать его более точным:
Закон Ома верен только «когда ток, протекающий в проводнике, остается прямо пропорциональным разности потенциалов, приложенной к его концам, — для изменений этой разности потенциалов .’
Почему V = IR не является законом Ома и почему это имеет значение
Я сбился со счета, сколько раз слышал, как люди говорят, что закон Ома равен \ (V = IR \). Я видел это во многих учебных материалах по электрике.
Этот пост объясняет, что закон Ома и \ (V = IR \) — не одно и то же, и разница имеет значение; мысль, что они одинаковы, может привести как минимум к двум неправильным представлениям, которые я опишу.
Сказав все это, я только что выполнил поиск в Интернете по запросу «что такое закон Ома?» и все 8 лучших результатов говорят, что закон Ома равен \ (V = IR \).Так что сейчас я довольно нервничаю из-за того, какое количество гнева может возникнуть на пути к этому посту … Тем не менее, если мне не хватит смелости, я всегда могу снять его снова!
Что такое закон Ома?
Закон Ома гласит, что ток (\ (I \)) через электрический проводник прямо пропорционален напряжению (\ (V \)) на нем. Математически мы можем записать это утверждение как \ (I \ propto V \).
Связь между \ (I \) и \ (V \) может быть показана на простом графике, который называется вольт-амперной характеристикой.Характеристика V-I для компонента, подчиняющегося закону Ома (например, резистора), будет выглядеть как любое другое пропорциональное соотношение — прямая линия, проходящая через начало координат, как показано ниже.
Пока все хорошо.
Что такое V = IR?
Эта формула представляет собой определение электрического сопротивления (часто обозначаемое как \ (R = \ frac {V} {I} \), но это то же самое, только с другой стороны). В системе СИ единицами измерения величин напряжения, тока и сопротивления являются вольты (В), амперы (А) — для краткости — амперы и омы (Ом), соответственно.Таким образом, если напряжение 10 В вызывает в резисторе ток 2 А, то его сопротивление составляет 5 Ом.
Почему закон Ома и V = IR выглядят одинаково?
Любая пропорциональная зависимость, такая как \ (I \ propto V \) закона Ома, может быть преобразована в уравнение (со знаком равенства) с помощью «константы пропорциональности». Если применить это к нашему утверждению закона Ома, получим:
\ (I = постоянная \ умноженная на V \)
И если мы скажем, что константа пропорциональности равна \ (1 / R \), тогда мы получим \ (I = V / R \), который просто переставлен в \ (V = IR \)! Итак, закон Ома и \ (V = IR \) на первый взгляд выглядят одинаково.
Теперь вернемся к нашему резистору, в котором напряжение 10 В вызывает ток 2 А…
Сопротивление резистора при токе 2 А составляет 5 Ом, как мы видели ранее. Это показано красной точкой на графике выше. (График представляет собой прямую линию, поскольку мы знаем, что резисторы подчиняются закону Ома.)
Когда ток выше, какое сопротивление? Посмотрим на оранжевую точку:
.\ (R = \ frac {V} {I} = \ frac {20 \ mathrm {V}} {4 \ mathrm {A}} = 5 \ Omega \)
Значит, сопротивление по-прежнему 5 Ом.Другими словами, каким бы ни был ток через резистор, сопротивление равно 5 Ом. Это постоянно. Точно так же, как константа пропорциональности в \ (I = константа \ умноженная на V \).
Поэтому вполне естественно думать, что закон Ома и \ (V = IR \) — одно и то же. Это просто неправда…
Так в чем проблема?
Характеристика V-I для лампы накаливания старого образца дает полезный способ увидеть проблему. Вот один…
\ (I \) не пропорционален \ (V \) (график не является прямой линией).Итак, закон Ома не выполняется. Но \ (V = IR \) по-прежнему применяется в каждой точке графика. Просто значения сопротивления в каждой точке графика разные. Мы можем убедиться в этом, рассчитав сопротивление в красной и оранжевой точках на этом графике:
Красный: \ (R = \ frac {V} {I} = \ frac {5 \ mathrm {V}} {3 \ mathrm {A}} = 1,67 \ Omega \)
Оранжевый: \ (R = \ frac {V} {I} = \ frac {20 \ mathrm {V}} {6 \ mathrm {A}} = 3.33 \ Omega \)
Таким образом, первое заблуждение, если предположить, что закон Ома и \ (V = IR \) — одно и то же:
«когда закон Ома не применяется, то \ (V = IR \) не применяется и .”
Тогда вы можете подумать, что нельзя использовать \ (V = IR \), например, для лампочки. Это правда, что в случае лампочки закон Ома неприменим. Но \ (V = IR \) делает . У лампочки просто есть сопротивление, которое изменяется с током, в отличие от постоянного сопротивления резистора.
В чем еще проблема?
Я сказал, что есть два заблуждения. Вот еще один. Это немного более тонко, но очень часто.
Когда у вас есть пропорциональная зависимость, скажем, \ (y \ propto x \), которая совпадает с \ (y = constant \ times x \), константа пропорциональности равна градиенту графика.Например, в графике \ (y = 3x \) градиент равен 3 (во всех точках на графике, потому что линия прямая).
Если вы думаете, что закон Ома равен \ (V = IR \), вы можете подумать, что градиент характеристики V-I дает вам \ (1 / R \).
Вернемся к нашему резистору.
Градиент характеристики V-I имеет значение (4/20 = 0,2), и это действительно равно \ (1 / R \) (вы можете видеть это из 1/5 = 0,2). Но не нужно думать о сопротивлении как о градиенте; вы просто считываете значения для \ (V \) и \ (I \).Для прямолинейного графика два подхода эквивалентны.
На самом деле, многие люди рисуют характеристики V-I «наоборот» с \ (I \) на оси \ (x \) -. Это нарушает общее соглашение о графиках, в которых независимая переменная откладывается на оси \ (x \). Напряжение вызывает ток, поэтому имеет смысл нанести \ (V \) на ось \ (x \). Единственная причина, по которой я могу «поменять местами оси», заключается в том, что для прямолинейного графика резистора градиент тогда дает вам напрямую \ (R \), а не \ (1 / R \).
Все это делает второе заблуждение весьма убедительным. Второе заблуждение:
«градиент = сопротивление или 1 / сопротивление, в зависимости от того, в каком направлении расположены оси».
Но это работает только для компонентов, которые подчиняются закону Ома . Это не общее правило. Для нашей лампочки, если мы попытаемся вычислить сопротивление по градиенту характеристики V-I, мы не получим правильный ответ.
При токе 6 А градиент графика имеет значение 0.08. Если мы попытаемся вычислить сопротивление, используя \ (1 / R \), мы получим значение 12,5 Ом. Это неправильный ответ сопротивлению. Это неправильный метод расчета сопротивления. Правильный метод — считать значения \ (V \) (20 В) и \ (I \) (6 A) и применить \ (V = IR \). Мы делали это раньше и получили значение 3,33 Ом (правильный ответ).
Вот три диаграммы, найденные на первой странице поиска изображений в Интернете «вольт-амперные характеристики».
Я думаю, они вводят в заблуждение.Да, градиент дает правильный результат, потому что рассматриваемая характеристика V-I подчиняется закону Ома. Но я думаю, что вы могли бы сделать вывод из диаграмм, что использование градиента для расчета сопротивления является общей техникой. И это не так.
(Там — это величина, равная градиенту — это называется дифференциальным сопротивлением. Но это не сопротивление \ (R \). Дифференциальное сопротивление \ (dV / dI \) и сопротивление \ (V / I \ ) имеют то же значение при \ (I \ propto V \), но не иначе.Полезность дифференциального сопротивления выходит за рамки этой статьи.)
Интересно, что я посмотрел на требования британской экзаменационной комиссии для 16-летних, и они вообще не упоминают закон Ома. Этот поразительно простой подход решает все вышеперечисленные проблемы. Все, что вам нужно, это \ (V = IR \), и знание того, что для некоторых компонентов \ (R \) постоянный, а для других он изменяется в зависимости от тока. Тогда никому бы не пришло в голову вычислить градиент или подумать, что иногда \ (V = IR \) не применяется.
Если вы все еще не думаете, что разница между законом Ома и \ (V = IR \) имеет значение, то этот пост показался бы самым педантичным в сети, и я прошу прощения …
Что такое закон Ома? Объяснение и ограничения закона Ома
Когда к проводнику приложена разность электрических потенциалов (В), , как показано на рисунке ниже, через него протекает некоторый ток (I) . Протеканию тока противостоит сопротивление проводника и цепи.Связь между напряжением, током и сопротивлением объясняется законом Ома.
ЗаконыОма гласят, что ток через любые две точки проводника прямо пропорционален разности потенциалов, приложенной к проводнику, при условии, что физические условия, то есть температура и т. Д., Не изменяются. Измеряется в ( Ом, ) Ом.
Математически это выражается как
Другими словами, закон Ома также можно сформулировать как;
Отношение разности потенциалов в конечной точке проводника к току, протекающему между ними, всегда постоянно, но физические условия проводника i.е. температура и т. д. остаются такими же.
Эта постоянная также называется сопротивлением (R) проводника (или цепи)
Его можно записать как
В цепи, когда ток протекает через резистор, разность потенциалов на резисторе известна как падение напряжения на нем, то есть В = IR.
Ограничения закона Ома
- Закон Ома не применяется в односторонних сетях.Односторонние сети позволяют току течь в одном направлении. Такие типы сетей состоят из таких элементов, как диод, транзистор и т. Д.
- Не применяется для нелинейной сети. В нелинейной сети параметр сети изменяется в зависимости от напряжения и тока. Их параметры, такие как сопротивление, индуктивность, емкость, частота и т. Д., Не остаются постоянными с течением времени. Так что закон Ома неприменим к нелинейной сети.
Закон Ома используется для определения сопротивления цепи, а также для определения напряжения и тока цепи.
Тест на законОм
- Изучив этот раздел, вы сможете:
- Расчет основных задач, связанных с законом Ома
- • Используйте соответствующие единицы и подъединицы.
- • Используйте научный калькулятор с инженерными обозначениями.
Рис. 3.2.1 Треугольник закона Ома
или (если хотите) дерево «ВИР»Попробуйте несколько вычислений на основе закона Ома.Для этого вам просто нужно использовать три основные формулы, описанные в модуле «Резисторы и схемы» 3.1. Надеюсь, это будет легкий ветерок. Важно помнить, что нужно использовать правильную версию формулы и поднять ее правильно (I = V / R хорошо, но I = R / V определенно НЕ!). Простым наглядным пособием для запоминания правильной формулы является треугольник закона Ома. Размещение V, I и R таким образом является напоминанием о том, что V = IR (I, умноженное на R), и I = V, превышающее (деленное на) R и R = V, превышающее (деленное на) I, как показано на рис.3.2.1.
Разработайте ответы с помощью карандаша и бумаги; если вы не запишете проблему, вы запутаетесь на полпути и получите неправильный ответ. Конечно, ответ будет не просто числом, это будет определенное количество Ом, Вольт или Ампер, но подождите, впереди еще худшее — эти Ом, Вольт или Ампер, скорее всего, будут в киломах, или милливольтах, или микроамперах, верно ? Так что вы должны показать это в своем ответе. Плохо просто писать 56. Пятьдесят шесть Что? может 56 Ом? Что ж, если реальный ответ был 56 кОм, вы все равно ошибаетесь, ваш ответ в тысячу раз меньше!
Но не волнуйтесь, чтобы встать на верный путь, вам следует загрузить нашу брошюру «Советы по математике», в которой показано, как использовать калькулятор с показателями степени и инженерной нотацией, чтобы каждый раз получать правильный ответ.
У вас нет научного калькулятора? Буклет «Подсказки по математике» объясняет, что вам нужно (и что вам не нужно, чтобы не тратить деньги без надобности). Если вы не хотите покупать научный калькулятор, вы всегда можете получить его бесплатно в сети. Пользователи ПК могут попробовать Calc98 на сайте www.calculator.org/download.html. Какой бы калькулятор вы ни выбрали, прочтите инструкции, чтобы ознакомиться с методами работы, которые вам следует использовать, поскольку они варьируются от калькулятора к калькулятору.
Хорошо, теперь вы прочитали эти инструкции, и вы готовы к работе. Вот способ изложить типичную проблему на бумаге, чтобы вы (с практикой) не запутались.
Сначала запишите, что известно из вопроса, а что неизвестно:
В =? (V — неизвестное количество.)
I = 500 мА (500 x 10 -3 Ампер) 500E-3 или 500EXP-3 при вводе его в калькулятор, в зависимости от того, какую модель вы используете.
R = 50 Ом
Итак, учитывая I и R, правильную формулу для нахождения V можно найти из треугольника закона Ома:
V = I x R , поэтому замена цифр, приведенных вместо I и R, дает:
V = 500E-3 x 50 (для E нажмите клавишу E, EE или EXP, а для — нажмите клавишу изменения знака +/- или (-), а НЕ клавишу минус (-). Таким образом, калькулятор на дисплее должно отображаться:
V = 500E-3 x 50 и нажатие = дает ответ 25
Следовательно, правильный ответ: 25V
Примечание: Если вы используете Calc98 для своих расчетов, вам необходимо установить в меню View> Option> Display значение Engineering (в разделе «Decimal»).
Было бы неплохо, находясь в этом меню, выбрать 2 в раскрывающемся списке «Десятичные знаки», чтобы установить количество цифр, отображаемых после десятичного разряда. Это округлит ваш ответ до двух десятичных знаков, что является достаточно точным для большинства применений и предотвратит получение глупых ответов, таких как 4,66666666667 мкА, что было бы слишком точной мерой в практической ситуации!
Практика расчетов по закону Ома — сопротивление, напряжение и ток.
(Подсчитайте свои ответы карандашом, бумагой и калькулятором, затем проверьте свои ответы ниже.)
1.
Какой будет разность потенциалов на резисторе 50 Ом, если через него протекает ток 500 мА? ЗаконОма: что это такое и почему это важно?
Обновлено 28 декабря 2020 г.
Ли Джонсон
Электрические цепи повсеместно встречаются в нашей повседневной жизни. От сложных интегральных схем, управляющих устройством, которое вы читаете в этой статье, до проводки, которая позволяет вам включать и выключать лампочку в вашем доме, вся ваша жизнь была бы радикально другой, если бы вы не были окружены цепями повсюду. ты иди.
Но большинство людей на самом деле не изучают мельчайших деталей того, как работают схемы, и довольно простые уравнения, такие как закон Ома, которые объясняют взаимосвязь между ключевыми понятиями, такими как электрическое сопротивление, напряжение и электрический ток. Однако более глубокое погружение в физику электроники может дать вам гораздо более глубокое понимание основных правил, лежащих в основе большинства современных технологий.
Что такое закон Ома?
Закон Ома — одно из самых важных уравнений, когда дело доходит до понимания электрических цепей, но если вы собираетесь его понять, вам понадобится хорошее понимание основных понятий, которые он связывает: напряжение , ток и сопротивление .Закон Ома — это просто уравнение, которое описывает соотношение между этими тремя величинами для большинства проводников.
Напряжение — это наиболее часто используемый термин для обозначения разности электрических потенциалов между двумя точками, который обеспечивает «толчок», который позволяет электрическому заряду перемещаться по проводящей петле.
Электрический потенциал — это форма потенциальной энергии, подобная гравитационной потенциальной энергии, и определяется как электрическая потенциальная энергия на единицу заряда. Единицей измерения напряжения в системе СИ является вольт (В), а 1 В = 1 Дж / Кл, или один джоуль энергии на кулон заряда.Иногда ее также называют электродвижущей силой , или ЭДС.
Электрический ток — это скорость протекания электрического заряда через заданную точку в цепи, которая имеет ампер (А) в системе СИ, где 1 А = 1 Кл / с (один кулон заряда в секунду). Он поставляется в форме постоянного (DC) и переменного (AC) тока, и хотя постоянный ток проще, цепи переменного тока используются для подачи энергии в большинство домашних хозяйств по всему миру, потому что его проще и безопаснее передавать на большие расстояния.
Последняя концепция, которую вам нужно понять, прежде чем приступить к рассмотрению закона Ома, — это сопротивление, которое является мерой сопротивления току, протекающему в цепи. Единицей измерения сопротивления в системе СИ является ом (в котором используется греческая буква омега, Ом), где 1 Ом = 1 В / А.
Уравнение закона Ома
Немецкий физик Георг Ом описал взаимосвязь между напряжением, током и сопротивлением в своем одноименном уравнении. Формула закона Ома:
В = IR
, где В, — напряжение или разность потенциалов, I — величина тока, а сопротивление R — конечная величина.
Уравнение можно легко переформулировать, чтобы получить формулу для расчета тока на основе напряжения и сопротивления или сопротивления на основе тока и напряжения. Если вам неудобно переставлять уравнения, вы можете найти треугольник закона Ома (см. Раздел «Ресурсы»), но это довольно просто для любого, кто знаком с основными правилами алгебры.
Ключевые моменты, которые показывает уравнение закона Ома, заключаются в том, что напряжение прямо пропорционально электрическому току (поэтому, чем выше напряжение, тем выше ток), и этот ток обратно пропорционален сопротивлению (поэтому чем выше сопротивление, тем ниже электрический ток).
Вы можете использовать аналогию с потоком воды, чтобы запомнить ключевые моменты, которые основаны на трубе с одним концом на вершине холма и одним концом внизу. Напряжение похоже на высоту холма (более крутой и высокий холм означает большее напряжение), ток подобен потоку воды (вода течет быстрее по крутому склону), а сопротивление похоже на трение между сторонами трубы. и вода (более тонкая труба создает большее трение и снижает скорость потока воды, как более высокое сопротивление для электрического тока).
Почему важен закон Ома?
Закон Ома жизненно важен для описания электрических цепей, поскольку он связывает напряжение с током, а значение сопротивления регулирует взаимосвязь между ними. Из-за этого вы можете использовать закон Ома для управления величиной тока в цепи, добавляя резисторы, чтобы уменьшить ток, и снимая их, чтобы увеличить величину тока.
Его также можно расширить, чтобы описать электрическую мощность (скорость потока энергии в секунду), потому что мощность P = IV, и поэтому вы можете использовать ее, чтобы гарантировать, что ваша схема обеспечивает достаточно энергии, скажем, для 60-ваттного прибора.
Для студентов-физиков наиболее важным в законе Ома является то, что он позволяет анализировать принципиальные схемы, особенно когда вы объединяете его с законами Кирхгофа, которые следуют из него.
Закон Кирхгофа по напряжению гласит, что падение напряжения вокруг любого замкнутого контура в цепи всегда равно нулю, а закон тока утверждает, что величина тока, протекающего в переходе или узле в цепи, равна величине, вытекающей из Это. Вы можете использовать закон Ома с законом напряжения, в частности, для расчета падения напряжения на любом компоненте схемы, что является общей проблемой, возникающей в классах электроники.
Примеры закона Ома
Вы можете использовать закон Ома, чтобы найти любую неизвестную величину из трех, при условии, что вам известны две другие величины для рассматриваемой электрической цепи. Работа с некоторыми базовыми примерами показывает, как это делается.
Во-первых, представьте, что у вас есть 9-вольтовая батарея, подключенная к цепи с общим сопротивлением 18 Ом. Сколько тока течет при подключении цепи? Изменив закон Ома (или используя треугольник), вы можете найти:
\ begin {align} I & = \ frac {V} {R} \\ & = \ frac {9 \ text {V}} {18 \ текст {Ω}} \\ & = 0.5 \ text {A} \ end {align}
Итак, 0,5 ампер тока течет по цепи. А теперь представьте, что это идеальная величина тока для компонента, который вы хотите запитать, но у вас есть только батарея на 12 В. Какое сопротивление вы должны добавить, чтобы убедиться, что компонент получает оптимальную силу тока? Опять же, вы можете переставить закон Ома и решить его, чтобы найти ответ:
\ begin {align} R & = \ frac {V} {I} \\ & = \ frac {12 \ text {V}} {0.5 \ text {A}} \\ & = 24 \ text {Ω} \ end {align}
Итак, вам понадобится резистор 24 Ом для завершения вашей схемы.Наконец, каково падение напряжения на резисторе 5 Ом в цепи с током 2 А, протекающим через нее? На этот раз стандартная форма закона V = IR работает нормально:
\ begin {выровнено} V & = IR \\ & = 2 \ text {A} × 5 \ text {Ω} \\ & = 10 \ text {V} \ end {align}
Омические и неомические резисторы
Вы можете использовать закон Ома в огромном количестве ситуаций, но есть ограничения на его применимость — это не действительно фундаментальный закон физики .

