Что такое таблица истинности. Как составить таблицу истинности для логических операций. Какие бывают типы логических функций. Где применяются таблицы истинности в информатике и электронике.
Что такое таблица истинности и для чего она нужна
Таблица истинности — это способ описания логической функции, который показывает все возможные комбинации значений входных переменных и соответствующие им значения функции. Таблицы истинности широко используются в математической логике, информатике и электронике для наглядного представления работы логических элементов и схем.
Основные преимущества использования таблиц истинности:
- Наглядно показывают все возможные варианты работы логической функции
- Позволяют легко сравнивать разные логические функции
- Помогают выявлять эквивалентные логические выражения
- Упрощают анализ и проектирование логических схем
Таким образом, таблицы истинности — это мощный инструмент для работы с логическими функциями в различных областях.
Основные логические операции и их таблицы истинности
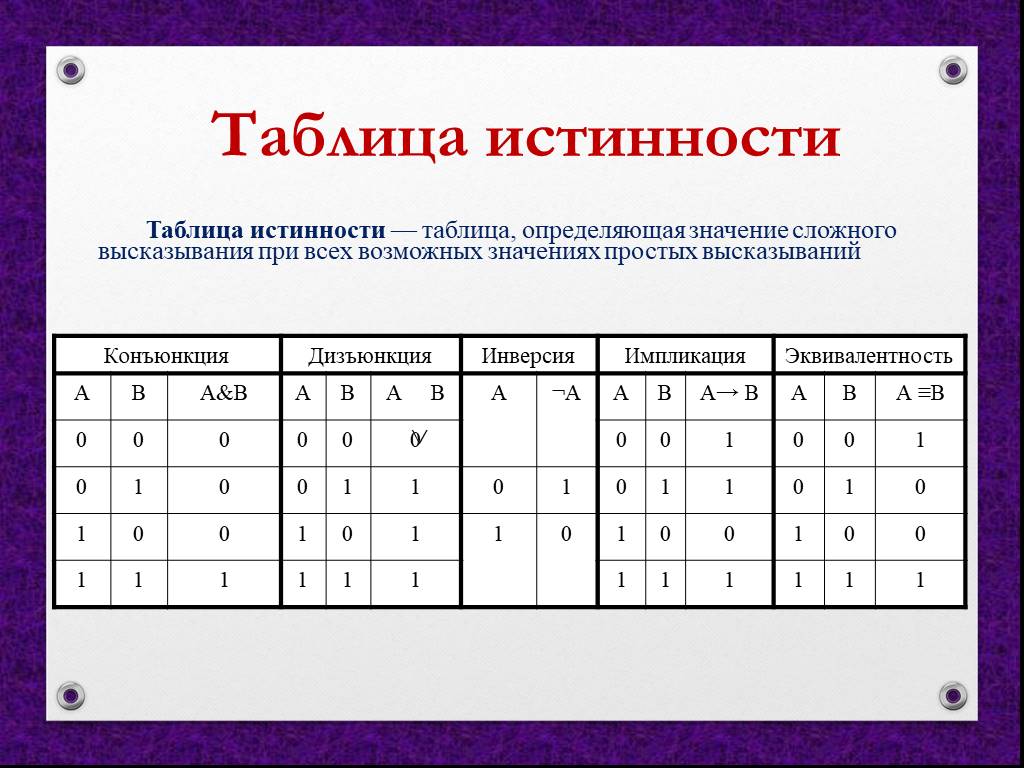
Рассмотрим таблицы истинности для базовых логических операций над двумя переменными A и B:
Конъюнкция (логическое И)
Обозначается: A & B или A ∧ B
| A | B | A & B |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Результат истинен только если оба входа истинны.
Дизъюнкция (логическое ИЛИ)
Обозначается: A | B или A ∨ B
| A | B | A | B |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Результат истинен если хотя бы один из входов истинен.
Отрицание (логическое НЕ)
Обозначается: ¬A
| A | ¬A |
|---|---|
| 0 | 1 |
| 1 | 0 |
Инвертирует входное значение.
Составные логические функции и их таблицы истинности
На основе базовых операций можно строить более сложные логические функции. Рассмотрим некоторые из них:
Исключающее ИЛИ (XOR)
Обозначается: A ⊕ B
| A | B | A ⊕ B |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Истинно когда входы различны.
Импликация
Обозначается: A → B
| A | B | A → B |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Ложна только когда из истины следует ложь.
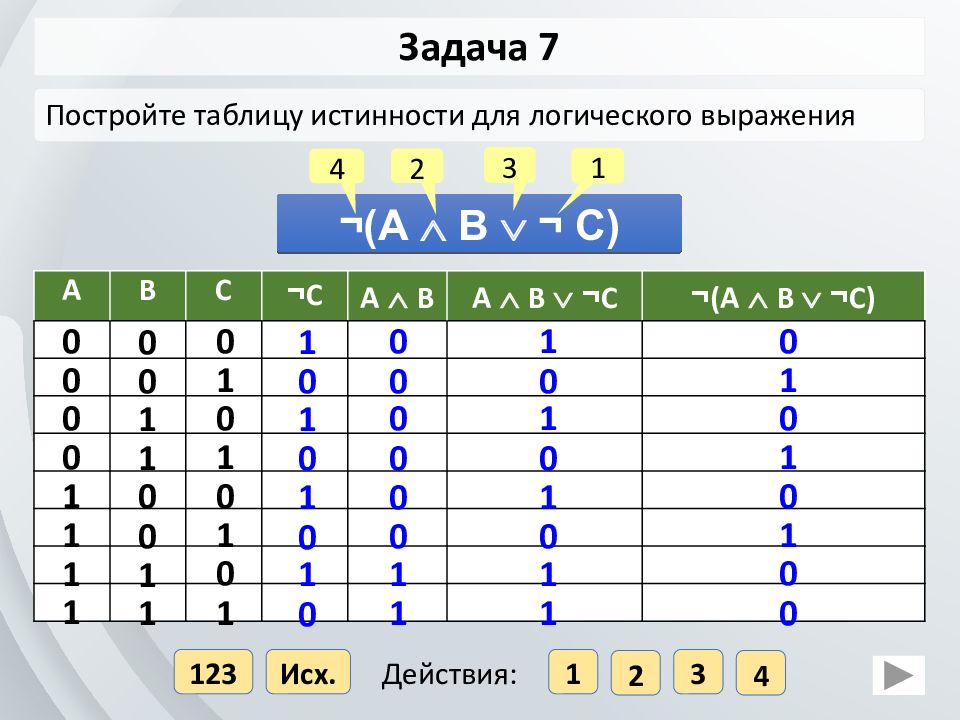
Как составить таблицу истинности для сложной логической функции
Для составления таблицы истинности сложной логической функции следуйте этому алгоритму:
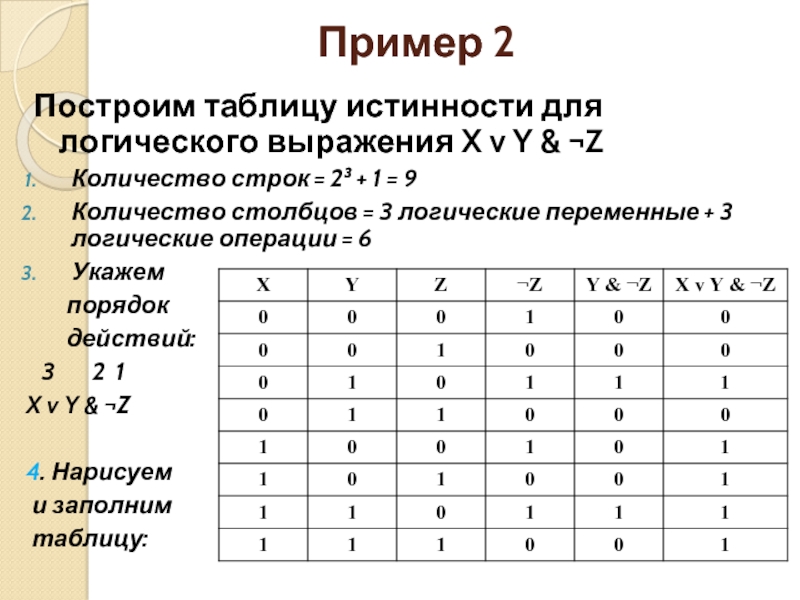
- Определите все входные переменные функции.
- Создайте столбцы для каждой переменной и выходной функции.
- Запишите все возможные комбинации значений входных переменных (2^n строк для n переменных).
- Вычислите значение функции для каждой комбинации входов, разбивая сложное выражение на элементарные операции.
- Запишите результаты в столбец выходной функции.
Пример для функции F = (A & B) | (¬A & C):
| A | B | C | A & B | ¬A | ¬A & C | F |
|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 0 | 1 | 1 | 1 |
| 0 | 1 | 0 | 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 0 | 0 | 1 |
Применение таблиц истинности в информатике и электронике
Таблицы истинности широко используются в следующих областях:
- Проектирование цифровых схем — для описания работы логических элементов и микросхем
- Анализ и минимизация булевых функций — для упрощения логических выражений
- Разработка алгоритмов — для описания логики работы программ
- Верификация и тестирование — для проверки корректности работы логических схем и программ
- Криптография — для анализа криптографических алгоритмов
Например, в цифровой электронике таблицы истинности используются для описания работы таких компонентов как:
- Логические вентили (И, ИЛИ, НЕ и др.)
- Мультиплексоры и демультиплексоры
- Шифраторы и дешифраторы
- Триггеры и регистры
- Сумматоры и АЛУ
Связь таблиц истинности с другими способами представления логических функций
Таблицы истинности тесно связаны с другими методами описания логических функций:
- Булевы выражения — таблица истинности может быть преобразована в булево выражение и наоборот
- Карты Карно — графический метод минимизации логических функций, основанный на таблицах истинности
- Диаграммы Венна — визуальное представление логических операций над множествами
- Логические схемы — графическое изображение логических функций в виде соединенных логических элементов
Эти различные представления дополняют друг друга и используются в зависимости от конкретной задачи.
Ограничения и недостатки таблиц истинности
Несмотря на свою полезность, таблицы истинности имеют некоторые ограничения:
- Размер таблицы экспоненциально растет с увеличением числа переменных (2^n строк для n переменных)
- Для функций с большим числом переменных таблицы становятся громоздкими и неудобными
- Не показывают внутреннюю структуру сложных логических выражений
- Затрудняют понимание закономерностей в работе функции
Поэтому для сложных функций часто используют другие методы анализа и представления, такие как карты Карно или алгебраические преобразования.
Заключение: важность понимания таблиц истинности
Таблицы истинности — фундаментальный инструмент в математической логике и цифровой технике. Их понимание критически важно для:
- Разработчиков цифровых схем и микропроцессорных систем
- Программистов, работающих с низкоуровневыми алгоритмами
- Специалистов по верификации и тестированию
- Студентов, изучающих информатику и электронику
Глубокое знание таблиц истинности и связанных с ними концепций позволяет эффективно анализировать, проектировать и оптимизировать логические системы различной сложности.
Таблица истинности. Базовые логические элементы.
Так же, как и стандартные Булевы выражения, информация на входах и выходах различных логических элементов или логических схем может быть собрана в единую таблицу – таблицу истинности.
Таблица истинности дает наглядное представление о системе логических функций. В таблице истинности отображаются сигналы на выходах логических элементов при всех возможных комбинациях сигналов на их входах.
В качестве примера, рассмотрим логическую схему с двумя входами и одним выходом. Входные сигналы отметим как «А» и «В», а выход «Q». Есть четыре (2²) возможных комбинаций входных сигналов, которые можно подать на эти два входа («ON — наличие сигнала» и «OFF — отсутствие сигнала»).
Однако, когда речь идет о логических выражениях и, особенно о таблице истинности логических элементов, вместо общего понятия «наличие сигнала» и «отсутствие сигнала» используют битные значения, которые представляют собой логический уровень «1» и логический уровень «0» соответственно.
Тогда четыре возможные комбинации «А» и «В» для 2-входного логического элемента можно представить в следующем виде:
- «OFF» — «OFF» или (0, 0)
- «OFF» — «ON» или (0, 1)
- «ON» — «OFF» или (1, 0)
- «ON» — «ON» или (1, 1)
Следовательно, у логической схемы имеющей три входа будет восемь возможных комбинаций (2³) и так далее. Для обеспечения легкого понимания сути таблицы истинности, мы будем изучать ее только на простых логических элементах с числом входов не превышающим двух. Но, несмотря на это, принцип получения логических результатов для многовходных элементов схемы остается таким же.
Практически, таблица истинности состоит из одного столбца для каждой из входных переменных (например, А и В), и один последний столбец для всех возможных результатов логической операции (Q). Следовательно, каждая строка таблицы истинности содержит один из возможных вариантов входных переменных (например, A = 1, B = 0), и результат операции с этими значениям.
Таблица истинности
Элемент «И»
Для логического элемента «И» выход Q будет содержать лог.1, только если на оба входа («А» и «В») будет подан сигнал лог.1
Микросхемы, содержащие логический элемент «И»:
- К155ЛИ1, аналог SN7408N
- К155ЛИ5 с открытым коллектором, аналог SN74451N
- К555ЛИ1, аналог SN74LS08N
- К555ЛИ2 с открытым коллектором, аналог SN74LS09N
Элемент «ИЛИ»
Выход Q, элемента «ИЛИ», будет иметь лог.1, если на любой из двух входов или же на оба входа сразу подать лог.1
Микросхемы, содержащие логический элемент «ИЛИ»:
- К155ЛЛ1, аналог SN7432N
- К155ЛЛ2 с открытым коллектором, аналог SN75453N
- К555ЛЛ1, аналог SN74LS32N
Элемент «НЕ»
В данном случае выход Q, логического элемента «НЕ», будет иметь сигнал противоположный входному сигналу.
Микросхемы, содержащие логический элемент «НЕ»:
- К155ЛН1, аналог SN7404N
- К155ЛН2 с открытым коллектором, аналог SN7405N
- К155ЛН3, аналог SN7406N
- К155ЛН5 с открытым коллектором, аналог SN7416N
- К155ЛН6, аналог SN7466N
Элемент «И-НЕ»
На выходе Q элемента «И-НЕ» будет лог.1 если на обоих входах одновременно отсутствует сигнал лог.1
Микросхемы, содержащие логический элемент «И-НЕ»:
- К155ЛА3, аналог SN7400N
- К155ЛА8, аналог SN7401N
- К155ЛА9 с открытым коллектором, аналог SN7403N
- К155ЛА11 с открытым коллектором, аналог SN7426N
- К155ЛА12 с открытым коллектором, аналог SN7437N
- К155ЛА13 с открытым коллектором, аналог SN7438N
- К155ЛА18 с открытым коллектором, аналог SN75452N
Элемент «ИЛИ-НЕ»
Только если на оба входа логического элемента «ИЛИ-НЕ» подать лог.0 мы получим на его выходе Q сигнал соответствующий лог.1
Микросхемы, содержащие логический элемент «ИЛИ-НЕ»:
- К155ЛЕ1, аналог SN7402N
- К155ЛЕ5, аналог SN7428N
- К155ЛЕ6, аналог SN74128N
Элемент «Исключающее ИЛИ»
В данном случае выход Q будет содержать лог.1, если на вход элемента «Исключающее ИЛИ» поданы два противоположных друг другу сигнала.
Микросхемы, содержащие логический элемент «Исключающее ИЛИ»:
- К155ЛП5, аналог SN7486N
Подведем итог, собрав все полученные ранее результаты работы логических элементов в единую таблицу истинности:
Логические функции алгебры логики: схемы и таблицы истинности
В данной статье мы начнем обозревать булевую алгебру или алгебру логики. Рассмотрим элементы функции на схеме, а так же приведем таблицы истинности для всех логических функций.
Введение в булевую алгебру
В 1854 году Джордж Буль провел исследование «законов мышления», которые основывались на упрощенной версии теории «групп» или «множеств», и из этого была выведена булевая алгебра.
Булева алгебра имеет дело, главным образом, с теорией, согласно которой логические операции и операции над множествами являются либо «ИСТИННЫМИ», либо «ЛОЖНЫМИ», но не обеими одновременно.
Например, A + A = A, а не 2A, как это было бы в обычной алгебре. Булева алгебра — это простой и эффективный способ представления действия переключения стандартных логических вентилей, а основные логические операторы, которые нас здесь интересуют, задаются операциями логических вентилей функций И , ИЛИ и НЕ.
Логическая функция «И» (умножение)
Функция логики И утверждает, что два или более события должны происходить вместе и одновременно, чтобы происходило выходное действие. Порядок, в котором происходят эти действия, не имеет значения, поскольку он не влияет на конечный результат. Например, & B = B & . В булевой алгебре функция логики И подчиняется коммутативному закону, который допускает изменение положения любой переменной.
Функция «И» представлена в электронике символом точки или полной остановки ( . ) Таким образом, 2-входное ( АВ ) «И» элемент имеет выходной термин, представленный логическим выражением A.B или просто AB.
Представление функции «И» на схеме


Здесь два переключателя A и B соединены вместе, образуя последовательную цепь. Поэтому в вышеупомянутой цепи оба выключателя A «И» B должны быть замкнуты (логика «1»), чтобы включить лампу. Другими словами, оба переключателя должны быть замкнуты или должны иметь логическую «1», чтобы лампа горела.
Тогда логический элемент этого типа (логический элемент «И» ) создает выход только тогда, когда все его входы истины. В терминах булевой алгебры вывод будет ИСТИНА, только когда все его входы ИСТИНА. В электрическом смысле логическая функция «И» равна последовательной цепи, как показано выше.
Поскольку имеется только два переключателя, каждый с двумя возможными состояниями «открытый» или «закрытый». Определяя логическую «0» как то, когда переключатель разомкнут, и логическую «1», когда переключатель замкнут, существует четыре различных способа или комбинации расположения двух переключателей вместе, как показано в таблице ниже.
Таблица истинности для функции «И»




Логические «И» элементы доступны как стандартные пакеты ic, такие как общие TTL 74LS08 Четырехпозиционные 2-входные положительные элементы «И» (или эквивалент CMOS 4081), TTL 74LS11 Тройные 3-входные положительные элементы «И» или 74LS21 Двойные 4-входные положительные элементы «И». «И» ворота можно также «каскадировать» вместе для создания цепей с более чем 4 входами.
Логическая функция «ИЛИ» (сложение)
Функция логического «ИЛИ» заявляет, что выходное действие станет ИСТИНОЙ, если одно «ИЛИ» больше событий ИСТИНЫ, но порядок, в котором они происходят, не имеет значения, поскольку он не влияет на конечный результат.
Так , например, А + В = В + А . В булевой алгебре функция логического «ИЛИ» подчиняется коммутативному закону так же, как и для логической функции «И», что позволяет изменять положение любой переменной.
Логика или логическое выражение, данное для логического элемента «ИЛИ», является логическим выражением, которое обозначается знаком плюс, ( + ). Таким образом, 2-входной ( АВ ) Логический элемент «ИЛИ» имеет выход термин, представленный булевой выражением: A + B = Q .
Представление функции «ИЛИ» на схеме


Здесь два переключателя А и B соединены параллельно и, либо переключатель A «ИЛИ» переключатель B может быть закрыт, чтобы включить лампу. Другими словами, выключатель может быть замкнут, либо быть на логике «1», чтобы лампа была включена.
Тогда этот тип логического элемента генерирует и выводит только тогда, когда присутствует «ЛЮБОЙ» из его входов, и в терминах Булевой алгебры выход будет ИСТИНА, если любой из его входов ИСТИНЕН. В электрическом смысле логическая функция «ИЛИ» равна параллельной цепи.
Как и в случае с функцией «И», есть два переключателя, каждый с двумя возможными положениями, открытыми или закрытыми, поэтому будет 4 различных способа расположения переключателей.
Таблица истинности для функции «ИЛИ»


Логические «ИЛИ» элементы доступны в виде стандартных пакетов ic, таких как общие TTL 74LS32 Четырехместные 2-входные положительные «ИЛИ» элементы. Как и в предыдущем логическом элементе «И», «ИЛИ» также может быть «каскадно» соединен для создания цепей с большим количеством входов, таких как системы охранной сигнализации (зона A или зона B или зона C и т.д.).
Логическая функция «НЕ» (отрицание)
Функция «Логическое НЕ» — это просто инвертор с одним входом, который изменяет вход логического уровня «1» на выход логического уровня «0» и наоборот.
«Функция логического НЕ» называется так, потому что ее выходное состояние НЕсовпадает с его входным состоянием с ее логическим выражением, обычно обозначаемым чертой или линией ( ¯ ) над его входным символом, который обозначает операцию инвертирования (отсюда ее название как инвертор).
Поскольку логическое «НЕ» выполняет логическую функцию инвертирования или комплементационной, их чаще называют инверторами, поскольку они инвертируют сигнал. В логических схемах это отрицание может быть представлено нормально замкнутым переключателем.
Представление функции «НЕ» на схеме


Если A означает, что переключатель замкнут, то «НЕ» A или А (с верхней чертой) говорит, что переключатель НЕ замкнут или, другими словами, он разомкнут. Функция логического НЕ имеет один вход и один выход, как показано на рисунке.
Таблица истинности для функции «НЕ»


Индикатор инверсии для логической функции «НЕ» является символом «пузыря», ( O) на выходе (или входе) символа логических элементов. В булевой алгебре инвертирующая логическая функция «НЕ» следует Закону дополнения, создающему инверсию.


Логические «НЕ» элементы или «Инверторы», как их чаще называют, могут быть связаны со стандартными элементами «И» и» ИЛИ» для создания элементов «НЕ И» и «НЕ ИЛИ» соответственно. Инверторы также могут использоваться для генерации «дополнительных» сигналов в более сложных декодерах / логических схемах, например, дополнение логики A — это «НЕ» A , а два последовательно соединенных инвертора дают двойную инверсию, которая выдает на своем выходе исходное значение A.
При проектировании логических схем вам может понадобиться только один или два инвертора в вашей конструкции, но если у вас нет места или денег для выделенного чипа инвертора, такого как 74LS04. Тогда вы можете легко заставить логику «НЕ» функционировать, используя любые запасные элементы «НЕ А» или «НЕ ИЛИ», просто соединяя их входы вместе, как показано ниже.


Логическая функция «НЕ И»
Функция «НЕ И» представляет собой комбинацию двух отдельных логических функций, функции «И» и функции «НЕ» последовательно. Логическая функция «НЕ И» может быть выражена логическим выражением AB (с верхней чертой)


Функция логического «НЕ И» генерирует выход, только когда «ЛЮБЫЕ» из ее входов отсутствуют, и в терминах булевой алгебры выход будет ИСТИНА, только когда любой из ее входов ЛОЖЬ (0).
Представление функции «НЕ И» на схеме


Таблица истинности — Википедия
Материал из Википедии — свободной энциклопедии
Таблица истинности — это таблица, описывающая логическую функцию.
Под «логической функцией» в данном случае понимается функция, у которой значения переменных (параметров функции) и значение самой функции выражают логическую истинность. Например, в двузначной логике они могут принимать значения «истина» либо «ложь» (true{\displaystyle true} либо false{\displaystyle false}, 1{\displaystyle 1} либо 0{\displaystyle 0}).
Табличное задание функций встречается не только в логике, но для логических функций таблицы оказались особенно удобными, и с начала XX века за ними закрепилось это специальное название. Особенно часто таблицы истинности применяются в булевой алгебре и в аналогичных системах многозначной логики.
Таблицы истинности для основных двоичных логических функций
В программировании:
- Конъюнкция = AND = И = ∧{\displaystyle \land } = &
- Дизъюнкция = OR = ИЛИ = ∨{\displaystyle \lor } = |
- Сложение по модулю 2 = XOR = ИСКЛЮЧАЮЩЕЕ ИЛИ = ⊕{\displaystyle \oplus } = ~
- Отрицание = NOT = НЕ = ¬{\displaystyle \neg } = !
Таблицы истинности для некоторых троичных логических функций
| x | 2 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 |
|---|---|---|---|---|---|---|---|---|---|
| y | 2 | 2 | 2 | 1 | 1 | 1 | 0 | 0 | |
| min(x,y) | 2 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 |
| x | 2 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 |
|---|---|---|---|---|---|---|---|---|---|
| y | 2 | 2 | 2 | 1 | 1 | 1 | 0 | 0 | 0 |
| max(x,y) | 2 | 2 | 2 | 2 | 1 | 1 | 2 | 1 | 0 |
| x | 2 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 |
|---|---|---|---|---|---|---|---|---|---|
| y | 2 | 2 | 2 | 1 | 1 | 1 | 0 | 0 | 0 |
| F2TN22310 | 0 | 0 | 0 | 0 | 2 | 2 | 0 | 2 | 1 |
См. также
Примечания
Литература
- Яблонский С. В., Гаврилов Г. П., Кудрявцев В. Б. Функции алгебры логики и классы Поста. — М.: Наука, 1966. — (Математическая логика и основания математики).
Ссылки
Таблица истинности — это… Что такое Таблица истинности?
Таблица истинности — это таблица, описывающая логическую функцию.
Под «логической функцией» в данном случае понимается функция, у которой значения переменных (параметров функции) и значение самой функции выражают логическую истинность. Например, в двузначной логике они могут принимать значения «истина» либо «ложь» ( либо , либо ).
Табличное задание функций встречается не только в логике, но для логических функций таблицы оказались особенно удобными, и с начала XX века за ними закрепилось это специальное название. Особенно часто таблицы истинности применяются в булевой алгебре и в аналогичных системах многозначной логики.
Таблицы истинности для основных двоичных логических функций
Таблицы истинности для некоторых троичных логических функций
| x | 2 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 |
|---|---|---|---|---|---|---|---|---|---|
| y | 2 | 2 | 2 | 1 | 1 | 1 | 0 | 0 | 0 |
| Минимум | 2 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 |
| x | 2 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 |
|---|---|---|---|---|---|---|---|---|---|
| y | 2 | 2 | 2 | 1 | 1 | 1 | 0 | 0 | 0 |
| Максимум Минус. | 2 | 2 | 2 | 2 | 1 | 1 | 2 | 1 | 0 |
| x | 2 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 |
|---|---|---|---|---|---|---|---|---|---|
| y | 2 | 2 | 2 | 1 | 1 | 1 | 0 | 0 | 0 |
| Webb(x,y) | 0 | 0 | 0 | 0 | 2 | 2 | 0 | 2 | 1 |
См. также
Примечания
Литература
- Яблонский С. В., Гаврилов Г. П., Кудрявцев В. Б. Функции алгебры логики и классы Поста. — М.: Наука, 1966. — (Математическая логика и основания математики).
Ссылки
iMath Wiki — Алгебра логики. Основные логические операции и их таблицы истинности. Основные законы алгебры логики.
Мы выяснили, как информация представляется в памяти вычислительных устройств и установили алгоритмы проведения операций над этими представлениями.
Теперь, давайте попробуем разобраться, как именно реализуются операции над двоичными представлениями. Для этого, для начала, нам придется разобраться с алгеброй логики.
Алгебра логики является частью дискретной математики – раздела математики, изучающего свойства структур конечного характера.
Сама алгебра логики изучает свойства функций, у которых значения как аргументов, так и самих функций ограничены двумя значениями, например, \(\{0,1\}\).
Отцом алгебры логики считается английский математик Джордж Буль (1815-1864), поэтому алгебру логики иногда называют булевой алгеброй.
Долгое время алгебра логики была известна лишь узкому кругу специалистов, и только в 1938 году американский математик Клод Шеннон (1916-2001), стоявший у истоков современной информатики, показал, что алгебра логики применима для описания самых разных процессов, в том числе релейных и транзисторных схем.
Исследования в области алгебры логики связаны с формальной логикой, а точнее, с понятием высказывания. Высказывание – это некое лексическое образование, которое устанавливает свойства и взаимосвязи между объектами. Высказывания могут быть истинными, если они адекватно описывают объекты, или ложными в противном случае.
Так, примерами высказываний могут служить такие фразы, как “сегодня идет дождь”, или “завтра я не пойду в институт”.
Определение истинности высказывания не всегда тривиально. Так, например:
Великая теорема Ферма
Для любого натурального числа \(n>2\) уравнение \[ a^n + b^n = c^n\] Не имеет решений в целых ненулевых числах \(a,\,b,\,c\)
Как известно, сформулированная Пьером Ферма в 1637 году, была окончательно доказана только в 1994.
Введем не совсем формальное, но достаточное для наших целей определение
- Высказывание
- это языковое образование, в отношении которого имеет смысл говорить о его истинности или ложности.
Это определение было предложено Аристотелем.
Проблема языковых образований в рамках алгебры логики в том, что они могут иметь весьма своеобразную структуру. Например, фраза “это высказывание является ложным” не может считаться высказыванием, поскольку бессмысленно говорить о его истинности или ложности. Причиной парадокса является структура фразы: она ссылается сама на себя. Подобные парадоксы могут быть устранены введением следующего определения:
- Элементарное высказывание
- это такое высказывание, никакая часть которого не является высказыванием.
Следует заметить, что высказыванием в строгом смысле является только утверждение о конкретных объектах. Если речь идет о неких переменных, например, “x – рациональное число”, то мы говорим о неких функциях, имеющих значение “истина” или “ложь”. Такие функции называются предикатами.
Так же следует заметить, что алгебра логики отвлекается от смыслового содержания высказываний, и занимается скорее связями между высказываниями. Если мы договоримся считать за аксиому, что “солнце светит ночью”, то есть, договоримся что это высказывание истинно, то в рамках нашей аксиоматики сможем делать какие-то обоснованные выводы. Эти выводы, конечно, не будут иметь много общего с действительностью.
Примерами таких отвлеченных, на первый взгляд, систем, может служить, например, геометрия Лобачевского, которая имеет не слишком много общего с нашим псевдоевклидовым пространством.
Различные языковые связки, такие, как “не”, “если …, то …”, “или”, “и”, и т.п. позволяют строить из элементарных высказываний более сложные.
В алгебре логики существуют соответствующие подобным связкам операции.
Введем некоторые из них.
- Конъюнкция, или логическое умножение
- логическая операция, ставящая в соответствие двум элементарным высказываниям новое высказывание, являющееся истинным тогда и только тогда, когда оба исходных высказывания истинны.
Конъюнкция обозначается различными способами, в частности, амперсандом \(a \,\&\,b\), точкой \(a \cdot b\), или “крышкой” \(a \wedge b\), и соответствует языковой связке “и”. Мы будем в основном использовать амперсанд.
Поскольку оба исходных высказывания имеют по два возможных значения, и конъюнкция имеет два возможных значения, мы можем записать это определение в виде таблицы истинности:
- Дизъюнкция, или логическое сложение
- логическая операция, ставящая в соответствие двум элементарным высказываниям новое высказывание, являющееся истинным тогда и только тогда, когда хотя бы одно из исходных высказываний истинно.
Дизъюнкция соответствует союзу “или”, и обозначается плюсом \(a+b\), или “галочкой” \(a\vee b\). Мы будем использовать в основном второй вариант.
Таблица истинности дизъюнкции, по определению:
- Строгая дизъюнкция, или сложение по модулю 2
- логическая операция, ставящая в соответствие двум элементарным высказываниям новое высказывание, являющееся истинным тогда и только тогда, когда только одно из исходных высказываний истинно.
Строгая дизъюнкция соответствует связке “либо …, либо …”, и обозначается плюсом в кружочке \(a\oplus b\), или треугольником \(a\vartriangle b\). Будем в основном пользоваться первым обозначением.
Таблица истинности, по определению:
- Импликация
- логическая операция, ставящая в соответствие двум элементарным высказываниям новое высказывание, являющееся ложным тогда и только тогда, когда первое из исходных высказываний (условие) истинно, а второе (следствие) – ложно.
Импликация соответствует связке “если …, то …”, и обозначается стрелкой \(a \rightarrow b\), или \(a \Rightarrow b\)
Таблица истинности, по определению:
Импликация, на первый взгляд, имеет не очевидное определение: как вдруг из ложных условий получается истинное следствие. Однако, в математике это никакая не новость. Например, возьмем очевидно ложное утверждение “один равен двум”:
\[1 = 2\] \[2 = 1\]
Складывая эти равенства, получим очевидно истинный результат:
\[3=3.\]
С другой стороны, из заведомо истинных посылок формально нельзя вывести ложный результат (конечно, человеческий фактор никто не отменял, но человеческий фактор выходит за пределы рассмотрения формальной логики).
- Эквивалентность
- логическая операция, ставящая в соответствие двум элементарным высказываниям новое высказывание, являющееся истинным тогда и только тогда, когда оба исходных высказывания одновременно истинны или одновременно ложны.
Эквивалентность соответствует связке “тогда и только тогда, когда”, и обозначается \(a \Leftrightarrow b\), или \(a \equiv b\), или \(a \sim b\), или \(a \leftrightarrow b\). Будем в основном пользоваться первыми двумя обозначениями.
Таблица истинности, по определению:
- Инверсия, или отрицание
- логическая операция, ставящая в соответствие элементарному высказыванию новое высказывание, являющееся истинным тогда и только тогда, исходное ложно.
Инверсия соответствует связке “не”, и обозначается \(\neg a\), или \(\;\overline{a}\;\), или \(!a\). Будем в основном пользоваться первыми двумя обозначениями.
Таблица истинности, по определению:
В заключение, таблица истинности основных логических операций:
| 0 | 0 | 1 | 0 | 0 | 0 | 1 | 1 |
| 0 | 1 | 1 | 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 |
| 1 | 1 | 0 | 1 | 1 | 0 | 1 | 1 |
Законы алгебры логики
Введем некоторые определения, аналогичные алгебре действительных чисел, для алгебры логики.
- Логическая переменная
- Переменная, значением которой может быть любое высказывание. Обозначать будем маленькими латинскими буквами.
- Логическая формула
- любая переменная, а так же любая из констант “0” (“ложь”) и “1” (“истина”)
- Любая комбинация логических формул, составленная с помощью логических операций.
- Эквивалентные формулы
- такие формулы, которые зависят от одного и того же набора переменных, и при одинаковых значениях этих переменных, формулы так же имеют одинаковые значения. Обозначать будем знаком равенства.
Существуют следующие “законы” алгебры логики, определяющие некий набор эквивалентных формул:
- Законы коммутативности
- \[x \,\&\,y = y \,\&\,x\] \[x \vee y = y\vee x\]
- Законы ассоциативности
- \[ (x \,\&\,y) \,\&\,z = x \,\&\,(y \,\&\,z)\] \[ (x \vee y) \vee z = x \vee(y \vee z)\]
- Законы поглощения
- \[x\vee 0 = x\] \[x\,\&\,1 = x\]
- Законы дистрибутивности
- \[ x\,\&\,(y\vee z) = (x\,\&\,y) \vee(x\,\&\,z)\] \[ x\vee(y\,\&\,z) = (x \vee y) \,\&\,(x\vee z)\]
- Закон противоречия
- \[ x \,\&\,\;\overline{x}\; = 0\]
- Закон исключения третьего
- \[ x \vee\;\overline{x}\; = 1\]
- Закон равносильности
- \[ x \,\&\,x = x\] \[ x \vee x = x \]
- Закон двойного отрицания
- \[\;\overline{\;\overline{x}\;}\; = x \]
- Законы де Моргана
- \[ \;\overline{x\,\&\,y}\; = \;\overline{x}\; \vee\;\overline{y}\; \] \[ \;\overline{x\vee y}\; = \;\overline{x}\; \,\&\,\;\overline{y}\; \]
- Законы поглощения
- \[ x\vee(x\,\&\,y) = x\] \[ x\,\&\,(x\vee y) = x\]
Все перечисленные законы элементарно доказываются составлением таблиц истинности.
Например, первый закон де Моргана:
| 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| 0 | 1 | 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 0 | 0 | 0 | 0 |
3 и 6 столбец одинаковы, следовательно, соответствующие формулы эквивалентны.
Введем еще одно определение
- Тавтология
- логическая формула, которая всегда истинна.
Например, тавтологией является формула, выражающая закон исключения третьего.
Оказывается, алгебра логики хорошо подходит для решения логических задач. Решение логических задач, конечно, умеренно бессмысленное времяпрепровождение (исключая случаи, когда на их примере рассматриваются более сложные вопросы), однако это хороший способ поработать с алгеброй логики и осмыслить основные концепции.
Итак, формальный способ решения логических задач:
- Из условий задачи выделяются простые высказывания и обозначаются как логические переменные.
- Условия задачи записываются в виде логических формул
- Составляется единое логическое выражение, соответствующее условию задачи. По условию задачи оно является истинным.
- Полученное выражение упрощается, либо составляется таблица истинности для него (либо и то, и другое)
- Выбирается решение задачи (случаи, когда условие истинно)
- Решение формулируется в исходных терминах задачи.
Пример: (источник)
На весеннем фестивале, четыре садовника показывали выращенные ими розы.
Всего розы были четырех цветов и у каждого садовника было по две розы.
Известно, что
- У первого была желтая роза
- У второго не было красной розы
- У третьего была синяя роза, но не было зеленой
- У одного из садовников с зеленой розой не было красной
- Ни у одного из садовников с желтой розой не было зеленой
- Ни у кого нет роз двух одинаковых цветов
Введем переменные, в которых название переменной соответствует цвету, а индекс – садовнику (номеру). Это автоматически учитывает условие “Ни у кого нет роз двух одинаковых цветов”. Тогда условия задачи запишутся в виде:
- \(y_1\)
- \(\;\overline{r_2}\;\)
- \(b_3 \,\&\,\;\overline{g_3}\;\)
- \((g_1\rightarrow\;\overline{r_1}\;) \oplus(g_2\rightarrow\;\overline{r_2}\;)\oplus(g_3\rightarrow\;\overline{r_3}\;)\oplus(g_4\rightarrow\;\overline{r_4}\;)\)
- \((y_1\rightarrow\;\overline{g_1}\;) \,\&\,(y_2\rightarrow\;\overline{g_2}\;)\,\&\,(y_3\rightarrow\;\overline{g_3}\;)\,\&\,(y_4\rightarrow\;\overline{g_4}\;)\)
Дополнительно, у каждого садовника по условиям задачи по две розы: Поэтому, если у садовника есть розы двух цветов, то роз двух других цветов у него нет. Учтем подразумеваемые импликации постфактум.
Далее для простоты записи, амперсанды опускаются (если между переменными нет ничего – значит там амперсанд). В случае отсутствия скобок, сначала применяется конъюнкция, потом все остальное.
Рассматривая последнее условие:
\((y_1\rightarrow\;\overline{g_1}\;) (y_2\rightarrow\;\overline{g_2}\;)(y_3\rightarrow\;\overline{g_3}\;)(y_4\rightarrow\;\overline{g_4}\;)\)
Первая импликация истинна, только если \(\;\overline{g_1}\;\) истинно. Предпоследняя импликация истинна всегда, \(\;\overline{g_3}\;\). Можем переписать в виде:
\(y_1 \;\overline{g_1}\; (y_2\rightarrow\;\overline{g_2}\;) (y_4\rightarrow\;\overline{g_4}\;)\)
Рассмотрим предпоследнее условие
\[ (g_1 \rightarrow\;\overline{r_1}\;) \oplus(g_2 \rightarrow\;\overline{r_2}\;) \oplus(g_3 \rightarrow\;\overline{r_3}\;) \oplus(g_4 \rightarrow\;\overline{r_4}\;) \]
Первая импликация всегда истинна, поскольку \(\;\overline{g_1}\;\), вторая всегда истинна, поскольку \(\;\overline{r_2}\;\), третья всегда истинна, поскольку \(\;\overline{g_3}\;\). Получаем:
\[ 1 \oplus 1 \oplus 1 \oplus(g_4 \rightarrow\;\overline{r_4}\;) \]
\[ 1 \oplus(g_4 \rightarrow\;\overline{r_4}\;) \]
Легко показать, что \(1 \oplus x = \;\overline{x}\;\). Тогда условие принимает вид
\[ \;\overline{g_4 \rightarrow\;\overline{r_4}\;}\; \]
Импликацию можно представить в виде \(x \rightarrow y = \;\overline{x}\; \vee y\)
Применяя закон де Моргана,
\[ r_4 g_4 \]
Записывая все условия вместе:
\[ y_1 \;\overline{g_1}\; \;\overline{r_2}\; (\;\overline{y_2}\; \vee\;\overline{g_2}\;) (\;\overline{y_4}\; \vee\;\overline{g_4}\;) b_3 \;\overline{g_3}\; g_4 r_4 \]
Учитывая \(g_4 (\;\overline{y_4}\; \vee\;\overline{g_4}\;) = g_4 \;\overline{y_4}\;\),
\[ y_1 \;\overline{g_1}\; \;\overline{r_2}\; (\;\overline{y_2}\; \vee\;\overline{g_2}\;) b_3 \;\overline{g_3}\; \;\overline{y_4}\; g_4 r_4 \]
Известно, что зеленые розы должны быть у двух садовников:
\[ \;\overline{g_1}\; \;\overline{g_2}\; g_3 g_4 \vee\;\overline{g_1}\; g_2 \;\overline{g_3}\; g_4 \vee\;\overline{g_1}\; g_2 g_3 \;\overline{g_4}\; \vee g_1 \;\overline{g_2}\; \;\overline{g_3}\; g_4 \vee g_1 \;\overline{g_2}\; g_3 \;\overline{g_4}\; \vee g_1 g_2 \;\overline{g_3}\; \;\overline{g_4}\; \]
А так как \(\;\overline{g_3}\;\) и \(\;\overline{g_1}\;\)
\[ \;\overline{g_1}\; g_2 \;\overline{g_3}\; g_4 \]
Получаем \(g_2\), тогда \(g_2 (\;\overline{y_2}\; \vee\;\overline{g_2}\;) = g_2 \;\overline{y_2}\;\)
Аналогично для желтых:
\[ y_1 \;\overline{y_2}\; y_3 \;\overline{y_4}\; \]
Получаем \(y_3\). Поскольку \(y_3 b_3\), можно утверждать \(\;\overline{r_3}\; \;\overline{g_3}\;\)
Для красных тогда:
\[ r_1 \;\overline{r_2}\; \;\overline{r_3}\; r_4 \]
Получаем \(r_1\). Поскольку \(r_1 y_1\), можем утверждать \(\;\overline{b_1}\; \;\overline{g_1}\;\)
Для синих:
\[ \;\overline{b_1}\; b_2 b_3 \;\overline{b_4}\; \]
Получаем \(b_2\).
Итого
\[ y_1 r_1 g_2 b_2 b_3 y_3 g_4 r_4 \]
Теория логики — Таблицы истинности. Часть III — Введение в… | Хесус Нахера
Теперь, когда мы ознакомились с принципами теории логики, а также с основными обозначениями, пора исследовать концепцию эквивалентности в логике. В частности, что делает два составных помещения равными?
Две составные посылки X и Y являются логически эквивалентными , если для каждого присвоения значений истинности примитивным посылкам, составляющим X и Y, утверждения X и Y имеют идентичные значения истинности.
Это определение сложно проглотить, но нам нужно изучить приложение этого определения. Чтобы добиться этого, мы рассмотрим множество все более сложных примеров. Но для начала давайте сделаем крюк и узнаем немного больше о нашем Экскалибуре для этого путешествия — одном из самых простых, но мощных инструментов для логиков для доказательства логической эквивалентности: таблиц истинности .
Таблица истинности — это визуальный инструмент в форме диаграммы со строками и столбцами, который показывает истинность или ложность составной предпосылки.Это способ организации информации, чтобы перечислить всех возможных сценариев из предоставленных помещений. Давайте начнем с самого простого примера, таблицы истинности, изображающей манипуляцию с одной предпосылкой: отрицание (~) примитивной предпосылки (P)
Таблицы истинности всегда читаются слева направо, с примитивной предпосылкой в первом столбце. В приведенном выше примере наша примитивная посылка ( P ) находится в первом столбце; а результирующая посылка ( ~ P ), пост-отрицание, составляет второй столбец.
Здесь легко переусердствовать — не забывайте, что посылка — это просто утверждение, которое либо истинно, , либо ложно. Так как в этом примере есть только единственная предпосылка , нам нужно отслеживать только два результата; в результате получается две строки, когда P истинно или когда ложно. Первая строка описывает слева направо, что если P истинно, то отрицание P ложно; в строке два показано, что если P уже ложно, то отрицание P истинно.
Давайте перейдем к более сложному примеру реальных таблиц истинности, вставив уже знакомую нам связку: импликацию (->).Чтобы сделать это немного более удобоваримым, давайте назначим нашим утверждениям P&Q некоторый контекст до построения нашей таблицы истинности:
P: Танос щелкнул пальцами
Q: 50% всех живых существ исчезло
Прежде чем смотреть ниже, продумайте эту структуру с учетом вышеперечисленных деталей. Во-первых, поскольку у нас есть две примитивные посылки (P, Q), мы знаем, что нам понадобится как минимум двух столбцов; Кроме того, мы должны подготовиться к результирующей посылке с импликационной связкой (P -> Q), для которой потребуется еще один столбец.Всего трех столбцов .
А как насчет строк? Поскольку у нас есть две посылки, каждая из которых может быть истинной или ложной, для учета всех возможных сценариев нам потребуется всего четырех строк (PS — из этого наблюдения можно вывести изящное следствие: таблица истинности, которая учитывает N помещений, требует N² строк) . Давайте теперь нарисуем эту таблицу и убедимся, что она понятна:
Просмотрите таблицу истинности выше строка за строкой.Первая строка подтверждает, что Танос щелкнул пальцами (P), и 50% всего живого исчезло (Q). Поскольку обе посылки верны, то результирующая посылка (импликация или условная) также верна:
Вторая строка одинаково прямолинейна в понимании. На этот раз P по-прежнему верно, однако Q теперь ложь. Интерпретация здесь такова: «Танос щелкнул пальцами, но 50% всех живых существ не исчезли». Поскольку мы собираемся доказать обоснованность импликации, логично, что предыдущее утверждение делает общую предпосылку однозначно ложной:
Последние две строки несколько более противоречивы.Здесь есть ярлык: нам нужно только посмотреть на первый столбец, чтобы убедиться, что значение истинно. В обеих строках 3 и 4 исходная посылка (P) — ложных — , и это все, что нам нужно знать, независимо от значения посылки Q, чтобы определить импликацию как истинных.
Почему ложное антецедент всегда приводит к истинному подтексту? Поскольку во вселенной нашего логического утверждения, поскольку предшествующего события не произошло, невозможно исключить всех возможных сценариев, которые могли вызвать Q.Например, в строке 3 сказано, что «Танос не щелкнул пальцами, но 50% всех живых существ все равно исчезло». Что ж, насколько нам известно, это вымирание могли быть вызваны метеоритом, стихийным бедствием, вторжением инопланетян или множеством других действий — в любых из этих сценариев, независимо от того, какой из них, последствия остаются верными, потому что мы все еще не можем докажи, что происходит, когда он щелкает пальцами.
Таблицы истинности — это удобные и удобные логические диаграммы, которые используются не только в математике, но и в информатике, электротехнике и философии.Обозначения могут различаться в зависимости от отрасли, в которой вы работаете, но основные концепции остаются теми же. Это универсальный междисциплинарный инструмент, но мы только прикоснулись к их полезности.
Теперь, когда есть таблицы истинности, пора перейти к доказательству эквивалентности между несколькими составными помещениями. В следующей статье этой серии мы используем наши знания о сложном соединении, чтобы доказать, что две различные составные предпосылки, такие как импликация и контрположительный, равны.
источников
Логика: теория формального вывода
Основы математики
Как использовать логические вентили с соответствующей таблицей истинности [Шаг за шагом]
Логические ворота — это цифровая электронная схема, которая используется для выполнения логических операций и задач.
Логические шлюзы работают с логическими функциями, чтобы выдавать логический выход для одного или более чем одного логического входа. Логическая функция использует один или несколько двоичных входов и создает новый двоичный выход в соответствии с применяемой функцией.
Ниже приведен метод, показывающий, как использовать логические вентили для построения вашей логической схемы, а также как тестировать их с помощью соответствующей таблицы истинности.
Шаги по использованию логического элемента в лаборатории
На следующем шаге мы берем логический вентиль или, чтобы продемонстрировать, как использовать логический вентиль в нашей виртуальной лаборатории.
Шаг 1: Прокрутите список компонентов выше и перейдите к логическим элементам, как показано на снимках экрана ниже.
Шаг 2: Щелкните логический вентиль, который вы хотите использовать, из списка. Логический вентиль появится на плате, как показано на скриншоте ниже.
Глава 5 Таблицы истинности | В поисках истины: руководство к критическому мышлению
Переводы в логике высказываний — это только средство для достижения цели. Наша цель — использовать переведенные формулы для определения справедливости аргументов. Для этого мы будем использовать инструмент, называемый таблицей истинности. По сути, таблица истинности — это список всех различных комбинаций значений истинности, которые может иметь предложение или набор предложений.
Одиночные предложения
Прежде чем мы сможем анализировать аргументы с помощью таблиц истинности, нам нужно знать, как построить таблицы истинности для отдельных предложений.Начнем с таблицы истинности отрицания. Сначала напишите формулу для анализа вверху.
\ [ \ begin {array} {cc} & \ neg P \\ & \\ & \ end {массив} \]
Слева от формулы перечислите буквы простого предложения в алфавитном порядке. В этом случае у нас есть только одна буква предложения.
\ [ \ begin {array} {cc} P & \ neg P \\ & \\ & \ end {массив} \]
Теперь нарисуйте горизонтальную линию под всем этим и вертикальную линию, отделяющую формулу от букв предложения, например:
\ [ \ begin {array} {c | c} P & \ neg P \\ \ hline & \\ & \ end {массив} \]
Следующий шаг — перечислить все возможные комбинации истинностных значений букв простого предложения.В этом случае у нас есть только одна буква, и она может быть истинной или ложной.
\ [ \ begin {array} {c | c} P & \ neg P \\ \ hline Т & \\ F & \ end {массив} \]
Наконец, введите значения истинности формулы для каждой строки, учитывая значения истинности простых предложений в этой строке. Поскольку отрицание просто изменяет значение истинности простого предложения, наша таблица истинности будет выглядеть так:
\ [ \ begin {array} {c | c} P & \ neg P \\ \ hline Т & Ф \\ F&T \ end {массив} \]
А теперь давайте построим таблицу истинности для конъюнкции.Снова запишем формулу вверху:
\ [ \ begin {array} {cccccc} & & P & \ & & Q \\ & & & & \\ & & & & \\ & & & & \\ & & & & \ end {массив} \]
Затем мы напишем простую букву предложения слева и проведем линии.
\ [ \ begin {array} {cc | cccc} P & Q & P & \ & & Q \\ \ hline & & & & \\ & & & & \\ & & & & \\ & & & & \ end {массив} \]
Затем нам нужно написать все возможные комбинации значений истинности этих простых букв предложения.Во-первых, они оба могут быть правдой.
\ [ \ begin {array} {cc | cccc} P & Q & P & \ & & Q \\ \ hline T & T & & & \\ & & & & \\ & & & & \\ & & & & \ end {массив} \]
Тогда \ (P \) может быть истинным, а \ (Q \) — ложным.
\ [ \ begin {array} {cc | cccc} P & Q & P & \ & & Q \\ \ hline T & T & & & \\ Т & Ф & & & \\ & & & & \\ & & & & \ end {массив} \]
Для следующей строки \ (P \) может быть ложным, а \ (Q \) истинным.
\ [ \ begin {array} {cc | cccc} P & Q & P & \ & & Q \\ \ hline T & T & & & \\ Т & Ф & & & \\ F & T & & & \\ & & & & \ end {массив} \]
Наконец, они оба могут быть ложными.
\ [ \ begin {array} {cc | cccc} P & Q & P & \ & & Q \\ \ hline T & T & & & \\ Т & Ф & & & \\ F & T & & & \\ Ф & Ф & & & \ end {массив} \]
А теперь заполним остальное.Конъюнкция истинна, когда оба конъюнкта истинны, и ложь в противном случае. Итак, завершенная таблица истинности выглядит так.
\ [ \ begin {array} {cc | cccc} P & Q & P & \ & & Q \\ \ hline T & T & & T & \\ T & F & & F & \\ F & T & & F & \\ F & F & & F & \ end {массив} \]
Вот таблица истинности дизъюнкции. Помните, что дизъюнкция истинна, когда хотя бы одна дизъюнкция истинна, и ложна в противном случае.Итак, дизъюнкция ложна только в нижней строке.
\ [ \ begin {array} {cc | cccc} P & Q & P & \ vee & Q \\ \ hline T & T & & T & \\ T & F & & T & \\ F & T & & T & \\ F & F & & F & \ end {массив} \]
Вот как выглядит таблица истинности условного оператора. Условные выражения ложны, когда антецедент истинен, а вывод ложен, но они истинны в любое другое время.
\ [ \ begin {array} {cc | cccc} P & Q & P & \ rightarrow & Q \\ \ hline T & T & & T & \\ T & F & & F & \\ F & T & & T & \\ F & F & & T & \ end {массив} \]
Наконец, вот таблица истинности для двусмысленных.Двуусловные выражения истинны, если обе стороны имеют одинаковое значение истинности. Это будет первая строка, где они оба истинны, и последняя строка, где они оба ложны.
\ [ \ begin {array} {cc | cccc} P & Q & P & \ leftrightarrow & Q \\ \ hline T & T & & T & \\ T & F & & F & \\ F & T & & F & \\ F & F & & T & \ end {массив} \]
Давайте сделаем то, что немного длиннее. Вот таблица истинности для \ (P \ mathbin {\ &} (Q \ vee R) \):
Мы продолжим и напишем буквы в формулах и предложениях и проведем линии.
\ [ \ begin {array} {ccc | ccccc} P & Q & R & P & \ & & (Q & \ vee & R) \\ \ hline & & & & & & & \\ & & & & & & & \\ & & & & & & & \\ & & & & & & & \\ & & & & & & & \\ & & & & & & & \\ & & & & & & & \\ & & & & & & & & \ end {массив} \]
По мере того, как таблицы становятся больше, становится все труднее заполнять комбинации значений истинности для букв предложения.Выполняйте по одной целой строке за раз, легко пропустить комбинацию. Лучше всего делать это по всей колонке за раз. Начните с крайнего правого столбца и чередуйте буквы T и F.
\ [ \ begin {array} {ccc | ccccc} P & Q & R & P & \ & & (Q & \ vee & R) \\ \ hline & & T & & & & & \\ & & F & & & & & \\ & & T & & & & & \\ & & F & & & & & \\ & & T & & & & & \\ & & F & & & & & \\ & & T & & & & & \\ & & F & & & & & \ end {массив} \]
Затем перейдите к следующему столбцу слева.Здесь чередуются пары букв Т и пары F.
\ [ \ begin {array} {ccc | ccccc} P & Q & R & P & \ & & (Q & \ vee & R) \\ \ hline & T & T & & & & & \\ & Т & Ф & & & & & \\ & F & T & & & & & \\ & F & F & & & & & \\ & T & T & & & & & \\ & Т & Ф & & & & & \\ & F & T & & & & & \\ & F & F & & & & & & \ end {массив} \]
Может, теперь вы видите картину.Затем мы перейдем к следующему столбцу и поставим четыре Т и четыре F.
\ [ \ begin {array} {ccc | ccccc} P & Q & R & P & \ & & (Q & \ vee & R) \\ \ hline T & T & T & & & & & \\ T & T & F & & & & & \\ T & F & T & & & & & \\ T & F & F & & & & & \\ Ф & Т & Т & & & & & \\ Ф & Т & Ф & & & & & \\ F & F & T & & & & & \\ F & F & F & & & & & & \ end {массив} \]
Обратите внимание, что у нас восемь строк.Если бы было четыре разных простых предложения, у нас было бы шестнадцать, тридцать два вместо пяти и так далее. Общая формула такова: если имеется n простых предложений, то будет 2 n строк.
Затем мы заполняем оставшуюся часть таблицы истинности. В более длинных таблицах может быть проще сначала скопировать столбцы букв предложения, например:
\ [ \ begin {array} {ccc | ccccc} P & Q & R & P & \ & & (Q & \ vee & R) \\ \ hline T & T & T & T & & T & & T \\ T & T & F & T & & T & & F \\ T & F & T & T & & F & & T \\ T & F & F & T & & F & & F \\ F & T & T & F & & T & & T \\ F & T & F & F & & T & & F \\ F & F & T & F & & F & & T \\ F & F & F & F & & F & & F \ end {массив} \]
Затем мы начинаем работу в круглых скобках.Поскольку это дизъюнкция, оно будет истинным, если хотя бы одно из Q и R истинно, и ложным, если оба они ложны.
\ [ \ begin {array} {ccc | ccccc} P & Q & R & P & \ & & (Q & \ vee & R) \\ \ hline T & T & T & T & & T & T & T \\ T & T & F & T & & T & T & F \\ T & F & T & T & & F & T & T \\ T & F & F & T & & F & F & F \\ F & T & T & F & & T & T & T \\ F & T & F & F & & T & T & F \\ F & F & T & F & & F & T & T \\ F & F & F & F & & F & F & F \ end {массив} \]
Теперь мы можем игнорировать столбцы под Q и R .Мы сосредоточились на P и столбце под символом дизъюнкции. Чтобы было понятно, я удалю остальные.
\ [ \ begin {array} {ccc | ccccc} P & Q & R & P & \ & & (Q & \ vee & R) \\ \ hline T & T & T & T & & & T & \\ T & T & F & T & & & T & \\ T & F & T & T & & & T & \\ T & F & F & T & & & F & \\ F & T & T & F & & & T & \\ F & T & F & F & & & T & \\ F & F & T & F & & & T & \\ F & F & F & F & & & F & \ end {массив} \]
Теперь мы завершаем столбец для соединения.Это правда, если оба \ (P \) и \ (Q \ vee R \) истинны.
\ [ \ begin {array} {ccc | ccccc} P & Q & R & P & \ & & (Q & \ vee & R) \\ \ hline T & T & T & T & T & & T & \\ T & T & F & T & T & & T & \\ T & F & T & T & T & & T & \\ T & F & F & T & F & & F & \\ F & T & T & F & F & & T & \\ F & T & F & F & F & & T & \\ F & F & T & F & F & & T & \\ F & F & F & F & F & & F & \ end {массив} \]
В конце концов, меня действительно интересует столбец под основным соединительным элементом.Я сделаю это смелым, чтобы внести ясность. Наша полная таблица истинности со всеми столбцами выглядит так:
\ [ \ begin {array} {ccc | ccccc} P & Q & R & P & \ & & (Q & \ vee & R) \\ \ hline T & T & T & T & \ textbf {T} & T & T & T \\ T & T & F & T & \ textbf {T} & T & T & F \\ T & F & T & T & \ textbf {T} & F & T & T \\ T & F & F & T & \ textbf {F} & F & F & F \\ F & T & T & F & \ textbf {F} & T & T & T \\ F & T & F & F & \ textbf {F} & T & T & F \\ F & F & T & F & \ textbf {F} & F & T & T \\ F & F & F & F & \ textbf {F} & F & F & F \ end {массив} \]
Обратите внимание, что столбец основной соединительной ткани состоит из букв T и F.Это называется непредвиденным обстоятельством. Условное утверждение верно для одних строк и ложно для других. Некоторые предложения верны во всех строках. Их называют тавтологиями. Вот простой пример:
\ [ \ begin {array} {c | ccc} P & P & \ vee & \ neg P \\ \ hline T & T & \ textbf {T} & F \\ F & F & \ textbf {T} & T \ end {массив} \]
Если предложение содержит букву F в каждой строке таблицы, это противоречие.
\ [ \ begin {array} {c | ccc} P & P & \ & & \ neg P \\ \ hline Т & Т & \ textbf {F} & F \\ F & F & \ textbf {F} & T \ end {массив} \]
Тавтологии не могут быть ложными, противоречия не могут быть истинными, а случайности могут быть истинными или ложными.
Логическая эквивалентность
Иногда полезно поместить пару предложений в одну и ту же таблицу истинности. Если столбцы под их основными связками идентичны, тогда предложения логически эквивалентны . Это означает, что они всегда имеют одинаковое значение истинности.
Вот пример. Предложения разделяются косой чертой.
\ [ \ begin {array} {cc | cccccccc} P & Q & \ neg & (P & \ & & Q) & / & \ neg P & \ vee & \ neg Q \\ \ hline T & T & \ textbf {F} & T & T & T & F & \ textbf {F} & F \\ T & F & \ textbf {T} & T & F & F & & F & \ textbf {T} & T \\ F & T & \ textbf {T} & F & F & T & T & \ textbf {T} & F \\ F & F & \ textbf {T} & F & F & F & T & \ textbf {T} & T \ end {массив} \]
Неудивительно, что эти предложения эквивалентны.Первый по существу утверждает, что это не тот случай, когда P и Q оба истинны, а второй утверждает, что по крайней мере один из них ложен. Это всего лишь два способа сказать одно и то же.
Таблицы истинности и действительности
Чтобы оценить аргумент с использованием таблицы истинности, поместите предпосылки в строку, разделенную одной косой чертой, а затем заключение, разделенное двумя косыми чертами.
Вот простой аргумент под названием Modus Ponens:
- P \ (\ rightarrow \) Q
- п.
- Q
Начнем таблицу истинности так:
\ [ \ begin {array} {cc | ccccccc} P & Q & (P & \ rightarrow & Q) & / & P & // & Q \\ \ hline & & & & & & & & \\ & & & & & & & & \\ & & & & & & & & \\ & & & & & & & & & \ end {массив} \]
Затем введите возможные значения истинности для простых предложений слева.
\ [ \ begin {array} {cc | ccccccc} P & Q & (P & \ rightarrow & Q) & / & P & // & Q \\ \ hline T & T & & & & & & & \\ Т & Ф & & & & & & & \\ Ф & Т & & & & & & & \\ F & F & & & & & & & & \ end {массив} \]
Мы можем легко заполнить столбцы для второй посылки и заключения, поскольку они включают просто копирование столбцов P и Q.
\ [ \ begin {array} {cc | ccccccc} P & Q & (P & \ rightarrow & Q) & / & P & // & Q \\ \ hline T & T & & & & & T & & T \\ T & F & & & & & T & & F \\ F & T & & & & & F & & T \\ F & F & & & & & F & & F \ end {массив} \]
Наконец, заполним столбец для первой посылки.Помните, что условие ложно только тогда, когда antecdent истинно, а следствие ложно. Итак, первая посылка ложна во второй строке и истинна в других строках.
\ [ \ begin {array} {cc | ccccccc} P & Q & (P & \ rightarrow & Q) & / & P & // & Q \\ \ hline T & T & & T & & & T & & T \\ T & F & & F & & & T & & F \\ F & T & & T & & & F & & T \\ F & F & & T & & & F & & F \ end {массив} \]
Итак, что говорит нам о том, что аргумент верен? Помните, что аргумент действителен, если невозможно, чтобы посылки были истинными, а вывод — ложным.Итак, мы проверяем, есть ли в таблице истинности строка, содержащая все истинные посылки и ложное заключение. Если да, значит, аргумент неверен. В этом аргументе единственная строка, в которой все предпосылки верны, — это строка 1. Однако в этой строке заключение также верно. Итак, этот аргумент верен.
Часто нет необходимости заполнять всю таблицу истинности для определения достоверности. Давайте посмотрим на ярлык, используя тот же аргумент. Я сразу вижу, что действительно есть только одна строка, с которой мне нужно работать.Посмотрим, сможешь ли ты выяснить, какой именно.
\ [ \ begin {array} {cc | ccccccc} P & Q & (P & \ rightarrow & Q) & / & P & // & Q \\ \ hline T & T & & & & & & & \\ Т & Ф & & & & & & & \\ Ф & Т & & & & & & & \\ F & F & & & & & & & & \ end {массив} \]
Мне нужно сосредоточиться только на строках, где я знаю, что посылки могут быть верными, а заключение — ложным.Итак, я могу спокойно игнорировать строки 3 и 4, потому что вторая посылка для этих строк неверна. Когда я смотрю на строки 1 и 2, я вижу, что вывод верен для строки 1. Итак, единственная строка, у которой есть шанс показать, что этот аргумент недействителен, — это строка 2. Итак, я буду работать над этим.
\ [ \ begin {array} {cc | ccccccc} P & Q & (P & \ rightarrow & Q) & / & P & // & Q \\ \ hline T & T & & & & & & & \\ T & F & & F & & & T & & F \\ Ф & Т & & & & & & & \\ F & F & & & & & & & & \ end {массив} \]
Поработав, вижу, что одно из помещений оказалось ложным.Итак, я знаю, что не существует ряда, в котором были бы все истинные предпосылки и ложное заключение.
А теперь посмотрим, что произойдет, если мы заменим вторую посылку заключением. Как вы думаете, на каких строках нам следует сосредоточиться?
\ [ \ begin {array} {cc | ccccccc} P & Q & (P & \ rightarrow & Q) & / & Q & // & P \\ \ hline T & T & & & & & & & \\ Т & Ф & & & & & & & \\ Ф & Т & & & & & & & \\ F & F & & & & & & & & \ end {массив} \]
Обратите внимание, что вывод неверен только для строк 3 и 4.Однако в строке 4 вторая посылка неверна. Итак, единственная строка, которая может сделать это недействительным, — это строка 3. Давайте поработаем и посмотрим, что получится.
\ [ \ begin {array} {cc | ccccccc} P & Q & (P & \ rightarrow & Q) & / & Q & // & P \\ \ hline T & T & & & & & & & \\ Т & Ф & & & & & & & \\ F & T & & T & & & T & & F \\ F & F & & & & & & & & \ end {массив} \]
Так как условие с ложным антецедентом истинно, первая посылка, если истинна, в строке 3.Вторая посылка также верна, но вывод неверен. Итак, этот аргумент неверен. Фактически, это настолько распространенный неверный аргумент, что у него есть название: «Предполагая, что следствие».
Вот еще пример:
- P \ (\ rightarrow \) Q
- ¬ Q
- ¬ P
\ [ \ begin {array} {cc | ccccccc} P & Q & (P & \ rightarrow & Q) & / & \ neg Q & // & \ neg P \\ \ hline T & T & & & & & & & \\ Т & Ф & & & & & & & \\ Ф & Т & & & & & & & \\ F & F & & & & & & & & \ end {массив} \]
Мы просто заполним все:
\ [ \ begin {array} {cc | ccccccc} P & Q & (P & \ rightarrow & Q) & / & \ neg Q & // & \ neg P \\ \ hline T & T & & T & & & F & & F \\ T & F & & F & & & T & & F \\ F & T & & T & & & F & & T \\ F & F & & T & & & T & & T \ end {массив} \]
Нет линии со всеми истинными предпосылками и ложным заключением, поэтому аргумент действителен.Этот тип аргумента называется латинским именем Modus Tollens . Давайте снова поменяем вторую посылку на вывод и посмотрим, что произойдет.
\ [ \ begin {array} {cc | ccccccc} P & Q & (P & \ rightarrow & Q) & / & \ neg P & // & \ neg Q \\ \ hline T & T & & T & & & F & & F \\ T & F & & F & & & F & & T \\ F & T & & T & & & T & & F \\ F & F & & T & & & T & & T \ end {массив} \]
В третьей строке есть все истинные посылки и ложный вывод, поэтому этот аргумент неверен.Это называется «отрицанием антецедента».
Давайте попробуем таблицу истинности для более сложного аргумента.
- A против B
- А → (В против С)
- ¬ (C&A)
- В
Таблица начинается так:
\ [ \ begin {array} {ccc | cccccccccccccccc} A & B & C & A & \ vee & B & / & A & \ rightarrow & (B & \ vee & C) & / & \ neg & (C & \ & & A) & // & B \\ \ hline Т & Т & Т & & & & & & & & & & & & & & & & & \\ Т & Т & Ф & & & & & & & & & & & & & & & & & \\ Т & Ф & Т & & & & & & & & & & & & & & & & & \\ Т & Ф & Ф & & & & & & & & & & & & & & & & & \\ Ф & Т & Т & & & & & & & & & & & & & & & & & \\ Ф & Т & Ф & & & & & & & & & & & & & & & & & \\ Ф & Ф & Т & & & & & & & & & & & & & & & & & \\ F & F & F & & & & & & & & & & & & & & & & & & \ end {массив} \]
Я расскажу вам первую строчку, а затем заполню остальные.В первой строке, поскольку оба A и B верны, верна первая посылка. Вторая посылка — это условие с истинным antecdent и истинным консеквентом (B и C истинны, что делает \ (B \ vee C \) истинным). Итак, верна и вторая посылка. Третья посылка ложна, поскольку это отрицание истинного союза. Наконец, вывод верный.
\ [ \ begin {array} {ccc | cccccccccccccccc} A & B & C & A & \ vee & B & / & A & \ rightarrow & (B & \ vee & C) & / & \ neg & (C & \ & & A) & // & B \\ \ hline T & T & T & T & T & T & & T & T & T & T & T & & F & T & T & T & & T \\ Т & Т & Ф & & & & & & & & & & & & & & & & & \\ Т & Ф & Т & & & & & & & & & & & & & & & & & \\ Т & Ф & Ф & & & & & & & & & & & & & & & & & \\ Ф & Т & Т & & & & & & & & & & & & & & & & & \\ Ф & Т & Ф & & & & & & & & & & & & & & & & & \\ Ф & Ф & Т & & & & & & & & & & & & & & & & & \\ F & F & F & & & & & & & & & & & & & & & & & & \ end {массив} \]
Заполненная таблица истинности выглядит так:
\ [ \ begin {array} {ccc | cccccccccccccccc} A & B & C & A & \ vee & B & / & A & \ rightarrow & (B & \ vee & C) & / & \ neg & (C & \ & & A) & // & B \\ \ hline T & T & T & T & T & T & & T & T & T & T & T & & F & T & T & T & & T \\ T & T & F & T & T & T & & T & T & T & T & F & & T & F & F & T & & T \\ T & F & T & T & T & F & & T & T & F & T & T & & F & T & T & T & & F \\ T & F & F & T & T & F & & T & F & F & F & F & & T & F & F & T & & F \\ F & T & T & F & T & T & & F & T & T & T & T & & T & T & F & F & & T \\ F & T & F & F & T & T & & F & T & T & T & F & & T & F & F & F & & T \\ F & F & T & F & F & F & & F & T & F & T & T & & T & T & F & F & & F \\ F & F & F & F & F & F & & F & T & F & F & F & & T & F & F & F & & F \ end {массив} \]
Нет линии со всеми истинными предпосылками и ложным заключением, поэтому аргумент действителен.
Краткие таблицы истинности
Таблицы истинности могут использоваться для определения достоверности любого аргумента в логике высказываний. Если вы внимательно будете следовать правилам , не допуская ошибок по неосторожности , вы гарантированно получите правильный ответ. Единственный недостаток — они очень быстро становятся очень большими. Таблица истинности аргумента с шестью простыми предложениями состоит из 64 строк — это не то, чего большинство из нас с нетерпением ждало бы.
Было бы хорошо, если бы был способ перейти прямо к строке, показывающей, что аргумент недействителен, если таковой имеется.К счастью, есть, хотя временами это может быть сложно.
Давайте попробуем следующий аргумент:
- А и В
- ¬ [A → (C v D)]
- C против D
Первый шаг — настроить таблицу истинности, как мы делали это раньше, но нам понадобится только одна строка.
\ [ \ begin {array} {ccc | cccccccccccccc} A & B & C & A & \ & & B & / & \ neg & [A & \ rightarrow & (C & \ vee & D)] & // & C & \ vee & D \\ \ hline & & & & & & & & & & & & & & & & & \ end {массив} \]
Следующий шаг — поставить букву «Т» под основным оператором всех помещений и букву «Т» под основным оператором заключения.
\ [ \ begin {array} {ccc | cccccccccccccc} A & B & C & A & \ & & B & / & \ neg & [A & \ rightarrow & (C & \ vee & D)] & // & C & \ vee & D \\ \ hline & & & & T & & & T & & & & & & & & & F & \ end {массив} \]
Когда мы делаем это, мы предполагаем, что существует линия, на которой все предпосылки аргумента истинны, а вывод ложен.Теперь посмотрим, приводит ли это предположение к противоречию. Если это так, то такой строки быть не может, и аргумент допустим. Если это не приведет к противоречию, то будет такая строчка, и аргумент будет недействительным.
Теперь мы начнем заполнять то, что должно быть правдой, если наши предположения верны. Первая посылка — истинное соединение, поэтому оба конъюнкта должны быть истинными.
\ [ \ begin {array} {ccc | cccccccccccccc} A & B & C & A & \ & & B & / & \ neg & [A & \ rightarrow & (C & \ vee & D)] & // & C & \ vee & D \\ \ hline & & & T & T & T & & T & & & & & & & & & F & \ end {массив} \]
Заключение является ложным дизъюнкцией, поэтому оба дизъюнкта должны быть ложными.
\ [ \ begin {array} {ccc | cccccccccccccc} A & B & C & A & \ & & B & / & \ neg & [A & \ rightarrow & (C & \ vee & D)] & // & C & \ vee & D \\ \ hline & & & T & T & T & & T & & & & & & & F & F & F \ end {массив} \]
Теперь мы знаем, какими должны быть A, B, C и D. Давайте перенесем эти ценности во вторую предпосылку.
\ [ \ begin {array} {ccc | cccccccccccccc} A & B & C & A & \ & & B & / & \ neg & [A & \ rightarrow & (C & \ vee & D)] & // & C & \ vee & D \\ \ hline & & & T & T & T & & T & T & & F & & F & & F & F & F \ end {массив} \]
Теперь нам нужно закончить вторую предпосылку. Мы начнем с дизъюнкции в антецеденте условного.
Затем само условие:
Теперь проверим, нет ли проблем. Мы ищем что-то вроде письма с разными значениями истинности или ложного дизъюнкта с истинным дизъюнктом. Здесь каждая буква имеет одинаковое значение истинности, где бы она ни встречалась. У нас есть соединение с двумя истинными союзами, два ложных дизъюнкции, оба с двумя ложными дизъюнкциями, ложное условное выражение с истинным антецедентом и ложным следствием и истинное отрицание с ложным отрицанием предложения.Все выглядит нормально, а это значит, что является возможным для аргумента , имеющего истинные предпосылки и ложное заключение, и определенно неверен. Проблемной строкой будет строка, в которой A истинно, B истинно, C ложно и D ложно. Это будет строка 4 всей таблицы истинности.
Давай попробуем другой. Вот классический аргумент, называемый конструктивной дилеммой:
- A ⊃ B
- C ⊃ D
- А против С
- B против D
Начните с построения основного заголовка таблицы.
\ [ \ begin {массив} {cccc | ccccccccccccccc} A & B & C & D & A & \ rightarrow & B & / & C & \ rightarrow & D & / & A & \ vee & C & // & B & \ vee & D \\ & & & & & & & & & & & & & & & & & & & \ end {массив} \]
Затем заполните T и F под основной связью помещения и вывода соответственно.
\ [ \ begin {массив} {cccc | ccccccccccccccc} A & B & C & D & A & \ rightarrow & B & / & C & \ rightarrow & D & / & A & \ vee & C & // & B & \ vee & D \\ & & & & & T & & & & T & & & & T & & & & F & \ end {массив} \]
Затем мы заполним то, что можем вычислить, исходя из этих предположений. Мы пока ничего не знаем о помещениях.Первые два являются истинными условными операторами, и есть три разных способа, которыми условное выражение может стать истинным. То же самое и с истинной дизъюнкцией в третьей посылке. Итак, начнем с вывода. Поскольку это ложная дизъюнкция, то и B, и D должны быть ложными.
\ [ \ begin {массив} {cccc | ccccccccccccccc} A & B & C & D & A & \ rightarrow & B & / & C & \ rightarrow & D & / & A & \ vee & C & // & B & \ vee & D \\ & & & & & T & & & & T & & & & T & & & F & F & F \ end {массив} \]
Затем мы можем заполнить эти значения везде, где встречаются B и D.
\ [ \ begin {массив} {cccc | ccccccccccccccc} A & B & C & D & A & \ rightarrow & B & / & C & \ rightarrow & D & / & A & \ vee & C & // & B & \ vee & D \\ & & & & & T & F & & & T & F & & & & T & & & F & F & F \ end {массив} \]
Теперь мы можем сделать первые два предположения. Обратите внимание, что у нас есть истинные условные выражения с ложными консеквентами.Это означает, что оба антецедента должны быть ложными.
\ [ \ begin {массив} {cccc | ccccccccccccccc} A & B & C & D & A & \ rightarrow & B & / & C & \ rightarrow & D & / & A & \ vee & C & // & B & \ vee & D \\ & & & & F & T & F & & F & T & F & & & T & & & & F & F & F \ end {массив} \]
Теперь мы можем заполнить это место там, где встречаются A и C в третьей посылке.
\ [ \ begin {массив} {cccc | ccccccccccccccc} A & B & C & D & A & \ rightarrow & B & / & C & \ rightarrow & D & / & A & \ vee & C & // & B & \ vee & D \\ & & & & F & T & F & & F & T & F & & F & T & F & & F & F & F \ end {массив} \]
Теперь у нас проблема. У нас есть истинная дизъюнкция в третьей посылке с двумя ложными дизъюнкциями.Это противоречие. Это означает, что мы не можем сделать этот аргумент имеющим истинные предпосылки и ложный вывод. Мы доказали, что аргумент верен.
Формы аргумента
Прежде чем мы оставим логику высказываний, вот несколько важных форм аргументов, которые могут быть полезны.
Действителен
Modus Ponens
- P \ (\ rightarrow \) Q
- п.
- Q
Modus Tollens
- P \ (\ rightarrow \) Q
- ¬ Q
- ¬ P
Дизъюнктивный силлогизм
- A против B
- ¬ B
- А
Гипотетический силлогизм
- A ⊃ B
- B C
- A ⊃ C
Конструктивная дилемма
- A ⊃ B
- C ⊃ D
- А против С
- B против D
Деструктивная дилемма
- A ⊃ B
- C ⊃ D
- ¬B v ¬ D
- ¬A v ¬ C
Неверно
Подтверждение Консультации
- P \ (\ rightarrow \) Q
- Q
- -п.
Отказ от предшествующего
- P \ (\ rightarrow \) Q
- ¬ П
- ¬ Q
Таблицы истинности — отрицание, соединение, дизъюнкция («не», «и», «или»)
Таблицы истинности — это способ анализа того, как обоснованность утверждений (называемых предложениями) ведет себя, когда вы используете логическое «или» или логическое «и» для их объединения. Утверждения либо полностью верны, либо полностью ложны, поэтому любая таблица истинности захочет показать обе эти возможности для всех сделанных утверждений.
Для всех этих примеров мы будем обозначать p и q предложениями.Это могут быть утверждения типа «Мне 25 лет» или «Сейчас теплее 70 °». Любые утверждения, которые являются правдой или ложью.
реклама
Отрицание — «не р»
Отрицание — это утверждение «не p», обозначаемое \ (\ neg p \), и поэтому оно будет иметь значение истинности, противоположное p. Если p истинно, то \ (\ neg p \), если ложно. Если p ложно, то \ (\ neg p \) истинно. Обратите внимание, что таблица истинности показывает все эти возможности.
Соединение — «и»
Рассмотрим утверждение «p и q», обозначенное \ (p \ wedge q \).Чтобы проанализировать это, мы сначала должны подумать обо всех комбинациях значений истинности для обоих утверждений, а затем решить, как эти комбинации влияют на утверждение «и». Прописью:
- Строка 1 : оба утверждения могут быть верными.
В этом случае имело бы смысл, что «p и q» также являются истинным утверждением. - Строка 2 : p может быть ложным, а q — истинным.
Для того, чтобы «p и q» были истинными, нам нужно, чтобы были истинными ОБА утверждения. Поскольку один из них ложен, «p и q» ложны. - Строка 3 : p может быть истинным, а q — ложным.
Если это так, то по тому же аргументу в строке 2 «p и q» ложны. - Строка 4 : оба утверждения могут быть ложными.
Если оба утверждения ложны, тогда «p и q» ложны.
Порядок строк не имеет значения — при условии, что мы систематичны таким образом, чтобы не пропустить никаких возможных комбинаций значений истинности для двух исходных утверждений p, q.
Дизъюнкция — «или»
Вы можете этого не осознавать, но есть два типа «или».Есть включительно или , где мы допускаем тот факт, что оба утверждения могут быть истинными, и есть исключительный или , где мы строго следим за тем, чтобы истинным было только одно или другое утверждение. В математике «или», с которым мы работаем, является включающим или, обозначаемым \ (p \ vee q \). Когда мы хотим работать с эксклюзивным или, мы конкретны и используем другую нотацию (вы можете прочитать об этом здесь: эксклюзивное или). Это показано в первой строке таблицы истинности, которую мы сейчас проанализируем:
- Строка 1 : оба утверждения могут быть верными.
Поскольку мы работаем с включающим или, утверждение «p или q» в этом случае будет истинным. - Строка 2 : p может быть ложным, а q — истинным.
Это суть или. Мы говорим «одно или оба утверждения верны». Следовательно, в данном случае верно «p или q». - Строка 3 : p может быть истинным, а q — ложным.
То же, что и второй ряд. - Строка 4 : оба утверждения могут быть ложными.
Принимая во внимание значение или, если оба утверждения ложны, тогда неверно, что «p или q», поэтому мы перечисляем ложные для этого утверждения.
Сводка
Чтобы отслеживать, как работают эти идеи, запомните следующее:
- «не p» всегда имеет значение истинности, противоположное p
- «p и q» верны только тогда, когда оба утверждения верны (в противном случае — ложь)
- «p или q» неверно, только если оба утверждения ложны (в противном случае — истина)
Понимание этих таблиц истинности позволит нам позже анализировать сложные составные композиции, состоящие из и, или, не, и, возможно, даже условного оператора, поэтому убедитесь, что у вас есть эти основы!
объявление
Продолжить рассмотрение отдельных математических тем
Далее: Таблицы истинности для условных и двусмысленных (подразумевает и если и только)
Подпишитесь на нашу рассылку!
Мы всегда публикуем новые бесплатные уроки и добавляем новые учебные пособия, руководства по калькуляторам и пакеты задач.
Подпишитесь, чтобы получать электронные письма (раз в пару или три недели) с информацией о новинках!

