Калькулятор электрических цепей: онлайн-инструмент для расчета параметров схем

Как рассчитать ток, напряжение и мощность в электрической цепи. Какие формулы использовать для последовательного и параллельного соединения. Как применять закон Ома и правила Кирхгофа. Онлайн-калькулятор для быстрых вычислений.

Основные принципы расчета электрических цепей

Расчет электрических цепей основан на применении нескольких фундаментальных законов и правил:

• Закон Ома, связывающий напряжение, ток и сопротивление: U = I * R
• Первый закон Кирхгофа: сумма токов, входящих в узел, равна сумме токов, выходящих из узла
• Второй закон Кирхгофа: сумма напряжений на элементах замкнутого контура равна нулю
• Формулы для последовательного и параллельного соединения резисторов

Применяя эти принципы, можно рассчитать токи, напряжения и мощности в любой электрической цепи. Рассмотрим основные типы расчетов на конкретных примерах.

Расчет простейших цепей постоянного тока

Простейшая электрическая цепь состоит из источника ЭДС, резистора и соединительных проводов. Для такой цепи справедлив закон Ома:

I = U / R

Где:

• I — сила тока в амперах (А)
• U — напряжение в вольтах (В)
• R — сопротивление в омах (Ом)

Например, если напряжение источника 12 В, а сопротивление 4 Ом, то ток в цепи составит:

I = 12 В / 4 Ом = 3 А

Последовательное и параллельное соединение резисторов

При последовательном соединении резисторов их общее сопротивление равно сумме сопротивлений:

R = R1 + R2 + R3 + …

При параллельном соединении обратная величина общего сопротивления равна сумме обратных величин сопротивлений отдельных резисторов:

1/R = 1/R1 + 1/R2 + 1/R3 + …

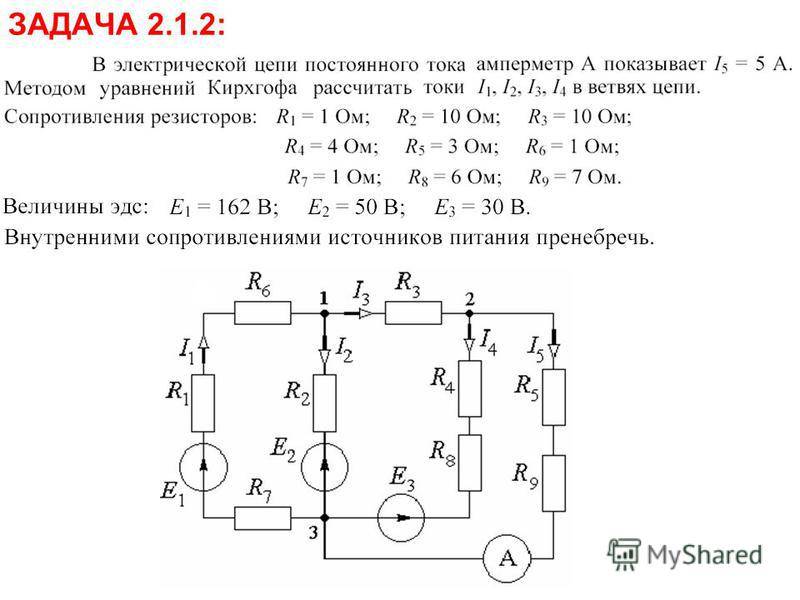
Расчет сложных цепей по правилам Кирхгофа

Для расчета сложных цепей с несколькими источниками ЭДС и резисторами применяют правила Кирхгофа:

1. Для каждого узла записывают уравнение по первому правилу Кирхгофа
2. Для каждого независимого контура записывают уравнение по второму правилу Кирхгофа
3. Решают полученную систему уравнений относительно неизвестных токов

Этот метод позволяет рассчитать любую линейную электрическую цепь, но для сложных схем вычисления могут быть громоздкими. В таких случаях удобно использовать онлайн-калькуляторы.

Онлайн-калькулятор для расчета электрических цепей

Для быстрого расчета параметров электрических цепей можно воспользоваться специальными онлайн-инструментами. Такие калькуляторы позволяют:

• Рассчитать токи, напряжения и мощности в простых и сложных цепях
• Определить эквивалентное сопротивление при различных соединениях резисторов
• Найти параметры элементов по заданным характеристикам цепи
• Построить векторные диаграммы для цепей переменного тока

Онлайн-калькуляторы значительно упрощают и ускоряют расчеты, избавляя от необходимости вручную решать системы уравнений.

Расчет цепей переменного тока

При расчете цепей переменного тока необходимо учитывать реактивные сопротивления катушек индуктивности и конденсаторов. Полное сопротивление цепи (импеданс) определяется по формуле:

Z = √(R^2 + (X_L — X_C)^2)

Где:

• R — активное сопротивление
• X_L = ωL — индуктивное сопротивление
• X_C = 1/(ωC) — емкостное сопротивление
• ω = 2πf — угловая частота

Ток и напряжение в цепи переменного тока могут быть сдвинуты по фазе. Для анализа таких цепей применяют метод векторных диаграмм.

Мощность в электрических цепях

Мощность, выделяемая на резисторе в цепи постоянного тока, рассчитывается по формуле:

P = I^2 * R = U^2 / R

В цепях переменного тока различают:

• Активную мощность P = I * U * cosφ
• Реактивную мощность Q = I * U * sinφ
• Полную мощность S = I * U

Где φ — угол сдвига фаз между током и напряжением.

Преимущества использования онлайн-калькуляторов

Применение онлайн-инструментов для расчета электрических цепей имеет ряд преимуществ:

• Высокая скорость вычислений даже для сложных схем
• Отсутствие ошибок, связанных с человеческим фактором
• Возможность быстро перебрать различные варианты параметров
• Наглядная визуализация результатов в виде графиков и диаграмм
• Доступность с любого устройства, подключенного к интернету

Это делает онлайн-калькуляторы незаменимым инструментом для инженеров, студентов и всех, кто работает с электрическими цепями.

Типичные задачи, решаемые с помощью калькуляторов

С помощью онлайн-калькуляторов можно решать следующие распространенные задачи:

• Расчет токов и напряжений в разветвленных цепях
• Определение эквивалентного сопротивления сложных схем
• Анализ резонансных явлений в RLC-цепях
• Расчет фильтров и делителей напряжения
• Определение мощности и коэффициента мощности
• Построение частотных и фазовых характеристик

Это позволяет существенно упростить проектирование и анализ электронных устройств.

РАСЧЕТ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ ОНЛАЙН

Наверное, каждый кто делал или делает ремонт электрики сталкивался с проблемой определения той или иной электрической величины. Для кого-то это становится настоящим камнем преткновения, а для кого-то все предельно ясно и каких-либо сложностей при определении той или иной величины нет. Данная статья посвящена именно первой категории – то есть для тех, кто не очень силен в теории электрических цепей и тех показателей, которые для них характерны.

Итак, для начала вернемся немного в прошлое и постараемся вспомнить школьный курс физики, касательно электрики. Как мы помним, основные электрические величины определяются на основании всего одного закона – закона Ома. Именно этот закон является базой проведения абсолютно для любых расчетов и имеет вид:

Отметим, что в данном случае речь идет о расчете самой простейшей электрической цепи, которая выглядит следующим образом:

Подчеркнем, что абсолютно любой расчет ведется именно посредством этой формулы. То есть путем не сложных математических вычислений можно определить ту или иную величину зная при этом два иных электрических параметра. Как бы там ни было, наш ресурс призван упростить жизнь тому кто делает ремонт, а поэтому мы упростим решение задачи определения электрических параметров, вывив основные формулы и предоставив возможность произвести расчет электрических цепей онлайн.

Мощность в цепи переменного тока

Внутри схемы переменного электротока различается три вида мощностей: активного типа или Р, реактивного типа или Q, и полного типа или S. В первом случае стандартной единицей замеров является Ватт (Вт или W), при этом формула для вычисления активных мощностных параметров:

P = U × I × cos φ.

Для замеров мощности реактивного типа применяется специальный вольт-ампер с обозначением «Вар» или Var.

Данной величиной характеризуются нагрузки, которые формируются внутри конструкций электротехнического типа под воздействием колебаний электромагнитных полей в цепях переменного синусоидального тока.

Расчет осуществляется на базе среднеквадратичных показателей напряжения и токовых параметров, умноженных на угловую синусоиду фазного сдвига, согласно значениям:

Q = U × I × sin φ.

В условиях значений на уровне 0/+90° синусовая величина будет положительной, а для показателей в пределах 0/-90° — только отрицательной. Замеры полной электромощности осуществляются исключительно в вольт-амперах (В·А или V·A).

Зависимость мощности от времени для переменного и постоянного тока

Величину, соответствующую произведению стандартного напряжения в зажимной области с показателями электротока периодического типа внутри цепи, целесообразно рассчитывать в соответствии с формулами:

S = U × I или S = √Р 2 + Q 2 , где

• значение Р представлено активной мощностью;
• значение Q 2 — показатель реактивной мощности.

Мощностные показатели электротока переменного типа являются произведением токовых данных на напряжение, при этом уровень будет нулевым в условиях прохождения через нуль, но обязательно максимальным на пиковой амплитуде.

Несмотря на сложность измерения мощности, важно помнить, что такие данные не показательны, поэтому с практической точки зрения интерес представляет активная средняя мощность в определенном периоде.

Формулы для расчётов цепи постоянного тока

Проще всего посчитать мощность для цепи постоянного тока. Если есть сила тока и напряжение, тогда нужно просто по формуле, приведенной выше, выполнить расчет:

P=UI

Но не всегда есть возможность найти мощность по току и напряжению. Если вам они не известны – вы можете определить P, зная сопротивление и напряжение:

P=U2/R

Также можно выполнить расчет, зная ток и сопротивление:

P=I2*R

Последними двумя формулами удобен расчёт мощности участка цепи, если вы знаете R элемента I или U, которое на нём падает.

Что такое мощность Ватт [Вт]

Мощность — величина, определяющая отношение работы, которую выполняет источник тока, за определённый промежуток времени.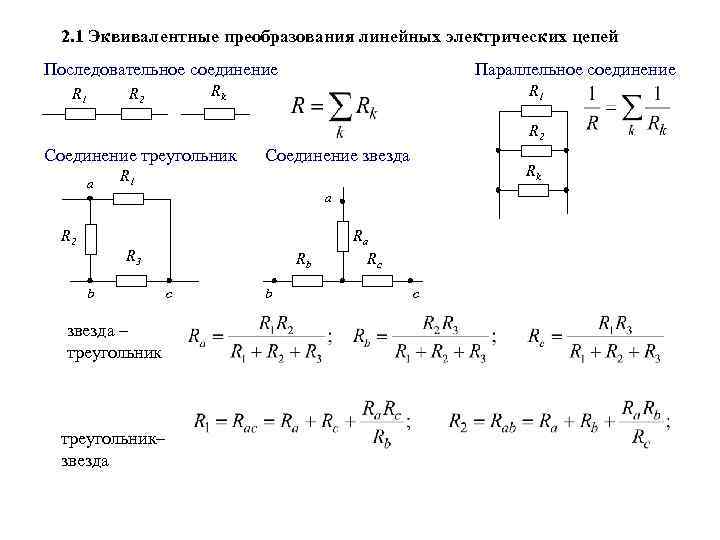 Один ватт соответствует произведению одного ампера на один вольт, но при определении трат на электроэнергию используется величина киловатт/час.

Она соответствует расходу одной тысячи ватт за 60 минут работы. Именно по этому показателю определяется стоимость услуг электроэнергии.

В большинстве случаев мощность, которую потребляет прибор, указана в технической документации или на упаковке. Указанное количество производится за один час работы.

Например, компьютер с блоком питания 500 Вт будет крутить 1 кВт за 2 часа работы.

Помочь определить силу тока при известной мощности поможет калькулятор, который делает перевод одной физической величины в другую.

Как узнать силу тока, зная мощность и напряжения

Чтобы ответить на вопрос, как определить ток, необходимо поделить электронапряжение на общее число ватт. При этом сделать все необходимые вычисления можно самостоятельно, а можно прибегнуть к специальному онлайн-калькулятору.

Расчет мощностного показателя по амперам и ваттам

Узнать потребление электроэнергии по токовой силе резистора можно умножением первой на сопротивление, выражаемое в Омах. В итоге, получится значение, представленное в вольтах, перемноженных на ом. Получится ампер.

Обратите внимание! Если нет сопротивления, нужно поделить ваттный показатель на токовую энергию, то есть следует поделить ватты на амперы и получится значение электроэнергии в вольтах. Понять мощностное показание через величину электричества с электронапряжением, можно умножив соответствующие показания с устройства.

Расчет электроэнергии через электромощность и электронапряжение

Что собой представляет мощность в электричестве

Под этим показателем подразумевают численную меру количества энергии, которая соответствует скорости изменения, или передачи ее в сети. У хозяйственно-бытовых приборов именно то количество электроэнергии, которое необходимо для их нормального функционирования — это и есть потребляемая мощность. В статичных приборах электричество трансформируется в свет или тепло. А в приборах с подвижными рабочими элементами — в энергию механического движения.

Формулировка выражается именно таким образом: за мощность (Р) принимают результат произведения моментальных значений напряжения (U) и силы тока (I) на части электроцепи.

P= U*I

Общая (полная) мощность образуется из таких собирательных элементов: активной и реактивной. Потребляемую (активную) измеряют в ваттах (Вт, кВт), реактивную — в вольт-амперах реактивных (ВАр, кВАр). Общая — в вольт-амперах (ВА).

Порядок вычисления электрической мощности в домашних условиях

Для выполнения предварительных расчетов следует первоначально собрать характеристики обо всех точках электропотребления, которые подключены к сети. Для этого следует придерживаться такого порядка:

1. Написать список всех приборов.
2. В каждом пункте списка следует указать эту необходимую величину, которую можно взять из паспортных данных.
3. Провести суммарный подсчет осветительных приборов.
4. Просуммировать показатели п.2 и п.3.
5. Полученное число следует округлить в большую сторону и добавить 15-25 % для избежания возможных перегрузок.

Чтобы рассчитать более верные показатели, следует учесть и такую величину, как коэффициент спроса. Эта величина обусловлена общей мощностью и устанавливается существующими нормативными параметрами.

Установленная (заявленная) мощность, кВт	до 14	>14 — 20	>20 — 30	>30 — 40	>40 — 50	>50 — 60	>70
Коэффициент спроса	0,8	0,65	0,6	0,55	0,5	0,48	0,45

Общую величину следует умножить на этот коэффициент. А итоговое число и будет отражением потребности в электричестве.

Расчет Мощности по Току и Напряжению | Схема | Таблица

Расчет электрических цепей | Физика

1.

Смешанное соединение проводников

Рассмотрим электрическую схему на рисунке 61.1. Некоторые проводники в ней соединены последовательно друг с другом, а некоторые – параллельно.

? 1. Какие проводники в этой схеме соединены последовательно друг с другом? Какие – параллельно?

Соединение проводников, при котором часть проводников соединена последовательно друг с другом, а часть – параллельно, называют смешанным.
При расчете сопротивления смешанного соединения проводников часто используют метод эквивалентного преобразования схем. При этом данную схему последовательно преобразуют в более простую, но имеющую такое же сопротивление.

Например, схему, изображенную на рисунке 61.1, можно преобразовать по следующему плану:
1. Заменить участок цепи с резисторами 1 и 2 одним резистором с сопротивлением, которое мы обозначим R₁₂.
2. Заменить участок цепи, содержащий резисторы с сопротивлениями R₁₂ и R₃, одним резистором с сопротивлением, которое мы обозначим R₁₂₃.
3. Заменить участок цепи с резисторами 4 и 5 одним резистором с сопротивлением, которое мы обозначим R₄₅.
4. Заменить участок цепи с резисторами сопротивлением R₁₂₃ и R₄₅ одним резистором. Его сопротивление и будет равно сопротивлению всего участка цепи.

? 2. В цепи, схема которой изображена на рисунке 61.1, сопротивление каждого резистора, выраженное в омах, примите равным номеру этого резистора. Начертите схемы, соответствующие каждому пункту намеченного выше плана; найдите R₁₂, R₁₂₃, R₄₅ и сопротивление всего участка.

Не всегда с первого взгляда на электрическую схему можно распознать вид соединения проводников.

В таком случае полезно найти точки с одинаковым потенциалом (например, соединенные проводами, сопротивление которых в таких задачах считают обычно пренебрежимо малым). Затем надо перечертить схему, объединив точки с одинаковым потенциалом.

Рассмотрим, например, схему участка цепи, изображенную на рисунке 61.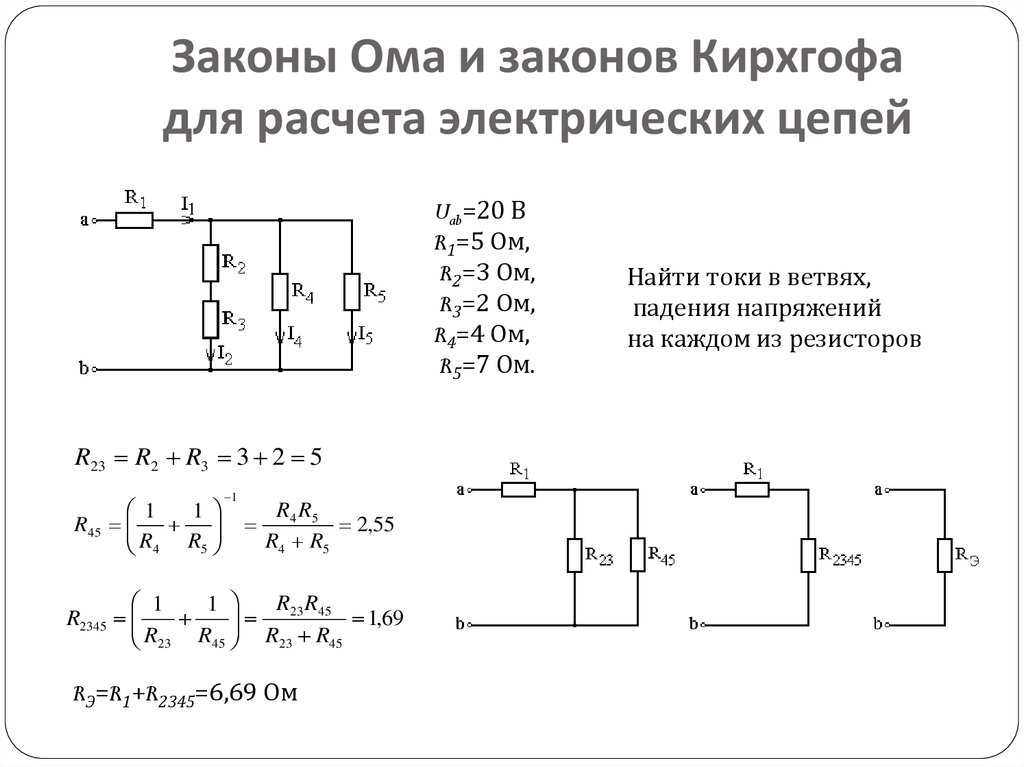 2.

Точки А и С соединены проводом с пренебрежимо малым сопротивлением, поэтому потенциалы этих точек равны. То же можно сказать и о точках В и D.

Следовательно, схему можно перечертить, объединив точки А и С в одну точку (обозначим ее АС), а точки В и D объединив в точку ВD. При этом, согласно исходной схеме, один конец каждого из трех резистов соединен с точкой АС, а другой – с точкой BD (рис. 61.3).

Теперь мы видим, что резисторы соединены параллельно.

? 3. Перенесите в тетрадь рисунок 61.2 и отметьте на нем направление тока в каждом резисторе, считая, что потенциал точки А выше потенциала точки D.

? 4. На рисунке 61.4 изображена схема участка электрической цепи. Сопротивление каждого резистора, выраженное в омах, равно номеру резистора. Обратите внимание: потенциалы точек А и С различны.

а) Перечертите схему, изображенную на рисунке 61.4, так, чтобы легко было распознать вид соединения резисторов.
б) Найдите сопротивление всего участка цепи.

К сожалению, не всякую электрическую схему можно поэтапно упрощать, используя только формулы для последовательного и параллельного соединений. На рисунке 61.5 приведен пример схемы участка цепи, которую нельзя упростить таим образом.

Но для некоторых частных случав можно найти сопротивление и такого участка цепи уже известными нам способами. Чтобы догадаться, каковы эти случаи, заменим резистор 5 идеальным вольтметром (рис. 61.6). (Напомним, что идеальным считают вольтметр, сопротивление которого можно принять бесконечно большим.)

? 5. Разность потенциалов между точками А и В равна 21 В. Сопротивления резисторов, выраженные в омах, равны их номерам.
а) Чему равна разность потенциалов между точками А и С?
б) Чему равна разность потенциалов между точками А и D?
в) Каковы показания вольтметра?
г) Резистором с каким сопротивлением надо заменить резистор 4, чтобы показания вольтметра были равны нулю?

? 6. Объясните, почему показания вольтметра будут равны нулю независимо от напряжения между точками А и В, если сопротивления резисторов на схеме, изображенной на рисунке 61. 6, удовлетворяют соотношению

R₁/R₂ = R₃/R₄.     (1)

Схему, изображенную на рисунке 61.6, называют мостиком Уитстона. С ее помощью можно измерить сопротивление одного из четырех резисторов, подбирая сопротивления остальных трех так, чтобы выполнялось соотношение (1).

? 7. Для сопротивлений резисторов 1 – 4 в цепи, изображенной на рисунке 61.5, выполняется соотношение (1).
а) Объясните, почему сопротивление данного участка цепи не зависит от сопротивления резистора 5.
б) Сопротивления резисторов 1 и 3 равны соответственно 10 Ом и 15 Ом. Подберите такие значения сопротивлений резисторов 2 и 4, чтобы сопротивление всего участка было равно 24 Ом независимо от сопротивления резистора 5.

2. Максимальная мощность во внешней цепи

? 8. К источнику с ЭДС ξ и внутренним сопротивлением r подключено внешнее сопротивление R (рис. 61.7).

а) Выразите мощность тока во внешней цепи через ξ, r и R.
б) Используя производную, найдите, при каком R мощность тока во внешней цепи будет максимальной.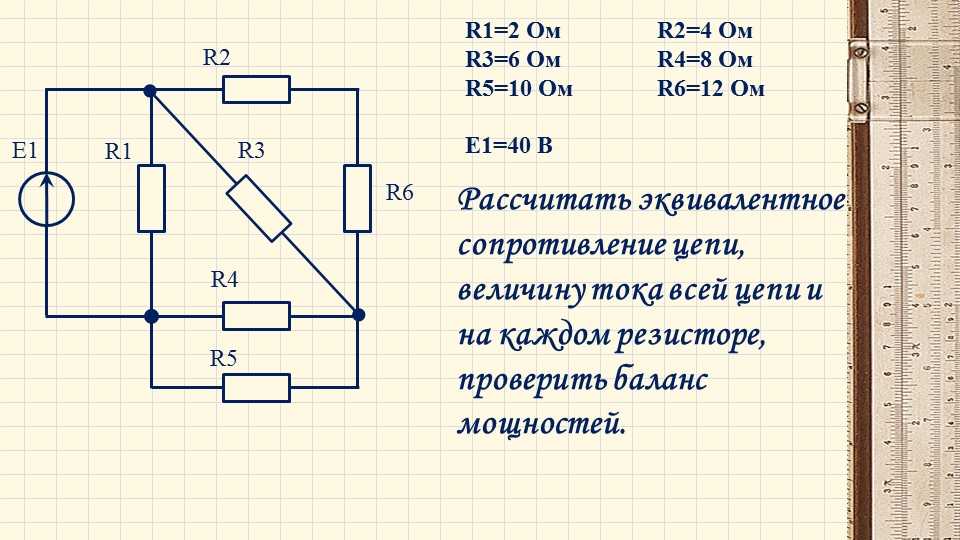

Эту задачу можно решить и без помощи производной. Для этого надо воспользоваться формулой для мощности тока во внешней цепи

P = UI,

где U – напряжение на внешнем сопротивлении (напомним, что оно равно напряжению на полюсах источника тока), I – сила тока в цепи.

? 9. Объясните, почему мощность тока во внешней цепи выражается формулой

P = (ξ – Ir)I.     (2)

Подсказка. Выразите напряжение на полюсах источника через ξ, I, r, используя закон Ома для всей цепи.

Правая часть равенства (2) представляет собой квадратичную функцию от силы тока I. Графиком ее является парабола.

? 10. Начертите график зависимости P(I) при изменении силы тока I от нуля до максимального значения (равного силе тока при коротком замыкании).
а) При каком значении I достигается максимум функции P(I)?
б) Какому сопротивлению внешней цепи соответствует это значение I?
Подсказка. Воспользуйтесь законом Ома для всей цепи.

Итак, максимальная мощность тока во внешней цепи достигается, когда сопротивление внешней цепи равно внутреннему сопротивлению источника тока.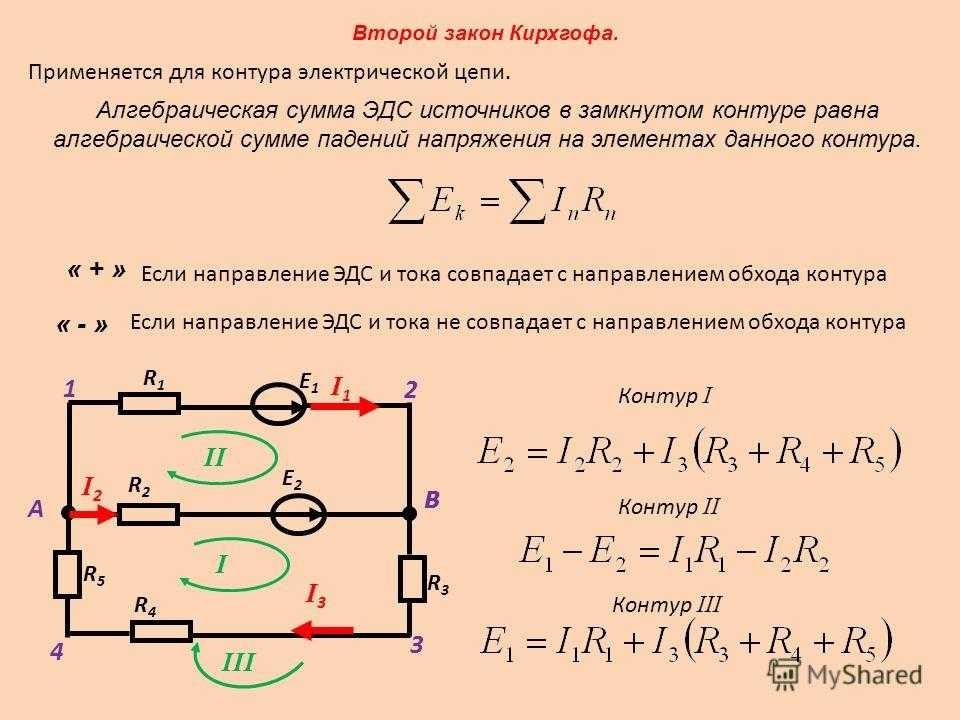

? 11. Чему при этом равен КПД источника тока?

3. Конденсаторы в цепи постоянного тока

Постоянный ток не может идти через конденсатор, потому что между его обкладками находится диэлектрик. Однако между обкладками конденсатора, включенного в цепь постоянного тока, может существовать разность потенциалов, и тога конденсатор будет заряженным. Начнем с самых простых случаев, когда в цепи, помимо конденсатора, есть только один резистор.

? 12. На рисунке 61.8 изображена схема электрической цепи. ЭДС источника тока ξ = 12 В, его внутреннее сопротивление r = 2 Ом, сопротивление резистора R = 10 Ом, электроемкость конденсатора С = 2 мкФ.
61.8
а) Чему равна разность потенциалов между точками А и В?
б) Чему равна разность потенциалов между точками А и D?
в) Чему равен заряд конденсатора?
г) Каков знак заряда обкладки конденсатора, соединенной с резистором?

? 13. На рисунке 61.9 изображена схема электрической цепи. ЭДС источника тока ξ, его внутреннее сопротивление r, сопротивление резистора R, электроемкость конденсатора C.

а) Чему равна разность потенциалов между точками А и В?
б) Чему равен заряд конденсатора?

Рассмотрим теперь более сложный случай, когда в цепи есть несколько резисторов, причем они по-разному подключены к конденсатору.

? 14. В цепи (рис. 61.10) ЭДС источника ξ = 6 В, его внутреннее сопротивление r = 1 Ом, сопротивления резисторов R₁ = 3 Ом, R₂ = 5 Ом, R₃ = 12 Ом, электроемкость конденсатора C = 8 мкФ.

а) Перенесите схему в тетрадь и обозначьте, через какие элементы цепи идет ток.
б) Какова сила тока в резисторе 3?
в) Чему равна разность потенциалов между точками А и D?
г) Чему равна разность потенциалов между точками А и В?
д) Чему равно напряжение на конденсаторе?
е) Чему равен заряд конденсатора?
ж) Каков знак заряда обкладки конденсатора, соединенной с резистором 2?

Дополнительные вопросы и задания

15. На рисунке 61.11 изображена схема участка электрической цепи. Сопротивление каждого резистора 1 Ом.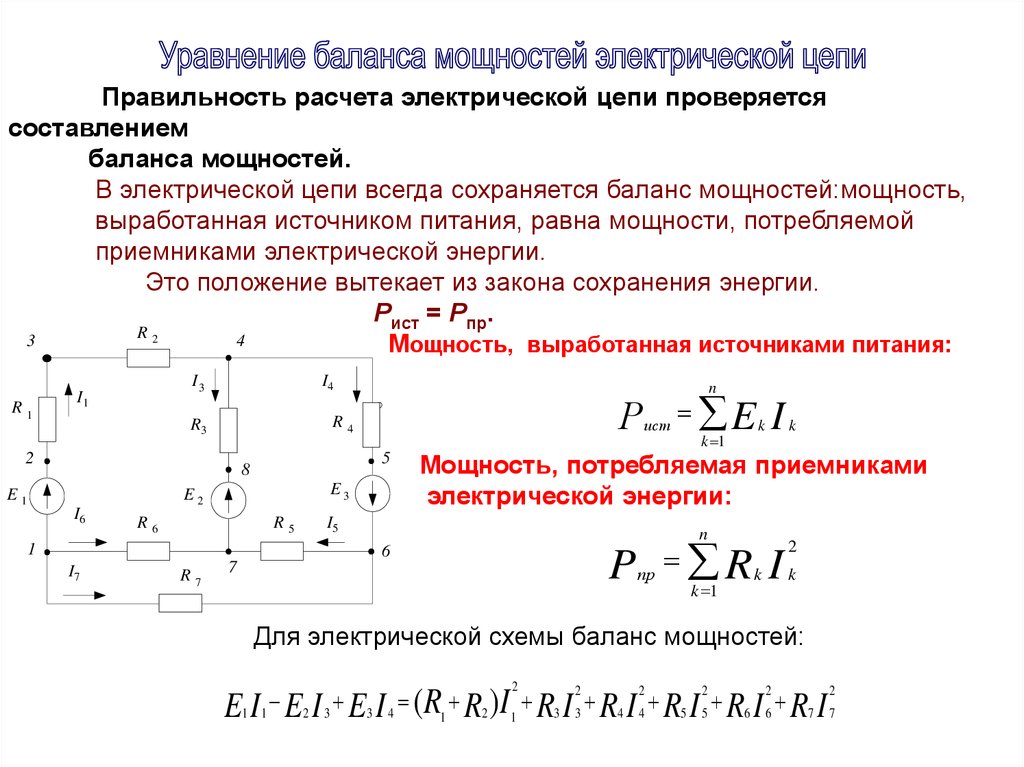 Используя метод эквивалентного преобразования схем:
а) начертите схемы последовательного упрощения данной схемы, содержащие меньше резисторов;
б) для каждой схемы рассчитайте ее сопротивление и найдите общее сопротивление всего участка.

16. На схеме участка цепи, изображенной на рисунке 61.5, сопротивления резисторов R₁ = 20 Ом, R₂ = 100 Ом, R₃ = 10 Ом, R₄ = 50 Ом, R₅ = 80 Ом. Каково общее сопротивление участка цепи?

17. Сопротивление внешней цепи в 4 раза больше того значения, при котором мощность тока во внешней цепи максимальна.
а) Чему равен КПД источника тока?
б) Во сколько раз при этом мощность тока во внешней цепи меньше максимально возможной?

‎App Store: Калькулятор схемы

Описание

Создайте электрическую цепь переменного или постоянного тока, добавляя, перетаскивая и вращая компоненты, а затем соединяя их вместе. Реакция в установившемся режиме рассчитывается мгновенно при нажатии кнопки. Потоки постоянного тока можно анимировать на экране.

Масштабирование и панорамирование стандартными жестами для просмотра напряжений и токов, отображаемых на схеме.

Калькулятор цепей является идеальным компаньоном для всех, кто изучает электротехнику, и отлично подходит для быстрой проверки ваших ответов, когда вы решили задачу анализа цепей вручную. Введите параметры компонента в виде вещественных и мнимых или модулей и аргументов, как в типичной домашней задаче. Обратите внимание, что это приложение не выполняет анализ переходных процессов.

Основные характеристики:

・Создание схемы на экране
・Решение и отображение результатов на схеме
・Расчет установившихся токов, напряжений и мощности
・Показ анимированных потоков постоянного тока
・Расчет значений эквивалентной схемы Тевенина/Нортона
・Выберите полярную или прямоугольную нотацию для AC
・Общий доступ к схемам через приложения «Сообщения» или «Почта»
・Распечатайте схему
・Скопируйте схему в буфер обмена
・Загрузите/сохраните схемы на устройстве или в iCloud
・Отменить/повторить действия
・Копировать/вставить компоненты
・Встроенное руководство пользователя

Доступные компоненты:

・Независимые идеальные источники тока
・Независимые идеальные источники напряжения
・Управляемые током источники напряжения 30 9 Токоуправляемые источники напряжения 10 Источники тока с регулируемым напряжением
・Источники напряжения с регулируемым напряжением
・Резисторы
・Конденсаторы
・Дроссели
・Взаимно связанные катушки индуктивности — только переменный ток
・Импедансы — только переменный ток
・Диоды — только для постоянного тока

Посетите http://circuitcalc. nwd-apps.co.uk или канал Circuit Calculator YouTube для получения дополнительной информации.

2 октября 2021 г.

Версия 2.92

Незначительные обновления совместимости для iOS 15

Рейтинги и обзоры

47 оценок

Отличное приложение для анализа цепей

Я думаю, что это приложение прекрасно подходит для построения схем для занятий на уровне колледжа. Это единственное приложение, с которым я столкнулся в AppStore, которое позволяет создавать простые схемы с интуитивно понятным управлением и полным анализом. Я столкнулся только с одной незначительной проблемой, и разработчик очень быстро отреагировал и обновил приложение, чтобы исправить проблему. Отличное приложение, отличный разработчик. Настоятельно рекомендуется!

Здравствуйте, приносим извинения за неудобства, вызванные этой проблемой, и спасибо за ваш конструктивный отзыв. Я исправил проблему и постараюсь внести дополнительные улучшения в то, как приложение выглядит в темном режиме в следующем выпуске. Я был бы признателен, если бы вы могли обновить свой отзыв после того, как вы проверили обновление.

Отличное приложение

Это приложение — все, что мне нужно для анализа цепей. Простота использования

Спасибо за отличный отзыв.

Стоит

Находка для проверки домашних заданий на вводных курсах

Разработчик Нил Вудкок указал, что политика конфиденциальности приложения может включать обработку данных, как описано ниже. Для получения дополнительной информации см. политику конфиденциальности разработчика.

Данные не собираются

Разработчик не собирает никаких данных из этого приложения.

Методы обеспечения конфиденциальности могут различаться, например, в зависимости от используемых вами функций или вашего возраста. Узнать больше

Информация

Продавец

Нил Вудкок

Размер

3 МБ

Категория

Образование

Возрастной рейтинг

4+

Авторское право

© 2014 Нил Вудкок

Цена

1,99 долл. США

• Сайт разработчика
• Тех. поддержка
• Политика конфиденциальности

Опоры

Еще от этого разработчика

Вам также может понравиться

Калькулятор тока в цепи Rl

Калькулятор тока в цепи RL рассчитает:

1. Ток, протекающий в любой момент в цепи RL, когда ток в цепи увеличивается
2. Ток, протекающий в любой момент в цепь RL, когда ток в цепи уменьшается

Рекомендации по расчету: Токопроводящий провод цепи и материал, из которого изготовлена ​​катушка индуктивности, однородны и везде имеют одинаковую толщину; Источник снабжает ток DC

7017011711101010101010101010101010101010101010101010101010101010101010101010101010101тели.

Ток в калькуляторе схемы RL

🖹 Нормальный просмотр полного просмотра страниц
Калькулятор (Decimal Place) 01234567891011121311415
Сопротивление схемы (r) ω
Индуктивность индуктора (L) H
ВРЕМЕНИ. Ток, протекающий в любой момент в цепи RL, когда ток в цепи увеличивается, составляет А [А]
Ток, протекающий в любой момент в цепи RL, когда ток в цепи уменьшается, составляет A [Ampere]
Current (when rising) in the circuit at any instant calculation
i 1 (t) = ε / R × 1 — e — R × t / L i 1 (t) = / × 1 — e — × / я 1 (t) = × 1 — e — / i 1 (t) = × 1 — e i 1 (t ) = × 1 — i 1 (t) = × i 1 (t) =
Current (when dropping) in the circuit at any instant calculation
i(t) = ε / R × e — R × t / L i 1 (t) = / × e — × / i 1 (t) = × e — / i 1 (t) = × e i 1 (t) = × i 1 (t) =
Ток в входных значениях калькулятора схемой RL
ЭМФ, полученные батареей (ε) В [Вольт]
Сопротивление схемы (R) 020171
Сопротивление схемы (R) 0 2
COURD (R) 0 2
. индуктора (L) H [Henry]
Прошедшее время (t) с [секунды]

Обратите внимание, что формулы для каждого расчета вместе с подробными расчетами доступны ниже. По мере того, как вы вводите конкретные коэффициенты каждого тока в расчет цепи RL, калькулятор тока в цепи Rl автоматически вычисляет результаты и обновляет элементы формулы Physics с каждым элементом тока в расчете цепи RL. Затем вы можете отправить по электронной почте или распечатать этот ток в расчете цепи rl, если это необходимо для последующего использования.

Мы надеемся, что калькулятор Current In A Rl Circuit Calculator оказался полезным для вашей версии физики. Если да, мы просим вас оценить этот калькулятор физики и, если у вас есть время, поделиться им в своей любимой социальной сети. Это позволяет нам распределять будущие ресурсы и сохранять эти калькуляторы по физике и учебные материалы бесплатными для всех по всему миру. Мы считаем, что у всех должен быть бесплатный доступ к учебным материалам по физике. Делясь с вами, вы помогаете нам охватить всех студентов-физиков и тех, кто интересуется физикой по всему миру.

★ ★ ★ ★ ★ [15 голосов]

Связанные секции. : Электроника

Раздел 22: Космология

Ток (при возрастании) в цепи в любой момент Формула и расчет

i ₁ (t) = ε / R × 1 — E ^{— R × T / L}

.

ε / R × E ^{— R × T / L}

Физики. ИСКЛЮЧИТЕЛЬНЫЕ.

• Калькулятор делителя напряжения
• Кинематика углового калькулятора SHM
• Эластичная сила и калькулятор энергии упругих потенциалов
• Джинсовый калькулятор массы
• Коррекция мощности. Кальциратор
• Столковой коэффициент. Калькулятор преобразования постоянной добротности
• Калькулятор кондуктивной теплопередачи
• Калькулятор среднего молекулярного свободного пробега
• Калькулятор частоты параллельного резонанса
• Интенсивность калькулятора поляризованного света
• Антенна калькулятор длины диполя
• Электрическое поле дипольного калькулятора
• Радиус BOHR.