Калькулятор параллельного включения резисторов: Калькулятор параллельных сопротивлений

Соединение резисторов последовательное, параллельное, смешанное. Пример расчета

Соединение резисторов — это взаимное расположение данных элементов в цепи относительно друг друга и источника питания. Можно по отдельности выделить последовательное и параллельное соединение резисторов. Когда в схеме присутствуют оба варианта, то такое соединение называется смешанным.

Нам известно, что резистор — это электронный компонент, который обладает электрическим сопротивлением и мощностью рассеивания. Если в цепи имеется несколько резисторов, то для получения общего сопротивления прибегают к расчетам по правилам последовательного или параллельного соединения. Помимо общего сопротивления, группы резисторов по закону Ома влияют на напряжение и силу тока на участках цепи. И в данном обзоре будет доступно рассмотрена методика расчета общего сопротивления при различных видах соединения резисторов. Также будет рассмотрен наглядный пример со смешанным соединением резисторов, где помимо сопротивлений будут просчитаны напряжения и сила тока на разных участках.

Стоит сразу отметить, что в данной теме рассеивающая мощность резисторов вынесена за скобки. Мощность важна при подборе и комбинировании резисторов в схеме, но это уже отдельная тема. К тому же все рассмотренные примеры взяты с учетом источника переменного напряжения 220 В. Почему так? Об этом вы узнаете в последнем пункте публикации.

Последовательное соединение резисторов

Последовательное соединение резисторов — это такое взаимное расположение компонентов, при котором ток движется в одном направлении и имеет общее значение для каждого резистора. При таком соединении напряжение на каждом участке будет пропорционально сопротивлению конкретного резистора в цепи.

Принципиальная схема последовательного соединения:

Как видно в цепи последовательно соединено три резистора (их может быть и больше). Сопротивление первого резистора R1 = 20 Ом. Второго R2 = 70 Ом. Третьего R3 = 10 Ом.

Для подсчета общего (эквивалентного) сопротивление при последовательном соединении нужно сложить все номинальные сопротивления резисторов входящих в цепь:

R = R1 + R2 + R3 + … + Rn.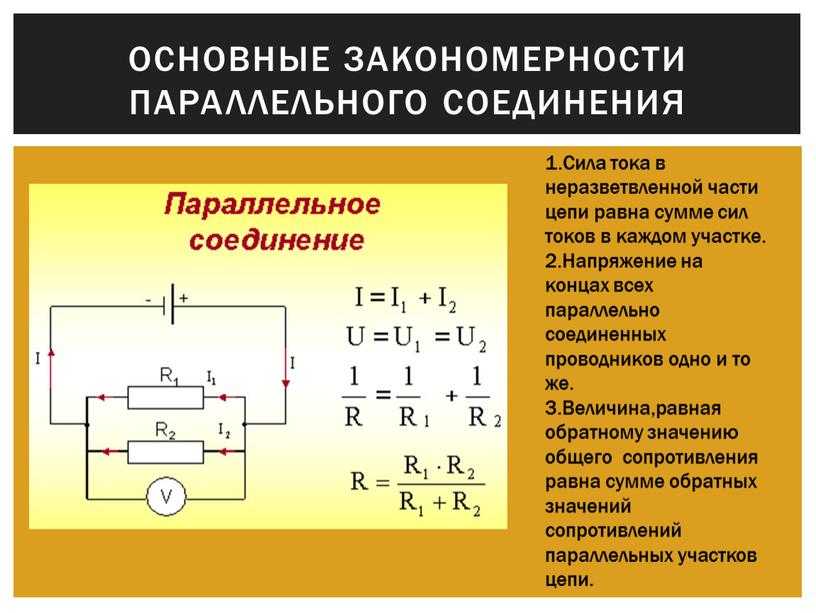

R = 20 + 70 + 10 = 100 Ом.

В представленной схеме для наглядности приведены напряжения на каждом из трех участков. И падение напряжения происходит в зависимости от сопротивления конкретного резистора. Сила тока в цепи общая для всех резисторов (I = I1 = I2 = I3). Поэтому согласно закону Ома сила тока при известном напряжении источника питания (в данном случае U = 220 В) определяется по формуле:

I = U / R = U / (R1 + R2 + R3 + … + Rn).

I = 220 / (20 + 70 + 10) = 220 / 100 = 2,2 A.

Формулы нахождения напряжения на участке цепи при известной силе тока (в данном случае I = I1 = I2 = I3 = 2,2 A):

• U1 = I × R1.
• U2 = I × R2.
• U3 = I × R3.
• Un = I × Rn.

Соответственно U1 = 2,2 × 20 = 44 В; U2 = 2,2 × 70 = 154 В; U3 = 2,2 × 10 = 22 В. В итоге сумма разностей потенциалов на резисторах равна общей разности потенциалов всей цепи (220 В).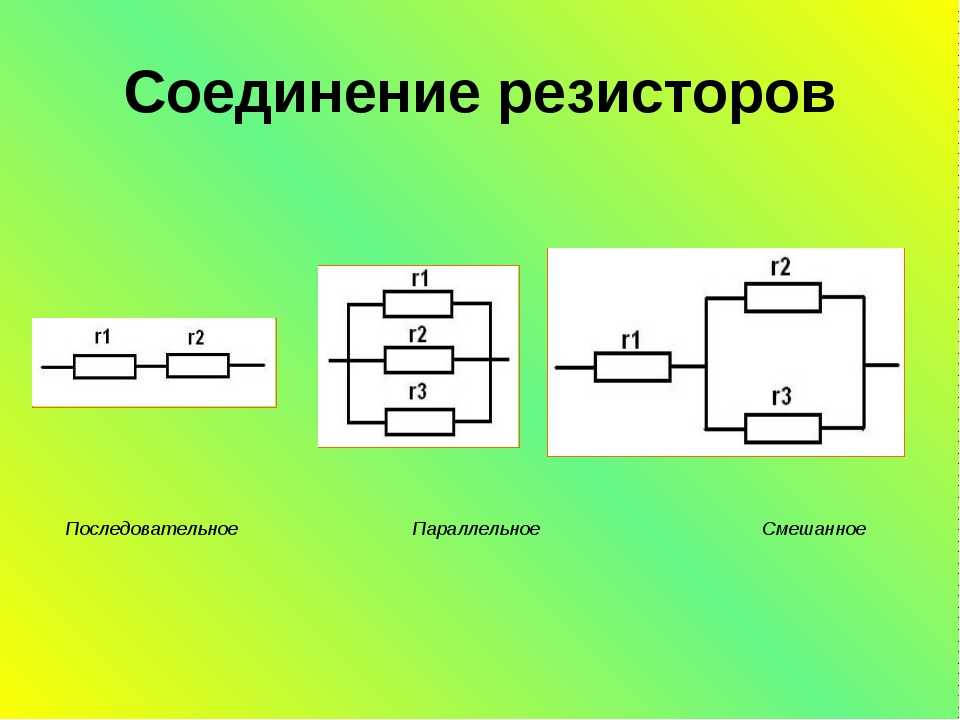

Рассмотренные три резистора в последовательной цепи можно заменить одним с сопротивлением 100 Ом:

Если можно несколько резисторов заменить одним, то возникает логичный вопрос, зачем применяется такое комбинирование. Простыми словами можно ответить, что иногда невозможно подобрать резистор с требуемыми параметрами или необходимо создать более сложные электронные схемы. В этом случае прибегают к последовательному, параллельному или смешанному соединению в цепи.

В цепи из последовательно соединенных резисторов главную роль играет тот, у которого самое большое сопротивление. Именно он в значительной степени влияет на общее сопротивление. К примеру, если соединить три резистора, номинал которых равен 1, 10 и 100 Ом, то в результате получиться составной с сопротивлением 111 Ом. Если убрать резистор на 100 Ом, то общее сопротивление цепочки резко уменьшиться до 11 Ом. А если убрать резистор на 10 Ом, то сопротивление незначительно уменьшиться до 101 Ом.

Объединение резистивных радиокомпонентов

https://youtube.com/watch?v=jJX6IsRhnhs

Параллельное соединение

Рассчитывается общее сопротивление при параллельном соединении по формуле: 1 / Rобщ = (1 / R1) + (1 / R2) + …+ (1 / Rn). Если выполнить математические преобразования и привести к общему знаменателю, то получится удобная формула параллельного соединения для расчета Rобщ. Она имеет следующий вид: Rобщ = (R1 * R2 * … * Rn) / (R1 + R2 + … + Rn). Если необходимо рассчитать величину Rобщ только для двух радиокомпонентов, то формула параллельного сопротивления имеет следующий вид: Rобщ = (R1 * R2) / (R1 + R2).

Последовательное и параллельное подключение резисторов. Как рассчитать с помощью формул?

При ремонте или проектировании схемы устройства возникает задача объединения нескольких резистивных элементов для получения конкретной величины сопротивления. Например, значение Rобщ для определенной цепочки элементов равно 8 Ом, которое получено при расчетах. Перед радиолюбителем стоит задача, какие нужно подобрать номиналы для получения нужного значения (в стандартном ряду резисторов отсутствует радиокомпонент с номиналом в 8 Ом, а только 7,5 и 8,2). В этом случае нужно найти сопротивление при параллельном соединении резистивных элементов. Посчитать значение Rобщ для двух элементов можно следующим образом:

1. Номинал резистора в 16 Ом подойдет.
2. Подставить в формулу: R = (16 * 16) / (16 + 16) = 256 / 32 = 8 (Ом).

В некоторых случаях следует потратить больше времени на подбор необходимых номиналов. Можно применять не только два, но и три элемента. Сила тока вычисляется с использованием первого закона Кирхгофа. Формулировка закона следующая: общее значение тока, входящего и протекающего по цепи, равен выходному его значению. Величина силы тока для цепи, состоящей из двух резисторов (параллельное соединение) рассчитывается по такому алгоритму:

• 
  Калькулятор соединения резисторов онлайн. параллельное соединение резисторов

1. Ток, протекающий через R1 и R2: I1 = U / R1 и I2 = U / R2 соответственно.
2. Общий ток — сложение токов на резисторах: Iобщ = I1 + I2.

Например, если цепь состоит из 2 резисторов, соединенных параллельно, с номиналами в 16 и 7,5 Ом. Они запитаны от источника питания напряжением в 12 В. Значение силы тока на первом резисторе вычисляется следующим способом: I1 = 12 / 16 = 0,75 (А). На втором резисторе ток будет равен: I2 = 12 / 7,5 = 1,6 (А). Общий ток определяется по закону Кирхгофа: I = I1 + I2 = 1,6 + 0,75 = 2,35 (А).

Последовательное подключение

Последовательное включение резисторов также применяется в радиотехнике. Методы нахождения общего сопротивления, напряжения и тока отличаются от параллельного подключения. Основные правила соединения следующие:

1. Ток не изменяется на участке цепи.
2. Общее напряжение равно сумме падений напряжений на каждом резисторе.
3. Rобщ = R1 + R2 + … + Rn.

Пример задачи следующий: цепочка, состоящая из 2 резисторов (16 и 7,5 Ом), питается от источника напряжением 12 В и током в 0,5 А. Необходимо рассчитать электрические параметры для каждого элемента. Порядок расчета следующий:

1. I = I1 = I2 = 0,5 (А).
2. Rобщ = R1 + R2 = 16 + 7,5 = 23,5 (Ом).
3. Падения напряжения: U1 = I * R1 = 0,5 * 16 = 8 (В) и U2 = I * R2 = 0,5 * 7,5 = 3,75 (В).

Не всегда выполняется равенство напряжений (12 В не равно 8 + 3,75 = 11,75 В), поскольку при этом расчете не учитывается сопротивление соединительных проводов. Если схема является сложной, и в ней встречается два типа соединений, то нужно выполнять расчеты по участкам. В первую очередь, рассчитать для параллельного соединения, а затем для последовательного.

Параллельное соединение резисторов

Параллельное соединение резисторов — это такое взаимное соединение компонентов, при котором оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов.

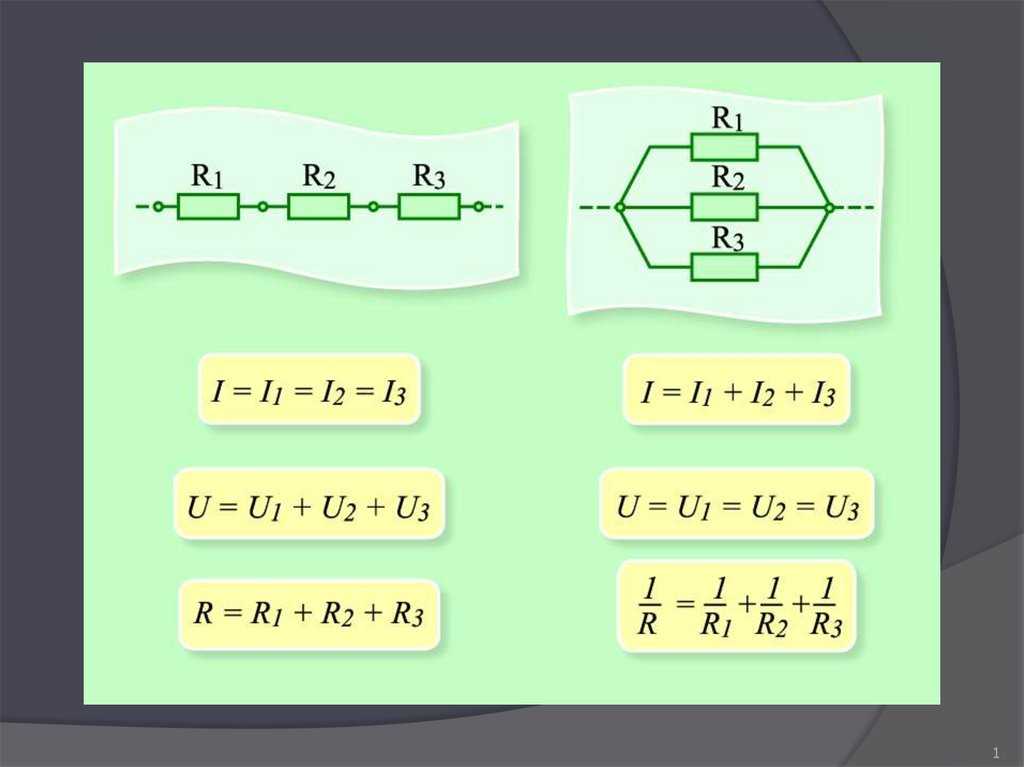
При таком соединении напряжение во всей цепи и на каждом участке одинаково и равно напряжению источника питания U = U1 = U2 = U3 = Un.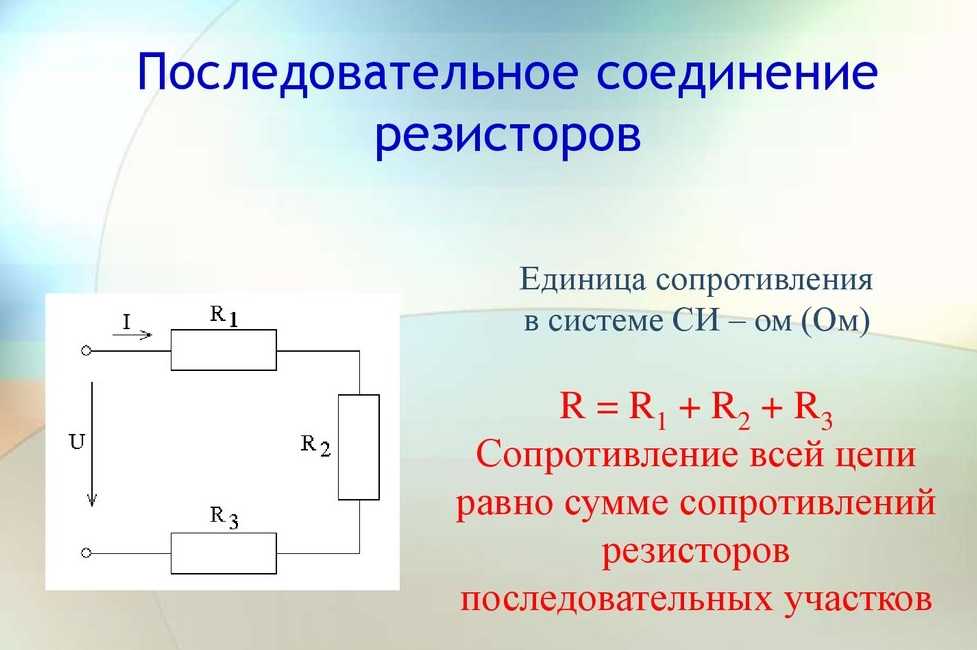 По каждому резистору течет свой ток. Сумма токов всех резисторов дает общую силу тока цепи: I = I1 + I2 + I3 + … + In. Соответственно общая проводимость параллельной цепи равна сумме ее отдельных проводимостей. Проводимость есть величина, обратная сопротивлению, поэтому эквивалентное сопротивление параллельно соединенных резисторов определяется следующим отношением:

1 / R = 1 / R1 + 1 / R2 + 1 / R3 + … + 1 / Rn. Величина, обратная общему сопротивлению цепи, равна сумме величин, обратных сопротивлениям параллельно включенных проводников.

Рассчитаем общее сопротивление для приведенного выше примера с параллельным соединением резисторов:

1 / R = 1 / 20 + 1 / 70 + 1 / 10 ≈ 0,164.

R ≈ 1 / 0,164 ≈ 6,097 Ом.

Для наглядности смоделируем в программе Electronics Workbench замену трех параллельно соединенных резисторов одним (R = 6,097 Ом):

Как видно, расчет был произведен правильно, так как сила тока в цепи с резистором 6,097 Ом равна силе тока в цепи с параллельным соединением (36,08 A ≈ 36,14 A).

Выделим основные особенности параллельного соединения резисторов:

• Общее сопротивление всегда меньше сопротивления любого параллельно включенного резистора.
• Увеличение числа параллельно соединенных резисторов ведет к уменьшению общего сопротивления и увеличению общей силы тока в цепи.
• Если параллельно соединены два резистора с одинаковым сопротивлением, то общее сопротивление этих резисторов будет ровно в два раза меньше, чем сопротивление каждого из резисторов, входящих в эту цепочку.
• Если в цепи используются резисторы одного номинала, то формула общего сопротивления упрощается и принимает вид R = R1 / N (R1 – номинальное сопротивление резистора; N – количество резисторов с одинаковым номинальным сопротивлением).

Как рассчитать сложные схемы соединения резисторов

Сложные схемы рассчитываются путем группировки по параллельному и последовательному способу соединения.

Перед нами сложная схема – задача рассчитать общее сопротивление:

1. R 2, R 3, R 4 объединим в последовательную группу – применим формулу R 2,3,4 = R 2+R 3+ R4.
2. R 5 и R 2,3,4 – параллельно соединенные резисторы, рассчитаем R 5,2,3,4 = 1/ (1/R 5+1/R 2,3,4).
3. R 5,2,3,4, R 1, R 6 опять объединяем в последовательную группу – суммируя величины, получаем Rобщ = R 5,2,3,4+R 1+R 6.

Смешанное соединение резисторов

Смешанное соединение резисторов — это комбинация последовательного и параллельного соединения. Иногда такую комбинацию называют последовательно-параллельным соединением.

Пример цепи со смешанным соединением резисторов:

Для расчета эквивалентного сопротивления таких соединений всю цепь разбивают на простейшие участки и придерживаются следующего алгоритма:

	Определяется общее сопротивление участков с параллельным соединением резисторов.
	Если эти участки содержат последовательно соединенные резисторы, то сначала вычисляют их общее сопротивление.
	После промежуточных расчетов схема перерисовывается, и получается цепь из последовательно соединенных эквивалентных сопротивлений.
	Далее рассчитывается сопротивление полученной простой схемы.

Схемы последовательного и параллельного соединения

Если рассматривать соединение на примере громкоговорителя, то при последовательном соединении с усилителем мощности подключается только один динамик, поскольку прохождение тока осуществляется только через один проводник. Подключение второго громкоговорителя может быть выполнено разными способами.

При последовательном соединении по обоим устройствам будет протекать одинаковый ток. В этом случае общее сопротивление приборов представляет собой сумму отдельно взятых сопротивлений. При параллельном соединении протекание тока будет происходить по двум направлениям. Здесь общее значение сопротивления в отличие от последовательного соединения, наоборот, будет уменьшаться. То есть, при параллельном соединении двух сопротивлений, их общее значение будет составлять половину каждого из них.

Если последовательное и параллельное соединение резисторов рассматривается с точки зрения радиоэлектроники, необходимо четко представлять себе, что представляет собой данный элемент и какова его роль в электронных схемах. Эта деталь является неотъемлемой частью многих устройств, благодаря такому свойству, как сопротивление электрическому току. Резисторы могут быть двух типов – постоянными и переменными, то есть подстроечными. При создании тех или иных электрических схем требуется резистор установленного номинала, которого в данный момент может не оказаться в наличии. Поэтому приходится использовать элементы с другими номинальными значениями, формула для каждого из которых подтверждает их физические свойства.

Последовательное соединение считается наиболее простым. Оно используется, когда необходимо увеличить общее сопротивление электрической цепи. В этом случае все сопротивления резисторов просто складываются и дают общую сумму. При параллельном соединении, наоборот, можно снизить результирующее сопротивление или увеличить мощность за счет нескольких подключенных резисторов.

Смешанное подключение

При смешанном подключении в одной схеме сочетаются несколько видов соединений – последовательное, параллельное соединение резисторов и их комбинации.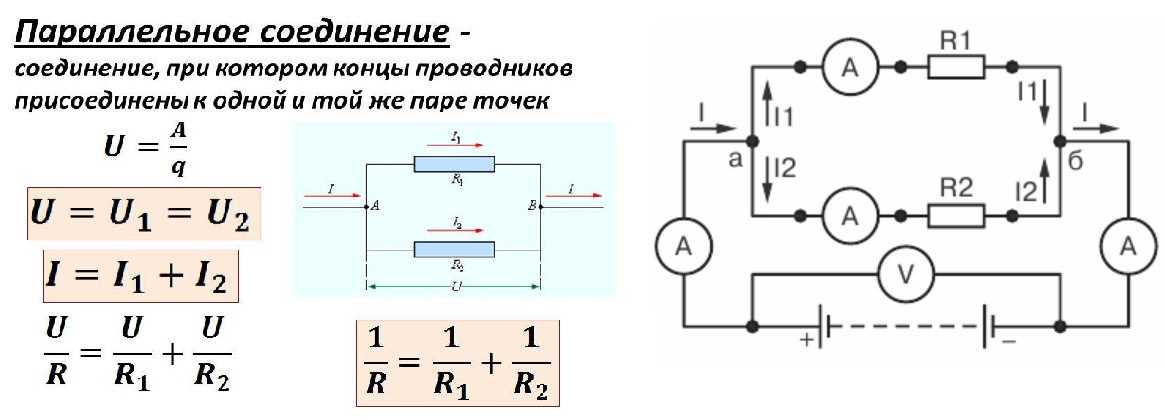 Самую сложную электрическую схему, состоящую из источников питания, диодов, транзисторов, конденсаторов и других радиоэлектронных элементов можно заменить резисторами и источниками напряжения, параметры которых изменяются в каждый момент времени. О параллельном соединении резистора и конденсатора читайте тут.

Смешанная схема делится на фрагменты, ток и напряжение рассчитывается для каждого отдельно в зависимости от того, как они соединены на выбранном сегменте электрической схемы.

Важно! Для расчета сопротивления резистора в схеме применяют отдельные формулы для каждого конкретного элемента в зависимости от вида соединения.

Эквивалентное сопротивление резисторов определить эквивалентное

Расчет реальной электрической цепи в идеальном виде невозможен по причине отсутствия математических методик учета индивидуальных параметров каждого составляющего элемента. Это естественно, так как любая деталь имеет свои паразитные характеристики, которые нереально учесть при расчетах. Для устранения этой проблемы было введено понятие эквивалентной замены. При этом в расчет принимается только одна определяющая характеристика элемента. Так, например, эквивалентное сопротивление резисторов в электрической схеме, отображает только величину сопротивления без влияния на него сторонних факторов.

В электротехнике существует два основных варианта включения деталей в электрической цепи – это последовательное и параллельное соединение. Объединяющей для них является смешанная схема, которая по сути может быть разбита на участки с вышеприведенными характеристиками.

Рассмотрим эквивалентное соединение резисторов в каждом отдельном случае.

Эквивалентное сопротивление при последовательно соединенных резисторов

При данном типе размещения резисторов в цепи условная схема будет соответствовать рис. 1.

Рисунок 1

Для того чтобы определить эквивалентное сопротивление резисторов необходимо вспомнить закон Ома. Для последовательного соединения он гласит что общее, а в нашем случае эквивалентное сопротивление, соответствует следующему уравнению:

R_экв= R₁+R₂+R₃+R_N-1+R_N

Рассмотрим пример последовательного соединения трех резисторов, сопротивление которых равно 10, 20 и 30 Ом, соответственно. Согласно выше приведенной формуле общее сопротивление всех этих резисторов на данном участке цепи будет равно 60 Ом. Таким образом, при расчетах параметров электрической схемы нет надобности использовать индивидуальные характеристики отдельных элементов. Их можно просто заменить одним значением эквивалентным их сумме.

Кроме теории, данное суммирование значений сопротивлений элементов, имеет и практическое применение – в случае необходимости всегда можно заменить несколько резисторов одним. Также имеет место и обратное утверждение – при отсутствии деталей с требуемой характеристикой ее можно заменить на несколько других, эквивалентное сопротивление которых будет соответствовать требуемому значению.  Все это справедливо и для параллельного соединения резисторов, только с некоторыми особенности.

Эквивалентное сопротивление при параллельном соединении резисторов

Общая схема при данном включении резисторов в цепь соответствует рис. 2.

Рисунок 2

Определить эквивалентное сопротивление параллельно соединенных резисторов позволяет закон Ома согласно которому, в данном варианте, справедливо равенство:

1/R _экв =1/R₁+1/R₂+1/R₃+1/R _N-1+1/R_N

Возвращаясь к нашему примеру с резисторами 10, 20 и 30 Ом.

Можно определить эквивалентное сопротивление для данного случая, преобразуя уравнение и получаем следующую формулу:

R _экв = R₁ х R₂ х R₃ / (R₁ x R₂) + (R₁ x R₃) + (R₂ x R₃) = 5,45 Ом

Важный момент: При параллельном включении резисторов в цепь эквивалентное сопротивление будет всегда меньше наименьшего значения отдельного элемента. При последовательном соединении R _экв обязательно больше самого большого параметра.

Эквивалентное сопротивление при смешанном соединении резисторов

Определение эквивалентного сопротивления при смешанном соединении резисторов не представляет особых сложностей. Для этого достаточно разбить существующую цепочку на логические составляющие – блоки. Т.е.

максимально упростить схему, приведя ее в соответствие с характеристиками свойственных тому или иному типу соединения. На рис. 3 приведена типичная схема упрощения, которая получила название метод свертывания цепи.

Рисунок 3

Данная схема позволяет наглядно понять, как можно определить эквивалентное сопротивление резисторов при смешанном соединении. Обращаем внимание, что начинать процесс упрощения можно в произвольном порядке. Так, например, объединение резисторов R₁ и R₂ не обязательно должно быть первым шагом. Можно совершенно смело на первом этапе найти R _экв сумме сопротивлений последовательно включенных в цепь резисторов R₄ и R₅.  Определение эквивалентного сопротивления для резисторов необходимо осуществлять в зависимости от типа соединения.

В заключение вернемся к самому понятию эквивалентной замены резисторов. В рассмотренных нами случаях речь шла об идеальном варианте. То есть в расчет принимается только величина сопротивления при нулевых значениях остальных характеристик.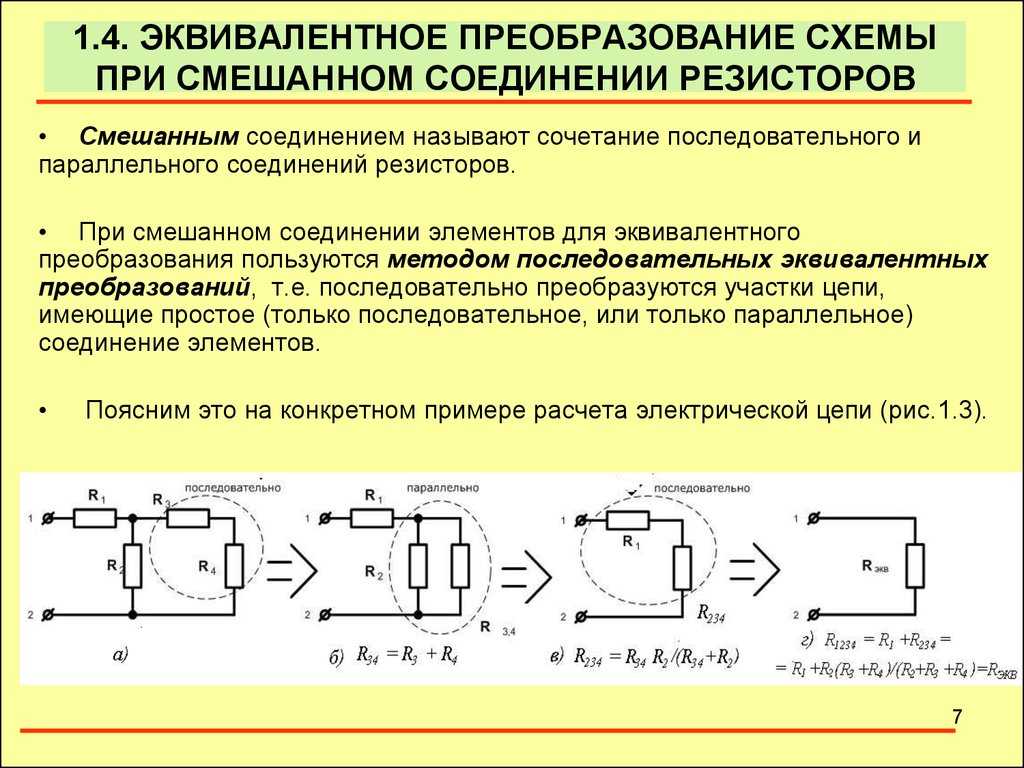 Также обращаем внимание, что при составлении эквивалентной схемы любых элементов электрической цепи, не только резисторов, можно вводить дополнительные переменные, которые будут влиять на конечные итоги.

Добавить отзыв

Калькулятор параллельного резистора

— Пайка Mind

Легко рассчитать параллельный

подключенный резистор сопротивление с помощью этого онлайн-калькулятора параллельного резистора. Вы можете рассчитать сопротивление параллельной цепи до 10 резисторов одновременно. Найдите правильные кодовые значения резисторов и введите их в данное поле калькулятора параллельного сопротивления, указанное ниже. Если вам сложно проверить значение резистора, воспользуйтесь онлайн-калькулятором цветового кода резистора 9. 0004 . Ссылка на цветовой код резистора приведена ниже.

Также проверьте: Калькулятор цветового кода резистора

Укажите Два значения резистора , будет рассчитано общее параллельное сопротивление.
( Вы можете даже войти в общее сопротивление R _Всего и одно известное сопротивление R

1 или R _21133.

Калькулятор расчета нескольких резисторов при параллельном подключении

Пожалуйста, введите несколько параллельных резисторов (в омах) для расчета параллельного сопротивления

Значащие цифры:

Резистор

Резисторы — это крошечные электронные компоненты, хорошо знакомые большинству людей. Любители электроники или просто не интересующиеся люди также видели резисторы во многих печатных платах. Так что я надеюсь, что вы знаете что-то о резисторах, хорошо. Теперь давайте перейдем к основной теме, параллельному соединению резистора. Зачем нужно параллельное соединение? Так что, прежде чем говорить о параллельном подключении, сначала расскажите об основном.

Резистор изготовлен из полупроводникового материала, который препятствует прохождению тока через одну клемму на другую. У резистора всего две клеммы. Сопротивление резистора обозначается цветовым кодом на самом резисторе. Цвет кольца на резисторе меняется, значение сопротивления тоже меняется. Высокое значение означает самое высокое сопротивление потенциальному току. Пройти через него очень сложно.

Резисторы в параллельном соединении

Резистор в параллельном соединении означает, что 2 или более резисторов подключены обоими концами с одинаковой ориентацией или параллельно к каждой клемме. Легко определить, соединены ли резисторы параллельно или последовательно? Если резисторы соединены встык друг с другом, как тележки поезда, это называется последовательным соединением. Теперь это очень ясно для понимания.

Схема подключения параллельного резистора

Если вы подключаете много резисторов параллельно, общее сопротивление резистора всегда будет меньше наименьшего значения резистора. Согласно уравнению,

P = VI и Резистор, подключенный параллельно, имеет одинаковое напряжение на них все время. Но меняющимся фактором является ток, протекающий через него. Многие резисторы соединены параллельно, крошечный ток, протекающий через каждый из транзисторов, создает огромный ток, возрождающийся на другом конце.

Пример: у вас есть батарея 10 В и резистор 1 кОм. Вы ставите резистор на последовательное соединение с полюсами батареи, измеряя протекающий ток, он показывает 1 мА. Если вы поместите резистор 10 кОм параллельно резистору 1 кОм, ток не изменится через батарею и цепь. Но резистор на 10 кОм потребляет ток всего 0,1 мА через батарею. Из уравнения V =IR оно общее для всех электронных устройств. Напряжение, ток и сопротивление также коррелируют друг с другом.

Резистор в параллельном расчете

Два резистора соединены параллельно R1 и R2, тогда уравнение для расчета параллельного сопротивления резистора:

1/Rобщ = 1/R1+1/R2

Решение формулы для получения формулы

Rобщ = (R1*R2)/(R1+R2)

Чтобы получить значение R1, формула будет

1/Rобщ = 1/R1+1/R2

Rобщ.*R1*R2 {1/Rобщ. = 1/R1+1/R2]

R1*R2 = Rобщ.*R2+Rобщ.*R1

R1*R2-Rобщ. *R1 =Rобщ. * R2

R1(R2-Rобщ.) = R2*Rобщ.

Итак, R1 = R2*Rобщ/(R2-Rобщ)

несколько резисторовпараллельный калькулятор параллельного сопротивлениякалькулятор параллельного резисторакалькулятор сопротивлениярезистор

домашнее задание и упражнения — Расчет сопротивления в последовательных и параллельных цепях

Задай вопрос

спросил 7 лет, 10 месяцев назад

Изменено 7 лет, 10 месяцев назад

Просмотрено 380 раз

$\begingroup$

У меня есть последовательная и параллельная схема.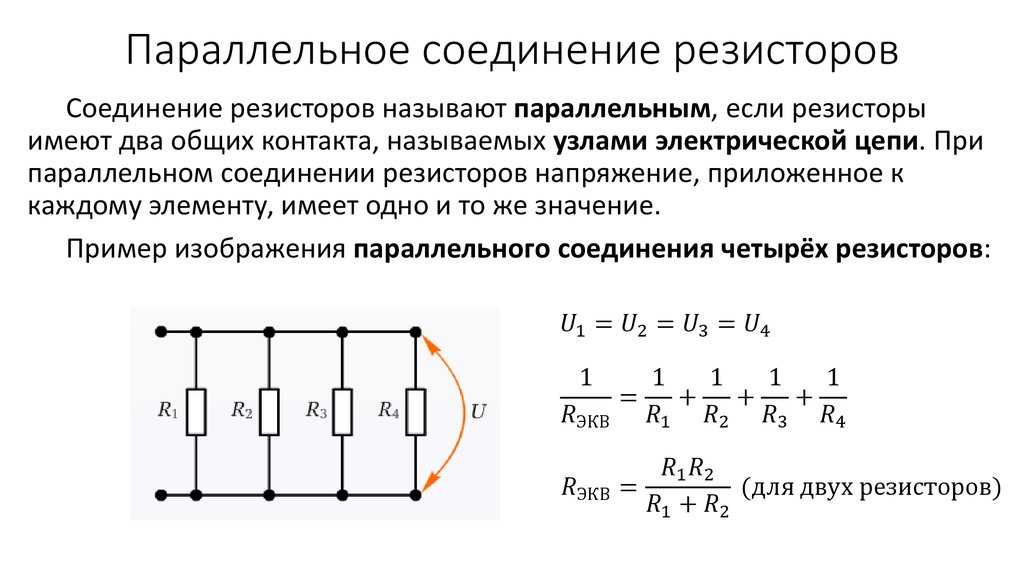 В обеих схемах я использую два резистора. Эти два резистора имеют одинаковое сопротивление $a$.

В обеих схемах я пробовал считывать величину тока с разным напряжением. Я получил следующие результаты.

$$ \begin{массив}{c|lcr} \text{Напряжение (В)} & \text{Последовательный (мА)} & \text{Параллельный (мА)} \\ \hline 1 и 0,42 и 2,91\ 2 и 0,98 и 4,83\ 3 и 1,47 и 6,8\ 4 и 2,03 и 8,96\\ 5 и 2,65 и 11,17\ 6 и 3.27 и 13.05\ 7 и 3,72 и 15,37\ 8 и 4,28 и 17,13 \\ 9 и 4,84 и 19.13\ 10 и 5.31 и 21.7 \конец{массив} $$

Общее сопротивление последовательной цепи составит $2a$. Для параллельной схемы это будет $\frac{a}{2}$.

Затем я использую формулу $V = IR$, чтобы найти сопротивление для каждого напряжения, которое я использовал, и тока, которые я считываю с амперметра (см. таблицу).

Как оказалось, среднее сопротивление последовательной цепи составляет: $1959$ Ом. В параллели это $440$ Ом.

$2а = 1959 \ тогда и только тогда, когда а = 979.5$

$\frac{2}{a} = 440 \iff a = 0,0045454545. ..$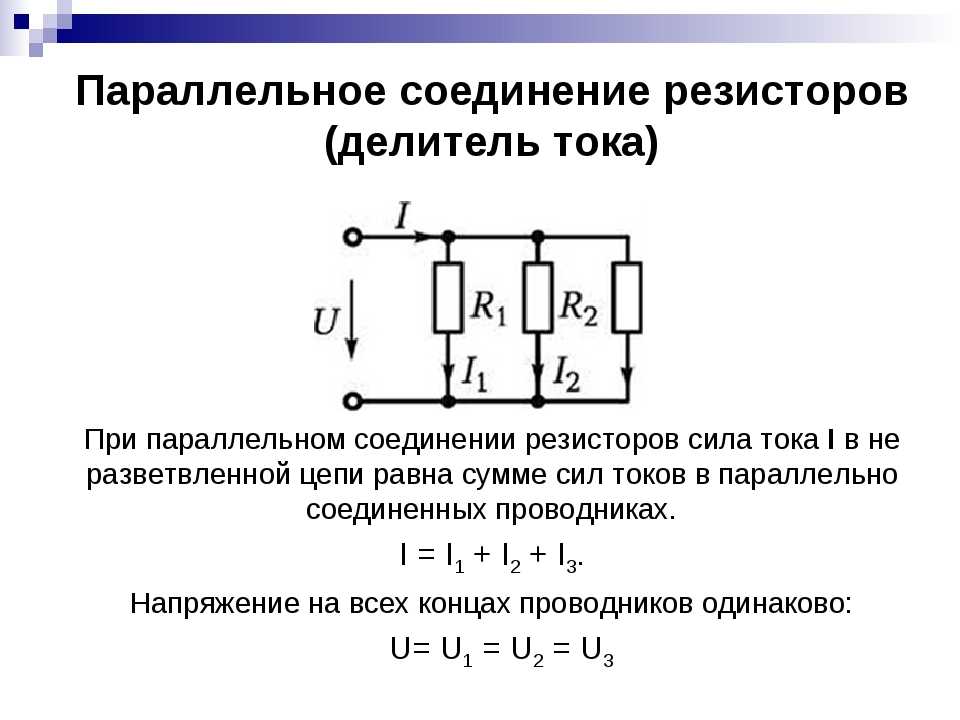

Почему сопротивление в параллельной цепи отличается от сопротивления в последовательной?

Мои показания неверны? Мои расчеты неверны? Я очень новичок в физике.

• домашние задания и упражнения
• электрические цепи
• электрические сопротивления

$\endgroup$

3

$\begingroup$

$\frac{2}{a} = 440$

Скорее должно быть

$\frac{a}{2} = 440$

Таким образом, вы получаете $a=880$ для параллельного контура. Между двумя измеренными сопротивлениями все еще есть некоторая разница. Похоже, что ваш амперметр имеет внутреннее сопротивление 66 Ом или ваш вольтметр имеет внутреннее сопротивление 13 кОм:

Если амперметр включен последовательно с вольтметром, вы измерите больший ток, чем ожидалось, потому что некоторые ток пойдет через вольтметр.