Как рассчитать общее сопротивление при последовательном и параллельном соединении резисторов. Какие формулы используются для вычисления эквивалентного сопротивления. Чем отличаются последовательное и параллельное соединение резисторов.
Последовательное соединение резисторов: принцип и расчет
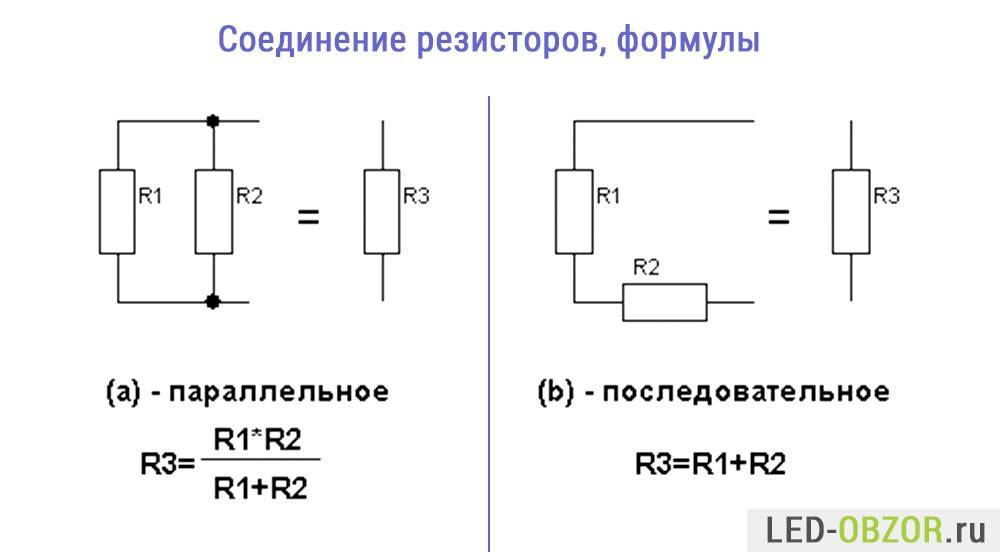
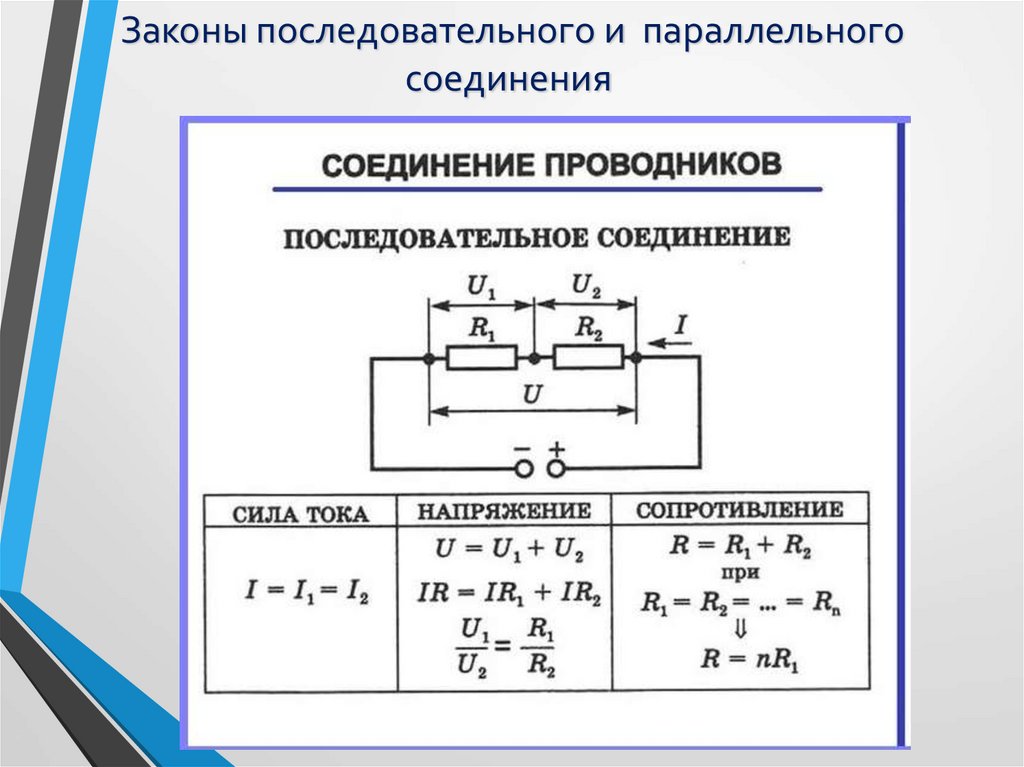
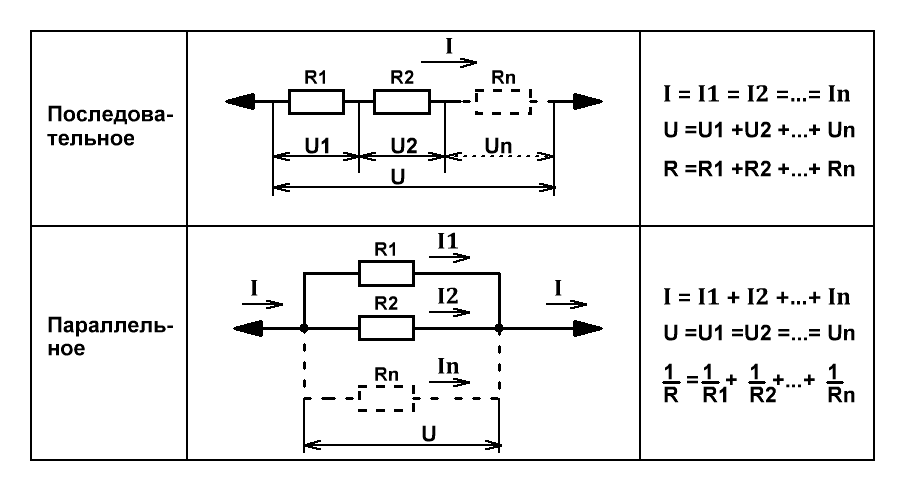
Последовательное соединение резисторов представляет собой такое подключение, при котором конец одного резистора соединяется с началом следующего. При этом через все резисторы протекает одинаковый ток. Рассмотрим основные особенности последовательного соединения:
- Общее сопротивление равно сумме сопротивлений всех резисторов
- Ток одинаков во всех резисторах
- Напряжение распределяется пропорционально сопротивлению каждого резистора
Формула для расчета общего сопротивления при последовательном соединении:
Rобщ = R1 + R2 + R3 + … + Rn
Где R1, R2, R3 и т.д. — сопротивления отдельных резисторов.
Параллельное соединение резисторов: особенности и вычисления
При параллельном соединении резисторов все их начала соединяются в одной точке, а все концы — в другой. Основные характеристики параллельного соединения:
- Напряжение одинаково на всех резисторах
- Общий ток равен сумме токов через каждый резистор
- Обратная величина общего сопротивления равна сумме обратных величин сопротивлений резисторов
Формула для расчета общего сопротивления при параллельном соединении:
1/Rобщ = 1/R1 + 1/R2 + 1/R3 + … + 1/Rn
Где R1, R2, R3 и т.д. — сопротивления отдельных резисторов.
Сравнение последовательного и параллельного соединения резисторов
Каковы основные отличия последовательного и параллельного соединения резисторов? Рассмотрим ключевые моменты:
- При последовательном соединении общее сопротивление всегда больше сопротивления любого из резисторов, а при параллельном — меньше
- В последовательной цепи ток одинаков, а напряжение распределяется, в параллельной — наоборот
- Последовательное соединение используется для увеличения общего сопротивления, параллельное — для уменьшения
Применение калькулятора для расчета резисторов
Для чего нужен калькулятор расчета последовательного и параллельного соединения резисторов? Он позволяет быстро и точно вычислить общее сопротивление цепи при различных комбинациях резисторов. Основные преимущества использования калькулятора:
- Экономия времени на ручных расчетах
- Исключение ошибок при вычислениях
- Возможность быстро перебрать разные варианты соединений
- Удобство при работе со сложными схемами с большим количеством резисторов
Практические примеры расчета сопротивлений
Рассмотрим несколько практических примеров использования калькулятора для расчета сопротивлений при последовательном и параллельном соединении резисторов:
Пример 1: Последовательное соединение
Rобщ = R1 + R2 + R3 = 100 + 200 + 300 = 600 Ом
Пример 2: Параллельное соединение
Дано: R1 = 10 Ом, R2 = 20 Ом
1/Rобщ = 1/R1 + 1/R2 = 1/10 + 1/20 = 3/20
Rобщ = 20/3 ≈ 6,67 Ом
Смешанное соединение резисторов: особенности расчета
Как рассчитать сопротивление при смешанном соединении резисторов? В этом случае в схеме присутствуют как последовательные, так и параллельные участки. Алгоритм расчета:
- Разбить схему на участки с однотипным соединением
- Рассчитать эквивалентное сопротивление для каждого участка
- Объединить полученные значения в соответствии с общей структурой схемы
Использование калькулятора значительно упрощает расчеты при смешанном соединении, позволяя быстро вычислить промежуточные значения для отдельных участков.
Влияние типа соединения на характеристики электрической цепи
Каким образом тип соединения резисторов влияет на основные характеристики электрической цепи? Рассмотрим ключевые аспекты:
- Распределение напряжения: при последовательном соединении напряжение распределяется между резисторами, при параллельном — одинаково на всех
- Сила тока: в последовательной цепи ток одинаков, в параллельной — распределяется между ветвями
- Общее сопротивление: последовательное соединение увеличивает сопротивление, параллельное — уменьшает
- Мощность: распределение мощности зависит от типа соединения и номиналов резисторов
Выбор оптимального соединения резисторов для различных задач
Как выбрать оптимальный тип соединения резисторов для конкретной задачи? Рассмотрим основные критерии:
- Требуемое общее сопротивление цепи
- Необходимое распределение напряжения и тока
- Доступные номиналы резисторов
- Ограничения по мощности рассеивания
- Особенности конструкции устройства
Используя калькулятор, можно быстро сравнить различные варианты соединений и выбрать наиболее подходящий для решения поставленной задачи.
последовательное и параллельное соединение + калькулятор
Резисторы представляют собой элементы с переменным или постоянным сопротивлением. С их помощью осуществляются различные действия, связанные с преобразованиями силы тока и напряжения, влияющих на работу всей схемы. Поэтому в большинстве случаев резисторы выполняют регулировочные функции. В большинстве цепей применяется последовательное и параллельное соединение резисторов. При необходимости они используются в комбинированном виде. Каждый вид соединения дает разные показатели сопротивления, в связи с чем для каждого из них разработана собственная методика расчетов.
Содержание
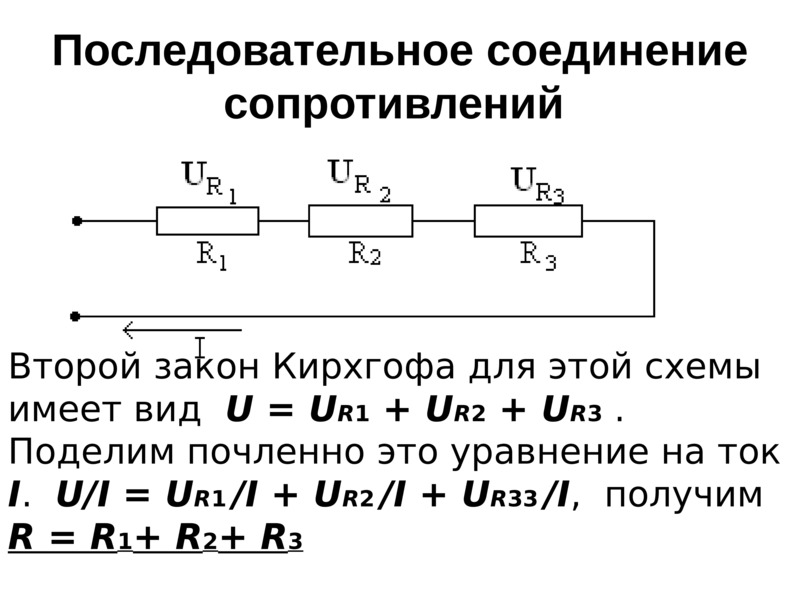
Последовательное соединение
Последовательным называется соединение двух и более резисторов, при котором конец первого элемента соединяется с началом второго и так далее. В результате получается последовательная цепочка, где по всем ее составляющим проходит одинаковый ток. В качестве примера можно взять последовательную цепь, состоящую из трех резисторов R1, R2 и R3.
Сопротивление в источнике тока принимается с нулевым значением. В соответствии со вторым законом Кирхгофа получается следующая формула: E = IR1 + IR2 + IR3 = I(R1 + R2 + R3) = IRэк.
В этой формуле значение эквивалентного сопротивления последовательной цепи составит сумму сопротивлений всех резисторов, имеющихся в данной цепи: Rэк = R1 + R2 + R3. По закону Ома напряжение при последовательном соединении на отдельных участках будет иметь следующее значение, поскольку E = U: U1=IR1; U2 = IR2, U3 = IRз, то есть U = U1 + U2 +U3. Данные формулы показывают, что в резисторах, последовательно соединенных между собой, напряжения распределяются пропорционально их сопротивлениям. То есть, чем выше сопротивление любого из резисторов, тем больше напряжение, приложенное к нему. В виде формулы — это утверждение будет выглядеть следующим образом: U1 : U2 : U3 = R1 : R2 : R3.
При последовательном соединении сопротивление R1 нескольких резисторов в количестве n, будет одинаковым. Следовательно, значение эквивалентного сопротивления цепи будет в n раз превышать сопротивление каждого из них: Rэк = nR1.
Следовательно напряжение на каждом отдельном резисторе будет в n раз меньше, чем общее напряжение цепи: U1 = U/n.
Таким образом, изменение сопротивления любого из резисторов при последовательном соединении, приводит к изменению напряжения на других резисторах, находящихся с ним в одной цепи. Поэтому, если электрическая цепь обрывается или выключается в одной из нагрузок, в других нагрузках также прекращается течение тока. Из-за этого последовательное соединение в электрических схемах используется довольно редко.
Параллельное соединение
Гораздо чаще в электрических цепях применяется параллельное соединение резисторов, отличающихся наличием общих точек, где соединяются начала и концы каждого элемента. Данный вид соединения характеризуется собственными физическими свойствами.
Основными из них являются следующие:
- Каждый из подключенных резисторов, обладает одинаковым напряжением: U = U1 = U2 = U3. То есть, напряжение в параллельном соединении на каждом участке будет одно и то же.
- Общая проводимость резисторов, соединенных параллельно, включает в себя сумму проводимостей каждого отдельного сопротивления, выраженную соотношением: 1/R = 1/R1 + 1/R2 + 1/R3 = R1R2 + R1R3 + R2R3/R1R2R3. Здесь R является эквивалентным или равнодействующим сопротивлением всех трех резисторов. Оно может полностью заменить их, без изменения величины силы тока в цепи. Значение эквивалентного сопротивления можно вычислить путем сложения проводимостей каждого участка. В результате, получится общая проводимость. Обратная ей величина и будет фактически общим сопротивлением.
- Существуют и особенности эквивалентной проводимости, когда используется параллельное соединение. Она составляет сумму проводимостей всех отдельно взятых ветвей. В этом случае при параллельном соединении сопротивление эквивалентное будет всегда ниже самого маленького сопротивления, включенного параллельно.
- соотношения касаются не только трех резисторов, соединенных параллельно, но и любого количества сопротивлений, соединенных этим способом. Этот способ широко используется в схемах радиотехнической аппаратуры. Параллельное включение двух и более резисторов используется при наличии слишком большой силы тока в цепи. В этом случае единственный резистор может перегреться и выйти из строя. Ярким примером служат электрические лампы освещения, включенные параллельно. Выключение ходя бы одной из них никак не повлияет на работу остальных ламп.
Этот способ широко используется в схемах радиотехнической аппаратуры. Параллельное включение двух и более резисторов используется при наличии слишком большой силы тока в цепи. В этом случае единственный резистор может перегреться и выйти из строя. Ярким примером служат электрические лампы освещения, включенные параллельно. Выключение ходя бы одной из них никак не повлияет на работу остальных ламп.Калькулятор вычисления параллельного соединения резисторов
Смешанное соединение
В радиоэлектронных и электрических схемах широко применяется последовательное, параллельное и смешанное соединение резисторов, наиболее подходящее на том или ином конкретном участке. Первые два соединения были рассмотрены выше, осталось лишь отметить характерные особенности комбинированного варианта.
В смешанных схемах нашли отражение свойства, присущие последовательному и параллельному соединениям. Частично выполняется последовательное подключение резисторов, а другая группа элементов подключается параллельно.
Резисторы R1 и R2, изображенные на схеме, включаются последовательно, а резисторы R1, R2 и R3 соединены параллельно.
Закон Ома для переменного тока
Как понять Закон Ома: простое объяснение для чайников с формулой и понятиями
Мультиметр: назначение, виды, обозначение, маркировка, что можно измерить мультиметром
Закон Ома для однородного участка цепи – формула
Закон Ома для полной и не полной электрической цепи, формула и правильное определение
Выключатель с подсветкой: установка, подключение, схема
Простой расчет параллельного соединения резисторов — калькулятор
В статье подробно рассмотрим, как параллельно соединять резисторы и научимся легко считать сопротивление тока в электрической цепи и узнаем, для чего вообще нужно параллельное соединение резисторов.
Содержание
Понятие и определение
Параллельное соединение резисторов имеет некоторый принцип, согласно которому, выводы одного изделия подключены и работают с аналогичными выводами другого. Создаются подобные решения, чтобы специально формировать более трудные по своему составу и компоновке схемы.
Что ещё нужно учитывать
Параллельное соединение определяет принцип, согласно которому величина, установленная обратной общему показателю цепи, будет равна непосредственно сумме величин, обратных значению включённых проводников. Такая же ситуация будет отмечена при значительно большем количестве проводниковых элементов.
Особенности включения
Параллельное соединение резисторов предусматривает, что показатель напряжения везде будет одинаковым, но ток фиксируется пропорциональным.
Отличия от иных вариантов подключения
В данной схеме, исключается подключение к источнику различных наименований реактивных компонентов.
Исключаются проблемные процессы колебания, сопряжённые ранее с фиксируемыми циклами смены уровня получения энергии в контексте подачи нагрузки.
Формула
Формула, согласно которой проводится расчёт и составляется схема резисторов в параллельном соединении:
\[ 1/Rобщ=1/R1+1/R2 \]
\[ Rобщ=1/(1/R1+1/R2) \]
\[ Rобщ=(R1*R2)/(R1+R2) \]
Онлайн-калькулятор расчета параллельного соединения резисторов
Как выполняется расчёт
Проводя расчёт сопротивления для рассматриваемого соединения резисторов, нужно учесть факт, общий параметр всегда будет несколько ниже, нежели параметр наименьшего в приведённом сочетании.
Пример №1
Потребуется включить резистор, имеющий сопротивление 8 Ом. Рассматривая номенклатуру изделий, отмечаем, резистор с подобным параметром в базовых наименованиях отсутствует. Необходимо использовать параллельную схему. В дальнейшем, расчёт выполняется:
\[ 1/R=1/R1+1/R2 \]
\[ 1/R=(R1+R2)/(R1*R2) \]
\[ R=(R1*R2)/(R1+R2) \]
В данном случае можно увидеть, что если оба значения равны между собой, то итог будет соответствовать половине одного из используемых двух резисторов.
Если ставится задача подобрать сопротивление 8 Ом, то значение 2*8=16 Ом.
\[ R=(R1*R2)/(R1+R2)=(16*16)/(16+16)=8 \]
Таким образом, чтобы получить значение равное 8 Ом, соединяем два резистора по 16 Ом параллельно.
Пример расчёта №2
Есть три элемента: R1=200, R2=470, R=220
Общее значение выводится по формуле:
\[ 1/R=1/R1+1/R2/1/R3 \]
\[ 1/R=1/200+1/470+1/220=0,0117 \]
\[ R=1/0,0117=85,67 Ом \]
Данный метод без проблем актуален для выполнения расчёта практически любой численности включённых в конструкцию элементов.
Ток в цепи параллельно соединенных резисторов
При параллельном соединении отмечается, что ток, приравнивается сумме из отдельных составляющих. Показатель в каждом ответвлении, не фиксируется идентичным значению в соседних ответвлениях. К отдельному резистору прикладывается идентичное напряжение.
Сила тока
Актуально выполнить расчёт для всех ветвей. Общий показатель силы тока составляет 8А, тогда предстоит распределить напряжения, показатель замеряется на отдельно рассмотренных участках.
\[ U12=I*Rэкв1=0,8*((2*4)/(2+4))=0,8*1,3=1,04 V \]
\[ I1=U12/R1=0,52 А \]
\[ I2=U12/R2=0,26 А \]
Корректность выполненных вычислений определяется:
\[ I=I1+I2=0,52+0,26≈0,8 А \]
Мощность
Для корректного выбора резисторов учитывается и мощность рассеивания. Данный показатель можно рассчитывать так:
\[ P=U*I \]
U — напряжение, В
I — сила тока, А
Показатель косвенным образом определяет некоторое количество энергии, она будет потребляться на выделение тепла.
Как найти сопротивление
Определение сопротивления выполняется по формулам:
\[ 1/G \]
\[ U/I \]
\[ U2/P \]
\[ P/I2 \]
Выбор параллельного подключения резисторов определяется с учётом входных параметров. Стоит только помнить о том, что показатель напряжения и уровень тока в отдельных ответвлениях идентичны.
Примеры применения при параллельном соединении
Конструктивно, каждый резистор рассчитан на некоторый рабочий диапазон температурного воздействия. Увеличение порога вызовет разрушение места пайки, соединения, самой детали, даже расположенных соседних блоков. Стоит помнить, что существуют одновременные соединения резисторов, приведённая компоновка способна нарушить функциональность и исправное состояние.
Благодаря использованию автоматических схем определения рабочих показателей можно переставлять резисторы, устанавливать в конкретном месте различные светодиоды, корректировать уровень сигнала на выходе.
Видео
Калькулятор параллельных и последовательных резисторов
Калькулятор параллельных и последовательных резисторов — идеальное решение для проектирования бесшовных электрических цепей и сетей резисторов. Этот интуитивно понятный инструмент легко вычисляет номиналы резисторов при параллельном или последовательном подключении, экономя ваше время и обеспечивая точность.
Быстро получайте значения полного сопротивления для различных приложений, используя всего несколько простых входных данных. Наш калькулятор упрощает сложные расчеты, позволяя вам сосредоточиться на разработке идеального электронного проекта.
Понимание параллельных и последовательных конфигураций резисторов
Как энтузиасты и профессионалы в области электроники, мы всегда ищем инструменты, которые могут упростить наш процесс проектирования и улучшить наше понимание поведения схемы. Калькулятор параллельных и последовательных резисторов является одним из таких незаменимых инструментов, позволяющих проводить эффективный и точный анализ резисторных цепей. В этом подробном руководстве мы рассмотрим концепцию параллельных и последовательных резисторов, важность калькуляторов резисторов и преимущества, которые они обеспечивают.
Параллельные резисторы
Параллельные резисторы — это резисторы, соединенные встык, с одинаковым напряжением на клеммах. Когда резисторы соединены параллельно, их общее сопротивление меньше наименьшего значения отдельного резистора.
Общее сопротивление в параллельной конфигурации определяется по формуле:
1/R_total = 1/R1 + 1/R2 + ... + 1/RnРезисторы серии Резисторы серии
подключаются таким образом, что конечный вывод одного резистора соединяется с начальным выводом следующего резистора. В последовательной конфигурации ток протекает последовательно через каждый резистор, и существует только один путь тока через всю сеть резисторов. Резисторы должны быть соединены встык, без точек соединения или ответвлений между ними. Стоит отметить, что в этой конфигурации через каждый резистор протекает одинаковый ток, а падение напряжения на каждом резисторе пропорционально его сопротивлению.
Общее сопротивление в последовательной конфигурации представляет собой просто сумму отдельных сопротивлений:
R_total = R1 + R2 + ... + Rn
Необходимость в калькуляторах параллельных и последовательных резисторов трудоемки и подвержены ошибкам, особенно при работе с несколькими резисторами или сложными схемами.
Здесь на помощь приходят калькуляторы параллельных и последовательных резисторов, предлагающие такие ценные преимущества, как:- Упрощенные и точные расчеты
- Экономия времени и усилий
- Расширенный анализ цепей
- Снижение риска ошибок при проектировании
Как работают калькуляторы параллельных и последовательных резисторов
Расчеты параллельных и последовательных резисторов предназначены для получения быстрых и точных результатов для резисторных цепей. Эти калькуляторы обычно включают следующие функции:
- Удобные интерфейсы для ввода номиналов резисторов
- Опции для выбора параллельной или последовательной конфигурации
- Автоматический расчет полного сопротивления
- Преобразование различных единиц измерения (например, омы, килоомы или мегаомы)
Применение параллельных и последовательных калькуляторов резисторов
Эти калькуляторы резисторов являются ценным инструментом как для профессионалов, так и для любителей.
Некоторые распространенные приложения включают:
- Проектирование и анализ цепей
- Поиск и устранение неисправностей существующих цепей
- Выбор компонентов для конкретных значений сопротивления
- Образовательные цели (например, обучение и изучение сетей резисторов)
Калькуляторы параллельных и последовательных резисторов являются важными инструментами для всех, кто работает с электронными схемами. Они упрощают расчеты, экономят время и силы и снижают риск ошибок при проектировании. Понимая их важность и выбирая правильный калькулятор, вы можете обеспечить бесперебойную и эффективную работу своих проектов. Итак, вперед, используйте мощь этих незаменимых инструментов, чтобы поднять свои навыки проектирования схем на новый уровень.
Напряжение на последовательном резисторе Пример
Серия
Соединение резистора:
Два компонента будут вызываться последовательно, если к узлу, к которому они подключены, не подключен другой компонент.
- 7 Меры предосторожности при ремонте электрооборудования в домашних условиях
- Краткое руководство по электронным генераторам и их разным типам
Предположим, два резистора подключены в точке b, а головка второго резистора соединена с хвостом первого резистора. Резисторы обычно не имеют головы и хвоста. Но когда течет ток, вы можете назначить им головы и хвосты, назначив положительные и отрицательные знаки в зависимости от падения напряжения, как показано.
Последовательная цепь обеспечивает только один путь для тока.
Обратите внимание, что ток может течь только по одному пути.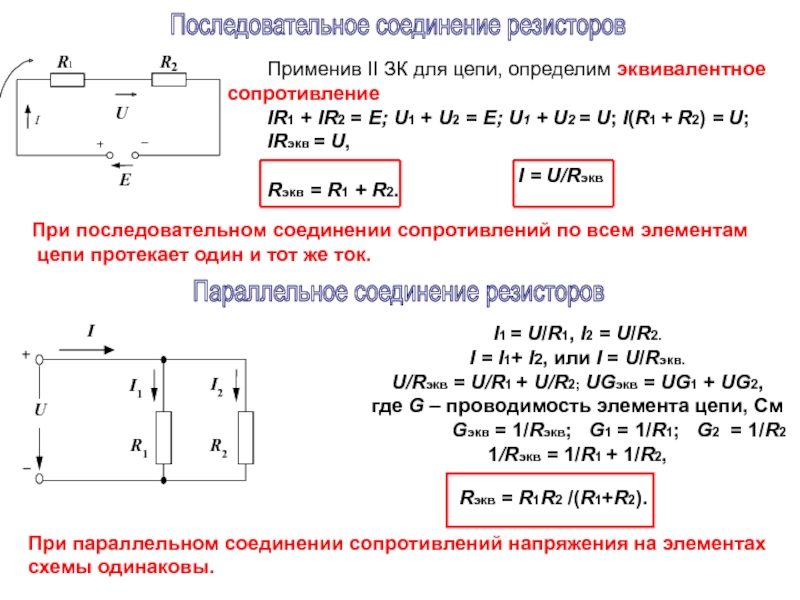
Положительная клемма R 2 соединена с отрицательной клеммой R 1 , и к этой точке не подключен ни один элемент цепи, исходя из предположения, что ток течет из точки a в точку c. Если к точке b подключен какой-либо третий компонент цепи (источник или резистор), R 1 и R 2 больше не будут последовательно друг с другом.
Калькулятор резисторов серии:
R 1
R 2
R 3
R 9009 7 Эквивалент
Резистор в последовательной цепи Формула:
До сих пор мы определили и попытались определить тип цепи. Следующий шаг — узнать, как найти эквивалентное сопротивление в сложной цепи? Предположим, у нас есть следующая сложная схема, и нас интересуют ответы на следующие вопросы.
Какой общий ток обеспечивает источник?
Чтобы узнать общий ток источника, во-первых, нам нужно знать, какое сопротивление испытывает источник? Общее сопротивление мы можем рассчитать по следующей формуле или использовать резистор в последовательном калькуляторе.
Здесь «n» — это общее количество резисторов, соединенных последовательно, в нашем случае n=3.
$R_{эквивалент}=R_{1}+R_{2}+\ldots +R_{n} $
$R_{Eq}=R_{1}+R_{2}+R_{3}$
Предположим $R_{1} R_{2}$ и $R_{3}$ равны 20, 40 и 10 $ \Omega $ соответственно. Подставляя значения в приведенную выше формулу, мы получаем:
$R_{Eq}=20\Omega +40\Omega +10\Omega $
$R_{Eq}=70\Omega $
После нахождения эквивалентного сопротивления схему можно свести к следующей схеме и найти общий ток.
- Как рассчитать KVA трансформатора: калькулятор KVA трансформатора
- Классификация трансформаторов тока на основе четырех параметров
$I_{T}=\frac{V}{R_{Eq}}$
$=\frac {140 В}{70 \Омега} $
$I_{T}=2 A$
Какова сила тока в каждом резисторе?
Для всех резисторов в последовательной цепи всегда есть только один путь для протекания тока. Из-за того, что они находятся на одном пути, ток всегда одинаков для всех последовательно соединенных резисторов, как показано в следующем уравнении.
$I_{T}=I_{1}=I_{2}=\ldots =I_{n} $
Здесь I 1 , I 2, и I n — ток резистора R1, R2 и Rn соответственно, а n представляет собой общее количество резисторов. В нашем случае ток для R1, R2 и R3 равен I1, а I 2 и I 3 2 ампера.
I T = 2 А
I 1 = 2 А,
I 2 = 2 А,
I 3 = 2 А
Какое напряжение на последовательном резисторе?
Это несложно, и закон Ома — лучший инструмент для этого, потому что у нас есть сопротивление и ток каждого резистора, поэтому мы можем легко найти соответствующее напряжение.
В 1 = I 1 R 1 = 2 А x 20 Ом = 40 В
В 3 = I 3 R 3 = 2 А x 10 Ом = 20 вольт
$V_{T}= V_{1}+V_{2}+V_{3} $
$V_{T}=40 В+80 В+20 В$
$V_{T}=120 В $
Обратите внимание, что полное падение напряжения на цепь точно равна приложенному к цепи напряжению.
