Калькулятор резисторов параллельное соединение. Соединение резисторов: параллельное, последовательное и смешанное подключение

Что такое последовательное соединение резисторов. Как рассчитать общее сопротивление при параллельном подключении. Какие особенности имеет смешанное соединение проводников. Как изменяется напряжение и ток в различных схемах подключения резисторов.

Особенности последовательного соединения резисторов

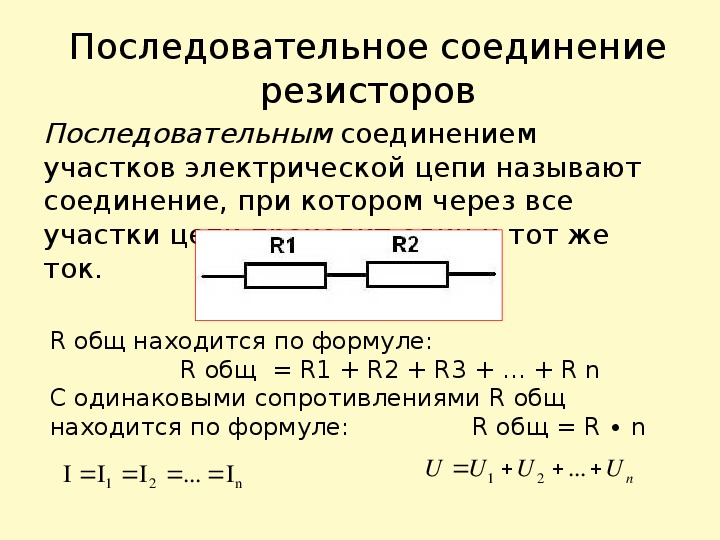
При последовательном соединении резисторы подключаются друг за другом в одну цепь. Конец одного резистора соединяется с началом следующего. Основные свойства такого соединения:

• Сила тока одинакова во всех резисторах
• Общее напряжение равно сумме напряжений на отдельных резисторах
• Общее сопротивление цепи равно сумме сопротивлений всех резисторов

Расчет общего сопротивления производится по формуле:

R = R1 + R2 + R3 + … + Rn

где R — общее сопротивление, R1, R2, R3 и т.д. — сопротивления отдельных резисторов.

Параллельное соединение резисторов

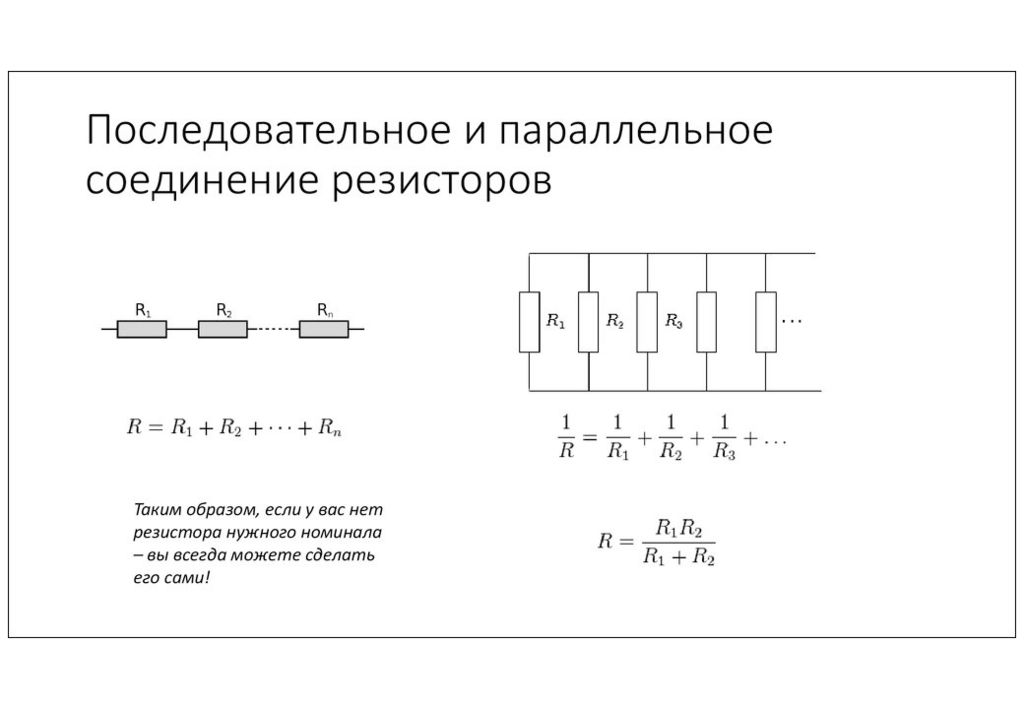
При параллельном соединении все резисторы подключаются к одним и тем же двум точкам цепи. Основные характеристики:

• Напряжение на всех резисторах одинаково
• Общий ток равен сумме токов через отдельные резисторы
• Обратная величина общего сопротивления равна сумме обратных величин сопротивлений резисторов

Формула для расчета общего сопротивления:

1/R = 1/R1 + 1/R2 + 1/R3 + … + 1/Rn

Как меняется напряжение при различных соединениях резисторов?

При последовательном соединении общее напряжение распределяется между резисторами пропорционально их сопротивлению. Чем больше сопротивление резистора, тем большее напряжение на нем падает.

При параллельном соединении напряжение на всех резисторах одинаково и равно напряжению источника питания. Это связано с тем, что все резисторы подключены к одним и тем же точкам цепи.

Особенности смешанного соединения проводников

Смешанное соединение представляет собой комбинацию последовательного и параллельного подключения резисторов. Основные свойства:

• Участки с последовательным соединением рассчитываются по правилам последовательного подключения
• Участки с параллельным соединением — по правилам параллельного
• Общее сопротивление находится путем последовательного применения формул для последовательного и параллельного соединения

Расчет смешанных цепей производится поэтапно, начиная с самых простых участков.

Как изменяется сила тока при разных схемах соединения?

При последовательном соединении сила тока одинакова на всех участках цепи. Это связано с тем, что заряды не могут накапливаться в узлах цепи.

При параллельном соединении общий ток распределяется между ветвями обратно пропорционально их сопротивлению. Чем меньше сопротивление ветви, тем больший ток через нее протекает.

Практическое применение различных схем соединения резисторов

Последовательное соединение резисторов применяется:

• Для увеличения общего сопротивления цепи
• В делителях напряжения
• Для ограничения тока в цепи

Параллельное соединение используется:

• Для уменьшения общего сопротивления
• В токовых шунтах
• Для распределения токов между потребителями

Смешанное соединение позволяет получить нужные характеристики цепи, комбинируя преимущества обоих типов подключения.

Как рассчитать мощность в цепях с различным соединением резисторов?

Расчет мощности производится по формуле P = I^2 * R или P = U^2 / R.

При последовательном соединении общая мощность равна сумме мощностей на отдельных резисторах:

P = P1 + P2 + P3 + … + Pn

При параллельном соединении общая мощность также равна сумме мощностей резисторов, но рассчитывается через напряжение:

P = U^2 * (1/R1 + 1/R2 + 1/R3 + … + 1/Rn)

В смешанных цепях мощность рассчитывается для каждого участка отдельно, а затем суммируется.

Преимущества и недостатки разных типов соединения резисторов

Последовательное соединение:

Преимущества:

• Простота подключения
• Возможность получить большое сопротивление

Недостатки:

• При выходе из строя одного резистора разрывается вся цепь
• Сложно получить малое общее сопротивление

Параллельное соединение:

Преимущества:

• Возможность получить малое общее сопротивление
• Выход из строя одного резистора не нарушает работу остальных

Недостатки:

• Сложнее в монтаже
• Трудно получить большое общее сопротивление

Выбор типа соединения зависит от конкретных задач и требований к электрической цепи.

Калькулятор параллельного сопротивления — электротехника и электроника

Калькулятор параллельных сопротивлений

Вычислите общее сопротивление резисторов параллельно с легкостью!

Вывод

Эквивалентное сопротивление

(Ω)

Как вычислить общее сопротивление резисторов в параллельном

Вычисление эквивалентного сопротивления (R _EQ ) резисторов параллельно вручную может быть утомительным. Этот инструмент был разработан, чтобы помочь вам быстро вычислить эквивалентное сопротивление, независимо от того, имеете ли вы два или десять резисторов параллельно. Чтобы использовать его, просто укажите количество параллельных резисторов и значение сопротивления для каждого из них.

Вы можете легко вычислить эквивалентное сопротивление, если параллельно два идентичных резистора: это половина индивидуального сопротивления. Это удобно, когда вам нужно определенное значение сопротивления и у него нет подходящей части. Например, если вы знаете, что вам нужно около 500 Ом, чтобы получить желаемую яркость из светодиодной схемы, вы можете использовать два резистора 1 кОм параллельно.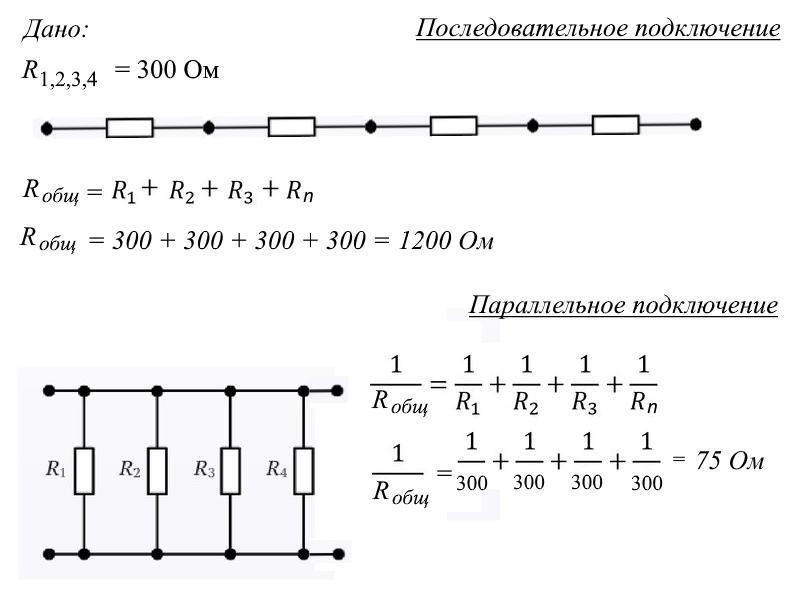

Имейте в виду, что ток через индивидуальный резистор не изменяется, когда вы добавляете резисторы параллельно, потому что одновременное добавление резисторов не влияет на напряжение на клеммах резисторов. Какими изменениями является общий ток, подаваемый источником питания, а не ток через один конкретный резистор.

уравнения

$$ \ frac {1} {R_ {EQ}} = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} + \ frac {1} {R_ {3}} + … + \ frac {1} {R_ {N}} $$

Когда параллельно параллельно два резистора: $$ R_ {EQ} = \ frac {R_1 \ times R_2} {R_1 + R_2} $$

Приложения

Резисторы в серии эквивалентны одному резистору, сопротивление которого является суммой каждого отдельного резистора. С другой стороны, резисторы, в свою очередь, приводят к эквивалентному сопротивлению, которое всегда ниже каждого отдельного резистора. Если вы думаете об этом, это имеет смысл: если вы применяете напряжение на резисторе, то происходит определенное количество текущих потоков. Если вы добавите еще один резистор параллельно с первым, вы по существу открыли новый канал, через который может протекать больше тока.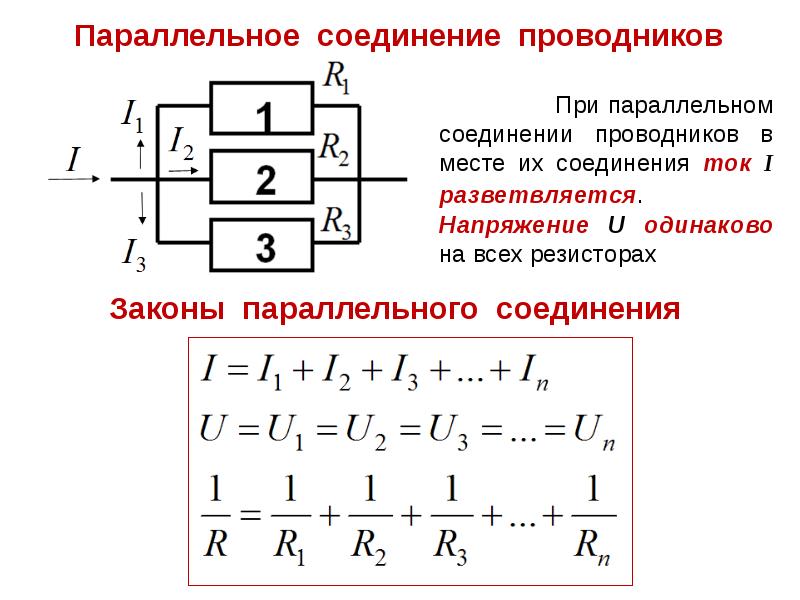 Независимо от того, насколько величен второй резистор, общий ток, протекающий от источника питания, будет по меньшей мере немного выше, чем ток через один резистор. И если общий ток выше, общее сопротивление должно быть ниже.

Дальнейшее чтение

• Учебник — Простые параллельные схемы
• Техническая статья — Сопротивление в параллельных сетях
• Параллельные схемы видеосигналов

Суммарное сопротивление при последовательном соединении. Онлайн калькулятор расчета сопротивления последовательно соединенных резисторов. Сопротивление параллельной цепи

Содержание:

Течение тока в электрической цепи осуществляется по проводникам, в направлении от источника к потребителям. В большинстве подобных схем используются медные провода и электрические приемники в заданном количестве, обладающие различным сопротивлением. В зависимости выполняемых задач, в электрических цепях используется последовательное и параллельное соединение проводников.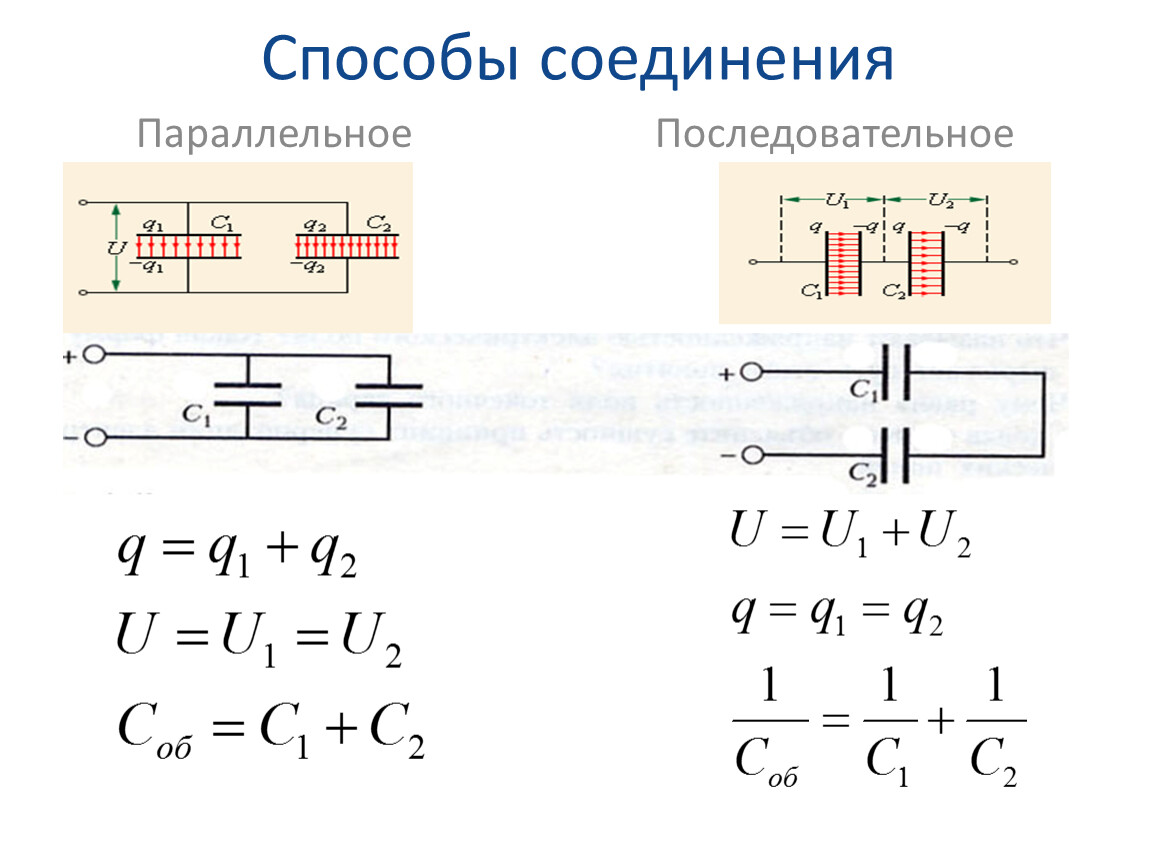

В некоторых случаях могут быть применены оба типа соединений, тогда этот вариант будет называться смешанным. Каждая схема имеет свои особенности и отличия, поэтому их нужно обязательно заранее учитывать при проектировании цепей, ремонте и обслуживании электрооборудования.

Последовательное соединение проводников

В электротехнике большое значение имеет последовательное и параллельное соединение проводников в электрической цепи. Среди них часто используется схема последовательного соединения проводников предполагающая такое же соединение потребителей. В этом случае включение в цепь выполняется друг за другом в порядке очередности. То есть, начало одного потребителя соединяется с концом другого при помощи проводов, без каких-либо ответвлений.

Свойства такой электрической цепи можно рассмотреть на примере участков цепи с двумя нагрузками. Силу тока, напряжение и сопротивление на каждом из них следует обозначить соответственно, как I1, U1, R1 и I2, U2, R2. В результате, получились соотношения, выражающие зависимость между величинами следующим образом: I = I1 = I2, U = U1 + U2, R = R1 + R2.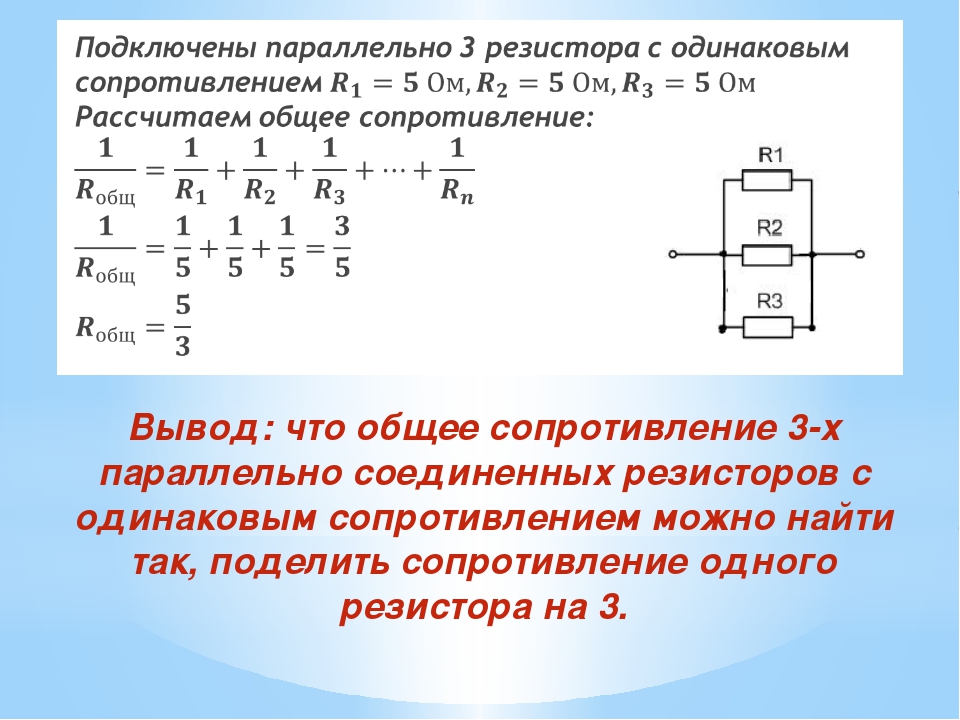

Полученные данные подтверждаются практическим путем с помощью проведения измерений амперметром и вольтметром соответствующих участков.

Таким образом, последовательное соединение проводников отличается следующими индивидуальными особенностями:

• Сила тока на всех участках цепи будет одинаковой.
• Общее напряжение цепи составляет сумму напряжений на каждом участке.
• Общее сопротивление включает в себя сопротивления каждого отдельного проводника.

Данные соотношения подходят для любого количества проводников, соединенных последовательно. Значение общего сопротивления всегда выше, чем сопротивление любого отдельно взятого проводника. Это связано с увеличением их общей длины при последовательном соединении, что приводит и к росту сопротивления.

Если соединить последовательно одинаковые элементы в количестве n, то получится R = n х R1, где R — общее сопротивление, R1 — сопротивление одного элемента, а n — количество элементов. Напряжение U, наоборот, делится на равные части, каждая из которых в n раз меньше общего значения.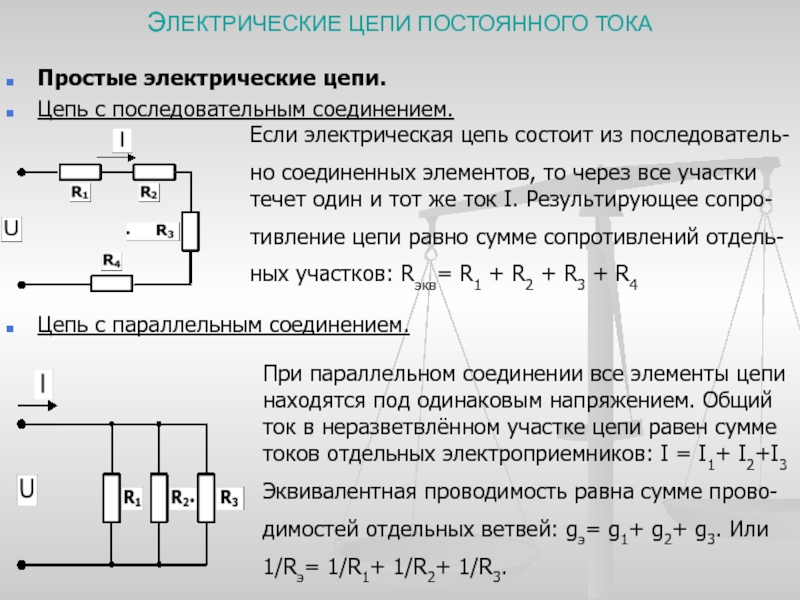 Например, если в сеть с напряжением 220 вольт последовательно включаются 10 ламп одинаковой мощности, то напряжение в любой из них составит: U1 = U/10 = 22 вольта.

Проводники, соединенные последовательно, имеют характерную отличительную особенность. Если во время работы отказал хотя-бы один из них, то течение тока прекращается во всей цепи. Наиболее ярким примером является , когда одна перегоревшая лампочка в последовательной цепи, приводит к выходу из строя всей системы. Для установления перегоревшей лампочки понадобится проверка всей гирлянды.

Параллельное соединение проводников

В электрических сетях проводники могут соединяться различными способами: последовательно, параллельно и комбинированно. Среди них параллельное соединение это такой вариант, когда проводники в начальных и конечных точках соединяются между собой. Таким образом, начала и концы нагрузок соединяются вместе, а сами нагрузки располагаются параллельно относительно друг друга. В электрической цепи могут содержаться два, три и более проводников, соединенных параллельно.

Если рассматривать последовательное и параллельное соединение, сила тока в последнем варианте может быть исследована с помощью следующей схемы. Берутся две лампы накаливания, обладающие одинаковым сопротивлением и соединенные параллельно. Для контроля к каждой лампочке подключается собственный . Кроме того, используется еще один амперметр, контролирующий общую силу тока в цепи. Проверочная схема дополняется источником питания и ключом.

После замыкания ключа нужно контролировать показания измерительных приборов. Амперметр на лампе № 1 покажет силу тока I1, а на лампе № 2 — силу тока I2. Общий амперметр показывает значение силы тока, равное сумме токов отдельно взятых, параллельно соединенных цепей: I = I1 + I2. В отличие от последовательного соединения, при перегорании одной из лампочек, другая будет нормально функционировать. Поэтому в домашних электрических сетях используется параллельное подключение приборов.

С помощью такой же схемы можно установить значение эквивалентного сопротивления.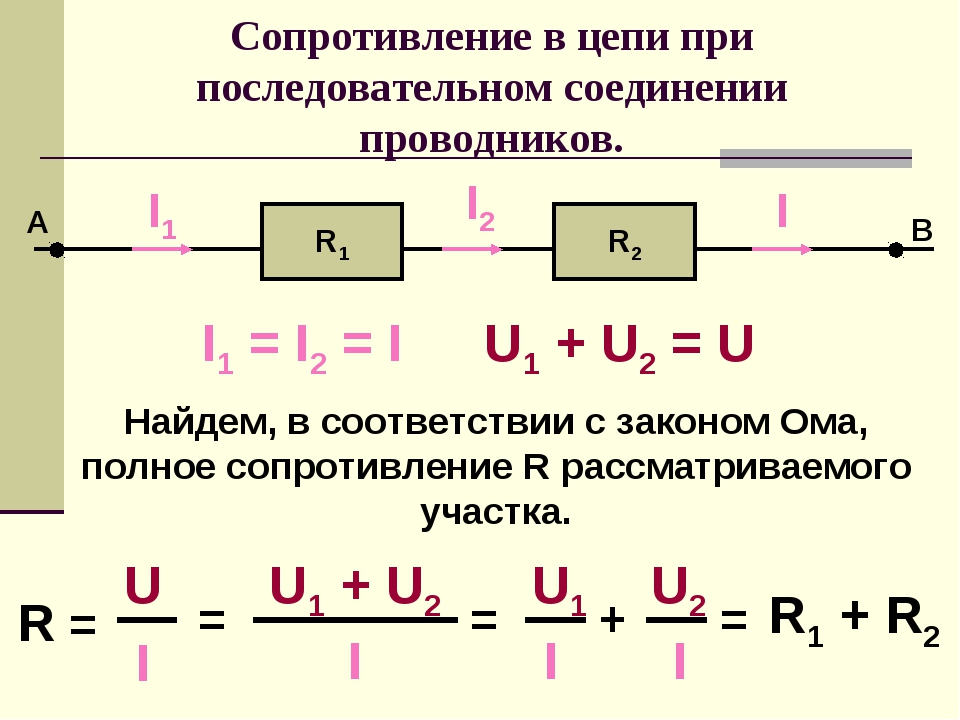 С этой целью в электрическую цепь добавляется вольтметр. Это позволяет измерить напряжение при параллельном соединении, сила тока при этом остается такой же. Здесь также имеются точки пересечения проводников, соединяющих обе лампы.

В результате измерений общее напряжение при параллельном соединении составит: U = U1 = U2. После этого можно рассчитать эквивалентное сопротивление, условно заменяющее все элементы, находящиеся в данной цепи. При параллельном соединении, в соответствии с законом Ома I = U/R, получается следующая формула: U/R = U1/R1 + U2/R2, в которой R является эквивалентным сопротивлением, R1 и R2 — сопротивления обеих лампочек, U = U1 = U2 — значение напряжения, показываемое вольтметром.

Следует учитывать и тот фактор, что токи в каждой цепи, в сумме составляют общую силу тока всей цепи. В окончательном виде формула, отражающая эквивалентное сопротивление будет выглядеть следующим образом: 1/R = 1/R1 + 1/R2. При увеличении количества элементов в таких цепях — увеличивается и число слагаемых в формуле.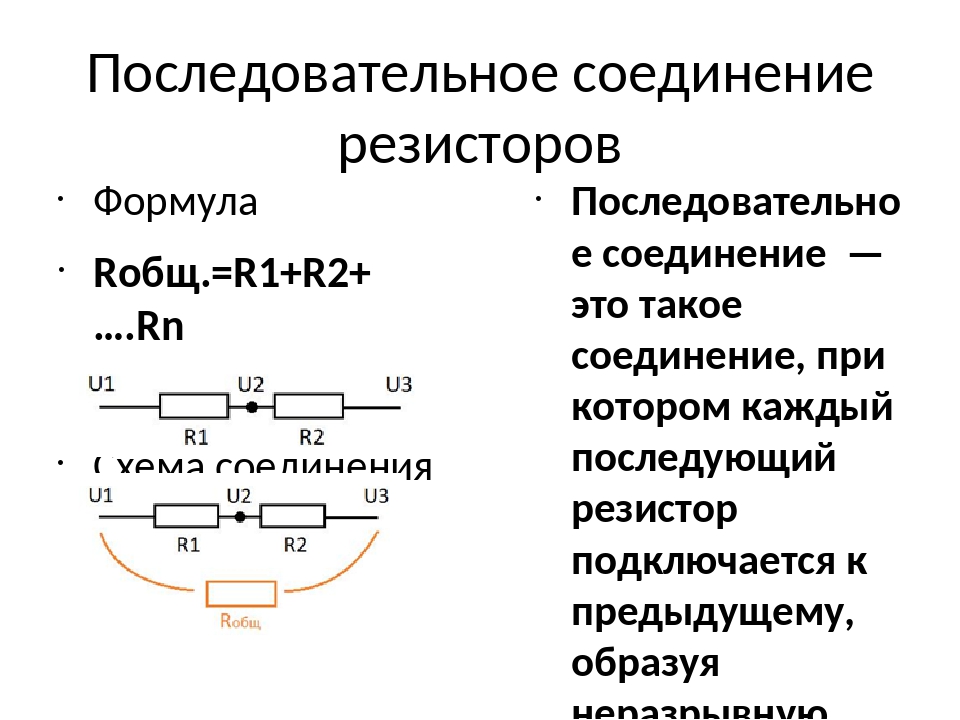 Различие в основных параметрах отличают друг от друга и источников тока, позволяя использовать их в различных электрических схемах.

Параллельное соединение проводников характеризуется достаточно малым значением эквивалентного сопротивления, поэтому сила тока будет сравнительно высокой. Данный фактор следует учитывать, когда в розетки включается большое количество электроприборов. В этом случае сила тока значительно возрастает, приводя к перегреву кабельных линий и последующим возгораниям.

Законы последовательного и параллельного соединения проводников

Данные законы, касающиеся обоих видов соединений проводников, частично уже были рассмотрены ранее.

Для более четкого их понимания и восприятия в практической плоскости, последовательное и параллельное соединение проводников, формулы следует рассматривать в определенной последовательности:

• Последовательное соединение предполагает одинаковую силу тока в каждом проводнике: I = I1 = I2.
• параллельное и последовательное соединение проводников объясняет в каждом случае по-своему. Например, при последовательном соединении, напряжения на всех проводниках будут равны между собой: U1 = IR1, U2 = IR2. Кроме того, при последовательном соединении напряжение составляет сумму напряжений каждого проводника: U = U1 + U2 = I(R1 + R2) = IR.
• Полное сопротивление цепи при последовательном соединении состоит из суммы сопротивлений всех отдельно взятых проводников, независимо от их количества.
• При параллельном соединении напряжение всей цепи равно напряжению на каждом из проводников: U1 = U2 = U.
• Общая сила тока, измеренная во всей цепи, равна сумме токов, протекающих по всем проводникам, соединенных параллельно между собой: I = I1 + I2.

Для того чтобы более эффективно проектировать электрические сети, нужно хорошо знать последовательное и параллельное соединение проводников и его законы, находя им наиболее рациональное практическое применение.

Смешанное соединение проводников

В электрических сетях как правило используется последовательное параллельное и смешанное соединение проводников, предназначенное для конкретных условий эксплуатации. Однако чаще всего предпочтение отдается третьему варианту, представляющему собой совокупность комбинаций, состоящих из различных типов соединений.

В таких смешанных схемах активно применяется последовательное и параллельное соединение проводников, плюсы и минусы которых обязательно учитываются при проектировании электрических сетей. Эти соединения состоят не только из отдельно взятых резисторов, но и довольно сложных участков, включающих в себя множество элементов.

Смешанное соединение рассчитывается в соответствии с известными свойствами последовательного и параллельного соединения. Метод расчета заключается в разбивке схемы на более простые составные части, которые считаются отдельно, а потом суммируются друг с другом.

Проверим справедливость показанных здесь формул на простом эксперименте.

Возьмём два резистора МЛТ-2 на 3 и 47 Ом и соединим их последовательно. Затем измерим общее сопротивление получившейся цепи цифровым мультиметром.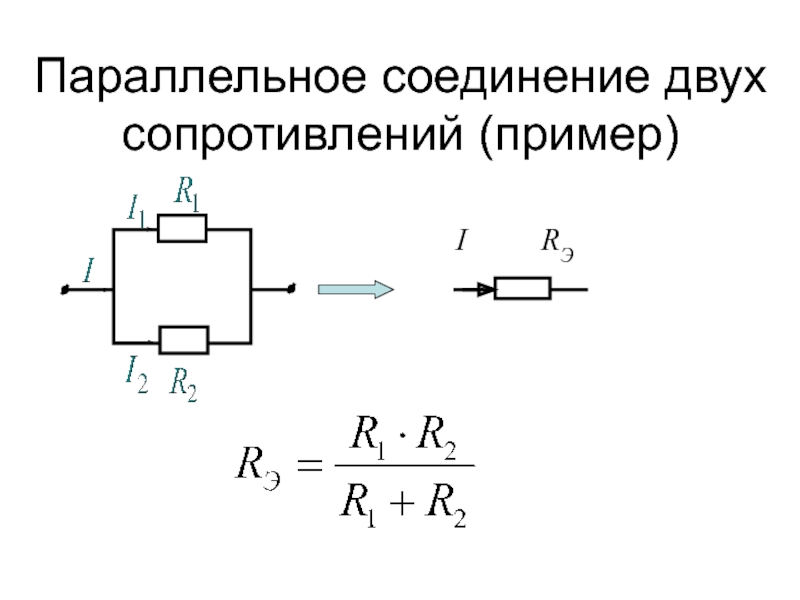 Как видим оно равно сумме сопротивлений резисторов, входящих в эту цепочку.

Замер общего сопротивления при последовательном соединении

Теперь соединим наши резисторы параллельно и замерим их общее сопротивление.

Измерение сопротивления при параллельном соединении

Как видим, результирующее сопротивление (2,9 Ом) меньше самого меньшего (3 Ом), входящего в цепочку. Отсюда вытекает ещё одно известное правило, которое можно применять на практике:

При параллельном соединении резисторов общее сопротивление цепи будет меньше наименьшего сопротивления, входящего в эту цепь.

Что ещё нужно учитывать при соединении резисторов?

Во-первых, обязательно учитывается их номинальная мощность. Например, нам нужно подобрать замену резистору на 100 Ом и мощностью 1 Вт . Возьмём два резистора по 50 Ом каждый и соединим их последовательно. На какую мощность рассеяния должны быть рассчитаны эти два резистора?

Поскольку через последовательно соединённые резисторы течёт один и тот же постоянный ток (допустим 0,1 А ), а сопротивление каждого из них равно 50 Ом , тогда мощность рассеивания каждого из них должна быть не менее 0,5 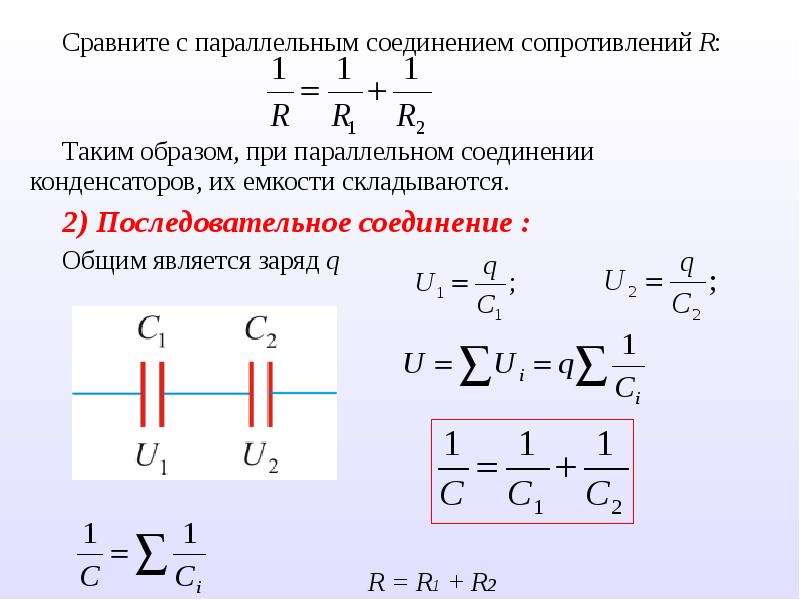Вт . В результате на каждом из них выделится по 0,5 Вт мощности. В сумме это и будет тот самый 1 Вт .

Данный пример достаточно грубоват. Поэтому, если есть сомнения, стоит брать резисторы с запасом по мощности.

Подробнее о мощности рассеивания резистора читайте .

Во-вторых, при соединении стоит использовать однотипные резисторы, например, серии МЛТ. Конечно, нет ничего плохого в том, чтобы брать разные. Это лишь рекомендация.

Темы кодификатора ЕГЭ : параллельное и последовательное соединение проводников, смешанное соединение проводников.

Есть два основных способа соединения проводников друг с другом — это последовательное и параллельное соединения. Различные комбинации последовательного и параллельного соединений приводят к смешанному соединению проводников.

Мы будем изучать свойства этих соединений, но сначала нам понадобится некоторая вводная информация.

Проводник, обладающий сопротивлением , мы называем резистором и изображаем следующим образом (рис.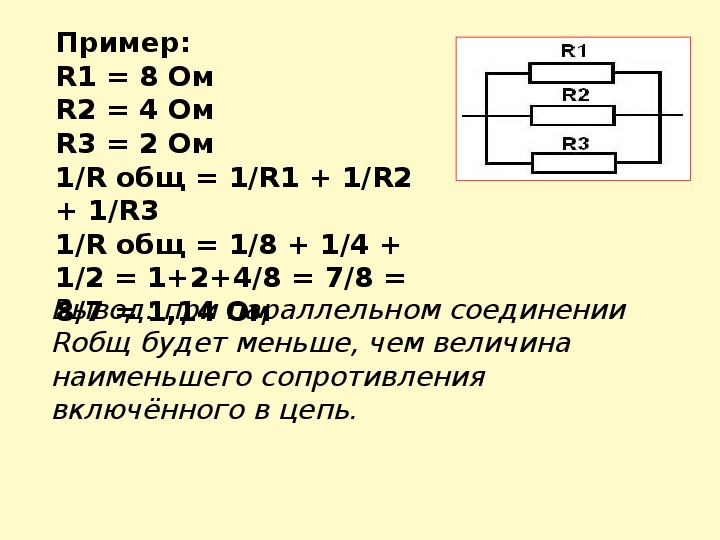 1 ):

Рис. 1. Резистор

Напряжение на резисторе — это разность потенциалов стационарного электрического поля между концами резистора. Между какими именно концами? В общем-то, это неважно, но обычно удобно согласовывать разность потенциалов с направлением тока.

Ток в цепи течёт от «плюса» источника к «минусу». В этом направлении потенциал стационарного поля убывает. Напомним ещё раз, почему это так.

Пусть положительный заряд перемещается по цепи из точки в точку , проходя через резистор (рис. 2 ):

Рис. 2.

Стационарное поле совершает при этом положительную работу .

Так как alt=»q > 0″> и alt=»A > 0″> , то и alt=»\varphi_a — \varphi_b > 0″> , т. е. alt=»\varphi_a > \varphi_b»> .

Поэтому напряжение на резисторе мы вычисляем как разность потенциалов в направлении тока: .

Сопротивление подводящих проводов обычно пренебрежимо мало; на электрических схемах оно считается равным нулю.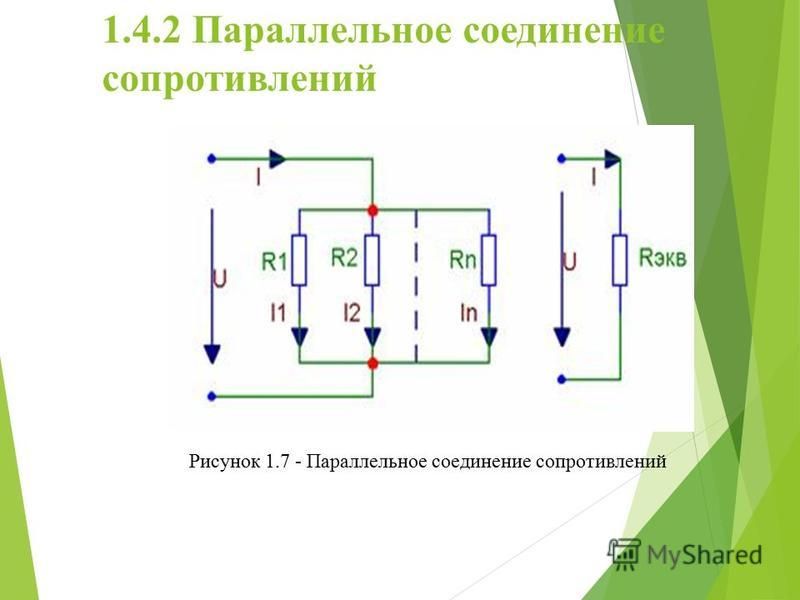 Из закона Ома следует тогда, что потенциал не меняется вдоль провода: ведь если и , то . (рис. 3 ):

Рис. 3.

Таким образом, при рассмотрении электрических цепей мы пользуемся идеализацией, которая сильно упрощает их изучение. А именно, мы считаем, что потенциал стационарного поля изменяется лишь при переходе через отдельные элементы цепи, а вдоль каждого соединительного провода остаётся неизменным . В реальных цепях потенциал монотонно убывает при движении от положительной клеммы источника к отрицательной.

Последовательное соединение

При последовательном соединении проводников конец каждого проводника соединяется с началом следующего за ним проводника.

Рассмотрим два резистора и , соединённых последовательно и подключённых к источнику постоянного напряжения (рис. 4 ). Напомним, что положительная клемма источника обозначается более длинной чертой, так что ток в данной схеме течёт по часовой стрелке.

Рис. 4. Последовательное соединение

Сформулируем основные свойства последовательного соединения и проиллюстрируем их на этом простом примере.

1. При последовательном соединении проводников сила тока в них одинакова.
В самом деле, через любое поперечное сечение любого проводника за одну секунду будет проходить один и тот же заряд. Ведь заряды нигде не накапливаются, из цепи наружу не уходят и не поступают в цепь извне.

2. Напряжение на участке, состоящем из последовательно соединённых проводников, равно сумме напряжений на каждом проводнике .

Действительно, напряжение на участке — это работа поля по переносу единичного заряда из точки в точку ; напряжение на участке — это работа поля по переносу единичного заряда из точки в точку . Складываясь, эти две работы дадут работу поля по переносу единичного заряда из точки в точку , то есть напряжение на всём участке:

Можно и более формально, без всяких словесных объяснений:

3. Сопротивление участка, состоящего из последовательно соединённых проводников, равно сумме сопротивлений каждого проводника.

Пусть — сопротивление участка . По закону Ома имеем:

что и требовалось.

Можно дать интуитивно понятное объяснение правила сложения сопротивлений на одном частном примере. Пусть последовательно соединены два проводника из одинакового вещества и с одинаковой площадью поперечного сечения , но с разными длинами и .

Сопротивления проводников равны:

Эти два проводника образуют единый проводник длиной и сопротивлением

Но это, повторяем, лишь частный пример. Сопротивления будут складываться и в самом общем случае — если различны также вещества проводников и их поперечные сечения.
Доказательство этого даётся с помощью закона Ома, как показано выше.
Наши доказательства свойств последовательного соединения, приведённые для двух проводников, переносятся без существенных изменений на случай произвольного числа проводников.

Параллельное соединение

При параллельном соединении проводников их начала подсоединяются к одной точке цепи, а концы — к другой точке.

Снова рассматриваем два резистора, на сей раз соединённые параллельно (рис. 5 ).

Рис. 5. Параллельное соединение

Резисторы подсоединены к двум точкам: и . Эти точки называются узлами или точками разветвления цепи. Параллельные участки называются также ветвями ; участок от к (по направлению тока) называется неразветвлённой частью цепи.

Теперь сформулируем свойства параллельного соединения и докажем их для изображённого выше случая двух резисторов.

1. Напряжение на каждой ветви одинаково и равно напряжению на неразветвлённой части цепи.
В самом деле, оба напряжения и на резисторах и равны разности потенциалов между точками подключения:

Этот факт служит наиболее отчётливым проявлением потенциальности стационарного электрического поля движущихся зарядов.

2. Сила тока в неразветвлённой части цепи равна сумме сил токов в каждой ветви.
Пусть, например, в точку за время из неразветвлённого участка поступает заряд . За это же время из точки к резистору уходит заряд , а к резистору — заряд .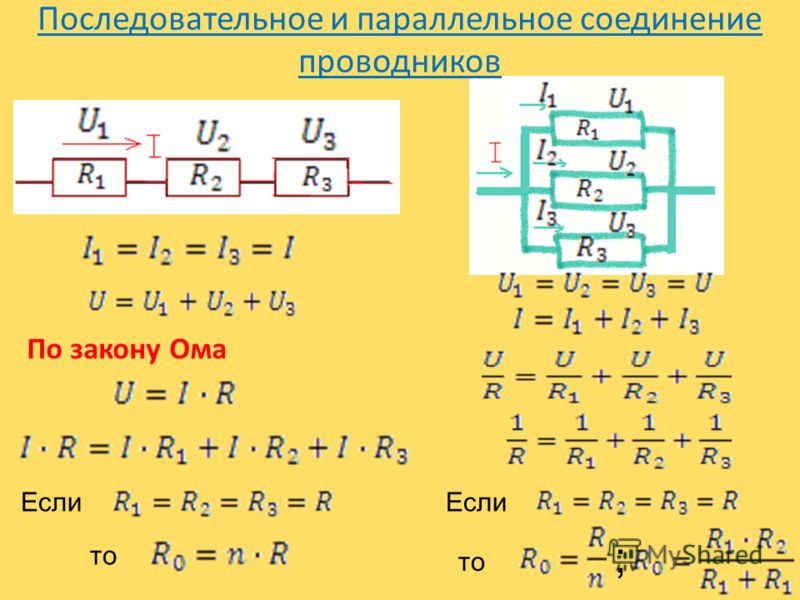

Ясно, что . В противном случае в точке накапливался бы заряд, меняя потенциал данной точки, что невозможно (ведь ток постоянный, поле движущихся зарядов стационарно, и потенциал каждой точки цепи не меняется со временем). Тогда имеем:

что и требовалось.

3. Величина, обратная сопротивлению участка параллельного соединения, равна сумме величин, обратных сопротивлениям ветвей.
Пусть — сопротивление разветвлённого участка . Напряжение на участке равно ; ток, текущий через этот участок, равен . Поэтому:

Сокращая на , получим:

(1)

что и требовалось.

Как и в случае последовательного соединения, можно дать объяснение данного правила на частном примере, не обращаясь к закону Ома.
Пусть параллельно соединены проводники из одного вещества с одинаковыми длинами , но разными поперечными сечениями и . Тогда это соединение можно рассматривать как проводник той же длины , но с площадью сечения . Имеем:

Приведённые доказательства свойств параллельного соединения без существенных изменений переносятся на случай любого числа проводников.

Из соотношения (1) можно найти :

(2)

К сожалению, в общем случае параллельно соединённых проводников компактного аналога формулы (2) не получается, и приходится довольствоваться соотношением

(3)

Тем не менее, один полезный вывод из формулы (3) сделать можно. Именно, пусть сопротивления всех резисторов одинаковы и равны . Тогда:

Мы видим, что сопротивление участка из параллельно соединённых одинаковых проводников в раз меньше сопротивления одного проводника.

Смешанное соединение

Смешанное сединение проводников, как следует из названия, может являться совокупностью любых комбинаций последовательного и параллельного соединений, причём в состав этих соединений могут входить как отдельные резисторы, так и более сложные составные участки.

Расчёт смешанного соединения опирается на уже известные свойства последовательного и параллельного соединений. Ничего нового тут уже нет: нужно только аккуратно расчленить данную схему на более простые участки, соединённые последовательно или параллельно.

Рассмотрим пример смешанного соединения проводников (рис. 6 ).

Рис. 6. Смешанное соединение

Пусть В, Ом, Ом, Ом, Ом, Ом. Найдём силу тока в цепи и в каждом из резисторов.

Наша цепь состоит из двух последовательно соединённых участков и . Сопротивление участка :

Ом.

Участок является параллельным соединением: два последовательно включённых резистора и подключены параллельно к резистору . Тогда:

Ом.

Сопротивление цепи:

Ом.

Теперь находим силу тока в цепи:

Для нахождения тока в каждом резисторе вычислим напряжения на обоих участках:

(Заметим попутно, что сумма этих напряжений равна В, т. е. напряжению в цепи, как и должно быть при последовательном соединении.)

Оба резистора и находятся под напряжением , поэтому:

(В сумме имеем А, как и должно быть при параллельном соединении.)

Сила тока в резисторах и одинакова, так как они соединены последовательно:

Стало быть, через резистор течёт ток A.

Последовательным называется такое соединение резисторов, когда конец одного проводника соединяется с началом другого и т.д. (рис. 1). При последовательном соединении сила тока на любом участке электрической цепи одинакова. Это объясняется тем, что заряды не могут накапливаться в узлах цепи. Их накопление привело бы к изменению напряженности электрического поля, а следовательно, и к изменению силы тока. Поэтому

Амперметр А измеряет силу тока в цепи и обладает малым внутренним сопротивлением (R A 0).

Включенные вольтметры V 1 и V 2 измеряют напряжение U 1 и U 2 на сопротивлениях R 1 и R 2 . Вольтметр V измеряет подведенное к клеммам М и N напряжение U. Вольтметры показывают, что при последовательном соединении напряжение U равно сумме напряжений на отдельных участках цепи:

Применяя закон Ома для каждого участка цепи, получим:

где R — общее сопротивление последовательно соединенной цепи. Подставляя U, U 1 , U 2 в формулу (1), имеем

Сопротивление цепи, состоящей из n последовательно соединенных резисторов, равно сумме сопротивлений этих резисторов:

Если сопротивления отдельных резисторов равны между собой, т. е. R 1 = R 2 = … = R n , то общее сопротивление этих резисторов при последовательном соединении в n раз больше сопротивления одного резистора: R = nR 1 .

При последовательном соединении резисторов справедливо соотношение

т.е. напряжения на резисторах прямо пропорциональны сопротивлениям.

Параллельным называется такое соединение резисторов, когда одни концы всех резисторов соединены в один узел, другие концы — в другой узел (рис. 2). Узлом называется точка разветвленной цепи, в которой сходятся более двух проводников. При параллельном соединении резисторов к точкам М и N подключен вольтметр. Он показывает, что напряжения на отдельных участках цепи с сопротивлениями R 1 и R 2 равны. Это объясняется тем, что работа сил стационарного электрического поля не зависит от формы траектории:

Амперметр показывает, что сила тока I в неразветвленной части цепи равна сумме сил токов I 1 и I 2 в параллельно соединенных проводниках R 1 и R 2:

Это вытекает и из закона сохранения электрического заряда. Применим закон Ома для отдельных участков цепи и всей цепи с общим сопротивлением R:

Подставляя I, I 1 и I 2 в формулу (2), получим.

Содержание:

Во всех электрических схемах используются резисторы, представляющие собой элементы, с точно установленным значением сопротивления. Благодаря специфическим качествам этих устройств, становится возможной регулировка напряжения и силы тока на любых участках схемы. Данные свойства лежат в основе работы практически всех электронных приборов и оборудования. Так, напряжение при параллельном и последовательном соединении резисторов будет отличаться. Поэтому каждый вид соединения может применяться только в определенных условиях, чтобы та или иная электрическая схема могла в полном объеме выполнять свои функции.

Напряжение при последовательном соединении

При последовательном соединении два резистора и более соединяются в общую цепь таким образом, что каждый из них имеет контакт с другим устройством только в одной точке. Иначе говоря, конец первого резистора соединяется с началом второго, а конец второго — с началом третьего и т.д.

Особенностью данной схемы является прохождение через все подключенные резисторы одного и того же значения электрического тока. С возрастанием количества элементов на рассматриваемом участке цепи, течение электрического тока становится все более затрудненным. Это происходит из-за увеличения общего сопротивления резисторов при их последовательном соединении. Данное свойство отражается формулой: R общ = R 1 + R 2 .

Распределение напряжения, в соответствии с законом Ома, осуществляется на каждый резистор по формуле: V Rn = I Rn x R n . Таким образом, при увеличении сопротивления резистора, возрастает и падающее на него напряжение.

Напряжение при параллельном соединении

При параллельном соединении, включение резисторов в электрическую цепь выполняется таким образом, что все элементы сопротивлений подключаются друг к другу сразу обоими контактами. Одна точка, представляющая собой электрический узел, может соединять одновременно несколько резисторов.

Такое соединение предполагает течение отдельного тока в каждом резисторе. Сила этого тока находится в обратно пропорциональной . В результате, происходит увеличение общей проводимости данного участка цепи, при общем уменьшении сопротивления. В случае параллельного соединения резисторов с различным сопротивлением, значение общего сопротивления на этом участке всегда будет ниже самого маленького сопротивления отдельно взятого резистора.

На представленной схеме, напряжение между точками А и В представляет собой не только общее напряжение для всего участка, но и напряжение, поступающее к каждому отдельно взятому резистору. Таким образом, в случае параллельного соединения, напряжение, подаваемое ко всем резисторам, будет одинаковым.

В результате, напряжение при параллельном и последовательном соединении будет отличаться в каждом случае. Благодаря этому свойству, имеется реальная возможность отрегулировать данную величину на любом участке цепи.

Последовательное и параллельное соединение проводников, резисторов, конденсаторов и катушек индуктивности. Онлайн расчёты.

«- Я тебе как электрику объясняю: Надя спит с мужиками последовательно, а Света параллельно. Кто из них шмара вавилонская?
— Ну, Света наверное.
— Вот! А мне, как кладовщику, видится немного другое: «поблядушка обыкновенная» — 2 штуки! »

«- А теперь скажи мне отрок, как течёт электричество по проводам электрическим, и цепям рукотворным, последовательным да параллельным, от плюса к минусу со скоростью света в вакууме?
— С Божьей помощью, батюшка! С Божьей помощью…»

Ну да ладно, достаточно! Шутки — штуками, а пора бы уже дело делать. Так что «Копайте пока здесь! А я тем временем схожу узнаю — где надо…», а заодно набросаю пару-тройку калькуляторов на заданную тему.

Итак.
При последовательном соединении проводников сила тока во всех проводниках одинакова, при этом общее напряжение в цепи равно сумме напряжений на концах каждого из проводников.
При параллельном соединении падение напряжения между двумя узлами, объединяющими элементы цепи, одинаково для всех элементов, а сила тока в цепи равна сумме сил токов в отдельных параллельно соединённых проводниках.
Поясним рисунком с распределением напряжений, токов и формулами.

Рис.1

Расчёт проведём для 4 резисторов (проводников), соединённых последовательно или параллельно. Если элементов в цепи меньше, то оставляем лишние поля в таблице не заполненными.
Заодно, при желании узнать распределение значений токов и напряжений на каждом из элементов при последовательном и параллельном соединениях, есть возможность ввести величину общего напряжения в цепи U. А есть возможность не вводить…
Короче, все вводные, помеченные * — к заполнению не обязательны.

РАСЧЁТ СОПРОТИВЛЕНИЙ ПРИ ПАРАЛЛЕЛЬНОМ И ПОСЛЕДОВАТЕЛЬНОМ СОЕДИНЕНИИ
проводников

Теперь, что касается последовательных и параллельных соединений конденсаторов и катушек индуктивности.
Схема, приведённая на Рис.1 для проводников и резисторов, остаётся в полной силе и для катушек с конденсаторами, распределение напряжений и токов тоже никуда не девается, трансформируется лишь осмысление того, что токи эти и напряжения обязаны быть переменными.
Почему переменными?
А потому, что для постоянных значений этих величин — сопротивление конденсаторов составляет в первом приближении бесконечность, а катушек — ноль, соответственно и токи будут равны либо нулю, либо бесконечности, а для переменных значений иметь ярко выраженную зависимость от частоты.

Поэтому, для желающих рассчитать величины напряжений и токов в последовательных или параллельных цепях, состоящих из конденсаторов и катушек индуктивности, имеет полный смысл выяснить на странице ссылка на страницу значения реактивных сопротивлений данных элементов при интересующей Вас частоте и подставить эти значения в таблицу для расчёта проводников и резисторов. А в качестве общего напряжения в цепи — подставлять действующее значение амплитуды переменного тока.

Ну а теперь приведём таблицы для расчёта значений ёмкостей и индуктивностей при условии последовательного и параллельного соединений конденсаторов и катушек в количестве от 2 до 4 штук.
Расчёт поведём на основании хрестоматийных формул:

С = С₁+ С₂+….+ С_n   и   1/L = 1/L₁+ 1/L₂ +…+ 1/L_n    для параллельных цепей и
L = L₁ + L₂ +….+ L_n   и   1/С = 1/С₁+ 1/С₂+…+ 1/С_n    для последовательных.

Как и в предыдущей таблице вводные, помеченные * — к заполнению не обязательны.

РАСЧЁТ ЁМКОСТИ ПРИ ПАРАЛЛЕЛЬНОМ И ПОСЛЕДОВАТЕЛЬНОМ СОЕДИНЕНИИ
конденсаторов

Ну и в завершении ещё одна таблица.

РАСЧЁТ ИНДУКТИВНОСТИ ПРИ ПАРАЛЛЕЛЬНОМ И ПОСЛЕДОВАТЕЛЬНОМ СОЕДИНЕНИИ
катушек

Тут важно заметить, что приведённые в последней таблице расчёты верны только для индуктивно не связанных катушек, то есть для катушек, намотанных на разных каркасах и расположенных на значительных расстояниях друг от друга, во избежание, пересечения взаимных магнитных полей.

 

Калькулятор параллельного включения резисторов

Как правильно соединять резисторы?

О том, как соединять конденсаторы и рассчитывать их общую ёмкость уже рассказывалось на страницах сайта. А как соединять резисторы и посчитать их общее сопротивление? Именно об этом и будет рассказано в этой статье.

Резисторы есть в любой электронной схеме, причём их номинальное сопротивление может отличаться не в 2 – 3 раза, а в десятки и сотни раз. Так в схеме можно найти резистор на 1 Ом, и тут же неподалёку на 1000 Ом (1 кОм)!

Поэтому при сборке схемы либо ремонте электронного прибора может потребоваться резистор с определённым номинальным сопротивлением, а под рукой такого нет. В результате быстро найти подходящий резистор с нужным номиналом не всегда удаётся. Это обстоятельство тормозит процесс сборки схемы или ремонта. Выходом из такой ситуации может быть применение составного резистора.

Для того чтобы собрать составной резистор нужно соединить несколько резисторов параллельно или последовательно и тем самым получить нужное нам номинальное сопротивление. На практике это пригождается постоянно. Знания о правильном соединении резисторов и расчёте их общего сопротивления выручают и ремонтников, восстанавливающих неисправную электронику, и радиолюбителей, занятых сборкой своего электронного устройства.

Последовательное соединение резисторов.

В жизни последовательное соединение резисторов имеет вид:

Последовательно соединённые резисторы серии МЛТ

Принципиальная схема последовательного соединения выглядит так:

На схеме видно, что мы заменяем один резистор на несколько, общее сопротивление которых равно тому, который нам необходим.

Подсчитать общее сопротивление при последовательном соединении очень просто. Нужно сложить все номинальные сопротивления резисторов входящих в эту цепь. Взгляните на формулу.

Общее номинальное сопротивление составного резистора обозначено как R_общ.

Номинальные сопротивления резисторов включённых в цепь обозначаются как R₁, R₂, R₃,…R_N.

Применяя последовательное соединение, стоит помнить одно простое правило:

Из всех резисторов, соединённых последовательно главную роль играет тот, у которого самое большое сопротивление. Именно он в значительной степени влияет на общее сопротивление.

Так, например, если мы соединяем три резистора, номинал которых равен 1, 10 и 100 Ом, то в результате мы получим составной на 111 Ом. Если убрать резистор на 100 Ом, то общее сопротивление цепочки резко уменьшиться до 11 Ом! А если убрать, к примеру, резистор на 10 Ом, то сопротивление будет уже 101 Ом. Как видим, резисторы с малыми сопротивлениями в последовательной цепи практически не влияют на общее сопротивление.

Параллельное соединение резисторов.

Можно соединять резисторы и параллельно:

Два резистора МЛТ-2, соединённых параллельно

Принципиальная схема параллельного соединения выглядит следующим образом:

Для того чтобы подсчитать общее сопротивление нескольких параллельно соединённых резисторов понадобиться знание формулы. Выглядит она вот так:

Эту формулу можно существенно упростить, если применять только два резистора. В таком случае формула примет вид:

Есть несколько простых правил, позволяющих без предварительного расчёта узнать, каково должно быть сопротивление двух резисторов, чтобы при их параллельном соединении получить то, которое требуется.

Если параллельно соединены два резистора с одинаковым сопротивлением, то общее сопротивление этих резисторов будет ровно в два раза меньше, чем сопротивление каждого из резисторов, входящих в эту цепочку.

Это правило исходит из простой формулы для расчёта общего сопротивления параллельной цепи, состоящей из резисторов одного номинала. Она очень проста. Нужно разделить номинальное сопротивление одного из резисторов на общее их количество:

Здесь R₁ – номинальное сопротивление резистора. N – количество резисторов с одинаковым номинальным сопротивлением.

Ознакомившись с приведёнными формулами, вы скажите, что все они справедливы для расчёта ёмкости параллельно и последовательно соединённых конденсаторов. Да, только в отношении конденсаторов всё действует с точностью до «наоборот”. Узнать подробнее о соединении конденсаторов можно здесь.

Проверим справедливость показанных здесь формул на простом эксперименте.

Возьмём два резистора МЛТ-2 на 3 и 47 Ом и соединим их последовательно. Затем измерим общее сопротивление получившейся цепи цифровым мультиметром. Как видим оно равно сумме сопротивлений резисторов, входящих в эту цепочку.

Замер общего сопротивления при последовательном соединении

Теперь соединим наши резисторы параллельно и замерим их общее сопротивление.

Измерение сопротивления при параллельном соединении

Как видим, результирующее сопротивление (2,9 Ом) меньше самого меньшего (3 Ом), входящего в цепочку. Отсюда вытекает ещё одно известное правило, которое можно применять на практике:

При параллельном соединении резисторов общее сопротивление цепи будет меньше наименьшего сопротивления, входящего в эту цепь.

Что ещё нужно учитывать при соединении резисторов?

Во-первых, обязательно учитывается их номинальная мощность. Например, нам нужно подобрать замену резистору на 100 Ом и мощностью 1 Вт. Возьмём два резистора по 50 Ом каждый и соединим их последовательно. На какую мощность рассеяния должны быть рассчитаны эти два резистора?

Поскольку через последовательно соединённые резисторы течёт один и тот же постоянный ток (допустим 0,1 А), а сопротивление каждого из них равно 50 Ом, тогда мощность рассеивания каждого из них должна быть не менее 0,5 Вт. В результате на каждом из них выделится по 0,5 Вт мощности. В сумме это и будет тот самый 1 Вт.

Данный пример достаточно грубоват. Поэтому, если есть сомнения, стоит брать резисторы с запасом по мощности.

Подробнее о мощности рассеивания резистора читайте тут.

Во-вторых, при соединении стоит использовать однотипные резисторы, например, серии МЛТ. Конечно, нет ничего плохого в том, чтобы брать разные. Это лишь рекомендация.

Интернет калькулятор для расчета параллельного сопротивления R1 + R2 в цепи. Вы можете определить общее эквивалентное сопротивление (R) до 2 резисторов параллельно.

Калькулятор параллельного соединения резисторов

Формула параллельных резисторов :

• R_p = Параллельное сопротивление
• R_{1 и} R₂ = Параллельно соединенные резисторы

Оставить Комментарий

Отменить Комментарий

Очень удобный калькулятор. Пользуюсь им несколько лет.

• Константин –> –>
• Ответить

l123l –> –>

Ответить

Примитивно. По тексту:»Вы можете определить общее эквивалентное сопротивление (R) до 2 резисторов параллельно.»А что параллельно бывает 1 резистор или 1,5 штуки?А что 3-4-5-…резисторов рассчитать нельзя?

Тебе не нужно знать –> –>

Ответить

А чего неработает?

pedgry –> –>

Ответить

Аноним –> –>

Ответить

До обыденного примитивно.Вот пример.
У меня есть R1=1500 омМне нужно Rобщее= 1250 омНу и какое сопротивление нужно добавить?R2= .
Если что-то делать, так делать.

Костя –> –>

Ответить

1. когда-то уменя был график общего R при двух параллельном подключении резисторов где можно увидеть такое повторение

2. григорий –> –>
3. Ответить

1. в любом калькуляторе .которых в сети немеряно.

   Соединение резисторов, при котором одноименные выводы каждого из элементов собираются в одну точку, называется параллельным. При этом ко всем резисторам подводится один и тот же потенциал, но величина тока через каждый из них будет отличаться. Для составления схем или при замене резисторов в уже существующих цепях важно знать их суммарное сопротивление, как показано на рисунке:

   Параллельное соединение резисторов

   Данный калькулятор позволяет рассчитать суммарное сопротивление параллельно соединенных резисторов с любым количеством элементов.

   Для этого вам необходимо:

2. Указать в графе “количество резисторов” их число, в нашем примере их три;
3. После того, как вы укажите количество элементов, в поле ниже появится три окошка для ввода значения сопротивления каждого из элементов, к примеру, у вас резисторы сопротивлением 20, 30 и 60 Ом;
4. Далее нажмите кнопку “рассчитать” и в окошке “параллельное сопротивление в цепи” вы получите значение сопротивления в 10 Ом.

Чтобы рассчитать другую цепь или при подборе других элементов, нажмите кнопку “сбросить”, чтобы обнулить значение параллельно включенных элементов калькулятора.

Для расчета суммарного сопротивления калькулятором используется такое соотношение:

• R_сум – суммарное сопротивление параллельно соединенных элементов
• R₁ – сопротивление первого резистора;
• R₂ – сопротивление второго резистора;
• R₃ – сопротивление третьего резистора;
• R_n – сопротивление n-ого элемента.

Таким образом, в рассматриваемом примере параллельно включены три резистора, поэтому формула для определения суммарного сопротивления будет иметь такой вид:

Чтобы выразить величину суммарного сопротивления необходимо умножить обе половины уравнения на произведение сопротивлений всех трех резисторов. После этого перенести составляющие элементы по правилу пропорции и получить значение сопротивления:

Как видите, расчет параллельного сопротивления резисторов вручную требует немалых усилий, поэтому куда проще его сделать на нашем онлайн калькуляторе.

Обратите внимание, при наличии элементов с сопротивлением в разной размерности Ом, кОм, МОм, их необходимо привести к одной величине, прежде чем производить расчет. К примеру, в Ом и указывать в поле калькулятора для расчета параллельного соединения резисторов значение непосредственно в Омах.

Калькулятор расчёта параллельного соединения резисторов

Уникальнvй софт / Калькулятор соединения резисторов

Калькулятор соединения резисторов v.1.0 – предоставляет возможность быстро вычислить и подобрать номиналы резисторов (до 10-ти резисторов в соединении) для параллельного и последовательного соединения. Вычисляет Rобщ на основе R1-R10 или подбирает нужный R1 для указанного Rобщ (с учетом резисторов R2-R10 при необходимости) для любого типа соединения резисторов (как последовательного так и параллельного). Вычисления делаются автоматически при вводе номиналов резисторов с возможностью отключения автоматического расчета при вводе. Возможен переход в диапазон кОм. Имеется возможность сохранения всех значений в текстовый файл. При необходимости, возможно включить параметр «Поверх всех окон».

Скачать программу Объём 167 кБ Всего загрузок: 1182

Интернет калькулятор для расчета параллельного сопротивления R1 + R2 в цепи. Вы можете определить общее эквивалентное сопротивление (R) до 2 резисторов параллельно.

Калькулятор параллельного соединения резисторов

Формула параллельных резисторов :

• R_p = Параллельное сопротивление
• R_{1 и} R₂ = Параллельно соединенные резисторы

8 комментариев

• Новые
• Старые
• Лучшие

• Приветствуем гость

• Маркер комментария
• Delete comment

• Маркер комментария
• Delete comment

Примитивно. По тексту:»Вы можете определить общее эквивалентное сопротивление (R) до 2 резисторов параллельно.»А что параллельно бывает 1 резистор или 1,5 штуки?А что 3-4-5-…резисторов рассчитать нельзя?

• Маркер комментария
• Delete comment

А чего неработает?

• Маркер комментария
• Delete comment

• Маркер комментария
• Delete comment

До обыденного примитивно.Вот пример.
У меня есть R1=1500 омМне нужно Rобщее= 1250 омНу и какое сопротивление нужно добавить?R2= .
Если что-то делать, так делать.

• Маркер комментария
• Delete comment

• Маркер комментария
• Delete comment

когда-то уменя был график общего R при двух параллельном подключении резисторов где можно увидеть такое повторение

• Маркер комментария
• Delete comment

в любом калькуляторе .которых в сети немеряно.

Каждый в этой жизни сталкивался с резисторами. Люди с гуманитарными профессиями, как и все, изучали в школе на уроках физики проводники электрического тока и закон Ома.

С резисторами также имеют дело студенты технических университетов и инженеры различных производственных предприятий. Перед всеми этими людьми, так или иначе, вставала задача расчёта электрической цепи при различных видах соединения резисторов. В данной статье речь пойдёт о расчёте физических параметров, характеризующих цепь.

Виды соединений

Резистор — пассивный элемент, присутствующий в каждой электрической цепи. Он предназначен для того, чтобы сопротивляться электрическому току. Существует два вида резисторов:

Зачем же спаивать проводники друг с другом? Например, если для какой-то электрической цепи нужно определённое сопротивление. А среди номинальных показателей нужного нет. В таком случае необходимо подобрать элементы схемы с определёнными значениями сопротивления и соединить их. В зависимости от вида соединения и сопротивлений пассивных элементов мы получим какое-то определённое сопротивление цепи. Оно называется эквивалентным. Его значение зависит от вида спайки проводников. Существует три вида соединения проводников:

Значение эквивалентного сопротивления в цепи считается достаточно легко. Однако, если резисторов в схеме очень много, то лучше воспользоваться специальным калькулятором, который считает это значение. При ведении расчёта вручную, чтобы не допускать ошибок, необходимо проверять, ту ли формулу вы взяли.

Последовательное соединение проводников

В последовательной спайке резисторы идут как бы друг за другом. Значение эквивалентного сопротивления цепи равно сумме сопротивлений всех резисторов. Особенность схем с такой спайкой заключается в том, что значение тока постоянно. Согласно закону Ома, напряжение в цепи равно произведению тока и сопротивления. Так как ток постоянен, то для вычисления напряжения на каждом резисторе, достаточно перемножить значения. После этого необходимо сложить напряжения всех резисторов, и тогда мы получим значение напряжения во всей цепи.

Расчёт очень простой. Так как с ним имеют дело в основном инженеры-разработчики, то для них не составит труда сосчитать всё вручную. Но если резисторов очень много, то проще воспользоваться специальным калькулятором.

Примером последовательного соединения проводников в быту является ёлочная гирлянда.

Параллельное соединение резисторов

При параллельном соединении проводников эквивалентное сопротивление в цепи считается по-другому. Немного сложнее, чем при последовательном.

Его значение в таких цепях равняется произведению сопротивлений всех резисторов, делённому на их сумму. А также есть и другие варианты этой формулы. Параллельное соединение резисторов всегда снижает эквивалентное сопротивление цепи. То есть, его значение всегда будет меньше, чем наибольшее значение какого-то из проводников.

В таких схемах значение напряжения постоянно. То есть значение напряжения во всей цепи равно значениям напряжений каждого из проводников. Оно задаётся источником напряжения.

Сила тока в цепи равна сумме всех токов, протекающих через все проводники. Значение силы тока, протекающего через проводник. равно отношению напряжения источника к сопротивлению этого проводника.

Примеры параллельного соединения проводников:

1. Освещение.
2. Розетки в квартире.
3. Производственное оборудование.

Для расчёта схем с параллельным соединением проводников лучше пользоваться специальным калькулятором. Если в схеме много резисторов, спаянных параллельно, то гораздо быстрее вы посчитаете эквивалентное сопротивление с помощью этого калькулятора.

Смешанное соединение проводников

Этот вид соединения состоит из каскадов резисторов. Например, у нас есть каскад из 10 проводников, соединённых последовательно, и после него идёт каскад из 10 проводников, соединённых параллельно. Эквивалентное сопротивление этой схемы будет равно сумме эквивалентных сопротивлений этих каскадов. То есть, по сути, здесь последовательное соединение двух каскадов проводников.

Многие инженеры занимаются оптимизацией различных схем. Её целью является уменьшение количества элементов в схеме за счёт подбора других, с подходящими значениями сопротивлений. Сложные схемы разбиваются на несколько небольших каскадов, ведь так гораздо проще вести расчёты.

Сейчас, в двадцать первом веке, инженерам стало гораздо проще работать. Ведь несколько десятилетий назад все расчёты производились вручную. А сейчас программисты разработали специальный калькулятор для расчёта эквивалентного сопротивления цепи. В нём запрограммированы формулы, по которым ведутся расчёты.

В этом калькуляторе можно выбрать вид соединения, и потом ввести в специальные поля значения сопротивлений. Через несколько секунд вы уже увидите это значение.

Калькулятор серий

и параллельных цепей

Калькулятор эквивалентной последовательной и параллельной цепей

Здесь мы изучаем расчет эквивалентной или полной последовательной цепи и параллельной цепи.

Во-первых, вы должны знать об основных понятиях, таких как последовательное и параллельное соединение цепей с соединенными различными элементами.

В предыдущем учебном пособии я объяснил последовательную цепь и параллельную схему на примере.

1. Калькулятор последовательной цепи —

При последовательном подключении электрические элементы или компоненты соединяются последовательно или последовательно.

Например, данная схема называется последовательной схемой, когда компоненты электроники (такие как сопротивление R1, R2 и R3) соединены одним путем с подключенным источником напряжения (Vs).

Когда в цепь подается напряжение, течет такой же ток (I). Но другое (или падение) напряжения (V1, V2 и V3) произошло на всем последовательно подключенном сопротивлении.

Сумма падений напряжения на отдельных последовательно соединенных сопротивлениях равна приложенному напряжению (т.е. V = V1 + V2 + V3).

Давайте проверим, вот несколько важных формул для различных компонентов, соединенных последовательно.

Для расчета тока в серии:

 Общий ток, (Ieq) = (I1 = I2 = I3 = I4 = 15 = ...... = In) (Единица - Ампер) 

Примечание: Один и тот же ток течет или возникает на разных подключенных компонентах в последовательной цепи.

Для расчета напряжения в серии:

 Общий ток, (Veq) = (V1 + V2 + V3 + V4 = V5 = ...... = Vn) (Единица - Вольт) 

Для расчета сопротивления в серии:

 Полное сопротивление, (Треб.) = (R1 + R2 + R3 + R4 + R5 + ...... + Rn) (Единица - Ом) 

Для расчета проводимости серий:

 Общая проводимость, (Geq) = [1 / ((1 / G1) + (1 / G2) + (1 / G3) + (1 / G4) + (1 / G5) +...... + (1 / Gn))] (Единица - Сименс) 

Для расчета емкости в серии:

 Общая емкость, (Ceq) = [1 / ((1 / C1) + (1 / C2) + (1 / C3) + (1 / C4) + (1 / C5) + ...... + ( 1 / Cn))] (Единица - Фарад) 

Для расчета индуктивности в серии:

 Общая индуктивность, (Leq) = (L1 + L2 + L3 + L4 + L5 ...... + Ln) (Единица - Генри) 

Это простое описание последовательной цепи с различными формулами.

2. Вычислитель параллельной цепи:

При параллельном подключении несколько электрических элементов или компонентов соединяются параллельно.

Например, когда электронные компоненты (такие как сопротивление R1, R2 и R3) подключены в параллельную ветвь с подключенным источником напряжения (Vs).

Когда в цепь подается напряжение, течет такой же ток (I). Но различное (или падение) напряжение (V1, V2 и V3) возникло на всем параллельно подключенном сопротивлении.

Сумма падений напряжения на отдельных параллельно соединенных сопротивлениях равна приложенному напряжению (т.е. V = V1 + V2 + V3).

Давайте проверим, вот несколько важных формул для различных подключенных компонентов в параллельной цепи.

Для расчета параллельного тока:

 Общий ток, (Ieq) = (I1 + I2 + I3 + I4 + 15 + ...... + In) (Единица - Ампер)   

Для расчета параллельного напряжения:

 Общее напряжение, (Veq) = (V1 = V2 = V3 = V4 = V5 =...... + Vn) (Единица- Вольт) 

Примечание: одинаковое напряжение или разность потенциалов возникают на разных подключенных компонентах.

Для расчета сопротивления параллельно:

 Общее сопротивление, (Треб.) = [1 / ((1 / R1) + (1 / R2) + (1 / R3) + (1 / R4) + (1 / R5) + ...... + ( 1 / Rn))] (Единица- Ом) 

Для расчета проводимости серий:

 Общая проводимость, (Geq) = (G1 + G2 + G3 + G4 + G5 +...... + Gn) (Единица - Сименс) 

Для расчета емкости в серии:

 Общая емкость, (Ceq) = (C1 + C2 + C3 + C4 + C5 + ...... + Cn) (Единица - Фарады) 

Для расчета индуктивности в серии:

 Общая индуктивность, (Leq) = [1 / ((1 / L1) + (1 / L2) + (1 / L3) + (1 / L4) + (1 / L5) + ...... + ( 1 / Ln))] (Блок - Генри) 

Это простое описание параллельной цепи с различными формулами.

RC параллельная цепь, онлайн калькулятор

Калькулятор и формулы для расчета тока и мощности параллельной RC-цепи

Расчет RC параллельной цепи

Калькулятор рассчитывает ток, мощность, импеданс и реактивное сопротивление. в параллельной цепи резистора и конденсатора.

Формулы для параллельной параллельной цепи

Общее сопротивление последовательной цепи RC в цепи переменного тока называется Импеданс Z. Закон Ома применяется ко всей цепи.

Ток и напряжение синфазны на омическом сопротивлении. При емкостном сопротивлении конденсатора напряжение отстает от тока на -90 °.

Полный ток I — это сумма геометрически сложенных парциальных токов.2} \)

\ (\ Displaystyle I \)	Общий ток
\ (\ Displaystyle I_R \)	Ток через резистор
\ (\ Displaystyle I_C \)	Ток через конденсатор

Треугольник проводимости

В параллельной цепи парциальные токи ведут себя как значения проводимости сопротивлений. 2} \)

\ (\ Displaystyle S \)	Полная мощность
\ (\ Displaystyle Р \)	Реальный сила
\ (\ Displaystyle Q \)	Реактивная сила

Реальная мощность

\ (\ Displaystyle П = U · I_R \)

\ (\ Displaystyle Р \)	Реальный сила
\ (\ Displaystyle U \)	Напряжение
\ (\ Displaystyle I_R \)	Ток через резистор

Реактивная мощность

\ (\ Displaystyle Q = U · I_C \)

\ (\ Displaystyle Q \)	Реактивная сила
\ (\ Displaystyle U \)	Напряжение
\ (\ Displaystyle I_C \)	Ток через конденсатор

Эта страница полезна? да Нет Спасибо за ваш отзыв! Извините за это Как мы можем это улучшить? послать

---

Серия

и параллельные схемы — узнайте.sparkfun.com

Добавлено в избранное Любимый 53

Практические правила для последовательных и параллельных резисторов

Есть несколько ситуаций, которые могут потребовать творческих комбинаций резисторов. Например, если мы пытаемся установить очень конкретное опорное напряжение, вам почти всегда потребуется очень конкретное соотношение резисторов, значения которых вряд ли будут «стандартными» значениями. И хотя мы можем получить очень высокую степень точности значений резисторов, мы, возможно, не захотим ждать X дней, необходимых для доставки чего-либо, или платить цену за нестандартные значения, отсутствующие на складе.Так что в крайнем случае мы всегда можем создать собственные номиналы резисторов.

Совет №1: Равные резисторы, включенные параллельно

Добавление N резисторов с одинаковым номиналом R , включенных параллельно, дает нам R / N Ом. Допустим, нам нужен 2,5 кОм; резистор, но все, что у нас есть, это ящик, полный 10 кОм. Объединение четырех из них параллельно дает нам 10 кОм / 4 = 2,5 кОм.

Совет № 2: Допуск

Знайте, какую терпимость вы можете терпеть.Например, если вам нужен 3.2k & ohm; резистор, можно было поставить 3 10кОм; резисторы параллельно. Это даст вам 3,3 кОм, что составляет около 4% отклонения от необходимого значения. Но если схема, которую вы строите, должна иметь допуск ближе, чем 4%, мы можем измерить наш запас в 10 кОм, чтобы увидеть, какие из них являются самыми низкими значениями, потому что они также имеют допуск. По идее, если заначка 10к & ом; резисторы имеют допуск 1%, мы можем получить только 3,3 кОм. Но производители запчастей, как известно, допускают именно такого рода ошибки, поэтому стоит немного покопаться.

Совет № 3: Номинальная мощность при последовательном / параллельном подключении

Такая комбинация резисторов последовательно и параллельно работает и с номинальной мощностью. Допустим, нам нужен 100 & Ом; резистор рассчитан на 2 Вт (Вт), но все, что у нас есть, это связка 1 кОм; резисторы на четверть ватта (Вт) (а сейчас 3 часа ночи, вся Mountain Dew исчезла, а кофе остыл). Вы можете объединить 10 из 1 кОм, чтобы получить 100 Ом; (1 кОм; / 10 = 100 Ом;), а номинальная мощность будет 10×0,25 Вт, или 2.5Вт. Не очень красиво, но это поможет нам завершить финальный проект и может даже принести нам дополнительные баллы за способность думать на ногах.

Нам нужно быть немного более осторожными, когда мы объединяем резисторы разных номиналов параллельно, когда речь идет об общем эквивалентном сопротивлении и номинальной мощности. Для читателя это должно быть совершенно очевидно, но …

Совет № 4: разные резисторы параллельно

Суммарное сопротивление двух резисторов разного номинала всегда меньше, чем резистор наименьшего номинала.Читатель будет поражен тем, сколько раз кто-то объединяет значения в своей голове и приходит к значению, которое находится посередине между двумя резисторами (1 кОм || 10 кОм; НЕ равняется чему-либо около 5 кОм ;!). Общее параллельное сопротивление всегда будет приближаться к резистору с наименьшим значением. Сделайте себе одолжение и прочитайте совет №4 10 раз.

Совет № 5: Параллельное рассеяние мощности

Мощность, рассеиваемая при параллельной комбинации резисторов разных номиналов, не распределяется между резисторами равномерно, поскольку токи не равны.Используя предыдущий пример (1k & ohm; || 10k & ohm;), мы видим, что 1k & ohm; будет потреблять в 10 раз больше тока 10 кОм. Поскольку закон Ома гласит, что мощность = напряжение x ток, отсюда следует, что 1 кОм; резистор рассеивает в 10 раз мощность, превышающую 10 кОм.

В конечном счете, уроки советов 4 и 5 заключаются в том, что мы должны уделять больше внимания тому, что мы делаем при параллельном соединении резисторов разного номинала. Но советы 1 и 3 предлагают несколько удобных ярлыков, когда значения совпадают.

---

← Предыдущая страница
Время эксперимента — Часть 2

Добавьте параллельные резисторы в схему

Если комбинация резисторов обеспечивает несколько путей для прохождения тока, она называется параллельными резисторами. Эквивалентное сопротивление всегда уменьшается, когда мы добавляем параллельные резисторы. Воспользуйтесь онлайн-калькулятором параллельных резисторов здесь.

Параллельная комбинация:

Комбинация резисторов будет называться резисторов, включенных параллельно , если к одному узлу в цепи подключено более двух компонентов.

Предположим, у нас есть три резистора, подключенных друг к другу в точке b, головка первого резистора подключена к головке второго и третьего резистора. Предполагая, что ток течет сверху вниз. В отличие от последовательной комбинации, положительный вывод R ₁ подключен к положительному выводу R ₂ и R ₃ . Комбинация приведет к трем различным путям для тока.

Обратите внимание, что в узле a и узле b присутствуют четыре компонента; источник, R ₁ , R _2, и R ₃ , как показано на диаграмме.

Параллельная цепь обеспечивает более одного пути для тока.

Онлайн-калькулятор параллельных резисторов:

Для расчета общего сопротивления резисторов, которые соединены параллельно, используйте следующий калькулятор параллельных резисторов. $ R_1, R_2 $ и $ R_3 $ — это три резистора, соединенных параллельно, а $ R_ {Total} $ — эквивалентное сопротивление.

Калькулятор тока параллельной цепи

После расчета общего сопротивления параллельных резисторов теперь вы можете рассчитать общий ток.Поместите общее сопротивление из онлайн-калькулятора параллельных резисторов, указанного выше. Также введите напряжение цепи, чтобы рассчитать ток.

Устранение резисторов в параллельной цепи:

Мы хотим знать несколько типов параметров для вышеуказанной схемы, как мы это делали для последовательной комбинации.

Общее эквивалентное сопротивление:

Каков общий ток, обеспечиваемый источником?

Чтобы ответить на вопрос, нам нужно рассчитать полное или эквивалентное сопротивление цепи.И формула для этого:

$ \ frac {1} {R_ {Equivalent}} = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} + \ ldots + \ frac {1} {R_ {n}} $

Если мы используем те же номиналы резисторов, которые мы использовали в последовательной схеме, то есть R $ _ {1} $, R $ _ {2,} $ и R $ _ {3 } $ равны 20, 40 и 10 $ \ Omega $ соответственно. И поместите эти значения в приведенную выше формулу, тогда:

$ \ frac {1} {R_ {Eq}} = \ frac {1} {20} + \ frac {1} {40} + \ frac {1} { 10} = \ frac {7} {40} $
$ R_ {Eq} = \ frac {40} {7} = 5.714 \ Omega $

Приведенная выше сложная схема теперь сведена к этой схеме с одним резистором.Теперь мы можем легко определить общий ток, потребляемый схемой по закону Ома, как показано ниже:

$ I_ {T} = \ frac {V} {R_ {Eq}} = \ frac {140 v} {5.714 \ Omega } $
$ I_ {T} = 24,5 A $

Общее сопротивление намного меньше, чем у последовательной цепи, а общий ток намного больше, чем у последовательной цепи.

Напряжение на каждом резисторе:

Какое напряжение на каждом резисторе?

Прежде всего, взгляните на схему, и вы поймете, что каждый резистор подключен к источнику напряжения.Напряжение на каждом резисторе совпадает с напряжением источника. Формула для напряжения:

$ V_ {T} = V_ {1} = V_ {2} = \ ldots = V_ {n} $

В нашем случае напряжение для R $ _ {1} $, R $ _ {2} $ и R $ _ {3} $: V $ _ {1} $ = 140 v, V $ _ {2} $ = 140 v и V $ _ {3} $ = 140 v соответственно.

Ток каждого резистора:

Каков ток каждого резистора?

Мы можем использовать закон Ома для определения тока. Предположим, что ток для R $ _ {1} $, R $ _ {2,} $ и R $ _ {3} $ равен I $ _ {1} $, I $ _ {2,} $ и I $ _ {3} $ соответственно.Итак, применяя закон Ома к каждому резистору, мы получаем

$ I_ {1} = \ frac {V_ {1}} {R_ {1}} = \ frac {140 v} {20 \ Omega} = 7 A $
. $ I_ {2} = \ frac {V_ {2}} {R_ {2}} = \ frac {140 v} {40 \ Omega} = 3,5 A $
$ I_ {3} = \ frac {V_ {3} } {R_ {3}} = \ frac {140 v} {10 \ Omega} = 14 A $

А что, если мы сложим все эти отдельные токи? Давай сделаем это.

$ I_ {T} = I_ {1} + I_ {2} + I_ {3}
$ I_ {T} = 7 A + 3,5 A + 14 A $
$ I_ {T} = 24,5 A $

Такой же ток может быть подтвержден с помощью вычислителя параллельных резисторов выше.

Наконец-то! Мы получили полный ток, потребляемый всеми этими резисторами, так как мы нашли первое место. Это означает, что полный ток цепи равен сумме токов отдельных резисторов. Мы можем обобщить формулу следующим образом:

$ I_ {T} = I_ {1} + I_ {2} + \ ldots + I_ {n} $

Индивидуальный ток каждого резистора можно найти с помощью правила делителя тока. (CDR).

Формула для добавления параллельных резисторов:

Мы наблюдали три параметра в приведенном выше обсуждении: первое общее сопротивление параллельно, второе, индивидуальное напряжение каждого резистора и, наконец, индивидуальный ток каждого резистора.Все эти формулы представлены здесь для вашей простоты с общей применимостью до n резисторов.

Полное сопротивление параллельной цепи:

$ \ frac {1} {R_ {Equivalent}} = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} + \ ldots + \ frac {1} {R_ {n}} $

Отдельное напряжение резисторов такое же, как и напряжение источника:

$ V_ {T} = V_ {1} = V_ {2} = \ ldots = V_ {n} $

Общий ток складывается из всех индивидуальных токов:

$ I_ {T} = I_ {1} + I_ {2} + \ ldots + I_ {n} $

Добавить параллельные резисторы То же значение:

Предположим, что схема, в которой все резисторы имеют одинаковое значение и все они подключены параллельно, каково будет общее сопротивление?

Предположим, что $ n $ количество параллельно подключенных резисторов с одинаковым сопротивлением.Общее сопротивление цепи будет

$ R_ {Total} = \ frac {R} {n} $

$ R $ — это значение сопротивления, которое одинаково для всех резисторов, а $ n $ равно количество резисторов, включенных параллельно.

Какой будет ток в каждом резисторе?

Ток каждого резистора будет

$ I = \ frac {I_ {Total}} {n} $

Вывод:

• Деление тока в параллельной цепи
• Добавьте параллельные резисторы, чтобы увеличить пути для тока
• Общий ток равен индивидуальному току параллельных цепей
• Напряжение остается неизменным в параллельных цепях электрической цепи
• Общее сопротивление уменьшается в параллельной цепи по сравнению с сопротивлением отдельных параллельных цепей

Сопротивление параллельной цепи переменного тока- Анализ цепи индуктора

Из этой статьи вы узнаете о поведении анализа параллельной цепи резистор-индуктор.Эта статья связана с предыдущей статьей о последовательной цепи резистор-индуктор. Возможно, вы захотите изучить цепи резистора-индуктора переменного тока.

Принципиальная схема

Рассмотрим параллельную цепь резистор-индуктор: (рисунок ниже)

Параллельная цепь R-L.

Поскольку источник питания имеет ту же частоту, что и схема последовательного примера, а резистор и катушка индуктивности имеют одинаковые значения сопротивления и индуктивности, соответственно, они также должны иметь одинаковые значения импеданса.Итак, мы можем начать нашу таблицу анализа с тех же «заданных» значений:

Расчет напряжения

Единственное отличие в нашей методике анализа на этот раз состоит в том, что мы будем применять правила параллельных цепей вместо правил для последовательных цепей. Принцип такой же, как и для DC. Мы знаем, что напряжение распределяется равномерно между всеми компонентами в параллельной цепи, поэтому мы можем передать значение общего напряжения (10 вольт ∠ 0 ^o ) во все столбцы компонентов:

Текущие расчеты

Теперь мы можем применить закон Ома (I = E / Z) по вертикали к двум столбцам таблицы, рассчитав ток через резистор и ток через катушку индуктивности:

Так же, как и в цепях постоянного тока, токи ответвления в параллельной цепи переменного тока складываются в общий ток (Закон Кирхгофа по току все еще сохраняется для переменного тока, как и для постоянного тока):

Расчет импеданса

Наконец, общий импеданс можно рассчитать с помощью закона Ома (Z = E / I) по вертикали в столбце «Всего».Между прочим, параллельный импеданс также можно рассчитать, используя обратную формулу, идентичную той, которая используется при вычислении параллельных сопротивлений.

Единственная проблема с использованием этой формулы заключается в том, что она обычно требует выполнения большого количества нажатий клавиш калькулятора. И если вы полны решимости использовать формулу, подобную этой «от руки», будьте готовы к очень большому объему работы! Но, как и в случае с цепями постоянного тока, у нас часто есть несколько вариантов расчета величин в наших таблицах анализа, и этот пример ничем не отличается.Независимо от того, каким способом вы рассчитываете полное сопротивление (закон Ома или обратная формула), вы получите одно и то же значение:

Резюме

• Импедансами (Z) управляют так же, как сопротивлениями (R) при анализе параллельной цепи: параллельные импедансы уменьшаются, чтобы сформировать общий импеданс, используя обратную формулу. Только обязательно выполняйте все вычисления в сложной (не скалярной) форме! Z _Всего = 1 / (1 / Z ₁ + 1 / Z ₂ +.