Что такое добротность катушки индуктивности. Как рассчитать энергию катушки. Какие существуют варианты соединения катушек индуктивности. Как влияет активное сопротивление на работу катушки. Чем отличаются последовательное и параллельное соединение катушек.
Добротность катушки индуктивности: ключевой параметр качества
Добротность является одной из важнейших характеристик катушки индуктивности. Она определяет качество катушки и эффективность ее работы в электрической цепи. Добротность катушки индуктивности рассчитывается по формуле:
Q = X_L / R
где X_L — реактивное (индуктивное) сопротивление катушки, R — активное сопротивление катушки.
Чем выше добротность, тем лучше катушка накапливает энергию магнитного поля и меньше рассеивает ее в виде тепла. Высокодобротные катушки имеют более острый резонанс и меньшие потери.
Энергия магнитного поля катушки индуктивности
Катушка индуктивности способна накапливать энергию в своем магнитном поле. Энергия магнитного поля катушки индуктивности определяется по формуле:

W = (L * I^2) / 2
где L — индуктивность катушки, I — ток, протекающий через катушку.
Эта энергия не рассеивается, а периодически преобразуется в энергию электрического поля и обратно. Именно способность накапливать и отдавать энергию магнитного поля позволяет катушкам индуктивности выполнять различные функции в электрических цепях.
Последовательное соединение катушек индуктивности
При последовательном соединении катушек индуктивности их общая индуктивность равна сумме индуктивностей отдельных катушек:
L_общ = L1 + L2 + L3 + …
Это справедливо, если катушки расположены достаточно далеко друг от друга и их магнитные поля не взаимодействуют. При близком расположении катушек необходимо учитывать их взаимную индуктивность.
Ток, протекающий через последовательно соединенные катушки, одинаков для всех катушек. Напряжение на участке цепи с последовательно соединенными катушками равно сумме напряжений на отдельных катушках.
Параллельное соединение катушек индуктивности
При параллельном соединении катушек индуктивности их общая индуктивность рассчитывается по формуле:

1/L_общ = 1/L1 + 1/L2 + 1/L3 + …
Эта формула аналогична формуле для расчета общего сопротивления параллельно соединенных резисторов. Общая индуктивность при параллельном соединении всегда меньше индуктивности наименьшей из катушек.
При параллельном соединении напряжение на всех катушках одинаково, а общий ток равен сумме токов через отдельные катушки.
Влияние активного сопротивления на работу катушки индуктивности
Реальные катушки индуктивности всегда обладают некоторым активным сопротивлением, которое влияет на их работу. Активное сопротивление катушки приводит к потерям энергии в виде тепла и снижает добротность катушки.
Для учета активного сопротивления реальную катушку индуктивности можно представить как идеальную катушку, последовательно соединенную с резистором. Величина этого резистора равна активному сопротивлению обмотки катушки.
При протекании постоянного тока через реальную катушку индуктивности на ней будет падение напряжения, равное произведению тока на активное сопротивление катушки:

U = I * R
Это необходимо учитывать при расчетах цепей постоянного тока, содержащих катушки индуктивности.
Смешанное соединение катушек индуктивности
На практике часто встречаются схемы со смешанным (последовательно-параллельным) соединением катушек индуктивности. В этом случае расчет общей индуктивности производится поэтапно:
- Сначала рассчитывают индуктивности параллельно соединенных групп катушек
- Затем суммируют индуктивности последовательно соединенных групп и отдельных катушек
Такой подход позволяет рассчитать общую индуктивность для любой комбинации соединения катушек.
Взаимная индуктивность катушек
При близком расположении катушек индуктивности их магнитные поля взаимодействуют, что приводит к появлению взаимной индуктивности. Взаимная индуктивность может как увеличивать, так и уменьшать общую индуктивность системы катушек.
Для двух катушек с взаимной индуктивностью M общая индуктивность при последовательном соединении равна:
L_общ = L1 + L2 ± 2M
Знак «+» используется при согласном включении катушек (их магнитные поля складываются), а знак «-» — при встречном включении (магнитные поля вычитаются).

Учет взаимной индуктивности особенно важен при проектировании трансформаторов и других устройств, где требуется тесная магнитная связь между катушками.
Применение катушек индуктивности в электронных схемах
Катушки индуктивности широко применяются в различных электронных устройствах и цепях. Вот некоторые из наиболее распространенных применений:
- Фильтры: катушки индуктивности используются в LC-фильтрах для подавления высокочастотных помех и выделения нужных частотных составляющих сигнала.
- Колебательные контуры: в сочетании с конденсаторами катушки образуют резонансные LC-контуры, применяемые в радиоприемниках и передатчиках.
- Трансформаторы: системы связанных катушек индуктивности используются для преобразования напряжения и гальванической развязки цепей.
- Дроссели: катушки индуктивности применяются для сглаживания пульсаций тока в источниках питания.
- Электромагниты: мощные катушки индуктивности используются для создания сильных магнитных полей в различных устройствах.
Правильный выбор и расчет параметров катушек индуктивности играет ключевую роль в обеспечении эффективной работы этих и многих других электронных устройств.

Добротность и энергия катушки индуктивности. Варианты соединения.
Продолжаем обсуждение катушек индуктивности! В первой статье (ссылка) мы обсудили все основные аспекты, а именно
Активное сопротивление и добротность катушки индуктивности.
Итак, начнем мы с того, что обсудим некоторые характеристики катушек индуктивности, с которыми мы не успели познакомиться в предыдущей статье. И для начала рассмотрим активное сопротивление катушки.
Рассматривая примеры включения катушек в различные цепи мы считали их активное сопротивление равным 0 (такие катушки называют идеальными). Но на практике любая катушка обладает ненулевым активным сопротивлением. Таким образом реальную катушку индуктивности можно представить как идеальную катушку и последовательно включенный резистор:
Таким образом реальную катушку индуктивности можно представить как идеальную катушку и последовательно включенный резистор:
Идеальная катушка, как вы помните, не оказывает никакого сопротивления постоянному току, и напряжение на ней равно 0. В случае с реальной катушкой ситуация несколько меняется. При протекании по цепи постоянного тока напряжение на катушке будет равно:
U_L = IR_а
Ну а поскольку частота тока равна 0 (постоянный ток), то реактивное сопротивление будет равно:
X_L = 2\pi f L = 0
А что же будет происходить при включении реальной катушки индуктивности в цепь переменного тока? Давай разбираться. Представим, что по данной цепи течет переменный ток i, тогда общее напряжение на цепи будет складываться из следующих компонент:
u = iR + u_L
Напряжение на идеальной катушке, как вы помните, выражается через ЭДС самоиндукции:
u_L = -\varepsilon_L = L\frac{di}{dt}
И мы получаем для напряжения на реальной катушке индуктивности:
u = iR + L\frac{di}{dt}
Отношение реактивного (индуктивного) сопротивления к активному называется
Q = \frac{X_L}{R}
Раз активное сопротивление R идеальной катушки равно 0, то значит ее добротность Q будет бесконечно большой. 2}{2}
2}{2}
Давайте переходить к вариантам соединения катушек между собой… Все расчеты мы будем производить для идеальных катушек индуктивности, то есть их активные сопротивления равны 0. К слову, в большинстве теоретических задач и примеров, рассматриваются именно идеальные катушки. Но не стоит забывать о том, что в реальных цепях активное сопротивление не равно 0 и его необходимо учитывать при проведении любых расчетов.
Последовательное соединение катушек индуктивности.
При последовательном соединении катушек индуктивности их можно заменить одной катушкой с величиной индуктивности, равной:
L_0 = L_1 + L_2
Вроде бы все просто, проще некуда, но тут есть один важный момент. Данная формула справедлива только в том случае, если катушки расположены на на таком расстоянии друг от друга, что магнитное поле одной катушки не пересекает витков другой:
Если же катушки расположены близко друг к другу и часть магнитного поля одной катушки пронизывает вторую, то тут ситуация совсем другая. Возможно два варианта:
Возможно два варианта:
- магнитные потоки катушек имеют одинаковое направление
- магнитные потоки направлены навстречу друг другу
Первый случай называется согласным включением катушек – начало второй катушки подключается к концу первой. А второй вариант называют встречным включением – конец второй катушки подключается к началу первой. На схемах начало катушки обозначают символом “*“. Таким образом, на схеме, которая представлена на рисунке мы имеем согласное включение катушек индуктивности. Для этого случая общая индуктивность определяется так:
L = L_1 + L_2 + 2M
L = L_1 + L_2\medspace-\medspace 2M
Можно заметить, что если потоки имеют одинаковое направление (согласное включение), то общая индуктивность увеличивается на двойную величину взаимной индуктивности. А если потоки направлены навстречу друг другу – уменьшается на ту же самую величину. 2}{L_1 + L_2 + 2M}
2}{L_1 + L_2 + 2M}
Также как и в случае с последовательным соединением, при согласном включении общая индуктивность будет больше, чем при встречном включении, поскольку знаменатель дроби будет меньше.
Собственно, на этом мы и заканчиваем рассмотрение катушек индуктивности. Ранее мы изучили конденсаторы и резисторы, а в будущих статьях нам предстоит работать с цепями, включающие все эти элементы в разных комбинациях 🙂 Так что подписывайтесь на обновления и не пропускайте новые статьи на нашем сайте!
|
Источник — Свободный взгляд Физическая природа индуктивности.Катушки индуктивности обладают свойством оказывать реактивное
сопротивление переменному току при незначительном сопротивлении
постоянному току. Совместно с конденсаторами они используются для
создания фильтров, осуществляющих частотную селекцию электрических
сигналов, а так же для создания элементов задержки сигналов и
запоминающих элементов, осуществления связи между цепями через
магнитный поток и т. Функционирование катушек индуктивности основано на взаимодействии тока и магнитного потока. Известно, что при изменении магнитного потока Ф в проводнике, находящемся в магнитном поле, возникает ЭДС, определяемая скоростью изменения магнитного потока
Поэтому при подключении к проводнику источника постоянного
напряжения ток в нем устанавливается не сразу, так как в момент
включения изменяется магнитный поток и в проводе индуцируется ЭДС,
препятствующая нарастанию тока, а спустя некоторое время, когда
магнитный поток перестает изменяться.
Она пропорциональна частоте w, а коэффициентом пропорциональности является индуктивность L. Следовательно, индуктивность характеризует способность проводника оказывать сопротивление переменному току. Величина этого сопротивления ХL=wL Индуктивность короткого проводника (мкГн) определяется его размерами:
где l -длина провода в см, d — диаметр провода в см. Если провод намотан на каркас, то образуется катушка
индуктивности. В этом случае магнитный поток концентрируется и
величина индуктивности возрастает. 2.3.2.Конструкции катушек индуктивности.Конструкционной основой катушки индуктивности является диэлектрический каркас, на который наматывается провод в виде спирали. Обмотка может быть как однослойной (рис.2.21,а), так и многослойной (рис.2.21,6). В некоторых случаях многослойная обмотка делается секционированной (рис.2.21,в). В интегральных схемах применяются плоские спиральные катушки индуктивности (рис.2.21,г). Для увеличения индуктивности применяют магнитные сердечники.
Помещенный внутрь катушки сердечник концентрирует магнитное поле и
тем самым увеличивает ее индуктивность. Перемещением сердечника
внутри каркаса можно изменяп, индуктивность. На рис.2.22
представлены три разнидности цилиндрических сердечников: С —
стержневой, Т — трубчатый и ПР — подстроечный резьбовой и две
разновидности броневых. Они могут иметь либо замкнутый магнитопровод (тип СБ — а), либо разомкнутый (тип С Б — б). Для изменения индуктивности служит подстроечный цилиндрический сердечник 1. Помимо цилиндрических и броневых сердечников применяют торроидальные (кольцевые) сердечники. На высоких частотах (десятки-сотни МГц) применяют подстроечные цилиндрические сердечники из диамагнетиков (латунь, медь). При введении этих сердечников внутрь катушки индуктивность уменьшается. В катушках индуктивности, работающих на низких в качестве сердечников используют пермаллои. При этом рается из тонких пластин толщиной 0,002-0,1мм. Для уменьшения влияния электромагнитного поля катушки на другие
элементы схемы, а также для уменьшения влияния внешних полей на
катушку индуктивности, ее располагают внутри металлического экрана,
как это показано на рис. 2.3.3. Индуктивность и собственная емкость катушек индуктивности.Индуктивность является основным параметром катушки индуктивности. Ее величина (мкТн) определяется соотношением где W — число витков, D — диаметр катушки в см, L0 — коэффициент, зависящий от отношения длины катушки / к ее диаметру О. Для однослойных катушек величина L0 определяется соотношением
Оптимальными в этом случае являются отношение а диаметр катушки в пределах от 1 до 2 см. При расчете диаметр катушки D принимается равным диаметру каркаса D0 Для многослойных катушек величина L0зависит не только от величины 1/D , но и от отношения толщины намотки t к диаметру катушки D. Она определяется по графикам (рис.2.24). В этом случае внешний диаметр катушки D=D0 + 2t При расчете катушки индуктивности предварительно задаются геометрическими размерами катушки и определяют коэффициент L0, а затем по заданной величине индуктивности L находят число витков:
где I, — в мкГн , D — в см. Для намотки катушки обычно применяют провод оптимального диаметра, который рассчитывается с помощью эмпирических формул и графиков. Для этого по графику S=f(t/D;l/D) (рис.2.25) находят вспомогательный коэффициент S. Затем рассчитывают коэффициент
где f -в мкГц , D — в см. Затем рассчитывают коэффициент a1 где f — частота в Гц. После чего по графику b1=f(a1) (рис. 2.26) находят вспомогательный коэффициент b1S и расчитывают оптимальный диаметр провода (мм)
Полученное значение округляется до ближайшего стандартного значения (табл.2.6) и выбирается марка провода с диаметром dиз Таблица 2.6 Основные параметры обмоточных проводов
После выбора оптимального диаметра провода проверяют возможность
размещения обмотки в заданных размерах l и t.
Если t>dиз; то обмотка размещается. В противном случае задаются большей величиной l и повторяют расчет. Для многослойных катушек рассчитывают толщину обмотки
где а — коэффициент неплотности обмотки ( a = 1,05…1,3), и находят фактическое значение
наружного диаметра катушки D=D0+2t. Если эта
величина отличается от выбранной в начале расчета более чем на 10%,
то задаю тся новыми значениями l и t и расчет
повторяют.
где h — коэффициент, зависящий от отношения l/D (рис.2.27), D — диаметр катушки, Dэк-диаметр экрана. Индуктивность уменьшается тем больше, чем меньше диаметр экрана. В большинстве случаев Dэк/D >1,6ё1,8.При этом индуктивность уменьшается не более чем на 20%. Многослойные катушки обычно выполняют с сердечниками броневого
типа, при использовании которых большая часть силовых линий
магнитного поля катушки замыкается через сердечник, а меньшая-через
воздух, вследствие чего влияние экрана на индуктивность катушки
значительно ослабляется. Применение сердечников из магнитных материалов позволяет уменьшить число витков катушки индуктивности и соответственно ее габариты. Основным параметром сердечника является магнитная проницаемость mс При его наличии индуктивность катушки становится равной Поскольку в расчетные формулы входят эмпирические коэффициенты, то индуктивность изготовленной катушки отличается от расчетной. Применение подстроечных магнитных сердечников позволяет получить требуемое значение индуктивности. Собственная емкость является паразитным параметром катушки
индуктивности, ограничивающим возможности ее применения. Ее
возникновение обусловлено конструкцией катушки индуктивности:
емкость существует между отдельными витками катушки, между витками и
сердечником, витками и экраном, витками и другими элементами
конструкции. Наименьшей собственной емкостью обладают однослойные катушки индуктивности Приближенно она рассчитывается по формуле (пФ)
где D — диаметр катушки в см. Обычно она не превышает 1-2пФ. Собственная емкость многослойных катушек значительно больше. При
многослойной рядовой намотке она достигает ЗОпФ; при намотке
«внавал» она несколько меньше. Существенное уменьшение емкости
многослойных катушек достигается при использовании универсальной
обмотки, при выполнении которой провод укладывается под некоторым
углом к образующей цилиндрического каркаса. Очевидно, что
Угол j , под которым осуществляется укладка провода, находится из соотношения
где l-осевая длина катушки, D — диаметр витка. Наименьшее значение угла j получается для витков, имеющих наименьший диаметр, равный диаметру каркаса D0. Обычно при использовании универсальной обмотки длину катушки принимают в пределах от 2 до 10мм. Количество циклов намотки связано с рачетнным числом витков W соотношением
Величина собственной емкости катушек с универсальной обмоткой составляет от 3 до 8пФ. Дополнительное снижение емкости достигается серкцонированием обмотки, как показано на рис.2.21,в. Совместное действие индуктивности и емкости можно учесть введением понятия об эквивалентной индуктивности катушки, определяемой из уравнения откуда
где -собственная резонансная частота катушки индуктивности. Если рабочая частота много ниже собственной резонансной частоты wL, то приближенно можно считать Lэ=L. В процессе работы на катушку действуют различные внешние факторы:температура, влага и другие, влияющие на ее индуктивность.Наиболее существенным является влияние температуры, которое оценивают температурным коэффициентом . Температурная нестабильность индуктивности обусловлена целым рядом факторов: при нагреве увеличивается длина и диаметр провода обмотки, увеличивается длина и диаметр каркаса, в результате чего изменяются шаг и диаметр витков; кроме того при изменении температуры изменяются диэлектрическая проницаемость материала каркаса, что ведет к изменению собственной емкости катушки. Для повышения температурной стабильности применяют каркасы из материала с малым значением коэффициента линейного расширения. Этим требованиям в наибольшей степени удовлетворяет керамика. Повышению температурной стабильности катушек способствует прочное сцепление обмотки с каркасом. С этой целью обмотку выполняют методом вжигания серебра в керамический каркас. В этом случае изменение размеров токопроводящего слоя определяется только линейным расширением каркаса. Такие катушки индуктивности имеют TKL >(5-100).10-6Стабильность многослойных катушек существенно хуже, так как в них невозможно избежать изменения линейных размеров провода обмотки. Многослойные катушки имеют TKL> (50-100).10-6 2.3.4. Потери в катушках индуктивности.В катушках индуктивности помимо основного эффекта взаимодействия тока и магнитного поля наблюдаются паразитные эффекты, вследствие которых сопротивление катушки не является чисто реактивным и равным ХL. Наличие паразитных эффектов ведет к появлению потерь в катушке, оцениваемых сопротивлением потерь RП , которое определяет добротность катушки индуктивности
Потери складываются из потерь в проводах, диэлектрике, сердечнике и экране. Потери в проводах вызваны тремя причинами. Во-первых, провода обмотки обладают омическим сопротивлением
где l -длина провода обмотки, d- диаметр провода, р- удельное сопротивление. Это сопротивление (Ом) можно выразить через число витков W и средний диаметр катушки DСР
где -диаметр провода в см. Во-вторых, сопротивление провода обмотки переменному току возрастает с ростом частоты, что обусловлено поверхностным эффектом, суть которого состоит в том, что ток протекает не по всему сечению проводника, а по кольцевой части поперечного сечения (рис.2.29), ширина (мм) которой равна
где f— частота в МГц, r— удельное сопротивление в мкOм· м. Вследствие этого провод длиной l имеет сопротивление переменному току равное
где SЭФ — площадь кольца, которая равна
где После преобразования получаем
В третьих, в проводах обмотки, свитой в спираль, проявляется эффект близости (рис.2.30), суть которого состоит в вытеснении тока под воздействием вихревых токов и магнитного поля к периферии провода, прилегающей к каркасу, в результате чего сечение, по которому протекает ток, принимает серповидный характер, что ведет к дополнительному возрастанию сопротивления провода. Сопротивление rБ, обусловленное эффектом близости, прямо пропорционально диаметру провода, а сопротивление rП, обусловленное эфектом, обратно пропорционально диаметру провода ( рис.2.31). Существует оптимальный диаметр провода dопт , при котором сопротивление провода току высокой частоты rf = rБ + rП оказывается минимальным. Для однослойных катушек dопт= 0,2-0,6мм, для многослойных dопт =0,08-0,2мм. Существенно уменьшить потери в проводах можно применяя провод «литцендрат», состоящий из большего числа жилок, скрученных в жгут. При небольшом диаметре тонких жилок ослабляется поверхностный эффект, а скручивание жилок в жгут ослабляет эффект близости. Существует методика расчета сопротивления rf , по которой предварительно рассчитывается вспомогательный коэффициент
где f — частота в Гц, d- диаметр провода в см. Затем по таблице находятся коэффициенты F(z) и G(z).
После этого по графику (рис.2.32) определяется вспомогательный коэффициент Кз , зависящий от геометрии катушки. По (2.50) рассчитывается сопротивление провода катушки току высокой частоты
где D— наружный диаметр катушки в см, d -диаметр провода в см. Если однослойная катушка намотана проводом оптимального диаметра и параметр z >5, то сопротивление rf можно определить по формуле
где D — в см, d — в см, f‘- в МГц. Потери в диэлектрике обусловлены тем, что между соседними витками катушки существует емкость, имеющая две составляющих-емкость через воздух Сов и емкость через диэлектрик Сод (рис.2.33). Потери в диэлектрике учитываются величиной tgd, зная которую можно рассчитать сопротивление потерь
где Сод — в пф, L — в мкГн, f — в МГц. Потери в сердечнике складываются из потерь на вихревые токи dв, потерь на гистерезис dг и начальных потерь dп и учитываются как тангенс угла потерь в сердечнике
В справочниках приводятся значения. tg dс для различных типов сердечников. Сопротивление потерь определяется по формуле Потери в экране обусловлены тем, что ток, протекающий по катушке, индуцирует ток в экране. Потери, вносимые экраном, определяются по формуле
где Dэ — диаметр экрана в см, lэ — длина экрана в см, f — частота в МГц. Величина h = f(l/D) определяется по графику (рис.2.27). Таким образом суммарное сопротивление потерь в катушке индуктивности, определяющее ее добротность, равно
Практически величина добротности лежит в пределах от 30 до 200. Повышение добротности достигается оптимальным выбором диаметра провода, увеличением размеров катушки индуктивности и применением сердечников с высокой магнитной проницаемостью и малыми потерями. С учетом потерь и паразитной емкости катушку индуктивности можно представить в виде эквивалент- ной схемы (рис.2.34,а), где Rп = rf + rд +rc + rэ. эта схема может быть приведена к более удобному виду (рис.2.34,б), где Lэ -эквивалентная индуктивность, учитывающая собственную емкость. Величины. Lэ и Rп, а следовательно, добротность Q = wL/Rп зависят от температуры. Зависимость Q от температуры определяется температурным коэффициентом добротности ТКД=DQ/QDТ 2.3.5.Разновидности катушек индуктивности.Контурные катушки индуктивности. Эти катушки используются совместно с конденсаторами для получения резонансных контуров. Они должны иметь высокую стабильность, точность и добротность. В диапазоне длинных и средних волн эти катушки многослойные, как правило, с намоткой типа «универсаль». Для повышения добротности применяют многожильные провода типа «литцендрат». Для изменения индуктивности применяют цилиндрические сердечники из альсифера или карбонильного железа. В диапазоне коротких и ультракоротких волн используются однослойные катушки с индуктивностью порядка единиц микрогенри и добротностью порядка 50 — 100. Число витков таких катушек не превышает одного-двух десятков, диаметр каркаса 10 — 20 мм. В качестве каркасов используют керамику, полиэтилен и полистирол. Для уменьшения собственной емкости применяют ребристые каркасы. Обмотка выполняется одножильным медным проводом диаметром около 1 мм. На УКВ применяют бескаркасные катушки из неизолированного провода. Катушки связи. Эти катушки применяются для обеспечения индуктивной связи между отдельными цепями и каскадами. Такая связь позволяет разделить по постоянному току цепи базы и коллектора и т.д. К таким катушкам не предъявляются жесткие требования на добротность и точность, поэтому они выполняются из тонкого провода в виде двух обмоток небольших габаритов. Основными параметрами этих катушек являются индуктивность и коэффициент связи где L1 и L2 — индуктивность связанных катушек, М — взаимная индуктивность между ними. Величина коэффициента связи зависит от расстояния между катушками, чем оно меньше, тем больше k. Вариометры. Это такие катушки, в которых предусмотрена возможность изменения индуктивности в процессе эксплуатации для перестройки колебательных контуров. Они состоят из двух катушек, соединенных последовательно. Одна из катушек неподвижная (статор), другая располагается внутри первой и вращается (ротор). При изменении положения ротора относительно статора изменяется величина взаимоиндукции, а следовательно, индуктивность вариометра Такая система позволяет изменять индуктивность в 4 — 5 раз. Дроссели. Это катушки индуктивности, обладающие высоким сопротивлением переменному току и малым сопротивлением постоянному . Обычно включаются в цепях питания усилительных устройств. Предназначены для защиты источников питания от попадания в них высокочастотных сигналов. На низких частотах они используются в фильтрах цепей питания и обычно имеют металлические сердечники. Катушки индуктивности для ГИС. На частотах порядка 10 — 100 МГц находят применение тонкопленочные спиральные катушки. На площади в 1 кв.см, располагается не более 10 витков. Добротность таких катушек не превышает 20-30. Поэтому они находят ограниченное применение. В ГИС предпочтительны миниатюрные торроидальные катушки на ферритовых сердечниках, индуктивность которых достигает десятков тысяч микрогенри. В последнее время наметилась тенденция замены катушек специальными схемами на транзисторах (гираторы) и электромеханическими, пьезоэлектрическими и акустоэлектронными фильтрами, основанными на принципе механических упругих колебаний и механического резонанса. Скорость распространения упругих колебаний в твердом теле примерно в 100 тысяч раз меньше скорости распространения электромагнитных волн, что позволяет создавать очень компактные механические резонаторы с распределенными параметрами, обладающие добротностью порядка 103. Развитие микроэлектроники привело к появлению фильтров на приборах с зарядовой связью и фильтров на поверхностных акустических волнах. Кроме того, в ИМС широкое применение находят активные RC — фильтры, в которых используются операционные усилители с глубокой частотно-зависимой обратной связью. Источник — Свободный взгляд | |||||
Индуктивность | Страница 2 из 3 | Electronov.net
Свойства индуктивности:
Индуктивность обладает комплексным импедансом (сопротивлением):
где:
j — мнимая единица;
ω — циклическая частота (рад/с) протекающего синусоидального тока;
f — частота в Гц;
L — индуктивность катушки (Генри).
Комплексный импеданс в общем случае записывается как сумма активного и реактивного сопротивлений:
Отсюда следует, что активное сопротивление идеальной индуктивности равно нулю, а реактивное сопротивление равно: Для постоянного тока частота равна нулю, следовательно, реактивное сопротивление равно нулю. Индуктивность по определению численно равна отношению создаваемого током потока магнитного поля, пронизывающего катушку, к силе протекающего тока. Отсюда следует, что применять катушки индуктивности имеет смысл только в цепях переменного тока.
Если Вы не привыкли слепо доверять формулам, то следующий абзац для Вас:
Спойлер
Чтобы разобраться, почему с ростом частоты тока у индуктивности растет реактивное сопротивление, необходимо вспомнить явление самоиндукции, которое можно сформулировать в 2 эквивалентных вариантах:
- Возникновение магнитного потока самоиндукции при протекании по цепи тока;
- Возникновение ЭДС индукции в том контуре, по которому протекает переменный ток.
По Закону электромагнитной индукции Фарадея, ЭДС индукции можно записать как:
где:
εi — величина ЭДС индукции;
Φ — величина магнитного потока.
В случае контура, содержащего N витков, используется понятие потокосцепления Ψs самоиндукции (Ψs = NΦs).
С учетом данных формул, можно записать ЭДС и ток самоиндукции:
Знак минуса показывает, что направление тока самоиндукции противоположно направлению основного тока.
Из этих формул следует, что любые изменения тока в цепи тормозятся, и тем сильнее, чем больше индуктивность цепи и меньше ее сопротивление.
Если сформулировать по научному:
Правило Ленца для явления самоиндукции – ток самоиндукции препятствует любым изменениям основного тока, текущего по цепи.
Можно также сказать, что индуктивность цепи является мерой ее электрической инертности, подобно тому, как масса в механике является мерой инертности тела при его поступательном движении.
И как Вы уже наверняка догадались, природа реактивного сопротивления индуктивности заключена в явлении ЭДС и тока самоиндукции, а скорость изменения величины тока – это его частота.
Схема замещения не идеальной (реальной) индуктивности:
Рисунок 1 — Схема замещения неидеальной (реальной) индуктивности.Сопротивление потерь:
В катушках индуктивности помимо основного эффекта взаимодействия тока и магнитного поля, наблюдаются паразитные эффекты, вследствие которых импеданс катушки не является чисто реактивным. Наличие паразитных эффектов ведет к появлению потерь в катушке, оцениваемых сопротивлением потерь:
где:
RCL – диэлектрические потери;
RL – индуктивные потери.
Диэлектрические потери вызваны магнитными свойствами диэлектрика, а также паразитной емкости, которая образуется между витками, вследствие наличия изоляции обмоточного провода, и соответственно появляются межвитковые утечки и прочие потери, характерные для диэлектриков конденсаторов. Однако для современных катушек общего применения эти потери пренебрежимо малы.
Индуктивные потери складываются из следующих составляющих:
- Потери в проводах:
В свою очередь, потери в проводах вызваны тремя причинами:
- Провода обмотки обладают омическим (активным) сопротивлением.
- Сопротивление провода обмотки возрастает с ростом частоты, что обусловлено поверхностным эффектом (скин-эффектом). Суть эффекта состоит в вытеснении тока в поверхностные слои провода. Как следствие, уменьшается полезное сечение проводника и растет сопротивление. Подробнее о поверхностном эффекте можно прочитать [гиперссылка]здесь[/гиперссылка].
- В проводах обмотки, свитой в спираль, проявляется эффект близости (англ. proximity effect), суть которого состоит в вытеснении тока под воздействием вихревых токов и магнитного поля, которые появляются из-за явления взаимной индуктивности, к периферии намотки. В результате сечение, по которому протекает ток, принимает серповидную форму, что ведет к дополнительному возрастанию сопротивления провода. Подробнее о эффекте близости можно прочитать [гиперссылка]здесь[/гиперссылка].
- Потери на перемагничивание ферромагнитного сердечника:
Данные потери связаны с эффектом гистерезиса в ферромагнетиках.
- Потери на вихревые токи (токи Фуко):
Переменное магнитное поле индуцирует вихревые ЭДС в окружающих проводниках, т.е. витках и сердечнике. При этом возникают вихревые (т.е. замкнутые в кольце) токи — токи Фуко, которые по физической природе ничем не отличаются от индукционных токов, возникающих в линейных проводах. Помимо электрических потерь, вихревые токи также разогревают каркас и обмотку катушки.
Резонансная частота индуктивности:
При f > fр катушка индуктивности в цепи переменного тока ведет себя как конденсатор. Следовательно, индуктивность целесообразно использовать лишь на частотах f < fp, на которых ее сопротивление носит индуктивный характер. Обычно максимальная рабочая частота индуктивности примерно в 2—3 раза ниже резонансной.
Добротность:
Добротность катушки индуктивности определяется отношением между ее реактивным и активным сопротивлениями:
Повышение добротности достигается оптимальным выбором диаметра провода, увеличением размеров катушки индуктивности и применением сердечников с высокой магнитной проницаемостью и малыми потерями, намоткой вида «универсаль», применением посеребренного провода, применением многожильного провода вида «литцендрат» для снижения потерь, вызванных скин-эффектом. Подробнее о проводе вида «литцендрат» можно прочитать [гиперссылка]здесь[/гиперссылка].
Необузданные гонки за всё более высокими параметрами добротности колебательных контуров не так просты, как могли бы показаться
на первый взгляд. — Потери в сердечнике складываются из потерь на вихревые токи и потерь на гистерезис, связанных с перемагничивание материала
в течение периода. Точный расчёт всех перечисленных параметров — дело весьма затруднительное, поэтому, с целью упрощения задачи, обычно учитываются только
потери в проводах, как вносящие основной вклад в общую сумму потерь. А теперь, что касается выбора параметра индуктивности катушки для достижения максимальной добротности. Глядя на формулу, описывающую величину добротности Q=2πfL/Rпот, а так же приведённую на рисунке, можно сделать преждевременный вывод — добротность катушки линейно растёт с ростом частоты и достигает максимума на частоте собственного резонанса, когда С минимальна и равна собственной паразитной ёмкости катушки и паразитных емкостей источника, нагрузки и монтажа. Однако, не всё так просто! При понижении частоты добротность уменьшается, но не линейно, а несколько медленнее, за счёт снижения влияния действия скин эффекта, гуляющего внутри провода, а при повышении — тоже плавно уменьшается из-за проявляющейся зависимости совокупных паразитных ёмкостей от частоты (варикапный эффект). К тому же эти паразитные ёмкости начинают доминировать в общей ёмкости колебательного контура, а образованный ими конденсатор, как известно, обладает далеко не самым выдающимся параметром добротности. И в заключение нашего теоретического экскурса, всё же не воздержусь и приведу основные факторы, определяющие сопротивление потерь в проводах катушек на высоких частотах: 1. Омическое (активное) сопротивление проводника постоянному току — классика жанра, рассчитать можно по длине и диаметру провода
на странице ссылка на страницу. Думаю, на этом хватит! 1. Очевидно, что из металла! 2. Катушка должна быть большой! Опять же, как и в первом пункте — излишний фанатизм не приветствуется. 3. Желание минимизировать эффект близости и уменьшить собственную ёмкость катушки сподвигло специалистов к следующему постулату: оптимальное отношение шага намотки (расстояние между центрами соседних витков) к диаметру провода равно ≈2. 4. И вот теперь главный вопрос радиолюбительства: Сколько мотать витков в оптимизированной катушке для достижения максимальной
добротности?
Данная таблица дошла до наших взоров благодаря стараниям латвийского радиолюбителя Юрия Балтина (YL2DX), опубликовавшим её в далёком 2003 году на своём сайте http://dx.ardi.lv, за что ему большое человеческое спасибо! Таблица эта — не догма и не абсолютная истина в последней инстанции, однако она позволяет достаточно наглядно пронаблюдать
зависимость параметра добротности катушки индуктивности от диаметра каркаса и толщины провода, а заодно и оценить оптимальное
значение индуктивности для того или иного частотного диапазона. А на следующей странице будем мотать высокодобротные катушки на ферритовых кольцах, а также на кольцах из распылённого железа.
|
|||||
Собственная паразитная ёмкость катушки индуктивности. Онлайн расчёт.
Собственная ёмкость — это паразитный параметр катушки индуктивности. Паразитный, но не так, чтобы уж очень: не домашнее животное в виде
таракана, не нежданный гость в виде татарина, а так… мелкий, но важный аспект, требующий учёта и внимания.
Возникновение собственной ёмкости обусловлено наличием ёмкостей между отдельными витками катушки, между витками и сердечником, витками
и экраном, а также витками и близлежащими элементами конструкции. Все эти распределённые ёмкости суммируются и называются собственной
ёмкостью катушки CL.
Паразитная собственная ёмкость всегда подключена параллельно катушке и образует с её собственной индуктивностью параллельный колебательный
контур, резонансная частота которого является частотой собственного резонанса катушки.
Несмотря на кажущуюся простоту, точный расчёт этого параметра — это вовсе: не плёвое дело, не поиск халявы и не комариная плешь, по крайней
мере, практически все отечественные авторы справочной литературы, дружно повернулись спиной к суровой правде бытия, выдавая за истину
теорию, никак не подкреплённую экспериментом.
Для примера приведу выдержку из подобного умного справочника.
Совсем другое дело — буржуйские пытливые умы, преимущественно американской этнической национальности. Эти ребята копают и вглубь и вширь похлеще азиатских хунвейбинов, восполняя нехватку теоретических обоснований многочисленными практическими экспериментами.
Вот как, к примеру, у них выглядит незамысловатая измерительная приблуда для определения собственной резонансной частоты катушки.
В результате всех этих раскопок из глубины на поверхность была извлечена совсем уж до неприличия простая формула определения собственной
ёмкости катушки:
CL(пф) ≈ 0,5×Dкат(см).
Казалось бы, вот оно — добро пожаловать «за грань добра и зла». Однако не всё так плохо — формула обеспечивает вполне приемлемую
точность вычислений и может быть использована для оценки собственных ёмкостей однослойных конструкций катушек с соотношением
длины намотки к диаметру:
0.5 нам/Dкат
А как посчитать нам величину собственной ёмкости при другом форм-факторе катушки?
Найти всеобъемлющую формулу, позволяющую рассчитать этот параметр для любых вариаций (включая частотную зависимость) оказалось делом
нереальным — по крайней мере мне этого сделать не удалось. Поэтому самым простым и точным методом, позволяющим оценить собственную
ёмкость катушки, я посчитал интерполяцию графика экспериментальной зависимости, полученной англичанином R.G.Medhurst-ом, в лаборатории
компании General Electric.
По шкале X — отношение длины к диаметру катушки;
По шкале Y — коэффициент H, равный отношению собственной ёмкости к диаметру катушки;
Шкала зависимости — логарифмическая.
Формула значения собственной ёмкости катушки в данном случае выглядит следующим образом:
CL(пф) = H×Dкат(см).
Зависимость снята для однослойных бескаркасных катушек в диапазоне частот, находящихся ниже частоты собственного резонанса катушки.
В этом же источнике приведена и удобная таблица, отражающая изменение коэффициента H в зависимости от форм-фактора катушки.
И, как результат — формула, позволяющая с 2-3% точностью описать полученные экспериментальные зависимости:
H = 0,1126×L/D+0,08+0,27/√L/D.
Это то, что касается бескаркасных катушек. При наличии гладкого каркаса расчётная ёмкость изделия увеличится на величину ≈10×ε (%), где ε — относительная диэлектрическая проницаемость материала каркаса. Для катушек, намотанных на каркасах с нарезкой для фиксации витков, коэффициент увеличения ёмкости уже может составлять величину ≈20×ε (%).
И в завершении мероприятия просуммируем вышеизложенные идеи калькулятором.
ТАБЛИЦА РАСЧЁТА ЗНАЧЕНИЯ СОБСТВЕННОЙ ЁМКОСТИ БЕСКАРКАСНОЙ КАТУШКИ.
Будьте внимательны — в качестве значения межвиткового расстояния принято считать расстояние между центрами соседних витков, а не зазор между ними, поэтому данное расстояние никак не может быть меньше величины диаметра провода.
Значение собственной ёмкости многослойной катушки значительно больше и может достигать нескольких десятков пФ.
Здесь, помимо всего прочего, вступают в сложное взаимодействие и ёмкости между соседними витками, и ёмкости между слоями, и разные другие
факторы, значительно усложняющие структуру длинной линии, описывающей свойства моточного изделия.
Наверно по этой причине никто никому и не выносит мозг, все отдыхают на расслабоне. Формул — нет!
Или я чего-то пропустил в этой жизни…
Соединение катушек — Основы электроники
Соединение катушек индуктивности при отсутствии взаимного влияния магнитных полей катушек.
Последовательное соединение катушек индуктивности.
Суммарная индуктивность двух или нескольких катушек, соединенных последовательно и расположенных на таком расстоянии друг от друга, что магнитное поле одной катушки не пересекает витков другой (рисунок 1), равна сумме их индуктивностей.
Рисунок 1. Последовательное соединение катушект индуктивности.
Цепь, изображенная на рисунке 1, обладает общей индуктивностью L, которая выражается так:
где L1, L2 и L3 — индуктивности отдельных катушек.
Параллельное соединение катушек индуктивности.
Индуктивность цепи, составленной из тех же катушек при параллельном их соединении (рисунок 2) и при соблюдении того же условия относительно их расположения (отсутствие магнитного взаимодействия), подсчитывается по следующей формуле:
Рисунок 2. Параллельное соединение катушек индуктивности.
Индуктивность двух катушек, соединенных параллельно, определяется по следующей формуле:
Как видим, формулы для подсчета результирующих индуктивностей катушек, соединенных последовательно или параллельно и не взаимодействующих между собой, совершенно тождественны с формулами для подсчета омического сопротивления цепи при последовательном и параллельном соединении резисторов.
Соединение катушек при наличии взаимного влияния их магнитных полей.
Если катушки, включенные в цепь последовательно, расположены близко друг к другу, т. е. так, что часть магнитного потока одной катушки пронизывает витки другой, т. е. между катушками существует индуктивная связь (рисунок 3а), то для определения их общей индуктивности приведенная выше формула будет уже непригодна. При таком расположении катушек могут быть два случая, а именно:
- Магнитные потоки обеих катушек имеют одинаковые направления
- Магнитные потоки обеих катушек направлены навстречу друг другу
Тот или другой случай будет иметь место в зависимости от направления витков обмотки катушек и от направлений токов в них.
Рисунок 3. Соединение катушек индуктивности: а)суммарная индуктивность увеличивается за счет взаимной индукции б)суммарная индуктивность уменьшается за счет взаимной индукции.
Если обе катушки намотаны в одну сторону и токи в них текут в одном направлении, то это будет соответствовать первому случаю; если же токи текут в противоположных направлениях (рисунок 3б), то будет иметь место второй случай.
Разберем первый случай, когда магнитные потоки направлены в одну сторону. Очевидно, при этих условиях витки каждой катушки будут пронизываться своим потоком и частью потока другой катушки, т. е. магнитные потоки в той и в другой катушке будут больше по сравнению с тем случаем, когда между катушками нет индуктивной связи. Увеличение магнитного потока, пронизывающего витки той или иной катушки, равносильно увеличению ее индуктивности. Поэтому общая индуктивность цепи в рассматриваемом случае будет больше суммы индуктивностей отдельных катушек, из которых составлена цепь.
Рассуждая таким же образом, мы придем к выводу, что для второго случая, когда потоки направлены навстречу друг другу, общая индуктивность цепи будет меньше суммы индуктивностей отдельных катушек.
Подсчет величины индуктивности цепи, составленной из двух соединенных последовательно катушек индуктивности L1 и L2 при наличии между ними индуктивной связи, производится по формуле:
В первом случае ставится знак + (плюс), а во втором случае знак — (минус).
Величина М, называемая коэффициентом взаимной индукции, представляет собой добавочную индуктивность, обусловленную частью магнитного потока, общей для обеих катушек.
На явлении взаимоиндукции основано устройство вариометров. Вариометр состоит из двух катушек, общая индуктивность которых может, по желанию, плавно изменяться в некоторых пределах. В радиотехнике вариометры применяются для настройки колебательных контуров приемников и передатчиков.
ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!
Похожие материалы:
Добавить комментарий
Калькулятор ВЧ индуктивности для однослойных спиральных круглых проволочных катушек
Серж Ю. Строобандт, ON4AA
Copyright 2007–2020, под лицензией Creative Commons BY-NC-SA
- Дом
- Калькулятор индуктивности
## Обеспечение высокого коэффициента качества Катушки, обеспечивающие наивысший коэффициент качества, требуют проволоки, ленты или трубки большого диаметра и обычно имеют кубическую форму ; я.е. длина катушки равна диаметру катушки.
Чем отличается этот калькулятор индуктивности от остальных?
- Д-р Джеймс Ф. Корум, K1AON
- Вычислитель индуктивности, представленный на этой странице, уникален тем, что использует волноводный режим со спиральной оболочкой n = 0 для определения индуктивности катушки независимо от ее электрической длины. В отличие от калькуляторов квазистатической индуктивности, этот калькулятор индуктивности RF позволяет более точно прогнозировать индуктивность на высоких частотах с помощью , включая эффекты линии передачи , проявляющиеся при более длинных катушках.Кроме того, калькулятор точно следует методологии Национального института стандартов и технологий (NIST) для применения коэффициентов коррекции круглой проволоки и неоднородности, а учитывает как эффект близости, так и скин-эффект.
Разработка этого калькулятора была в основном основана на статье IEEE Microwave Review 2001 г. братьев Корум 7 и формулах коррекции, представленных в книге Дэвида Найта, G3YNH, теоретический обзор, 1 , дополненной несколькими личными дополнениями.
Какую схему замещения следует использовать?
Обе эквивалентные схемы дают точно такое же полное сопротивление катушки на расчетной частоте.
Для узкополосных приложений с единственной расчетной частотой может использоваться эффективная эквивалентная схема. При необходимости могут быть рассчитаны дополнительные эквивалентные схемы для дополнительных расчетных частот.
Схема замещения с сосредоточенными параметрами приведена здесь в основном для сравнения с другими калькуляторами.За счет параллельного добавления сосредоточенной паразитной емкости эта эквивалентная схема пытается имитировать частотную характеристику импеданса катушки. Это будет точно только для ограниченного диапазона частот, сосредоточенного вокруг проектной частоты.
Для чего можно использовать этот калькулятор?
- спиральная антенна
- Калькулятор возвращает значения для коэффициента осевого распространения β и характеристического импеданса Z c волновода со спиральной оболочкой n = 0 (T 0 ) для любых размеров спирали и любой частоты.
Данная информация пригодится при проектировании:
- High-Q загрузочные катушки для уменьшения размера антенны (детали конструкции),
- Одинарная или многоядерная — рамочные приемные антенны с известной резонансной частотой,
- Спиральные антенны, , эквивалентные стержневой диэлектрической антенне,
- Катушка Тесла источники высокого напряжения (см. Рисунок далее),
- РЧ катушки для магнитно-резонансной томографии (МРТ),
- Лампа бегущей волны (ЛБВ) спиралей (рисунок ниже).
В чем проблема других калькуляторов индуктивности?
- Том Раух, W8JI
- Том Раух, W8JI, в своем известном исследовании индукторов с высокой добротностью однажды пожаловался, что многие программы моделирования индукторов не учитывают два важных эффекта:
- Паразитная емкость через катушку индуктивности,
- Эффект близости , вызывает уменьшение Q по мере сближения витков.
Например, JavaScript-калькулятор RF Coil Design от VE3KL игнорирует эти эффекты.
Точно так же некогда очень популярная компьютерная программа, названная «COIL» Брайаном Бизли ex-K6STI, оказалась основана на наборе ошибочных формул, 1,10,11 , как было тщательно указано Дэвидом Найтом, G3YNH. К счастью, эта программа больше не продается.
Как рассчитывается мода спирального волновода?
- Фридрих Вильгельм Бессель
- Катушку лучше всего рассматривать как спиральный волновод, по которому распространяется своего рода спиральная поверхностная волна. Фазовая скорость распространения такого спирального волновода составляет с дисперсией, что означает, что она разная для разных частот. (Это не относится к обычным линиям передачи, таким как коаксиальный или открытый провод.) Более низкие частоты распространяются медленнее по катушке. Фактическая фазовая скорость на определенной частоте для конкретной волновой моды получается путем решения трансцендентного уравнения на собственные значения, включающего модифицированные функции Бесселя первого (I n ) и второго рода (K n ) соответственно для внутреннего и снаружи спирали. 7,8
- Dr T. J. Dekker
- Поскольку такое уравнение не может быть решено обычными аналитическими средствами, настоящий калькулятор определит фазовую скорость β моды спирали оболочки самого низкого порядка (n = 0) на расчетной частоте, используя метод Теодора (Дирк) Дж. Деккера 12–14 комбинированный метод определения корня пополам и секущей . Для этого калькулятора версия SLATEC FORTRAN 15 алгоритма Деккера была переведена Дэвидом Биннером в код JavaScript, а затем, с уважением, в код Brython.
Аналогичный алгоритм также используется для определения частоты, на которой катушка выглядит как четвертьволновой резонатор. Это первая собственная резонансная частота катушки.
Более подробную информацию об используемых формулах и алгоритмах можно получить непосредственно из исходного кода Brython этого калькулятора.
Почему все еще нужны поправочные коэффициенты?
Несмотря на то, что модель волновода со спиральной оболочкой является наиболее точной из имеющихся на сегодняшний день, она определенно страдает рядом ограничений.Они берут свое начало в самом определении — спирали оболочки, — это: идеализированная анизотропно проводящая цилиндрическая поверхность, которая проводит только в спиральном направлении. 7
Выбирая спираль оболочки в качестве модели для цилиндрической катушки из круглой проволоки, делаются следующие допущения:
- Провод отлично проводит.
- Провод бесконечно тонкий.
- Витки катушки бесконечно замкнуты.
- Наконец, поскольку более высокие (n> 0) моды волновода со спиральной оболочкой не принимаются во внимание, концевые эффекты в виде неоднородностей поля не рассматриваются. Следовательно, спираль оболочки должна быть очень длинной и относительно тонкой, чтобы концевые эффекты стали незначительными.
- К счастью, эти допущения совпадают с допущениями, сделанными при использовании формулы геометрической индуктивности. Это означает, что те же поправочные коэффициенты могут быть применены к результатам модели волновода со спиральной оболочкой, а именно:
- Поправочный коэффициент неравномерности поля k L согласно Lundin 1,3 для моделирования конечных эффектов коротких и толстых катушек (высокий \ (\ frac {D} {\ ell} \) соотношение),
- A Поправочный коэффициент самоиндукции круглой проволоки k с согласно Rosa, 1,4,5
- A Поправочный коэффициент взаимной индуктивности круглого провода k м по Knight, 1,6
- Уменьшенный эффективный диаметр катушки для моделирования гашения тока в проводе под действием близости соседних обмоток,
- Последовательное сопротивление переменному току для моделирования скин-эффекта, включая дополнительную концевую коррекцию для двух концевых витков, которые подвержены только половинному эффекту близости.
Есть небольшой разрыв в расчетных индуктивностях?
Да, есть; около ℓ = D. Thomas Bruhns, K7ITM обнаружил этот небольшой недостаток. Это полностью из-за по сути прерывистой формулировки справочной формулы Лундина. Эта приближенная формула используется для получения поправочного коэффициента неоднородности поля k L без особых вычислительных затрат. Неравномерность расчетных индуктивностей появляется только тогда, когда ℓ = D. Она проявляется только тогда, когда сумма поправочных коэффициентов (k s + k m ) относительно мала по сравнению с k L ; я.е. для очень толстых витков с закрытым интервалом. Однако даже в этом случае ошибка не превышает ± 0,0003%. 1
Делаются ли какие-то другие приближения?
- Д-р Дэвид В. Найт, G3YNH
- Да, есть еще несколько приближений. Они вводятся только тогда, когда вычислительная выгода существенна и когда влияние на точность меньше любого допустимого производственного допуска. Помимо ранее обсуждавшейся формулы из справочника Лундина, аппроксимационная формула Дэвида Найта 1 используется для определения поправочного коэффициента k m для взаимной индуктивности круглого провода. 1 Эффективный диаметр D eff также оценивается просто потому, что в настоящее время нет известного способа его расчета (см. Ниже).
Основывается ли этот калькулятор на каких-либо эмпирических данных?
Коэффициент близости Φ, используемый для расчета сопротивления катушки переменному току, интерполируется из таблицы экспериментальных данных Медхерста. 2 Коэффициент близости Φ определяется как отношение общего сопротивления переменного тока, включая вклад эффекта близости к сопротивлению переменного тока без вклада эффекта близости.
\ [\ Phi \ Equiv \ frac {R_ {ac, \ Phi}} {R_ {ac}} \]
Как эффективный диаметр D eff связан с коэффициентом близости Φ?
Другие вычислители индуктивности обычно используют средний и внутренний физические диаметры (соответственно: D и D — d), чтобы ограничить индуктивность катушки между двумя широко разнесенными теоретическими пределами. 1 . Однако часто упоминается, что фактический эффективный диаметр D eff катушки должен быть связан с коэффициентом близости Φ.Чтобы избавиться от неоднозначности результата измерения диапазона индуктивности, была выведена новая наивная формула аппроксимации. В этом приближении эффективный диаметр D eff является простой функцией фактора близости Φ. В результате этих усилий этот калькулятор индуктивности вернет только одно значение индуктивности.
Эффективный диаметр и его предполагаемое отношение к коэффициенту близости Φ (см. Текст)
Хотя расчет индуктивности по этой формуле более конкретен, чем брекетинг эффективного диаметра, он остается приблизительным по двум причинам:
- Как и в случае с брекетингом диаметра, эта формула в равной степени предполагает, что ток под действием эффекта близости гаснет, сохраняя при этом круговое поперечное распределение.Скорее всего, это не так.
- Как и в случае брекетинга диаметра, формула не учитывает частотно-зависимые возмущения поперечного распределения тока, такие как скин-эффект.
Эти нарушения в поперечном распределении тока не учитываются и могут перемещать центр распределения тока дальше внутрь. Это уменьшает эффективный диаметр и, как следствие, индуктивность еще больше. Следовательно, индуктивность, полученная с помощью этого калькулятора, будет немного завышена.Тем не менее, указанная индуктивность в большинстве случаев будет более точной и, безусловно, менее неоднозначной, чем теоретические крайние значения (или их среднее значение), указанные другими вычислителями индуктивности.
Индуктивность и, следовательно, добротность вблизи резонанса огромны; Это может быть правильно?
Как объяснялось ранее, правильный способ увидеть катушку индуктивности — это спиральный волновод, закороченный на одном конце, поскольку предполагается, что он питается от источника напряжения. На любой частоте можно определить коэффициент осевого распространения β и характеристический импеданс Z c эквивалентной линии передачи.
Входной импеданс на другом конце будет тангенциальной функцией электрической длины катушки. Следовательно, когда электрическая длина приближается к четверти длины волны или \ (\ frac {\ pi} {2} \) рад, результирующий входной импеданс и, следовательно, индуктивность будут чрезвычайно высокими. Омические потери остаются сравнительно низкими, поэтому добротность Q будет огромной вблизи резонанса.
Катушка Тесла использует это явление для создания чрезвычайно высоких напряжений в диапазоне нескольких сотен кВ. 7 Калькуляторы индуктивности, которые не показывают такого реального поведения, основаны на геометрических формулах.
Пробой напряжения воздуха на одном конце катушки Тесла. Источник: oneTesla
Расчетная индуктивность отрицательна; Это может быть правильно?
Вы работаете с катушкой выше ее первой собственной резонансной частоты. Катушка с электрической длиной между 90 ° и 180 ° (и нечетными кратными этому) будет вести себя как конденсатор, а не как катушка индуктивности. Это еще раз указывает на то, что первый собственный резонанс катушки на самом деле является параллельным резонансом. Из-за емкостного поведения в этом диапазоне индуктивность катушки будет отрицательной.
Паразитная емкость C p намного выше, чем у других калькуляторов; Это может быть правильно?
Понятие паразитной емкости — вот что это такое; корректирующий элемент в схеме с сосредоточенными параметрами катушки, эквивалентный для решения проблемы частотной независимости формулы худшей геометрической индуктивности. 7
Используя формулы на основе спирального волновода, настоящий калькулятор работает намного лучше при оценке индуктивности на высоких частотах. Таким образом, калькулятор компенсирует эквивалент схемы с сосредоточенными параметрами даже больше, чем другие калькуляторы. Это приводит к более высоким значениям для C p .
В конце концов, со старомодной концепцией эквивалента сосредоточенной схемы лучше отказаться. Вместо этого фокусируется на эффективных значениях на проектной частоте для индуктивности, реактивного сопротивления, последовательного сопротивления и ненагруженной Q.
В чем проблема проектирования катушек с использованием EZNEC?
Прагматики среди нас, вероятно, хотели бы использовать EZNEC, программу моделирования антенн, которая позволяет вам очень удобно определять спиральные структуры катушек. Однако этот ценный метод не лишен недостатков:
- Катушки в EZNEC определены как полилинии. Спроецированный многоугольник полилинии должен иметь ту же площадь, что и спроецированный круг реальной спиральной катушки. Я предоставлю читателю возможность выполнить это тригонометрическое упражнение.
- Чем больше сегментов в полилинии, тем точнее модель будет представлять реальную спиральную катушку. Однако EZNEC имеет нижний предел длины сегмента, который пропорционален длине волны.
- С учетом двух предыдущих пунктов, довольно громоздко оптимизировать конструкцию змеевика с помощью EZNEC.
Катушка EZNEC модель
На практике часто гораздо проще, быстрее и точнее прибегнуть к вышеуказанному калькулятору вместо создания геометрической модели змеевика EZNEC. После получения результатов с помощью этого калькулятора катушку можно легко смоделировать как нагрузку Лапласа в любой модели антенны EZNEC.
Шаг намотки однослойной катушки определяется как
\ [\ begin {уравнение} p \ эквив \ frac {\ ell} {N} \ end {уравнение} \]
Фактор близости \ (\ Phi \) интерполирован на основе эмпирических данных Медхерста. 1,2
\ [\ begin {уравнение} \ Phi = f_ \ text {Medhurst} \ left (\ frac {\ ell} {D}, \ frac {p} {d} \ right) \ end {уравнение} \]
Наивная приближенная формула для эффективного диаметра \ (D_ \ text {eff} \) была выведена автором:
\ [\ begin {уравнение} D_ \ text {eff} = D — d \ cdot \ left (1 — \ frac {1} {\ sqrt {\ Phi}} \ right) \ end {уравнение} \]
Поправочные коэффициенты
\ (k_ \ text {L} \) — коэффициент коррекции неоднородности поля по Лундину.2} — \ frac {4D_ \ text {eff}} {3 \ pi \ ell} \ end {формула} \]
\ (k_ \ text {s} \) — поправочный коэффициент для самоиндукции круглого проводника по Найту и Розе. 2} {4 \ ell} — D_ \ text {eff} N \ frac {k_ \ текст {s} + k_ \ text {m}} {2} \ right] \]
Характеристический импеданс волноводной моды спиральной оболочки
Эффективный угол наклона рассчитывается по тригонометрии:
\ [\ psi = \ arctan {\ frac {p} {\ pi \, D_ \ text {eff}}} \]
Герц показал, что произвольное электромагнитное поле в однородной линейной изотропной среде без источника может быть определено в терминах единственного векторного потенциала \ (\ Pi \). 16 Предполагая временную зависимость \ (\ e {\, \ j \ omega t} \), волна в поле векторного потенциала Герца может быть записана как:
\ [\ vec {\ Pi} (x) = \ vec {\ Pi} (0) \ e {- \ gamma x} \]
Постоянная распространения \ (\ gamma \) — комплексная величина:
\ [\ gamma = \ alpha + \ j \ beta \]
где:
\ (\ alpha \) — постоянная затухания, а
\ (\ beta \) — фазовая постоянная.
Однако, поскольку затухание в воздушной среде незначительно, принято записывать волновое уравнение исключительно в функции комплексной фазовой постоянной \ (\ beta \):
\ [\ vec {\ Pi} (x) = \ vec {\ Pi} (0) \ e {- \ j \ beta x} \]
, где \ (\ beta = \ beta ‘- \ j \ beta’ ‘\),
такой, что \ (\ gamma \ Equiv \ j \ beta = \ j (\ beta’ — \ j \ beta ») = \ бета » + \ j \ beta ‘\ Rightarrow \ beta’ ‘\ Equiv \ alpha \).2} \]
Характеристический импеданс \ (Z_ \ text {c} \) волновода со спиральной оболочкой \ (n = 0 \) на расчетной частоте равен: 7
\ [Z_ \ text {c} = \ frac {60 \ beta} {k_0} \, \ text {I} _0 (\ tau a) \; \ text {K} _0 (\ tau a) \]
Формула волновода со спиральной оболочкой и скорректированной оболочкой
\ [L_ \ text {eff, s} = \ frac {Z_ \ text {c}} {\ omega} \, \ tan (\ beta \, \ ell) \; k_ \ text {L} — \ mu_0 D_ \ text {eff} N \ frac {k_ \ text {s} + k_ \ text {m}} {2} \]
Эффективная эквивалентная схема
\ [X_ \ text {eff, s} = \ omega L_ \ text {eff, s} \]
\ [Q_ \ text {eff} \ Equiv \ frac {X_ \ text {eff, s}} {R_ \ text {eff, s}} \]
Схема замещения с сосредоточенными параметрами
Чтобы вычислить концентрированную эквивалентную схему, сначала известную последовательную эффективную эквивалентную схему преобразуют в ее параллельную версию:
\ [R_ \ text {eff, p} = \ left (Q_ \ text {eff} ^ 2 + 1 \ right) R_ \ text {eff, s} \ qquad X_ \ text {eff, p} = \ frac {Q_ \ text {eff} ^ 2 + 1} {Q_ \ text {eff} ^ 2} X_ \ text {eff, s} \]
Аналогично, эквивалентная схема с сосредоточенными параметрами может быть преобразована в схему только с параллельными компонентами, в которой \ (Q_L \) и \ (R_ \ text {s} \) остаются неизвестными:
\ [R_ \ text {p} = \ left (Q_L ^ 2 + 1 \ right) R_ \ text {s} \ qquad X_ {L_ \ text {p}} = \ frac {Q_L ^ 2 + 1} {Q_L ^ 2} X_ {L_ \ text {s}} \]
Можно записать еще три тождества; первая гласит, что параллельные резисторы в обеих схемах замещения одни и те же:
\ [R_ \ text {p} = R_ \ text {eff, p} \ qquad Q_L \ Equiv \ frac {X_ {L_ \ text {s}}} {R_ \ text {s}} \ qquad X_ {L_ \ text {s}} = \ omega L_ \ text {s} \]
Подстановка позволяет записать сокращенное квадратное уравнение в \ (Q_L \):
\ [R_ \ text {p} = \ left (Q_L ^ 2 + 1 \ right) \ frac {X_ {L \ text {s}}} {Q_L} \ quad \ Rightarrow \ quad Q_L ^ 2 — \ frac {R_ \ text {p}} {X_ {L \ text {s}}} Q_L +1 = 0 \]
Это дает следующие решения для \ (Q_L \) и \ (R_ \ text {s} \):
\ [Q_L = \ frac {R_ \ text {p}} {2 X_ {L \ text {s}}} + \ sqrt {\ left (\ frac {R_ \ text {p}} {2 X_ {L \ текст {s}}} \ right) ^ 2 — 1} \ qquad R_ \ text {s} = \ frac {X_ {L_ \ text {s}}} {Q_L} \]
На данный момент известны как \ ({X_ \ text {eff, p}} \), так и его компонент \ (X_ {L_ \ text {p}} \). 2} \),
дисперсионная функция трансцендентной спирали оболочки решается численно для поперечного (радиального) волнового числа 𝜏,
\ (\ omega = k_0 c_0 \) и \ (f_ \ text {res} = \ frac {\ omega} {2 \ pi} \).
Код Brython этого калькулятора доступен ниже. Код Brython не предназначен для автономной работы, хотя он выглядит почти идентично Python 3. Код Brython выполняется на стороне клиента в браузере, где он транскодируется для защиты Javascript.
8. Роберт Э. Коллин. Основы микроволновой техники. В: 2-е изд. Wiley-IEEE Press; 2001: 580-583.
12. T. J. Dekker, W. Hoffmann. Алгол 60 Процедуры числовой алгебры, часть 2 .Mathematisch Centrum Amsterdam; 1968.
13. T. J. Dekker. Нахождение нуля с помощью последовательной линейной интерполяции. В: Б. Дежон, П. Хенрици, ред. Конструктивные аспекты основной теоремы алгебры . Нью-Йорк; 1969.
16. Дж. А. Страттон. Электромагнитная теория . Макгроу-Хилл; 1941.
Как рассчитать индуктивность катушки (однослойные индукторы с цилиндрическим сердечником)
Индуктивность катушки зависит от ее геометрических характеристик, количества витков и способа намотки катушки.Чем больше диаметр, длина и большее количество витков обмотки, тем больше ее индуктивность.
Если катушка намотана плотно, от поворота к витку, то она будет иметь большую индуктивность, чем катушка с неплотной намоткой, с промежутками между витками. Иногда вам нужно намотать катушку с заданной геометрией, а у вас нет провода с требуемым диаметром, тогда, если вы используете более толстую проволоку, вам следует немного увеличить количество витков, а если использовать более тонкую проволоку, это нужно, чтобы уменьшить количество витков катушки, чтобы получить требуемую индуктивность.
Все вышеперечисленное относится к катушкам намотки без ферритовых сердечников.
Индуктивность однослойных катушек на цилиндрических формах обмоток можно рассчитать по формуле:
L = ( D /10) 2 * n 2 /( 4.5 * D + 10 * l ) (1)
Где
L — индуктивность катушки, мкГн;
D — диаметр витка (диаметр бывшего), мм;
л — длина змеевика, мм;
n — количество витков обмоток.
В расчете может быть две задачи:
А. Приведена геометрия катушки, найти индуктивность;
В. Дана индуктивность катушки, посчитайте количество витков и диаметр провода.
В случае «A» все данные указаны, индуктивность легко найти.
Пример 1. Рассчитаем индуктивность катушки, показанной на рисунке выше. Подставьте значения в формулу 1:
L = (18/10) 2 * 20 2 / (4.5 * 18 + 10 * 20) = 4,6 мкГн
Во втором случае известны диаметр катушки и длина намотки. Длина намотки зависит от количества витков и диаметра проволоки. Поэтому рекомендуется производить расчет именно в таком порядке. Исходя из геометрических соображений, определите размер катушки, диаметр и длину намотки, а затем подсчитайте количество витков по формуле:
n = 10 * (5 * L * (0,9 * D + 2 * L )) 1/2 / D (2)
После того, как вы нашли количество витков, определите диаметр провода с изоляцией по формуле:
d = l / n (3)
Где
d — диаметр проволоки, мм;
l — длина намотки, мм;
n — количество витков.
Пример 2. Нам нужно сделать катушку диаметром 10 мм и длиной намотки 20 мм, катушка должна иметь индуктивность 0,8 мкГн. Обмотка однослойная, от поворота к повороту.
Подставляем значения в формулу 2, получаем:
n = 10 * (5 * 0,8 * (0,9 * 10 + 2 * 20)) 1/2 /10 = 14
Диаметр проволоки: d = 20/14 = 1,43 мм
Для намотки катушки проводом меньшего диаметра необходимо разместить полученные расчетным путем 14 витков по всей длине катушки (20 мм) с равными интервалами между витками (шаг намотки).Индуктивность катушки будет на 1-2% меньше номинальной, это следует учитывать при изготовлении этих катушек. Чтобы намотать катушку проволокой толще 1,43 мм, новый расчет следует производить с увеличенным диаметром или длиной обмотки катушки. Вам также может потребоваться увеличить диаметр и длину одновременно, пока не получите желаемые размеры катушки для данной индуктивности.
Следует отметить, что приведенные выше формулы предназначены для расчета катушек с длиной витка l равной половине диаметра или более.Если длина намотки меньше половины диаметра намотки D /2, более точные результаты можно получить, используя следующие формулы:
L = (D /10) 2 * n 2 / ((4 D +11 l )) (4)
и
n = (10 L * (4 D +11 l )) 1/2 / D (5)
Артикул: «300 практических советов»
ЗначениеAL [Энциклопедия электромагнетизма]
A L , A L значение , коэффициент индуктивности , индуктивность на виток , индуктивность на квадратный виток , а также индуктивность — обратная величина магнитное сопротивление , характерное для данного магнитопровода (тип, размер, воздушный зазор и т.), часто предоставляемые производителем.
Ферритовый сердечник RM8 с зазором изготовителя так, что коэффициент индуктивности A L = 250 нГн / виток 2 (надпись A250 на сердечнике)С. Зурек, Encyclopedia Magnetica, CC-BY-3.0
Значение A L обычно используется при проектировании электронных трансформаторов на основе ферритовых сердечников, для которых значение часто выражается в наногенри.
Значение A L широко используется применительно к магнитопроводам из мягкого феррита. Название проницаемость физически и математически является синонимом значения A L , но является более общим термином, относящимся к свойству данной магнитной цепи.
| Поддержите us с всего за 1 доллар США через PayPal или кредитную карту: |
Единицы и уравнения
Математически A L имеет единицу СИ генри (H), но отношение к индуктивности нелинейно, и практическая единица измерения — наногенри на квадратный виток или нГн / виток 2 .2} $$
Таким образом, значение A L для данного сердечника можно рассчитать, если известно количество витков и можно измерить индуктивность.
Калькулятор индуктивности по значению ШС и количеству витков
Практическое применение
При проектировании трансформаторов и катушек индуктивности для импульсных источников питания параметры переключения и уровень мощности определяют значения индуктивности, необходимые для такого компонента.
Следовательно, значение индуктивности известно на следующем этапе проектирования. Использование значения A L позволяет быстро вычислить необходимое количество витков для данного размера сердечника.
Следует отметить, что значение A L часто указывается в единицах (нГн) или аналогичных единицах, подразумевая «на квадратный оборот». Важно помнить, что соотношение между значением A L и индуктивностью не пропорционально из-за квадрата витков.2 ⋅ \ mu_0 ⋅ \ mu_r ⋅ A} {l} $$
где: N — число витков, μ 0 — магнитная проницаемость свободного пространства (H / м), μ r — относительная проницаемость материала (безразмерная), A — поперечная площадь сечения (м 2 ), l — длина магнитного пути (м).
Приведенное выше уравнение можно переписать как:
где:
| $$ x = \ frac {\ mu_0 ⋅ \ mu_r ⋅ A} {l} $$ | (Вт) |
И сравнивая уравнения, можно увидеть, что значение $ x = A_L $, и оно является константой для данного магнитного сердечника с фиксированными параметрами, если это не влияет на эффективную магнитную проницаемость (например,г. насыщения избегается).
Следовательно, если производитель предоставляет A L , это упрощает расчеты.
Типичное обозначение A L = 160 нГн ± 3% означает, что сердечник имеет такой воздушный зазор, что A L = 160 нГн (на квадратный виток). Для сердечника ER14.5-3-7 это синоним воздушного зазора 150 мкм.
Точный допуск в ± 3% возможен для пропорционально больших зазоров.В приведенном выше примере 150 мкм — это относительно большое значение для магнитного пути сердечника, которое составляет 19 мм. Это снижает эффективную проницаемость с более чем 1000 до примерно 137 (см. Также калькулятор эффективной проницаемости).
Для меньших зазоров влияние сердечника увеличивается, и допуск может достигать ± 25%. То же самое относится к сердечникам без зазоров.
Пример техпаспорта
Пример таблицы данных, в которой указано значение A L .
См. Также
Список литературы
Страница не найдена | MIT
Перейти к содержанию ↓- Образование
- Исследование
- Инновации
- Прием + помощь
- Студенческая жизнь
- Новости
- Выпускников
- О MIT
- Подробнее ↓
- Прием + помощь
- Студенческая жизнь
- Новости
- Выпускников
- О MIT
Попробуйте поискать что-нибудь еще! Что вы ищете? Увидеть больше результатов
Предложения или отзывы?
Микроволны101 | Математика индуктивности
Нажмите здесь, чтобы перейти на страницу с основной индуктивностью
В марте 2016 года наши друзья из Keysight Technologies предоставили нам видео о том, как моделировать спиральные индукторы.Спасибо, Keysight!
Ниже приведен индекс нашего математического обсуждения индукторов:
Индуктивное сопротивление
Индуктивность ЛЭП (отдельная страница)
Индуктивность соленоида
Спиральный индуктор (проволока)
Спиральные индукторы на подложке (Новинка марта 2016!)
Индуктивность тороида
Индуктивность Wirebond (теперь на отдельной странице)
Индуктивность воздушного моста (отдельная страница)
Индуктивность через отверстие (отдельная страница)
Индуктивность проводов (отдельная страница)
Сопротивление индуктивности постоянному току и ВЧ
Резонансы
Индуктивное сопротивление
Воспользуйтесь нашим калькулятором реактивного сопротивления, если вам интересна эта тема!
Хорошо известное уравнение для индуктивного реактивного сопротивления показано ниже.Обратите внимание, что индуктивное реактивное сопротивление положительное, полярность противоположная емкостному. На диаграмме Смита это означает, что последовательная индуктивность имеет тенденцию изменять коэффициент отражения по часовой стрелке.
Более полезная форма уравнения индуктивного реактивного сопротивления приведена ниже, где частота выражается в ГГц, а индуктивность — в наногенри. К счастью, все эти десятичные знаки просто отменяют друг друга!
Индуктивность соленоида
Соленоид цилиндрической формы намотан проволокой для создания индуктивности.Он может иметь один слой обмоток или многослойный, и он может использовать воздушный сердечник или сердечник с высокой магнитной проницаемостью для увеличения индуктивности. Самыми полезными (читай, «наивысшей добротностью») соленоидами для микроволновых приложений являются миниатюрные однослойные индукторы с воздушным сердечником. Рисунок ниже предоставлен Себастьяном. Большое спасибо!
Классическая формула для однослойной индуктивности (воздушный сердечник) называется формулой Уиллера, которая восходит к временам радио-индустрии 1920-х годов:
где:
L = индуктивность в микро-Генри (не нано-Генри!)
N = количество витков провода
R = радиус катушки в дюймах
H = высота катушки в дюймах
Вот это в пересчете на D, диаметр катушки:
(Эта формула исправлена 9 апреля 2006 г. благодаря KB!)
ФормулаУиллера не учитывает диаметр проволоки и расстояние между витками.В формуле Уиллера витки касаются друг друга, но предполагается, что некоторая изоляция предотвращает короткое замыкание. На практике необходимо некоторое расстояние между витками, чтобы уменьшить межвитковую емкость и увеличить рабочую частоту. Посмотрим правде в глаза, Уиллера не интересовала точность нано-катушек Генри для микроволнового оборудования.
Предположительно более точный метод расчета индуктивности однослойных индукторов с воздушным сердечником для микроволновых компонентов можно найти на веб-сайте Microwave Components Incorporated:
где:
L = индуктивность в нано-Генри
N = количество витков провода
D = внутренний диаметр катушки (дюймы)
D1 = диаметр неизолированного провода (дюймы)
S = расстояние между витками (дюймы)
По формуле MCI применительно к проводу 47 калибра (1.Диаметр неизолированного провода 2 мил) и расстояние между витками 0,5 мил, обертывая витки вокруг штифтовых тисков 20 мил, можно получить следующие значения для воздушной катушки:
1 оборот = 2 нГн
2 оборота = 5 нГн
3 оборота = 8 нГн
4 оборота = 12 нГн
5 оборотов = 16 нГн
6 оборотов = 20 нГн
7 оборотов = 25 нГн
8 оборотов = 30 нГн
9 оборотов = 35 нГн
10 оборотов = 40 нГн
Щелкните здесь, чтобы перейти к нашей таблице калибра проводов (AWG) для Америки.
Дроссель спиральный (проволочный)
Эта формула и рисунок также были предоставлены Себастьяном (единицы также являются микро-Генри): Мы должны признать, что мы лично не проверяли точность некоторых формул на этой странице по сравнению с измеренными данными.Также обратите внимание, что любая модель индуктора, не учитывающая паразитную емкость и сопротивление, будет иметь ограниченную точность на микроволновых частотах.
Спиральные индукторы на подложке
Спиральные индукторы часто используются в конструкциях MIC, MMIC и RFIC, особенно ниже 18 ГГц. Катушки индуктивности могут быть прямоугольными или круглыми, если вы умеете их моделировать. Модель спирального индуктора с сосредоточенными элементами может иметь множество элементов конденсатора и резистора, чтобы учесть все паразиты, которые делают ее все менее и менее идеальной по мере увеличения частоты.Для моделирования индуктора требуются хорошие извлеченные данные об одном или нескольких значениях индуктивности, что приводит к масштабируемой модели, позволяющей прогнозировать характеристики произвольных значений индуктивности, необходимых для вашей конструкции.
Хотите немного более практического описания того, как моделировать спиральные индукторы? Посмотрите это видео ТОЧНО ЭТО. Франц Сишка из SisConsult проведет вас через полную модель спирального индуктора с сосредоточенными элементами, включая скин-эффекты, вихревые токи подложки и соединение с металлическим экраном 1.Программа Keysight для определения характеристик и анализа интегральных схем (IC-CAP) используется для соответствия двум примерам измерений. Элементы настраиваются вручную с последующей оптимизацией. Предоставляются методы проверки модели и файлы примеров можно скачать.
Индуктивность тороида
Тороид похож на соленоид, но имеет форму пончика. Еще не все!
Сопротивление катушек индуктивности постоянному току и ВЧ
Вычислить сопротивление спирального индуктора постоянному току просто, и разработчики часто упускают из виду его, пока не построят схему усилителя, и деталь не смещается правильно на первой итерации.Вам нужно знать сопротивление листа вашей металлизации в Ом на квадрат и вычислить количество квадратов в катушке индуктивности. Количество квадратов — это общая длина (если вы ее раскрутили), деленная на ширину, и может легко исчисляться сотнями для большой катушки индуктивности.
При вычислении радиочастотного сопротивления вам, возможно, придется учитывать эффект глубины скин-слоя.
Показанная ниже модель является классической моделью спиральных индукторов. Вычислить элементы не так просто, как вы могли бы надеяться.
Резонансы индуктора
Еще впереди!
Расчет индуктивности утечки сложных конструкций трансформатора на основе простой модели индуктора с двумя катушками
AN2866 Примечание по применению
Замечания по применению Как спроектировать 13.Антенна с настраиваемой меткой 56 МГц Введение Метки RFID (радиочастотная идентификация) извлекают всю свою энергию из поля считывающего устройства. Бирки и антенны считывателя
ПодробнееEisflisfræði 2, vor 2007 г.
[Просмотр задания] [Печать] Eðlisfræði 2, vor 2007 30. Назначение индуктивности должно быть произведено в 2:00 ночи в среду, 14 марта 2007 г. Кредит за проблемы, представленные с опозданием, уменьшится до 0% после того, как крайний срок достигнет
ПодробнееРасчет схемы трансформатора
Расчеты схемы трансформатора Эта таблица и все связанные файлы находятся под лицензией Creative Commons Attribution License, версия 1.0. Чтобы просмотреть копию этой лицензии, посетите http://creativecommons.org/licenses/by/1.0/,
Подробнееd di Поток (B) Ток (H)
Сравнение методов расчета индуктивности Tony Morcos Magnequench Technology Center Research Triangle Park, North Carolina 1 VCM Baseline: Geometry Аксиально намагниченный диск MQ3-F 42 NdFeB Br = 131kG
ПодробнееГЛАВА 28 ЭЛЕКТРИЧЕСКИЕ ЦЕПИ
ГЛАВА 8 ЭЛЕКТРИЧЕСКИЕ ЦЕПИ 1.Нарисуйте принципиальную схему цепи, которая включает в себя резистор R 1, подключенный к положительному выводу батареи, пару параллельных резисторов R и R, подключенных к
. ПодробнееГлава 4. LLC Резонансный преобразователь.
Глава 4 LLC-резонансный преобразователь 4.1 Введение В предыдущих главах обсуждались тенденции и технические проблемы, связанные с преобразователем постоянного тока в постоянный. Высокая удельная мощность, высокая эффективность и высокая мощность
ПодробнееВывод решения для Capa # 11
Выводы решения для Capa # 11 Внимание: символ E используется попеременно для обозначения энергии и ЭДС.1) ДАННЫЕ: V b = 5,0 В, = 155 Ом, L = 8,400 · 10 2 Н. На схеме выше показано напряжение на
ПодробнееИндукторы. Теория переменного тока. Модуль 3
Модуль 3 Теория переменного тока Что вы узнаете в Модуле 3. Раздел 3.1 Электромагнитная индукция. Магнитные поля вокруг проводников. Соленоид. Раздел 3.2 Индуктивность и обратная э.д.с. Единица индуктивности. Факторы
ПодробнееНаведенные напряжения и закон Фарадея индуктивности
Наведенные напряжения и индуктивность Закон Фарадея Концепция # 1, 4, 5, 8, 13 Задача # 1, 3, 4, 5, 6, 9, 10, 13, 15, 24, 23, 25, 31, 32a, 34, 37, 41, 43, 51, 61 В прошлой главе мы видели, что ток производит магнитное поле
ПодробнееEMI в электромобилях
EMI в электромобилях S.Guttowski, S. Weber, E. Hoene, W. John, H. Reichl Fraunhofer Institute for Reliability and Microintegration Gustav-Meyer-Allee 25, 13355 Berlin, Germany Телефон: ++ 49 (0) 3046403144,
ПодробнееЛаборатория физики законов Кирхгофа IX
Лаборатория физики законов Кирхгофа IX Цель В серии экспериментов теоретические соотношения между напряжениями и токами в цепях, содержащих несколько батарей и резисторов в сети,
ПодробнееСетевые реакторы и приводы переменного тока
Сетевые реакторы и приводы переменного тока Rockwell Automation Mequon Wisconsin Довольно часто линейные и нагрузочные реакторы устанавливаются на приводы переменного тока без четкого понимания того, почему и каковы положительные и отрицательные последствия.
Подробнее5.Измерение магнитного поля
H 5. Измерение магнитного поля 5.1 Введение Магнитные поля играют важную роль в физике и технике. В этом эксперименте исследуются три различных метода измерения
ПодробнееЧто такое индуктивность?
Богатин Энтерпрайзис, д-р Эрик Богатин 26235 З 110 терр. Olathe, KS 66061 Голос: 913-393-1305 Факс: 913-393-1306 eric @ bogent.com www.bogatinenterprises.com Тренинг по целостности сигнала и межсоединению
ПодробнееГлава 15: Конструкция трансформатора
Глава 15 Конструкция трансформатора Некоторые более сложные вопросы проектирования, не рассмотренные в предыдущей главе: n Учет потерь в сердечнике + + Выбор рабочего потока i 1 плотность для оптимизации общих потерь v 1 v Несколько
ПодробнееОбратный преобразователь
Примечания к лекции по обратноходовому преобразователю ECEN4517! Получение обратного преобразователя: версия повышающего преобразователя с трансформаторной изоляцией! Типичные формы сигналов и вывод M (D) = V /! Обратный трансформатор
ПодробнееГенераторы переменного тока.Базовый генератор
Генераторы переменного тока Базовый генератор Базовый генератор состоит из магнитного поля, якоря, контактных колец, щеток и резистивной нагрузки. Магнитное поле обычно представляет собой электромагнит. Арматура любая номер
ПодробнееМодуль 11: Наведенные выбросы.
Модуль 11: Кондуктивная эмиссия 11.1 Обзор Термин кондуктивная эмиссия относится к механизму, который позволяет создавать электромагнитную энергию в электронном устройстве и связывать его с его шнуром питания переменного тока.
ПодробнееЛекция 2 Матричные операции
Лекция 2 Операции с матрицами транспонирование, сумма и разность, скалярное умножение, умножение матриц, обратная матрица-векторное произведение, матрица 2 1 Транспонирование матрицы, транспонирование m n матрицы A, обозначенное A T или
ПодробнееИзмерение емкости
Предварительные вопросы по измерению емкости Название страницы: Класс: Номер в реестре: Инструктор :.Конденсатор используется для хранения. 2. Какова единица СИ для емкости? 3. Конденсатор в основном состоит из двух
ПодробнееТеория асинхронного двигателя
Курс PDHonline E176 (3 PDH) Инструктор по теории асинхронных двигателей: Джерри Р. Беднарчик, P.E. 2012 PDH Online PDH Center 5272 Meadow Estates Drive Fairfax, VA 22030-6658 Телефон и факс: 703-988-0088 www.pdhonline.org
ПодробнееГлава 14: Конструкция индуктора
Глава 14 Конструкция индуктора 14.1 Ограничения при проектировании индуктора фильтра 14.2 Пошаговая процедура проектирования 14.3 Расчет многообмоточного магнитного устройства с использованием метода Kg 14.4 Примеры 14.5 Краткое изложение ключевых моментов
Подробнее .
 д. В отличие от резисторов и конденсаторов они
не являются стандартизованными изделиями, а изготавливаются для
конкретных целей и имеют такие параметры, которые необходимы для
осуществления тех или иных преобразований электрических сигналов,
токов и напряжений.
д. В отличие от резисторов и конденсаторов они
не являются стандартизованными изделиями, а изготавливаются для
конкретных целей и имеют такие параметры, которые необходимы для
осуществления тех или иных преобразований электрических сигналов,
токов и напряжений. Если же к проводнику подключен
источник переменного напряжения, то ток и магнитный поток будут
изменяться непрерывно и наводимая в проводнике ЭДС будет
препятствовать протеканию переменного тока, что эквивалентно
увеличению сопротивления проводника. Чем выше частота изменения
напряжения, приложенного к проводнику,, тем больше величина ЭДС,
наводимая в нем, следовательно, тем больше сопротивление,
оказываемое проводником протекающему току. Это сопротивление
XL не связано с потерями энергии, поэтому является
реактивным. При изменении тока по синусоидальному закону наводимая
ЭДС будет равна
Если же к проводнику подключен
источник переменного напряжения, то ток и магнитный поток будут
изменяться непрерывно и наводимая в проводнике ЭДС будет
препятствовать протеканию переменного тока, что эквивалентно
увеличению сопротивления проводника. Чем выше частота изменения
напряжения, приложенного к проводнику,, тем больше величина ЭДС,
наводимая в нем, следовательно, тем больше сопротивление,
оказываемое проводником протекающему току. Это сопротивление
XL не связано с потерями энергии, поэтому является
реактивным. При изменении тока по синусоидальному закону наводимая
ЭДС будет равна 26)
26)
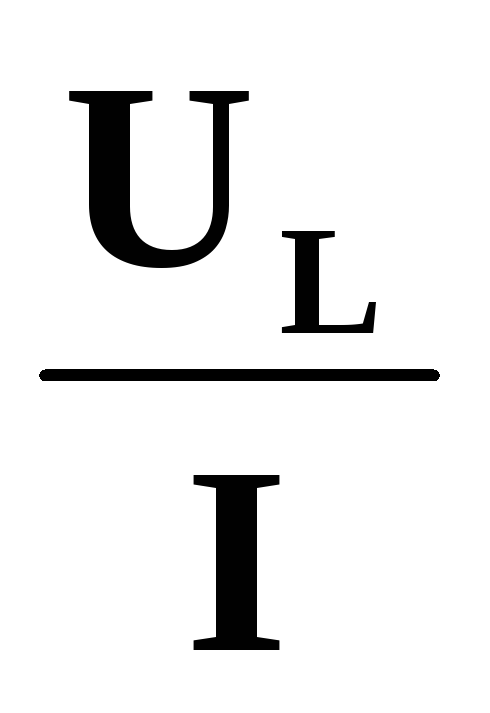 Броневые сердечники состоят из двух чашек 2,
изготовленных из карбонильного железа или ферритаов.
Броневые сердечники состоят из двух чашек 2,
изготовленных из карбонильного железа или ферритаов. 2.23 (1 — заглушка, 2 — экран, 3 — корпус, 4
— обмотка, 5 — каркас, 6 -подстроечный стержень, 7 — чашка
сердечника, 8 — основание, 9 — заливка).
2.23 (1 — заглушка, 2 — экран, 3 — корпус, 4
— обмотка, 5 — каркас, 6 -подстроечный стержень, 7 — чашка
сердечника, 8 — основание, 9 — заливка). 29)
29)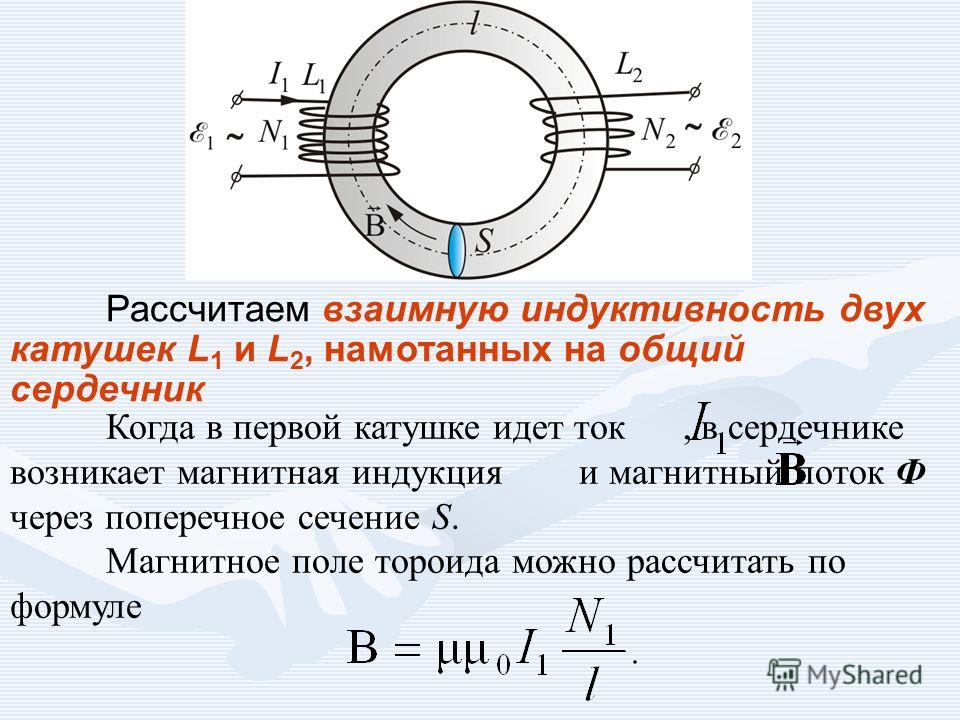 30)
30)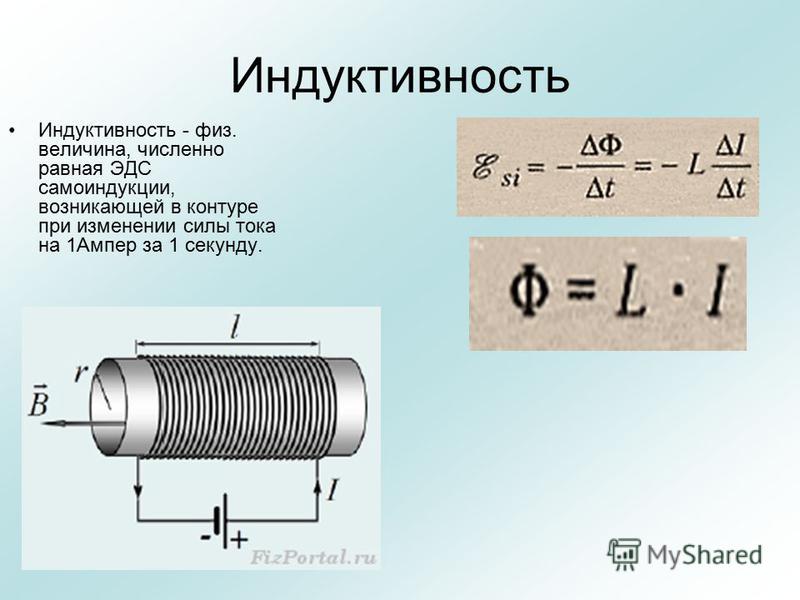 32)
32) 11
11 435
435 Для однослойных катушек рассчитывают шаг намотки
Для однослойных катушек рассчитывают шаг намотки При помещении катушки в экран индуктивность катушки
уменьшается
При помещении катушки в экран индуктивность катушки
уменьшается
 Все эти распределенные емкости можно объединить в одну,
называемую собственной емкостью катушки CL
Все эти распределенные емкости можно объединить в одну,
называемую собственной емкостью катушки CL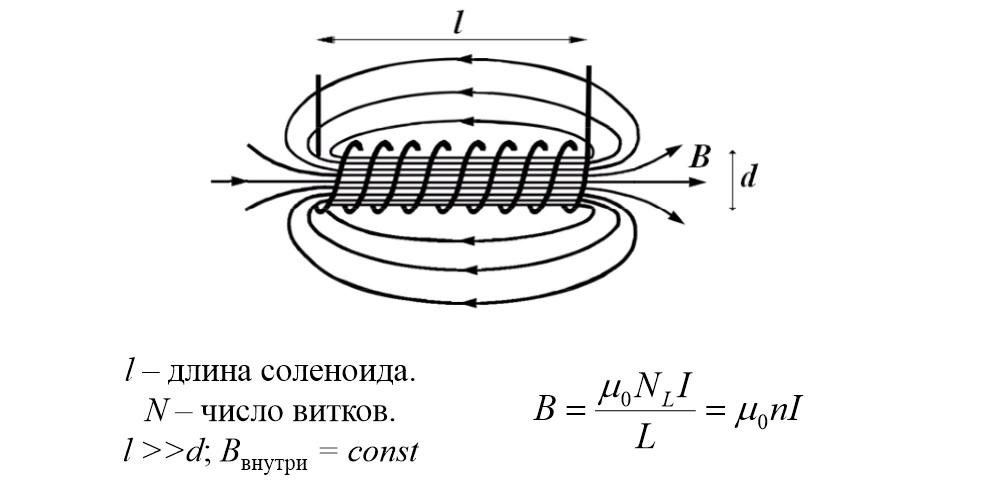 Схема такой намотки
показана на рис.2.28. Как только провод доходит до края катушки,
направление укладки меняется. Цикл универсальной обмотки выбирается
таким, что, совершив один оборот вокруг каркаса, провод возвращается
к положение, отличающееся от исходного на угол b. Этот угол выбирается таким, чтобы каждый
последующий виток находился рядом с предыдущим.
Схема такой намотки
показана на рис.2.28. Как только провод доходит до края катушки,
направление укладки меняется. Цикл универсальной обмотки выбирается
таким, что, совершив один оборот вокруг каркаса, провод возвращается
к положение, отличающееся от исходного на угол b. Этот угол выбирается таким, чтобы каждый
последующий виток находился рядом с предыдущим. 39)
39)