Как работает катушка индуктивности в цепи переменного тока. Какие основные характеристики имеет катушка индуктивности. Чем отличается поведение катушки в цепях постоянного и переменного тока. Какие эффекты возникают при прохождении переменного тока через катушку.
Что такое катушка индуктивности и для чего она нужна
Катушка индуктивности — это один из базовых элементов электрических цепей, представляющий собой проводник, намотанный в виде спирали на каркас. Основные функции катушки индуктивности:
- Накопление энергии магнитного поля
- Ограничение переменного тока
- Сглаживание пульсаций тока
- Фильтрация высокочастотных помех
- Создание колебательных контуров
Катушка индуктивности обладает свойством электромагнитной инерции — она препятствует изменениям силы тока в цепи. Это свойство и определяет ее основные применения.
Основные характеристики катушки индуктивности
Ключевыми параметрами, характеризующими катушку индуктивности, являются:

- Индуктивность (L) — основной параметр, измеряемый в Генри (Гн)
- Активное сопротивление обмотки (R)
- Добротность (Q) — отношение реактивного сопротивления к активному
- Собственная емкость
- Максимальный допустимый ток
- Частотный диапазон работы
Индуктивность катушки зависит от числа витков, геометрических размеров и свойств сердечника. Чем больше индуктивность, тем сильнее катушка противодействует изменениям тока.
Катушка индуктивности в цепи постоянного тока
В цепи постоянного тока катушка индуктивности ведет себя следующим образом:
- В момент включения ток через катушку нарастает постепенно из-за возникающей ЭДС самоиндукции
- После завершения переходного процесса катушка пропускает постоянный ток, как обычный проводник
- При отключении ток в катушке спадает не мгновенно, а постепенно
То есть в установившемся режиме катушка не оказывает существенного влияния на постоянный ток, кроме небольшого падения напряжения на активном сопротивлении обмотки.
Принцип работы катушки индуктивности в цепи переменного тока
В цепи переменного тока поведение катушки индуктивности кардинально отличается:

- При прохождении переменного тока в катушке постоянно возникает ЭДС самоиндукции, препятствующая изменениям тока
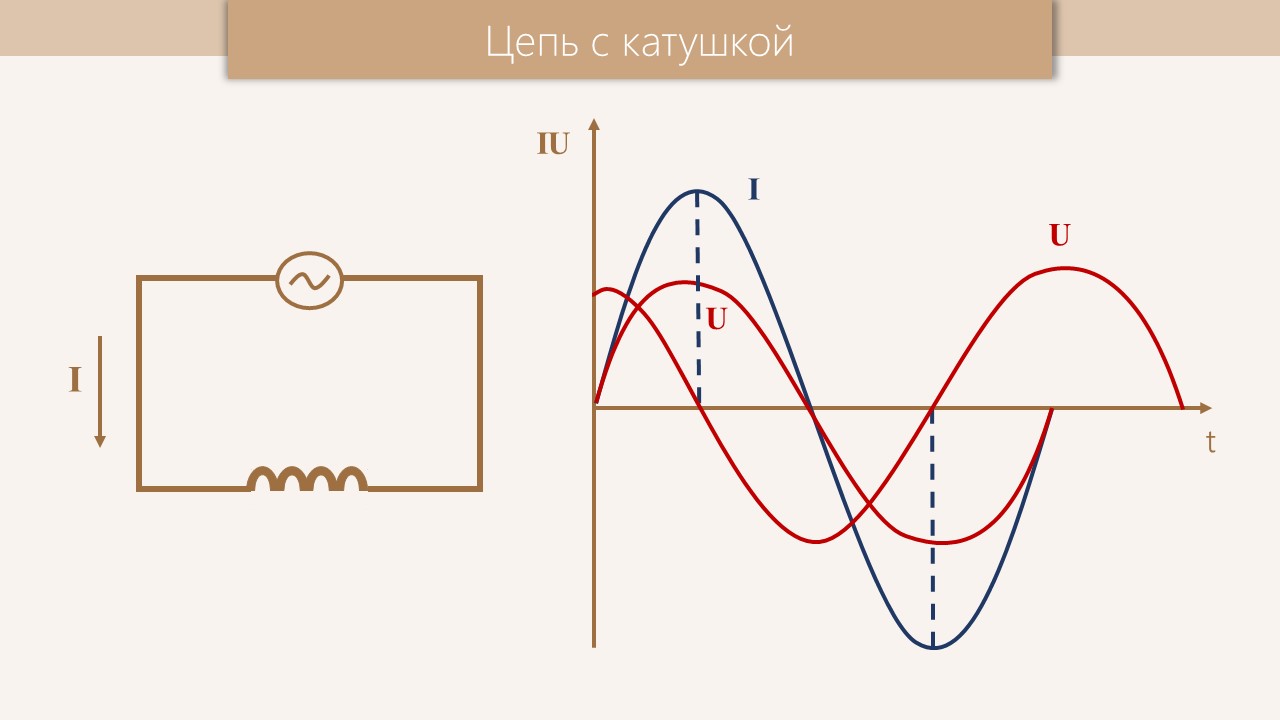
- Возникает сдвиг фаз между током и напряжением — ток отстает от напряжения на 90°
- Катушка обладает индуктивным сопротивлением, пропорциональным частоте тока
- Возникают потери энергии на активном сопротивлении обмотки и в сердечнике
Таким образом, в цепи переменного тока катушка индуктивности выступает как реактивный элемент, ограничивающий ток.
Индуктивное сопротивление катушки
Ключевой характеристикой катушки индуктивности в цепи переменного тока является ее индуктивное сопротивление:
XL = ωL = 2πfL
Где:
- XL — индуктивное сопротивление (Ом)
- ω — угловая частота (рад/с)
- f — частота тока (Гц)
- L — индуктивность катушки (Гн)
Индуктивное сопротивление прямо пропорционально частоте тока и индуктивности катушки. Чем выше частота, тем больше сопротивление катушки переменному току.
Векторная диаграмма тока и напряжения
Для наглядного представления соотношения между током и напряжением на катушке индуктивности используется векторная диаграмма:
 «`
«`
«`
«`
На диаграмме видно, что вектор тока I отстает от вектора напряжения UL на катушке на 90°. Это ключевая особенность поведения идеальной катушки индуктивности в цепи переменного тока.
Мощность в цепи с катушкой индуктивности
В цепи с идеальной катушкой индуктивности возникают следующие виды мощности:
- Активная мощность P = 0 (в идеальной катушке)
- Реактивная мощность Q = ULI = I2XL
- Полная мощность S = ULI
Идеальная катушка не потребляет активную мощность, а лишь обменивается реактивной мощностью с источником. В реальных катушках присутствуют потери активной мощности на сопротивлении обмотки и в сердечнике.
Применение катушек индуктивности
Благодаря своим свойствам, катушки индуктивности широко применяются в различных электронных устройствах:
- Фильтры высоких и низких частот
- Колебательные контуры
- Трансформаторы
- Дроссели в источниках питания
- Электромагнитные реле
- Датчики
- Антенны
Понимание принципов работы катушки индуктивности в цепях переменного тока критически важно для разработки и анализа многих электронных схем.

Катушка индуктивности в цепи постоянного тока
Катушка индуктивности – это элемент характеризующимся своим свойством накапливать энергию магнитной поля.
Первый закон коммутации гласит: ток, протекающий в катушке индуктивности, в момент коммутации не может измениться скачком.
Это понятно из формулы:
Предположим, что ток iL изменился скачком, то есть:
А значит, что и напряжение в данном случае будет бесконечно велико:
Чего в природе быть не может, так как, следуя закону сохранения энергии, для этого бы потребовался источник энергии бесконечной мощности.
На схеме представлена RL – цепь, запитанная от источника постоянного тока. При замыкании ключа в положение 1, ток протекает по цепи “плюс” источника – резистор R – катушка индуктивности — “минус” источника. Тем самым, происходит накопление энергии магнитного поля в катушке индуктивности.
Напряжение и ток, протекающие в данной цепи, изменяются по экспоненциальному закону. Причем, их изменения взаимообратные, т.е. с увеличением тока, падение напряжения на катушке уменьшается.
Если мы переведем ключ в положение 2, то ток, не изменив своего направления, начнет уменьшаться по экспоненте до нуля. С физической точки зрения, в данном случае катушка отдает накопленную энергию магнитного поля в цепь, где она расходуется на тепловые потери в резисторе.
Одной из характеристик данной цепи является постоянная времени τ. Она зависит от величины индуктивности и активного сопротивления. Примерно за 5 τ ток в цепи достигает своего минимума или максимума.
Реализуем эту схему в программной среде Multisim 13.0 , взяв значения R = 10 Ом, L = 0,1 Гн.
Скачать файл Multisim 13.0
Рассчитаем время, за которое ток в цепи достигает установившегося значения:
Собранная схема запитана от батареи 12 В. Для снятия значений тока, использовался инструмент “current probe”. Внутреннее активное сопротивление катушки индуктивности, принято равным нулю.
Катушка индуктивности в цепи постоянного и переменного тока
Как ведет себя катушка индуктивности в цепи постоянного и переменного тока?
Катушка индуктивности в цепи постоянного тока
Итак, для этого опыта нам понадобится блок питания, который выдает постоянное напряжение, лампочка накаливания и собственно сама катушка индуктивности.
Чтобы сделать катушку индуктивности с хорошей индуктивностью, нам надо взять ферритовый сердечник:
Намотать на него лакированного медного провода и зачистить выводы:
Замеряем индуктивность нашей катушки с помощью LC метра:
132 микрогенри.
Теперь собираем все это вот по такой схеме:
где
L – катушка индуктивности
La – лампочка накаливания на напряжение 12 Вольт
Bat – блок питания, с выставленным напряжением 12 Вольт
Лампочка засветилась!
Как вы помните из прошлой статьи, конденсатор у нас не пропускал постоянный электрический ток:
Делаем вывод: постоянный электрический ток почти беспрепятственно течет через катушку индуктивности. Сопротивлением обладает только сам провод, из которого намотана катушка.
[quads id=1]
Катушка индуктивности в цепи переменного тока
Для того, чтобы узнать, как ведет себя катушка индуктивности в цепи переменного тока, нам понадобится осциллограф, генератор частоты, собственно сама катушка индуктивности и резистор на 100 Ом. Чем больше сопротивление, тем меньше будет проседать напряжение с моего генератора частоты, поэтому я взял резистор на 100 Ом.Он у меня будет в качестве шунта. Падение напряжения на этом резисторе будет зависеть от тока, протекающего через него
Собираем все это дело по такой схеме:
Получилось как то так:
Сразу договоримся, что у нас первый канал будет красным цветом, а второй канал – желтым. Следовательно, красная синусоида – это частота, которую нам выдает генератор частоты, а желтая синусоида – это сигнал, который снимается с резистора.
Мы с вами узнали, что при нулевой частоте (постоянный ток), катушка почти беспрепятственно пропускает через себя электрический ток. В нашем опыте мы будем подавать с генератора частоты синусоидальный сигнал с разной частотой и смотреть, меняется ли напряжение на резисторе.
Опыт N1
Для начала подаем сигнал с частотой в 1 Килогерц.
Давайте разберемся, что есть что. В зеленой рамочке я вывел автоматические замеры, которые делает осциллограф
Красный кружок с цифрой “1” – это замеры “красного”канала. Как мы видим, F (частота) =1 Килогерц, а Ма (амплитуда) = 1,96 Вольт. Ну грубо скажем 2 Вольта. Смотрим на кружочек с цифрой “2”. F=1 Килогерц, а Ма=1,96 Вольт. То есть можно сказать, что сигнал на выходе точно такой же, как и на входе.
Увеличиваем частоту до 10 Килогерц
Амплитуда не уменьшилась. Сигнал какой есть, такой и остался.
Увеличиваем до 100 Килогерц
Заметили разницу? Амплитуда желтого сигнала стала меньше, да еще и график желтого сигнала сдвигается вправо, то есть запаздывает, или научным языком, появляется
Сдвиг фаз – это разность между начальными фазами двух измеряемых величин. В данном случае напряжения. Для того, чтобы произвести замер сдвига фаз, должно быть условие, что у этих сигналов одна и та же частота. Амплитуда может быть любой. Ниже на рисунке приведен этот самый сдвиг фаз или, как еще его называют, разность фаз:
Увеличиваем частоту до 200 Килогерц
На частоте 200 Килогерц амплитуда упала вдвое, да и разность фаз стала больше.
Увеличиваем частоту до 300 Килогерц.
Амплитуда желтого сигнала упала уже до 720 милливольт. Разность фаз стала еще больше.
Увеличиваем частоту до 500 Килогерц
Амплитуда уменьшилась до 480 милливольт.
Добавляем еще частоту до 1 Мегагерц
Амплитуда желтого канала стала 280 милливольт.
Ну и добавляем частоту до предела, который позволяет выдать генератор частоты: 2 Мегагерца
Амплитуда “желтого” сигнала стала настолько маленькой, что мне пришлось ее даже увеличить в 5 раз.
И можно сказать, что сдвиг фаз стал почти 90 градусов или π/2.
[quads id=1]
Но станет ли сдвиг фаз больше, чем 90 градусов, если подать очень-очень большую частоту? Эксперименты говорят, что нет. Если сказать просто, то при бесконечной частоте сдвиг фаз будет равняться 90 градусов. Если совместить наши графики на бесконечной частоте, то можно увидеть примерно вот такой рисунок:
Так какой вывод можно сделать?
С увеличением частоты сопротивление катушки растет, а также увеличивается сдвиг фаз. И чем больше частота, тем больше будет сдвиг фазы, но не более, чем 90 градусов.
Опыт N2
Давайте же уменьшим индуктивность катушки. Прогоним еще раз по тем же самым частотам. Я убрал половину витков и сделал витки на край феррита, тем самым уменьшил индуктивность до 33 микрогенри.
Итак, прогоняем все по тем же значениям частоты
При частоте в 1 Килогерц у нас значение почти не изменилось.
10 Килогерц
Здесь тоже ничего не изменилось.
100 Килогерц
Тоже почти ничего не изменилось, кроме того, что желтый сигнал стал тихонько сдвигаться.
200 Килогерц
Здесь уже видим, что амплитуда на желтом сигнале начинает проседать и сдвиг фаз наращивает обороты.
300 Килогерц
Сдвиг фаз стал больше и амплитуда просела еще больше
500 Килогерц
Сдвиг стал еще больше и амплитуда желтого сигнала тоже просела.
1 Мегагерц
Амплитуда желтого сигнала падает, сдвиг фаз прибавляется. 😉
2 Мегагерца, предел моего генератор частоты
Сдвиг фаз стал почти равен 90 градусов, а амплитуда стала даже меньше, чем пол Вольта.
Обратите внимание на амплитуду в Вольтах на тех же самых частотах. В первом случае у нас индуктивность была больше, чем во втором случае, но амплитуда желтого сигнала во втором случае больше, чем в первом.
Отсюда вывод напрашивается сам собой:
При уменьшении индуктивности, сопротивление катушки индуктивности также уменьшается.
Реактивное сопротивление катушки индуктивности
С помощью нехитрых умозаключений, физиками была выведена формула:
где
ХL – реактивное сопротивление катушки, Ом
П – постоянная и равна приблизительно 3,14
F – частота, Гц
L – индуктивность, Гн
В данном опыте мы с вами получили фильтр низких частот (ФНЧ). Как вы видели сами, на низких частотах катушка индуктивности почти не оказывает сопротивление напряжению, следовательно амплитуда и мощность на выходе такого фильтра будет почти такой же, как и на входе. Но с увеличением частоты у нас амплитуда гасится. Применив такой фильтр на динамик, можно с уверенностью сказать, что будет усиливаться только бас, то есть низкая частота звука.
Видео про катушку индуктивности:
Заключение
Постоянный ток протекает через катушку индуктивности без каких-либо проблем. Сопротивлением обладает только сам провод, из которого намотана катушка.
Сопротивление катушки зависит от частоты протекающего через нее тока и выражается формулой:
Катушка индуктивности в цепи переменного тока
Если катушка индуктивности включена в цепь переменного тока, то в такой цепи, фаза тока всегда отстает от фазы напряжения. Разберем причины этого отставания на простейшем примере, когда в цепи имеется только индуктивное сопротивление, а омического сопротивления нет вовсе, или вернее омическим сопротивлением провода катушки самоиндукции можно пренебречь, так как оно мало.
Для удобства рассмотрения явлений будем считать, что мы присоединяем катушку индуктивности к источнику переменного тока в тот момент, когда напряжение U на его зажимах имеет максимальное амплитудное значение (рис. 1а.). Этот момент будем считать началом периода.
Рисунок 1. Самоиндукция-инерция. а) соотношения фаз тока, напряжения и ЭДС самоиндукции при включение катушки индуктивности в цепь переменного тока; б) соотношение фаз скорости движения, внешней силы и силы инерции
В момент включения катушки в ней немедленно возникнет электрический ток. Но ток не может сразу достичь своего амплитудного значения потому, что при его возникновении вокруг катушки начнет появляться магнитное поле, которое будет наводить в катушке ЭДС самоиндукции, направленную против внешнего напряжения, т. е. напряжения источника переменного тока. Электродвижущая сила самоиндукции будет препятствовать быстрому нарастанию силы тока в катушке. Поэтому нарастание тока будет длиться целую четверть периода.
По мере приближения к концу первой четверти периода скорость нарастания тока в катушке постепенно уменьшается.
Но вместе с тем ослабевает и ЭДС самоиндукции, так как величина ее зависит от скорости изменения силы тока.
Итак, в конце первой четверти периода внешнее напряжение, приложенное к катушке, будет равно нулю, ЭДС самоиндукции также будет, равна нулю, а ток в катушке и магнитный поток вокруг нее будут иметь максимальные амплитудные значения. В магнитном поле катушки будет запасено некоторое количество энергии, полученной от источника тока.
С началом второй четверти периода внешнее напряжение, переменив свое направление, будет возрастать, вследствие чего ток в катушке, текущий все еще в прежнем направлении, начнет уменьшаться. Но теперь в катушке снова возникнет ЭДС самоиндукции, обусловленная уменьшением магнитного потока, которая будет поддерживать ток в прежнем направлении.
В течение всей второй четверти периода внешнее напряже¬ние будет увеличиваться, а сила тока — уменьшаться. Ско¬рость уменьшения силы тока, оставаясь небольшой в начале второй четверти, станет постепенно нарастать и в конце этой четверти достигнет наибольшей величины.
Итак, к концу второй четверти периода внешнее напряжение приближается к амплитудному значению, а сила тока и магнитный ноток приближаются к нулю, убывая все с большей скоростью, вследствие чего ЭДС самоиндукции достигает своего амплитудного значения. Направление ЭДС самоиндукции, как всегда, остается противоположным направлению внешнего напряжения. Энергия, запасенная в магнитном поле за первую четверть периода, теперь возвращается обратно в цепь.
В течение второй половины (третья и четвертая четверти) периода все явления будут происходить в том же порядке, с той лишь разницей, что направления тока, внешнего напряжения и ЭДС самоиндукции изменяются на противоположные (рис. 1а.).
Таким образом, фаза тока все время отстает от фазы напряжения, причем нетрудно заметить, что сдвиг фаз тока и напряжения равен 90°.
Представим себе, что мы толкаем вдоль по рельсам груженую вагонетку. В первый момент, когда вагонетка только начинает трогаться с места, мы прилагаем к ней максимум усилий, которые по мере увеличения скорости вагонетки будем постепенно уменьшать. При этом мы почувствуем, что вагонетка, обладая инерцией, как бы сопротивляется нашим усилиям. Это противодействие (реакция) вагонетки будет особенно сильным вначале, по мере же ослабления наших усилий будет ослабевать и противодействие вагонетки, она постепенно будет переставать «упрямиться» и покорно покатится по рельсам.
Затем мы вовсе перестанем толкать вагонетку и даже, наоборот, начнем понемногу тянуть ее в обратном направлении. При этом мы почувствуем, что вагонетка снова сопротивляется нашим усилиям. Если мы будем все сильнее и сильнее тянуть вагонетку назад, то и ее противодействие будет соответственно все более и более возрастать. Наконец, нам удастся остановить вагонетку и даже изменить направление ее движения. Когда вагонетка покатится обратно, мы будем постепенно ослаблять наши усилия, т. е. будем тянуть ее все слабее и слабее, однако, несмотря на это, скорость вагонетки будет все-таки увеличиваться (при слабом трении в подшипниках).
Когда вагонетка пройдет половину пути в обратном направлении, мы совсем перестанем тянуть ее и снова переменим направление наших усилий, т. е. начнем ее снова задерживать, постепенно увеличивая силу торможения до тех пор, пока вагонетка не остановится, заняв первоначальное (исходное) положение. После этого мы можем продолжать все наши действия сначала.
В этом примере наши усилия, прилагаемые к вагонетке, соответствуют внешней ЭДС, противодействие вагонетки, обусловленное ее инерцией, — ЭДС самоиндукции, а скорость вагонетки — электрическому току. Если изобразить графически изменение наших усилий, а также изменение противодействия вагонетки и ее скорости с течением времени, то мы получим графики (рис. 1б), в точности соответствующие графикам рис.1а.
Из этого примера становится более понятной сущность реактивного (безваттного) сопротивления. В самом деле, в течение первой четверти периода мы толкали вагонетку, а она противодействовала нашим усилиям; в течение второй четверти периода она катилась сама, а мы «упирались»; в течение третьей четверти периода мы опять тянули ее, а вагонетка снова оказывала противодействие нашим усилиям и, наконец, в течение четвертой четверти периода она снова катилась сама, а мы ее тормозили.
Короче говоря, в течение первой и третьей четверти периода мы работали «на вагонетку», а в течение второй и четвертой четвертей она работала «на нас», возвращая обратно полученную то нас энергию. В результате наша работа оказалась «безваттной».
Таким образом катушка индуктивности в цепи переменного тока может работать как безваттный резистор.
ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!
Похожие материалы:
Добавить комментарий
Катушка Индуктивности в Цепи Переменного Тока: Принцип Действия
Катушки индуктивности различных модификаций
Сегодня нами будет рассмотрена катушка индуктивности в цепи переменного тока, узнаем, в чем бы была разница, если бы цепь питалась от постоянного тока, а также много интересных особенностей этого простого, но очень важного радиоэлемента.
Теоретика
Для начала давайте определим назначение этой детали, а также основные понятия и термины, связанные с ней.
Что такое катушка индуктивности
Разнообразие размеров катушек
Катушка индуктивности – это радиоэлемент, применяющийся в разных схемах для следующего:
- Сглаживание биений;
- Подавление помех;
- Ограничение переменного тока;
- Накопление энергии и прочее.
Представляет собой данный элемент спиральную, винтовую или винтоспиральную катушку, сделанную из изолированного проводника. Деталь обладает относительно малой емкостью и малым активным сопротивлением, при этом у него имеет высокая индуктивность, то есть способность возникновения ЭДС (электродвижущей силы) в проводнике, при протекании в цепи электрического тока.
Дроссели на печатной плате
- Катушка индуктивности, в зависимости от места и цели применения может иметь и другие названия. Например, если элемент используется для изоляции по высокой частоте в разных частях схемы, накоплении энергии магнитного поля сердечника, сглаживания пульсаций и подавления помех, катушку называют дросселем либо реактором (второе название употребляется редко).
- Если говорить про силовую электротехнику, то там устоялось название ректор – его применяют при необходимости ограничения тока, например, если произошло замыкание на ЛЭП.
Соленоид
- Бывают также и цилиндрические катушки индуктивности, называемые соленоидами. Длина такого цилиндра в несколько раз превышает его диаметр.
Интересно знать! Магнитное поле внутри соленоида однородно. Данное магнитное поле может выполнять механическую работу, втягивая ферритовый сердечник.
Обмотка с втягивающего реле на стартере
- Применяются катушки индуктивности и в электромагнитных реле, где их называют обмоткой реле.
- Устанавливаются подобные элементы и в индукционные нагреватели – тут их называют нагревательными индукторами.
Схема сверхпроводящего индуктивного накопителя
- Также можно услышать термины вроде индукционного накопителя или накопительного дросселя, если речь идет об устройствах импульсной стабилизации напряжения.
Конструкционные особенности
Строение катушки индуктивности
Конструкционно катушка индуктивности представляет собой намотанную по спирали или винтом изолированную одножильный или многожильный проводник (чаще, лакированная медная проволока), вокруг диэлектрического сердечника (каркаса). Форма сердечника может быть круглой, тороидальной, прямоугольной, квадратной. Материалы, применяемые для сердечника, имеют магнитную проницаемость выше, чем у воздуха, что дополнительно удерживает магнитное поле возле катушки, а значит, увеличивается и индуктивность.
Существуют и катушки, вовсе не имеющие сердечника, или же он является регулируемым, что позволяет менять индуктивность детали.
Тороидальная катушка
Намотка проводника может быть как однослойной, ее еще называют рядовой с шагом, или многослойной (применяются названия универсал, внавал, рядовая). Расстояние между витками называется шагом.
Интересно знать! Шаг намотки может быть прогрессивным, то есть его величина изменяется по длине катушки. Применяется такая намотка для снижения «паразитной» емкости.
Применение
Используются катушки в схемах обработки сигналов и аналоговых схемах. В сочетании с конденсаторами и прочими радиокомпонентами могут формировать участки схем, которые усиливают или отфильтровывают определенные сигналы.
Широко применяются дроссели в источниках питания, где они вместе с конденсаторами фильтра призваны устранить остаточные помехи и прочие колебания, возникающие на выходе.
Строение трансформатора
Если две катушки соединить одним магнитным полем, то получится трансформатор – устройство, способное передавать электричество от одной части цепи к другой, за счет электромагнитной индукции, попутно меняя величину напряжения.
Для справки! Трансформаторы способны функционировать только с переменным током.
Основные характеристики катушек индуктивности
Прежде чем разбираться с тем, как ведет себя ток, проходя в цепи через катушку индуктивности, давайте сначала узнаем главные характеристики этого элемента.
Определение индуктивности: формула
- Прежде всего, нас интересует индуктивность – значение, численно выражающаяся соотношением потока магнитного поля, которое создается протекающим током, к силе этого самого тока. Измеряется этот параметр в Генри (Гн).
- Если говорить более простым языком, то это явление можно описать так. При протекании тока через катушку индуктивности создается электромагнитное поле, которое напрямую связано с ЭДС, которая оказывает противодействие изменению переменного напряжения, то есть в цепи возникает ток, который течет в обратном направлении основному.
- Измерение силы тока на катушке индуктивности и переменного напряжения, противостоят данной силе, точнее наоборот. Это свойство элемента называется индуктивным сопротивлением, которое находится в противофазе реактивному емкостному сопротивлению конденсатора, включенному в цепь переменного тока.
Совет! Изменение величины индуктивности катушки происходит пропорционально изменению числа витков.
Расчет энергии магнитного поля катушки
- Давно известно, что любое магнитное поле обладает некоторой энергией. Отсюда следует, что магнитное поле катушки тоже имеет определенный запас магнитной энергии. Величина этого запаса равна затраченной энергии на обеспечение протекания тока (I) в противодействие ЭДС. Расчеты производятся по приведенной выше формуле.
Гидротурбина
- Чтобы было еще понятнее давайте сравним катушку с гидротурбиной. Итак, водяной поток, который направлен через турбину, будет ощущать ее сопротивление, пока турбина до конца не раскрутится. Она имеет некоторую инерцию, а значит, будет вращаться синхронно с потоком воды, не оказывая ему практически никакого сопротивления.
- Если вы попробуете остановить поток воды или сменить его направление, то увидите, что турбина продолжит вращаться по инерции, заставляя двигаться воду в прежнем направлении. Чем выше инерция у турбины, тем сильнее она будет сопротивляться изменению направления потока воды.
- Ровно то же самое происходит в катушке индуктивности, когда переменный ток начинает течь в обратном направлении.
При последовательном соединении катушек их индуктивность складывается
- Влияние тока на индуктивность катушки выражается не только в виде основного эффекта взаимодействия. Часто наблюдаются паразитные эффекты, из-за которых сопротивление переменному току катушки индуктивности чисто реактивным назвать нельзя. Из-за этих эффектов в катушке возникают некоторые потери, оценивающиеся как сопротивление потерь. Данное значение составляет сумму потерь в сердечнике, проводе, экране и диэлектрике.
- Каждая из потерь вызвана разными причинами. В проводах их целых три: они обладают хоть и малым, но все же активным омическим сопротивлением; данное сопротивление растет с увеличением частоты, что обусловлено уменьшением амплитуды электромагнитных волн, по мере того как они проникают в глубину проводящей среды (это явление называется скин-эффектом) – другими словами, ток вытесняется на верхние слои провода, из-за чего изменяется площадь проводника, а значит, и его сопротивление; если провода свиты в спираль, возникает эффект близости, из-за которого тоже меняется активное сечение проводника, и общее сопротивление.
Дроссель сварочного аппарата
- Потери в диэлектрике могут возникать из-за межвиткового конденсатора, или по причине его электромагнитных свойств. Однако справедливости ради стоит отметить, что потери в этой части детали настолько малы, что ими часто пренебрегают при расчетах.
- Потери на сердечнике складываются из двух величин: потери на перемагничивание ферромагнетика (потери на гистерезис) и потери на вихревые токи. Переменное магнитное поле, возникающее от протекающего в проводнике тока, индуцирует вихревые ЭДС в соседних проводниках – сердечнике, проводах ближайших витков, и даже экране. Возникшие токи, имеющие название помимо вихревых, токи Фуко, также являются причиной потерь, из-за активного сопротивления провода.
- С потерями на сопротивление связана и другая характеристика, называемая добротностью. Ее величина – это соотношение реактивного и активного сопротивления катушки индуктивности.
Паразитная емкость катушки индуктивности
- Следующий параметр – это паразитная емкость. Явление состоит в том, что между витками катушки возникает некоторая нежелательная емкостная связь.
- ТКИ (температурный коэффициент индуктивности) – все мы знаем, что при нагревании вещества увеличиваются в размерах. Когда это происходит с катушкой, мы получаем нестабильность индуктивности, из-за изменения длины и диаметра проводника, длины и диаметра каркаса, а значит, изменения диаметра и шага витков. Помимо этого перемена температуры влияет на диэлектрическую проницаемость материала каркаса, что влечет изменение емкости катушки и влияет на проницаемость магнитным полем ферромагнетика сердечника.
- ТКД (температурный коэффициент дробности) – тут все понятно! Это изменение параметров добротности в зависимости от температуры.
Включение катушки индуктивности в цепи с постоянным и переменным током
В целом, мы определили, что такое катушка индуктивности, для чего она нужна, и какие характеристики для расчета ее параметров важны, однако до сих пор неискушенному читателю наверняка не понятно, как будут изменяться параметры протекающего через эту деталь тока.
Цепь, питаемая постоянным током
Катушка индуктивности в цепи постоянного тока
Чтобы упростить изложение, будем проводить очень простой опыт:
- Для начала нам потребуется блок питания, способный выдавать стабильные 12 Вольт напряжения на выходе, 12-ти вольтовая лампочка накаливания для создания сопротивления, а также сама катушка индуктивности.
Стержень из феррита
- Катушку мы соберем своими руками из куска лакированной медной проволоки и ферритового стержня.
Изготовление катушки индуктивности
- Инструкция предельно проста — берем проволоку и наматываем ее на стержень, после чего зачищаем ножом концы, чтобы можно было подсоединить клеммы от блока питания и подпаять провода.
- Цена такой схемы минимальна, так что можете без проблем повторить опыт при желании дома.
Измерение индуктивности собранной катушки
- При помощи LC-метра измеряем индуктивность полученной детали. Как видно из фото выше, в рассматриваемом примере она составила 132 мкГн.
Схема с включенной катушкой индуктивности
- Теперь берем все наши детали и соединяем их по приведенной выше схеме.
Схема включена в сеть
- Вот что получилось на практике. Как видим, постоянный ток протекает через катушку практически беспрепятственно, если не учитывать естественное сопротивление проводника, ведь ток не меняет своего направления на противоположное.
На данной схеме лампочку заменяет резистор, но это не важно
- Значит ли это, что катушка индуктивности неприменима в цепях с постоянным током? Вовсе нет! Вот другая схема, в которую, как мы видим, уже включен некий выключатель, способный размыкать цепь. Именно в момент замыкания и происходит самое интересное.
- Поскольку до этого ток был равен нулю, он начнет изменяться и расти, из-за чего изменится магнитное поле катушки, что в свою очередь приведет к возникновению ЭДС. В катушке появится индукционный ток, который потечет в обратном направлении основного потока от источника питания.
- Именно в момент включения величина ЭДС будет максимальной, так как скорость изменения тока в этот момент наиболее высока, а значит, ток катушки индуктивности равен нулю.
- Что произойдет дальше? А дальше мы увидим, что ток в катушке индуктивности начнет расти, тогда как ЭДС, наоборот, снижаться. Вот как это выглядит на графике.
Uвх – входное напряжение питания; Il- изменение величины тока; Ul – напряжение на катушке
- На верхнем графике изображено изменение напряжения входной сети, сразу после включения. Как видим, моментально появляется постоянное значение.
- Дальше показано, как меняется величина тока, протекающего через катушку. Он тоже достигает постоянно значения, но не сразу, а спустя какое-то время.
- Напряжение на катушке (нижний график) также вырастает моментально, но тут же начинает падать. При этом обратите внимание, что графики силы тока и напряжения зеркально противоположны.
- Если все это перенести на наш опыт с лампой, то мы увидим, что после соединения цепи через выключатель, она загорится не сразу, а с некоторой задержкой.
Похожая ситуация будет и при размыкании цепи.
Физические процессы в катушке при размыкании цепи
По графикам видна противоположная ситуация, означающая, что лампочка продолжить гореть еще какое-то время после размыкания цепи.
Дело в том, что при прекращении подачи питания, в катушке снова возникнет ЭДС, однако ток индукции потечет теперь в том же направлении, что и от источника питания, то есть запасенная энергия в катушке, поддержит питание цепи.
Включение в цепь с переменным током
Теперь давайте проведем другой опыт, в котором подключим сделанную ранее катушку к источнику питания переменного тока.
Схема включения катушки индуктивности в цепь переменного тока
- Для создания приведенной схемы и снятия показаний нам потребуются: генератор частоты, осциллограф, резистор на 100 Ом и сама катушка.
Схема в сборе
- На фото выше виден осциллограф, отображающий 2 синусоиды. Это каналы, соответствующие частотам генератора (красная) и резистора (желтая), который включен в цепь уже после катушки индуктивности.
- Опыт с постоянным током показал, что катушка индуктивности при неизменном токе, никак не изменяет параметры тока, то есть не оказывает ему никакого сопротивления, а изменения случаются лишь во время включения и выключения питания.
- Теперь же, при помощи генератора, мы сможем посмотреть, как изменится сопротивление катушки, вследствие увеличения частот.
Ток имеет частоту 1 кГц
- Для начала подадим ток частотой в 1 кГц. Как видно из показаний, сигнал на выходе ничем не отличается от входного – сохранились и частота, и амплитуда.
Частота в 100 кГц
- Наращиваем частоту, останавливаясь на 100 кГц-ах. По графикам видно, что произошло какое-то изменение. А именно, уменьшилась амплитуда (ток стал выравниваться) и желтый график сместился вправо (появилась задержка) – это явление называет сдвигом фаз, то есть разницей между начальными и итоговыми замерами величин.
Интересно знать! Чтобы иметь возможность измерить сдвиг фаз, необходимо чтобы сигналы имели одинаковую частоту. Амплитуда значения не имеет.
Сдвиг фаз
Давайте посмотрим, что произойдет, если частоту увеличить еще.
Частота в 500 кГц
- По графикам видно, что тенденция сохранилась. Фаза сдвинулась еще сильнее, а амплитуда упала до 480 милливольт, хотя изначально равнялась практически 2 Вольтам.
Частота в 2 Мегагерца
- Выставляем максимальную частоту, что способен выдать наш генератор, и видим падение амплитуды до 120 мВ, и смещение фазы практически на 90 градусов.
- Отсюда можно сделать вывод, что с увеличением частоты питающего тока сопротивление катушки индуктивности будет расти. При этом происходит сдвиг фаз, максимальное значение которого составляет 90 градусов.
Сопротивление катушки напрямую зависит от ее индуктивности и рассчитывается по следующей формуле.
Расчет сопротивления катушки индуктивности
Работает при этом катушка все по тому же принципу.
Изменение тока и ЭДС самоиндукции
На графике показана зависимость тока и ЭДС от времени. Почему она выглядит именно так?
- Мы уже выяснили на примере постоянного тока, что ЭДС прямопропорциональна скорости, с которой изменяется сила тока. Собственно на графике и показывается эта зависимость.
- Рассмотрим часть графика. Между точками 1 и 2 ток изменяется, причем вначале изменение весьма резкое, но чем ближе к точке 2, тем оно сильнее замедляется, а в некотором промежутке времени и вовсе остается почти одинаковым.
- Отсюда следует, что скорость изменения тока выше около точки 1, а значит, в тот момент времени ЭДС и будет самым высоким.
- Также мы помним, что направление ЭДС противоположно основному току, то есть принимает отрицательное значение. Вот собственно и показанная зависимость – ток от точки 1 до точки 2 растет, а ЭДС падает, при прямой зависимости от скорости изменения тока.
- Идем дальше – промежуток 2-3. Ток у нас падает – сначала с медленной, а затем быстрой скоростью. ЭДС же, наоборот, растет, принимая положительное значение. И так далее, по аналогии.
Теперь, что касается знаков. На участке 1-2, у тока и ЭДС они противоположные, а значит, ЭДС тормозит ток, препятствуя его возрастанию, из-за того что они направлены навстречу друг другу. Далее идет участок 2-3, на котором ток и ЭДС выравниваются по знакам, а значит ЭДС побежит в ту же сторону, поддерживая убывающий ток.
Вот мы и пришли к тому факту, что току, протекающему в цепи, катушка индуктивности оказывает индуктивное или реактивное сопротивление. Возвращаясь к формуле расчета этого сопротивления, видим, что, так как частота в постоянном токе равно 0, сопротивление не оказывается, и наоборот, высокая частота переменного тока, увеличивает сопротивление катушки.
Так, мы что-то забыли! Да, конечно же! Что будет в это время с напряжением?
Зависимость напряжения и тока от времени
Из графика видно, что ток относительно напряжения сдвинут по фазе на ¼ такта, или на 90 градусов (отстает), что является одним из важнейших свойств цепей переменного тока, с включенной катушкой индуктивности.
Как все это можно задействовать на практике. Самый банальный пример – это фильтр низких частот (ФНЧ). Мы увидели, что сигнал с высокой частотой проходит намного хуже, тогда как низкочастотный, не испытывает никакого сопротивления. Если включить катушку индуктивности в цепь, запитывающую динамик, то мы получим обрезку высоких частот, превращая конструкцию в сабвуфер, играющий только басы.
На этом все. Мы разобрали, как меняется ток катушки индуктивности, ЭДС и напряжение. Кто бы мог подумать, что это простое устройство совершает такую работу? Этим то и прекрасен мир электротехники. Изучайте его, и вам откроется много интересного! В дополнение просмотрите лекцию из видео в этой статье. Удачи!
Урок 9. конденсатор и катушка индуктивности в цепи переменного электрического тока — Физика — 11 класс
Физика, 11 класс
Урок 9. Конденсатор и катушка индуктивности в цепи переменного электрического тока
Перечень вопросов, рассматриваемых на уроке:
Процессы, происходящие в цепи переменного электрического тока при наличии конденсатора и катушки индуктивности;
Устройство и принцип действия генератора переменного тока и трансформатора;
Автоколебания;
Проблемы передачи электроэнергии и способы повышения эффективности её использования.
Глоссарий по теме
Автоколебания – незатухающие колебания в системе, поддерживаемые за счет постоянного источника энергии.
Электрические машины преобразующие механическую энергию в электрическую называются генераторами.
Трансформатор – устройство, применяемое для повышения или понижения переменного напряжения.
Коэффициент трансформации – величина равная отношению напряжений в первичной и вторичной обмотках трансформатора.
Основная и дополнительная литература по теме урока:
Мякишев Г.Я., Буховцев Б.Б., Чаругин В.М. Физика.11 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2014. – С. 86 – 95.
Рымкевич А.П. Сборник задач по физике. 10-11 класс. — М.: Дрофа, 2014. – С. 128 – 132.
Степанова. Г.Н. Сборник задач по физике. 10-11 класс. М., Просвещение 1999 г.
Е.А. Марон, А.Е. Марон. Контрольные работы по физике. М., Просвещение, 2004
Основное содержание урока
Переменный ток, которым мы пользуемся, вырабатывается с помощью генераторов переменного тока на электростанциях. Для передачи произведенной электроэнергии строятся линии электропередачи. В каждом населенном пункте имеются трансформаторы. Какую роль играют трансформаторы при передаче электроэнергии? Об этом мы поговорим на данном уроке.
В июле 1832 года Фарадей получил анонимное письмо, в котором автор описывал устройство созданного им генератора постоянного тока. Ознакомившись с содержанием письма Фарадей тут же отослал его в редакцию научного журнала. Автор этого письма не назвал себя, его фамилия осталась неизвестной.
Электрические машины преобразующие механическую энергию в электрическую называются генераторами. Впоследствии генераторы постоянного тока непрерывно совершенствовались. Потом, когда начали использовать переменный ток они уступили место генераторам переменного тока. Переменный ток в основном вырабатывается генераторами переменного тока. Простой моделью генератора может служить прямоугольная рамка, вращающаяся в магнитном поле. При вращении рамки, магнитный поток пронизывающий площадь поверхности, ограниченную рамкой, меняется по гармоническому закону:
N- число витков.
Возникает ЭДС индукции который меняется по гармоническому закону.
ЭДС индукции в рамке равна:
Если с помощью контактных колец и скользящих по ним щёток соединить концы рамки с электрической цепью, то в цепи возникнет переменный ток.
В современной энергетике для производства электроэнергии используются электромеханические индукционные генераторы. Принцип действия таких генераторов основан на явлении электромагнитной индукции. Основными частями генератора являются статор и ротор. Неподвижная часть генератора называется статором, а вращающаяся – ротором.
Постоянный ток не может идти по цепи содержащей конденсатор, т. к. цепь оказывается разомкнутой. При включении конденсатора в цепь переменного тока конденсатор будет периодически заряжаться и разряжаться с частотой равной частоте приложенного напряжения. В результате периодически меняющихся процессов зарядки и разрядки конденсатора в цепи течет переменный ток. Лампа накаливания, включенная в цепь переменного тока последовательно с конденсатором кажется горящей непрерывно, т.к. при высокой частоте колебаний силы тока человеческий глаз не способен заметить периодического ослабления нити накала. Конденсатор оказывает сопротивление прохождению тока. Это сопротивление называют ёмкостным.
Величину ХC, обратную произведению циклической частоты на электрическую ёмкость конденсатора называют ёмкостным сопротивлением.
Ёмкостное сопротивление не является постоянной величиной. Мы видим, что конденсатор оказывает бесконечно большое сопротивление постоянному току. Чем больше ёмкость конденсатора и частота колебаний, тем больше ток перезарядки. При наличии в цепи переменного тока конденсатора колебания силы тока опережают по фазе колебания напряжения конденсаторе на 90º. Сдвиг фазы колебаний силы тока на 90º относительно фазы колебания напряжения на конденсаторе приводит к тому, что мощность переменного тока в течение одной четверти периода имеет положительный знак, а в течение второй четверти – отрицательный. Поэтому среднее значение мощности за период равно нулю.
Индуктивность в цепи, так же, как и ёмкость, влияет на силу переменного тока. Объясняется это явлением самоиндукции. В любом проводнике, по которому протекает переменный ток, возникает ЭДС самоиндукции. При подключении катушки к источнику постоянного напряжения сила тока в цепи нарастает постепенно. Возникающее при этом вихревое электрическое поле тормозит движение электронов. Лишь спустя некоторое время сила тока достигает максимального значения, соответствующего данному постоянному напряжению. Если напряжение быстро меняется, то сила тока не будет успевать достигать тех значений, которые она приобрела бы при постоянном напряжении. Следовательно, максимальное значение силы переменного тока ограничивается индуктивностью цепи и его частотой колебаний.
Величину ХL, равную произведению циклической частоты на индуктивность, называют индуктивным сопротивлением.
Если частота равна нулю, то индуктивное сопротивление тоже равно нулю. Поэтому постоянный ток как бы не «замечает» катушку индуктивности в цепи.
Колебания напряжения на катушке опережают по фазе колебания силы тока на 90º.
Сдвиг фазы колебаний приводит к тому, что средняя мощность за период колебаний равна нулю.
Генератор на транзисторе используется для создания высокочастотных электромагнитных колебаний.
Для потребления электрической энергии нужно доставить его от источника к потребителю. Для этого строят линии электропередачи. При передаче электроэнергии на расстояние возникают потери энергии вследствие нагревания проводов. Тепловые потери можно определить используя закон Джоуля – Ленца:
Из этой формулы следует, что для уменьшения потерь энергиинужно уменьшить сопротивление или повысить напряжение. Уменьшения сопротивления проводов ЛЭП требует увеличения их площади поперечного сечения, что приведет к увеличению массы проводов. Увеличение массы проводов связано с большими расходами на укрепление столбов линии электропередачи, для их удержания и на производство металла для них. Наиболее эффективным является увеличение напряжения.
Для изменения напряжения в сети используют трансформаторы. Трансформатор был изобретен в 1876 году Яблочковым и в 1882 году усовершенствован Усагиным. Простейший трансформатор состоит из двух катушек, надетых на общий замкнутый стальной сердечник. Эти катушки называются обмотками трансформатора. Обмотка трансформатора, подключаемая к источнику переменного напряжения, называют первичной, а другая к которой присоединяют нагрузку – вторичной. Действие трансформатора основано на явлении электромагнитной индукции. При прохождении переменного тока по первичной обмотке в трансформаторе возникает переменное магнитное поле. Это поле пронизывает обе обмотки и в них возникает вихревое электрическое поле, которое действуя на заряженные частицы во вторичной обмотке способствует возникновению в ней переменного напряжения.
Величина равная отношению напряжений в первичной и вторичной обмотках трансформатора называют коэффициентом трансформации. Его обозначают буквой «k».
k– коэффициент трансформации.
U1 иU2 – напряжения на первичной и на вторичной обмотке.
N1 и N2— число витков на первичной и на вторичной обмотке.
Если k < 1 — трансформатор повышающий,
k > 1 — трансформатор понижающий.
КПД трансформатора равен отношению мощности в нагрузке к мощности, подаваемой из сети на первичную обмотку:
Для передачи электроэнергии на расстояние напряжение повышают с помощью трансформатора, а для потребления — понижают. В массивных проводниках при изменении магнитного поля возникают индукционные токи (токи Фуко), которые нагревают проводник. Чтобы эти индукционные токи не нагревали сердечник трансформатора его делают не сплошным, а из отдельных пластин, скрепленных вместе.
Закон Ома гласит: значение тока в цепи переменного тока прямо пропорционально напряжению в цепи и обратно пропорционально полному сопротивлению цепи.
Из формулы закона Ома для переменного тока мы видим, что при постоянной амплитуде напряжения, амплитуда силы тока зависит от частоты. Амплитуда силы тока будет максимальной, если полное сопротивление минимально. Полное сопротивление цепи минимально при равенстве индуктивного и ёмкостного сопротивления. В этом заключается условие возникновения резонанса в электрической цепи.
Резонанс в электрической цепи – это явление резкого возрастания амплитуды колебаний силы тока в контуре при совпадении частоты вынужденных колебаний с частотой собственных колебаний контура.
Явление резонанса широко используется в радиотехнике, в схемах настройки радиоприемников. Меняя электроемкость конденсатора в колебательном контуре можно настроить его на нужную волну, т.е. выделить частоту на которой работает передающая станция
Разбор тренировочных заданий
1. Каково амплитудное значение ЭДС, возникающей в рамке из 50 витков, если она вращается с циклической частотой 180 рад/с в магнитном поле индукцией 0,4 Тл? Площадь рамки 0,02 м2.
Дано:
N=50
ω=180 рад/с
B=0,4 Тл
S=0,02 м2
_________
Ԑm=?
Решение:
Ответ: 72 В.
2. Катушка с индуктивностью 0,08 Гн присоединена к источнику переменного тока частотой 1000 Гц. При этом вольтметр показывает 100 В. Определить амплитуду тока в цепи. Ответ округлить до десятых.
Дано:
L=0,08 Гн
ν= 1000 Гц
U=100 В
__________
Im=?
Решение:
Напишем закон Ома для переменного тока
Т.к. ХC и R равны нулю, то
Учитывая, что , получаем:
Найдем амплитудное значение напряжения:
Подставим числовые данные в формулу для расчета амплитуды силы тока:
Ответ: Im = 0,3 А.
2. Катушка индуктивности в цепи переменного тока | 3. Реактивное сопр. и импеданс — Индуктивность | Часть2
2. Катушка индуктивности в цепи переменного тока
Катушка индуктивности в цепи переменного тока
Катушка индуктивности в цепи переменного тока ведет себя не так, как резистор. Если резисторы просто противостоят потоку электронов (напряжение на них прямопропорционально току), то катушки индуктивности противостоят изменению проходящего через них тока (напряжение на них прямопропоционально скорости изменения тока). Согласно Закону Ленца, индуцированное напряжение всегда имеет такую полярность, которая пытается сохранить текущее значение силы тока. То есть, если величина тока возрастает, то индуцированное напряжение будет «тормозить» поток электронов; если величина тока уменьшается, то полярность напряжения развернется и будет «помогать» электронному потоку оставаться на прежнем уровне. Такое противостояние изменению величины тока называется реактивным сопротивлением.
Математическая взаимосвязь между напряжением на катушке индуктивности и скоростью изменения тока через нее выглядит следующим образом:
Отношение di/dt представляет собой скорость изменения мгновенного тока (i) с течением времени, и измеряется в амперах в секунду. Индуктивность (L) измеряется в Генри, а мгновенное напряжение (u) — в вольтах. Чтобы показать, что происходит с переменным током, давайте проанализируем простую индуктивную схему:
Простая индуктивная цепь: ток катушки отстает от напряжения на 90o.
Если мы построим график тока и напряжения для этой простой цепи, то он будет выглядеть примерно так:
Как вы помните, изменение напряжения на катушке индуктивности является реакцией на изменение тока, проходящего через нее. Отсюда можно сделать вывод, что мгновенное напряжение равно нулю всякий раз, когда мгновенное значение тока находится в пике (нулевое изменение, или нулевой наклон синусоидальной волны тока), и мгновенное напряжение равно своему пиковому значению всякий раз, когда мгновенный ток находится в точках максимального изменения (точки самого крутого наклона волны тока, в которых она пересекает нулевую линию). Все это приводит к тому, что волна напряжения на 90o не совпадает по фазе с волной тока. На графике видно, как волна напряжения дает «фору» волне тока: напряжение «ведет» ток, а ток «запаздывает» за напряжением.
Ели мы на этот график нанесем значения мощности нашей схемы, то все станет еще более интересным:
Поскольку мгновенная мощность представляет собой произведение мгновенного напряжения и мгновенного тока (p = iu), она будет равна нулю, если мгновенное напряжение или ток будут равны нулю. Всякий раз, когда мгновенные значения тока и напряжения имеют положительные значения (выше нулевой линии), мощность так же будет положительна. Аналогично примеру с резистивной цепью, мощность примет положительное значение и в том случае, если мгновенный ток и напряжение будут иметь отрицательные значения (ниже нулевой линии). Однако, вследствие того, что волны напряжения и тока не совпадают по фазе на 90o, бывают случаи, когда ток положителен, а напряжение отрицательно (или наоборот), в результате чего появляются отрицательные значения мгновенной мощности.
Но, что такое отрицательная мощность? Отрицательная мощность означает, что катушка индуктивности отдает энергию обратно в цепь. Положительная же мощность означает, что катушка индуктивности поглощает энергию из цепи. Так как положительные и отрицательные циклы питания равны по величине и продолжительности, в течение полного цикла катушка индуктивности отдает обратно в схему столько же энергии, сколько она потребляет из нее. В практическом смысле это означает, что реактивное сопротивление катушки не рассеивает никакой энергии, чем оно и отличается от сопротивления резистора, рассеивающего энергию в виде тепла. Однако, все вышесказанное справедливо только для идеальных катушек индуктивности, провода которых не имеют никакого сопротивления.
Сопротивление катушки индуктивности, изменяющее силу тока, интерпретируется как сопротивление переменному току в целом, у которого по определению постоянно меняется мгновенная величина и направление. Это сопротивление переменному току похоже на обычное сопротивление, но отличается от него тем, что всегда приводит к фазовому сдвигу между током и напряжением, а так же рассеивает нулевую мощность. Из-за указанных различий, данное сопротивление носит несколько иное название — реактивное сопротивление. Реактивное сопротивление, как и обычное, измеряется в Омах, только обозначается оно символом Х, а не R. Для большей конкретики, реактивное сопротивление катушки индуктивности обычно обозначают заглавной буквой Х с буквой L в качестве индекса: XL.
Поскольку напряжение на катушке индуктивности пропорционально скорости изменения тока, оно будет больше для быстро меняющихся токов, и меньше — для токов с более медленным изменением. Это означает, что реактивное сопротивление любой катушки индуктивности (в Омах) прямопропорционально частоте переменного тока. Точная формула расчета реактивного сопротивления выглядит следующим образом:
Если на катушку индуктивностью 10 мГн воздействовать частотами 60, 120 и 2500 Гц, то ее реактивное сопротивление примет следующие значения:
| Частота (Гц) | Реактивное сопротивление (Ом) |
|---|---|
| 60 | 3.7699 |
| 120 | 7.5398 |
| 2500 | 157.0796 |
В уравнении реактивного сопротивления выражение “2πf” имеет важное значение. Оно означает число в радианах в секунду, характеризующее «вращение» переменного тока (один полный цикл переменного тока представляет собой одно полное круговое вращение). Радиан — это единица измерения углов: в одном полном круге есть 2π радиан, точно так же, как в нем есть 360o. Если генератор переменного тока двухполюсный, то он произведет один полный цикл для каждого полного оборота вала, что будет означать 2π радиан или 360o. Если постоянную 2π умножить на частоту в герцах (циклах в секунду), то результатом будет число в радианах в секунду, известное как угловая (циклическая) частота переменного тока.
Помимо выражения 2πf, угловая частота переменного тока может обозначаться строчной греческой буквой ω (Омега). В этом случае формула XL = 2πfL может быть написана как XL = ωL.
Необходимо понимать, что угловая частота является выражением того, насколько быстро проходит полный цикл волны, равный 2π радиан. Она необязательно представляет фактическую скорость вала генератора, производящего переменный ток. Если генератор имеет более двух полюсов, его угловая частота будет кратной скорости вращения вала. По этой причине ω иногда выражается в единицах электрических радиан в секунду, чтобы отличить ее от механического движения.
При любом способе выражения угловой частоты очевидно, что она прямопропорциональна реактивному сопротивлению катушки индуктивности. При увеличении частоты переменного тока (или скорости вращения вала генератора), катушка индуктивности будет оказывать большее сопротивление прохождению тока и наоборот. Переменный ток в простой индуктивной цепи равен напряжению (в Вольтах) поделенному на реактивное сопротивление катушки индуктивности (в Омах). Как видите, это аналогично тому что переменный или постоянный ток в простой резистивной цепи равен напряжению (в Вольтах) поделенному на сопротивление (в Омах). В качестве примера давайте рассмотрим следующую схему:
Однако, мы должны иметь в виду, что напряжение и ток имеют разные фазы. Как было сказано ранее, напряжение имеет фазовый сдвиг +90o по отношению к току (рисунок ниже). Если представить фазовые углы напряжения и тока математически (в виде комплексных чисел), то мы увидим, что сопротивление катушки индуктивности переменному току обладает следующим фазовым углом:
Ток на катушке индуктивности отстает от напряжения на 90o.
Математически можно сказать, что фазовый угол сопротивления катушки индуктивности переменному току составляет 90o. Фазовый угол реактивного сопротивления току очень важен при анализе цепей. Особенно эта важность проявляется при анализе сложных цепей переменного тока, где реактивные и простые сопротивления взаимодействуют друг с другом. Он также окажется полезным для представления сопротивления любого компонента электрическому току с точки зрения комплексных чисел (а не скалярных величин сопротивления и реактивного сопротивления).
Катушка индуктивности в цепи переменного тока: индуктивное сопротивление
Индуктивность в цепи переменного тока будет влиять на силу переменного тока. Проверим это на следующем опыте.
Возьмем два источника питания. Один из них пусть будет источником постоянного напряжения, а второй – переменного. Причем подберем источники так, чтобы постоянное значение напряжения равнялось действующему значению переменного напряжения. Подключим к ним с помощью переключателя цепь, состоящую из лампочки и катушки индуктивности.
Причем лампочка и катушка подключены последовательно. Переключатель включим так, чтобы при одном положении цепь питалась от источника постоянного тока, а при другом – от источника переменного тока.
рисунок
При включении питания от источника постоянного тока лампочка загорится очень ярко. Если подключить цепь к источнику тока с переменным напряжением, то лампочка будет гореть, но заметно слабее. Можем сделать вывод, что действующее значение силы тока при переменном токе меньше, чем сила тока при постоянном источнике.
Индуктивность катушки
Это можно объяснить с помощью явления самоиндукции. ЭДС самоиндукции катушки будет достаточно большим, и будет препятствовать нарастанию силы тока, поэтому свое максимальное значение сила тока достигнет только спустя некоторое время. Если напряжение будет быстро меняться, то сила тока не будет успевать достигнуть своего максимального значения.
Можно сделать вывод, что индуктивность катушки будет ограничивать максимальное значение силы тока. Чем больше индуктивность катушки и частота изменения напряжения, тем меньше будет максимальное значение силы тока.
Рассмотрим цепь, в которой есть только катушка индуктивности. При этом значение сопротивления катушки и соединительных проводов пренебрежимо мало.
рисунок
Выясним, как будут связаны напряжение на катушке с ЭДС самоиндукции в ней. При сопротивлении катушки равном нулю, напряженность электрического поля внутри проводника тоже будет равна нулю. Равенство нулю напряженности возможно.
Напряженности электрического поля создаваемого зарядами Eк будет соответствовать такая же по модулю и противоположно направленная напряженность вихревого электрического поля, которое появится вследствие изменения магнитного поля.
Следовательно, ЭДС самоиндукции ei будет равна по модулю и противоположна по знаку удельной работе кулоновского поля.
Следовательно:
ei = -u.
Сила тока будет изменяться по гармоническому закону:
I = Im*sin(ω*t).
ЭДС самоиндукции будет равна:
Ei = -L*i’ = -L*ω*im*cos(ω*t).
Следовательно, напряжение будет равно:
U = L*ω*Im*cos(ω*t) = L*ω*Im*sin(ω*t+pi/2).
Отсюда значение действующего напряжения будет равняться Um = L*ω*Im. Видим, что между колебаниями тока и напряжения получилась разность фаз равная pi/2.
Индуктивное сопротивление
Следовательно, колебания силы тока отстают от колебания напряжения на pi/2. Это наглядно представлено на следующем рисунке.
рисунок
Im = Um/(ω*L). Введем обозначение XL = ω*L. Эта величина называется индуктивное сопротивление.
Нужна помощь в учебе?
Предыдущая тема: Конденсатор в цепи переменного тока: изменение силы тока в цепи
Следующая тема:   Резонанс в электрической цепи: генератор на транзисторе
Индуктор
и влияние индуктивности на индуктор
В наших уроках по электромагнетизму мы видели, что когда электрический ток течет по проводнику, вокруг этого проводника создается магнитный поток. Этот эффект создает взаимосвязь между направлением магнитного потока, циркулирующего вокруг проводника, и направлением тока, протекающего через тот же проводник. Это приводит к взаимосвязи между током и направлением магнитного потока, называемой «правилом правой руки Флеминга».
Но есть еще одно важное свойство, относящееся к намотанной катушке, которое также существует, а именно, что вторичное напряжение индуцируется в той же катушке движением магнитного потока, поскольку оно противодействует или сопротивляется любым изменениям электрического тока, протекающего по ней.
Типовой индуктор
В своей основной форме индуктор представляет собой не что иное, как катушку с проволокой, намотанную вокруг центрального сердечника. Для большинства катушек ток (i), протекающий через катушку, создает вокруг нее магнитный поток (NΦ), который пропорционален этому потоку электрического тока.
Катушка индуктивности , также называемая дросселем, представляет собой другой электрический компонент пассивного типа, состоящий из катушки с проволокой, предназначенной для использования преимущества этого отношения, создавая магнитное поле в себе или внутри сердечника в результате тока, протекающего через катушка проволоки. Превращение проволочной катушки в катушку индуктивности приводит к гораздо более сильному магнитному полю, чем то, которое создается простой катушкой с проволокой.
Катушки индуктивностисостоят из проволоки, плотно намотанной вокруг твердого центрального сердечника, который может быть либо прямым цилиндрическим стержнем, либо непрерывной петлей, либо кольцом для концентрации их магнитного потока.
Схематическое обозначение катушки индуктивности — это катушка с проводом, поэтому катушку с проволокой также можно назвать Inductor . Индукторы обычно классифицируются в зависимости от типа внутреннего сердечника, вокруг которого они намотаны, например, полый сердечник (на открытом воздухе), твердый железный сердечник или мягкий ферритовый сердечник, при этом различные типы сердечников выделяются путем добавления непрерывных или пунктирных параллельных линий рядом с катушка с проволокой, как показано ниже.
Символ индуктивности
Ток i, протекающий через катушку индуктивности, создает пропорциональный ему магнитный поток.Но в отличие от конденсатора, который препятствует изменению напряжения на своих пластинах, индуктор противодействует скорости изменения тока, протекающего через него, из-за накопления самоиндуцированной энергии в его магнитном поле.
Другими словами, катушки индуктивности сопротивляются изменениям тока или противодействуют им, но легко пропускают установившийся постоянный ток. Эта способность катушки индуктивности противостоять изменениям тока и которая также связывает ток, i с его магнитной индукционной связью, NΦ как константу пропорциональности, называется индуктивностью , которая обозначается символом L с единицами измерения Генри , ( H ) после Джозефа Генри.
Поскольку Генри является относительно большой единицей индуктивности сам по себе, для меньших индуктивностей используются подъединицы Генри для обозначения ее значения. Например:
Префиксы индуктивности
| Префикс | Обозначение | Множитель | Мощность десяти |
| милли | м | 1 / 1,000 | 10 -3 |
| микро | µ | 1/1 000 000 | 10 -6 |
| нано | n | 1/1 000 000 000 | 10 -9 |
Итак, чтобы отобразить подъединицы Генри, мы будем использовать в качестве примера:
- 1 мГн = 1 милли-Генри, что равно одной тысячной (1/1000) части Генри.
- 100 мкГн = 100 микро-Генри, что равно 100 миллионной (1/1 000 000) Генри.
Катушки индуктивности или катушки очень распространены в электрических цепях, и существует множество факторов, определяющих индуктивность катушки, например, форма катушки, количество витков изолированного провода, количество слоев проволоки, расстояние между ними. витки, проницаемость материала сердечника, размер или площадь поперечного сечения сердечника и т. д., и это лишь некоторые из них.
Катушка индуктивности имеет центральную площадь сердечника (A) с постоянным числом витков провода на единицу длины (l).Таким образом, если катушка из N витков связана посредством магнитного потока Φ, тогда катушка имеет потокосцепление NΦ, и любой ток, (i), который течет через катушку, будет создавать индуцированный магнитный поток в направлении, противоположном направлению поток тока. Затем, согласно закону Фарадея, любое изменение в этой магнитной потокосцепке вызывает самоиндуцированное напряжение в единственной катушке:
- Где:
- N — количество витков
- А — площадь поперечного сечения, м 2
- Φ — количество флюса в Webers
- мкм — проницаемость материала сердечника
- l Длина змеевика в метрах
- di / dt — скорость изменения тока в амперах в секунду
Изменяющееся во времени магнитное поле индуцирует напряжение, которое пропорционально скорости изменения тока, создающего его, с положительным значением, указывающим на увеличение ЭДС, и отрицательным значением, указывающим на уменьшение ЭДС.Уравнение, связывающее это самоиндуцированное напряжение, ток и индуктивность, можно найти, заменив мкН 2 А / л на L, обозначающую константу пропорциональности, называемую индуктивностью катушки.
Связь между потоком в катушке индуктивности и током, протекающим через катушку индуктивности, определяется следующим образом: NΦ = Li. Поскольку катушка индуктивности состоит из катушки с проводящим проводом, это затем уменьшает приведенное выше уравнение, чтобы получить самоиндуцированную ЭДС, иногда называемую обратной ЭДС , также индуцированную в катушке:
Обратная ЭДС, генерируемая индуктором
Где: L — самоиндукция, а di / dt — скорость изменения тока.
Катушка индуктивности
Итак, из этого уравнения мы можем сказать, что «Самоиндуцированная ЭДС равна индуктивности, умноженной на скорость изменения тока», и цепь с индуктивностью в один Генри будет иметь ЭДС в один вольт, индуцированную в цепи, когда ток, протекающий через цепь меняется со скоростью один ампер в секунду.
Одно важное замечание по поводу приведенного выше уравнения. Он только связывает ЭДС, создаваемую на катушке индуктивности, с изменениями тока, потому что, если течение тока в катушке индуктивности является постоянным и не изменяется, например, в установившемся режиме постоянного тока, то индуцированное напряжение ЭДС будет равно нулю, поскольку мгновенная скорость изменения тока равна ноль, di / dt = 0.
При постоянном постоянном токе, протекающем через катушку индуктивности и, следовательно, нулевом индуцированном напряжении на ней, индуктор действует как короткое замыкание, равное отрезку провода или, по крайней мере, с очень низким сопротивлением. Другими словами, сопротивление протеканию тока, обеспечиваемое катушкой индуктивности, сильно различается между цепями переменного и постоянного тока.
Постоянная времени индуктора
Теперь мы знаем, что ток не может мгновенно измениться в катушке индуктивности, потому что для того, чтобы это произошло, ток должен измениться на конечную величину за нулевое время, что приведет к тому, что скорость изменения тока будет бесконечной, di / dt = ∞ , что делает наведенную ЭДС бесконечной, а бесконечные напряжения не существуют.Однако, если ток, протекающий через катушку индуктивности, изменяется очень быстро, например, при срабатывании переключателя, на катушке индуктора могут возникать высокие напряжения.
Рассмотрим схему чистого индуктора справа. Когда переключатель (S1) разомкнут, ток через катушку индуктивности не протекает. Поскольку через катушку индуктивности не течет ток, скорость изменения тока (di / dt) в катушке будет равна нулю. Если скорость изменения тока равна нулю, в катушке индуктивности нет самоиндуцированной обратной ЭДС (V L = 0).
Если мы теперь замкнем переключатель (t = 0), ток будет течь по цепи и медленно поднимется до своего максимального значения со скоростью, определяемой индуктивностью катушки индуктивности. Эта скорость тока, протекающего через катушку индуктивности, умноженная на индуктивность катушки индуктивности в системе Генри, приводит к возникновению в катушке некоторой самоиндуцированной ЭДС фиксированного значения, как это определено приведенным выше уравнением Фарадея: V L = -Ldi / dt.
Эта самоиндуцированная ЭДС на катушке индуктора (V L ) борется с приложенным напряжением до тех пор, пока ток не достигнет своего максимального значения и не будет достигнуто состояние устойчивого состояния.Ток, который теперь протекает через катушку, определяется только постоянным током или «чистым» сопротивлением обмоток катушек, поскольку значение реактивного сопротивления катушки уменьшилось до нуля, потому что скорость изменения тока (di / dt) равна нулю в состояние устойчивого состояния. Другими словами, в реальной катушке существует только сопротивление катушки постоянному току, которое препятствует прохождению тока через себя.
Аналогичным образом, если переключатель (S1) разомкнут, ток, протекающий через катушку, начнет падать, но индуктор снова будет бороться с этим изменением и попытается сохранить текущее значение тока на его предыдущем значении, создавая другое напряжение в другом направлении. .Наклон падения будет отрицательным и связан с индуктивностью катушки, как показано ниже.
Ток и напряжение в индукторе
Сколько наведенного напряжения будет создаваться катушкой индуктивности, зависит от скорости изменения тока. В нашем руководстве по электромагнитной индукции Закон Ленца гласил: «Направление индуцированной ЭДС таково, что она всегда будет противодействовать вызывающему ее изменению». Другими словами, индуцированная ЭДС всегда будет ПРОТИВ движению или изменению, которые изначально привели к возникновению индуцированной ЭДС.
Таким образом, при уменьшении тока полярность напряжения будет действовать как источник, а при увеличении тока полярность напряжения будет действовать как нагрузка. Таким образом, при одинаковой скорости изменения тока через катушку увеличение или уменьшение величины наведенной ЭДС будет одинаковым.
Пример индуктора No1
Установившийся постоянный ток 4 ампера проходит через соленоидную катушку 0,5H. Каким было бы среднее напряжение обратной ЭДС, индуцированное в катушке, если бы переключатель в приведенной выше схеме был разомкнут на 10 мс и ток, протекающий через катушку, упал до нуля ампер.
Мощность в индукторе
Мы знаем, что индуктор в цепи противодействует прохождению тока, (i) через него, потому что поток этого тока индуцирует противодействующую ему ЭДС, закон Ленца. Затем должен работать внешний аккумуляторный источник, чтобы поддерживать ток, протекающий против этой наведенной ЭДС. Мгновенная мощность, используемая для создания тока, (i) против этой самоиндуцированной ЭДС (V L ), дается сверху как:
Мощность в цепи определяется как, P = V * I, следовательно:
Идеальный индуктор не имеет сопротивления, только индуктивность, поэтому R = 0 Ом, и, следовательно, внутри катушки не рассеивается мощность, поэтому мы можем сказать, что идеальный индуктор имеет нулевые потери мощности.
Энергия в индукторе
Когда мощность поступает в индуктор, энергия накапливается в его магнитном поле. Когда ток, протекающий через катушку индуктивности, увеличивается и di / dt становится больше нуля, мгновенная мощность в цепи также должна быть больше нуля (P> 0), т. Е. Положительная величина, что означает, что энергия накапливается в катушке индуктивности.
Аналогично, если ток через катушку индуктивности уменьшается и di / dt меньше нуля, то мгновенная мощность также должна быть меньше нуля (P <0), т. Е. Отрицательная, что означает, что индуктор возвращает энергию обратно в цепь. .Затем, интегрируя приведенное выше уравнение для мощности, общая магнитная энергия, которая всегда положительна, хранится в индукторе, поэтому определяется как:
Энергия, запасаемая индуктором
Где: W — в джоулях, L — в Генри, а i — в амперах
Энергия фактически накапливается в магнитном поле, окружающем катушку индуктивности, за счет протекающего через нее тока. В идеальной катушке индуктивности, которая не имеет сопротивления или емкости, по мере того, как ток увеличивается, энергия течет в индуктор и сохраняется там в его магнитном поле без потерь, она не высвобождается до тех пор, пока ток не уменьшится и магнитное поле не исчезнет.
Тогда в цепи переменного тока переменного тока индуктор постоянно накапливает и доставляет энергию в каждом цикле. Если ток, протекающий через катушку индуктивности, постоянный, как в цепи постоянного тока, то запасенная энергия не изменяется, поскольку P = Li (di / dt) = 0.
Таким образом, индукторы можно определить как пассивные компоненты, поскольку они могут как накапливать, так и передавать энергию в цепь, но не могут генерировать энергию. Идеальный индуктор классифицируется как без потерь, что означает, что он может хранить энергию неограниченное время, поскольку энергия не теряется.
Однако настоящие катушки индуктивности всегда будут иметь некоторое сопротивление, связанное с обмотками катушки, и всякий раз, когда ток течет через сопротивление, энергия теряется в виде тепла из-за Закона Ома (P = I 2 R) независимо от того, ток переменный или постоянный.
Затем индукторы в основном используются в цепях фильтрации, резонансных цепях и для ограничения тока. Катушка индуктивности может использоваться в схемах для блокировки или изменения формы переменного тока или диапазона синусоидальных частот, и в этой роли катушка индуктивности может использоваться для «настройки» простого радиоприемника или различных типов генераторов.Он также может защитить чувствительное оборудование от разрушительных скачков напряжения и высоких пусковых токов.
В следующем уроке по индукторам мы увидим, что эффективное сопротивление катушки называется индуктивностью, а индуктивность, которая, как мы теперь знаем, является характеристикой электрического проводника, который «препятствует изменению тока», может быть либо внутренне индуцированная, называемая самоиндукцией, или внешняя, называемая взаимной индуктивностью.
Индуктор в цепи постоянного тока
DC-Circuits> Индуктор в цепи постоянного тока
Индуктор — это пассивное устройство, которое накапливает энергию в своем магнитном поле и возвращает энергию в цепь, когда это необходимо.Индуктор образован цилиндрическим сердечником с множеством витков проводящего провода. Рисунки 1 и 2 представляют собой базовую структуру и схематический символ индуктора.
Рисунок 1: Базовая конструкция индуктора
Рисунок 2: Условное обозначение индуктора
Когда индуктор подключен к цепи с источником постоянного тока (DC), в определенных условиях происходят два процесса, которые называются «накоплением» и «затуханием» энергии.
Катушка индуктивности подключена к источнику питания постоянного тока, рис. 3. Внезапное увеличение тока в индукторе создает саминдуцированную электродвижущую силу, v , ЭДС , противодействующую изменению тока, рис. 1. Это проявляется как напряжение на индукторе. , vL = — v ЭДС . Это — v emf замедлит текущее изменение, и, в свою очередь, замедление текущего изменения сделает vL меньше. Когда ток становится стабильным, индуктор больше не создает противодействия и vL становится равным нулю, фаза накопления завершается.
Рисунок 3: Индуктор накапливает энергию
Катушка индуктивности эквивалентна короткому замыканию на постоянный ток, потому что после завершения фазы накопления ток, iL, который протекает через него, является стабильным, iL = V / R, без самонаводящейся ЭДС. производится и vL равен нулю. Индуктор действует как обычный соединительный провод, его сопротивление равно нулю. Ток iL через индуктор не может резко измениться.
Когда индуктор отключен от источника питания, рис. 4, vL меняет полярность и мгновенно падает с нуля до отрицательного значения, но iL сохраняет то же направление и величину.Энергия, запасенная в индукторе, затухает через резистор R D . vL постепенно увеличивается до нуля, а iL постепенно падает до нуля.
Рисунок 4: Индуктор теряет энергию
На рисунках 3 и 4 сопротивление R S и R D влияет на скорость сохранения и скорость затухания индуктора соответственно.
Частное индуктивности L и сопротивления R называется постоянной времени τ, которая характеризует скорость накопления энергии и затухания энергии в индукторе, рисунок 5.
Рисунок 5: Напряжение V L и ток i L во время фазы хранения и фазы разряда (спада)
Чем больше сопротивление, тем меньше постоянная времени, тем быстрее индуктор накапливает энергию и затухает энергию, и наоборот.
Катушки индуктивности используются во многих электронных схемах. Например, два индуктора могут образовывать трансформатор, который используется для преобразования высокого и низкого напряжения и наоборот.
DC-Circuits> Индуктор в цепи постоянного тока
Что такое индуктор? — ES Components
Индуктор , также называемый катушкой , дросселем или реактором , представляет собой пассивный двухконтактный электрический компонент, который накапливает энергию в магнитном поле, когда через него протекает электрический ток.Индуктор обычно состоит из изолированного провода, намотанного в катушку вокруг сердечника.
Когда ток, протекающий через индуктор, изменяется, изменяющееся во времени магнитное поле индуцирует в проводнике электродвижущую силу ( э.д.с. ) (напряжение), описываемую законом индукции Фарадея. Согласно закону Ленца, индуцированное напряжение имеет полярность (направление), которая противодействует изменению тока, который его создал. В результате катушки индуктивности препятствуют любым изменениям тока через них.
Катушка индуктивности характеризуется своей индуктивностью, которая представляет собой отношение напряжения к скорости изменения тока.В Международной системе единиц (СИ) единицей индуктивности является генри (Н), названный в честь американского ученого 19 века Джозефа Генри. При измерении магнитных цепей он эквивалентен Веберу / Амперу. Индукторы имеют значения, которые обычно находятся в диапазоне от 1 мкГн (10-6 Гн) до 20 Гн. Многие индукторы имеют магнитный сердечник из железа или феррита внутри катушки, который служит для увеличения магнитного поля и, следовательно, индуктивности. Наряду с конденсаторами и резисторами, индукторы являются одним из трех пассивных элементов линейной цепи, составляющих электронные схемы.Индукторы широко используются в электронном оборудовании переменного тока (AC), особенно в радиооборудовании. Они используются для блокировки переменного тока, позволяя проходить постоянному току; индукторы, предназначенные для этой цели, называются дросселями. Они также используются в электронных фильтрах для разделения сигналов разных частот и в сочетании с конденсаторами для создания настроенных схем, используемых для настройки радио и ТВ-приемников.
Катушки индуктивности широко используются в аналоговых схемах и обработке сигналов. Применения варьируются от использования больших катушек индуктивности в источниках питания, которые в сочетании с фильтрующими конденсаторами устраняют пульсации, кратные частоте сети (или частоте переключения для импульсных источников питания) на выходе постоянного тока, до небольшой индуктивности. ферритовой бусины или торца, установленных вокруг кабеля, чтобы предотвратить передачу радиочастотных помех по проводу.Индукторы используются в качестве накопителя энергии во многих импульсных источниках питания для выработки постоянного тока. Катушка индуктивности подает энергию в цепь, чтобы поддерживать ток во время периодов выключения, и позволяет создавать топографии, в которых выходное напряжение выше входного.
Источник: Википедия
Что такое индуктор? — Простое и легкое руководство по индуктору
Я получил несколько писем с вопросом «Что такое индуктор?». И я понял, что это действительно хороший вопрос.Потому что это какой-то странный компонент.
Катушка индуктивности — это просто катушка с проводом.
Сделать его невероятно просто — достаточно сделать несколько петель из проволоки. Но поскольку провода создают магнитные поля, вы скоро увидите, что они могут делать кое-что интересное.
Индуктор в цепи
Если вы изучаете электронику, первый важный вопрос: что делает катушка индуктивности в цепи?
Катушка индуктивности будет сопротивляться изменениям тока.
В схеме ниже у вас есть светодиод и резистор, соединенные последовательно с индуктором. И есть переключатель для включения и выключения питания.
Без индуктора это была бы обычная светодиодная цепь, и светодиод включился бы сразу же, когда вы щелкаете выключателем.
Но индуктор — это компонент, который сопротивляется изменениям тока.
Когда переключатель выключен, ток не течет. Когда вы включаете выключатель, начинает течь ток.Это означает, что существует изменение тока, которому индуктор будет сопротивляться.
Таким образом, вместо того, чтобы ток сразу пошел от нуля до максимума, он будет постепенно увеличиваться до максимального значения.
(Максимальный ток для этой цепи устанавливается резистором и светодиодом.)
Поскольку сила тока определяет интенсивность света светодиода, индуктор заставляет светодиод постепенно загораться, а не мгновенно.
Примечание: Вам понадобится очень большая катушка индуктивности, чтобы можно было видеть, как светодиоды гаснут в приведенной выше схеме.Это не то, для чего вы бы использовали индуктор. Но используйте это как мысленный образ того, что индуктор делает в цепи.
Что происходит при отключении индуктора?
Катушка индуктивности также препятствует мгновенному отключению тока. Ток не просто перестанет течь в катушке индуктивности в одно мгновение.
Таким образом, когда вы выключаете питание, индуктор будет пытаться продолжить прохождение тока.
Это достигается за счет быстрого увеличения напряжения на его выводах.
На самом деле он настолько увеличивается, что вы можете получить небольшую искру на контактах вашего переключателя!
Эта искра позволяет току течь (через воздух!) В течение доли секунды, пока магнитное поле вокруг индуктора не разорвется.
Вот почему диод обычно помещают в обратном направлении через катушку реле или двигателя постоянного тока. Таким образом, индуктор может разряжаться через диод вместо того, чтобы создавать в цепи высокое напряжение и искры.
БЕСПЛАТНЫЙ бонус: Загрузите основные электронные компоненты [PDF] — мини-книгу с примерами, которая научит вас, как работают основные компоненты электроники.
Как работают индукторы
Любой провод, по которому протекает ток, окружен небольшим магнитным полем.
Когда вы наматываете провод в катушку, поле становится сильнее.
Если вы намотаете провод на магнитопровод, например, из стали или железа, вы получите еще более сильное магнитное поле.
Так создается электромагнит.
Магнитное поле вокруг индуктора зависит от силы тока. Итак, когда меняется ток, меняется магнитное поле.
Когда магнитное поле изменяется, на выводах индуктора создается напряжение, которое препятствует этому изменению.
Для чего можно использовать индукторы?
В типичных схемах для начинающих не так уж часто можно увидеть дискретные индукторы. Так что, если вы только начинаете, вы, вероятно, еще не встретите их.
Но они очень распространены в блоках питания. Например, для создания понижающего или повышающего преобразователя. И они распространены в радиосхемах для создания генераторов и фильтров.
Но гораздо чаще вы встретите электромагниты. И они в основном индукторы. Вы найдете их почти во всем, что движется от электричества. Например, реле, двигатели, соленоиды, динамики и многое другое.
А трансформатор — это, по сути, две катушки индуктивности, намотанные на один и тот же сердечник.
Если вы хотите узнать, как работают другие электронные компоненты, перейдите к основным компонентам в электронике.
Что такое схемы индуктивности? | Универсальный класс
Ключевые термины
o Индуктор
o Индуктивность
o Генри
Цели
o Примените принципы магнетизма, чтобы понять функцию катушек индуктивности
o Изучить поведение простых цепей, содержащих катушки индуктивности
Обратите внимание: не пытайтесь воспроизвести схемы, иллюстрации или инструкции из этой статьи в реальной жизни.Это может привести к поражению электрическим током, травме или смерти. Эти примеры предназначены только для теоретического обсуждения, а не для фактического / физического использования.
Другим важным устройством в электрических цепях является индуктор, который в некоторых отношениях похож на конденсаторы, но сильно отличается в других. Катушки индуктивности важны для цепей связи, а также для трансформаторов — это лишь пара примеров. Опираясь на концепции магнетизма, мы рассмотрим, как индукторы работают в цепях.
Катушки индуктивности
Проволочная петля создает магнитное поле, когда через нее протекает ток, и ток может индуцироваться в ней, когда магнитное поле через петлю изменяется (увеличивается или уменьшается).Теперь представьте, что мы берем кусок проволоки и наматываем его, как катушку с ниткой: это, по сути, индуктор . Обратите внимание, что индуктор по-прежнему является проводящим путем — у него нет сопротивления (если предположить, что он сделан из идеального проводника), и ток может течь через него, в отличие от конденсатора. Поскольку индуктор имеет несколько контуров, он создает большее магнитное поле для данного тока, чем одиночный контур.
Катушка индуктивности похожа на конденсатор в том, что она накапливает энергию — в этом случае индуктор накапливает энергию в виде магнитного поля (а не за счет накопления заряда в случае конденсатора, который эффективно накапливает энергию в виде электрическая сила или поле).Давайте посмотрим, как это работает с точки зрения электрической цепи. Во-первых, обратите внимание, что мы будем использовать следующий символ для обозначения индуктора:
Точно так же, как конденсатор измеряется его емкостью, индуктивность измеряется его индуктивностью , , которая имеет единицы генри (представлен символом H — мы не будем углубляться в то, что такое генри, но достаточно это означает, что это уровень магнитного поля, создаваемого катушкой индуктивности на ампер тока).Теперь мы рассмотрим схему с катушкой индуктивности (представленной L ) и резистором, включенным последовательно с источником напряжения.
Запуск путем включения выключателя S 1 ; как обычно, это позволит току течь. Но индуктор будет реагировать, эффективно преобразовывая кинетическую энергию тока в магнитную энергию. В результате вместо тока «мгновенно» становится (вспомните закон Ома), он будет медленно увеличиваться до , поскольку индуктор «крадет» энергию для хранения в магнитном поле.(Вспомните, как ток через петлю «противостоит» обратному току из-за изменяющегося магнитного поля.) В это время некоторая часть общего падения напряжения В, будет на катушке индуктивности: сначала она будет полностью на катушке индуктивности, но это будет меняться по мере увеличения тока и все больше и больше общего падения напряжения приходится на резистор. Наконец, все падение напряжения будет на R, , а катушка индуктивности будет фактически проводом (помните, что это не что иное, как свернутый в спираль проводящий провод), но все равно будет иметь магнитное поле, сила которого связана с индуктивность L .
Теперь давайте одновременно закроем S 2 и откроем S 1 . Обычно, поскольку катушка индуктивности представляет собой просто свернутый в спираль провод, мы ожидаем, что ток просто перестанет течь немедленно, потому что источник питания был отключен от цепи. Но помните, что индуктор отбирал энергию движения у заряда и сохранял ее в магнитном поле. Поскольку источник питания больше не поддерживает этот ток, магнитное поле будет распадаться, возвращая свою энергию в кинетическую энергию заряда — другими словами, оно будет подавать ток в цепь до тех пор, пока магнитное поле не «истощится», и в этот момент нет больше тока будет течь.
В этом смысле катушка индуктивности похожа на конденсатор в том, что в ней накапливается энергия, которую он может высвободить, как если бы он был источником питания, хотя напряжение питания которого со временем уменьшается. К сожалению, физические концепции, связанные с индукторами и магнетизмом, очень сложны, поэтому мы представили только «ручное» обсуждение того, как работают индукторы. Тем не менее, этот несколько упрощенный взгляд на индукторы и магнетизм будет служить нашим целям.
Практическая проблема : Переключатель S замкнут на долгое время, а затем разомкнулся.Что случится?
Решение : Эта проблема требует от нас применения ряда понятий, которые мы изучили до сих пор. Во-первых, обратите внимание, что, поскольку переключатель S был замкнут в течение длительного времени, катушка индуктивности полностью «заряжена» (т.е. для тока , протекающего через R 2 , катушка индуктивности окружена своим максимальным магнитным полем). Когда переключатель S разомкнут, происходит несколько вещей.
Во-первых, источник питания больше не подает ток на резисторы, но индуктор высвобождает накопленную энергию магнитного поля в виде кинетической энергии заряда (тока).Так же, как он «украл» ток для создания магнитного поля при подключении источника питания, он «вернет» этот ток в цепь в том же направлении.
Этот ток будет уменьшаться по мере затухания магнитного поля, в конечном итоге достигая нуля, когда вся накопленная энергия будет израсходована. Точно так же падение напряжения на резисторах одновременно упадет до нуля. Обратите внимание, что, хотя индуктор работает по другому механизму, он во многом похож на конденсатор в том, что он накапливает энергию, которая позже может быть высвобождена.
Учебное пособие по индуктору: работа и использование в практических схемах
Индуктор — это пассивный компонент в электронике, который считается самым важным после резисторов и конденсаторов. Говоря об индукторах, это не что иное, как проволока, плотно намотанная на сердечник. Это руководство написано, чтобы дать хорошее представление о работе индукторов и их использовании в практических схемах. В этом руководстве рассматриваются три важных вопроса, которые могут возникнуть у энтузиастов об индукторах.
- Что такое индуктор? — 3 минуты
- Как работает индуктор? — 5 минут
- Как использовать их в схемах? — 7 минут
К концу этого руководства вы получите хорошее представление о работе индукторов. Также вы сможете распознать использование индукторов в любых цепях, которые вы увидите. Вы можете ознакомиться с нашими руководствами по другим компонентам
ЧТО ТАКОЕ ИНДУКТОР
Как уже говорилось, индуктор — это не что иное, как изолированный провод, плотно намотанный на сердечник.Этот сердечник может быть из ферромагнитного материала или пластмассы или, в некоторых случаях, полый (воздушный). Это основано на принципе «Магнитный поток возникает вокруг проводника с током» . Если вы знаете о конденсаторах, вы должны знать, что конденсатор накапливает энергию, накапливая на своих пластинах одинаковые и противоположные заряды. Точно так же индуктор накапливает энергию в виде магнитного поля, развивающегося вокруг него. Индукторы по-разному реагируют на переменный и постоянный ток. Но прежде чем углубиться в «Работу индукторов».Посмотрим на его конструкцию и характеристики.
КОНСТРУКЦИЯ ИНДУКТОРА:
Индуктор
довольно просто собрать из всех других компонентов, используемых в электронике. Вот руководство по созданию простого индуктора. Все, что требуется, — это изолированный провод и материал сердечника, чтобы намотать катушку. Сердечник — это не что иное, как материал, на который намотана проволока, как показано на схеме выше. Существуют различные типы индукторов в зависимости от материала сердечника, из которого они изготовлены. Некоторые из распространенных материалов сердечника — это железо, ферромагниты и т. Д.Помимо типов материала сердечника, он бывает разных размеров и форм: Циклиндрический, Стержневой, Торроидный и Листовой. В отличие от этого есть также индукторы, у которых нет физических ядер. Они известны как индукторы с полым сердечником или воздушным сердечником. Ядро играет важную роль в изменении индуктивности индуктора.
КАК РАБОТАЕТ ИНДУКТОР
Начнем с констатации того факта, что «Магнитный поток будет развиваться через проводник с током».Точно так же, когда ток подается через индуктор, вокруг него создается магнитный поток. Другими словами, энергия, приложенная к индуктору, сохраняется в виде магнитного потока. Направление развиваемого магнитного потока будет противоположным направлению потока тока. Поэтому индукторы сопротивляются резкому изменению тока, протекающего через них. Эта способность индуктора называется индуктивностью, и каждый индуктор будет иметь некоторую индуктивность. Это обозначается символом L и измеряется в Генри.
Индуктивность индуктора зависит от формы катушки, количества витков обмотки на сердечнике, площади сердечника и коэффициента проницаемости материала сердечника.Индуктивность индуктора равна
.L = мкН 2 А / л
L — Индуктивность катушки
μ — Проницаемость материала сердечника
A — Площадь змеевика в квадратных метрах
N — Количество витков в катушке
л — Средняя длина змеевика в метрах
ИНДУКТОРЫ В ЦЕПИ ПЕРЕМЕННОГО ТОКА:
Как было сказано ранее, индуктор действует иначе, чем переменный ток, по сравнению с источником сигнала постоянного тока. Когда сигнал переменного тока подается на индуктор, он создает магнитное поле, которое изменяется во времени, потому что ток, создающий поле, сам изменяется во времени.Это явление согласно закону Фарадея вызывает самоиндуцированное напряжение на индукторе. Это самоиндуцированное напряжение обозначается V L . Фактически, напряжение, возникающее на катушке индуктивности, действует в направлении, противоположном току, сопротивляющемуся им. Это напряжение на индукторе определяется формулой
.В L = L di / dt
VL — Напряжение самоиндукции
di / dt — Изменение тока относительно времени
Если 1 ампер тока по отношению к одной секунде, когда он протекает через один индуктор Генри, разовьется на 1 В.Теперь вы видите, как ток, протекающий через катушку индуктивности, влияет на развиваемое на ней напряжение. Это возникающее напряжение действует противоположно току, протекающему через индуктор.
V-I ХАРАКТЕРИСТИКИ ИНДУКТОРА:
Давайте лучше поймем вышеупомянутые концепции, обратившись к характеристической кривой VI индуктора. Когда положительный цикл сигнала переменного тока проходит через индуктор, ток увеличивается. Мы знаем, что Inductor ненавидит изменение тока, поэтому он вырабатывает индуцированное напряжение, чтобы действовать против тока, который его вызывает.На графике выше при 0 ° вы можете заметить, что индуцированное напряжение будет максимальным, когда ток начнет расти. Как только ток достигает максимума, индуцированное напряжение становится отрицательным, чтобы предотвратить уменьшение тока.
Этот цикл повторяется, и из приведенного выше графика мы можем видеть, что индуцированное напряжение, возникающее в индукторе, будет действовать против изменяющегося тока, протекающего через него. А здесь напряжение и ток сдвинуты по фазе на 90 °. Таким образом, с сигналом переменного тока индуктор накапливает и высвобождает энергию в виде магнитного поля в непрерывном цикле.
ИНДУКТОР В ЦЕПИ ПОСТОЯННОГО ТОКА:
Теперь у нас есть представление о том, как индуктор работает с источником сигнала переменного тока. Давайте посмотрим, как он реагирует при использовании с источником сигнала постоянного тока. Напомним, формула наведенного напряжения на индукторе равна
.В L = L di / dt
При использовании источника сигнала постоянного тока изменение тока во времени будет равно нулю, в результате чего индуцированное напряжение на индукторе будет равно нулю. Проще говоря, в цепях постоянного тока индуктор ведет себя как простой простой провод с некоторым сопротивлением, вызванным его проводом.Но это еще не все, когда в практических схемах используется индуктор с источником сигнала постоянного тока. В практических схемах будет короткий период времени, необходимый току для достижения максимального значения от нуля. В этот момент на индукторе будет индуцированное напряжение, которое будет отрицательным максимумом, когда ток начнет двигаться от нуля до максимального значения. Как только ток достигает стабильного состояния постоянного тока, индуцированное напряжение резко падает до нуля и обнуляется. Этот короткий промежуток индуцированного напряжения будет проявляться как всплеск напряжения на индукторе при использовании с источником сигнала постоянного тока.
ИНДУКТИВНАЯ РЕАКТИВНОСТЬ:
Еще одна важная вещь, которую нужно знать об индукторах, — это реактивность. Это резистивное свойство, проявляемое такими компонентами, как конденсатор и индуктор для сигнала переменного тока. Реактивное сопротивление, отображаемое индуктором, называется индуктивным реактивным сопротивлением и выражается формулой
.X L = 2πFL
Из уравнения вы можете вывести, что реактивное сопротивление увеличивается с частотой сигнала переменного тока, помните, что индуктор ненавидит изменение тока, поэтому он проявляет большее реактивное сопротивление к высокочастотным сигналам.Тогда как, когда частота близка к нулю или сигнал постоянного тока проходит через реактивное сопротивление становится равным нулю, действуя как проводник для прохождения входного сигнала.
ПРИМЕНЕНИЕ ИНДУКТОРА
Теперь мы прошли немного скучную и расплывчатую рабочую часть индуктора. Давайте узнаем, как использовать индукторы в схемах. Для этого давайте взглянем на его приложения. Применение индуктора — самая захватывающая часть этого руководства. В этом разделе обсуждаются наиболее важные приложения / схемы, в которых используется индуктор.Если вы где-нибудь найдете индуктор в цепи, велика вероятность, что он подпадает под одно из следующих применений индукторов.
ОСЦИЛЛЯТОРЫ / НАСТРОЕННЫЕ ЦЕПИ:
Это схемы, которые используются в радиопередатчиках, приемниках, генераторах и приложениях, где важен выбор частоты. Здесь индуктор работает вместе с конденсатором. Если вы знаете о работе конденсатора, вы знаете, что он демонстрирует высокое реактивное сопротивление к низкочастотным сигналам, тогда как индуктор предлагает высокое реактивное сопротивление к высокочастотным сигналам.В этой схеме значение индуктора и конденсатора должно быть выбрано таким образом, чтобы обеспечить равное реактивное сопротивление при заданной входной частоте. Это состояние называется разумной частотой, а соответствующая частота называется разумной частотой. В Reasonance эта схема способна генерировать сигналы соответствующей частоты, чтобы действовать как осциллятор или принимать сигналы этой частоты из сложного сигнала.
Когда конденсатор в этой цепи заряжается, он накапливает заряды между пластинами.После отключения питания ток от конденсатора проходит через индуктор, в результате чего вокруг него создается магнитное поле. К этому времени заряд, хранящийся в конденсаторе, будет исчерпан, и ток перестанет течь к индуктору. Как мы знаем, индуктор любит постоянный ток, и в результате он будет пытаться поддерживать постоянный ток, сжимая свое магнитное поле и позволяя току течь обратно к конденсатору. Конденсатор снова будет полностью заряжен. Заряд течет назад и вперед между конденсатором и индуктором, что приводит к генерации сигнала фиксированной разумной частоты.
Причина определяется по формуле f 0 = 1 / 2π√ (LC)
ОГРАНИЧИТЕЛЬ ПУСКОВОГО ТОКА:
Пусковые токи, также известные как импульсный ток или входной импульсный ток, в значительной степени способны разрушать цепи. Это мгновенные токи, потребляемые нагрузкой или электрическим устройством при их включении. Поразительно, что этот пусковой ток может быть в 40-50 раз выше, чем ток в установившемся режиме, и потенциально способен разрушать устройства.Пусковой ток обычно возникает из-за мгновенного высокого тока, необходимого для работы конденсаторов большой емкости, трансформаторов, которые должны быть защищены от попадания в оборудование.
Индуктор — широко распространенный способ предотвращения повреждения цепи пусковым током. Когда цепь включена, течет мгновенный сильный ток, который изменяется во времени. Индуктор противодействует этому изменению тока, создавая вокруг себя магнитное поле, которое создает самоиндуцированное напряжение, которое противодействует этому высокому току от источника питания.Через некоторое время, когда ток возвращается в установившееся состояние, магнитное поле схлопывается и высвобождает накопленную энергию в цепь в виде тока. Как только ток станет постоянным, индуктор больше не будет противодействовать ему и предлагает свободный путь для тока, протекающего через него.
ФИЛЬТРЫ:
Это особый тип цепей, используемых для фильтрации или устранения сигналов нежелательной частоты, которые позволяют сигналам проходить только в желаемых пределах. Используя индуктор вместе с пассивными компонентами, такими как резистор и конденсатор, мы можем создать три различных типа фильтров, которые могут служить нашей цели фильтрации сигнала.
ФИЛЬТР НИЗКОГО ПРОХОДА:
Как следует из названия, этот фильтр используется в схемах, где вам необходимо отфильтровать сигналы с частотой выше, чем частота среза из входящего сигнала. Термин частота среза относится к пределу частоты, установленному значением компонентов, используемых в этом фильтре. Итак, здесь значение индуктора и резистора определяет частоту среза. Этот фильтр пропускает сигнал, частота которого ниже этого предела среза, а частота выше этого предела блокируется этим фильтром.
В этом фильтре происходит то, что когда входящий сигнал имеет высокую частоту, реактивное сопротивление индуктора будет очень высоким. Реактивное сопротивление определяется значением индуктивности и частотой, как мы видели в формуле X L = 2πFL. Катушка индуктивности вместе с резистором образует делитель напряжения, где при более высокой частоте реактивное сопротивление (сопротивление) индуктора будет выше. Более высокое реактивное сопротивление позволяет индуктору эффективно ослаблять сигналы, и поэтому на выходе будет нулевое напряжение или близкое к нулю.
Частота среза этого фильтра нижних частот может быть рассчитана с использованием f c = R / 2πL
ФИЛЬТР ВЫСОКОГО ПРОХОДА:
Здесь в этом фильтре верхних частот поменяны местами индуктор и резистор. Этот фильтр пропускает только высокочастотные сигналы, в отличие от фильтра нижних частот. Здесь разрешены сигналы с частотой выше частоты среза. А сигналы с частотой ниже этой будут ослабляться / блокироваться. Когда сигнал низкой частоты проходит через цепь, реактивное сопротивление индуктора будет очень низким по сравнению с сопротивлением резистора, поэтому падение напряжения на резисторе будет очень высоким, а выходной сигнал будет нулевым или близким к нулю.
Когда через цепь проходит высокочастотный сигнал, индуктор демонстрирует высокое реактивное сопротивление по сравнению с резистором R1. Следовательно, резистор обеспечивает очень меньшее затухание входящих сигналов, заставляя высокочастотные сигналы выходить с очень меньшим или нулевым затуханием. Таким образом, пропускается высокочастотный сигнал, а низкочастотный сигнал блокируется.
Частоту среза этого фильтра можно рассчитать, используя f c = R / 2πL
ПОЛОСНЫЙ ПРОХОДНОЙ ФИЛЬТР:
В этом фильтре через них может проходить только полоса частот, и все, что находится за пределами этой частоты, будет отклонено.В отличие от фильтра низких и высоких частот, полосовой фильтр имеет две частоты среза. Будет разрешено проходить только верхнюю и нижнюю частоту среза и сигнал частоты между этими частотами.
Работа этого фильтра в основном зависит от параллельно подключенных индуктора и конденсатора. Это контур резервуара, как мы видели ранее в настроенном контуре. Если вы помните, что вы видели в разделе «Настроенная схема», резонансная частота — это частота, при которой реактивное сопротивление индуктора и конденсатора на входящий сигнал будет одинаковым.Реактивное сопротивление, определяемое парой индуктивности и конденсатора, будет высоким по сравнению с сопротивлением резистора, когда входящий сигнал близок к разумной частоте или около нее. Следовательно, полоса частот, близкая к разумной, будет проходить через фильтр. Частоты вне этого диапазона будут заблокированы.
УСИЛИТЕЛЬ НАПРЯЖЕНИЯ:
Бустеры напряжения — это схемы, которые используются для повышения входящего напряжения до определенного уровня. Он показывает более высокое выходное напряжение, чем входное.Катушки индуктивности являются наиболее важным элементом в схемах повышения напряжения из-за их способности создавать самоиндуцированную ЭДС при протекании через них тока переменного тока. Выше показана типичная схема усилителя, в которой на индуктор подается постоянный ток. С другой стороны, к нему подключен полевой МОП-транзистор. MOSFET будет включаться и выключаться с постоянными интервалами от источника сигнала.
Когда MOSFET включен, ток течет от источника питания к индуктору, а затем проходит через MOSFET.Это создает магнитный поток, а также самоиндуцированное напряжение на индукторе. Когда MOSFET выключен с помощью источника сигнала, это приводит к уменьшению протекания тока. Индуктор теперь будет пытаться поддерживать постоянный ток. В результате самоиндуцированное напряжение переключает полярность, заставляя его действовать как напряжение, последовательно подключенное к источнику питания G1.
Это комбинированное напряжение (напряжение от источника питания G1 и самоиндуцированное напряжение на L1) будет пропускать ток через диод и заряжать конденсатор до этого уровня напряжения.Когда полевой МОП-транзистор включается и выключается достаточно быстро, конденсатор будет сохранять это напряжение и показывать этот уровень напряжения на выходе. Таким образом, используя такие схемы, вы получите повышенное напряжение на выходе.
КРАТКОЕ ОПИСАНИЕ ИНДУКТОРОВ:
- Индуктор — это пассивный элемент, что означает, что он не может генерировать энергию самостоятельно.
- Противодействует изменениям тока, протекающего через него. Индуктор
- обеспечивает путь с низким сопротивлением при подаче на него сигнала постоянного тока.
- При подаче сигнала переменного тока вокруг индуктора формируется магнитное поле, в результате чего возникает самоиндуцированное напряжение, которое противодействует изменению тока, протекающего через него.
- В отличие от конденсатора, индуктор предлагает высокое реактивное сопротивление к высокочастотным сигналам и низкое реактивное сопротивление к низкочастотным сигналам.
- Важные области применения индукторов — в радиопередатчиках, приемниках, источниках питания, фильтрах сигналов и т. Д.
Это в основном об индукторах и их применении в практических схемах.Мы предлагаем вам дважды прочитать это руководство по работе с индукторами и по применению, чтобы получить четкое представление об индукторах. Этот учебник, должно быть, помог вам определить цель использования индуктора в любых схемах в будущем. Есть также другие приложения Inductor, которые мы не рассмотрели в этом руководстве, но мы рассмотрим их в другом руководстве, которое будет опубликовано в ближайшие дни.
Здесь вы можете найти учебные материалы по другим электронным компонентам на нашем веб-сайте. В будущем мы будем публиковать больше электронных руководств.Подпишитесь на нашу рассылку новостей и следите за нами через каналы социальных сетей, чтобы получать регулярные обновления с нашего веб-сайта. Если у вас есть какие-либо сомнения, требующие разъяснения или дальнейшего объяснения, оставьте свои вопросы в поле для комментариев ниже. Или, если вы считаете, что мы упустили что-то важное в этом уроке, дайте нам знать, мы добавим их.
Переходная характеристика индуктора| Постоянные времени RC и L / R
Катушки индуктивности имеют прямо противоположные характеристики конденсаторов. В то время как конденсаторы накапливают энергию в электрическом поле (создаваемом напряжением между двумя пластинами), индукторы накапливают энергию в магнитном поле (создаваемом током через провод).Таким образом, в то время как накопленная в конденсаторе энергия пытается поддерживать постоянное напряжение на его выводах, накопленная энергия в катушке индуктивности пытается поддерживать постоянный ток через его обмотки.
Из-за этого катушки индуктивности противодействуют изменениям тока и действуют в точности противоположно конденсаторам, которые противодействуют изменениям напряжения. Полностью разряженная катушка индуктивности (без магнитного поля) с нулевым током через нее первоначально будет действовать как разомкнутая цепь при подключении к источнику напряжения (поскольку она пытается поддерживать нулевой ток), снижая максимальное напряжение на своих выводах.
Со временем ток катушки индуктивности увеличивается до максимального значения, допустимого для схемы, и соответственно уменьшается напряжение на клеммах. Как только напряжение на клеммах катушки индуктивности снизится до минимума (ноль для «идеальной» катушки индуктивности), ток останется на максимальном уровне, и это будет вести себя по существу как короткое замыкание.
Когда переключатель в первый раз замкнут, напряжение на катушке индуктивности немедленно перескакивает до напряжения батареи (действуя как разомкнутая цепь) и со временем спадает до нуля (в конечном итоге действуя так, как если бы это было короткое замыкание).Напряжение на катушке индуктивности определяется путем расчета, сколько напряжения падает на резисторе R с учетом тока, протекающего через катушку индуктивности, и вычитания этого значения напряжения из батареи, чтобы увидеть, что осталось.
Когда переключатель в первый раз замкнут, ток равен нулю, затем он увеличивается со временем, пока не станет равным напряжению батареи, деленному на последовательное сопротивление 1 Ом. Это поведение прямо противоположно тому, что происходит в цепи последовательного резистора-конденсатора, где ток начинается с максимума, а напряжение конденсатора равно нулю.Давайте посмотрим, как это работает, используя реальные значения:
| Время (секунды) | Напряжение аккумулятора | Напряжение индуктора | Текущий |
|---|---|---|---|
| 0 | 15 В | 15 В | 0 |
| 0,5 | 15 В | 9,098 В | 5,902 А |
| 1 | 15 В | 5,518 В | 9,482 А |
| 2 | 15 В | 2.030 В | 12,97 А |
| 3 | 15 В | 0,747 В | 14,25 А |
| 4 | 15 В | 0,275 В | 14,73 А |
| 5 | 15 В | 0,101 В | 14,90 А |
| 6 | 15 В | 37,181 мВ | 14,96 А |
| 10 | 15 В | 0,681 мВ | 14,99 А |
Как и в случае RC-цепи, приближение напряжения индуктора к 0 вольт и приближение тока к 15 ампер с течением времени составляет асимптотика .Однако для всех практических целей мы можем сказать, что напряжение на катушке индуктивности в конечном итоге достигнет 0 вольт, а ток в конечном итоге составит максимум 15 ампер.
Опять же, мы можем использовать программу анализа цепей SPICE, чтобы составить график этого асимптотического спада напряжения катушки индуктивности и нарастания тока катушки индуктивности в более графической форме (ток катушки индуктивности отображается как падение напряжения на резисторе, используя резистор как шунт для измерения тока):
Обратите внимание на то, как напряжение сначала очень быстро падает (слева от графика), а затем постепенно спадает с течением времени.Ток также сначала изменяется очень быстро, затем со временем стабилизируется, но он приближается к максимуму (справа от шкалы), в то время как напряжение приближается к минимуму.
ОБЗОР:
- Полностью «разряженная» катушка индуктивности (без тока через нее) первоначально действует как разомкнутая цепь (падение напряжения без тока) при внезапном приложении напряжения.

