Код баркера. Коды Баркера: эффективное кодирование для цифровой связи

Что такое коды Баркера и как они используются в цифровой связи. Каковы основные свойства и преимущества кодов Баркера. Как формируются коды Баркера различной длины. Где применяются коды Баркера на практике.

Что такое коды Баркера

Коды Баркера представляют собой специальные последовательности двоичных символов, обладающие уникальными корреляционными свойствами. Они были предложены ирландским физиком Рональдом Хью Баркером в 1953 году.

Основные свойства кодов Баркера:

• Состоят из последовательности +1 и -1 (или 1 и 0)
• Имеют небольшую длину — от 2 до 13 символов
• Обладают идеальной автокорреляционной функцией
• Боковые лепестки автокорреляционной функции не превышают 1 по модулю

Благодаря этим свойствам коды Баркера широко применяются в системах цифровой связи для синхронизации, обнаружения сигналов и подавления помех.

Формирование кодов Баркера

Известны коды Баркера следующей длины:

• 2 символа: +1 -1
• 3 символа: +1 +1 -1
• 4 символа: +1 +1 -1 +1
• 5 символов: +1 +1 +1 -1 +1
• 7 символов: +1 +1 +1 -1 -1 +1 -1
• 11 символов: +1 +1 +1 -1 -1 -1 +1 -1 -1 +1 -1
• 13 символов: +1 +1 +1 +1 +1 -1 -1 +1 +1 -1 +1 -1 +1

Более длинных кодов Баркера математически не существует. Наиболее часто используются коды длиной 11 и 13 символов.

Автокорреляционные свойства

Ключевым свойством кодов Баркера является их идеальная автокорреляционная функция. Она характеризуется следующими особенностями:

• Максимальное значение при нулевом сдвиге равно длине кода N
• Боковые лепестки не превышают по модулю 1
• Отношение максимума к боковым лепесткам составляет N

Как рассчитать автокорреляционную функцию кода Баркера?

1. Берем код Баркера и его копию
2. Сдвигаем копию на определенное число позиций
3. Умножаем соответствующие элементы исходного кода и сдвинутой копии
4. Суммируем полученные произведения
5. Повторяем для всех возможных сдвигов

Применение кодов Баркера

Основные области применения кодов Баркера в системах связи:

• Синхронизация приемника и передатчика
• Маркировка начала пакетов данных
• Обнаружение слабых сигналов на фоне шумов
• Подавление межсимвольных помех
• Формирование расширенного спектра сигнала
• Сжатие импульсов в радиолокации

В частности, коды Баркера используются в следующих системах:

• WiFi (стандарт IEEE 802.11) — код длиной 11 символов
• Импульсные радиолокаторы — коды длиной 13 символов
• Системы спутниковой навигации GPS
• Цифровое телевидение
• Мобильная связь

Преимущества использования кодов Баркера

Почему коды Баркера так эффективны в цифровой связи? Ключевые преимущества:

• Высокая помехоустойчивость за счет хороших корреляционных свойств
• Возможность обнаружения слабых сигналов на фоне шумов
• Простота формирования и обработки
• Эффективное использование полосы частот
• Хорошие спектральные характеристики сигнала
• Возможность разделения сигналов от разных источников

Это делает коды Баркера оптимальным выбором для многих приложений цифровой связи.

Модуляция с использованием кодов Баркера

Как применяются коды Баркера для модуляции сигналов? Основные варианты:

1. Фазовая манипуляция (BPSK):
   • +1 соответствует фазе 0°
   • -1 соответствует фазе 180°
2. Частотная манипуляция (FSK):
   • +1 соответствует частоте f1
   • -1 соответствует частоте f2
3. Амплитудная манипуляция (ASK):
   • +1 соответствует амплитуде A
   • -1 соответствует амплитуде -A

Чаще всего используется фазовая манипуляция BPSK, так как она обеспечивает наилучшую помехоустойчивость.

Обнаружение сигналов с кодами Баркера

Как происходит обнаружение сигналов, закодированных кодами Баркера?

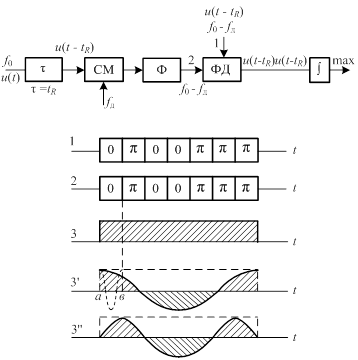
1. Принятый сигнал коррелируется с опорной последовательностью кода Баркера
2. При совпадении кодов формируется острый корреляционный пик
3. Амплитуда пика в N раз превышает уровень боковых лепестков
4. Положение пика определяет момент прихода сигнала
5. Высота пика характеризует мощность принятого сигнала

Это позволяет надежно обнаруживать даже очень слабые сигналы на фоне шумов и помех.

Сравнение кодов Баркера с другими кодовыми последовательностями

Чем коды Баркера отличаются от других кодовых последовательностей?

Характеристика	Коды Баркера	M-последовательности	Коды Голда
Длина	2-13 символов	2^n — 1 символов	2^n — 1 символов
Автокорреляция	Идеальная	Хорошая	Средняя
Взаимная корреляция	—	Средняя	Низкая
Количество кодов	Ограничено	Среднее	Большое

Коды Баркера имеют наилучшие автокорреляционные свойства, но ограничены по длине и количеству.

Ограничения кодов Баркера

Несмотря на свои преимущества, коды Баркера имеют ряд ограничений:

• Максимальная длина кода — 13 символов
• Всего существует 7 различных кодов
• Невозможно создать большой набор слабо коррелированных кодов
• Сложно использовать для разделения сигналов многих пользователей
• При больших скоростях передачи возрастают межсимвольные искажения

Поэтому в современных системах связи коды Баркера часто комбинируются с другими методами кодирования.

Основные принципы цифровой беспроводной связи. Ликбез / Хабр

Всем привет. В этой статье я хотел бы рассказать немного об основных приемах и идеях современной цифровой беспроводной связи — на примере стандарта IEEE 802.11. В наше время очень часто люди живут на довольно высоких уровнях абстракции, плохо представляя как именно работают окружающие нас вещи. Ну что ж — попытаюсь принести в массы свет просвещения. В статье будут использоваться вещи и терминология, объясненные в этой статье. Так что людям, далеким от радиотехники рекомендуется сначала прочитать её.
DANGER: в статье присутствует матан — особо впечатлительным не нажимать на эту кнопку:

Цифровые сигналы и спектры

Аналоговые сигналы

До развития компьютеров — посредством радиоволн передавались обычно аналоговые сигналы — то есть

сигналы, множество значений которых непрерывно

.

Например — звук — зависимость давления от времени. Полученный с приемника сигнал (напряжение) поступает на усилитель звуковой частоты и заставляет колебаться динамик.

Или видеосигнал для кинескопа. Уровень сигнала определяет значение мощности, бегающего по экрану лучика, который в нужные моменты времени засвечивает люминофор, формируя изображение на экране

Основной минус такого способа передачи информации — низкая помехоустойчивость — передающая среда всегда вносит в наш сигнал какую то случайную составляющую — изменение формы видеосигнала меняет цвета отдельных пикселей(все мы помним шумы радиоприемника и рябь на экране телевизора).

Цифровые сигналы

Цифровые сигналы — то есть

сигналы, имеющие дискретное множество значений

— по этому параметру значительно лучше аналоговых, так как нас интересует не непосредственно значение сигнала, а

диапазон

в котором находится это значение и помеха нам не страшна(например в диапазоне напряжений 0В — 1. 6В мы считаем, что это лог 0, а в диапазоне 3.3В — 5В лог 1). Расплата за это — увеличение требуемой скорости передачи и обработки информации.

Первое, что люди научились делать — естественно передавать такие сигналы по проводам, просто переключая состояние линии данных и синхронизации из единицы в ноль.
На этом небольшой ликбез закончен — далее речь пойдет о том — а как же передается цифровой сигнал при помощи радиоволн. Как работает WiFi.

Спектр единичного импульса

В радиосвязи нас часто интересует спектр сигнала — цифровой сигнал — последовательность прямоугольных импульсов — для начала рассмотрим спектр одного прямоугольного импульса.
Вспомним — что такое спектр(коэффициент перед интегралом опущен):

Спектр прямоугольного импульса длительностью T и амплитудой A:

Вывод

Выносим константу за интеграл и делаем замену дифференциала


Считаем определенный интеграл

Далее делаем замену на синус по Формуле Эйлера

Таак — а как же быть с отрицательной амплитудой? Вспомним что в действительных числах спектр раскладывается на сумму синусов и косинусов с нулевыми фазами —

в такой форме на самом деле удобней представлять в компьютере, но для анализа такая форма совершенно неудобна — при изменениях сигнала во временнОй области — спектры будут меняться совершенно непонятным для человека образом, поэтому два спектра синусных компонент и косинусных компонент преобразуют в полярные координаты, сворачивая пары синусов и косинусов с нулевой фазой в синус с ненулевой фазой, получая амплитудный спектр и фазовый, а теперь вспомним, что домножение сигнала на -1 — эквивалентно скачку фазы на 180 градусов, поэтому отрицательная часть отразится относительно горизонтальной оси, а в точках перегиба — фаза будет испытывать скачок на 180 градусов.

Также видим, что спектр одиночного импульса представляет собой sinc функцию, довольно часто встречающуюся в цифровой обработке сигналов и радиотехнике.

Почти вся энергия импульса содержится в центральном пике спектра — его ширина обратно пропорциональна длительности импульса. А высота — прямо пропорциональна — то есть — чем длиннее импульс — тем уже и выше его спектр, а чем короче — тем ниже и шире.
Спектр последовательности импульсов с хорошей степенью точности можно считать совокупностью гармоник в спектральной полосе, ширина которой обратно пропорциональна длительности импульса T.

Итак — вывод — уменьшая длину импульсов нашего цифрового сигнала мы можем размазывать сигнал по широкой полосе спектра — при этом пропорционально уменьшается его высота — при увеличении полосы в N раз — во столько же уменьшится высота спектра вплоть до уровня шумов. Широкополосная передача имеет довольно много плюсов — один из них — устойчивость к узкополосным помехам — так как информация размазана по спектру — узкополосная помеха портит только малую часть этой информации.

Если тупо уменьшить длину импульсов нашего информационного сигнала — спектр, конечно, уширится, но ведь приемник не знает какую информацию мы ему передаем и не сможет выделить её из шумов. Поэтому необходим способ — преобразовать узкополосный сигнал в широкополосный шумоподобный — для передачи по радиоканалу, а после приема преобразовать обратно в узкополосный — нужно добавлять в сигнал избыточную информацию, то есть информацию, известную и приемнику и передатчику, при помощи которой приемник может отличить сигнал от шумов. Закодируем каждый бит информации известной и приемнику и передатчику последовательностью.

Автокорреляционная функция. Коды Баркера

Наша задача — найти в длинной последовательности входных данных заранее известную короткую последовательность.
Автокорреляция — статистическая взаимосвязь между случайными величинами из одного ряда, но взятых со сдвигом.
Особое значение данный параметр имеет в локации — вот сгенерировали мы какой то сигнал и засекли время — скорость распространения сигнала нам известна, значит зная время, которое потребовалось сигналу, чтобы сбегать до препятствия и обратно — мы можем вычислить расстояние для препятствия. Но вот незадача — идеальных условий в жизни не бывает — как правило вокруг очень много шумов и вместе с отраженным сигналом на вход приемника поступает всякий мусор. А мы во-первых не должны спутать наш сигнал ни с чем другим, во вторых — достаточно точно определить момент времени, когда он вернулся назад.

Математически — автокорреляция определяется так:

То есть мы накладываем функцию на саму себя, но со сдвигом — перемножаем и вычисляем интеграл, отмечаем точку, затем опять сдвигаем, опять вычисляем интеграл и так для всех возможных сдвигов. Если мы прикладываем функцию не к самой себе, а к какой то другой, то это называется просто

корреляция

.
На приведенной ниже картинке демонстрируются операции

свертки

,

корреляции

и

автокорреляции

.
Отличие свертки и корреляции — в направлении — свертка функций f(x) и g(x) — это та же корреляция, только функций f(x) и g(-x), автокорреляция — корреляция функции с самой собой

То есть в момент времени, когда входной сигнал наиболее похож на нужную нам функцию — корреляционная функция будет иметь пик. 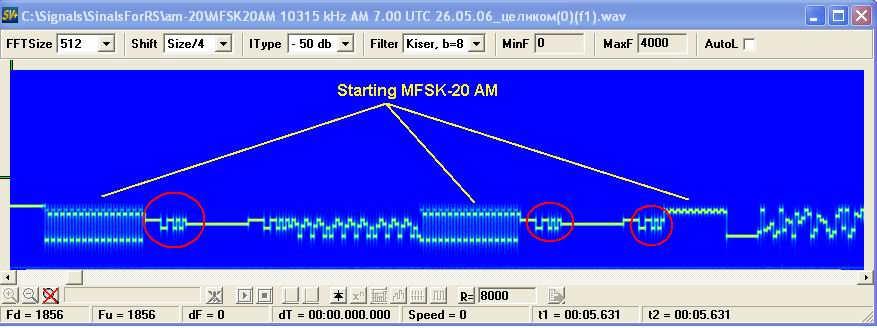Ширина этого пика, если не брать во внимание шум — будет равна удвоенной длине зондирующего импульса и будет симметричной относительно центрального пика — даже если исследуемый сигнал не является симметричным. К слову — пиков может быть несколько — центральный пик и так называемые

боковые лепестки

— зависит от функции. Корреляционный метод является самым оптимальным методом определения сигнала известной формы на фоне

белого шума

— другими словами метод имеет наилучшее отношение сигнал/шум. Зондирующий импульс должен удовлетворять следующим требованиям — иметь как можно более узкий центральный пик и при этом иметь минимальный уровень боковых лепестков, то есть функция похожа сама на себя только в очень коротком интервале времени — чуть сдвинуть и она становится совершенно непохожа. В локации этим требованиям удовлетворяет ЛЧМ сигнал.

Имеющий минимальный уровень боковых лепестков, автокорреляционная функция ЛЧМ сигнала имеет следующий вид:

Аналогом ЛЧМ сигнала в дискретных системах является последовательность Баркера
Например — известная последовательность длинной 11 бит: 11100010010.
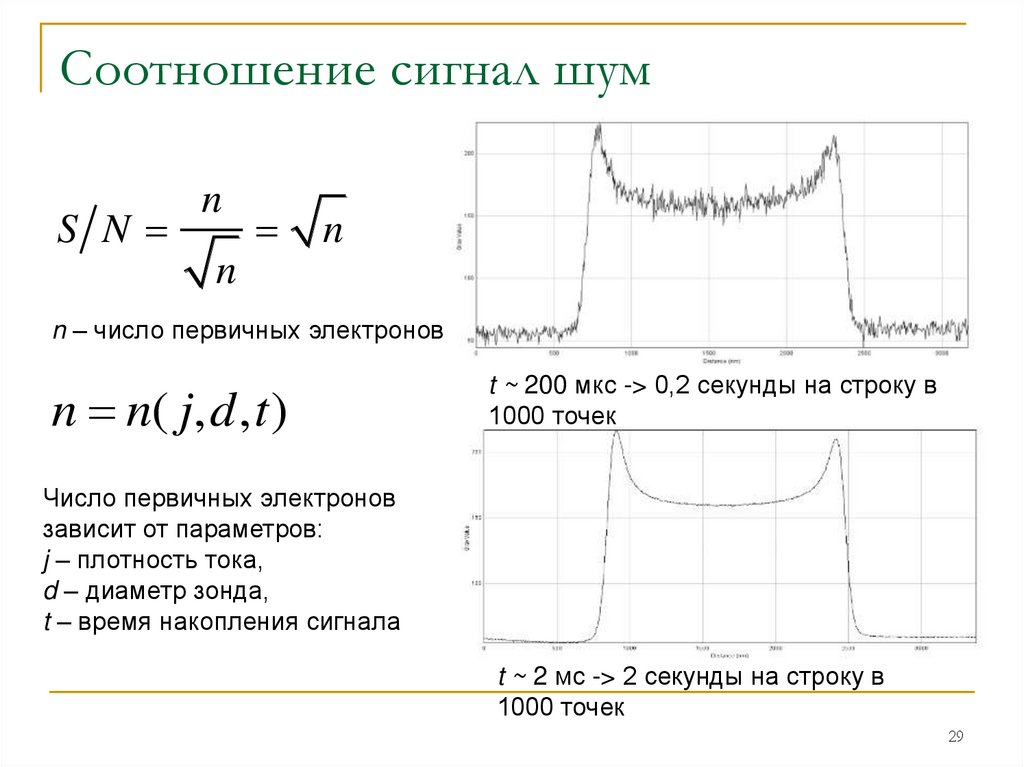
Найдем автокорреляционную функцию этой последовательности, циклически сдвигая её и считая сумму попарных произведений, при этом заменив 0 на -1
11100010010
11100010010
11
11100010010
01110001001
-1
11100010010
10111000100
-1
11100010010
01011100010
-1
11100010010
00101110001
-1
11100010010
10010111000
-1
…
И так далее — в общем автокорреляционная функция имеет значение 11 только при полном совпадении, во всех остальных случаях — -1.
То же самое справедливо и для инверсии последовательности, то есть для 00011101101. Плюс ко всему — прямая и инверсная последовательности слабо коррелируют между собой — мы их не спутаем.
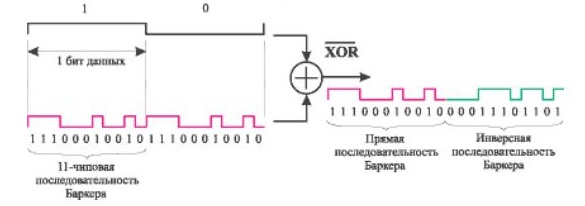
Получается, что мы можем каждый бит информации кодировать 11 битами последовательности Баркера — прямой для единиц и инверсной для нулей. Элементы последовательности Баркера называют

чипами

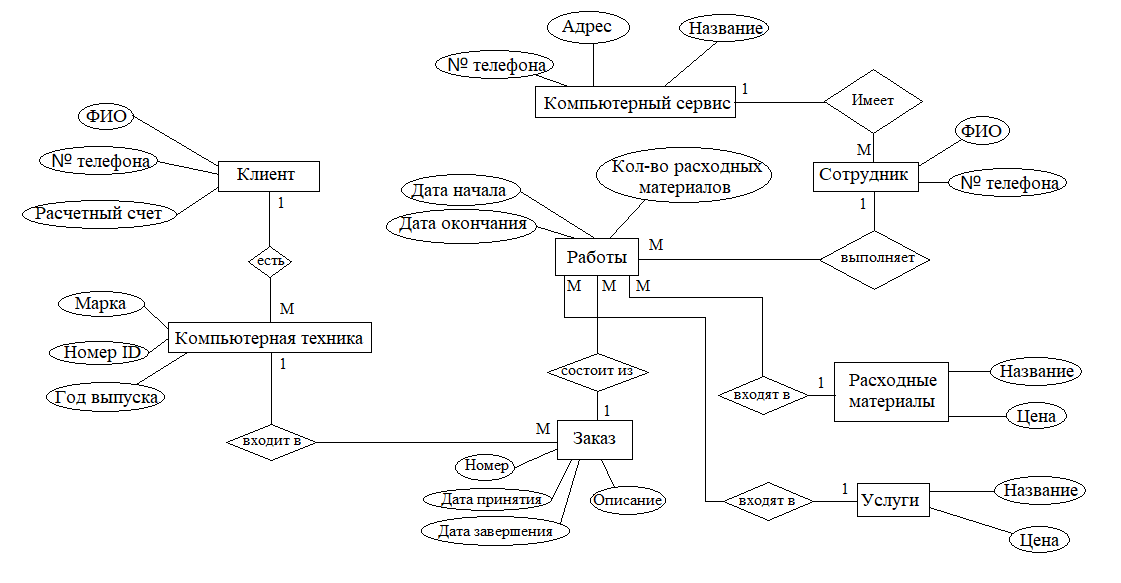. На практике кодирование происходит примерно так:

Приемник просто может считать корреляцию последовательностей Баркера(прямой и инверсной) и входного сигнала и по пикам корреляционной функции определять — где во входном сигнале закодированы нули, а где — единицы

Модуляция

В общем — как сделать из узкополосного информационного сигнала — широкополосный шумоподобный, а потом его восстановить — разобрались. Теперь поговорим немного о способах передачи данных через среду — средой может быть вакуум, воздух, оптоволокно, провод и т.д. Для того чтобы передавать сигнал при помощи радиоволн нам нужна несущая частота, промодулировав её — мы насаживаем нашу информацию на несущую. Есть 3 основных типа модуляции — амплитудная, частотная и фазовая.
Можно наш готовый к передаче сигнал направить на переключатель и просто включать-выключать передачу несущей — тем самым промодулировав амплитуду

Достоинства и недостатки амплитудной модуляции рассматривались в этой статье, так что подробно здесь останавливаться на ней не будем — в настоящее время амплитудная модуляция почти не применяется.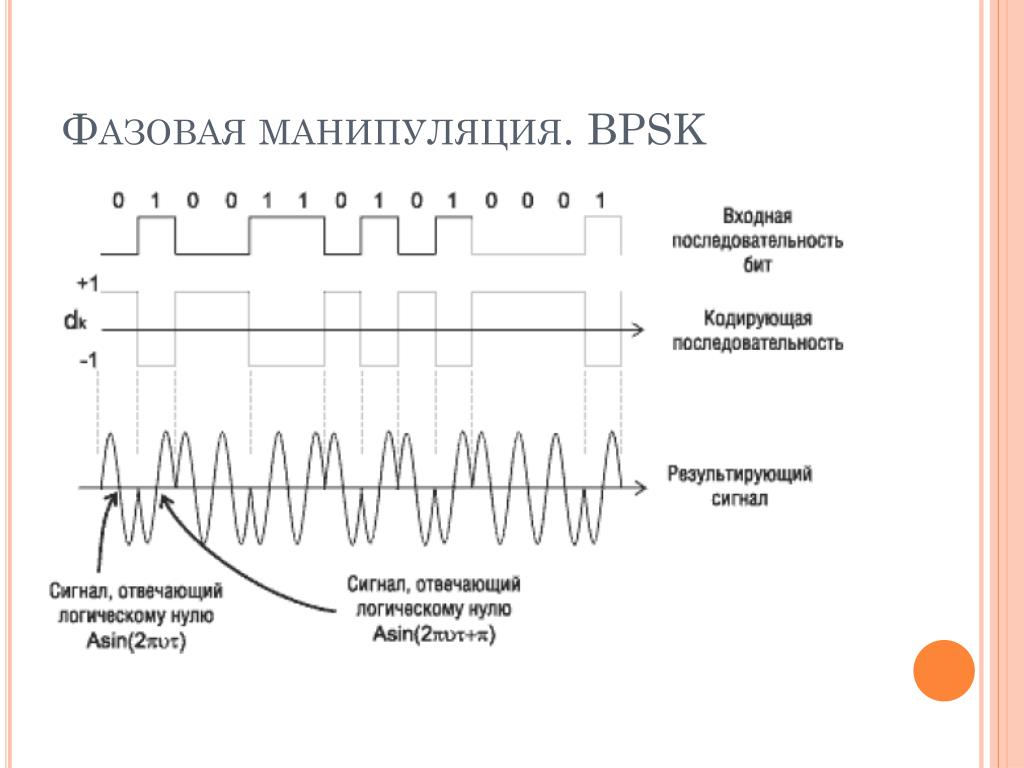

Следующий тип модуляции — частотная, когда сигнал данных управляет частотой несущей — либо напрямую (ГУН), либо переключаясь между двумя разными генераторами(при этом происходит скачок фазы)

Тут тоже есть что сказать, но как нибудь в другой раз — иначе статья получится слишком уж большой.

Фазовая модуляция

Несложно догадаться — что тут мы кодируем информацию в фазе сигнала — например нуль соответствует нулевому сдвигу по фазе, а единица — сдвигу на 180 градусов — такой способ кодировки легко реализовать технически — например умножая сигнал на 1 — имеем нулевой фазовый сдвиг, а умножая на -1 — сдвиг на 180 градусов. Такая модуляция называется Binary Phase Shift Key или BPSK

А что если мы хотим иметь больше фазовых сдвигов? Для начала объясню логику инженеров, которые придумали следующие танцы с бубном — у вас всего 2 управляющих сигнала — 1 и -1 и при помощи них нужно наиболее простым способом закодировать произвольное число фазовых сдвигов — можно конечно поставить какой нибудь супер ЦАП и управлять генерируемой частотой напрямую, но математика предлагает нам кое что получше.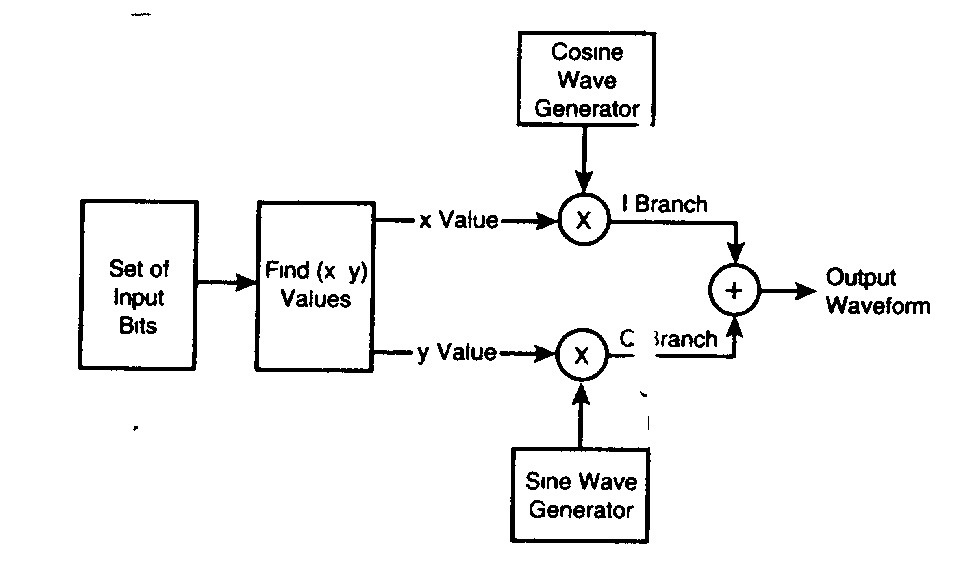 А именно вот эту формулу:

К слову — на ее основе мы произвели переход от спектров синусоид и косинусоид с нулевыми фазами к спектру синусоид с ненулевыми фазами и фазовому спектру — теперь мы просто делаем обратное преобразование.

На этом основана Квадратурная Модуляция

— вместе с несущей мы генерируем еще один сигнал, который сдвинут относительно несущей на 90 градусов, то есть находится с ней в квадратуре. Теперь — управляя амплитудой каждого сигнала(In phase и Quadrature) — умножая на 1 или -1, а затем суммируя — мы можем получить уже 4 возможных фазовых сдвига.

Теперь за раз мы можем кодировать 2 бита. То есть скорость передачи возрастает вдвое. Но и вероятность ошибки при тоже неизбежно возрастет.

Аналогичным образом можно получить большее число фазовых сдвигов. Возможные состояния сигнала обычно показывают на векторной диаграмме или на плоскости сигнального созвездия

Обратите внимание, что последовательность бинарных слов на диаграмме представляет собой Код Грея, что минимизирует вероятность ошибки. Кроме того — есть дополнительный сдвиг на 45 градусов — это делается для того, чтобы уменьшить паразитную амплитудную модуляцию при скачках фазы на 180 градусов

На практике синхронный способ передачи не используется — потому что есть привязка к какой то начальной фазе, а со временем набегает ошибка и фаза уплывает, нужно постоянно переустанавливать начальную фазу — синхронизировать приемник и передатчик. Поэтому носителем информации в реальных системах является не фаза, а изменение фазы — дифференциальный способ передачи сигнала позволяет избавиться от синхронизации. Например при каждом появлении нуля — фаза делает скачок на 180 градусов (BPSK).

Далее уже можно начать говорить о тонкостях реализации — как всегда — на практике все оказывается сложнее, чем в теории, данная статья — скорее небольшой ликбез для расширения кругозора.

UPD Отличное наглядное видео про квадратурную модуляцию

Презентация на тему: Сигналы Баркера при

			N2 11
и	N1	5

	Общая теория связи/Радиотехнические цепи	21
	и сигналы Практическое занятие № 3

Расчёт КФ сигналов Баркера

	Общая теория связи/Радиотехнические цепи и	22
	сигналы Практическое занятие № 3

АКФ действительного сигнала

	Общая теория связи/Радиотехнические цепи и	23
	сигналы Практическое занятие № 3

Общая теория связи/Радиотехнические цепи и	24
сигналы Практическое занятие № 3

Графический расчёт АКФ сигнала

с5-и значным кодом Баркера

•Формула дискретной свёртки

Rn	N t Sk Sk n
		N 1
	N 1 n	k 0

•1 клеточка – длительность одного дискрета или в Wi-Fi – длительность одного чипа

•Дома: чётные номера строят АКФ для 11- значного, нечётные — для 13-значного кода Баркера

	Общая теория связи/Радиотехнические цепи и	25
	сигналы Практическое занятие № 3

5-и значный код Баркера

	Общая теория связи/Радиотехнические цепи	26
	и сигналы Практическое занятие № 3

	Общая теория связи/Радиотехнические цепи	27
	и сигналы Практическое занятие № 3

R			N t		N	1		S S		Расчёт АКФ сигнала с
n					k					k n
		N 1 n
					k 0				использованием формулы
	0		1		2				3	4
	1		1		1				-1	1
n=			+		*				+						=5
0	1		1		1				1	1	1	-1	-1	1	1
			1					1			1		1		1
n=			+		*				+						=0
1	1		0		1				1	1	1
			0					1			1		-1		-1
n=			+		*				+						=1
2	1		0		1				0	1	1	-1	1	1	1
			0					0			1		-1		1
							Общая теория связи/Радиотехнические								28
n=			+		*				+
															=0
3						цепи и сигналы Практическое занятие № 3

Расчитать АКФ сигнала с использованием формулы

•На Mathcad для 11

•13 значных кодов Баркера

	Общая теория связи/Радиотехнические цепи и	29
	сигналы Практическое занятие № 3

Линейная Дискретная свёртка (свёртка дискретных сигналов) Длина первого N отсчетов, длина второго M отсчетов

Круговая (циклическая )Дискретная свертка

Обе последовательности имеют одинаковую длину N отсчетов

Чтобы выровнять длину последовательностей их дополняют нулями до длины M+N-1.

	Общая теория связи/Радиотехнические цепи	30
	и сигналы Практическое занятие № 3

Коды Баркера

Filter by alphabets Filter by categories

• All
• 1-9
• A
• B
• C
• D
• E
• F
• G
• H
• I
• J
• K
• L
• M
• N
• O
• P
• Q
• R
• S
• T
• U
• V
• W
• Д
• З

закрыть

Нажмите здесь, чтобы перейти на нашу главную страницу, посвященную радиолокации

Нажмите здесь, чтобы перейти на нашу главную страницу, посвященную радиосвязи

Новое в ноябре 2022 года. и посмотрите, что на самом деле происходит в системе, использующей микроволновое оборудование… на этой странице приведен один из таких примеров.

https://www.radartutorial.eu/08.transmitters/pic/kor7.gif

Коды Баркера названы в честь ирландского физика доктора Рональда Хью Баркера. Работая с первыми компьютерами и разрабатывая радары, телеметрию и даже цифровые речевые системы в Британском научно-исследовательском центре сигналов (SRDE), Баркер в 1953 году представил статью под названием «Групповая синхронизация двоичных систем». запланировать двоичную последовательность в поток цифровых данных, чтобы «умный» приемник мог точно сопоставить, где начинаются и заканчиваются передаваемые данные. «Код Баркера» является ключом к корреляции данных. Баркер предложил семь различных кодов длиной 2, 3, 4, 5, 7, 11 и 13 бит, каждый из которых обладает тем свойством, что все боковые лепестки одинаково низки (также известное как «идеальная автокорреляция»). Вы можете увидеть коды здесь, в Википедии. Чем больше длина кода, тем выше вероятность того, что он не будет случайно воспроизведен в потоке данных, что может привести к ошибкам синхронизации. В радиочастотном мире коды Баркера обычно реализуются с фазовой модуляцией, где сигналы имеют значение «1» (фаза 0 градусов) или «-1» (фаза 180 градусов). Интересно, что в течение многих десятилетий после статьи Баркера никому не удавалось разработать код Баркера с более чем 13 битами.

Пока мы разрабатываем более подробное объяснение кодов Баркера, вот видео, объясняющее концепцию и ее использование в сжатии импульсов радара. Спасибо Rohde and Schwarz за отличную презентацию!

Понимание кодов Баркера от Rohde and Schwarz

Мы скоро добавим на эту страницу, мы работаем над электронной таблицей кодов Баркера в Excel, которая не готова для прайм-тайм…

Пока мы обсуждаем эту тему «Зазывалы», вот видео Винсента Прайса, играющего карнавального зазывалу в 1969 фильм «Больше мертв, чем жив». Не путайте коды Баркера с карнавальной жизнью!

Баркер, Р. Х., «Групповая синхронизация двоичных цифровых систем». Теория коммуникации , 1953 г., Лондон: Баттерворт. стр. 273–287.

Автор : Неизвестный редактор

Реклама

Реклама

энциклопедии-подробности

Код Баркера — HandWiki

Из HandWiki

Пространства имен

• Страница
• Обсуждение

Действия

• Читать
• Просмотр Источник
• ИСТОРИЯ
• ZWI EXPORT

Графическое представление кода Barker-7

Функция AutoCorretation Spectrute SpectReplation Spectrute SpectRELER SpectRELER SpectRELEUM SpectRELER SPEPTRELEUM DAPTRELER SPEPTRELEUM. Код Баркера 13

В телекоммуникационных технологиях код Баркера или последовательность Баркера представляет собой конечную последовательность цифровых значений с идеальным свойством автокорреляции. Он используется в качестве шаблона синхронизации между отправителем и получателем.

Содержание

• 1 Пояснение
• 2 Определение
• 3 Известные коды Баркера
• 4 Модуляция Баркера
• 5 Каталожные номера

Объяснение

Двоичные цифры имеют очень мало значения, если не известно значение отдельных цифр. Передача предварительно подготовленного синхронизирующего шаблона цифр может позволить регенерировать сигнал. приемником с низкой вероятностью ошибки. Проще говоря, это эквивалентно привязыванию метки к одной цифре, после которой другие могут быть связаны путем подсчета. Это достигается за счет передачи специального набора цифр, который однозначно распознается приемником. Чем длиннее шаблон, тем точнее можно синхронизировать данные и исключить ошибки из-за искажений. Эти шаблоны, называемые последовательностями Баркера, более известны как код Баркера в честь изобретателя Рональда Хью Баркера. Это процесс «Групповая синхронизация двоичных цифровых систем», впервые опубликованный в 1953. {N-v} a_j a_{j+v} }[/math]

как можно меньше:

[математика]\displaystyle{ |c_v| \le 1\, }[/math]

для всех [math]\displaystyle{ 1 \le v \lt N }[/math]. ^[1]

Известно только девять последовательностей Баркера ^[2] , все длиной N не более 13. ^[3] В статье Баркера 1953 г. запрашивались последовательности с более сильным условием

[математика]\displaystyle{ c_v \in \{-1, 0\}. }[/math]

Известны только четыре таких последовательности, выделенные жирным шрифтом в таблице ниже. ^[4]

Известные коды Баркера

Вот таблица всех известных кодов Баркера, в которой опущены отрицания и обращения кодов. Код Баркера имеет максимальную автокорреляционную последовательность, боковые лепестки которой не превышают 1. Принято считать, что других совершенных двоичных фазовых кодов не существует. ^{[5] [6]} (Было доказано, что не существует других кодов нечетной длины, ^[7] , а также кодов четной длины N < 10 ²² .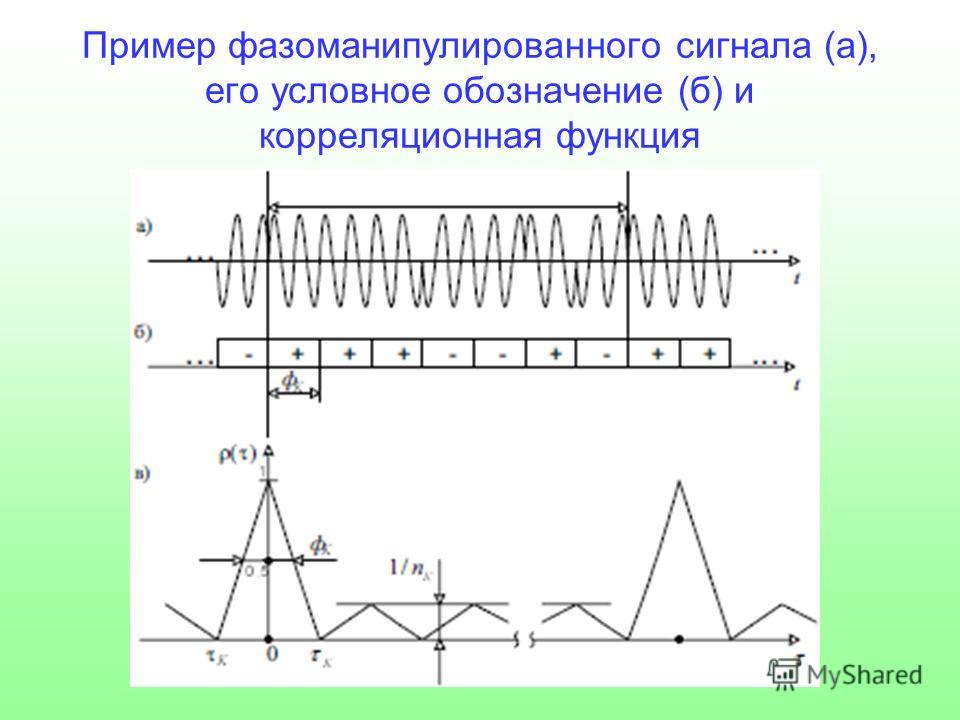 ^[8] )

Известные коды Баркера

Длина	Коды		Отношение уровней боковых лепестков [9] [10]
2	+1 −1	+1 +1	−6 дБ
3	+1 +1 −1		−9,5 дБ
4	+1 +1 −1 +1	+1 +1 +1 −1	−12 дБ
5	+1 +1 +1 −1 +1		−14 дБ
7	+1 +1 +1 −1 −1 +1 −1		−16,9 дБ
11	+1 +1 +1 −1 −1 −1 +1 −1 −1 +1 −1		−20,8 дБ
13	+1 +1 +1 +1 +1 −1 −1 +1 +1 −1 +1 −1 +1		−22,3 дБ

Коды Баркера длиной N , равные 11 и 13, используются в радиолокационных системах с расширенным спектром прямой последовательности и со сжатием импульсов из-за их низких автокорреляционных свойств (уровень амплитуды боковых лепестков кодов Баркера составляет 1/9). 0061 N пикового сигнала). ^[11] Код Баркера напоминает дискретную версию непрерывного щебета, другого сигнала с низкой автокорреляцией, используемого в других радарах со сжатием импульсов.

Положительная и отрицательная амплитуды импульсов, формирующих коды Баркера, предполагают использование двухфазной модуляции или двоичной фазовой манипуляции; то есть изменение фазы несущей волны составляет 180 градусов.

Подобным кодам Баркера являются комплементарные последовательности, которые точно гасят боковые лепестки при суммировании; пары кодов Баркера четной длины также являются дополнительными парами. Существует простой конструктивный метод создания произвольно длинных комплементарных последовательностей. 9n-1 }[/math] последовательности максимальной длины (MLS). Можно построить сколь угодно длинные циклические последовательности.

Модуляция Баркера

Код Баркера, используемый в модуляции BPSK

В беспроводной связи последовательности обычно выбираются по их спектральным свойствам и низкой взаимной корреляции с другими последовательностями, которые могут создавать помехи. В стандарте 802.11 для скоростей 1 и 2 Мбит/с используется последовательность Баркера из 11 чипов. Значение автокорреляционной функции для последовательности Баркера равно 0 или −1 при всех смещениях, кроме нуля, где оно равно +11. Это обеспечивает более однородный спектр и лучшую производительность приемников. ^[12]

Ссылки

1. ↑ ^{1,0 1,1} Barker, R. H. (1953). «Групповая синхронизация двоичных цифровых систем». Теория общения . Лондон: Баттерворт. стр. 273–287.
2. ↑ Sloane, NJA, изд. «Последовательность A091704». Фонд ОИС. https://oeis.org/A091704.
3. ↑ Борвейн, Питер; Моссингхофф, Майкл Дж. (2008). «Последовательности Баркера и плоские многочлены». в Джеймсе Макки. Теория чисел и многочлены . Конспекты лекций LMS. 352 . Издательство Кембриджского университета. стр. 71–88. ISBN 978-0-521-71467-9.
4. ↑ Использование другой формы импульса в коде Баркера также улучшает некоторые свойства автокорреляции.