Конденсатор емкостной. Основы емкости в электронике: характеристики, формулы и применение конденсаторов — Производство и поставка электростанций, Бензиновые и дизельные генераторы от 1 до 100 кВт. Мини ТЭЦ на базе двигателя Стирлинга.

Что такое емкость в электронике. Как рассчитать емкость конденсатора. Какие бывают типы конденсаторов. Где применяются конденсаторы в электронных схемах. Как работают конденсаторы на переменном и постоянном токе.

Содержание

Что такое емкость в электронике и как она измеряется

Емкость — это способность электронного компонента накапливать и хранить электрический заряд. Основной единицей измерения емкости является фарад (Ф). Один фарад — это очень большая емкость, поэтому на практике чаще используются микрофарады (мкФ), нанофарады (нФ) и пикофарады (пФ).

Емкость конденсатора зависит от следующих факторов:

Площади обкладок
Расстояния между обкладками
Диэлектрической проницаемости материала между обкладками

Чем больше площадь обкладок и чем ближе они расположены друг к другу, тем выше емкость. Также емкость увеличивается при использовании диэлектрика с высокой диэлектрической проницаемостью.

Основные формулы для расчета емкости конденсатора

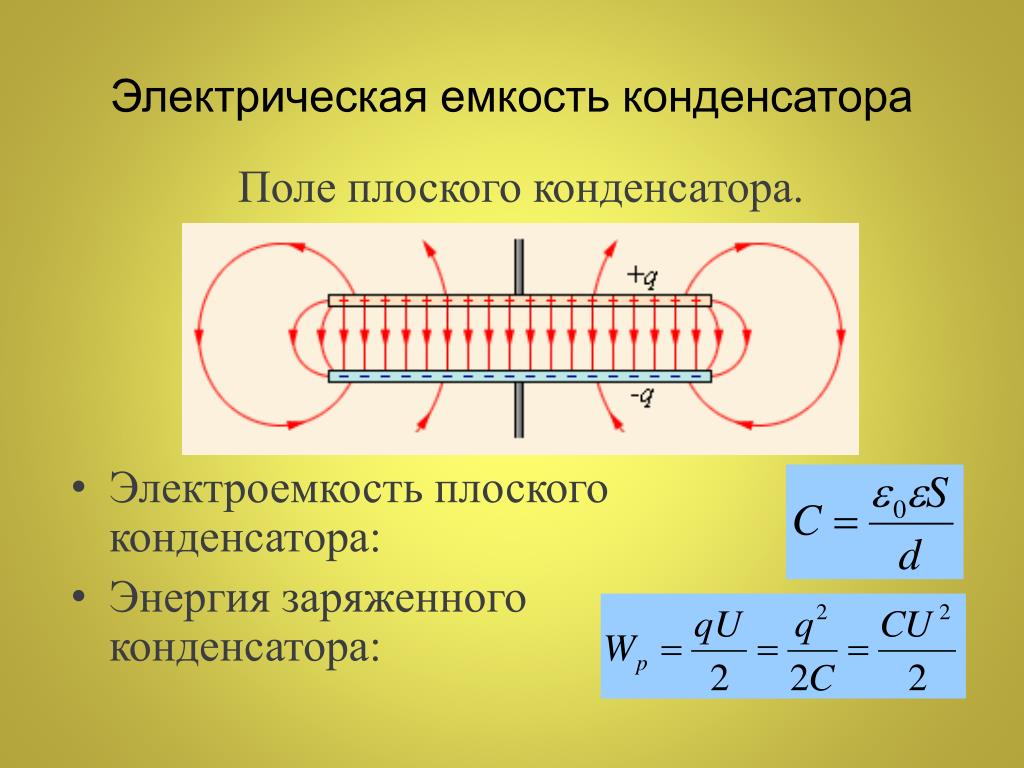
Емкость плоского конденсатора рассчитывается по формуле:

C = εε0S / d

где:

C — емкость в фарадах
ε — относительная диэлектрическая проницаемость материала между обкладками
ε0 — электрическая постоянная (8.85 * 10^-12 Ф/м)
S — площадь перекрытия обкладок в м^2
d — расстояние между обкладками в метрах

Для цилиндрического конденсатора используется формула:

C = 2πεε0L / ln(R2/R1)

где L — длина цилиндра, R1 и R2 — радиусы внутреннего и внешнего цилиндров.

Типы конденсаторов и их характеристики

Основные типы конденсаторов, используемых в электронике:

Керамические — компактные, недорогие, для высокочастотных цепей
Пленочные — стабильные, для фильтров и развязки
Электролитические — большая емкость, для источников питания
Танталовые — компактные, для поверхностного монтажа
Подстроечные — с регулируемой емкостью

При выборе конденсатора учитывают следующие параметры:

Номинальная емкость
Допустимое напряжение
Температурный коэффициент емкости
Частотные характеristики
Габариты и тип корпуса

Применение конденсаторов в электронных схемах

Конденсаторы широко используются в электронике для выполнения следующих функций:

Накопление энергии
Фильтрация помех и сглаживание пульсаций
Разделение постоянной и переменной составляющих сигнала
Частотная коррекция в фильтрах и цепях обратной связи
Создание резонансных контуров
Подавление помех по цепям питания

Например, в источниках питания электролитические конденсаторы большой емкости используются для сглаживания пульсаций выпрямленного напряжения. В радиоприемниках конденсаторы образуют колебательные контуры для настройки на нужную частоту.

Поведение конденсатора на постоянном и переменном токе

На постоянном токе идеальный конденсатор ведет себя как разрыв цепи — он заряжается до напряжения источника и ток через него не протекает. На переменном токе конденсатор пропускает переменную составляющую, но блокирует постоянную.

Емкостное сопротивление конденсатора на переменном токе зависит от частоты и рассчитывается по формуле:

Xc = 1 / (2πfC)

где f — частота, C — емкость.

Чем выше частота, тем меньше емкостное сопротивление. Поэтому конденсаторы используют для частотной фильтрации сигналов.

Последовательное и параллельное соединение конденсаторов

При параллельном соединении конденсаторов их емкости складываются:

C = C1 + C2 + C3 + …

При последовательном соединении суммарная емкость уменьшается и рассчитывается по формуле:

1/C = 1/C1 + 1/C2 + 1/C3 + …

Эти формулы позволяют получить требуемую емкость, комбинируя стандартные номиналы конденсаторов.

Заряд и разряд конденсатора

При подключении конденсатора к источнику постоянного напряжения через резистор происходит его зарядка. Напряжение на конденсаторе при этом изменяется по экспоненциальному закону:

U = U0(1 — e^(-t/RC))

где U0 — напряжение источника, R — сопротивление, C — емкость конденсатора.

Время зарядки до 63% от U0 называется постоянной времени τ = RC.

Разряд конденсатора через резистор происходит по аналогичному закону:

U = U0 * e^(-t/RC)

Знание этих процессов важно при расчете времязадающих и интегрирующих цепей.

Паразитные параметры реальных конденсаторов

Реальный конденсатор отличается от идеального наличием паразитных параметров:

Последовательное сопротивление (ESR) — вызывает потери энергии
Последовательная индуктивность (ESL) — ограничивает работу на высоких частотах
Параллельное сопротивление утечки — приводит к саморазряду
Диэлектрические потери — характеризуются тангенсом угла потерь

Учет этих параметров необходим при проектировании высокочастотных и прецизионных схем.

влияние на переменный и постоянный ток, формулы для расчета

Конденсатор используется в схемах для разделения переменной и постоянной составляющей напряжения, при этом он хорошо проводит высокочастотный сигнал, и плохо — низкочастотный. Находясь в цепи постоянного тока, его импеданс принимается бесконечно большим. Для переменного тока ёмкостное сопротивление конденсатора не имеет постоянной величиной. Поэтому расчёт этого значения крайне важен при проектировании различных радиоэлектронных приборов.

Общее описание
Характеристики прибора
Импеданс элемента
- Ёмкостное сопротивление
- Индуктивная составляющая
Пример расчёта

Общее описание

Физически электронное устройство — конденсатор — представляет собой две обкладки, выполненные из проводящего материала, между которыми находится диэлектрический слой. С поверхности пластин выводятся два электрода, предназначенные для подключения в электрическую цепь. Конструктивно прибор может быть различного размера и формы, но его структура остаётся неизменной, то есть всегда происходит чередование проводящего и диэлектрического слоев.

Слово «конденсатор» произошло от латинского «condensatio» — «накопление». Научное определение гласит, что накопительный электрический прибор — это двухполюсник, характеризующийся постоянным и переменным значениями ёмкости и большим сопротивлением. Предназначен он для накопления энергии и заряда. За единицу измерения ёмкости принят фарад (F).

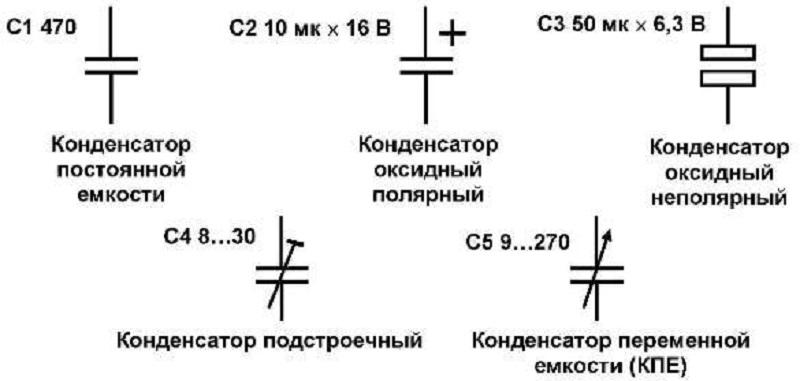
На схемах конденсатор изображается в виде двух прямых, соответствующих проводящим пластинам прибора, и перпендикулярно к их серединам нарисованными отрезками — выводами устройства.

Принцип действия конденсатора заключается в следующем: при включении прибора в электрическую цепь напряжение в ней будет иметь нулевую величину. В этот момент устройство начинает получать и накапливать заряд. Электрический ток, подающийся в схему, будет максимально возможным.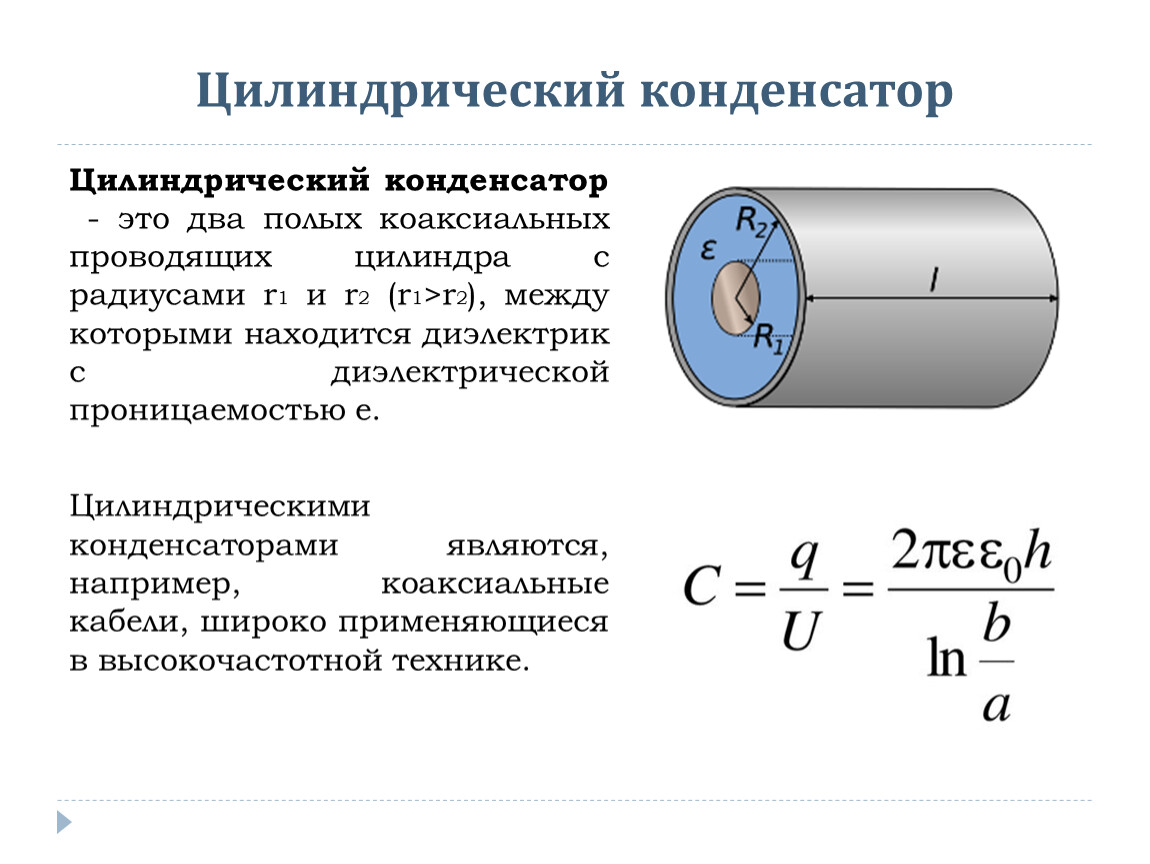 Через некоторое время на одном из электродов прибора начнут накапливаться заряды положительного знака, а на другом — отрицательного.

Длительность этого процесса зависит от ёмкости прибора и активного сопротивления. Расположенный между выводами диэлектрик мешает перемещению частиц между обкладками. Но это будет происходить лишь до того момента, пока разность потенциалов источника питания и напряжение на выводах конденсатора не сравняются. В этот момент ёмкость станет максимально возможной, а электроток — минимальным.

Если на элемент перестают подавать напряжение, то при подключении нагрузки конденсатор начинает отдавать свой накопленный заряд ей. Его ёмкость уменьшается, а в цепи снижаются уровни напряжения и тока. Иными словами, накопительный прибор сам превращается в источник питания. Поэтому если конденсатор подключить к переменному току, то он начнёт периодически перезаряжаться, то есть создавать определённое сопротивление в цепи.

Характеристики прибора

Важнейшей характеристикой накопительного прибора является ёмкость.

От неё зависит время заряда при подключении устройства к источнику тока. Время разряда напрямую связано со значением сопротивления нагрузки: чем оно выше, тем быстрее происходит процесс отдачи накопленной энергии. Определяется эта ёмкость следующим выражением:

C = E*Eo*S / d, где E — относительная диэлектрическая проницаемость среды (справочная величина), S — площадь пластин, d — расстояние между ними.

Кроме ёмкости конденсатор характеризуется рядом параметров, такими как:

удельная ёмкость — определяет отношение величины ёмкости к массе диэлектрика;
рабочее напряжение — номинальное значение, которое может выдержать устройство при подаче его на обкладки элемента;
температурная стабильность — интервал, в котором ёмкость конденсатора практически не изменяется;
сопротивление изоляции — характеризуется саморазрядом устройства и определяется током утечки;

эквивалентное сопротивление — состоит из потерь, образуемых на выводах прибора и слое диэлектрика;
абсорбция — процесс возникновения разности потенциалов на обкладках после разряда устройства до нуля;
ёмкостное сопротивление — уменьшение проводимости при подаче переменного тока;
полярность — из-за физических свойств материала, используемого при изготовлении, конденсатор сможет правильно работать, только если к обкладкам приложен потенциал с определённым знаком;
эквивалентная индуктивность — паразитный параметр, появляющийся на контактах устройства и превращающий конденсатор в колебательный контур.

Импеданс элемента

Общее сопротивление конденсатора (импеданс) переменному сигналу складывается из трёх составляющих: ёмкостного, резистивного и индуктивного сопротивления. Все эти величины при конструировании схем, содержащих накопительный элемент, необходимо учитывать. В ином случае в электрической цепи, при соответствующей обвязке, конденсатор может вести себя как дроссель и находится в резонансе. Из всех трёх величин наиболее значимой является ёмкостное сопротивление конденсатора, но при определённых обстоятельствах индуктивное тоже оказывает влияние.

Часто при расчётах паразитные значения вроде индуктивности или активного сопротивления принимаются ничтожно малыми, а конденсатор в этом случае называется идеальным.

Полное сопротивление элемента выражается в формуле Z = (R2 + (Xl-Xc) ² ) ^½, где

Xl — индуктивность;
Xс — ёмкость;
R — активная составляющая.

Последняя возникает из-за появления электродвижущей силы (ЭДС) самоиндукции. Непостоянство тока приводит к изменению магнитного потока, поддерживающего ток ЭДС самоиндукции постоянным. Это значение определяется индуктивностью L и частотой протекающих зарядов W. Xl = wL = 2*p*f*L. Xc — ёмкостное сопротивление, зависящее от ёмкости накопителя C и частоты тока f. Xc = 1/wC = ½*p*f*C, где w — круговая частота.

Разница между ёмкостным и индуктивным значениями называется реактивным сопротивлением конденсатора: X = Xl-Xc. По формулам можно увидеть, что при увеличении частоты f сигнала начинает преобладать индуктивное значение, при уменьшении — ёмкостное. Поэтому если:

X > 0, в элементе проявляются индуктивные свойства;
X = 0, в ёмкости присутствует только активная величина;
X < 0, в элементе проявляется ёмкостное сопротивление.

Активное сопротивление R связывается с потерями мощности, превращением её электрической энергии в тепловую.
Реактивное — с обменом энергии между переменным током и электромагнитным полем. Таким образом, полное сопротивление можно найти, используя формулу Z = R +j*X, где j — мнимая единица.

Ёмкостное сопротивление

Для понимания процесса следует представить конденсатор в электрической цепи, по которой течёт переменный ток. Причём в этой цепи нет других элементов. Значение тока, проходящего через конденсатор, и напряжения, приложенного к его обкладкам, изменяется по времени. Зная любое из этих значений, можно найти другое.

Пускай ток изменяется по синусоидальной зависимости I (t) = Im * sin (w*t+ f 0). Тогда напряжение можно описать как U (t) = (Im/C*w) *sin (w*t+ f 0 -p/2). При учёте в формуле сдвига фаз на 90 градусов, возникающего между сигналами, вводится комплексная величина j, называемая мнимой единицей. Поэтому формула для нахождения тока будет выглядеть как I = U /(1/j*w*C). Но учитывая, что комплексное число только обозначает смещение напряжения относительно тока, а на их амплитудные значения не влияет, его можно убрать из формулы, тем самым значительно её упростив.

Так как по закону Ома сопротивление прямо пропорционально напряжению на участке цепи и обратно пропорционально току, то преобразуя формулы, можно будет получить следующее выражение:

Xc = 1/w*C = ½*p*f*C. Единица измерения — ом.

Становится понятно, что ёмкостное сопротивление зависит не только от ёмкости, но и от частоты. При этом чем больше эта частота, тем меньшее сопротивление конденсатор будет оказывать проходимому через него току. По отношению к ёмкости это утверждение будет обратным. Вот поэтому для постоянного тока, частота которого равна нулю, сопротивление накопителя будет бесконечно большим.

На практике всё немного по-другому. Чем ближе частота сигнала приближается к нулевому значению, тем больше становится сопротивление конденсатора, но при этом разрыв цепи наступить всё равно не может. Связанно это с током утечки. В случае когда частота стремится к бесконечности, сопротивление конденсатора должно становиться нулевым, но этого тоже не происходит — из-за присутствия паразитной индуктивности и всё того же тока утечки.

Индуктивная составляющая

При прохождении переменного сигнала через накопитель, его можно представить в виде последовательно включённой с источником питания катушки индуктивности. Эта катушка характеризуется большим сопротивлением в цепи переменного сигнала, чем постоянного. Значение силы тока в определённой точке времени находится как I = I 0 * sinw .

Приняв во внимание, что мгновенная величина напряжения U 0 обратна по знаку мгновенному значению ЭДС самоиндукции E 0, а также используя правило Ленца, можно получить выражение E = L * I, где L — индуктивность.

Следовательно: U = L*w * I 0 *cosw*t = U 0 *sin (wt + p /2) , причём ток отстаёт от напряжения на p /2. Используя закон Ома и приняв, что сопротивление катушки равно w * L, получится формула для участка электрической цепи, имеющая только индуктивную составляющую: U 0 = I 0 / w * L.

Таким образом, индуктивное сопротивление будет равно Xl = w * L, измеряется оно также в омах. Из полученного выражения видно, что чем больше частота сигнала, тем сильнее будет сопротивление прохождению тока.

Пример расчёта

Ёмкостное и индуктивное сопротивления относятся к реактивным, то есть таким, которые не потребляют мощности. Поэтому закон Ома для участка схемы с ёмкостью имеет вид I = U/Xc, где ток и напряжение обозначают действующие значения. Именно из-за этого конденсаторы используются в цепях для разделения не только постоянных и переменных токов, но и низкой и высокой частот. При этом чем ёмкость будет ниже, тем более высокой частоты сможет пройти ток. Если же последовательно с конденсатором включено активное сопротивление, то общий импеданс цепи находится как Z = (R ² +Xc ² ) ^½.

Практическое применение формул можно рассмотреть при решении задачи. Пусть имеется RC цепочка, состоящая из ёмкости C = 1 мкФ и сопротивления R = 5 кОм. Необходимо найти импеданс этого участка и ток цепи, если частота сигнала равна f = 50 Гц, а амплитуда U = 50 В.

В первую очередь понадобится определить сопротивление конденсатора в цепи переменного тока для заданной частоты. Подставив данные в формулу, получим, что для частоты 50 Гц сопротивление будет

Xc = 1/ (2*p*F*C) = 1/ (2*3,14*50*1* 10 ⁻⁶ ) = 3,2 кОм.

По закону Ома можно найти ток: I = U /Xc = 50 /3200 = 15,7 мА.

Напряжение берётся изменяемым по закону синуса, поэтому: U (t) = U * sin (2*p*f*t) = 50*sin (314*t). Соответственно, ток будет I (t) = 15,7* 10 ⁻³ + sin (314*t+p/2). Используя полученные результаты, можно построить график тока и напряжения при этой частоте. Общее сопротивление участка цепи находим как Z = (5000²+3200²)½ = 5 936 Ом =5,9 кОм.

Таким образом, подсчитать полное сопротивление на любом участке цепи несложно. При этом можно воспользоваться и так называемыми онлайн-калькуляторами, куда вводят начальные данные, такие как частота и ёмкость, а все расчёты выполняются автоматически. Это удобно, так как нет необходимости запоминать формулы и вероятность ошибки при этом стремится к нулю.

«Конденсатор аналогичной емкости занял бы несколько шкафов»: в Дубне изобрели новый тип «батареек»

Скачки потребления энергии представляют проблему для многих электросистем, поскольку большинство источников тока рассчитаны на стабильную генерацию. Российские ученые разработали накопитель для сглаживания таких пульсаций на основе сверхпроводящего магнита. Он гораздо компактнее конденсаторов и способен отдавать и принимать энергию во много раз быстрее аккумуляторов. Такую «батарейку» создали для нового дубненского коллайдера NICA, но потенциально ее можно применять где угодно, от электроавтобусов до промышленных предприятий.

Объединенный институт ядерных исследований ведет строительство коллайдера NICA, флагманской российской физической установки. При проектировании было разработано множество технологий, которым можно найти применение за пределами фундаментальной науки. В том числе, ученые из Дубны начали создавать новый накопитель энергии с рекордной для своего класса емкостью.

Магнитные системы ускорительных колец коллайдера NICA – «Нуклотрона» и «Бустера» – потребляют энергию крайне неравномерно. Они создают импульсное поле с периодом колебаний от четырех секунд и выше, что вызывает пульсации энергии в сети. Это приводит к нагрузке на систему и ухудшает работу самих ускорителей и измерительной аппаратуры.

Чтобы сглаживать пики потребления, можно установить накопитель энергии. Поскольку колебания происходят слишком быстро, химические аккумуляторы не в состоянии их скомпенсировать: они слишком долго заряжаются и недостаточно быстро отдают заряд.

100%

«В нашей системе питания накопителя будет два: емкостной, то есть, конденсаторы, и индуктивный. Индуктивный накопитель – это магнитная катушка, или соленоид. Его полная энергия будет равна 3,65 МДж, а полезная – 1,7. Ее он будет перебрасывать из «Нуклотрона» в «Бустер» и обратно, предварительно накапливая», – рассказал старший научный сотрудник ОИЯИ Михаил Новиков, создатель накопителя.

Индуктивный накопитель энергии создан на основе главного элемента ускорителя NICA – мощных магнитов.

«Обмотки магнитов NICA сделаны из сверхпроводящего кабеля. Магнит представляет собой мельхиоровую трубку, обмотанную проводником из сплава ниобия и титана, внутри течет жидкий гелий при температуре -269 градусов по Цельсию – практически абсолютный ноль. Из этого кабеля можно создавать изделия сложной геометрии, и в нем могут течь очень большие, килоамперные токи. Мы предложили помимо основных магнитов из этого кабеля сделать «батарейку» на несколько мегаватт. То есть, это накопитель энергии, в который вы можете завести ток, накопить несколько мегаджоулей, и потом от него запитать потребителя – например, огромный ускоритель», – пояснил «Газете.Ru» директор ОИЯИ академик Григорий Трубников.

Наглядным аналогом этого накопителя можно считать индукционную катушку, которую многие видели на школьном уроке физики. Если подключить лампочку не прямо к аккумулятору, а через катушку, то при замыкании и размыкании цепи она будет зажигаться и гаснуть не сразу, а плавно.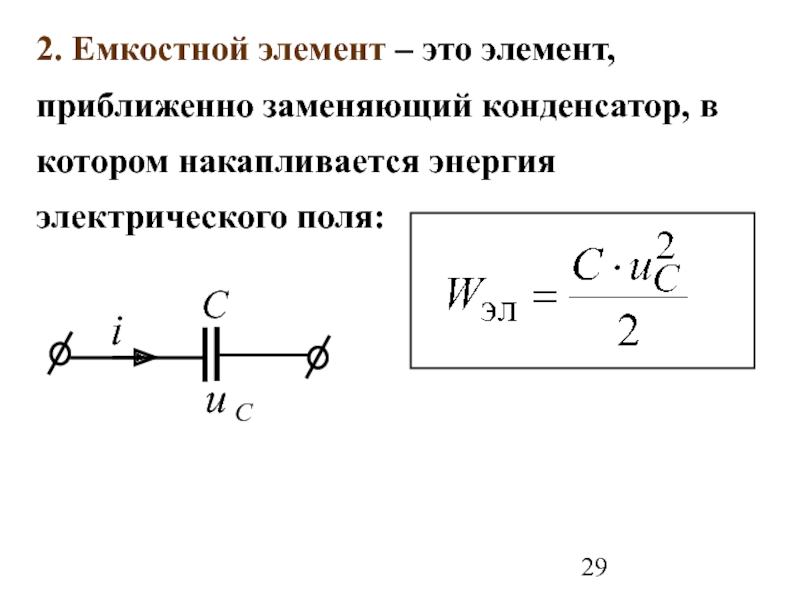 Это происходит потому, что катушка накапливает энергию в свое магнитное поле при замыкании электроцепи, и затем отдает. Аналогичным образом работает и индуктивный накопитель коллайдера NICA, с той лишь разницей, что обмотка этой катушки сделана из высокотемпературного сверхпроводника (работающего при температуре жидкого неона, около 20 кельвинов), что приводит к неизмеримо меньшим потерям энергии.

100%

«Наша катушка сохраняет энергию примерно в течение часа. Долгое хранение нам не требуется, но если бы мы сделали сверхпроводящими не только обмотку, но и контакты, запасенная энергия хранилась бы бесконечно и без потерь»,

– пояснил Новиков. Для сохранения запасенной мощности катушку необходимо замкнуть с наименьшим сопротивлением.

Устройство работает одновременно как накопитель энергии и как сетевой фильтр. В качестве примера Трубников приводит схему работы гидроаккумулирующих станций: «Такие станции работают круглые сутки, днем энергия расходуется, а ночью, когда потребление меньше, выработанная, но не востребованная энергия собирается в накопителе. Им может быть как аккумулятор, так и водоем».

Загадочный звуковой канал: как услышать старт ракеты за сотни километров

Волноводы позволяют передать звук (или свет) на огромное расстояние, заключив их будто бы в узкий…

13 мая 09:48

Установка весит около полутора тонн и способна запасать несколько мегаджоулей. Это не много, если сравнивать с аккумуляторами: например, батарея Tesla Model S хранит до cотни киловатт-час (360 МДж) при весе в 540 килограмм. Однако накопитель ОИЯИ относится к совсем другому классу, и его задача отдавать и принимать энергию максимально быстро. Таким образом, его нужно сравнивать не с химическими источниками тока, а с конденсаторами и механическими маховиками.

«В нем нет вращающегося «волчка», в отличие от кинетических накопителей, и потому нет опасности взрыва или возникновения опасных вибраций. Наш магнит надежен, и должен выдержать 70 миллионов циклов разрядки-зарядки.

Этими преимуществами обладают и конденсаторы, но наш накопитель превосходит их с точки зрения плотности энергии. Емкостный накопитель с аналогичной энергией занял бы не кубический метр, а несколько больших шкафов»,

– рассказал Новиков.

В нынешнем состоянии индуктивному накопителю требуется массивная криогенная установка, но в будущем ее можно заменить на миниатюрный криокулер, помещающийся в невысокую тумбочку. В этом случае накопитель можно будет устанавливать в электрические системы для сглаживания пульсаций, в том числе в городские, промышленные и транспортные. Например, с его помощью можно будет создать систему рекуперации энергии для электрического автобуса. Современные электродвигатели умеют вырабатывать ток при торможении, но аккумуляторы не в состоянии быстро его потребить. Поэтому добавление в схему мощного и быстрого накопителя позволит экономить заряд батарей. Кроме того, на его основе можно изготовить источники бесперебойного питания для промышленности, где требуется высокая токоотдача.

Основные понятия емкости » Заметки по электронике

Емкость является одним из основных понятий электроники и широко используется, о чем свидетельствует количество конденсаторов, используемых в электронных схемах

Емкость Учебное пособие Включает:
Емкость Формулы конденсаторов Емкостное реактивное сопротивление Параллельные и последовательные конденсаторы Диэлектрическая проницаемость и относительная диэлектрическая проницаемость Коэффициент рассеяния, тангенс угла потерь, ESR Таблица преобразования конденсаторов

Сопротивление, емкость и индуктивность — это три основных параметра, связанных с электрическими и электронными цепями.

В отличие от двух других, емкость связана с хранением электрического заряда, а атрибуты используются в электронных компонентах, называемых конденсаторами, которые, в свою очередь, используются во многих электрических цепях и практически во всех электронных схемах.

Эффекты емкости можно использовать различными способами в схемах, начиная от электродвигателей и заканчивая электронными схемами, такими как источники питания, аудиосхемы, радиочастотные схемы, логические и цифровые схемы и многие другие.

В связи с этим емкость является особенно важным параметром, который используется во многих областях.

Что такое емкость

Глядя на емкость, в первую очередь необходимо посмотреть, что она собой представляет. Емкость — это фактически способность накапливать заряд. В простейшей форме конденсатор состоит из двух параллельных пластин. Обнаружено, что когда батарея или любой другой источник напряжения подключены к двум пластинам, как показано, ток течет в течение короткого времени, и одна пластина получает избыток электронов, а другая — слишком мало.

Таким образом, одна пластина с избытком электронов становится отрицательно заряженной, а другая положительно заряженной.

Заряд сохраняется на двух обкладках конденсатора

Если снять батарею, конденсатор сохранит свой заряд. Однако, если резистор помещен между пластинами, ток будет течь до тех пор, пока конденсатор не разрядится.

Соответственно можно определить, что такое емкость:

Определение емкости:

Емкость — это способность компонента или цепи собирать и хранить энергию в виде электрического заряда. Это количество электрического заряда, хранящегося на проводнике при установленной разности электрических потенциалов.

Чем больше пластины, тем больше заряда они могут хранить, а также чем ближе они друг к другу, тем больше заряда они сохраняют. Хранение заряда также зависит от материала между двумя пластинами.

Единицы или емкость

Необходимо уметь определять «размер» конденсатора. Емкость конденсатора является мерой его способности накапливать заряд, а основной единицей измерения емкости является фарад, названный в честь Майкла Фарадея.

Стоит определить фарад, который является основной единицей измерения емкости.

Емкость: Фарад определение:

Конденсатор имеет емкость в один фарад, когда разность потенциалов в один вольт заряжает его одним кулоном электричества (т. е. один ампер за одну секунду).

Конденсатор емкостью один фарад слишком велик для большинства электронных приложений, и обычно используются компоненты с гораздо меньшими значениями емкости. Используются три префикса (множителя): µ (микро), n (нано) и p (пико):

Префиксы и множители единиц измерения емкости
Префикс	Множитель	Терминология
µ	10 ^-6 (миллионная)	1000000 мкФ = 1Ф
нет	10 ^-9 (тысячно-миллионная)	1000 нФ = 1 мкФ
р	10 ^-12 (миллион-миллионный)	1000 пФ = 1 нФ

Электрические поля и диэлектрики

Поскольку на обкладках конденсатора имеется потенциал, существует соответствующее электрическое поле. В случае параллельных пластин силовые линии электрического поля обычно параллельны друг другу и проходят под прямым углом к пластинам.

Пластины конденсатора с линиями электрического поля

Конденсаторам требуется некоторый изолятор между двумя пластинами, иначе заряд не мог бы оставаться на пластинах, он рассеивался бы через среду между двумя пластинами.

Хотя воздух является хорошим изолятором, часто пластины конденсатора необходимо отделять друг от друга каким-либо жестким изолятором.

Упрощенный вид конструкции конденсатора с пластинами и изолирующим диэлектриком

Материал между двумя пластинами называется диэлектриком. Это не только действует как изолятор, но и определяет многие другие свойства. Мера, известная как диэлектрическая проницаемость, влияет на уровень емкости, достижимый для данного размера пластин конденсатора и расстояния между ними.

Высокие уровни относительной диэлектрической проницаемости/диэлектрической проницаемости могут многократно увеличить емкость.

Тема относительной диэлектрической проницаемости, диэлектрической проницаемости и т. д. является самостоятельной темой, и хотя ее легко понять, ее, возможно, следует рассмотреть отдельно.

Подробнее о . . . . Относительная диэлектрическая проницаемость и диэлектрическая проницаемость.

Конденсаторы для зарядки и разрядки

Также можно посмотреть напряжение на конденсаторе, а также посмотреть заряд. Ведь напряжение на нем проще измерить простым измерителем. Когда конденсатор разряжен, на нем нет напряжения. Точно так же, когда он полностью заряжен, ток не течет от источника напряжения, и поэтому он имеет то же напряжение на нем, что и источник.

В идеальной цепи без паразитного сопротивления или индуктивности, когда напряжение подается на конденсатор, он мгновенно заряжается, и напряжение на нем будет таким же, как и на источнике электрического потенциала.

В действительности в цепи всегда будет какое-то сопротивление, и поэтому конденсатор будет подключен к источнику напряжения через резистор.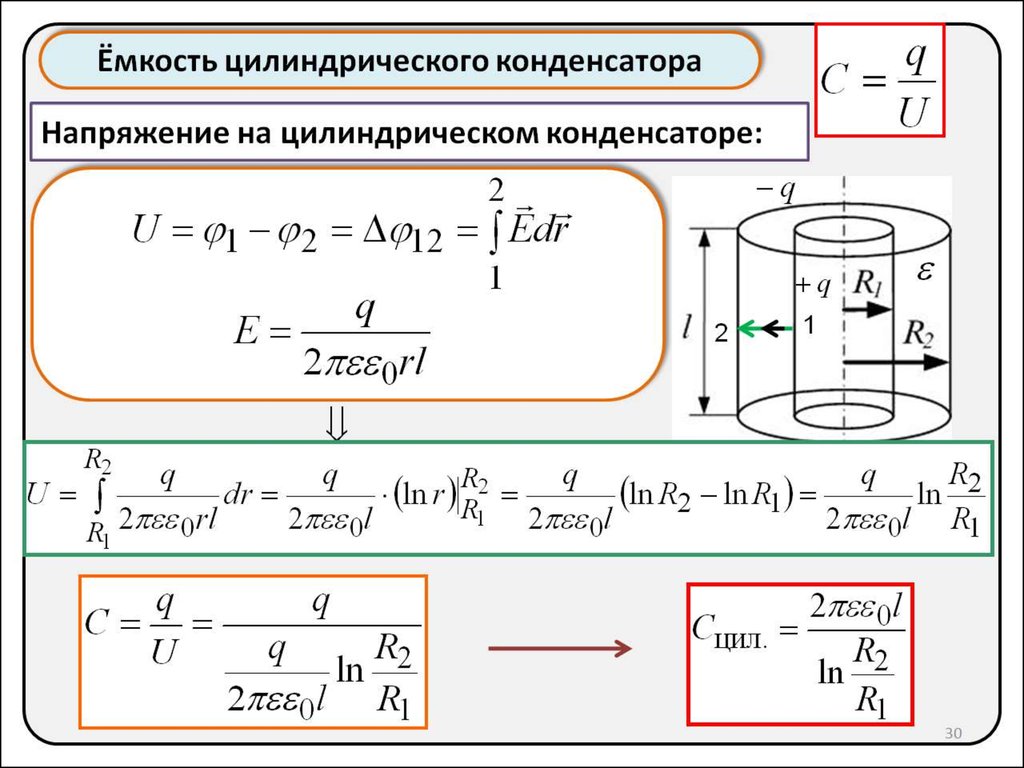 Это означает, что для зарядки конденсатора потребуется конечное время, и повышение напряжения не происходит мгновенно.

Обнаружено, что скорость, с которой повышается напряжение, сначала намного выше, чем после того, как он заряжался в течение некоторого времени. В конце концов он достигает точки, когда он практически полностью заряжен, и ток почти не течет.

Теоретически конденсатор никогда не заряжается полностью, так как кривая асимптотическая. Однако на самом деле он достигает точки, когда его можно считать полностью заряженным или разряженным, и ток не течет.

Напряжение конденсатора при зарядке и разрядке

Точно так же конденсатор всегда будет разряжаться через сопротивление. Когда заряд конденсатора падает, напряжение на пластинах уменьшается. Это означает, что ток будет уменьшаться, и, в свою очередь, скорость уменьшения заряда падает.

Это означает, что напряжение на конденсаторе падает экспоненциально, постепенно приближаясь к нулю.

Скорость нарастания или спада напряжения зависит от сопротивления в цепи. Чем больше сопротивление, тем меньше количество передаваемого заряда и тем больше времени требуется конденсатору для зарядки или разрядки.

Подача переменного сигнала на конденсатор

До сих пор рассматривался случай, когда батарея была подключена для зарядки конденсатора и отключена, а для его зарядки был применен резистор. Если к конденсатору приложить переменный сигнал, который по своей природе постоянно меняется, то он будет постоянно заряжаться и разряжаться.

Для этого в цепи должен протекать ток. Таким образом, конденсатор пропускает переменный ток, но блокирует постоянный. Таким образом, конденсаторы используются для передачи сигнала переменного тока между двумя цепями, которые имеют разные постоянные потенциалы.

Кривые тока и напряжения для идеального конденсатора
Примечание: ток опережает кривую напряжения на 90°.

Установлено, что при первом применении синусоидальной волны скорость изменения напряжения максимальна, а это означает, что заряд увеличивается с максимальной скоростью, и, следовательно, ток, протекающий через конденсатор, будет равен в наибольшей степени. Другими словами, ток максимален.

По мере увеличения напряжения на конденсаторе скорость изменения напряжения уменьшается и в результате увеличивается заряд и, следовательно, падает ток. В конце концов достигается пик синусоиды напряжения, при котором напряжение не меняется, и, соответственно, ток в этой точке равен нулю.

После пика напряжения напряжение начинает снижаться, соответственно уровень заряда падает и это означает, что из этой точки вытекает ток из конденсатора.

Остальная часть сигнала повторяется аналогичным образом. В результате видно, что напряжение и ток не совпадают по фазе друг с другом. Ток отстает от напряжения на четверть цикла, т. е. на 90°.

Зависимость тока и напряжения идеального конденсатора можно выразить следующим образом:

Vt=sin(ωt)

It=sin(ωt+90)

Реальные конденсаторы

Конденсаторы — это электронные компоненты, которые обеспечивают емкость, необходимую в электрических и электронных цепях.

Конденсаторы

бывают самых разных форм, каждая со своими свойствами. Физические конденсаторы могут быть либо для поверхностного монтажа, либо с традиционными выводами, а также иметь различные форм-факторы и электрические характеристики.

Примечание по типам конденсаторов:

Доступно множество различных типов конденсаторов. Хотя емкость является универсальной мерой, разные конденсаторы имеют разные характеристики с точки зрения таких элементов, как максимально допустимый ток, частотная характеристика, размер, напряжение, стабильность, допуски и тому подобное. Чтобы соответствовать этим параметрам, некоторые типы конденсаторов в некоторых приложениях лучше других,

Подробнее о Типы конденсаторов.

Выбор правильного конденсатора зависит не только от выбора правильного уровня емкости, но и от многих других аспектов, включая диэлектрическую проницаемость, размер, уровни эквивалентного последовательного сопротивления и многое другое.

Принимая во внимание все эти требования, существует очень широкий выбор этих электронных компонентов, доступных для использования в электрических и электронных схемах и т. д.

Емкость является одним из основных параметров, связанных с электротехникой и электроникой. Уравнения и расчеты емкости используются каждый день при проектировании электронных схем и во многих других областях, и емкость не является мерой, связанной только с конденсаторами, могут быть уровни емкости во многих других электронных компонентах, включая резисторы, катушки индуктивности, провода, печатные платы. и многие другие предметы.

Дополнительные основные понятия и руководства по электронике:
Напряжение Текущий Власть Сопротивление Емкость Индуктивность Трансформеры Децибел, дБ Законы Кирхгофа Q, добротность РЧ-шум Сигналы
Вернуться в меню основных понятий электроники . . .

Емкость | Определение, формула, единица измерения и факты

Связанные темы:: фарада электрический проводник цепь переменного тока

См. весь связанный контент →

емкость , свойство электрического проводника или набора проводников, которое измеряется количеством отделенного электрического заряда, который может храниться на нем на единицу изменения электрического потенциала. Емкость также подразумевает связанное с ней хранение электрической энергии. При переносе электрического заряда между двумя первоначально незаряженными проводниками оба становятся одинаково заряженными, один положительно, другой отрицательно, и между ними устанавливается разность потенциалов. Емкость Кл есть отношение количества заряда q на любом проводнике к разности потенциалов В между проводниками, или просто Кл = q / В.

В обоих практических и метр–килограмм–секунда в научных системах, единицей электрического заряда является кулон, а единицей разности потенциалов – вольт, так что единица измерения емкости, называемая фарад (обозначается символом Ф), равна одному кулону на вольт. Один фарад — очень большая емкость. Удобные в обычном использовании подразделения составляют одну миллионную часть фарада, называемую микрофарадой ( мк Ф) и одна миллионная микрофарад, называемая пикофарад (пФ; более старый термин, микромикрофарад, мкмк Ф). В электростатической системе единиц емкость имеет размерность расстояния.

Еще из Britannica

электричество: емкость

Емкость в электрических цепях преднамеренно вводится устройством, называемым конденсатором. Он был открыт прусским ученым Эвальдом Георгом фон Клейстом в 1745 году и независимо голландским физиком Питером ван Мушенбруком примерно в то же время в процессе исследования электростатических явлений. Они обнаружили, что электричество, полученное от электростатической машины, может накапливаться в течение определенного периода времени, а затем высвобождаться. Устройство, которое стало известно как лейденская банка, состояло из закрытого пробкой стеклянного флакона или банки, наполненной водой, с гвоздем, протыкающим пробку и погружаемым в воду. Держа банку в руке и прикасаясь гвоздем к проводнику электростатической машины, они обнаружили, что от гвоздя можно получить удар после его отсоединения, касаясь его свободной рукой. Эта реакция показала, что часть электричества от машины была сохранена.

Простой, но фундаментальный шаг в эволюции конденсатора был сделан английским астрономом Джоном Бевисом в 1747 году, когда он заменил воду металлической фольгой, образующей подкладку на внутренней поверхности стекла и другую, покрывающую внешнюю поверхность. Эта форма конденсатора с проводником, выступающим из горлышка банки и касающимся облицовки, имела в качестве основных физических особенностей два проводника протяженной площади, почти одинаково разделенных изолирующим или диэлектрическим слоем, сделанным настолько тонким, насколько это практически возможно. Эти особенности были сохранены в каждой современной форме конденсатора.

Конденсатор, также называемый конденсатором, таким образом, представляет собой сэндвич из двух пластин из проводящего материала, разделенных изолирующим материалом или диэлектриком.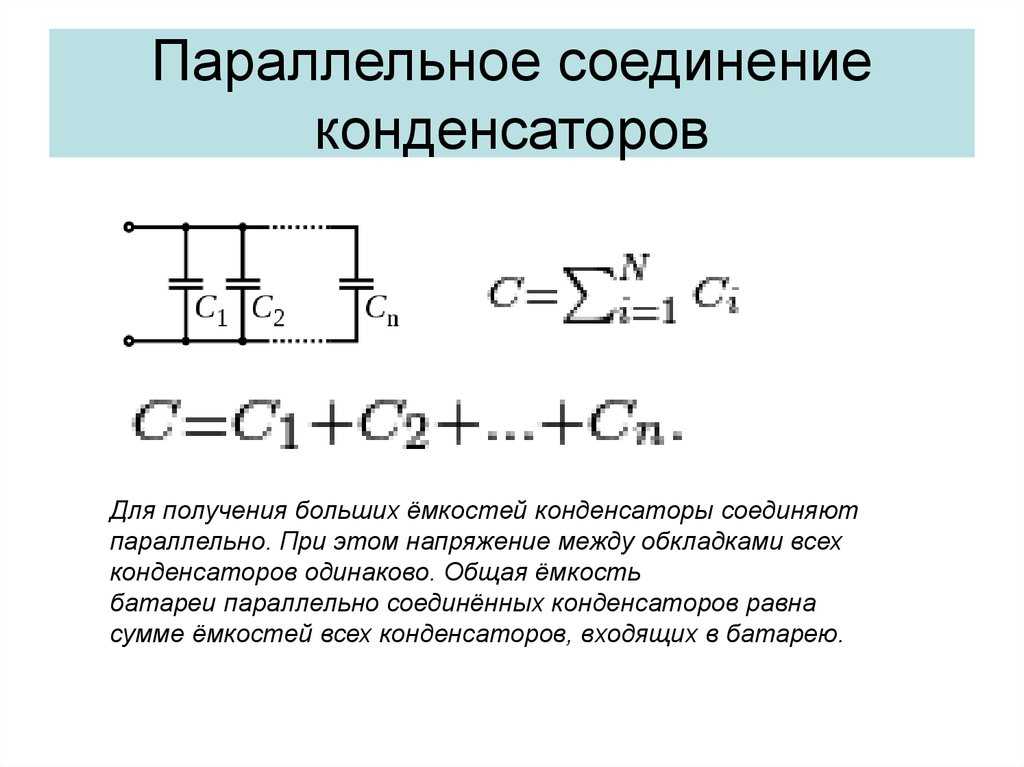 Его основная функция заключается в хранении электрической энергии. Конденсаторы различаются размерами и геометрическим расположением пластин, а также видом используемого диэлектрического материала. Отсюда и такие названия, как слюдяные, бумажные, керамические, воздушные и электролитические конденсаторы. Их емкость может быть фиксированной или регулируемой в диапазоне значений для использования в схемах настройки.

Энергия, накопленная конденсатором, соответствует работе, выполненной (например, батареей) по созданию противоположных зарядов на двух пластинах при приложенном напряжении. Количество заряда, которое может быть сохранено, зависит от площади пластин, расстояния между ними, диэлектрического материала в пространстве и приложенного напряжения.

Оформите подписку Britannica Premium и получите доступ к эксклюзивному контенту.

Подпишитесь сейчас

Конденсатор, включенный в цепь переменного тока (AC), попеременно заряжается и разряжается каждые полпериода.