Чем отличается конденсатор от резистора. Как работают эти радиодетали. Какие бывают типы конденсаторов и резисторов. Как обозначаются на схемах. Какие параметры важны при выборе.
Конденсатор и резистор: ключевые различия
Конденсаторы и резисторы — два важнейших пассивных компонента электрических цепей. Хотя они часто используются вместе, их функции и принципы работы существенно различаются:
- Конденсатор накапливает и хранит электрический заряд, а резистор ограничивает протекание тока
- Конденсатор пропускает переменный ток и блокирует постоянный, резистор одинаково влияет на оба вида тока
- Основной параметр конденсатора — емкость (в фарадах), резистора — сопротивление (в омах)
- Конденсатор не рассеивает энергию, резистор преобразует часть энергии в тепло
Рассмотрим подробнее особенности каждого компонента.
Что такое конденсатор и как он работает
Конденсатор — это электронный компонент, способный накапливать электрический заряд. Простейший конденсатор состоит из двух проводящих пластин, разделенных диэлектриком:

- При подаче напряжения на пластины они приобретают противоположные заряды
- Диэлектрик препятствует протеканию тока между пластинами
- В результате энергия накапливается в электрическом поле конденсатора
Ключевые свойства конденсатора:
- Пропускает переменный ток, но блокирует постоянный
- Может быстро заряжаться и разряжаться
- Не потребляет энергию в идеальном случае
Основные типы и параметры конденсаторов
Конденсаторы различаются по типу диэлектрика и конструкции. Основные разновидности:
- Керамические — компактные, недорогие, для высоких частот
- Пленочные — стабильные, для фильтров и развязки
- Электролитические — большая емкость, полярные
- Танталовые — малые габариты, стабильность
Ключевые параметры при выборе конденсатора:
- Емкость — способность накапливать заряд, измеряется в фарадах
- Рабочее напряжение — максимально допустимое напряжение
- Допуск — отклонение реальной емкости от номинала
- Температурный коэффициент — зависимость емкости от температуры
Принцип работы и назначение резистора
Резистор — это компонент, создающий сопротивление протеканию электрического тока. Его работа основана на преобразовании электрической энергии в тепловую:
- При протекании тока часть энергии рассеивается в виде тепла
- Чем выше сопротивление, тем сильнее ограничивается ток
- Сопротивление не зависит от направления тока
Основные функции резисторов в схемах:
- Ограничение тока через компоненты
- Деление напряжения
- Задание рабочих точек активных элементов
- Согласование импедансов
Разновидности и характеристики резисторов
Резисторы бывают постоянные и переменные. Основные типы постоянных резисторов:
- Углеродистые — недорогие, для общего применения
- Металлопленочные — точные, малошумящие
- Проволочные — высокомощные
Ключевые параметры при выборе резистора:
- Номинальное сопротивление — измеряется в омах
- Допустимая мощность рассеивания
- Температурный коэффициент сопротивления
- Допуск — отклонение от номинала
Как обозначаются конденсаторы и резисторы на схемах
На принципиальных схемах применяются следующие обозначения:
- Конденсаторы — буква C и порядковый номер (C1, C2 и т.д.)
- Постоянные резисторы — буква R и номер (R1, R2…)
- Переменные резисторы — буквы VR и номер
Рядом с условным обозначением указывается номинал компонента:
- Для конденсаторов — емкость в фарадах или производных единицах
- Для резисторов — сопротивление в омах
Области применения конденсаторов и резисторов
Эти компоненты широко используются в различных электронных устройствах:
Применение конденсаторов:
- Фильтрация пульсаций в источниках питания
- Разделение постоянной и переменной составляющих сигнала
- Накопление энергии для импульсных схем
- Частотная коррекция в усилителях
Применение резисторов:
- Ограничение тока через светодиоды
- Создание делителей напряжения
- Задание режимов работы транзисторов
- Демпфирование колебаний в фильтрах
Как правильно выбрать конденсатор или резистор
При подборе компонентов для схемы следует учитывать:
Для конденсаторов:
- Требуемую емкость и допуск
- Максимальное рабочее напряжение
- Тип диэлектрика в зависимости от назначения
- Частотные характеристики для ВЧ-схем
Для резисторов:
- Номинальное сопротивление и точность
- Допустимую мощность рассеяния
- Температурную стабильность
- Уровень шумов для прецизионных схем
Правильный выбор этих базовых компонентов — ключ к надежной работе электронных устройств.

|
главная основы элементы примеры расчетов любительская технология общая схемотехника радиоприем конструкции для дома и быта связная аппаратура телевидение измерения обзор радиолюбительских схем в журналах обратная связь реклама
|
резисторы и конденсаторы полупроводниковые приборы акустические приборы микросхемы солнечные фотоэлементы SMD компоненты реле электромагнитные полупроводниковые оптоприборы
ЗНАКОМСТВО С РАДИОДЕТАЛЯМИ Резистор.
Эта деталь встречается
практически в каждой конструкции.
Представляет собой фарфоровую трубочку (или
стержень), на которую снаружи напылена
тончайшая пленка металла или сажи (углерода).
Резистор обладает сопротивлением и
используется для того, чтобы установить
нужный ток в электрической цепи. Вспомните
пример с резервуаром: изменяя диаметр трубы
(сопротивление нагрузки), можно получить ту
или иную скорость потока воды (электрический
ток различной силы). Чем тоньше пленка на
фарфоровой трубочке или стержне, тем больше
сопротивление току. На схемах резистор
обозначается латинской буквой R (от слова
Resistans — сопротивляться).
Сопротивление резистора проставляют на
схемах рядом с его условным обозначением. К группе резисторов относятся и так называемые терморезисторы.
В принципе, у любого резистора имеется определенная зависимость
номинала от окружающей температуры. Эта зависимость называется
Температурный Коэффициент Сопротивления — сокращенно — ТКС и носит
величину в процентах на градус
(как правило — градус Цельсия!). В процессе изготовления стараются
снизить ТКС у резисторов до минимума… Довольно высокий ТКС
имеют некоторые металлы (например — медь). Это свойство часто
используется для контроля за температурой внутри аппаратуры, а также
дает возможность косвенным путем вычислить температуру, например,
силового трансформатора или электродвигателя. Используя некоторые из
полупроводниковых материалов можно создать терморезисторы как с
положительным, так и с отрицательным ТКС.
Конденсатор.
Надо сказать, что эту деталь,
как и резистор, можно увидеть во многих
самоделках. Как правило, самый простой
конденсатор — это две металлические
пластинки (обкладки) и воздух между ними. Как вы знаете, у резистора основной
параметр — сопротивление, у конденсатора же
— емкость. Конденсаторы бывают постоянной и
переменной емкости. У переменных
конденсаторов емкость изменяется при
вращении выступающей наружу оси. Кроме этих
двух типов, в наших конструкциях
используется еще одна разновидность
конденсаторов — подстроечный. Обычно его
устанавливают в то или иное устройство для
того, чтобы при налаживании точнее
подобрать нужную емкость и больше
конденсатор не трогать. На схемах для них указывают не только
емкость, но и максимальное напряжение, на
которое их можно использовать . Например,
надпись 5,0×10 В означает, что конденсатор
емкостью 5 мкФ нужно взять на напряжение 10 В. Необходимо
иметь в виду, что электролитичесие конденсаторы (за исключением
специально изготовленных, так называемых «неполярных»!) не могут
работать в цепях переменного тока значительной величины! Использование
полярных электролитических конднсаторов в цепях переменного тока
приводит к их разрушению и даже к взрыву!!! Номинальные значения емкости конденсаторов и сопротивления резисторов показаны на рисунке внизу: Цифры номиналов зависят от допустимого отклонения (получается при изготовлении и последующей отбраковки элементов) от номинального значения в процентах. вверх |
Разница между конденсатором и резистором
Конденсаторы и резисторы являются двумя важными пассивными компонентами электрической цепи. Оба играют разные роли в определении поведения цепи и связаны проводящими проводами, по которым проходит электричество.
Оба играют разные роли в определении поведения цепи и связаны проводящими проводами, по которым проходит электричество.
Научная викторина
Проверьте свои знания по темам, связанным с наукой
1 / 10
Ферментация – это процесс ______.
Превращение крахмала в сахар
Превращение сахара в спирт
Превращение белка в сахар
добавление дрожжей для приготовления вина
2 / 10
Каково научное название человека?
Mangifera Indica
Рана тигрина
Хомо сапиенс
виды человека
3 / 10
Химическая реакция с выделением энергии называется:
эндотермический
экзотермический
4 / 10
Какая из перечисленных желез находится во рту человека?
Надпочечник
Гипофиз
Половые
слюнный
5 / 10
Какое из следующих соединений в основном используется в дезинфицирующих средствах для рук?
Альдегид
Уксусная кислота
Алкоголь
кетонов
6 / 10
Какое топливо на Солнце?
гелий
водород
Oxygen
Углекислый газ
7 / 10
Воздушные шары наполнены
азот
гелий
кислород
аргон
8 / 10
Где происходит фотосинтез?
Ядро
вакуоль
Хлоропласты/хлорофилл
Митохондрии
9 / 10
Газированная вода содержит
Углекислота
Серная кислота
Углекислый газ
Азотная кислота
10 / 10
Каков диапазон рН кислот?
0 — 7
7 — 14
1 — 7
7 — 15
ваш счет
Конденсатор против резистораОсновные выводы
- Конденсатор — это электронный компонент, который хранит и высвобождает электрическую энергию, характеризующуюся его способностью пропускать сигналы переменного тока (AC) и блокировать сигналы постоянного тока (DC).

- Резистор — это электронный компонент, который противодействует протеканию электрического тока, помогая контролировать уровни напряжения и тока в цепи.
- И конденсаторы, и резисторы являются основными компонентами электронных схем, но они выполняют разные функции: конденсаторы управляют накоплением энергии, а резисторы контролируют протекание тока.
Разница между конденсатором и резистором заключается в том, что конденсатор — это электронное устройство, используемое для хранения электрической энергии в виде зарядов, а резистор — это электронное устройство, используемое для сопротивления или блокировки тока в цепи. Конденсаторы могут хранить электрический счет в течение короткого периода времени, в то время как резисторы блокируют поток ветра.
Хотите сохранить эту статью на потом? Нажмите на сердечко в правом нижнем углу, чтобы сохранить в свой собственный блок статей!
Когда конденсатор подключен к цепи, цепь постоянного тока не может протекать по цепи из-за его изолирующего слоя и сохраняется в виде заряда на проводящих проводах.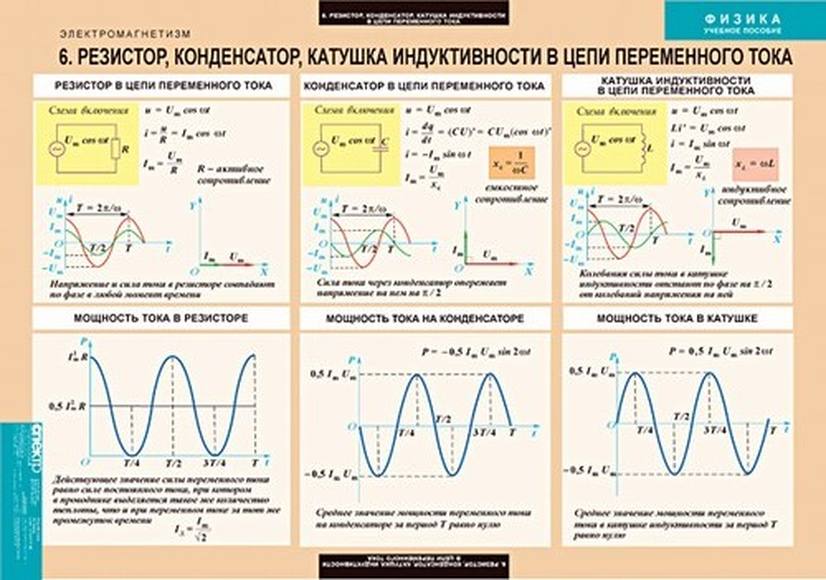
С другой стороны, когда резистор подключен к цепи, он поглощает электрический ток и рассеивает энергию в виде тепла.
Сравнительная таблица
| Параметр сравнения | Конденсатор | резистор |
|---|---|---|
| Какие? | A Конденсатор представляет собой электрический компонент, используемый для хранения электрического заряда. | Резистор — это электрический компонент, который ограничивает протекание тока в электрический схема. Это создает трение, подобное силе, которая блокирует ток. |
| Влияние на цепь | Конденсатор накапливает электрическую энергию за счет зарядов на проводящей пластине при добавлении. | При добавлении резистор поглощает электрическую энергию и рассеивает ее в виде тепла. |
| Используйте | Конденсаторы используются для фильтрации, сглаживания, соединения различных участков цепи и ограничения переходных процессов высокого напряжения в цепи. | Резисторы уменьшают ток, делят напряжения, ограничивают линии передачи и регулируют уровень сигнала. |
| Потеря мощности | Конденсатор не дает потерь электроэнергии. | Резистор создает потери мощности и создает тепло. |
| Зависимость от частоты | Противодействие протеканию тока зависит от применяемой частоты. | Противодействие протеканию тока не зависит от применяемой частоты. |
| Единицы | Емкость измеряется в фарадах. | Сопротивление измеряется в омах. |
| Формула | C = Q / V | R = V / I |
| Объем | Он может блокировать только постоянный ток. | Он может блокировать как постоянный, так и переменный ток. |
Что такое конденсатор?
Конденсатор — это пассивный компонент электрической цепи, который может накапливать энергию в виде электрического заряда, производящего потенциальные различия по его тарелке.
Доступны конденсаторы различных размеров, от крошечных, используемых в резонансных цепях, до больших конденсаторов, используемых для коррекции коэффициента мощности.
Он состоит из двух (или более) параллельных металлических пластин, которые не соприкасаются друг с другом, но электрически разнесены друг от друга (по воздуху или каким-либо другим материалом, таким как слюда, пластик и т. д.). Этот изолирующий слой между проводящими пластинами называется диэлектрический.
Из-за изолирующего слоя постоянный ток не может проходить через конденсатор; вместо этого вокруг пластин возникает напряжение в виде электрического заряда.
С другой стороны, когда конденсаторы подключены к цепи переменного тока, ток проходит через конденсатор с небольшим сопротивлением.
Он создает электрический заряд, используя внешнее напряжение. Следовательно, он хранит только электроны для хранения энергии и испускает заряды позже, когда это необходимо.
Конденсатор можно классифицировать как фиксированный конденсатор, емкость которого имеет фиксированное значение и не регулирует поведение, и переменный конденсатор. Такие конденсаторы предлагают регулируемое поведение для операций схемы.
Формула для нахождения емкости: С=Q/V. Емкость (в фарадах) равна заряду (в кулонах), деленному на напряжение (в вольтах).
Что такое резистор?
Резистор является еще одним основным компонентом электрической цепи. Он ограничивает и блокирует прохождение электрического тока по цепи. Энергия измеряет сопротивление резистора. Он может рассеиваться в электрической цепи.
Он способствует ограничению скорости заряда конденсатора, регулировке частотной характеристики ВЧ-цепей и действует как делитель напряжения для схемы.
Когда резистор подключен к цепи, он управляет потоком заряда, поглощая количество электричества и рассеивая его в виде тепла.
Двумя основными измерениями, связанными с резисторами, являются сопротивление (измеряется в омах) и мощность рассеивания энергии (измеряется в ваттах).
Резистор может быть классифицирован как постоянный резистор, в котором значение сопротивления является фиксированным, и переменный резистор, который обеспечивает регулируемое сопротивление при подключении к любой цепи.
Формула для расчета сопротивления: Р=В/И. Сопротивление (в Ом) равно напряжению (в вольтах), деленному на ток (в амперах).
Основные различия между конденсатором и резистором
- Конденсатор — это электронный компонент, который накапливает электрическую энергию в заряде. В то же время Резистор — это электронный компонент, который ограничивает, регулирует или блокирует ток в цепи.
- Конденсатор используется для разделения положительных и отрицательных зарядов, а резистор используется для управления потоком тока к другим компонентам цепи.
- Конденсатор хранит электрический ток в виде зарядов на проводящих проводах, в то время как резистор поглощает электрическую энергию и рассеивает ее в виде тепла.
- Конденсатор не приводит к потере мощности, в отличие от резистора.
- Емкость измеряется в фарадах путем деления заряда на напряжение, а сопротивление измеряется в омах путем деления напряжения на ток. непристойный
Рекомендации
- https://ieeexplore.
 ieee.org/abstract/document/1355709/
ieee.org/abstract/document/1355709/ - https://ieeexplore.ieee.org/abstract/document/4768889/
Один запрос?
Я приложил столько усилий, чтобы написать этот пост в блоге, чтобы предоставить вам ценность. Это будет очень полезно для меня, если вы подумаете о том, чтобы поделиться им в социальных сетях или со своими друзьями/родными. ДЕЛИТЬСЯ ♥️
Пиюш Ядав
Пиюш Ядав последние 25 лет работал физиком в местном сообществе. Он физик, увлеченный тем, чтобы сделать науку более доступной для наших читателей. Он имеет степень бакалавра естественных наук и диплом о высшем образовании в области наук об окружающей среде. Подробнее о нем можно прочитать на его био страница.
Разница между резистором и конденсатором
Резисторы и конденсаторы являются двумя наиболее распространенными компонентами электронных устройств, и каждый из них играет пассивную роль, воздействуя на электрические заряды в электрической или электронной цепи. Вот краткий обзор различий между конденсатором и резистором.
Что такое конденсаторы?
Конденсаторы в основном предназначены для накопления электрического заряда или энергии. Затем они могут высвобождать заряд или энергию, когда это необходимо. Конденсатор состоит из двух проводящих параллельных пластин, разделенных диэлектрической средой, которая по своей конструкции является плохим проводником электричества. Как только на конденсатор подается потенциал, положительные и отрицательные заряды накапливаются на сторонах пластин. Состояние, которое создает конденсатор, называется емкостью (С), которая измеряет способность компонента накапливать электрический заряд. Емкость эквивалентна электрическому заряду (Q), деленному на напряжение (В). Измеряется в фарадах (F), микрофарадах и нанофарадах. Два типа конденсаторов фиксированные и переменные. Фиксированный конденсатор допускает только фиксированную емкость, тогда как переменный конденсатор допускает регулируемую емкость.
Что такое резисторы?
Резисторы поглощают электрический заряд или энергию и преобразуют их в тепло. Они обычно используются для ограничения протекания тока в цепи. Резисторы — это, по сути, переключатели, которые включают или выключают ток. Они создают сопротивление, которое измеряется в омах. Уравнение для сопротивления: R (для сопротивления) = V (для напряжения), деленное на I (для тока, измеряемого в амперах). Два типа резисторов фиксированные и переменные. Фиксированный резистор создает фиксированное и неизменное значение сопротивления, измеряемое в омах, представленное символом Ω. Переменный резистор, напротив, предлагает переменные значения сопротивления.
Они обычно используются для ограничения протекания тока в цепи. Резисторы — это, по сути, переключатели, которые включают или выключают ток. Они создают сопротивление, которое измеряется в омах. Уравнение для сопротивления: R (для сопротивления) = V (для напряжения), деленное на I (для тока, измеряемого в амперах). Два типа резисторов фиксированные и переменные. Фиксированный резистор создает фиксированное и неизменное значение сопротивления, измеряемое в омах, представленное символом Ω. Переменный резистор, напротив, предлагает переменные значения сопротивления.
См.: Схемы с переключаемыми конденсаторами: преимущества и области применения
Основные различия между конденсатором и резистором
Основные различия между резисторами и конденсаторами заключаются в том, как эти компоненты влияют на электрический заряд. В то время как резисторы применяют сопротивление для ограничения протекания тока, конденсаторы хранят энергию в электрическом поле до тех пор, пока она не понадобится. Добавление резисторов и конденсаторов последовательно увеличивает влияние их соответствующих функций. Это означает, что последовательное добавление резисторов увеличивает сопротивление, а последовательное добавление конденсаторов увеличивает емкость. Резисторы и конденсаторы обычно используются в радиокоммуникационном оборудовании и логических схемах, наряду с катушками индуктивности. Резисторы преобразуют электрическую энергию в тепло, которое затем рассеивается. Конденсаторы часто используются для фильтрации частот, разделяя положительные и отрицательные заряды. Конденсаторы также могут использоваться для пропускания переменного тока при блокировании постоянного тока.
Добавление резисторов и конденсаторов последовательно увеличивает влияние их соответствующих функций. Это означает, что последовательное добавление резисторов увеличивает сопротивление, а последовательное добавление конденсаторов увеличивает емкость. Резисторы и конденсаторы обычно используются в радиокоммуникационном оборудовании и логических схемах, наряду с катушками индуктивности. Резисторы преобразуют электрическую энергию в тепло, которое затем рассеивается. Конденсаторы часто используются для фильтрации частот, разделяя положительные и отрицательные заряды. Конденсаторы также могут использоваться для пропускания переменного тока при блокировании постоянного тока.
Заключение
Знание различий между резисторами и конденсаторами дает вам фундаментальное понимание того, как энергия передается в электрических или электронных цепях. Оба являются полезными компонентами для управления потоком электронов. Если вы ищете высокоомные резисторы или конденсаторы, посетите веб-сайт Allied Components International уже сегодня.
Allied Components International
Allied Components International специализируется на разработке и производстве широкого спектра магнитных компонентов и модулей, соответствующих отраслевым стандартам, таких как микросхемы индуктивности, заказные магнитные катушки индуктивности и заказные трансформаторы. Мы стремимся предоставлять нашим клиентам высококачественную продукцию, обеспечивать своевременные поставки и предлагать конкурентоспособные цены.
Мы являемся растущим предприятием в магнитной промышленности с более чем 20-летним опытом.
4.11 Цепи постоянного тока, содержащие резисторы и конденсаторы – Douglas College Physics 1207
Глава 4 Электрический ток, сопротивление и закон Ома
Резюме
- Объясните важность постоянной времени τ и рассчитайте постоянную времени для данного сопротивления и емкости.
- Объясните, почему батарейки в фонарике постепенно разряжаются, а свет со временем тускнеет.

- Опишите, что происходит с графиком зависимости напряжения на конденсаторе от времени при его зарядке.
- Объясните, как работает схема синхронизации, и перечислите некоторые приложения.
- Рассчитайте необходимую скорость стробоскопической вспышки, необходимую для «остановки» движения объекта на определенной длине.
При использовании камеры со вспышкой для зарядки конденсатора, питающего вспышку, требуется несколько секунд. Световая вспышка разряжает конденсатор за доли секунды. Почему зарядка занимает больше времени, чем разрядка? Этот вопрос и ряд других явлений, связанных с зарядкой и разрядкой конденсаторов, обсуждаются в этом модуле.
Цепь RC содержит резистор R и конденсатор C . Конденсатор представляет собой электрический компонент, хранящий электрический заряд.
На рис. 1 показана простая схема RC , в которой используется источник постоянного напряжения. Конденсатор изначально не заряжен. Как только ключ замыкается, ток течет к и от первоначально незаряженного конденсатора. По мере увеличения заряда на пластинах конденсатора увеличивается сопротивление потоку заряда за счет отталкивания одинаковых зарядов на каждой пластине.
Конденсатор изначально не заряжен. Как только ключ замыкается, ток течет к и от первоначально незаряженного конденсатора. По мере увеличения заряда на пластинах конденсатора увеличивается сопротивление потоку заряда за счет отталкивания одинаковых зарядов на каждой пластине.
С точки зрения напряжения это связано с тем, что напряжение на конденсаторе определяется как В c = Q/C , где Q — это количество заряда, накопленного на каждой пластине, а C — это емкость . Это напряжение противодействует батарее, возрастая от нуля до максимальной ЭДС при полной зарядке. Таким образом, ток уменьшается от своего начального значения до нуля, когда напряжение на конденсаторе достигает того же значения, что и ЭДС. Когда нет тока, нет IR падение, поэтому напряжение на конденсаторе должно быть равно ЭДС источника напряжения. Это также можно объяснить вторым правилом Кирхгофа (правилом петли), обсуждаемым в Правилах Кирхгофа, которое гласит, что алгебраическая сумма изменений потенциала вокруг любой замкнутой петли должна быть равна нулю.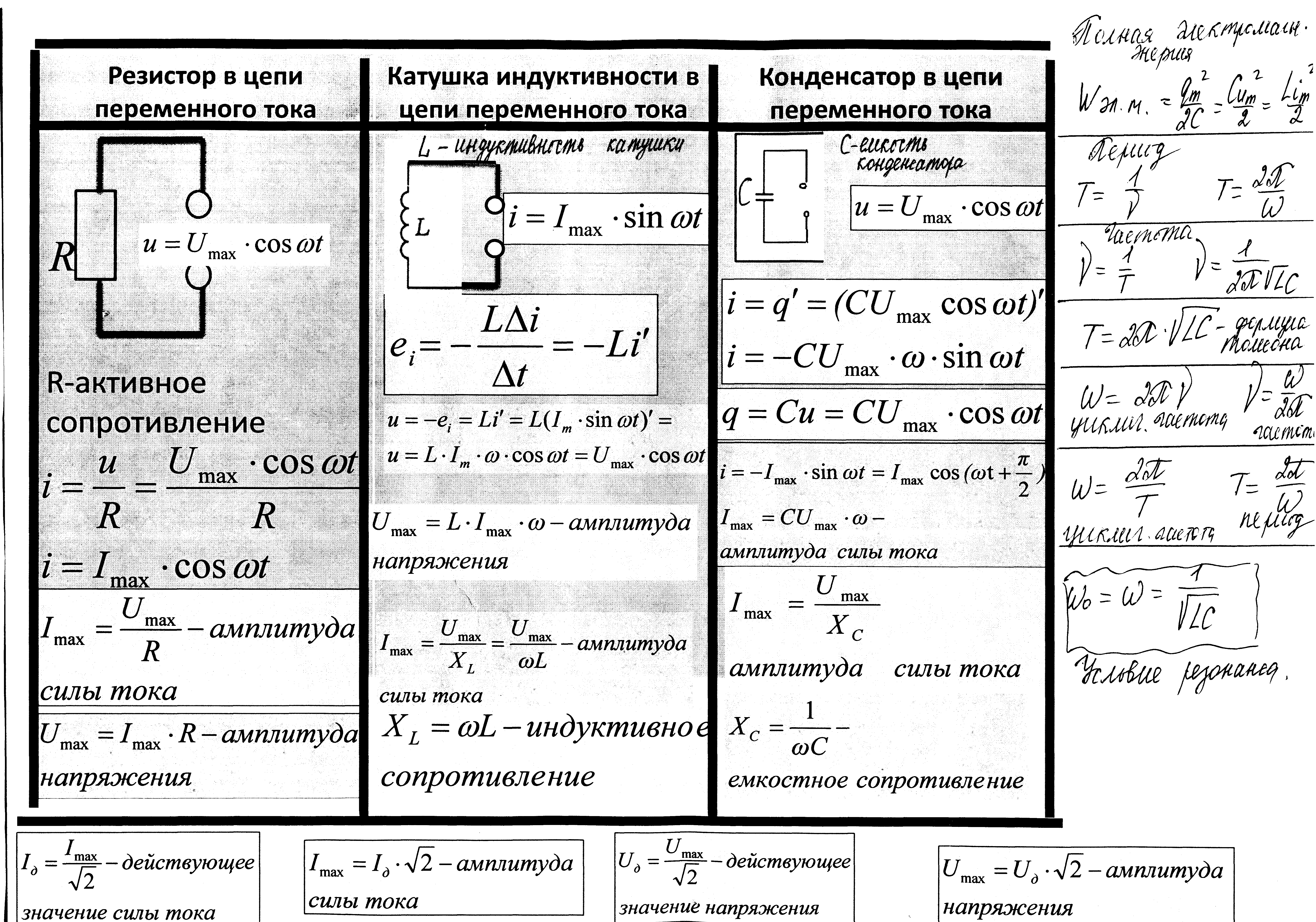
Начальный ток равен I 0 = эдс / R , потому что все падение IR приходится на сопротивление. Следовательно, чем меньше сопротивление, тем быстрее будет заряжаться данный конденсатор. Обратите внимание, что внутреннее сопротивление источника напряжения включено в R , а также сопротивления конденсатора и соединительных проводов. В приведенном выше сценарии камеры со вспышкой, когда батареи питания камеры начинают изнашиваться, их внутреннее сопротивление возрастает, уменьшая ток и увеличивая время, необходимое для подготовки к следующей вспышке.
Рис. 1. (a) Цепь RC с изначально незаряженным конденсатором. Ток течет в указанном направлении (противоположном потоку электронов), как только переключатель замыкается. Взаимное отталкивание одноименных зарядов в конденсаторе постепенно замедляет поток по мере заряда конденсатора, останавливая ток, когда конденсатор полностью заряжен и Q = C эдс . (Помните, что Q=CV) (b) График зависимости напряжения на конденсаторе от времени с замыканием ключа в момент времени t = 0 . (Обратите внимание, что в двух частях рисунка заглавная буква E обозначает ЭДС, q обозначает заряд, хранящийся в конденсаторе, а τ обозначает постоянную времени RC .)
(Помните, что Q=CV) (b) График зависимости напряжения на конденсаторе от времени с замыканием ключа в момент времени t = 0 . (Обратите внимание, что в двух частях рисунка заглавная буква E обозначает ЭДС, q обозначает заряд, хранящийся в конденсаторе, а τ обозначает постоянную времени RC .) Напряжение на конденсаторе изначально равна нулю и сначала быстро возрастает, так как начальный ток максимален. На рис. 1(b) показан график зависимости напряжения конденсатора от времени (t ) начиная с замыкания переключателя в t=0 . Напряжение приближается к ЭДС асимптотически, поскольку чем ближе оно приближается к ЭДС, тем меньше протекает ток. Уравнение зависимости напряжения от времени при зарядке конденсатора C через резистор R , полученное с помощью вычислений, равно
., где В — напряжение на конденсаторе, ЭДС равна ЭДС источника постоянного напряжения, а экспонента e = 2,718 … — основание натурального логарифма. Обратите внимание, что единицы RC — секунды. Определяем
Обратите внимание, что единицы RC — секунды. Определяем
τ = RC
, где τ (греческая буква тау) называется постоянной времени для цепи RC . Как отмечалось ранее, небольшое сопротивление R позволяет конденсатору заряжаться быстрее. Это разумно, так как больший ток протекает через меньшее сопротивление. Также разумно, что чем меньше конденсатор C , тем меньше времени требуется для его зарядки. Оба фактора содержатся в τ = RC.
Более количественно рассмотрим, что происходит, когда t = τ = RC. Тогда напряжение на конденсаторе равно
Это означает, что за время τ = RC напряжение возрастает до 0,632 от своего конечного значения. Напряжение увеличится на 0,632 остатка в следующем времени τ = RC . Характеристика экспоненциальной функции заключается в том, что конечное значение никогда не достигается, но 0,632 остатка от этого значения достигается каждый раз, τ. Таким образом, всего за несколько кратных постоянной времени τ окончательное значение почти достигается, как показано на графике на рисунке 1(b).
Таким образом, всего за несколько кратных постоянной времени τ окончательное значение почти достигается, как показано на графике на рисунке 1(b).
Разрядка конденсатора через резистор происходит аналогичным образом, как показано на рис. 2. Первоначально ток составляет I o = V o / R , управляемый начальным напряжением V o на конденсаторе. По мере уменьшения напряжения ток и, следовательно, скорость разряда уменьшаются, что подразумевает другую экспоненциальную формулу для В . Используя вычисление, напряжение В на конденсаторе C разряжается через резистор R оказывается
Рисунок 2. (a) Замыкание ключа разряжает конденсатор C через резистор R . Взаимное отталкивание одноименных зарядов на каждой пластине вызывает ток. (b) График зависимости напряжения на конденсаторе от времени, где В = В 0 при t = 0 . Напряжение уменьшается экспоненциально, падая на фиксированную долю пути до нуля в каждую последующую постоянную времени т .
Напряжение уменьшается экспоненциально, падая на фиксированную долю пути до нуля в каждую последующую постоянную времени т . График на рис. 2(b) является примером такого экспоненциального затухания. Опять же, постоянная времени равна τ = RC . Небольшое сопротивление R позволяет конденсатору разрядиться за малое время, так как ток больше. Точно так же малой емкости требуется меньше времени для разряда, поскольку сохраняется меньше заряда. В первом временном интервале τ = RC . после замыкания ключа напряжение падает до 0,368 от исходного значения, так как В = Vo e -1 = 0,368 В o .
В течение каждого последующего времени τ напряжение падает до 0,368 от предыдущего значения. Через несколько кратных τ напряжение становится очень близким к нулю, как показано на графике на рисунке 2(b).
Теперь мы можем объяснить, почему фотовспышка в нашем сценарии заряжается гораздо дольше, чем разряжается; сопротивление при зарядке значительно больше, чем при разрядке. Внутреннее сопротивление батареи составляет большую часть сопротивления во время зарядки. По мере старения батареи увеличивающееся внутреннее сопротивление еще больше замедляет процесс зарядки. (Возможно, вы это заметили.)
Внутреннее сопротивление батареи составляет большую часть сопротивления во время зарядки. По мере старения батареи увеличивающееся внутреннее сопротивление еще больше замедляет процесс зарядки. (Возможно, вы это заметили.)
Вспыхивающий разряд происходит через ионизированный газ с низким сопротивлением в импульсной трубке и происходит очень быстро. Фотографии со вспышкой, такие как на рис. 3, могут запечатлеть краткий момент быстрого движения, потому что вспышка может длиться менее микросекунды. Такие вспышки можно сделать чрезвычайно интенсивными.
Во время Великой Отечественной войны проводились ночные разведывательные фотосъемки с воздуха с одной вспышкой, освещавшей более квадратного километра территории противника. Краткость вспышки устранила размытие из-за движения самолета-разведчика. Сегодня важным применением мощных импульсных ламп является накачка энергии в лазер. Короткая интенсивная вспышка может быстро активировать лазер и позволить ему переизлучать энергию в другой форме.
Интегрированная концептуальная задача: расчет размера конденсатора — стробоскопы Массачусетский технологический институт. Вы могли видеть примеры его работы в удивительных кадрах движущихся колибри, капли молока, разбрызгивающейся на стол, или пули, пронзающей яблоко (см. рис. 3). Чтобы остановить движение и сделать эти снимки, нужна мощная вспышка с очень коротким импульсом, как упоминалось ранее в этом модуле.
Предположим, кто-то хочет запечатлеть пулю (движущуюся со скоростью 500 м/с) , которая проходит сквозь яблоко. Продолжительность вспышки связана с постоянной времени RC , τ = RC . Конденсатор какой емкости потребуется в цепи RC , чтобы добиться успеха, если сопротивление лампы-вспышки составляет 10,0 Ом? Предположим, что яблоко представляет собой сферу диаметром 8,0 x 10 -2 м .
Стратегия
Начнем с определения задействованных физических принципов. Этот пример имеет дело со стробоскопом, как обсуждалось выше. На рис. 2 показана схема этого пробника. Характерное время τ строба определяется как τ = RC .
Решение
Мы хотим найти C , но не знаем τ = RC .. Мы хотим, чтобы вспышка горела только тогда, когда пуля пересекает яблоко. Поэтому нам нужно использовать кинематические уравнения, описывающие связь между расстоянием x , постоянная скорость V и время T :
x = VT или T = x / V
Скорость пули приведена как 5,0 x 10 2 м / с , а также — 5,0 x 100204 2 м / с , и — расстояние x равно 8,0 x 10 -2 м . Таким образом, время прохождения равно
t = x / v = ( 8,0 x 10 -2 м) / (5,0 x 10 2 м/с) = 1,6 x 10 -4 с Мы устанавливаем это значение для времени пересечения t равно τ . Следовательно,
Следовательно,
C = τ / R = t / R = (1,6 x 10 -4 с) (10,0 Ом) = 16 мкФ.
(Примечание: емкость C обычно измеряется в фарадах, F определяется как кулоны на вольт. Из уравнения видно, что C также может быть выражено в секундах на ом.)
Обсуждение
Интервал вспышки 160 мкс (время прохождения пули) относительно легко получить сегодня. Стробоскопы открыли новые миры от науки до развлечений. Информация с изображения яблока и пули была использована в отчете Комиссии Уоррена об убийстве президента Джона Ф. Кеннеди в 1963, чтобы подтвердить, что была выпущена только одна пуля.
RC Цепи обычно используются для синхронизации. Приземленный пример этого можно найти в вездесущих прерывистых системах стеклоочистителей современных автомобилей. Время между протирками регулируется путем регулировки сопротивления в цепи RC . Другой пример схемы RC можно найти в ювелирных украшениях, костюмах для Хэллоуина и различных игрушках с мигалками на батарейках. (См. схему синхронизации на рис. 4.)
Другой пример схемы RC можно найти в ювелирных украшениях, костюмах для Хэллоуина и различных игрушках с мигалками на батарейках. (См. схему синхронизации на рис. 4.)
Более важным применением цепей RC для целей синхронизации является искусственный кардиостимулятор, используемый для контроля частоты сердечных сокращений. Частота сердечных сокращений в норме контролируется электрическими сигналами, генерируемыми синоатриальным (СА) узлом, который находится на стенке камеры правого предсердия. Это заставляет мышцы сокращаться и перекачивать кровь. Иногда сердечный ритм ненормальный, а сердцебиение слишком высокое или слишком низкое.
Искусственный кардиостимулятор вставляется рядом с сердцем, чтобы подавать электрические сигналы сердцу, когда это необходимо, с соответствующей постоянной времени. У кардиостимуляторов есть датчики, которые обнаруживают движение тела и дыхание, чтобы увеличить частоту сердечных сокращений во время упражнений, чтобы удовлетворить повышенные потребности организма в крови и кислороде.
Расчетное время:
RC Цепь в дефибрилляторе сердцаДефибриллятор сердца используется для реанимации жертвы несчастного случая путем разряда конденсатора через туловище ее тела. Упрощенный вариант схемы показан на рис. 2. (а) Чему равна постоянная времени, если используется конденсатор 8,00 – мкФ , а сопротивление пути через ее тело составляет 1,00 x 10 3 Ом ? (b) Если начальное напряжение равно 10,0 кВ, сколько времени потребуется, чтобы снизиться до 5,00 x 10 2 В ?
Стратегия
Поскольку сопротивление и емкость известны, их просто перемножить, чтобы получить постоянную времени, требуемую в части (а). Чтобы найти время снижения напряжения до 5,00 x 10 2 В , мы многократно умножаем начальное напряжение на 0,368, пока напряжение не станет меньше или равно 5,00 x 10 2 V получен. Каждое умножение соответствует времени τ секунд.
Чтобы найти время снижения напряжения до 5,00 x 10 2 В , мы многократно умножаем начальное напряжение на 0,368, пока напряжение не станет меньше или равно 5,00 x 10 2 V получен. Каждое умножение соответствует времени τ секунд.
Решение для (a)
Постоянная времени τ определяется уравнением RC . Ввод заданных значений сопротивления и емкости (и помня, что единицы измерения фарад можно выразить как с/Ом, дает
τ = RC = (1,00 x 10 3 Ом) (8,00 мкФ) = 8,00 мс
Решение для (б)
За первые 8,00 мс напряжение (10,0 кВ) снижается до 0,368 от исходного значения. То есть:
В = 0,368 В o = 3,680 x 10 3 В при t = 8,00 мс.
(Обратите внимание, что мы вносим дополнительную цифру для каждого промежуточного вычисления. ) Еще через 8,00 мс мы снова умножаем на 0,368, и напряжение равно
) Еще через 8,00 мс мы снова умножаем на 0,368, и напряжение равно
Аналогично, еще через 8,00 мс напряжение равно
Обсуждение
Таким образом, всего через 24,0 мс напряжение падает до 49 В.8 В, или 4,98 % от исходного значения. Такое короткое время полезно при дефибрилляции сердца, потому что короткий, но интенсивный ток вызывает кратковременное, но эффективное сокращение сердца. Фактическая схема сердечного дефибриллятора немного сложнее, чем схема на рисунке 2, чтобы компенсировать магнитные эффекты и эффекты переменного тока, которые будут рассмотрены в магнетизме.
PhET Explorations: Circuit Construction Kit (только DC)
Комплект электроники для вашего компьютера. Создавайте схемы с резисторами, лампочками, батареями и переключателями.
Прямая ссылка: https://phet.colorado.edu/sims/html/capacitor-lab-basics/latest/capacitor-lab-basics_en.html
Проведите измерения с помощью реалистичного амперметра и вольтметра. Просмотрите схему в виде схемы или переключитесь на реалистичный вид. Прямая ссылка: https://phet.colorado.edu/sims/html/circuit-construction-kit-dc/latest/circuit-construction-kit-dc_en.html
Просмотрите схему в виде схемы или переключитесь на реалистичный вид. Прямая ссылка: https://phet.colorado.edu/sims/html/circuit-construction-kit-dc/latest/circuit-construction-kit-dc_en.html
Концептуальные вопросы
1: Что касается единиц, участвующих в соотношении τ = RC , убедитесь, что единицами измерения сопротивления, умноженного на емкость, являются время, то есть Ом • F = с.
2: Постоянная времени RC при дефибрилляции сердца имеет решающее значение для ограничения времени прохождения тока. Если емкость дефибриллятора фиксирована, как бы вы манипулировали сопротивлением в цепи, чтобы отрегулировать константу RC ? Будет ли также необходима регулировка приложенного напряжения, чтобы гарантировать, что подаваемый ток имеет соответствующее значение?
3: При измерении ЭКГ важно измерять колебания напряжения за небольшие промежутки времени. Время ограничено константой цепи RC — невозможно измерить колебания времени меньше RC . Как бы вы манипулировали R и C в цепи, чтобы обеспечить необходимые измерения?
Время ограничено константой цепи RC — невозможно измерить колебания времени меньше RC . Как бы вы манипулировали R и C в цепи, чтобы обеспечить необходимые измерения?
4: Нарисуйте два графика зависимости заряда конденсатора от времени. Нарисуйте один для заряда первоначально незаряженного конденсатора последовательно с резистором, как в схеме на рисунке 1, начиная с t=0 секунд . Нарисуйте другой для разряда конденсатора через резистор, как в схеме на рисунке 2, начиная с t = 0 , с начальным зарядом Q o . Покажите не менее двух интервалов τ .
5: При зарядке конденсатора, как обсуждалось в связи с рис. 1, сколько времени требуется, чтобы напряжение на конденсаторе достигло ЭДС? Это проблема?
6: При разрядке конденсатора, как описано в связи с рис. 2, сколько времени требуется, чтобы напряжение на конденсаторе достигло нуля? Это проблема?
2, сколько времени требуется, чтобы напряжение на конденсаторе достигло нуля? Это проблема?
7: Ссылаясь на рисунок 1, нарисуйте график зависимости разности потенциалов на резисторе от времени, показав не менее двух интервалов τ . Также нарисуйте график зависимости тока от времени для этой ситуации.
8: Длинный недорогой удлинитель подключается изнутри дома к холодильнику снаружи. Холодильник не работает как надо. В чем может быть проблема?
9: Показывает ли график на рисунке 4, что постоянная времени для разрядки короче, чем для зарядки? Можно ли ожидать, что ионизированный газ будет иметь низкое сопротивление? Как бы вы отрегулировали R , чтобы увеличить время между вспышками? Повлияет ли настройка R на время разряда?
10: Электронное устройство может иметь большие конденсаторы под высоким напряжением в секции питания, представляющие опасность поражения электрическим током, даже когда устройство выключено. Таким образом, на такой конденсатор помещают «спускной резистор», как схематично показано на рис. 6, чтобы стравливать с него заряд после выключения устройства. Почему сопротивление прокачки должно быть намного больше, чем эффективное сопротивление остальной части цепи? Как это влияет на постоянную времени разряда конденсатора?
Таким образом, на такой конденсатор помещают «спускной резистор», как схематично показано на рис. 6, чтобы стравливать с него заряд после выключения устройства. Почему сопротивление прокачки должно быть намного больше, чем эффективное сопротивление остальной части цепи? Как это влияет на постоянную времени разряда конденсатора?
Упражнения с задачами
1: Таймер в автомобильной системе стеклоочистителя основан на постоянной времени RC и использует конденсатор 0,500 – мкФ и переменный резистор. В каком диапазоне необходимо варьировать R , чтобы получить постоянные времени от 2,00 до 15,0 с?
2: Кардиостимулятор срабатывает 72 раза в минуту, каждый раз, когда конденсатор емкостью 25,0 нФ заряжается (аккумулятором последовательно с резистором) до 0,632 полного напряжения.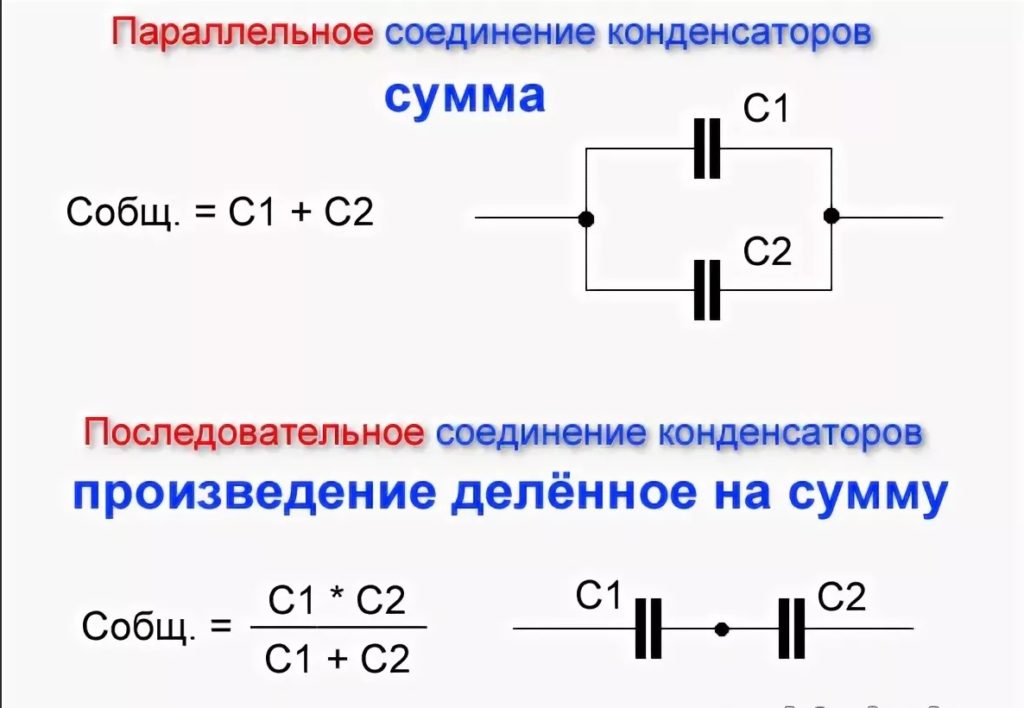 Каково значение сопротивления?
Каково значение сопротивления?
3: Продолжительность фотовспышки связана с постоянной времени RC , которая для определенной камеры составляет 0,100 мкс . (a) Если сопротивление лампы-вспышки составляет 0,0400 Ом во время разряда, какова емкость конденсатора, питающего ее энергией? б) Чему равна постоянная времени зарядки конденсатора, если зарядное сопротивление равно 800 кОм ?
4: A 2,00 мкФ и конденсатор 7,50 мкФ могут быть соединены последовательно или параллельно, как и резистор 25,0 кОм и 100 кОм. Рассчитайте четыре постоянные времени RC , возможные при последовательном соединении результирующих емкости и сопротивления.
5: Какой процент конечного напряжения, ЭДС, после двух постоянных времени приходится на первоначально незаряженный конденсатор C , заряженный через сопротивление Р ?
6: Резистор 500 Ом, незаряженный конденсатор 1,50 мкФ и ЭДС 6,16 В соединены последовательно. а) Чему равен начальный ток? (b) Какова постоянная времени RC ? в) Чему равен ток после одной постоянной времени? г) Чему равно напряжение на конденсаторе после одной постоянной времени?
а) Чему равен начальный ток? (b) Какова постоянная времени RC ? в) Чему равен ток после одной постоянной времени? г) Чему равно напряжение на конденсаторе после одной постоянной времени?
7: Дефибриллятор сердца, используемый на пациенте, имеет постоянную времени RC 10,0 мс из-за сопротивления пациента и емкости дефибриллятора. (a) Если дефибриллятор имеет 8,00 мкФ емкость, каково сопротивление пути через пациента? (Емкостью пациента и сопротивлением дефибриллятора можно пренебречь.) (b) Если начальное напряжение равно 12,0 кВ, сколько времени потребуется, чтобы снизиться до 6,00 x 10 2 В?
8: Монитор ЭКГ должен иметь постоянную времени RC менее 1,00 x 10 2 мкс, чтобы иметь возможность измерять изменения напряжения за небольшие интервалы времени. (a) Если сопротивление цепи (в основном из-за сопротивления грудной клетки пациента) составляет 1,00 кОм, какова максимальная емкость цепи? (b) Будет ли трудно на практике ограничить емкость меньше значения, указанного в (а)?
9: На рис. 7 показано, как разрядный резистор используется для разрядки конденсатора после отключения электронного устройства, что позволяет человеку работать с электроникой с меньшим риском поражения электрическим током. а) Чему равна постоянная времени? б) Сколько времени потребуется, чтобы уменьшить напряжение на конденсаторе до 0,250 % (5 % от 5 %) его полного значения после начала разрядки? (c) Если конденсатор заряжается до напряжения или В через сопротивление 100 Ом , рассчитайте время, необходимое для повышения до 0,865 В (это примерно две постоянные времени.)
7 показано, как разрядный резистор используется для разрядки конденсатора после отключения электронного устройства, что позволяет человеку работать с электроникой с меньшим риском поражения электрическим током. а) Чему равна постоянная времени? б) Сколько времени потребуется, чтобы уменьшить напряжение на конденсаторе до 0,250 % (5 % от 5 %) его полного значения после начала разрядки? (c) Если конденсатор заряжается до напряжения или В через сопротивление 100 Ом , рассчитайте время, необходимое для повышения до 0,865 В (это примерно две постоянные времени.)
11: Используя точную экспоненциальную обработку, найдите время, необходимое для зарядки первоначально незаряженного конденсатора емкостью 100 пФ через резистор 75,0 МОм до 90,0% от конечного напряжения.
12: Интегрированные концепции
Если вы хотите сфотографировать пулю, летящую со скоростью 500 м/с, то очень короткая вспышка света, создаваемая RC разрядом через фотовспышку, может ограничить размытие. Если предположить, что 1,00 мм движение в течение одного RC является приемлемым, и учитывая, что вспышка приводится в действие конденсатором 600 – мкФ , каково сопротивление в импульсной трубке?
Если предположить, что 1,00 мм движение в течение одного RC является приемлемым, и учитывая, что вспышка приводится в действие конденсатором 600 – мкФ , каково сопротивление в импульсной трубке?
13: Комплексные концепции
Мигающая лампа в рождественской сережке основана на RC разряде конденсатора через его сопротивление. Эффективная продолжительность вспышки составляет 0,250 с, в течение которых она производит в среднем 0,500 Вт из среднего 3,00 В. (а) Какую энергию она рассеивает? б) Сколько зарядов проходит через лампу? в) Найдите емкость. г) Чему равно сопротивление лампы?
14: Integrated Concepts
Конденсатор емкостью 160 мкФ, заряженный до 450 В, разряжается через резистор 31,2 кОм. а) Найдите постоянную времени. б) Рассчитайте повышение температуры резистора, если его масса 2,50 г, а удельная теплоемкость 1,67 кДж/кг o С, отметив, что большая часть тепловой энергии сохраняется за короткое время разряда. (c) Рассчитайте новое сопротивление, предполагая, что это чистый углерод. (d) Представляется ли это изменение сопротивления значительным?
(c) Рассчитайте новое сопротивление, предполагая, что это чистый углерод. (d) Представляется ли это изменение сопротивления значительным?
16: необоснованные результаты
(a) Рассчитайте емкость, необходимую для получения постоянной времени RC 1,00 x 10 3 с с резистором 0,100 Ом. б) Что неразумного в этом результате? (c) Какие предположения ответственны?
17: Создайте свою собственную задачу
Рассмотрим фотовспышку. Составьте задачу, в которой вы вычисляете размер конденсатора, хранящего энергию для лампы-вспышки. Среди факторов, которые необходимо учитывать, — напряжение, подаваемое на конденсатор, энергия, необходимая для вспышки, и соответствующий заряд, необходимый для конденсатора, сопротивление лампы-вспышки во время разряда и требуемая постоянная времени RC .
18: Создайте свою собственную проблему
Рассмотрим перезаряжаемый литиевый элемент, который будет использоваться для питания видеокамеры.

 .. Из
многообразия радиодеталей надо уметь
быстро отличить по внешнему виду нужную,
расшифровать надпись на ее корпусе,
определить выводы. О том, как это сделать, и
будет кратко рассказано ниже. Более же
подробные сведения о радиодеталях вы
найдете в описании конструкций самоделок.
.. Из
многообразия радиодеталей надо уметь
быстро отличить по внешнему виду нужную,
расшифровать надпись на ее корпусе,
определить выводы. О том, как это сделать, и
будет кратко рассказано ниже. Более же
подробные сведения о радиодеталях вы
найдете в описании конструкций самоделок.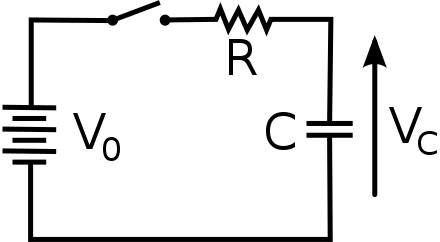
 Если сопротивление менее 1 кОм, цифрами
указывают число ом без единицы измерения.
При сопротивлении 1 кОм и более — до 1 МОм
указывают число килоом и ставят рядом букву
«к». Сопротивление 1 МОм и выше выражают
числом мегаом с добавлением буквы «М».
Например, если на схеме рядом с
обозначением резистора написано 510, значит,
сопротивление резистора 510 Ом. Обозначениям
3,6 к и 820 к соответствует сопротивление 3,6
кОм и 820 кОм. Надпись на схеме 1 М или 4,7 М
означает, что используются сопротивления 1
МОм -и 4,7 МОм.
Если сопротивление менее 1 кОм, цифрами
указывают число ом без единицы измерения.
При сопротивлении 1 кОм и более — до 1 МОм
указывают число килоом и ставят рядом букву
«к». Сопротивление 1 МОм и выше выражают
числом мегаом с добавлением буквы «М».
Например, если на схеме рядом с
обозначением резистора написано 510, значит,
сопротивление резистора 510 Ом. Обозначениям
3,6 к и 820 к соответствует сопротивление 3,6
кОм и 820 кОм. Надпись на схеме 1 М или 4,7 М
означает, что используются сопротивления 1
МОм -и 4,7 МОм. Когда же ось поворачивают обратно,
происходит обратное явление. Это свойство
переменного резистора используется,
например, для регулирования громкости
звука в усилителях, приемниках,
электрофонах.
Когда же ось поворачивают обратно,
происходит обратное явление. Это свойство
переменного резистора используется,
например, для регулирования громкости
звука в усилителях, приемниках,
электрофонах. Резисторы с положительным ТКС
часто используют в цепях защиты аппаратуры от перегрева. При увеличении
температуры сопротивление такого резистора увеличивается до величины
иногда в несколько раз большей, чем начальная, что ограничивает ток,
например в цепи пусковой обмотки электродвигателя… Терморезисторы с
отрицательным ТКС часто используются для обеспечения так называемого
«мягкого» пуска электродвигателей а также для продления службы обычных
ламп накаливания. Такой резистор при комнатной температуре имеет
некоторое начальное сопротивление, уменьшающееся в процессе нагрева.
Таким образом мы имеем некоторое ограничение пускового тока…
Справочные данные некоторых из отечественных терморезисторов можно скачать по этой ссылке.
Резисторы с положительным ТКС
часто используют в цепях защиты аппаратуры от перегрева. При увеличении
температуры сопротивление такого резистора увеличивается до величины
иногда в несколько раз большей, чем начальная, что ограничивает ток,
например в цепи пусковой обмотки электродвигателя… Терморезисторы с
отрицательным ТКС часто используются для обеспечения так называемого
«мягкого» пуска электродвигателей а также для продления службы обычных
ламп накаливания. Такой резистор при комнатной температуре имеет
некоторое начальное сопротивление, уменьшающееся в процессе нагрева.
Таким образом мы имеем некоторое ограничение пускового тока…
Справочные данные некоторых из отечественных терморезисторов можно скачать по этой ссылке. Вместо воздуха может быть фарфор, слюда или
другой материал, не проводящий ток. Если
резистор пропускает постоянный ток, то
через конденсатор он не проходит. А вот
переменный ток через конденсатор проходит.
Благодаря такому свойству конденсатор
ставят там, где нужно отделить постоянный
ток от переменного.
Вместо воздуха может быть фарфор, слюда или
другой материал, не проводящий ток. Если
резистор пропускает постоянный ток, то
через конденсатор он не проходит. А вот
переменный ток через конденсатор проходит.
Благодаря такому свойству конденсатор
ставят там, где нужно отделить постоянный
ток от переменного. В любительских
конструкциях подстроечный конденсатор
нередко используют как переменный — он
дешев и доступен. На схемах конденсатор
обозначается буквой С (от латинского слова
Capacitor — накопитель).
В любительских
конструкциях подстроечный конденсатор
нередко используют как переменный — он
дешев и доступен. На схемах конденсатор
обозначается буквой С (от латинского слова
Capacitor — накопитель). Они
отличаются материалом между пластинами и
конструкцией. Бывают конденсаторы
воздушные, слюдяные, керамические и др. Одна
из разновидностей постоянных
конденсаторов — электролитический.
Такие
конденсаторы выпускают большой емкости — от
0,5 до 68000 мкФ.
Они
отличаются материалом между пластинами и
конструкцией. Бывают конденсаторы
воздушные, слюдяные, керамические и др. Одна
из разновидностей постоянных
конденсаторов — электролитический.
Такие
конденсаторы выпускают большой емкости — от
0,5 до 68000 мкФ. Например, надпись 5 — 180
свидетельствует о том, что в одном крайнем
положении оси емкость конденсатора
составляет 5 пФ, а в другом — 180 пФ. При
плавном повороте из одного положения в
другое емкость конденсатора будет также
плавно изменяться от 5 до 180 пФ или от 180 до 5
пФ.
Например, надпись 5 — 180
свидетельствует о том, что в одном крайнем
положении оси емкость конденсатора
составляет 5 пФ, а в другом — 180 пФ. При
плавном повороте из одного положения в
другое емкость конденсатора будет также
плавно изменяться от 5 до 180 пФ или от 180 до 5
пФ.